7. Approximation periodischer Funktionen
|
|
|
- Roland Armbruster
- vor 5 Jahren
- Abrufe
Transkript
1 H.J. Oberle Approximation WS 13/14 7. Approximation periodischer Funktionen Fourier Reihen. Wir betrachten wieder den Raum aller stetigen, -periodischen Funktionen C := {f C(R) : t R : f(t + ) = f(t)} (7.1) mit dem Standard-Skalarprodukt f, g := 1 f(t) g(t) dt. (7.) Die zugehörige Norm auf C werde wieder mit oder besser bezeichnet. Der folgende Satz fasst nochmals das Beipiel (6.14) zusammen Satz (7.3) Die Funktionen 1, cos t, sin t,..., cos(n t), sin(n t) bilden ein Orthonormalsystem bzgl.,. Sie sind somit zugleich eine ONB des von ihnen aufgespannten linearen Teilraumes T n := {f C : f(t) = a n + [a k cos(kt) + b k sin(kt)], a k, b k R}. (7.4) Die L Bestapproximation einer Funktion f C aus T n lautet daher S n (f)(t) = f n (t) = a + n a k = 1 f(t) cos(kt) dt, b k = 1 [a k cos(kt) + b k sin(kt)] f(t) sin(kt) dt. (7.5) Für n erhält man hieraus formal die Fourier-Entwicklung einer Funktion f C (Jean-Baptiste-Joseph Fourier; ) f(t) a + [a k cos(kt) + b k sin(kt)]. (7.6) Wir fragen nach der Konvergenz dieser Fourier-Reihe, nach der Konvergenzgeschwindigkeit und untersuchen, unter welchen Voraussetzungen in (7.6) punktweise bzw. gleichmäßige Konvergenz vorliegt. 7
2 Zunächst können wir analog zu Satz (6.33) die L -Konvergenz der Fourier-Reihe feststellen. Satz (7.7) Zu f C bezeichne T n (f) die (bzw. eine) Bestapproximation von f aus T n bezüglich. Dann gelten a) f T n (f) (n ), b) f T n (f) (n ), c) f S n (f) (n ). Beweis: Der Beweis erfolgt analog zu dem von Satz (6.33). Teil a) ergibt sich aus dem zweiten Weierstraßschen Approximationssatz (4.). Teil b) folgt aus der Abschätzung f T n (f) f T n (f). Teil c) folgt schließlich aus der Minimaleigenschaft von S n (f), nämlich f S n (f) f T n (f). Erinnert sei auch an die Parseval Gleichung (6.13), die sich aus der Dichtheit der trigonometrischen Polynome in C ergibt, a + ( ) a k + b k = f. (7.8) Aus (7.8) folgt insbesondere, dass die Fourier-Koeffizienten a k, b k Nullfolgen bilden. Nun zur Untersuchung der punktweisen bzw. gleichmäßigen Konvergenz der Fourier- Reihe. Zunächst ist klar, dass Satz (7.7) lediglich die Konvergenz im quadratischen Mittel zeigt, woraus nicht auf die punktweise Konvergenz geschlossen werden kann. Tatsächlich hat Paul du Bois-Reymond ( ) eine stetige Funktion f C angegeben, deren Fourier-Reihe in mindestens einem Punkt divergiert. Die Jackson Sätze. Ausgangspunkt für die folgenden Untersuchungen ist das Lemma von Lebesgue (3.4). Hierbei ist zu beachten, dass S n : C T n ein stetiger linearer Projektor ist. Die Stetigkeit ergibt sich beispielsweise aus der Integraldarstellung (vgl. (4.16)) S n (f)(t) = 1 f(t + θ) D n (θ) dθ, D n (θ) := sin[(n + 1/)θ]. (7.9) sin[θ/] 73
3 Das Lemma von Lebesgue ist also anwendbar und lautet hier konkret f S n (f) ( 1 + S n ) En (f), E n (f) := inf p T n f p. (7.1) Dabei bezeichnet E n (f) den Minimalabstand von f zu T n bezüglich der Maximumsnorm. Wir beginnen mit einer Abschätzung für S n. Satz (7.11) a) S n = 1 b) Beweis: sin[(n + 1/) θ ] sin(θ/) d θ 4 ln(1 + n) S n 1 + ln( n + 1). zu a) Dies folgt direkt aus der Integraldarstellung (7.9). Man beachte, dass D n (θ) eine gerade, -periodische Funktion ist. zu b) Seien θ k := (k )/(n + 1/) die Nullstellen von D n (θ). Damit gilt S n 1 n 1 k= n 1 k= = 4 n 1 k= θ k+1 θ k 1 θ k+1 sin[(n + 1/) θ ] θ/ θ k+1 θ k d θ sin[(n + 1/) θ ] d θ 1 k ln(n + 1). Für die rechte Seite verwenden wir die folgenden beiden Abschätzungen sin[(n + 1/) θ ] sin(θ/) = n cos(k θ) n + 1, k= sowie sin[(n + 1/) θ ] sin(θ/) Für irgendein µ ], 1[ folgt somit 1 θ/ = θ. S n 1 ( µ ( n + 1) dθ + µ θ dθ) = ( n + 1) µ + ln µ. Speziell für µ = /( n + 1) ergibt sich die angegebene obere Schranke. 74
4 Um nun mittels (7.1) Konvergenz zu zeigen, benötigen wir die hinreichend schnelle Konvergenz von E n (f) (n ). Hierzu dienen die verschiedenen Sätze von Jackson, benannt nach Dunham Jackson ( ), einem Schüler von Edmund Landau. Satz (7.1) (Jackson I) Für f C (1) := C C 1 (R) und n N gilt E n (f) (n + 1) f. Beweis: Zunächst zeigt man mittels partieller Integration die Darstellung f(t) = 1 f(θ) dθ + 1 θ f (θ + t + ) dθ. (7.13) Der erste Summand ist konstant. Da T n die konstanten Funktionen enthält, genügt es, den zweiten Summanden durch trigonometrische Polynome aus T n zu approximieren. E n (f) = inf { 1 θ f (θ + t + ) dθ q(t) : q T n }. (7.14) Nun ist für g C und p T n die folgende Funktion q(t) := p(θ) g(θ + t) dθ auch stets wieder ein trigonometrisches Polynom in T n. Aufgrund der Periodizität von p und g hat man nämlich q(t) = p(θ t) g(θ) dθ p(θ t) = a (θ) + n a k (θ) cos(kt) + b k (θ) sin(kt). Wir reduzieren also die Infimumsbildung in (7.14) auf die trigonometrischen Polynome q der obigen Form, wobei wir g(t) := f (t + ) wählen. Damit erhalten wir aus (7.14) E n (f) inf { 1 1 f inf { (θ p(θ)) f (θ + t + ) dθ : p T n } θ p(θ) dθ : p T n }. (7.15) 75
5 Damit ist nun unser Problem, eine obere Schranke für E n (f) zu finden, zurückgeführt worden auf eine L 1 -Approximationsaufgabe, nämlich auf das Problem, die Funktion g(t) = t in L 1 -Sinn auf dem Intervall [, ] durch ein trigonometrisches Polynom p T n zu approximieren. Wir verzichten darauf, die L 1 -Optimalität der folgenden Konstruktion zu beweisen, und geben statt dessen nur die Lösung dieser Approximationsaufgabe an. Dazu bedarf es noch einiger Vorbemerkungen über trigonometrischer Interpolation. (a) Zu (n + 1) Knoten t < t 1 <... < t n [, [ und Funktionswerten f j gibt es genau ein trigonometrisches Polynom p T n mit p(t j ) = f j, j =,..., n. (Beweis: Transformation in ein komplexes Polynom.) (b) Ein trigonometrisches Polynom p T n, p, kann in [, [ höchstens n Nullstellen haben. (Beweis: Gäbe es mehr als n Nullstellen, hätte man einen Widerspruch zu (a).) (c) Wir setzen t k := k, k = 1,..., n. Dann gibt es genau ein trigonometrisches n + 1 Polynom p T n der Form p(t) = n 1 b k sin(kt) mit p(t k ) = t k, k = 1,..., n. (Beweis: Wende (a) an auf die Stützstellen (±t k, ±t k ) und (, ) und zeige ebenfalls mittels (a), dass alle a k verschwinden müssen.) (d) Die Fehlerfunktion e(t) := t p(t) hat in ], [ genau die Nullstellen t k, k = 1,..., n. (Beweis: e hat nach Konstruktion die Nullstellen t k und. Hätte e noch eine weitere Nullstelle in ], [, so wäre e (t) = 1 p (t) ein gerades trigonometrisches Polynom in T n und hätte nach dem Satz von Rolle wenigstens (n + 1) Nullstellen in ], [, also wenigstens (n + ) Nullstellen in [, [; Widerspruch!) Für die obige Konstruktion werten wir nun die L 1 Norm aus e 1 = θ p(θ) dθ = θ p(θ) dθ. Dazu setzen wir σ n+1 (t) := sign[sin((n + 1)t)] und finden t p(t) dt = σ n+1 (t) (t p(t)) dt = σ n+1 (t) t dt n b k σ n+1 (t) sin(k t) dt = = n ( 1) k k= (n + 1). t k+1 t k t dt 76
6 Zur vorletzten Gleichung zeigt man explizit, dass sämtliche Integrale σn+1 (t) sin(k t) dt verschwinden. Die letzte Gleichheit ist ebenfalls durch explizite Berechnung der Integrale t dt zu zeigen. Insgesamt ist damit eine obere Schranke, nämlich e 1 /(n + 1) bewiesen, wobei diese Schranke (ohne Beweis) bestmöglich ist. Setzt man diese nun in (7.15) ein, so ergibt sich schließlich die Behauptung des Satzes. Bemerkung (7.16) Der in der Abschätzung (7.1) auftretende Faktor /(n + ) lässt sich nicht verbessern. Beweis: Zu ε > lässt sich eine Funktion f ε C (1) konstruieren mit den Eigenschaften f ε (k/(n + 1)) = ( 1) k, k =, ±1,..., ±(n + 1), f ε (n + 1) (1 + ε). Sei p ε nun eine Bestapproximation von f ε aus T n bzgl.. Wäre f ε p ε < 1, so hätte p ε in den t k das gleiche Vorzeichen wie f ε und somit nach Zwischenwertsatz wenigstens n + Nullstellen in ], [. Widerspruch! Damit folgt aber E n (f ε ) 1 (n + 1) (1 + ε) f ε. Für ε geht die Abschätzung gegen die des ersten Jackson-Satzes. Satz (7.17) (Jackson II) Ist f C Lipschitz-stetig mit einer Lipschitz-Konstanten L, so gilt für n N E n (f) (n + 1) L. Beweis: Für δ > setze man F δ (t) := 1 δ und es gilt F δ (t) = 1 δ Ist p T n t+δ t δ ( f(t + δ) f(t δ) ), also F δ L. f(θ) dθ. Dann ist F δ C (1) nun Bestapproximation von F δ aus T n bzgl., so folgt E n (f) f p f F δ + F δ p f F δ + Ferner lässt sich abschätzen f F δ = max t 1 δ t+δ t δ und somit f F δ (δ ). (f(t) f(θ))dθ max t 77 L δ t+δ t δ (n + 1) L. t θ dθ = Lδ
7 Satz (7.18) (Jackson III) Ist f C, so gilt für n N E n (f) 3 ω( n + 1 ). Dabei ist ω(δ) := sup{ f(x) f(y) : x y δ} der Stetigkeitsmodul von f. Beweis: Für δ > sei F δ wie im Beweis zu (7.17) erklärt. Dann folgt mit F δ (t) = ( f(t + δ) f(t δ) ) /( δ) die Abschätzung F δ ω( δ) δ ω(δ) δ. Die letzte Ungleichung ist eine direkte Folge aus der Definition des Stetigkeitsmoduls. Nach dem Jackson-Satz I gilt damit E n (F δ ) ω(δ). Weiterhin ist (n + 1)δ f F δ = max t Insgesamt ergibt sich somit wieder max t 1 δ 1 δ t+δ t δ t+δ t δ E n (f) f F δ + E n (F δ ) ( 1 + ( f(t) f(θ) ) dθ ω(δ) dθ = ω(δ). ) ω(δ). (n + 1) δ Speziell für δ = /(n + 1) ergibt sich die Behauptung des Satzes. Bemerkung (7.19) Da für eine stetige Funktion f C der Stetigkeitsmodul gegen Null konvergiert ω(/(n + 1)) (n ) folgt aus dem dritten Jackson-Satz auch der zweite Weierstraßsche Approximationssatz zurück: Jede stetige, -periodische Funktion lässt sich bzgl. der Maximumsnorm beliebig genau durch trigonometrische Polynome approximieren. Kombiniert man nun diese Abschätzung für die Minimalabweichung E n (f) mit der Abschätzung (7.11b) für die Operatornorm S n, so ergibt sich der folgende Satz von Dini und Lipschitz. Satz (7.) (Dini, Lipschitz) Erfüllt f C die Dini-Lipschitz-Bedingung, lim [ ω(δ) ln δ ] =, δ so konvergiert die Fourier-Reihe S n (f) gleichmäßig gegen f für n. 78
8 Beweis: Aufgrund des Lemmas von Lebesgue (7.1) sowie der Abschätzungen (7.11) und (7.18) ergibt sich f S n (f) ( 1 + S n ) En (f) ( + ln( n + 1) ) 3 ω( n + 1 ). Für n 3 stellt man fest, dass ln( n + 1) ln( ) ln( ) und ln( ) < n + 1 gelten. Somit folgt f S n (f) 6 ω( ) 1.5 ln( n + 1 n + 1 ) ω( n + 1 ) (n ). Bemerkung (7.1) Über die Konvergenzgeschwindigkeit der Fourier-Entwicklung, wenn weitere Glattheitsvoraussetzungen an die Funkton f gestellt werden, gibt schließlich der vierte Jackson-Satz Auskunft, den wir nur kurz zitieren wollen f C (k) := C C k (R) E n (f) ( ) k f (k). n + Berechnung von Fourier Koeffizienten. Wir beginnen mit der komplexen Darstellung der Partialsumme S n (f) = a + n [a k cos(kt) + b k sin(kt)] (7.) der Fourier-Entwicklung einer Funktion f C. Stellt man cos t und sin t als Real- und Imaginärteil von e it dar, so ergibt sich S n (f) = a + n = a + n = n k= n c k e ikt. [ a k (eikt + e ikt ) + b k i (eikt e ikt ) ] [ a k i b k e ikt + a k + i b k e ikt ] (7.3) 79
9 Umrechnung der Koeffizienten: (k = 1,,..., n) c = a, c k = 1 (a k i b k ), c k = 1 (a k + i b k ), a = c, a k = c k + c k, b k = i (c k c k ). (7.4) Fourier Koeffizienten: (k N, j Z) a k = 1 b k = 1 f(t) cos(kt) dt, f(t) sin(kt) dt, (7.5) c j = 1 f(t) e i j t dt. Die Grundidee zur numerischen Berechnung der Fourier-Koeffizienten besteht darin, die Integrale in (7.5) durch Trapezsummen zu approximieren. Wegen der Periodizität der Integranden sind diese zur numerischen Quadratur besonders gut geeignet. Für hinreichend große N N setzen wir h := N, t k := k h, f k := f(t k ), k =, 1,..., N. (7.6) Mit f = f N (Periodizität) ergeben sich dann die folgenden Näherungen durch die Trapezsumme { } a k h N 1 f + f j cos(k t j ) + f N = N b k N N 1 j= N 1 j= S n (f) A + n j=1 f j cos(j k h) =: A k, k =,..., n, f j sin(j k h) =: B k, k = 1,..., n, [ A k cos(k t) + B k sin(k t) ] =: Sn (f)(t). (7.7) Man beachte, dass die Approximationen A k a k und B k b k i. Allg. nur für kleine k brauchbar sind. So sind die A k, B k gemäß Definition periodisch im Index, A k+n = A k, B k+n = B k, während die tatsächlichen Fourier-Koeffizienten Nullfolgen bilden. Eine Faustregel besagt, dass man N n wählen sollte. 8
10 Andere Interpretationen: a) Man kann die diskreten Fourier-Koeffizienten A k, B k (eigentlich A k,n, B k,n ) auch als exakte Fourier-Koeffizienten einer diskretisierten Approximationsaufgabe interpretieren. Zu N n + 1 werde definiert { } R := C (B), B := k : k =, 1,..., N 1, N f, g := N N 1 k= f(k h) g(k h). (7.8) Die Funktionen 1, cos t, sin t,..., cos(n t), sin(n t) bilden eine ONB des von ihnen aufgespannten (diskreten) Raumes T n bzgl.,. Die A k, B k liefern dann die Lösung der L Approximationsaufgabe, ein vorgebenes f R durch ein Element aus Tn zu approximieren. Genauer ist die Lösung der Approximationsaufgabe gegeben durch wobei die A k, B k S n (f)(t) = A + n durch (7.7) gegeben sind. [ A k cos(k t) + B k sin(k t) ], b) Die A k, B k lassen sich auch als Lösung einer trigonometrischen Interpolationaufgabe interpretieren. Zu Interpolationsdaten (t k, f k ), k =, 1,..., N 1, mit t k aus (7.6), ist eine interpolierende trigonometrische Summe der Form A n + [ A k cos(k t) + B k sin(k t) ], für N = n + 1, q(t) = n 1 A + [ A k cos(k t) + B k sin(k t) ] + A n cos(n t), für N = n. (7.9) Es lässt sich dann zeigen, dass diese Interpolationsaufgabe eine eindeutig bestimmte Lösung besitzt, welche gerade durch die A k, B k gemäß (7.7) gegeben ist. Komplexe Variante: Man sucht ein (komplexes) trigonometrisches Polynom der Form p(t) = N 1 k= C k e ikt, (7.3) das die gegebenen Daten (t k, f k ), k =,..., N 1, interpoliert. Man erhält wieder eine eindeutig bestimmte Lösung, nämlich C k = 1 N N 1 j= f j e i j k h, k =, 1,..., N 1. (7.31) 81
11 Auch hier lässt sich die reelle Lösung (7.7) und die komplexe Lösung (7.31) ineinander umrechnen. Man erhält analog zum kontinuierlichen Approximationsproblem, vgl. (7.), (k = 1,..., n) C = A, C k = 1 (A k i B k ), C N k = 1 (A k + i A k ), A = C, A k = C k + C N k, B k = i (C k C N k ). (7.3) Fazit: Sowohl für die numerische Berechnung der Fourier-Koeffizienten wie auch für die Auswertung der trigonometrischen Partialsummen sind jeweils trigonometrische Summen der Form (7.7) bzw. (7.31) auf einem festen Gitter - oder kontinuierlich (7.) bzw. (7.3) auszuwerten. Dabei ist es gleichgültig, ob man die reelle oder die komplexe Darstellung verwendet, da beide inneinander umgerechnet werden können. Der Algorithmus von Goertzel und Reinsch. Der Algorithmus berechnet zu gegebenen Daten f,..., f N 1 R und t R die trigonometrischen Summen A(t) := N 1 k= f k cos(k t), B(t) := N 1 k= f k sin(k t). (7.33) Die Grundidee des Algorithmus ist ganz analog zum Clenshaw Verfahren die Verwendung einer Dreiterm-Rekursion für die Terme c k := cos(k t) und s k := sin(k t). Mittels trigonometrischer Umformung zeigt man c = 1, c 1 = cos t, c k+1 = c 1 c k c k 1, k 1, s =, s 1 = sin t, s k+1 = c 1 s k s k 1, k 1. (7.34) Mit der gleichen Technik, die wir für den Algorithmus von Clenshaw angewendet haben, vgl. (6.3), erhalten wir den folgenden Algorithmus von Goertzel (1958): Algorithmus von Goertzel (7.35) U N :=, U N 1 := f n 1, c := cos t, F := c, für k = N, N 3,..., 1 U k := f k + F U k+1 U k+ A(t) := f + c U 1 U, B(t) := U 1 sin t. 8
12 Anmerkungen: Zu Berechnung aller A k, B k, t = t k = k/n, benötigt der Algorithmus O(N ) wesentliche Operationen. Für kleine t ist der Algorithmus numerisch instabil. Der Grund liegt darin, dass der Algorithmus mit c = cos t arbeitet. Kleine Änderungen in c 1 entsprechen dabei großen Änderungen in t. Stabilisierung nach Reinsch (1968) Man ersetzt die Rekursion (7.34) durch eine solche, die mit sin (t/) bzw. cos (t/) anstelle von cos t arbeitet. Hintergrund sind die trigonometrischen Relationen sin ( t ) = 1 (1 cos t), cos ( t ) = 1 (1 + cos t). Fall 1: cos t >. U k = f k + c 1 U k+1 U k+ = f k + (c 1 1) U k+1 + U k+1 U k+ (U k U k+1 ) = f k + (c 1 1) U k+1 + (U k+1 U k+ ). Mit D k := U k U k+1 gilt somit D k = f k 4 sin (t/) U k+1 + D k+1 und A = f + c 1 U 1 U = U c 1 U 1 = D + sin (t/) U 1. Fall : cos t. U k = f k + c 1 U k+1 U k+ = f k + (c 1 + 1) U k+1 U k+1 U k+ (U k + U k+1 ) = f k + (c 1 + 1) U k+1 (U k+1 + U k+ ). Mit D k := U k + U k+1 gilt somit D k = f k + 4 cos (t/) U k+1 D k+1 und A = f + C 1 U 1 U = U C 1 U 1 = D cos (t/) U 1. Algorithmus von Goertzel und Reinsch (7.36) Falls cos t > : σ := 1, F := 4 sin (t/), sonst : σ := 1, F := 4 cos (t/), U N :=, D N 1 := f N 1, 83
13 für k = N, N 3,..., U k+1 := D k+1 + σ U k+, D k := f k + F U k+1 + σ D k+1, A(t) := D.5 F U 1, B(t) := U 1 sin t. In dieser Form ist der Algorithmus numerisch stabil und nur wenig aufwendiger als die ursprüngliche Version von Goertzel. Die schnelle Fourier-Transformation (FFT). Der Algorithmus von Goertzel und Reinsch wertet die trigonometrischen Summen an beliebigen Stellen t R aus. Er ist jedoch mit O(N ) Operationen immer noch recht aufwendig. Ist man jedoch nur an den diskreten Fourier-Koeffizienten A k, B k interessiert, oder möchte man das trigonometrische Polynom nur auf dem Gitter k h, h = /N auswerten, so lassen sich effizientere Algorithmen angeben, die mit O(N log N) Operationen auskommen. Solche Verfahren sind unter dem Namen FFT (fast Fourier transform) bekannt. Sie sind durch eine Arbeit von J.W. Cooley und J.W. Tuckey (Math. Comput. 19, 1965) populär geworden und bilden auch heute ein aktuelles Forschungsgebiet. Wir gehen im Folgenden von der komplexen Darstellung aus und nehmen an, dass N eine Zweierpotenz ist. Der reelle Fall wird mittels der Rücktransformation (7.3) erledigt. Gegeben: N = r+1, r N h = /N, t k = k h, f k = f(t k ), k =,..., N 1, Gesucht: C k = 1 N N 1 j= f j e i j k h, k =,..., N 1. Die Grundidee besteht darin, die Summe in zwei Summanden aufzuteilen, die selber als Fourier-Koeffizienten zu einem gröberen Gitter mit doppelter Schrittweite interpretiert werden können. Setzen wir m := N/ und sortieren die Summe C k Indizes, so ergibt sich für k =,..., N 1 nach geraden und ungeraden 84
14 C k = 1 N = [ 1 N [ m 1 j= m 1 j= f j e i (j) k h + f j e i j k (h) ] m 1 j= f j+1 e i (j+1) k h ] + e i k /m [ 1 N m 1 = G k + e i k /m U k, wobei definiert wird j= f j+1 e i j k (h) ] G k := 1 N m 1 j= f j e i j k (/m), U k := 1 N m 1 j= f j+1 e i j k (/m). Nun sind die G k und U k periodisch im Index: G k+m = G k, U k+m = U k, k =, 1,..., m 1, so dass sich der Rechenaufwand zur Berechnung der G k und U k gegenüber der Berechnung der C k im Wesentlichen halbiert. Wir fassen den Reduktionsschritt noch einmal zusammen. Reduktionsschritt (7.37) Mit m := N/ berechne man für k =, 1,..., m 1 G k := 1 N U k := 1 N m 1 j= m 1 j= f j e i j k (/m), f j+1 e i j k (/m), C k := G k + e i k /m U k, end k. C k+m := G k e i k /m U k. Dieser Reduktionsschritt wird nun iteriert bis nur noch triviale Fourier- Transformationen (also m = 1) auszuführen sind. Die einzelnen Fourier- Transformationen für m = 1,, 4,..., r werden aus diesem gemäß (7.37) zusammengesetzt. Der Algorithmus besteht aus zwei Phasen: Zunächst werden die Daten so umsortiert, wie sie nach Durchführung aller Reduktionsschritte auftreten. In der zweiten Phase werden diese Daten dann gemäß (7.37) wieder zusammengesetzt. Phase 1: Sortieren der Daten: Wir betrachten zunächst den Sortierschritt für N = 8: 85
15 Ausgangsdaten: f f 1 f f 3 f 4 f 5 f 6 f 7 Schritt 1: f f f 4 f 6 f 1 f 3 f 5 f 7 Schritt : f f 4 f f 6 f 1 f 5 f 3 f 7 Schritt 3: f f 4 f f 6 f 1 f 5 f 3 f 7 Betrachtet man die Dualdarstellung der Indizes bei den obigen Sortierschritten, so sieht man für den ersten Schritt (j)... (j + 1)... 1 (j)... (m + j) 1... Für sämtliche r Sortierschritte erhält man die Index-Zuordnung j = (j r j r 1... j 1 j ) j = (j j 1... j r 1 j r ), d.h. der Index des f-wertes in Anfangsposition j ergibt sich durch Bitumkehr der Ziffernfolge in der Dualdarstellung des Index j. Für das Beispiel N = 8 ergibt sich Algorithmus FFT 1.Teil (7.38) j (j) (j) j ( ) ( ) 1 ( 1) (1 ) 4 ( 1 ) ( 1 ) 3 ( 1 1) (1 1 ) 6 4 (1 ) ( 1) 1 5 (1 1) (1 1) 5 6 (1 1 ) ( 1 1) 3 7 (1 1 1) (1 1 1) 7 C = f /N; j = ; for j = 1,,..., N 1 end j l = N/; while l + j N, end l = l/; j = j + 3 l N; C j := f j /N; 86
16 Erläuterung: In Schritt j wird zum Index j der neues Index j berechnet. Dabei wird in der while Schleife der alte Index j auf führende Einsen getestet j = (1,..., 1,, j l+,..., j r ) l = (,...,, 1,,..., ) jneu = (,...,, 1, j l+,..., j r ) j + 3 l n = (,...,, 1, j l+,..., j r ) Phase : Nachdem die f j Werte nun in die richtige Reihenfolge gebracht worden sind, erfolgen die Reduktionsschritte (7.37) Algorithmus FFT.Teil (7.39) for l =, 1,..., r m = l ; m = m; for k =, 1,..., m 1 c = exp( i k /m); for j = : m : N m G = C j+k ; U = c C j+k+m ; C j+k = G + U; C j+k+m = G U; end j end k end l Joseph Fourier ( ) 87
T n (1) = 1 T n (cos π n )= 1. deg T n q n 1.
 KAPITEL 3. INTERPOLATION UND APPROXIMATION 47 Beweis: Wir nehmen an qx) für alle x [, ] und führen diese Annahme zu einem Widerspruch. Es gilt nach Folgerung ii) T n ) T n cos π n ). Wir betrachten die
KAPITEL 3. INTERPOLATION UND APPROXIMATION 47 Beweis: Wir nehmen an qx) für alle x [, ] und führen diese Annahme zu einem Widerspruch. Es gilt nach Folgerung ii) T n ) T n cos π n ). Wir betrachten die
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung
 Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
Konvergenz im quadratischen Mittel und Parsevalsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Prof Dr Picard, gehalten von Helena Malinowski In vorhergehenden Vorträgen und dazugehörigen
Periodische Funktionen, Fourier Reihen
 Kapitel 1: Periodische Funktionen, Fourier Reihen 1.1 Grundlegende Begriffe Periodische Funktionen Definition: Eine Funktion f : R R oder f : R C) heißt periodisch mit der Periode T, falls für alle t R
Kapitel 1: Periodische Funktionen, Fourier Reihen 1.1 Grundlegende Begriffe Periodische Funktionen Definition: Eine Funktion f : R R oder f : R C) heißt periodisch mit der Periode T, falls für alle t R
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung
 Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Konvergenz im quadratischen Mittel und die Parsevelsche Gleichung Skript zum Vortrag im Proseminar Analysis bei Dr. Gerhard Mülich Christian Maaß 6.Mai 8 Im letzten Vortrag haben wir gesehen, dass das
Beispiel: Die Sägezahnfunktion.
 Beispiel: Die Sägezahnfunktion. Betrachte die Sägezahnfunktion : für t = oder t = π S(t) := 1 (π t) : für < t < π Die Sägezahnfunktion ist ungerade, also gilt (mit ω = 1) a k = und b k = π π und damit
Beispiel: Die Sägezahnfunktion. Betrachte die Sägezahnfunktion : für t = oder t = π S(t) := 1 (π t) : für < t < π Die Sägezahnfunktion ist ungerade, also gilt (mit ω = 1) a k = und b k = π π und damit
8. Tschebyscheff-Approximation: Theorie
 HJ Oberle Approximation WS 2013/14 8 Tschebyscheff-Approximation: Theorie Im Folgenden untersuchen wir Bestapproximationen bezüglich der Maximumsnorm Die Wurzeln dieser Theorie gehen auf Pafnuti Lwowitsch
HJ Oberle Approximation WS 2013/14 8 Tschebyscheff-Approximation: Theorie Im Folgenden untersuchen wir Bestapproximationen bezüglich der Maximumsnorm Die Wurzeln dieser Theorie gehen auf Pafnuti Lwowitsch
VIII. Fourier - Reihen
 VIII. Fourier - Reihen Dieses Kapitel enthält eine kurze Einführung in die mathematische Beschreibung von Schwingungen. Übersicht über den Inhalt von Kapitel VIII: 5. Der Satz von Fejér 53. Die Parsevalsche
VIII. Fourier - Reihen Dieses Kapitel enthält eine kurze Einführung in die mathematische Beschreibung von Schwingungen. Übersicht über den Inhalt von Kapitel VIII: 5. Der Satz von Fejér 53. Die Parsevalsche
8 Polynominterpolation
 8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
f(t) = a 2 + darstellen lasst Periodische Funktionen.
 7. Fourier-Reihen Viele Prozesse der Ingenieur- und Naturwissenschaften verlaufen periodisch oder annahernd periodisch, wie die Schwingungen einer Saite, Spannungs- und Stromverlaufe in Wechselstromkreisen
7. Fourier-Reihen Viele Prozesse der Ingenieur- und Naturwissenschaften verlaufen periodisch oder annahernd periodisch, wie die Schwingungen einer Saite, Spannungs- und Stromverlaufe in Wechselstromkreisen
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 7. Übungsblatt
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
8. Spezielle Funktionen
 H.J. Oberle Differentialgleichungen II SoSe 2013 8. Spezielle Funktionen Spezielle Funktionen (der mathematischen Physik) entstehen zumeist aus Separationsansätzen für PDG bei Vorliegen von Symmetrie-Eigenschaften.
H.J. Oberle Differentialgleichungen II SoSe 2013 8. Spezielle Funktionen Spezielle Funktionen (der mathematischen Physik) entstehen zumeist aus Separationsansätzen für PDG bei Vorliegen von Symmetrie-Eigenschaften.
9. Tschebyscheff-Approximation: Numerik
 HJ Oberle Approximation WS 213/14 9 Tschebyscheff-Approximation: Numerik Der Remez Algorithmus Der meist verwendete Algorithmus zur Lösung von Approximationsaufgaben bezüglich der Tschebyscheff-Norm ist
HJ Oberle Approximation WS 213/14 9 Tschebyscheff-Approximation: Numerik Der Remez Algorithmus Der meist verwendete Algorithmus zur Lösung von Approximationsaufgaben bezüglich der Tschebyscheff-Norm ist
2 Tschebyscheff-Approximation durch Polynome
 Approximationstheorie 71 2 Tschebyscheff-Approximation durch Polynome 2.1 Tschebyscheff-Polynome In diesem Abschnitt: explizit lösbare Tschebyscheff-Approximationsprobleme durch Polynome. Bezeichnungen:
Approximationstheorie 71 2 Tschebyscheff-Approximation durch Polynome 2.1 Tschebyscheff-Polynome In diesem Abschnitt: explizit lösbare Tschebyscheff-Approximationsprobleme durch Polynome. Bezeichnungen:
12.2 Gauß-Quadratur. Erinnerung: Mit der Newton-Cotes Quadratur. I n [f] = g i f(x i ) I[f] = f(x) dx
![12.2 Gauß-Quadratur. Erinnerung: Mit der Newton-Cotes Quadratur. I n [f] = g i f(x i ) I[f] = f(x) dx 12.2 Gauß-Quadratur. Erinnerung: Mit der Newton-Cotes Quadratur. I n [f] = g i f(x i ) I[f] = f(x) dx](/thumbs/71/65291080.jpg) 12.2 Gauß-Quadratur Erinnerung: Mit der Newton-Cotes Quadratur I n [f] = n g i f(x i ) I[f] = i=0 b a f(x) dx werden Polynome vom Grad n exakt integriert. Dabei sind die Knoten x i, 0 i n, äquidistant
12.2 Gauß-Quadratur Erinnerung: Mit der Newton-Cotes Quadratur I n [f] = n g i f(x i ) I[f] = i=0 b a f(x) dx werden Polynome vom Grad n exakt integriert. Dabei sind die Knoten x i, 0 i n, äquidistant
Ferienkurs Seite 1. Technische Universität München Ferienkurs Analysis 1 Stetigkeit, Konvergenz, Topologie
 Ferienkurs Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit, Konvergenz, Topologie Lösung 2.03.202. Gleichmäßige Konvergenz Entscheiden Sie, ob die folgenden auf (0,
Ferienkurs Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit, Konvergenz, Topologie Lösung 2.03.202. Gleichmäßige Konvergenz Entscheiden Sie, ob die folgenden auf (0,
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
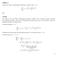 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Konvergenz im quadratischen Mittel - Hilberträume
 CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
8 Interpolation. 8.1 Problemstellung. Gegeben: Diskrete Werte einer Funktion f : R R an n + 1 Stützstellen. x 0 < x 1 <... < x n.
 8 Interpolation 81 Problemstellung Gegeben: Diskrete Werte einer Funktion f : R R an n + 1 Stützstellen x 0 < x 1 < < x n Eingabedaten: (x 0, f 0 ),(x 1, f 1 ),,(x n, f n ) Gegebene Daten (x j, f j ) Analysis
8 Interpolation 81 Problemstellung Gegeben: Diskrete Werte einer Funktion f : R R an n + 1 Stützstellen x 0 < x 1 < < x n Eingabedaten: (x 0, f 0 ),(x 1, f 1 ),,(x n, f n ) Gegebene Daten (x j, f j ) Analysis
53 Die Parsevalsche Gleichung
 53 Die Parsevalsche Gleichung 53 Die Parsevalsche Gleichung 5 53. Skalarprodukte auf Räumen quadratintegrierbarer Funktionen. a) Die Orthogonalitätsrelationen (5.5) legen die Interpretation des Ausdrucks
53 Die Parsevalsche Gleichung 53 Die Parsevalsche Gleichung 5 53. Skalarprodukte auf Räumen quadratintegrierbarer Funktionen. a) Die Orthogonalitätsrelationen (5.5) legen die Interpretation des Ausdrucks
Die Interpolationsformel von Lagrange
 Die Interpolationsformel von Lagrange Zentrale Aussage: Zu beliebigen n + Stützpunkten (x i,f i ), i =,...,n mit paarweise verschiedenen Stützstellen x i x j, für i j, gibt es genau ein Polynom π n P n
Die Interpolationsformel von Lagrange Zentrale Aussage: Zu beliebigen n + Stützpunkten (x i,f i ), i =,...,n mit paarweise verschiedenen Stützstellen x i x j, für i j, gibt es genau ein Polynom π n P n
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Westfälische Wilhelms-Universität Münster. Seminararbeit. Fourier-Reihen. vorgelegt von. Stefan Marczinzik
 Westfälische Wilhelms-Universität Münster Seminararbeit Fourier-Reihen vorgelegt von Stefan Marczinzik Fachbereich Mathematik und Informatik Seminar: Integraltransformationen (WS /3) Seminarleiter: Prof.
Westfälische Wilhelms-Universität Münster Seminararbeit Fourier-Reihen vorgelegt von Stefan Marczinzik Fachbereich Mathematik und Informatik Seminar: Integraltransformationen (WS /3) Seminarleiter: Prof.
Höhere Mathematik I für die Fachrichtung Informatik. Lösungsvorschläge zum 10. Übungsblatt. < 0 für alle t > 1. tan(x) tan(0) x 0
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
7. Die eindimensionale Wärmeleitungsgleichung
 H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
H.J. Oberle Differentialgleichungen II SoSe 2013 7. Die eindimensionale Wärmeleitungsgleichung Als Beispiel für eine parabolische PDG betrachten wir die eindimensionale Wärmeleitungsgleichung u t (x, t)
Inhalt Kapitel IV: Interpolation
 Inhalt Kapitel IV: Interpolation IV Interpolation IV. Polynom-Interpolation IV. Spline-Interpolation Kapitel IV (InhaltIV) Die Interpolationsformel von Lagrange Zentrale Aussage: Zu beliebigen n + Stützpunkten
Inhalt Kapitel IV: Interpolation IV Interpolation IV. Polynom-Interpolation IV. Spline-Interpolation Kapitel IV (InhaltIV) Die Interpolationsformel von Lagrange Zentrale Aussage: Zu beliebigen n + Stützpunkten
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Numerische Verfahren und Grundlagen der Analysis
 Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 26 1. Folgen R. Steuding (HS-RM)
Numerische Verfahren und Grundlagen der Analysis Rasa Steuding Hochschule RheinMain Wiesbaden Wintersemester 2011/12 R. Steuding (HS-RM) NumAna Wintersemester 2011/12 1 / 26 1. Folgen R. Steuding (HS-RM)
Die Interpolationsaufgabe besteht darin, eine (einfache) Funktion u n U n zu finden,
 Kapitel 3 Interpolation 31 Einführung Bemerkung 31 Motivation, Aufgabenstellung Gegeben seien eine Funktion f C([a,b]) und x i [a,b], i = 0,n, mit a x 0 < x 1 < < x n b (31) Die Interpolationsaufgabe besteht
Kapitel 3 Interpolation 31 Einführung Bemerkung 31 Motivation, Aufgabenstellung Gegeben seien eine Funktion f C([a,b]) und x i [a,b], i = 0,n, mit a x 0 < x 1 < < x n b (31) Die Interpolationsaufgabe besteht
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
Fourier-Integrale: Ausgangsdaten und Transformierte sind jeweils Funktionen über der ganzen reellen Achse.
 Fourier-Reihen Fourier-Transformation Die Fourier-Transformation ist eines der wichtigsten Instrumente zur Behandlung linearer Systeme, seien es gewöhnliche oder partielle lineare Differentialgleichungen
Fourier-Reihen Fourier-Transformation Die Fourier-Transformation ist eines der wichtigsten Instrumente zur Behandlung linearer Systeme, seien es gewöhnliche oder partielle lineare Differentialgleichungen
11. Darstellung von Kurven und Flächen
 H.J. Oberle Approximation WS 23/4. Darstellung von Kurven und Flächen Bézier Kurven. Unser Ziel ist es, polynomiale Kurven auf dem Rechner möglichst effizient darzustellen. Hierzu nutzen wir die Basisdarstellung
H.J. Oberle Approximation WS 23/4. Darstellung von Kurven und Flächen Bézier Kurven. Unser Ziel ist es, polynomiale Kurven auf dem Rechner möglichst effizient darzustellen. Hierzu nutzen wir die Basisdarstellung
Höhere Mathematik I/II
 Markus Stroppel Höhere Mathematik I/II Z. Zusätze. Z.. Skalarprodukte in Funktionenräumen. Wir wollen an einigen Beispielen zeigen, dass es nützlich sein kann, Skalarprodukte auch in ganz allgemeinen (reellen)
Markus Stroppel Höhere Mathematik I/II Z. Zusätze. Z.. Skalarprodukte in Funktionenräumen. Wir wollen an einigen Beispielen zeigen, dass es nützlich sein kann, Skalarprodukte auch in ganz allgemeinen (reellen)
Lösungen zur Übungsserie 9
 Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag,? November Lösungen zur Übungsserie 9 Aufgaben 1,2,3,5,6,8,9,11 Aufgabe 1. Sei a R. Berechnen Sie die folgenden Grenzwerte, falls sie existieren.
Analysis 1 Herbstsemester 2018 Prof. Peter Jossen Montag,? November Lösungen zur Übungsserie 9 Aufgaben 1,2,3,5,6,8,9,11 Aufgabe 1. Sei a R. Berechnen Sie die folgenden Grenzwerte, falls sie existieren.
Fourier-Reihen: Definitionen und Beispiele
 Fourier-Reihen: Definitionen und Beispiele Die Fourieranalysis beschäftigt sich mit dem Problem Funktionen in Kosinus und Sinus zu entwickeln. Diese Darstellungen sind in der Mathematik sowie in der Physik
Fourier-Reihen: Definitionen und Beispiele Die Fourieranalysis beschäftigt sich mit dem Problem Funktionen in Kosinus und Sinus zu entwickeln. Diese Darstellungen sind in der Mathematik sowie in der Physik
Analysis I für Studierende der Ingenieurwissenschaften
 Analysis I für Studierende der Ingenieurwissenschaften Ingenuin Gasser Department Mathematik Universität Hamburg Technische Universität Hamburg Harburg Wintersemester 2008/2009 1 Definition: Sei M R, alsom
Analysis I für Studierende der Ingenieurwissenschaften Ingenuin Gasser Department Mathematik Universität Hamburg Technische Universität Hamburg Harburg Wintersemester 2008/2009 1 Definition: Sei M R, alsom
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
Kugelfunktionen und Kugelflächenfunktionen
 Kugelfunktionen und Kugelflächenfunktionen Wir beschreiben jetzt die Konstruktion von Orthonormalsystemen, die insbesondere in der Geophysik bedeutsam sind, wenn Effekte auf der Erdoberfläche, der Erdkugel
Kugelfunktionen und Kugelflächenfunktionen Wir beschreiben jetzt die Konstruktion von Orthonormalsystemen, die insbesondere in der Geophysik bedeutsam sind, wenn Effekte auf der Erdoberfläche, der Erdkugel
Karlsruher Institut für Technologie (KIT) WS 2012/13 Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning
 Karlsruher Institut für Technologie (KIT) WS 202/3 Institut für Analysis 26..202 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 7. Übungsblatt Aufgabe Untersuchen
Karlsruher Institut für Technologie (KIT) WS 202/3 Institut für Analysis 26..202 Prof. Dr. Tobias Lamm Dr. Patrick Breuning Höhere Mathematik I für die Fachrichtung Physik 7. Übungsblatt Aufgabe Untersuchen
Die Fakultät. Thomas Peters Thomas Mathe-Seiten 13. September 2003
 Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 3. September 2003 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
Die Fakultät Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 3. September 2003 Dieser Artikel gibt die Definition der klassischen Fakultät und führt von dort aus zunächst zu der Anwendung in Taylor-Reihen
6. Lineare DGL-Systeme erster Ordnung
 HJ Oberle Differentialgleichungen I WiSe 22/3 6 Lineare DGL-Systeme erster Ordnung A Allgemeines Wir betrachten ein lineares DGL System erster Ordnung y (t = A(t y(t + b(t (6 und setzen voraus, dass die
HJ Oberle Differentialgleichungen I WiSe 22/3 6 Lineare DGL-Systeme erster Ordnung A Allgemeines Wir betrachten ein lineares DGL System erster Ordnung y (t = A(t y(t + b(t (6 und setzen voraus, dass die
V. Claus, Juli 2005 Einführung in die Informatik II 45
 Um die Größenordnung einer reellwertigen oder ganzzahligen Funktion zu beschreiben, verwenden wir die so genannten Landau-Symbole (nach dem deutschen Mathematiker Edmund Landau, 1877-1938). Hierbei werden
Um die Größenordnung einer reellwertigen oder ganzzahligen Funktion zu beschreiben, verwenden wir die so genannten Landau-Symbole (nach dem deutschen Mathematiker Edmund Landau, 1877-1938). Hierbei werden
Orthogonalität von Kosinus und Sinus
 Orthogonalität von Kosinus und Sinus Die Funktionen 1, cos(kx), sin(kx), k >, bilden ein Orthogonalsystem im Raum der quadratintegrierbaren π-periodischen Funktionen: cos(jx) cos(kx) dx = cos(jx) sin(lx)
Orthogonalität von Kosinus und Sinus Die Funktionen 1, cos(kx), sin(kx), k >, bilden ein Orthogonalsystem im Raum der quadratintegrierbaren π-periodischen Funktionen: cos(jx) cos(kx) dx = cos(jx) sin(lx)
Übungsblatt 1 Musterlösung
 Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
Numerik gewöhnlicher Differentialgleichungen MA234 - SS6 Übungsblatt Musterlösung Aufgabe (Interpolationspolynom) a) Bestimmen Sie die Hilfspolynome L i, i =,,2, für x =, x = 2 und x 2 = 3 nach der Formel
3 Grenzwert und Stetigkeit 1
 3 Grenzwert und Stetigkeit 3. Grenzwerte bei Funktionen In diesem Abschnitt gilt: I ist immer ein beliebiges Intervall, 0 I oder einer der Endpunkte. 3.. Definition Sei I Intervall, 0 IR und 0 I oder Endpunkt
3 Grenzwert und Stetigkeit 3. Grenzwerte bei Funktionen In diesem Abschnitt gilt: I ist immer ein beliebiges Intervall, 0 I oder einer der Endpunkte. 3.. Definition Sei I Intervall, 0 IR und 0 I oder Endpunkt
Musterlösungen zur Leistungsnachweisklausur vom Studiengang Informatik, Ingenieurinformatik, Lehramt
 TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
TU ILMENAU Institut für Mathematik Numerische Mathematik PD Dr. W. Neundorf Musterlösungen zur Leistungsnachweisklausur vom.0.006 Studiengang Informatik, Ingenieurinformatik, Lehramt 1. Lineare Algebra
30 Die Gammafunktion und die Stirlingsche Formel
 3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
3 Die Gammafunktion und die Stirlingsche Formel 35 Charakterisierung der Gammafunktion 36 Darstellung der Gammafunktion 38 Beziehung zwischen der Gammafunktion und der Zetafunktion 3 Stirlingsche Formel
Numerik SS Übungsblatt 3
 PROF. DR. BERND SIMEON CHRISTIAN GOBERT THOMAS MÄRZ Numerik SS 9 Übungsblatt 3 Aufgabe 1 Clenshaw-Curtis-Quadratur Wie bereits bei der Polynominterpolation bietet es sich auch zur Quadratur an Tschebysheff-
PROF. DR. BERND SIMEON CHRISTIAN GOBERT THOMAS MÄRZ Numerik SS 9 Übungsblatt 3 Aufgabe 1 Clenshaw-Curtis-Quadratur Wie bereits bei der Polynominterpolation bietet es sich auch zur Quadratur an Tschebysheff-
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 11. Übungsblatt. { wachsend fallend
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 8/9 Aufgabe Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 8/9 Aufgabe Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
Konvergenz interpolierender Polynome
 Technische Universität Berlin Institut für Mathematik Konvergenz interpolierender Polynome Seminar Differentialgleichungen im Sommersemester 2012 bei Prof. Dr. Etienne Emmrich vorgelegt von David Breiter
Technische Universität Berlin Institut für Mathematik Konvergenz interpolierender Polynome Seminar Differentialgleichungen im Sommersemester 2012 bei Prof. Dr. Etienne Emmrich vorgelegt von David Breiter
Fourier-Transformation
 ANHANG A Fourier-Transformation In diesem Anhang werden einige Definitionen Ergebnisse über die Fourier-Transformation dargestellt. A. Definition Theorem & Definition: Sei f eine integrable komplexwertige
ANHANG A Fourier-Transformation In diesem Anhang werden einige Definitionen Ergebnisse über die Fourier-Transformation dargestellt. A. Definition Theorem & Definition: Sei f eine integrable komplexwertige
Lösung zu Kapitel 5 und 6
 Lösung zu Kapitel 5 und 6 (1) Sei f eine total differenzierbare Funktion. Welche Aussagen sind richtig? f ist partiell differenzierbar f kann stetig partiell differenzierbar sein f ist dann immer stetig
Lösung zu Kapitel 5 und 6 (1) Sei f eine total differenzierbare Funktion. Welche Aussagen sind richtig? f ist partiell differenzierbar f kann stetig partiell differenzierbar sein f ist dann immer stetig
n=1 a n mit reellen Zahlen a n einen
 4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
3 Numerisches Rechnen
 E Luik: Numerisches Rechnen 65 3 Numerisches Rechnen 31 Zahlen und ihre Darstellung Grundlage der Analysis bilden die reellen Zahlen Wir sind heute daran gewöhnt, eine reelle Zahl im Dezimalsystem als
E Luik: Numerisches Rechnen 65 3 Numerisches Rechnen 31 Zahlen und ihre Darstellung Grundlage der Analysis bilden die reellen Zahlen Wir sind heute daran gewöhnt, eine reelle Zahl im Dezimalsystem als
$Id: reihen.tex,v /06/12 10:59:50 hk Exp $ unendliche Summe. a 1 + a 2 + a 3 +.
 Mathematik für Informatiker B, SS 202 Dienstag 2.6 $Id: reihen.tex,v.8 202/06/2 0:59:50 hk Exp $ 7 Reihen Eine Reihe ist eine unendliche Summe a + a 2 + a 3 +. Die Summanden a i können dabei reell oder
Mathematik für Informatiker B, SS 202 Dienstag 2.6 $Id: reihen.tex,v.8 202/06/2 0:59:50 hk Exp $ 7 Reihen Eine Reihe ist eine unendliche Summe a + a 2 + a 3 +. Die Summanden a i können dabei reell oder
15 Hauptsätze über stetige Funktionen
 15 Hauptsätze über stetige Funktionen 15.1 Extremalsatz von Weierstraß 15.2 Zwischenwertsatz für stetige Funktionen 15.3 Nullstellensatz von Bolzano 15.5 Stetige Funktionen sind intervalltreu 15.6 Umkehrfunktionen
15 Hauptsätze über stetige Funktionen 15.1 Extremalsatz von Weierstraß 15.2 Zwischenwertsatz für stetige Funktionen 15.3 Nullstellensatz von Bolzano 15.5 Stetige Funktionen sind intervalltreu 15.6 Umkehrfunktionen
Komplexe Analysis für ITET und RW/CSE. Serie 11
 Prof. Dr. F. Da Lio R. Gantner Frühlingssemester 5 Komplexe Analysis für ITET und RW/CSE ETH Zürich D-MATH Serie Aufgabe. Fourierreihen (.a Sei f p die ungerade periodische Fortsetzung der Funktion f :
Prof. Dr. F. Da Lio R. Gantner Frühlingssemester 5 Komplexe Analysis für ITET und RW/CSE ETH Zürich D-MATH Serie Aufgabe. Fourierreihen (.a Sei f p die ungerade periodische Fortsetzung der Funktion f :
Inexakte Newton Verfahren
 Kapitel 3 Inexakte Newton Verfahren 3.1 Idee inexakter Newton Verfahren Wir betrachten weiterhin das nichtlineare Gleichungssystem F (x) = mit einer zumindest stetig differenzierbaren Funktion F : R n
Kapitel 3 Inexakte Newton Verfahren 3.1 Idee inexakter Newton Verfahren Wir betrachten weiterhin das nichtlineare Gleichungssystem F (x) = mit einer zumindest stetig differenzierbaren Funktion F : R n
15. Bereichsintegrale
 H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
H.J. Oberle Analysis III WS 212/13 15. Bereichsintegrale 15.1 Integrale über uadern Ziel ist die Berechnung des Volumens unterhalb des Graphen einer Funktion f : R n D R, genauer zwischen dem Graphen von
Fourierreihen. Die erste dieser Aussagen folgt direkt aus der Definition. Für die zweite bemerken
 Fachbereich Mathematik SS 0 J. Latschev Analysis II Fourierreihen In diesem Kapitel der Vorlesung widmen wir uns der Frage, inwieweit man jede periodische Funktion als Reihe in gewissen Standardfunktionen
Fachbereich Mathematik SS 0 J. Latschev Analysis II Fourierreihen In diesem Kapitel der Vorlesung widmen wir uns der Frage, inwieweit man jede periodische Funktion als Reihe in gewissen Standardfunktionen
Grenzwerte und Stetigkeit
 KAPITEL 3 Grenzwerte und Stetigkeit 3.1 Grenzwerte..................................... 49 3.2 Stetigkeit....................................... 57 Lernziele 3 Grenzwerte ε-δ-definition des Grenzwerts,
KAPITEL 3 Grenzwerte und Stetigkeit 3.1 Grenzwerte..................................... 49 3.2 Stetigkeit....................................... 57 Lernziele 3 Grenzwerte ε-δ-definition des Grenzwerts,
a 0, a 1, a 2, a 3,... Dabei stehen die drei Pünktchen für unendlich oft so weiter.
 7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
Finite Elemente I Konvergenzaussagen
 Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
Finite Elemente I 195 5 onvergenzaussagen 5 onvergenzaussagen TU Bergakademie Freiberg, SoS 2006 Finite Elemente I 196 5.1 Interpolation in Sobolev-Räumen Wesentlicher Baustein der FE-onvergenzanalyse
Fourierreihen. Definition. Eine Funktion f(x) heißt periodisch mit der Periode T, wenn f(x + T ) = f(x)
 Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
1. Hierarchische Basen. 1. Hierarchische Basen Perlen der Informatik I, Hans-Joachim Bungartz page 1 of 33
 Perlen der Informatik I, Hans-Joachim Bungartz page 1 of 33 1.1. Quadratur nach Archimedes Näherungsweise Berechnung von F 1 := 1 0 4 x (1 x) dx = 2 3 1 t=1 t=2 ¼ 0 ½ 1 ¼ 0 ½ 1 0 ½ 1 Perlen der Informatik
Perlen der Informatik I, Hans-Joachim Bungartz page 1 of 33 1.1. Quadratur nach Archimedes Näherungsweise Berechnung von F 1 := 1 0 4 x (1 x) dx = 2 3 1 t=1 t=2 ¼ 0 ½ 1 ¼ 0 ½ 1 0 ½ 1 Perlen der Informatik
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Analysis I. 7. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 207 Erinnerung Satz. (Zwischenwertsatz) Sei f : [a, b] R stetig mit f(a) f(b). Dann gibt es zu jedem
Analysis I 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 26, 207 Erinnerung Satz. (Zwischenwertsatz) Sei f : [a, b] R stetig mit f(a) f(b). Dann gibt es zu jedem
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 Reelle und komplexe Zahlenfolgen
 Mathematik für Physiker I, WS 200/20 Freitag 0.2 $Id: folgen.tex,v. 200/2/06 :2:5 hk Exp $ $Id: reihen.tex,v. 200/2/0 4:4:40 hk Exp hk $ 6 Reelle und komplexe Zahlenfolgen 6. Cauchyfolgen Wir kommen nun
Mathematik für Physiker I, WS 200/20 Freitag 0.2 $Id: folgen.tex,v. 200/2/06 :2:5 hk Exp $ $Id: reihen.tex,v. 200/2/0 4:4:40 hk Exp hk $ 6 Reelle und komplexe Zahlenfolgen 6. Cauchyfolgen Wir kommen nun
Musterlösungen zu Blatt 15, Analysis I
 Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme
 6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme 6.1 Nullstellen reeller Funktionen Bemerkung 6.1 (Problemstellung) geg.: f C[a, b] ges.: x [a, b] mit f(x ) = 0 Lösungstheorie f linear
6 Iterationsverfahren für lineare und nichtlineare Gleichungssysteme 6.1 Nullstellen reeller Funktionen Bemerkung 6.1 (Problemstellung) geg.: f C[a, b] ges.: x [a, b] mit f(x ) = 0 Lösungstheorie f linear
2 Der Weierstraßsche Produktsatz
 4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
7. Übungsblatt zur Mathematik II für Inf, WInf
 Fachbereich Mathematik Prof. Dr. Streicher Dr. Sergiy Nesenenko Pavol Safarik SS 2010 27.-31.05.10 7. Übungsblatt zur Mathematik II für Inf, WInf Gruppenübung Aufgabe G24 (Grundlegende Definitionen) Betrachten
Fachbereich Mathematik Prof. Dr. Streicher Dr. Sergiy Nesenenko Pavol Safarik SS 2010 27.-31.05.10 7. Übungsblatt zur Mathematik II für Inf, WInf Gruppenübung Aufgabe G24 (Grundlegende Definitionen) Betrachten
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
2 Polynome und rationale Funktionen
 Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
Gleichungen spielen auch in der Ingenieurmathematik eine große Rolle. Sie beschreiben zum Beispiel Bedingungen, unter denen Vorgänge ablaufen, Gleichgewichtszustände, Punktmengen. Gleichungen für eine
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Das Additionstheorem für die Weierstrass sche -Funktion und elliptische Integrale. Peychyn Lai
 Das Additionstheorem für die Weierstrass sche -Funktion und elliptische Integrale Peychyn Lai 10. Oktober 2007 1 Einleitung Wir haben im letzten Vortrag die Weierstrass sche -Funktion kennengelernt, die
Das Additionstheorem für die Weierstrass sche -Funktion und elliptische Integrale Peychyn Lai 10. Oktober 2007 1 Einleitung Wir haben im letzten Vortrag die Weierstrass sche -Funktion kennengelernt, die
Computer-orientierte Mathematik
 Computer-orientierte Mathematik 6. Vorlesung - Christof Schuette 30.11.18 Memo: Relative und Absolute Kondition Relative Kondition der Grundrechenarten: Addition, Multiplikation und Division liefern beruhigende
Computer-orientierte Mathematik 6. Vorlesung - Christof Schuette 30.11.18 Memo: Relative und Absolute Kondition Relative Kondition der Grundrechenarten: Addition, Multiplikation und Division liefern beruhigende
PRÜFUNG AUS MATHEMATIK 3
 (8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
(8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
3.6 Approximationstheorie
 3.6 Approximationstheorie Bisher haben wir uns im Wesentlichen mit der Interpolation beschäftigt. Die Approximation ist weiter gefasst: wir suchen eine einfache Funktion p P (dabei ist der Funktionenraum
3.6 Approximationstheorie Bisher haben wir uns im Wesentlichen mit der Interpolation beschäftigt. Die Approximation ist weiter gefasst: wir suchen eine einfache Funktion p P (dabei ist der Funktionenraum
KAPITEL 9 Splinefunktionen
 KAPITEL 9 Splinefunktionen 9.1 Splineräume und Approximationsgüte Bei der Behandlung von Splines ist es bequemer, statt mit dem Grad von Polynomen, mit der Ordnung k := Grad + 1 zu arbeiten. Für eine Knotenmenge
KAPITEL 9 Splinefunktionen 9.1 Splineräume und Approximationsgüte Bei der Behandlung von Splines ist es bequemer, statt mit dem Grad von Polynomen, mit der Ordnung k := Grad + 1 zu arbeiten. Für eine Knotenmenge
c < 1, (1) c k x k0 c k = x k0
 4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
4.14 Satz (Quotientenkriterium). Es sei (x k ) Folge in K. Falls ein k 0 existiert, so dass für k k 0 gilt x k 0 und x k+1 x k c < 1, (1) so ist x k absolut konvergent. Beweis. Aus (1) folgt mit vollständiger
11 Fourier-Analysis Grundlegende Begriffe
 11 Fourier-Analysis 11.1 Grundlegende Begriffe Definition: Eine Funktion f : R R (oder f : R C) heißt periodisch mit der Periode T (oder T-periodisch), falls f(t + T) = f(t) für alle t R. Ziel: Entwicklung
11 Fourier-Analysis 11.1 Grundlegende Begriffe Definition: Eine Funktion f : R R (oder f : R C) heißt periodisch mit der Periode T (oder T-periodisch), falls f(t + T) = f(t) für alle t R. Ziel: Entwicklung
3.5 Schnelle Fouriertransformation (FFT, DFT)
 3.5 Schnelle Fouriertransformation (FFT, DFT) 3.5.1 Grundlagen Ein Polynom P = i a ix i C[x] vom Grad n ist eindeutig durch seine Koeffizienten a i bestimmt, d.h. man hat eine Bijektion {Polynome C[x]
3.5 Schnelle Fouriertransformation (FFT, DFT) 3.5.1 Grundlagen Ein Polynom P = i a ix i C[x] vom Grad n ist eindeutig durch seine Koeffizienten a i bestimmt, d.h. man hat eine Bijektion {Polynome C[x]
2.5 Komplexe Wurzeln. Mathematik für Naturwissenschaftler I 2.5
 Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
KAPITEL 8. Interpolation
 KAPITEL 8. Interpolation 8.2 Lagrange-Interpolationsaufgabe für Polynome Wir beschränken uns auf die Lagrange-Interpolation mit Polynomen. Der Raum der Polynome vom Grad n: Stützstellen: Π n = { n j=0
KAPITEL 8. Interpolation 8.2 Lagrange-Interpolationsaufgabe für Polynome Wir beschränken uns auf die Lagrange-Interpolation mit Polynomen. Der Raum der Polynome vom Grad n: Stützstellen: Π n = { n j=0
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1. Anhang: Spline-Funktionen
 C:\D\DOKU\NUM KURS\SPLINE.TEX C:\UG\.AI 20. Juli 1998 Vorbemerkung: Wenn der Satz stimmt, daß jede Formel eines Textes die Leserzahl halbiert, dann brauche ich bei grob geschätzt 40 Formeln etwa 2 40 =
C:\D\DOKU\NUM KURS\SPLINE.TEX C:\UG\.AI 20. Juli 1998 Vorbemerkung: Wenn der Satz stimmt, daß jede Formel eines Textes die Leserzahl halbiert, dann brauche ich bei grob geschätzt 40 Formeln etwa 2 40 =
4.5 Schranken an die Dichte von Kugelpackungen
 Gitter und Codes c Rudolf Scharlau 19. Juli 2009 341 4.5 Schranken an die Dichte von Kugelpackungen Schon in Abschnitt 1.4 hatten wir die Dichte einer Kugelpackung, speziell eines Gitters bzw. einer quadratischen
Gitter und Codes c Rudolf Scharlau 19. Juli 2009 341 4.5 Schranken an die Dichte von Kugelpackungen Schon in Abschnitt 1.4 hatten wir die Dichte einer Kugelpackung, speziell eines Gitters bzw. einer quadratischen
cos(kx) sin(nx)dx =?
 3.5 Fourierreihen 3.5.1 Vorbemerkungen cos(kx) sin(nx)dx =? cos gerade Funktion x cos(kx) gerade Funktion sin ungerade Funktion x sin(nx) ungerade Funktion x cos(kx) sin(nx) ungerade Funktion Weil [, π]
3.5 Fourierreihen 3.5.1 Vorbemerkungen cos(kx) sin(nx)dx =? cos gerade Funktion x cos(kx) gerade Funktion sin ungerade Funktion x sin(nx) ungerade Funktion x cos(kx) sin(nx) ungerade Funktion Weil [, π]
bekannt Analog reduzieren wir die Randwerte im 2d-System. Man erhält dann eine Blocktridia-
 3.. Jetzt: Eliminiere 1. und 2. wie folgt u 2 + 2u 1 = h 2 f 1 + α }{{} bekannt Nun: Au = b mit A R n,n, b R n, u R n und A hat die Gestalt 2 1 1 2 1 A =......... =: tridiag( 1, 2, 1)...... 1 1 2 Analog
3.. Jetzt: Eliminiere 1. und 2. wie folgt u 2 + 2u 1 = h 2 f 1 + α }{{} bekannt Nun: Au = b mit A R n,n, b R n, u R n und A hat die Gestalt 2 1 1 2 1 A =......... =: tridiag( 1, 2, 1)...... 1 1 2 Analog
72 Orthonormalbasen und Konvergenz im quadratischen Mittel
 72 Orthonormalbasen und Konvergenz im quadratischen Mittel 30 72 Orthonormalbasen und Konvergenz im quadratischen Mittel Wir untersuchen nun die Konvergenz von Fourier-Reihen im quadratischen Mittel in
72 Orthonormalbasen und Konvergenz im quadratischen Mittel 30 72 Orthonormalbasen und Konvergenz im quadratischen Mittel Wir untersuchen nun die Konvergenz von Fourier-Reihen im quadratischen Mittel in
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Technische Universität Berlin. Klausur Analysis I
 SS 2008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis I 4.07.2008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
SS 2008 Prof. Dr. John M. Sullivan Kerstin Günther Technische Universität Berlin Fakultät II Institut für Mathematik Klausur Analysis I 4.07.2008 Name: Vorname: Matr.-Nr.: Studiengang: Mit der Veröffentlichung
Approximationstheorie und Approximationspraxis
 Approximationstheorie und Approximationspraxis Martin Wagner Bergische Universität Wuppertal Fachbereich C - Mathematik und Naturwissenschaften AG Optmierung und Approximation 3. Februar 2010 1 / 20 Motivation
Approximationstheorie und Approximationspraxis Martin Wagner Bergische Universität Wuppertal Fachbereich C - Mathematik und Naturwissenschaften AG Optmierung und Approximation 3. Februar 2010 1 / 20 Motivation
ANALYSIS I FÜR TPH WS 2016/17 3. Übung Übersicht
 ANALYSIS I FÜR TPH WS 206/7 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Untersuchung von Reihen mittels Konvergenzkriterien Aufgabe 2: Konvergenz und Berechnung von Reihen I Aufgabe 3: ( )
ANALYSIS I FÜR TPH WS 206/7 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Untersuchung von Reihen mittels Konvergenzkriterien Aufgabe 2: Konvergenz und Berechnung von Reihen I Aufgabe 3: ( )
