Hausaufgabe 1 (Induktion):
|
|
|
- Richard Winkler
- vor 5 Jahren
- Abrufe
Transkript
1 Prof Dr J Giesl M Brokshmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgben sollen in Gruppen von je 2 Studierenden us dem gleihen Tutorium berbeitet werden Die Lösungen der Husufgben müssen bis Fr, , 11:45 in der Globlübung bgegeben werden Alterntiv ist es möglih, die Lösungen in den Tutorien m Mittwoh bzugeben oder bis Fr, Uhr im Abgbeksten im Flur des LuFG I2 einzuwerfen (Ahornstr 55, E1, 2 Etge) Nmen und Mtrikelnummern der Studierenden sowie die Nummer der Übungsgruppe sind uf jedes Bltt der Abgbe zu shreiben Heften bzw tkern Sie die Blätter! Die Tutorufgben werden in den jeweiligen Tutorien gemeinsm besprohen und berbeitet Am finden die letzten Tutorien zur Vorlesung Formle Systeme, Sprhen, Prozesse sttt Dort werden Sie die Möglihkeit hben, unter Anleitung des Tutors vershiedene klusurrelevnte Aufgben us dem Semester zu wiederholen Am findet die letzte Vorlesung Formle Systeme, Sprhen, Prozesse im Sommersemester 2010 sttt Husufgbe 1 (Induktion): (5 Punkte) Gegeben sei ein NFA M = (Q, Σ, δ, q 0, F ) Wir konstruieren dmit die linkslinere Grmmtik G = (Q, Σ, P, q o ) mit den Produktionen P = {q p p δ(q, ), q Q, Σ} {q ɛ q F } Beweisen Sie, dss für lle p, q Q, w Σ gilt: p ˆδ(q, w) q G wp1 Hinweis: Beweisen Sie beide Rihtungen getrennt Verwenden Sie für eine Induktion über die Wortlänge und für eine Induktion über die Ableitungslänge Wir zeigen zuerst p ˆδ(q, w) q G wp ( ) per Induktion über die Länge des Wortes w Induktionsnfng: Sei w = 0, dh w = ɛ Sei p ˆδ(q, ɛ) Dnn gilt p = q und die Ableitung q 0 G q = p existiert Wir nehmen nun ls Induktionshypothese n, dss für beliebige n N 0 die Aussge ( ) für Wörter der Länge n bereits gilt Induktionsshritt: Sei w = n + 1 mit w = w, w Σ n, Σ Dnn gibt es ein q mit p δ(q, ) und q ˆδ(q, w ) Nh Induktionshypothese gilt q G w q Nh Konstruktion gilt ußerdem q p P Dmit können wir die Ableitung q G w q q p w p = wp bilden Wir zeigen nun die Rükrihtung q G wp p ˆδ(q, w) ( ) per Induktion über die Länge n der Ableitung Induktionsnfng: Sei n = 0, dh q 0 g q = ɛq Es gilt offensihtlih q ˆδ(q, ɛ) Wir nehmen nun ls Induktionshypothese n, dss für beliebige n N 0 die Aussge ( ) für Ableitungen der Länge n bereits gilt Induktionsshritt: Nh Konstruktion von G gibt es nur linkslinere Regeln Es gibt lso ein q Q mit einer Regel q p mit q n G w q q p w p = wp Nh Induktionshypothese gilt q ˆδ(q, w ) und nh Konstruktion der Regel q p gilt uh p δ(q, ) Dmit gilt dnn direkt p ˆδ(q, w) 1 Dies ist Lemm 404 us der Vorlesung 1
2 Tutorufgbe 2 (Kontextsensitive Sprhen): Um zu zeigen, dss L i für i {1, 2} eine kontextsensitive Sprhe ist, geben Sie jeweils eine monotone Grmmtik G i n, so dss L(G i ) = L i gilt Geben Sie ußerdem eine Ableitung für ds Wort w i mit Ihrer Grmmtik n ) L 1 = { n b n n n N 0 } und w 1 = bb b) L 2 = { n b m n d m n, m N >0 } und w 2 = bbbddd ) S ɛ (1) S T (2) T T BC (3) T BC (4) CB BC (5) B b (6) bb bb (7) bc b (8) C (9) Hier werden mit Regeln (3) und (4) für jedes Terminlsymbol jeweils gleih viele B und C erzeugt Diese sind noh niht notwendigerweise in der rihtigen Ordnung, können ber mit Regel (5) Shritt für Shritt so geordnet werden, dss kein B mehr rehts von einem C steht Nun knn mn von den -Symbolen uf der linken Seite usgehend jeweils ds erste Nonterminl in ein Terminl umwndeln Beispielbleitung für bb (bgeleitete Teile sind jeweils unterstrihen): S (2) T (3) T BC (4) BCBC (5) BBCC (6) bbcc (7) bbcc (8) bbc (9) bb 2
3 b) S NM (1) S M (2) N NY (3) N Y (4) M bmd (5) M bxd (6) Y b by (7) Y X X (8) X (9) Hier werden die Teillängen n, m durh die Anzhl der N- bzw M-Produktionen festgelegt Während die -, b- und -Terminle bereits beim Verwenden der N und M-Produktionen ufgebut werden, wird ds Nonterminl Y verwendet, um die Anzhl der noh zu erzeugenden -Terminle zu zählen Ds Nonterminl X wird genu einml erzeugt und mrkiert die Stelle, n der die -Terminle eingefügt werden müssen Mit Hilfe von Produktion (7) werden dnn die vor den bereits erzeugten b stehenden Y im Wort nh rehts vershoben, bis sie X erreihen Dort werden sie dnn durh ein ersetzt Zuletzt knn X durh ein einziges ersetzt werden Beispielbleitung für bbbddd (bgeleitete Teile sind jeweils unterstrihen): S (1) NM (4) Y M (5) Y bmd (5) Y bbmdd (6) Y bbbxddd (7) by bbxddd (7) bby bxddd (7) bbby Xddd (8) bbbxddd (9) bbbddd Husufgbe 3 (Kontextsensitive Sprhen): ( = 9 Punkte) Um zu zeigen, dss L i für i {3, 4, 5} eine kontextsensitive Sprhe ist, geben Sie jeweils eine monotone Grmmtik G i n, so dss L(G i ) = L i gilt Geben Sie ußerdem eine Ableitung für ds Wort w i mit Ihrer Grmmtik n ) L 3 = {w {, b, } (w) = b (w) = (w)} und w 3 = bb b) L 4 = {(b) n (b) n () n n N 0 } und w 4 = bbbb 3
4 ) L 5 = { n b m k n, m, k N >0 n m k} und w 5 = bb ) S ɛ (1) S T (2) T T T (3) T ABC (4) AB BA (5) AC CA (6) BA AB (7) BC CB (8) CA AC (9) CB BC (10) A (11) B b (12) C (13) Hier werden mit den Regeln (3) und (4) eine beliebige Anzhl von ABC-Gruppen erzeugt Mit Hilfe der Regeln (5)-(10) können diese dnn frei vertusht werden Mit den Regeln (11)-(13) werden die Nonterminle dnn in die entsprehenden Terminle übersetzt Beispielbleitung für bb (bgeleitete Teile sind jeweils unterstrihen): S (2) T (3) T T (4) ABCT (4) ABCABC (8) ACBABC (6) CABABC (7) CAABBC (8) CAABCB bb 4
5 b) S ɛ (1) S T (2) T bt HK (3) T bhk (4) KH HK (5) bh bb (6) bh bb (7) bk b (8) K (9) Die Grmmtik ist bis uf die Terminlsymbole identish zur Grmmtik für L 1 = { n b n n n N 0 } Beispielbleitung für bbbb (bgeleitete Teile sind jeweils unterstrihen): S (2) T (3) bt HK (4) bbhkhk (5) bbhhkk (6) bbbhkk (7) bbbbkk (8) bbbbk (9) bbbb ) S T bx (1) S bx (2) T T bc (3) T T bc (4) T T C (5) T bc (6) T C (7) Cb bc (8) CX X (9) X (10) Hier werden - und b-symbole erneut beim initilen Aufbu mit Hilfe der Produktionen für S und G generiert Mit X wird die Stelle im Wort mrkiert, in der im Folgenden die -Symbole erzeugt werden müssen, deren Zhl von der Anzhl der erzeugten C-Nonterminle bhängt Diese werden mitten im Wort erzeugt und können dnn mit Regel 8 nh rehts bewegt werden 5
6 Beispielbleitung für bb (bgeleitete Teile sind jeweils unterstrihen): S (1) T bx (3) T bcbx (4) CbCbX (8) CbbCX (8) bcbcx (8) bbccx (9) bbcx (9) bbx (10) bb Tutorufgbe 4 (Synhronisiertes Produkt): while (true) { ; /* wit for x!= 1 */ while (x = 1); print ( ); } x := 0; /* wit for x!= 0 */ while (x = 0); print ( b ); Progrmm P 1 Progrmm P 2 ) Modellieren Sie den Kontrollfluss von P 1 durh einen NFA M 1 mit 3 Zuständen, sowie den den Kontrollfluss von P 2 durh einen NFA M 2 mit 4 Zuständen Verwenden Sie hierbei für beide Automten die Signtur Σ = {,, x := 0,, print( ), print( b )} b) Berehnen Sie ds unsynhronisierte Produkt M 1 M 2 Geben Sie den resultierenden NFA n ) Modellieren Sie die booleshe Vrible x des Progrmms durh den NFA B x Berehnen Sie den NFA M := (M 1 M 2 ) B x und geben Sie die Automten B x und M n d) Ist es möglih, dss Progrmm P 1 und P 2 (wenn sie gleihzeitig usgeführt werden) die Zeihenfolge b usgeben? Begründen Sie ihre Antwort mit dem NFA M ) 6
7 q 0 q 1 q 2 print( ) q x := 0 3 q 4 q print( b ) 5 q 6 b) (q 0, q 3 ) (q 1, q 3 ) (q 2, q 3 ) x := 0 print( ) x := 0 x := 0 (q 0, q 4 ) (q 1, q 4 ) (q 2, q 4 ) print( ) (q 0, q 5 ) (q 1, q 5 ) (q 2, q 5 ) print( b ) print( ) print( b ) print( b ) (q 0, q 6 ) (q 1, q 6 ) (q 2, q 6 ) print( ) ) 7
8 x := 0 b 0 b 1 x := 0 (q 0, q 3, b 0 ) (q 1, q 3, b 1 ) x := 0 x := 0 (q 0, q 4, b 0 ) (q 1, q 4, b 0 ) print( ) (q 2, q 4, b 0 ) (q 1, q 4, b 1 ) (q 1, q 5, b 1 ) print( b ) (q 1, q 6, b 1 ) d) Nein, der NFA M beshreibt keinen Pfd, uf dem nh einem print( b ) noh ein print( ) folgen knn Husufgbe 5 (Synhronisiertes Produkt): (4 Punkte) q 3 q 4 b b q 1 q 2 q 5 Gegeben seien die DFAs M 1 und M 2 Berehnen Sie: ) M 1 M 2 8
9 b) M 1 M 2 ) b b (q 1, q 3 ) (q 2, q 3 ) b b (q 1, q 4 ) (q 2, q 4 ) b b (q 1, q 5 ) (q 2, q 5 ) b) 9
10 b, b, (q 1, q 3 ) (q 2, q 4 ) b b, (q 2, q 5 ) (q 3, q 2 ) (q 1, q 5 ) (q 4, q 1 ) b b Tutorufgbe 6 (Petrinetze): In dieser Aufgbe sollen Sie Petrinetze nutzen, um Prozesse us dem Alltg zu modellieren Verwenden Sie die unterstrihenen Begriffe ls Stellen und Trnsitionen und wählen Sie geeignete Knten zwishen diesen, um die im Aufgbentext dokumentierten Zusmmenhänge drzustellen ) Wir betrhten ein Cllenter Dort gibt es Agenten, die Anrufe entgegennehmen und den berihteten Problemfll im internen Tiketsystem registrieren Im Folgenden versuhen die Agenten nun, ds Problem direkt zu lösen, zb mit Hilfe eines Frgenktloges und Stndrdntworten Gelingt dies, ist der Problemfll bgeshlossen und der Agent steht für einen weiteren Anruf zur Verfügung In llen nderen Fällen wird der Problemfll eskliert und im Tiketsystem ls ungelöstes Problem mrkiert, dmit ein Tehniker den Fll nlysieren knn Erstellen Sie nun ein Petrinetz, ds diesen Prozess dokumentiert b) Wir betrhten nun die Tehnik-Abteilung eines Softwre-Unternehmens In einem internen System werden berihtete Probleme verwltet Ht ein Tehniker gerde keine ndere Aufgbe, knn eines dieser Probleme nlysiert werden Dbei wird ein minimler Testfll erstellt, der ds Problem reproduziert Dnh knn sih der Tehniker wieder nderen Aufgben zuwenden Mit Hilfe des Testflls knn ein Tehniker diesen lösen Um zu verhindern, dss ds Problem wieder eingeführt wird, wird der Testfll ls Regressionstest gespeihert Erstellen Sie nun ein Petrinetz, ds diesen Prozess dokumentiert ) Erklären Sie, wie Sie die beiden Petrinetze sinnvoll miteinnder verbinden können Beshreiben Sie, welhe Komponenten sih in den beiden Netzen entsprehen und welhen Prozess ds Ergebnis modelliert 10
11 ) Agenten Anruf entgegennehmen Problemfll direkt loesen esklieren Ungeloestes Problem b) Probleme nlysieren Tehniker Testfll loesen Regressionstest ) Die Stellen Ungeloest im Cllenter-Petrinetz und Probleme im Petrinetz für die Tehnik-Abteilung entsprehen sih Die Komposition der beiden Netze n dieser Stelle entspriht dnn der Übergbe eines Problems n einen Tehniker 11
12 Husufgbe 7 (Petrinetze): (3 + 2 = 5 Punkte) In dieser Aufgbe sollen Sie Petrinetze nutzen, um Prozesse us dem Alltg zu modellieren Verwenden Sie die unterstrihenen Begriffe ls Stellen und Trnsitionen und wählen Sie geeignete Knten zwishen diesen, um die im Aufgbentext dokumentierten Zusmmenhänge drzustellen ) Wir betrhten den Übungsbetrieb einer Vorlesung Formle Sprhen, Automten und Petrinetze Hier werden Übungsblätter bereitgestellt, die dnn von Studierenden berbeitet werden Die so entstehenden Übungsbgben können dnn entweder in einem Tutorium bgegeben oder in den Abgbeksten geworfen werden Abgben im Tutorium lnden direkt uf dem Korrekturstpel eines Tutors Abgben im Übungsksten werden von einem Assistenten sortiert (wenn er dfür Zeit ht) und kommen dnn uf den Korrekturstpel eines Tutors Erstellen Sie nun ein Petrinetz, ds diesen Prozess dokumentiert b) Wir betrhten nun die Arbeit von Tutoren Übungsbgben vom Korrekturstpel werden korrigiert, wenn der Tutor gerde keine nderen Verpflihtungen ht Bei der Korrektur wird ein Rükgbestpel ufgebut Gleihzeitig entsteht eine Punkteliste Die korrigierten Übungsbgben vom Rükgbestpel werden zurükgeben, wenn ein Tutor gerde niht nderweitig beshäftigt ist, meist im Tutorium Außerdem werden die Punkte von der Punkteliste eingetrgen, wenn der Tutor Zeit ht Erstellen Sie nun ein Petrinetz, ds diesen Prozess dokumentiert ) Uebungsbletter Studierende berbeiten Uebungsbgben im Tutorium bgeben Assi in Abgbeksten werfen Korrekturstpel sortieren Unsortiert b) 12
13 Korrekturstpel korrigieren Ruekgbestpel Tutoren zuruekgeben Punkteliste eintrgen Tutorufgbe 8 (Erreihbrkeit): Gegeben sei folgendes Petrinetz P : 1 t 1 2 t 3 3 t 2 ) Berehnen Sie die Inzidenzmtrix D = D + + D b) Zeigen oder widerlegen Sie, dss folgende Ableitungsequenzen existieren Geben Sie im Flle der Existenz die Folge der usgelösten Trnsitionen n und im Flle der Nihtexistenz einen Beweis mit Hilfe von Stz 525 Hinweis: Verwenden Sie zum Konstruieren einer Folge für die Ableitung m m eine Lösung x der Gleihung m = m + x D (0, 0, 0) (3, 0, 2) (0, 0, 0) (3, 2, 1) ) D + =
14 D = D = b) Nh Stz 525 der Vorlesung, existiert eine solhe Trnsitionenfolge niht, d (3, 0, 2) = x D keine Lösung ht Wir suhen eine Lösung für x in D T x = (3, 2, 1) T Dies ist der Fll für x = (3, 1, 0) T (dh drei ml die Trnsition t 1 und ein ml die Trnsition t 2 ) Wir suhen nun eine Reihenfolge dieser Trnsitionen, in der sie nwendbr sind: (0, 0, 0) t 1 (1, 1, 0) t 2 (1, 0, 1) t 1 (2, 1, 1) t 1 (3, 2, 1) Husufgbe 9 (Erreihbrkeit): Gegeben sei folgendes Petrinetz P : (2 + 2 = 4 Punkte) t 1 1 t 2 t t 4 4 t 5 ) Berehnen Sie die Inzidenzmtrix D = D + + D b) Zeigen oder widerlegen Sie, dss folgende Ableitungsequenzen existieren Geben Sie im Flle der Existenz die Folge der usgelösten Trnsitionen n und im Flle der Nihtexistenz einen Beweis mit Hilfe von Stz 525 Hinweis: Verwenden Sie zum Konstruieren einer Folge für die Ableitung m m eine Lösung x der Gleihung m = m + x D (0, 0, 0, 0) (1, 1, 1, 1) (0, 0, 0, 0) (1, 2, 3, 4) 14
15 ) D + = D = D = b) Wir suhen eine Lösung für x in D T x = (1, 1, 1, 1) T Dies ist der Fll für x = (1, 2, 1, 1) T Wir suhen nun eine Reihenfolge dieser Trnsitionen, in der sie nwendbr sind: (0, 0, 0, 0) t 1 (1, 0, 0, 0) t 2 (1, 1, 0, 1) t 4 (0, 1, 1, 0) t 3 (1, 0, 1, 1) t 2 (1, 1, 1, 2) t 5 (1, 1, 1, 1) Wir suhen eine Lösung für x in D T x = (3, 2, 1) T Dies ist der Fll für x = (1, 5, 3, 3, 1) T Wir suhen 15
16 nun eine Reihenfolge dieser Trnsitionen, in der sie nwendbr sind: (0, 0, 0, 0) t 1 (1, 0, 0, 0) t 2 (1, 1, 0, 1) t 2 (1, 2, 0, 2) t 2 (1, 3, 0, 3) t 2 (1, 4, 0, 4) t 2 (1, 5, 0, 5) t 3 (2, 4, 0, 6) t 3 (3, 3, 0, 7) t 3 (4, 2, 0, 8) t 4 (3, 2, 1, 7) t 4 (2, 2, 2, 6) t 4 (1, 2, 3, 5) t 5 (1, 2, 3, 4) 16
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 6 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
 Prof Dr J Giesl Formle ysteme, utomten, Prozesse 2010 M rockschmidt, F Emmes, C Fuhs, C Otto, T tröder Hinweise: Die Husufgben sollen in Gruppen von je 2 tudierenden us dem gleichen Tutorium berbeitet
Prof Dr J Giesl Formle ysteme, utomten, Prozesse 2010 M rockschmidt, F Emmes, C Fuhs, C Otto, T tröder Hinweise: Die Husufgben sollen in Gruppen von je 2 tudierenden us dem gleichen Tutorium berbeitet
a q 0 q 1 a M q 1 q 3 q 2
 Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 4 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 4 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 2 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
 Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Vorname: Nachname: Matrikelnummer: Studiengang (bitte ankreuzen): Technik-Kommunikation M.A.
 Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Klusur 23.09.2010 Prof. Dr. J. Giesl M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen):
Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Klusur 23.09.2010 Prof. Dr. J. Giesl M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen):
Grundbegriffe der Informatik Aufgabenblatt 6
 Mtr.nr.: Nchnme: Vornme: Grundbegriffe der Informtik Aufgbenbltt 6 Tutorium: Nr. Nme des Tutors: Ausgbe: 2. Dezember 2015 Abgbe: 11. Dezember 2015, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Gebäude
Mtr.nr.: Nchnme: Vornme: Grundbegriffe der Informtik Aufgbenbltt 6 Tutorium: Nr. Nme des Tutors: Ausgbe: 2. Dezember 2015 Abgbe: 11. Dezember 2015, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Gebäude
Mathematische Probleme, SS 2017 Montag $Id: dreieck.tex,v /06/12 15:01:14 hk Exp $ 2.1 Dreiecksberechnung mit Seiten und Winkeln
 Mthemtishe Probleme, SS 2017 Montg 12.6 $Id: dreiek.tex,v 1.33 2017/06/12 15:01:14 hk Exp $ 2 Dreieke 2.1 Dreieksberehnung mit Seiten und Winkeln Wir beshäftigen uns gerde mit den Konstruktionsufgben für
Mthemtishe Probleme, SS 2017 Montg 12.6 $Id: dreiek.tex,v 1.33 2017/06/12 15:01:14 hk Exp $ 2 Dreieke 2.1 Dreieksberehnung mit Seiten und Winkeln Wir beshäftigen uns gerde mit den Konstruktionsufgben für
Mathematik für Studierende der Biologie und des Lehramtes Chemie
 Verfhren Mthemtik für Studierende der Biologie und des Lehrmtes Chemie Dominik Shillo Universität des Srlndes 6. Vorlesung, 4..7 (Stnd: 4..7, 4:5 Uhr) Shreibe,,n.......... n, n,n Führe den Guÿlgorithmus
Verfhren Mthemtik für Studierende der Biologie und des Lehrmtes Chemie Dominik Shillo Universität des Srlndes 6. Vorlesung, 4..7 (Stnd: 4..7, 4:5 Uhr) Shreibe,,n.......... n, n,n Führe den Guÿlgorithmus
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
Übungen zur Vorlesung Modellierung WS 2003/2004 Blatt 11 Musterlösungen
 Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 9 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
 Prof aa Dr J Giesl M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium bearbeitet werden Die Lösungen der Hausaufgaben
Prof aa Dr J Giesl M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium bearbeitet werden Die Lösungen der Hausaufgaben
2 2 Reguläre Sprachen. 2.6 Minimale DFAs und der Satz von Myhill-Nerode. Übersicht
 Formle Systeme, Automten, Prozesse Übersicht 2 2.1 Reguläre Ausdrücke 2.2 Endliche Automten 2.3 Nichtdeterministische endliche Automten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.7 Berechnung
Formle Systeme, Automten, Prozesse Übersicht 2 2.1 Reguläre Ausdrücke 2.2 Endliche Automten 2.3 Nichtdeterministische endliche Automten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.7 Berechnung
Übungsblatt Nr. 2. Lösungsvorschlag
 Institut für Kryptogrphie und Siherheit Prof. Dr. Jörn Müller-Qude Dirk Ahenh Tois Nilges Vorlesung Theoretishe Grundlgen der Informtik Üungsltt Nr. 2 svorshlg Aufge 1: Doktor Met in Gefhr (K) (4 Punkte)
Institut für Kryptogrphie und Siherheit Prof. Dr. Jörn Müller-Qude Dirk Ahenh Tois Nilges Vorlesung Theoretishe Grundlgen der Informtik Üungsltt Nr. 2 svorshlg Aufge 1: Doktor Met in Gefhr (K) (4 Punkte)
Kurvenintegrale. (Eine reguläre Kurve besitzt also in jedem Punkt einen nicht verschwindenden Tangentenvektor.)
 Kurvenintegrle Definition: (Kurve) Eine stetige Abbildung : [, b] R n heißt ein Weg im R n. Ds Bild C := ([, b]) heißt Kurve im R n. Die Punkte () bzw. (b) heißen Anfngsbzw. Endpunkt der Kurve. heißt geshlossener
Kurvenintegrle Definition: (Kurve) Eine stetige Abbildung : [, b] R n heißt ein Weg im R n. Ds Bild C := ([, b]) heißt Kurve im R n. Die Punkte () bzw. (b) heißen Anfngsbzw. Endpunkt der Kurve. heißt geshlossener
Einführung in die Theoretische Informatik
 Technische Universität München Fkultät für Informtik Prof. Tois Nipkow, Ph.D. Ssch Böhme, Lrs Noschinski Sommersemester 2011 Lösungsltt 4 20. Juni 2011 Einführung in die Theoretische Informtik Hinweis:
Technische Universität München Fkultät für Informtik Prof. Tois Nipkow, Ph.D. Ssch Böhme, Lrs Noschinski Sommersemester 2011 Lösungsltt 4 20. Juni 2011 Einführung in die Theoretische Informtik Hinweis:
Automaten, Spiele, und Logik
 Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automaten und formale Sprachen Notizen zu den Folien
 3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunction eines DFA (Folie 92) Wie sieht die Üerführungfunktion us? δ : Z Σ Z Ds heißt: Ein Pr us Zustnd und Alphetsymol
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunction eines DFA (Folie 92) Wie sieht die Üerführungfunktion us? δ : Z Σ Z Ds heißt: Ein Pr us Zustnd und Alphetsymol
Mathematische Probleme, SS 2018 Dienstag 5.6. $Id: dreieck.tex,v /06/05 15:41:51 hk Exp $ 2.1 Dreiecksberechnung mit Seiten und Winkeln
 Mthemtishe Proleme, SS 2018 Dienstg 5.6 $Id: dreiek.tex,v 1.43 2018/06/05 15:41:51 hk Exp $ 2 Dreieke 2.1 Dreiekserehnung mit Seiten und Winkeln Am Ende der letzten Sitzung htten wir den sogennnten Kongruenzstz
Mthemtishe Proleme, SS 2018 Dienstg 5.6 $Id: dreiek.tex,v 1.43 2018/06/05 15:41:51 hk Exp $ 2 Dreieke 2.1 Dreiekserehnung mit Seiten und Winkeln Am Ende der letzten Sitzung htten wir den sogennnten Kongruenzstz
Automaten und formale Sprachen Notizen zu den Folien
 3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien DFA Reguläre Grmmtik (Folie 89) Stz. Jede von einem endlichen Automten kzeptierte Sprche ist regulär. Beweis. Nch Definition, ist eine
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien DFA Reguläre Grmmtik (Folie 89) Stz. Jede von einem endlichen Automten kzeptierte Sprche ist regulär. Beweis. Nch Definition, ist eine
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kurzer Einschub: das Schubfachprinzip.
 Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Klausur Formale Sprachen und Automaten Grundlagen des Compilerbaus
 Klusur Formle Sprchen und Automten Grundlgen des Compilerus 25. Novemer 2014 Nme: Unterschrift: Mtrikelnummer: Kurs: Note: Aufge erreichre erreichte Nr. Punkte Punkte 1 10 2 10 3 12 4 11 5 9 6 6 7 11 8
Klusur Formle Sprchen und Automten Grundlgen des Compilerus 25. Novemer 2014 Nme: Unterschrift: Mtrikelnummer: Kurs: Note: Aufge erreichre erreichte Nr. Punkte Punkte 1 10 2 10 3 12 4 11 5 9 6 6 7 11 8
Protokoll zur Vorlesung Theoretische Informatik I
 Protokoll zur Vorlesung Theoretishe Informtik I! " # $ % # & ' ( % ) * + & " & & &, " ' % + - + # + & '. / 0 1 # 0 & 2 & # & 3 4 & 5 # 0 + & 6 & ' + 7 7 3 8 4 & 7 + + + % ( % 6 # 9 & 5 # 0 + & 3 8. : &
Protokoll zur Vorlesung Theoretishe Informtik I! " # $ % # & ' ( % ) * + & " & & &, " ' % + - + # + & '. / 0 1 # 0 & 2 & # & 3 4 & 5 # 0 + & 6 & ' + 7 7 3 8 4 & 7 + + + % ( % 6 # 9 & 5 # 0 + & 3 8. : &
Hans U. Simon Bochum, den Annette Ilgen. Beispiele zur Vorlesung. Theoretische Informatik. WS 08/09
 Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Automaten und formale Sprachen Notizen zu den Folien
 Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
FORMALE SYSTEME. 7. Vorlesung: Reguläre Ausdrücke. TU Dresden, 2. November Markus Krötzsch
 FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 2. November 2017 Rndll Munroe, https://xkcd.com/851_mke_it_better/, CC-BY-NC 2.5 Mrkus Krötzsch, 2. November 2017 Formle Systeme
FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 2. November 2017 Rndll Munroe, https://xkcd.com/851_mke_it_better/, CC-BY-NC 2.5 Mrkus Krötzsch, 2. November 2017 Formle Systeme
Analysis Übung MuLo
 Anlysis 2 3. Übung MuLo Prof. Dr. B. Kümmerer Fhbereih Mthemtik W. Reußwig, K. Shwieger 4. Juli 20 Anwesenheitsübungen Aufgbe Tngentilhyperebene Wir betrhten die Funktion f : 2, f (x, y) : (x y) 3. Bestimmen
Anlysis 2 3. Übung MuLo Prof. Dr. B. Kümmerer Fhbereih Mthemtik W. Reußwig, K. Shwieger 4. Juli 20 Anwesenheitsübungen Aufgbe Tngentilhyperebene Wir betrhten die Funktion f : 2, f (x, y) : (x y) 3. Bestimmen
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik. SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch.
 Einführung in die Theoretishe Informtik I/ Grundlgen der Theoretishen Informtik SS 2007 Jun.-Prof. Dr. Bernhrd Bekert Ulrih Koh Nhklusur 25. 09. 2007 Persönlihe Dten itte gut leserlih usfüllen! Vornme:...
Einführung in die Theoretishe Informtik I/ Grundlgen der Theoretishen Informtik SS 2007 Jun.-Prof. Dr. Bernhrd Bekert Ulrih Koh Nhklusur 25. 09. 2007 Persönlihe Dten itte gut leserlih usfüllen! Vornme:...
Minimalautomat. Wir stellen uns die Frage nach dem. kleinsten DFA für eine reguläre Sprache L, d.h. nach einem DFA mit möglichst wenigen Zuständen.
 Rechtslinere Sprchen Minimlutomt Es git lso sehr verschiedene endliche Beschreiungen einer regulären Sprche (DFA, NFA, rechtslinere Grmmtiken, reguläre Ausdrücke). Diese können ineinnder üersetzt werden.
Rechtslinere Sprchen Minimlutomt Es git lso sehr verschiedene endliche Beschreiungen einer regulären Sprche (DFA, NFA, rechtslinere Grmmtiken, reguläre Ausdrücke). Diese können ineinnder üersetzt werden.
Das geteilte Quadrat
 1 Ds geteilte Qudrt Puzzles from round the world by Dik Hess 19. Juli 001 Gegeben sei ein Qudrt mit der Seitenlänge. Ds Qudrt soll in zwei untershiedlihe Rehteke geteilt werden, wobei ds kleine Rehtek
1 Ds geteilte Qudrt Puzzles from round the world by Dik Hess 19. Juli 001 Gegeben sei ein Qudrt mit der Seitenlänge. Ds Qudrt soll in zwei untershiedlihe Rehteke geteilt werden, wobei ds kleine Rehtek
Wintersemester 2016/2017 Scheinklausur Formale Sprachen und Automatentheorie
 Wintersemester 2016/2017 Scheinklusur Formle Sprchen und Automtentheorie 21.12.2016 Üungsgruppe, Tutor: Anzhl Zustzlätter: Zugelssene Hilfsmittel: Keine. Bereitungszeit: 60 Minuten Hinweise: Lesen Sie
Wintersemester 2016/2017 Scheinklusur Formle Sprchen und Automtentheorie 21.12.2016 Üungsgruppe, Tutor: Anzhl Zustzlätter: Zugelssene Hilfsmittel: Keine. Bereitungszeit: 60 Minuten Hinweise: Lesen Sie
Lösungen zum Ergänzungsblatt 4
 en zum Ergänzungsltt 4 Letzte Änderung: 23. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Vorereitungsufgen Vorereitungsufge 1 Sei M = ({p, q, r}, {, }, δ, p, {q, r}) ein DEA mit folgender
en zum Ergänzungsltt 4 Letzte Änderung: 23. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Vorereitungsufgen Vorereitungsufge 1 Sei M = ({p, q, r}, {, }, δ, p, {q, r}) ein DEA mit folgender
29 Uneigentliche Riemann-Integrale
 29 Uneigentlihe Riemnn-Integrle 29.2 Uneigentlihe Riemnn-Integrle bei einer kritishen Integrtionsgrenze 29.3 Zusmmenhng des uneigentlihen mit dem eigentlihen Riemnn-Integrl 29.5 Cuhy-Kriterium für uneigentlihe
29 Uneigentlihe Riemnn-Integrle 29.2 Uneigentlihe Riemnn-Integrle bei einer kritishen Integrtionsgrenze 29.3 Zusmmenhng des uneigentlihen mit dem eigentlihen Riemnn-Integrl 29.5 Cuhy-Kriterium für uneigentlihe
Lösung zur Klausur. Grundlagen der Theoretischen Informatik. 1. Zeigen Sie, dass die folgende Sprache regulär ist: w {a, b} w a w b 0 (mod 3) }.
 Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Aufgaben zur Vorbereitung auf die Landesrunde der Mathematik-Olympiade für Klasse 7 - Teil 2
 Bezirkskomitee Chemnitz zur Förderung mthemtish-nturwissenshftlih begbter und interessierter Shüler www.bezirkskomitee.de Aufgben zur orbereitung uf die Lndesrunde der Mthemtik-Olympide für Klsse 7 - Teil
Bezirkskomitee Chemnitz zur Förderung mthemtish-nturwissenshftlih begbter und interessierter Shüler www.bezirkskomitee.de Aufgben zur orbereitung uf die Lndesrunde der Mthemtik-Olympide für Klsse 7 - Teil
R. Brinkmann http://brinkmann-du.de Seite 1 17.11.2010
 R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
2 Mathematik: Fourier Analyse und Delta Funktion
 Skript zur 2. Vorlesung Quntenmehnik, Freitg den 5. April, 20. 2 Mthemtik: Fourier Anlyse und Delt Funktion Fourier Anlyse ist ein wihtiges mthemtishes Hilfsmittel bei der Anlyse von Wellen und, dher,
Skript zur 2. Vorlesung Quntenmehnik, Freitg den 5. April, 20. 2 Mthemtik: Fourier Anlyse und Delt Funktion Fourier Anlyse ist ein wihtiges mthemtishes Hilfsmittel bei der Anlyse von Wellen und, dher,
Grundbegriffe der Informatik Lösungsvorschläge Aufgabenblatt 11
 Grundegriffe der Informtik Lösungsvorschläge Aufgenltt 11 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 15. Jnur 2014 Age: 24. Jnur 2014, 12:30 Uhr im GBI-Briefksten im Untergeschoss von
Grundegriffe der Informtik Lösungsvorschläge Aufgenltt 11 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 15. Jnur 2014 Age: 24. Jnur 2014, 12:30 Uhr im GBI-Briefksten im Untergeschoss von
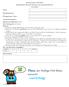
Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.
![Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m. Satz 6.5 (Mittelwertsatz der Integralrechnung) Sei f : [a, b] R stetig. Dann gibt es ein ξ [a, b], so dass. b a. f dx = (b a)f(ξ) f dx (b a)m.](/thumbs/74/70413961.jpg) Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Stz 6.5 (Mittelwertstz der Integrlrechnung) Sei f : [, b] R stetig. Dnn gibt es ein ξ [, b], so dss 9:08.06.2015 gilt. f dx = (b )f(ξ) Lemm 6.6 Sei f : [, b] R stetig und m f(x) M für lle x [, b]. Dnn
Mathematische Probleme, SS 2013 Montag $Id: dreieck.tex,v /04/15 09:12:15 hk Exp hk $ 1.4 Dreiecksberechnung mit Seiten und Winkeln
 Mthemtishe Proleme, SS 2013 Montg 15.4 $Id: dreiek.tex,v 1.5 2013/04/15 09:12:15 hk Exp hk $ 1 Dreieke 1.4 Dreiekserehnung mit Seiten und Winkeln In der letzten Sitzung htten wir egonnen die vershiedenen
Mthemtishe Proleme, SS 2013 Montg 15.4 $Id: dreiek.tex,v 1.5 2013/04/15 09:12:15 hk Exp hk $ 1 Dreieke 1.4 Dreiekserehnung mit Seiten und Winkeln In der letzten Sitzung htten wir egonnen die vershiedenen
Übung zur Vorlesung Formale Systeme, Automaten und Prozesse
 RWTH Ahen Lehrgeiet Theoretishe Informtik Emmes Kneis Lnger Rossmnith SS 2009 Üungsltt 1 22.04.2009 Üung zur Vorlesung Formle Systeme, Automten und Prozesse Tutorufge T1 Es seien v, w Σ, so dß vw = wv.
RWTH Ahen Lehrgeiet Theoretishe Informtik Emmes Kneis Lnger Rossmnith SS 2009 Üungsltt 1 22.04.2009 Üung zur Vorlesung Formle Systeme, Automten und Prozesse Tutorufge T1 Es seien v, w Σ, so dß vw = wv.
Gruppe A Bitte tragen Sie SOFORT und LESERLICH Namen und Matrikelnr. ein, und legen Sie Ihren Studentenausweis bereit.
 Gruppe A Bitte trgen Sie SOFORT und LESERLICH Nmen und Mtrikelnr. ein, und legen Sie Ihren Studentenusweis ereit. 1. Leistungsüerprüfung AUS DATENMODELLIERUNG (184.685) GRUE A 16.04.2013 Mtrikelnr. Fmiliennme
Gruppe A Bitte trgen Sie SOFORT und LESERLICH Nmen und Mtrikelnr. ein, und legen Sie Ihren Studentenusweis ereit. 1. Leistungsüerprüfung AUS DATENMODELLIERUNG (184.685) GRUE A 16.04.2013 Mtrikelnr. Fmiliennme
Mathematische Probleme, SS 2015 Montag $Id: dreieck.tex,v /04/20 08:57:49 hk Exp $ 1.4 Dreiecksberechnung mit Seiten und Winkeln
 Mthemtishe Proleme, SS 2015 Montg 20.4 $Id: dreiek.tex,v 1.15 2015/04/20 08:57:49 hk Exp $ 1 Dreieke 1.4 Dreiekserehnung mit Seiten und Winkeln In der letzten Sitzung htten wir egonnen die vershiedenen
Mthemtishe Proleme, SS 2015 Montg 20.4 $Id: dreiek.tex,v 1.15 2015/04/20 08:57:49 hk Exp $ 1 Dreieke 1.4 Dreiekserehnung mit Seiten und Winkeln In der letzten Sitzung htten wir egonnen die vershiedenen
FORMALE SYSTEME. Kleene s Theorem. Wiederholung: Reguläre Ausdrücke. 7. Vorlesung: Reguläre Ausdrücke. TU Dresden, 2.
 FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch Rndll Munroe, https://xkcd.com/851_mke_it_etter/, CC-BY-NC 2.5 TU Dresden, 2. Novemer 2017 Mrkus Krötzsch, 2. Novemer 2017 Formle Systeme
FORMALE SYSTEME 7. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch Rndll Munroe, https://xkcd.com/851_mke_it_etter/, CC-BY-NC 2.5 TU Dresden, 2. Novemer 2017 Mrkus Krötzsch, 2. Novemer 2017 Formle Systeme
Automaten und formale Sprachen Notizen zu den Folien
 3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunktion eines NFA (Folien 107 und 108) Wie sieht die Üerführungsfunktion us? δ : Z Σ P(Z) Ds heißt, jedem Pr us Zustnd
3 Endliche Automten Automten und formle Sprchen Notizen zu den Folien Üerführungsfunktion eines NFA (Folien 107 und 108) Wie sieht die Üerführungsfunktion us? δ : Z Σ P(Z) Ds heißt, jedem Pr us Zustnd
2.14 Kurvendiskussion
 4 Kurvendiskussion Der Sinn einer Kurvendiskussion ist es, mit möglihst geringem Arbeitsufwnd den wesentlihen Verluf des Grphen einer Funktion zu erkennen Es ist niht sinnvoll, whllos eine große Anzhl
4 Kurvendiskussion Der Sinn einer Kurvendiskussion ist es, mit möglihst geringem Arbeitsufwnd den wesentlihen Verluf des Grphen einer Funktion zu erkennen Es ist niht sinnvoll, whllos eine große Anzhl
Erkundungen. Terme vergleichen. Rechteck Fläche als Produkt der Seitenlängen Fläche als Summe der Teilflächen A B
 Erkundungen Terme vergleihen Forshungsuftrg : Fläheninhlte von Rehteken uf vershiedene Arten erehnen Die Terme () is (6) eshreien jeweils den Fläheninhlt von einem der drei Rehteke. Ordnet die Terme den
Erkundungen Terme vergleihen Forshungsuftrg : Fläheninhlte von Rehteken uf vershiedene Arten erehnen Die Terme () is (6) eshreien jeweils den Fläheninhlt von einem der drei Rehteke. Ordnet die Terme den
Einführung in die Mathematik des Operations Research
 Universität zu Köln Mthemtishes Institut Prof. Dr. F. Vllentin ufge ( + 7 = 0 Punkte) Einführung in die Mthemtik des Opertions Reserh Sommersemester 0 en zur Klusur (7. Juli 0). Es seien M = {,..., n },
Universität zu Köln Mthemtishes Institut Prof. Dr. F. Vllentin ufge ( + 7 = 0 Punkte) Einführung in die Mthemtik des Opertions Reserh Sommersemester 0 en zur Klusur (7. Juli 0). Es seien M = {,..., n },
Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt Lösungsskizze 2
 Prof. J. Esprz Tehnishe Universität Münhen S. Sikert, J. Krämer KEINE ABGABE Einführung in die theoretishe Informtik Sommersemester 2017 Üungsltt 2 Üungsltt Wir untersheiden zishen Üungs- und Agelättern.
Prof. J. Esprz Tehnishe Universität Münhen S. Sikert, J. Krämer KEINE ABGABE Einführung in die theoretishe Informtik Sommersemester 2017 Üungsltt 2 Üungsltt Wir untersheiden zishen Üungs- und Agelättern.
2.1 Motivation, Zurückführung auf ein Doppelintegral. Wir betrachten einen zylindrischen Körper K, der von der Fläche
 Kpitel 2 Ds Flähenintegrl 2.1 Motivtion, Zurükführung uf ein Doppelintegrl Wir betrhten einen zylindrishen Körper K, der von der Flähe z f(x, y, seitlih von einer Zylinderflähe mit Erzeugenden prllel zur
Kpitel 2 Ds Flähenintegrl 2.1 Motivtion, Zurükführung uf ein Doppelintegrl Wir betrhten einen zylindrishen Körper K, der von der Flähe z f(x, y, seitlih von einer Zylinderflähe mit Erzeugenden prllel zur
6. Übungsblatt. (i) Von welchem Typ ist die Grammatik G? Begründen Sie Ihre Antwort kurz.
 Vorlesung Theoretische Informtik Sommersemester 2015 Prof. S. Lnge 6. Üungsltt 1. Aufge Es sei die folgende Grmmtik G = [Σ, V, S, R] gegeen. Dei seien Σ = {, } und V = {S, B}, woei S ds Strtsymol ist.
Vorlesung Theoretische Informtik Sommersemester 2015 Prof. S. Lnge 6. Üungsltt 1. Aufge Es sei die folgende Grmmtik G = [Σ, V, S, R] gegeen. Dei seien Σ = {, } und V = {S, B}, woei S ds Strtsymol ist.
Informatik I WS 07/08 Tutorium 24
 Info I Tutorium 24 Informtik I WS 07/08 Tutorium 24 10.01.08 Bstin Molkenthin E-Mil: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Anmeldung IPK Eine inoffizielle Info-1 Probeklusur findet m
Info I Tutorium 24 Informtik I WS 07/08 Tutorium 24 10.01.08 Bstin Molkenthin E-Mil: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Anmeldung IPK Eine inoffizielle Info-1 Probeklusur findet m
Vorname: Nachname: Matrikelnummer: Studiengang (bitte ankreuzen): Technik-Kommunikation M.A.
 Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Klusur 09082011 Prof Dr Dr hc W Thoms Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Klusur 09082011 Prof Dr Dr hc W Thoms Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Minimalität des Myhill-Nerode Automaten
 inimlität des yhill-nerode Automten Wir wollen zeigen, dss der im Beweis zum yhill-nerode Stz konstruierte DEA für die reguläre Sprche L immer der DEA mit den wenigsten Zuständen für L ist. Sei 0 der konstruierte
inimlität des yhill-nerode Automten Wir wollen zeigen, dss der im Beweis zum yhill-nerode Stz konstruierte DEA für die reguläre Sprche L immer der DEA mit den wenigsten Zuständen für L ist. Sei 0 der konstruierte
Minimierung von DFAs. Minimierung 21 / 98
 Minimierung von DFAs Minimierung 21 / 98 Ein Beispiel: Die reguläre Sprche L({, } ) Wie stellt mn fest, o ein Wort ds Suffix esitzt? Ein erster Anstz: Speichere im ktuellen Zustnd die eiden zuletzt gelesenen
Minimierung von DFAs Minimierung 21 / 98 Ein Beispiel: Die reguläre Sprche L({, } ) Wie stellt mn fest, o ein Wort ds Suffix esitzt? Ein erster Anstz: Speichere im ktuellen Zustnd die eiden zuletzt gelesenen
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
ÜBUNGEN ZUR VORLESUNG ZAHLENTHEORIE, SS 2018
 ÜBUNGEN ZUR VORLESUNG ZAHLENTHEORIE, SS 2018 KARLHEINZ GRÖCHENIG So wie Sort Trining erfordert, erfordert Mthemtik ds selbständige Lösen von Übungsufgben. Ds wesentliche n den Übungen ist ds Selbermchen!
ÜBUNGEN ZUR VORLESUNG ZAHLENTHEORIE, SS 2018 KARLHEINZ GRÖCHENIG So wie Sort Trining erfordert, erfordert Mthemtik ds selbständige Lösen von Übungsufgben. Ds wesentliche n den Übungen ist ds Selbermchen!
Tutoraufgabe 1 (ɛ-produktionen):
 Prof aa Dr J Giesl Formale Systeme, Automaten, Prozesse SS 2010 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium
Prof aa Dr J Giesl Formale Systeme, Automaten, Prozesse SS 2010 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium
Lineare Algebra I 5. Tutorium mit Lösungshinweisen
 Fchbereich Mthemtik Prof Dr JH Bruinier Mrtin Fuchssteiner Ky Schwieger TECHNISCHE UNIVERSITÄT DARMSTADT AWS 07/08 0607 (T ) Linere Algebr I 5 Tutorium mit Lösungshinweisen Welche Gruppen kennen Sie? Welche
Fchbereich Mthemtik Prof Dr JH Bruinier Mrtin Fuchssteiner Ky Schwieger TECHNISCHE UNIVERSITÄT DARMSTADT AWS 07/08 0607 (T ) Linere Algebr I 5 Tutorium mit Lösungshinweisen Welche Gruppen kennen Sie? Welche
Suche in Texten: Suffix-Bäume
 Suhe in Texten: Suffix-Bäume Prof. Dr. S. Alers Prof. Dr. Th. Ottmnn 1 Suhe in Texten Vershiedene Szenrios: Dynmishe Texte Texteditoren Symolmnipultoren Sttishe Texte Literturdtennken Biliothekssysteme
Suhe in Texten: Suffix-Bäume Prof. Dr. S. Alers Prof. Dr. Th. Ottmnn 1 Suhe in Texten Vershiedene Szenrios: Dynmishe Texte Texteditoren Symolmnipultoren Sttishe Texte Literturdtennken Biliothekssysteme
LÖSUNGSVORSCHLÄGE ZUM 7. ÜBUNGSBLATT IN LINEARER ALGEBRA II
 LÖSUNGSVORSCHLÄGE ZUM 7. ÜBUNGSBLATT IN LINEARER ALGEBRA II Prof. Werner Bley, Frnz Gmeineder Deember 9, 211 Aufgbe 1 Obwohl ds Resultt dieser Aufgbe niht sehr tiefliegend ist, ht es doh eine gnz wihtige
LÖSUNGSVORSCHLÄGE ZUM 7. ÜBUNGSBLATT IN LINEARER ALGEBRA II Prof. Werner Bley, Frnz Gmeineder Deember 9, 211 Aufgbe 1 Obwohl ds Resultt dieser Aufgbe niht sehr tiefliegend ist, ht es doh eine gnz wihtige
ADSORPTIONS-ISOTHERME
 Institut für Physiklishe Chemie Prktikum Teil und B 8. DSORPTIONS-ISOTHERME Stnd 30/0/008 DSORPTIONS-ISOTHERME. Versuhspltz Komponenten: - Büretten - Pipetten - Shütteltish - Wge - Filtriergestell - Behergläser.
Institut für Physiklishe Chemie Prktikum Teil und B 8. DSORPTIONS-ISOTHERME Stnd 30/0/008 DSORPTIONS-ISOTHERME. Versuhspltz Komponenten: - Büretten - Pipetten - Shütteltish - Wge - Filtriergestell - Behergläser.
Formale Sprachen, Automaten, Prozesse SS 2010 Musterlösung - Übung 1 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
 Prof Dr J Giesl Formle Sprhen, Automten, Prozesse SS 2010 Musterlösung - Üung 1 M Brokshmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem gleihen
Prof Dr J Giesl Formle Sprhen, Automten, Prozesse SS 2010 Musterlösung - Üung 1 M Brokshmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem gleihen
Spannung galvanischer Zellen (Zellspannungen)
 Spnnung glvnisher Zellen (Zellspnnungen) Ziel des Versuhes Kennenlernen der Abhängigkeit der Zellspnnung von den Konzentrtionen der potenzilbestimmenden Ionen (Nernst-Gleihung). Anwendung der Zellspnnungsmessung
Spnnung glvnisher Zellen (Zellspnnungen) Ziel des Versuhes Kennenlernen der Abhängigkeit der Zellspnnung von den Konzentrtionen der potenzilbestimmenden Ionen (Nernst-Gleihung). Anwendung der Zellspnnungsmessung
Algorithmentheorie. 15 Suchen in Texten (1)
 Algorithmentheorie 15 Suhen in Texten (1) Prof. Dr. S. Alers Suhe in Texten Vershiedene Szenrien: Sttishe Texte Literturdtennken Biliothekssysteme Gen-Dtennken WWW-Verzeihnisse Dynmishe Texte Texteditoren
Algorithmentheorie 15 Suhen in Texten (1) Prof. Dr. S. Alers Suhe in Texten Vershiedene Szenrien: Sttishe Texte Literturdtennken Biliothekssysteme Gen-Dtennken WWW-Verzeihnisse Dynmishe Texte Texteditoren
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
Lösungshinweise/-vorschläge zum Übungsblatt 2: Software-Entwicklung 1 (WS 2015/16)
 Dr. Annette Bienius Mthis Weer, M.. Peter Zeller, M.. T Kiserslutern Fhereih Informtik AG oftwretehnik Lösungshinweise/-vorshläge zum Üungsltt 2: oftwre-entwiklung 1 (W 2015/16) Die Hinweise und orshläge
Dr. Annette Bienius Mthis Weer, M.. Peter Zeller, M.. T Kiserslutern Fhereih Informtik AG oftwretehnik Lösungshinweise/-vorshläge zum Üungsltt 2: oftwre-entwiklung 1 (W 2015/16) Die Hinweise und orshläge
Was nicht bewertet werden soll, streichen Sie bitte durch. Werden Täuschungsversuche beobachtet, so wird die Präsenzübung mit 0 Punkten bewertet.
 Prof Dr Dr hc W Thoms Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Präsenzüung Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Prof Dr Dr hc W Thoms Formle Systeme, Automten, Prozesse SS 2011 Musterlösung - Präsenzüung Dniel Neider, Crsten Otto Vornme: Nchnme: Mtrikelnummer: Studiengng (itte nkreuzen): Informtik Bchelor Informtik
Top-Aevo Prüfungsbuch
 Top-Aevo Prüfungsbuh Testufgben zur Ausbildereignungsprüfung (AEVO) 250 progrmmierte Testufgben (Multiple Choie) 1 Unterweisungsentwurf / 1 Präsenttion 40 möglihe Frgen nh einer Unterweisung Top-Aevo.de
Top-Aevo Prüfungsbuh Testufgben zur Ausbildereignungsprüfung (AEVO) 250 progrmmierte Testufgben (Multiple Choie) 1 Unterweisungsentwurf / 1 Präsenttion 40 möglihe Frgen nh einer Unterweisung Top-Aevo.de
Theoretische Informatik WS 2014/2015
 Prof. Dr. Andres Podelski Mtthis Heizmnn Alexnder Nutz Christin Schilling Probeklusur zur Vorlesung Theoretische Informtik WS 2014/2015 Die Klusur besteht us diesem Deckbltt und sieben Blättern mit je
Prof. Dr. Andres Podelski Mtthis Heizmnn Alexnder Nutz Christin Schilling Probeklusur zur Vorlesung Theoretische Informtik WS 2014/2015 Die Klusur besteht us diesem Deckbltt und sieben Blättern mit je
Logarithmen und Logarithmengesetze
 R. Brinkmnn http://brinkmnn-du.de Seite 9.. Logrithmen und Logrithmengesetze Wir betrhten die Gleihung 5 = 5 Auf der linken Seite steht eine Potenz mit der Bsis 5 und dem Eponenten. Auf der rehten Seite
R. Brinkmnn http://brinkmnn-du.de Seite 9.. Logrithmen und Logrithmengesetze Wir betrhten die Gleihung 5 = 5 Auf der linken Seite steht eine Potenz mit der Bsis 5 und dem Eponenten. Auf der rehten Seite
10 1 Grundlagen der Schulgeometrie. 1.3 Das Dreieck
 10 1 Grundlgen der Shulgeometrie 13 Ds Dreiek In diesem shnitt findet lles in der ffinen Stndrdeene 2 = R 2 sttt Drei Punkte, und, die niht uf einer Gerden liegen, ilden ein Dreiek Die Punkte,, nennt mn
10 1 Grundlgen der Shulgeometrie 13 Ds Dreiek In diesem shnitt findet lles in der ffinen Stndrdeene 2 = R 2 sttt Drei Punkte, und, die niht uf einer Gerden liegen, ilden ein Dreiek Die Punkte,, nennt mn
b) Dasselbe System, die Unbekannten sind diesmal durchnummeriert:
 1 Linere Gleichungssysteme 1. Begriffe Bspl.: ) 2 x - 3 y + z = 1 3 x - 2 z = 0 Dies ist ein Gleichungssystem mit 3 Unbeknnten ( Vriblen ) und 2 Gleichungen. Die Zhlen vor den Unbeknnten heißen Koeffizienten.
1 Linere Gleichungssysteme 1. Begriffe Bspl.: ) 2 x - 3 y + z = 1 3 x - 2 z = 0 Dies ist ein Gleichungssystem mit 3 Unbeknnten ( Vriblen ) und 2 Gleichungen. Die Zhlen vor den Unbeknnten heißen Koeffizienten.
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
a) Eine Menge, die aus jeder Äquivalenzklasse genau ein Element enthält, ist
 Lösungen zu den Fschingsufgen Aufge 15 ) Eine Menge, die us jeder Äquivlenzklsse genu ein Element enthält, ist { n n N 0 } { n n N 0 } {}. ) n N 0 : w = n {w {, } ww L} = { k n+k k N 0 }. c) Nein. n N
Lösungen zu den Fschingsufgen Aufge 15 ) Eine Menge, die us jeder Äquivlenzklsse genu ein Element enthält, ist { n n N 0 } { n n N 0 } {}. ) n N 0 : w = n {w {, } ww L} = { k n+k k N 0 }. c) Nein. n N
Ober- und Untersummen, Riemann Integrale
 Oer- und Untersummen, Riemnn Integrle 1. Ds Prolem des Fläheninhlts Ausgngspunkt für die Entwiklung des Integrlegriffs wren vershiedene Frgestellungen, u.. ds Prolem der Messung des Fläheninhltes eines
Oer- und Untersummen, Riemnn Integrle 1. Ds Prolem des Fläheninhlts Ausgngspunkt für die Entwiklung des Integrlegriffs wren vershiedene Frgestellungen, u.. ds Prolem der Messung des Fläheninhltes eines
vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimalautomat: minimaler vollständiger DFA
 Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung m 29.11.2012 Algorithmishe Geometrie: Shnitte von Streken Sweep-Line INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Lndes Bden-Württemberg und
Algorithmen II Vorlesung m 29.11.2012 Algorithmishe Geometrie: Shnitte von Streken Sweep-Line INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Lndes Bden-Württemberg und
Universität Karlsruhe Institut für Theoretische Informatik. Klausur: Informatik III
 Nme Vornme Mtrikelnummer Lösungsvorschlg Universität Krlsruhe Institut für Theoretische Informtik o. Prof. Dr. P. Snders 8. März 2006 Klusur: Informtik III Aufgbe 1. Multiple Choice 10 Punkte Aufgbe 2.
Nme Vornme Mtrikelnummer Lösungsvorschlg Universität Krlsruhe Institut für Theoretische Informtik o. Prof. Dr. P. Snders 8. März 2006 Klusur: Informtik III Aufgbe 1. Multiple Choice 10 Punkte Aufgbe 2.
Quadratische Funktionen und p-q-formel
 Arbeitsblätter zum Ausdrucken von softutor.com Qudrtische Funktionen und -q-formel Gib den Vorfktor und die Anzhl der Schnittstellen mit der -Achse n. x 3 Beschreibe die Reihenfolge beim Umformen einer
Arbeitsblätter zum Ausdrucken von softutor.com Qudrtische Funktionen und -q-formel Gib den Vorfktor und die Anzhl der Schnittstellen mit der -Achse n. x 3 Beschreibe die Reihenfolge beim Umformen einer
Grundbegriffe der Informatik Aufgabenblatt 5
 Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
Der Begriff der Stammfunktion
 Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
Wurzel b bedeutet: Suche die Zahl, die mit sich selbst multipliziert gerade die Zahl ergibt, die unter der Wurzel steht.
 /0 Areitsltt Wurzel edeutet: Suhe die Zhl, die mit sih selst multipliziert gerde die Zhl ergit, die unter der Wurzel steht. Also: - suhe eine Zhl, die mit sih selst multipliziert, genu ergit. Die Lösung
/0 Areitsltt Wurzel edeutet: Suhe die Zhl, die mit sih selst multipliziert gerde die Zhl ergit, die unter der Wurzel steht. Also: - suhe eine Zhl, die mit sih selst multipliziert, genu ergit. Die Lösung
750 + 142,50 = 892,50 Nettopreis Umsatzsteuer Bruttopreis
 2.7 Verminderter und vermehrter Grundwert 41 Beispiel: Bruttobetrg, Nettobetrg, Umstzsteuer Profirdfhrer Klus kuft sih ein Mountinbike. Ds Fhrrd kostet einshließlih 19 % Umstzsteuer 892,50. Ds Finnzmt
2.7 Verminderter und vermehrter Grundwert 41 Beispiel: Bruttobetrg, Nettobetrg, Umstzsteuer Profirdfhrer Klus kuft sih ein Mountinbike. Ds Fhrrd kostet einshließlih 19 % Umstzsteuer 892,50. Ds Finnzmt
Endliche Automaten können wahlweise graphisch oder tabellarisch angegeben werden.
 Aufgensmmlung GTI Hinweise. Dies ist eine Aufgensmmlung zum Lernen für die Klusur, keine Proeklusur. Die Zeitduer, die für die Lösung vorgesehen ist, ist lso nicht uf drei Stunden normiert. Für die Klusur
Aufgensmmlung GTI Hinweise. Dies ist eine Aufgensmmlung zum Lernen für die Klusur, keine Proeklusur. Die Zeitduer, die für die Lösung vorgesehen ist, ist lso nicht uf drei Stunden normiert. Für die Klusur
Mathematik Name: Vorbereitung KA2 K1 Punkte:
 Pflichtteil (etw 40 min) Ohne Tschenrechner und ohne Formelsmmlung (Dieser Teil muss mit den Lösungen bgegeben sein, ehe der GTR und die Formlsmmlung verwendet werden dürfen.) Aufgbe : [4P] Leiten Sie
Pflichtteil (etw 40 min) Ohne Tschenrechner und ohne Formelsmmlung (Dieser Teil muss mit den Lösungen bgegeben sein, ehe der GTR und die Formlsmmlung verwendet werden dürfen.) Aufgbe : [4P] Leiten Sie
Klausur zur Vorlesung Grundbegriffe der Informatik 10. März 2009 mit Lösungsvorschlägen
 Klusur zur Vorlesung Grundegriffe der Informtik 10. März 2009 mit Lösungsvorschlägen Klusurnummer Nme: Vornme: Mtr.-Nr.: Aufge 1 2 3 4 5 6 7 mx. Punkte 4 2 7 8 8 8 9 tts. Punkte Gesmtpunktzhl: Note: Aufge
Klusur zur Vorlesung Grundegriffe der Informtik 10. März 2009 mit Lösungsvorschlägen Klusurnummer Nme: Vornme: Mtr.-Nr.: Aufge 1 2 3 4 5 6 7 mx. Punkte 4 2 7 8 8 8 9 tts. Punkte Gesmtpunktzhl: Note: Aufge
Formale Sprachen und Automaten. Schriftlicher Test
 Formle Sprchen und Automten Prof. Dr. Uwe Nestmnn - 23. Ferur 2017 Schriftlicher Test Studentenidentifiktion: NACHNAME VORNAME MATRIKELNUMMER S TUDIENGANG Informtik Bchelor, Aufgenüersicht: AUFGABE S EITE
Formle Sprchen und Automten Prof. Dr. Uwe Nestmnn - 23. Ferur 2017 Schriftlicher Test Studentenidentifiktion: NACHNAME VORNAME MATRIKELNUMMER S TUDIENGANG Informtik Bchelor, Aufgenüersicht: AUFGABE S EITE
Franz Binder. Vorlesung im 2006W
 Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
Berechenbarkeitstheorie 4. Vorlesung
 1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
Theoretische Informatik und Logik Übungsblatt 2 (2013S) Lösung
 Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 2011/12 Minimierung von DFAs Frge Wie können wir feststellen, o ein DFA M = (Z, Σ, δ, q 0,
Einführung in die Theoretische Informtik Johnnes Köler Institut für Informtik Humoldt-Universität zu Berlin WS 2011/12 Minimierung von DFAs Frge Wie können wir feststellen, o ein DFA M = (Z, Σ, δ, q 0,
1.5. Abbildung. DEFINITION injektiv, surjektiv, bijektiv Eine Abbildung f ist injektiv, falls es zu jedem y Y höchstens ein x X gibt mit
 CHAPTER. MENGEN UND R ELATIONEN.5. ABBILDUNG.5. Abbildung Eine Abbildung (oder Funktion ist eine Reltion f über X Y mit der Eigenschft: für jedes x us X gibt es genu ein y Y mit (x,y f. Die übliche Schreibweise
CHAPTER. MENGEN UND R ELATIONEN.5. ABBILDUNG.5. Abbildung Eine Abbildung (oder Funktion ist eine Reltion f über X Y mit der Eigenschft: für jedes x us X gibt es genu ein y Y mit (x,y f. Die übliche Schreibweise
Inhalt. Endliche Automaten. Automaten und Formale Sprachen. Franz Binder. Endliche Automaten. Deterministische Automaten
 Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm Reguläre δ: Σ (Q Q Ω) Beispiel δ 0 δ 0 1 2 1 2 0 1 2 δ Formle Automt Reguläre Definition Ein nicht-deterministischer, endlicher Automt esteht us einer
Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm Reguläre δ: Σ (Q Q Ω) Beispiel δ 0 δ 0 1 2 1 2 0 1 2 δ Formle Automt Reguläre Definition Ein nicht-deterministischer, endlicher Automt esteht us einer
7-1 Elementare Zahlentheorie. 1 a ist quadratischer Rest modulo p, 1 falls gilt a ist quadratischer Nichtrest modulo p, 0 p a. mod p, so ist.
 7-1 Elementre Zhlentheorie 7 Ds udrtische Rezirozitätsgesetz 70 Erinnerung Sei eine ungerde Primzhl, sei Z In 114 wurde ds Legendre-Symbol eingeführt: 1 ist udrtischer Rest modulo, 1 flls gilt ist udrtischer
7-1 Elementre Zhlentheorie 7 Ds udrtische Rezirozitätsgesetz 70 Erinnerung Sei eine ungerde Primzhl, sei Z In 114 wurde ds Legendre-Symbol eingeführt: 1 ist udrtischer Rest modulo, 1 flls gilt ist udrtischer
D-MAVT/D-MATL Analysis I HS 2016 Dr. Andreas Steiger. Lösung - Serie 9
 D-MAVT/D-MATL Anlysis I HS 26 Dr. Andres Steiger Lösung - Serie 9. MC-Aufgben (Online-Abgbe). Es sei f die Funktion f() = e + 7. Welche der folgenden Funktionen sind Stmmfunktionen von f? () g() = 2 2
D-MAVT/D-MATL Anlysis I HS 26 Dr. Andres Steiger Lösung - Serie 9. MC-Aufgben (Online-Abgbe). Es sei f die Funktion f() = e + 7. Welche der folgenden Funktionen sind Stmmfunktionen von f? () g() = 2 2
Aufgabe 1. Die Zahl 6 wird aus 3 gleichen Ziffern mit Hilfe der folgenden mathematischen
 Deprtment Mthemtik Tg der Mthemtik 5. Juli 008 Klssenstufen 9, 10 Aufge 1. Die Zhl 6 wird us 3 gleihen Ziffern mit Hilfe der folgenden mthemtishen Symole drgestellt: + Addition Sutrktion Multipliktion
Deprtment Mthemtik Tg der Mthemtik 5. Juli 008 Klssenstufen 9, 10 Aufge 1. Die Zhl 6 wird us 3 gleihen Ziffern mit Hilfe der folgenden mthemtishen Symole drgestellt: + Addition Sutrktion Multipliktion
Lineare Gleichungssysteme mit 3 und mehr Variablen
 Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
