Einführung in die numerische Modellierung
|
|
|
- Alexa Holtzer
- vor 5 Jahren
- Abrufe
Transkript
1 Numerische Modellierung von Naturgefahren mit dem Softwaresystem BASEMENT Workshop vom 6. Oktober 2006 an der VAW ETH Zürich Einführung in die numerische Modellierung von Strömung und Sedimenttransport in offenen Gerinnen in einem Gebirgsland von Naturge.. mit BASEM Ziel: Begriffe einführen Gleichungen und numerische Probleme erläutern Schwierigkeiten aus Sicht des Anwenders Fokus: Sedimenttransport Roland Fäh
2 Flood-Routing-Verfahren Hydrologische Verfahren Z (t) ( ) St () = K xzt () + 1 x At () A (t) Z (t) A (t) Hydrodynamische Verfahren
3 Prozesse
4 1d resp. 2d Abflusstiefe h (x,y,t) (x,t) Fliessgeschwindigkeit u (x,y,t),v(x,y,t) (x,t) Kontrollvolumen y x
5 Massenerhaltung dh Q in h Q out h: Abflusstiefe [m] Q: Volumenfluss [m 3 /s] Δx ( ) dh B Δ x = Q Q Δt in out Volumenänderung in der Zeit Δt B: Breite [m] A: Durchströmte Fläche [m 2 /s] A Q + = qlat t x Bietet kaum Probleme Lässt sich leicht überprüfen
6 Druck Druck Impulserhaltung m* b ( ) d mv = = Kräfte dt P l I Fl G I Fr ΔI Δt = ΔI Konvektive Konvektive Beschleunig. fbeschleunig. +ΔP + G R Gewicht Gewicht Reibung Reibung R x P r S + S = b f 0 Normalabfluss (Strickler) 2/3 v = k h S st f Zeitliche Zeitliche Änderung Änderung des des Impulses Impulses Q t 2 Q + ga( h Sb + Sf ) = 0 Staukurve: Q(t)=const. x A x 2 Q h + + ga Sb + S f = 0 De Sain-Venant Gleichung x A x Problem: Nichtlinearität Schliessbedingung
7 Reibung Kornreibung: c f ks 12h = 5.75log ks = (1.5 4.) d 90 Reibungskoeffizient f laminar Übergang Übergang glatt rauh k s /h Formreibung: Re=uh/ν h Riffel λ Δ λ: Wellenlänge der Düne Δ: Wellenhöhe Δ/λ: Steilheit
8 Feststofftransport Gliederung nach Transportmechanismen Strömungsinduziert Schwebstofftransport Geschiebetransport Gesamttransport Strömungs- und Gravitationsinduziert Seitlicher Transport Murgang Gravitationsinduziert Böschungskollaps Hangstabilität/Bergsturz 8
9 Geschiebe- vs. Schwebstofftransport Altes Thurquerprofil [m ü.m.] [m] Übergang fliessend > Murgang 9
10 Mehrkornmodell d m
11 Massenerhaltung im Activelayer dh Δx β k %-Volumen der Fraktion k qs in qs in Q in h zb zb Δx hm hm S k Sf k Q out qsout qsout am Gesamtvolumen [-] p Porosität [-] S k Austausch Suspension [ms -1 ] Sf k Austausch Boden [ms -1 ] Sl k lokaler Zu- oder Wegfluss [ms -1 ] ( 1 p) ( β hm) k + t qs x k +S k Sf Sl = 0 k k k Sortiergleichungen: Bestimmungsgleichung für β k
12 Bestimmungsgleichung für zb Δx qs in zus 2 zb hm Sf k qsout zb: Sohlenkote [m] qs: Geschiebefluss [m 3 /ms] hm: Dicke des Activelayers [m] S k : Austausch Suspension [ms -1 ] Sf k : Austausch Boden [ms -1 ] Sl k : lokaler Zu- oder Wegfluss [ms -1 ] ( p) ( zb hm zus ) Sfk = 0 t ( ) nk k = 1 nk k = 1 zb qsk 1 p + + Sk + Slk = 0 t x Bodenevolutionsgleichung Exnergleichung
13 Gesuchte Grössen Primäre Unbekannte Wasser h q r Sediment C g zb β g β g Sekundäre Unbekannte Geschiebetrieb qbx qby Austauschschicht hm Quellterme S g Sf g Sekundäre Unbekannte sind Funktionen der primären Variabeln F(h,q,r,zb,β g,c g )
14 Empirische Schliessbedingungen Geschiebetrieb qsxk = qsxxk + qsxyk + qsxgk qsx xk : Geschiebetrieb aufgrund der Strömung in x-richtung qsx yk : lateraler Geschiebetrieb aufgrund Strömung in y-richtung qsx gk: Rein gravitationsinduzierter Feststofftransport
15 Schliessbedingungen: Geschiebetransport Geschiebetransport aufgrund Strömung in x-richtung qsx k xk k = β k ϕ = + (1 ϕ k ) ξ qb k ( ) 3/2 qb τ τ cr ( ) τ = θ ρ ρ cr cr s w m τ = ξ kkτ cr k β γ cr, h d ξ k = 0.85 m d u w * ln( ) k k k gd qb k : Transportkapazität (z.b. Meyer-Peter) β k : Anteil der Kornklasse k ϕ k : Faktor für Zuweisung zur Transportart (Geschiebe/Suspension) ξ k : Hiding Function w k : Sinkgeschwindigkeit wk = F( dk, ν, ρ, C) Kalibrierung?
16 Beispiel zum Thema Geschiebetriebformel Meyer-Peter vs. Meyer-Peter-Hunziker 0.3 Thur bei Altikon Geschiebetrieb QP03 MP QP55 MP QP03 MPH QP53 MPH Zeit [h] Hydrograph Mittlere Sohlenlage [m ü.m.] Endlage Messung Ausgangslage Endlage MP Endlage MPH Was ist richtig? Längsprofil [km] Q (m3/s) Time (s)
17 Gleichungen Lösung Modell Ausschnitt der Wirklichkeit Zeitlich Anfangsbedingungen: h(t 0,x,y), q(t 0,x,y)... Räumlich Randbedingungen: Q(t), Qs(t) Hydrologie Sedimentzufluss? RB beinhalten grösste Unsicherheit
18 Randbedingungen Typ der RB: Charakteristiken > schiessen/strömen
19 Probleme bei Messung der Feststoffe Q, C Q, C Grosse Abweichungen in der Bilanz!
20 Schwebstoffbeziehung C = a Q b Konzentration [g/m3] Abfluss [m3/s] Datum
21 Randbedingung Geschiebe Thur: Längenprofil Aufweitung Altikon Mittlere Sohlenkote RB: Geschiebzufluss Transportkapazität Messung 2004 Simulation 2005 Messung [km] Mittlere Sohlenkote RB: Geschiebezufluss Transportkapazität - 1% Messung 2005 Messung 2004 Simulation [km] RB Feststofftransport > sensitiv
22 Mathematik Numerik u t F( u) + = x 0 explizit implizit Finite Differenzen Finite Volumen Finite Elemente Δu Δt ΔF( u) + = Δx 0 Welches ist das beste Verfahren?
23 Lösungsstrategie Flachwassergleichungen lösen Abflusstiefe h Fliessgeschwindigkeit u,v Transportgleichung für Suspension Konzentration C k Massenbilanz in Austauschschicht Kornverteilung β k Globale Massenbilanz Sohlenkote zb Iteration Loop über Zeitschritte Reibungsbeiwert Entkoppelt vs. Simultan
24 Grundsätzliches zu numerischen Methoden Zeitintegration Räumliche Diskretisierung Genauigkeit Stabilität Konvergenz Modellgleichungen u t u t F( u) + = 0 x u + c = 0 x Lineare Wellengleichung
25 Zeitdiskretisierung n+1 t Δt v cr P u t u + vch = x 0 n A Δx Δt U = U v U U 2Δx ( ) n+ 1 n n n i i Ch i i Explizit: Implizit: i-1 i i+1 (, ) + 1, 1 U = f U U U n+ 1 n n n i i i i Kein Gleichungssystem vchδt Δx (..., ) + 1, 1,..., + 1, 1... U = f U U U U U U n 1 n n n n 1 n 1 n 1 i i i i i i i x vchδt 1 Δx Gleichungssystem: falls nichtlinear > Iteration Courant-Friedrich-Levy Zahl (CFL)
26 Berechnungszeit Δx Δt = v Ch Strömungsfeld Suspension Exnergl. v Ch = v± gh 7 m/s v Ch = v 1 m/s df(u) u v du Ch = 1 km/year 2 h1-fr ( ) 1d: Δx = m Δt= 10 s 2d: Δx = 5-30 m Δt= 1 s Geschiebehaushaltstudie? Parallelisieren
27 Mathematik Numerik u t F( u) + = x 0 explizit implizit Finite Volumen Δu Δt ΔF( u) + = Δx 0
28 Rechengitter Gitterqualität: Genauigkeit und Konvergenz hängen ab von Orthogonalität α 45º < α <135º aspect ratio: dx b /dy b <2 dy a A B expansion ratio: dx b /dx a < 1.2 dx a dx b
29 Beispiel zum Thema Gitterqualität Längsprofil [m ü.m.] Sohle krit. Wasserspiegel Wasserspiegel Energielinie Längsprofil [km] 667 [m ü.m.] Sohle krit. Wasserspiegel Wasserspiegel Energielinie [km]
30 Räumliche Diskretisierung Δt C C F F Δx Fluss über Zellseite ( ) 1/2 + 1/2 n+ 1 n n n i = i + i i (,, ) n n n n i+ 1/2 = i 1 i i+ 1 F f C C C Upwind scheme (1. Ord.) n i+ 1/2 = n ( i ) n ( i ) F f C n i+ 1/2 = + 1 F f C if u>0 if u<0 C i-1 u i-1 C i Ci+1 i-1/2 i i+1/2 i+1 Central scheme ( ) ( ) F f C f C n n n i+ 1/2 = 0.5 i + i+ 1 Higher order Upwind scheme C i-1 i-1 C i C L C R C i+1 i-1/2 i i+1/2 i+1
31 Einfluss verschiedener Rechenschemen C t C + u = 0 x mit Anfangsbedingung: Cx (,0) = 1 für 0 x 0.3 Cx (,0) = 0.2 für 0 x 0.3 und Randbedingung: C(0, x) = 1.0 und u(0, t) = konst. = 1.0 C central 2. order C upwind 1. order 1.0 t= t= t0 0.5 t x x C upwind 3. order C higher order 1.0 t= t= t0 0.5 t x x
32 Zur Genauigkeit von Rechenschemen u t u + c = 0 x ux (, t) U i n i n Richtige Lösung Näherungs Lösung U U U U Δt 2Δx n+ 1 n n n i i + c i+ 1 i 1 = 0 2 u u Δt Δx + c = utt uxx +... t x 2 6 Abbruchfehler 2 3 n+ 1 Δx Δx Ui = u+δx ux + uxx + uxxx n Δx Δx Ui 1 = u Δx ux + uxx uxxx n+ 1 Δt Ui = u+δt ut + utt Fehler (numerische Diffusion) proportional zu Δt und Δx 2 1. Ordnung in der Zeit 2. Ordnung im Raum
33 Numerische Diffusion: Einfluss Gitter V Ch vchδ t=δx dx Numerical diffusion
34 Schlussbemerkungen Modell: Physik Mathematik Numerik Randbed. Ermessenspielraum Erfahrung Keep it simple!
35 Danke Roland Fäh
1D-BASEMENT. Renata Müller
 Numerische Modellierung von Naturgefahren mit dem Softwaresystem BASEMENT Workshop vom 6. Oktober 2006 an der VAW ETH Zürich 1D-BASEMENT Renata Müller Überblick Einführung Mathematische Beschreibung Gleichungen
Numerische Modellierung von Naturgefahren mit dem Softwaresystem BASEMENT Workshop vom 6. Oktober 2006 an der VAW ETH Zürich 1D-BASEMENT Renata Müller Überblick Einführung Mathematische Beschreibung Gleichungen
Hybride Geschiebemodellierung der Sihl am HB Zürich
 Basement-Anwendertreffen 2016 Hybride Geschiebemodellierung der Sihl am HB Zürich Masterarbeit FS15 Andrea Irniger Abb. 1: Zusammenfluss Limmat und Sihl, Aug. 2005, Quelle: AWEL Betreuung: Florian Hinkelammert
Basement-Anwendertreffen 2016 Hybride Geschiebemodellierung der Sihl am HB Zürich Masterarbeit FS15 Andrea Irniger Abb. 1: Zusammenfluss Limmat und Sihl, Aug. 2005, Quelle: AWEL Betreuung: Florian Hinkelammert
Unstetige Galerkin-Verfahren und die lineare Transportgleichung. Tobias G. Pfeiffer Freie Universität Berlin
 Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Hyperbolische Erhaltungsgleichungen und die Wellengleichung
 Hyperbolische Erhaltungsgleichungen und die Wellengleichung Stefanie Günther Universität Trier 11.November 2010 Stefanie Günther (Universität Trier) Seminar Numerik 1/29 11.November 2010 1 / 29 Inhaltsverzeichnis
Hyperbolische Erhaltungsgleichungen und die Wellengleichung Stefanie Günther Universität Trier 11.November 2010 Stefanie Günther (Universität Trier) Seminar Numerik 1/29 11.November 2010 1 / 29 Inhaltsverzeichnis
Angewandte Strömungssimulation
 Angewandte Strömungssimulation 7. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung Auswertung Parameter und Kennzahlen
Angewandte Strömungssimulation 7. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung Auswertung Parameter und Kennzahlen
Angewandte Strömungssimulation
 Angewandte Strömungssimulation 6. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung Auswertung Parameter und Kennzahlen
Angewandte Strömungssimulation 6. Vorlesung Stefan Hickel Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung Auswertung Parameter und Kennzahlen
Dual-Mesh Ansatz zur numerischen Simulation von Sedimenttransport auf unstrukturierten Berechnungsgittern
 1 Dual-Mesh Ansatz zur numerischen Simulation von Sedimenttransport auf unstrukturierten Berechnungsgittern Christian Volz, Patric Rousselot, David Vetsch, Renata Müller, Roland Fäh Zusammenfassung Für
1 Dual-Mesh Ansatz zur numerischen Simulation von Sedimenttransport auf unstrukturierten Berechnungsgittern Christian Volz, Patric Rousselot, David Vetsch, Renata Müller, Roland Fäh Zusammenfassung Für
Effiziente Diskretisierungs- und Lösungstechniken für die Lattice-Boltzmann Equation auf unstrukturierten Gittern
 Effiziente Diskretisierungs- und Lösungstechniken für die Lattice-Boltzmann Equation auf unstrukturierten Gittern Thomas Hübner, Stefan Turek (thomas.huebner@math.uni-dortmund.de, ture@featflow.de) LS
Effiziente Diskretisierungs- und Lösungstechniken für die Lattice-Boltzmann Equation auf unstrukturierten Gittern Thomas Hübner, Stefan Turek (thomas.huebner@math.uni-dortmund.de, ture@featflow.de) LS
Transport Einführung
 Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Numerische Modellierung von Grundwasserströmungen
 Numerische Modellierung von Grundwasserströmungen Heiko Berninger Berlin, 23. Juni 2004 Elbe Hochwasser August 2002 Ökosystem Untere Havel Unteres Havelland als natürliches Überschwemmungsgebiet Hydrologische
Numerische Modellierung von Grundwasserströmungen Heiko Berninger Berlin, 23. Juni 2004 Elbe Hochwasser August 2002 Ökosystem Untere Havel Unteres Havelland als natürliches Überschwemmungsgebiet Hydrologische
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
 8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
Burgers Gleichung. Juri Chomé, Olaf Merkert. 2. Dezember J. Chomé, O. Merkert () Burgers Gleichung 2. Dezember / 25
 Burgers Gleichung Juri Chomé, Olaf Merkert 2. Dezember 2009 J. Chomé, O. Merkert () Burgers Gleichung 2. Dezember 2009 1 / 25 Gliederung 1 Geschichte 2 Herleitung 3 Charakteristiken 4 Numerische Lösung
Burgers Gleichung Juri Chomé, Olaf Merkert 2. Dezember 2009 J. Chomé, O. Merkert () Burgers Gleichung 2. Dezember 2009 1 / 25 Gliederung 1 Geschichte 2 Herleitung 3 Charakteristiken 4 Numerische Lösung
Übungsblatt 6 Musterlösung
 MSE SS7 Übungsblatt 6 Musterlösung Lösung Methode der Charakteristiken) a) Hier ist c = x, d =. Also sind die Gleichungen für die Charakteristiken durch ẋt) = xt), żt) =, mit Anfangsbedingungen x) = x,
MSE SS7 Übungsblatt 6 Musterlösung Lösung Methode der Charakteristiken) a) Hier ist c = x, d =. Also sind die Gleichungen für die Charakteristiken durch ẋt) = xt), żt) =, mit Anfangsbedingungen x) = x,
Angewandte Strömungssimulation
 Angewandte Strömungssimulation 6. Vorlesung Stefan Hickel Finite - Volumen - Methode Finite - Volumen - Methode! Das Rechengebiet wird in nicht überlappende Bereiche (= finite Volumina) unterteilt.! Jedem
Angewandte Strömungssimulation 6. Vorlesung Stefan Hickel Finite - Volumen - Methode Finite - Volumen - Methode! Das Rechengebiet wird in nicht überlappende Bereiche (= finite Volumina) unterteilt.! Jedem
Berechnungsmethoden der Energie- und Verfahrenstechnik Methode der gewichteten Residuen
 Berechnungsmethoden der Energie- und Verfahrenstechnik Methode der gewichteten Residuen Giuseppe Bonfigli IFD, ETH-Zürich 3. Juni 21 Giuseppe Bonfigli (IFD, ETH-Zürich) Gewichtete Residuen 3. Juni 21 1
Berechnungsmethoden der Energie- und Verfahrenstechnik Methode der gewichteten Residuen Giuseppe Bonfigli IFD, ETH-Zürich 3. Juni 21 Giuseppe Bonfigli (IFD, ETH-Zürich) Gewichtete Residuen 3. Juni 21 1
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Randwertbedingungen und Ghost Cells
 Randwertbedingungen und Ghost Cells Olaf Kern Universität Trier 16.Dezember 2010 Olaf Kern (Universität Trier) Seminar Numerik 1/23 16.Dezember 2010 1 / 23 Inhaltsverzeichnis 1 Einführung 2 Periodische
Randwertbedingungen und Ghost Cells Olaf Kern Universität Trier 16.Dezember 2010 Olaf Kern (Universität Trier) Seminar Numerik 1/23 16.Dezember 2010 1 / 23 Inhaltsverzeichnis 1 Einführung 2 Periodische
Klassifikation von partiellen Differentialgleichungen
 Kapitel 2 Klassifikation von partiellen Differentialgleichungen Die meisten partiellen Differentialgleichungen sind von 3 Grundtypen: elliptisch, hyperbolisch, parabolisch. Betrachte die allgemeine Dgl.
Kapitel 2 Klassifikation von partiellen Differentialgleichungen Die meisten partiellen Differentialgleichungen sind von 3 Grundtypen: elliptisch, hyperbolisch, parabolisch. Betrachte die allgemeine Dgl.
VORLESUNGEN. Numerische. Diplomarbeit. Strömungsmechanik Kolleg
 VORLESUNGEN Strömungslehre 5 Angewandte Strömungsmechanik Math. Methoden der Strömungslehre 6 Numerische Strömungsmechanik 7 Trainings-Kurs 8 Diplomarbeit Strömungsmechanik Kolleg Mathematische Methoden
VORLESUNGEN Strömungslehre 5 Angewandte Strömungsmechanik Math. Methoden der Strömungslehre 6 Numerische Strömungsmechanik 7 Trainings-Kurs 8 Diplomarbeit Strömungsmechanik Kolleg Mathematische Methoden
Einige grundlegende partielle Differentialgleichungen
 Einige grundlegende partielle Differentialgleichungen H. Abels 17. Oktober 2010 H. Abels (U Regensburg) Grundlegende PDGLn 17. Oktober 2010 1 / 14 Transportgleichung Eine der einfachsten Differentialgleichungen
Einige grundlegende partielle Differentialgleichungen H. Abels 17. Oktober 2010 H. Abels (U Regensburg) Grundlegende PDGLn 17. Oktober 2010 1 / 14 Transportgleichung Eine der einfachsten Differentialgleichungen
Numerik von Anfangswertaufgaben Teil II
 Institut für Numerische Mathematik und Optimierung Numerik von Anfangswertaufgaben Teil II Numerik partieller Differentialgleichungen Oliver Ernst Hörerkreis: 6. Mm, 8. Mm Sommersemester 2012 Inhalt 1.
Institut für Numerische Mathematik und Optimierung Numerik von Anfangswertaufgaben Teil II Numerik partieller Differentialgleichungen Oliver Ernst Hörerkreis: 6. Mm, 8. Mm Sommersemester 2012 Inhalt 1.
D-MAVT NUMERISCHE MATHEMATIK FS 14 K. Nipp, A. Hiltebrand Lösung vom Test 1
 D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
D-MAVT NUMERISCHE MATHEMATIK FS 4 K. Nipp, A. Hiltebrand Lösung vom Test. Sei eps die Maschinengenauigkeit in Matlab. Dann gilt: eps/4 = Richtig / Falsch + eps/2 = Richtig / Falsch 8 + eps = 8 Richtig
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
Numerik gewöhnlicher Differentialgleichungen 4.4 Anfangsrandwertprobleme Die Diskretisierung von zeitabhängigen partiellen Differentialgleichungen mit der Linienmethode führt auf Systeme gewöhnlicher Dgl
1D-Transportgleichung
 Analytische Lösungen der Transportgleichung 1-Transportgleichung Wenn ein gelöster Stoff sich sowohl advektiv, als auch diffusiv in einer Flüssigkeit bewegt, dann gilt folgende Gleichung ( nc t + x x &
Analytische Lösungen der Transportgleichung 1-Transportgleichung Wenn ein gelöster Stoff sich sowohl advektiv, als auch diffusiv in einer Flüssigkeit bewegt, dann gilt folgende Gleichung ( nc t + x x &
2. Vorlesung Partielle Differentialgleichungen
 2. Vorlesung Partielle Differentialgleichungen Wolfgang Reichel Karlsruhe, 22. Oktober 204 Institut für Analysis KIT University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz
2. Vorlesung Partielle Differentialgleichungen Wolfgang Reichel Karlsruhe, 22. Oktober 204 Institut für Analysis KIT University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz
3. Berechnen Sie auch die Beschleunigung a als Funktion der Zeit t. 4. Erstellen Sie ein SIMULINK Modell, das x(t) numerisch berechnet.
 unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Hydroinformatik II Prozess-Simulation und Systemanalyse
 Version 9.01-5. August 2018 Hydroinformatik II Prozess-Simulation und Systemanalyse Prof. Dr.-Ing. Olaf Kolditz TU Dresden / UFZ Leipzig Angewandte Umweltsystemanalyse Department Umweltinformatik Sommersemester
Version 9.01-5. August 2018 Hydroinformatik II Prozess-Simulation und Systemanalyse Prof. Dr.-Ing. Olaf Kolditz TU Dresden / UFZ Leipzig Angewandte Umweltsystemanalyse Department Umweltinformatik Sommersemester
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm
 Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
2. Vorlesung Partielle Differentialgleichungen
 2. Vorlesung Partielle Differentialgleichungen Wolfgang Reichel 2.Transatlantische Vorlesung aus Oaxaca, Mexiko, 20. Oktober 2010 Institut für Analysis KIT University of the State of Baden-Wuerttemberg
2. Vorlesung Partielle Differentialgleichungen Wolfgang Reichel 2.Transatlantische Vorlesung aus Oaxaca, Mexiko, 20. Oktober 2010 Institut für Analysis KIT University of the State of Baden-Wuerttemberg
4. Transiente Analyse
 4. Transiente Analyse Bei der transienten Analyse wird der zeitliche Verlauf der Antwort auf eine zeitlich veränderliche Last bestimmt. Die zu lösende Bewegungsgleichung lautet: [ M ] [ü ]+[ D ] [ u ]+
4. Transiente Analyse Bei der transienten Analyse wird der zeitliche Verlauf der Antwort auf eine zeitlich veränderliche Last bestimmt. Die zu lösende Bewegungsgleichung lautet: [ M ] [ü ]+[ D ] [ u ]+
Partielle Differentialgleichungen. Hofer Joachim/Panis Clemens
 9.11.2010 Contents 1 Allgemein 2 1.1 Definition................................................. 2 1.2 Klassifikation............................................... 2 1.3 Lösbarkeit.................................................
9.11.2010 Contents 1 Allgemein 2 1.1 Definition................................................. 2 1.2 Klassifikation............................................... 2 1.3 Lösbarkeit.................................................
Hydroinformatik II Prozess-Simulation und Systemanalyse
 Version 7.01-10. August 2016 Hydroinformatik II Prozess-Simulation und Systemanalyse Prof. Dr.-Ing. Olaf Kolditz TU Dresden / UFZ Leipzig Angewandte Umweltsystemanalyse Department Umweltinformatik Sommersemester
Version 7.01-10. August 2016 Hydroinformatik II Prozess-Simulation und Systemanalyse Prof. Dr.-Ing. Olaf Kolditz TU Dresden / UFZ Leipzig Angewandte Umweltsystemanalyse Department Umweltinformatik Sommersemester
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulation reaktiver und nichtreaktiver Strömungen
 Statustreffen IWRMM, Karlsruhe, 15.4.2005 Simulation reaktiver und nichtreaktiver Strömungen Jochen Fröhlich Universität Karlsruhe Arbeitsbereiche des TCP Zusammenschluss 1.1.2004 Institut für Chemische
Statustreffen IWRMM, Karlsruhe, 15.4.2005 Simulation reaktiver und nichtreaktiver Strömungen Jochen Fröhlich Universität Karlsruhe Arbeitsbereiche des TCP Zusammenschluss 1.1.2004 Institut für Chemische
Angewandte Strömungssimulation
 Angewandte Strömungssimulation 9. Vorlesung Stefan Hickel Validierung und Fehlererkennung Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung
Angewandte Strömungssimulation 9. Vorlesung Stefan Hickel Validierung und Fehlererkennung Numerische Strömungsberechnung Physikalische Modellierung Mathematische Modellierung Numerische Modellierung Lösung
m d2 x dt 2 = K( x), d 2 x j dt 2 = K i.
 P m d2 x dt 2 = K( x), m δ ij d 2 x j dt 2 = K i. C W C = C K i dx i δ ij δ ij λδ ij, m m λ d v dt K BA = K AB R 4 E 3 R Σ Σ x = R x a, R T R = I, R... E 3 T 1, 3 + 3 + 1 = 7 E 3 = O 3 T 3,... E 3 O 3
P m d2 x dt 2 = K( x), m δ ij d 2 x j dt 2 = K i. C W C = C K i dx i δ ij δ ij λδ ij, m m λ d v dt K BA = K AB R 4 E 3 R Σ Σ x = R x a, R T R = I, R... E 3 T 1, 3 + 3 + 1 = 7 E 3 = O 3 T 3,... E 3 O 3
Analytische Lösungen der Transportgleichung Transportmodellierung
 Analytische Lösungen der Transportgleichung 1D-Transportgleichung Wenn ein gelöster Stoff sich sowohl advektiv, als auch diffusiv in einer Flüssigkeit bewegt, dann gilt folgende Gleichung ( nc) t + x x
Analytische Lösungen der Transportgleichung 1D-Transportgleichung Wenn ein gelöster Stoff sich sowohl advektiv, als auch diffusiv in einer Flüssigkeit bewegt, dann gilt folgende Gleichung ( nc) t + x x
Glättung durch iterative Verfahren
 Numerische Methoden in der Finanzmathematik II Sommersemester 211 Glättung durch iterative Verfahren Vorlesung Numerische Methoden in der Finanzmathematik II Sommersemester 211 Numerische Methoden in der
Numerische Methoden in der Finanzmathematik II Sommersemester 211 Glättung durch iterative Verfahren Vorlesung Numerische Methoden in der Finanzmathematik II Sommersemester 211 Numerische Methoden in der
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Differentialgleichungen
 Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Numerik und Simulation in der Geoökologie
 1/25 Rekapitulation Simulation des Wärmetransportes Methode der finiten Volumen Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 11 WS 2007/2008 2/25 Rekapitulation Simulation des Wärmetransportes
1/25 Rekapitulation Simulation des Wärmetransportes Methode der finiten Volumen Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 11 WS 2007/2008 2/25 Rekapitulation Simulation des Wärmetransportes
Serie 4: Gradient und Linearisierung
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
Hamilton-Systeme. J. Struckmeier
 Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Invarianten für zeitabhängige Hamilton-Systeme J. Struckmeier Vortrag im Rahmen des Winterseminars des Instituts für Angewandte Physik der Johann-Wolfgang-Goethe-Universität Frankfurt a.m. Hirschegg, 04.
Nichtlineare Gleichungen in einer und mehreren Unbekannten
 Gleichungen in einer und mehreren Unbekannten 2. Vorlesung 170004 Numerische Methoden I Clemens Brand 26. Februar 2009, Gliederung,, Gleichungen in einer Variablen Was ist... Wie geht... eine lineare (nichtlineare,
Gleichungen in einer und mehreren Unbekannten 2. Vorlesung 170004 Numerische Methoden I Clemens Brand 26. Februar 2009, Gliederung,, Gleichungen in einer Variablen Was ist... Wie geht... eine lineare (nichtlineare,
Mehrgitter-Verfahren für DG Finite-Elemente-Diskretisierungen von turbulenten Strömungen
 www.dlr.de Folie 1 > STAB Workshop, 12.11.2013 > Marcel Wallraff, Tobias Leicht 12.11.2013 Mehrgitter-Verfahren für DG Finite-Elemente-Diskretisierungen von turbulenten Strömungen Marcel Wallraff, Tobias
www.dlr.de Folie 1 > STAB Workshop, 12.11.2013 > Marcel Wallraff, Tobias Leicht 12.11.2013 Mehrgitter-Verfahren für DG Finite-Elemente-Diskretisierungen von turbulenten Strömungen Marcel Wallraff, Tobias
Anwendung von Lattice-Boltzmann Methoden in der Strömungsakustik. Andreas Wilde
 Anwendung von Lattice-Boltzmann Methoden in der Strömungsakustik Andreas Wilde Einführung/Überblick Frage: Kann man mit Lattice-Boltzmann Strömungsakustik machen? 2 Einführung/Überblick Frage: Kann man
Anwendung von Lattice-Boltzmann Methoden in der Strömungsakustik Andreas Wilde Einführung/Überblick Frage: Kann man mit Lattice-Boltzmann Strömungsakustik machen? 2 Einführung/Überblick Frage: Kann man
Möglichkeiten der numerischen Lösung der Navier-Stokes- Gleichungen am Beispiel einer inkompressiblen Strömung über eine rückspringende Stufe
 Möglichkeiten der numerischen Lösung der Navier-Stokes- Gleichungen am Beispiel einer inkompressiblen Strömung über eine rückspringende Stufe Dr. rer. nat. Frank Morherr Bingen, 11.01.2016 Die Navier-Stokes-Gleichungen
Möglichkeiten der numerischen Lösung der Navier-Stokes- Gleichungen am Beispiel einer inkompressiblen Strömung über eine rückspringende Stufe Dr. rer. nat. Frank Morherr Bingen, 11.01.2016 Die Navier-Stokes-Gleichungen
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Dr. A. Caspar ETH Zürich, Januar D BIOL, D CHAB Lösungen zu Mathematik I/II. ( Punkte) a) Wir benutzen L Hôpital lim x ln(x) L Hôpital x 3 = lim 3x + x L Hôpital = lim x ln(x) x 3x 3 = lim ln(x) x 3 x
Neues numerisches Verfahren zur Modellierung von Suspensionstransport
 1 Neues numerisches Verfahren zur Modellierung von Suspensionstransport Renata Müller, Patric Rousselot, David Vetsch, Christian Volz, Roland Fäh Zusammenfassung Zur numerischen Modellierung von Suspensionstransport
1 Neues numerisches Verfahren zur Modellierung von Suspensionstransport Renata Müller, Patric Rousselot, David Vetsch, Christian Volz, Roland Fäh Zusammenfassung Zur numerischen Modellierung von Suspensionstransport
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 6. Teil Die Berechnung des Geschwindigkeitsfeldes
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 6. Teil Die Berechnung des Geschwindigkeitsfeldes
Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator
 Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Joel H. Ferziger. Milovan Petie. Numerische. Stromungsmechanik. ~ Springer
 Joel H. Ferziger. Milovan Petie Numerische Stromungsmechanik ~ Springer Vorwort V 1. Physikalische Grundlagen der St.rdrnungen................ 1 1.1 Einftihrung :::... 1 1.2 Erhaltungsprinzipien... 3 1.3
Joel H. Ferziger. Milovan Petie Numerische Stromungsmechanik ~ Springer Vorwort V 1. Physikalische Grundlagen der St.rdrnungen................ 1 1.1 Einftihrung :::... 1 1.2 Erhaltungsprinzipien... 3 1.3
Thermodynamik II Musterlösung Rechenübung 9
 Thermodynamik II Musterlösung Rechenübung 9 Aufgabe 1 Der Wärmetransfer des Festkörpers und diejenige des finiten Fluidvolumens sind über den konvektiven Wärmeübergang, der von A und α abhängt, gekoppelt.
Thermodynamik II Musterlösung Rechenübung 9 Aufgabe 1 Der Wärmetransfer des Festkörpers und diejenige des finiten Fluidvolumens sind über den konvektiven Wärmeübergang, der von A und α abhängt, gekoppelt.
1 Die Problemstellung
 Institut für Wissenschaftliches Rechnen Technische Universität Braunschweig Prof. Hermann G. Matthies, Ph.D. ScientifiComputing Wir wollen als erstes das in diesem Praktikum zu behandelnde Problem aus
Institut für Wissenschaftliches Rechnen Technische Universität Braunschweig Prof. Hermann G. Matthies, Ph.D. ScientifiComputing Wir wollen als erstes das in diesem Praktikum zu behandelnde Problem aus
Spezialisierte adaptive Algorithmen für die Modellprädiktive Regelung von PDEs
 Spezialisierte adaptive Algorithmen für die Modellprädiktive Regelung von PDEs Lehrstuhl für Angewandte Mathematik Mathematisches Institut Universität Bayreuth 28.02.2018 12. Elgersburg Workshop (26.02.
Spezialisierte adaptive Algorithmen für die Modellprädiktive Regelung von PDEs Lehrstuhl für Angewandte Mathematik Mathematisches Institut Universität Bayreuth 28.02.2018 12. Elgersburg Workshop (26.02.
Hydrodynamik Kontinuitätsgleichung. Massenerhaltung: ρ. Massenfluss. inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms : v
 Hydrodynamik Kontinuitätsgleichung A2, rho2, v2 A1, rho1, v1 Stromröhre Massenerhaltung: ρ } 1 v {{ 1 A } 1 = ρ } 2 v {{ 2 A } 2 m 1 inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms
Hydrodynamik Kontinuitätsgleichung A2, rho2, v2 A1, rho1, v1 Stromröhre Massenerhaltung: ρ } 1 v {{ 1 A } 1 = ρ } 2 v {{ 2 A } 2 m 1 inkompressibles Fluid: (ρ 1 = ρ 2 = konst) Erhaltung des Volumenstroms
reibungsbehaftete Strömungen bisher: reibungsfreie Fluide und Strömungen nur Normalkräfte Druck nun: reibungsbehaftete Strömungen
 reibungsbehaftete Strömungen bisher: reibungsfreie Fluide und Strömungen nur Normalkräfte Druck 000000000000000 111111111111111 000000000000000 111111111111111 u 000000000000000 111111111111111 000000000000000
reibungsbehaftete Strömungen bisher: reibungsfreie Fluide und Strömungen nur Normalkräfte Druck 000000000000000 111111111111111 000000000000000 111111111111111 u 000000000000000 111111111111111 000000000000000
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, August D BIOL, D CHAB Lösungen zu Mathematik I/II Aufgaben. ( Punkte) a) Wir berechnen lim sin(x ) x 3 + 4x L Hôpital = lim x cos(x ) 3x + 8x = 4. b) Wir benutzen L Hôpital lim
Dr. A. Caspar ETH Zürich, August D BIOL, D CHAB Lösungen zu Mathematik I/II Aufgaben. ( Punkte) a) Wir berechnen lim sin(x ) x 3 + 4x L Hôpital = lim x cos(x ) 3x + 8x = 4. b) Wir benutzen L Hôpital lim
Bachelor Modulprüfung. Höhere Mathematik III für die Fachrichtung Physik. Lösungsvorschläge
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE (KIT) Institut für Analysis Priv.-Doz. Dr. Peer Kunstmann Markus Antoni WS 22/23 Bachelor Modulprüfung Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge
KARLSRUHER INSTITUT FÜR TECHNOLOGIE (KIT) Institut für Analysis Priv.-Doz. Dr. Peer Kunstmann Markus Antoni WS 22/23 Bachelor Modulprüfung Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge
Einführung in einige Teilbereiche der Wirtschaftsmathematik für Studierende des Wirtschaftsingenieurwesens
 in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2013 Hochschule Augsburg : Gliederung 1 Finanzmathematik 2 Lineare Programme 3 Differentialgleichungen 4 Statistik:
in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2013 Hochschule Augsburg : Gliederung 1 Finanzmathematik 2 Lineare Programme 3 Differentialgleichungen 4 Statistik:
1. Die Wellengleichung
 1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
1. Die Wellengleichung Die Wellengleichung ist eine partielle Differenzialgleichung für das Schallfeld. Sie lässt sich durch Linearisierung aus der Massenbilanz, der Impulsbilanz und der Energiebilanz
Unterschiede bei der Geschiebemodellierung an flachen und steilen Fliessgewässern mit Hydro_GS-2D
 Unterschiede bei der Geschiebemodellierung an flachen und steilen Fliessgewässern mit Hydro_GS-2D Anwendertreffen Hydro_AS-2D in München am 05.10.2016 Dr. sc. techn. Roni Hunziker, Andrea Irniger, dipl.
Unterschiede bei der Geschiebemodellierung an flachen und steilen Fliessgewässern mit Hydro_GS-2D Anwendertreffen Hydro_AS-2D in München am 05.10.2016 Dr. sc. techn. Roni Hunziker, Andrea Irniger, dipl.
Der Einfluss der natürlichenvarianz von Tide und Wind auf den Sedimenttransport in der inneren Deutschen Bucht. Dr.-Ing. A. D.
 Der Einfluss der natürlichenvarianz von Tide und Wind auf den Sedimenttransport in der inneren Deutschen Bucht Dr.-Ing. A. D. Plüß AK - K3 / 22-11 Folie-Nr. 1 Gliederung Analyse der Varianz auf der Grundlage
Der Einfluss der natürlichenvarianz von Tide und Wind auf den Sedimenttransport in der inneren Deutschen Bucht Dr.-Ing. A. D. Plüß AK - K3 / 22-11 Folie-Nr. 1 Gliederung Analyse der Varianz auf der Grundlage
Modellieren in der Angewandten Geologie II. Sebastian Bauer
 Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Modellieren in der Angewandten Geologie II Geohydromodellierung Institut für Geowissenschaften Christian-Albrechts-Universität zu Kiel CAU 3-1 Die Finite Elemente Method (FEM) ist eine sehr allgemeine
Dierentialgleichungen 2. Ordnung
 Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
Dierentialgleichungen 2. Ordnung haben die allgemeine Form x = F (x, x, t. Wir beschränken uns hier auf zwei Spezialfälle, in denen sich eine Lösung analytisch bestimmen lässt: 1. reduzible Dierentialgleichungen:
System von Differentialgleichungen erster Ordnung
 System von Differentialgleichungen erster Ordnung Die Standardform eines Systems von Differentialgleichungen ist u (t) = f (t, u(t)) mit der Anfangsbedingung u(t 0 ) = a. Dabei ist u = (u 1,..., u n )
System von Differentialgleichungen erster Ordnung Die Standardform eines Systems von Differentialgleichungen ist u (t) = f (t, u(t)) mit der Anfangsbedingung u(t 0 ) = a. Dabei ist u = (u 1,..., u n )
Kapitel 3. Diskretisierungsverfahren. 3.1 Elliptische Differentialgleichung
 Kapitel 3 Diskretisierungsverfahren 3.1 Elliptische Differentialgleichung Wir beschränken uns auf elliptische Randwertaufgaben. Gesucht ist eine Funktion u (x, y) in R 2, welche die allgemeine partielle
Kapitel 3 Diskretisierungsverfahren 3.1 Elliptische Differentialgleichung Wir beschränken uns auf elliptische Randwertaufgaben. Gesucht ist eine Funktion u (x, y) in R 2, welche die allgemeine partielle
Thermodynamik II Musterlösung Rechenübung 10
 Thermodynamik II Musterlösung Rechenübung 0 Aufgabe Seitenansicht: Querschnitt: Annahmen: stationärer Zustand Wärmeleitung in axialer Richtung ist vernachlässigbar konstante Materialeigenschaften Wärmeleitungswiderstand
Thermodynamik II Musterlösung Rechenübung 0 Aufgabe Seitenansicht: Querschnitt: Annahmen: stationärer Zustand Wärmeleitung in axialer Richtung ist vernachlässigbar konstante Materialeigenschaften Wärmeleitungswiderstand
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Experimentalphysik 1 für MSE
 Physik-Department LS für Funktionelle Materialien WS 2017/18 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Dr. Neelima Paul, Sebastian Grott, Lucas Kreuzer,
Physik-Department LS für Funktionelle Materialien WS 2017/18 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Dr. Neelima Paul, Sebastian Grott, Lucas Kreuzer,
Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder
 DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
DGL Schwingung Physikalische Felder Mathematik-Tutorium für Maschinenbauer II: Differentialgleichungen und Vektorfelder Johannes Wiedersich 23. April 2008 http://www.e13.physik.tu-muenchen.de/wiedersich/
Wir betrachten das Anfangsrandwertproblem auf dem Halbraum R + :
 Die Reflektionsmethode für den Halbraum R + = x > 0}: Wir betrachten das Anfangsrandwertproblem auf dem Halbraum R + : u tt u xx = 0 in R + (0, ) u = g, u t = h auf R + t = 0} u = 0 auf x = 0} (0, ) mit
Die Reflektionsmethode für den Halbraum R + = x > 0}: Wir betrachten das Anfangsrandwertproblem auf dem Halbraum R + : u tt u xx = 0 in R + (0, ) u = g, u t = h auf R + t = 0} u = 0 auf x = 0} (0, ) mit
Numerische Methoden I FEM/REM
 Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 27.0.206 Klausur Datum: 2.3.206 Numerische Methoden RES, SM, MT (DPO 203),
Numerische Methoden I FEM/REM Dr.-Ing. Markus Kästner ZEU 353 Tel.: 035 463 32656 E-Mail: Markus.Kaestner@tu-dresden.de Dresden, 27.0.206 Klausur Datum: 2.3.206 Numerische Methoden RES, SM, MT (DPO 203),
Hydroinformatik II: Finite Differenzen Methode
 Hydroinformatik II: Finite Differenzen Methode 1 Helmholtz Centre for Environmental Research UFZ, Leipzig 2 Technische Universität Dresden TUD, Dresden Dresden, 05. Juni 2015 1/24 Prof. Dr.-Ing. habil.
Hydroinformatik II: Finite Differenzen Methode 1 Helmholtz Centre for Environmental Research UFZ, Leipzig 2 Technische Universität Dresden TUD, Dresden Dresden, 05. Juni 2015 1/24 Prof. Dr.-Ing. habil.
Numerische Simulation der Störungsausbreitung. Berücksichtigung nichtlinearer Effekte
 DGLR Fachausschußsitzung T 2.3 Strömungsakustik/Fluglärm Numerische Simulation der Störungsausbreitung in Düsenströmungen unter Berücksichtigung nichtlinearer Effekte Hermann-Föttinger-Intitut Technische
DGLR Fachausschußsitzung T 2.3 Strömungsakustik/Fluglärm Numerische Simulation der Störungsausbreitung in Düsenströmungen unter Berücksichtigung nichtlinearer Effekte Hermann-Föttinger-Intitut Technische
Kapitel 4: Nichtlineare Nullstellenprobleme
 Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Klausur Strömungsmechanik II u x + v. y = 0. ρ u u x + v u ) ρ c p. x + v T ) v ; ρ = ρ ; x = x u ρ L ; ȳ = y L ; u ; v = λ λ Konti:
 ...... Name, Matr.-Nr, Unterschrift Klausur Strömungsmechanik II 05. 08. 011 1. Aufgabe a Konti: Impuls: Energie: u x + v = 0 ρ u u x + v u ρ c p u T x + v T = η u = λ T dimensionslose Größen: ū = u u
...... Name, Matr.-Nr, Unterschrift Klausur Strömungsmechanik II 05. 08. 011 1. Aufgabe a Konti: Impuls: Energie: u x + v = 0 ρ u u x + v u ρ c p u T x + v T = η u = λ T dimensionslose Größen: ū = u u
Höhere Mathematik III für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Ioannis Anapolitanos Dipl.-Math. Sebastian Schwarz WS 5/6 6..5 Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Ioannis Anapolitanos Dipl.-Math. Sebastian Schwarz WS 5/6 6..5 Höhere Mathematik III für die Fachrichtung Physik Lösungsvorschläge zum. Übungsblatt
Strömung mit Ablösung Eine Grenzschicht, der ein positiver Druckgradient aufgeprägt ist, kann ablösen: z.b.: Strömung in einem Diffusor
 Strömung mit Ablösung Eine Grenzschicht, der ein positiver Druckgradient aufgeprägt ist, kann ablösen: z.b.: Strömung in einem Diffusor reibungsfreie Strömung: Grenzschicht A(x) u a ρu a x = p x A(x) x
Strömung mit Ablösung Eine Grenzschicht, der ein positiver Druckgradient aufgeprägt ist, kann ablösen: z.b.: Strömung in einem Diffusor reibungsfreie Strömung: Grenzschicht A(x) u a ρu a x = p x A(x) x
Kompressible Strömungen
 Kompressible Strömungen Problemstellungen: - Wie lassen sich Überschallströmungen realisieren? - Welche Windkanalgeometrie ist notwendig? - Thermodynamische Beziehungen in Überschallströmungen? - Unterschall
Kompressible Strömungen Problemstellungen: - Wie lassen sich Überschallströmungen realisieren? - Welche Windkanalgeometrie ist notwendig? - Thermodynamische Beziehungen in Überschallströmungen? - Unterschall
Mathematische Modellierung in der Hämodynamik...
 Mathematische Modellierung in der Hämodynamik... Ergänzunsgvorlesung SoSe 2014 Dienstag 10.00-12.00 Dr. Anna Hundertmark Institut für Mathematik, AG Numerik Themen Wir werden erarbeiten: Themen Wir werden
Mathematische Modellierung in der Hämodynamik... Ergänzunsgvorlesung SoSe 2014 Dienstag 10.00-12.00 Dr. Anna Hundertmark Institut für Mathematik, AG Numerik Themen Wir werden erarbeiten: Themen Wir werden
κ Κα π Κ α α Κ Α
 κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ
κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ
Modellierung und Simulation von Mischvorgängen in einem Rührer - Bachelorarbeit -
 Modellierung und Simulation von Mischvorgängen in einem Rührer - Bachelorarbeit - Dies Mathematicus 211 25. November 211 Gliederung 1 Motivation: Mischvorgänge in einem Rührer 2 Mathematische Modellierung
Modellierung und Simulation von Mischvorgängen in einem Rührer - Bachelorarbeit - Dies Mathematicus 211 25. November 211 Gliederung 1 Motivation: Mischvorgänge in einem Rührer 2 Mathematische Modellierung
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 6. Teil Die Berechnung des Geschwindigkeitsfeldes
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 6. Teil Die Berechnung des Geschwindigkeitsfeldes
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Lyapunov-Exponenten. Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems:
 Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Bildverarbeitung: Diffusion Filters. D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10
 Bildverarbeitung: Diffusion Filters D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10 Diffusion Idee Motiviert durch physikalische Prozesse Ausgleich der Konzentration eines Stoffes. Konzentration
Bildverarbeitung: Diffusion Filters D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10 Diffusion Idee Motiviert durch physikalische Prozesse Ausgleich der Konzentration eines Stoffes. Konzentration
3D-Simulationen magneto-hydrodynamischer Instabilitäten in Akkretionsscheiben
 3D-Simulationen magneto-hydrodynamischer Instabilitäten in Akkretionsscheiben Wilhelm Kley, Jochen Peitz Daniel Marik Institut für Astronomie & Astrophysik Universität Tübingen Andreas Dedner, Dietmar
3D-Simulationen magneto-hydrodynamischer Instabilitäten in Akkretionsscheiben Wilhelm Kley, Jochen Peitz Daniel Marik Institut für Astronomie & Astrophysik Universität Tübingen Andreas Dedner, Dietmar
Hydraulik I. Roman Stocker. Gerinneströmung (ohne Reibung)
 Hydraulik I Roman Stocker Gerinneströmung (ohne Reibung) Begriffe der Gerinneströmung (1) z o = Sohlhöhe h = Wassertiefe v 2 /(2g) = Geschwindigkeitshöhe (Annahme: α = 1) H E = Energiehöhe H 0 = spezifische
Hydraulik I Roman Stocker Gerinneströmung (ohne Reibung) Begriffe der Gerinneströmung (1) z o = Sohlhöhe h = Wassertiefe v 2 /(2g) = Geschwindigkeitshöhe (Annahme: α = 1) H E = Energiehöhe H 0 = spezifische
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
KAPITEL 5. Nichtlineare Gleichungssysteme
 KAPITEL 5. Nichtlineare Gleichungssysteme Beispiel 5.1. Gravitationskraft zwischen zwei Punktmassen m 1 und m 2 mit gegenseitigem Abstand r: F = G m 1m 2 r 2, wobei G = 6.67 10 11 Nm 2 /kg. Gravitationsfeld
KAPITEL 5. Nichtlineare Gleichungssysteme Beispiel 5.1. Gravitationskraft zwischen zwei Punktmassen m 1 und m 2 mit gegenseitigem Abstand r: F = G m 1m 2 r 2, wobei G = 6.67 10 11 Nm 2 /kg. Gravitationsfeld
Dipl.-Ing. Christoph Erath 10. November FVM-BEM Kopplung. Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln?
 Dipl.-Ing. Christoph Erath 10. November 2007 FVM-BEM Kopplung Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln? Seite 2 FVM-BEM Kopplung 10. November 2007 Dipl.-Ing. Christoph Erath
Dipl.-Ing. Christoph Erath 10. November 2007 FVM-BEM Kopplung Was gewinnen wir, wenn wir zwei numerische Methoden miteinander koppeln? Seite 2 FVM-BEM Kopplung 10. November 2007 Dipl.-Ing. Christoph Erath
3. Lineare Mehrschrittverfahren 3.1 Begriffe
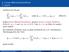 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
14 Numerik hyperbolischer Differentialgleichungen
 Numerik II 256 14 Numerik hyperbolischer Differentialgleichungen Während parabolische PDG Diffusionsvorgänge modellieren stellen hyperbolische PDG Modelle für Wellenphänomene dar. Wichtigste Anwendungsgebiete
Numerik II 256 14 Numerik hyperbolischer Differentialgleichungen Während parabolische PDG Diffusionsvorgänge modellieren stellen hyperbolische PDG Modelle für Wellenphänomene dar. Wichtigste Anwendungsgebiete
Numerik für Ingenieure II
 Numerik für Ingenieure II Prof. Dr. Dimitri Kuzmin Lehrstuhl für Angewandte Mathematik III Universität Erlangen-Nürnberg kuzmin@am.uni-erlangen.de http://www.mathematik.uni-dortmund.de/ kuzmin/numingii.html
Numerik für Ingenieure II Prof. Dr. Dimitri Kuzmin Lehrstuhl für Angewandte Mathematik III Universität Erlangen-Nürnberg kuzmin@am.uni-erlangen.de http://www.mathematik.uni-dortmund.de/ kuzmin/numingii.html
Newton- und und Quasi-Newton-Methoden in der Optimierung. János Mayer
 Newton- und und Quasi-Newton-Methoden in der Optimierung János Mayer 1 GLIEDERUNG Newton-Methode für nichtlineare Gleichungen nichtlineare Gleichungssysteme freie Minimierung. Quasi-Newton-Methoden für
Newton- und und Quasi-Newton-Methoden in der Optimierung János Mayer 1 GLIEDERUNG Newton-Methode für nichtlineare Gleichungen nichtlineare Gleichungssysteme freie Minimierung. Quasi-Newton-Methoden für
