Reihen und Finanzmathematik
|
|
|
- Luisa Egger
- vor 7 Jahren
- Abrufe
Transkript
1 Kapitel 4. Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Die entsprechenden Beispiele werden im nächsten Abschnitt behandelt. Grundkurs Mathematik WiSe 2007/ Sei (a n ) n N eine Folge. Wir definieren die n-te Partialsumme (oder: Teilsumme) der Folge (a n ) n N durch Aufaddieren der ersten n Folgenglieder, also n s n = a + a a n = a k für alle n N. k= Die Folge (s n ) n N der Partialsummen heißt eine (unendliche) ( n ) Reihe und wird auch als a k geschrieben. k= n N Die Bezeichnung n-te Partialsumme bezieht sich auf die Anzahl der aufsummierten Folgenglieder. Beachten Sie, dass zur Darstellung der n-ten Partialsumme mit dem Summenzeichen ein zweiter Laufindex, hier k, benötigt wird. Grundkurs Mathematik WiSe 2007/
2 Bei Reihen treten also immer zwei verschiedene Folgen auf: die Folge (a n ) n N der einzelnen Glieder und die Folge (s n ) n N der Partialsummen, das ist dann die Reihe. Beispiel 4.. Sei a n = n. Dann ist s n = n = n s 3 = = 6, k= k etwa s 0 = = s 00 5, 9 s ,79. 2, 93, Die Reihe (s n ) n N heißt harmonische Reihe. Grundkurs Mathematik WiSe 2007/ Ist a n = 2 n, dann ist s 3 = = 7 8 = 0, 875 s 0 = ,999 s 00 0, Sei a n = n. Dann ist s 2 = 3, s 0 = = 55, s 00 = Grundkurs Mathematik WiSe 2007/
3 4. Sei a n = ( ) n n. Dann ist s 3 = = 5 6, s 0 = s ,6930, s ,693. 0, 6456, In diesem Fall heißt die Folge (s n ) n N alternierende harmonische Reihe. 5. Ist a n = ( ) n, dann ist die Folge der Partialsummen gegeben durch s =, s 2 = + = 0, s 3 = + + ( ) =, s 4 = 0 und allgemein s 2n = 0 und s 2n = für alle n N. Die Graphen der Folgen in Beispiel 4.., 2 und 4 sehen folgendermaßen aus. Grundkurs Mathematik WiSe 2007/ Beispiel 4.: Harmonische Reihe x Beispiel x Grundkurs Mathematik WiSe 2007/
4 Beispiel 4.4: Alternierende harmonische Reihe x Ist (a n ( n N n ) a k k= n N Ist (a n ( n N n ) a k k= n N eine geometrische Folge, so heißt geometrische Reihe. eine arithmetische Folge, so heißt arithmetische Reihe. Da bei geometrischen bzw. arithmetischen Folgen alle Folgenglieder bereits durch Grundkurs Mathematik WiSe 2007/ a und den Quotienten q bzw. die Differenz d vollständig festgelegt sind, lassen sich auch die Partialsummen allein aus a und q bzw. d berechnen. Grundkurs Mathematik WiSe 2007/
5 . Sei (a n ) eine arithmetische Folge mit a n+ = a n + d. Dann ist n ( ) (n ) d s n = a k = n a +. 2 k= 2. Ist (a n ) eine geometrische Folge mit a n+ a n ist n na falls q =, s n = a k = q k= n a falls q. q = q, so Grundkurs Mathematik WiSe 2007/ Beispiel 4.2. Die Folge a n = 2 n ist geometrisch. Daher bilden die zugehörigen Partialsummen eine geometrische Reihe und lassen sich berechnen durch siehe etwa s 0 in Beispiel s n = 2 (/2)n /2 = 2n 2 n, 2. Die Folge a n = n aus Beispiel 4..3 ist arithmetisch mit d = und a =. Folglich ist die Folge (s n ) n N der Partialsummen eine arithmetische Reihe und die Summen lassen sich berechnen durch ( s n = n + n 2 ) = n(n + ). 2 Grundkurs Mathematik WiSe 2007/
6 3. Für die geometrische Folge a n = 5 3 n ergeben sich die Partialsummen s n = 5 3n, 2 etwa s 0 = Ist a n = 3 4n+, dann ist mit Hilfe der Rechenregeln für Summen aus Abschnitt.2 s n = n k= 3 4 = n k+ k= = ( 4 )n () k 3 = 4 4 n k= () k 4 = 3 6 4( ( 4 )n ) 4 = ( 4 )n 4 Grundkurs Mathematik WiSe 2007/ Zum Beispiel ist s 5 = ( 4 )5 4 = , Da Reihen nur eine spezielle Form von Folgen sind, lassen sich die Begriffe aus dem letzten Abschnitt übertragen. Eine Reihe (s n ) n N mit s n = n k= a k heißt (streng) monoton steigend oder fallend bzw. beschränkt, falls die Folge (s n ) n N diese Eigenschaften hat. Grundkurs Mathematik WiSe 2007/
7 Beispiel 4.3 ( n ) Die harmonische Reihe ist streng monoton steigend, da in jedem k n N k= Schritt eine positive Zahl addiert wird. ( n ) Allgemein ist jede Reihe a k k= n N wenn a n > 0 (bzw. a n < 0) für alle n N ist. streng monoton steigend (bzw. fallend), Für alle a, q > 0 ist die geometrische Reihe steigend. ( n aq k) streng monoton k= Grundkurs Mathematik WiSe 2007/ Für a > 0 und q < 0 ist die geometrische Reihe ( n aq k) weder streng monoton steigend noch fallend, denn es wird abwechselnd eine positive Zahl addiert oder subtrahiert. So ist etwa für q = 2 k= s = 0, 5, s 2 = 0,25, s 3 = 0,375, s 4 = 0, 325, s 5 = 0, Auch der Grenzwertbegriff lässt sich übertragen. Grundkurs Mathematik WiSe 2007/
8 Eine Reihe (s n ) n N mit s n = n k= a k heißt konvergent (bzw. divergent), wenn sie als Folge konvergiert (bzw. divergiert). Ist sie konvergent, so schreiben wir für den Grenzwert lim s n = lim n Beachten Sie, dass das Symbol n k= k= Reihe selbst) bezeichnet, sofern er existiert. n a k = a k. k= a k den Grenzwert der Reihe (und nicht die Grundkurs Mathematik WiSe 2007/ Entsprechend wird die bestimmte Divergenz für Folgen auf Reihen übertragen. Beispiel 4.4. Harmonische Reihe: Die zur Folge ( k ) k N gehörende Reihe ( n k= k ) n N ist divergent, genauer k= k =. 2. Dezimalzahlen: Eine Zahl r = r 0,r r 2 r 3 mit r 0 N 0 und r n {0,...,9} für n hat den Wert r = r 0 + r 0 + r = r k 0 k k=0 Grundkurs Mathematik WiSe 2007/
9 Sie ist also gerade der Grenzwert der zur Folge (r k 0 k ) k N0 gehörenden Reihe ( n k=0 r k 0 k ) n N0. Dass diese Reihe tatsächlich immer konvergiert, wird später in Beispiel noch mal begründet. 3. Die zur Folge ( k 2 +k ) k N gehörende Reihe ( n also k= k= k 2 + k =, k 2 +k ) n N konvergiert gegen, Grundkurs Mathematik WiSe 2007/ denn k 2 +k = k k+ und daher n k= k 2 + k = n k= = + n k k + n k= k= = n + n k + k= k + n + und somit k= k 2 + k =. Grundkurs Mathematik WiSe 2007/
10 Dabei haben wir benutzt: n k= n k = + k +. k= Analog zeigt man die Konvergenz der Reihe ( n k=2 ) k 2 k n N indem man k 2 k = k k benutzt. Es gibt eine sehr einfache notwendige Bedingung für die Konvergenz einer Folge. Grundkurs Mathematik WiSe 2007/ Satz 4. Ist die Reihe ( n k= a k) n N konvergent, dann gilt lim a n = 0. n Achtung: die Umkehrung gilt nicht! Wir erinnern daran, dass eine Implikation AµB äquivalent zu BµA ist. Daher lässt sich obige Aussage auch formulieren als Beispiel 4.5 Ist (a n ) n N keine Nullfolge, dann konvergiert die Reihe ( n k= a k) n N nicht.. Die Folge (a n ) n N mit a n = 3n+5 6n Reihe nicht konvergent. ist keine Nullfolge, daher ist die zugehörige Grundkurs Mathematik WiSe 2007/
11 2. Die Folge (a n ) n N mit a n = n ist eine Nullfolge, aber die zugehörige Reihe (das ist genau die harmonische Reihe) ist nicht konvergent. Es folgt nun sofort: Die arithmetische Reihe zu der Folge mit a n+ = a n + d konvergiert nur für a = d = 0. Die Beschreibung des Konvergenzverhaltens geometrischer Reihen ist etwas aufwändiger. Grundkurs Mathematik WiSe 2007/ Grenzwert geometrischer Reihen: Sei (a n ) n N eine geometrische Folge mit a n+ a n = q R und a 0.. Ist q <, dann konvergiert die geometrische Reihe ( n k= a k) n N, und es gilt a k = lim k= n n k= a k = lim a q n n q = a q. 2. Für q ist die geometrische Reihe divergent. Grundkurs Mathematik WiSe 2007/
12 Beachten Sie, dass hier a n = a q n gilt. Setzen wir a =, so erhalten wir q k = k= q k = k=0 für q < q für q Beachten Sie bitte den kleinen Unterschied, wenn die Summation mit k = beginnt: { q q k für q < = q k= für q Beispiel 4.6 Sei a n = ( ) 2 n 7 und sn = n k= a k. Dann ist lim s (2) k n = a k = = n 7 2 = 7 =, k=0 k=0 Grundkurs Mathematik WiSe 2007/ Die Konvergenz ist sehr schnell. Es ist zum Beispiel s 0, , s 6, Durch einige Umformungen lässt sich auch Konvergenzverhalten und Grenzwert der Reihe 2 k 3 7 k+ k=0 k=0 bestimmen. Diese Reihe ist nicht geometrisch, setzt sich aber aus geometrischen Reihen zusammen. Setze s n = n k=0 2k 3. Dann ist nach den Rechenregeln für 7 Summen k+ n ( 2 k s n = 7 3 ) n = k+ 7 k+ = 7 n ( 2 ) k k=0 k=0 n ( ) k. 7 k=0 2 ) k 7( n 3 ) k 7 7( 7 k=0 Grundkurs Mathematik WiSe 2007/
13 Also folgt nach den Grenzwertformeln für die geometrische Reihe sowie nach den Rechenregeln für Grenzwerte von Folgen lim n s n = 7 ( 2 ) k k=0 ( k 7) k=0 = = 5 2 = 0,3. 7 Für Reihen gibt es einige einfache Kriterien für Konvergenz. Sie besagen allerdings nur, ob eine gegebene Reihe konvergiert, geben aber nicht den zugehörigen Grenzwert an. Ein hinreichendes Kriterium für spezielle Reihen ist das Grundkurs Mathematik WiSe 2007/ Leibnizsches Konvergenzkriterium für alternierende Reihen: Sei (a n ) n N eine monoton fallende Folge nichtnegativer Zahlen mit lim a n = 0. Dann ist die n alternierende Reihe ( n ) ( ) k a k konvergent. k= n N Es ist wichtig, dass a n > 0 für alle n N. Grundkurs Mathematik WiSe 2007/
14 Beispiel 4.7 Die alternierende harmonische Reihe ( n ( ) k ) konvergiert. k= k Ohne den genauen Grenzwert zu kennen, zeigen die in Beispiel 4..4 ausgerechneten Partialsummen, dass die Konvergenz der alternierenden harmonischen Reihe sehr langsam ist. Die Partialsummen s 5000 und s 0000 unterscheiden sich noch in der 4. Dezimalstelle. Vergleichen Sie dies auch mit der Konvergenz der geometrischen Reihe in Beispiel 4.6 n N Grundkurs Mathematik WiSe 2007/ Quotientenkriterium I Sei ( n k= a k) n N eine Reihe, und es gebe ein k 0 N mit a k 0 für alle k k 0. Gibt es ein c (0, ) mit a k+ a k c für alle k k 0, dann konvergiert die Reihe ( n k= a k) n N. Grundkurs Mathematik WiSe 2007/
15 Quotientenkriterium II Gibt es eine Zahl c > mit a k+ a k c für alle k k 0, dann ist die Reihe ( n k= a k) n N divergent. Wenn weder Quotientenkriterium I noch II erfüllt sind, ist auf den ersten Blick keine Aussage über das Konvergenzverhalten der Reihe möglich. Als Folgerung erhalten wir: Grundkurs Mathematik WiSe 2007/ Ist die Folge der Quotienten Q k := konvergent, dann gilt: ( a k+ a k )k N ist lim Q k <, so konvergiert die Reihe ( n ) a k k k= ist lim Q k >, so divergiert die Reihe ( n ) a k k k= ist lim k Q k =, so ist keine Aussage möglich. n N n N Grundkurs Mathematik WiSe 2007/
16 Beispiel 4.8. Die Reihe (s n ) n N mit s n = k 3 2k n k= k 3 2k 3 k ist konvergent, denn es ist a k = > 0 für alle k > und 3 k a k+ a k = (k + ) 3 2(k + ) 3 k 3 k+ k 3 2k = 3 k (k 3 + 3k 2 + 3k + 2k 2) 3 k+ (k 3 2k) = k 3 + 3k 2 + k 3(k 3 2k) k 3. Also ist für genügend großes k der Quotient a k+ a k stets kleiner als und die Reihe konvergiert. Grundkurs Mathematik WiSe 2007/ Die Reihe (s n ) n N mit s n = alle k N und a k+ a k n k= 3 k k 2 konvergiert nicht, denn a k = 3k k 2 > 0 für = 3k+ (k + ) k2 2 3 = 3k 2 k k 2 + 2k + k 3 Also ist für genügend großes k der Quotient echt größer als. 3. Für die Reihe (s n ) n N mit s n = n k= ist keine Aussage möglich, denn k2 a k+ a k = (k + ) k2 2 = k 2 k 2 + 2k + Übrigens konvergiert diese Reihe, und zwar gegen π2 6. k. Grundkurs Mathematik WiSe 2007/
17 Besonders wichtig ist das folgende Beispiel. Beispiel 4.9 Die Reihe ( n k=0 x k ) k! n N konvergiert für jedes feste x R nach dem Quotientenkriterium, denn mit a k = xk k! ist a k+ a k = x k+ k! x k (k + )! = x k +. Also ist für k 2 x a k+ a k x 2 x + < x 2 x = 2 Somit ist mit c = 2 das Quotientenkriterium erfüllt, und die Reihe konvergiert. ) Der Grenzwert der Reihe stimmt mit dem früher definierten Wert ( n k=0 xk k! n N Grundkurs Mathematik WiSe 2007/ e x bzw. exp(x) überein, es gilt also ( e x = lim + x ) n= x k x2 = + x + n n k! 2! + x3 3! +. k=0 Insbesondere ist für x = ( e= lim + ) n= n n k! = k=0 Beachten Sie wieder, dass die Summation hier mit dem Index k = 0 beginnt. Für die Frage nach der Konvergenz der Reihe ist das unerheblich, es ist aber wichtig, wenn man konkret den Grenzwert ausrechnen will. Für kleine Werte von x wie sie z.b. in der Zinsrechnung auftreten liefert die Reihendarstellung von e x bessere Näherungswerte für die Exponentialfunktion Grundkurs Mathematik WiSe 2007/
18 ( als die Folge + n) x n. Das zeigen etwa folgende Näherungswerte von e 2, indem man x = einsetzt: n ( + n n )n k=0 k! , 25 2, 5 3 2,370 2, ,44 2, ,488 2,77 0 2,594 2, Ein sehr praktisches Hilfsmittel zur Bestimmung des Konvergenzverhaltens einer Reihe ist noch Grundkurs Mathematik WiSe 2007/ Majoranten-Kriterium: Sei (a n ) n N eine gegebene Folge. Außerdem sei ( n k= b k) n N eine konvergente Reihe, und es gebe ein n 0 N mit a n b n für alle n n 0. Dann konvergiert auch die Reihe ( n k= a k) n N. Grundkurs Mathematik WiSe 2007/
19 Beispiel 4.0. Die zur Folge ( ) n 2 n N gehörende Reihe ( n k= ) k 2 n N konvergiert, denn k für alle k 2 2 k 2 k und die Reihe ( n k=2 k 2 k ) n N konvergiert nach Beispiel Die Reihe für Dezimalzahlen r = r 0 + r 0 + r = r k 0 k, wobei r k {0,...,9} für k N, konvergiert, da r k 0 k 9 0 k für alle k N und ( ) k 9 0 k 9 = 9 = 0 = 0 0 k=0 k=0 k=0 Grundkurs Mathematik WiSe 2007/ aufgrund der Formel für den Grenzwert einer geometrischen Reihe. 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p 00 Zinssatz pro Zeiteinheit q = + d Aufzinsungsfaktor n Anzahl der Zeiteinheiten (i.a. Jahre) Z n Zinsen nachnzeiteinheiten Kapital nachn Zeiteinheiten K n Grundkurs Mathematik WiSe 2007/
20 Zinsrechnung (A) Die lineare (einfache) Verzinsung, bei der innerhalb eines Kapitalüberlassungszeitraumes kein Zinszuschlagtermin (oder Zinsverrechnungstermin) liegt, wird durch eine arithmetische Folge beschrieben. Beispiel 4. Zum Zinssatz d = 0,06 = 6% p.a. wird das Kapital K 0 = ( oder Maltesische Lira) für einen Zeitraum von 6 Jahren ausgeliehen. Damit ergibt sich K 0 = , K = K 0 ( + d), Z = K 0 d, K 2 = K 0 ( + 2 d), Z 2 = K 0 2 d, K 3 = K 0 ( + 3 d), Z 3 = K 0 3 d,.. Nach 6 Jahren belaufen sich die Zinsen auf Z 6 = K 0 6 d = Grundkurs Mathematik WiSe 2007/ und das (End)-Kapital beträgt K 6 = K 0 ( + 6 d) = Lineare Verzinsung: Bei der linearen Verzinsung zum Zinssatz d ergeben sich die folgenden expliziten Formeln für das Kapital und die Zinsen nach n Jahren: K n = K 0 ( + n d) und Z n = K 0 n d. Beispiel 4.2 Welches Anfangskapital K 0 muss bei einfacher Verzinsung angelegt werden, wenn nach 7 Jahren ein Kapital von vorhanden sein soll und der Zinssatz 0, 05 bzw. 0, 06 beträgt? Grundkurs Mathematik WiSe 2007/
21 Im ersten Fall muss die Gleichung K 7 = = K 0 ( + 7 0,05) = K 0,35 nach K 0 aufgelöst werden. Das ergibt ein benötigtes Anfangskapital von Im zweiten Fall ergibt sich analog K 0 = 00000, K 0 = 00000, Grundkurs Mathematik WiSe 2007/ (B) Neben der einfachen Verzinsung spielt natürlich die Zinseszinsrechnung eine wichtige Rolle. Hier gibt es innerhalb der Kapitalüberlassungsfrist weitere Zinsverrechnungs- oder Zinszuschlagtermine, in denen die bis dahin entstandenen Zinsen dem Kapital als Zinszuschlag hinzugefügt werden und mit ihm zusammen das weiter zu verzinsende Kapital bilden. Wir betrachten noch einmal das obige Beispiel, wobei diesmal die Zinsen jährlich nachträglich dem Kapital zugeschlagen und ebenfalls verzinst werden. Beispiel 4.3 Es wird das Kapital K 0 = für einen Zeitraum von 6 Jahren angelegt. Nach jeder Zinsperiode ( Jahr) erfolgt ein Zinszuschlag von d = 0, 06 = 6%. Damit ergibt sich K 0 = , K = K 0 ( + d), K 2 = K ( + d) = K 0 ( + d) 2,. Grundkurs Mathematik WiSe 2007/
22 Nach 6 Jahren ist also das Gesamtkapital K 6 = K 0 ( + d) Zinseszinsrechnung: Bei Berücksichtigung nachschüssiger Zinseszinsen ergeben sich die folgenden Formeln für das Kapital und die Zinsen nach n Jahren: K n = K 0 ( + d) n und Z n = K n K 0. Nachschüssigkeit bedeutet, dass die Zinsen am Ende des Jahres gezahlt werden. Beispiel 4.4 Der Unterschied zwischen einfacher Verzinsung und (nachschüssigem) Zinseszins bezogen auf einen Zeitraum von bis zu 50 Jahren ist Grundkurs Mathematik WiSe 2007/ in der folgenden Tabelle für zu erkennen. K 0 =.000 und d = 0,05 = 5% n K 0 ( + nd) K 0 ( + d) n Grundkurs Mathematik WiSe 2007/
23 Beispiel 4.5 Welches Anfangskapital K 0 muss bei nachschüssigem Zinseszins angelegt werden, wenn nach 7 Jahren ein Kapital von vorhanden sein soll und der Zinssatz 0, 05 bzw. 0, 06 beträgt? Im ersten Fall muss die Gleichung K 7 = = K 0 ( + 0, 05) 7 nach K 0 aufgelöst werden. Das ergibt ein benötigtes Anfangskapital von Analog ergibt sich im zweiten Fall K 0 = 00000, K 0 = 00000, Grundkurs Mathematik WiSe 2007/ Die Berechnung von K 0 aus gegebenem n, d und K n wird auch als Bestimmung des Barwertes einer zukünftigen Zahlung bezeichnet. Barwertformel der Zinseszinsrechnung: Der heute zahlbare Betrag K 0, der benötigt wird, um eine in n Zeitperioden fällige Schuld K n abzulösen, beträgt K 0 = K n ( + d) n = K n( + d) n, wobei d der Zinssatz pro Zeitperiode ist. K 0 heißt Barwert des nach n Zeitperioden fälligen Betrags K n oder auch n-mal abgezinstes bzw. diskontiertes Kapital K n. Grundkurs Mathematik WiSe 2007/
24 Das Abzinsen erlaubt den Vergleich von Zahlungen zu unterschiedlichen Zeitpunkten: eine Zahlung K, fällig in n 0 Zeitperioden, und eine Zahlung K, fällig in ñ 0 Zeitperioden, heißen äquivalent bzgl. eines Zinssatzes d, wenn gilt K( + d) ñ 0 = K( + d) n 0 oder, anders geschrieben, K = K( + d)ñ0 n 0. Ebenso wie das Anfangskapital K 0 lassen sich auch der Zinssatz d sowie die Anzahl n der Jahre aus den anderen Größen in der Zinseszinsformel ermitteln d = n Kn K 0, n = Kn ln K 0 ln( + d) = lnk n lnk 0 ln( + d). Grundkurs Mathematik WiSe 2007/ Beispiel 4.6 Sie bringen ein Anfangskapital von 500 zur Bank und erhalten 8% jährliche nachschüssige Zinseszinsen. Wie lange müssen Sie warten, bis Sie ein Kapital von 900 besitzen? Wir berechnen die Anzahl der Jahre durch n = ln 900 ln 500 ln(, 08) 7, 637. Sie müssen also 8 Jahre warten. Geben Sie bei einer Aufgabe wie dieser Ihr Ergebnis bitte nicht in der Form n = 7, 637 an. Die hier verwendeten Formeln sagen zunächst nur etwas aus über die Kapitalentwicklung zu festen Zeitpunkten, also z.b. nach 7 und nach 8 Jahren, und nicht, nach welcher Formel sich das Kapital dazwischen entwickelt. Außerdem Grundkurs Mathematik WiSe 2007/
25 suggeriert eine Angabe wie 7, 637 Jahre eine unangemessene Genauigkeit: Sie rechnen hier genauer als bis auf einen Tag genau, obwohl in der Regel bei (kleineren) Finanzgeschäften nur bis auf den Tag genau und nicht etwa Stundengenau gerechnet wird! (C) Werden die Zinsen dem Kapital auch nach Zeitintervallen gutgeschlagen, die kleiner sind als ein Jahr (oder die dem angegebenen Zinssatz zugrunde liegende Zeiteinheit) und im weiteren mitverzinst, so spricht man von unterjähriger Verzinsung. Beispiel 4.7 Eine Bank gibt für die Verzinsung eines Kapitals K 0 einen nominellen Jahreszinssatz d an. Der Zinszuschlag erfolgt allerdings nicht jährlich, sondern nach jedem Quartal. Dann ergibt sich nach einem Jahr als Kapital K 0 ( + d ) 4 4 Grundkurs Mathematik WiSe 2007/ ( und der effektive Jahreszins beträgt + d 4. 4) Ist zum Beispiel K 0 = 000 und d = 0,05, so ergibt sich ( ) K = K 0 + 0, K 2 = K ( + 0,05 4 K 3 = K 2 ( + 0,05 4 ) 4 ( ) = K0 + 0, ) 4 ( ) = K0 + 0, Der effektive Jahreszins ist hier ( )4 0.05, also etwa 5.%. Anders gesagt: Ein nomineller Zinssatz von 5% bei vierteljährlicher Zinszahlung ist dasselbe wie ein Zinssatz von 5.%, der nur einmal jährlich gutgeschrieben wird. Grundkurs Mathematik WiSe 2007/
26 Unterjährige Verzinsung: Erfolgt bei einem nominellen Jahreszinssatz d an m Zeitpunkten eines Jahres ein nachschüssiger Zinszuschlag, dann beträgt das Kapital nach Ablauf des n-ten Jahres ( K n = K 0 + m) d m n. Der effektive Jahreszins ist gleich ( + d m) m. Lässt man die Zeitintervalle der Zinszuschläge immer kürzer werden (d. h. m ), so kommt man zur stetigen Verzinsung. Der effektive Jahreszins ist dann ( + m) d m = e d. lim m Grundkurs Mathematik WiSe 2007/ Die folgende Tabelle gibt den effektiven Zinssatz bei unterjähriger Verzinsung zu verschiedenen Zeitintervallen sowie bei stetiger Verzinsung an. Die nominellen Zinssätze sind 2%, 5% und 0%. m 2% 5% 0% 2 2, 00 5, 063 0, , 05 5, 095 0, , 08 5, 6 0, , 020 5, 27 0, 57 (e d )% 2,020 5,27 0, 57 Grundkurs Mathematik WiSe 2007/
27 Rentenrechnung Unter einer n-maligen Rente versteht man eine regelmäßige, in n gleichen Zeitabständen fällige Zahlung, die aus n Teilzahlungen R j, mit j =,..., n, besteht, den Rentenraten. Bei der nachschüssigen Rente erfolgt die Zahlung R j am Ende des j-ten Zeitabschnitts, bei der vorschüssigen Rente dagegen am Beginn des j-ten Zeitabschnitts. Im Zusammenhang mit Renten interessiert man sich vor allem für den Gesamtwert, unter Berücksichtigung von Zinseszins, den eine Rente am Anfang bzw. Ende der Rentenzahlungen hat. Hierbei kommt es darauf an, ob die Rente nach- oder vorschüssig gezahlt wird. Denn bei nachschüssiger Zahlung einer n-maligen Rente Grundkurs Mathematik WiSe 2007/ wird die erste Rentenzahlung nur n Jahre verzinst, bei vorschüssiger aber n Jahre. Entsprechendes gilt für die weiteren Zahlungen. Im folgenden betrachten wir nur den Fall konstanter Rentenzahlungen, also R j = R für alle j. Grundkurs Mathematik WiSe 2007/
28 Rentenendwertformel bei nach- und vorschüssiger Zahlung: Bei dem Aufzinsungsfaktor q = + d und der konstanten Rentenzahlung R ergibt sich bei nachschüssiger Zahlung der Gesamtwert K n = Rq n + Rq n 2 + Rq n R n n = Rq n k = Rq k = R qn q k= und bei vorschüssiger Zahlung k= K n = Rq n + Rq n + Rq n Rq = n k=0 Rq n k = n k= Rq k = Rq qn q Grundkurs Mathematik WiSe 2007/ Falls zu Beginn des Zeitraums auch noch ein Anfangskapital K 0 vorliegt (wie oft bei Ratensparverträgen), so ergeben sich als Endwerte bei nach- und vorschüssiger Zahlung K n = K 0 q n + R qn q, K n = K 0 q n + Rq qn q. Beispiel 4.8 Sie schließen mit Ihrer Bank einen Ratensparvertrag über 0 Jahre zu einem Zinsfuß von 6% ab. Zu Beginn des ersten Jahres zahlen Sie einen Einmalbetrag von 500 ein und anschließend jeweils am Ende des Jahres eine Rate von 200. Welchen Wert hat das Kapital nach 0 Jahren? Grundkurs Mathematik WiSe 2007/
29 Da es sich um nachschüssige Ratenzahlung handelt, ergibt sich als Endwert K 0 = 500, ,060, Das von Ihnen eingezahlte Kapital beträgt = Der Rest stammt aus den Zinseszinsen. Löst man die Rentenendwertformeln (ohne Anfangskapital) nach R auf, so kann man bestimmen, welche jährliche Rate zu zahlen ist, um bei einem Zinsfuß von p% nach n Jahren ein gewünschtes Kapital zu erhalten. Mit dem Aufzinsungsfaktor q = + d = + p 00 ergeben sich bei nach- und vorschüssiger Zahlung q R = K n q n und R = K n q q q n Bei Berücksichtigung eines Anfangskapitals K 0 erhalten wir Grundkurs Mathematik WiSe 2007/ R = (K n K 0 q n ) q q n (nachschüssig) R = (K n K 0 q n ) q q(q n ) (vorschüssig) Wenn Sie wissen wollen, nach wie vielen Jahren Sie bei konstanter Rentenzahlung R ein Kapital K angespart haben, müssen Sie nach n auflösen: Grundkurs Mathematik WiSe 2007/
30 ( K + R ) q n = ln K 0 + R / ln(q) (nachschüssig) q ( K q n = ln + R ) q K 0 + R / ln(q) (vorschüssig) q Eine einfache Formel, um q aus R, n, K n und K 0 auszurechnen, gibt es nicht. Grundkurs Mathematik WiSe 2007/ Tilgungsrechnung Tilgung, Annuität: Werden Schulden in Teilbeträgen, den sogenannten Raten zurückgezahlt, so spricht man von einer Tilgung, bei der die Schulden auf eine Restschuld vermindert werden. Die in einem Zeitabschnitt vom Schuldner aufzubringende Leistung wird als Annuität bezeichnet. Die Annuität A setzt sich aus der Tilgungsrate T und den Zinsen Z für den Zeitabschnitt zusammen: A = T + Z. Eine Zusammenstellung der in den einzelnen Zeitabschnitten zu erbringenden Annuitäten, Zinsen und Tilgungsraten heißt Tilgungsplan. Bei der Ratentilgung ist die Tilgungsrate während der gesamten Tilgungsdauer konstant. Bei der Annuitätentilgung erfolgt die Tilgung am Ende jeder Periode so, dass die Annuität über den gesamten Zeitraum konstant bleibt. Grundkurs Mathematik WiSe 2007/
31 Da die Restschuld und damit die Zinsen im Laufe der Zeit sinken, wird bei der Annuitätentilgung von Jahr zu Jahr ein größerer Betrag getilgt. Soll eine Schuld K 0 in n Jahren mit einer Ratentilgung getilgt werden, so beträgt die jährliche Tilgungsrate T = K 0 n. Da die zu verzinsende Restschuld von Jahr zu Jahr abnimmt, werden die Annuitäten mit der Zeit geringer. Beispiel 4.9 (Ratentilgung) Der Tilgungsplan für eine Schuld K 0 = Grundkurs Mathematik WiSe 2007/ bei 8% Zinsen und einer Laufzeit von 0 Jahren hat folgende Form Jahr Tilgungsrate Zinsen Annuität Restschuld Grundkurs Mathematik WiSe 2007/
32 Wie man an der Tabelle sieht, sind die Belastungen des Schuldners ungleichmäßig über die Tilgungsdauer verteilt. Ratentilgung: Sei K 0 die Schuld und T die Tilgungsrate, um die Schuld in n Jahren zu tilgen, also T = K 0 n. Bei der Ratentilgung bilden Zinsen, Annuitäten und Restschuld jeweils arithmetische Folgen: Sei d der Zinssatz, K m die Restschuld am Ende der m-ten Periode, Z m die zu zahlenden Zinsen für die (m + )-te Periode und A m die Annuität, also Grundkurs Mathematik WiSe 2007/ A m = T + Z m. Dann ist K m = K m T, Z 0 = K 0 d, m =,...,n Z m = Z m T d, m =,...,n, A 0 = Z 0 + T, A m = A m T d, m =,...,n, wobei d = q (q Aufzinsungsfaktor). Beispiel 4.20 (Annuitätentilgung) Will man nun in der gleichen Situation wie in Beispiel 4.9 die Schuld mit der Annuitätentilgung ableisten, so benötigt man diejenige konstante Annuität A, die nach 0 Jahren zur Gesamttilgung der Schuld mit den aufgelaufenen Zinsen führt. Dieser Wert A berechnet sich wie folgt: Grundkurs Mathematik WiSe 2007/
33 In 0 Jahren wird aus der Schuld K 0 = bei nachschüssigem Zinseszins K n = K 0, 08 0 = 25892, 50. Die Tilgung dieser Gesamtschuld in 0 Jahren kann man sich nun als eine n-malige Rente vorstellen. Daher ist die gesuchte Annuität A gerade diejenige konstante Rentenzahlung, die zu einem Endwert von 25892, 50 führt. Bei nachschüssiger Zahlung muss also die erste Formel auf Seite 345 angewendet werden und liefert A = K n q q n = 25892, 50 0, 08, , 95. (typischerweise begleicht man nicht gleich bei Aufnahme des Kredits eine Schuld, sondern beginnt nach dem ersten Zeitintervall, daher nachschüssige Zahlung). Damit hat der Tilgungsplan für eine Schuld von K 0 = bei 8% Zinsen und einer Laufzeit von 0 Jahren die Form Grundkurs Mathematik WiSe 2007/ Jahr Tilgung Zinsen Annuität Restschuld 6.902, , , , , , , , , , , , , , , , , , , , , , , , , 3.948, , , , , , , , , , , , 02.03, , 95 0, , , 50 Grundkurs Mathematik WiSe 2007/
34 Annuitätentilgung: Sei K 0 die Schuld, d der jährliche Zinssatz, q = + d der Aufzinsungsfaktor, und sei A die konstante Annuität, die erforderlich ist, um die Schuld nach n Jahren zu tilgen. Dann ist K 0 q n = A qn q. Bei der Annuitätentilgung bildet die Tilgung eine geometrische Folge. Sei K m die Restschuld am Ende der m-ten Periode, Z m die zu zahlenden Zinsen für die (m+)-te Periode und T m die zu zahlende Tilgungsrate für die (m+)-te Grundkurs Mathematik WiSe 2007/ Periode. Dann gilt K m = K 0 q m A qm q, Z 0 = K 0 (q ) m =,...,n Z m = Z m q A (q ), m =,...,n T 0 = A K 0 (q ) T m = T m q, m =,...,n Beispiel 4.2 Statt die Situation eines Schuldners und seiner Bank zu betrachten, können die Rollen auch vertauscht werden, d.h. wir behandeln nun folgende Situation: Sei K 0 ein Anfangskapital, das zu Beginn eines Jahres eingezahlt und mit dem jährlichen Zinssatz d verzinst wird. Innerhalb eines Jahres vermehrt sich das Grundkurs Mathematik WiSe 2007/
35 Kapital um den Aufzinsungsfaktor q = + d. Am Ende jeden Jahres wird dem Kapital ein fester Betrag R entnommen (die Rente ). Dieser Betrag R entspricht der konstanten Annuität in der Situation der Annuitätentilgung. Wie groß ist dann das Kapital nach n Jahren? Die Formel aus dem obigen Satz liefert unmittelbar die Antwort; dies ist die sogenannte Sparkassenformel für den Kapitalabbau durch Auszahlung einer festen Rente bei einem Zinssatz d: K n = K 0 q n R qn q = K 0 ( + d) n R ( + d)n d Grundkurs Mathematik WiSe 2007/ Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess, so ist die Wachstumsgeschwindigkeit von Interesse oder auch die relative Wachstumsrate. Ist f eine Steuerfunktion, so ist die Frage bedeutend, welcher Steuerprozentsatz auf einen kleinen Zuverdienst zu zahlen ist. Für ein Unternehmen ist interessant, wie sich die (relative) Nachfrage nach einem Produkt bei (relativ) kleinen Preisänderungen ändert. Wichtig ist auch die Bestimmung von Extremwerten ökonomischer Größen, etwa die Minimierung von Kosten oder die Maximierung von Gewinnen. Bei der Beantwortung dieser Fragen ist die Differenzialrechnung nützlich. Alle Funktionen in diesem Kapitel sind stets von der Form f : D R wobei D R der Definitionsbereich ist. Also gibt es für jedes x D einen Funktionswert Grundkurs Mathematik WiSe 2007/
36 f(x). Beispiel 5. Angenommen, die Kostenfunktion eines Unternehmens für die Produktion von x Stücken eines Gutes sei gegeben durch K(x) = 20 x Nun ist das Unternehmen daran interessiert, wie sich die Kosten bei kleiner Änderung der Produktionsmenge verändern. Eine standardisierte Information ist hierbei zum Beispiel, wie sich K(x) ändert, wenn man x um eine Einheit erhöht. Die Änderung ist dann K(x + ) K(x). Es sollte klar sein, dass eine solche Änderung von der Ausgangszahl x abhängt. Etwa ist K(0) K(00) = 20( 0 00) 0, 998, K(00) K(000) = 20( ) 0, 36. Grundkurs Mathematik WiSe 2007/ Zieht man auch andere Änderungen von x in Betracht, so ist es sinnvoll, die relative Änderung der Kosten im Verhältnis zur Änderung von x zu berechnen. Das ist der Quotient K(x + h) K(x) (x + h) x = K(x + h) K(x) h (etwa für die Werte h =, 0., 0.0) und gibt die durchschnittliche Kostenänderung pro zusätzlicher Mengeneinheit an. In der folgenden Tabelle sind diese relativen Änderungen für einige Werte von x angegeben. K(x+) K(x) K(x+0,) K(x) 0, K(x+0,0) K(x) 0,0 x 0 3,087 3,54 3,6 00 0,998 0, 0, 000 0,36 0,36 0,36 Grundkurs Mathematik WiSe 2007/
37 Man sieht, dass sich für kleine Werte von x die Änderung von x stärker auf die relative Änderung der Kosten auswirkt als für große Werte. Das kann man auch am Graphen sehen, denn die Funktionswerte unterscheiden sich in der Nähe von x = 0 stärker voneinander als etwa bei x = 00 oder x = x Man sieht, dass die obige Situation durch die Steigung des Graphen erklärt wird. Grundkurs Mathematik WiSe 2007/ Differenziation Bevor wir eine formale Definition der Ableitung einer Funktion angeben, soll zunächst beschrieben werden, wie man die Steigung einer (krummlinigen) Funktion in einem Punkt festlegen und bestimmen kann. Steigung einer Funktion in einem Punkt. Ist f : R R eine Gerade, so ist die Steigung des zugehörigen Graphen an jeder Stelle gleich und lässt sich durch ein Steigungsdreieck ermitteln. Grundkurs Mathematik WiSe 2007/
38 70 60 x0=2, h=2 x=5,h = f(x+h )-f(x) h h f(x0+h)-f(x0) x Die Steigung ist definiert als Höhe durch Breite des Steigungsdreiecks, also f(x 0 + h) f(x 0 ) = f(x 0 + h) f(x 0 ). (x 0 + h) x 0 h Hierbei spielt es offensichtlich keine Rolle, wo das Dreieck eingezeichnet wird Grundkurs Mathematik WiSe 2007/ und wie weit die beiden Stellen x 0 und x 0 + h auseinanderliegen. Sie ist also unabhängig von x 0 und h. Ist f(x) = cx + d, so ist f(x 0+h) f(x 0 ) h = ch h = c. 2. Ist nun f : D R eine Funktion mit einem krummlinigen Graphen, so lassen sich immer noch Steigungsdreiecke zu gegebenen Stellen x 0 und x 0 + h zeichnen; die daraus resultierende Größe f(x 0 + h) f(x 0 ) h (5.) hängt nun aber im allgemeinen sowohl von x 0 als auch von h ab (siehe Beispiel 5.). Sie gibt die (relative) Veränderung der Funktionswerte im Verhältnis zu den x-werten an. Außerdem lässt sie sich als durchschnittliche Steigung von f auf dem Abschnitt [x 0,x 0 + h] auffassen. Das ist die Steigung der Geraden, die durch die Punkte (x 0, f(x 0 )) und (x 0 + h, f(x 0 + h)) geht. In diesem Zusammenhang heißen diese Geraden auch Sekanten. Man benutzt nun diese Grundkurs Mathematik WiSe 2007/
39 Steigungsdreiecke für einen Grenzprozess: wählt man h immer kleiner, so rückt der Punkt x 0 + h immer näher an x 0, das Steigungsdreieck wird immer kleiner und die Größe (5.) liefert die Steigung auf einem sehr kleinen Abschnitt in der Nähe von x 0. Falls dieser Grenzprozess einen Grenzwert hat, etwa f(x 0 + h) f(x 0 ) lim h 0 h = a, so nennt man a die Ableitung von f an der Stelle x 0. Als Grenzwert der Sekanten erhält man dann gerade die Tangente an den Graphen von f an der Stelle x 0. Deren Steigung ist a. Grundkurs Mathematik WiSe 2007/ Differenzenquotient, Differenzialquotient, Ableitung Sei D ein offenes Intervall, f : D R eine Funktion und x 0 D.. Für h R\{0} heißt f(x 0+h) f(x 0 ) h f. ein Differenzenquotient von 2. Die Funktion f heißt an der Stelle x 0 differenzierbar, falls der Grenzwert f(x 0 + h) f(x 0 ) lim h 0 h existiert. In diesem Fall wird die Notation f (x 0 ) := lim h 0 f(x 0 + h) f(x 0 ) h benutzt. Grundkurs Mathematik WiSe 2007/
40 Der Grenzwert f (x 0 ) heißt Ableitung von f an der Stelle x 0. Ist f an jeder Stelle x D differenzierbar, dann heißt f differenzierbar auf D, und die Funktion f : D R heißt Ableitung von f. Beachte, dass das Symbol lim h 0 für den beidseitigen Grenzwert steht. Man muss also sowohl positive als auch negative Werte für h betrachten! Die Größe h wird in der Literatur oft als x geschrieben. Sie steht für eine (kleine) Änderung der Argumente x. Für die zugehörige Änderung der Funktionswerte f(x + h) f(x) wird dann f geschrieben. Grundkurs Mathematik WiSe 2007/ Bemerkung: Oft werden statt der Bezeichnungen x 0 und x 0 + h für die zwei Stellen auch x 0 und x gewählt. Setzt man h := x x 0, also x = x 0 + h, so lautet dann der Differenzenquotient f(x) f(x 0 ) x x 0 und die Ableitung, falls sie existiert, ist der Grenzwert f(x) f(x 0 ) lim. x x 0 x x 0 Für kleine Werte von h (oder für x nahe bei x 0 ) ist der Differenzenquotient eine Grundkurs Mathematik WiSe 2007/
41 Annäherung an die Ableitung: f (x 0 ) f(x 0 + h) f(x 0 ) h = f(x) f(x 0) x x 0. Geometrisch bedeutet diese Approximation, dass die Funktion in der Nähe von x 0 durch die Tangente an der Stelle x 0 angenähert wird. Denn f(x) f(x 0 ) + f (x 0 ) (x x 0 ) und der Ausdruck auf der rechten Seite ist die Gleichung der Geraden mit Steigung f (x 0 ) durch den Punkt (x 0, f(x 0 )). Beispiel 5.2. Lineare Funktion: Eine Funktion der Form f : R R, f(x) = cx + d ist eine lineare Funktion. Grundkurs Mathematik WiSe 2007/ Der Funktionsgraph ist die Gerade {(x, cx + d) x R} mit Steigung c. Sei nun x 0 R, dann ist für alle h R \ {0} der Differenzenquotient gegeben durch c(x 0 + h) + d (cx 0 + d) h = ch h = c. Der Differenzenquotient hängt weder von x 0 noch von h ab. Insbesondere ist f (x 0 ) = c für alle x 0 R. Die Funktion hat überall die gleiche Steigung. Die Ableitung f : R R ist somit die konstante Funktion f (x) = c für alle x R. Grundkurs Mathematik WiSe 2007/
42 2. f(x) = x 3 : Mithilfe des binomischen Lehrsatzes erhält man für den Differenzenquotienten an der Stelle x f(x + h) f(x) h Damit ist der Grenzwert = (x + h)3 x 3 h f(x + h) f(x) lim h 0 h = x3 + 3x 2 h + 3xh 2 + h 3 x 3 h = h(3x2 + 3xh + h 2 ) h = 3x 2 + 3xh + h 2 = 3x 2 = f (x). Grundkurs Mathematik WiSe 2007/ Ähnlich lässt sich zeigen: f(x) = x n, dann ist f (x) = nx n. 3. f(x) = x : Die Betragsfunktion f : R R mit f(x) = x ist an der Stelle x 0 = 0 nicht differenzierbar x 4 Grundkurs Mathematik WiSe 2007/
43 Offensichtlich lässt sich an der Stelle x 0 = 0 keine eindeutige Tangente einzeichnen. Die Steigung springt hier abrupt von auf. Genauer gesagt: Steigungsdreiecke, die links von x 0 = 0 liegen, liefern alle die Steigung, die, die rechts liegen, die Steigung. Daher existiert der beidseitige Grenzwert des Differenzenquotienten an der Stelle x 0 = 0 nicht und die Funktion ist dort nicht differenzierbar. Etwas genauer: 0 + h 0 lim hր0 h weil h = h für h < 0 gilt. Entsprechend gilt 0 + h 0 lim hց0 h weil h = h für h > 0 gilt. h = lim hր0 h = lim h hր0 h =, h = lim hց0 h = lim h hց0 h =, Grundkurs Mathematik WiSe 2007/ Hat eine Funktion eine Sprungstelle an der Stelle x 0, so hat sie dort sicherlich keine Tangente. Genauer: Ist die Funktion f : D R in x 0 D differenzierbar, dann ist f auch stetig im Punkt x 0. Aber nicht jede stetige Funktion ist auch differenzierbar, wie die Betragsfunktion in Beispiel zeigt. Beispiel 5.3 (Ableitung einiger Grundfunktionen) Die Definitionsbereiche der unten stehenden Funktionen haben wir bereits in Grundkurs Mathematik WiSe 2007/
44 Kapitel 2 untersucht. f(x) c x n x α (α R) e x f (x) 0 n x n α x α e x f(x) a x (a > 0) ln( x ) log a ( x ) (a > 0, a ) f (x) ln(a) a x x x ln(a) f(x) sin(x) cos(x) tan(x) cot(x) f (x) cos(x) sin(x) cos 2 (x) sin 2 (x) Speziell ist für f(x) = x = x die Ableitung f (x) = x 2 = x 2 und allgemein Grundkurs Mathematik WiSe 2007/ f(x) = x n = x n, dann f (x) = nx n = n x n+. Mit den obigen Grundfunktionen und folgenden Rechenregeln lassen sich leicht die Ableitungen vieler Funktionen berechnen. Grundkurs Mathematik WiSe 2007/
45 Seien f, g : D R in einem Punkt x D differenzierbar. Dann sind auch die Funktionen f + g, f g : D R in x differenzierbar, und es gilt: Summenregel: (f + g) (x) = f (x) + g (x), Produktregel: (fg) (x) = f (x) g(x) + f(x) g (x) Als Spezialfall der Produktregel ergibt sich (λ f) (x) = λ f (x) für jede differenzierbare Funktion f und jede Zahl λ R. Grundkurs Mathematik WiSe 2007/ Ist zusätzlich g(x) 0 für alle x D, dann ist die Funktion : D R in x differenzierbar mit f g Quotientenregel: ( ) f (x) = f (x) g(x) f(x) g (x) g g(x) 2 Etwas komplizierter ist die folgende Regel: Grundkurs Mathematik WiSe 2007/
46 Seien f : D R und g : E R Funktionen mit f(d) E, d.h. f(x) E für alle x D). Sei f in x D differenzierbar, und sei g in f(x) E differenzierbar. Dann ist auch g f an der Stelle x differenzierbar und es gilt Kettenregel: (g f) (x) = g (f(x)) f (x). Beispiel 5.4. Für f(x) = 3x 5 0x 4 + 2x 3 7x ist 2. Sei f(x) = 3x2 2x +. Dann ist 7x 5 f (x) = 5x 4 40x 3 + 6x 2 4x. Grundkurs Mathematik WiSe 2007/ f (x) = (6x 2)(7x 5) 7(3x2 2x + ) (7x 5) 2 = 2x2 30x + 3 (7x 5) 2 3. Für S(x) = sin 2 (x) können wir schreiben S = g f mit f(x) = sin(x) und g(x) = x 2. Daher ist S (x) = 2 sin(x) cos(x) Allgemein ist für eine Funktion f(x) = g(x) n f (x) = ng(x) n g (x). 4. Für f(x) = e (ax2 +bx+c) 2 ist mit der Kettenregel f (x) = e (ax2 +bx+c) 2 2 (ax 2 + bx + c) (2ax + b) Grundkurs Mathematik WiSe 2007/
47 Als letzte Differenziationsregel betrachten wir Ableitung der Umkehrfunktion: Sei f : D R eine injektive stetige Abbildung, und sei f : f(d) R die Umkehrfunktion von f. Ist f in einem Punkt x D differenzierbar mit f (x) 0, dann ist f im Punkt y = f(x) differenzierbar, und es gilt (f ) (y) = f (f (y)) = f (x). Beispiel 5.5 Sei f(x) = e x. Die Funktion ist injektiv. Die Umkehrfunktion ist gegeben durch g(x) = f (x) = ln(x). Nach Beispiel 5.3 ist f (x) = e x und Grundkurs Mathematik WiSe 2007/ daher f (x) 0 für alle x R. Die obige Rechenregel liefert g (y) = f (g(y)) = e ln(y) = y, wie es auch schon in Beipiel 5.3 angegeben ist. Es gilt soger g ( y ) = y. Als neue Ableitungen erhält man die der trigonometrischen Umkehrfunktionen. Grundkurs Mathematik WiSe 2007/
48 Beispiel 5.6 (Ableitung der Arcusfunktionen) f sin(x) cos(x) tan(x) cot(x) D(f) [ π 2, ] π 2 [0,π] ( π 2, ) π 2 (0, π) W(f) [, ] [,] R R f arcsin(x) arccos(x) arctan(x) arccot(x) (f ) x 2 x 2 +x 2 +x 2 Wir wollen uns dies für den Tangens etwas genauer anschauen. Die Rechenregel Grundkurs Mathematik WiSe 2007/ für die Ableitung der Umkehrfunktion zeigt arctan (y) = tan (x), wobei y = tan(x), also x = arctan(y). Wir erhalten mittels der Quotientenregel und tan(x) = sin(x) cos(x) tan (x) = cos2 (x) + sin 2 (x) cos 2 (x) = + tan 2 (x) = + y 2, weil x = arctan(y) und somit tan(x) = y. Das liefert arctan (y) = + y 2. Grundkurs Mathematik WiSe 2007/
49 Die anderen Fälle sind ähnlich. Man kann den Differenziationsprozess unter Umständen auch auf die Ableitung anwenden. Grundkurs Mathematik WiSe 2007/ Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f im Punkt x und die Funktion f : D R heißt zweite Ableitung von f. Allgemein heißt eine Funktion f : D R n-mal differenzierbar, n N, wenn die (n )-te Ableitung differenzierbar ist. Die n-te Ableitung wird auch mit f (n) : D R bezeichnet. Insbesondere wird f (0) = f gesetzt und es ist f () = f und f (2) = f. Die Funktion f heißt oft differenzierbar, wenn alle Ableitungen f (n), n N, existieren. Grundkurs Mathematik WiSe 2007/
50 Die geometrische Bedeutung der zweiten Ableitung wird im nächsten Abschnitt erklärt. Beispiel 5.7 Mithilfe von Beispiel 5.3 und den üblichen Rechenregeln lassen sich folgende Ableitungen berechnen.. f(x) = ln(x): f (x) = x, f (x) = x 2, f (3) (x) = 2 x 3 = 2x 3, f (4) (x) = 6 x 4,... f (n) (x) = ( ) n (n )! x n Grundkurs Mathematik WiSe 2007/ f(x) = x 5 2x 3 + x 2 0: 3. f(x) = 3e x : f (x) = 5x 4 6x 2 + 2x, f (x) = 20x 3 2x + 2, f (3) (x) = 60x 2 2, f (4) (x) = 20x, f (5) (x) = 20, f (6) (x) = 0 = f (n) (x), für n 6 f (x) = 3e x, f (x) = 3e x,..., f (n) (x) = 3e x. Polynome, rationale Funktionen, die Exponentialfunktion und die trigonometrischen Funktionen sind auf ihrem Definitionsbereich unendlich oft differenzierbar. Grundkurs Mathematik WiSe 2007/
51 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten von Funktionen, wo Zähler und Nenner für x x 0 beide gegen Null (oder beide gegen unendlich) konvergieren. Mithilfe der Differentiation ist es nun möglich, weitere Grenzwertregeln aufzustellen, mit denen sich etwa sin(x) lim x 0 x x 3 oder lim x e x bestimmen lassen. Grundkurs Mathematik WiSe 2007/ Regeln von de L Hospital: Seien D = (a,b)\{x 0 } mit a < x 0 < b und f, g : D R differenzierbare Funktion, sowie g (x) 0 auf D. Außerdem gelte lim f(x) = lim g(x) = 0 (5.2) x x 0 x x 0 oder Dann gilt lim x x 0 f(x) = ±, Rµ f (x) lim x x 0 g (x) = a lim x x 0 g(x) = ±. (5.3) f(x) lim x x 0 g(x) = a. (5.4) Die gleichen Aussagen gelten auch für Grenzwerte der Form f(x) lim xցx0 g(x), lim f(x) xրx 0 g(x) und lim x ± f(x) g(x). Grundkurs Mathematik WiSe 2007/
52 Man beachte, dass die Implikation (5.4) auch beinhaltet, dass im Falle der f (x) f(x) Konvergenz von lim x x 0 g der Grenzwert lim überhaupt existiert. (x) x x 0 g(x) Es ist ganz wichtig, dass die Voraussetzungen (5.2) oder (5.3) erfüllt sind. Andernfalls liefert die Implikation (5.4) ein falsches Ergebnis. Das wird in Beispiel illustriert. Wenn (5.2) und (5.3) beide nicht gelten, lässt sich der Grenzwert sowieso direkt bestimmen. Beispiel Seien f(x) = sin(x), g(x) = x und x 0 = 0. Dann ist (5.2) erfüllt und wegen f (x) lim x 0 g (x) = lim cosx x 0 = Grundkurs Mathematik WiSe 2007/ ist mit (5.4): sin(x) lim x 0 x = lim x 0 f(x) g(x) =. 2. Seien f(x) = x3 und g(x) = e x. Dann ist (5.3) für x erfüllt und iterative Anwendung der Regel von de L Hospital liefert: x 3 lim x e = lim f(x) x x g(x) = lim f (x) x g (x) = lim 3x 2 x e x f (x) = lim x g (x) = lim 6x x e x f (3) (x) = lim x g (3) (x) = lim 6 x e = 0. x Grundkurs Mathematik WiSe 2007/
53 3. Seien f(x) = ex + 2 und g(x) = e 2x 2. Dann ist (5.3) für x erfüllt und daher lim x e x + 2 e 2x 2 = lim x e x = lim 2e2x x 2e x = Seien f(x) = ln(x), g(x) = x und x 0 = 0. Es soll lim xց0 ln(x)x bestimmt werden. Dies ist zwar kein Quotient, aber durch Umformen erhält man ln(x) lim ln(x) x = lim xց0 xց0 x = x = lim xց0 = lim( x) = 0. xց0 x 2 Grundkurs Mathematik WiSe 2007/ Seien f(x) = + a x und g(x) = x. Dann ist ( lim + a x = lim x x) x f(x)g(x) = lim eln(f(x)) g(x) x = lim x eln(+a x ) x. Nun ist der Exponent für x vom Typ 0 und daher ist wie in 3. lim ( ln + a ) x = lim x x x lim x ln ( + a x a x 2 + a x x 2 x ) = = lim x a + a x = a. Grundkurs Mathematik WiSe 2007/
54 Also ist ( lim + a x = e x x) a Seien f(x) = x + und g(x) = 2 ln(x). Dann gilt 2 lim (x + ) ln(x) = lim x x f(x)g(x) = lim eln(f(x)) g(x) x = lim eln(x+) 2 ln(x). x Der Exponent ist für x vom Typ. Somit ist 2 ln(x + ) lim x ln(x) x+ x = lim 2 x = lim x 2 x x + = 2. Grundkurs Mathematik WiSe 2007/ Also ist 2 lim (x + ) ln(x) = e 2. x Für f(x) = x 3 x und g(x) = ln(x) gilt ( lim ) x3 x ln(x) = lim f(x) g(x) = lim e ln(f(x)) g(x) xց0 xց0 xց0 = lim e ln( x3 x ) ln(x) = lim e xց0 xց0 2 ln(x)+x ln(3) ln(x). Grundkurs Mathematik WiSe 2007/
55 Der Exponent ist für x ց 0 vom Typ, also 2 ln(x) + xln(3) lim xց0 ln(x) = lim xց0 = lim xց0 2x + ln(3) x ( 2 + xln(3) ) = 2. ( Damit ist lim ) x3 x ln(x) = e. xց0 8. Abschließend noch ein Beispiel, das die Notwendigkeit der Voraussetzung (5.2) oder (5.3) zeigt. Betrachte f(x) = e 2x 2 und g(x) = e x + 2. Es soll f(x) lim x g(x) (5.5) Grundkurs Mathematik WiSe 2007/ bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x x e x = lim x 2ex = 0 den Grenzwert 0 für (5.5) liefern. Das ist aber falsch, denn wegen lim x ex = 0 ist lim f(x) = 2 und lim g(x) = 2, folglich erhalten wir den korrekten x x Grenzwert f(x) lim x g(x) =. Offensichtlich sind weder (5.2) noch (5.3) erfüllt, deshalb darf man (5.4) nicht anwenden. Grundkurs Mathematik WiSe 2007/
56 5.2 Kurvendiskussion Viele ökonomischen Zusammenhänge werden durch Funktionen beschrieben. Daher ist es wichtig, das Verhalten der Funktionen bestimmen zu können. Hierzu gehören. Definitionsbereich 2. Nullstellen 3. Monotonieverhalten und (lokale) Extremwerte, 4. Krümmungsverhalten und Wendepunkte, 5. Asymptotisches Verhalten, d. h. das Aussehen des Graphen an den Rändern des Definitionsbereichs, 6. Verhalten von f an Sprungstellen, Polstellen und Definitionslücken Grundkurs Mathematik WiSe 2007/ Dabei ist die Differenzialrechnung ein nützliches Hilfsmittel. An dem folgenden Beispiel (wir nennen es Beispiel A) werden alle Begriffe illustriert. Grundkurs Mathematik WiSe 2007/
57 Beispiel A: g(x) = 2x 2 x 2 2x x Grundkurs Mathematik WiSe 2007/ Der maximale Definitionsbereich einer gegebenen Funktion und seine Bestimmung wurde bereits in Abschnitt 2.2 behandelt. Beispiel A: Da das Nennerpolynom keine Nullstellen hat, ist D(g) = R. 2. Die Bestimmung der Nullstellen, also der Schnittpunkte des Graphen mit der x-achse, kann ein schwieriges Problem sein. Für Polynome (und folglich auch rationale Funtionen) wurde dies in Abschnitt 2.4 diskutiert. Beispiel A: Das Zählerpolynom und damit die Funktion g hat die einzige Nullstelle x 0 =. Im allgemeinen lassen sich graphisch Näherungswerte für die Nullstellen finden. Ein Verfahren zur approximativen Bestimmung der Nullstellen einer gegebenen Grundkurs Mathematik WiSe 2007/
58 Funktion ist das Newtonverfahren: Sei f : D R eine differenzierbare Funktion. Wähle einen Wert x D und setze für alle n N x n+ = x n f(x n) f (x n ) (Newtoniteration) Dann gilt: Wenn die Newtonfolge (x n ) n N konvergiert, dann ist der Grenzwert eine Nullstelle von f. Die dieser Methode zugrunde liegende Idee ist wie folgt: Ist x n ein Schätzwert für eine Nullstelle, dann wird in (x n,f(x n )) die Tangente an den Graphen von f Grundkurs Mathematik WiSe 2007/ gelegt. Sie hat die Gleichung y = f (x n )(x x n ) + f(x n ). Ihre Nullstelle ist gerade obiger Wert x n+, der dann als neue Schätzung benutzt wird. Die Frage, in welchen Situationen die Newtoniteration (x n ) n N konvergiert, bleibt hier unbehandelt. Beispiel 5.9 Sei f(x) = x 2 a mit a R +. Dann ist die Newtoniteration x n+ = x n x2 n a = ) (x n + axn 2x n 2 Man kann zeigen, dass die Folge gegen a konvergiert. 3. Monotonieverhalten und lokale Extremwerte Monotonie einer Funktion auf einem Intervall ist bereits in Abschnitt 2.2 definiert Grundkurs Mathematik WiSe 2007/
59 worden. Im Falle einer differenzierbaren Funktion lässt sich Monotonie mithilfe der ersten Ableitung klären. Grundkurs Mathematik WiSe 2007/ Monotonieverhalten Sei f : D R eine differenzierbare Funktion, I D ein Intervall. Dann gilt: f ist konstant in I genau dann, wenn f = 0 auf I. f ist monoton wachsend in I genau dann, wenn f (x) 0 für alle x I. f ist monoton fallend in I genau dann, wenn f (x) 0 für alle x I. f ist streng monoton wachsend in I, wenn f (x) > 0 für alle x I. f ist streng monoton fallend in I, wenn f (x) < 0 für alle x I. Grundkurs Mathematik WiSe 2007/
5 Differenzialrechnung für Funktionen einer Variablen
 5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen
 Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
4 Reihen und Finanzmathematik
 4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei
4 Reihen und Finanzmathematik
 4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Die
4 Reihen und Finanzmathematik 4. Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Die
3.2 Reihen. Mathematik I WiSe 2005/
 3.2 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Die entsprechenden Beispiele werden
3.2 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Die entsprechenden Beispiele werden
4 Reihen und Finanzmathematik
 4 Reihen und Finanzmathematik 4.1 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle.
4 Reihen und Finanzmathematik 4.1 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle.
Da die Restschuld und damit die Zinsen im Laufe der Zeit sinken, wird bei der Annuitätentilgung von Jahr zu Jahr ein größerer Betrag getilgt.
 Tilgung, Annuität: Werden Schulden in Teilbeträgen, den sogenannten Raten zurückgezahlt, so spricht man von einer Tilgung, bei der die Schulden auf eine Restschuld vermindert werden. Die in einem Zeitabschnitt
Tilgung, Annuität: Werden Schulden in Teilbeträgen, den sogenannten Raten zurückgezahlt, so spricht man von einer Tilgung, bei der die Schulden auf eine Restschuld vermindert werden. Die in einem Zeitabschnitt
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
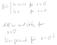 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Man schreibt dann lim. = bzw. lim
 Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
4 Reihen. s n = a 1 + a 2 + + a n = Die Folge (s n ) n N der Partialsummen heißt eine (unendliche) Reihe und wird auch als a k. k=1. )n N geschrieben.
 4 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei (a k ) k N eine Folge. Wir definieren
4 Reihen Aus Folgen lassen sich durch Aufaddieren weitere Folgen konstruieren. Das sind die sogenannten Reihen, sie spielen in der Finanzmathematik eine wichtige Rolle. Sei (a k ) k N eine Folge. Wir definieren
2 Differenzialrechnung für Funktionen einer Variablen
 2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
Tilgungsrechnung. (K n + R n = ln. / ln(q) (nachschüssig) + R. / ln(q) (vorschüssig)
 (K n + R n = ln n = ln q 1 K 0 + R q 1 (K n q + R q 1 K 0 q + R q 1 ) / ln(q) (nachschüssig) ) / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
(K n + R n = ln n = ln q 1 K 0 + R q 1 (K n q + R q 1 K 0 q + R q 1 ) / ln(q) (nachschüssig) ) / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
Tilgungsrechnung. n = ln. K 0 + R / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. q 1. q 1.
 (K + R ) q 1 n = ln K 0 + R / ln(q) (nachschüssig) q 1 n = ln ( K q + R ) q 1 K 0 + R / ln(q) (vorschüssig) q 1 Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
(K + R ) q 1 n = ln K 0 + R / ln(q) (nachschüssig) q 1 n = ln ( K q + R ) q 1 K 0 + R / ln(q) (vorschüssig) q 1 Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
3. Mit c n = ( 1) n ist. 4. Mit d n = 2 n ist. 5. Mit y n = ( 1 3) n. 6. Ist x n = (1 + 1 n )n, dann ist. Die Zahl a n heißt die n-te Fibonaccizahl.
 Kapitel 3. Folgen und Reihen 3. Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als a, a, a 3,...) = a n ) n N. Es ist also a n R. Der Index n gibt
Kapitel 3. Folgen und Reihen 3. Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als a, a, a 3,...) = a n ) n N. Es ist also a n R. Der Index n gibt
1 k = = Sie ist also gerade der Grenzwert der zur Folge (r k 10 k ) k N0 gehörenden Reihe( n
 Die zur Folge ( k ) k N gehörende Reihe ( n k ) n N ist divergent, genauer k =. 2. Dezimalzahlen: Eine Zahl r = r 0,r r 2 r 3 mit r 0 N 0 und r n {0,...,9} für n hat den Wert r = r 0 +r 0 +r 2 00 +...
Die zur Folge ( k ) k N gehörende Reihe ( n k ) n N ist divergent, genauer k =. 2. Dezimalzahlen: Eine Zahl r = r 0,r r 2 r 3 mit r 0 N 0 und r n {0,...,9} für n hat den Wert r = r 0 +r 0 +r 2 00 +...
Im weiteren werden die folgenden Bezeichnungen benutzt: Zinsrechnung
 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
1 Folgen und Stetigkeit
 1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 2. Zinsrechnung 2.1. Grundbegriffe K... Kapital (caput das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen eines Kapitals für
2. Zinsrechnung 2.1. Grundbegriffe K... Kapital (caput das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen eines Kapitals für
5 Differenzialrechnung für Funktionen einer Variablen
 5 Differenzialrecnung für Funktionen einer Variablen Ist f eine ökonomisce Funktion, so ist oft wictig zu wissen, wie sic die Funktion bei kleinen Änderungen verält. Bescreibt etwa f einen Wacstumsprozess,
5 Differenzialrecnung für Funktionen einer Variablen Ist f eine ökonomisce Funktion, so ist oft wictig zu wissen, wie sic die Funktion bei kleinen Änderungen verält. Bescreibt etwa f einen Wacstumsprozess,
Kapitel 4. Folgen und Reihen. Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38
 Kapitel 4 Folgen und Reihen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38 Folgen Eine Folge ist eine Anordnung von reellen Zahlen. Die einzelnen Zahlen heißen Glieder
Kapitel 4 Folgen und Reihen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38 Folgen Eine Folge ist eine Anordnung von reellen Zahlen. Die einzelnen Zahlen heißen Glieder
2.6 Stetigkeit und Grenzwerte
 2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
2.6 Stetigkeit und Grenzwerte Anschaulich gesprochen ist eine Funktion stetig, wenn ihr Graph sich zeichnen lässt, ohne den Stift abzusetzen. Das ist natürlich keine präzise mathematische Definition und
3.1 Folgen. ,...) die Folge der sogenannten Hauptbrüche in Q. Mathematik I WiSe 2005/ y = (y n ) n N = ( 1 3, 1 9, 1 27, 1 81, 1
 Kapitel 3. Folgen und Reihen 3.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als a = (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index
Kapitel 3. Folgen und Reihen 3.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als a = (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index
Kapitel 4. Reihen 4.1. Definition und Beispiele
 Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Kapitel 4. Reihen 4.1. Definition und Beispiele Ist (a n ) eine Folge von Zahlen, so heißt der formale Ausdruck a ν = a 0 + a 1 + a 2 +... eine Reihe; die einzelnen a ν sind die Glieder dieser Reihe. Um
Folgen und Reihen. Kapitel Zahlenfolgen
 Kapitel 2 Folgen und Reihen 2. Zahlenfolgen Definition. Eine Folge reeller Zahlen a 0,a,a 2,..., die gewonnen wird durch eine Vorschrift, die jeder natürlichen Zahl n N genau eine reelle Zahl a n zuordnet,
Kapitel 2 Folgen und Reihen 2. Zahlenfolgen Definition. Eine Folge reeller Zahlen a 0,a,a 2,..., die gewonnen wird durch eine Vorschrift, die jeder natürlichen Zahl n N genau eine reelle Zahl a n zuordnet,
3 Reihen. 3.1 Konvergenz und Divergenz. Die Eindeutigkeit nach Satz 13 ergibt schließlich (5). (6) folgt aus (2) und (1) wegen. 1 a +log ba.
 Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Die Eindeutigkeit nach Satz 3 ergibt schließlich (5). (6) folgt aus (2) und () wegen Aussage (7) ergibt sich aus () und (6). 0 = log b = log b ( a a) = log b a +log ba. 3 Reihen 3. Konvergenz und Divergenz
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
3 Folgen und Stetigkeit
 3 Folgen und Stetigkeit 3.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
3 Folgen und Stetigkeit 3.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
3 Folgen, Reihen und stetige Funktionen
 Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
f(f 1 (w)) = w f 1 (f(z)) = z Abbildung 21: Eine Funktion und ihre Umkehrfunktion
 Mathematik für Naturwissenschaftler I 2.8 2.8 Umkehrfunktionen 2.8. Definition Sei f eine Funktion. Eine Funktion f heißt Umkehrfunktion, wenn f (w) = z für w = f(z). f darf nicht mit f(z) = (f(z)) verwechselt
Mathematik für Naturwissenschaftler I 2.8 2.8 Umkehrfunktionen 2.8. Definition Sei f eine Funktion. Eine Funktion f heißt Umkehrfunktion, wenn f (w) = z für w = f(z). f darf nicht mit f(z) = (f(z)) verwechselt
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
bestimmt werden. Allein die Regel (5.4) würde wegen g(x) = 2, folglich erhalten wir den korrekten lim
 bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathematik 1 Folgen, Reihen und Finanzmathematik
 Wirtschaftswissenschaftliches Zentrum 1 Universität Basel Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Folgen, Reihen und Finanzmathematik Inhaltsverzeichnis 1 Zahlenfolgen 2 1.1 Grundlegende
Wirtschaftswissenschaftliches Zentrum 1 Universität Basel Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Folgen, Reihen und Finanzmathematik Inhaltsverzeichnis 1 Zahlenfolgen 2 1.1 Grundlegende
Differentialrechnung
 Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 205/6 7 Differentialrechnung / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f () f ( 0) 0 heißt
Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 205/6 7 Differentialrechnung / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f () f ( 0) 0 heißt
1 Folgen und Stetigkeit
 1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
Die anderen Folgen in Beispiel 3.1 sind nicht geometrisch. So ist etwa für die Folge mit b n = 1 n b 3 = 2 b 2 3, aber b 4
 Ebenso ist jede Folge mit der Vorschrift d n = q n für ein festes q R geometrisch. Die anderen Folgen in Beispiel 3.1 sind nicht geometrisch. So ist etwa für die Folge mit b n = 1 n b 3 = 2 b 2 3, aber
Ebenso ist jede Folge mit der Vorschrift d n = q n für ein festes q R geometrisch. Die anderen Folgen in Beispiel 3.1 sind nicht geometrisch. So ist etwa für die Folge mit b n = 1 n b 3 = 2 b 2 3, aber
Stetigkeit von Funktionen
 Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Wirtschaftsmathematik: Formelsammlung (V1.40)
 Wirtschaftsmathematik: Formelsammlung (V.40) Grundlagen n! = 2 3... n = 0! = n i für n N, n 0, i= pq-formel Lösung von x 2 + px + q = 0 x /2 = p p 2 ± 2 4 q abc-formel Lösung von ax 2 + bx + c = 0 Binomische
Wirtschaftsmathematik: Formelsammlung (V.40) Grundlagen n! = 2 3... n = 0! = n i für n N, n 0, i= pq-formel Lösung von x 2 + px + q = 0 x /2 = p p 2 ± 2 4 q abc-formel Lösung von ax 2 + bx + c = 0 Binomische
11 Spezielle Funktionen und ihre Eigenschaften
 78 II. ANALYSIS 11 Spezielle Funktionen und ihre Eigenschaften In diesem Abschnitt wollen wir wichtige Eigenschaften der allgemeinen Exponentialund Logarithmusfunktion sowie einiger trigonometrischer Funktionen
78 II. ANALYSIS 11 Spezielle Funktionen und ihre Eigenschaften In diesem Abschnitt wollen wir wichtige Eigenschaften der allgemeinen Exponentialund Logarithmusfunktion sowie einiger trigonometrischer Funktionen
Kapitel 6 Folgen und Stetigkeit
 Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (0.09.03 0.09.03) Dr. Jörg Horst WS 03-04 Mathematischer Vorkurs TU Dortmund Seite / 5 Mathematischer Vorkurs TU Dortmund Seite 6 / 5 Schenkel Winkelbereich Scheitel S
Mathematischer Vorkurs NAT-ING II (0.09.03 0.09.03) Dr. Jörg Horst WS 03-04 Mathematischer Vorkurs TU Dortmund Seite / 5 Mathematischer Vorkurs TU Dortmund Seite 6 / 5 Schenkel Winkelbereich Scheitel S
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
2.5 Komplexe Wurzeln. Mathematik für Naturwissenschaftler I 2.5
 Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
Mathematik für Naturwissenschaftler I 2.5 Die Periodizität von e z ist der Grund, warum im Komplexen Logarithmen etwas schwieriger zu behandeln sind als im Reellen: Der natürliche Logarithmus ist die Umkehrung
= = x 2 = 2x x 2 1 = x 3 = 2x x 2 2 =
 1 Lösungsvorschläge zu den Aufgaben 28, 29, 30 b), 31, 32, 33, 35, 36 i) und 37 a) von Blatt 4: 28) a) fx) := x 3 10! = 0 Wir bestimmen eine Näherungslösung mit dem Newtonverfahren: Als Startwert wählen
1 Lösungsvorschläge zu den Aufgaben 28, 29, 30 b), 31, 32, 33, 35, 36 i) und 37 a) von Blatt 4: 28) a) fx) := x 3 10! = 0 Wir bestimmen eine Näherungslösung mit dem Newtonverfahren: Als Startwert wählen
Modul Grundbildung Analysis WiSe 10/11. A.: Wurde in diesem Kapitel behandelt. C.: Weitere Fragen (Nicht nur für die Klausur interessant)
 Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 1 2. Zinsrechnung 2.1. Grundbegriffe K... Kapital (caput das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen eines Kapitals
1 2. Zinsrechnung 2.1. Grundbegriffe K... Kapital (caput das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen eines Kapitals
Kapitel 5 Trigonometrie
 Mathematischer Vorkurs TU Dortmund Seite / 7 Schenkel Winkelbereich Scheitel S α Winkel werden in Grad oder im Bogenmaß (auch Rad) angegeben: 360 =. y cot α r = sin α α cos α tan α x Durch diese Betrachtungen
Mathematischer Vorkurs TU Dortmund Seite / 7 Schenkel Winkelbereich Scheitel S α Winkel werden in Grad oder im Bogenmaß (auch Rad) angegeben: 360 =. y cot α r = sin α α cos α tan α x Durch diese Betrachtungen
Differentialrechnung
 Katharina Brazda 5. März 007 Inhaltsverzeichnis Motivation. Das Tangentenproblem................................... Das Problem der Momentangeschwindigkeit.......................3 Differenzenquotient und
Katharina Brazda 5. März 007 Inhaltsverzeichnis Motivation. Das Tangentenproblem................................... Das Problem der Momentangeschwindigkeit.......................3 Differenzenquotient und
Kapitel 7. Differentialrechnung. Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56
 Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
Analysis I. Vorlesung 9. Reihen
 Prof. Dr. H. Brenner Osnabrück WS 20/204 Analysis I Vorlesung 9 Reihen Wir haben in der siebten Vorlesung gesagt, dass man eine Dezimalentwicklung, also eine (unendliche) Ziffernfolge mit Ziffern zwischen
Prof. Dr. H. Brenner Osnabrück WS 20/204 Analysis I Vorlesung 9 Reihen Wir haben in der siebten Vorlesung gesagt, dass man eine Dezimalentwicklung, also eine (unendliche) Ziffernfolge mit Ziffern zwischen
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
LAF Mathematik. Näherungsweises Berechnen von Nullstellen von Funktionen
 LAF Mathematik Näherungsweises Berechnen von Nullstellen von Funktionen von Holger Langlotz Jahrgangsstufe 12, 2002/2003 Halbjahr 12.1 Fachlehrer: Endres Inhalt 1. Vorkenntnisse 1.1 Nicht abbrechende Dezimalzahlen;
LAF Mathematik Näherungsweises Berechnen von Nullstellen von Funktionen von Holger Langlotz Jahrgangsstufe 12, 2002/2003 Halbjahr 12.1 Fachlehrer: Endres Inhalt 1. Vorkenntnisse 1.1 Nicht abbrechende Dezimalzahlen;
V.1 Konvergenz, Grenzwert und Häufungspunkte
 V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
Kapitel 5 Reihen 196
 Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Mathematik I Herbstsemester 2018 Kapitel 3: Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 39 3. Differentialrechnung Einführung Ableitung elementarer Funktionen Ableitungsregeln Kettenregel Ableitung
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 39 3. Differentialrechnung Einführung Ableitung elementarer Funktionen Ableitungsregeln Kettenregel Ableitung
Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Univariate Analysis. Analysis und nichtlineare Modelle Sommersemester
 Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Ist die Funktion f : R R injektiv, hat den Definitionsbereich D und den Wertebereich W, so ist f : D W bijektiv. Dann heißt
 Ist die Funktion f : R R injektiv, hat den Definitionsbereich D und den Wertebereich W, so ist f : D W bijektiv. Dann heißt f 1 : W D, y wobei D mit f() = y die Umkehrfunktion zu f. Der Graph G f 1 = {(y,
Ist die Funktion f : R R injektiv, hat den Definitionsbereich D und den Wertebereich W, so ist f : D W bijektiv. Dann heißt f 1 : W D, y wobei D mit f() = y die Umkehrfunktion zu f. Der Graph G f 1 = {(y,
Analysis 1 für Informatiker (An1I)
 Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Biostatistik, Winter 2011/12
 Biostatistik, Winter 2011/12 Summen, Exponentialfunktion, Ableitung Prof. Dr. Achim Klenke http://www.aklenke.de 2. Vorlesung: 04.11.2011 1/46 Inhalt 1 Summen und Produkte Summenzeichen Produktzeichen
Biostatistik, Winter 2011/12 Summen, Exponentialfunktion, Ableitung Prof. Dr. Achim Klenke http://www.aklenke.de 2. Vorlesung: 04.11.2011 1/46 Inhalt 1 Summen und Produkte Summenzeichen Produktzeichen
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathemati PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Höhere Mathemati für Informatier II (Sommersemester 00) Lösungen zu Aufgabenblatt
Exponentialfunktion, Logarithmus
 Exponentialfunktion, Logarithmus. Die Exponentialfunktion zu einer Basis > 0 Bei Exponentialfunktionen ist die Basis konstant und der Exponent variabel... Die Exponentialfunktion zu einer Basis > 0. Sei
Exponentialfunktion, Logarithmus. Die Exponentialfunktion zu einer Basis > 0 Bei Exponentialfunktionen ist die Basis konstant und der Exponent variabel... Die Exponentialfunktion zu einer Basis > 0. Sei
16. Differentialquotient, Mittelwertsatz
 16. Differentialquotient, Mittelwertsatz Gegeben sei eine stetige Funktion f : R R. Wir suchen die Gleichung der Tangente t an die Kurve y = f(x) im Punkt (x, f(x ), x R. Das Problem dabei ist, dass vorderhand
16. Differentialquotient, Mittelwertsatz Gegeben sei eine stetige Funktion f : R R. Wir suchen die Gleichung der Tangente t an die Kurve y = f(x) im Punkt (x, f(x ), x R. Das Problem dabei ist, dass vorderhand
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Definition der Reihe Gegeben: (a n) unendliche Folge in R Dann heißt (s n) mit Beispiel: eine unendliche Reihe. s n
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Definition der Reihe Gegeben: (a n) unendliche Folge in R Dann heißt (s n) mit Beispiel: eine unendliche Reihe. s n
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Rechenregeln für Grenzwerte Gegeben: lim (a n) = a und lim (b n) = b n n kurz:
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Rechenregeln für Grenzwerte Gegeben: lim (a n) = a und lim (b n) = b n n kurz:
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 5. x 1 2x 3 = lim 6x
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
Viele Statistiken werden durch endliche Folgen beschrieben. (z.b. Anzahl der Studierenden an der TU München in den Jahren 1962 bis 1976)
 Kapitel 9 Folgen und Reihen 9.1 Folgen 9.1.1 Was ist eine Folge? Abbildungen, die auf N definiert sind (mit Werten z.b. in R), heißen (unendliche) Folgen. Abb., die auf einer endlichen Menge aufeinander
Kapitel 9 Folgen und Reihen 9.1 Folgen 9.1.1 Was ist eine Folge? Abbildungen, die auf N definiert sind (mit Werten z.b. in R), heißen (unendliche) Folgen. Abb., die auf einer endlichen Menge aufeinander
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Mathematischer Vorkurs
 Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite / 50 Kapitel 5 Mathematischer Vorkurs TU Dortmund Seite 54 / 50 Scheitel S Schenkel α Winkelbereich Winkel werden in Grad
Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite / 50 Kapitel 5 Mathematischer Vorkurs TU Dortmund Seite 54 / 50 Scheitel S Schenkel α Winkelbereich Winkel werden in Grad
Mathematik I - Woche 10
 Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16)
 1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen
 Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen Susanna Pohl Vorkurs Mathematik TU Dortmund 12.03.2015 Folgen und Reihen Folgen und Grenzwerte Rechenregeln für konvergente Folgen
Vorbereitungskurs Mathematik zum Sommersemester 2015 Folgen und Reihen Susanna Pohl Vorkurs Mathematik TU Dortmund 12.03.2015 Folgen und Reihen Folgen und Grenzwerte Rechenregeln für konvergente Folgen
FH Gießen-Friedberg, Sommersemester 2010 Skript 9 Diskrete Mathematik (Informatik) 30. April 2010 Prof. Dr. Hans-Rudolf Metz.
 FH Gießen-Friedberg, Sommersemester 010 Skript 9 Diskrete Mathematik (Informatik) 30. April 010 Prof. Dr. Hans-Rudolf Metz Funktionen Einige elementare Funktionen und ihre Eigenschaften Eine Funktion f
FH Gießen-Friedberg, Sommersemester 010 Skript 9 Diskrete Mathematik (Informatik) 30. April 010 Prof. Dr. Hans-Rudolf Metz Funktionen Einige elementare Funktionen und ihre Eigenschaften Eine Funktion f
Stetige Funktionen. Definition. Seien (X, d) und (Y, ϱ) metrische Räume und f : X Y eine Abbildung. D(f) X sei der Definitionsbereich von f.
 Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Stetige Funktionen Abbildungen f : X Y, wobei X und Y strukturierte Mengen sind (wie z.b. Vektorräume oder metrische Räume), spielen eine zentrale Rolle in der Mathematik. In der Analysis sind Abbildungen
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Definition der Reihe Gegeben: (a n) unendliche Folge in R Dann heißt (s n) mit Beispiel: eine unendliche Reihe. s n heißt
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Definition der Reihe Gegeben: (a n) unendliche Folge in R Dann heißt (s n) mit Beispiel: eine unendliche Reihe. s n heißt
2 Stetigkeit und Differenzierbarkeit
 2.1) Sei D R. a) x 0 R heißt Häufungspunkt von D, wenn eine Folge x n ) n N existiert mit x n D,x n x 0 und lim n x n = x 0. D sei die Menge der Häufungspunkte von D. b) x 0 D heißt innerer Punkt von D,
2.1) Sei D R. a) x 0 R heißt Häufungspunkt von D, wenn eine Folge x n ) n N existiert mit x n D,x n x 0 und lim n x n = x 0. D sei die Menge der Häufungspunkte von D. b) x 0 D heißt innerer Punkt von D,
6 Di erentialrechnung, die Exponentialfunktion
 6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
Kapitel 4 Folgen, Reihen & Funktionen
 Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Mathematik I für Wirtschaftswissenschaftler Klausur am , bzw
 1 Mathematik I für Wirtschaftswissenschaftler Klausur am 21.2.28, 9. 11. bzw. 9. 9.. Bitte unbedingt beachten: a) Gewertet werden alle acht bzw. drei gestellten Aufgaben. b) Lösungswege sind anzugeben.
1 Mathematik I für Wirtschaftswissenschaftler Klausur am 21.2.28, 9. 11. bzw. 9. 9.. Bitte unbedingt beachten: a) Gewertet werden alle acht bzw. drei gestellten Aufgaben. b) Lösungswege sind anzugeben.
Jede beschränkte und monotone Folge (a n ) n N konvergiert, d.h. es gibt ein a R, so dass lim
 Beispiel 3.10 ( 1) n n a n a+nd aq n 1 (a > 0) n monoton steigend d 0 q 1 nein nein streng monoton steigend d > 0 q > 1 nein nein monoton fallend d 0 0 q 1 streng monoton fallend d < 0 0 < q < 1 ja nein
Beispiel 3.10 ( 1) n n a n a+nd aq n 1 (a > 0) n monoton steigend d 0 q 1 nein nein streng monoton steigend d > 0 q > 1 nein nein monoton fallend d 0 0 q 1 streng monoton fallend d < 0 0 < q < 1 ja nein
Tutorium: Analysis und lineare Algebra. Differentialrechnung. Steven Köhler. mathe.stevenkoehler.de Steven Köhler
 Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Analysis für Informatiker und Statistiker Nachklausur
 Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Ableitung und Steigung. lim h
 Ableitung und Steigung Aufgabe 1 Bestimme die Ableitung der Funktion f(x) = x über den Differentialquotienten. f (x f '(x ) lim h h) f (x h ) (x lim h h) h x x lim h hx h h x h(x lim h h h) lim x h h x
Ableitung und Steigung Aufgabe 1 Bestimme die Ableitung der Funktion f(x) = x über den Differentialquotienten. f (x f '(x ) lim h h) f (x h ) (x lim h h) h x x lim h hx h h x h(x lim h h h) lim x h h x
