Bachelorarbeit. Generierung von synchronisierten Trajektorien aus geplanten Via- Punkten. Bachelorarbeit. Christian Breu
|
|
|
- Michaela Solberg
- vor 7 Jahren
- Abrufe
Transkript
1 Bachelorarbeit Generierung von ynchroniierten Trajektorien au geplanten Via- Punkten Bachelorarbeit Chritian Breu
2
3 Hochchule für angewandte Wienchaften Fachhochchule Deggendorf Fakultät Elektro- und Medientechnik Generierung von ynchroniierten Trajektorien au geplanten Via-Punkten Generation of ynchronized trajectorie from planned via-point Bachelorarbeit zur Erlangung de akademichen Grade: Bachelor of Engineering an der Hochchule Deggendorf vorgelegt von: Breu, Chritian Prüfer: Prof. Dr.-Ing. Nikolau Müller am:
4 Erklärung Name de Studierenden: Name de Betreuer: Fall extern: Name de Betreuer: Chritian Breu Prof. Dr.-Ing. Nikolau Müller Dipl.-Ing. Andrea Stemmer Thema der Bachelorarbeit: Generierung von ynchroniierten Trajektorien au geplanten Via-Punkten 1. Ich erkläre hiermit, da ich die Bachelorarbeit gemäß 11 APO (Allgemeine Prüfungordnung der Hochchule für Angewandte Wienchaften Fachhochchule Deggendorf) elbtändig verfat, noch nicht anderweitig für Prüfungzwecke vorgelegt, keine anderen al die angegebenen Quellen oder Hilfmittel benutzt owie wörtliche und inngemäße Zitate al olche gekennzeichnet habe. Deggendorf, (Datum) (Unterchrift de Studierenden). Ich bin damit einvertanden, da die von mir angefertigte Bachelorarbeit über die Bibliothek der Hochchule einer breiteren Öffentlichkeit zugänglich gemacht wird. Ja Nein Fall Ja: Ich erkläre und tehe dafür ein, da ich alleiniger Inhaber aller Rechte an der Bachelorarbeit, einchließlich de Verfügungrecht über Vorlagen an beigefügten Abbildungen, Plänen o. ä. bin und durch deren öffentliche Zugänglichmachung weder Rechte und Anprüche Dritter noch geetzliche Betimmungen verletzt werden. Deggendorf, (Datum) (Unterchrift de Studierenden) Nur bei Einvertändni de Verfaer mit einer Veröffentlichung der Bachelorarbeit vom Betreuer auzufüllen: Eine Aufnahme eine Exemplar der Bachelorarbeit in den Betand der Bibliothek und die Auleihe de Exemplar wird befürwortet. nicht befürwortet. Deggendorf, (Datum) (Unterchrift de Prüfer) II
5 Dankagung An dieer Stelle möchte ich mich bei allen Peronen bedanken, die mich bei der Anfertigung meiner Bachelorarbeit untertützt haben. Mein beonderer Dank gilt Herrn Dipl.-Ing. Andrea Stemmer, der mich al fachlicher Betreuer beim Deutchen Zentrum für Luft- und Raumfahrt in zahlreichen Dikuionen mit Rat und Tat untertützt und omit maßgeblich zum Gelingen dieer Arbeit beigetragen hat. Schwierige Fragen und Probleme konnten Dank einer Hilfe beantwortet und gelöt werden. De Weiteren bedanke ich mich bei Prof. Dr.-Ing. Nikolau Müller, meinem Betreuer an der Hochchule Deggendorf, der durch eine Betreuung diee Arbeit ermöglichte. Beonder der unkomplizierte Umgang bei organiatorichen Fragen und ein tet offene Ohr waren mir eine große Hilfe. Auch da ehr angenehme Arbeitklima in der Abteilung mit den tet hilfbereiten und freundlichen Kollegen erleichterte die Anfertigung der Bachelorarbeit. Ein beonderer Dank geht an meine Familie, die mir mein Studium ermöglicht und mich vielfältig untertützt hat. Auch bei meiner Freundin und meinen Freunden möchte ich mich für die motivierenden Worte während der Enttehungzeit dieer Arbeit bedanken. III
6 Inhaltverzeichni 1 Einleitung Motivation Aufgabentellung Vorgehenweie... Grundlagen der Robotik Erklärung von Begriffen Trajektorienplanung Stand der Technik Analytiche Anätze Punkt zu Punkt Mit Via-Punkt Anwendung auf mehrere Achen Vor- und Nachteile Mögliche Erweiterungen Weitere Funktionen Trajektoriengenerierung mit nichtlinearem Filter Optimale Trajektorienplanung Entkoppelte Trajektorienplanung Eigenchaften Pfaderzeugung Berechnung de zeitlichen Verlauf Kontante Skalierung IV
7 Inhaltverzeichni 4.3. Variable Skalierung durch Integration Beipiel einer Trajektorie Umetzung in einen Algorithmu Polynom-Generator Vorgehen zur Pfaderzeugung Bogentück mit zwei Polynomen dritten Grade Erzeugung voll-ynchroner Achen Optimierung der Krümmung im Übergang Integration Filter Zuammenfaung und Aublick... 8 Literaturverzeichni Abbildungverzeichni V
8 1 Einleitung 1.1 Motivation Roboter ind au dem heutigen Alltag nicht mehr wegzudenken. Den größten Anteil beitzen Indutrieroboter, die verchiedene Tätigkeiten, wie zum Beipiel Schweißen, Lackieren oder Verpacken verrichten. Aber auch in der Medizin halten Roboter Einzug. Sei e al Träger von Röntgengeräten oder für die Durchführung von minimal-invaiver Chirurgie, durch Roboter ind neuartige, chonendere Eingriffe möglich. Ein weiterer Arbeitbereich für Roboter it der Weltraum. Dort können Roboter autonom auf entfernten Planenten Raumtationen errichten oder ferngeteuert von der Erde au Satelliten reparieren. Zukünftig wird der Bereich von Service-Robotern zunehmend an Bedeutung gewinnen, vor allem im Hinblick auf den bevortehenden demografichen Wandel und dem damit verbundenen Engpa an Pflegeperonal. Roboter könnten einfache Hol- und Bringdiente verrichten und o beipielweie bettlägerige Menchen untertützen. In allen vorgetellten Bereichen it e notwendig, da der Roboter ein Potential voll aunutzen kann. In der Indutrie it e erwüncht, da die Tätigkeiten in kürzeter Zeit abgewickelt werden, ein Service-Roboter oll ich möglicht menchlich bewegen. Bei beiden Tätigkeiten it e erforderlich, da ein Roboterarm eine geplante bzw. vorgegebene Bahn genau verfolgt und nicht von ihr abweicht. Um die zu erreichen müen die Gelenke ynchron angeteuert werden, die Bewegung eine jeden Gelenke mu genau die gleiche Zeit benötigen und dabei aber chnelltmöglich vontatten gehen. In dieer Bachelorarbeit wird ein Algorithmu entwickelt, der diee Vorgaben erfüllt und al Grundlage für weitere Optimierungen dient. 1
9 1 Einleitung 1. Aufgabentellung Die Arbeit enttand beim Deutchen Zentrum für Luft- und Raumfahrt in Oberpfaffenhofen am Intitut für Robotik und Mechatronik. Ziel dieer Bachelorarbeit it die Erarbeitung und Implementierung eine Algorithmu, der au einer Folge von Punkten im Gelenkraum eine auführbare Trajektorie für den Roboter generiert. Die Trajektorie oll dabei die vorgegebenen Punkte in allen Gelenken ynchron mit einer eintellbaren Maximalabweichung erreichen und den Roboter unter Einhaltung von Gechwindigkeit-, Bechleunigung- und wenn möglich auch Ruckbegrenzungen möglicht chnell zum Zielpunkt bewegen. 1.3 Vorgehenweie Die Bachelorarbeit umfat mehrere Arbeitchritte. Im erten Schritt werden die grundlegenden Begriffe der Aufgabentellung erläutert und kurz auf die Trajektorienplanung eingegangen. Anchließend wird auf den aktuellen Stand der Technik eingegangen. Dabei gilt e die Vielzahl an derzeit exitierenden Anätzen zu analyieren und zu vergleichen. Im nächten Arbeitpaket wird der augewählte Anatz genauer vorgetellt und die dazu notwendige mathematiche Vorgehenweie erörtert. Anchließend müen nun die erarbeiteten mathematichen Bechreibungen zur Vorunteruchung und zum leichteren Erweitern in einen Algorithmu umgewandelt werden. In dieem Fall wird die plattformunabhängige Software Matlab verwendet. Abchließend werden die Ergebnie der Arbeit zuammengefat und ein Aublick auf mögliche Erweiterungen gegeben.
10 Grundlagen der Robotik In dieem Abchnitt werden die grundlegenden Begriffe der Aufgabentellung erläutert und kurz auf die Trajektorienplanung eingegangen..1 Erklärung von Begriffen Um ein genauere Vertändni für die Forderungen der Aufgabentellung zu erhalten, müen noch einige Begriffe geklärt werden. Dabei wird unter anderem der Titel dieer Bachelorarbeit Generierung von ynchroniierten Trajektorien au geplanten Via-Punkten aufgearbeitet. Zunächt wird die Herkunft der geplanten Punkte erläutert. E kann für einen Roboterarm an jedem rotatorichen Gelenk ein Winkel vorgegeben werden. Bei einem tranlatorichen Gelenk wird antatt einem Winkel die Länge de Gelenk vorgegeben. Die Untercheidung von dieen zwei Bewegungformen it für nachfolgende Betrachtungen ohne Bedeutung. E werden aber au Gründen der Überichtlichkeit meiten Gelenkwinkel, alo rotatoriche Gelenke betrachtet. Diee Winkel ollen in dieem Programm nicht berechnet, ondern lediglich weiter verarbeitet werden. Die Werte, alo die Soll-Winkeltellungen, werden bereit von einem übergeordneten Planer geliefert. Dieer Planer generiert für eine geplante Bewegung de Roboter für jede Gelenk die dazugehörigen Winkeltellungen. Der Planer kann dabei ein eigene Programm ein, welche zum Beipiel elbttändig durch Bildverarbeitung einen Weg für den Roboterarm durch den Raum ermittelt. Möglich it aber auch, da ein Benutzer Werte vorgibt, die der Roboterarm einnehmen oll. Zur Veranchaulichung de Zuammenhang eine geplanten Wege mit den dazugehörigen Gelenkwinkeln wird al Beipiel ein Roboter mit zwei rotatorichen Achen herangezogen. Dabei it ein Motor für da erte Gelenk, ein zweiter für da zweite Gelenk verantwortlich. Die beiden Gelenkwinkel werden mit q 1 und q bezeichnet. Bei Robotern mit n Achen heißt der Gelenkwinkel in der letzten Ache q n. In dem unten dargetellten Beipiel oll ich der Endpunkt 3
11 Grundlagen der Robotik de Roboter, alo der Endeffektor, vom Startpunkt zum Endpunkt bewegen. Dazu mu nur da zweite Gelenk verändert werden, da beide Punkte auf einem Krei liegen, deen Mittelpunkt da zweite Gelenk it. Der Gelenkwinkel q 1 bleibt während de geamten Bewegungvorgang auf einem kontanten Wert. Nur der Winkel q mu ich vom Itwert zu einer neuen Winkeltellung bewegen, um den Endpunkt zu erreichen. Der tatächlich nötige Wert für q, damit der Roboter diee Poition einnimmt, it von allen vorhandenen Achen und dehalb vom Aufbau de Roboter abhängig. Die Umrechnung auf die Poition de Endeffektor anhand de Roboteraufbau it durch die Rücktranformation bechrieben. Endpunkt Startpunkt q q Startwerte q Endwerte q 1 q 1 t Ende t Abbildung.1: Zuammenhang Gelenkwinkel zur Bewegung im Raum Der Planer liefert allerding nicht den geamten Verlauf für die Gelenkwinkel, ondern nur die neuen benötigten Sollwerte für da Einnehmen der Endpoition. E liegen alo lediglich zwei neue Werte für q 1 und q vor. In dem in Abbildung.1 auf der rechten Seite dargetellten Koordinatenytem it über die x-ache die Zeit t, über die y-ache die Gelenkwinkel q aller Achen aufgetragen. Da in dieer Arbeit die Gelenkwinkel von großer Bedeutung ind und diee für Berechnungen und zur Veranchaulichung in einen Graphen eingetragen werden, dient der Aufbau diee Koordinatenytem al Grundlage für alle weiteren Betrachtungen. 4
12 Grundlagen der Robotik Für komplexe Bewegungabläufe liefert der Planer aber nicht nur zwei, ondern gleich mehrere Werte. Die it chon bei relativ einfachen Bewegungabläufen nötig. Soll der Roboter beipielweie um eine Ecke fahren, o ind mindeten drei Winkeltellungen nötig. Die ind der Anfang- und Endwert und der Winkel im Eckpunkt. Diee Soll-Winkeltellung zwichen dem Start- und dem Zielwert wird Via-Punkt genannt [6]. In der Literatur exitieren unterchiedliche Definitionen für einen Via-Punkt. Zum einen gibt e die Vorgabe, da die Trajektorie genau durch dieen Punkt verlaufen oll. Dabei oll die Gechwindigkeit, mit der ich der Antrieb dreht, aber nicht null werden, wie e zum Beipiel der Fall wäre, wenn zwei Punkt zu Punkt Verbindungen nacheinander augeführt werden [6]. Eine andere Definition gibt an, da diee Winkeltellung im Via- Punkt nicht genau eingenommen, ondern nur angenähert wird, die Gechwindigkeit it hierbei aber auch nicht null [6]. In dieer Arbeit dient die zweite Definition al Grundlage, jedoch mit dem Zuatz, da eine maximale Abweichung vorgegeben werden kann. Zur Veranchaulichung eine Via-Punkte wird al Beipiel ein x-y-portal, ähnlich dem Aufbau eine Kran in einer Halle, herangezogen. Dabei it ein Motor für die Bewegung in x-richtung, ein zweiter für die Bewegung in y-richtung verantwortlich. Da Portal oll ich von einem Startpunkt über einen Via-Punkt zum Endpunkt bewegen. Die Motoren an den Antriebachen müen dabei den Winkel vom Itwert zum erten Sollwert für den Via-Punkt und anchließend zum zweiten Sollwert für den Endpunkt einnehmen. Schematich dargetellt it ein olche Portal in Abbildung.. Eingezeichnet ind dabei der Verfahrweg mit Via-Punkt und die dazu nötigen Gelenkwinkel. Die Winkeltellung q 1 gehört zu dem erten Motor, q it für den zweiten. Die Itwerte der beiden Antriebe ind bei einer Zeit von t = eingezeichnet. Die Soll-Winkeltellungen für den Via-Punkt ind über den Zeitpunkt t via, für den Endwert über t Ende eingetragen. 5
13 Grundlagen der Robotik y 3 Endpunkt q Via-Punkte q y Via-Punkt Hinderni q 1 y 1 Startpunkt x x 1 x 3 x t Start t via t Ende t Abbildung.: Bahnverlauf eine x-y-portal mit Via-Punkt Da in dieer Arbeit der Via-Punkt o definiert it, da eine maximale Abweichung vorgegeben werden kann, mu noch kurz auf die Auwirkung einer Toleranz eingegangen werden. Auch für diee Beipiel wird ein x-y-portal zu Rate gezogen. Die Toleranz wird für die Soll-Gelenkwinkel vorgegeben. Bei dem Portal ind zwei Gelenkwinkel für die Poition verantwortlich. Werden nun für beide Achen Toleranzen zugelaen, o ergibt ich au einem einzigen Startpunkt ein ganzer Bereich. Bei gleicher Dimenionierung der Achen und gleichen Toleranzen it dieer Bereich quadratich. In der folgenden Abbildung ind die die grauen Quadrate. y /y 3 Via-Punkt Endpunkt q Toleranz q Toleranz q 1 y 1 Startpunkt x 1 /x x 3 x t Start t via t Ende t Abbildung.3: Poitionabweichungen durch Toleranzen im Gelenkwinkel Die Toleranz oll nicht nur an den einzelnen Punkten, die der Planer vorgibt, eingehalten werden oll, ondern auch in den Übergangbereichen. Dehalb 6
14 Grundlagen der Robotik wird im Koordinatenytem, in dem die Winkel eingetragen werden, nicht nur die Abweichung an den Punkten, ondern auch dazwichen begrenzt. Dadurch ergibt ich ein Toleranzband, welche nicht verlaen werden darf. Die Dartellung de Toleranzbande im Koordinatenytem und de dazugehörigen möglichen Bereich, den da Portal einnehmen kann, it nachfolgend dargetellt. Beipielhaft it die Auwirkung auf den Verlauf de Pfade, wenn die Gelenkwinkel nicht exakt eingehalten werden, in rot eingezeichnet. Diee Toleranzband it von großer Bedeutung, da e ehr viele mathematiche Möglichkeiten gibt, um zwei Punkte, alo zwei Gelenkwinkel im Koordinatenytem, miteinander zu verbinden. Mögliche Funktionen ind in Abbildung.5 dargetellt. Die getrichelten Verbindungen halten diee Toleranzband eventuell nicht ein. y /y 3 Via-Punkt Endpunkt q Toleranzband q Toleranz q 1 y 1 Startpunkt x 1 /x x 3 x t Start t via t Ende t Abbildung.4: Zuläige Toleranzband zum Einhalten einer vorgegebenen Abweichung q q Ende q t t Ende t Abbildung.5: Verchiedene Möglichkeiten für Punkt zu Punkt Verbindungen 7
15 Grundlagen der Robotik Al nächte folgt die Erklärung, wehalb überhaupt Trajektorien generiert werden müen. Wie oeben bechrieben, dienen al Auganglage verchiedene Winkelwerte für jede Ache de Roboter. Im einfachten Fall oll ich der Roboter von einem Startpunkt zu einem Endpunkt bewegen. Der Planer liefert alo zunächt einen Startwinkel in einem Robotergelenk. Im Normalfall it der Startwert auch der Itwert de Gelenk. Der zweite Wert, den der Planer liefert, it der Gelenkwinkel, den der Roboter einnehmen mu, um zum Endpunkt zu gelangen, alo der Sollwert. E ind zwei Winkeltellungen für ein Gelenk vorgegeben, die ichertellen, da der Roboter im Raum genau der geplanten Bahn folgt. Der Motor, der die Ache antreibt, mu o angeteuert werden, da ich diee zur Endtellung dreht. Derzeitige Motorregler benötigen jede Milliekunde einen Sollwert. Wird dieem Regler der neue Soll-Winkel übergeben, o bedeutet die eine prunghafte Änderung de Sollwert. Da der neue Wert möglicht chnell erreicht werden oll, it e üblich, da der Regler einen Überchwinger erzeugt, alo die Auganggröße den Sollwert überteigt. Ein Verhindern de Überchwingen bedeutet, da der neue Sollwert aymptotich erreicht wird, wa allerding erheblich mehr Zeit benötigt. Beer it e nicht einfach nur die neue Winkeltellung zu übergeben, ondern au dem It- und dem Sollwert eine tetige Funktion zu generieren, die zu jedem Abtatzeitpunkt de Regler eine neue Soll-Winkeltellung liefert, o da die Fähigkeiten de Antrieb optimal genutzt werden. Diee Funktion bechreibt nicht nur den zeitlichen Verlauf der Winkeltellungen, ondern durch die erte und zweite Ableitung auch die Gechwindigkeit, mit der ich die Motoren drehen ollen, owie die Bechleunigung, mit denen diee beaufchlagt werden. Die dritte Ableitung entpricht dem Ruck j. Für die Forderung von ynchroniierten Trajektorien gilt e die verchiedenen Arten der Synchroniation zu erörtern. Diee Betrachtung it ert bei der Planung von mehreren Achen notwendig. Bei der Bewegung eine Roboterarm werden nicht nur die Winkeltellungen in einer Ache, ondern meiten ogar in jeder Ache verändert. In dieem Fall wird für jeden Motorregler an jeder Ache eine Trajektorie geplant. Soll eine jede Ache genau zum gleichen Zeitpunkt mit der Bewegung beginnen und auch wieder enden, o pricht man von 8
16 Grundlagen der Robotik halb-ynchron bzw. von zeit-ynchronen Trajektorien [7]. Voll-ynchron bedeutet, da eine jede Trajektorie nicht nur die gleiche Geamtzeit benötigt, ondern da alle Bewegungphaen gleich lange dauern. Da bedeutet, da alle Achen genau die gleiche Zeit zum Bechleunigen und zum Verzögern benötigen, ie bewegen ich auch exakt die gleich lange Zeit mit kontanter Gechwindigkeit. Zur Verdeutlichung der unterchiedlichen Auwirkungen von aynchronen, zeit-ynchronen und voll-ynchronen Trajektorien wird al Beipiel wieder ein x-y-portal herangezogen. Die Motoren an den Antriebachen müen dabei den Winkel von einem Startwert zu einem Endwert ändern, um da Portal vom Startpunkt zum Endpunkt zu bewegen. Eingezeichnet ind in Abbildung.6 die verchiedenen Verfahrwege, die ich mit unterchiedlicher Synchronität ergeben. Der Verlauf mit der Nummer ein kommt zutande, wenn zuert Motor ein und ert nach Beenden diee Verfahrvorgang Motor zwei mit dem neuen Sollwinkel angeteuert wird. Typich für die Anteuerung mit aynchronen Trajektorien it dabei der Verlauf zwei. Die Bewegung in y-richtung wird zuert beendet, die Bewegung in x-richtung it dabei noch nicht abgechloen. Zeit-ynchron it der Verlauf der Bahn drei. Hier beginnen und beenden beide Antriebe zum gleichen Zeitpunkt ihre Bewegung, jedoch ind die einzelnen Bewegungphaen nicht ynchron. Die Bewegung in x-richtung verläuft chon kontant, während ich der Antrieb in y-richtung noch in der Bechleunigungphae befindet. Ert im Bewegungverlauf Nummer vier, welcher eine direkte Gerade zwichen dem Start- und Endpunkt bechreibt, handelt e ich um eine Anteuerung mit voll-ynchronen Trajektorien. Beide Antriebe benötigen die gleiche Zeit für den Bechleunigungvorgang. Die Phae, in der die Gechwindigkeit einen kontanten Wert beitzt, dauert ebeno bei beiden Achen gleich lange. Auch der Verzögerungvorgang it zeitlich ynchron. Die Abbildung verdeutlicht, da ich unterchiedliche Synchronitäten gravierend auf den realen Bahnverlauf eine Roboter auwirken. Der Wegplaner geht aber immer von einer direkten Verbindung von Start- und Endpunkt au. Werden alo nicht voll-ynchrone Trajektorien geplant, o it e möglich, da der Roboter von der Bahn abweicht und dadurch eventuell Hindernie 9
17 Grundlagen der Robotik durchfahren würde, wa zu einer Bechädigung de Roboter oder de Hindernie führen kann. y Endpunkt Startpunkt x Abbildung.6: Bahnverläufe mit unterchiedlichen Synchronitäten Die Schwierigkeiten, die bei der Generierung von ynchroniierten Trajektorien auftreten, ind im Abchnitt bechrieben. E ei aber bereit jetzt erwähnt, da voll-ynchrone Trajektorien zeitlich geehen nicht der chnellten Verbindung von Start- und Endpunkt entprechen. Halb-ynchrone Trajektorien wie Nummer zwei und drei ind meit chneller. Neben den Bedingungen, die ich au dem Titel der Bachelorarbeit ergeben, gibt e aber noch weitere Eigenchaften, die erfüllt werden müen. Diee wären zum Beipiel, da für die Trajektorienplanung die Grenzen der Antriebe berückichtigt werden müen. Die ind im Beonderen die maximale Gelenkwinkelgechwindigkeit, alo wie chnell ich ein Antrieb drehen kann, um den Gelenkwinkel zu verändern. Außerdem mu die maximale Bechleunigung de Motor eingehalten werden. Wünchenwert wäre auch noch eine Begrenzung de Ruck, alo der Ableitung der Bechleunigung, die kann aber al optional betrachtet werden. Darau folgt, da die Trajektorie glatt, alo tetig differenzierbar ein mu. Diee Forderung berückichtigt, da der Motor keinen Sprung in der Gechwindigkeit oder dem Gelenkwinkel auführen kann, die Änderung der Gechwindigkeit it immer tetig. Für eine Begrenzung de 1
18 Grundlagen der Robotik Ruck mu die Trajektorie dreimal ableitbar ein. Die zweite Ableitung, alo die Bechleunigung mu dann tetig, aber nicht differenzierbar ein.. Trajektorienplanung Prinzipiell kann zwichen Pfadplanung und Trajektorienplanung unterchieden werden. Vor allem in Kapitel 4 bei der entkoppelten Trajektorienplanung it diee Untercheidung ehr wichtig, wehalb chon jetzt kurz darauf eingegangen wird. Die Pfadplanung legt die geometriche Bahn fet, auf der ich der Roboter zwichen einem Start- und einem Zielpunkt bewegen oll. Die Trajektorienplanung bechreibt den Verlauf der Gechwindigkeit und Bechleunigung, mit der der Roboter entlang der Bahn verfahren oll. Da heißt bei der Pfadplanung wird der geometriche Verlauf der Bahn unabhängig von der Gechwindigkeit bzw. de zeitlichen Verlauf fetgelegt [8]. In den meiten nachfolgend vorgetellten Anätzen wird aber ofort verucht da Erreichen de vorgegebenen Winkel zeitabhängig zu betimmen, e wird alo direkt eine Trajektorie geplant. Im Koordinatenytem, in dem die Gelenkwinkel eingezeichnet ind, it die Untercheidung zwichen Pfad- und Trajektorienplanung an der Bechriftung der x-ache zu erkennen. Wird eine Trajektorie geplant, o repräentiert die x-ache die Zeit t, bei der Pfadplanung werden die Gelenkwinkel über den Bahnparameter aufgetragen. 11
19 3 Stand der Technik Für die Trajektorien- bzw. die Pfadplanung gibt e bereit eine Vielzahl von Anätzen. In dieem Kapitel wird ein Überblick über die meiten derzeit in der Literatur vertretenen Löungvorchläge gegeben. Sie werden in kurzen Beipielen erläutert und e wird außerdem auf die Vor- und Nachteile eingegangen. Anhand dieer Unteruchung oll verdeutlicht werden, wehalb die Wahl auf den Anatz der entkoppelten Trajektorienplanung gefallen it. 3.1 Analytiche Anätze Zur Veranchaulichung aller hier vorgetellten Verfahren werden die Gelenkwinkel wieder in Koordinatenytemen dargetellt. Wie in Abbildung.6 im Kapitel.1 dargetellt, oll eine mathematiche Funktion gefunden werden, die zwei Punkte, welche verchiedene Winkeltellungen eine Robotergelenke repräentieren, miteinander verbinden. Da heißt da Gelenk dreht ich von einer vorgegebenen Auganglage in eine gewünchte Endlage. Bei einigen Beipielen ollen zwichen dieem Verfahrweg weitere Winkeltellungen eingenommen werden. Die it vor allem dann nötig, wenn z. B. der Roboterarm eine weite Strecke zurücklegt und dabei ein Hinderni umfahren oll. Diee gewünchten Winkel zwichen der Anfang- und der Endpoition werden Via-Punkte genannt. Da Gelenk oll alo verchiedene vorgegebene Poitionen einnehmen. Diee Bedingungen werden im Kapitel.1 abgehandelt. Gültig für alle Anätze it die Bedingung, da die Gechwindigkeit de Gelenk am Anfang und am Ende null it, e ich alo au dem Stilltand herau in Rotation veretzt, und am Ende wieder zum Stehen kommt. Der Gelenkwinkel wird mit q bezeichnet, die Gelenkwinkelgechwindigkeit v oder q, die Gelenkwinkelbechleunigung a bzw. q Punkt zu Punkt Die einfachte Aufgabentellung bei der Trajektorienplanung it die Verbindung von Punkt zu Punkt. Die einfachte mathematiche Funktion, die zwei Punkte 1
20 3 Stand der Technik miteinander verbindet, it eine Gerade. Da diee Gerade überall die gleiche Steigung und damit eine kontante Gechwindigkeit aufweit, wird die Bedingung, da Start- und Endgechwindigkeit null ein oll, nicht erfüllt. E wird eine Funktion benötigt, welche vier Bedingungen erfüllt. Nämlich da Erreichen der vorgegebenen Start- und Endwinkel owie die, da Start- und Endgechwindigkeit, alo die 1. Ableitung der Funktion, null it. Um diee vier Bedingungen zu erfüllen it eine Funktion mit vier freien Koeffizienten nötig, alo z. B. ein Polynom dritten Grade. Siehe hierzu Formel (3.1). Wird dazu noch die Zeit vorgegeben die benötigt wird um vom Startpunkt zum Endpunkt zu gelangen, o kann da Polynom folgendermaßen berechnet werden [6]. Ein kubiche Polynom hat die Form: q( t) t Die erte und zweite Ableitung ergeben ich zu: 3 a a1t at a3 (3.1) q ( t) a 1 q ( t) a a t 3a t 6a t 3 3 (3.) Da Erreichen der Start- und Endwinkel q a und q e ergibt folgende Audrücke: q( t q() q ende ) q a e (3.3) Die Vorgabe der Start- und Endgechwindigkeit von /: q () q ( ) t ende (3.4) Dadurch ergeben ich folgende Gleichungen: q q a e a a a a 1 1 a t a 1 a t ende t a t 3 3a t 3 3 ende (3.5) 13
21 3 Stand der Technik Aufgelöt ergibt ich dann für die 4 Koeffizienten: a a a a 1 3 q a 3 ( q ) e qa tende ( q ) 3 e qa t ende (3.6) Geplottet für eine Zeit von 4 Sekunden ergibt ich dabei der nachfolgend dargetellte Verlauf. 1 Gelenkwinkel q in Gechwindigkeit v in / Bechleunigung a in / Zeit in Abbildung 3.1: Punkt zu Punkt Verbindung mit Polynome dritten Grade Der Verlauf de Gelenkwinkel beginnt und endet bei den gewünchten Werten, die Gechwindigkeit, alo die 1. Ableitung it in dieen Punkten Null. Für die Zeit wurde t = 4 vorgegeben. Außerdem it noch die. Ableitung abgebildet, alo der Verlauf der Bechleunigung. Allgemein kann die Auage getroffen werden, da der Verlauf de Gelenkwinkel ehr glatt it. Al größter Nachteil bei dieem Anatz gilt, da die Zeit vorgegeben werden mu. Der 14
22 3 Stand der Technik Spitzenwert der Gelenkwinkelgechwindigkeit, al auch die Spitzenwerte bei der Bechleunigung, ergeben ich aufgrund der Vorgabe der Zeit. E könnte zwar, durch Auflöen von (3.), eine Zeit ermittelt werden, die entweder eine maximale Gechwindigkeit oder die Bechleunigung berückichtigt, beide it jedoch nicht möglich. Genau die it unerwüncht, e ollen die maximal zuläigen Werte für die Bechleunigung und die Gechwindigkeit de Gelenke vorgegeben werden können. Die Zeit oll, mit der Bedingung möglicht kurz zu dauern, au dieen Größen ermittelt werden. Ein anderer gebräuchlicher Anatz für die Punkt zu Punkt Verbindung it der Anatz einer Geraden mit parabolichen Enden [6]. Siehe hierzu Abbildung 3.. Dabei etzt ich die Funktion au parabolichen Teiltücken, welche für die Bechleunigung zutändig ind, und au einer Geraden, welche für eine kontante Gechwindigkeit orgt, zuammen. Die parabolichen Teile ind in blau, da gerade Teiltück it in rot eingezeichnet. Auch bei dieer Funktion mu für die Berechnung die Zeit vorgegeben werden, die Gechwindigkeit wird darau ermittelt. Ein Vorteil bei dieem Anatz it allerding, da die Bechleunigung chon begrenzt werden kann. Durch Variation der maximalen Bechleunigung a max kann die Dauer der Bechleunigung und der Verzögerung beeinflut werden. Ein größere a max verkürzt diee Vorgänge, eine Verkleinerung bewirkt eine Verlängerung. Die Berechnung der einzelnen Funktionen it nachfolgend aufgeführt. Die Gechwindigkeit am Ende de Parabelbogen mu gleich groß der Gechwindigkeit de linearen Teil ein. Der Wert von q b it gegeben durch: q q h b qt b (3.7) th tb q b q q t (3.8) 1 b Der Hilfpunkt q h kann ermittelt werden mit: q h q f q (3.9) 15
23 3 Stand der Technik Durch Kombination von (3.7) mit (3.8), einetzen von (3.9) owie der Bedingung t = t h ergibt ich: b q q q t qt t (3.1) b Dabei it t die geamte Zeit für die Bewegung, im folgenden Beipiel it t = 4. Die. Ableitung von q, alo die Bechleunigung kann vorgegeben werden. Damit eine Löung exitiert, mu diee groß genug ein. Mit dieen Werten kann die Dauer de Bechleunigungvorgang berechnet werden. t b f t q t 4q q f q (3.11) q Die Bechleunigung mu dabei folgende Bedingung erfüllen. Beträgt die Bechleunigung genau gleich der Bedingung (3.1), chrumpft der lineare Anteil auf die Länge Null. Die Kurve beteht nur au einem Bechleunigung- und Verzögerungvorgang. 4 q f q (3.1) t q 16
24 3 Stand der Technik Geplottet ergibt ich folgender Verlauf. 1 Gelenkwinkel q in v in / q q h qf-b f 5 q b q t b t h t f -t b Gechwindigkeit Bechleunigung a in / Zeit in Abbildung 3.: Punkt zu Punkt Verbindung durch Gerade mit parabolichen Enden 3.1. Mit Via-Punkt Bei den beiden in Abchnitt vorgetellten Anätzen wird der Gelenkwinkel nur von einem Anfangwert auf einen Endwert vertellt. Im Folgenden werden diee beiden Anätze o erweitert, da auch vorgegebene Werte zwichen dieen beiden Zutänden, o genannte Via-Punkte, eingenommen werden. Al erte wird da Polynom dritten Grade betrachtet. Um nun alo einen weiteren Punkt im Gelenkwinkelraum einzunehmen, müte entweder die Ordnung de Polynom erhöht werden oder e werden mehrere Polynome dritter Ordnung aneinander gefügt [6]. Im Folgenden wird davon augegangen, da ein Via-Punkt vorhanden it. Dafür werden zwei Polynome dritten Grade verwendet, welche folgende Bedingungen erfüllen müen. Die Gechwindigkeit mu am Anfang- und am Endpunkt null ein, im Via-Punkt, alo dort wo ich die zwei Polynome treffen, mu die Gechwindigkeit tetig differenzierbar ein. 17
25 3 Stand der Technik Die Bechleunigung mu im Übergangpunkt tetig ein. De Weiteren oll da erte Polynom den Startwert und den Via-Punkt erreichen, da zweite oll vom Via-Punkt bi zum Endpunkt gehen. Somit ergeben ich zwei Funktionen dritten Grade mit je vier Koeffizienten. Da oben genau acht Bedingungen bechrieben wurden, können die ingeamt acht Koeffizienten berechnet werden. Die it nachfolgend dargetellt [6]. Die erte Funktion berechnet ich mit: Die zweite it: q( t) t 3 a1 a11t a1t a13 (3.13) q( t) t 3 a a1t at a3 (3.14) Jede Formel beginnt bei t = und endet bei t = t ende a 11 a t 1 ende1 a 1 3a 6a t 13 ende1 t q q q q v v e 13 ende1 a a a a a a a a a a a t 11 ende1 t 1 ende t a ende a t 1 ende1 t ende 3a t a a 3 ende t 3 13 ende1 t 3 3 ende (3.15) 18
26 3 Stand der Technik Aufgelöt mit der Bedingung t ende1 it genau o lang wie t ende ergibt ich o für die Koeffizienten: a a a a a a a a q 1qv 3qe 9q 4tende 8qv 3qe 5q 3 4tende qv 3qe 3q 4tende 1qv 6qe 6q 4t ende 8qv 5q 3q 4t e 3 ende (3.16) Wird nun wieder eine Zeit für jede Funktion von vier Sekunden vorgegeben, o ergibt ich der in Abbildung 3.3 dargetellte Verlauf. Dabei it in blau die erte, in rot die zweite Funktion dargetellt. Im Übergang der beiden Funktionen it der Via-Punkt q v. Bei dieem Vorgehen ergeben ich allerding die gleichen Nachteile wie bei dem Polynom dritter Ordnung ohne Via-Punkt. Die Zeit mu vorgegeben werden, owohl der Spitzenwert der Gelenkwinkelgechwindigkeit al auch die Spitzenwerte bei der Bechleunigung ergeben ich aufgrund der vorgegebenen Zeit. Die Maximalwerte können nicht begrenzt werden. 19
27 3 Stand der Technik 1 Gelenkwinkel q in 5 q q v qe Gechwindigkeit v in / Bechleunigung a in / Zeit in Abbildung 3.3: Verbindung mit Via-Punkt mit Polynome dritten Grade Bei dem Verfahren mit Geraden und parabolichen Enden it folgende Vorgehen üblich [6]. Der erte und der letzte Parabelbogen werden äquivalent der Berechnung der Parabelbögen ohne Via-Punkt durchgeführt. Für die Via- Punkte wird eine andere Vorgehenweie angewandt. Im Beipiel in Abbildung 3.4 werden die Punkte zwei und drei owie die Punkte drei und vier mit einer Geraden verbunden. Die Steigungen dieer Geraden werden entweder über die Vorgabe der Zeit oder durch Vorgabe einer maximalen Winkelgechwindigkeit berechnet, wobei die Steigung die Gechwindigkeit repräentiert. Die Steigung m berechnet ich mit Vorgabe der Zeit folgendermaßen: q m (3.17) t Vorgabe der maximalen Gelenkwinkelgechwindigkeit v ergibt die Zeit t. q t (3.18) v max
28 3 Stand der Technik Da heißt bei dieem Anatz kann bereit eine Maximalgechwindigkeit vorgegeben werden, die Zeit wird darau ermittelt. Üblich it die Vorgabe der Zeit. Die Vorgabe der maximalen Bechleunigung hat Einflu auf die Krümmung der Parabelbögen und it omit für die Verbindungtücke zwichen den Geraden zutändig. Im Übergang von der Geraden auf die Parabel mu al Bedingung berückichtigt werden, da die Gechwindigkeit gleich groß it. q in v in / Gelenkwinkel Gechwindigkeit Bechleunigung a in / Zeit in Abbildung 3.4: Verbindung von Via-Punkten durch Geraden mit parabolichen Enden Anwendung auf mehrere Achen Üblicherweie wird bei der Bewegung eine Roboterarm nicht nur eine Ache verändert, ondern mehrere. In dieem Fall mu natürlich für jede Ache der Bewegungablauf geplant werden. Werden mit dem oben vorgetellten Anatz der Geraden mit parabolichen Enden mehrere Achen berechnet, lät ich in Abbildung 3.5 ehr chnell die Problematik erkennen, die bei einer geforderten ynchronen Berechnung von zwei Achen auftritt. Gerade in dem unten dargetellten Beipiel wird der chlechtete Fall gezeigt. Die erte Ache, alo der 1
29 3 Stand der Technik blaue Verlauf, hat eine maximale Winkelgechwindigkeit von 15 / und eine Bechleunigung von /. Die zweite, rot eingezeichnete Ache, erlaubt eine maximale Gechwindigkeit von / bei einer Bechleunigung von 15 /. Da Verhältni von Bechleunigung zur Gechwindigkeit it alo genau entgegengeetzt. Die Forderung nach Halb-Synchronität etzt vorau, da beide Achen die gleiche Zeit benötigen [7]. Die kann durch Herabkalieren der Gechwindigkeit der zweiten Ache realiiert werden. Wird aber wie in der Aufgabentellung volle Synchronität gefordert, müen auch die Phaen der Bechleunigung und die Phaen mit kontanter Gechwindigkeit bei beiden Achen gleich lange dauern [7]. Im eben vorgetellten Beipiel würde da (bei dem verwendeten Anatz) die Verfahrdauer beider Achen maximal verlängern. E mu nämlich die Gechwindigkeit der chnelleren Ache herunter kaliert werden, während die Ache mit der größeren Bechleunigung diee verkleinern mu. Da heißt, da bei voller Synchronität beide Achen mehr Zeit benötigen, al davor die langamere benötigt hat. 1 Gelenkwinkel q in Gechwindigkeit v in / Bechleunigung a in / Zeit in Abbildung 3.5: Zwei Achen mit unterchiedlichen Grenzwerten
30 3 Stand der Technik Ein reine Begrenzen der maximalen Gechwindigkeit auf die geringte Gechwindigkeit von allen Achen owie die Begrenzung der Bechleunigung auf die geringte Bechleunigung it dabei nicht zielführend. Im oben dargetellten Beipiel würde die zwar ehr gut funktionieren. Wenn aber zum Beipiel die langamte Ache nur eine geringe oder keine Änderung de Gelenkwinkel vornehmen mu, o kann eine chnellere Ache ehr wohl mit ihrer maximalen Gechwindigkeit bewegt werden. Möglich wäre, da die langamte Ache immer die gleiche Winkeltellung beitzen oll, während ich eine andere Ache bewegt. In dieem Fall dürfen die chnelleren Achen nur eingebremt werden, wenn die langamen Achen auch tatächlich den Gelenkwinkel verändern Vor- und Nachteile Bei den Anätzen von Polynomen 3. Ordnung it der größte Vorteil, da die Löung analytich ehr einfach berechnet werden kann. Al Nachteil mu zum einen erwähnt werden, da die Zeiten zwichen den einzelnen gewünchten Gelenkwinkeln vorgegeben werden müen und ich die Gechwindigkeiten owie die Bechleunigungen darau ableiten. Genau diee Eigenchaften ind bei einem Trajektorien-Planer am wenigten erwüncht. Viel mehr ollte nur anhand der Vorgabe von gewünchten Winkeln und der maximalen Gechwindigkeit und Bechleunigung eine Trajektorie geplant werden, welche die kürzete Zeit benötigt. Al anderer Nachteil it die Unvorherehbarkeit der Trajektorie zu nennen. Bei dieem Anatz wird zwar ichergetellt, da die gewünchten Winkeltellungen ohne Abweichung eingenommen werden, auf den Verlauf zwichen dieen Punkten kann o aber kein Einflu genommen werden. Da Toleranzband würde unter Umtänden verlaen werden. Siehe hierzu nachfolgende Abbildung. In dieem Beipiel werden drei Winkel vorgegeben. Diee ind, 9 und 5. Nach dem Erreichen de zweiten Werte von 9 nimmt der Betrag der Winkeltellung weiter zu, hier auf 38, und verringert ich ert päter auf den Endwert. Werden von einem übergeordneten Planer diee drei Werte vorgegeben, o it e nicht erwüncht, da dazwichen andere Maximalwerte eingenommen werden, zumindet mu aber ichergetellt werden, da da Toleranzband nicht verlaen wird. Die kann mit dieem 3
31 3 Stand der Technik Anatz aber nicht garantiert werden. In der Abbildung beträgt die zuläige Toleranz ogar beachtliche ± und wird trotzdem überchritten. Würden diee Werte auf einen Roboterarm übertragen werden, o wäre e möglich, da dieer dadurch von der eigentlich geplanten Bahn abweicht und Hindernie durchfährt. 4 Gelenkwinkel q in v in / X: Y: X: 4 Y: 9 X: 4.91 Y: 38. X: 8 Y: Gechwindigkeit Bechleunigung 1 a in / Zeit in Abbildung 3.6: Abweichung vom Toleranzband bei zwei Polynome dritten Grade Beim Anatz der Geraden mit parabolichen Enden bzw. Übergängen ergeben ich mehrere Vorteile. Bereit bei dieem relativ einfachen Anatz kann die Gechwindigkeit und die Bechleunigung begrenzt werden. Anhand dieer Grenzen wird nun die Zeit ermittelt, die zum Erreichen der vorgegebenen Winkelwerte benötigt wird. Da entpricht bereit den grundlegenden Eigenchaften eine Trajektorienplaner. Trotzdem eignet ich diee Vorgehenweie nicht für die zu unteruchende Aufgabentellung. Einereit können o mehrere Achen nicht bzw. nur chlecht berückichtigt werden, wie im Abchnitt bechrieben. Anderereit kann da Erreichen der Via-Punkte nicht garantiert werden. Die Abweichung, dargetellt in Abbildung 3.7, beruht auf dem Abrunden de 4
32 3 Stand der Technik Schnittpunkte der Geraden mit einem Parabelbogen. Der Abtand vom Via- Punkt zum Scheitelpunkt der Parabel it abhängig von der vorgegebenen Maximalbechleunigung. Bei einer geringeren Bechleunigung wird der Abtand größer und e kann bei Vorgabe einer maximal zuläigen Toleranz nicht garantiert werden, da diee eingehalten wird. E wäre zwar denkbar, da durch Einfügen weiterer Peudo-Punkte die eigentlichen Via-Punkte getroffen werden [6], zeitoptimal wäre der Planer dadurch allerding nicht mehr. 9 Gelenkwinkel q in Zeit in Abbildung 3.7: Abweichung vom Toleranzband bei Geraden mit parabolichen Enden Außerdem mu die maximale Gechwindigkeit und Bechleunigung in einem einigermaßen innvollen Zuammenhang tehen, anonten wird der Abtand zu den Via-Punkten viel zu groß und die Trajektorie chwingt nur zwichen den einzelnen Sollwerten hin und her. In Abbildung 3.8 it die Bechleunigung zu klein um die Maximalgechwindigkeit erreichen zu können. Durch einen vermichten Anatz von Vorgabe der Zeitwerte und der Gechwindigkeiten ließe ich diee Problem zwar eventuell umgehen, allerding oll die Zeit elbttändig errechnet werden. Ein weiterer Nachteil it außerdem, da immer die 5
33 3 Stand der Technik maximal mögliche Bechleunigung verwendet wird. Diee Verhalten kann zu einem erhöhten Verchleiß der Robotertruktur führen [8]. 5 Gelenkwinkel q in Gechwindigkeit v in / Bechleunigung a in / Zeit in Abbildung 3.8: Abweichung vom Sollverlauf durch unangepate Werte Eine kurze Übericht über alle Vor- und Nachteile der vorgetellten Anätze, aber auch chon der Anätze im Kapitel owie de Anatze im Kapitel 3., Trajektoriengenerierung mit nichtlinearem Filter, gibt die nachfolgende Tabelle. Polynome dritten Grade Gerade parabelförmige Enden Funktionen höherer Ordnung Nichtlineare Filter Ermittlung der Zeit Analytiche Löung Abweichung von Via- Punkten Begrenzung der Maximalwerte Berückichtigung mehrer Achen Nein Ja Nein Nein Nein Teil Ja Ja Teil Nein Nein Ja Nein Nein Nein Nein Nein Ja Ja Nein 6
34 3 Stand der Technik Mögliche Erweiterungen In dieem Abatz wird vorgetellt wie bei einer geplanten Trajektorie die Zeit iterativ o verlängert bzw. verkürzt wird, bi die maximalen Werte der Bechleunigung und der Gechwindigkeit erreicht werden [1]. Al Grundlage kann hier der Anatz von den Polynomen dritten Grade, aber auch die im nächten Abchnitt vorgetellten Anätze verwendet werden. E wird im erten Schritt eine Trajektorie geplant, die eine betimmte Verfahrdauer hat. Im nächten Schritt wird geprüft, ob ich die Werte der Bechleunigung und der Gechwindigkeit innerhalb der fetgeetzten Grenzen befinden. Befinden ie ich innerhalb der Grenzen, o wird die Zeit für die Trajektorie um eine betimmte Schrittweite verkürzt. Überchreiten die Werte bereit die Grenzen, o mu die Zeit um eine fetgelegte Schrittweite verlängert werden. Die mit dieer neuen Dauer neu berechnete Trajektorie wird wieder auf die Grenzen geprüft. Dieer Vorgang wird o lange wiederholt, bi die Grenzen erreicht werden, ie dürfen aber nicht überchritten werden. Durch dieen Vorgang kann die kürzete Zeit für eine Trajektorie ermittelt werden, welche die Grenzen für die maximale Gechwindigkeit und Bechleunigung einhält. In der Abbildung 3.9 link wird eine chrittweie Verkürzung der Zeit dargetellt. In der rechten Abbildung it die neue Trajektorie mit der kürzeten möglichen Zeit abgebildet. In dieem Beipiel werden al Grenzen für die maximal Winkelgechwindigkeit ±3 / und für die maximale Winkelbechleunigung ± / angenommen. Die Zeit wird o lange verkürzt, bi diee Grenzen genau erreicht werden. Gelenkwinkel Gelenkwinkel q in 1 q in Gechwindigkeit Gechwindigkeit 5 v in / v in / Bechleunigung Bechleunigung a in / Zeit in a in / Zeit in Abbildung 3.9: Iterative Anpaen an Grenzwerte mit darau reultierendem Verlauf 7
35 3 Stand der Technik Weitere Funktionen In den vorherigen Abchnitten wurden Polynome dritten Grade und Geraden mit parabolichen Enden vorgetellt. Neben dieen Funktionen gibt e noch eine Vielzahl an weiteren mathematichen Vorgehenweien, mit denen Punkte im Gelenkwinkelraum verbunden werden können. In dieem Abchnitt wird ein kurzer Überblick über weitere Möglichkeiten gegeben. Al erte wird ein Polynom fünften Grade vorgetellt. Diee Polynom kann ech Bedingungen erfüllen. Die wäre der gewünchte Anfang- und Endwinkel, die Anfang- und Endgechwindigkeit owie die Anfang- und Endbechleunigung [1]. Bei einem Polynom iebten Grade kann neben den oeben vorgetellten Bedingungen auch noch der Anfang- und Endruck vorgegeben werden [1]. Der Ruck tellt die Ableitung der Bechleunigung dar. Ebeno können auch Polynome noch höheren Grade verwendet werden. Bei dieen drei vorgetellten Berechnungen bleiben aber die Nachteile wie beim Polynom dritten Grade betehen. Hinzu kommt, da die maximalen Werte der Ableitungen mit teigendem Grad anteigen [1]. Eine weitere Möglichkeit, Punkte im Gelenkwinkelraum zu verbinden, bieten trigonometriche Funktionen. Al Vorteil kann dabei angeehen werden, da für diee Funktionen jede beliebige Ableitung gebildet werden kann. Al Nachteil mu aber gelten, da mit dieen Funktionen nur zwei Punkte im Gelenkwinkelraum verbunden werden können. Via-Punkte können omit nicht berückichtigt werden. Außerdem können die Ableitungen am Start- und Endwert einen Sprung aufweien. Im Folgenden werden trotz der Nachteile drei verchiedene Anätze von trigonometrichen Funktionen vorgetellt [1]. Dabei it der erte Winkel q, der zweite it q 1. Harmoniche Bewegung: q h ( t) 1 co q t t T (3.19) Dabei gilt h = q 1 q und T = t 1 t 8
36 3 Stand der Technik Zykloidiche Trajektorie: q t t 1 ( t) in q T t t T (3.) Elliptiche Trajektorie: h tt co T q( t) 1 q tt 1 in T (3.1) Mit α = (n - 1)/n, n it da Verhältni von großer zu kleiner Ache. Neben dem vorgetellten Anatz der Gerade mit parabolichen Enden können auch weitere zuammengeetzte Funktionen verwendet werden. Diee ind z. B. Geraden mit kreiförmigen Enden oder auch Geraden mit polynomichen Enden. Der Grad der polynomichen Funktionen kann dabei nahezu beliebig gewählt werden. Antatt dem geraden Abchnitt in der Mitte kann auch eine Funktion dritten Grade verwendet werden. Die Endtücke werden dabei mit Funktionen vierten Grade berechnet [1]. Diee oeben vorgetellten Anätze eignen ich aber nur für Punkt zu Punkt Verbindungen und ind dewegen für die gegebene Aufgabentellung unbrauchbar. Für die Verbindung von Via-Punkten können weitere, unterchiedliche Anätze verwendet werden. Um beipielweie acht Punkte zu verbinden würde au rein mathematicher Sicht ein Polynom iebten Grade genügen. Müen nun mehrere Via-Punkte verbunden werden, o teigt auch der Grad der Funktion. Die kann zu einem tarken Ozillieren der Funktion führen. Au dieem Grund it dieer Anatz zu verwerfen. Anätze, welche die Via-Punkte nur approximieren, können von vornherein augechloen werden, da damit die maximal zuläige Toleranz an den einzelnen Punkten nicht mehr garantiert werden kann. Eine normalerweie ehr beliebte Form verchiedene Punkte miteinander zu verbinden it die Spline-Funktion. Mit dieem Anatz kann eine beliebige Anzahl von Punkten verbunden werden. Al Ergebni werden abchnittweie de- 9
37 3 Stand der Technik finierte Funktionen dritten Grade geliefert, wobei ogar die Krümmung minimiert wird. Wie aber nachfolgend in Abbildung 3.1 dargetellt, kann auch hier der Verlauf nicht vorhergeagt werden. E ergibt ich derelbe Nachteil wie bei zuammengeetzten Polynomen dritten Grade. Der Verlauf der Funktion nach dem dritten Punkt, hier bei 4, it o nicht erwüncht. Die Trajektorie ollte bei dieem Punkt ein lokale Minimum haben und nicht ert danach bzw. die Höhe de neuen lokalen Minimum ollte zumindet vorherehbar ein. Ein Verlaen de Toleranzbande it ehr wahrcheinlich. Lediglich bei ehr großen zuläigen Abweichungen bleibt die Funktion innerhalb de Bande. Die im Beipiel gewählte Abweichung von ±5 wird hier überchritten. 8 Gelenkwinkel q in Zeit in Abbildung 3.1: Abweichung von Spline-Polynome vom Toleranzband Wird antelle der Spline-Funktion die B-Spline-Funktion verwendet, ergibt ich daelbe Problem. E könnte zwar eventuell durch gechickte Vergabe der Eckpunkte der konvexen Hülle von B-Spline erreicht werden, da ich diee innerhalb der geforderten Toleranzen befinden, dennoch getaltet ich diee Vorgehen al äußert kompliziert [4]. Weitere ehr intereante Anätze ind mit Sicherheit Bezier-Kurven oder Nurb []. Hierbei ergibt ich aber auch da Problem, da die Abweichung an 3
38 3 Stand der Technik den einzelnen Punkten nicht immer eingehalten wird. Diee Funktionen folgen zwar ihrem Kontroll-Polygon, ie durchlaufen aber nicht genau die Punkte. Die Abweichung an dieen kann nicht vorhergeagt werden. 3. Trajektoriengenerierung mit nichtlinearem Filter Für die Planung von Trajektorien für Automatiierungmachinen mit mehreren Achen it die Einhaltung der Bechränkungen der Gechwindigkeit, der Bechleunigung und im beten Fall auch de Ruck von großem Interee. Normalerweie wird diee Problem offline berechnet. Ändert ich eine der Bedingungen, mu die komplette Trajektorie neu berechnet werden. Zum Einhalten der Grenzen wird in dieem Abchnitt ein neuartige Konzept vorgetellt, da dynamiche, nichtlineare Filter [1]. Diee Filter wird in Kakade zu einem Generator gechaltet, welcher Bai-Bewegungprofile erzeugt. Diee Profile ind beipielweie Sprünge oder Rampen. Die Anordnung it nachfolgend dargetellt. Da Ziel de Filter it die online Verarbeitung der Bewegungprofile und orgt o für eine auführbare Trajektorie, welche die gegebenen Grenzen einhält. v max a max j max Generator Bai- Bewegungprofile r(t) e(t) q(t) Filter Abbildung 3.11: Anordnung eine nichtlinearen Filter Da nichtlineare Filter baiert auf einer Rückkopplung und orgt dafür, da da Augangignal q(t) dem externen Referenzignal r(t) folgt und dabei da Einhalten der Grenzen der drei Ableitungen garantiert. Da Bai-Referenzignal kann in kürzeter Zeit vorgegeben werden. Sollen nun die Bechleunigung, die Gechwindigkeit und der Ruck berückichtigt werden, o wird ein Filter dritter Ordnung benötigt. In der nächten Abbildung it 31
39 3 Stand der Technik der Aufbau de Filter dargetellt. Im Anchlu werden nur die für die Implementierung notwendigen Rechenchritte erläutert [1]. r k r k r k u k T z k T 1 z k T 1 z C z q 1 z q 1 z q k Abbildung 3.1: Aufbau eine nichtlinearen Filter Da Filter kann in Echtzeit jede beliebige Standard Referenzignal r(t) in ein glatte Augangignal q(t) umwandeln und dabei folgende Bedingungen erfüllen: U v a j min min min q ( t) v q ( t) a q( t) j max max max U (3.) Der Signal-Generator kann dabei einfache Bewegungprofile wie Rampen oder Stufen erzeugen. Da Filter kann aber auch anderweitig erzeugte Signale verarbeiten, beipielweie direkt vom Bediener vorgegebene Bewegungen. E kann ebeno al Überwachungeinheit eingeetzt werden, welche da von einem eigentändigen Planer erzeugte Augangignal auf Einhalten der Grenzwerte überprüft und nur auführbare Trajektorien an die Motorregler weiterreicht. Da diee Filter digital vorliegt, mu die Zeit dikretiiert werden. Zu jedem Zeitpunkt t k = kt mit k = 1,, erhält die Variablentruktur de Regler C3 da Referenzignal r k und deen erte und zweite Ableitung, genauo wie die Werte der Poition bzw. de Gelenkwinkel q k, der Gechwindigkeit q k und der Bechleunigung q k und berechnet den Wert der Auganggröße u k, wa dem Ruck entpricht. Der Ruck mu nun dreimal integriert werden um den Gelenkwinkel zu erhalten. Dazu wird die Bechleunigung durch Rechteck- Approximation integriert, die Gechwindigkeit und die Poition mit Trapez- 3
40 3 Stand der Technik Approximation. Alternativ kann die Poition auch mit der quadratichen Approximation integriert werden. q q q k k k q q q k 1 k 1 k 1 Tu T q T q k 1 k k q q k 1 k 1 (3.3) Der Regler C 3 baiert auf der Regeldifferenz zwichen dem Referenzignal und dem Wert de Gelenkwinkel q k, bezogen auf U. Die Variable U it der maximale Wert der Augang-Variable u k und repräentiert omit den Ruck j. e k qk rk q k r k, e k, U U e k q k rk (3.4) U Die Grenzen für die maximale bzw. minimale Gechwindigkeit und Bechleunigung werden auf die Variablen ė k und ė k übertragen. e e min min v a min r k, U rk, U min e e max max v a max U r max U r k k (3.5) Die Grenzen ind nicht kontant, hängen aber von ṙ k und ṙ k ab und müen zu jeder Abtatzeit neu berechnet werden. Anderereit können o während der Laufzeit die Grenzen der Gechwindigkeit und der Bechleunigung verändert werden. Der Regler ändert dann die aktuelle Gechwindigkeit oder Bechleunigung um diee neuen Grenzen wieder einzuhalten. 33
Ableitungsberechnung mit der Grenzwertmethode. Besonders wichtig ist der Zentraltext über Ableitungen Datei Stand 30.
 Analyi Ableitungfunktionen Ableitungberechnung mit der Grenzwertmethode Beonder wichtig it der Zentraltet über Ableitungen 400 Datei 40 Stand 0. Dezember 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 40 Ableitungfunktionen
Analyi Ableitungfunktionen Ableitungberechnung mit der Grenzwertmethode Beonder wichtig it der Zentraltet über Ableitungen 400 Datei 40 Stand 0. Dezember 00 INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 40 Ableitungfunktionen
Beispiel-Schulaufgabe 2
 Anregungen zur Ertellung von Aufgaben Aufgaben für Leitungnachweie Die zeichnet ich durch eine augewogene Berückichtigung der allgemeinen mathematichen Kompetenzen au. Aufgaben, deren Bearbeitung in auffallendem
Anregungen zur Ertellung von Aufgaben Aufgaben für Leitungnachweie Die zeichnet ich durch eine augewogene Berückichtigung der allgemeinen mathematichen Kompetenzen au. Aufgaben, deren Bearbeitung in auffallendem
K l a u s u r N r. 2
 17.11.008 K l a u u r N r. Aufgabe 1 Ein Fahrzeug durchfährt eine überhöhte Kurve, die gegenüber der Horizontalen einen Winkel von 5 hat. Da Fahrzeug wird dabei mit der Kraft F ge 1000 N enkrecht auf die
17.11.008 K l a u u r N r. Aufgabe 1 Ein Fahrzeug durchfährt eine überhöhte Kurve, die gegenüber der Horizontalen einen Winkel von 5 hat. Da Fahrzeug wird dabei mit der Kraft F ge 1000 N enkrecht auf die
Fachhochschule Wedel. Seminararbeit. Flussprobleme in Graphen und ihre Anwendung auf 0/1-Netzwerken
 Fachhochchule Wedel Seminararbeit Thema: Fluprobleme in Graphen und ihre Anwendung auf 0/-Netzwerken Eingereicht von: Erarbeitet im: Claudia Padberg (wi09) An der Windmühle 880 Wedel Tel. (00) 98897 E-Mail:
Fachhochchule Wedel Seminararbeit Thema: Fluprobleme in Graphen und ihre Anwendung auf 0/-Netzwerken Eingereicht von: Erarbeitet im: Claudia Padberg (wi09) An der Windmühle 880 Wedel Tel. (00) 98897 E-Mail:
( ) = ( ) ( ) ( ) ( )
 R. Brinkmann http://brinkmann-du.de Seite 0.0.0 Löungen Grundaufgaben für lineare und quadratiche Funktionen I e: E e f( x) = x+ Py 0 f( x) = x+ Px 0 E E E E E6 E7 E8 E9 E0 f x = mx + b mit m = und P(
R. Brinkmann http://brinkmann-du.de Seite 0.0.0 Löungen Grundaufgaben für lineare und quadratiche Funktionen I e: E e f( x) = x+ Py 0 f( x) = x+ Px 0 E E E E E6 E7 E8 E9 E0 f x = mx + b mit m = und P(
Jan Auffenberg. Die Lösung der Bewegungsgleichung eines einzelnen Pendels liefert wie in Versuch M1 betrachtet die Eigenfrequenz der Pendel zu:
 Protokoll zu Veruch M: Gekoppelte Pendel. Einleitung Im folgenden Veruch werden Schwingungen von durch eine weiche Feder gekoppelten Pendeln unterucht, deren Schwingungebenen eich ind. Die chwache Kopplung
Protokoll zu Veruch M: Gekoppelte Pendel. Einleitung Im folgenden Veruch werden Schwingungen von durch eine weiche Feder gekoppelten Pendeln unterucht, deren Schwingungebenen eich ind. Die chwache Kopplung
Definition: Die Bewegung eines Körpers, die sich in festen Zeitabständen wiederholt und symmetrisch zu einer Ruhelage abläuft heißt Schwingung.
 9 Schwingungen 9.1 Beipiele und Grundlagen Ruhelage Ruhelage Fadenpendel Ruhelage Federpendel Federpendel Ruhelage orionpendel Charakteritika: Die Bewegung it periodich; d.h. die Bewegung wiederholt ich
9 Schwingungen 9.1 Beipiele und Grundlagen Ruhelage Ruhelage Fadenpendel Ruhelage Federpendel Federpendel Ruhelage orionpendel Charakteritika: Die Bewegung it periodich; d.h. die Bewegung wiederholt ich
Regelungstechnik (A)
 Intitut für Elektrotechnik und Informationtechnik Aufgabenammlung zur Regelungtechnik (A) Prof. Dr. techn. F. Gauch Dipl.-Ing. C. Balewki Dipl.-Ing. R. Berat 08.01.2014 Übungaufgaben in Regelungtechnik
Intitut für Elektrotechnik und Informationtechnik Aufgabenammlung zur Regelungtechnik (A) Prof. Dr. techn. F. Gauch Dipl.-Ing. C. Balewki Dipl.-Ing. R. Berat 08.01.2014 Übungaufgaben in Regelungtechnik
Abschlussprüfung Berufliche Oberschule 2014 Physik 12 Technik - Aufgabe I - Lösung
 Abchluprüfung Berufliche Oberchule 204 Phyik 2 Technik - Aufgabe I - Löung Ein Motorrad tartet zum Zeitpunkt t 0 0 au dem Silltand herau Der Schwerpunkt von Motorrad und Fahrer befindet ich zu dieem Zeitpunkt
Abchluprüfung Berufliche Oberchule 204 Phyik 2 Technik - Aufgabe I - Löung Ein Motorrad tartet zum Zeitpunkt t 0 0 au dem Silltand herau Der Schwerpunkt von Motorrad und Fahrer befindet ich zu dieem Zeitpunkt
Aufgabe 2.4: Temposünder?
 Idee, Aufgabenentwurf und Foto: Barbara Mathea, Ferdinand Weber Weil da Radargerät defekt war, filmte die Polizei in einer 30-km-Zone alle vorbeifahrenden Auto. Von 4 Auto ind je 5 aufeinander folgende
Idee, Aufgabenentwurf und Foto: Barbara Mathea, Ferdinand Weber Weil da Radargerät defekt war, filmte die Polizei in einer 30-km-Zone alle vorbeifahrenden Auto. Von 4 Auto ind je 5 aufeinander folgende
Kooperatives Lernen SINUS Bayern
 Kooperative Lernen SINUS Bayern Mathematik Fachoberchule/Berufoberchule Jgt. 11/1 Partnerpuzzle zu quadratichen Funktionen Mit der Methode Partnerpuzzle wird die Betimmung der Nulltellen und de Scheitelpunkte
Kooperative Lernen SINUS Bayern Mathematik Fachoberchule/Berufoberchule Jgt. 11/1 Partnerpuzzle zu quadratichen Funktionen Mit der Methode Partnerpuzzle wird die Betimmung der Nulltellen und de Scheitelpunkte
Grundkurs Codierung Lösungsvorschläge zu den Fragen in den Unterkapiteln Was blieb? Stand Unterkapitel 4.4 Seite 261
 Grundkur Codierung Löungvorchläge zu den Fragen in den Unterkapiteln Wa blieb? Stand 22.04.2007 Unterkapitel 4.4 Seite 261 Zu Frage 1: Nein, damit bleibt da one time pad-verfahren nicht perfekt. Man kann
Grundkur Codierung Löungvorchläge zu den Fragen in den Unterkapiteln Wa blieb? Stand 22.04.2007 Unterkapitel 4.4 Seite 261 Zu Frage 1: Nein, damit bleibt da one time pad-verfahren nicht perfekt. Man kann
Grundlagen: Algorithmen und Datenstrukturen
 Grundlagen: Algorithmen und Datentrukturen Prof. Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Sommeremeter H. Täubig
Grundlagen: Algorithmen und Datentrukturen Prof. Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Sommeremeter H. Täubig
PHYSIK Gekoppelte Bewegungen 2
 PHYSIK Gekoppelte Bewegungen Gekoppelte Bewegungen auf chiefer Ebene Datei Nr. 93 Friedrich W. Buckel ktober 00 Internatgynaiu Schloß Torgelow Inhalt Grundwien Bewegung ohne äußeren Antrieb (Beipiel )
PHYSIK Gekoppelte Bewegungen Gekoppelte Bewegungen auf chiefer Ebene Datei Nr. 93 Friedrich W. Buckel ktober 00 Internatgynaiu Schloß Torgelow Inhalt Grundwien Bewegung ohne äußeren Antrieb (Beipiel )
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zentrale chriftliche Abiturprüfungen i Fach Matheatik Analyi Grundkur Aufgabe 5: Helikopter In der Abbildung it ein Auchnitt de Graphen einer quadratichen Funktion zu ehen, der i Zeitinterall on 0 bi 60
Zentrale chriftliche Abiturprüfungen i Fach Matheatik Analyi Grundkur Aufgabe 5: Helikopter In der Abbildung it ein Auchnitt de Graphen einer quadratichen Funktion zu ehen, der i Zeitinterall on 0 bi 60
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
 Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Übungsmaterial. Lösen von Anfangswertproblemen mit Laplacetransformation
 Prof. Dr. W. Roenheinrich 30.06.2009 Fachbereich Grundlagenwienchaften Fachhochchule Jena Übungmaterial Löen von Anfangwertproblemen mit Laplacetranformation Nachtehend ind einige Anfangwertprobleme zu
Prof. Dr. W. Roenheinrich 30.06.2009 Fachbereich Grundlagenwienchaften Fachhochchule Jena Übungmaterial Löen von Anfangwertproblemen mit Laplacetranformation Nachtehend ind einige Anfangwertprobleme zu
V6.4 - Erzwungene Schwingungen, Resonanz
 V6.4 - Erzwungene Schwingungen, Reonanz Michael Baron, Sven Pallu 31. Mai 2006 Zuammenfaung Im folgenden Veruch betrachten wir da Schwingungverhalten eine gedämpften, periodich erregten Ozillator in Form
V6.4 - Erzwungene Schwingungen, Reonanz Michael Baron, Sven Pallu 31. Mai 2006 Zuammenfaung Im folgenden Veruch betrachten wir da Schwingungverhalten eine gedämpften, periodich erregten Ozillator in Form
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sytemtheorie Teil A - Zeitkontinuierliche Signale und Syteme - Muterlöungen Manfred Strohrmann Urban Brunner Inhalt 8 Muterlöungen rundlagen de Filterentwurf 3 8. Entwurf eine paiven Filter mit kriticher
Sytemtheorie Teil A - Zeitkontinuierliche Signale und Syteme - Muterlöungen Manfred Strohrmann Urban Brunner Inhalt 8 Muterlöungen rundlagen de Filterentwurf 3 8. Entwurf eine paiven Filter mit kriticher
Der Kugelring. Verfasser: Praxelius. Beschreibung des Kugelrings und Herleitung der Formeln
 Der Kugelring Verfaer: Praxeliu Bechreibung de Kugelring und Herleitung der Formeln PDF-Dokument: Kugelring.pdf Da Dokument it urheberrechtlich gechützt. Alle Rechte vorbehalten. KR-850-00 Dieen Beitrag
Der Kugelring Verfaer: Praxeliu Bechreibung de Kugelring und Herleitung der Formeln PDF-Dokument: Kugelring.pdf Da Dokument it urheberrechtlich gechützt. Alle Rechte vorbehalten. KR-850-00 Dieen Beitrag
Lösungen zu Übungs-Blatt Differentialgleichungen 2. Ordnung und PBZ
 Prof.Dr. B.Grabowki Mathematik III/MST Übung Löungen Löungen zu Übung-Blatt Differentialgleichungen. Ordnung und PBZ Zu Aufgabe ) Geben Sie jeweil mindeten eine Löung folgender Differentialgleichung an
Prof.Dr. B.Grabowki Mathematik III/MST Übung Löungen Löungen zu Übung-Blatt Differentialgleichungen. Ordnung und PBZ Zu Aufgabe ) Geben Sie jeweil mindeten eine Löung folgender Differentialgleichung an
Prof. Liedl Lösung Blatt 8. Übungen zur Vorlesung PN1. Lösung zum Übungsblatt 8. Besprochen am
 11.12.212 Löung Blatt 8 Übungen zur Vorleung PN1 Löung zum Übungblatt 8 Beprochen am 11.12.212 Aufgabe 1: Moleküle al tarre rotierende Körper Durch Mikrowellen laen ich Rotationen von Molekülen mit einem
11.12.212 Löung Blatt 8 Übungen zur Vorleung PN1 Löung zum Übungblatt 8 Beprochen am 11.12.212 Aufgabe 1: Moleküle al tarre rotierende Körper Durch Mikrowellen laen ich Rotationen von Molekülen mit einem
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2014/2015 Prof. Dr. Peter Gritzmann 07.
 Note: Name Vorname Matrikelnummer Studiengang Unterchrift der Kandidatin/de Kandidaten Höraal Reihe Platz Techniche Univerität München Fakultät für Mathematik Algorithmiche Dikrete Mathematik WS 1/1 Prof.
Note: Name Vorname Matrikelnummer Studiengang Unterchrift der Kandidatin/de Kandidaten Höraal Reihe Platz Techniche Univerität München Fakultät für Mathematik Algorithmiche Dikrete Mathematik WS 1/1 Prof.
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 15. Übungsblatt
 Karlruher Intitut für Technologie (KIT) Intitut für Analyi Dr. A. Müller-Rettkowki Dipl.-Math. M. Uhl WS 9/ Höhere Mathematik I für die Fachrichtungen Elektroingenieurween, Phyik und Geodäie Löungvorchläge
Karlruher Intitut für Technologie (KIT) Intitut für Analyi Dr. A. Müller-Rettkowki Dipl.-Math. M. Uhl WS 9/ Höhere Mathematik I für die Fachrichtungen Elektroingenieurween, Phyik und Geodäie Löungvorchläge
Diplomhauptprüfung. "Regelung linearer Mehrgrößensysteme" 17. März Aufgabenblätter
 Diplomhauptprüfung "Regelung linearer Mehrgrößenyteme" 7. Mär 008 Aufgabenblätter Die Löungen owie der volltändige und nachvolliehbare Löungweg ind in die dafür vorgeehenen Löungblätter einutragen. Nur
Diplomhauptprüfung "Regelung linearer Mehrgrößenyteme" 7. Mär 008 Aufgabenblätter Die Löungen owie der volltändige und nachvolliehbare Löungweg ind in die dafür vorgeehenen Löungblätter einutragen. Nur
Überlegungen zum Bremsweg eines Wagens Seite 1. Rechnung Bremsweg. F g. m g,m=0,8 1000kg 10 N Hy. =μ H
 Überlegungen zum Bremweg eine Wagen Seite 1 Rechnung Bremweg Ein Auto mit v=72km/h und m=1000kg Mae macht eine Vollbremung. Der Reibfaktor zwichen Reifen und Straße beträgt dabei μ H =0,8. Impultrom Impul
Überlegungen zum Bremweg eine Wagen Seite 1 Rechnung Bremweg Ein Auto mit v=72km/h und m=1000kg Mae macht eine Vollbremung. Der Reibfaktor zwichen Reifen und Straße beträgt dabei μ H =0,8. Impultrom Impul
An welchen Wirkungen können wir Kräfte erkennen? Ergebnis Verformung, Beschleunigung, abbremsen, Bewegungsrichtung ändern.
 R. Brinkann http://brinkann-du.de Seite 1 5.11.013 Obertufe: e und auführliche Löungen zur Klaenarbeit zur Mechanik II (Variante A) e: E1 E E3 E4 E5 E6 E7 An welchen Wirkungen können wir Kräfte erkennen?
R. Brinkann http://brinkann-du.de Seite 1 5.11.013 Obertufe: e und auführliche Löungen zur Klaenarbeit zur Mechanik II (Variante A) e: E1 E E3 E4 E5 E6 E7 An welchen Wirkungen können wir Kräfte erkennen?
2. Praktikum. Maximal drei Personen in jeder Gruppe. Matrikelnummer: Die Vorbereitungsaufgaben sind vor dem Praktikumstermin zu lösen!
 Prof. Dr.-Ing. Jörg Raich Dipl.-Ing. Stephanie Geit Behrang Monajemi Nejad Fachgebiet Regelungyteme Fakultät IV Elektrotechnik und Informatik Techniche Univerität Berlin Integrierte Lehrverantaltung Grundlagen
Prof. Dr.-Ing. Jörg Raich Dipl.-Ing. Stephanie Geit Behrang Monajemi Nejad Fachgebiet Regelungyteme Fakultät IV Elektrotechnik und Informatik Techniche Univerität Berlin Integrierte Lehrverantaltung Grundlagen
R. Brinkmann Seite Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di
 R. Brinkmann http://brinkmann-du.de Seite 0..0 Klaenarbeit Mathematik Bearbeitungzeit 90 min. Di.06.0 SB Z NAME: A A A A Gerade durch Punkte. Gegeben ind die Punkte P (- ) P ( - ). Berechnen Sie die Funktiongleichung.
R. Brinkmann http://brinkmann-du.de Seite 0..0 Klaenarbeit Mathematik Bearbeitungzeit 90 min. Di.06.0 SB Z NAME: A A A A Gerade durch Punkte. Gegeben ind die Punkte P (- ) P ( - ). Berechnen Sie die Funktiongleichung.
Übungsblatt 7 Besprechung am /
 PN - Phyik für Chemiker und Biologen Prof. J. Lipfert WS 07/8 Übungblatt 7 Übungblatt 7 Beprechung am..07/4..07 Aufgabe Raketentechnik: Raketenantriebe funktionieren nach dem Rücktoßprinzip: Der Treibtoff
PN - Phyik für Chemiker und Biologen Prof. J. Lipfert WS 07/8 Übungblatt 7 Übungblatt 7 Beprechung am..07/4..07 Aufgabe Raketentechnik: Raketenantriebe funktionieren nach dem Rücktoßprinzip: Der Treibtoff
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analytische Geometrie / Stochastik Aufgabe B 1 - Lösungen
 1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
K l a u s u r N r. 2 G k P h 12
 10.1.10 K l a u u r N r. G k P h 1 Aufgabe 1 Bechreiben Sie einen Veruch, mit dem man die Schallgechwindigkeit mit Hilfe einer fortchreitenden Welle betimmen kann. (Veruchkizze mit Bechriftung, Veruchdurchführung,
10.1.10 K l a u u r N r. G k P h 1 Aufgabe 1 Bechreiben Sie einen Veruch, mit dem man die Schallgechwindigkeit mit Hilfe einer fortchreitenden Welle betimmen kann. (Veruchkizze mit Bechriftung, Veruchdurchführung,
Besprechung am /
 PN1 - Phyik 1 für Chemiker und Biologen Prof. J. Lipfert WS 018/19 Übungblatt 8 Übungblatt 8 Beprechung am 18.1.018/0.1.018 Aufgabe 1 Magnetiche Fetplatten, auch al HDD (Hard Drive Dik) bezeichnet, tellten
PN1 - Phyik 1 für Chemiker und Biologen Prof. J. Lipfert WS 018/19 Übungblatt 8 Übungblatt 8 Beprechung am 18.1.018/0.1.018 Aufgabe 1 Magnetiche Fetplatten, auch al HDD (Hard Drive Dik) bezeichnet, tellten
mit dem Betrag v 0 Die Anordnung befindet sich im Vakuum. Die auf die Ionen wirkenden Gravitationskräfte sind vernachlässigbar klein.
 athphy-online Abchluprüfung Berufliche Oberchule 00 Phyik Technik - Aufgabe II - Löung Teilaufgabe.0 Mit der unten dargetellten Anordnung kann die Mae von Protonen betit werden. Eine Waertoffionenquelle
athphy-online Abchluprüfung Berufliche Oberchule 00 Phyik Technik - Aufgabe II - Löung Teilaufgabe.0 Mit der unten dargetellten Anordnung kann die Mae von Protonen betit werden. Eine Waertoffionenquelle
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sytemtheorie eil - Zeitkontinuierliche Signale und Syteme - Muterlöungen Manfred Strohrmann Urban Brunner Inhalt Muterlöungen - Laplace-ranformation zeitkontinuierlicher Signale... 3. Berechnung der Laplace-ranformierten
Sytemtheorie eil - Zeitkontinuierliche Signale und Syteme - Muterlöungen Manfred Strohrmann Urban Brunner Inhalt Muterlöungen - Laplace-ranformation zeitkontinuierlicher Signale... 3. Berechnung der Laplace-ranformierten
Abschnittsweise definierte Funktionen - Aufgaben aus der Physik -
 Abchnittweie definierte Funktionen GS - 0.05.06 - Radfahrer_anw_.cd Abchnittweie definierte Funktionen - Aufgaben au der Phyik - Aufgabe : Ein Radfahrer hat zur Zeit t = 0 die kontante Gechwindigkeit v
Abchnittweie definierte Funktionen GS - 0.05.06 - Radfahrer_anw_.cd Abchnittweie definierte Funktionen - Aufgaben au der Phyik - Aufgabe : Ein Radfahrer hat zur Zeit t = 0 die kontante Gechwindigkeit v
K l a u s u r N r. 1 Gk Ph 11
 1.10.008 K l a u u r N r. 1 Gk Ph 11 Aufgabe 1 Drei Kräfte F 1 100 N, F 70 N und F 3 48 N wirken in einer Ebene und greifen an einem gemeinamen Punkt A an. Die Kräfte F 1 und F chließen dabei den Winkel
1.10.008 K l a u u r N r. 1 Gk Ph 11 Aufgabe 1 Drei Kräfte F 1 100 N, F 70 N und F 3 48 N wirken in einer Ebene und greifen an einem gemeinamen Punkt A an. Die Kräfte F 1 und F chließen dabei den Winkel
Vorbereitung Mathematik Cusanus-Gymnasium Wittlich Fachlehrer : W. Zimmer
 Vorbereitung Mathematik Cuanu-Gymnaium Wittlich Fachlehrer W. Zimmer Den folgenden Katalog habe ich bei www.lehrer.uni-karlruhe.de gefunden. Er oll Beipiele dafür aufzeigen, wa konkret verlangt werden
Vorbereitung Mathematik Cuanu-Gymnaium Wittlich Fachlehrer W. Zimmer Den folgenden Katalog habe ich bei www.lehrer.uni-karlruhe.de gefunden. Er oll Beipiele dafür aufzeigen, wa konkret verlangt werden
1. MECHANISCHE ENERGIE
 KAITL III NRGI . MCHANISCH NRGI Wird ein Körper mit der Kraft entlang de Wege bewegt, o it die dafür benötigte mechaniche nergie da kalare rodukt au der Kraft und dem Weg : co und ind in dieer Definition
KAITL III NRGI . MCHANISCH NRGI Wird ein Körper mit der Kraft entlang de Wege bewegt, o it die dafür benötigte mechaniche nergie da kalare rodukt au der Kraft und dem Weg : co und ind in dieer Definition
FOS: Die harmonische Schwingung. Wir beobachten die Bewegung eines Fadenpendels
 R. Brinkmann http://brinkmann-du.de Seite 1 25.11.213 Bechreibung von Schwingungen. FOS: Die harmoniche Schwingung Veruch: Wir beobachten die Bewegung eine Fadenpendel Lenken wir die Kugel au und laen
R. Brinkmann http://brinkmann-du.de Seite 1 25.11.213 Bechreibung von Schwingungen. FOS: Die harmoniche Schwingung Veruch: Wir beobachten die Bewegung eine Fadenpendel Lenken wir die Kugel au und laen
Fachhochschule Hannover Übungen zur Klausur im WS0809 am
 Fachhochchule Hannover Übungen zur Klauur im WS0809 am 5.0.09 Fachbereich Machinenbau Zeit: 90 min Fach: Phyik (Prof. Schrewe) Hilfmittel: Formelammlung zur Vorleung Verwenden Sie zur Vereinfachung bei
Fachhochchule Hannover Übungen zur Klauur im WS0809 am 5.0.09 Fachbereich Machinenbau Zeit: 90 min Fach: Phyik (Prof. Schrewe) Hilfmittel: Formelammlung zur Vorleung Verwenden Sie zur Vereinfachung bei
Grundlagen der Technischen Chemie - Praktikum WS2015/ Februar Protokoll. Nitritreduktion
 2. Faung Protokoll Nitritreduktion Gruppe 29 Guido Petri, Matrikelnummer 364477 Rami Michael Saoudi, Matrikelnummer 356563 1 Aufheizgechwindigkeit Gruppe 29 Inhaltverzeichni Aufgabentellung...2 1. Theorie...2
2. Faung Protokoll Nitritreduktion Gruppe 29 Guido Petri, Matrikelnummer 364477 Rami Michael Saoudi, Matrikelnummer 356563 1 Aufheizgechwindigkeit Gruppe 29 Inhaltverzeichni Aufgabentellung...2 1. Theorie...2
Zur Bestimmung der ungünstigsten Toleranz zusammengesetzter Systeme können die Einzeltoleranzen entsprechend ihres Zusammenwirkens addiert werden.
 Vorauetzung und verwandte Themen Für diee Bechreibungen ind Vorkenntnie der Statitik und der Verteilungen erforderlich. Weiterführende Thema it: www.veruchmethoden.de/prozedaten_toleranzimulation.pdf Einführung
Vorauetzung und verwandte Themen Für diee Bechreibungen ind Vorkenntnie der Statitik und der Verteilungen erforderlich. Weiterführende Thema it: www.veruchmethoden.de/prozedaten_toleranzimulation.pdf Einführung
Aufgabenblatt 4: Wachstum
 Aufgabenblatt 4: Wachtum Löungkizze Bitten beachten Sie, da diee Löungkizze lediglich al Hilfetellung zur eigentändigen Löung der Aufgaben gedacht it. Sie erhebt weder Anpruch auf Volltändigkeit noch auf
Aufgabenblatt 4: Wachtum Löungkizze Bitten beachten Sie, da diee Löungkizze lediglich al Hilfetellung zur eigentändigen Löung der Aufgaben gedacht it. Sie erhebt weder Anpruch auf Volltändigkeit noch auf
Aufgaben zum Impuls
 Aufgaben zu Ipul 593. Ein Wagen (Mae 4kg) prallt it einer Gechwindigkeit, / auf einen zweiten ( 5 kg), der ich in gleicher Richtung it der Gechwindigkeit 0,6 / bewegt. a) Wie groß ind die Gechwindigkeiten
Aufgaben zu Ipul 593. Ein Wagen (Mae 4kg) prallt it einer Gechwindigkeit, / auf einen zweiten ( 5 kg), der ich in gleicher Richtung it der Gechwindigkeit 0,6 / bewegt. a) Wie groß ind die Gechwindigkeiten
Aufgabenblatt zum Seminar 01 PHYS70356 Klassische und relativistische Mechanik (Physik, Wirtschaftsphysik, Physik Lehramt, Nebenfach Physik)
 Aufgabenblatt zum Seminar 01 PHYS70356 Klaiche und relativitiche Mechanik Phyik, Wirtchaftphyik, Phyik Lehramt, Nebenfach Phyik) Othmar Marti, othmar.marti@uni-ulm.de) 20. 10. 2008 1 Aufgaben 1. Sie ehen
Aufgabenblatt zum Seminar 01 PHYS70356 Klaiche und relativitiche Mechanik Phyik, Wirtchaftphyik, Phyik Lehramt, Nebenfach Phyik) Othmar Marti, othmar.marti@uni-ulm.de) 20. 10. 2008 1 Aufgaben 1. Sie ehen
1.1.4 Potential; Äquipotentiallinien bzw. -flächen; potentielle Energie eines geladenen Teilchens im homogenen elektrischen Feld
 1.1.4 Potential; Äquipotentiallinien bzw. -flächen; potentielle nergie eine geladenen Teilchen im homogenen elektrichen Feld Die Charakteriierung eine elektrichen Felde in einem Raumpunkt durch Angabe
1.1.4 Potential; Äquipotentiallinien bzw. -flächen; potentielle nergie eine geladenen Teilchen im homogenen elektrichen Feld Die Charakteriierung eine elektrichen Felde in einem Raumpunkt durch Angabe
Autonome Mobile Systeme
 Autonome Mobile Syteme Teil II: Sytemtheorie für Informatiker Dr. Mohamed Oubbati Intitut für Neuroinformatik Univerität Ulm SS 2007 Warum Sytemtheorie? Informatiker werden zunehmend mit Sytemen konfrontiert,
Autonome Mobile Syteme Teil II: Sytemtheorie für Informatiker Dr. Mohamed Oubbati Intitut für Neuroinformatik Univerität Ulm SS 2007 Warum Sytemtheorie? Informatiker werden zunehmend mit Sytemen konfrontiert,
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sytemtheorie Teil A - Zeitkontinuierliche Signale und Syteme - Muterlöungen Manfred Strohrmann rban Brunner Inhalt 5 Muterlöungen Syteme im Laplace-Bereich 3 5. Löen einer homogenen linearen Differentialgleichung...
Sytemtheorie Teil A - Zeitkontinuierliche Signale und Syteme - Muterlöungen Manfred Strohrmann rban Brunner Inhalt 5 Muterlöungen Syteme im Laplace-Bereich 3 5. Löen einer homogenen linearen Differentialgleichung...
Gliederung. Gliederung (cont.) Gliederung (cont.)
 - Gliederung Jianwei Zhang zhang@informatik.uni-hamburg.de Fakultät für Mathematik, Informatik und Naturwissenschaften Technische Aspekte Multimodaler Systeme 11. Mai 2010 Allgemeine Informationen Einführung
- Gliederung Jianwei Zhang zhang@informatik.uni-hamburg.de Fakultät für Mathematik, Informatik und Naturwissenschaften Technische Aspekte Multimodaler Systeme 11. Mai 2010 Allgemeine Informationen Einführung
Geschwindigkeit v = kurz:
 Mechanik 1 Gechwindigkeit Die Gechwindigkeit v gibt an, wie chnell ich ein Körper bewegt. Sie it fetgelegt durch: Gechwindigkeit v = zurückgelegter Weg dafür benötigte Zeit t übliche Einheiten: m km 1
Mechanik 1 Gechwindigkeit Die Gechwindigkeit v gibt an, wie chnell ich ein Körper bewegt. Sie it fetgelegt durch: Gechwindigkeit v = zurückgelegter Weg dafür benötigte Zeit t übliche Einheiten: m km 1
K T 1 s + 1. G S (s) = G S (s) = 1 2s + 1. T n s + 1 T n s. G R (s) = K R. G R (s) = 2s + 1 s. F ω (s) = 1/s 1 + 1/s = 1
 Aufgabe : a) Au und K = und T = 2 folgt: Mit und K R = 2, T n = 2 : G S () = K T G S () = 2 G R () = K R T n T n G R () = 2 G 0 () = G R ()G S () = F ω () = / + / = b) Y () = F ω ()W() Die Sprungantwort
Aufgabe : a) Au und K = und T = 2 folgt: Mit und K R = 2, T n = 2 : G S () = K T G S () = 2 G R () = K R T n T n G R () = 2 G 0 () = G R ()G S () = F ω () = / + / = b) Y () = F ω ()W() Die Sprungantwort
23. Kürzeste Wege. Flussüberquerung (Missionare und Kannibalen) Das ganze Problem als Graph. Formulierung als Graph
 Fluüberquerung (Miionare und Kannibalen). Kürzete Wege Problem: Drei Kannibalen und drei Miionare tehen an einem Ufer eine Flue. Ein dort bereittehende Boot fat maimal zwei Peronen. Zu keiner Zeit dürfen
Fluüberquerung (Miionare und Kannibalen). Kürzete Wege Problem: Drei Kannibalen und drei Miionare tehen an einem Ufer eine Flue. Ein dort bereittehende Boot fat maimal zwei Peronen. Zu keiner Zeit dürfen
LMPG_SI-Einheiten (Technische Mathematik S ) LAB1A/B
 LMPG_SI-Einheiten (Techniche Matheatik S. 7-78) LAB1A/B Gebräuchliche, abgeleitete Gröen: Au den Baigröen und Baieinheiten laen ich eine Vielzahl weiterer Gröen und Einheiten ab- und herleiten, die zu
LMPG_SI-Einheiten (Techniche Matheatik S. 7-78) LAB1A/B Gebräuchliche, abgeleitete Gröen: Au den Baigröen und Baieinheiten laen ich eine Vielzahl weiterer Gröen und Einheiten ab- und herleiten, die zu
Zweiatomige Moleküle
 Zweiatomige Moleküle Nicola Wink 16. November 2014 Inhaltverzeichni 1 Einleitung 2 2 Born-Oppenheimer Näherung 2 3 Rotation- und Vibrationbewegung zweiatomiger Moleküle 5 4 LCAO Näherung 7 5 Zuammenfaung
Zweiatomige Moleküle Nicola Wink 16. November 2014 Inhaltverzeichni 1 Einleitung 2 2 Born-Oppenheimer Näherung 2 3 Rotation- und Vibrationbewegung zweiatomiger Moleküle 5 4 LCAO Näherung 7 5 Zuammenfaung
Taschenbuch der Statistik
 Tachenbuch der Statitik von Werner Voß 2., verbeerte Auflage Haner München 2003 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 22605 0 Zu Inhaltverzeichni chnell und portofrei erhältlich bei
Tachenbuch der Statitik von Werner Voß 2., verbeerte Auflage Haner München 2003 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 22605 0 Zu Inhaltverzeichni chnell und portofrei erhältlich bei
Mechanik 2. Addition von Geschwindigkeiten 1
 Mechanik. Addition on Gechwindigkeiten 1. Addition on Gechwindigkeiten Wa beeinflut die Gechwindigkeit de Boote? a. Wind b. Waergechwindigkeit Haben beide die gleiche Richtung, o addieren ie ich. Haben
Mechanik. Addition on Gechwindigkeiten 1. Addition on Gechwindigkeiten Wa beeinflut die Gechwindigkeit de Boote? a. Wind b. Waergechwindigkeit Haben beide die gleiche Richtung, o addieren ie ich. Haben
) + d(v s0...s n ) 2. Bedingung B ist in der Anwendung mühsam zu verifizieren. Ist ' jedoch ein Diffeomorphismus, so genügt folgende Sektorbedingung.
 248 8 HomoklinePunkteundShiftabbildungen und daher mit Lemma 2 k qk 1 1 µ d(u 1... n ) + d(v... n ) 2 1 µ n. Alo it h tetig. Die Stetigkeit von h 1 folgt chließlich au der Eindeutigkeit der Zuordnung $
248 8 HomoklinePunkteundShiftabbildungen und daher mit Lemma 2 k qk 1 1 µ d(u 1... n ) + d(v... n ) 2 1 µ n. Alo it h tetig. Die Stetigkeit von h 1 folgt chließlich au der Eindeutigkeit der Zuordnung $
Greensche Funktion. Frank Essenberger FU Berlin. 30.September Nomenklatur 1. 2 Greensche Theoreme 1. 3 Anwendung in der Elektrostatik 2
 Greenche Funktion Frank Eenberger FU Berlin 30.September 2006 Inhalterzeichni Nomenklatur 2 Greenche Theoreme 3 Anwendung in der Elektrotatik 2 4 Anpaung an Randbedingungen 3 5 Eindeutigkeit der Löung
Greenche Funktion Frank Eenberger FU Berlin 30.September 2006 Inhalterzeichni Nomenklatur 2 Greenche Theoreme 3 Anwendung in der Elektrotatik 2 4 Anpaung an Randbedingungen 3 5 Eindeutigkeit der Löung
Physik I Übung 3 - Lösungshinweise
 Phyik I Übung 3 - Löunghinweie Moritz Kütt WS / Stefan Reutter Stand:.. Franz Fujara Aufgabe Der erte Blick Ein Fahrradfahrer fährt die Hälfte einer Strecke mit km/h, die zweite Hälfte mit km/h. Schätze
Phyik I Übung 3 - Löunghinweie Moritz Kütt WS / Stefan Reutter Stand:.. Franz Fujara Aufgabe Der erte Blick Ein Fahrradfahrer fährt die Hälfte einer Strecke mit km/h, die zweite Hälfte mit km/h. Schätze
Einfacher loop-shaping Entwurf
 Intitut für Sytemtheorie technicher Prozee Univerität Stuttgart Prof. Dr.-Ing. F. Allgöwer 6.4.24 Regelungtechnik I Loophaping-Entwurf t http://www.it.uni-tuttgart.de/education/coure/rti/ Einfacher loop-haping
Intitut für Sytemtheorie technicher Prozee Univerität Stuttgart Prof. Dr.-Ing. F. Allgöwer 6.4.24 Regelungtechnik I Loophaping-Entwurf t http://www.it.uni-tuttgart.de/education/coure/rti/ Einfacher loop-haping
Vektorrechnung Theorie Manfred Gurtner 2011 Seite 1. Vektorrechnung
 Vektorrechnung Theorie Manfred Gurtner Seite Vektorrechnung ink: http://member.chello.at/gut.jutta.gerhard/kur/vektoren.htm http://member.chello.at/gut.jutta.gerhard/kur/vektoren.htm http://www.mathematik.net/vektoral/va.htm
Vektorrechnung Theorie Manfred Gurtner Seite Vektorrechnung ink: http://member.chello.at/gut.jutta.gerhard/kur/vektoren.htm http://member.chello.at/gut.jutta.gerhard/kur/vektoren.htm http://www.mathematik.net/vektoral/va.htm
PlaNeT SimTech. Team 28
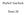 PlaNeT SimTech Team 28 Inhaltverzeichni 1. Einführung...3 2. Hauptteil...3 3. Schlufolgerung...3 1. Zuammenfaung Um die Wiedervereinigung einer Nation zu feiern, wird die trennende Mauer zwichen den beiden
PlaNeT SimTech Team 28 Inhaltverzeichni 1. Einführung...3 2. Hauptteil...3 3. Schlufolgerung...3 1. Zuammenfaung Um die Wiedervereinigung einer Nation zu feiern, wird die trennende Mauer zwichen den beiden
Lösungsvorschlag TECHNISCHE UNIVERSITÄT MÜNCHEN. Fakultät für Informatik ... Midterm-Klausur Final-Klausur
 Name Studiengang (Hauptfach) Vorname Fachrichtung (Nebenfach)... Note Matrikelnummer Unterchrift der Kandidatin/de Kandidaten 1 I II TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Informatik Midterm-Klauur
Name Studiengang (Hauptfach) Vorname Fachrichtung (Nebenfach)... Note Matrikelnummer Unterchrift der Kandidatin/de Kandidaten 1 I II TECHNISCHE UNIVERSITÄT MÜNCHEN Fakultät für Informatik Midterm-Klauur
Versuch 16 (früher I9) Aufbauten 16/36 (früher I7a/I7b) Logikschaltungen mit dem Bipolartransistor
 Hochchule Augburg Veruch 16 (früher I9) Aufbauten 16/36 (früher I7a/I7b) Logikchaltungen mit dem Bipolartranitor Phyikaliche Praktikum Die Funktionweie von Bipolartranitoren ollte vor Veruch 9 im Theorieteil
Hochchule Augburg Veruch 16 (früher I9) Aufbauten 16/36 (früher I7a/I7b) Logikchaltungen mit dem Bipolartranitor Phyikaliche Praktikum Die Funktionweie von Bipolartranitoren ollte vor Veruch 9 im Theorieteil
Nach der Bearbeitung dieses Kapitels soll der Leser in der Lage sein,
 3 1 Einführung Nach der Bearbeitung diee Kapitel oll der Leer in der Lage ein, die Funktionen Invetition und Finanzierung in die Geamtheit der Betriebwirtchaftlehre einzuordnen, ihre Bedeutung für die
3 1 Einführung Nach der Bearbeitung diee Kapitel oll der Leer in der Lage ein, die Funktionen Invetition und Finanzierung in die Geamtheit der Betriebwirtchaftlehre einzuordnen, ihre Bedeutung für die
Studienarbeit. Thema: Bestimmung der Schichtdicke von Aluminium auf Siliziumoxid mit dem Vier-Spitzen-Messgerät VSM100
 Studienarbeit Thema: Betimmung der Schichtdicke von Aluminium auf Siliziumoxid mit dem Vier-Spitzen-Megerät VSM00 angefertigt von: Robert Uath Matrikelnummer: 99047 Betreuer: Prof. Dr.-Ing. B. K. Glück
Studienarbeit Thema: Betimmung der Schichtdicke von Aluminium auf Siliziumoxid mit dem Vier-Spitzen-Megerät VSM00 angefertigt von: Robert Uath Matrikelnummer: 99047 Betreuer: Prof. Dr.-Ing. B. K. Glück
Landeswettbewerb Mathematik Baden-Württemberg. Runde 2
 1994 Runde ufgabe 1 Zeige, da 1!! 3!... 1995! mindeten 1 Teiler hat. Hinwei: Unter n! verteht man da Produkt der erten n natürlichen Zahlen. eipiel: 5! = 1 3 4 5 = 10 Löung Die Summe S = 1!! 3!... 1995!
1994 Runde ufgabe 1 Zeige, da 1!! 3!... 1995! mindeten 1 Teiler hat. Hinwei: Unter n! verteht man da Produkt der erten n natürlichen Zahlen. eipiel: 5! = 1 3 4 5 = 10 Löung Die Summe S = 1!! 3!... 1995!
Luftbewegungen bei barokliner Schichtung
 Luftbewegungen bei barokliner Schichtung Bilancierte Wirbeln Diagnotiche Gleichungen Prognotiche Gleichungen Luftbewegungen bei barokliner Schichtung In den baroklinen Bereichen der Atmophäre chneiden
Luftbewegungen bei barokliner Schichtung Bilancierte Wirbeln Diagnotiche Gleichungen Prognotiche Gleichungen Luftbewegungen bei barokliner Schichtung In den baroklinen Bereichen der Atmophäre chneiden
Figurierte Zahlen, Urnen und Kugelfarben
 Figurierte Zahlen, Urnen und Kugelfarben KLAUS-ULRICH UDER, Lüneburg HANS HUMENBERER und BERTHOLD SCHUPPAR, Dortmund Zuammenfaung: Bei einem elementaren tochatichen Problem (Ziehung von zei Kugeln au einer
Figurierte Zahlen, Urnen und Kugelfarben KLAUS-ULRICH UDER, Lüneburg HANS HUMENBERER und BERTHOLD SCHUPPAR, Dortmund Zuammenfaung: Bei einem elementaren tochatichen Problem (Ziehung von zei Kugeln au einer
Lösungsvorschlag. Qq r 2 F C = 1
 Löungvorchlag 1. Zunächt zwei Skizzen zur Verdeutlichung der Situation: Link it da Kügelchen mit der Ladung q zu ehen. Recht it die Kugel mit der Ladung Q 1 µc an die Stelle de Kügelchen gebracht worden.
Löungvorchlag 1. Zunächt zwei Skizzen zur Verdeutlichung der Situation: Link it da Kügelchen mit der Ladung q zu ehen. Recht it die Kugel mit der Ladung Q 1 µc an die Stelle de Kügelchen gebracht worden.
Grundfertigkeiten Physik Jahrgangsstufe 7
 Robert-Koch-Gymnaium Grundfertigkeiten Phyik Jahrgangtufe 7 Fachchaft Phyik 2013 Serie A 1 Grundfertigkeiten Phyik Jahrgangtufe 7 Serie A Hilfe: Hookeche Geetz: Einfache Formelgleichungen Elektricher Widertand
Robert-Koch-Gymnaium Grundfertigkeiten Phyik Jahrgangtufe 7 Fachchaft Phyik 2013 Serie A 1 Grundfertigkeiten Phyik Jahrgangtufe 7 Serie A Hilfe: Hookeche Geetz: Einfache Formelgleichungen Elektricher Widertand
Aufgabe 1 Bestimmen Sie die Laplace-Transformierte der Rampenfunktion
 Übung /Grundgebiete der Elektrotechnik 3 (WS7/8 aplace-tranformation Dr Alexander Schaum, ehrtuhl für vernetzte elektroniche Syteme Chritian-Albrecht-Univerität zu Kiel Aufgabe Betimmen Sie die aplace-tranformierte
Übung /Grundgebiete der Elektrotechnik 3 (WS7/8 aplace-tranformation Dr Alexander Schaum, ehrtuhl für vernetzte elektroniche Syteme Chritian-Albrecht-Univerität zu Kiel Aufgabe Betimmen Sie die aplace-tranformierte
Mathematik und angewandte Mathematik 1. HAK (1. Jahrgang) 1. AUL (1. Jahrgang) Mathematik und angewandte Mathematik 1. HLW (1.
 Unterrichtfach Lehrplan HAK: Mathematik und angewandte Mathematik 1. HAK (1. Jahrgang) 1. AUL (1. Jahrgang) Lehrplan HLW: Mathematik und angewandte Mathematik 1. HLW (1. Jahrgang) Lehrplan HTL: Mathematik
Unterrichtfach Lehrplan HAK: Mathematik und angewandte Mathematik 1. HAK (1. Jahrgang) 1. AUL (1. Jahrgang) Lehrplan HLW: Mathematik und angewandte Mathematik 1. HLW (1. Jahrgang) Lehrplan HTL: Mathematik
3.4. Flächen und Umfang. 3 Planung Rechnen KAPITEL 3.4 1
 KAPITEL 3.4 1 3.4 Flächen und Umfang Einleitung In dieem Kapitel lernen Sie, den Flächeninhalt und den Umfang von geometrichen Formen zu berechnen. Dafür lernen Sie den Umgang mit Formeln kennen. Flächen-
KAPITEL 3.4 1 3.4 Flächen und Umfang Einleitung In dieem Kapitel lernen Sie, den Flächeninhalt und den Umfang von geometrichen Formen zu berechnen. Dafür lernen Sie den Umgang mit Formeln kennen. Flächen-
Robotersteuerung mit online Bahnvorgabe durch Kraftsensorik und / oder Bildverarbeitung
 Roboterteuerung mit online Bahnvorgabe urch Kraftenorik un / oer Bilverarbeitung Frierich Lange Intitut für Robotik un Mechatronik, DLR Oberpfaffenhofen Gerthofen, 26. Januar 2005 1. Einleitung: Aufgabe,
Roboterteuerung mit online Bahnvorgabe urch Kraftenorik un / oer Bilverarbeitung Frierich Lange Intitut für Robotik un Mechatronik, DLR Oberpfaffenhofen Gerthofen, 26. Januar 2005 1. Einleitung: Aufgabe,
Zentralabitur 2014 Physik Schülermaterial Aufgabe II ga Nachschreibtermin Bearbeitungszeit: 220 min
 Thema: Interferenz In Aufgabe 1 wird Interferenz von Licht am Gitter behandelt. In Aufgabe 2 geht e um die Eigenchaften verchiedener Quantenobjete. Aufgabe 3 befat ich mit Michelon-Interferometern. Aufgabentellung
Thema: Interferenz In Aufgabe 1 wird Interferenz von Licht am Gitter behandelt. In Aufgabe 2 geht e um die Eigenchaften verchiedener Quantenobjete. Aufgabe 3 befat ich mit Michelon-Interferometern. Aufgabentellung
2. Klausur Physik Leistungskurs Klasse Dauer. 90 min. Name:... Teil 1 Hilfsmittel: alles verboten
 . Klauur Phyik Leitungkur Klae 0..05 Dauer. 90 in Nae:... Teil Hilfittel: alle verboten. Gleich chwere Pakete werden vo Fußboden in ein Regal gehoben, deen Fächer untereinander den gleichen Abtand haben.
. Klauur Phyik Leitungkur Klae 0..05 Dauer. 90 in Nae:... Teil Hilfittel: alle verboten. Gleich chwere Pakete werden vo Fußboden in ein Regal gehoben, deen Fächer untereinander den gleichen Abtand haben.
Klausur Strömungsmaschinen I SoSe 2012
 Klauur Strömungmachinen I SoSe 01. Augut 01, Beginn 13:30 Uhr Prüfungzeit: 90 Minutenn Zugelaene Hilfmittel ind: Tachenrechner, Geodreieck, Zeichenmaterial Andere Hilfmittel, inbeondere: Alte Klauuren
Klauur Strömungmachinen I SoSe 01. Augut 01, Beginn 13:30 Uhr Prüfungzeit: 90 Minutenn Zugelaene Hilfmittel ind: Tachenrechner, Geodreieck, Zeichenmaterial Andere Hilfmittel, inbeondere: Alte Klauuren
Gegeben: v 1 = 120 km h. und v 2 = 150 km h. 2. Ein Radfahrer fährt 40 s mit der gleichbleibenden Geschwindigkeit von 18 km.
 Übungen (en ohne Gewähr) ================================================================== 1. Ein Auto teigert eine Gechwindigkeit gleichmäßig von 120 km auf 150 km. h h Wie groß it die Bechleunigung
Übungen (en ohne Gewähr) ================================================================== 1. Ein Auto teigert eine Gechwindigkeit gleichmäßig von 120 km auf 150 km. h h Wie groß it die Bechleunigung
15. Physikolympiade des Landes Sachsen-Anhalt Schuljahr 2018/2019 Runde 1 Lösungen Klasse 8
 Hinweie für die Korrektoren: - Kommt eine Schülerin oder ein Schüler bei der Bearbeitung der Aufgaben auf einem anderen al dem angegebenen Weg zum richtigen Ergebni, o it da al richtig zu werten. - Die
Hinweie für die Korrektoren: - Kommt eine Schülerin oder ein Schüler bei der Bearbeitung der Aufgaben auf einem anderen al dem angegebenen Weg zum richtigen Ergebni, o it da al richtig zu werten. - Die
Lösungsblatt 04 Mechanik (Physik, Wirtschaftsphysik, Physik Lehramt) (WS2007/08)
 Löungblatt 4 Mechanik Phyik, Wirtchaftphyik, Phyik Lehramt WS27/8 Wolfgang v. Soden wolfgang.oden@uni-ulm.de 13. 11. 27 15 Abchlag vom Tor 2P Der Urprung de Kordinatenytem wird in den Torwart gelegt, der
Löungblatt 4 Mechanik Phyik, Wirtchaftphyik, Phyik Lehramt WS27/8 Wolfgang v. Soden wolfgang.oden@uni-ulm.de 13. 11. 27 15 Abchlag vom Tor 2P Der Urprung de Kordinatenytem wird in den Torwart gelegt, der
6. Klasse 1. Schularbeit 1999-10-20 Gruppe A + 40.! Bestimme das Monotonieverhalten und berechen den Grenzwert! 4 Punkte
 6. Klae 1. Schularbeit 1999-10-0 Gruppe A 1) Betrachte da Wettrennen zwichen Achille und der Schildkröte für folgende Angaben: Gechwindigkeit von Achille 10 m, Gechwindigkeit der Schildkröte m Vorprung
6. Klae 1. Schularbeit 1999-10-0 Gruppe A 1) Betrachte da Wettrennen zwichen Achille und der Schildkröte für folgende Angaben: Gechwindigkeit von Achille 10 m, Gechwindigkeit der Schildkröte m Vorprung
Protokoll zu Versuch M4: Stoßgesetze
 Protokoll zu Veruch M4: toßgeetze. Einleitung In dieem Veruch läßt man zwei tahlkugeln zentral aufeinandertoßen. Dabei werden die Kugeln an Fäden aufgehängt und können omit al Fadenpendel angeehen werden.
Protokoll zu Veruch M4: toßgeetze. Einleitung In dieem Veruch läßt man zwei tahlkugeln zentral aufeinandertoßen. Dabei werden die Kugeln an Fäden aufgehängt und können omit al Fadenpendel angeehen werden.
Versuch 1: Drehzahlregelung eines Gleichstrommotors
 Techniche Univerität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungyteme Leitung: Prof. Dr.-Ing. Jörg Raich Praktikum Grundlagen der Regelungtechnik Sommeremeter 2012 Veruchbechreibung
Techniche Univerität Berlin Fakultät IV Elektrotechnik und Informatik Fachgebiet Regelungyteme Leitung: Prof. Dr.-Ing. Jörg Raich Praktikum Grundlagen der Regelungtechnik Sommeremeter 2012 Veruchbechreibung
Physikpraktikum. Versuch 2) Stoß. F α F * cos α
 Phyikpraktikum Veruch ) Stoß Vorbereitung: Definition von: Arbeit: wenn eine Kraft einen Körper auf einem betimmten Weg verchiebt, o verrichtet ie am Körper Arbeit Arbeit = Kraft * Weg W = * S = N * m
Phyikpraktikum Veruch ) Stoß Vorbereitung: Definition von: Arbeit: wenn eine Kraft einen Körper auf einem betimmten Weg verchiebt, o verrichtet ie am Körper Arbeit Arbeit = Kraft * Weg W = * S = N * m
Besprechung am
 PN2 Einführung in die Phyik für Chemiker 2 Prof. T. Weitz SS 2017 Übungblatt 8 Übungblatt 8 Beprechung am 03.07.2017 Aufgabe 1 Elektromotor. Ein Elektromotor wandelt elektriche Energie in mechaniche Energie
PN2 Einführung in die Phyik für Chemiker 2 Prof. T. Weitz SS 2017 Übungblatt 8 Übungblatt 8 Beprechung am 03.07.2017 Aufgabe 1 Elektromotor. Ein Elektromotor wandelt elektriche Energie in mechaniche Energie
MATHEMATIK-WETTBEWERB 2016/2017 DES LANDES HESSEN
 MATHEMATIK-WETTBEWERB 206/207 DES LANDES HESSEN 3. RUNDE LÖSUNGEN AUFGABENGRUPPE A. a) L { 2; ; 0; ;...}, denn b) L Z G, denn. Fall: 3 (x 7) (x 3)(x 7) x 7 oder 3 x 3 x 7 oder x 6 2. Fall: 3 (x 7) < (x
MATHEMATIK-WETTBEWERB 206/207 DES LANDES HESSEN 3. RUNDE LÖSUNGEN AUFGABENGRUPPE A. a) L { 2; ; 0; ;...}, denn b) L Z G, denn. Fall: 3 (x 7) (x 3)(x 7) x 7 oder 3 x 3 x 7 oder x 6 2. Fall: 3 (x 7) < (x
Lehreinheit 09 Prozesssimulation II: Prozesssimulation mit einfachen Petri-Netzen Wintersemester 2012/2013
 Dynamiche Unternehmenmodellierung und -imulation (ehemal: Buine Dynamic - Dynamiche Modellierung und Simulation komplexer Gechäftyteme, Arbeitwienchaft V) Lehreinheit 09 Prozeimulation : Prozeimulation
Dynamiche Unternehmenmodellierung und -imulation (ehemal: Buine Dynamic - Dynamiche Modellierung und Simulation komplexer Gechäftyteme, Arbeitwienchaft V) Lehreinheit 09 Prozeimulation : Prozeimulation
Klausur zur Vorlesung Verkehrsdynamik und -simulation, SS 2016 Lösungsvorschlag
 Aufgabe 1 (40 Punkte) Klauur zur Vorleung Verkehrdynamik und -imulation, SS 2016 Löungvorchlag Gegeben it eine zweitreifige Richtungfahrbahn mit zwei im Weentlichen geraden Abchnitten I und III owie dem
Aufgabe 1 (40 Punkte) Klauur zur Vorleung Verkehrdynamik und -imulation, SS 2016 Löungvorchlag Gegeben it eine zweitreifige Richtungfahrbahn mit zwei im Weentlichen geraden Abchnitten I und III owie dem
Der Stein müsste aus einer Höhe von etwa 5892 m fallen.
 R. Brinkann http://brinkann-du.de Seite 1 5.11.013 Obertue: Ergebnie und auührliche Löungen zu den n zu reien Fall Ergebnie: E1 Ergebni Der Stein üte au einer Höhe von etwa 589 allen. E E3 E4 E5 E6 E7
R. Brinkann http://brinkann-du.de Seite 1 5.11.013 Obertue: Ergebnie und auührliche Löungen zu den n zu reien Fall Ergebnie: E1 Ergebni Der Stein üte au einer Höhe von etwa 589 allen. E E3 E4 E5 E6 E7
12.6 Aufgaben zur Laplace-Transformation
 292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
Übungsblatt - Stabilität des Standardregelkreises
 Prof. Dr.-Ing. Jörg Raich Dr.-Ing. Thoma Seel Fachgebiet Regelungyteme Fakultät IV Elektrotechnik und Informatik Techniche Univerität Berlin Integrierte Verantaltung Mehrgrößenregelyteme Übungblatt - Stabilität
Prof. Dr.-Ing. Jörg Raich Dr.-Ing. Thoma Seel Fachgebiet Regelungyteme Fakultät IV Elektrotechnik und Informatik Techniche Univerität Berlin Integrierte Verantaltung Mehrgrößenregelyteme Übungblatt - Stabilität
Verschiebungssatz: Ist F (s) die Laplace-Transformierte von f (t), dann gilt für t 0 > 0
 3.6 Tranformationätze 853 3.6 Tranformationätze In dieem Abchnitt werden weitere Eigenchaften der Laplace-Tranformation vorgetellt, die in vielen technichen Bechreibungen ihre Anwendung finden. Oftmal
3.6 Tranformationätze 853 3.6 Tranformationätze In dieem Abchnitt werden weitere Eigenchaften der Laplace-Tranformation vorgetellt, die in vielen technichen Bechreibungen ihre Anwendung finden. Oftmal
So verstehen Sie die Leistung einer Stromquelle
 Univerität amburg, Fachbereich Informatik Arbeitbereich Techniche Apekte Multimodaler yteme (TAM) Praktikum der Technichen Informatik T2 3 MO-Tranitor: Kennlinien, Vertärker igitale rundchaltungen Name:...
Univerität amburg, Fachbereich Informatik Arbeitbereich Techniche Apekte Multimodaler yteme (TAM) Praktikum der Technichen Informatik T2 3 MO-Tranitor: Kennlinien, Vertärker igitale rundchaltungen Name:...
Jahresarbeit im Fach Physik. Erstellung eines Videos zu Experimenten in der Kinematik
 Jahrearbeit im Fach Phyik Ertellung eine Video zu Experimenten in der Kinematik Fachlehrer: Herr Meuer Kur: Leitungkur Phyik 12/2 Namen: Martin Böhme und Maik Münch Datum: 21.12.2001 1. VORWORT 4 2. DIE
Jahrearbeit im Fach Phyik Ertellung eine Video zu Experimenten in der Kinematik Fachlehrer: Herr Meuer Kur: Leitungkur Phyik 12/2 Namen: Martin Böhme und Maik Münch Datum: 21.12.2001 1. VORWORT 4 2. DIE
Beobachten und Messen mit dem Mikroskop
 Phyikaliche Grundpraktikum Veruch 006 Veruchprotokolle Beobachten und een mit dem ikrokop Aufgaben 1. Betimmen de ildungmaßtabe der vorhandenen ektive mit Hilfe eine echraubenokular. Vergleich mit den
Phyikaliche Grundpraktikum Veruch 006 Veruchprotokolle Beobachten und een mit dem ikrokop Aufgaben 1. Betimmen de ildungmaßtabe der vorhandenen ektive mit Hilfe eine echraubenokular. Vergleich mit den
8.6.5 Diffusion von Bromdampf ******
 8.6.5 ****** Motivation Die Langamkeit der Diffuion wird mit Hilfe von Bromdampf veranchaulicht. Die quantitative Meung der Diffuion erlaubt die Betimmung der mittleren freien Weglänge und die Meung der
8.6.5 ****** Motivation Die Langamkeit der Diffuion wird mit Hilfe von Bromdampf veranchaulicht. Die quantitative Meung der Diffuion erlaubt die Betimmung der mittleren freien Weglänge und die Meung der
Fortgeschrittene Netzwerk- und Graph-Algorithmen
 Fortgechrittene Netzwerk- und Graph-Algorithmen Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Winteremeter 2010/11 H.
Fortgechrittene Netzwerk- und Graph-Algorithmen Dr. Hanjo Täubig Lehrtuhl für Effiziente Algorithmen (Prof. Dr. Ernt W. Mayr) Intitut für Informatik Techniche Univerität München Winteremeter 2010/11 H.
