Kugeldreieck. (a) München (λ = 11,5 ö. L., φ = 48,1 ) (b) New York (λ = 74,0 w. L., φ = 40,4 ) (c) Moskau (λ = 37,4 ö. L.
|
|
|
- Christa Meinhardt
- vor 6 Jahren
- Abrufe
Transkript
1 Kugeldreieck 1. Berechnen Sie die Fläche des vom Äquator, vom Nullmeridian und dem Längenkreis durch den angegebenen Ort begrenzten Kugeldreiecks. Geben Sie den sphärischen Exzeß des Dreiecks im Grad- und Bogenmaß an. (a) München (λ = 11,5 ö. L., φ = 48,1 ) (b) New York (λ = 74,0 w. L., φ = 40,4 ) (c) Moskau (λ = 37,4 ö. L., φ = 55,5 ) Lösung: (a) A = 0, km 2,ε = 11,5 = 0,2 (b) A = 5, km 2,ε = 74 = 1,29 (c) A = 2, km 2,ε = 37,4 = 0,65 2. Welchen prozentualen Anteil der Kugeloberfläche nimmt ein Kugeldreieck mit (a) α = ,β = und γ = ein? (b) α = ,β = und γ = ein? Lösung: (a) 9,3% (b) 19% 3. Welche Winkel hat ein gleichwinkliges Kugeldreieck (α = β = γ), wenn die Fläche (a) 1 der Kugeloberfläche beträgt. 8 (b) 1 der Kugeloberfläche beträgt. 6 (c) 15% der Kugeloberfläche beträgt. (d) 20% der Kugeloberfläche beträgt. Lösung: (a) 90 (b) 100 (c) 96 (d) (a) Was ist die größtmögliche Fläche, die ein Kugeldreieck auf der Kugeloberfläche (r = 1) einnehmen kann? Begründen Sie ihre Antwort. (b) Zwischen welchen Werten liegt die Winkelsumme im Kugeldreieck? (c) Zwischen welchen Werten liegt die Winkelsumme im Kugelviereck? (d) Zwischen welchen Werten liegt die Winkelsumme im Kugelfünfeck? (e) Zwischen welchen Werten liegt die Winkelsumme im Kugel-n-eck? 1
2 Lösung: (a) 2π (b) < α 1 +α 2 +α 3 < 3 (c) 2 < α 1 +α 2 +α 3 < 4 (d) 3 < α 1 +α 2 +α 3 < 5 (e) (n 2) < α 1 +α 2 +α 3 < n 5. (a) Gegeben ist folgendes Dreieck auf der Erde (r = 6370km 2 ): A : Südpol B : Schnittpunkt des Meridians zu 100 ö. Länge mit dem Äquator C : Schnittpunkt des Meridians zu 30 w. Länge mit dem Äquator Wo liegen die Ecken des Linkspolardreiecks A B C zu ABC (Orientierung A B C)? Bezeichnen Sie die Ecken. (b) Berechnen Sie die Fläche des Polardreiecks. (c) Wo liegen die Ecken des Linkspolardreiecks A B C zu A B C (Orientierung A B C )? Bezeichnen Sie die Ecken. Lösung: (a) A : Nordpol B : Schnittpunkt des Meridians zu 120 w. Länge mit Äquator C : Schnittpunkt des Meridians zu 170 w. Länge mit Äquator (b) Im Dreieck ABC ist a = 130, b = c = 90 α = 50, β = γ = 90 A = (6370km) 2 π = 3, km 2 (c) A : Nordpol B : Schnittpunkt des Meridians zu 80 w. Länge mit Äquator C : Schnittpunkt des Meridians zu 150 ö. Länge mit Äquator 6. (a) In einem Kugeldreieck beträgt a = 80 und b = 120. Welche Werte kann c annehmen? Welche Werte kann die Fläche des Polardreiecks annehmen? (b) In einem Kugeldreieck beträgt a = 100 und c = 110. Welche Werte kann b annehmen? Welche Werte kann die Fläche des Polardreiecks annehmen? (c) In einem Kugeldreieck beträgt α = 160 und β = 130. Welche Werte kann γ annehmen? Welche Werte kann die Fläche des Kugeldreiecks annehmen? (d) In einem Kugeldreieck beträgt α = 170 und γ = 150. Welche Werte kann β annehmen? Welche Werte kann die Fläche des Kugeldreiecks annehmen? Lösung: (a) a+b+c = c = 200 +c < 360 c < 160 α = 100, β = 60, 20 < γ < A = γ r 2 π 0 < A < 8 9 r2 π 2
3 (b) a+b+c = 100 +b+110 = 210 +b < 360 b < 150 α = 80, γ = 70, 30 < β < A = 80 +β +70 r 2 π 0 < A < 5 6 r2 π (c) α+β < γ 110 < γ < r2 π < A < r2 π (d) α+γ < β 140 < β < r2 π < A < r2 π 7. Berechnen Sie für folgende Kugeldreiecke die fehlenden Seiten und Winkel: (a) α = 90, b = 60, c = 100 (b) α = 90, b = 140, c = 100 (c) α = 40, β = 90, c = 70 (d) α = 40, β = 90, c = 110 Lösung: (a) β = 60,38, γ = 98,68, a = 94,98 (b) β = 139,57, γ = 96,47, a = 82,36 (c) γ = 77,30, a = 38,26, b = 74,42 (d) γ = 102,70, a = 38,26, b = 105,58 8. Berechnen Sie für folgende Dreiecke auf der Einheitskugel den Umfang des Polardreiecks: (a) α = 70, β = 120, γ = 100 (b) α = 120, β = 80, A = 2 3 π (c) α = 110, γ = 150, A = 8 9 π Lösung: (a) U = 250 (b) γ = 100 U = 240 (c) β = 80 U = Berechnen SiedieFlächenfolgenderSehnenvierecke P 1 P 2 P 3 P 4 aufdereinheitskugel: (a) α 1 = 100, α 3 = 130 (b) α 2 = 80, α 4 = 170 Lösung: (a) A = 2(α 1+α 3 ) 360 π = 5 9 π (b) A = 2(α 2+α 4 ) 360 π = 7 9 π 10. Was kann über die Winkel in folgenden Sehnenvierecken P 1 P 2 P 3 P 4 auf der Einheitskugel ausgesagt werden: 3
4 (a) α 1 = 80, Fläche A = 5 9 π (b) α 2 = 130, Fläche A = 4 9 π (c) P 1 P 2 = 30, P 2 P 3 = 90, Radius des Umkreises r = 50, Fläche 2 3 π (d) P 2 P 3 = 60, P 3 P 4 = 30, Radius des Umkreises r = 60, Fläche 4 9 π Lösung: (a) A = 2(α 1+α 3 ) 360 π = 5 9 π α 3 = ( ) : 2 α 1 = 150 α 2 +α 4 = 230 (b) A = 2(α 2+α 4 ) 360 π = 4 9 π α 4 = ( ) : 2 α 2 = 90 α 2 +α 4 = 220 (c) Vom sphärischen Mittelpunkt Lot auf die Seiten P 1 P 2 und P 2 P 3 fällen. cosα 21 = tan15 tan50 α 21 = 77 cosα 22 = tan45 tan50 α 22 = 33 α 2 = 110 A = 2(α 2+α 4 ) 360 π = 2 3 π α 4 = 130 α 1 +α 3 = 240 (d) Vom sphärischen Mittelpunkt Lot auf die Seiten P 2 P 3 und P 3 P 4 fällen. cosα 31 = tan30 tan60 α 21 = 70,53 cosα 32 = tan15 tan60 α 22 = 81,10 α 3 = 151,63 A = 2(α 1+α 3 ) 360 π = 4 9 π α 1 = 68,37 α 2 +α 4 = Berechnen Sie die Flächen folgender Sehnenvierecke P 1 P 2 P 3 P 4 : (a) α 1 = 120, P 2 P 3 = P 3 P 4 = 40, Radius des Umkreises r = 50 (b) α 2 = 50, P 3 P 4 = P 4 P 1 = 30, Radius des Umkreises r = 70 Lösung: (a) Vom sphärischen Mittelpunkt Lot auf die Seite P 2 P 3 fällen. cos α 3 2 = tan20 tan50 α 3 = 144,43 α 1 +α 3 = 264,43 A = 2(α 1+α 3 ) 360 π = 2,95 (b) Vom sphärischen Mittelpunkt Lot auf die Seite P 3 P 4 fällen. cos α 4 2 = tan15 tan70 α 4 = 168,81 α 2 +α 4 = 218,81 A = 2(α 2+α 4 ) 360 π = 1, Gegeben ist ein Kugeldreieck P 1 P 2 P 3 mit a 2 = 100, a 1 = 60 und α 2 = 120. Berechnen Sie α 1, a 3, α 3, die Länge der Seitenhalbierenden s 1 und der Höhe h 2. Lösung: α 1 = 49,6, a 3 = 64,3, α 3 = 52,4, s 1 = 81,4, h 2 = 43,3. 4
5 13. Berechnen Sie die fehlenden Stücke des Kugeldreiecks! a b c α β γ a) 62,83 61,43 96,60 b) 74,53 80,62 98,87 c) 43,03 21,17 135,32 d) 81,98 53,12 85,52 e) 51,89 109,88 146,13 f) 30,23 67,91 58,69 g) 87,57 115,81 82,17 h) 132,02 86,98 92,54 Lösung: a b c α β γ a) 62,83 61,43 96,60 54,10 53,09 115,25 b) 74,53 80,62 98,87 72,58 77,62 102,00 c) 74,48 30,66 96,85 43,03 21,17 135,32 d) 76,48 51,76 78,21 81,98 53,12 85,52 e) 145,51 51,89 109,88 146,13 50,75 67,76 f) 30,23 67,91 55,43 31,49 105,98 58,69 g) 115,35 83,98 87,57 115,81 82,17 84,43 h) 83,67 132,02 96,11 86,98 131,72 92, Aus der sphärischen Geometrie erhält man als Grenzfall für R (R: Kugelradius) und gleichbleibende Längen die ebene Geometrie. (a) Was wird aus sin a, tan a und cos a (a: Mittelpunktswinkel eines Großkreisbogens im Bogenmaß) beim Übergang zur ebenen Geometrie. (b) Was erhält man aus den Formeln sinα = sina tanb tana, cosα = und tanα = sinc tanc sinb für rechtwinklige Dreiecke mit γ = 90 beim Übergang zur Ebene? (c) Was erhält man aus der Formel cosa cosb = cosc für rechtwinklige Dreiecke mit γ = 90 beim Übergang zur Ebene? (d) Was erhält man aus der Formel sina Ebene? = sinα sinb sinβ für Dreiecke beim Übergang zur (e) Was erhält man aus der Formel cosc = cosa cosb + sina sinb cosγ für Dreiecke beim Übergang zur Ebene? Lösung: (a) a = a R (a : Länge des Großkreisbogens) wird für große Kugelradien R sehr klein. Also wird sina zu a, tana zu a und cosa zu a2. (b) sinα = a c, cosα = b c, tanα = a b (c) Satz des Pythagoras: c 2 = a 2 +b 2 (d) Sinussatz: a b = sinα sinβ (e) Kosinussatz: c 2 = a 2 +b 2 2abcosγ 5
6 15. Beweisen Sie den folgenden Satz: Ist in einem Kugeldreieck ABC der Winkel γ = 90, so liegt die Länge der Hypothenuse c zwischen a und π a bzw. zwischen b und π b. Lösung: sinα = sina sinc sina = sinαsinc Es gilt also: sina sinc, was mit der Behauptung äquivalent ist. sinβ = sinb sinc sinb = sinβsinc Es gilt also: sinb sinc, was mit der Behauptung äquivalent ist. 16. Leiten Sie durch Übergang zum Polardreieck aus der Neperschen Regel eine neue Regel her. Lösung: Geht man bei einem rechtwinkligen Kugeldreieck zum Polardreieck über, erhält man ein rechtsseitiges Kugeldreieck. In der Neperschen Regel ergeben sich dabei die folgenden Ersetzungen: c γ, α a, β b, 90 b β 90 und 90 a α 90 Nun schreibt man sich die zehn zugehörigen Formeln entsprechend der Neperschen Regel auf und nutzt die Eigenschaften der trigonometrischen Funktionen. Man erkennt, dass die Formeln bei den folgenden Ersetzungen richtig bleiben: b b, a a, β β und α α. Im Neperschen Kreis stehen also der Reihe nach die Größen: γ, b, 90 α, 90 β und a. 17. In ebenen rechtwinkligen Dreiecken mit γ = 90 gilt der Kathetensatz: a 2 = cq und b 2 = cp Suchen Sie nach einem analogen Satz für sphärische rechtwinklige Dreiecke. Lösung: sinα = sina sinc = sinq sina sin2 a = sinc sinq. Analog folgt sin 2 b = sinc sinp. 18. Zeigen Sie, dass in einem rechtwinkligen Kugeldreieck die Winkelsumme zwischen π und 2π liegt. Lösung: In jedem Kugeldreieck gilt α+β+γ > π, da die Fläche eines Kugeldreiecks α+β+γ π π stets positiv ist. Die Fläche eines rechtwinkligen Dreiecks ist offensichtlich kleiner als r 2 π α+β+γ π π < 1 α+β +γ < 2 π r 2 π 6
7 19. (a) In einem Kugeldreieck ABC wird ein beliebiger Punkt T auf der Seite c ergänzt. Zeigen Sie, dass mit CT= t, AT= p und TB= q gilt: sinc cost = sinp cosa+sinq cosb (b) Berechnen Sie mit diesem Zusammenhang allgemein die Länge einer Seitenhalbierenden im Kugeldreieck. (c) Welchen Zusammenhang erhält man durch analoge Rechnung in der ebenen Geometrie? (d) Zeigen Sie, dass man den Zusammenhang aus Teilaufgabe (c) auch aus dem Zusammenhang aus Teilaufgabe (a) durch Übergang zur ebenen Geometrie erhält. Lösung: (a) Wendet man den Kosinussatz auf die Teildreiecke an, erhält man cosb = cosp cost+sinpsintcosµ und cosa = cosq cost+sinqsintcos(π µ). Durch Ersetzung von cos µ erhält man daraus cosa sinp+sinq cosb = cost(cosq sinp+cosp sinq) = cost sinc (b) sinc cost = sin c 2 cosa+sin c 2 cosb = sin c 2 (cosa+cosb) Wegen sinc = 2sin c 2 cos c 2 folgt 2cos c cosa+cosb 2 cost = cosa+cosb cost = 2cos c 2 (c) ct 2 +cpq = a 2 p+b 2 q (d) Berücksichtigt man Terme bis zur dritten Potenz, erhält man aus dem Zusammenhang aus (a): (c 1 6 c3 )(1 1 2 t2 ) = (p 1 6 p3 )(1 1 2 a2 )+(q 1 6 q6 )(1 1 2 b2 ) ct 2 +cpq = a 2 p+b 2 q 20. (a) Wie sieht das Polardreieck zu einem gleichschenkligen Kugeldreieck mit α = β und γ = 90 aus? (b) Wie sieht das Polardreieck zu einem gleichschenkligen Kugeldreieck mit α = β = 90 aus? (c) Wie sieht das Polardreieck zu einem rechtwinkligen Kugeldreieck mit α = β = γ = 90 aus? Lösung: (a) gleichschenkliges Kugeldreieck mit c = 90 (b) gleichschenkliges Kugeldreieck mit a = b = 90 (c) Kugeldreieck mit a = b = c = 90, also Kugeloktant 7
Lösungen IV ) β = 54,8 ; γ = 70,4 106) a) 65 b) 65 (115?) d) 57,5
 (Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
(Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.4 2013/06/24 23:05:24 hk Exp hk $ 5 Sphärische Trigonometrie 5.2 Sphärische Dreiecksberechnung Wir behandeln gerade die Berechnung sphärischer Dreiecke und haben zu diesem Zweck bereits
$Id: sphaere.tex,v 1.4 2013/06/24 23:05:24 hk Exp hk $ 5 Sphärische Trigonometrie 5.2 Sphärische Dreiecksberechnung Wir behandeln gerade die Berechnung sphärischer Dreiecke und haben zu diesem Zweck bereits
Aufgaben mit Lösungen zum Themengebiet: Geometrie bei rechtwinkligen Dreiecken
 Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
Das Vektorprodukt und Sphärische Geometrie
 Das Vektorprodukt und Sphärische Geometrie Proseminar zu Algebra von Methnani Lassaad Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf 12. April 2010 Betreuung: Prof. Dr. Bogopolski Ÿ1)
Das Vektorprodukt und Sphärische Geometrie Proseminar zu Algebra von Methnani Lassaad Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf 12. April 2010 Betreuung: Prof. Dr. Bogopolski Ÿ1)
Trigonometrie. bekannte Zusammenhänge. 4-Streckensatz: groß/klein = groß/klein. Zusammenhänge im allgemeinen Dreieck:
 Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Sphärische Geometrie und Trigonometrie
 1 Sphärische Geometrie und Trigonometrie Die Sphärische Trigonometrie befasst sich mit der erechnung von Kugeldreiecken. Sie ist von stronomie und Seefahrern entwickelt worden, um die Lage von Punkten
1 Sphärische Geometrie und Trigonometrie Die Sphärische Trigonometrie befasst sich mit der erechnung von Kugeldreiecken. Sie ist von stronomie und Seefahrern entwickelt worden, um die Lage von Punkten
Mathematische Probleme, SS 2013 Montag $Id: dreieck.tex,v /04/22 20:37:01 hk Exp hk $
 $Id: dreieck.tex,v 1.7 013/04/ 0:37:01 hk Exp hk $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck In der letzten Sitzung hatten wir den sogenannten Inkreis eines Dreiecks eingeführt, dies ist der Kreis
$Id: dreieck.tex,v 1.7 013/04/ 0:37:01 hk Exp hk $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck In der letzten Sitzung hatten wir den sogenannten Inkreis eines Dreiecks eingeführt, dies ist der Kreis
Repetition Begriffe Geometrie. 14. Juni 2012
 Repetition Begriffe Geometrie 14. Juni 2012 Planimetrie 1. Strahlensatz Planimetrie 1. Strahlensatz Werden zwei sich schneidende Geraden von zwei Parallelen geschnitten, so verhalten sich die Abschnitte
Repetition Begriffe Geometrie 14. Juni 2012 Planimetrie 1. Strahlensatz Planimetrie 1. Strahlensatz Werden zwei sich schneidende Geraden von zwei Parallelen geschnitten, so verhalten sich die Abschnitte
fakultät für physik bernhard emmer mathematik vorkurs für physiker Übungsblatt 1 für beliebiges k N und x 0. a 2 x 1 x 3 y 2 ) 2
 fakultät für physik bernhard emmer mathematik vorkurs für physiker Übungsblatt Aufgabe Induktion). a) Beweisen Sie, dass + 3 + 5 +... + n )) ein perfektes Quadrat genauer n ) ist. b) Zeigen Sie: + + +...
fakultät für physik bernhard emmer mathematik vorkurs für physiker Übungsblatt Aufgabe Induktion). a) Beweisen Sie, dass + 3 + 5 +... + n )) ein perfektes Quadrat genauer n ) ist. b) Zeigen Sie: + + +...
Trigonometrie. In der Abbildung: der Winkel 120 (Gradenmaß) ist 2π = 2π (Bogenmaß).
 Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
Sphärische Trigonometrie. Berechnungen. Hans Walser
 Sphärische Trigonometrie. Berechnungen Hans Walser Sphärische Trigonometrie. Berechnungen ii Inhalt 1 Sphärische Trigonometrie... 1 1.1 Worum geht es?... 1 1.2 Der Seiten-Cosinus-Satz... 1 1.3 Zusammenhang
Sphärische Trigonometrie. Berechnungen Hans Walser Sphärische Trigonometrie. Berechnungen ii Inhalt 1 Sphärische Trigonometrie... 1 1.1 Worum geht es?... 1 1.2 Der Seiten-Cosinus-Satz... 1 1.3 Zusammenhang
Elemente der Mathematik - Sommer 2016
 Elemente der Mathematik - Sommer 2016 Prof Dr Matthias Lesch, Regula Krapf Übungsblatt 7 Aufgabe 23 9 Punkte In der folgenden Aufgabe sei mit baryzentrischen Koordinaten immer die baryzentrischen Koordinaten
Elemente der Mathematik - Sommer 2016 Prof Dr Matthias Lesch, Regula Krapf Übungsblatt 7 Aufgabe 23 9 Punkte In der folgenden Aufgabe sei mit baryzentrischen Koordinaten immer die baryzentrischen Koordinaten
DIPLOMARBEIT. Sphärische Kegelschnitte - didaktisch aufbereitet
 DIPLOMARBEIT Sphärische Kegelschnitte - didaktisch aufbereitet Ausgeführt am Institut für Diskrete Mathematik und Geometrie der Technischen Universität Wien unter Anleitung von Ao. Univ.-Prof. Dr. Wolfgang
DIPLOMARBEIT Sphärische Kegelschnitte - didaktisch aufbereitet Ausgeführt am Institut für Diskrete Mathematik und Geometrie der Technischen Universität Wien unter Anleitung von Ao. Univ.-Prof. Dr. Wolfgang
2 Geometrie und Vektoren
 Geometrie und Vektoren Vorbemerkung: Begriffe wie die folgenden werden hier als bekannt vorausgesetzt: Punkt, Strecke, Strahl, Gerade, Ebene, Kreis, Winkel, rechter Winkel, etc..1 Grundlegende Sätze Satz
Geometrie und Vektoren Vorbemerkung: Begriffe wie die folgenden werden hier als bekannt vorausgesetzt: Punkt, Strecke, Strahl, Gerade, Ebene, Kreis, Winkel, rechter Winkel, etc..1 Grundlegende Sätze Satz
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
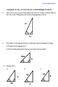 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.5 2013/08/13 17:21:33 hk Exp $ 5 Sphärische Trigonometrie m Ende der letzten Sitzung hatten wir mit der Untersuchung sphärischer Dreiecke begonnen. Gegeben war eine Sphäre K, oder
$Id: sphaere.tex,v 1.5 2013/08/13 17:21:33 hk Exp $ 5 Sphärische Trigonometrie m Ende der letzten Sitzung hatten wir mit der Untersuchung sphärischer Dreiecke begonnen. Gegeben war eine Sphäre K, oder
1. Unterteilung von allgemeinen Dreiecken in rechtwinklige
 Trigonometrie am allgemeinen Dreieck Wir können auch die Seiten und Winkel von allgemeinen Dreiecken mit Hilfe der Trigonometrie berechnen. Die einfachste Variante besteht darin, ein beliebiges Dreieck
Trigonometrie am allgemeinen Dreieck Wir können auch die Seiten und Winkel von allgemeinen Dreiecken mit Hilfe der Trigonometrie berechnen. Die einfachste Variante besteht darin, ein beliebiges Dreieck
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.15 2016/07/08 13:57:53 hk Exp $ 5 Sphärische Trigonometrie 5.3 Kleinkreise als sphärische Kreise In der letzten Sitzung hatten wir eingesehen das die sphärischen Kreise auf einer Sphäre
$Id: sphaere.tex,v 1.15 2016/07/08 13:57:53 hk Exp $ 5 Sphärische Trigonometrie 5.3 Kleinkreise als sphärische Kreise In der letzten Sitzung hatten wir eingesehen das die sphärischen Kreise auf einer Sphäre
Lösungen der Übungsaufgaben III
 Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
1.4 Trigonometrie. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 3
 1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
Trigonometrische Funktionen
 Trigonometrische Funktionen Rainer Hauser September 013 1 Einleitung 1.1 Der Begriff Funktion Eine Funktion ordnet jedem Element m 1 einer Menge M 1 ein Element m einer Menge M zu. Man schreibt dafür f:
Trigonometrische Funktionen Rainer Hauser September 013 1 Einleitung 1.1 Der Begriff Funktion Eine Funktion ordnet jedem Element m 1 einer Menge M 1 ein Element m einer Menge M zu. Man schreibt dafür f:
Grundwissen 10. Überblick: Gradmaß rπ Länge eines Bogens zum Mittelpunktswinkels α: b = α
 Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
1.4 Trigonometrie I. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 4
 1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
Arbeitsblatt Geometrie / Trigonometrie
 Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Arbeitsbltt Geometrie / Trigonometrie Dozent: - rückenkurs Mthemtik 2016 Modul: Mthemtik Dtum: 2016
Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Arbeitsbltt Geometrie / Trigonometrie Dozent: - rückenkurs Mthemtik 2016 Modul: Mthemtik Dtum: 2016
D i e W e l t s t ä d t e r o s e
 D i e W e l t s t ä d t e r o s e Eine Besonderheit der APG-Sonnenuhr ist die Weltstädterose. Um den Polos sind in die Bodenplatten kreisförmig Pfeile aus Edelstahl, die Richtung und Entfernung von ausgewählten
D i e W e l t s t ä d t e r o s e Eine Besonderheit der APG-Sonnenuhr ist die Weltstädterose. Um den Polos sind in die Bodenplatten kreisförmig Pfeile aus Edelstahl, die Richtung und Entfernung von ausgewählten
Trigonometrische Funktionen: Sinus und Cosinus. Dieter Harig (Dipl. Math.) HD MINT-Projekt 5. Dezember 2013
 Trigonometrische Funktionen: Sinus und Cosinus Dieter Harig (Dipl. Math.) HD MINT-Projekt 5. Dezember 0 4 5 4 4 Grad- und Bogenmaß Wir betrachten den Einheitskreis (Radius r = ) und einen beliebigen Winkel
Trigonometrische Funktionen: Sinus und Cosinus Dieter Harig (Dipl. Math.) HD MINT-Projekt 5. Dezember 0 4 5 4 4 Grad- und Bogenmaß Wir betrachten den Einheitskreis (Radius r = ) und einen beliebigen Winkel
Eine Methode zur Positionsberechnung aus Relativmessungen. Von Eckhardt Schön, Erfurt
 Eine Methode zur Positionsberechnung aus Relativmessungen Von Eckhardt Schön, Erfurt Mit 4 Abbildungen Die Bewegung der Sterne und Planeten vollzieht sich für einen irdischen Beobachter scheinbar an einer
Eine Methode zur Positionsberechnung aus Relativmessungen Von Eckhardt Schön, Erfurt Mit 4 Abbildungen Die Bewegung der Sterne und Planeten vollzieht sich für einen irdischen Beobachter scheinbar an einer
3. Erweiterung der trigonometrischen Funktionen
 3. Erweiterung der trigonometrischen Funktionen 3.1. Polarkoordinaten 1) Rechtwinklige und Polarkoordinaten Üblicherweise gibt man die Koordinaten eines Punktes in der Ebene durch ein Zahlenpaar vor: P(x
3. Erweiterung der trigonometrischen Funktionen 3.1. Polarkoordinaten 1) Rechtwinklige und Polarkoordinaten Üblicherweise gibt man die Koordinaten eines Punktes in der Ebene durch ein Zahlenpaar vor: P(x
Themenbereich: Besondere Dreiecke Seite 1 von 6
 Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Themenbereich: Besondere Dreiecke Seite 1 von 6 Lernziele: - Kenntnis der Bezeichnungen für besondere Dreiecke - Kenntnis der Seiten- und Winkelbezeichnungen bei besonderen Dreiecken - Kenntnis der Eigenschaften
Trigonometrische Berechnungen
 Trigonometrische Berechnungen Aufgabe 1 Berechnen Sie im rechtwinkligen Dreieck die fehlenden Seiten und Winkel: a) p = 4,93, β = 70,3 b) p = 28, q = 63 c) a = 12,5, p = 4,4 d) h = 9,1, q = 6,0 e) a =
Trigonometrische Berechnungen Aufgabe 1 Berechnen Sie im rechtwinkligen Dreieck die fehlenden Seiten und Winkel: a) p = 4,93, β = 70,3 b) p = 28, q = 63 c) a = 12,5, p = 4,4 d) h = 9,1, q = 6,0 e) a =
Fit in Mathe. Mai Klassenstufe 9. Körper ohne π
 Thema Musterlösungen 1 Körper ohne π Ein rechtwinkliges Dreieck besteht aus den Seiten a, b und c, wobei der Seite c ein rechter Winkel gegenüberliegt. Berechne jeweils die Länge der fehlenden Seite(n).
Thema Musterlösungen 1 Körper ohne π Ein rechtwinkliges Dreieck besteht aus den Seiten a, b und c, wobei der Seite c ein rechter Winkel gegenüberliegt. Berechne jeweils die Länge der fehlenden Seite(n).
Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher Umlaufsinn!
 Berechnungen in Dreiecken Allgemeines zu Dreiecken Innenwinkelsatz α + β + γ = 180 Besondere Dreiecke Gleichschenkliges Dreieck Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher
Berechnungen in Dreiecken Allgemeines zu Dreiecken Innenwinkelsatz α + β + γ = 180 Besondere Dreiecke Gleichschenkliges Dreieck Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher
Der Flächeninhalt eines Sehnenvierecks auf den Spuren des indischen Mathematikers Brahmagupta ( )
 Den Flächeninhalt eines allgemeinen Vierecks bestimmt man meistens durch Zerlegung in Dreiecke. Geht es auch anders? Für den Fall, dass das Viereck ein Sehnenviereck ist, hat der indische Mathematiker
Den Flächeninhalt eines allgemeinen Vierecks bestimmt man meistens durch Zerlegung in Dreiecke. Geht es auch anders? Für den Fall, dass das Viereck ein Sehnenviereck ist, hat der indische Mathematiker
und der Kosinussatz cos(γ) = a2 + b 2 c 2 2 a b Sinussatz sin(β) = a b
 Blatt Nr 1906 Mathematik Online - Übungen Blatt 19 Dreieck Geometrie Nummer: 41 0 2009010074 Kl: 9X Aufgabe 1911: (Mit GTR) In einem allgemeinen Dreieck ABC sind a = 18782, c = 1511 und β = 33229 gegeben
Blatt Nr 1906 Mathematik Online - Übungen Blatt 19 Dreieck Geometrie Nummer: 41 0 2009010074 Kl: 9X Aufgabe 1911: (Mit GTR) In einem allgemeinen Dreieck ABC sind a = 18782, c = 1511 und β = 33229 gegeben
Mathematische Probleme, SS 2015 Montag $Id: dreieck.tex,v /04/27 13:26:30 hk Exp $
 $Id: dreieck.tex,v 1.17 2015/04/27 13:26:30 hk Exp $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck m Ende der letzten Sitzung hatten wir eingesehen das die drei Mittelsenkrechten eines Dreiecks = sich
$Id: dreieck.tex,v 1.17 2015/04/27 13:26:30 hk Exp $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck m Ende der letzten Sitzung hatten wir eingesehen das die drei Mittelsenkrechten eines Dreiecks = sich
Mathematische Probleme, SS 2013 Donnerstag $Id: dreieck.tex,v /04/18 15:03:29 hk Exp hk $
 $Id: dreieck.tex,v 1.6 2013/04/18 15:03:29 hk Exp hk $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck Wir hatten gerade begonnen uns mit den speziellen Punkten im Dreieck zu beschäftigen. Dabei beschränken
$Id: dreieck.tex,v 1.6 2013/04/18 15:03:29 hk Exp hk $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck Wir hatten gerade begonnen uns mit den speziellen Punkten im Dreieck zu beschäftigen. Dabei beschränken
I. Reelle Zahlen GRUNDWISSEN MATHEMATIK - 9. KLASSE
 I. Reelle Zahlen 1. Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen. Nenne Beispiele für rationale und irrationale Zahlen.. Aus negativen
I. Reelle Zahlen 1. Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen. Nenne Beispiele für rationale und irrationale Zahlen.. Aus negativen
f(x nk ) = lim y nk ) = lim Bemerkung 2.14 Der Satz stimmt nicht mehr, wenn D nicht abgeschlossen oder nicht beschränkt ist, wie man z.b.
 Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
3. Mathematikschulaufgabe
 Arbeitszeit 40min 1.0 Gegeben sind die Punkte A (-I1) und B (6I-1), sowie die Gerade g mit der Gleichung y = 0,5x + 3. Führe die folgenden Berechnungen jeweils auf zwei Stellen gerundet aus. 1.1 Berechne
Arbeitszeit 40min 1.0 Gegeben sind die Punkte A (-I1) und B (6I-1), sowie die Gerade g mit der Gleichung y = 0,5x + 3. Führe die folgenden Berechnungen jeweils auf zwei Stellen gerundet aus. 1.1 Berechne
ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese Aufgabenblätter
 Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 2005 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 2005 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
(von Punkt A nach Punkt B) gemessen und auch die entsprechenden Zenitwinkel z B
 Aufgabe a.1 Verwendet dieses elementare geometrische Verhältnis der Strecken, um die Höhe eines Turmes oder eines sonstigen hohen Gebäudes in eurer Nähe zu bestimmen. Dokumentiert euer Experiment. Wiederholt
Aufgabe a.1 Verwendet dieses elementare geometrische Verhältnis der Strecken, um die Höhe eines Turmes oder eines sonstigen hohen Gebäudes in eurer Nähe zu bestimmen. Dokumentiert euer Experiment. Wiederholt
KREISFUNKTIONEN. Allgemeines
 KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
Beispiel: Bestimmung des Werts 3 2 ( 2 1, 4142) Es gilt 3 1,41 = 3 141/100 = , 707. Es gilt 3 1,42 = 3 142/100 = , 759.
 (4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
(4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 14 VERMESSUNGSAUFGABEN
 Mathematik Mag. Schmid Wolfgang Arbeitsblatt 4 3. Semester ARBEITSBLATT 4 VERMESSUNGSAUFGABEN Nun wollen wir unser Wissen über recht- und schiefwinkelige Aufgaben an einigen Aufgaben beweisen Beispiel
Mathematik Mag. Schmid Wolfgang Arbeitsblatt 4 3. Semester ARBEITSBLATT 4 VERMESSUNGSAUFGABEN Nun wollen wir unser Wissen über recht- und schiefwinkelige Aufgaben an einigen Aufgaben beweisen Beispiel
Elemente der Mathematik - Sommer 2016
 Elemente der Mathematik - Sommer 06 Prof. Dr. Matthias Lesch, Regula Krapf Übungsblatt 8 Aufgabe 7 (8 Punkte). Ein Parallelogramm ist ein Rechteck ABCD mit Seiten a, b, c, d wie unten dargestellt, mit
Elemente der Mathematik - Sommer 06 Prof. Dr. Matthias Lesch, Regula Krapf Übungsblatt 8 Aufgabe 7 (8 Punkte). Ein Parallelogramm ist ein Rechteck ABCD mit Seiten a, b, c, d wie unten dargestellt, mit
Trigonometrie. 3. Kapitel aus meinem Lehrgang Geometrie. Ronald Balestra CH St. Peter
 Trigonometrie 3. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch 17. August 2008 Inhaltsverzeichnis 3 Trigonometrie 46 3.1 Warum Trigonometrie........................
Trigonometrie 3. Kapitel aus meinem Lehrgang Geometrie Ronald Balestra CH - 7028 St. Peter www.ronaldbalestra.ch 17. August 2008 Inhaltsverzeichnis 3 Trigonometrie 46 3.1 Warum Trigonometrie........................
Das Problem der dreizehn Kugeln
 Clemens Hauser Das Problem der dreizehn Kugeln Vortrag im Seminar für Didaktik der Mathematik an der Universität Freiburg 1.12.2009 Kepler (1611): Dichteste Kugelpackung (?) Kepler (1611): Dichteste Kugelpackung
Clemens Hauser Das Problem der dreizehn Kugeln Vortrag im Seminar für Didaktik der Mathematik an der Universität Freiburg 1.12.2009 Kepler (1611): Dichteste Kugelpackung (?) Kepler (1611): Dichteste Kugelpackung
Konstruktionen am Dreieck
 Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Sphärische Trigonometrie
 Sphärische Trigonometrie Bei geodätischen Messungen, die sich über größere Entfernungen erstrecken, muss die Kugelgestalt der Erde berücksichtigt werden. Dazu ist eine Geometrie auf der Kugel erforderlich.
Sphärische Trigonometrie Bei geodätischen Messungen, die sich über größere Entfernungen erstrecken, muss die Kugelgestalt der Erde berücksichtigt werden. Dazu ist eine Geometrie auf der Kugel erforderlich.
9.5 Graphen der trigonometrischen Funktionen
 9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Mathematische Einführung
 und euklidische Geometrie 13.04.2011 Motivation Warum braucht man eine mathematische Einführung? Die Physik ist in der Sprache der Mathematik formuliert. Mathematische Methoden essentiell zur Lösung von
und euklidische Geometrie 13.04.2011 Motivation Warum braucht man eine mathematische Einführung? Die Physik ist in der Sprache der Mathematik formuliert. Mathematische Methoden essentiell zur Lösung von
Lösungen V.1. Pfeile bedeuten ist auch ein. (Lambacher-Schweizer Geometrie 2, S. 150)
 Lösungen V.1 I: Trapez (zwei parallele Seiten; keine Symmetrie) II: gleichschenkliges Trapez (zwei parallele Seiten, die anderen beiden gleich lang; achsensymmetrisch) III: Drachen(viereck) (jeweils zwei
Lösungen V.1 I: Trapez (zwei parallele Seiten; keine Symmetrie) II: gleichschenkliges Trapez (zwei parallele Seiten, die anderen beiden gleich lang; achsensymmetrisch) III: Drachen(viereck) (jeweils zwei
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Berechnungen am Dreieck
 1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
Trigonometrie und Planimetrie
 Trigonometrie und Planimetrie Hinweis: Die Aufgaben sind in 3 Gruppen gegliedert (G): Grundlagen, Basiswissen einfache Aufgaben (F): Fortgeschritten mittelschwere Aufgaben (E): Experten schwere Aufgaben
Trigonometrie und Planimetrie Hinweis: Die Aufgaben sind in 3 Gruppen gegliedert (G): Grundlagen, Basiswissen einfache Aufgaben (F): Fortgeschritten mittelschwere Aufgaben (E): Experten schwere Aufgaben
11. Sphärische Geometrie und das Problem der guten Karten.
 11. Sphärische Geometrie und das Problem der guten Karten. Im 15. Jahrhundert hatte man die Technologie um sich von der Küstenschiffahrt zu lösen und Fernreisen zu machen. Kopernikus machte sich auf, um
11. Sphärische Geometrie und das Problem der guten Karten. Im 15. Jahrhundert hatte man die Technologie um sich von der Küstenschiffahrt zu lösen und Fernreisen zu machen. Kopernikus machte sich auf, um
Didaktik der Geometrie
 Didaktik der Geometrie 7.1 Didaktik der Geometrie Didaktik der Geometrie 7.2 Inhalte Didaktik der Geometrie 1 Ziele und Inhalte 2 Begriffsbildung 3 Konstruieren 4 Argumentieren und Beweisen 5 Problemlösen
Didaktik der Geometrie 7.1 Didaktik der Geometrie Didaktik der Geometrie 7.2 Inhalte Didaktik der Geometrie 1 Ziele und Inhalte 2 Begriffsbildung 3 Konstruieren 4 Argumentieren und Beweisen 5 Problemlösen
O A B. Ableitung der Winkelfunktionen
 Ableitung der Winkelfunktionen Das Verständnis der Herleitung der Ableitung der Winkelfunktionen sett einiges an Mittelstufenkenntnissen voraus; das meiste davon wird häufig im Unterricht geschlabbert
Ableitung der Winkelfunktionen Das Verständnis der Herleitung der Ableitung der Winkelfunktionen sett einiges an Mittelstufenkenntnissen voraus; das meiste davon wird häufig im Unterricht geschlabbert
Passerelle Mathematik Frühling 2005 bis Herbst 2006
 Passerelle Mathematik Frühling 2005 bis Herbst 2006 www.mathenachhilfe.ch info@mathenachhilfe.ch 079 703 72 08 Inhaltsverzeichnis 1 Algebra 3 1.1 Termumformungen..................................... 3
Passerelle Mathematik Frühling 2005 bis Herbst 2006 www.mathenachhilfe.ch info@mathenachhilfe.ch 079 703 72 08 Inhaltsverzeichnis 1 Algebra 3 1.1 Termumformungen..................................... 3
Konstruktion des isoperimetrischen Punktes
 Konstruktion des isoperimetrischen Punktes C. und M. Reinsch Dreieck in der komplexen Ebene Ecken: A, B, C. Seiten: a = B C, b = C A, c = A B. Kreise: A(u) um A mit Radius u, B(v) um B mit Radius v, C(w)
Konstruktion des isoperimetrischen Punktes C. und M. Reinsch Dreieck in der komplexen Ebene Ecken: A, B, C. Seiten: a = B C, b = C A, c = A B. Kreise: A(u) um A mit Radius u, B(v) um B mit Radius v, C(w)
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Klausur zur Einführung in die Geometrie im SS 2002
 Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Lernmodul 4, Kapitel
 1 Lernmodul 4, Kapitel 14 5 Konstruktion Die wichtigsten Konstruktionselemente bei der Konstruktion mit Zirkel und Lineal sind: 1 Mittelsenkrechte zwischen zwei Punkten auf einer Geraden Lot fällen: einen
1 Lernmodul 4, Kapitel 14 5 Konstruktion Die wichtigsten Konstruktionselemente bei der Konstruktion mit Zirkel und Lineal sind: 1 Mittelsenkrechte zwischen zwei Punkten auf einer Geraden Lot fällen: einen
Dr. O. Wittich Aachen, 12. September 2017 S. Bleß, M. Sc. Analysis. Übungsaufgaben. im Vorkurs Mathematik 2017, RWTH Aachen University
 Dr. O. Wittich Aachen,. September 7 S. Bleß, M. Sc. Analysis Übungsaufgaben im Vorkurs Mathematik 7, RWTH Aachen University Intervalle, Beschränktheit, Maxima, Minima Aufgabe Bestimmen Sie jeweils, ob
Dr. O. Wittich Aachen,. September 7 S. Bleß, M. Sc. Analysis Übungsaufgaben im Vorkurs Mathematik 7, RWTH Aachen University Intervalle, Beschränktheit, Maxima, Minima Aufgabe Bestimmen Sie jeweils, ob
Inhaltsverzeichnis. iii
 Inhaltsverzeichnis 1 Geometrie auf der Kugeloberfläche 1 11 Grundlagen der sphärischengeometrie 2 111 Kugel, Sphäre, Kugelkoordinaten 2 112 Klein- und Großkreise, diametrale Punktepaare, Geraden, Strecken
Inhaltsverzeichnis 1 Geometrie auf der Kugeloberfläche 1 11 Grundlagen der sphärischengeometrie 2 111 Kugel, Sphäre, Kugelkoordinaten 2 112 Klein- und Großkreise, diametrale Punktepaare, Geraden, Strecken
α π r² Achtung: Das Grundwissen steht im Lehrplan! 1. Kreis und Kugel
 Achtung: Das Grundwissen steht im Lehrplan! Tipps zum Grundwissen Mathematik Jahrgangsstufe 10 Folgende Begriffe und Aufgaben solltest Du nach der 10. Klasse kennen und können: (Falls Du Lücken entdeckst,
Achtung: Das Grundwissen steht im Lehrplan! Tipps zum Grundwissen Mathematik Jahrgangsstufe 10 Folgende Begriffe und Aufgaben solltest Du nach der 10. Klasse kennen und können: (Falls Du Lücken entdeckst,
Sphärische Geometrie
 Sphärische Geometrie Nikolai Nowaczyk http://math.nikno.de/ Lars Wallenborn http://math.wallenborn.net/ 03.-05. Dezember 2010 Dies ist ein Skript zum gleichnamigen
Sphärische Geometrie Nikolai Nowaczyk http://math.nikno.de/ Lars Wallenborn http://math.wallenborn.net/ 03.-05. Dezember 2010 Dies ist ein Skript zum gleichnamigen
KOMPETENZHEFT ZUR TRIGONOMETRIE, II
 KOMPETENZHEFT ZUR TRIGONOMETRIE, II 1. Aufgabenstellungen Aufgabe 1.1. Bestimme alle Winkel in [0 ; 360 ], die Lösungen der gegebenen Gleichung sind, und zeichne sie am Einheitskreis ein. 1) sin(α) = 0,4
KOMPETENZHEFT ZUR TRIGONOMETRIE, II 1. Aufgabenstellungen Aufgabe 1.1. Bestimme alle Winkel in [0 ; 360 ], die Lösungen der gegebenen Gleichung sind, und zeichne sie am Einheitskreis ein. 1) sin(α) = 0,4
Sinus-und Kosinussatz
 Sinus-und Kosinussatz Referentin: Theresia Herrmann a sinα = b sin β = c sinγ = 2r r 1 = r 2 = r a 2 = b 2 +c 2 2 b c cosα b 2 = a 2 +c 2 2 a c cosβ c 2 = a 2 +b 2 2 a b cosγ Gliederung: 1.Sinussatz 2.Beweis
Sinus-und Kosinussatz Referentin: Theresia Herrmann a sinα = b sin β = c sinγ = 2r r 1 = r 2 = r a 2 = b 2 +c 2 2 b c cosα b 2 = a 2 +c 2 2 a c cosβ c 2 = a 2 +b 2 2 a b cosγ Gliederung: 1.Sinussatz 2.Beweis
Sphärische Trigonometrie
 Spezialgebiet in Mathematik Sphärische Trigonometrie Von Christoph Saulder Inhalt Inhalt... 2 Historischer Hintergrund... 3 Grundlagen... 3 Großkreise... 3 Kugelzweiecke... 4 Kleinkreise... 4 Begriffe...
Spezialgebiet in Mathematik Sphärische Trigonometrie Von Christoph Saulder Inhalt Inhalt... 2 Historischer Hintergrund... 3 Grundlagen... 3 Großkreise... 3 Kugelzweiecke... 4 Kleinkreise... 4 Begriffe...
Lösung zur Übung 3 vom
 Lösung zur Übung 3 vom 28.0.204 Aufgabe 8 Gegeben ist ein Dreieck mit den nachfolgenden Seiten- und Winkelbezeichnung. Der Cosinussatz ist eine Verallgemeinerung des Satzes des Pythagoras: a) c 2 = a 2
Lösung zur Übung 3 vom 28.0.204 Aufgabe 8 Gegeben ist ein Dreieck mit den nachfolgenden Seiten- und Winkelbezeichnung. Der Cosinussatz ist eine Verallgemeinerung des Satzes des Pythagoras: a) c 2 = a 2
Was bedeutet Trigonometrie und mit was beschäftigt sich die Trigonometrie?
 Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Trigonometrie. Winkelfunktionen und Einheitskreis
 Trigonometrie Die Trigonometrie ist die Lehre der Winkel- oder Kreisfunktionen. Die auffälligste Eigenschaften der Funktionen der Trigonometrie ist die Periodizität: Trigonometrische Funktionen zeigen
Trigonometrie Die Trigonometrie ist die Lehre der Winkel- oder Kreisfunktionen. Die auffälligste Eigenschaften der Funktionen der Trigonometrie ist die Periodizität: Trigonometrische Funktionen zeigen
6. Orbits und die Runge-Lenz Vektor
 Übungen zur T: Theoretische Mechani, SoSe3 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physi.uni-muenchen.de 6. Orbits und die Runge-Lenz Vetor Übung 6.: Die Rücehr der Kanonenugel
Übungen zur T: Theoretische Mechani, SoSe3 Prof. Dr. Dieter Lüst Theresienstr. 37, Zi. 45 Dr. James Gray James.Gray@physi.uni-muenchen.de 6. Orbits und die Runge-Lenz Vetor Übung 6.: Die Rücehr der Kanonenugel
Ebene und Sphärische Trigonometrie
 Ebene und Sphärische Trigonometrie Prof. Udo Hebisch TU Bergakademie Freiberg Dies ist ein vorläufiges Skript zur zweistündigen Vorlesung Sphärische Trigonometrie für Markscheider im WS 005/006. Anfragen,
Ebene und Sphärische Trigonometrie Prof. Udo Hebisch TU Bergakademie Freiberg Dies ist ein vorläufiges Skript zur zweistündigen Vorlesung Sphärische Trigonometrie für Markscheider im WS 005/006. Anfragen,
Grundwissen. 10. Jahrgangsstufe. Mathematik
 Grundwissen 10. Jahrgangsstufe Mathematik 1 Kreis und Kugel 1.1 Kreissektor und Bogenmaß Kreis Umfang U = π r=π d Flächeninhalt A=π r Kreissektor mit Mittelpunktswinkel α Bogenlänge b= α π r 360 Flächeninhalt
Grundwissen 10. Jahrgangsstufe Mathematik 1 Kreis und Kugel 1.1 Kreissektor und Bogenmaß Kreis Umfang U = π r=π d Flächeninhalt A=π r Kreissektor mit Mittelpunktswinkel α Bogenlänge b= α π r 360 Flächeninhalt
Gerade, Strecke, Halbgerade, Winkel (in (R n,, ))
 Gerade, Strecke, Halbgerade, Winkel (in (R n,, )) A B Winkel Gerade Halbgerade Strecke A A A Gerade ist Punktmenge L A,v := {A+t v t R}, wobei v 0. Halbgerade (Strahl) ist Punktmenge H A,v := {A+t v t
Gerade, Strecke, Halbgerade, Winkel (in (R n,, )) A B Winkel Gerade Halbgerade Strecke A A A Gerade ist Punktmenge L A,v := {A+t v t R}, wobei v 0. Halbgerade (Strahl) ist Punktmenge H A,v := {A+t v t
Die Trigonometrie behandelt das Problem der Berechnung von Dreiecken. Es bestehen schöne Anwendungen in der Vermessung oder Astronomie.
 1 Trigonometrie 1 1. Einleitung, Definition Die Trigonometrie behandelt das Problem der Berechnung von Dreiecken. Es bestehen schöne Anwendungen in der Vermessung oder Astronomie. Aufgabe: Zeichne ein
1 Trigonometrie 1 1. Einleitung, Definition Die Trigonometrie behandelt das Problem der Berechnung von Dreiecken. Es bestehen schöne Anwendungen in der Vermessung oder Astronomie. Aufgabe: Zeichne ein
Lösung Arbeitsblatt Geometrie / Trigonometrie
 Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Lösung Arbeitsbltt Geometrie / Trigonometrie Dozent: - Brückenkurs Mthemtik 016 Winkelbeziehugen
Fchhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Mthemtik und Nturwissenschften Lösung Arbeitsbltt Geometrie / Trigonometrie Dozent: - Brückenkurs Mthemtik 016 Winkelbeziehugen
Übungsblatt 1: Lösungswege und Lösungen
 Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
12 Übungen zu Gauß-Algorithmus
 Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
Landeswettbewerb Mathematik Bayern Lösungsbeispiele 1. Runde 2006
 Landeswettbewerb Mathematik Bayern Lösungsbeispiele 1. Runde 2006 Aufgabe 1 Die Ziffern von 1 bis 5 sollen so in einer Reihe angeordnet werden, dass jedes Paar benachbarter Ziffern eine Zahl ergibt, die
Landeswettbewerb Mathematik Bayern Lösungsbeispiele 1. Runde 2006 Aufgabe 1 Die Ziffern von 1 bis 5 sollen so in einer Reihe angeordnet werden, dass jedes Paar benachbarter Ziffern eine Zahl ergibt, die
Ein Beispiel: In einem rechtwinkligen Dreieck ist die Hypotenuse halb so lang wie die Hypotenuse.
 Item 2 Schreibe so viele Verallgemeinerungen (Sätze, Definitionen, Eigenschaften, Folgerungen) wie du kannst auf, die mit rechtwinkligen Dreiecken zu tun haben. Ein Beispiel: In einem rechtwinkligen Dreieck
Item 2 Schreibe so viele Verallgemeinerungen (Sätze, Definitionen, Eigenschaften, Folgerungen) wie du kannst auf, die mit rechtwinkligen Dreiecken zu tun haben. Ein Beispiel: In einem rechtwinkligen Dreieck
8. Sphärische Geometrie und das Problem der guten Karten.
 8. Sphärische Geometrie und das Problem der guten Karten. Im 15. Jahrhundert hatte man in der Seefahrt die Technologie bereit, um von Fahrten entlang von Küsten zu Fahrten über das offene Meer überzugehen.
8. Sphärische Geometrie und das Problem der guten Karten. Im 15. Jahrhundert hatte man in der Seefahrt die Technologie bereit, um von Fahrten entlang von Küsten zu Fahrten über das offene Meer überzugehen.
Definition von Sinus und Cosinus
 Definition von Sinus und Cosinus Definition 3.16 Es sei P(x y) der Punkt auf dem Einheitskreis, für den der Winkel von der positiven reellen Halbachse aus (im Bogenmaß) gerade ϕ beträgt (Winkel math. positiv,
Definition von Sinus und Cosinus Definition 3.16 Es sei P(x y) der Punkt auf dem Einheitskreis, für den der Winkel von der positiven reellen Halbachse aus (im Bogenmaß) gerade ϕ beträgt (Winkel math. positiv,
befasst sich mit den Beziehungen zwischen den Seiten und Winkeln in einem Dreieck.
 Trigonometrie Lernziele befasst sich mit den Beziehungen zwischen den Seiten und Winkeln in einem Dreieck. Selbständiges Erarbeiten der Kurztheorie Kenntnis der wichtigsten Begriffe, Definitionen und Formeln
Trigonometrie Lernziele befasst sich mit den Beziehungen zwischen den Seiten und Winkeln in einem Dreieck. Selbständiges Erarbeiten der Kurztheorie Kenntnis der wichtigsten Begriffe, Definitionen und Formeln
2.2C. Das allgemeine Dreieck
 .C. Das allgemeine Dreieck Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = ( 0, z ) (x, y, z > 0) transformieren. Die
.C. Das allgemeine Dreieck Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = ( 0, z ) (x, y, z > 0) transformieren. Die
Übung 2 vom
 Übung vom.0.04 Aufgabe 5 Gegeben ist die Gleichung sin(α) + sin(α + β) + sin(α + β) = 0 Für welches Argument β ist diese Gleichung für jedes α erfüllt? Wo findet diese Gleichung Anwendung in der Technik?
Übung vom.0.04 Aufgabe 5 Gegeben ist die Gleichung sin(α) + sin(α + β) + sin(α + β) = 0 Für welches Argument β ist diese Gleichung für jedes α erfüllt? Wo findet diese Gleichung Anwendung in der Technik?
Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2)
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 2815 Bremen Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2) Name: Ich 1. 2. 3. So schätze ich meinen Lernzuwachs ein. kann die
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 2815 Bremen Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2) Name: Ich 1. 2. 3. So schätze ich meinen Lernzuwachs ein. kann die
Koordinatensysteme der Erde
 Koordinatensysteme der Erde Es gibt verschiedene Arten, die Position eines Punktes auf der Oberfläche einer Kugel (manchmal auch Sphäre genannt) darzustellen, jede hat ihre Vor-und Nachteile und ist für
Koordinatensysteme der Erde Es gibt verschiedene Arten, die Position eines Punktes auf der Oberfläche einer Kugel (manchmal auch Sphäre genannt) darzustellen, jede hat ihre Vor-und Nachteile und ist für
FACHHOCHSCHULE ZÜRICH Musterprüfung Geometrie * Klasse ZS K2 18. März 2011
 1 FACHHOCHSCHULE ZÜRICH Musterprüfung Geometrie * Klasse ZS K2 18. März 2011 A Name:... 1. Teil: Winkelberechnungen Aufgabe W-1: In nebenstehendem Sehnenviereck sei = 80º und = 70º. Wie gross sind dann
1 FACHHOCHSCHULE ZÜRICH Musterprüfung Geometrie * Klasse ZS K2 18. März 2011 A Name:... 1. Teil: Winkelberechnungen Aufgabe W-1: In nebenstehendem Sehnenviereck sei = 80º und = 70º. Wie gross sind dann
HTBLA VÖCKLABRUCK STET
 HTBLA VÖCKLABRUCK STET Trigonometrie INHALTSVERZEICHNIS 1. WINKELFUNKTIONEN IM RECHTWINKELIGEN DREIECK... 3. BOGENMASS... 3 3. TRIGONOMETRISCHE FUNKTIONEN BELIEBIGER WINKEL... 4 3.1. Einheitskreis (r =
HTBLA VÖCKLABRUCK STET Trigonometrie INHALTSVERZEICHNIS 1. WINKELFUNKTIONEN IM RECHTWINKELIGEN DREIECK... 3. BOGENMASS... 3 3. TRIGONOMETRISCHE FUNKTIONEN BELIEBIGER WINKEL... 4 3.1. Einheitskreis (r =
Vektoren, Skalarprodukt, Ortslinien
 .0 Gegeben sind die Punkte A(0/-4), C(0/4), sowie die Pfeile mit α [ 90 ; 90 ]. 4cosα AB = 4sinα+ 4. Zeichne die drei Punkte B, B und B 3 mit α { 30;0;30 } in ein KOS.. Zeige: 4cosα CB =. 4sinα 4.3 Zeige,
.0 Gegeben sind die Punkte A(0/-4), C(0/4), sowie die Pfeile mit α [ 90 ; 90 ]. 4cosα AB = 4sinα+ 4. Zeichne die drei Punkte B, B und B 3 mit α { 30;0;30 } in ein KOS.. Zeige: 4cosα CB =. 4sinα 4.3 Zeige,
6. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 12 Saison 1966/1967 Aufgaben und Lösungen
 6. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 12 Saison 1966/1967 Aufgaben und Lösungen 1 OJM 6. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 12 Aufgaben Hinweis: Der Lösungsweg mit
6. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 12 Saison 1966/1967 Aufgaben und Lösungen 1 OJM 6. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 12 Aufgaben Hinweis: Der Lösungsweg mit
Mathematische Probleme, SS 2013 Donnerstag $Id: dreieck.tex,v /04/12 15:30:18 hk Exp hk $
 $Id: dreieck.tex,v 1.3 2013/04/12 15:30:18 hk Exp hk $ 1 Dreiecke 1.2 Der Strahlensatz Nachdem wir in der letzten Sitzung rechtwinklige Dreiecke betrachtet haben, kommen wir nun zur Einführung der trigonometrischen
$Id: dreieck.tex,v 1.3 2013/04/12 15:30:18 hk Exp hk $ 1 Dreiecke 1.2 Der Strahlensatz Nachdem wir in der letzten Sitzung rechtwinklige Dreiecke betrachtet haben, kommen wir nun zur Einführung der trigonometrischen
Geometrie und Zahlentheorie. Ganzzahlige geometrische Objekte
 1 Geometrie und Zahlentheorie. Ganzzahlige geometrische Objekte Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin 19. Tag der Mathematik 17. Mai 014, TU Berlin Pythagoräische
1 Geometrie und Zahlentheorie. Ganzzahlige geometrische Objekte Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin 19. Tag der Mathematik 17. Mai 014, TU Berlin Pythagoräische
1. Aufgabe: Grundwissen
 NAME: Mathematik 3. Klassenarbeit Klasse 10e- Gr. A 06. Feb. 2007 Trigonometrie für Winkel bis 90 Grad - ups - Teil A: Arbeitsblatt ohne Nutzung von Tafelwerk, Formelsammlung und Taschenrechner 1. Aufgabe:
NAME: Mathematik 3. Klassenarbeit Klasse 10e- Gr. A 06. Feb. 2007 Trigonometrie für Winkel bis 90 Grad - ups - Teil A: Arbeitsblatt ohne Nutzung von Tafelwerk, Formelsammlung und Taschenrechner 1. Aufgabe:
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.8 2015/07/09 15:09:47 hk Exp $ 5 Sphärische Trigonometrie 5.3 Geographische Koordinaten b γ a P α c β P 2 P 1 λ ϕ ϕ2 Längengrad λ und Breitengrad ϕ Abstand auf Großkreis Wir betrachten
$Id: sphaere.tex,v 1.8 2015/07/09 15:09:47 hk Exp $ 5 Sphärische Trigonometrie 5.3 Geographische Koordinaten b γ a P α c β P 2 P 1 λ ϕ ϕ2 Längengrad λ und Breitengrad ϕ Abstand auf Großkreis Wir betrachten
