Mathematik für Ingenieure A III Wintersemester 2008
|
|
|
- Klaudia Krämer
- vor 6 Jahren
- Abrufe
Transkript
1 1 / 80 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III
2 2 / 80 Technisches Vorlesungswebsite: Mittwochs gibt s ein Aufgabenblatt: Drei live in den Übungen, drei Hausaufgaben, davon zwei Pflicht. Abgabe der alten Hausaufgaben in kleinen ruppen ebenfalls am Mittwoch in der Vorlesung Schein: 60% der Punkte in den Pflichthausaufgaben.
3 3 / 80 Technisches Übungsgruppen: Beginn Mi nächste Woche Bitte bis spätestens per WebAnmeldeSystem. Reihenfolge angeben! Die ersten zwei ausgewählten Termine sollten auf jeden Fall gehen! Termine: Siehe auch Univis! Di 14:15 15:45 im E1.12 Mi 10:00 12:00 im R4.11 Do 10:00 12:00 im E1.12 Fr 10:15 11:45 im E1.12 Fr 10:15 11:45 im R4.15
4 4 / 80 Literatur Wie im letzten Semester Burg, Haf, Wille: Höhere Mathematik für Ingenieure I IV, B..Teubner, Stuttgart, raf Finck v. Finckenstein, Lehn, Schellhaas, Wegmann: Arbeitsbuch Mathematik für Ingenieure I II, B..Teubner, Stuttgart Hoffmann, Marx, Vogt: Mathematik für Ingenieure 1 2, Pearson Studium Bronstein, Semendjajew, Musiol: Taschenbuch der Mathematik, Verlag Harri Deutsch, 6.Auflage: verschiedene Skripte im Web der Uni Erlangen...
5 Wiederholung Sommersemester 5 / 80
6 6 / 80 Wiederholung Folgen, Reihen, Potenzreihen, Taylorreihen (1d) Differentialrechnung (1d und n-d) Integralrechnung (1d) gewöhnliche Dln
7 7 / 80 Parameterintegrale I R sei ein Intervall und f : [a,b] I R sei eine Funktion f (t,x) von zwei Variablen. Wir untersuchen die Integralfunktion F : I R mit für x I F(x) = b a f (t,x)dt }{{} Parameterintegral
8 8 / 80 Eigentliche Parameterintegrale Beispiel: für x R 2 F(x) = 1 e tx t dt
9 9 / 80 Uneigentliche Parameterintegrale Beispiel: Die amma-funktion Γ(x) = e t t x 1 dt für x (0, ). Hier nicht mehr vgl. 2. Semester! 0
10 10 / 80 Eigenschaften eigentlicher Parameterintegrale Satz f : [a,b] I R sei eine gegebene Funktion, und F : I R bezeichne die zugehörge Integralfunktion. Dann gilt: a) Ist f auf [a,b] I stetig, so ist F auf I stetig. b) Ist f auf [a,b] I stetig, existiert auf [a,b] I die partielle Ableitung f x und ist diese dort stetig, so ist F auf I differenzierbar und es gilt: F (x) = df b dx (x) = a f (t,x) dt x
11 11 / 80 Beispiel 2 F(x) = 1 e tx t dt für x 0. (F läßt sich nicht analytisch integrieren!) F (x) = 2 1 e tx 2 x t dt = e tx dt 1 = 1 x etx t=2 t=1 = 1 x ( e 2x e x)
12 12 / 80 Satz von Fubini Hier nehmen wir speziell I = [c,d] an. Satz: Ist f : [a,b] [c,d] R eine stetige Funktion, so folgt für die zugehörige Integralfunktion F : [c, d] R: d c F(x)dx = d c b a f (t,x)dt dx = b a d c f (t,x)dx dt
13 13 / 80 Variable Integrationsgrenzen F(x) = ψ(x) ϕ(x) f (t,x)dt Satz: I R sei ein gegebenes Intervall, ϕ : I R und ψ : I R seien auf I stetig differenzierbare Funktionen, und f sei eine gegebene reellwertige Funktion, die auf der Menge M := {(t,x) R I t [ϕ(x),ψ(x)] oder t [ψ(x),ϕ(x)]} stetig ist und dort eine stetige partielle Ableitung f x besitzt.
14 14 / 80 Variable Integrationsgrenzen Dann ist die Integralfunktion F : I R mit F(x) = differenzierbar auf I und es gilt F (x) = ψ(x) ϕ(x) ψ(x) ϕ(x) f (t,x)dt f (t,x) dt + ψ (x) f (ψ(x),x) ϕ (x) f (ϕ(x),x) x
15 15 / 80 Beispiel x2 F(x) = cos(t 2 x)dt 0 F (x) = x2 0 x cos(t2 x)dt + 2xcos(x 4 x) 0 x2 = t 2 sin(t 2 x)dt + 2xcos(x 5 ) 0
16 16 / 80 Integration von Funktionen mehrerer Variabler
17 17 / 80 Zweidimensionale Integrale Im R 2 betrachten wir ein Rechteck der Form I := { (x,y) R 2 a x b,c y d } f : I R sei eine beschränkte Funktion. Zur Integration von f auf I gehen wir wie folgt vor: 1. Wir bilden eine Zerlegung Z 1 von [a,b] in n + 1 Teilpunkte a = x 0 < x 1 <... < x n = b und eine Zerlegung Z 2 von [c,d] in m + 1 Teilpunkte c = y 0 < y 1 <... < y m = d. Wir bezeichnen wieder die rößen Z 1 := max 1 i n (x i x i 1 ) und Z 2 := max 1 j m (y j y j 1 ) als die Normen dieser Zerlegungen.
18 18 / 80 Zweidimensionale Integrale I ij := {(x,y) x i 1 x x i,y j 1 y y j } für i = 1,...,n und j = 1,...,m
19 19 / 80 Zweidimensionale Integrale 2. Wir wählen für jedes i und j ein x i [x i 1,x i ] und ein y j [y j 1,y j ] und bilden die Riemannsche Summe S Z1 Z 2 = n m i=1 j=1 f (x i,y j ) (x i x i 1 ) (y j y j 1 ) f (x i,y j ) (x i x i 1 ) (y j y j 1 ) beschreibt das Volumen des Quaders mit den rundseiten x i x i 1,y j y j 1 und der Höhe f (x i,y j )
20 20 / 80 Zweidimensionale Integrale Wir gehen zu immer feineren Zerlegungen über, d.h. Z 1 0 und Z 2 0 Definition: f sei eine auf I beschränkte reellwertige Funktion. Streben die Riemann schen Summen S Z1 Z 2 für alle Zerlegungen Z 1 von [a,b] mit Z 1 0 und alle Zerlegungen Z 2 von [c,d] mit Z 2 0 sowie jede Wahl der Zwischenstellen (x i,y j ) einem gemeinsamen renzwert S zu, so heißt f integrierbar auf I. Die Zahl S heißt bestimmtes Integral über f auf I. Wir schreiben S = lim n m Z 1 0 Z 2 0 i=1 j=1 = f (x,y)d(x,y) I f (x i,y j ) (x i x i 1 ) (y j y j 1 )
21 21 / 80 Zweidimensionale Integrale Eine nichtleere Teilmenge des R 2 heißt beschränkt, falls es ein Rechteck I := {(x,y) R 2 a x b,c y d} mit I gibt.
22 22 / 80 Zweidimensionale Integrale Definition: R 2 sei eine beschränkte Menge (mit I) und f : R sei eine beschränkte Funktion. Existiert für die Erweiterungsfunktion f I von f auf I mit { } f (x,y) falls (x,y) f I (x,y) := 0 falls (x,y) I \ das Integral S = I f I (x,y)d(x,y) so heißt f integrierbar auf und wir setzen S = f (x,y)d(x,y)
23 23 / 80 Zweidimensionale Integrale Ist die Funktion f : R nichtnegativ auf, f (x,y) 0 (x,y) so beschreibt das Integral f (x,y)d(x,y) das Volumen des Raumstücks über und unter der Fläche z = f (x,y). Weitere Schreibweise: S = f (x,y)d(x,y) = f (xy)d
24 24 / 80 Zweidimensionale Integrale Definition: Ist R 2 eine beschränkte Menge, und ist die Funktion f (x,y) 1 integrierbar auf, so heißt meßbar. Der Wert des Integrals µ() = d(x, y) heißt der zweidimensionale Inhalt oder das Maß von.
25 25 / 80 Rechenregel Satz: f und g seien integrierbar auf R 2. Dann ist für alle α,β R die Funktion αf + βg ebenfalls integrierbar auf, und es gilt [αf (x,y) + βg(x,y)]d(x,y) = α f (x,y)d(x,y) + β g(x, y)d(x, y)
26 26 / 80 Projizierbare Mengen Berechnung zweidimensionaler Integrale Definition: Eine nichtleere Teilmenge R 2 a) heißt y-projizierbar, wenn es auf einem Intervall [a, b] der x-achse stetige Funktionen y(x) und y(x) mit so gibt, dass gilt y(x) y(x) x [a,b] = { (x,y) x [a,b],y(x) y y(x) }
27 27 / 80 Projizierbare Mengen b) heißt x-projizierbar, wenn es auf einem Intervall [c,d] der y-achse stetige Funktionen x(y) und x(y) mit x(y) x(y) y [x,d] so gibt, dass gilt = {(x,y) y [c,d],x(y) x x(y)}
28 28 / 80 Projizierbare Mengen c) heißt projizierbar, falls y-projizierbar oder x-projizierbar ist. d) heißt Standardmenge im R 2, falls sowohl y-projizierbar als auch x-projizierbar ist.
29 29 / 80 Projizierbare Mengen Man beachte, dass eine Menge R 2 weder y- noch x-projizierbar sein muss.
30 30 / 80 Integralberechnung Satz: R 2 sei eine projizierbare Menge und f : R sei eine stetige Funktion. Dann existiert das Integral f (x,y)d(x,y) und es gilt, a) falls y-projizierbar ist: f (x,y)d(x,y) = b y(x) a y(x) b) falls x-projizierbar ist: f (x,y)d(x,y) = d x(y) c x(y) f (x,y)dy dx f (x,y)dx dy
31 Beispiel 1 Man berechne (x 2 + y 2 )d(x,y) für := { (x,y) R 2 0 x 2,x 2 y 4 } ist y- und x-projizierbar. 31 / 80
32 32 / 80 Beispiel 1 (x 2 + y 2 )d(x,y) = = = = (x 2 + y 2 )dy dx x 2 [x 2 y + 13 ] y=4 y3 y=x 2 dx ( 4x x4 1 ) 3 x6 dx [ 4 3 x x 1 5 x x7 ] x=2 x=0 = =
33 33 / 80 Beispiel 1 (x 2 + y 2 )d(x,y) = = = y (x 2 + y 2 )dx dy 0 [ 1 3 x3 + y 2 x [ y y 7 2 ] x= y x=0 ] y=4 y=0 = = = dy = 4 0 ( ) 1 3 y y 2 dy
34 34 / 80 Beispiel 2 esucht ist das Volumen I, das durch das Paraboloid f (x,y) = 1 x 2 y 2 und durch die (x,y)-ebene begrenzt wird. ist der Einheitskreis in der (x,y)-ebene und kann wie folgt dargestellt werden: { } = (x,y) R 2 x [ 1,1], 1 x 2 y 1 x 2
35 35 / 80 Beispiel 2 I = = (1 x 2 y 2 )d(x,y) 1 1 = x 2 (1 x 2 y 2 )dy dx 1 x (1 x 2 ) 3 2 dx
36 36 / 80 Beispiel 2 Substitution mit x = sin(ϕ) (Integral Nr. 171, Bronstein, 19. Aufl. ergibt I = = (1 x 2 ) 3 2 dx [ x(1 x 2 ) x 1 x arcsinx ] x=1 = arcsin1 }{{} 3 2 arcsin( 1) }{{} = π 2 = π 2 = π 4 + π 4 = π 2 x= 1
37 37 / 80 Projizierbare Mengen Ist R 2 nicht projizierbar, aber zerlegbar in N projizierbare Mengen 1,..., N, so gilt f (x,y)d(x,y) = f (x,y)d(x,y) f (x,y)d(x,y) 1 N
38 38 / 80 Die Substitutionsregel Substitutionsregel für zweidimensionale Integrale f (x,y)d(x,y) x = x(u,v) und y = y(u,v) seien stetige Funktionen, die auf einer Menge H der (u, v)-ebene stetige partielle Ableitungen erster Ordnung besitzen. Die Funktionen seien umkehrbar eindeutig: Jedem (u 0,v 0 ) H ist genau ein (x(u 0,v 0 ),y(u 0,v 0 )) zugeordnet und umgekehrt. Für die Jacobische Funktionalmatrix gelte det x(u,v) (x,y) (u,v) = u y(u,v) u ( ) (x,y) (u,v) 0 für alle (u,v) H. x(u,v) v y(u,v) v
39 39 / 80 Die Substitutionsregel Dann gilt f (x,y)d(x,y) = H ( ) f (x(u,v),y(u,v)) (x,y) det d(u,v) (u,v)
40 40 / 80 Beispiel Berechne e x2 +y 2 d(x,y) für = { (x,y) R 2 1 x 2 + y 2 4,y 0 } Wir führen Polarkoordinaten ein, d.h. x = r cos(ϕ) und y = r sin(ϕ) mit 1 r 2 und 0 ϕ π.
41 41 / 80 Beispiel Dann ist H = { (r,ϕ) R 2 1 r 2,0 ϕ π } und es gilt det ( ) ( (x,y) cosϕ r sinϕ = det (r,ϕ) sinϕ r cosϕ ) = r cos 2 ϕ + r sin 2 ϕ = r e x2 +y 2 d(x,y) = e r2 rd(r,ϕ) = H 2 π e r2 rdϕ dr = = π 2 er2 2 = π 1 2 (e4 e) e r2 rπdr
42 42 / 80 Dreidimensionale Integrale Integrale über Funktionen f (x, y, z) mit drei Variablen werden ähnlich wie im zweidimensionalen Fall definiert. Zur Berechnung von f (x,y,z)d(x,y,z) führen wir projizierbare Mengen im R 3 ein.
43 43 / 80 Projizierbare Mengen Definition: sei eine nichtleere Teilmenge des R 3. a) heißt z-projizierbar, wenn es eine projizierbare Menge z in der (x,y)-ebene und auf z stetige Funktionen z(x,y) und z(x,y) mit z(x,y) z(x,y) (x,y) z so gibt, dass gilt = { (x,y,z) R 3 (x,y) z,z(x,y) z z(x,y) }
44 44 / 80 Projizierbare Mengen b) heißt y-projizierbar, wenn es eine projizierbare Menge y in der (x,z)-ebene und auf y stetige Funktionen y(x,z) und y(x,y) mit y(x,z) y(x,z) (x,z) y so gibt, dass gilt = { (x,y,z) R 3 (x,z) y,y(x,z) y y(x,z) } c) heißt x-projizierbar, wenn es eine projizierbare Menge x in der (y,z)-ebene und auf x -stetige Funktionen x(y,z) und x(y,z) mit x(y,z) x(y,z) (y,z) x so gibt, dass gilt = { (x,y,z) R 3 (y,z) x,x(y,z) x x(y,z) }
45 45 / 80 Projizierbare Mengen d) heißt projizierbar, wenn sie z-projizierbar oder y-projizierbar oder x-projizierbar ist. e) heißt Standardmenge im R 3, wenn sie sowohl z-projizierbar als auch y-projizierbar und x-projizierbar ist.
46 46 / 80 Projizierbare Mengen Satz: R 3 sei eine projizierbare Menge, und f : R sei eine stetige Funktion. Dann existiert das Integral f (x,y,z)d(x,y,z), und es gilt a) falls z-projizierbar ist: f (x,y,z)d(x,y,z) = z z(x,y) z(x,y) f (x,y,z)dz d(x,y)
47 47 / 80 Projizierbare Mengen b) falls y-projizierbar ist: f (x,y,z)d(x,y,z) = c) falls x-projizierbar ist: y f (x,y,z)d(x,y,z) = x y(x,z) y(x,z) x(y,z) x(y,z) f (x,y,z)dy d(x,z) f (x,y,z)dx d(y,z)
48 48 / 80 Projizierbare Mengen f (x,y,z)d(x,y,z) = z z(x,y) z(x,y) f (x,y,z)dz d(x,y) Man beachte, dass die Integrale in Klammern eindimensional und die äußeren Integrale zweidimensional sind. Ist z.b. z-projizierbar und z y-projizierbar, so folgt f (x,y,z)d(x,y,z) = b a y(x) y(x) z(x,y) z(x,y) f (x,y,z)dz dy dx
49 49 / 80 Beispiel Man berechne xd(x,y,z) für = {(x,y,z) R 3 x 0,y 0,z 0, x a + y b + z } c 1 mit a,b,c > 0. beschreibt das nachstehend dargestellte Tetraeder.
50 50 / 80 Beispiel ist z-projizierbar mit z = { ( (x,y) R 2 x 0,y 0, x a + y b 1} z(x,y) = 0, z(x,y) = c 1 x a y ). b
51 51 / 80 Beispiel Die Menge z ist y-projizierbar, denn es ist z = {(x,y) R 2 x [0,a],0 y b(1 x } a )
52 52 / 80 Beispiel xd(x,y,z) = = z a 0 c(1 x a y b ) 0 b(1 a x ) 0 xdz d(x,y) c(1 x a y b ) xd(x,y,z) = 1 24 a2 bc 0 xdz dy dx
53 Volumen einer Menge Definition: Ist R 3 eine beschränkte Menge (d.h., ist Teilmenge eines Quaders im R 3 ), und ist die Funktion f (x,y,z) 1 integrierbar auf, so heißt messbar. Der Wert des Integrals µ() := d(x,y,z) heißt der dreidimensionale Inhalt oder das Maß von oder das Volumen von. 53 / 80
54 54 / 80 Beispiel esucht ist der dreidimensionale Inhalt (Volumen) von := { (x,y,z) R 3 0 x 1,0 y x, y 2 z x 2} µ() = = 1 0 d(x,y,z) = x 0 = 1 3 x x 0 [ x 2 + y 2] dy dx = 0 = 1 3 x2 y 2 dz 1 0 dy dx (x x3 )dx }{{} 4 3 x3
55 55 / 80 Die Substitutionsregel Substitutionsregel für dreidimensionale Integrale f (x,y,z)d(x,y,z) Man substituiert x = x(u,v,w), y = y(u,v,w) und z = z(u,v,w). Dabei seien x,y und z stetige Funktionen, die auf einer Menge H R 3 stetige partielle Ableitungen erster Ordnung besitzen und die Menge H eineindeutig auf die Menge abbilden. Für die Jacobische Funktionalmatrix (x,y,z) (u,v,w) = x u y u z u x v y v z v ( ) sei det (x,y,z) (u,v,w) 0 für alle (u,v,w) H. x w y w z w
56 56 / 80 Zylinderkoordinaten x = r cosϕ y = r ϕ z = t 0 ϕ 2π, r 0, < t < det ( ) (x,y,z) (r,ϕ,t) = det cosϕ r sinϕ 0 sinϕ r cosϕ = r cos 2 ϕ + r sin 2 ϕ = r
57 57 / 80 Kugelkoordinaten x = r sinϕ cosϑ y = r sinϕ sinϑ z = r cosϕ 0 ϕ π, 0 ϑ 2π, r 0
58 58 / 80 Kugelkoordinaten ( ) (x,y,z) det = det (r,ϕ,ϑ) sinϕ cosϑ r cosϕ cosϑ r sinϕ sinϑ sinϕ sinϑ r cosϕ sinϑ r sinϕ cosϑ cosϕ r sinϕ 0 = cosϕ(r 2 cosϕ cos 2 ϑ sinϕ + r 2 cosϕ sin 2 ϑ sinϕ) + r sinϕ(r sin 2 ϕ cos 2 ϑ + r sin 2 ϕ sin 2 ϑ) = r 2 cos 2 ϕ sinϕ(cos 2 ϑ + sin 2 ϑ) + r 2 sin 3 ϕ(cos 2 ϑ + sin 2 ϑ) = r 2 cos 2 ϕ sinϕ + r 2 sin 3 ϕ = r 2 sinϕ(cos 2 ϕ + sin 2 ϕ) = r 2 sinϕ
59 Beispiel für z ln(x2 + y 2 ) x 2 + y 2 d(x,y,z) = { (x,y,z) R 3 1 x 2 + y 2 e 2, x 0, y 0, 0 z 4 } 59 / 80
60 60 / 80 Beispiel Führen wir Zylinderkoordinaten ein, d.h. x = r cosϕ,y = r sinϕ,z = t so entspricht der Menge die Menge H = {(r,ϕ,t) R 3 1 r e,0 ϕ π } 2,0 t 4 Dann folgt z ln(x2 + y 2 ) x 2 + y 2 d(x,y,z) = H t ln(r2 cos 2 ϕ + r 2 sin 2 ϕ) r 2 cos 2 ϕ + r 2 sin 2 ϕ rd(r,ϕ,t)
61 61 / 80 Beispiel für e (x2 +y 2 +z 2 ) 32 d(x,y,z) = { (x,y,z) R 3 x 2 + y 2 + z 2 1 }
62 62 / 80 Beispiel beschreibt im R 3 eine Kugel um 0 mit dem Radius 1. Unter Verwendung von Kugelkoordinaten x = r sinϕ cosϑ, y = r sinϕ sinϑ, z = r cosϕ entspricht der Menge Wegen H := { (r,ϕ,ϑ) R 3 0 r 1,0 ϕ π,0 ϑ 2π } x 2 + y 2 + z 2 = r 2 sin 2 ϕ cos 2 ϑ + r 2 sin 2 ϕ sin 2 ϑ + r 2 cos 2 ϕ erhalten wir e (x2 +y 2 +z 2 ) 32 d(x,y,z) = = r 2 sin 2 ϕ(cos 2 ϑ + sin 2 ϑ) + r 2 cos 2 ϕ = r 2 H e (r2 ) 32 r 2 sinϕd(r,ϕ,ϑ)
63 Beispiel für z ln(x2 + y 2 ) x 2 + y 2 d(x,y,z) = { (x,y,z) R 3 1 x 2 + y 2 e 2, x 0, y 0, 0 z 4 } 63 / 80
64 64 / 80 Beispiel Führen wir Zylinderkoordinaten ein, d.h. x = r cosϕ,y = r sinϕ,z = t so entspricht der Menge die Menge H = {(r,ϕ,t) R 3 1 r e,0 ϕ π } 2,0 t 4 Dann folgt z ln(x2 + y 2 ) x 2 + y 2 d(x,y,z) = H t ln(r2 cos 2 ϕ + r 2 sin 2 ϕ) r 2 cos 2 ϕ + r 2 sin 2 ϕ rd(r,ϕ,t)
65 65 / 80 Beispiel für e (x2 +y 2 +z 2 ) 32 d(x,y,z) = { (x,y,z) R 3 x 2 + y 2 + z 2 1 }
66 66 / 80 Beispiel beschreibt im R 3 eine Kugel um 0 mit dem Radius 1. Unter Verwendung von Kugelkoordinaten x = r sinϕ cosϑ, y = r sinϕ sinϑ, z = r cosϕ entspricht der Menge Wegen H := { (r,ϕ,ϑ) R 3 0 r 1,0 ϕ π,0 ϑ 2π } x 2 + y 2 + z 2 = r 2 sin 2 ϕ cos 2 ϑ + r 2 sin 2 ϕ sin 2 ϑ + r 2 cos 2 ϕ erhalten wir e (x2 +y 2 +z 2 ) 32 d(x,y,z) = = r 2 sin 2 ϕ(cos 2 ϑ + sin 2 ϑ) + r 2 cos 2 ϕ = r 2 H e (r2 ) 32 r 2 sinϕd(r,ϕ,ϑ)
67 67 / 80 Beispiel für e (x2 +y 2 +z 2 ) 32 d(x,y,z) = { (x,y,z) R 3 x 2 + y 2 + z 2 1 }
68 Beispiel beschreibt im R 3 eine Kugel um 0 mit dem Radius 1. Unter Verwendung von Kugelkoordinaten x = r sinϕ cosϑ, y = r sinϕ sinϑ, z = r cosϕ entspricht der Menge H := { (r,ϕ,ϑ) R 3 0 r 1,0 ϕ π,0 ϑ 2π } 68 / 80
69 69 / 80 Beispiel Wegen H := { (r,ϕ,ϑ) R 3 0 r 1,0 ϕ π,0 ϑ 2π } x 2 + y 2 + z 2 = r 2 sin 2 ϕ cos 2 ϑ + r 2 sin 2 ϕ sin 2 ϑ + r 2 cos 2 ϕ erhalten wir = r 2 sin 2 ϕ(cos 2 ϑ + sin 2 ϑ) + r 2 cos 2 ϕ = r 2 e (x2 +y 2 +z 2 ) 32 d(x,y,z) = H e (r2 ) 32 r 2 sinϕd(r,ϕ,ϑ)
70 70 / 80 Beispiel = H e (x2 +y 2 +z 2 ) 32 d(x,y,z) e (r2 ) 32 r 2 sinϕd(r,ϕ,ϑ) = 4 π(e 1) 3
71 Masse eines Körpers R 3 sei eine messbare Menge ( Körper ). Dann berechnet sich das Volumen V von als V = d(x,y,z) Ist in eine Dichteverteilung ρ = ρ(x,y,z) gegeben, so wird M := als Masse von bezeichnet. Bei konstanter Dichte ρ ist M = ρ V. ρ(x,y,z)d(x,y,z) 71 / 80
72 72 / 80 Schwerpunkt eines Körpers Unter dem Schwerpunkt von bezüglich der Dichteverteilung ρ(x,y,z) versteht man einen Punkt (x s,y s,z s ) R 3 mit den Koordinaten x s = 1 M y s = M z s = M xρ(x,y,z)d(x,y,z) yρ(x,y,z)d(x,y,z) zρ(x,y,z)d(x,y,z)
73 73 / 80 Beispiel Schwerpunkt des Kugeloktanten := {(x,y,z) R 3 x 0,y 0,z 0,x 2 + y 2 + z 2 R 2} vom Radius R > 0 bezüglich der konstanten Dichteverteilung ρ.
74 74 / 80 Beispiel Kugelkoordinaten: x = r sinϕ cosϑ y = r sinϕ sinϑ z = r cosϕ 0 ϕ π 2 0 ϑ π 2 0 r R
75 75 / 80 Beispiel Masse M von : M = ρ d(x,y,z) = ρ π 2 0 R 0 M = ρπr3 6 π 2 0 r 2 sinϕ dϑ dr dϕ
76 76 / 80 Beispiel x-koordinate des Schwerpunkts xρ d(x,y,z) = ρ π 2 R π r sinϕ cosϑ r 2 sinϕ dϑ dr dϕ xρ d(x,y,z) = ρr4 π 16
77 77 / 80 Beispiel x s = 1 M xρ d(x,y,z) = 6 ρπr 3 ρr4 π 16 = 3 8 R y s = 3 8 R z s = 3 8 R
78 78 / 80 Trägheitsmomente Sei R 3 wieder eine messbare Menge mit einer Dichteverteilung ρ(x, y, z). Die Trägheitsmomente T x bezüglich der x-achse, T y bezüglich der y-achse und T z bezüglich der z-achse sind definiert als T x = T y = T z = (y 2 + z 2 )ρ(x,y,z)d(x,y,z) (x 2 + z 2 )ρ(x,y,z)d(x,y,z) (x 2 + y 2 )ρ(x,y,z)d(x,y,z)
79 79 / 80 Beispiel Trägheitsmoment T z bezüglich der z-achse einer Kugel := { (x,y,z) R 3 x 2 + y 2 + z 2 R 2} vom Radius R > 0 mit konstanter Dichteverteilung ρ(x,y,z) = 1. Wir verwenden Kugelkoordinaten: x = r sinϕ cosϑ y = r sinϕ sinϑ 0 ϕ π,0 ϑ 2π,0 r R z = r cosϕ x 2 + y 2 = r 2 sin 2 ϕ cos 2 ϑ + r 2 sin 2 ϕ sin 2 ϑ = r 2 sin 2 ϕ
80 80 / 80 Beispiel x 2 + y 2 = r 2 sin 2 ϕ cos 2 ϑ + r 2 sin 2 ϕ sin 2 ϑ = r 2 sin 2 ϕ T z = = = (x 2 + y 2 )ρ(x,y,z)d(x,y,z) π (x 2 + y 2 )d(x,y,z) R π r 2 sin 2 ϕ r 2 sinϕ dϑ dr dϕ T z = 8 15 πr5
Mathematik für Ingenieure A III Wintersemester 2008
 1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
1 / 61 Mathematik für Ingenieure A III Wintersemester 2008 J. Michael Fried Lehrstuhl Angewandte Mathematik III 17.10.2008 2 / 61 Wiederholung Parameterintegrale Zweidimensionale Riemann Integrale 3 /
Höhere Mathematik Vorlesung 4
 Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
Höhere Mathematik Vorlesung 4 März 217 ii In der Mathematik versteht man die inge nicht. Man gewöhnt sich nur an sie. John von Neumann 4 as oppelintegral Flächen, Volumen, Integrale Ob f für a x b definiert
Vorlesung: Analysis II für Ingenieure. Wintersemester 07/08. Michael Karow. Thema: Transformationsformel für Gebietsintegrale
 Vorlesung: Analysis II für Ingenieure Wintersemester 7/8 Michael Karow Thema: Transformationsformel für Gebietsintegrale Transformation von Gebietsintegralen im 2 (Satz 24 im Skript) Seien, 2 kompakte
Vorlesung: Analysis II für Ingenieure Wintersemester 7/8 Michael Karow Thema: Transformationsformel für Gebietsintegrale Transformation von Gebietsintegralen im 2 (Satz 24 im Skript) Seien, 2 kompakte
ein geeignetes Koordinatensystem zu verwenden.
 1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
x + y + z = 6, x = 0, z = 0, x + 2y = 4, indem Sie das Volumen als Dreifachintegral schreiben.
 Übungen (Aufg. u. Lösungen) zur Ingenieur-Mathematik II SS 8 Blatt 1 3.7.8 Aufgabe 47: Berechnen Sie das Volumen des von den folgenden Flächen begrenzten Körpers x + y + z 6, x, z, x + y 4, indem Sie das
Übungen (Aufg. u. Lösungen) zur Ingenieur-Mathematik II SS 8 Blatt 1 3.7.8 Aufgabe 47: Berechnen Sie das Volumen des von den folgenden Flächen begrenzten Körpers x + y + z 6, x, z, x + y 4, indem Sie das
Integralrechnung für GLET
 Freitagsrunden Tech Talk November 2, 2012 1 Grundlagen Rechenregeln für Integrale 2 Mehrdimensionale Integrale Flächenintegrale Volumenintegrale Lösbar? 3 Kugel- und Zylinderkoordinaten Kugelkoordinaten
Freitagsrunden Tech Talk November 2, 2012 1 Grundlagen Rechenregeln für Integrale 2 Mehrdimensionale Integrale Flächenintegrale Volumenintegrale Lösbar? 3 Kugel- und Zylinderkoordinaten Kugelkoordinaten
Integralrechnung für Funktionen mehrerer Variabler
 Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
Inhaltsverzeichnis 9 Integralrechnung für Funktionen mehrerer ariabler 36 9. Integration über ebene Bereiche in kartesischen Koordinaten.............. 36 9. Integration über ebene Bereiche in Polarkoordinaten..................
Integration über allgemeine Integrationsbereiche.
 Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
Integration über allgemeine Integrationsbereiche. efinition: Sei R n eine kompakte und messbare Menge. Man nennt Z = { 1,..., m } eine allgemeine Zerlegung von, falls die Mengen k kompakt, messbar und
1 Lösungsskizzen zu den Übungsaufgaben
 Lösungsskizzen zu den Übungsaufgaben. Lösungen zu den Aufgaben zum Kapitel.. Tutoraufgaben. Man stellt fest: fx, y x, y G. omit ist f beschränkt auf G a Da f auf G beschränkt, ist f auf G Riemann-Integrabel
Lösungsskizzen zu den Übungsaufgaben. Lösungen zu den Aufgaben zum Kapitel.. Tutoraufgaben. Man stellt fest: fx, y x, y G. omit ist f beschränkt auf G a Da f auf G beschränkt, ist f auf G Riemann-Integrabel
Serie 6. x 2 + y 2, 0 z 4.
 Analysis D-BAUG Dr. Cornelia Busch FS 6 Serie 6. Wir betrachten drei verschiedene Flaschen in der Form eines Paraboloids P, eines Hyperboloids H und eines Kegels K. Diese sind wie folgt gegeben: P = {
Analysis D-BAUG Dr. Cornelia Busch FS 6 Serie 6. Wir betrachten drei verschiedene Flaschen in der Form eines Paraboloids P, eines Hyperboloids H und eines Kegels K. Diese sind wie folgt gegeben: P = {
Rückblick auf die letzte Vorlesung
 Rückblick auf die letzte Vorlesung 1. Integration (Fortsetzung) 2. Existenz von Integralen auf Quadern und allgemeineren Mengen 3. Satz von Fubini 4. Berechnung von Integralen 5. Volumina 6. Normalgebiete
Rückblick auf die letzte Vorlesung 1. Integration (Fortsetzung) 2. Existenz von Integralen auf Quadern und allgemeineren Mengen 3. Satz von Fubini 4. Berechnung von Integralen 5. Volumina 6. Normalgebiete
19.3 Oberflächenintegrale
 19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
19.3 Oberflächenintegrale Definition: Sei D R 2 ein Gebiet und p : D R 3 eine C 1 -Abbildung x = p(u) mit x R 3 und u = (u 1, u 2 ) T D R 2 Sind für alle u D die beiden Vektoren und u 1 linear unabhängig,
Serie 5. Figure 1: 1.a)
 Analsis D-BAUG Dr. Cornelia Busch FS 16 Serie 5 1. Bei den folgenden Integralen ist die Reihenfolge der Integrationen umzukehren: Die innere Variable soll zur äusseren werden und umgekehrt. Wie lautet
Analsis D-BAUG Dr. Cornelia Busch FS 16 Serie 5 1. Bei den folgenden Integralen ist die Reihenfolge der Integrationen umzukehren: Die innere Variable soll zur äusseren werden und umgekehrt. Wie lautet
Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang. Sommersemester
 Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang Sommersemester 3 8.6.3 Höhere Mathematik II für die Fachrichtungen Elektrotechnik und Informationstechnik
Karlsruher Institut für Technologie Institut für Analysis Dr. Andreas Müller-Rettkowski Dr. Vu Hoang Sommersemester 3 8.6.3 Höhere Mathematik II für die Fachrichtungen Elektrotechnik und Informationstechnik
Analysis II für M, LaG/M, Ph 12. Übungsblatt
 Analysis II für M, La/M, Ph. Übungsblatt Fachbereich Mathematik WS / Prof. Dr. Christian Herrmann 8.. Vassilis regoriades Horst Heck ruppenübung Aufgabe. erechnen Sie das ebietsintegral sin (x y) d, wobei
Analysis II für M, La/M, Ph. Übungsblatt Fachbereich Mathematik WS / Prof. Dr. Christian Herrmann 8.. Vassilis regoriades Horst Heck ruppenübung Aufgabe. erechnen Sie das ebietsintegral sin (x y) d, wobei
Höhere Mathematik Vorlesung 5
 Höhere Mathematik Vorlesung 5 März 2017 ii Gibt es etwa eine bessere Motivation als den rfolg?. Ion Tiriac 5 Das Dreifachintegral Ähnlich wie im zweindimensionalen Fall definieren wir das Dreifachintegral
Höhere Mathematik Vorlesung 5 März 2017 ii Gibt es etwa eine bessere Motivation als den rfolg?. Ion Tiriac 5 Das Dreifachintegral Ähnlich wie im zweindimensionalen Fall definieren wir das Dreifachintegral
Das mehrdimensionale Riemann-Integral. 1. Volumenintegrale
 Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Das mehrdimensionale Riemann-Integral. Volumenintegrale Es sei ein uader im R n gegeben durch := [a, b ] [a 2, b 2 ] [a n, b n ] = {(x,... x n ) a j x j b j } mit rellen Zahlen a j, b j, j =,... n. Offenbar
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen 1. Juni 13 *Aufgabe 1. erechnen Sie durch Übergang zu Polar-, Kugel- oder Zylinderkoordinaten die Fläche bzw. das Volumen (a) der von der Lemniskate x y (x + y ) = umschlossenen
Tutorium Mathematik II, M Lösungen 1. Juni 13 *Aufgabe 1. erechnen Sie durch Übergang zu Polar-, Kugel- oder Zylinderkoordinaten die Fläche bzw. das Volumen (a) der von der Lemniskate x y (x + y ) = umschlossenen
Höhere Mathematik II für die Fachrichtung Informatik. Lösungsvorschläge zum 10. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 4 Höhere Mathematik II für die Fachrichtung Informatik Lösungsvorschläge zum. Übungsblatt Aufgabe 37
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 4 Höhere Mathematik II für die Fachrichtung Informatik Lösungsvorschläge zum. Übungsblatt Aufgabe 37
mit 0 < a < b um die z-achse entsteht.
 Übungen (Aufg. u. Lösungen) zu Mathem. u. Lin. Alg. II SS 6 Blatt 8 13.6.6 Aufgabe 38: Berechnen Sie das Volumen des Volltorus, der durch Rotation der reisscheibe { (x, y, z) R 3 y, (x b) + z a } mit
Übungen (Aufg. u. Lösungen) zu Mathem. u. Lin. Alg. II SS 6 Blatt 8 13.6.6 Aufgabe 38: Berechnen Sie das Volumen des Volltorus, der durch Rotation der reisscheibe { (x, y, z) R 3 y, (x b) + z a } mit
11. Übungsblatt zur Mathematik II für MB
 Fachbereich Mathematik Prof. Dr. U. Reif R. Hartmann, T. Koch SS 8.6.. Übungsblatt zur Mathematik für MB Aufgabe 5 ntervall im R egeben sei das ntervall { (x, y, z) R : π x π, y, z π}. Berechnen Sie x
Fachbereich Mathematik Prof. Dr. U. Reif R. Hartmann, T. Koch SS 8.6.. Übungsblatt zur Mathematik für MB Aufgabe 5 ntervall im R egeben sei das ntervall { (x, y, z) R : π x π, y, z π}. Berechnen Sie x
Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe / r. Hanna Peywand Kiani.. Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften Bereichsintegrale, Transformationssatz, Potentiale
Fachbereich Mathematik der Universität Hamburg WiSe / r. Hanna Peywand Kiani.. Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften Bereichsintegrale, Transformationssatz, Potentiale
7 Differential- und Integralrechung für Funktionen
 Differential- und Integralrechung für Funktionen mehrer Veränderlicher 7 7 Differential- und Integralrechung für Funktionen mehrer Veränderlicher Die Differential- und Integralrechung für Funktionen mehrer
Differential- und Integralrechung für Funktionen mehrer Veränderlicher 7 7 Differential- und Integralrechung für Funktionen mehrer Veränderlicher Die Differential- und Integralrechung für Funktionen mehrer
Serie 4: Gradient und Linearisierung
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
9 Integralrechnung für Funktionen mehrerer Variabler Integration über ebene Bereiche in kartesischen Koordinaten
 Inhaltsverzeichnis 6 Integralrechnung 6. Einführung.............................................. 6. Unbestimmte Integrale........................................ 6.. Unbestimmte Integrale der rundfunktionen.......................
Inhaltsverzeichnis 6 Integralrechnung 6. Einführung.............................................. 6. Unbestimmte Integrale........................................ 6.. Unbestimmte Integrale der rundfunktionen.......................
R 1. 3 x 1+9. y 1 (x) = x 2, y 2(x) = x 3, y 3(x) = p x
 Studiengang: ME/MB Semester: SS 9 Analysis II Serie: Thema: bestimmtes Integral. Aufgabe: Berechnen Sie den Wert der folgenden bestimmten Integrale: d) g) j) R (x e x )dx, b) R sinx cos7xdx, e) R e R p
Studiengang: ME/MB Semester: SS 9 Analysis II Serie: Thema: bestimmtes Integral. Aufgabe: Berechnen Sie den Wert der folgenden bestimmten Integrale: d) g) j) R (x e x )dx, b) R sinx cos7xdx, e) R e R p
12 Integralrechnung, Schwerpunkt
 Dr. Dirk Windelberg Leibniz Universität Hannover Mathematik für Ingenieure Mathematik http://www.windelberg.de/agq Integralrechnung, Schwerpunkt Schwerpunkt Es sei ϱ die Dichte innerhalb der zu untersuchenden
Dr. Dirk Windelberg Leibniz Universität Hannover Mathematik für Ingenieure Mathematik http://www.windelberg.de/agq Integralrechnung, Schwerpunkt Schwerpunkt Es sei ϱ die Dichte innerhalb der zu untersuchenden
Mathematik 3 für Informatik
 Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 15
 5. Es sei Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 5 f(x, y) : x y, : x, y, x + y, y x. erechnen Sie f(x, y) d. Wir lösen diese Aufgabe auf zweierlei Art. Zuerst betrachten wir das Gebiet
5. Es sei Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 5 f(x, y) : x y, : x, y, x + y, y x. erechnen Sie f(x, y) d. Wir lösen diese Aufgabe auf zweierlei Art. Zuerst betrachten wir das Gebiet
Lösungsvorschlag Klausur MA9802
 Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Lehrstuhl für Numerische Mathematik Garching, den 3.8.22 Prof. Dr. Herbert Egger Dr. Matthias Schlottbom Lösungsvorschlag Klausur MA982 Aufgabe [3 + 3 Punkte] Berechnen Sie, falls existent, die folgenden
Lösung zur Klausur zur Analysis II
 Otto von Guericke Universität Magdeburg 9.7.4 Fakultät für Mathematik Lösung zur Klausur zur Analysis II Vorlesung von Prof. L. Tobiska, Sommersemester 4 Bitte benutzen Sie für jede Aufgabe ein eigenes
Otto von Guericke Universität Magdeburg 9.7.4 Fakultät für Mathematik Lösung zur Klausur zur Analysis II Vorlesung von Prof. L. Tobiska, Sommersemester 4 Bitte benutzen Sie für jede Aufgabe ein eigenes
8.2 Integralrechnung für mehrere Variable
 8.2 Integralrechnung für mehrere Variable Der bisher behandelte Begriff des Integrals einer Funktion mit einer einzigen Variablen lässt sich auf mehrere Arten verallgemeinern. Zunächst führt die Erweiterung
8.2 Integralrechnung für mehrere Variable Der bisher behandelte Begriff des Integrals einer Funktion mit einer einzigen Variablen lässt sich auf mehrere Arten verallgemeinern. Zunächst führt die Erweiterung
Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 4/5 r. Hanna Peywand Kiani 6..5 Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften Bereichsintegrale, Transformationssatz,
Fachbereich Mathematik der Universität Hamburg WiSe 4/5 r. Hanna Peywand Kiani 6..5 Anleitung zu Blatt 6 Analysis III für Studierende der Ingenieurwissenschaften Bereichsintegrale, Transformationssatz,
x(t) := 1 k definierte Funktion. (a) Berechnen Sie ẋ(t) und ẍ(t). (b) Zeigen Sie, daß die Funktion x = x(t) eine Lösung der Differentialgleichung
 Übungen (Aufg. u. Lösungen) zu Mathem. u. Lin. Algebra II SS 26 Blatt 7 3.5.26 Aufgabe 33: Die Funktion f : R R sei stetig. Betrachten Sie die durch x(t) : 1 k f(u) sin (k(t u)) du definierte Funktion.
Übungen (Aufg. u. Lösungen) zu Mathem. u. Lin. Algebra II SS 26 Blatt 7 3.5.26 Aufgabe 33: Die Funktion f : R R sei stetig. Betrachten Sie die durch x(t) : 1 k f(u) sin (k(t u)) du definierte Funktion.
2 x x 2 y 2 vol(a) = d(x, y, z) = 4 3 x3 dx = [ 1
 UNIVERSITÄT ARLSRUHE Institut für Analsis HDoz Dr P C unstmann Dipl-Math M Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Phsik und Geodäsie inklusive omplexe Analsis
UNIVERSITÄT ARLSRUHE Institut für Analsis HDoz Dr P C unstmann Dipl-Math M Uhl Sommersemester 9 Höhere Mathematik II für die Fachrichtungen Elektroingenieurwesen, Phsik und Geodäsie inklusive omplexe Analsis
D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Serie 8: Satz von Green und Oberflächenintegrale
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 8: Satz von Green und Oberflächenintegrale Bemerkungen: Die Aufgaben der Serie 8 bilden den Fokus der Übungsgruppen vom./3. April.. Den Satz
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 8: Satz von Green und Oberflächenintegrale Bemerkungen: Die Aufgaben der Serie 8 bilden den Fokus der Übungsgruppen vom./3. April.. Den Satz
12. Übungsblatt zur Analysis II
 Facbereic atematik Prof. Dr. R. Farwig C. omo J. Prasiswa R. Sculz SS 29 6.7.29 2. Übungsblatt zur Analysis II Gruppenübung Aufgabe G (Jordan-essbarkeit Die enge R n sei Jordan-messbar. Zeigen Sie, dass
Facbereic atematik Prof. Dr. R. Farwig C. omo J. Prasiswa R. Sculz SS 29 6.7.29 2. Übungsblatt zur Analysis II Gruppenübung Aufgabe G (Jordan-essbarkeit Die enge R n sei Jordan-messbar. Zeigen Sie, dass
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 7. Das Gauss-Integral e x2 dx TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (nalysis 3 http://www.ma.tum.de/hm/m924 2W/
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 7. Das Gauss-Integral e x2 dx TECHNISCHE UNIVESITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (nalysis 3 http://www.ma.tum.de/hm/m924 2W/
Aufgaben zu Kapitel 25
 Aufgaben zu Kapitel 5 Aufgaben zu Kapitel 5 Verständnisfragen Aufgabe 5. Mit W R 3 bezeichnen wir das Gebiet, das von den Ebenen x, x, x 3 und der Fläche x 3 x + x, x, x begrenzt wird. Schreiben Sie das
Aufgaben zu Kapitel 5 Aufgaben zu Kapitel 5 Verständnisfragen Aufgabe 5. Mit W R 3 bezeichnen wir das Gebiet, das von den Ebenen x, x, x 3 und der Fläche x 3 x + x, x, x begrenzt wird. Schreiben Sie das
Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form. ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können.
 142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
142 Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten x, y, z vertauscht sein können. efinition
B Lösungen. Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R 2 Berechnen Sie zur Abbildung. f(x, y) := x sin(xy) f : R 2 R,
 B en Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R Berechnen Sie zur Abbildung f : R R, f(x, y) : x sin(xy) das totale Differenzial f df, die Jacobi-Matrix J f (x, y) und den Gradienten ( f)(x,
B en Aufgabe 1 (Begriffe zur Differenziation) Sei (x, y) R Berechnen Sie zur Abbildung f : R R, f(x, y) : x sin(xy) das totale Differenzial f df, die Jacobi-Matrix J f (x, y) und den Gradienten ( f)(x,
Topologie und Differentialrechnung mehrerer Veränderlicher, SS 2009 Modulprüfung/Abschlussklausur. Aufgabe Punkte
 Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
Universität München 22. Juli 29 Topologie und Differentialrechnung mehrerer Veränderlicher, SS 29 Modulprüfung/Abschlussklausur Name: Aufgabe 2 3 4 Punkte Gesamtpunktzahl: Gesamturteil: Schreiben Sie unbedingt
3 Lebesgue-Integration im IR n
 33 3 Lebesgue-Integration im IR n 3.1 Vorbemerkung Zuerst eine heuristische Betrachtung: Wir betrachten eine nichtnegative stetige Funktion f(x, y, die über einem kompakten, also beschränkten und abgeschlossenen
33 3 Lebesgue-Integration im IR n 3.1 Vorbemerkung Zuerst eine heuristische Betrachtung: Wir betrachten eine nichtnegative stetige Funktion f(x, y, die über einem kompakten, also beschränkten und abgeschlossenen
Seite 1. sin 2 x dx. b) Berechnen Sie das Integral. e (t s)2 ds. (Nur Leibniz-Formel) c) Differenzieren Sie die Funktion f(t) = t. d dx ln(x + x3 ) dx
 Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =
Ferienkurs Analysis 3 für Physiker. Übung: Integralsätze
 Ferienkurs Analysis 3 für Physiker Übung: Integralsätze Autor: enjamin Rüth Stand: 7. März 4 Aufgabe (Torus) Zu festem R > werden mittels ϱ T : [, R] [, π] [, π] R 3, ϕ ϑ Toruskoordinaten eingeführt. estimmen
Ferienkurs Analysis 3 für Physiker Übung: Integralsätze Autor: enjamin Rüth Stand: 7. März 4 Aufgabe (Torus) Zu festem R > werden mittels ϱ T : [, R] [, π] [, π] R 3, ϕ ϑ Toruskoordinaten eingeführt. estimmen
Mathematik II: Übungsblatt 01: Lösungen
 N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
12 Gewöhnliche Differentialgleichungen
 2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
2 2 Gewöhnliche Differentialgleichungen 2. Einleitung Sei f : D R wobei D R 2. Dann nennt man y = f(x, y) (5) eine (gewöhnliche) Differentialgleichung (DGL) erster Ordnung. Als Lösung von (5) akzeptiert
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt
 Übungen zur Ingenieur-Mathematik III WS 9/ Blatt 4..9 Aufgabe : Berechnen Sie das Volumen des Volltorus, der durch Rotation der reisscheibe { x,, z R 3, x b + z a } mit < a < b um die z-achse entsteht.
Übungen zur Ingenieur-Mathematik III WS 9/ Blatt 4..9 Aufgabe : Berechnen Sie das Volumen des Volltorus, der durch Rotation der reisscheibe { x,, z R 3, x b + z a } mit < a < b um die z-achse entsteht.
1 Das Prinzip von Cavalieri
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 14 11.6.14 Höhere Mathematik II für die Fachrichtung Informatik 5. Saalübung 11.6.14 1 Das Prinzip von
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann SS 14 11.6.14 Höhere Mathematik II für die Fachrichtung Informatik 5. Saalübung 11.6.14 1 Das Prinzip von
Aufgaben für die 14. Übung zur Vorlesung Mathematik 2 für Informatiker: Analysis Sommersemester 2010
 Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
Mathematik II für Inf und WInf
 Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Gruppenübung Mathematik II für Inf und WInf 8. Übung Lösungsvorschlag G 28 (Partiell aber nicht total differenzierbar) Gegeben sei die Funktion f : R 2 R mit f(x, ) := x. Zeige: f ist stetig und partiell
Klausurenkurs zum Staatsexamen (SS 2015): Differential und Integralrechnung 6
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 205): Differential und Integralrechnung 6 6. (Frühjahr 2009, Thema, Aufgabe 3) Sei r > 0. Berechnen Sie die Punkte auf der Parabel y = x 2 mit dem
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 205): Differential und Integralrechnung 6 6. (Frühjahr 2009, Thema, Aufgabe 3) Sei r > 0. Berechnen Sie die Punkte auf der Parabel y = x 2 mit dem
Karlsruher Institut für Technologie (KIT) SS 2013 Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning
 Karlsruher Institut für Technologie KIT SS 3 Institut für Analysis.6.3 Prof. Dr. Tobias Lamm Dr. Patrick reuning Aufgabe Höhere Mathematik II für die Fachrichtung Physik 9. Übungsblatt Ein Heißluftballon
Karlsruher Institut für Technologie KIT SS 3 Institut für Analysis.6.3 Prof. Dr. Tobias Lamm Dr. Patrick reuning Aufgabe Höhere Mathematik II für die Fachrichtung Physik 9. Übungsblatt Ein Heißluftballon
Abbildung 10.1: Das Bild zu Beispiel 10.1
 Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Analysis 3, Woche Mannigfaltigkeiten I. Definition einer Mannigfaltigkeit Die Definition einer Mannigfaltigkeit braucht den Begriff Diffeomorphismus, den wir in Definition 9.5 festgelegt haben. Seien U,
Analysis II für Ingenieure Übersicht: Integration. 1 Kurvenintegral über ein Skalarfeld
 Analysis II für Ingenieure Übersicht: Integration 1 Kurvenintegral über ein Skalarfeld 1.1 erechnung c f ds = b a f ( c(t) ) c(t) dt 1. Kurve c parametrisieren: c : [a, b] R n, t c(t). 2. c(t) und dann
Analysis II für Ingenieure Übersicht: Integration 1 Kurvenintegral über ein Skalarfeld 1.1 erechnung c f ds = b a f ( c(t) ) c(t) dt 1. Kurve c parametrisieren: c : [a, b] R n, t c(t). 2. c(t) und dann
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz WS 5/6 8..6 Höhere Mathematik II für die Fachrichtung Physik Bachelor-Modulprüfung Aufgabe
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz WS 5/6 8..6 Höhere Mathematik II für die Fachrichtung Physik Bachelor-Modulprüfung Aufgabe
PROBEPRÜFUNG MATHEMATIK I UND II
 PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form
 155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
Mehrdimensionale Integralrechnung 2
 Mehrdimensionale Integralrechnung Quiz Wir wollen die Dynamik zweier Teilchen beschreiben, die über ein hoch elastisches Seil verbunden sind und sich wild im Raum bewegen! Ein Kollege schlägt dazu vor
Mehrdimensionale Integralrechnung Quiz Wir wollen die Dynamik zweier Teilchen beschreiben, die über ein hoch elastisches Seil verbunden sind und sich wild im Raum bewegen! Ein Kollege schlägt dazu vor
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Klausurenkurs zum Staatsexamen (WS 2014/15): Differential und Integralrechnung 6
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 204/5): Differential und Integralrechnung 6 6. (Frühjahr 2009, Thema, Aufgabe 3) Sei r > 0. Berechnen Sie die Punkte auf der Parabel y = x 2 mit dem
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 204/5): Differential und Integralrechnung 6 6. (Frühjahr 2009, Thema, Aufgabe 3) Sei r > 0. Berechnen Sie die Punkte auf der Parabel y = x 2 mit dem
Technische Universität Berlin
 Technische Universität Berlin Fakultät II Institut für Mathematik WS /5 G. Bärwol, A. Gündel-vom-Hofe..5 Februar Klausur Analysis II für Ingenieurswissenschaften Lösungsskizze. Aufgabe 6Punkte Bestimmen
Technische Universität Berlin Fakultät II Institut für Mathematik WS /5 G. Bärwol, A. Gündel-vom-Hofe..5 Februar Klausur Analysis II für Ingenieurswissenschaften Lösungsskizze. Aufgabe 6Punkte Bestimmen
Lösungen zu Koordinatentrafo und Integration im R n
 Lösungen zu Koordinatentrafo und Integration im R n für Freitag, 8.9.9 von Carla Zensen Aufgabe : Verschiedene Parametrisierungen a) Zylinderkoordinaten ρ Ψ ϕ Ψ z Ψ cos ϕ ρ sin ϕ DΨρ, ϕ, z) = ρ Ψ ϕ Ψ z
Lösungen zu Koordinatentrafo und Integration im R n für Freitag, 8.9.9 von Carla Zensen Aufgabe : Verschiedene Parametrisierungen a) Zylinderkoordinaten ρ Ψ ϕ Ψ z Ψ cos ϕ ρ sin ϕ DΨρ, ϕ, z) = ρ Ψ ϕ Ψ z
Mehrdimensionale Analysis
 KAPITEL IV Mehrdimensionale Analsis 15 Mehrdimensionale Differentialrechnung Wir wollen in diesem Abschnitt einige Aspekte der Differentialrechnung von Abbildungen von R n nach R oder nach R m ansprechen
KAPITEL IV Mehrdimensionale Analsis 15 Mehrdimensionale Differentialrechnung Wir wollen in diesem Abschnitt einige Aspekte der Differentialrechnung von Abbildungen von R n nach R oder nach R m ansprechen
Analysis II. Mehrdimensionale Differenzialund Integralrechnung
 Übungen zur Vorlesung Analysis II Aufgaben Mehrdimensionale Differenzialund Integralrechnung gelesen von Prof. Dr. Heinrich Freistühler Martin Gubisch Konstanz, Sommersemester 28 Übungsaufgaben. Aufgabe
Übungen zur Vorlesung Analysis II Aufgaben Mehrdimensionale Differenzialund Integralrechnung gelesen von Prof. Dr. Heinrich Freistühler Martin Gubisch Konstanz, Sommersemester 28 Übungsaufgaben. Aufgabe
Lösungsvorschläge zur Klausur für bau, fmt, IuI, mach, tema, umw, verf und zugehörige Technikpädagogik
 Prüfung in Höhere Mathematik 3 9. März 21 Lösungsvorschläge zur Klausur für bau, fmt, IuI, mach, tema, umw, verf und zugehörige Technikpädagogik Aufgabe 1: (7 Punkte Gegeben ist die Menge G : {(x,y R 2
Prüfung in Höhere Mathematik 3 9. März 21 Lösungsvorschläge zur Klausur für bau, fmt, IuI, mach, tema, umw, verf und zugehörige Technikpädagogik Aufgabe 1: (7 Punkte Gegeben ist die Menge G : {(x,y R 2
Serie 6: MC-Zwischentest - Kapitel I und II
 D-ERDW, D-HEST, D-USYS Mathematik II FS 14 Dr. Ana Cannas Serie 6: MC-Zwischentest - Kapitel I und II Einsendeschluss: 11. April 14, 17 Uhr Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des
D-ERDW, D-HEST, D-USYS Mathematik II FS 14 Dr. Ana Cannas Serie 6: MC-Zwischentest - Kapitel I und II Einsendeschluss: 11. April 14, 17 Uhr Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des
Ferienkurs Analysis 3 Lösung Vektoranalysis 19. März Die Einheitssphäre werde parametrisiert mithilfe von Kugelkoordina- ten
 Ferienkurs Analysis 3 Lösung Vektoranalysis 19. März 1 Die Einheitssphäre werde parametrisiert mithilfe von Kugelkoordina- Lösung 1. ten Ψ(θ, φ) sin θ cos φ sin θ sin φ cos θ Dann gilt 1 Ψ(θ, φ) cos θ
Ferienkurs Analysis 3 Lösung Vektoranalysis 19. März 1 Die Einheitssphäre werde parametrisiert mithilfe von Kugelkoordina- Lösung 1. ten Ψ(θ, φ) sin θ cos φ sin θ sin φ cos θ Dann gilt 1 Ψ(θ, φ) cos θ
Klausur zu Analysis II - Lösungen
 Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Dr. Axel Grünrock WS 1/11 11..11 Klausur zu Analysis II - Lösungen 1. Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind.
Mathematisches Institut der Heinrich-Heine-Universität Düsseldorf Dr. Axel Grünrock WS 1/11 11..11 Klausur zu Analysis II - Lösungen 1. Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind.
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
1 = z = y + e. Nabla ist ein Vektor, der als Komponenten keine Zahlen sondern Differentiationsbefehle
 Anmerkung zur Notation Im folgenden werden folgende Ausdrücke äquivalent benutzt: r = x y = x 1 x 2 z x 3 1 Der Vektoroperator Definition: := e x x + e y y + e z z = x y z. Nabla ist ein Vektor, der als
Anmerkung zur Notation Im folgenden werden folgende Ausdrücke äquivalent benutzt: r = x y = x 1 x 2 z x 3 1 Der Vektoroperator Definition: := e x x + e y y + e z z = x y z. Nabla ist ein Vektor, der als
Analysis I & II Lösung zur Basisprüfung
 FS 6 Aufgabe. [8 Punkte] (a) Bestimmen Sie den Grenzwert ( lim x x ). [ Punkte] log x (b) Beweisen Sie, dass folgende Reihe divergiert. n= + n + n + sin(n) n 3 + [ Punkte] (c) Finden Sie heraus, ob die
FS 6 Aufgabe. [8 Punkte] (a) Bestimmen Sie den Grenzwert ( lim x x ). [ Punkte] log x (b) Beweisen Sie, dass folgende Reihe divergiert. n= + n + n + sin(n) n 3 + [ Punkte] (c) Finden Sie heraus, ob die
Höhere Mathematik 3 Herbst 2014
 IMNG, Fachbereich Mathematik Universität Stuttgart Prof. Dr. K. Höllig Höhere Mathematik 3 Herbst 214 Aufgabe 1 Entscheiden Sie, welche der folgenden Aussagen richtig und welche falsch sind. (i) rot(2
IMNG, Fachbereich Mathematik Universität Stuttgart Prof. Dr. K. Höllig Höhere Mathematik 3 Herbst 214 Aufgabe 1 Entscheiden Sie, welche der folgenden Aussagen richtig und welche falsch sind. (i) rot(2
Mathematik 2 für Wirtschaftsinformatik
 für Wirtschaftsinformatik Sommersemester 2012 Hochschule Augsburg : Gliederung 1 Folgen und Reihen 2 Komplexe Zahlen 3 Reelle Funktionen 4 Differenzieren 1 5 Differenzieren 2 6 Integration 7 Zinsen 8
für Wirtschaftsinformatik Sommersemester 2012 Hochschule Augsburg : Gliederung 1 Folgen und Reihen 2 Komplexe Zahlen 3 Reelle Funktionen 4 Differenzieren 1 5 Differenzieren 2 6 Integration 7 Zinsen 8
2 Koordinatentransformationen
 Mathematik für Ingenieure III, WS 9/1 Montag 3.11 $Id: transform.tex,v 1.5 9/11/3 16:9: hk Exp $ Koordinatentransformationen. ie Transformationsformel In der letzten Sitzung hatten wir die Transformationsformel
Mathematik für Ingenieure III, WS 9/1 Montag 3.11 $Id: transform.tex,v 1.5 9/11/3 16:9: hk Exp $ Koordinatentransformationen. ie Transformationsformel In der letzten Sitzung hatten wir die Transformationsformel
Kleine Formelsammlung zu Mathematik für Ingenieure IIA
 Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
Kleine Formelsammlung zu Mathematik für Ingenieure IIA Florian Franzmann 5. Oktober 004 Inhaltsverzeichnis Additionstheoreme Reihen und Folgen 3. Reihen...................................... 3. Potenzreihen..................................
Serie 9: Der Satz von Green und Parametrisierungen von Flächen im Raum
 : Der Satz von Green und Parametrisierungen von Flächen im Raum Bemerkung: Die Aufgaben der sind der Fokus der Übungsstunden vom 6./8. April.. Überprüfung des Satzes von Green Der Satz von Green besagt
: Der Satz von Green und Parametrisierungen von Flächen im Raum Bemerkung: Die Aufgaben der sind der Fokus der Übungsstunden vom 6./8. April.. Überprüfung des Satzes von Green Der Satz von Green besagt
6 Integration auf Untermannigfaltigkeiten
 6 Integration auf Untermannigfaltigkeiten 6.1 annigfaltigkeiten. Eine k dimensionale C α annigfaltigkeit ist ein metrischer Raum mit einer Überdeckung {V : J} durch offene engen und Homöomorphismen ϕ :
6 Integration auf Untermannigfaltigkeiten 6.1 annigfaltigkeiten. Eine k dimensionale C α annigfaltigkeit ist ein metrischer Raum mit einer Überdeckung {V : J} durch offene engen und Homöomorphismen ϕ :
Übungen zum Ferienkurs Analysis II 2014
 Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Übungen zum Ferienkurs Analysis II 4 Probeklausur Allgemein Hinweise: Die Arbeitszeit beträgt 9 Minuten. Falls nicht anders angegeben, sind alle en ausführlich und nachvollziehbar zu begründen. Schreiben
Thema 12 Differentialrechnung, Partielle Ableitungen, Differenzierbarkeit, Taylor-Formel, Lokale Extrema
 Thema 12 Differentialrechnung, Partielle Ableitungen, Differenzierbarkeit, Taylor-Formel, Lokale Extrema In diesem Kapitel befassen wir uns mit der Ableitung von Funktionen f : R m R n. Allein die Schreibweise
Thema 12 Differentialrechnung, Partielle Ableitungen, Differenzierbarkeit, Taylor-Formel, Lokale Extrema In diesem Kapitel befassen wir uns mit der Ableitung von Funktionen f : R m R n. Allein die Schreibweise
12. Mehrfachintegrale
 - 1-1. Mehrfachintegrale Flächen- und Volumenelemente Naive Gemüter sind geneigt, den Flächeninhalt dx dy (kartesische Koordinaten) in den neuen Koordinaten durch du dv anzugeben. Das ist i.a. falsch!
- 1-1. Mehrfachintegrale Flächen- und Volumenelemente Naive Gemüter sind geneigt, den Flächeninhalt dx dy (kartesische Koordinaten) in den neuen Koordinaten durch du dv anzugeben. Das ist i.a. falsch!
Vorkurs Mathematik Übungen zu Kurven im R n
 Vorkurs Mathematik Übungen zu urven im R n Als bekannt setzen wir die folgende Berechnung voraus: Sei f : [a, b] R eine urve im R. Die Länge L der urve berechnet sich durch L b a f t dt urven in R Aufgabe.
Vorkurs Mathematik Übungen zu urven im R n Als bekannt setzen wir die folgende Berechnung voraus: Sei f : [a, b] R eine urve im R. Die Länge L der urve berechnet sich durch L b a f t dt urven in R Aufgabe.
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
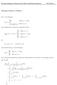 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Analysis IV. Gruppenübungen
 Fachbereich Mathematik Prof. B. Farkas Martin Fuchssteiner Lisa Steiner TECHNISCHE UNIVESITÄT DAMSTADT ASS 6 7.7.26 Analysis IV 3. Übung mit Lösungshinweisen (G ) Berechnung einiger Volumina Gruppenübungen
Fachbereich Mathematik Prof. B. Farkas Martin Fuchssteiner Lisa Steiner TECHNISCHE UNIVESITÄT DAMSTADT ASS 6 7.7.26 Analysis IV 3. Übung mit Lösungshinweisen (G ) Berechnung einiger Volumina Gruppenübungen
Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen
 Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen In diesem Kapitel betrachten wir die Invertierbarkeit von glatten Abbildungen bzw. die Auflösbarkeit von impliziten Gleichungen.
Thema14 Der Satz über inverse Funktionen und der Satz über implizite Funktionen In diesem Kapitel betrachten wir die Invertierbarkeit von glatten Abbildungen bzw. die Auflösbarkeit von impliziten Gleichungen.
46 Der Satz von Fubini
 46 Der Satz von Fubini 227 46 Der Satz von Fubini Die Berechnung des n-dimensionalen Integrals einer Funktion f L (R n ) kann auf die eindimensionaler Integrale zurückgeführt werden. Dazu werden für R
46 Der Satz von Fubini 227 46 Der Satz von Fubini Die Berechnung des n-dimensionalen Integrals einer Funktion f L (R n ) kann auf die eindimensionaler Integrale zurückgeführt werden. Dazu werden für R
Mathematik 2 SS 2016
 Mathematik 2 SS 2016 2. Übungsblatt Gruppe 1 18. Man zeige, dass die Gleichung f(x, y) = y 5 e y (2x 2 + 3) sin y + x 2 y 2 x cos x = 0 in einer Umgebung des Punktes P (0, 0) nach y aufgelöst werden kann,
Mathematik 2 SS 2016 2. Übungsblatt Gruppe 1 18. Man zeige, dass die Gleichung f(x, y) = y 5 e y (2x 2 + 3) sin y + x 2 y 2 x cos x = 0 in einer Umgebung des Punktes P (0, 0) nach y aufgelöst werden kann,
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 23 (5.8.23). Gegeben seien die Matrizen A = 2 3 3 und B = 5 2 5 (a) Bestimmen Sie die Eigenwerte von A und B sowie die
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 23 (5.8.23). Gegeben seien die Matrizen A = 2 3 3 und B = 5 2 5 (a) Bestimmen Sie die Eigenwerte von A und B sowie die
4 Absolutstetige Verteilungen und Zufallsvariablen 215/1
 4 Absolutstetige Verteilungen und Zufallsvariablen 215/1 23. Bemerkung Integralbegriffe für Funktionen f : R d R (i) Lebesgue-Integral (Vorlesung Analysis IV). Spezialfall: (ii) Uneigentliches Riemann-Integral
4 Absolutstetige Verteilungen und Zufallsvariablen 215/1 23. Bemerkung Integralbegriffe für Funktionen f : R d R (i) Lebesgue-Integral (Vorlesung Analysis IV). Spezialfall: (ii) Uneigentliches Riemann-Integral
Der metrische Raum (X, d) ist gegeben. Zeigen Sie, dass auch
 TECHNISCHE UNIVERSITÄT BERLIN SS 07 Institut für Mathematik Stand: 3. Juli 007 Ferus / Garcke Lösungsskizzen zur Klausur vom 6.07.07 Analysis II. Aufgabe (5 Punkte Der metrische Raum (X, d ist gegeben.
TECHNISCHE UNIVERSITÄT BERLIN SS 07 Institut für Mathematik Stand: 3. Juli 007 Ferus / Garcke Lösungsskizzen zur Klausur vom 6.07.07 Analysis II. Aufgabe (5 Punkte Der metrische Raum (X, d ist gegeben.
Umkehrfunktion. g (y) = f (x) 1, x = g(y), Umkehrfunktion 1-1
 Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Umkehrfunktion Ist für eine stetig differenzierbare n-variate Funktion f : D R n die Jacobi-Matrix f (x ) für einen Punkt x im Innern des Definitionsbereiches D R n nicht singulär, so ist f lokal invertierbar,
Technische Universität Berlin Fakultät II Institut für Mathematik SS 13 G. Bärwolff, C. Mehl, G. Penn-Karras
 Technische Universität Berlin Fakultät II Institut für Mathematik SS 3 G. Bärwolff, C. Mehl, G. Penn-Karras 9..3 Oktober Klausur Analysis II für Ingenieure Rechenteil. Aufgabe Punkte i) Wir berechnen zunächst
Technische Universität Berlin Fakultät II Institut für Mathematik SS 3 G. Bärwolff, C. Mehl, G. Penn-Karras 9..3 Oktober Klausur Analysis II für Ingenieure Rechenteil. Aufgabe Punkte i) Wir berechnen zunächst
Übungen zur Ingenieur-Mathematik III WS 2011/12 Blatt N dl. y 3
 Übungen zur Ingenieur-Mathematik III WS / Blatt 9.. Aufgabe 5: Berechnen Sie das Integral K ( x y N dl über den Rand des Kreises K {(x, y x + y } einmal direkt mit Hilfe einer geeigneten Parametrisierung
Übungen zur Ingenieur-Mathematik III WS / Blatt 9.. Aufgabe 5: Berechnen Sie das Integral K ( x y N dl über den Rand des Kreises K {(x, y x + y } einmal direkt mit Hilfe einer geeigneten Parametrisierung
Parametrisierung und Integralsätze
 Parametrisierung und Integralsätze 2. März 2 Integration in der Ebene. Defintion: eien w,..., w n stückweise reguläre, einfach geschlossene Kurven in R 2, seien W,..., W n die von diesen Wegen umschlossene
Parametrisierung und Integralsätze 2. März 2 Integration in der Ebene. Defintion: eien w,..., w n stückweise reguläre, einfach geschlossene Kurven in R 2, seien W,..., W n die von diesen Wegen umschlossene
Prüfung Modul A, Teil 2 (Mathematik 2) (Fernstudium Bauingenieurwesen)
 Name: Vorname: Matrikelnummer: TU Dresden, Fachrichtung Mathematik, Dr. N. Koksch 6. Februar 8 Prüfung Modul A, Teil (Mathematik ) (Fernstudium auingenieurwesen) ewertet werden nur solche Lösungsschritte,
Name: Vorname: Matrikelnummer: TU Dresden, Fachrichtung Mathematik, Dr. N. Koksch 6. Februar 8 Prüfung Modul A, Teil (Mathematik ) (Fernstudium auingenieurwesen) ewertet werden nur solche Lösungsschritte,
(u, v) z(u, v) u Φ(u, v) (v = const.) Parameterlinie v = const. v Φ(u, v) (u = const.) Parameterlinie u = const.
 13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
6.4 Koordinatentransformationen
 6.4 Koordinatentransformationen Koordinatentransformationen benötigt man vor allem, um sich einigen Rechenaufwand zu ersparen. Wer möchte schon freiwillig eine Kugel in kartesischen Koordinaten beschreiben?
6.4 Koordinatentransformationen Koordinatentransformationen benötigt man vor allem, um sich einigen Rechenaufwand zu ersparen. Wer möchte schon freiwillig eine Kugel in kartesischen Koordinaten beschreiben?
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
1. Übungsblatt zur Analysis 3
 Hannover, den 2. Oktober 23 Aufgabe. Übungsblatt zur Analysis 3 Abgabe am 27./28. Oktober 23 vor den Stundenübungen (je 5 Punkte) Man zeige: a) Die Funktion f : N N N, f(m, n) := 2 (m + n)(m + n + ) +
Hannover, den 2. Oktober 23 Aufgabe. Übungsblatt zur Analysis 3 Abgabe am 27./28. Oktober 23 vor den Stundenübungen (je 5 Punkte) Man zeige: a) Die Funktion f : N N N, f(m, n) := 2 (m + n)(m + n + ) +
