9 SLAM Simultaneous Localization and Mapping
|
|
|
- Adolph Bauer
- vor 5 Jahren
- Abrufe
Transkript
1 9 SLAM Simultaneous Localization and Mapping
2 Einleitung eines der aktivsten Forschungsgebiete innerhalb der Robotik Roboterlokalisierung bei gegebener Karte (Kap. 8 und Karte aus Sensordaten bei bekannter Position (Kap. 7 sind relativ einfach beide Probleme aber gleichzeitig zu lösen ist schwierig aktuelle Algorithmen verwenden probabilistische Ansätze, um Unsicherheiten explizit zu modellieren deterministische Ansätze sind meist schlechter
3 Einleitung Eingabe: Sensordaten Kontrollkommandos des Roboters (Fahren Gesucht: Schätzung der Karte Pfad des Roboters (alle bisherigen Positionen
4 Probleme Sowohl Positionen der Landmarken als auch Roboterweg sind unbekannt Die Zuordnung von Sensordaten zu Landmarken sind in der Regel unbekannt Roboter muss entscheiden, ob Sensordaten zu einer bereits beobachteten Landmarke zugeordnet werden können oder zu einer noch nicht gesehenen Landmarke Zuordnungsproblematik wird durch Fehler im Roboterweg verstärkt Fehler kann prinzipiell unbegrenzt wachsen
5 SLAM Graph 1 E Fehler A Rob C D B Roboter sieht die Landmarken A und B.
6 SLAM Graph 2 Fehler E A C D Rob B Nach Bewegung des Roboters nimmt die Genauigkeit der Lokalisierung ab Die Unsicherheit der Positionsschätzungen der Landmarken C und D steigt
7 SLAM Graph 3 A C E D Rob B Roboter erkennt eine bereits gesehene Landmarke wieder
8 SLAM Graph 4 A C E D Rob wird genauer B rekursive Verbesserung (Optimierung
9 Problem Datenassoziation Sobald Landmarken nicht eindeutig unterscheidbar sind, muss die Frage beantwortet werden, in welchen Fällen zwei gleich aussehende Landmarken tatsächlich dieselbe Landmarke waren Macht der Roboter hier Fehler, kann das starke Auswirkungen auf die Lösung (Karte haben
10 Lösung des SLAM Problems Aufbau des Graphen Optimierung
11 SLAM Simultaneous Localization and Mapping p( x t, m z 1:t, u 1:t p ( x t, m, c t z 1:t, u 1:t Online SLAM Problem (inkrementelles SLAM p ( x 1:t, m z 1: t, u 1:t p ( x 1:t, m, c 1 :t z 1 :t, u 1 :t Full SLAM Problem (vollständiges SLAM
12 Full SLAM
13 Online SLAM
14 Verfahren EKF SLAM verwendet Extended Kalman Filter Online Fast SLAM verwendet Partikel Filter Graph SLAM vollständiges SLAM
15 Verfahren Niko Sünderhauf
16 9.1 Simple SLAM Einfaches Modell
17 Simple SLAM Roboterposition ( x r, y r N Landmarken (Positionen: ( x l 1, y l1 ( x l 2, y l 2 ( x l, y l N N
18 Simple SLAM - Zustand x t =( x r (t, y r (t, x l 1, y l1,, x li, y li, x l N, y l N T Bewegung Omnidirektionales Bewegungsmodell (Antrieb in alle Richtungen (Roboterfront zeigt immer in gleiche Richtung u t =(v x (t, v y (t T
19 Simple SLAM Bewegungsgleichung x t = A t x t 1 +B t u t +ε t Bt=( A t =( Landmarken bewegen sich nicht 0 0 ε t =(ε rx (t, ε ry (t,0,0,,0 T (ε rx (t, ε ry (t T N (0,V rt ε t N (0, V t V t =(V rt
20 Simple SLAM Sensordaten Landmarken seien eindeutig identifizierbar, für jede Landmarke wird ihre Position relativ zum Roboter gemessen =( z1(t x r (t y y r (t z t z i (t x l x N r (t z N (t =(xl1 y l N y r (t
21 Simple SLAM - Messgleichung z t = H t x t +δ t H t =(H 1(t H 2 (t H N (t H i =( (2i+1-te Spalte
22 Simple SLAM Messgleichung δ t N (0, W t δ t =(δ 1 (t, δ 2 (t,, δ N (t T z t = H t x t +δ t δ i (t N (0, W it 1t W W t =(W 2t W Nt
23 Simple SLAM Kalmanfilter Damit sind alle alle Systemparameter (lineares System! festgelegt und der lineare Kalman-Filter-Algorithmus kann direkt verwendet werden.
24 Simple SLAM Erweiterungen Das Bewegungsmodel kann erweitert werden. Zur Roboterposition kommt dann noch die Orientierung dazu. Statt bei jeder Landmarke die relative Position zu messen, kann auch Abstand und Orientierung gemessen werden. Zusätzlich kann noch das Problem der Zuordnung der Messdaten zu den Landmarken- Nummern dazukommen. EKF SLAM
25 9.2 EKF SLAM
26 EKF SLAM erster SLAM Algorithmus verwendet erweiterten Kalmanfilter Online SLAM bekannte Korrespondenzen zu den Landmarken unbekannte Korrespondenzen zu den Landmarken
27 Beispiel Roboterposition Landmarken (8 Hier sieht der Roboter die erste Landmarke erneut, sämtliche Unsicherheiten werden erheblich kleiner.
28 EKF SLAM zu berechnen: p( y t z 1: t,u 1:t =( y x m t t y t =( x, y,θ,m 1, x, m 1, y, s 1,, m N, x, m N, y, s N T
29 EKF SLAM μ 0 =(0,0,,0 T 3N+3 - Vektor (3N+3 (3N Σ 0 =( Matrix
30 EKF SLAM y t = y t 1 + F x T ( v t w t sin θ + v t w t sin (θ +w t Δt v t w t cosθ v t w t cos(θ +w t Δt w t Δt y t =g (u t, y t 1 +N (0, F x T R t F x +N (0, F T x R t F x F x =( N
31 EKF SLAM y t =g (u t, y t 1 +N (0, F x T R t F x g (u t, y t 1 g (u t, μ t 1 +G t ( y t 1 μ t 1 G t = I +F x T g t F x v t ( cos( μ w t 1,θ +cos( μ t 1, θ +w t Δt t v t 0 0 ( sin( μ w t 1,θ +sin ( μ t 1,θ +w t Δt t g t =(0 0
32 EKF SLAM μ t =g ( u t, μ t 1 = μ t 1 + F x T ( v t w t sin θ + v t w t sin (θ +w t Δt v t w t cosθ v t w t cos(θ +w t Δt w t Δt θ= μ t 1,θ Σ t =G t Σ t 1 G t T +F x T R t F x
33 Sensorbeobachtungen
34 EKF SLAM Landmarke j wird zum ersten Mal gesehen: ( μ j, x μ j, y, x t, y i μ j, s=( μt s t +(rt i cos(φ i t + μ t, θ r i t sin (φ i t + μ t,θ 0 δ=( δ x y δ = j, x μ t, x ( μ y μ j, y μ t, q=δ T δ
35 EKF SLAM =( i s t i t z i i t =(r φ t (m j, x x 2 +(m j, y y 2 atan 2( m j, y y, m j, x x θ+n (0, Q t m j, s m={m 1,, m N } m j =(m j, x, m j, y, m j, s T j=c t i z t i =h( y t, j +N (0, Q t h ( y t, j h( μ t, j+h t i ( y t μ t 2 r Q t =(σ 0 σ φ σ s 2
36 EKF SLAM h( y t, j h( μ t, j+h t i ( y t μ t H t i =h t i F x, j q( H i t = 1 q δ x q δ y 0 q δ x q δ y 0 δ y δ x 1 δ y δ x 0 x, j F
37 EKF SLAM H t i =h t i F x, j F x, j =( j 3 3 N 3 j
38 EKF SLAM for all features z t i : S t i = H t i Σ t (H ti T +Q t K t i = Σ t (H ti T (S ti 1 q ( μ t = μ t +K i t ( z i t atan 2(δ y,δ x μ t,θ Σ t =( I K t i H t i Σ t μ j, s μ t = μ t Σ t = Σ t
39 9.3 Graph SLAM
40 9.3.1 Pose Graph SLAM Problem
41 Idee Karte alle Roboterpositionen, keine Landmarken Graph (Pose Graph zur Repräsentation des Problems Knoten Roboterpositionen Kante Constraint zwischen 2 Knoten (Odometrie Messung Konstruiere den Graphen und finde eine Knotenmenge, die einen Fehler über alle Constraints minimiert
42 Karte und Pose Graph 2D Welt: x =( x, y,θ T Roboterpositionen: x 0, x 1, Pose Graph: x 0 x 1 x 2 x 3 x 4 Odometrie Constraints
43 Weg des Roboters
44 Roboter sieht Positionen erneut
45 Kanten Constraints x 0 x 1 x 2 x 3 x 4 Bewegungsmodell Odometrie: x i+ 1 =g( x i,u i +w i w i N (0,Σ i x i+ 1 N (g ( x i,u i, Σ i Normalverteilung
46 Kanten Constraints Loop closure constraints: x 0 x 1 x 2 x 3 x 4 Der Roboter sieht eine Position erneut. x j N (g (x i, u i, j, Λ ij
47 Graph SLAM Optimierung Gegeben: u i, u ij U Gesucht: X * X *=argmax X x i X P ( X U
48 Graph SLAM Optimierung X *=argmax X P ( X U P ( X U =α i P (x i +1 x i,u i i, j P (x j x i,u i, j Odometry Constraints Loop Closure Constraints
49 Graph SLAM Optimierung P ( X U =α i Squared Mahalanobis distance: P (x i +1 x i,u i i, j P (x j x i,u i, j a b Σ 2 =(a b T Σ 1 (a b P (x i +1 x i,u i =ηe 1 2 g (x i, u i x i+1 Σ i 2 P (x j x i,u ij =ηe 1 2 g (x i, u ij x j Λ i, j 2
50 Graph SLAM Optimierung P ( X U =η i e 1 2 g( x i,u i x i+1 Σ i 2 i, j e 1 2 g ( x i,u i, j x j Λ ij 2 log(p( X U =η( g (x i,u i x i +1 Σi i 2 + i, j g ( x i,u i, j x j 2 Λij X *=argmax X P ( X U X *=argmin log P( X U X
51 Graph SLAM Optimierung X *=argmin log P( X U X X *=argmin( g ( x i,u i x i+ 1 Σi X i 2 + i, j g ( x i, u i, j x j 2 Λij (weighted least squares optimization problem
52 Least Squares Optimization Problem f i : R m R x R m x =( x 1,, x m T n F (x = 1 2 i=1 f i ( x 2 F (x = 1 2 f ( xt f (x f (x =( f 1 (x, f 2 (x,, f n ( x T Optimierungsproblem: x *=argmin x F (x =argmin x 1 2 f (x T f ( x
53 Weighted Least Squares Optimization Problem x *=argmin x F (x =argmin x 1 2 f (x T Ω f (x F = 1 2 i f i 2 Σi = 1 2 f T Σ 1 f = 1 2 f T Ω f covariance matrix information matrix
54 Lösung Gauss Newton x *=argmin x F (x =argmin x 1 2 f (x T Ω f (x Iteration: x 0 x x+δ x J = f x J T Ω J Δ x= J T Ω T f (x
55 Beispiel u 0 u x 0 x 1 u 1 x 2 u 2 x 3 3 x 4 u 0,4 prior constraint odometry constraints loop closure constraints
56 Beispiel u 0 u x 0 x 1 u 1 x 2 u 2 x 3 3 x 4 u 0,4 exakter Wert Messung u u u u u 0,4 0 0
57 Beispiel u 0 u x 0 x 1 u 1 x 2 u 2 x 3 3 x 4 u 0,4 exakter Wert Messung x x x x x
58 Beispiel u 0 u x 0 x 1 u 1 x 2 u 2 x 3 3 x 4 u 0,4 Constraints: g (x i, u i x i +1 Σi 2 2 = x i +u i x i +1 Σi i=0,1,2,3 g (x 0,u 0,4 x 4 Λ0,4 2 2 = x 0 +u 0,4 x 4 Λ0,4 x 0 0 Π 2 prior constraint
59 Beispiel u 0 u x 0 x 1 u 1 x 2 u 2 x 3 3 x 4 x *=argmin x x0+u0 x1 x 1 +u 1 x 2 x f (x =( 2 +u 2 x 3 x 3 +u 3 x 4 x 0 +u 0,4 x 4 x 0 0 Ω=(0.01 u 0,4 F (x=argmin x 1 2 f (x T Ω f (x
60 Beispiel u 0 u x 0 x 1 u 1 x 2 u 2 x 3 3 x 4 x *=argmin x x0+u0 x1 x 1 +u 1 x 2 x f (x =( 2 +u 2 x 3 x 3 +u 3 x 4 x 0 +u 0,4 x 4 x 0 0 Ω=(100 u 0,4 F (x=argmin x 1 2 f (x T Ω f (x
61 x *=argmin x x0+u0 x1 x 1 +u 1 x 2 x f (x =( 2 +u 2 x 3 x 3 +u 3 x 4 x 0 +u 0,4 x 4 x 0 0 J = f x = ( f x 0 F (x=argmin x f x 1 Ω=(100 f x 2 Beispiel 1 2 f (x T Ω f (x f x 3 =( f x
62 Beispiel Iteration J T Ω J Δ x= J T Ω T f (x x x+δ x x 0 =( T
63 9.3.2 Graph SLAM mit Landmarken
64 Graph SLAM mit Landmarken Full SLAM Knoten sind Roboterpositionen und Landmarken Kanten beschreiben Bewegungen und Sensorbeobachtungen Kanten sind nichtlineare Constraints zugeordnet
65 Graph SLAM mit Landmarken wird minimiert
66 Konstruktion
67 Konstruktion
68 Konstruktion
SLAM-Verfahren Synchrone Lokalisierung und Kartenerstellung
SLAM-Verfahren Synchrone Lokalisierung und Kartenerstellung EKF-SLAM: Landmarkenbasiertes SLAM-Verfahren mit einem erweiterten Kalmanfilter Fast-Slam: Gitterbasiertes SLAM-Verfahren mit einem Partikelfilter
Fast-SLAM: Synchrone Lokalisierung und Kartenerstellung mit einem Partikel-Filter
Fast-SLAM: Synchrone Lokalisierung und Kartenerstellung mit einem Partikel-Filter! Landmarkenbasiertes Fast-SLAM! Gitterbasiertes Fast-Slam! Optimierungen Prof. Dr. O. Bittel, HTWG Konstanz Autonome Roboter
SLAM. Simultaneous Localization and Mapping. KogSys-Sem-M2: Reading Club - SLAM - Andreas Habermann
SLAM Simultaneous Localization and Mapping KogSys-Sem-M2: Reading Club - SLAM - Andreas Habermann Simultaneous Localization And Mapping SLAM Problematik SLAM Arten SLAM Methoden: (E)KF SLAM GraphSLAM Fast
HAW Hamburg Anwendung 1 - Vortrag Andrej Rull
HAW Hamburg Anwendung 1 - Vortrag Andrej Rull 02122008 1 Gliederung o Motivation o Der Anwendungsfall o Das SLAM Problem o Lösungsansätze und Algorithmen o Zusammenfassung o Ausblick auf AW2 2 Motivation
Lokalisierung. von Matthias Heine, Norbert Müller, Silvia Schreier, Oliver Zöllner
Lokalisierung von Matthias Heine, Norbert Müller, Silvia Schreier, Oliver Zöllner Was ist Lokalisierung? Fähigkeit eines autonomen Roboters seine Position in Bezug auf ein festes (Koordinaten-)System zu
κ Κα π Κ α α Κ Α
κ Κα π Κ α α Κ Α Ζ Μ Κ κ Ε Φ π Α Γ Κ Μ Ν Ξ λ Γ Ξ Ν Μ Ν Ξ Ξ Τ κ ζ Ν Ν ψ Υ α α α Κ α π α ψ Κ α α α α α Α Κ Ε α α α α α α α Α α α α α η Ε α α α Ξ α α Γ Α Κ Κ Κ Ε λ Ε Ν Ε θ Ξ κ Ε Ν Κ Μ Ν Τ μ Υ Γ φ Ε Κ Τ θ
HAW Hamburg Anwendung 2 - Vortrag Andrej Rull
HAW Hamburg Anwendung 2 - Vortrag Andrej Rull 25062009 1 Gliederung o Motivation o Das SLAM Problem o Related Works ATLAS Framework o Abgrenzung der eigenen o Zusammenfassung 2 Motivation Wofür überhaupt
Kalman-Filter und Target Tracking
Kalman-Filter und Target Tracking Peter Poschmann Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik/Mathematik 23. März 2016 Inhalt 1 Kalman-Filter Einleitung Eindimensionaler Kalman-Filter
Klasse WI06b MLAN2 zweite-klausur 13. Juni 2007
Klasse WI6b MLAN zweite-klausur 3. Juni 7 Name: Aufgabe Gegeben sind die beiden harmonischen Schwingungen ( y = f (t) = +3 sin ωt + π ) (), ( 4 y = f (t) = 8 cos ωt + π ) (). 4 a) Bestimmen Sie mit Hilfe
Visuelle Information zur robusten Zuordnung von Landmarken für die Navigation mobiler Roboter
Visuelle Information zur robusten Zuordnung von Landmaren für die Navigation mobiler Roboter Forum Bildverarbeitung 2010 Thomas Emter Thomas Ulrich Loalisierung Herausforderungen Relative Sensoren (Dead
Simultaneous Localisation And Mapping SLAM
Simultaneous Localisation And Mapping SLAM https://www.youtube.com/watch?v=8w2pqtbaybe https://www.youtube.com/watch?v=lpg0hzokito Sebastian Thrun, Gewinner der DARPA Grand Challenge 2005 SLAM Problemdefinition
Algorithmen für Sensornetze
Algorithmen für Sensornetze Markus Völker 02. Februar 2010 Lokalisierung in Gebäuden Lokalisierung Ausgangssituation? Lokalisierung Ziel! Lokalisierung Signalabfall in Gebäuden Signalabfall mit ca. 1/d
Grundlagen der Objektmodellierung
Grundlagen der Objektmodellierung Daniel Göhring 30.10.2006 Gliederung Grundlagen der Wahrscheinlichkeitsrechnung Begriffe zur Umweltmodellierung Bayesfilter Zusammenfassung Grundlagen der Wahrscheinlichkeitsrechnung
Anordnungstechniken für konvektionsdominante Probleme im Ê 3. Dimensionsunabhängige Verfahren. Algorithmen für planare Graphen. Numerische Beispiele
Anordnungstechniken für konvektionsdominante Probleme im Ê 3 Inhalt: Einführung Dimensionsunabhängige Verfahren Algorithmen für planare Graphen Anordnungen im Ê 3 Numerische Beispiele 2 Einführung betrachtet
Aufgabe 4.1 Robotermodell (1)
Aufgabe 4.1 Robotermodell (1)! Erstellen Sie ein Simulationsmodell für einen mobilen Roboter (z.b. Pioneer 3DX), der sich über Geschwindigkeit v und Rotationsgeschwindigkeit ω steuern lässt. v ω Pioneer
Stochastische Selbstlokalisation I
Stochastische Selbstlokalisation I Thomas Röfer Unsicherheit Probabilistischer Ansatz Modelle für Bewegung und Wahrnehmung Gitterkarten Monte Carlo Methode Rückblick Architektur der Rollstühle Verteilt
Algorithmische Methoden zur Netzwerkanalyse
Algorithmische Methoden zur Netzwerkanalyse Prof. Dr. Henning Meyerhenke Institut für Theoretische Informatik 1 KIT Henning Universität desmeyerhenke, Landes Baden-Württemberg Institutund für Theoretische
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
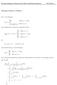Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Algorithmen zur Visualisierung von Graphen
Algorithmen zur Visualisierung von Graphen Kombinatorische Optimierung mittels Flussmethoden II Vorlesung im Wintersemester 2011/2012 10.11.2011 Orthogonale Zeichnungen II letztes Mal: Satz G Maxgrad-4-Graph
1 Ableitungen. Definition: Eine Kurve ist eine Abbildung γ : I R R n, γ besteht also aus seinen Komponentenfunktionen. a 1 + tx 1. eine Kurve.
1 Ableitungen Definition: Eine Kurve ist eine Abbildung γ : I R R n, γ besteht also aus seinen Komponentenfunktionen γ 1 (t) γ(t) = γ n (t) Bild(γ) = {γ(t) t I} heißt auch die Spur der Kurve Beispiel:1)
Der diskrete Kalman Filter
Der diskrete Kalman Filter Fachbereich: Informatik Betreuer: Marc Drassler Patrick Winkler 1168954 6. Dezember 2004 Technische Universität Darmstadt Simulation und Systemoptimierung Darmstadt Dribbling
GNSS/IMU Integration für die präzise Bestimmung einer Flugtrajektorie
GNSS/IMU Integration für die präzise Bestimmung einer Flugtrajektorie Fabian Hinterberger Institut für Geodäsie und Geophysik, Tu Wien 18. Nov. 2011 1 Motivation Motivation Gegenüberstellung Eigenschaften
1.8 Shift-And-Algorithmus
.8 Shift-And-Algorithmus nutzt durch Bitoperationen mögliche Parallelisierung Theoretischer Hintergrund: Nichtdeterministischer endlicher Automat Laufzeit: Θ(n), falls die Länge des Suchwortes nicht größer
Stabilitätsfragen bei autonomen Systemen
1 Stabilitätsfragen bei autonomen Systemen M. Schuster 09.08.2006 Inhaltsverzeichnis 1 Allgemeines über autonome Systeme 1 1.1 Oft übliche Bezeichnungen mit Übersetzung.......................... 1 2 Stabilität
Nichtlineare Ausgleichsrechnung
10. Großübung Nichtlineare Ausgleichsrechnung Allgemeines Problem: Wir betrachten ein nichtlineares System F : R n R m mit (m > n, d.h. das System ist überbestimmt und F i (x g(t i ; x g i! 0 i 1,.., m.
09. Lineare Abbildungen und Koordinatentransformationen
09. Lineare Abbildungen und Koordinatentransformationen Definition. Seien V und W Vektorräume. Unter einer linearen Abbildung versteht man eine Abbildung F : V W, v F v w mit folgender Eigenschaft: F λ
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 7 vom Abgabe:
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 03 Blatt 7 vom 0.06.3 Abgabe: 7.06.3 Aufgabe 9 3 Punkte Keplers 3. Gesetz Das 3. Keplersche Gesetz für die Planetenbewegung besagt, dass das
47 Singulärwertzerlegung
47 Singulärwertzerlegung 47.1 Motivation Wir haben gesehen, dass symmetrische Matrizen vollständig mithilfe ihrer Eigenwerte und Eigenvektoren beschrieben werden können. Diese Darstellung kann unmittelbar
Odometrie und lokale Karten
Odometrie und lokale Karten Thomas Röfer Metrische Positionen Odometrie Navigation mit Odometrie Lokale Karten Rückblick Verhaltensbasierte Robotik II Subsumption Architecture Spatial Semantic Hierarchy
Teach-In für die 3D-Scan Akquise mit einem Roboter. Teach-In für die 3D-Scanakquise mit einem mobilen Roboter
Teach-In für die 3D-Scan Akquise mit einem Roboter DoritStruckmeier, Borrmann Dorit Oldenburger 2017 Oliver Borrmann,3D-Tage Andreas Nüchter 1 Zielsetzung der Arbeit Ein mobiler Roboter fährt einen angelernten
Modellierung von Unsicherheit in Systemen
Modellierung von Unsicherheit in Systemen Motivation Systeme Zeitdiskrete, lineare und nicht-lineare Systeme, Beispiele Wahrscheinlichkeiten Zufallsvariablen, Wahrscheinlichkeitsdichten, mehrdimensionale
KLAUSUR. Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.:
KLAUSUR Lineare Algebra (E-Techniker/Mechatroniker/W-Ingenieure/Informatiker).3. (W. Koepf) Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Für jede Aufgabe gibt es Punkte. Zum Bestehen der Klausur
Was ist Robotik? Robotik heute:
Grundlagen Was ist Robotik? Das Wort Robot / Roboter entstand 92 in einer Geschichte von Karel Ċapek und geht auf das tschechische Wort robota (rbeit, Fronarbeit) zurück. Dessen Ursprung ist das altkirchenslawische
Kalmanfilter und Nichtparametrische Filter. Bayesfilter
Kalmanfilter und Nichtparametrische Filter Daniel Göhring 06.11.2006 Bayesfilter Zustand zur Zeit t ist Zufallvariable x t Wahrscheinlichkeitsfunktion Bel (Belief) über x t : Bel(x t ) repräsentiert die
Quadrocopters and it s Applications: Overview of State of the Art Techniques
: Overview of State of the Art Techniques Visual Tracking for Robotic Applications Sebastian Brunner Lehrstuhl für Echtzeitsysteme und Robotik Technische Universität München Email: brunnese@in.tum.de Date:
Ausgleichungsrechnung - nach der Methode der kleinsten Quadrate -
Computer Vision Ausgleichungsrechnung - nach der Methode der kleinsten Quadrate -.6.5 Problem Beispiel: Bestimmung der Parameter einer Gerade bei gegebenen x und fehlerhaften y y = ax+ b Beschreibung der
DSGE-Modelle. Linearisierung und Lösung. Institut für Ökonometrie und Wirtschaftsstatistik Münster
DSGE-Modelle Linearisierung und Lösung Dr. Andrea Beccarini Willi Mutschler, M.Sc. Institut für Ökonometrie und Wirtschaftsstatistik Münster willi.mutschler@uni-muenster.de Sommersemester 2012 Willi Mutschler
Radgetriebene Systeme
Radgetriebene Systeme Mobilität, Räder Räder benötigen weniger Energie und erlauben eine schnellere Fortbewegung (auf entsprechendem Terrain) Benötigen Kinematische Gleichungen, d.h. Beschreibungen wie
Übungen zur Ingenieur-Mathematik III WS 2011/12 Blatt Aufgabe 25: Berechnen Sie den kritischen Punkt der Funktion
Übungen zur Ingenieur-Mathematik III WS 11/1 Blatt 8 3.11.11 Aufgabe 5: Berechnen Sie den kritischen Punkt der Funktion fx, y 3x 5xy y + 3 und entscheiden Sie, ob ein Maximum, Minimum oder Sattelpunkt
Lösungen zu den Hausaufgaben zur Analysis II
Christian Fenske Lösungen zu den Hausaufgaben zur Analysis II Blatt 6 1. Seien 0 < b < a und (a) M = {(x, y, z) R 3 x 2 + y 4 + z 4 = 1}. (b) M = {(x, y, z) R 3 x 3 + y 3 + z 3 = 3}. (c) M = {((a+b sin
Statistics, Data Analysis, and Simulation SS 2017
Statistics, Data Analysis, and Simulation SS 2017 08.128.730 Statistik, Datenanalyse und Simulation Dr. Michael O. Distler Mainz, May 29, 2017 Dr. Michael O. Distler
3. Übungsblatt Aufgaben mit Lösungen
. Übungsblatt Aufgaben mit Lösungen Aufgabe : Gegeben sind zwei Teilmengen von R : E := {x R : x x = }, und F ist eine Ebene durch die Punkte A = ( ), B = ( ) und C = ( ). (a) Stellen Sie diese Mengen
Aufgabe 1. Die Determinante ist eine lineare Abbildung von C n n nach C? Nein (außer für n = 1). Es gilt det(λa) = (λ) n det(a).
Aufgabe Die Determinante ist eine lineare Abbildung von C n n nach C? Nein (außer für n = Es gilt det(λa = (λ n det(a det I n = n? Nein (außer für n = Es gilt deti n = det(ab = det A det B? Ja det(a =
Lösungsskizzen zu den Klausuraufgaben zum Kurs 1142 Algorithmische Mathematik. a 0 = 0 =
Lösungsskizzen zu den Klausuraufgaben zum Kurs 4 Algorithmische Mathematik 4KSL3 6 Punkte Aufgabe. Die Folge (a n ) n N natürlicher Zahlen a n sei rekursiv definiert durch a 0 = 0, a n = a n + n falls
Blatt 1. Kinematik- Lösungsvorschlag
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Lineare Klassifikationsmethoden
Verena Krieg Fakultät für Mathematik und Wirtschaftswissenschaften 08. Mai 2007 Inhaltsverzeichnis 1. Einführung 2. Lineare Regression 3. Lineare Diskriminanzanalyse 4. Logistische Regression 4.1 Berechnung
12 Lineare Differentialgleichungen mit periodischen Koeffizienten
56 Gewöhnliche Differentialgleichungen / Sommersemester 28 12 Lineare Differentialgleichungen mit eriodischen Koeffizienten 12.1 Homogene lineare Systeme mit eriodischen Koeffizienten haben für > die Form
Autonom-Explorierender Hexapod-Roboter
Fachbereich 4: Informatik Autonom-Explorierender Hexapod-Roboter Bachelorarbeit zur Erlangung des Grades Bachelor of Science im Studiengang Computervisualistik vorgelegt von Christian Schlöffel Betreuer:
Graphbasiertes SLAM mit integrierter Kalibrierung für mobile Roboter
Graphbasiertes SLAM mit integrierter Kalibrierung für mobile Roboter Diplomarbeit von Leonie Sautter Fakultät für Informatik Institut für Anthropomatik und FZI Forschungszentrum Informatik Erstgutachter:
Einführung in die Robotik
Einführung in die Robotik Vorlesung 7 13 Januar 2009 Dr. Mohamed Oubbati Institut für Neuroinformatik WS 2008/2009 Wiederholung vom letzten Mal! Signalverarbeitungskette Bewegungsregelung A/D Wandler D/A
Institut für Geometrie und Praktische Mathematik
RWTH Aachen Verständnisfragen-Teil Institut für Geometrie und Praktische Mathematik 4 Punkte Es gibt zu jeder der Aufgaben vier Teilaufgaben. Diese sind mit bzw. zu kennzeichnen hinschreiben. Es müssen
Gaußsche Ausgleichsrechnung
Kapitel 6 Gaußsche Ausgleichsrechnung 6. Gaußsche Methode der kleinsten Fehlerquadrate Die Gaußsche Methode der kleinsten Fehlerquadrate wurde 89 von C.F. Gauß in dem Aufsatz Theorie der Bewegung der Himmelkörper
Fortgeschrittene Netzwerk- und Graph-Algorithmen
Fortgeschrittene Netzwerk- und Graph-Algorithmen Prof. Dr. Hanjo Täubig Lehrstuhl für Effiziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester
Theoretische Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
1 Analytische Geometrie und Grundlagen
$Id: vektor.tex,v 1.44 2018/05/17 14:11:13 hk Exp $ 1 Analytische Geometrie und Grundlagen 1.6 Bewegungen und Kongruenzbegriffe Wir untersuchen gerade die Spiegelung an einer Hyperebene h R d. Ist ein
Brownsche Bewegung. Satz von Donsker. Bernd Barth Universität Ulm
Brownsche Bewegung Satz von Donsker Bernd Barth Universität Ulm 31.05.2010 Page 2 Brownsche Bewegung 31.05.2010 Inhalt Einführung Straffheit Konvergenz Konstruktion einer zufälligen Funktion Brownsche
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen
Kurztest zur Numerik I WiR AG, Dep. Mathematik, NT-Fakultät, Universität Siegen Wintersemester 2012/201 Zwischentest Teil 1: 1. Was bedeuten die Bezeichnungen O(h) und o(h)? (Definition) (siehe Skript!)
Simultane Mehrgleichungssysteme: Parameterschätzung
Simultane Mehrgleichungssysteme: Parameterschätzung Stichwörter: Eigenschaften des OLS-Schätzers Hilfsvariablenschätzer 2SLS limited information Methoden 3SLS FIML full information Methoden o1-21.tex/0
Lineare Gleichungssysteme
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 5. Dezember 2007 Definition : Tomographie (Fortsetzung) : Tomographie Definition: Ein lineares Gleichungssystem (LGS) ist ein System von n
2.3.4 Drehungen in drei Dimensionen
2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
Gaußsche Felder und Simulation
3 2 data_2d_1.dat data_2d_2.dat data_2d_64.dat data_2d_128.dat 1-1 -2-3 1 2 3 4 5 6 7 Gaußsche Felder und Simulation Benedikt Jahn, Aaron Spettl 4. November 28 Institut für Stochastik, Seminar Zufällige
Identifizierbarkeit von Modellen
Identifizierbarkeit von Modellen Stichwörter: Simultanes Mehrgleichungsmodell Struktur- und reduzierte Form Vollständigkeit Identifizierbarkeit Abzählbedingung Rangbedingung o1-19.tex/0 Interdependente
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 2016
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 1 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Übungsblatt 3 Maschinelles Lernen und Klassifikation Abgabe online
Beispiel: Positionsschätzung
Das Kalman Filter Beispiel: Positionsschätzung Beispiel: Positionsschätzung. Messung: mit Varianz Daraus abgeleitete Positionsschätzung: mit Varianz ˆX = = f f ( y ) y 3 Beispiel: Positionsschätzung. Messung:
6.3.1 Allgemeiner Bayes-Filter
6.3 Baes Fler 6.3. Allgemener Baes-Fler Sa von Baes ' ' ' η Sa über de oale Wahrschenlchke Besel oen oen oen Beobachung lecher u ermeln Besel oen.6 oen. 3 oen.5 oen. 5 oen oen oen oen oen oen oen.6.5 oen.6.5.3.5
1.3 Knuth-Morris-Pratt-Algorithmus
1.3 Knuth-Morris-Pratt-Algorithmus Präprozessing bestimmt längste Ränder der Präfixe von P Die Kenntnis der Ränder erspart Vergleiche bei periodischen Suchwörtern Laufzeit: Θ(m) für das Präprozessing,
Numerische Mathematik
Numerische Mathematik SS 999 Augabe 6 Punkte Das Integral I ln d soll numerisch bis au eine Genauigkeit von mindestens - approimiert werden. a Wie groß muss die Anzahl N der Teilintervalle sein damit mit
TECHNISCHE UNIVERSITÄT MÜNCHEN
TECHNSCHE UNVERSTÄT MÜNCHEN Zentrum Mathematik PROF DRDR JÜRGEN RCHTER-GEBERT, VANESSA KRUMMECK, MCHAEL PRÄHOFER Höhere Mathematik für nformatiker Wintersemester 23/24 Aufgabenblatt 2 23 Januar 24 Präsenzaufgaben
Lineare Algebra für D-ITET, D-MATL, RW. Beispiellösung für Serie 4. Aufgabe 4.1. Dr. V. Gradinaru D. Devaud A. Hiltebrand.
Dr V Gradinaru D Devaud A Hiltebrand Herbstsemester 4 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie 4 Aufgabe 4 Multiple Choice: Online abzugeben 4a) Wir betrachten
Innere-Punkt-Methoden
Innere-Punkt-Methoden Johannes Stemick 26.01.2010 Johannes Stemick () Innere-Punkt-Methoden 26.01.2010 1 / 28 Übersicht 1 Lineare Optimierung 2 Innere-Punkt-Methoden Path-following methods Potential reduction
Vorlesung Wissensentdeckung
Vorlesung Wissensentdeckung Klassifikation und Regression: nächste Nachbarn Katharina Morik, Uwe Ligges 14.05.2013 1 von 24 Gliederung Funktionsapproximation 1 Funktionsapproximation Likelihood 2 Kreuzvalidierung
Wintersemester 2004/ Februar 2005
Lehrstuhl für Praktische Informatik III Norman May B6, 29, Raum C0.05 68131 Mannheim Telefon: (0621) 181 2517 Email: norman@pi3.informatik.uni-mannheim.de Matthias Brantner B6, 29, Raum C0.05 68131 Mannheim
Charakteristische Funktionen
Kapitel 9 Charakteristische Funktionen Jeder Wahrscheinlichkeitsverteilung auf (, B 1 ) (allgemeiner: (R n, B n )) ist eine komplexwertige Funktion, ihre charakteristische Funktion, zugeordnet, durch die
Biologisch motivierter SLAM Algorithmus
HAW Hamburg 01. Dezember 2011 Gliederung 1 Einführung 2 RatSLAM 3 Aussicht für Master 2 / 23 Einführung Was ist SLAM SLAM bedeutet: Simultaneous Localization and Mapping Erstellung einer Karte durch mobilen
Drehung. Die orthogonale n n-matrix 1 0. c s. Zeile j. s c
Drehung Die orthogonale n n-matrix Q i,j... Zeile i c s... Zeile j s c... mit c = cos ϕ und s = sin ϕ beschreibt eine Drehung um den Winkel ϕ in der x i x j -Ebene des R n. Drehung - Drehung Die orthogonale
Brückenkurs Mathematik. Mittwoch Freitag
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Adaptive Systeme. Prof. Dr.-Ing. Heinz-Georg Fehn Prof. Dr. rer. nat. Nikolaus Wulff
Adaptive Systeme Evolutionäre Algorithmen: Überlebenskampf und Evolutionäre Strategien Prof. Dr.-Ing. Heinz-Georg Fehn Prof. Dr. rer. nat. Nikolaus Wulff Überblick Einleitung Adaptive Filter Künstliche
(u, v) z(u, v) u Φ(u, v) (v = const.) Parameterlinie v = const. v Φ(u, v) (u = const.) Parameterlinie u = const.
13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
Wir betrachten hier den Polarisationszustand einer Normalmode
Kapitel 5 Die Polarisation elektromagnetischer Wellen 5.1 Einführung Der zeitliche Verlauf des reellen elektrischen Feldvektors E r r,t) bestimmt den Polarisationszustand des Feldes. Wir betrachten hier
Numerik III trifft inverse Probleme
Numerik III trifft inverse Probleme Michael Hönig Heinrich-Heine-Universität Düsseldorf Bad Neuenahr-Ahrweiler, Juli 2009 Inverse Probleme Schließen von einer beobachteten Wirkung auf deren Ursache Beispiel:
Basen von Schnitt und Summe berechnen
Basen von Schnitt und Summe berechnen 1 / 8 Voraussetzung Es seien U 1, U 2 Untervektorräume von K n. Wir wollen Basen des Schnittes U 1 U 2 und der Summe bestimmen. U 1 + U 2 2 / 8 Bezeichnung Der Einfachheit
Die Klasse NP und die polynomielle Reduktion. Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen
Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 26 Optimierungsprobleme und ihre Entscheidungsvariante Beim Rucksackproblem
Orthogonalreihendarstellung eines zentrierten Gauß-Prozesses
Orthogonalreihendarstellung eines zentrierten Gauß-Prozesses Thomas Steinle Seminar Zufällige Felder Universität Ulm 18. November, 2008 Einleitung Inhalt Einleitung Wiederholung und Themenvorstellung Wichtiges
Kapitel 9: Lineare Programmierung Gliederung
Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Algorithmische Methoden zur Netzwerkanalyse Vorlesung 13, Henning Meyerhenke
Algorithmische Methoden zur Netzwerkanalyse Vorlesung 13, 01.02.2012 Henning Meyerhenke 1 KIT Henning Universität desmeyerhenke: Landes Baden-Württemberg und nationales Algorithmische Forschungszentrum
KAPITEL 5. Nichtlineare Gleichungssysteme
KAPITEL 5. Nichtlineare Gleichungssysteme Beispiel 5.1. Gravitationskraft zwischen zwei Punktmassen m 1 und m 2 mit gegenseitigem Abstand r: F = G m 1m 2 r 2, wobei G = 6.67 10 11 Nm 2 /kg. Gravitationsfeld
Die Klasse NP und die polynomielle Reduktion
Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Dezember 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
10. Übung zur Linearen Algebra I -
. Übung zur Linearen Algebra I - en Kommentare an Hannes.Klarner@FU-Berlin.de FU Berlin. WS 29-. Aufgabe 37 i Für welche α R besitzt das lineare Gleichungssystem 4 αx + αx 2 = 4x + α + 2x 2 = α genau eine,
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler
Kommentierte Musterlösung zur Klausur HM II für Naturwissenschaftler Sommersemester 7 (7.8.7). Gegeben ist die Matrix A 3 3 3 (a) Bestimmen Sie sämtliche Eigenwerte sowie die zugehörigen Eigenvektoren.
Kapitel 4: Nichtlineare Nullstellenprobleme
Vorlesung Höhere Mathematik: Numerik (für Ingenieure) Kapitel 4: Nichtlineare Nullstellenprobleme Jun.-Prof. Dr. Stephan Trenn AG Technomathematik, TU Kaiserslautern Sommersemester 2015 HM: Numerik (SS
Das Prinzip der Suchmaschine Google TM
/9 Das Prinzip der Suchmaschine Google TM Numerische Mathematik WS 20/2 Basieren auf dem Paper The $25,000,000,000 Eigenvector: The Linear Algebra behind Google von Kurt Bryan und Tanya Leise (SIAM Review,
Computer Vision: Kalman Filter
Computer Vision: Kalman Filter D. Schlesinger TUD/INF/KI/IS D. Schlesinger () Computer Vision: Kalman Filter 1 / 8 Bayesscher Filter Ein Objekt kann sich in einem Zustand x X befinden. Zum Zeitpunkt i
Lösungen zu Übungsblatt 9 Höhere Mathematik2/Stochastik 2 Master KI/PI
Lösungen zu Übungsblatt 9 Höhere Mathematik/Stochastik Anpassung von Verteilungen Zu Aufgabe ) a) Zeichnen des Histogranmmes: Um das Histogramm zu zeichnen, benötigen wir die Höhe der Balken. Die Höhe
Vorlesung Maschinelles Lernen
Vorlesung Maschinelles Lernen Strukturelle Modelle Conditional Random Fields Katharina Morik LS 8 Informatik Technische Universität Dortmund 17.12. 2013 1 von 27 Gliederung 1 Einführung 2 HMM 3 CRF Strukturen
Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern
Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern Vorlesung Robotik SS 016 Kalmanfiter () Kalman-Filter: optimaler rekursiver Datenverarbeitungsalgorithmus optimal hängt vom gewählten
Lösung Semesterendprüfung (Nachprüfung)
MLAE Mathematik: Lineare Algebra für Ingenieure Frühlingssemester 6 Dr. Christoph Kirsch ZHAW Winterthur Lösung Semesterendprüfung (Nachprüfung Aufgabe : Aufgabe : a Gemäss Def. der Vorlesung müssen wir
Algebraische und arithmetische Algorithmen
Kapitel 1 Algebraische und arithmetische Algorithmen 1.1 Das algebraische Berechnungsmodell Struktur: Körper (oder Ring) mit den Operationen +,,, (/) Eingabe: endliche Folge von Zahlen Ausgabe: endliche
Seite 1. sin 2 x dx. b) Berechnen Sie das Integral. e (t s)2 ds. (Nur Leibniz-Formel) c) Differenzieren Sie die Funktion f(t) = t. d dx ln(x + x3 ) dx
Seite Aufgabe : a Berechnen Sie das Integral b Berechnen Sie das Integral +x x+x dx. π sin x dx. c Differenzieren Sie die Funktion ft = t e t s ds. Nur Leibniz-Formel a + x x + x dx = d dx lnx + x dx =