Zeichne einen Würfel unter Parallelprojektion
|
|
|
- Angelika Esser
- vor 7 Jahren
- Abrufe
Transkript
1 Ulrich Schoenwaelder GEONExT-Fortbildung 15. April 2005 Lst. D für Mathematik Zeichne einen Würfel unter Parallelprojektion Klassenstufe: Methodische Ziele: Raumvorstellung stärken. Genaues Beobachten, Beschreiben und Argumentieren bei der Modellierung: Raumpunkte, Leinwandpunkte und Geonextpunkte unterscheiden, aber auch durch die Parallelprojektion in Beziehung setzen. Stoffliche Ziele: räumliche und ebene Affine Geometrie, Studium der folgenden Hilfsabbildungen. Parallelprojektion als Effekt einer räumlichen Drehung einer Ebene um eine ihrer Geraden als Achse. Achsenaffinitäten einer Ebene, die durch räumliche Parallelprojektionen entstanden sind. Ebene Bilder räumlicher Objekte begegnen uns tagtäglich, und wir lernen, solche Bilder zu verstehen, sie eben räumlich zu sehen. Aber welche Prinzipien stecken hinter ihrer zeichnerischen Konstruktion? Am häufigsten wird die Zentralprojektion verwandt, bei der (fast) alle Punkte des Raumes (insbesondere die markanten Punkte des Objektes) von einem festen Punkt aus, dem Zentrum, längs Geraden auf eine feste Ebene projiziert werden. Vgl. hierzu z. B. [3]. Als Grenzfall, bei dem der feste Punkt unendlich weit weg liegt und die Geraden zu Parallelen in einer festen Richtung werden, hat man eine Parallelprojektion. In diesem Text soll die Theorie der Parallelprojektionen entwickelt und mit der dynamischen Geometriesoftware GEONExT [1] an Beispielen erlebt werden. Als Anwendungbeispiele haben wir zwei Situationen: 1. Ich sehe aus großer Entfernung ein Objekt vor einem vertikalen Hintergrund, den ich mir als Leinwand vorstelle, auf die parallel projiziert wird. 2. Eine entfernte Lichtquelle (Sonne) sendet parallele Strahlen auf eine ebene Wand und produziert dort den Schatten eines davor befindlichen Objektes. Der Unterschied der beiden Situationen besteht darin, dass ich beim Sehen mich doch in der Mitte (weit) vor dem Objekt befinde und das Objekt somit senkrecht auf den Hintergrund projiziert wird, während eine Lichtquelle in der Regel schräg von der Seite leuchten wird. 1
2 I. Das Kinderhaus Grundschulkinder zeichnen ein Haus gerne so, wie es das linke Bild zeigt, von älteren Personen könnte das rechte Bild stammen. Beide Bilder stellen den Betrachter nicht ganz zufrieden. Obwohl sie viele wichtige Merkmale des Hauses enthalten und obwohl man schon versteht, was gemeint ist, kann man folgende Kritik äußern: Links sieht man zwei Seiten des Hauses gleichzeitig von vorne, als stünde man jeweils zentral davor. Abgesehen davon, dass man beim Sehen in der Regel nicht sehr weit weg vom Objekt ist und deshalb eher eine Zentralprojektion angebracht wäre, handelt es sich auch beim linken Haus um eine legitime Parallelprojektion: man stelle sich statt der Hausgrundfläche eine Tischplatte vor und die Projektionsgeraden so, dass sie parallel zur Tischplatte verlaufen. Beim rechten Haus verlaufen die Projektionsgeraden nicht parallel zur Grundfläche, aber auch nicht senkrecht zur Traufe (sonst könnte man die Seitenwand nicht sehen), also offenbar etwas von rechts oben nach links unten. Der Betrachter befindet sich also rechts vom Haus in einem Baum (sog. Kavalierperspektive, Schreckbild [2]). Das ist nicht die übliche Sicht eines Hauses, wo man eher zentral davor steht. Wie ist also ein Haus richtig zu zeichnen? Dazu mehr in den Abschnitten II bis IV. Zuvor noch ein technischer Hinweis. K Wie werden obige Hausbilder mit GEONExT erstellt? Es reicht zu wissen, wie man ein Rechteck bekommt. Dazu (Start) Strecke [A, B] als eine Rechteckseite. (1. Konstruktion) Senkrechte (Perpendicular Line) in beiden Endpunkten. Gleiter C auf der Senkrechten in B und Parallele durch ihn zur Grundseite [A, B]. Schnittpunkt D als vierten Rechteckpunkt. 2
3 (2. Konstruktion) Senkrechte in einem Endpunkt, etwa B. Gleiter C auf dieser Senkrechten. Pfeil von B nach C darüber legen; Senkrechte verstecken. Parallelpfeil von A aus setzen. Spitzen der Pfeile durch Strecke verbinden. (Verschönerung) Man möchte aber Strecken statt Geraden oder Pfeile haben. Also legt man Strecken [B, C], [C, D], [D, A] darüber und versteckt anschließend die Geraden bzw. Pfeile mit den Befehlen Objects - Object Properties - im neuen Fenster Object Properties den Namen der Geraden anklicken - Hide Object markieren. Nun möchte man noch die Kreuzchen für Punkte und die Namen der Punkte entfernen. Das geht mit den Befehlen Objects - Special Properties - Hide (das Hide- Symbol erscheint am linken Rand) - dieses Hide-Symbol verwenden. II. Militärprojektion eines Hauses Wir stellen uns vor, ein Bauklotz-Haus steht auf unserer Zeichenfläche, die vor uns auf der Tischplatte liegt. Wir schauen aus einer vergleichsweise großen Entfernung darauf. Diese Situation modellieren wir durch eine Parallelprojektion von oben schräg auf die Tischplatte/Zeichenfläche. F Wie wird der Hausklotz auf der Zeichenfläche dargestellt? Wie die Grundfläche? Wie die vertikalen Kanten? A Die Grundfläche des Hausklotzes wird in realer Größe und Form dargestellt, weil sie ja praktisch in der Zeichenfläche liegt. Vertikale Kanten werden auch vertikal dargestellt, da wir zentral von vorne schauen. - Die Sache wäre anders, wenn die Parallelprojektion nicht von vorne, sondern etwas von rechts auf die Zeichenfläche verliefe wie bei einer entfernten Lichtquelle, bezüglich der wir den Schatten des Hausklotzes auf der Zeichenfläche ermitteln wollten. Die zu zeichnende Höhe des Hauses hängt davon ab, von wie weit oben ich auf den Klotz schaue. Sie kann also in der Zeichnung vorgegeben werden. K Konstruiere das Schaubild oder/und allgemeiner das Schattenbild des Hausklotzes mit GEO- NExT. Ziehe am Bildpunkt einer Dachecke, um zu verfolgen, wie sich das Schattenbild bei verschiedenen Einfallsrichtungen der Lichtstrahlen verändert. Eine solche Projektion, bei der die Grundflächen formtreu und maßstabsgerecht und vertikale Kanten auch vertikal dargestellt werden, nennt man Militärperspektive. Sie findet oft bei Stadtplänen mit eingezeichneten Gebäuden Anwendung. 3
4 Bei der Konstruktion der vorstehenden Zeichnung wurden - vielleicht umbewusst - Geraden des Raumes durch Geraden in der Zeichnung sowie parallele Geraden des Raumes durch Parallelen in der Zeichnung dargestellt. Ich stelle in Abschnitt V abstrakte Eigenschaften von Parallelprojektionen zusammen, die bei der Bildkonstruktion Verwendung finden, und begründe sie dort. III. Normalprojektion eines Quadrates Wir wollen im folgenden Abschnitt IV einen Würfel, der irgenwie vor einer vertikalen Leinwand schwebt, per Parallelprojektion senkrecht zur Leinwand auf die Leinwand projizieren, genauer ein entsprechendes Bild mit GEONE X T konstruieren. Eine Parallelprojektion senkrecht auf die Leinwand nennt man Normalprojektion (Orthogonalprojektion, Riss). Ziel dabei ist es, alle rechten Winkel und alle gleich langen Strecken des Raumes relativ zueinander richtig darzustellen. Dazu beginnen wir mit der Darstellung eines schräg im Raum liegenden Quadrates Q. Das Quadrat sei Q = [ D A C B ] und habe die Seitenlänge s. Wenn die Ebene ABCD parallel zur vertikalen Leinwand liegt, erscheint auch das Bild des Quadrates unter der Normalprojektion auf die Leinwand als ein Quadrat mit der Seitenlänge s. Nun nehmen wir aber an, dass die Ebene ABCD die Leinwandebene in einer Geraden trifft. Diese könnte weit weg von unserem Quadrat liegen. Um das zu vermeiden, betrachten wir eine zur Leinwand parallele Hilfsebene L 1, die durch eine Ecke des Quadrates Q geht, etwa durch C. Die Ebene des Quadrates treffe die Hilfsebene L 1 in der Geraden f. Auf ihr liegt C. Es genügt, die Normalprojektion des Quadrates auf L 1 zu konstruieren, sie liefert ja das deckungsgleiche Bild unter der Normalprojektion auf die Leinwand. Wir studieren also die durch die Normalprojektion gegebene Abbildung α = (P P ): ABCD L 1 von Punkten P des Raumes, insbesondere der Ebene ABCD des Quadrates, auf die entsprechenden Punkte P der Hilfsebene L 1. Gesucht ist das Bildparallelogramm Q = [ D A C B ] des Quadrates Q. Wie in Abschnitt V dargestellt, ist α als Parallelprojektion parallelitätstreu, also ist das Bild von Q in der Tat ein Parallelogramm; aber welches? Wir können Quadrate gut zeichnen, wenn sie in der Hilfsebene L 1 liegen; es wird ja auf L 1 projiziert. Deshalb stellen wir eine Beziehung her zwischen unserem Quadrat Q und einem Quadrat Q 1 in der Hilfsebene L 1, indem wir uns die Ebene ABCD nach einer der beiden Seiten um die 4
5 Gerade f als Achse in die Ebene L 1 gedreht denken. Dabei bewegt sich ein Punkt P der Ebene ABCD auf einem Kreisbogen einer Kreisscheibe, die senkrecht zur Achse f zu denken ist und ihren Mittelpunkt auf der Achse hat, bis zu einem Punkt P 1 in der Hilfsebene L 1. Auf diese Weise wird jedem Punkt P der Ebene ABCD ein Punkt P 1 der Ebene L 1 zugeordnet. Diese Abbildung (P P 1 ) nenne ich δ: δ = (P P 1 ): ABCD L 1. Sie erhält alle Abstände und Winkelmaße in diesen Ebenen. Eine Analyse dieser Abbildung in Abschnitt VI ergibt, dass δ eine Parallelprojektion ist, nämlich in Richtung AA 1 BB 1 DD 1. C = C 1 bleibt unter δ fix. Die gedachten Strecken [A, A 1 ], [B, B 1 ] und [D, D 1 ] werden unter der Parallelprojektion α auf parallele Strecken [A, A 1 ] [B, B 1 ] [D, D 1 ] in L 1 abgebildet; A 1, B 1, C 1 bleiben als Punkte von L 1 fix. Diese Strecken liegen ganz in der Hilfsebene L 1 : die Zuordnung π = (P P 1 ): L 1 L 1 ist der Schlüssel zum α-bild unseres Quadrates Q. Wie wir nämlich in Abschnitt V zeigen, ist π eine Achsenaffinität (Definition in Abschnitt V) der Ebene L 1 zur Achse f und Richtung A A 1 B B 1 D D 1 ; sie ist durch ein einziges Punkt-Bildpunkt-Paar (X, X 1 ), das nicht auf f liegt, festgelegt, wie die folgende Konstruktion zeigen wird; vgl. dazu auch [5]. Welche Lage soll die Strecke [A, A 1 ] relativ zur Achse f haben? Im Raum bewegte sich A auf einem Kreisbogen in A 1, der sich in einer zur Achse f senkrechten Ebene befindet. Unter unserer Normalprojektion α geht diese Ebene in eine zur Achse f senkrechte Gerade über: in ihr liegt die Strecke [A, A 1 ]. Die Richtung der Achsenaffinität π von L 1 ist also orthogonal zu f. (Bei einer nichtnormalen Parallelprojektion wäre das nicht so, etwa dann, wenn wir das Schattenbild eines Würfels unter schräg einfallenden parallelen Lichtstrahlen zeichnen wollten.) Um das Bildparallelogramm Q zu konstruieren, geben wir uns also in der Hilfsebene L 1 eine Gerade f als Achse und ein Quadrat (!) Q 1 = [ D1 C 1 A 1 B 1 ] vor mit C 1 auf f; außerdem wird der Punkt A auf der Lotgeraden von A 1 auf f vorgegeben und zwar zwischen A 1 und f. Denn der Abstand des Bildes A von f ist eher kleiner als der wahre Abstand von A (und A 1 ) zu f. Die Gerade f und der Punkt A beschreiben in der Bildebene L 1 die räumliche Lage der Ebene ABCD. Aber nun kommen wir endlich zur Konstruktion von B und D, allgemein von P zu gegebenem Punkt P 1. K Vorbereitung Zeichne eine Gerade C 1 M = f und ein Quadrat Q 1 = [ D1 C 1 A 1 B 1 ] durch Vorgabe von D 1 in der Entfernung s von C 1. Wähle außerdem einen Punkt X 1, der nicht auf f liegt, etwa A 1. Konstruiere seinen Lotfußpunkt X auf f, die Strecke [X 1, X ] und einen Punkt X hierauf als Gleiter. Wir betrachten die durch (X, X 1 ) definierte Achsenaffinität π und wollen allgemein für gegebene Punkte P 1 die Punkte P konstruieren, speziell für B 1 und D 1. K1 Wähle einen Punkt P 1, für den X 1 P 1 nicht parallel zu f ist, etwa D 1. Es sei S = f X 1 P 1 der Schnittpunkt. Da P 1 auf X 1 S liegt, liegt P auf X S (Geradentreue der Achsenaffinität π). Außerdem hat π die Richtung X 1 X ; also liegt P auf der Parallelen zu [X 1, X ] durch 5
6 P 1. (Der vierte Parallelogrammpunkt B kann aus D, A, C in dieser Reihenfolge mit der GEONExT-Funktion Parallelogram Point leicht erhalten werden, ohne über die Abbildung π zu gehen.) K2 Wenn S nicht mehr auf dem Geonextblatt zu sehen ist, zeichnen wir parallele Geraden durch X 1 und P 1, die nicht in der Richtung von π verlaufen, mit Schnittpunkten X bzw. P mit f. Diese parallelen Geraden werden unter π auf parallele Geraden (Parallelitätstreue von π) abgebildet: die eine ist X X, die andere demnach die Parallele hierzu durch P. Wie vorher liegt P andererseits in Richtung X 1 X von P 1. K3 Wenn für den Punkt P 1 die Gerade X 1 P 1 parallel zu f verläuft, kann man zunächst das Bild eines Punktes R 1 wie unter K1 konstruieren und dann zur Konstruktion von P das Paar (R, R 1 ) benutzen statt (X, X 1 ). Auf diese Weise konstruieren wir das Bildparallelogramm Q = [ D A C B ]. Nun können wir an dem Punkt D 1 ziehen, der das Quadrat Q 1 festgelegt hat, damit es gut in der Mitte des Blattes zu liegen kommt. Interessanter ist es zu sehen, wie sich das Bildparallelogramm Q verändert, wenn wir an X = A ziehen. Im folgenden Abschnitt IV wird das Bild des Quadrates Q zum Bild eines Würfels ergänzt; die nötige Theorie dazu wird in den Abschnitten V und VI dargestellt. 6
7 IV. Ein taumelnder Würfel Wir kommen jetzt dazu, das Bild eines taumelnden Würfels, der also irgendwie vor einer Leinwand schwebt, zu konstruieren. Eine Seitenfläche des Würfels W sei das Quadrat Q = [ D A C B ], ihre Gegenseite sei [ H E G F ], wobei die Ecken A und E benachbart seien, entsprechend B und F, C und G, D und H. Das Bildparallelogramm Q von Q unter der Normalprojektion α auf eine zur Leinwand parallele Hilfsebene L 1 durch C = C 1 = C haben wir schon in Abschnitt III konstruiert. Es geht jetzt darum, die Lage des dazu parallel verschobenen Bildparallelogramms [ H E G F ] festzulegen, also die Richtung und Länge der Strecke [C, G ] in L 1. Im Urbild W ist ja [C, G] senkrecht auf ABCD und gleich lang wie [C, B]. F Für das α-bild G von G fragen wir also: 1. In welcher Richtung von C aus liegt G? 2. In welcher Entfernung von C aus liegt G? A Dazu entsprechend stellen wir die folgende Analyse an: 1. Im Würfel W steht die Kante [C, G] senkrecht auf der Grundfläche ABCD, also erst recht senkrecht auf ihrer Geraden f. Unter der Normalprojektion α wird die zu f in C senkrechte Ebene in die zu f in C = C senkrechte Gerade von L 1 abgebildet. Also liegt G auf dieser Geraden. Genau so liegen E, F und H auf den zu f senkrechten Geraden durch A, B bzw. D, die wir auch schon zur Konstruktion der α-bildpunkte aus A 1, B 1 und D 1 benutzt hatten. 2. Damit der Bildwürfel seine richtige Höhe bekommt, denken wir uns die Seitenfläche [ H D G C ] um eine neue Achse f 2 durch C = C in L 1 in die Hilfsebene L 1 gedreht, wo das Bildquadrat [ H2 G 2 D 2 C 2 ] mit richtiger Seitenlänge s erscheint. Als Achse f 2 wählen wir die zu B C in C = C senkrechte Gerade von L 1. Das α-bild des Kreisbogens von D nach D 2 liegt - analog früher bei Drehung um f - in der zu f 2 senkrechten Geraden durch D. M. a. W., der Punkt D 2 liegt auf der Geraden A D. Da seine Entfernung von C = C 2 bekannt ist (gleich s), können wir D 2 als einen der beiden Schnittpunkte mit dem Kreis um C = C 2 vom Radius s einzeichnen. Wir ergänzen [C 2, D 2 ] auf der gewünschten Seite zu einem Quadrat mit den weiteren Ecken G 2 und H 2. Dann liegt G auf der zu f 2 senkrechten Geraden durch G 2 (und H auf der zu f 2 senkrechten Geraden durch H 2 ). Durch A1 und A2 ist G als Schnittpunkt zweier Geraden festgelegt. K Wir konstruieren das Bild eines taumelnden Würfels unter der Normalprojektion α. Kopiere die GEONExT-Konstruktion des Bildparallelogramms Q = [ D A C B ] unter neuem Namen auf ein neues Blatt. Färbe die alte Achse f rot und die Kanten des Quadrats Q grün, damit sie sich besser von späteren blauen Konstruktionsgeraden abheben. Zeichne (gemäß A2) die Achse f 2 durch C senkrecht zu B C. Färbe sie ebenfalls rot. Zeichne D 2 auf der Parallelen zu B C (also orthogonal zu f 2 ) durch D in der richtigen Entfernung s von C. Die Hilfsgerade und der Hilfskreis können durch die Befehle Objects - Special Properties -Draft als graue Linien in den Hintergrund geschickt werden. 7
8 Ergänze die Quadratecke G 2. Zeichne die Lotgerade von G 2 auf f 2. Markiere ihren Schnittpunkt G mit der Senkrechten auf f in C (gemäß A1). Ergänze die anderen Würfeleckenbilder E, F, H durch Parallelogrammkonstruktionen. Färbe die Würfelkanten grün. Ziehe an A, um zu sehen, wie sich der ganze Würfel verändert. V. Wesentliche Eigenschaften von Parallelprojektionen (Theorie) D Definition Eine Parallelprojektion α im Raum ist gegeben durch eine Ebene E [auf die die Raumpunkte (oder auch nur die Punkte einer weiteren Ebene) abgebildet werden] und eine Gerade r [in deren Richtung projiziert wird]; sie darf nicht parallel zu E sein, damit für einen Raumpunkt P die Parallele zu r durch P einen Schnittpunkt P mit E hat: α(p ) = P. Um das α-bild von Raumkörpern beschreiben zu können, braucht man Kenntnis darüber, wie die gegenseitige Lage von Raumpunkten von α berücksichtigt wird. F Welche Eigenschaften hat α? 8
9 A Der Definition von Parallelprojektion und der Raumanschauung können wir entnehmen: (Richtung) Alle Geraden P P sind untereinander parallel (zu r). (Entartung) Punkte P und R, für die die Gerade P R parallel zu r ist, haben dasselbe α-bild P = R. Die Gerade P R wird durch diesen Punkt dargestellt. (Geradentreue) Nun interessieren uns Punkte einer Geraden g, die nicht parallel zu r ist. Betrachte einen Punkt P von g, der nicht auf E liegt, und die Parallele r zu r durch P. Die Geraden g und r definieren eine Hilfsebene G, die E in einer Geraden g trifft. Deshalb liegen die α-bilder der Punkte von g auf einer Geraden, nämlich g. (Parallelitätstreue) Parallele Geraden des Raumes haben parallele Bilder in E. Denn parallele Hilfsebenen haben parallele Schnittgeraden mit E. Insbesondere gehen Parallelogramme des Raumes in Parallelogramme von E über, wenn sie nicht entarten. Wir brauchen noch eine Eigenschaft der Hintereinanderausführung zweier Parallelprojektionen α 1 = (P 1 P 2 ): E 1 E 2 und α 2 = (P 2 P 3 ): E 2 E 3 zwischen Ebenen E 1, E 2 und E 3, die sich in einer Geraden f = E 1 E 2 = E 2 E 3 treffen. Es darf E 1 = E 3 sein. Die uns interessierende Zuordnung ist β = (P 1 P 3 ): E 1 E 3. Nach Voraussetzung sind alle Geraden P 1 P 2 untereinander parallel (zu r 1 = X 1 X 2 ) und alle Geraden P 2 P 3 untereinander parallel (zu r 2 = X 2 X 3 ). F Sind auch alle Geraden P 1 P 3 untereinander parallel (zu r 3 = X 1 X 3 )? A (Richtung) Die Gerade P 1 X 1 von E 1 treffe f im Punkt S. Da die Punkte von f bei α 1 fix bleiben, liegt P 2 auf X 3 S. Da α 1 und α 2 Parallelprojektionen sind, ist P 1 P 2 X 1 X 2 und P 2 P 3 X 2 X 3. Damit ist die Ebene P 1 P 2 P 3 parallel zur Ebene X 1 X 2 X 3. Diese beien Ebenen schneiden die von den Geraden SP 1 X 1 und SP 3 X 3 erzeugte Ebene F in parallelen Geraden P 1 P 3 X 1 X 3 = r 3. Die Abbildung β ist also eine Achsenaffiniät der Ebene F im Sinne der folgenden Definition. D Eine Achsenaffinität einer Ebene F ist eine Abbildung von F nach F, bei der (Achse) die Punkte einer festen Geraden f fix bleiben, (Geradentreue) die Punkte einer jeden Geraden auf die Punkte einer Geraden abgebildet werden und (Richtung) alle durch Punkt und Bildpunkt (nicht auf f) definierten Geraden zueinander parallel sind. Satz Man stellt durch Konstruktionen wie in Abschnitt III leicht fest, dass eine Achsenaffinität durch 9
10 ihre Achse, ihre Richtung und ein Punkt-Bildpunkt-Paar, das nicht auf der Achse liegt, festgelegt ist. Vgl. [5], Literaturhinweise zur Darstellenden Geometrie in [4]. VI. Die Hilfsabbildung δ (Theorie) Wir betrachten wie in Abschnitt III zwei Ebenen des Raumes, die sich in einer Geraden schneiden: die Leinwandebene L 1 und eine Ebene L 0 (in Abschnitt III die Ebene ABCD des Quadrates Q) mit der Schnittgeraden f. Wir denken uns die Ebene L 0 längs der Achse f in die Ebene L 1 verdreht: auf diese Weise entspricht jedem Punkt P von L 0 ein verdrehter Punkt P 1 von L 1. Es soll jetzt gezeigt werden, dass die Zuordnung eine Parallelprojektion in Richtung P P 1 ist. δ = (P P 1 ): L 0 L 1 F Vergleiche eine (feste) Gerade AA 1 (für einen Punkt A in L 0 ) mit einer beliebigen weiteren Geraden P P 1 (P in L 0 ) mit dem Ziel, ihre Parallelität zu zeigen. Es bezeichne A den Fußpunkt des Lotes von A auf f und analog P den Fußpunkt des Lotes von P auf f. A1 (1. Fall) Wir nehmen zunächst einen Punkt P, für den die Verbindungsgerade AP einen Schnittpunkt S mit f hat (in L 0 ), der nicht mit A zusammen fällt. P ist also von A verschieden. Bei dem gedachten Drehvorgang bleiben A, P und S als Punkte der Achse f fix. Es ist AA P P und A 1 A P 1 P. Die Gerade AP S geht in die Gerade A 1 P 1 S über. Ich fasse zusammen: Wir haben einen Punkt S, die drei Geraden AP S, A P S, A 1 P 1 S durch S und die beiden Dreiecke (im Raum) [A, A, A 1 ] und [P, P, P 1 ], wo zweimal entsprechende Seiten parallel sind. In solchen Situationen sind aus unserer Erfahrung mit Ebenen auch die dritten Seiten zueinander parallel: AA 1 P P 1. Denn parallele Ebenen schneiden eine weitere Ebene in parallelen Geraden: bei uns sind die durch parallele Geradenpaare (A A, A A 1 ) und (P P, P P 1 ) definierten Ebenen parallel; sie schneiden die durch die Geraden AP S und A 1 P 1 S definierte Ebene in den (somit) parallelen Geraden AA 1 und P P 1. (Man nennt dies den Großen Satz von Desargues [6, S. 22].) 10
11 A2 (2. Fall) Nun sei P auf AA. Dann ist P P 1 AA 1 nach der Umkehrung des 1. Strahlensatzes. A3 (3. Fall) Nun sei AP f. Dann ist auch A 1 P 1 f. Wir haben eine ähnliche Situation wie im 1. Fall, nur dass die drei Geraden AP, A P, A 1 P 1 nicht durch einen gemeinsamen Punkt gehen, sondern zueinander parallel sind. Auch hier kennt man die Parallelität der dritten Dreiecksseiten. (Man nennt dies den Kleinen Satz von Desargues.) Fazit. Die Abbildung δ von der ersten Ebene L 0 auf die zweite Ebene L 1 ist die Parallelprojektion in Richtung AA 1. Literatur [1] Peter Baptist et al. GEONExT. Programm, Einführung, Beispiele. [2] H. Bergold. Schrägbild Schreckbild. Didaktik der Mathematik, 17(Heft 3): , HB: Z5339. [3] Hans-Jürgen Elschenbroich. Zentralperspektive mit EUKLID. Mit einem zweidimensionalen Geometrieprogramm Raumvorstellung entwickeln. Praxis der Mathematik: PM Computerpraxis, 40(4): , MB: Z 101. Der Verfasser zeigt an verschiedenen Beispielen, wie man mit Hilfe eines 2-dimensionalen Geometrie-Programms (im Beispiel EUKLID) die Raumvorstellung entwickeln kann. [4] H. Klement. Ebene Affinitäten in der Darstellenden Geoemtrie. Praxis der Mathematik, 45(6): , HB: Z1757; MB: Z
12 [5] U. Schoenwaelder. Von Achsenspiegelungen zu Achsenaffinitäten. Manuskript zur Lehrerfortbildung am in Aachen, Ulrich.Schoenwaelder/Fachdidaktik/index.html. [6] E. M. Schröder. Vorlesungen über Geometrie, Band 2: Affine und projektive Geometrie. BI, Wissenschaftsverlag, ISBN HB: Bd1495-2; MB: 16319b. 12
Schrägbilder zeichnen
 Was sind Schrägbilder und welchen Zweck haben sie? Durch ein Schrägbild wird auf einer ebenen Fläche (z.b. Blatt Papier) ein Körper räumlich dargestellt (räumliche Perspektive des Körpers). Es gibt sehr
Was sind Schrägbilder und welchen Zweck haben sie? Durch ein Schrägbild wird auf einer ebenen Fläche (z.b. Blatt Papier) ein Körper räumlich dargestellt (räumliche Perspektive des Körpers). Es gibt sehr
Konstruktionen am Dreieck
 Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Winkelhalbierende Die Winkelhalbierende halbiert den jeweiligen Innenwinkel des Dreiecks. Sie agieren als Symmetrieachse. Dadurch ist jeder Punkt der Winkelhalbierenden gleich weit von den beiden Schenkeln
Achsen- und punktsymmetrische Figuren
 Achsensymmetrie Der Punkt P und sein Bildpunkt P sind symmetrisch bzgl. der Achse s, wenn ihre Verbindungsstrecke [PP ] senkrecht auf der Achse a steht und von dieser halbiert wird. Zueinander symmetrische......strecken
Achsensymmetrie Der Punkt P und sein Bildpunkt P sind symmetrisch bzgl. der Achse s, wenn ihre Verbindungsstrecke [PP ] senkrecht auf der Achse a steht und von dieser halbiert wird. Zueinander symmetrische......strecken
Klausurenkurs zum Staatsexamen (WS 2016/17): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Klausur zur Einführung in die Geometrie im SS 2002
 Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Anwendungen der Vektorrechnung in R 3 mit GeoGebra
 Anwendungen der Vektorrechnung in R 3 mit GeoGebra 1. Parallelogramm Die Punkte A = ( 2, 1,0), B = (3, 2,2), C = (5,4,3) sind Eckpunkte eines Parallelogramms. Gesucht ist der fehlende Eckpunkt D sowie
Anwendungen der Vektorrechnung in R 3 mit GeoGebra 1. Parallelogramm Die Punkte A = ( 2, 1,0), B = (3, 2,2), C = (5,4,3) sind Eckpunkte eines Parallelogramms. Gesucht ist der fehlende Eckpunkt D sowie
Lösungen zum Thema Geometrie. Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt.
 Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Analytische Geometrie
 Analytische Geometrie 1 Punkte und Vektoren im Raum G 1.1 Gegeben sind die Vektoren in nebenstehender Abbildung. Drücke die Vektoren AC durch a und b AB durch z und w BC durch c und d DB durch b und u
Analytische Geometrie 1 Punkte und Vektoren im Raum G 1.1 Gegeben sind die Vektoren in nebenstehender Abbildung. Drücke die Vektoren AC durch a und b AB durch z und w BC durch c und d DB durch b und u
Parallelprojektive Schattenbilder von Körpern mit Cabri 3D
 Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
2.5. Aufgaben zu Dreieckskonstruktionen
 2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Qualiaufgaben Konstruktionen
 Qualiaufgabe 2008 Aufgabengruppe I Trage in ein Koordinatensystem mit der Einheit 1 cm die Punkte A (-2/2) und C (1/3) ein. a) Zeichne das gleichseitige Dreieck AMC. b) Ein regelmäßiges Sechseck mit der
Qualiaufgabe 2008 Aufgabengruppe I Trage in ein Koordinatensystem mit der Einheit 1 cm die Punkte A (-2/2) und C (1/3) ein. a) Zeichne das gleichseitige Dreieck AMC. b) Ein regelmäßiges Sechseck mit der
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel
 Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
Konvexes Viereck Trapez Drachenviereck Parallelogramm Sehnenviereck Tangentenviereck Überraschung? Haus der Vierecke. Dr.
 Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 40 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck Überraschung? 2 / 40 Wir betrachten nur
Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 40 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck Überraschung? 2 / 40 Wir betrachten nur
Abitur 2016 Mathematik Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Gundlagen Klasse 5/6 Geometrie. nach oben. Inhaltsverzeichnis
 Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Anschauliche Parallelrisse und Hauptrisse
 Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
7.6. Prüfungsaufgaben zu Normalenformen
 7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Bild 1: Gegeben ist der in der Zentralperspektive zentrale Fluchtpunkt, der Distanzpunkt und der Grundriss des zu zeichnenden Vierecks.
 Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Geometrie-Dossier Kreis 2
 Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Geometrie-Dossier Kreis 2 Name: Inhalt: Konstruktion im Kreis (mit Tangenten, Sekanten, Passanten und Sehnen) Grundaufgaben Verwendung: Dieses Geometriedossier orientiert sich am Unterricht und liefert
Die Kapitel 1 und 2.1 haben wir im Jahr 2012 behandelt. Im Zirkel am haben wir mit Kapitel 2.2 begonnen.
 Das vorliegende Skript beschäftigt sich mit dem Thema Elementargeometrie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Schuljahr 2012/2013. Die vorliegende
Das vorliegende Skript beschäftigt sich mit dem Thema Elementargeometrie. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft(MSG) im Schuljahr 2012/2013. Die vorliegende
Hans Delfs. Übungen zu Mathematik III für Medieninformatik
 Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
1.1 Geradenspiegelungen
 1.1 Geradenspiegelungen 1.1.1 Eigenschaften Definition 1.1 Eine Abbildung der Ebene ist eine Vorschrift, die jedem Punkt P der Ebene einen Bildpunkt P zuordnet. Beispiel 1.1 Zentrische Streckung mit Zentrum
1.1 Geradenspiegelungen 1.1.1 Eigenschaften Definition 1.1 Eine Abbildung der Ebene ist eine Vorschrift, die jedem Punkt P der Ebene einen Bildpunkt P zuordnet. Beispiel 1.1 Zentrische Streckung mit Zentrum
1.10 Geometrie. 1 Die zentrische Streckung Einführung und Definition der zentrischen Streckung... 2
 1.10 Geometrie Inhaltsverzeichnis 1 Die zentrische Streckung 2 1.1 Einführung und Definition der zentrischen Streckung..................... 2 1.2 Flächeninhalte bei zentrischer Streckung............................
1.10 Geometrie Inhaltsverzeichnis 1 Die zentrische Streckung 2 1.1 Einführung und Definition der zentrischen Streckung..................... 2 1.2 Flächeninhalte bei zentrischer Streckung............................
Name: Bearbeitungszeitraum:
 Meine Geomappe Name: Bearbeitungszeitraum: vom bis zum Aufgabe 1 Zeichne einen Kreis mit a) Radius 2 cm. b) Radius 3,5 cm. c) Radius 1,7 cm. Aufgabe 2 a.) Zeichne einen Kreis mit einem Durchmesser von
Meine Geomappe Name: Bearbeitungszeitraum: vom bis zum Aufgabe 1 Zeichne einen Kreis mit a) Radius 2 cm. b) Radius 3,5 cm. c) Radius 1,7 cm. Aufgabe 2 a.) Zeichne einen Kreis mit einem Durchmesser von
mentor Lernhilfe: Mathematik 7. Klasse Baumann
 mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
mentor Lernhilfen mentor Lernhilfe: Mathematik 7. Klasse Geometrie: Achsen- und Punktspiegelung, Drehung, Verschiebung, Winkelgesetze von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 7. Klasse
Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D
 Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Thema: Ein Ausblick auf die Möglichkeiten durch den Software-Einsatz im Mathematikunterricht.
 Vorlesung 2 : Do. 10.04.08 Thema: Ein Ausblick auf die Möglichkeiten durch den Software-Einsatz im Mathematikunterricht. Einführung in GeoGebra: Zunächst eine kleine Einführung in die Benutzeroberfläche
Vorlesung 2 : Do. 10.04.08 Thema: Ein Ausblick auf die Möglichkeiten durch den Software-Einsatz im Mathematikunterricht. Einführung in GeoGebra: Zunächst eine kleine Einführung in die Benutzeroberfläche
Seite 10 Aufgaben Zentrische Streckung 1 a) Konstruktionsbericht (Vorschlag):
 Seite 10 1 a) Konstruktionsbericht (Vorschlag): 1. Alle Eckpunkte mit Z verbinden 2. Die Strecke ZC halbieren (das entspricht der Streckung mit k 0.5) C 3. Parallelverschieben CB // durch C B 4. AB //
Seite 10 1 a) Konstruktionsbericht (Vorschlag): 1. Alle Eckpunkte mit Z verbinden 2. Die Strecke ZC halbieren (das entspricht der Streckung mit k 0.5) C 3. Parallelverschieben CB // durch C B 4. AB //
Übungen. Löse folgende Aufgaben mit GeoGebra
 Übungen Löse folgende Aufgaben mit GeoGebra A1 Die Fachbegriffe in den Kästchen sollen den untenstehenden Aussagen bezüglich eines Dreiecks ABC zugeordnet werden. Du darfst die Kärtchen mehrfach verwenden
Übungen Löse folgende Aufgaben mit GeoGebra A1 Die Fachbegriffe in den Kästchen sollen den untenstehenden Aussagen bezüglich eines Dreiecks ABC zugeordnet werden. Du darfst die Kärtchen mehrfach verwenden
Von Achsenspiegelungen zu Achsenaffinitäten
 Ulrich Schoenwaelder GEONExT-Fortbildung 15. April 2005 Lst. D für Mathematik Von Achsenspiegelungen zu Achsenaffinitäten Klassenstufe: 7-8 und 9-10. Ziele: Hinführung zum punktweisen Abbilden. Eine neue
Ulrich Schoenwaelder GEONExT-Fortbildung 15. April 2005 Lst. D für Mathematik Von Achsenspiegelungen zu Achsenaffinitäten Klassenstufe: 7-8 und 9-10. Ziele: Hinführung zum punktweisen Abbilden. Eine neue
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Elemente der Zweitafelprojektion
 Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Teil I Elemente der Zweitafelprojektion 1 Einleitung Darstellende Geometrie: Eindeutige Darstellung der Geometrie des Raumes auf einer Zeichenebene ohne primäre Anschaulichkeit. Eine DG-Zeichnung muss
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Die Strahlensätze. Ben Hambrecht. 1 Zentrische Streckungen 2. 2 Der 1. Strahlensatz 7. 3 Der Streckfaktor Der 2.
 Die Strahlensätze Ben Hambrecht Inhaltsverzeichnis 1 Zentrische Streckungen 2 2 Der 1. Strahlensatz 7 3 Der Streckfaktor 11 4 Der 2. Strahlensatz 14 5 Der 3. Strahlensatz 18 6 Die Umkehrungen der Strahlensätze
Die Strahlensätze Ben Hambrecht Inhaltsverzeichnis 1 Zentrische Streckungen 2 2 Der 1. Strahlensatz 7 3 Der Streckfaktor 11 4 Der 2. Strahlensatz 14 5 Der 3. Strahlensatz 18 6 Die Umkehrungen der Strahlensätze
Name: Bearbeitungszeitraum:
 Meine Geomappe Name: Bearbeitungszeitraum: vom bis zum Aufgabe 1 Zeichne einen Kreis mit a) Radius 2 cm. b) Radius 3,5 cm. c) Radius 1,7 cm. Aufgabe 2 Zeichne einen Kreis mit einem Durchmesser von 5 cm
Meine Geomappe Name: Bearbeitungszeitraum: vom bis zum Aufgabe 1 Zeichne einen Kreis mit a) Radius 2 cm. b) Radius 3,5 cm. c) Radius 1,7 cm. Aufgabe 2 Zeichne einen Kreis mit einem Durchmesser von 5 cm
Inhaltsverzeichnis. Inhaltsverzeichnis
 Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Prüfungsteil 2, Aufgabe 4 Analytische Geometrie
 Abitur Mathematik: Prüfungsteil, Aufgabe 4 Analytische Geometrie Nordrhein-Westfalen 0 GK Aufgabe a (). SCHRITT: MITTELPUNKT DER GRUNDFLÄCHE BERECHNEN Die Spitze befindet sich einen Meter senkrecht über
Abitur Mathematik: Prüfungsteil, Aufgabe 4 Analytische Geometrie Nordrhein-Westfalen 0 GK Aufgabe a (). SCHRITT: MITTELPUNKT DER GRUNDFLÄCHE BERECHNEN Die Spitze befindet sich einen Meter senkrecht über
Sekundarschulabschluss für Erwachsene. Geometrie A 2012
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2012 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2012 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Sekundarschulabschluss für Erwachsene
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
K2 ÜBUNGSBLATT 2 F. LEMMERMEYER
 K2 ÜBUNGSBLATT 2 F. LEMMERMEYER Aufgabe 1. Hier ein knappes Beispiel, wie man einen Punkt P an einer Geraden g spiegelt (Wer sich gerne was merkt: Lotfußpunkte auf Ebene mit Lotgerade, Lotfußpunkte auf
K2 ÜBUNGSBLATT 2 F. LEMMERMEYER Aufgabe 1. Hier ein knappes Beispiel, wie man einen Punkt P an einer Geraden g spiegelt (Wer sich gerne was merkt: Lotfußpunkte auf Ebene mit Lotgerade, Lotfußpunkte auf
1 Dreiecke. 1.6 Ähnliche Dreiecke. Mathematische Probleme, SS 2019 Donnerstag 2.5. $Id: dreieck.tex,v /05/03 14:05:29 hk Exp $
 $Id: dreieck.tex,v 1.60 2019/05/03 14:05:29 hk Exp $ 1 Dreiecke 1.6 Ähnliche Dreiecke Wir hatten zwei Dreiecke kongruent genannt wenn in ihnen entsprechende Seiten jeweils dieselbe Länge haben und dann
$Id: dreieck.tex,v 1.60 2019/05/03 14:05:29 hk Exp $ 1 Dreiecke 1.6 Ähnliche Dreiecke Wir hatten zwei Dreiecke kongruent genannt wenn in ihnen entsprechende Seiten jeweils dieselbe Länge haben und dann
Konvexes Viereck Trapez Drachenviereck Parallelogramm Sehnenviereck Tangentenviereck. Haus der Vierecke. Dr. Elke Warmuth. Sommersemester 2018
 Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 39 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck 2 / 39 Wir betrachten nur konvexe Vierecke:
Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 39 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck 2 / 39 Wir betrachten nur konvexe Vierecke:
Aufgabe 1 Erstelle mit Hilfe von GEOGEBRA ein dynamisches Geometrie-Programm, das die Mittelsenkrechte
 AB Mathematik Experimentieren mit GeoGebra Merke Alle folgenden Aufgaben sind mit dem Programm GEOGEBRA auszuführen! Eine ausführliche Einführung in die Bedienung des Programmes erfolgt im Unterricht.
AB Mathematik Experimentieren mit GeoGebra Merke Alle folgenden Aufgaben sind mit dem Programm GEOGEBRA auszuführen! Eine ausführliche Einführung in die Bedienung des Programmes erfolgt im Unterricht.
. Wo liegt das Zentrum S? d) E ist das Bild von I mit
 Zentrische Streckung, Ähnlichkeit 1. Eine gegebene Strecke ist durch Konstruktion im Verhältnis 5 3 harmonisch zu teilen. 1 U und V teilen die Strecke mit der Länge 24 cm harmonisch im Verhältnis 5 3.
Zentrische Streckung, Ähnlichkeit 1. Eine gegebene Strecke ist durch Konstruktion im Verhältnis 5 3 harmonisch zu teilen. 1 U und V teilen die Strecke mit der Länge 24 cm harmonisch im Verhältnis 5 3.
Konstruktion von Kreistangenten
 Konstruktion von Kreistangenten 1 Gegeben sind die Punkte A und B mit AB = 5cm Konstruiere die Geraden durch B, die von A den Abstand 3cm haben! 2 Eine Ecke einer Rasenfläche, an der die geraden Ränder
Konstruktion von Kreistangenten 1 Gegeben sind die Punkte A und B mit AB = 5cm Konstruiere die Geraden durch B, die von A den Abstand 3cm haben! 2 Eine Ecke einer Rasenfläche, an der die geraden Ränder
Grundrissebene und Aufrissebene
 Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Grundrissebene und Aufrissebene x 3 (bzw. z) - Höhe Aufrissebene 2 (bzw. yz-ebene) Rissachse x 12 O x 2 (bzw. y) - Breite Grundrissebene 1 (bzw. xy-ebene) x 1 (bzw. x) - Tiefe Grund- / Aufrissverfahren
Sekundarschulabschluss für Erwachsene. Geometrie A b) Strecken Sie das Dreieck ABC (Streckfaktor: -1/ Streckzentrum Z) (3 Punkte)
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2013 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Einleitung. Aufgaben: Vergrössern / Verkleinern. 1. Die Geo-Maus
 Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Zentrische Streckung und Ähnlichkeit Einleitung Aufgaben: Vergrössern / Verkleinern 1. Die Geo-Maus a) Zeichne die Geo-Maus noch
Kantonsschule Solothurn Geometrie: Zentrische Streckung und Ähnlichkeit RYS Zentrische Streckung und Ähnlichkeit Einleitung Aufgaben: Vergrössern / Verkleinern 1. Die Geo-Maus a) Zeichne die Geo-Maus noch
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 24 Unter den drei klassischen Problemen der antiken Mathematik versteht man (1) die Quadratur des Kreises, (2) die Dreiteilung
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 24 Unter den drei klassischen Problemen der antiken Mathematik versteht man (1) die Quadratur des Kreises, (2) die Dreiteilung
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
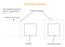 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
2.6. Aufgaben zu Kongruenzabbildungen
 Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Aufgabe.6. Aufgaben zu Kongruenzabbildungen Gegeben sind die Dreiecke ABC mit A(0 ), B( 0) und C(3 0) sowie A B C mit A ( ), B (3 ) und C ( ). Beschreibe die Abbildung, die das Dreieck ABC auf das Dreieck
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler Problem
 Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler roblem von Reimund Albers, Bremen Im Baseler roblem geht es um die Summe der reziproken Quadrate, also + + 2 3 + 2 4 + +..., und ein exaktes
Die Kraft der Geometrie oder Eine geometrische Lösung zum Baseler roblem von Reimund Albers, Bremen Im Baseler roblem geht es um die Summe der reziproken Quadrate, also + + 2 3 + 2 4 + +..., und ein exaktes
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Themen: Geometrie (Kongruenzabbildungen, Winkelsätze, Flächenberechnungen)
 Klasse 7 Mathematik Vorbereitung zur Klassenarbeit Nr. 4 im Mai 2019 Themen: Geometrie (Kongruenzabbildungen, Winkelsätze, Flächenberechnungen) Checkliste Was ich alles können soll Ich kenne den Begriff
Klasse 7 Mathematik Vorbereitung zur Klassenarbeit Nr. 4 im Mai 2019 Themen: Geometrie (Kongruenzabbildungen, Winkelsätze, Flächenberechnungen) Checkliste Was ich alles können soll Ich kenne den Begriff
Didaktik der Geometrie
 Jürgen Roth Didaktik der Geometrie Modul 5: Fachdidaktische Bereiche 3.1 Inhalt Didaktik der Geometrie 1 Ziele und Inhalte 2 Begriffsbildung 3 Konstruieren 4 Argumentieren und Beweisen 5 Problemlösen 6
Jürgen Roth Didaktik der Geometrie Modul 5: Fachdidaktische Bereiche 3.1 Inhalt Didaktik der Geometrie 1 Ziele und Inhalte 2 Begriffsbildung 3 Konstruieren 4 Argumentieren und Beweisen 5 Problemlösen 6
Demo-Text für Inversion (Spiegelung am Kreis) Ein Spezialthema INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Inversion (Spiegelung am Kreis) Ein Spezialthema Teil 1 Grundlagen Text Nr. 1400 Stand: 4. Februar 016 FIEDICH W. BUCKEL INTENETBIBLIOTHEK FÜ SCHULMATHEMATIK 1400 Inversion 1 Vorwort Die Inversion, die
Inversion (Spiegelung am Kreis) Ein Spezialthema Teil 1 Grundlagen Text Nr. 1400 Stand: 4. Februar 016 FIEDICH W. BUCKEL INTENETBIBLIOTHEK FÜ SCHULMATHEMATIK 1400 Inversion 1 Vorwort Die Inversion, die
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Geometrie Winkel und Vierecke PRÜFUNG 02. Ohne Formelsammlung! Name: Klasse: Datum: Punkte: Note: Klassenschnitt/ Maximalnote : Ausgabe: 2.
 GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
Einführung in Geonext
 Einführung in Geonext von Konrad Brunner Downloadquelle: Regionale Lehrerfortbildung Neue Unterrichtsmethoden im Mathematikunterricht Termin: Ort: 27.03.2003 von 09.30 Uhr bis 16.00 Uhr Städtische Rudolf-Diesel-Realschule,
Einführung in Geonext von Konrad Brunner Downloadquelle: Regionale Lehrerfortbildung Neue Unterrichtsmethoden im Mathematikunterricht Termin: Ort: 27.03.2003 von 09.30 Uhr bis 16.00 Uhr Städtische Rudolf-Diesel-Realschule,
Abituraufgaben bis 2018 Baden-Württemberg. Geraden, Ebenen, Abstand
 Abituraufgaben bis 8 Baden-Württemberg Geraden, Ebenen, Abstand allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com August 8 Aufgabe : (Abiturprüfung 8) Gegeben sind die Ebenen E: xx x
Abituraufgaben bis 8 Baden-Württemberg Geraden, Ebenen, Abstand allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com August 8 Aufgabe : (Abiturprüfung 8) Gegeben sind die Ebenen E: xx x
Geometrie (4b) Wintersemester 2015/16. Kapitel 2. Abbildungsgeometrie. Teil 2
 Kapitel 2 Abbildungsgeometrie Teil 2 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Kapitel 2 Abbildungsgeometrie 2.1 2,3,4 Geradenspiegelungen 2.2 Sinn & Orientierung
Kapitel 2 Abbildungsgeometrie Teil 2 1 Maximilian Geier, Institut für Mathematik, Campus Landau, Universität Koblenz Landau Kapitel 2 Abbildungsgeometrie 2.1 2,3,4 Geradenspiegelungen 2.2 Sinn & Orientierung
Elemente der SchulgeometrieGrundschule. Aufgabenblatt 8 Körper und Kippen
 Elemente der SchulgeometrieGrundschule Aufgabenblatt 8 Körper und Kippen Aufgabe 1: a) Zeichnen Sie als Schrägbild (Winkel 45,Verkürzungsfaktor 0.5) einen Oktaeder mit der Seitenlänge 10 cm. (Achtung!
Elemente der SchulgeometrieGrundschule Aufgabenblatt 8 Körper und Kippen Aufgabe 1: a) Zeichnen Sie als Schrägbild (Winkel 45,Verkürzungsfaktor 0.5) einen Oktaeder mit der Seitenlänge 10 cm. (Achtung!
Klausurenkurs zum Staatsexamen (WS 2013/14): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Bearbeitungszeit: Name: Erklärung
 Ausgabe: Mittwoch, 05.05.2004 Abgabe: Freitag, 14.05.2004 Am Freitag den 14.05.2004 halte ich die Mathestunde. Bring deshalb auch dann dein Übungsblatt mit! Bearbeitungszeit: Name: Erklärung 1 2 3 Pflichtaufgabe
Ausgabe: Mittwoch, 05.05.2004 Abgabe: Freitag, 14.05.2004 Am Freitag den 14.05.2004 halte ich die Mathestunde. Bring deshalb auch dann dein Übungsblatt mit! Bearbeitungszeit: Name: Erklärung 1 2 3 Pflichtaufgabe
100 % Mathematik - Lösungen
 100 % Mathematik: Aus der Geometrie Name: Klasse: Datum: 1 Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm
100 % Mathematik: Aus der Geometrie Name: Klasse: Datum: 1 Ordne die gemessenen Längenangaben den beschriebenen Objekten zu. 22 m 37 cm Tischdicke 22 mm Breite eines Turnsaals 2 m 45 cm Sitzhöhe 258 mm
Achtung: Die Aufgabenkarten werden nacheinander ausgegeben! 1
 Achtung: Die Aufgabenkarten werden nacheinander ausgegeben! 1 Aufgabe 1 Zeichne in Geogebra ein beliebiges Dreieck und konstruiere den Umkreismittelpunkt U, den Schwerpunkt S und den Höhenschnittpunkt
Achtung: Die Aufgabenkarten werden nacheinander ausgegeben! 1 Aufgabe 1 Zeichne in Geogebra ein beliebiges Dreieck und konstruiere den Umkreismittelpunkt U, den Schwerpunkt S und den Höhenschnittpunkt
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg
 Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
3 Die Theorie des Spiegelbuches
 3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
3 Die Theorie des Spiegelbuches 41 3 Die Theorie des Spiegelbuches Fügt man zwei Spiegel unter einem Winkel zusammen, so spricht man von einem Spiegelbuch. Blickt man in diese Spiegelanordnung, so kann
Klausurenkurs zum Staatsexamen (WS 2012/13): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS /3): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 a)
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS /3): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 a)
D C. Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
 V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
V. Körper, Flächen und Punkte ================================================================= 5.1 Körper H G E F D C A B Man unterscheidet in der Geometrie zwischen Körpern, Flächen, Linien und Punkten.
Kapitel 4: Dreieckslehre. 4.1 Bedeutung der Dreiecke
 Kapitel 4: Dreieckslehre 4.1 edeutung der Dreiecke Durch Triangulation lassen sich Vielecke in Dreiecke zerlegen ( n Eck in n- Dreiecke) eweis von Sätzen mittels Sätzen über Dreiecke (z.. Winkelsumme,
Kapitel 4: Dreieckslehre 4.1 edeutung der Dreiecke Durch Triangulation lassen sich Vielecke in Dreiecke zerlegen ( n Eck in n- Dreiecke) eweis von Sätzen mittels Sätzen über Dreiecke (z.. Winkelsumme,
E r g ä n z u n g. zur Trigonometrie
 E r g ä n z u n g zur Trigonometrie Klasse 10 b 2018 / 19 Deyke www.deyke.com Trigonometrie.pdf W I N K E L F U N K T I O N E N Die Strahlensätze und der Satz des Pythagoras sind bisher die einzigen Hilfsmittel
E r g ä n z u n g zur Trigonometrie Klasse 10 b 2018 / 19 Deyke www.deyke.com Trigonometrie.pdf W I N K E L F U N K T I O N E N Die Strahlensätze und der Satz des Pythagoras sind bisher die einzigen Hilfsmittel
Übungsblatt 3 (Vektorgeometrie)
 Fachhochschule Nordwestschweiz (FHNW Hochschule für Technik Institut für Mathematik- und Naturwissenschaft Übungsblatt (Vektorgeometrie Roger Burkhardt 08 Mathematik. Aufgabe Gegeben seien die Vektoren
Fachhochschule Nordwestschweiz (FHNW Hochschule für Technik Institut für Mathematik- und Naturwissenschaft Übungsblatt (Vektorgeometrie Roger Burkhardt 08 Mathematik. Aufgabe Gegeben seien die Vektoren
Aufgaben für die Klassenstufen 11/12
 Aufgaben für die Klassenstufen 11/12 mit Lösungen Einzelwettbewerb Gruppenwettbewerb Speedwettbewerb Aufgaben OE1, OE2, OE3 Aufgaben OG1, OG2, OG3, OG4 Aufgaben OS1, OS2, OS3, OS4, OS5, OS6, OS7, OS8 Aufgabe
Aufgaben für die Klassenstufen 11/12 mit Lösungen Einzelwettbewerb Gruppenwettbewerb Speedwettbewerb Aufgaben OE1, OE2, OE3 Aufgaben OG1, OG2, OG3, OG4 Aufgaben OS1, OS2, OS3, OS4, OS5, OS6, OS7, OS8 Aufgabe
1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: m (ausgesprochen: T von t und m)
 Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Darstellende Geometrie Übungen. Tutorial 06. Übungsblatt: Schatten - Perspektive 04. Wohnhaus
 Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Lk Mathematik 12 Analytische Geometrie Arbeitsblatt A.1
 Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
Kapitel 5: Dreieckslehre. 5.1 Bedeutung der Dreiecke
 edeutung+winkelsumme 1 Kapitel 5: Dreieckslehre 5.1 edeutung der Dreiecke Durch Triangulation lassen sich Vielecke in Dreiecke zerlegen ( n Eck in n- Dreiecke) eweis von Sätzen mittels Sätzen über Dreiecke
edeutung+winkelsumme 1 Kapitel 5: Dreieckslehre 5.1 edeutung der Dreiecke Durch Triangulation lassen sich Vielecke in Dreiecke zerlegen ( n Eck in n- Dreiecke) eweis von Sätzen mittels Sätzen über Dreiecke
Körper erkennen und beschreiben
 Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Zum Einstieg. Mittelsenkrechte
 Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Zum Einstieg Mittelsenkrechte 1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB. 2. Zeichne einen Kreis um B mit dem gleichen Radius. 3. Die Gerade durch
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Abitur 2017 Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur 7 Mathematik Geometrie VI Gegeben sind die beiden bezüglich der x x 3 -Ebene symmetrisch liegenden Punkte A( 3 ) und B( 3 ) sowie der Punkt C( ). Teilaufgabe
Seite http://www.abiturloesung.de/ Seite Abitur 7 Mathematik Geometrie VI Gegeben sind die beiden bezüglich der x x 3 -Ebene symmetrisch liegenden Punkte A( 3 ) und B( 3 ) sowie der Punkt C( ). Teilaufgabe
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Mitten-Dreiund Vier-Ecke
 Alle Ergebnisse - dazu gehören auch Kopiene der Zeichnungen - sind im Heft zu notieren Du wirst im Folgenden einiges selbst herausfinden müssen. Nutze dazu auch die Hilfen, dei dir kig liefert. 1 Mittendreieck
Alle Ergebnisse - dazu gehören auch Kopiene der Zeichnungen - sind im Heft zu notieren Du wirst im Folgenden einiges selbst herausfinden müssen. Nutze dazu auch die Hilfen, dei dir kig liefert. 1 Mittendreieck
Städtewettbewerb Frühjahr 2009
 Städtewettbewerb Frühjahr 2009 Lösungsvorschläge Hamburg 4. März 2009 [Version 1. April 2009] M Mittelstufe Aufgabe M.1 (3 P.). In ein konvexes 2009-Eck werden sämtliche Diagonalen eingezeichnet. (Diagonalen
Städtewettbewerb Frühjahr 2009 Lösungsvorschläge Hamburg 4. März 2009 [Version 1. April 2009] M Mittelstufe Aufgabe M.1 (3 P.). In ein konvexes 2009-Eck werden sämtliche Diagonalen eingezeichnet. (Diagonalen
Strahlensätze und Ähnliches
 Strahlensätze und Ähnliches Dr. Elke Warmuth Sommersemester 2018 1 / 27 Zentrische Streckung Strahlensätze Ähnliche Figuren 2 / 27 Was ist hier passiert? 3 / 27 Zentrische Streckung mit Streckungszentrum
Strahlensätze und Ähnliches Dr. Elke Warmuth Sommersemester 2018 1 / 27 Zentrische Streckung Strahlensätze Ähnliche Figuren 2 / 27 Was ist hier passiert? 3 / 27 Zentrische Streckung mit Streckungszentrum
Aufgabe A6/13. Aufgabe A7/13. Aufgabe A6/14
 Aufgabe A6/ Gegeben sind die Ebene 4 : Abituraufgaben Analytische Geometrie (Pflichtteil) ab und : 8. Bestimmen Sie eine Gleichung der Schnittgeraden. (Quelle Abitur BW Aufgabe 6) Aufgabe A7/ Gegeben sind
Aufgabe A6/ Gegeben sind die Ebene 4 : Abituraufgaben Analytische Geometrie (Pflichtteil) ab und : 8. Bestimmen Sie eine Gleichung der Schnittgeraden. (Quelle Abitur BW Aufgabe 6) Aufgabe A7/ Gegeben sind
Oktaeder. Bernhard Möller. 22. Dezember 2010
 Oktaeder Bernhard Möller. Dezember 00 Ein Oktaeder ist ein regelmäßiges Polyeder, dessen Oberfläche aus acht kongruenten, gleichseitigen Dreiecken besteht. Jedes Oktaeder kann einem Würfel so einbeschrieben
Oktaeder Bernhard Möller. Dezember 00 Ein Oktaeder ist ein regelmäßiges Polyeder, dessen Oberfläche aus acht kongruenten, gleichseitigen Dreiecken besteht. Jedes Oktaeder kann einem Würfel so einbeschrieben
