Grundlagen der Elektrotechnik 3
|
|
|
- Evagret Hausler
- vor 5 Jahren
- Abrufe
Transkript
1 Grundlagen der Elekroechnik 3 Prof. Dr.-Ing. Ingolf Willms und Prof. Dr.-Ing. Adalber Beyer und basierend auf dem Scrip von Prof. Dr.-Ing. Ingo Wolff Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
2 Grundlagen der Elekroechnik 3 Inhal Einleiung Grundlagen der Signalheorie deerminierer Signale 3 Schalvorgänge 4 Orskurven 5 Nezwerksäze Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
3 Lieraur Lieraur zur Vorlesung: R. Paul Elekroechnik, Grundlagenbuch Nezwerke Springer-Verlag, Heidelberg 994 I. Wolff Grundlagen der Elekroechnik Band Verlag Dr. Wolff, Aachen 5 Weierführende Lieraur : W. Ameling Grundlagen der Elekroechnik II G. Bosse Grundlagen der Elekroechnik IV B.I. Wissenschafverlag Mannheim, Wien Zürich 996 R. UnbehauenGrundlagen der Elekroechnik I Springer-Verlag, Heidelberg 994 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 3
4 Einleiung GE3 enhäl überwiegend heoreische Grundlagen zu informaionsechnischen Fragesellungen Informaionsechnik: Ensanden aus Informaik (I- Verarbeiungsechnik) und Nachrichenechnik (I- Übermilungsechnik) I: Effiziene Daenverarbeiung, Speicherung und ranspor I beinhale 4 Gruppen: Grundlagen und echnologien (G) Srukuren, Verfahren, Programme (G) Geräe, Einrichungen, Anlagen (G3) Anwendungen (G4) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 4
5 Einleiung G: heoreische Grundlagen, Mehoden, SW- und HW-echnologien, Physiologische Grundlagen G: Rechensyseme, Sofwaresyseme, Archiekuren, Aufnahme-, Wiedergabe und Speicherung, Vermilungsund Überragungsverfahren G3: Rechenanlagen, Einrichungen zu Ein- und Ausgabe, End- und Meßeinrichungen, Einrichungen zur Auomaisierung, Vermilung und Überragung, G4: Kommerzielle, adminisraive, indusrielle Anwendungen, Prozeßdaen, echnisch/wissenschafliche Anwendungen, Kommunikaion, Orung und Navigaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 5
6 Grundlagen der Signalheorie deerminierer Signale Kapielübersich:. Vorbemerkungen Modell für die Informaions-Überragung Signalklassen. Beschreibung nichsinusförmiger, periodischer Zeivorgänge Approximaion von Funkionen mi Fourier-Reihe Anwendungen auf Nezwerke.3 Beschreibung aperiodischer Zeivorgänge Das Fourier-Inegral in verschiedenen Formen Beispiele dazu Eigenschafen der Fourier-ransformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 6
7 . Vorbemerkungen Sörer Quelle Sender Kanal Empfänger Senke Bereich der elekrischen ors- und zeiabhängigen Signale Signale: räger der Informaionen Signalklassen: Deerminiere, sochasische Signale Werkoninuierlich, Werdiskre Zeikoninuierlich, zeidiskre Periodisch, aperiodisch Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 7
8 . Vorbemerkungen coninuous ime-(space-) domain discree s s k od. k Analog signal Analog signal sequence Werebereich s s k od. k signal wih discree values Digial signal Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 8
9 .. Das Exponenialsignal jω s() = e = cosω+ jsinω Für Spannungen gil: ( + u ) jω { } { } u ( ) = uˆ cos( ω+ ϕ ) = Re uˆ e = Re u e where u= uˆ e Für anseigende/abfallende Signale gil: u j ω ϕ jϕ u e = e e = e ( σ+ j ω ) σ j ω p Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 9
10 .. Die Dirac Funkion Definiion: + Φ ( ) = δ ( ) Φ( ) d Eigenschafen: δ ( a) = δ ( ) a Für a = gil: δ ( ) = δ ( ) + s() = δ ( τ ) s( τ) dτ Folg aus der Definiionsgleichung. Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
11 .. Die Dirac Funkion + δτ ( ) dτ= s() = mi δτ ( ) für τ δ () = lim rec δ ( τ ) τ Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
12 ..3 Die Sprungfunkion for < ε() = for ε() = δτ ( ) dτ ε () Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
13 ..4 Periodische Signale Allgemeine Formel: s ( ) = s ( + n) where n=,...,, +,..., + Beispiele: + s () = s ( n ) n= + s () = c s ( n ) n n= Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 3
14 ..4 Periodische Signale s ( ) = rec n + s() = rec n= + = rec n n= s () n = n = n = Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 4
15 ..5 Impulsarige Signale rec( x) for x = for x > rec( x) x Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 5
16 ..5 Impulsarige Signale s () = ( / ) e s( ) 3 3 / Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 6
17 ..5 Impulsarige Signale for > s ( ) = sign ( ) = for = for < sign() Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 7
18 ..5 Impulsarige Signale s () für =Λ = sons s () =Λ Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 8
19 ..5 Impulsarige Signale () = cos( ω ( )) s e s () 3 4 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 9
20 ..6 Anpassung von Zei- und Frequenz Funcionen Fall: Kompression & Dehnung s() = a s b Beispiel: s() = u rec Fall : Verschiebung s = s ν () ( ) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
21 ..6 Anpassung von Zei- und Frequenz Funcionen Beispiel: s () = rec s() = u s = u rec u rec( x) s () x Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
22 ..6 Anpassung von Zei- und Frequenz Funcionen Fall 3: Spiegelung (b = -) s () = s ( ) Beispiel: s () = ε() s () = s ( ) = ε( ) s () Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
23 ..6 Anpassung von Zei- und Frequenz Funcionen Dehnung & Verschiebung: s() = rec s() = rec 3 ν s3() = s( ν ) = rec 3 s3 ( ) 3 v Verschiebung & Dehnung: s = s ν () ( ) s3( ) = as Ersezung von mi in s( ) b b = as ν b Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 3
24 ..6 Anpassung von Zei- und Frequenz Funcionen Beispiel: s( ) = rec ; a = u ; b= () ν ν s = rec = rec ν ν s3() = arec = urec b u s () 3 v Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 4
25 ..6 Anpassung von Zei- und Frequenz Funcionen Spiegelung & Verschiebung: s () = s ( ) s ( ) = s ( ) = s ( ( )) = s ( ) 3 ν ν ν Neue Abfolge: Verschiebung & Spiegelung: s4 = s ν () ( ) s () = s ( ) = s ( ) s () 5 4 ν 3 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 5
26 ..6 Anpassung von Zei- und Frequenz Funcionen Beispiel mi der Rampenfunkion r(): r = () ε () s = r s() = s( ) = r s () s () 3 s () ν s3() = s( ν ) = r v Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 6
27 ..6 Anpassung von Zei- und Frequenz Funcionen ν s4() = s( ν ) = r ν s5() = s5( ) = r s5 ( ) s4 ( ) v v Es gib 4 Fälle: ± ± v Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 7
28 ..6 Anpassung von Zei- und Frequenz Funcionen Alle o.a. Mehoden können auch auf Frequenzfunkionen angewende werden: f( x) = f( y) mi y = f3( x) f ( x) = f ( f ( x)) 3 Beispiel: f ( ω) ω ω = rec ω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 8
29 . Beschreibung nichsinusförmiger, periodischer Zeivorgänge.. Approximaion von Funkionen Moivaion: Kennfunkionen, Exrakion von Kenndaen Daenkompression Ansaz: Gegeben sei f() Gesuch is g(),die f() im Inervall approximier mi n g() = αigi() bei Vorgabe der gi( ) i= g() f() Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 9
30 .. Approximaion von Funkionen - Anforderung: Möglichs kleiner Fehler der Approximaion - Definiion Fehlerfunkion: Φ () = f() g() - Milerer Fehler: Φ = [ f () ()] m min - Milerer absoluer Fehler : g d min Φ = f () g() d ma min min Φ = f () g() d mq min - Milerer Quadraischer Fehler : [ ] - Voreile/Nacheile der Fehlermaße Aufheben der Fehler möglich bei milerem Fehler Absol. Fehler ergib Unseigkeien (beim par. Differenzieren) Quadr. Fehler is häufigse Anwendung min Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 3
31 .. Approximaion von Funkionen Besimmung der Koeffizienen Hieraus folgen die unen angegebenen Schrie: φ mq = i =,,..., n α i α υ αi n f() α jg j() d = j= n ( ) ( ) ( ) f α jg j gi d = j= n f() gi() d = gi() α jg j() d j= Dies ensprich einem Gleichungssysem, das nach den Koeffizienen aufgelös werden kann Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 3
32 .. Approximaion von Funkionen = α + α + + α ν α ν + + n f g() d g () d g() g() d... g() g() d... g() g() d n f () g () d = α g () g () d + α g () g () d α g () g () d α g () g () d ν ν n n... f() g () d = α g () g () d+ α g () g () d α g () g () d α g () g () d n n n ν ν n n n n Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 3
33 .. Approximaion miels orhogonaler Funkionensyseme Definiion orhogonaler Funkionen in Inervall (, ) miels reeller Funkionen g(). Diese Funkionen sollen seig im Inervall sein. Dabei wird Chronecker sche Delafunkion benuz: Ansaz für die Approximaion: δ µν g () g () d = δ h µ ν µν µ und geeigneem h für µ ν = für µ = ν () = n g αigi() i= µ Dami folg für die Koeffizienen (infolge Wegfalls aller Inegrale je Zeile bis auf zwei Inegrale): α = i f g() d g i i () d Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 33
34 .. Approximaion miels orhogonaler Funkionensyseme Man erhäl orhonormale Funkionensyseme miels der Feslegungen g () g () gν () gn() G ( ) =, G ( ) =,..., Gν ( ) =,..., Gn ( ) = h h h h ν n Für diese gil dann: G () G () d µ ν µν für µ ν = δ = für µ = ν Dami läss sich eine Funkion f() im Inervall mi Hilfe von geeigneen Koeffizienen in eine Reihe von orhonormalen Funkionen enwickeln. Das Ergebnis der Approximaion is dann eine Funkion G(). Zusammenfassend gil: Die Koeffizienen A sind die sog. verallgemeineren Fourierkoeffizienen: f() G() AG () A i n = i= = f() Gi() d i i Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 34
35 ..3 Approximaion von periodischen, nichsinusförmigen Funkionen Beispiel einer Funkion mi der Periodendauer. Diese Funkion is als nich endende Wiederholung einer Periode inerpreierbar. f() Für eine periodische Funkion gil: f( ) = f( ± ν) ν =,,,..., Nach Fourier kann eine beliebige Funkion, die die Dirichle schen Bedingungen erfüll, u.a. in der folgenden rigonomerischen Form dargesell werden: a f () = + [ aν cos( νω) + bν sin( νω) ] ν = Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 35
36 .. Approximaion von periodischen, nichsinusförmigen Funkionen (Fourier-Reihe) Dirichle sche Bedingungen (in der Praxis erfüll) Funkion f() is im Inervall enweder seig oder ha endlich viele Unseigkeissellen Endliche Grenzwere von f() exisieren, wenn von rechs oder von links gegen die Unseigkeisselle sreb Das Inervall läss sich derar in eile zerlegen, so dass dor f() monoon is Saz von Dirichle Bei Erfüllung der Dirichle schen Bedingungen konvergier die Fourierreihe im gesamen Inervall Der Wer der Fourier-Reihe is idenisch mi Funkion f() an seigen Sellen An Unseigkeissellen is der Wer gleich:.5 f( + ) + f( ) [ ] An Endpunken des Inervalls is der Wer gleich: [ f + + f ].5 ( ) ( ) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 36
37 ..3 Fourier Reihe Analogie zur Reihenenwicklung orhogonaler Funkionen Für die Reihenenwicklung gil bei orhogonalen Funkionen Für die benuzen Funkionen läß sich die Orhogonaliä zeigen: Ansonsen gil wie o.a. : Dadurch is gesicher, dass Fourier- Reihe die besmögliche Approximaion im quadraischen Miel is (auch bei abgebrochener Reihe) g () g () d = δ h µ ν µν µ () = n g αigi() i= mi = + = + sin( µω)sin( νω ) d = cos( µω)cos( νω) d = δµν = = α = i f g() d g i i () d a f a b () = + ν cos( ) + ν sin( ) ν = [ νω νω ] Es sind Koeffizienensäze nöig, dami gerade und ungerade Funkionsaneile dargesell werden können. Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 37
38 ..3 Fourier Reihe Dami gil für die Besimmung der Fourier-Koeffizienen der rigonomerischen Form: a = + = = = = + = f() d d = + = f() d Dies is der Gleichaneil (arihm. Mielwer) = + f()cos( µω) d = + = aν = = ()cos( ) = + f µω d = µω d = cos ( ) = + f()sin( µω) d = + = bν = = ()sin( ) f µω d = d = + sin ( µω ) = Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 38
39 ..4 Die Polar-Form der Fourier Reihe (Fourier-Cosinus-Reihe) Miels der Beziehung A x B x A B x B A cos( ) + sin( ) = + cos( arcan( / )) läss sich die rigon. Fourier-Reihe umschreiben von a f( ) = + [ aν cos( νω) + bν sin( νω) ] zu ν = f() = d + dν cos( νω+ ψν) mi d = a und ν = d = a + b b ν ν ν ν ; ψν = arcan ( + / π für negaive aν ) aν Darüber hinaus is obige Formel auch in der Version der Fourier-Sinus- Reihe bekann: f( ) = e + e sin( νω+ ϕ ) mi e = d sowie ϕ = π / + ψ ν = ν ν ν ν ν ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 39
40 ..5 Beispiele zur Berechnung der Fourier- Reihe mi symmer. Funkionen B: f() is eine gerade Funkion mi f ( ) = f( ) und f() -f() f() -/ - / aν = f ()cos( νω) d bν = f()sin( νω) d = = Die Fourier-Reihe ha dami die Form: Grund: Darsellbarkei gerader Funkionen nur durch andere gerade Funkionen a f a () = + ν cos( νω ) ν = Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 4
41 ..5 Beispiele zur Berechnung der Fourier- Reihe mi symmer. Funkionen B: f() is eine ungerade Funkion mi f () = f( ) und -/ - f() f() -f() / a = a ν = Somi resulier: 4 bν = f ()sin( νω) d f() = bν sin( νω) ν = Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 4
42 ..5 Beispiele zur Berechnung der Fourier-Reihe mi symmer. Funkion B3: f() is vollsymmerische Funkion mi f()= - f( + /) f() +/ f(+/) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 4
43 ..5 Beispiele zur Berechnung der Fourier-Reihe mi symmer. Funkion Es gil dafür : aν = f()cos( νω) d oder nach Aufeilung des Inervalls: für ν = k gil: aν = f()cos( νω) d f()cos( νω) d + o ak = f( )cos( kω) d f( )cos( kω) d + = o 4 sowie für ν = k + : a = k + f ()cos( [ k ) ω] d + Grund: Geradzahlige k ergeben sich nach / wiederholende cos-funkionen. Auslöschung der erme wegen zu / negaiven und sich wiederholendem f()! Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 43
44 ..5 Beispiele zur Berechnung der Fourier- Reihe mi symmer. Funkion - Auf ähnlicher Weise läß sich die Güligkei folgender Aussagen einsehen (auch sin-funkion wiederhol sich für gerade k nach /): 4 b k = und b = k + f()sin [(k ) ω] d + - Es kommen daher in dieser Fourier-Reihe nur ungeradzahlige Schwingungen vor, für die ν = k + gil: k = { k+ [ ω ] k+ [ ω ]} f () = a cos(k+ ) + b sin (k+ ) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 44
45 ..5 Beispiele zur Berechnung der Fourier-Reihe mi symmer. Funkion B4 : Funkion is vollsymmerisch mi f() = f( + / ). Daraus folg dann: f() 8 # 4 ak f()cos( kω) d = und a + = k / +/ 4 b k f()sin( kω) d = und b + = Grund: Nach / erfolg Wiederholung der cos/sin-funkionen mi den Indizes k. Cos/sin-Funkionen mi Indizes k+ haben bei / Absand jeweils andere Halbwelle! Die Fourier-Reihe von f() ha dann eine Form mi allein geradzahligen Koeffizienen: a f ( ) = + { ak cos [( k) ω] + bk sin [( k) ω] } k = k Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 45
46 ..5 Beispiele zur Berechnung der Fourier- Reihe mi symmer. Funkion B5 : f() is gerade und vollsymmerisch [ f() = - f( + /) ] : Resula: Nur ungeradzahlige Kosinusschwingungen kommen vor f() / a Somi laue die ensprechende Fourier-Reihe hier: k = ( ) f () = ak + cos k+ ω = a = und b ν = k 4 8 a = k + f ()cos[( k ) ω] d + Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 46
47 ..5 Beispiele zur Berechnung der Fourier- Reihe mi symmer. Funkion B6 : f() is ungerade und vollsymmerisch [ f() = -f( + /) ] : Hier reen in der Fourier-Reihe nur ungeradzahlige Sinuschwingungen auf f() / a = = und b = a ν 4 8 b = k + f()sin[( k ) ω] d + k Für die Fourier-Reihe läß sich hier schreiben : k = ( ) f() = bk + sin k+ ω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 47
48 ..5 Beispiele zur Berechnung der Fourier- Reihe mi symmer. Funkion B7: f() wird auf der Zeiachse verschoben : Beräg die Verschiebung ± dann gil mi ' = ± a g f a b ( ') = ( ± ) = + ν cos[ ( ± )] + ν sin[ ( ± )] ν = { νω νω } Ein einfacherer Ausdruck resulier für die kompl. Koeffizienen: f c e m jvω ( ± ) ergib { n } Dieser Ausdruck ermöglich es, die Fourier-Reihenenwicklung für den neuen Koordinaenursprung zu ermieln. Es is of von Voreil, den Koordinaenursprung zu verschieben, z.b. wenn sich dami symmerische Eigenschafen der Funkion ergeben. Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 48
49 ..6 Fourier-Analyse Es beseh die Möglichkei, eine periodische nich-sinusförmige Funkion hinsichlich ihres Informaionsgehales auf zwei Aren darsellen: ) Im Zeibereich ( s. folgendes Bild) f() d -/4 / /4 3/4 -A ) Im Spekralbereich (Frequenzbereich): Darsellung der Ampliuden aν, b bzw. der cos-ampliude d ν und der Phase ψν in Abhängigkei von der Frequenz. ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 49
50 ..6 Fourier-Analyse Weiere Beispiele Beispiel: Fourier-Analyse der rapezfunkion Diese is gerade und vollsymmerisch (s. B5) mi 4 a, = a = = 8 k b ν und a = k + f()cos[( k ) ω] d + Für f() gil in der ersen Vierelperiode: A = cons für < d 4 f() = A für d < + d d Dami resulier: d 4 4 a 8 + = A cos[( k A k + ) ω ] d + ( )cos[( + ) ] 4 k ω d d d 4 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 5
51 ..6 Fourier-Analyse Als Endergebnis ergib sich (nach par. Inegraion ec.): a 4A a = k cos[(k ) ω( d)] + π(k+ ) ωd + 4 bzw. nach Auflösung des Argumens im cos in zwei Ausdrücke und Umschreiben des dami resulierenden erms cos (x-y) in cos und sin Produkerme: 4Asin[(k+ ) ωd] π = sin[( k+ ) ] π(k+ ) ωd k + Die Fourier-Reihe der rapezfunkion laue dami: 4A f( ) = [sin( ωd)cos( ω) sin(3 ωd)cos(3 ω) + sin(5 ωd)cos(5 ω) ) πωd 9 5 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 5
52 ..6 Fourier-Analyse Sonderfall der rapezfunkion : Die Dreiecksfunkion (d = /4) : f() d A -/4 /4 / 3/4 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 5
53 π /..6 Fourier-Analyse Dafür ergib sich das folgende Ampliuden und Phasenspekrum: d v 8A = π ² v² π ϕ v 3 7 ν π 5 7 Koeffizienen der Sinus-Reihe erfordern ν = k + π Endergebnisse : Phase von: 8A 8A π ak =, b, k = dk =, ϕ k =, ψk = + π (k+ ) + π (k+ ) ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 53
54 ..6 Fourier-Analyse Sonderfall der rapezfunkion : Recheckfunkion mi d f() A d -/4 /4 / 3/4 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 54
55 ..6 Fourier-Analyse Bildung des Grenzüberganges miels der Regel von Bernoulli- L Hospial: c v c v 4A = vπ π v ' sin[(k + ) ωd] { sin[(k + ) ωd] } lim = lim = lim si((k + ) ωd) = si() = d ' (k + ) ωd d d (k + ) ωd π { } ϕ v v Dami folg: k+ 4 A π a = sin[(k + ) ], bk = π (k + ) 4 A π π dk+ =, ϕk+ =± sin[(k + ) ], ψ k+ = π (k + ) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 55
56 ..7 Die komplexe Form der Fourier- Reihe Allgemein gil für die Fourierreihen-Darsellung a f a b () = + ν cos( ) + ν sin( ) ν = [ νω νω ] Ausserdem gil: cos( νω) jνω jνω e + e = sin( νω) = e e j jνω jνω a e + e e e und dami : f() = + aν bν + ν = j jνω jνω jνω jνω bzw. a a + jb a jb = + + ν = ν ν jνω ν ν jνω f() e e Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 56
57 ..7 Die komplexe Form der Fourier- Reihe Nunmehr werden auch negaive Were für ν einbezogen. a c =, Mi den Abkürzungen aν jbν cν = für posiive ν aν + jbν cν = für negaive ν erhäl man Paare von Koeffizienen. Also: c ν = c * ν Dies lassen sich in der sehr kompaken Darsellung der Fourier-Reihe in ihrer komplexen Form schreiben: f() j c e νω ν ν = = Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 57
58 ..7 Die komplexe Form der Fourier- Reihe Es gil außerdem: a = R ( c ) b = I( c ) > Für die komplexen Koeffizienen resulieren dami die Besimmungsgleichungen: + a c = = (), f d ν ν ν ν ν + + aν jbν jνω cν = = ( )[cos( ) sin( )] = ( ), f νω j νω d f e d c ν + jνω = f( ) e, ν =,,,... Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 58
59 ..8 Inerpreaion der Fourier-Koeffizienen Es werden dami folgende Darsellungen der Fourier-Reihe benuz: a f a b () = + ν cos( ) + ν sin( ) ν = oder f() = oder ν = c e ν ν = [ νω νω ] jνω f() = d + d cos( νω+ ψ ) ν Verabredung ab hier: c sa c ν ν ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 59
60 ..8 Inerpreaion der Fourier-Koeffizienen - a Gleichaneil des Signals : = c = d - Scheielwere oder Ampliuden der Fourier-Komponenen: a, b, c und d - Nullphasenwinkel (Phase) der cosinusförmigen Schwingungen: ψν - Grundschwingung: d cos( ω+ ψ ) ν ν ν ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 6
61 ..9 Anwendung der Fourier-Reihe bei einem Nezwerk Bei cosinus-förmiger Spannung u () = uˆ cos( νω+ ϕu ) wird üblicherweise ein j u j komplexer Scheielwer uˆ ue ˆ ϕ ω = mi u( ) = Re{ ue ˆ } zugeordne. Nun kann man für jede periodische Funkion ansezen: Auch bei elekrische Nezwerken nuz man die Darsellung (der Spannungen und Sröme) in Kosinusform: u () = ue jνω mi ν = v u () = u + uˆ cos( νω+ ϕ ) ν = i () = i + iˆ cos( νω+ ϕ ) ν = v v * uˆ v, für ν uv = u für ν = uˆ v für ν iν uν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 6
62 ..9 Anwendung der Fourier-Reihe bei einem Nezwerk Beispiel-Nezwerk: Reihen-Schwingkreis u () i() u () u () L R û C / Hier is gegeben : u () u sin( ω) mi ω= π/ ˆ = Daraus folg: Zu berechnen sind : i () und u () uˆ 4uˆ u () = cos( kω) (4 ) π k = π k L Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 6
63 ..9 Anwendung der Fourier-Reihe bei einem Nezwerk Lösungsansaz : - Verwendung der Impedanz für jede Frequenz kω : - Angabe der Fourier-Reihe zu u () 4uˆ in komplexer Form mi: uˆ k = π (4k ) u () = k= π k ˆ u e (4 ) jkω Z k uˆ = k iˆ k Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 63
64 ..9 Anwendung der Fourier-Reihe bei einem Nezwerk Impedanz bzw. Srom des Reihen-Schwingkreises für eine besimme Frequenz kω : Zk = R+ jx mi k Xk = kωl k ω C Dann gil für den Srom : und i = u / Z uˆ i () = ik =. π (4k ) R+ jx jkω e k= k= k Mi der Euler schen Formel resulier: uˆ i ( ) =..[cos( kω) + jsin( kω)] π k R+ jx k = (4 ) k k k k Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 64
65 ..9 Anwendung der Fourier-Reihe bei einem Nezwerk Nach einer Umformung (per konjugier komplexer Erweierung des Nenners) ergib sich : uˆ Rcos( k ) Xksin( k ) Rsin( k ) Xk cos( k ) i () ω + ω j ω ω = + k= π (4k ) R + Xk R + Xk Werden die Eigenschafen der Funkionen ( cos, sin ) für +/- k ausgenuz, so gil mi X k = Xk (mi Wegfall der Imaginäreils!): i () = 4uˆ Rcos( kω) + X sin( kω) k k = π (4k ) R + Xk Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 65
66 ..9 Anwendung der Fourier-Reihe bei Die Spannung an der Spule erhäl man über: einem Nezwerk u L () = () di() ul = L d 4uˆ kωl[ Rsin( kω) Xk cos( kω)] π (4k ) R + X k = k Die Ergebnisse lassen sich auch in Polarform darsellen: 4uˆ kωl R ul( ) =. cos[( kω) + arcan( )] π (k ) + X k = R Xk k 4uˆ k ( ) =. cos[( kω) arcan( )] k = π (k ) R + X R k i X Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 66
67 .. Formulierung der Parseval schen Gleichung - Berache werden zwei im allgemeinen nich-sinusförmige periodische Funkionen f () und f () mi gleicher Periodendauer : - Die ensprechenden Fourier-Reihen lauen: + jνω jνω () = ν ν = () ν = f C e mi C f e d und + jµω jµω () = µ µ = () µ = f D e mi D f e d - Für das Produk beider Funkionen gil : und zugleich da periodisch : jνω jµω ν µ ν = µ = f () f () C e. D e = + jkω jkω () () = k mi k = () () k = f f E e E f f e d Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 67
68 .. Formulierung der Parseval schen Gleichung Weierhin gil: + jνω jµω jkω Ek = Cν e. Dµ e e d ν = µ = + j( ν + µ k) ω Ek = Cν Dµ e d ν = µ = bzw. + j( ν + µ k) ω Ek = CI ν mi I= Dµ e d ν = µ = Man kann zeigen, dass I verschieden von Null is nur bei: (wg. Orhogonaliä von cos(nx) und sin(nx) ) ν + µ k = Dami wird der Inegrand idenisch mi und es gil: I= D = D µ= µ µ µ= Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 68
69 .. Formulierung der Parseval schen Gleichung die Fourier-Koeffizienen des Produkes f () f () E = C D = C D k ν µ ν k ν ν = µ = ν= infolge ν + µ k = bzw. µ = k v Besimmung des Gleichaneils (zeil. Mielwer) des Produkes f ( ) f ( ) über k = : E + E = f (). f () d = Cν. D ν = ν Es gib diverse Anwendungen dieser Beziehung (Besimmung des Inegrals im Zei- oder Frequenzbereich)! Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 69
70 .. Formulierung der Parseval schen Gleichung Alle komplexen Fourier-Koeffizienen besizen die Eigenschaf : * * C = C und D = D ν ν ν ν Dami läß sich die folgende Formel umschreiben von + E = f() f() d = CνD ν = CνD ν + CD + CνD v = zu: * * { ν ν} { ν ν} E = Re C D = Re C D ν= ν= ν= ν= * * C νdν CD CD ν v CD ( C νdv C vdv) ν= ν= ν= + + = + + = * ( ν v ( v v) ) Re ν v ν= ν= ν= Dies is die Parseval sche Gleichung { } = CD + C D + C D = CD + C D Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 7
71 .. Die Leisung bei nich-sinusförmigen periodischen Nezwerkgrößen Die elekrische Energie pro Periode (Wirkleisung) an einem ohmschen Widersand beräg: ()() () () PW = u i d u d R i d = = R Anwendung der Parseval schen Gleichung für diesen Sonderfall: f () = f () = f () und dami f f f () () = () ergib: + * E = f () d Re C C Re C e = = ν= ν= Cν C Cν ν= ν= = = + { } { j( C C )} ν ν ν v v Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 7
72 .. Die Leisung bei nich-sinusförmigen periodischen Nezwerkgrößen Mi a, aν jbν c = = C cν = Cν = ν folg: + a av + bv a av + bv f () d = c + cν = + = + 4 ν= ν= ν= Wenn f() Spannungs- oder Sromcharaker ha, werden die ensprechenden Spekralgrößen aν, bν und cν die Wirkleisungsverhälnisse des ensprechenden Nezwerkelemenes beschreiben. Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 7
73 .. Die Leisung bei nich-sinusförmigen periodischen Nezwerkgrößen Berache wird nun ein Einor (nich nur ohmsch) mi nichsinusförmigen periodischen Nezwerkgrößen u() und i(): U() i() Für die Wirkleisung gil: Einor und + + u( ) = f ( ) = C e ν = i( ) = f ( ) = D e ν = ν = PW = uid ()() f() f() d CD Re C D = = + ν * { ν ν} = CD + Re ν = µ jν ω jvω * { CD ν ν } Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 73
74 .. Die Leisung bei nich-sinusförmigen periodischen Nezwerkgrößen Uner Berücksichigung der Zusammenhänge ensprechend S. 4 C = U ˆ, D = I, C = u, D = i ˆ folg : ν ν ν ν * * { ˆ ˆ } Re{ ˆ ˆ } P = U I + Re u i = U I + u i W v v v v ν= ν= Dami is die Gesamleisung über die Summe aller Einzelleisungen jeder Spekrallinie zu besimmen! Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 74
75 .. Die Beureilung der Abweichung vom sinusförmigen Verlauf periodischer Funkionen Definiion des Effekivwers einer periodischen Funkion: + () eff = () f f d Die Parseval sche Gleichung gesae die Besimmung des Effekivwers über die Fourier-Koeffizienen (bzw. über die zugehörigen Effekivwere): f () eff = ν = c ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 75
76 .. Die Beureilung der Abweichung vom sinusförmigen Verlauf periodischer Funkionen - Der Effekivwer für eine periodische Spannung u() beräg: uˆ ν eff ν ν= ν= Ueff = U + = U U û ν : Gleichaneil von u() : Scheielwer Ueff ν = uˆ ν / : Effekivwer der ν -en eilspannung (Frequenz: νω) - Der Effekivwer für einen periodischen Srom beräg sinngemäß: ˆ i ν eff ν ν= ν= I = Ieff = I + = I Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 76
77 .. Die Beureilung der Abweichung vom sinusförmigen Verlauf periodischer Funkionen Bei reinen Wechselgrössen, also ohne Gleichaneil gil: a = Ansonsen is f() eine Mischgrösse (Gleichaneil und Wechselaneil der nich-periodischen Funkion f() is zugleich vorhanden). a Also gil für Mischgrößen: Dafür is der Schwingungsgehal s definier (Aneil AC am Gesamsignal): s Ueff ν Ueff ν ν= ν= = = U eff ν = U eff ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 77
78 .. Die Beureilung der Abweichung vom sinusförmigen Verlauf periodischer Funkionen Die Abweichung vom sinusförmigen Ablauf kann durch den Grundschwingungsgehal g beschrieben werden: g U = = U eff eff eff U ν = U effν Der Oberschwingungsgehal k ( Klirrfakor ) beräg: k U eff ν U effν ν = ν = = = U eff ν = U effν g + k = Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 78
79 .. Die Beureilung der Abweichung vom sinusförmigen Verlauf periodischer Funkionen Zusäzlich gib es weiere Definiionen mi Formfakor und Scheielfakor: Formfakor : k f = ν = U eff ν u ( ) d Scheielfakor für Signale ohne Gleichaneil: k a = u () ν = max U eff ν Bei rein sinusförmigen Verlauf erhäl man: π k f =, und ka = =, 4 Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 79
80 ..3 Zusäzliche Eigenschafern der Fourier-Reihe Lineariä Zeiverschiebung k s( ) ergib Reihe mi k c v a s ( ) + b s () ergib Reihe mi a c + b c v v s ( ) ergib Reihe mi c e v jvω Spiegelung s( ) ergib Reihe mi c * v Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 8
81 Grundlagen der Elekroechnik 3 Kapiel.3 Beschreibung aperiodischer Zeivorgänge miels der Fourier-ransformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 8
82 .3. Vorbemerkungen Ansaz: Enwicklung der Fourier-ransformaion aus der Fourier-Reihe durch Überführung periodischer Funkion in aperiodischen Impuls Beispiel : Berache wird ein periodischer Recheckimpuls u() sei hier eine gerade Funkion f() U für < < = sons i i () u ρ ρ ρ - Es soll eine Fourier-Analyse dieses Signals durchgeführ werden Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 8
83 .3. Vorbemerkungen Lösung : c =+ i i = = U d = U i ν = i = sin( νω ) cos( νω ) νω i = aν jbν aν U cν = = = U d = b π mi ω = πv i πv i sin sin i sin νπ U Ui = = c ν νω i νπ i i Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 83
84 .3. Vorbemerkungen bzw: i sin νπ U = = U aν c = si νω i i i ν ( νω ) i Dami gil: U i = νπ e ν = ν = i () si u jνω C C C C 3 C 4 C 5 = C = sin( ν x) ν x C 5 =. 5 Skizze des Spekrums von u() für den Fall, ν i =, Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 84
85 .3. Das Fourier-Inegral Im folgenden wird weier die Fourier-Reihe einer periodischen Funkion f() unersuch. Die Periode sei hier: -o/ f() / f() Dabei sollen die nachsehenden Voraussezungen gemach werden : ) f() sei seig. ) In jeder endlichen Periodendauer möge die Funkion = c e jνω den Dirichle schen Bedingungen genügen 3 ) Bei beliebiger Periodendauer sei f() absolu inegrierbar ν = = π ω ν Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 85
86 .3. Das Fourier-Inegral Die folgende Darsellung geh aus von einem periodischem Signal welches in ein nich-periodisches Signals überführ wird. Ansaz: Vergrößerung der Periodendauer - also per: lim Jeder erm in komplexer Fourier-Reihe ensprich einer Linie im Spekrum. Die Linienabsände beragen: ω = π / In einem Inervall ω um einen beliebigen Frequenzpunk ω liegen m Linien mi der Anzahl: ω m = = ω ω π Bei genügend kleinem Inervall resulier dann nur geringer Unerschied der m einzelnen erme der komplexer Fourier-Reihe zueinander. Konsequenz: Zusammenfassung dieser erme is erlaub! Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 86
87 Für.3. Das Fourier-Inegral In jedem Inervall mi m Linien gil dami für dessen Beirag zur Reihe: jvω jvω m c ve = ω c ve π kann man dann die Inervalle infiniesimal klein wählen (wenn m unveränder bleiben soll) Dami ergib sich für den Beirag jedes Inervalls zur Reihe: jv ω mi daher: j ω dω c ve vω ω c ve dω π π Außerdem läß sich abkürzend schreiben: c v = F ( ω ) Insgesam resulier dami: + jω f () = ( ) F ω e dω π Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 87
88 .3. Das Fourier-Inegral Es gil also: + jω f() = F( ω) e dω π jνω mi c ν = f ( e ) d = + = Nunmehr folg wegen c ( ) und lim : v= Fω Das Fourierspekrum bzw. die Fourier ransformiere der Funkion f() kann auch dargesell werden über: F { } + jω ƒ( ) = F( ω) = f ( e ) d Das Symbol dazu: f() F( ω) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 88
89 .3.3 Die Fourier-Rückransformaion Die Funkion f() läß sich also miels ihres Fourierspekrums darsellen über: jω f () = ( ) F ω e dω π Die (Rück)ransformaion zwischen Bildbereich und Originalbereich kennzeichne man so: F( ω ) f () F ( ω ) Ampliude x Zei oder Ampliude Frequenz Die Exisenz des Fourier-Inegrals is dann gesicher wenn f() absolu inegrierbar is: Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 + ha nich Ampliudencharaker (wie bei F.-Reihe), sondern es is eine Ampliudendiche mi der Dimension : + f () d S = cons Fachgebie Nachrichenechnische Syseme S. 89
90 .3.4 Inerpreaion und Zusammenfassung Berachung eines Signals s() aus dem per idealer BP-Filerung nur Aneile innerhalb eines besimmen Frequenzbandes exrahier werden. Die Filerung erfolge so schmalbandig, dass sich darin das Spekrum (und die Exponenialfunkion) nur unwesenlich änder. Für diesen exrahieren Aneil g() folg: + + jω jω jω g ( ) = S( ω) e dω S( ω) e dω S( ω) e dω π = π + π ω jω jω ( S( ω) e + S( ω) e ) π ω jω * = Re{ S( ω) e } wegen S( ω) = S ( ω) π ω ω = S ω e e = S ω ω+ S ω π π j S( ω) jω Re{ ( ) } ( ) cos( ( )) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 9
91 .3.4 Zusammenfassung und Inerpreaion Die Fourierransformaion is (uner gegebenen Vorr.) also uner Bezug auf die berachee Bandbreie und bei der beracheen Frequenz ein Maß für die Ampliude und die Phasenlage einer Signalaneils (Signalkomponene). Die Anwendung der Fourierransformaion erlaub: ) Ein im Zeibereich bekannes Signal gleichwerig im Frequenzbereich über die zugeordnee Fourierransformaion zu beschreiben ) Aus einer bekannen Fourier-ransformieren die Zeifunkion zurückzugewinnen Die Fourierransformaion is ein wichiges Werkzeug der Elekroechnik, Regelungsechnik, Physik ( Opik, Mechanik, ). Zugleich bilde diese die Grundlage der Laplace-ransformaion, Z- ransformaion und der diskreen Fourierransformaion incl. der FF. Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 9
92 .3.5 Beispiele zur Fourierransformaion Beispiel : ρ f() U ρ ρ ρ jω jω e jω ρ F( ω) = U e d = U = U e ρ jω jω e jω ρ ρ ρ sin ω ( ) F ω U U si ω ω ρ = ρ = ρ ρ Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 9
93 .3.5 Beispiele zur Fourierransformaion Unersuchung der Hüllkurve von 9% der Impulsenergie innerhalb roen Bereichs F ( ω) U si ω ρ = ρ F ( ω ) 9% 9% F( ω).64 ρ π π ρ π ρ ρ π ω ρ π ρ π ω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 93
94 .3.5 Beispiele zur Fourierransformaion Beispiel : Der Diracimpuls ' A f () " A " ρ ' ρ δ () = lim rec( ) p A= A = A = = = = = ' '' ' '' ρ. ρ.... ' ρ '' ρ ρ ρ + + jω ( ω) = δ() = δ() = F e d ed p p A ρ Also gil: δ () ρ ' ρ " ρ ρ ρ " ' ρ ω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 94
95 .3.5 Beispiele zur Fourierransformaion δ() ha diverse Namen: Soßfunkion, Dirac-Disribuion oder Diracimpuls ec. f ( x) x x x x x x + Weierhin gil: h = x x für x < ( x x) x x f x rec für x x x x x für ( x + x) < x + ( ) = ( ) = ( ) < < ( + ) x x x Normale Schreibweise: f ( xdx ) = f( x) = δ ( x x ) Ausserdem δ( x x ) g ( xdx ) = δ( x x) g ( x ) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 95
96 .3.5 Beispiele zur Fourierransformaion Beispiel 3 : f() für < = a e für < und endlichem a F { } + + jω jω a jω f() = F( ω) = f() e d = e d+ e e d ( a+ jω ) ( a+ jω ) e = e d = = ( a+ jω) a+ jω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 96
97 .3.5 Beispiele zur Fourierransformaion Die Spekralfunkion in reeller Form laue dami für: jω F( ω) = f( ) e d = f( )(cos( ω) jsin( ω)) d= a( ω) jb( ω)! + a( ω) = f ( )cos( ω) d { F ω } = Re ( ) + b( ω) = f( )sin( ω) d { F ω } = Im ( ) Für die ransformiere auf der lezen Seie gil: a jω a ω F( ω) =. = j = a( ω) jb( ω) a+ jω a jω a² + ω² a² + ω² Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 97
98 .3.5 Beispiele zur Fourierransformaion Die Spekralfunkion in reeller Form: a( ω) a( ω) b( ω) = = a a² + ω² ω a² + ω² a a b( ω) a ω ω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 98
99 .3.5 Beispiele zur Fourierransformaion Beispiel 4 : Sprungfunkion f () = ε () Hier gil nich: + f () d S = cons Daher besonderer Ansaz mi Grenzwerbildung zur Beschreibung der Sprungfunkion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 99
100 .3.5 Beispiele zur Fourierransformaion Ansaz für die Sprungfunkion: für < f() = e a für < Die Sprungfunkion ergib sich dami zu : f() = ε () = lim { f() } a F ( ω ) F( ω ) = a + jω a ω = j a² + ω ² a² + ω ² Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
101 .3.5 Beispiele zur Fourierransformaion a ) Besimmung des Realeils der Fourier-ransformieren für den Einheissprung : a Re { F( f( )) } = a² + ω² a für ω = lim Re { F( f( )) } = lim = a a a² + ω² für ω Dies läß sich miels eines Diracsoßes beschreiben. Dazu Besimmung dessen Flächeninhales (Gewiches) A: a ω π π A= dω = arcan = = π a² + ω² a Dami gil : { F } + Re ( f ( )) = πδ( ω) Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
102 .3.5 Beispiele zur Fourierransformaion b ) Besimmung des Imaginäreils der Fourier-ransformieren für den Einheisprung: ω Im { F( f( )) } = lim Im { F( f( )) } = lim = a a a² + ω² ω Dami gil: F{ } f() = πδ ( ω) j ω { F{ f }} Re ( ) πδ( ω) ω { F{ f }} Im ( ) ω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S.
103 .3.5 Beispiele zur Fourierransformaion Beispiel 5 : α f() = f e für α > + jω F( ω) = f( ) e d + + a j ω a j ω j ω = f e e d = f e ( e + e ) d a jω a jω fe e fe e f f = + = + a jω a+ jω a+ jω a jω α f f α f () α F( ω) f 3f e α F( ω) = f a + ω a α 3 α 3 ω Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 Fachgebie Nachrichenechnische Syseme S. 3
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Prof. Dr.-Ing. Ingolf Willms und Prof. Dr.-Ing. Adalber Beyer und basierend auf dem Scrip von Prof. Dr.-Ing. Ingo Wolff Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik
Grundlagen der Elekroechnik 3 Prof. Dr.-Ing. Ingolf Willms und Prof. Dr.-Ing. Adalber Beyer und basierend auf dem Scrip von Prof. Dr.-Ing. Ingo Wolff Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik
Kontinuierliche Fourier Transformation
 Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Kapitel 2: Fourieranalyse. Analoge, nichtperiodische Signale
 ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Charakterisierung des Systems R C. Faltungsintegral. Faltungsintegral (anschaulich) Faltungsintegral (anschaulich) 1. Übertragungsfunktion zb
 Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
5. Signalverarbeitung
 5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
1. Signalbeschreibung im Zeitbereich
 . Signalbeschreibung im Zeibereich SiSy, Signal, - Inhalsverzeichnis. Signalklassen * Kapiel 3.4 (Energie und Leisung).2 Symmerie-Eigenschafen von Signalen.3 Verschiebung und Dehnung eines Zeisignals *
. Signalbeschreibung im Zeibereich SiSy, Signal, - Inhalsverzeichnis. Signalklassen * Kapiel 3.4 (Energie und Leisung).2 Symmerie-Eigenschafen von Signalen.3 Verschiebung und Dehnung eines Zeisignals *
Leseprobe. Ines Rennert, Bernhard Bundschuh. Signale und Systeme. Einführung in die Systemtheorie. ISBN (Buch):
 Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Fouerierreihen - eine Einführung
 HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
10. Wechselspannung Einleitung
 10.1 Einleiung In Sromnezen benuz man sa Gleichspannung eine sinusförmige Wechselspannung, uner anderem weil diese wesenlich leicher zu erzeugen is. Wie der Name es sag wechsel bei einer Wechselspannung
10.1 Einleiung In Sromnezen benuz man sa Gleichspannung eine sinusförmige Wechselspannung, uner anderem weil diese wesenlich leicher zu erzeugen is. Wie der Name es sag wechsel bei einer Wechselspannung
Vielseitige Darstellungen von Drehstromsignalen
 Vielseiige Darsellungen von Drehsromsignalen Die Leisungs- und Energie-Analysaoren Qualisar+ dienen zur soforigen Darsellung aller wesenlichen Eigenschafen eines Drehsromnezes. Zeiliche Darsellung Die
Vielseiige Darsellungen von Drehsromsignalen Die Leisungs- und Energie-Analysaoren Qualisar+ dienen zur soforigen Darsellung aller wesenlichen Eigenschafen eines Drehsromnezes. Zeiliche Darsellung Die
Kennzeichnung stochastischer Prozesse
 . Kennzeichnung sochasischer Prozesse...1.0. Der Plaz der sochasischen Prozesse in der Regelungsechnik...1.1. Beschreibung sochasischer Prozesse im Zeibereich...3.1.1. Die Auokorrelaionsfunkion (AKF)...3.1..
. Kennzeichnung sochasischer Prozesse...1.0. Der Plaz der sochasischen Prozesse in der Regelungsechnik...1.1. Beschreibung sochasischer Prozesse im Zeibereich...3.1.1. Die Auokorrelaionsfunkion (AKF)...3.1..
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Grundlagen der Nachrichtentechnik 1 Communications 1
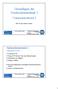 Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
Leseprobe. Daniel von Grünigen. Digitale Signalverarbeitung. mit einer Einführung in die kontinuierlichen Signale und Systeme
 Leseprobe Daniel von Grünigen Digiale Signalverarbeiung mi einer Einführung in die koninuierlichen Signale und Syseme ISBN (Buch: 978-3-446-4479- ISBN (E-Book: 978-3-446-4399-7 Weiere Informaionen oder
Leseprobe Daniel von Grünigen Digiale Signalverarbeiung mi einer Einführung in die koninuierlichen Signale und Syseme ISBN (Buch: 978-3-446-4479- ISBN (E-Book: 978-3-446-4399-7 Weiere Informaionen oder
Von der Fourier-Reihe zum Fourier-Integral
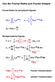 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Näherung einer Wechselspannung
 HL Seyr Wechselsromparabel Seie 1 von 1 Nieros Bernhard bernhard.nieros@hl-seyr.ac.a Näherung einer Wechselspannung Mahemaische / Fachliche Inhale in Sichworen: Polynomfunkion, allgemeine Sinusschwingung,
HL Seyr Wechselsromparabel Seie 1 von 1 Nieros Bernhard bernhard.nieros@hl-seyr.ac.a Näherung einer Wechselspannung Mahemaische / Fachliche Inhale in Sichworen: Polynomfunkion, allgemeine Sinusschwingung,
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Leistungselektronik Grundlagen und Standardanwendungen. Übung 3: Kommutierung
 Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
1 Abtastung, Quantisierung und Codierung analoger Signale
 Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Diskrete Integratoren und Ihre Eigenschaften
 Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
PHYSIK III. Serie 12, Musterlösung
 Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Signal- und Systemtheorie for Dummies
 FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
4.2.5 Energie und Energiedichte im Magnetfeld
 4..5 Energie und Energiediche im Magnefeld - die magneische Energie W ui dψ ( ) i i d m ψ ψ Ψ d dw mag V dφ V V Φ Wmag V ( Φ ) dφ Tuorium jeweils Miwoch 3: Uhr Hu - die Energiediche im magneischen Feld
4..5 Energie und Energiediche im Magnefeld - die magneische Energie W ui dψ ( ) i i d m ψ ψ Ψ d dw mag V dφ V V Φ Wmag V ( Φ ) dφ Tuorium jeweils Miwoch 3: Uhr Hu - die Energiediche im magneischen Feld
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Fourier- und Laplace- Transformation
 Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Ministerium für Schule und Weiterbildung NRW M LK HT 4 Seite 1 von 9. Unterlagen für die Lehrkraft. Abiturprüfung Mathematik, Leistungskurs
 Seie von 9 Unerlagen für die Lehrkraf Abiurprüfung 9 Mahemaik, Leisungskurs. Aufgabenar Lineare Algebra/Geomerie ohne Alernaive. Aufgabensellung siehe Prüfungsaufgabe. Maerialgrundlage 4. Bezüge zu den
Seie von 9 Unerlagen für die Lehrkraf Abiurprüfung 9 Mahemaik, Leisungskurs. Aufgabenar Lineare Algebra/Geomerie ohne Alernaive. Aufgabensellung siehe Prüfungsaufgabe. Maerialgrundlage 4. Bezüge zu den
Grundlagen der Elektrotechnik II Übungsaufgaben
 Grundlagen der Elekroechnik II Übungsaufgaben 24) ransiene -eihenschalung Die eihenschalung einer Indukiviä ( = 100 mh) und eines Widersands ( = 20 Ω) wird zur Zei = 0 an eine Gleichspannungsquelle geleg.
Grundlagen der Elekroechnik II Übungsaufgaben 24) ransiene -eihenschalung Die eihenschalung einer Indukiviä ( = 100 mh) und eines Widersands ( = 20 Ω) wird zur Zei = 0 an eine Gleichspannungsquelle geleg.
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
Aufgabensammlung. Signale und Systeme 1. Einführung in die Signal- und Systemtheorie. Kontaktinformation: Dr. Mike Wolf, Tel. 2619
 Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Kapitel 2: Spektrum periodischer Signale (Fourierreihe)
 ZHW, SiSy, Rumc, - Kapiel : Sperum periodischer Signale (Fourierreihe) Signale önnen im Zeibereich analysier werden. Es is aber häufig voreilhaf, Signale im Frequenzbereich zu analysieren. In diesem Kapiel
ZHW, SiSy, Rumc, - Kapiel : Sperum periodischer Signale (Fourierreihe) Signale önnen im Zeibereich analysier werden. Es is aber häufig voreilhaf, Signale im Frequenzbereich zu analysieren. In diesem Kapiel
Seminar Praktikum Communications 1. Signalparameter im Zeit- und Frequenzbereich
 Seminar Prakikum Communicaions 1 Seminarversuch 2 Signalparameer im Zei- und Frequenzbereich Fachgebie: Nachrichenechnische Syseme Name: Mar.-Nr.: Bereuer: Daum: N S Die Vorbereiungsaufgaben müssen vor
Seminar Prakikum Communicaions 1 Seminarversuch 2 Signalparameer im Zei- und Frequenzbereich Fachgebie: Nachrichenechnische Syseme Name: Mar.-Nr.: Bereuer: Daum: N S Die Vorbereiungsaufgaben müssen vor
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Flugzeugaerodynamik I Lösungsblatt 2
 Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
5 Stromrichter. (Gl. (5.1)) Beispiel 5.2: An den gezeigten Diodenkennlinien sind folgende Berechnungen anzustellen:
 5 Sromricher Sromricher haben beim Seuern und egeln von Elekroenergiesysemen eine große Bedeuung. Sie werden zum Gleich- wie auch zum Wechselrichen eingesez. In Sromrichern werden Dioden, ransisoren (IGBs
5 Sromricher Sromricher haben beim Seuern und egeln von Elekroenergiesysemen eine große Bedeuung. Sie werden zum Gleich- wie auch zum Wechselrichen eingesez. In Sromrichern werden Dioden, ransisoren (IGBs
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
i(t) t 0 t 1 2t 1 3t 1
 Aufgabe 1: i 0 0 1 2 1 3 1 1. Eine Kapaziä werde mi einem recheckförmigen Srom gespeis (s.o.). Berechnen Sie den Verlauf der Spannung für den Anfangswer u( 0 )=0V mi 0 = 0s. 2. Skizzieren Sie den eisungsverlauf
Aufgabe 1: i 0 0 1 2 1 3 1 1. Eine Kapaziä werde mi einem recheckförmigen Srom gespeis (s.o.). Berechnen Sie den Verlauf der Spannung für den Anfangswer u( 0 )=0V mi 0 = 0s. 2. Skizzieren Sie den eisungsverlauf
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Grundlagen zeitveränderlicher Signale, Analyse von Systemen der Audio- und Videotechnik
 3. Nichperiodische Signale 3.1 ω ω ω dω Nichperiodische Signale endlicher Länge Die Fourierransformaion zerleg nichperiodische Signale endlicher Länge in ein koninuierliches endliches Frequenzspekrum.
3. Nichperiodische Signale 3.1 ω ω ω dω Nichperiodische Signale endlicher Länge Die Fourierransformaion zerleg nichperiodische Signale endlicher Länge in ein koninuierliches endliches Frequenzspekrum.
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
7. Funktionalgleichung der Zeta-Funktion
 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Nachrichtentechnik 2 5 Zwei Zufallsvariablen, Folgen von Zufallsvar.
 Nachrichenechnik 5 Zwei Zufallsvariablen, Folgen von Zufallsvar. Folgen von Zufallsvariablen Definiion 5.: Gemeinsame Wahrscheinlichkeisvereilung F x,x,x 3,...,x N (x,x,x 3,..., x N P({x x } {x x } {x
Nachrichenechnik 5 Zwei Zufallsvariablen, Folgen von Zufallsvar. Folgen von Zufallsvariablen Definiion 5.: Gemeinsame Wahrscheinlichkeisvereilung F x,x,x 3,...,x N (x,x,x 3,..., x N P({x x } {x x } {x
Vom singenden Draht zum DVB-C
 Vom singenden Drah zum DVB-C Is digiale Kommunikaion effiziener? Gerolf Ziegenhain TU Kaiserslauern Übersich Einleiung Begriffsklärung Ziel Analoge Modulaion AM FM Muliplexverfahren Digiale Modulaion QPSK
Vom singenden Drah zum DVB-C Is digiale Kommunikaion effiziener? Gerolf Ziegenhain TU Kaiserslauern Übersich Einleiung Begriffsklärung Ziel Analoge Modulaion AM FM Muliplexverfahren Digiale Modulaion QPSK
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Zeitreihenökonometrie
 Zeireihenökonomerie Kapiel 4 Schäzung univariaer Zeireihenmodelle Y = c+ α Y + + α Y + ε + βε + + β ε p p q q Problem: Direke Schäzung der Parameer α,, αp und β,, βq über OLS nich möglich, da die Residuen
Zeireihenökonomerie Kapiel 4 Schäzung univariaer Zeireihenmodelle Y = c+ α Y + + α Y + ε + βε + + β ε p p q q Problem: Direke Schäzung der Parameer α,, αp und β,, βq über OLS nich möglich, da die Residuen
Elektrodynamik II - Wechselstromkreise
 Physik A VL36 (18.1.13 Elekrodynamik II - Wechselspannung und Wechselsrom Wechselspnnung durch Indukion Drehsrom Schalungen mi Wechselsrom Kirchhoff sche h egeln Maschenregel bei Indukiviäen und Kapaziäen
Physik A VL36 (18.1.13 Elekrodynamik II - Wechselspannung und Wechselsrom Wechselspnnung durch Indukion Drehsrom Schalungen mi Wechselsrom Kirchhoff sche h egeln Maschenregel bei Indukiviäen und Kapaziäen
Informationstechnik. Script zur Vorlesung
 Informaionsechnik Scrip zur Vorlesung Prof. J. Waler Sand April 4 6.4.4 Prof. J. Waler, FH Karlsruhe, Molkesr. 3, 7633 Karlsruhe; el.: 7-95-79 Daei:445_k_info.doc Seie Einführung in die Informaionsechnik
Informaionsechnik Scrip zur Vorlesung Prof. J. Waler Sand April 4 6.4.4 Prof. J. Waler, FH Karlsruhe, Molkesr. 3, 7633 Karlsruhe; el.: 7-95-79 Daei:445_k_info.doc Seie Einführung in die Informaionsechnik
Signale - Fourieranalyse. Roland Küng, 2010
 Signale - Fourieranalyse Roland Küng, Moivaion Digial Radio Mondial Analog Modulaion AM/FM Digial Modulaion hp://www.drm.org/?page_id5 Moivaion Grenzfrequenz Filer? Bandbreie MIC?.5. 5.. 5. -.5. 5 -.5..5..5
Signale - Fourieranalyse Roland Küng, Moivaion Digial Radio Mondial Analog Modulaion AM/FM Digial Modulaion hp://www.drm.org/?page_id5 Moivaion Grenzfrequenz Filer? Bandbreie MIC?.5. 5.. 5. -.5. 5 -.5..5..5
7. Gewöhnliche Differentialgleichungen
 1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
Zeit (in h) Ausflussrate (in l/h)
 Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
sin = cos = tan = Sinus und Cosinus im rechtwinkligen Dreieck Aufgabe: Berechnen Sie die fehlende Seitenlänge und den Winkel. Gegenkathete Hypotenuse
 Sinus und Cosinus im rechwinkligen Dreieck Ankahee Hpoenuse. Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Aufgabe: Berechnen Sie die fehlende Seienlänge und den Winkel.
Sinus und Cosinus im rechwinkligen Dreieck Ankahee Hpoenuse. Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Aufgabe: Berechnen Sie die fehlende Seienlänge und den Winkel.
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Die Untersuchungen beschränken sich auf harmonische Wechselspannungen und -ströme
 WS 8. Wechselsröme 8.1 Einleiung n Wechselsromkreisen spielen neben Ohmschen Widersänden auch Kondensaoren (Kapaziäen) und Spulen (ndukiviäen) wichige Rolle. n diesem Versuch soll am Beispiel einfacher
WS 8. Wechselsröme 8.1 Einleiung n Wechselsromkreisen spielen neben Ohmschen Widersänden auch Kondensaoren (Kapaziäen) und Spulen (ndukiviäen) wichige Rolle. n diesem Versuch soll am Beispiel einfacher
Kondensator und Spule im Gleichstromkreis
 E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
Zeitreihenökonometrie
 Zeireihenökonomerie Kapiel 1 - Grundlagen Einführung in die Verfahren der Zeireihenanalyse (1) Typischerweise beginn man mi einer Beschreibung der jeweils zu unersuchenden Zeireihe (graphisch) Trendverhalen,
Zeireihenökonomerie Kapiel 1 - Grundlagen Einführung in die Verfahren der Zeireihenanalyse (1) Typischerweise beginn man mi einer Beschreibung der jeweils zu unersuchenden Zeireihe (graphisch) Trendverhalen,
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Dr.-Ing. habil. Jörg Wollnack S.1. Fourier-Reihen, und Maschinendynamik. Kuka. Schaublin
 .6.8 S. Fourier-Reihen, Fourier- und Laplace-Transformaion und Maschinendynamik Kuka Schaublin .6.8 S. Fourier-Reihe .6.8 S.3 Allgemeine Fourier-Reihe K g ( ) ag( ), a = k k k k = R Minimierungsproblem:
.6.8 S. Fourier-Reihen, Fourier- und Laplace-Transformaion und Maschinendynamik Kuka Schaublin .6.8 S. Fourier-Reihe .6.8 S.3 Allgemeine Fourier-Reihe K g ( ) ag( ), a = k k k k = R Minimierungsproblem:
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Regelungstechnik. Steuerung. Regelung. Beim Steuern bewirkt eine Eingangsgröße eine gewünschte Ausgangsgröße (Die nicht auf den Eingang zurückwirkt.
 Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Sinus und Cosinus im rechtwinkligen Dreieck ( )
 Sinus und Cosinus im rechwinkligen Dreieck (6.8.8) Ankahee. Hpoenuse Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Was ha das rechwinklige Dreieck mi Schwingungen
Sinus und Cosinus im rechwinkligen Dreieck (6.8.8) Ankahee. Hpoenuse Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Was ha das rechwinklige Dreieck mi Schwingungen
Theoretische Physik I/II
 Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Bildmaterial zur Vorlesung Regelungstechnik Teil I Die Regelstrecke. Wintersemester 2014 Prof. Dr.-Ing. habil. Klaus-Peter Döge
 Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Praktikum Grundlagen der Elektrotechnik Versuch 5. Matrikelnummer:... ...
 FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
Übungsblatt 4 Lösungsvorschläge
 Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Der kinetische Ansatz zur Beschreibung von Selbstorganisationsprozessen. mögliche Variationen und Erweiterungen: diskrete Gleichungen (endliches t):
 Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Prüfung Finanzmathematik und Investmentmanagement 2011
 Prüfung Finanzmahemaik und Invesmenmanagemen 0 Aufgabe : (0 Minuen) a) Auf der Grundlage einer Lagrange-Opimierung ergib sich die folgende funkionale Form für die (, ) -Koordinaen der (rein riskanen) Randporfolios
Prüfung Finanzmahemaik und Invesmenmanagemen 0 Aufgabe : (0 Minuen) a) Auf der Grundlage einer Lagrange-Opimierung ergib sich die folgende funkionale Form für die (, ) -Koordinaen der (rein riskanen) Randporfolios
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Regelungstechnik 1 - Grundglieder: Analyse im Zeit und Frequenzbereich
 Regelungsechnik - Grundglieder: Analyse im Zei und Frequenzbereich Vorberachungen: Das Überragungsverhalen von linearen Regelkreiselemenen wird vorwiegend durch Sprunganworen bzw. Übergangsfunkionen sowie
Regelungsechnik - Grundglieder: Analyse im Zei und Frequenzbereich Vorberachungen: Das Überragungsverhalen von linearen Regelkreiselemenen wird vorwiegend durch Sprunganworen bzw. Übergangsfunkionen sowie
Systemtheorie: Übertragungssystem: Beispiele
 Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
