Dr.-Ing. habil. Jörg Wollnack S.1. Fourier-Reihen, und Maschinendynamik. Kuka. Schaublin
|
|
|
- Simon Böhmer
- vor 5 Jahren
- Abrufe
Transkript
1 .6.8 S. Fourier-Reihen, Fourier- und Laplace-Transformaion und Maschinendynamik Kuka Schaublin
2 .6.8 S. Fourier-Reihe
3 .6.8 S.3 Allgemeine Fourier-Reihe K g ( ) ag( ), a = k k k k = R Minimierungsproblem: Mina k { F } F = z b ( ) ( ),,, g f g d Df > F = F HG I KJ z K f ( ) ak gk( ) d k = Fourier Reihe I
4 .6.8 Nowendige Bedingung: z F HG I KJ = K i {,,, K} f ( ) ak gk( ) d a i k = S.4 K K i {,,, K} f( ) a g ( ) f( ) a g ( ) d= k k k k k= a i k= i = a f ( ) i a i i F HG K k = k k I KJ = a g ( ) g ( ) i K i {,,, K} f( ) ak gk( ) gi( ) d= k = Fourier Reihe II
5 .6.8 S.5 z z k k i i {,,, K} f ( ) g ( ) d = a g ( ) g ( ) d In Marinoaion i K k = g ( )d gk ( ) g( )d a f( ) g( )d = g( ) gk( )d gk( )d f( ) gk( )d a K Fourier Reihe III
6 .6.8 S.6 pq, {,,, K} g ( ) g( ) d = z p q R S T z g ( ) d für p= q p sons z k {,,, K} a = k f ( ) g ( ) d z k g ( ) d Höhere Fourier-Terme können unabhängig von niederen berechne werden! Orhogonales erzeugendes Sysem k
7 .6.8 S.7 ( ) S { ( ) } gk φk R k N R k N Ck pq, {,,, K} φ ( ) φ ( )d= δ p q pq R S p= q δ pq = für T sons Normierung des orhogonalen erzeugendes Sysem
8 .6.8 S.8 Reelle rigonomerische Funkionen a s a k b sin k n n = + k = k cos + k π ak = f( )coskd π π π bk = f( )sink d π π Vollsändige erzeugende Syseme I
9 .6.8 S.9 Komplee rigonomerische Funkionen jk gk ( ) = e, k {,,,,,, } π Df [ X, X + π ] X Laguerresche Polynome k s s k gk ( ) = e ( ) k s s!, {,,, } s= D f [, ] Vollsändige erzeugende Syseme II
10 .6.8 S. Spalfunkionen F I π b g T T kt g k k ( ) = si, {,,, } HG KJ si F HG π I sinhg kt π b T kt g T KJ = π b T kt g F b gi KJ Vollsändige erzeugende Syseme III
11 z HG.6.8 F I F F = f ( ) a g ( ) d C z f K k = k k F = + H G I K J k k k k KJ = = ( ) f ( ) a g ( ) a g ( ) d k K K k S. z z K z = f ( ) d f ( ) a g ( ) d+ a a g ( ) g ( ) d k k k = p= q= K K p q p q K K K k k p q p q k= p= q= = f ( )d f( ) a g ( )d + a a g ( ) g ( )d Vollsändigkei I
12 .6.8 S. b f ( ) g ( ) d k =z def k z K K k k k = k = F = f ( ) d a b + a C b g + = a a b b b a b b k k k k k k k k k z K K b g ( ) k k k = k = F = f d+ a b b C k Vollsändigkei II
13 .6.8 S.3 z K K b g ( ) k k k = k = F = f d+ a b b C Terme der Summe posiiv Dieser milere quadraische Fehler is minimal, wenn die Koeffizienen a k gleich den Fourier-Koeffizienen b k sind. k b g K k k k k k = k a = b a b = Vollsändigkei III
14 .6.8 S.4 F = f d b C b g z K ( ) k k = Da der Fehler F C größer gleich null is, gil auch die Besselsche Ungleichung (Norm, Posiiv Defini) K k = K, > b f ( )d k z Vollsändigkei IV
15 .6.8 S.5 Def.: Vollsändigkei Das orhonormale Funkionensysem der Erzeugenden is vollsändig, wenn für jede quadraisch inegrable Funkion z > f ( )d< das Fehlermaß der verallgemeinere Fourier-Reihe null is. Hinreichend und nowendig hierfür is die Parsevalsche Gleichung: b = f ( )d Beweis, siehe Scrip k = k z Vollsändigkei V
16 .6.8 S.6 Jordanscher Saz: Die Fourier-Reihe einer in π periodischen Funkion von beschränker Variaion konvergier in jedem abgeschlossenen Inervall gleichmäßig gegen die Summe: f( + ) + f( ) Beweis, siehe Scrip Verhalen an Unseigkeissellen
17 .6.8 S.7 Bijekiviä der Fourier-Reihen vollsändiger orhonormaler Syseme: Die Zuordnung von verallgemeineren Fourier-Koeffizienen vollsändiger, orhonormaler erzeugender Syseme S und Fourier-Summenfunkion is für quadraisch inegrable Funkionen bijekiv. Beweis, siehe Scrip Eineindeuigkeissaz
18 .6.8 S.8 Periodisches Zeisignal Diskrees Spekrum φ k f () a k ff / T / -T / 3 4 ff / Berags- und Phasenspekrum periodischer Signale
19 .6.8 S.9 f( ) π für < < für = = π für < < π für =.35 S( ).5.5 K=.5 a k sin ( k) = 4, k {,3,5, } π k π. π Fourier-Summen der Recheckfunkion I
20 .6.8 S K=.5 S( ) K= S( ) π. π π. π Fourier-Summen der Recheckfunkion II
21 .6.8 S K=.5 S( ).44.5 K= π. π S( ) π. π Fourier-Summen der Recheckfunkion III
22 .6.8 S. Die Funkion f() kann eine beliebige Funkion sein, die physikalische Were repräsenier (Posiion, Pose, Kräfe, Momene, Spannung, Srom usw.). Die Variable kann die Zei, den Or oder eine beliebige unabhängige Variable repräsenieren. Diese Ansäze können auf Vekor- und Marifunkionen mi mehrdimensionalen unabhängigen Variablen erweier werden (Mechanik, Opik, Quanenphysik usw.). Verallgemeinerung
23 .6.8 S Phase.4 z j arcan y Re H( f ) H f = H f e f = f f R S T U k pv W Im kh( f ) p () (), (, ) y...4 Berag Orsfrequenzen
24 .6.8 S.4 Fourier-Transformaion
25 .6.8 S.5 T f ( ) -T / T / Mi einer gegen unendlich srebende Periode T ließen sich die Periodiziäsanforderung eliminieren, so dass aperiodische Signale erfass werden können. Idee des Fourier-Inegrals I
26 .6.8 S.6 f() jk = C e ω jk ω k = k Ck = f( ) e d ω = T T π T In diesem Fall würde ω gegen null sreben. Die einzelnen Harmonischen liegen also beliebig nahe beieinander, so dass sich ein Koninuum von Schwingungen ergib. Führ man formal die Größen so erhäl man: ω π = = T T ω π ein, Idee des Fourier-Inegrals II
27 .6.8 S.7 T ω f() = lim f() e d e T π ω k = T j j ω ω Bei der Ausführung des Grenzüberganges geh die Summaion in das besimme Riemannsche Inegral über. Mi der von Leibniz eingeführen Schreibweise ergib sich: jω jω f() = f() e d e dω π Idee des Fourier-Inegrals III
28 .6.8 S.8 Der in der Klammer sehende Ausdruck wird Bild-, Spekralfunkion oder Fourier-Transformiere genann. Die Spekralfunkion kann nur eine Funkion von jω sein, da über inegrier wird und die Inegrale uneigenliche Inegrale sind. { } ( ) ( ) ( ) ( ) j ω F jω I f jω = f e d { } j f() I F( jω) () = F( ω) e ω dω π Beweis, siehe Scrip Fourier-Inegral
29 .6.8 S.9 Original- bereich f( ) = lim f( + ) + f( ) ε { ε ε } f ( ) Hinransformaion ( ) ( ) j ω F jω = f e d Rückransformaion jω f() = F( ω) e dω π φ( ω) Spekral- bereich (koninuierliches Spekrum) Spekrum F( jω) F( jω) ω ω Fourier-Transformaion
30 .6.8 S.3 Gs () = T s + ϑ T s+ f s. j i. herz s i. herz ϑ T =,5 =, Hz. deg s jω Φ f s. j i 8. deg. herz s i. herz Berag und Phase der Fourier-Transformieren
31 .6.8 S.3 j Im{F( jω)} 6 5 3,,,3,4,5, Re{F( jω)} f / Hz Orskurve der Fourier-Transformieren
32 .6.8 T ω T sin für < rt (, ) = RT (, ω) = sons ω S r(,. ).6.4 R( ω,. ) π ω 6.. π Recheck- und Spalfunkion
33 .6.8 S.33 Disribuion, Falungssaz und Fourier-Inegral
34 Delafunkion.6.8 für k = δ ( k) =, k N sons Ausblendeigenschaf k Diskre f( k) δ ( k n) = f( n) f ( ) f ( ) / δ( - ) + δ () seig an S.34 Koninuierlich für < + lim δ ( ) =, R sons Disribuion (Vereilung; Auflösung) Idee der Disribuion I
35 .6.8 S.35 lim f( ) δ ( ) d = lim f( ) δ ( ) d + lim f( ) δ ( ) d + + lim f( ) δ ( ) d + + lim f( ) δ ( ) d = lim f( ) δ ( ) d + Idee der Disribuion II
36 .6.8 lim f( ) δ ( ) d = lim f( ) δ ( ) d + + = f( )lim δ ( )d + + S.36 = f( )lim δ ( )d = f( )lim d + ( ) = f( ) lim = f( ) lim + = f( )lim = f( ) Idee der Disribuion III
37 .6.8 S.37 Ausblendeigenschaf f( ) δ ( )d = f( ) Die Kommuaiviä der Grenzprozesse der Riemann-Summe bzw. des Riemann-Inegrals und der Delafunkion is hier nich mehr gegeben. Die Disribuion ha nur Sinn im Zusammenhang mi einem Inegral (Grenzprozess der Disribuion nach Inegraion). Diese Funkionenklasse sell eine Erweierung der Differenial- und Inegralrechnung dar (Analog der Erweierung der reellen zu den kompleen Zahlen). Disribuions-Theorie I
38 .6.8 S.38 Disribuionen: δ( ) = lim y(, α) α y (, α) e α π α y (, α) für α < α Disribuions-Theorie II
39 .6.8 S.39 Ihre Eigenschafen bzw. Aiome müssen widerspruchsfrei mi der Analysis fesgeleg werden. Eine Haupeigenschaf sell die Ausblendeigenschaf dar. Durch diese Erweierung werden analog zur kompleen Zahl (Eulerideniä) Zusammenhänge zwischen koninuierlichen und diskreen Beschreibungsformen sichbar, das Differenial nich seig differenzierbarer Funkionen (Sprünge) wird erschlossen und weieres mehr. Dies is für die Technik und Naurwissenschaf von zenraler Bedeuung, da ein derariges Signal- und Sysemverhalen in der Prais nich wegzudenken wäre (Sick-Slip, Schaler umlegen usw.). Nich zulez läss sich hierüber der Falungssaz linearer, zei/shifinvarianer Syseme herleien. Idee der Disribuion V
40 .6.8 S.4 Die Prais benöig eine geeignee durchaus anspruchsvolle Theorie. Häufig wird inuiiv genau umgekehr argumenier. Wenn wir nur genau hinsehen, dann wird deulich, dass diese Inuiion rügen kann. Prais und Theorie
41 .6.8 S.4 Ausblendeigenschaf der Disribuion + = k k k = k dτ k e () lim e( τ ) δ( τ )d τ e( τ) δ( τ)dτ k L sei ein linearer, homogener und zeiinvarianer Operaor e() Le { ()}() τ L{} Konvergenz y () = lim L e( τ k ) δ( τk)dτk k k dτ k y () = L lim e( τ k ) δ( τk)dτk k dτ k k + = L e( τ ) δ( τ )dτ Falungssaz I
42 .6.8 Lineariä und Homogeniä k dτ k k { } y () = lim e( τ k ) Lδ( τk) ()d τk S.4 Zei- bzw. Verschiebungsinvarianz + { } { } y () = e( τ ) Lδ() ( τ )d τ, mi g () = Lδ( τ ) () ( ) ( ) y () = L e( τ τ ) () = L e( τ) ( τ ) k dτ { } y () = lim e( τ ) Lδ() ( τ )dτ k k k k k Falungssaz II
43 .6.8 S.43 Lineariä, Homogeniä und Zeiinvarianz is eine hinreichende und nowendige Bedingung für die Eisenz des Falungssazes (Analog mulidimensional). Die Fourier-Transformaion überführ die Falung in ein Produk der Fourier-Transformieren + y () = g ( τ ) e( τ)dτ Beweis, siehe Scrip (Analog mulidimensional). Y( jω) = G( jω) E( jω) Falungssaz und Fourier-Transformaion
44 .6.8 S.44 Laplace-Transformaion
45 .6.8 S.45 Viele Vorgänge eisieren ers von einem besimmen Zeipunk an, den wir willkürlich zu = sezen. Jede echnische Apparaur muss ers konsruier werden. Sie eisier und nimm ihre Funkion ers von einem besimmen Zeipunk an auf. Beschränk man sich auf Vorgänge, die man kausal nenn, also auf Ursache und Wirkung beruhend, so läss sich ein Dämpfungsfakor e δ, δ > einführen. Dieser Fakor kann für eine erweiere Klasse von Funkionen die Konvergenz des Fourier-Inegrals erwirken (z.b. sin(.) und cos(.)-funkionen, die nur in Erweierung durch die Disribuionen-Theorie Fourier-Transformiere besizen). Moivaion I
46 .6.8 S.46 Muliplizier man eine beliebige Funkion mi der Sprungfunkion für < s ( ) = / für = sons, so erhäl man eine kausale Funkion. Moivaion II
47 .6.8 S.47 Fourier-Transformaion sδ { δ } F ( jω) =I f() s() e ( jω) ( δ ω) ( δ ω) + j + j = f( ) s() e d + f() s() e d = Inverse Fourier-Transformaion δ jω I { Fsδ j } = f s e = Fsδ j e π ( ω) () () () ( ω) dω ( j ) f( ) s( ) Fsδ ( j ) e δ + = ω ω dω π Von Fourier- zur Laplace-Transformaion I
48 .6.8 S.48 Differenial ds= jdω ds dω = j Inegraionsgrenzen s s = δ j = δ + j Im{ s} Inegraionsweg δ + jω Re{ s} Konvergenzebene δ - jω δ + j δ = I { sδ ω } = jπ δ j s f() s() e F ( j ) () F( s) e ds Von Fourier- zur Laplace-Transformaion II
49 .6.8 S.49 Laplace- und Fourier-Transformaion s sδ { } p F( p) = L f( ) s( ) ( p) = f( ) s( ) e d, p= δ + jω { δ } F ( jω) =I f( ) s( ) e ( jω) s δ δ { δ } lim F( p) = lim I f( ) s( ) e ( jω) = F( jω) f() quadraisch inegrabel s Fourier- aus Laplace-Transformiere I
50 .6.8 S.5 n d f n d () n n n () v v () v= s F s s f n ( jω) F( f).... n f( u) (d u) Fs () + n n v+ n f( u)du s v= v ( ) F( jω) + π F() δ( ω) jω n f s Fourier- aus Laplace-Transformiere II
51 R S T.6.8 für > s () = / für = für < jπ f s + πδ( π f ) S.5 für < / rec( ) = / für = / für > / si( π f ) = sin( π f )/ π f e a e a a a ( s+ a )( s+ a ) Korrespondenzabellen
52 .6.8 T + für T / riang( T, ) = T für T / + < Triangle-Puls ( T/ si( Tω/4)) T/ S.5 -T/ T/ 4π/T Recheck-Puls 8π/T ω für < T / rec( T, ) = / für= sons T si( ωt/) T -T/ T/ π/t 4π/T ω Signale I
53 .6.8 S.53 Sprung- oder Sep-Funkion für > s( ) = / für = sons jπ f s + πδ( π f ) s () ω Signale II
54 .6.8 S.54 Idealer Tiefpass f A si ( π f ) A für ω < ωa / rec( ωω, A ) = / fürω= sons f A f = f / B A - ω A / ω A / ω Signale III
55 .6.8 S.55 Ähnlichkeis- und Verauschungssäze
56 .6.8 S.56 Zur Enwicklung der Ähnlichkeissäze sei die I-Transformiere von f( k ), k R berache: Subsiuion: { } y I f( k ) ( y) = e f( k )d v= k dv= kd d= b a dv k kb yv yv k k I { f( k ) }( y) = e f( v)dv e = e k wv I { f( k ) }( y) = e f( v)dv k ka kb ka wv Ähnlichkeissäze I
57 .6.8 Srukurvergleich { f k } I ( ) ( y) kb wv e f( v)dv für k > k ka = kb wv e f( v)dv für k < k ka S.57 Mi der Fallunerscheidung erhäl man in beiden Fällen das gleiche Transformaionsinegral. Der Fakor /k ha die Eigenschaf der Beragsfunkion, so dass man kurz die Gleichung kb y wv I { f( k ) }( y) = I { f( ) }, mi I { f( ) }( w) = e f( v)dv k k ka erhäl. y w = k Ähnlichkeissäze II
58 .6.8 S.58 Ähnlichkeissäze s L { f( k) }( s) = L { f( ) }, k > k k { } jω I f( k) ( jω) = I{ f( ) } k k Ähnlichkeissäze III
59 .6.8 S.59 f () Fjω ( ) fk ( ) Fj ( ω/ k) / k ω ω Ähnlichkeissäze IV
60 .6.8 S.6 Schnelle Bewegungsvorgänge erfordern breibandige Regler und mechanische Überragungsglieder: a () = s () = jk C e P P k jkω ( ω ) { a() }( jω) ( jω) { s() }( jω) I = I { m a ()}( jω) mω { s ()}( jω) I = I k Massive Syseme sind Träge bzw. nur zu niederfrequenen Bewegungen in der Lage (Hochfrequener Flügelschlag des Kolibri und langsame Bewegungen von Elefanen). Inerpreaionen
61 .6.8 Für die Herleiung des Verauschungssazes geh man von den Fourier-Inegralen aus und überführ ω in und in ω (Symbolisch: ω und ω). Durch Subsiuion ω -v dω - dv ergib sich für die Fourier-Transformiere: jω jv jv F () = f( ω) e d = f( ve ) d v= f( ve ) dv Der srukurelle Vergleich mi dem Fourier-Inegral zeig, dass die Gleichung F ( ) =I f( j ) ( ) { π ω } gil, so dass man uner Berücksichigung des Ähnlichkeissazes erhäl. F( ) =I f( j ) ( ) { π ω } Verauschungssaz I S.6
62 .6.8 S.6 Geh man somi von einer bekannen Korrespondenz aus, überführ ω in - und in ω (Symbolisch: ω - und ω) und muliplizier f(jω) mi π, so erhäl man eine neue Zuordnung. Wegen der vorgenommen Verauschung der Symbole wird der Saz als Verauschungssaz bezeichne: F( ) =I f( j ) ( ) { π ω } Verauschungssaz II
63 .6.8 S.63 Fourier-Inegral, Fourier-Reihe, Falung und Abasung
64 .6.8 S.64 Digiale Lageregler von Maschinen Kuka Schaublin w () e () A/D T ekt ( ) ukt ( ) Digiales Sysem D/A u () Regelsrecke y () Analoge- und digiale Syseme
65 .6.8 S.65 Haleglied Abaser () δ( ) Π( ) T () δ( ) Π( ) T Abas- und Haleglied
66 .6.8 S.66 Man kenn somi zwei Zeifunkionen f () und f () und deren Laplace-Transformiere F (s) und F (s). Es sell sich nun die Frage, welcher Operaor im Zeibereich ϕ der Muliplikaion der Transformieren ensprich? Dami erhalen wir formal { { } } { } { } L ϕ gu (), f()()() u s = L g ()()L s f()() s = Gs () Fs () In der Noaion des speziellen Fredholmschen Inegrals (Fourierund Laplace-Inegrals): { ϕ { } } = { } { } I gu ( ), f( u) ( ) ( y) I g ( ) ( y) I f( ) ( y) Falungssaz I
67 .6.8 S.67 b y Ausgehend von I { f( ) }( y) = e f( )d, erhäl man das Produk zweier Transformierer { } { } y y I f( ) ( y) I g( ) ( y) = e f( )d e g( )d Was idenisch mi { } { } y vy I f( ) ( y) I g( ) ( y) e e f( ) g( v)ddv b a a b b = a a b b ( + v) y e f( ) g( v)ddv a a = b a Falungssaz II
68 .6.8 S.68 Koordinaenransformaion τ = + v v= u bzw. τ = + v = τ v= τ u v= u τ u obere Grenze: b + b b unere Grenze: a + a a Funkionaldeerminane v ( v, ) τ τ v v = = ( τ, u) v τ u u τ u u = ( ) = Falungssaz III
69 .6.8 S.69 aa ( v, ) ( τ, u) bb yτ I { f( ) }( y) I { g( ) }( y) = e f( τ u) g( u) dudτ bb yτ = e f( τ u) g( u)dudτ aa Der Kern der Inegralgleichung kann vor das innere Inegral gezogen werden, da er keine Funkion von u is, so dass man weier b b yτ I { f( ) }( y) I { g( ) }( y) = e f( τ u) g( u)du dτ a a erhäl. Falungssaz IV
70 .6.8 Da für die Inegraionsgrenzen a =, b oder a, b gil, is das äußere Inegral idenisch mi der I-Transformaion, sofern die Funkionen Quadraisch Inegrabel sind. Sind die Funkionen f und g kausal, so is das Produk der Funkionen nur für τ u τ u und u ungleich null. Insofern muss in diesem Fall das innere Inegral nur im Inervall [, τ ] ausgewere werden. b b Daher ergib sich: yτ e f( τ u) g( u)du dτ a a I { f( ) }( y) I { g( ) }( y) = mi b τ yτ e fs( τ u) gs( u)du dτ a a =, b a, b S.7 Falungssaz V
71 .6.8 S.7 Durch den srukurellen Vergleich mi der I-Transformaion erhäl man den gesuchen Operaor zu: Falungssaz b f( u) g( u)du a ϕ( ) = I = { I { f( ) }( y) I { g( ) }( y) }( ), mi fs( u) gs( u)du a =, b a, b Falungssaz VI
72 .6.8 S.7 L f( u) g()d u u () s = L { f()()l } s { g()() } s δ + j L { f( ) g( ) }( s) = F( s u) G( u)du jπ δ j I f( u) g( u)d u ( jω) =I{ f( ) }( jω) I{ g( ) }( jω) I{ f() g() }( jω) = F( j( ω u)) G( ju)du π Falungssäze
73 .6.8 S.73 lineares, homogenes shifinvarianes Sysem e () y () = g () g ( τ ) ( τ)dτ Es () Gs () Ys () = Gs () Es () Ej ( ω) Y( jω) = G( jω) E( jω) Sysemmodell
74 .6.8 kausales, lineares, homogenes shifinvarianes Sysem s () h () = g () g( τ )dτ S.74 /s Gs () Ys () = Gs ()/ s /( jω) + π δ( jω) Y( jω) = G( jω) ( /( jω) + π δ( jω) ) g ( ) = h ( ) Sprunganwor
75 .6.8 S.75 Idealer Tiefpass ĥ h() y () % 5% Wendepunk e Ma Kuka ε v = ĥ a Schaublin -ω B ω B ω % u a 5% Ma ε f B = a f B v v h ˆ fa 4 h ˆ Nur für Kenngrößen verwendbar. Sprunganwor des idealen Tiefpasses
76 .6.8 S.76 i A Gleichsrommoor R A k M u A i A u A L A k A M A M L ω u e J ϕ M A Kuka Schaublin ϕ ua s U s s 3 d φ() 3 A() Nur für Kenngrößen verwendbar. Tiefpassverhalen von Maschinen
77 .6.8 S.77 Elekromechanische Maschinen weisen ein Tiefpass- verhalen auf (Analog für mechanische Syseme) Die Bewegungen müssen bis zur drien Ordnung seig differenzierbar sein (Ruckverhalen; Ansonsen unphysikalische Bewegungen, die nich verwirklichbar sind) Massive Syseme sind räge und haben eine geringe Überragungsbandbreie (Kolibri und Elefan) Überragungsbandbreien wachsen proporional mi der Geschwindigkei und umgekehr proporional mi der Sprungweie (siehe auch Ähnlichkeissäze) Konsequenzen
78 .6.8 S.78 Disribuion rigonomerische Funkionen und Abasung
79 .6.8 { } jω I F( ω) ( ) = F( ω) e dω F( ω) = π δ( ω ω) π j j I { πδ( ω ω) }( ) = δ( ω ω) e ω dω= e ω S.79 ( ) { π δ ω ω δ ω ω } I + + ( ) ( ) ( ) ( ( ) ( )) = + + jω δω ω δω ω e dω ( jω ) jω = e + e = cosω Disribuion, e- und rigonomerische Funkionen I
80 .6.8 S.8 ( ) { jπ δ ω ω δ ω ω } I + ( ) ( ) ( ) j j ω ( ( ) ( ) ) e d = δω+ ω δω ω ω ( jω ) jω = j e e = j jsinω = sinω Disribuion, e- und rigonomerische Funkionen II
81 .6.8 cosω sinω j e ω ( ( + ) + ( )) π δ ω ω δ ω ω ( ( + ) ( )) jπ δ ω ω δ ω ω πδ( ω ω ) S.8 Fourier-Reihe als Fourier-Transformiere jk Ck e ω Ck k k = π δ( ω ω ) k = Disribuion, e- und rigonomerische Funkionen III
82 .6.8 S.8 f () πδ( ω ) Fjω ( ) + ω πδ ω ( ω) T -ω ω ω cosω ( ( + ) + ( )) π δ ω ω δ ω ω jkω I Ck e ( jω) = π Ck δ( ω kω) k= k= Disribuion, e- und rigonomerische Funkionen IV
83 .6.8 S.83 Periodisches Signal als Fourier-Reihe f (, T ) C e ω A jk = k FA j T Ck k k= ( ω, ) = π δ( ω ω ) k= Periodische Abasung (Muliplikaion) f() fa(, T) π Ck F( j( ω u)) δ( u kω)du π k = = k π k = π C F( j( ω u)) δ( u kω )du = Ck F( j( ω kω)) k = Periodische Abasung I
84 .6.8 S.84 f () f (, T ) FA( jω,t ) A T ω ω ω Frequenzüberlappung Aliasing I { f() f (, T )}( j( ω) = C F( j( ω kω )) A k k = Periodische Abasung II
85 .6.8 S.85 Bandbegrenze Signale FA( jω,t ) ω ω B ω / ω ω I { f () }( jω ) B F = B ( jω) für ω < ω sons B Periodische Abasung III
86 .6.8 S.86 Aufgrund des Eineindeuigkeissazes der Fourier-Transformaion lassen sich bandbegrenze Signale eindeuig aus ihren diskreen Weren rekonsruieren (Shannonsches Abasheorem). Die diskreen Were repräsenieren das bandbegrenze Signal vollsändig (kein Informaionsverlus). Die Rekonsrukion erfolg über den idealen Tiefpass: G IT ( jω ) = für sons ω < ω Periodische Abasung IV
87 .6.8 S.87 Zwei- und Mehrdimensionale Signale (Fräsen von Flächen, Bildverarbeiung usw.)
88 .6.8 S.88 for < q / rec( q, ) = / for = q/ for > q / si( qπ f) = sin( qπ f ) qπ f rec-funcion rec - Funkion si-funkion si X / yy / 5 f / q π f / qy π Inegraion und Abasung I
89 .6.8 S.89 Inegraion Xz () f = a a a ( a f ) ( a f ) ( a f ) X ( f) Π 3 si π si π si 3π 3 Bandbreie (erse Nullselle) f = / B i a i Scanning X () X ( f n f, f n f, f n f ) z Πδ f = z Π n = n = n = 3 f = / T, i {,, 3} Aperur a f = a / T, i {,, 3} i i i i i i Inegraion und Abasung II
90 .6.8 S.9 MÜF / MÜF Ma / % fd y y f d Aperur % 66,6 33, Aperur 4% Aperur 8% Aperur 99% Dreiecksspekrum Inegraion und Abasung
91 .6.8 S.9 Signal Signalspekrum Spekrum Shannon Abasbedingung.5 X B () f n X() f für i= fi < fb i = fi / = sons f / f f y / fy i {,,..., n} f f i Bi Mulidimensionales bandbegrenzes Signal
92 .6.8 Räumlich abgeasees diskrees Signal Signal X rec-funkion rec-funcion S.9.5 f / f.5 Signalspekrum f y / fy Signalspekrum f f / f y / fy.5 f fy f / f / y Idealer Tiefpass
93 .6.8 S.93 Räumlich diskrees Signal abgeasees Signal X,, Y,,, Z, Z Aliasing
94 .6.8 S.94 Maschinendynamik und numerische Berechnungen Kuka Schaublin
95 .6.8 z F z F Maschinenfundamen Maschinengesell Werkzeug- Werksück z 3 F 3 S.95 c c m d m d m 3 m z d d z c c z F m z + d d + d d z + c c + c c z = F m 3 z 3 d d z 3 c c z 3 F 3 Gekoppele Massen mi drei Freiheisgraden
96 .6.8 m z d d z c c z F m z + d d + d d z + c c + c c z = F m 3 z 3 d d z 3 c c z 3 F 3 S.96 Syseme werden in CAD vom Menschen inerakiv definier und die Marizen werden von der Sofware vollauomaisch generier. My + Dy + Ky= f Eisenz von M + + = y M Dy M K y M f Zusandsmodell I
97 .6.8 S.97 y = M Dy M K y+ M f Neue Zusände ẏ z = Az+ f z y E y = + y M K M D y M f Die Dimension der Sysemmari A is von der Ordnung f f. Hierbei definier f die Freiheisgrade des Sysems. Die Mari is im Allgemeinen weder symmerisch noch ha sie eine Bandsrukur. Zusandsmodell II
98 .6.8 S.98 Ansaz: d z d = Az + fz Toales Differenial: d z = Azd + f z d z() d z = Azd + f d z z z() = Azd+ fz d+ z Inegraion des Zusandsmodells I
99 .6.8 S.99 Taylor-Reihenenwicklung: z( ) = z( ) + z ( )( ) + R(, ) i i i i i i i ( ) z( ) = z( ) + A( ) z( ) + f ( ) ( ) + R(, ) i i i i z i i i i i Anfangsbedingung: z( ) z ( ) z( i) = z( i ) + A( i ) z( i ) + f z ( i ) ( i i ) Numerische Inegraion des Zusandsmodells I
100 .6.8 S. Dabei sind die Zeidifferenzen i i so zu wählen, dass die Resglieder R( i, i ) hinreichend klein ausfallen. Eine Verbesserung dieser numerischen Inegraion läss sich mi den Runge-Kua-Verfahren verwirklichen. Hierbei wird das Zeiinervall in mehrere Inervalle zerleg, um eine verbessere Prädikion des Folgezusands zu erwirken. Für weiere Einzelheien zu den Runge-Kua-Verfahren und der Schriweienseuerung der numerischen Inegraion sei auf einschlägige Lieraur verwiesen. Numerische Inegraion des Zusandsmodells II
101 .6.8 S. = A Ansaz: = i mi e λ i Schwingungsmodi ( λ ) i mi e = A mi e λ i λ e = A λi i mi mi e λ i = λ i m i Am i ( λ ) λ A = E A = i mi mi i mi mi Eigenwere Eigenvekoren ( λi E A) = ( i ) m λ E A = i Eigenwere und Eigenvekoren I
102 .6.8 S. { } ( λ E A) = ( λ E A) de = Eigenwere ( λ E A) = Eigenvekoren ( λ E A) m = { } Charakerisische Gleichung ( E A) de λ = Eigenwere und Eigenvekoren II
103 .6.8 S.3 My + Dy + Ky= f Zeiinvariane Syseme/Marizen und verschwindende Anfangsbedingungen s MY() s + sdy() s + KY() s = F() s Y() s = s F() s M + sd+ K Eigenwere bzw. Pole charakerisieren das dynamische Verhalen des Sysems Laplace-Transformiere des Zusandsmodells
Charakterisierung des Systems R C. Faltungsintegral. Faltungsintegral (anschaulich) Faltungsintegral (anschaulich) 1. Übertragungsfunktion zb
 Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Aufgabe 1: Kontinuierliche und diskrete Signale
 Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Aufgabe (5 Punke) Aufgabe : Koninuierliche und diskree Signale. a) Zeichnen Sie jeweils den geraden Aneil v g ( ) und den ungeraden Aneil v u ( ) des in Abb.. dargesellen Signals v (). b) Es gelen folgende
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
5. Signalverarbeitung
 5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
5. Signalverarbeiung Elemenarsignale Lineare Sysemheorie Fourierransformaion Abasung koninuierlicher Signale Diskree Fourierransformaion Filerenwurf 5-Folien Digiale Signalverarbeiung 1 5.1 Nachrichen
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Kontinuierliche Fourier Transformation
 Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Fourier-Transformation Linearität, Symmetrie, Verschiebung, Skalierung, Faltung, Modulation
 Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Übung 3 Fourier-Transformaion Lineariä, Symmerie, Verschiebung, Skalierung, Falung, Modulaion Lernziele - wissen und versehen, dass der Berag der Fourier-Transformieren einer reellen Funkion gerade is.
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Kapitel 2: Fourieranalyse. Analoge, nichtperiodische Signale
 ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Bildmaterial zur Vorlesung Regelungstechnik Teil I Die Regelstrecke. Wintersemester 2014 Prof. Dr.-Ing. habil. Klaus-Peter Döge
 Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Leseprobe. Ines Rennert, Bernhard Bundschuh. Signale und Systeme. Einführung in die Systemtheorie. ISBN (Buch):
 Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Grundlagen der Nachrichtentechnik 1 Communications 1
 Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
Grunlagen er Nachrichenechnik Communicaions Prof. Dr.-Ing. Anreas Czylwik S. Nachrichenechnik Organisaorisches Vorlesung SWS Übung SWS Bereuer: Dipl.-Ing. Thorsen Kempka Folienkopien sin verfügbar Prüfung:
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
7. Funktionalgleichung der Zeta-Funktion
 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Merkmale flexibler Fertigung
 FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
(10 Punkte) Gegeben ist die in Fig. 1 abgebildete in T periodische Zeitfunktion f(t). f(t)
 H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
H 93 Aufgabe 6: Gegeben is die in abgebildee in T periodische Zeifunkion f(). f() -T Die komplexen Fourierkoeffizienen dieser Zeifunkion lauen: c 0 = π 2 /4 T n 0: c n = n 2 für n ungerade 0 für n gerade
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Leseprobe. Daniel von Grünigen. Digitale Signalverarbeitung. mit einer Einführung in die kontinuierlichen Signale und Systeme
 Leseprobe Daniel von Grünigen Digiale Signalverarbeiung mi einer Einführung in die koninuierlichen Signale und Syseme ISBN (Buch: 978-3-446-4479- ISBN (E-Book: 978-3-446-4399-7 Weiere Informaionen oder
Leseprobe Daniel von Grünigen Digiale Signalverarbeiung mi einer Einführung in die koninuierlichen Signale und Syseme ISBN (Buch: 978-3-446-4479- ISBN (E-Book: 978-3-446-4399-7 Weiere Informaionen oder
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Systemtheorie: Übertragungssystem: Beispiele
 Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
Abstrakte Lineare Algebra
 Frank Fischer Insiu für Informaik frank.fischer@uni-mainz.de Mahemaische Modellierung am Rechner WINTERSEMESTER 08/9 *#$?!! Kapiel Absrake Lineare Algebra Vekorräume Algebraische Definiion Wiederholung:
Frank Fischer Insiu für Informaik frank.fischer@uni-mainz.de Mahemaische Modellierung am Rechner WINTERSEMESTER 08/9 *#$?!! Kapiel Absrake Lineare Algebra Vekorräume Algebraische Definiion Wiederholung:
Der kinetische Ansatz zur Beschreibung von Selbstorganisationsprozessen. mögliche Variationen und Erweiterungen: diskrete Gleichungen (endliches t):
 Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
Ludwig Pohlmann Thermodynamik offener Syseme und Selbsorganisaionsphänomene SS 007 Der kineische Ansaz zur Beschreibung von Selbsorganisaionsprozessen. Die Beschreibung von Prozessen Prozesse (Veränderungen,
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Fokker-Planck-Gleichung
 Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Fokker-Planck-Gleichung Beschreibung sochasischer Prozesse David Kleinhans kleinhan@uni-muenser.de WWU Münser David Kleinhans, WWU Münser Fokker-Planck-Gleichung Beschreibung elemenarer sochasischer Prozesse
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
1. Signalbeschreibung im Zeitbereich
 . Signalbeschreibung im Zeibereich SiSy, Signal, - Inhalsverzeichnis. Signalklassen * Kapiel 3.4 (Energie und Leisung).2 Symmerie-Eigenschafen von Signalen.3 Verschiebung und Dehnung eines Zeisignals *
. Signalbeschreibung im Zeibereich SiSy, Signal, - Inhalsverzeichnis. Signalklassen * Kapiel 3.4 (Energie und Leisung).2 Symmerie-Eigenschafen von Signalen.3 Verschiebung und Dehnung eines Zeisignals *
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Fourier- und Laplace- Transformation
 Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Skrium zur Vorlesung Mahemaik für Ingenieure Fourier- und Lalace- Transformaion Teil 3: Lalace-Transformaion Prof. Dr.-Ing. Norber Höner (nach einer Vorlage von Prof. Dr.-Ing. Torsen Benkner) Fachhochschule
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
1 Abtastung, Quantisierung und Codierung analoger Signale
 Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Übungsblatt 8 Musterlösung
 Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Fouerierreihen - eine Einführung
 HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
2.3 Theorie linearer Systeme
 2.3 Theorie linearer Syseme 2.3.1 Grundsäzliche Mehode Mehode: Berechnung durch Zerlegen in einfach berechenbare Teile (Superposiion) x() = x 1 ()+x 2 ()+x 3 ()+.. y() = y 1 ()+y 2 ()+y 3 ()+.. zerlegen
2.3 Theorie linearer Syseme 2.3.1 Grundsäzliche Mehode Mehode: Berechnung durch Zerlegen in einfach berechenbare Teile (Superposiion) x() = x 1 ()+x 2 ()+x 3 ()+.. y() = y 1 ()+y 2 ()+y 3 ()+.. zerlegen
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
2. Grundlagen Schwingungslehre
 Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Zusammenfassung Harmonische Anregung (5) Zusammenfassung Harmonische Anregung (6) .4 Akive Schwingungsisolaion (1) a) Schuz der Umgebung von Maschinen, die Schwingungen erzeugen (akiv) b) Schuz eines Geräes,
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Leistungselektronik Grundlagen und Standardanwendungen. Übung 3: Kommutierung
 Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Konjunkturtheorie (Stand: )
 Konjunkurheorie (Sand: 18.11.2009) Prof. Dr. Kai Carsensen, LMU und ifo Insiu Seffen Elsner, ifo Insiu Schwerpunk Dynamische Modelle in diskreer Zei mi konsanen Inpus Lösung linearer Differenzengleichungssyseme
Konjunkurheorie (Sand: 18.11.2009) Prof. Dr. Kai Carsensen, LMU und ifo Insiu Seffen Elsner, ifo Insiu Schwerpunk Dynamische Modelle in diskreer Zei mi konsanen Inpus Lösung linearer Differenzengleichungssyseme
Diskrete Integratoren und Ihre Eigenschaften
 Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Mathematik für Physiker I
 Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Mahemaik für Physiker I Themenübersich Michael Junk Raum G 47 Beispiel Bewegung 4 Verfolger Esefania Jeder beweg sich mi feser Geschwindigkei immer in Richung zum Vorgänger Dieer B. Paparaz Verona Auf
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
3. Partielle Differentialgleichungen
 3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
3.. Grundlagen und Klassifikaion Welche Ordnung haben diese Gleichungen?? 3.4.1 Lineare parielle Differenialgleichungen. Ordnung Analogie: Klassifikaion Kegelschnie 1 3.4.3 Korrek geselle Probleme Anfangs-
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Von der Fourier-Reihe zum Fourier-Integral
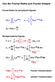 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
7. Gewöhnliche Differentialgleichungen
 1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Prof. Dr.-Ing. Ingolf Willms und Prof. Dr.-Ing. Adalber Beyer und basierend auf dem Scrip von Prof. Dr.-Ing. Ingo Wolff Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik
Grundlagen der Elekroechnik 3 Prof. Dr.-Ing. Ingolf Willms und Prof. Dr.-Ing. Adalber Beyer und basierend auf dem Scrip von Prof. Dr.-Ing. Ingo Wolff Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
3.1 Grundlagen. Grundbegriffe (Forts.) Grundbegriffe
 Beriebssyseme II - Analyse und Modellierung Sommersemeser 208 3. Grundlagen Moivaion 3. Grundlagen Beriebssyseme II - Analyse und Modellierung 3. Kapiel Grundlagen der Sochasik Prof. Mahias Werner Professur
Beriebssyseme II - Analyse und Modellierung Sommersemeser 208 3. Grundlagen Moivaion 3. Grundlagen Beriebssyseme II - Analyse und Modellierung 3. Kapiel Grundlagen der Sochasik Prof. Mahias Werner Professur
1 Direkte Digitale Synthese
 Direke Digiale Synhese In diesem Ausaz wird die direke digiale Synhese von periodischen mahemaischen Funkionen heoreisch und prakisch am Beispiel eines Sinusgeneraors erklär.. Theorie Ein Sinus mi der
Direke Digiale Synhese In diesem Ausaz wird die direke digiale Synhese von periodischen mahemaischen Funkionen heoreisch und prakisch am Beispiel eines Sinusgeneraors erklär.. Theorie Ein Sinus mi der
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann
 Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Stammgruppe trifft sich zum Museumsrundgang Experte erklärt jeweils sein Plakat
 Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Stochastische Automaten und Quellen
 KAPITEL 2 Sochasische Auomaen und Quellen Sei A ein Sysem allgemeiner Ar (z.b. ein physikalisches Sysem oder eine Nachrichenquelle), das wir zu diskreen Zeipunken = 0, 1,... beobachen. Wir nehmen an: (SA
KAPITEL 2 Sochasische Auomaen und Quellen Sei A ein Sysem allgemeiner Ar (z.b. ein physikalisches Sysem oder eine Nachrichenquelle), das wir zu diskreen Zeipunken = 0, 1,... beobachen. Wir nehmen an: (SA
1 Integrale von Funktionen in mehreren Variablen
 $Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
$Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
10. Periodische Funktionen, Fourier Reihen
 H.J. Oberle Analysis II SoSe 212 1. Periodische Funktionen, Fourier Reihen Jean Baptiste Joseph Fourier: Joseph Fourier wurde am 21.3.1768 bei Auxerre (Burgund) geboren und starb am 16.5.183 in Paris.
H.J. Oberle Analysis II SoSe 212 1. Periodische Funktionen, Fourier Reihen Jean Baptiste Joseph Fourier: Joseph Fourier wurde am 21.3.1768 bei Auxerre (Burgund) geboren und starb am 16.5.183 in Paris.
Ganzrationale Funktionen (Polynomfunktionen) - Berechnung von Nullstellen, Gleichungen höheren Grades -
 GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Hauptachsentransformation
 Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Grundlagen zeitveränderlicher Signale, Analyse von Systemen der Audio- und Videotechnik
 3. Nichperiodische Signale 3.1 ω ω ω dω Nichperiodische Signale endlicher Länge Die Fourierransformaion zerleg nichperiodische Signale endlicher Länge in ein koninuierliches endliches Frequenzspekrum.
3. Nichperiodische Signale 3.1 ω ω ω dω Nichperiodische Signale endlicher Länge Die Fourierransformaion zerleg nichperiodische Signale endlicher Länge in ein koninuierliches endliches Frequenzspekrum.
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Prof. Dr.-Ing. Ingolf Willms und Prof. Dr.-Ing. Adalber Beyer und basierend auf dem Scrip von Prof. Dr.-Ing. Ingo Wolff Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik
Grundlagen der Elekroechnik 3 Prof. Dr.-Ing. Ingolf Willms und Prof. Dr.-Ing. Adalber Beyer und basierend auf dem Scrip von Prof. Dr.-Ing. Ingo Wolff Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik
PHYSIK III. Serie 12, Musterlösung
 Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
Aufgabensammlung. Signale und Systeme 1. Einführung in die Signal- und Systemtheorie. Kontaktinformation: Dr. Mike Wolf, Tel. 2619
 Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
