Theoretische Physik. Zur Vorbereitung der Vordiplomsprüfung. Hanno Rein
|
|
|
- Günther Dunkle
- vor 5 Jahren
- Abrufe
Transkript
1 Theoretsche Physk Zur Vorberetung der Vordplomsprüfung 6. Aprl 005
2 Vordplom - Theoretsche Physk Mechank - Sete Inhaltsverzechns Newton sche Mechank. Koordnatensysteme Newton sche Axome Konservatve Kraftfelder Phasenraum Keplersche Gesetze Veltelchensysteme Vralsatz Rotatonen 3. Orthogonale Transformatonen Zetabletung m roterenden Koordnatensystem Schenkräfte Starre Körper 3 3. Träghetstensor Satz von Stener Knetsche Energe Lagrange Formalsmus 4 4. Zwangsbedngungen Vrtuelle Verrückungen D Alembertsches Prnzp Lagrange Bewegungsglechungen. Art Lagrange Bewegungsglechungen. Art Geschwndgketsabhängge Kräfte Hamltonsches Prnzp Erhaltungssätze Hamlton Formalsmus 6 5. Hamltonsche Bewegungsglechungen Modfzertes Hamltonsches Prnzp Kanonsche Transformaton Posson Klammer Noether Theorem Klene Schwngungen 8 6. Harmonsche Näherung Normalschwngungen Nchtlneare Systeme, Chaos 8 7. Logstsche Glechung Physkalsche Systeme Satz von Louvlle Stabltät Spezelle Relatvtätstheore 9 8. Verdmensonaler Raum Lorentz Transformaton Zetdlataton Längenkontrakton Relatvstsche Bewegungsglechung Newton sche Mechank. Koordnatensysteme De Enhetsvektoren normert snd: ê q rq, q, q 3 rq, q, q 3 Geschwndgket n belebgen Koordnaten d r r dq q + r dq q + r dq 3 q 3 Zylnderkoordnaten und Kugelkoordnaten: r ρ cos φ sn θ cos φ ρ sn φ r rê r r sn θ sn φ z cos θ. Newton sche Axome. Alle Körper verharren m Zustand der Ruhe oder der glechförmgen, geradlngen Bewegung, wenn kene äußeren Enflüsse vorhanden snd.. F m a 3. FA B F B A acto reacto Das Inertalsystem ruht oder bewegt sch mt konstanter Geschwndgket kene Rotaton oder Beschleungung. Im Intertalsystem glt das Träghetsgesetzt, als se es der ruhende Mttelpunkt der Welt..3 Konservatve Kraftfelder Kraftfeld F st konservatv Energeerhaltung st gültg, wenn es sch folgendermaßen schreben lässt F r V r. Es st Bewes mt Hlfe lnearer Näherung von V dv V d r. Wegntegral über Potental V r st wegunabhängg. Bewes: r r F r d r V r d r r r r r dv V r V r Es glt Drehmpulserhaltung: d l m d r v m [ v v + r a] r F {{ f r r r 0 Drehmoment Zentrales konservatves Kraftfeld F : F r f r r
3 Vordplom - Theoretsche Physk Mechank - Sete.4 Phasenraum Abbldung : Trajektoren m Phasenraum für ungedämpften, schwach und stark gedämpften harmonschen Oszllator.5 Keplersche Gesetze. De Planeten durchlaufen Ellpsenbahnen. Ellpsenbahn: C st Lenz scher Vektor und legt n der Bewegungsebene und st parallel zum Ortsvektor des Perhels. Durch skalare Multplkaton mt r ergbt sch de Ellpsenglechung: r p l m r r r C l r p mr rc cos φ l r l /m C/m cos φ.6 Veltelchensysteme De reduzerte Masse st µ m m m + m. ρ P ɛ cos φ P b a ɛ a b a Be enem elastschen Stoß glecher Massen glt de Impuls- und Energeerhaltung:. Der Fahrstrahl überstrecht n glechen Zeten gleche Flächen df Impulserhaltung. Bewes: df r v r m v m m l const πab T. 3. Mt der großen Halbachse a und der Umlaufzet T glt für alle Planeten a3 T const. Bewes: a 3 T a l 4m π b 4π l m P De Radalbeschleungung lässt sch berechnen zu a ρ ρ ρ φ l m P ρ Das Gravtatonsgesetz sagt nun, dass der erste Faktor konstant st. Des entsprcht aber auch genau dem Faktor n der Glechung von a3 T. Aus der Bewegungsglechung folgt durch Multplkaton mt l: p p + p p m p m + p m Durch Quadreren der Impulserhaltung folgt p p + p + p p 0 p p p p cos φ Handelt es sch ncht um enen zentralen Stoß, st somt φ Vralsatz Befnden sch alle Telchen n enem endlchen Volumen, so gbt der Vralsatz de mttlere knetsche Energe der Telchen an: T F r Bewes: Berechne Abletung von G p r dg T + F r + m r F r d p l p r r 3 p l r 3 r p r r p d m r r p l m r r C Der absolute zetlche Mttelwert ergbt sch somt zu dg τ dg lm τ τ 0 τ p r 0 T + 0 F r
4 Vordplom - Theoretsche Physk Mechank - Sete 3 Rotatonen. Orthogonale Transformatonen Koordnatentransformaton st orthogonal wenn D D T und det D. Drehmatrx um z-achse: cos sn 0 R z sn cos Ene belebge Rotaton wrd beschreben durch dre Eulerwnkel: R Euler, β, γ R z γ R x β R z. Zetabletung m roterenden Koordnatensystem { d f Lab { d f RK + ω f Bewes: Den um den Wnkel ωt transformerten Vektor m RK ableten und Summanden dentfzeren..3 Schenkräfte De Beschleungung m Laborsystem errechnet sch durch -malges Anwenden und Ausmultplzeren der obgen Glechung zu: a Lab a RK + d ω r + ω v + ω [ ω r] Lneare Beschleungung. Corolsbeschleungung 3. Zentrfugalbeschleungung 3 Starre Körper 3. Träghetstensor Der Gesamtdrehmpuls L st de Summe der enzelnen Drehmpulse: L l m [ r ω r ] m y ω x y ω y x z ω z x ω x z z ω y z ω z y x ω x y ω y x x ω z x ω x z y ω y z ω z y m y + z x y x z x y x + z y z ω I ω x z y z x + y Transformaton des Drehmpulses: L R L RI ω R I {{ R R ω I ω Der Träghetstensor st also en Tensor zweter Stufe. Der Vektor ω st en Tensor erster Stufe. Be ener Hauptträghetsachse st L ω. Zur Bestmmung der Haupträghetsachsen und Hauptträghetsmomente st folgendes Egenwertproblem zu lösen: deti λ ˆ 0 Für ene belebge Drehachse errechnet sch das Träghetsmoment zu I ω ê ω Iê ω m r r ê ω De Berechnung enes Träghetsmoments enes Körpers mt kontnuerlcher Massenvertelung erfolgt mt Hlfe enes Volumenntegrals. Der Integrand st dann Volumenelement Dchte Abstand zu ω 3. Satz von Stener Das Träghetsmoment enes starren Körpers mt Masse M um de Drehachse ê ω mt Anstand b zum Schwerpunkt st I ω I Schwerpunkt ω + Mb. Bewes: Se ρ der Ortsvektor enes Massenpunktes m Schwerpunktsystem, und r der Ortsvektor m um den Vektor R verschobenen Koordnatensystem also r R + ρ, so glt: I ω M R + m r r ê ω m [R + R ρ ] + ρ Knetsche Energe m m ρ ρ ê ω M R + I SP ω De knetsche Energe des gesamten starren Körpers st: T Kn m d r dr + d ρ m d { R + d ρ + ω ρ RK M d R + d R ω m ρ + m ω ρ
5 Vordplom - Theoretsche Physk Mechank - Sete 4 4 Lagrange Formalsmus 4. Zwangsbedngungen Holonome Zwangbedngung: f r,..., r N, t 0 Ncht holonome Zwangsbedngung: f r,..., r N, t > 0 Ene skeleronome Zwangsbedngung st zetunabhängg, ene rheonome zetabhängg. 4. Vrtuelle Verrückungen De vrtuelle Verrückung st ene nfntesmale Veränderung des Systems, de mt den Zwangsbedngungen verträglch st. δ r 3N k r q δq Damt de Zwangsbedngungen erfüllt bleben muss für alle l... k gelten f l r,..., r N, t f l r + δ r,..., r N + δ r N, t 0. De Entwcklung an der Stelle r + δ r um den Punkt r ergbt f l r + δ r,..., r N + δ r N, t N f f l r,..., r N, t + δ r. r Daraus folgt de Bestmmungsglechung für de erlaubten vrtuellen Verrückungen N f l δ r 0 l... k D Alembertsches Prnzp De zetlche Entwcklung des Systems erfolgt n Rchtung solcher vrtuellen Verrückungen δ r, für de de Zwangskräfte kene Arbet lesten: N F Zwang δ r 0 Das D Alembertsche Prnzp st en Postulat. 4.4 Lagrange Bewegungsglechungen. Art Das D Alembertsche Prnzp st ene Lnearkombnaton der Bestmmunsglechung der vrtueller Verrückungen: N k N F Zwang δ r λ l f l δ r F Zwang l k λ l f l l..n De Zwangskräfte snd so konstruert, dass sch das Telchen bewegt, als ob ene Gesamtkraft F Gesamt F + F Zwang auf es wrkt. De Lagrange Bewegungsglechungen. Art snd somt m a F + f l r, t 0. k λ l f l r, t l {{ F Zwang 4.5 Lagrange Bewegungsglechungen. Art De Geschwndgket enes Telchens berechnet sch zu v d r 3N k r dq j q j + r j Multplzert man alle Lagrange Bewegungsglechungen. Art mt der zugehörgen vrtuellen Verrückung und addert dese, so st N m a δ r N N F δ r + F Zwang δ r 0 D Alembert Setzt man de Defnton der vrtuellen Verrückungen en, so erhällt man r m a δq r F δq q, q, { d r m r m d r r δq q, q Als Nebenrechnungen st zu zegen: d r q j k sowe r d r q j q j q j dqj, r dq k q j q k + r q j { r dq k q k + r r r q j k Setzt man des oben en, so ergbt sch mt der knetschen Energe T m v : { d r m r m d r r δq q q
6 Vordplom - Theoretsche Physk Mechank - Sete 5 { d m r r m r r δq q, q { d q, m r q m r δq { d T T δq q q Da de vrtuellen Verrückungen belebg snd, glt de Glechung auch für jede generalserte Koordnate enzeln: d T T q q F r q Q Herbe st Q de generalserte Kraft, für de sch m Falle enes konservatven Kraftfeldes mt dem Potental V ergbt Q F r q V r r q V q. Lässt man n enem transformerten Koordnatensystem alle bs auf ene Koordnate q β fx, so beschrebt x q,..., q β,... ene Raumkurve, wobe x / q β der Tangentenvektor an dese Kurve st. Das nnere Produkt der Kraft mt desem Tangentenvektor ergbt de Projekton der Kraft, de generalserte Kraft. Erwetert man das Konzept der Potenzalfunkton V, ndem man de Geschwndgketsabhänggket zulässt, so ergbt sch de generalserte Kraft zu: Q d V V q q Setzt man L T V so lässt sch de Lagrange Bewegungsglechung zweter Art aufstellen: d L L 0 q q 4.6 Geschwndgketsabhängge Kräfte En geladenes Telchen m elektromagnetschen Feld erfährt das verallgemenerte Potenzal M eφ e v A De Lagrangefunkton st somt 4.7 Hamltonsches Prnzp De Bewegungsglechung für en Telchen, auf das de Kraft F und de Zwangskraft F Zwang wrkt lautet 0 F + F Zwang m a Summert über alle Telchen und multplzert mt der vrtuellen Verrückung δ r glt 0 F + F Zwang m a δ r F m a δ r Integrert man über de Zet, wendet zwemal partelle Integraton an und setzt de vertuellen Verrückungen zum Anfangs und Endzetpunkt glech null, so st 0 F m a δ r V δ r r + d V r δ r m a δ r V δ r V r r δ r {{ δ δ δ δ V + V + V + m a δ r V + δ δ V m v δ r v m v δ r T δ r v T δ L 0 De Varaton des Potentals δ V und de entsprechende Varaton der knetschen Energe st verträglch mt den Zwangs- und den Randbedngungen. Mt der Euler-Lagrangeschen Varatonsglechung folgt daraus wederum Lagrange. L T M m v eφ + e v A De relatvstsche Betrachtung lefert L m 0 c v c eφ + e v A
7 Vordplom - Theoretsche Physk Mechank - Sete Erhaltungssätze Der generalserte/kanonsche/konjungerte Impuls p j st defnert zu p j L q j. Ist de Lagrange Funkton ncht von ener generalserten Varablen q j abhängg, so st dese Varable zyklsch. Der zugrhörge generalserte Impuls st ene Erhaltungsgröße. 0 L q j Lagrange II d L d q j p j De Zetabletung der Lagrangefunkton ergbt unter der Annahme, dass L ncht explzt von der Zet abhängt und das Potenzal geschwndgketsunabhängg st zu dl L + d p q. L q q + L q Daraus folgt p q L const. E T + V Zum Bewes, dass es sch be deser Konstanten um de Gesammtenerge handelt, wrd de knetsche Energe berechnet: T lk m j m r q l r q k r q j q j lk Der generalserte Impuls berechnet sch zu p j L q j T q j k Somt st p q T kj q k. lk q l q k und de obge Konstante kann als de Gesammtenerge dentfzert werden. 5 Hamlton Formalsmus 5. Hamltonsche Bewegungsglechungen Um de gekoppelten Lagrange Bewegungsglechungen zu verenfachen, defnert man de Hamltonfunkton n Hq, p, t p q Lq, q, t de nur von den generalserten Koordnaten und den generalserten Impulsen abhängt. Bewes durch Berechnung der Dfferenzalform dh dp q + p d q L dq L q d q L dp q L dq p dp L + dq + Aus dem Verglech der letzten mt der zweten Zele folgen de Hamltonschen Bewegungsglechungen: p q L d L d q p ṗ 5. Modfzertes Hamltonsches Prnzp Aus dem Hamltonschen Prnzp δ L 0 erhällt man das modfzerte Hamltonsche Prnzp n δ p q Hq, p, t 0. 0 Um von desem modfzerten Hamltonprnzp auf de Hamltonschen Bewegungsglechungen zu kommen, parametrsert man den Weg q,p mt ener belebgen Varaton um den rchtgen Weg: q q 0 + η p p 0 + ɛ Damt st: 0 δ n 0 n 0 n 0 n 0 n p q Hq, p, t 0 ɛ q + p η p p ɛ q + p η η p ɛ ɛ q ṗ η η p ɛ ɛ q p η ṗ + Durch ene passende Wahl der Varatonen η und ɛ folgen de Hamltonschen Bewegungsglechungen.
8 Vordplom - Theoretsche Physk Mechank - Sete Kanonsche Transformaton Ene Transformaton heßt kanonsch, wenn mt den neuen Koordnaten Q und P wederum de Hamltonschen Bewegungsglechungen gelten. Des st der Fall wenn das modfzerte Hamltonsche Prnzp gültg st. Es blebt be der Transformaton gültg, wenn sch das Integral nach der Integraton nur noch um enen konstanten Faktor unterschedet. Es muss also gelten: p q h df q, p, Q, P, t P Q H + Im folgenden se F q, p, Q, P, t F q, Q, t o.b.d.a da de Varablen ncht unabhängg snd. Somt st H h F F q p + q Q F + P. Q De Glechung st genau dann dentsch null, wenn glt de Transformatonsglechungen gelten: p F P F Q H h F 5.4 Posson Klammer De Posson Klammer st für de dynamschen Varablen f und g defnert als n f g {f, g : f g p p Es glt de Jacob Identtät {f, {g, h + {g, {h, f + {h, {f, g 0 Ene dynamsche Varable f de ncht explzt von der Zet abhängt st genau dann ene Konstante der Bewegung wenn de Possonklammer mt der Hammltonfunkton verschwndet. Bewes: df f 0 nach Vor. n {f, H! 0 + n [ f p f p De Fundamentalklammern snd [ f q + f ] ṗ p {p, p j {q, q j 0, {q, p j δ j Ene Transformaton st genau dann kanonsch, wenn auch für de neuen Koordnaten de Fundamentalklammern gelten. Zum Bewes wrd berechnet: Q j {Q j, H H p p k ] Q j p Q j p H Q k + H P k Q k p P k p Setzt man de zwete Glechung n de erste en, so ergbt sch nach Umformungen: Q j k H Q k {Q j, Q k + H P k {Q j, P k! H P j. De Bedngung, dass de Bewegungsglechungen gelten, st genau dann erfüllt, wenn de Fundamentalklammern gelten. 5.5 Noether Theorem De nfntesmale kanonsche Transformaton wrd defnert zu p q p + δp β q + δq De erzeugende Funkton F, mt ener belebgen Funkton f de von den alten Koordnaten und den neuen Impulsen abhängt, se n F q, q + ɛfq, Mt den Regeln der kanonschen Transformaton ergbt sch somt p F + ɛ fq, q {{ δp β F q + ɛ fq, {{ δq Durch ene Taylorentwcklung von f ergbt sch durch konsequentes Vernachlässgen quadratscher nfntesmaler Größen: δp ɛ fq, ɛ fq, p ɛ {p, f δq ɛ fq, p ɛ fq, p p ɛ {q, f Betrachtet man nun de Änderung ener dynamschen Varablen g, so ergbt sch wederum nach Taylor: δg g, β gp, q gp, q + [ g δp + g ] δq gp, q p [ g ɛ fq, p + g ɛ fq ], p p p ɛ {g, f Jetzt lässt sch das Noether Theorem formuleren: δh 0 {f, H 0 df f + {f, H 0 De Hamltonfunkton H st genau dann nvarant unter der nfntesmalen Transformaton de durch f erzeugt wrd, wenn f ene Konstante der Bewegung st.
9 Vordplom - Theoretsche Physk Mechank - Sete 8 6 Klene Schwngungen 6. Harmonsche Näherung Be ener mnmalen Auslenkung η q q 0 der generalserten Koordnaten q um en Mnmum q 0 des Potentals V lässt sch deses nähern durch V q V q 0 + V q0 q j q 0j q j j 0 + V q0 q j q 0j q q q j,j const + K j η η j.,j Herbe st K der Kraftkonstantentensor. De knetsche Energe st T m r M j q q j,j 7 Nchtlneare Systeme, Chaos 7. Logstsche Glechung De logstsche Glechung lautet x n+ f a x ax n x n Fxpunkte x n x n+ snd Attraktoren, wenn se Iteratonen anzehen. Bedngung für enen Attraktor fx + ɛ fx < x + ɛ x ɛ Daraus folgt: fx + ɛ fx ɛ df dx < Entwckeln sch durch Verändern des Parameters a aus enem Attraktor zwe Attraktoren, so sprcht man von ener Bfurkaton. mt M j r r m q q j a j q 0 + Taylor De Lagrange Funkton ergbt sch somt zu: L T V M j η η j K j η η j,j Engesetzt n Lagrange II folgt de Vektorglechung M η K η Mt dem harmonschen Ansatz ηt η 0 exp ωt lässt sch de Glechung umformen zu K ω M η 0 0 De Matrx K ω M st symmetrsch und postv defnt. Alle Egenwerte ω snd größer oder glech 0. Um ncht nur de trvale Lösung für ω zu erhallten, muss de Determnante unglech null sen. 6. Normalschwngungen Um de Komponenten A j der Normalschwngungen η 0 der zugehörgen Wnkelfrequenz ω zu bestmmen, glt A j +j det [ K ωm ] j Herbe st [ K ω M ] j de Matrx K ω M,wobe de erste Zele und de j-te Spalte gestrchen st. Der Bewes erfolgt durch Ensetzen. Abbldung : Bfurkatonen der logstschen Abletung 7. Physkalsche Systeme Se x 0 en Fxpunkt enes physkalschen System m s- Phasenraum, so st x F x 0. Um nun festzustellen, ob en Fxpunkt auch en Attraktor st, entwckelt man de Funkton F um den Fxpunkt x 0 n ener Taylorrehe: s F x F x 0 + β 0 Es st x A x x 0 Der Ansatz F x β A,β x β x β 0 xt x 0 exp [A t t 0 ] xt 0 x 0
10 Vordplom - Theoretsche Physk Mechank - Sete 9 löst de obge DGL. De Matrx kann so transformert werden, dass nur noch n deren Dagonalen de komplexen Egenwerte λ ν c + d stehen. Somt st x ν t x ν 0 exp [c + d t t 0 ] x ν t 0 x ν 0 Snd also alle Realtele der Egenwerte negatv, so handelt es sch um gedämpfte Schwngungen um den Fxpunkt. Der Fxpunkt st somt en Attraktor. 7.3 Satz von Louvlle Betrachtet man ene Bahn xt q,..., q s, p,..., p s m Phasenraum, so blebt das Volumen dv n ener nfntesmalen Umgebung enes Bahnpunktes erhalten. De Phasenraumdchte st ρ Anzahl der Trajektoren dv const. 8 Spezelle Relatvtätstheore 8. Verdmensonaler Raum Kontravaranter und kovaranter Verervektor: ct ct x µ x y x µ x y z z Betragsquadrat: r x µ x µ µ x µ x µ c t x y z Der metrsche Tensor g µν wandelt enen kovaranten n enen kontravaranten Vektor um: x µ g µν x ν De Zetlche Änderung von ρ st dρ ρ + ρ q + ρ ṗ p Durch Betrachtung der Ströme durch en Rechteck m Phasenunterraum mt q k, p k ergbt sch ρ dρ 0 s [ ρ q k + q k s [ ρ k k ] ρ ṗ k p k q k q k + q k q k ρ + ρ p k ṗ k + ṗ k p k ρ s [ ρ q k + q k ρ H ρ H + ρ ] ṗ k q k p k p k q k p k k Somt st de zetlche Änderung der Dchte dentsch null. 7.4 Stabltät Bahnstabltät: mn At Bt < ɛ t Asymptotsche Stabltät: lm At lm Bt t t Lyapunov Stabltät: lm At Bt 0 t ] Abbldung 3: Weltlne m Mnkowskraum Punkte mt negatver Mnkowskabstand s.o. snd raumartg, Punkte mt postvem zetartg. 8. Lorentz Transformaton Das Koordnatensystem K bewege sch mt der Geschwndgket vê x m Bezug auf das Koordnatensystem K. De Transformaton x ν a ν µx µ st lnear mt β 0 0 β β a β 0 0 β β β v c. Der Betrag des Vektors m Mnkowskraum st bezüglch deser Transformaton nvarant. Eregnsse m Ursprung von K haben de Koordnaten ct β, 0, 0, 0, befnden sch also tatsächlch m Ursprung.
11 Vordplom - Theoretsche Physk Mechank - Sete Zetdlataton In enem mt der Geschwndgket v geboosteten Koordnatensystem K glt: c t x c t x c t v t. Daraus folgt für zwe Eregnsse de sch aus Scht des ruhenden Koordnatensystems K m Urspung und m zetlchen Abstand t eregnen: c t x c t v t 0 t t v c zu vervollständgen Längenkontrakton De Länge st maxmal n dem Koordnatensystem, n dem der Körper ruht. De Längenmessung fndet n jedem Koordnatensystem glechzetg statt. Im mtbewegten Koordnatensystem glt also x 0, x! l 0 t t 0 Durch de Lorentztransformaton vom bewegten n das ruhende Koordnatensystem zurück, ergbt sch unter der Vorderung der Glechzetgket der Messung de Länge m relatv bewegten Koordnatensystem zu x 0 x v c l Relatvstsche Bewegungsglechung Da de normale Geschwndgket 3er Vektor ken kovaranter Lorentz Vektor st, defnert man de 4er Geschwndgket zu: u d dτ x dτ β d d x ct r β d x β c v Der 4er Impuls ergbt sch dann zu p m u. Letet man desen nach der Egenzet τ ab, so erhällt man de Mnkowskkraft. Im Ruhesystem des Telchens v 0 glt: 0 0 m a F Durch de Lorentztransformaton erhällt man de Kraft n enem belebgen Koordnatensystem: K 0 v F β c K F + β v v F v
Die Hamilton-Jacobi-Theorie
 Kaptel 7 De Hamlton-Jacob-Theore Ausgearbetet von Rolf Horn und Bernhard Schmtz 7.1 Enletung Um de Hamlton schen Bewegungsglechungen H(q, p q k = p k H(p, q ṗ k = q k zu verenfachen, führten wr de kanonschen
Kaptel 7 De Hamlton-Jacob-Theore Ausgearbetet von Rolf Horn und Bernhard Schmtz 7.1 Enletung Um de Hamlton schen Bewegungsglechungen H(q, p q k = p k H(p, q ṗ k = q k zu verenfachen, führten wr de kanonschen
Theoretische Physik: Mechanik
 Ferenkurs Theoretsche Physk: Mechank Sommer 2017 Vorlesung 2 (mt freundlcher Genehmgung von Merln Mtscheck und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme
Ferenkurs Theoretsche Physk: Mechank Sommer 2017 Vorlesung 2 (mt freundlcher Genehmgung von Merln Mtscheck und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
Theoretische Physik: Mechanik
 Merln Mtschek, Verena Walbrecht Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 3 Technsche Unverstät München 1 Fakultät für Physk Merln Mtschek, Verena Walbrecht Inhaltsverzechns 1 Symmetren
Merln Mtschek, Verena Walbrecht Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 3 Technsche Unverstät München 1 Fakultät für Physk Merln Mtschek, Verena Walbrecht Inhaltsverzechns 1 Symmetren
Der starre Körper. 1 Grundlagen. Dominik Fauser. 1.1 Denition. 1.2 Freiheitsgrade
 Der starre Körper Domnk Fauser 1 Grundlagen 1.1 Denton Als enen starren Körper bezechnet man en System von Massepunkten m, deren Abstände zuenander konstant snd: r j = r r j. Mest betrachtet man ene sehr
Der starre Körper Domnk Fauser 1 Grundlagen 1.1 Denton Als enen starren Körper bezechnet man en System von Massepunkten m, deren Abstände zuenander konstant snd: r j = r r j. Mest betrachtet man ene sehr
Kreisel. koerperfestes KS. z y. raumfestes KS. Starrer Körper: System von Massepunkten m i, deren Abstände r i r j untereinander konstant sind.
 Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
Noethertheorem. 30. Januar 2012
 Noethertheorem 30. Januar 2012 1 Inhaltsverzechns 1 Symmetre 3 1.1 Symmetre n der Geometre................... 3 1.2 Symmetre n der Mathematk.................. 3 1.3 Symmetre n der Physk.....................
Noethertheorem 30. Januar 2012 1 Inhaltsverzechns 1 Symmetre 3 1.1 Symmetre n der Geometre................... 3 1.2 Symmetre n der Mathematk.................. 3 1.3 Symmetre n der Physk.....................
18. Vorlesung Sommersemester
 8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
Zusammenfassung. 1) Falls Zwangsbedinungen die Freiheitsgrade einschränken, kann man die abhängige Koordinaten aus der Lagrangfunktion elimieren;
 Zusammenfassung 1) Falls Zwangsbednungen de Frehetsgrade enschränken, kann man de abhängge Koordnaten aus der Lagrangfunkton elmeren; 2) Es st auch möglch de Zwangsbednungen mt Hlfe der Lagrangefaktoren
Zusammenfassung 1) Falls Zwangsbednungen de Frehetsgrade enschränken, kann man de abhängge Koordnaten aus der Lagrangfunkton elmeren; 2) Es st auch möglch de Zwangsbednungen mt Hlfe der Lagrangefaktoren
Dynamik starrer Körper
 Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
3. Vorlesung Sommersemester
 3. Vorlesung Sommersemester 1 Bespele (Fortsetzung) 1. Der starre Körper: Formulerung der Zwangsbedngungen später. Anschaulch snd schon de Frehetsgrade: dre der Translaton (z. B. Schwerpuntsoordnaten)
3. Vorlesung Sommersemester 1 Bespele (Fortsetzung) 1. Der starre Körper: Formulerung der Zwangsbedngungen später. Anschaulch snd schon de Frehetsgrade: dre der Translaton (z. B. Schwerpuntsoordnaten)
Theoretische Physik 1 Mechanik
 Technsche Unverstät München Fakultät für Physk Ferenkurs Theoretsche Physk 1 Mechank Skrpt zu Vorlesung 4: Starrer Körper, Hamlton-Formalsmus gehalten von: Markus Krottenmüller & Markus Perner 30.08.01
Technsche Unverstät München Fakultät für Physk Ferenkurs Theoretsche Physk 1 Mechank Skrpt zu Vorlesung 4: Starrer Körper, Hamlton-Formalsmus gehalten von: Markus Krottenmüller & Markus Perner 30.08.01
Kapitel 5. Symmetrien und Erhaltungsgrößen. 5.1 Symmetrietransformationen
 Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
Klassische Theoretische Physik II (Theorie B) Sommersemester 2016
 Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
d Alambert: Variationsprinzip in Differentialform (äquivalent zum Hamilton-Prinzip) = 0 (d Alambertsches Prinzip; δw = Z δr = 0 )
 Zusammenfassung Theoretsche Mechan d Alambert: Varatonsprnzp n Dfferentalform (äuvalent zum amlton-prnzp) δw ( F p ) * δr 0 (d Alambertsches Prnzp; δw Z δr 0 ) m allg.: p m * r m statschen Fall st: p 0
Zusammenfassung Theoretsche Mechan d Alambert: Varatonsprnzp n Dfferentalform (äuvalent zum amlton-prnzp) δw ( F p ) * δr 0 (d Alambertsches Prnzp; δw Z δr 0 ) m allg.: p m * r m statschen Fall st: p 0
Allgemeine Formulierung der Punktmechanik
 Kaptel 3 Allgemene Formulerung der Punktmechank Axom 2.2 besagt, daß der zetlche Bewegungsablauf enes Massenpunktes berechnet werden kann, wenn de Kräfte, welche auf den Massenpunkt wrken, vorgegeben snd.
Kaptel 3 Allgemene Formulerung der Punktmechank Axom 2.2 besagt, daß der zetlche Bewegungsablauf enes Massenpunktes berechnet werden kann, wenn de Kräfte, welche auf den Massenpunkt wrken, vorgegeben snd.
Rotation (2. Versuch)
 Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Physik A VL11 ( )
 Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
Hamiltonsche Mechanik
 Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materalen zur Vorlesung Theoretsche Mechank, WS 005/06 Dörte Hansen Semnar 0 Starrer Körper und Kreseltheore. Der starre Körper.. A dfferent pont of vew Raum -und körperfeste Koordnatensysteme
Ergänzende Materalen zur Vorlesung Theoretsche Mechank, WS 005/06 Dörte Hansen Semnar 0 Starrer Körper und Kreseltheore. Der starre Körper.. A dfferent pont of vew Raum -und körperfeste Koordnatensysteme
3 Elastizitätstheorie
 3 Elastztätstheore Für en elastsches Medum nmmt man enen spannungsfreen Referenzzustand an, der n Eulerkoordnaten durch x = Ax, t) gegeben st. Abwechungen werden beschreben durch de Verschebung ux, t)
3 Elastztätstheore Für en elastsches Medum nmmt man enen spannungsfreen Referenzzustand an, der n Eulerkoordnaten durch x = Ax, t) gegeben st. Abwechungen werden beschreben durch de Verschebung ux, t)
4. Lagrange-Formalismus
 y(t) ϑ 4. Lagrange-Formalsmus 4.0 Enführung Abbldung 4.1: Das sphärsche Pendel mt bewegtem Aufhängepunkt. R F mg Zel st es, enen enfachen Zugang zu komplzerten mechanschen Systemen zu entwckeln. Nach ener
y(t) ϑ 4. Lagrange-Formalsmus 4.0 Enführung Abbldung 4.1: Das sphärsche Pendel mt bewegtem Aufhängepunkt. R F mg Zel st es, enen enfachen Zugang zu komplzerten mechanschen Systemen zu entwckeln. Nach ener
1 Mehrdimensionale Analysis
 1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
Kapitel 5 Systeme von Massenpunkten, Stöße
 Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
I) Mechanik 1.Kinematik (Bewegung)
 I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
Experimentalphysik II (Kip SS 2007)
 permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
Lagrangesche Mechanik
 Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
Theoretische Physik II: Analytische Mechanik und Spezielle Relativitätstheorie
 Theoretsche Physk II: Analytsche Mechank und Spezelle Relatvtätstheore Drk H. Rschke Sommersemester 2010 Inhaltsverzechns 1 Lagrange-Mechank 1 1.1 Zwangskräfte, Zwangsbedngungen und generalserte Koordnaten.....
Theoretsche Physk II: Analytsche Mechank und Spezelle Relatvtätstheore Drk H. Rschke Sommersemester 2010 Inhaltsverzechns 1 Lagrange-Mechank 1 1.1 Zwangskräfte, Zwangsbedngungen und generalserte Koordnaten.....
Theoretische Physik B MECHANIK. Vorlesung SS 2003
 Theoretsche Physk B MECHANIK Vorlesung SS 2003 P. Wölfle Insttut für Theore der Kondenserten Matere Fakultät für Physk Unverstät Karlsruhe Homepage: http://www.tkm.un-karlsruhe.de/lehre/ Textverarbetung:
Theoretsche Physk B MECHANIK Vorlesung SS 2003 P. Wölfle Insttut für Theore der Kondenserten Matere Fakultät für Physk Unverstät Karlsruhe Homepage: http://www.tkm.un-karlsruhe.de/lehre/ Textverarbetung:
MOD-01 LAGRANGE FORMALISMUS -- TEIL 1
 MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
I)1. Kinematik. EP WS 2009/10 Dünnweber/Faessler
 I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
Vorlesung 3 Differentialgeometrie in der Physik 13
 Vorlesung 3 Dfferentalgeometre n der Physk 13 Bemerkung. Ist M Manngfaltgket, p M und φ : U R n Karte mt p U, so nennt man U auch Koordnatenumgebung und φ auch Koordnatensystem n p. Bespel 2.4 Seen R >
Vorlesung 3 Dfferentalgeometre n der Physk 13 Bemerkung. Ist M Manngfaltgket, p M und φ : U R n Karte mt p U, so nennt man U auch Koordnatenumgebung und φ auch Koordnatensystem n p. Bespel 2.4 Seen R >
Holonome Mehrkörpersysteme
 Kaptel 6 Holonome Mehrkörpersysteme In Anlehnung an de Vorgehenswese be Massenpunktsystemen n Kaptel 5 werden n desem Kaptel de Formulerungen der Bewegungsglechungen von Mehrkörpersystemen mt holonomen
Kaptel 6 Holonome Mehrkörpersysteme In Anlehnung an de Vorgehenswese be Massenpunktsystemen n Kaptel 5 werden n desem Kaptel de Formulerungen der Bewegungsglechungen von Mehrkörpersystemen mt holonomen
Theoretische Physik II Elektrodynamik Blatt 2
 PDDr.S.Mertens M. Hummel Theoretsche Physk II Elektrodynamk Blatt 2 SS 29 8.4.29 1. Rechnen mt Nabla. Zegen Se durch Auswertung n kartesschen Koordnaten de folgende Relaton und werten Se de anderen Relatonen
PDDr.S.Mertens M. Hummel Theoretsche Physk II Elektrodynamk Blatt 2 SS 29 8.4.29 1. Rechnen mt Nabla. Zegen Se durch Auswertung n kartesschen Koordnaten de folgende Relaton und werten Se de anderen Relatonen
Fachbereich Mathematik Prof. K. Grosse-Brauckmann D. Frisch WS 2007/08 10./ Gruppenübung
 Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
Stand: gern gestellte Prüfungsfragen & Definitionen
 Stand: 7.0.98 gern gestellte Prüfungsfragen & Defntonen Klasssche Mechan (mt & ohne Gravtaton, aber: v > h) Stat: Lehre vom Glechgewcht der Kräfte. Se beschäftgt sch mt Kräften an starren
Stand: 7.0.98 gern gestellte Prüfungsfragen & Defntonen Klasssche Mechan (mt & ohne Gravtaton, aber: v > h) Stat: Lehre vom Glechgewcht der Kräfte. Se beschäftgt sch mt Kräften an starren
3 Vorlesung: Lagrange Mechanik I. 3.1 Zwangsbedingungen. Beispiele (nach Kuypers)
 3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
Multilineare Algebra und ihre Anwendungen. Nr. 6: Normalformen. Verfasser: Yee Song Ko Adrian Jenni Rebecca Huber Damian Hodel
 ultlneare Algebra und hre Anwendungen Nr. : Normalformen Verfasser: Yee Song Ko Adran Jenn Rebecca Huber Daman Hodel 9.5.7 - - ultlneare Algebra und hre Anwendungen Jordan sche Normalform Allgemene heore
ultlneare Algebra und hre Anwendungen Nr. : Normalformen Verfasser: Yee Song Ko Adran Jenn Rebecca Huber Daman Hodel 9.5.7 - - ultlneare Algebra und hre Anwendungen Jordan sche Normalform Allgemene heore
Einführung in die theoretische Physik 1
 Enführung n de theoretsche hysk 1 rof. Dr. L. Mathey Denstag 15:45 16:45 und Donnerstag 10:45 12:00 Begnn: 23.10.12 Jungus 9, Hörs 2 Mathey Enführung n de theor. hysk 1 1 Grundhypothese der Thermostatk
Enführung n de theoretsche hysk 1 rof. Dr. L. Mathey Denstag 15:45 16:45 und Donnerstag 10:45 12:00 Begnn: 23.10.12 Jungus 9, Hörs 2 Mathey Enführung n de theor. hysk 1 1 Grundhypothese der Thermostatk
Experimentalphysik 1. Vorlesung 1
 Technsche Unverstät München Fakultät für Physk Ferenkurs Expermentalphysk 1 WS 2016/17 Vorlesung 1 Ronja Berg (ronja.berg@tum.de) Katharna Sche (katharna.sche@tum.de) Inhaltsverzechns 1 Klasssche Mechank
Technsche Unverstät München Fakultät für Physk Ferenkurs Expermentalphysk 1 WS 2016/17 Vorlesung 1 Ronja Berg (ronja.berg@tum.de) Katharna Sche (katharna.sche@tum.de) Inhaltsverzechns 1 Klasssche Mechank
Für jeden reinen, ideal kristallisierten Stoff ist die Entropie am absoluten Nullpunkt gleich
 Drtter Hauptsatz der Thermodynamk Rückblck auf vorherge Vorlesung Methoden zur Erzeugung tefer Temperaturen: - umgekehrt laufende WKM (Wärmepumpe) - Joule-Thomson Effekt bs 4 K - Verdampfen von flüssgem
Drtter Hauptsatz der Thermodynamk Rückblck auf vorherge Vorlesung Methoden zur Erzeugung tefer Temperaturen: - umgekehrt laufende WKM (Wärmepumpe) - Joule-Thomson Effekt bs 4 K - Verdampfen von flüssgem
29 zweite Ableitungen der thermodynamischen Potentiale spezifische Wärme (thermischer response) E = = = T V N V N V N = = κ T.
 hermodynamsche resonse -unktonen: 9 zwete Abletungen der thermodynamschen Potentale sezfsche Wärme (thermscher resonse) E C S be konstantem olumen (sochor):,,, be konstantem Druck (sobar): C S Komressbltät
hermodynamsche resonse -unktonen: 9 zwete Abletungen der thermodynamschen Potentale sezfsche Wärme (thermscher resonse) E C S be konstantem olumen (sochor):,,, be konstantem Druck (sobar): C S Komressbltät
4. Musterlösung. Problem 1: Kreuzende Schnitte **
 Unverstät Karlsruhe Algorthmentechnk Fakultät für Informatk WS 05/06 ITI Wagner 4. Musterlösung Problem 1: Kreuzende Schntte ** Zwe Schntte (S, V \ S) und (T, V \ T ) n enem Graph G = (V, E) kreuzen sch,
Unverstät Karlsruhe Algorthmentechnk Fakultät für Informatk WS 05/06 ITI Wagner 4. Musterlösung Problem 1: Kreuzende Schntte ** Zwe Schntte (S, V \ S) und (T, V \ T ) n enem Graph G = (V, E) kreuzen sch,
1 Definition und Grundbegriffe
 1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
Klassische Mechanik. von Herbert Goldstein, Charles P Poole, Jr, John L Safko, Sr. 1. Auflage
 Klasssche Mechank von Herbert Goldsten, Charles P Poole, Jr, John L Safko, Sr 1. Auflage Klasssche Mechank Goldsten / Poole, Jr / Safko, Sr schnell und portofre erhältlch be beck-shop.de DIE FACHBUCHHANDLUNG
Klasssche Mechank von Herbert Goldsten, Charles P Poole, Jr, John L Safko, Sr 1. Auflage Klasssche Mechank Goldsten / Poole, Jr / Safko, Sr schnell und portofre erhältlch be beck-shop.de DIE FACHBUCHHANDLUNG
Ergänzungskurs Physik Teil 1: Theoretische Mechanik
 Vorlesungsskrpt Ergänzungskurs Physk Tel 1: Theoretsche Mechank Angewandte Naturwssenschaft TU Bergakademe Freberg Sandra Glles nach ener Vorlesung von Prof. J. Monecke m Sommersemester 2003 Ma 2004 Inhaltsverzechns
Vorlesungsskrpt Ergänzungskurs Physk Tel 1: Theoretsche Mechank Angewandte Naturwssenschaft TU Bergakademe Freberg Sandra Glles nach ener Vorlesung von Prof. J. Monecke m Sommersemester 2003 Ma 2004 Inhaltsverzechns
Zusammenfassung der ersten Vorlesung
 Zusammenfassung der ersten Vorlesung 1. Es geht um de Mechank.. Jedes mechansche System kann mttels ener Lagrangefunkton charaktersert werden. De Lagrangefunkton hängt von den verallgemenerten Koordnaten,
Zusammenfassung der ersten Vorlesung 1. Es geht um de Mechank.. Jedes mechansche System kann mttels ener Lagrangefunkton charaktersert werden. De Lagrangefunkton hängt von den verallgemenerten Koordnaten,
Ko- und kontravariante Darstellung
 Ko- und kontravarante Darstellung Physkalsche Sachverhalte snd vom verwendeten Koordnatensystem unabhängg. Sehr oft st es snnvoll, se n verschedenen Koordnatensystemen darzustellen. Berets erwähnt wurden
Ko- und kontravarante Darstellung Physkalsche Sachverhalte snd vom verwendeten Koordnatensystem unabhängg. Sehr oft st es snnvoll, se n verschedenen Koordnatensystemen darzustellen. Berets erwähnt wurden
Grundgedanke der Regressionsanalyse
 Grundgedanke der Regressonsanalse Bsher wurden durch Koeffzenten de Stärke von Zusammenhängen beschreben Mt der Regressonsrechnung können für ntervallskalerte Varablen darüber hnaus Modelle geschätzt werden
Grundgedanke der Regressonsanalse Bsher wurden durch Koeffzenten de Stärke von Zusammenhängen beschreben Mt der Regressonsrechnung können für ntervallskalerte Varablen darüber hnaus Modelle geschätzt werden
Vermessungskunde für Bauingenieure und Geodäten
 Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
9 Komplexe Zahlen ( ) ( ) 9.1 Ziele. 9.2 Warum braucht man komplexe Zahlen? 9.3 Darstellung von komplexen Zahlen. r 2. j 2. j 1.
 Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Übungsklausur zur Vorlesung Wahrscheinlichkeit und Regression Lösungen. Übungsklausur Wahrscheinlichkeit und Regression Die Lösungen
 Übungsklausur Wahrschenlchket und Regresson De Lösungen. Welche der folgenden Aussagen treffen auf en Zufallsexperment zu? a) En Zufallsexperment st en emprsches Phänomen, das n stochastschen Modellen
Übungsklausur Wahrschenlchket und Regresson De Lösungen. Welche der folgenden Aussagen treffen auf en Zufallsexperment zu? a) En Zufallsexperment st en emprsches Phänomen, das n stochastschen Modellen
Zur Erinnerung: System von Massenpunkten. dt i dt. 1 dt. Massenschwerpunkt
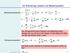 Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
6. Übungsblatt zur VL Einführung in die Klassische Mechanik und Wärmelehre Modul P1a, 1. FS BPh 17. November 2009
 6. Übungsblatt zur VL Enführung n de Klasssche Mechank und Wärmelehre Modul P1a, 1. FS BPh 17. November 2009 Aufgabe 6.1: Schlepplft In enem Wntersportgebet soll en neuer Schlepplft für Schfahrer gebaut
6. Übungsblatt zur VL Enführung n de Klasssche Mechank und Wärmelehre Modul P1a, 1. FS BPh 17. November 2009 Aufgabe 6.1: Schlepplft In enem Wntersportgebet soll en neuer Schlepplft für Schfahrer gebaut
Die mathematischen Grundlagen der Wellenmechanik
 De mathematschen Grundlagen der Wellenmechank Zustände und deren Darstellung En physkalsches System wrd durch enen Zustand u charaktersert, ndem es durch ene bestmmte expermentelle Präparaton gebracht
De mathematschen Grundlagen der Wellenmechank Zustände und deren Darstellung En physkalsches System wrd durch enen Zustand u charaktersert, ndem es durch ene bestmmte expermentelle Präparaton gebracht
3. Lineare Algebra (Teil 2)
 Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
5. Gruppenübung zur Vorlesung. Höhere Mathematik 1. Wintersemester 2012/2013
 O. Alaya, S. Demrel M. Fetzer, B. Krnn M. Wed 5. Gruppenübung zur Vorlesung Höhere Mathematk Wntersemester /3 Dr. M. Künzer Prof. Dr. M. Stroppel Lösungshnwese zu den Hausaufgaben: Aufgabe H 6. Darstellungen
O. Alaya, S. Demrel M. Fetzer, B. Krnn M. Wed 5. Gruppenübung zur Vorlesung Höhere Mathematk Wntersemester /3 Dr. M. Künzer Prof. Dr. M. Stroppel Lösungshnwese zu den Hausaufgaben: Aufgabe H 6. Darstellungen
Vermessungskunde für Bauingenieure und Geodäten
 Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
Theoretische Mechanik WS 2007/08. Inhaltsverzeichnis
 Theoretsche Mechank Inhaltsverzechns 0 Lteratur 6 WS 007/08 Harald Jeschke, Unverstät des Saarlandes/Unverstät Frankfurt auf Grundlage enes Skrpts von Claudus Gros, Unverstät Frankfurt 1 Bewegungsglechungen
Theoretsche Mechank Inhaltsverzechns 0 Lteratur 6 WS 007/08 Harald Jeschke, Unverstät des Saarlandes/Unverstät Frankfurt auf Grundlage enes Skrpts von Claudus Gros, Unverstät Frankfurt 1 Bewegungsglechungen
9 Komplexe Zahlen ( ) ( ) 9.1 Ziele. 9.2 Warum braucht man komplexe Zahlen? 9.3 Darstellung von komplexen Zahlen. r 2. j 2. j 1.
 Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Andreas Schulz. 18. Juni Lokal- orthogonale Koordinatesysteme Math. Hilfsmittel: Antisymmetrischer Tensor: Kreuzprodukt, Spatprodukt,
 Tutorum zur G2 Srker - SS3 Mathematscher Notfallkoffer : Dfferentaloperatoren und Integraton n allgemenen, krummlng-orthogonalen Korrdnatensystemen Andreas Schulz 8. Jun 23 Inhaltsverzechns Bevor es losgeht...
Tutorum zur G2 Srker - SS3 Mathematscher Notfallkoffer : Dfferentaloperatoren und Integraton n allgemenen, krummlng-orthogonalen Korrdnatensystemen Andreas Schulz 8. Jun 23 Inhaltsverzechns Bevor es losgeht...
Regressionsgerade. x x 1 x 2 x 3... x n y y 1 y 2 y 3... y n
 Regressonsgerade x x x x 3... x n y y y y 3... y n Bem Auswerten von Messrehen wrd häufg ene durch theoretsche Überlegungen nahegelegte lneare Bezehung zwschen den x- und y- Werten gesucht, d.h. ene Gerade
Regressonsgerade x x x x 3... x n y y y y 3... y n Bem Auswerten von Messrehen wrd häufg ene durch theoretsche Überlegungen nahegelegte lneare Bezehung zwschen den x- und y- Werten gesucht, d.h. ene Gerade
1.4 Dynamik, Newton sche Axiome ( Postulate) der klassischen (Punkt)Mechanik
 Woche.doc, 1/.1.14 1.4 Dynamk, Newton sche Aome ( Postulate) der klassschen (Punkt)Mechank Ausgangspunkt: De Knematk sagt nchts über de Ursache der Bewegung von Körpern n Raum und Zet. In der Dynamk wrd
Woche.doc, 1/.1.14 1.4 Dynamk, Newton sche Aome ( Postulate) der klassschen (Punkt)Mechank Ausgangspunkt: De Knematk sagt nchts über de Ursache der Bewegung von Körpern n Raum und Zet. In der Dynamk wrd
Aufgabenkomplex 2: Umrechung von Einheiten, Ungleichungen, Komplexe Zahlen
 Technsche Unverstät Chemntz 0. Oktober 009 Fakultät für Mathematk Höhere Mathematk I.1 Aufgabenkomplex : Umrechung von Enheten, Unglechungen, Komplexe Zahlen Letzter Abgabetermn: 19. November 009 n Übung
Technsche Unverstät Chemntz 0. Oktober 009 Fakultät für Mathematk Höhere Mathematk I.1 Aufgabenkomplex : Umrechung von Enheten, Unglechungen, Komplexe Zahlen Letzter Abgabetermn: 19. November 009 n Übung
NSt. Der Wert für: x= +1 liegt, erkennbar an dem zugehörigen Funktionswert, der gesuchten Nullstelle näher.
 PV - Hausaugabe Nr. 7.. Berechnen Se eakt und verglechen Se de Werte ür de Nullstelle, de mttels dem Verahren von Newton, der Regula als und ener Mttelung zu erhalten snd von der! Funkton: ( ) Lösungs
PV - Hausaugabe Nr. 7.. Berechnen Se eakt und verglechen Se de Werte ür de Nullstelle, de mttels dem Verahren von Newton, der Regula als und ener Mttelung zu erhalten snd von der! Funkton: ( ) Lösungs
1.11 Beispielaufgaben
 . Bespelaufgaben Darstellung komplexer Zahlen Aufgabe. Man stelle de komplexe Zahl z = +e 5f n algebrascher Form, also als x + y dar. Damt man de Formel für de Dvson anwenden kann, muss zunächst der Nenner
. Bespelaufgaben Darstellung komplexer Zahlen Aufgabe. Man stelle de komplexe Zahl z = +e 5f n algebrascher Form, also als x + y dar. Damt man de Formel für de Dvson anwenden kann, muss zunächst der Nenner
12 LK Ph / Gr Elektrische Leistung im Wechselstromkreis 1/5 31.01.2007. ω Additionstheorem: 2 sin 2 2
 1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
Abbildung 3.1: Besetzungszahlen eines Fermigases im Grundzustand (a)) und für eine angeregte Konfiguration (b)).
 44 n n F F a) b) Abbldung 3.: Besetzungszahlen enes Fermgases m Grundzustand (a)) und für ene angeregte Konfguraton (b)). 3.3 Ferm Drac Statstk In desem Abschntt wollen wr de thermodynamschen Egenschaften
44 n n F F a) b) Abbldung 3.: Besetzungszahlen enes Fermgases m Grundzustand (a)) und für ene angeregte Konfguraton (b)). 3.3 Ferm Drac Statstk In desem Abschntt wollen wr de thermodynamschen Egenschaften
Zwischen dem Kronecker Symbol und dem Levi-Cevita Symbol besteht der Zusammenhang
 Ü bung zur Vorlesung Aufgabe Schreben Se folgende Ausdrücke n Indexschrebwese unter Verwendung der Ensten schen Summatonskonventon und der Kommadarstellung für partelle Abletungen! a) C AB b) C T A B c)
Ü bung zur Vorlesung Aufgabe Schreben Se folgende Ausdrücke n Indexschrebwese unter Verwendung der Ensten schen Summatonskonventon und der Kommadarstellung für partelle Abletungen! a) C AB b) C T A B c)
Herbert Goldstein, Charles P. Poole, Jr., und John L. Safko. Klassische Mechanik
 Herbert Goldsten, Charles P. Poole, Jr., und John L. Safko Klasssche Mechank Wetere Ttel zu desem Thema Kuypers, F. Klasssche Mechank Mt 103 Bespelen und 167 Aufgaben mt Lösungen 608 Seten mt 286 Abbldungen
Herbert Goldsten, Charles P. Poole, Jr., und John L. Safko Klasssche Mechank Wetere Ttel zu desem Thema Kuypers, F. Klasssche Mechank Mt 103 Bespelen und 167 Aufgaben mt Lösungen 608 Seten mt 286 Abbldungen
2 Zufallsvariable und Verteilungen
 Zufallsvarable und Vertelungen 7 Zufallsvarable und Vertelungen Wr wollen uns jetzt mt Zufallsexpermenten beschäftgen, deren Ausgänge durch (reelle) Zahlen beschreben werden können, oder be denen man jedem
Zufallsvarable und Vertelungen 7 Zufallsvarable und Vertelungen Wr wollen uns jetzt mt Zufallsexpermenten beschäftgen, deren Ausgänge durch (reelle) Zahlen beschreben werden können, oder be denen man jedem
Methoden der innerbetrieblichen Leistungsverrechnung
 Methoden der nnerbetreblchen Lestungsverrechnung In der nnerbetreblchen Lestungsverrechnung werden de Gemenosten der Hlfsostenstellen auf de Hauptostenstellen übertragen. Grundlage dafür snd de von den
Methoden der nnerbetreblchen Lestungsverrechnung In der nnerbetreblchen Lestungsverrechnung werden de Gemenosten der Hlfsostenstellen auf de Hauptostenstellen übertragen. Grundlage dafür snd de von den
10 Einführung in die Statistische Physik
 10 Enführung n de Statstsche Physk More s dfferent! P.W. Anderson, Nobelpres 1977 10.1 Prolegomena Technsch gesehen st de Rolle der Statstschen Mechank der Glechgewchtssysteme, ausgehend von unseren Kenntnsse
10 Enführung n de Statstsche Physk More s dfferent! P.W. Anderson, Nobelpres 1977 10.1 Prolegomena Technsch gesehen st de Rolle der Statstschen Mechank der Glechgewchtssysteme, ausgehend von unseren Kenntnsse
Asymptotische Stochastik (SS 2010) Übungsblatt 1 P X. 0, n.
 Insttut für Stochastk PD. Dr. Deter Kadelka Danel Gentner Asymptotsche Stochastk (SS 2) Übungsblatt Aufgabe (Arten von Konvergenz reeller Zufallsvarablen und deren Zusammenhänge) Es seen X,, n N reelle
Insttut für Stochastk PD. Dr. Deter Kadelka Danel Gentner Asymptotsche Stochastk (SS 2) Übungsblatt Aufgabe (Arten von Konvergenz reeller Zufallsvarablen und deren Zusammenhänge) Es seen X,, n N reelle
Determinanten - I. den i-ten Zeilenvektor der n n-matrix A bezeichnet.
 Determnanten - I Ene Determnante st ene Abbldung, welche ener quadratschen (!) Matrx ene Zahl zuordnet. Wr verwenden n desem Zusammenhang de Schrebwese A = a 2, wobe den -ten Zelenvektor der n n-matrx
Determnanten - I Ene Determnante st ene Abbldung, welche ener quadratschen (!) Matrx ene Zahl zuordnet. Wr verwenden n desem Zusammenhang de Schrebwese A = a 2, wobe den -ten Zelenvektor der n n-matrx
4. Energie, Arbeit, Leistung, Impuls
 34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
6. Übung zur Linearen Algebra II
 Unverstät Würzburg Mathematsches Insttut Prof. Dr. Peter Müller Dr. Peter Fleschmann SS 2006 30.05.2006 6. Übung zur Lnearen Algebra II Abgabe: Bs Mttwoch, 14.06.2006, 11:00 Uhr n de Brefkästen vor der
Unverstät Würzburg Mathematsches Insttut Prof. Dr. Peter Müller Dr. Peter Fleschmann SS 2006 30.05.2006 6. Übung zur Lnearen Algebra II Abgabe: Bs Mttwoch, 14.06.2006, 11:00 Uhr n de Brefkästen vor der
Runge-Kutta-Theorie: Adjungierte Verfahren, A-Stabilität, Steife Systeme
 Runge-Kutta-Teore: Adjungerte Verfaren, A-Stabltät, Stefe Systeme Andre Neubert bat@un-paderborn.de Semnar Numerk für Informatker, SS2004: Runge-Kutta-Teore Sete Glederung : - Adjungerte Verfaren / Symmetrsce
Runge-Kutta-Teore: Adjungerte Verfaren, A-Stabltät, Stefe Systeme Andre Neubert bat@un-paderborn.de Semnar Numerk für Informatker, SS2004: Runge-Kutta-Teore Sete Glederung : - Adjungerte Verfaren / Symmetrsce
12 UMPU Tests ( UMP unbiased )
 89 1 UMPU Tests ( UMP unbased ) Nach Bemerkung 11.8(b) exstert m Allgemenen ken zwesetger UMP- Test zu enem Nveau α. Deshalb Enschränkung auf unverfälschte Tests: ϕ Φ α heßt unverfälscht (unbased) zum
89 1 UMPU Tests ( UMP unbased ) Nach Bemerkung 11.8(b) exstert m Allgemenen ken zwesetger UMP- Test zu enem Nveau α. Deshalb Enschränkung auf unverfälschte Tests: ϕ Φ α heßt unverfälscht (unbased) zum
( ) γ. (t 1 ) (t 2 ) = Arg γ 2(t 2 )
 Funktonentheore, Woche 10 Bholomorphe Abbldungen 10.1 Konform und bholomorph Ene konforme Abbldung erhält Wnkel und Orenterung. Damt st folgendes gement: Wenn sch zwe Kurven schneden, dann schneden sch
Funktonentheore, Woche 10 Bholomorphe Abbldungen 10.1 Konform und bholomorph Ene konforme Abbldung erhält Wnkel und Orenterung. Damt st folgendes gement: Wenn sch zwe Kurven schneden, dann schneden sch
50 Matrixnormen und Eigenwertabschätzungen
 50 Matrxnormen und Egenwertabschätzungen 501 Motvaton De Berechnung der Egenwerte ener Matrx st aufwändg (vgl Kaptel 45, Kaptel 51) Kann man de Egenwerte ener Matrx mt gerngem Aufwand abschätzen? Des spelt
50 Matrxnormen und Egenwertabschätzungen 501 Motvaton De Berechnung der Egenwerte ener Matrx st aufwändg (vgl Kaptel 45, Kaptel 51) Kann man de Egenwerte ener Matrx mt gerngem Aufwand abschätzen? Des spelt
Elemente der Mathematik - Sommer 2016
 Elemente der Mathematk - Sommer 2016 Prof Dr Matthas Lesch, Regula Krapf Lösungen Übungsblatt 3 Aufgabe 9 (10 Punkte) Das Horner-Schema st ene Methode zum Auswerten enes Polynoms n a0 x an der Stelle s
Elemente der Mathematk - Sommer 2016 Prof Dr Matthas Lesch, Regula Krapf Lösungen Übungsblatt 3 Aufgabe 9 (10 Punkte) Das Horner-Schema st ene Methode zum Auswerten enes Polynoms n a0 x an der Stelle s
Schriftliche Prüfung aus Systemtechnik am
 U Graz, Insttut egelungs- und Automatserungstechnk Schrftlche Prüfung aus Systemtechnk am 4.. 5 Name / Vorname(n): Kenn-Matr.Nr.: Bonuspunkte: 4 errechbare Punkte 4 5 7 5 errechte Punkte U Graz, Insttut
U Graz, Insttut egelungs- und Automatserungstechnk Schrftlche Prüfung aus Systemtechnk am 4.. 5 Name / Vorname(n): Kenn-Matr.Nr.: Bonuspunkte: 4 errechbare Punkte 4 5 7 5 errechte Punkte U Graz, Insttut
e dt (Gaußsches Fehlerintegral)
 Das Gaußsche Fehlerntegral Φ Ac 5-8 Das Gaußsche Fehlerntegral Φ st denert als das Integral über der Standard-Normalvertelung j( ) = -,5 n den Grenzen bs, also F,5 t ( ) = - e dt (Gaußsches Fehlerntegral)
Das Gaußsche Fehlerntegral Φ Ac 5-8 Das Gaußsche Fehlerntegral Φ st denert als das Integral über der Standard-Normalvertelung j( ) = -,5 n den Grenzen bs, also F,5 t ( ) = - e dt (Gaußsches Fehlerntegral)
5.3.3 Relaxationsverfahren: das SOR-Verfahren
 53 Iteratve Lösungsverfahren für lneare Glechungssysteme 533 Relaxatonsverfahren: das SOR-Verfahren Das vorangehende Bespel zegt, dass Jacob- sowe Gauß-Sedel-Verfahren sehr langsam konvergeren Für de Modellmatrx
53 Iteratve Lösungsverfahren für lneare Glechungssysteme 533 Relaxatonsverfahren: das SOR-Verfahren Das vorangehende Bespel zegt, dass Jacob- sowe Gauß-Sedel-Verfahren sehr langsam konvergeren Für de Modellmatrx
Schriftliche Prüfung aus Signaltransformationen Teil: Dourdoumas am
 TU Graz, Insttut für Regelungs- und Automatserungstechnk 1 Schrftlche Prüfung aus Sgnaltransformatonen Tel: Dourdoumas am 1. 10. 01 Name / Vorname(n): Kennzahl / Matrkel-Nummer: 1 errechbare Punkte 4 errechte
TU Graz, Insttut für Regelungs- und Automatserungstechnk 1 Schrftlche Prüfung aus Sgnaltransformatonen Tel: Dourdoumas am 1. 10. 01 Name / Vorname(n): Kennzahl / Matrkel-Nummer: 1 errechbare Punkte 4 errechte
Diskrete Mathematik 1 WS 2008/09
 Ruhr-Unverstät Bochum Lehrstuhl für Kryptologe und IT-Scherhet Prof. Dr. Alexander May M. Rtzenhofen, M. Mansour Al Sawad, A. Meurer Lösungsblatt zur Vorlesung Dskrete Mathematk 1 WS 2008/09 Blatt 7 /
Ruhr-Unverstät Bochum Lehrstuhl für Kryptologe und IT-Scherhet Prof. Dr. Alexander May M. Rtzenhofen, M. Mansour Al Sawad, A. Meurer Lösungsblatt zur Vorlesung Dskrete Mathematk 1 WS 2008/09 Blatt 7 /
Vorlesung Theoretische Mechanik
 Vorlesung Theoretsche Mechank Verson vom WS 2014/2015 Unverstät Manz Insttut für Physk Theore der kondenserten Matere Prof. Dr. Frederke Schmd Inhalt: Newtonsche Mechank De Newtonschen Axome Bezugssysteme
Vorlesung Theoretsche Mechank Verson vom WS 2014/2015 Unverstät Manz Insttut für Physk Theore der kondenserten Matere Prof. Dr. Frederke Schmd Inhalt: Newtonsche Mechank De Newtonschen Axome Bezugssysteme
Lineare Regression - Mathematische Grundlagen
 FKULTÄT FÜR MTHEMTIK U TURWISSESCHFTE ISTITUT FÜR PHYSIK FCHGEBIET EXPERIMETLPHYSIK I r. rer. nat. orbert Sten, pl.-ing (FH) Helmut Barth Lneare Regresson - Mathematsche Grundlagen. llgemene Gerade Wr
FKULTÄT FÜR MTHEMTIK U TURWISSESCHFTE ISTITUT FÜR PHYSIK FCHGEBIET EXPERIMETLPHYSIK I r. rer. nat. orbert Sten, pl.-ing (FH) Helmut Barth Lneare Regresson - Mathematsche Grundlagen. llgemene Gerade Wr
6. Hilbertraum und lineare Operatoren (mathematische Grundlagen QM)
 6. Hlbertraum und lneare Operatoren (mathematsche Grundlagen QM) 6.1 Hlbertraum Raum = mathematsches Konstrukt: Vektorraum a) Der lneare komplexe Raum st de Menge von mathematschen Objekten mt folgenden
6. Hlbertraum und lneare Operatoren (mathematsche Grundlagen QM) 6.1 Hlbertraum Raum = mathematsches Konstrukt: Vektorraum a) Der lneare komplexe Raum st de Menge von mathematschen Objekten mt folgenden
Wiederholung: Newtonsche Mechanik
 Kaptel 1 Weerholung: Newtonsche Mechank c Copyrght 2012 Freerke Schm 1 1.1 De Newtonschen Axome 1.1.1 Wortlaut (übersetzt) aus: prncpa mathematca phlosophae naturals I) Jeer Körper verharrt m Zustan er
Kaptel 1 Weerholung: Newtonsche Mechank c Copyrght 2012 Freerke Schm 1 1.1 De Newtonschen Axome 1.1.1 Wortlaut (übersetzt) aus: prncpa mathematca phlosophae naturals I) Jeer Körper verharrt m Zustan er
Statistik und Wahrscheinlichkeitsrechnung
 Statstk und Wahrschenlchketsrechnung Statstk und Wahrschenlchketsrechnung 5. Vorlesung Dr. Jochen Köhler.03.0 Statstk und Wahrschenlchketsrechnung Wchtg!!! Vorlesung Do 4.03.0 HCI G3 Übung 5 D 9.03.0 Fnk
Statstk und Wahrschenlchketsrechnung Statstk und Wahrschenlchketsrechnung 5. Vorlesung Dr. Jochen Köhler.03.0 Statstk und Wahrschenlchketsrechnung Wchtg!!! Vorlesung Do 4.03.0 HCI G3 Übung 5 D 9.03.0 Fnk
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 009 UNIVERSITÄT KARLSRUHE Blatt 4 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 16: (Success Run, Fortsetzung)
INSTITUT FÜR STOCHASTIK SS 009 UNIVERSITÄT KARLSRUHE Blatt 4 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 16: (Success Run, Fortsetzung)
Physik für Studierende der Biologie und Chemie Universität Zürich, HS 2009, U. Straumann Version 26. Oktober 2009
 Physk für Studerende der Bologe und Cheme Unverstät Zürch, HS 009, U. Straumann erson 6. Oktober 009 Inhaltsverzechns 3. Systeme von Telchen................................ 3. 3.. Schwerpunkt..................................
Physk für Studerende der Bologe und Cheme Unverstät Zürch, HS 009, U. Straumann erson 6. Oktober 009 Inhaltsverzechns 3. Systeme von Telchen................................ 3. 3.. Schwerpunkt..................................
9. Der starre Körper; Rotation I
 Mechank De stae Köpe; Rotaton I 9. De stae Köpe; Rotaton I 9.. Enletung bshe: (Systeme on) Punktmassen jetzt: Betachtung ausgedehnte Köpe, übe de de Masse glechmäßg etelt st (kene Atome). Köpe soll sch
Mechank De stae Köpe; Rotaton I 9. De stae Köpe; Rotaton I 9.. Enletung bshe: (Systeme on) Punktmassen jetzt: Betachtung ausgedehnte Köpe, übe de de Masse glechmäßg etelt st (kene Atome). Köpe soll sch
INTELLIGENTE DATENANALYSE IN MATLAB. Mathematische Grundlagen
 INTELLIGENTE DATENANALYSE IN MATLAB Mathematsche Grundlagen Überblck Lneare Algebra: Vektoren, Matrzen, Analyss & Optmerung: Dstanzen, konvexe Funktonen, Lagrange-Ansatz, Stochastk: Wahrschenlchketstheore,
INTELLIGENTE DATENANALYSE IN MATLAB Mathematsche Grundlagen Überblck Lneare Algebra: Vektoren, Matrzen, Analyss & Optmerung: Dstanzen, konvexe Funktonen, Lagrange-Ansatz, Stochastk: Wahrschenlchketstheore,
Invariantentheorie. Vorlesung 3. Lineare Operationen
 Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invarantentheore Vorlesung 3 Lneare Operatonen Ene Operaton ener Gruppe G auf ener (geometrschen) Menge M st das gleche we en Gruppenhomomorphsmus der Gruppe
Prof. Dr. H. Brenner Osnabrück WS 2012/2013 Invarantentheore Vorlesung 3 Lneare Operatonen Ene Operaton ener Gruppe G auf ener (geometrschen) Menge M st das gleche we en Gruppenhomomorphsmus der Gruppe
Eine Kompassnadel, die sich nur um eine vertikale Achse drehen kann, richtet sich entlang der Horizontalkomponente des Erdmagnetfeldes B E,
 IYPT 009 Problem Nr..: Coupled compasses Place a compass on a table. Place a smlar compass next to the frst one and shake t gently to make the needle start oscllatng. The orgnal compass' needle wll start
IYPT 009 Problem Nr..: Coupled compasses Place a compass on a table. Place a smlar compass next to the frst one and shake t gently to make the needle start oscllatng. The orgnal compass' needle wll start
