Vorlesung Theoretische Mechanik
|
|
|
- Paula Braun
- vor 7 Jahren
- Abrufe
Transkript
1 Vorlesung Theoretsche Mechank Verson vom WS 2014/2015 Unverstät Manz Insttut für Physk Theore der kondenserten Matere Prof. Dr. Frederke Schmd Inhalt: Newtonsche Mechank De Newtonschen Axome Bezugssysteme Energe und Potental Erhaltungssätze und Symmetren Anwendung: Das Zwekörperproblem Lagrange-Mechank Zwangsbedngungen und Zwangskräfte Lagrange-Glechungen erster Art Invaranzen und Erhaltungsgrößen Das Hamltonsche Prnzp Verallgemenerte Lagrange-Formalsmen Starre Körper Knematk: Beschrebung der Bewegung Dynamsche Größen und Träghetstensor Bewegungsglechungen und Kreseltheore Hamltonsche Mechank Generalserter Impuls Legendre-Transformaton und Hamlton-Funkton Posson-Klammern Kanonsche Transformatonen Der Louvlle-Satz De symplektsche Struktur des Phasenraums Anwendung: Klene Schwngungen Ausblck: En Ausflug ns Hamltonsche Chaos Grundbegrffe der Hydrodynamk Elektronsch: Letzte Änderung am Staudngerweg 9, ,
2 Copyrght 2014 Frederke Schmd De Vertelung deses Dokuments n elektronscher oder gedruckter Form st gestattet, solange sen Inhalt enschleßlch Autoren- und Copyrght-Angabe unverändert blebt und de Vertelung kostenlos erfolgt, abgesehen von ener Gebühr für den Datenträger, den Kopervorgang usw.
3 Inhaltsverzechns Vorbemerkungen 1 1 Newtonsche Mechank De Newtonschen Axome Wortlaut (übersetzt) Präzserung der knematschen Begrffe Dskusson der Postulate Bespele: Anwendungen des Kraftgesetzes Freer Fall m homogenen Schwerefeld Freer Fall m homogenen Schwerefeld mt Rebung Pendel Bezugssysteme Inertalsysteme und Galle-Transformaton Roterende Bezugssysteme Belebg beschleungte Bezugssysteme Energe und Potental Potentelle Energe Knetsche Energe Wetere Begrffe Erhaltungssätze und Symmetren Homogentät der Zet und Energeerhaltung Homogentät des Raumes und Impulserhaltung Isotrope des Raumes und Drehmpulserhaltung Skalennvaranz und Vralsatz Bespele für Anwendungen von Symmetreprnzpen Zusammenfassung: Newtonsche Mechank Anwendung: Das Zwekörperproblem Redukton auf en endmensonales Problem Das Kepler-Problem Elastsche Streuung von Telchen Wssensfragen Lagrange-Mechank Zwangsbedngungen und Zwangskräfte Klassfzerung von Zwangsbedngungen Zwangskräfte
4 v INHALTSVERZEICHNIS Prnzp der vrtuellen Verrückungen d Alembertsches Prnzp Lagrange-Glechungen erster Art Allgemen Bespele Lagrange-Glechungen zweter Art Generalserte Koordnaten Generalserte Kräfte Generalsertes Prnzp der vrtuellen Verrückungen d Alembertsches Prnzp und Bewegungsglechungen Bespele Invaranzen und Erhaltungsgrößen Zyklsche Varablen Zetunabhänggket Der Satz von Emmy Noether Das Hamltonsche Prnzp Das Prnzp Hamlton-Prnzp mt zusätzlchen Zwangsbedngungen Verallgemenerte Lagrange-Formalsmen Telchen m elektromagnetschen Feld Rebung und Dsspatonsfunkton Zusammenfassung: Lagrange-Mechank Wssensfragen Starre Körper Beschrebung der Bewegung (Knematk) Charakterserung des Körpers Beschrebung des momentanen Zustandes Beschrebung der Bewegung Dynamsche Größen Impuls Drehmpuls Knetsche Energe Der Träghetstensor Defnton Zusammenhang mt Träghetsmoment Bespel: Träghetstensor des Zylnders Physkalsche Skalare, Vektoren, Tensoren Hauptachsentransformaton Zusammenfassung und Folgerungen Dynamk und Bewegungsglechungen Zugang drekt über Kräfte Zugang über Lagrange-Funkton Wssensfragen
5 INHALTSVERZEICHNIS v 4 Hamltonsche Mechank Generalserter Impuls Hamlton-Funkton Vorbemerkung: Legendre-Transformaton Anwendung auf Lagrange-Funkton Hamltonsche Bewegungsglechungen Modfzertes Hamltonsches Prnzp Posson-Klammern Defnton Bedeutung und Egenschaften der Possonklammer Bespele für Possonklammern Kanonsche Transformatonen Defnton und enfache Bespele Elementare Egenschaften Konstrukton kanonscher Transformatonen Der Hamlton-Jacob Formalsmus Der Phasenraum Der Louvlle-Satz Hntergrund: Symplektsche Struktur des Phasenraums Zusammenfassung: Hamltonsche Mechank Anwendung: Klene Schwngungen Lneare Näherung Normalmodenzerlegung Lösung m Hamlton-Jacob Formalsmus Zusammenfassung: Klene Schwngungen Ausblck: En Ausflug ns Hamltonsche Chaos Identfzerung von Chaos Egenarten von Hamltonschem Chaos Integrable Systeme Klene Störungen und KAM-Theorem Wssensfragen Grundbegrffe der Hydrodynamk Flude und Kontnuumshypothese Knematk der Flude Dynamk: Bewegungsglechungen für Flude Kräfte n allgemenen Flüssgketen Spannungstensor und Deformatonstensor Ideale Flüssgketen und Euler-Glechungen Newtonsche Flüssgketen und Naver-Stokes Glechungen Ideale Flüssgketen Bernoull-Funkton und Bernoull-Glechung Wrbel- und Zrkulatonserhaltung Zugkraft und Auftreb
6 v INHALTSVERZEICHNIS
7 Vorbemerkungen Theoretsche Mechank : Erste Vorlesung aus Zyklus Theoretsche Physk, bestehend aus: - Mechank (dese Vorlesung) - Elektrodynamk - Quantenmechank - Thermodynamk und Statstsche Physk - Höhere Quantenmechank (ncht mehr verpflchtend; evtl. Master) - Höhere Statstsche Physk (ncht mehr verpflchtend; Master) Frage: Was sollen Se dort lernen? Oder: Was st theoretsche Physk? Warum extra Vorlesungen dafür? Generell: Unterschedung Physk und theoretsche Physk st unglücklch. Besser: Vertefte Beschäftgung mt Grundthemen der Physk auf der Bass der mttlerwele erworbenen mathematschen Kenntnsse Also nächste Frage: Warum st Mathematk so wchtg? Dazu grundsätzlcher: Was st egentlch Physk? Nach Fredrch Hund ( Grundbegrffe der Physk ): De Physk st de Lehre von solchen Dngen der Wrklchket, be denen man hoffen darf, dass se auf Grund wenger Prnzpen n Gedanken nachkonstruert werden können. (NB: Wäre auch heute noch de aktuellste Defnton von Physk. Umfasst moderne, nterdszplnäre Gebete we Econophyscs etc.) Grunderfahrung n der Physk: De Sprache der Physk st de Mathematk oder (Jeans) The great archtect sems to be a mathematcan macht de Fasznaton aus, de für vele von der Physk ausgeht: Warum kann de Natur so gut rechnen? 1
8 2 INHALTSVERZEICHNIS Es gbt Bereche, n denen de Bedeutung der Mathematk nachvollzehbar st: Veltelchensysteme z.b. Dffuson: Gesamtdchtevertelung ergbt sch aus Mttelung über alle möglchen Wege, de enzelne Partkel nehmen Falls Anfangsvertelung punktförmg, erhält man ene sch verbreternde Gaußvertelung ϱ( r, t) e r2 /4Dt (D=Dffusonskonstante), unabhängg davon, we sch Partkel m enzelnen bewegen Allgemener: Dffusonsglechung tϱ( r, t) = D ϱ( r, t) Jedoch: Mathematk beschrebt auch de fundamentalen Naturgesetze, und das st sehr vel erstaunlcher. z.b. Gravtatonsgesetz F 12 = γ m 1m 2 r 2 12 NB: Gravtatonsgesetz lässt sch auch n lokale Form brngen: F = U; (U=Potental) U = 0 fast überall, U = 4πγm 1 m 2 δ( r) be r 0 gewsse Ähnlchket mt Dffusonsglechung legt nahe, dass fundamentales Gesetz statstschen Ursprung haben könnte (so etwas we dffunderende Potentaltelchen ) Aber: Solche Gedanken verstoßen gegen ene grundlegende Regel des physkalschen Weltbldes : Physkalsche Realtät hat nur, was physkalsch gemessen werden kann. Dffunderende Potentaltelchen snd nur real, wenn se m Prnzp nachgewesen werden können. Anderenfalls handelt es sch um phlosophsche Spekulatonen mt dem großen Nachtel, dass se das Denkbare enschränken. In enem solchen Bld hätte z.b. Allgemene Relatvtätstheore ncht entwckelt werden können. Frage, warum Naturgesetze mathematsch snd, blebt offen Bezehung Mathematk - Physk: Mathematk Axome Physk Wchtg für neue Entwcklungen n der Physk: Unvorengenommenhet Physkalsche Realtät physkalsche Messung nchts hnnehmen, was ncht gemessen werden kann Physk m Entwcklungsstadum ncht axomatsch. Erst etablerte Gebete der Physk können m Nachhnen eventuell axomatsch aufgebaut werden. Völlg anderes Vorgehen als n der Mathematk
9 INHALTSVERZEICHNIS 3 Grundfragen / Grundbegrffe n der Physk: Struktur von Raum und Zet Kausaltät (nachher vorher)? Symmetren (abgeletet) Erhaltungssätze Extremalprnzpen In desem Snne: Überblck über de Vorlesungen der theoretschen Physk 1) Mechank (Matere) klasssche Struktur von Raum und Zet Symmetren und Erhaltungssätze Gallesches Relatvtätsprnzp 2) Elektrodynamk (Felder) Felder: zusätzlche nnere Egenschaften des Raums Verborgene Symmetren, Echnvaranz Zusätzlch: Spezelle Relatvtätstheore Enstensches Relatvtätsprnzp 3) Quantenmechank Physkalsche Realtät n mkroskopschen Dmensonen Hesenbergsche Unschärferelaton 4) Thermodynamk und statstsche Physk Neue Phänomene n makroskopschen Veltelchensystemen Zetpfel, Entrope Komplextät Mathematscher Rahmen (grob) 1),2) Analyss 3) Funktonalanalyss 4) Stochastk
10 4 INHALTSVERZEICHNIS Enge empfohlene Bücher zur Theoretschen Mechank W. Noltng: Grundkurs Theoretsche Physk Bd. 1, 2 & 4. (Veweg) H. Goldsten: Klasssche Mechank. (Akademsche Verlagsgesellschaft) F. Scheck: Mechank. (Sprnger) L. D. Landau/ E. M. Lfshtz: Mechank. (Veweg) F. Kuypers: Klasssche Mechank. (VCH) H. Stephan, G. Kluge: Theoretsche Mechank. (Spektrum) u.a.
11 Kaptel 1 Newtonsche Mechank Copyrght 2014 Frederke Schmd De Newtonschen Axome Wortlaut (übersetzt) aus: Phlosophae Naturals Prncpa Mathematca (1687) I) Jeder Körper verharrt m Zustand der Ruhe oder der glechförmgen Bewegung, wenn er ncht durch enwrkende Kräfte gezwungen wrd, senen Bewegungszustand zu ändern. II) De Änderung der Bewegung st der enwrkenden Kraft proportonal und gescheht längs jener geraden Lne, nach welcher de Kraft wrkt. III) De Reakton auf ene Akton st mmer entgegengesetzt und glech, d.h. de Aktonen (Kraftwrkungen) zweer Körper aufenander snd mmer glech groß und entgegengesetzt gerchtet Präzserung der knematschen Begrffe Wr verstehen unter a) enem Körper : Enen Massenpunkt dealserte Objekte mt Masse, aber ohne räumlche Ausdehnung ( Rotaton spelt kene Rolle) Generell gute Näherung, wenn Ausdehnung des Körpers sehr vel klener als andere typsche Längenskalen des Systems Wr werden n Kaptel 3 S.57 sehen, dass man unter gewssen Umständen auch ausgedehnte Körper we Massenpunkte behandeln kann (mt Zentrum am Massenschwerpunkt). 1 Prof. Dr. Frederke Schmd, Vorlesung Theoretsche Mechank, Unverstät Manz, WS 2014/2015. Letzte Änderung am
12 6 KAPITEL 1. NEWTONSCHE MECHANIK b) Bewegung : De Bahnkurve bzw. Trajektore r(t) enes Massenpunktes Dahnter steht ene Abbldung Welt R 3 R physkalscher Raum ( Ort ) R 3 ( r) physkalsche Zet R (t) Bahnkurve r(t) Notwendg für dese Abbldung: Defnton ener Referenzlänge und enes Referenz-Zetntervalls Enheten (z.b. SI-System: [r]= 1 m, [t] = 1 s) Bemerkung: Der Ort r st ene vektorelle Größe n 3 Dmensonen. Des st an zwe Egenschaften erkennbar: Darstellung durch 3 Koordnaten (r 1, r 2, r 3 ) n ener Orthonormalbass E = ( e 1, e 2, e 3 ). (Egenschaften: E T E =EE T =1, det(e)=±1 E O(3)) Darstellung von r: r = r 1 e 1 + r 2 e 2 + r 3 e 3 = E Berechnung der Koordnaten: r = r e r 1 r 2 r 3 Transformatonsverhalten be Wechsel der Bass Neue Orthonormalbass: E = ( e 1, e 2, e 3 ). Neue Darstellung: r 1 r 2 r 3 = U r 1 r 2 r 3 r 1 r 2 r 3 = E T r mt Transformatonsmatrx U = E T E bzw. U j = e e j r 1 (Bewes: r 2 r 3 c) Bewegungszuständen = E T r = E T E T E 1 r 1 r = U r 2 r 3 Egenschaften der Transformatonsmatrx: U T U =UU T =1 ) (Bewes: U T U = (E T E) T (E T E) = E T E E T E = E T E = 1 UU T = (U T T ) T = 1 T = 1 ) 1 Defnere zunächst von der Bahnkurve r(t) abgeletete Größen - Geschwndgket: v(t) = d dt r(t) = r (Enhet 1 m/s) - Beschleungung: a(t) = d dt v(t) = r (Enhet 1 m/s 2 )
13 1.1. DIE NEWTONSCHEN AXIOME 7 Wr verstehen unter - Zustand der Ruhe : Bahnkurve r(t) = r 0 = const. - glechförmge Bewegung : Bahnkurve mt v(t) = v 0 = const. r(t) = r 0 + v 0 t - Änderung der Bewegung : Beschleungung a(t) Dskusson der Postulate a) Dskusson des Postulats II Begrff der Kraft F Angelehnt an unsere Wahrnehmung, Erfahrung aus dem Alltag Bespele Postulat: Schwerkraft an der Erdoberfläche zeht nach unten erschent überall glech groß Expermentelle Beobachtung (Galle): führt bem freen Fall zu konstanter Beschleungung Angelegte Kraft Erfahrung: Beschleungung erfolgt n Rchtung der Kraft Kraft st ene vektorelle Größe F Effekt ener Kraft auf Bahnkurve enes Massenpunkts st F = m a mt m: zunächst nur Proportonaltätsfaktor Folgerung: Superpostonsprnzp Nmm an, auf Körper wrken verschedene Kräfte Beschleungungen adderen sch vektorell auf Kräfte adderen sch vektorell auf: F = F 1 + F 2 b) Dskusson des Postulats III Zwe Aspekte: Beschrebt Wahrnehmung: Wenn ch ene Kraft ausübe, erfahre ch ene Gegenkraft, z.b. Tauzehen Glechung: F12 = F 21 Ermöglcht den Verglech der Wrkung von Kräften auf verschedene Körper Aussage über Proportonaltätskonstante m: m st ene Egenschaft von Körpern: Träge Masse
14 8 KAPITEL 1. NEWTONSCHE MECHANIK Messvorschrft für de träge Masse Aufbau: - Zehe so, dass Aufbau n Ruhe ˆ F = F21 = F 12 = F - Schnede Faden durch: F - Mss Beschleungungen a 1 = F m 1 und a 2 = m 2 Verhältns a 1 a 2 gbt Verhältns m 2 m 1 Damt können m Prnzp de Massen aller Körper n Enheten der Masse enes Referenzkörpers gemessen werden. Masse hat physkalsche Realtät Enhet der Masse: Referenzmasse, z.b. SI-System: 1 kg Zusammenfassend: Newtonsches Kraftgesetz: F = m a mt m: träge Masse, physkalsche Egenschaft enes Körpers (Enhet: [F ] = 1 kg m/s 2 ) Alternatve Formulerung des Newtonschen Kraftgesetzes Defnere Impuls p = m v Newtonsches Kraftgesetz: c) Dskusson des Postulats I Wahrnehmungserfahrung F = p - In enem Karussell: sehr starke Kraft nach außen - Am Boden: wenger Kraft, fast nur noch Schwerkraft nach unten - Auf dem Mond: noch wenger Kraft Postulat: Es gbt Bezugssysteme, n denen kräftefree Körper n glechförmger Bewegung verharren. Dese Bezugssysteme nennt man Inertalsysteme. Problem mt Inertalsystem Verschedene Inertalsysteme bewegen sch relatv zuenander mt glechförmger Geschwndgket. Ursprünglch gng Newton sogar noch weter und postulerte enen absoluten Raum, also en ausgezechnetes Inertalsystem, das n Ruhe st. Problem: Man kann deses ncht von anderen Bezugssystemen unterscheden, es hat also kene physkalsche Realtät. In der klassschen Mechank kann auf absoluten Raum ohne weteres verzchtet werden.
15 1.1. DIE NEWTONSCHEN AXIOME 9 Aber: Selbst wenn man enen relatven Raum akzeptert, bleben noch wetere grundlegende Probleme: Inertalsysteme m Snne der klassschen Mechank können expermentell m Unversum prnzpell ncht realsert werden. Das legt daran, dass es kene kräftefreen Körper geben kann, da Gravtatonskräfte we 1/r 2 abfallen und sch ncht abschrmen lassen. (NB: Gravtatonskräfte snd de enzgen ncht abschrmbaren Kräfte. Alle anderen Kräfte lassen sch abschrmen.) En ästhetsches Problem: Es gbt kenen absoluten Raum, aber ene absolute Zet. Mt welchem Recht? Lösung: Relatvtätstheore Klasssche Mechank Relatver Raum, absolute Zet Problem mt Inertalsystem Spezelle Relatvtätstheore Kene absolute Zet mehr Asymmetre zwschen Raum und Zet wetgehend aufgehoben Problem mt Inertalsystem besteht Allgemene Relatvtätstheore Gravtaton st Egenschaft des Raums Inertalsystem (kräftfree Bewegung) realsert m freen Fall gbt dem Inertalsystem physkalsche Realtät
16 10 KAPITEL 1. NEWTONSCHE MECHANIK 1.2 Bespele: Anwendungen des Kraftgesetzes Freer Fall m homogenen Schwerefeld Kraft: Schwerkraft an Erdoberfläche Bahnkurve F grav = m s g mt m s : Schwere Masse Expermentell stellt man fest: Alle Körper fallen glech (Galle) g st ene Beschleungung (konkret: g = 9.81 m/s 2 ) und m s m (träge Masse) Enstensches Äquvalenzprnzp: m s = m (allgemene Relatvtätstheore) Anfangsbedngungen zur Zet t = 0: Ort r 0, Geschwndgket v 0 - Beschleungung: a(t) = g - Geschwndgket: v(t) = v 0 + τ 0 dτ a(τ) = v 0 + g t - Ort: r(t) = r 0 + τ dτ v(τ) = r 0 + v 0 t g t Freer Fall m homogenen Schwerefeld mt Rebung Kräfte: Schwerkraft F grav = m g Rebungskraft F reb = α(v) v Nmm an, α = const. (Stokessche Rebung) Berechne Geschwndgketsverlauf Glechung: v(t) + α m v(t) = g nhomogene lneare Dfferentalglechung 1. Ordnung Vorgehen: () Löse zunächst homogene DGL: v(t) + α m v(t) = 0 Schar von homogenen Lösungen v hom (t) () Suche spezelle Lösung für nhomogene DGL v s (t) Allgemene Lösung hat Form v nh (t) = v s (t) + v hom (t)
17 1.2. BEISPIELE: ANWENDUNGEN DES KRAFTGESETZES 11 Umsetzung: () homogene DGL: v(t) + α m v(t) = 0 Ansatz: v = w e λt v = λ w e λt Ensetzen: w e λt (λ + α m ) = 0 λ = α m Allgemene Lösung hat Form v hom (t) = w e α m t () Spezelle Lösung v s (t): z.b. de Lösung, be der v g und Rebungskraft de Schwerkraft genau aufwegt F reb = F grav v s = const. und α v s = m g v s = m α g Allgemene Lösung hat Form v nh (t) = m α g + w e α m t Bahnkurve mt Anfangsbedngungen r 0, v 0 zur Zet t = 0 - Geschwndgket: v 0 = v(t = 0) = m α g + w w = v 0 m α g v(t) = m α g + ( v 0 m α g) e α m t - Bahnkurve: Pendel r(t) = r 0 + τ 0 dτ v(τ) = r 0 + m α gt + ( v 0 m α g)( m α ) e α m τ τ=t τ=0 = r 0 + m α gt + ( v 0 m α g) m α (1 e α m t ) Charaktersere zunächst Bahnkurve r(t): Kresbewegung Wähle mtroterendes Bezugssystem: e r = r r, e ϕ e r - Bahn: r(t) = l e r (l: Fadenlänge) - Geschwndgket: r = r 2 = const. d r 2 dt v e r v e ϕ v(t) = l ϕ(t) e ϕ - Beschleungung: d eϕ dt = d er und: d eϕ dt dt = d( r/r) dt a(t) = l ϕ(t) e ϕ Tangentalbeschleungung Folgerung für Kraft = r r d r = er v = 0 dt ( ϕ(t): Wnkelgeschwndgket) = d r dt 1 l = v = ϕ(t) l e r, zegt Rchtung e r für ϕ > 0 l ϕ 2 e r Normalbeschleungung F = m a = m ϕ l e ϕ m ϕ 2 l e r! = m g f Faden e r Schwerkraft Fadenkraft
18 12 KAPITEL 1. NEWTONSCHE MECHANIK Zerlegung: Normalkraft: Fr! = m ( g e r ) e r + f Faden e r = m ϕ 2 l e r g cos ϕ sorgt dafür, dass Körper auf Kresbahn blebt Tangentalkraft: F! ϕ = m ( g e ϕ ) e ϕ = m ϕ l e ϕ g sn ϕ Lösung für Bahnkurve ϕ(t) Newtonsche Glechung für Tangentalkraft Dfferentalglechung ϕ + g l sn ϕ = 0 Exakte Lösung kann noch ncht (aber bald) berechnet werden Im Moment beschränken wr uns auf den Spezalfall klener Auslenkungen sn ϕ ϕ Genäherte Dfferentalglechung: ϕ + g l ϕ = 0 Ansatz: ϕ(t) = e λt Ensetzen: λ = ± g/l magnär Allgemene Lösung hat de Form: ϕ(t) = C + e g/l t + C e g/l t Anfangsbedngungen: ϕ(0) = ϕ 0, ϕ(0) = ω 0 ϕ 0 = C + + C, ω 0 = g/l(c + + C ) C + = 1 2 ϕ ω 0 l g, C = 1 2 ϕ ω 0 l g Lösung: ϕ(t) = ϕ 0 cos Ωt + ω 0 Ω sn Ωt mt Ω = g l
19 1.3. BEZUGSSYSTEME Bezugssysteme An den Bespelen 1.2 S.10 wurde deutlch: Je nach Stuaton beten sch verschedene Koordnatensysteme an. Bespel Pendel: Mtroterendes Bezugssystem ( e r, e ϕ ) Bahnkurve r(t) = l e r : Für den mtroterenden Beobachter konstant Beobachter spürt Kraft auf Faden: m (g cos ϕ) e r : Schwerkraft m ϕ 2 l e r : Zusätzlche Schenkraft - Zentrfugalkraft Beobachter spürt kene Kraft n Rchtung e ϕ : Schwerkraft wrd durch wetere Schenkraft genau aufgehoben. Wr wollen dese Zusammenhänge nun systematsch untersuchen: We hängen Schenkräfte mt Bezugssystemen zusammen, oder allgemener: We transformert man zwschen verschedenen Bezugssystemen? Ausgangspunkt: 1. Newtonsches Axom: Es gbt Inertalsysteme Es gbt mndestens en Inertalsystem Σ (Newton: absoluter Raum, her: egal, rgendens) Deses soll unser Referenzsystem sen De Koordnaten ener Bahnkurve m Referenzsystem Σ seen: r Σ (t) Betrachte nun Bezugssystem Σ Allgemene Koordnatentransformaton: r Σ (t) = D(t) r Σ (t) + d(t) Drehung Translaton r Σ (t) = D 1 (t)[ r Σ (t) d(t)] = D T (t) r Σ (t) d (t) mt d (t) = D T (t) d(t) Inertalsysteme und Galle-Transformaton Herletung : Koordnatentransformatonen zwschen Inertalsystemen Falls Σ en Inertalsystem st, glt generell: r Σ = 0 Bahn st kräftefre r Σ = 0 Ensetzen: r Σ = D T ( r Σ d) r Σ = ḊT ( r Σ d) + D T ( r Σ d) r Σ = D T ( r Σ d) + 2ḊT ( r Σ d) + D T ( r Σ d)! = 0, falls r Σ = 0 für alle r Σ, r Σ D T = 0, Ḋ T = 0, d = 0 D = const. (feste Drehung); d = r 0 + v 0 t Transformaton: r Σ = D T ( r Σ (t) r 0 v 0 t)
20 14 KAPITEL 1. NEWTONSCHE MECHANIK Allgemene Formulerung (Zet enbezogen): Galle-Transformaton t Σ = t Σ + t 0 r Σ = D r Σ + r 0 + v 0 t Σ bzw. t Σ = t Σ t 0 r Σ = D T r Σ r 0 v 0 t Σ mt t 0 = t 0, r 0 = DT ( r 0 v 0 t 0 ) und v 0 = DT v 0 bzw. n Matrxform: t Σ x Σ y Σ z Σ t Σ x Σ yσ zσ v = 0x v 0y D = v 0z D T v 0x v 0y v 0z t Σ x Σ yσ + zσ t Σ x Σ y Σ z Σ t 0 x 0 y 0 z 0 t 0 x 0 y 0 z 0 NB: t 0 = t 0 bedeutet: Zetdfferenzen snd absolut! t Σ = t Σ + t 0 bedeutet: Zet st absolut, unabhängg von r und v 0. Folgerungen : () Zu jedem Satz (D, v 0, r 0, t 0 ) gehört en Inertalsystem Wenn es en Inertalsystem gbt, gbt es unendlch vele () Transformaton von - Geschwndgketen: v Σ (t) = D v Σ (t) + v 0 v Σ (t) = r Σ (t) = D T ( v Σ (t) v 0 ) = D T v Σ (t) v 0 - Beschleungungen: a Σ (t) = r Σ (t) = D r Σ (t) - Kräften: we Beschleungungen: FΣ (t) = D F Σ (t) Roterende Bezugssysteme r Σ (t) = D(t) r Σ (t) bzw. r Σ (t) = D T (t) r Σ (t) D st Drehung: D(t)D T (t) = D T (t)d(t) = 1; det(d) = +1 Enfachhetshalber: Betrachte Bahnkurve, Kräfte etc. zu enem bestmmten Zetpunkt t 0. Wähle Inertalsystem Σ, welches zu desem Zetpunkt mt Σ überenstmmt. (We man von enem anderen Inertalsystem dahntransformert, wssen wr ja.)
21 1.3. BEZUGSSYSTEME 15 Vorabklärung : Zetlche Abletungen von Vektorfunktonen u(t) u Σ (t) t=t 0 = D(t 0 ) u Σ (t 0 ) = u Σ (t 0 ), da D(t 0 ) = 1 u Σ (t) t=t0 = Ḋ(t 0) u Σ (t 0 ) + D(t 0 ) u Σ (t 0 ) Es glt: D T D = 1 (D T D) = ḊT D + DT Ḋ = 0 zu allen Zeten t (wegen D(t 0 ) = 1): Ḋ T (t 0 ) + Ḋ(t 0) = 0 0 a b Ḋ(t 0) hat de Form a 0 c : schefsymmetrsche Matrx b c 0 x 1 Damt glt für belebge Vektoren x = x 2 x 3 0 a b x 1 ax 2 + bx 3 c Ḋ(t 0 ) x = a 0 c x 2 = ax 1 + cx 3 ω x mt ω = b b c 0 x 3 bx 1 cx 2 a = ω u Σ (t 0 ) + u Σ (t 0 ) Also Schrebwese: Ḋ(t 0 ) = ω Zu dem Zetpunkt, an dem Σ und Σ dentsch snd, glt: ( d dt ) Σ = ω + ( d dt ) Σ Bemerkungen () Anschaulche Bedeutung von ω Betrachte nfntesmale Drehung D = 1 + dt Ḋ Für Vektoren x ω glt: Ḋ x = ω x = 0 D x = x ω zegt n Rchtung der Drehachse Berechne Kreuzprodukt enes gedrehten und ungedrehten Enhetsvektors e, der auf ω senkrecht steht. ω ω e (D e ) = sn ( e, D e ) = ϕ dt ω ω ϕ dt ω = ϕ = e ( e + dt ω e ) = dt ω ω entsprcht der Wnkelgeschwndgket () ω st strenggenommen ken Vektor, sondern von Matrx abgeletet. Trotzdem transformert es unter Drehungen we en Vektor. Unter Spegelungen transformert es we en Vektor, aber mt umgedrehtem Vorzechen. Allgemen (Drehung + evtl. Spegelung) glt für Koordnatentransformatonen U: ω 1 ω 2 ω 3 = U ω 1 ω 2 ω 3 det(u) (Grund: Betrachte Vektor a, transformert we en solcher. b = ω a st auch Vektor, transformert we en solcher ω muss we Vektor transformeren, außer wenn Koordnatensystem Händgket ändert z.b. Punktspegelung: U = 1 a = a, b = b = ω a ω = ω) Größen mt enem solchen Transformatonsverhalten nennt man auch Pseudovektoren. Wr werden noch mehrere kennenlernen.
22 16 KAPITEL 1. NEWTONSCHE MECHANIK Anwendung auf Bahnkurve r(t) - Geschwndgket: r Σ (t 0 ) = ( d dt r) Σ = ω r + ( d dt r) Σ = ω r + r Σ (t 0 ) - Beschleungung: r Σ (t 0 ) = ( d dt r Σ ) Σ = ω r Σ + ( d dt r Σ ) Σ = ω [ ω r + r Σ ] + ( d dt [ ω r + r Σ ]) Σ = ω ( ω r) + ω r Σ + ω r + ω r Σ + ( d dt r Σ ) Σ = ω ( ω r) + 2 ω r Σ + ω r + r Σ - Kräfte: F = m r Σ = m ω ( ω r) + 2m ω r Σ + m ω r + m r Σ bzw. Bewegungsglechung m System Σ: m r Σ = F m ω ( ω r) 2m ω r Σ m ω r echte Kraft ()Zentrfugalkraft ()(namenlos) Anschaulch: ()Corolskraft Belebg beschleungte Bezugssysteme Allgemener Fall r Σ (t) = D(t) r Σ (t) + d(t) Um Kräfte zu berechnen und Bewegungsglechung aufzustellen: Betrachte weder Inertalsystem, das zur Zet t 0 mt Σ überenstmmt (D(t 0 ) = 1, d(t0 ) = 0) Verfahren we vorher, Ergebns fast glech: m r Σ = F m ω ( ω r) 2m ( ω r) m ( ω r) m d
23 1.4. ENERGIE UND POTENTIAL Energe und Potental Potentelle Energe Vorbemerkung : Wr nehmen m folgenden an, dass wr n enem Inertalsystem snd, und wollen uns auf geschwndgketsunabhängge Kräfte beschränken. De allgemene Form enes Kraftfeldes lautet zwar F ( r, r, t) (en Telchen) bzw. { F ( r 1 r N, r 1 r N, t)} (N Telchen); makroskopsch kennt man jedoch nur zwe Arten von geschwndgketsabhänggen Feldern: De Rebungskraft und de Lorentzkraft (Magnetsmus). Dese sollen gesondert behandelt werden. Betrachte Kraftfeld der Form F ( r, t) (en Telchen) bzw. { F ( r 1 r N, t)} (N Telchen) Erfahrung : Geschwndgketsunabhängge Kräfte lassen sch n der Regel von enem Potental ableten. En Telchen: F ( r, t) = U( r, t) N Telchen: F ( r 1 r N, t) = U( r 1 r N, t) ( = / r x / r y ) / r z Häufg snd Kräfte und Potental zudem ncht explzt zetabhängg, d.h. F ( r 1 r N ) = U( r 1 r N ). Solche Kraftfelder heßen auch konservatv. Bespele: - En Telchen n ener Dmenson x d trval. F (x, t) = dxu(x, t) mt U(x, t) = F ( x, t)d x + U 0 x 0 - En Telchen, auf das Zentralkraft der Form F ( r, t) = f(r, t) e r wrkt. Dann glt: F ( r, t) = U( r, t) mt U(r, t) = r r 0 f( r, t)d r + U 0 (Check: U = d dr U(r, t) r d dr U(r, t) = d r dr f( r, t)d r = f(r, t) r 0 r = r 2 1 = 2 2 r = r/r = er ) r 2 Bemerkung: Ncht jede Funkton F ( r, t) lässt sch auf en Potental zurückführen. Bespel für ene hypothetsche Kraft, für de das ncht glt: F ( r, t) = f(r, t) e ϕ (f(r, t) ncht Null) Betrachte Lnenntegral entlang enes Kreses mt Radus R. d r F ( r, t) = 2π dϕ d r F ( r(ϕ), t) = 2π dϕ dϕ R e ϕf(r, t) e ϕ = 2πRf(R). 0 0 Gäbe es en Potental U mt F = U, dann müsste aber gelten: 2π dϕ d r F ( r(ϕ), t) = 2π dϕ dϕ d r U( r(ϕ), t) = 2π dϕ dϕ d U( r(ϕ), t) = U( r(ϕ), t) 2π dϕ =
24 18 KAPITEL 1. NEWTONSCHE MECHANIK Bedngung dafür, dass en Potental exstert () Globale Formulerung: Wegntegral über de Kraft muss auf geschlossenenen Wegen verschwnden. En Telchen: d r F ( r, t) = 0 N Telchen: d r F ( r 1 r N, t) = 0 Bewes: Bedngung st notwendg: Betrachte geschlossene Kurve { r (s)} (s [0, S]) d r S F ( r 1 r N, t) = ds d r ds F ( r 1 (s) r N (s), t) 0 = (falls Potental exstert) S d r ds ds U( r 1 r N, t) 0 = S 0 ds d ds U( r 1(s) r N (s), t) = U( r 1 (s) r N (s), t) S 0 = 0 Bedngung st hnrechend: Konstruktonsbewes Konstruere U( r 1 r N ) folgendermassen über Wegntegral: Wähle Referenzpunkt { r 1 0 r0 N }, setze U 0 = U( r 1 0 r0 N ) Wähle belebgen Verbndungsweg { r 1 (s) r N (s)} zwschen { r 1 0 r0 N } und { r 1 r N } (s [0 S]) Bestmme U( r 1 r N, t) = U 0 j S 0 ds d r j ds F j ( r 1 (s) r N { r 1 r N } (s), t) = U 0 d r j F j ( r 1 r N, t) j { r 1 0 r0 N } Falls Integrale über alle geschlossenen Wege verschwnden, st das Ergebns endeutg. Dann glt auch: F ( r 1 r N, t) = U( r 1 r N, t) (Denn: Für belebge klene Verschebungen d r glt: d r U = U( r 1 r + d r r N ) U( r 1 r r N ) = { r 1 r +d r r N } { r 1 r r N } j Glt für alle d r U = F ) d r j F j = d r F () Lokale Formulerung: Rotaton muss verschwnden En Telchen F = 0 N Telchen: F α r jβ = F jβ r α Des snd notwendge Bedngungen für de Exstenz enes Potentals, aber se snd allen noch ncht hnrechend. Ene hnrechende Zusatzbedngung st, dass das betrachtete Gebet enfach zusammenhängend snd, d.h. jede geschlossene Kurve läßt sch n dem Gebet stetg auf Null zusammenzehen. (Anschaulch: Gebet hat kene Löcher).
25 1.4. ENERGIE UND POTENTIAL 19 Bespele : Bewes: Bedngung st notwendg: Falls Potental exstert, glt F α = U r α, F jβ = U F α r jβ = 2 U r jβ r α = 2 U r α r jβ = F jβ r α r jβ Bedngung st hnrechend: Zege erst: Falls F α r jβ = F jβ r α, dann snd Lnenntegrale B A d r F für verschedene Integratonswege glech, wenn se sch stetg nenander überführen lassen. Dazu: betrachte nfntesmal deformertes Telstück I 1 = (1) I 2 = (2) I 1 = I 2, falls F α r jβ d r F = F α dr α + (F jβ + F jβ dr r α )dr jβ α d r F = F jβ dr jβ + (F α + F α dr r jβ )dr α jβ = F jβ r α. Lnenntegral st glech für Integratonswege, de sch durch vele nfntesmale Deformatonen nenander überführen lassen. Daraus folgt, dass de globale Bedngung () erfüllt st (da sch n enem enfach zusammenhängenden Gebet alle geschlossenen Lnenntegrale stetg auf Null zusammenzehen lassen.) Weder Zentralkräfte: Defnton ener allgemenen Zentralkraft: F ( r, t) e r Wr zegen, dass ene Zentralkraft F ( r, t) = f( r, t) e r genau dann en Potental hat, wenn f( r, t) nur von r abhängt. Bewes: F = (f e r) = ( f) e r + f ( e r) =! 0 e r = 1 r ( r) + ( 1 r ) r = 0 r r 3 r = 0 f e r = 0 f e r e r f steht senkrecht auf Fläche f = const. f = const. st Kugeloberfläche f hängt nur von r ab. N-Telchen-System mt Paarwechselwrkungen f j = f( r r j ) ( r r j ) r r j Kraftfeld F = f j hat Potental j Bewes: j: F α = d r jβ dr ( f r ) (r β r jβ )(r α r jα ) f r r j r j r δ αβ = F jβ r α = j: F α r β = [ d dr ( f r ) (r β r jβ )(r α r jα ) + f j r r j r j r δ αβ] = F β r α NB: Potental dazu: U = 1 2 φ( r r j ) mt φ(r) = φ 0 r d rf( r) dφ j r 0 1 ( k U = k 2 φ( r r j ) j dr = f(r) = 1 2 dφ {δ k dr dφ r r j + δ kj j r dr j r r j } j r j = 1 2 dφ dr { ( r k r j ) ( r j r k ) j k r r kj k r j r j r k } = f( r k r j ) ( r k r j ) ) r j k k r j
26 20 KAPITEL 1. NEWTONSCHE MECHANIK Knetsche Energe Herletung und Motvaton Betrachte en N-Telchen-System mt enem Potental, das ncht explzt von der Zet abhängt: t U = 0 bzw. U = U( r 1 r N ) Dynamsche Entwcklung Trajektore { r 1 (t) r N (t)} Zetlche Änderung des Potentals: d dt U( r 1(t) r N (t), t) = N U d r dt = N F r = N m r r =1 =1 =1 = N =1 mt T = d m 2 m r 2 dt r 2 = d dt T : Knetsche Energe De Größe T + U st zetlch konstant ( d dt (T + U) = 0). Motvert Defnton der Gesamtenerge E = T + U. Falls U ncht explzt zetabhängg st (d.h. U t = 0), st de Gesamtenerge E ene Konstante der Bewegung Energeerhaltung NB: Nur wegen deser Egenschaft defnert man überhaupt ene knetsche Energe und ene Gesamtenerge. Wenn E ncht m allgemenen erhalten wäre, wären dese Größen unnteressant. Anwendungsbespele : Endmensonales System mt Potental U(x) E = T + U = m 2 ẋ2 + U(x) ẋ 2 = 2 m (E U(x)) dx dt = ± 2 m m (E U(x)) dt = ± Bahnkurve x(t) aus t = t 0 ± x(t) x(0) 2(E U(x)) dx dx m 2(E U(x)) Spezell: Pendel, Anfangsbedngungen ϕ 0, ϕ 0 (zur Zet t = 0) Potentelle Energe: Schwerkraft F = m g U = mgz = mgl(1 cos ϕ) Knetsche Energe: v = ϕl T = 1 2m( ϕl)2 Energeerhaltung: U + T = ml 2 ( ϕ2 2 + g l (1 cos ϕ)) = const. Bewegungsglechung aus d dt (U + T ) = 0 ϕ + g l sn ϕ = 0 (vgl. 1.2 S.10) Bewegungskonstante: am Umkehrpunkt: zur Zet t = 0: ϕ 2 2 g l Umkehrpunkt: cos ϕ max = cos ϕ 0 l 2g ϕ2 0 cos ϕ = const. = g l cos ϕ max = ϕ g l cos ϕ 0 Wnkelgeschwndgket: ϕ 2 = 2 g l (cos ϕ cos ϕ max) dt = ±dϕ/ 2 g l (cos ϕ cos ϕ max)
27 1.4. ENERGIE UND POTENTIAL 21 ϕ max 0 Perode: T = T dt = 4 dϕ/ 2 g l (cos ϕ cos ϕ max) 0 = 4 l ϕmax g K(sn 2 ) = 2π l g ( ϕ2 max + ) wobe K(x) = π 2 ( x2 +...) vollständges ellptsches Integral Bahnkurve: Aus Umkehrung von t(ϕ) NB: Bs zum ersten Umkehrpunkt: ϕ t(ϕ) = ± d ϕ/ 2 g l (cos ϕ cos ϕmax) (+ ϕ 0 > 0 ϕ 0 ϕ 0 < 0 ) ±ϕ max Erster Umkehrpunkt: t 0 = ± ϕ 0 dϕ/ 2 g (cos ϕ cos ϕmax) l Bs zum zweten Umkehrpunkt: ϕ t(ϕ) = t 0 d ϕ/ ±ϕ max 2 g (cos ϕ cos ϕmax) l Bs zum drtten Umkehrpunkt: ϕ t(ϕ) = t 0 + T /2 ± d ϕ/ ϕ max 2 g (cos ϕ cos ϕmax) l etc. ϕ 0 d ϕ/ cos ϕ cos ϕ max = sn ϕ/2 2 F (arcsn( sn ϕ max/2 ϕmax ), sn ) 2 ellptsches Integral mt Maxmum: F ( π 2, sn ϕmax 2 ) = K(sn ϕmax 2 ) Wetere Begrffe (vollständgketshalber) Betrachte nun allgemene Kraftfelder F ( r 1 r N, r 1 r N, t) mt Trajektoren { r 1 (t) r N (t)} Arbet: W = t 1 dt F ( r 1 r N, r 1 r N, t) r t 0 (Arbet, de n der Zet von t 0 bs t 1 verrchtet wurde) Lestung: P = dw dt = Dsspatves Kraftfeld F ( r 1 r N, r 1 r 1, t) r Allgemenes Kraftfeld wrd manchmal zerlegt n konservatven Antel und Rest F = F kons, + F R, mt F kons, = U( r 1 r N ) d Dann glt: dt (U + T ) = F R, jr (Lestung der ncht-konservatven Kräfte) Auf geschlossenen Trajektoren, d.h. r (t 1 ) = r (t 0 ) t 1 t 1 st dt F r = dt F R, r t 0 t 0 (der konservatve Antel der Kraft verrchtet kene Arbet). Nchtkonservatve Kräfte, de dauerhaft Arbet verrchten, nennt man dsspatve Kräfte. Se wandeln mechansche Energe n ene andere Energeform um, z.b. Wärme (Rebungskräfte) oder Strahlung.
28 22 KAPITEL 1. NEWTONSCHE MECHANIK 1.5 Erhaltungssätze und Symmetren In desem Kaptel nehmen wr an: Das Bezugssystem st en Intertalsystem. Kräfte haben en Potental (Potentalkräfte). Ernnerung an S.20 Enführung der knetschen Energe T über Energeerhaltung. Falls en Potental U( r 1 r N ) exstert und ncht explzt zetabhängg st, dann st E = U + T ene Erhaltungsgröße. Nähere Betrachtung: - Potental U( r 1 r N ) charaktersert dynamsche Entwcklung des Systems legt Bewegungsglechungen fest. - Kene explzte Zetabhänggket bedeutet: ken ausgezechneter Zetpunkt, kene absolute Zet Bewegungsglechungen translatonsnvarant bzgl. Zettranslatonen oder homogen n der Zet - Aus der Homogentät der Zet folgt: Es exstert ene Erhaltungsgröße de Energe Bespel für en allgemeneres Prnzp ( Noethersches Theorem): Zu jeder kontnuerlchen Symmetre gehört ene Erhaltungsgröße. Dabe st ene kontnuerlche Symmetre: Transformaton K a : ( r 1 r N, t) a ( r 1 r N, t ), welche Bewegungsglechungen nvarant lässt mt a: kontnuerlcher Parameter; a = 0 Identtät Im Fall der Homogentät der Zet: U( r 1 r N, t) hängt ncht von t ab Bewegungsglechung nvarant unter ( r 1 r N, t) ( r 1 r N, t ) = ( r 1 r N, t + a) Wetere Symmetren/Invaranzen Homogentät des Raumes ( S.23) Invaranz unter räumlchen Translatonen r = r + a Impulserhaltung Isotrope des Raumes ( S.24) Invaranz unter Drehungen r = D a ( r ) (D 0 = 1) Drehmpulserhaltung Echnvaranz m elektromagnetschen Feld (ncht n deser Vorlesung) Ladungserhaltung
29 1.5. ERHALTUNGSSÄTZE UND SYMMETRIEN 23 Grundlegende Symmetren unserer Raumzet: Für abgeschlossene Systeme (kene oder fast kene Wechselwrkungen mt der Außenwelt), erwartet man, dass de Bewegungsglechungen nvarant snd unter allgemenen Galle-Transformatonen r Σ = D r Σ + r 0 + v 0 t Σ. NB: Ncht erfüllt für de Glechungen der Elektrodynamk Motvert Entwcklung der spezellen Relatvtätstheore Invaranz unter Lorentz-Transformatonen (sehe Theore II). Daraus folgen (nchtrelatvstsch und relatvstsch) Erhaltungssätze: t 0 Invaranz unter Zettranslatonen Energe r 0 + v 0 t Σ Invaranz unter Raumtranslatonen Impuls D Invaranz unter Drehungen Drehmpuls Homogentät der Zet und Energeerhaltung Berets besprochen (1.4.2 S.20) Homogentät des Raumes und Impulserhaltung Homogentät des Raumes: In enem abgeschlossenen System snd de Bewegungsglechungen nvarant unter der Transformaton ( r 1 r N, t) ( r 1 + a r N + a, t) (Es gbt kenen ausgezechneten Raumpunkt). Daraus folgt: U( r 1,, r N, t) = U( r 1 + a,, r N + a, t) a 0 = du da α aα=0 = d dt p = 0 U d(r α +a α) r α da = α aα=0 p = const. U r α d = da α U( r 1 + a,, r N + a, t) 0 F α = ṗ α = d dt p α Der Gesamtmpuls P = p st ene Erhaltungsgröße. Folgerung: Schwerpunktsatz Gegeben en System von N Telchen, Massen m Defnere Schwerpunkt R = m r m, Gesamtmasse M = m Falls das System abgeschlossen st, glt R = P /M = const.. Der Schwerpunkt enes abgeschlossenen Systems bewegt sch glechförmg mt der Geschwndgket P /M Das Schwerpunktsystem, n dem R am Ursprung stzt, st en Inertalsystem (d.h. r r = r R(t) st ene Galletransformaton)
30 24 KAPITEL 1. NEWTONSCHE MECHANIK Isotrope des Raumes und Drehmpulserhaltung Isotrope des Raumes: In enem abgeschlossenen System snd de Bewegungsglechungen nvarant unter ( r 1 r N, t) (D a r 1 D a r N, t) D a : Drehung mt Drehachse a a, Drehwnkel a (Es gbt kene ausgezechnete Raumrchtung). Daraus folgt: NR: U( r 1 r N, t) = U(D a r 1 D a r N, t) a Spezell a 0 (nfntesmal): D a [1 + a ] d da α U( r 1 + a r 1,, r N + a r N, t) = 0 a=0 0 = β(x,y,z) U r β Fβ d [r da α β + ( a r ) β ] = β F β d da α γδ (nach S.13) ε γδβ a γr δ = F β ε γδβ δ αγr δ βγδ = ε αδβ r δ F β = ε δβα r δ F β = ( r F ) α = ( r p ) α βδ βδ d dt ( r p ) = ( r p ) + ( r p ) 0 wegen oben 0 wel r p = 0 r p = const. Der Gesamtdrehmpuls Allgemener glt: L = r p st ene Erhaltungsgröße. Falls n enem System kene Raumrchtung ausgezechnet st, glt Drehmpulserhaltung. Falls en System nvarant st bzgl. Drehungen um ene Drehachse n, st n L erhalten (Bewes analog). Bespel: En Telchen m Zentralpotental U(r) Kene Impulserhaltung (da Ort ausgezechnet), aber Drehmpulserhaltung (kene ausgezechnete Rchtung) l = r p = const.. Folgerungen: () Bahn r(t) st mmer n ener Ebene ( r(t) l) () Flächensatz : r(t) überstrecht zu glechen Zeten gleche Flächen Fläche A( t) = t+ t da = t+ t 1 2 ( r v)dt t t = 1 t+ t 2m t r p dt = l l 2m t
31 1.5. ERHALTUNGSSÄTZE UND SYMMETRIEN Skalennvaranz und Vralsatz Skalennvaranz: Ene wenger allgemene Symmetre Angenommen, Potental hat Egenschaft U(λ r 1 λ r N ) = λ K U( r 1 r N ) Bespele: Gravtatonskraft: U = γ m m j r j r j U(λ r 1 λ r N ) = λ 1 U( r 1 r N ) gekoppelte Oszllatoren: U = k j ( r r j ) 2 j U(λ r 1 λ r N ) = λ 2 U( r 1 r N ) Bewegungsglechungen snd nvarant unter Skalentransformatonen ( r 1 r N, t) (λ r 1 λ r N, λ 1 K 2 t) kontnuerlche Symmetre K a mt λ = e a ; Identtät be a = 0 bzw. λ = 1 (Check: Setze r α = λr α, t = λ r t d Aus Bewegungsglechung m 2 dt 2 r α = U( r r 1 r N ) folgt: α folgt: m λ 1+2r d2 d t r 2 α = λ U( r r 1 /λ r N /λ) = λ λ K U( r α r 1 r N ) α d Bewegungsglechungen snd nvarant, wenn glt: m 2 d t r 2 α = U( r r 1 r N ) α Es muss gelten: λ 1+2r = λ 1 K λ r = 1 K 2 ) Be Skalennvaranz glt (Rechnung analog we n den vorgen Kapteln) d dλ U(λ r 1 λ r N ) = d dλ [λk U( r 1 r N )] = Kλ K 1 U( r 1 r N ) d dλ U(λ r 1 λ r N ) = U(λ r 1 λ r N ) d(λ r ) = dλ U(λ r 1 λ r N ) r (λ=1) KU( r 1 r N ) = U( r 1 r N ) r = r p = r p r p = KU + 2T d dt K U + m r 2 F r = p r d dt ( r p ) = K U + 2T Folgerungen: Ken rchtg brauchbarer Erhaltungssatz ( r p + t 0 dτ(ku 2T ) = const.) T 1 Aber: nützlcher Satz für zetlche Mttelwerte = lm T T dt : 0 Für räumlch beschränkte Systeme glt der Vralsatz: T = K 2 U (Rechnung: Falls System räumlch beschränkt r p endlch t 0 dτ(ku 2T ) endlch t T lm dτ(ku 2T ) = lm T [K U 2 T ] endlch T 0 T K U 2 T = 0 )
32 26 KAPITEL 1. NEWTONSCHE MECHANIK Bespele für Anwendungen von Symmetreprnzpen Anwendungen der Symmetreprnzpen auf verschedene Stuatonen N nchtwechselwrkende Telchen n ener quaderförmgen Box Invaranz gegen Zettranslatonen, Kene Invaranz gegen Ortstranslatonen, kene Isotrope Energeerhaltung, kene Impulserhaltung, kene Drehmpulserhaltung N nchtwechselwrkende Telchen zwschen zwe unendlch ausgedehnten parallelen Platten, de n (x, y)-ebene orentert snd Invaranz gegen Translatonen von Zet und Ort n x, y Rchtung Invaranz gegen Drehungen um z-achse (belebger Ursprung) Kene Invaranz gegen Ortstranslatonen n z-rchtung Kene Invaranz gegen Drehungen um x, y-achse Erhalten snd: Energe, P x,y, L z, ncht erhalten snd: P z, L x,y N nchtwechselwrkende Telchen n enem unendlch langen Rohr mt kresförmgem Querschntt, das n x-rchtung orentert st Invaranz gegen Translatonen von Zet und Ort n x-rchtung Kene Invaranz gegen Ortstranslatonen n y, z-rchtung Kene Drehnvaranz außer bzgl. Drehungen um zentrale Rohrachse Erhalten snd: Energe, P x, L x bzgl. Ursprung n der zentralen Achse Ncht erhalten: P y,z, L y,z, L x bzgl. anderem Ursprung 2 Telchen mt enem Paarpotental der Form U gesamt ( r 1, r 2 ) = U( r 1 r 2 ) sn(ωt) Invaranz gegen Ortstranslaton und Drehungen Kene Invaranz gegen Zettranslatonen Impuls- und Drehmpulserhaltung, kene Energeerhaltung
33 1.6. ZUSAMMENFASSUNG: NEWTONSCHE MECHANIK Zusammenfassung: Newtonsche Mechank Konzepte: Technken: Beschrebung klassscher Systeme von N Telchen durch Massenpunkte mt Ortskoordnaten r 1,, r N, wobe r R Newtonsche Postulate, nsbesondere: Konzept des Inertalsystems Newtonsche Bewegungsglechungen m r = F (n Inertalsystemen n kartesschen Koordnaten) Kraftfelder (konservatv und dsspatv) Zentrale Größe, de de Dynamk charaktersert: (falls Kraftfelder konservatv)) Potental U( r 1, r N, t) m r = U Zusammenhang von Symmetren bzw. Homogentäten mt Erhaltungssätzen Begrffe von Energe, Impuls, Drehmpuls Lösen von Dfferentalglechungen Wechsel von Bezugssystemen Physk: (nächster Abschntt 1.7 S.28) Lösung des Zwekörperproblems Spezell: Lösung des Keplerproblems
34 28 KAPITEL 1. NEWTONSCHE MECHANIK 1.7 Anwendung: Das Zwekörperproblem Wchtger Spezalfall: Abgeschlossenes System aus zwe Telchen Potental: U gesamt ( r 1, r 2 ) = U( r 1 r 2 ), Massen m 1, m 2 Besondere Bedeutung - In allgemener Form lösbar (st ab dre Körpern schon ncht mehr möglch) - Beschrebt n guter Näherung Planetenbahnen (Keplerproblem: Sonne-Planet) Streuung an enem Telchen Vorbemerkungen Es glt erlaubt Rückschlüsse auf Lage des Streuzentrums und auf Form des Potentals (ncht endeutg) - Impulserhaltung: m 1 r 1 + m 2 r 2 = const. Schwerpunktsatz - Energeerhaltung: 1 2 m 1 r m 2 r U( r 1 r 2 ) = const. - Drehmpulserhaltung: r 1 (m 1 r 1 ) + r 2 (m 2 r 2 ) = const. Defnere Gesamtmasse: M = m 1 + m Redukton auf en endmensonales Problem Schwerpunkt- und Relatvkoordnaten Impulserhaltung und Schwerpunktsatz Schwerpunkt R = 1 M (m 1 r 1 + m 2 r 2 ) bewegt sch mt glechförmger Geschwndgket Gesamtmpuls P = M R = const. Nutze dese Informaton aus: De Bewegungsglechungen snd für ene Lnearkombnaton von r 1 und r 2 schon gelöst. Brauche nur noch ene wetere Kombnaton zu betrachten. Nahelegende Wahl für zwete Kombnaton ergbt sch aus Form des Potentals U gesamt = U( r 1 r 2 ): Relatvkoordnaten r = r 1 r 2. Dann st U gesamt = U( r )
35 1.7. ANWENDUNG: DAS ZWEIKÖRPERPROBLEM 29 Umrechnung: R = m 1 M r 1 + m 2 r = r 1 r 2 ( r m 1 1 ) = ( M r 2 M r 2 r 1 = R + m 2 M r r 2 = R m 1 M r m 2 1 M 1 1 ) bzw. (Matrxschrebwese) ( R m1 r ) = ( M R ( m1 m r ) ; ( 2 1 M M 1 1 ) m 2 M 1 1 ) ( r 1 ) r 2 = ( 1 m 2 M 1 m 1 M ) Bewegungsglechungen für Relatvkoordnaten Herletung über Energeerhaltung - Potentelle Energe: U = U(r) - Knetsche Energe: T = 1 2 m 1 r m 2 r 2 2 muss noch n Schwerpunkt- und Relatvkoordnaten ausgedrückt werden Dazu: Matrxschrebwese T = 1 2 ( r 1 r 2 ) ( m m 2 ) ( r 1 r 2 ) Es glt: ( r 1 r 2 ) = ( 1 m 2/M 1 m 2 /M ) ( R r ) ( r 1 ) == ( 1 m 2/M r 2 1 m 1 /M ) ( Ṙ r ) und ( r 1 r 2 ) == ( R 1 1 r) ( m 2 /M m 1 /M ) T = 1 2 ( R 1 1 r) ( m 2 /M m 1 /M ) (m 1 0 ) ( 1 m 2/M 0 m 2 1 m 1 /M ) ( Ṙ r ) M 0 0 m 1 m 2 /M T = 1 2 M R 2 gesamt µ r 2 = 1 2 ( R r) ( M 0 0 m 1 m 2 /M ) ( Ṙ r ) = 1 2 M R m 1 m 2 r 2 2 M mt der reduzerten Masse: µ = m 1m 2 m 1 + m 2 Gesamtenerge: E gesamt = T + U = 1 2 M R µ r 2 + U(r) = const. Wegen R = const. glt: 1 2 µ r 2 + U(r) = const. d dt [ 1 2 µ r 2 + U(r)] = µ r r + U r 0 r[µ r + U] 0 (mmer!) µ r + U 0 Bewegungsglechung: µ r = U De Relatvbewegung st dentsch mt der Bewegung enes enzelnen Massenpunktes der reduzerten Masse µ m Potental U(r). Problem reduzert auf Bewegung enes Telchens m Zentralpotental U(r) Kraft (vgl S.17): Zentralkraft F = U = du dr r = du r dr r
36 30 KAPITEL 1. NEWTONSCHE MECHANIK Bewegung m Zentralpotental Vorbemerkung: Da U(r) konservatves Zentralpotental, snd nach S.24 der Relatvdrehmpuls l = r (µ r) und de Relatvenerge E = 1 2 µ r 2 +U(r) erhalten. NB: Gesamtdrehmpuls: L = r 1 (m 1 r 1 ) + r 2 (m 2 r 2 ) = l + R (M R) (Bewes: Ensetzen) Folgerung: Fallunterschedung () l 0 r r r bewegt sch auf Geraden durch Ursprung. Endmensonale Bewegung: µ r = du dr () l 0 wegen l r r st r l und r l r(t) legt n Ebene durch Ursprung, de senkrecht zu l steht Ebene Bewegung Wähle Koordnatensystem mt z-achse n Rchtung l Benutze Polarkoordnaten: cos ϕ sn ϕ 0 e r = sn ϕ ; e ϕ = cos ϕ ; e z = r cos ϕ r(t) = r sn ϕ = r e r 0 r cos ϕ ṙ cos ϕ r ϕ sn ϕ r(t) = r sn ϕ = r e r ; r(t) = ṙ sn ϕ + r ϕ cos ϕ = ṙ e r + r ϕ e ϕ 0 0 r r = r e r (ṙ e r + r ϕ e ϕ) = rṙ( e r / e r) + r 2 ϕ( e r e ϕ) = r 2 ϕ e z r 2 = (ṙ e r + r ϕ e ϕ)) 2 = ṙ 2 e 2 r +2ṙr ϕ e r e ϕ) + r 2 ϕ 2 e 2 ϕ = ṙ 2 + r 2 ϕ Nutze Drehmpulserhaltung aus: µ r r = l e z = µr 2 ϕ e z ϕ = l/µr 2 Nutze Energeerhaltung aus: E = const. = 1 2 µ r 2 + U(r) = 1 2 µṙ2 + µr2 2 ϕ 2 + U(r) = 1 2 µṙ2 + 1 l 2 2 µr 2 + U(r) = µ 2 ṙ2 + U eff (r) mt U eff (r) = U(r) + l 2 /2µr 2 d dt ( µ 2 ṙ2 + U eff (r)) = µṙ r + ṙ du eff = 0 dr Bewegungsglechung: µ r = du eff dr Zusammenfassung von () und () Bewegung der Relatvkoordnate r(t) - Ebene Bewegung n derjengen Ebene durch den Ursprung, de senkrecht auf dem Relatvdrehmpuls l steht (bzw. für l = 0: Endmensonale Bewegung auf Geraden r)
37 1.7. ANWENDUNG: DAS ZWEIKÖRPERPROBLEM 31 - Betrag von r bewegt sch we endmensonale Masse µ m effektven Potental U eff (r) = U(r) + l 2 /2µr 2 Radalglechung: µ r = du eff dr - Wnkelkoordnate folgt aus l = µ r r = const.. n Polarkoordnaten mt cos ϕ l e z, r = r sn ϕ : ϕ = l 0 µr Integraton der Bewegungsglechungen - Radalglechung Über Energe der Relatvbewegung: E = µ 2 ṙ2 + U eff (r) = const. ṙ = ± 2 µ (E U eff(r)) = dr dt dt = ±dr/ 2 µ (E U eff(r)) t = t 0 ± - Wnkelglechung r(t) r(t 0 ) 2 d r/ µ (E U eff( r)) Implzte Glechung für r(t) Über ϕ = l = dϕ µr 2 dt = dϕ dr ṙ = ± dϕ 2 dr µ (E U eff(r)) dϕ dr = ± l µr 2 / 2 µ (E U eff(r)) dϕ = ±dr l/r 2 2µ(E U eff (r)) ϕ = ϕ 0 ± r(ϕ) r(ϕ 0 ) l d r r 2 2µ(E U eff ( r)) Implzte Glechung für r(ϕ) Das Kepler-Problem Wchtgster Spezalfall des Zwekörperproblems: Potental der Form U(r) = α/r Bespele: Gravtatonskraft: U(r) = γm 1 m 2 /r Coulombkraft: U(r) = q 1 q 2 /r Qualtatve Analyse Betrachte das effektve Potental U eff = α r + Fall α < 0: l2 2µr 2 Nur Energen E > 0 möglch Alle Bahnen ungebunden
38 32 KAPITEL 1. NEWTONSCHE MECHANIK Fall α > 0: Mnmum: r 0 = l2 µα U 0 = µα2 2l 2 Energe E muss größer als U 0 sen Möglche Bahnen: () E = U 0 r(t) r 0 Kresbahn () U 0 < E < 0 r(t) blebt beschränkt gebundene Bahn () E > 0 r(t) recht ns Unendlche ungebundene Bahn Semquanttatve Analyse Betrachte Bewegung mt Energe E Bestmme maxmale und mnmale Entfernung vom Ursprung E = U eff (r) E + α r l2 = 0 1 = µα 2µr 2 r ± l 2 (1 ± 1 + 2El2 µα 2 ) Fälle: () U 0 < E < 0 (α > 0) r + und r reell und postv Zwe Umkehrpunkte, gebundene Bahn () E > 0 (α 0) r + postv, r negatv unphyskalsche Lösung Nur en Umkehrpunkt, ungebundene Bahn Quanttatve Lösung Benutze Wnkelglechung ϕ = φ 0 ± r(ϕ) r(ϕ 0 ) d r l r 2 2µ(E U eff ( r)) Verenfache: E U eff (r) = E + α r l2 2µr 2 = l2 2µ ( 1 1 r + r )( 1 r 1 ) (mt 1 we oben n ) r r ± Varablentransformaton: r = 1 τ d r/ r2 = dτ; Wähle x-achse so, dass r(ϕ = 0) = r + 1/r Ensetzen mt ϕ 0 = 0: ϕ = dτ/ ( 1 τ)(τ 1 ) = ±( π 2 r + r 2 arcsn r 1 1/r + 2 r r+ 1 r 1 1 r+ r 1 = sn(ϕ π 2 ) = cos(ϕ) 1 r = 1 2 ( 1 r r ) = 1/p ± 1 2 ( 1 1 ) r + r = ε/p Setze en (s.o.) 1 = µα r ± l 2 (1 ± 1 + 2El2 µα 2 ) p = l2 µα, ɛ = 1 + 2El2 µα 2 r+ 1 r 1 r+ r 1 cos(ϕ) )
39 1.7. ANWENDUNG: DAS ZWEIKÖRPERPROBLEM 33 Lösung für r(ϕ) folgt p r l2 = 1 + ε cos(ϕ) mt p = µα ; ε = 1 + 2El2 µα 2 Glechung für enen Kegelschntt mt Brennpunkt m Ursprung! p = Parameter ε = Exzentrztät ϕ = 0 = Perhel : r legt Zentrum am nächsten Umrechnung n kartessche Koordnaten (x = r cos ϕ, y = r sn ϕ) p = r + ε r cos ϕ (p εx) 2 = r 2 = x 2 + y 2 y 2 + x 2 (1 ε 2 ) + 2εpx p 2 = 0 x { ε 1 y2 ( 1 ε2 p 2 Fallunterschedung ε = 1 y 2 = p 2 2px ) + (x + pε 1 ε 2 ) 2 ( 1 ε2 p )2 = 1 () ε 2 < 1 (E < 0) Glechung der Form ( y a )2 + ( x+x 0 b ) 2 = 1 Ellpsen-Bahn mt Halbachsen a und b a = b = p = l 1 ε 2 2µ E p 1 ε 2 = α 2 E Spezell: Berechne Umlaufzet aus Flächensatz (1.5.3 S.24) Überstrchene Fläche pro Zet dt: da = l Gesamtfläche: A = πab = π lα 8µ E 3 Umlaufzet: T = 2µ l A = π α µ 2 E 3 T hängt ncht vom Drehmpuls l ab 2µ dt T 2 E 3 b 3 : Drttes Keplersches Gesetz () ε 2 = 1 (E = 0) Glechung x = p 2 y2 2p Parabel ungebunden, Geschwndgket verschwndet m Unendlchen () ε 2 > 1 (E > 0) Glechung der Form ( y a )2 + ( x x 0 b ) 2 = 1 Hyperbel mt Halbachsen a und b µα Ablenkwnkel: ϑ = 2 arctan 2 2El 2 l a = 2µE, b = α /2E ungebundene Bahn, am Potental abgelenkt um ϑ mt tan(ϑ/2) = b/a
40 34 KAPITEL 1. NEWTONSCHE MECHANIK Rückrechnung auf absolute Koordnaten Im Schwerpunktsystem ( R(t) 0) r 1 (t) = r(t) m 2 /M r 2 (t) = r(t) m 1 /M } Bahnen von r 1, r 2 gleche Form we r(t), nur reskalert Bespel gebundene Bahnen (Ellpsen) Falls Massen sehr unterschedlch, z.b. Planeten: m Sonne m Planet Große Masse steht nahezu (sehr enge Bahn) Benahe echtes Zentralkraftproblem mt reduzerter Masse µ = m Planetm Sonne m Planet +m Sonne m Planet In belebgem System ( R(t) = R 0 + P /M t) r 1 (t) = r(t) m 2 /M + R(t) r 2 (t) = r(t) m 1 /M + R(t) } Addere glechförmge Bewegung zu r(t) dazu Bemerkung: Im ungebundenen Fall snd bede Massen n jedem Inertalsystem zur Zet t = ± m Unendlchen. Selbst be sehr großem Massenuntersched gbt es ken Inertalsystem, n dem de schwerere Masse asymptotsch ruht. Egenart der langen Rechwete des Potentals α/r. (Bewes: Übungsaufgabe) Elastsche Streuung von Telchen Betrachte nun belebges Potental U(r) mt lm r U(r) = 0 Frage: We lenken sch ungebundene Telchen gegensetg ab? Vorweg: Rückführung auf Entelchenproblem gemäß S Streuung enes enzelnen Telchen m Zentralpotental Geometre Der Stoßparameter b st der Abstand, mt dem das Telchen am Streuzentrum vorbeflegen würde, wenn deses ncht streuen würde.
41 1.7. ANWENDUNG: DAS ZWEIKÖRPERPROBLEM 35 Grundsätzlch glt: Energeerhaltung: E = const. = { t p2 /2µ t + p 2 /2µ } p = p const. = { t r(t) p Drehmpulserhaltung: l = t + r(t) p } Bahn legt n ener Streuebene, aufgespannt von p und p Betrag von l: l = bp = b p b = b Streuwnkel ϑ hängt vom Stoßparameter b ab: Berechnung nach S.31: ϑ = π 2ϕ mt ϕ = r mn d r r 2 l/ 2µ(E U( r) l 2 /2µ r 2 ) Mt l = bp, E = p2 2µ folgt: ϑ = π 2 d r b r 2 r 1 2µU( r)/p 2 b 2 / r 2 mn Streuung enes Strahls von Telchen In der Praxs typscherwese vele glechartge Streueregnsse Streuung enes Strahls von glechartgen Telchen Charakterserung durch dfferentellen Streuquerschntt : Zahl der Telchen, de n enem bestmmten Wnkelberech gestreut werden, pro enlaufendem Telchenstrom - Enfallender Strahl Impuls p Telchenstromdchte J = - Auslaufende Telchen Telchen Zet Querschnttsfläche A 0 Impulse p mt p = p Kugel von möglchen Rchtungen p / p Telberech von Impulsen p wrd durch Raumwnkel charaktersert: Flächenantel auf Enhetskugel von möglchen p / p Infntesmaler Raumwnkel: dω = sn ϑ dϑ dϕ
42 36 KAPITEL 1. NEWTONSCHE MECHANIK - Dfferenteller Streuquerschntt Aus der Zahl der Telchen dn pro Zet, de n den Raumwnkel dω gestreut werden: dn = dω J dσ dω dσ dω Berechnung von dσ dω : Dfferenteller Streuquerschntt, Egenschaft des Streupotentals - Für gegebenes Potental U(r) se Zusammenhang zwschen Streuwnkel und Stoßparameter bekannt: ϑ(b) - Anzahl der Telchen mt Stoßparameter n [b, b + db] und Azmutwnkel n [ϕ, ϕ + dϕ]: dn = J b db dϕ - Dese Telchen werden n Raumwnkel dω = sn ϑ dϑ dϕ gestreut () Falls ϑ(b) endeutg umkehrbar st: b(ϑ) dn = J b db dϕ = dω J dσ dσ dω = sn ϑ dϑ dϕ J dω dσ dω = b(ϑ) sn ϑ db dϑ () Falls es zu enem gegebenen ϑ mehrere b gbt mehrere Stoßparameterbereche streuen n den glechen Wnkelberech Beträge (b α =Lösungen von ϑ(b α ) = ϑ 0 ) müssen aufsummert werden: dσ dω = bα(ϑ) db α sn ϑ dϑ b α Bespel: () Spezalfälle: (1) dϑ db = 0 dσ dω : Regenbogenstreuung (2) sn ϑ = 0, b 0 dσ dω : Glory (θ = 0) oder Rückwärtsstreuung (θ = π) (3) sn ϑ = 0, b = 0 alles möglch!
43 1.7. ANWENDUNG: DAS ZWEIKÖRPERPROBLEM Rutherfordstreuung Streuung spezell an enem Potental der Form U(r) = α/r (z.b. Streuung an geladenen Telchen) Zusammenhang ϑ(b) bekannt aus S.32: ϑ = 2 arctan b(ϑ) = α µα 2 2El 2 2E 1 tan(ϑ/2) db dϑ = α 4E 1 sn 2 (ϑ/2) α mt l = bp, E = p2 2µ ϑ = 2 arctan 2Eb Berechne Dfferentellen Streuquerschntt dσ sn ϑ db durch Ensetzen (mt sn(θ) = 2 sn(θ/2) cos(θ/2)): dσ dω = α 2 16E 2 1 sn 4 (ϑ/2) dω = b(ϑ) dϑ
44 38 KAPITEL 1. NEWTONSCHE MECHANIK 1.8 Wssensfragen 1. Was versteht man unter enem Massenpunkt? 2. We kann man de Bahn enes Massenpunktes parametrseren? We berechnet man n ener solchen Parametrserung Geschwndgket und Beschleungung? 3. Was versteht man unter ener Orthonormalbass? 4. We transformeren sch de Koordnaten enes physkalschen Vektors unter Koordnatentransformaton zwschen zwe Orthonormalbasen? 5. Nennen Se enge physkalsche Größen, de durch Vektoren beschreben werden. 6. We lautet das Superpostonsprnzp für Kräfte? 7. Was versteht man unter der trägen Masse? 8. We st der Newtonsche Impuls enes Massenpunktes defnert? 9. We lautet das Newtonsche Kraftgesetz? 10. Was st en Inertalsystem? 11. Beschreben und dskuteren Se de dre Newtonschen Postulate. 12. Was versteht man unter der Galle-Transformaton und we lautet se? 13. Warum treten n beschleungten Bezugssystemen Schenkräfte auf? 14. Was st de Zentrfugalkraft und de Corolskraft? Geben Se Bespele. We lauten de Glechungen dafür? 15. Was st en Kraftfeld? Was versteht man konkret unter enem konservatven und enem dsspatven Kraftfeld? Geben Se jewels en Bespel. 16. Was versteht man unter enem Potental? 17. Unter welchen Bedngungen bestzt en Kraftfeld en Potental? (Erläutern Se de lokale und de globale Formulerung). 18. Welche Form muß ene konservatve Zentralkraft haben? Warum? 19. We st de knetsche Energe defnert? 20. We snd Arbet und Lestung defnert? 21. Erläutern Se den Zusammenhang zwschen Erhaltungssätzen (z.b. Energe, Impuls, Drehmpuls) und den Symmetreegenschaften n enem System. 22. Was versteht man konkret unter Homogentät der Zet, Homogentät des Raums, und Isotrope des Raums? 23. We st der Schwerpunkt enes Systems von Massenpunkten defnert? 24. We bewegt sch der Schwerpunkt enes Systems, n dem der Impuls erhalten st? 25. Unter welchen Voraussetzungen glt Energeerhaltung? 26. Unter welchen Voraussetzungen glt Impulserhaltung? 27. Unter welchen Voraussetzungen glt Drehmpulserhaltung? 28. Geben Se en Bespel für en System, n dem nur Energeerhaltung glt, aber kene Impuls- und Drehmpulserhaltung. 29. Welche Erhaltungssätze gelten n enem System von N Telchen zwschen zwe parallelen Platten und warum?
45 1.8. WISSENSFRAGEN Welche Erhaltungssätze gelten n enem Zentralpotental U(r)? 31. Was besagt der Keplersche Flächensatz? 32. Warum bewegen sch Telchen, deren Drehmpuls erhalten st, mmer n ener Ebene? We kann man dese Ebene beschreben? 33. Was versteht man unter Schwerpunkt- und Relatvkoordnaten? 34. Was st de reduzerte Masse? 35. Was versteht man unter enem Zentralpotental? Welche Form muss ene konservatve Zentralkraft haben? 36. Was für möglche Bahnen kann en Telchen n enem Zentralpotental der Form U(r) = α/r ausführen? 37. Was versteht man unter dem dfferentellen Streuquerschntt? 38. Was versteht man unter dem totalen Streuquerschntt? 39. Was st Rutherford-Streuung?
46 40 KAPITEL 1. NEWTONSCHE MECHANIK
47 Kaptel 2 Lagrange-Mechank Copyrght 2014 Frederke Schmd 1 Motvaton: Bespele: Bs jetzt: Newtonsche Mechank N Telchen, Koordnaten r, Kräfte F = m r (ggf. Potental F = U( r 1 r N ) kartessche Koordnaten (manchmal umgeschreben) So kann man m Prnzp alles beschreben Aber: Oft ungünstg. Besser wäre es häufg, von vornheren mt anderen Varablen ( Koordnaten ) zu arbeten. Pendel Kräfte: Schwerkraft F g, Fadenkraft F Faden Aber: FFaden egentlch unnteressant Interessant st nur, dass F Faden gerade dafür sorgt, dass l konstant blebt! Zwangsbedngung l = const.. wrd gewährlestet durch Zwangskraft F Faden Ökonomsche Behandlung nutzt Kenntns der Zwangsbedngung aus und arbetet nur noch mt ener Koordnate ϕ. Bewegung auf strukturerter Oberfläche Körper gletet auf enem Gebrge feste Höhe: z = H(x, y) Kräfte: Schwerkraft F g, Normalkraft von Ebene F N Normalkraft sorgt dafür, dass Körper mmer auf Ebene blebt. 1 Prof. Dr. Frederke Schmd, Vorlesung Theoretsche Mechank, Unverstät Manz, WS 2014/2015. Letzte Änderung am
48 42 KAPITEL 2. LAGRANGE-MECHANIK Auto Bewegungsglechungen nach Newton: Man müsste F g zerlegen n Antel F parallel zur Oberfläche und F senkrecht zur Oberfläche. F beschleungt den Körper parallel zur Oberfläche. Dann muss dese Bewegung noch umgerechnet werden n de entsprechende Bewegung n x-rchtung. komplzertes geometrsches Problem, fehleranfällg Frage: Gbt es en enfaches, scheres Verfahren, de Bewegungsglechungen für enen solchen Fall aufzustellen? Frehetsgrade: Zwe (n der Ebene) Aber: Nur Bewegung entlang der Vorderräder bzw. quer zur Radachse e (Achse) st erlaubt. (kene setlche Bewegung) 2.1 Zwangsbedngungen und Zwangskräfte Klassfzerung von Zwangsbedngungen skleronom: zetunabhängg rheonom: zetabhängg holonom: lassen sch durch geschlossene Glechung der Form f( r 1 r N, t) = 0 beschreben (z.b. Pendel: f(x, z) = x 2 + z 2 l 2 = 0 Strukturerte Oberfläche: f(x, y, z) = z H(x, y) = 0) ncht holonom: Kene Glechung der Form f( r 1 r N, t) = 0 möglch. Eventuell lässt sch dfferentelle Glechung aufstellen ( a ( r 1 r N, t)d r = a 0 ( r 1 r N, t)dt ) (z.b. Auto: d r e Achse (t) = 0) Zwangskräfte Kräfte Z, de zusätzlch zu den bekannten Kräften F wrken, um de Zwangsbedngungen scherzustellen. (z.b. Pendel: Fadenkraft Strukturerte Oberfläche: Normalkraft auf Oberfläche etc.) Es glt: p = F + Z m Allgemenen unnteressant, Berechnung nur manchmal nötg (z.b. bem Pendel, wenn Faden nur gewsse Spannung aushält!)
49 2.2. LAGRANGE-GLEICHUNGEN ERSTER ART Prnzp der vrtuellen Verrückungen Bshergen Bespele haben gezegt: Zwangskräfte senkrecht auf möglchen Verrückungen des Systems (alle möglchen Verrückungen, ncht zu verwechseln mt tatsächlcher Bewegung) Etwa be strukturerter Oberfläche Konkreter: Defnere Vrtuelle Verrückungen δ r : Alle nfntesmalen Verrückungen, de mt den Zwangsbedngungen zu gegebenem festen Zetpunkt verenbar snd. Falls Zwangsbedngungen skleronom: Vrtuellen Verrückungen δ r schleßen tatsächlche Bewegungen d r en. Falls Zwangsbedngungen rheonom (zetabhängg): Tatsächlche Bewegungen d r u.u. vrtuell (be engefrorener Zet) ncht möglch, d r δ r Prnzp der vrtuellen Verrückungen: Zwangskräfte stehen senkrecht auf allen möglchen vrtuellen Verrückungen: Z δ r = 0 δ r d Alembertsches Prnzp Alternatve Formulerung des Prnzps der vrtuellen Verrückungen, n der unbekannte Zwangskräfte ncht mehr explzt vorkommen. Aus Z δ r = 0 und p = F + Z folgt: ( p F ) δ r = 0 für alle erlaubten vrtuellen Verrückungen δ r Verallgemenerung der Newtonschen Bewegungsglechungen Spezell: Kene Zwangsbedngungen alle δ r erlaubt ( p F ) δ r = 0 für alle δ r p = F (Newtonsche Glechungen) 2.2 Lagrange-Glechungen erster Art Verfahren, Zwangskräfte aus dem Prnzp der vrtuellen Verrückungen zu gewnnen und Bewegungsglechungen aufzustellen Allgemen Gegeben seen K Zwangsbedngungen n der dfferentellen Form: ( ) N =1 a(α) ( r 1 r N, t) d r = a (α) 0 ( r 1 r N, t)dt (α = 1 K) Vrtuelle Verrückungen δ r erfüllen a (α) δ r = 0 (feste Zet dt = 0) Vergleche mt Prnzp der vrtuellen Verrückungen: Z δ r = 0 Ansatz für Zwangskräfte: Z = α λ (α) a (α) Lagrange-Glechungen erster Art: p = F + λ (α) a (α) α
50 44 KAPITEL 2. LAGRANGE-MECHANIK Bemerkung: Holonome Zwangsbedngungen f (α) ( r 1 r N, t) = 0 lassen sch n de Form ( ) brngen mt a (α) = f (α), a (α) 0 = f t (f (α) 0 df (α) dt Vorgehenswese n der Praxs = 0 = ( f (α) (α) f ) r + t ( f (α) )d r = f t dt) () Stelle Zwangsbedngung auf, brnge se n de Form ( ) () Stelle Lagrange-Glechung erster Art auf () Wähle λ (α) so, dass Zwangsbedngungen erfüllt snd (v) Löse de Glechungen ( () und (v) können u.u. auch vertauscht werden.) Bespele Bewegung n Gebrge n 2 Dmensonen (x, z) Bekannte Kraft: Schwerkraft F = (0, mg) () Zwangsbedngung: f(x, z) = z H(x) = 0 df = H (x)dx + dz = 0 Dfferentelle Bedngung: a d r = 0 mt a = ( H (x), 1) () Lagrange-Glechung erster Art: p = F + λ a = ( λh, mg + λ) () Bestmmung von λ aus Zwangsbedngung a d r = 0 a d r = 0 a m d r dt = a p = 0 ( a p) = 0 und d t=0 dt ( a p) = 0 a p + a p = a p + d a dx ẋ p = 0 a(x) = ( H 1 ) ; d a dx = ( H 0 ) ; p = m (ẋ ż ) ; p = F + λ a = ( λh mg + λ ) λh 2 mg + λ H mẋ 2 = 0 λ = m(g + H ẋ 2 )/(1 + H 2 ) Zwangskraft: Z = m 1+H 2 ( g Antel der Schwerkraft + H ẋ 2 ) ( H 1 ) Zentrpetalkraft Bewegungsglechung: p = F + Z = ( 0 mg ) + m(g+ẋ2 H (x)) ( H (x) ) 1+H 2 1 Auto, das mt ener Kraft F angeschoben wrd () Zwangsbedngung: e Achse (t) d r = 0 a = e Achse (t). () Lagrange-Glechung 1. Art: p = F + λ a = λ e Achse (t) + F () Bestmmung von λ aus a d r = 0 a p = 0 d dt ( a p) = a p + a p = a p + a ( F + λ a) =! 0 λ = 1 ( F a + p a) a 2 = a = e Achse =1 F e Achse m v e Achse Bewegungsglechung: p = F + λ a = F e Achse ( F e Achse + m v e Achse )
51 2.3. LAGRANGE-GLEICHUNGEN ZWEITER ART 45 Auto auf schefer Ebene z = κx unter Enfluss der Schwerkraft F g = mg e z () Zwe Zwangsbedngungen: (1): e Achse (t) d r = 0 a (1) = e Achse (t) (2): f(x, y, z) = z + κx = 0 κdx + dz = 0 a (2) = (κ, 0, 1) () Lagrange-Glechung 1. Art: p = F g + λ (1) a (1) + λ (2) a (2) () Bestmme λ (1) und λ (2) so, dass d r a (α) = 0 für α = 1, 2 p a (α) d = 0 bzw. dt ( p a(α) ) = p a (α) d + p dt a(α) = 0 d (Her: dt a(1) = e Achse d, dt a(2) = 0) Mt p = F g + 2 α=1 a(α) λ (α) Lneares Glechungssystem für λ (1,2). Atwoodsche Fallmaschne Bespel für Lagrange-Glechungen erster Art n enem System mt mehreren Massenpunkten Betrachte nur z-koordnaten z Bekannte Kraft: Schwerkraft F = m g () Zwangsbedngung: f(z 1, z 2 ) = z 1 + z 2 + l =! 0 bzw. dfferentell: dz 1 + dz 2 = 0. 2 =1 a dz mt a = 1 () Lagrangeglechung erster Art: ṗ = F + λa = m g + λ () Bestmmung von λ aus Zwangsbedngung dz 1 + dz 2 = 0 ż 1 + ż 2 = 0 p 1 m 1 + p 2 m 2 = 0 ( p 1 m 1 + p 2 m 2 ) = 0 und d t=0 dt ( p 1 m 1 + p 2 m 2 ) = ṗ1 m 1 + ṗ2 m 2 = 0 (Ensetzen) m 1g+λ m 1 + m 2g+λ m 2 = 0 λ = 2g/( 1 m m 2 ) Zwangskraft: Z 1 = Z 2 = 2g/( 1 m m 2 ) Bewegungsglechung: m z = m g + 2g/( 1 m m 2 ) 2.3 Lagrange-Glechungen zweter Art Voraussetzungen m Folgenden: Betrachte Systeme mt holonomen Zwangsbedngungen lassen sch n K Glechungen f (α) ( r 1 r N, t) = 0 fassen (α = 1 K) Alle Kräfte bs auf de Zwangskräfte lassen sch auf en Potental zurückführen. Ohne Zwangsbedngungen: 3N Frehetsgrade, 3N Bewegungsglechungen Mt Zwangsbedngungen: m = 3N K Frehetsgrade Beschrebung durch nur noch m Bewegungsglechungen sollte rechen. Zel: Allgemenes Verfahren, dese m Bewegungsglechungen aufzustellen.
52 46 KAPITEL 2. LAGRANGE-MECHANIK Vorgehen: Beschrebe System durch m Varablen q 1 q m. Folge schrttwese Defntonen n 2.1 S.42. Das d Alembertsche Prnzp (2.1.4 S.43) wrd zu Bewegungsglechungen für de q führen Generalserte Koordnaten Beschrebe durch Varablen (q 1 q m ) mt r = r (q 1 q m, t) ( Bespel Pendel: Raumkoordnaten x, z Zwangsbedngung x 2 + z 2 l 2 = 0 Generalserte Koordnate: ϕ mt { x = l sn ϕ z = l cos ϕ } ) Potental U( r 1 r N ) lässt sch auch als Funkton der generalserten Koordnaten ausdrücken: U(q 1 q m, t) ( Bespel Pendel: U(x, z) = z m g = l cos ϕ m g = U(ϕ) ) Generalserte Kräfte Defnton: Reale Kräfte F N r Generalserte Kräfte: Q j = F =1 q j Defnton lässt sch auf belebge Kräfte (Zwangskräfte und Potentalkräfte) anwenden. Motvaton wrd weter unten erschtlch. Spezell Potentalkräfte: F = U( r 1 r N, t) Q j = q j U(q 1 q m, t) (Q j = N U( r 1 r N, t) r = U( r q =1 j q 1 (q 1 q j m, t) r N (q 1 q m, t), t)) Generalsertes Prnzp der vrtuellen Verrückungen Erlaubte vrtuelle Verrückungen δ r hängen zusammen mt Verschebungen ( Varatonen ) δq j der Varablen q j : δ r = m r q j=1 j δq j Aus dem Prnzp der vrtuellen Verrückungen wrd N =1 Z Zwangskräfte r Z! q j ) δq j = 0 generalserte Zwangskräfte nach δ r = m ( N j=1 = d Alembertsches Prnzp und Bewegungsglechungen Das d Alembertsche Prnzp besagt: ( p F ) δ r = 0 für erlaubte δ r Daraus folgt analog zu m δq j [ N q j=1 =1 j p N q =1 j F ] = 0 () () Betrachte erst (): Laut Voraussetzung glt F = U (Potentalkraft) Daraus folgt N =1 r q F j = Q j = q j U(q 1 q m, t) nach (2.3.2 S.46) r r
53 2.3. LAGRANGE-GLEICHUNGEN ZWEITER ART 47 r T q =1 j T q j (Bewes: Betrachte T = 1 2 m r 2 Ferner: () N q j p = d dt mt T (q 1 q m, q 1 q m, t): knetsche Energe Aus r = d dt r (q 1 q m, t) = m r q q j + r j=1 j t T q j Daraus folgt: Fazt: folgt: r = r q k q k und r = m q 2 r q k q j=1 k q j + 2 r j q k t = m q j [ r ] + q j=1 j q k t [ r ] = d q k dt [ r ] q k r = m r q j d T r = dt q j m r + q j m j=1 δq j [ d dt r = m r ; q j T q j m r d dt ( r q j ) = T q j T q j + U r = m r q j d = m r dt ( r ) q j p r q j + T q j ) q j ] = 0 für alle δq j [ ] = 0 q j (T U) = d dt q j T = d dt q j (T U) Defnere Lagrange-Funkton: L(q 1 q m, q 1 q m, t) = T U Dann gelten: Lagrange-Glechungen zweter Art: Gewünschter Satz von m Bewegungsglechungen!!! (wg. U q j = 0) d L L = 0 dt q j q j Bemerkung: Glt unabhängg davon, ob tatsächlch Zwangsbedngungen vorlegen. Zum Bespel kann ( r 1 r N ) (q 1 q 3N ) enfach Umwandlung von kartesschen Koordnaten n andere, günstgere Varablen sen. Lagrange-Glechungen lefern zugehörgen Bewegungsglechungen Bespele Pendel Knetsche Energe: T = m 2 v2 = m 2 l2 ϕ 2 Potental U = mlg cos ϕ Lagrange-Funkton: L = T U = m 2 l2 ϕ 2 + mlg cos ϕ = L(ϕ, ϕ) Lagrange-Glechung: d L dt ϕ = ml2 ϕ =! L ϕ = mlg sn ϕ ϕ = g l sn ϕ Perle auf roterendem Stab Stab rotert mt Wnkelgeschwndgket ω = ϕ Perle gletet rebungsfre auf dem Stab, Lage r (Bespel für rheonome Zwangsbedngungen) Geschwndgket der Perle: v = ṙ e r + rω e ϕ ( e r = r r ; e ϕ e r : Enhetsvektor n Drehebene) Knetsche Energe: T = m 2 v2 = m 2 (ṙ2 + r 2 ω 2 ) Potental: U = 0 (Stab st waagerecht, Schwerkraft spelt kene Rolle) Lagrange-Funkton: L = T U = m 2 (ṙ2 + r 2 ω 2 ) = L(r, ṙ) d L Lagrange-Glechung: dt ṙ = m r =! L r = mω2 r r = ω 2 r NB: Lösung hat allgemene Form r(t) = a e ωt + b e ωt a e ωt t Energe blebt ncht erhalten. (Zwangsbedngung zerstört Homogentät der Zet)
54 48 KAPITEL 2. LAGRANGE-MECHANIK 2.4 Invaranzen und Erhaltungsgrößen Betrachte en System, das durch ene Lagrange-Funkton L(q 1 q m, q 1 q m, t) beschreben wrd. Aus Invaranzen der Lagrange-Funkton be bestmmten Varablentransformatonen ( Symmetren des Systems) lassen sch Erhaltungsgrößen ableten (Verallgemenerung und Erweterung von 1.5 S.22) Zyklsche Varablen Falls L von ener Varablen q ncht explzt abhängt: L q = 0 L Dann st ene Erhaltungsgröße (wegen d dt q De Varable q heßt dann zyklsche Varable. L q = L q = 0) Bespel: N Nchtwechselwrkende free Telchen (1 Raumdmenson) Lagrange-Funkton: L(x 1 x N ) = 1 2 N =1 m ẋ 2 L x = 0 alle x snd zyklsche Varablen! L ẋ = m ẋ st erhalten für alle Zetunabhänggket Falls L von der Zet t ncht explzt abhängt: L t = 0 Dann st H = (wegen: dh dt m j=1 L q j L ene Erhaltungsgröße q j = m j=1 d dt ( q j L ) d q j dt L(q 1 q m, q 1 q m, t) = m j=1 ( q j L + q q j j Spezell: L = 1 2 m ẋ 2 U L ẋ d L dt q j L/ q j ) m j=1 ( q j L q j + q j L ) L = 0 ) q j t 0 E = ẋ L = m ẋ2 1 2 m ẋ 2 + U = 1 2 m ẋ 2 + U = T + U m ẋ Allgemener: Be skleronomen glechbedeutend mt der nach Homogentät der Zet, und de Erhaltungsgröße st de Energe. Be rheonomen Zwangsbedngungen st das ncht unbedngt der Fall! Bespele: Pendel (sehe S.47) L(ϕ, ϕ) = m 2 l2 ϕ 2 + mlg cos(ϕ) ncht explzt zetabhängg! H = ϕ L ϕ L L (mt ϕ = ml2 ϕ 2 ) = m 2 l2 φ2 mlg cos(ϕ) = E (Energe) s erhalten. Perle auf roterendem Stab (sehe S.47) L(r, ṙ) = m 2 (ṙ2 + r 2 ω 2 ) ncht explzt zetabhängg! H = ṙ L ṙ L = m 2 (ṙ2 r 2 ω 2 ) st erhalten. Aber: H st ncht de Energe (H E)! Energe E = T = m 2 (ṙ2 + r 2 ω 2 ) st ncht erhalten!
55 2.4. INVARIANZEN UND ERHALTUNGSGRÖSSEN Der Satz von Emmy Noether Vorab: Addert man zu der Lagrange-Funkton ene totale Zetabletung hnzu, L L = L + d dt D(q 1 q m, t), so bleben de Bewegungsglechungen unverändert. (Bewes: n Lagrange-Glechungen 2. Art ensetzen, Übungsaufgabe) Satz: De Lagrange-Funkton L(q 1 q m, q 1 q m, t) enes Systems se quasnvarant unter ener kontnuerlchen Symmetre-Transformaton K a (q 1 q m ) ( q 1 (a) q m (a)) (her st a en kontnuerlcher Parameter, q = q (a) und ( q (0) = q ), vgl. 1.5 S.22). Quas-nvarant hesst, L st nvarant bs auf ene totale Zetabletung L( q 1 q m, q 1 q m, t) = L(q 1 q m, q 1 q m, t) + d dt D(q 1 q m, t; a) Dann gbt es en Integral der Bewegung (ene Erhaltungsgröße) J(q 1 q m, q 1 q m, t) = m L j=1 ( d q j(a) q j da ) a=0 ( D a ) a=0 d (Bewes: Aus Quas-Invaranz folgt: da L( q 1(a) q m(a), q 1 (a) q m(a), t) = d D a=0 dt a a=0 d da L( q 1(a) q m(a), q 1 (a) q m(a), t) = m j=1 ( L d q j q j da + L d q j q j da ) a=0 Folgerungen: = m j=1 ( d q j da ( d L dt d dt [ m L j=1 q j ( d q j )+ q L ( j q d d j dt da q j)) a=0 = m j=1 d dt ( L da ) ( D a=0 a ) ] = 0 [ m L a=0 j=1 q j ( d q j q j d q j da ) = d a=0 dt [ m L j=1 q j ( d q j da ) a=0 ] da ) a=0 ( D a ) a=0 ] = const. ) () Zet-Translatonen: q (t) = q (t + a) a 0 = q (t) + a q (t) Allgemen glt: L( q 1 q m, q 1 q m, t + a) = L(q 1 q m, q 1 q m, t) + a d dt L Falls L ncht explzt zetabhängg, ( L t = 0), st L quas-nvarant: L( q 1 q m, q 1 q m ) = L(q 1 q m, q 1 q m )+ d dtd(t, a) mt D(t, a) = al Erhaltungsgröße: J = m L q j=1 j ( d q j(a) da ) ( D a=0 a ) L = a=0 q j=1 j q j L = H (Reproduzert 2.4.2!) q j L () Falls (q 1 q m ) = kartessche Raumkoordnaten ( r 1 r N ) Aus Noether-Theorem folgt 1.5 S.22 (Homogentät der Zet Energeerhaltung (s. ()) Homogentät des Raums Impulserhaltung Isotrope des Raums Drehmpulserhaltung) z.b. Impulserhaltung n ener Dmenson: L(x 1 x N, ẋ 1 ẋ N, t) = 1 2 m ẋ 2 U(x 1 x N, t) Falls L nvarant unter K a x x (a) = x + a Erhaltungsgröße: J = N =1 L ẋ ( d x (a) da ) a=0 mt L ẋ = m ẋ = p, d x (a) da = 1 J = N =1 p : Gesamtmpuls blebt erhalten. Allgemen: Rechnungen analog zu 1.5, daher ncht wederholt.
56 50 KAPITEL 2. LAGRANGE-MECHANIK 2.5 Das Hamltonsche Prnzp Alternatver Zugang, äquvalent zu Lagrange-Glechungen zweter Art Gegeben se en System mt m Frehetsgraden q j (generalserte Koordnaten) und bekannter Lagrange-Funkton L(q, q, t); Notaton q = (q 1 q m )). Defnere Wrkung ener Trajektore q(t) n dem Zetntervall [t 0, t 1 ]: Das Prnzp t 1 I = dt L(q(t), q(t), t) t 0 De Bewegung enes Systems zwschen zwe Zeten t 0 und t 1 be vorgegebenen Anfangs- und Endpunkten q(t 0 ), q(t 1 ) verläuft derart, dass de Wrkung I = t 1 t 0 dt L(q, q, t) extremal wrd. (m Allgemenen mnmal. Prnzp der klensten Wrkung ) Was bedeutet das? tatsächlche Bahn q(t) Wrkung I[ q(t)] benachbarte Bahnen q(t) + δq(t) δq(t) nfntesmale Varaton Wrkung I[ q(t) + δq(t)] I mnmal heßt: I[ q] < I[ q + δq] für alle δq I extremal heßt: δi = I[ q + δq] I[ q] = 0 + O((δq)2 ) Abwechung der Ordnung (δq) 2 Mathematsch etwas präzser Wrkung I st extremal, wenn für de dfferenzerbaren Wege η(t) mt η(t 0 ) = η(t 1 ) = 0 glt: lm 1 ε 0 ε (I[ q + εη] I[ q]) = 0. Se nun I[ q + δq] I[ q] = 0 für alle Varatonen δq 0 = t 1 t 0 dt{l( q + δq, q + δ q, t) L( q, q, t)} - Taylorentwcklung des Integranden um q j (t) = t 1 dt{ m ( L q t 0 j=1 j δq j + L q j δ q j ) + O((δq) 2 )} - Partelle Integraton bzgl. δ q j = d dt δq j = m dt L q j=1 j δq j + [ L q j δ q j ] t 1 t 0 - δq j (t 0 ) = δq j (t 1 ) = 0 { t 1 t1 t 0 = t 1 dt( L q j d L dt q j )δq j für alle {δq j } t 0 Da de δq j unabhängg snd, folgt: L L dt( d dt q j )δq j } t 0 q j d L dt q j = 0 Hamlton-Prnzp st äquvalent zu Lagrange-Glechungen zweter Art.
57 2.5. DAS HAMILTONSCHE PRINZIP 51 Bemerkung: Rechnung oben st en Bespel für de Lösung enes Extremalproblems mt Hlfe von Varatonsrechnung. Führt oft (we her) auf Dfferentalglechungen, den sogenannten Euler-Lagrange Glechungen. Bespele für Extremalprobleme n anderen Berechen der Physk: Castglano-Prnzp (Elastostatk), Fermatsches Prnzp (Strahlenoptk), Jaynesches Prnzp (statstsche Physk) Hamlton-Prnzp mt zusätzlchen Zwangsbedngungen Zugang über Hamlton-Prnzp ermöglcht Kombnaton von Lagrange-Glechungen erster und zweter Art - z.b. wenn Zwangsbedngungen telwese holonom und telwese ncht holonom snd. Gegeben: m generalserte Koordnaten q j, und Lagrange-Funkton L(q, q, t) Aber: q j ncht unabhängg, zusätzlche Zwangsbedngungen legen vor. Enfachketshalber zunächst nur ene Zusatzbedngung. Unterschede zwschen () Zwangsbedngung holonom: f(q, t) = 0 Erwetere Hamlton-Prnzp um Lagrange-Multplkator Term λ(t) (sehe Vorlesung Mathematsche Rechenmethoden ) Fordere, dass I t 0 t 1 dt λ(t)f(q, t) extremal Varatonsrechnung: I[ q + δq] I[ q] t 1 dt λ(t) m f! q t 0 =1 δq = 0 L Bewegungsglechungen: d L = λ(t) f q j dt q j q j Wähle λ(t) so, dass Zwangsbedngung erfüllt st. () Zwangsbedngungen nchtholonom, aber lassen sch n dfferenteller Form ausdrücken: m j=1 a j (q, t)dq j = a 0 (q, t)dt Vergleche mt dfferenteller Form der holonomen Zwangsbedngung: q m f j=1 dq = f t dt df (aus: f 0 dt 0) Legt Verallgemenerung von () nahe: I[ q + δq] I[ q] t 1 dt λ(t) m! a δq = 0 t 0 =1 Bewegungsglechungen: Mehrere Zwangsbedngungen a (α) j : Analog L L d L = λ(t) a j (q, t) q j dt q j d L q j dt q j = α (für jede Zwangsbedngung en Lagrange-Multplkator λ (α) (t)) λ (α) (t)a (α) j
58 52 KAPITEL 2. LAGRANGE-MECHANIK 2.6 Verallgemenerte Lagrange-Formalsmen Bs jetzt: Exstenz enes geschwndgketsunabhänggen Potentals U(q 1 q m, t) wurde gefordert, war notwendg zur Herletung der Lagrange-Glechungen. Aber: Exstenz enes Potentals ncht a pror zwngend. De Hauptsache st, dass de Lagrange-Funkton de rchtgen Bewegungsglechungen lefert. Unter deser Voraussetzung dürfen auch andere Systeme mt dem Lagrange- Formalsmus behandelt werden. Wetere Möglchket: Erweterung der Lagrange-Glechungen zweter Art um enen Betrag aus zusätzlchen Kräften F (R), de sch ncht auf en Potental zurückführen lassen. Erweterte Lagrangeglechung hat dann de Form L d L = R j mt (vgl S.46) R j = q j dt q j N =1 F (R) r q j (Herletung analog S.46: Tele Kräfte F n konservatve und sonstge Kräfte auf: F = U + F (R). Aus dem d Alembertschen Prnzp N =1 ( p F )δ r = 0 folgt zunächst d T dt T Q q j = 0 mt der generalserten Kraft (vgl S.46) Q j = j N r =1 F = U + R q j q j.) j q j Promnente Bespele für geschwndgketsabhängge Kräfte: Lorentzkraft (Kraft auf en Telchen m elektromagnetschen Feld) und Rebungskräfte Telchen m elektromagnetschen Feld Promnentestes Bespel ener verallgemenerten Lagrange-Funkton für en System mt geschwndgketsabhänggen Kräften. Ladung q; elektrsches Feld E( r, t); magnetsches Feld B( r, t); Bewegungsglechung: m r = q E + elektrsche Kraft q c v B Lorentz- Kraft geschwndgketsabhängg! Es glt (Vorgrff auf Vorlesung Elektrodynamk (Theore 2)): E, B lassen sch durch Potentale φ( r, t), A( r, t) ausdrücken: B = A; E 1 = A c t φ Damt lässt sch ene Lagrange-Funkton aufstellen, de de rchtgen Bewegungsglechungen ( ) erzeugt: L = m 2 r 2 q φ + q c r A( r, t) ( L = q φ + q r α r α c A ṙ β β ; r β α 0 =! d L dt L ṙ α r α m r α = q ( φ = m r α + q c β 1 A α r α c t ) E α m r = q E + q c v B ) L = mṙ ṙ α + q α c Aα A α ṙ r β + q A α + q φ q β c t r α c A ṙ β β r β α + q c A β A β(ṙ β ṙ α r α β ) r β [ r ( A)] α=[ v B] α ( )
59 2.6. VERALLGEMEINERTE LAGRANGE-FORMALISMEN Rebung und Dsspatonsfunkton Rebungskräfte: Bespele für geschwndgketsabhängge Kräfte, de sch ncht auf ene Lagrangefunkton zurückführen lassen. (NB: Snd allerdngs auch ncht fundamental m Gegensatz zu z.b. Gravtatonskräften oder elektromagnetsche Kräften). Allgemen: Rebungskraft F (R) verallgemenerte Rebungskraft R j = N =1 r (R) q j F. Berechnung von R j über dese Formel st m Allgemenen mühsam! Häufger Spezalfall: Rebungskräfte auf Telchen snd der Geschwndgket des Telchens entgegengesetzt: F (R) r. In desem Fall kann man ene Dsspatonsfunkton P bestmmen, so dass R j = P. q j Konkret: F (R) = λ r Rayleghsche Dsspatonsfunkton: P = 1 2 N =1 λ r 2 Allgemener: F (R) = λ (v ) r P = N =1 r (Rechnung: Für r (q 1,, q m, t) glt: r = q q j + r j t r = r. q j q j r R j = λ (v ) r r = q j λ (v ) r = 1 q j 2 λ (v ) ( r ) 2 q j 0 v λ (v ) v dv Anderersets P = q j q j v 0 λ (v )v dv v = λ (v )v = 1 q j 2 v λ (v )v 2. q j Mt r 2 = v 2 folgt R j = P/ q j.) Folgerung für desen Spezalfall: Lagrange-Glechung kann durch enfachen d L Dsspatonsterm ergänzt werden: L + P = 0. dt q j q j q j Zur Bestmmung der Bewegungsglechungen braucht man zwe Funktonen L und P. Bespel: Pendel (vgl S.47) mt Luftrebung F (R) = λ r. Lagrange-Funkton (sehe S.47): L(φ, φ) = T U = m 2 l2 φ2 + mlg cos φ Dsspatonsfunkton: P = λ 2 v2 = λ 2 l2 φ2. Verallgemenerte Lagrange-Glechung: d L L dt φ φ = ml2 φ + mlg sn φ = P φ = λl2 φ. φ = g l sn φ λ φ. m
60 54 KAPITEL 2. LAGRANGE-MECHANIK 2.7 Zusammenfassung: Lagrange-Mechank Konzepte: Technken: Verallgemenerte Koordnaten q 1, q m (ermöglcht u.a. eleganten Enbau von Zwangsbedngungen) Zentrale Größe, de de Dynamk charaktersert: L q = L Lagrange-Funkton L(q 1,, q m, q 1, q m, t) d d q (NB: Allgemener als Potental U( r 1, r N, t) aus der Newtonschen Mechank (1.7 S.28). Damt kann u.a. auch Lorentzkraft m elektromagnetschen Feld beschreben werden (2.6.1 S.52)). Wrkung I = t 1 t 0 dt L und Hamltonsches Prnzp (I extremal) Systematscher Satz zum Zusammenhang zwschen Symmetren und Erhaltungsgrößen: Noether-Theorem Lösung von Extremalproblemen mttels Varatonsrechnung Umgang mt Nebenbedngungen über Lagrange-Parameter
61 2.8. WISSENSFRAGEN Wssensfragen 40. Was snd rheonome, skleronome, holonome Zwangsbedngungen? Geben Se jewels konkrete Bespele. 41. Was snd Zwangskräfte? Nennen Se de Zwangskräfte n Ihren Bespelen aus der vorgen Frage und geben Se de Rchtung an, n de dese zegen. 42. Was snd vrtuelle Verrückungen? 43. Unter welchen Umständen gehören tatsächlche Bewegungen enes Systems ncht zur Klasse der vrtuellen Verrückungen? Begründen Se Ihre Antwort. 44. We lautet das d Alembertsche Prnzp? 45. Erklären Se de Lagrange-Glechungen erster Art 46. Was versteht man unter generalserten Koordnaten? 47. Was st ene Lagrange-Funkton und we berechnet man se? 48. Unter welchen Bedngungen kann man Lagrange-Glechungen zweter Art aufstellen? We lauten dese Glechungen? 49. Welche Größe st erhalten wenn ene Lagrange-Funkton ncht von der Zet abhängt? 50. Was st ene zyklsche Varable? 51. Was besagt das Noethersche Theorem? Geben Se Bespele. 52. We lautet das Hamltonsche Prnzp bzw. Wrkungsprnzp? We st n desem Kontext de Lagrangesche Wrkung defnert? 53. We kann man das Hamltonsche Prnzp formuleren, wenn de generalserten Koordnaten zusätzlchen Zwangsbedngungen unterlegen? 54. We lautet de Lagrange-Funkton für en Telchen m elektromagnetschen Feld? 55. Was versteht man unter der Dsspatonsfunkton? Wann kann man se formuleren und we kann man n desem Fall de Lagrange-Glechungen zweter Art um Rebungskräfte ergänzen? 56. We kann man Rebungskräfte enführen, wenn kene Dsspatonsfunkton gefunden werden kann?
62 56 KAPITEL 2. LAGRANGE-MECHANIK
63 Kaptel 3 Starre Körper Copyrght 2014 Frederke Schmd 1 Starre Körper: En Bespel für Zwangsbedngungen Defnton enes starren Körpers (ähnlch we bem Massenpunkt en dealsertes Konzept) - System von Massenpunkten m mt festen Abständen z.b. Gesamtmasse M = m offenschtlch klarer Fall von holonomen Zwangsbedngungen - Verallgemenerung: Kontnuerlche starre Massenvertelung z.b. Dchtevertelung ϱ( r) Gesamtmasse M = d 3 r ϱ( r) In beden Fällen: Insgesamt sechs Frehetsgrade Dre für Poston Dre für Orenterung ( u = 1 und Rchtung des Henkels) 3.1 Beschrebung der Bewegung (Knematk) Charakterserung des Körpers Wähle en Bezugssystem, das sch mt dem Körper mtbewegt ( körperfestes Koordnatensystem) In desem Bezugssystem glt: - Dskreter Fall: Jeder Massenpunkt m hat feste Koordnate s - Kontnuerlcher Fall: Unveränderlche Dchtevertelung ϱ( s) 1 Prof. Dr. Frederke Schmd, Vorlesung Theoretsche Mechank, Unverstät Manz, WS 2014/2015. Letzte Änderung am
64 58 KAPITEL 3. STARRE KÖRPER Snnvoll st es, den Ursprung des körperfesten Koordnatensystems n den Schwerpunkt zu legen ( R = 1 M m r bzw. R = 1 M d 3 r ϱ( r) r). So soll es n Zukunft geschehen Beschrebung des momentanen Zustandes Zustand bzgl- raumfestem Koordnatensystem Σ (Inertalsystem) () Lage des Schwerpunktes R Dre Frehetsgrade R x, R y, R z Defnere: u = r R : Koordnaten relatv zum Schwerpunkt () Orenterung des körperfesten Bezugssystems Σ Drehmatrx D mt D T u = s bzw. u = D s ( s: körperfeste Koordnaten) D beschrebt Koordnatentransformaton Σ Σ Dre Frehetsgrade Konkret z.b. Eulersche Wnkel (z.b. Goldsten, Noltng) cos ϕ sn ϕ 0-1. Drehung um z-achse, Wnkel ϕ: Dϕ T = sn ϕ cos ϕ Drehung um x-achse, Wnkel ϑ: Dϑ T = 0 cos ϑ sn ϑ 0 sn ϑ cos ϑ cos ψ sn ψ 0-3. Drehung um z-achse, Wnkel ψ: Dψ T = sn ψ cos ψ Insgesamt: D T = D T ψ DT ϑ DT ϕ Frehetsgrade: (ψ, ϑ, ϕ)
65 3.2. DYNAMISCHE GRÖSSEN 59 Drehachse und Drehwnkel: Jede Drehung lässt sch als Drehung um ene Drehachse und enen Drehwnkel beschreben. ϕ x ϕ Frehetsgrade ϕ ϕ y mt ϕ : Drehwnkel, ϕ : Drehachse ϕ z Cayley-Klen Parameter oder Quaternonen (sehe z.b. Goldsten) Beschrebung der Bewegung Bewegung enes starren Körpers setzt sch zusammen aus: () Translatonsbewegung des Schwerpunkts R () Rotaton um ene Achse, de durch den Schwerpunkt geht. Also: Für dskrete Massenpunkte: r = R + ω u Für kontnuerlche Vertelung: r = R + ω u Anschaulch: r = R + u r = R + u Aber: u = const.. (Abstand zum Schwerpunkt unveränderlch) d dt u2 = 2 u u = 0 u u Rotaton Formal: r = R + u, u = D T s mt s = const. r = R () + u () mt u = ḊT s (körperfeste Koordnaten) - Für en Inertalsystem Σ, das zur Zet t 0 mt dem körperfesten Bezugssystem überenstmmt (D(t 0 ) = 1, u = s zur Zet t 0 ), glt: Ḋ T wrkt gemäß u = ḊT u = Ω u für en Ω - In anderen Koordnatensystemen muss deses mmer noch gelten mt entsprechend koordnatentransformertem Ω: u = ω u mt ω = D Ω 3.2 Dynamsche Größen Impuls Dskrete Massenvertelung: P = m r = m ( R + ω u ) = Kontnuerlche Vertelung: Analog P = d 3 u ϱ( u) M M m R + ω m u = M R 0 R + ω d 3 u ϱ( u) u = M R 0 P = M R
66 60 KAPITEL 3. STARRE KÖRPER Drehmpuls Dskrete Massenvertelung: L = r p = m [ r r ] = m [( R + u ) ( R + ω u )] = m R R + R ( ω m u ) + m u R + m u ( ω u ) u 2 M 0 0 ω u ( u ω) = R P + m [ ω( u 2 ) u ( ω u )] L = R P + I ω mt I αβ = m [ u 2 δ αβ u α u β ] : Träghetstensor Kontnuerlche Vertelung: Analoge Rechnung mt m d 3 u ϱ( u) L = R P + I ω mt I αβ = d 3 u ϱ( u)[ u 2 δ αβ u α u β ] : Träghetstensor L = R P + I ω Knetsche Energe Dskrete Massenvertelung: T = 1 2 m r 2 = 1 2 m ( R + ω u ) 2 R 2 + R ω m u = 1 2 m M = 1 2 M R m ( ω u ) 2 ω 2 u 2 ( ω u ) 2 m [ ω 2 u 2 ( ω u ) 2 ] = 1 2 M R m [ u 2 δ αβ u α u β ]ω α ω β αβ = 1 2 M R ω I ω mt I : Träghetstensor we oben Kontnuerlche Vertelung: Weder analoge Rechnung T = T Transl + T Rot mt T Transl = 1 2 M R 2 T Rot = 1 2 ω I ω Translaton Rotaton
67 3.3. DER TRÄGHEITSTENSOR Der Träghetstensor Defnton Gemäß 3.2 S.59: dskrete Massenvertelung: kontnuerlche Vertelung: I αβ = m (δ αβ u 2 u αu β ) I αβ = d 3 u ϱ( u)(δ αβ u 2 u α u β ) Alternatv n Vektorschrebwese: dskret: kontnuerlch: I = m (1 u 2 u u ) I = d 3 u ϱ( u)(1 u 2 u u) a 1 a 1 b 1 a 1 b 2 mt a b = a 2 (b 1 b 2 ) = a 2 b 1 a 2 b 2 : dyadsches Produkt Üblcherwese wrd Träghetstensor we oben bzgl. dem Schwerpunkt defnert. Aber: allgemene Defnton bzgl. (belebgem) Ursprung auch möglch Dskreter Fall: kontnuerlch: ˆ I = m (1 r 2 r r ) ˆ I = d 3 r ϱ( r)(1 r 2 r r) Nützlch vor allem be Drehung um festen Drehpunkt Wähle Ursprung Drehpunkt; ˆ ω: Wnkelgeschwndgket der Drehung Dann glt: Drehmpuls L = ˆ I ˆ ω ; knetsche Energe T = 1 2 ˆ ω ˆ I ˆ ω (Dskreter Fall: L = m ( r r ) = r =ˆ ω r m ( r (ˆ ω r )) = m ( r 2 ˆ ω r ( r ˆ ω)) = ˆ I ˆ ω T = 1 2 m r 2 = 1 2 m (ˆ ω r ) 2 = 1 2 m (ˆ ω 2 r 2 (ˆ ω r ) 2 ) = 1 2 ˆ ω ˆ I ˆ ω Kontnuerlcher Fall: analog ) Zusammenhang von I und ˆ I : Verallgemenerter Satz von Stener: ˆ I = I +1 M R 2 M R R (Dskreter Fall: ˆ I = m (1 r 2 r r ) = m (1( u + R) 2 ( u + R) ( u + R)) = m (1 u 2 u u ) + 21 m u R + m 1R 2 ( m u R 0 M 0 + R m u ) m R R 0 M Kontnuerlcher Fall: analog ) Zusammenhang mt Träghetsmoment Träghetsmoment aus der Vorlesung Expermentalphysk I bekannt Bezüglch ener Achse n durch den Schwerpunkt θ = d 3 u ϱ( u) d 2 = d 3 u ϱ( u)( n u) 2 = d 3 u ϱ( u)( n 2 u 2 ( n u) 2 ) θ = n I n
68 62 KAPITEL 3. STARRE KÖRPER Bezüglch ener Achse n durch den Ursprung Analog: ˆθ = n ˆ I n = n( I +1 M R 2 M R R) n = n I n + M( R 2 n1 n n 2 = n I n + M( R n) 2 ˆθ = θ + M( R n) 2 : Satz von Stener n R R n ) ( n R) Bespel: Träghetstensor des Zylnders Länge L, Radus R, Masse M Volumen V = LπR 2, Dchte ϱ = M V Wähle Koordnatensystem mt z-achse=längsachse (Bld) ϱ 2 z < L/2, x 2 + y 2 < R 2 Massenvertelung: ϱ( u) = 0 sonst u x τ cos ϕ Benutze Zylnderkoordnaten u y = τ sn ϕ u 2 = τ 2 + z 2 ; d 3 L/2 u ϱ( u) = ϱ dz 2π dϕ R dτ τ u z z L/2 0 0 I xx = d 3 u ϱ( u) { u 2 u 2 x} z 2 +τ 2 sn 2 ϕ = ϱ( L3 πr LπR4 4 I xy = d 3 u ϱ( u) { u xu y} τ 2 cos ϕ sn ϕ L/2 = ϱ dz z 2 2π R L/2 2π dϕ dτ τ + ϱ dz dϕ sn 2 R ϕ dτ τ 3 L/2 0 0 L/2 0 0 L 3 2π /12 R 2 /2 L π R 4 /4 ) = M 12 (L2 + 3R 2 ) L/2 = ϱ L/2 I xz = d 3 L/2 u ϱ( u) { u xu z} = ϱ L/2 τz cos ϕ dz 2π 0 dz 2π 0 R dϕ cos ϕ sn ϕ dτ τ 3 = 0 = I yx 0 0 R dϕ cos ϕ dτ τ = 0 = I zx 0 0 I yy = I xx und I yz = I xz aus Symmetregründen (da x- und y-rchtung äquvalent) I zz = d 3 u ϱ( u) { u 2 u 2 L/2 2π R z} = ϱ dz dϕ dτ τ 3 = ϱ LπR4 = MR2 L/2 0 0 τ 2 L 2π R 4 /4 1 Zusammenfassend: 12 M(L2 + 3R 2 ) I = 0 12 M(L2 + 3R 2 ) MR2 (NB: Her kene Nchtdagonalelemente, aber m allgemenen Fall natürlch schon!) Anwendung: Knetsche Energe enes rollenden Zylnders T = 1 2 Mv I zz ω ) MR /2( 2 = 3 4 Mv2 2 v/r
69 3.3. DER TRÄGHEITSTENSOR Enschub und Ernnerung: Physkalsche Skalare, Vektoren, und Tensoren Betrachte ene Koordnatentransformaton Σ Σ zwschen zwe orthonormalen Systemen mt demselben Ursprung Basen: Σ ( e 1, e 2, e 3 ), Σ ( e 1, e 2, e 3 ) Darstellung enes Ortsvektors r n Σ: Koordnaten (r 1, r 2, r 3 ) mt r α = ( e α r) r = α e α r α n Σ : Koordnaten (r 1, r 2, r 3 ) mt r α = ( e α r) r = α e αr α Transformaton Σ Σ : r α = ( e α r) = ( e α β e β r β ) = β mt Transformatonsmatrx: U αβ = ( e α e β ) = cos( ( e α, e β )) Wnkel NB: U st orthonormal: UU T = U T U = 1 Defntonen: U αβ r β ( [UU T ] αβ = U αγu βγ = ( e α eγ)( eγ e β ) = e α e γ( e γ e β ) = e α e β = δ αβ ) γ γ e β () Physkalscher Skalar: Enkomponentge Größe a, de sch unter der Koordnatentransformaton Σ Σ ncht verändert: a = a () Physkalscher Vektor: Drekomponentge Größe u, de sch unter Σ Σ gemäß u α = U αβ u β β bzw. u = Uu verändert. (d.h.: Transformert sch unter Drehung we en Ortsvektor) () Physkalscher Tensor: Neunkomponentge Größe A, de sch unter Σ Σ gemäß A αβ = γδ U αγ U βδ A γδ bzw. A = UAU T verändert. (Falls u Vektor, A Tensor, st A u weder Vektor, A u = UA U T U 1 u = UA u) (v) Physkalscher Tensor nter Stufe: 3 n komponentge Größe T α1 α n, de sch unter Σ Σ gemäß T α 1 α n = U α1 β 1 U αnβn T β1 β n verändert. β 1 β n Folgerungen 1 st en Skalar (klar) 1 st en Tensor (1 U1U T = 1 nvarant) Falls u und v Vektoren snd, st u v en Skalar. v 1 (u v = (u 1 u 2 u 3 ) v 2 v 3 = u T v Σ Σ u T v = (Uu) T (Uv) = u T U T U 1 v = u T v) Falls u und v Vektoren snd, st u v en Tensor. u 1 (u v = u 2 (v 1 v 2 v 3 ) = u v T u 3 Σ Σ u v T = (Uu)(Uv) T = Uu v T U T )
70 64 KAPITEL 3. STARRE KÖRPER Darstellung von Skalaren, Vektoren, Tensoren n ener Bass Σ () Skalar a: klar a () Vektor u: u α = ( u e α ) u = u α e α α (sehe oben) () Tensor A: A αβ = e α A eα A= A αβ e α e β α,β ( Glt für Bass Σ: ( e 1, e 2, e 3 ) = ( ( 1 0), ( 0 1), ( 0 0) ) check durch Ensetzen Andere Bass Σ : A αβ = U αγu βδ A γδ = ( e α eγ)( e β e δ) e γ A eδ γδ γδ = e γ( e γ e α) A e δ ( e δ e β ) = e α A e β ) γ δ e α e β Hauptachsentransformaton Transformatonsverhalten des Träghetstensors Zur Ernnerung: m (1 u 2 I = u u ) (dskreter Fall) d 3 u ϱ( u)(1 u 2 u u) (kontnuerlcher Fall) Nun glt: 1 st en Tensor, u 2 en Skalar, u u en Tensor 1 u 2 u u st en Tensor analog natürlch auch 1 u 2 u u I st en Tensor! (Daher natürlch der Name Träghetstensor ) Hauptachsentransformaton Fazt bs jetzt: I transformert sch unter Basswechsel gemäß I UIU T Weterhn: I st symmetrsch: I αβ = I βα Spektralsatz der lnearen Algebra I hat reelle Egenwerte Egenvektoren spannen den dredmensonalen Raum auf Egenvektoren zu verschedenen Egenwerten stehen senkrecht aufenander Erklärung : Egenwerte und Egenvektoren Ausgangspunkt: Egenwertglechung I p = λ p hat Lösungen für spezelle Werte von λ: Egenwerte De Lösungen p zu enem Wert λ heßen Egenvektoren zu λ
71 3.3. DER TRÄGHEITSTENSOR 65 Es glt: Falls p 1, p 2 Egenvektoren zum glechen Egenwert a p 1 + b p 2 st auch Egenvektor Falls p 1, p 2 Egenvektoren zu verschedenen Egenwerten und I symmetrsch p 1 p 2 = 0, also p 1 p 2 ( I symmetrsch p 1 I p2 = p 2 I p1 p 1 λ 2 p 2 = p 2 λ 1 p 1 (λ 2 λ 1 ) p 1 p 2 = 0 p 1 p 2 = 0 da λ 1 λ 2 ) Folgerung: Aus den Egenvektoren kann man ene Orthonormalbass ( p 1, p 2, p 3 ) konstrueren. In deser Bass st I dagonal. Nomenklatur: Bassvektoren p 1, p 2, p 3 heßen Hauptträghetsachsen (beten sch an als Achsen enes körperfesten Bezugssystems) Zugehörge Egenwerte λ α = I α heßen Hauptträghetsmomente Zusammenfassung und Folgerungen Allgemene Darstellung des Träghetstensors: I = 3 I α p α p α α=1 I α: Hauptträghetsachsen, p α: Enhetsvektoren entlang Hauptträghetsachsen Koordnaten des Träghetstensors n belebgem Bezugssystem ( e 1, e 2, e 3 ) I αβ = e α I eβ = γ I γ e α p γ p γ e β I αβ = Rotatonsantel der knetschen Energe T Rot = 1 2 ω I ω = 1 2 I γ ( ω p α ) 2 γ Rotatonsantel des Drehmpulses L Rot = I ω = α I α ( p α ω) p α 3 I γ ( e α p γ )( e β p γ ) γ=1 zegt ncht unbedngt n Rchtung von ω Berets be kräftefreer Bewegung mt L = const. komplzerte Bewegungen möglch Falls ω L: Drehachse muss sch ständg drehen
72 66 KAPITEL 3. STARRE KÖRPER 3.4 Dynamk und Bewegungsglechungen Zugang drekt über Kräfte Drehmoment Zunächst dskrete Massenvertelung Impuls: d P dt = d dt p = p = F = F : Gesamtkraft Drehmpuls: d L dt = d dt r p = ( r p + r p ) = r F = M: Drehmoment 0 da parallel Falls Ursprung m Schwerpunkt legt, glt spezell dl dt = d dt ( I ω) = u F = M (0) Allgemen (belebger Ursprung) dl dt = d dt ( R P + I ω) = R P + d dt ( I ω) d L dt = M = R F + M (0) Kontnuerlche Massenvertelung: analog Kraftdchte f( r): Auf Massenelement ϱ( r)d 3 r wrkt Kraft f( r)d 3 r Gesamtkraft: F = d 3 r f( r) P = F Drehmoment: M (0) = d 3 u( u f( u)) L = R F + M (0) Eulersche Glechungen Ausgangspunkt: M (0) = d dt ( I ω) (raumfestes Schwerpunktsystem) Transformaton n roterendes körperfestes System mttels ( d dt ) = ω +( d raumfest dt ) (sehe S.14) körperfest d Daraus folgt: dtm (0) = d dt ( I ω) = ω ( I ω) + d dt ( körperfest I ω). NB: Im Hauptachsensystem st I I = 0 I 2 0 ω ( I 1 ω 1 I ω) = ω I 2 ω I 3 I 3 ω 3 und d dt körperfest( I ω) = I ( d dt ω ω ω) = I Bewegungsglechungen m körperfesten Hauptachsensystem d dt ω. dω Eulersche Glechungen I 1 1 dt + (I 3 I 2 )ω 2 ω 3 = M (0) 1 dω I 2 2 dt + (I 1 I 3 )ω 3 ω 1 = M (0) 2 dω I 3 3 dt + (I 2 I 1 )ω 1 ω 2 = M (0) 3
73 3.4. DYNAMIK UND BEWEGUNGSGLEICHUNGEN Bespel: Kräftefreer, symmetrscher Kresel Betrachte enen unaxalen Kresel mt Symmetreachse e s = e 3 m körperfesten System, d.h. den Hauptträghetsmomenten I 1 = I 2 I 3 (a) Körperfestes Bezugssystem Drtte Euler-Glechung: I 3 dω 3 dt = 0 ω 3 = const.. Defnere Ω = I 3 I 1 I 1 ω 3 1. und 2. Euler-Glechung: dω 1 dt + Ωω 2 = 0, dω 2 dt Ωω 1 = 0. Defnere komplexe Funkton ω = ω 1 +ω 2 d ω dt Ω ω = 0 ω(t) eωt Im körperfesten System st ω 1 ω 2 ω 3 = (mt Integratonskonstangen ω und α). ω cos(ωt + α) ω sn(ωt + α) Insbesondere: Der Antel ω 3 der Wnkelgeschwndgket um de Symmetreachse st konstant. Weterhn: Betrag ω = ω 2 + ω3 2 st fest. ω rotert glechmäßg um Symmetreachse e s = e 3 mt Wnkelgeschwndgket Ω. (b) Raumfestes Bezugssystem (raumfestes Inertalsystem) Fester Drehmpuls: L = I ω = ω 3 const., Symmetreachse e s Wähle raumfestes Bezugssystem so, dass es zum Zetpunkt t 0 dentsch mt dem körperfesten Hauptachsensystem st mt e s = e 3. L = I 1 ω + I 3 ω 3 e s mt ω = ω ω 3 e s (ω e s ) Verwende Ω = I 3 I 1 I 1 ω 3 L = I 1 ( ω + (ω 3 + Ω) e s ) Vergleche damt ω = ω + ω 3 e s Daraus folgt: ω = L/I 1 Ω e s ω, L und e s (Symmetreachse) legen n ener Ebene! Falls L ncht parallel zu Kreselachse e s : e s führt Präzesson um (raumfeste) Achse L/L durch. NB: Allgemen versteht man unter Präzesson de Drehende Bewegung der Achse enes Kresels um ene außerhalb des Kresels legende feste Achse. Wr dskuteren her den Fall der drehmoment-freen Präzesson. Präzesson kann auch durch en äußeres Drehmoment nduzert werden, z.b. durch en Schwerefeld. Unter Enfluss enes Drehmoments macht auch der Drehmpuls L ene kresende Bewegung (sehe ). Wnkelgeschwndgket der Präzesson ω Präzesson = L/I 1 (da d es L dt = ω e s = I 1 e s ) Wnkelgeschwndgket der Drehung um Symmetreachse m raumfesten System: ω Symmetre = Ω.
74 68 KAPITEL 3. STARRE KÖRPER Zugang über Lagrange-Funkton Allgemen: L = T U = 1 2 M R ω I ω U( R, Wnkelvarablen) U und ω müssen als Funkton der Wnkelvarablen und hrer zetlchen Abletungen ausgedrückt werden Lagrange-Funkton starrer Körper n Eulerschen Wnkeln Konkrete Form der Lagrange-Funkton, falls als Wnkelvarablen de Eulerschen Wnkel gewählt werden (vgl S.58) und als körperfestes Koordnatensystem das Hauptachsensystem. Ernnerung: Euler-Wnkel φ, θ, ψ beschreben sukzessve Drehung des Koordnatensystems vom raumfesten System Σ zum körperfesten System Σ mttels cos ϕ sn ϕ 0 Drehung um z-achse, Wnkel ϕ: Dϕ T = sn ϕ cos ϕ Drehung um x-achse, Wnkel ϑ: Dϑ T = 0 cos ϑ sn ϑ 0 sn ϑ cos ϑ cos ψ sn ψ 0 Drehung um z-achse, Wnkel ψ: Dψ T = sn ψ cos ψ Zusammenhang zwschen raumfesten Koordnaten u und körperfesten Koordnaten u : u = D T u mt D T = D T ψ DT ϑ DT ϕ Dre zetlch veränderlche Wnkelvarablen dre Beträge zur Wnkelgeschwndgket: ω = ω ψ + ω θ + ω φ. Betrachte nun Koordnaten von ω m körperfesten System. Betrag von φ: Im raumfesten System st ω φ = (0, 0, φ) = Dφ T ω φ Körperfestes System: ω φ = DT = Dψ T DT θ = φ sn θ sn ψ sn θ cos ψ. cos θ 0 0 φ 0 0 φ Betrag von θ: ω θ = ( θ, 0, 0) = Dθ T ω θ n enem Koordnatensystem Σ, n dem Drehung bzgl. φ schon stattgefunden hat. Körperfestes System: ω θ = DT ψ θ 0 0 = θ cos ψ sn ψ 0. Betrag von ψ: ω ψ = (0, 0, ψ) = D T ψ ω ψ m körperfesten System.
75 3.4. DYNAMIK UND BEWEGUNGSGLEICHUNGEN 69 Knetscher Betrag der Rotaton: T Rot = 1 2 ω I ω = 1 2 (I 1ω I 2 ω I 3 ω 2 3) mt ω = ω ψ + ω θ + ω φ = φ sn θ sn ψ + θ cos ψ φ sn θ cos ψ θ sn ψ φ cos θ + ψ Lagrange-Funkton: L = 1 2 M R α=1 I α ω 2 α U Bespel: Symmetrscher Kresel m Schwerefeld Symmetrscher Kresel (I 1 = I 2 I 3 ), wrd an enem Unterstützungspunkt festgehalten, der den Abstand l zum Schwerpunkt hat. Wähle als Nullpunkt aller Koordnatensysteme (körperfest und raumfest) den Unterstützungspunkt (ncht den Schwerpunkt). Überlegungen aus S.68 können trotzdem übernommen werden. I 1, I 2, I 3 snd nun Hauptträghetsmomente für Drehungen um den Unterstützungspunkt. Rotatonsenerge: T Rot = I 1 2 ( φ 2 sn 2 θ + θ 2 ) + I 3 2 ( φ cos θ + ψ) 2 Potentelle Energe: U = Mgl cos θ L = I 1 2 ( φ 2 sn 2 θ + θ 2 ) + I 3 2 ( φ cos θ + ψ) 2 Mgl cos θ Bewegungsglechungen können nur numersch gelöst werden. Her: Analyse anhand der Erhaltungssätze. Erhaltungsgrößen: Zyklsche Varablen: φ, ψ p ψ = L ψ = I 3( φ cos θ + ψ) = I 3 ω 3 = const. (Rotaton um Symmetreachse) p φ = L φ = I 1 φ sn 2 θ + p ψ cos θ = const. (Präzesson von φ be gegebenem θ) Energe: E = I 1 2 ( φ 2 sn 2 θ + θ 2 ) + I 3 2 ( φ cos θ + ψ) 2 + Mgl cos θ = (p φ p ψ cos θ) 2 2I 1 sn 2 θ + I 1 2 θ2 + p2 ψ 2I 3 + Mgl cos θ Analyse: Substtuere u = cos θ θ 2 = u 2 /(1 u 2 ) E = (p φ p ψ u) 2 2I 1 (1 u 2 ) + I 1 u p2 ψ 1 u 2 2I 3 + Mgl u 1 2 u2 + V eff (u) = 0 mt V eff (u) = 1 I 1 [( p2 ψ 2I 3 E + Mglu)(1 u 2 ) + (p φ p ψ u) 2 2I 1 ] entsprcht Bewegung enes Telchens der Gesamtenerge 0 m effektven Potental V eff (u), u [ 1, 1]. NB: V eff (u) st en Polynom 3. Grades, V eff (± ), V eff (±1) = (p φ p ψ ) 2 2I 2 1 > 0 maxmal zwe Nullstellen m Berech u [ 1, 1]
76 70 KAPITEL 3. STARRE KÖRPER Dskusson: Nullstellen von V eff (±1) entsprechen den Umkehrpunkten ener oszllatorschen Bewegung n θ: Nutaton zusätzlch zur Präzesson. Nutatonsfree Bewegung möglch, wenn de Nullstellen von V eff (u) aufenanderfallen. Weterhn glt wegen p φ p ψ u = φi 1 (1 u 2 ): φ wechselt perodsch das Vorzechen, falls p φ p ψ u das Vorzechen wechselt. Verschedene Kategoren von Kurven. Vorzechen von φ blebt glech: Wellenförmge Bewegung. Vorzechen von φ wechselt: Schraubenförmge Bewegung. Unter sehr spezellen Bedngungen auch möglch: Umkehrpunkte von u fallen aufenander, nutatonsfree Präzesson. Drehmpuls L = I ω st ncht erhalten! (es lohnt sch ncht enmal, L her auszurechnen!) 3.5 Wssensfragen 57. Was versteht man unter enem starren Körper? 58. Was snd de Eulerschen Wnkel? 59. Was zechnet enen physkalschen Tensor aus? 60. We st der Träghetstensor enes starren Körpers mt der Massenvertelung ρ( r) defnert? 61. We hängt der Träghetstensor mt dem Träghetsmoment zusammen? 62. Geben Se den allgemenen Ausdruck für den Drehmpuls und de knetsche Energe enes starren Körpers an. Welches st der Translatonsantel? Welches st der Rotatonsantel? 63. Was st ene Hauptachsentransformaton? 64. Was snd Hauptträghetsmomente? Was snd Hauptträghetsachsen? 65. We lautet der Satz von Stener und der verallgemenerte Satz von Stener? 66. We st das Drehmoment defnert? 67. We stellt man allgemen de Lagrangeglechung für starre Körper auf? 68. We lauten de Eulerschen Glechungen? Was beschreben se?
77 Kaptel 4 Hamltonsche Mechank Copyrght 2014 Frederke Schmd 1 Annahme n desem Kaptel: Es exstert ene Lagrange-Funkton L(q 1 q m, q 1 q m, t), de de Zetentwcklung des Systems vollständg beschrebt. (Also nsbesondere: alle Zwangsbedngungen snd holonom) Lagrange-Mechank recht völlg aus, um Dynamk zu beschreben und Bewegungsglechungen aufzustellen ( L q j = d L dt q j j ) Aber: Lagrange-Formalsmus hat enge Nachtele : - Grundlegende Erhaltungsgrößen (Energe, Impuls) tef vergraben - L hat kene physkalsche Interpretaton - q und q gehen ncht glech en, asymmetrsch unästhetsch Her: Enführung enes alternatven Formalsmus ohne dese Nachtele. Varablenwechsel ( q j, q j ) ( q j, p j ) generalserte Orte und generalserte Impulse. Wrd nchts brngen für de Bewegungsglechungen, aber: - Erhaltungsgrößen schtbarer - Neue charakterstsche Funkton H(q 1 q m, p 1 p m ), de oft ene physkalsche Interpretaton bestzt: Energe - Verdeutlchung der mathematschen Struktur der klassschen Mechank Besserer Ausgangspunkt für manche mechanschen Probleme. Natürlcher Ausgangspunkt für statstsche Mechank und Quantenmechank (wrd n entsprechenden Vorlesungen klar werden) 1 Prof. Dr. Frederke Schmd, Vorlesung Theoretsche Mechank, Unverstät Manz, WS 2014/2015. Letzte Änderung am
78 72 KAPITEL 4. HAMILTONSCHE MECHANIK 4.1 Generalserter Impuls Defnton: Bespele: Gegeben Lagrange-Funkton L(q 1 q m, q 1 q m, t) Bewegungsglechungen d dt L q j = L q j d Formaler Verglech mt Newtonschen Glechungen: dt p = F mt p = gewöhnlcher Impuls motvert Verallgemenerung: Generalserter Impuls: p j = L q j NB: Falls L q j = 0, st p j ene Erhaltungsgröße: p j = const. () N Massenpunkte m Potental U( r 1 r N ), kartessche Koordnaten L = 1 2,α m ṙ 2,α U( r 1 r N ) p,α = dl dṙ,α = m ṙ,α gewöhnlche Impulse p = m r () Geladener Massenpunkt m elektromagnetschen Feld (2.6.1 S.52) L = m 2 r 2 qφ( r, t) + q c r A( r, t) p α = L ṙ α = mṙ α + q c A α bzw. p = m r + q c A generalserter Impuls gewöhnlcher Impuls! ( p gewöhnlch = m r) () Perle auf roterendem Stab (Bespel n S.47) L(r, ṙ) = m 2 (ṙ2 + r 2 ω 2 ) p = L ṙ = mṙ = Radalmpuls p r weder verscheden vom gewöhnlchen Impuls p = m v = mṙ e r + mωr e ϕ Generalserter Impuls p j st oft unglech dem gewöhnlchen Impuls. Aber: hat Ausschten, Erhaltungsgröße zu sen (falls q j zyklsch st, sehe S.48) Wunsch: Formalsmus, n dem q j durch p j ersetzt st. 4.2 Legendre-Transformaton und Hamlton-Funkton Ausgangspunkt: Lagrange-Funkton L(q 1 q m, q 1 q m, t), de en bestmmtes dynamsches System vollständg beschrebt. Gesucht: Funkton H(q 1 q m, p 1 p m, t) mt p = L q, de dasselbe lestet Weg: Legendre-Transformaton
79 4.2. HAMILTON-FUNKTION Vorbemerkung: Legendre-Transformaton Zunächst n nur ener Varablen Gegeben stetg dfferenzerbare Funkton f(x), streng konvex oder konkav (f (x) 0 x) f (x) streng monoton stegend oder fallend ξ = f (x) endeutg umkehrbar: x = x(ξ) Wunsch: Ene Funkton F (ξ) fnden, de deselbe Informaton we f(x) enthält aus F (ξ) muss f(x) sch endeutg rekonstrueren lassen 1. Versuch: Ordne jeder Stegung ξ den Wert f(x(ξ)) zu: F (ξ) = f(x(ξ)) Problem: f(x) kann aus F (ξ) ncht endeutg rekonstruert werden: Falls f(x) Lösung von F (ξ) = f, st f(x a) auch Lösung für alle a! Informatonsverlust: ncht akzeptabel Ausweg: Ordne jeder Stegung ξ den zugehörgen Achsenabschntt zu Angabe des Achsenabschntts defnert f(x) vollständg: Konvexe/Konkave Enhüllende der Tangentenschar mt Stegung ξ und Achsenabschntt F (ξ) F (ξ) = f ξ x mt ξ = f (x) : Legendre-Transformaton Verallgemenerung auf mehrere Varablen Se f(x 1 x k ) konvex: det 2 f x x k 0 überall f(x 1 x k ) F ( f f ) = f x 1 x 1 k =1 f x x Anwendung auf Lagrange-Funkton Zurück zur Lagrange-Funkton L(q 1 q m, q 1 q m, t) Nmm an: L konvex n q j det ( 2 L q j q k ) 0 überall (für knetsche Energe 1 2 m ẋ 2 Dann lässt sch p j = L q j angewendet werden bzgl. p j = L q j : typscherwese erfüllt) endeutg nach q j auflösen und Legendre-T. kann L L j L q j q j = L p j q j Führt zur Hamltonfunkton H(q 1 q m, p 1 p m, t) = p j q j L enthält de gesamte Informaton über das dynamsche System
80 74 KAPITEL 4. HAMILTONSCHE MECHANIK Bemerkung: H = L q j q j L st gerade de Erhaltungsgröße, de nach S.48 aus Zetunabhänggket von L folgt. (H = const., falls L t = 0). Be skleronomen (zetunabhänggen) Zwangsbedngungen kann der Wert von H mt der Energe E dentfzert werden. Bespele: () N Massenpunkte m Potental U( r 1 r N ) L = 1 2 m r 2 U; p = m r 2 H = p r L = 1 2 p2 m + U: Energe () Geladener Massenpunkt m elektromagnetschen Feld L = m r 2 2 qφ + q r c A; p = m r + q c A bzw. r = 1 m ( p q c A) H = p r L = 1 2m ( p q A) c 2 + qφ ( = m r qφ Energe ) () Perle auf roterendem Stab L(r, ṙ) = m 2 (ṙ2 + r 2 ω 2 ); p = mṙ H = pṙ L = p2 2m m 2 r2 ω 2 H st Erhaltungsgröße, aber ncht de Energe (E = m r 2 2 = L const.) Hamltonsche Bewegungsglechungen Im Lagrange-Formalsmus glt: Lagrange-Funkton: L(q 1 q m, q 1 q m, t) d L Lagrange-Glechungen: dt q j = L q j Daraus folgt m Hamlton-Formalsmus: Hamlton-Funkton: H(q 1 q m, p 1 p m, t) Hamlton-Glechungen: H q j = ṗ j ; H p j = q j ( Rechnung: Schrebe L(q 1 q m, p 1 p m) = L(q 1 q m, q 1 q m) mt q j = q j (q 1 q m, p 1 p m) (L, L: glecher Zahlenwert, andere funktonale Form) H = p j q j (q 1 q m, p 1 p m) L(q 1 q m, p 1 p m) H q k = ( p j q q q j + p j j ) L j k q k q k = j = L = d L = ṗ q k dt q k k H Analog: = p ( p j q q k p j + p j j ) j k p k j δjk ( p j q k 0 ( L q j q q j + p j j ) q ( L k q j j q j + L p k q j 0 pj q j + L q k q j δjk pj q j p k ) = q k ) q j q k ) Folgerung: Zetentwcklung des Werts von H d dt H(q 1(t) q m (t), p 1 (t) p m (t), t) = j ( H q j ṗj q j + H p j qj ṗ j ) + H t = H t dh dt = H t H = const., falls H ncht explzt zetabhängg ( H t = 0)
81 4.2. HAMILTON-FUNKTION 75 Bespele () N Massenpunkte m Potental U( r 1 r N ) H = 1 2 p2 m + U( r 1 r N ) H p α = p α m ṙ α & H r α = U r α ṗ α () Geladener Massenpunkt m elektromagnetschen Feld H = 1 2m ( p q c A) 2 + qφ H p α = 1 m (p α q c A α) ṙ α & H r α = q mc ( p q c A) A r α + q φ r α ṗ α () Perle auf roterendem Stab H = p2 2m m 2 r2 ω 2 H p = p m ṙ & H r = mrω2 ṗ Modfzertes Hamltonsches Prnzp Dynamk m Lagrange-Formalsmus L(q 1 q m, q 1 q m, t) Zwe äquvalente Formulerungen: (2.5 S.50) - Lagrange-Glechungen: L q j = d L dt q j - Hamlton-Prnzp: I{q 1 (t) q m (t)} = t 1 t 0 dt L extremal, d.h. δi = I{q + δq} I{q} = 0 für alle Varatonen δq j, de be t 0, t 1 verschwnden (δq j (t 0 ) = δq j (t 1 ) = 0) (Notaton her: q = q 1 q m ) Im Hamlton-Formalsmus H(q 1 q m, p 1 p m, t) Weder Äquvalenz zw. Bewegungsglechungen und Varatonsprnzp: - Hamlton-Glechungen: H q j = ṗ j ; - Modfzertes Hamlton-Prnzp: H p j = q j I {q 1 (t) q m (t), p 1 (t) p m (t)} = t 1 dt( p j q j H) extremal, t 0 j d.h. δi = I {q + δq, p + δp} I {q, p} = 0 für alle Varatonen δq j, δp k mt δq j (t 0 ) = δq j (t 1 ) = 0 (kene Bedngungen an δp k (t)!) (Notaton weder: q = q 1 q m, p = p 1 p m ) (Nachwes der Äquvalenz: δi = I {q + δq, p + δp} I {q, p} t 1 = dt[ (δp j q j + p j δ q j ) ( H δp p j + H δq t 0 j j j q j )] j partelle Integraton bzgl. δ q j. Benutze δq j (t 0 ) = δq j (t 1 ) = 0 t 1 = dt[ δp j ( q j H ) + p t 0 j j δq j ( ṗ j H )] q j j verschwndet genau dann für alle δq j, δp j (mt δq j (t 0 ) = δq j (t 1 ) = 0), wenn q j H 0 und ṗ p j + H 0 ) j q j
82 76 KAPITEL 4. HAMILTONSCHE MECHANIK 4.3 Posson-Klammern Defneren mathematsche Struktur der klassschen Mechank Ab jetzt häufg Kurznotaton: q = q 1 q m, p = p q p m, q = q 1 q m, p = p 1 p m, Defnton Motvaton: Zetlche Entwcklung von dynamschen Größen. Dynamsche Größe oder Observable : Funkton f(q 1 q m, p 1 p m, t) = f(q, p, t) (z.b. knetsche Energe, Schwerpunkt, Drehmpuls,...) Es glt: df dt = j ( f q j q j + f p j ṗ j ) + f t = j ( f H q j p j f H p j q j ) + f t Allgemener Ausdruck für zetlche Entwcklung ener Observablen: df dt = {f, H} + f t mt {, }: Possonklammer {f, g} = ( f g f g ) = f j q j p j p j q j q f p f p f q für belebge dfferenzerbare Funktonen f und g Spezell: Falls f ncht explzt zetabhängg (f(q, p)), glt df dt f st genau dann ene Erhaltungsgröße, wenn {f, H} = 0 = {f, H} Allgemenes Krterum, mt dem man schnell feststellen kann, ob ene gegebene Observable erhalten st Bedeutung und Egenschaften der Possonklammer Grundlegender Raum: Menge der unendlch oft dfferenzerbaren dynamschen Größen f(q 1 q m, p 1 p m, t), d.h. de Menge C (D) mt D = Ω R, wobe Ω = {(q 1 q m, p 1 p m )} der 2m-dmensonale Phasenraum der zugänglchen Orts/Impulskoordnaten (mehr zu desem Begrff sehe 4.5 S.82). blden Vektorraum V über R (oder C) Possonklammern: Defneren Produkt : V V V (f, g) {f, g} mt den folgenden Egenschaften: (Bewes: (),() klar, (): Ensetzen) () Blnear: {αf 1 + βf 2, g} = α{f 1, g} + β{f 2, g} {f, αg 1 + βg 2 } = α{f, g 1 } + β{f, g 2 } für alle α, β R (bzw. C); f, f 1, f 2, g, g 1, g 2 V () Antsymmetrsch: {f, g} = {g, f} () Jacob-Identtät: {f, {g, h}} + {g, {h, f}} + {h, {f, g}} = 0 für alle f, g, h V
83 4.4. KANONISCHE TRANSFORMATIONEN 77 Enen Vektorraum mt enem Produkt (ener nneren Verknüpfung), das de Egenschaften ()-() erfüllt, nennt man ene Le-Algebra. (Weteres Bespel ener Le-Algebra: R 3 mt Vektorprodukt a b) Mathematsche Struktur der klassschen Mechank: - Vektorraum über R oder C: Menge C der unendlch oft dfferenzerbaren Funktonen f(q, p) - Le-Algebra darn, Possonklammer Bespele für Possonklammern Fundamentale Possonklammern {q j, q k } = {p j, p k } = 0 {q j, p k } = δ jk ; {p j, q k } = δ jk Drehmpulskomponenten {L x, L y } = L z ; {L y, L z } = L x ; {L z, L x } = L y (Bewes: Ensetzen) Partelle Abletungen dynamscher Größen f q j = {p j, f} f p j = {q j, f}; (Bewes: Ensetzen) 4.4 Kanonsche Transformatonen Defnton und enfache Bespele Ausgangspunkt: Phasenraum {(q 1 q m, p 1 p m )} = {(q, p)} Defnton : Ene kanonsche Transformaton st ene Koordnatentransformaton (q 1 q m, p 1 p m ) (Q 1 Q m, P 1 P m ) bzw. (q, p) (Q, P ) de Hamltonsche Strukturen erhält. Das hesst, dass es für jedes dynamsche System, dessen Bewegung durch ene Hamltonfunkton H(q, p, t) bestmmt wrd, ene Hamltonfunkton H (Q, P, t) gbt, so dass de Bewegungsglechungen des Systems bzgl. Q und P weder Hamlton-Glechungen snd ( H Q j = P j ; H P j = Q j ). Falls sogar H = H (dem Wert nach), sprcht man von ener kanonschen Transformaton m engeren Snne. Bespele für kanonsche Transformatonen - Vertauschung von Ort und Impuls (q 1 q m, p 1 p m ) (p 1 p m, q 1 q m ) bzw. (q, p) (p, q) Bewegungsglechungen: Hamltonglechungen mt H = H Dagegen: Vertauschung (q, p) (p, q) st ncht kanonsch: Man kann kene Hamltonfunkton H fnden, so dass Bewegungsglechungen de kanonsche Hamltonsche Form haben.
84 78 KAPITEL 4. HAMILTONSCHE MECHANIK - Punkttransformatonen m Lagrange-Formalsmus können de generalserten Koordnaten belebg gewählt werden. alle Transformatonen (q 1 q m ) (Q 1 Q m ) erlaubt! m Hamlton-Formalsmus entsprcht das (q, p) (Q, P ) mt P = L Q = Q ( p q H) = Q H ( p p H) (partelle Abletung Q ausgeführt be festgehaltenem Q ). Neue Hamltonfunkton: H = P Q L = P Q p q + H Elementare Egenschaften Es glt: Possonklammern snd unter kanonschen Transformatonen nvarant. {f, g} p,q = {f, g} P,Q bzw. ( f q j j g p j f p j g q j ) = j (Bewes her nur für kanonsche Transformatonen m engeren Snne zunächst se f ncht explzt zetabhängg g defnert fktves dynamsches System mt Ĥ = g In desem System st df = {f, Ĥ} = {f, g} dt darf von der Wahl der Koordnaten ncht abhängen {f, g} koordnatenunabhängg ( f Q j g P j f P j g Q j ) falls f doch explzt zetabhängg: Fasse explzten Parameter t enfach als zusätzlchen (unabhänggen) Parameter auf, darf nchts ändern an Invaranz von {f, g}. ) Umgekehrt glt: Ene Transformaton st genau dann kanonsch, wenn für de neuen Koordnaten glt: {Q j, P k } = δ jk, {Q j, Q k } = 0, {P j, P k } = 0 (Possonklammern n alten Koordnaten ausgewertet.) Allgemenes Krterum dafür, ob ene Transformaton kanonsch st. Falls de Transformaton darüber hnaus noch zetunabhängg st, st se sogar kanonsch m engeren Snn. (Bewes: Notwendg - klar, da Possonklammer nvarant Hnrechend - soll her nur für zetunabhängge Transformatonen gezegt werden also Q j = Q j (q, p); P j = P j (q, p) bzw. Q j = P j = 0 t t (und Umkehrung q j = q j (Q, P ); p j = p j (Q, P )) Dann glt: Q j = {Q j, H} und P j = {P j, H} nach S.76 Weterhn glt für H (Q, P ) = H(q, p): H p l = ( H Q k + H P k ), Q k k p l P k p l H q l = ( H Q k + H P k ) Q k k q l P k q l Ensetzen: Q j = [ Q j ( H Q k + H P k ) Q j ( H Q k + H P k q kl l Q k p l P k p l p l Q k q l P k [ H {Q Q j, Q k } k = k 0 + H H {Q P j, P k }] = k P j δ jk Analog: P j = H Q j Hamltonglechungen mt transformerter Hamltonfunkton H = H Transformaton kanonsch m engeren Snne! (für zetunabhängge Transformatonen) ) q l )]
85 4.4. KANONISCHE TRANSFORMATIONEN Konstrukton kanonscher Transformatonen Ausgangspunkt: Modfzertes Hamlton-Prnzp (4.2.4 S.75): Für kanonsche Transformatonen (q, p) (Q, P ) muss mt I alt = t 1 t 0 dt( j p j q j H) auch I neu = t 1 t 0 dt ( j P j Q j H ) extremal sen. Also dürfen sch ( j p j q j H) und ( j P j Q j H ) maxmal um ene totale Zetabletung unterscheden. df dt = ( j p j q j H) ( P j Q j H ) j Motvert folgendes Konstruktonsprnzp: In ( ) st F ene Funkton von 2m unabhänggen Phasenraumkoordnaten (und evtl. der Zet). Wähle als Argumente m alte Varablen und m neue Varablen (Kombnaton belebg). Dann st F ene Erzeugende, de über ( ) ene kanonsche Transformaton vermttelt (Bewes dazu sehe Ende des Abschntts (4.4.3)) NB: De Exstenz ener Erzeugenden F st ene notwendge und hnrechende Bedngung dafür, dass ene Transformaton kanonsch st. Anwendung usw. () Erzeugende F n Gl. ( ) hängt von den q j und Q j ab: F (q, Q, t) df = j p j dq j P j dq j + (H H)dt j F F = p j = P j q j Q j defneren Zusammenhang Q j (q,p,t), P j (q,p,t) F t = H H legt H fest () Erzeugende F n Gl. ( ) hängt von den q j und P j ab: F (q, P, t) Konstruere neue Erzeugende Φ(q, P, t) = F + P j Q j j dφ = df + (P j dq j + Q j dp j ) j = j Φ q j = p j p j dq j j P j dq j + (H H)dt + (P j dq j + Q j dp j ) j Φ P j = Q j Φ t = H H () Erzeugende F hängt von den Q j und p j ab: F (Q, p, t) Konstruere neue Erzeugende Ψ(Q, p, t) = F p j q j j dψ = df (p j dq j + q j dp j ) j = j Ψ p j = q j p j dq j j P j dq j + (H H)dt (p j dq j + q j dp j ) j Ψ Q j = P j Ψ t = H H Beachte: Falls F ncht explzt zetabhängg ( F t = 0), st H = H Transformaton st kanonsch m engeren Snne ( )
86 80 KAPITEL 4. HAMILTONSCHE MECHANIK Zum Schluss wrd nun noch der Bewes nachgelefert, dass de Glechung ( ) ene gültge Konstrukton vermttelt. Startpunkt: Modfzertes Hamltonprnzp (4.2.4 S.75) Es glt: I alt = t 1 t 0 dt( j p j q j H) extremal bzgl. Varatonen δq, δp mt δq(t 0 ) = δq(t 1 ) = 0. Zu zegen: I neu extremal bzgl. Varatonen δq, δp mt δq(t 0 ) = δq(t 1 ) = 0, wobe I neu = t 1 t 0 dt( j P j Q j H ) = I alt t 1 t 0 dt df dt = I alt F t 1 laut ( ) t 0 NB: δq(t 0 ) = δq(t 1 ) = 0 mplzert ncht automatsch δq(t 0 ) = δq(t 1 ) = 0! Zege vorab: δf = j (p j δq j P j δq j ) unabhängg von der Wahl der Argumente von F bzgl. allgemener Varatonen δq, δp. (δq, δp snd dann von δq, δp abhängg, z.b. δq = q(q + δq, P + δp ) q(q, P )) Dazu: Fallunterschedung nach Argumenten we oben () F (q, Q, t) δf = j ( F q j pj δq j + F Q j Pj δq j ) = j (p j δq j P j δq j ) () F (q, P, t) = Φ(q, P, t) j P j Q j δf = j ( Φ q j δq j + Φ δp P j ) j j (P j δq j + Q j δp j ) = j (p j δq j P j δq j ) pj Qj () F (Q, p, t) = Ψ(Q, p, t) + j p j q j δf = j ( Ψ δq Q j + Ψ δp j p j ) + j j (p j δq j + q j δp j ) = j (p j δq j P j δq j ) Pj qj (v) übrge Fälle analog! Dann: Berechne Varaton von I neu = I alt F t 1 t0 bzgl. δq, δp mt δq(t 0 ) = δq(t 1 ) = 0. Es glt: δi alt = t 1 t 0 dt j (p j δ q j + q j δp j H q j δq j H δp p j ) j ṗj qj Partelle Integraton: t 1 t 0 dt p j δ q j = t 1 t 0 dt ṗ j δq j + p j δq j t 1 t0 = j p j δq j t 1 t0 (NB: δi alt 0, da wr δq(t 0,1) = 0 fordern und ncht δq(t 0,1 ) = 0!) δi neu = δi alt δf t 1 t0 = j p j δq j j (p j δq j P j δq j ) = j P j δq j = 0 für δq(t 0 ) = δq(t 1 ) = Der Hamlton-Jacob Formalsmus Idee der Hamlton-Jacob Theore: Suche spezelle kanonsche Transformatonen (q, p) (Q, P ) mt H (Q, P, t) 0. Voraussetzung: Es gbt m unabhängge Erhaltungsgrößen P j de Possonkommuteren, d.h. {P j, P k } = 0. (notwendg, da mt H 0 folgt: H Q j = P j = 0 P j = const.) Systeme, de das erfüllen, nennt man Louvlle-ntegrabel. sehr starke Enschränkung, für m > 1 n der Regel ncht der Fall! Motvaton: (Warum soll man sch trotzdem damt beschäftgen?) Guter Ausgangspunkt für Theore des Hamltonschen Chaos Formale Ähnlchket zu Glechungen der Quantenmechank NB: Wenn enmal en Satz Koordnaten Q, P mt H (Q, P ) 0 gefunden st, st de Lösung der Hamltonglechungen trval. ( Q = 0, Ṗ = 0 Q j = const., P j = const.) Problem wrd verlagert auf Ermttlung der Erzeugendenfunkton
87 4.4. KANONISCHE TRANSFORMATIONEN 81 Konkret: Hamlton-Jacob-Glechungen Allgemen: Suche Erzeugendenfunkton Φ(q, P, t) W P (q, t) (Index P steht für festen Satz von Erhaltungsgrößen P j ). Mt W t = H H, H 0, p j = W q j und Notaton q = q 1 q m folgt W W + H(q, t q, t) = 0 zetabhängge Hamlton-Jacob Glechung Physkalsche Bedeutung von W : dw dt = ( j p j q j H) ( j P j Q j H ) = j p j q j H = L W = t t 0 dt L: Wert entsprcht der Lagrangesche Wrkung! Spezell konservatves System: Kene explzte Zetabhänggket Bespele: H = E = const. W t E = H(q, S q ) = E W (q, t) = Et+S(q) mt W q = S q zetunabhängge Hamlton-Jacob-Glechung Nun kann S(q) selbst als Erzeugende genutzt werden. De Erzeugendenfunkton Φ(q, P ) = S P (q) vermttelt ene kanonsche Transformaton m engeren Snne (q, p) (Q, P ) mt H(q, p) = H(Q, P ) = E. Wegen H Q j = P j = 0 folgt: H = H(P ): alle Varablen Qj snd zyklsch! 1) Frees Telchen n ener Dmenson: H(x, p) = p 2 /2m Hamlton-Jacob-Glechung: E = H(x, S x ) = 1 2m ( ds dx )2. Lösung: ds dx = 2mE S(x) = 2mE x = S E (x) Setze P = E und defnere Erzeugende Φ(x, E) = S E (x) Φ generert Transformaton (x, p) (Q, E) mt Q = Φ E = m Es glt H(Q, E) = E Q = H P = 1 Q = t t 0 Rekonstruere Bahnkurve: Kombnere Ausdrücke für Q x = m 2E (t t 0) Nutze noch E = m 2 v2 x = v(t t 0 ) = x 0 + vt 2) Harmonscher Oszllator: H(x, p) = p 2 /2m mω2 x 2 2E x Hamlton-Jacob-Glechung: E = H(x, S x ) = 1 2m ( ds dx ) mω2 x 2. Lösung: S E (x) = x 2 2mE m 2 ω 2 x 2 + E ω arctan( mωx ) 2mE m 2 ω 2 x 2 Setze P = E/ω = I (Konventon), defnere Erzeugende Φ(x, I) = S E (x) Φ(x, I) generert (x, p) (Q, I) mt Q = Φ I = arctan( x ) 2I/mω x 2 Es glt H(Q, I) = E = Iω Rekonstruere Bahnkurve: Kombnere Ausdrücke für Q x = Q = H I = ω Q = ωt θ 0 2I mω sn(ωt θ 0) Nutze I = E/ω = 1 2 mω2 x 2 max x = x max sn(ωt θ 0 ) Bemerkung: Varable Q = ωt θ 0 st de facto en Wnkel! I = E/ω hat de Dmenson ener Wrkung! Bespel von sogenannten Wnkel/Wrkungs-Varablen (mehr dazu n Kaptel S.91!)
88 82 KAPITEL 4. HAMILTONSCHE MECHANIK 4.5 Der Phasenraum Wchtge Begrffe - Phasenraum: 2m-dmensonaler Raum der {(q 1 q m, p 1 p m )} = {q, p} (z.b. N free Telchen n 3 Dmensonen Phasenraum hat 6N Dmensonen) - Phasenraumpunkt: Γ = (q 1 q m, p 1 p m ) = (q, p) charaktersert Zustand enes Systems und gesamte zukünftge und vergangene Entwcklung (determnstsche Dynamk, Anfangsbedngungen bekannt) - Phasenraumtrajektore: Γ(t), beschrebt Zetentwcklung enes Systems, z.b. harmonscher Oszllator, H = p2 2m + U(x) mt U(x) = 1 2 mω2 x 2 perodsche Schwngung = geschlossene Trajektore - Phasenraumdchte: ϱ(γ, t) = ϱ(q 1 q m, p 1 p m, t) Gleches Bespel, aber nun Schar unabhängger glecher Oszllatoren mt lecht verschedenen Anfangsbedngungen. Dchtevertelung m Phasenraum charaktersert durch ϱ(x, p, t) NB: Solche Überlegungen macht man ncht nur, wenn man es mt! ener Schar unabhängger Systeme zum tun hat, sondern auch be enem enzelnen System, wenn Anfangsbedngung ncht genau bekannt Wahrschenlchketsvertelung ϱ(γ, t) Der Louvlle-Satz Ener der wchtgsten Sätze der Mechank. Beschrebt charakterstschste Egenschaft enes Hamltonschen Systems, also enes dynamschen Systems mt ener Zetentwcklung, de durch enen Hamltonoperator defnert wrd. Zentrale Frage: We entwckelt sch de Phasenraumdchte mt der Zet bzw. we verformt sch en Volumen m Phasenraum, dessen Punkte sch gemäß ener Hamltonschen Dynamk fortentwckeln? Zunächst m 2-dmensonalen Phasenraum {(x, p)} (Bespel der harmonschen Oszllatoren) Zetentwcklung von ϱ(x, p, t) an festem Phasenraumpunkt (x,p) n gegebenem Zetraum [t, t + dt] laufen Trajektoren n Volumenelement dx dp hnen, und andere heraus Bewrkt Änderung ϱ t Quantfzerung: Defnere Geschwndgket ener Trajektore, Γ = ẋ ṗ
89 4.5. DER PHASENRAUM 83 Strom m Phasenraum: J = ϱ Γ = ϱ(x, p, t) ẋ ṗ Dchteänderung ϱ ϱ t t : = {Herenfleßender Strom - Herausfleßender Strom} = J = x (ϱẋ) p (ϱṗ) Kontnutätsglechung: Sorgt dafür, dass kene Trajektoren verloren gehen. Glt allgemen (auch n ncht-hamltonschen Systemen)! Zetentwcklung von ϱ(x(t), p(t), t) entlang ener Trajektore Γ(t) Rechnung: d dt ϱ (ϱ(x(t), p(t), t)) = xẋ + ϱ pṗ + ϱ t Kontnutätsglechung = xẋ ϱ + ϱ pṗ (ϱẋ) x ẋ (ϱṗ) p ϱ(x(t), p(t), t) = const. ṗ = ϱ( ẋ Hamltonglechungen: ẋ = H p, ṗ = H x = ϱ( 2 H x p 2 H p x ) = 0 Louvlle-Satz Allgemen: 2m-dmensonaler Phasenraum Selbes Resultat! Geschwndgket m Phasenraum: Γ = dγ dt Strom m Phasenraum: J = ϱ Γ Kontnutätsglechung: bzw. ϱ t = m ϱ t + J = 0 ( (ϱ q j) q j=1 j + (ϱṗ j) p j ) Phasenraumdchte entlang ener Trajektore d ϱ dtϱ(γ(t), t) = t + ( ϱ q j j q j + ϱ p j ṗ j ) Kontnutätsglechung = ϱ ( q j j q j + p j ṗ j ) = ϱ j ( 2 H q j p j 2 H x + ṗ p ) p j q j ) = 0 Louvllescher Satz: De Phasenraumdchte entlang ener gegebenen Hamltonschen Trajektore m Phasenraum st konstant! Das Phasenraumvolumen ener Menge Phasenraumpunkte, de sch gemäß ener Hamlton-Dynamk entwckeln, blebt zetlch erhalten! Bedeutung des Louvlle-Satzes - Wchtge Konsequenzen für dynamsche Egenschaften - Grundvoraussetzung für de Gültgket der klassschen statstschen Mechank ( Entrope, Temperatur,... )
90 84 KAPITEL 4. HAMILTONSCHE MECHANIK Hntergrund: Symplektsche Struktur des Phasenraums Louvlle-Satz: Äußerer Ausdruck ener strukturellen Egenschaft der Hamlton- Dynamk: Symplektztät Erheblch wetrechender als Louvlle-Satz, benhaltet Louvlle-Satz als wchtgste Konsequenz Defnton: Betrachte dre nfntesmal benachbarte Punkte m Phasenraum Γ = (q, p); Γ + dγ = (q + dq, p + dp); Γ + dγ = (q + dq, p + dp ) (q, p kurz für q 1 q m, p 1 p m) De dfferentelle symplektsche Fläche von (dγ, dγ ) st defnert als: dσ = dp dq dq dp (= (dp j dq j dq jdp j )) j dγ S m dγ mt S m = ( 0 1 m ) (1m: m m-enhetsmatrx) 1 m 0 z.b. Endmensonales System: dσ = ( dx dp ) (dx dp ) = Fläche (NB: Mathematsch gesehen stellt dσ ene Dfferentalform vom Grad 2 (ene 2-Form) dar.) Ene Varablentransformaton heßt symplektsch, wenn se alle dfferentellen symplektschen Flächen dσ nvarant lässt. Nun glt (Behauptung): (1) Alle kanonschen Transformatonen snd symplektsch (2) De Zetentwcklung defnert ene kanonsche Transformaton, d.h. de Transformaton (q 0, p 0 ) (Q, P ) = (q(t), p(t)) mt {Q j = q j (t), P j = p j (t)} be Anfangsbedngung: q(0) = q 0, p(0) = p 0 st kanonsch. Bewes zu Behauptung (1) Zu zegen: Für kanonsche Transformatonen (q, p) (Q, P ) glt: dq dp dq dp = dq dp dq dp Benutze: Transformaton kanonsch Possonklammer nvarant Vorweg: Für belebge Größen glt: (Bewes durch Ensetzen: {p j, f} = Analog natürlch auch: f Q j Daraus folgt nsbesondere: Qα q und analog Pα p j = q j Q α, Pα q f q j ( p j q 0 = {P j, f}; = {p j, f}; f p j p p δj f f p j = {q j, f} f ) = f q q j etc.) P j = {Q j, f} = {p, Q α } = {Q α, p } = p P α = p Q α, Qα p j = q j P α
91 4.5. DER PHASENRAUM 85 dq dp dp dq = α (dq α dp α dp α dq α) Entwckle: dq α = ( Qα dq q + Qα q j und analog auch dp α, dp α; Sammle und sortere: Terme dq dq j, dp dp j fallen raus p dp ), dq α = j ( Qα dq j + Qα p j dp j ) = {dq dp j [ Qα P α q jα p j Pα Q α q p j ] + dp dq j [ Qα P α q p j Pα Q α p q j ]} Verwende Qα q [ Qα q α α [ Qα q = p, Pα = q j, Pα P α p j Q α q P α p j P α p j Pα Q α ] = q p j [ p P α α Pα p Q α ] = q j [ p P α α = (dq dp dp dq ) = dq dp dp dq Bewes zu Behauptung (2): = p, Qα Q α p j q j q j Q α P α = q j P α p Q α ] = {q j, p } = δ j q j q p j ] = {p Q α Q α P α, q j } = δ j Es genügt zu zegen, dass nfntesmale Zetentwcklung kanonsch st. Also: (q, p) (Q, P ) mt (Q = q + q dt, P = p + ṗ dt) Berechne fundamentale Possonklammern {Q, P j } = {q, p j } + d dt {q, p j } dt +... = {q, ṗ j } + [{ q, p j } + {q, p j }]dt +... Folgerungen = δ j + [ q q k k q = H, ṗ p = H, {q q, p j } = δ j δk 2 H p k q j + q p k 0 2 H q k q j + 2 H q k p p j p k δjk 2 H p k p = δ j + [ 2 H p q j + 2 H q j p ]dt +... = δ j +... (O(dt 2 )) Analog {Q, Q j } = 0, {P, P j } = 0 p j q k 0 ]dt +... () De Hamltonsche Dynamk st symplektsch: Für dre nfntesmal benachbarte Trajektoren Γ(t), Γ(t) + dγ(t), Γ(t) + dγ (t) glt: dσ(t) = dγ S m dγ = const. de dfferentelle symplektsche Fläche zwschen den Trajektoren st zetlch konstant. () Daraus kann man den Louvlle-Satz ableten: Betrachte nfntesmales Volumen, aufgespannt von (2m + 1) nfntesmal benachbarten Trajektoren Γ(t), Γ(t) + dγ (1) (t),..., Γ(t) + dγ (m) (t) Volumen st dv = det(dγ (1) dγ (m) ) = det ( dq(1) dq (m) dp (1) dp (m)) lässt sch ausdrücken als Summe von Produkten von dγ () S m dγ (j) = A (j) (t) (sehe dazu Scheck, Mechank, S. 102) Aus da (j) (t) = const. folgt dv = const. Phasenraumvolumen ändert sch zetlch ncht, damt blebt auch Phasenraumdchte entlang Γ(t) konstant.
92 86 KAPITEL 4. HAMILTONSCHE MECHANIK 4.6 Zusammenfassung: Hamltonsche Mechank Defnert mathematsche Struktur der klassschen Mechank - Raum: Phasenraum (q 1 q m, p 1 p m ) (q, p) Γ (q: generalserte Koordnaten, p: generalserte Impulse) Funktonen f(q, p, t) C (unendlch oft dfferenzerbar) blden Vektorraum über R oder C - Struktur: Le-Algebra, vermttelt durch äußeres Produkt der Possonklammer: {f, g} = j ( f q j g p j f p j - Dynamk: Hamltonfunkton H(q, p) Hamltonglechungen ṗ = H q ; q = H p Belebge Observable: df dt Kanonsche Transformatonen: = {f, H} + f t g q j ) Koordnatentransformatonen (q, p) (Q, P ) m Phasenraum, de dese Struktur unverändert lassen. Also nsbesondere: Posson-Klammer nvarant NB: Dann blebt ene Hamltonsche Dynamk auch Hamltonsch, d.h.: Falls se n dem System (q, p) durch Hamltonan H beschreben wrd, gbt es m System (Q, P ) ene Hamltonan H, de deselbe Dynamk beschrebt. Louvlle-Satz Phasenraumdchte ϱ(γ, t) Louvlle-Satz: d dtϱ(γ(t), t) = 0, falls Dynamk Hamltonsch st.
93 4.7. ANWENDUNG: KLEINE SCHWINGUNGEN Anwendung: Klene Schwngungen Als Anwendung des bsher Gelernten: Betrachte stables System von N Telchen (d.h. en System, das weder explodert noch mplodert) nahe an dem Zustand nedrgster Energe. Enfachketshalber Beschränkung auf ene Raumdmenson (wenger Indzes). Verallgemenerung auf dre Dmensonen st trval. Beschrebung durch Potental U(x 1 x N ) mt Mnmum U 0 be (x 1 x N ) Lneare Näherung Ausgangspunkt: Hamltonfunkton H(x 1 x N, p 1 p N ) = N j=1 p 2 j 2m j + U(x 1 x N ) Annahme: Konfguraton des Systems wecht nur lecht ab von (x 1 x N ) Entwckle U(x 1 x N ) um Mnmum U 0 = U(x 1 x N ) U(x 1 x N ) U U j x x j (x x ) (x j x j ) x1 x N Motvert erste kanonsche Transformaton (m Wesentlchen Reskalerung) p p = p / m x q = (x x ) m ( Kanonsch, da { q, q j } = { p, p j } = 0 und { q, p j } = k ( q x k δ k m H( q 1 q N, p 1 p N ) = U j p 2 j j q q j p j q p k p k δ jk / m j 0 p j x k 0 ) = δ j ) 2 U x x j 1 x1 x m m j N Matrxnotaton: Defnere Matrx Φ = {Φ j } mt Φ j = 1 m m j und Vektoren q = ( q 1 q N ), p = ( p 1 p N ) 2 U x x j x1 x N H( q, p) = U pt p qt Φ q Normalmodenzerlegung Nutze nun: Φ st symmetrsch (Φ j = Φ j ) Φ st postv semdefnt (u T Φ u 0 u) Φ kann dagonalsert werden: Φ = U T Ω U mt U T U = 1 (orthogonal) und Ω: Dagonale Matrx mt postven Egenwerten Ω j = δ j ω 2 Schrebe H um als H = U pt U T U p qt U T Ω U q Motvert zwete kanonsche Transformaton q ξ = U q p p ξ = U p ( Kanonsch, da {ξ, ξ j } = {p ξ, p ξj } = 0 und {ξ, p ξj } = k ( ξ q k Uk p ξj p k Ujk ξ p k 0 p ξj ) = q k U k U jk = δ j k ) 0 H = U (pt ξ p ξ + ξt Ωξ) = U 0 + N k=1 H k mt H k = 1 2 p2 ξk ξ2 k ω2 k N unabhängge harmonsche Oszllatoren, mt Hamltonfunktonen H k! Koordnaten ξ k hessen Normalmoden
94 88 KAPITEL 4. HAMILTONSCHE MECHANIK Bemerkung: Häufg betrachtet man Systeme, de translatonsnvarant snd, d.h. U(x 1 + a,, x N + a) = U(x 1,, x N ) für alle a. Dann muss es ene Mode ξ j geben mt ω j = 0: Entsprcht der kollektven Verschebung aller Telchen um a, beschrebt konstante Schwerpunktsbewegung R(t) = V s (t t 0 ). Dese Mode wrd üblcherwese separat behandelt. H = U 0 + H Schwerpunkt + k H k mt k : Summe ohne Schwerpunktbewegung. Analog n dre Dmensonen: Dort gbt es sechs Moden, für de aus Symmetregründen oft ω j = 0 gelten muss und de dann aus der Summe k H k ausgenommen werden: Dre für de Schwerpunktbewegung und dre für kollektve Rotatonen Lösung m Hamlton-Jacob Formalsmus System H = k H k st Louvlle-ntegrabel, denn: Es gbt N Erhaltungsgrößen H j ( d dt H j = {H j, H} = 0) Dese snd Posson-kommuterend ({H j, H k } = 0}) Der Hamlton-Jacob-Formalsmus (4.4.4 S.80) kann angewendet werden. Hamlton-Jacob Glechung: E = H(ξ, S ξ ) = U 0 + k H k (ξ k, S ξ k ) Setze an S(ξ) = k S k (ξ k ) und defnere E k = H k (= const..) N entkoppelte Glechungen E k = H k (ξ k, S k ξ k ) berets n S.80, Bespel 2 gelöst! Beschrebung n Wnkel/Wrkungs-Varablen θ k, I k mt I k = E k /ω k, θ k = ω k t θ k,0 n Koordnaten ξ k erhält man ξ k (t) = 2Ik ω k sn(ω k t θ k,0 ) Zurückgerechnet auf ursprünglchen Koordnaten x (t) (benutze (x x ) m = q mt q = U T ξ, I j = E j /ω j ) x (t) = x + 1 m j j U 2Ej sn(ω ωj 2 j t θ j,0 ) + V s (t t 0 ) (NB: Man hätte de entkoppelten Hamlton-Glechungen natürlch auch lecht drekt lösen können!) Zusammenfassung: Klene Schwngungen Klene Schwngungen: Häufge Näherung zur Beschrebung von Systemen be ncht zu hohen Energen (z.b. Moleküle, Krstalle) exakt lösbares Problem guter Ausgangspunkt für allgemenere Behandlung Ergebns: Zerlegung n Normalmoden: Entsprechen den Egenschwngungen des Systems bzw. den Resonanzen, falls de Systeme angeregt werden. Kontnuerlche Symmetren (z.b. Translatonsnvaranz, Isotrope) führen zu Moden mt Frequenzen ω k = 0.
95 4.8. AUSBLICK: EIN AUSFLUG INS HAMILTONSCHE CHAOS 89 Lneare Näherung führ zu Louvlle-ntegrablen Systemen Integrabltätsegenschaft geht n der Regel verloren, wenn höhere Terme n der Entwcklung des Potentals U berückschtgt werden Nchtlneare Dynamk, evtl. Übergang ns Chaos (nächstes Kaptel!) 4.8 Ausblck: En Ausflug ns Hamltonsche Chaos Geschchtlche Bemerkungen: 1687 Isaac Newton: Phlosophae Naturals Prncpa Mathematca Begründung der Newtonschen Mechank und Gravtatonsgesetz. Mathematsche Erklärung der Keplerschen Gesetze Lösung des Zwekörperproblems (Kaptel 1.7 S.28) Danach (Newton und vele andere): Versuche, das Drekörperproblem zu lösen (z.b. Erde + Sonne + Jupter) Zentrale Frage: Ist das Sonnensystem stabl? 1888 Henr Poncaré: (Betrag zu enem Wettbewerb zu desem Thema) Es gbt kene analytsche Lösung des Drekörperproblems. Bewes, dass das planare Drekörper-Problem n der Regel ncht ntegrabel st. (Bs dahn wurde vermutet, dass jedes Hamltonsche System ntegrabel st!) Bewes, dass es Bereche m Phasenraum gbt, n denen klenste Änderungen der Parameter große Konsequenzen haben und sch deshalb de Entwcklung enes Systems ncht genau vorhersagen lässt. (NB: Parameter snd prnzpell ne genau bekannt!) Ene sehr klene Ursache, de uns entgehen mag, bewrkt enen beachtlchen Effekt, den wr ncht gnoreren können, und wr sagen dann, dass deser Effekt auf Zufall beruht ( Wssenschaft und Methode, 1903) Begründung der Chaostheore Geret danach weder etwas n Vergessenhet Edward Lorenz: Wederbelebung des Chaosgedanken Beobachtung n Smulatonen des Wetterprogramms Royal Mc Bee (Enes der ersten Wettermodelle: Ideal glatte Erde, mmer Sonne, ken Sommer/Wnter Aber: Berets Tefdruckgebete, wechselnde Wndrchtungen etc.) Verglech zweer Smulatonen mt fast dentschen Startbedngungen: Tage (aufgetragen st rgendene Größe) nach enger Zet wechen de Ergebnsse stark vonenander ab! Butterfly-Effekt Set 1970: Aktves Forschungsgebet der Physk: ( Nchtlneare Dynamk ) Fundamentalen Ergebnsse aus der mathematschen Theore snd allerdngs telwese älter (z.b. KAM Theorem, 4.8.3)
96 90 KAPITEL 4. HAMILTONSCHE MECHANIK Identfzerung von Chaos Defnerendes Kennzechen von Chaos: Trajektoren reageren sehr senstv auf klenste Veränderungen der Anfangsbedngungen ( exponentell dvergent ) Quantfzerung allgemen: Zunächst dynamsches System mt nur ener Dmenson x: (NB: ncht Hamltonsch, dazu bräuchte es 2m Dmensonen!) Betrachte zwe Trajektoren mt Abstand x 0 0 zur Zet t = 0. Zur Zet t se der Abstand x(t) Defnere Lyapunov-Exponent: 1 x(t) λ = lm ln [ lm ] t t x 0 0 x 0 ( Verhalten be t : x(t) x 0 e λt ) System hesst chaotsch, wenn λ > 0 ( x(t) dvergert) Vele (2m) Dmensonen: Man erhält 2m Lyapunov-Exponenten System st chaotsch, wenn ener davon postv stt. Bespele: Getrebenes gedämpftes Pendel, Doppelpendel Egenarten von Hamltonschem Chaos In Hamltonschen Systemen glt der Louvlle-Satz starke Enschränkung! 1) Phasenraumvolumen blebt mmer glech. Fundamentaler Untersched zu dsspatven Systemen, wo das Phasenraumvolumen mt der Zet klener wrd und sch Systeme nach langer Zet oft auf enen nederdmensonalen Unterraum zurückzehen (enen Attraktor ) sowohl m chaotschen als auch m nchtchaotschen Fall. Kennzechen von dsspatvem Chaos (Hausaufgabe: Internetrecherche): Seltsame Attraktoren mt fraktaler Dmenson So etwas kann es m Hamltonschen Chaos ncht geben! 2) Poncarésches Wederkehrtheorem In endlchen Systemen glt: In jeder Umgebung V 0 enes Phasenraumpunktes Γ 0 kann mndestens ene Trajektore gestartet werden, de nach endlcher Zet weder n V 0 zurückführt. (Bewes: Zerlege Zet n Zetschrtte t dskrete Zetentwcklung V 0 V 1 V 2 V n t t Nmm an V 1 V 2 = Wegen des Louvllesatzes muss es en Paar (m, n) geben mt V m V n Verfolge V n V m rückwärts n der Zet V n m V 0 0 ) Ausgangspunkt der Theore des Hamltonschen Chaos st oft en ntegrables Referenzsystem, welches mt der Hamlton-Jacob Theore (4.4.4 S.80) gelöst wurde. Daher m nächsten Abschntt (4.8.3) zunächst ene allgemene Dskusson ntegrabler Systeme.
97 4.8. AUSBLICK: EIN AUSFLUG INS HAMILTONSCHE CHAOS Integrable Systeme 1) Defnton (Ernnerung an S.80): Louvlle-Integrabltät En Hamltonsches System m 2m-dmensonalen Phasenraum hesst ntegrabel, wenn es m unabhängge Erhaltungsgrößen P j gbt, de Possonkommuteren, d.h. {P j, P k } = 0 j, k ( Dann hat Hamlton-Jacob Glechung ene Lösung) 2) Invarante Tor und Wnkel/Wrkungsvarablen Untersuche nun topologsche Struktur der Hyperflächen mt P j = const. j Trajektoren bleben auf desen Flächen nvarante Flächen Hamltonfunkton H(Q, P ) = H(P ) Q j = H P j = u j Q j = u j t+q j,0 Nmm an, endlches System bzw. räumlch begrenzte Bewegung. Q j kehrt zurück, geschlossene Bahn Q j muss perodsch sen! Normere so, dass de Perodztät genau 2π st (Q j + 2π = Q j ). z.b. we n 4.4.4, Bespel 2 (harmonscher Oszllator) Wnkel/Wrkungs-Varablen θ j, I j : H(q, p) = H(I) mt H I j = ω j Trajektoren: θ j (t) = (ω j t + θ j,0 ) mod 2π Struktur der nvaranten Fläche: Torus Jeder Satz I defnert enen separaten Torus NB: Alternatve Defnton enes ntegrablen Systems: En System, dessen Phasenraum n nvarante Tor aufblättert. 3) Folgerungen für Trajektoren Alle Koordnaten θ j zusammengenommen: Trajektoren wnden sch um m-dmensonalen Torus Trajektoren snd ncht unbedngt geschlossen. (nur, falls Wndungsfrequenzen kommensurabel) Varable θ j perodsch Belebge Funktonen f(t) = f(q(t), p(t)) = f(θ(t), I(t)) kann man n ener multdmensonalen Fourer-Rehe entwckeln: f(θ, I) = k Z m f k (I)e k θ mt k θ = j k j θ j f(t) = k Z m e k (ωt+θ 0 ) f k Motvert Klassfzerung nach der Topologe der Trajektoren: Möglchketen Torus nchtresonant, ratonal unabhängg ω k 0 für alle k Z m, k 0 Jede Trajektore füllt den gesamten Torus! Torus resonant, ratonal abhängg ω k = 0 für en k Z m (k 0) Trajektoren füllen jewels nur enen Tel des Torus Torus zerfällt n Untertor
98 92 KAPITEL 4. HAMILTONSCHE MECHANIK Spezell: Es gbt m 1 unabhängge resonante Relatonen ω k = 0 Dann st jede Frequenz en Velfaches ener Grundfrequenz ω Torus gefüllt mt perodschen Orbts der Perode 2π/ω 4) Ncht-entartete Systeme Angenommen, ω(i) se als Funkton von I stetg dfferenzerbar und endlch, und det ω I 0 für alle I Resonante Tor legen dcht n der Menge aller Tor (analog ratonale Zahlen / reelle Zahlen) Klene Störungen und KAM-Theorem Betrachte nun ntegrables System H 0 (q, p) mt klener Störung: H(q, p) = H 0 (q, p) + ɛ H 1 (q, p) (alles zetunabhängg) Frage: Blebt das System ntegrabel? We wrkt sch de Störung auf nvarante Tor aus? 1) Hstorsch 1892 Poncaré ( Vater des Chaos ); 1937 Brkhoff Resonante Tor werden durch belebg klene Störung zerstört! Folgerung: In nchtentarteten Systemen wrd ene dchte Menge der Tor zerstört.a. st Hamltonsystem ncht ntegrabel! 1954 Kolmogorov: Dennoch überlebt Mehrzahl der Tor ene endlche Störung, wrd nur verformt ( stark nchtresonante Tor ) 1962 Moser, 1963 Arnold: KAM-Theorem 2) Anschaulch In resonanten Tor wrd mmer derselbe Untertorus durchlaufen. Klene Störung (z.b. zusätzlcher Planet m Drekörperproblem) gbt der Trajektore an mmer der glechen Stelle enen klenen Kck das destablsert de Torus-Trajektore! In nchtresonanten Tor wrkt der Kck jedesmal en weng anders Effekt mttelt sch heraus, Torus-Trajektore kann überleben! 3) Zugang mttels Störungstheore Wderspruchsbewes: Zege, dass H.A. ncht ntegrabel st! Her nur grobe Idee des Arguments. Tatsächlche saubere mathematsche Behandlung st aufwendger! H 0 ntegrabel Lässt sch kanonsch n Wnkel/Wrkungsvarablen (θ, I) darstellen mt θ = ωt + θ 0 Vermute, dass H(θ, I) = H 0 (I) + ɛ H 1 (θ, I) auch ntegrabel st: Dann exsteren m Erhaltungsgrößen I und ene kanonsche Transformaton (θ, I) (θ, I ), so dass H(θ, I) = H (I )
99 4.8. AUSBLICK: EIN AUSFLUG INS HAMILTONSCHE CHAOS 93 Dann kann der Hamlton-Jacob Formalsmus (4.4.4 S.80) angewendet werden: Es exstert ene Erzeugende S(θ, I ) mt S = θ, I S S θ = I, de de Hamlton-Jacob Glechung löst: E = H(θ, θ ), wobe E = H (θ ) Störungsentwcklung: Setze an S = S 0 + ɛ S 1 mt S 0 = I θ (S 0 vermttelt de Identtät: θ = S 0 I = θ ) H (I )! = H(θ, S θ ) = H 0( S θ ) + ɛ H 1(θ, S = H 0 ( S 0 θ I = H 0 (I ) + ɛ H 0 I θ ) +ɛ S 1 θ + ) + ɛ H 1(θ, S 0 θ H 0 I +O(ɛ)=ω+O(ɛ) I + ) S 1 θ + ɛ H 1(θ, I ) + O(ɛ 2 ) = H 0 (I ) + ɛ ω S 1 θ + ɛ H 1(θ, I ) + O(ɛ 2 ) Entwcklung n Fourer-Rehe analog S.91 H 1 = k H 1,k (I )e k θ ; S 1 = k S 1,k (I )e k θ S 1 θ = k k S 1,k e k θ Ensetzen: H (I ) H 0 (I ) = ɛ k [ω k S 1,k (I ) + H 1,k (I )] e k θ θ unabhängg von θ [ ] = 0 S 1,k (I ) = H 1,k (I )/ω k S 1 (θ, I H 1,k ) = k ω k ek θ S 1 dvergert, falls ω k = 0 für en k 0 (resonante Tor). S 1 kann möglcherwese konvergeren, falls ω k hnrechend groß für alle k ( stark nchtresonante Tor ) Folgerung: Resonante Tor werden schon durch klenste Störungen zerstört! Stark nchtresonante Tor bleben möglcherwese erhalten und werden nur verformt. 4) Das KAM-Theorem (ganz ohne Bewes) Se Ω ene beschränkte Menge Ω R m Defnere Ω τ α: Menge aller ω Ω mt ω k > Abstand α zum Rand von Ω haben. ( k = m j=1 k j, τ > m 1 fest) α k τ, de mndestens den Se en nchtentartetes ntegrables Hamltonsches System H 0 mt Störung H = H 0 +ɛh. Dann exstert en δ > 0 so, dass für alle ɛ < δα 2 glt: Alle Tor des ungestörten Systems mt ω Ω α bleben erhalten oder werden nur lecht deformert! Fazt: Klene Störungen de mesten Tor verformen sch nur! Große Störungen mmer mehr Tor gehen ns Chaos über. Je resonanter en Torus, desto schneller kommt das Chaos!
100 94 KAPITEL 4. HAMILTONSCHE MECHANIK 5) Bespel: Resonanzen m Asterodengürtel Promnente Stuaton, n der Resonanzen ene Rolle spelen: Asterodengürtel m Sonnensystem zwschen Mars und Jupter Beobachtung: Vertelung der Halbbahnachsen west deutlche Lücken auf (Krkwoodlücken, gefunden von Danel Krkwood 1866). Lücken treten dann auf, wenn de Bahn der Asteroden n Resonanz mt der Bahn des Jupters kommt! Bldquelle: Wkpeda Grund: Resonanzen m Drekörpersystem Sonne/Asterod/Jupter Jupter stört das System Sonne/Asterod (NB: Jupter verengt n sch 70% der Masse aller Planeten.) Resonante Tor treten auf, wenn de Umlauffrequenz von Jupter und de Umlauffrequenz des Asterods kommensurabel snd! Anschaulch (sehe Bld): In resonanten Konfguratonen hat man perodsch wederkehrend ene Konstellaton, n der der Jupter dem Asterod besonders nahe st und hn ablenkt. Effekt st besonders stark, wenn Asterod zu desem Zetpunkt m Aphel sener Bahn steht (sonnenfernster Punkt, gegenüber vom Perhel (sehe S.32)). Schematsche Zechnung ener 2:1 Resonanz m Drekörpersystem Sonne (gelb), Asterod (schwarz) und Jupter (braun)
101 4.9. WISSENSFRAGEN Wssensfragen 69. We defnert man m Lagrange-formalsmus den generalserten Impuls? 70. Was st ene Hamlton-Funkton? 71. We hängen Lagrange-Funkton und Hamlton-Funkton zusammen? 72. We lauten de Hamltonschen Bewegungsglechungen? 73. We snd de Possonklammern defnert? 74. Nennen Se enge wchtge Egenschaften der Possonklammern. 75. Was st ene kanonsche Transformaton? Was versteht man spezell unter ener kanonschen Transformaton m engeren Snne? 76. We verhalten sch Possonklammern unter kanonschen Transformatonen? 77. Was versteht man unter ener Erzeugenden Funkton m Kontext der kanonschen Transformatonen? 78. Nach welchem allgemenen Krterum können Se entscheden, ob ene Transformaton kanonsch st? 79. Erklären Se den Hamlton-Jacob Formalsmus. 80. We lauten de zetunabhängge und de zetabhängge Hamlton-Jacob- Glechungen? Wann snd se lösbar? 81. Was versteht man unter dem Phasenraum? 82. Was versteht man unter ener Phasenraumtrajektore? 83. Was versteht man unter der Phasenraumdchte? 84. Erklären Se den Louvlleschen Satz. 85. We behandelt man en System, das nahe an dem Zustand mnmaler Energe st, n lnearer Näherung? 86. Was st ene Normalmodenzerlegung? 87. Was versteht man unter dem Begrff Louvlle-ntegrabel? 88. Erklären Se den Begrff der Wnkel/Wrkungs-Varablen. 89. Was st generell das Kennzechen von Chaos? 90. We lautet das Poncarésche Wederkehrtheorem? 91. Skzzeren Se de wesentlche Aussage des KAM-Theorems.
102 96 KAPITEL 4. HAMILTONSCHE MECHANIK
103 Kaptel 5 Grundbegrffe der Hydrodynamk Copyrght 2014 Frederke Schmd 1 Hydrodynamk oder Mechank der Flude : Ene der wchtgsten makroskopschen Theoren mt Anwendungen quer durch alle naturwssenschaftlchen Dszplnen und Ingeneurwssenschaften (Mathematk, Physk, Meteorologe, Geophysk, Cheme, Luft/Raumfahrt, Umweltwssenschaften) Bespel ener Kontnuumstheore Beschrebung von Veltelchensystemen durch Dchte und Flüssen bzw. Geschwndgketsprofle vergröberte, unscharfe Schtwese (NB:Wetere promnente Kontnuumstheore: Elastztätstheore für feste Körper, oft als Lagrange Feldtheore formulert. (mehr zu klassschen Feldtheoren sehe Vorlesung Theore 2) Hydrodynamk dagegen basert mest auf Newtonscher Mechank, z.b. wel Rebung dann lechter berückschtgt werden kann.) 5.1 Flude und Kontnuumshypothese 1) Flude - umfassen Flüssgketen und Gase Kennzechen verglchen mt Festkörpern nedrge Bndungsenergen zwschen Partkeln kene festen Nachbarn, fre scherbar kene Formbeständgket ; können Behälter n jede Ecke ausfüllen Flüssgketen: wetgehend nkompressbel. Gase: kompressbel. Bemerkung: De Trennung flud-fest st ncht mmer endeutg, z.b. Plastsches Fleßen: Unter starken Scherkräften fangen vele Festkörper an zu fleßen, z.b. metallsche Werkstoffe, Gletscher, Erdkruste 1 Prof. Dr. Frederke Schmd, Vorlesung Theoretsche Mechank, Unverstät Manz, WS 2014/2015. Letzte Änderung am
104 98 KAPITEL 5. GRUNDBEGRIFFE DER HYDRODYNAMIK Vskoelastsche Materalen Verhalten sch unter hochfrequenten Kräften we Festkörper, unter nederfrequenten we Flüssgketen (z.b. Stärke) Granulare Materalen, z. B. Sand 2) Übergang zum Kontnuum Fragestellung: Dynamk enes Fluds auf makroskopschen Längenund Zetskalen ( µm-km, µs-h). Im Prnzp N-Telchen Problem (mt N ), mt mkroskopscher Dynamk: Stöße zwschen Telchen mttlere Zet zwschen Stößen: τ Stoß s mttlere free Weglänge: λ nm. Aber: Mkroskopsche Dynamk nteressert uns ncht. Uns nteresseren nur wenge, langsam veränderlche Größen, z.b. Dchte oder Strömungsgeschwndgket (typscherwese Dchten von Erhaltungsgrößen we Masse oder Impuls!) Kontnuumshypothese: Grundannahme der Hydrodynamk Es gbt langsame und schnelle Prozesse, de man klar trennen kann. ( Trennung der Längen- und Zetskalen ). Trennung der Längenskalen Bld: Se A V rgendene Größe, gemttelt über das Volumen V Annahme: Es gbt en Plateau Irgendwo m Plateau st das Volumen enes Flüssgketselementes angesedelt. Trennung der Zetskalen Entsprechende Annahme: Es gbt ene charakterstsche Zetskala τ τ Stoß, auf der sch de mkroskopsche Dynamk ausmttelt und de auf en Flüssgketselement wrkenden Kräfte durch makroskopsche Konzepte we Druck und Scherung beschreben werden können. Das Flüssgketselement st auf deser Zetskala lokal m Glechgewcht (mechansch und thermsch). 3) Gegenstand der Hydrodynamk Zetlche Entwcklung von Dchten ρ( r, t) und Strömungsproflen v( r, t), gemttelt über Flüssgketselemente, unter Enfluss äußerer Kräfte (z.b. Schwerkraft) und nnerer gemttelter Kräfte (z.b. Druck, Scherkräfte). Wr kennen schon ene Glechung für ρ( r, t): De Kontnutätsglechung ρ t + j = 0 mt j = ρ v Suche nun entsprechende Glechung für v( r, t).
105 5.2. KINEMATIK DER FLUIDE Knematk der Flude Zunächst: Beschrebung von Strömungen v( r, t) 1) Euler-Beschrebung vs. Lagrange-Beschrebung Zwe Schtwesen Lagrangesche Beschrebung Koordnatensystem wrd mt Strömung mttransportert. Bezeht sch mmer auf dasselbe Flüssgketselement. Konkret: Wähle Referenzzet t 0, Ordne Flüssgketselemente hrem Ort r 0 zur Zet t 0 zu ( r 0 markert das Flüssgketselement) Strömung zur Zet t wrd beschreben durch Geschwndgket V ( r 0, t) des Flüssgketselementes r 0 Analog andere Größen A L ( r 0, t) Entsprcht der Schtwese enes mtschwmmenden Beobachters Eulersche Beschrebung Koordnatensystem blebt ortsfest (üblche Schtwese) Strömungsprofl v( r, t) beschrebt zu verschedenen Zeten verschedene Flüssgketselemente Entsprcht der Schtwese enes ruhenden Beobachters 2) Zetlche Abletungen Betrachte nun belebge Größe A( r, t), de (lokal) de Egenschaften enes Flüssgketselementes beschrebt (z.b. v( r, t)) Frage: Um welchen Wert A ändert sch dese Größe auf dem Flüssgketselement während der Zet t (mt t 0; Flüssgketselement bewegt sch n deser Zet um r = v t weter.) Lagrange-Koordnaten (mtbewegt) A = A L ( r 0, t + t) A L ( r 0, t) = A t t (+O( t2 )) Euler-Koordnaten (ruhend) A = A( r + r, t + t) A( r, t) = A( r + v t, t + t) A( r, t) = 3 α=1 A r α v α t + A A t t = t ( t + ( v )A) Notaton: Zetlche Abletungen entlang des Strömungspfades: d dt A = A + ( v )A t d dt (entsprcht totaler Abletung!) Spezell: Beschleungung enes Flüssgketselementes: d v dt = v + ( v ) v t (wchtg wegen des Newtonschen Kraftgesetzes: d v dt = Kraftdchte!)
106 100 KAPITEL 5. GRUNDBEGRIFFE DER HYDRODYNAMIK 3) Charakterserung von Strömungsfeldern Dvergenz: v: Volumenänderung enes Flüssgketselementes (Kontnutätsglechung ρ ρ + (ρ v) = 0 + ( v )ρ +ρ v = 0 t t v = 1 dρ 1 dv = ) ρ dt dρ ρ=n/v V dt dt Rotaton: v = ω: Rotatonsstrom bzw. Vortztät Beschrebt Wrbel m Strömungsprofl (Stokesscher Satz: Fläche A d A( v) = A d s v 0 für v 0 ) Potentalströmungen: Strömungen v( r, t) mt v = 0 und v = 0. Lassen sch lokal als Gradent enes Potentals Φ( r, t) darstellen entsprechend v = Φ mt Φ = 0. NB: Man kann zegen: Allgemene Strömungsfelder können zerlegt werden n dre Antele v = v 1 + v 2 + v 3 mt v 1 : Rener Rotatonsstrom ( v 1 = 0, v 1 = v = ω) v 2 : Rene Kompresson/Dlataton ( v 2 = 0, v 2 = v = 1 ρ v 3 : Potentalstrom ( v 3 = 0, v 3 = 0; v 3 = Φ mt Φ = 0) (ohne Bewes: Dazu wären de Werkzeuge aus Theore 2 nötg!) dρ dt ) 5.3 Dynamk: Bewegungsglechungen für Flude Ausgangspunkt: Newtonsches Kraftgesetz für Punkttelchen: m d v dt = F d v Zel: Übertragen auf Flüssgketselement: ρ dt = f Frage: Was st f? Massendchte Kraft pro Volumen Kräfte n allgemenen Flüssgketen Beträge zur Nettokraft F V = f V auf Flüssgketselement V Externe Kräfte ( Volumenkräfte ) auf Partkel z.b. Schwerkraft: f = ρ g mt g = g e z Innere Kräfte aus Wechselwrkungen zwschen Telchen Bespel: Druck P ( r, t) Berechne Nettokraft F V = f p V auf Flüssgketselement V : ( V = x y z = A x x mt A x = y z etc.) F V = e x A x x xp e y A y y yp e z A z z zp V V V = V P fp = P Verallgemenerung: Spannungstensor Gegeben belebge (nfntesmale) Oberfläche A (Flächennhalt A, Flächennormale n = A/A) Kraft auf dese Fläche F A se ncht unbedngt parallel zu A Defnere Spannungstensor über FA = σ A bzw. FA /A = σ n
107 5.3. DYNAMIK: BEWEGUNGSGLEICHUNGEN FÜR FLUIDE 101 (NB: σ hängt ncht von n ab, da sch Kräfte n verschedene Rchtungen lnear aufadderen, sehe Bld) Nettokraft auf Flüssgketselement V : F V = V da σ n = Gauss V d3 r σ= V σ= f V f = σ Spezell Druck: f P = σ P mt σ P = P 0 P 0 P (Spezalfall) Konkret gbt es n gewöhnlchen Fluden.A. nur zwe Arten von nneren Kräften: Druckkräfte und Rebungskräfte Motvert Trennung n σ P und vskosen Spannungstensor σ Folgerung für Bewegungsglechungen Lagrange-Beschrebung: ρ d v dt = f ext P + σ Euler-Beschrebung: ρ v t + ρ( v ) v = f ext P + σ Drekte lokale Geschwndgketsänderung Konvekton Externe Kraft Druckgradent Rebungskräfte Im Allgemenen kann der Druck P ( r, t) berechnet werden (z.b. drekt aus ener thermschen Zustandsglechung P (ρ), oder ndrekt aus ener Inkompressbltätsbedngung für das Flud). Zur Vervollständgung der Theore brauchen wr dann noch enen Ausdruck für σ. Bemerkung: Ohne σ zu kennen, können wr nun schon ruhende Flüssgketen behandeln: Für v( r, t) 0 gbt es kene Rebungskräfte σ = 0 fext = P Fundamentalsatz der Hydrostatk Spannungstensor und Deformatonstensor Zunächst: Allgemene Aussagen zum Spannungstensor und zum Zusammenhang zwschen Spannung und Scherung 1) Allgemene Egenschaften des Spannungstensors Spannungstensor: Allgemenes Konzept der Kontnuumsmechank Wrd auch n der Elastztätstheore und n Feldtheoren we der Elektrodynamk benutzt ( Maxwellscher Spannungstensor). Im Glechgewcht: Isotrop, σ= P 1 (Flüssgket n Ruhe oder glechförmg bewegt). Im Nchtglechgewcht gbt es zusätzlche Antele. n Festkörpern: Elastsche Kräfte Elastscher Spannungstensor n Fluden: Rebungskräfte Vskoser Spannungstensor σ (s.o.)
108 102 KAPITEL 5. GRUNDBEGRIFFE DER HYDRODYNAMIK Allgemen: σ muss symmetrsch sen. Anderenfalls müssten nfntesmale Volumenelemente mt unendlcher Geschwndgket roteren! 0 S 3 S 2 (Bewes: Angenommen, es gäbe enen antsymmetrschen Antel σ A = S 3 0 S 1 S 2 S 3 0 σ A n kann geschreben werden als S n mt S = (S 1, S 2, S 3 ) Betrachte Flüssgketselement mt Volumen V (V 0) Kräfte F A = σ A A = S A auf Oberflächen erzeugen Drehmoment M 2) Deformatonstensor M = V ( r df A ) = df A = σ A da= S d A V r ( S da) = V (da S) r = Gauss V d3 r ( S) r = V d 3 r [ S ( r) ( S r) ] = 2SV Drehmoment wrkt auf Drehmpuls: M = d dt L Im Schwerpunktsystem st L = I Ω 3 S mt Ω: Wnkelgeschwndgket und I : Träghetstensor (vgl. 3.2 S.59, Konzept glt ncht nur für starre Körper). I j = ρ d 3 r (r 2 δ j r r j ) I d 3 rr 2 rmax 5 V 5/3 2SV = d dt I Ω V 5/3 Wnkelgeschwndgket Ω muss we V 2/3 skaleren Ω für V 0 Das st ncht möglch, also muss S = 0 sen bzw. σ A = 0 ) Scherkräfte bzw. vskoser Spannungstensor wrd durch Scherströmungen, d.h. Geschwndgketsgradenten bestmmt (NB: ncht absoluten Geschwndgketen wegen Galle-Invaranz: Ene mt glechförmger Geschwndgket bewegte Flüssgket sollte sch ncht von ener ruhenden Flüssgket unterscheden!) Baserend auf dem Geschwndgketsprofl v( r, t) defnere Deformatonstensor G über G j = j v = e j + ω j mt e j = 1 2 ( jv + v j ) ω j = 1 2 ( jv v j ) Interpretaton: : symmetrscher Antel : antsymmetrscher Antel Sp( e ) = v: Kompresson/Dlataton von Flüssgketselementen Nebendagonalelemente von e : Beschreben Scherung von Flüssgketselementen Antsymmetrscher Antel ω 0 ω 3 ω 2 mt ω = (ω 1, ω 2, ω 3 ) = v: ω 3 0 ω 1 Vortztät (vgl. 5.2 S.99) ω= ω 2 ω 1 0 (Check: ω k = j ɛ jk ω j = 1 2 j ɛ jk ( j v v j ) = j ɛ jk v j ) Beschrebt Drehung von Flüssgketselementen 3) Bezehung zwschen Spannungstensor und Deformatonstensor Wechselspel: Geschwndgketsgradent erzeugt Rebungskräfte ( σ ) Spannung (Scherkräfte) erzeugen Geschwndgketsgradenten
109 5.3. DYNAMIK: BEWEGUNGSGLEICHUNGEN FÜR FLUIDE 103 Grundannahme der Kontnuumshypothese: Trennung der Zetskalen, Flüssgketselemente snd lokal m Glechgewcht Es gbt endeutgen Zusammenhang zwschen σ und G Konkret: Antsymmetrscher Antel ω von G trägt ncht be (be rener Rotaton trtt kene Rebung auf). Hydrodynamsche Theore wrd vervollständgt durch Konsttutve Glechung σ e, System- bzw. materalabhängg Ideale Flüssgketen und Euler-Glechungen Enfachster Fall: Rebung vernachlässgt Ideale Flüssgket Konsttutve Glechung: σ = 0 Bewegungsglechung: d v dt = v t + ( v ) v = f ext ρ 1 ρ P Euler-Glechungen Häufg nmmt man zusätzlch an, dass de Flüssgket nkompressbel st, d.h. v = 0. Wr werden das her ncht notwendg voraussetzen Newtonsche Flüssgketen und Naver-Stokes Glechungen Zweter promnenter Fall: Enfache sotrope Flüssgket σ hängt lnear und nstantan von e ab ( σ e ) Allgemener Ansatz: σ j = kl C jkl e kl mt C jkl : konstante Koeffzenten Istropes Medum allgemene Form (ohne Bewes) C jkl = A δ k δ jl + A δ l δ jk + B δ j δ kl σ symmetrsch (, j) können vertauscht werden A = A σ j = 2Ae j + B δ j l e ll bzw. σ = 2A e +B 1 Sp( e ) Tele σ auf nach Betrag von Sp( e ) = v und spurlosem Rest Konsttutve Glechung: σ = µ (2 e 2 3 1Sp( e )) spurlos Flüssgketselement verformt sch kene Volumenänderung + ζ 1 Sp( e ) Rene sotrope Dlataton/Kompresson mt µ: Schervskostät ζ: Volumen-Vskostät (Betrag verschwndet n nkompressblen Flüssgketen) Bewegungsglechung: ρ d v dt = f ext P + σ mt [ σ ] j = [2µe j + (ζ 2 3 µ)δ j Sp( e ) e j = 1 2 ( v j + j v ) v = µ( v j + jv ) + (ζ 2 3 µ) j( v) = µ v j + (ζ µ) j( v) v j j ( v)
110 104 KAPITEL 5. GRUNDBEGRIFFE DER HYDRODYNAMIK Naver-Stokes-Glechungen ρ v t + ρ( v ) v = f ext P + µ v + (ζ + µ ) ( v) 3 bzw. spezell für nkompressble Flüssgketen ( v = 0) v t + ( v ) v = f ext ρ 1 P + ν v ρ mt ν = µ/ρ: knematsche Vskostät Bemerkung: Grenzfälle der Naver-Stokes Glechungen Falls ν 0 Verhalten we deale Flüssgket Falls ν Rechte Sete der Naver-Stokes Glechungen domnert. Lnke Sete kann vernachlässgt werden. Führt m nkompressblen Fall zu Stokes-Glechungen: fext P + µ v = 0 mt v = 0 lamnare Strömungen De Bedeutung von Rebung verglchen zur Träghet wrd üblcherwese durch de Reynoldszahl charaktersert! Se en konkretes Strömungsproblem, z.b. Fluss durch Kanal Defnere charakterstsche Länge L (z.b. Kanaldurchmesser) charakterstsche Geschwndgket U (z.b. v n der Mtte des Kanals) Folgerungen: Defnert Reynoldszahl Re = U Lρ/µ Reskalere r r/l, v = v/u, P = P /ρu 2 Dann erhält man m nkompressblen Fall de Glechung v t + ( v ) v = f ext P + 1 Re v Re : Verhalten we deale Flüssgket Re 0: Hochvskose, lamnare Flüssgket Mkroskopsche Strömungen (z.b. n nanotechnologschen Anwendungen oder n Zellen bzw. klenen Blutgefäßen) snd mest lamnar! Makroskopsche Strömungen, z.b. umströmte Flugzeuge, kann man oft n guter Näherung als deale Flüssgketen beschreben außer n der Nähe der Oberflächen. Dort setzt der Abstand zur Oberfläche de charakterstsche Längenskala und es bldet sch ene lamnare Grenzschcht.
111 5.4. IDEALE FLÜSSIGKEITEN Ideale Flüssgketen Zum Abschluss deses Ausflugs n de Hydrodynamk wollen wr konkret am Bespel der dealen Flüssgketen en paar Anwendungen der n 5.3 hergeleteten Glechungen zegen. Ideale Flüssgketen: Kene Vskostät. Kommt n der Natur.A. ncht vor, st aber trotzdem manchmal ene ganz gute Näherung, z.b. falls... Reynoldszahlen groß snd und de Strömung trotzdem ncht turbulent st, z.b. wet weg von Wänden ( Längenskala L gross ) charakterstsche Zetskalen so kurz snd, dass Störungen der Geschwndgket kene Zet haben, über Rebungskräfte wegtransportert zu werden (nchtstatonärer Strom be kurzen Zeten, hochfrequenter Strom) echte deale Flüssgketen: Supraflüssgketen z.b. He 4 be tefen Temperaturen Folgen nach S.103 den Euler-Glechungen: d v dt = f ext ρ 1 ρ P Bernoull-Funkton und Bernoull-Glechung Annahme m Folgenden (her und m Rest des Kaptels 5.4): Strömung se zusätzlch barotrop, d.h. es exstert ene endeutge Bezehung ρ P (ρ = ρ(p )), und de externe Kraft lässt sch auf en Potental U zurückführen, d.h. es glt f ext /ρ = U (z.b. Schwerkraft: U = gz). f Dann kann man schreben ext ρ 1 ρ P = (W +U) mt W = P 0 dp /ρ(p ) Alternatve Formulerungen der Euler-Glechungen: () () d v dt Folgerungen: = (W + U) (klar) v t + B = v ω mt B = W + U v2 Bernoull-Funkton und ω = v (Vortztät) we gehabt (sehe 5.2) (Check: v ω = v ( v) = v v ( v ) v = 1 2 v2 ( v ) v 0 = d v v v + (W + U) = + ( v ) v + (W + U) = dt t t Spezell: Inkompressble Flüssgket m Schwerefeld v2 + (W + U + ) v ω ) 2 W = P dp /ρ = P /ρ; U = g z B = 1 2 v2 + P ρ + g z Für Statonäre Ströme glt: (da db dt db dt = 0 = B +( v )B = v [( v ω v ] = 0 ) t t 0 statonär 0 statonär
112 106 KAPITEL 5. GRUNDBEGRIFFE DER HYDRODYNAMIK Spezell für nkompressble Flüssgket m Schwerefeld: Entlang der Bahn von Flüssgketselementen (auf Bahnlnen) glt de Bernoull-Glechung: B = 1 2 v2 + P ρ + g z = const. (beschreben von Bernoull 1738, hergeletet von Euler) In Berechen, n denen de Flüssgket schneller strömt (z.b. Rohrverengungen), ernedrgt sch der Druck! Anwendungen: Wasserstrahlpumpe, Zerstäuber, Wrbel- und Zrkulatonserhaltung Defnere Zrkulaton um ene geschlossene Kontur C: Γ = C d l v Annahmen we n 5.4.1: Barotroper Fluss. f ext /ρ st Potentalkraft. Dann glt der Satz von Thomson (Lord Kelvn), 1869 Entlang ener mt der Strömung mtgewegten Kontur C(t) d blebt de Zrkulaton erhalten: dt C(t) v d l = 0 (Herletung: Folgerungen d dt C(t) v d l = d v dt Euler (W +U) d l(t + dt) = r 1 (t + dt) r 0 (t + dt) = r 1 (t) + v( r 1 )dt r 0 (t) v( r 0 )dt = d l(t) + ( v( r 1 ) v( r 0 ))dt d dt d l = ( v( r 1 ) v( r 0 )) = d v dl dl d d l + v dt d l = d l (W + U) d v 2 = 0 ) d v dl dl Stokesscher Satz 0 da (W +U)=0 Vortztät ω = v blebt auf Bahnlnen erhalten (da ω nach dem Stokesschen Satz der Zrkulaton auf nfntesmaler Kurve entsprcht. Alternatver, drekter Bewes: d ω dt = d v = (W + U) = 0 ) dt Spezell: Falls ω = 0 auf enem Punkt, st ω = 0 auf der Bahnlne! Deshalb st der Begrff der Potentalströmung überhaupt snnvoll. Im Volumen blebt ene Potentalströmung.A. ene Potentalströmung. Beachte: Man könnte versucht sen, zu folgern, dass alle statonären Strömungen, für de v = const. m Unendlchen st, Potentalströmungen sen müssen. (Ist ω = 0 m Unendlchen, so blebt ω = 0 bem Durchströmen). Aber: In der Nähe von Oberflächen brcht das Argument zusammen. Für Flusslnen, de drekt von der Oberfläche abgehen, st ω umdefnert. Bespel: Umströmung ener Kugel. Nahelegende Lösung: Potentalströmung Möglch snd aber auch Lösungen zu, be denen Flüssgketselemente verschedener Geschwndgket anenander entlanggleten: Tangentale Dskontnutäten mt ω 0 (snd n Gegenwart von Rebung nstabl, dort entstehen Turbulenzen)
113 5.4. IDEALE FLÜSSIGKEITEN Zugkraft und Auftreb Untersuche Körper der Geschwndgket u, der von dealer Flüssgket umströmt wrd. Im Unendlchen se v gegeben und konstant. An der Oberfläche des Körpers glt als Randbedngung: Flüssgket darf ncht hnenströmen, d.h. v = n v = n u ( n st de Oberflächennormale). Enfachketshalber kene Gravtaton. Frage: Welche Kraft F übt de Strömung auf den Körper aus? Zugkraft F D (D: drag) Auftreb F L (L: lft) Her spezell: Potentalströmungen: v = 0 und ω = v = 0 überall. (kene tangentalen Instabltäten etc.) Das bedeutet: Lokal exstert Potental Φ mt v = Φ. Es glt: Falls das Gebet der Potentalströmung enfach zusammenhängend st, exstert auch en globales Potental (Bewes analog 1.4.1). Da de Randbedngungen v an den Rändern des Gebets vorgegeben snd, st das Potental endeutg bs auf ene Konstante. (Bewes: Randbedngungen v = n v vorgegeben Φ = n Φ vorgegeben. n Angenommen, es gäbe zwe Lösungen Φ 1, Φ 2 von Φ = 0 mt desen Randbedngungen. Φ = Φ 1 Φ 2 löst Φ = 0 und n Φ = 0 an den Rändern des Gebetes. 0 = da Gauss Φ Φ = d 3 r ( Φ Φ) = d 3 r[( Φ) 2 + Φ Φ ] = d 3 r( Φ) 2 Φ = 0 Φ = const. ) Das D Alembertsche Paradox Zurück zu unserem Problem: Betrachte endlchen Körper n enem dredmensonalen unendlchen Gebet, der von ener Potentalströmung umströmt wrd. Dann zegt sch: De Gesamtkraft auf den Körper st Null! Alle Beträge müssen enander aufheben. (Bewes dazu: Zunächst Galle-Transformaton, so dass de Strömung m Unendlchen n Ruhe st v 0 und der Körper sch mt Geschwndgket u bewegt. Egenvolumen des Körpers se V 0, Rand des Körpers V 0 Gesamtsystem se Kugel mt Radus R, Volumen V = 4/3πR 3, Rand V R Zusammenhängendes Gebet Potental Φ mt Φ = 0 st endeutg bs auf Konstante. Konstante kann so gewählt werden, dass VR da Φ = 0 Randbedngungen lnear und Φ = 0 lnear Φ u Vorgrff auf Vorlesung Theore II: Lösungen der Laplace-Glechung mt Φ 0 für r können entwckelt werden: Φ(r) = b r + B r r 3 + bzw. v = Φ = b ˆr B 3( r 2 + B ˆr)ˆr r 3 + mt ˆr = r/r. Multpolentwcklung mt Koeffzenten b, B, wobe b, B u wegen Φ u. Wegen Φ = 0 glt: 0 = d 3 Φ Gauss = da n Φ da n Φ = R da v V V R da v V 0 0 Randbedngung Fluss durch Kugel R muss verschwnden: VR da v 4πb + O( 1 R ) = 0 R b = 0 Führender Term st der zwete Term: Φ(r) B r/r 3
114 108 KAPITEL 5. GRUNDBEGRIFFE DER HYDRODYNAMIK Berechne Energe der Flüssgket (knetsche Energe): E = T = 1 2 ρ d 3 r v 2 Zerlege v 2 = u 2 + ( v u) ( v + u) E = 1 2 ρ(u2 (V V 0 ) + I) mt I = d 3 ( v u) ( v + u) Benutze ( v u) = 0 und ( v + u) = (Φ u r) I = d 3 r [( v u)(φ u r)] Gaußscher Satz I = VR da n ( v u)(φ u r ) + V0 da n ( v u) (Φ u r) R 2 ( u n)r S dω (Enhetskugel) 0 Randbedngung Auf der Oberfläche der Kugel R glt: Φ 1 R 2 B n und v 1 R 3 ( B 3( B n) n) n ( v u) = 2 R 3 ( B n) ( u n), (Φ u r) = 1 R 2 ( B n) ( u n)r I = R 3 S dω ( u n) 2 3 dω ( u n) ( B n) + O( 1 Nutze S dω n n j = 4π 3 δ j I = R 3 4π 3 u2 + 4π( B u) = V u 2 + 4π( B u) E = 1 2 ρ(u2 (V V 0 ) u 2 V + 4π( B u) = 1 2 ρu2 V ρ4π( B u)) Da B u, folgt, dass T quadratsch n u st: E = 1 2 m ku u k Zusammenhang mt Gesamtmpuls P der Flüssgket: de = u d P (Grund: Flüssgket rebungsfre Impulsänderung d P wrd vollständg n Energeänderung de umgesetzt. Bedes wrd durch Kraft F auf Körper vermttelt. Arbet dw = F udt = de und Impulsübertrag d P = F dt de = u d P ) P = m k u k bzw. konkret P = 4πρ B ρv 0 u (NB: P st endlch!) Daraus folgt: Wenn u = const., blebt P konstant, d.h. es wrd kene Kraft auf de Flüssgket übertragen. Umgekehrt heßt das aber auch (acto=reacto), dass auch de Flüssgket kene Kraft auf den Körper überträgt! ) Dskusson: Zumndest de Abwesenhet von Zugkraft st enleuchtend: Gäbe es ene Zugkraft F D, dann müsste der Körper permanent Arbet F D udt verrchten Energe müsste über Rebungskräfte dsspert bzw. abtransportert werden. Aber: Energedsspaton gbt es n dealen Flüssgketen ncht. Abtransport st ncht möglch, da v m Unendlchen zu schnell verschwndet. R 3 ) Ver wchtge Voraussetzungen gngen n den Bewes en: () Potentalströmung. () Körper st endlch ausgedehnt. De Flüssgket strömt nnerhalb enes enfach zusammenhängenden Gebetes darum herum. () De Flüssgket st unendlch ausgedehnt. Falls () ncht zutrfft (z.b. tangentale Instabltäten) kann man gar nchts sagen. (Aber n desem Fall muss man soweso de vollen Naver-Stokes-Glechungen rechnen). Falls () ncht zutrfft, z.b. unendlch langer Zylnder sehe nächster Abschntt (zwedmensonale Strömungen) Falls () ncht zutrfft, z.b. n der Nähe ener Oberfläche: En Körper, der parallel zu ener Oberfläche bewegt wrd, erfährt ene Zugkraft! Das hängt damt zusammen, dass Oberflächenwellen erzeugt werden, de kontnuerlch Energe abtransporteren können ( Wellenzugkraft ) Nach dem d Alembertsche Paradoxon sollte es n dealen Flüssgketen auch kenen Auftreb geben. Warum können dann aber Flugzeuge flegen?
115 5.4. IDEALE FLÜSSIGKEITEN Warum Flugzeuge flegen Argument: Auf sehr großen Skalen (vel größer als das Flugzeug) kann man de Luftströmungen ncht mehr als Potentalströmungen annähern Lokal, n der Umgebung der Flügel, st de Darstellung als Potentalströmung zwar ganz gut. Auf deser Skala sollte man aber das Flugzeug ncht mehr als dredmensonales Objekt beschreben. De Strömungsverhältnsse werden besser durch zwedmensonale Strömungen um enen quas unendlch ausgedehnten Flugzeugflügel beschreben. Untersuche daher Auftreb und Zugkraft be Objekten, de von zwedmensonalen Strömungen umströmt werden. Betrachte Objekt (z.b. Querschntt durch unendlchen langer Zylnder oder Flugzeugflügel), dass sch mt glechförmger Geschwndgket durch ene Potentalströmung bewegt ( v = 0, ω = 0). NB: De Voraussetzung () für das d Alembertsche Paradoxon trfft dann ncht mehr zu. Insbesondere muss es ken endeutges Potental Φ mehr geben, da das Strömungsgebet ncht mehr enfach zusammenhängend st Möglchket von Zrkulaton trotz ω 0. Frage: Was ändert sch dadurch? Wähle desmal das Bezugssystem so, dass das Objekt n Ruhe st. Im Unendlchen ströme das Flud n x-rchtung mt Geschwndgket v F D = F e x : Kraft Strömung; FL = F e y : Kraft Strömung a) Das Theorem von Blasus Betrachte ruhenden Körper n ener Strömung (zwe Dmensonen) Defnere komplexe Geschwndgket w(z) = v x v y mt z = x + y. NB: Mt v = x v x + y v y = 0 und v = x v y y v x = 0 snd de Cauchy-Remannschen Dfferentalglechunen erfüllt. w(z) st ene analytsche (holomorphe) Funkton von z. Dann glt: F D F L = ρ 2 w 2 (z) dz Rand d. Körpers (Bewes: Kraftblanz: Kräfte auf Rand snd Normalkräfte df = np dl (P : Druck, dl: Länge enes Oberflächenelementes, n dl = ( dy dx )) Betrag zur Zugkraft: df D = P dy Betrag zum Auftreb: df L = P dx Kombnere df D df L = P dy P dx = P dz F D F L = P dz Bernoullglechung (ohne Gravtaton): P + ρ 2 v2 = Bρ = const. P dz = Bρ dz + ρ 2 dz (vx 2 + vy) 2 = ρ 2 dz (v x + v y)(v x v y) 0 Randbedngungen: ( vx ) ( dx vx+vy= v exp(θ) ) v y dy dx+dy= dz exp(θ) } selbes θ dz (v x + v y) = dz (v x v y) = ρ 2 dz(v x v y) 2 = ρ 2 dz w 2 )
Wiederholung: Newtonsche Mechanik
 Kaptel 1 Weerholung: Newtonsche Mechank c Copyrght 2012 Freerke Schm 1 1.1 De Newtonschen Axome 1.1.1 Wortlaut (übersetzt) aus: prncpa mathematca phlosophae naturals I) Jeer Körper verharrt m Zustan er
Kaptel 1 Weerholung: Newtonsche Mechank c Copyrght 2012 Freerke Schm 1 1.1 De Newtonschen Axome 1.1.1 Wortlaut (übersetzt) aus: prncpa mathematca phlosophae naturals I) Jeer Körper verharrt m Zustan er
Inhaltsverzeichnis. Vorbemerkungen 1
 Inhaltsverzechns Vorbemerkungen 1 1 Newtonsche Mechank 5 1.1 De Newtonschen Axome........................ 5 1.1.1 Wortlaut (übersetzt)...................... 5 1.1.2 Präzserung der knematschen Begrffe...........
Inhaltsverzechns Vorbemerkungen 1 1 Newtonsche Mechank 5 1.1 De Newtonschen Axome........................ 5 1.1.1 Wortlaut (übersetzt)...................... 5 1.1.2 Präzserung der knematschen Begrffe...........
Theoretische Physik: Mechanik
 Merln Mtschek, Verena Walbrecht Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 3 Technsche Unverstät München 1 Fakultät für Physk Merln Mtschek, Verena Walbrecht Inhaltsverzechns 1 Symmetren
Merln Mtschek, Verena Walbrecht Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 3 Technsche Unverstät München 1 Fakultät für Physk Merln Mtschek, Verena Walbrecht Inhaltsverzechns 1 Symmetren
Theoretische Physik: Mechanik
 Ferenkurs Theoretsche Physk: Mechank Sommer 018 Vorlesung 4 (mt freundlcher Genehmgung von Gramos Qerm, Jakob Unfred und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns
Ferenkurs Theoretsche Physk: Mechank Sommer 018 Vorlesung 4 (mt freundlcher Genehmgung von Gramos Qerm, Jakob Unfred und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns
Inhaltsverzeichnis. Vorbemerkungen 1
 Inhaltsverzechns Vorbemerkungen 1 1 Newtonsche Mechank 5 1.1 De Newtonschen Axome........................ 5 1.1.1 Wortlaut (übersetzt)...................... 5 1.1.2 Präzserung der knematschen Begrffe...........
Inhaltsverzechns Vorbemerkungen 1 1 Newtonsche Mechank 5 1.1 De Newtonschen Axome........................ 5 1.1.1 Wortlaut (übersetzt)...................... 5 1.1.2 Präzserung der knematschen Begrffe...........
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
Theoretsche Physk 2 (Theoretsche Mechank Prof. Dr. Th. Feldmann 28. Oktober 2013 Kurzzusammenfassung Vorlesung 4 vom 25.10.2013 1.6 Dynamk mehrerer Massenpunkte Dynamk für = 1... N Massenpunkte mt.a. komplzerter
Die Hamilton-Jacobi-Theorie
 Kaptel 7 De Hamlton-Jacob-Theore Ausgearbetet von Rolf Horn und Bernhard Schmtz 7.1 Enletung Um de Hamlton schen Bewegungsglechungen H(q, p q k = p k H(p, q ṗ k = q k zu verenfachen, führten wr de kanonschen
Kaptel 7 De Hamlton-Jacob-Theore Ausgearbetet von Rolf Horn und Bernhard Schmtz 7.1 Enletung Um de Hamlton schen Bewegungsglechungen H(q, p q k = p k H(p, q ṗ k = q k zu verenfachen, führten wr de kanonschen
Theoretische Physik: Mechanik
 Ferenkurs Theoretsche Physk: Mechank Sommer 2017 Vorlesung 2 (mt freundlcher Genehmgung von Merln Mtscheck und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme
Ferenkurs Theoretsche Physk: Mechank Sommer 2017 Vorlesung 2 (mt freundlcher Genehmgung von Merln Mtscheck und Verena Walbrecht) Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme
Noethertheorem. 30. Januar 2012
 Noethertheorem 30. Januar 2012 1 Inhaltsverzechns 1 Symmetre 3 1.1 Symmetre n der Geometre................... 3 1.2 Symmetre n der Mathematk.................. 3 1.3 Symmetre n der Physk.....................
Noethertheorem 30. Januar 2012 1 Inhaltsverzechns 1 Symmetre 3 1.1 Symmetre n der Geometre................... 3 1.2 Symmetre n der Mathematk.................. 3 1.3 Symmetre n der Physk.....................
Theoretische Physik: Mechanik
 Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 2 Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme von Massenpunkten 3 1.1 Schwerpunktsmpuls..............................
Ferenkurs Theoretsche Physk: Mechank Sommer 2013 Vorlesung 2 Technsche Unverstät München 1 Fakultät für Physk Inhaltsverzechns 1 Systeme von Massenpunkten 3 1.1 Schwerpunktsmpuls..............................
18. Vorlesung Sommersemester
 8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
8. Vorlesung Sommersemester Der Drehmpuls des starren Körpers Der Drehmpuls des starren Körpers st etwas komplzerter. Wenn weder de Wnkelgeschwndgket um de feste Rotatonsachse st, so wrd mt Hlfe des doppelten
Dynamik starrer Körper
 Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
Dynamk starrer Körper Bewegungen starrer Körper können n Translaton und Rotaton zerlegt werden. De Rotaton stellt enen nneren Frehetsgrad des Körpers dar, der be Punktmassen ncht exstert. Der Schwerpunkt
Klassische Theoretische Physik II (Theorie B) Sommersemester 2016
 Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
Karlsruher Insttut für Technologe Insttut für Theore der Kondenserten Matere Klasssche Theoretsche Physk II Theore B Sommersemester 016 Prof. Dr. Alexander Mrln Musterlösung: Blatt 7. PD Dr. Igor Gorny,
Theoretische Physik. Zur Vorbereitung der Vordiplomsprüfung. Hanno Rein
 Theoretsche Physk Zur Vorberetung der Vordplomsprüfung http://hanno-ren.de 6. Aprl 005 Vordplom - Theoretsche Physk Mechank - Sete Inhaltsverzechns Newton sche Mechank. Koordnatensysteme............. Newton
Theoretsche Physk Zur Vorberetung der Vordplomsprüfung http://hanno-ren.de 6. Aprl 005 Vordplom - Theoretsche Physk Mechank - Sete Inhaltsverzechns Newton sche Mechank. Koordnatensysteme............. Newton
Experimentalphysik 1. Vorlesung 1
 Technsche Unverstät München Fakultät für Physk Ferenkurs Expermentalphysk 1 WS 2016/17 Vorlesung 1 Ronja Berg (ronja.berg@tum.de) Katharna Sche (katharna.sche@tum.de) Inhaltsverzechns 1 Klasssche Mechank
Technsche Unverstät München Fakultät für Physk Ferenkurs Expermentalphysk 1 WS 2016/17 Vorlesung 1 Ronja Berg (ronja.berg@tum.de) Katharna Sche (katharna.sche@tum.de) Inhaltsverzechns 1 Klasssche Mechank
I) Mechanik 1.Kinematik (Bewegung)
 I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
Kapitel 5. Symmetrien und Erhaltungsgrößen. 5.1 Symmetrietransformationen
 Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
Kaptel 5 Symmetren un Erhaltungsgrößen 5.1 Symmetretransformatonen Betrachte en mechansches System mt en Koornaten q 1,... q f un er Lagrangefunkton L(q 1,... q f, q 1,... q f, t). Nun soll ene Transformaton
Kreisel. koerperfestes KS. z y. raumfestes KS. Starrer Körper: System von Massepunkten m i, deren Abstände r i r j untereinander konstant sind.
 Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
Kresel z y koerperfestes KS z y x raumfestes KS x Starrer Körper: System von Massepunkten m, deren Abstände r r j unterenander konstant snd. Der Zustand läßt sch beschreben durch: Poston des Schwerpunktes,
Der starre Körper. 1 Grundlagen. Dominik Fauser. 1.1 Denition. 1.2 Freiheitsgrade
 Der starre Körper Domnk Fauser 1 Grundlagen 1.1 Denton Als enen starren Körper bezechnet man en System von Massepunkten m, deren Abstände zuenander konstant snd: r j = r r j. Mest betrachtet man ene sehr
Der starre Körper Domnk Fauser 1 Grundlagen 1.1 Denton Als enen starren Körper bezechnet man en System von Massepunkten m, deren Abstände zuenander konstant snd: r j = r r j. Mest betrachtet man ene sehr
Physik A VL11 ( )
 Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
Physk A VL11 (0.11.01) Dynamk der Rotatonsbewegung I Kresbewegung und Kräfte Drehmoment und räghetsmoment Kresbewegung und Kräfte en Massepunkt (Schwerpunkt) führt nur ene ranslatonsbewegung aus ausgedehnte
I)1. Kinematik. EP WS 2009/10 Dünnweber/Faessler
 I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
I)1. Knematk I) Mechank 1.Knematk (Bewegung) 2. Dynamk on Massenpunkten (Enfluss on Kräften) 3. Starre Körper 4.Deformerbare Meden 5. Schwngungen, Wellen, Akustk I)1. Knematk Bewegungslehre (Zel: Quanttate
d Alambert: Variationsprinzip in Differentialform (äquivalent zum Hamilton-Prinzip) = 0 (d Alambertsches Prinzip; δw = Z δr = 0 )
 Zusammenfassung Theoretsche Mechan d Alambert: Varatonsprnzp n Dfferentalform (äuvalent zum amlton-prnzp) δw ( F p ) * δr 0 (d Alambertsches Prnzp; δw Z δr 0 ) m allg.: p m * r m statschen Fall st: p 0
Zusammenfassung Theoretsche Mechan d Alambert: Varatonsprnzp n Dfferentalform (äuvalent zum amlton-prnzp) δw ( F p ) * δr 0 (d Alambertsches Prnzp; δw Z δr 0 ) m allg.: p m * r m statschen Fall st: p 0
Theoretische Physik 1 Mechanik
 Technsche Unverstät München Fakultät für Physk Ferenkurs Theoretsche Physk 1 Mechank Skrpt zu Vorlesung 4: Starrer Körper, Hamlton-Formalsmus gehalten von: Markus Krottenmüller & Markus Perner 30.08.01
Technsche Unverstät München Fakultät für Physk Ferenkurs Theoretsche Physk 1 Mechank Skrpt zu Vorlesung 4: Starrer Körper, Hamlton-Formalsmus gehalten von: Markus Krottenmüller & Markus Perner 30.08.01
3. Vorlesung Sommersemester
 3. Vorlesung Sommersemester 1 Bespele (Fortsetzung) 1. Der starre Körper: Formulerung der Zwangsbedngungen später. Anschaulch snd schon de Frehetsgrade: dre der Translaton (z. B. Schwerpuntsoordnaten)
3. Vorlesung Sommersemester 1 Bespele (Fortsetzung) 1. Der starre Körper: Formulerung der Zwangsbedngungen später. Anschaulch snd schon de Frehetsgrade: dre der Translaton (z. B. Schwerpuntsoordnaten)
16. Vorlesung Sommersemester
 16. Vorlesung Sommersemester 1 Das Egenwertproblem In allgemener Form hat das Egenwertproblem de Form A x = λ x, (1) wobe A ene n n-matrx, x en n-dmensonaler Vektor und λ der Egenwert st (n Englsch: egenvector,
16. Vorlesung Sommersemester 1 Das Egenwertproblem In allgemener Form hat das Egenwertproblem de Form A x = λ x, (1) wobe A ene n n-matrx, x en n-dmensonaler Vektor und λ der Egenwert st (n Englsch: egenvector,
Zusammenfassung. 1) Falls Zwangsbedinungen die Freiheitsgrade einschränken, kann man die abhängige Koordinaten aus der Lagrangfunktion elimieren;
 Zusammenfassung 1) Falls Zwangsbednungen de Frehetsgrade enschränken, kann man de abhängge Koordnaten aus der Lagrangfunkton elmeren; 2) Es st auch möglch de Zwangsbednungen mt Hlfe der Lagrangefaktoren
Zusammenfassung 1) Falls Zwangsbednungen de Frehetsgrade enschränken, kann man de abhängge Koordnaten aus der Lagrangfunkton elmeren; 2) Es st auch möglch de Zwangsbednungen mt Hlfe der Lagrangefaktoren
Kapitel 5 Systeme von Massenpunkten, Stöße
 Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
Katel 5 ystee von Massenunkten, töße Drehoente und Drehuls enes Telchensystes O t : z r r r F x r F F F y F F t (acto = reacto) : F t äußeren Kräften F und F und nneren Kräften F = -F Drehoente : D D r
Rotation (2. Versuch)
 Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Rotaton 2. Versuch Bekannt snd berets Vektorfelder be denen das Lnenntegral über ene geschlossene Kurve Null wrd Stchworte: konservatve Kraft Potentalfelder Gradentenfeld. Es gbt auch Vektorfelder be denen
Vorlesung 3 Differentialgeometrie in der Physik 13
 Vorlesung 3 Dfferentalgeometre n der Physk 13 Bemerkung. Ist M Manngfaltgket, p M und φ : U R n Karte mt p U, so nennt man U auch Koordnatenumgebung und φ auch Koordnatensystem n p. Bespel 2.4 Seen R >
Vorlesung 3 Dfferentalgeometre n der Physk 13 Bemerkung. Ist M Manngfaltgket, p M und φ : U R n Karte mt p U, so nennt man U auch Koordnatenumgebung und φ auch Koordnatensystem n p. Bespel 2.4 Seen R >
Allgemeine Formulierung der Punktmechanik
 Kaptel 3 Allgemene Formulerung der Punktmechank Axom 2.2 besagt, daß der zetlche Bewegungsablauf enes Massenpunktes berechnet werden kann, wenn de Kräfte, welche auf den Massenpunkt wrken, vorgegeben snd.
Kaptel 3 Allgemene Formulerung der Punktmechank Axom 2.2 besagt, daß der zetlche Bewegungsablauf enes Massenpunktes berechnet werden kann, wenn de Kräfte, welche auf den Massenpunkt wrken, vorgegeben snd.
22. Vorlesung Sommersemester
 22 Vorlesung Sommersemester 1 Bespel 2: Würfel mt festgehaltener Ecke In desem Fall wählt man den Koordnatenursprung n der Ecke und der Würfel st durch den Berech x = 0 a, y = 0 a und z = 0 a bestmmt De
22 Vorlesung Sommersemester 1 Bespel 2: Würfel mt festgehaltener Ecke In desem Fall wählt man den Koordnatenursprung n der Ecke und der Würfel st durch den Berech x = 0 a, y = 0 a und z = 0 a bestmmt De
3 Elastizitätstheorie
 3 Elastztätstheore Für en elastsches Medum nmmt man enen spannungsfreen Referenzzustand an, der n Eulerkoordnaten durch x = Ax, t) gegeben st. Abwechungen werden beschreben durch de Verschebung ux, t)
3 Elastztätstheore Für en elastsches Medum nmmt man enen spannungsfreen Referenzzustand an, der n Eulerkoordnaten durch x = Ax, t) gegeben st. Abwechungen werden beschreben durch de Verschebung ux, t)
1.4 Dynamik, Newton sche Axiome ( Postulate) der klassischen (Punkt)Mechanik
 Woche.doc, 1/.1.14 1.4 Dynamk, Newton sche Aome ( Postulate) der klassschen (Punkt)Mechank Ausgangspunkt: De Knematk sagt nchts über de Ursache der Bewegung von Körpern n Raum und Zet. In der Dynamk wrd
Woche.doc, 1/.1.14 1.4 Dynamk, Newton sche Aome ( Postulate) der klassschen (Punkt)Mechank Ausgangspunkt: De Knematk sagt nchts über de Ursache der Bewegung von Körpern n Raum und Zet. In der Dynamk wrd
Experimentalphysik II (Kip SS 2007)
 permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
permentalphsk II (Kp SS 007) Zusatvorlesungen: Z-1 n- und mehrdmensonale Integraton Z- Gradent, Dvergen und Rotaton Z-3 Gaußscher und Stokesscher Integralsat Z-4 Kontnutätsglechung Z-5 lektromagnetsche
Theoretische Mechanik WS 2007/08. Inhaltsverzeichnis
 Theoretsche Mechank Inhaltsverzechns 0 Lteratur 6 WS 007/08 Harald Jeschke, Unverstät des Saarlandes/Unverstät Frankfurt auf Grundlage enes Skrpts von Claudus Gros, Unverstät Frankfurt 1 Bewegungsglechungen
Theoretsche Mechank Inhaltsverzechns 0 Lteratur 6 WS 007/08 Harald Jeschke, Unverstät des Saarlandes/Unverstät Frankfurt auf Grundlage enes Skrpts von Claudus Gros, Unverstät Frankfurt 1 Bewegungsglechungen
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 009 UNIVERSITÄT KARLSRUHE Blatt 4 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 16: (Success Run, Fortsetzung)
INSTITUT FÜR STOCHASTIK SS 009 UNIVERSITÄT KARLSRUHE Blatt 4 Prv.-Doz. Dr. D. Kadelka Dpl.-Math. W. Lao Übungen zur Vorlesung Stochastsche Prozesse Musterlösungen Aufgabe 16: (Success Run, Fortsetzung)
Lösungen der Aufgaben zu Kapitel 2
 Lösungen der Aufgaben zu Kaptel Abschntt 1 Aufgabe 1 Wr benutzen de Potenzrechenregeln, um ene Potenz von mt geradem Eponenten n oder mt ungeradem Eponenten n + 1 we folgt darzustellen: n n und n+1 n n
Lösungen der Aufgaben zu Kaptel Abschntt 1 Aufgabe 1 Wr benutzen de Potenzrechenregeln, um ene Potenz von mt geradem Eponenten n oder mt ungeradem Eponenten n + 1 we folgt darzustellen: n n und n+1 n n
Zusammenfassung. 1. Die Bewegungsintegrale sind eng mit den Symmetrien der Wirkung verbunden. Was das genau bedeutet, zeigt das Noether-Theorem.
 Zusaenfassung 1. De Bewegungsntegrale snd eng t den Syetren der Wrkung verbunden. Was das genau bedeutet, zegt das Noether-Theore. Noether-Theore: Falls de Wrkung enes echansches Systes unter der folgenden
Zusaenfassung 1. De Bewegungsntegrale snd eng t den Syetren der Wrkung verbunden. Was das genau bedeutet, zegt das Noether-Theore. Noether-Theore: Falls de Wrkung enes echansches Systes unter der folgenden
9 Komplexe Zahlen ( ) ( ) 9.1 Ziele. 9.2 Warum braucht man komplexe Zahlen? 9.3 Darstellung von komplexen Zahlen. r 2. j 2. j 1.
 Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
9 Komplexe Zahlen ( ) ( ) 9.1 Ziele. 9.2 Warum braucht man komplexe Zahlen? 9.3 Darstellung von komplexen Zahlen. r 2. j 2. j 1.
 Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Mathematk I / Komplexe Zahlen 9 Komplexe Zahlen 9. Zele Am Ende deses Kaptels hast Du ene Grundvorstellung was komplexe Zahlen snd. Du kannst se grafsch darstellen und enfache Berechnungen durchführen.
Holonome Mehrkörpersysteme
 Kaptel 6 Holonome Mehrkörpersysteme In Anlehnung an de Vorgehenswese be Massenpunktsystemen n Kaptel 5 werden n desem Kaptel de Formulerungen der Bewegungsglechungen von Mehrkörpersystemen mt holonomen
Kaptel 6 Holonome Mehrkörpersysteme In Anlehnung an de Vorgehenswese be Massenpunktsystemen n Kaptel 5 werden n desem Kaptel de Formulerungen der Bewegungsglechungen von Mehrkörpersystemen mt holonomen
4. Lagrange-Formalismus
 y(t) ϑ 4. Lagrange-Formalsmus 4.0 Enführung Abbldung 4.1: Das sphärsche Pendel mt bewegtem Aufhängepunkt. R F mg Zel st es, enen enfachen Zugang zu komplzerten mechanschen Systemen zu entwckeln. Nach ener
y(t) ϑ 4. Lagrange-Formalsmus 4.0 Enführung Abbldung 4.1: Das sphärsche Pendel mt bewegtem Aufhängepunkt. R F mg Zel st es, enen enfachen Zugang zu komplzerten mechanschen Systemen zu entwckeln. Nach ener
10 Einführung in die Statistische Physik
 10 Enführung n de Statstsche Physk More s dfferent! P.W. Anderson, Nobelpres 1977 10.1 Prolegomena Technsch gesehen st de Rolle der Statstschen Mechank der Glechgewchtssysteme, ausgehend von unseren Kenntnsse
10 Enführung n de Statstsche Physk More s dfferent! P.W. Anderson, Nobelpres 1977 10.1 Prolegomena Technsch gesehen st de Rolle der Statstschen Mechank der Glechgewchtssysteme, ausgehend von unseren Kenntnsse
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materalen zur Vorlesung Theoretsche Mechank, WS 005/06 Dörte Hansen Semnar 0 Starrer Körper und Kreseltheore. Der starre Körper.. A dfferent pont of vew Raum -und körperfeste Koordnatensysteme
Ergänzende Materalen zur Vorlesung Theoretsche Mechank, WS 005/06 Dörte Hansen Semnar 0 Starrer Körper und Kreseltheore. Der starre Körper.. A dfferent pont of vew Raum -und körperfeste Koordnatensysteme
19. Vorlesung Sommersemester
 19. Vorlesung Sommersemester 1 Allgemene Bewegung des starren Körpers Bsher wurde nur der Fall behandelt, dass de Drehachse festgehalten wrd. Im allgemenen Fall kommen als Probleme hnzu, dass 1. de Drehachse
19. Vorlesung Sommersemester 1 Allgemene Bewegung des starren Körpers Bsher wurde nur der Fall behandelt, dass de Drehachse festgehalten wrd. Im allgemenen Fall kommen als Probleme hnzu, dass 1. de Drehachse
Klassische Mechanik. von Herbert Goldstein, Charles P Poole, Jr, John L Safko, Sr. 1. Auflage
 Klasssche Mechank von Herbert Goldsten, Charles P Poole, Jr, John L Safko, Sr 1. Auflage Klasssche Mechank Goldsten / Poole, Jr / Safko, Sr schnell und portofre erhältlch be beck-shop.de DIE FACHBUCHHANDLUNG
Klasssche Mechank von Herbert Goldsten, Charles P Poole, Jr, John L Safko, Sr 1. Auflage Klasssche Mechank Goldsten / Poole, Jr / Safko, Sr schnell und portofre erhältlch be beck-shop.de DIE FACHBUCHHANDLUNG
Arbeitsgruppe Radiochemie Radiochemisches Praktikum P 06. Einführung in die Statistik. 1. Zählung von radioaktiven Zerfällen und Statistik 2
 ETH Arbetsgruppe Radocheme Radochemsches Praktkum P 06 Enführung n de Statstk INHALTSVERZEICHNIS Sete 1. Zählung von radoaktven Zerfällen und Statstk 2 2. Mttelwert und Varanz 2 3. Momente ener Vertelung
ETH Arbetsgruppe Radocheme Radochemsches Praktkum P 06 Enführung n de Statstk INHALTSVERZEICHNIS Sete 1. Zählung von radoaktven Zerfällen und Statstk 2 2. Mttelwert und Varanz 2 3. Momente ener Vertelung
MOD-01 LAGRANGE FORMALISMUS -- TEIL 1
 MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
MOD- LAGRAGE FORMALISMUS -- EIL. Zustandsfunktonen Defnton -: Zustandsfunkton Ene Zustandsfunkton W( () t, t) = W(, t) bzw. W ( ) st jede belebge skalare Funkton der Zustandsgrößen () t und der Zet t,
1 Mehrdimensionale Analysis
 1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
1 Mehrdmensonale Analyss Bespel: De Gesamtmasse der Erde st ene Funton der Erddchte ρ Erde und des Erdradus r Erde De Gesamtmasse der Erde st dann m Erde = V Erde ρ Erde Das Volumen ener Kugel mt Radus
3.6 Molekulare Dynamik
 3.6 Molekulare Dynamk In den letzten 5 Jahrzehnten wurden drekte numersche Smulatonen zur statstschen Auswertung von Veltelchensystemen mmer wchtger. So lassen sch Phasenübergänge, aber auch makroskopsche
3.6 Molekulare Dynamk In den letzten 5 Jahrzehnten wurden drekte numersche Smulatonen zur statstschen Auswertung von Veltelchensystemen mmer wchtger. So lassen sch Phasenübergänge, aber auch makroskopsche
( ) γ. (t 1 ) (t 2 ) = Arg γ 2(t 2 )
 Funktonentheore, Woche 10 Bholomorphe Abbldungen 10.1 Konform und bholomorph Ene konforme Abbldung erhält Wnkel und Orenterung. Damt st folgendes gement: Wenn sch zwe Kurven schneden, dann schneden sch
Funktonentheore, Woche 10 Bholomorphe Abbldungen 10.1 Konform und bholomorph Ene konforme Abbldung erhält Wnkel und Orenterung. Damt st folgendes gement: Wenn sch zwe Kurven schneden, dann schneden sch
Hamiltonsche Mechanik
 Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
Kaptel 3 Hamltonsche Mechank Das Lagrange-Formalsmus lefert uns de Bewegungsglechungen n der Form von enem System von Dfferentalglechungen zweter Ordnung für verallgemenerte Koordnaten. Solches System
Theoretische Physik B MECHANIK. Vorlesung SS 2003
 Theoretsche Physk B MECHANIK Vorlesung SS 2003 P. Wölfle Insttut für Theore der Kondenserten Matere Fakultät für Physk Unverstät Karlsruhe Homepage: http://www.tkm.un-karlsruhe.de/lehre/ Textverarbetung:
Theoretsche Physk B MECHANIK Vorlesung SS 2003 P. Wölfle Insttut für Theore der Kondenserten Matere Fakultät für Physk Unverstät Karlsruhe Homepage: http://www.tkm.un-karlsruhe.de/lehre/ Textverarbetung:
Einführung in die theoretische Physik 1
 Enführung n de theoretsche hysk 1 rof. Dr. L. Mathey Denstag 15:45 16:45 und Donnerstag 10:45 12:00 Begnn: 23.10.12 Jungus 9, Hörs 2 Mathey Enführung n de theor. hysk 1 1 Grundhypothese der Thermostatk
Enführung n de theoretsche hysk 1 rof. Dr. L. Mathey Denstag 15:45 16:45 und Donnerstag 10:45 12:00 Begnn: 23.10.12 Jungus 9, Hörs 2 Mathey Enführung n de theor. hysk 1 1 Grundhypothese der Thermostatk
Fachbereich Mathematik Prof. K. Grosse-Brauckmann D. Frisch WS 2007/08 10./ Gruppenübung
 Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
Fachberech Mathematk Prof. K. Grosse-Brauckmann D. Frsch WS 27/8./.. 6. Übungsblatt zur Lnearen Algebra für Physker Gruppenübung Aufgabe G7 (Kern, Bld, Rang und Orthogonaltät) Gegeben se ene lneare Abbldung
Theoretische Physik II: Analytische Mechanik und Spezielle Relativitätstheorie
 Theoretsche Physk II: Analytsche Mechank und Spezelle Relatvtätstheore Drk H. Rschke Sommersemester 2010 Inhaltsverzechns 1 Lagrange-Mechank 1 1.1 Zwangskräfte, Zwangsbedngungen und generalserte Koordnaten.....
Theoretsche Physk II: Analytsche Mechank und Spezelle Relatvtätstheore Drk H. Rschke Sommersemester 2010 Inhaltsverzechns 1 Lagrange-Mechank 1 1.1 Zwangskräfte, Zwangsbedngungen und generalserte Koordnaten.....
Bilderbuch zur Vorlesung Experimentalphysik -1. Struktur der Materie. Verhalten von Materie und Strahlung. Wintersemester 2012/13
 Fragestellung der Physk Blderbuch zur Vorlesung Expermentalphysk - Struktur der Matere Verhalten von Matere und Strahlung Wntersemester / Prof. Dr. Hanspeter Helm Un-Freburg quanttatve Beobachtung (Messung)
Fragestellung der Physk Blderbuch zur Vorlesung Expermentalphysk - Struktur der Matere Verhalten von Matere und Strahlung Wntersemester / Prof. Dr. Hanspeter Helm Un-Freburg quanttatve Beobachtung (Messung)
3 Vorlesung: Lagrange Mechanik I. 3.1 Zwangsbedingungen. Beispiele (nach Kuypers)
 3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
3 Vorlesung: Lagrange Mechank I 3.1 Zwangsbedngungen Im folgenden Kaptel werden wr uns mt Bewegungen beschäftgen, de geometrschen Zwangsbedngungen unterlegen, we etwa der Pendelbewegung, der Bewegung auf
3. Lineare Algebra (Teil 2)
 Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
Mathematk I und II für Ingeneure (FB 8) Verson /704004 Lneare Algebra (Tel ) Parameterdarstellung ener Geraden Im folgenden betrachten wr Geraden m eukldschen Raum n, wobe uns hauptsächlch de Fälle n bzw
4.6 Das Pumping-Lemma für reguläre Sprachen:
 Theoretsche Informatk 1 Vorlesungsskrpt vom Fretag, 30 Jun 000 Index: Erstellt von: (Matrkelnummer: 70899) Sete : 46 Das Pumpng-Lemma für reguläre Sprachen 1 Satz W 1 Zugrundelegende Idee des Pumpng-Lemma
Theoretsche Informatk 1 Vorlesungsskrpt vom Fretag, 30 Jun 000 Index: Erstellt von: (Matrkelnummer: 70899) Sete : 46 Das Pumpng-Lemma für reguläre Sprachen 1 Satz W 1 Zugrundelegende Idee des Pumpng-Lemma
29 zweite Ableitungen der thermodynamischen Potentiale spezifische Wärme (thermischer response) E = = = T V N V N V N = = κ T.
 hermodynamsche resonse -unktonen: 9 zwete Abletungen der thermodynamschen Potentale sezfsche Wärme (thermscher resonse) E C S be konstantem olumen (sochor):,,, be konstantem Druck (sobar): C S Komressbltät
hermodynamsche resonse -unktonen: 9 zwete Abletungen der thermodynamschen Potentale sezfsche Wärme (thermscher resonse) E C S be konstantem olumen (sochor):,,, be konstantem Druck (sobar): C S Komressbltät
Stand: gern gestellte Prüfungsfragen & Definitionen
 Stand: 7.0.98 gern gestellte Prüfungsfragen & Defntonen Klasssche Mechan (mt & ohne Gravtaton, aber: v > h) Stat: Lehre vom Glechgewcht der Kräfte. Se beschäftgt sch mt Kräften an starren
Stand: 7.0.98 gern gestellte Prüfungsfragen & Defntonen Klasssche Mechan (mt & ohne Gravtaton, aber: v > h) Stat: Lehre vom Glechgewcht der Kräfte. Se beschäftgt sch mt Kräften an starren
1 Finanzmathematik. 1.1 Das Modell. Sei Xt
 1.1 Das Modell Se Xt der Pres enes Assets zur Zet t und X = X ) 1 d der Rd +-dmensonale Presprozess. Das Geld kann auch zu dem rskolosen Znssatz r be ener Bank angelegt werden. Der Wert deser Anlage wrd
1.1 Das Modell Se Xt der Pres enes Assets zur Zet t und X = X ) 1 d der Rd +-dmensonale Presprozess. Das Geld kann auch zu dem rskolosen Znssatz r be ener Bank angelegt werden. Der Wert deser Anlage wrd
2 Zufallsvariable und Verteilungen
 Zufallsvarable und Vertelungen 7 Zufallsvarable und Vertelungen Wr wollen uns jetzt mt Zufallsexpermenten beschäftgen, deren Ausgänge durch (reelle) Zahlen beschreben werden können, oder be denen man jedem
Zufallsvarable und Vertelungen 7 Zufallsvarable und Vertelungen Wr wollen uns jetzt mt Zufallsexpermenten beschäftgen, deren Ausgänge durch (reelle) Zahlen beschreben werden können, oder be denen man jedem
Die kanonische Zustandssumme (System) und ihr Zusammenhang mit der molekularen Zustandssumme (Einzelmolekül) unterscheidbare Teilchen:
 De molekulare Zustandssumme βε = e mt β = De kanonsche Zustandssumme (System) und hr Zusammenhang mt der molekularen Zustandssumme (Enzelmolekül) unterschedbare elchen: Q = ununterschedbareelchen Q : =!
De molekulare Zustandssumme βε = e mt β = De kanonsche Zustandssumme (System) und hr Zusammenhang mt der molekularen Zustandssumme (Enzelmolekül) unterschedbare elchen: Q = ununterschedbareelchen Q : =!
Theoretische Physik II Elektrodynamik Blatt 2
 PDDr.S.Mertens M. Hummel Theoretsche Physk II Elektrodynamk Blatt 2 SS 29 8.4.29 1. Rechnen mt Nabla. Zegen Se durch Auswertung n kartesschen Koordnaten de folgende Relaton und werten Se de anderen Relatonen
PDDr.S.Mertens M. Hummel Theoretsche Physk II Elektrodynamk Blatt 2 SS 29 8.4.29 1. Rechnen mt Nabla. Zegen Se durch Auswertung n kartesschen Koordnaten de folgende Relaton und werten Se de anderen Relatonen
Ko- und kontravariante Darstellung
 Ko- und kontravarante Darstellung Physkalsche Sachverhalte snd vom verwendeten Koordnatensystem unabhängg. Sehr oft st es snnvoll, se n verschedenen Koordnatensystemen darzustellen. Berets erwähnt wurden
Ko- und kontravarante Darstellung Physkalsche Sachverhalte snd vom verwendeten Koordnatensystem unabhängg. Sehr oft st es snnvoll, se n verschedenen Koordnatensystemen darzustellen. Berets erwähnt wurden
Zusammenfassung der ersten Vorlesung
 Zusammenfassung der ersten Vorlesung 1. Es geht um de Mechank.. Jedes mechansche System kann mttels ener Lagrangefunkton charaktersert werden. De Lagrangefunkton hängt von den verallgemenerten Koordnaten,
Zusammenfassung der ersten Vorlesung 1. Es geht um de Mechank.. Jedes mechansche System kann mttels ener Lagrangefunkton charaktersert werden. De Lagrangefunkton hängt von den verallgemenerten Koordnaten,
Konkave und Konvexe Funktionen
 Konkave und Konvexe Funktonen Auch wenn es n der Wrtschaftstheore mest ncht möglch st, de Form enes funktonalen Zusammenhangs explzt anzugeben, so kann man doch n velen Stuatonen de Klasse der n Frage
Konkave und Konvexe Funktonen Auch wenn es n der Wrtschaftstheore mest ncht möglch st, de Form enes funktonalen Zusammenhangs explzt anzugeben, so kann man doch n velen Stuatonen de Klasse der n Frage
Ergänzungskurs Physik Teil 1: Theoretische Mechanik
 Vorlesungsskrpt Ergänzungskurs Physk Tel 1: Theoretsche Mechank Angewandte Naturwssenschaft TU Bergakademe Freberg Sandra Glles nach ener Vorlesung von Prof. J. Monecke m Sommersemester 2003 Ma 2004 Inhaltsverzechns
Vorlesungsskrpt Ergänzungskurs Physk Tel 1: Theoretsche Mechank Angewandte Naturwssenschaft TU Bergakademe Freberg Sandra Glles nach ener Vorlesung von Prof. J. Monecke m Sommersemester 2003 Ma 2004 Inhaltsverzechns
Vorlesung Theoretische Mechanik
 Julus-Maxmlans-Unverstät Würzburg Vorlesung Theoretsche Mechank Wntersemester 17/18 Prof. Dr. Johanna Erdmenger Vorläufges Skrpt - wrd laufend aktualsert 1 Enletung Aufgeschreben von Floran Wrth, 20. 10.
Julus-Maxmlans-Unverstät Würzburg Vorlesung Theoretsche Mechank Wntersemester 17/18 Prof. Dr. Johanna Erdmenger Vorläufges Skrpt - wrd laufend aktualsert 1 Enletung Aufgeschreben von Floran Wrth, 20. 10.
Die mathematischen Grundlagen der Wellenmechanik
 De mathematschen Grundlagen der Wellenmechank Zustände und deren Darstellung En physkalsches System wrd durch enen Zustand u charaktersert, ndem es durch ene bestmmte expermentelle Präparaton gebracht
De mathematschen Grundlagen der Wellenmechank Zustände und deren Darstellung En physkalsches System wrd durch enen Zustand u charaktersert, ndem es durch ene bestmmte expermentelle Präparaton gebracht
Herbert Goldstein, Charles P. Poole, Jr., und John L. Safko. Klassische Mechanik
 Herbert Goldsten, Charles P. Poole, Jr., und John L. Safko Klasssche Mechank Wetere Ttel zu desem Thema Kuypers, F. Klasssche Mechank Mt 103 Bespelen und 167 Aufgaben mt Lösungen 608 Seten mt 286 Abbldungen
Herbert Goldsten, Charles P. Poole, Jr., und John L. Safko Klasssche Mechank Wetere Ttel zu desem Thema Kuypers, F. Klasssche Mechank Mt 103 Bespelen und 167 Aufgaben mt Lösungen 608 Seten mt 286 Abbldungen
Theoretische Mechanik
 Theoretsche Mechank (Bachelor of Educaton) C. Tmm Technsche Unverstät Dresden, Insttut für Theoretsche Physk Satz: Chrstna Krüger mt engen Korrekturen gesetzt von Martn Körber Sommersemester 009 Stand:
Theoretsche Mechank (Bachelor of Educaton) C. Tmm Technsche Unverstät Dresden, Insttut für Theoretsche Physk Satz: Chrstna Krüger mt engen Korrekturen gesetzt von Martn Körber Sommersemester 009 Stand:
-70- Anhang: -Lineare Regression-
 -70- Anhang: -Lneare Regressn- Für ene Messgröße y f(x) gelte flgender mathematsche Zusammenhang: y a+ b x () In der Regel läßt sch durch enen Satz vn Messwerten (x, y ) aber kene Gerade zechnen, da de
-70- Anhang: -Lneare Regressn- Für ene Messgröße y f(x) gelte flgender mathematsche Zusammenhang: y a+ b x () In der Regel läßt sch durch enen Satz vn Messwerten (x, y ) aber kene Gerade zechnen, da de
Sei T( x ) die Tangente an den Graphen der Funktion f(x) im Punkt ( x 0, f(x 0 ) ) : T( x ) = f(x 0 ) + f (x 0 ) ( x - x 0 ).
 Taylorentwcklung (Approxmaton durch Polynome). Problemstellung Se T( x ) de Tangente an den Graphen der Funkton f(x) m Punkt ( x 0, f(x 0 ) ) : T( x ) = f(x 0 ) + f (x 0 ) ( x - x 0 ). Dann kann man de
Taylorentwcklung (Approxmaton durch Polynome). Problemstellung Se T( x ) de Tangente an den Graphen der Funkton f(x) m Punkt ( x 0, f(x 0 ) ) : T( x ) = f(x 0 ) + f (x 0 ) ( x - x 0 ). Dann kann man de
Abbildung 3.1: Besetzungszahlen eines Fermigases im Grundzustand (a)) und für eine angeregte Konfiguration (b)).
 44 n n F F a) b) Abbldung 3.: Besetzungszahlen enes Fermgases m Grundzustand (a)) und für ene angeregte Konfguraton (b)). 3.3 Ferm Drac Statstk In desem Abschntt wollen wr de thermodynamschen Egenschaften
44 n n F F a) b) Abbldung 3.: Besetzungszahlen enes Fermgases m Grundzustand (a)) und für ene angeregte Konfguraton (b)). 3.3 Ferm Drac Statstk In desem Abschntt wollen wr de thermodynamschen Egenschaften
Lagrangesche Mechanik
 Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
Kaptel Lagrangesche Mechank De Newtonsche Mechank hat enge Nachtele. 1) De Bewegungsglechungen snd ncht kovarant, d.h. se haben n verschedenen Koordnatensystemen verschedene Form. Z.B., zwedmensonale Bewegungsglechungen
Bedingte Entropie. Bedingte Entropie. Bedingte Entropie. Kapitel 4: Bedingte Entropie I(X;Y) H(X Y) H(Y) H(X) H(XY)
 Bedngte Entrope Kaptel : Bedngte Entrope Das vorherge Theorem kann durch mehrfache Anwendung drekt verallgemenert werden H (... H ( = Ebenso kann de bedngt Entrope defnert werden Defnton: De bedngte Entrope
Bedngte Entrope Kaptel : Bedngte Entrope Das vorherge Theorem kann durch mehrfache Anwendung drekt verallgemenert werden H (... H ( = Ebenso kann de bedngt Entrope defnert werden Defnton: De bedngte Entrope
Seminar Analysis und Geometrie Professor Dr. Martin Schmidt - Markus Knopf - Jörg Zentgraf. - Fixpunktsatz von Schauder -
 Unverstät Mannhem Fakultät für Mathematk und Informatk Lehrstuhl für Mathematk III Semnar Analyss und Geometre Professor Dr. Martn Schmdt - Markus Knopf - Jörg Zentgraf - Fxpunktsatz von Schauder - Ncole
Unverstät Mannhem Fakultät für Mathematk und Informatk Lehrstuhl für Mathematk III Semnar Analyss und Geometre Professor Dr. Martn Schmdt - Markus Knopf - Jörg Zentgraf - Fxpunktsatz von Schauder - Ncole
Werkstoffmechanik SS11 Baither/Schmitz. 5. Vorlesung
 Werkstoffmechank SS11 Bather/Schmtz 5. Vorlesung 0.05.011 4. Mkroskopsche Ursachen der Elastztät 4.1 Energeelastztät wrd bestmmt durch de Wechselwrkungspotentale zwschen den Atomen, oft schon auf der Bass
Werkstoffmechank SS11 Bather/Schmtz 5. Vorlesung 0.05.011 4. Mkroskopsche Ursachen der Elastztät 4.1 Energeelastztät wrd bestmmt durch de Wechselwrkungspotentale zwschen den Atomen, oft schon auf der Bass
Eine kurze Einführung in die Dichtefunktionaltheorie (DFT)
 Ene kurze Enführung n de Dchtefunktonaltheore (DFT) Mchael Martns Lteratur: W. Koch, M.C. Holthausen A Chemst s Gude to Densty Functonal Theory Wley-VCH 2001 Dchtefunktonaltheore p.1 Enletung Im Falle
Ene kurze Enführung n de Dchtefunktonaltheore (DFT) Mchael Martns Lteratur: W. Koch, M.C. Holthausen A Chemst s Gude to Densty Functonal Theory Wley-VCH 2001 Dchtefunktonaltheore p.1 Enletung Im Falle
1 Definition und Grundbegriffe
 1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
1 Defnton und Grundbegrffe Defnton: Ene Glechung n der ene unbekannte Funkton y y und deren Abletungen bs zur n-ten Ordnung auftreten heßt gewöhnlche Dfferentalglechung n-ter Ordnung Möglche Formen snd:
Denavit-Hartenberg-Notation
 DENAVIT und HARTENBERG haben ene Methode engeführt, de es erlaubt für alle knematsche Ketten de Lagen der Gleder zuenander enhetlch auszudrücken. De Gelenke, de de Gleder mtenander verbnden, dürfen dabe
DENAVIT und HARTENBERG haben ene Methode engeführt, de es erlaubt für alle knematsche Ketten de Lagen der Gleder zuenander enhetlch auszudrücken. De Gelenke, de de Gleder mtenander verbnden, dürfen dabe
Elemente der Mathematik - Sommer 2016
 Elemente der Mathematk - Sommer 2016 Prof Dr Matthas Lesch, Regula Krapf Lösungen Übungsblatt 3 Aufgabe 9 (10 Punkte) Das Horner-Schema st ene Methode zum Auswerten enes Polynoms n a0 x an der Stelle s
Elemente der Mathematk - Sommer 2016 Prof Dr Matthas Lesch, Regula Krapf Lösungen Übungsblatt 3 Aufgabe 9 (10 Punkte) Das Horner-Schema st ene Methode zum Auswerten enes Polynoms n a0 x an der Stelle s
Zur Erinnerung: System von Massenpunkten. dt i dt. 1 dt. Massenschwerpunkt
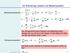 Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
Massenschwerunkt r Zur rnnerung: yste on Massenunkten r dr dt r t M, M dr P dt M M M F dp d dt d M dt dt Ma chwerunktsyste Der chwerunkt enes ystes aus Massenunkten bewegt sch so, als ob er en Körer t
Das zum dualen Problem (10.2) gehörige Barriere-Problem lautet analog
 60 Kaptel 2. Lneare Optmerung 10 Innere-Punkte-Verfahren Lteratur: Geger, Kanzow, 2002, Kaptel 4.1 Innere-Punkte-Verfahren (IP-Verfahren) oder nteror pont methods bewegen sch m Gegensatz zum Smplex-Verfahren
60 Kaptel 2. Lneare Optmerung 10 Innere-Punkte-Verfahren Lteratur: Geger, Kanzow, 2002, Kaptel 4.1 Innere-Punkte-Verfahren (IP-Verfahren) oder nteror pont methods bewegen sch m Gegensatz zum Smplex-Verfahren
Asymptotische Stochastik (SS 2010) Übungsblatt 1 P X. 0, n.
 Insttut für Stochastk PD. Dr. Deter Kadelka Danel Gentner Asymptotsche Stochastk (SS 2) Übungsblatt Aufgabe (Arten von Konvergenz reeller Zufallsvarablen und deren Zusammenhänge) Es seen X,, n N reelle
Insttut für Stochastk PD. Dr. Deter Kadelka Danel Gentner Asymptotsche Stochastk (SS 2) Übungsblatt Aufgabe (Arten von Konvergenz reeller Zufallsvarablen und deren Zusammenhänge) Es seen X,, n N reelle
Facility Location Games
 Faclty Locaton Games Semnar über Algorthmen SS 2006 Klaas Joeppen 1 Abstract Wr haben berets sehr häufg von Nash-Glechgewchten und vor allem von deren Exstenz gesprochen. Das Faclty Locaton Game betet
Faclty Locaton Games Semnar über Algorthmen SS 2006 Klaas Joeppen 1 Abstract Wr haben berets sehr häufg von Nash-Glechgewchten und vor allem von deren Exstenz gesprochen. Das Faclty Locaton Game betet
Eine Kompassnadel, die sich nur um eine vertikale Achse drehen kann, richtet sich entlang der Horizontalkomponente des Erdmagnetfeldes B E,
 IYPT 009 Problem Nr..: Coupled compasses Place a compass on a table. Place a smlar compass next to the frst one and shake t gently to make the needle start oscllatng. The orgnal compass' needle wll start
IYPT 009 Problem Nr..: Coupled compasses Place a compass on a table. Place a smlar compass next to the frst one and shake t gently to make the needle start oscllatng. The orgnal compass' needle wll start
Physik A VL7 (23.10.2012)
 Physk A VL7 (3.0.0) Kräfte und Kräfte-Glechgewchte, Newton sche Axome Kräfte Kräfte-Glechgewchte Hebel und Drehmoment De Newton schen Axome Kräfte De Kraft - st ene gerchtete physkalsche Größe (en Vektor!)
Physk A VL7 (3.0.0) Kräfte und Kräfte-Glechgewchte, Newton sche Axome Kräfte Kräfte-Glechgewchte Hebel und Drehmoment De Newton schen Axome Kräfte De Kraft - st ene gerchtete physkalsche Größe (en Vektor!)
1. Relativität von Raum und Zeit
 K.Bräuer: Phlosophsche Aspekte der modernen Physk, SS 01 1. Relatvtät von Raum und Zet Lcht bretet sch ncht n enem Medum aus, we etwa Wasser. De Ausbretung von Lchtsgnalen st als Kausalzusammenhang zwschen
K.Bräuer: Phlosophsche Aspekte der modernen Physk, SS 01 1. Relatvtät von Raum und Zet Lcht bretet sch ncht n enem Medum aus, we etwa Wasser. De Ausbretung von Lchtsgnalen st als Kausalzusammenhang zwschen
Definition des linearen Korrelationskoeffizienten
 Defnton des lnearen Korrelatonskoeffzenten r xy x y y r x xy y 1 x x y y x Der Korrelatonskoeffzent st en Indkator dafür, we gut de Punkte (X,Y) zu ener Geraden passen. Sen Wert legt zwschen -1 und +1.
Defnton des lnearen Korrelatonskoeffzenten r xy x y y r x xy y 1 x x y y x Der Korrelatonskoeffzent st en Indkator dafür, we gut de Punkte (X,Y) zu ener Geraden passen. Sen Wert legt zwschen -1 und +1.
4. Energie, Arbeit, Leistung, Impuls
 34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
34 35 4. Energe, Arbet, Lestung, Ipuls Zentrale Größen der Physk: Energe E, Enhet Joule ( [J] [N] [kg /s ] Es gbt zwe grundsätzlche Foren on Energe: knetsche Energe: entelle Energe: Arbet, Enhet Joule
Vermessungskunde für Bauingenieure und Geodäten
 Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
Vermessungskunde für Baungeneure und Geodäten Übung 4: Free Statonerung (Koordnatentransformaton) und Flächenberechnung nach Gauß Mlo Hrsch Hendrk Hellmers Floran Schll Insttut für Geodäse Fachberech 13
12 LK Ph / Gr Elektrische Leistung im Wechselstromkreis 1/5 31.01.2007. ω Additionstheorem: 2 sin 2 2
 1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
1 K Ph / Gr Elektrsche estng m Wechselstromkres 1/5 3101007 estng m Wechselstromkres a) Ohmscher Wderstand = ˆ ( ω ) ( t) = sn ( ω t) t sn t ˆ ˆ P t = t t = sn ω t Momentane estng 1 cos ( t) ˆ ω = Addtonstheorem:
