6 Korrektheit des Simplexalgorithmus

Transkript

1 6 Korrektheit des Simplexalgorithmus Folgerung: Es sei L: Ax = b, c T x max LP und A B nicht-degenerierte PZB von L und es gebe c r := c r c B A B A r > 0 a) Falls a r := A B a r 0, dann L unbeschränkt b) Falls es eine positive Komponente in a r gibt, dann ist A B (r) derart, dass c B(r) x B(r) > c B x B. a) x B = A B b (A B a r ), x r =, x j = 0 für alle j N \ {r} ist zulässig für alle > 0 mit c BT x B + c r x r = c BT A B b + c r >0 b) c B (r) x B (r) = c BT (A B b) + c r c BT (A B b) = c B x B. >0 >0 80

2 6 Korrektheit des Simplexalgorithmus Laufzeit: in der bisherigen Version können Endlosschleifen auftreten. Anti-Cycling-Regel: 1) Schreibe alle Variablen in eine Liste L := (l 1,..,l m+n ) = (x 1,..,x n,t 1,..,t m ) 2) Auswahl des Pivotelements: 2a) Auswahl der Spalte r Wähle r {1,...,n} mit c r > 0. Gibt es mehr als eine Möglichkeit für r, wähle r so, dass die zur Spalte r gehörende NBV möglichst weit vorn in L liegt. 2b) Auswahl der Zeile s: Wähle s {1,...,m} mit = min {b i /a ir a ir > 0} =: b s /a sr 1 i m Gibt es mahr als eine Möglichkeit für s, wähle s so, dass die zur Zeile s gehörige BV möglichst weit vorn in L steht. damit: keine Endlosschleifen mehr im schlimmsten Fall O(2 m ) Pivotschritte (kostruierte Eingaben) in Praxis: polynomielles Verhalten 81

3 6 Korrektheit des Simplexalgorithmus Laufzeit: in der Praxis ist der Simplex mit Anti-Cycling oft spürbar langsamer als ohne. deshalb: um Kreisen z uverhindern muss man die Anticycling-Regel nicht in jedem Schritt anwenden. Stattdessen nur, wenn man eine vorgegebene Anzahl Pivotschritte durchgeführt hat, ohne die Ecke zu verlassen. Alternative Anti-Cycling-Regel: Wähle von möglichen Zeilen/Spalten-Kandidaten einen zufälligen aus. Dann wird Ecke mit Wahrscheinlichkeit 1 verlassen. -> hat keine Fans 82

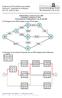
4 7 Das duale Problem Def 5.1. Es sei (L): Ax x max ein LP in kanonischer Form. L heißt primales Problem Das LP (D): b T u min A T u c, u u T A = (A T u) T heißt das zu L duale LP (D = dual(l)). b 1 b 2 c 1 c 2 u 1 u 2 u 3 min c 1 c 2 max 83

5 7 Das duale Problem Lemma 5.1. Es sei (L): Ax max ein LP. Dann ist dual(dual(l)) = L Beweis: dual(l): A T u c, b T u min äquivalent zu D : (-A) T u -c (-b) T u max Dann ist dual(d ): ((-A) T ) T y -b Ay b (-c) T y min c T y max = (L) 84

6 7 Das duale Problem Satz 7.1. Schwache Dualität : Es sei (L): Ax max ein LP. D := dual(l). Seien z L und z D die optimalen Zielfunktionswerte für L und D. Ist beliebiges x zulässig für L und beliebiges u zulässig für D, dann ist Bew: c T x z L z D b T u (a) Wegen x 0 und u T A c T ist c T x u T Ax (b) Wegen u 0 und Ax b ist u T Ax u T b = b T u, weil u,b. Erinnerung: L: Ax max D: A T u c, b T u min Es ist also c T x b T u für alle x und u (jeweils zulässig) Insbesondere ist damit auch z L b T u für alle zulässigen u und damit auch z L z D 85

7 7 Das duale Problem Folgerungen: (a) Wenn x primal zulässige Lösung ist, und y dual zulässige Lösung, und c T x = b T u dann sind x und u optimale Lösungen. (kleiner kann b T u wegen Satz 7.1 nicht werden, und c T x auch nicht größer.) (b) Es sei (L) ein LP, D = dual(l). Ist L unbeschränkt, so hat D keine Lösung. (Wegen Satz 7.1 ist z D α für alle α 86

8 7 Das duale Problem Erinnerung: L: Ax max D: A T u c, b T u min Satz 7.2. Starke Dualität : Wenn das primale oder das duale Problem eine optimale Lösung mit endlichem Wert besitzt, dann besitzt auch das Gegenstück eine optimale Lösung und max c T x = min b T u. Bew: Gezeigt wird: Wenn das primale Problem eine optimale Lösung x besitzt, dann gibt es eine dual zulässige Lösung u, so dass c T x = b T u. Sei x eine optimale primal zulässige Basislösung, generiert vom Simplexalgorithmus. Also: Ax = (A B,A N ) b mit x B = A B b, x N =0. Sei u := (A B ) T c B. x B x N Reduzierte Kosten: c NT c B T c B c N A T B A T N Dann: c A T u = - (A B ) T c B. = 0 c N A NT (A B ) T c B = c N (c B T und c T x = c BT (A B b) = (c BT A B ) T b = u T b 87

9 7 Das duale Problem dual endliches unbegrenzt keine Optimum Lösung primal endliches Optimum unbegrenzt keine Lösung 88

10 7 Das duale Problem Beispiel für: primales und duales Problem haben beide keine Lösung: Maximiere 3x 1 + 2x 2 u.d.n.: 2x 1 2x 2-2x 1 + 2x 2-4 x 1, x 2 0 Minimiere w 1-4w 2 u.d.n. 2w 1 2w 2 3-2w 1 + 2w 2 2 w 1, w

11 7 Das duale Problem, dualer Simplex-Algorithmus Vorbereitung: geg. L: Ax max, mit Schlupfvariablen t 1,...,t m, t i MAX x 1... x n L: Ax b Ax - b = -t x 0 bzw. x 0, t 0 c T x max c T x max primal zulässig, wenn b 0 a a 1n b 1 = -t a m1... a mn b m = -t m c 1... c n z D: A T u c A T u c = s u 0 bzw. u 0, s 0 b T u min -b T u max dual zulässig, wenn c 0 Überschussvariablen MAX x 1... x n u 1... u m a a 1n b 1 = -t a m1... a mn b m = -t m c 1... c n z =...= s 1... s n 90

12 7 Das duale Problem, dualer Simplex-Algorithmus Dualer Simplex-Algorithmus für dual zulässige Tableaus: Ein Tableau heißt dual zulässig, wenn c

13 7 Das duale Problem, Beispiel L: Max -4x 1 2x 2 udn. -x 1 2x 2-2 -x 1 + x 2 MAX x 1 x 2 x 3 x = -x = -x D: Min -2u 1 u 2 Max 2u 1 + u 2 udn. u 1 + u 2 4 2u 1 - u 2 2 MAX u 1 u 2 u 3 u = -u = -u MAX x 1 x 2 x 3 x 4 1/2 1 /2 0 1 = -x 2-3/2 0 1/2 1-2 = -x MAX u 1 u 2 u 3 u 4 0 3/2 1 /2 3 = -u 3 1 /2 0 1/2 1 = -u MAX x 1 x 2 x 3 x /3 /3 1/3 = -x /3-2/3 4/3 = -x MAX u 1 u 2 u 3 u /3 /3 2 = -u /3 1/3 2 = -u /3 /3-6 92