Teil II: Quantenmechanik
|
|
|
- Anke Stieber
- vor 7 Jahren
- Abrufe
Transkript
1 Teil II: Quantenmechanik Historisches [Weinberg 1] Den ersten Hinweis auf die Unmöglichkeit der klassischen Physik fand man in der Thermodynamik des elektromagnetischen Feldes: Das klassische Strahulungsfeld im thermischen Gleichgewicht hat unendliche Energiedichte. Planck konnte das korrekte Energiespektrum der Wärmestrahlung zunächst,,erraten (1900). Später hat er dann eine Herleitung mit mit Hilfe der Quantenhypothese gefunden: Emission und Absorption von Licht mit der Kreisfrequenz ω erfolgt nur in ganzahligen Vielfachen von ω mit dem Planckschen Wirkungsquantum = h 2π = 1, J s Einstein postulierte dann 1905: Licht der Wellenlänge λ besteht aus Paketen, Teilchen der Energie ω und Impuls k mit k = 2π/λ = ω/c Bohr postulierte 1913 Quantenbedingungen für im Atom gebundene Elektronen und konnte so die Energienieveaus im Wasserstoff erklären. De Broglie hat 1924 Materieteilchen wie z.b. Elektronen Welleneigenschaften zugeschrieben: ω = E/, k = p/. Aus E = p 2 /() ergab sich ω = k 2 /(). Bis dahin waren das Hypothesen und Kochrezepte die für manche Systeme korrekte Resultate lieferten, für andere nicht, aber keine Theorie. Der Durchbruch zur Quantentheorie gelang 1925 Heisenberg mit der,,matrizenmechanik, die von Heisenberg, Born und Jordan ( ) und unabhängig von Dirac (1926) ausgearbeitet wurde. Schrödinger hat 1926 die Quantenmechanik ein zweites Mal in Form der,,wellenmechanik entdeckt, aufbauend auf den Ideen von de Broglie. Er fand die Schrödingergleichung und zeigte später, dass diese mathematisch äuquivalent zur Matrizenmechanik ist. In dieser Vorlesung werden wir die Formulierungen von Schrödinger und später auch die von Dirac benutzen. Born fand 1926 die Wahrscheinlichkeitsinterpretation der Quantenmechanik. Die weitgehend anerkannte Deutung der Quantenmechanik ist die sogenannte Kopenhagener Interpretation, die von Born und Heisenberg abgeschlossen wurde. 1 Die Wellenfunktion [Griffiths 1.1] Betrachte ein nichtrelativistisches Teilchen der Masse M, das sich in einer Raumdimension im Potential V (x) bewegt. In der klassischen Physik hat das Teilchen zu jedem Zeitpunkt t eine bestimmte Position x(t), die durch das Newtonsche Gesetz Mẍ(t) = F ( t, x(t) ) 1
2 mit der Kraft F = V x bestimmt ist. Kennt man V, sowie x(t 0 ), ẋ(t 0 ) für ein t 0, ist dadurch x(t) für alle Zeiten t festgelegt. In der Quantenmechanik ist das ganz anders. Hierzu gibt es unzählige Beispiele, ich erwähne an dieser Stelle nur zwei: 1. Betrachte ein freies Neutron in Ruhe. Wenn man noch dazu sagt, in welche Richtung sein Spin zeigt, ist der Zustand des Neutrons vollständig bestimmt. Jedes freie Neutron zerfällt früher oder später in ein Proton, ein Elektron und ein Antineutrino. Man kann aber nicht sagen wann, obwohl man den Zustand vollständig kennt! Was man sagen kann, dass der Zerfall im Mittel nach knapp 15 Minuten erfolgt, aber es kann auch kürzer dauern oder auch länger. 2. Licht besteht aus Photonen. Nehmen wir an wir haben einen monochromatischen zirkular polarisierten Lichtstrahl, der auf einen halbdurchlässigen Spiegel fällt. Dann ist der Zustand jedes Photons vollständig bestimmt. Alle Photonen sind gleich. Trotzdem werden manche vom Spiegel reflektiert und die anderen werden durchgelassen. Was mit einem einzelnen Photon passiert, kann man nicht vorhersagen, obwohl man seinen Zustand kennt. 1.1 Die Schrödingergleichung Ein Teilchen, das sich einer Raumrichtung bewegen kann, wird in der Quantemechanik durch eine komplexwertige Wellenfunktion ψ(t, x) beschrieben. ψ ist durch eine lineare partielle Differentialgleichung bestimmmt. Diese kann man nicht herleiten, aber durch die de Broglie-Relationen motivieren: Ein freies, d.h. kräftefreies Teilchen hat einen konstanten Impuls p = k. Es wird beschrieben durch die ebene Welle ψ = Ae ikx iωt wobei Nun ist ψ ist also Lsg. der DGL ω = ( k)2 ωψ = t, ( k) 2 t = 2 ψ 2 x 2 = 2 ψ 2 x 2 ( ) 2
3 Die Energie als Funktion von p und x ist die Hamiltonfunktion H(p, x). Für freie Teilchen ist H(p, x) = p2 Ersetzt man hierin p i x dann kann man ( ) schreiben als t = H ( i ) x, x ψ Schrödinger postutierte dass dies allgemein gilt, also auch für den Fall mit Potential V (x) Das ergibt die Schrödingergleichung H(p, x) = p2 + V (x) t = 2 2 ψ 2 x + V ψ Wie versprochen ist dies eine partielle DGL. Sie ist linear wenn ψ 1, ψ 2 Lösungen sind, dann auch c 1 ψ 1 + c 2 ψ 2 mit beliebigen komplexen Zahlen c 1, c 2. Sie genügt also dem Superpositionsprinzip. Jetzt haben wir eine Gleichung für ψ, wissen aber noch nicht was ψ bedeutet. 1.2 Die statistische Interpretation [Griffiths 1.2] Die Bedeutung kommt jetzt: ψ(t, x) 2 = ψ (t, x)ψ(t, x) ist die Wahrscheinlichkeitsdichte, das Teilchen zur Zeit t am Ort x zu finden. Anders ausgedrückt: b a dx ψ(t, x) 2 ist die Wahrscheinlichkeit, das Teilchen zur Zeit t zwischen a und b (a < b) zu finden. Mehr kann man nicht sagen! Der Ort des Teilchens ist i.a. nicht bestimmt. Man kann nur sagen, mit welcher Wahrscheinlichkeit man es in einem bestimmten Gebiet findet. Das Ergebnis einer Messung (hier des Ortes) kann i.a. nicht vorhergesagt werden. 3
4 Es gibt aber eine Ausnahme: Angenommen man macht eine Ortsmessung, findet den Wert d und wiederholt die Ortsmessung unmittelbar danach. Dann erhält man den gleichen Wert d. D.h. durch die Messung ändert sich die Wellenfunktion i.a. radikal! Diese Änderung bezeichnet man als Kollaps der Wellenfunktion. Eine Konsequenz der Schrödingergleichung und der Interpretation der Wellenfunktion sind Beugungseffekte von Materieteilchen, z.b. am Doppelspalt: 4
5 Das gleiche Experiment mit Fußbällen, die blindlings auf eine Torwand mit zwei Löchern geschossen werden: 22. April
Die Macht und Ohnmacht der Quantenwelt
 Die Macht und Ohnmacht der Quantenwelt Prof. Dr. Sebastian Eggert Tag der Physik, TU Kaiserslautern, 5. Dezember 2015 Quantenmechanik heute Quanteninformatik Ultrakalte Quantengase Supraleitung und Vielteilchenphysik
Die Macht und Ohnmacht der Quantenwelt Prof. Dr. Sebastian Eggert Tag der Physik, TU Kaiserslautern, 5. Dezember 2015 Quantenmechanik heute Quanteninformatik Ultrakalte Quantengase Supraleitung und Vielteilchenphysik
Fazit: Wellen haben Teilchencharakter
 Die Vorgeschichte Maxwell 1865 sagt elektromagnetische Wellen vorher Hertz 1886 beobachtet verstärkten Funkenüberschlag unter Lichteinstrahlung Hallwachs 1888 studiert den photoelektrischen Effekt systematisch
Die Vorgeschichte Maxwell 1865 sagt elektromagnetische Wellen vorher Hertz 1886 beobachtet verstärkten Funkenüberschlag unter Lichteinstrahlung Hallwachs 1888 studiert den photoelektrischen Effekt systematisch
Quantenmechanik. Eine Kurzvorstellung für Nicht-Physiker
 Quantenmechanik Eine Kurzvorstellung für Nicht-Physiker Die Quantenvorstellung Der Ursprung: Hohlraumstrahlung Das Verhalten eines Von Interesse: idealen Absorbers Energiedichte in Abhängigkeit zur Wellenlänge
Quantenmechanik Eine Kurzvorstellung für Nicht-Physiker Die Quantenvorstellung Der Ursprung: Hohlraumstrahlung Das Verhalten eines Von Interesse: idealen Absorbers Energiedichte in Abhängigkeit zur Wellenlänge
Der Welle-Teilchen-Dualismus
 Quantenphysik Der Welle-Teilchen-Dualismus Welle-Teilchen-Dualismus http://bluesky.blogg.de/2005/05/03/fachbegriffe-der-modernen-physik-ix/ Welle-Teilchen-Dualismus Alles ist gleichzeitig Welle und Teilchen.
Quantenphysik Der Welle-Teilchen-Dualismus Welle-Teilchen-Dualismus http://bluesky.blogg.de/2005/05/03/fachbegriffe-der-modernen-physik-ix/ Welle-Teilchen-Dualismus Alles ist gleichzeitig Welle und Teilchen.
Die Wellenfunktion ψ(r,t) ist eine komplexe skalare Größe, da keine Polarisation wie bei elektromagnetischen Wellen beobachtet wurde.
 2. Materiewellen und Wellengleichung für freie Teilchen 2.1 Begriff Wellenfunktion Auf Grund des Wellencharakters der Materie können wir den Zustand eines physikalischen Systemes durch eine Wellenfunktion
2. Materiewellen und Wellengleichung für freie Teilchen 2.1 Begriff Wellenfunktion Auf Grund des Wellencharakters der Materie können wir den Zustand eines physikalischen Systemes durch eine Wellenfunktion
Was sind Quantenobjekte?
 Quantenobjekte Was sind Quantenobjekte? Die Quantentheorie beschreibt das Verhalten von Quantenobjekten in Raum und Zeit. Als Quantenobjekte oder Mikroteilchen werden in der Physik Objekte bezeichnet,
Quantenobjekte Was sind Quantenobjekte? Die Quantentheorie beschreibt das Verhalten von Quantenobjekten in Raum und Zeit. Als Quantenobjekte oder Mikroteilchen werden in der Physik Objekte bezeichnet,
Einführung in die Quantentheorie der Atome und Photonen
 Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
1 Die Schrödinger Gleichung
 1 Die Schrödinger Gleichung 1.1 Die Wellenfunktion und ihre Wahrscheinlichkeitsinterpretation Aus den Versuchen der Elektronenbeugung, hat ein Elektron auch Welleneigenschaften. Für freie Elektronen mit
1 Die Schrödinger Gleichung 1.1 Die Wellenfunktion und ihre Wahrscheinlichkeitsinterpretation Aus den Versuchen der Elektronenbeugung, hat ein Elektron auch Welleneigenschaften. Für freie Elektronen mit
ν und λ ausgedrückt in Energie E und Impuls p
 phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
1 Physikalische Hintergrunde: Teilchen oder Welle?
 Skript zur 1. Vorlesung Quantenmechanik, Montag den 11. April, 2011. 1 Physikalische Hintergrunde: Teilchen oder Welle? 1.1 Geschichtliches: Warum Quantenmechanik? Bis 1900: klassische Physik Newtonsche
Skript zur 1. Vorlesung Quantenmechanik, Montag den 11. April, 2011. 1 Physikalische Hintergrunde: Teilchen oder Welle? 1.1 Geschichtliches: Warum Quantenmechanik? Bis 1900: klassische Physik Newtonsche
Übungen Quantenphysik
 Ue QP 1 Übungen Quantenphysik Kernphysik Historische Entwicklung der Atommodelle Klassische Wellengleichung 5 Schrödinger Gleichung 6 Kastenpotential (Teilchen in einer Box) 8 Teilchen im Potentialtopf
Ue QP 1 Übungen Quantenphysik Kernphysik Historische Entwicklung der Atommodelle Klassische Wellengleichung 5 Schrödinger Gleichung 6 Kastenpotential (Teilchen in einer Box) 8 Teilchen im Potentialtopf
14. Teilchen und Wellen
 Inhalt 14.1 Strahlung schwarzer Körper 14.2 Der Photoeffekt 14.3 Der Comptoneffekt 14.4 Materiewellen 14.5 Interpretation von Teilchenwellen 14.6 Die Schrödingergleichung 14.7 Heisenberg sche Unschärferelation
Inhalt 14.1 Strahlung schwarzer Körper 14.2 Der Photoeffekt 14.3 Der Comptoneffekt 14.4 Materiewellen 14.5 Interpretation von Teilchenwellen 14.6 Die Schrödingergleichung 14.7 Heisenberg sche Unschärferelation
1.4. Die Wahrscheinlichkeitsinterpretation
 1.4. Die Wahrscheinlichkeitsinterpretation 1.4.1. Die Heisenbergsche Unschärferelation Wie kann der Welle-Teilchen-Dualismus in der Quantenmechanik interpretiert werden? gibt die Wahrscheinlichkeit an,
1.4. Die Wahrscheinlichkeitsinterpretation 1.4.1. Die Heisenbergsche Unschärferelation Wie kann der Welle-Teilchen-Dualismus in der Quantenmechanik interpretiert werden? gibt die Wahrscheinlichkeit an,
Die Schrödinger Gleichung
 Die Schrödinger Gleichung Eine Einführung Christian Hirsch Die Schrödinger Gleichung p. 1/16 Begriffserklärung Was ist die Schrödingergleichung? Die Schrödinger Gleichung p. 2/16 Begriffserklärung Was
Die Schrödinger Gleichung Eine Einführung Christian Hirsch Die Schrödinger Gleichung p. 1/16 Begriffserklärung Was ist die Schrödingergleichung? Die Schrödinger Gleichung p. 2/16 Begriffserklärung Was
Von der kosmischen Hintergrundstrahlung zur Heisenbergschen Unbestimmtheitsrelation. eine Einführung in die Quantenmechanik
 Von der kosmischen Hintergrundstrahlung zur Heisenbergschen Unbestimmtheitsrelation eine Einführung in die Quantenmechanik 1) Die Hohlraumstrahlung: Geburt der Quantenmechanik Die kosmische Hintergrundstrahlung
Von der kosmischen Hintergrundstrahlung zur Heisenbergschen Unbestimmtheitsrelation eine Einführung in die Quantenmechanik 1) Die Hohlraumstrahlung: Geburt der Quantenmechanik Die kosmische Hintergrundstrahlung
Zur Philosophie der Quantenmechanik
 Zur Philosophie der Quantenmechanik Vortrag in der Q12 am Gymnasium Geretsried Tobias Jung Lehrstuhl für Philosophie und Wissenschaftstheorie Technische Universität München (TUM) 18. Dezember 2012 Tobias
Zur Philosophie der Quantenmechanik Vortrag in der Q12 am Gymnasium Geretsried Tobias Jung Lehrstuhl für Philosophie und Wissenschaftstheorie Technische Universität München (TUM) 18. Dezember 2012 Tobias
Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit. An einigen Beispielen erläutern
 Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit An einigen Beispielen erläutern 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Wichtige Punkte: u( ν, T ) = 8πh c
Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit An einigen Beispielen erläutern 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Wichtige Punkte: u( ν, T ) = 8πh c
Die Schrödingergleichung
 Die Schrödingergleichung Wir werden in dieser Woche die grundlegende Gleichung der Quantenmechanik kennenlernen, die Schrödingergleichung. Sie beschreibt das dynamische Verhalten von Systemen in der Natur.
Die Schrödingergleichung Wir werden in dieser Woche die grundlegende Gleichung der Quantenmechanik kennenlernen, die Schrödingergleichung. Sie beschreibt das dynamische Verhalten von Systemen in der Natur.
14 Teilchen und Wellen
 14 Teilchen und Wellen 14.1 Teilchencharakter von elektromagnetischen Wellen 1411 14.1.1 Strahlung schwarzer Körper 14.1.2 Der Photoeffekt 14.1.3 Technische Anwendungen 14.2 Wellencharakter von Teilchen
14 Teilchen und Wellen 14.1 Teilchencharakter von elektromagnetischen Wellen 1411 14.1.1 Strahlung schwarzer Körper 14.1.2 Der Photoeffekt 14.1.3 Technische Anwendungen 14.2 Wellencharakter von Teilchen
Physik IV Einführung in die Atomistik und die Struktur der Materie
 Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 011 Vorlesung 04 1.04.011 Physik IV - Einführung in die Atomistik Vorlesung 4 Prof. Thorsten Kröll 1.04.011 1 Versuch OH
Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 011 Vorlesung 04 1.04.011 Physik IV - Einführung in die Atomistik Vorlesung 4 Prof. Thorsten Kröll 1.04.011 1 Versuch OH
= 6,63 10 J s 8. (die Plancksche Konstante):
 35 Photonen und Materiefelder 35.1 Das Photon: Teilchen des Lichts Die Quantenphysik: viele Größen treten nur in ganzzahligen Vielfachen von bestimmten kleinsten Beträgen (elementaren Einheiten) auf: diese
35 Photonen und Materiefelder 35.1 Das Photon: Teilchen des Lichts Die Quantenphysik: viele Größen treten nur in ganzzahligen Vielfachen von bestimmten kleinsten Beträgen (elementaren Einheiten) auf: diese
1. Auf dem Weg zur Quantentheorie Grundlegende Experimente und Erkenntnisse
 1. Auf dem Weg zur Quantentheorie Grundlegende Experimente und Erkenntnisse 1.1. Theorie der Wärmestrahlung Plancksche Strahlenhypothese Untersuchungen der Hohlraumstrahlung vor 1900 zeigten, dass das
1. Auf dem Weg zur Quantentheorie Grundlegende Experimente und Erkenntnisse 1.1. Theorie der Wärmestrahlung Plancksche Strahlenhypothese Untersuchungen der Hohlraumstrahlung vor 1900 zeigten, dass das
5 Der quantenmechanische Hilbertraum
 5 Der quantenmechanische Hilbertraum 5.1 Die Wellenfunktion eines Teilchens Der Bewegungs- Zustand eines Teilchens Elektrons zu einem Zeitpunkt t, in der klassischen Mechanik das Wertepaar r,p von Ort
5 Der quantenmechanische Hilbertraum 5.1 Die Wellenfunktion eines Teilchens Der Bewegungs- Zustand eines Teilchens Elektrons zu einem Zeitpunkt t, in der klassischen Mechanik das Wertepaar r,p von Ort
10 Teilchen und Wellen. 10.1 Strahlung schwarzer Körper
 10 Teilchen und Wellen Teilchen: m, V, p, r, E, lokalisierbar Wellen: l, f, p, E, unendlich ausgedehnt (harmonische Welle) Unterscheidung: Wellen interferieren 10.1 Strahlung schwarzer Körper JEDER Körper
10 Teilchen und Wellen Teilchen: m, V, p, r, E, lokalisierbar Wellen: l, f, p, E, unendlich ausgedehnt (harmonische Welle) Unterscheidung: Wellen interferieren 10.1 Strahlung schwarzer Körper JEDER Körper
Thema heute: Aufbau der Materie: Das Bohr sche Atommodell
 Wiederholung der letzten Vorlesungsstunde: Erste Atommodelle, Dalton Thomson, Rutherford, Atombau, Coulomb-Gesetz, Proton, Elektron, Neutron, weitere Elementarteilchen, atomare Masseneinheit u, 118 bekannte
Wiederholung der letzten Vorlesungsstunde: Erste Atommodelle, Dalton Thomson, Rutherford, Atombau, Coulomb-Gesetz, Proton, Elektron, Neutron, weitere Elementarteilchen, atomare Masseneinheit u, 118 bekannte
Vorlesung Allgemeine Chemie (CH01)
 Vorlesung Allgemeine Chemie (CH01) Für Studierende im B.Sc.-Studiengang Chemie Prof. Dr. Martin Köckerling Arbeitsgruppe Anorganische Festkörperchemie Mathematisch-Naturwissenschaftliche Fakultät, Institut
Vorlesung Allgemeine Chemie (CH01) Für Studierende im B.Sc.-Studiengang Chemie Prof. Dr. Martin Köckerling Arbeitsgruppe Anorganische Festkörperchemie Mathematisch-Naturwissenschaftliche Fakultät, Institut
Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e [
 Vorlesung 4 Teilchen im externen Elektromagnetischen Feld Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e v B c ]. 1) Das elektrische
Vorlesung 4 Teilchen im externen Elektromagnetischen Feld Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e v B c ]. 1) Das elektrische
Das Meßproblem in der Kopenhagener Deutung
 Das Meßproblem in der Kopenhagener Deutung Angenommen, ein quantenmechanisches System kann nur zwei Werte annehmen, z.b. Spin oben oder Spin unten... Dieses Teilchen wird in Bezug auf den Spin durch eine
Das Meßproblem in der Kopenhagener Deutung Angenommen, ein quantenmechanisches System kann nur zwei Werte annehmen, z.b. Spin oben oder Spin unten... Dieses Teilchen wird in Bezug auf den Spin durch eine
(a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle?
 FK Ex 4-07/09/2015 1 Quickies (a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle? (b) Wie groß ist die Energie von Lichtquanten mit einer Wellenlänge von
FK Ex 4-07/09/2015 1 Quickies (a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle? (b) Wie groß ist die Energie von Lichtquanten mit einer Wellenlänge von
6 Der Harmonische Oszillator
 6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
Periodensystem, elektromagnetische Spektren, Atombau, Orbitale
 Periodensystem, elektromagnetische Spektren, Atombau, Orbitale Als Mendelejew sein Periodensystem aufstellte waren die Edelgase sowie einige andere Elemente noch nicht entdeck (gelb unterlegt). Trotzdem
Periodensystem, elektromagnetische Spektren, Atombau, Orbitale Als Mendelejew sein Periodensystem aufstellte waren die Edelgase sowie einige andere Elemente noch nicht entdeck (gelb unterlegt). Trotzdem
Wiederholung der letzten Vorlesungsstunde:
 Wiederholung der letzten Vorlesungsstunde: Das (wellen-) quantenchemische Atommodell Orbitalmodell Beschreibung atomarer Teilchen (Elektronen) durch Wellenfunktionen, Wellen, Wellenlänge, Frequenz, Amplitude,
Wiederholung der letzten Vorlesungsstunde: Das (wellen-) quantenchemische Atommodell Orbitalmodell Beschreibung atomarer Teilchen (Elektronen) durch Wellenfunktionen, Wellen, Wellenlänge, Frequenz, Amplitude,
Zum Bahnbegriff eines Teilchens in der Physik
 11. Februar 2009 Abschlussvorlesung Mathematik I für Physiker Kann man auch in der Quantenmechanik von der Bahn eines Teilchens sprechen? Zitate zum Bahnbegriff in der Quantenmechanik Das Wort Bahn hat
11. Februar 2009 Abschlussvorlesung Mathematik I für Physiker Kann man auch in der Quantenmechanik von der Bahn eines Teilchens sprechen? Zitate zum Bahnbegriff in der Quantenmechanik Das Wort Bahn hat
Vorlesung 21: Roter Faden: Das Elektron als Welle Heisenbergsche Unsicherheitsrelation. Versuch: Gasentladung
 Vorlesung 21: Roter Faden: Das Elektron als Welle Heisenbergsche Unsicherheitsrelation Versuch: Gasentladung Juli 7, 2006 Ausgewählte Kapitel der Physik, Prof. W. de Boer 1 Erste Experimente mit Elektronen
Vorlesung 21: Roter Faden: Das Elektron als Welle Heisenbergsche Unsicherheitsrelation Versuch: Gasentladung Juli 7, 2006 Ausgewählte Kapitel der Physik, Prof. W. de Boer 1 Erste Experimente mit Elektronen
Alternative Interpretationen der Quantentheorie
 1 von 12 Physiker und Physiklehrertagung, Dornach, 26.2.2015 Alternative Interpretationen der Quantentheorie Oliver Passon Bergische Universität Wuppertal Physik und ihre Didaktik Warum gibt es alternative
1 von 12 Physiker und Physiklehrertagung, Dornach, 26.2.2015 Alternative Interpretationen der Quantentheorie Oliver Passon Bergische Universität Wuppertal Physik und ihre Didaktik Warum gibt es alternative
Wiederholung der letzten Vorlesungsstunde:
 Wiederholung der letzten Vorlesungsstunde: Das Bohr sche Atommodell: Strahlenabsorption, -emission, Elektromagentische Strahlung, Wellen, Wellenlänge, Frequenz, Wellenzahl. Postulate: * Elektronen bewegen
Wiederholung der letzten Vorlesungsstunde: Das Bohr sche Atommodell: Strahlenabsorption, -emission, Elektromagentische Strahlung, Wellen, Wellenlänge, Frequenz, Wellenzahl. Postulate: * Elektronen bewegen
Relativistische Mechanik und Quantenmechanik
 Sommersemester 2010 Beginn: Donnerstag, 22. April, 14.00-15.30 Klaus Keller Seminarraum IAM (1.12) des Relativistische Mechanik und Albert Einstein (1879-1955). Max Planck (1858-1947) Nils Bohr (1885-1962)
Sommersemester 2010 Beginn: Donnerstag, 22. April, 14.00-15.30 Klaus Keller Seminarraum IAM (1.12) des Relativistische Mechanik und Albert Einstein (1879-1955). Max Planck (1858-1947) Nils Bohr (1885-1962)
12.8 Eigenschaften von elektronischen Übergängen. Übergangsfrequenz
 phys4.024 Page 1 12.8 Eigenschaften von elektronischen Übergängen Übergangsfrequenz betrachte die allgemeine Lösung ψ n der zeitabhängigen Schrödinger-Gleichung zum Energieeigenwert E n Erwartungswert
phys4.024 Page 1 12.8 Eigenschaften von elektronischen Übergängen Übergangsfrequenz betrachte die allgemeine Lösung ψ n der zeitabhängigen Schrödinger-Gleichung zum Energieeigenwert E n Erwartungswert
Inhaltsverzeichnis. Einleitung 1
 Inhaltsverzeichnis Einleitung 1 1 Licht und Materie 7 Was ist eigentlich Licht? 8 Aber was schwingt da wie? 9 Was sind Frequenz und Wellenlänge des Lichts? 11 Was ist eigentlich Materie? 12 Woraus besteht
Inhaltsverzeichnis Einleitung 1 1 Licht und Materie 7 Was ist eigentlich Licht? 8 Aber was schwingt da wie? 9 Was sind Frequenz und Wellenlänge des Lichts? 11 Was ist eigentlich Materie? 12 Woraus besteht
1.2 Grenzen der klassischen Physik Michael Buballa 1
 1.2 Grenzen der klassischen Physik 23.04.2013 Michael Buballa 1 1.2 Grenzen der klassischen Physik Die Konzepte klassischer Teilchen und Wellen haben ihren Ursprung in unserer Alltagserfahrung, z.b. Teilchen:
1.2 Grenzen der klassischen Physik 23.04.2013 Michael Buballa 1 1.2 Grenzen der klassischen Physik Die Konzepte klassischer Teilchen und Wellen haben ihren Ursprung in unserer Alltagserfahrung, z.b. Teilchen:
Festkörperelektronik 2008 Übungsblatt 1
 Lichttechnisches Institut Universität Karlsruhe (TH) Prof. Dr. rer. nat. Uli Lemmer Dipl.-Phys. Alexander Colsmann Engesserstraße 13 76131 Karlsruhe Festkörperelektronik 1. Übungsblatt 17. April 2008 Dozent:
Lichttechnisches Institut Universität Karlsruhe (TH) Prof. Dr. rer. nat. Uli Lemmer Dipl.-Phys. Alexander Colsmann Engesserstraße 13 76131 Karlsruhe Festkörperelektronik 1. Übungsblatt 17. April 2008 Dozent:
Die Geschichte der Quantenmechanik
 Die Geschichte der Quantenmechanik Kurt Bräuer Institut für Theoretische Physik 5.04.006 www.kbraeuer.de 1 'Urväter' 5.04.006 www.kbraeuer.de Strahlung schwarzer Körper: Max Plank 1900 Plank'sches Strahlungsgesetz:
Die Geschichte der Quantenmechanik Kurt Bräuer Institut für Theoretische Physik 5.04.006 www.kbraeuer.de 1 'Urväter' 5.04.006 www.kbraeuer.de Strahlung schwarzer Körper: Max Plank 1900 Plank'sches Strahlungsgesetz:
Grundlagen der Quantentheorie
 Grundlagen der Quantentheorie Ein Schwarzer Körper (Schwarzer Strahler, planckscher Strahler, idealer schwarzer Körper) ist eine idealisierte thermische Strahlungsquelle: Alle auftreffende elektromagnetische
Grundlagen der Quantentheorie Ein Schwarzer Körper (Schwarzer Strahler, planckscher Strahler, idealer schwarzer Körper) ist eine idealisierte thermische Strahlungsquelle: Alle auftreffende elektromagnetische
Der Lebensraum von Quantenteilchen
 Der Lebensraum von Quantenteilchen Michael Eder - Vortrag bei PRO SCIENTIA, Graz am 17.04.2018 Einführung: Die Quantenmechanik gilt als eine der erfolgreichsten Theorien der Physik. Sie ist tatsächlich
Der Lebensraum von Quantenteilchen Michael Eder - Vortrag bei PRO SCIENTIA, Graz am 17.04.2018 Einführung: Die Quantenmechanik gilt als eine der erfolgreichsten Theorien der Physik. Sie ist tatsächlich
Ein Unterrichtsprojekt zur Quantenmechanik am Begabungsstützpunkt
 Ein Unterrichtsprojekt zur Quantenmechanik am Begabungsstützpunkt Andreas Kellerer (BSG Memmingen) Prof. Dr. Reinhold Rückl (Universität Würzburg) Die Rahmenbedingungen: Unterrichtsprojekt für den Kurs
Ein Unterrichtsprojekt zur Quantenmechanik am Begabungsstützpunkt Andreas Kellerer (BSG Memmingen) Prof. Dr. Reinhold Rückl (Universität Würzburg) Die Rahmenbedingungen: Unterrichtsprojekt für den Kurs
Strahlungsformel von M. Planck (1900) E = h ν = ω E = Energie ν = Frequenz ω = 2πν h = Wirkungsquantum 6.62608 10 34 Js = h/2π
 Max Planck (1858 1947, Nobelpreis 1918) Hypothetische Erklärung des (klassisch nicht erklärbaren) Strahlungsverhaltens schwarzer Körper : eletromagnetische Strahlung wird nur in diskreten Portionen ( Quanten
Max Planck (1858 1947, Nobelpreis 1918) Hypothetische Erklärung des (klassisch nicht erklärbaren) Strahlungsverhaltens schwarzer Körper : eletromagnetische Strahlung wird nur in diskreten Portionen ( Quanten
Abb.15: Experiment zum Rutherford-Modell
 6.Kapitel Atommodelle 6.1 Lernziele Sie kennen die Entwicklung der Atommodelle bis zum linearen Potentialtopf. Sie kennen die Bohrschen Postulate und können sie auch anwenden. Sie wissen, wie man bestimmte
6.Kapitel Atommodelle 6.1 Lernziele Sie kennen die Entwicklung der Atommodelle bis zum linearen Potentialtopf. Sie kennen die Bohrschen Postulate und können sie auch anwenden. Sie wissen, wie man bestimmte
Klassische Mechanik. Elektrodynamik. Thermodynamik. Der Stand der Physik am Beginn des 20. Jahrhunderts. Relativitätstheorie?
 Der Stand der Physik am Beginn des 20. Jahrhunderts Klassische Mechanik Newton-Axiome Relativitätstheorie? Maxwell-Gleichungen ok Elektrodynamik Thermodynamik Hauptsätze der Therm. Quantentheorie S.Alexandrova
Der Stand der Physik am Beginn des 20. Jahrhunderts Klassische Mechanik Newton-Axiome Relativitätstheorie? Maxwell-Gleichungen ok Elektrodynamik Thermodynamik Hauptsätze der Therm. Quantentheorie S.Alexandrova
Quantenmechanik. Seminar Interpretation der QM, Goethe-Universität Frankfurt am Main. Daniel Guterding. 26. Mai Die Kopenhagener Deutung der
 Seminar Interpretation der QM, Goethe-Universität Frankfurt am Main Daniel Guterding 26. Mai 2011 Väter der Interpretation Niels Bohr ( 1885 1962) Werner Heisenberg ( 1901 1976) Entstehungsgeschichte QM
Seminar Interpretation der QM, Goethe-Universität Frankfurt am Main Daniel Guterding 26. Mai 2011 Väter der Interpretation Niels Bohr ( 1885 1962) Werner Heisenberg ( 1901 1976) Entstehungsgeschichte QM
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie
 Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Bohm sche Mechanik. Determinismus in der Quantenmechanik. Sven Köppel Mirko Pohland. 9. Juni, Fachbereich 13, Physik
 Determinismus in Quantenmechanik Sven Köppel Mirko Pohland Fachbereich 13, Physik 9. Juni, 2011 Ergebnisse an landläufigen Quantenmechanik ähnlich wie in Thermodynamik wäre es möglich, dass die Quantenmechanik
Determinismus in Quantenmechanik Sven Köppel Mirko Pohland Fachbereich 13, Physik 9. Juni, 2011 Ergebnisse an landläufigen Quantenmechanik ähnlich wie in Thermodynamik wäre es möglich, dass die Quantenmechanik
Die Schrödingergleichung
 Vortrag im Rahmen der Vorlesung zu Spektralmethoden Magdalena Sigg Wanja Chresta 20. Mai 2008 Zusammenfassung ist die zentrale Gleichung der Quantenmechanik. Mit ihrer Hilfe werden Teilchen in gegebenen
Vortrag im Rahmen der Vorlesung zu Spektralmethoden Magdalena Sigg Wanja Chresta 20. Mai 2008 Zusammenfassung ist die zentrale Gleichung der Quantenmechanik. Mit ihrer Hilfe werden Teilchen in gegebenen
Silvia Arroyo Camejo. Skurrile Quantenwelt ABC
 Silvia Arroyo Camejo Skurrile Quantenwelt ABC Inhaltsverzeichnis Einleitung.................................................... 1 1 Licht und Materie......................................... 7 Was ist
Silvia Arroyo Camejo Skurrile Quantenwelt ABC Inhaltsverzeichnis Einleitung.................................................... 1 1 Licht und Materie......................................... 7 Was ist
Atommodell führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen.
 Atommodell nach Rutherford 1911 führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen. Beobachtung: Fast alle Teilchen fliegen ungestört durch.
Atommodell nach Rutherford 1911 führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen. Beobachtung: Fast alle Teilchen fliegen ungestört durch.
Bohrsches Atommodell / Linienspektren. Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
 Bohrsches Atommodell / Linienspektren Quantenstruktur der Atome: Atomspektren Emissionslinienspektren von Wasserstoffatomen im sichtbaren Bereich Balmer Serie (1885): 1 / λ = K (1/4-1/n 2 ) 656.28 486.13
Bohrsches Atommodell / Linienspektren Quantenstruktur der Atome: Atomspektren Emissionslinienspektren von Wasserstoffatomen im sichtbaren Bereich Balmer Serie (1885): 1 / λ = K (1/4-1/n 2 ) 656.28 486.13
Theoretische Physik mit Maple, WS 2010/ Übungsblatt (Besprechung am ) R( ) ( ( ( ) ( ))) ( ) u ( x)
 Theoretische Physik mit Maple, WS 2010/2011 9. Übungsblatt (Besprechung am 24.1.2011) Quantenmechanische Streuung am Kastenpotential Wir betrachten die zeitunabhängige Schrödinger-Gleichung (ZuSG) und
Theoretische Physik mit Maple, WS 2010/2011 9. Übungsblatt (Besprechung am 24.1.2011) Quantenmechanische Streuung am Kastenpotential Wir betrachten die zeitunabhängige Schrödinger-Gleichung (ZuSG) und
Die Lösungen der S.-Glg. für das freie Teilchen
 Die Lösungen der S.-Glg. für das freie Teilchen Zeitabhängige S- G l g., ħ ħ x (, (, m i = + Vrt rt Analogie zu den eletromagnetischen Wellen, Materiewellen, intuitives Raten etc. Ansatz f ü r W e l l
Die Lösungen der S.-Glg. für das freie Teilchen Zeitabhängige S- G l g., ħ ħ x (, (, m i = + Vrt rt Analogie zu den eletromagnetischen Wellen, Materiewellen, intuitives Raten etc. Ansatz f ü r W e l l
7.3 Der quantenmechanische Formalismus
 Dieter Suter - 389 - Physik B3 7.3 Der quantenmechanische Formalismus 7.3.1 Historische Vorbemerkungen Die oben dargestellten experimentellen Hinweise wurden im Laufe der ersten Jahrzehnte des 20. Jahrhunderts
Dieter Suter - 389 - Physik B3 7.3 Der quantenmechanische Formalismus 7.3.1 Historische Vorbemerkungen Die oben dargestellten experimentellen Hinweise wurden im Laufe der ersten Jahrzehnte des 20. Jahrhunderts
Kapitel 10. Potentiale Elektronen im Potentialtopf
 Kapitel 10 Potentiale 10.1 Elektronen im Potentialtopf Mit dem Aufstellen der Schrödinger-Gleichung ist man der realistischen Beschreibung von Quantenobjekten ein großes Stück nähergekommen. Unser Interesse
Kapitel 10 Potentiale 10.1 Elektronen im Potentialtopf Mit dem Aufstellen der Schrödinger-Gleichung ist man der realistischen Beschreibung von Quantenobjekten ein großes Stück nähergekommen. Unser Interesse
2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten
 Inhalt: 1. Regeln und Normen Modul: Allgemeine Chemie 2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten 3.Bausteine der Materie Atomkern: Elementarteilchen, Kernkräfte,
Inhalt: 1. Regeln und Normen Modul: Allgemeine Chemie 2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten 3.Bausteine der Materie Atomkern: Elementarteilchen, Kernkräfte,
Martinovsky Nicole. Schwarzmann Tobias. Thaler Michael
 Themen: Unbestimmtheitsrelationen, Materiewellen, Materieteilchen als Welle, Wellenfunktion, Dispersionsrelation, Wellenpaket, Wahrscheinlichkeitsinterpretation, Materie-Quanteninterferenz Martinovsky
Themen: Unbestimmtheitsrelationen, Materiewellen, Materieteilchen als Welle, Wellenfunktion, Dispersionsrelation, Wellenpaket, Wahrscheinlichkeitsinterpretation, Materie-Quanteninterferenz Martinovsky
Von der Kerze zum Laser: Die Physik der Lichtquanten
 Von der Kerze zum Laser: Die Physik der Lichtquanten Jörg Weber Institut für Angewandte Physik/Halbleiterphysik Technische Universität Dresden Was ist Licht? Wie entsteht Licht? Anwendungen und offene
Von der Kerze zum Laser: Die Physik der Lichtquanten Jörg Weber Institut für Angewandte Physik/Halbleiterphysik Technische Universität Dresden Was ist Licht? Wie entsteht Licht? Anwendungen und offene
Erkenntnistheoretische Implikationen der Quantentheorie. Oliver Passon Zentralinstitut für Angewandte Mathematik Forschungszentrum Jülich
 Erkenntnistheoretische Implikationen der Quantentheorie Zentralinstitut für Angewandte Mathematik Forschungszentrum Jülich Vorbemerkungen In erster Näherung gilt: Quantenmechanik = Quantenphysik = Quantentheorie
Erkenntnistheoretische Implikationen der Quantentheorie Zentralinstitut für Angewandte Mathematik Forschungszentrum Jülich Vorbemerkungen In erster Näherung gilt: Quantenmechanik = Quantenphysik = Quantentheorie
1.4. Das freie quantenmechanische Elektron
 1.4. Das freie quantenmechanische Elektron 1.4.3. Dispersionsrelation Damit ist die Basis gelegt, um sich mit den grundlegenden Eigenschaften eines quantenmechanischen Teilchens vertraut zu machen. Die
1.4. Das freie quantenmechanische Elektron 1.4.3. Dispersionsrelation Damit ist die Basis gelegt, um sich mit den grundlegenden Eigenschaften eines quantenmechanischen Teilchens vertraut zu machen. Die
Für Geowissenschaftler. EP WS 2009/10 Dünnweber/Faessler
 Für Geowissenschaftler Termin Nachholklausur Vorschlag Mittwoch 14.4.10 25. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung und Quantenmechanik Photometrie Plancksches Strahlungsgesetze, Welle/Teilchen
Für Geowissenschaftler Termin Nachholklausur Vorschlag Mittwoch 14.4.10 25. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung und Quantenmechanik Photometrie Plancksches Strahlungsgesetze, Welle/Teilchen
lichen auf sehr engem Raum konzentriert ist und die positive Ladung trägt
 lichen auf sehr engem Raum konzentriert ist und die positive Ladung trägt Kanalstrahlexperimente hatten schwere, positiv geladene Teilchen beim Wasserstoff nachgewiesen Aufgrund von Streuexperimenten postulierte
lichen auf sehr engem Raum konzentriert ist und die positive Ladung trägt Kanalstrahlexperimente hatten schwere, positiv geladene Teilchen beim Wasserstoff nachgewiesen Aufgrund von Streuexperimenten postulierte
Eichinvarianz in der Quantenmechanik. abgeleitet aus der Maxwell-Theorie
 Eichinvarianz in der Quantenmechanik abgeleitet aus der Maxwell-Theorie Seminarvortrag Quantenelektrodynamik 1. Teil: Schrödingergleichung Motivation: Eichtheorien sind ein inhaltsreicher Gedankenkomplex
Eichinvarianz in der Quantenmechanik abgeleitet aus der Maxwell-Theorie Seminarvortrag Quantenelektrodynamik 1. Teil: Schrödingergleichung Motivation: Eichtheorien sind ein inhaltsreicher Gedankenkomplex
ATOMPHYSIK. Gábor Talián Univ. Pécs, Institut für Biophysik September 2016
 ATOMPHYSIK Gábor Talián Univ. Pécs, Institut für Biophysik 15-22. September 2016 PRÜFUNGSTHEMA Die Temperaturstrahlung. Das plancksche Wirkungsquantum. Derphotoelektrische Effekt. Experimentelle Beobachtungen
ATOMPHYSIK Gábor Talián Univ. Pécs, Institut für Biophysik 15-22. September 2016 PRÜFUNGSTHEMA Die Temperaturstrahlung. Das plancksche Wirkungsquantum. Derphotoelektrische Effekt. Experimentelle Beobachtungen
Im Folgenden finden Sie den Text der am geschriebenen Theorie D-Klausur, sowie Lösungen zu den einzelnen Aufgaben. Diese Lösungen sind
 Im Folgenden finden Sie den Text der am 28.7.2010 geschriebenen Theorie D-Klausur, sowie Lösungen zu den einzelnen Aufgaben. Diese Lösungen sind unter Umständen nicht vollständig oder perfekt, und sie
Im Folgenden finden Sie den Text der am 28.7.2010 geschriebenen Theorie D-Klausur, sowie Lösungen zu den einzelnen Aufgaben. Diese Lösungen sind unter Umständen nicht vollständig oder perfekt, und sie
27. Wärmestrahlung. rmestrahlung, Quantenmechanik
 25. Vorlesung EP 27. Wärmestrahlung V. STRAHLUNG, ATOME, KERNE 27. Wä (Fortsetzung) Photometrie Plancksches Strahlungsgesetz Welle/Teilchen Dualismus für Strahlung und Materie Versuche: Quadratisches Abstandsgesetz
25. Vorlesung EP 27. Wärmestrahlung V. STRAHLUNG, ATOME, KERNE 27. Wä (Fortsetzung) Photometrie Plancksches Strahlungsgesetz Welle/Teilchen Dualismus für Strahlung und Materie Versuche: Quadratisches Abstandsgesetz
27. Wärmestrahlung. rmestrahlung, Quantenmechanik
 24. Vorlesung EP 27. Wärmestrahlung rmestrahlung, Quantenmechanik V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung, Quantenmechanik Photometrie Plancksches Strahlungsgesetz Welle/Teilchen Dualismus für Strahlung
24. Vorlesung EP 27. Wärmestrahlung rmestrahlung, Quantenmechanik V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung, Quantenmechanik Photometrie Plancksches Strahlungsgesetz Welle/Teilchen Dualismus für Strahlung
T2 Quantenmechanik Lösungen 3
 T2 Quantenmechanik Lösungen LMU München, WS 1/18.1. Wellenfunktion und Wahrscheinlichkeit Prof. D. Lüst / Dr. A. Schmidt-May version: 2. 11. Es seien x 1, x 2, N drei reelle Konstanten und x 2 > x 1 >.
T2 Quantenmechanik Lösungen LMU München, WS 1/18.1. Wellenfunktion und Wahrscheinlichkeit Prof. D. Lüst / Dr. A. Schmidt-May version: 2. 11. Es seien x 1, x 2, N drei reelle Konstanten und x 2 > x 1 >.
6 Einige Gleichungen der mathematischen Physik
 203 6 Einige Gleichungen der mathematischen Physik Wir haben verschiedene dynamische Gleichungen kennengelernt, die die Bewegung eines physikalischen Systems wir betrachten in diesem Kapitel nur Systeme
203 6 Einige Gleichungen der mathematischen Physik Wir haben verschiedene dynamische Gleichungen kennengelernt, die die Bewegung eines physikalischen Systems wir betrachten in diesem Kapitel nur Systeme
Das Bohrsche Atommodell
 Das Bohrsche Atommodell Auf ein Elektron, welches im elektrischen Feld eines Atomkerns kreist wirkt ein magnetisches Feld. Der Abstand zum Atomkern ist das Ergebnis, der elektrostatischen Coulomb-Anziehung
Das Bohrsche Atommodell Auf ein Elektron, welches im elektrischen Feld eines Atomkerns kreist wirkt ein magnetisches Feld. Der Abstand zum Atomkern ist das Ergebnis, der elektrostatischen Coulomb-Anziehung
Die Welt der Quanten Murmeln oder Wellen? Max Camenzind Senioren Uni WS2013
 Die Welt der Quanten Murmeln oder Wellen? Max Camenzind Senioren Uni Würzburg @ WS2013 Die Krise des mechanischen Weltbildes und die Gründerväter der modernen Physik. Elektromagnetische Strahlung Maxwell,
Die Welt der Quanten Murmeln oder Wellen? Max Camenzind Senioren Uni Würzburg @ WS2013 Die Krise des mechanischen Weltbildes und die Gründerväter der modernen Physik. Elektromagnetische Strahlung Maxwell,
WKB-Methode. Jan Kirschbaum
 WKB-Methode Jan Kirschbaum Westfälische Wilhelms-Universität Münster Fachbereich Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie 1 Einleitung Die WKB-Methode, unabhängig und fast
WKB-Methode Jan Kirschbaum Westfälische Wilhelms-Universität Münster Fachbereich Physik Seminar zur Theorie der Atome, Kerne und kondensierten Materie 1 Einleitung Die WKB-Methode, unabhängig und fast
Vorlesung 6: Roter Faden: Schrödingergleichung als Wellengleichung der Materie. Messungen in der Quantenmechanik
 Vorlesung 6: Roter Faden: Schrödingergleichung als Wellengleichung der Materie Messungen in der Quantenmechanik Folien auf dem Web: http://www-ekp.physik.uni-karlsruhe.de/~deboer/ Wim de Boer, Karlsruhe
Vorlesung 6: Roter Faden: Schrödingergleichung als Wellengleichung der Materie Messungen in der Quantenmechanik Folien auf dem Web: http://www-ekp.physik.uni-karlsruhe.de/~deboer/ Wim de Boer, Karlsruhe
Einführung in die Quantenphysik
 Einführung in die Quantenphysik Klassische Optik Der lichtelektrische Effekt Effekte elektromagnetischer Strahlung Kopenhagen-Interpretation Elektronen Quantenphysik und klassische Physik Atomphysik Klassische
Einführung in die Quantenphysik Klassische Optik Der lichtelektrische Effekt Effekte elektromagnetischer Strahlung Kopenhagen-Interpretation Elektronen Quantenphysik und klassische Physik Atomphysik Klassische
SS 2015 Supplement to Experimental Physics 2 (LB-Technik) Prof. E. Resconi
 Quantenmechanik des Wasserstoff-Atoms [Kap. 8-10 Haken-Wolf Atom- und Quantenphysik ] - Der Aufbau der Atome Quantenmechanik ==> Atomphysik Niels Bohr, 1913: kritische Entwicklung, die schließlich Plancks
Quantenmechanik des Wasserstoff-Atoms [Kap. 8-10 Haken-Wolf Atom- und Quantenphysik ] - Der Aufbau der Atome Quantenmechanik ==> Atomphysik Niels Bohr, 1913: kritische Entwicklung, die schließlich Plancks
Quantenmechanik& Wahrscheinlichkeit. Der liebe Gott würfelt nicht! Albert Einstein um 1923
 Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Mit diesem Ausspruch
Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Quantenmechanik& Wahrscheinlichkeit Der liebe Gott würfelt nicht! Albert Einstein um 1923 Mit diesem Ausspruch
Das Doppelspalt-Gedankenexperiment...
 Universität Hamburg Physik im Alltag Das Doppelspalt-Gedankenexperiment... Ψ... und seine Konsequenzen Prof. Dr. Michael Potthoff I. Institut für Theoretische Physik p. 1 Experimentalphysik p. 2 Experimentalphysik
Universität Hamburg Physik im Alltag Das Doppelspalt-Gedankenexperiment... Ψ... und seine Konsequenzen Prof. Dr. Michael Potthoff I. Institut für Theoretische Physik p. 1 Experimentalphysik p. 2 Experimentalphysik
Feynman Vorlesungen über Physik
 Feynman Vorlesungen über Physik Band llhouantenmechanik. Definitive Edition von Richard R Feynman, Robert B. Leighton und Matthew Sands 5., verbesserte Auflage Mit 192 Bildern und 22Tabellen Oldenbourg
Feynman Vorlesungen über Physik Band llhouantenmechanik. Definitive Edition von Richard R Feynman, Robert B. Leighton und Matthew Sands 5., verbesserte Auflage Mit 192 Bildern und 22Tabellen Oldenbourg
Moderne Physik. von Paul A. Tipler und Ralph A. LIewellyn. Oldenbourg Verlag München Wien
 Moderne Physik von Paul A. Tipler und Ralph A. LIewellyn Oldenbourg Verlag München Wien Inhaltsverzeichnis I Relativitätstheorie und Quantenmechanik: Die Grundlagen der modernen Physik 1 1 Relativitätstheorie
Moderne Physik von Paul A. Tipler und Ralph A. LIewellyn Oldenbourg Verlag München Wien Inhaltsverzeichnis I Relativitätstheorie und Quantenmechanik: Die Grundlagen der modernen Physik 1 1 Relativitätstheorie
Die seltsame Welt der Quanten
 Saturday Morning Physics Die seltsame Welt der Quanten Wie spielt Gott sein Würfelspiel? 12. 11. 2005 Gernot Alber und Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt [email protected]
Saturday Morning Physics Die seltsame Welt der Quanten Wie spielt Gott sein Würfelspiel? 12. 11. 2005 Gernot Alber und Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt [email protected]
Durch welchen Schlitz ist das Teilchen geflogen? Beobachtung
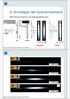 ) Grundlagen der Quantenmechanik Welle-Teilchen-Dualismus: das Doppelspaltexperiment Teilchen Welle Durch welchen Schlitz ist das Teilchen geflogen? Beobachtung Welle-Teilchen-Dualismus: 1) P =... Wahrscheinlichkeitsamplitude
) Grundlagen der Quantenmechanik Welle-Teilchen-Dualismus: das Doppelspaltexperiment Teilchen Welle Durch welchen Schlitz ist das Teilchen geflogen? Beobachtung Welle-Teilchen-Dualismus: 1) P =... Wahrscheinlichkeitsamplitude
Ein schwarzer Körper und seine Strahlung
 Quantenphysik 1. Hohlraumstrahlung und Lichtquanten 2. Max Planck Leben und Persönlichkeit 3. Das Bohrsche Atommodell 4. Niels Bohr Leben und Persönlichkeit 5. Wellenmechanik 6. Doppelspaltexperiment mit
Quantenphysik 1. Hohlraumstrahlung und Lichtquanten 2. Max Planck Leben und Persönlichkeit 3. Das Bohrsche Atommodell 4. Niels Bohr Leben und Persönlichkeit 5. Wellenmechanik 6. Doppelspaltexperiment mit
3. Klausur in K2 am
 Name: Punkte: Note: Ø: Profilfach Physik Abzüge für Darstellung: Rundung: 3. Klausur in K am 4.3. 05 Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: h =
Name: Punkte: Note: Ø: Profilfach Physik Abzüge für Darstellung: Rundung: 3. Klausur in K am 4.3. 05 Achte auf die Darstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Angaben: h =
Verschiedene Interpretationen der Quantenmechanik
 Verschiedene Interpretationen der Quantenmechanik Albert Steiner Handout 18.01.2012 1 Einleitung Der Beginn des Welle-Teilchen Dualismus ist das Strahlungsgesetz für einen schwarzen Körper von Max Plank.
Verschiedene Interpretationen der Quantenmechanik Albert Steiner Handout 18.01.2012 1 Einleitung Der Beginn des Welle-Teilchen Dualismus ist das Strahlungsgesetz für einen schwarzen Körper von Max Plank.
10. Das Wasserstoff-Atom Das Spektrum des Wasserstoff-Atoms. im Bohr-Modell:
 phys4.016 Page 1 10. Das Wasserstoff-Atom 10.1.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
phys4.016 Page 1 10. Das Wasserstoff-Atom 10.1.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
22. Wärmestrahlung. rmestrahlung, Quantenmechanik
 22. Wärmestrahlung rmestrahlung, Quantenmechanik Plancksches Strahlungsgesetz: Planck (1904): der Austausch von Energie zwischen dem strahlenden System und dem Strahlungsfeld kann nur in Einheiten von
22. Wärmestrahlung rmestrahlung, Quantenmechanik Plancksches Strahlungsgesetz: Planck (1904): der Austausch von Energie zwischen dem strahlenden System und dem Strahlungsfeld kann nur in Einheiten von
Vorlesung: Festkörperelektronik
 Vorlesung: Festkörperelektronik I.0 Allgemeine Informationen: Prof. Uli Lemmer Lichttechnisches Institut, Geb. 30.34, Raum 223 Tel: 0721-608-2530 E-Mail: [email protected], URL: www.lti.uni-karlsruhe.de
Vorlesung: Festkörperelektronik I.0 Allgemeine Informationen: Prof. Uli Lemmer Lichttechnisches Institut, Geb. 30.34, Raum 223 Tel: 0721-608-2530 E-Mail: [email protected], URL: www.lti.uni-karlsruhe.de
RELATIVITÄT und QUANTEN
 FAKULTÄT FÜR PHYSIK PHYSIK AM SAMSTAG RELATIVITÄT und QUANTEN Konzepte der Teilchenphysik J. H. KÜHN http://www-ttp.physik.uni-karlsruhe.de/slides PHYSIK Reduktion der Beobachtungen auf einfache Naturgesetze
FAKULTÄT FÜR PHYSIK PHYSIK AM SAMSTAG RELATIVITÄT und QUANTEN Konzepte der Teilchenphysik J. H. KÜHN http://www-ttp.physik.uni-karlsruhe.de/slides PHYSIK Reduktion der Beobachtungen auf einfache Naturgesetze
