SCHRIFTENREIHE SCHIFFBAU
|
|
|
- Heinz Baumann
- vor 7 Jahren
- Abrufe
Transkript
1 August 2008 SCHRIFTENREIHE SCHIFFBAU Stefan Krüger Hydrostatik von Schiffen
2 Institut für Entwerfen von Schiffen und Schiffssicherheit Prof Dr-Ing Stefan Krüger Hydrostatik von Schiffen Prof Dr-Ing Stefan Krüger 23 April 2013
3 Inhaltsverzeichnis 1 Grundlagen 4 11 Hauptabmessungen 4 12 Koordinatensystem 5 13 Ansichten 6 14 Linienriss 7 15 Völligkeitsgrade 8 16 Flächenträgheitsmomente 9 2 Gesetz des Archimedes Druckverteilung im Wasser Schwimmender Körper 11 3 Kleine Änderungen der Schwimmlage Beliebige, kleine Änderung der Schwimmlage Tiefertauchung um δt Verdrehung um δϕ Verdrehung um δψ Schwimmkörper unter äußeren Einwirkungen 23 4 Stabilität von Schwimmlagen 27 5 Kleine Schwimmlagenänderungen intakter Schiffe Krängung um δϕ : Trimm um δψ : Einheitstrimmmoment Stabilitätsbedingungen 37 6 Pantokarenen und Stabilitätshebelarme Pantokarenen Stabilitätshebelarme Schiffskörper unter der Wirkung eines krängenden Momentes M ξ und außermittiger Lage y G des Gewichtsschwerpunktes Pantokarenen und Hebelarme unvertrimmter Quader Berechnung des Verdrängungsschwerpunkts und der Pantokarenen gekrängter Quader (Formschwerpunktskurve) Berechnung der Schwerpunktskoordinaten des Verdrängungsschwerpunktes und der Pantokarenen für die Bereiche I und Berechnung der Schwerpunktskoordinaten des Verdrängungsschwerpunktes und der Pantokarenen für die Bereiche II und Berechnung der Schwerpunktskoordinaten des Verdrängungsschwerpunkts und der Pantokarenen für die Bereiche III und 3 51 Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 2/77
4 635 Krümmung, Krümmungsradius der Formschwerpunktskurve (Metazentrische Evolute) Metazentrische Evolute eines Quaders für die Bereiche I und Metazentrische Evolute für die Bereiche II und Metazentrische Evolute eines Quaders für die Bereiche III und Stabilitätskurven bzw Pantokarenen Hebel des aufrichtenden Momentes Schiff und Quader 61 7 Krängende Momente Moment durch seitlichen Winddruck Moment bei Drehkreisfahrt Verschiebung von Flüssigkeiten in Tanks mit freien Oberflächen Moment durch Verrutschen von Ladung Moment durch Wasser an Deck Moment durch Vereisung Moment durch Personen Moment durch hängende Lasten Moment durch Trossenzug Moment durch Propellerdrehmoment Momentenbilanz Stabilitätsforderungen 67 8 Schiff mit Grundberührung Schiff sitzt mit der ganzen Länge des Kiels auf (Schiff im Dock) Schiff sitzt auf einem Punkt des Kiels fest (Strandung, Aufdrehen beim Stapellauf) 70 9 Stapellauf Allgemeines Ablauf Erweiterungen und Notizen Pantokarenen 77 Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 3/77
5 1 Grundlagen 11 Hauptabmessungen Abbildung 1: Hauptabmessungen, nach Normentwurf DIN Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 4/77
6 Bezeichnung Einheit Bedeutung deutsch englisch L OA L OA m Länge über alles, vom vordersten zum hintersten festen Punkt L PP L PP m Länge zwischen den Loten (Perpendiculars) L WL L WL m Länge in der Schwimmwasserlinie DWL CWL m Konstruktionswasserlinie VL FP m Vorderes Lot (Fore Perpendicular), Schnittpunkt CWL mit Mallkante Vordersteven HL AP m Hinteres Lot (After perpendicular), Mitte Ruderschaft B OA B OA m Breite über alles T, T DWL T, d, T D m Konstruktionstiefgang gemessen auf halber Länge zwischen den Loten H D m Seitenhöhe F F m Freibord m 3 Verdrängtes Volumen des Schiffes auf Spanten t Deplacement: Verdrängte Masse MS CL Mittschiffsebene (Centreline plane) HS, MF Hauptspant WL WL Wasserlinie SB SB Steuerbordseite (starboard) BB, XB PS, XB Backbordseite (portside) Tabelle 1: Einige wichtige Abmessung In der Seefahrt wird das gebunkerte Süßwasser als Frischwasser bezeichnet, in Anlehnung an das englische Wort freshwater für Süßwasser 12 Koordinatensystem Man führt ein schiffsfestes Koordinatensystem ein Üblicherweise liegt der Koordinatenursprung im hinteren Lot (HL) auf der Höhe der Basis in der Schiffsmitte Die x- Achse geht entlang der Schiffslängsachse, die y-achse ist die Querachse und die z-achse die Hochachse Da der Ursprung in der Schiffsmitte liegt, können die y-werte sowohl positiv als auch negativ sein Für die Backbordseite sind die y-werte positiv und für die Steuerbordseite negativ Die x-werte werden zum Bug hin positiv gezählt, alles was hinter HL liegt wird negativ Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 5/77
7 Abbildung 2: Schiffsfestes Achsensystem, nach Normentwurf DIN Ansichten Man denkt sich den Schiffsrumpf von Ebenen parallel zu den Ebenen des kartesischen Koordinatensystems zerschnitten Die Projektionen der so entstandenen Umrisslinien auf jeweils eine gemeinsame Zeichenebene ergeben drei Ansichten des Schiffskörpers (siehe Abbildung 3): Spantenriss (body plan) in der y,z-ebene (Spanten, frames,sections), Längsriss (sheer plan) in der x,z-ebene (Schnitte, buttocks), Wasserlinienriss (half-breadth plan, water-line plan) in der x,y-ebene (Wasserlinien, waterlines) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 6/77
8 Abbildung 3: Projektion des Schiffskörpers in die drei Ebenen des kartesischen Koordinatensystems Wegen der Übersichtlichkeit ist der Ursprung verschoben gezeichnet Ein weiterer Schnitt, der in einem Winkel zur Mittschiffsebene gelegt wird, dient der Kontrolle des Linienverlaufs und wird Sentenriss (plan of diagonals) genannt Ausgehend von der Mittschiffsebene werden geneigte Schnitte geführt, die möglichst viele Spanten möglichst senkrecht schneiden Es ergeben sich den Wasserlinien ähnliche Kurven 14 Linienriss Der Linienriss enthält den Spantenriss, den Längsriss und den Wasserlinienriss Bei der Entwicklung des Linienrisses müssen die Linien straken, dh sie müssen stetig verlaufen Spanten: L pp wird in eine gerade Anzahl gleicher Abstände eingeteilt (zb 10 oder 20); es entstehen 10 bzw 20 Konstruktionsspanten, wobei man mit der Zählung am AP mit 0 beginnt Da an den Schiffsenden starke Krümmungen der Außenhaut auftreten, werden hier meist weitere Spanten in engeren Abständen angeordnet Im Spantenriss wird das Vorschiff rechts und das Hinterschiff links dargestellt Schnitte: Der Umriss stellt Vor- und Hintersteven, die Aufbauten und den Decksverlauf dar Dabei werden die halben Schnitte durch die vordere Schiffshälfte rechts und die durch die hintere Schiffshälfte links dargestellt Wasserlinien: Glatte Abstände, zb 0,5 m oder 1 m usw Zusätzlich wird die Konstruktionswasserlinie CWL eingezeichnet Es wird jeweils nur die Backbordhälfte Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 7/77
9 dieser Kurven in den Linienriss eingezeichnet Abbildung 4: Linienriss 15 Völligkeitsgrade Unter dem Völligkeitsgrad oder der Völligkeit versteht man im Schiffbau das Verhältnis einer beliebig geformten Fläche zur Fläche des umschreibenden Rechtecks, eines beliebig geformten Körpers zum Volumen des umschreibenden Quaders Die Völligkeitsgrade charakterisieren die Schiffsform Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 8/77
10 Definition Bezeichnung Erläuterung Völligkeitsgrad der Wasserlinienfläche C WP = A W L B Verhältnis der auf Mallkante bezogenen Wasserlinienfläche zum umschreibenden Rechteck C M = A M B T Völligkeitsgrad der eingetauchten Hauptspantfläche Verhältnis der auf Mallkante bezogenen eingetauchten Hauptspantfläche zu dem Rechteck aus Breite und Tiefgang C B = V L B T Blockkoeffizient Verhältnis des Volumens des Unterwasserschiffes zum umschriebenen Quader C P = V A M L Zylinderkoeffizient oder Schärfegrad Verhältnis des Volumens des Unterwasserschiffes zum Volumen des aus Hauptspantfläche und Länge gebildeten Körpers 16 Flächenträgheitsmomente Im Schiffbau gibt es für die Flächenträgheitsmomente der Wasserlinienfläche verschiedene übliche Bezeichnungen So wird das Flächenträgheitsmoment um die x-achse auch Breitenträgheitsmoment genannt, übliche Bezeichnungen sind: I xs = I W L = I T Das Flächenträgheitsmoment um die y-achse wird auch Längenträgheitsmoment genannt und hat die Bezeichnungen: I ys = I W LL = I L Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 9/77
11 2 Gesetz des Archimedes Diese Dokumentation wurde erstellt aufgrund der Vorlage von Prof Kloppenburg, ehem Inst f Schiffbau 21 Druckverteilung im Wasser Neben dem bereits in Kapitel 1 erwähnten schiffsfesten Koordinatensystem wird ein ortsfestes Koordinatensystem eingeführt Das globale Koordinatensystem ξ, η, ζ (xi, eta, zeta) orientiert sich an der Wasseroberfläche Die ξ, η-ebene ist die Wasseroberfläche oder eine dazu parallele Ebene, ζ weist senkrecht nach unten (zum Erdmittelpunkt) Das ruhende Wasser besitzt die Dichte ρ und damit das spezifische Gewicht (ρg) Das spezifische Gewicht gibt den Quotienten aus Gewichtskraft (gravity, Abkürzung G) und Volumen an: G V = m g = ρg V Die Flüssigkeitssäule hat den Querschnitt A und die Höhe ζ Dann existieren an der Wassersäule folgende Vertikalkräfte (Kräfte, die nach oben zeigen, werden positiv gezählt), siehe Abbildung 5 Luftdruck p B η ξ ζ Globales Koordinatensystem ζ A Wasserdruck p Abbildung 5: Absoluter Wasserdruck F 0 = p 0 A (Druckkraft an der Oberseite) (21) F G = G = (ρg) V = (ρg)a ζ (Gewicht) (22) F S = p A (Druckkraft an der Unterseite) (23) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 10/77
12 Das statische Gleichgewicht liefert: F = p0 A (ρg)a ζ + p A = 0 (24) Damit erhält man in der Tiefe ζ einen Überdruck von: (p p 0 ) = (ρg) ζ (25) Der Überdruck ist die Differenz zwischen dem Umgebungsdruck p 0 und dem Druck p in der Tiefe ζ 22 Schwimmender Körper Es gibt zwei Schwimmzustände für Schwimmkörper: voll getaucht und teilweise getaucht Ein voll getauchter Schwimmkörper befindet sich in nur einem Medium, wie zb ein U- Boot ganz unter Wasser, ein teilweise getauchter Schwimmkörper befindet sich in zwei Medien, wie zb ein konventionelles Frachtschiff in Luft und Wasser Daraus ergeben sich für das Schwimmverhalten, zb die Schwimmstabilität, unterschiedliche Zusammenhänge Bei einer Krängung eines Überwasserschwimmkörpers verändert sich die Form des eingetauchten Volumens, entsprechend muss sich auch die Lage des Auftriebsschwerpunktes ändern Wird ein Unterwasserschwimmkörper gekrängt, so ändert sich die Lage des Auftriebsschwerpunktes nicht, da sich die Wasser verdrängende Form nicht ändert Im Auftriebsschwerpunkt greift die Auftriebskraft F B an Es existiert ein schwimmender/teilweise eingetauchter Körper mit einer Unterwasserform S(ξ,η) siehe Abbildung 6 p B da Körper η ξ G ξ B da dv G B W F B ξ S(ξ,η) ζ pda Abbildung 6: Auftrieb Denkt man sich eine Säule mit dem Querschnitt da aus dem Körper herausgeschnitten, wirken an der Säule folgende Vertikalkräfte, wobei die Kräfte, die nach oben zeigen, Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 11/77
13 wieder positiv gezählt werden: df B = (p p B ) da = (ρg)ζ da = (ρg) dv (26) Momente von df B um die ξ und η Achse: dm Bξ = ηdf B = (ρg)ηζda = (ρg)ηdv, dm Bη = ξdf B = (ρg)ξζda = (ρg)ξdv (27) Hier bedeutet dv den eingetauchten/schraffierten Volumenanteil Für den Gesamtauftrieb gilt dann: F B = df B = (ρg) ζda = (ρg)v ; ζ > 0 (28) S S F B ist die Gesamtauftriebskraft S ist der eingetauchte, benetzte Oberflächenanteil des Körpers V ist das eingetauchte Körpervolumen, dh seine Verdrängung B(ξ B ; η B ; ζ B ) ist der Auftriebsschwerpunkt, dh der Volumenschwerpunkt der verdrängten Flüssigkeit Momente des Gesamtauftriebs F B um die ξ bzw η Achse: M Bξ = dm Bξ = (ρg) ηζda = (ρg) ηdv = (ρg)m V ξ = (ρg)η B V, S S S M Bη = dm Bη = (ρg) ξζda = (ρg) ξdv = (ρg)m V η = (ρg)ξ B V (29) S S M Bξ bzw M Bη nennt man Auftriebsmoment, bei M V ξ bzw M V η spricht man vom Volumenmoment S Gleichgewichtsbedingungen am Gesamtkörper: Drei Gleichgewichtsbedingungen definieren die hydrostatische Schwimmlage eines teilgetauchten Körpers: Eine translatorische (Kräftegleichgewicht in ζ-richtung) und zwei rotatorische (Momentengleichgewicht um die ξ-achse und um die η-achse) Gleichgewichtsbedingungen Kräftegleichgewicht: Daraus folgt das Gesetz des Archimedes: G + F B = G + (ρg)v = 0 G = g = (ρg)v (210) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 12/77
14 In Worten: Das Gewicht eines Schwimmkörpers ist gerade so groß wie das Gewicht des von ihm verdrängten Wassers Anders: Die Auftriebskraft eines schwimmenden Körpers ist gleich der Gewichtskraft des verdrängten Flüssigkeitsvolumens G ist die Gewichtskraft - kurz das Gewicht - des Schwimmkörpers, = ρv ist sein Deplacement (Masse; Einheit in t), V ist das eingetauchte Volumen (wird im Schiffbau auch mit dem Symbol gekennzeichnet) Momentengleichgewicht: G(ξ G ; η G ; ζ G ) ist der Gewichtsschwerpunkt Moment um die ξ Achse: G η G + M Bξ = G η G + (ρg)η B V = 0 Daraus folgt: Moment um die η Achse: η G = η B (211) G ξ G + M Bη = G ξ G + (ρg)ξ B V = 0 Daraus folgt: ξ G = ξ B (212) In der Gleichgewichtslage liegen Gewichtsschwerpunkt G und Auftriebsschwerpunkt B auf einer gemeinsamen vertikalen Wirkungslinie Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 13/77
15 Beispiele: Beispiel 1: Ein Holzfloß mit dem Volumen V F l = 0,8m 3 und der Dichte von Holz ρ H = 0,7 t m 3 schwimmt in Süßwasser (engl freshwater; ρ F W = 1 t ); g = 9,81 m = 9,81 N m 3 s 2 kg = 9,81 kn t Bei welcher Beladung F geht das Floß unter? Man betrachtet das Kräftegleichgewicht F B G F = 0 kurz bevor das Floß untergeht, also wenn es vollständig getaucht ist; das eingetauchte Volumen entspricht dann dem Gesamtvolumen des Floßes Daraus folgt: F = F B G = (ρ F W ρ H )g V F l = (1,0 0,7) t m 3 9,81kN t 0,8m 3 = 2,35kN Beispiel 2: Ein Ponton (L = 7m; B = 2m; = 6t) schwimmt in Seewasser (ρ SW = 1,03t/m 3 ) a) Welcher Tiefgang stellt sich ein? b) Welche Masse m muss zu-/abgeladen werden, damit eine Tiefgangszu-/abnahme von δt = 0,15m erreicht wird? Zu a): Mit = ρ SW V = ρ SW L B T findet man: Zu b): T = ρ SW L B = 6t 1,03 t 7m 2m = 0,416m m 3 m = ρ SW L B δt = 1,03 t 7m 2m 0,15m = 2,16t m3 Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 14/77
16 3 Kleine Änderungen der Schwimmlage Dieses Kapitel beschäftigt sich mit der Betrachtung der Kräfte und Momente an einem beliebig geformten Körper, wenn dieser kleine Änderungen seiner Schwimmlage erfährt Hier wird also die Theorie hergeleitet, die dann im Kapitel Kleine Schwimmlageänderungen intakter Schiffe auf Schiffe angewendet wird Wichtig ist, dass die Formeln dieser beiden Kapitel nur für kleine Neigungen gelten Wie in der Einführung bereits benutzt, ist bei der Betrachtung schwimmender Körper im allgemeinen eine Unterscheidung zwischen einem globalen/ortsfesten (ξ; η; ζ) und einem lokalem/körperfesten (x; y; z) Koordinatensystem nötig oder nützlich Die einschränkende Aussage hier, dass nämlich nur kleine Änderungen der Schwimmlage betrachtet werden sollen, ist dagegen so gemeint, dass diese Unterscheidung zwischen den beiden Koordinatensystemen nicht erforderlich ist Der Unterschied beider Systeme sei also klein und vernachlässigbar Deshalb wird im Folgenden immer nur vom globalen Koordinatensystem gesprochen werden Die ξ; η Ebene sei wieder horizontal, also parallel zur Wasseroberfläche, die ihrerseits als unveränderlich angesehen wird Dagegen kann der Koordinatenursprung beliebig gewählt werden Nach der Wahl bleibt das Koordinatensystem (ξ; η; ζ) fest Veränderungen der Schwimmlage werden als Veränderungen im gewählten Koordinatensystem angegeben, s Abb 7 Ausgehend von einer statischen Gleichgewichtslage, ΣF = 0; ΣM = 0, sollen kleine Veränderungen / Abweichungen von einer erwarteten/gewollten Schwimmlage betrachtet werden Der Schwimmkörper erfahre kleine Verschiebungen (Translationen) und Verdrehungen (Rotationen) Er besitzt sechs Freiheitsgrade, drei translatorische und drei rotatorische Verschiebungen in ξ und η Richtung (also Bewegungen parallel zur Wasseroberfläche), sowie Drehung um die ζ Achse bewirken keine Veränderung des eingetauchten Volumens/ Auftriebs, dadurch ergeben sich keine zusätzlichen Kraft- bzw Momentenwirkungen Bezüglich dieser drei Freiheitsgrade befindet sich der Körper im indifferenten Gleichgewicht 31 Beliebige, kleine Änderung der Schwimmlage Eine beliebige, kleine Veränderung der Lage des Schwimmkörpers enthält ein δt als Verschiebung in ζ Richtung und Drehungen δϕ um die ξ Achse und δψ um die η Achse Jede dieser anteiligen Lageänderungen des Schwimmkörpers liefert eine Veränderung des eingetauchten Volumens um δv und führt dadurch zu Änderungen des Auftriebs δf B und der Auftriebsmomente δm Bξ und δm Bη Es werden nun also die Änderungen des Auftriebs und der Auftriebsmomente für die drei Änderungen der Schwimmlage näher betrachtet: 1 Tiefertauchung um δt (translatorische Bewegung in Richtung der ζ-achse), 2 Verdrehung um δϕ (rotatorische Bewegung um die ξ-achse), 3 Verdrehung um δψ (rotatorische Bewegung um die η-achse) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 15/77
17 32 Tiefertauchung um δt δt Aw ζ Schwimmwasserlinie ursprglwl da ξ η Körper Abbildung 7: Tiefertauchung um δt Vergrößerung des Tiefgangs T um δt liefert eine Veränderung des Volumens um δv, siehe Abbildung 7: δv = δt da = δt A w da = δt A w A w (31) mit A w als Fläche der Schwimmwasserlinie (WL-Fläche) Auftriebsänderung: Mit dem Gesetz des Archimedes findet man den Differenzenquotienten δf B δt F B = (ρg)v (32) deltaf B = (ρg)δv (33) = (ρg)δv δt = (ρg)a w (34) Beim Grenzübergang δt 0 wird daraus der Differentialquotient: F B T = (ρg)a w (35) δf B sei positiv bei einer Tiefgangszunahme, dann ist δf B nach oben gerichtet Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 16/77
18 Änderung des Momentes M Bη des Auftriebs F B (Auftriebsmoment um die η-achse): δm Bη = ξδf B = ξ(ρg)δv = (ρg)δt ξ da A w (36) Der Schwerpunkt der WL-Fläche habe die Koordinaten F (ξ w ; η w ), berechnet aus A w ξ w = ξ da; A w A w η w = η da A w (37) Damit wird und beim Grenzübergang δt 0 : δm Bη δt M Bη T = (ρg) ξ w A w, (38) = (ρg) ξ w A w (39) Damit wird Änderung des Auftriebsmomentes M Bξ ( um die ξ-achse): δm Bξ = ηδf B = η(ρg)δv = (ρg)δt η da, A w δm Bξ δt und beim Grenzübergang δt 0 : = (ρg) η w A w, M Bξ T = (ρg) η w A w Zusammenstellung : Aufgrund einer Tiefertauchung T ergibt sich: F B T = (ρg)a w; M Bη T = (ρg) ξ w A w ; M Bξ T = (ρg) η w A w 33 Verdrehung um δϕ Rechts-(Links-)Drehung des Körpers um die negative (positive) ξ Achse um δϕ (Eine Verdrehung um die horizontale ξ Achsen liefert zunächst eine Horizontalverschiebung des Körpers um ζdϕ, womit keine Änderung des eingetauchten Volumens verbunden ist Allerdings ist als zusätzlicher Effekt mit der Verdrehung auch eine parallele Tiefertauchung um ζ(dϕ) 2 verbunden Letztere ist jedoch von höherer Ordnung klein und damit vernachlässigbar Gleiches gilt auch für eine Verdrehung um die η Achse) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 17/77
19 ζ δϕ WL ursprgl WL da h= ηδϕ ζ δϕ r r B B δη Β ξ η Körper ξ ϕ η Körper Abbildung 8: Verdrehung um δϕ (links) und Auswanderung des Auftriebsschwerpunktes (rechts) Verdrehung um δϕ liefert, siehe Abbildung 8 (links): δv = h da = δϕ A w ηda = δϕ η w A w A w Auftriebsänderung: bzw δf B δϕ = (ρg)δv δϕ = (ρg) η w A w F B ϕ = (ρg) η w A w Änderung des Auftriebsmomentes M Bη : δm Bη = ξδf B = ξ(ρg)δv = (ρg)δϕ ξ η da A w bzw I ξη = A w ξ η da δm Bη δϕ M Bη ϕ = (ρg)j ξη = (ρg)j ξη Zentrifugalmoment der WL-Fläche, bezogen auf die ξ und η Achse Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 18/77
20 Änderung des Auftriebsmomentes M Bξ : Moment des eintauchenden Volumens δv : δm Bξ1 = ηδf B = η(ρg)δv = (ρg)δϕ η 2 da A w bzw I ξ = A w η 2 da δm Bξ1 δϕ = (ρg)i ξ M Bξ1 ϕ = (ρg)i ξ Trägheitsmoment der WL-Fläche bezogen auf die ξ Achse Moment durch Änderung der Lage des Auftriebsschwerpunktes B, s Abb 8 (rechts), (Änderung des Momentes M Bξ der Gesamtverdrängung V ) : ζ Β δη B ξ ϕ r r δϕ η B =rcosϕ r δϕ ζ B =rsinϕ δηb ϕ B η Abbildung 9: Änderung δη B bei Verdrehung um δϕ Der Auftriebsschwerpunkt habe die Koordinaten B(ξ B ; η B ; ζ B ) Durch Drehung um δϕ wandert er nach B, r bleibt erhalten, ϕ ändert sich um ( δϕ), siehe Abbildung 9 δη B = dη B dϕ η B = r cos ϕ; ζ B = r sin ϕ cos ϕ) ( δϕ) = d(r δϕ = r sin ϕ δϕ = ζ B δϕ; dϕ dη B dϕ = ζ B; dη B dt = dη B dψ = 0 Bei diesem Anteil der Änderung des Auftriebsmomentes ist die Gesamtverdrängung beteiligt! δm Bξ2 = δη B (ρg)v = (ρg)δϕ ζ B V Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 19/77
21 bzw δm Bξ2 δϕ M Bξ2 ϕ = (ρg)ζ BV = (ρg)ζ BV Zusammenstellung : Aufgrund einer Verdrehung δϕ um die negative ξ Achse ergibt sich: F B ϕ = (ρg)η wa w ; M Bη ϕ = (ρg)i ξη; M Bξ ϕ = (ρg)(i ξ + ζ B V ) 34 Verdrehung um δψ Rechtsdrehung des Körpers um die positive η Achse um δψ Verdrehung um δψ liefert, s Abb 10 (links): η ζ δψ ξ da WL ursprgl WL Körper h= ξδψ ζ η δψ ψ r r Β ξ B=rcosψ δξ B r δψ ζ B =rsinψ B ψ B ξ Abbildung 10: Verdrehung um δψ δv = h da = δψ A w ξ da = δψ ξ w A w A w Auftriebsänderung: δf B δψ = (ρg)δv δψ = (ρg) ξ w A w bzw F B ψ = (ρg)ξ w A w Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 20/77
22 Änderung des Auftriebsmomentes M Bη : Moment des eintauchenden Volumens: δm Bη1 = ξδf B = ξ(ρg)δv = (ρg)δψ ξ 2 da A w bzw I η = A w ξ 2 da δm Bη1 δψ = (ρg)i η M Bη1 ψ = (ρg)i η Trägheitsmoment der WL-Fläche bezogen auf die η Achse Moment durch Änderung der Lage des Auftriebsschwerpunktes B Durch Drehung um δψ wandert der Auftriebsschwerpunkt nach B, r bleibt erhalten, ψ ändert sich um δψ, s Abb 10 (rechts) ξ B = r cos ψ; ζ B = r sin ψ δξ B = dξ B dψ ( δψ) = r sin ψ δψ = ζ B δψ dξ B dψ = ζ B; dξ B dt = dξ B dψ = 0 δm Bη2 = δξ B (ρg)v = (ρg)δψ ζ B V bzw δm Bη2 δψ M Bη2 ψ = (ρg)ζ BV = (ρg)ζ BV Änderung des Auftriebsmomentes M Bξ: δm Bξ = ηδf B = η(ρg)δv = (ρg)δψ ξ η da A w bzw δm Bξ δψ M Bξ ψ = (ρg)i ξη = (ρg)i ξη Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 21/77
23 Zusammenstellung : Aufgrund einer Verdrehung δψ um die positive η Achse ergibt sich: F B ψ = (ρg)ξ w A w ; M Bη ψ = (ρg)(i η + ζ B V ); M Bξ ψ = (ρg)i ξη Gesamtänderung df B (totales Differential) des Auftriebs aufgrund von dt ; dψ; dϕ : df B = F B T dt + F B ψ dψ + F B ϕ dϕ = (ρg)[a w dt + ξ w A w dψ + η w A w dϕ] (310) Gesamtänderung dm Bη des Auftriebsmomentes: dm Bη = M Bη T dt + (M Bη1 + M Bη2 ) dψ + M Bη ψ ϕ dϕ = (ρg)[ξ w A w dt + (I η + ζ B V )dψ + I ξη dϕ] (311) Gesamtänderung dm Bξ des Auftriebsmomentes: dm Bξ = M Bξ T dt + M Bξ ψ dψ + (M Bξ1 + M Bξ2 ) dϕ ϕ = (ρg)[η w A w dt + I ξη dψ + (I ξ + ζ B V )dϕ] (312) Die neun Ableitungen von F B ; M Bη ; M Bξ nach T ; ψ; ϕ lassen sich in folgender Kurzschreibweise zusammenfassen: (F B ; M Bη ; M Bξ ) (T ; ψ; ϕ) A = F B T M Bη T M Bξ T F B ψ M Bη ψ M Bξ ψ F B ϕ M Bη ϕ M Bξ ϕ = A A w ξ w A w η w A w = (ρg) ξ w A w (I η + ζ B V ) I ξη (313) η w A w I ξη (I ξ + ζ B V ) Die Matrix A der Ableitungen ist quadratisch und symmetrisch Die drei Gleichungen 310, 311, 312 zur Berechnung der Änderungen von Auftrieb und Auftriebsmomenten lassen sich damit in folgender Kurzschreibweise zusammenfassen: df B dm Bη dm Bξ = A dt dψ dϕ (314) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 22/77
24 35 Schwimmkörper unter äußeren Einwirkungen Bisher wurde statisches Gleichgewicht angenommen, F = 0; M = 0 Jetzt soll der Fall behandelt werden, dass sich endliche Resultierende ergeben, dh von außen wird auf den Körper eingewirkt Resultierende Vertikalkraft: bzw F ζ = F B W δf ζ = δf B δw Da sich durch Änderung der Schwimmlage das Gewicht des Schwimmkörpers nicht ändert (G = konst), verschwinden auch alle Ableitungen G T = G ψ = G ϕ 0 und es kann δg 0 gesetzt werden und somit: δf ζ = δf B Die Definition von F ζ ist: Wenn eine Tiefertauchung δt eintritt, ist F B > G F ζ > 0 Damit weist F ζ positiv nach oben, was jedoch auch bedeutet, dass die äußere Einwirkung den Schwimmkörper nach unten drückt Resultierende Momente : η Achse: bzw ξ Achse: bzw M η = M Bη ξ G G δm η = δm Bη δξ G G M ξ = M Bξ η G G δm ξ = δm Bξ δη G G Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 23/77
25 Änderung der Schwerpunktskoordinaten : ζ G δη G r δϕ r ϕ G ξ ϕ δϕ r η G = rcosϕ ζ G =rsinϕ δηg η Abbildung 11: Änderung δη G bei Verdrehung um δϕ Der Gewichtsschwerpunkt habe die Koordinaten G(ξ G ; η G ; ζ G ) Drehung um δϕ um die negative ξ Achse, siehe Abbildung 11: η G = r cos ϕ; ζ G = r sin ϕ; δη G = dη G dϕ ( δϕ) = r sin ϕ δϕ = ζ G δϕ Bei einer Verschiebung um δt ändert sich η G nicht, auch nicht durch Verdrehung um δψ Zusammengefasst: dη G dϕ = ζ dη G G; dt = dη G dψ = 0 Drehung um δψ um die positive η Achse: ξ G = r cos ψ; ζ G = r sin ψ δξ G = dξ G dψ ( δψ) = r sin ψ δψ = ζ G δψ Bei einer Verschiebung um δt ändert sich ξ G nicht, auch nicht durch Verdrehung um δϕ Zusammengefasst: dξ G dψ = ζ G; dξ G dt = dξ G dϕ = 0 Die Gesamtänderungen von F ζ ; M η ; M ξ (totales Differential) aufgrund von dt ; dψ; dϕ: df ζ = df B = F ζ T dt + F ζ ψ dψ + F ζ ϕ dϕ dmη = dm Bη Gdξ G = (ρg)[a w dt + ξ w A w dψ + η w A w dϕ] (315) = M η T dt + M η ψ dψ + M η ϕ dϕ = (ρg)[ξ w A w dt + (I η + ζ B V )dψ + I ξη dϕ] Gζ G dψ (316) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 24/77
26 dm ξ = dm Bξ Gdη G = M ξ T dt + M ξ ψ dψ + M ξ ϕ dϕ = (ρg)[η w A w dt + I ξη dψ + (I ξ + ζ B V )dϕ] Gζ G dϕ (317) Hier wurden df B ; dm Bη und dm Bξ von vorne übernommen, s Gl (310); (311) und (312) Die neun Ableitungen von F ζ ; M η ; M ξ nach T ; ψ; ϕ lassen sich in folgender Kurzschreibweise zusammenfassen: (F ζ ; M η ; M ξ ) (T ; ψ; ϕ) S = F ζ T M η T M ξ T M ζ ψ M η ψ M ξ ψ F ζ ϕ M η ϕ M ξ ϕ = S (318) A w ξ w A w η w A w ξ w A w (I η + ζ B V ) I ξη = (ρg) Gζ G /(ρg) η w A w I ξη (I ξ + ζ B V ) Gζ G /(ρg) Die Matrix S der Ableitungen ist quadratisch und symmetrisch, dh: S = S S ist die transponierte Matrix zu S Für die Elemente der Matrix S gilt deshalb: a ik = a ki Hier bedeutet i den Zeilenzähler und k den Spaltenzähler Für Gleichgewicht der Vertikalkräfte gilt: G = (ρg)v = F B (319) Dann wird aus der Matrix S: (ρg)a w (ρg)ξ w A w (ρg)η w A w S = (ρg)ξ w A w G(I η /V + ζ B ζ G ) (ρg)i ξη (320) (ρg)η w A w (ρg)i ξη G(I ξ /V + ζ B ζ G ) Das Gleichungssystem 315; 316; 317 lässt sich analog zu Gl314 ebenfalls in kurzer Matrizenschreibweise darstellen: df ζ dm η dm ξ = S dt dψ (321) dϕ Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 25/77
27 Zu gegebenen dt ; dψ; dϕ lassen sich hiermit direkt die aus Gewicht G und Auftrieb F B resultierenden Kräfte und Momente bestimmen, indem die Matrix S mit dem Vektor dt dψ multipliziert wird Sind jedoch resultierende Kräfte oder Momente gegeben, dϕ ist die Schwimmlagenänderung durch Lösung des resultierenden Gleichungssystems zu ermitteln Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 26/77
28 4 Stabilität von Schwimmlagen Stabilität ist die Fähigkeit eines Schwimmkörpers, sich aus einer geneigten Lage (Krängung) wieder selbstständig aufzurichten Allgemein wird die Stabilität von folgenden Faktoren beeinflusst: die Form des Unterwasserschiffes, zb völlige oder weniger völlige Hauptspantform, die Verhältniswerte der Hauptabmessungen, zb B/T, T/D, vom Freibord; bei geringem Freibord taucht Seite Deck zu früh ein, die Lage des Gewichtsschwerpunktes; ein tiefliegender Gewichtsschwerpunkt führt zu starken aufrichtenden Momenten (Schiff ist steif ), ein hochliegender Gewichtsschwerpunkt bewirkt nur ein geringes aufrichtendes Moment (Schiff ist rank), äußere Einflussgrößen wie Winddruck, überkommende Wassermassen bei Seegang Der Schwimmkörper befinde sich in der Gleichgewichtslage: F ζ = M η = M ξ 0 Die Schwimmlage ist stabil, wenn kleine Schwimmlageänderungen (δt ; δψ; δϕ) in beliebiger Kombination eine positive (zu leistende) Arbeit erfordern, dh der Schwimmkörper wird versuchen in die aufrechte Position zurückzukehren Wiederholung der Vorzeichendefinitionen, s Abb 12: δt δψ Tiefertauchung des Körpers: Kraft δf ζ nach oben Rechtsdrehung um η Achse: Moment δm η linksdrehend um η δϕ Linksdrehung um ξ Achse: Moment δm ξ rechtsdrehend um ξ Schwimmlageänderungen (δt ; δψ; δϕ) und daraus resultierende Kräfte/Momente sind entgegengesetzt gerichtet Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 27/77
29 ζ R ζ ζ δt δt δϕ R ξ δψ R η ξ ϕ η η ψ ξ Abbildung 12: Vorzeichendefinition Tiefertauchung δt erfordert die Arbeit, s Abb13: L 1 = T0 +δt T 0 F ζ dt = 1 2 δt δf ζ Hier ist T 0 der Gleichgewichtstiefgang Treten außerdem Änderungen (δψ; δϕ) auf, so ist die Gesamtarbeit: L = 1 2 (δt δf ζ + δψδm η + δϕδm ξ ) In Matrizenschreibweise: (siehe Kapitel Kleine Änderung der Schwimmlage ) δf ζ 2L = (δt δψ δϕ) δm η δm ξ δt 2L = (δt δψ δϕ) S δψ δϕ Die Schwimmlage ist dann und nur dann stabil, wenn 2L für beliebige Vektoren (δt ; δψ; δϕ) (0; 0; 0); positiv ist: dh wird S von rechts mit einem Vektor (0; 0; 0) und von links mit demselben Vektor multipliziert, muss sich eine positive Zahl ergeben S ist positiv definit Eine Dreiecksmatrix mit nur positiven Elementen in der Hauptdiagonalen ist positiv definit Deshalb muss S in eine Dreiecksmatrix umgeformt werden a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 = a 11 a 12 a 13 a 12 a 22 a 23 a 13 a 23 a 33 E 1 A B 0 E 2 C 0 0 E 3 Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 28/77
30 R ζ T 0 δt L 1 δr ζ T Abbildung 13: Arbeit bei Tiefertauchung δt 1Index i =Zeile, 2Index k =Spalte Da die Matrix S symmetrisch ist, sind die Elemente a ik = a ki 1) 2) 3) a 11 a 12 a 13 a 12 a 22 a 23 a 13 a 23 a 33 (a 12 /a 11 ) (a 13 /a 11 ) (2 1) (3 1) Damit sind aus der zweiten und dritten Zeile die jeweils ersten Elemente a 12 ; a 13 entfernt und man erhält: ) 1) 2) 3) a 11 a 12 a 13 ( 0 (a 22 a 2 12 /a 11) (a 23 a 12 a 13 /a 11 ) a23 a 12 a 13 /a 11 0 (a 23 a 12 a 13 /a 11 ) (a 33 a 2 13 /a a 22 a ) /a 11 Die Dreiecksmatrix wird schließlich zu: a 11 a 12 a 13 0 (a 22 a 2 12 /a 11) (a 23 a 12 a 13 /a 11 ) 0 0 (a 33 a 2 13 /a 11) ( (a23 a 12 a 13 /a 11 ) 2 a 22 a 2 12 /a 11 ) (3 2) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 29/77
31 Damit werden die Elemente der Hauptdiagonalen der Dreiecksmatrix und nach dem Ersetzen der a ik aus der Matrix S zu: E 1 = a 11 = (ρg)a w E 2 = a 22 a 2 12/a 11 = (ρg)(i η + ζ B V ) Gζ G (ρg)ξ 2 wa w E 3 = a 33 a 2 13/a 11 1 E 2 (a 23 a 12 a 13 /a 11 ) 2 = (ρg)(i ξ + ζ B V ) Gζ G (ρg)η 2 wa w 1 E 2 ((ρg)i ξη (ρg)ξ w η w A w ) 2 E 2 ; E 3 lassen sich mit Hilfe des Steinerschen Satzes vereinfachen: I η ξ 2 wa w = I ηs I ηs ist das Flächenträgheitsmoment der WL-Fläche A w um eine zur η Achse parallele Achse durch den Schwerpunkt der WL-Fläche I ξ η 2 wa w = I ξs I ξs ist das Flächenträgheitsmoment der WL-Fläche A w um eine zur ξ Achse parallele Achse durch den Schwerpunkt der WL-Fläche I ξη ξ w η w A w = I ξηs I ξηs ist das Zentrifugalmoment der WL-Fläche A w bezüglich der Schwerpunktsachsen der WL-Fläche E 1 E 2 E 3 = (ρg)a w = (ρg)(i ηs + ζ B V ) Gζ G = (ρg)(i ξs + ζ B V ) Gζ G 1 E 2 (ρg) 2 I 2 ξηs Da G = (ρg)v > 0 und für die stabile Schwimmlage die E i > 0; (i = 1; 2; 3) sein müssen, wird durch G bzw (ρg)v geteilt Damit ist die Schwimmlage nur und nur dann stabil, wenn 1) A w > 0; 2) I ηs /V + ζ B ζ G > 0; ) 2 3) I ξs /V + ζ B ζ G /(IηS /V + ζ B ζ G ) > 0 ( IξηS V Ist eine der drei Größen gleich Null, die anderen jedoch größer Null, so kann die Schwimmlage stabil, instabil oder indifferent sein Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 30/77
32 So ist zb bei einem Fisch A w = 0 Er befindet sich in einem indifferenten Gleichgewicht Da G = (ρg)v, kann der Fisch ohne Arbeitsaufwand vertikal verschoben werden Ist nur eine der drei Größen kleiner Null, so ist die Schwimmlage instabil, dh die Schwimmlage verändert sich ohne Arbeitsaufwand in eine neue, stabile Gleichgewichtslage Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 31/77
33 5 Kleine Schwimmlagenänderungen intakter Schiffe Wir betrachten symmetrische, aufrecht schwimmende Schiffe, bei denen das Archimedische Gesetz G = (ρg)v = F B erfüllt ist Sie sollen kleine Änderungen (δt ; δϕ; δψ) der Schwimmlage erfahren Alle Formeln sind nur gültig für kleine Änderungen der Schwimmlage Praktisch bedeutet das, dass beispielsweise die Formänderung der Wasserline durch Ein- bzw Austauchen infolge von Trimm, Krängung oder Tiefertauchung verschwindend gering ist und im Wesentlichen der Ausgangsform entspricht Absolute Zahlenwerte können für moderne Schiffslinien nicht angegeben werden Beim Schiff nennt man die Änderung um δt Tiefertauchung, die Änderung um δϕ Krängung und die Änderung um δψ Trimm Das schiffsfeste Koordinatensystem (x; y; z) und das an der Wasseroberfläche orientierte raumfeste Koordinatensystem (ξ; η; ζ) fallen ungefähr zusammen Somit können (M ξ ; M η ; F ζ ) durch (M x ; M y ; F z ) ersetzt werden Dabei ist: Schiffslängsrichtung x; nach Backbord y; nach oben z Die x,z Ebene ist die Mittschiffs- und Symmetrieebene; dafür gilt: y w = 0; I xy = 0, da das Flächendeviationsmoment I xy für symmetrische Körper gleich Null wird Da y w = 0 und I xy = 0, vereinfacht sich die Matrix der Auftriebs-/Momentenänderungen zu (siehe Kapitel Kleine Änderungen der Schwimmlage ): F z / T F z / ψ F z / ϕ M y / T M y / ψ M y / ϕ = S M x / T M x / ψ M x / ϕ A w x w A w 0 S = (ρg) x w A w G (ρg) (I y/v + z B z G ) G (ρg) (I x/v + z B z G ) Multipliziert man S mit der Spaltenmatrix (δt ; δψ; δϕ) ergibt sich: δf z δm y δm x = (ρg)a w (δt + x w δψ); = (ρg)x w A w δt + G(I y /V + z B z G )δψ; = G(I x /V + z B z G )δϕ Legt man den Koordinatenursprung in den Schwerpunkt der WL-Fläche so wird: x w = 0; I x I xs = I W L ; I y I ys = I W LL Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 32/77
34 Dann gilt: δf z = (ρg)a w δt ; δm y δm x = G(I W LL /V + z B z G )δψ; = G(I W L /V + z B z G )δϕ Danach bewirkt eine Vertikalkraft im WL-Schwerpunkt nur eine Änderung des Tiefgangs um (δt ) Trimm und Krängung bleiben unverändert Ein Moment um Queroder Längsachse (y, oder x Achse) ändert nur Trimm oder Krängung um (δψ) oder (δϕ) Der Tiefgang am WL-Schwerpunkt bleibt unverändert, da das Schiff um den WL- Schwerpunkt dreht 51 Krängung um δϕ : Durch die Krängung ändert sich die Form des eingetauchten Volumens des Schiffes; der Auftriebsschwerpunkt B wandert nach B (s Abb 10) Die neue Wirklinie der Auftriebskraft geht durch den Punkt B und schneidet die bisherige Wirklinie der Auftriebskraft im Punkt M, dem Metazentrum Der Begriff meta (griech: scheinbar) weist darauf hin, dass dieser Schnittpunkt kein wirkliches Zentrum ist, also nicht festliegt Die Bahn, auf der sich das Metazentrum bewegt, heißt Evolvente Bei Schiffsformen ist das Metazentrum aber für kleine Krängungswinkel bis etwa 10 ein fester Punkt Vor allem in älterer Literatur wird das Metazentrum als scheinbarer Drehpunkt oder Aufhängepunkt gedeutet Durch die Krängung erfolgt eine Verschiebung eines Keilvolumens von der austauchenden Seite zur eintauchenden Seite Die Keilvolumina setzen sich aus Volumenteilchen δv zusammen, die alle horizontal und vertikal verschoben werden; es entstehen so horizontale und vertikale Verschiebungsmomente Die Summe der Verschiebungsmomente der Teilvolumen entspricht dem Verschiebungsmoment der Gesamtverdrängung Mit der Gesamtverschiebung des Autriebsschwerpunktes (y B,z B ) gilt für die Verschiebungsmomente in y-richtung y B V und in z-richtung z B V (siehe Abbildung 14): Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 33/77
35 M δϕ δϕ W G B z K x h y B z B y B F B da Abbildung 14: Krängung um δϕ 1 Die Verschiebung in y-richtung: y B V = ydv = A w ydz da = A w yyδϕ da = δϕ A w y 2 da = δϕi T A w Daraus folgt: y B = I W L V δϕ In dem annäherungsweise rechtwinkligen Dreieck BB M sieht man, dass für kleine Winkel gilt: y B = sin(δϕ) δϕ BM Damit ist: BM = y B δϕ = I W L V 2 Die Verschiebung in z-richtung: In z-richtung wandert der Auftriebsschwerpunkt kaum aus, so dass z B z B ist Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 34/77
36 Metazentrum: Die z-koordinate von M ist: Beim Schiff bedeuten: z M = y B δϕ + z B I W L V + z B I xs V = I W L V = BM; z B = KB; z G = KG; z M = KM KM = BM + KB = I W L + KB Eine Krängung um δϕ ruft ein aufrichtendes Moment M A hervor: δr x = M A = F B h = G h Aus der Abbildung liest man ab: h = GM δϕ Daraus folgt: M A = G GM δϕ GM nennt man die (Breiten-)Metazentrische Höhe GM = KB+BM KG Wird allegemein vom Metazentrum oder der metazentrischen Höhe gesprochen, so ist in aller Regel das Breitenmetazentrum gemeint Für übliche Handelsschiffe ist GM wenige Dezimeter bis wenige Meter 52 Trimm um δψ : Hier bedeuten δm y = G( I W LL V + z B z G )δψ = GGM L δψ GM L = KB + BM L KG I ys V = I W LL V = BM L, M L das Längenmetazentrum und GM L die Längenmetazentrische Höhe Für übliche Handelsschiffe ist GM L von der Größe der Schiffslänge oder größer Bei kleinen Drehungen (δψ; δϕ) ist die Lage von M; M L etwa konstant, aber nicht gleich M und M L unterscheiden sich erheblich Als Abschätzung dient: BM LB 3 ; BM L L 3 B BM L BM ( ) L 2 B Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 35/77
37 53 Einheitstrimmmoment Das Einheitstrimmmoment E T ist dasjenige Trimmmoment, das eine gesamte Trimmänderung von t = 1m hervorruft Herleitung: t sei der Unterschied der Tiefgänge an vorderer und hinterer Ahming (Ahming: Tiefgangsmarken, die am Bug, am Heck und mittschiffs angebracht sind Die Tiefgangsangabe wird vom Kiel gerechnet), L A L pp sei der Abstand zwischen den Ahmingen, siehe Abbildung 15) t = T v T h = tan ψl A Für kleine Trimmänderungen gilt dann mit tan ψ ψ: δt = L A δψ ψ t L A Abbildung 15: Trimmänderung Das trimmende Moment errechnet sich dann δm y = G GM L δψ = G GM L δt L A Trimmende Momente δm y werden durch Längsverschiebung von Massen m i hervorgerufen: δm y = g i m i x i = g GM L δt L A Mit = ρv als Masse (Deplacement) des Schiffes wird das Trimmmoment zu: δm y g = i m i x i = GM L δt L A bzw das Einheitstrimmmoment E T (Trimmmoment für 1m Tiefgangsunterschied) wird zu: Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 36/77
38 E T = GM L L A = L A (KB + BM L KG) Da (KB KG) BM L ist, kann vereinfacht berechnet werden: E T L A BM L = L A IW LL V = ρi W LL L A Einheitskrängungsmoment: Analog zum Einheitstrimmmoment kann auch ein Einheitskrängungsmoment berechnet werden: E K = B (KB + BM KG) = B (KB + I W L V KG) B ist die Breite des Schiffes Das Einheitskrängungsmoment findet in der Praxis nahezu keine Verwendung 54 Stabilitätsbedingungen Stabilitätsbedingungen für die Schwimmlage eines intakten Schiffes: 1) A w > 0; 2) I W LL V + z B z G = BM L + KB KG = GM L > 0; ( ) 3) I W L IxyS 2 ( ) V + z B z G V / IW LL V + z B z G > 0 Für zur Mittschiffsebene symmetrische Schiffe wird J xys = 0, so dass sich die Stabilitätsbedingung 3) vereinfacht: 3) I W L V + z B z G = BM + KB KG = GM > 0 Falls M unterhalb von G liegt (negatives GM), ist das Schiff instabil, der Krängungswinkel vergrößert sich dann eventuell bis zum Kentern Falls G und M an derselben Stelle liegen, befindet sich das Schiff im indifferenten Gleichgewicht Damit sind Schiffe stabil, wenn A w, GM L und GM > 0 Da GM GM L, bleibt im Wesentlichen die Berechnung von GM zur Überprüfung der Stabilität Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 37/77
39 6 Pantokarenen und Stabilitätshebelarme Die Bedingung für kleine Neigungen ist nun nicht mehr erfüllt; die Formeln aus dem Kapitel Kleine Schwimmlageänderungen intakter Schiffe können nicht benutzt werden Die Änderungen der Schwimmlage sind also nun nicht mehr klein, dh das schiffsfeste (lokale) x; y; z Koordinatensytem und das globale ξ; η; ζ -Koordinatensystem fallen nicht mehr zusammen Der Koordinatenursprung ist für beide Systeme gleich, nämlich Kielpunkt K im Schnitt von Mittschiffs- und Hauptspantebene, siehe Abbildung 16 und Abbildung 17 WL ζ z B F B x ϕ ξ η Β η y Abbildung 16: Lokales und globales Koordinatensystem in der y; z Ebene ζ z WL y ψ ξ x η Abbildung 17: Lokales und globales Koordinatensystem in der x; z Ebene x; y; z Koordinatensystem x Längsachse, positiv nach vorn, Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 38/77
40 y Querachse,positiv nach Bb, z Hochachse, positiv nach oben ξ; η; ζ Koordinatensystem ξ; η Achsen, parallel zur Wasseroberfläche, ζ Achse, senkrecht nach oben 61 Pantokarenen Bei den Pantokarenen handelt es sich um das Lot vom Kielpunkt auf die Wirklinie der Auftriebskraft F B, sie werden im Allgemeinen mit w abgekürzt Diese Strecke w ändert sich mit der Krängung, dem Trimm und dem Tiefgang Für eine konstante Krängung ϕ kann dann die zugehörige Pantokarene bestimmt werden Die aus Auftrieb (ρg)v und Gewicht G resultierenden Kräfte und Momente sind (siehe auch Kapitel Kleine Schwimmlageänderungen intakter Schiffe ): die resultierende Vertikalkraft F ζ = (ρg)v G; das resultierende Moment um die Querachse (Trimmmoment) M η = (ρg)ξ B V ξ G G; das resultierende Moment um die Längsachse (krängendes Moment) M ξ = (ρg)η B V η G G Mit F B = (ρg)v = G folgt: F ζ = 0; M η = (ξ B ξ G )G; M ξ = (η B η G )G Hier wird η B = w bezeichnet w ist das Lot vom Kielpunkt K auf die Wirkungslinie von F B bei vorgegebener Neigung ϕ, aus Abbildung 18 liest man ab: w = y B cos ϕ + z B sin ϕ Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 39/77
41 WL ζ z η B =w y B B Κ y B cosϕ ϕ zb ϕ z B sinϕ η y Abbildung 18: Berechnung von w aus den lokalen Koordinaten von B Die Bestimmung der Pantokarene w ist eine geometrische Aufgabe, dh Berechnung von Volumen und Volumenschwerpunkten (y B ; z B ) Die Pantokarene ist vom Tiefgang bzw eingetauchten Volumen, dem Trimm bzw Gewichtsschwerpunkt in Schifflängsrichtung und der Krängung abhängig: w = f(t ; ψ; ϕ) = f(v,x G ; ϕ) Die Pantokarene für vorgegebene konstante Krängung ϕ hängt damit nur noch vom Tiefgang bzw eingetauchten Volumen und dem Trimm bzw Gewichtsschwerpunkt in Schifflängsrichtung ab: w = f(v ; x G ) mit ϕ = konst Berechnung der Pantokarenen: Die Berechnung der Pantokarenen erfolgt also über die Bestimmung des Verdrängungsschwerpunkts B(y B ; z B ) Dies geschieht zunächst im lokalen System, dann erfolgt mit w = y B cos ϕ + z B sin ϕ die Umrechnung über den Krängungswinkel ϕ ins globale System Trimmausgleich: Für alle Volumina V und Krängungswinkel ϕ wird der Trimmwinkel ψ = konst; in der Regel ψ = 0 angenommen Da aber im Allgemeinen die Längskoordinate des Auftriebsschwerpunktes ξ B vom verdrängten Volumen und vom Krängungswinkel abhängt ξ B = f(v,ϕ); wobei die Änderungen allerdings klein sind, bleibt ein kleines resultierendes Trimmmoment, da der Gewichtsschwerpunkt ja konstant bleibt für alle Änderungen der Schwimmlage (ξ G = konst) In der Regel wird diese Abhängigkeit des Auftriebsschwerpunktes vom Trimmwinkel jedoch vernachlässigt Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 40/77
42 Pantokarenen ohne Trimmausgleich: Rechnet man die Pantokarene ohne Trimmausgleich, tut man damit so, als verhielte sich ξ B wie ξ G Die Lage des Auftriebsschwerpunktes bleibt dann konstant Pantokarenen mit Trimmausgleich: Rechnet man mit Trimmausgleich, wird nur für ϕ = 0 der Trimmwinkel ψ = konst, in der Regel ψ = 0 angenommen Für ϕ > 0 wird das Trimmmoment durch einen veränderten Trimmwinkel ausgeglichen Pantokarenen mit Trimmausgleich fallen immer kleiner aus als ohne Der Unterschied ist dann besonders deutlich, wenn die Unterwasserform stark asymmetrisch zur Lage x w des Wasserlinienschwerpunktes ist Bei Symmetrie von Vor- und Hinterschiff ist immer M η 0, dann liegt für alle ϕ der Verdrängungsschwerpunkt B in der Symmetrie- /Hauptspantebene 62 Stabilitätshebelarme Eine Gleichgewichtslage mit der Krängung ϕ = ϕ EQ (EQ als Abkürzung für Equi Librium) ist dadurch gegeben, dass Auftrieb und Gewicht gleich groß sind und die jeweiligen Schwerpunkte erdfest übereinander liegen, siehe Abbildung 19 G G G G B B K F B K F B LC LC Abbildung 19: Gleichgewichtslage; links: y G = 0 rechts: y G 0 Bildet man nun das Moment um den Kielpunkt K, ergibt sich: MK = 0 = B(y B cos ϕ EQ + z B sin ϕ EQ ) G(y G cos ϕ EQ + z G sin ϕ EQ ) Daraus folgt die Gleichgewichtsbeziehung: y B cos ϕ EQ + z B sin ϕ EQ = y G cos ϕ EQ + z G sin ϕ EQ Für einen Winkel, in dem sich das Schiff nicht in einer Gleichgewichtslage befindet, gilt für den Stabilitätshebelarm h: h = y B cos ϕ + z B sin ϕ y }{{} G cos ϕ z G sin ϕ w=pantokarene Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 41/77
43 Liegt der Massenschwerpunkt auf Center Line, dh y G = 0, vereinfacht sich h zu: h = w z G sin ϕ = 0 Gleichgewichtslage h > 0 aufrichtender Hebel (stabil; rückdrehendes Moment) < 0 krängender Hebel (instabil; krängendes Moment) Ist h > 0, so nimmt der Schwimmkörper eine Schwimmlage mit kleinerer Krängung ϕ, für h < 0 mit größerer Krängung ϕ ein Eine stabile Gleichgewichtslage erfordert zusätzlich dh = dh aufrichtend + dh krängend dϕ EQ dϕ dϕ Trägt man die Hebel h über die Winkel ϕ auf, entsteht die sog Hebelarmkurve Bestimmt man bei ϕ = 0 die Steigung der Tangente an die Hebelarmkurve, ergibt sich daraus das Anfangsmetazentrum GM (siehe Abbildung 22) > 0 GM = dh dϕ = dw dϕ z G sin ϕ = dw dϕ dϕ z G cos ϕ GM = dw dϕ KG cos ϕ Der maximale Hebel gibt das maximal ertragbare Moment an 621 Schiffskörper unter der Wirkung eines krängenden Momentes M ξ und außermittiger Lage y G des Gewichtsschwerpunktes Die Koordinaten des Massenschwerpunktes sind G(x G ; y G ; z G = KG) Im globalen System wird aus η G = y G cos ϕ + KG sin ϕ Mit y G 0 wird eine außermittige Lage des Gewichtsschwerpunktes zugelassen, wie sie sich aus einer seitlichen Verschiebung einer Masse m ergibt Für die Gleichgewichtslage eines Schiffes, auf das zusätzlich ein äußeres krängendes Moment M ξ wirkt, gilt für das Momentengleichgewicht um K: MK = 0 = F B w G(KG sin ϕ + y G cos ϕ) M ξ 0 = w KG sin ϕ y G cos ϕ M ξ G w = KG sin ϕ + y G cos ϕ + M ξ G h aufr = h kr (61) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 42/77
44 m WL R ξ ζ z G y G cosϕ y G KGsin ϕ Κ W ϕ B h w F B η y Abbildung 20: Schiffskörper unter der Wirkung eines krängenden Momentes M ξ außermittiger Lage y G des Gewichtsschwerpunktes und Damit wird in der Gleichgewichtslage der aufrichtende Hebel gleich dem krängenden Hebel Das Momentengleichgewicht kann um jeden beliebigen Punkt gebildet werden, wie bisher um den Kielpunkt K, so wird der aufrichtende Hebel (als derjenige Hebel, der zur aufrichtenden Kraft F B gehört) gleich der Pantokarene Bildet man das Momentengleichgewicht um den Punkt X, so ergibt sich der aufrichtende Hebel (Hebel zur Kraft F B ) zu w KG sin ϕ Im Grunde sind diese nur verschiedene Notationen Beispiel: Das Deplacement eines Schiffes beträgt in Seewasser (ρ SW = 1025kg/m 3 ) = 1025t Eine Ladung m = 102,5t werde parallel zum Doppelboden um y k = 5m seitlich verschoben, KG = 5m, die Pantokarenen seien bekannt Die Verdrängung beträgt V = /ρ = 1000m 3 Durch die Ladungsverschiebung krängt das Schiff, der Krängungswinkel der neuen Gleichgewichtslage wird nun gesucht Wird in einer Masse eine Teilmasse verschoben, so erfährt der Gesamtschwerpunkt eine gleichsinnige, parallel gerichtete Verschiebung, vergleiche Verschiebungssatz formuliert von Herner Die beiden Momente, gebildet aus Verschiebungsweg und Masse sind gleich groß: y G = y k m Daraus folgt: Die außermittige Lage des Gewichtsschwerpunktes beträgt nach der Verschiebung y G = (y k m)/ = 5 102,5/1025m = 0,5m Mit den gegebenen Pantokarenen können dann die Hebelarme h = w z G sin ϕ y G cos ϕ bestimmt werden: Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 43/77
45 ϕ w in [m] 1,0 2,0 2,95 3,82 4,40 h in [m] -0,36-0,18 0,02 0,28 0,24 Trägt man nun den Hebel h über den Winkel ϕ auf, so ergibt sich die Hebelarmkurve für ein Schiff mit außermittiger Lage des Gewichtsschwerpunktes Der Schnittpunkt bei h = 0 mit der ϕ-achse zeigt den Krängungswinkel der Gleichgewichtsschwimmlage mit ϕ EQ 29, also der Winkel, den das Schiff aufgrund der Ladung einnehmen wird, siehe Abbildung 21 h [m] 0,3 0,2 0,1 0-0,1-0,2-0, ö Abbildung 21: Hebelarmkurve Alternativ lässt sich die Hebelarmkurve des Schiffes ohne Ladeverschiebung mit h = w z G sin ϕ (y G = 0) berechnen (siehe Abbildung 22) Zusätzlich wird der Hebelarm der Ladeverschiebung y G cos ϕ als eigene Kurve über den Krängungswinkel ϕ aufgetragen: ϕ w in [m] 1,0 2,0 2,95 3,82 4,40 h in [m] 0,13 0,29 0,45 0,61 0,57 y G cos ϕ in [m] 0,49 0,47 0,43 0,38 0,32 So liefert der Schnittpunkt der beiden Kurven h(ϕ) und y G cos ϕ auch hier den Krängungswinkel der Gleichgewichtsschwimmlage mit ϕ EQ 29 Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 44/77
46 m h 0,5 0,4 0,3 0,2 0,1 0 y G cosϕ m y G cosϕ 29 o h 10 o 20 o 40 o 30 o 50 o 57,3 o GM ϕ Abbildung 22: Bestimmung des Krängungswinkels Beide Betrachtungen liefern als Gleichgewichtsschwimmlage denselben Krängungswinkel; im ersten Fall werden für das Schiff direkt die Hebelarme mit Ladeverschiebung berechnet, indem angenommen wird, der Gewichtsschwerpunkt des Schiffes habe sich verschoben Im zweiten Fall hingegen wird die Ladeverschiebung als ein krängendes Moment aufgefasst (siehe Kapitel Krängende Momente ) und mit der Hebelarmkurve des ungekrängten Schiffes aufgetragen Bei in aufrechter Schwimmlage symmetrischen Körpern ist die Mittschiffsebene (ξ,ζ Ebene) die Symmetrieebene M ξ = G h G y G cos ϕ Für die Änderung des krängenden Momentes gilt: dm ξ dϕ = G dh dϕ + G y G sin ϕ Für kleine Krängungen (ϕ 0) und verschwindendes y G wird daraus mit ξ = x : dm x dϕ = G dh dϕ ϕ=0 Für kleine Winkel war früher gefunden worden: δm x = G GM δϕ bzw für ϕ 0 : dm x dϕ = G dh ϕ=0 dϕ = G GM ϕ=0 Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 45/77
47 Dann wird dh dϕ = GM = tan α = GM ϕ=0 1 Die Fläche unter der Hebelarmkurve gibt die Arbeit an 1 im Bogenmaß entspricht einem Winkel von ϕ = 57,3 Zeichnet man bei ϕ = 0 die Tangente an die Hebelarmkurve, so läßt sich bei ϕ = 57,3 das GM der aufrechten Schwimmlage ablesen, siehe Abbildung 22 Betrachtet man die Hebelarmkurve mit der Ladungsverschiebung, erkennt man, dass die Steigung im Punkt 0 negativ ist, das Schiff hat also aufgrund der verschobenen Ladung ein negatives GM und seine Gleichgewichtslage nicht mehr bei ϕ = 0 sondern bei ϕ Pantokarenen und Hebelarme unvertrimmter Quader 631 Berechnung des Verdrängungsschwerpunkts und der Pantokarenen gekrängter Quader (Formschwerpunktskurve) Hier wird zunächst nun für unvertrimmte Quader gezeigt wie der Verdrängungsschwerpunkt bestimmt werden kann Daraus ergeben sich mit den Krängungswinkeln ϕ dann unmittelbar die Pantokarenen Die Bezeichnungen Verdrängungs- oder Auftriebs- oder Formschwerpunkt werden in gleicher Bedeutung benutzt und bezeichnen den Schwerpunkt des eingetauchten Volumens des Quaders bzw des Schwimmkörpers Übergeordnetes Kriterium ist, dass der Betrag des eingetauchten Volumens V 0 = LBT = konst (62) für alle Neigungen ϕ erhalten bleibt Es kommt nur zur Änderung der Form des eingetaucheten Volumens Implizit heißt das jedoch auch, dass das Volumen des Überwasserschiffes Vü = LBF = konst für alle Neigungen ϕ erhalten bleibt, beide Volumen sind einander komplementär Für das Gesamtvolumen V des Quaders gilt immer V = V 0 + Vü (63) Es wird nun zwischen zwei Fällen unterschieden: 1 Fall: Das Volumen das oberhalb der Wasseroberfäche liegt ist größer als das Volumen unterhalb der Wasseroberfläche, das bedeutet Freibord F ist größer als Tiefgang T 2 Fall: Das Volumen das oberhalb der Wasseroberfäche liegt ist kleiner als das Volumen unterhalb der Wasseroberfläche, das bedeutet Freibord F ist kleiner als Tiefgang T 1 Fall 2 Fall F/T > 1 : (Abb 23, links) Bereich I: 0 tan ϕ < T/(B/2) (Kimm taucht aus) Bereich II: T/(B/2) tan ϕ < H 2 /(2BT ) (Seite Deck taucht ein) Bereich III: H 2 /(2BT ) tan ϕ tan(90 o ) F/T < 1 : (Abb 23, rechts) Bereich 1: 0 tan ϕ < F/(B/2) (Seite Deck taucht ein) Bereich 2: F/(B/2) tan ϕ < H 2 /(2BF ) (Kimm taucht aus) Bereich 3: H 2 /(2BF ) tan ϕ tan(90 o ) Prof Dr-Ing Stefan Krüger wwwssitu-harburgde Seite: 46/77
Koordinatenysteme und elementare Stabilitätsgrundlagen
 Koordinatenysteme und elementare Stabilitätsgrundlagen 1 Inhalt Diese Dokumentation beschreibt zunächst die allen Methoden zugrundeliegenden Koordinatensysteme. Ferner werden die elementaren Beziehungen
Koordinatenysteme und elementare Stabilitätsgrundlagen 1 Inhalt Diese Dokumentation beschreibt zunächst die allen Methoden zugrundeliegenden Koordinatensysteme. Ferner werden die elementaren Beziehungen
Stabilität beim Schiff wie beim Menschen: die Fähigkeit, sich aus einem gekrän(g)kten Zustand wieder aufzurichten ;-)
 Stabilität beim Schiff wie beim Menschen: die Fähigkeit, sich aus einem gekrän(g)kten Zustand wieder aufzurichten ;-) Windstärke um die 6 Bft - auflandig vor Kühlungsborn. Eine 24 ft. Yacht fährt quer
Stabilität beim Schiff wie beim Menschen: die Fähigkeit, sich aus einem gekrän(g)kten Zustand wieder aufzurichten ;-) Windstärke um die 6 Bft - auflandig vor Kühlungsborn. Eine 24 ft. Yacht fährt quer
5.3 Drehimpuls und Drehmoment im Experiment
 5.3. DREHIMPULS UND DREHMOMENT IM EXPERIMENT 197 5.3 Drehimpuls und Drehmoment im Experiment Wir besprechen nun einige Experimente zum Thema Drehimpuls und Drehmoment. Wir betrachten ein System von N Massenpunkten,
5.3. DREHIMPULS UND DREHMOMENT IM EXPERIMENT 197 5.3 Drehimpuls und Drehmoment im Experiment Wir besprechen nun einige Experimente zum Thema Drehimpuls und Drehmoment. Wir betrachten ein System von N Massenpunkten,
0,6 m. 0,4m. Gegeben seien die obigen drei auf den Balken wirkenden Kräfte mit:
 Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
4.9 Der starre Körper
 4.9 Der starre Körper Unter einem starren Körper versteht man ein physikalische Modell von einem Körper der nicht verformbar ist. Es erfolgt eine Idealisierung durch die Annahme, das zwei beliebig Punkte
4.9 Der starre Körper Unter einem starren Körper versteht man ein physikalische Modell von einem Körper der nicht verformbar ist. Es erfolgt eine Idealisierung durch die Annahme, das zwei beliebig Punkte
5.1 Gruppe paralleler Kräfte 5.2 Körperschwerpunkt 5.3 Flächenschwerpunkt. 5. Schwerpunkt. Prof. Dr. Wandinger 1. Statik TM 1.5-1
 5.1 Gruppe paralleler Kräfte 5.2 Körperschwerpunkt 5.3 Flächenschwerpunkt 5. Schwerpunkt Prof. Dr. Wandinger 1. Statik TM 1.5-1 5.1 Gruppe paralleler Kräfte G 1 G 2 G R G i G n P x x 1 S x S Gesucht: Angriffspunkt,
5.1 Gruppe paralleler Kräfte 5.2 Körperschwerpunkt 5.3 Flächenschwerpunkt 5. Schwerpunkt Prof. Dr. Wandinger 1. Statik TM 1.5-1 5.1 Gruppe paralleler Kräfte G 1 G 2 G R G i G n P x x 1 S x S Gesucht: Angriffspunkt,
2. Translation und Rotation
 2. Translation und Rotation 2.1 Rotation eines Vektors 2.2 Rotierendes ezugssystem 2.3 Kinetik Prof. Dr. Wandinger 2. Relativbewegungen Dynamik 2 2.2-1 2.1 Rotation eines Vektors Gesucht wird die zeitliche
2. Translation und Rotation 2.1 Rotation eines Vektors 2.2 Rotierendes ezugssystem 2.3 Kinetik Prof. Dr. Wandinger 2. Relativbewegungen Dynamik 2 2.2-1 2.1 Rotation eines Vektors Gesucht wird die zeitliche
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 2008 Theoretische Mechanik 9. Übung 9.1 d alembertsches Prinzip: Flaschenzug Wir betrachten
Flüssigkeitsteilchen sind frei gegeneinander verschiebbar. Flüssigkeitsoberfläche stets senkrecht zur wirkenden Kraft. F G
 2.9.3 Flüssigkeiten Flüssigkeitsteilchen sind frei gegeneinander verschiebbar. Flüssigkeitsoberfläche stets senkrecht zur wirkenden Kraft. F Abbildung 2.46: Kräfte bei Rotation von Flüssigkeiten F Z =
2.9.3 Flüssigkeiten Flüssigkeitsteilchen sind frei gegeneinander verschiebbar. Flüssigkeitsoberfläche stets senkrecht zur wirkenden Kraft. F Abbildung 2.46: Kräfte bei Rotation von Flüssigkeiten F Z =
K U R S S T A T I K / F E S T I G K E I T S L E H R E
 BAULEITER HOCHBAU K U R S S T A T I K / F E S T I G K E I T S L E H R E QUERSCHNITTSWERTE ) Schwerpunktsbestimmungen ) Trägheitsmoment 3) Widerstandsmoment 4) Das statische Moment 5) Beispiele von Querschnittstabellen
BAULEITER HOCHBAU K U R S S T A T I K / F E S T I G K E I T S L E H R E QUERSCHNITTSWERTE ) Schwerpunktsbestimmungen ) Trägheitsmoment 3) Widerstandsmoment 4) Das statische Moment 5) Beispiele von Querschnittstabellen
Klausur Schiffshydrostatik Beginn: ca Ende : ca Allgemeine Hinweise:
 TUHH - Institut für Entwerfen von Schiffen und Schiffsicherheit - D-21073 Hamburg Klausur Schiffshydrostatik 28.07.2006 Beginn: ca. 10.00 Ende : ca. 13.00 Allgemeine Hinweise: 1. Alle Hilfsmittel außer
TUHH - Institut für Entwerfen von Schiffen und Schiffsicherheit - D-21073 Hamburg Klausur Schiffshydrostatik 28.07.2006 Beginn: ca. 10.00 Ende : ca. 13.00 Allgemeine Hinweise: 1. Alle Hilfsmittel außer
2. Trägheitstensor. Prof. Dr. Wandinger 3. Kinetik des starren Körpers Dynamik
 2. Trägheitstensor Der Drall hängt ab von der Verteilung der Masse und der Geschwindigkeit über den örper. Die Geschwindigkeitsverteilung ergibt sich aus der Überlagerung einer Translation und einer Rotation.
2. Trägheitstensor Der Drall hängt ab von der Verteilung der Masse und der Geschwindigkeit über den örper. Die Geschwindigkeitsverteilung ergibt sich aus der Überlagerung einer Translation und einer Rotation.
2. Schiffshebewerk Das Schiff verdrängt genau die selbe Masse an Wasser, die es wiegt, also 4500t. M ges. M Wasser ITrog. M verdrängteswasser
 1. Archimedes und die goldene Krone von Hiero Die Krone und das überlassene Gold haben die gleiche Masse. Gold hat aber eine wesentlich größere Dichte als Silber, nämlich Gold 19,3 t/m³ zu Silber mit 10,5
1. Archimedes und die goldene Krone von Hiero Die Krone und das überlassene Gold haben die gleiche Masse. Gold hat aber eine wesentlich größere Dichte als Silber, nämlich Gold 19,3 t/m³ zu Silber mit 10,5
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Gewerbliche Lehranstalten Bremerhaven, Georg-Büchner-Str. 7, Bremerhaven
 1.1 Schiffsgröße und Darstellung der Schiffsform 1.1.2 Zeichnerische Darstellung der Schiffsform - Linienriss Der Schiffskörper und die ihn begrenzende Schiffsaußenhaut stellen freie Körper dar, d. h.
1.1 Schiffsgröße und Darstellung der Schiffsform 1.1.2 Zeichnerische Darstellung der Schiffsform - Linienriss Der Schiffskörper und die ihn begrenzende Schiffsaußenhaut stellen freie Körper dar, d. h.
4. Verzerrungen. Der Abstand von zwei Punkten ändert sich. Der Winkel zwischen drei Punkten ändert sich
 4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
Grundlagen der Physik 1 Lösung zu Übungsblatt 8
 Grundlagen der Physik 1 Lösung zu Übungsblatt 8 Daniel Weiss 1. Dezember 29 Inhaltsverzeichnis Aufgabe 1 - inhomogener hängender Balken 1 a) Seilkräfte...................................... 1 b) Schwerpunkt....................................
Grundlagen der Physik 1 Lösung zu Übungsblatt 8 Daniel Weiss 1. Dezember 29 Inhaltsverzeichnis Aufgabe 1 - inhomogener hängender Balken 1 a) Seilkräfte...................................... 1 b) Schwerpunkt....................................
Kreis - Tangente. 2. Vorbemerkung: Satz des Thales Eine Möglichkeit zur Bestimmung der Tangente benutzt den Satz des Thales.
 Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
3. Trägheitstensor. Starrkörperdynamik Prof. Dr. Wandinger. 2. Der starre Körper
 3. Trägheitstensor Im Beispiel der rollenden Scheibe hängt der Drall linear von der Winkelgeschwindigkeit ab. Bei der Berechnung des Dralls treten Integrale über die Geometrie des starren örpers auf. Es
3. Trägheitstensor Im Beispiel der rollenden Scheibe hängt der Drall linear von der Winkelgeschwindigkeit ab. Bei der Berechnung des Dralls treten Integrale über die Geometrie des starren örpers auf. Es
Physik für Biologen und Zahnmediziner
 Physik für Biologen und Zahnmediziner Kapitel 5: Drehmoment, Gleichgewicht und Rotation Dr. Daniel Bick 16. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 16. November 2016 1 / 39 Impuls
Physik für Biologen und Zahnmediziner Kapitel 5: Drehmoment, Gleichgewicht und Rotation Dr. Daniel Bick 16. November 2016 Daniel Bick Physik für Biologen und Zahnmediziner 16. November 2016 1 / 39 Impuls
Kräftepaar und Drehmoment
 Kräftepaar und Drehmoment Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Kräftepaar
Kräftepaar und Drehmoment Vorlesung und Übungen 1. Semester BA Architektur KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Kräftepaar
3. Allgemeine Kraftsysteme
 3. Allgemeine Kraftsysteme 3.1 Parallele Kräfte 3.2 Kräftepaar und Moment 3.3 Gleichgewicht in der Ebene Prof. Dr. Wandinger 1. Statik TM 1.3-1 3.1 Parallele Kräfte Bei parallelen Kräften in der Ebene
3. Allgemeine Kraftsysteme 3.1 Parallele Kräfte 3.2 Kräftepaar und Moment 3.3 Gleichgewicht in der Ebene Prof. Dr. Wandinger 1. Statik TM 1.3-1 3.1 Parallele Kräfte Bei parallelen Kräften in der Ebene
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Welche Gesamtmasse ist in dem Schiffshebewerk zu heben?
 1. Archimedes und die goldene Krone von Hiero Archimedes (285v. Chr. 212 v. Chr.) wurde vom König von Syrakus zur Lösung folgenden Problems beauftragt: Der König von Syrakus hat bei einem Goldschmied eine
1. Archimedes und die goldene Krone von Hiero Archimedes (285v. Chr. 212 v. Chr.) wurde vom König von Syrakus zur Lösung folgenden Problems beauftragt: Der König von Syrakus hat bei einem Goldschmied eine
M1 Maxwellsches Rad. 1. Grundlagen
 M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
M1 Maxwellsches Rad Stoffgebiet: Translations- und Rotationsbewegung, Massenträgheitsmoment, physikalisches Pendel. Versuchsziel: Es ist das Massenträgheitsmoment eines Maxwellschen Rades auf zwei Arten
Physik 1 Mechanik Tutorium Gravitation Schweredruck - Wasser. Diesmal 6 Aufgaben, davon 2 sehr leicht zu beantworten.
 Seite1(6) Übung 7 Gravitation Schweredruck - Wasser. Diesmal 6 Aufgaben, davon 2 sehr leicht zu beantworten. Aufgabe 1 ISS (IRS) Die ISS (IRS) hat eine Masse von 455 t und fliegt aktuell in einer mittleren
Seite1(6) Übung 7 Gravitation Schweredruck - Wasser. Diesmal 6 Aufgaben, davon 2 sehr leicht zu beantworten. Aufgabe 1 ISS (IRS) Die ISS (IRS) hat eine Masse von 455 t und fliegt aktuell in einer mittleren
Dietmar Gross, Werner Hauger, Jörg Schröder und Wolfgang A. Wall
 Spannungszustand 2 Dietmar Gross, Werner Hauger, Jörg Schröder und Wolfgang A. Wall Springer-Verlag GmbH Deutschland 2017 D. Gross et al., Technische Mechanik 2, DOI 10.1007/978-3-662-53679-7_2 35 36 2
Spannungszustand 2 Dietmar Gross, Werner Hauger, Jörg Schröder und Wolfgang A. Wall Springer-Verlag GmbH Deutschland 2017 D. Gross et al., Technische Mechanik 2, DOI 10.1007/978-3-662-53679-7_2 35 36 2
Mathematische Probleme, SS 2015 Montag $Id: quadratisch.tex,v /06/22 12:08:41 hk Exp $
 Mathematische Probleme, SS 15 Montag 6 $Id: quadratischtex,v 111 15/06/ 1:08:41 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen In der letzten Sitzung hatten wir die Normalform (1 ɛ )x + y pɛx p =
Mathematische Probleme, SS 15 Montag 6 $Id: quadratischtex,v 111 15/06/ 1:08:41 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen In der letzten Sitzung hatten wir die Normalform (1 ɛ )x + y pɛx p =
Grundsätzliches Produkte Anwendungen in der Geometrie. Vektorrechnung. Fakultät Grundlagen. Juli 2015
 Vektorrechnung Fakultät Grundlagen Juli 205 Fakultät Grundlagen Vektorrechnung Übersicht Grundsätzliches Grundsätzliches Vektorbegriff Algebraisierung der Vektorrechnung Betrag 2 Skalarprodukt Vektorprodukt
Vektorrechnung Fakultät Grundlagen Juli 205 Fakultät Grundlagen Vektorrechnung Übersicht Grundsätzliches Grundsätzliches Vektorbegriff Algebraisierung der Vektorrechnung Betrag 2 Skalarprodukt Vektorprodukt
1 Schwimmfähigkeit 1.1 Die physikalischen Grundlagen der Schwimmfähigkeit
 1 Schwimmfähigkeit 1.1 Die physikalischen Grundlagen der Schwimmfähigkeit Warum schwimmt ein Körper? Auch ein Laie wird ohne Weiteres darauf kommen, dass Schwimmfähigkeit etwas mit dem Gewicht zu tun hat.
1 Schwimmfähigkeit 1.1 Die physikalischen Grundlagen der Schwimmfähigkeit Warum schwimmt ein Körper? Auch ein Laie wird ohne Weiteres darauf kommen, dass Schwimmfähigkeit etwas mit dem Gewicht zu tun hat.
Übungsblatt 1: Lösungswege und Lösungen
 Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
Übungsblatt : Lösungswege und Lösungen 5..6 ) Hier geht es weniger um mathematisch-strenge Beweise als darum, mit abstrakten Vektoren ohne Komponenten) zu hantieren und damit die Behauptungen plausibel
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Berechnungsformeln der Hydrostatik
 1 Berechnungsformeln der Hydrostatik Hydrostatik ist die Lehre vom ruhenden Fluid. Damit ein Fluid in Ruhe sein kann, muß seine Umgebung Druckkräfte aufbringen, die der Volumenkraft auf das Fluid im folgenden
1 Berechnungsformeln der Hydrostatik Hydrostatik ist die Lehre vom ruhenden Fluid. Damit ein Fluid in Ruhe sein kann, muß seine Umgebung Druckkräfte aufbringen, die der Volumenkraft auf das Fluid im folgenden
Analytische Geometrie II
 Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
1. Bewegungsgleichung
 1. Bewegungsgleichung 1.1 Das Newtonsche Grundgesetz 1.2 Dynamisches Gleichgewicht 1.3 Geführte Bewegung 1.4 Massenpunktsysteme 1.5 Schwerpunktsatz Prof. Dr. Wandinger 2. Kinetik des Massenpunkts Dynamik
1. Bewegungsgleichung 1.1 Das Newtonsche Grundgesetz 1.2 Dynamisches Gleichgewicht 1.3 Geführte Bewegung 1.4 Massenpunktsysteme 1.5 Schwerpunktsatz Prof. Dr. Wandinger 2. Kinetik des Massenpunkts Dynamik
3. Impuls und Drall. Prof. Dr. Wandinger 2. Kinetik des Massenpunkts Dynamik 2.3-1
 3. Impuls und Drall Die Integration der Bewegungsgleichung entlang der Bahn führte auf die Begriffe Arbeit und Energie. Die Integration der Bewegungsgleichung bezüglich der Zeit führt auf die Begriffe
3. Impuls und Drall Die Integration der Bewegungsgleichung entlang der Bahn führte auf die Begriffe Arbeit und Energie. Die Integration der Bewegungsgleichung bezüglich der Zeit führt auf die Begriffe
3.2 Das physikalische Pendel (Körperpendel)
 18 3 Pendelschwingungen 32 Das physikalische Pendel (Körperpendel) Ein starrer Körper (Masse m, Schwerpunkt S, Massenträgheitsmoment J 0 ) ist um eine horizontale Achse durch 0 frei drehbar gelagert (Bild
18 3 Pendelschwingungen 32 Das physikalische Pendel (Körperpendel) Ein starrer Körper (Masse m, Schwerpunkt S, Massenträgheitsmoment J 0 ) ist um eine horizontale Achse durch 0 frei drehbar gelagert (Bild
KAPITEL 1: Die Welt, in der wir uns bewegen
 KAPITEL 1: Die Welt, in der wir uns bewegen Kugel Kugel Tischplatte Zug beschleunigt Tischplatte Zug bremst Die Kugel möchte ihren Bewegungszustand beibehalten. Bestimmen der Masse mit einer Balkenwaage...
KAPITEL 1: Die Welt, in der wir uns bewegen Kugel Kugel Tischplatte Zug beschleunigt Tischplatte Zug bremst Die Kugel möchte ihren Bewegungszustand beibehalten. Bestimmen der Masse mit einer Balkenwaage...
2. Flächenträgheitsmomente
 . Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
. Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
2. Flächenträgheitsmomente
 . Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
. Flächenträgheitsmomente.1 Definitionen. Zusammengesette Querschnitte.3 Hauptachsen Prof. Dr. Wandinger 3. Balken TM 3.-1 .1 Definitionen Flächenträgheitsmomente: Die ur Berechnung der Spannungen eingeführten
Mechanik 1. Übungsaufgaben
 Mechanik 1 Übungsaufgaben Universitätsprofessor Dr.-Ing. habil. Jörg Schröder Universität Duisburg-Essen, Standort Essen Fachbereich 10 - Bauwesen Institut für Mechanik Übung zu Mechanik 1 Seite 1 Aufgabe
Mechanik 1 Übungsaufgaben Universitätsprofessor Dr.-Ing. habil. Jörg Schröder Universität Duisburg-Essen, Standort Essen Fachbereich 10 - Bauwesen Institut für Mechanik Übung zu Mechanik 1 Seite 1 Aufgabe
- Durchführung und Auswertung eines Krängungsversuches -
 - Durchführung und Auswertung eines Krängungsversuches - Die Durchführung erfolgt analog zu den Richtlinien für die Durchführung eines Krängungsversuches gemäß IMO Res. MSC.267(85) (IS Code 2008). Checkliste
- Durchführung und Auswertung eines Krängungsversuches - Die Durchführung erfolgt analog zu den Richtlinien für die Durchführung eines Krängungsversuches gemäß IMO Res. MSC.267(85) (IS Code 2008). Checkliste
Potentialströmung und Magnuseffekt
 Potentialströmung und Magnuseffekt (Zusammengefasst und ergänzt nach W Albring, Angewandte Strömungslehre, Verlag Theodor Steinkopff, Dresden, 3 Aufl 1966) Voraussetzungen Behandelt werden reibungs und
Potentialströmung und Magnuseffekt (Zusammengefasst und ergänzt nach W Albring, Angewandte Strömungslehre, Verlag Theodor Steinkopff, Dresden, 3 Aufl 1966) Voraussetzungen Behandelt werden reibungs und
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
rechnerisch, ob weitere Lösungen dieser Gleichung im Bereich 0 x l existieren.
 Anwendungs- und Optimierungsaufgaben (Technik) 1. Ein Balken der Länge l ist auf zwei Stützen gelagert (siehe Bild). Der Balken wird durch sein Eigengewicht auf Biegung beansprucht. Die Durchbiegung ist
Anwendungs- und Optimierungsaufgaben (Technik) 1. Ein Balken der Länge l ist auf zwei Stützen gelagert (siehe Bild). Der Balken wird durch sein Eigengewicht auf Biegung beansprucht. Die Durchbiegung ist
& sind die Vektorkomponenten von und sind die Vektorkoordinaten von. A x. a) Der Betrag eines Vektors
 Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
3 Matrizenrechnung. 3. November
 3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
3. November 008 4 3 Matrizenrechnung 3.1 Transponierter Vektor: Die Notation x R n bezieht sich per Definition 1 immer auf einen stehenden Vektor, x 1 x x =.. x n Der transponierte Vektor x T ist das zugehörige
Kapitel 2: Mathematische Grundlagen
 [ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
[ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat.
 1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II. x 2
 Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Lernmaterialblatt Mathematik. Vektorrechnung eine Einführung. Anwendung Mathematik I. Einleitung:
 Vektorrechnung eine Einführung Einleitung: Um beispielsweise das Dreieck ABC in der Abbildung an die Position A'B'C' zu verschieben, muss jeder Punkt um sieben Einheiten nach rechts und drei nach oben
Vektorrechnung eine Einführung Einleitung: Um beispielsweise das Dreieck ABC in der Abbildung an die Position A'B'C' zu verschieben, muss jeder Punkt um sieben Einheiten nach rechts und drei nach oben
Mathematische Probleme, SS 2013 Donnerstag $Id: quadratisch.tex,v /08/12 09:49:46 hk Exp $ c a b = 1 3. tan(2φ) =
 Mathematische Probleme SS 13 Donnerstag 136 $Id: quadratischtexv 18 13/08/1 09:49:46 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen Nachdem wir in der letzten Sitzung die Hauptachsentransformation
Mathematische Probleme SS 13 Donnerstag 136 $Id: quadratischtexv 18 13/08/1 09:49:46 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen Nachdem wir in der letzten Sitzung die Hauptachsentransformation
Zum Schluss berechnen wir die Steigung, indem wir
 Einführung Grafisches Differenzieren (auch grafische Ableitung genannt) gibt uns zum einen die Möglichkeit, die Steigung des Graphen einer Funktion in einem bestimmten Punkt zu ermitteln, ohne dass wir
Einführung Grafisches Differenzieren (auch grafische Ableitung genannt) gibt uns zum einen die Möglichkeit, die Steigung des Graphen einer Funktion in einem bestimmten Punkt zu ermitteln, ohne dass wir
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
11. Vorlesung Wintersemester
 11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
Der Spannungszustand. (traction vector) [N/mm²] k Volumskraftdichte [N/mm³] Mechanik IA
![Der Spannungszustand. (traction vector) [N/mm²] k Volumskraftdichte [N/mm³] Mechanik IA Der Spannungszustand. (traction vector) [N/mm²] k Volumskraftdichte [N/mm³] Mechanik IA](/thumbs/70/63003006.jpg) Der Spannungszustand σ na Spannungsvektor (traction vector) [N/mm²] k Volumskraftdichte [N/mm³] σ x σ x x + dx, y, z σ x x, y, z + σ x dx x x dx, y, z σ x x, y, z + σ x dx x etc df (R) = kdxdydz + σ x
Der Spannungszustand σ na Spannungsvektor (traction vector) [N/mm²] k Volumskraftdichte [N/mm³] σ x σ x x + dx, y, z σ x x, y, z + σ x dx x x dx, y, z σ x x, y, z + σ x dx x etc df (R) = kdxdydz + σ x
Kinematik des starren Körpers
 Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Technische Mechanik II Kinematik des starren Körpers Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes
Physikalisches Praktikum M 7 Kreisel
 1 Physikalisches Praktikum M 7 Kreisel Versuchsziel Quantitative Untersuchung des Zusammenhangs von Präzessionsfrequenz, Rotationsfrequenz und dem auf die Kreiselachse ausgeübten Kippmoment Literatur /1/
1 Physikalisches Praktikum M 7 Kreisel Versuchsziel Quantitative Untersuchung des Zusammenhangs von Präzessionsfrequenz, Rotationsfrequenz und dem auf die Kreiselachse ausgeübten Kippmoment Literatur /1/
1.3. DAS COULOMBSCHE GESETZ, ELEKTROSTATISCHES FELD 9
 8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
8 KAPITEL. ELEKTROSTATIK.3 Das Coulombsche Gesetz, elektrostatisches Feld Zur Einführung verschiedener Grundbegriffe betrachten wir zunächst einmal die Kraft, die zwischen zwei Ladungen q an der Position
Inhaltsverzeichnis INHALTSVERZEICHNIS 1
 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis 1 Die Parabel 2 1.1 Definition................................ 2 1.2 Bemerkung............................... 3 1.3 Tangenten................................ 3 1.4
INHALTSVERZEICHNIS 1 Inhaltsverzeichnis 1 Die Parabel 2 1.1 Definition................................ 2 1.2 Bemerkung............................... 3 1.3 Tangenten................................ 3 1.4
Unregelmäßig geformte Scheibe Best.- Nr. MD02256
 Unregelmäßig geformte Scheibe Best.- Nr. MD02256 Momentenlehre Ziel Die unregelmäßig geformte Scheibe wurde gewählt, um den Statik-Kurs zu vervollständigen und um einige praktische Versuche durchzuführen.
Unregelmäßig geformte Scheibe Best.- Nr. MD02256 Momentenlehre Ziel Die unregelmäßig geformte Scheibe wurde gewählt, um den Statik-Kurs zu vervollständigen und um einige praktische Versuche durchzuführen.
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
2. Der ebene Spannungszustand
 2. Der ebene Spannungszustand 2.1 Schubspannung 2.2 Dünnwandiger Kessel 2.3 Ebener Spannungszustand 2.4 Spannungstransformation 2.5 Hauptspannungen 2.6 Dehnungen 2.7 Elastizitätsgesetz Prof. Dr. Wandinger
2. Der ebene Spannungszustand 2.1 Schubspannung 2.2 Dünnwandiger Kessel 2.3 Ebener Spannungszustand 2.4 Spannungstransformation 2.5 Hauptspannungen 2.6 Dehnungen 2.7 Elastizitätsgesetz Prof. Dr. Wandinger
Vektorgeometrie. 1. Vektoren eingeben, Norm, Skalarprodukt. 2 In einem kartesischen Koordinatensystem sind die Vektoren. , v. und. gegeben.
 Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
1.1. Geradengleichung aus Steigung und y-achsenabschnitt
 Version vom 4. Januar 2007 Gleichungen von Geraden in der Ebene 1999 Peter Senn * 1.1. Geradengleichung aus Steigung und y-achsenabschnitt In dieser Form lautet die Gleichung der Geraden wie folgt: g:
Version vom 4. Januar 2007 Gleichungen von Geraden in der Ebene 1999 Peter Senn * 1.1. Geradengleichung aus Steigung und y-achsenabschnitt In dieser Form lautet die Gleichung der Geraden wie folgt: g:
5.2 Druck in Flüssigkeiten Kap5_2_Druck_in_:Flüss_fs3_06_01_05
 5.2 Druck in Flüssigkeiten Kap5_2_Druck_in_:Flüss_fs3_06_01_05 Höheres W kin der Moleküle in Flüssigkeit (Brownsche Molekularbewegung!) leichte Verschiebbarkeit: Flüssigkeit hat nur Volums- keine Gestaltselastizität.
5.2 Druck in Flüssigkeiten Kap5_2_Druck_in_:Flüss_fs3_06_01_05 Höheres W kin der Moleküle in Flüssigkeit (Brownsche Molekularbewegung!) leichte Verschiebbarkeit: Flüssigkeit hat nur Volums- keine Gestaltselastizität.
Probeklausur zur T1 (Klassische Mechanik)
 Probeklausur zur T1 (Klassische Mechanik) WS 006/07 Bearbeitungsdauer: 10 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Probeklausur zur T1 (Klassische Mechanik) WS 006/07 Bearbeitungsdauer: 10 Minuten Prof. Stefan Kehrein Name: Matrikelnummer: Gruppe: Diese Klausur besteht aus vier Aufgaben. In jeder Aufgabe sind 10 Punkte
Matrizen und Drehungen
 Matrizen und Drehungen 20. Noember 2003 Diese Ausführungen sind im wesentlichen dem Skript zur Vorlesung Einführung in die Theoretische Physik I und II on PD Dr. Horst Fichtner entnommen. Dieses entstand
Matrizen und Drehungen 20. Noember 2003 Diese Ausführungen sind im wesentlichen dem Skript zur Vorlesung Einführung in die Theoretische Physik I und II on PD Dr. Horst Fichtner entnommen. Dieses entstand
Abitur Mathematik Baden-Württemberg 2012
 Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
1. Prinzip von d'alembert
 1. Prinzip von d'alembert 1.1 Freiheitsgrade 1.2 Zwangsbedingungen 1.3 Virtuelle Geschwindigkeiten 1.4 Prinzip der virtuellen Leistung Prof. Dr. Wandinger 5. Prinzipien der Mechanik Dynamik 2 5.1-1 1.1
1. Prinzip von d'alembert 1.1 Freiheitsgrade 1.2 Zwangsbedingungen 1.3 Virtuelle Geschwindigkeiten 1.4 Prinzip der virtuellen Leistung Prof. Dr. Wandinger 5. Prinzipien der Mechanik Dynamik 2 5.1-1 1.1
1. Kinematik. Untersucht wird die Bewegung eines Punktes P in Bezug auf zwei Bezugssysteme: Bezugssystem Oxyz ist ruhend:
 Untersucht wird die ewegung eines Punktes P in ezug auf zwei ezugssysteme: ezugssystem Oxyz ist ruhend: Ursprung O Einheitsvektoren e x, e y, e z Koordinaten x, y, z ezugssystem ξηζ bewegt sich: Ursprung
Untersucht wird die ewegung eines Punktes P in ezug auf zwei ezugssysteme: ezugssystem Oxyz ist ruhend: Ursprung O Einheitsvektoren e x, e y, e z Koordinaten x, y, z ezugssystem ξηζ bewegt sich: Ursprung
2 Wirkung der Kräfte. 2.1 Zusammensetzen von Kräften Kräfte mit gemeinsamer Wirkungslinie
 2 Wirkung der Kräfte Kräfte, die auf einen Körper wirken, werden diesen verschieben, wenn kein gleichgroßer Widerstand dagegen wirkt. Dabei wird angenommen, dass die Wirkungslinie der Kraft durch den Schwerpunkt
2 Wirkung der Kräfte Kräfte, die auf einen Körper wirken, werden diesen verschieben, wenn kein gleichgroßer Widerstand dagegen wirkt. Dabei wird angenommen, dass die Wirkungslinie der Kraft durch den Schwerpunkt
y (t) Wie berechnet sich die Ableitung von F aus den Ableitungen von x (t) und y (t)? Die Antwort gibt die erste Kettenregel
 103 Differenzialrechnung 553 1035 Kettenregeln Die Kettenregel bei Funktionen einer Variablen erlaubt die Berechnung der Ableitung von verketteten Funktionen Je nach Verkettung gibt es bei Funktionen von
103 Differenzialrechnung 553 1035 Kettenregeln Die Kettenregel bei Funktionen einer Variablen erlaubt die Berechnung der Ableitung von verketteten Funktionen Je nach Verkettung gibt es bei Funktionen von
Koordinatengeometrie. Aufgabe 4 Untersuchen Sie die Funktion f(x) = x² 9.
 Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
I.1.3 b. (I.7a) I.1 Grundbegriffe der Newton schen Mechanik 9
 I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
 Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
a 2β... a n ω alle Permutationen von α β γ... ω a 3 γ ( 1) k a 1α
 Mathematik 1 - Übungsblatt 7 Lösungshinweise Tipp: Verwenden Sie zur Kontrolle Scilab, wo immer es möglich ist. Aufgabe 1 (Definitionsformel für Determinanten) Determinanten quadratischer Matrizen sind
Mathematik 1 - Übungsblatt 7 Lösungshinweise Tipp: Verwenden Sie zur Kontrolle Scilab, wo immer es möglich ist. Aufgabe 1 (Definitionsformel für Determinanten) Determinanten quadratischer Matrizen sind
Lösungen der Übungsaufgaben III
 Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Projektionen von geometrischen Objekten
 Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
Prüfung zum Thema Druck (total 36 P möglich)
 Prüfung zum Thema Druck (total 36 P möglich) Verwenden Sie beim Ortsfaktor g 10 N/kg, ausser bei den Aufgaben 1. und 2. 1. Luftdruck und gesamte Masse der Luft der Erdatmosphäre (5 P) a) Wie kommt der
Prüfung zum Thema Druck (total 36 P möglich) Verwenden Sie beim Ortsfaktor g 10 N/kg, ausser bei den Aufgaben 1. und 2. 1. Luftdruck und gesamte Masse der Luft der Erdatmosphäre (5 P) a) Wie kommt der
Selbsteinschätzungstest Auswertung und Lösung
 Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Vorkurs Mathematik Intensiv. Geraden, Ebenen und lineare Gleichungssysteme - Musterlösung
 Prof. Dr. J. Dorfmeister und Tutoren Vorkurs Mathematik Intensiv TU München WS 06/07 Geraden, Ebenen und lineare Gleichungssysteme - Musterlösung. Gegeben seien die Gerade G und die Ebene E : G : x (0,
Prof. Dr. J. Dorfmeister und Tutoren Vorkurs Mathematik Intensiv TU München WS 06/07 Geraden, Ebenen und lineare Gleichungssysteme - Musterlösung. Gegeben seien die Gerade G und die Ebene E : G : x (0,
Die Erweiterung vom Satz des Pythagoras anhand der resultierenden Kraft FR
 Michael B. H. Middendorf 1 Die Erweiterung vom Satz des Pthagoras anhand der resultierenden Kraft FR Bei meinen Überlegungen als Maschinenbauer bzgl. eines Impulsantriebes, stieß ich auf das Problem, ständig
Michael B. H. Middendorf 1 Die Erweiterung vom Satz des Pthagoras anhand der resultierenden Kraft FR Bei meinen Überlegungen als Maschinenbauer bzgl. eines Impulsantriebes, stieß ich auf das Problem, ständig
Testprüfung (Abitur 2013)
 Testprüfung (Abitur 2013) Steve Göring, stg7@gmx.de 3. April 2013 Bearbeitungszeit: Zugelassene Hilfsmittel: 270 Minuten Taschenrechner (nicht programmierbar, nicht grafikfähig), Tafelwerk Name: Punkte:
Testprüfung (Abitur 2013) Steve Göring, stg7@gmx.de 3. April 2013 Bearbeitungszeit: Zugelassene Hilfsmittel: 270 Minuten Taschenrechner (nicht programmierbar, nicht grafikfähig), Tafelwerk Name: Punkte:
E1 Mechanik Lösungen zu Übungsblatt 2
 Ludwig Maimilians Universität München Fakultät für Physik E1 Mechanik en u Übungsblatt 2 WS 214 / 215 Prof. Dr. Hermann Gaub Aufgabe 1 Drehbewegung einer Schleifscheibe Es werde die Schleifscheibe (der
Ludwig Maimilians Universität München Fakultät für Physik E1 Mechanik en u Übungsblatt 2 WS 214 / 215 Prof. Dr. Hermann Gaub Aufgabe 1 Drehbewegung einer Schleifscheibe Es werde die Schleifscheibe (der
2. Die Steifigkeitsmatrix
 . Die Steifigkeitsmatrix Freiheitsgrade der Gesamtstruktur: Bei einem ebenen Fachwerk hat jeder Knoten zwei Freiheitsgrade, nämlich die Verschiebungen u x und u y, zu denen die Kräfte F x und F y gehören.
. Die Steifigkeitsmatrix Freiheitsgrade der Gesamtstruktur: Bei einem ebenen Fachwerk hat jeder Knoten zwei Freiheitsgrade, nämlich die Verschiebungen u x und u y, zu denen die Kräfte F x und F y gehören.
6 Mechanik des Starren Körpers
 6 Mechanik des Starren Körpers Ein Starrer Körper läßt sich als System von N Massenpunkten m (mit = 1,...,N) auffassen, die durch starre, masselose Stangen miteinander verbunden sind. Dabei ist N M :=
6 Mechanik des Starren Körpers Ein Starrer Körper läßt sich als System von N Massenpunkten m (mit = 1,...,N) auffassen, die durch starre, masselose Stangen miteinander verbunden sind. Dabei ist N M :=
Kräfte. Vorlesung und Übungen 1. Semester BA Architektur. Institut Entwerfen und Bautechnik, Fachgebiet Bautechnologie/Tragkonstruktionen
 Kräfte Vorlesung und Übungen 1. Semester BA Architektur Institut Entwerfen und Bautechnik, / KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Kräfte Vorlesung und Übungen 1. Semester BA Architektur Institut Entwerfen und Bautechnik, / KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Abiturprüfung 2000 LK Mathematik Baden-Württemberg
 Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Mathematik II: Übungsblatt 01: Lösungen
 N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
10.2 Linearkombinationen
 147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
7.6. Prüfungsaufgaben zu Normalenformen
 7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
1 Ableitungen. Definition: Eine Kurve ist eine Abbildung γ : I R R n, γ besteht also aus seinen Komponentenfunktionen. a 1 + tx 1. eine Kurve.
 1 Ableitungen Definition: Eine Kurve ist eine Abbildung γ : I R R n, γ besteht also aus seinen Komponentenfunktionen γ 1 (t) γ(t) = γ n (t) Bild(γ) = {γ(t) t I} heißt auch die Spur der Kurve Beispiel:1)
1 Ableitungen Definition: Eine Kurve ist eine Abbildung γ : I R R n, γ besteht also aus seinen Komponentenfunktionen γ 1 (t) γ(t) = γ n (t) Bild(γ) = {γ(t) t I} heißt auch die Spur der Kurve Beispiel:1)
Physik für Biologen und Zahnmediziner
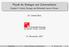 Physik für Biologen und Zahnmediziner Kapitel 4: Arbeit, Energie und Meachnik starrer Körper Dr. Daniel Bick 17. November 2017 Daniel Bick Physik für Biologen und Zahnmediziner 17. November 2017 1 / 39
Physik für Biologen und Zahnmediziner Kapitel 4: Arbeit, Energie und Meachnik starrer Körper Dr. Daniel Bick 17. November 2017 Daniel Bick Physik für Biologen und Zahnmediziner 17. November 2017 1 / 39
35 Matrixschreibweise für lineare Abbildungen
 35 Matrixschreibweise für lineare Abbildungen 35 Motivation Wir haben gesehen, dass lineare Abbildungen sich durch ihre Wirkung auf die Basisvektoren ausdrücken lassen Mithilfe von Matrizen können wir
35 Matrixschreibweise für lineare Abbildungen 35 Motivation Wir haben gesehen, dass lineare Abbildungen sich durch ihre Wirkung auf die Basisvektoren ausdrücken lassen Mithilfe von Matrizen können wir
