Klausurrepetitorium ABWL

Transkript

1 Klausurrepetitorium ABWL Planungs- und Südwestfälische Industrie- und Handelskammer 2. Februar 25 Dr. Friedhelm Kulmann, Sandra Rudolph 2.2.5

2 Gliederung. Netzplantechnik.. Grundlagen der Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen.3. Zeitanalyse bei Vorgangspfeilnetzen 2. Lösung von linearen Optimierungsproblemen mit Hilfe des Simplex-Algorithmus 2.. Lineare Optimierungsprobleme 2.2. Simplex-Verfahren 2.3. Sonderfälle 3. Planung von Güterströmen als Lineares Optimierungsproblem 2.2.5

3 Gliederung. Netzplantechnik.. Grundlagen der Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen.3. Zeitanalyse bei Vorgangspfeilnetzen 2. Lösung von linearen Optimierungsproblemen mit Hilfe des Simplex-Algorithmus 2.. Lineare Optimierungsprobleme 2.2. Simplex-Verfahren 2.3. Sonderfälle 3. Planung von Güterströmen als Lineares Optimierungsproblem

4 .. Grundlagen der Netzplantechnik Planungs- und.netzplantechnik Strukturelemente eines Projekts Vorgänge: Zeit und Betriebsmittel beanspruchende, nicht mehr weiter zerlegbare Geschehen mit definiertem Anfang und Ende Ereignisse: Wohldefinierte Zustände im Zeitablauf Darstellungsweisen von Netzplänen Vorgangspfeilnetzplan: Pfeile repräsentieren Vorgänge, Knoten kennzeichnen (künstliche) Ereignisse (CPM - Critical Path Methode) Vorgangsknotennetzplan: Knoten repräsentieren Vorgänge, Pfeile kennzeichnen Abhängigkeiten zwischen Vorgängen (MPM - Metra Potential Methode) 3

5 .Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen Definition Netzplanelement Ein Netzplanelement besteht aus einem Vorgang i-j und dessen Anfangs- und Endereignis Ein Vorgang wird eindeutig identifiziert, indem er eine eigene Benennung erhält oder durch Nummern i und j der beiden zugehörigen Ereignisse (Knoten) bezeichnet wird

6 .Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen Grundregeln () Jeder Vorgang beginnt mit einem Ereignis und endet mit einem nachfolgenden Ereignis. Grundregeln (2) Müssen mehrere Vorgänge beendet sein, bevor ein nachfolgender beginnen kann, so enden diese im Anfangsknoten des nachfolgenden Vorgangs

7 .Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen Grundregeln (3) Können mehrere Vorgänge beginnen, nachdem ein vorausgegangener beendet ist, so beginnen alle in dem Endknoten dieses gemeinsamen Vorgängers

8 .Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen Grundregeln (4) 2 Knoten dürfen nur durch einen Pfeil miteinander verbunden werden. Parallel verlaufende Vorgänge müssen daher durch Einführung eines Scheinvorgangs dargestellt werden. Dieser dient nur zur Strukturierung und hat die Dauer Null

9 .Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen Grundregeln (5) Enden und beginnen in einem Ereignis mehrere Vorgänge, die nicht unabhängig von einander sind, so werden auch hier Scheinvorgänge als Strukturierungshilfe eingesetzt. A,B,C,D gegeben; C kann erst nach Abschluss von A und B beginnen; D nach Abschluss von B

10 .2. Strukturanalyse bei Vorgangspfeilnetzen Grundregeln (6) Der Netzplan muss schleifenfrei sein Planungs- und.netzplantechnik

11 .2. Strukturanalyse bei Vorgangspfeilnetzen Grundregeln (7) Ein Netzplan besitzt genau eine Quelle und eine Senke Planungs- und.netzplantechnik 2.2.5

12 .Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen Grundregeln (8) Das Scheinvorgänge nur zur Strukturierung dienen, sollen so wenige wie möglich eingesetzt werden, um die Übersichtlichkeit des Netzplans zu erhalten

13 .Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen Topologische Sortierung - Eine topologische Sortierung der Knoten dient der Orientierung - Prinzip: Jeder Knoten, der keinen nicht-numerierten Vorgänger hat, erhält die nächsthöhere Knotennummer

14 .2. Strukturanalyse bei Vorgangspfeilnetzen Beispiel Vorgang A B C D E F G H J.Netzplantechnik Vorgänger - - A,B C B D C,E C,E G,H

15 .3. Zeitanalyse bei Vorgangspfeilnetzen Planungs- und.netzplantechnik Notationen i - j Vorgang zwischen den Ereignissen i und j D i-j Dauer des Vorgangs i - j FZ k Früheste Zeit des Ereignisses k im Projekt SZ k Späteste Zeit des Ereignisses k im Projekt FAZ i-j frühester Anfangszeitpunkt des Vorgangs i - j SAZ i-j spätester Anfangszeitpunkt des Vorgangs i - j FEZ i-j frühester Endzeitpunkt des Vorgangs i - j SEZ i-j spätester Endzeitpunkt des Vorgangs i - j Gleichungen FAZ i-j :=FZ i FEZ i-j :=FAZ i-j + D i-j SEZ i-j :=SZ j SAZ i-j := SEZ i-j -D i-j

16 .3. Zeitanalyse bei Vorgangspfeilnetzen Vorwärtsrechnung Planungs- und.netzplantechnik Hat ein Vorgang mehrere Vorgänger, so kann dieser erst begonnen werden, wenn alle Vorgänger abgeschlossen sind. ( ) FZ : = FAZ : = max FZ + D j j k i i j i V j

17 .3. Zeitanalyse bei Vorgangspfeilnetzen Vorwärtsrechnung - Beispiel Vorgang A B C D E F G H J Dauer [ZE] Netzplantechnik Vorgänger - - A,B C B D C,E C,E G,H

18 .3. Zeitanalyse bei Vorgangspfeilnetzen Rückwärtsrechnung Planungs- und.netzplantechnik Ein Vorgang muss spätestens dann beendet sein, wenn der zeitlich nächste Nachfolger spätestens beginnen muss. ( ) SZ : = SEZ : = min SZ D i h i j i j j N i

19 .3. Zeitanalyse bei Vorgangspfeilnetzen Rückwärtsrechnung - Beispiel Vorgang A B C D E F G H J Dauer [ZE] Netzplantechnik Vorgänger - - A,B C B D C,E C,E G,H

20 .3. Zeitanalyse bei Vorgangspfeilnetzen Puffer Planungs- und.netzplantechnik Gesamtpuffer (GP i-j ) GPi j : = SZ j FZi Di j gibt an, um wie viele ZE der Vorgang i-j maximal verschoben werden darf, ohne die späteste Zeit von j zu gefährden und damit das Projektende hinauszuzögern Freier Vorwärtspuffer (FVP i-j ) FVPi j : = FZ j FZi Di j gibt an, um wie viele ZE der Beginn eines Vorgangs i-j hinausgezögert werden darf, ohne den frühesten Beginn des Nachfolgers zu gefährden Freier Rückwärtspuffer (FRP i-j ) FRPi j : = SZ j SZi D gibt an, um wie viele ZE das Ende eines Vorgangs i-j verschoben werden darf, ohne das späteste Ende des Nachfolgers zu verzögern i j 9

21 .3. Zeitanalyse bei Vorgangspfeilnetzen Gesamtpufferberechnung - Beispiel Vorgang A B C D E F G H J.Netzplantechnik Dauer [ZE] Vorgänger A,B 5 C 7 B 5 D 3 C,E C,E 8 G,H

22 .3. Zeitanalyse bei Vorgangspfeilnetzen Freier Vorwärtspufferberechnung - Beispiel Vorgang A B C D E F G H J.Netzplantechnik Dauer [ZE] Vorgänger A,B 5 C 7 B 5 D 3 C,E C,E 8 G,H

23 .3. Zeitanalyse bei Vorgangspfeilnetzen Puffer Planungs- und.netzplantechnik Gesamtpuffer (GP i-j ) Freier Vorwärtspuffer (FVP i-j ) GP i j FVP i j : = SZ : = j FZ j FZ i FZ i D i j D i j GP 2-3 FVP

24 Gliederung. Netzplantechnik.. Grundlagen der Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen.3. Zeitanalyse bei Vorgangspfeilnetzen 2. Lösung von linearen Optimierungsproblemen mit Hilfe des Simplex-Algorithmus 2.. Lineare Optimierungsprobleme 2.2. Simplex-Verfahren 2.3. Sonderfälle 3. Planung von Güterströmen als Lineares Optimierungsproblem

25 2.. Lineare Optimierungsprobleme Lineare Optimierungsprobleme (LOP) Planungs- und.netzplantechnik Optimierung einer linearen Zielfunktion unter linearen Nebenbedingungen (Restriktionen). Betriebswirtschaftliche Probleme - Optimale Produktionsprogrammplanung bei Kapazitätsoder Absatzbeschränkungen (Kostenminimierung, Gewinnmaximierung) - Optimierung von Materialmischungen unter Berücksichtigung bestimmter Qualitäts- und Mengenanforderungen und mit dem Ziel der Gesamtkostenminimierung - Verschnittoptimierung unter Berücksichtigung bestimmter Verschnittmuster und mit dem Ziel der Faktoreinsatzminimierung bzw. Abfallminimierung

26 2.2. Simplex-Verfahren Planungs- und.netzplantechnik Beispiel Eine Tischlerei produziert zwei Typen von Schränke. Typ A erwirtschaftet einen Stückgewinn von 5 (Hundert Euro), Typ B einen Stückgewinn von 6 (Hundert Euro). Beide Typen benötigen im Holzzuschnitt jeweils Arbeitsstunden. In der Tischlerei findet die eigentliche Montage der Holzzuschnitte statt. Für Typ A müssen Arbeitsstunden, für Typ B aufgrund der Holzverzierungen an den Türen 2 Arbeitsstunden aufgewendet werden. Im Holzzuschnitt steht ein Mitarbeiter mit 4 Stunden, in der Tischlerei ein Meister sowie ein Geselle mit insgesamt 6 Arbeitsstunden die Woche zur Verfügung. Des Weiteren bestehen Fixkosten für die Miete der Werkstatt in Höhe von 7 (Hundert Euro). Der Inhaber der Tischlerei plant die optimalen Produktionsmengen für Typ A und B unter Berücksichtigung der genannten Restriktionen. 25

27 2.2. Simplex-Verfahren Planungs- und.netzplantechnik Modellierung des LOP Entscheidungsvariablen x : Anzahl der zu produzierenden Schränke vom Typ A x 2 : Anzahl der zu produzierenden Schränke vom Typ B Ziel: Maximierung des Gesamtgewinns max x = 5x + 6x 2 7 Restriktionen x + x 2 x + 2x 2 x,x () Arbeitsstunden Holzzuschnitt (2) Arbeitsstunden Tischlerei (3) Produktionsmengen sind nichtnegativ

28 2.2. Simplex-Verfahren Graphische Lösung Planungs- und.netzplantechnik () (2)

29 .Netzplantechnik 2.2. Simplex-Verfahren Grundlegende Idee des Verfahrens - Suche nach der optimalen Lösung durch Durchwanderung der Ecken und Prüfung auf Verbesserung () (2)

30 .Netzplantechnik 2.2. Simplex-Verfahren Standardform des LOP - In Vorbereitung auf die Anwendung des Simplex-Verfahrens wird das LOP in die sogenannte Standardform gebracht - Ungleichungen durch Einführung von Schlupfvariable in Gleichungen überführen - n Strukturvariablen und m Restriktionen max x u.d.n. a x ij j x j = b = c jx i n j= für alle i =,.., n für alle j =,.., n j + m max x u.d.n. Ax = b x = c T x

31 2.2. Simplex-Verfahren LOP Standardform des LOP.Netzplantechnik max x u.d.n. x x x,x + x 2 = 5x 2 + 2x 2 + 6x max x = 5x + 6x 7 udn x + x + x =4 2 3 x + 2 x + x =6 2 4 x, x

32 .Netzplantechnik 2.2. Simplex-Verfahren Bedeutung der Schlupfvariablen x + x

33 2.. Lineare Optimierungsprobleme Planungs- und.netzplantechnik A Begriff Basis Jede nichtsinguläre m x m Teilmatrix von A heißt Basis. Nichtsingularität bedeutet, dass die m-dimensionalen Spaltenvektoren von B linear unabhängig sind. Es kann sich also kein Spaltenvektor als Linearkombination der anderen darstellen lassen. x + x + x = x + 2x + + x = B

34 .Netzplantechnik Simplex-Verfahren Grundzüge des Simplex-Verfahrens () Maximierungsproblem: max u.d.n. x x x,x x + x 2 = 5x 2 + 2x 2 + 6x Zielfunktion wird in die Nebenbedingungen mit aufgenommen, Maximierung von x max x udn... x 5x 6x2 = 7 x+ x2 + x3 =4 x+ 2 x2 + x 4 =6 x, x 2

35 2.2. Simplex-Verfahren Grundzüge des Simplex-Verfahrens (2).Netzplantechnik Simplex-Tableau x x x 2 x 3 x 4 RHS = =

36 2.2. Simplex-Verfahren Grundzüge des Simplex-Verfahrens (3).Netzplantechnik Pivotisieren x x -5 x 2-6 x 3 x 4 RHS x x x 2 x 3 x 4 RHS -2 6/2 5 -/2 /2 /

37 2.2. Simplex-Verfahren Grundzüge des Simplex-Verfahrens (4) Planungs- und.netzplantechnik Basistausch NBV x,x NBV x,x 2 36

38 2.2. Simplex-Verfahren Grundzüge des Simplex-Verfahrens (5).Netzplantechnik Pivotisieren x x -2 x 2 x 3 x 4 6/2 RHS 5 -/2 /2 /2 3 x x x 2 x 3 x 4 RHS 2/5 / 5 /5 -/ / / 2 37

39 2.2. Simplex-Verfahren Grundzüge des Simplex-Verfahrens (6) Planungs- und.netzplantechnik Basistausch NBV x,x 3 NBV x 3,x

40 2.2. Simplex-Verfahren Grundzüge des Simplex-Verfahrens (7) Planungs- und.netzplantechnik Interpretation der Schattenpreise x x x 2 x 3 x 4 2/5 / RHS 5 /5 -/ 2 -/ /

41 .Netzplantechnik 2.3. Sonderfälle. Minimierungsproblem Ein Minimierungsproblem der Form minx kann in ein Maximierungsproblem transformiert werden min = T T x c x + d [max -x = c x d] = T c x T [max -x = c x d] min Zielfunktionswerte T x = c x + d

42 .Netzplantechnik 2.3. Sonderfälle 2. Unzulässige Ausgangslösung Eine unzulässige Ausgangslösung ist dann gegeben, wenn die Ausgangslösung, die sich durch Nullsetzen der Strukturvariablen ergibt, nicht im zulässigen Bereich liegt max x = 5x + 6x 7 2 udn... x + x 4 2 x + 2x 6 x 2 + x 2 x, x 2 2 max x = 5x + 6x 7 2 udn... x + x + x = x + 2 x + x = x + x -x = x, x

43 2.3. Sonderfälle Geometrische Bedeutung der >= -Restriktion Planungs- und.netzplantechnik

44 2.3. Sonderfälle Ausgangstableau bei unzulässiger Ausgangslösung.Netzplantechnik x x -5 x 2-6 x 3 x 4 x 5 RHS

45 2.3. Sonderfälle.Netzplantechnik X - x x x 2 x 3 x 4 x 5 x H RHS

46 2.3. Sonderfälle X - x x x 2 x 3 x 4 x 5 x H RHS.Netzplantechnik X - -2 x x x 2 x 3 x 4 x 5 x H RHS

47 2.3. Sonderfälle X - -2 x x x 2 x 3 x 4 x 5 x H RHS.Netzplantechnik X - x x x 2 x 3 x 4 x 5 x H RHS

48 2.3. Sonderfälle Planungs- und.netzplantechnik

49 .Netzplantechnik 2.3. Sonderfälle 3. Freie Variable Sind einige der Strukturvariablen nichtnegativ und einige frei, dann werden die freien Variable in die Basis mit aufgenommen und verbleiben im Laufe des Iterationsprozesses auch dort

50 .Netzplantechnik 2.3. Sonderfälle 4. Entartung Zu einer Basis gehört jeweils genau eine Ecke, im Falle der Entartung jedoch ist eine Ecke mehreren Basen zugeordnet

51 Gliederung. Netzplantechnik.. Grundlagen der Netzplantechnik.2. Strukturanalyse bei Vorgangspfeilnetzen.3. Zeitanalyse bei Vorgangspfeilnetzen 2. Lösung von linearen Optimierungsproblemen mit Hilfe des Simplex-Algorithmus 2.. Lineare Optimierungsprobleme 2.2. Simplex-Verfahren 2.3. Sonderfälle 3. Planung von Güterströmen als Lineares Optimierungsproblem

52 3. Planung von Güterströmen als LOP Planungs- und.netzplantechnik Betriebswirtschaftliche Probleme - Planung kürzester Wege eines Konsumgüterherstellers von verschiedenen Produktionsstandorten zu verschiedenen Großhändlern - Planung der Zuordnung von Mitarbeitern auf Tätigkeiten gemäß ihrer Eignung Darstellung - Transportsysteme werden mittels Graphen dargestellt - Knoten sind Orte, Kanten Wegeverbindungen - Haben die Wege Einbahnstraßencharakter, so werden sie als Pfeile dargestellt

53 3. Planung von Güterströmen als LOP Planungs- und.netzplantechnik Kostenminimaler Fluss - (Gerichtete) Kanten repräsentieren Transportwege; Knoten Orte, an denen Angebot oder Nachfrage eines Gutes besteht bzw. an denen ein Gut nur umgeschlagen wird - Menge der Orte V = V + V 2 + V 3 Notationen und Bedingungen - In Quellort i V können max. a i Gütereinheiten pro Zeiteinheit eingespeist werden - Aus Senke i V 3 können maximal b i Gütereinheiten pro ZE entnommen werden -x ij bezeichnet den Güterstrom in Kante <i,j> von Knoten i zu Knoten j - Der Güterstrom sei durch Wegekapazität κ ij beschränkt -c ij bezeichne die Kosten des Transports einer Gütereinheit von i nach j 52

54 3. Planung von Güterströmen als LOP Lineare Optimierungsaufgabe Planungs- und.netzplantechnik min x u.d.n. = i V j N() i a für i V x ij xli = für i V j N(i) l N( i) -b für i V x κ für alle (i,j) ij ij c x ij ij i 2 i

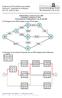
55 3. Planung von Güterströmen als LOP Beispiel.Netzplantechnik +4 2, 3 5, , 3 2, 4 27, 5 5 4, , 6 25, , ,

56 3. Planung von Güterströmen als LOP Lösung.Netzplantechnik +4 2, 3 5, , 3 27, 5 4, , 6 25, , ,

57 3. Planung von Güterströmen als LOP Planungs- und.netzplantechnik min 3x + 4x + 6x + x + 5x + x + 2x + 7x + 5x + 2x + 3x udn x 2, x 5, x 5, x 2, x 27, x 2, x 25, x 4, x 3, x 25, x x + x + x x x + x + x x + x x x x x x x x + x + x x x x x = x, x, x, x, x, x, x, x, x, x, x

58 3. Planung von Güterströmen als LOP Planungs- und.netzplantechnik Ausblick - Transportprobleme können sehr komplex sein - Finden einer zulässigen Ausgangslösung nicht trivial - Um eine zulässige Anfangslösung zu finden, können Heuristiken eingesetzt werden