Matematický časopis. Václav Medek Darstellende Geometrie eines Raumes mit Orthogonalgeometrie
|
|
|
- Bettina Beutel
- vor 7 Jahren
- Abrufe
Transkript
1 Matematický časopis Václav Medek Darstellende Geometrie eines Raumes mit Orthogonalgeometrie Matematický časopis, Vol. 19 (1969), No. 3, Persistent URL: Terms of use: Mathematical Institute of the Slovak Academy of Sciences, 1969 Institute of Mathematics of the Academy of Sciences of the Czech Republic provides access to digitized documents strictly for personal use. Each copy of any part of this document must contain these Terms of use. This paper has been digitized, optimized for electronic delivery and stamped with digital signature within the project DML-CZ: The Czech Digital Mathematics Library
2 Matematický časopis 19 (1969). No. 3 DARSTELLENDE GEOMETRIE EINES RAUMES MIT ORTHOGONALGEOMETRIE VACLAV MEDEK, Bratislava 1. Einige Bemerkungen zur Orthogonalgeometrie eines dreidimensionalen Raumes. Wir werden von Lenzschen Axiomen (vgl. [1], S. 138) eines affinen Raumes 21 ausgehen; da wir uns mit einem dreidimensionalen Räume beschäftigen werden, werden wir anstatt des Axioms 8, dieses Axiom 8' benützen: Zwei verschiedene Ebenen haben entweder keinen gemeinsamen Punkt, oder eine gemeinsame Gerade. Im Räume 21 gelten alle Grundeigenschaften der Lage aus dem euklidischen dreidimensionalen Räume (über dem Körper von reellen Zahlen), was unmittelbar aus den Axiomen folgt. Der Begriff der Parallelität wird bekannterweise eingeführt, wobei wir auch zwei inzidente Figuren als parallel betrachten. Wir werden diese in 21 geltenden Sätze benützen: Satz 1. Wenn oc, oc f zwei parallele Ebenen sind und die Gerade a die Ebene oc in einem Punkte A schneidet, dann schneidet die Gerade a auch die Ebene oc f. Aus diesem Satz folgt die Eindeutigkeit der Ebene oc f durch den Punkt A und parallel zur Ebene oc. Satz 2. Eine notwendige und hinreichende Bedingung für die Parallelität von Ebenen oc, oc f ist die Existenz von solchen sich schneidenden Geraden a'', b f e oc f, dass a' \\ oc, b' \\ oc ist. Satz 3. Eine notwendige und hinreichende Bedingung für die Parallelität einer Geraden a und einer Ebene oc ist die Existenz einer solchen Geraden a f e oc, dass a\\a' ist. Satz 4. Wenn eine Gerade a die Ebene oc schneidet (a^ oc), dann schneidet diese Ebene auch jede mit der Geraden a parallele Gerade. Satz 5. Wenn die Ebenen oc, oc f parallel sind und eine Ebene ß mit der Ebene x nicht parallel ist, dann sind auch die Ebenen oc f, ß nicht parallel und die Schnittgeraden a = [oc, ß], a f = [oc f, ß] sind parallel. Unter einem Vektor des Raumes 21 verstehen wir eine Abbildung V : 21 -> 21, wobei jedes Punktepaar A, B die Eigenschaft [)TA, yb] \\[A, B] hat und die Abbildung y entweder eine Identität ist, oder keinen invarianten Punkt hat. Es ist gut bekannt, dass ein Vektor durch einen Punkt und sein Bild bestimmt ist und dass alle Vektoren eine abelsche Gruppe bilden. Wenn wir im Räume
3 einen willkürlichen festen Punkt O wählen, dann können wir Punkte des Raumes 21 eineindeutig in Vektoren des Raumes 2i so abbilden, dass dem Punkte A e2l der Vektor A, welcher den Punkt O auf den Punkt A abbildet, zugeordnet wird. Vektoren des Raumes 21 bilden einen Vektorraum 2} über einem Körper T. In weiteren Überlegungen werden wir voraussetzen, dass der Körper T kommutativ der Charakteristik #= 2 ist; ausserdem werden wir in den Vektorraum 2} eine Orthogonalgeometrie einführen (vgl. z. B. [2], S. 111). Das Skalarprodukt von Vektoren A, B werden wir mit AB bezeichnen und wir werden voraussetzen, dass das Radikal des Raumes 2J der Nullvektor ist; der Raum 2? ist also regulär. Wenn es zu keinem Missverständniss führen kann, werden wir die Punkte des Raumes 21 mit zugeordneten Vektoren identifizieren und dann können wir sagen, dass jede Isometrie des Raumes 21 in eine orthogonale Transformation des Raumes 2) und eine Translation des Raumes 21 zerlegt werden kann. Definition 1. Zwei Punktepaare (A, B), (C, D) heissen kongruent, wenn (ß - Af - (D - C)2. Die Kongruenz von Punktepaaren ist eine Äquivalenzrelation und für zwei zugeordnete Punktepaare schreiben wir dann (A, B) ~ (C, D). Definition 2. Seien die Vektoren A, B, C, D #= 0 und nicht isotrop; dann heissen die Vektorenpaare (A, B), (C, D) kongruent, wenn (Aß)2_(CD)2 A2ß2 C^D 2 Zwei von Null verschiedene Vektoren heissen xrthogonal, wenn AB = 0. Das Vektorenpaar (A, B) ist mit jedem Paar (ka, IB) kongruent, wo k, l zwei von Null verschiedene Elemente des Körpers T sind. Die Kongruenzrelation von Vektorenpaaren ist wieder eine Äquivalenzrelation und wir schreiben daher (A, B) ~ (C, D). Ein Paar von Null verschiedenen, nicht isotropen orthogonalen Vektoren ist mit jedem solchen Paar kongruent. Definition 3. Sei a eine willkürliche Gerade des Raumes 21 und sei a f die Parallele zu a durch den Punkt 0; wenn A #= 0 ein beliebiger Punkt der Geraden a f ist, dann heisst der Vektor A ein Richtungsvektor der Geraden a. Die Gerade a heisst gerade dann isotrop, wenn ihr Richtungsvektor isotrop ist; jede nicht isotrope Gerade heisst regulär. Sei oc eine willkürliche Ebene des Raumes 21 und oc' sei die zu ihr parallele Ebene durch d n Punkt 0; dann heisst der Unterraum d s Raumes 23, wzlchen die Vektoren der Ebene oc' bilden, die Richtungsebene der Eb ne oc. Die Ebene oc heisst regulär, wenn das Radikal ihrer Richtungsebene qleich Nidl ist; jede nicht reguläre Ebene heisst singulär. Diese Definition ermöglicht eine Kongruenzrelation zwischen Geradenpaaren einzuführen; zwei Geradenpaare (a, b), (c, d) heissen kongruent, wenn 217
4 die Paare ihrer Richtungsvektoren kongruent sind. Auch diese Relation ist eine Äquivalenzrelation und wir schreiben (a, b) ~ (c, d). Wenn wir zwei Geraden mit zueinander orthogonalen Geraden als orthogonale Geraden bezeichnen, dann sind jede zwei Paare von zueinander orthogonalen Geraden kongruent. Es gibt zwei Arten von regulären Ebenen; entweder enthält die Ebene keine isotrope Gerade, oder sie enthält gerade zwei Systeme zueinander paralleler isotropen Geraden; im letzten Falle heisst die Ebene hyperbolisch. In einer singulären Ebene a können nicht alle Vektoren isotrop sein; dann würde nämlich rad a = a, a* = a und dim a + dim a* = 4 > 3. Deshalb enthält eine jede singulare Ebene gerade ein System von parallelen isotropen Geraden. Definition 4. Eine Gerade a ist zu einer Ebene oc gerade dann orthogonal, wenn ihr Eichtungsvektor auf zwei linear unabhängige Vektoren der Eichtungsebene a' orthogonal ist. Aus dieser Definition folgt dieses Kriterium für Orthogonalität von Geraden und Ebenen: Eine Gerade ist gerade dann zu einer Ebene orthogonal, wenn sie zu zwei sich schneidenden Geraden orthogonal ist. Eine Senkrechte (orthogonale Gerade) auf eine Ebene ist gerade dann mit dieser Ebene nicht parallel., wenn die Ebene (und daher auch die Senkrechte auf sie) regulär ist. Wenn die Ebene singulär ist, dann ist auch jede Senkrechte auf sie isotrop und mit ihr parallel. 2, Die Parallelprojektion im 21. Definition 5. Unter einer Parallelprojektion des Eaumes 21 auf eine Ebene n e 21 verstehen wir eine Abbildung & des Eaumes 21 auf n, welche diese Bedingungen erfüllt: 1) Die Punkte werden in Punkte abgebildet; die Punkte der Ebene n (Bildebene) sind invariant. 2) Die Geraden werden auf Geraden oder auf Punkte abgebildet; das Bild einer Geraden ist dann und nur dann ein Punkt, wenn Bilder von zwei ihrer verschiedenen Punkte zusammenfallen. 3) Keine drei nichtkollineare Punkte haben ein gemeinsames Bild. 4) Die Inzidenz wird bei SP erhalten. Bemerkung 1. Die Abbildung SP vermittelt eine Zerlegung des Raumes 2T in disjunkte Untermengen mit der Eigenschaft, dass alle Punkte einer Untermenge in einen Punkt abgebildet sind. Diese Untermengen heissen Abbildungsuntermengen der Abbildung SP. Satz 6. Die Abbildungsuntermengen Geraden. der Abbildung SP sind zueinander parallele 218
5 Beweis. Die Bilder von Figuren bei der Abbildung SP werden wir mit einem Index 1 rechts unten bezeichnen. Wählen wir einen beliebigen Punkt A e 21, A^n; sein Bild ist A\ en. Beschäftigen wir uns jetzt mit der Verbindungsgeraden der Punkte A,A\. Da die Bilder der Punkte A, A\ im Punkte A\ zusammenfallen, wird nach 2) das Bild der Geraden z A = [A, A\] der Punkt A\. Die Gerade z A ist eine Abbildungsuntermenge, da nach 3) kein weiterer Punkt in den Punkt A\ abgebildet werden kann. Wählen wir weiter eine willkürliche Gerade p e n, A\< p und es sei a eine Ebene durch den Punkt A und durch die Gerade p. Sei jetzt B\ + A\ ein willkürlicher Punkt aus n und seii?i $ p (das ist möglich, da der Körper T von Charakteristik 4= 2 ist). Sei P b = [b\,p]; dann ist das Bild der Geraden b = [P b, A] (nach 2) und 4)) die Gerade bi. Nach 2) kann kein Punkt M e b, M 4= A, P b weder in den Punkt A\, noch in den Punkt P b projiziert werden. Alle Geraden vom Typ z M = [M, M\], wo M e b, M #= P b liegen in einer Ebene q b = [b, b\] und da sie keinen gemeinsamen Punkt haben, sind sie zueinander parallel. Wenn wir dann die Parallele z B mit z M durch B\ konstruieren, schneidet sie die Gerade b im Punkte B, dessen Bild gerade der Punkt B\ ist. Zwischen den Punkten einer Geraden b und den Punkten ihres Bildes b\ besteht eine eineindeutige Verwandschaft, welche durch zueinander parallele Abbildungsgeraden vermittelt ist. Sei jetzt C\en ein solcher Punkt, dass die Verbindungsgerade [A\,C\] parallel zur Geraden p ist; ähnlich werden wir dann mit Hilfe vom Punkt B\ beweisen, dass die Abbildungsuntermenge z c eine Gerade ist. Da die Wahl der Geraden p ganz willkürlich war, ist der Satz vollständig bewiesen. Bemerkung 2. Satz 6 gilt nicht für einen Raum 21 über einem Körper T der Restklassen mod 2. Bezeichnen wir die Punkte des Raumes 21 als A, B, C, D, E, F, G, H und die Ebene n möge die Punkte A, B,C, D enthalten. Seien die Geraden [A,E], [B,F], [C, G], [D, H] Parallelen. Die Abbildung E->A, F->C, G->B, H -> D erfüllt alle Bedingungen 1) 4) und doch sind die Abbildungsuntermengen keine zueinander parallele Geraden. Bemerkung 3. Die Abbildung & kann man durch die Ebene n und durch die Richtung s der projizierenden Geraden bestimmen. Definition 6. Der Schnittpunkt einer Geraden mit. der Bildebene heisst Spurpunkt und die Schnittgerade einer Ebene mit der Bildebene heisst Spur. Definition 7. Die Projektion einer Figur ist die Menge von Projektionen, aller Punkte der Figur. Bemerkung 4. Über die Projektionen von Punkten und Geraden spricht man in 1) und 2) in der Definition 5. Die folgenden zwei Sätze beweist man genau so wie in der darstellenden Geometrie eines affinen Raumes über dem Körper von reellen Zahlen. 219
6 Satz 7. Die Projektion einer Ebene ist die Bildebene, bzw. eine Gerade je nachdem, ob die Ebene nicht parallel, bzw. parallel mit der Projektionsrichtung ist. Satz 8. Zwei Parallelen mit der Projektionsrichtung projizieren sich in Punkte; in jedem anderen Falle sind Projektionen von zwei zueinander parallelen Geraden wieder zueinander parallele Geraden. Definition 8. Sei die Ebene oc nicht mit der Bildebene n parallel; dann geht durch jeden Punkt der Ebene oc eine Gerade n h e oc parallel mit der Bildebene. Die Geraden n h e oc heissen Hauptgeraden der Ebene bezüglich der Bildebene n. Offenbar gilt der Satz 9. Die Projektionen von Hauptgeraden sind zueinander parallele Geraden. Definition 9. Wenn eine Ebene oc die Bildebene n in einer regulären Geraden schneidet, dann heissen die Geraden in der Ebene oc, welche orthogonal zu ihren Hauptgeraden bezüglich der Bildebene n sind, Neigungsgeraden bezüglich der Bildebene n und werden mit n s bezeichnet. Bemerkung 5. Wenn eine Ebene oc die Bildebene in einer isotropen Geraden schneidet, hat es keinen Sinn über die Neigungsgeraden zu sprechen. Wenn die Ebene a singulär ist, dann eine jede ihre Gerade orthogonal zu ihren Hauptgeraden ist und wenn die Ebene oc regulär ist (also hyperbolisch), dann sind ihre Hauptgeraden isotrop und also zu sich selbst orthogonal. Bemerkung 6. Die Neigungsgeraden sind isotrop, wenn die Ebene oc singulär ist, im entgegensetzten Falle sind sie regulär. In beiden Fällen gibt es eine einzige Richtung von Neigungsgeraden bezüglich der Bildebene n. Satz 10. Sei die Ebene oc parallel zur Bildebene n; seien A, B zwei beliebige Punkte der Ebene oc und seien A\, B\ ihre Projektionen in n; dann sind die Punktepaare (A, B), (A\,B\) kongruent. Beweis. Wir können voraussetzen, dass die Ebenen n. a verschieden sind. Sei S der Vektor A A\; dann der Vektor B -> B\ ist ks, wo k G T. Die Verbindungsgeraden [A, B] und [A\, B\] sind zueinander parallel nach Satz 8 (nach Satz 4 gibt es nämlich in n eine zur Geraden [.4, B] parallele Gerade und beide müssen sich parallel projizieren); daraus folgt ßi Ai = k'(ß A). Weiter ßi = ß + ks, -Ai = A + S. Daraus folgt ßi A 1 = ß A + (k \)S, oder (1 k') (ß A) + (k 1)S = O und da die Vektoren ß A und S linear unabhängig sind, muss k' = k = l werden, oder ßi Ai - B A. In weiteren Überlegungen werden wir uns mit einer Orthogonalprojektion beschäftigen, d. h. mit einer solcher Projektion, w r o die Projektionsrichtung s zur Bildebene n orthogonal ist. Daraus folgt, dass die Bildebene und auch alle Projektionsgeraden regulär sind. Satz 11. Die orthogonale Projektion einer isotropen Geraden ist gerade dann eine isotrope Gerade, wenn sie zur Bildebene n parallel ist; in jedem anderen 220
7 Falle ist die orthogonale Projektion einer isotropen Geraden eine reguläre Gerade. Die orthogonale Projektion einer regulären Geraden kann ein Punkt, eine isotrope, oder eine reguläre Gerade sein. Beweis. Wenn es isotrope Geraden parallel zur Bildebene gibt, dann ist die Bildebene eine hyperbolische Ebene und die orthogonalen Projektionen der isotropen Geraden sind die isotropen Geraden der Bildebene. Da es in projizierenden Ebenen durch istorope Geraden nur ein System von isotropen Parallelen gibt (diese Ebenen sind nämlich singulär), projiziert sich eine jede andere isotrope Gerade orthogonal in eine reguläre Gerade. Der weitere Teil des Satzes ist evident. Satz 12. Die Neigungsgeraden einer Ebene projizieren sich entweder in Punkte (wenn die Ebene orthogonal zur Bildebene ist), oder auf Geraden, die orthogonal zu Projektionen der Hauptgeraden der gegebenen Ebene sind. Beweis. Wenn die Ebene a orthogonal zur Bildebene n ist, ist sie nur dann regulär, wenn sie die Bildebene n in einer regulären Geraden schneidet. Dann sind die Neigungsgeraden von der Ebene a regulär und zur Bildebene orthogonal ; sie projizieren sich daher in Punkte. Sei jetzt die Ebene a nicht zur Bildebene orthogonal und ihre Schnittgerade n p a mit der Bildebene n sei isotrop; dann ist die Ebene a regulär. Die Ebene x J_ n durch die Gerade n p a ist nämlich singulär. Wenn es durch die Gerade n p a noch eine weitere singulare Ebene gäbe, müsste die Gerade n p* zu allen Geraden des Raumes % orthogonal sein, was ein Widerspruch ist. Die Ebene x ist daher zu allen Ebenen durch die Gerade n p a orthogonal. Sei jetzt s a eine willkürliche Neigungsgeradö der Ebene a und sei P = [ n p a, s a ]. Die Senkrechte zur Bildebene n durch den Punkt P und die Gerade s a bestimmen die orthogonalprojizierende Ebene a der Geraden s a und diese Ebene ist zur Spur n p a orthogonal. Dann ist auch die Schnittgerade s\ [a, n] orthogonal zur Spur n p a. Sei die Schnittgerade n p a von Ebenen n, oc regulär; dann sind die Neigungsgeraden regulär, wenn die Ebene a regulär ist und sie sind isotrop, wenn die Ebene singulär ist. Sei s a eine willkürliche Neigungsgerade der Ebene a und sei P = [s a, n p a ]. Sei s die Senkrechte durch P zur Bildebene n und sei a [s, s a ]. Die Ebene a ist die orthogonalprojizierende Ebene der Neigungsgeraden und nach dem Kriterium für Orthogonalität von Geraden und Ebenen ist n p a J_ a und daher ist auch s\ = [o, n] zur n p a orthogonal. Satz 13. Eine Senkrechte zu einer Ebene projiziert sich orthogonal in die Bildebene entweder in einen Punkt (wenn die Ebene mit der Bildebene parallel ist), oder auf eine Senkrechte zu Projektionen der Hauptgeraden der gegebenen Ebene. Beweis. Der erste Teil des Satzes ist evident. Sei jetzt die Spur der Ebene a isotrop. Dann kann die Ebene singulär sein, wenn sie orthogonal zur Bilde- 221
8 bene ist. In diesem Falle ist die Gerade n p a gleichzeitig eine Senkrechte zur Ebene a und der Satz ist bewiesen. W 7 enn die Ebene a regulär ist, ist die Senkrechte zu ihr auch regulär und liegt in einer singulären Ebene durch die Gerade n p a (anders gehört die Gerade n p 0i zum Radikal des Raumes 21, was ein Widerspruch ist). Die Projektion der Senkrechten ist dann die Spur n p (X und die Behauptung ist bewiesen. Wenn die Spur n p 0L regulär und die Ebene a singulär sind, dann ist die isotrope Gerade der Ebene a gleichzeitig orthogonal zu ihr und nach dem Beweis des vorigen Satzes ist ihre Projektion zur Spur n p oc orthogonal. Wenn die Ebene a regulär ist, führt man den Beweis wie im Satz 12. Satz 14. Zwei zueinander orthogonale Geraden projizieren sich wieder auf zwei zueinander orthogonale Geraden gerade dann, wenn keine von ihnen zur Bildebene orthogonal und mindestens eine von ihnen mit der Bildebene parallel ist. Beweis. Wenn beide gegebenen Geraden parallel zur Bildebene sind, ist die Behauptung des Satzes evident. Wählen wir jetzt eine willkürliche isotrope Gerade a, die mit der Bildebene nicht parallel ist; ihre orthogonale Projektion (nach Satz 11) ist eine reguläre Gerade a\. Alle Geraden orthogonal zur Geraden a liegen in einer singulären Ebene a durch die Gerade a (bzw. sie liegen in einer mit ihr parallelen Ebene); es gibt gerade eine solche Ebene. Nach dem Beweis des Satzes 12 ist die Spur n p a der Ebene a orthogonal zur Geraden a\. Sei P = [ n p a, a\\. Keine von den Geraden der Ebene a durch den Punkt P (also keine der Senkrechten zur Geraden a), mit Ausnahme der Geraden n p a. projiziert sich auf die Parallele zur n p a und die Behauptung ist bewiesen. Sei die Gerade a eine willkürliche reguläre Gerade, die nicht zur Bildebene parallel ist. Wählen wir auf der Geraden a einen willkürlichen Punkt A; dann liegen alle Senkrechten zur Geraden a durch den Punkt A in einer regulären Ebene oc, die orthogonal zur Geraden a ist. Nach Satz 12 hat die Hauptgerade n h a der Ebene a durch den Punkt A die Projektion n h\ orthogonal zur a\. Alle anderen Geraden der Ebene a durch den Punkt A (ohne Rücksicht darauf,ob sie isotrop sind oder nicht) projizieren sich auf reguläre Geraden und daher kann sich keine von ihnen auf die Senkrechte zu a\ projizieren. Satz. 15. Ein Paar von orthogonalen Projektionen (A\, B\) von zwei verschiedenen Punkten A, B ist gerade dann mit dem Paar (A, B) kongruent, wenn die Verbindungsgerade [A, B] mit der Bildebene parallel ist. Beweis. Wenn die Verbindungsgerade [A, B] mit der Bildebene parallel ist, dann folgt die Behauptung des Satzes aus dem Satz 10. Sei jetzt die Verbindungsgerade [-4,.B] nicht mit der Bildebene parallel; ohne Beschränkung der Allgemeinheit können wir voraussetzen, dass der Punkt B in der Bildebene liegt und dass B = 0. Sei K der Vektor A -> A\; dann A\ = A -\- K ist. Weiter 222
9 folgt A\ = A 2 + 2AK + K 2 = A 2 + AK + (A + K)K = A 2 + AK + A±K = = A 2 + AK; da AK * 0, ist A\ 4= A 2 und daher sind die Paare (A, B), (A u B±) nicht kongruent. Konstruktion. Sei jedes Element des Körpers T ein Quadrat; dann kann man in der Bildebene ein Paar von Punkten kongruent zum willkürlichen Paar der Punkte konstruieren, deren Verbindungsgerade nicht isotrop ist und deren Projektion keine isotrope Gerade ist. Beweis. Ohne Beschränkung der Allgemeinheit können wir voraussetzen, dass die Bildebene n durch einen von gegebenen Punkten geht und diesen Punkt können wir als den Punkt 0 wählen. Dann benützen wir die Bezeichnung des vorigen Satzes und wir wählen in n einen willkürlichen Vektor C orthogonal zum Vektor A±. Ein solcher Vektor existiert, denn der Vektor _Ai ist nicht isotrop. Suchen wir jetzt einen solchen Vektor n A, dass n A 2 = A 2 und n A = = A x + kc. Dann muss A\ + k 2 C 2 = A 2 sein, oder k 2 = (A 2 A\)/C 2. Nach unserer Voraussetzung gibt es ein Element k et, das diese Gleichung erfüllt. Es gilt auch k 2 C 2 = K 2, denn A 2 = (A ± K) 2 = A ± + K 2 ; daraus folgt K 2 = A 2 - A\ = k 2 C 2. Bemerkung 7. Diese Konstruktion führt zur bekannten Konstruktion im euklidischen Räume, wo man die umgeklappte Strecke so bekommt, dass wir auf der Senkrechten zu ihrer Projektion durch A\ eine Strecke derselben Länge wie die Höhe des Punktes A über die Bildebene konstruieren. Satz 16. Bei der Bezeichnung des vorigen Satzes sind die Paare (A, A±) und ( n A, Ai) kongruent. Beweis. AA X = (A + K)A X = A\; n AA x = (A x + kc)a l = A\. Da nach vorigem Satze n A 2 = A 2 gilt, folgt die Behauptung aus Definition 2. Bemerkung 8. Dieser Satz führt im euklidischen Räume zur bekannten Xonstruktion des Winkels kongruent mit dem Winkel einer Geraden mit der Bildebene. Satz 17. Sei die reguläre Eb ne oc nicht zur Bildzbene n orthogonal und sei ihre Schnittgerade mit der Bildebene eine reguläre Gerade n p 0L ; sei jedes Element des Körpers T ein Quadrat; dann gibt es eine solche Isometrie dzr Ebene oc auf die Ebene n (die Bild^r von Figuren in der Isometrie oc -> n werden wir mit eimm Kreischen rechts unten bzzeichnen), dass die Verbindungsgerade der orthogonalen Projektion eines Punktes dar Ebene oc und seines Bildes (in der Isomztrie) zur Spur n p 0L orthogonal ist und dass die Spur n p 0L punktweise invariant ist. Beweis. Wählen wir in der Ebene oc zwei willkürliche verschiedene Punkte A, B so, dass A, B $ n p a, die Verbindungsgerade [A, B] und auch die Neigungsgerade von oc nicht isotrop sind und dass die Neigungsgerade die Spur n p (X schneidet; ohne Beschränkung der Allgemeinheit können wir diesen Schnittpunkt zum Punkt 0 wählen. Sei s A die Neigungsgerade von oc durch den Punkt 223
10 A und sei P = [s A, 7l p (X ]. Ebenso sei s B die Neigungsgerade von a durch den Punkt B und sei R = [s B, *p«]. Bezeichnen wir S A = A P, s Ai = A x P? K = Ai - A. Zuerst gilt es, dass die Vektoren s Ai und P zueinander orthogonal sind (nach unserer Voraussetzung gilt S AP = AP P 2 = 0; s AiP = AiP P 2 = AiP AP = (Ai A)P = KP = 0). Suchen wir weiter auf der Geraden sf einen solchen Punkt Ao, dass die Punktepaare (Ao,P) und (A, P) kongruent werden. Dafür bezeichnen wir S A 0 = Ao P; dann < s Ao = k s A\. Weiter muss «A = S A 2 sein, oder k 2 S A\ = S A 2, woraus k 2 = *A 2 j*a\ folgt. Nach Voraussetzung existiert ein solches Element k e T und A 0 = P -{- k s A\. Dann gilt, dass auch die Paare (O, A) und (O, A 0 ) kongruent sind; wirklich: A 2 = (P + *A) 2 = P 2 + 2P*A + *A 2 = P 2 + *A 2 ; A 2 0 = (P + k*ai) 2 =- P 2 -f + 2kP*Ai + k 2 S A* = P 2 + k 2 S A\ = P 2 + *A 2 = A 2. Sei ß = ca; dann, da A = P + S A, ist ß = cp + c*ai, oder R = cp. Ähnlich setzen wir fest, dass S B = c s A, s ßi = c«ai, ß 0 = ca 0, ßi = cai, woraus (ßi ß 0 )R = 0folgt. Wählen wir jetzt einen beliebigen Punkt X A auf der Geraden s A und sei l A = P + l s A; dann l A 0 = P -f Z S A. Wenn ein solcher Punkt **4 existiert, dass die Verbindungsgerade [M,O] isotrop ist, dann ist auch die Verbindungsgerade [^0,0] isotrop. Für den Punkt >A muss nämlich *A 2 = (P + i*a) 2 = P 2 + -f i 2^A 2 = 0 gelten. Dann aber gilt <A = (P + ^A 0 ) 2 = P 2 + i 2s A 2 = P 2 + _ _ ^2s^2 _ o. In unserer Isometrie entsprechen einander also isotrope Geraden. Bemerkung 9. Mit Hilfe dieser Sätze kann man im Falle aller Paare der Grundfiguren festsetzen, ob sie kongruent sind oder nicht. Bemerkung 10. Da eine einzige Projektion zur Rekonstruktion der Figuren nicht genügt, muss mann noch eine Projektion, oder irgendwelche Analogie der kotierten Projektion einführen. Da wir die Anordnung des Körpers T nicht voraussetzen, können wir nicht den Raum 21 in zwei Halbräume teilen. Doch können wir im Räume 2J einen von Null verschiedenen willkürlichen, zur Bildebene n orthogonalen, Vektor K wählen. Dann können wir jeden Punkt A e 21 durch seine orthogonale Projektion A\ und ein Element A ket charakterisieren, wobei der Vektor A kk den Punkt A in den Punkt A\ transformiert. LITERATUR [1] Lenz H., Grundlagen der Elementarmathematik, Berlin [2] Artin E., Geometrie Algebra, New York [3] Pickert G., Analytische Geometrie, Leipzig Eingegangen am Katedra matematiky a deskriptivnej geometrie Stavebnej fakulty Slovenskej vysokej skoly technickej, Bratislava 224
Archivum Mathematicum
 Archivum Mathematicum Robert Karpe Zwei Typen der Kombinationen zur bestimmten Summe, deren Anzahl durch direkte Formel festgestellt werden kann Archivum Mathematicum, Vol. 8 (1972), No. 1, 51--56 Persistent
Archivum Mathematicum Robert Karpe Zwei Typen der Kombinationen zur bestimmten Summe, deren Anzahl durch direkte Formel festgestellt werden kann Archivum Mathematicum, Vol. 8 (1972), No. 1, 51--56 Persistent
8. Kleinsche Geometrie I: Hyperbolische Geometrie. Das Erlanger Programm.
 8. Kleinsche Geometrie I: Hyperbolische Geometrie Nach den bisherigen Ergebnissen müssen wir uns nun um die Gruppe PSL 2 C kümmern. Das Studium dieser Gruppe wird uns in dieser Vorlesung zu einem neuen
8. Kleinsche Geometrie I: Hyperbolische Geometrie Nach den bisherigen Ergebnissen müssen wir uns nun um die Gruppe PSL 2 C kümmern. Das Studium dieser Gruppe wird uns in dieser Vorlesung zu einem neuen
Elementare Geometrie Vorlesung 13
 Elementare Geometrie Vorlesung 13 Thomas Zink 7.6.2017 1.Vektoren Es sei E eine Ebene. Eine Translation T : E E wird auch als Vektor bezeichnet. Wenn O, A E, so gibt es genau einen Vektor T, so dass T
Elementare Geometrie Vorlesung 13 Thomas Zink 7.6.2017 1.Vektoren Es sei E eine Ebene. Eine Translation T : E E wird auch als Vektor bezeichnet. Wenn O, A E, so gibt es genau einen Vektor T, so dass T
Grundlagen der Gruppoid- und Gruppentheorie
 Grundlagen der Gruppoid- und Gruppentheorie 12. Grundbegriffe über Gruppoide In: Otakar Borůvka (author): Grundlagen der Gruppoid- und Gruppentheorie. (German). Berlin: VEB Deutscher Verlag der Wissenschaften,
Grundlagen der Gruppoid- und Gruppentheorie 12. Grundbegriffe über Gruppoide In: Otakar Borůvka (author): Grundlagen der Gruppoid- und Gruppentheorie. (German). Berlin: VEB Deutscher Verlag der Wissenschaften,
Definition und gemeinsame Eigenschaften der Symplektischen und Orthogonalen Geometrie
 Universität Duisburg-Essen, Campus Essen, Fachbereich Mathematik, IEM AG Zahlentheorie Definition und gemeinsame Eigenschaften der Symplektischen und Orthogonalen Geometrie Proseminar Algebra WS 2008/2009,
Universität Duisburg-Essen, Campus Essen, Fachbereich Mathematik, IEM AG Zahlentheorie Definition und gemeinsame Eigenschaften der Symplektischen und Orthogonalen Geometrie Proseminar Algebra WS 2008/2009,
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Modulprüfung zum Lehrerweiterbildungskurs Geometrie am
 Modulprüfung zum Lehrerweiterbildungskurs Geometrie am 28.6.17 Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Punkte Bearbeiten Sie bitte drei der vier folgenden Aufgaben!
Modulprüfung zum Lehrerweiterbildungskurs Geometrie am 28.6.17 Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Punkte Bearbeiten Sie bitte drei der vier folgenden Aufgaben!
4.3 Affine Punkträume
 4.3. AFFINE PUNKTRÄUME 185 4.3 Affine Punkträume Es wird jetzt der Übergang von der linearen Algebra zur analytischen Geometrie beschrieben. 4.3.1 Definition (affiner Punktraum) Sei V ein K-Vektorraum,
4.3. AFFINE PUNKTRÄUME 185 4.3 Affine Punkträume Es wird jetzt der Übergang von der linearen Algebra zur analytischen Geometrie beschrieben. 4.3.1 Definition (affiner Punktraum) Sei V ein K-Vektorraum,
Musterlösung zur Klausur Grundwissen Schulmathematik am
 Musterlösung zur Klausur Grundwissen Schulmathematik am 24.2.2012 Aufgabe 1 (10 Punkte) Zeigen Sie: Für alle n N ist n 3 3n 2 +2n durch 6 teilbar. svorschläge Beweis durch Induktion nach n n = 1. Es ist
Musterlösung zur Klausur Grundwissen Schulmathematik am 24.2.2012 Aufgabe 1 (10 Punkte) Zeigen Sie: Für alle n N ist n 3 3n 2 +2n durch 6 teilbar. svorschläge Beweis durch Induktion nach n n = 1. Es ist
Kapitel 11. Bilinearformen über beliebigen Bilinearformen
 Kapitel 11 Bilinearformen über beliebigen Körpern Wir können in diesem Kapitel rasch vorgehen, weil die meisten Konzepte im Zusammenhang mit Sesquilinearformen bereits eingeführt wurden. In diesem Abschnitt
Kapitel 11 Bilinearformen über beliebigen Körpern Wir können in diesem Kapitel rasch vorgehen, weil die meisten Konzepte im Zusammenhang mit Sesquilinearformen bereits eingeführt wurden. In diesem Abschnitt
4.3 Bilinearformen. 312 LinAlg II Version Juni 2006 c Rudolf Scharlau
 312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
Unterlagen zur Vorlesung Algebra und Geometrie in der Schule: Grundwissen über Affine Geometrie. Sommersemester Franz Pauer
 Unterlagen zur Vorlesung Algebra und Geometrie in der Schule: Grundwissen über Affine Geometrie Sommersemester 2009 Franz Pauer INSTITUT FÜR MATHEMATIK, UNIVERSITÄT INNSBRUCK, TECHNIKERSTRASSE 13, 6020
Unterlagen zur Vorlesung Algebra und Geometrie in der Schule: Grundwissen über Affine Geometrie Sommersemester 2009 Franz Pauer INSTITUT FÜR MATHEMATIK, UNIVERSITÄT INNSBRUCK, TECHNIKERSTRASSE 13, 6020
1 Angeordnete Körper und Anordnung
 1 ANGEORDNETE KÖRPER UND ANORDNUNG 1 1 Angeordnete Körper und Anordnung Die nächste Idee, die wir interpretieren müssen ist die Anordnung. Man kann zeigen, dass sie nicht über jeden Körper möglich ist.
1 ANGEORDNETE KÖRPER UND ANORDNUNG 1 1 Angeordnete Körper und Anordnung Die nächste Idee, die wir interpretieren müssen ist die Anordnung. Man kann zeigen, dass sie nicht über jeden Körper möglich ist.
Elementare Geometrie - Die Gerade & das Dreieck Teil I
 Proseminar zur Linearen Algebra und Elementargeometrie Elementare Geometrie - Die Gerade & das Dreieck Teil I Eingereicht von: Alexandra Kopp 178294 alexandra.kopp@tu-dortmund.de Eingereicht bei: Prof.
Proseminar zur Linearen Algebra und Elementargeometrie Elementare Geometrie - Die Gerade & das Dreieck Teil I Eingereicht von: Alexandra Kopp 178294 alexandra.kopp@tu-dortmund.de Eingereicht bei: Prof.
zur Modulprüfung zum Lehrerweiterbildungskurs Geometrie am
 Nachklausur zur Modulprüfung zum Lehrerweiterbildungskurs Geometrie am 12.7.17 Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Punkte Bearbeiten Sie bitte drei der vier folgenden
Nachklausur zur Modulprüfung zum Lehrerweiterbildungskurs Geometrie am 12.7.17 Name, Vorname Matrikel-Nr. Aufg.1 Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Punkte Bearbeiten Sie bitte drei der vier folgenden
Wiederholungsblatt Elementargeometrie LÖSUNGSSKIZZE
 Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
1.2 Modulare Arithmetik
 Algebra I 8. April 2008 c Rudolf Scharlau, 2002 2008 11 1.2 Modulare Arithmetik Wir erinnern an die Notation für Teilbarkeit: m c für m, c Z heißt, dass ein q Z existiert mit qm = c. Definition 1.2.1 Sei
Algebra I 8. April 2008 c Rudolf Scharlau, 2002 2008 11 1.2 Modulare Arithmetik Wir erinnern an die Notation für Teilbarkeit: m c für m, c Z heißt, dass ein q Z existiert mit qm = c. Definition 1.2.1 Sei
Commentationes Mathematicae Universitatis Carolinae
 Commentationes Mathematicae Universitatis Carolinae Jiří Novák Über gewisse minimale Systeme von k-tupeln Commentationes Mathematicae Universitatis Carolinae, Vol. 11 (1970), No. 3, 397--402 Persistent
Commentationes Mathematicae Universitatis Carolinae Jiří Novák Über gewisse minimale Systeme von k-tupeln Commentationes Mathematicae Universitatis Carolinae, Vol. 11 (1970), No. 3, 397--402 Persistent
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Geometrie WiSe 2014/2015 am
 Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Geometrie WiSe 2014/2015 am 23.1.2015 Bearbeiten Sie bitte zwei der drei folgenden Aufgaben! Falls Sie alle drei Aufgaben bearbeitet haben sollten, kennzeichnen
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Geometrie WiSe 2014/2015 am 23.1.2015 Bearbeiten Sie bitte zwei der drei folgenden Aufgaben! Falls Sie alle drei Aufgaben bearbeitet haben sollten, kennzeichnen
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Geometrie kubischer Kurven
 Geometrie kubischer Kurven Werner Hoffmann Wir wollen die Theorie nur soweit entwickeln, wie es zum Verständnis der Gruppenoperation auf einer irreduziblen kubischen Kurve nötig ist. Satz 1 In der affinen
Geometrie kubischer Kurven Werner Hoffmann Wir wollen die Theorie nur soweit entwickeln, wie es zum Verständnis der Gruppenoperation auf einer irreduziblen kubischen Kurve nötig ist. Satz 1 In der affinen
Geometrische Objekte im 3-dimensionalen affinen Raum oder,... wie nützlich ist ein zugehöriger Vektorraum der Verschiebungen
 Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 2009
 I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
Acta Universitatis Carolinae. Mathematica et Physica
 Acta Universitatis Carolinae. Mathematica et Physica E. Vavřinec Elektrische Erscheinungen bei der plastischen Deformation von Silberchloridkristallen Acta Universitatis Carolinae. Mathematica et Physica,
Acta Universitatis Carolinae. Mathematica et Physica E. Vavřinec Elektrische Erscheinungen bei der plastischen Deformation von Silberchloridkristallen Acta Universitatis Carolinae. Mathematica et Physica,
12. R n als EUKLIDISCHER VEKTORRAUM
 12. R n als EUKLIDISCHER VEKTORRAUM 1 Orthogonalität in der Ebene. Die Vektoren in der Ebene, die (im üblichen Sinne) senkrecht zu einem Vektor x = (x 1, x 2 ) T stehen, lassen sich leicht angeben. Sie
12. R n als EUKLIDISCHER VEKTORRAUM 1 Orthogonalität in der Ebene. Die Vektoren in der Ebene, die (im üblichen Sinne) senkrecht zu einem Vektor x = (x 1, x 2 ) T stehen, lassen sich leicht angeben. Sie
Ebene und. Gerade, 2. Punkte A, B, C,..., die auf einer Geraden liegen, heißen kollinear.
 16 3 Das Axiomensystem Motiviert von den Elementen des Euklid, wollen wir jetzt ein modernes Axiomensystem für die Ebene Geometrie aufstellen. Zum ersten Mal wurde das um 1900 von David Hilbert geleistet,
16 3 Das Axiomensystem Motiviert von den Elementen des Euklid, wollen wir jetzt ein modernes Axiomensystem für die Ebene Geometrie aufstellen. Zum ersten Mal wurde das um 1900 von David Hilbert geleistet,
DEUTSCHE SCHULE MONTEVIDEO BIKULTURELLES DEUTSCH-URUGUAYISCHES ABITUR ( AUF SPANISCH )
 Grundlegende Bemerkungen : Der Begriff des Vektors wurde in den vergangenen Jahren im Geometrieunterricht eingeführt und das mathematische Modell des Vektors wurde vor allem auch im Physikunterricht schon
Grundlegende Bemerkungen : Der Begriff des Vektors wurde in den vergangenen Jahren im Geometrieunterricht eingeführt und das mathematische Modell des Vektors wurde vor allem auch im Physikunterricht schon
Klausurenkurs zum Staatsexamen (WS 2013/14): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Quadriken Polarität Transformationen Klassifikation von Quadriken Geraden in Regelquadriken Die kubische Wendelinie (twisted
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Quadriken Polarität Transformationen Klassifikation von Quadriken Geraden in Regelquadriken Die kubische Wendelinie (twisted
Mathematische Grundlagen
 Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 06.12.2013 Alexander Lytchak 1 / 16 Wiederholung Ist V ein Vektorraum, so heißen Abbildungen T v : V V der Form w w
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 06.12.2013 Alexander Lytchak 1 / 16 Wiederholung Ist V ein Vektorraum, so heißen Abbildungen T v : V V der Form w w
Lineare Algebra II Lösungen der Aufgaben 42 und 43
 D Blottière SS 7 P Schützdeller Universität Paderborn Lineare Algebra II Lösungen der Aufgaben 4 und 43 Aufgabe 4 : Bemerkungen : Es sei V ein n-dimensionaler Vektorraum über einem Körper K und β : V V
D Blottière SS 7 P Schützdeller Universität Paderborn Lineare Algebra II Lösungen der Aufgaben 4 und 43 Aufgabe 4 : Bemerkungen : Es sei V ein n-dimensionaler Vektorraum über einem Körper K und β : V V
Ebene Elementargeometrie
 Ebene Elementargeometrie Im Folgenden unterscheiden wir neben Definitionen (Namensgebung) und Sätzen (nachweisbaren Aussagen) so genannte Axiome. Axiome stellen der Anschauung entnommene Aussagen dar,
Ebene Elementargeometrie Im Folgenden unterscheiden wir neben Definitionen (Namensgebung) und Sätzen (nachweisbaren Aussagen) so genannte Axiome. Axiome stellen der Anschauung entnommene Aussagen dar,
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
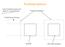 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
Physikalischer Raum. Euklidischer Raum
 Physikalischer Raum Aus unserer Erfahrung schreiben wir dem Raum intuitiv bestimmte Eigenschaften zu. Intuition ist aber nicht ausreichend zum Aufbau einer Theorie. Es bedarf vielmehr einer präzisen mathematischen
Physikalischer Raum Aus unserer Erfahrung schreiben wir dem Raum intuitiv bestimmte Eigenschaften zu. Intuition ist aber nicht ausreichend zum Aufbau einer Theorie. Es bedarf vielmehr einer präzisen mathematischen
Aufgabe 1: Multiple Choice Test
 PH Heidelberg, Fach Mathematik, Klausur zur Teilprüfung Modul, Einführung in die Geometrie, SS010, 30.07.010 Aufgabe 1: Multiple Choice Test Kennzeichnen Sie die Ihrer Meinung nach richtigen Antworten.
PH Heidelberg, Fach Mathematik, Klausur zur Teilprüfung Modul, Einführung in die Geometrie, SS010, 30.07.010 Aufgabe 1: Multiple Choice Test Kennzeichnen Sie die Ihrer Meinung nach richtigen Antworten.
Mathematisches Kaleidoskop II Materialien Teil 3. Dr. Hermann Dürkop
 Mathematisches Kaleidoskop II Materialien Teil 3 Dr. Hermann Dürkop E-Mail: info@ermanus.de .3.3 Noch zwei Isomorphie-Beispiele Beispiel : Wir betrachten die Symmetrien eines nichtquadratischen Rechtecks.
Mathematisches Kaleidoskop II Materialien Teil 3 Dr. Hermann Dürkop E-Mail: info@ermanus.de .3.3 Noch zwei Isomorphie-Beispiele Beispiel : Wir betrachten die Symmetrien eines nichtquadratischen Rechtecks.
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Kössler, Miloš: Scholarly works
 Kössler, Miloš: Scholarly works Miloš Kössler Ein Beitrag zur Theorie der schlichten Potenzreihen Věstník Král. čes. spol. nauk 1932, No. 5, 8 p. Persistent URL: http://dml.cz/dmlcz/501251 Terms of use:
Kössler, Miloš: Scholarly works Miloš Kössler Ein Beitrag zur Theorie der schlichten Potenzreihen Věstník Král. čes. spol. nauk 1932, No. 5, 8 p. Persistent URL: http://dml.cz/dmlcz/501251 Terms of use:
Sphärische Zwei - und Dreiecke
 TECHNISCHE UNIVERSITÄT DORTMUND Sphärische Zwei - und Dreiecke Proseminar innerhalb des Lehramtsstudiums im Fach Mathematik Meryem Öcal Matrikelnummer 168833 Studiengang LABG 2009 Prüfer: Prof. Dr. Lorenz
TECHNISCHE UNIVERSITÄT DORTMUND Sphärische Zwei - und Dreiecke Proseminar innerhalb des Lehramtsstudiums im Fach Mathematik Meryem Öcal Matrikelnummer 168833 Studiengang LABG 2009 Prüfer: Prof. Dr. Lorenz
Elementare Geometrie Vorlesung 19
 Elementare Geometrie Vorlesung 19 Thomas Zink 28.6.2017 1.Gleichungen von Kreisen Es sei OAB ein kartesisches Koordinatensystem der Ebene E. Für einen Punkt P mit den Koordinaten (x, y) schreiben wir auch
Elementare Geometrie Vorlesung 19 Thomas Zink 28.6.2017 1.Gleichungen von Kreisen Es sei OAB ein kartesisches Koordinatensystem der Ebene E. Für einen Punkt P mit den Koordinaten (x, y) schreiben wir auch
γ(p) = {(P,g) P G P g}. π(g) = {(P,g) P G P g}.
 Lösungsvorschläge zur Klausur Elementare Geometrie vom 02.08.2017 Aufgabe 1 Es sei P eine nicht kollineare endliche Menge von Punkten in einer affinen Ebene. Weiter sei G die Menge aller Geraden PQ mit
Lösungsvorschläge zur Klausur Elementare Geometrie vom 02.08.2017 Aufgabe 1 Es sei P eine nicht kollineare endliche Menge von Punkten in einer affinen Ebene. Weiter sei G die Menge aller Geraden PQ mit
Übungen zu Geometrie (LGy) Universität Regensburg, Sommersemester 2014 Dr. Raphael Zentner, Dr. Olaf Müller
 Übungen zu Geometrie (LGy) Universität Regensburg, Sommersemester 2014 Dr. Raphael Zentner, Dr. Olaf Müller Übungsblatt 13 Dieses Übungsblatt wird nicht mehr zur Abgabe vorgesehen. Es dient der Wiederholung
Übungen zu Geometrie (LGy) Universität Regensburg, Sommersemester 2014 Dr. Raphael Zentner, Dr. Olaf Müller Übungsblatt 13 Dieses Übungsblatt wird nicht mehr zur Abgabe vorgesehen. Es dient der Wiederholung
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Kapitel 1. Erste algebraische Strukturen. 1.2 Ringe und Körper
 Kapitel 1 Lineare Algebra individuell M. Roczen und H. Wolter, W. Pohl, D.Popescu, R. Laza Erste algebraische Strukturen Hier werden die grundlegenden Begriffe eingeführt; sie abstrahieren vom historisch
Kapitel 1 Lineare Algebra individuell M. Roczen und H. Wolter, W. Pohl, D.Popescu, R. Laza Erste algebraische Strukturen Hier werden die grundlegenden Begriffe eingeführt; sie abstrahieren vom historisch
Affine Geometrie (Einfachere, konstruktive Version)
 Affine Geometrie (Einfachere, konstruktive Version) Def. Affiner Raum der Dimension n über Körper K ist nach Definition K n. Bemerkung. Man könnte Theorie von affinen Raumen auch axiomatisch aufbauen mit
Affine Geometrie (Einfachere, konstruktive Version) Def. Affiner Raum der Dimension n über Körper K ist nach Definition K n. Bemerkung. Man könnte Theorie von affinen Raumen auch axiomatisch aufbauen mit
Zusammenfassung Mathe III. Themenschwerpunkt 3: Analytische Geometrie / lineare Algebra (ean) 1. Rechenregeln mit Vektoren
 Zusammenfassung Mathe III Themenschwerpunkt 3: Analytische Geometrie / lineare Algebra (ean) 1. Rechenregeln mit Vektoren Definition: (1) anschaulich: Ein Vektor ist eine direkt gerichtete Verbindung zweier
Zusammenfassung Mathe III Themenschwerpunkt 3: Analytische Geometrie / lineare Algebra (ean) 1. Rechenregeln mit Vektoren Definition: (1) anschaulich: Ein Vektor ist eine direkt gerichtete Verbindung zweier
Lineare Algebra. 1 Lineare Abbildungen
 Lineare Algebra Die lineare Algebra ist ein Teilgebiet der Mathematik, welches u. A. zur Beschreibung geometrischer Abbildungen und diverser Prozesse und zum Lösen linearer Gleichungssysteme mit Hilfe
Lineare Algebra Die lineare Algebra ist ein Teilgebiet der Mathematik, welches u. A. zur Beschreibung geometrischer Abbildungen und diverser Prozesse und zum Lösen linearer Gleichungssysteme mit Hilfe
Erste Schnittpunktsätze und Anfänge einer Dreiecksgeometrie
 Christoph Vogelsang Matr.Nr. 66547 Nils Martin Stahl Matr.Nr. 664 Seminar: Geometrie Dozent: Epkenhans Wintersemester 005/006 Erste Schnittpunktsätze und Anfänge einer Dreiecksgeometrie Ausarbeitung der
Christoph Vogelsang Matr.Nr. 66547 Nils Martin Stahl Matr.Nr. 664 Seminar: Geometrie Dozent: Epkenhans Wintersemester 005/006 Erste Schnittpunktsätze und Anfänge einer Dreiecksgeometrie Ausarbeitung der
Übungen zur Geometrie
 Aufgabe 1.1. Beweisen Sie die folgende Aussage: Die Diagonalen eines Parallelogrammes schneiden sich in ihren Mittelpunkten. Aufgabe 1.2. Beweis von: rechter Winkel = stumpfer Winkel D A E M F B C AB beliebige
Aufgabe 1.1. Beweisen Sie die folgende Aussage: Die Diagonalen eines Parallelogrammes schneiden sich in ihren Mittelpunkten. Aufgabe 1.2. Beweis von: rechter Winkel = stumpfer Winkel D A E M F B C AB beliebige
Lineare Algebra und Numerische Mathematik für D-BAUG
 P Grohs T Welti F Weber Herbstsemester 25 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 8 Aufgabe 8 Basen für Bild und Kern Gegeben sind die beiden 2 Matrizen:
P Grohs T Welti F Weber Herbstsemester 25 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie 8 Aufgabe 8 Basen für Bild und Kern Gegeben sind die beiden 2 Matrizen:
Die Strahlensätze. Ben Hambrecht. 1 Zentrische Streckungen 2. 2 Der 1. Strahlensatz 7. 3 Der Streckfaktor Der 2.
 Die Strahlensätze Ben Hambrecht Inhaltsverzeichnis 1 Zentrische Streckungen 2 2 Der 1. Strahlensatz 7 3 Der Streckfaktor 11 4 Der 2. Strahlensatz 14 5 Der 3. Strahlensatz 18 6 Die Umkehrungen der Strahlensätze
Die Strahlensätze Ben Hambrecht Inhaltsverzeichnis 1 Zentrische Streckungen 2 2 Der 1. Strahlensatz 7 3 Der Streckfaktor 11 4 Der 2. Strahlensatz 14 5 Der 3. Strahlensatz 18 6 Die Umkehrungen der Strahlensätze
1.3 Relationen und Funktionen
 1.3. RELATIONEN UND FUNKTIONEN 1 1.3 Relationen und Funktionen Es gibt eine Konstruktion (Übungsaufgabe!) einer Klasse (a, b) mit der Eigenschaft (a, b) = (c, d) a = c b = d. Diese Klasse (a, b) heißt
1.3. RELATIONEN UND FUNKTIONEN 1 1.3 Relationen und Funktionen Es gibt eine Konstruktion (Übungsaufgabe!) einer Klasse (a, b) mit der Eigenschaft (a, b) = (c, d) a = c b = d. Diese Klasse (a, b) heißt
Aufgabe I.1 (4 Punkte) Gegeben seien die Matrix H := und die Menge L := {A R 4 4 A HA = H} Zeigen Sie:
 Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Aufgabe I (4 Punkte Gegeben seien die Matrix und die Menge Zeigen Sie: H := L := {A R 4 4 A HA = H} a L ist bezüglich der Matrizenmultiplikation eine Gruppe b Die Matrizen der Form ( E O, O B wobei E R
Vorlesung Mathematik 2 für Informatik
 Vorlesung Mathematik für Informatik Inhalt: Lineare Algebra Rechnen mit Vektoren und Matrizen Lineare Gleichungssysteme, GauÿAlgorithmus Vektorräume, Lineare Abbildungen Eigenwerte und Eigenvektoren Literatur
Vorlesung Mathematik für Informatik Inhalt: Lineare Algebra Rechnen mit Vektoren und Matrizen Lineare Gleichungssysteme, GauÿAlgorithmus Vektorräume, Lineare Abbildungen Eigenwerte und Eigenvektoren Literatur
Prof. S. Krauter Endliche Geometrie. SS 05. Blatt Wiederholen Sie die Abschnitte zum Rechnen mit Restklassen aus der Einführungsveranstaltung.
 Prof. S. Krauter Endliche Geometrie. SS 05. Blatt03 1. Wiederholen Sie die Abschnitte zum Rechnen mit Restklassen aus der Einführungsveranstaltung. 2. Die zahlentheoretische Kongruenz ist folgendermaßen
Prof. S. Krauter Endliche Geometrie. SS 05. Blatt03 1. Wiederholen Sie die Abschnitte zum Rechnen mit Restklassen aus der Einführungsveranstaltung. 2. Die zahlentheoretische Kongruenz ist folgendermaßen
MAT746 Seminar über Euklidische Geometrie Philipp Becker
 MAT746 Seminar über Euklidische Geometrie Philipp Becker R David Hilbert (1862-1943) Den Begriffen aus der Anschauungswelt fehlt die notwendige mathematische Exaktheit. Gebäude der Geometrie soll nicht
MAT746 Seminar über Euklidische Geometrie Philipp Becker R David Hilbert (1862-1943) Den Begriffen aus der Anschauungswelt fehlt die notwendige mathematische Exaktheit. Gebäude der Geometrie soll nicht
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
Lineare Algebra und analytische Geometrie II
 Prof Dr H Brenner Osnabrück SS 26 Lineare Algebra und analytische Geometrie II Vorlesung 2 Orthogonalität Mit dem Skalarprodukt kann man die Eigenschaft zweier Vektoren, aufeinander senkrecht zu stehen,
Prof Dr H Brenner Osnabrück SS 26 Lineare Algebra und analytische Geometrie II Vorlesung 2 Orthogonalität Mit dem Skalarprodukt kann man die Eigenschaft zweier Vektoren, aufeinander senkrecht zu stehen,
Prüfung Lineare Algebra 2
 1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
Polaren am Kreis. Helmut Frühinsfeld (aka ottogal) September x 2. , usw.) a 2. = a 1 b 1 + a 2 b 2 (1) a = 1 + a 2 2 (2) a 2 a.
 Polaren am Kreis Helmut Frühinsfeld aka ottogal September 017 1 Vorbemerkungen Wir verwenden ein kartesisches x 1, x -Koordinatensystem. Zu jedem Punkt Xx 1 x gehört der Ortsvektor OX = Analog hat Aa 1
Polaren am Kreis Helmut Frühinsfeld aka ottogal September 017 1 Vorbemerkungen Wir verwenden ein kartesisches x 1, x -Koordinatensystem. Zu jedem Punkt Xx 1 x gehört der Ortsvektor OX = Analog hat Aa 1
Übungen zu Einführung in die Lineare Algebra und Geometrie
 Übungen zu Einführung in die Lineare Algebra und Geometrie Andreas Cap Sommersemester 2010 Kapitel 1: Einleitung (1) Für a, b Z diskutiere analog zur Vorlesung das Lösungsverhalten der Gleichung ax = b
Übungen zu Einführung in die Lineare Algebra und Geometrie Andreas Cap Sommersemester 2010 Kapitel 1: Einleitung (1) Für a, b Z diskutiere analog zur Vorlesung das Lösungsverhalten der Gleichung ax = b
Symmetrien der Ebene und des Raumes
 Kapitel 2 Symmetrien der Ebene und des Raumes 2.1. Affine Abbildungen und Schwerpunkte Wir erinnern daran, dass E n den affinen Raum aller Punkte und V (E n ) den zugrunde liegenden euklidischen Vektorraum
Kapitel 2 Symmetrien der Ebene und des Raumes 2.1. Affine Abbildungen und Schwerpunkte Wir erinnern daran, dass E n den affinen Raum aller Punkte und V (E n ) den zugrunde liegenden euklidischen Vektorraum
~ v 2. Abbildung 3: Zweiter Schritt des Gram-Schmidt-Verfahrens. k 1. i=1. v k = w k
 v 1 v 1 v 2 v 2 W 2 -v (v, v ) 1 1 2 Abbildung 3: Zweiter Schritt des Gram-Schmidt-Verfahrens. k. Schritt: Subtraktion der Komponenten von ṽ k in Richtung von v 1,v 2,...,v k 1 und Normierung von w k auf
v 1 v 1 v 2 v 2 W 2 -v (v, v ) 1 1 2 Abbildung 3: Zweiter Schritt des Gram-Schmidt-Verfahrens. k. Schritt: Subtraktion der Komponenten von ṽ k in Richtung von v 1,v 2,...,v k 1 und Normierung von w k auf
Lineare Algebra I 5. Tutorium Die Restklassenringe /n
 Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Lineare Algebra I 5. Tutorium Die Restklassenringe /n Fachbereich Mathematik WS 2010/2011 Prof. Dr. Kollross 19. November 2010 Dr. Le Roux Dipl.-Math. Susanne Kürsten Aufgaben In diesem Tutrorium soll
Affine Eigenschaften ( stets K = R)
 Affine Eigenschaften ( stets K = R) Def. 15 Sei M eine Teilmenge eines affinen Raums A über V (über K). Eine Eigenschaft der Menge M heißt affin, wenn für jede Affinität F : A A 1 die Bildmenge {F(a)wobei
Affine Eigenschaften ( stets K = R) Def. 15 Sei M eine Teilmenge eines affinen Raums A über V (über K). Eine Eigenschaft der Menge M heißt affin, wenn für jede Affinität F : A A 1 die Bildmenge {F(a)wobei
einführendes Beispiel: In der Skizze ist die durch die Punkte A(2, 4, 3) B(2, 6, 2) C(4, 4, 2) festgelegte Ebene ε dargestellt.
 6 4. Darstellung der Ebene 4. Die Parametergleichung der Ebene einführendes Beispiel: In der Skizze ist die durch die Punkte A(2, 4, 3) B(2, 6, 2) C(4, 4, 2) festgelegte Ebene ε dargestellt. 0 2 r uuur
6 4. Darstellung der Ebene 4. Die Parametergleichung der Ebene einführendes Beispiel: In der Skizze ist die durch die Punkte A(2, 4, 3) B(2, 6, 2) C(4, 4, 2) festgelegte Ebene ε dargestellt. 0 2 r uuur
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel
 Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
Lösungen Übung 6 Aufgabe 1. a.) Idee: Gesucht sind p, q mit pq = 6 2 und p + q = 13. Dies entspricht genau der Situation im Höhensatz. Konstruktion: 1. Punkte A, B mit AB = 13 2. Gerade g AB mit dist(g,
Definition von R n. Parallelverschiebungen in R n. Definition 8.1 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R... R (n-mal), d.h.
 8 Elemente der linearen Algebra 81 Der euklidische Raum R n Definition von R n Definition 81 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R R (n-mal), dh R n = {(x 1, x 2,, x n ) : x
8 Elemente der linearen Algebra 81 Der euklidische Raum R n Definition von R n Definition 81 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R R (n-mal), dh R n = {(x 1, x 2,, x n ) : x
Mit Skalarprodukt und Vektorprodukt lässt sich ein weiteres, kombiniertes Produkt, das Spatprodukt
 Mit Skalarprodukt und Vektorprodukt lässt sich ein weiteres, kombiniertes Produkt, das Spatprodukt a ( b c) bilden. Aus der geometrischen Interpretation von Skalarprodukt und Vektorprodukt ist sofort ersichtlich,
Mit Skalarprodukt und Vektorprodukt lässt sich ein weiteres, kombiniertes Produkt, das Spatprodukt a ( b c) bilden. Aus der geometrischen Interpretation von Skalarprodukt und Vektorprodukt ist sofort ersichtlich,
5. Gegenseitige Lage von Geraden und Ebenen. 5.1 Gegenseitige Lage zweier Geraden (siehe Kap. 3.2) 5.2: Schnittpunkt einer Geraden mit einer Ebene
 5 5. Gegenseitige Lage von Geraden und Ebenen 5. Gegenseitige Lage zweier Geraden (siehe Kap..) 5.: Schnittpunkt einer Geraden mit einer Ebene Beispiel: : x + y + 4z - 4 = g = P(6, -, )Q(, 6, 4) geometrisch:
5 5. Gegenseitige Lage von Geraden und Ebenen 5. Gegenseitige Lage zweier Geraden (siehe Kap..) 5.: Schnittpunkt einer Geraden mit einer Ebene Beispiel: : x + y + 4z - 4 = g = P(6, -, )Q(, 6, 4) geometrisch:
Elementare Geometrie Vorlesung 2
 Elementare Geometrie Vorlesung 2 Thomas Zink 24.4.2017 Vierecke Definition Ein Viereck ABCD ist ein Streckenzug aus vier Strecken AB, BC,CD, DA ohne Selbstüberschneidungen. Vierecke Definition Ein Viereck
Elementare Geometrie Vorlesung 2 Thomas Zink 24.4.2017 Vierecke Definition Ein Viereck ABCD ist ein Streckenzug aus vier Strecken AB, BC,CD, DA ohne Selbstüberschneidungen. Vierecke Definition Ein Viereck
Übersicht zur Vorlesung
 Stand: 19.1.2012 Übersicht zur Vorlesung Ausgewählte Kapitel der Geometrie Definitionen/Axiome Anordnungsaxiome Archimedisches Axiom Definition von größer in den reellen Zahlen Intervalle Punkte, Geraden
Stand: 19.1.2012 Übersicht zur Vorlesung Ausgewählte Kapitel der Geometrie Definitionen/Axiome Anordnungsaxiome Archimedisches Axiom Definition von größer in den reellen Zahlen Intervalle Punkte, Geraden
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik
 Aufgabe 50. Projektivspiegelung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern Projektive Geometrie WS 2010/11 Lösungen zu Aufgabenblatt 12 (24.
Aufgabe 50. Projektivspiegelung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Martin von Gagern Projektive Geometrie WS 2010/11 Lösungen zu Aufgabenblatt 12 (24.
Mathematik für Anwender II
 Prof Dr H Brenner Osnabrück SS 22 Mathematik für Anwender II Vorlesung Euklidische Vektorräume Im Anschauungsraum kann man nicht nur Vektoren addieren und skalieren, sondern ein Vektor hat auch eine Länge,
Prof Dr H Brenner Osnabrück SS 22 Mathematik für Anwender II Vorlesung Euklidische Vektorräume Im Anschauungsraum kann man nicht nur Vektoren addieren und skalieren, sondern ein Vektor hat auch eine Länge,
Funktionentheorie auf Riemannschen Flächen
 Funktionentheorie auf Riemannschen Flächen Universität Regensburg Sommersemester 2014 Daniel Heiß: 5: Maximale analytische Fortsetzung 20.05.2014 Abstract Zunächst werden Garben und weitere benötigte Begriffe
Funktionentheorie auf Riemannschen Flächen Universität Regensburg Sommersemester 2014 Daniel Heiß: 5: Maximale analytische Fortsetzung 20.05.2014 Abstract Zunächst werden Garben und weitere benötigte Begriffe
Lineare Algebra und Numerische Mathematik für D-BAUG
 P. Grohs T. Welti F. Weber Herbstsemester 5 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe. Skalarprodukt und Orthogonalität.a) Bezüglich des euklidischen
P. Grohs T. Welti F. Weber Herbstsemester 5 Lineare Algebra und Numerische Mathematik für D-BAUG ETH Zürich D-MATH Beispiellösung für Serie Aufgabe. Skalarprodukt und Orthogonalität.a) Bezüglich des euklidischen
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C /07
 Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C - 6/7. Gegenseitige Lage von Geraden Gesucht ist die gegenseitige Lage der Geraden g durch die beiden Punkte A( ) und B( 5 9 ) und der Geraden
Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C - 6/7. Gegenseitige Lage von Geraden Gesucht ist die gegenseitige Lage der Geraden g durch die beiden Punkte A( ) und B( 5 9 ) und der Geraden
Institut für Mathematik Geometrie und Lineare Algebra J. Schönenberger-Deuel
 Lösungen Übung 7 Aufgabe 1. Skizze (mit zusätzlichen Punkten): Die Figur F wird begrenzt durch die Strecken AB und BC und den Kreisbogen CA auf l. Wir werden die Bilder von AB, BC und CA unter der Inversion
Lösungen Übung 7 Aufgabe 1. Skizze (mit zusätzlichen Punkten): Die Figur F wird begrenzt durch die Strecken AB und BC und den Kreisbogen CA auf l. Wir werden die Bilder von AB, BC und CA unter der Inversion
Übungen zu Einführung in die Lineare Algebra und Geometrie
 Übungen zu Einführung in die Lineare Algebra und Geometrie Andreas Cap Wintersemester 2014/15 Kapitel 1: Einleitung (1) Für a, b Z diskutiere analog zur Vorlesung das Lösungsverhalten der Gleichung ax
Übungen zu Einführung in die Lineare Algebra und Geometrie Andreas Cap Wintersemester 2014/15 Kapitel 1: Einleitung (1) Für a, b Z diskutiere analog zur Vorlesung das Lösungsverhalten der Gleichung ax
Lineare Algebra: Theorie und Anwendungen
 Lineare Algebra: Theorie und Anwendungen Sommersemester 2012 Bernhard Burgeth Universität des Saarlandes c 2010 2012, Bernhard Burgeth 1 VEKTOREN IN DER EBENE UND IM RAUM 2 1 Vektoren in der Ebene und
Lineare Algebra: Theorie und Anwendungen Sommersemester 2012 Bernhard Burgeth Universität des Saarlandes c 2010 2012, Bernhard Burgeth 1 VEKTOREN IN DER EBENE UND IM RAUM 2 1 Vektoren in der Ebene und
Analytische Geometrie II
 Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Mathematische Probleme, SS 2013 Donnerstag $Id: dreieck.tex,v /04/18 15:03:29 hk Exp hk $
 $Id: dreieck.tex,v 1.6 2013/04/18 15:03:29 hk Exp hk $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck Wir hatten gerade begonnen uns mit den speziellen Punkten im Dreieck zu beschäftigen. Dabei beschränken
$Id: dreieck.tex,v 1.6 2013/04/18 15:03:29 hk Exp hk $ 1 Dreiecke 1.5 Einige spezielle Punkte im Dreieck Wir hatten gerade begonnen uns mit den speziellen Punkten im Dreieck zu beschäftigen. Dabei beschränken
Kapitel 5. Vektorräume mit Skalarprodukt
 Kapitel 5 Vektorräume mit Skalarprodukt 119 120 Kapitel V: Vektorräume mit Skalarprodukt 5.1 Elementare Eigenschaften des Skalarprodukts Dienstag, 20. April 04 Wollen wir in einem Vektorraum wie in der
Kapitel 5 Vektorräume mit Skalarprodukt 119 120 Kapitel V: Vektorräume mit Skalarprodukt 5.1 Elementare Eigenschaften des Skalarprodukts Dienstag, 20. April 04 Wollen wir in einem Vektorraum wie in der
S c h u l b i b l i o t h e k
 S c h u l b i b l i o t h e k Eine Schüler und Lehrerhandreichung aus dem Math-College zur Einführ ung in die Di f fer enz ia lrec hnu ng unter Anwendung eines Computeralgebrasystems Eine Einführung in
S c h u l b i b l i o t h e k Eine Schüler und Lehrerhandreichung aus dem Math-College zur Einführ ung in die Di f fer enz ia lrec hnu ng unter Anwendung eines Computeralgebrasystems Eine Einführung in
Modulteilprüfung Geometrie (BaM-GS), Probeklausur
 HRZ-Benutzername: Modulteilprüfung Geometrie (BaM-GS), Probeklausur Dr. Patrik Hubschmid // SoSe 2013, 4. Juli 2013 Kontrollieren Sie, ob Sie alle Blätter (8 einschlieÿlich zweier Deckblätter) erhalten
HRZ-Benutzername: Modulteilprüfung Geometrie (BaM-GS), Probeklausur Dr. Patrik Hubschmid // SoSe 2013, 4. Juli 2013 Kontrollieren Sie, ob Sie alle Blätter (8 einschlieÿlich zweier Deckblätter) erhalten
4.2 Quotientenvektorräume
 306 LinAlg II Version 1 6. Juni 2006 c Rudolf Scharlau 4.2 Quotientenvektorräume Zum Verständnis der folgenden Konstruktion ist es hilfreich, sich noch einmal den Abschnitt 1.4 über Restklassen vom Beginn
306 LinAlg II Version 1 6. Juni 2006 c Rudolf Scharlau 4.2 Quotientenvektorräume Zum Verständnis der folgenden Konstruktion ist es hilfreich, sich noch einmal den Abschnitt 1.4 über Restklassen vom Beginn
Geometrie 1.1. Homepage zur Veranstaltung: Lehre Geometrie
 Geometrie 1.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 1.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Geometrie 1.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 1.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Lineare Algebra und analytische Geometrie I
 Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Vorlesung 3 Gruppen In der linearen Algebra wird im Allgemeinen ein Grundkörper K zugrunde gelegt, über den sich
Prof. Dr. H. Brenner Osnabrück WS 2015/2016 Lineare Algebra und analytische Geometrie I Vorlesung 3 Gruppen In der linearen Algebra wird im Allgemeinen ein Grundkörper K zugrunde gelegt, über den sich
42 Orthogonalität Motivation Definition: Orthogonalität Beispiel
 4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 31 Vektorräume mit Skalarprodukt Im R n kann man nicht nur Vektoren addieren und skalieren, sondern ein Vektor
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 31 Vektorräume mit Skalarprodukt Im R n kann man nicht nur Vektoren addieren und skalieren, sondern ein Vektor
Analytische Geometrie, Vektorund Matrixrechnung
 Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Lineare Algebra und analytische Geometrie
 Lineare Algebra und analytische Geometrie von Günther Eisenreich Mit 107 Abbildungen und 2 Tabellen 3., erweiterte und berichtigte Auflage Akademie Verlag Inhaltsverzeichnis A. Allgemeine Vorbemerkungen
Lineare Algebra und analytische Geometrie von Günther Eisenreich Mit 107 Abbildungen und 2 Tabellen 3., erweiterte und berichtigte Auflage Akademie Verlag Inhaltsverzeichnis A. Allgemeine Vorbemerkungen
Definition Sei V ein Vektorraum, und seien v 1,..., v n V. Dann heißt eine Linearkombination. n λ i = 1. mit. v = v i λ i.
 Kapitel Geometrie Sei V ein Vektorraum, z.b. V = R 3. Wenn wir uns für geometrische Eigenschaften von R 3 interessieren, so stört manchmal die Ausnahmerolle des Nullvektors, die es ja in V gibt. Beispielsweise
Kapitel Geometrie Sei V ein Vektorraum, z.b. V = R 3. Wenn wir uns für geometrische Eigenschaften von R 3 interessieren, so stört manchmal die Ausnahmerolle des Nullvektors, die es ja in V gibt. Beispielsweise
Lineare Schieberegisterfolgen
 Lineare Schieberegisterfolgen Sei K ein endlicher Körper. Man nehme zwei Vektoren x 0 a0 x n 1, a n 1 K n n 1 x n := a i x i und betrachte die lineare Abbildung : K n K n, die durch i=0, berechne x 0 x
Lineare Schieberegisterfolgen Sei K ein endlicher Körper. Man nehme zwei Vektoren x 0 a0 x n 1, a n 1 K n n 1 x n := a i x i und betrachte die lineare Abbildung : K n K n, die durch i=0, berechne x 0 x
4.2 Die adjungierte Abbildung
 4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
4.2. DIE ADJUNGIERTE ABBILDUNG 177 4.2 Die adjungierte Abbildung Die Vektorräume dieses Paragraphen seien sämtlich euklidisch, die Norm kommt jetzt also vom inneren Produkt her, v = v v. Zu f Hom R (V,
