Dynamische Risikomaße
|
|
|
- Tristan Geiger
- vor 6 Jahren
- Abrufe
Transkript
1 Dynamische Risikomaße in der Unternehmenssteuerung Jochen Wolf FH Koblenz Ulm, Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
2 statische Risikomaße Agenda 1 statische Risikomaße Erinnerungen Einsatzmöglichkeiten und Grenzen 2 Allgemeine dynamische Risikomaße 3 Filtrationen - revisited 4 dynamische Risikomaße auf Produktökonomien Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
3 statische Risikomaße Erinnerungen prominente Beispiele (1) Definition Der Value at Risk zum Niveau α (0, 1) ist definiert als der minimale Verlust, der in den 100 (1 α)% der schlechtesten Szenarien entsteht: VaR α (X ) := F X (α) := inf{x R : F X (x) α}, wobei F X die Verteilungsfunktion und F X ihre Pseudoinverse ist. Definition Der Tail Value at Risk (TVaR) zum Niveau α (0, 1) ist definiert als der erwartete Verlust in den 100 (1 α)% schlechtesten Szenarien: TVaR α (X ) := E(X X > VaR α (X )) Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
4 statische Risikomaße Erinnerungen prominente Beispiele (2) Definition Der Expected Shortfall (Average Value at Risk) zum Niveau α (0, 1) ist definiert durch ES α (X ) = 1 1 VaR z (X ) dz. 1 α α Satz Es gilt mit λ α = ES α (X ) = λ α TVaR α (X ) + (1 λ α ) VaR α (X ) P(X >VaRα(X )) 1 α. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
5 statische Risikomaße Erinnerungen prominente Beispiele (3) alternative Berechnungsmethode für den Expected Shortfall: Lemma Es sei X : Ω R eine Zufallsvariable und x R. Wir setzen 1 X,x,α = 1 {X >x} + β X,α (x) 1 {X =x}, wobei β X,α (x) = { P(X x) α P(X =x) falls P(X = x) > 0 0 sonst. Dann gilt 1 1 X,VaRα(X ),α(ω) [0, 1] für alle ω Ω, 2 E ( 1 X,VaRα(X ),α) = 1 α, 3 E ( X 1 X,VaRα(X ),α) = (1 α) ESα (X ). Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
6 statische Risikomaße Erinnerungen Axiomatik nach Artzner et al. Artzner, Delbaen, Eber und Heath (1999) begründen eine Axiomatik des Risikomaßes, die Eigenschaften eines intuitiven Risikobegriffs aufgreift. Definition Ein Risikomaß ϱ : M R heißt kohärent, falls es die folgenden Eigenschaften erfüllt: Translationsinvarianz: ϱ(x + c) = ϱ(x ) + c Monotonie: X 1 X 2 f.ü. ϱ(x 1 ) ϱ(x 2 ) X M, c R X 1, X 2 M positive Homogenität: ϱ(cx ) = cϱ(x ) X M, c R + Subadditivität: ϱ(x 1 + X 2 ) ϱ(x 1 ) + ϱ(x 2 ) X 1, X 2 M Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
7 statische Risikomaße Einsatzmöglichkeiten und Grenzen klassische Einsatzfelder Risikomaße werden eingesetzt zum Vergleich verschiedener Risiken, als Input für risikoadjustierte Erfolgsgrößen, zur Prämienberechnung, zur Ermittlung der Risikomarge versicherungstechnischer Rückstellungen, zur Ermittlung des benötigten Risikokapitals (Solvenzkapital, ökonomisches Kapital). Das ökonomische Sicherheitsniveau der Risikokapitalausstattung wird dabei durch folgende Faktoren festgelegt: Typ des Risikomaßes technisches Konfidenzniveau Zeithorizont Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
8 statische Risikomaße Einsatzmöglichkeiten und Grenzen Grenzen Die Wahl einer Periode als Zeithorizont wirft angesichts des langfristigen Charakters des Versicherungsgeschäfts Fragen auf, z.b. Risikokapitalausstattung in künftigen Perioden? (ORSA, ökonomische Steuerung) Abhängigkeiten zwischen den Perioden? Änderungen des eigenen Risikoprofils? Änderungen des Umfelds (Kapitalmarkt)? zentrale Perspektive: Informationszuwachs im Laufe der Zeit Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
9 Allgemeine dynamische Risikomaße Agenda 1 statische Risikomaße 2 Allgemeine dynamische Risikomaße 3 Filtrationen - revisited 4 dynamische Risikomaße auf Produktökonomien Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
10 Allgemeine dynamische Risikomaße Definition Definition Seien (Ω, P) ein Wahrscheinlichkeitsraum und (F t ) t {0,...,n} eine Filtration auf Ω. Für jedes t sei M t (Ω, R) ein Vektorraum F t -messbarer Funktionen. Ein dynamisches Risikomaß ist eine Familie (ρ t ) t {0,...,n} von Abbildungen so dass gilt: ρ t : M n (Ω, R) M t (Ω, R), 1 X 1 X 2 f.s. ρ t (X 1 ) ρ t (X 2 ) f.s. (Monotonie); 2 Für K M t (Ω, R) gilt ρ t (X + K) = ρ t (X ) + K f.s. (Translationsinvarianz). Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
11 Allgemeine dynamische Risikomaße Kohärenz Definition Ein dynamisches Risikomaß (ρ t ) t {0,...,n} heißt kohärent, falls gilt: 1 ρ t (KX ) = Kρ t (X ) f.s. für alle K M t (Ω, R) mit K 0 f.s. und KX M n (Ω, R) (Homogenität); 2 ρ t (X 1 + X 2 ) ρ t (X 1 ) + ρ t (X 2 ) f.s. (Subadditivität). Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
12 Allgemeine dynamische Risikomaße Konstruktionsmöglichkeit (1) duale Darstellung Satz Sei W eine Teilmenge von Wahrscheinlichkeitsmaßen auf (Ω, A, P) mit folgenden Eigenschaften: 1 Für jedes X M(Ω, R) und jedes Q W existiert E Q (X ). 2 Q P für alle Q W. Dann ist durch ein kohärentes Risikomaß definiert. ρ W (X ) = sup {E Q (X )} Q W Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
13 Allgemeine dynamische Risikomaße Konstruktionsmöglichkeit (2) Satz (Ω, A, P) sei ein Wahrscheinlichkeitsraum und (F t ) t {0,...,n} sei eine Filtration mit F n = A. Für t {0,..., n} sei M t (Ω, R) der Vektorraum der f.s. beschränkten, F t -messbaren Funktionen. W sei eine Menge von Wahrscheinlichkeitsmaßen auf Ω. Dann ist die Familie von Abbildungen ρ W t : M n (Ω, R) M t (Ω, R), X ρ W t (X ) = esssup Q W E Q (X F t ) ein kohärentes, dynamisches Risikomaß. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
14 Allgemeine dynamische Risikomaße Ist der ES problematisch? Beispiel. (Ω, A, P) = (]0, 1[ ]0, 1[, B(]0, 1[ ]0, 1[), λ 2 ) mit der Produktfiltration F 0 = {, Ω}, F 1 = {A ]0, 1[: A B(]0, 1[)}, F 2 = B(]0, 1[ ]0, 1[) Für α ]0, 1[ sei { W α = Q: Q ist ein W.maß mit Q P und dq dp 1 }. 1 α Dann gilt ρ Wα 0 (X ) = ES α (X ), ρ Wα 1 (X ) = sup ω Ω X (ω). Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
15 Allgemeine dynamische Risikomaße Braucht man also Zusatzbedingungen? In der Literatur finden sich axiomatisch eingeführte Bedingungen zur zeitlichen Konsistenz. Definition Ein dynamisches Risikomaß ρ t heißt vergleichskonsistent, falls für alle Zufallsvariablen X, Y M(Ω, R) gilt. ρ t+1 (X ) ρ t+1 (Y ) f.s. ρ t (X ) ρ t (Y ) f.s. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
16 Filtrationen - revisited Agenda 1 statische Risikomaße 2 Allgemeine dynamische Risikomaße 3 Filtrationen - revisited 4 dynamische Risikomaße auf Produktökonomien Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
17 Filtrationen - revisited Erinnerung (1) Sei T = {0,..., n} und F 0 = {, Ω}. Eine Filtration (F t ) t T ist eine Menge von σ-algebren auf Ω mit F 0 F 1 F n. Ein adaptierter stochastischer Prozess mit Werten in R k ist eine Abbildung X : Ω T R k, (ω, t) X t (ω), wobei für jedes t T die Abbildung X t : Ω R k bezüglich F t messbar ist. E(X F t ) als Best Estimate für das Endergebnis zum Zeitpunkt t Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
18 Filtrationen - revisited Erinnerung (2) A 1,..., A k seien σ-algebren auf den Mengen Ω 1,..., Ω k. Die Produkt-σ-Algebra auf der Produktmenge Ω 1 Ω 2 Ω k ist dann durch k A t = A 1 A k = σ (A 1 A k A t A t für t {1,....k}) t=1 gegeben, wobei wir die Konvention benutzen. A 1 A t 1 A t+1 A k = Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
19 Filtrationen - revisited Modellierung des Informationszuwachses (1) Definition Sei T = {0,..., n} und für t T \ {0} A t eine σ-algebra auf der Menge Ω t. Die Produktfiltration auf dem kartesischen Produkt Ω = n t=1 Ω t ist durch { {, Ω} falls t = 0, F t = t s=1 A s n s=t+1 {, Ω s} sonst gegeben. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
20 Filtrationen - revisited Modellierung des Informationszuwachses (2) Definition Sei Ω = n t=1 Ω t und π t : Ω t Ω s ω π t (ω) = (ω 1,..., ω t ) s=1 die Projektion auf die ersten t Faktoren. Für ω Ω und t {1,..., n} ist die t-faser durch ω durch F t (ω) = πt 1 (π t (ω)) gegeben, und wir setzen F 0 (ω) = Ω. Für w π t (Ω) ist die t-faser über w die Menge F t (w) = πt 1 (w). Schreibweise: Ω t B = t s=1 Ω s, und Ω t B = n s=t+1 Ω s, π t (ω) = ωb t Ωt B ω = (ωb t, ωt F ) mit ωt F Ωt F Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
21 Filtrationen - revisited Modellierung des Informationszuwachses (3) Es gilt: Eine Abbildung g : Ω R ist genau dann F t -messbar, wenn sie F n -messbar und auf den Fasern F t (ω) konstant ist. Ist (F t ) t T eine Produktfiltration auf Ω = n t=1 Ω t und (ω, t) X t (ω) ein adaptierter stochastischer Prozess, so hängt X t (ω) nur von den ersten t Komponenten ω 1,..., ω t ab. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
22 Filtrationen - revisited Produktökonomie (1) Definition Für t {1,..., n} sei (Ω t, µ t ) ein Maßraum und (F t ) t T die Produktfiltration auf Ω = n t=1 Ω t. Das Wahrscheinlichkeitsmaß P auf (Ω, F n ) sei bzgl. des Produktmaßes µ = n ( t=1 µ t absolut stetig. Dann ist Ω, (Ft ) t T, P ) eine filtrierte Produktökonomie. Wir schreiben µ t B = t s=1 µ s und µ t F = n s=t+1 µ s. Die Zufallsquellen µ t der einzelnen Perioden sind unabhängig. gute Eignung für Simulationsmodelle hinreichend allgemeine Modellierungsstruktur: AR(1)-Prozess: S t = αs t 1 + sω t, t = 1,..., n Schadenprozess (X 1, X 2 ) über zwei Perioden mit der Dichte p(x 1, x 2 ) = exp( x 1 ) 10 11x 1 exp( 10x 2 /(11x 1 ))1 (0, ) (0, ) (x 1, x 2 ) Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
23 Filtrationen - revisited Produktökonomie (2) Lemma Sei ( Ω, (F t ) t T, P ) eine filtrierte Produktökonomie und P = pµ. Dann gilt: 1 Auf der Faser F t (ω) ist bezüglich der von F n induzierten σ-algebra durch P ω t B (A) = 1A p(ω t B, ωt F ) dµt F p(ω t B, ω t F ) dµt F 2 ein Wahrscheinlichkeitsmaß gegeben. E (g F t ) ω t B = Ω t F g (ω) p (ω) dµ t F p (ω) dµ t F Ω t F P-f.ü. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
24 dynamische Risikomaße auf Produktökonomien Agenda 1 statische Risikomaße 2 Allgemeine dynamische Risikomaße 3 Filtrationen - revisited 4 dynamische Risikomaße auf Produktökonomien Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
25 dynamische Risikomaße auf Produktökonomien dynamischer Value at Risk Definition Es sei ( Ω, (F t ) t T, P ) eine filtrierte Produktökonomie, α ]0, 1[ und M t (Ω, R) der Raum der F t -messbaren Funktionen. Die durch t T parametrisierte Familie von Abbildungen VaR α,t : M n (Ω, R) M t (Ω, R), X VaR α,t (X ) mit VaR α,t (X ) ω t B = inf { ( ( x R: P ω t B X ω t B, ) x ) } α heißt dynamischer Value at Risk. Der dynamische Value at Risk ist ein dynamisches Risikomaß. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
26 dynamische Risikomaße auf Produktökonomien dynamischer Expected Shortfall Definition Sei ( Ω, (F t ) t T, P ) eine filtrierte Produktökonomie, α ]0, 1[ und M t (Ω, R) der Raum der integrierbaren, F t -messbaren Funktionen. Die durch t T parametrisierte Familie von Abbildungen ES α,t : M n (Ω, R) M t (F t, R), X ES α,t (X ) mit ES α,t (X ) ω t B = 1 ( 1 α E P ω t X ( ωb t, ) ) 1 X(ω t B B, ),VaR α,t(x ) ω t,α B heißt dynamischer Expected Shortfall, wobei 1 X,x,α definiert ist wie auf Folie 5. Der dynamische Expected Shortfall ist ein kohärentes dynamisches Risikomaß. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
27 dynamische Risikomaße auf Produktökonomien Zeitkonsistenz (1) Definition Sei (F t ) t T eine Produktfiltration auf Ω = n s=1 Ω s. Ein dynamisches Risikomaß (ρ t ) t T ist 1 zeitkonsistent, falls es für jede Zufallsvariable X, fast jedes ω Ω und jede F t+1 -messbare Teilmenge B F t (ω) mit P ω t B (B) > 0 und essinf B (ρ t+1 (X )) > ρ t (X ) ω eine F t+1 -messbare Teilmenge C F t (ω) gibt mit P ω t B (C) > 0 und esssup C (ρ t+1 (X )) < ρ t (X ) ω. 2 schwach zeitkonsistent, falls für fast jedes ω und jedes Paar (X, t) gilt: essinf Ft(ω) (ρ t+1 (X )) ρ t (X ) ω. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
28 dynamische Risikomaße auf Produktökonomien Zeitkonsistenz (2) Der dynamische Value at Risk ist schwach zeitkonsistent, der dynamische Expected Shortfall zeitkonsistent. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
29 dynamische Risikomaße auf Produktökonomien Beispiel (1) Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
30 dynamische Risikomaße auf Produktökonomien Beispiel (2) Zum Zeitpunkt t = 1 gilt: ES 80%,1 (X ) (U) = = = 17, ES 80%,1 (X ) (D) = = = 11.5, ES 80%,1 (Y ) (U) = = = 17, ES 80%,1 (Y ) (D) = = = 11.5, Es liegt keine Vergleichskonsistenz vor, da gilt: ES 80%,0 (X ) (r) = ES 80%,0 (Y ) (r) = 100 Für Ỹ := Y c mit c ]0, 3[ erhalten wir ES 80%,0 (Ỹ ) > ES 80%,0 (X ), = = 15.6 = = 12.6 aber ES 80%,1 (Ỹ ) < ES 80%,1 (X ) f.s. Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
31 dynamische Risikomaße auf Produktökonomien Quelle Kriele, M., Wolf, J., Wertorientiertes Risikomanagement von Versicherungsunternehmen, Springer, Wolf FH Koblenz Dynamische Risikomaße Ulm, / 31
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Kompaktskript zur Vorlesung Stochastische Risikoanalyse
 Kompaktskript zur Vorlesung Stochastische Risikoanalyse Friedrich-Schiller-Universität Jena Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Wirtschafts- und Sozialstatistik Prof. Dr. P. Kischka Sommersemester
Kompaktskript zur Vorlesung Stochastische Risikoanalyse Friedrich-Schiller-Universität Jena Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Wirtschafts- und Sozialstatistik Prof. Dr. P. Kischka Sommersemester
Unabhängige Zufallsvariablen
 Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Brownsche Bewegung. Satz von Donsker. Bernd Barth Universität Ulm
 Brownsche Bewegung Satz von Donsker Bernd Barth Universität Ulm 31.05.2010 Page 2 Brownsche Bewegung 31.05.2010 Inhalt Einführung Straffheit Konvergenz Konstruktion einer zufälligen Funktion Brownsche
Brownsche Bewegung Satz von Donsker Bernd Barth Universität Ulm 31.05.2010 Page 2 Brownsche Bewegung 31.05.2010 Inhalt Einführung Straffheit Konvergenz Konstruktion einer zufälligen Funktion Brownsche
Risikomaß. Kapitel Die Idee des Risikomaßes
 Kapitel 2 Risikomaß 2.1 Die Idee des Risikomaßes Umgangssprachlich wird unter Risiko einfach die Möglichkeit verstanden, dass ungünstige Ereignisse auftreten. Abweichungen hin zum Positiven Chance werden
Kapitel 2 Risikomaß 2.1 Die Idee des Risikomaßes Umgangssprachlich wird unter Risiko einfach die Möglichkeit verstanden, dass ungünstige Ereignisse auftreten. Abweichungen hin zum Positiven Chance werden
Kapitel II. Brownsche Bewegung. Literatur: Karatzas, Shreve (1999, Chap. 2).
 Kapitel II Brownsche Bewegung Literatur: Karatzas, Shreve (1999, Chap. 2). Gegeben: Wahrscheinlichkeitsraum (Ω, A, P) mit Filtration F = (F t ) t I, wobei I = [0, [. Definition 1. W = (W t ) t I Brownsche
Kapitel II Brownsche Bewegung Literatur: Karatzas, Shreve (1999, Chap. 2). Gegeben: Wahrscheinlichkeitsraum (Ω, A, P) mit Filtration F = (F t ) t I, wobei I = [0, [. Definition 1. W = (W t ) t I Brownsche
Solvency II und die Standardformel
 Fakultät Mathematik und Naturwissenschaften Institut für Mathematische Stochastik Solvency II und die Standardformel Festkolloquium 20 Jahre (neue) Versicherungsmathematik an der TU Dresden Sebastian Fuchs
Fakultät Mathematik und Naturwissenschaften Institut für Mathematische Stochastik Solvency II und die Standardformel Festkolloquium 20 Jahre (neue) Versicherungsmathematik an der TU Dresden Sebastian Fuchs
Ljapunov Exponenten. Reiner Lauterbach
 Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Ljapunov Exponenten Reiner Lauterbach 28. Februar 2003 2 Zusammenfassung n diesem Teil betrachten wir ein wichtiges Thema: sensitive Abhängigkeit. Zunächst hat man ja stetige Abhängigkeit, wie man sie
Risikomessung mit dem Conditional Value-at-Risk
 Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Jendrik Hanisch Risikomessung mit dem Conditional Value-at-Risk Implikationen für das Entscheidungsverhalten. Bibliothek j k Mit einem Geleitwort von \* \, -^ Prof. Dr. Wolfgang Kürsten A; Verlag Dr. Kovac
Kapitel 6 Martingale
 Kapitel 6 Martingale Martingale spielen eine große Rolle in der Finanzmathematik, und sind zudem ein wichtiges Hilfsmittel für die statistische Inferenz stochastischer Prozesse, insbesondere auch für Zählprozesse
Kapitel 6 Martingale Martingale spielen eine große Rolle in der Finanzmathematik, und sind zudem ein wichtiges Hilfsmittel für die statistische Inferenz stochastischer Prozesse, insbesondere auch für Zählprozesse
Varianz und Kovarianz
 KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
Nachteile: STD existiert nur für Verteilungen mit E(FL 2 ) <, d.h. nicht ansetzbar bei leptokurtischen ( fat tailed ) Verlustverteilungen;
 Risikomaße basierend auf die Verlustverteilung Sei F L := F Ln+1 die Verteilung der Verlust L n+1. Die Parameter von F Ln+1 werden anhand von historischen Daten entweder direkt oder mit Hilfe der Risikofaktoren
Risikomaße basierend auf die Verlustverteilung Sei F L := F Ln+1 die Verteilung der Verlust L n+1. Die Parameter von F Ln+1 werden anhand von historischen Daten entweder direkt oder mit Hilfe der Risikofaktoren
Übungen zu bedingten Erwartungswerten. Tutorium Stochastische Prozesse 13. Dezember 2016
 Übungen zu bedingten Erwartungswerten Tutorium Stochastische Prozesse 13. Dezember 2016 Bedingter Erwartungswert Definition Sei X eine reellwertige Zufallsvariable auf (Ω, A, P), so dass E[ X ]
Übungen zu bedingten Erwartungswerten Tutorium Stochastische Prozesse 13. Dezember 2016 Bedingter Erwartungswert Definition Sei X eine reellwertige Zufallsvariable auf (Ω, A, P), so dass E[ X ]
σ-algebren, Definition des Maßraums
 σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
TU Darmstadt FB Mathematik, AG 9 WS 2004/2005 Jakob Creutzig (1 + ρ)
 TU Darmstadt FB Mathematik, AG 9 WS 2004/2005 Jakob Creutzig 9..04 Lösungsvorschläge zum 3. Aufgabenblatt der Vorlesung,,Einführung in die Finanzmathematik Gruppenübungen Aufgabe : Es sei Ω = {, +} n,
TU Darmstadt FB Mathematik, AG 9 WS 2004/2005 Jakob Creutzig 9..04 Lösungsvorschläge zum 3. Aufgabenblatt der Vorlesung,,Einführung in die Finanzmathematik Gruppenübungen Aufgabe : Es sei Ω = {, +} n,
Bewertung von biometrischen Risiken in der bav
 Bewertung von biometrischen Risiken in der bav Ralf Knobloch Fachhochschule Köln Gliederung 1. Biometrische Risiken in der bav 2. Das Modell 3. Risikomaße 4. Einfaches Beispiel 5. Schlussbemerkungen 2
Bewertung von biometrischen Risiken in der bav Ralf Knobloch Fachhochschule Köln Gliederung 1. Biometrische Risiken in der bav 2. Das Modell 3. Risikomaße 4. Einfaches Beispiel 5. Schlussbemerkungen 2
Mathematik für Naturwissenschaften, Teil 2
 Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Wahrscheinlichkeitstheorie Kapitel V - Stetige Verteilungen
 Wahrscheinlichkeitstheorie Kapitel V - Stetige Verteilungen Georg Bol georg.bol@statistik.uni-karlsruhe.de Markus Höchstötter hoechstoetter@statistik.uni-karlsruhe.de Stetige Verteilungen Definition: Sei
Wahrscheinlichkeitstheorie Kapitel V - Stetige Verteilungen Georg Bol georg.bol@statistik.uni-karlsruhe.de Markus Höchstötter hoechstoetter@statistik.uni-karlsruhe.de Stetige Verteilungen Definition: Sei
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban
 Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
3 Markov-Eigenschaft der Brownschen Bewegung
 Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
Stochastik. 1. Wahrscheinlichkeitsräume
 Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Bestimmung des Conditional Value-at-Risk (CVaR) bei Normal- bzw. Lognormalverteilung
 Mannheimer Manuskripte u Risikotheorie, Portfolio Management und Versicherungswirtschaft r. 4 Bestimmung des Conditional Value-at-Risk (CVaR bei ormal- bw. Lognormalerteilung on PETER ALBRECHT UD SVE KORYCIORZ
Mannheimer Manuskripte u Risikotheorie, Portfolio Management und Versicherungswirtschaft r. 4 Bestimmung des Conditional Value-at-Risk (CVaR bei ormal- bw. Lognormalerteilung on PETER ALBRECHT UD SVE KORYCIORZ
BERECHNUNG VON SCHWANKUNGSZUSCHLÄGEN IM PRICING VON RV-VERTRÄGEN
 BERECHNUNG VON SCHWANKUNGSZUSCHLÄGEN IM PRICING VON RV-VERTRÄGEN SAV-Prüfungskolloquium am 19.11.2009 Dr. Katja Lord Aktuar Corporate Underwriting / Corporate Pricing Agenda 1. Schwankungszuschlag als
BERECHNUNG VON SCHWANKUNGSZUSCHLÄGEN IM PRICING VON RV-VERTRÄGEN SAV-Prüfungskolloquium am 19.11.2009 Dr. Katja Lord Aktuar Corporate Underwriting / Corporate Pricing Agenda 1. Schwankungszuschlag als
Übersicht Wahrscheinlichkeitsheorie
 Übersicht Wahrscheinlichkeitsheorie Gunther Leobacher und Friedrich Pillichshammer Universität Linz, Institut für Finanzmathematik, Altenbergerstrasse 69, 4040 Linz, Austria E-mail: gunther.leobacher@jku.at,
Übersicht Wahrscheinlichkeitsheorie Gunther Leobacher und Friedrich Pillichshammer Universität Linz, Institut für Finanzmathematik, Altenbergerstrasse 69, 4040 Linz, Austria E-mail: gunther.leobacher@jku.at,
KONSTRUKTION VON MASSEN
 KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
Primzahlen Primzahlsatz Satz von Szemerédi Verallg. von Green/Tao Anwendung. Arithmetische Progressionen von Primzahlen
 Arithmetische Progressionen von Primzahlen Sei N := {1, 2, 3,... } die Menge der natürlichen Zahlen. Definition Eine Primzahl ist eine natürliche Zahl > 1, die nur durch 1 und durch sich selbst teilbar
Arithmetische Progressionen von Primzahlen Sei N := {1, 2, 3,... } die Menge der natürlichen Zahlen. Definition Eine Primzahl ist eine natürliche Zahl > 1, die nur durch 1 und durch sich selbst teilbar
Diskrete Wahrscheinlichkeitstheorie - Probeklausur
 Diskrete Wahrscheinlichkeitstheorie - robeklausur Sommersemester 2007 - Lösung Name: Vorname: Matrikelnr.: Studiengang: Hinweise Sie sollten insgesamt Blätter erhalten haben. Tragen Sie bitte Ihre Antworten
Diskrete Wahrscheinlichkeitstheorie - robeklausur Sommersemester 2007 - Lösung Name: Vorname: Matrikelnr.: Studiengang: Hinweise Sie sollten insgesamt Blätter erhalten haben. Tragen Sie bitte Ihre Antworten
Definition Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) :=
 Definition 2.34. Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) := x f(x)dx der Erwartungswert von X, sofern dieses Integral existiert. Entsprechend wird die Varianz V(X)
Definition 2.34. Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) := x f(x)dx der Erwartungswert von X, sofern dieses Integral existiert. Entsprechend wird die Varianz V(X)
Stochastische Finanzmathematik I
 Notizen zu der Vorlesung Stochastische Finanzmathemati I 1 Zum Ein-perioden-Modell 1.1 Beispiel: Zwei-wertiges Modell: π 0 = 1, S 0 =, { b Wahrs. p S 1 = a Wahrs. 1 p Arbitrage frei: Es gibt p 0, 1) mit
Notizen zu der Vorlesung Stochastische Finanzmathemati I 1 Zum Ein-perioden-Modell 1.1 Beispiel: Zwei-wertiges Modell: π 0 = 1, S 0 =, { b Wahrs. p S 1 = a Wahrs. 1 p Arbitrage frei: Es gibt p 0, 1) mit
Beispiel 5 Europäische Call Option (ECO) in einer Aktie S mit Laufzeit T und Ausübungspreis (Strikepreis) K.
 Beispiel 5 Europäische Call Option (ECO) in einer Aktie S mit Laufzeit T und Ausübungspreis (Strikepreis) K. Wert der Call Option zum Zeitpunkt T: max{s T K,0} Preis der ECO zum Zeitpunkt t < T: C = C(t,
Beispiel 5 Europäische Call Option (ECO) in einer Aktie S mit Laufzeit T und Ausübungspreis (Strikepreis) K. Wert der Call Option zum Zeitpunkt T: max{s T K,0} Preis der ECO zum Zeitpunkt t < T: C = C(t,
Martingal-Maße. Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Manuel Müller Mathematisches Institut
 Martingal-Maße Manuel Müller 29.04.2016 Mathematisches Institut Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Seite 2 Martingal-Maße 29.04.2016 Inhaltsverzeichnis
Martingal-Maße Manuel Müller 29.04.2016 Mathematisches Institut Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Seite 2 Martingal-Maße 29.04.2016 Inhaltsverzeichnis
Vergleich von Entscheidungsträgern bzgl. ihrer Risikoaversion:
 Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
Ist das Arrow-Pratt-Maß der absoluten Risikoaversion bekannt, so lässt sich daraus die Nutzenfunktion bestimmen: Mithilfe der Substitution y := U (w) dy = U (w)dw gilt: und daher U (w) U (w) dw = A a (w)dw
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung
 2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
2.2 Binomialverteilung, Hypergeometrische Verteilung, Poissonverteilung Die einfachste Verteilung ist die Gleichverteilung, bei der P(X = x i ) = 1/N gilt, wenn N die Anzahl möglicher Realisierungen von
2 Zufallsvariable, Verteilungen, Erwartungswert
 2 Zufallsvariable, Verteilungen, Erwartungswert Bisher: Zufallsexperimente beschrieben durch W-Räume (Ω, A, P) Häufig interessiert nur eine zufällige Größe X = X(ω), die vom Ergebnis ω des Zufallsexperiments
2 Zufallsvariable, Verteilungen, Erwartungswert Bisher: Zufallsexperimente beschrieben durch W-Räume (Ω, A, P) Häufig interessiert nur eine zufällige Größe X = X(ω), die vom Ergebnis ω des Zufallsexperiments
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
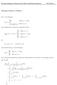 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
3. Kombinatorik und Wahrscheinlichkeit
 3. Kombinatorik und Wahrscheinlichkeit Es geht hier um die Bestimmung der Kardinalität endlicher Mengen. Erinnerung: Seien A, B, A 1,..., A n endliche Mengen. Dann gilt A = B ϕ: A B bijektiv Summenregel:
3. Kombinatorik und Wahrscheinlichkeit Es geht hier um die Bestimmung der Kardinalität endlicher Mengen. Erinnerung: Seien A, B, A 1,..., A n endliche Mengen. Dann gilt A = B ϕ: A B bijektiv Summenregel:
Mathematische Ökonometrie
 Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen
 Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Fraktale Geometrie. 9: Metrische äußere Maße II. Universität Regensburg Sommersemester Daniel Heiß:
 Universität Regensburg Sommersemester 013 Daniel Heiß: 9: Metrische äußere Maße II I Das mehrdimensionale Lebesguemaß 1.1 Definition (i) Für reelle Zahlen a b, c d ist ein Rechteck im R die Menge R = a,
Universität Regensburg Sommersemester 013 Daniel Heiß: 9: Metrische äußere Maße II I Das mehrdimensionale Lebesguemaß 1.1 Definition (i) Für reelle Zahlen a b, c d ist ein Rechteck im R die Menge R = a,
3 Bedingte Wahrscheinlichkeit, Unabhängigkeit
 3 Bedingte Wahrscheinlichkeit, Unabhängigkeit Bisher : (Ω, A, P) zur Beschreibung eines Zufallsexperiments Jetzt : Zusatzinformation über den Ausgang des Experiments, etwa (das Ereignis) B ist eingetreten.
3 Bedingte Wahrscheinlichkeit, Unabhängigkeit Bisher : (Ω, A, P) zur Beschreibung eines Zufallsexperiments Jetzt : Zusatzinformation über den Ausgang des Experiments, etwa (das Ereignis) B ist eingetreten.
Gesetze der großen Zahlen
 Kapitel 0 Gesetze der großen Zahlen 0. Einführung Im ersten Kapitel wurde auf eine Erfahrungstatsache im Umgang mit zufälligen Erscheinungen aufmerksam gemacht, die man gewöhnlich als empirisches Gesetz
Kapitel 0 Gesetze der großen Zahlen 0. Einführung Im ersten Kapitel wurde auf eine Erfahrungstatsache im Umgang mit zufälligen Erscheinungen aufmerksam gemacht, die man gewöhnlich als empirisches Gesetz
Stochastische Analysis
 Stochastische Analysis SS1 von Steffen Dereich Fachbereich Mathematik und Informatik Philipps-Universität Marburg Version vom 6. Mai 21 Inhaltsverzeichnis 1 Motivation / Einführung 4 1.1 Motivation anhand
Stochastische Analysis SS1 von Steffen Dereich Fachbereich Mathematik und Informatik Philipps-Universität Marburg Version vom 6. Mai 21 Inhaltsverzeichnis 1 Motivation / Einführung 4 1.1 Motivation anhand
Appendix I: Eine etwas komprimierte Einführung in die Wahrscheinlichkeitstheorie
 Appendix I: Eine etwas komprimierte Einführung in die Wahrscheinlichkeitstheorie Vorbemerkung: Die folgenden Seiten sind nicht zur Abschreckung gedacht, sondern als Ergänzung zu den Darstellungen, die
Appendix I: Eine etwas komprimierte Einführung in die Wahrscheinlichkeitstheorie Vorbemerkung: Die folgenden Seiten sind nicht zur Abschreckung gedacht, sondern als Ergänzung zu den Darstellungen, die
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Kapitel 8 Probabilistische und Possibilistische Logik. 23. Juni 2005
 Kapitel 8 Probabilistische und Possibilistische Logik 23. Juni 2005 Zusammenfassung Kapitel 1-2 Grundlagen, Kapitel 3 Fuzzy-Mengen und -Relationen, Kapitel 4 Erweiterung des klassischen Beweisbegriffes,
Kapitel 8 Probabilistische und Possibilistische Logik 23. Juni 2005 Zusammenfassung Kapitel 1-2 Grundlagen, Kapitel 3 Fuzzy-Mengen und -Relationen, Kapitel 4 Erweiterung des klassischen Beweisbegriffes,
Simulation von Zufallsvariablen und Punktprozessen
 Simulation von Zufallsvariablen und Punktprozessen 09.11.2009 Inhaltsverzeichnis 1 Einleitung 2 Pseudozufallszahlen 3 Punktprozesse Zufallszahlen Definition (Duden): Eine Zufallszahl ist eine Zahl, die
Simulation von Zufallsvariablen und Punktprozessen 09.11.2009 Inhaltsverzeichnis 1 Einleitung 2 Pseudozufallszahlen 3 Punktprozesse Zufallszahlen Definition (Duden): Eine Zufallszahl ist eine Zahl, die
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Beweis. Bauer (4. Auflage, 1991), S , Hoffmann-Jørgensen, Vol. I, S. 457.
 Exkurs A: Bedingte Erwartungswerte, bedingte Verteilungen (Ω, A, P ) sei W-Raum, X : Ω IR P-quasiintegrierbar, F A Unter - σ- Algebra. E(X F) = E P (X F) (Version des) bedingter Erwartungswert von X unterf
Exkurs A: Bedingte Erwartungswerte, bedingte Verteilungen (Ω, A, P ) sei W-Raum, X : Ω IR P-quasiintegrierbar, F A Unter - σ- Algebra. E(X F) = E P (X F) (Version des) bedingter Erwartungswert von X unterf
17 Lineare Abbildungen
 Chr.Nelius: Lineare Algebra II (SS2005) 1 17 Lineare Abbildungen Wir beginnen mit der Klärung des Abbildungsbegriffes. (17.1) DEF: M und N seien nichtleere Mengen. Eine Abbildung f von M nach N (in Zeichen:
Chr.Nelius: Lineare Algebra II (SS2005) 1 17 Lineare Abbildungen Wir beginnen mit der Klärung des Abbildungsbegriffes. (17.1) DEF: M und N seien nichtleere Mengen. Eine Abbildung f von M nach N (in Zeichen:
Kompaktskript zur Vorlesung Statistische Verfahren der Risikoanalyse
 Kompaktskript zur Vorlesung Statistische Verfahren der Risikoanalyse Friedrich-Schiller-Universität Jena Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Wirtschafts- und Sozialstatistik Prof. Dr. P.
Kompaktskript zur Vorlesung Statistische Verfahren der Risikoanalyse Friedrich-Schiller-Universität Jena Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Wirtschafts- und Sozialstatistik Prof. Dr. P.
Optimale Steuerung, Prof.Dr. L. Blank 1. II Linear-quadratische elliptische Steuerungsprobleme
 Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
Optimale Steuerung, Prof.Dr. L. Blank 1 II Linear-quadratische elliptische Steuerungsprobleme Zuerst: Zusammenstellung einiger Begriffe und Aussagen aus der Funktionalanalysis (FA), um dann etwas über
8. Stetige Zufallsvariablen
 8. Stetige Zufallsvariablen Idee: Eine Zufallsvariable X ist stetig, falls ihr Träger eine überabzählbare Teilmenge der reellen Zahlen R ist. Beispiel: Glücksrad mit stetigem Wertebereich [0, 2π] Von Interesse
8. Stetige Zufallsvariablen Idee: Eine Zufallsvariable X ist stetig, falls ihr Träger eine überabzählbare Teilmenge der reellen Zahlen R ist. Beispiel: Glücksrad mit stetigem Wertebereich [0, 2π] Von Interesse
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 11. Oktober 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Multivariate Verteilungen
 Multivariate Verteilungen Zufallsvektoren und Modellierung der Abhängigkeiten Ziel: Modellierung der Veränderungen der Risikofaktoren X n = (X n,1, X n,2,..., X n,d ) Annahme: X n,i und X n,j sind abhängig
Multivariate Verteilungen Zufallsvektoren und Modellierung der Abhängigkeiten Ziel: Modellierung der Veränderungen der Risikofaktoren X n = (X n,1, X n,2,..., X n,d ) Annahme: X n,i und X n,j sind abhängig
Regulär variierende Funktionen
 KAPITEL 4 Regulär variierende Funktionen Unser nächstes Ziel ist es, die Max-Anziehungsbereiche der Extremwertverteilungen zu beschreiben. Dies wird im nächsten Kapitel geschehen. Wir haben bereits gesehen,
KAPITEL 4 Regulär variierende Funktionen Unser nächstes Ziel ist es, die Max-Anziehungsbereiche der Extremwertverteilungen zu beschreiben. Dies wird im nächsten Kapitel geschehen. Wir haben bereits gesehen,
Einführung in die Stochastik 6. Übungsblatt
 Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Maß und Integral I und II. SS 2004 und WS 2004/05
 Maß und Integral I und II SS 2004 und WS 2004/05 Vorlesung von Priv.-Doz. Dr. J. Dippon unter Verwendung einer Vorlesung von Prof. Dr. H. Walk im SS 2003 Inhaltsverzeichnis Bezeichnungen 3 1 Grundbegriffe
Maß und Integral I und II SS 2004 und WS 2004/05 Vorlesung von Priv.-Doz. Dr. J. Dippon unter Verwendung einer Vorlesung von Prof. Dr. H. Walk im SS 2003 Inhaltsverzeichnis Bezeichnungen 3 1 Grundbegriffe
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
2 Brownsche Bewegung. Wahrscheinlichkeitstheorie III Teil Der Wienerraum
 8 Wahrscheinlichkeitstheorie III Teil 3 Brownsche Bewegung Wir haben die Brownsche Bewegung bereits als Grenzwert reskalierter Irrfahrten in der VL WTH II kennengelernt siehe dazu Abschnitt 5.. In diesem
8 Wahrscheinlichkeitstheorie III Teil 3 Brownsche Bewegung Wir haben die Brownsche Bewegung bereits als Grenzwert reskalierter Irrfahrten in der VL WTH II kennengelernt siehe dazu Abschnitt 5.. In diesem
Institut für Stochastik, SoSe K L A U S U R , 13:
 Institut für Stochastik, SoSe 2014 Mathematische Statistik Paravicini/Heusel 1. K L A U S U R 12.7.2014, 13:00-16.00 Name: Geburtsdatum: Vorname: Matrikelnummer: Übungsgruppe bei: Studiengang & angestrebter
Institut für Stochastik, SoSe 2014 Mathematische Statistik Paravicini/Heusel 1. K L A U S U R 12.7.2014, 13:00-16.00 Name: Geburtsdatum: Vorname: Matrikelnummer: Übungsgruppe bei: Studiengang & angestrebter
Stochastik für Wirtschaftswissenschaftler
 Stochastik für Wirtschaftswissenschaftler Hartmut Lanzinger Wintersemester 0/ Inhaltsverzeichnis Wahrscheinlichkeiten Einführung.......................................... Laplacesche Wahrscheinlichkeitsräume...........................
Stochastik für Wirtschaftswissenschaftler Hartmut Lanzinger Wintersemester 0/ Inhaltsverzeichnis Wahrscheinlichkeiten Einführung.......................................... Laplacesche Wahrscheinlichkeitsräume...........................
Terminologie Stochastischer Prozesse
 Terminologie Stochastischer Prozesse Nikolai Nowaczyk 2014-03-31 Dieses Script ist die Ausarbeitung zum einem Vortrag, gehalten im Seminar zur Wahrscheinlichkeitstheorie im SS 14 an der Uni Regensburg.
Terminologie Stochastischer Prozesse Nikolai Nowaczyk 2014-03-31 Dieses Script ist die Ausarbeitung zum einem Vortrag, gehalten im Seminar zur Wahrscheinlichkeitstheorie im SS 14 an der Uni Regensburg.
Teil II. Wahrscheinlichkeitsrechnung
 Teil II Wahrscheinlichkeitsrechnung Deskriptive Statistik und Wahrscheinlichkeitsrechnung (SS 2014) Folie 129 5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) 5 Zufallsexperimente Ergebnisse Ereignisse
Teil II Wahrscheinlichkeitsrechnung Deskriptive Statistik und Wahrscheinlichkeitsrechnung (SS 2014) Folie 129 5 Zufallsexperimente Inhaltsverzeichnis (Ausschnitt) 5 Zufallsexperimente Ergebnisse Ereignisse
Satz von Borel-Cantelli. Limes inferior von Mengen. Limes superior von Mengen. Stetigkeit. Konvergenz von Zufallsvariablen. Kolmogorow-Ungleichung
 Satz von Borel-Cantelli Limes inferior von Mengen Limes superior von Mengen Stetigkeit Konvergenz von Zufallsvariablen Kolmogorow-Ungleichung Tschebyschow-Ungleichung Konvergenzkriterien Starkes Gesetz
Satz von Borel-Cantelli Limes inferior von Mengen Limes superior von Mengen Stetigkeit Konvergenz von Zufallsvariablen Kolmogorow-Ungleichung Tschebyschow-Ungleichung Konvergenzkriterien Starkes Gesetz
Analysis 3 - Klausur - Lösung
 Wintersemester 23/24, Universität Bonn Analysis 3 - Klausur - Lösung Aufgabe : Sigma-Algebren (4+6 Punkte) a) Sei X eine Menge. Sei F = {{} : X}. Bestimmen Sie σ(f). b) Sei X eine Menge, Sei S P(X). Zeigen
Wintersemester 23/24, Universität Bonn Analysis 3 - Klausur - Lösung Aufgabe : Sigma-Algebren (4+6 Punkte) a) Sei X eine Menge. Sei F = {{} : X}. Bestimmen Sie σ(f). b) Sei X eine Menge, Sei S P(X). Zeigen
Wahrscheinlichkeitstheorie und Statistik vom
 INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator
 Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Universität Bielefeld Regularitätsresultate für parabolische Gleichungen mit nichtlokalem Operator Matthieu Felsinger Universität Bielefeld Mathematisches Kolloquium, TU Clausthal 05. Februar 2014 1 Einleitung
Vorlesung 8a. Kovarianz und Korrelation
 Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Vorlesung 8a Kovarianz und Korrelation 1 Wir erinnern an die Definition der Kovarianz Für reellwertige Zufallsvariable X, Y mit E[X 2 ] < und E[Y 2 ] < ist Cov[X, Y ] := E [ (X EX)(Y EY ) ] Insbesondere
Normalverteilung. 1 2πσ. Gauß. 2 e 1 2 ((x µ)2 σ 2 ) Werkzeuge der empirischen Forschung. W. Kössler. Einleitung. Datenbehandlung. Wkt.
 Normalverteilung Diskrete Stetige f(x) = 1 2πσ 2 e 1 2 ((x µ)2 σ 2 ) Gauß 91 / 169 Normalverteilung Diskrete Stetige Satz: f aus (1) ist Dichte. Beweis: 1. f(x) 0 x R und σ > 0. 2. bleibt z.z. lim F(x)
Normalverteilung Diskrete Stetige f(x) = 1 2πσ 2 e 1 2 ((x µ)2 σ 2 ) Gauß 91 / 169 Normalverteilung Diskrete Stetige Satz: f aus (1) ist Dichte. Beweis: 1. f(x) 0 x R und σ > 0. 2. bleibt z.z. lim F(x)
7.5 Erwartungswert, Varianz
 7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
Analysis III. Vorlesung 72. Korollar Es sei (M,A,µ) ein σ-endlicher Maßraum und v: M R n eine messbare Abbildung. Dann ist die Abbildung
 Prof. Dr. H. Brenner Osnabrück WS 15/16 Analysis III Vorlesung 7 Korollar 7.1. Es sei (,A,µ) ein σ-endlicher aßraum und v: R n eine messbare Abbildung. Dann ist die Abbildung bijektiv und maßtreu. ϕ v
Prof. Dr. H. Brenner Osnabrück WS 15/16 Analysis III Vorlesung 7 Korollar 7.1. Es sei (,A,µ) ein σ-endlicher aßraum und v: R n eine messbare Abbildung. Dann ist die Abbildung bijektiv und maßtreu. ϕ v
Klausur im Grundwissen Wert- und risikoorientierte Unternehmenssteuerung
 Klausur im Grundwissen Wert- und risikoorientierte Unternehmenssteuerung 14.05.2010 Hinweise: Als Hilfsmittel ist ein Taschenrechner zugelassen. Die Gesamtpunktzahl beträgt 90. Die Klausur ist bestanden,
Klausur im Grundwissen Wert- und risikoorientierte Unternehmenssteuerung 14.05.2010 Hinweise: Als Hilfsmittel ist ein Taschenrechner zugelassen. Die Gesamtpunktzahl beträgt 90. Die Klausur ist bestanden,
K8 Stetige Zufallsvariablen Theorie und Praxis
 K8 Stetige Zufallsvariablen Theorie und Praxis 8.1 Theoretischer Hintergrund Wir haben (nicht abzählbare) Wahrscheinlichkeitsräume Meßbare Funktionen Zufallsvariablen Verteilungsfunktionen Dichten in R
K8 Stetige Zufallsvariablen Theorie und Praxis 8.1 Theoretischer Hintergrund Wir haben (nicht abzählbare) Wahrscheinlichkeitsräume Meßbare Funktionen Zufallsvariablen Verteilungsfunktionen Dichten in R
Übungsscheinklausur,
 Mathematik IV für Maschinenbau und Informatik (Stochastik) Universität Rostock, Institut für Mathematik Sommersemester 27 Prof. Dr. F. Liese Übungsscheinklausur, 3.7.27 Dipl.-Math. M. Helwich Name:...
Mathematik IV für Maschinenbau und Informatik (Stochastik) Universität Rostock, Institut für Mathematik Sommersemester 27 Prof. Dr. F. Liese Übungsscheinklausur, 3.7.27 Dipl.-Math. M. Helwich Name:...
Kompaktskript zur Vorlesung Stochastische Risikoanalyse
 Kompaktskript zur Vorlesung Stochastische Risikoanalyse Friedrich-Schiller-Universität Jena Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Wirtschafts- und Sozialstatistik Prof. Dr. P. Kischka Sommersemester
Kompaktskript zur Vorlesung Stochastische Risikoanalyse Friedrich-Schiller-Universität Jena Wirtschaftswissenschaftliche Fakultät Lehrstuhl für Wirtschafts- und Sozialstatistik Prof. Dr. P. Kischka Sommersemester
Die Varianz (Streuung) Definition
 Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Schätzer und Konfidenzintervalle
 Kapitel 2 Schätzer und Konfidenzintervalle Bisher haben wir eine mathematische Theorie entwickelt, die es uns erlaubt, gewisse zufällige Phänomene zu modellieren. Zum Beispiel modellieren wir die Anzahl
Kapitel 2 Schätzer und Konfidenzintervalle Bisher haben wir eine mathematische Theorie entwickelt, die es uns erlaubt, gewisse zufällige Phänomene zu modellieren. Zum Beispiel modellieren wir die Anzahl
4 Unabhängige Zufallsvariablen. Gemeinsame Verteilung
 4 Unabhängige Zufallsvariablen. Gemeinsame Verteilung Häufig werden mehrere Zufallsvariablen gleichzeitig betrachtet, z.b. Beispiel 4.1. Ein Computersystem bestehe aus n Teilsystemen. X i sei der Ausfallzeitpunkt
4 Unabhängige Zufallsvariablen. Gemeinsame Verteilung Häufig werden mehrere Zufallsvariablen gleichzeitig betrachtet, z.b. Beispiel 4.1. Ein Computersystem bestehe aus n Teilsystemen. X i sei der Ausfallzeitpunkt
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
3 Das n-dimensionale Integral
 3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
Grundbegriffe der Wahrscheinlichkeitstheorie. Karin Haenelt
 Grundbegriffe der Wahrscheinlichkeitstheorie Karin Haenelt 1 Inhalt Wahrscheinlichkeitsraum Bedingte Wahrscheinlichkeit Abhängige und unabhängige Ereignisse Stochastischer Prozess Markow-Kette 2 Wahrscheinlichkeitsraum
Grundbegriffe der Wahrscheinlichkeitstheorie Karin Haenelt 1 Inhalt Wahrscheinlichkeitsraum Bedingte Wahrscheinlichkeit Abhängige und unabhängige Ereignisse Stochastischer Prozess Markow-Kette 2 Wahrscheinlichkeitsraum
Vorlesung im SoSe 2010 Stochastische Analysis & Zeitstetige Finanzmathematik
 Univ. Leipzig Mathematisches Institut Vertretung Professur Stochastische Prozesse Max v. Renesse email: mrenesse@math.tu-berlin.de Vorlesung im SoSe 2010 Stochastische Analysis & Zeitstetige Finanzmathematik
Univ. Leipzig Mathematisches Institut Vertretung Professur Stochastische Prozesse Max v. Renesse email: mrenesse@math.tu-berlin.de Vorlesung im SoSe 2010 Stochastische Analysis & Zeitstetige Finanzmathematik
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
mathematik und informatik
 Prof. Dr. Otto Moeschlin et al. Kurs 0359 Testtheorie LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung
Prof. Dr. Otto Moeschlin et al. Kurs 0359 Testtheorie LESEPROBE mathematik und informatik Das Werk ist urheberrechtlich geschützt. Die dadurch begründeten Rechte, insbesondere das Recht der Vervielfältigung
ETWR Teil B. Spezielle Wahrscheinlichkeitsverteilungen (stetig)
 ETWR Teil B 2 Ziele Bisher (eindimensionale, mehrdimensionale) Zufallsvariablen besprochen Lageparameter von Zufallsvariablen besprochen Übertragung des gelernten auf diskrete Verteilungen Ziel des Kapitels
ETWR Teil B 2 Ziele Bisher (eindimensionale, mehrdimensionale) Zufallsvariablen besprochen Lageparameter von Zufallsvariablen besprochen Übertragung des gelernten auf diskrete Verteilungen Ziel des Kapitels
7.2 Moment und Varianz
 7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
STOCHASTISCHE UNABHÄNGIGKEIT. Annika Pohlmann Philipp Oel Wilhelm Dück
 STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
Stochastische Analysis
 PD Dr. Jürgen Dippon, Universität Stuttgart Stochastische Analysis Stuttgart, Wintersemester 211/212 Version: 15. Februar 212 Für Hinweise auf Druckfehler und Kommentare jeder Art bin ich dankbar. 1 Viel
PD Dr. Jürgen Dippon, Universität Stuttgart Stochastische Analysis Stuttgart, Wintersemester 211/212 Version: 15. Februar 212 Für Hinweise auf Druckfehler und Kommentare jeder Art bin ich dankbar. 1 Viel
1 2. Körpererweiterungen
 1 2. Körpererweiterungen 1 2. 1. Definition: Sind K, L Körper und i: K L ein Ringhomomorphismus, so ist i injektiv, wir fassen K vermöge i als Unterkörper von L auf, schreiben dafür L K und nennen L eine
1 2. Körpererweiterungen 1 2. 1. Definition: Sind K, L Körper und i: K L ein Ringhomomorphismus, so ist i injektiv, wir fassen K vermöge i als Unterkörper von L auf, schreiben dafür L K und nennen L eine
Höhere Analysis. dω = Reiner Lauterbach. Vorlesung. Universität Hamburg, WS 2015/2016
 Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
5 Erwartungswerte, Varianzen und Kovarianzen
 47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
Wahrscheinlichkeitstheorie 2 & 3. Prof. Dr. Barbara Gentz mitgeschrieben von Arthur Sinulis 30. Januar 2015
 Wahrscheinlichkeitstheorie 2 & 3 Prof. Dr. Barbara Gentz mitgeschrieben von Arthur Sinulis 3. Januar 215 Inhaltsverzeichnis. Bedingte Erwartungswerte 4 1. Martingale, Stoppzeiten und Filtrierungen 9 1.1.
Wahrscheinlichkeitstheorie 2 & 3 Prof. Dr. Barbara Gentz mitgeschrieben von Arthur Sinulis 3. Januar 215 Inhaltsverzeichnis. Bedingte Erwartungswerte 4 1. Martingale, Stoppzeiten und Filtrierungen 9 1.1.
Box-Plots. Werkzeuge der empirischen Forschung. W. Kössler. Einleitung. Datenbehandlung. Wkt.rechnung. Beschreibende Statistik 174 / 258
 174 / 258 Box-Plots Ziel: übersichtliche Darstellung der Daten. Boxplot zu dem Eingangsbeispiel mit n=5: Descr_Boxplot0.sas Prozeduren: UNIVARIATE, GPLOT, BOXPLOT 174 / 258 Box-Plots Ziel: übersichtliche
174 / 258 Box-Plots Ziel: übersichtliche Darstellung der Daten. Boxplot zu dem Eingangsbeispiel mit n=5: Descr_Boxplot0.sas Prozeduren: UNIVARIATE, GPLOT, BOXPLOT 174 / 258 Box-Plots Ziel: übersichtliche
Vollständiger Raum, Banachraum
 Grundbegriffe beschränkte Menge Cauchyfolge Vollständiger Raum, Banachraum Kriterium für die Vollständigkeit Präkompakte Menge Kompakte Menge Entropiezahl Eigenschaften kompakter und präkompakter Mengen
Grundbegriffe beschränkte Menge Cauchyfolge Vollständiger Raum, Banachraum Kriterium für die Vollständigkeit Präkompakte Menge Kompakte Menge Entropiezahl Eigenschaften kompakter und präkompakter Mengen
Mathematik III. Produkt-Präringe
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 66 Es ist unser Ziel zu zeigen, dass auf der Produktmenge von Maßräumen unter recht allgemeinen Voraussetzungen ein Maß definiert ist,
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 66 Es ist unser Ziel zu zeigen, dass auf der Produktmenge von Maßräumen unter recht allgemeinen Voraussetzungen ein Maß definiert ist,
Einiges über die Brown sche Bewegung
 Einiges über die Brown sche Bewegung Gunther Leobacher und Friedrich Pillichshammer Inhaltsverzeichnis Definition und Existenz einer Brown schen Bewegung Einige elementare Eigenschaften der Brown schen
Einiges über die Brown sche Bewegung Gunther Leobacher und Friedrich Pillichshammer Inhaltsverzeichnis Definition und Existenz einer Brown schen Bewegung Einige elementare Eigenschaften der Brown schen
Einführung in die Statistik Gliederung zur Vorlesung im Sommersemester Markus Reiß Universität Heidelberg
 Einführung in die Statistik Gliederung zur Vorlesung im Sommersemester 2005 Markus Reiß Universität Heidelberg 9. Januar 2006 Inhaltsverzeichnis 1 Diskrete Wahrscheinlichkeitsräume 1 1.1 Grundbegriffe.............................
Einführung in die Statistik Gliederung zur Vorlesung im Sommersemester 2005 Markus Reiß Universität Heidelberg 9. Januar 2006 Inhaltsverzeichnis 1 Diskrete Wahrscheinlichkeitsräume 1 1.1 Grundbegriffe.............................
2 Die Dimension eines Vektorraums
 2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
2 Die Dimension eines Vektorraums Sei V ein K Vektorraum und v 1,..., v r V. Definition: v V heißt Linearkombination der Vektoren v 1,..., v r falls es Elemente λ 1,..., λ r K gibt, so dass v = λ 1 v 1
