Hans Walser, [ ] Lemniskate 1 Worum geht es Es werden Konstruktionen der Lemniskate mit Hilfe von Ellipsen und deren Brennpunkten
|
|
|
- Curt Schneider
- vor 6 Jahren
- Abrufe
Transkript
1 Hans alser, [ ] Lemniskate 1 orum geht es s werden Konstruktionen der Lemniskate mit Hilfe von llipsen und deren Brennpunkten besprochen. 2 Das Vorgehen ir zeichnen den inheitskreis mit Mittelpunkt (0, 0) und die Punkte (1, 0), ( 1, 0), (0, 1), (0, 1) (Abb. 1). Auf dem inheitskreis wählen wir einen beliebigen Punkt P. P Abb. 1: in Punkt P auf dem inheitskreis un zeichnen wir die llipse mit den konjugierten Halbmessern und P sowie deren Brennpunkte F 1 und F 2 (Abb. 2).
2 Hans alser: Lemniskate 2 / 10 P F 1 F 2 Abb. 2: llipse mit Brennpunkten Die beiden Brennpunkte liegen auf der zu den Punkten und gehörenden Lemniskate (Abb. 3). P F 1 F 2 Abb. 3: Brennpunkte auf Lemniskate
3 Hans alser: Lemniskate 3 / 10 Durch Variation von P erhalten wir so alle Punkte der Lemniskate (rtslinie). 3 Lemniskate inige Fakten zur Lemniskate (Abb. 4). L 1 1 Abb. 4: Lemniskate Für einen Punkt L auf der Lemniskate gilt (definierende igenschaft): L L = 1 (1) In Polarkoordinaten hat die Lemniskate die Gleichung: r = 2cos( 2ϕ ) (2) In kartesischen Koordinaten hat die Lemniskate die Gleichung: ( ) 2 2( 2 2 ) = 0 (3) 4 Beweis der Brennpunkteigenschaft Der Punkt P (Abb. 2) habe die Koordinaten:
4 Hans alser: Lemniskate 4 / 10 ( ( )) (4) P cos( 2t),sin 2t Der Faktor 2 beim Parameter t ist aus technischen Gründen dabei. r vereinfacht die Formeln. Da die beiden konjugierten Halbmesser und P die gleiche Länge haben, sind die Hauptachsenrichtungen der llipse die inkelhalbierenden der Halbmesser. Die Halbachsen a und b haben die Länge: a = 2 cos( t), b = 2 sin( t) (5) Daraus erhalten wir die halbe Brennpunktweite c: c = a 2 b 2 = 2 cos 2 ( t) sin 2 ( t) = 2 cos( 2t) (6) Vergleich mit (2) beweist die Behauptung. 5 Umriss Die Hüllkurve der sich durch die Variation von P ergebenden llipsenschar (rote llipse in Abb. 2 und 3) ist ihrerseits eine llipse (Abb. 5). P F 1 F 2 Abb. 5: Umrissellipse
5 Hans alser: Lemniskate 5 / 10 ie hat die Punkte und als Brennpunkte und verläuft durch die Punkt und. Die lange Halbachse ist 2, die kurze Halbachse ist 1. ir können das durch eine kartografische Überlegung einsehen. 6 chrägbild der rdkugel ir stellen die rdkugel auf den Tisch (Projektionsebene) und beleuchten von recht oben unter einem inkel von 45 (Abb. 6a, Aufriss). In der Projektionsebene erhalten wir so ein chrägbild der rdkugel (Abb. 6b, Grundriss).
6 Hans alser: Lemniskate 6 / 10 a) b) Abb. 6: chrägbild der rdkugel Die Abbildung 7 zeigt das chrägbild allein.
7 Hans alser: Lemniskate 7 / 10 Abb. 7: o ist das schöne Tirol? Die Breitenkreise sind in diesem chrägbild als Kreise dargestellt. Der Äquator erscheint als inheitskreis in der Mitte. Der Kartenumriss ist eine llipse mit der langen Halbachse 2 und der kurzen Halbachse 1 (chrägschnitt des sich durch die Projektionsstrahlen ergebenden Umrisszlinders). Die Brennpunkte dieser llipse sind die Bilder der beiden Pole (Überlegung mit Kugeln von Dandelin). Die Meridiane erscheinen als llipsen durch die beiden Pole, welche die Umrissellipse von innen berühren. Die Abbildung 8 zeigt das etz (15 -Maschenweite) der Meridiane und Breitenkreise ohne die rde. egen der Projektionsrichtung 45 und der Maschenweite 15 berühren sich die Bilder der Breitenkreise.
8 Hans alser: Lemniskate 8 / 10 Abb. 8: Meridiane und Breitenkreise Die Figur der Abbildung 8 passt genau auf die Figur der Abbildung 5. Die rote llipse in der Abbildung 5 entspricht einem Meridianbild im chrägbild. omit erhalten wir eine Variante der Lemniskaten-Konstruktion. 7 Variante der Lemniskaten-Konstruktion ir zeichnen die Punkte (1, 0), ( 1, 0), (0, 1), (0, 1) und dazu die llipse mit den Brennpunkten und durch. Auf der llipse wählen wir einen beliebigen Punkt Q (Abb. 9).
9 Hans alser: Lemniskate 9 / 10 Q Abb. 9: tart mit llipse un zeichnen wir eine zweite llipse mit dem Mittelpunkt durch, welche die erste llipse in Q berührt (Abb. 10). benso zeichnen wir die Brennpunkte G 1 und G 2 dieser llipse. Q G 2 G 1 Abb. 10: Berührende Inellipse
10 Hans alser: Lemniskate 10 / 10 Die Brennpunkte G 1 und G 2 liegen auf unserer Lemniskate (Abb. 11). Q G 2 G 1 Abb. 11: Brennpunkte auf Lemniskate ebsites Kartenprojektionen ( ): ikipedia, Lemniskate ( ):
Winkelteilung 1 Worum geht es? 2 Mit Zirkel und Lineal 3 Winkeldrittelung 3.1 Konstruktion einer Kurve
 Hans Walser, [208084] Winkelteilung Anregung: Jo Niemeyer, Berlin Worum geht es? Es wird eine Methode besprochen, einen Winkel in eine ungerade Anzahl gleicher Teile zu unterteilen. 2 Mit Zirkel und Lineal
Hans Walser, [208084] Winkelteilung Anregung: Jo Niemeyer, Berlin Worum geht es? Es wird eine Methode besprochen, einen Winkel in eine ungerade Anzahl gleicher Teile zu unterteilen. 2 Mit Zirkel und Lineal
Eine anallagmatische Kurve. Eckart Schmidt
 Eine anallagmatische Kurve Eckart Schmidt Man bezeichnet eine Kurve als anallagmatisch, wenn sie durch eine Inversion auf sich abgebildet werden kann. Eine anallagmatische Kurve kann als Inverses eines
Eine anallagmatische Kurve Eckart Schmidt Man bezeichnet eine Kurve als anallagmatisch, wenn sie durch eine Inversion auf sich abgebildet werden kann. Eine anallagmatische Kurve kann als Inverses eines
Die Kugel. Mathematische Betrachtungen von Peter Franzke
 Die Kugel Mathematische Betrachtungen von Die Einheitssphäre S 1. Die Kugel Geometrie: gekrümmte geschlossene Fläche, deren Punkte von einem festen Punkt M (Kugelmittelpunkt) einen festen Abstand r (Kugelradius)
Die Kugel Mathematische Betrachtungen von Die Einheitssphäre S 1. Die Kugel Geometrie: gekrümmte geschlossene Fläche, deren Punkte von einem festen Punkt M (Kugelmittelpunkt) einen festen Abstand r (Kugelradius)
Kartografie I. Hans Walser. Koordinatensysteme und Transformationen
 Kartografie I Hans Walser Koordinatenssteme und Transformationen Hans Walser: Koordinatenssteme und Transformationen ii Inhalt Koordinatenssteme.... Kartesische Koordinaten....2 Polarkoordinaten... 2.3
Kartografie I Hans Walser Koordinatenssteme und Transformationen Hans Walser: Koordinatenssteme und Transformationen ii Inhalt Koordinatenssteme.... Kartesische Koordinaten....2 Polarkoordinaten... 2.3
Abb. 1: Stereografische Projektion
 Hans Walser, [20160808] Stereografische Projektion 1 Ausgangslage Wir projizieren die Erde (Geodaten) vom Nordpol aus auf die Tangentialebene im Südpol. Die Abbildung 1 zeigt die Projektion exemplarisch
Hans Walser, [20160808] Stereografische Projektion 1 Ausgangslage Wir projizieren die Erde (Geodaten) vom Nordpol aus auf die Tangentialebene im Südpol. Die Abbildung 1 zeigt die Projektion exemplarisch
φ(ζ, η) = (ζ η, η) = (x, y), bijektiv und stetig differenzierbar ist. Die Jacobi-Matrix von φ lautet: f(ζ) det(dφ(ζ, η)) dζ dη f(ζ) dζ dη.
 Übungen (Aufg und Lösungen zu Mathem u Lin Alg II SS 6 Blatt 9 66 Aufgabe 43: Sei f : R R eine stetige Funktion Formen Sie das Integral f(x + y dx dy in ein einfaches Integral um Lösung: Führe neue Koordinaten
Übungen (Aufg und Lösungen zu Mathem u Lin Alg II SS 6 Blatt 9 66 Aufgabe 43: Sei f : R R eine stetige Funktion Formen Sie das Integral f(x + y dx dy in ein einfaches Integral um Lösung: Führe neue Koordinaten
Komplexe Zahlen. Darstellung
 Komplexe Zahlen Die Zahlenmengen, mit denen wir bis jetzt gearbeitet haben lassen sich zusammenfassen als N Z Q R Die natürlichen Zahlen sind abgeschlossen bezüglich der Operation des Addierens. Das heisst
Komplexe Zahlen Die Zahlenmengen, mit denen wir bis jetzt gearbeitet haben lassen sich zusammenfassen als N Z Q R Die natürlichen Zahlen sind abgeschlossen bezüglich der Operation des Addierens. Das heisst
Ebene Schnitte einer Kugel
 Ebene Schnitte einer Kugel Eine Kugel Φ(M,r) und eine Ebene Σschneiden sich in einem Kreis k(σ, M k, r k ), falls der Abstand d des Kugelmittelpunkts von Σ kleiner r ist. Φ Φ k r=r k d M k r k M=M k k
Ebene Schnitte einer Kugel Eine Kugel Φ(M,r) und eine Ebene Σschneiden sich in einem Kreis k(σ, M k, r k ), falls der Abstand d des Kugelmittelpunkts von Σ kleiner r ist. Φ Φ k r=r k d M k r k M=M k k
Vorkurs Mathematik Übungen zu Komplexen Zahlen
 Vorkurs Mathematik Übungen zu Komplexen Zahlen Komplexe Zahlen Koordinatenwechsel Aufgabe. Zeichnen Sie die folgende Zahlen zunächst in ein (kartesisches) Koordinatensystem. Bestimmen Sie dann die Polarkoordinaten
Vorkurs Mathematik Übungen zu Komplexen Zahlen Komplexe Zahlen Koordinatenwechsel Aufgabe. Zeichnen Sie die folgende Zahlen zunächst in ein (kartesisches) Koordinatensystem. Bestimmen Sie dann die Polarkoordinaten
3.2. Polarkoordinaten
 3.2. Polarkoordinaten Die geometrische Bedeutung der komplexen Multiplikation versteht man besser durch die Einführung von Polarkoordinaten. Der Betrag einer komplexen Zahl z x + i y ist r: z x 2 + y 2.
3.2. Polarkoordinaten Die geometrische Bedeutung der komplexen Multiplikation versteht man besser durch die Einführung von Polarkoordinaten. Der Betrag einer komplexen Zahl z x + i y ist r: z x 2 + y 2.
Implizite Differentiation
 Implizite Differentiation -E -E Implizite Darstellung Eine Funktion ist in impliziter Form gegeben, wenn ie Funktionsgleichung nach keiner er beien Variablen x un y aufgelöst ist. Beispielsweise x y =
Implizite Differentiation -E -E Implizite Darstellung Eine Funktion ist in impliziter Form gegeben, wenn ie Funktionsgleichung nach keiner er beien Variablen x un y aufgelöst ist. Beispielsweise x y =
Hans Walser, [ a] Grafische Lösung einer quadratischen Gleichung Anregung: D. M. und M. P.
![Hans Walser, [ a] Grafische Lösung einer quadratischen Gleichung Anregung: D. M. und M. P. Hans Walser, [ a] Grafische Lösung einer quadratischen Gleichung Anregung: D. M. und M. P.](/thumbs/69/61462793.jpg) Hans Walser, [007067a] Grafische Lösung einer quadratischen Gleichung Anregung: D. M. und M. P. Problemstellung Wir lösen die Gleichung: x px + q = 0 Die Gleichung ist in einer in den Schulen unüblichen
Hans Walser, [007067a] Grafische Lösung einer quadratischen Gleichung Anregung: D. M. und M. P. Problemstellung Wir lösen die Gleichung: x px + q = 0 Die Gleichung ist in einer in den Schulen unüblichen
A = Eine symmetrische Matrix ist gleich ihrer transponierten Matrix: A t = A
 Hans Walser, [07] Smmetrische Matri Die Matri Wir arbeiten mit der smmetrischen Matri: A = 3 6 Eine smmetrische Matri ist gleich ihrer transponierten Matri: A t = A Die Abbildung. Verzerrungsellipse Wir
Hans Walser, [07] Smmetrische Matri Die Matri Wir arbeiten mit der smmetrischen Matri: A = 3 6 Eine smmetrische Matri ist gleich ihrer transponierten Matri: A t = A Die Abbildung. Verzerrungsellipse Wir
Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen.
 10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
10.1. Ebene Kurven Mathematische Kurven sind uns aus den verschiedensten Zusammenhängen vertraut. Wir stellen hier kurz die wichtigsten Begriffe zusammen. Parameterdarstellungen einer Kurve sind stetige
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
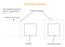 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 1. Übung: Woche vom (komplexe Zahlen):
 Übungsaufgaben 1. Übung: Woche vom 17.-21.10.16 (komplexe Zahlen): Heft Ü1: 3.9 (a,b); 3.10, 3.12 (a-c); 3.13 (a-c); 3.2 (a,b,d); 3.3 (c,d,f) Wiederholung Komplexe Zahlen Definition (Imaginäre Einheit,
Übungsaufgaben 1. Übung: Woche vom 17.-21.10.16 (komplexe Zahlen): Heft Ü1: 3.9 (a,b); 3.10, 3.12 (a-c); 3.13 (a-c); 3.2 (a,b,d); 3.3 (c,d,f) Wiederholung Komplexe Zahlen Definition (Imaginäre Einheit,
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Kegelschnitte - Teil 7
 7.1 Kegelschnitte - Gemeinsame Gleichung Kegelschnitte - Teil 7 Die verschiedenen Kegelschnitte entstehen, indem die Schnittebene eine verschiedene Neigung zur Hauptachse des Kreiskegels hat. Von senkrecht
7.1 Kegelschnitte - Gemeinsame Gleichung Kegelschnitte - Teil 7 Die verschiedenen Kegelschnitte entstehen, indem die Schnittebene eine verschiedene Neigung zur Hauptachse des Kreiskegels hat. Von senkrecht
2.1 Steigung 1. Die Geraden mit Steigung ±1 folgen den Diagonalen der Netzquadrate (Abb. 2). Abb. 1: Plattkarte. Abb. 2: Situation auf der Karte
 Hans Walser, [20131216a], [20140308] Sphärische Spiralen 1 Idee Die Idee ist einfach: Wir zeichnen auf einer Weltkarte eine schräg ansteigende Gerade und studieren deren Bild auf der Kugel. Je nach Kartentyp
Hans Walser, [20131216a], [20140308] Sphärische Spiralen 1 Idee Die Idee ist einfach: Wir zeichnen auf einer Weltkarte eine schräg ansteigende Gerade und studieren deren Bild auf der Kugel. Je nach Kartentyp
Es wird versucht, die geometrischen Grundlagen zur Entscheidung dieser Frage aufzuarbeiten.
 Hans Walser, [20160609] Gestalt der Erde 1 Worum geht es? Im späten 17. Jahrhundert entspann sich ein wissenschaftlicher treit um die Gestalt der Erde (Brotton 2012,. 308): Die Anhänger von Descartes (1596-1650)
Hans Walser, [20160609] Gestalt der Erde 1 Worum geht es? Im späten 17. Jahrhundert entspann sich ein wissenschaftlicher treit um die Gestalt der Erde (Brotton 2012,. 308): Die Anhänger von Descartes (1596-1650)
Koordinatensysteme der Erde
 Koordinatensysteme der Erde Es gibt verschiedene Arten, die Position eines Punktes auf der Oberfläche einer Kugel (manchmal auch Sphäre genannt) darzustellen, jede hat ihre Vor-und Nachteile und ist für
Koordinatensysteme der Erde Es gibt verschiedene Arten, die Position eines Punktes auf der Oberfläche einer Kugel (manchmal auch Sphäre genannt) darzustellen, jede hat ihre Vor-und Nachteile und ist für
Unterrichtsreihe zur Parabel
 Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Transformation von Gauß-Krüger(GK)- Koordinaten des Systems MGI in Universal Transversal Mercator(UTM)- Koordinaten des Systems ETRS89
 Transformation von Gauß-Krüger(GK)- Koordinaten des Systems MGI in Universal Transversal Mercator(UTM)- Koordinaten des Systems ETRS89 Inhaltsverzeichnis Leitfaden... 3 Ellipsoidparameter und abgeleitete
Transformation von Gauß-Krüger(GK)- Koordinaten des Systems MGI in Universal Transversal Mercator(UTM)- Koordinaten des Systems ETRS89 Inhaltsverzeichnis Leitfaden... 3 Ellipsoidparameter und abgeleitete
Lemniskaten und eine Strophoide des Dreiecks
 Lemniskaten und eine Strophoide des Dreiecks Eckart Schmidt Spiegelt man Umkegelschnitte eines Dreiecks am Umkreis, so erhält man im allgemeinen Kurven vierter Ordnung. Hier werden nur gleichseitige Umhyperbeln
Lemniskaten und eine Strophoide des Dreiecks Eckart Schmidt Spiegelt man Umkegelschnitte eines Dreiecks am Umkreis, so erhält man im allgemeinen Kurven vierter Ordnung. Hier werden nur gleichseitige Umhyperbeln
Die Abbildung 2 zeigt das Spiegelbild des Innenhofes auf der Kugel in der Bildmitte der Abbildung 1.
 Hans Walser, [20161017] Reflexion an Kugel Idee und Anregung: W. K., F. 1 Worum geht es? Im Innenhof eines Wiener Hotels sind reflektierende Kugeln aufgehängt (Abb. 1). Abb. 1: Reflektierende Kugeln Die
Hans Walser, [20161017] Reflexion an Kugel Idee und Anregung: W. K., F. 1 Worum geht es? Im Innenhof eines Wiener Hotels sind reflektierende Kugeln aufgehängt (Abb. 1). Abb. 1: Reflektierende Kugeln Die
1.5. Relationen, Abbildungen und Flächen
 .5. Relationen, Abbildungen und Flächen In Verallgemeinerung der reellen Situation nennt man jede Teilmenge F eines kartesischen Produkts A B eine Relation zwischen A und B, und man spricht von einer Abbildung
.5. Relationen, Abbildungen und Flächen In Verallgemeinerung der reellen Situation nennt man jede Teilmenge F eines kartesischen Produkts A B eine Relation zwischen A und B, und man spricht von einer Abbildung
2 Kegelschnitte, Normalformen und Konstruktion
 Mathematik fur Ingenieure Institut fur Algebra, Zahlentheorie und Diskrete Mathematik Dr. Dirk Windelberg Universitat Hannover Stand: 8. August 008 http://www.iazd.uni-hannover.de/windelberg/teach/ing
Mathematik fur Ingenieure Institut fur Algebra, Zahlentheorie und Diskrete Mathematik Dr. Dirk Windelberg Universitat Hannover Stand: 8. August 008 http://www.iazd.uni-hannover.de/windelberg/teach/ing
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
Übung 1. Man nde die gesuchten Funktionswerte. (ii) f(x, y) = sin(xy)
 Man nde die gesuchten Funktionswerte. Übung (i) f(, ) = + 3 f(, ) f(, ) f(, 3) f( 3, ) f(, ) = sin() f(, π/6) f( 3, π/) f(π, /) f( π/, 7) Übung Man nde und skizziere den enitionsbereich und nde den Wertebereich
Man nde die gesuchten Funktionswerte. Übung (i) f(, ) = + 3 f(, ) f(, ) f(, 3) f( 3, ) f(, ) = sin() f(, π/6) f( 3, π/) f(π, /) f( π/, 7) Übung Man nde und skizziere den enitionsbereich und nde den Wertebereich
7 Beziehungen im Raum
 Lange Zeit glaubten die Menschen, die Erde sei eine Scheibe. Heute zeigen dir Bilder aus dem Weltall sehr deutlich, dass die Erde die Gestalt einer Kugel hat. 7 Beziehungen im Raum Gradnetz der Erde Längengrade
Lange Zeit glaubten die Menschen, die Erde sei eine Scheibe. Heute zeigen dir Bilder aus dem Weltall sehr deutlich, dass die Erde die Gestalt einer Kugel hat. 7 Beziehungen im Raum Gradnetz der Erde Längengrade
Serie 3 - Komplexe Zahlen II
 Analysis D-BAUG Dr. Meike Akveld HS 2015 Serie - Komplexe Zahlen II 1. Wir betrachten die komplexe Gleichung z 6 = 4 4i. a) Bestimmen Sie alle en z C dieser Gleichung. b) Zeichnen Sie die en in die komplexe
Analysis D-BAUG Dr. Meike Akveld HS 2015 Serie - Komplexe Zahlen II 1. Wir betrachten die komplexe Gleichung z 6 = 4 4i. a) Bestimmen Sie alle en z C dieser Gleichung. b) Zeichnen Sie die en in die komplexe
Hans Walser. Raumgeometrie. Modul 1 Der Würfel Lernumgebung, Teil 1
 Hans Walser Raumgeometrie Modul 1 Der Würfel Lernumgebung, Teil 1 Hans Walser: Modul 1, Der Würfel. Lernumgebung, Teil 1 ii Inhalt 1 Der 12-7-5-Würfel... 1 2 Schnittpunkte am Quader... 2 3 Zwölf oder dreizehn
Hans Walser Raumgeometrie Modul 1 Der Würfel Lernumgebung, Teil 1 Hans Walser: Modul 1, Der Würfel. Lernumgebung, Teil 1 ii Inhalt 1 Der 12-7-5-Würfel... 1 2 Schnittpunkte am Quader... 2 3 Zwölf oder dreizehn
Schwerpunkt homogener ebener Flächen: Teil 2
 Celle, Stadtkirche St. Marien, Fragment Schwerpunkt homogener ebener Flächen: Teil 3 E Ma Lubov Vassilevskaya Flächeninhalt 3 E Ma Lubov Vassilevskaya Schwerpunkt einer homogenen ebenen Fläche: Aufgaben
Celle, Stadtkirche St. Marien, Fragment Schwerpunkt homogener ebener Flächen: Teil 3 E Ma Lubov Vassilevskaya Flächeninhalt 3 E Ma Lubov Vassilevskaya Schwerpunkt einer homogenen ebenen Fläche: Aufgaben
2.9 Die komplexen Zahlen
 LinAlg II Version 1 3. April 2006 c Rudolf Scharlau 121 2.9 Die komplexen Zahlen Die komplexen Zahlen sind unverzichtbar für nahezu jede Art von höherer Mathematik. Systematisch gehören sie zum einen in
LinAlg II Version 1 3. April 2006 c Rudolf Scharlau 121 2.9 Die komplexen Zahlen Die komplexen Zahlen sind unverzichtbar für nahezu jede Art von höherer Mathematik. Systematisch gehören sie zum einen in
Abitur 2010 Mathematik LK Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Serie 6. x 2 + y 2, 0 z 4.
 Analysis D-BAUG Dr. Cornelia Busch FS 6 Serie 6. Wir betrachten drei verschiedene Flaschen in der Form eines Paraboloids P, eines Hyperboloids H und eines Kegels K. Diese sind wie folgt gegeben: P = {
Analysis D-BAUG Dr. Cornelia Busch FS 6 Serie 6. Wir betrachten drei verschiedene Flaschen in der Form eines Paraboloids P, eines Hyperboloids H und eines Kegels K. Diese sind wie folgt gegeben: P = {
(u, v) z(u, v) u Φ(u, v) (v = const.) Parameterlinie v = const. v Φ(u, v) (u = const.) Parameterlinie u = const.
 13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
13 Flächenintegrale 64 13 Flächenintegrale Im letzten Abschnitt haben wir Integrale über Kurven betrachtet. Wir wollen uns nun mit Integralen über Flächen beschäftigen. Wir haben bisher zwei verschiedene
K A N T O N S S C H U L E I M L E E MATHEMATIK. Grafiktaschenrechner ohne CAS, beliebige Formelsammlung
 K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 017 Klasse: g Profil: MN / M Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 017 Klasse: g Profil: MN / M Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
Abitur 2016 Mathematik Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
2.1 Radienverhältnis 2 1 In diesem Fall berühren sich die grünen Kreise untereinander (Abb. 2). Der rote Radius ist 2 1, der grüne Radius 1.
 Hans Walser, [20170526] Kreispackungen Anregung: Heinz Klaus Strick, Leverkusen. Siehe auch (Strick 2017, S. 269f). 1 Ausgangslage Wir arbeiten mit zwei Kreisscharen (Abb. 1). Abb. 1: Zwei Kreisscharen
Hans Walser, [20170526] Kreispackungen Anregung: Heinz Klaus Strick, Leverkusen. Siehe auch (Strick 2017, S. 269f). 1 Ausgangslage Wir arbeiten mit zwei Kreisscharen (Abb. 1). Abb. 1: Zwei Kreisscharen
Ferienkurs Theoretische Mechanik 2009 Hamilton Formalismus und gekoppelte Systeme
 Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
Fakultät für Physik Technische Universität München Michael Schrapp Übungsblatt 3 Ferienkurs Theoretische Mechanik 009 Hamilton Formalismus und gekoppelte Systeme Hamilton-Mechanik. Aus Doctoral General
2.2A. Das allgemeine Dreieck
 .A. Das allgemeine Dreieck Koordinatentransformation eines Dreiecks Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = (
.A. Das allgemeine Dreieck Koordinatentransformation eines Dreiecks Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den Eckpunkten A = ( x, 0 ), B = ( y, 0 ), C = (
Brückenkurs Mathematik. Freitag Freitag
 Brückenkurs Mathematik Freitag 9.09. - Freitag 13.10.017 Vorlesung 10 Komplexe Zahlen Kai Rothe Technische Universität Hamburg-Harburg Freitag 13.10.017 0 Brückenkurs Mathematik, K.Rothe, Vorlesung 10
Brückenkurs Mathematik Freitag 9.09. - Freitag 13.10.017 Vorlesung 10 Komplexe Zahlen Kai Rothe Technische Universität Hamburg-Harburg Freitag 13.10.017 0 Brückenkurs Mathematik, K.Rothe, Vorlesung 10
10.5 Differentialgeometrie ebener Kurven Tangente, Normale
 1.5 1.5 Differentialgeometrie ebener Kurven 1.5.1 Tangente, Normale Gegeben: Kurve C C := C := { (x { (x y) } y = f(x), a x b y ) x = ϕ(t) y = ψ(t), t 1 t t } oder C heißt glatte Kurve, wenn f stetig differenzierbar
1.5 1.5 Differentialgeometrie ebener Kurven 1.5.1 Tangente, Normale Gegeben: Kurve C C := C := { (x { (x y) } y = f(x), a x b y ) x = ϕ(t) y = ψ(t), t 1 t t } oder C heißt glatte Kurve, wenn f stetig differenzierbar
x 1 Da y nur in der 2.Potenz vorkommt, ist die Kurve achsensymmetrisch zur x-achse.
 .6. Klausur Kurs Ma Mathematik Lk Lösung Gegeben ist die Gleichung x y y x. [] Verschaffen Sie sich einen Überblick über den Kurvenverlauf, indem Sie die Kurve auf Asymptoten und waagrechte sowie senkrechte
.6. Klausur Kurs Ma Mathematik Lk Lösung Gegeben ist die Gleichung x y y x. [] Verschaffen Sie sich einen Überblick über den Kurvenverlauf, indem Sie die Kurve auf Asymptoten und waagrechte sowie senkrechte
mathphys-online Aufgaben zur Differentialrechnung - Lösung Tangentenaufgaben Aufgabe 1 Definition des Feldindex in Vektoren und Matrizen: ORIGIN 1
 Aufgaben zur Differentialrechnung - Lösung Tangentenaufgaben Definition es Felinex in Vektoren un Matrizen: ORIGIN Aufgabe Gegeben ist ie Funktion f mit em Funktionsterm f( x) = x x, wobei x IR. a) Bestimmen
Aufgaben zur Differentialrechnung - Lösung Tangentenaufgaben Definition es Felinex in Vektoren un Matrizen: ORIGIN Aufgabe Gegeben ist ie Funktion f mit em Funktionsterm f( x) = x x, wobei x IR. a) Bestimmen
Berechnungen am rechtwinkligen Dreieck Der Einheitskreis. VI Trigonometrie. Propädeutikum Holger Wuschke. 21. September 2018
 Propädeutikum 018 1. September 018 Denition Trigonometrie Die Trigonometrie beschäftigt sich mit dem Messen (µɛτ ρoν) von dreiseitigen (τ ρίγωνo) Objekten. Zunächst gilt in Dreiecken: A = 1 g h Abbildung:
Propädeutikum 018 1. September 018 Denition Trigonometrie Die Trigonometrie beschäftigt sich mit dem Messen (µɛτ ρoν) von dreiseitigen (τ ρίγωνo) Objekten. Zunächst gilt in Dreiecken: A = 1 g h Abbildung:
Komplexe Funktionen. Freitag Vorlesung 1. Kai Rothe. Sommersemester Technische Universität Hamburg-Harburg
 Komplexe Funktionen Freitag 13.04.018 Vorlesung 1 Kai Rothe Sommersemester 018 Technische Universität Hamburg-Harburg K.Rothe, komplexe Funktionen, Vorlesung 1 Nullstellen quadratischer Gleichungen Beispiel
Komplexe Funktionen Freitag 13.04.018 Vorlesung 1 Kai Rothe Sommersemester 018 Technische Universität Hamburg-Harburg K.Rothe, komplexe Funktionen, Vorlesung 1 Nullstellen quadratischer Gleichungen Beispiel
Mathematik für die Sekundarstufe 1
 Hans Walser Mathematik für die Sekundarstufe 1 Modul 05 Schnecken und Spiralen Lernumgebung Hans Walser: Modul 05, Schnecken und Spiralen. Lernumgebung ii Inhalt 1 Spiralen in der Umwelt... 1 Archimedische
Hans Walser Mathematik für die Sekundarstufe 1 Modul 05 Schnecken und Spiralen Lernumgebung Hans Walser: Modul 05, Schnecken und Spiralen. Lernumgebung ii Inhalt 1 Spiralen in der Umwelt... 1 Archimedische
Weitere Ableitungsregeln. Kapitel 4
 Weitere Ableitungsregeln Kapitel . Die Kettenregel L f() = u(v()) g() = v(u()) a) + + b) cos [( + ) ] (cos + ) c) sin ( ) [sin ()] d) e) ( = _ ) _ ( f) cos [π( + )] cos (π) + g) ( ) = h) ( + ) + = + +
Weitere Ableitungsregeln Kapitel . Die Kettenregel L f() = u(v()) g() = v(u()) a) + + b) cos [( + ) ] (cos + ) c) sin ( ) [sin ()] d) e) ( = _ ) _ ( f) cos [π( + )] cos (π) + g) ( ) = h) ( + ) + = + +
Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel.
 1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
5 Sphärische Trigonometrie
 $Id: sphaere.tex,v 1.4 2013/06/24 23:05:24 hk Exp hk $ 5 Sphärische Trigonometrie 5.2 Sphärische Dreiecksberechnung Wir behandeln gerade die Berechnung sphärischer Dreiecke und haben zu diesem Zweck bereits
$Id: sphaere.tex,v 1.4 2013/06/24 23:05:24 hk Exp hk $ 5 Sphärische Trigonometrie 5.2 Sphärische Dreiecksberechnung Wir behandeln gerade die Berechnung sphärischer Dreiecke und haben zu diesem Zweck bereits
9.5 Graphen der trigonometrischen Funktionen
 9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
9.5 Graphen der trigonometrischen Funktionen 9.5 Graphen der trigonometrischen Funktionen. Unter dem Bogenmass eines Winkels versteht man die Länge des Winkelbogens von auf dem Kreis mit Radius (Einheitskreis).
[ ] (1) ( ) ( ) ( ) π 2, π 2 ( )
![[ ] (1) ( ) ( ) ( ) π 2, π 2 ( ) [ ] (1) ( ) ( ) ( ) π 2, π 2 ( )](/thumbs/72/66438745.jpg) Hans Walser, [20170718] Kosinusspindel Indirekte Anregung: F. H., B. 1 Worum geht es? Rotationsfläche mit einer Kosinuskurve als Meridian. 2 Parameterdarstellungen 2.1 Einheitskugel Wir gehen aus von der
Hans Walser, [20170718] Kosinusspindel Indirekte Anregung: F. H., B. 1 Worum geht es? Rotationsfläche mit einer Kosinuskurve als Meridian. 2 Parameterdarstellungen 2.1 Einheitskugel Wir gehen aus von der
2λx cos(y) + (4 2λ)y sin(y) e x harmonisch in R 2 ist. Dazu berechnen wir. = e x (2λ(x 2) cos(y) + (4 2λ)y sin(y))
 Mathematik für Ingenieure IV, Kurs-Nr. 094 SS 008 Lösungsvorschläge zu den Aufgaben für die Studientage am 30./3.08.008 Kurseinheit 6: Die Potentialgleichung Aufgabe : Wir untersuchen, für welche λ R die
Mathematik für Ingenieure IV, Kurs-Nr. 094 SS 008 Lösungsvorschläge zu den Aufgaben für die Studientage am 30./3.08.008 Kurseinheit 6: Die Potentialgleichung Aufgabe : Wir untersuchen, für welche λ R die
P 2. Bemerkung 3: Im Folgenden wird das Konstruktionsverfahren beschrieben. Die Beweise überlassen wir dem der Lust hat.
 Hans Walser, [20150318] Brennpunkte der Ellipse 1 Worum geht es? Eine Ellipse sei durh fünf Punkte,...,P 5 gegeben (Abb. 1). P5 P 4 P 3 Abb. 1: Eine Ellipse durh fünf Punkte Gesuht sind die Brennpunkte
Hans Walser, [20150318] Brennpunkte der Ellipse 1 Worum geht es? Eine Ellipse sei durh fünf Punkte,...,P 5 gegeben (Abb. 1). P5 P 4 P 3 Abb. 1: Eine Ellipse durh fünf Punkte Gesuht sind die Brennpunkte
Abb. 1: St. Galler-Brot. 2.1 Formelsammlung In der Formelsammlung finden wir für den Flächeninhalt A einer Kugelzone: A = 2πRh (1)
 Hans Walser, [20180112] Brotkruste Anregungen: Sebastian Baader, Bern, und Anselm Lambert, Saarbrücken 1 Worum geht es? In einigen Gegenden der Schweiz gibt es ein annähernd kugelförmiges Brot, das so
Hans Walser, [20180112] Brotkruste Anregungen: Sebastian Baader, Bern, und Anselm Lambert, Saarbrücken 1 Worum geht es? In einigen Gegenden der Schweiz gibt es ein annähernd kugelförmiges Brot, das so
Cassini-Kurven Lemniskate
 Cassini-Kurven Lemniskate Text Nr. 510 Stand 1. April 016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 510 Cassini-Kurven und Lemniskate Vorwort Der Namen Lemniskate ist sicher bekannter
Cassini-Kurven Lemniskate Text Nr. 510 Stand 1. April 016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK 510 Cassini-Kurven und Lemniskate Vorwort Der Namen Lemniskate ist sicher bekannter
Höhere Mathematik für technische Studiengänge Vorbereitungsaufgaben für die Übungen
 Höhere Mathematik für technische Studiengänge Vorbereitungsaufgaben für die Übungen Komplexe Zahlen Lösungshinweise. Sei z = + i und z = i. Berechnen Sie z + z, z z, z z, z z, z /z, z + z, z z, z z, z
Höhere Mathematik für technische Studiengänge Vorbereitungsaufgaben für die Übungen Komplexe Zahlen Lösungshinweise. Sei z = + i und z = i. Berechnen Sie z + z, z z, z z, z z, z /z, z + z, z z, z z, z
Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B
 Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Gymnasium Muttenz Maturitätsprüfung 2016 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Die einleitend angesprochenen Zusammenhänge sind in der folgenden Tabelle zusammengestellt:
 Ein konstantes Abstandsrodukt Eckart Schmidt Zu zwei fest vorgegebenen Punkten sind die Ortslinien für Punkte mit konstanten Abstandssummen, Abstandsdifferenzen oder Abstandsverhältnissen Kegelschnitte;
Ein konstantes Abstandsrodukt Eckart Schmidt Zu zwei fest vorgegebenen Punkten sind die Ortslinien für Punkte mit konstanten Abstandssummen, Abstandsdifferenzen oder Abstandsverhältnissen Kegelschnitte;
Übungen 3. Vektoren. 1) Gesucht sind alle möglichen Vektoren c mit der Länge 6, die senkrecht auf den Vektoren a und b stehen.
 Vektoren Übungen ) Gesucht sind alle möglichen Vektoren c mit der Länge, die senkrecht auf den Vektoren a und b stehen. a = ( ); b = ( ) a) Ein Dreieck in R ist durch die Punkte O( ), A( ), B( ) definiert.
Vektoren Übungen ) Gesucht sind alle möglichen Vektoren c mit der Länge, die senkrecht auf den Vektoren a und b stehen. a = ( ); b = ( ) a) Ein Dreieck in R ist durch die Punkte O( ), A( ), B( ) definiert.
Angewandte Geometrie Semestralprüfung am 5. Juli 2005, Uhr
 Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Technische Universität München SS 2005 Zentrum Mathematik Blatt 7 apl. Prof. Dr. J. Hartl Angewandte Geometrie Semestralprüfung am 5. Juli 2005, 12.00-1.0 Uhr 1. In einem dreidimensionalen euklidischen
Algebra 3.
 Algebra 3 www.schulmathe.npage.de Aufgaben 1. In einem kartesischen Koordinatensystem sind die Punkte A( 3), B( ) sowie für jedes a (a R) ein Punkt P a (a a a) gegeben. a) Zeigen Sie, dass alle Punkte
Algebra 3 www.schulmathe.npage.de Aufgaben 1. In einem kartesischen Koordinatensystem sind die Punkte A( 3), B( ) sowie für jedes a (a R) ein Punkt P a (a a a) gegeben. a) Zeigen Sie, dass alle Punkte
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Aufgabe 5.1 Geben Sie zu folgenden komplexen Zahlen die Polarkoordinatendarstellung an, w z w z.
 Kapitel 5 Aufgaben Verständnisfragen Aufgabe 5. Geben Sie zu folgenden komplexen Zahlen die Polarkoordinatendarstellung an z i z + i z 3 + 3i). Zu den komplexen Zahlen mit Polarkoordinaten r 4 ϕ 4 π r
Kapitel 5 Aufgaben Verständnisfragen Aufgabe 5. Geben Sie zu folgenden komplexen Zahlen die Polarkoordinatendarstellung an z i z + i z 3 + 3i). Zu den komplexen Zahlen mit Polarkoordinaten r 4 ϕ 4 π r
Abitur 2011 G8 Musterabitur Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Aufgaben für die Klassenstufen 11/12
 Aufgaben für die Klassenstufen 11/12 Einzelwettbewerb Gruppenwettbewerb Speedwettbewerb Aufgaben OE1, OE2, OE3 Aufgaben OG1, OG2, OG3, OG4 Aufgaben OS1, OS2, OS3, OS4, OS5, OS6, OS7, OS8 Aufgabe OE1: Ein
Aufgaben für die Klassenstufen 11/12 Einzelwettbewerb Gruppenwettbewerb Speedwettbewerb Aufgaben OE1, OE2, OE3 Aufgaben OG1, OG2, OG3, OG4 Aufgaben OS1, OS2, OS3, OS4, OS5, OS6, OS7, OS8 Aufgabe OE1: Ein
Gymnasium Muttenz Maturitätsprüfung 2014 Mathematik Profile A und B
 Gymnasium Muttenz Maturitätsprüfung 2014 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
Gymnasium Muttenz Maturitätsprüfung 2014 Mathematik Profile A und B Name, Vorname:... Hinweise: Klasse:... Die Prüfung dauert 4 Stunden. Es können maximal 48 Punkte erreicht werden. Es werden alle Aufgaben
14.3 Berechnung gekrümmter Flächen
 4.3 Berechnung gekrümmter Flächen Gekrümmte Flächen werden berechnet, indem sie als Graph einer Funktion zweier Veränderlicher aufgefasst werden. Fläche des Graphen einer Funktion zweier Veränderlicher
4.3 Berechnung gekrümmter Flächen Gekrümmte Flächen werden berechnet, indem sie als Graph einer Funktion zweier Veränderlicher aufgefasst werden. Fläche des Graphen einer Funktion zweier Veränderlicher
Funktionen mehrerer Variablen: Integralrechnung. Aufgaben mit Lösungen. Jörg Gayler, Lubov Vassilevskaya
 Funktionen mehrerer Variablen: Integralrechnung ufgaben mit Lösungen Jörg Gayler, Lubov Vassilevskaya Inhaltsverzeichnis ii Doppelintegrale. Doppelintegrale.. Doppelintegrale mit konstanten Integrationsgrenzen
Funktionen mehrerer Variablen: Integralrechnung ufgaben mit Lösungen Jörg Gayler, Lubov Vassilevskaya Inhaltsverzeichnis ii Doppelintegrale. Doppelintegrale.. Doppelintegrale mit konstanten Integrationsgrenzen
Ein Maß für die Krümmung von Funktionsgraphen Helmut Umla 2015
 Ein Maß für die Krümmung von Funktionsgraphen Helmut Umla 015 Halbkreise Der Kreis mit Mittelpunkt und Radius hat die Gleichung + (Satz des Pythagoras). Die Gleichung nach aufgelöst: ± Der untere Halbkreis
Ein Maß für die Krümmung von Funktionsgraphen Helmut Umla 015 Halbkreise Der Kreis mit Mittelpunkt und Radius hat die Gleichung + (Satz des Pythagoras). Die Gleichung nach aufgelöst: ± Der untere Halbkreis
Komplexe Zahlen und Geometrie
 Komplexe Zahlen und Geometrie Dr. Axel Schüler, Univ. Leipzig März 1998 Zusammenfassung Ziel dieses Beitrages ist es, die komplexen Zahlen bei einfachen geometrischen Aufgaben einzusetzen. Besonderes Augenmerk
Komplexe Zahlen und Geometrie Dr. Axel Schüler, Univ. Leipzig März 1998 Zusammenfassung Ziel dieses Beitrages ist es, die komplexen Zahlen bei einfachen geometrischen Aufgaben einzusetzen. Besonderes Augenmerk
Aufgaben zu Kapitel 5
 Aufgaben zu Kapitel 5 Aufgaben zu Kapitel 5 Verständnisfragen Aufgabe 5. Geben Sie zu folgenden komplexen Zahlen die Polarkoordinatendarstellung an z i z + i z 3 + 3i). r 5 ϕ 5 4 3 π bzw. r 6 3 ϕ 6 4 5
Aufgaben zu Kapitel 5 Aufgaben zu Kapitel 5 Verständnisfragen Aufgabe 5. Geben Sie zu folgenden komplexen Zahlen die Polarkoordinatendarstellung an z i z + i z 3 + 3i). r 5 ϕ 5 4 3 π bzw. r 6 3 ϕ 6 4 5
Kartografie I. Hans Walser. Kartenprojektionen Lernumgebung
 Kartografie I Hans Walser Kartenprojektionen Lernumgebung Hans Walser: Kartenprojektionen. Lernumgebung ii Inhalt Parameterdarstellung der Kugel... 2 Geodätische Linien... 3 Kegelprojektion: Variante mit
Kartografie I Hans Walser Kartenprojektionen Lernumgebung Hans Walser: Kartenprojektionen. Lernumgebung ii Inhalt Parameterdarstellung der Kugel... 2 Geodätische Linien... 3 Kegelprojektion: Variante mit
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Mathematik. Abiturprüfung Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten
 Mathematik Abiturprüfung 2015 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
Mathematik Abiturprüfung 2015 Prüfungsteil A (CAS) Arbeitszeit: 90 Minuten Bei der Bearbeitung der Aufgaben dürfen keine Hilfsmittel verwendet werden. Zu den Themengebieten Analysis, Stochastik und Geometrie
A. N. Danilewsky 31. Fortsetzung von Kapitel 2
 A. N. Danilewsky 31 Fortsetzung von Kapitel 2 2.3 Darstellung von Körpern... 32 2.3.1 Othogonale Parallelprojektion... 32 2.3.2 Stereographische Projektion... 34 2.3.3 Gnomonische Projektion... 42 32 Kristallographie
A. N. Danilewsky 31 Fortsetzung von Kapitel 2 2.3 Darstellung von Körpern... 32 2.3.1 Othogonale Parallelprojektion... 32 2.3.2 Stereographische Projektion... 34 2.3.3 Gnomonische Projektion... 42 32 Kristallographie
Transformation von Gauß-Krüger(GK)- Koordinaten des Systems MGI in Universal Transversal Mercator(UTM)- Koordinaten des Systems ETRS89
 Transformation von Gauß-Krüger(GK)- Koordinaten des Systems MGI in Universal Transversal Mercator(UTM)- Koordinaten des Systems ETRS89 1. Inhaltsverzeichnis 1. Inhaltsverzeichnis...2 2. Leitfaden...3 3.
Transformation von Gauß-Krüger(GK)- Koordinaten des Systems MGI in Universal Transversal Mercator(UTM)- Koordinaten des Systems ETRS89 1. Inhaltsverzeichnis 1. Inhaltsverzeichnis...2 2. Leitfaden...3 3.
Lösungsvorschlag Theoretische Physik A Neuntes Übungsblatt
 Lösungsvorschlag Theoretische Physik A Neuntes Übungsblatt Aufgabe 3 Prof. Dr. Schön und Dr. Eschrig Wintersemester 004/005 Durch Trennung der Veränderlichen und anschließende Integration ergibt sich aus
Lösungsvorschlag Theoretische Physik A Neuntes Übungsblatt Aufgabe 3 Prof. Dr. Schön und Dr. Eschrig Wintersemester 004/005 Durch Trennung der Veränderlichen und anschließende Integration ergibt sich aus
Hans Walser, [ ], [ ], [ b] Zerlegungsgleichheit
![Hans Walser, [ ], [ ], [ b] Zerlegungsgleichheit Hans Walser, [ ], [ ], [ b] Zerlegungsgleichheit](/thumbs/93/111644499.jpg) Hans Walser, [20130516], [20130520], [20130525b] Zerlegungsgleichheit 1 Worum es geht In der Ebene sind flächengleiche Polygone immer auch zerlegungsgleich. Wie finden wir bei Dreiecken und Rechtecken
Hans Walser, [20130516], [20130520], [20130525b] Zerlegungsgleichheit 1 Worum es geht In der Ebene sind flächengleiche Polygone immer auch zerlegungsgleich. Wie finden wir bei Dreiecken und Rechtecken
a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g(x) = f(x)
 Vertikale Verschiebung a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g() = f() b) Zeichne den Graphen der Funktion h mit h() = f() ein. Oben oder unten? f() +
Vertikale Verschiebung a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g() = f() b) Zeichne den Graphen der Funktion h mit h() = f() ein. Oben oder unten? f() +
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen 1. Juni 13 *Aufgabe 1. erechnen Sie durch Übergang zu Polar-, Kugel- oder Zylinderkoordinaten die Fläche bzw. das Volumen (a) der von der Lemniskate x y (x + y ) = umschlossenen
Tutorium Mathematik II, M Lösungen 1. Juni 13 *Aufgabe 1. erechnen Sie durch Übergang zu Polar-, Kugel- oder Zylinderkoordinaten die Fläche bzw. das Volumen (a) der von der Lemniskate x y (x + y ) = umschlossenen
Mathematik II: Übungsblatt 01: Lösungen
 N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
Linien- oder Kurvenintegrale: Aufgaben
 Linien- oder Kurvenintegrale: Aufgaben 4-E Das ebene Linienintegral Im Fall eines ebenen Linienintegrals liegt der Integrationsweg C häufig in Form einer expliziten Funktionsgleichung y = f (x) vor. Das
Linien- oder Kurvenintegrale: Aufgaben 4-E Das ebene Linienintegral Im Fall eines ebenen Linienintegrals liegt der Integrationsweg C häufig in Form einer expliziten Funktionsgleichung y = f (x) vor. Das
Komplexe Zahlen und Funktionen
 Komplexe Zahlen und Funktionen 1. komplexes Gleichungssystem z 1 iz 2 = i 2 z 2 + 3z 3 = 6 6i 2iz 1 3iz 3 = 1 8i 2. komplexe Gleichung Welche z C erfüllen die Gleichung 4z 2 4 z + 1 = 0? 3. konjugiert-komplexe
Komplexe Zahlen und Funktionen 1. komplexes Gleichungssystem z 1 iz 2 = i 2 z 2 + 3z 3 = 6 6i 2iz 1 3iz 3 = 1 8i 2. komplexe Gleichung Welche z C erfüllen die Gleichung 4z 2 4 z + 1 = 0? 3. konjugiert-komplexe
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
12 Übungen zu Gauß-Algorithmus
 Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 15
 5. Es sei Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 5 f(x, y) : x y, : x, y, x + y, y x. erechnen Sie f(x, y) d. Wir lösen diese Aufgabe auf zweierlei Art. Zuerst betrachten wir das Gebiet
5. Es sei Übungen zu Doppel- und Dreifachintegralen Lösungen zu Übung 5 f(x, y) : x y, : x, y, x + y, y x. erechnen Sie f(x, y) d. Wir lösen diese Aufgabe auf zweierlei Art. Zuerst betrachten wir das Gebiet
Abiturprüfung Mathematik 2012 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
10 Der Satz von Fubini
 er Satz von Fubini ie Bezeichnungen seien wie in den Paragraphen 8 und 9. Satz. (Satz von Tonelli Es sei f : d [, + ] messbar. (Aus 8 folgt dann, dass f, f y messbar sind, wobei klar ist, dass f, f y sind.
er Satz von Fubini ie Bezeichnungen seien wie in den Paragraphen 8 und 9. Satz. (Satz von Tonelli Es sei f : d [, + ] messbar. (Aus 8 folgt dann, dass f, f y messbar sind, wobei klar ist, dass f, f y sind.
Ministerium für Schule und Berufsbildung Schleswig-Holstein Kernfach Mathematik. Schriftliche Abiturprüfung 2015
 Bei der Bearbeitung der Aufgabe dürfen alle Funktionen des Taschenrechners genutzt werden. Aufgabe 3: Analytische Geometrie Das Modell einer Gartenlaterne kann als Stumpf einer regelmäßigen quadratischen
Bei der Bearbeitung der Aufgabe dürfen alle Funktionen des Taschenrechners genutzt werden. Aufgabe 3: Analytische Geometrie Das Modell einer Gartenlaterne kann als Stumpf einer regelmäßigen quadratischen
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 2005/06
 Übungen zu: Theoretische Physik I klassische Mechanik W 223 Tobias Spranger - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teaching.html 25. Janua6 Übungsblatt Lösungsvorschlag 3 Aufgaben,
Übungen zu: Theoretische Physik I klassische Mechanik W 223 Tobias Spranger - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teaching.html 25. Janua6 Übungsblatt Lösungsvorschlag 3 Aufgaben,
Ptolemäus (2. Jhdt. n. Chr.) gilt als erster Hersteller eines Globus und führt Längen- und Breitengrade zur Positionsangabe ein.
 Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
Ptolemäus (2. Jhdt. n. Chr.) gilt als erster Hersteller eines Globus und führt Längen- und Breitengrade zur Positionsangabe ein.
 Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
Die Gestalt der Erde Früheste Vorstellung: Ebene ( Erdscheibe ) Spätestens seit Pythagoras (6. Jhdt. v. Chr.) bzw. Aristoteles (4. Jhdt. v. Chr.) setzte sich die Ansicht durch, die Erde sei kugelförmig.
2 Das Bild In Schulbüchern und Arbeitsblättern sieht man oft Würfel -Darstellungen wie etwa in der Abbildung 1. Abb. 1: Was ist denn das?
 Hans Walser, [20131013], [20160331], [20160401] Quetschwürfel 1 Worum geht es? Es wird auf die Problematik der in Schulen weitverbreiteten Schrägbilder eingegangen. 2 Das Bild In Schulbüchern und Arbeitsblättern
Hans Walser, [20131013], [20160331], [20160401] Quetschwürfel 1 Worum geht es? Es wird auf die Problematik der in Schulen weitverbreiteten Schrägbilder eingegangen. 2 Das Bild In Schulbüchern und Arbeitsblättern
Räumliche Bereichsintegrale mit Koordinatentransformation
 Räumliche Bereichsintegrale mit Koordinatentransformation Gegeben seien ein räumlicher Bereich, das heißt ein Körper K im R 3, und eine von drei Variablen abhängige Funktion f f(,, z). Die Aufgabe bestehe
Räumliche Bereichsintegrale mit Koordinatentransformation Gegeben seien ein räumlicher Bereich, das heißt ein Körper K im R 3, und eine von drei Variablen abhängige Funktion f f(,, z). Die Aufgabe bestehe
