Koordinatensysteme. Grundkurs Architektur & Darstellung: Darstellende Geometrie. Lehrveranstaltungsinhalte
|
|
|
- Sven Schräder
- vor 6 Jahren
- Abrufe
Transkript
1 Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Lehrveranstaltungsinhalte Grundkurs Architektur & Darstellung: Darstellende Geometrie Koordinatensysteme Projektionen und Risse Parametrische Grundkörper Boolesche Operationen Raumtransformationen Schattenkonstruktion Perspektive Splines Flächen im Bauwesen Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Ebene kartesische Koordinaten Kugel/Zylinderkoordinaten Kartesische Normalkoordinaten Ebene, Raum Koordinatensysteme y e y x P E y E x P y P x-achse, y-achse: zwei (zueinander) orthogonale, im Gegenuhrzeigersinn orientierte Geraden (Strahlen) einer Ebene Ebenes kartesisches Rechtskoordinatensystem Welt/Benutzer Rechts/Links Polarkoordinaten e x x e x, e y... Einheitsstrecken Damit können Punkte der Ebene durch Zahlenpaare (Koordinaten) festgelegt werden. E x, E y... Einheitspunkte Bsp: P(x P = 3, y P = 2.3) 3 4
2 Räumliche kartesische Koordinaten Koordinatensysteme z P x-achse, y-achse, z-achse: drei (zueinander) orthogonale, orientierte Geraden durch einen gemeinsamen Punkt U (Koordinatenursprung) y z z y x U y Räumliches kartesisches Rechtskoordinatensystem Rechte Hand Regel x - + x Rechte Hand Regel: x-achse, y-achse und z-achse eines Rechtskoordinatensystems sind orientiert wie Daumen, Zeigefinger und Mittelfinger der rechten Hand Linkskoordinatensystem Rechtskoordinatensystem 5 6 Räumliche kartesische Koordinaten Ebene Polarkoordinaten P x z U P P P P, P, P... Grundriss, Aufriss, Kreuzriss des Punktes P Koordinatenweg: Ein in U beginnender und in P endender Streckenzug aus drei Kanten eines Koordinatenquaders, welcher alle drei Koordinaten von P zeigt y Koordinatenquader: Die Kantenlängen am Quader zeigen die Absolutbeträge der Koordinaten des Punktes P(x P, y P, z P ) 7 Pol ϕ r Q (r; ϕ) positiver Drehsinn Bsp: Q(7,5; 39º) Nullrichtung Zusammenhang kartesische/polarkoordinaten: x Q = r cos(ϕ) r 2 = x 2 Q + y 2 Q Ein Punkt der Ebene kann auch in Polarkoordinaten festgelegt werden: Q(r; ϕ) r... Abstand des Punktes zum Pol ϕ... Winkel zwischen der Nullrichtung und dem Vektor Pol - Punkt y Q = r sin(ϕ) tan(ϕ) = y Q / x Q ϕ x y r x Q Q y Q 8
3 Zylinderkoordinaten Kugelkoordinaten z z P r x U ϕ r P z P P y x U ϕ ψ P P(r; ϕ; ψ) y Kugelkoordinaten entsprechen der geographischen Länge und Breite auf der Erdkugel P(r; ϕ; z P ) Bsp: Tragen Sie den Punkt Q(r; 90; z p /2) ein! Bsp: Tragen Sie den Punkt Q(r; 100; 30) ein 9 10 Welt / Benutzer- Koordinatensysteme formz Koordinatensystem BKS x y z z WKS x z y BKS A absolute/relative Koordinaten W Weltkoordinaten-/ Benutzerkoordinatensystem C Kartesische- /Polarkoordinaten Frank O. Gehry DESIGN MUSEUM Weil am Rhein, Germany x y 11 12
4 Tipp für CAD Konstruktionen Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Vereinfachung der CAD Konstruktion durch Verwendung geeigneter Koordinatensysteme Möglichkeit der Koordinateneingabe über Tastatur und Maus Projektionen und Risse passende Wahl von Benutzerkoordinatensystemen (in formz über die Wahl der Referenzebene) Parallelprojektion Zentralprojektion Zentralprojektion Zentralprojektion O Zentralprojektion ist die Projektion aus einem Punkt (Zentrum) O auf eine zur Blickachse (optischen Achse) normale Bildebene (vgl. Filmebene in Fotografie) ist dem einäugigen Sehen nachgebildet (Netzhaut ist jedoch gekrümmt; Projektion auf gekrümmte Flächen tritt bei Panoramabildern auf) Bsp: Schattenwurf einer punktförmigen Lichtquelle Grundlegende Begriffe: O Projektionszentrum π Bildebene s = OP Sehstrahlen (Geraden durch O, werden projizierend abgebildet) Eigenschaften: geradentreu für allgemeine Geraden speziell: nicht mittelpunktstreu allgemein: nicht teilverhältnisstreu nicht parallelentreu s P c =s c P Π 15 16
5 F 2 Zentralprojektion Parallelprojektion Parallelprojektion ist die Projektion mittels paralleler Geraden auf eine (Bild-)ebene F i Fluchtpunkt (Zentralriss des Fernpunktes einer Geraden g) Parallele Geraden haben denselben Fluchtpunkt F 1 Bsp: Schattenwurf bei Sonnenschein P P s Q Q s Π Mario Botta EINFAMILIENHAUS RIVA SAN VITALE Tessin, Schweiz Nicholas Grimshaw SPORTHALLE FUER IBM Hampshire, England Parallelprojektion Parallelprojektion geradentreu teilverhältnistreu mittelpunktstreu parallelentreu Π Π 19 20
6 Teilverhältnis Sind A, B, C drei verschiedene Punkte auf einer Geraden g, so bezeichnet man mit TV(A,B,C) das Teilverhältnis der Punkte A,B,C. TV(A,B,C) := AC / BC > 0 TV(A,B,C) < 0 C liegt zwischen A und B Um welches Objekt handelt es sich hier? Motivation für Normalrisse z A M B C Beispiel: TV(A,B,C) = 5:2 = 2,5 Ist speziell M der Mittelpunkt der Strecke AB, so ist TV(A,B,M) = -1 x Aus einem Bild kann die Raumsituation nicht eindeutig rekonstruiert werden! y Normalrisse formz -- Views z Π 3 Π 2 P P P Kreuzriss Axonometrie Aufriss Grundriss x y P Π
7 Projektionen in formz Tipp für CAD Konstruktionen Verwendung geeigneter Normalrisse als Konstruktionsprinzip im CAD z.b.: Würfel auf eine Raumdiagonale stellen Tipp für CAD Konstruktionen Axonometrie Verwendung geeigneter Snapfunktionen als Konstruktionsprinzip im CAD Normale Axonometrie: Parallelprojektion mit zur Bildebene normalen Projektionsstrahlen Würfel minus Kugel (welche die Kanten berührt) Würfel- und Kugelmittelpunkt identisch wählen, den Kugelradius über Snap-Midpoint interaktiv Schiefe Axonometrie: Parallelprojektion mit zur Bildebene nicht parallelen Projektionsstrahlen eingeben 27 28
8 Abbildungsvorschrift Horizontalriss Axonometrische Methode: 1. Das abzubildende Objekt wird mit einem kartesischen Koordinatensystem {U; E x,e y,e z } verbunden. z P spezielle schiefe Axonometrie 2. Der Parallelriss des Koordinatensystems wird entweder durch Angabe von U p,e xp,e yp, E zp oder durch Angabe der orientierten Achsenbilder x P,y P,z P samt Verzerrungen v x, v y,v z so festgelegt, dass keine der Koordinatenebenen projizierend ist (d.h. die Geraden x P,y P,z P müssen paarweise verschieden sein.) 3. Die Risse von Objektpunkten werden über die Risse von Koordinatenwegen eingemessen ( axonometrisches Aufbauverfahren). x P E P z E P x E P y P P P(2/5/3) y P Gustav Peichl ORF-Studio, Graz z P x P y P x P y P v x =v y Frontalriss Isometrie spezielle schiefe Axonometrie z n spezielle normale Axonometrie x n y n z P y P y P z P Gustav Peichl Behördenzentrum, Frankfurt am Main x P v y =v z Christian de Portzamparc Cite de la Musique, Paris z n,x n = x n,y n = y n,z n v x =v y =v z 31 32
9 Schlagschatten einer Kugel bei Parallelbeleuchtung Umriss einer Kugel Lichtstrahlen, welche die Kugel berühren, bilden einen Drehzylinder (berührt längs eines Großkreises). Der Schlagschatten auf eine Ebene (ebener Schnitt des Lichtzylinders) wird von einer Ellipse berandet (Kreis, falls die Lichtstrahlen normal zur Schirmebene) 33 axonometric Normale Axonometrie Umriss der Kugel = Kreis oblique Schiefe Axonometrie Umriss der Kugel = Ellipse 34 Aufbauverfahren Aufbauverfahren z z z p z p y y y y Angabe y p x p v x = 1, v y =v z = 3/2 x 35 Konstruktion v x = 1, v y =v z = 3/2 x p y p x 36
10 Aufbauverfahren Einschneideverfahren z p z P P n Q Designertisch y y Q n P Ergebnis v x = 1, v y = v z = 3/2 x p y p x 37 Q 38 Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Parametrische Grundkörper Was sind parametrische Grundkörper? Parametrische Grundkörper sind als Grundelemente in CAD-Paketen enthalten werden über die Festlegung der sie bestimmenden Parameter konstruiert können nachträglich durch Veränderung der Parameter manipuliert werden Parametrische Grundkörper in formz Quader (cube), Kegel (cone), Zylinder (cylinder), Kugel (sphere), Torus (torus),... Geodätische Kuppel (spheric geodesic sphere), Platonische Körper (spheric ) 39 40
11 Parametrische Grundkörper Quader ( Cube ) Drei verschiedene Angabemöglichkeiten Quader Höhe h 1 Breite h Länge 1 1 Sears Tower, Chicago, US Flächenmodell (Surface) Volumsmodell (Solid) Flächen- und Volumsmodelle Parametrische Grundkörper Für die CAD Modellierung Flächenmodell (surface) stellt die Oberfläche (Haut) eines Objektes dar Volumsmodell (solid) Objekt als Vollkörper Kegel Vor allem für Darstellungszwecke Kantenmodell (wireframe) repräsentiert Kanten und ausgewählte Kurven auf der Oberfläche eines Objektes Norman Foster Millenium Tower Tokyo, Japan 43 44
12 Kegel (Cone) Drei verschiedene Angabemöglichkeiten Geometrie der Kegelflächen Höhe Mittelpunkt des Basiskreises Radius 1 2 h 1 2 h Angabe durch Spitze S und Leitkurve l: Die Kegelfläche besteht aus allen Geraden (Erzeugenden), welche durch die Spitze S gehen und die Leitkurve l treffen. S l Flächenmodell Volumsmodell Tangentialebenen In allen Punkten einer Erzeugenden berührt dieselbe Tangentialebene Parametrische Grundkörper Zylinder (Cylinder) Drei verschiedene Angabemöglichkeiten Zylinder 3 3 Höhe h h 1 1 Mittelpunkt des Basiskreises Radius 2 2 Hans Hollein HAAS-HAUS Wien, Oesterreich 47 Flächenmodell Volumsmodell 48
13 Geometrie der Zylinderflächen Angabe durch Erzeugendenrichtung und Leitkurve: Die Zylinderfläche besteht aus allen Geraden (Erzeugenden), welche die Leitkurve l treffen und die gegebene Richtung besitzen Moderne CAD-Pakete speichern auch den Konstruktionsgang Dadurch wird die nachträgliche Manipulation eines fertigen Objektes durch die Variation der verwendeten Parameter einfach möglich Beispiel: Parametrisches Konstruieren im CAD Tangentialebenen In allen Punkten einer Erzeugenden berührt dieselbe Tangentialebene Radius vergrößern Extrusion paralleles Extrudieren Eine Punktmenge der Ebene (Polygon, Kurve, Bereich, ) wird in Extrusionsrichtung stetig parallelverschoben und überstreicht dabei ein Extrusionsobjekt Extrusion zentrales Extrudieren alle Punkte einer Punktmenge der Ebene (Polygon, Kurve, Bereich, ) werden durch geradlinige Strecken mit dem Extrusionszentrum verbunden, diese bilden das Extrusionsobjekt 51 52
14 Extrusion als Konstruktionsprinzip Parametrische Grundkörper Erkennen von Extrusionskörpern im Objektaufbau vereinfacht die Modellierung Bsp: Die Profile p 1 und p 2 werden parallel extrudiert, die beiden Extrusionskörper zum fertigen Objekt vereinigt Kugel p 1 p 2 Adrian Fainsilber CITE DES SCIENCES ET DE'L INDUSTRIE, Paris, Frankreich Kugel (Sphere) Drei verschiedene Angabemöglichkeiten Parametrische Grundkörper Mittelpunkt 4 Santiago Calatrava Funk - Fernsehturm Montjuic Spanien Torus Radius 2 Flächenmodell Volumsmodell Takasaki Masaharu ASTRONOMICAL MUSEUM Kihoku-cho, Japan 55 56
15 Torus - Erzeugung Rotiert ein Kreis k um eine Achse a, die in der Kreisebene liegt, aber kein Kreisdurchmesser ist, so entsteht ein Torus. a...achse Mittelpunkt Torus - Bezeichnungen Je nachdem ob die Anzahl der Schnittpunkte von k und a gleich 0,1, oder 2 ist, sprechen wir von einem Ringtorus, Dorntorus, oder Spindeltorus k...meridiankreis m Mittenkreis Ringtorus Dorntorus Spindeltorus Torus (Torus) Drei verschiedene Angabemöglichkeiten Flächen/Volumsmodelle 1 3 Mittenkreisradius Meridiankreisradius 2 Ringtorus Dorntorus Spindeltorus
16 Ebene Schnitte des Torus Villarceau-Kreise: Jeder Schnitt eines Ringtorus mit einer Doppeltangentialebene zerfällt in zwei kongruente Kreise, welche von Y. Villarceau (1848) entdeckt wurden. Ein Ringtorus enthält mithin neben den Parallelund Meridiankreisen noch unendlich viele weitere Kreise. Konvexität Konvexer Bereich: Punktmenge welche die Verbindungsstrecke von je zwei beliebig in ihr gewählten Punkten zur Gänze enthält (in 2D, 3D, ) konvex nicht konvex 61 Polyeder: ebenflächig begrenztes Objekt in 3D Konvexes Polyeder: Polyeder, dessen Volumsmodell ein konvexer Bereich in 3D ist 62 Konvexe und nichtkonvexe Polyeder Topologisch äquivalente Körper sind durch stetige Deformation ineinander überführbar Tetraeder Platonische Körper Oktaeder Ikosaeder konvex (stets topologisch äquivalent zu Kugel, Quader, ) nicht konvex (topologisch verschieden) Würfel Pentagondodekaeder 63 64
17 Platonische Körper Die konvexen Polyeder, deren sämtliche Seitenflächen von kongruenten regelmäßigen Polygonen berandet werden und bei denen von jeder Ecke gleich viele Kanten ausgehen sind genau die 5 Platonischen Polyeder (Platonische Körper). Tetraeder: 4 gleichseitige Dreiecke, 4 Ecken, 6 Kanten Hexaeder (Würfel): 6 Quadrate, 8 Ecken, 12 Kanten Oktaeder: 8 gleichseitige Dreiecke, 6 Ecken, 12 Kanten Pentagondodekaeder: 12 regelmäßige Fünfecke, 20 Ecken, 30 Kanten Ikosaeder: 20 gleichseitige Dreiecke, 12 Ecken, 30 Kanten Dualität der Platonischen Körper Die Mittelpunkte der Seitenflächen eines Platonischen Körpers (Polyeders) sind ebenfalls die Ecken eines Platonischen Körpers (Polyeders). Tetraeder Tetraeder Würfel Oktaeder Sie besitzen eine Umkugel, Inkugel und Kantenkugel. Dodekaeder Ikosaeder Platonische Körper im Bauwesen Tetraeder im Kunstturm Mito Eulersche Polyederformel Architekt Arata Isozaki Unter der Voraussetzung, dass das Polyeder topologisch äquivalent zur Kugel ist ( kein Loch hat ) gilt: Pentagondodekaeder in einer Wohnsiedlung Architekt Zvi Hecker e k + f = 2 e... k... f... Anzahl der Ecken Anzahl der Kanten Anzahl der Flächen 67 68
18 Parametrische Grundkörper Geodesic Spheres Geodesic Sphere Geodesic Spheres entstehen aus den platonischen Grundkörpern durch Teilung der Flächen in kleinere Dreiecke und Verlagern der eingefügten Punkte auf die den Grundkörper einhüllende Kugel Verallgemeinerung dieses Prinzips führt uns später zu den Unterteilungsflächen (subdivision surfaces) Geodesic Spheres im CAD In vielen CAD Paketen werden Geodesic Spheres aus dem Grundkörper Ikosaeder erzeugt Seitenflächen einer Geodesic Sphere keine gleichseitigen Dreiecke! 2 Unterteilungsvarianten Variante 1: Seitenflächen des Ausgangspolyeders werden immer feiner unterteilt (z.b. 3DSMax) Variante 2: Seitenflächen aus dem vorigen Unterteilungsschritt werden nach demselben Schema weitergeteilt (z.b. formz) 71 72
19 Geodesic Sphere Level Unterteilungsvariante 1 Geodesic Sphere Level Unterteilungsvariante 2 Geodesic Spheres mit Basisobjekt Ikosaeder Anzahl der Dreiecke im Level k 20*(k+1)^2 Geodesic Spheres mit Basisobjekt Ikosaeder Anzahl der Dreiecke im Level k 20*4^k (oder rekursiv 4 mal die Anzahl der Dreiecke aus dem vorigen Schritt) Level 1 (20*4 = 80 triangles) Level 2 (20*9 = 180 triangles) Level 3 (20*16 = 320 triangles) Level 1 (20*4 = 80 triangles) Level 2 (20*16 = 4*80 = 320 triangles) Level 3 (20*64 = 4*320 = 1280 triangles) Level 4 (20*256 = 4*1280 = 5120 triangles) Geodesic Spheres in formz Befehl Spherical Object Geodesic Spheres weitere Ausgangskörper Als Basisobjekte auch Tetraeder oder Oktaeder Unterteilungsvarianten wie Ikosaeder Tetraeder Oktaeder Anzahl der Level definieren 75 Grundkörper Level 1 Level 2 Level 3 76
20 Geodesic-Spheres in der Architektur Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Boolesche Operationen Durchschnitt Kugel Würfel Differenz Kugel \ Würfel Differenz Würfel \ Kugel Boolesche Operationen Die Mengenoperationen Vereinigung, Durchschnitt und Differenz treten im computergestützten Konstruieren im Zusammenhang mit geometrischen Objekten auf. Ebene: z.b. bei Vielecken Raum: Volumenkörper 2D Ausgangsobjekte A B Boolesche Operation Vereinigung (Union) Vereinigung A B A B 3D Vereinigung A B Durchschnitt A B Differenz A \ B Differenz B \ A 79 80
21 Boolesche Operation Durchschnitt (Intersection) Boolesche Operation Differenz (Difference) Ausgangsobjekte Durchschnitt A B Ausgangsobjekte Differenz A \ B 2D A A 2D A A B B B B 3D 3D Boolesche Operation Differenz (Difference) Boolean Split 2D Ausgangsobjekte A Differenz B \ A A CAD Pakete stellen oft auch noch eine Zerlegung in die einzelnen Schnittelemente zur Verfügung B B 3D One-way B-Split B / A One-way B-Split A / B Two-way B-Split 83 84
22 Boolean Operations in formz Boolesche Operationen in der Architektur Union Intersection Difference Boolean split Ossarium im Friedhof von San Cataldo Modena, Italien Trim, Split für Flächenmodelle Ausgangsobjekte Übungsbeispiele zu den Booleschen Operationen Kennzeichnen Sie (durch Anmalen) das Ergebnis nach Anwendung der angeführten Booleschen Operationen auf die Ausgangsobjekte (= Bereiche mit den gegebenen Linien als Rand) 1 Split both objects (Explosionsdarstellung) Trim first object Differenz: Ellipse minus Polygon Durchschnitt der drei Bereiche 87 88
23 Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Kongruenztransformation Schiebung Vektor Drehung Punkt / Gerade Spiegelung gleichsinnig / ungleichsinnig Schraubung Skalierung Achse Faktor Punkt / Gerade / Ebene Raumtransformationen Wird ein Objekt aus einer Position des Raumes in eine andere Position so übergeführt, dass Längen erhalten bleiben, dann spricht man von einer Kongruenztransformation Als Folge der Längentreue ergibt sich die Winkeltreue Man unterscheidet zwischen gleichsinnigen und ungleichsinnigen Kongruenzen: eine gleichsinnige Kongruenztransformation bildet ein Rechtssystem auf ein Rechtssystem ab eine ungleichsinnige Kongruenztransformation bildet ein Rechtssystem auf ein Linkssystem ab Kongruenztransformationen Raumtransformationen Gleichsinnige Kongruenztransformationen: Schiebung Drehung um eine Gerade Spiegelung an einer Geraden Schraubung Ungleichsinnige Kongruenztransformationen: Spiegelung an einer Ebene Punktspiegelung Gleitspiegelung Schiebung (Translation) Eine Schiebung wird durch einen Schiebvektor festgelegt
24 Schiebung (Translation) Raumtransformationen Drehung (Rotation) Eine Drehung wird durch eine Drehachse und den Drehwinkel bestimmt. Fa. Herold, Mödling, Austria Drehung (Rotation) Raumtransformationen Spiegelung an einer Geraden Eine Spiegelung an einer Geraden kann durch eine Drehung ersetzt werden (Drehwinkel 180 ; Drehachse = Spiegelachse). Tower Dallas, US Bemerkung: Die Spiegelung an einer Geraden im Raum ist gleichsinnig! 95 96
25 Diskrete Schraubung Je zwei gleichsinnig kongruente Lagen eines starren Körpers lassen sich im allgemeinen durch eine diskrete Schraubung ineinander überführen Diese setzt sich zusammen aus einer Drehung um eine Achse a und einer Schiebung längs dieser Achse In Sonderfällen hängen zwei gleichsinnig kongruente Lagen durch eine reine Schiebung oder eine reine Drehung zusammen a 97 Ein räumlicher Bewegungsvorgang, der aus einer gleichförmigen Drehung um eine Achse a und einer gleichförmigen Schiebung parallel zu a zusammengesetzt ist, heißt Schraubung. Der Drehwinkel φ (gemessen im Bogenmaß) und die zugehörige Länge s der Schiebstrecke sind direkt proportional: wird um den Winkel φ gedreht, so wird um die Strecke s = p φ verschoben. Der konstante Quotient p = s / φ heißt Schraubparameter. Zu einer vollen Umdrehung (Drehwinkel 2π) gehört als Länge der Schiebstrecke die Ganghöhe h. Stetige Schraubung (Screw) φ a... Schraubachse h... Ganghöhe 98 Raumtransformationen Spiegelung (Reflection) Spiegelung (an einer Ebene) z z x Eine Spiegelung an einer Ebene wird durch die Spiegelebene angegeben. y x y Die Spiegelung an einer Ebene ist gegensinnig! 99 Cesar Pelli PETRONAS TOWERS Kuala Lumpur, Malaysia 100
26 Raumtransformationen Raumtransformationen z Punktspiegelung Gleitspiegelung Die Punktspiegelung im Raum kann auch durch drei Spiegelungen (an zueinander normalen Spiegelebenen) erzeugt werden und ist daher ungleichsinnig. x y* y x* P P P* Bemerkung: Die Punktspiegelung in der Ebene ist zugleich eine Drehung um 180 Grad und daher gleichsinnig. z* Eine Gleitspiegelung setzt sich aus einer Spiegelung an einer Ebene und einer Schiebung parallel zu dieser Ebene zusammen Gleitspiegelung in der Ebene Skalierung (Scale) C 1 B 1 M 1 = M 2 A 2 B 2 C 2 Gegeben sind drei Skalierungsfaktoren s x, s y, s z Die zugehörige Skalierung bildet dann einen Punkt P(x/y/z) auf den Punkt P (s x x/s y y/s z z) ab z A 1 a Spiegelung an a + Schiebung längs a a Bei gleichen Faktoren, s=s x =s y =s z, ergibt sich eine zentrische Ähnlichkeit mit dem Koordinatenursprung als Zentrum, diese Abbildung ist winkeltreu x y Die Mittelpunkte der Verbindungsstrecken entsprechender Punkte X 1,X 2 liegen auf a
27 Zusammensetzung von Raumtransformationen Zusammensetzung von Raumtransformationen Durch Zusammensetzen (Hintereinanderausführen) von Kongruenztransformationen entsteht wieder eine Kongruenztransformation: 1) gleichsinnig gleichsinnig gleichsinnig 2) ungleichsinnig ungleichsinnig gleichsinnig 3) gleichsinnig ungleichsinnig ungleichsinnig Zusammensetzung ist i.a. nicht kommutativ (auf die Reihenfolge kommt es an) Drehachse Drehachse Beispiel: Gleitspiegelung = Spiegelung an Ebene Schiebung (ungleichsinnig = ungleichsinnig gleichsinnig) zuerst Schiebung, dann Drehung Schiebvektor zuerst Drehung, dann Schiebung Schiebvektor Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Grundbegriffe der Schattenkonstruktion Schatten bei Parallelbeleuchtung Eigenschatten Dem Licht abgewandte Teile eines Objektes (lokal zu entscheiden) liegen im Eigenschatten; die Eigenschattengrenze trennt Eigenschattenbereiche von den dem Licht zugewandten Bereichen Schlagschatten Zur Konstruktion der Schlagschattengrenze brauchen nur die Schlagschatten für die Punkte der Eigenschattengrenze konstruiert zu werden
28 Grundbegriffe der Schattenkonstruktion Wichtige Schattenregeln Bei Parallelbeleuchtung sind alle Lichtstrahlen zu einer orientierten Geraden parallel Lichtstrahl s durch einen Punkt P schneidet eine Schirmebene im Schlagschattenpunkt P s Die Lichtstrahlen, welche eine Gerade treffen sind Teil einer Ebene (Lichtebene) Der Schlagschatten einer Geraden geht durch den Spurpunkt G der Geraden auf der Schirmebene. G P s P s Bei Parallelbeleuchtung haben parallele Geraden parallele Schatten z Schatten bei Parallelbeleuchtung z Eigenschatten P l l l l l Q l x y x y Angabe: Objekt & Lichtrichtung
29 z Schlagschatten 1.Teil z Schlagschatten 2.Teil l l l l l l x y x y z Schlagschatten 3.Teil z Ergebnis (mit Lichtstrahlen) l l l l l l x Doppelschattenpunkt y x y
30 z Ergebnis (ohne Lichtstrahlen) l l l Übungsbeispiel Schatten bei Parallelbeleuchtung l Konstruieren Sie für die Parallelbeleuchtung mit Lichtrichtung l alle am Objekt auftretenden Schlagund Eigenschatten, sowie den Schlagschatten des Objektes in die xy-ebene z l l x y y x Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Zentralprojektion O Perspektive Grundlegende Begriffe: O Projektionszentrum π Bildebene s = OP Sehstrahlen (Geraden durch O, werden projizierend abgebildet) s P π Eigenschaften: geradentreu für Geraden allgemeiner Lage gilt: nicht teilverhältnistreu (speziell: nicht mittelpunktstreu) nicht parallelentreu P c =s c
31 Fluchtpunkt einer Geraden Fluchtpunkt einer Geraden F 2 Fluchtpunkt F g der Geraden g: O Verschiebe g durch O und schneide mit der Bildebene π g F 1 F g π Parallele Geraden haben denselben Fluchtpunkt F i g c π Hauptgeraden Hauptgerade = Gerade h parallel zur Bildebene Perspektive bei lotrechter Bildebene In der Aufnahmesituation ist das Bild h c einer Hauptgeraden zur Raumlage h parallel. Parallele Hauptgeraden haben parallele Zentralrisse h O π π Horizont O Wir beziehen das Objekt im folgenden auf ein kartesisches x,y,z- Koordinatensystem, dessen z-achse lotrecht und nach oben orientiert ist. Die Koordinatenebene π 1 ist dabei horizontal. h c π 1 Der Horizont enthält die Fluchtpunkte aller horizontalen Geraden
32 1. Perspektive bei horizontaler Blickachse Durchschnittverfahren π a d π 1 Der Abstand zwischen Augpunkt O und der Koordinatenebene π 1 heißt Aughöhe a Der Abstand zwischen Augpunkt O und der Bildebene Π heißt Distanz d Durchschnittverfahren Durchschnittverfahren 1. Wahl des Augpunktes O der horizontalen Blickachse (Hauptsehstrahl) und der lotrechten Bildebene π O O π 2. In Grund- und Aufriss: Ermittlung der Schnittpunkte der Sehgeraden durch den Augpunkt O mit der erstprojizierenden Bildebene π O O π P c P P c P
33 Durchschnittverfahren 3. Wir legen in die Bildebene ein kartesisches Rechtskoordinatensystem ξ,η Hauptpunkt H als Ursprung Horizont als ξ-achse η H ξ H =η ξ Durchschnittverfahren 4. Die ξ- bzw. η-koordinate des Zentralrisses P c eines Objektpunkts P oder eines Fluchtpunkts Y uc kann im Grundriss bzw. im Aufriss unverzerrt abgelesen werden P c η ξ P c 5. Im Zeichenfeld können die unverzerrte ξ- bzw. η-koordinate des Zentralrisses P c ins (ξ,η)- Koordinatensystem eingetragen werden η H ξ P c η ξ z C L =P A Durchschnittverfahren Beispiel aus den Übungen Vervollständigen einer vorliegenden Perspektive Vervollständigen Sie von dem im axonometrischen Riss gegebenen Objekt die vorliegende Perspektive! z p J I 1 z c x p y p K =N F D =M y B =E =G C c A c F J x π, C =I M P =N K =L D G y H A =B =1 E Y u c D c L c J c E c K c P c N c B c H G c a=2,5 c X u a a 2a 131 x c y c 132
34 Übungsbeispiel: Vervollständigen einer vorliegenden Perspektive Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Vervollständigen Sie von dem im axonometrischen Riss gegebenen Objekt die vorliegende Perspektive! z c x p z p y p Splines x c y c Schiffbau Automobilbau Architektur Interpolierende Kurve Interpolation & Approximation Geg: Menge von Punkten Ges: Kurve, welche die Punkte interpoliert (d.h. die Kurve enthält die gegebenen Punkte) oder approximiert (d.h. der Verlauf der Punkte wird durch die Kurve nur angenähert) Es gibt unendlich viele interpolierende oder approximierende Kurven. CAD-Pakete bieten verschiedene Lösungen an, die Auswahl hängt vom Designzweck ab Approximierende Kurve Beispiel zur Approximation Geg: Datenpunkte Ges: Linearer Ausgleich, sodass die Punkte von der Ausgleichsgerade möglichst wenig abweichen f(x) f(x) = *x x Methode (Gauß): Minimierung der Summe der Fehlerquadrate Fehler eines Punktes: Abstand zur Ausgleichsgeraden in Richtung parallel zur y-achse
35 Bézier-Kurven Grad einer Bézier-Kurve Bézier-Kurven wurden aus dem Bedarf für Freiformkurven in der CAD/CAM/CAE-Technik entwickelt: P. de Casteljau (1959) bei Citroën, P. Bézier (1962) bei Renault Standardmäßig sind Bézier-Kurven in vielen CAD-Paketen enthalten Bézier-Kurven werden durch Angabe eines Polygons gesteuert. Dieses Polygon heisst Kontrollpolygon, seine Ecken werden Kontrollpunkte genannt Eine Bézier-Kurve mit n+1 Kontrollpunkten besitzt den Grad n (= Grad der in der mathematischen Beschreibung auftretenden Polynome) 2 Kontrollpunkte Grad 1 Bezier- Kurve ist Verbindungsstrecke der beiden Kontrollpunkte b 1 3 Kontrollpunkte Grad 2 Bezier- Kurve ist Parabelbogen; Kontrollpunkte: Endpunkte b 0 b 2 und Schnittpunkt b 1 der Tangenten T 0, T 2 in den Endpunkten b 0 T 0 T 2 b Grad einer Bézier-Kurve Geometrischer Algorithmus zur Konstruktion von Bezier-Kurven Grad 1 lineare Bézier-Kurve Grad 2 quadratische Bézier- Kurve Grad 3 kubische Bézier-Kurve Für eine quadratische Bezier-Kurve (Parabelbogen) ist der verwendetet Algorithmus die Fadenkonstruktion einer Parabel Dieser wird später auf höhere Grade verallgemeinert (Algorithmus von de Casteljau)
36 Fadenkonstruktion einer Parabel Fadenkonstruktion einer Parabel b 1 Geg: 2 Linienelemente (b 0, T 0 ), (b 2, T 2 ) einer Parabel b 1 Methode: Übertragen von Teilverhältnissen Ges: weitere Linienelemente (d.h. Punkte mit Tangenten) b 11 (0.25) T 0 T 2 Konstruktion für t = 0.25, 0.5, 0.75 b 01 (0.25) b 0 2 (0.25) Kurvenpunkt b 0 b 0 b 2 b 2 0 t TV(b 0, b 1, b 0 1 ) = TV(b 1, b 2, b 1 1 ) = TV(b 0 1, b 1 1, b 0 2 ) 142 b 0 b 01 (0.5) b 01 (0.25) b 01 (0.75) Fadenkonstruktion einer Parabel b 1 b Kurven punkt b 11 (0.25) b 11 (0.5) b 11 (0.75) b Algorithmus von de Casteljau Ist eine Verallgemeinerung der Fadenkonstruktion der Parabel. 1) Teilverhältnis TV(0,1,t) auf die Strecken des Polygons übertragen 2) Verbinden der erhaltenen Teilungspunkte zu einem neuen Polygon Wiederholtes Anwenden von 1 und 2 liefert schrittweise (oberer Index) Polygone mit absteigender Eckenzahl bis schließlich nur noch der Kurvenpunkt übrigbleibt. b 1 1 Geg: Kontrollpunkte b 0,...,b n Ges: Punkte der Bezier-Kurve n-ten Grades Jeder Punkt ist genau einem Parameter t aus dem Intervall [0,1] zugeordnet: t=0 entspricht b 0 t=1 entspricht b n b 1 b 2 b 0 1 b 0 b 0 2 b t 1 b 1 2 b 3 b
37 Algorithmus von de Casteljau Beispiele von Bézier-Kurven Kurven vom Grad 3 de Casteljau-Schema: b 0 b 1 b 1 0 b 2 b 1 1 b 2 0 b 3 b 1 2 b 2 1 b 3 0 b 1 1 b 1 b 2 b 2 0 b 2 1 b 3 0 b 1 0 b 1 2 Kurven vom Grad 4 b 3 0 t 1 b b 0 Linienelement Bézier-Kurven Eigenschaften Endpunktinterpolation + Tangenteneigenschaft (endpoint interpolation): Eine Bézier-Kurve interpoliert den ersten und den letzten Punkt des Kontrollpolygons und besitzt dort die erste bzw. letzte Strecke des Kontrollpolygons als Tangente. Bézier-Kurve Kontrollpolygon b n Linienelement 147 Wiederholung: Konvexe Hülle konvexer Bereich ist eine Punktmenge, welche die Verbindungsstrecken aller ihrer Punktepaare enthält konvexe Hülle ist der kleinste konvexe Bereich, welcher eine gegebene (Punkt-) Menge enthält 148
38 Bézier-Kurven Eigenschaften Konvexe Hülle Eigenschaft (convex hull property): Eine Bézier-Kurve liegt in der konvexen Hülle ihres Kontrollpolygons. Bézier-Kurven Eigenschaften Variationsreduzierende Eigenschaft in der Ebene [im Raum] (variation diminishing property): Geg: Bézier-Kurve, beliebige Gerade [Ebene] Eine Bézier-Kurve wechselt die Seite jeder beliebigen Gerade [Ebene] nicht öfter als das Kontrollpolygon. 2 Testgeraden Bézier-Kurven Eigenschaften Lineare Präzision (linear precision): Liegen die Kontrollpunkte b 0,...,b n einer Bézier- Kurve kollinear (= auf einer Geraden), dann liegt die Bézier-Kurve auf der Strecke b 0 b n b 0 Kontrollpolygon Bézier-Kurve b n 151 Unterteilung (subdivision): Gegeben sei eine Bézier- Kurve mit Kontrollpolygon (b 0,...,b n ) bzgl. [0,1]. Manchmal ist es notwendig, eine einzelne Bézier-Kurve so in zwei Teilstücke zu zerlegen, dass sie gemeinsam identisch sind zur Ausgangskurve. 1. Unterteilungsalgorithmus von de Casteljau liefert auch die Kontrollpolygone (c 0,...,c n ) und (d 0,...,d n ) der Bézier-Kurve bzgl. der Intervalle [0,t] bzw. [t,1]. Bézier-Kurven Eigenschaften b 0 b 2 b 1 c 2 c 3 c 1 c 0 d 0 Beispiel: n=3 b 3 d 1 d 2 d 3 152
39 Bézier-Kurven Eigenschaften Bézier-Kurven Eigenschaften Unterteilung (subdivision): Unterteilung (subdivision): Gegeben sei eine Bézier- Kurve mit Kontrollpolygon (b 0,...,b n ) b 1 b 2 Gegeben sei eine Bézier- Kurve mit Kontrollpolygon (b 0,...,b n ) b 1 b 2 2. Wiederholte Unterteilung mit de Casteljau liefert eine rasch gegen die Kurve konvergierende Polygonfolge. 3. Durch Eckenabschneiden entstehen keine zusätzlichen Seitenwechsel Variationsreduzierende Eigenschaft gilt b 3 b 3 b 0 b Übungsbeispiele zu Freiformkurven Übungsbeispiel zu Bézier-Kurven Begründen Sie, warum es sich bei den folgenden Kurven jeweils nicht um eine Bézier Kurve mit zugehörigem Kontrollpolygon handelt: Gegeben ist das Kontrollpolygon einer Bézier-Kurve Konstruieren Sie mit dem Algorithmus von de Casteljau zum Parameterwert t=1/3 einen Punkt der Bézier-Kurve Skizzieren Sie die zugehörige Bézier-Kurve
40 3D-Bézier-Kurven Spline-Kurven Geg: Kontrollpunkte im 3-Raum Ges: Bézier-Kurve b 2 b 3 Bézier- Kurve Bézier-Kurven sind durch das Kontrollpolygon bestimmt. Damit bewirkt die Änderung eines Kontrollpunktes eine Veränderung des gesamten Kurvenverlaufes (global). ungünstig für Designzwecke b 0 b 1 Die Bézier-Kurve liegt in der konvexen Hülle Kontrollpolygon ihres Kontrollpolygons (hier: Tetraeder) 157 Eine mögliche Abhilfe: Kurven niedrigen Grades zu einer Kurve zusammensetzen Spline-Kurve, lokale Kontrolle, an den Segmenttrennstellen geeignete Übergangsbedingung (z.b. gemeinsame Tangente). 158 Grad und Kontrollpunkte von Splines Grad und Kontrollpunkte von B-Spline Kurven Viele Splinetypen (B-Spline, NURBS, continuous Bezier in FormZ, interpolierende kubische Splines) sind aus Bezierkurven zusammengesetzt Der Grad der Bezier- Segmente heißt Grad der Splinekurve Die Kontrollpunkte des Splines sind oft von den Kontrollpunkten der Beziersegmente verschieden kubische B-Spline Kurve mit B-Spline Kontrollpolygon kubische B-Spline Kurve mit Kontrollpolygonen der kubischen Beziersegmente
41 Spline-Kurven Beispiel: 2 mögliche Kurven zum selben Kontrollpolygon B-Spline Kurven, NURBS B-Spline-Kurven wurden ins Computer Aided Design von J. Ferguson (1964) bei Boeing eingeführt. In CAD-Systemen taucht auch oft der Name NURBS (= Non-Uniform Rational B-Splines) auf. Bézier-Kurve (Grad 13) B-Spline-Kurve Grad 2 B-Spline-Kurve Grad 3 Kurve ist aus Parabelsegmenten mit tangentenstetigem Übergang zusammengesetzt. B-Spline (Grad 2) 161 B-Spline-Kurve Grad 7 (= Bézier) 162 B-Spline Kurven Eine B-Spline-Kurve vom Grad n besteht aus Bezier-Kurven vom Grad n, welche mit optimaler Glattheit zusammengesetzt sind: Grad 2: stetige Tangente Grad 3: stetige Krümmung... Angabe: Kontrollpolygon, Grad, Knoten (hängt mit mathematischer Beschreibung zusammen, für Design kaum verwendbar) B-Spline Kurven B-Spline-Kurven können offen oder geschlossen sein: Bei einer geschlossenen B-Spline-Kurve wird ein geschlossenes Kontrollpolygon zur Gänze geglättet Im offenen Modus hat ein geschlossenes Polygon einen Anfangspunkt und einen damit identischen Endpunkt; dort wird nicht geglättet geschlossen offen offen
42 B-Spline-Kurven Eigenschaften NURBS Gewichte (weights) Bei offenen B-Spline Kurven: Endpunkte mit Tangenten werden durch das Kontrollpolygon angegeben Kurve liegt in der konvexen Hülle des Kontrollpolygons Es gilt die variationsreduzierende Eigenschaft B-Spline-Kurven und somit auch die Bézier-Kurven sind Spezialfälle von NURBS (= Non-Uniform Rational B- Splines) NURBS haben einen zusätzlichen Designparameter Gewichte. Standardmäßig sind alle Gewichte gleich 1, dann stimmt die NURBS- Kurve mit der gewöhnlichen B-Spline- Kurve überein Das Erhöhen des Gewichtes eines Kontrollpunktes bewirkt, dass die Kurve zu diesem Kontrollpunkt hingezogen wird Multipliziert man die Gewichte aller Punkte mit demselben Faktor, so erhält man die ursprüngliche Kurve Kegelschnitte als NURBS Tipps zum CAD Konstruieren mit Splinekurven b 1 w 1 > 1 w 1 = 1 0 < w 1 < 1 Von den Kegelschnitten (Kreis, Ellipse, Parabel, Hyperbel) kann nur die Parabel als Bézier-Kurve (vom Grad 2) repräsentiert werden. Durch das Verwenden von Gewichten können alle Kegelschnittstypen als NURBS vom Grad 2 erhalten werden. Komplexe Kurvenformen mittels NURBS modellieren, und Feinabstimmungen durch Veränderung der Kontrollpunkte und der Gewichte vornehmen. w 1 > 1 Hyperbelbogen w 1 = 1 Parabelbogen 0 < w 1 < 1 Ellipsenbogen b 0 b
43 Splines in der Architektur Unterteilungskurven (Subdivision curves) Grundideen der Unterteilung gehen zurück in die 40er Jahre als G. Rahm corner cutting dazu verwendete glatte Kurven zu beschreiben Anwendungen im CAD, geometrischen Modellieren und in der Computergraphik Grand Arbour, Brisbane, Australia Chaikins Algorithmus Chaikins Algorithmus stationäres Unterteilungsschema, d.h. in jedem Iterationsschritt k=1,2, wird dieselbe Methode (corner cutting) angewendet für k erhält man so eine quadratische B-Spline Kurve P 1 P 2 Q 1 R 1 R 0 Q 2 Q 0 P 0 R 2 Q 3 P 3 R 3 P 4 In jedem Iterationsschritt werden die einzelnen Strecken bei ¼ bzw. ¾ geteilt und die neuen Punkte verbunden
44 Chaikins Algorithmus Unterteilungskurven Weitere Unterteilungsalgorithmen für Kurven (und auch Flächen) werden im Wahlpflichtfach CAAD und Geometrie vorgestellt Bsp: Interpolierender Unterteilungsalgorithmus k = 0 k = 1 k = k = 3 k = 4 k = Übungsbeispiel Unterteilungskurven Konstruieren Sie für das gegebene Polygon den ersten Verfeinerungsschritt im Chaikin Algorithmus In welchem Verhältnis werden die Seiten jeweils unterteilt? Welche Art von Freiformkurve erhält man so bei fortgesetzter Unterteilung? Institut für Diskrete Mathematik und Geometrie Geometrisches Modellieren und Industrielle Geometrie Prof. Dr. H. Pottmann Flächen im Bauwesen SECC Conference Center, Glasgow, Scotland Office Building, Prague, Czech Republic Reorganized Church of Jesus Christ of Latter Day Saints Temple, Independance, Missouri, USA
45 a Drehflächen (Rotational Surfaces) Eine Drehfläche entsteht durch stetige Drehung einer erzeugenden Kurve e um eine feste Achse a. e Drehflächen Die einzelnen Punkte der Erzeugenden e beschreiben dabei der Fläche angehörende Kreise, die ihre Parallelkreise heißen, weil sie in parallelen, zu a normalen Ebenen liegen. Jede durch die Achse gelegte Ebene schneidet die Drehfläche Meridian nach einem Meridian. Alle Meridiane einer Drehfläche sind untereinander kongruent, weil sie durch Drehung auseinander hervorgehen. a Flachkreis Kehlkreis Äquatorkreis Spezielle Parallelkreise: Äquatorkreis, Kehlkreis, Flachkreis Spezielle Drehflächen Gebaute Drehflächen Drehzylinder Kugel Drehkegel Torus Bonaventure Hotel, Los Angeles, USA Melbourne Central, Melbourne, Australia Oriental Pearl Tower, Shanghai, China
46 Drehquadriken Drehparaboloid Eine Drehfläche, die bei stetiger Drehung eines Kegelschnittes um eine seiner Achsen entsteht, heißt Drehquadrik. Ebene Schnitte dieser Flächen sind Kegelschnitte. Außer den Kugeln gibt es folgende Typen: Ein Drehparaboloid entsteht bei Drehung einer Parabel um ihre Achse. Eigenschaft: Strahlen parallel zur Achse werden in den Brennpunkt reflektiert (Anwendung: Satelliten-Parabolspiegel) Drehellipsoid Drehparaboloid Drehhyperboloide Drehparaboloid Drehparaboloide im Bauwesen Drehellipsoid Ein eiförmiges bzw. abgeplattetes Drehellipsoid entsteht durch Drehung einer Ellipse um ihre Hauptachse bzw. Nebenachse. Very Large Array Plains of San Augustin, New Mexico Erdefunkstelle Aflenz (Steiermark) Gustav Peichl, 1980 (Antennen 32m) Kirche, Oklahoma City, USA Quelle: Telekom Austria Planetarium, Bochum, Deutschland 183 eiförmiges Drehellipsoid abgeplattetes Drehellipsoid 184
47 Drehellipsoide im Bauwesen Drehhyperboloid Ein zweischaliges bzw. einschaliges Drehhyperboloid entsteht bei Drehung einer Hyperbel um ihre Hauptachse bzw. Nebenachse. Rockhalle im Gasometer B (Durchschnitt von 2 Drehellipsoiden) Fukui Prefectural Museum of Dinosaurs, Katsuyama, Fukui, Japan Museum of Ftuit, Yamanashi, Itsuko Hasegawa Atomei (Forschungsreaktor) Garching, Deutschland 185 zweischaliges Drehhyperboloid einschaliges Drehhyperboloid 186 Regeldrehflächen Eine Drehfläche, deren erzeugende Kurve e eine Gerade ist, heißt Regeldrehfläche. Die einzelnen Lagen von e heißen Erzeugenden der Fläche. Ist die Gerade e zur Drehachse parallel bzw. schneidet e die Drehachse in einem Punkt S, so ist die Regeldrehfläche ein Drehzylinder bzw. ein Drehkegel mit der Spitze S. Drehhyperboloide im Bauwesen Kühltürme Atomkraftwerk Temelin, Tschechien Ist die Erzeugende e zur Achse windschief (aber nicht normal), dann erhalten wir ein einschaliges Drehhyperboloid. In einer solchen Fläche liegen zwei Drehscharen von Erzeugenden. e-schar f-schar e- und f-schar 187 Kathedrale Sacre-Coeur, Algier, Algerien 188
48 Rohrflächen (Pipe Surfaces) Rohrflächen (Pipe Surfaces) m Eine Rohrfläche ist bestimmt durch die Ortslinie m der Kugelzentren (Mittellinie der Rohrfläche) und den Kugelradius r. Eine Rohrfläche kann auf zwei Arten erzeugt werden: 1. als das Hüllgebilde einer Schar kongruenter Kugeln 2. indem ein Kreis in einer Ebene normal zur Mittellinie bewegt wird Beispiele: Drehzylinder, Torus, Rohrflächen Kanalflächen Als Verallgemeinerung der Rohrflächen sind jene Flächen anzusehen, die das Hüllgebilde einer Schar von Kugeln sind, deren Radius von der Lage des Kugelmittelpunktes abhängt. Sie werden Kanalflächen genannt. Sonderfälle der Kanalflächen sind die Rohr-, und Drehflächen. Eine Drehfläche ist eine Kanalfläche mit gerader Mittellinie. Wasserrutsche Spielgerät: Teil einer Rohrfläche
49 Wiederholung Schraubung Schraublinie/Schraubzylinder Schraubung = räumlicher Bewegungsvorgang, der durch Zusammensetzen einer gleichförmigen Drehung um eine Achse a mit einer gleichförmigen Schiebung parallel zu a entsteht Begriffe: Drehwinkel ϕ Schraubparameter p Ganghöhe h Jede Schraublinie liegt auf einem sogenannten Schraubzylinder mit der Schraubachse als Achse. In diesem Beispiel ist die Säule der Schraubzylinder. Schraublinie = Bahnkurve eines Punktes, der einer Schraubung unterworfen wird Pestsäule, Karlskirche in Wien, Rechts-/Linksschraubung Rechts-/Linksschraubung Rechtsschraubung Linkssschraubung Besitzen Drehung und Schiebung in Bezug auf ein Rechtskoordinatensystem, dessen z-achse die Schraubachse a ist, gleiches Vorzeichen, dann spricht man von einer Rechtsschraubung, andernfalls von einer Linksschraubung Betrachtet man die Säulen der Karlskirche, so sieht man, dass die rechte Säule eine Rechtsschraublinie, die linke eine Linksschraublinie trägt. Durch eine Bewegung kann eine Rechtsschraublinie nicht in eine Linksschraublinie übergeführt werden!
50 Abwicklung einer Schraublinie Schraubflächen (Helical Surfaces) Die Tangenten längs einer Schraublinie schließen mit einer zur Achse normalen Ebene einen konstanten Winkel ein Schneidet man den Schraubzylinder längs einer Erzeugenden auf und wickelt man diesen Mantel in eine Ebene ab, dann ist die Abwicklung der Schraublinie eine Gerade ϕ ϕ α ϕ α Unterwirft man eine Kurve e einer stetigen Schraubung, wobei e keine Bahnkurve dieser stetigen Schraubung ist, so heißt die Menge der Punkte der dabei entstehenden, zu e kongruenten Kurven eine Schraubfläche. Die Schnittkurven mit Ebenen normal zur Schraubachse bzw. durch die Schraubachse heißen Querschnitte bzw. Meridiane der Schraubfläche. Doppelwendeltreppe, Grazer Burg, 1499 DNA Beispiele: Regelschraubflächen (z.b. Wendelfläche) Kreisschraubflächen Schraubtorsen Wendelflächen Gebaute Wendelflächen Die Geraden durch die Punkte einer Schraublinie, welche die Schraubachse orthogonal schneiden, bilden eine Wendelfläche. Wendelflächen treten als Unterseiten von Wendeltreppen, als Wendelrampen und als flachgängige Schrauben auf. 199 Solomon R. Guggenheim Museum von Frank Lloyd Wright ( ), N.Y. City. Eine langläufig gewendelte Rampe zieht sich über sechs Geschosse durch den gesamten Innenraum des Museums und stellt nicht nur die Erschließung der daran angrenzenden Ausstellungsräume bzw. Nebenräume dar, sondern ist zugleich Ausstellungsbereich für Bilder und/oder Skulpturen. Das Museum wurde 1959 fertiggestellt und beinhaltet seither Wechselausstellungen Moderner Kunst. 200
51 Doppelwendeltreppe Der Stiegenaufgang im Vatikanischen Museum in Rom ist als Doppelwendeltreppe ausgeführt. So werden die Besucherströme beim Betreten bzw. Verlassen des Gebäudes auf getrennten Treppen geführt. Weitere Anwendungen finden sich bei den Auf-/Abfahrtsrampen in Parkhäusern. Anwendungen der Schraubung Bei Treppen gehen Stufen oft durch Schraubung auseinander hervor. Stiegenaufgang des Vatikanischen Museums Rom, Italien Auftreten von Schraubflächen im Bauwesen Kreisschraubflächen Parkhaus... Grundriss Parkhaus Meridiankreisschraubfläche: Entsteht durch Verschraubung eines Kreises in einer durch die Schraubachse gehenden Ebene Schichtenkreisschraubfläche: Entsteht durch Verschraubung eines Kreises in einer zur Schraubachse normalen Ebene 204
52 Kreisschraubflächen Rohrschraubflächen Schneidet der erzeugende Kreis die Schraubachse, dann entstehen die für den Barock typischen Säulen 1. Art der Erzeugung: Man bewegt einen Kreis, welcher in einer zur Bahnschraublinie m seines Mittelpunktes M normalen Ebene liegt, entlang m Innenansicht der Jesuitenkirche (ehemalige Universitätskirche, Wien I, zwischen 1623 und 1631) mit gewundenen Barocksäulen 205 Rutsche Ravenna von Grünzig Spielgeräte 2. Art der Erzeugung: Rohrschraubfläche ist eine Einhüllende einer Kugel, die längs einer Schraublinie bewegt wird 206 Regelflächen Wird eine Gerade im Raum bewegt so überstreift sie im Laufe dieser Bewegung eine Regelfläche (außer die Gerade wird nur in sich verschoben) Durch jeden Punkt einer Regelfläche geht mindestens eine Flächengerade, die Erzeugende genannt wird Tangentialebenen von Regelflächen Berührt in allen Punkten einer Erzeugenden dieselbe Tangentialebene, so spricht man von einer torsalen Erzeugenden (z.b. Kegel, Zylinder) Sind alle Erzeugenden einer Regelfläche torsal, spricht man von einer torsalen Regelfläche (einfach gekrümmte Regelfläche) City Link Melbourne, Australia
53 Tangentialebenen von Regelflächen Sind die Tangentialebenen in den einzelnen Punkten einer Erzeugenden verschieden, so spricht man von einer nichttorsalen Erzeugenden. Jede Ebene durch eine solche Erzeugende ist in genau einem Punkt der Erzeugenden Tangentialebene. Regelflächen, deren Erzeugende nichttorsal sind, heißen windschiefe Regelflächen (zweifach gekrümmte Regelflächen) 209 A g Erzeugung von Regelflächen Die Bewegung einer Geraden im Raum kann durch zwei Leitkurven samt einer Punktkorrespondenz zwischen den Kurven angegeben werden: X Die Gerade muss stets beide Leitkurven treffen Die Punktkorrespondenz gibt an, welche Punkte der zwei Kurven gleichzeitig von der Geraden durchlaufen werden (z.b. Durchlaufgeschwindigkeit auf jeder Kurve). A* X* l 1 l 2 B* B Beispiel: Gegeben sind zwei Leitkurven l 1,l 2 sowie die Gerade g in ihrer Startlage AA* und Endlage BB*. Korrespondierende Punkte werden durch Abtragen von Bogenlängen mit einem fixem Ähnlichkeitsfaktor λ gefunden: (hier: λ = ½ ) * * AX=λ AX 210 Beispiele zur Erzeugung von Regelflächen durch Leitkurven Die HP-Fläche Zylinder: Leitkurven: Zwei kongruente Kreise in parallelen Ebenen Die Zuordnung erfolgt durch Bogenlängenähnlichkeit Drehkegel: Leitkurven : Punkt und Kreis in geeigneter Lage Treffgeradenmenge aus der Spitze an den Basiskreis Betrachten wir nun zwei Geraden als Leitkurven: Parallele Leitgeraden ebenes Flächenstück (trivialer Fall) Drehhyperboloid: Leitkurven: Zwei kongruente Kreise in geeigneter Lage Die Zuordnung erfolgt durch Bogenlängenähnlichkeit Wendelfläche: Leitkurven: Schraublinie und deren Achse Die Zuordnung erfolgt durch Bogenlängenähnlichkeit windschiefe Leitgeraden Windschiefe Leitgeraden hyperbolisches Paraboloid oder kurz HP-Fläche Bemerkung: Zu jeder Regelfläche kann eine Schar von geeigneten Leitkurven gefunden werden. 211 Erzeugenden 212
54 Teilverhältnisregel für HP-Flächen HP-Flächen als zweifache Regelflächen B ε X A z x B* X* y y A* Die Zuordnung zwischen den Leitgeraden erfolgt nun durch Abtragen von Teilstrecken (analog zur Bogenlänge bei Leitkurven): Die Leitgeraden werden durch die Erzeugenden teilverhältnisgleich aufeinander bezogen TV(A,B,X) = TV(A*,B*,X*) Es gibt einen Parallelriss, in dem die Erzeugenden als untereinander parallele Geraden erscheinen. D.h. die Erzeugenden sind alle parallel zu einer Ebene, der sogenannten Richtebene ε (hier: erstprojizierend). 213 z x y y Es gibt eine Schar von Leitgeraden welche auf der Fläche liegen. Bezüglich je zwei dieser Leitgeraden gilt die Teilverhältnisregel. Auf der Fläche gibt es zwei gleichberechtigte Scharen von Erzeugenden je zwei Geraden derselben Schar sind windschief je zwei Geraden verschiedener Scharen schneiden in einem Flächenpunkt Durch jeden Flächenpunkt gehen zwei Erzeugende, welche die Tangentialebene in diesem Punkt aufspannen 214 D HP-Fläche durch windschiefes Vierseit C A B Eine HP-Fläche ist durch ein windschiefes Erzeugendenvierseit eindeutig festgelegt. Das windschiefe Vierseit ist durch 4 nicht in einer Ebene liegende Punkte A, B, C, D festgelegt Eine Schar von Erzeugenden besitzt AB und DC als Leitgeraden. Konstruktion mittels Teilverhältnisregel Die andere Schar von Erzeugenden besitzt AD und BC als Leitgeraden. Konstruktion von Erzeugenden mittels Teilverhältnisregel 215 x Optimale Aufstellung von HP-Flächen z In dieser besonderen Aufstellung gibt es genau einen Punkt S mit horizontaler Tangentialebene. Dieser heißt Scheitel S der HP-Fläche. Die Flächennormale im Scheitel (lotrecht in der besonderen Aufstellung) heißt Achse a der HP-Fläche y Jede der beiden Erzeugendenscharen besitzt eine Richtebene Werden die Richtebenen beide lotrecht gewählt, so hat die HP-Fläche besonders günstige statische Eigenschaften (große Spannweite bei geringer Schalendicke) S a 216
55 Ebene Schnitte von HP-Flächen Gebaute HP-Flächen Der Schnitt einer HP-Fläche mit einer Ebene parallel zur Achse ist eine Parabel (oder eine Erzeugende falls die Ebene eine Richtebene ist) schräg zur Achse ist eine Hyperbel (Ausnahme: Ist die Ebene eine Tangentialebene so schneidet sie die Fläche nach 2 Erzeugenden) Philips-Pavillon (Le Corbusier) Weltausstellung 1958 Brüssel Aufbahrungshalle, Wien 21 Dachkonstruktion: HP-Schale aus Holz Restaurant Los Manantiales (Felix Candela) 1958, Xochimilco, Mexico Entertainment Center (Felix Candela) Konoidale Regelflächen Wendelflächen x z Leitgerade 1 y Richtebene Richtebene Regelflächen, deren Erzeugende zu einer Ebene ε parallel sind, heißen konoidale Regelflächen. Beispiel: HP-Fläche Die Ebene ε und jede zu ihr parallele Ebene heißt Richtebene der Fläche. Durch Angabe der Richtebene und zweier Leitkurven ist eine konoidale Regelfläche bestimmt. Die Geraden durch die Punkte einer Schraublinie, welche die Schraubachse orthogonal schneiden, bilden eine Wendelfläche. Die Wendelfläche ist eine konoidale Regelfläche, die eine Schraublinie und deren Achse als Leitkurven besitzt. Die Richtebenen sind zur Schraubachse normale Ebenen. Leitkurve
56 Erzeugende parallel zur Richtebene Leitkurven e Olympic Train Station, Homebush, Sydney, Australia Sheddächer Sheddächer sind häufig Ausschnitte von konoidalen Regelflächen mit lotrechten Richtebenen Meist ist eine Richtebene gemeinsame Symmetrieebene der Leitkurven und somit auch Symmetrieebene der Fläche. lotrechte Richtebene 221 Wird eine Kurve k (Profilkurve) entlang einer Kurve l (Leitkurve) zu sich parallel verschoben, so heißt die Menge der Punkte der dabei entstehenden zu k kongruenten Kurven eine Schiebfläche. Halle 26, Deutsche Messe Hanover, Germany Schiebflächen Dulles Airport von Eero Saarinen, Chantilly, Virginia, Wird speziell eine Gerade k längs einer Leitkurve l verschoben, so ist diese Schiebfläche eine allgemeine Zylinderfläche. 222 Schiebflächen Gegeben sind eine Leitkurve l und eine Profilkurve k, die einen Punkt O gemeinsam haben: Wir wenden auf k Schiebungen an, welche O in Punkte der Leitkurve l überführen. Dadurch entstehen neue Lagen der Profilkurve, welche eine Schiebfläche bilden. Zweifache Erzeugung von Schiebflächen Die Rollen von Profil- und Leitkurve können vertauscht werden: Bei Verschiebung von k längs l entsteht dieselbe Fläche wie bei Verschiebung von l längs k. Die Fläche trägt demnach zwei Scharen von Kurven, welche zu k bzw. l schiebungsgleich sind L Leitkurve l P K Profilkurve k K Profilkurve k P Leitlinie l L O 224
57 HP-Flächen als Schiebflächen HP-Fläche als Schiebfläche p 2 p 1 Bei Verschiebung einer Parabel p 1 längs einer Parabel p 2 entsteht eine HP-Fläche, sofern die beiden Parabeln parallele Achsen besitzen als Schiebfläche HP-Flächen im CAD Schiebparabeln als Bezierkurven 2. Grades modellieren HP-Fläche durch sweepen (verschieben) einer Parabel längs der anderen erzeugen Abwickelbare Flächen Unter der Abwicklung oder Verebnung einer krummen Fläche versteht man, anschaulich gesprochen, ihre längentreue (und somit auch winkeltreue) Ausbreitung in eine Ebene. Raumkurve P als Regelfläche durch Einspannen einer Bezierfläche vom Grad (1,1) in ein windschiefes Vierseit Abwickelbare krumme Flächen: τ Zylinderflächen, Kegelflächen,Tangentenflächen von Raumkurven Kennzeichnende Eigenschaft: Regelflächen die nur torsale Erzeugenden besitzen (Tangentialebene berührt jeweils längs der gesamten Erzeugenden)
58 Abwickelbare Flächen Zylinderfläche entsteht durch Verfeinerung einer Prismenfläche Kegelfläche entsteht durch Verfeinerung einer Pyramidenfläche Abwickelbare Flächen Tangentenfläche einer Raumkurve entsteht durch Verfeinerung eines Torsenpolyeders: Die Kanten des Torsenpolyeders sind die Seitengeraden eines räumlichen Polygons. Die Seitenflächen werden von jeweils zwei aufeinanderfolgenden Polygonseiten aufgespannt. Durch Verfeinerung entsteht aus einem räumlichen Polygon eine Raumkurve. Die Polygonseiten gehen dabei in Kurventangenten über. Aus dem Torsenpolyeder des Polygons entsteht die Tangentenfläche der Raumkurve. Das erzeugende Polygon bildet eine Rückkehrkante auf dem Torsenpolyeder Die erzeugende Raumkurve ist eine scharfe Kante (Gratlinie) der Tangentenfläche Abwickelbare Flächen im Bauwesen Abwickelbare Flächen sind für das Bauwesen interessant, weil sie... eine Schar von Geraden tragen und daher leichter zu bauen sind als ganz freie Formen (z.b. Verschalungen, Stahlbeton, Holzbau, ) mit Blech leicht zu verkleiden sind Abwicklungen Die Animation zeigt die Abwicklung eines Drehzylinders bzw. eines Drehkegels in eine Ebene Weisman Art Museum
59 Abwicklung eines Kegels Netz eines Polyeders Ein Polyeder, also ein aus lauter ebenen Flächenstücken begrenzter Körper, lässt sich mit verhältnismäßig geringem Aufwand nachbilden, indem man die einzelnen Oberflächenteile aus Karton oder Blech ausschneidet und aneinanderheftet. Die in einer Ebene möglichst zusammenhängend aneinandergereihten Flächenstücke bilden das Netz des Polyeders Fußball = Ikosaederstumpf 233 In FormZ kann für die Abwicklung von Flächen der Befehl Unfold verwendet werden. 234 Übungsbeispiele Netze von Polyedern Abwicklung - Netz Skizzieren Sie die 11 verschiedenen Netze eines Würfels Netze von Tetraeder, Oktaeder, Pentagondodekaeder und Ikosaeder ein Netz des untenstehenden Objektes Von jeder Fläche kann man ein Näherungspolyeder bilden und für dieses ein Netz konstruieren Dabei entstehen zwischen den verebneten Seitenflächen Lücken, welche auch bei noch so feiner Approximation auftreten Dieser Vorgang kann also nicht als Beweis für die Abwickelbarkeit beliebiger Flächen dienen Beispiel: Eine Kugel ist nicht in die Ebene abwickelbar, daher gibt es keine verzerrungsfreien Landkarten
60 Freiformflächen Bézier-Flächen Karin Zeitlhuber, Reinhard Bernsteiner; Die Welle: Berufsschule Villach Preston Scott Cohen; Torus House; Old Chatham Frank O. Gehry; Experience Music Project Bezier-Kurven werden von einem Kontrollpolygon ausgehend konstruiert. Es liegt also nahe für Bezier-Flächen ein Kontrollnetz zu verwenden. Allgemein wird eine Bézier-Fläche vom Grad (m,n) durch ein Vierecksnetz mit Eckpunkten P i,j (i = 0,...,m; j = 0,...,n) angegeben. Das Bézier-Flächenstück besitzt i.a. 4 Randkurven. Diese sind Bézier-Kurven mit den Randpolygonen des Netzes als Kontrollpolygonen Freiformflächen sind wegen ihrer großen Bedeutung im industriellen Design entwickelt worden (z.b. Automobilindustrie, Schiffbau). Sie finden inzwischen auch großes Interesse bei repräsentativer Architektur Freiformmodule findet man in allen CAD-Systemen Bézier-Flächen Zur Konstruktion eines Flächenpunktes kann man jede der m+1 Zeilen (verbinden jeweils n+1 Punkte mit festem Index i) als Kontrollpolygone auffassen und zum selben Teilverhältnis Kurvenpunkte konstruieren. Dies liefert m+1 Punkte, welche die Kontrollpunkte einer Bézier-Kurve m-ten Grades sind, die ganz auf der Fläche liegt. Bézier-Flächen Randkurven eines Bézier-Flächenstücks sind Bézier-Kurven Eckpunkte des Kontrollnetzes sind Punkte des zugehörigen Bézier-Flächenstücks Damit sieht man, dass auf einer Bézier-Fläche vom Grad (m,n) eine Schar von Bézier-Kurven vom Grad m liegt. Analog erhält man über die Spalten des Kontrollnetzes eine Schar von Bézier-Kurven vom Grad n, die ganz auf der Fläche liegen
61 Bézier-Regelflächen HP-Fläche als Bezier-Fläche Eine Bézier-Kurve ersten Grades ist eine geradlinige Strecke. Daher ist eine Bézier-Fläche vom Grad (1,n) oder (m,1) ein Regelflächenstück. Eine Bézierfläche vom Grad (1,1) ist eine HP-Fläche B 1, 0 B 0, 1 Eine Bézier-Fläche vom Grad (1,1) ist durch vier Kontrollpunkte B 0,0, B 0,1, B 1,0, B 1,1 gegeben, welche zu einem Kontrollvierseit verbunden werden. Sind bei einer Bézier-Fläche vom Grad (1,n) die n+1 Spaltenstrecken parallel, so erhält man ein Stück einer Zylinderfläche. Die Randkurven sind die Bézier-Kurven zu den Randpolygonen des Netzes. B 0, 0 Falls dieses Vierseit nicht in einer Ebene liegt, ist die Bézier-Fläche das HP-Flächenstück mit dem B 1, 1 Kontrollvierseit als Erzeugendenvierseit B-Spline-Flächen Die Bézier-Methode ist zum Design komplizierterer Formen kaum geeignet, weil bei höherem Grad die Bezier-Fläche die Form der Eingabefigur nicht gut wiedergibt. Oft ist auch der globale Einfluss der Kontrollpunkte unerwünscht: Änderung eines einzigen Punktes beeinflusst das gesamte Flächenstück. B-Spline-Flächen Die mathematische Beschreibung einer B-Spline-Fläche basiert auf einem Vierecksnetz. Dieses besitzt im allgemeinen vier Randpolygone und beschreibt demnach ein Flächenstück, dass von vier Randkurven begrenzt wird. Fallen ein oder zwei Paare gegenüberliegender Randpolygone des Vierecksnetzes zusammen, so entstehen schlauchförmige bzw. torusförmige Flächen. In der Praxis verwendet man daher oft B-Spline-Flächen. Auf dieselbe Art wie man von Bezier-Kurven auf Bezier- Flächen erweitert gelangt man von B-Spline-Kurven auf B-Spline-Flächen
62 NURBS-Flächen So wie bei den NURBS-Kurven kann man die Form einer NURBS-Fläche durch Gewichte, die den Kontrollpunkten zugeordneten sind, steuern. Effekt der Gewichte wie bei NURBS-Kurven Das Bild zeigt eine NURBS-Fläche mit einem Kontrollnetz bestehend aus 5*7 = 35 Kontrollpunkten Gebaute Freiformflächen Ausblick: Geometrie & CAAD Vorlesung Vertiefung Freiformflächen Subdivision Surfaces Sweep- und Skinflächen Spiralung Netze und Modellbau Animation Übung Modellierung gebauter Objekte Durchführung eines umfangreicheren CAD-Projektes Unterteilungsflächen (Subdivision Surfaces) Können im Gegensatz zu klassischen Freiformflächen (NURBS-Flächen, ) Flächen beliebiger Topologie darstellen Methode: Ausgehend von einem Mesh wird dieses nach gegebenen Unterteilungsregeln verfeinert bis man eine hinreichend glatte Fläche erhält
63 Sweepflächen entstehen, indem eine erzeugende Kurve längs einer oder mehrerer beliebiger Kurven bewegt wird. Lage und Form der erzeugenden Kurve kann sich während der Bewegung ändern Sweepflächen Skinning Skinning eignet sich besonders zur Erstellung von organischen und komplexen 3D-Formen Skin ist gegenüber Sweep die mächtigere Operation City Link, Melbourne, Australia 249 Guggenheimmuseum (Bilbao) 250 Ausblick: Erschließung neuer Geometrien 3D Photographie Wiener Trio 3D-Photographie & 3D-Druck Visualisierung und Analyse von geometrischen Objekten Geometrische Topologie Minimalflächen Fraktale Mathematische Morphologie Kunstwerk am Schottenring 3D-Scannen CAD-Modell Rekonstruktion 3D-Drucken
64 Einseitige Flächen Fraktale Geometrie Möbiusband Kleinsche Flasche Euklidische Geometrie 2000 Jahre alt verwendbar für künstliche Objekte glatte Oberflächen analytische Gesetzmäßigkeiten Fraktale Geometrie ~ 30 Jahre alt verwendbar für natürliche Objekte rauhe Oberflächen Algorithmen
Splines. Bézier-Kurven. Beispiel zur Approximation. Interpolation & Approximation. Schiffbau Automobilbau Architektur. f(x) f(x) =
 Institut für Geometrie Abteilung für Geometrie im Bauwesen und im Scientific Computing Prof. Dr. H. Pottmann Interpolation & Approximation Splines Geg: Menge von Punkten Ges: Kurve, welche die Punkte interpoliert
Institut für Geometrie Abteilung für Geometrie im Bauwesen und im Scientific Computing Prof. Dr. H. Pottmann Interpolation & Approximation Splines Geg: Menge von Punkten Ges: Kurve, welche die Punkte interpoliert
Die Geometrieausbildung der Architekturstudenten an der TU Wien
 Die ausbildung der Architekturstudenten an der TU Wien Andreas Asperl, Wien Vorgeschichte vor etwa 3 Jahren: Intention der neuen STUKO Architektur Keine verpflichtende ausbildung Kontakte über ARCHICAD-Jourfixe
Die ausbildung der Architekturstudenten an der TU Wien Andreas Asperl, Wien Vorgeschichte vor etwa 3 Jahren: Intention der neuen STUKO Architektur Keine verpflichtende ausbildung Kontakte über ARCHICAD-Jourfixe
Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung
 Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Jahresplanung Vorschlag 1
 Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16. Prüfer: Mag.
 Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
Externistenprüfungen aus Darstellender Geometrie
 Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Inhaltsverzeichnis. geometrischer Objekte auszufüllen. Die Liste der Lösungen kann auch eine ABC Liste zu diesen Themen sein.
 Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
16. Platonische Körper kombinatorisch
 16. Platonische Körper kombinatorisch Ein Würfel zeigt uns, daß es Polyeder gibt, wo in jeder Ecke gleich viele Kanten zusammenlaufen, und jede Fläche von gleich vielen Kanten berandet wird. Das Tetraeder
16. Platonische Körper kombinatorisch Ein Würfel zeigt uns, daß es Polyeder gibt, wo in jeder Ecke gleich viele Kanten zusammenlaufen, und jede Fläche von gleich vielen Kanten berandet wird. Das Tetraeder
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
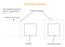 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
37 II.1. Abbildungen
 37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
37 II.1. Abbildungen "Abbildung" und "Funktion" sind verschiedene Namen für denselben Begriff, der charakterisiert ist durch die Angabe der Definitionsmenge ("Was wird abgebildet?"), der Wertemenge ("Wohin
Polynome im Einsatz: Bézier-Kurven im CAD
 Polynome im Einsatz: Bézier-Kurven im CAD Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 25 Kurven im Raum Eine Kurve im
Polynome im Einsatz: Bézier-Kurven im CAD Dipl.-Inform. Wolfgang Globke Institut für Algebra und Geometrie Arbeitsgruppe Differentialgeometrie Universität Karlsruhe 1 / 25 Kurven im Raum Eine Kurve im
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Featurebasierte 3D Modellierung
 1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
11: Die Euler sche Polyederformel für planare Graphen
 Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Chr.Nelius: Graphentheorie (WS 2016/17) 38 11: Die Euler sche Polyederformel für planare Graphen (11.1) BEM: a) Ein Polyeder (auch Vielflach oder Vielflächner) ist ein geometrischer Körper, der nur von
Polyeder, Konvexität, Platonische und archimedische Körper
 Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
Unter einem Polyeder verstehen wir einen zusammenhängenden Teil des dreidimensionalen Raumes der durch Polygone begrenzt wird. Seine Oberfläche besteht also aus Punkten (Ecken genannt), Strecken (Kanten
DARSTELLENDE GEOMETRIE
 1 von 8 Anlage A Sechster Teil A Pflichtgegenstände 2. Oberstufe a) Pflichtgegenstände Bildungs- und Lehraufgabe (7. und 8. Klasse): DARSTELLENDE GEOMETRIE Die Bedeutung der Darstellenden Geometrie in
1 von 8 Anlage A Sechster Teil A Pflichtgegenstände 2. Oberstufe a) Pflichtgegenstände Bildungs- und Lehraufgabe (7. und 8. Klasse): DARSTELLENDE GEOMETRIE Die Bedeutung der Darstellenden Geometrie in
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Kurs zur Ergänzungsprüfung Darstellende Geometrie CAD. Ebenes Zeichnen (2D-CAD) und die ersten Befehle
 CAD Ebenes Zeichnen (2D-CAD) und die ersten Befehle Schnellzugriff-Werkzeugkasten (Quick Access Toolbar) Registerkarten (Tabs) Gruppenfenster (Panels) Zeichenfläche Befehlszeile: für schriftl. Eingabe
CAD Ebenes Zeichnen (2D-CAD) und die ersten Befehle Schnellzugriff-Werkzeugkasten (Quick Access Toolbar) Registerkarten (Tabs) Gruppenfenster (Panels) Zeichenfläche Befehlszeile: für schriftl. Eingabe
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
Klausurenkurs zum Staatsexamen (WS 2013/14): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 3/4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
11. Geometrische Extremalprobleme I
 11. Geometrische Extremalprobleme I Die hier behandelten geometrischen Extremalprobleme beruhen auf der Dreiecksungleichung Satz 1. Sind A, B, C drei Punkte der euklidischen Ebene mit A B, dann ist (1)
11. Geometrische Extremalprobleme I Die hier behandelten geometrischen Extremalprobleme beruhen auf der Dreiecksungleichung Satz 1. Sind A, B, C drei Punkte der euklidischen Ebene mit A B, dann ist (1)
Zwei Aufgaben, die auf windschiefe Regelflächen führen,
 Zwei Aufgaben, die auf windschiefe Regelflächen führen, von À. KIEFER (Zürich). (Als Manuskript eingegangen am 25. Januar 1926.) I. Gesucht im Raum der Ort des Punktes, von dem aus die Zentralprojektionen
Zwei Aufgaben, die auf windschiefe Regelflächen führen, von À. KIEFER (Zürich). (Als Manuskript eingegangen am 25. Januar 1926.) I. Gesucht im Raum der Ort des Punktes, von dem aus die Zentralprojektionen
Stereometrie. Rainer Hauser. Dezember 2010
 Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Geometrie. 1 Vektorielle analytische Geometrie der Ebene, Kegelschnitte
 Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Mathematische Probleme, SS 2013 Donnerstag $Id: quadratisch.tex,v /08/12 09:49:46 hk Exp $ c a b = 1 3. tan(2φ) =
 Mathematische Probleme SS 13 Donnerstag 136 $Id: quadratischtexv 18 13/08/1 09:49:46 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen Nachdem wir in der letzten Sitzung die Hauptachsentransformation
Mathematische Probleme SS 13 Donnerstag 136 $Id: quadratischtexv 18 13/08/1 09:49:46 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen Nachdem wir in der letzten Sitzung die Hauptachsentransformation
Darstellung von Kurven und Flächen
 Darstellung von Kurven und Flächen Technische Universität Dresden Fakultät Informatik Institut für Software- und Multimediatechnik Dozent: Dr. Mascolous Referent: Gliederung / Einleitung 1 / 25 1. Kurven
Darstellung von Kurven und Flächen Technische Universität Dresden Fakultät Informatik Institut für Software- und Multimediatechnik Dozent: Dr. Mascolous Referent: Gliederung / Einleitung 1 / 25 1. Kurven
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Polyeder und Platonische Körper
 Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
Polyeder und Platonische Körper Ausarbeitung zum 30.11.2016 Linus Leopold Boes Matrikelnummer: 2446248 Algorithmen für planare Graphen Institut für Informatik HHU Düsseldorf Inhaltsverzeichnis 1 Einleitung
Einleitung 8 1. Grundlagen Fundamental Terms of Geometry. 2. Projektionen Types of Projections
 Einleitung 8 1. Grundlagen Fundamental Terms of Geometry 1.1 Koordinatensysteme Systems of Coordinates 0 Koordinatensysteme Systems of Coordinates 10 1 Beispiel: Kartesische Koordinaten - Ablesen von Koordinaten
Einleitung 8 1. Grundlagen Fundamental Terms of Geometry 1.1 Koordinatensysteme Systems of Coordinates 0 Koordinatensysteme Systems of Coordinates 10 1 Beispiel: Kartesische Koordinaten - Ablesen von Koordinaten
Lehrveranstaltung Darstellende Geometrie I SS 2011 CAD. I. Arbeiten mit Catia
 I. Arbeiten mit Catia Wir verwenden das -Paket Catia in der Version V5. Die Grafik unten zeigt eine Übersicht der Benutzeroberfläche des Part Design Packages dieses Programmes. Sketcher Block (Extrusionskörper)
I. Arbeiten mit Catia Wir verwenden das -Paket Catia in der Version V5. Die Grafik unten zeigt eine Übersicht der Benutzeroberfläche des Part Design Packages dieses Programmes. Sketcher Block (Extrusionskörper)
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Parallelprojektive Schattenbilder von Körpern mit Cabri 3D
 Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
2.4A. Reguläre Polyeder (Platonische Körper)
 .A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
.A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
Lösungen der Übungsaufgaben III
 Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Regelflächen theoretisch, exemplarisch, visuell
 GRG3 KUNDMANNGASSE, WIEN 3 Regelflächen theoretisch, exemplarisch, visuell Fachbereichsarbeit aus dem Fach Mathematik Verfasst von Anna Niggas Betreut von Dr. Gerhard Pillwein Schuljahr 2013/14 I. Zusammenfassung
GRG3 KUNDMANNGASSE, WIEN 3 Regelflächen theoretisch, exemplarisch, visuell Fachbereichsarbeit aus dem Fach Mathematik Verfasst von Anna Niggas Betreut von Dr. Gerhard Pillwein Schuljahr 2013/14 I. Zusammenfassung
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Schriftliche Reifeprüfung Darstellende Geometrie
 SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
Darstellungsarten für 3D-Körper. Boundary Representation (BRep):
 Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
Oktaeder. Bernhard Möller. 22. Dezember 2010
 Oktaeder Bernhard Möller. Dezember 00 Ein Oktaeder ist ein regelmäßiges Polyeder, dessen Oberfläche aus acht kongruenten, gleichseitigen Dreiecken besteht. Jedes Oktaeder kann einem Würfel so einbeschrieben
Oktaeder Bernhard Möller. Dezember 00 Ein Oktaeder ist ein regelmäßiges Polyeder, dessen Oberfläche aus acht kongruenten, gleichseitigen Dreiecken besteht. Jedes Oktaeder kann einem Würfel so einbeschrieben
1. Winkel (Kapitel 3)
 1. Winkel (Kapitel 3) 1.1 Winkel Einführung 1.2 Winkel an Geraden bjak 1 1.3 Winkel am Dreieck bjak 2 1.4 Winkel am Kreis bjak 3 bjak 4 2. Dreiecke (Kapitel 3) 2.1 Linien am Dreieck bjak 5 2.2 Flächeninhalt
1. Winkel (Kapitel 3) 1.1 Winkel Einführung 1.2 Winkel an Geraden bjak 1 1.3 Winkel am Dreieck bjak 2 1.4 Winkel am Kreis bjak 3 bjak 4 2. Dreiecke (Kapitel 3) 2.1 Linien am Dreieck bjak 5 2.2 Flächeninhalt
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Konstruktionslehre 1
 Prof. Dr.-Ing. Dipl.-Math. P. Köhler V Folie Gliederung. Einführung. Geometrische Grundlagen. Wiederholung geometrischer Grundkonstruktionen. Besondere Punktmengen. Projektionsarten.. Überblick.. Axonometrische
Prof. Dr.-Ing. Dipl.-Math. P. Köhler V Folie Gliederung. Einführung. Geometrische Grundlagen. Wiederholung geometrischer Grundkonstruktionen. Besondere Punktmengen. Projektionsarten.. Überblick.. Axonometrische
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
Mathematische Probleme, SS 2013 Montag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
$Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
3. Ähnlichkeitsabbildungen
 3. Ähnlichkeitsabbildungen 3.1 Definitionen: Ähnlichkeitsabbildungen, Dilatationen Bis jetzt haben wir Isometrien (Kongruenzabbildungen) betrachtet. Diese bbildungen wurden aufgebaut aus den Geradenspiegelungen.
3. Ähnlichkeitsabbildungen 3.1 Definitionen: Ähnlichkeitsabbildungen, Dilatationen Bis jetzt haben wir Isometrien (Kongruenzabbildungen) betrachtet. Diese bbildungen wurden aufgebaut aus den Geradenspiegelungen.
Prüfungsdauer: 120 Minuten
 Computergraphik und Multimediasysteme Seite 1 von 6 Klausur: Computergraphik II Probeklausur Semester: Prüfer: Prüfungsdauer: 1 Minuten Hilfsmittel: Schreibgeräte, Lineal, nichtprogrammierbarer Taschenrechner
Computergraphik und Multimediasysteme Seite 1 von 6 Klausur: Computergraphik II Probeklausur Semester: Prüfer: Prüfungsdauer: 1 Minuten Hilfsmittel: Schreibgeräte, Lineal, nichtprogrammierbarer Taschenrechner
Gundlagen Klasse 5/6 Geometrie. nach oben. Inhaltsverzeichnis
 Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Tutorial. Übungsblatt CAD: Faltwerkdach für Bühne
 Tutorial Übungsblatt CAD: Faltwerkdach für Bühne 1. REVERSE FOLDING Für das Reverse Folding nimmt man eine gefaltete Ebene schneidet diese mit einer geeigneten schrägen Ebene α in zwei Teile und spiegelt
Tutorial Übungsblatt CAD: Faltwerkdach für Bühne 1. REVERSE FOLDING Für das Reverse Folding nimmt man eine gefaltete Ebene schneidet diese mit einer geeigneten schrägen Ebene α in zwei Teile und spiegelt
Die Konstruktion der Schnittgeraden zweier Ebenen ist auf unterschiedliche Art und Weise möglich:
 Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Ebene Ebene Zwei Ebenen sind entweder Elemente eines Parallelenebenenbüschels oder sie schneiden einander. Im letzteren Fall existiert eine eindeutig bestimmte eigentliche Gerade als Schnittmenge beider
Mathematische Grundlagen
 Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Übungen mit dem Applet Kurven in Polarkoordinaten
 Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
Mathematische Probleme, SS 2015 Montag $Id: quadratisch.tex,v /06/22 12:08:41 hk Exp $
 Mathematische Probleme, SS 15 Montag 6 $Id: quadratischtex,v 111 15/06/ 1:08:41 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen In der letzten Sitzung hatten wir die Normalform (1 ɛ )x + y pɛx p =
Mathematische Probleme, SS 15 Montag 6 $Id: quadratischtex,v 111 15/06/ 1:08:41 hk Exp $ 4 Kegelschnitte 41 Quadratische Gleichungen In der letzten Sitzung hatten wir die Normalform (1 ɛ )x + y pɛx p =
3 Planare Graphen die Eulersche Polyederformel
 3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
3 Planare Graphen die Eulersche Polyederformel Planare Graphen sind solche Graphen, die sich ohne Überkreuzungen von Kanten in eine Ebene zeichnen lassen. Wir nehmen hierbei an, dass die Knoten als Punkte
Einige Grundlagen der Verzahnungstheorie
 Einige Grundlagen der Verzahnungstheorie 1 Wichtige Kenngrößen Die Relativbewegung zweier Zahnräder entsteht durch das Abrollen der beiden zugrundeliegenden Wälzkreise, aufeinander (Abb. 1). Die Zahnflanken,
Einige Grundlagen der Verzahnungstheorie 1 Wichtige Kenngrößen Die Relativbewegung zweier Zahnräder entsteht durch das Abrollen der beiden zugrundeliegenden Wälzkreise, aufeinander (Abb. 1). Die Zahnflanken,
FormZ-Workshop Strobl 2002
 FormZ-Workshop Strobl 2002 Lehrziele: Das sollten Sie am Ende der Übungen beherrschen: Eintragen und Ablesen von Kugelkoordinaten Ablesen von Teilverhältnissen Kennenlernen und Einrichten der Arbeitsoberfläche
FormZ-Workshop Strobl 2002 Lehrziele: Das sollten Sie am Ende der Übungen beherrschen: Eintragen und Ablesen von Kugelkoordinaten Ablesen von Teilverhältnissen Kennenlernen und Einrichten der Arbeitsoberfläche
-dimensionale Darstellungen
 1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
Lk Mathematik 12 Analytische Geometrie Arbeitsblatt A.1
 Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
Lk Mathematik 2 Analytische Geometrie Arbeitsblatt A.. Die Grundäche eines Spielplatzes liegt in der x - -Ebene. Auf ihm steht eine innen begehbare, senkrechte, quadratische Pyramide aus Holz mit den Eckpunkten
Hans Delfs. Übungen zu Mathematik III für Medieninformatik
 Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Eulerscher Polyedersatz
 Eigenschaften als reguläre Parkettierungen der Sphäre Seien E die der Ecken, F die der Flächen und K die der Kanten eines konvexen Polyeders, dann gilt: K E = F 2 als reguläre Parkettierungen der Sphäre
Eigenschaften als reguläre Parkettierungen der Sphäre Seien E die der Ecken, F die der Flächen und K die der Kanten eines konvexen Polyeders, dann gilt: K E = F 2 als reguläre Parkettierungen der Sphäre
8.Kreisdarstellung in Perspektive
 8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
Kompetenzmodell. Geometrisches Zeichnen. Arbeitsblätter
 Kompetenzmodell Geometrisches Zeichnen Arbeitsblätter 4.10.2012 Inhaltsdimension Arbeitsblätter Risse Lesen und Skizzieren Bausteine Länge von Strecken Flächenmodelle Bedienung eines CAD-Programms 3D-CAD-Software:
Kompetenzmodell Geometrisches Zeichnen Arbeitsblätter 4.10.2012 Inhaltsdimension Arbeitsblätter Risse Lesen und Skizzieren Bausteine Länge von Strecken Flächenmodelle Bedienung eines CAD-Programms 3D-CAD-Software:
Unterrichtsreihe zur Parabel
 Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Unterrichtsreihe zur Parabel Übersicht: 1. Einstieg: Satellitenschüssel. Konstruktion einer Parabel mit Leitgerade und Brennpunkt 3. Beschreibung dieser Punktmenge 4. Konstruktion von Tangenten 5. Beweis
Zeichnung: Malte Kittelmann AXONOMETRIE
 Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
SCHRIFTLICHE ABITURPRÜFUNG Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten
 Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten L 1, L 2 und L 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
Mathematik (Leistungskurs) Arbeitszeit: 300 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten L 1, L 2 und L 3 zur Bearbeitung aus. Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Projektion des Torus in isotroper Richtung
 Projektion des Torus in isotroper Richtung Autor(en): Objekttyp: Hohenberg, Fritz Article Zeitschrift: Elemente der Mathematik Band (Jahr): 27 (1972) Heft 4 PDF erstellt am: 30.09.2017 Persistenter Link:
Projektion des Torus in isotroper Richtung Autor(en): Objekttyp: Hohenberg, Fritz Article Zeitschrift: Elemente der Mathematik Band (Jahr): 27 (1972) Heft 4 PDF erstellt am: 30.09.2017 Persistenter Link:
3 Kurven und Flächen. HS Heilbronn - Prof. Dr. P. Fleischmann CAD-K3 10/2011 3/1. Bild 3.1: 3D-Flächen. Bild 3.2: Freiformkurven
 HS Heilbronn - Prof. Dr. P. Fleischmann CAD-K3 10/2011 3/1 3 Kurven und Flächen 3.1 Flächenmodell 3.1.1 Ebene 3.1.2 Zylinder, Kegel, Torus.2 Freiformkurven und -flächen 3.2.1 Interpolierende Kurven/Flächen
HS Heilbronn - Prof. Dr. P. Fleischmann CAD-K3 10/2011 3/1 3 Kurven und Flächen 3.1 Flächenmodell 3.1.1 Ebene 3.1.2 Zylinder, Kegel, Torus.2 Freiformkurven und -flächen 3.2.1 Interpolierende Kurven/Flächen
Bestimme ferner die Koordinaten des Bildpunktes von B bei der Spiegelung
 Vektoren - Skalar- und Vektorprodukt ================================================================== 1. Gegeben sind die Punkte A 1 2 3 und B 3 4 1 bzgl. eines kartesischen Koordina- tensystems mit
Vektoren - Skalar- und Vektorprodukt ================================================================== 1. Gegeben sind die Punkte A 1 2 3 und B 3 4 1 bzgl. eines kartesischen Koordina- tensystems mit
Geometrie kubischer Kurven
 Geometrie kubischer Kurven Werner Hoffmann Wir wollen die Theorie nur soweit entwickeln, wie es zum Verständnis der Gruppenoperation auf einer irreduziblen kubischen Kurve nötig ist. Satz 1 In der affinen
Geometrie kubischer Kurven Werner Hoffmann Wir wollen die Theorie nur soweit entwickeln, wie es zum Verständnis der Gruppenoperation auf einer irreduziblen kubischen Kurve nötig ist. Satz 1 In der affinen
Seminar für LAGym/LAB: Analytische Geometrie
 Seminar für LAGym/LAB: Analytische Geometrie Ingo Runkel und Peter Stender Euklidische Vektorräume und Geometrie E1: Lineare Gleichungssysteme - Affiner Unterraum eines Vektorraumes. Lineare Gleichungssysteme
Seminar für LAGym/LAB: Analytische Geometrie Ingo Runkel und Peter Stender Euklidische Vektorräume und Geometrie E1: Lineare Gleichungssysteme - Affiner Unterraum eines Vektorraumes. Lineare Gleichungssysteme
DG für Kunstpädagogik
 DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
Einige Ergebnisse der euklidischen Geometrie
 1 Teil I Einige Ergebnisse der euklidischen Geometrie In Teil I setzen wir den euklidischen Raum als bekannt voraus (aus der Schule oder aus der Vorlesung Lineare lgebra und nalytische Geometrie). Da wir
1 Teil I Einige Ergebnisse der euklidischen Geometrie In Teil I setzen wir den euklidischen Raum als bekannt voraus (aus der Schule oder aus der Vorlesung Lineare lgebra und nalytische Geometrie). Da wir
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Vorkurs aus Darstellender Geometrie Übungen
 Beispielsammlung für CAD Beispiele und Freihandzeichnen aus Vorkurs aus Darstellender Geometrie Übungen Mag. Susanne Vanovsek Mag. Dr. Martin Pfurner WS 2008/2009 Einführung in Rhinoceros 3D Merkwürdige
Beispielsammlung für CAD Beispiele und Freihandzeichnen aus Vorkurs aus Darstellender Geometrie Übungen Mag. Susanne Vanovsek Mag. Dr. Martin Pfurner WS 2008/2009 Einführung in Rhinoceros 3D Merkwürdige
Flächenklassen mit Solid Edge
 Flächenklassen in Solid Edge: Einführung Flächenklassen mit Solid Edge Prinzipiell muss in Solid Edge, wie in jedem CAD Paket, zwischen Volumskörpern und Flächen unterschieden werden. Volumskörper (Solids)
Flächenklassen in Solid Edge: Einführung Flächenklassen mit Solid Edge Prinzipiell muss in Solid Edge, wie in jedem CAD Paket, zwischen Volumskörpern und Flächen unterschieden werden. Volumskörper (Solids)
Darstellende Geometrie Übungen. Tutorial 09. CAD 2 - Archimedische Körper
 Tutorial 09 CAD 2 - Archimedische Körper Achtung: In diesem Tutorial wird die Konstruktion eines Pentagondodekaeders erklärt. Diese ist der Konstruktion des Fußballes aus der Übung 09 sehr ähnlich und
Tutorial 09 CAD 2 - Archimedische Körper Achtung: In diesem Tutorial wird die Konstruktion eines Pentagondodekaeders erklärt. Diese ist der Konstruktion des Fußballes aus der Übung 09 sehr ähnlich und
5 5 5 Abbildung : Raumkurve Abbildung 5: Tangente t existiert nur dann, wenn _ ~x(t ) = ist. Ein Punkt mit f _x; _y; _zg = f; ; g heißt ein regulärer
 3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
3 Differentialgeometrische Eigenschaften von Kurven und Flächen Ziel dieses Abschnittes ist es, eine kurze Einführung in die Anfangsgründe der mathematischen Theorie der Raumkurven und Flächen zu geben.
Perspektive Vertiefung
 Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Projektionskurve Abiturprüfung LK Bayern 2003
 Projektionskurve Abiturprüfung LK Bayern 03 In einem kartesischen Koordinatensystem des R 3 ist die Ebene H: x 1 + x 2 + x 3 8 = 0 sowie die Schar von Geraden ( a 2 ) ( ) 3a g a : x = 0 a 2 + λ 3a 8, λ
Projektionskurve Abiturprüfung LK Bayern 03 In einem kartesischen Koordinatensystem des R 3 ist die Ebene H: x 1 + x 2 + x 3 8 = 0 sowie die Schar von Geraden ( a 2 ) ( ) 3a g a : x = 0 a 2 + λ 3a 8, λ
2. Isometrien oder Kongruenzabbildungen
 6 2. Isometrien oder Kongruenzabbildungen 2.1 Einführende Überlegungen Kongruente Figuren sind deckungsgleiche Figuren. Eine Figur wird so bewegt, dass sie mit einer anderen Figur zur Deckung gebracht
6 2. Isometrien oder Kongruenzabbildungen 2.1 Einführende Überlegungen Kongruente Figuren sind deckungsgleiche Figuren. Eine Figur wird so bewegt, dass sie mit einer anderen Figur zur Deckung gebracht
Modellierung. Oliver Hartmann
 Modellierung Oliver Hartmann oliver.hartmann@uni-ulm.de Inhalt Boolesche Operationen Splines B-Splines Bezier-Kurven NURBS Anwendung Sculpting Volumengrafik Marching Cubes Ray Casting Texture Mapping Boolesche
Modellierung Oliver Hartmann oliver.hartmann@uni-ulm.de Inhalt Boolesche Operationen Splines B-Splines Bezier-Kurven NURBS Anwendung Sculpting Volumengrafik Marching Cubes Ray Casting Texture Mapping Boolesche
Die einleitend angesprochenen Zusammenhänge sind in der folgenden Tabelle zusammengestellt:
 Ein konstantes Abstandsrodukt Eckart Schmidt Zu zwei fest vorgegebenen Punkten sind die Ortslinien für Punkte mit konstanten Abstandssummen, Abstandsdifferenzen oder Abstandsverhältnissen Kegelschnitte;
Ein konstantes Abstandsrodukt Eckart Schmidt Zu zwei fest vorgegebenen Punkten sind die Ortslinien für Punkte mit konstanten Abstandssummen, Abstandsdifferenzen oder Abstandsverhältnissen Kegelschnitte;
Projektion. Ebene geometrische Projektionen
 Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Schwerpunktfach AM/PH, 2011 KEGELSCHNITTE
 Schwerpunktfach AM/PH, 011 KEGELSCHNITTE 5. Kreis und Ellipse 5.1. Grundkonstruktionen am Kreis Konstruktion 1: Konstruiere einen Kreis, welcher durch die gegebenen 3 Punkte A,B und C verläuft: C B A Konstruktionsbericht:
Schwerpunktfach AM/PH, 011 KEGELSCHNITTE 5. Kreis und Ellipse 5.1. Grundkonstruktionen am Kreis Konstruktion 1: Konstruiere einen Kreis, welcher durch die gegebenen 3 Punkte A,B und C verläuft: C B A Konstruktionsbericht:
Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel.
 1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
1 3 Die Parabel 3.1 Die Parabel als Kegelschnitt Wird ein Kreiskegel von einer Ebene geschnitten, welche zu einer Mantellinie des Kegels parallel ist, so entsteht als Schnittkurve eine Parabel. Sei SP
