2. Mathematische Grundlagen
|
|
|
- Judith Bruhn
- vor 7 Jahren
- Abrufe
Transkript
1 2. Mathematische Grundlagen Erforderliche mathematische Hilfsmittel: Summen und Produkte Exponential- und Logarithmusfunktionen 21
2 2.1 Endliche Summen und Produkte Betrachte n reelle Zahlen a 1, a 2,..., a n R. Zahlen notiert man wie folgt: Die Summe der a 1 + a a n = a i = i I a i Bezeichnungen: i heißt Summationsindex I = {1,..., n} heißt Indexmenge 22
3 Bemerkungen: Die Indexmenge I darf eine beliebige Menge ganzer Zahlen sein (I Z), z.b. I = { 4, 3, 2, 1, 0, 1, 2, 3}. Für die Summe gilt dann: i I a i = 3 i= 4 a i = a 4 + a 3 + a 2 + a 1 + a 0 + a 1 + a 2 + a 3 Die Indexmenge I kann auch leer sein, d.h. I = {}. Für die Summe definiert man dann i I a i = 0. 23
4 Fragen: Warum ist das Summenzeichen wichtig? Wie kann man formal mit Summen rechnen? Antworten: Das Summenzeichen vereinfacht die Schreibweise in der gesamten Statistik Es gibt Rechenregeln für Summen, die allesamt formal bewiesen werden müssen (Aufgabe der Mathematik) 24
5 Rechenregeln für endliche Summen: [I] Dazu seien a 1,..., a n sowie b 1,..., b n reelle Zahlen Mit den beliebigen reellen Zahlen α, β gilt: (α a i + β b i ) = = α α a i + β b i a i + β b i Falls a 1 = a 2 =... = a n a, so folgt: a i = a = n a 25
6 Rechenregeln für endliche Summen: [II] Für jedes (ganzzahlige) m mit 0 m n gilt: a i = m a i + a i i=m+1 Für jedes ganzzahlige m gilt: a i = n+m a i m +m 26
7 Spezielle endliche Summen: [I] i = n = n (n + 1) 2 i 2 = n (n + 1) (2n + 1) 6 i 3 = n2 (n + 1)
8 Spezielle endliche Summen: [II] Es seien a 1, b R, a i = a 1 + (i 1) b für i = 2,..., n. Dann heißt a 1, a 2,..., a n endliche arithmetische Folge 1. Ordnung und es gilt: a i = n 2 (2a 1 + (n 1) b) Es seien a 1, q R, a i = a 1 q i 1 für i = 2,..., n. Dann heißt a 1, a 2,..., a n endliche geometrische Folge und es gilt für q 1: a i = a 1 qn 1 q 1 28
9 Doppelsummen: [I] Es sei a 11 a 12 a 1m a 21 a 22 a 2m a n1 a n2 a nm eine Matrix (Tabelle) reeller Zahlen 29
10 Doppelsummen: [II] Die Summe über alle diese Zahlen notiert man als Doppelsumme: m j=1 a ij = a 11 + a a 1m + a 21 + a a 2m. + a n1 + a n a nm Es gilt: m j=1 a ij = m a ij j=1 30
11 Weiteres Beispiel für eine Doppelsumme: j=i a ij = a a 1n + a a 2n + a a 3n. + a nn (Der Laufbereich des 2. Index hängt vom 1. Index ab) 31
12 Endliche Produkte Betrachte n reelle Zahlen a 1, a 2,..., a n R. Mit der Indexmenge I = {1, 2,..., n} notiert man das Produkt der Zahlen wie folgt: a 1 a 2... a n = n a i = i I a i Bemerkung: Die Indexmenge I kann wiederum leer sein, d.h. I = {}. Für das Produkt definiert man dann i I a i = 1 32
13 Rechenregeln für endliche Produkte: Es seien a 1,..., a n sowie b 1,..., b n reelle Zahlen Mit den beliebigen reellen Zahlen α, β gilt: n α a i β b i = α n β n n a i n b i Falls a 1 = a 2 =... = a n a, so folgt: n a i = n a = a n 33
14 2.2 Exponentialfunktion und Logarithmus Zwei wichtige mathematische Funktionen: Natürliche Exponentialfunktion Natürlicher Logarithmus Hier: Mathematische Definition und Eigenschaften 34
15 Anwendung in der gesamten Wirtschaftstheorie, z.b. in der Wachstumstheorie (VWL) in Mikro- und Makromodellen (VWL) im gesamten Finance-Bereich (BWL) im Operations-Research (BWL) in der Statistik / Ökonometrie 35
16 Definition der Exponentialfunktion: [I] Betrachte die unendliche Reihe k=0 x k k! = 1 + x + x2 2 + x3 6 + x (k! bezeichnet das Produkt der ersten k ganzen Zahlen, also k! = k) Man kann zeigen, dass die Summe für jedes x R gegen eine endliche Zahl konvergiert 36
17 Definition der Exponentialfunktion: [II] Für jedes x R definiert man exp(x) = k=0 x k k! Die Funktion exp : R R heißt natürliche Exponentialfunktion 37
18 Graph der natürlichen Exponentialfunktion exp(x) x 38
19 Eigenschaften der Exponentialfunktion: [I] Es gilt: exp(0) = 1 exp(1) = e (Eulersche Zahl) Für alle x R gilt: exp(x) > 0 Für alle x R gilt: exp (x) d exp(x) = exp(x) d x (Ableitung ist gleich der Funktion selbst) 39
20 Eigenschaften der Exponentialfunktion: [II] Die Funktion exp ist streng monoton wachsend Für beliebige x, y R gilt die Beziehung: (Funktionalgleichung) exp(x + y) = exp(x) exp(y) Für alle x R gilt ( exp(x) = lim 1 + x ) n n n (Äquivalente Darstellung zur Summendefinition) 40
21 Jetzt: Die exp-funktion besitzt eine eindeutig bestimmte Umkehrfunktion Diese Umkehrfunktion ist definiert auf (0, ) Definition des natürlichen Logarithmus Die Umkehrfunktion der natürlichen Exponentialfunktion exp : R (0, ) heißt natürlicher Logarithmus und wird bezeichnet mit ln : (0, ) R 41
22 Graph des natürlichen Logarithmus ln(x) x 42
23 Eigenschaften des natürlichen Logarithmus: Die Funktion ln ist streng monoton wachsend Für x > 0 gilt: ln (x) = d ln(x) d x = 1 x Für beliebige x, y > 0 gilt die Beziehung (Funktionalgleichung) ln(x y) = ln(x) + ln(y) 43
24 Weitere Definitionen und Eigenschaften: [I] Die allgemeine Potenz ist für alle x > 0, y R definiert durch x y = exp(y ln(x)) Insbesondere ist für x R e x = exp(x) Es sei a > 0 und a 1. Der allgemeine Logarithmus von x > 0 zur Basis a ist definiert durch y = log a (x) x = a y 44
25 Weitere Definitionen und Eigenschaften: [II] Es gelten die folgenden Beziehungen: ln(x) = loge(x) ln(x) = log a (x) ln(a) log a (x) = ln(x) ln(a) Es sei f : R (0, ) eine differenzierbare Funktion. jedes x R heißt die Ableitung (ln(f(x)) = d ln(f(x)) = f (x) d x f(x) die logarithmische Ableitung von f an der Stelle x (auch: stetige Wachstumsrate) Für 45
Exponential- und Logarithmusfunktion. Biostatistik, WS 2010/2011. Inhalt. Matthias Birkner Mehr zur Eulerschen Zahl und natürliche
 Biostatistik, WS 2010/2011 Exponential- und Logarithmusfunktion Matthias Birkner http://www.mathematik.uni-mainz.de/~birkner/biostatistik1011/ 5.11.2010 Inhalt 1 Exponential- und Logarithmusfunktion Potenzen
Biostatistik, WS 2010/2011 Exponential- und Logarithmusfunktion Matthias Birkner http://www.mathematik.uni-mainz.de/~birkner/biostatistik1011/ 5.11.2010 Inhalt 1 Exponential- und Logarithmusfunktion Potenzen
Mathematik für Anwender I
 Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
Biostatistik, WS 2010/2011 Exponential- und Logarithmusfunktion
 1/22 Biostatistik, WS 2010/2011 Exponential- und Logarithmusfunktion Matthias Birkner http://www.mathematik.uni-mainz.de/~birkner/biostatistik1011/ 5.11.2010 2/22 Inhalt Exponential- und Logarithmusfunktion
1/22 Biostatistik, WS 2010/2011 Exponential- und Logarithmusfunktion Matthias Birkner http://www.mathematik.uni-mainz.de/~birkner/biostatistik1011/ 5.11.2010 2/22 Inhalt Exponential- und Logarithmusfunktion
Biostatistik, Winter 2011/12
 Biostatistik, Winter 2011/12 Summen, Exponentialfunktion, Ableitung Prof. Dr. Achim Klenke http://www.aklenke.de 2. Vorlesung: 04.11.2011 1/46 Inhalt 1 Summen und Produkte Summenzeichen Produktzeichen
Biostatistik, Winter 2011/12 Summen, Exponentialfunktion, Ableitung Prof. Dr. Achim Klenke http://www.aklenke.de 2. Vorlesung: 04.11.2011 1/46 Inhalt 1 Summen und Produkte Summenzeichen Produktzeichen
11 Spezielle Funktionen und ihre Eigenschaften
 78 II. ANALYSIS 11 Spezielle Funktionen und ihre Eigenschaften In diesem Abschnitt wollen wir wichtige Eigenschaften der allgemeinen Exponentialund Logarithmusfunktion sowie einiger trigonometrischer Funktionen
78 II. ANALYSIS 11 Spezielle Funktionen und ihre Eigenschaften In diesem Abschnitt wollen wir wichtige Eigenschaften der allgemeinen Exponentialund Logarithmusfunktion sowie einiger trigonometrischer Funktionen
17 Logarithmus und allgemeine Potenz
 7 Logarithmus und allgemeine Potenz 7. Der natürliche Logarithmus 7.3 Die allgemeine Potenz 7.4 Die Exponentialfunktion zur Basis a 7.5 Die Potenzfunktion zum Exponenten b 7.6 Die Logarithmusfunktion zur
7 Logarithmus und allgemeine Potenz 7. Der natürliche Logarithmus 7.3 Die allgemeine Potenz 7.4 Die Exponentialfunktion zur Basis a 7.5 Die Potenzfunktion zum Exponenten b 7.6 Die Logarithmusfunktion zur
Der natürliche Logarithmus. logarithmus naturalis
 Der natürliche Logarithmus ln logarithmus naturalis Zur Erinnerung: Die Exponentialfunktion y = exp(x) ist festgelegt durch 2 y = exp(x) y (x) = y(x) 0 x y(0) = 2 Zur Erinnerung: e := y() 2.78 exp(x) =
Der natürliche Logarithmus ln logarithmus naturalis Zur Erinnerung: Die Exponentialfunktion y = exp(x) ist festgelegt durch 2 y = exp(x) y (x) = y(x) 0 x y(0) = 2 Zur Erinnerung: e := y() 2.78 exp(x) =
Beispiel: Bestimmung des Werts 3 2 ( 2 1, 4142) Es gilt 3 1,41 = 3 141/100 = , 707. Es gilt 3 1,42 = 3 142/100 = , 759.
 (4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
(4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
Inhaltsverzeichnis. Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden. Mathematischer Vorkurs.
 Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Exponentialfunktionen und Logarithmen Inhaltsverzeichnis 1 Einführung 2 2
Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Exponentialfunktionen und Logarithmen Inhaltsverzeichnis 1 Einführung 2 2
Mathematischer Vorbereitungskurs für Ökonomen. Exponentialfunktionen und Logarithmen
 Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Exponentialfunktionen und Logarithmen Inhalt:. Zinsrechnung. Exponential- und Logaritmusfunktionen
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Exponentialfunktionen und Logarithmen Inhalt:. Zinsrechnung. Exponential- und Logaritmusfunktionen
Exponentialfunktion, Logarithmus
 Exponentialfunktion, Logarithmus. Die Exponentialfunktion zu einer Basis > 0 Bei Exponentialfunktionen ist die Basis konstant und der Exponent variabel... Die Exponentialfunktion zu einer Basis > 0. Sei
Exponentialfunktion, Logarithmus. Die Exponentialfunktion zu einer Basis > 0 Bei Exponentialfunktionen ist die Basis konstant und der Exponent variabel... Die Exponentialfunktion zu einer Basis > 0. Sei
Grundkurs Mathematik II
 Prof. Dr. H. Brenner Osnabrück SS 2017 Grundkurs Mathematik II Vorlesung 53 Die rationalen Exponentialfunktionen Zu einer positiven Zahl b K aus einem angeordenten Körper K haben wir in der 27. Vorlesung
Prof. Dr. H. Brenner Osnabrück SS 2017 Grundkurs Mathematik II Vorlesung 53 Die rationalen Exponentialfunktionen Zu einer positiven Zahl b K aus einem angeordenten Körper K haben wir in der 27. Vorlesung
$Id: stetig.tex,v /06/26 15:40:18 hk Exp $
 $Id: stetig.tex,v 1.11 2012/06/26 15:40:18 hk Exp $ 9 Stetigkeit 9.1 Eigenschaften stetiger Funktionen Am Ende der letzten Sitzung hatten wir eine der Grundeigenschaften stetiger Funktionen nachgewiesen,
$Id: stetig.tex,v 1.11 2012/06/26 15:40:18 hk Exp $ 9 Stetigkeit 9.1 Eigenschaften stetiger Funktionen Am Ende der letzten Sitzung hatten wir eine der Grundeigenschaften stetiger Funktionen nachgewiesen,
Mathematik für Wirtschaftswissenschaftler
 Mathematik für Wirtschaftswissenschaftler Yves Schneider Universität Luzern Frühjahr 2016 Repetition Kapitel 1 bis 3 2 / 54 Repetition Kapitel 1 bis 3 Ausgewählte Themen Kapitel 1 Ausgewählte Themen Kapitel
Mathematik für Wirtschaftswissenschaftler Yves Schneider Universität Luzern Frühjahr 2016 Repetition Kapitel 1 bis 3 2 / 54 Repetition Kapitel 1 bis 3 Ausgewählte Themen Kapitel 1 Ausgewählte Themen Kapitel
3. DER NATÜRLICHE LOGARITHMUS
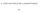 3. DER NATÜRLICHE LOGARITHMUS ln Der natürliche Logarithmus ln(x) betrachtet als Funktion in x, ist die Umkehrfunktion der Exponentialfunktion exp(x). Das bedeutet, für reelle Zahlen a und b gilt b = ln(a)
3. DER NATÜRLICHE LOGARITHMUS ln Der natürliche Logarithmus ln(x) betrachtet als Funktion in x, ist die Umkehrfunktion der Exponentialfunktion exp(x). Das bedeutet, für reelle Zahlen a und b gilt b = ln(a)
f : x 2 x f : x 1 Exponentialfunktion zur Basis a. Für alle Exponentialfunktionen gelten die Gleichungen (1) a x a y = a x+y (2) ax a y = ax y
 5. Die natürliche Exponentialfunktion und natürliche Logarithmusfunktion ================================================================== 5.1 Die natürliche Exponentialfunktion f : x 2 x f : x 1 2 x
5. Die natürliche Exponentialfunktion und natürliche Logarithmusfunktion ================================================================== 5.1 Die natürliche Exponentialfunktion f : x 2 x f : x 1 2 x
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Kapitel 5 GRENZWERTE
 Kapitel 5 GRENZWERTE Fassung vom 3. Februar 2006 Mathematik für Humanbiologen und Biologen 69 5. Der Begri des Grenzwertes 5. Der Begri des Grenzwertes An den Messungen der Hefevermehrung (vgl. Beispiel
Kapitel 5 GRENZWERTE Fassung vom 3. Februar 2006 Mathematik für Humanbiologen und Biologen 69 5. Der Begri des Grenzwertes 5. Der Begri des Grenzwertes An den Messungen der Hefevermehrung (vgl. Beispiel
differenzierbare Funktionen
 Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Der lange Weg zu den Potenz- und Logarithmengesetzen
 Der lange Weg zu den Potenz- und Logarithmengesetzen. Schritt: x n, n N, also eine natürliche Zahl ungleich Null). Wie jeder weiß gilt: 0 6 0 3 = } 0 0 0 {{ 0 0 0} 0 } 0 {{ 0} = } 0 0 0 0 0 {{ 0 0 0 0}
Der lange Weg zu den Potenz- und Logarithmengesetzen. Schritt: x n, n N, also eine natürliche Zahl ungleich Null). Wie jeder weiß gilt: 0 6 0 3 = } 0 0 0 {{ 0 0 0} 0 } 0 {{ 0} = } 0 0 0 0 0 {{ 0 0 0 0}
Kapitel 4 Folgen, Reihen & Funktionen
 Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Kapitel 4. Folgen und Reihen. Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38
 Kapitel 4 Folgen und Reihen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38 Folgen Eine Folge ist eine Anordnung von reellen Zahlen. Die einzelnen Zahlen heißen Glieder
Kapitel 4 Folgen und Reihen Josef Leydold Auffrischungskurs Mathematik WS 2017/18 4 Folgen und Reihen 1 / 38 Folgen Eine Folge ist eine Anordnung von reellen Zahlen. Die einzelnen Zahlen heißen Glieder
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Zahlenfolgen, endliche Summen und deren Grenzwerte
 Zahlenfolgen, endliche Summen und deren Grenzwerte Wichtige Begriffsbildungen, darunter die reellen Zahlen R, Exponentialfunktion und Logarithmus sowie Stetigkeit, Ableitung und Integral von Funktionen
Zahlenfolgen, endliche Summen und deren Grenzwerte Wichtige Begriffsbildungen, darunter die reellen Zahlen R, Exponentialfunktion und Logarithmus sowie Stetigkeit, Ableitung und Integral von Funktionen
Kapitel 6. Exponentialfunktion
 Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Potenzen, Wurzeln, Logarithmen
 KAPITEL 3 Potenzen, Wurzeln, Logarithmen 3.1 Funktionen und Umkehrfunktionen.............. 70 3.2 Wurzeln............................ 72 3.3 Warum ist a 2 + b 2 a + b?................. 73 3.4 Potenzfunktion........................
KAPITEL 3 Potenzen, Wurzeln, Logarithmen 3.1 Funktionen und Umkehrfunktionen.............. 70 3.2 Wurzeln............................ 72 3.3 Warum ist a 2 + b 2 a + b?................. 73 3.4 Potenzfunktion........................
11 Logarithmus und allgemeine Potenzen
 Logarithmus und allgemeine Potenzen Bevor wir uns mit den Eigenschaften von Umkehrfunktionen, und insbesondere mit der Umkehrfunktion der Eponentialfunktion ep : R R + beschäftigen, erinnern wir an den
Logarithmus und allgemeine Potenzen Bevor wir uns mit den Eigenschaften von Umkehrfunktionen, und insbesondere mit der Umkehrfunktion der Eponentialfunktion ep : R R + beschäftigen, erinnern wir an den
Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16)
 1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Monotone Funktionen. Definition Es sei D R. Eine Funktion f : D R heißt. (ii) monoton fallend, wenn für alle x, x D gilt. x < x f (x) f (x ).
 Monotone Funktionen Definition 4.36 Es sei D R. Eine Funktion f : D R heißt (i) monoton wachsend, wenn für alle x, x D gilt x < x f (x) f (x ). Wenn sogar die strikte Ungleichung f (x) < f (x ) folgt,
Monotone Funktionen Definition 4.36 Es sei D R. Eine Funktion f : D R heißt (i) monoton wachsend, wenn für alle x, x D gilt x < x f (x) f (x ). Wenn sogar die strikte Ungleichung f (x) < f (x ) folgt,
Thema 4 Limiten und Stetigkeit von Funktionen
 Thema 4 Limiten und Stetigkeit von Funktionen Wir betrachten jetzt Funktionen zwischen geeigneten Punktmengen. Dazu wiederholen wir einige grundlegende Begriffe und Schreibweisen aus der Mengentheorie.
Thema 4 Limiten und Stetigkeit von Funktionen Wir betrachten jetzt Funktionen zwischen geeigneten Punktmengen. Dazu wiederholen wir einige grundlegende Begriffe und Schreibweisen aus der Mengentheorie.
1 Beschreibung der Grundlagen
 Westsächsische Hochschule Zwickau Fachgruppe Mathematik Grundlagen Inhaltsverzeichnis Aufgaben zu den Grundlagen findet man über den folgenden Link: Aufgaben zu den Grundlagen 01 1 Beschreibung der Grundlagen
Westsächsische Hochschule Zwickau Fachgruppe Mathematik Grundlagen Inhaltsverzeichnis Aufgaben zu den Grundlagen findet man über den folgenden Link: Aufgaben zu den Grundlagen 01 1 Beschreibung der Grundlagen
Surjektive, injektive und bijektive Funktionen.
 Kapitel 1: Aussagen, Mengen, Funktionen Surjektive, injektive und bijektive Funktionen. Definition. Sei f : M N eine Funktion. Dann heißt f surjektiv, falls die Gleichung f(x) = y für jedes y N mindestens
Kapitel 1: Aussagen, Mengen, Funktionen Surjektive, injektive und bijektive Funktionen. Definition. Sei f : M N eine Funktion. Dann heißt f surjektiv, falls die Gleichung f(x) = y für jedes y N mindestens
Exponentialfunktion & Logarithmus
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen & 31. Oktober 2011 & Potenzen Definitionsbereiche Potenzrechenregeln Beispiel exp Beispiel: Lichtabsorption Definition Injektivität Beispiel:
Mathematik I für Biologen, Geowissenschaftler und Geoökologen & 31. Oktober 2011 & Potenzen Definitionsbereiche Potenzrechenregeln Beispiel exp Beispiel: Lichtabsorption Definition Injektivität Beispiel:
Klausur zur Analysis I WS 01/02
 Klausur zur Analysis I WS 0/0 Prof. Dr. E. Kuwert. Februar 00 Aufgabe (4 Punkte) Berechnen Sie unter a) und b) jeweils die Ableitung von f für x (0, ): a) f(x) = e sin x b) f(x) = x α log x a) f (x) =
Klausur zur Analysis I WS 0/0 Prof. Dr. E. Kuwert. Februar 00 Aufgabe (4 Punkte) Berechnen Sie unter a) und b) jeweils die Ableitung von f für x (0, ): a) f(x) = e sin x b) f(x) = x α log x a) f (x) =
e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme sin(x+y) = cos(x) sin(y)+sin(x) cos(y). und f. Für eine reelle Zahl x R gilt e ix = 1.
 8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
8. GRENZWERTE UND STETIGKEIT VON FUNKTIONEN 51 e. Für zwei reelle Zahlen x,y R gelten die Additionstheoreme cos(x+y) = cos(x) cos(y) sin(x) sin(y) und sin(x+y) = cos(x) sin(y)+sin(x) cos(y). f. Für eine
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION
 Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Kapitel 3 EXPONENTIAL- UND LOGARITHMUS-FUNKTION Fassung vom 3 Dezember 2005 Mathematik für Humanbiologen und Biologen 39 3 Exponentialfunktion 3 Exponentialfunktion Wir betrachten als einführendes Beispiel
Viele Statistiken werden durch endliche Folgen beschrieben. (z.b. Anzahl der Studierenden an der TU München in den Jahren 1962 bis 1976)
 Kapitel 9 Folgen und Reihen 9.1 Folgen 9.1.1 Was ist eine Folge? Abbildungen, die auf N definiert sind (mit Werten z.b. in R), heißen (unendliche) Folgen. Abb., die auf einer endlichen Menge aufeinander
Kapitel 9 Folgen und Reihen 9.1 Folgen 9.1.1 Was ist eine Folge? Abbildungen, die auf N definiert sind (mit Werten z.b. in R), heißen (unendliche) Folgen. Abb., die auf einer endlichen Menge aufeinander
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Die elementaren Funktionen (Überblick)
 Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
Die elementaren Funktionen (Überblick)
 Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Monotonie, Konkavität und Extrema
 Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
Kapitel 8 Monotonie, Konkavität und Extrema Josef Leydold Auffrischungskurs Mathematik WS 2017/18 8 Monotonie, Konkavität und Extrema 1 / 55 Monotonie Eine Funktion f heißt monoton steigend, falls x 1
2.4 Exponential - und Logarithmus - Funktionen
 25.05.20 2.4 Eponential - und Logarithmus - Funktionen Mit Hilfe der Potenz a t definiert man eine weitere Funktionsart, indem man statt der Basis den Eponenten durch die Variable ersetzt: Für a ε R >
25.05.20 2.4 Eponential - und Logarithmus - Funktionen Mit Hilfe der Potenz a t definiert man eine weitere Funktionsart, indem man statt der Basis den Eponenten durch die Variable ersetzt: Für a ε R >
23 Konvexe Funktionen und Ungleichungen
 23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
10 Kriterien für absolute Konvergenz von Reihen
 10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
17 Exponentialfunktion und Logarithmus
 17 Exponentialfunktion und Logarithmus Die Exponentialfunktion gilt als die wichtigste Funktion der Analysis. Sie hat sowohl theoretische als auch praktische Bedeutung. Sie tritt in vielen Anwendungen
17 Exponentialfunktion und Logarithmus Die Exponentialfunktion gilt als die wichtigste Funktion der Analysis. Sie hat sowohl theoretische als auch praktische Bedeutung. Sie tritt in vielen Anwendungen
Vektorräume und lineare Abbildungen
 Kapitel 11. Vektorräume und lineare Abbildungen 1 11.1 Vektorräume Sei K ein Körper. Definition. Ein Vektorraum über K (K-Vektorraum) ist eine Menge V zusammen mit einer binären Operation + einem ausgezeichneten
Kapitel 11. Vektorräume und lineare Abbildungen 1 11.1 Vektorräume Sei K ein Körper. Definition. Ein Vektorraum über K (K-Vektorraum) ist eine Menge V zusammen mit einer binären Operation + einem ausgezeichneten
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
Univariate Analysis. Analysis und nichtlineare Modelle Sommersemester
 Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Analysis und nichtlineare Modelle Sommersemester 9 5 Univariate Analysis C. Berechnen Sie ohne Taschenrechner(!). Runden Sie die Ergebnisse auf ganze Zahlen. (a) 7 :, (b) 795 :.. Berechnen Sie ohne Taschenrechner(!):
Kapitel 7. Exponentialfunktion
 Kapitel 7. Exponentialfunktion 7.1. Potenzreihen In Kap. 5 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 7. Exponentialfunktion 7.1. Potenzreihen In Kap. 5 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Mathematik für Wirtschaftswissenschaftler. Universität Trier Wintersemester 2013 / 2014
 Mathematik für Universität Trier Wintersemester 2013 / 2014 Inhalt der Vorlesung 1. Gleichungen und Summen 2. Grundlagen der Funktionslehre 3. Rechnen mit Funktionen 4. Optimierung von Funktionen 5. Funktionen
Mathematik für Universität Trier Wintersemester 2013 / 2014 Inhalt der Vorlesung 1. Gleichungen und Summen 2. Grundlagen der Funktionslehre 3. Rechnen mit Funktionen 4. Optimierung von Funktionen 5. Funktionen
Folgen und Reihen. Mathematik-Repetitorium
 Folgen und Reihen 1.1 Vollständige Induktion 1.2 Zahlenfolgen 1.3 Eigenschaften konvergenter Zahlenfolgen 1.4 Konvergenzkriterien 1.5 Unendliche Reihen 1.6 Eigenschaften unendlicher Reihen 1.7 Rechnen
Folgen und Reihen 1.1 Vollständige Induktion 1.2 Zahlenfolgen 1.3 Eigenschaften konvergenter Zahlenfolgen 1.4 Konvergenzkriterien 1.5 Unendliche Reihen 1.6 Eigenschaften unendlicher Reihen 1.7 Rechnen
$Id: reihen.tex,v /06/12 10:59:50 hk Exp $ unendliche Summe. a 1 + a 2 + a 3 +.
 Mathematik für Informatiker B, SS 202 Dienstag 2.6 $Id: reihen.tex,v.8 202/06/2 0:59:50 hk Exp $ 7 Reihen Eine Reihe ist eine unendliche Summe a + a 2 + a 3 +. Die Summanden a i können dabei reell oder
Mathematik für Informatiker B, SS 202 Dienstag 2.6 $Id: reihen.tex,v.8 202/06/2 0:59:50 hk Exp $ 7 Reihen Eine Reihe ist eine unendliche Summe a + a 2 + a 3 +. Die Summanden a i können dabei reell oder
f(x 0 ) = lim f(b k ) 0 0 ) = 0
 5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
Systemwissenschaften, Mathematik und Statistik
 Systemwissenschaften, Mathematik und Statistik Systemwissenschaften: 1 WS: Systemwissenschaften 1, VO 2std 2 SS: Systemwissenschaften 2, VO 2std Übung zu Systemwissenschaften, UE 2std 3 WS: Systemwissenschaften
Systemwissenschaften, Mathematik und Statistik Systemwissenschaften: 1 WS: Systemwissenschaften 1, VO 2std 2 SS: Systemwissenschaften 2, VO 2std Übung zu Systemwissenschaften, UE 2std 3 WS: Systemwissenschaften
a 0, a 1, a 2, a 3,... Dabei stehen die drei Pünktchen für unendlich oft so weiter.
 7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
Übungen zur Vorlesung MATHEMATIK II
 Fachbereich Mathematik und Informatik der Philipps-Universität Marburg Übungen zur Vorlesung MATHEMATIK II Prof. Dr. C. Portenier unter Mitarbeit von Michael Koch Marburg, Sommersemester 2005 Fassung vom
Fachbereich Mathematik und Informatik der Philipps-Universität Marburg Übungen zur Vorlesung MATHEMATIK II Prof. Dr. C. Portenier unter Mitarbeit von Michael Koch Marburg, Sommersemester 2005 Fassung vom
3. Folgen und Reihen. 3.1 Folgen und Grenzwerte. Denition 3.1 (Folge) Kapitelgliederung
 Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Die Exponentialfunktion und ihre Anwendung in der Biologie
 Die Exponentialfunktion und ihre Anwendung in der Biologie Escheria coli (kurz E. coli) sind Bakterien, die im Darm von Säugetieren und Menschen leben. Ein junges E. coli Bakterium wächst mit einer konstanten
Die Exponentialfunktion und ihre Anwendung in der Biologie Escheria coli (kurz E. coli) sind Bakterien, die im Darm von Säugetieren und Menschen leben. Ein junges E. coli Bakterium wächst mit einer konstanten
Kapitel 6 Folgen und Stetigkeit
 Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Vorkurs Mathematik. Übungen Teil IV
 Vorkurs Mathematik Herbst 009 M. Carl E. Bönecke Skript und Übungen Teil IV. Folgen und die Konstruktion von R Im vorherigen Kapitel haben wir Z und Q über (formale) Lösungsmengen von Gleichungen der Form
Vorkurs Mathematik Herbst 009 M. Carl E. Bönecke Skript und Übungen Teil IV. Folgen und die Konstruktion von R Im vorherigen Kapitel haben wir Z und Q über (formale) Lösungsmengen von Gleichungen der Form
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 3. Übung: Woche vom bis
 Übungsaufgaben 3. Übung: Woche vom 27. 10. bis 31. 10. 2010 Heft Ü1: 3.14 (c,d,h); 3.15; 3.16 (a-d,f,h,j); 3.17 (d); 3.18 (a,d,f,h,j) Übungsverlegung für Gruppe VIW 05: am Mo., 4.DS, SE2 / 022 (neuer Raum).
Übungsaufgaben 3. Übung: Woche vom 27. 10. bis 31. 10. 2010 Heft Ü1: 3.14 (c,d,h); 3.15; 3.16 (a-d,f,h,j); 3.17 (d); 3.18 (a,d,f,h,j) Übungsverlegung für Gruppe VIW 05: am Mo., 4.DS, SE2 / 022 (neuer Raum).
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
4.1. Grundlegende Definitionen. Elemente der Analysis I Kapitel 4: Funktionen einer Variablen. 4.2 Graphen von Funktionen
 4.1. Grundlegende Definitionen Elemente der Analysis I Kapitel 4: Funktionen einer Variablen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 22./29. November 2010 http://www.mathematik.uni-trier.de/
4.1. Grundlegende Definitionen Elemente der Analysis I Kapitel 4: Funktionen einer Variablen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 22./29. November 2010 http://www.mathematik.uni-trier.de/
x A, x / A x ist (nicht) Element von A. A B, A B A ist (nicht) Teilmenge von B. A B, A B A ist (nicht) echte Teilmenge von B.
 SBP Mathe Grundkurs 1 # 0 by Clifford Wolf # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das Lernen mit Lernkarten
SBP Mathe Grundkurs 1 # 0 by Clifford Wolf # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das Lernen mit Lernkarten
SBP Mathe Grundkurs 1 # 0 by Clifford Wolf. SBP Mathe Grundkurs 1
 SBP Mathe Grundkurs 1 # 0 by Clifford Wolf SBP Mathe Grundkurs 1 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
SBP Mathe Grundkurs 1 # 0 by Clifford Wolf SBP Mathe Grundkurs 1 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
4.4 Umkehrfunktion 77. Sei o.b.d.a. f(a) > 0 und f(b) < 0, setzen M = {y [a, b] mit f(x) > 0 für alle x [a, y]}
![4.4 Umkehrfunktion 77. Sei o.b.d.a. f(a) > 0 und f(b) < 0, setzen M = {y [a, b] mit f(x) > 0 für alle x [a, y]} 4.4 Umkehrfunktion 77. Sei o.b.d.a. f(a) > 0 und f(b) < 0, setzen M = {y [a, b] mit f(x) > 0 für alle x [a, y]}](/thumbs/73/68945497.jpg) . Umkehrfunktion 77 B e w e i s : Sei o.b.d.a. fa) > und fb) für alle [a, y] M a M), M beschränkt y b) Aiom V ξ [a, b] : ξ sup M fa) f) n.z.z. : i) fξ) ii) ξ a, b) zu i):
. Umkehrfunktion 77 B e w e i s : Sei o.b.d.a. fa) > und fb) für alle [a, y] M a M), M beschränkt y b) Aiom V ξ [a, b] : ξ sup M fa) f) n.z.z. : i) fξ) ii) ξ a, b) zu i):
Übungen zur Vorlesung Differential und Integralrechnung I Lösungsvorschlag
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner WS 203/4 Blatt 20.0.204 Übungen zur Vorlesung Differential und Integralrechnung I Lösungsvorschlag 4. a) Für a R betrachten wir die Funktion
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner WS 203/4 Blatt 20.0.204 Übungen zur Vorlesung Differential und Integralrechnung I Lösungsvorschlag 4. a) Für a R betrachten wir die Funktion
6.7 Isolierte Singularitäten
 6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 016/17 Dr. K. Rothe Analsis I für Studierende der Ingenieurwissenschaften Hörsaalübung mit Beispielaufgaben zu Blatt 3 Gegeben sei eine Funktion f :
Fachbereich Mathematik der Universität Hamburg WiSe 016/17 Dr. K. Rothe Analsis I für Studierende der Ingenieurwissenschaften Hörsaalübung mit Beispielaufgaben zu Blatt 3 Gegeben sei eine Funktion f :
Wiederholung von Linearer Algebra und Differentialrechnung im R n
 Wiederholung von Linearer Algebra und Differentialrechnung im R n 1 Lineare Algebra 11 Matrizen Notation: Vektor x R n : x = x 1 x n = (x i ) n i=1, mit den Komponenten x i, i {1,, n} zugehörige Indexmenge:
Wiederholung von Linearer Algebra und Differentialrechnung im R n 1 Lineare Algebra 11 Matrizen Notation: Vektor x R n : x = x 1 x n = (x i ) n i=1, mit den Komponenten x i, i {1,, n} zugehörige Indexmenge:
ist streng monoton fallend.
 Beispiel 3.5 Betrachte die Folgen aus Beispiel 3.1 Die Folgen a und d mit a n = n 2 und d n = 2 n sowie die Fibonacci-Folge sind streng monoton wachsend. Die Folge b mit b n = 1 n ist streng monoton fallend.
Beispiel 3.5 Betrachte die Folgen aus Beispiel 3.1 Die Folgen a und d mit a n = n 2 und d n = 2 n sowie die Fibonacci-Folge sind streng monoton wachsend. Die Folge b mit b n = 1 n ist streng monoton fallend.
Analysis I. Vorlesung 13. Gleichmäßige Stetigkeit
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 13 Gleichmäßige Stetigkeit Die Funktion f: R + R +, x 1/x, ist stetig. In jedem Punkt x R + gibt es zu jedem ǫ > 0 ein δ > 0 mit f(u (x,δ))
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Analysis I Vorlesung 13 Gleichmäßige Stetigkeit Die Funktion f: R + R +, x 1/x, ist stetig. In jedem Punkt x R + gibt es zu jedem ǫ > 0 ein δ > 0 mit f(u (x,δ))
3. DIE EXPONENTIALFUNKTION UND VERWANDTES
 3. DIE EXPONENTIALFUNKTION UND VERWANDTES (1) DIE KOMPLEXE EXPONENTIALFUNKTION Für α = (a n ) n=0mit a n := 1, (n IN) gilt r α = lim n (n + 1)! = lim n (n + 1) =. Damit konvergiert die zugehörige Potenzreihe
3. DIE EXPONENTIALFUNKTION UND VERWANDTES (1) DIE KOMPLEXE EXPONENTIALFUNKTION Für α = (a n ) n=0mit a n := 1, (n IN) gilt r α = lim n (n + 1)! = lim n (n + 1) =. Damit konvergiert die zugehörige Potenzreihe
lim Der Zwischenwertsatz besagt folgendes:
 2.3. Grenzwerte von Funktionen und Stetigkeit 35 Wir stellen nun die wichtigsten Sätze über stetige Funktionen auf abgeschlossenen Intervallen zusammen. Wenn man sagt, eine Funktion f:[a,b] R, definiert
2.3. Grenzwerte von Funktionen und Stetigkeit 35 Wir stellen nun die wichtigsten Sätze über stetige Funktionen auf abgeschlossenen Intervallen zusammen. Wenn man sagt, eine Funktion f:[a,b] R, definiert
Veranschaulichen Sie die de Morgan schen Regeln anhand von Venn-Diagrammen:
 Formalisierungspropädeutikum Aufgabensammlung Prof. Dr. Th. Augustin, Dr. R. Poellinger, C. Jansen, J. Plaß, G. Schollmeyer Oktober 2016 Aufgabe 1 (de Morgan sche Regeln) Veranschaulichen Sie die de Morgan
Formalisierungspropädeutikum Aufgabensammlung Prof. Dr. Th. Augustin, Dr. R. Poellinger, C. Jansen, J. Plaß, G. Schollmeyer Oktober 2016 Aufgabe 1 (de Morgan sche Regeln) Veranschaulichen Sie die de Morgan
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 13.1.016 Zwischenwertsatz und klassische Funktionen In diesem Abschnitt haben wir es mit Funktionen zu tun, die auf einem Intervall definiert sind. Eine Menge I R ist genau dann ein
Universität Freiburg 13.1.016 Zwischenwertsatz und klassische Funktionen In diesem Abschnitt haben wir es mit Funktionen zu tun, die auf einem Intervall definiert sind. Eine Menge I R ist genau dann ein
Der Abschluss D ist die Menge, die durch Hinzunahme der Intervallränder entsteht, in den obigen Beispielen also
 Festlegung Definitionsbereich 11.1 Festlegung Definitionsbereich Festlegung: Wir betrachten Funktionen f : D Ñ R, deren Definitionsbereich eine endliche Vereinigung von Intervallen ist, also z.b. D ra,
Festlegung Definitionsbereich 11.1 Festlegung Definitionsbereich Festlegung: Wir betrachten Funktionen f : D Ñ R, deren Definitionsbereich eine endliche Vereinigung von Intervallen ist, also z.b. D ra,
Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1. 1 Grundlagen 2. 2 Der Graph einer Funktion 4. 3 Umkehrbarkeit 5
 Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1 Inhaltsverzeichnis 1 Grundlagen 2 2 Der Graph einer Funktion
Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1 Inhaltsverzeichnis 1 Grundlagen 2 2 Der Graph einer Funktion
Funktionalgleichungen
 Funktionalgleichungen Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 10. Mai 2010 Funktionalgleichungen sind Gleichungen, mit denen Funktionen charakterisiert oder bestimmt werden können. In diesem
Funktionalgleichungen Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 10. Mai 2010 Funktionalgleichungen sind Gleichungen, mit denen Funktionen charakterisiert oder bestimmt werden können. In diesem
5 Stetigkeit und Differenzierbarkeit
 5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
Einleitung. Einige grundlegende Konzepte ziehen sich durch die gesamte Finanzmathematik:
 1 Einleitung Finanzmathematik durchzieht gewissermaßen das ganze Leben: Wir legen Geld auf ein zinsbringendes Konto, wir zahlen wiederholt denselben Betrag oder unterschiedliche Beträge zu beliebigen Zeitpunkten
1 Einleitung Finanzmathematik durchzieht gewissermaßen das ganze Leben: Wir legen Geld auf ein zinsbringendes Konto, wir zahlen wiederholt denselben Betrag oder unterschiedliche Beträge zu beliebigen Zeitpunkten
Einführung in die Stochastik 6. Übungsblatt
 Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Mathematische Anwendersysteme Einführung in MuPAD
 Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
Mathematische Anwendersysteme Einführung in MuPAD Tag 6 Folgen Konvergenzkriterien Reihen Potenzreihen 2322004 Gerd Rapin grapin@mathuni-goettingende Gerd Rapin Mathematische Anwendersysteme: Einführung
Weitere einfache Eigenschaften elementarer Funktionen
 Kapitel 6 Weitere einfache Eigenschaften elementarer Funktionen 6.1 Polynome Geg.: Polynom vom Grad n p(x) = a 0 + a 1 x +... + a n 1 x n 1 + a n x n, also mit a n 0. p(x) = x n ( a 0 x + a 1 n x +...
Kapitel 6 Weitere einfache Eigenschaften elementarer Funktionen 6.1 Polynome Geg.: Polynom vom Grad n p(x) = a 0 + a 1 x +... + a n 1 x n 1 + a n x n, also mit a n 0. p(x) = x n ( a 0 x + a 1 n x +...
Funktionen. Kapitel Der Funktionsbegriff
 Kapitel 6 Funktionen 6. Der Funktionsbegriff Eine Funktion f(x) ist durch eine Vorschrift f definiert, die jedem Element x D (Definitionsbereich) ein Element f(x) W (Wertebereich) zuordnet. Für reelle
Kapitel 6 Funktionen 6. Der Funktionsbegriff Eine Funktion f(x) ist durch eine Vorschrift f definiert, die jedem Element x D (Definitionsbereich) ein Element f(x) W (Wertebereich) zuordnet. Für reelle
Das Newton Verfahren.
 Das Newton Verfahren. Ziel: Bestimme eine Nullstelle einer differenzierbaren Funktion f :[a, b] R. Verwende die Newton Iteration: x n+1 := x n f x n) f x n ) für f x n ) 0 mit Startwert x 0. Das Verfahren
Das Newton Verfahren. Ziel: Bestimme eine Nullstelle einer differenzierbaren Funktion f :[a, b] R. Verwende die Newton Iteration: x n+1 := x n f x n) f x n ) für f x n ) 0 mit Startwert x 0. Das Verfahren
Kapitel 5 Reihen 196
 Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
2. Funktionen einer Variablen
 . Funktionen einer Variablen Literatur: [SH, Kapitel 4].1. Definitionen.. Typen von Funktionen..1. Lineare Funktionen... Quadratische Funktionen..3. Polynome..4. Potenzfunktionen..5. Exponentialfunktionen..6.
. Funktionen einer Variablen Literatur: [SH, Kapitel 4].1. Definitionen.. Typen von Funktionen..1. Lineare Funktionen... Quadratische Funktionen..3. Polynome..4. Potenzfunktionen..5. Exponentialfunktionen..6.
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Betriebswirtschaft International Business Dresden 05 . Mengen
Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik / Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Betriebswirtschaft International Business Dresden 05 . Mengen
: das Bild von ) unter der Funktion ist gegeben durch
 % 1.3 Funktionen Seien und Mengen nennt man Funktion oder Abbildung. Beachte: Zuordnung ist eindeutig. Bezeichnungen: : Definitionsbereich : Bildbereich (Zielmenge) von Der Graph einer Funktion: graph!
% 1.3 Funktionen Seien und Mengen nennt man Funktion oder Abbildung. Beachte: Zuordnung ist eindeutig. Bezeichnungen: : Definitionsbereich : Bildbereich (Zielmenge) von Der Graph einer Funktion: graph!
KAPITEL 2. Folgen und Reihen
 KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
Folgen und Reihen. Katharina Brazda 9. März 2007
 Katharina Brazda 9. März 2007 Inhaltsverzeichnis 1 Folgen 2 1.1 Definition von Folgen - explizite und rekursive Darstellung.............. 2 1.2 Wachstumsverhalten von Folgen - Monotonie und Beschränktheit..........
Katharina Brazda 9. März 2007 Inhaltsverzeichnis 1 Folgen 2 1.1 Definition von Folgen - explizite und rekursive Darstellung.............. 2 1.2 Wachstumsverhalten von Folgen - Monotonie und Beschränktheit..........
1 Folgen und Stetigkeit
 1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
1 Folgen und Stetigkeit 1.1 Folgen Eine Folge ist eine durchnummerierte Zusammenfassung von reellen Zahlen. Sie wird geschrieben als (a 1, a 2, a 3,...) = (a n ) n N. Es ist also a n R. Der Index n gibt
Folgen und Reihen von Funktionen
 Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
Höhere Mathematik für Physiker II
 Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
