Theoretische Einleitung Fachwerkbrücken Parabelbrücken
|
|
|
- Jörn Schäfer
- vor 6 Jahren
- Abrufe
Transkript
1 Quellen: www1.pictures.gi.zimbio.com
2 Quellen: www1.pictures.gi.zimbio.com
3 Kräfte in unserer Umgebung C. Hauck, F. Stefanica Universität Stuttgart 14. Juli 2011
4 Agenda 1 Theoretische Einleitung Kräfte sind Vektoren Kräfteüberlagerung Kräftezerlegung Beispiel Kräftezerlegung 2 Fachwerkbrücken Theorie Beispiel 3 Parabelbrücken
5 Kräfte sind charakterisiert durch...
6 Kräfte sind charakterisiert durch... Betrag (Länge, Größe)
7 Kräfte sind charakterisiert durch... Betrag (Länge, Größe) Orientierung
8 Kräfte sind charakterisiert durch... Betrag (Länge, Größe) Orientierung : Richtung + Richtungssinn
9 Kräfte sind charakterisiert durch... Betrag (Länge, Größe) Orientierung : Richtung + Richtungssinn Kräfte können als Vektoren dargestellt werden.
10 Vektordarstellung einer Kraft
11 Vektordarstellung einer Kraft
12 Vektordarstellung einer Kraft F = ( Fx F y )
13 Vektordarstellung einer Kraft F = ( Fx F y )
14 Vektordarstellung einer Kraft F = ( Fx F y ) F x = F cos α, F y = F sin α
15 Vektordarstellung einer Kraft F = ( Fx F y ) F x = ( F cos ) α, F y = F sin α Fx F x = 0
16 Vektordarstellung einer Kraft F = ( Fx F y ) F x = ( F cos ) α, F y = F sin α Fx F x = 0 ( ) 0 F y = F y
17 Vektordarstellung einer Kraft F = ( Fx F y ) F x = ( F cos ) α, F y = F sin α Fx F x = 0 ( ) 0 F y = F = F y F 2 x + F 2 y
18 Beispiel Kräfteüberlagerung Auf einen punktförmigen Gegenstand wirken die folgenden zwei Kräfte: F 1 = 8N F 2 = 8N.
19 Beispiel Kräfteüberlagerung Auf einen punktförmigen Gegenstand wirken die folgenden zwei Kräfte: F 1 = 8N F 2 = 8N. Wie groß ist die resultierende Kraft?
20 Beispiel Kräfteüberlagerung F 1 und F 2 haben gleiche Richtung, gleichen Richtungssinn:
21 Beispiel Kräfteüberlagerung F 1 und F 2 haben gleiche Richtung, gleichen Richtungssinn:
22 Beispiel Kräfteüberlagerung F 1 und F 2 haben gleiche Richtung, gleichen Richtungssinn: F R = 8N + 8N = 16N
23 Beispiel Kräfteüberlagerung F 1 und F 2 haben gleiche Richtung, gleichen Richtungssinn: F R = 8N + 8N = 16N F 1 und F 2 haben gleiche Richtung, entgegengesetzten Richtungssinn:
24 Beispiel Kräfteüberlagerung F 1 und F 2 haben gleiche Richtung, gleichen Richtungssinn: F R = 8N + 8N = 16N F 1 und F 2 haben gleiche Richtung, entgegengesetzten Richtungssinn:
25 Beispiel Kräfteüberlagerung F 1 und F 2 haben gleiche Richtung, gleichen Richtungssinn: F R = 8N + 8N = 16N F 1 und F 2 haben gleiche Richtung, entgegengesetzten Richtungssinn: F R = 8N 8N = 0N
26 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen:
27 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen:
28 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen:
29 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen: F 1x = 4N, F 1y 6, 928N F 2x 6, 928N, F 2y = 4N
30 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen: F 1x = 4N, F 1y 6, 928N F 2x 6, 928N, F 2y = 4N
31 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen: F 1x = 4N, F 1y 6, 928N F 2x 6, 928N, F 2y = 4N F Rx 10, 928N, F Ry 10, 928N
32 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen: F 1x = 4N, F 1y 6, 928N F 2x 6, 928N, F 2y = 4N F Rx 10, 928N, F Ry 10, 928N
33 Beispiel Kräfteüberlagerung F 1 und F 2 haben verschiedene Richtungen: F 1x = 4N, F 1y 6, 928N F 2x 6, 928N, F 2y = 4N F Rx 10, 928N, F Ry 10, 928N F R = FR 2 x + FR 2 y 15, 454N
34 Kräfteüberlagerung Allgemeines Vorgehen:
35 Kräfteüberlagerung Allgemeines Vorgehen: Zerlegung der Kräfte in Richtung der Koordinatenachsen
36 Kräfteüberlagerung Allgemeines Vorgehen: Zerlegung der Kräfte in Richtung der Koordinatenachsen Addition der Komponenten entlang jeder einzelnen Achse Komponenten der resultierenden Kraft
37 Kräfteüberlagerung Allgemeines Vorgehen: Zerlegung der Kräfte in Richtung der Koordinatenachsen Addition der Komponenten entlang jeder einzelnen Achse Komponenten der resultierenden Kraft Berechnung der Resultierenden als Hypotenuse in einem rechtwinkligen Dreieck
38 Kräfteüberlagerung Allgemeines Vorgehen: Zerlegung der Kräfte in Richtung der Koordinatenachsen Addition der Komponenten entlang jeder einzelnen Achse Komponenten der resultierenden Kraft Berechnung der Resultierenden als Hypotenuse in einem rechtwinkligen Dreieck Im Dreidimensionalen: F R ist Diagonale im Quader.
39 Kräftezerlegung in vorgegebene Richtungen Es ist die Kraft F R gegeben, deren Betrag und Orientierung bekannt sind.
40 Kräftezerlegung in vorgegebene Richtungen Es ist die Kraft F R gegeben, deren Betrag und Orientierung bekannt sind. Diese soll in zwei sich überlagernde Komponenten zerlegt werden, wobei die Komponenten mit FR die Winkel α und β bilden.
41 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen:
42 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R
43 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R
44 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen
45 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen
46 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms
47 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms
48 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms - Berechnen des dritten Winkels im Dreieck ABC:
49 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms - Berechnen des dritten Winkels im Dreieck ABC:
50 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms - Berechnen des dritten Winkels im Dreieck ABC: γ = 180 α β
51 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms - Berechnen des dritten Winkels im Dreieck ABC: γ = 180 α β - Berechnen der gesuchten Komponenten mit Hilfe des Sinussatzes:
52 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms - Berechnen des dritten Winkels im Dreieck ABC: γ = 180 α β - Berechnen der gesuchten Komponenten mit Hilfe des Sinussatzes: AB = AC sin β sin γ AB = AC sin β sin γ = F 1
53 Kräftezerlegung in vorgegebene Richtungen Allgemeines Vorgehen: - Einzeichnen von F R - Einzeichnen der vorgegebenen Richtungen - Einzeichnen des Parallelogramms - Berechnen des dritten Winkels im Dreieck ABC: γ = 180 α β - Berechnen der gesuchten Komponenten mit Hilfe des Sinussatzes: AB = AC sin β sin γ analog: BC = AC sin α sin γ = F 2 AB = AC sin β sin γ = F 1
54 Gleichgewichtszustand
55 Gleichgewichtszustand Problematik Körper bzw. Kräftegruppe ist im Gleichgewicht, wenn F = 0. Zerlegung in die Komponenten: Fx = 0, F y = 0, F Z = 0 Die z-komponente entfällt bei ebenen Probleme.
56 Beispiel Kräftezerlegung: Straßenlaterne Problematik Straßenlaterne 100N ist an einem Seil mittig über der Straße gespannt.
57 Beispiel Kräftezerlegung: Straßenlaterne Problematik Straßenlaterne 100N ist an einem Seil mittig über der Straße gespannt. Seil hat einen Scheitelwinkel von 140.
58 Beispiel Kräftezerlegung: Straßenlaterne Problematik Straßenlaterne 100N ist an einem Seil mittig über der Straße gespannt. Seil hat einen Scheitelwinkel von 140. Wie groß ist die Kraft im Seil?
59 Freikörperbild Vorgang Koordinatensystem festlegen. Freilegen der Reaktionskräfte und innere Kräfte durch gedankliches Aufschneiden. Freikörperbild = Darstellung aller eingeprägten und inneren Kräfte am freigeschnittenen Körper.
60 Gleichgewichtsgleichung Aufstellen des Gleichgewichts F = 0
61 Gleichgewichtsgleichung Aufstellen des Gleichgewichts ( S1 cos(α) S 1 sin(α) F = 0 ) ( S2 cos(β) + S 2 sin(β) ) ( 0 G ) = ( 0 0 )
62 Gleichgewichtsgleichung Komponentenweise Aufstellen des linearen Gleichungssystems (LGS): α = β (Symmetrie) Fx = 0 : S 1 cos(α) S 2 cos(α) = 0 (1) Fy = 0 : S 1 sin(α) + S 2 sin(α) G = 0 (2) Aus 1: S 1 = S 2 cos(α) cos(α) = S 2 = S (3)
63 Gleichgewichtsgleichung Komponentenweise Aufstellen des linearen Gleichungssystems (LGS): α = β (Symmetrie) Fx = 0 : S 1 cos(α) S 2 cos(α) = 0 (1) Fy = 0 : S 1 sin(α) + S 2 sin(α) G = 0 (2) Aus 1: S 1 = S 2 cos(α) cos(α) = S 2 = S (3) Mit 3 in 2: 2 S sin(α) = G G S = 2 sin(α) = 100N 2 sin(20 ) = 146N
64 Fachwerkbrücke Informationen Alte Eisenbahnbrücken
65 Fachwerkbrücke Informationen Alte Eisenbahnbrücken Gute Montierbarkeit
66 Fachwerkbrücke Informationen Alte Eisenbahnbrücken Gute Montierbarkeit Einfache Berechnung Knotenpunktverfahren
67 Knotenpunktverfahren Grundidee Koordinatensystem festlegen
68 Knotenpunktverfahren Grundidee Koordinatensystem festlegen An einem Knoten kommen mehrere Stäbe zusammen
69 Knotenpunktverfahren Grundidee Koordinatensystem festlegen An einem Knoten kommen mehrere Stäbe zusammen Nummerierung Stäbe und Knoten
70 Knotenpunktverfahren Grundidee Koordinatensystem festlegen An einem Knoten kommen mehrere Stäbe zusammen Nummerierung Stäbe und Knoten Freischneiden jedes Knotens (Stäbe auf Zug belastet)
71 Knotenpunktverfahren Grundidee Koordinatensystem festlegen An einem Knoten kommen mehrere Stäbe zusammen Nummerierung Stäbe und Knoten Freischneiden jedes Knotens (Stäbe auf Zug belastet) Aufstellen der Gleichgewicht für jeden Knoten F = 0
72 Knotenpunktverfahren Grundidee Koordinatensystem festlegen An einem Knoten kommen mehrere Stäbe zusammen Nummerierung Stäbe und Knoten Freischneiden jedes Knotens (Stäbe auf Zug belastet) Aufstellen der Gleichgewicht für jeden Knoten F = 0 Bestimmung Stab- und Lagerkräfte mittels LGS
73 Anwendungsbeispiel Informationen Lagerung durch Festlager A und Loslager B
74 Theoretische Einleitung Fachwerkbrücken Anwendungsbeispiel Informationen Lagerung durch Festlager A und Loslager B Parabelbrücken
75 Theoretische Einleitung Fachwerkbrücken Anwendungsbeispiel Informationen Lagerung durch Festlager A und Loslager B Parabelbrücken
76 Anwendungsbeispiel Informationen Lagerung durch Festlager A und Loslager B Besteht aus 5 Stäbe und 4 Knoten (A, B, I und II)
77 Anwendungsbeispiel Informationen Lagerung durch Festlager A und Loslager B Besteht aus 5 Stäbe und 4 Knoten (A, B, I und II) Die Stäbe 1 und 2 haben die Länge 2a
78 Anwendungsbeispiel Informationen Lagerung durch Festlager A und Loslager B Besteht aus 5 Stäbe und 4 Knoten (A, B, I und II) Die Stäbe 1 und 2 haben die Länge 2a Der Stab 3 hat die Länge a
79 Anwendungsbeispiel Informationen Lagerung durch Festlager A und Loslager B Besteht aus 5 Stäbe und 4 Knoten (A, B, I und II) Die Stäbe 1 und 2 haben die Länge 2a Der Stab 3 hat die Länge a Belastung Knoten I mit 2F = 30000N; Knoten II mit F
80 Geometrie Für den Winkel α gilt: tan(α) = a 2a = 1 2 sin(α) = α 26, 565 tan(α) 5 = tan 2 (α) 1 5 cos(α) = = tan 2 5 (α)
81 Gleichgewichtsbedingung Knoten A: ( Ax A y ) ( S1 + 0 ) ( S4 cos(α) + S 4 sin(α) ) = ( 0 0 )
82 Gleichgewichtsbedingung Knoten I: ( S1 0 ) ( S2 + 0 ) ( 0 + S 3 ) ( 0 2F ) = ( 0 0 )
83 Gleichgewichtsbedingung Knoten II: ( F 0 ) ( S4 cos(α) S 4 sin(α) ) ( S5 cos(α) + S 5 sin(α) ) ( 0 S 3 ) = ( 0 0 )
84 Gleichgewichtsbedingung Knoten B: ( 0 B y ) ( S2 0 ) ( S5 cos(α) + S 5 sin(α) ) = ( 0 0 )
85 Gleichungssystem Knoten A: : A x + S 1 + S 4 cos(α) = 0 (1) : A y + S 4 sin(α) = 0 (2) Knoten I: : S 1 + S 2 = 0 (3) : S 3 2F = 0 (4) Knoten II: : F S 4 cos(α) + S 5 cos(α) = 0 (5) : S 4 sin(α) S 5 sin(α) S 3 = 0 (6) Knoten B: : S 2 S 5 cos(α) = 0 (7) : B y + S 5 sin(α) = 0 (8)
86 Gleichungssystem LGS Matrizendarstellung: A x A y S 1 S 2 S 3 S 4 S 5 B y Kraft cos(α) sin(α) F cos(α) cos(α) 0 F sin(α) sin(α) cos(α) sin(α) 1 0
87 Lösung des Gleichungssystem Lösung Matrizendarstellung: A x A y S 1 S 2 S 3 S 4 S 5 B y Kraft [N]
88 Gleichungssystem Knoten A: : A x + S 1 + S 4 cos(α) = 0 (1) : A y + S 4 sin(α) = 0 (2) Knoten I: : S 1 + S 2 = 0 (3) : S 3 2F = 0 (4) Knoten II: : F S 4 cos(α) + S 5 cos(α) = 0 (5) : S 4 sin(α) S 5 sin(α) S 3 = 0 (6) Knoten B: : S 2 S 5 cos(α) = 0 (7) : B y + S 5 sin(α) = 0 (8)
89 Lösen des Gleichungssystems Aus 4: S 3 2F = 0 S 3 = 2F = 30000N Aus 6: S 4 sin(α) S 5 sin(α) S 3 = 0 S 4 = S 5 S 3 sin(α) (9)
90 Lösen des Gleichungssystems Mit 9 in 5: S 4 = S 5 S 3 sin(α) F + S 5 cos(α) + S 3 sin(α) cos α + S 5 cos α = 0 2 S 5 cos α = F S 3 sin(α) cos(α) F S 5 = 2 cos(α) S 3 = 41926N (10) 2 sin(α) Mit 10 in 9: S 4 = 25156N (11)
91 Lösen des Gleichungssystems Mit 10 in 7: S 2 S 5 cos(α) = 0 S 2 = S 5 cos(α) = 37500N (12) Mit 12 in 3: S 1 + S 2 = 0 S 1 = S 2 = 37500N (13) Mit 10 in 8: B y + S 5 sin(α) = 0 B y = S 5 sin(α) = 18749N
92 Lösen des Gleichungssystems Mit 11 und 13 in 1: A x + S 1 + S 4 cos(α) = 0 A x = S 1 S 4 cos α = 15000N Mit 11 in 2: A y + S 4 sin(α) = 0 A y = S 4 sin(α) = 11250N
93 Übersicht über die Kräfte Stab bzw. Lager Kraft [N] Belastung A x A y B y S Zug S Zug S Zug S Druck S Druck
94 Theoretische Einleitung Fachwerkbrücken Parabelbrücken Quellen: Parabelbrücken
95 Parabelbrücke und Kräfte
96 Parabelbrücke und Kräfte
97 Parabelbrücke und Kräfte
98 Parabelbrücke und Kräfte Im Punkt P 0 wirkt( die Kraft ) 0 F =. F
99 Parabelbrücke und Kräfte Im Punkt P 0 wirkt( die Kraft ) 0 F =. F Welche Kräfte wirken in den anderen Stützpunkten?
100 Parabelbrücke und Kräfte Kräfte im Punkt P 1 :
101 Parabelbrücke und Kräfte Kräfte im Punkt P 1 :
102 Parabelbrücke und Kräfte Kräfte im Punkt P 1 :
103 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke:
104 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 a = x F 2
105 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: x = F 2a 1 a = x F 2
106 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( ) F 0 = 2a 1 F = F 2a a 2
107 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( F 0 = 2a 1 F = F 2a a 2 ) Resultierende im Punkt P 1 :
108 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( F 0 = 2a 1 F = F 2a a 2 ) Resultierende im Punkt P 1 : F 1 = F 0 + F
109 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( F 0 = 2a 1 F = F 2a a 2 ) Resultierende im Punkt P 1 : F 1 = F 0 + ( F) ( ) 1 0 = F + 2a a F
110 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( F 0 = 2a 1 F = F 2a a 2 ) Resultierende im Punkt P 1 : F 1 = F 0 + ( F) ( ) 1 0 = F + 2a a F ( ) ( ) 1 0 = F + F 2a a 2a 2a
111 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( F 0 = 2a 1 F = F 2a a 2 ) Resultierende im Punkt P 1 : F 1 = F 0 + ( F) ( ) 1 0 = F + 2a a F ( ) ( ) 1 0 = F + F 2a a 2a 2a ( ) 1 = F 2a 3a
112 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( F 0 = 2a 1 F = F 2a a 2 ) Resultierende im Punkt P 1 : F 1 = F 0 + ( F) ( ) 1 0 = F + 2a a F ( ) ( ) 1 0 = F + F 2a a 2a 2a ( ) 1 = F 2a 3a F 1 ist parallel zu P 1 P 2
113 Parabelbrücke und Kräfte Kräfte im Punkt P 1 : Ähnlichkeit der Dreiecke: 1 = x a F x = F 2a 2 ( F ) ( F 0 = 2a 1 F = F 2a a 2 ) Resultierende im Punkt P 1 : F 1 = F 0 + ( F) ( ) 1 0 = F + 2a a F ( ) ( ) 1 0 = F + F 2a a 2a 2a ( ) 1 = F 2a 3a F 1 ist parallel zu P ( ) ( 1 P) 2 = ( ) = 4a a 3a
114 Parabelbrücke und Kräfte Resultierende im Punkt P 2 :
115 Parabelbrücke und Kräfte Resultierende im Punkt P 2 : F 2 = F 1 + F
116 Parabelbrücke und Kräfte Resultierende im Punkt P 2 : F 2 = F 1 + ( F ) ( ) = F 1 0 2a + 3a F
117 Parabelbrücke und Kräfte Resultierende im Punkt P 2 : F 2 = F 1 + ( F ) ( ) = F 1 0 2a + 3a F ( ) ( ) = F 1 2a + F 0 3a 2a 2a
118 Parabelbrücke und Kräfte Resultierende im Punkt P 2 : F 2 = F 1 + ( F ) ( ) = F 1 0 2a + 3a F ( ) ( = F 1 2a + F 0 3a 2a 2a ( ) = F 1 2a 5a )
119 Parabelbrücke und Kräfte Resultierende im Punkt P 2 : F 2 = F 1 + ( F ) ( ) = F 1 0 2a + 3a F ( ) ( = F 1 2a + F 0 2a 2a = F 2a 3a ( ) 1 5a F 2 ist parallel zu P 2 P 3 = ) ( 3 9a ) ( 2 4a ) = ( 1 5a )
120 Parabelbrücke und Kräfte Resultierende im Punkt P 2 : F 2 = F 1 + ( F ) ( ) = F 1 0 2a + 3a F ( ) ( = F 1 2a + F 0 2a 2a = F 2a 3a ( ) 1 5a F 2 ist parallel zu P 2 P 3 = ) ( 3 9a ) ( 2 4a ) = ( 1 5a ) Parallelität
121 Parabelbrücke und Kräfte Resultierende im Punkt P 2 : F 2 = F 1 + ( F ) ( ) = F 1 0 2a + 3a F ( ) ( = F 1 2a + F 0 2a 2a = F 2a 3a ( ) 1 5a F 2 ist parallel zu P 2 P 3 = ) ( 3 9a ) ( 2 4a ) = ( 1 5a ) Parallelität keine Biegemomente
122 Parabelbrücke und Kräfte F 1 < F 2
123 Parabelbrücke und Kräfte F 1 < F 2 < F 3
124 Parabelbrücke und Kräfte F 1 < F 2 < F 3 < F 4
125 Parabelbrücke und Kräfte F 1 < F 2 < F 3 < F 4 <...
126 Parabelbrücke und Kräfte F 1 < F 2 < F 3 < F 4 <...
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
Aufgaben zur Statik S 1. Seilkräfte 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn Am Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. Addition
3. Zentrales ebenes Kräftesystem
3. Zentrales ebenes Kräftesystem Eine ruppe von Kräften, die an einem starren Körper angreifen, bilden ein zentrales Kräftesystem, wenn sich die Wirkungslinien aller Kräfte in einem Punkt schneiden. f
1. Einfache ebene Tragwerke
Die Ermittlung der Lagerreaktionen einfacher Tragwerke erfolgt in drei Schritten: Freischneiden Aufstellen der Gleichgewichtsbedingungen Auflösen der Gleichungen Prof. Dr. Wandinger 3. Tragwerksanalyse
Aufgaben mit Lösungen zum Themengebiet: Geometrie bei rechtwinkligen Dreiecken
Übungsaufgaben zur Satzgruppe des Pythagoras: 1) Seiten eines rechtwinkligen Dreiecks Sind folgende Aussagen richtig oder falsch? Verbessere, wenn notwendig! Die Katheten grenzen an den rechten Winkel.
4. Verzerrungen. Der Abstand von zwei Punkten ändert sich. Der Winkel zwischen drei Punkten ändert sich
4. Verzerrungen Wird ein Körper belastet, so ändert sich seine Geometrie. Die Punkte des Körpers ändern ihre Lage. Sie erfahren eine Verschiebung. Ist die Verschiebung für benachbarte Punkte unterschiedlich,
und der Kosinussatz cos(γ) = a2 + b 2 c 2 2 a b Sinussatz sin(β) = a b
Blatt Nr 1906 Mathematik Online - Übungen Blatt 19 Dreieck Geometrie Nummer: 41 0 2009010074 Kl: 9X Aufgabe 1911: (Mit GTR) In einem allgemeinen Dreieck ABC sind a = 18782, c = 1511 und β = 33229 gegeben
Vorlesung Technische Mechanik 1 Statik, Wintersemester 2007/2008. Technische Mechanik
Technische Mechanik 1. Einleitung 2. Statik des starren Körpers 3. Statik von Systemen starrer Körper 3.1 Gleichgewichtsbedingungen, das Erstarrungsprinzip 3.2 Lager 3.2.1 Lagerung in der Ebene 3.2.2 Allgemeiner
3. Allgemeine Kraftsysteme
3. Allgemeine Kraftsysteme 3.1 Parallele Kräfte 3.2 Kräftepaar und Moment 3.3 Gleichgewicht in der Ebene Prof. Dr. Wandinger 1. Statik TM 1.3-1 3.1 Parallele Kräfte Bei parallelen Kräften in der Ebene
Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher Umlaufsinn!
Berechnungen in Dreiecken Allgemeines zu Dreiecken Innenwinkelsatz α + β + γ = 180 Besondere Dreiecke Gleichschenkliges Dreieck Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher
entspricht der Länge des Vektorpfeils. Im R 2 : x =
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Brückenkurs Mathematik. Mittwoch Freitag
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
0,6 m. 0,4m. Gegeben seien die obigen drei auf den Balken wirkenden Kräfte mit:
Kurs: Statik Thema: Resultierende bestimmen Aufgabe 1) Wo liegt bei der Berechnung der Resultierenden der Unterschied zwischen Kräften mit einem gemeinsamen Angriffspunkt und Kräften mit unterschiedlichen
Analytische Geometrie II
Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
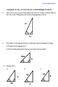Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Lösungen der Übungsaufgaben III
Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
TECHNISCHE MECHANIK A (STATIK)
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 3 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 31 5,5 15,5 10,5 11,5 6 80 Davon erreicht Punkte: Gesamtergebnis
Technische Mechanik. Statik
Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
4. Das (symmetrische) - im Querschnitt dreieckige - Dach eines Hauses ist 3,50 Meter
1. Eine 7 Meter lange Leiter lehnt an einer Hauswand. Sie schließt mit dem Boden eine Winkel von 70 ein. a) In welcher Höhe lehnt die Leiter an der Wand? b) Wie weit ist der Fußpunkt der Leiter von der
Trigonometrie. bekannte Zusammenhänge. 4-Streckensatz: groß/klein = groß/klein. Zusammenhänge im allgemeinen Dreieck:
Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
1.4 Trigonometrie. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 3
1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
Symmetrien und Winkel
1 10 Symmetrien 301 Zeichne Grossbuchstaben des Alphabets, sortiert nach vier Typen: achsensymmetrisch punktsymmetrisch achsen- und punktsymmetrisch weder achsen- noch punktsymmetrisch Trage bei den symmetrischen
1.4 Trigonometrie I. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 4
1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
TECHNISCHE MECHANIK A (STATIK)
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Formelsammlung Mathematik Grundkurs Inhalt
Formelsammlung Mathematik Grundkurs Inhalt Inhalt...1 Trigonometrie Grundlagen... Vektoren...3 Skalarprodukt...4 Geraden...5 Abstandsberechnungen...6 Ebenen...7 Lineare Gleichungssysteme (LGS)...8 Gauß'sches
52 5 Gleichgewicht des ebenen Kraftsystems. Festlager
52 5 Gleichgewicht des ebenen Kraftsystems Loslager A estlager B BH Einspannung A M A AH A BV AV Abbildung 5.11: Typische Lagerungen eines starren Körpers in der Ebene (oben) und die zugehörigen Schnittskizzen
2.3.4 Drehungen in drei Dimensionen
2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
4. In einem Parallelogramm ABCD sind die Seiten a = c = 6 und
Sinus, Cosinus und Tangens 1. In einem gleichschenkligen Dreieck ABCsind die Seiten c = 4 und a = b = gegeben. Berechne die Winkel im Dreieck ABC und den Flächeninhalt des Dreiecks. In einem Parallelogramm
1 lineare Gleichungssysteme
Hinweise und Lösungen: http://mathemathemathe.de/lineare-algebra-grundlagen 1 lineare Gleichungssysteme Übung 1.1: Löse das lineare Gleichungssystem: I 3x + 3y + 7z = 13 II 1x 2y + 2, 5z = 1, 5 III 4x
Hochschule Karlsruhe Technische Mechanik Statik. Aufgaben zur Statik
S 1. Seilkräfte ufgaben zur Statik 28 0 F 1 = 40 kn 25 0 F 2 = 32 kn m Mast einer Überlandleitung greifen in der angegebenen Weise zwei Seilkräfte an. Bestimmen Sie die resultierende Kraft. S 2: Zentrales
Grundwissen 10. Überblick: Gradmaß rπ Länge eines Bogens zum Mittelpunktswinkels α: b = α
Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
3D-Transformationen. Kapitel Translation Skalierung
Kapitel 13 3D-Transformationen Wie im weidimensionalen Fall, werden die Definitionspunkte der Objekte als Spaltenvektoren mit homogener Koordinate geschrieben. Die notwendigen Transformationen werden wieder
Mechanik 1. Übungsaufgaben
Mechanik 1 Übungsaufgaben Universitätsprofessor Dr.-Ing. habil. Jörg Schröder Universität Duisburg-Essen, Standort Essen Fachbereich 10 - Bauwesen Institut für Mechanik Übung zu Mechanik 1 Seite 1 Aufgabe
Lineare Funktionen. Das rechtwinklige (kartesische) Koordinatensystem. Funktionen
Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
Lösung zur Übung 3 vom
Lösung zur Übung 3 vom 28.0.204 Aufgabe 8 Gegeben ist ein Dreieck mit den nachfolgenden Seiten- und Winkelbezeichnung. Der Cosinussatz ist eine Verallgemeinerung des Satzes des Pythagoras: a) c 2 = a 2
f(x nk ) = lim y nk ) = lim Bemerkung 2.14 Der Satz stimmt nicht mehr, wenn D nicht abgeschlossen oder nicht beschränkt ist, wie man z.b.
Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
KREISFUNKTIONEN. Allgemeines
KREISFUNKTIONEN Allgemeines Um die Graphen der Winkelfunktionen zeichnen und verstehen zu können, ist es wichtig, den Einheitskreis zu kennen. Zunächst stellt man sich einen Kreis mit dem Radius 1 vor.
2. Räumliche Bewegung
2. Räumliche Bewegung Prof. Dr. Wandinger 1. Kinematik des Punktes TM 3 1.2-1 2. Räumliche Bewegung Wenn die Bahn des Punkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort
Koordinatengeometrie. Aufgabe 4 Untersuchen Sie die Funktion f(x) = x² 9.
Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Mathematik I Pflichtteil - Nachtermin Aufgabe P 1. Klasse: Platzziffer: Punkte:
Prüfungsdauer: Abschlussprüfung 2006 150 Minuten an den Realschulen in Bayern R4/R6 Mathematik I Pflichtteil - Nachtermin Aufgabe P 1 Name: Vorname: Klasse: Platzziffer: Punkte: P 1.0 Gegeben sind der
Prof. Dr. K. Melzer IWB 1 Blatt 1 Vektorrechnung Aufgaben
Prof. Dr. K. Melzer IWB Blatt Vektorrechnung Aufgaben Aufgabe : Ermitteln Sie die Koordinatendarstellung der skizzierten Vektoren a und b. Aufgabe 2: Ein Vektor r mit r = 7 und dem Anfangspunkt (2 ) hat
Trigonometrische Berechnungen
Trigonometrische Berechnungen Aufgabe 1 Berechnen Sie im rechtwinkligen Dreieck die fehlenden Seiten und Winkel: a) p = 4,93, β = 70,3 b) p = 28, q = 63 c) a = 12,5, p = 4,4 d) h = 9,1, q = 6,0 e) a =
Lösbarkeit linearer Gleichungssysteme
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Grundwissen Abitur Geometrie 15. Juli 2012
Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
Brückenkurs Mathematik
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Kugeldreieck. (a) München (λ = 11,5 ö. L., φ = 48,1 ) (b) New York (λ = 74,0 w. L., φ = 40,4 ) (c) Moskau (λ = 37,4 ö. L.
Kugeldreieck 1. Berechnen Sie die Fläche des vom Äquator, vom Nullmeridian und dem Längenkreis durch den angegebenen Ort begrenzten Kugeldreiecks. Geben Sie den sphärischen Exzeß des Dreiecks im Grad-
1. Ebene gerade Balken
1. Ebene gerade Balken Betrachtet werden gerade Balken, die nur in der -Ebene belastet werden. Prof. Dr. Wandinger 4. Schnittlasten bei Balken TM 1 4.1-1 1. Ebene gerade Balken 1.1 Schnittlasten 1.2 Balken
(x 1. Vektoren. g: x = p + r u. p r (u1. x 2. u 2. p 2
Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Trigonometrie. In der Abbildung: der Winkel 120 (Gradenmaß) ist 2π = 2π (Bogenmaß).
Trigonometrie. Winkel: Gradmaß oder Bogenmaß In der Schule lernt man, dass Winkel im Gradmass, also als Zahlen zwischen 0 und 60 Grad angegeben werden. In der Mathematik arbeitet man lieber mit dem Bogenmaß,
3. Erweiterung der trigonometrischen Funktionen
3. Erweiterung der trigonometrischen Funktionen 3.1. Polarkoordinaten 1) Rechtwinklige und Polarkoordinaten Üblicherweise gibt man die Koordinaten eines Punktes in der Ebene durch ein Zahlenpaar vor: P(x
ELEMENTE. Grundkompetenzen DER MATHEMATIK. für die neue Reifeprüfung. Mit Lösungen
5 ELEMENTE DER MATHEMATIK GK Grundkompetenzen für die neue Reifeprüfung Mit Lösungen Die Formulierung der Grundkompetenzen (GK) bezieht sich auf den Stand von August 2010. 1. Auflage, 2010 Gesamtherstellung:
4. Allgemeines ebenes Kräftesystem
4. llgemeines ebenes Kräftesystem Eine Gruppe von Kräften, die an einem starren Körper angreifen, bilden ein allgemeines Kräftesystem, wenn sich ihre Wirkungslinien nicht in einem gemeinsamen Punkt schneiden.
Rudolf Brinkmann Seite und W = {x 3 x 6}
Rudolf Brinkmann Seite 0.0.008 Lineare Funktionen Es soll der Graph der Funktion f = {,y y = f() = } in den Bereichen D { } = und W = { 6} - - 0 f() = -6-0 6 9 erstellt werden. 6 6 5 0 Definition Eine
Wiederholungsaufgaben Klasse 10
Wiederholungsaufgaben Klasse 10 (Lineare und quadratische Funktionen / Sinus, Kosinus, Tangens und Anwendungen) 1. In welchem Punkt schneiden sich zwei Geraden, wenn eine Gerade g durch die Punkte A(1
H. Gruber, R. Neumann. Erfolg im Mathe-Abi. Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen
H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Themen des Pflichtteils... Analysis Von der Gleichung
Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C /07
Übungsblatt Analytische Geometrie - Geraden und Ebenen - 6C - 6/7. Gegenseitige Lage von Geraden Gesucht ist die gegenseitige Lage der Geraden g durch die beiden Punkte A( ) und B( 5 9 ) und der Geraden
Vektoren und Matrizen
Universität Basel Wirtschaftswissenschaftliches Zentrum Vektoren und Matrizen Dr. Thomas Zehrt Inhalt: 1. Vektoren (a) Einführung (b) Linearkombinationen (c) Länge eines Vektors (d) Skalarprodukt (e) Geraden
d 2 b 2 c 2 d 3 b 3 c 3 , D a 1 d 1 c 1 v 3 Definiton (Verbindungsvektor): Zwei Punkte A(a 1 a 2 a 3 ) und B(b 1 b 2 b 3 ) legen den Vektor b 1 a 1
2008/2009 Das Wichtigste in Kürze Klasse 3 Lineare Gleichungssysteme und Determinanten Definiton (Lineare Gleichungssysteme: Lineare Gleichungssysteme löst man entweder mit dem Gauß-Algorithmus oder nach
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 14 VERMESSUNGSAUFGABEN
Mathematik Mag. Schmid Wolfgang Arbeitsblatt 4 3. Semester ARBEITSBLATT 4 VERMESSUNGSAUFGABEN Nun wollen wir unser Wissen über recht- und schiefwinkelige Aufgaben an einigen Aufgaben beweisen Beispiel
Teil 2. Metrik mit Skalarprodukt. Für moderne Geometrie-Kurse am Gymnasium. und für Realschulen in Bayern! (Prüfungsstoff!)
Vektor-Geometrie für die Sekundarstufe 1 Teil 2 Metrik mit Skalarprodukt Für moderne Geometrie-Kurse am Gymnasium und für Realschulen in Bayern! (Prüfungsstoff!) Dieser Text setzt Kenntnisse der Trigonometrie
TECHNISCHE MECHANIK A (STATIK)
Probeklausur im Fach TECHNISCHE MECHANIK A (STATIK) Nr. 5 Matrikelnummer: Vorname: Nachname: Ergebnis Klausur Aufgabe: 1 2 3 4 5 6 Summe Punkte: 31 7,5 17,5 9 10 5 80 Davon erreicht Punkte: Gesamtergebnis
Grundsätzliches Produkte Anwendungen in der Geometrie. Vektorrechnung. Fakultät Grundlagen. Juli 2015
Vektorrechnung Fakultät Grundlagen Juli 205 Fakultät Grundlagen Vektorrechnung Übersicht Grundsätzliches Grundsätzliches Vektorbegriff Algebraisierung der Vektorrechnung Betrag 2 Skalarprodukt Vektorprodukt
Lernkarten. Analytische Geometrie. 6 Seiten
Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
Mehmet Maraz. MechanikNachhilfe
Mehmet Maraz MechanikNachhilfe 1. Auflage 015 Inhaltsverzeichnis 1 Statik 1 1.1 Lagerungen und Lagerreaktionen................. 1. Kräftegleichgewichte......................... 5 1..1 Drehmoment.........................
KLAUSUR. Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.:
KLAUSUR Lineare Algebra (E-Techniker/Mechatroniker/W-Ingenieure/Informatiker).3. (W. Koepf) Name: Vorname: Matr. Nr./Studiengang: Versuch Nr.: Für jede Aufgabe gibt es Punkte. Zum Bestehen der Klausur
I. Reelle Zahlen GRUNDWISSEN MATHEMATIK - 9. KLASSE
I. Reelle Zahlen 1. Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen. Nenne Beispiele für rationale und irrationale Zahlen.. Aus negativen
Vektoren, Skalarprodukt, Ortslinien
.0 Gegeben sind die Punkte A(0/-4), C(0/4), sowie die Pfeile mit α [ 90 ; 90 ]. 4cosα AB = 4sinα+ 4. Zeichne die drei Punkte B, B und B 3 mit α { 30;0;30 } in ein KOS.. Zeige: 4cosα CB =. 4sinα 4.3 Zeige,
3.6 Einführung in die Vektorrechnung
3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
2. Momentanpol. Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: y A ), v Py. =v Ay
ufgabenstellung: Für die Geschwindigkeit eines beliebigen Punktes P eines starren Körpers gilt: Gesucht ist der Punkt П, dessen momentane Geschwindigkeit null ist. Lösung: v Px =x ( y P y ), v Py =y +
Übungen zur Analysis II Blatt 27 - Lösungen
Prof. Dr. Torsten Wedhorn SoSe 22 Daniel Wortmann Übungen zur Analysis II Blatt 27 - Lösungen Aufgabe 5: 6+6+6* Punkte Bestimme alle lokalen Extrema der folgenden Funktionen: a b c* f : R 3 R g : R 2 R
Übungsaufgaben Statik zentrales Kräftesystem
I zentralen Kräftesyste liegen alle Kräfte in derselben Ebene und wirken auf einen geeinsaen Punkt. Lösen Sie alle Aufgaben zeichnerisch und rechnerisch. Kräfte zusaensetzen c) Eierziehen Bei Eierziehen
Lösung zur Übung 1. In einem Würfel der Kantenlänge a wird ein Methanmolekül so platziert, dass das Kohlenstoffatom. r = a 2. d = 2 a (3) 2 = 2 a (4)
Lösung zur Übung 1 Aufgabe 1 In einem Würfel der Kantenlänge a wird ein Methanmolekül so platziert, dass das Kohlenstoffatom im Zentrum des Würfels liegt. Wie groß ist der Tangens des halben H-C-H Bindungswinkels?
Octave/Matlab-Übungen
Aufgabe 1a Werten Sie die folgenden Ausdrücke mit Octave/Matlab aus: (i) 2 + 3(5 11) (ii) sin π 3 (iii) 2 2 + 3 2 (iv) cos 2e (v) ln π log 10 3,5 Aufgabe 1b Betrachten Sie (i) a = 0.59 + 10.06 + 4.06,
3 Analytische Geometrie der Kongruenzabbildungen
3 Analytische Geometrie der Kongruenzabbildungen 4 3 Analytische Geometrie der Kongruenzabbildungen 3. Grundlagen, Begriffe, Schreibweisen 3.. Achsenkreuz Die Achsen heißen in dieser Darstellung x und
Dynamik Lehre von den Kräften
Dynamik Lehre von den Kräften Physik Grundkurs Stephie Schmidt Kräfte im Gleichgewicht Kräfte erkennt man daran, dass sie Körper verformen und/oder ihren Bewegungszustand ändern. Es gibt Muskelkraft, magnetische
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 17. März 2012 Die Bearbeitungszeit für alle drei Aufgaben beträgt 90 Minuten.
KLAUSUR ZUR TECHNISCHEN MECHANIK I Termin: 7. März Die Bearbeitungszeit für alle drei Aufgaben beträgt 9 Minuten. AUFGABE (6 Punkte) Der Stab in Abb. mit l =,5 m ist in gelenkig gelagert und in abgestützt.
Vordiplom Mechanik/Physik WS 2010/2011
Vordiplo Mechanik/Physik WS / Aufgabe a Ein zentrales Kräftesyste besteht aus folgenden Kräften: Betrag Zwischenwinkel F 4 N α = 48 F 37 N β = F 3 37 N γ = 68 F 4 5 N δ = 37 F 5 N a) Erstelle eine grobassstäbliche
Arbeitsblatt 1 Einführung in die Vektorrechnung
Arbeitsblatt Einführung in die Vektorrechnung Allgemein Vektoren sind physikalische Größen und durch ihre Richtung und ihren Betrag festgelegt. Geometrisch wird ein Vektor durch einen Pfeil dargestellt,
fakultät für physik bernhard emmer mathematik vorkurs für physiker Übungsblatt 1 für beliebiges k N und x 0. a 2 x 1 x 3 y 2 ) 2
fakultät für physik bernhard emmer mathematik vorkurs für physiker Übungsblatt Aufgabe Induktion). a) Beweisen Sie, dass + 3 + 5 +... + n )) ein perfektes Quadrat genauer n ) ist. b) Zeigen Sie: + + +...
Drei Flugzeuge unterwegs
Anwendungsaufgaben: R. 3. 1 Drei Flugzeuge unterwegs Um die Bewegungen dreier Flugzeuge zu analysieren, wird ein räumliches kartesisches Koordinatensystem gewählt, das an die Navigation auf bzw. über der
Demo: Mathe-CD KOMPLEXE ZAHLEN
KMPLEXE ZAHLEN Diese Datei gibt einige Seiten Einblick in die Serie Komplexe Zahlen, und, die gegen Zusatbestellung auf der CD u haben ist. Abonnenten erhalten sie automatisch. Datei Nr. 50000 Januar 00
AnKa Hyp. , tan α= Weil die Ankathete des einen Winkels der Gegenkathete des anderen entspricht, gilt auch: sin α = cos β und sinβ = cosα.
Trigonometrie Wenn mn die Trigonometrischen Funktionen Sinus, Kosinus und Tngens berechnen will, ist es wichtig, uf welchen Winkel sie sich beziehen. Die Kthete, die direkt m Winkel nliegt, heißt Ankthete
Rechnen mit Vektoren. 1. Vektoren im Koordinatensystem Freie Vektoren in der Ebene
Rechnen mit 1. im Koordinatensystem 1.1. Freie in der Ebene 1) Definition Ein Vektor... Zwei sind gleich, wenn... 2) Das ebene Koordinatensystem Wir legen den Koordinatenursprung fest, ferner zwei zueinander
a 2β... a n ω alle Permutationen von α β γ... ω a 3 γ ( 1) k a 1α
Mathematik 1 - Übungsblatt 7 Lösungshinweise Tipp: Verwenden Sie zur Kontrolle Scilab, wo immer es möglich ist. Aufgabe 1 (Definitionsformel für Determinanten) Determinanten quadratischer Matrizen sind
Kapitel II. Vektoren und Matrizen
Kapitel II. Vektoren und Matrizen Vektorräume A Körper Auf der Menge R der reellen Zahlen hat man zwei Verknüpfungen: Addition: R R R(a, b) a + b Multiplikation: R R R(a, b) a b (Der Malpunkt wird oft
mentor Lernhilfe: Mathematik 10. Klasse Baumann
mentor Lernhilfe: Mathematik 10. Klasse Geometrie: Winkelfunktionen, Trigonometrie, Additionstheoreme, Vektorrechnung von Rolf Baumann 1. Auflage mentor Lernhilfe: Mathematik 10. Klasse Baumann schnell
Repetition Begriffe Geometrie. 14. Juni 2012
Repetition Begriffe Geometrie 14. Juni 2012 Planimetrie 1. Strahlensatz Planimetrie 1. Strahlensatz Werden zwei sich schneidende Geraden von zwei Parallelen geschnitten, so verhalten sich die Abschnitte
Lösungen IV ) β = 54,8 ; γ = 70,4 106) a) 65 b) 65 (115?) d) 57,5
(Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
2 Geometrie und Vektoren
Geometrie und Vektoren Vorbemerkung: Begriffe wie die folgenden werden hier als bekannt vorausgesetzt: Punkt, Strecke, Strahl, Gerade, Ebene, Kreis, Winkel, rechter Winkel, etc..1 Grundlegende Sätze Satz
Vektorielle Addition von Kräften
Vektorielle Addition von Kräften (Begleitende schriftliche Zusammenfassung zum Online-Video) Was wir bisher betrachtet haben: (a) Kräfte wirken entlang derselben Wirkungslinie (parallel oder antiparallel)
Lösungen V.1. Pfeile bedeuten ist auch ein. (Lambacher-Schweizer Geometrie 2, S. 150)
Lösungen V.1 I: Trapez (zwei parallele Seiten; keine Symmetrie) II: gleichschenkliges Trapez (zwei parallele Seiten, die anderen beiden gleich lang; achsensymmetrisch) III: Drachen(viereck) (jeweils zwei
Analytische Geometrie I
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Einstiegsvoraussetzungen für das 3. Semester Angewandte Mathematik AM
Einstiegsvoraussetzungen für das 3. Semester Angewandte Mathematik AM 1. Siehe: Einstiegsvoraussetzungen für das 1. Semester 2. Bereich: Zahlen und Maße 2.1. Fehlerrechnung (Begriffe absoluter und relativer
Technische Mechanik I
Technische Mechanik I m.braun@uni-duisburg.de Wintersemester 2003/2004 Lehrveranstaltung Zeit Hörsaal Beginn Technische Mechanik I V 3 Mi 14:00 15:30 LB 104 15.10.2003 r 08:15 09:45 LB 104 17.10.2003 14tägig
B Die Grundaufgaben der Statik
-I.B1- B Die Grundaufgaben der Statik 1 Begriffserklärungen 1.1 Zentrales und allgemeines Kräftesystem Unter einem Kräftesystem versteht man beliebig viele Kräfte, die gleichzeitig an einem Bauteil wirken.
ÜTA: B - Schlauch für Cluster 1 (tw.) und 3
bernhard.nietrost@htl-steyr.ac.at Seite 1 von 9 ÜTA: B - Schlauch für Cluster 1 (tw.) und 3 Mathematische / Fachliche Inhalte in Stichworten: allgemeine Sinusfunktion, Winkelfunktionen im schiefwinkeligen
Trigonometrie Sachaufgaben Vektor. Kräfte sind Vektoren
Trigonometrie Sachaufgaben Vektor Man kann die trigonometrischen Beziehungen direkt für die Vektorrechnung heranziehen, indem man die Katheten eines rechtwinkligen Dreiecks als Komponenten eines Vektors