: C C, z = x + iy z = x iy.
|
|
|
- Sabine Böhler
- vor 5 Jahren
- Abrufe
Transkript
1 Komplexe Zahlen (C, +, ): Körper der komplexen Zahlen mit C = R 2, R C Unterkörper, und z C mit z = 0. genannt ±i. z, w C, z = x + iy, w = u + iv, (x, y), (u, v) R 2 : z + w = (x + u) + i(y + v), z w = (xu yv) + i(xv + yu). Komplexe Konjugation Betrag z = zz. : C C, z = x + iy z = x iy. Polarkoordinatendarstellung: z = r(cos ϕ + i sin ϕ), r = z, ϕ = Arg(z), Hauptwert des Arguments, falls ϕ ( π, π]. n-te Einheitswurzeln ζ k = cos 2πk 2πk n + i sin n, (ζ k) n = 1, 0 k < n.
2 Elementare komplexe Funktionen Eigenschaften von (konvergenten) Folgen und Reihen sind analog zur reellen Analysis. Polynome p(z) = n ν=0 a νz ν, a ν C. exp(z) = n=0 zn n!, sin(z) = cos(z) = z=0 ( 1) n (2n)! z2n. exp(iz) = cos(z) + i sin(z). z=0 ( 1) n (2n+1)! z2n+1, exp ist nicht injektiv, periodisch mit Perioden 2πik, k Z. sin, cos haben genau dieselben Nullstellen wie in R. Es existiert eine Umkehrfunktion Log : C C zu exp z, der Hauptzweig des Logarithmus, eindeutig bestimmt durch π < Im Log z π und exp(log z) = z. Log(z) = log z + iarg(z). Log ist nicht stetig entlang der negativen reellen Achse.
3 Komplexe Differenzierbarkeit f : D C, D C heisst komplex differenzierbar in a D, f (z) f (a) falls lim z a =: f (a) existiert. z a Für D offen ist dies äquivalent zu: f ist total differenzierbar in a und es gilt für die Tangentialabb.: Tf (a)z = l z mit l = f (a), d.h. Tf (a) ist C linear. f ist total differenzierbar in a und für u = Ref, v = Imf gelten: die Cauchy Riemannschen Differentialgleichungen x u(a) = y v(a), y u(a) = x v(a). f = f, f = 0, mit f := 1 2 ( xf i y f ), f := 1 2 ( xf + i y f ). Für D offen heisst f holomorph in D, falls f für alle a D komplex differenzierbar ist. O(D) := {f : D C f holomorph }. Rechenregeln für f : = O(D) C(D) ist C Unteralgebra.
4 Folgerungen aus komplexer Differenzierbarkeit f lokal konstant, wenn a D U D : f U ist konstant. Äquivalent zu: f O(D), f (z) = 0 z D. D heisst zusammenhängend, wenn jede lokal konstante Funktion D C konstant ist. Satz über die Umkehrfunktion: f O(D), injektiv, f (z) 0 für alle z D. Dann ist f (D) C offen, f 1 O(f (D)) und (f 1 ) (f (z)) = 1 f (z). Log(z) : C C ist holomorph, nicht stetig entlang der negativen reellen Achse. f O(D), f = u + iv. Dann sind u, v harmonisch, d.h. u = v = 0 mit = 2 x + 2 y.
5 Konforme Abbildungen Eine lineare, bijektive Abb. T : R n R n heisst konform, wenn sie orientierungstreu (det T > 0) und winkelerhaltend ( x y Tx, Ty = Tx Ty x, y, x, y R n ) ist. f : D D, D, D R n offen, ist (im Kleinen) konform, falls Tf (a) für alle a D konform ist. f ist im Grossen konform, falls f auch noch bijektiv ist. D C offen, zusammenhängend, f : D C total differenzierbar. Dann gilt: f O(D) mit f (z) 0 z D f ist konform. (Für eine Verallgemeinerung siehe weiter unten.)
6 Kurvenintegrale Glatte Kurve: γ : [a, b] C stetig differenzierbar. Geschlossen, falls γ(a) = γ(b). Bogenlänge: L(γ) = b a γ (t) dt. Komplexes Integral: g : [a, b] C stetig. b a g(t)dt := b a Re g(t)dt + i b a Im g(t)dt, f : D C, D C, f stetig, imγ D. Kurvenintegral: γ f (ζ)dζ := b a f (γ(t))γ (t)dt. C linear. Standardabschätzung: γ f (ζ)dζ C L(γ), falls f (z) < C für z im γ. Verallgemeinerung des Riemann Integrals. Transformationsinvarianz: γ f (ζ)dζ = γ φ f (ζ)dζ Fundamentalsatz: f (ζ)dζ = F (γ(b)) F (γ(a)), falls eine γ Stammfunktion F von f existiert. γ 1±γ 2 f (ζ)dζ := γ 1 f (ζ)dζ ± γ 2 f (ζ)dζ
7 Der Cauchysche Integralsatz Es gilt für alle Kreisscheiben B = B r (c), c C, r > 0: { (ζ c) n 0 falls n 1 dζ = 2πi falls n = 1 B D C heisst wegzusammenhängend, falls für alle z, w D: γ : [a, b] C, im γ D mit γ(a) = z, γ(b) = w. D wegzusammenhängend = D zusammenhängend. Eine wegzusammenhgd., offene Menge D C heisst Gebiet. f : D C stetig, D ein Gebiet. Dann sind äquivalent: f besitzt eine Stammfunktion f (ζ)dζ = 0 für alle γ geschlossen, im γ D γ f (ζ)dζ hängt für alle Kurven γ nur von deren Anfangs- und γ Endpunkt ab. Für f O(D) gilt der Cauchysche Integralsatz für Dreieckswege: f (ζ)dζ = 0 für alle Dreiecke D.
8 Cauchyscher Integralsatz und logarithmische Ableitung Ein Gebiet D C heisst Sterngebiet, falls es z D gibt, so daß für alle z D: {z + t(z z ) t [0, 1]} D. Für f O(D), D ein Sterngebiet, gilt der Cauchysche Integralsatz für Sterngebiete: f (ζ)dζ = 0 für alle geschlossenen Kurven γ, im γ D. γ Ein Gebiet D C heisst Elementargebiet, falls jedes f O(D) eine Stammfunktion besitzt. Sei D ein Elementargebiet, f O(D), f (z) 0 für alle z D. h O(D) heisst holomorpher Zweig des Logarithmus von f, falls f = exp h, f f heisst logarithmische Ableitung von f. Ein holomorpher Zweig des Logarithmus von f existiert genau dann, wenn f f eine Stammfunktion besitzt. Sei f O(D), f (z) 0 für alle z D. Dann gilt für alle 1 f geschlossenen Kurven γ mit im γ D: (ζ) 2πi γ f (ζ) dζ Z
9 Die Cauchysche Integralformel f O(D), B r (z 0 ) D, r > 0. Dann gilt z B r (z 0 ) die die Cauchysche Integralformel f (z) = 1 f (ζ) 2πi ζ z dζ. B r (z 0 ) f ist beliebig oft differenzierbar, jede Ableitung von f ist wieder holomorph, und für n N 0 und z B r (z 0 ) gilt die verallgemeinerte Cauchysche Integralformel f (n) (z) = n! 2πi B r (z 0 ) f (ζ) dζ. (ζ z) n+1 Leibnizregel für die Differentiation unter dem Integral g : [a, b] D C stetig, D offen, t [a, b] fest sei g(t, ) O(D), g z : [a, b] D C stetig. Dann gilt: G(z) = b a g(t, z)dt O(D) und G (z) = b g a z dt.
10 Anwendungen der Cauchyschen Integralformeln Satz von Liouville: Jede beschränkte ganze Funktion ist konstant. Fundamentalsatz der Algebra Jedes nicht konstante Polynom p C[z] besitzt eine Nullstelle. Falls deg p = n 1, dann existieren C C, α k C, k = 1,..., n so dass p(z) = C n k=1 (z α k). Satz von Morera: Für D C offen, f : D C stetig und jeden Dreiecksweg z 1, z 2, z 3 mit zugehöriger Dreiecksfläche D gelte f (ζ)dζ = 0. Dann ist f holomorph in D.
11 Gleichmässige Approximation (f n ) n N, f n : D C heisst gleichmässig konvergent gegen f : D C, falls gilt: ε > 0 N N : f (z) f n (z) < ε für alle n N und alle z D. (f n ) konvergiert lokal gleichmässig gegen f, falls (f n U D ) gleichmässig konvergiert für eine offene Umgebung U C. (f n ) n N lokal gleichmässig konvergente Folge stetiger Funktionen f n : D C. Grenzfunktion ist stetig und darf mit Kurvenintegral (für alle γ stückweise glatt ) vertauscht werden: lim n γ f n (ζ)dζ = γ lim f n(ζ)dζ n Satz von Weierstraß: (f n ) n N lokal gleichmässig konvergente Folge holomorpher Funktionen f n : D C. Der Grenzfunktion f ist holomorph. Weiter dürfen Grenzwert und Ableitung vertauscht werden: ( f = lim n f n ) = lim n f n.
12 Normale Konvergenz Eine Reihe n=0 f n, f n : D C heisst (lokal) gleichmässig konvergent, falls die Folge der Partialsummen (lokal) gleichmässig konvergent ist. Eine Reihe heisst normal konvergent in D, falls gilt: a D U(a) D offen und (M n ) n 0, M n 0, so dass n=0 M n < und f n (z) M n z U(a) D, n N 0. Eine normal konvergente Reihe konvergiert absolut und lokal gleichmässig. Satz von Weierstraß: Sei f = n=0 f n eine normal konvergente Reihe mit f n O(D). Dann ist f O(D), Grenzfunktion und Ableitung dürfen vertauscht werden ( ) f n = n=0 und n=0 f n konvergiert normal. n=0 f n
13 Cauchyscher Entwicklungssatz Zu jeder Potenzreihe um 0, f = n=0 a nz n, a n C, existiert eine eindeutige bestimmte Zahl R [0, ) { }, der Konvergenzradius, so dass f in B R (0) normal konvergiert und für alle z C mit z > R divergiert. Formel für Konvergenzradius: Sei n=0 a nz n eine Reihe mit Konvergenzradius R. Dann gilt: 1. R = lim sup n a n. (Cauchy Hadamard) a 2. R = lim n n a, falls a n+1 n 0 n N und der Grenzwert existiert. f O(D), B r (a) D, r > 0. Dann gilt der Cauchysche Entwicklungssatz z B r (a), 0 < ρ < r und n N 0 ist f (z) = n=0 a nz n mit a n = 1 n! f (n) (a) = 1 f (ζ) dζ 2πi ζ a =ρ (ζ a) n+1 Insbesondere ist der Konvergenzradius R r.
14 Holomorphie Sei D C offen, f : D C. Dann sind äquivalent: f ist holomorph, d.h komplex differenzierbar in jedem z D. f ist total differenzierbar und u = Ref, v = Imf erfüllen die Cauchy Riemannschen DGL f ist stetig und für jeden Dreiecksweg, D gilt f (ζ)dζ = 0 f besitzt lokal eine Stammfunktion f ist stetig und besitzt eine Integraldarstellung durch die Cauchysche Integralformel f ist lokal durch eine konvergente Potenzreihe darstellbar f besitzt für alle B r (a) D eine konvergente Cauchysche Potenzreihenentwicklung f ist konform, falls f (z) 0 z D
15 Rechenregeln für Potenzreihen Seien f = n=0 a nz n, g = n=0 b nz n Potenzreihenentwicklungen holomorpher Funktionen auf D. Identitätssatz: Falls f = g, dann a n = b n für alle n N. Multiplikationssatz von Cauchy: Formel für Koeff. von fg Inversionssatz: Rekursionsformel für Koeff. von 1/f Doppelreihensatz von Weierstrass Umordnungssatz: a n (z a) n = b n (z b) n für a, b D. Verkettungssatz: Rekursionsformel für Koeff. von f g Umkehrungssatz: Rekursionsformel für Koeff. von f 1.
16 Abbildungseigenschaften holomorpher Funktionen Seien im folgenden f, g O(D), D C ein Gebiet, D. Identitätssatz: f = g {z D f (z) = g(z)} hat Häufungspunkt in D z 0 D mit f (n) (z 0 ) = g (n) (z 0 ) n N. Satz von der Gebietstreue Sei f nicht konstant. Dann ist f (D) wieder ein Gebiet. Maximumprinzip: Gilt f (a) f (z) für ein a D und alle z D, dann ist f konstant. Maximumprinzip für beschränkte Gebiete: Sei D beschränkt, f stetig auf D. Dann nimmt f ihr Maximum auf D an. Minimumprinzip: Ist f nicht konstant und gilt f (a) f (z) für ein a D und alle z D, dann ist f (a) = 0. Aut(D) :={ {f : D D f bijektiv, f, f 1 O(D)}. Aut(E) = z eiϕ z a āz 1 }. a E, 0 ϕ < 2π
17 Singularitäten holomorpher Funktionen Seien f O(D), a C \ D, so dass die punktierte Kreisscheibe B r (a) = {z C 0 < z a < r} in D liegt. a heisst isolierte Singularität von f a heisst hebbar, falls f O(D {a}) mit f D = f. Riemannscher Hebbarkeitssatz: f ist hebbar in a punktierte Umgebung Ů D von a, so dass f U beschränkt. a heisst ausserwesentlich, falls m Z, so dass g(z) = (z a) m f (z) in a hebbar ist. Eine nicht-hebbare, ausserwesentliche Singularität a heisst Pol(stelle) von f. a heisst wesentlich, falls a nicht ausserwesentlich ist. Sei k Z die kleinste Zahl mit dieser Eigenschaft, dann heisst ord a (f ) := k Ordnung von f in a. a ist ein Pol von f limz a f (z) =. z D Satz von Casorati Weierstraß: Für eine wesentliche Singularität a von f ist das Bild f (Ů D) einer beliebigen punktierten Umgebung Ů dicht in C.
18 Laurent Zerlegung Seien 0 r < R. Sei R = {z C r < z < R} ein Ringgebiet und f O(R). Cauchyscher Integralsatz für Ringgebiete: Sind ρ, P so gewählt, dass r < ρ < P < R, dann gilt: f (ζ)dζ = f (ζ)dζ. ζ =ρ ζ =P Es existieren g O(B R (0)) und h O(B 1 (0)) (eindeutig, r falls h(0) = 0), so dass f (z) = g(z) + h ( ) 1 z. Die Zerlegung f (z) = g(z) + h ( ) 1 z heisst Laurent Zerlegung, h ihr Hauptteil, g ihr Nebenteil. Die Laurentreihe von f in R um 0 ist f = n= a nz n mit a n bestimmt durch g = n=0 a nz n für z < R, und h = n=1 a nz n für z < 1 r. Es gilt: a n = 1 f (ζ) 2πi ζ =ρ dζ für alle n Z und r < ρ < R. ζ n+1
19 Anwendungen der Laurentreihe Sei a C \ D eine isolierte Singularität von f O(D). a ist hebbar a n = 0, n < 0. ein Pol der Ordnung k > 0 a k 0, a n = 0, n < k. wesentlich a n 0 für unendlich viele n < 0. Seien (a, b) R, D = {z C a < Im z < b} und f O(D) mit f (z + 1) = f (z) für alle z D. Dann lässt sich f in eine normal konvergente, komplexe Fourierreihe entwickeln: f (z) = a n exp(2πinz) n= mit a n = 1 0 f (z) exp( 2πinz)dx für alle y (a, b) wobei z = x + iy.
20 Meromorphe Funktionen Die Riemannsche Zahlenkugel C = C { } ist homöomorph zu S 2 mit der Topologie auf C gegeben durch die offenen Mengen U C, U offen, und {z C z > R}, R > 0. f : D C, D C offen, heisst meromorph, falls S(f ) = f 1 ( ) ist diskret in D f D\S(f ) C ist holomorph Die Punkte aus S(f ) sind Pole von f D\S(f ). f (z) := f ( 1 z ) ist in der offenen Menge D = { z C 1 z D} holomorph. M(D) := {f : D C f meromorph} ist ein C Körper, O(D) M(D) ein C Unterring. f = p q M(D) heisst rationale Fkt. auf D, falls p, q C[z], q 0. Es gilt: M(C) = {f : C C f rational} =: C(z) Jede bijektive rationale Abb. f : C C ist eine Möbiustransf. z az+b cz+d für a, b, c, d C, ad bc 0. Aut(C) = GL(2, C)/{ ( λ 0 0 λ) λ C } als Gruppe.
21 Residuensatz Sei γ eine geschlossene glatte Kurve, z C \ imγ. Die Umlaufzahl von γ bezügl. z ist ind γ (z) = 1 2πi γ 1 ζ z dζ Z. ind γ (z) ist lokal konstant. Sei a eine isolierte Singularität von f O(D). Der Koeffizient a 1 in der Laurententwicklung von f um a heisst Residuum von f in a, Res a f = 1 2πi ζ a =ρ f (ζ)dζ, ρ klein genug. Für f O(D \ {a}) mit ausserwesentlicher Singularität in a, ord a (f ) = k, k N gilt: Res a (f ) = 1 f (k 1)! (k 1) (a), ( ) f (z) = (z a) k f (z). Weiter Res f a = ord a f für f 0. Residuensatz Es sei D C ein Elementargebiet, z 1,..., z k D, f O(D \ {z 1,..., z k }), γ : [a, b] D \ {z 1,..., z k } eine geschlossene glatte Kurve. Dann gilt die Residuenformel k f (ζ)dζ = 2πi Res zj (f )ind γ (z j ). γ j=1 f
22 Anwendungen des Residuensatzes Satz von Hurwitz: D ein Gebiet, (f n ) n N, f n O(D) lokal gleichmässig konvergent mit Grenzfkt. f O(D). fn (z) 0, z D, n N, = f 0 oder f (z) 0 z D. fn (z) injektiv n N = f = const oder f injektiv Sei D C ein Elem.gebiet f M(D), γ eine Kurve, die alle Pol- und Nullstellen von f genau einmal umläuft. Dann gilt: die Anzahlformel für Pol- und Nullstellen 1 2πi γ f (ζ) dζ = N(0) N( ). f (ζ) Sei D ein Gebiet, f O(D), f const, a D, b = f (a), ord a (f (z) b) = n. Dann gibt es offene Umg. U D von a und V C von b, so dass w V, w b, z 1,..., z n U mit f (z j ) = w und ord zj (f (z) w) = 1, 1 j n. Satz von Rouché: Sei D ein Elem.gebiet, f, g O(D), γ eine geschlossene Kurve in D mit ind γ z = 1 z Int(γ). Sei g(ζ) < f (ζ), ζ imγ. Dann haben f, f + g keine Nullstelle auf imγ und gleich viele Nullstellen in Intγ.
23 Berechnung von reellen Integralen Seien p, q Polynome in zwei Variablen, q(x, y) 0 (x, y) R 2 mit x 2 + y 2 = 1. Dann gilt: 2π 0 p(cos t, sin t) q(cos t, sin t) dt = 2πi Res a f a E mit f (z) = 1 p( 1 2 (z+z 1 ), 1 2i (z z 1 )) iz q( 1 2 (z+z 1 ), 1 2i (z z 1 )) Sei D C ein Elem. gebiet mit H D, a j D, 1 j k, f O(D \ {a 1,..., a k }), so dass f (x)dx < und lim z z f (z) = 0. Dann gilt: k f (x)dx = 2πi Res aj f. Es seien p, q Polynome vom Grad m, n. Dann gibt es reelle Zahlen K, L, R > 0, so dass gilt: K z m n p(z) q(z) L z m n, z C, z R. j=1
24 Berechnung von reellen Integralen Seien a j C \ R, 1 j k, f O(C \ {a 1,..., a k }), lim z f (z) = 0. Dann gilt: e iλx f (x)dx = 2πi w H Res w (f (z)e iλz ), λ > 0. Sei f M(C) mit endlicher Polstellenmenge S(f ) C + = C \ R +, sei λ C \ Z so dass lim z 0 ( z) λ f (z) = 0, lim z ( z) λ f (z) = 0. Dann gilt: f (x)x λ 1 2πi dx = 0 1 e 2πiλ res w (f (z)( z) λ 1 ). w C + Für alle z C \ Z gilt: die Partialbruchentwicklung des Kotangens π cot πz = 1 z + ( 1 z n + 1 ). n n Z n 0
25 Unendliche Produkte Das unendliche Produkt (1 + a 0 )(1 + a 1 )... konvergiert absolut, wenn die Reihe n=0 a n konvergiert. Der Grenzwert m 1 (1 + a n ) = (1 + a n ) exp( Log(1 + a n )) N 1 lim N n=0 n=0 n=m existiert und wird mit n=1 (1 + a n) bezeichnet. Ein Produkt n=0 f n, f n = 1 + g n O(D) heisst normal konvergent, wenn die Reihe n=1 g n normal konvergiert. In diesem Fall existiert die Grenzfunktion f mit f O(D). Insbesondere konvergiert jedes Produkt f N = n N f n normal und f = f 0 f 1... f N 1 fn. Sei f = n=0 f n, f n O(D), f n 0, normal konvergent. Dann gilt: f 0, N(f ) = alle a D. Falls f 0, dann ist und es gilt f f = n=0 n=0 N(f n) und ord a f = n=0 ord af n, für n=0 f n f n. f n f n normal konvergent in D \ N(f )
26 Die Gamma Funktion Γ(z) = 0 t z 1 e t dt, Re z > 0 heisst Gamma Funktion. Γ(z) ist für Re z > 0 eine holomorphe Fkt. und ist in C \ S, S = {0, 1, 2,... } holomorph fortsetzbar, es gilt: Γ(z + 1) = zγ(z), z C \ S Γ(z) hat Pole 1. Ordnung in S mit Res n Γ = ( 1)n n!. Γ(1) = 1. Γ(z) ist durch diese Eigenschaften und Beschränktheit in {z C 1 Rez < 2} eindeutig charakterisiert. Für alle z C besitzt Γ(z) die Produktdarstellungen 1 Γ(z) = z exp(γz) n=1 ( ) 1 + z n exp( z n ) m!m z Γ(z) = lim m z(z + 1)... (z + m) Weitere Eigenschaften: Γ(z)Γ(1 z) = π sin πz n 1 k=0 Γ(z + k n 1 n ) = (2π) 2 n 1 2 nz Γ(nz)
: C C, z = x + iy z = x iy.
 Komplexe Zahlen (C, +, ): Körper der komplexen Zahlen mit C = R 2, i 2 = 1, R C Unterkörper z, w C, z = x + iy, w = u + iv, (x, y), (u, v) R 2 : z + w = (x + u) + i(y + v), z w = (xu yv) + i(xv + yu).
Komplexe Zahlen (C, +, ): Körper der komplexen Zahlen mit C = R 2, i 2 = 1, R C Unterkörper z, w C, z = x + iy, w = u + iv, (x, y), (u, v) R 2 : z + w = (x + u) + i(y + v), z w = (xu yv) + i(xv + yu).
4 Anwendungen des Cauchyschen Integralsatzes
 4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
4 Anwendungen des Cauchyschen Integralsatzes Satz 4. (Cauchysche Integralformel) Es sei f : U C komplex differenzierbar und a {z C; z z 0 r} U. Dann gilt f(a) = z z 0 =r z a dz. a z 0 9 Beweis. Aus dem
Funktionentheorie - Zusammenfassung
 Funktionentheorie - Zusammenfassung Diese Zusammenfassung erhebt keinen Anspruch auf Vollständigkeit oder Korrektheit. Solltet ihr Fehler finden oder Ergänzungen haben, teilt sie mir bitte mit: richard.gebauer@student.kit.edu
Funktionentheorie - Zusammenfassung Diese Zusammenfassung erhebt keinen Anspruch auf Vollständigkeit oder Korrektheit. Solltet ihr Fehler finden oder Ergänzungen haben, teilt sie mir bitte mit: richard.gebauer@student.kit.edu
2. Klausur zur Funktionentheorie SS 2009
 Aufgabe : Finden Sie ein Beispiel für eine meromorphe Funktion f M(C), die auf den Kreisringen A 0, (0) und A,2 (0) unterschiedliche Laurentreihenentwicklungen besitzt. Beweisen Sie, dass Ihr Beispiel
Aufgabe : Finden Sie ein Beispiel für eine meromorphe Funktion f M(C), die auf den Kreisringen A 0, (0) und A,2 (0) unterschiedliche Laurentreihenentwicklungen besitzt. Beweisen Sie, dass Ihr Beispiel
Funktionentheorie I. M. Griesemer
 Funktionentheorie I M. Griesemer Übersicht der wichtigsten Definitionen und Sätze der Vorlesung Funktionentheorie I, SS 2001, Fachbereich Mathematik, Johannes Gutenberg - Universität Mainz. Inhalt der
Funktionentheorie I M. Griesemer Übersicht der wichtigsten Definitionen und Sätze der Vorlesung Funktionentheorie I, SS 2001, Fachbereich Mathematik, Johannes Gutenberg - Universität Mainz. Inhalt der
4 Isolierte Singularitäten und Laurentreihen
 35 4 Isolierte Singularitäten und Laurentreihen Wir beginnen mit einer lokalen Beschreibung der Nullstellen holomorpher Funktionen. 4. Lokale Beschreibung von Nullstellen. Sei U C offen, f : U C holomorph
35 4 Isolierte Singularitäten und Laurentreihen Wir beginnen mit einer lokalen Beschreibung der Nullstellen holomorpher Funktionen. 4. Lokale Beschreibung von Nullstellen. Sei U C offen, f : U C holomorph
Proseminar Komplexe Analysis 1
 Proseminar Komplexe Analysis 1 Bernhard Lamel und Gerald Teschl SS27 Bemerkung: Die meisten Beispiel sind aus dem Buch von K. Jähnich, Funktionentheorie, Springer. 1. Beweise folgende Eigenschaften des
Proseminar Komplexe Analysis 1 Bernhard Lamel und Gerald Teschl SS27 Bemerkung: Die meisten Beispiel sind aus dem Buch von K. Jähnich, Funktionentheorie, Springer. 1. Beweise folgende Eigenschaften des
Ferienkurs Analysis 3 - Funktionentheorie
 Ferienkurs Analysis 3 - Funktionentheorie Ralitsa Bozhanova, Max v. Vopelius 12.08.2009 1 Grundbegriffe und Differenzierbarkeit 1.1 R-lineare und C-lineare Abbildungen C C Da C sowohl VR über R als auch
Ferienkurs Analysis 3 - Funktionentheorie Ralitsa Bozhanova, Max v. Vopelius 12.08.2009 1 Grundbegriffe und Differenzierbarkeit 1.1 R-lineare und C-lineare Abbildungen C C Da C sowohl VR über R als auch
Themen Potenzreihen Laurentreihen Residuenkalkül
 5 Reihenentwicklungen und der Residuensatz Themen Potenzreihen Laurentreihen Residuenkalkül folgen 5.1 Potenzreihen und Taylorreihen Satz Sei und sei f(z) = a n (z z 0 ) n, a n, n=0 R = 1 lim sup n a n,
5 Reihenentwicklungen und der Residuensatz Themen Potenzreihen Laurentreihen Residuenkalkül folgen 5.1 Potenzreihen und Taylorreihen Satz Sei und sei f(z) = a n (z z 0 ) n, a n, n=0 R = 1 lim sup n a n,
Proseminar Komplexe Analysis 1
 Proseminar Komplexe Analysis 1 Michael Kunzinger und Gerald Teschl WS215/16 Bemerkung: Die meisten Beispiele sind aus dem Buch von K. Jänich, Funktionentheorie, Springer. 1. Bereiten Sie eine Kurzpräsentation
Proseminar Komplexe Analysis 1 Michael Kunzinger und Gerald Teschl WS215/16 Bemerkung: Die meisten Beispiele sind aus dem Buch von K. Jänich, Funktionentheorie, Springer. 1. Bereiten Sie eine Kurzpräsentation
Funktionentheorie I - Prüfungsprotokolle Skript Dr. Herzog
 Funktionentheorie I - Prüfungsprotokolle Skript Dr. Herzog 1 Komplexe Zahlen 2 Topologische Begriffe Offene Menge Abgeschlossene Menge Kompakte Teilmenge: Überdeckungskompaktheit 3 Die Riemann sche Zahlenkugel
Funktionentheorie I - Prüfungsprotokolle Skript Dr. Herzog 1 Komplexe Zahlen 2 Topologische Begriffe Offene Menge Abgeschlossene Menge Kompakte Teilmenge: Überdeckungskompaktheit 3 Die Riemann sche Zahlenkugel
ÜBUNGSBEISPIELE ZUR KOMPLEXEN ANALYSIS. Komplexe Zahlen. (x, y) + (u, v) := (x + u, y + v) (x, y) (u, v) := (xu yv, xv + yu)
 ÜBUNGSBEISPIELE ZUR KOMPLEXEN ANALYSIS ARMIN RAINER Sommersemester 05 Komplexe Zahlen Sei z = i und w = 3 + 4i. Berechne: (a) z + w, zw, z w, w z, z 3, w. (b) z, z, w, w, z, w. Zeige, dass R mit der Addition
ÜBUNGSBEISPIELE ZUR KOMPLEXEN ANALYSIS ARMIN RAINER Sommersemester 05 Komplexe Zahlen Sei z = i und w = 3 + 4i. Berechne: (a) z + w, zw, z w, w z, z 3, w. (b) z, z, w, w, z, w. Zeige, dass R mit der Addition
Lösungen zur Klausur Funktionentheorie I SS 2005
 Universität Karlsruhe 29 September 25 Mathematisches Institut I Prof Dr M von Renteln Dr C Kaiser Aufgabe en zur Klausur Funktionentheorie I SS 25 Sei S die Möbiustransformation, die durch S(z) = i i z
Universität Karlsruhe 29 September 25 Mathematisches Institut I Prof Dr M von Renteln Dr C Kaiser Aufgabe en zur Klausur Funktionentheorie I SS 25 Sei S die Möbiustransformation, die durch S(z) = i i z
Einige Standard-Aufgabentypen der Funktionentheorie I
 Matthias Stemmler SS 6 stemmler@mathematik.uni-marburg.de Einige Standard-Aufgabentypen der Funktionentheorie I I. Untersuchung von Funktionen auf komplexe Differenzierbarkeit/Holomorphie gegeben: gesucht:
Matthias Stemmler SS 6 stemmler@mathematik.uni-marburg.de Einige Standard-Aufgabentypen der Funktionentheorie I I. Untersuchung von Funktionen auf komplexe Differenzierbarkeit/Holomorphie gegeben: gesucht:
86 Klassifizierung der isolierten Singularitäten holomorpher
 86 Klassifizierung der isolierten Singularitäten holomorpher Funktionen 86. Isolierte Singulariäten holomorpher Funktionen 86.3 Klassifizierung der isolirerten Singularitäten 86.5 Charakterisierung hebbarer
86 Klassifizierung der isolierten Singularitäten holomorpher Funktionen 86. Isolierte Singulariäten holomorpher Funktionen 86.3 Klassifizierung der isolirerten Singularitäten 86.5 Charakterisierung hebbarer
3 Meromorphe Funktionen und der Residuenkalkül
 $Id: mero.tex,v 1.3 2016/06/22 16:12:36 hk Exp $ 3 Meromorphe Funktionen und der Residuenkalkül 3.3 Hauptteile und Residuen Am Ende der letzten Sitzung hatten wir die Laurententwicklung einer holomorphen
$Id: mero.tex,v 1.3 2016/06/22 16:12:36 hk Exp $ 3 Meromorphe Funktionen und der Residuenkalkül 3.3 Hauptteile und Residuen Am Ende der letzten Sitzung hatten wir die Laurententwicklung einer holomorphen
Übungen zur Vorlesung Funktionentheorie Sommersemester Klausurvorbereitungsblatt Lösungsvorschläge
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Dr. Tobias Mai M.Sc. Felix Leid Übungen zur Vorlesung Funktionentheorie Sommersemester 7 Klausurvorbereitungsblatt Lösungsvorschläge (5) Bestimmen
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Dr. Tobias Mai M.Sc. Felix Leid Übungen zur Vorlesung Funktionentheorie Sommersemester 7 Klausurvorbereitungsblatt Lösungsvorschläge (5) Bestimmen
Funktionentheorie. Wolfram Decker
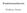 Funktionentheorie Wolfram Decker Inhaltsverzeichnis Kapitel. Grundlagen 7 1. Komplexe Zahlen 7 1.1. Der Körper C 7 1.2. Konjugation 7 1.3. Euklidischer Abstand, C als metrischer Raum 8 1.4. Zusammenhang
Funktionentheorie Wolfram Decker Inhaltsverzeichnis Kapitel. Grundlagen 7 1. Komplexe Zahlen 7 1.1. Der Körper C 7 1.2. Konjugation 7 1.3. Euklidischer Abstand, C als metrischer Raum 8 1.4. Zusammenhang
D-MATH Funktionentheorie HS 2018 Prof. Michael Struwe. Lösungen Serie 8. Laurentreihen, isolierte Singularitäten, meromorphe Funktionen
 D-MATH Funktionentheorie HS 208 Prof. Michael Struwe Lösungen Serie 8 Laurentreihen, isolierte Singularitäten, meromorphe Funktionen. Bestimmen Sie die Laurentreihenentwicklung der folgenden Funktionen:
D-MATH Funktionentheorie HS 208 Prof. Michael Struwe Lösungen Serie 8 Laurentreihen, isolierte Singularitäten, meromorphe Funktionen. Bestimmen Sie die Laurentreihenentwicklung der folgenden Funktionen:
10 Logarithmus- und Potenzfunktion
 4 Logarithmus- und Potenzfunktion. Satz: Sei G einfach zusammenhängend, f H(G) und z G. Dann existiert genau eine Stammfunktion F von f mit F(z ) =. Für z G sei γ z ein beliebiger Integrationsweg in G,
4 Logarithmus- und Potenzfunktion. Satz: Sei G einfach zusammenhängend, f H(G) und z G. Dann existiert genau eine Stammfunktion F von f mit F(z ) =. Für z G sei γ z ein beliebiger Integrationsweg in G,
Kapitel I. Holomorphe Funktionen. 1 Potenzreihen
 Kapitel I Holomorphe Funktionen Potenzreihen Definition. Sei f a (z) = c n (z a) n eine Potenzreihe mit Entwicklungspunkt a. Die Zahl R := sup{r 0 z C, so daß f a (z) konvergent und r = z a ist.} heißt
Kapitel I Holomorphe Funktionen Potenzreihen Definition. Sei f a (z) = c n (z a) n eine Potenzreihe mit Entwicklungspunkt a. Die Zahl R := sup{r 0 z C, so daß f a (z) konvergent und r = z a ist.} heißt
c r Addiert man nun beide Reihendarstellungen, so folgt f (ζ) Nach dem Cauchyschen Integralsatz gilt dann auch
 Residuen V Beweis Einsetzen in das Kurvenintegral über c r ergibt demnach f (ζ) 2πi ζ z dζ = f (ζ) 2πi (ζ z 0 ) c r k= c r k+ dζ Addiert man nun beide Reihendarstellungen, so folgt a k (z z 0 ) k, r z
Residuen V Beweis Einsetzen in das Kurvenintegral über c r ergibt demnach f (ζ) 2πi ζ z dζ = f (ζ) 2πi (ζ z 0 ) c r k= c r k+ dζ Addiert man nun beide Reihendarstellungen, so folgt a k (z z 0 ) k, r z
Funktionentheorie, Woche 11. Funktionen mit Singularitäten Meromorphe Funktionen
 Funktionentheorie, Woche Funktionen mit Singularitäten. Meromorphe Funktionen Definition. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P = f ( hat keine
Funktionentheorie, Woche Funktionen mit Singularitäten. Meromorphe Funktionen Definition. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P = f ( hat keine
Komplexe Funktionen für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg SoSe 214 Dr K Rothe Komplexe Funktionen für Studierende der Ingenieurwissenschaften Aufgaben und Theoriehinweise zu Blatt 6 Komplexe Funktionen, K Rothe,
Fachbereich Mathematik der Universität Hamburg SoSe 214 Dr K Rothe Komplexe Funktionen für Studierende der Ingenieurwissenschaften Aufgaben und Theoriehinweise zu Blatt 6 Komplexe Funktionen, K Rothe,
3 Windungszahlen und Cauchysche Integralformeln
 3 3 Windungszahlen und Cauchysche Integralformeln 3. Definition: Sei geschlossener Integrationsweg oder Zyklus mit z 0 C \ Sp. Dann heißt n(, z 0 ) := dz z z 0 Windungszahl (oder: Index, Umlaufszahl) von
3 3 Windungszahlen und Cauchysche Integralformeln 3. Definition: Sei geschlossener Integrationsweg oder Zyklus mit z 0 C \ Sp. Dann heißt n(, z 0 ) := dz z z 0 Windungszahl (oder: Index, Umlaufszahl) von
23 Laurentreihen und Residuen
 23 Laurentreihen und Residuen 23. Laurentreihen Ist eine Funktion f in einem Punkt z nicht holomorph (oder nicht einmal definiert), so läßt sich f nicht durch eine Potenzreihe mit Entwicklungspunkt z darstellen.
23 Laurentreihen und Residuen 23. Laurentreihen Ist eine Funktion f in einem Punkt z nicht holomorph (oder nicht einmal definiert), so läßt sich f nicht durch eine Potenzreihe mit Entwicklungspunkt z darstellen.
5 Meromorphe Funktionen
 $Id: mero.tex,v.8 202/06/26 9:08:48 hk Exp $ $Id: residuum.tex,v.3 202/06/26 9:5:40 hk Exp hk $ 5 Meromorphe Funktionen 5.2 Laurentreihen In der letzten Sitzung hatten wir Laurentreihen eingeführt und
$Id: mero.tex,v.8 202/06/26 9:08:48 hk Exp $ $Id: residuum.tex,v.3 202/06/26 9:5:40 hk Exp hk $ 5 Meromorphe Funktionen 5.2 Laurentreihen In der letzten Sitzung hatten wir Laurentreihen eingeführt und
Funktionentheorie Nachholklausur
 Prof. Dr. Thomas Vogel Sommersemester 2014 Robert Schmidt 6.10.2014 Funktionentheorie Nachholklausur Nachname: Matrikelnr.: Vorname: Fachsemester: Abschluss: Bachelor, PO 2007 2010 2011 Master, PO 2010
Prof. Dr. Thomas Vogel Sommersemester 2014 Robert Schmidt 6.10.2014 Funktionentheorie Nachholklausur Nachname: Matrikelnr.: Vorname: Fachsemester: Abschluss: Bachelor, PO 2007 2010 2011 Master, PO 2010
Übungen zur Funktionentheorie
 Mathematisches Institut SS 29 Universität München Prof. Dr. M. Schottenloher C. Paleani M. Schwingenheuer A. Stadelmaier Übungen zur Funktionentheorie Lösungen zu Übungsblatt. Sei fz) = z ) z 2) 2 eine
Mathematisches Institut SS 29 Universität München Prof. Dr. M. Schottenloher C. Paleani M. Schwingenheuer A. Stadelmaier Übungen zur Funktionentheorie Lösungen zu Übungsblatt. Sei fz) = z ) z 2) 2 eine
10. Isolierte Singularitäten
 0. Isolierte Singularitäten 57 0. Isolierte Singularitäten Der wichtigste Spezialfall von Laurent-Reihen (und in der Tat auch der, den wir ab jetzt nur noch betrachten werden) ist der, bei dem der innere
0. Isolierte Singularitäten 57 0. Isolierte Singularitäten Der wichtigste Spezialfall von Laurent-Reihen (und in der Tat auch der, den wir ab jetzt nur noch betrachten werden) ist der, bei dem der innere
6.7 Isolierte Singularitäten
 6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
6.7 Isolierte Singularitäten Definition: Eine analytische Funktion f hat in einem Punkt a C eine isolierte Singularität, falls f in einem Kreisring B r (a) \ {a} = {z C : 0 < z a < r} für r > 0, definiert
Analytische Zahlentheorie
 4. April 005. Übungsblatt Aufgabe (4 Punkte Sei k N. Beweisen Sie, dass f : N C mit f(n := n k streng multiplikativ ist. Sei τ die Funktion, die der natürlichen Zahl n die Anzahl der Teiler von n zuordnet
4. April 005. Übungsblatt Aufgabe (4 Punkte Sei k N. Beweisen Sie, dass f : N C mit f(n := n k streng multiplikativ ist. Sei τ die Funktion, die der natürlichen Zahl n die Anzahl der Teiler von n zuordnet
9 Ergänzungen zur Funktionentheorie
 9 Ergänzungen zur Funktionentheorie 9. Herausziehen von Polen und Nullstellen Das folgende Lemma hatten wir an zahlreichen Stellen verwendet, ohne es jemals streng bewiesen zu haben. Lemma 9. Die Funktion
9 Ergänzungen zur Funktionentheorie 9. Herausziehen von Polen und Nullstellen Das folgende Lemma hatten wir an zahlreichen Stellen verwendet, ohne es jemals streng bewiesen zu haben. Lemma 9. Die Funktion
Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi
![Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi Bemerkung Als Folge von Satz 6.2 kann man jede ganze Funktion schreiben als Potenzreihe. α m z m. f(z) = m=0. 2πi. re it t [0,2π] 2πi](/thumbs/92/110521610.jpg) Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Funktionentheorie, Woche 7 Eigenschaften holomorpher Funktionen 7.1 Ganze Funktionen Definition 7.1 Eine Funktion f : C C, die holomorph ist auf C, nennt man eine ganze Funktion. Bemerkung 7.1.1 Als Folge
Potenzreihenentwicklung im Reellen und Komplexen
 Potenzreihenentwicklung im Reellen und Komplexen Christoph Lassnig 26. Januar 20 Zusammenfassung Dieses Dokument bietet einen kleinen Überblick über Potenzreihen, sowie auf ihnen aufbauenden Sätzen und
Potenzreihenentwicklung im Reellen und Komplexen Christoph Lassnig 26. Januar 20 Zusammenfassung Dieses Dokument bietet einen kleinen Überblick über Potenzreihen, sowie auf ihnen aufbauenden Sätzen und
Studienbegleitende Prüfung / Modulprüfung / Diplomprüfung Funktionentheorie I SS 2010 Lösungsvorschläge Version vom
 Studienbegleitende Prüfung / Modulprüfung / Diplomprüfung Funktionentheorie I SS 2010 svorschläge Version vom 2382010 Aufgabe 1 (2+2 Punkte) a) Sei f : C C gegeben durch f(z) := 5 5i 1 2i + ez z Geben
Studienbegleitende Prüfung / Modulprüfung / Diplomprüfung Funktionentheorie I SS 2010 svorschläge Version vom 2382010 Aufgabe 1 (2+2 Punkte) a) Sei f : C C gegeben durch f(z) := 5 5i 1 2i + ez z Geben
Formelsammlung Analysis III - Funktionentheorie für Physiker und Mathematiker
 Formelsammlung Analysis III - Funktionentheorie für Physiker und Mathematiker Stand: 2.07.2006 - Version:.0. Erhältlich unter http://privat.macrolab.de Diese Formelsammlung
Formelsammlung Analysis III - Funktionentheorie für Physiker und Mathematiker Stand: 2.07.2006 - Version:.0. Erhältlich unter http://privat.macrolab.de Diese Formelsammlung
Typ der Residuum Funktion Test Singularität bei a bei a. ; a = i, Res(f; i) = lim z 2 +1 (z i)(z+i) z i 2i
 A: Berechnung von Residuen (f Singularität in a, meist f = g, g, h analytisch in a) h Typ der Residuum Funktion Test Singularität bei a bei a. f(z) lim(z a)f(z) = hebbar z a f(z) = sin z, a = ; lim zf(z)
A: Berechnung von Residuen (f Singularität in a, meist f = g, g, h analytisch in a) h Typ der Residuum Funktion Test Singularität bei a bei a. f(z) lim(z a)f(z) = hebbar z a f(z) = sin z, a = ; lim zf(z)
1.3 Isolierte Singularitäten
 6.3 Isolierte Singularitäten Definition Sei U C offen, z 0 U und f : U \ {z 0 } C holomorph. Dann nennt man z 0 eine isolierte Singularität von f. Zunächst einmal ist z 0 nur eine Definitionslücke für
6.3 Isolierte Singularitäten Definition Sei U C offen, z 0 U und f : U \ {z 0 } C holomorph. Dann nennt man z 0 eine isolierte Singularität von f. Zunächst einmal ist z 0 nur eine Definitionslücke für
Funktionentheorie I - Formelsammlung
 Funktionentheorie I - Formelsammlung von Julian Merkert, Skript Dr. Herzog Komplexe Zahlen R 2 = {(x, y) : x, y R}: Vektorraum der Dimension 2 über R Körper C der komplexen Zahlen: (R 2, +, ) mit... (i)
Funktionentheorie I - Formelsammlung von Julian Merkert, Skript Dr. Herzog Komplexe Zahlen R 2 = {(x, y) : x, y R}: Vektorraum der Dimension 2 über R Körper C der komplexen Zahlen: (R 2, +, ) mit... (i)
Lösungen zum 11. Übungsblatt Funktionentheorie I
 Universität Karlsruhe SS 2005 Mathematisches Institut I Prof. Dr. M. von Renteln Dr. C. Kaiser Lösungen zum 11. Übungsblatt Funktionentheorie I Aufgabe 11.1 a) Nach dem Maximumprinzip nimmt die Funktion
Universität Karlsruhe SS 2005 Mathematisches Institut I Prof. Dr. M. von Renteln Dr. C. Kaiser Lösungen zum 11. Übungsblatt Funktionentheorie I Aufgabe 11.1 a) Nach dem Maximumprinzip nimmt die Funktion
AUFGABEN ZUR FUNKTIONENTHEORIE. von. Prof. Dr. H.-W. Burmann
 AUFGABEN ZUR FUNKTIONENTHEORIE von Prof. Dr. H.-W. Burmann Bei den folgenden Aufgaben handelt es sich um Reste, die bei der Erstellung der Aufgabenblätter übriggeblieben sind. Der Schwierigkeitsgrad der
AUFGABEN ZUR FUNKTIONENTHEORIE von Prof. Dr. H.-W. Burmann Bei den folgenden Aufgaben handelt es sich um Reste, die bei der Erstellung der Aufgabenblätter übriggeblieben sind. Der Schwierigkeitsgrad der
Wir wollen jetzt die Cauchys che Integralformel in mehreren Veränderlichen formulieren. (ζ 1 z 1 ) (ζ n z n ) dζ 1 (ζ 1 z 1 ) dζ n.
 4 Kapitel Holomorphe Funktionen 2 Das Cauchy-Integral Wir wollen jetzt die Cauchys che Integralformel in mehreren Veränderlichen formulieren. Sei r (r,..., r n ) R n +, P P n (0, r), n (0, r), und f eine
4 Kapitel Holomorphe Funktionen 2 Das Cauchy-Integral Wir wollen jetzt die Cauchys che Integralformel in mehreren Veränderlichen formulieren. Sei r (r,..., r n ) R n +, P P n (0, r), n (0, r), und f eine
X. Funktionentheorie. Übersicht über den Inhalt von Kapitel X: 57. Holomorphe Funktionen. 58. Cauchy-Formeln und Anwendungen
 56 Integralsätze im Raum 273 X. Funktionentheorie Übersicht über den Inhalt von Kapitel X: 57. Holomorphe Funktionen 58. Cauchy-Formeln und Anwendungen 59. Laurent-Entwicklungen und Residuensatz 274 X.
56 Integralsätze im Raum 273 X. Funktionentheorie Übersicht über den Inhalt von Kapitel X: 57. Holomorphe Funktionen 58. Cauchy-Formeln und Anwendungen 59. Laurent-Entwicklungen und Residuensatz 274 X.
Prüfungsvorbereitungskurs Höhere Mathematik 3
 Prüfungsvorbereitungskurs Höhere Mathematik 3 Funktionentheorie Marco Boßle Jörg Hörner Mathematik Online Frühjahr 20 PV-Kurs HM 3 Funktionentheorie - Zusammenfassung Grundlagen Komplexe Funktion f (z)
Prüfungsvorbereitungskurs Höhere Mathematik 3 Funktionentheorie Marco Boßle Jörg Hörner Mathematik Online Frühjahr 20 PV-Kurs HM 3 Funktionentheorie - Zusammenfassung Grundlagen Komplexe Funktion f (z)
Kapitel 3. Die Stammfunktion
 Kapitel 3 Die Stammfunktion Nachdem wir im vorigen Kapitel die Grundlagen von Kurvenintegralen erarbeitet haben, befassen wir uns nun mit der konkreten Berechnung eines solchen Integrals. Besonderes Augenmerk
Kapitel 3 Die Stammfunktion Nachdem wir im vorigen Kapitel die Grundlagen von Kurvenintegralen erarbeitet haben, befassen wir uns nun mit der konkreten Berechnung eines solchen Integrals. Besonderes Augenmerk
4 Funktionen mit isolierten Singularitäten
 4 Funktionen mit isolierten Singularitäten Funktionen wie z +z 2, z tanz oder z e /z sind mit Ausnahme einzelner Punkte in C holomorph. In diesem Abschnitt untersuchen wir solche Funktionen in der Nähe
4 Funktionen mit isolierten Singularitäten Funktionen wie z +z 2, z tanz oder z e /z sind mit Ausnahme einzelner Punkte in C holomorph. In diesem Abschnitt untersuchen wir solche Funktionen in der Nähe
Vertiefung der Funktionentheorie
 Vertiefung der Funktionentheorie Wintersemester 2009/2010 Universität Bayreuth Michael Stoll Inhaltsverzeichnis 0. Wiederholung 2 1. Der Residuensatz 4 2. Anwendungen des Residuensatzes 7 3. Das Null-
Vertiefung der Funktionentheorie Wintersemester 2009/2010 Universität Bayreuth Michael Stoll Inhaltsverzeichnis 0. Wiederholung 2 1. Der Residuensatz 4 2. Anwendungen des Residuensatzes 7 3. Das Null-
4 Der globale Cauchysche Integralsatz 56
 Inhaltsverzeichnis Vorbemerkung ii 0 Abbildungen f : U lc lc, (x, y) f(x, y) 2 1 Holomorphe Funktionen 10 2 Kurvenintegrale 18 3 Die Stammfunktion 27 3.1 Stammfunktionen und der Cauchysche Integralsatz........
Inhaltsverzeichnis Vorbemerkung ii 0 Abbildungen f : U lc lc, (x, y) f(x, y) 2 1 Holomorphe Funktionen 10 2 Kurvenintegrale 18 3 Die Stammfunktion 27 3.1 Stammfunktionen und der Cauchysche Integralsatz........
1. Aufgabe 9 Punkte. Musterlösung Analysis III f. Ing., 09. Oktober Partialbruchzerlegung: 4 z 1 1. (z 1)(z +3) =
 Musterlösung Analysis III f. Ing., 09. Oktober 0. Aufgabe 9 Punkte Partialbruchzerlegung: (z )(z +3) z z +3 Um eine im Ringgebiet < z < 5 konvergente Laurent-Reihe zu erhalten, entwickelt man den Term
Musterlösung Analysis III f. Ing., 09. Oktober 0. Aufgabe 9 Punkte Partialbruchzerlegung: (z )(z +3) z z +3 Um eine im Ringgebiet < z < 5 konvergente Laurent-Reihe zu erhalten, entwickelt man den Term
Meromorphe Funktionen
 Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
Kapitel Meromorphe Funktionen Der Satz von Mittag-Leffler Zur Erinnerung: Die holomorphe Funktion f habe in z 0 C eine isolierte Singularität. Liegt eine Polstelle vor, so gibt es eine offene Umgebung
3.4 Analytische Fortsetzung
 3.4 Analytische Fortsetzung 3.4. Analytische Fortsetzung 49 Es kann vorkommen, dass eine holomorphe Funktion f, definiert durch eine Potenzreihe um den Punkt z 0 mit Konvergenzradius R, über den Rand der
3.4 Analytische Fortsetzung 3.4. Analytische Fortsetzung 49 Es kann vorkommen, dass eine holomorphe Funktion f, definiert durch eine Potenzreihe um den Punkt z 0 mit Konvergenzradius R, über den Rand der
Ferienkurs Analysis 3 - Übungen Funktionentheorie - Musterlösung
 Ferienkurs Analysis 3 - Übungen Funktionentheorie - Musterlösung Ralitsa Bozhanova, Ma v. Vopelius.8.9 Differenzierbarkeit (a Sei A (a ij i,j, R. Zeigen Sie, dass die von A durch die Matrimultiplikation
Ferienkurs Analysis 3 - Übungen Funktionentheorie - Musterlösung Ralitsa Bozhanova, Ma v. Vopelius.8.9 Differenzierbarkeit (a Sei A (a ij i,j, R. Zeigen Sie, dass die von A durch die Matrimultiplikation
Skriptum. Funktionentheorie I. Definitionen und Sätze
 Skriptum Funktionentheorie I Definitionen und Sätze c Stefan Englert Würzburg, 2009 Inhaltsverzeichnis Komplexe Zahlen 2 2 Holomorphe Funktionen 2 3 Kurvenintegrale 3 4 Der Cauchysche Integralsatz 4 5
Skriptum Funktionentheorie I Definitionen und Sätze c Stefan Englert Würzburg, 2009 Inhaltsverzeichnis Komplexe Zahlen 2 2 Holomorphe Funktionen 2 3 Kurvenintegrale 3 4 Der Cauchysche Integralsatz 4 5
3 Meromorphe Funktionen und der Residuenkalkül
 $Id: mero.tex,v.5 203/05/4 3:0:42 hk Exp hk $ 3 Meromorphe Funktionen und der Residuenkalkül 3.2 Isolierte Singularitäten In der letzten Sitzung hatten wir die drei Typen isolierter Singularitäten und
$Id: mero.tex,v.5 203/05/4 3:0:42 hk Exp hk $ 3 Meromorphe Funktionen und der Residuenkalkül 3.2 Isolierte Singularitäten In der letzten Sitzung hatten wir die drei Typen isolierter Singularitäten und
Anhang. ν=1,...,n z ν.
 Komplexe Analysis von mehreren Veränderlichen 121 Anhang Komplexe Analysis von mehreren Veränderlichen 1 Holomorphe Funktionen Definition. Die euklidische Norm eines Vektors z C n wird gegeben durch z
Komplexe Analysis von mehreren Veränderlichen 121 Anhang Komplexe Analysis von mehreren Veränderlichen 1 Holomorphe Funktionen Definition. Die euklidische Norm eines Vektors z C n wird gegeben durch z
Kapitel 24. Entwicklungen holomorpher Funktionen Taylor-Reihen (Potenzreihen und holomorphe Funktionen;
 Kapitel 24 Entwicklungen holomorpher Funktionen Reihenentwicklungen spielen in der Funktionentheorie eine ganz besodere Rolle. Im Reellen wurden Potenzreihen in Kapitel 5.2 besprochen, das komplexe Gegenstück
Kapitel 24 Entwicklungen holomorpher Funktionen Reihenentwicklungen spielen in der Funktionentheorie eine ganz besodere Rolle. Im Reellen wurden Potenzreihen in Kapitel 5.2 besprochen, das komplexe Gegenstück
Windungszahl. Windungszahl II. Bemerkung. Beispiel
 Windungszahl Bemerkung. Für einen beliebigen z 0 homotopen Weg in G \ {z 0 }, der den Punkt z 0 niht notwendigerweise genau einmal durhläuft, gilt 2πi Uml (, z 0 ) f (z 0 ) 2. Nützlih ist folgende heuristishe
Windungszahl Bemerkung. Für einen beliebigen z 0 homotopen Weg in G \ {z 0 }, der den Punkt z 0 niht notwendigerweise genau einmal durhläuft, gilt 2πi Uml (, z 0 ) f (z 0 ) 2. Nützlih ist folgende heuristishe
3. VORLESUNG,
 1.3.9. Satz (Parametrisierung der Kreislinie). 3. VORLESUNG, 23.04.2009 (i) Die Abbildung p : R S 1, p(ϕ) = e iϕ = cosϕ+isinϕ ist ein Gruppenmorphismus der additiven Gruppe (R,+) auf die multiplikative
1.3.9. Satz (Parametrisierung der Kreislinie). 3. VORLESUNG, 23.04.2009 (i) Die Abbildung p : R S 1, p(ϕ) = e iϕ = cosϕ+isinϕ ist ein Gruppenmorphismus der additiven Gruppe (R,+) auf die multiplikative
Übungen zur Vorlesung Funktionentheorie Sommersemester Musterlösung zu Blatt 10. f(z) f(z) dz
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Musterlösung zu Blatt 0 Aufgabe. Berechnen Sie
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Kapitel 4. Der globale Cauchysche Integralsatz
 Kapitel 4 Der globale Cauchysche Integralsatz Die Ergebnisse, die wir im vorigen Kapitel gewonnen haben, leben in der Regel davon, dass über einfach geschlossene Kurven integriert wird. Wie sich die Aussagen
Kapitel 4 Der globale Cauchysche Integralsatz Die Ergebnisse, die wir im vorigen Kapitel gewonnen haben, leben in der Regel davon, dass über einfach geschlossene Kurven integriert wird. Wie sich die Aussagen
γ j γ j (f) = f(z) dz.
 27 6. Globale Versionen des Cauchyschen Integralsatzes. Residuensatz 6.. Ketten und Zyklen. Es seien γ,...,γ n Wege in der Ebene und K =Bildγ... Bild γ n. Jedes γ j liefert eine lineare Abbildung γ j :
27 6. Globale Versionen des Cauchyschen Integralsatzes. Residuensatz 6.. Ketten und Zyklen. Es seien γ,...,γ n Wege in der Ebene und K =Bildγ... Bild γ n. Jedes γ j liefert eine lineare Abbildung γ j :
Diplom-Prüfung Physik Nebenfach Mathematik. Funktionentheorie Gewöhnliche DGL s und dynamische Systeme
 Diplom-Prüfung Physik Nebenfach Mathematik Funktionentheorie Gewöhnliche DGL s und dynamische Systeme Martin-I. Trappe (Dated: 30. September 2005) Quellen: E. Freitag, R. Busam, Funktionentheorie, Springer
Diplom-Prüfung Physik Nebenfach Mathematik Funktionentheorie Gewöhnliche DGL s und dynamische Systeme Martin-I. Trappe (Dated: 30. September 2005) Quellen: E. Freitag, R. Busam, Funktionentheorie, Springer
Funktionentheorie erkunden mit Maple
 Springer-Lehrbuch Funktionentheorie erkunden mit Maple Bearbeitet von Wilhelm Forst, Dieter Hoffmann 1. Auflage 2012. Taschenbuch. xviii, 328 S. Paperback ISBN 978 3 642 29411 2 Format (B x L): 15,5 x
Springer-Lehrbuch Funktionentheorie erkunden mit Maple Bearbeitet von Wilhelm Forst, Dieter Hoffmann 1. Auflage 2012. Taschenbuch. xviii, 328 S. Paperback ISBN 978 3 642 29411 2 Format (B x L): 15,5 x
Die j-funktion, Abschätzung der Fourierkoeffizienten. 1 Grundlagen
 Die j-funktion, Abschätzung der Fourierkoeffizienten Vortrag zum Seminar zur Funktionentheorie, 0.04.00 Felix Voigtländer Diese Ausarbeitung beschäftigt sich zunächst mit der j-funktion. Diese stellt einerseits
Die j-funktion, Abschätzung der Fourierkoeffizienten Vortrag zum Seminar zur Funktionentheorie, 0.04.00 Felix Voigtländer Diese Ausarbeitung beschäftigt sich zunächst mit der j-funktion. Diese stellt einerseits
Funktionentheorie 1 - Übung SS 2015 Marcel Marohn
 Funktionentheorie 1 - Übung SS 2015 Marcel Marohn 7. April 2015 Inhaltsverzeichnis 1 Der topologische Raum C 3 1.1 Grundlagen über Komplexe Zahlen...................... 3 1.2 Topologische Grundbegriffe..........................
Funktionentheorie 1 - Übung SS 2015 Marcel Marohn 7. April 2015 Inhaltsverzeichnis 1 Der topologische Raum C 3 1.1 Grundlagen über Komplexe Zahlen...................... 3 1.2 Topologische Grundbegriffe..........................
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik 6. Hauptzweig des Logarithmus Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik 6. Hauptzweig des Logarithmus Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
28: Holomorphe Funktionen, Potenzreihen und Laurentreihen
 Einleitung 28: Holomorphe Funktionen, Potenzreihen und Laurentreihen 28.1 Einleitung Wir wissen bereits, dass eine holomorphe Funktion f : M C unendlich oft komplex differenzierbar ist. Für jedes z 0 M
Einleitung 28: Holomorphe Funktionen, Potenzreihen und Laurentreihen 28.1 Einleitung Wir wissen bereits, dass eine holomorphe Funktion f : M C unendlich oft komplex differenzierbar ist. Für jedes z 0 M
6.1 Komplexe Funktionen
 118 6 Funktionentheorie 6.1 Komplexe Funktionen Wir kennen die komplexen Zahlen als Erweiterung des Körpers der reellen Zahlen. Man postuliert die Existenz einer imaginären Größe i mit der Eigenschaft
118 6 Funktionentheorie 6.1 Komplexe Funktionen Wir kennen die komplexen Zahlen als Erweiterung des Körpers der reellen Zahlen. Man postuliert die Existenz einer imaginären Größe i mit der Eigenschaft
Analysis IV. Walter Bergweiler. Sommersemester 2014 Fassung vom 18. Juli Überblick 1. 1 Komplexe Differenzierbarkeit 2
 Analysis IV Walter Bergweiler Sommersemester 204 Fassung vom 8. Juli 204 Inhaltsverzeichnis Überblick Komplexe Differenzierbarkeit 2 2 Kurven, Zusammenhang und Wegzusammenhang 5 3 Kurvenintegrale 9 4 Stammfunktionen
Analysis IV Walter Bergweiler Sommersemester 204 Fassung vom 8. Juli 204 Inhaltsverzeichnis Überblick Komplexe Differenzierbarkeit 2 2 Kurven, Zusammenhang und Wegzusammenhang 5 3 Kurvenintegrale 9 4 Stammfunktionen
6. VORLESUNG,
 27 6. VORLESUNG, 1.5.217 2.2.9. Beispiel. Die Funktion f : C C, f(z) = 1 hat keine Stammfuntkion, da z dz (2.9) z =. B 1 () B 1 () Hätte f eine Stammfunktion, so wäre das Integral Null. Die Formel (2.9)
27 6. VORLESUNG, 1.5.217 2.2.9. Beispiel. Die Funktion f : C C, f(z) = 1 hat keine Stammfuntkion, da z dz (2.9) z =. B 1 () B 1 () Hätte f eine Stammfunktion, so wäre das Integral Null. Die Formel (2.9)
Komplexe Funktionen. Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg
 Komplexe Funktionen Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 12. Juni 2009 Reihenentwicklung komplexer Funktionen
Komplexe Funktionen Michael Hinze (zusammen mit Peywand Kiani) Department Mathematik Schwerpunkt Optimierung und Approximation, Universität Hamburg 12. Juni 2009 Reihenentwicklung komplexer Funktionen
Funktionentheorie. Daniel Scholz im Sommer Überarbeitete Version vom 19. September 2007.
 Funktionentheorie Daniel Scholz im Sommer 25 Überarbeitete Version vom 9. September 27. Inhaltsverzeichnis Komplexe Zahlen 4. Grundlegende Definitionen.................... 4.2 Anordnung in C.........................
Funktionentheorie Daniel Scholz im Sommer 25 Überarbeitete Version vom 9. September 27. Inhaltsverzeichnis Komplexe Zahlen 4. Grundlegende Definitionen.................... 4.2 Anordnung in C.........................
Übungen zur Vorlesung Funktionentheorie Sommersemester Lösungshinweise zum Klausurvorbereitungsblatt. (z) i f. 2xe (x2 +y 2) i2ye (x2 +y 2 ) 2
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Lösungshinweise zum Klausurvorbereitungsblatt (3
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6. MATHEMATIK Prof. Dr. Roland Speicher M.Sc. Tobias Mai Übungen zur Vorlesung Funktionentheorie Sommersemester 0 Lösungshinweise zum Klausurvorbereitungsblatt (3
Höhere Mathematik II für die Fachrichtung Physik. Lösungsvorschläge zum 11. Übungsblatt
 Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 7.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc. Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
Institut für Analysis SS17 PD Dr. Peer Christian Kunstmann 7.7.17 Dipl.-Math. Leonid Chaichenets, Johanna Richter, M.Sc. Tobias Ried, M.Sc., Tobias Schmid, M.Sc. Höhere Mathematik II für die Fachrichtung
3 Der Riemannsche Abbildungssatz
 24 Biholomorphe Abbildungen 3 Der Riemannsche Abbildungssatz Definition. Sei G C ein Gebiet, G. Eine holomorphe oder meromorphe Funktion f auf U \ { } heißt holomorph (bzw. meromorph) im Unendlichen, falls
24 Biholomorphe Abbildungen 3 Der Riemannsche Abbildungssatz Definition. Sei G C ein Gebiet, G. Eine holomorphe oder meromorphe Funktion f auf U \ { } heißt holomorph (bzw. meromorph) im Unendlichen, falls
Kurzscript zur Funktionentheorie im SS Sebastian Goette
 Kurzscript zur Funktionentheorie im SS 2014 Sebastian Goette KAPITEL 1 Holomorphe und Analytische Funktionen 1a Analytische Funktionen 11 Wiederholung Setze C = R 2 Für z = (x, y) und w = (u, v) C seien
Kurzscript zur Funktionentheorie im SS 2014 Sebastian Goette KAPITEL 1 Holomorphe und Analytische Funktionen 1a Analytische Funktionen 11 Wiederholung Setze C = R 2 Für z = (x, y) und w = (u, v) C seien
Musterlösung zu Übungsblatt 11
 Prof. R. Pandharipande J. Schmitt, C. Schießl Funktionentheorie 2. Dezember 16 HS 2016 Musterlösung zu Übungsblatt 11 Aufgabe 1. Sei U C offen und a U. Seien f, g : U {a} folgende Formeln zur Berechnung
Prof. R. Pandharipande J. Schmitt, C. Schießl Funktionentheorie 2. Dezember 16 HS 2016 Musterlösung zu Übungsblatt 11 Aufgabe 1. Sei U C offen und a U. Seien f, g : U {a} folgende Formeln zur Berechnung
2 Der Weierstraßsche Produktsatz
 4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
4 Kapitel Meromorphe Funktionen Der Weierstraßsche Produktsatz Unser nächstes Problem soll sein, zu einer vorgegebenen Menge von Punkten eine holomorphe Funktion zu suchen, die genau in den Punkten Nullstellen
Sätze der Funktionentheorie. Daniel Jaud
 Sätze der Funktionentheorie Daniel Jaud August 2, 2013 2 Contents 1 Komplexe Differenzierbarkeit und Holomorphie 7 1.1 Körper der komplexen Zahlen.................... 7 1.2 Algebraische Abgeschlossenheit...................
Sätze der Funktionentheorie Daniel Jaud August 2, 2013 2 Contents 1 Komplexe Differenzierbarkeit und Holomorphie 7 1.1 Körper der komplexen Zahlen.................... 7 1.2 Algebraische Abgeschlossenheit...................
Laurent-Reihen und isolierte Singularitaten
 Seminar zu Analysis III LA Gym Laurent-Reihen und isolierte Singularitaten Eingereicht von: Judith Krischke Matrikelnr.: 295 Email: judith.krischke@tudortmund.de Eingereicht bei: JP Dr. Tomas Dohnal 7.
Seminar zu Analysis III LA Gym Laurent-Reihen und isolierte Singularitaten Eingereicht von: Judith Krischke Matrikelnr.: 295 Email: judith.krischke@tudortmund.de Eingereicht bei: JP Dr. Tomas Dohnal 7.
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Analysis III für Physik
 Analysis III für Physik Prof Dr Uwe Jannsen Wintersemester 2014/15 Inhaltsverzeichnis 0 Erinnerung/Einstimmung 1 1 Komplexe Funktionen 4 2 Komplexe Differenzierbarkeit 6 3 Komplexe Potenzreihen 10 4 Der
Analysis III für Physik Prof Dr Uwe Jannsen Wintersemester 2014/15 Inhaltsverzeichnis 0 Erinnerung/Einstimmung 1 1 Komplexe Funktionen 4 2 Komplexe Differenzierbarkeit 6 3 Komplexe Potenzreihen 10 4 Der
Gesucht ist eine holomorphe oder meromorphe Funktion, die die Fakultäten interpoliert. z z + m 1 f(z +m+1) = ( 1)m 1
 23 3 Die Γ-Funktion Gesucht ist eine holomorphe oder meromorphe Funktion, die die Fakultäten interpoliert. f(n) = (n )! für n N. Das wird durch die Funktionalgleichung erreicht. Bemerkungen. f(z + ) =
23 3 Die Γ-Funktion Gesucht ist eine holomorphe oder meromorphe Funktion, die die Fakultäten interpoliert. f(n) = (n )! für n N. Das wird durch die Funktionalgleichung erreicht. Bemerkungen. f(z + ) =
Holomorphe Funktionen
 1 Kapitel 1 Holomorphe Funktionen 1 Komplexe Differenzierbarkeit Ist z = (z 1,..., z n ) ein Element des C n und z ν = x ν + i y ν, so können wir auch schreiben: z = x + i y, mit x = (x 1,..., x n ) und
1 Kapitel 1 Holomorphe Funktionen 1 Komplexe Differenzierbarkeit Ist z = (z 1,..., z n ) ein Element des C n und z ν = x ν + i y ν, so können wir auch schreiben: z = x + i y, mit x = (x 1,..., x n ) und
Laurent-Reihen und isolierte Singularitäten
 Laurent-Reihen und isolierte Singularitäten Seminar Analysis III (SoSe 203) Pascal Niehus - Vortrag vom 27.05.203 - Kontaktdaten: Name: Studiengang: Fächer: E-Mail: Pascal Niehus BfP Mathematik, Physik
Laurent-Reihen und isolierte Singularitäten Seminar Analysis III (SoSe 203) Pascal Niehus - Vortrag vom 27.05.203 - Kontaktdaten: Name: Studiengang: Fächer: E-Mail: Pascal Niehus BfP Mathematik, Physik
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
ANALYSIS III. Teil I: Funktionentheorie
 H ANALYSIS III 995/96 Teil I: Funktionentheorie Vorspann der für das WS 993/94 erstellten. Auflage: Im Wintersemester 993/94 wurde, einem Beschluß der Mathematischen Fakultät der Universität Tübingen folgend,
H ANALYSIS III 995/96 Teil I: Funktionentheorie Vorspann der für das WS 993/94 erstellten. Auflage: Im Wintersemester 993/94 wurde, einem Beschluß der Mathematischen Fakultät der Universität Tübingen folgend,
Einführung in die Funktionentheorie 1
 Einführung in die Funktionentheorie Martin Ziegler Freiburg, WS 994/95, WS 2000/0, SS 2006 Literatur [] Klaus Jänich. Funktionentheorie. Springer Verlag, 993. [2] H.Behnke und F.Sommer. Theorie der analytischen
Einführung in die Funktionentheorie Martin Ziegler Freiburg, WS 994/95, WS 2000/0, SS 2006 Literatur [] Klaus Jänich. Funktionentheorie. Springer Verlag, 993. [2] H.Behnke und F.Sommer. Theorie der analytischen
Prof. D. Salamon Funktionentheorie ETH Zürich MATH, PHYS 27. Oktober Musterlösung 5
 Prof. D. Salamon Funktionentheorie ETH Zürich MATH, PHYS 27. Oktober 2009 Musterlösung 5 1. Sei f : C C eine holomorphe Funktion, so dass f(z) < z n für ein n N und alle hinreichend grossen z. Dann ist
Prof. D. Salamon Funktionentheorie ETH Zürich MATH, PHYS 27. Oktober 2009 Musterlösung 5 1. Sei f : C C eine holomorphe Funktion, so dass f(z) < z n für ein n N und alle hinreichend grossen z. Dann ist
D-MATH Funktionentheorie HS 2018 Prof. Michael Struwe. Lösungen Serie 5. Korollare der Integralformel von Cauchy
 D-MATH Funktionentheorie HS 08 Prof. Michael Struwe Lösungen Serie 5 Korollare der Integralformel von Cauchy. (a) Berechnen Sie für folgende Funktionen die Taylorreihe bei z 0 und bestimmen Sie den Konvergenzradius.
D-MATH Funktionentheorie HS 08 Prof. Michael Struwe Lösungen Serie 5 Korollare der Integralformel von Cauchy. (a) Berechnen Sie für folgende Funktionen die Taylorreihe bei z 0 und bestimmen Sie den Konvergenzradius.
1. Übungsblatt zur Funktionentheorie I
 Hannover, den 9. April 24. Übungsblatt zur Funktionentheorie I Abgabe am 26./27. April 24 vor den Stundenübungen Leider können nur die mit Punkten versehenen Aufgaben korrigiert werden. Aufgabe (2,3,5
Hannover, den 9. April 24. Übungsblatt zur Funktionentheorie I Abgabe am 26./27. April 24 vor den Stundenübungen Leider können nur die mit Punkten versehenen Aufgaben korrigiert werden. Aufgabe (2,3,5
H.J. Oberle Komplexe Funktionen SoSe Residuensatz
 H.J. Oberle Komplexe Funktionen SoSe 2013 Partialbruch-Zerlegung. 10. Residuensatz Wir setzen unsere Untersuchung der isolierten Singularitäten einer holomorphen Funktion mit einer Methode fort, die komplexe
H.J. Oberle Komplexe Funktionen SoSe 2013 Partialbruch-Zerlegung. 10. Residuensatz Wir setzen unsere Untersuchung der isolierten Singularitäten einer holomorphen Funktion mit einer Methode fort, die komplexe
Laurent-Reihen. Definition 1 (Laurent-Reihe) Unter einer Laurent-Reihe versteht man eine Reihe der Form. c n (z z 0 ) n (2) n=0
 Laurent-Reihen Definition (Laurent-Reihe Unter einer Laurent-Reihe versteht man eine Reihe der Form c n (z z 0 n. ( n Man nennt die Teile c n (z z 0 n n bzw. c n (z z 0 n ( n0 den Haupt- bzw. Nebenteil
Laurent-Reihen Definition (Laurent-Reihe Unter einer Laurent-Reihe versteht man eine Reihe der Form c n (z z 0 n. ( n Man nennt die Teile c n (z z 0 n n bzw. c n (z z 0 n ( n0 den Haupt- bzw. Nebenteil
Mathematik IV für Studierende der Physik Vorlesungsskript
 Mathematik IV für Studierende der Physik Vorlesungsskript Ralf Holtkamp Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/holtkamp Hamburg, Sommersemester 217 Inhaltsverzeichnis 1
Mathematik IV für Studierende der Physik Vorlesungsskript Ralf Holtkamp Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/holtkamp Hamburg, Sommersemester 217 Inhaltsverzeichnis 1
Hans Joachim Oberle Universität Hamburg. Komplexe Funktionen. Vorlesung an der TUHH im Sommersemester 2013 Freitags, 9:45-11:15, Audimax II
 Hans Joachim Oberle Universität Hamburg Komplexe Funktionen Vorlesung an der TUHH im Sommersemester 2013 Freitags, 9:45-11:15, Audimax II Literatur. R. Ansorge, H.J. Oberle, K. Rothe, T. Sonar: Mathematik
Hans Joachim Oberle Universität Hamburg Komplexe Funktionen Vorlesung an der TUHH im Sommersemester 2013 Freitags, 9:45-11:15, Audimax II Literatur. R. Ansorge, H.J. Oberle, K. Rothe, T. Sonar: Mathematik
5.1 Anwendung auf die Berechnung uneigentlicher
 Kapitel 5 Anwendungen des Residuenkalküls Wie sich am Ende des vorigen Kapitels in Beispiel 4.17 bereits angedeutet hat, bietet der Residuenkalkül ein mächtiges Werkzeug, um uneigentliche Integrale mit
Kapitel 5 Anwendungen des Residuenkalküls Wie sich am Ende des vorigen Kapitels in Beispiel 4.17 bereits angedeutet hat, bietet der Residuenkalkül ein mächtiges Werkzeug, um uneigentliche Integrale mit
