1 Exponentielles Wachstum
|
|
|
- Kajetan Voss
- vor 7 Jahren
- Abrufe
Transkript
1 Schülerbuchseite Lösungen vorläufig VI Anwendungen der Differential- und Integralrechnung Exponentielles Wachstum S. 56 S. 58 a) H (t) = 4000,0 t b),0 t = e k t,0 = e k k = ln,0 0,0 H (t) = 4000 e 0,0 t c) k = ln,0 = ln ( + %) a) c = ; k = ln,05 0,05; f (t) = e 0,05 t Anmerkung: Die Bank rechnet nicht mit g (t) = ,05 t, durch die unzulässige Rundung auf 0,05 entsteht eine Differenz z. B. bei f (0) g (0) 700 zu Ungunsten der Bank. b) f () = e 0,05 05,40 ; f () 03,40 ; f (3) 3 36,70 ; f (5) 5 680,50 ; f (0) 3 974,40 ; f (0) ,60 c) f (t + ) f (t) > e 0,05 (t + ) e 0,05 t > e 0,05 t (e 0,05 ) > 000 e 0,05 t >,95 t > 3,36 Im 4. Jahr beträgt das mittlere Wachstum mehr als 000. d) f (t) = e 0,05 t 0,05 = 000 e 0,05 t f (t) = e 0,05 t = 000 e 0,05 t = t 0,05 = ln t 3,86 Nach 4 Jahren erreicht die momentane Wachstumsrate 000 pro Jahr. 3 a) Prüfe die Quotienten der Bakterienzahlen jeweils aufeinander folgender Zeitschritte: 7,7 : 7,,08; 8,3 : 7,7,08; 9,0 : 8,3,08 b) k = ln,08 0,08; f (t) = 7, e 0,08 t c) = 7, e 0,08 t,69 = e 0,08 t ln,69 = 0,08 t _ ln,69 t = 0,08 6,6 Nach etwas weniger als 7 Stunden werden es mehr als Millionen Bakterien sein. 4 rot: Ablesen zweier Punkte: P (0,5) und P (4 0,5); einsetzen in f (x) = a e k x ergibt zwei Gleichungen: (I),5 = a e 0 a =,5; (II) 0,5 =,5 e 4 b b 0,4 Gleichung: f (x) =,5 e 0,4 x analoge Vorgehensweise bei dem gelben und blauen Graphen. gelb: P (0 ); P (4 5,5); f (x) = e 0,5 x blau: P (0 ); P (4,5 6); f (x) = e 0,4 x 5 a) f (t) = c e k t f (0) = 88,9 c = 88,9 f (5) = 88,9 e k 5 = 40; e k 5 _ ln,57 =,57; k = 5 0,03 a = e 0,03,03 Die jährliche Zuwachsrate beträgt 3 %. b) Neue Funktion g, die das Wachstum ab 006 beschreibt: g (t) = 40 e 0,03 t bzw. g (t) = 40 e 0,05 t g (4) = 40 e 0, Millionen oder: g (4) = 40 e 0, Millionen Die Prognosewerte für das Jahr 00 schwanken zwischen 99 Millionen und 3 Millionen. Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 8
2 Schülerbuchseite 59 Lösungen vorläufig S a) Vergleiche die Quotienten des relativen Risikos für Lungenkrebs aufeinander folgender gleicher Zeitschritte: 30 : 38 0,79; : 30 0,73; 7 : 0,77; 3 : 7 0,76; 0 : 3 0,77 f (t) = 38 e ln 0,77 t = 38 e 0,6 t ; t š Jahre b) f (7,5) = 38 e 0,6 7,5 5,4 5 Jahre nach der letzten Zigarette beträgt das Risiko an Lungenkrebs zu erkranken ca. 5,4 %. c) = 38 e 0,6 t t = ln ( _ 38 ) _ 0,6 4 Nach 8 Jahren wird etwa das Lungenkrebsrisiko eines Nichtrauchers erreicht. 7 a) f (t) = c e k t f (0) = 400 c = 400 f () = 400 e k = 30000; e k = 75; k = _ ln 75,6 f (t) = 400 e,6 t b) f (5) 9,6 Millionen c) f (t) = 400 e,6 t,6 = 864 e,6 t f (0) 860; f () = 864 e,6 7500; f () = 864 e, d) f (0) = 400 e,6 0 9,6 0 f (00) = 400 e,6 00, Die Berechnung ist weniger sinnvoll, weil sich das exponentielle Wachstum sicher nicht allzu lange fortsetzen kann. 8 a = 0,96; k = ln 0,96 0,04 f (t) = e 0,04 t (t in s) f (0) = e 0,04 0 0,8 % Die Pumpe arbeitet nicht normal. 9 a) f (0) > g (0) und die Wachstumskonstante von f ist kleiner als die Wachstumskonstante von g. b) f (t S ) = g (t S ); 800 e 0,8 t S = 800 e, t S ;,5 = e 0,4 t S _ ln,5 ; t S = 0,4,073; S (,0 9) c) f (t) = 800 e 0,8 t 0,8 = 440 e 0,8 t ; f (,073) 790; tan α = 790 α = 89,99 g (t) = 800 e, t, = 960 e, t ; g (,073) 0 935; tan α = α = 89,9948 Schnittwinkel: φ = α α 0,003,073 d) A = : (f(t) g (t)) dt = 4 50 e 0,8 t 666,7 e, t, a) h (0) = 0,0 e k 0 = 0,0 Die Pflanze ist zu Beobachtungsbeginn cm hoch. b) h (6) = 0,0 e k 6 = 0,4; e k 6 = 0; k = _ ln 0 6 0,5 c) h (9) = 0,0 e 0,5 9,80 Nach 9 Wochen ist die Pflanze,80 m hoch. d) 3 0,0 e 0,5 t ; e 0,5 t = 50; t = _ ln 50 0,5 0 Nach etwa 0 Wochen ist die Pflanze 3 m hoch. e) f (t + ) f (t) =,5 0,0 e 0,5 (t + ) 0,0 e 0,5 t =,5; 0,0 e 0,5 t (e 0,5 ) =,5; t = 9,5 Zwischen 9,5 und 0,5 Wochen wächst die Pflanze 50 cm. f) f (t) = 0,0 e 0,5 t 0,5 = 0,0 e 0,5 t 0,0 e 0,5 t = ; e 0,5 t = 00; t = _ ln 00 0,5 9, Nach 9, Wochen ist die momentane Wachstumsrate m Woche. g) 3 = 3,5 8, e 0,75 t ; 0,5 = 8, e 0,75 t ; e 0,75 t _ ln 0,06 = 0,06; t = 0,75 6 Nach dieser Modellierung ist die Pflanze erst nach etwa 6 Wochen 3 m hoch. Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 83
3 Schülerbuchseite 59 6 Lösungen vorläufig t Die Zufallsgröße X beschreibt die Anzahl der entdeckten Fahrräder mit beiden Mängeln. Es wird das Gegenereignis betrachtet: Keines der untersuchten Fahrräder hat beide Mängel, d. h. X = 0 Für die Wahrscheinlichkeit dieses Ereignisses soll gelten: P (X = 0) 0 % X ist binomialverteilt mit p = 0,05. P (X = 0) = ( n 0 ) 0,05 0 ( 0,05) n! 0 % n 45 Es müssen wenigstens 45 Fahrräder überprüft werden. a) Fehler im Schülerbuch bis Auflage. Richtig muss es heißen: x 3 3 x = 4 x Die ganzrationale Funktion x 3 3 x 4 x (vom Grad 3) besitzt höchstens 3 Nullstellen; es gibt also maximal 3 Lösungen. x 3 3 x 4 x = x (x 3 x 4) = 0 x = 0 oder x 3 x 4 = 0 Lösung der quadratischen Gleichung liefert: x = ; x = 4 L = { ; 0; 4} b) L = [ 7, ; + [ Bestimmung von Halbwerts- und Verdoppelungszeiten S. 60 a) f (0) = 8; f () = 4; f (4) = ; f (6) = Innerhalb von Zeiteinheiten halbiert sich der Bestand. b) f (t) = 3 e 0,5 t ; f (0) = 3 e 0 = 3 6 = 3 e 0,5 t = e 0,5 t ; t = ln 0,5,4 = 3 e 0,5 t 4 = e 0,5 t ; t = ln 4 0,5,8 S. 6 a) a = 5 % = 0,85; k = ln a = ln 0,85 0,6 T H = _ ln 0,6 4,3 Nach 4,3 Jahren ist der Wert des Autos auf die Hälfte gesunken. b) a = + 4,5 % =,045; k = ln,045 0,04 T V = ln 5,7 ln,045 Nach 5,7 Jahren hat sich das angelegte Geld verdoppelt. c) T V = _ ln ; k = _ ln k 0,06; a = e k = e 0,06,06 Der Zinssatz beträgt 6 %. d) f (t) = c e k t _ ln 0,5 ; f (0) = f (8,5) = 0,5 k = 8,5 0,075 a = e k 0,978; a 0,07 Es zerfallen täglich etwa 7, %. 3 Anmerkung: Es wird mit dem exakten TR-Wert weitergearbeitet! a) T H = _ ln = 4400; k = _ ln 5 k 4400,8 0 f (t) = 30 e,8 0 5 t f ( 0) = 30 e,8 0 5 ( 0) 30,0 kg f (00) = 30 e, ,9 kg b) f (000) = e, ,97 Nach 000 Jahren sind noch 97 % vorhanden. f (0000) = e, ,75 Nach Jahren sind noch 75 % vorhanden. c) 0, = e,8 0 5 t ln 0, ; t =, Nach ca Jahren sind 90 % einer Menge zerfallen. Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 84
4 Schülerbuchseite 6 Lösungen vorläufig 4 a) a = + 0,04 =,04: k = ln,04 0,04 T V = _ ln 0,04 50 Nach etwa 50 Jahren hätte sich die Bevölkerung Indiens erneut verdoppelt. b) T V = _ ln = 33; k = ln _ k 33 0,0; a = e k = e 0,0,0 Die jährliche Zunahme betrug etwa, %. 5 g (t) = c e k t (I) g () = c e k = 85 c = _ 85 e k in (II): 85 (II) g (5) = c e 5 k = 35 g (t) = 6 e 0,54 t T V = _ ln 0,54 4 _ e k e 5 k = 35 e 3 k,59 _ ln,59 k = 3 0,54 85 c = e 0, blauer Graph: f (0) =,5; f () = 5 a,86 k 0,6 f (t) =,5 e 0,6 t ; T V = ln 0,6,6 relative Zunahme: a 83 % lila Graph: f (0) = ; f () = 3 a,5 k 0, f (t) = e 0, t ; T V = ln 0, 3,5 relative Zunahme: a 3 % roter Graph: f () = ; f (3) = a 0,707 k 0,35 f (t) =,84 e 0,35 t ; T H = _ ln 0,35 relative Abnahme: a 0,9 30 % 7 T H = _ ln =,3; k = _ ln k,3 0,056 f (t) = e 0,056 t a = e k 0,945; a 0,055 Jährlich zerfällt ein Anteil von 5,5 %. 8 a) Ansatz: f (x) = a x 4 + b x 3 + c x + d x + e Wegen f (0) = 0 und f (0) = 0 d = e = 0 f (x) = a x 4 + b x 3 + c x f (x) = 4 a x b x + c x f (x) = a x + 6 b x + c f () = 0: Å6 a + 8 b + 4 c = 0 f () = : a + b + c = Å a = ; b = ; c = 0 f () = 0: Å a + 6 b + c = 0 f (x) = x 4 + x 3 (roter Graph zugehörig) b) Blauer Graph: f (0) = a = f blau (x) = x 4 + x 3 x + c) f a (x) = x + x Wendepunkte: f a (x) = 0 x ( x + ) = 0 x = 0; x = W (0 a); W ( a) d a = _ W W = a 4 a + Extremwertuntersuchung mithilfe der Ersatzfunktion E (a) = 4 a 4 a + E (a) = 8 a 4 E (a) = 0 a = _ Für a = _ ergibt sich ein minimaler Abstand (E (a) = 8 > 0). Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 85
5 Schülerbuchseite 6 63 Lösungen vorläufig 3 Wiederholung: Extremwertprobleme S. 6 a) Die nach unten geöffnete Parabel ist symmetrisch zur y-achse, ihr Scheitel S (0 9), ihre Schnittpunkte mit der x-achse sind N ( 3 0) und N (3 0). Somit kann für jedes u (0 u 3) ein Rechteck einbeschrieben werden. Für u = 0 und u = 3 ist der Flächeninhalt gleich 0. Für einen Wert u 0, 0 < u 0 < 3, ist der Flächeninhalt dann maximal. b) ) Man stellt eine Funktion f auf, die den Flächeninhalt des Rechtecks in Abhängigkeit von u beschreibt. ) Man bestimmt die Extremwerte dieser Funktion f. u 0 ist dann eine der Stellen, für die f ein lokales Maximum bestitzt, nämlich diejenige mit dem größten Funktionswert. S. 63 a) y Da 0 x P 3 liegt auch Q auf der x-achse so, dass x Q 3. Der Flächeninhalt beträgt A = 3 für x = 0 bzw. A = 0 für x = 3. Für einen Wert x 0 besitzt das Rechteck maximalen P S Flächeninhalt, entweder an einem lokalen Maximum der Flächeninhaltsfunktion oder am Rand für x = 0. Q R x 4 3 O 3 b) A (x) = (3 x) f (x) = (3 x) (0,4 x + ) A (x) =, x + 3 0,4 x 3 x = 0,4 x 3 +, x x + 3 A (x) =, x +,4 x A (x) = 0 wenn, x,4 ± ,76 4,8,4 ± 0,98 +,4 x = 0; x / =,4 =,4 x =,4; x = 0,6 x ist zwar lokales Maximum, wegen A (x ),85 besitzt das Rechteck für P (0 ) maximale Fläche. 3 a) V = a h = 40 ø; 0 = a + 4 a h a h = 40 h = _ 40 a O (a) = a + 4 a 40 _ a = a + 60 _ a O (a) = a 60 _ a O (a) = 0 wenn a _ 60 a = 0 a3 = 60; a 3 = 80; a 4,3; O (a) = + _ 30 a 3 > 0 h = _ 40 4,3, Die Kiste muss mit den Maßen a = 4,3 dm (Grundkante) und der Höhe h =, dm gebaut werden. b) V = r π h = 500 ø h = _ 500 r π (h in dm, da ø = dm3 ) ohne Deckel: O = r π + r π h O (r) = r π + r π _ 500 r π = r π mit Deckel: _ r O (r) = r π _ 000 r O (r) = 0 wenn r π _ 000 r = 0; r 3 π = 000; r = ,4 h = _ ( 500 _ = 500_ 3 = r _ 500 π )_ 3 π _ 3 Der Materialverbrauch für die Tonne ohne Deckel wird für r = h 5,4 dm möglichst gering. O = r π + r π h O (r) = r π + r π _ 500 r π = r π O (r) = 4 r π _ 000 r O (r) = 0 wenn 4 r π _ 000 r = 0; 4 r 3 π = 000; r = ,3 _ r Mit Deckel wird der Materialverbrauch für die Tonne für r = 4,3 dm und h = 8,6 dm möglichst gering. _ π _ π Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 86
6 Schülerbuchseite 63 Lösungen vorläufig 4 rπ r U = a + r + r 0 r ( + π r) π = a + r ( + π r) = 0 a = Maximale Lichtmenge für S = 60 % _ r π + 80 % a r S (r) = 0,3 π r + 0,8 (0 r ( + π r)) r = (0,3 π 0,8 ( + π r)) r + 8 r S (r) = 0,6 π r r 3 π r ; S (r) < 0 a S (r) = 0 r 0,86 Für r 0,86 m und a 3,4 m würde eine maximale Lichtmenge ins Innere gelangen. r r 5 a) Schnittpunkte von f b (x) und g b (x) im Intervall 4 π_ ; π_ 5: b cos ( x) = _ b cos ( x) b cos ( x) + _ cos ( x) = 0; b also: ( b + _ b ) cos ( x) = 0; cos ( x) = 0 für x = π_ 4 ; x = π_ 4 Die Fläche liegt also im Intervall 4 π_ 4 ; π_ 4 5: Da die gesuchte Fläche symmetrisch zur y-achse ist, gilt: 0 π_ 4 A (b) = : ( ( b + _ b ) cos ( x) ) dx = ( b + _ b ) 4 _ sin ( x) 5 π_ 4 = ( b + _ b ) 4 _ sin 0 _ sin ( π_ ) 5 = ( b + _ b ) _ = b + _ b Da die Funktionen für b < 0 nur die Rolle tauschen, der Flächeninhalt jedoch gleich bleibt, genügt es, b > 0 zu betrachten. 0 A (b) = _ b ; A (b) = 0 wenn _ b = 0; b = ; b = A (b) = _ 3 ; A () = ; also liegt für b = ein Tiefpunkt/Minimum vor. b Für b = wird der Flächeninhalt minimal. A () =. b) Da kein lokales Maximum existiert und lim A (b) = + und lim A (b) = + existiert kein b 0 b + maximaler Flächeninhalt, sondern dieser kann beliebig groß werden. 6 a) f (x) = 4_ 3 x + 4; B (x f (x)) A (x) = x ( 4_ 3 x + 4 )= 4_ 3 x + 4 x A (x) = 8_ 3 x + 4 A (x) = 0 wenn 8_ 3 x + 4 = 0 x =,5; A (,5) = 8_ 3 < 0 maximale Rechtecksfläche: A (,5) = 3 FE; B (,5 ) b) A Dreieck = _ 4 3 = 6 FE Variante : P (0 3); P (4 0); f (x) = 3_ 4 x + 3 A (x) = x ( 3_ 4 x + 3 )= 3_ 4 x + 3 x A (x) = 3_ x + 3; A (x) = 0 wenn 3_ x + 3 = 0 x = maximale Rechtecksfläche: A () = 3 FE; B (,5) Variante : P (0 ); P (6 0); f (x) = _ 3 x + A (x) = x ( _ 3 x + )= _ 3 x + x A (x) = _ 3 x + ; A (x) = 0 wenn _ 3 x + = 0 x = 3 maximale Rechtecksfläche: A (3) = 3 FE; B (3 ) Ergebnis: Die maximale Rechtecksfläche bleibt immer gleich, nämlich 3 FE; der x-wert von B ist stets der halbe x-wert der Nullstelle von f. Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 87
7 Schülerbuchseite Lösungen vorläufig 7 f (x) = 5 (00 5 x) (70 Passagieren + 0 x) f (x) = 5 ( 500 x + 50 x ) f (x) = 5 ( 000 x + 50) f (x) = 0 wenn 000 x + 50 = 0 x =,5 Eine Preissenkung auf 00 5,5 = 43,75 würde ca ,5 = 5 Passagiere pro Flug bringen und damit tägliche Einnahmen von ,75. 8 a) 3 x 3_ cos x b) (cos x) (sin x) x_ c) x + f) cos x (x ) + sin x x d) x sin x + 4 x 3 cos x e) _ ( _ x sin x ) t 9 Ansatz: α_ 360 r π = r α = _ 360 π 4,6 4 Untersuchung verknüpfter Funktionen S. 64 S. 67 grüner Graph: drei einfache Nullstellen: x = ; x 0,7; x 3, drei Extremwerte: Tiefpunkte bei x 4 0,7; x 5,6 lim f (x) = + x + blauer Graph: zwei einfache Nullstellen: x = ; x = Schnittpunkt mit der y-achse bei (0 ) lim f (x) = ; lim f (x) = 0 (x-achse ist Asymptote) x + x ein Hochpunkt bei x 3 0,4 roter Graph: Symmetrie zur y-achse zwei einfache Nullstellen: x,6; x,6 x-achse ist Asymptote a) f (x) = sin x + ( + x) cos x b) g (x) = sin ( + x ) x c) h (x) = e x ( + e x ) + e x e x = e x ( + e x + e x ) = e x ( + e x ) d) f (x) = 3 (sin x) cos x e) g (x) = 3 e + x f) h (x) = e x (x x + ) + e x ( x ) = e x (x ) 3 Nullstellen: g (x) = 0 wenn x + = 0 oder ln x = 0; Nullstelle: ( 0) x = n. d. x =??? Extremwerte: g (x) = _ x + x + ln x ; g (x) > 0 für alle x * D g Grenzwerte: y keine Extremwerte; G g ist echt monoton steigend. lim x 0 +g (x) = ; lim g (x) = + x + G f O x 3 4 Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 88
8 Schülerbuchseite xx xx Lösungen vorläufig S a) f (x) = 0 wenn e x (x + x) = 0; e x < 0 für alle x * D x + x = 0 x (x + ) = 0; x = 0; x = b) f (x) = e x (x + x) e x ( x + ) = e x (x + 4 x + ) f (x) = 0 wenn e x (x + 4 x + ) = 0; x + 4 x + = 0; x / = 4 ± ; x = ; x = f (x) = e x (x + 4 x + ) e x ( x + 4) = e x (x + 6 x + 6) f ( ) < 0, also Hochpunkt bei ( ,9) f ( ) > 0, also Tiefpunkt bei ( ,3) c) f (x) = 0 wenn e x (x + 6 x + 6) = 0; x + 6 x + 6 = 0; x / = Wendepunkt bei ( ,3) und ( ,5) d) lim x e x (x + x) = ; lim + x e x (x + x) = 0 e) F (x) = 4x e x x e x = e x ( x + x ) = f (x) 0 f) : f (x) dx = 4 x e x 0 5 = 0 ( ( ) e ) = (,08) =,08 g) A k = : k f(x) dx = 4 x e x 5 k = ( ) e ( k e k ) = 8 e + k e k lim 8 e + k e k = 8 e k 5 Nullstellen bei x = ; x = Extremwerte: Tiefpunkt bei ( 0,4 5); Hochpunkt bei (,,7) Wendepunkte: W ( 0,5 ); W (4,) : f(x) dx = : f(x) dx = ; x = ; x = a) f (x) = 3 e x + 3 x e x ( ) = 3 e x 6 e x = 3 e x ( x) f () = 3 e ( ) = 3 e 3 e = 3 e + t t = 6 e Tangente: f (x) = 3 e x + 6 e b) f (0,5) = 3 e (0,5) ( 0,5) = 0 Der Graph hat bei (0,5 e ) eine waagrechte Tangente. Normale: x =,5 e c) f (x) = 3 e x ( ) ( x) + 3 e x ( ) = 6 e x ( x) 6 e x = 6 e x ( x) = e x ( x) f (x) = 0 wenn x = 0; x = Tangente aus a) ist auch Wendetangente; f (x) = 3 e x + 6 e 7 Senkrechte Asymptote bei x = _ Waagrechte Asymptote bei y = 3 x a f (x) = ; f (0) = _ 3 ( _ a x + _ ) _ 3 _ = a = _ 3 f (0) = ; x + 3 f (x) = _ 3 ( = 3 x + x + _ ) ( x + _ ) b) g (x) = e lim x e ± 3 x + ( x + _ ) 3 x + ( x + _ ) ; D f = R \ 6 _ 7 = e 3_ zu d) O 3 y G f x Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 89
9 Schülerbuchseite xx xx Lösungen vorläufig c) h (x) = ln ( 3 x + ( x + _ )) 3 x + > 0 und ( x + _ )> 0 x = _ 3 und x + _ < 0 x < _ D h = ] _ ; _ 3 [ Die innere Funktion ist in D h streng monoton abnehmend. Die äußere Funktion x ln x ist streng monoton abnehmend. Daher ist g (x) in D h streng monoton abnehmend. d) XXX 8 a) f (x) = 0 wenn x + x = 0; x (x + ) = 0; x = 0; x = b) g (x) = 0 wenn e 3 x e x = 0; e 3 x = e x 3 x = x; x = 0 c) f (x) = 0 wenn x 3 e x x e x = 0; x e x = 0; x = 0; x = d) g (x) = 0 wenn ln (x + x ) = 0; also x + x = x + x 3 = 0 x / = ± ; x = ; x = e) h (x) = 0 wenn e x e x = 0; e x = e x x = ln x; x = ln f) f (x) = 0 wenn x x _ = 0; x x = 0; x / = ± _ ; x = _ ; x = ; 9 a) f (x) = 00 e 0,05 x + 00 (x 0) e 0,05 x ( 0,05) = 00 e 0,05 x ( 0,05 (x 0)) = 00 e 0,05 x (,5 0,05 x) f (x) = 0 wenn 00 e 0,05 x (,5 0,05 x) = 0,5 0,05 x = 0 x = 30 Nach 30 Tagen rechnet man mit der höchsten Besucherzahl. f (30) = 00 (30 0) e 0, Die Besucherzahl ist dann etwa b) Kurz vor und auch nach dem Besuchermaximum bleiben die Besucherzahlen fast auf dem Höchststand. c) f (x) = 00 e 0,05 x (0,05) ( 0,05 x) + 00 e 0,05 x (0,05) f (x) = 5 e 0,05 x (,5 0,05 x) f (x) = 0 wenn,5 0,05 x = 0 x = 50 S a) g ist echt monoton zunehmend für x *] ; 0,6 [, für x *] 0,6 ; + [ monoton abnehmend. Der Graph schneidet bei x 0,4 die x-achse und bei (0 ) die y-achse. lim g (x) = 0, d. h. die x-achse ist Asymptote. x + b) Bei einem Startwert x nähern sich die x n -Werte keinem Wert (der gesuchten Nullstelle) an, sondern sie wandern immer mehr ins Unendliche. a) f (x) = 0 wenn x e x = 0 x = 0 b) lim x x + e x = 0; lim x x e x = c) f (x) = x e x + x e x ( ) = e x ( x) f (x) = 0 wenn e x ( x) = 0 x = ; E ( ) f (x) = e x ( x) ( ) = e x (x ) f (x) = ( ) = Hochpunkt bei ( ) d) f (x) = 0 wenn e x (x ) = 0 x = ; Wendepunkt: ( 4 e ) f (x) > 0 für x > G f ist linksgekrümmt; f (x) < 0 für x < G f ist rechtsgekrümmt. Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 90
10 Schülerbuchseite xx xx Lösungen vorläufig e) zu e) + g)? f ( 0,5) = 0,5 e,5,75 y f (5) = 0 e 4 0,8 3 G Ø G f O x f) : f (x) dx _ = ; : f(x) dx _ 4 = 4 g) Ø (x) = f (x) Ø (x) = 0 für x = 0; Ø (x) = f (x); f (x) = e > 0 Die Integralfunktion hat an der Stelle (0 0) ein Minimum. y Der abgebildete Graph drückt die Ableitung Ø (x) aus. Da f an der Stelle x = 3 eine Nullstelle hat, hat Ø (x) bei x = 3 einen Extremwert. x Für x < 3 besitzt G f negative Werte, somit fällt G Ø, für x > 3 steigt G Ø. O 3 4 An der Stelle x = hat G f einen Tiefpunkt, somit hat G Ø einen G Ø Wendepunkt. G Ø hat an der Stelle x = 0 eine Nullstelle. v v 3 Beide Begriffe werden beim Testen von Hypothesen verwendet. Ein Fehler. Art liegt vor, wenn die Nullhypothese wahr ist, jedoch irrtümlich (aufgrund der Testergebnisse) verworfen wird. Das Signifikanzniveau α (für einen zu konstruierenden Test) ist die vorgegebene maximale Wahrscheinlichkeit für diesen Fehler. Art, die man bereit ist, zu tolerieren. 4 a) E: _ X = ( ) + λ ( ) + μ ( 3 ) b) z. B. AB AC = ( ) ist ein Normalenvektor ( ) = Mit dem Aufpunkt ( ) ergibt sich n 0 = (( 8) ) = 4 Hesse sche Normalenform (Koordinatendarstellung): 8 x + 4 x 8 x 3 4 = 0 _ ( Im Nenner Vorzeichen, damit n 0 = _ 4 < 0 ) x x + x = 0 c) d (R; E) = = ; d (S ; E) = d) AB AC = ist auch Normalenvektor von H: ( ) ( _ X ( 4 3 ) ) = 0 e) Nein. Der Punkt S hat von E den gleichen Abstand wie der Punkt R. R und S könnten aber auf verschiedenen Seiten von E liegen. Ernst Klett Verlag GmbH, Stuttgart 00 Lösungen Klasse ISBN Integralrechung 9
1 Die natürliche Exponentialfunktion und ihre Ableitung
 Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
1 Die zweite Ableitung
 Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
= 4 0 = 4. Hinweis: Dieses Ergebnis folgt auch aus der Punktsymmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ].
![= 4 0 = 4. Hinweis: Dieses Ergebnis folgt auch aus der Punktsymmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ]. = 4 0 = 4. Hinweis: Dieses Ergebnis folgt auch aus der Punktsymmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ].](/thumbs/96/129050460.jpg) 73. a) dx = d x = [x] = = b) sin x dx = [ cos x] = cos + cos ( ) = ( ) + ( ) = Hinweis: Dieses Ergebnis folgt auch aus der Punktsmmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ]. e
73. a) dx = d x = [x] = = b) sin x dx = [ cos x] = cos + cos ( ) = ( ) + ( ) = Hinweis: Dieses Ergebnis folgt auch aus der Punktsmmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ]. e
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Diskussion einzelner Funktionen
 Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
a) Begründen Sie, dass der Graph von f symmetrisch zum Punkt S 0 2 f) Ermitteln Sie eine Gleichung der Tangente im Punkt B
 I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
Natürliche Exponential- und Logarithmusfunktion. Kapitel 5
 Natürliche Eponential- und Logarithmusfunktion Kapitel . Die natürliche Eponentialfunktion und ihre Ableitung 48 Arbeitsaufträge. Individuelle Lösungen Jahr 908 90 90 930 90 960 970 990 000 00 in Sekunden
Natürliche Eponential- und Logarithmusfunktion Kapitel . Die natürliche Eponentialfunktion und ihre Ableitung 48 Arbeitsaufträge. Individuelle Lösungen Jahr 908 90 90 930 90 960 970 990 000 00 in Sekunden
Analysis 5.
 Analysis 5 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch f(x) = 2 e 2 x 2 (x D f ) a) Geben Sie den größtmöglichen Definitionsbereich der Funktion f an und führen Sie für die Funktion
Analysis 5 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch f(x) = 2 e 2 x 2 (x D f ) a) Geben Sie den größtmöglichen Definitionsbereich der Funktion f an und führen Sie für die Funktion
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Hauptprüfung 2007 Aufgabe 3
 Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abitur 2013 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS. 16. Jänner Mathematik. Teil-2-Aufgaben. Korrekturheft
 Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS 16. Jänner 2018 Mathematik Teil-2-Aufgaben Korrekturheft Aufgabe 1 Funktion a) Lösungserwartung: Mögliche Vorgehensweise: f (x) = 2 a
Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS 16. Jänner 2018 Mathematik Teil-2-Aufgaben Korrekturheft Aufgabe 1 Funktion a) Lösungserwartung: Mögliche Vorgehensweise: f (x) = 2 a
Übungsaufgaben zur Kurvendiskussion
 SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
SZ Neustadt Mathematik Torsten Warncke FOS 12c 30.01.2008 Übungsaufgaben zur Kurvendiskussion 1. Gegeben ist die Funktion f(x) = x(x 3) 2. (a) Untersuchen Sie die Funktion auf Symmetrie. (b) Bestimmen
LÖSUNGEN Kurvendiskussion
 M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
streng monoton steigend. streng monoton fallend. Ist f eine in einem Intervall stetige und im Innern des Intervalls differenzierbare Funktion mit
 3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
3. Anwendungen ================================================================= 3.1 Monotonie Eine Funktion f heißt in ihrem Definitionsbereich D monoton steigend, wenn für alle x 1, x 2 D mit x 1 < x
Technische Universität München Zentrum Mathematik. Übungsblatt 4
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 4 Hausaufgaben Aufgabe 4. Gegeben sei die Funktion f : D R mit f(x) :=
Abschlussprüfung Berufliche Oberschule 2017 Mathematik 12 Technik - A II - Lösung mit CAS. e 2x mit der maximalen Definitionsmenge D f = IR.
 Abschlussprüfung Berufliche Oberschule 07 Mathematik Technik - A II - Lösung mit Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( ) e mit der maimalen Definitionsmenge D f IR. Teilaufgabe. ( BE)
Abschlussprüfung Berufliche Oberschule 07 Mathematik Technik - A II - Lösung mit Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( ) e mit der maimalen Definitionsmenge D f IR. Teilaufgabe. ( BE)
I. Verfahren mit gebrochen rationalen Funktionen:
 I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
I. Verfahren mit gebrochen rationalen Funktionen: 1. Definitionslücken bestimmen: Nenner wird gleich 0 gesetzt! 2. Prüfung ob eine hebbare Definitionslücke vorliegt: Eine hebbare Definitionslücke liegt
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen
 ZK M A (mit CAS) Seite von 5 Nr. Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen Punkte a Nullstellen von f: f ( = 0 x = x = x = + Lokale Extrempunkte:,7
ZK M A (mit CAS) Seite von 5 Nr. Beispielklausur für zentrale Klausuren Mathematik Unterlagen für die Lehrkraft - Modelllösungen Punkte a Nullstellen von f: f ( = 0 x = x = x = + Lokale Extrempunkte:,7
Volumen und Oberflächeninhalt der Kugel 10_01
 Volumen und Oberflächeninhalt der Kugel 10_01 Alle Punkte (des dreidimensionalen Raums), die von einem Punkt M die gleiche Entfernung r besitzen, liegen auf einer Kugel mit Mittelpunkt M und Radiuslänge
Volumen und Oberflächeninhalt der Kugel 10_01 Alle Punkte (des dreidimensionalen Raums), die von einem Punkt M die gleiche Entfernung r besitzen, liegen auf einer Kugel mit Mittelpunkt M und Radiuslänge
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
(Quelle Abitur BW 2004) Gegeben sind die Schaubilder der Funktion mit, ihrer Ableitungsfunktion, einer Stammfunktion von und der Funktion mit.
 Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Übungsaufgaben zu Kapitel 1 bis 4 (Studiengang Produktionstechnik)
 Hochschule für Technik und Wirtschaft Dresden Wintersemester 8/9 Fakultät Informatik/Mathematik Prof. Dr. B. Jung Übungsaufgaben zu Kapitel bis 4 (Studiengang Produktionstechnik) Aufgabe : Vereinfachen
Hochschule für Technik und Wirtschaft Dresden Wintersemester 8/9 Fakultät Informatik/Mathematik Prof. Dr. B. Jung Übungsaufgaben zu Kapitel bis 4 (Studiengang Produktionstechnik) Aufgabe : Vereinfachen
B Anwendungen der Differenzialrechnung
 B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Polynome. Ein Term der Form. mit n und a 0 heißt Polynom. Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms.
 Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
1.2 Weisen Sie rechnerisch nach, dass das Schaubild der Funktion mit 4P! bei 1 einen Sattelpunkt aufweist.
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Analysis 7. f(x) = 4 x (x R)
 Analysis 7 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch fx) = 4 x R) a) Führen Sie für die Funktion f eine Kurvendiskussion durch Nullstellen, Koordinaten der lokalen Extrempunkte,
Analysis 7 www.schulmathe.npage.de Aufgaben Gegeben ist die Funktion f durch fx) = 4 x R) a) Führen Sie für die Funktion f eine Kurvendiskussion durch Nullstellen, Koordinaten der lokalen Extrempunkte,
5.5. Abituraufgaben zu ganzrationalen Funktionen
 .. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
.. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Abitur 2015 Mathematik Infinitesimalrechnung I
 Seite 1 Abiturloesung.de - Abituraufgaben Abitur 215 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion f : x ( x 3 8 ) (2 + ln x) mit maximalem Definitionsbereich D. Teilaufgabe Teil A 1a (1
Seite 1 Abiturloesung.de - Abituraufgaben Abitur 215 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion f : x ( x 3 8 ) (2 + ln x) mit maximalem Definitionsbereich D. Teilaufgabe Teil A 1a (1
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf. SBP Mathe Grundkurs 2
 SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
Anwendungen der Differentialrechnung
 KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
Lösungen 0.1. g) x 1 = 1,82; x 2 = 1,9. + q = 0 x 2 p
 Lösungen 0.1 c) Gleichungen lösen Quadratische Gleichungen: (Buch 11. Klasse) 98/1 a) x 1, = 1,3 b) x 1, = 3,5 c) x 1, = k d) x 1, =,5 e) x 1, = a f) x 1, = t 8 56 98/ a) x 1 = 3; x = 4 b) x 1 = 3; x =
Lösungen 0.1 c) Gleichungen lösen Quadratische Gleichungen: (Buch 11. Klasse) 98/1 a) x 1, = 1,3 b) x 1, = 3,5 c) x 1, = k d) x 1, =,5 e) x 1, = a f) x 1, = t 8 56 98/ a) x 1 = 3; x = 4 b) x 1 = 3; x =
Aufgabenstellung Teilaufgabe a) Anforderungsprofil Teilaufgabe a) Modelllösung Teilaufgabe a) (1)
 Aufgabenstellung Teilaufgabe a) Anforderungsprofil Teilaufgabe a) Modelllösung Teilaufgabe a) (1) Seite 1/8 Heinz Klaus Strick 2011 Die Wertetabelle des Graphen ergibt sich über die I-Option des WTR: Dass
Aufgabenstellung Teilaufgabe a) Anforderungsprofil Teilaufgabe a) Modelllösung Teilaufgabe a) (1) Seite 1/8 Heinz Klaus Strick 2011 Die Wertetabelle des Graphen ergibt sich über die I-Option des WTR: Dass
Mathematik Übungsklausur 2013 Ausführliche Lösungen
 Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
Mathematik Übungsklausur 0 Ausführliche Lösungen Analysis Aufgabe Die Nullstellen einer Funktion f mit Definitionsbereich D f sind die Lösungen der Gleichung f(x) = 0 in D f. Damit erhält man: a) f: x
GF MA Differentialrechnung A2
 Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Kurvendiskussion Nullstellen: Für die Nullstellen x i ( i! ) einer Funktion f gilt: Steigen bzw. Fallen: f ( x i ) = 0 f '( x) > 0 im Intervall I f ist streng monoton wachsend in I f '( x) < 0 im Intervall
Analysis II. Abitur Mathematik Bayern 2012 Musterlösung. Bayern Teil 1. Aufgabe 1. Aufgabe 2. Abitur Mathematik: Musterlösung.
 Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
Extremstellenbestimmung: A'(a) = 50 2a = 0 a = 25 und damit b = 25.
 6. Anwendungen der Differentialrechnung 6. Extremwertaufgben Eine Größe G hänge von mehreren Variablen ab. Wenn man sich dafür interesssiert, für welche Werte dieser Variablen die davon abhängige Größe
6. Anwendungen der Differentialrechnung 6. Extremwertaufgben Eine Größe G hänge von mehreren Variablen ab. Wenn man sich dafür interesssiert, für welche Werte dieser Variablen die davon abhängige Größe
1.4 Schaubild von Schaubild von Schaubild von 1., /
 Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
Lösung A1 1.1 Das Integral ist größer als Null, da die Fläche die der Graph der - Funktion oberhalb der -Achse größer ist als die Fläche unterhalb der -Achse. 1.2 Aussagen über das Schaubild von sind:
ist symmetrisch bezüglich der y-achse, da f( x) = f(x) ist. e x + e x = 2 2 (Substitution: a = e x )
 Problemstellung. f() e + e ist symmetrisch bezüglich der y-achse, da f( ) f() ist. Es ist f () e e. Aus f () folgt ; f(). f () e + e vor.
Problemstellung. f() e + e ist symmetrisch bezüglich der y-achse, da f( ) f() ist. Es ist f () e e. Aus f () folgt ; f(). f () e + e vor.
Analysis 8.
 Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i
![C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5. = 4 + i, z 2. = i](/thumbs/96/129296716.jpg) ETH-Aufnahmeprüfung Herbst 18 Mathematik I (Analysis) D C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5 α. A 1 Aufgabe [1 Punkte] Geben Sie die Lösungsmenge folgender Gleichungen in!
ETH-Aufnahmeprüfung Herbst 18 Mathematik I (Analysis) D C Aufgabe 1 [6 Punkte] Bestimmen Sie den Winkel α im Trapez ABCD. 5 α. A 1 Aufgabe [1 Punkte] Geben Sie die Lösungsmenge folgender Gleichungen in!
Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften:
 1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
Matur-/Abituraufgaben Analysis
 Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
waagrechte Asymptote: y = ln 2 senkrechte Asymptoten: x = 1 Nullstelle der Tangente in P: x = 3
 Abiturprüfung 006 - - Aufgabe GM.I a) ----- b) 7 x + > 0 für x < oder x > 0 ( x = ist einzige Nullstelle) x lim x ± g(x) = ln ; lim x g(x) = ; lim x 0+ waagrechte Asymptote: y = ln senkrechte Asymptoten:
Abiturprüfung 006 - - Aufgabe GM.I a) ----- b) 7 x + > 0 für x < oder x > 0 ( x = ist einzige Nullstelle) x lim x ± g(x) = ln ; lim x g(x) = ; lim x 0+ waagrechte Asymptote: y = ln senkrechte Asymptoten:
Lösungen 0.1. g) x 1 = 1,82; x 2 = 1,9. + q = 0 x 2 p
 Lösungen 0.1 c) Gleichungen lösen Quadratische Gleichungen: (Buch 11. Klasse) 98/1 a) x 1, = 1,3 b) x 1, = 3,5 c) x 1, = k d) x 1, =,5 e) x 1, = a f) x 1, = t 8 56 98/ a) x 1 = 3; x = 4 b) x 1 = 3; x =
Lösungen 0.1 c) Gleichungen lösen Quadratische Gleichungen: (Buch 11. Klasse) 98/1 a) x 1, = 1,3 b) x 1, = 3,5 c) x 1, = k d) x 1, =,5 e) x 1, = a f) x 1, = t 8 56 98/ a) x 1 = 3; x = 4 b) x 1 = 3; x =
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Analysis: Klausur Analysis
 Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Förderaufgaben EF Arbeitsblatt 1 Abgabe Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung.
 Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Grundwissen 10. Überblick: Gradmaß rπ Länge eines Bogens zum Mittelpunktswinkels α: b = α
 Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
Grundwissen 0. Berechnungen an Kreis und Kugel a) Bogenmaß Beispiel: Gegeben ist ein Winkel α=50 ; dann gilt: b = b = π 50 0,8766 r r 360 Die (reelle) Zahl ist geeignet, die Größe eines Winkels anzugeben.
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
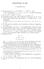 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 10
 RMG Haßfurt Grundwissen Mathematik Jahrgangsstufe 0 Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 0 Wissen und Können. Berechnungen am Kreis Bogenmaß Das Bogenmaß ist das zu
RMG Haßfurt Grundwissen Mathematik Jahrgangsstufe 0 Regiomontanus - Gymnasium Haßfurt - Grundwissen Mathematik Jahrgangsstufe 0 Wissen und Können. Berechnungen am Kreis Bogenmaß Das Bogenmaß ist das zu
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
Prüfungsteil 1, Aufgabe 3. Analysis. Nordrhein-Westfalen 2012 GK. Aufgabe a (1) Aufgabe a (2) Abitur Mathematik: Musterlösung
 Abitur Mathematik: Prüfungsteil 1, Aufgabe 3 Nordrhein-Westfalen 2012 GK Aufgabe a (1) 1. SCHRITT: BEDINGUNG FÜR PUNKTSYMMETRIE ZUM URSPRUNG PRÜFEN Der Graph der Funktion : ist genau dann punktsymmetrisch
Abitur Mathematik: Prüfungsteil 1, Aufgabe 3 Nordrhein-Westfalen 2012 GK Aufgabe a (1) 1. SCHRITT: BEDINGUNG FÜR PUNKTSYMMETRIE ZUM URSPRUNG PRÜFEN Der Graph der Funktion : ist genau dann punktsymmetrisch
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1
 Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1 Lehrplan: M 11.1.1 Graphen gebrochen-rationaler Funktionen M 11.1.2 Lokales Differenzieren Passende Kapitel im Schulbuch Fokus Mathematik 11:
Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1 Lehrplan: M 11.1.1 Graphen gebrochen-rationaler Funktionen M 11.1.2 Lokales Differenzieren Passende Kapitel im Schulbuch Fokus Mathematik 11:
Kurvendiskussion von Polynomfunktionen
 Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Analysis: Klausur Analysis
 Analysis Klausur zur Integralrechnung Stammfunktionsberechnung, Flächenberechnung, Rotationsvolumen, Funktionen zu Änderungsraten (Bearbeitungszeit: 9 Minuten) Gymnasium J1 Aleander Schwarz www.mathe-aufgaben.com
Analysis Klausur zur Integralrechnung Stammfunktionsberechnung, Flächenberechnung, Rotationsvolumen, Funktionen zu Änderungsraten (Bearbeitungszeit: 9 Minuten) Gymnasium J1 Aleander Schwarz www.mathe-aufgaben.com
a) Im Berührungspunkt müssen die y-werte und die Steigungen übereinstimmen:
 . ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
. ANALYSIS Gegeben ist die kubische Parabel f: y = x 3 6x + 8x + a) Die Gerade g: y = k x + berührt die Parabel an der Stelle x = x 0 > 0. Bestimmen Sie den Parameter k. b) Berechnen Sie den Inhalt der
Hauptprüfung Fachhochschulreife Baden-Württemberg
 Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Abschlussaufgabe Nichttechnik - Analysis II
 Analysis NT GS - 0.06.06 - m06_ntalsg_gs.mcd Abschlussaufgabe 006 - Nichttechnik - Analysis II.0 Gegeben sind die reellen Funktionen fx ( ) mit ID f = ID g = IR. ( ) = x und gx ( ) = fx ( ) +. Zeigen Sie,
Analysis NT GS - 0.06.06 - m06_ntalsg_gs.mcd Abschlussaufgabe 006 - Nichttechnik - Analysis II.0 Gegeben sind die reellen Funktionen fx ( ) mit ID f = ID g = IR. ( ) = x und gx ( ) = fx ( ) +. Zeigen Sie,
Abschlussprüfung Berufliche Oberschule 2017 Mathematik 12 Nichttechnik - A I - Lösung
 Abschlussprüfung Berufliche Oberschule Mathematik Nichttechnik - A I - Lösung Teilaufgabe. Gegeben ist die ganzrationale Funktion g dritten Grades mit D g IR, deren Graph G g in untenstehender Abbildung
Abschlussprüfung Berufliche Oberschule Mathematik Nichttechnik - A I - Lösung Teilaufgabe. Gegeben ist die ganzrationale Funktion g dritten Grades mit D g IR, deren Graph G g in untenstehender Abbildung
K2 MATHEMATIK KLAUSUR 2. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
1 2 x x. 1 2 x 4
 S. Potenzfunktionen mit rationalen Exponenten und ihre Ableitung Zuordung f(x) = x g(x) = x h(x) = x k(x) = x p(x) = x 0, q(x) = x r(x) = x s(x) = x, 6 7 Wurzelfunktionen a) f(x) = x + D = [ ; [ f '(x)
S. Potenzfunktionen mit rationalen Exponenten und ihre Ableitung Zuordung f(x) = x g(x) = x h(x) = x k(x) = x p(x) = x 0, q(x) = x r(x) = x s(x) = x, 6 7 Wurzelfunktionen a) f(x) = x + D = [ ; [ f '(x)
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
Aufgaben zur e- und ln-funktion
 Aufgaben zur e- und ln-funktion 1.0 Gegeben ist die Funktion f(x) = 2x2 2 mit D. Ihr Graph sei G f. (Abitur 2008 AI) e x f =! 1.1 Geben Sie die Schnittpunkte von G f mit den Koordinatenachsen an. 1.2 Untersuchen
Aufgaben zur e- und ln-funktion 1.0 Gegeben ist die Funktion f(x) = 2x2 2 mit D. Ihr Graph sei G f. (Abitur 2008 AI) e x f =! 1.1 Geben Sie die Schnittpunkte von G f mit den Koordinatenachsen an. 1.2 Untersuchen
Mathematik für Studierende technischer Fächer und Studierende der Chemie. Prof. Dr. Kathrin Klamroth Britta Schulze, M.Sc.
 Mathematik für Studierende technischer Fächer und Studierende der Chemie Lösungen zum Vorkurs WS 6/7 Prof. Dr. Kathrin Klamroth Britta Schulze, M.Sc. Bergische Universität Wuppertal Fakultät für Mathematik
Mathematik für Studierende technischer Fächer und Studierende der Chemie Lösungen zum Vorkurs WS 6/7 Prof. Dr. Kathrin Klamroth Britta Schulze, M.Sc. Bergische Universität Wuppertal Fakultät für Mathematik
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
1 Differenzenquotient und mittlere Änderungsrate
 Schülerbuchseite 8 9 Lösungen vorläufig Differenzenquotient und mittlere Änderungsrate S. 8 a) Da der dargestellte Graph keine Gerade ist, verläuft die Temperaturzunahme nicht gleichmäßig. Temperaturzunahme
Schülerbuchseite 8 9 Lösungen vorläufig Differenzenquotient und mittlere Änderungsrate S. 8 a) Da der dargestellte Graph keine Gerade ist, verläuft die Temperaturzunahme nicht gleichmäßig. Temperaturzunahme
Zusammenfassung: Differenzialrechnung 2
 LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
)e2 (3 x2 ) a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen Sie das Verhalten von f für x.
 Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
Analysis Aufgabe aus Abiturprüfung Bayern GK (abgeändert). Gegeben ist die Funktion f(x) = ( x )e ( x ). a) Untersuchen Sie den Graphen auf Symmetrie, ermitteln Sie die Nullstellen von f und bestimmen
HTWD, FB Informatik/Mathematik. Mathematik für Bauingenieure. Wiederholungsaufgaben: Mathematik I
 HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik I Wiederholung Mathematik für Bauingenieure Wiederholungsaufgaben: Mathematik I Aufgabe : Für die Aussagenverbindung T = (A B) ( A) gebe man
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik I Wiederholung Mathematik für Bauingenieure Wiederholungsaufgaben: Mathematik I Aufgabe : Für die Aussagenverbindung T = (A B) ( A) gebe man
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT. Abitur April/Mai Mathematik (Grundkurs) Arbeitszeit: 210 Minuten
 KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT Abitur April/Mai 004 Mathematik (Grundkurs) Arbeitszeit: 0 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten G, G und G 3 zur Bearbeitung aus. Gewählte
KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT Abitur April/Mai 004 Mathematik (Grundkurs) Arbeitszeit: 0 Minuten Der Prüfling wählt je eine Aufgabe aus den Gebieten G, G und G 3 zur Bearbeitung aus. Gewählte
Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[
![Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[ Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) < 0 x ]a, b[](/thumbs/76/73058958.jpg) Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
Monotonie und erste Ableitung: Satz: Eine Funktion f ist monoton wachsend auf einem Intervall ]a, b[, wenn gilt: f (x) 0 x ]a, b[ Eine Funktion f ist monoton fallend auf einem Intervall ]a, b[, wenn gilt:
Beispielseite (Band 1) 2. Ganzrationale Funktionen 2.4 Nullstellen bei Funktionen 3. Grades
 Beispielseite (Band ). Ganzrationale Funktionen.4 Nullstellen bei Funktionen. Grades Funktionen. Grades ohne Absolutglied Bei ganzrationalen Funktionen. Grades ohne Absolutglied beginnt die Nullstellenberechnung
Beispielseite (Band ). Ganzrationale Funktionen.4 Nullstellen bei Funktionen. Grades Funktionen. Grades ohne Absolutglied Bei ganzrationalen Funktionen. Grades ohne Absolutglied beginnt die Nullstellenberechnung
Mathematik im Berufskolleg II
 Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
K2 KLAUSUR 2. Aufgabe Punkte (max) Punkte. (1) Bestimmen Sie die Ableitung von f(x) = 2 x
 K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
1. Aufgabe Niederschlag Diagramm I
 1. Aufgabe Niederschlag Diagramm I a) Die Gesamtmenge entspricht der Fläche zwischen Graphen und x-achse. Diese kann durch entweder durch Kästchenzählen ermittelt werden oder durch ein Dreieck angenähert
1. Aufgabe Niederschlag Diagramm I a) Die Gesamtmenge entspricht der Fläche zwischen Graphen und x-achse. Diese kann durch entweder durch Kästchenzählen ermittelt werden oder durch ein Dreieck angenähert
Aufgabe A2 1.1 Die Funktion ist gegeben durch 3P 21 mit Berechne die Gleichung der Tangente an das Schaubild von im Schnittpunkt mit der -Achse. 1.2 E
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
1.2 Einfache Eigenschaften von Funktionen
 1.2 Einfache Eigenschaften von Funktionen 1.2.1 Nullstellen Seien A und B Teilmengen von R und f : A B f : Df Wf eine Funktion. Eine Nullstelle der Funktion f ist ein 2 D f, für das f ( = 0 ist. (Eine
1.2 Einfache Eigenschaften von Funktionen 1.2.1 Nullstellen Seien A und B Teilmengen von R und f : A B f : Df Wf eine Funktion. Eine Nullstelle der Funktion f ist ein 2 D f, für das f ( = 0 ist. (Eine
Analysis Aufgabengruppe 1.. Der Graph von f wird mit G f bezeichnet.
 BE 1 Gegeben ist die Funktion mit x Analysis Augabengruppe 1 1 1 und Deinitionsbereich x 1 x 3 D IR\ 3; 1. Der Graph von wird mit G bezeichnet. x zu jedem der drei olgenden Terme äquivalent ist: 2 2 1
BE 1 Gegeben ist die Funktion mit x Analysis Augabengruppe 1 1 1 und Deinitionsbereich x 1 x 3 D IR\ 3; 1. Der Graph von wird mit G bezeichnet. x zu jedem der drei olgenden Terme äquivalent ist: 2 2 1
p x 1,25x 5. Der Graph von p wird mit G p bezeichnet. BE Teil 2
 BE Teil 2 1 An einer Wand im Innenhof der von Antoni Gaudi gestalteten Casa Batlló in Barcelona findet man ein Keramikkunstwerk (vgl. Abbildung 1). Der annähernd parabelförmige obere Rand des Kunstwerks
BE Teil 2 1 An einer Wand im Innenhof der von Antoni Gaudi gestalteten Casa Batlló in Barcelona findet man ein Keramikkunstwerk (vgl. Abbildung 1). Der annähernd parabelförmige obere Rand des Kunstwerks
