Computersimulationen biologischer Musterbildung HANS MEINHARDT
|
|
|
- Angela Giese
- vor 7 Jahren
- Abrufe
Transkript
1 Strukturbildungsprozesse Computersimulationen biologischer Musterbildung HANS MEINHARDT INTERNET Mit einfachen Mitteln lassen sich mit dem Computer Prozesse der biologischen Musterbildung simulieren. Biologische Prozesse beruhen auf der Wechselwirkung von Molekülen. Das gilt natürlich auch für solche, die eine Ausbildung lokaler Signale für die Steuerung der Zelldifferenzierung ermöglichen. In dem vorangegangenen Aufsatz (Seite 22) wurde beschrieben, dass diese Prozesse Wechselwirkungen erfordern, bei denen Substanzen direkt oder indirekt eine starke positive Rückwirkung auf ihre eigene Produktion haben. Parallel dazu müssen antagonistische Substanzen synthetisiert werden, die diese selbstverstärkenden Reaktionen in ein neues Gleichgewicht bringen. Unsere Intuition ist ein sehr unvollkommenes Instrument, um die Eigenschaften solcher rückgekoppelten und nicht linearen Systeme vorauszusagen. Wie in anderen Wissenschaften auch ist eine mathematische Formulierung der Hypothesen notwendig. Eine Gleichung ist eindeutig. Im Folgenden soll an einfachen Beispielen gezeigt werden, wie eine solche Formulierung aussehen und wie man sie für eine Computersimulation aufbereiten kann. Mithilfe des einfachen, hier abgedruckten Programms können einige elementare Simulationen ausgeführt werden. Es ist in BASIC geschrieben. Von der BIUZ-Webseite kann ein noch etwas umfangreicheres Programm und eine unter DOS lauffähige Version heruntergeladen werden. Auch die Simulationen können dort eingesehen werden. Wenn während der Entwicklung eines Organismus an einer Stelle etwas geschieht, was an einer anderen Stelle Von der BIUZ-Webseite können Sie ein Programm und eine unter DOS lauffähige Version herunterladen, mit dessen Hilfe einige elementare Simulationen ausgeführt werden können. Die im Artikel vorgestellten Simulationen können dort eingesehen werden. Weitere Simulationen an der Homepage des Max-Planck- Instituts für Entwicklungsbiologie Theoretical aspects of pattern formation and neuronal development. theory.html nicht erfolgt, so müssen wir davon ausgehen, dass unterschiedliche Konzentrationen von Signalmolekülen aufgebaut wurden. Die mathematische Formulierung muss eine Berechnung dieser Konzentrationsverteilungen als Funktion der Zeit ermöglichen. Dazu muss man die Konzentrationsänderungen innerhalb eines kurzen Zeitraums als Funktion der anderen beteiligten Stoffe berechnen. Addiert man diese Änderungen zu gegebenen Ausgangskonzentrationen, so erhält man die Konzentrationsverteilung zu einem etwas späteren Zeitpunkt. Durch vielfache Wiederholung solcher Rechenschritte (Iterationen) erhält man die Konzentrationen der beteiligten Substanzen als Funktion des Ortes und der Zeit. Bei den Konzentrationsänderungen spielen drei Faktoren eine wichtige Rolle: die Produktion, der Abbau und der Austausch mit benachbarten Zellen, beispielsweise durch Diffusion. Gleichung für ein Aktivator-Inhibitor-System Wie in dem vorhergehenden Aufsatz im Detail beschrieben, erfordert eine spontane Musterbildung eine örtlich begrenzte Selbstverstärkung, die mit einer sich schnell ausbreitenden inhibitorischen Reaktion gekoppelt ist. Es bilden sich Muster, weil kleine Abweichungen von einer homogenen Verteilung eine starke positive Rückwirkung auf ihr weiteres Anwachsen haben. Der weitreichende antagonistische Effekt sorgt dafür, dass die selbstverstärkende Reaktion weder beliebig anwachsen noch sich beliebig ausbreiten kann. Das folgende Gleichungssystem beschreibt Konzentrationsänderungen pro Zeiteinheit eines hypothetischen Aktivators a(x) und des entsprechenden Inhibitors b(x) [1, 2, 5]. a s a a = 2 2 b r a D t + b a a + a 2 x 2 b 2 b = sa r b D t b + b 2 x 48 Biologie in unserer Zeit 31. Jahrgang 2001 Nr. 1
2 STRUKTURBILDUNGSPROZESSE DAS EXPERIMENT In diesen Gleichungen bedeutet t die Zeit, x die räumliche Koordinate, D a und D b die Diffusionskoeffizienten, r a und r b die Zerfallsraten von a und b. Solche Gleichungen sind leicht zu lesen. Die erste Gleichung besagt, dass der Aktivator nicht linear auf seine eigene Produktion zurückwirkt (a 2 ). Eine solche Nicht-Linearität entsteht, wenn zwei Aktivatormoleküle einen Komplex bilden müssen, um die Synthese weiterer Moleküle anzuregen. Um die Autokatalyse bei sehr niedrigen Aktivatorkonzentrationen in Gang zu setzen, ist eine kleine aktivatorunabhängige Grundproduktion b a notwendig. Diese spielt eine Rolle beim Zünden neuer Maxima während des Wachstums, für das periodische Aktivieren bei Oszillationen oder bei der Regeneration von Mustern. Die Produktion wird durch den Inhibitor verlangsamt (1/b). Der Faktor s, die Quelldichte, beschreibt die Fähigkeit der Zellen zur Autokatalyse. Die Rate, mit der Moleküle verschwinden, ist in der Regel proportional zur Anzahl der vorhandenen Moleküle (-r a a). Diese Annahme ist unmittelbar einleuchtend. So ist beispielsweise auch die Zahl der Menschen, die im Mittel pro Jahr in einer Stadt sterben, proportional zur Zahl der Einwohner. Musterbildung kann nur stattfinden, wenn die Zellen miteinander Signale austauschen können. Eine Möglichkeit dazu ist die Diffusion. Dieser Austausch ist proportional zur zweiten Ableitung der Konzentrationsänderung. Auch das ist leicht einsehbar. Der Nettoaustausch von Molekülen durch Diffusion ist natürlich null, wenn alle Zellen die gleiche Konzentration besitzen. Er ist jedoch ebenfalls null, wenn zwischen benachbarten Zellen eine konstante Konzentrationsdifferenz besteht, wenn also ein linearer Konzentrationsgradient vorliegt. Dann erhält jede Zelle von ihrer Nachbarzelle mit der höheren Konzentration die gleiche Stoffmenge, die sie an ihre Nachbarzelle mit der niedrigeren Konzentration verliert. Mit anderen Worten, für einen Verlust oder Zuwachs durch Diffusion ist nicht die Konzentrationsänderung, sondern die Änderung der Konzentrationsänderung zwischen Nachbarzellen entscheidend. Die Gleichung für die Änderung der Inhibitorkonzentration kann entsprechend gelesen werden. Sie unterscheidet sich im Wesentlichen nur dadurch, dass die Produktionsrate nur vom Aktivator, nicht aber vom Inhibitor selbst abhängig ist. Berechnung einer Musterentwicklung Um mit Hilfe einer solchen Gleichung die zeitliche Entwicklung eines räumlichen Musters berechnen zu können, müssen zunächst die Konstanten wie die Produktions-, Zerfalls- und Diffusionsraten festgelegt werden. Die Wahl ist natürlich nicht willkürlich. Damit eine räumliche Musterbildung möglich ist, muss der Inhibitor viel schneller diffundieren als der Aktivator (D b >> D a ). Ferner muss der Inhibitor sehr schnell auf eine Veränderung der Aktivatorkonzentration reagieren, sonst beginnt das System zu oszillieren. Das bedeutet, dass die Lebensdauer des Inhibitors kürzer sein muss als die des Aktivators. Das heißt, für die Abbauraten muss die Relation r b > r a gelten. Da die Gleichungen nur Veränderungen beschreiben, müssen bestimmte Anfangskonzentrationen angenommen werden. Von diesen Anfangsverteilungen ausgehend, wird der weitere zeitliche Verlauf berechnet. Um die spontane Musterbildung zu demonstrieren, wird bis auf die kleinen statischen Schwankungen in der Quelldichte s immer von homogenen Anfangsbedingungen ausgegangen. Der Computer kann nicht mit einem kontinuierlichen Feld, sondern nur mit diskreten Zellen rechnen, was für biologische Anwendungen ohnehin nicht ganz falsch ist. Dazu werden in dem Programm die Aktivatorkonzentrationen der einzelnen Zellen in Arrays gespeichert, im Programm heißen diese a(i), b(i) usw. Hierbei gibt i=1 n an, um welche Zelle es sich handelt. Im vorliegenden Programm wird nur von einer Kette von Zellen ausgegangen. ABB. 1 MUSTERBILDUNG Eine schichtartige Ausdehnung wird nicht berücksichtigt. Bevor die jeweilige Rechnung für eine bestimme Zelle und ein bestimmtes Zeitintervall ausgeführt wird, werden die aktuellen Konzentrationen der Substanzen a, b, c,. als a, b, c, zwischengespeichert. Die lokale Produktionsrate (Quelldichte) wird in dem Feld s(i) gespeichert und während einer Simulation nicht verändert. In der Regel wird die Produktionsrate s des Aktivators gleich seiner Zerfallsrate r a gesetzt. Das hat den Vorteil, dass in den Simulationen Absolutkonzentrationen in der Größenordnung von 1 entstehen. Der Wert von s wird lokal noch durch zufällige Schwankungen von 1% moduliert. Mit jeder neuen Simulation werden nach einer Zufallsfunktion neue Fluktuationen festgelegt. Darum kann eine Wiederholung mit gleichen Parametern durchaus zu einem etwas anderen Muster führen. Bei der Berechnung des Austauschs durch Diffusion treten statt der zweiten Ableitungen die Differenz der Kon- Bildschirmkopien von Simulationen, produziert mit dem beschriebenen Programm: Bildung gradierter (obere Reihe) und periodischer Verteilungen (unten). Dargestellt sind die Anfangs-, eine intermediäre und die endgültige stabile Verteilung des Aktivators und des Inhibitors. Die Musterbildung wird jeweils durch kleine statistische Schwankungen (blaue Kurve) ausgelöst. Nr Jahrgang 2001 Biologie in unserer Zeit 49
3 zentrationsdifferenzen zwischen Nachbarzellen auf. Damit erhält man statt der kontinuierlichen Differentialgleichungen diskrete Differenzengleichungen für die Änderungen der Aktivatorkonzentration in einem kleinen Zeitintervall in der jeweiligen Zelle i. Diese Konzentrationsänderungen werden zu den ursprünglichen Konzentrationen addiert und es ergibt sich die neue Konzentrationen a (i) in der Zelle i a (i) = a(i) + s(i) * (a(i) 2 + BA)/b(i)- RA * a(i) + DA * ((a(i-1)-a(i)) + (a(i+1))-a(i)) Zunächst muss in einer Schleife diese neue Konzentration für alle Zellen i, i=1 n ausgerechnet werden. Anschließend werden in einer weiteren Schleife die Konzentrationsänderungen für das nächste Zeitintervall berechnet usw. Der Austausch von Molekülen durch Diffusion zwischen Nachbarzellen erfordert bestimmte Bedingungen für die Zellen am Rand des Feldes. Für Rechnungen auf einem Ring wird angenommen, dass die letzte Zelle n die Zelle 1 als Nachbarn hat. Bei einer offenen Kette von Zellen soll der Rand undurchlässig sein, das heißt, es gehen weder Moleküle durch den Rand verloren noch werden Moleküle von außen aufgenommen. Dazu werden hypothetische Zellen neben den Randzellen angenommen, die immer die gleichen Konzentrationen wie die Randzellen selbst haben. Zwischen Zellen mit gleichen Konzentrationen findet kein Nettoaustausch statt. Damit ist die Bedingung erfüllt, dass durch die Grenzen kein Austausch stattfindet. Die Simulation erfordert kleine Zeitschritte Bei einer solchen Simulation geht man von schrittweisen Änderungen aus. Das ist natürlich nur eine Näherung. Man darf die Schritte also nicht zu groß machen, sonst können numerische Instabilitäten auftreten. Das ist am leichtesten bei den Diffusionskonstanten zu verstehen. Nehmen wir zum Beispiel eine Kette von Zellen an, in der anfänglich nur eine Zelle eine hohe Konzentration hatte. Mit einer numerischen Diffusionskonstante von 1 nimmt diese Zelle nach der ersten Iteration eine negative Konzentration von gleicher Größe an. Dagegen werden die beiden Nachbarzellen die gleiche Konzentration haben wie die ursprüngliche Zelle. Damit ist aber die Konzentrationsdifferenz zwischen benachbarten Zellen auf 2 gewachsen. Das ist natürlich Unsinn, denn durch Diffusion müssen sich Konzentrationsdifferenzen ausgleichen und nicht weiter erhöhen. Um solche numerischen Instabilitäten zu vermeiden, darf der numerische Wert der Diffusionskonstante 0,4 (0,2 bei zweidimensionalen Simulationen) nicht übersteigen. Der numerische Wert besagt ja, wieviel der Substanz während eines Zeitschrittes ausgetauscht wird. Ein kleinerer numerischer Wert entspricht also einer kleineren Schrittlänge. Die Diffusion der schnell diffundierenden Substanz bestimmt also die maximale mögliche Schrittlänge. Ob beispielsweise eine gradierte Verteilung oder eine periodische Verteilung entsteht, hängt von den Reichweiten der beteiligten Substanzen ab (Abbildung 1). Die Reichweite ist die Strecke, die ein Molekül im Mittel zwischen seiner Entstehung und seinem Zerfall zurücklegt, und ist sowohl von der Diffusionsgeschwindigkeit als auch von der Lebensdauer abhängig. Ein Blick auf die im Programm verwendeten Konstanten zeigt, dass die Abbauraten für die Simulation der periodischen Strukturen als wesentlich größer angenommen wurden. Also reicht die Inhibition nicht so weit, und mehrere Maxima haben im gleichen Feld Platz. Umgekehrt, wenn die Reichweite des Aktivators ungefähr der Feldgröße entspricht, ist nur Platz für ein Maximum an einer Seite des Feldes vorhanden. Es bildet sich ein polares Muster aus. Für eine biologische Anwendung ist das sehr wichtig, da so in einem Teil eines sich entwickelnden Embryos eine andere Entwicklung initiiert werden kann als auf der gegenüberliegenden Seite, obwohl in allen Zellen die gleiche genetische Information vorhanden ist. Selbst-löschende Muster Wie im vorangegangenen Aufsatz gezeigt, tritt durch einen weiteren Inhibitor, der eine kurze Reichweite und eine lange Lebensdauer hat, eine Vergiftung eines einmal gebildeten Maximums auf. Das Maximum verschwindet wieder, dafür wird am anderen Ende ein neues gebildet usw. In dem Beispielprogramm wird dieser Inhibitor c(x) durch den Aktivator produziert und wirkt additiv zu dem Inhibitor mit langer Reichweite b(x). Statt 1/b ergibt sich eine Gesamtinhibition von 1/(b+c). Das ist aber nur eine der denkbaren Möglichkeiten. Bei der Simulation treten Maxima abwechselnd an dem einen und anderen Ende des Feldes auf (Abbildung 2). Eine solche Oszillation eines polaren Musters wurde in E.coli als Teil eines Systems gefunden, mit dem das Bakterium seine geometrische Mitte bestimmt. Das ist notwendig, um die nächste Zellteilung zu lokalisieren [3]. Bei einem solchen System bleibt im zeitlichen Mittel die Aktivatorkonzentration in der Mitte des stabförmigen Gebildes am geringsten. Da die abwechselnd gebildeten Maxima notwendigerweise symmetrisch sind, erscheint das Minimum immer genau in der Mitte. In einem weiten Bereich ist diese unabhängig von der tatsächlichen Länge des Bakteriums. Dieses Minimum kann von anderen Komponenten zur Festlegung der Teilungsebene benutzt werden. Wird dagegen die Simulation auf einer ringförmig geschlossenen Kette von Zellen durchgeführt, so erscheinen die Maxima entweder an en, die um jeweils etwa 137,5 versetzt sind, in paarweiser, jeweils um 90 versetzter Anordnung, oder abwechselnd an gegenüberliegenden en. Diese Muster entsprechend den häufigsten phyllotaktischen Anordnungen von Blättern. Die helikale Anordnung kann mit dem Programm, das von der Webseite verfügbar ist, simuliert werden. 50 Biologie in unserer Zeit 31. Jahrgang 2001 Nr. 1
4 STRUKTURBILDUNGSPROZESSE DAS EXPERIMENT ABB. 2 DAS OSZILLIERENDE POLARE MUSTER Zeit Durch einen zweiten Inhibitor (violett), der sich langsam lokal ansammelt, wird ein Maximum kurz nach seiner Bildung vergiftet. Ein neues Maximum entsteht an der gegenüber liegenden Seite. Im weiteren (hier nicht gezeigten) Verlauf wird auch das wieder verschwinden und ein neues Maximum wird an der ursprünglichen Stelle erscheinen usw. Die graphische Darstellung Jeweils nach einer bestimmten Anzahl von Iterationen sollen die aktuell errechneten Verteilungen dargestellt werden. In dem abgedruckten Programm wird eine Darstellung verwendet, mit der die Konzentrationen in einer Kette von Zellen wiedergeben werden können (Abbildung 1, 2). Dazu wird die jeweilige Aktivatorkonzentration der Zelle i durch ein (grünes) Rechteck dargestellt, dessen Höhe proportional zur aktuellen Konzentration ist. Um Reste früherer Rechtecke zu löschen, wird über diesem Rechteck noch ein weißes Rechteck bis zum oberen Rand gemalt. Da die Inhibitorverteilung die Aktivatorverteilung nicht vollständig überdecken soll, wird diese nur als schmaler (roter) Balken in einer Höhe entsprechend der jeweiligen Konzentration aufgetragen. In Blau ist die lokale Produktionsrate mit ihren minimalen Fluktuationen angegeben. Wie leicht zu sehen ist, ist in diesen Fluktuationen das endgültige Muster nicht schon in einer verborgenen Weise vorhanden. Die Konzentration des langlebigen, vergiftenden Inhibitors, der zu dem dynamischen Auf- und Abbau von Maxima führt, ist violett angegeben (Abbildung 2). In Abbildung 1 ist die ursprüngliche Verteilung, ein Zwischenzustand und die am Ende stabile Verteilung gezeigt. Interessanter ist aber die vollständige dynamische Entwicklung auf dem eigenen Computer zu beobachten. Da die Fluktuationen mit jeder Simulation neu bestimmt werden, ist der detaillierte Verlauf jeweils etwas verschieden. Beispielsweise ist es Zufall, ob sich bei der gradierten Verteilung das Maximum auf der rechten oder der linken Seite bildet. Bei der zweiten Art der graphischen Darstellung wird die Musterbildung in der ringförmigen Blattbildungszone simuliert (siehe Abbildung 3 des vorhergehenden Aufsatzes). Durch die perspektivische Betrachtung erscheinen die Kreise als Ellipsen. Im Laufe der Simulation werden viele solcher Ellipsen jeweils etwas nach oben verschoben übereinander gezeichnet. Dadurch entsteht der Eindruck eines wachsenden Zylinders. Wenn die Aktivatorkonzentration einen bestimmten Wert übersteigt, wird dieser Teil der Ellipse als dicker grauer Strich gemalt. Es erscheint so eine dunkle Fläche auf dem Zylinder entsprechend einem Signal zur Blattbildung. Um den zylinderartigen Eindruck zu verbessern, sind die Flächen, die einer Ansicht auf eine innere Zylinderwand entsprechen, in hellerem Grau gehalten. Gegenständige, kreuzständige und helikale Anordnung können simuliert werden. Wenn man mit statistischen Anfangsbedingungen beginnt, benötigt die Reaktion gegebenenfalls einige Zeit, bis sich das endgültige Muster stabil eingestellt hat. Deshalb sollte man dann mit der Taste w ggf. einen weiteren Satz von Iterationen rechnen. Die Ausbildung des stabilen Musterns ist dabei gut zu beobachten. Vom Programmcode zum ausführbaren Programm Das kurze Programm wurde auf die wesentlichen Elemente beschränkt, damit es leicht zu verstehen ist. Ausführliche Kommentare sind eingefügt, so dass zusammen mit den obigen Erklärungen die einzelnen Teile verständlich sein sollten. Es kann mit den DOS-Programmen der Microsoft Nr Jahrgang 2001 Biologie in unserer Zeit 51
5 DAS COMPUTER-PROGRAMM DEFINT H-N Variablen mit diesen Anfangsbuchstaben sind ganzzahlig i = 1 n= Zellen imax = 200: DIM a(imax), b(imax), c(imax), s(imax) simtyp$ = p Anfang mit periodischer Verteilung start: RANDOMIZE TIMER Durch verschiedene Fluktuationen wird jede Simulation etwas anders Festlegung der Konstanten wie Diffusion, Lebensdauer, etc - SELECT CASE simtyp$ fuer periodische, gradierte und oszilierende Muster CASE p : text$ = Periodisches Muster kt = 100 Zahl der Darstellungen kp = 20 Zahl der Iterationen zwischen den Darstellungen Zahl der Iterationen insgesamt = kt * kp! n = 40 Zahl der Zellen DA =.01 Diffusion des Aktivator RA =.02 Zerfallsrate des Aktivators BA =.001 kleine Aktivator-unabhängige Produktionsrate des Aktivators DB =.4 Diffusion des lokalen Inhibitors B RB =.03 Zerfallsrate des lokalen Inhibitors B RC = 0 Substanz C nicht gebraucht fa = 60: fb = 60: fc = 0 Graphik-Normierung CASE g : text$ = Gradierte Verteilung kt = 50: n = 12: kp = 200 DA =.004: RA =.0015: BA =.0001: DB =.4: RB =.0025: RC = 0 fa = 60: fb = 60: fc = 0 CASE o : text$ = Muster vergiftet sich: 2.Inhibitor = rosa kt = 200: kp = 500: n = 12: DA =.003: RA =.002: BA =.085 DB =.4: RB =.003: DC =.001: RC =.0001: fa = 40: fb = 50: fc = 50 Graph-Normierung CASE ELSE: END jede andere Taste: Ende END SELECT REM - Anfangsbedingungen FOR i = 1 TO n s(i) = RA * ( * RND) Quelldichte = Aktivatorproduktion proportional zur Zerfallsrate + 1% statistische Fluktuationen a(i) = 1 Aktivator, generelle Anfangskonzentration b(i) = 1 Inhibitor, generelle Anfangskonzentration c(i) = 0 NEXT i t = TIMER SCREEN 12: WINDOW (1, 1)-(640, 480) Koordinaten-System continuo: idx = 600 / n Zellenbreite in Pixel fs = 350 / RA Normierung der Quelldichte fuer Darstellung LINE (1, 1)-(640, 480), 15, BF Hintergrund weiss LOCATE 30, 1: PRINT gruen = Aktivator, rot = Inhibitor, blau = Quelldichte ; PRINT jede Taste: Unterbrechung ; LOCATE 1, 1: textprint$ = text$ + SPACE$(80) PRINT LEFT$(textprint$, 80); FOR itot = 0 TO kt Schleifen fuer darzustellende Verteilung FOR iprint% = 1 TO kp Rechnung zwischen den Darstellungen REM Rand-ist-dicht al = a(1): bl = b(1): cl = c(1) al ist die Konzentration einer Zelle links von der aktuellen Zelle = linke Zelle = Rand ist dicht a(n + 1) = a(n) Konzentrationen in einer virtueller Zelle rechts b(n + 1) = b(n) gleich Konzentration der ganz rechten Zelle c(n + 1) = c(n) und das für alle Substanzen REM - Reaktionen in den Zellen 1.n FOR i = 1 TO n i = laufende Zelle, n = rechte Zelle a = a(i) lokale Aktivator-Konzentration b = b(i) lokale Inhibitor1-Konzentration c = c(i) lokale Inhibitor2-Konzentration Ausrechnen der neuen Aktivator- und Inhibitorkonz. in Zelle i Diffaktivator = DA * ((al a) + (a(i + 1) a)) Austausch mit Nachbarz. a(i) = a + s(i) * (a * a + BA) / (b + c) RA * a + Diffaktivator b(i) = b + s(i) * a * a RB * b + DB * ((bl b) + (b(i + 1) b)) IF RC > 0 THEN c nur bei oszillierenden Mustern und Phyllotaxis c(i) = c + RC * (a c) + DC * ((cl c) + (c(i + 1) c)) END IF al = a: bl = b: cl = c Es sind die noch nicht geaenderten Konzentrationen die fuer die Berechnung der Diffusion in der naechsten Zelle NEXT i verwendet werden muessen NEXT iprint% REM Graphische Darstellung = jede Zelle ein Rechteck LINE (20, 45)-(620, 50), 7, BF Basis-Linie blau x1 = 20 des ersten Rechtecks FOR i = 1 TO n x2 = x1 + idx afl = 51 + a(i) * fa: LINE (x1, 51)-(x2, afl), 2, BF (Gruener Block = Aktivator) LINE (x1, afl)-(x2, 462), 15, BF Block weiss malen=alten Wert loeschen bfl = 51 + b(i) * fb: LINE (x1, bfl)-(x2, bfl + 10), 12, BF sfl = 51 + s(i) * fs: LINE (x1, sfl)-(x2, sfl + 3), 1, BF IF RC > 0 THEN nur wenn 2 Inhibitoren verwendet werden cfl = 51 + c(i) * fc LINE (x1, cfl)-(x2, cfl + 3), 13, BF END IF x1 = x2: NEXT DO UNTIL TIMER t >.1: LOOP: t = TIMER Bremse; sonst ggf. zu schnell t = TIMER Neue Zeitmessung IF INKEY$ > THEN EXIT FOR Jeder Tastendruck dazwischen macht Abbruch NEXT itot LOCATE 30, 1: PRINT w = Weiter; n = Neustart; s = Start einer anderen ; PRINT Simulation, andere Taste=Ende ; a$ = : DO UNTIL a$ > : a$ = INKEY$: LOOP Warten auf Taste SELECT CASE a$ CASE c, w, W : GOTO continuo Weiter rechnen CASE n, N : GOTO start Neu anfangen CASE s, S : LOCATE 30, 1: PRINT p = Periodische Verteilung; g = Gradient, ; Auswahl der Muster PRINT o = Oszillierende polare V.; e = Ende ; simtyp$ = : DO UNTIL simtyp$ > : simtyp$ = INKEY$: LOOP Warten auf Taste GOTO start END SELECT 52 Biologie in unserer Zeit 31. Jahrgang 2001 Nr. 1
6 STRUKTURBILDUNGSPROZESSE DAS EXPERIMENT BASIC-Familie (QB oder Professional BASIC) sowie mit Power-BASIC übersetzt werden. Nach leichtem Umbau kann der Code auch in ein Visual Basic Projekt für Windows integriert werden. Auch der Interpreter QBASIC ist geeignet. Er wurde früher standardmäßig mit Windows ausgeliefert (im DOS-Ordner) und ist vermutlich noch auf dem einen oder anderen älteren Rechner verfügbar. Die Ausführungsgeschwindigkeit mit diesem Interpreter ist aber etwas langsamer als bei Verwendung der anderen Compiler. Die fertig übersetzte Version, die vom Internet heruntergeladen werden kann, wurde mit Power-Basic übersetzt (patt-ex.exe; das Programm entpackt sich selbst und stellt dann die lauffähige Version (pattern.exe) und den Quellcode (pattern.bas) zur Verfügung). Da das Programm sehr einfach ist, sollte eine Umsetzung in eine andere Programmsprache keine Schwierigkeiten bereiten. Programme, bei denen die Parameter interaktiv geändert werden können und die auch zweidimensionale Simulationen erlauben, sind an anderer Stelle zu finden [2]. Dieses Programme erlauben auch Manipulationen wie beispielsweise das Entfernen von Zellen, um die Regeneration zu simulieren. Literatur [1] A. Gierer und H. Meinhardt, A theory of biological pattern formation. Kybernetik 1972, 12, (Eine Kopie dieser Arbeit ist über [5] erhältlich). [2] H. Meinhardt, Wie Schnecken sich in Schale werfen, (mit PC- Programmen), Springer-Verlag, Heidelberg, [3] D.M. Raskin and P. de Boer, Rapid pole-to-pole oscillation of a protein required for directing division to the middle of escherichia coli, PNAS 1999, 96, Autor Der Autor ist den Lesern aus BIUZ 2001, 31, Seite 29, bekannt. Anschrift: Prof. Dr. Hans Meinhardt, Max-Planck-Institut für Entwicklungsbiologie, Spemannstraße 35, D Tübingen. Hans.Meinhardt@Tuebingen.mpg.de Nr Jahrgang 2001 Biologie in unserer Zeit 53
Kopf- & Fußbildung der Hydra
 Kopf- & Fußbildung der Hydra Übersicht I. Die Biologie der Hydra II. Modellierung der Hydra III. Experiment vs. Theorie Übersicht I. Die Biologie der Hydra II. Modellierung der Hydra III. Experiment vs.
Kopf- & Fußbildung der Hydra Übersicht I. Die Biologie der Hydra II. Modellierung der Hydra III. Experiment vs. Theorie Übersicht I. Die Biologie der Hydra II. Modellierung der Hydra III. Experiment vs.
Wie Schnecken sich in Schale werfen
 Hans Meinhardt Wie Schnecken sich in Schale werfen Muster tropischer Meeresschnecken als dynamische Systeme Mit Beiträgen und Bildern von Przemyslaw Prusinkiewicz und Deborah R. Fowler Mit 120 Abbildungen,
Hans Meinhardt Wie Schnecken sich in Schale werfen Muster tropischer Meeresschnecken als dynamische Systeme Mit Beiträgen und Bildern von Przemyslaw Prusinkiewicz und Deborah R. Fowler Mit 120 Abbildungen,
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Synthetische Muster für lokale Suchalgorithmen
 Medizin Michael Dienst Synthetische Muster für lokale Suchalgorithmen Wissenschaftlicher Aufsatz Synthetische Muster für lokale Suchalgorithmen Beuth-Hochschule für Technik FB VIII Maschinenbau, Umwelt-
Medizin Michael Dienst Synthetische Muster für lokale Suchalgorithmen Wissenschaftlicher Aufsatz Synthetische Muster für lokale Suchalgorithmen Beuth-Hochschule für Technik FB VIII Maschinenbau, Umwelt-
Dynamische Strukturbildung in Zellen. Teilungsprozess der Bakteriezelle E.coli. Referent:Janosch Deeg 23.Mai 2006
 Teilungsprozess der Bakteriezelle E.coli. Referent: 23.Mai 2006 Gliederung Zellbiologie 1 Einleitung Zellbiologie 2 MinCDE-System 3 Zellteilung Zellbiologie Kontrollsystem periodisch ablaufende biochemische
Teilungsprozess der Bakteriezelle E.coli. Referent: 23.Mai 2006 Gliederung Zellbiologie 1 Einleitung Zellbiologie 2 MinCDE-System 3 Zellteilung Zellbiologie Kontrollsystem periodisch ablaufende biochemische
Beispiellösungen zu Blatt 77
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 77 Die Zahl 9 ist sowohl als Summe der drei aufeinanderfolgenden Quadratzahlen,
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 77 Die Zahl 9 ist sowohl als Summe der drei aufeinanderfolgenden Quadratzahlen,
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Übungen mit dem Applet Vergleich von zwei Mittelwerten
 Vergleich von zwei Mittelwerten 1 Übungen mit dem Applet Vergleich von zwei Mittelwerten 1 Statistischer Hintergrund... 2 1.1 Typische Fragestellungen...2 1.2 Fehler 1. und 2. Art...2 1.3 Kurzbeschreibung
Vergleich von zwei Mittelwerten 1 Übungen mit dem Applet Vergleich von zwei Mittelwerten 1 Statistischer Hintergrund... 2 1.1 Typische Fragestellungen...2 1.2 Fehler 1. und 2. Art...2 1.3 Kurzbeschreibung
So viel wie möglich Extremwertaufgaben aus Geometrie
 So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
So viel wie möglich Extremwertaufgaben aus Geometrie Andreas Ulovec 1 Einführung Die meisten Leute sind mit Extremwertaufgaben vertraut: Was ist das flächengrößte Dreieck, das man in einen Kreis einschreiben
Musterbildung. Vom Kleinen zum Großen. 4. Lange Nacht der Mathematik. Thomas Westermann. Formen u. Muster. Differenzialgleichungen.
 bildung Vom Kleinen zum Großen Thomas Westermann 4. Lange Nacht der Mathematik HS Karlsruhe 12. Mai 2006 Formen und Formen und Formen und Formen und A R U B L R L UB = UR + UL U B U = RI() t + LI'() t
bildung Vom Kleinen zum Großen Thomas Westermann 4. Lange Nacht der Mathematik HS Karlsruhe 12. Mai 2006 Formen und Formen und Formen und Formen und A R U B L R L UB = UR + UL U B U = RI() t + LI'() t
Dieses Kapitel vermittelt:
 2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
Systemwissenschaften, Mathematik und Statistik
 Systemwissenschaften, Mathematik und Statistik Systemwissenschaften: 1 WS: Systemwissenschaften 1, VO 2std 2 SS: Systemwissenschaften 2, VO 2std Übung zu Systemwissenschaften, UE 2std 3 WS: Systemwissenschaften
Systemwissenschaften, Mathematik und Statistik Systemwissenschaften: 1 WS: Systemwissenschaften 1, VO 2std 2 SS: Systemwissenschaften 2, VO 2std Übung zu Systemwissenschaften, UE 2std 3 WS: Systemwissenschaften
Bildverarbeitung: Diffusion Filters. D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10
 Bildverarbeitung: Diffusion Filters D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10 Diffusion Idee Motiviert durch physikalische Prozesse Ausgleich der Konzentration eines Stoffes. Konzentration
Bildverarbeitung: Diffusion Filters D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10 Diffusion Idee Motiviert durch physikalische Prozesse Ausgleich der Konzentration eines Stoffes. Konzentration
$Id: linabb.tex,v /01/09 13:27:34 hk Exp hk $
 Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
3. Diffusion und Brechungsindex
 3. Diffusion und Brechungsinde Die Diffusion in und aus einer Schicht ist die Grundlage vieler Sensoreffekte, wobei sich die einzelnen Sensoren dann nur noch in der Art der Übersetzung in ein meßbares
3. Diffusion und Brechungsinde Die Diffusion in und aus einer Schicht ist die Grundlage vieler Sensoreffekte, wobei sich die einzelnen Sensoren dann nur noch in der Art der Übersetzung in ein meßbares
GRUNDLEGENDE MODELLE. Caroline Herbek
 GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
Der Algorithmus von Bresenham
 Der Algorithmus von Bresenham Das Bresenham-Verfahren beruht im wesentlichen auf zwei grundsätzliche Beobachtungen: - Es reicht ein Verfahren aus um Geraden mit einer Steigung im Bereich von null bis eins
Der Algorithmus von Bresenham Das Bresenham-Verfahren beruht im wesentlichen auf zwei grundsätzliche Beobachtungen: - Es reicht ein Verfahren aus um Geraden mit einer Steigung im Bereich von null bis eins
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Der Weg eines Betrunkenen
 Der Weg eines Betrunkenen 2 Hätte es damals schon Computer gegeben, wäre es für unseren Mathematiker um einiges leichter gewesen, den Weg des Betrunkenen zu bestimmen. Er hätte nicht nur eine beliebige
Der Weg eines Betrunkenen 2 Hätte es damals schon Computer gegeben, wäre es für unseren Mathematiker um einiges leichter gewesen, den Weg des Betrunkenen zu bestimmen. Er hätte nicht nur eine beliebige
Mathematische Werkzeuge für Computergrafik 2016/17. Gleitkommzahlen
 Mathematische Werkzeuge für Computergrafik 2016/17 Gleitkommzahlen 1 Grundlagen 1 Da im Computer nur endliche Ressourcen zur Verfügung stehen, können reelle Zahlen in vielen Fällen nicht exakt dargestellt
Mathematische Werkzeuge für Computergrafik 2016/17 Gleitkommzahlen 1 Grundlagen 1 Da im Computer nur endliche Ressourcen zur Verfügung stehen, können reelle Zahlen in vielen Fällen nicht exakt dargestellt
I.1.3 b. (I.7a) I.1 Grundbegriffe der Newton schen Mechanik 9
 I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
I. Grundbegriffe der Newton schen Mechanik 9 I..3 b Arbeit einer Kraft Wird die Wirkung einer Kraft über ein Zeitintervall oder genauer über die Strecke, welche das mechanische System in diesem Zeitintervall
Was ist eine Funktion?
 Lerndomino zum Thema Funktionsbegriff Kopiereen Sie die Seite (damit Sie einen Kontrollbogen haben), schneiden Sie aus der Kopie die "Dominosteine" zeilenweise aus, mischen Sie die "Dominosteine" und verteilen
Lerndomino zum Thema Funktionsbegriff Kopiereen Sie die Seite (damit Sie einen Kontrollbogen haben), schneiden Sie aus der Kopie die "Dominosteine" zeilenweise aus, mischen Sie die "Dominosteine" und verteilen
Wenn man den Kreis mit Radius 1 um (0, 0) beschreiben möchte, dann ist. (x, y) ; x 2 + y 2 = 1 }
 A Analsis, Woche Implizite Funktionen A Implizite Funktionen in D A3 Wenn man den Kreis mit Radius um, beschreiben möchte, dann ist { x, ; x + = } eine Möglichkeit Oft ist es bequemer, so eine Figur oder
A Analsis, Woche Implizite Funktionen A Implizite Funktionen in D A3 Wenn man den Kreis mit Radius um, beschreiben möchte, dann ist { x, ; x + = } eine Möglichkeit Oft ist es bequemer, so eine Figur oder
[A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration
![[A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration [A] = c(a) in den Einheiten mol/l (1) Eine tiefgestellte Null wie bei [A] 0 zeigt an, dass es sich um eine Anfangskonzentration](/thumbs/66/55829074.jpg) 1 Ableitung des Massenwirkungsgesetzes Mit dem Umfüllexperiment haben wir herausgefunden, dass die Stoffmengen oder die Stoffmengenkonzentrationen im Gleichgewicht auf einen Grenzwert zulaufen. Außerdem
1 Ableitung des Massenwirkungsgesetzes Mit dem Umfüllexperiment haben wir herausgefunden, dass die Stoffmengen oder die Stoffmengenkonzentrationen im Gleichgewicht auf einen Grenzwert zulaufen. Außerdem
7.11. Extrema unter Nebenbedingungen
 7.11. Extrema unter Nebenbedingungen Randextrema Wir haben schon bemerkt, daß die üblichen Tests mit Hilfe von (eventuell höheren) Ableitungen nur Kriterien für (lokale) Extrema im Inneren des Definitionsgebietes
7.11. Extrema unter Nebenbedingungen Randextrema Wir haben schon bemerkt, daß die üblichen Tests mit Hilfe von (eventuell höheren) Ableitungen nur Kriterien für (lokale) Extrema im Inneren des Definitionsgebietes
Klausur Mathematik I
 Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Nullstellen von algebraischen Gleichungen
 Kapitel 2 Nullstellen von algebraischen Gleichungen 2.1 Vorbemerkungen Suche Lösung der Gleichung f(x) = 0 (2.1) Dies ist die Standardform für eine Dimension. - typisch nichtlineare Gleichung, sonst elementar
Kapitel 2 Nullstellen von algebraischen Gleichungen 2.1 Vorbemerkungen Suche Lösung der Gleichung f(x) = 0 (2.1) Dies ist die Standardform für eine Dimension. - typisch nichtlineare Gleichung, sonst elementar
Intensivübung zu Algorithmen und Datenstrukturen
 Intensivübung zu Algorithmen und Datenstrukturen Silvia Schreier Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Übersicht Programmierung Fallunterscheidung Flussdiagramm Bedingungen Boolesche
Intensivübung zu Algorithmen und Datenstrukturen Silvia Schreier Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Übersicht Programmierung Fallunterscheidung Flussdiagramm Bedingungen Boolesche
Schleifeninvarianten. Dezimal zu Binär
 Schleifeninvarianten Mit vollstandiger Induktion lasst sich auch die Korrektheit von Algorithmen nachweisen. Will man die Werte verfolgen, die die Variablen beim Ablauf eines Algorithmus annehmen, dann
Schleifeninvarianten Mit vollstandiger Induktion lasst sich auch die Korrektheit von Algorithmen nachweisen. Will man die Werte verfolgen, die die Variablen beim Ablauf eines Algorithmus annehmen, dann
Zelluläre Automaten. Sommerakademie Ftan Daniel Abler
 Zelluläre Automaten Sommerakademie Ftan 2004 Daniel Abler Zelluläre Automaten 1.Merkmale komplexer Systeme bzw. zellulärer Automaten 2.Grundcharakteristika - Game of Life 3.Definition 4.Eigenschaften und
Zelluläre Automaten Sommerakademie Ftan 2004 Daniel Abler Zelluläre Automaten 1.Merkmale komplexer Systeme bzw. zellulärer Automaten 2.Grundcharakteristika - Game of Life 3.Definition 4.Eigenschaften und
Einiges zu den Potenzfunktionen. Exponentialfunktionen
 Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
A2.3 Lineare Gleichungssysteme
 A2.3 Lineare Gleichungssysteme Schnittpunkte von Graphen Bereits weiter oben wurden die Schnittpunkte von Funktionsgraphen mit den Koordinatenachsen besprochen. Wenn sich zwei Geraden schneiden, dann müssen
A2.3 Lineare Gleichungssysteme Schnittpunkte von Graphen Bereits weiter oben wurden die Schnittpunkte von Funktionsgraphen mit den Koordinatenachsen besprochen. Wenn sich zwei Geraden schneiden, dann müssen
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Anleitung zum Applet. Rangwerte
 Rangwerte 1 Anleitung zum Applet Rangwerte bearbeitet von: Erwin Wagner WS 2006/2007 E/TI betreut von: Prof. Dr. Wilhelm Kleppmann Rangwerte 2 Inhaltsverzeichnis 1 VORWORT... 3 2 BENUTZEROBERFLÄCHE...
Rangwerte 1 Anleitung zum Applet Rangwerte bearbeitet von: Erwin Wagner WS 2006/2007 E/TI betreut von: Prof. Dr. Wilhelm Kleppmann Rangwerte 2 Inhaltsverzeichnis 1 VORWORT... 3 2 BENUTZEROBERFLÄCHE...
Füllen von Primitiven
 Füllen von Primitiven Basisproblem der 2D-Graphik Anwendung: füllen beliebiger Flächen (Polygone, Freiformkurven) Darstellung von Buchstaben dicke Primitive (Linien, Kreise, Kurven), Teilproblem in der
Füllen von Primitiven Basisproblem der 2D-Graphik Anwendung: füllen beliebiger Flächen (Polygone, Freiformkurven) Darstellung von Buchstaben dicke Primitive (Linien, Kreise, Kurven), Teilproblem in der
Lineare Gleichungssysteme (Teschl/Teschl 11.1)
 Lineare Gleichungssysteme (Teschl/Teschl.) Ein Lineares Gleichungssystem (LGS) besteht aus m Gleichungen mit n Unbekannten x,...,x n und hat die Form a x + a 2 x 2 +... + a n x n b a 2 x + a 22 x 2 +...
Lineare Gleichungssysteme (Teschl/Teschl.) Ein Lineares Gleichungssystem (LGS) besteht aus m Gleichungen mit n Unbekannten x,...,x n und hat die Form a x + a 2 x 2 +... + a n x n b a 2 x + a 22 x 2 +...
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Arbeitsblatt 6: Programmierung geometrischer Figuren
 Arbeitsblatt 6: Programmierung geometrischer Figuren Die Karten, auf denen die Lärmmessungen dargestellt werden, bestehen aus einer Vielzahl geometrischer Formen. Diese geometrischen Formen ergeben zusammen
Arbeitsblatt 6: Programmierung geometrischer Figuren Die Karten, auf denen die Lärmmessungen dargestellt werden, bestehen aus einer Vielzahl geometrischer Formen. Diese geometrischen Formen ergeben zusammen
1 Spannung messen mit Grenzwertüberwachung
 1 Spannung messen mit Grenzwertüberwachung 1.1 Spannung simulieren Der Drehregler liefert eine Wert zwischen 0 und 10. Die Messinstrument- Anzeige und die Tankanzeige zeigen diesen Wert an. 3 LEDs neben
1 Spannung messen mit Grenzwertüberwachung 1.1 Spannung simulieren Der Drehregler liefert eine Wert zwischen 0 und 10. Die Messinstrument- Anzeige und die Tankanzeige zeigen diesen Wert an. 3 LEDs neben
Optimieren unter Nebenbedingungen
 Optimieren unter Nebenbedingungen Hier sucht man die lokalen Extrema einer Funktion f(x 1,, x n ) unter der Nebenbedingung dass g(x 1,, x n ) = 0 gilt Die Funktion f heißt Zielfunktion Beispiel: Gesucht
Optimieren unter Nebenbedingungen Hier sucht man die lokalen Extrema einer Funktion f(x 1,, x n ) unter der Nebenbedingung dass g(x 1,, x n ) = 0 gilt Die Funktion f heißt Zielfunktion Beispiel: Gesucht
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
HAK, HUM, HLSF, BAKIP (HTL1) Geogebra
 Finale Vorbereitung auf die srdp 2016 HAK, HUM, HLSF, BAKIP (HTL1) Geogebra Lösung der Bewegungsaufgabe a) Ansicht: Algebra und Grafik Eingabefenster : s(t)= Funktion[- x^3/180+x^2/2,0,100] ENTER 0der
Finale Vorbereitung auf die srdp 2016 HAK, HUM, HLSF, BAKIP (HTL1) Geogebra Lösung der Bewegungsaufgabe a) Ansicht: Algebra und Grafik Eingabefenster : s(t)= Funktion[- x^3/180+x^2/2,0,100] ENTER 0der
Satz über implizite Funktionen und seine Anwendungen
 Satz über implizite Funktionen und seine Anwendungen Gegeben sei eine stetig differenzierbare Funktion f : R 2 R, die von zwei Variablen und abhängt. Wir betrachten im Folgenden die Gleichung f(,) = 0.
Satz über implizite Funktionen und seine Anwendungen Gegeben sei eine stetig differenzierbare Funktion f : R 2 R, die von zwei Variablen und abhängt. Wir betrachten im Folgenden die Gleichung f(,) = 0.
(auch: Zellularautomaten, Polyautomaten, cellular automata, CA)
 4. Zelluläre Automaten Einordnung: Modell mit räumlich konstantem Medium, raumorientiert, diskret, mit fester Nachbarschaft der Zellen, mit kontextsensitiven Wachstumsregeln. Zelluläre Automaten (auch:
4. Zelluläre Automaten Einordnung: Modell mit räumlich konstantem Medium, raumorientiert, diskret, mit fester Nachbarschaft der Zellen, mit kontextsensitiven Wachstumsregeln. Zelluläre Automaten (auch:
Ideen und Konzepte der Informatik. Programme und Algorithmen Kurt Mehlhorn
 Ideen und Konzepte der Informatik Programme und Algorithmen Kurt Mehlhorn November 2016 Algorithmen und Programme Algorithmus = Schritt-für-Schritt Vorschrift zur Lösung eines Problems. Formuliert man
Ideen und Konzepte der Informatik Programme und Algorithmen Kurt Mehlhorn November 2016 Algorithmen und Programme Algorithmus = Schritt-für-Schritt Vorschrift zur Lösung eines Problems. Formuliert man
Diese Gleichung hat für einige a nur Lösungen aus C und nicht aus R.
 Aufgabe 1 Zahlenmengen, quadratische Gleichungen Gegeben ist eine quadratische Gleichung a 0 mit a R. Kreuzen Sie die beiden zutreffenden Aussagen an! Diese Gleichung hat für einige a nur Lösungen aus
Aufgabe 1 Zahlenmengen, quadratische Gleichungen Gegeben ist eine quadratische Gleichung a 0 mit a R. Kreuzen Sie die beiden zutreffenden Aussagen an! Diese Gleichung hat für einige a nur Lösungen aus
Diffusion. Prüfungsfrage
 Prüfungsfrage Diffusion Die Diffusion. Erstes Fick sches Gesetz. Der Diffusionskoeffizient. Die Stokes-Einstein Beziehung. Diffusion durch die Zellmembrane: passive, aktive und erleichterte Diffusion Lehrbuch
Prüfungsfrage Diffusion Die Diffusion. Erstes Fick sches Gesetz. Der Diffusionskoeffizient. Die Stokes-Einstein Beziehung. Diffusion durch die Zellmembrane: passive, aktive und erleichterte Diffusion Lehrbuch
Musterbildung in biologischen Systemen
 Musterbildung in biologischen Systemen Praktikum: Nichtlineare Modellierung in den Naturwissenschaften Jan Hendrik Bongers, Fabian Eustermann Westfälische Wilhelms-Universität Münster 25. Juli 2013 J.
Musterbildung in biologischen Systemen Praktikum: Nichtlineare Modellierung in den Naturwissenschaften Jan Hendrik Bongers, Fabian Eustermann Westfälische Wilhelms-Universität Münster 25. Juli 2013 J.
Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen
 MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
MATHEMATISCHES INSTITUT SoSe 24 DER UNIVERSITÄT MÜNCHEN Probeklausur zu Funktionentheorie, Lebesguetheorie und gewöhnlichen Differentialgleichungen Musterlösung Prof. Dr. P. Pickl Aufgabe Zeigen Sie, dass
Zur Berechnung der Wertziffern bei Teamturnieren
 Zur Berechnung der Wertziffern bei Teamturnieren Wolfhart Umlauft und Michael Stieglitz 30. März 2009 1 Das Problem Die in der Rangliste für Teamturniere angegebenen Zahlen sind sog. Wertziffern. Sie spiegeln
Zur Berechnung der Wertziffern bei Teamturnieren Wolfhart Umlauft und Michael Stieglitz 30. März 2009 1 Das Problem Die in der Rangliste für Teamturniere angegebenen Zahlen sind sog. Wertziffern. Sie spiegeln
Beschränktheit, Monotonie & Symmetrie
 Beschränktheit, Monotonie & Symmetrie ein Referat Dies ist eine Beilage zum Gruppen-SOL - Projekt Potenz- & Exponentialfunktionen Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch November 2015 Inhaltsverzeichnis
Beschränktheit, Monotonie & Symmetrie ein Referat Dies ist eine Beilage zum Gruppen-SOL - Projekt Potenz- & Exponentialfunktionen Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch November 2015 Inhaltsverzeichnis
Die Lösungen der Gleichung b x = log b (x)
 Die Lösungen der Gleichung b = log b () wgnedin@math.uni-koeln.de 17. Januar 2014 In der ersten Vorlesung des Wintersemesters wurde folgende Frage gestellt: Wieviele Lösungen hat die Gleichung ( ) 1 =
Die Lösungen der Gleichung b = log b () wgnedin@math.uni-koeln.de 17. Januar 2014 In der ersten Vorlesung des Wintersemesters wurde folgende Frage gestellt: Wieviele Lösungen hat die Gleichung ( ) 1 =
u v w v = 1 w u w u v schon in der Mathematik gesehen?
 Die Kettenregel für die Thermodynamik Ziel ist die in der Thermodynamik benutzten Differentiationsregeln die auf den ersten Blick nicht denen aus der Mathematik ähneln doch als dieselben zu beschreiben
Die Kettenregel für die Thermodynamik Ziel ist die in der Thermodynamik benutzten Differentiationsregeln die auf den ersten Blick nicht denen aus der Mathematik ähneln doch als dieselben zu beschreiben
Lineare Differenzengleichungen und Polynome. Franz Pauer
 Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck, Technikerstr. 13/7, A-600 Innsbruck, Österreich. Franz.Pauer@uibk.ac.at Vortrag beim ÖMG-LehrerInnenfortbildungstag
Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck, Technikerstr. 13/7, A-600 Innsbruck, Österreich. Franz.Pauer@uibk.ac.at Vortrag beim ÖMG-LehrerInnenfortbildungstag
Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
5 Erwartungswerte, Varianzen und Kovarianzen
 47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
10.6. Implizite ebene Kurven und Tangenten
 0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
Vierte Schularbeit Mathematik Klasse 7A G am xx
 Vierte Schularbeit Mathematik Klasse 7A G am xx.05.2016 SCHÜLERNAME: Punkte im ersten Teil: Punkte im zweiten Teil: Davon Kompensationspunkte: Note: Notenschlüssel: Falls die Summe der erzielten Kompensationspunkte
Vierte Schularbeit Mathematik Klasse 7A G am xx.05.2016 SCHÜLERNAME: Punkte im ersten Teil: Punkte im zweiten Teil: Davon Kompensationspunkte: Note: Notenschlüssel: Falls die Summe der erzielten Kompensationspunkte
Aufgaben / Lösungen der Klausur Nr. 4 vom Juni 2002 im LK 12. nx ln(x)dx
 Aufgaben / Lösungen der Klausur Nr. 4 vom Juni 2002 im LK 2 Aufgabe ) a) Berechne für alle natürlichen Zahlen n N das Integral e nx ln(x)dx. Mit Hilfe der partiellen Integration für f (x) = nx, somit f(x)
Aufgaben / Lösungen der Klausur Nr. 4 vom Juni 2002 im LK 2 Aufgabe ) a) Berechne für alle natürlichen Zahlen n N das Integral e nx ln(x)dx. Mit Hilfe der partiellen Integration für f (x) = nx, somit f(x)
Atmung, Dissimilation
 Atmung, Dissimilation Peter Bützer Abbildung 1: Atmung Inhalt 1 Physiologisches... 1 2 Atmung, eine Reaktion 0. Ordnung... 2 3 Simulation... 2 4 Interpretation... 4 5 Mikroökologie im Zimmer... 4 6 Interpretation...
Atmung, Dissimilation Peter Bützer Abbildung 1: Atmung Inhalt 1 Physiologisches... 1 2 Atmung, eine Reaktion 0. Ordnung... 2 3 Simulation... 2 4 Interpretation... 4 5 Mikroökologie im Zimmer... 4 6 Interpretation...
Übungen mit dem Applet Kurven in Polarkoordinaten
 Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
Kurven in Polarkoordinaten 1 Übungen mit dem Applet Kurven in Polarkoordinaten 1 Ziele des Applets...2 2 Wie entsteht eine Kurve in Polarkoordinaten?...3 3 Kurvenverlauf für ausgewählte r(ϕ)...4 3.1 r
Mathematik für Wirtschaftswissenschaftler
 Mathematik für Wirtschaftswissenschaftler Yves Schneider Universität Luzern Frühjahr 2016 Repetition Kapitel 1 bis 3 2 / 54 Repetition Kapitel 1 bis 3 Ausgewählte Themen Kapitel 1 Ausgewählte Themen Kapitel
Mathematik für Wirtschaftswissenschaftler Yves Schneider Universität Luzern Frühjahr 2016 Repetition Kapitel 1 bis 3 2 / 54 Repetition Kapitel 1 bis 3 Ausgewählte Themen Kapitel 1 Ausgewählte Themen Kapitel
Geordnetes Chaos Untersuchungen zur Langton Ameise
 Geordnetes Chaos Untersuchungen zur Langton Ameise Die sogenannte "Langton Ameise" ist die Umsetzung einfacher Regeln, nach denen sich ein Punkt auf dem Bildschirm bewegen soll und Spuren hinterlässt.
Geordnetes Chaos Untersuchungen zur Langton Ameise Die sogenannte "Langton Ameise" ist die Umsetzung einfacher Regeln, nach denen sich ein Punkt auf dem Bildschirm bewegen soll und Spuren hinterlässt.
Biochemische Oszillationen
 Biochemische Oszillationen Al-Aifari Reema 16. November 2008 Bakkalaureatsarbeit aus Mathematische Modelle in der Technik, Johannes Kepler Universität Linz, WS 2007/08. Name: Al-Aifari Reema Matr.Nr.:
Biochemische Oszillationen Al-Aifari Reema 16. November 2008 Bakkalaureatsarbeit aus Mathematische Modelle in der Technik, Johannes Kepler Universität Linz, WS 2007/08. Name: Al-Aifari Reema Matr.Nr.:
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I
 Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Simulation von Brownscher Dynamik und Assoziationsraten von PP-Komplexen. Alexander Baldauf Montag
 Simulation von Brownscher Dynamik und Assoziationsraten von PP-Komplexen Alexander Baldauf Montag 25.04.2005 Motivation Typen von Interaktionen Verschiedene Methoden zur Vorhersage Wie kommen die beiden
Simulation von Brownscher Dynamik und Assoziationsraten von PP-Komplexen Alexander Baldauf Montag 25.04.2005 Motivation Typen von Interaktionen Verschiedene Methoden zur Vorhersage Wie kommen die beiden
Simulation. Lineare Regression Methode der kleinsten Quadrate (Excel-Matrix-Formel) Verknüpfung des Euler- und Newton-Verfahrens. Das Euler-Verfahren
 Simulation Lineare Regression Methode der kleinsten Quadrate (Excel-Matrix-Formel) Verknüpfung des Euler- und Newton-Verfahrens Dynamische Prozesse: Prozesse, bei denen sich das zeitliche und örtliche
Simulation Lineare Regression Methode der kleinsten Quadrate (Excel-Matrix-Formel) Verknüpfung des Euler- und Newton-Verfahrens Dynamische Prozesse: Prozesse, bei denen sich das zeitliche und örtliche
FACHCURRICULUM KL. 9. Raum und Form Figuren zentrisch strecken Üben und Festigen. Strahlensätze. Rechtwinklige Dreiecke.
 MATHEMATIK Schönbuch-Gymnasium Holzgerlingen Seite 1/5 Ähnliche Figuren - Strahlensätze Figuren zentrisch strecken Eigenschaften der zentrischen Streckung kennen und Zentrische Streckung anwenden Strahlensätze
MATHEMATIK Schönbuch-Gymnasium Holzgerlingen Seite 1/5 Ähnliche Figuren - Strahlensätze Figuren zentrisch strecken Eigenschaften der zentrischen Streckung kennen und Zentrische Streckung anwenden Strahlensätze
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Tutorial zum Umgang mit Scratch
 Tutorial zum Umgang mit Scratch In diesem Tutorial sollst du die grundlegenden Funktionen von Scratch ausprobieren und kennen lernen Danach solltest du gut mit dem Programm umgehen können und eigene Programme
Tutorial zum Umgang mit Scratch In diesem Tutorial sollst du die grundlegenden Funktionen von Scratch ausprobieren und kennen lernen Danach solltest du gut mit dem Programm umgehen können und eigene Programme
Ebenengleichungen und Umformungen
 Ebenengleichungen und Umformungen. Januar 7 Ebenendarstellungen. Parameterdarstellung Die Parameterdarstellung einer Ebene ist gegeben durch einen Stützvektor r, der einen Punkt auf der Ebene angibt und
Ebenengleichungen und Umformungen. Januar 7 Ebenendarstellungen. Parameterdarstellung Die Parameterdarstellung einer Ebene ist gegeben durch einen Stützvektor r, der einen Punkt auf der Ebene angibt und
Chemische Oszillationen
 Ludwig Pohlmann Thermodynamik offener Systeme und Selbstorganisationsphänomene SS 007 Chemische Oszillationen. Chemische (Formal-)Kinetik Die chemische Kinetik untersucht die Geschwindigkeit und den Mechanismus
Ludwig Pohlmann Thermodynamik offener Systeme und Selbstorganisationsphänomene SS 007 Chemische Oszillationen. Chemische (Formal-)Kinetik Die chemische Kinetik untersucht die Geschwindigkeit und den Mechanismus
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 6. Teil Die Berechnung des Geschwindigkeitsfeldes
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 6. Teil Die Berechnung des Geschwindigkeitsfeldes
Der folgende Vortrag basiert auf dem Text A Polynomial Time Algorithm for the N-Queens Problem von Rok Sosic und Jun Gu aus dem Jahre 1990.
 Ein polynomieller Algorithmus für das N-Damen Problem 1 Einführung Der folgende Vortrag basiert auf dem Text A Polynomial Time Algorithm for the N-Queens Problem von Rok Sosic und Jun Gu aus dem Jahre
Ein polynomieller Algorithmus für das N-Damen Problem 1 Einführung Der folgende Vortrag basiert auf dem Text A Polynomial Time Algorithm for the N-Queens Problem von Rok Sosic und Jun Gu aus dem Jahre
6 Differentialgleichungen
 93 6 Differentialgleichungen Eine Differentialgleichung ist eine Gleichung, in der eine unbekannte Funktion y = y(x) und Ableitungen (die erste oder auch höhere) von y vorkommen. Lösungen einer Differentialgleichung
93 6 Differentialgleichungen Eine Differentialgleichung ist eine Gleichung, in der eine unbekannte Funktion y = y(x) und Ableitungen (die erste oder auch höhere) von y vorkommen. Lösungen einer Differentialgleichung
Übungsaufgaben zur Analysis
 Serie Übungsaufgaben zur Analysis. Multiplizieren Sie folgende Klammern aus: ( + 3y)( + 4a + 4b) (a b )( + 3y 4) (3 + )(7 + y) + (a + b)(3 + ). Multiplizieren Sie folgende Klammern aus: 6a( 3a + 5b c)
Serie Übungsaufgaben zur Analysis. Multiplizieren Sie folgende Klammern aus: ( + 3y)( + 4a + 4b) (a b )( + 3y 4) (3 + )(7 + y) + (a + b)(3 + ). Multiplizieren Sie folgende Klammern aus: 6a( 3a + 5b c)
Lineare (Un-)Gleichungen und lineare Optimierung
 Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-6020 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung In der linearen
Lineare (Un-)Gleichungen und lineare Optimierung Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-6020 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung In der linearen
Etwas Spezielles: Zielwertsuche und Solver. Zielwertsuche
 Etwas Spezielles: Zielwertsuche und Solver Zielwertsuche EXCEL kann auch Beziehungen indirekt auflösen. Die einfache Variante ist die Zielwertsuche. Für eine bestimmte Zelle ("Zielzelle") wird ein anderer
Etwas Spezielles: Zielwertsuche und Solver Zielwertsuche EXCEL kann auch Beziehungen indirekt auflösen. Die einfache Variante ist die Zielwertsuche. Für eine bestimmte Zelle ("Zielzelle") wird ein anderer
Numerische Integration
 A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
1 Differentialrechnung
 BT/MT SS 6 Mathematik II Klausurvorbereitung www.eah-jena.de/~puhl Thema: Üben, üben und nochmals üben!!! Differentialrechnung Aufgabe Differenzieren Sie folgende Funktionen: a y = ln( b f( = a a + c f(
BT/MT SS 6 Mathematik II Klausurvorbereitung www.eah-jena.de/~puhl Thema: Üben, üben und nochmals üben!!! Differentialrechnung Aufgabe Differenzieren Sie folgende Funktionen: a y = ln( b f( = a a + c f(
Fit in Mathe. Januar Klassenstufe 11 Umkehrfunktion. f x ist 2,5 also Buchstabenpaar GA.
 Thema Musterlösungen 1 Umkehrfunktion Bestimme zur Funktion f die Umkehrfunktion f, dargestellt als Tabelle. x 0 1 2 3 4 f x 1 3 5 7 9 x 0 1 2 3 4 f x -0,5 0 0,5 1 1,5 Die Summe der 5 Werte von f x ist
Thema Musterlösungen 1 Umkehrfunktion Bestimme zur Funktion f die Umkehrfunktion f, dargestellt als Tabelle. x 0 1 2 3 4 f x 1 3 5 7 9 x 0 1 2 3 4 f x -0,5 0 0,5 1 1,5 Die Summe der 5 Werte von f x ist
1 Umkehrfunktionen und implizite Funktionen
 Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
1/2 2 v 1/5 0 0 E H I E H I
 Lineare Algebra 1. Chemische Reaktionen Bei einer hypothetischen Reaktion zwischen Molekülen A und Molekülen B geht pro Zeiteinheit der Bruchteil p = 0.3 der Moleküle A in Moleküle B und der Bruchteil
Lineare Algebra 1. Chemische Reaktionen Bei einer hypothetischen Reaktion zwischen Molekülen A und Molekülen B geht pro Zeiteinheit der Bruchteil p = 0.3 der Moleküle A in Moleküle B und der Bruchteil
Lösungen 10 (Kinetik)
 Chemie I WS 2003/2004 Lösungen 10 (Kinetik) Aufgabe 1 Verschiedenes 1.1 Als Reaktionsgeschwindigkeit v c wird die Ableitung der Konzentration eines Reaktanden A nach der Zeit t, dividiert durch dessen
Chemie I WS 2003/2004 Lösungen 10 (Kinetik) Aufgabe 1 Verschiedenes 1.1 Als Reaktionsgeschwindigkeit v c wird die Ableitung der Konzentration eines Reaktanden A nach der Zeit t, dividiert durch dessen
Aufgaben zum Wasserstoffatom
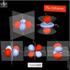 Aufgaben zum Wasserstoffatom Hans M. Strauch Kurfürst-Ruprecht-Gymnasium Neustadt/W. Aufgabenarten Darstellung von Zusammenhängen, Abgrenzung von Unterschieden (können u.u. recht offen sein) Beantwortung
Aufgaben zum Wasserstoffatom Hans M. Strauch Kurfürst-Ruprecht-Gymnasium Neustadt/W. Aufgabenarten Darstellung von Zusammenhängen, Abgrenzung von Unterschieden (können u.u. recht offen sein) Beantwortung
Anhang 2: Modellierung: Der Kurs des DAX
 Anhang 2: Modellierung: Der Kurs des DAX Die Abbildungen A2.1 A2.10 zeigen, wie man mit dem Computertool Vensim dynamische Systeme an Hand von Daten (DAX-Entwicklung) modelliert und simuliert. In Abb.
Anhang 2: Modellierung: Der Kurs des DAX Die Abbildungen A2.1 A2.10 zeigen, wie man mit dem Computertool Vensim dynamische Systeme an Hand von Daten (DAX-Entwicklung) modelliert und simuliert. In Abb.
Einführung: Wovon handelt die Thermodynamik? Was sind thermodynamische Systeme?
 Einführung: Wovon handelt die Thermodynamik? Was sind thermodynamische Systeme? Thermodynamische Systeme: 1. Charakteristikum: - sehr große Anzahl von Freiheitsgraden: N = 6 10 23 Teilchen pro Mol - es
Einführung: Wovon handelt die Thermodynamik? Was sind thermodynamische Systeme? Thermodynamische Systeme: 1. Charakteristikum: - sehr große Anzahl von Freiheitsgraden: N = 6 10 23 Teilchen pro Mol - es
Verbindung Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1
 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
Mathematik II Frühlingsemester 2015 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren
 Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Aufgaben zur Übung der Anwendung von GeoGebra
 Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
In dieser Aufgabe geht es darum, das einfache Meteor-Spiel zu verstehen und anzupassen. Lade als erstes das Spiel sample12 und spiele es.
 In dieser Aufgabe geht es darum, das einfache Meteor-Spiel zu verstehen und anzupassen. Lade als erstes das Spiel sample12 und spiele es. Im Spiel fällt ein Meteor vom oben zum unteren Rand. Das Raumschiff
In dieser Aufgabe geht es darum, das einfache Meteor-Spiel zu verstehen und anzupassen. Lade als erstes das Spiel sample12 und spiele es. Im Spiel fällt ein Meteor vom oben zum unteren Rand. Das Raumschiff
ARBEITSBLATT 6-5. Kurvendiskussion
 ARBEITSBLATT 6-5 Kurvendiskussion Die mathematische Untersuchung des Graphen einer Funktion heißt Kurvendiskussion. Die Differentialrechnung liefert dabei wichtige Dienste. Intuitive Erfassung der Begriffe
ARBEITSBLATT 6-5 Kurvendiskussion Die mathematische Untersuchung des Graphen einer Funktion heißt Kurvendiskussion. Die Differentialrechnung liefert dabei wichtige Dienste. Intuitive Erfassung der Begriffe
Nichtlineare Prozesse in der Elektrochemie II
 Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
49 Mathematik für Biologen, Biotechnologen und Biochemiker
 49 Mathematik für Biologen, Biotechnologen und Biochemiker 43 Momentane Wachstumsrate, Zuwachsrate pro Zeiteinheit und die Verdoppelungszeit Jede Exponentialfunktion f(t) = c exp(t) ist durch die beiden
49 Mathematik für Biologen, Biotechnologen und Biochemiker 43 Momentane Wachstumsrate, Zuwachsrate pro Zeiteinheit und die Verdoppelungszeit Jede Exponentialfunktion f(t) = c exp(t) ist durch die beiden
Stetigkeit von Funktionen
 Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Frequenzbewertung von Luftschallsignalen
 04/17 von Luftschallsignalen Das menschliche Ohr empfindet Töne mit gleichem Schalldruck aber unterschiedlichen Tonhöhen unterschiedlich laut. Dieser frequenzabhängige Empfindlichkeitsverlauf des menschlichen
04/17 von Luftschallsignalen Das menschliche Ohr empfindet Töne mit gleichem Schalldruck aber unterschiedlichen Tonhöhen unterschiedlich laut. Dieser frequenzabhängige Empfindlichkeitsverlauf des menschlichen
Lösungsskizzen zu den Klausuraufgaben zum Kurs 1142 Algorithmische Mathematik. a 0 = 0 =
 Lösungsskizzen zu den Klausuraufgaben zum Kurs 4 Algorithmische Mathematik 4KSL3 6 Punkte Aufgabe. Die Folge (a n ) n N natürlicher Zahlen a n sei rekursiv definiert durch a 0 = 0, a n = a n + n falls
Lösungsskizzen zu den Klausuraufgaben zum Kurs 4 Algorithmische Mathematik 4KSL3 6 Punkte Aufgabe. Die Folge (a n ) n N natürlicher Zahlen a n sei rekursiv definiert durch a 0 = 0, a n = a n + n falls
Relaxation. Dominik Weishaupt. 2.1 T1: Longitudinale Relaxation T2/T2*: Transversale Relaxation 8
 2 Relaxation 7 7 2 Relaxation Dominik Weishaupt 2.1 T1: Longitudinale Relaxation 8 2.2 T2/T2*: Transversale Relaxation 8 D. Weishaupt, V. D. Köchli, B. Marincek, Wie funktioniert MRI?, DOI 10.1007/978-3-642-41616-3_2,
2 Relaxation 7 7 2 Relaxation Dominik Weishaupt 2.1 T1: Longitudinale Relaxation 8 2.2 T2/T2*: Transversale Relaxation 8 D. Weishaupt, V. D. Köchli, B. Marincek, Wie funktioniert MRI?, DOI 10.1007/978-3-642-41616-3_2,
