Grundlagen der Signalverarbeitung und Robotik
|
|
|
- Hans Dieter
- vor 7 Jahren
- Abrufe
Transkript
1 Grundlagen der Signalverarbeitung und Robotik Grundlagen der Signalverarbeitung und Robotik lectures/2011ss/vorlesung/gdsr Jianwei Zhang Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Technische Aspekte Multimodaler Systeme Sommersemester 2011 J. Zhang 1
2 Gliederung Grundlagen der Signalverarbeitung und Robotik 1. Einführung 2. Grundlagen der Robotik 3. Grundlagen der Sensorik 4. Scandaten verarbeiten 5. Rekursive Zustandsschätzung 6. Fuzzy-Logik 7. Steuerungsarchitekturen J. Zhang 2
3 5 Rekursive Zustandsschätzung Grundlagen der Signalverarbeitung und Robotik Gliederung 1. Einführung 2. Grundlagen der Robotik 3. Grundlagen der Sensorik 4. Scandaten verarbeiten 5. Rekursive Zustandsschätzung Grundlagen der Wahrscheinlichkeitsrechnung Stochastische Fortpflanzungsgesetze und Belief Bayes-Filter Selbst-Lokalisierung mobiler Roboter Literatur 6. Fuzzy-Logik 7. Steuerungsarchitekturen J. Zhang 206
4 5 Rekursive Zustandsschätzung Grundlagen der Signalverarbeitung und Robotik Rekursive Zustandsschätzung Idee: Schätzung eines Systemzustands, der nicht direkt gemessen werden kann, aber aus den Messungen ableitbar ist Beobachtungen bestimmter Aspekte des Systems Steueraktionen, die das System beeinflussen Unsicherheit in Beobachtungen und Aktionen. Probabilistische Algorithmen zur Zustandsschätzungen berechnen eine belief distribution über die möglichen Zustände Der belief beschreibt das Wissen eines Systems über seinen Zustand J. Zhang 207
5 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung Sensorwerte, Stellgrößen, der Zustand eines Systems und von dessen Umgebung können als Zufallsvariable modelliert werden Sei X eine Zufallsvariable und ein Wert, den diese annehmen kann Ist der Wertebereich W von X diskret mit W = { 1, 2,..., m }, so schreibt man: p(x = ) um die Wahrscheinlichkeit anzugeben, dass X den Wert hat J. Zhang 208
6 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Die Summe diskreter Wahrscheinlichkeiten ist 1: p(x = ) = 1 Wahrscheinlichkeiten sind immer nicht-negativ, d.h. p(x = ) 0 Wir schreiben p() anstelle von p(x = ) J. Zhang 209
7 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Eine Funktion F, die durch die diskrete Zufallsvariable X bestimmt ist, heißt Verteilungsfunktion von X. Beispiel: Wert der Zufallsvariablen als vorgegebener Wert: F () = P(X ), R F () = P(X ) = P(X = i ) i Eine Funktion f : R R, die über eine reellwertige Zufallsvariable X definiert ist, heißt Wahrscheinlichkeitsdichte oder Dichtefunktion Beispiel: Wert der stetigen Zufallsvariablen im Intervall [a, b]: P(a X b) = b a f ()d J. Zhang 210
8 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Der Erwartungswert einer Zufallsvariablen ist gegeben als: E[X] = µ = p() (diskret) E[X] = µ = p() d (kontinuierlich) Der Erwartungswert ist eine lineare Funktion einer Zufallsvariablen, d.h. es gilt: E[aX + b] = ae[x] + b J. Zhang 211
9 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Die Varianz σ 2 von X berechnet sich wie folgt: σ 2 = E[X µ] 2 = E[X 2 ] µ 2 Die Varianz misst das erwartete Quadrat der Abweichung vom Erwartungswert Für die Standardabweichung oder Streuung von X gilt: σ = σ 2 = E[X µ] 2 J. Zhang 212
10 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Für die Kovarianz Cov zweier reeller Zufallsvariablen X, Y gilt: Cov(X, Y ) = E((X E(X)) (Y E(Y ))) unter der Voraussetzung, dass E(X), E(Y ) und E(XY ) eistiert. Cov(X, Y ) > 0, falls monoton wachsender linearer Zusammenhang Cov(X, Y ) = 0, falls kein linearer Zusammenhang zwischen den Variablen; möglicherweise aber ein nichtlinearer Zusammenhang, d. h. die Variablen sind nicht notwendigerweise stochastisch unabhängig. Cov(X, Y ) < 0, falls monoton fallender linearer Zusammenhang keine Aussage über die Stärke des Zusammenhanges Cov(X, X) = Var(X) = σ 2 falls X, Y stochastisch unabhängig, folgt Cov(X, Y ) = 0 J. Zhang 213
11 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Entropie einer Wahrscheinlichkeitsverteilung Sei P = {p 1,, p n } eine Wahrscheinlichkeitsverteilung, dann gilt für die Entropie von P: H(P) = n p i log 2 p i i=1 was dem Erwartungswert des Informationsgehaltes (E[I()] mit 1 I() = log 2 p() = log 2p() [bit]) entspricht. Die Entropie ist die erwartete Information, die die Werte von tragen J. Zhang 214
12 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Für P = {p 1,, p n } gelten folgende Schranken: 0 H(p 1,, p n ) log 2 n untere Schranke von H(p1,, p n ) = 0 genau dann, wenn die W-Verteilung entartet ist; also wenn ein i eistiert mit p i = 1 obere Schranke von H(p1,, p n ) = log 2 n genau dann, wenn p i = 1 n, i, 1 i n Im diskreten Fall ist log 2 p() die Anzahl der Bits, die notwendig sind, um optimal zu kodieren, wenn p() die Wahrscheinlichkeit für die Beobachtung von ist J. Zhang 215
13 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Kann die Zufallsvariable einen kontinuierlichen Wert annehmen, dann wird sie durch eine Dichtefunktion beschrieben (engl. probability density function, PDF) Eine typische Dichtefunktion ist die Normalverteilung mit Mittelwert µ und Varianz σ 2 : { } p() = (2πσ 2 ) 1 2 ep 1 ( µ) 2 2 σ 2 Im mehrdimensionalen Fall mit Mittelwertsvektor µ und Kovarianzmatri Σ: p() = det(2πσ) 1 2 ep { 1 2 ( µ)σ 1 ( µ) T } J. Zhang 216
14 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Die Kovarianzmatri Σ ist die Matri der paarweisen Kovarianzen eines Zufallsvektors X = (X 1,, X n ) Cov(X 1, X 1 ) Cov(X 1, X n ) Σ =..... Cov(X n, X 1 ) Cov(X n, X n ) Die Kovarianzmatri Σ ist positiv semidefinit und symmetrisch (A T 0, diagonalisierbar, Eigenwerte 0) Für eine PDF gilt: p()d = 1 Der Funktionswert einer PDF ist nicht wie bei diskreten Wahrscheinlichkeiten nach oben durch 1 begrenzt J. Zhang 217
15 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Für die Wahrscheinlichkeit, dass X den Wert und Y den Wert y hat, schreibt man p(, y) = p(x = und Y = y) Sind die beiden Zufallsvariablen X und Y von einander unabhängig gilt: p(, y) = p()p(y) Die Wahrscheinlichkeit für X unter der Voraussetzung, dass Y den Wert y besitzt (bedingte Wahrscheinlichkeit), wird wie folgt beschrieben p( y) = p(x = Y = y) J. Zhang 218
16 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Gilt für diese bedingte Wahrscheinlichkeit, dass p(y) > 0 ist, gilt: p(, y) p( y) = p(y) Sind X und Y voneinander unabhängig, gilt: p( y) = p()p(y) p(y) = p() Das bedeutet, wenn X und Y unabhängig voneinander sind, sagt uns Y nichts über X J. Zhang 219
17 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Gesetz der totalen Wahrscheinlichkeit: p() = y p( y)p(y) (diskret) p() = p( y)p(y)dy (kontinuierlich) Satz von Bayes: (mit p(y) > 0) p( y) p( y) = p(y )p() p(y) = = p(y )p() p(y) = p(y )p() p(y )p( ) p(y )p() p(y )p( )d (diskret) (kontinuierlich) Satz von Bayes beschreibt Umkehrung von Schlussfolgerungen die Berechnung von p(ereignis Ursache) ist oft einfach aber gesucht ist p(ursache Ereignis) J. Zhang 220
18 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Der Satz von Bayes spielt eine hervorgehobene Rolle Sei die Größe, die wir aus y ableiten wollen, dann bezeichnet man die Grundwahrscheinlichkeit p() als A-Priori-Wahrscheinlichkeit und y als Daten (z.b. Sensormessungen) Die Verteilung der p() beschreibt das Wissen über X, bevor die Messung y berücksichtigt wird Die Verteilung der p( y) wird als A-Posteriori-Wahrscheinlichkeit von X bezeichnet Der Satz von Bayes erlaubt die bedingte Wahrscheinlichkeit p( y) zu berechnen, wenn die Wahrscheinlichkeit für eine Messung y bei einem Zustand (p(y )) und die Grundwahrscheinlichkeiten p() und p(y) bekannt sind J. Zhang 221
19 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Im Satz von Bayes hängt die Grundwahrscheinlichkeit p(y) nicht von ab Daher ist der Faktor p(y) 1 für jeden Wert in p( y) gleich Dieser Faktor wird meist als Normaliserungsfaktor im Satz von Bayes notiert: p( y) = ηp(y )p() Der Faktor η wird derart gewählt, dass die Normierung der Verteilung auf 1 erhalten bleibt η bezeichnet im Folgenden immer solche Normalisierungsfaktoren, deren eigentliche Werte sich aber unterscheiden können J. Zhang 222
20 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) Alle bisherigen Regeln können durch eine weitere Zufallsvariable Z bedingt sein Dies bedeutet für den Satz von Bayes mit Z = z: p( y, z) = p(y, z)p( z) p(y z) solange p(y z) > 0 Für die Regel zur Kombination unabhängiger Zufallsvariablen (p(a, b) = p(a)p(b)) gilt analog: p(, y z) = p( z)p(y z) J. Zhang 223
21 5.1 Rekursive Zustandsschätzung - Grundlagen der Wahrscheinlichkeitsrechnung Grundlagen der Signalverarbeitung und Robotik Grundlagen der Wahrscheinlichkeitsrechnung (cont.) p(, y z) = p( z)p(y z) besagt, dass y keine Information über trägt, wenn z bekannt ist Obige Formel beschreibt eine bedingte Unabhängigkeit und ist äquivalent zu p( z) = p( z, y) p(y z) = p(y z, ) Die Formel impliziert nicht, dass X unabhängig von Y ist: p(, y z) = p( z)p(y z) p(, y) = p()p(y) und die Umkehrung gilt generell auch nicht: p(, y) = p()p(y) p(, y z) = p( z)p(y z) J. Zhang 224
22 5.2 Rekursive Zustandsschätzung - Stochastische Fortpflanzungsgesetze und Belief Grundlagen der Signalverarbeitung und Robotik Stochastische Fortpflanzunggesetze Der Zustand eines Systems lässt sich durch eine Wahrscheinlichkeitsverteilung p( t 0:t 1, z 1:t 1, u 1:t ) beschreiben, die abhängig ist von den bisherigen Zuständen 0:t 1 allen bisherigen Messungen z1:t 1 und allen bisherigen Stellgrößen (Steuerkommandos) u 1:t J. Zhang 225
23 5.2 Rekursive Zustandsschätzung - Stochastische Fortpflanzungsgesetze und Belief Grundlagen der Signalverarbeitung und Robotik Stochastische Fortpflanzunggesetze (cont.) Ist der Zustand t komplett, dann fasst die Stellgröße u t und der Zustand t 1 alle bisherigen Ereignisse zusammen: p( t 0:t 1, z 1:t 1, u 1:t ) = p( t t 1, u t ) Für die Messungen gilt dann entsprechend: p(z t 0:t, z 1:t 1, u 1:t ) = p(z t t ) Der Zustand t ist ausreichend um die Messung z t vorherzusagen Die bedingte Wahrscheinlichkeit p( t t 1, u t ) wird als Zustandsübergangswahrscheinlichkeit bezeichnet Sie beschreibt wie sich der Zustand der Umgebung abhängig von den Stellgrößen ändert Die Wahrscheinlichkeit p(z t t ) wird Wahrscheinlichkeit der Messung genannt J. Zhang 226
24 5.2 Rekursive Zustandsschätzung - Stochastische Fortpflanzungsgesetze und Belief Grundlagen der Signalverarbeitung und Robotik Stochastische Fortpflanzunggesetze (cont.) Zustandsübergangswahrscheinlichkeit und Wahrscheinlichkeit der Messung beschreiben zusammen ein dynamisches stochastisches System Eine solche Systembeschreibung ist auch bekannt als hidden Markov model (HMM) oder dynamic Bayes network (DBN) t 1 t t+1 ut 1 ut u t+1 z t 1 z t z t+1 J. Zhang 227
25 5.2 Rekursive Zustandsschätzung - Stochastische Fortpflanzungsgesetze und Belief Grundlagen der Signalverarbeitung und Robotik Belief Als belief bezeichnet man das Wissen (Schätzung) eines Systems über seinen Zustand Der wahre Zustand eines Systems ist nicht dasselbe Der belief ist die A-Posteriori-Wahrscheinlichkeit der Zustandsvariablen anhand der bisherigen Daten: bel( t ) = p( t z 1:t, u 1:t ) Diese Definition berechnet den belief (als Wahrscheinlichkeit) nach der aktuellen Messung t J. Zhang 228
26 5.2 Rekursive Zustandsschätzung - Stochastische Fortpflanzungsgesetze und Belief Grundlagen der Signalverarbeitung und Robotik Belief (cont.) Der belief vor der Messung wird als bel( t ) = p( t z 1:t 1, u 1:t ) definiert und meist als Vorhersage (engl. prediction) bezeichnet Der Schritt zur Berechung von bel( t ) aus der Vorhersage bel( t ) wird als Korrektur (engl. correction oder measurement update) bezeichnet J. Zhang 229
27 5.3 Rekursive Zustandsschätzung - Bayes-Filter Grundlagen der Signalverarbeitung und Robotik Bayes-Filter Ein allgemeiner Algorithmus, um beliefs zu berechnen, ist der Bayes-Filter-Algorithmus Der Algorithmus ist rekursiv und berechnet bel( t ) zum Zeitpunkt t aus folgenden Größen bel(t 1 ) zum Zeitpunkt t 1 (alter belief) der Stellgröße ut (aktuelle Stellgröße) der Messung z t (aktuelle Messung) J. Zhang 230
28 Universität Hamburg Rekursive Zustandsschätzung - Bayes-Filter - Algorithmus Grundlagen der Signalverarbeitung und Robotik Bayes-Filter-Algorithmus Bayes-Filter (bel( t 1 ), u t, z t ): 1. for all t do 2. bel( t ) = p( t u t, t 1 ) bel( t 1 ) d t 1 3. bel( t ) = η p(z t t )bel( t ) 4. endfor 5. return bel( t ) J. Zhang 231
29 5.3.1 Rekursive Zustandsschätzung - Bayes-Filter - Algorithmus Grundlagen der Signalverarbeitung und Robotik Bayes-Filter-Algorithmus (cont.) In Zeile 2 wird die Stellgröße u t verarbeitet bel( t ) ist das Integral des Produktes zweier Wahrscheinlichkeitsverteilungen: die Wahrscheinlichkeit für Zustand t 1 und die Wahrscheinlichkeit das mit u t in den Zustand t gewechselt wird Das ist die Vorhersage In Zeile 3 findet die Korrektur statt Vorhersage (bel(t )) wird mit der Wahrscheinlichkeit multipliziert, dass die Messung z t in diesem Zustand wahrgenommen wird J. Zhang 232
30 5.3.1 Rekursive Zustandsschätzung - Bayes-Filter - Algorithmus Grundlagen der Signalverarbeitung und Robotik Bayes-Filter-Algorithmus (cont.) Der Algorithmus muss mit einem belief zum Zeitpunkt t = 0 initialisiert werden In den meisten Fällen ist der Startzustand 0 bekannt und die Wahrscheinlichkeit kann für alle anderen Zustände gleich 0 gesetzt werden Oder der Zustand ist unbekannt und alle Zustände werden mit der gleichen Wahrscheinlichkeit initialisiert J. Zhang 233
31 5.3.1 Rekursive Zustandsschätzung - Bayes-Filter - Algorithmus Grundlagen der Signalverarbeitung und Robotik Bayes-Filter-Algorithmus (cont.) Der Algorithmus kann in dieser Form nur für sehr einfache Probleme implementiert werden Entweder muss die Integration in Zeile 2 und die Multiplikation in Zeile 3 in geschlossener Form möglich sein oder ein endlicher Zustandsraum muss gegeben sein, so dass das Integral in Zeile 2 zu einer Summe wird J. Zhang 234
32 5.3.2 Rekursive Zustandsschätzung - Bayes-Filter - Mathematische Herleitung Grundlagen der Signalverarbeitung und Robotik Mathematische Herleitung des Bayes-Filter Beweis durch Induktion: Zeige, dass bel( t ) = p( t z 1:t, u 1:t ) aus p( t 1 z 1:t 1, u 1:t 1 ) hergeleitet werden kann Beweis-Basis: Korrekte Initialisierung von bel( o ) zum Zeitpunkt t = 0 Bedingungen: Zustand t ist komplett und die Stellgrößen werden zufällig gewählt Nach dem Satz von Bayes gilt: bel( t ) = p( t z 1:t, u 1:t ) = p(z t t, z 1:t 1, u 1:t )p( t z 1:t 1, u 1:t ) p(z t z 1:t 1, u 1:t ) = ηp(z t t, z 1:t 1, u 1:t )p( t z 1:t 1, u 1:t ) J. Zhang 235
33 5.3.2 Rekursive Zustandsschätzung - Bayes-Filter - Mathematische Herleitung Grundlagen der Signalverarbeitung und Robotik Mathematische Herleitung des Bayes-Filter (cont.) bel( t ) = p( t z 1:t, u 1:t ) = ηp(z t t, z 1:t 1, u 1:t )p( t z 1:t 1, u 1:t ) Da der Zustand komplett ist, gilt (bedingte Unabhängigkeit) p(z t t, z 1:t 1, u 1:t ) = p(z t t ) Daraus folgt: p( t z 1:t, u 1:t ) = ηp(z t t )p( t z 1:t 1, u 1:t ) und damit bel( t ) = ηp(z t t )bel( t ) was Zeile 3 des Bayes-Filter-Algorithmus entspricht J. Zhang 236
34 5.3.2 Rekursive Zustandsschätzung - Bayes-Filter - Mathematische Herleitung Grundlagen der Signalverarbeitung und Robotik Mathematische Herleitung des Bayes-Filter (cont.) Nach dem Gesetz der totalen Wahrscheinlichkeit gilt: bel( t ) = p( t z 1:t 1, u 1:t ) = p( t t 1, z 1:t 1, u 1:t ) p( t 1 z 1:t 1, u 1:t ) d t 1 Wieder gilt, wenn wir t 1 kennen, liefern z 1:t 1 und u 1:t 1 keine zusätzliche Information Daher gilt die Vereinfachung p( t t 1, z 1:t 1, u 1:t ) = p( t t 1, u t ) u t bleibt, da diese Stellgröße erst zum Zustandsübergang führt J. Zhang 237
35 5.3.2 Rekursive Zustandsschätzung - Bayes-Filter - Mathematische Herleitung Grundlagen der Signalverarbeitung und Robotik Mathematische Herleitung des Bayes-Filter (cont.) Bei zufällig gewählten Stellgrößen kann u t daher auch in den Bedingungen für p( t 1 z 1:t 1, u 1:t ) weggelassen werden Es ergibt sich mit bel( t ) = p( t t 1, u t ) p( t 1 z 1:t 1, u 1:t 1 ) d t 1 die 2. Zeile des Bayes-Filter-Algoritmus J. Zhang 238
36 5.3.2 Rekursive Zustandsschätzung - Bayes-Filter - Mathematische Herleitung Grundlagen der Signalverarbeitung und Robotik Mathematische Herleitung des Bayes-Filter (cont.) Für konkrete Implementierungen des Bayes-Filter-Algoritmus werden drei Wahrscheinlichkeitsverteilungen benötigt: der initiale belief p(0 ) die Wahrscheinlichkeit der Messungen p(z t t ) die Zustandsübergangswahrscheinlichkeiten p( t u t, t 1 ) J. Zhang 239
37 5.3.3 Rekursive Zustandsschätzung - Bayes-Filter - Markov Annahme Grundlagen der Signalverarbeitung und Robotik Markov-Annahme Die Annahme, dass ein Zustand komplett ist, wird Markov-Annahme (engl. Markov assumption) genannt Die Annahme fordert, dass vergangene und zukünftige Daten unabhängig sind, wenn man den aktuellen Zustand t kennt J. Zhang 240
38 5.3.3 Rekursive Zustandsschätzung - Bayes-Filter - Markov Annahme Grundlagen der Signalverarbeitung und Robotik Markov-Annahme (cont.) Das folgende Beispiel soll verdeutlichen, wie hart diese Annahme ist: Zur Lokalisierung mobiler Roboter werden Bayes-Filter eingesetzt Dabei ist t die Position im Raum (Pose) des Roboters mit Bezug auf eine feste Karte Es gibt Effekte die die Sensormessungen systematisch verfälschen und damit die Markov-Annahme zunichte machen: Einfluss sich bewegender Personen auf die Sensormessungen Ungenauigkeiten in den probabilistischen Modellen p(z t t) und p( t u t, t 1) Rundungsfehler, wenn Näherungen für die Repräsentation des beliefs verwendet werden Variablen innerhalb der Software, die mehrere Stellgrößen beeinflussen J. Zhang 241
39 5.3.3 Rekursive Zustandsschätzung - Bayes-Filter - Markov Annahme Grundlagen der Signalverarbeitung und Robotik Markov-Annahme (cont.) Einige dieser Variablen könnten im Zustand berücksichtigt werden, werden aber oft fallen gelassen, um den rechnerischen Aufwand zu verringern In der Prais sind Bayes-Filter erstaunlich robust gegen die Verletzung der Markov-Annahme J. Zhang 242
40 5.3.4 Rekursive Zustandsschätzung - Bayes-Filter - Darstellung und Berechnung Grundlagen der Signalverarbeitung und Robotik Darstellung und Berechnung Bayes-Filter können auf unterschiedliche Weise implementiert werden Die Techniken basieren auf unterschiedlichen Annahmen über die Wahrscheinlichkeiten für die Messungen, die Zustandsübergänge und den belief Die Algorithmen besitzen dadurch unterschiedliche rechnerische Eigenschaften In den meisten Fällen müssen die beliefs angenähert werden Dies hat Auswirkungen auf die Kompleität der Algorithmen Keine der verschiedenen Techniken ist generell zu bevorzugen J. Zhang 243
41 5.3.4 Rekursive Zustandsschätzung - Bayes-Filter - Darstellung und Berechnung Grundlagen der Signalverarbeitung und Robotik Beispiele Kalman-Filter Fehlerverteilung der Messfehler durch Gaussverteilung modelliert Veränderung des Zustandes linear und a-priori bekannt Partikelfilter von gitterbasierter Lokalisierung abgeleitet keine Annahme der Normalverteilung des geschätzten Wertes Schätzung wird als Wahrscheinlichkeitsverteilung modelliert Verteilung wird an ausgewählten Stellen, den sog. Partikeln diskretisiert und zwischen diesen wird interpoliert. J. Zhang 244
42 5.3.4 Rekursive Zustandsschätzung - Bayes-Filter - Darstellung und Berechnung Grundlagen der Signalverarbeitung und Robotik Effizienz Einige Näherungen bedingen polynomiale Laufzeiten in Abhängigkeit von der Dimension des Zustands (z.b. Kalman-Filter) Einige haben eponentielle Laufzeiten (z. B. gridbasierte Techniken) Partikel-basierte Verfahren haben eine Laufzeit, die von der gewünschten Genauigkeit abhängt J. Zhang 245
43 5.3.4 Rekursive Zustandsschätzung - Bayes-Filter - Darstellung und Berechnung Grundlagen der Signalverarbeitung und Robotik Genauigkeit Einige Näherungen eignen sich besser, um eine Reihe von Wahrscheinlichkeitsverteilungen anzunähern Beispielsweise eignen sich Normalverteilungen für uni-modale Wahrscheinlichkeitsverteilungen Histogramme können multimodale Verteilungen besser annähern, aber auf Kosten der Genauigkeit Partikel-Techniken können eine Vielzahl von Verteilungen annähern, wodurch allerdings die Anzahl der Partikel sehr groß werden kann J. Zhang 246
44 5.3.4 Rekursive Zustandsschätzung - Bayes-Filter - Darstellung und Berechnung Grundlagen der Signalverarbeitung und Robotik Einfachheit der Implementierung Abhängig von der Form der Verteilungen kann die Implementierung der Verfahren aufwändig sein Weil Partikel-Techniken meist sehr einfach für nicht-lineare Systeme implementiert werden können, sind sie zurzeit sehr populär J. Zhang 247
45 5.3.5 Rekursive Zustandsschätzung - Bayes-Filter - Zusammenfassung Grundlagen der Signalverarbeitung und Robotik Zusammenfassung Die Interaktion zwischen einem Roboter und dessen Umgebung wird modelliert als gekoppeltes dynamisches System. Der Roboter setzt dazu Stellgrößen um die Umgebung zu manipulieren und nimmt die Umgebung über Sensormessungen war. Die Dynamiken werden charakterisiert durch zwei wahrscheinlichkeitstheoretische Gesetze die Wahrscheinlichkeitsverteilungen für den Zustandsübergang die " die Messungen Erstere beschreibt wie der Zustand sich mit der Zeit ändert, die Zweite, wie Messungen wahrgenommen werden. J. Zhang 248
46 5.3.5 Rekursive Zustandsschätzung - Bayes-Filter - Zusammenfassung Grundlagen der Signalverarbeitung und Robotik Zusammenfassung (cont.) Der belief ist die A-Posteriori-Wahrscheinlichkeit des Zustands; gegeben: Alle bisherigen Messungen und Stellgrößen. Der Bayes-Filter ist ein Algorithmus um den belief zu berechnen. Er ist rekursiv, d.h. der belief zum Zeitpunkt t wird aus dem belief zum Zeitpunkt t-1 berechnet. Der Bayes-Filter macht eine Markov-Annahme, d.h. der Zustand ist eine komplette Zusammenfassung der Vergangenheit. Diese Annahme trifft in der Prais meist nicht zu. Bayes-Filter sollten vor ihrm Einsatz in speziellen Anwendungen anhand verschiedener Kriterien wie Genauigkeit, Effizienz und Einfachheit evaluiert werden. J. Zhang 249
47 5.4.1 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Markov-Lokalisierung Grundlagen der Signalverarbeitung und Robotik Markov-Lokalisierung Wahrscheinlichkeitstheoretische Lokalisierungsverfahren sind Varianten des Bayes-Filters Die direkte Anwendung des Bayes-Filters wird Markov-Lokalisierung genannt Markov-Lokalisierungen benötigen zusätzlich eine Karte der Umgebung Die Karte spielt eine Rolle im Messmodell (teilweise auch im Bewegungsmodell) Markov-Lokalisierung wird verwendet für globale Lokalisierung Positions-Tracking das Kidnapped-Robot-Problem J. Zhang 250
48 5.4.1 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Markov-Lokalisierung Grundlagen der Signalverarbeitung und Robotik Markov-Lokalisierung (cont.) bel() p(z ) bel() bel() p(z ) bel() bel() J. Zhang 251
49 5.4.2 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Etended Kalman Filter Lokalisierung Grundlagen der Signalverarbeitung und Robotik Etended Kalman Filter Lokalisierung Ein besonderer Fall der Markov-Lokalisierung ist der etended Kalman filter localisation Algorithmus (oder EKF-Lokalisierung) Die EKF-Lokalisierung repräsentiert den belief bel( t ) durch den Mittelwert µ t und die Kovarianzmatri Σ t Die Karte ist dabei eine Sammlung von Merkmalen Der Roboter misst die Entfernung und Richtung einiger Merkmale in seiner Nähe J. Zhang 252
50 5.4.2 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Etended Kalman Filter Lokalisierung Grundlagen der Signalverarbeitung und Robotik Etended Kalman Filter Lokalisierung (cont.) bel() bel() p(z ) bel() bel() J. Zhang 253
51 5.4.3 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Grid-Lokalisierung Grundlagen der Signalverarbeitung und Robotik Grid-Lokalisierung Grid-Lokalisierung approimiert den belief durch einen Histogram-Filter über die Grid-Dekomposition des Zustandsraumes Dieser diskrete Bayes-Filter verwaltet eine Menge diskreter Wahrscheinlichkeitswerte: bel t = {p k,t } wobei jedes p k,t zu einer Grid-Zelle k gehört Typische Wertefür die Zellengröße in der Prais sind 15cm Kantenlänge und 5 Winkelauflösung J. Zhang 254
52 5.4.3 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Grid-Lokalisierung Grundlagen der Signalverarbeitung und Robotik Grid-Lokalisierung (cont.) bel() Robot position p(z ) bel() bel() Robot position p(z ) bel() Robot position bel() J. Zhang 255
53 5.4.4 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Monte-Carlo-Lokalisierung Grundlagen der Signalverarbeitung und Robotik Monte-Carlo-Lokalisierung Monte-Carlo-Lokalisierung (MCL) approimiert den belief durch eine Menge von Partikeln Sehr populär Mit MCL können nahezu beliebige Verteilungsfunktionen angenähert werden Es können multimodale und unimodale Verteilungen approimiert und übergangslos zwischen ihnen gewechselt werden Eine höhere Anzahl von Partikeln erhöht die Genauigkeit J. Zhang 256
54 5.4.4 Rekursive Zustandsschätzung - Selbst-Lokalisierung mobiler Roboter - Monte-Carlo-Lokalisierung Grundlagen der Signalverarbeitung und Robotik Monte-Carlo-Lokalisierung (cont.) bel() p(z ) bel() bel() p(z ) bel() bel() J. Zhang 257
55 5.5 Rekursive Zustandsschätzung - Literatur Grundlagen der Signalverarbeitung und Robotik [TBF05] Sebastian Thrun, Wolfram Burgard, Dieter Fo, Ronald C. Arkin (Hrsg.): Probabilistic Robotics. MIT Press; Cambridge, Massachusetts, 2005 (Intelligent Robotics and Autonomous Agents). Kapitel 2 J. Zhang 258
Intelligente Roboter
 64-424 Intelligente Roboter 64-424 Intelligente Roboter http://tams.informatik.uni-hamburg.de/ lectures/2010ws/vorlesung/ir Jianwei Zhang Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften
64-424 Intelligente Roboter 64-424 Intelligente Roboter http://tams.informatik.uni-hamburg.de/ lectures/2010ws/vorlesung/ir Jianwei Zhang Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften
Grundlagen der Objektmodellierung
 Grundlagen der Objektmodellierung Daniel Göhring 30.10.2006 Gliederung Grundlagen der Wahrscheinlichkeitsrechnung Begriffe zur Umweltmodellierung Bayesfilter Zusammenfassung Grundlagen der Wahrscheinlichkeitsrechnung
Grundlagen der Objektmodellierung Daniel Göhring 30.10.2006 Gliederung Grundlagen der Wahrscheinlichkeitsrechnung Begriffe zur Umweltmodellierung Bayesfilter Zusammenfassung Grundlagen der Wahrscheinlichkeitsrechnung
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Zusammenfassung: diskrete und stetige Verteilungen. Woche 4: Gemeinsame Verteilungen. Zusammenfassung: diskrete und stetige Verteilungen
 Zusammenfassung: e und e Verteilungen Woche 4: Gemeinsame Verteilungen Wahrscheinlichkeitsverteilung p() Wahrscheinlichkeitsdichte f () WBL 15/17, 11.05.2015 Alain Hauser P(X = k
Zusammenfassung: e und e Verteilungen Woche 4: Gemeinsame Verteilungen Wahrscheinlichkeitsverteilung p() Wahrscheinlichkeitsdichte f () WBL 15/17, 11.05.2015 Alain Hauser P(X = k
Teil VI. Gemeinsame Verteilungen. Lernziele. Beispiel: Zwei Würfel. Gemeinsame Verteilung
 Zusammenfassung: diskrete und stetige Verteilungen Woche 4: Verteilungen Patric Müller diskret Wahrscheinlichkeitsverteilung p() stetig Wahrscheinlichkeitsdichte f ()
Zusammenfassung: diskrete und stetige Verteilungen Woche 4: Verteilungen Patric Müller diskret Wahrscheinlichkeitsverteilung p() stetig Wahrscheinlichkeitsdichte f ()
Mehrdimensionale Zufallsvariablen
 Mehrdimensionale Zufallsvariablen Im Folgenden Beschränkung auf den diskreten Fall und zweidimensionale Zufallsvariablen. Vorstellung: Auswerten eines mehrdimensionalen Merkmals ( ) X Ỹ also z.b. ω Ω,
Mehrdimensionale Zufallsvariablen Im Folgenden Beschränkung auf den diskreten Fall und zweidimensionale Zufallsvariablen. Vorstellung: Auswerten eines mehrdimensionalen Merkmals ( ) X Ỹ also z.b. ω Ω,
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.)
 Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Wiederh.) 1 Zusammenfassung Bedingte Verteilung: P (y x) = P (x, y) P (x) mit P (x) > 0 Produktsatz P (x, y) = P (x y)p (y) = P (y x)p (x) Kettenregel
Kalmanfilter und Nichtparametrische Filter. Bayesfilter
 Kalmanfilter und Nichtparametrische Filter Daniel Göhring 06.11.2006 Bayesfilter Zustand zur Zeit t ist Zufallvariable x t Wahrscheinlichkeitsfunktion Bel (Belief) über x t : Bel(x t ) repräsentiert die
Kalmanfilter und Nichtparametrische Filter Daniel Göhring 06.11.2006 Bayesfilter Zustand zur Zeit t ist Zufallvariable x t Wahrscheinlichkeitsfunktion Bel (Belief) über x t : Bel(x t ) repräsentiert die
Mathematische Grundlagen Kalman Filter Beispielprogramm. Kalman Filter. Stephan Meyer
 Kalman Filter Stephan Meyer FWPF Ortsbezogene Anwendungen und Dienste Georg-Simon-Ohm-Hochschule Nürnberg 07.12.2007 Outline 1 Mathematische Grundlagen 2 Kalman Filter 3 Beispielprogramm Mathematische
Kalman Filter Stephan Meyer FWPF Ortsbezogene Anwendungen und Dienste Georg-Simon-Ohm-Hochschule Nürnberg 07.12.2007 Outline 1 Mathematische Grundlagen 2 Kalman Filter 3 Beispielprogramm Mathematische
Kapitel 8. Parameter multivariater Verteilungen. 8.1 Erwartungswerte
 Kapitel 8 Parameter multivariater Verteilungen 8.1 Erwartungswerte Wir können auch bei mehrdimensionalen Zufallsvariablen den Erwartungswert betrachten. Dieser ist nichts anderes als der vektor der Erwartungswerte
Kapitel 8 Parameter multivariater Verteilungen 8.1 Erwartungswerte Wir können auch bei mehrdimensionalen Zufallsvariablen den Erwartungswert betrachten. Dieser ist nichts anderes als der vektor der Erwartungswerte
Mathematik für Naturwissenschaften, Teil 2
 Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Lösungsvorschläge für die Aufgaben zur Vorlesung Mathematik für Naturwissenschaften, Teil Zusatzblatt SS 09 Dr. J. Schürmann keine Abgabe Aufgabe : Eine Familie habe fünf Kinder. Wir nehmen an, dass die
Bestimmte Zufallsvariablen sind von Natur aus normalverteilt. - naturwissenschaftliche Variablen: originär z.b. Intelligenz, Körpergröße, Messfehler
 6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
Universität Basel Wirtschaftswissenschaftliches Zentrum. Zufallsvariablen. Dr. Thomas Zehrt
 Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Universität Basel Wirtschaftswissenschaftliches Zentrum Zufallsvariablen Dr. Thomas Zehrt Inhalt: 1. Einführung 2. Zufallsvariablen 3. Diskrete Zufallsvariablen 4. Stetige Zufallsvariablen 5. Erwartungswert
Zufallsgröße X : Ω R X : ω Anzahl der geworfenen K`s
 X. Zufallsgrößen ================================================================= 10.1 Zufallsgrößen und ihr Erwartungswert --------------------------------------------------------------------------------------------------------------
X. Zufallsgrößen ================================================================= 10.1 Zufallsgrößen und ihr Erwartungswert --------------------------------------------------------------------------------------------------------------
I Grundbegriffe 1 1 Wahrscheinlichkeitsräume Bedingte Wahrscheinlichkeiten und Unabhängigkeit Reellwertige Zufallsvariablen...
 Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit
 3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
3. Gemeinsame und bedingte Verteilung, stochastische Unabhängigkeit Lernziele dieses Kapitels: Mehrdimensionale Zufallsvariablen (Zufallsvektoren) (Verteilung, Kenngrößen) Abhängigkeitsstrukturen Multivariate
2 Zufallsvariable und Verteilungsfunktionen
 8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
8 2 Zufallsvariable und Verteilungsfunktionen Häufig ist es so, dass den Ausgängen eines Zufallexperiments, d.h. den Elementen der Ereignisalgebra, eine Zahl zugeordnet wird. Das wollen wir etwas mathematischer
Übungsklausur zur Vorlesung Wahrscheinlichkeit und Regression Thema: Wahrscheinlichkeit. Übungsklausur Wahrscheinlichkeit und Regression
 Übungsklausur Wahrscheinlichkeit und Regression 1. Welche der folgenden Aussagen treffen auf ein Zufallsexperiment zu? a) Ein Zufallsexperiment ist ein empirisches Phänomen, das in stochastischen Modellen
Übungsklausur Wahrscheinlichkeit und Regression 1. Welche der folgenden Aussagen treffen auf ein Zufallsexperiment zu? a) Ein Zufallsexperiment ist ein empirisches Phänomen, das in stochastischen Modellen
Modellierung von Unsicherheit in Systemen
 Modellierung von Unsicherheit in Systemen Motivation Systeme Zeitdiskrete, lineare und nicht-lineare Systeme, Beispiele Wahrscheinlichkeiten Zufallsvariablen, Wahrscheinlichkeitsdichten, mehrdimensionale
Modellierung von Unsicherheit in Systemen Motivation Systeme Zeitdiskrete, lineare und nicht-lineare Systeme, Beispiele Wahrscheinlichkeiten Zufallsvariablen, Wahrscheinlichkeitsdichten, mehrdimensionale
Wahrscheinlichkeitsverteilungen
 Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern
 Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern Vorlesung Robotik SS 016 Kalmanfiter () Kalman-Filter: optimaler rekursiver Datenverarbeitungsalgorithmus optimal hängt vom gewählten
Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern Vorlesung Robotik SS 016 Kalmanfiter () Kalman-Filter: optimaler rekursiver Datenverarbeitungsalgorithmus optimal hängt vom gewählten
Dynamische Systeme und Zeitreihenanalyse // Multivariate Normalverteilung und ML Schätzung 11 p.2/38
 Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Woche 2: Zufallsvariablen
 Woche 2: Zufallsvariablen Patric Müller ETHZ WBL 17/19, 24.04.2017 Wahrscheinlichkeit und Statistik Patric Müller WBL 2017 Teil III Zufallsvariablen Wahrscheinlichkeit
Woche 2: Zufallsvariablen Patric Müller ETHZ WBL 17/19, 24.04.2017 Wahrscheinlichkeit und Statistik Patric Müller WBL 2017 Teil III Zufallsvariablen Wahrscheinlichkeit
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Review)
 Einige Konzepte aus der Wahrscheinlichkeitstheorie (Review) 1 Diskrete Zufallsvariablen (Random variables) Eine Zufallsvariable X(c) ist eine Variable (genauer eine Funktion), deren Wert vom Ergebnis c
Einige Konzepte aus der Wahrscheinlichkeitstheorie (Review) 1 Diskrete Zufallsvariablen (Random variables) Eine Zufallsvariable X(c) ist eine Variable (genauer eine Funktion), deren Wert vom Ergebnis c
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik. PD Dr. U. Ludwig. Vorlesung 7 1 / 19
 Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
Wahrscheinlichkeitsrechnung und Statistik für Studierende der Informatik PD Dr. U. Ludwig Vorlesung 7 1 / 19 2.2 Erwartungswert, Varianz und Standardabweichung (Fortsetzung) 2 / 19 Bedingter Erwartungswert
STOCHASTISCHE UNABHÄNGIGKEIT. Annika Pohlmann Philipp Oel Wilhelm Dück
 STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
STOCHASTISCHE UNABHÄNGIGKEIT Annika Pohlmann Philipp Oel Wilhelm Dück 1 GLIEDERUNG 1) Bedingte Wahrscheinlichkeiten 2) Unabhängigkeit für mehr als zwei Ereignisse 3) Unabhängigkeit für Zufallsvariable
SLAM. Simultaneous Localization and Mapping. KogSys-Sem-M2: Reading Club - SLAM - Andreas Habermann
 SLAM Simultaneous Localization and Mapping KogSys-Sem-M2: Reading Club - SLAM - Andreas Habermann Simultaneous Localization And Mapping SLAM Problematik SLAM Arten SLAM Methoden: (E)KF SLAM GraphSLAM Fast
SLAM Simultaneous Localization and Mapping KogSys-Sem-M2: Reading Club - SLAM - Andreas Habermann Simultaneous Localization And Mapping SLAM Problematik SLAM Arten SLAM Methoden: (E)KF SLAM GraphSLAM Fast
Grundbegriffe der Wahrscheinlichkeitsrechnung
 Algorithmen und Datenstrukturen 349 A Grundbegriffe der Wahrscheinlichkeitsrechnung Für Entwurf und Analyse randomisierter Algorithmen sind Hilfsmittel aus der Wahrscheinlichkeitsrechnung erforderlich.
Algorithmen und Datenstrukturen 349 A Grundbegriffe der Wahrscheinlichkeitsrechnung Für Entwurf und Analyse randomisierter Algorithmen sind Hilfsmittel aus der Wahrscheinlichkeitsrechnung erforderlich.
Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung
 Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung Version: 22. September 2015 Evelina Erlacher 1 Mengen Es sei Ω eine Menge (die Universalmenge ) und A, B seien Teilmengen von Ω. Dann schreiben
Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung Version: 22. September 2015 Evelina Erlacher 1 Mengen Es sei Ω eine Menge (die Universalmenge ) und A, B seien Teilmengen von Ω. Dann schreiben
4. Gemeinsame Verteilung und Grenzwertsätze
 4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze
 4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
4. Gemeinsame Verteilung und Grenzwertsätze Häufig in der Praxis: Man muss mehrere (n) ZV en gleichzeitig betrachten (vgl. Statistik I, Kapitel 6) Zunächst Vereinfachung: Betrachte n = 2 Zufallsvariablen
Zufallsvariablen [random variable]
![Zufallsvariablen [random variable] Zufallsvariablen [random variable]](/thumbs/52/29710821.jpg) Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Wahrscheinlichkeit und Statistik: Zusammenfassung
 HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
Überblick. Überblick. Bayessche Entscheidungsregel. A-posteriori-Wahrscheinlichkeit (Beispiel) Wiederholung: Bayes-Klassifikator
 Überblick Grundlagen Einführung in die automatische Mustererkennung Grundlagen der Wahrscheinlichkeitsrechnung Klassifikation bei bekannter Wahrscheinlichkeitsverteilung Entscheidungstheorie Bayes-Klassifikator
Überblick Grundlagen Einführung in die automatische Mustererkennung Grundlagen der Wahrscheinlichkeitsrechnung Klassifikation bei bekannter Wahrscheinlichkeitsverteilung Entscheidungstheorie Bayes-Klassifikator
Der diskrete Kalman Filter
 Der diskrete Kalman Filter Fachbereich: Informatik Betreuer: Marc Drassler Patrick Winkler 1168954 6. Dezember 2004 Technische Universität Darmstadt Simulation und Systemoptimierung Darmstadt Dribbling
Der diskrete Kalman Filter Fachbereich: Informatik Betreuer: Marc Drassler Patrick Winkler 1168954 6. Dezember 2004 Technische Universität Darmstadt Simulation und Systemoptimierung Darmstadt Dribbling
Varianz und Kovarianz
 KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
Zufallsvariablen. Diskret. Stetig. Verteilung der Stichprobenkennzahlen. Binomial Hypergeometrisch Poisson. Normal Lognormal Exponential
 Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Stetige Zufallsvariable Verteilungsfunktion: Dichtefunktion: Integralrechnung:
Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Stetige Zufallsvariable Verteilungsfunktion: Dichtefunktion: Integralrechnung:
Teil VIII. Zentraler Grenzwertsatz und Vertrauensintervalle. Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle. Lernziele. Typische Situation
 Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Übung 1: Wiederholung Wahrscheinlichkeitstheorie
 Übung 1: Wiederholung Wahrscheinlichkeitstheorie Ü1.1 Zufallsvariablen Eine Zufallsvariable ist eine Variable, deren numerischer Wert solange unbekannt ist, bis er beobachtet wird. Der Wert einer Zufallsvariable
Übung 1: Wiederholung Wahrscheinlichkeitstheorie Ü1.1 Zufallsvariablen Eine Zufallsvariable ist eine Variable, deren numerischer Wert solange unbekannt ist, bis er beobachtet wird. Der Wert einer Zufallsvariable
Diskrete Zufallsvariablen (Forts.) I
 9 Eindimensionale Zufallsvariablen Diskrete Zufallsvariablen 9.4 Diskrete Zufallsvariablen (Forts.) I T (X ) ist endlich oder abzählbar unendlich, die Elemente von T (X ) werden daher im Folgenden häufig
9 Eindimensionale Zufallsvariablen Diskrete Zufallsvariablen 9.4 Diskrete Zufallsvariablen (Forts.) I T (X ) ist endlich oder abzählbar unendlich, die Elemente von T (X ) werden daher im Folgenden häufig
Fast-SLAM: Synchrone Lokalisierung und Kartenerstellung mit einem Partikel-Filter
 Fast-SLAM: Synchrone Lokalisierung und Kartenerstellung mit einem Partikel-Filter! Landmarkenbasiertes Fast-SLAM! Gitterbasiertes Fast-Slam! Optimierungen Prof. Dr. O. Bittel, HTWG Konstanz Autonome Roboter
Fast-SLAM: Synchrone Lokalisierung und Kartenerstellung mit einem Partikel-Filter! Landmarkenbasiertes Fast-SLAM! Gitterbasiertes Fast-Slam! Optimierungen Prof. Dr. O. Bittel, HTWG Konstanz Autonome Roboter
WAHRSCHEINLICHKEITSRECHNUNG
 WAHRSCHEINLICHKEITSRECHNUNG Mathematischer Teil In der Wahrscheinlichkeitsrechnung haben wir es mit Zufallsexperimenten zu tun, d.h. Ausgang nicht vorhersagbar. Grundbegriffe Zufallsexperiment und Ergebnisse
WAHRSCHEINLICHKEITSRECHNUNG Mathematischer Teil In der Wahrscheinlichkeitsrechnung haben wir es mit Zufallsexperimenten zu tun, d.h. Ausgang nicht vorhersagbar. Grundbegriffe Zufallsexperiment und Ergebnisse
Zuverlässigkeitstheorie
 3. Grundbegriffe der Wahrscheinlichkeitsrechnung Prof. Jochen Seitz Fachgebiet Kommunikationsnetze 20. November 2008 Übersicht Gesetz der großen Zahlen von Bernoulli 1 Gesetz der großen Zahlen von Bernoulli
3. Grundbegriffe der Wahrscheinlichkeitsrechnung Prof. Jochen Seitz Fachgebiet Kommunikationsnetze 20. November 2008 Übersicht Gesetz der großen Zahlen von Bernoulli 1 Gesetz der großen Zahlen von Bernoulli
K8 Stetige Zufallsvariablen Theorie und Praxis
 K8 Stetige Zufallsvariablen Theorie und Praxis 8.1 Theoretischer Hintergrund Wir haben (nicht abzählbare) Wahrscheinlichkeitsräume Meßbare Funktionen Zufallsvariablen Verteilungsfunktionen Dichten in R
K8 Stetige Zufallsvariablen Theorie und Praxis 8.1 Theoretischer Hintergrund Wir haben (nicht abzählbare) Wahrscheinlichkeitsräume Meßbare Funktionen Zufallsvariablen Verteilungsfunktionen Dichten in R
Wahrscheinlichkeitsrechnung und Quantentheorie
 Physikalische Chemie II: Atombau und chemische Bindung Winter 2013/14 Wahrscheinlichkeitsrechnung und Quantentheorie Messergebnisse können in der Quantenmechanik ganz prinzipiell nur noch mit einer bestimmten
Physikalische Chemie II: Atombau und chemische Bindung Winter 2013/14 Wahrscheinlichkeitsrechnung und Quantentheorie Messergebnisse können in der Quantenmechanik ganz prinzipiell nur noch mit einer bestimmten
Wirtschaftsmathematik
 Einführung in einige Teilbereiche der Wintersemester 206 Prof. Dr. Stefan Etschberger HSA Unabhängigkeit von Ereignissen A, B unabhängig: Eintreten von A liefert keine Information über P(B). Formal: P(A
Einführung in einige Teilbereiche der Wintersemester 206 Prof. Dr. Stefan Etschberger HSA Unabhängigkeit von Ereignissen A, B unabhängig: Eintreten von A liefert keine Information über P(B). Formal: P(A
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen
 Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Einführung in die Stochastik für Informatiker Übungsaufgaben mit Lösungen David Geier und Sven Middelberg RWTH Aachen, Sommersemester 27 Inhaltsverzeichnis Information 2 Aufgabe 4 Aufgabe 2 6 4 Aufgabe
Veranstaltung: Statistik für das Lehramt Dozent: Martin Tautenhahn Referenten: Belinda Höher, Thomas Holub, Maria Böhm.
 Veranstaltung: Statistik für das Lehramt 16.12.2016 Dozent: Martin Tautenhahn Referenten: Belinda Höher, Thomas Holub, Maria Böhm Erwartungswert Varianz Standardabweichung Die Wahrscheinlichkeitsverteilung
Veranstaltung: Statistik für das Lehramt 16.12.2016 Dozent: Martin Tautenhahn Referenten: Belinda Höher, Thomas Holub, Maria Böhm Erwartungswert Varianz Standardabweichung Die Wahrscheinlichkeitsverteilung
Kapitel 12 Erwartungswert und Varianz
 Kapitel 12 Erwartungswert und Varianz Vorlesung Wahrscheinlichkeitsrechnung I vom 4/10. Juni 2009 Lehrstuhl für Angewandte Mathematik 1 FAU 12.1 Der Erwartungswert Der Erwartungswert einer Zufallsvariablen
Kapitel 12 Erwartungswert und Varianz Vorlesung Wahrscheinlichkeitsrechnung I vom 4/10. Juni 2009 Lehrstuhl für Angewandte Mathematik 1 FAU 12.1 Der Erwartungswert Der Erwartungswert einer Zufallsvariablen
Wahrscheinlichkeitsrechnung und Statistik
 5. Vorlesung Verteilungsfunktion (VF) Definition 9 Die Verteilungsfunktion (VF) einer Zufallsgröße X ist F : R R definiert als F (x) := P({ω Ω : X (ω) x}) = P( X x ) für jedes x R. Satz 9 - Eigenschaften
5. Vorlesung Verteilungsfunktion (VF) Definition 9 Die Verteilungsfunktion (VF) einer Zufallsgröße X ist F : R R definiert als F (x) := P({ω Ω : X (ω) x}) = P( X x ) für jedes x R. Satz 9 - Eigenschaften
Zusatzmaterial zur Vorlesung Statistik II
 Zusatzmaterial zur Vorlesung Statistik II Dr. Steffi Höse Professurvertretung für Ökonometrie und Statistik, KIT Wintersemester 2011/2012 (Fassung vom 15.11.2011, DVI- und PDF-Datei erzeugt am 15. November
Zusatzmaterial zur Vorlesung Statistik II Dr. Steffi Höse Professurvertretung für Ökonometrie und Statistik, KIT Wintersemester 2011/2012 (Fassung vom 15.11.2011, DVI- und PDF-Datei erzeugt am 15. November
Lösungsskizzen zur Präsenzübung 09
 Lösungsskizzen zur Präsenzübung 09 Hilfestellung zur Vorlesung Anwendungen der Mathematik im Wintersemester 2015/2016 Fakultät für Mathematik Universität Bielefeld Veröffentlicht am 07. Februar 2016 von:
Lösungsskizzen zur Präsenzübung 09 Hilfestellung zur Vorlesung Anwendungen der Mathematik im Wintersemester 2015/2016 Fakultät für Mathematik Universität Bielefeld Veröffentlicht am 07. Februar 2016 von:
Chi-Quadrat-Verteilung
 Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
Kenngrößen von Zufallsvariablen
 Kenngrößen von Zufallsvariablen Die Wahrscheinlichkeitsverteilung kann durch die sogenannten Kenngrößen beschrieben werden, sie charakterisieren sozusagen die Verteilung. Der Erwartungswert Der Erwartungswert
Kenngrößen von Zufallsvariablen Die Wahrscheinlichkeitsverteilung kann durch die sogenannten Kenngrößen beschrieben werden, sie charakterisieren sozusagen die Verteilung. Der Erwartungswert Der Erwartungswert
1 Verteilungsfunktionen, Zufallsvariable etc.
 4. Test M3 ET 27 6.6.27 4. Dezember 27 Regelung für den.ten Übungstest:. Wer bei den Professoren Dirschmid, Blümlinger, Vogl oder Langer die UE aus Mathematik 2 gemacht hat, sollte dort die WTH und Statistik
4. Test M3 ET 27 6.6.27 4. Dezember 27 Regelung für den.ten Übungstest:. Wer bei den Professoren Dirschmid, Blümlinger, Vogl oder Langer die UE aus Mathematik 2 gemacht hat, sollte dort die WTH und Statistik
Die Varianz (Streuung) Definition
 Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
KAPITEL 5. Erwartungswert
 KAPITEL 5 Erwartungswert Wir betrachten einen diskreten Wahrscheinlichkeitsraum (Ω, P) und eine Zufallsvariable X : Ω R auf diesem Wahrscheinlichkeitsraum. Die Grundmenge Ω hat also nur endlich oder abzählbar
KAPITEL 5 Erwartungswert Wir betrachten einen diskreten Wahrscheinlichkeitsraum (Ω, P) und eine Zufallsvariable X : Ω R auf diesem Wahrscheinlichkeitsraum. Die Grundmenge Ω hat also nur endlich oder abzählbar
7.2 Moment und Varianz
 7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
7.2 Moment und Varianz Def. 21 Es sei X eine zufällige Variable. Falls der Erwartungswert E( X p ) existiert, heißt der Erwartungswert EX p p tes Moment der zufälligen Variablen X. Es gilt dann: + x p
Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung
 R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
R. Brinkmann http://brinkmann-du.de Seite 5.05.0 Erwartungswert, Umgebungswahrscheinlichkeiten und die Normalverteilung Erwartungswert binomialverteilter Zufallsgrößen Wird ein Bernoulli- Versuch, bei
Zusammenfassung Mathe II. Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen
 Zusammenfassung Mathe II Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen Zufallsexperiment: Ein Vorgang, bei dem mindestens zwei Ereignisse möglich sind
Zusammenfassung Mathe II Themenschwerpunkt 2: Stochastik (ean) 1. Ein- und mehrstufige Zufallsexperimente; Ergebnismengen Zufallsexperiment: Ein Vorgang, bei dem mindestens zwei Ereignisse möglich sind
5 Erwartungswerte, Varianzen und Kovarianzen
 47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
47 5 Erwartungswerte, Varianzen und Kovarianzen Zur Charakterisierung von Verteilungen unterscheidet man Lageparameter, wie z. B. Erwartungswert ( mittlerer Wert ) Modus (Maximum der Wahrscheinlichkeitsfunktion,
Kapitel 6. Verteilungsparameter. 6.1 Der Erwartungswert Diskrete Zufallsvariablen
 Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
Kapitel 6 Verteilungsparameter Wie bei einem Merkmal wollen wir nun die Lage und die Streuung der Verteilung einer diskreten Zufallsvariablen durch geeignete Maßzahlen beschreiben. Beginnen wir mit Maßzahlen
1. Grundbegri e der Stochastik
 Wiederholung von Grundwissen der Stochastik. Grundbegri e der Stochastik Menge der Ereignisse. Die Elemente! der Menge heißen Elementarereignisse und sind unzerlegbare Ereignisse. Das Ereignis A tritt
Wiederholung von Grundwissen der Stochastik. Grundbegri e der Stochastik Menge der Ereignisse. Die Elemente! der Menge heißen Elementarereignisse und sind unzerlegbare Ereignisse. Das Ereignis A tritt
1. Grundbegri e. T n i=1 A i = A 1 \ A 2 \ : : : \ A n alle A i treten ein. na = A das zu A komplementäre Ereignis; tritt ein, wenn A nicht eintritt.
 . Grundbegri e Menge der Ereignisse. Die Elemente! der Menge heißen Elementarereignisse und sind unzerlegbare Ereignisse. Das Ereignis A tritt ein, wenn ein! A eintritt. ist auch das sichere Ereignis,
. Grundbegri e Menge der Ereignisse. Die Elemente! der Menge heißen Elementarereignisse und sind unzerlegbare Ereignisse. Das Ereignis A tritt ein, wenn ein! A eintritt. ist auch das sichere Ereignis,
Programm. Wiederholung. Gleichverteilung Diskrete Gleichverteilung Stetige Gleichverteilung. Binomialverteilung. Hypergeometrische Verteilung
 Programm Wiederholung Gleichverteilung Diskrete Gleichverteilung Stetige Gleichverteilung Binomialverteilung Hypergeometrische Verteilung Wiederholung verschiedene Mittelwerte für verschiedene Skalenniveaus
Programm Wiederholung Gleichverteilung Diskrete Gleichverteilung Stetige Gleichverteilung Binomialverteilung Hypergeometrische Verteilung Wiederholung verschiedene Mittelwerte für verschiedene Skalenniveaus
Unabhängigkeit von Zufallsvariablen
 Unabhängigkeit von Zufallsvariablen Seminar Gegenbeispiele in der Wahrscheinlichkeitstheorie Pascal Beckedorf 12. November 2012 Pascal Beckedorf Unabhängigkeit von Zufallsvariablen 12. November 2012 1
Unabhängigkeit von Zufallsvariablen Seminar Gegenbeispiele in der Wahrscheinlichkeitstheorie Pascal Beckedorf 12. November 2012 Pascal Beckedorf Unabhängigkeit von Zufallsvariablen 12. November 2012 1
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilungen stetiger Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilungen stetiger Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
7.5 Erwartungswert, Varianz
 7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
7.5 Erwartungswert, Varianz Def. 7.5.: a) X sei eine diskrete ZV, die bei unendl. vielen Werten x k folgende Zusatzbedingung erfüllt: x k p k
Kapitel 8: Zufallsvektoren
 Folie zur Vorlesung Wahrscheinlichkeitsrechnung und Stoch. Prozesse 03.12.2015 Kapitel 8: Zufallsvektoren Statt einem Merkmal werden häufig mehrere Merkmale gleichzeitig betrachtet, z.b. Körpergröße und
Folie zur Vorlesung Wahrscheinlichkeitsrechnung und Stoch. Prozesse 03.12.2015 Kapitel 8: Zufallsvektoren Statt einem Merkmal werden häufig mehrere Merkmale gleichzeitig betrachtet, z.b. Körpergröße und
0 für t < für 1 t < für 2 t < für 3 t < für 4 t < 5 1 für t 5
 4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
4 Verteilungen und ihre Kennzahlen 1 Kapitel 4: Verteilungen und ihre Kennzahlen A: Beispiele Beispiel 1: Eine diskrete Zufallsvariable X, die nur die Werte 1,, 3, 4, 5 mit positiver Wahrscheinlichkeit
Wahrscheinlichkeitstheorie und Statistik vom
 INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
INSTITUT FÜR STOCHASTIK SS 2007 UNIVERSITÄT KARLSRUHE Priv.-Doz. Dr. D. Kadelka Dipl.-Math. oec. W. Lao Klausur (Maschineningenieure) Wahrscheinlichkeitstheorie und Statistik vom 2.9.2007 Musterlösungen
1. Grundbegri e der Stochastik
 . Grundbegri e der Stochastik Raum der Ereignisse. Die einelementigen Teilmengen f!g heißen auch Elementarereignisse. Das Ereignis A tritt ein, wenn ein! A eintritt. A ist ein geeignetes System von Teilmengen
. Grundbegri e der Stochastik Raum der Ereignisse. Die einelementigen Teilmengen f!g heißen auch Elementarereignisse. Das Ereignis A tritt ein, wenn ein! A eintritt. A ist ein geeignetes System von Teilmengen
Fit for Abi & Study Stochastik
 Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
Kalman-Filter und Target Tracking
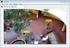 Kalman-Filter und Target Tracking Peter Poschmann Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik/Mathematik 23. März 2016 Inhalt 1 Kalman-Filter Einleitung Eindimensionaler Kalman-Filter
Kalman-Filter und Target Tracking Peter Poschmann Hochschule für Technik und Wirtschaft Dresden Fakultät Informatik/Mathematik 23. März 2016 Inhalt 1 Kalman-Filter Einleitung Eindimensionaler Kalman-Filter
Prüfungsvorbereitungskurs Höhere Mathematik 3
 Prüfungsvorbereitungskurs Höhere Mathematik 3 Stochastik Marco Boßle Jörg Hörner Marcel Thoms Mathematik Online Herbst 211 PV-Kurs HM 3 Stochastik 1-1 Zusammenfassung Wahrscheinlichkeitsraum (WR): Menge
Prüfungsvorbereitungskurs Höhere Mathematik 3 Stochastik Marco Boßle Jörg Hörner Marcel Thoms Mathematik Online Herbst 211 PV-Kurs HM 3 Stochastik 1-1 Zusammenfassung Wahrscheinlichkeitsraum (WR): Menge
Statistik und Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
ETWR Teil B. Spezielle Wahrscheinlichkeitsverteilungen (stetig)
 ETWR Teil B 2 Ziele Bisher (eindimensionale, mehrdimensionale) Zufallsvariablen besprochen Lageparameter von Zufallsvariablen besprochen Übertragung des gelernten auf diskrete Verteilungen Ziel des Kapitels
ETWR Teil B 2 Ziele Bisher (eindimensionale, mehrdimensionale) Zufallsvariablen besprochen Lageparameter von Zufallsvariablen besprochen Übertragung des gelernten auf diskrete Verteilungen Ziel des Kapitels
Unabhängige Zufallsvariablen
 Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Kapitel 9 Unabhängige Zufallsvariablen Die Unabhängigkeit von Zufallsvariablen wird auf die Unabhängigkeit von Ereignissen zurückgeführt. Im Folgenden sei Ω, A, P ) ein Wahrscheinlichkeitsraum. Definition
Begriffe aus der Informatik Nachrichten
 Begriffe aus der Informatik Nachrichten Gerhard Goos definiert in Vorlesungen über Informatik, Band 1, 1995 Springer-Verlag Berlin Heidelberg: Die Darstellung einer Mitteilung durch die zeitliche Veränderung
Begriffe aus der Informatik Nachrichten Gerhard Goos definiert in Vorlesungen über Informatik, Band 1, 1995 Springer-Verlag Berlin Heidelberg: Die Darstellung einer Mitteilung durch die zeitliche Veränderung
3.3 Bedingte Wahrscheinlichkeit
 28 3.3 Bedingte Wahrscheinlichkeit Oft ist die Wahrscheinlichkeit eines Ereignisses B gesucht unter der Bedingung (bzw. dem Wissen), dass ein Ereignis A bereits eingetreten ist. Man bezeichnet diese Wahrscheinlichkeit
28 3.3 Bedingte Wahrscheinlichkeit Oft ist die Wahrscheinlichkeit eines Ereignisses B gesucht unter der Bedingung (bzw. dem Wissen), dass ein Ereignis A bereits eingetreten ist. Man bezeichnet diese Wahrscheinlichkeit
Statistik III. Walter Zucchini Fred Böker Andreas Stadie
 Statistik III Walter Zucchini Fred Böker Andreas Stadie Inhaltsverzeichnis 1 Zufallsvariablen und ihre Verteilung 1 1.1 Diskrete Zufallsvariablen........................... 1 1.2 Stetige Zufallsvariablen............................
Statistik III Walter Zucchini Fred Böker Andreas Stadie Inhaltsverzeichnis 1 Zufallsvariablen und ihre Verteilung 1 1.1 Diskrete Zufallsvariablen........................... 1 1.2 Stetige Zufallsvariablen............................
Wahrscheinlichkeitsfunktion. Binomialverteilung. Binomialverteilung. Wahrscheinlichkeitshistogramme
 Binomialverteilung Wahrscheinlichkeitsfunktion Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder
Binomialverteilung Wahrscheinlichkeitsfunktion Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder
Statistik 2 für SoziologInnen. Normalverteilung. Univ.Prof. Dr. Marcus Hudec. Themen dieses Kapitels sind:
 Statistik 2 für SoziologInnen Normalverteilung Univ.Prof. Dr. Marcus Hudec Statistik 2 für SoziologInnen 1 Normalverteilung Inhalte Themen dieses Kapitels sind: Das Konzept stetiger Zufallsvariablen Die
Statistik 2 für SoziologInnen Normalverteilung Univ.Prof. Dr. Marcus Hudec Statistik 2 für SoziologInnen 1 Normalverteilung Inhalte Themen dieses Kapitels sind: Das Konzept stetiger Zufallsvariablen Die
Stochastik. 1. Wahrscheinlichkeitsräume
 Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
Stochastik 1. Wahrscheinlichkeitsräume Ein Zufallsexperiment ist ein beliebig oft und gleichartig wiederholbarer Vorgang mit mindestens zwei verschiedenen Ergebnissen, bei dem der Ausgang ungewiß ist.
1. Was ist eine Wahrscheinlichkeit P(A)?
 1. Was ist eine Wahrscheinlichkeit P(A)? Als Wahrscheinlichkeit verwenden wir ein Maß, welches die gleichen Eigenschaften wie die relative Häufigkeit h n () besitzt, aber nicht zufallsbehaftet ist. Jan
1. Was ist eine Wahrscheinlichkeit P(A)? Als Wahrscheinlichkeit verwenden wir ein Maß, welches die gleichen Eigenschaften wie die relative Häufigkeit h n () besitzt, aber nicht zufallsbehaftet ist. Jan
4. Verteilungen von Funktionen von Zufallsvariablen
 4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
4. Verteilungen von Funktionen von Zufallsvariablen Allgemeine Problemstellung: Gegeben sei die gemeinsame Verteilung der ZV en X 1,..., X n (d.h. bekannt seien f X1,...,X n bzw. F X1,...,X n ) Wir betrachten
Übungsblatt 9 (25. bis 29. Juni)
 Statistik 2 Dr. Andrea Beccarini Dipl.-Vw. Dipl.-Kffr. Heike Bornewasser-Hermes Sommersemester 2012 Übungsblatt 9 (25. bis 29. Juni) Stetiges Verteilungsmodell und Gemeinsame Verteilung Stetiges Verteilungsmodell
Statistik 2 Dr. Andrea Beccarini Dipl.-Vw. Dipl.-Kffr. Heike Bornewasser-Hermes Sommersemester 2012 Übungsblatt 9 (25. bis 29. Juni) Stetiges Verteilungsmodell und Gemeinsame Verteilung Stetiges Verteilungsmodell
P (X = 2) = 1/36, P (X = 3) = 2/36,...
 2.3 Zufallsvariablen 2.3 Zufallsvariablen Meist sind die Ereignisse eines Zufallseperiments bereits reelle Zahlen. Ist dies nicht der Fall, kann man Ereignissen eine reelle Zahl zuordnen. Zum Beispiel
2.3 Zufallsvariablen 2.3 Zufallsvariablen Meist sind die Ereignisse eines Zufallseperiments bereits reelle Zahlen. Ist dies nicht der Fall, kann man Ereignissen eine reelle Zahl zuordnen. Zum Beispiel
Forschungsstatistik I
 Prof. Dr. G. Meinhardt 2. Stock, Nordflügel R. 02-429 (Persike) R. 02-431 (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de WS 2008/2009
Prof. Dr. G. Meinhardt 2. Stock, Nordflügel R. 02-429 (Persike) R. 02-431 (Meinhardt) Sprechstunde jederzeit nach Vereinbarung Forschungsstatistik I Dr. Malte Persike persike@uni-mainz.de WS 2008/2009
Mehrdimensionale Verteilungen und Korrelation
 Vorlesung: Computergestützte Datenauswertung Mehrdimensionale Verteilungen und Korrelation Günter Quast Fakultät für Physik Institut für Experimentelle Kernphysik SS '17 KIT Die Forschungsuniversität in
Vorlesung: Computergestützte Datenauswertung Mehrdimensionale Verteilungen und Korrelation Günter Quast Fakultät für Physik Institut für Experimentelle Kernphysik SS '17 KIT Die Forschungsuniversität in
13 Grenzwertsätze Das Gesetz der großen Zahlen
 13 Grenzwertsätze 13.1 Das Gesetz der großen Zahlen Der Erwartungswert einer zufälligen Variablen X ist in der Praxis meist nicht bekannt. Um ihn zu bestimmen, sammelt man Beobachtungen X 1,X 2,...,X n
13 Grenzwertsätze 13.1 Das Gesetz der großen Zahlen Der Erwartungswert einer zufälligen Variablen X ist in der Praxis meist nicht bekannt. Um ihn zu bestimmen, sammelt man Beobachtungen X 1,X 2,...,X n
Probeklausur Statistik II
 Prof. Dr. Chr. Müller PROBE-KLAUSUR 1 1 2 3 4 5 6 7 8 Gesamt: 15 8 16 16 7 8 15 15 100 Probeklausur Statistik II Name: Vorname: Fachrichtung: Matrikel-Nummer: Bitte beachten Sie folgendes: 1) Die Klausur
Prof. Dr. Chr. Müller PROBE-KLAUSUR 1 1 2 3 4 5 6 7 8 Gesamt: 15 8 16 16 7 8 15 15 100 Probeklausur Statistik II Name: Vorname: Fachrichtung: Matrikel-Nummer: Bitte beachten Sie folgendes: 1) Die Klausur
Beispiel 6 (Einige Aufgaben zur Gleichverteilung)
 Beispiel 6 (Einige Aufgaben zur Gleichverteilung) Aufgabe (Anwendung der Chebyshev-Ungleichung) Sei X eine Zufallsvariable mit E(X) = µ und var(x) = σ a) Schätzen Sie die Wahrscheinlichkeit dafür, daß
Beispiel 6 (Einige Aufgaben zur Gleichverteilung) Aufgabe (Anwendung der Chebyshev-Ungleichung) Sei X eine Zufallsvariable mit E(X) = µ und var(x) = σ a) Schätzen Sie die Wahrscheinlichkeit dafür, daß
Prüfungsvorbereitungskurs Höhere Mathematik 3
 Prüfungsvorbereitungskurs Höhere Mathematik 3 Stochastik Marco Boßle Jörg Hörner Mathematik Online Frühjahr 2011 PV-Kurs HM 3 Stochastik 1-1 Zusammenfassung Wahrscheinlichkeitsraum (WR): Menge der Elementarereignisse
Prüfungsvorbereitungskurs Höhere Mathematik 3 Stochastik Marco Boßle Jörg Hörner Mathematik Online Frühjahr 2011 PV-Kurs HM 3 Stochastik 1-1 Zusammenfassung Wahrscheinlichkeitsraum (WR): Menge der Elementarereignisse
Biostatistik, Sommer 2017
 1/52 Biostatistik, Sommer 2017 Prof. Dr. Achim Klenke http://www.aklenke.de 7. Vorlesung: 02.06.2017 2/52 Inhalt 1 Wahrscheinlichkeit Bayes sche Formel 2 Diskrete Stetige 3/52 Wahrscheinlichkeit Bayes
1/52 Biostatistik, Sommer 2017 Prof. Dr. Achim Klenke http://www.aklenke.de 7. Vorlesung: 02.06.2017 2/52 Inhalt 1 Wahrscheinlichkeit Bayes sche Formel 2 Diskrete Stetige 3/52 Wahrscheinlichkeit Bayes
67 Zufallsvariable, Erwartungswert, Varianz
 67 Zufallsvariable, Erwartungswert, Varianz 67.1 Motivation Oft möchte man dem Resultat eines Zufallsexperiments eine reelle Zahl zuordnen. Der Gewinn bei einem Glücksspiel ist ein Beispiel hierfür. In
67 Zufallsvariable, Erwartungswert, Varianz 67.1 Motivation Oft möchte man dem Resultat eines Zufallsexperiments eine reelle Zahl zuordnen. Der Gewinn bei einem Glücksspiel ist ein Beispiel hierfür. In
Statistik für Ingenieure Vorlesung 2
 Statistik für Ingenieure Vorlesung 2 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 24. Oktober 2016 2.4 Bedingte Wahrscheinlichkeiten Häufig ist es nützlich, Bedingungen
Statistik für Ingenieure Vorlesung 2 Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut für Stochastik 24. Oktober 2016 2.4 Bedingte Wahrscheinlichkeiten Häufig ist es nützlich, Bedingungen
Univariates Datenmaterial
 Univariates Datenmaterial 1.6.1 Deskriptive Statistik Zufallstichprobe: Umfang n, d.h. Stichprobe von n Zufallsvariablen o Merkmal/Zufallsvariablen: Y = {Y 1, Y 2,..., Y n } o Realisationen/Daten: x =
Univariates Datenmaterial 1.6.1 Deskriptive Statistik Zufallstichprobe: Umfang n, d.h. Stichprobe von n Zufallsvariablen o Merkmal/Zufallsvariablen: Y = {Y 1, Y 2,..., Y n } o Realisationen/Daten: x =
