Warping im Detail $KNFXGTCTDGKVWPIWPF#NIQTKVJOGP 2TQH &T9QNHICPI-QPGP. Bildverarbeitung und Algorithmen SS Konen, Zielke
|
|
|
- Maria Frank
- vor 6 Jahren
- Abrufe
Transkript
1 $KNFXGTCTDGKVWPIWPF#NIQTKVJOGP 2TQH &T9QNHICPI-QPGP Warping im Detail SS Konen, Zielke SS Konen, Zielke
2 &KG5EJTKVVGFGU9CTRKPI#NIQTKVJOWU 6FKULWW: Passpunkte finden automatisch oder manuell 6FKULWW: Suche zu den Passpunkten die beste Transformation analytisch (z.b. Vertreter aus Klasse der affinen Transformationen) oder stückweise linear für jeden Pixelort [ im Zielbild (*ULGGLQJ) 6FKULWW: Grauwerte der Zielpixel festlegen durch Interpolation am Quellort (nächster Nachbar, bilinear, bikubisch, ) Aus didaktischen Gründen gehen wir nachfolgend diese Schritte in umgekehrter Reihenfolge durch SS Konen, Zielke 6TCPUHQTOCVKQPGP6WPF6 UGKGPIGIGDGP Backwards-Warp: Zielpixelort [ wird durch Quellort [ koloriert Quelle I Ziel I [ 7 [µ ƒ Wieso nicht Vorwärts-Warp? s. Vorlesung. Quelle: aufg_loes.htm ƒ Grauwert durch z.b. bilineare Interpolation um Quellort [ herum Formel in Vorlesung SS Konen, Zielke
3 )GQOGVTKUEJG6TCPUHQTOCVKQP6 Typisierung analytischer Transformationen SS Konen, Zielke )GQOGVTKUEJG6TCPUHQTOCVKQP6 Typisierung analytischer Transformationen Euklid / Procrustes Affin Bilinear perspektivisch (projektiv) Geraden bleiben Geraden, Quadrate bleiben Quadrate Geraden bleiben Geraden, Parallelen bleiben parallel, Rechteck Parallelogramm Geraden bleiben Geraden, Rechteck allg. Viereck Geraden bleiben Geraden, Parallelen Geraden mit gemeinsamen Fluchtpunkt Biquadratisch Geraden werden zu Kurven SS Konen, Zielke
4 )GQOGVTKUEJG6TCPUHQTOCVKQP6 Typisierung analytischer Transformationen Euklid / Procrustes Affin Kombination Translation + Rotation + globale Skalierung Kombination Translation + Rotation + x-skalierung + y- Skalierung mind. 2 Kontrollpunkte mind. 3 Kontrollpunkte Bilinear mind. 4 Kontrollpunkte perspektivisch (projektiv) mind. 5 Kontrollpunkte Biquadratisch mind. 6 Kontrollpunkte SS Konen, Zielke )GQOGVTKUEJG6TCPUHQTOCVKQP6 Wie genau macht man den Warp in MATLAB?. wenn T gegeben ist 2. wenn T aus Passpunkten zu berechnen ist a) beste Transformation im LS-Sinne aus bestimmter Klasse von Transformationen suchen >> s. Übung b) stückweise-linear interpolieren zwischen Passpunkten (*ULGGLQJ) *ULGGLQJ ist der Vorgang, bei dem eine Funktion, deren Werte nur an einigen Stellen gegeben sind, für alle Punkte in einem regelmäßigen Gitter (*ULG) berechnet wird. SS Konen, Zielke
5 XQTIGIGDGPGU6 Zu 2..: Sei T als homogene 3x3-Matrix bekannt [h,w] = size(i); [Xp,Yp] = ndgrid(:w,:h); n = h*w; X = T \ [Xp(:),YP(:),ones(n,)] ; <S ;S Lösung ; für Xp 7; = Yp Xp2 Yp2 SS Konen, Zielke C$GUVGU6OKV.5(KV Zu 2.2.a): Seien mehr Passpunkte gegeben als man zur Bestimmung von T braucht. Bsp. Rotationsstreckung: x a = y b b x a y x = ax + by y = bx + ay x x = y y y a x b Übergang auf mehrere Passpunkte: x x x n x = y y yn y n n y y n x x n a b ;= =W Dieses i.d.r. überbestimmte System für Parametervektor W =(a,b) T wird durch den MATLAB-Befehl t = Z \ Xp; im LS-Sinne gelöst. Der Trick: Jeder freie Parameter a,b, taucht genau x auf SS Konen, Zielke
6 DUV EMYGKUGNKPGCTG6TCPUHQTOCVKQP6 Zu 2.2.b): Aufgabe: Die Bildmitte vergrößert abbilden (Fovea) Definiere einige Passpunkte [xpr,ypr] [xr,yr] Q u e l l e Z i e l Delaunay-Triangulation SS Konen, Zielke DUV EMYGKUGNKPGCTG6TCPUHQTOCVKQP6 Zwischen den Dreieckspunkten linear interpolieren an Dreieckspunkten ist durch (X,X2,X3 ) die Ebene der X -Koordinatenfunktion gegeben Pixel (x,y) erhält Ebenenwert x'=x'(x,y) analog für (Y',Y2',Y3') und Y'-Koordinatenfunktion *ULGGLQJ in MATLAB (foveawarp.m): X (X,Y) X2 X - Ebene X3 X,,Xn Y,,Yn X,,Xn gleiche Dim wie xg [xg,yg] = ndgrid(:28,:28); xi = griddata(xr,yr, xpr, xg,yg); yi = griddata(xr,yr, ypr, xg,yg); Ip(:,:,)=interp2(I(:,:,), yi, xi, bilinear,255); Ip(:,:,2)=interp2(I(:,:,2), yi, xi, bilinear,255); Ip(:,:,3)=interp2(I(:,:,3), yi, xi, bilinear,255); griddata macht Delaunay-Triang. für alle (Xi,Yi) und interpoliert damit neue X'-Werte xi an Orten (xg,yg) SS Konen, Zielke
7 'TI¼P\WPI Fragen / Aufgaben Wieso muss es ",yi,xi," heißen und nicht ",xi,yi,"? Können Sie eine Fovealisierungs-Funktion angeben, d.h. eine Funktion, die aus dem Gitter [xr,yr] das Gitter [xpr,ypr] berechnet? Aufgabe Warping: aufgaben.htm, Lsg.: euclideanwarp2.m zum Schmunzeln foveawarp2.m SS Konen, Zielke 2CUURWPMVGHKPFGP manuell o.k. für BildEHarbeitung, aber keine (automatisierte) BildYHUarbeitung mühsam, wenn viele Bilder optional: Passpunkte per Kreuzkorrelation verbessern automatisch: möglich, wenn korrespondierende Punkte in 2 Bildern vorliegen diese Aufgabe heißt 0DWFKLQJ oder 5HJLVWULHUXQJ 2 Teilprobleme: das Auffinden geeigneter Punkte im Bild "salient points", Landmarken >> Aperturproblem (!) das genaue Wiederfinden im anderen Bild Template Matching s. Projekt Tracking SS Konen, Zielke
8 #PYGPFWPIGP9CTRKPI Kamerakalibrierung (Kissen- oder Tonnenverzeichnung korrigieren) industrielle Prüfaufgaben für deformierbare Objekte Inverse Perspektive medizinische Bildverarbeitung Matching und Registrierung bei multimodalen, multitemporalen Aufnahmen >> s. Projekt Matching Zwischenbilder berechnen >> s. Projekt Morphing Facial Animation, 3D-MM (Morphable Models) [Blanz, Vetter] >> s. reanim_exercise.mpg Mosaicing (mehrere Bilder zusammensetzen) >> s. Projekt Panoramic View SS Konen, Zielke
Einführung in die medizinische Bildverarbeitung WS 12/13
 Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Prozess einer räumliche Transformation zu finden um ein Bild auf ein anderes Bild abzubilden Eingabe: Fixed und
Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Prozess einer räumliche Transformation zu finden um ein Bild auf ein anderes Bild abzubilden Eingabe: Fixed und
Projektive Geometrie
 Projektive Geometrie Einleitung Was ist projektive Geometrie? eine alternative algebraische Repräsentation von geometrischen Objekten (Punkt, Gerade,...) und Transformationen (Translation, Rotation,...)
Projektive Geometrie Einleitung Was ist projektive Geometrie? eine alternative algebraische Repräsentation von geometrischen Objekten (Punkt, Gerade,...) und Transformationen (Translation, Rotation,...)
Computergrafik Inhalt Achtung! Kapitel ist relevant für CG-2!
 Coputergrafik Inhalt Achtung! Kapitel ist relevant für CG-2! 1 2 3 4 5 6 7 8 Historie, Überblick, Beispiele Begriffe und Grundlagen Objekttransforationen Objektrepräsentation und -Modellierung Sichttransforationen
Coputergrafik Inhalt Achtung! Kapitel ist relevant für CG-2! 1 2 3 4 5 6 7 8 Historie, Überblick, Beispiele Begriffe und Grundlagen Objekttransforationen Objektrepräsentation und -Modellierung Sichttransforationen
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Punkte Ebenen im Raum Dualismus im Raum Die unendlich ferne Ebene Parametrische Darstellung (Span) Die Gerade im Raum -
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 5 Punkte Ebenen im Raum Dualismus im Raum Die unendlich ferne Ebene Parametrische Darstellung (Span) Die Gerade im Raum -
Bildverarbeitung Herbstsemester. Mustererkennung
 Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Mustererkennung 1 Inhalt Einführung Mustererkennung in Grauwertbildern Ähnlichkeitsmasse Normalisierte Korrelation Korrelationskoeffizient Mustererkennung
Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Mustererkennung 1 Inhalt Einführung Mustererkennung in Grauwertbildern Ähnlichkeitsmasse Normalisierte Korrelation Korrelationskoeffizient Mustererkennung
Projektion. Ebene geometrische Projektionen
 Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Animation ist das Erzeugen von Filmen mit Hilfe der Computergrafik. Objekte bewegen sich hierbei oder Beleuchtung, Augpunkt, Form,... ändern sich.
 Kapitel 1 Animation (Belebung) Animation ist das Erzeugen von Filmen mit Hilfe der Computergrafik. Objekte bewegen sich hierbei oder Beleuchtung, Augpunkt, Form,... ändern sich. Anwendungen findet die
Kapitel 1 Animation (Belebung) Animation ist das Erzeugen von Filmen mit Hilfe der Computergrafik. Objekte bewegen sich hierbei oder Beleuchtung, Augpunkt, Form,... ändern sich. Anwendungen findet die
Grundlagen der Computergraphik Klausur SS08
 Grundlagen der Computergraphik Klausur SS08 Prof. Dr. Holger Theisel 23. Juli 2008 Vorname: Nachname: Matrikelnummer: Anzahl zusätzlicher Blätter: Die Tabelle wird bei der Korrektur ausgefüllt! Aufgabe
Grundlagen der Computergraphik Klausur SS08 Prof. Dr. Holger Theisel 23. Juli 2008 Vorname: Nachname: Matrikelnummer: Anzahl zusätzlicher Blätter: Die Tabelle wird bei der Korrektur ausgefüllt! Aufgabe
-dimensionale Darstellungen
 1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
Methode der kleinsten Quadrate
 1. Phase: Methode der kleinsten Quadrate Einführung Im Vortrag über das CT-Verfahren hat Herr Köckler schon auf die Methode der kleinsten Quadrate hingewiesen. Diese Lösungsmethode, welche bei überbestimmten
1. Phase: Methode der kleinsten Quadrate Einführung Im Vortrag über das CT-Verfahren hat Herr Köckler schon auf die Methode der kleinsten Quadrate hingewiesen. Diese Lösungsmethode, welche bei überbestimmten
Kapitel 2: Mathematische Grundlagen
 [ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
[ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Hans Delfs. Übungen zu Mathematik III für Medieninformatik
 Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 6 Endliche Kameras Die Lochkamera Die Projektive Kamera Die projektive Kamera Spalten von P Zeilen von P Hauptpunkt und Hauptachse
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 6 Endliche Kameras Die Lochkamera Die Projektive Kamera Die projektive Kamera Spalten von P Zeilen von P Hauptpunkt und Hauptachse
3 Systeme linearer Gleichungen
 3 Systeme linearer Gleichungen Wir wenden uns nun dem Problem der Lösung linearer Gleichungssysteme zu. Beispiel 3.1: Wir betrachten etwa das folgende System linearer Gleichungen: y + 2z = 1 (1) x 2y +
3 Systeme linearer Gleichungen Wir wenden uns nun dem Problem der Lösung linearer Gleichungssysteme zu. Beispiel 3.1: Wir betrachten etwa das folgende System linearer Gleichungen: y + 2z = 1 (1) x 2y +
R.Wagner, Mathematik in der Astronomie
 Mathematik in der Astronomie Roland Wagner Johann Radon Institute for Computational and Applied Mathematics (RICAM) Österreichische Akademie der Wissenschaften (ÖAW) Linz, Austria Linz, 20.Mai 2016 Übersicht
Mathematik in der Astronomie Roland Wagner Johann Radon Institute for Computational and Applied Mathematics (RICAM) Österreichische Akademie der Wissenschaften (ÖAW) Linz, Austria Linz, 20.Mai 2016 Übersicht
12 Übungen zu Gauß-Algorithmus
 Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
Aufgaben zum Vorkurs B S. 2 Übungen zu Gauß-Algorithmus 2x x 2 = 7x +, 5x 2 = 7 Aufgabe 6: Aufgabe 7: Aufgabe 8: Aufgabe 9: 2x x 2 = x +2x 2 = 2 2x x 2 = 7x +, 5x 2 =, 5 x 2x 2 = x +x 2 = 5 2x +x 2 = 4
Erweiterte Koordinaten
 Erweiterte Koordinaten Sei K n ein n dimensionaler affiner Raum Die erweiterten Koordinaten des Punktes x x n K n sind x x n Kn+ (Das ist für alle K sinnvoll, weil in jedem Körper K wohldefiniert ist In
Erweiterte Koordinaten Sei K n ein n dimensionaler affiner Raum Die erweiterten Koordinaten des Punktes x x n K n sind x x n Kn+ (Das ist für alle K sinnvoll, weil in jedem Körper K wohldefiniert ist In
Computer-Graphik I Baryzentrische Koordinaten
 /7/ lausthal omputer-raphik I Zachmann lausthal University, ermany zach@intu-clausthalde Def: affin unabhängig n n dadurch eg: k+ Punkte Pi R, 0 i k, kseien k Vektoren vi definiert: vi : Pi P0, i,, k Die
/7/ lausthal omputer-raphik I Zachmann lausthal University, ermany zach@intu-clausthalde Def: affin unabhängig n n dadurch eg: k+ Punkte Pi R, 0 i k, kseien k Vektoren vi definiert: vi : Pi P0, i,, k Die
Vorkurs Mathematik Übungen zu linearen Gleichungssystemen
 Vorkurs Mathematik Übungen zu linearen Gleichungssystemen Lineare Gleichungssysteme lösen Aufgabe. Lösen sie jeweils das LGS A x = b mit ( ( a A =, b = b A =, b = 6 Aufgabe. Berechnen Sie für die folgenden
Vorkurs Mathematik Übungen zu linearen Gleichungssystemen Lineare Gleichungssysteme lösen Aufgabe. Lösen sie jeweils das LGS A x = b mit ( ( a A =, b = b A =, b = 6 Aufgabe. Berechnen Sie für die folgenden
Entwicklung einer Programmbibliothek zur Simulation von Hautdeformation durch Knochen und Muskeln
 Entwicklung einer Programmbibliothek zur Simulation von Hautdeformation durch Knochen und Muskeln Universität Koblenz Institut für Computervisualistik Arbeitsgruppe Computergraphik Betreuer und Prüfer
Entwicklung einer Programmbibliothek zur Simulation von Hautdeformation durch Knochen und Muskeln Universität Koblenz Institut für Computervisualistik Arbeitsgruppe Computergraphik Betreuer und Prüfer
Bildverarbeitung: 3D-Geometrie. D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13
 Bildverarbeitung: 3D-Geometrie D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Bildverarbeitung: 3D-Geometrie D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Rekonstruktion kontinuierlicher Daten Interpolation multivariater Daten Ulrich Rüde Lehrstuhl für Systemsimulation Sommersemester
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Rekonstruktion kontinuierlicher Daten Interpolation multivariater Daten Ulrich Rüde Lehrstuhl für Systemsimulation Sommersemester
Bildtransformationen. Geometrische Transformationen Grauwert-Interpolation
 Bildtransformationen Geometrische Transformationen Grauwert-Interpolation Transformation Transformation zwei Schritte geometrische Transformation (Trafo der Koordinaten) Neuberechnung der Pielwerte an
Bildtransformationen Geometrische Transformationen Grauwert-Interpolation Transformation Transformation zwei Schritte geometrische Transformation (Trafo der Koordinaten) Neuberechnung der Pielwerte an
Prüfungsdauer: 120 Minuten
 Computergraphik und Multimediasysteme Seite 1 von 6 Klausur: Computergraphik II Probeklausur Semester: Prüfer: Prüfungsdauer: 1 Minuten Hilfsmittel: Schreibgeräte, Lineal, nichtprogrammierbarer Taschenrechner
Computergraphik und Multimediasysteme Seite 1 von 6 Klausur: Computergraphik II Probeklausur Semester: Prüfer: Prüfungsdauer: 1 Minuten Hilfsmittel: Schreibgeräte, Lineal, nichtprogrammierbarer Taschenrechner
Interaktives, echtzeitnahes Morphen verschiedenartiger Bildfolgen
 Interaktives, echtzeitnahes Morphen verschiedenartiger Bildfolgen André Viergutz 1 Inhalt Motivation und Grundlagen Registrierung mittels Optischem Fluss Vorverarbeitung der Bilder Synthese der Verarbeitungsschritte
Interaktives, echtzeitnahes Morphen verschiedenartiger Bildfolgen André Viergutz 1 Inhalt Motivation und Grundlagen Registrierung mittels Optischem Fluss Vorverarbeitung der Bilder Synthese der Verarbeitungsschritte
Quadratische Gleichungen. Üben. Lösung. Quadratische Gleichungen. Klasse. Schwierigkeit. Art. math. Thema. Nr. Löse mit der Lösungsformel:
 1a Löse mit der sformel: a) x 2 + 6x + 5 = 0 b) y 2 + 6y + 7 = 0 c) z 2 13z 48 = 0 1a a) a = 1, b = 6, c = 5 2 6 ± 6 4 1 5 x 1/ 2 = ; x1 5 ; x2 = 1 2 1 b) x 1 = 3 2 ; x 2 = 3+ 2 c) x1 = - 3 ; x2 = 16 1b
1a Löse mit der sformel: a) x 2 + 6x + 5 = 0 b) y 2 + 6y + 7 = 0 c) z 2 13z 48 = 0 1a a) a = 1, b = 6, c = 5 2 6 ± 6 4 1 5 x 1/ 2 = ; x1 5 ; x2 = 1 2 1 b) x 1 = 3 2 ; x 2 = 3+ 2 c) x1 = - 3 ; x2 = 16 1b
YOUNG SCIENTISTS. 4 dimensionale komplexe Zahlen in der Computergrafik. Bastian Weiß 19. Mai 2017 INSTITUT FÜR ANGEWANDTE GEOMETRIE
 YOUNG SCIENTISTS 4 dimensionale komplexe in der Computergrafik Bastian Weiß 19. Mai 2017 INSTITUT FÜR ANGEWANDTE GEOMETRIE Programm Vorbereitung (Wiederholung) Komplexe Vektoren Quaternionen Quaternionen
YOUNG SCIENTISTS 4 dimensionale komplexe in der Computergrafik Bastian Weiß 19. Mai 2017 INSTITUT FÜR ANGEWANDTE GEOMETRIE Programm Vorbereitung (Wiederholung) Komplexe Vektoren Quaternionen Quaternionen
Prof. J. Zhang zhang@informatik.uni-hamburg.de. Universität Hamburg. AB Technische Aspekte Multimodaler Systeme. 16. Dezember 2003
 zhang@informatik.uni-hamburg.de Universität Hamburg AB Technische Aspekte Multimodaler Systeme zhang@informatik.uni-hamburg.de Inhaltsverzeichnis 5. Sichtsysteme in der Robotik....................307 Industrielle
zhang@informatik.uni-hamburg.de Universität Hamburg AB Technische Aspekte Multimodaler Systeme zhang@informatik.uni-hamburg.de Inhaltsverzeichnis 5. Sichtsysteme in der Robotik....................307 Industrielle
Darstellung von Kurven und Flächen
 Darstellung von Kurven und Flächen Technische Universität Dresden Fakultät Informatik Institut für Software- und Multimediatechnik Dozent: Dr. Mascolous Referent: Gliederung / Einleitung 1 / 25 1. Kurven
Darstellung von Kurven und Flächen Technische Universität Dresden Fakultät Informatik Institut für Software- und Multimediatechnik Dozent: Dr. Mascolous Referent: Gliederung / Einleitung 1 / 25 1. Kurven
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 8 Projektive Invarianz und das kanonische Kamerapaar Kanonisches Kamerapaar aus gegebener Fundamentalmatrix Freiheitsgrade
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 8 Projektive Invarianz und das kanonische Kamerapaar Kanonisches Kamerapaar aus gegebener Fundamentalmatrix Freiheitsgrade
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Transformationen im 3D-Raum
 Thomas Jung Repräsentation von 3D-Oberflächen Aufbau von Szenen Transformationen im 3D-Raum Projektionstranformationen Anwendung in OpenGL Geometrietransformationen bilden die Basis für die Computergrafik
Thomas Jung Repräsentation von 3D-Oberflächen Aufbau von Szenen Transformationen im 3D-Raum Projektionstranformationen Anwendung in OpenGL Geometrietransformationen bilden die Basis für die Computergrafik
bilinear interpoliert ideal interpoliert
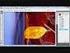 Bildverarbeitung und Objekterkennung Privatdozent (PD) Dr.-Ing. habil. K.-H. Franke Technische Universität Ilmenau Fakultät für Informatik und Automatisierung Institut für Prakt. Inf. und Medieninf. Fachgebiet
Bildverarbeitung und Objekterkennung Privatdozent (PD) Dr.-Ing. habil. K.-H. Franke Technische Universität Ilmenau Fakultät für Informatik und Automatisierung Institut für Prakt. Inf. und Medieninf. Fachgebiet
6. Vektor- und Koordinaten-Geometrie.
 6. Vektor- und Koordinaten-Geometrie. Jeder endlichen Menge, etwa der Menge kann man durch M = {,,, }. R 4 (M) = { a 1 + a 2 + a 3 + a 4 a i R } die Menge der formalen Linearkombinationen zuordnen. Es
6. Vektor- und Koordinaten-Geometrie. Jeder endlichen Menge, etwa der Menge kann man durch M = {,,, }. R 4 (M) = { a 1 + a 2 + a 3 + a 4 a i R } die Menge der formalen Linearkombinationen zuordnen. Es
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Geometrie WiSe 2014/2015 am
 Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Geometrie WiSe 2014/2015 am 23.1.2015 Bearbeiten Sie bitte zwei der drei folgenden Aufgaben! Falls Sie alle drei Aufgaben bearbeitet haben sollten, kennzeichnen
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Geometrie WiSe 2014/2015 am 23.1.2015 Bearbeiten Sie bitte zwei der drei folgenden Aufgaben! Falls Sie alle drei Aufgaben bearbeitet haben sollten, kennzeichnen
Lernkarten. Analytische Geometrie. 6 Seiten
 Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
d) Produkte orthogonaler Matrizen sind wieder orthogonal.
 Die orthogonale Matrizen Definition: Eine Matrix Q R n n heißt orthogonal, falls QQ T = Q T Q = I gilt. Die Eigenschaften orthogonaler Matrizen: a) det(q) = ±1; b) Qx 2 = x 2 für alle x R n, also Q 2 =
Die orthogonale Matrizen Definition: Eine Matrix Q R n n heißt orthogonal, falls QQ T = Q T Q = I gilt. Die Eigenschaften orthogonaler Matrizen: a) det(q) = ±1; b) Qx 2 = x 2 für alle x R n, also Q 2 =
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Inverse und implizite Funktionen
 Kapitel 8 Inverse und implizite Funktionen Josef Leydold Mathematik für VW WS 2017/18 8 Inverse und implizite Funktionen 1 / 21 Inverse Funktion Sei f : D f R n W f R m, x y f(x). Eine Funktion f 1 : W
Kapitel 8 Inverse und implizite Funktionen Josef Leydold Mathematik für VW WS 2017/18 8 Inverse und implizite Funktionen 1 / 21 Inverse Funktion Sei f : D f R n W f R m, x y f(x). Eine Funktion f 1 : W
4 Affine Koordinatensysteme
 4 Affine Koordinatensysteme Sei X φ ein affiner Raum und seien p,, p r X Definition: Nach ( c ist der Durchschnitt aller affinen Unterräume Z X, welche die Menge {p,,p r } umfassen, selbst ein affiner
4 Affine Koordinatensysteme Sei X φ ein affiner Raum und seien p,, p r X Definition: Nach ( c ist der Durchschnitt aller affinen Unterräume Z X, welche die Menge {p,,p r } umfassen, selbst ein affiner
Computer Vision: Kalman Filter
 Computer Vision: Kalman Filter D. Schlesinger TUD/INF/KI/IS D. Schlesinger () Computer Vision: Kalman Filter 1 / 8 Bayesscher Filter Ein Objekt kann sich in einem Zustand x X befinden. Zum Zeitpunkt i
Computer Vision: Kalman Filter D. Schlesinger TUD/INF/KI/IS D. Schlesinger () Computer Vision: Kalman Filter 1 / 8 Bayesscher Filter Ein Objekt kann sich in einem Zustand x X befinden. Zum Zeitpunkt i
Geoinformatik I /Geoinformationsysteme
 Geoinformatik I /Geoinformationsysteme SS 2005 1 Georeferenzieren a) Sie haben ein Feature, das mit den Angaben [WGS-1984, UTM-Zone 12N] georeferenziert ist. Was bedeuten die beiden Angaben? (Was ist ein
Geoinformatik I /Geoinformationsysteme SS 2005 1 Georeferenzieren a) Sie haben ein Feature, das mit den Angaben [WGS-1984, UTM-Zone 12N] georeferenziert ist. Was bedeuten die beiden Angaben? (Was ist ein
Digitale Bildverarbeitung Einheit 12 3D-Modellierung
 Digitale Bildverarbeitung Einheit 12 3D-Modellierung Lehrauftrag WS 05/06 Fachbereich M+I der FH-Offenburg Dipl.-Math. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Einen Eindruck
Digitale Bildverarbeitung Einheit 12 3D-Modellierung Lehrauftrag WS 05/06 Fachbereich M+I der FH-Offenburg Dipl.-Math. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Einen Eindruck
Musterlösung zum Übungsblatt Interpolation nach Newton, Nevill, Lagrange.
 Angewandte Mathematik Ing.-Wiss., HTWdS Dipl.-Math. Dm. Ovrutskiy Musterlösung zum Übungsblatt Interpolation nach Newton, Nevill, Lagrange. Aufgabe 1 Approximieren Sie cos(x) auf [ /, /] an drei Stützstellen
Angewandte Mathematik Ing.-Wiss., HTWdS Dipl.-Math. Dm. Ovrutskiy Musterlösung zum Übungsblatt Interpolation nach Newton, Nevill, Lagrange. Aufgabe 1 Approximieren Sie cos(x) auf [ /, /] an drei Stützstellen
6. Vorlesung. Rechnen mit Matrizen.
 6. Vorlesung. Rechnen mit Matrizen. In dieser Vorlesung betrachten wir lineare Gleichungs System. Wir betrachten lineare Gleichungs Systeme wieder von zwei Gesichtspunkten her: dem angewandten Gesichtspunkt
6. Vorlesung. Rechnen mit Matrizen. In dieser Vorlesung betrachten wir lineare Gleichungs System. Wir betrachten lineare Gleichungs Systeme wieder von zwei Gesichtspunkten her: dem angewandten Gesichtspunkt
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Lineare Gleichungssysteme Sei K ein Körper, a ij K für 1 i m, 1 j n. Weiters seien b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2... a m1
Euklidische Algorithmus, Restklassenringe (Z m,, )
 Euklidische Algorithmus, Restklassenringe (Z m,, ) Manfred Gruber http://www.cs.hm.edu/~gruber SS 2008, KW 14 Gröÿter gemeinsamer Teiler Denition 1. [Teiler] Eine Zahl m N ist Teiler von n Z, wenn der
Euklidische Algorithmus, Restklassenringe (Z m,, ) Manfred Gruber http://www.cs.hm.edu/~gruber SS 2008, KW 14 Gröÿter gemeinsamer Teiler Denition 1. [Teiler] Eine Zahl m N ist Teiler von n Z, wenn der
große Vielfalt von Daten für die Visualisierung möglich
 4. Charakterisierung von Datensätzen und Darstellungsformen 4.1 Charakterisierung von Datensätzen große Vielfalt von Daten für die Visualisierung möglich Überblick Typisierungen von Daten: hierin nicht
4. Charakterisierung von Datensätzen und Darstellungsformen 4.1 Charakterisierung von Datensätzen große Vielfalt von Daten für die Visualisierung möglich Überblick Typisierungen von Daten: hierin nicht
Transformationen. 09-Transformationen
 Transformationen 9-Transformationen Als Transformationen werden affine Transformationen im R n betrachtet. Alle derartigen Transformationen lassen sich darstellen als: A + b wobei A die quadratische Transformationsmatri
Transformationen 9-Transformationen Als Transformationen werden affine Transformationen im R n betrachtet. Alle derartigen Transformationen lassen sich darstellen als: A + b wobei A die quadratische Transformationsmatri
Lineare Abbildungen (Teschl/Teschl 10.3, 11.2)
 Lineare Abbildungen (Teschl/Teschl.3,.2 Eine lineare Abbildung ist eine Abbildung zwischen zwei Vektorräumen, die mit den Vektoroperationen Addition und Multiplikation mit Skalaren verträglich ist. Formal:
Lineare Abbildungen (Teschl/Teschl.3,.2 Eine lineare Abbildung ist eine Abbildung zwischen zwei Vektorräumen, die mit den Vektoroperationen Addition und Multiplikation mit Skalaren verträglich ist. Formal:
Skalierbarkeit virtueller Welten
 $86=8*'(5 )2/,(1 9505 9RUOHVXQJ Dr. Ralf Dörner *RHWKH8QLYHUVLWlWÃ)UDQNIXUW *UDSKLVFKHÃ'DWHQYHUDUEHLWXQJ hehueolfn Der Begriff VR Perspektivisches Sehen in 3D Skalierbarkeit virtueller Welten Echtzeitanforderungen
$86=8*'(5 )2/,(1 9505 9RUOHVXQJ Dr. Ralf Dörner *RHWKH8QLYHUVLWlWÃ)UDQNIXUW *UDSKLVFKHÃ'DWHQYHUDUEHLWXQJ hehueolfn Der Begriff VR Perspektivisches Sehen in 3D Skalierbarkeit virtueller Welten Echtzeitanforderungen
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Definition. Sei K ein Körper, a ij K für 1 i m, 1 j n und b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2......
Lineare Gleichungssysteme Definition. Sei K ein Körper, a ij K für 1 i m, 1 j n und b 1,..., b m K. Dann heißt a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2......
Navigation anhand natürlicher Landmarken mit Hilfe der Scale Invariant Feature Transform. Thorsten Jost INF-M2 AW1 Sommersemester
 Navigation anhand natürlicher Landmarken mit Hilfe der Scale Invariant Feature Transform Thorsten Jost INF-M2 AW1 Sommersemester 2008 Agenda Motivation Feature Detection Beispiele Posenbestimmung in Räumen
Navigation anhand natürlicher Landmarken mit Hilfe der Scale Invariant Feature Transform Thorsten Jost INF-M2 AW1 Sommersemester 2008 Agenda Motivation Feature Detection Beispiele Posenbestimmung in Räumen
12 Der Abstand eines Punktes von einer Geraden Seite 1 von Der Abstand eines Punktes von einer Geraden
 12 Der Abstand eines Punktes von einer Geraden Seite 1 von 5 12 Der Abstand eines Punktes von einer Geraden Die Bestimmung des Abstands eines Punktes von einer Geraden gehört zu den zentralen Problemen
12 Der Abstand eines Punktes von einer Geraden Seite 1 von 5 12 Der Abstand eines Punktes von einer Geraden Die Bestimmung des Abstands eines Punktes von einer Geraden gehört zu den zentralen Problemen
6 Symmetrische Matrizen und quadratische Formen
 Mathematik für Ingenieure II, SS 9 Freitag 9.6 $Id: quadrat.tex,v. 9/6/9 4:6:48 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6. Symmetrische Matrizen Eine n n Matrix heißt symmetrisch wenn
Mathematik für Ingenieure II, SS 9 Freitag 9.6 $Id: quadrat.tex,v. 9/6/9 4:6:48 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6. Symmetrische Matrizen Eine n n Matrix heißt symmetrisch wenn
Geometrische Objekte im 3-dimensionalen affinen Raum oder,... wie nützlich ist ein zugehöriger Vektorraum der Verschiebungen
 Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Computer-Graphik I Transformationen & Viewing
 lausthal Motivation omputer-raphik I Transformationen & Viewing Man möchte die virtuelle 3D Welt auf einem 2D Display darstellen. Zachmann lausthal University, ermany zach@in.tu-clausthal.de. Zachmann
lausthal Motivation omputer-raphik I Transformationen & Viewing Man möchte die virtuelle 3D Welt auf einem 2D Display darstellen. Zachmann lausthal University, ermany zach@in.tu-clausthal.de. Zachmann
Volumenverarbeitung und Optimierung II
 Volumenverarbeitung und Optimierung II Praktikum Medizinische GPU Verfahren Susanne Fischer sanne@uni-koblenz.de Institut für Computervisualistik Universität Koblenz-Landau 9. Dezember 2006 Susanne Fischer
Volumenverarbeitung und Optimierung II Praktikum Medizinische GPU Verfahren Susanne Fischer sanne@uni-koblenz.de Institut für Computervisualistik Universität Koblenz-Landau 9. Dezember 2006 Susanne Fischer
Kamerakalibrierung. Messen in Videobildern, Leobots-Projekt Version 1.0. Matthias Jauernig, 03INB, HTWK Leipzig
 Kamerakalibrierung Messen in Videobildern, Leobots-Projekt 2006 Version 1.0 Matthias Jauernig, 03INB, HTWK Leipzig Copyright (c) 2006, Matthias Jauernig Kamerakalibrierung, Matthias Jauernig 3 Begriffe
Kamerakalibrierung Messen in Videobildern, Leobots-Projekt 2006 Version 1.0 Matthias Jauernig, 03INB, HTWK Leipzig Copyright (c) 2006, Matthias Jauernig Kamerakalibrierung, Matthias Jauernig 3 Begriffe
Klausuraufgaben zur Vorlesung Computer Vision. Prüfung I W772, I 2M54. Termin: 17. Juli bzw. 90 Minuten Maximal mögliche Punktzahl: 48
 Klausuraufgaben zur Vorlesung Computer Vision Prüfung I W772, I 2M54 Prüfer: Laubenheimer Termin: 17. Juli 2008 Beginn: 8:00 Uhr Dauer: 60 bzw. 90 Minuten Maximal mögliche Punktzahl: 48 Name Matrikelnummer
Klausuraufgaben zur Vorlesung Computer Vision Prüfung I W772, I 2M54 Prüfer: Laubenheimer Termin: 17. Juli 2008 Beginn: 8:00 Uhr Dauer: 60 bzw. 90 Minuten Maximal mögliche Punktzahl: 48 Name Matrikelnummer
Mathematische Probleme lösen mit Maple
 Mathematische Probleme lösen mit Maple Ein Kurzeinstieg Bearbeitet von Thomas Westermann überarbeitet 2008. Buch. XII, 169 S. ISBN 978 3 540 77720 5 Format (B x L): 15,5 x 23,5 cm Weitere Fachgebiete >
Mathematische Probleme lösen mit Maple Ein Kurzeinstieg Bearbeitet von Thomas Westermann überarbeitet 2008. Buch. XII, 169 S. ISBN 978 3 540 77720 5 Format (B x L): 15,5 x 23,5 cm Weitere Fachgebiete >
5. Gitter, Gradienten, Interpolation Gitter. (Rezk-Salama, o.j.)
 5. Gitter, Gradienten, Interpolation 5.1. Gitter (Rezk-Salama, o.j.) Gitterklassifikation: (Bartz 2005) (Rezk-Salama, o.j.) (Bartz 2005) (Rezk-Salama, o.j.) Allgemeine Gitterstrukturen: (Rezk-Salama, o.j.)
5. Gitter, Gradienten, Interpolation 5.1. Gitter (Rezk-Salama, o.j.) Gitterklassifikation: (Bartz 2005) (Rezk-Salama, o.j.) (Bartz 2005) (Rezk-Salama, o.j.) Allgemeine Gitterstrukturen: (Rezk-Salama, o.j.)
6 Symmetrische Matrizen und quadratische Formen
 Mathematik für Ingenieure II, SS 009 Dienstag 3.6 $Id: quadrat.tex,v.4 009/06/3 4:55:47 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6.3 Quadratische Funktionen und die Hauptachsentransformation
Mathematik für Ingenieure II, SS 009 Dienstag 3.6 $Id: quadrat.tex,v.4 009/06/3 4:55:47 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6.3 Quadratische Funktionen und die Hauptachsentransformation
Kapitel II. Vektoren und Matrizen
 Kapitel II. Vektoren und Matrizen Vektorräume A Körper Auf der Menge R der reellen Zahlen hat man zwei Verknüpfungen: Addition: R R R(a, b) a + b Multiplikation: R R R(a, b) a b (Der Malpunkt wird oft
Kapitel II. Vektoren und Matrizen Vektorräume A Körper Auf der Menge R der reellen Zahlen hat man zwei Verknüpfungen: Addition: R R R(a, b) a + b Multiplikation: R R R(a, b) a b (Der Malpunkt wird oft
Technische Universität Chemnitz im April 2013
 Dr. Neidhart Kamprath Technisches Gymnasium an der Handwerkerschule Chemnitz Technische Universität Chemnitz im April 2013 Ausgangspunkt Änderung der Bildgröße mittels Photoshop Berechnungsverfahren zur
Dr. Neidhart Kamprath Technisches Gymnasium an der Handwerkerschule Chemnitz Technische Universität Chemnitz im April 2013 Ausgangspunkt Änderung der Bildgröße mittels Photoshop Berechnungsverfahren zur
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eine Familie von Gleichungen der Form a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2............ a m1 x 1 + a m2 x 2 +... + a mn x n = b m
Lineare Gleichungssysteme Eine Familie von Gleichungen der Form a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2............ a m1 x 1 + a m2 x 2 +... + a mn x n = b m
Das Gruppengesetz auf elliptischen Kurven: Assoziativität
 Ausarbeitung des Seminarvortrags Das Gruppengesetz auf elliptischen Kurven: Assoziativität Seminar Kryptographie, TU Kaiserslautern Sommersemester 2011 Pablo Luka Version vom 14. 05. 2011 Inhaltsverzeichnis
Ausarbeitung des Seminarvortrags Das Gruppengesetz auf elliptischen Kurven: Assoziativität Seminar Kryptographie, TU Kaiserslautern Sommersemester 2011 Pablo Luka Version vom 14. 05. 2011 Inhaltsverzeichnis
3D-Modellierung / Motion-Capturing. von Kevin O Brien
 3D-Modellierung / Motion-Capturing von Kevin O Brien Inhalt 1. Animationsfilme Geschichte der Animation 3D-Modellierung 2. Special Effects Vorkommen Blue- / Greenscreen Motion-Capturing Kameraführung 2/36
3D-Modellierung / Motion-Capturing von Kevin O Brien Inhalt 1. Animationsfilme Geschichte der Animation 3D-Modellierung 2. Special Effects Vorkommen Blue- / Greenscreen Motion-Capturing Kameraführung 2/36
Orientierung der Vektoren b 1,..., b n. Volumen des von den Vektoren aufgespannten Parallelotops
 15. DETERMINANTEN 1 Für n Vektoren b 1,..., b n im R n definiert man ihre Determinante det(b 1,..., b n ) Anschaulich gilt det(b 1,..., b n ) = Orientierung der Vektoren b 1,..., b n Volumen des von den
15. DETERMINANTEN 1 Für n Vektoren b 1,..., b n im R n definiert man ihre Determinante det(b 1,..., b n ) Anschaulich gilt det(b 1,..., b n ) = Orientierung der Vektoren b 1,..., b n Volumen des von den
MATLAB-Toolskurs HS17
 7 Analysis 1. Programmieren Sie für folgendes Polynom eine MATLAB Funktion oder eine anonyme Funktion: y(x) = 0.001x 5 + 0.05x 4 + 0.2x 3 x 2 0.8x + 4 Die Variable x ist der Eingabeparameter und y der
7 Analysis 1. Programmieren Sie für folgendes Polynom eine MATLAB Funktion oder eine anonyme Funktion: y(x) = 0.001x 5 + 0.05x 4 + 0.2x 3 x 2 0.8x + 4 Die Variable x ist der Eingabeparameter und y der
Ornamente zeichnen und hyprbolisieren
 Ornamente zeichnen und hyprbolisieren Martin von Gagern TU München in Zusammenarbeit mit Prof. Jürgen Richter-Gebert www.mathe-vital.de u.a. mit Applet zu Sierpinski-Dreieck per IFS... ist nicht Thema
Ornamente zeichnen und hyprbolisieren Martin von Gagern TU München in Zusammenarbeit mit Prof. Jürgen Richter-Gebert www.mathe-vital.de u.a. mit Applet zu Sierpinski-Dreieck per IFS... ist nicht Thema
Viele wichtige Operationen können als lineare Abbildungen interpretiert werden. Beispielsweise beschreibt die lineare Abbildung
 Kapitel 3 Lineare Abbildungen Lineare Abbildungen sind eine natürliche Klasse von Abbildungen zwischen zwei Vektorräumen, denn sie vertragen sich per definitionem mit der Struktur linearer Räume Viele
Kapitel 3 Lineare Abbildungen Lineare Abbildungen sind eine natürliche Klasse von Abbildungen zwischen zwei Vektorräumen, denn sie vertragen sich per definitionem mit der Struktur linearer Räume Viele
Affine Hülle. x x 1 ist lineare Kombination der Vektoren x 2 x 1,x 3 x 1,...,x k x 1. Tatsächlich, in diesem Fall ist λ 1 = 1 λ 2 λ 3...
 Affine Hülle Wiederholung. Der Vektor x K n ist eine lineare Kombination der Vektoren x,...,x k K n, wenn es Zahlen λ,...,λ k K gibt mit x = λ x +... + λ k x k. Def. Gibt es solche Zahlen λ,...,λ k K mit
Affine Hülle Wiederholung. Der Vektor x K n ist eine lineare Kombination der Vektoren x,...,x k K n, wenn es Zahlen λ,...,λ k K gibt mit x = λ x +... + λ k x k. Def. Gibt es solche Zahlen λ,...,λ k K mit
c) Der Umfang einer quadratförmigen Rabatte misst 60,4 m. Wie lange ist eine Seitenlänge?
 13.3 Übungen zur Flächenberechnung 13.3.1 Übungen Quadrat Berechnen Sie für diese Quadrate das gesuchte Maß, geben Sie das Resultat in der verlangten Einheit an. a) l 4,8 dm, A? cm 2, U? m A l 2 4,8 2
13.3 Übungen zur Flächenberechnung 13.3.1 Übungen Quadrat Berechnen Sie für diese Quadrate das gesuchte Maß, geben Sie das Resultat in der verlangten Einheit an. a) l 4,8 dm, A? cm 2, U? m A l 2 4,8 2
1 Singulärwertzerlegung und Pseudoinverse
 Singulärwertzerlegung und Pseudoinverse Singulärwertzerlegung A sei eine Matrix mit n Spalten und m Zeilen. Zunächst sei n m. Bilde B = A A. Dies ist eine n n-matrix. Berechne die Eigenwerte von B. Diese
Singulärwertzerlegung und Pseudoinverse Singulärwertzerlegung A sei eine Matrix mit n Spalten und m Zeilen. Zunächst sei n m. Bilde B = A A. Dies ist eine n n-matrix. Berechne die Eigenwerte von B. Diese
Computergraphik 1 2. Teil: Bildverarbeitung. Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation
 Computergraphik 1 2. Teil: Bildverarbeitung Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS2009 1 2 Repräsentation
Computergraphik 1 2. Teil: Bildverarbeitung Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS2009 1 2 Repräsentation
Bei der Registrierung werden zwei Bilder betrachtet, von denen eines üblicherweise als Referenzbild
 3.4 egistrierung 3.4 egistrierung In diesem Abschnitt beschäftigen wir uns mit dem Problem der egistrierung von Bildern, d.h. der Aufgabe zwei Bilder derselben Szene, oder zumindest ähnlicher Szenen, bestmöglich
3.4 egistrierung 3.4 egistrierung In diesem Abschnitt beschäftigen wir uns mit dem Problem der egistrierung von Bildern, d.h. der Aufgabe zwei Bilder derselben Szene, oder zumindest ähnlicher Szenen, bestmöglich
II. Lineare Gleichungssysteme. 10 Matrizen und Vektoren. 52 II. Lineare Gleichungssysteme
 52 II Lineare Gleichungssysteme II Lineare Gleichungssysteme 10 Matrizen und Vektoren 52 11 Der Gaußsche Algorithmus 58 12 Basen, Dimension und Rang 62 13 Reguläre Matrizen 66 14 Determinanten 69 15 Skalarprodukte
52 II Lineare Gleichungssysteme II Lineare Gleichungssysteme 10 Matrizen und Vektoren 52 11 Der Gaußsche Algorithmus 58 12 Basen, Dimension und Rang 62 13 Reguläre Matrizen 66 14 Determinanten 69 15 Skalarprodukte
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
Inhaltsverzeichnis. Kapitel 1: Rechnen mit Zahlen. Kapitel 2: Umformen von Ausdrücken. Kapitel 3: Gleichungen, Ungleichungen, Gleichungssysteme
 Kapitel 1: Rechnen mit Zahlen 1.1 Rechnen mit reellen Zahlen 1.2 Berechnen von Summen und Produkten 1.3 Primfaktorzerlegung 1.4 Größter gemeinsamer Teiler 1.5 Kleinstes gemeinsames Vielfaches 1.6 n-te
Kapitel 1: Rechnen mit Zahlen 1.1 Rechnen mit reellen Zahlen 1.2 Berechnen von Summen und Produkten 1.3 Primfaktorzerlegung 1.4 Größter gemeinsamer Teiler 1.5 Kleinstes gemeinsames Vielfaches 1.6 n-te
Normalengleichungen. Für eine beliebige m n Matrix A erfüllt jede Lösung x des Ausgleichsproblems Ax b min die Normalengleichungen A t Ax = A t b,
 Normalengleichungen Für eine beliebige m n Matrix A erfüllt jede Lösung x des Ausgleichsproblems Ax b min die Normalengleichungen A t Ax = A t b, Normalengleichungen 1-1 Normalengleichungen Für eine beliebige
Normalengleichungen Für eine beliebige m n Matrix A erfüllt jede Lösung x des Ausgleichsproblems Ax b min die Normalengleichungen A t Ax = A t b, Normalengleichungen 1-1 Normalengleichungen Für eine beliebige
Bildverarbeitung. Fachschaftsrat Informatik. Professor Fuchs. Fragen TECHNISCHE UNIVERSITÄT DRESDEN. Unterteilung der Filter in Klassen
 Professor Fuchs Unterteilung der Filter in Klassen Wie erstellt man bei der Segmentierung objektumschreibende Formen? Eigenschaften der Zellkomplextopologie Was ist ein Histogramm? Wozu ist es gut? Unterschied
Professor Fuchs Unterteilung der Filter in Klassen Wie erstellt man bei der Segmentierung objektumschreibende Formen? Eigenschaften der Zellkomplextopologie Was ist ein Histogramm? Wozu ist es gut? Unterschied
7. Wie lautet die Inverse der Verkettung zweier linearer Abbildungen? 9. Wie kann die Matrixdarstellung einer linearen Abbildung aufgestellt werden?
 Kapitel Lineare Abbildungen Verständnisfragen Sachfragen Was ist eine lineare Abbildung? Erläutern Sie den Zusammenhang zwischen Unterräumen, linearer Unabhängigkeit und linearen Abbildungen! 3 Was ist
Kapitel Lineare Abbildungen Verständnisfragen Sachfragen Was ist eine lineare Abbildung? Erläutern Sie den Zusammenhang zwischen Unterräumen, linearer Unabhängigkeit und linearen Abbildungen! 3 Was ist
Computer Vision: 3D-Geometrie. D. Schlesinger () Computer Vision: 3D-Geometrie 1 / 17
 Computer Vision: 3D-Geometrie D. Schlesinger () Computer Vision: 3D-Geometrie 1 / 17 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Computer Vision: 3D-Geometrie D. Schlesinger () Computer Vision: 3D-Geometrie 1 / 17 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Computer Vision: Optische Flüsse
 Computer Vision: Optische Flüsse D. Schlesinger TUD/INF/KI/IS Bewegungsanalyse Optischer Fluss Lokale Verfahren (Lukas-Kanade) Globale Verfahren (Horn-Schunck) (+ kontinuierliche Ansätze: mathematische
Computer Vision: Optische Flüsse D. Schlesinger TUD/INF/KI/IS Bewegungsanalyse Optischer Fluss Lokale Verfahren (Lukas-Kanade) Globale Verfahren (Horn-Schunck) (+ kontinuierliche Ansätze: mathematische
Repräsentation und Transformation von geometrischen Objekten
 Repräsentation und Transformation von geometrischen Objekten Inhalt: Grundlagen Überblick Einfache Transformationen in der Ebene Homogene Koordinaten Einfache Transformationen in der Ebene mit homogenen
Repräsentation und Transformation von geometrischen Objekten Inhalt: Grundlagen Überblick Einfache Transformationen in der Ebene Homogene Koordinaten Einfache Transformationen in der Ebene mit homogenen
5 Quadriken. K = { R 2 ax 2 + bxy + cy 2 + dx + ey + f = 0} wobei a, b, c, d, e, f reelle Zahlen sind mit (a, b, c) (0, 0, 0).
 5 Quadriken Kegelschnitte Ein Kegelschnitt ist eine Teilmenge K R 2, welche durch eine quadratische Gleichung in zwei Unbestimmten beschrieben werden kann: x K = { R 2 ax 2 + bxy + cy 2 + dx + ey + f =
5 Quadriken Kegelschnitte Ein Kegelschnitt ist eine Teilmenge K R 2, welche durch eine quadratische Gleichung in zwei Unbestimmten beschrieben werden kann: x K = { R 2 ax 2 + bxy + cy 2 + dx + ey + f =
3 Bilinearformen und quadratische Formen
 3 Bilinearformen und quadratische Formen Sei V ein R Vektorraum. Definition: Eine Bilinearform auf V ist eine Abbildung s : V V R, welche linear in beiden Variablen ist, d.h.: Für u, v, w V und λ, µ R
3 Bilinearformen und quadratische Formen Sei V ein R Vektorraum. Definition: Eine Bilinearform auf V ist eine Abbildung s : V V R, welche linear in beiden Variablen ist, d.h.: Für u, v, w V und λ, µ R
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg,
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg, Literatur Richard Hartle and Andrew Zisserman. Multiple View Geometr in computer vision, Cambridge Universit Press, 2 nd Ed., 23. O.D.
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg, Literatur Richard Hartle and Andrew Zisserman. Multiple View Geometr in computer vision, Cambridge Universit Press, 2 nd Ed., 23. O.D.
Lineares Gleichungssystem
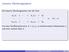 Lineares Gleichungssystem Ein lineares Gleichungssystem hat die Form a 1,1 x 1 + + a 1,n x n = b 1...... Ax = b a m,1 x 1 + + a m,n x n = b m mit einer Koeffizientenmatrix A = (a i,j ), zu bestimmenden
Lineares Gleichungssystem Ein lineares Gleichungssystem hat die Form a 1,1 x 1 + + a 1,n x n = b 1...... Ax = b a m,1 x 1 + + a m,n x n = b m mit einer Koeffizientenmatrix A = (a i,j ), zu bestimmenden
Chapter 1 : þÿ b e t a t h o m e. c o m B i n g o c h a p t e r
 Chapter 1 : þÿ b e t a t h o m e. c o m B i n g o c h a p t e r þÿ W e t t m a r k t. E i n e k o s t e n l o s e T e i l n a h m e i s t e b e n f a l l s m ö g l i c h, w e n n m a n a k t i v. n o d
Chapter 1 : þÿ b e t a t h o m e. c o m B i n g o c h a p t e r þÿ W e t t m a r k t. E i n e k o s t e n l o s e T e i l n a h m e i s t e b e n f a l l s m ö g l i c h, w e n n m a n a k t i v. n o d
mathbu.ch 7 Aufgabensammlung 8 Parallelogramme untersuchen
 1. Für die gezeichneten Parallelogramme gelten die Masse: I s = 7.5 cm II a = 3 cm b = 5 cm h = 2 cm III c = 8.6 cm d = 47 mm IV s = 28 mm t = 6.5 cm Beantworte zu jeder Figur die folgenden Fragen. A Wie
1. Für die gezeichneten Parallelogramme gelten die Masse: I s = 7.5 cm II a = 3 cm b = 5 cm h = 2 cm III c = 8.6 cm d = 47 mm IV s = 28 mm t = 6.5 cm Beantworte zu jeder Figur die folgenden Fragen. A Wie
Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof. Dr. Ulrich Reif
 14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
Kapitel 3. Transformationen
 Oyun Namdag Am 08.11.2007 WS 07/08 Proseminar Numerik: Mathematics for 3D game programming & computer graphics Dozenten: Prof. Dr. V. Schulz, C. Schillings Universität Trier Kapitel 3 Transformationen
Oyun Namdag Am 08.11.2007 WS 07/08 Proseminar Numerik: Mathematics for 3D game programming & computer graphics Dozenten: Prof. Dr. V. Schulz, C. Schillings Universität Trier Kapitel 3 Transformationen
Übersicht der Vorlesung
 Übersicht der Vorlesung 1. Einführung 2. Bildverarbeitung 3. orphologische Operationen 4. Bildsegmentierung 5. erkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Übersicht der Vorlesung 1. Einführung 2. Bildverarbeitung 3. orphologische Operationen 4. Bildsegmentierung 5. erkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
7.1.2 Lineare Funktionen Schnittpunkte mit den Achsen - Lösungen
 7.. Lineare Funktionen Schnittpunkte mit den Achsen - Lösungen. Bestimme von den nachfolgenden Funktionsgleichungen zunächst die Schnittpunkte mit den Achsen; stelle sie danach im Koordinatensystem dar.
7.. Lineare Funktionen Schnittpunkte mit den Achsen - Lösungen. Bestimme von den nachfolgenden Funktionsgleichungen zunächst die Schnittpunkte mit den Achsen; stelle sie danach im Koordinatensystem dar.
Medizinische Bildverarbeitung. FH-Campus Hagenberg
 Medizinische Bildverarbeitung Campus Hagenberg 20 km nordöstlich von Linz 7 Bachelor-Studiengänge + 5 Masterstudiengänge 3 Cluster: Software / Systeme / Medien Medizin-Informatik, Bioinformatik Derzeit
Medizinische Bildverarbeitung Campus Hagenberg 20 km nordöstlich von Linz 7 Bachelor-Studiengänge + 5 Masterstudiengänge 3 Cluster: Software / Systeme / Medien Medizin-Informatik, Bioinformatik Derzeit
Projektive Räume und Unterräume
 Projektive Räume und Unterräume Erik Slawski Proseminar Analytische Geometrie bei Prof. Dr. Werner Seiler und Marcus Hausdorf Wintersemester 2007/2008 Fachbereich 17 Mathematik Universität Kassel Inhaltsverzeichnis
Projektive Räume und Unterräume Erik Slawski Proseminar Analytische Geometrie bei Prof. Dr. Werner Seiler und Marcus Hausdorf Wintersemester 2007/2008 Fachbereich 17 Mathematik Universität Kassel Inhaltsverzeichnis
Elemente der Algebra und Zahlentheorie Musterlösung, Serie 5, Wintersemester vom 21. Januar 2006
 Prof. E.-W. Zink Institut für Mathematik Humboldt-Universität zu Berlin Elemente der Algebra und Zahlentheorie Musterlösung, Serie 5, Wintersemester 2005-06 vom 21. Januar 2006 1. Sei (N, v) Peano-Menge
Prof. E.-W. Zink Institut für Mathematik Humboldt-Universität zu Berlin Elemente der Algebra und Zahlentheorie Musterlösung, Serie 5, Wintersemester 2005-06 vom 21. Januar 2006 1. Sei (N, v) Peano-Menge
