Computergraphik 1 2. Teil: Bildverarbeitung. Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation
|
|
|
- Bettina Frank
- vor 7 Jahren
- Abrufe
Transkript
1 Computergraphik 1 2. Teil: Bildverarbeitung Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS2009 1
2 2 Repräsentation als Exponentialfunktion
3 3 1D-Basisfunktionen
4 4 2D-Basisfunktionen
5 5 2D-Fouriertransformationspaar
6 6 Phase und Amplitude
7 7 Beispiele f. Amplitude
8 8 Darstellungsweise Original Amplitude (zentriert, d.h. von N/2 bis N/2) Amplitude (log. Skala) Amplitude (zentriert, log. Skala)
9 9 Beispiele Amplitude Phase
10 10 Einfluss von Amplitude und Phase
11 11 Translation
12 12
13 13 Phasenverschiebung
14 14
15 15 Periodizität und Symmetrie
16 16 Separabilität
17 17 Konvolution und Korrelation Worst case Aufwand im Ortsraum: N 4 für Kantenlänge N des Bildes
18 18 Konvolution und Korrelation Konvolution und Korrelation sind zwei eng verwandte Filter-Operationen. Beide können im Ortsraum und im Frequenzraum ausgeführt werden. Die Operation im Frequenzraum ist eine einfache Multiplikation (Aufwand N 2 ).
19 19 Konvolution im Frequenzraum
20 20 Konvolutionskern
21 21 Konvolution am Bildrand
22 22
23 23 Diskrete Kosinustransformation (DCT) Zerlegung in Wellen unterschiedlicher Frequenz. Sehr ähnlich zur Fouriertransformation. Basisfunktionen sind reell. Wird vor allem bei Kompressionsverfahren verwendet(jpeg). Wie lassen sich genügend reellwertige Basisfunktionen finden?
24 24 Basisfunktionen der DCT Basisfunktionen sind Wellen, deren Wert für jede zweite Frequenz u am Anfang und am Ende des Intervalls unterschiedliches Vorzeichen haben.
25 25 Basisfunktionen der DCT
26 26 Literatur Klaus D. Tönnies: "Grundlagen der Bildverarbeitung", ISBN (daraus auch viele Abbildungen der heutigen Vorlesung)
27 27 FFT und Anwendungen der Fouriertransformation
28 28 Fouriertransformation: Grundidee Beschreibe beliebige Funktion als gewichtete Summe periodischer Grundfunktionen (Basisfunktionen) mit untersch. Frequenz
29 Überlagerung von Schwingungen: anschaulich LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
30 30 Fourier Transformation zum Anschauen exploratories/
31 31 Fast Fourier Transformation
32 32 Vorgehensweise generell Vereinfachende Annahme: N=2 k, k>1 Nutze Separabilität, um 2D-FT auf 1D zurückzuführen (O(n 4 ) O(n 3 )) Teile Summe in zwei Teilsummen auf Finde Gemeinsamkeiten in den Teilsummen und berechne beide Teilsummen miteinander Betrachte die Teilsumme und unterteile rekursiv bis N=1 (O(n 3 ) O(n 2 log n)
33 Separabilität Vorgehensweise: F u (m) für alle Spalten m berechnen und dann bei den Zeilen verwenden. LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
34 34 Divide Schritt Teile Summe in zwei Teilsummen auf Finde Gemeinsamkeiten in den Teilsummen
35 35 Ausnutzen der Periodizität Also kann man F(u+K) mithilfe F(u) berechnen (einmal F even + F odd, einmal F even F odd ) Betrachte die Teilsumme [0 K-1] und unterteile rekursiv bis K=1 (O(n 3 ) O(n 2 log n)
36 36 Restauration linearer Bildstörungen
37 Beispiel I: Bewegungsunschärfe Über einen Zeitraum Δt wird ein Objektpunkt p auf immer andere Punkte auf dem CCD-Chip abgebildet. Bei unbewegter Kamera sei die Bildhelligkeit des abgebildeten Punkts h. Dann ist sie bei bewegter Kamera h/δs, wobei Δs die zurückgelegte Strecke ist. Wenn Δs für alle Punkte gleich ist, dann lässt sich die Veränderung durch eine Faltung beschreiben. LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
38 38 Bewegungsunschärfe Faltungskern ist eine Funktion w mit Der Winkel α gibt die Bewegungsrichtung an. Die Strecke Δs gibt die Strecke an, um die sich der Punkt bewegt hat:
39 39 Bewegungsunschärfe = * Gestörtes Bild Original Faltungskern
40 40 Repräsentation linearer Störungen Jede verschiebungsinvariante lineare Operation wird vollständig durch die Faltungsfunktion beschrieben. Die Faltungsfunktion beschreibt die Operation für beliebige Bilder Die Faltungsfunktion kann als Resultat der Veränderung eines Punkts erzeugt werden Punktantwort = Point Spread Function (PSF)
41 Beispiel II: Fokussierungsunschärfe Maß der Unschärfe hängt vom Punktabstand z, der Brennweite der Linse f und der Kammerkonstante f k ab. Linsengesetz: Größe des Unschärfekreises: Unschärfe kann durch Aufnahme eines punktförmigen Testobjekts angenähert werden. LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
42 42 Fokussierungsunschärfe Wie kann die Störung rückgängig gemacht werden?
43 43 Bildrestauration Ziel: Korrektur des Bildsignals um bekannte und unbekannte Störungen Annahme: Störung kann durch einen verschiebungsinvarianten linearen Operator h beschrieben werden. g(x,y) (Störung durch PSF h) g'(x,y) g'(x,y) = [h*g] (x,y) PSF beschreibt die Störung Wie kann die PSF bestimmt werden?
44 44 Gesucht: PSF
45 PSF von Testbildern Annahme: Störung ist unveränderlich und Testaufnahme ist möglich. Durch die Aufnahme eines punktförmigen Objekts kann ein δ-impuls approximiert werden. Aufnahme ist eine Näherung für die PSF. LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
46 46 PSF aus dem aufgenommenen Bild Testaufnahme ist nicht möglich: Näherungsweise Bestimmung der PSF durch Betrachtung von Punkten oder Linien im gestörten Bild.
47 47 Kanten Die meisten Bilder weisen wenige Linien oder Punkte auf, aber Kanten können in fast jedem Bild gefunden werden.
48 48 1D-Kanten
49 49 Kanten im 2D-Raum: Gradienten Gradient im kontinuierlichen Raum (x,y): Vektor der partiellen Ableitungen der Bildfunktion in x- und y-richtung: (f(x,y)) = ( f/ x f/ y) Approximation des Gradienten: Differential wird durch Differenz approximiert:
50 50 Elemente des Gradienten
51 51 PSF aus Kanten PSF kann auch aus dem Verlauf einer als ideal angenommenen Kante approximiert werden.
52 52 Invertierung der Störung Überführung der Repräsentation in den Frequenzraum: G'(u,v) = FT[g'(m,n)] = FT[[h*g](m,n)] = H(u,v) G(u,v) Invertierung: g(m,n) = FT -1 [G'(u,v)/H(u,v)] (Inverse Filterung)
53 53 Inverse Filterung FT -1 ( / )= Theoretisch: vollständige Rückgewinnung der Information aus den gestörten Daten
54 54 Bewegungsunschärfe PSF FT(PSF)
55 Bewegungsunschärfe Resultat der inversen Filterung FT -1 [FT (g )(u,v)/ft(psf)(u,v)] LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
56 Numerische Probleme bei der inversen Filterung Problem: Nullstellen von H Treten auf, falls h als Matrix nicht den vollen Rang hat Auch kleine Werte von H sind numerisch schon ein Problem Deswegen in der Praxis: LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
57 Rauschen Problem: Inverse Filterung geht von idealen (ungestörten) Daten aus In Wirklichkeit enthalten Bilddaten Rauschen Dieses Rauschen wird bei der inversen Filterung extrem verstärkt Rauschen lässt sich nicht herausrechnen, da es nicht wiederholbar ist LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
58 58 Rauschen
59 59 Ad-hoc Lösung Gewichte die Wirkung der inversen Filterung mit der Amplitude der Störungsfunktion im Verhältnis zur mittleren Amplitude Problem: Gewichtung nimmt keine Rücksicht auf die Signalstärke von F
60 Wiener Filter Wobei S η und S f die Spektren des Rauschens bzw. der ungestörten Funktion sind S η =0 (ungestört) perfekte inverse Filterung Leider ist S η in der Praxis meist unbekannt Lösung: heuristisches Wiener Filter mit k LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
61 61
62 62
63 63 Transformation und Interpolation
64 64 Transformation und Interpolation Die Transformationen Translation, Rotation und Skalierung sind auf reellen Zahlen definiert: Digitale Bilder haben einen ganzzahligen Definitionsbereich. Nach Transformation ist eine Interpolation notwendig.
65 Interpolation Konstante Interpolation (Wert des nächsten Nachbarpixels) Lineare Interpolation Interpolation durch Polynome höheren Grades. Interpolation im Frequenzraum. LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
66 66 Konstante Interpolation
67 67 Bilineare Interpolation
68 Polynome höheren Grades Interpolation der Bildfunktion durch mehr als 2 Stützpunkte Polynom n-ten Grades interpoliert n+1 Punkte Die Bildfunktion wird besser angenähert, wenn mehr Terme der Taylor-Approximation berücksichtigt werden. Ableitungen für die Taylor-Reihe werden durch Differenzen angenähert. Grad des Polynoms ist ein Kompromiss zwischen steigender Anzahl berücksichtigter Terme der Taylor-Reihe. steigender Ungenauigkeit der geschätzten Ableitungen. bilinear bikubisch LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
69 69 Interpolation im Frequenzraum Die Basisfunktionen der Fouriertransformation haben einen reellen Definitionsbereich. Ein Funktionswert kann an beliebiger Stelle (x,y) bestimmt werden durch Die Interpolation ist exakt, falls die ursprüngliche Funktion f bandbegrenzt ist (was die meisten Funktionen jedoch nicht sind).
70 Literatur Klaus D. Tönnies: "Grundlagen der Bildverarbeitung", ISBN page=booksites/ selectchapter&isbn= &pszielgruppe=studen t LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS
Computergrafik 2: Filtern im Frequenzraum
 Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Fourier-Transformation
 Computergrafik 2: Fourier-Transformation Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Fourier-Transformation Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Übung 6. Korrelation im Orts- und Frequenzraum, Filtern im Frequenzraum, Wiener Filter
 Computergrafik : Übung 6 Korrelation im Orts- und Frequenzraum, Filtern im Frequenzraum, Wiener Filter Quiz Warum Filtern im Frequenzraum? Ideales Tiefpassfilter? Parameter? Eigenschaften? Butterworth-Filter?
Computergrafik : Übung 6 Korrelation im Orts- und Frequenzraum, Filtern im Frequenzraum, Wiener Filter Quiz Warum Filtern im Frequenzraum? Ideales Tiefpassfilter? Parameter? Eigenschaften? Butterworth-Filter?
Computergrafik 2: Filtern im Frequenzraum
 Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Fourier-Transformation Graphische DV und BV, Regina Pohle, 8. Fourier-Transformation 1 Einordnung in die Inhalte der Vorlesung Einführung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Fourier-Transformation Graphische DV und BV, Regina Pohle, 8. Fourier-Transformation 1 Einordnung in die Inhalte der Vorlesung Einführung
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Computergrafik 2: Filtern im Ortsraum
 Computergrafik 2: Filtern im Ortsraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Filtern im Ortsraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Grundlagen der Computer-Tomographie
 Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Einführung in die medizinische Bildverarbeitung WS 12/13
 Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Pipeline Pipelinestufen können sich unterscheiden, beinhalten aber i.d.r. eine Stufe zur Bildvorverarbeitung zur
Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Pipeline Pipelinestufen können sich unterscheiden, beinhalten aber i.d.r. eine Stufe zur Bildvorverarbeitung zur
Motivation. Diskretisierung. Überblick. Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen. Diskretisierung und Quantisierung
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Computergrafik 2: Filtern im Ortsraum
 Computergrafik 2: Filtern im Ortsraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Filtern im Ortsraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
R.Wagner, Mathematik in der Astronomie
 Mathematik in der Astronomie Roland Wagner Johann Radon Institute for Computational and Applied Mathematics (RICAM) Österreichische Akademie der Wissenschaften (ÖAW) Linz, Austria Linz, 20.Mai 2016 Übersicht
Mathematik in der Astronomie Roland Wagner Johann Radon Institute for Computational and Applied Mathematics (RICAM) Österreichische Akademie der Wissenschaften (ÖAW) Linz, Austria Linz, 20.Mai 2016 Übersicht
Technische Universität München. Fakultät für Informatik
 Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik IX Thema: Filterung im Bildraum: Konvolution Proseminar: Grundlagen Bildverstehen/Bildgestaltung Jonas Zaddach
Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik IX Thema: Filterung im Bildraum: Konvolution Proseminar: Grundlagen Bildverstehen/Bildgestaltung Jonas Zaddach
Bildverarbeitung Herbstsemester 2012. Fourier-Transformation
 Bildverarbeitung Herbstsemester 2012 Fourier-Transformation 1 Inhalt Fourierreihe Fouriertransformation (FT) Diskrete Fouriertransformation (DFT) DFT in 2D Fourierspektrum interpretieren 2 Lernziele Sie
Bildverarbeitung Herbstsemester 2012 Fourier-Transformation 1 Inhalt Fourierreihe Fouriertransformation (FT) Diskrete Fouriertransformation (DFT) DFT in 2D Fourierspektrum interpretieren 2 Lernziele Sie
1. Filterung im Ortsbereich 1.1 Grundbegriffe 1.2 Lineare Filter 1.3 Nicht-Lineare Filter 1.4 Separabele Filter 1.
 . Filterung im Ortsbereich. Grundbegriffe. Lineare Filter.3 Nicht-Lineare Filter.4 Separabele Filter.5 Implementierung. Filterung im Frequenzbereich. Fouriertransformation. Hoch-, Tief- und Bandpassfilter.3
. Filterung im Ortsbereich. Grundbegriffe. Lineare Filter.3 Nicht-Lineare Filter.4 Separabele Filter.5 Implementierung. Filterung im Frequenzbereich. Fouriertransformation. Hoch-, Tief- und Bandpassfilter.3
Systemtheorie abbildender Systeme
 Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Diskrete Signalverarbeitung und diskrete Systeme
 Diskrete Signalverarbeitung und diskrete Systeme Computer- basierte Verarbeitung von Signalen und Realisierung von Systemverhalten erfordern diskrete Signale und diskrete Systembeschreibungen. Wegen der
Diskrete Signalverarbeitung und diskrete Systeme Computer- basierte Verarbeitung von Signalen und Realisierung von Systemverhalten erfordern diskrete Signale und diskrete Systembeschreibungen. Wegen der
Bildverarbeitung: Fourier-Transformation. D. Schlesinger () BV: Fourier-Transformation 1 / 16
 Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
Bildverarbeitung. Fachschaftsrat Informatik. Professor Fuchs. Fragen TECHNISCHE UNIVERSITÄT DRESDEN. Unterteilung der Filter in Klassen
 Professor Fuchs Unterteilung der Filter in Klassen Wie erstellt man bei der Segmentierung objektumschreibende Formen? Eigenschaften der Zellkomplextopologie Was ist ein Histogramm? Wozu ist es gut? Unterschied
Professor Fuchs Unterteilung der Filter in Klassen Wie erstellt man bei der Segmentierung objektumschreibende Formen? Eigenschaften der Zellkomplextopologie Was ist ein Histogramm? Wozu ist es gut? Unterschied
Computergraphik 1 2. Teil: Bildverarbeitung
 1 Computergraphik 1 2. Teil: Bildverarbeitung Bildverbesserung 2 Themen jetzt gleich Rauschen, Entropie Bildverbesserung Punktbasiert Flächenbasiert Kantenbasiert 3 Was ist Rauschen? Rauschen n(m,n) ist
1 Computergraphik 1 2. Teil: Bildverarbeitung Bildverbesserung 2 Themen jetzt gleich Rauschen, Entropie Bildverbesserung Punktbasiert Flächenbasiert Kantenbasiert 3 Was ist Rauschen? Rauschen n(m,n) ist
Filter. Industrielle Bildverarbeitung, Vorlesung No M. O. Franz
 Filter Industrielle Bildverarbeitung, Vorlesung No. 5 1 M. O. Franz 07.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Lineare Filter 2 Formale
Filter Industrielle Bildverarbeitung, Vorlesung No. 5 1 M. O. Franz 07.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Lineare Filter 2 Formale
Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
Grundlagen der Bildverarbeitung
 Grundlagen der Bildverarbeitung Inhaltsverzeichnis Vorwort 9 Kapitel 1 Einführung 13 1.1 Anwendungen der digitalen Bildverarbeitung 16 1.2 Algorithmische Verarbeitung von Bildinformation 17 1.3 Zu diesem
Grundlagen der Bildverarbeitung Inhaltsverzeichnis Vorwort 9 Kapitel 1 Einführung 13 1.1 Anwendungen der digitalen Bildverarbeitung 16 1.2 Algorithmische Verarbeitung von Bildinformation 17 1.3 Zu diesem
Computergrafik 2: Morphologische Operationen
 Computergrafik 2: Morphologische Operationen Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies
Computergrafik 2: Morphologische Operationen Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies
Nichtmonotone Grauwertabbildung
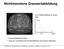 LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
Bildrekonstruktion & Multiresolution
 Bildrekonstruktion & Multiresolution Verkleinern von Bildern? Was ist zu beachten? Es kann aliasing auftreten! Das Abtasttheorem sagt wie man es vermeidet? ===> Page 1 Verkleinern von Bildern (2) Vor dem
Bildrekonstruktion & Multiresolution Verkleinern von Bildern? Was ist zu beachten? Es kann aliasing auftreten! Das Abtasttheorem sagt wie man es vermeidet? ===> Page 1 Verkleinern von Bildern (2) Vor dem
Inhaltsverzeichnis. Kapitel 1: Rechnen mit Zahlen. Kapitel 2: Umformen von Ausdrücken. Kapitel 3: Gleichungen, Ungleichungen, Gleichungssysteme
 Kapitel 1: Rechnen mit Zahlen 1.1 Rechnen mit reellen Zahlen 1.2 Berechnen von Summen und Produkten 1.3 Primfaktorzerlegung 1.4 Größter gemeinsamer Teiler 1.5 Kleinstes gemeinsames Vielfaches 1.6 n-te
Kapitel 1: Rechnen mit Zahlen 1.1 Rechnen mit reellen Zahlen 1.2 Berechnen von Summen und Produkten 1.3 Primfaktorzerlegung 1.4 Größter gemeinsamer Teiler 1.5 Kleinstes gemeinsames Vielfaches 1.6 n-te
5. Fourier-Transformation
 Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Mathematik für Wirtschaftswissenschaftler
 Mathematik für Wirtschaftswissenschaftler Yves Schneider Universität Luzern Frühjahr 2016 Repetition Kapitel 1 bis 3 2 / 54 Repetition Kapitel 1 bis 3 Ausgewählte Themen Kapitel 1 Ausgewählte Themen Kapitel
Mathematik für Wirtschaftswissenschaftler Yves Schneider Universität Luzern Frühjahr 2016 Repetition Kapitel 1 bis 3 2 / 54 Repetition Kapitel 1 bis 3 Ausgewählte Themen Kapitel 1 Ausgewählte Themen Kapitel
Bildpunkt auf dem Gitter: Pixel (picture element) (manchmal auch Pel)
 4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt
 Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Computergrafik 1 2. Teil: Bildverarbeitung
 1 Computergrafik 1 2. Teil: Bildverarbeitung Digitalfotografie, Abtastung von Bildern, Konvolution und Korrelation, Fouriertransformation 2 Themen heute Bilder aus der Digitalfotografie Kontrastumfang,
1 Computergrafik 1 2. Teil: Bildverarbeitung Digitalfotografie, Abtastung von Bildern, Konvolution und Korrelation, Fouriertransformation 2 Themen heute Bilder aus der Digitalfotografie Kontrastumfang,
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Struktur des menschlichen Auges. Bildgebende Verfahren in der Medizin und medizinische Bildverarbeitung Bildverbesserung 2 / 99
 Struktur des menschlichen Auges 2 / 99 Detektoren im Auge Ca. 100 150 Mio. Stäbchen Ca. 1 Mio. Zäpfchen 3 / 99 Zapfen Entlang der Sehachse, im Fokus Tagessehen (Photopisches Sehen) Scharfsehen Farbsehen
Struktur des menschlichen Auges 2 / 99 Detektoren im Auge Ca. 100 150 Mio. Stäbchen Ca. 1 Mio. Zäpfchen 3 / 99 Zapfen Entlang der Sehachse, im Fokus Tagessehen (Photopisches Sehen) Scharfsehen Farbsehen
Signale und Systeme Signale
 Signale und Systeme Signale Gerhard Schmidt Christian-Albrechts-Universität zu Kiel Technische Fakultät Elektrotechnik und Informationstechnik Digitale Signalverarbeitung und Systemtheorie Inhalt der Vorlesung
Signale und Systeme Signale Gerhard Schmidt Christian-Albrechts-Universität zu Kiel Technische Fakultät Elektrotechnik und Informationstechnik Digitale Signalverarbeitung und Systemtheorie Inhalt der Vorlesung
Digitale Signalverarbeitung Bernd Edler
 Digitale Signalverarbeitung Bernd Edler Wintersemester 2008/2009 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
Digitale Signalverarbeitung Bernd Edler Wintersemester 2008/2009 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
Mathematische Probleme lösen mit Maple
 Mathematische Probleme lösen mit Maple Ein Kurzeinstieg Bearbeitet von Thomas Westermann überarbeitet 2008. Buch. XII, 169 S. ISBN 978 3 540 77720 5 Format (B x L): 15,5 x 23,5 cm Weitere Fachgebiete >
Mathematische Probleme lösen mit Maple Ein Kurzeinstieg Bearbeitet von Thomas Westermann überarbeitet 2008. Buch. XII, 169 S. ISBN 978 3 540 77720 5 Format (B x L): 15,5 x 23,5 cm Weitere Fachgebiete >
GMA. Grundlagen Mathematik und Analysis. Nullstellen und Fixpunkte Reelle Funktionen 3. Christian Cenker Gabriele Uchida
 GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
Grundlagen Kondition Demo. Numerisches Rechnen. (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang
 Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Technische Universität
 Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik IX Filterung im Frequenzraum: Fouriertransformation Proseminar: Grundlagen Bildverarbeitung / Bildverstehen
Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik IX Filterung im Frequenzraum: Fouriertransformation Proseminar: Grundlagen Bildverarbeitung / Bildverstehen
3.3 Das Abtasttheorem
 17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
Technische Universität München Fakultät für Informatik
 Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik IX Proseminar: Grundlagen Bildverarbeitung/Bildverstehen Rückgewinnung/Restauration von Informationen Markus
Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik IX Proseminar: Grundlagen Bildverarbeitung/Bildverstehen Rückgewinnung/Restauration von Informationen Markus
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson 2004
 4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
Fourier Optik. Zeit. Zeit
 Fourier Optik Beispiel zur Fourier-Zerlegung: diskretes Spektrum von Sinus-Funktionen liefert in einer gewichteten Überlagerung näherungsweise eine Rechteckfunktion Sin t Sin 3t Sin 5t Sin 7t Sin 9t Sin
Fourier Optik Beispiel zur Fourier-Zerlegung: diskretes Spektrum von Sinus-Funktionen liefert in einer gewichteten Überlagerung näherungsweise eine Rechteckfunktion Sin t Sin 3t Sin 5t Sin 7t Sin 9t Sin
Grundlagen der Bildverarbeitung Klaus D. Tönnies
 Grundlagen der Bildverarbeitung Klaus D. Tönnies ein Imprint von Pearson Education München Boston San Francisco Harlow, England Don Mills, Ontario Sydney Mexico City Madrid Amsterdam Grundlagen der Bildverarbeitung
Grundlagen der Bildverarbeitung Klaus D. Tönnies ein Imprint von Pearson Education München Boston San Francisco Harlow, England Don Mills, Ontario Sydney Mexico City Madrid Amsterdam Grundlagen der Bildverarbeitung
Numerisches Programmieren, Übungen
 Technische Universität München SS 2012 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Alexander Breuer Dipl.-Math. Dipl.-Inf. Jürgen Bräckle Dr.-Ing. Markus
Technische Universität München SS 2012 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Alexander Breuer Dipl.-Math. Dipl.-Inf. Jürgen Bräckle Dr.-Ing. Markus
Übungsblatt 1 Geometrische und Technische Optik WS 2012/2013
 Übungsblatt 1 Geometrische und Technische Optik WS 2012/2013 Gegeben ist eine GRIN-Linse oder Glasaser) mit olgender Brechzahlverteilung: 2 2 n x, y, z n0 n1 x y Die Einheiten der Konstanten bzw. n 1 sind
Übungsblatt 1 Geometrische und Technische Optik WS 2012/2013 Gegeben ist eine GRIN-Linse oder Glasaser) mit olgender Brechzahlverteilung: 2 2 n x, y, z n0 n1 x y Die Einheiten der Konstanten bzw. n 1 sind
Modulprüfung Numerische Mathematik 1
 Prof. Dr. Klaus Höllig 18. März 2011 Modulprüfung Numerische Mathematik 1 Lösungen Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. 1. Die Trapezregel
Prof. Dr. Klaus Höllig 18. März 2011 Modulprüfung Numerische Mathematik 1 Lösungen Aufgabe 1 Geben Sie (ohne Beweis an, welche der folgenden Aussagen richtig und welche falsch sind. 1. Die Trapezregel
Institut für Geometrie und Praktische Mathematik
 RWTH Aachen Institut für Geometrie und Praktische Mathematik Diplom VP Numerik 13. September 004 Aufgabe 1 10 0 40 Gegeben sei die Matrix A = 80 10 10. 10 5 5 (6 Punkte) a) Skalieren (Zeilenäquilibrierung)
RWTH Aachen Institut für Geometrie und Praktische Mathematik Diplom VP Numerik 13. September 004 Aufgabe 1 10 0 40 Gegeben sei die Matrix A = 80 10 10. 10 5 5 (6 Punkte) a) Skalieren (Zeilenäquilibrierung)
Segmentierung. Vorlesung FH-Hagenberg SEM
 Segmentierung Vorlesung FH-Hagenberg SEM Segmentierung: Definition Die Pixel eines Bildes A={a i }, i=1:n, mit N der Anzahl der Pixel, werden in Teilmengen S i unterteilt. Die Teilmengen sind disjunkt
Segmentierung Vorlesung FH-Hagenberg SEM Segmentierung: Definition Die Pixel eines Bildes A={a i }, i=1:n, mit N der Anzahl der Pixel, werden in Teilmengen S i unterteilt. Die Teilmengen sind disjunkt
Digitale Bildverarbeitung Einheit 8 Lineare Filterung
 Digitale Bildverarbeitung Einheit 8 Lineare Filterung Lehrauftrag SS 2008 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, wie lineare
Digitale Bildverarbeitung Einheit 8 Lineare Filterung Lehrauftrag SS 2008 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, wie lineare
Mathematischer Vorkurs für Physiker WS 2012/13
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13 Übungsblatt 2 Wichtige Formeln aus der Vorlesung: Basisaufgaben Beispiel 1: 1 () grad () = 2 (). () () = ( 0 ) + grad ( 0 ) ( 0 )+
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13 Übungsblatt 2 Wichtige Formeln aus der Vorlesung: Basisaufgaben Beispiel 1: 1 () grad () = 2 (). () () = ( 0 ) + grad ( 0 ) ( 0 )+
6. Polynom-Interpolation
 6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
6. Polynom-Interpolation 1 6.1. Klassische Polynom-Interpolation 2 6.2. Lösung mit Hilfe Lagrange scher Basisfunktionen 3 6.3. Lösung mit Hilfe Newton scher Basisfunktionen 4 6.4. Fehlerabschätzung für
Spektralanalyse. Spektralanalyse ist derart wichtig in allen Naturwissenschaften, dass man deren Bedeutung nicht überbewerten kann!
 Spektralanalyse Spektralanalyse ist derart wichtig in allen Naturwissenschaften, dass man deren Bedeutung nicht überbewerten kann! Mit der Spektralanalyse können wir Antworten auf folgende Fragen bekommen:
Spektralanalyse Spektralanalyse ist derart wichtig in allen Naturwissenschaften, dass man deren Bedeutung nicht überbewerten kann! Mit der Spektralanalyse können wir Antworten auf folgende Fragen bekommen:
Funktionen. Mathematik-Repetitorium
 Funktionen 4.1 Funktionen einer reellen Veränderlichen 4.2 Eigenschaften von Funktionen 4.3 Die elementaren Funktionen 4.4 Grenzwerte von Funktionen, Stetigkeit Funktionen 1 4. Funktionen Funktionen 2
Funktionen 4.1 Funktionen einer reellen Veränderlichen 4.2 Eigenschaften von Funktionen 4.3 Die elementaren Funktionen 4.4 Grenzwerte von Funktionen, Stetigkeit Funktionen 1 4. Funktionen Funktionen 2
Inhaltsübersicht. Deltafunktion Gammafunktion Fehlerfunktion. Kapitel 13: Spezielle Funktionen
 Inhaltsübersicht Kapitel 13: Spezielle Funktionen Deltafunktion Gammafunktion Fehlerfunktion Notizen zur Vorlesung Mathematik für Materialwissenschaftler 2 1 Die Bezeichnung Delta-Funktion ist streng genommen
Inhaltsübersicht Kapitel 13: Spezielle Funktionen Deltafunktion Gammafunktion Fehlerfunktion Notizen zur Vorlesung Mathematik für Materialwissenschaftler 2 1 Die Bezeichnung Delta-Funktion ist streng genommen
5. Numerische Differentiation. und Integration
 5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
5. Numerische Differentiation und Integration 1 Numerische Differentiation Problemstellung: Gegeben ist eine differenzierbare Funktion f : [a,b] R und x (a,b). Gesucht sind Näherungen für die Ableitungen
Bildverarbeitung: Filterung. D. Schlesinger () Bildverarbeitung: Filterung 1 / 17
 Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Theoretische Physik 1, Mechanik
 Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
Tutorium Mathematik II, M Lösungen
 Tutorium Mathematik II, M Lösungen 7. Juni 201 *Aufgabe 1. Gegeben seien fx, y = xy 2 8e x+y und P = 1, 2. Der Gradient von f ist genau an der Stelle P Null. a Untersuchen Sie mit Hilfe der Hesse-Matrix,
Tutorium Mathematik II, M Lösungen 7. Juni 201 *Aufgabe 1. Gegeben seien fx, y = xy 2 8e x+y und P = 1, 2. Der Gradient von f ist genau an der Stelle P Null. a Untersuchen Sie mit Hilfe der Hesse-Matrix,
FILTER UND FALTUNGEN
 Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Morphologische Operatoren Graphische DV und BV, Regina Pohle, 5. Morphologische Operatoren Einordnung in die Inhalte der Vorlesung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Morphologische Operatoren Graphische DV und BV, Regina Pohle, 5. Morphologische Operatoren Einordnung in die Inhalte der Vorlesung
12.2 Gauß-Quadratur. Erinnerung: Mit der Newton-Cotes Quadratur. I n [f] = g i f(x i ) I[f] = f(x) dx
![12.2 Gauß-Quadratur. Erinnerung: Mit der Newton-Cotes Quadratur. I n [f] = g i f(x i ) I[f] = f(x) dx 12.2 Gauß-Quadratur. Erinnerung: Mit der Newton-Cotes Quadratur. I n [f] = g i f(x i ) I[f] = f(x) dx](/thumbs/71/65291080.jpg) 12.2 Gauß-Quadratur Erinnerung: Mit der Newton-Cotes Quadratur I n [f] = n g i f(x i ) I[f] = i=0 b a f(x) dx werden Polynome vom Grad n exakt integriert. Dabei sind die Knoten x i, 0 i n, äquidistant
12.2 Gauß-Quadratur Erinnerung: Mit der Newton-Cotes Quadratur I n [f] = n g i f(x i ) I[f] = i=0 b a f(x) dx werden Polynome vom Grad n exakt integriert. Dabei sind die Knoten x i, 0 i n, äquidistant
Vorlesung: Analysis II für Ingenieure. Wintersemester 07/08. Michael Karow. Themen: Niveaumengen und Gradient
 Vorlesung: Analysis II für Ingenieure Wintersemester 07/08 Michael Karow Themen: Niveaumengen und Gradient Wir betrachten differenzierbare reellwertige Funktionen f : R n G R, G offen Zur Vereinfachung
Vorlesung: Analysis II für Ingenieure Wintersemester 07/08 Michael Karow Themen: Niveaumengen und Gradient Wir betrachten differenzierbare reellwertige Funktionen f : R n G R, G offen Zur Vereinfachung
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 1 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 2010 Prof. Dr. Klaus Höllig (IMNG)
Numerische Lineare Algebra Vorlesung 1 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 2010 Prof. Dr. Klaus Höllig (IMNG)
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Rekonstruktion kontinuierlicher Daten Interpolation multivariater Daten Ulrich Rüde Lehrstuhl für Systemsimulation Sommersemester
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Rekonstruktion kontinuierlicher Daten Interpolation multivariater Daten Ulrich Rüde Lehrstuhl für Systemsimulation Sommersemester
REPETITORIUM DER HÖHEREN MATHEMATIK. Gerhard Merziger Thomas Wirth
 REPETITORIUM DER HÖHEREN MATHEMATIK Gerhard Merziger Thomas Wirth 6 INHALTSVERZEICHNIS Inhaltsverzeichnis Fl Formelsammlung F2 Formelsammlung Alphabete 11 Zeichenindex 12 1 Grundbegriffe 14 1.1 Logische
REPETITORIUM DER HÖHEREN MATHEMATIK Gerhard Merziger Thomas Wirth 6 INHALTSVERZEICHNIS Inhaltsverzeichnis Fl Formelsammlung F2 Formelsammlung Alphabete 11 Zeichenindex 12 1 Grundbegriffe 14 1.1 Logische
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
5. Gitter, Gradienten, Interpolation Gitter. (Rezk-Salama, o.j.)
 5. Gitter, Gradienten, Interpolation 5.1. Gitter (Rezk-Salama, o.j.) Gitterklassifikation: (Bartz 2005) (Rezk-Salama, o.j.) (Bartz 2005) (Rezk-Salama, o.j.) Allgemeine Gitterstrukturen: (Rezk-Salama, o.j.)
5. Gitter, Gradienten, Interpolation 5.1. Gitter (Rezk-Salama, o.j.) Gitterklassifikation: (Bartz 2005) (Rezk-Salama, o.j.) (Bartz 2005) (Rezk-Salama, o.j.) Allgemeine Gitterstrukturen: (Rezk-Salama, o.j.)
Analysis II. 8. Klausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis II 8. Klausur mit en 1 2 Aufgabe 1. Definiere die folgenden kursiv gedruckten) Begriffe. 1) Eine Metrik auf einer Menge M. 2) Die Kurvenlänge
INTELLIGENTE DATENANALYSE IN MATLAB
 INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
Perlen der Informatik I Wintersemester 2012 Aufgabenblatt 6
 Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
SCHWINGUNGEN. Version 2.0 Herbert Paukert. Sinusfunktion y = sin(x) [ 03 ]
![SCHWINGUNGEN. Version 2.0 Herbert Paukert. Sinusfunktion y = sin(x) [ 03 ] SCHWINGUNGEN. Version 2.0 Herbert Paukert. Sinusfunktion y = sin(x) [ 03 ]](/thumbs/55/37142779.jpg) Schwingungen Herbert Paukert 1 SCHWINGUNGEN Version 2.0 Herbert Paukert Sinusfunktion y = sin(x) [ 03 ] Sinusfunktion y = a*sin(x) [ 08 ] Sinusfunktion y = sin(b*x) [ 09 ] Sinusfunktion y = sin(x+c) [
Schwingungen Herbert Paukert 1 SCHWINGUNGEN Version 2.0 Herbert Paukert Sinusfunktion y = sin(x) [ 03 ] Sinusfunktion y = a*sin(x) [ 08 ] Sinusfunktion y = sin(b*x) [ 09 ] Sinusfunktion y = sin(x+c) [
Klausur zur Vorlesung Lineare Algebra und Geometrie I
 Klausur zur Vorlesung Lineare Algebra und Geometrie I Ruhr-Universität Bochum Prof. Dr. Peter Eichelsbacher 3. April 2007, 9.00-13.00 Uhr, 240 Minuten Name und Geburtsdatum: Matrikelnummer: Hinweise: Überprüfen
Klausur zur Vorlesung Lineare Algebra und Geometrie I Ruhr-Universität Bochum Prof. Dr. Peter Eichelsbacher 3. April 2007, 9.00-13.00 Uhr, 240 Minuten Name und Geburtsdatum: Matrikelnummer: Hinweise: Überprüfen
Approximation durch Polynome
 durch n Anwendungen: zur Vereinfachung einer gegebenen Funktion durch einen Polynomausdruck. Dann sind übliche Rechenoperation +,,, / möglich. zur Interpolation von Daten einer Tabelle n Beispiel Trotz
durch n Anwendungen: zur Vereinfachung einer gegebenen Funktion durch einen Polynomausdruck. Dann sind übliche Rechenoperation +,,, / möglich. zur Interpolation von Daten einer Tabelle n Beispiel Trotz
Diskrete Fourier-Transformation Stefanie Dourvos Institut für Informatik FU Berlin
 Diskrete Fourier-Transformation Stefanie Dourvos Institut für Informatik FU Berlin 28.04.09 Übersicht Einleitung Problem: polynomiale Multiplikation Crashkurs Diskrete Fourier-Transformation DFT mit FFT
Diskrete Fourier-Transformation Stefanie Dourvos Institut für Informatik FU Berlin 28.04.09 Übersicht Einleitung Problem: polynomiale Multiplikation Crashkurs Diskrete Fourier-Transformation DFT mit FFT
EVC Repetitorium Blender
 EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
Analysis III. Teil I. Rückblick auf das letzte Semester. Themen aus dem SS Inhalt der letzten Vorlesung aus dem SS.
 Analysis III für Studierende der Ingenieurwissenschaften Technische Universität Hamburg-Harburg Reiner Lauterbach Teil I Rückblick auf das letzte Semester Fakultät für Mathematik, Informatik und Naturwissenschaften
Analysis III für Studierende der Ingenieurwissenschaften Technische Universität Hamburg-Harburg Reiner Lauterbach Teil I Rückblick auf das letzte Semester Fakultät für Mathematik, Informatik und Naturwissenschaften
Digitale Bildverarbeitung
 Bernd Jahne Digitale Bildverarbeitung 6., überarbeitete und erweiterte Auflage Mit 248 Abbildungen und 155 Übungsaufgaben und CD-ROM Sy Springer Inhaltsverzeichnis I Grundlagen 1 Anwendungen und Werkzeuge
Bernd Jahne Digitale Bildverarbeitung 6., überarbeitete und erweiterte Auflage Mit 248 Abbildungen und 155 Übungsaufgaben und CD-ROM Sy Springer Inhaltsverzeichnis I Grundlagen 1 Anwendungen und Werkzeuge
Bildverarbeitung Herbstsemester 2012. Kanten und Ecken
 Bildverarbeitung Herbstsemester 01 Kanten und Ecken 1 Inhalt Einführung Kantendetektierung Gradientenbasierende Verfahren Verfahren basierend auf der zweiten Ableitung Eckpunkterkennung Harris Corner Detector
Bildverarbeitung Herbstsemester 01 Kanten und Ecken 1 Inhalt Einführung Kantendetektierung Gradientenbasierende Verfahren Verfahren basierend auf der zweiten Ableitung Eckpunkterkennung Harris Corner Detector
Einführung in die Physik I. Schwingungen und Wellen 1
 Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Biosignalverarbeitung (Schuster)
 Biosignalverarbeitung (Schuster) 9. FOURIER - TRANSFORMATION: 4 Ausprägungen der Transformation: Zeitbereich Frequenzbereich Laplace-Transformation Fourier-Transformation kontinuierlicher Signale (FT,
Biosignalverarbeitung (Schuster) 9. FOURIER - TRANSFORMATION: 4 Ausprägungen der Transformation: Zeitbereich Frequenzbereich Laplace-Transformation Fourier-Transformation kontinuierlicher Signale (FT,
Warum z-transformation?
 -Transformation Warum -Transformation? Die -Transformation führt Polynome und rationale Funktionen in die Analyse der linearen eitdiskreten Systeme ein. Die Faltung geht über in die Multiplikation von
-Transformation Warum -Transformation? Die -Transformation führt Polynome und rationale Funktionen in die Analyse der linearen eitdiskreten Systeme ein. Die Faltung geht über in die Multiplikation von
SEMINAR COMPUTATIONAL PHOTOGRAPHY
 Beseitigung von Bewegungsunschärfe Oliver Kelling, Mirco Menze SEMINAR COMPUTATIONAL PHOTOGRAPHY 1 Einführung Milderung bzw. Vermeidung von Unschärfe durch: 1. Kürze Belichtungszeiten 2. Stabilisierende
Beseitigung von Bewegungsunschärfe Oliver Kelling, Mirco Menze SEMINAR COMPUTATIONAL PHOTOGRAPHY 1 Einführung Milderung bzw. Vermeidung von Unschärfe durch: 1. Kürze Belichtungszeiten 2. Stabilisierende
Kap. 7: Wavelets. 2. Diskrete Wavelet-Transformation (DWT) 4. JPEG2000. H. Burkhardt, Institut für Informatik, Universität Freiburg DBV-I 1
 Kap. 7: Wavelets. Die kontinuierliche Wavelet-Transformation (WT). Diskrete Wavelet-Transformation (DWT) 3. Sh Schnelle Wavelet-Transformation ltt ti (FWT) 4. JPEG000 H. Burkhardt, Institut für Informatik,
Kap. 7: Wavelets. Die kontinuierliche Wavelet-Transformation (WT). Diskrete Wavelet-Transformation (DWT) 3. Sh Schnelle Wavelet-Transformation ltt ti (FWT) 4. JPEG000 H. Burkhardt, Institut für Informatik,
Faltung, Korrelation, Filtern
 Faltung, Korrelation, Filtern Wie beschreibe ich lineare Systeme (z.b. Seismometer) -> Faltung, Konvolution, Dekonvolution? Wie quantifiziere ich die Ähnlichkeit von Zeitreihen (-> Korrelation) Wie quantifiziere
Faltung, Korrelation, Filtern Wie beschreibe ich lineare Systeme (z.b. Seismometer) -> Faltung, Konvolution, Dekonvolution? Wie quantifiziere ich die Ähnlichkeit von Zeitreihen (-> Korrelation) Wie quantifiziere
Mathematik für Anwender II
 Prof. Dr. H. Brenner Osnabrück SS 2012 Mathematik für Anwender II Vorlesung 49 Zu einer reellwertigen Funktion Extrema auf einer offenen Menge G R n interessieren wir uns, wie schon bei einem eindimensionalen
Prof. Dr. H. Brenner Osnabrück SS 2012 Mathematik für Anwender II Vorlesung 49 Zu einer reellwertigen Funktion Extrema auf einer offenen Menge G R n interessieren wir uns, wie schon bei einem eindimensionalen
Bildverarbeitung 5 Frequenzraum und Bildrestauration
 Bildverarbeitung 5 Frequenzraum und Bildrestauration Frühjahrssemester 04 ETH Zürich Jan Dirk Wegner und Michal Havlena ETH Zürich Institut ür Geodäsie und Photogrammetrie (mit Material von Uwe Sörgel
Bildverarbeitung 5 Frequenzraum und Bildrestauration Frühjahrssemester 04 ETH Zürich Jan Dirk Wegner und Michal Havlena ETH Zürich Institut ür Geodäsie und Photogrammetrie (mit Material von Uwe Sörgel
Merkmale von Bildregionen, Einführung in Spektraltechniken
 Merkmale von Bildregionen, Einführung in Spektraltechniken Industrielle Bildverarbeitung, Vorlesung No. 10 1 M. O. Franz 12.12.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger
Merkmale von Bildregionen, Einführung in Spektraltechniken Industrielle Bildverarbeitung, Vorlesung No. 10 1 M. O. Franz 12.12.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
1 Potenzen und Polynome
 1 Potenzen und Polynome Für eine reelle Zahl x R und eine natürliche Zahl n N definieren wir x n := x x x... x }{{} n-mal Einschub über die bisher aufgetretenen mathematischen Symbole: Definition mittels
1 Potenzen und Polynome Für eine reelle Zahl x R und eine natürliche Zahl n N definieren wir x n := x x x... x }{{} n-mal Einschub über die bisher aufgetretenen mathematischen Symbole: Definition mittels
Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik
![Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik](/thumbs/55/37142352.jpg) Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 2 Zeitkontinuierliche
Nachrichtentechnik [NAT] Kapitel 2: Zeitkontinuierliche Signale Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 2 Zeitkontinuierliche
"Kanten- und Linienerkennung in Grauwertbildern für Bildverarbeitungsstufen im Antikollissionssystem des Faustfahrzeugs"
 "Kanten- und Linienerkennung in Grauwertbildern für Bildverarbeitungsstufen im Antikollissionssystem des Faustfahrzeugs" Ning Liu HAW-Hamburg Seminarvortrag December 15, 2006 Ning Liu Kanten- und Linienerkennung
"Kanten- und Linienerkennung in Grauwertbildern für Bildverarbeitungsstufen im Antikollissionssystem des Faustfahrzeugs" Ning Liu HAW-Hamburg Seminarvortrag December 15, 2006 Ning Liu Kanten- und Linienerkennung
Hilfsblätter Lineare Algebra
 Hilfsblätter Lineare Algebra Sebastian Suchanek unter Mithilfe von Klaus Flittner Matthias Staab c 2002 by Sebastian Suchanek Printed with L A TEX Inhaltsverzeichnis 1 Vektoren 1 11 Norm 1 12 Addition,
Hilfsblätter Lineare Algebra Sebastian Suchanek unter Mithilfe von Klaus Flittner Matthias Staab c 2002 by Sebastian Suchanek Printed with L A TEX Inhaltsverzeichnis 1 Vektoren 1 11 Norm 1 12 Addition,
Fourierreihen periodischer Funktionen
 Fourierreihen periodischer Funktionen periodische Funktion: (3.1) Fourierkoeffizienten und (3.2) (3.3) Fourier-Reihenentwicklungen Cosinus-Reihe: (3.4) (3.5) Exponentialreihe: (3.6) (3.7-3.8) Bestimmung
Fourierreihen periodischer Funktionen periodische Funktion: (3.1) Fourierkoeffizienten und (3.2) (3.3) Fourier-Reihenentwicklungen Cosinus-Reihe: (3.4) (3.5) Exponentialreihe: (3.6) (3.7-3.8) Bestimmung
