Lebensversicherungsmathematik. Kurseinheit 4 Prospektive Kalkulation (Aktuarielles Standardverfahren)
|
|
|
- Fritzi Sternberg
- vor 6 Jahren
- Abrufe
Transkript
1 Lebensversicherungsmathematik Kurseinheit 4 (Aktuarielles Standardverfahren)
2 Inhalt Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen) Berechnung von (stochastischen) Leistungsbarwerten und der Nettoeinmalprämie Prämienbarwert und Äquivalenzprinzip Pricing via Äquivalenz zwischen Prämien- und Leistungsbarwert Traditionelle Formeln zur Berechnung der Prämien für Standardprodukte Prospektive Reserve und das Theorem von Cantelli Die prospektiven Reserve als Barwert aller zukünftigen vertraglichen Zahlungsströme Äquivalenz zwischen prospektiver und retrospektiver Reserve Hinweis: Die Inhalte dieser Kurseinheit, die Konzept von Prämien- und Leistungsbarwert, deren Verknüpfung via Äquivalenzprinzip sowie die prospektive Reserve bilden essentielle Grundlagen der traditionellen LV-Mathematik. Diese Vorlesung verknüpft den traditionellen Ansatz einerseits mit dem stochastischen Ansatz (nach Gerber) und dem Zugang via Thielscher Gleichung Zum Nachlesen: Recht 2, Gerber 3 & 5 (auch Führer D) 2
3 Thema (i) Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen) Berechnung von (stochastischen) Leistungsbarwerten und der Nettoeinmalprämie Prämienbarwert und Äquivalenzprinzip Pricing via Äquivalenz zwischen Prämien- und Leistungsbarwert Traditionelle Formeln zur Berechnung der Prämien für Standardprodukte Prospektive Reserve und das Theorem von Cantelli Die prospektiven Reserve als Barwert aller zukünftigen vertraglichen Zahlungsströme Äquivalenz zwischen prospektiver und retrospektiver Reserve 3
4 - Grundidee Nutzung analytischer Formeln zur Kalkulation von Beiträgen und Reserven von Lebensversicherungen an Stelle des rekursiven Konzepts der Thielschen Gleichungen. Vorteil: Mathematische Ästhetik durch Verwendung geschlossener Formel (auch bei stochastischen Ansatz) Vorteil: Reduktion auf wenige Basisgrößen erlaubte einfache manuelle Kalkulation von Prämien direkt durch den Vermittler ( Tarifbücher analog Logarithmentafeln) Nachteil: z.t. recht komplexe Summenformeln ( merken statt rechnen ) Nachteil: Inflation von Symbolen die erforderlich sind, um Produktvarianten vollständig beschreiben zu können Nachteil: Komplexere Vertragsvarianten wie variable Prämien- und Leistungsvektoren, Vertragsübergänge etc. sind nicht mehr sinnvoll darstellbar Nachteil: Modell funktioniert nur mit starrem Rechnungszins und Kostenmodellen => Das Prospektive Modell spielt heute in der mathematischen Tarifbeschreibung eine zentrale Rolle, bei der Produktentwicklung und Vertragsverwaltung (IT Systeme) ist es weitgehend überholt. 4
5 Todesfallversicherung Stochastischer Leistungsbarwert Fragestellung: Welche Bedarfsprämie (ohne Zillmerung und Kosten) ist erforderlich, um eine n-jährige Todesfallversicherung zu finanzieren. Schritt 1: Bestimmung des Barwerts der Todesfall-Leistung (stochastisch bzw. als Erwartungswert) bezogen auf den Vertragsbeginn Schritt 2: Umrechnung auf eine laufende Prämienzahlung Leistungsbarwert im stochastischen Modell: Interpretation: Λ(ω) = v T(ω) * SI falls T(ω)* < n Λ(ω) = 0 falls T(ω) n Im Todesfall (Bedingung T(ω) = t wird die Sum Insured fällig. Zu Vertragsbeginn ist der Barwert der zukünftigen Zahlung durch Diskontierung mit dem Rechnungszins zu bestimmen. Gegeben die Verteilungsfunktion G(t) für T(ω) so ist die stochastische Funktion v T(ω) unmittelbar auszuwerten und damit der Leistungsbarwert als stochastische Größe zu modellieren. * Zur Vereinfachung der Darstellung steht in diesem Kapital T(ω) grundsätzlich für T x (ω) 5
6 Todesfallversicherung - Nettoeinmalprämie Für langfristige Verträge ist die Nettoeinmalprämie NEP ist das Analogon zur Bedarfsprämie bei YRT-Verträge. Analog zu KE 2 ist diese definiert als der Erwartungswert des stochastischen Leistungsbarwerts NEP (LPT) := Erw{Λ(ω)} = SI * = SI * k p x q x+k = =: SI * A (x,n) A (x,n), definiert über die obige Formel, ist ein aktuarielles Standardsymbol und wird für die üblichen Sterbetafeln und Rechnungszinsen tabelliert dargestellt. 6
7 Endowment Leistungsbarwert & Nettoeinmalprämie Leistungsbarwert im stochastischen Modell: Λ(ω) = v T(ω) * SI falls T(ω) < n Λ(ω) = vn *SI falls T(ω) n Interpretation ergibt sich automatisch aus dem Term Life Beispiel Nettoeinmalprämie NEP (End) = SI * ) + v n *SI Pr( [T(ω)] n] = SI * kp x q x+k v k +1 + v n * SI * n p x = SI * (A (x,n) + v n np x ) 7
8 Varianz des Leistungsbarwerts Leistungsbarwert (Endowment) im stochastischen Modell: Λ(ω) = SI * (v T(ω) Ind [T(ω) < n] + v n Ind [T(ω) n] ) mit Ind [ ] als Indikatorfunktion (1, wenn Bedingung erfüllt, 0 sonst) => Λ 2 (ω) = SI 2 *(v 2T(ω) * Ind [T(ω) < n] + v 2n *Ind [T(ω) n] ) Mischterm verschwindet wegen Disjunktheit der Bedingung für die Indikatorfunktion Varianz des Leistungsbarwerts Var{ Λ 2 (ω) } = NEP 2 Erw{ Λ 2 (ω)} = NEP 2 SI *{ kp x q x+k v 2k+2 + v 2n np x } Die Varianz des Leistungsbarwerts für eine Term Life Versicherung ergibt sich automatisch durch weglassen den letzten Terms. 8
9 Thema (ii) Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen) Berechnung von (stochastischen) Leistungsbarwerten und der Nettoeinmalprämie Prämienbarwert und Äquivalenzprinzip Pricing via Äquivalenz zwischen Prämien- und Leistungsbarwert Traditionelle Formeln zur Berechnung der Prämien für Standardprodukte Prospektive Reserve und das Theorem von Cantelli Die prospektiven Reserve als Barwert aller zukünftigen vertraglichen Zahlungsströme Äquivalenz zwischen prospektiver und retrospektiver Reserve 9
10 Prämienbarwert Analog zum Leistungsbarwert ergibt sich der stochastische Barwert der Prämie (unterstellt eine vertraglich konstante Prämiezahlung) für das Jahr k zu Π(ω,k) = v k * P falls T(ω) > k Π(ω,k) = 0 sonst Daraus ist der Prämienbarwert PPV zu Vertragsbeginn als Erwartungswert über die Summe aller stochastischen Prämien über die Vertragsdauer bestimmt als PPV(x,0,n) := Erw { Π(ω,k) } = P * v k Pr [T(ω) > k] = P * v k kp x =: P * ä (x,n) ä (x,n), wie oben definiert, ist ein aktuarielles Standardsymbol und wird für üblichen Sterbetafeln und Rechnungszinsen tabelliert dargestellt. 10
11 Äquivalenzprinzip Die Bedarfsprämie eine beliebigen Versicherung bestimmt sich durch Gleichsetzen von Leistungsbarwert und Prämienbarwert. Äquivalenzprinzip Allgemeines Prinzip NEP = PPV Anwendung: Term Life SI * A (x,n) = P * ä (x,n) Anwendung:Endowment SI * (A (x,n) + v n np x ) = P * ä (x,n) Risikozuschläge sind entweder durch implizit vorsichtige Annahmen bereits im Prämienbarwert enthalten oder zusätzlich zur Prämie zu addieren. Der Leistungsbarwert kann kalkulatorisch auch Kostenzuschläge enthalten. 11
12 Thema (iii) Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen) Berechnung von (stochastischen) Leistungsbarwerten und der Nettoeinmalprämie Prämienbarwert und Äquivalenzprinzip Pricing via Äquivalenz zwischen Prämien- und Leistungsbarwert Traditionelle Formeln zur Berechnung der Prämien für Standardprodukte Prospektive Reserve und das Theorem von Cantelli Die prospektiven Reserve als Barwert aller zukünftigen vertraglichen Zahlungsströme Äquivalenz zwischen prospektiver und retrospektiver Reserve 12
13 Barwerte während der Vertragslaufzeit Das Äquivalenzprinzip gilt per Konstruktion zum Vertragsbeginn t=0. Während der Vertragslaufzeit sind verallgemeinerte Barwert relevant: PPV(x,n,s) NEP TL (x,n,s) := P * ä(x+s,n-s) := SI * A (x+s,n-s) Barwert der am Ende der Periode ss- 1 noch fälligen Beiträge Barwert zum Zeitpunkt s zu erwartenden Leistungen (Term Life) NEP End (x,n,s) := SI * { A (x+s,n-s) + v s n-sp x+s } Barwert zum Zeitpunkt s zu erwartenden Leistungen (Endowment) Im Normalfall übersteigt der Leistungsbarwert den Prämienbarwert zu jedem Zeitpunkt s = 1... (n-1). Die (barwertige) Different aus ist vom Versicherer als Reserve zu halten (aufsichtsrechtliche bzw. bilanzielle Vorschrift). 13
14 Prospektive Reserve und Theorem von Cantelli Definition: Die Differenz zwischen dem vertraglichen Leistungsbarwert zum Zeitpunkt s und dem Barwert der zukünftigen Prämien V(x,n,s) := NEP(x,n,s) PPV(x,n,s) wird als die prospektive Reserve bezeichnet. Theorem von Cantelli: Die prospektive Reserve und die nach dem Äquivalenzprinzip bestimmte Prämie, berechnet auf Basis der Rechnungsgrundlagen Sterblichkeit und Rechnungszins, ist für einen Lebensversicherungsvertrag mit festen Leistungen L Erleb und L Tod identisch mit der Rückstellung und der Bedarfsprämie, die sich aus dem Thielschen Gleichungs- System ergeben. 14
15 Umrechnung des Prämienbarwerts Lemma 1: v p x+s-1 PPV(x,n,s) = PPV(x,n,s-1) P Prosp Beweis: Mit p x+s-1 * k p x+s = k+1 p x+s-1 ergibt sich durch Verschiebung der Summenindizes v p x+s-1 PPV(x,n,s) = v p x+s-1 P Prosp * ä(x+s,n-s) = P Prosp * v k+1 p x+s-1 * k p x+s = P Prosp * v k+1 k+1p x+s-1 = P Prosp ( v r rp x+s-1 - v 0 0 p x+s-1 ) = PProsp (ä(x+s-1,n-(s-1)) 1) = PPV (x,n,s-1) P Prosp 15
16 Umrechnung des Leistungsbarwerts Lemma 2: v p x+s-1 NEP Tod (x,n,s) = NEP Tod (x,n,s-1) - q x+s-1 SI v p x+s-1 NEP Erl (x,n,s) = NEP Erl (x,n,s-1) Beweis: Analog zu Lemma 1 gilt für die Todesfalldeckung: v p x+s-1 NEP Tod (x,s) = SI v p x+s-1 A(x+s,n-s) = SI v k+2 p x+s-1 k p x+s q x+s+k = SI v k+2 k+1p x+s-1 q x+s+k = SI v r+1 rp x+s-1 q x+s+r-1 = SI (A(x+s-1;n-(s-1)) v q x+s-1 ) und für die Erlebensfalldeckung gilt v p x+s-1 v s n-sp x+s = v s+1 n-s+1p x+s-1. 16
17 Beweis des Theorems von Cantelli Es gilt per Definition der prospektiven Reserve und unter Verwendung von Lemma 1 und 2: v p x+s-1 V(x,n,s) = v p x+s-1 ( NEP Tod (x,n,s) + NEP Erl (x,n,s) - PPV(x,n,s)) = NEP Tod (x,n,s-1) v q x+s-1 SI +NEP Erl (x,n,s-1) - PPV(x,n,s-1) + P Prosp = V(x,n,s+1) + P Prosp v q x+s-1 SI Somit genügt der Vektor {P Prosp,V (x,n,s-1) s=1 n } bei gegebener SI dem Thielschen Gleichungssystem. Die Randbedingungen s=n ist trivial und aus der Definition von P Prosp folgt, dass aus die Randbedingung V(x,n,0)=0 erfüllt ist. Wegen der Existenz und Eindeutigkeit der Lösung des Thielschen Gleichungssystems beweist dies, dass { P Prosp, V(x,n,s) } = { P Thiel, Res(s)} q.e.d. 17
18 Kurseinheit 4 - Übungsaufgabe Barwertformel für die Zillmerprämie Bestimmen Sie die Differenz Zillmer-Prämie P Z für eine Level Term Life Versicherung analytisch unter Verwendung der Barwertformel aus dem Äquivalenzprinzip und der Bedingung V(0) = Res (0) = α * n * P Z 18
Lebensversicherungsmathematik. Vorbemerkungen, Literaturhinweise und Symbolverzeichnis
 Lebensversicherungsmathematik Vorbemerkungen, Literaturhinweise und Symbolverzeichnis Inhalt Datum Themen 14.Okt KE 1: Modellierung von Sterblichkeit KE 2: Modellierung von Todesfall-Versicherungen 28.Okt
Lebensversicherungsmathematik Vorbemerkungen, Literaturhinweise und Symbolverzeichnis Inhalt Datum Themen 14.Okt KE 1: Modellierung von Sterblichkeit KE 2: Modellierung von Todesfall-Versicherungen 28.Okt
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
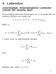 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 20 Versicherungstechnik Übungsblatt 6 Abgabe bis zum Dienstag, dem 29.11.2016 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 20 Versicherungstechnik Übungsblatt 6 Abgabe bis zum Dienstag, dem 29.11.2016 um 10 Uhr im Kasten
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 37 Versicherungstechnik Übungsblatt 11 Abgabe bis zum Dienstag, dem 10.01.2017 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 37 Versicherungstechnik Übungsblatt 11 Abgabe bis zum Dienstag, dem 10.01.2017 um 10 Uhr im Kasten
Lebensdauer eines x-jährigen
 Lebensdauer eines x-jährigen Sabrina Scheriau 20. November 2007, Graz 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 Einleitung 3 2 Sterbewahrscheinlichkeiten 4 2.1 Definition und Ermittlung....................
Lebensdauer eines x-jährigen Sabrina Scheriau 20. November 2007, Graz 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 Einleitung 3 2 Sterbewahrscheinlichkeiten 4 2.1 Definition und Ermittlung....................
Folgen. Kapitel 2. Folgen. Peter Becker (H-BRS) Analysis Sommersemester / 543
 Kapitel 2 Folgen Peter Becker (H-BRS) Analysis Sommersemester 2016 89 / 543 Inhalt Inhalt 1 Folgen Definition kriterien in C, R d und C d Peter Becker (H-BRS) Analysis Sommersemester 2016 90 / 543 Definition
Kapitel 2 Folgen Peter Becker (H-BRS) Analysis Sommersemester 2016 89 / 543 Inhalt Inhalt 1 Folgen Definition kriterien in C, R d und C d Peter Becker (H-BRS) Analysis Sommersemester 2016 90 / 543 Definition
2.2 Kollineare und koplanare Vektoren
 . Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
. Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
Kapitalversicherungen
 Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung (Grundwissen)
 Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte
 III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
Kapitalversicherungen
 Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
$Id: linabb.tex,v /01/09 13:27:34 hk Exp hk $
 Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Cashflows von Versicherungsverträgen in der Lebensversicherung
 Cashflows von Versicherungsverträgen in der Lebensversicherung 5. Juni 2015 1 / 37 Inhalt Geschäftsmodell der Lebensversicherung Produkte der Lebensversicherung Zahlungsströme unter Unsicherheit Deckungsrückstellung
Cashflows von Versicherungsverträgen in der Lebensversicherung 5. Juni 2015 1 / 37 Inhalt Geschäftsmodell der Lebensversicherung Produkte der Lebensversicherung Zahlungsströme unter Unsicherheit Deckungsrückstellung
VERSICHERUNGEN AUF MEHRERE LEBEN. Marta Ja lowiecka. 23 Januar 2009
 VERSICHERUNGEN AUF MEHRERE LEBEN Marta Ja lowiecka 23 Januar 2009 1 1 Einführung Im Folgenden werden betrachtet- basierend auf Modellen und Formeln für einfache Versicherungen auf ein Leben- verschiedene
VERSICHERUNGEN AUF MEHRERE LEBEN Marta Ja lowiecka 23 Januar 2009 1 1 Einführung Im Folgenden werden betrachtet- basierend auf Modellen und Formeln für einfache Versicherungen auf ein Leben- verschiedene
Assets Liability Management für Versicherungsunternehmen (VU) Lecture 7 Lebensversicherungsprodukte
 Assets Liability Management für Versicherungsunternehmen (VU) Lecture 7 Lebensversicherungsprodukte Inhalt # Topic What is it about 7 (i) Lebensversicherung Kalkulatorischen Grundlagen 7 (ii) Reservierung
Assets Liability Management für Versicherungsunternehmen (VU) Lecture 7 Lebensversicherungsprodukte Inhalt # Topic What is it about 7 (i) Lebensversicherung Kalkulatorischen Grundlagen 7 (ii) Reservierung
Kapitel 5 KONVERGENZ
 Kapitel 5 KONVERGENZ Fassung vom 21. April 2002 Claude Portenier ANALYSIS 75 5.1 Metrische Räume 5.1 Metrische Räume DEFINITION 1 Sei X eine Menge. Eine Abbildung d : X X! R + heißt Metrik oder Distanz
Kapitel 5 KONVERGENZ Fassung vom 21. April 2002 Claude Portenier ANALYSIS 75 5.1 Metrische Räume 5.1 Metrische Räume DEFINITION 1 Sei X eine Menge. Eine Abbildung d : X X! R + heißt Metrik oder Distanz
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Zinsratentheorie in der Versicherung
 Zinsratentheorie in der Versicherung Julia Eisenberg 04.05.2010 Gliederung 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip
Zinsratentheorie in der Versicherung Julia Eisenberg 04.05.2010 Gliederung 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip
 Nichtlebenversicherungsmathematik Aus welchen Teilen besteht eine Prämie Zufallsrisiko, Parameterrisiko, Risikokapital Risikomasse (VaR, ES) Definition von Kohärenz Zusammengesetze Poisson: S(i) CP, was
Nichtlebenversicherungsmathematik Aus welchen Teilen besteht eine Prämie Zufallsrisiko, Parameterrisiko, Risikokapital Risikomasse (VaR, ES) Definition von Kohärenz Zusammengesetze Poisson: S(i) CP, was
00. Einiges zum Vektorraum R n
 00. Einiges zum Vektorraum R n In diesem einleitenden Kapitel werden die in der LV Einführung in die mathematischen Methoden erwähnten Konzepte über Vektoren (im R 2 und R 3 ) im Rahmen des n-dimensionalen
00. Einiges zum Vektorraum R n In diesem einleitenden Kapitel werden die in der LV Einführung in die mathematischen Methoden erwähnten Konzepte über Vektoren (im R 2 und R 3 ) im Rahmen des n-dimensionalen
Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr E Schörner WS / Blatt 6 Übungen zur Vorlesung Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag Wir verwenden das Unterraumkriterium,
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr E Schörner WS / Blatt 6 Übungen zur Vorlesung Lineare Algebra und analytische Geometrie I (Unterrichtsfach) Lösungsvorschlag Wir verwenden das Unterraumkriterium,
Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik II für biw/ciw/mach/mage/vt
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Explizite Formeln für rekursiv definierte Folgen
 Schweizer Mathematik-Olympiade Explizite Formeln für rekursiv definierte Folgen Aktualisiert: 6 Juni 014 In diesem Skript wird erklärt, wie man explizite Formeln für rekursiv definierte Folgen findet Als
Schweizer Mathematik-Olympiade Explizite Formeln für rekursiv definierte Folgen Aktualisiert: 6 Juni 014 In diesem Skript wird erklärt, wie man explizite Formeln für rekursiv definierte Folgen findet Als
1 Stochastische Konvergenz 2. 2 Das Gesetz der grossen Zahlen 4. 3 Der Satz von Bernoulli 6
 Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Mathematik Dr. Thomas Zehrt Grenzwertsätze Benötigtes Vorwissen: Der Stoff der Vorlesung,,Statistik wird als bekannt vorausgesetzt, insbesondere
Wirtschaftswissenschaftliches Zentrum 0 Universität Basel Mathematik Dr. Thomas Zehrt Grenzwertsätze Benötigtes Vorwissen: Der Stoff der Vorlesung,,Statistik wird als bekannt vorausgesetzt, insbesondere
6 Lineare Gleichungssysteme
 6 LINEARE GLEICHUNGSSYSTEME 3 6 Lineare Gleichungssysteme Unter einem linearen Gleichungssystem verstehen wir ein System von Gleichungen α ξ + + α n ξ n = β α m ξ + + α mn ξ n = β m mit Koeffizienten α
6 LINEARE GLEICHUNGSSYSTEME 3 6 Lineare Gleichungssysteme Unter einem linearen Gleichungssystem verstehen wir ein System von Gleichungen α ξ + + α n ξ n = β α m ξ + + α mn ξ n = β m mit Koeffizienten α
2. Spezielle anwendungsrelevante Funktionen
 2. Spezielle anwendungsrelevante Funktionen (1) Affin-lineare Funktionen Eine Funktion f : R R heißt konstant, wenn ein c R mit f (x) = c für alle x R existiert linear, wenn es ein a R mit f (x) = ax für
2. Spezielle anwendungsrelevante Funktionen (1) Affin-lineare Funktionen Eine Funktion f : R R heißt konstant, wenn ein c R mit f (x) = c für alle x R existiert linear, wenn es ein a R mit f (x) = ax für
$Id: vektor.tex,v /01/21 14:35:13 hk Exp $
 Mathematik für Physiker I, WS 2/2 Freitag 2 $Id: vektortex,v 5 2//2 4:35:3 hk Exp $ Vektorräume 2 Untervektorräume und Erzeugendensysteme Am Ende der letzten Sitzung hatten wir wieder einmal den Lösungsraum
Mathematik für Physiker I, WS 2/2 Freitag 2 $Id: vektortex,v 5 2//2 4:35:3 hk Exp $ Vektorräume 2 Untervektorräume und Erzeugendensysteme Am Ende der letzten Sitzung hatten wir wieder einmal den Lösungsraum
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Inhaltsverzeichnis Teil 1 Teil
3. Übungsblatt Aufgaben mit Lösungen
 . Übungsblatt Aufgaben mit Lösungen Aufgabe : Gegeben sind zwei Teilmengen von R : E := {x R : x x = }, und F ist eine Ebene durch die Punkte A = ( ), B = ( ) und C = ( ). (a) Stellen Sie diese Mengen
. Übungsblatt Aufgaben mit Lösungen Aufgabe : Gegeben sind zwei Teilmengen von R : E := {x R : x x = }, und F ist eine Ebene durch die Punkte A = ( ), B = ( ) und C = ( ). (a) Stellen Sie diese Mengen
Symplektische Geometrie
 Symplektische Geometrie Def. Eine symplektische Form auf U R 2n ist eine geschlossene, nichtausgeartete 2-Differentialform. }{{}}{{} d.h. dω = 0 wird gleich definiert Wir bezeichnen sie normalerweise mit
Symplektische Geometrie Def. Eine symplektische Form auf U R 2n ist eine geschlossene, nichtausgeartete 2-Differentialform. }{{}}{{} d.h. dω = 0 wird gleich definiert Wir bezeichnen sie normalerweise mit
3.9 Elementarmatrizen
 90 Kapitel III: Vektorräume und Lineare Abbildungen 3.9 Elementarmatrizen Definition 9.1 Unter einer Elementarmatrix verstehen wir eine Matrix die aus einer n n-einheitsmatrix E n durch eine einzige elementare
90 Kapitel III: Vektorräume und Lineare Abbildungen 3.9 Elementarmatrizen Definition 9.1 Unter einer Elementarmatrix verstehen wir eine Matrix die aus einer n n-einheitsmatrix E n durch eine einzige elementare
Statistik und Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Spieltheorie. Nash-Gleichgewichts-Berechnung. Bernhard Nebel und Robert Mattmüller. Arbeitsgruppe Grundlagen der Künstlichen Intelligenz 14.
 Spieltheorie Nash-Gleichgewichts-Berechnung Albert-Ludwigs-Universität Freiburg Bernhard Nebel und Robert Mattmüller Arbeitsgruppe Grundlagen der Künstlichen Intelligenz 14. Mai 2012 14. Mai 2012 B. Nebel,
Spieltheorie Nash-Gleichgewichts-Berechnung Albert-Ludwigs-Universität Freiburg Bernhard Nebel und Robert Mattmüller Arbeitsgruppe Grundlagen der Künstlichen Intelligenz 14. Mai 2012 14. Mai 2012 B. Nebel,
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie
 Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Kapitalversicherungen
 10. Dezember 2008 Inhalt des Vortrags Wichtige Begriffe Warum Lebensversicherungen? Wichtigste Versicherungsformen Inhalt des Vortrags Wichtige Begriffe Warum Lebensversicherungen? Wichtigste Versicherungsformen
10. Dezember 2008 Inhalt des Vortrags Wichtige Begriffe Warum Lebensversicherungen? Wichtigste Versicherungsformen Inhalt des Vortrags Wichtige Begriffe Warum Lebensversicherungen? Wichtigste Versicherungsformen
8 Polynominterpolation
 8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
8 Polynominterpolation Interpolations-Aufgabe: Von einer glatten Kurve seien nur lich viele Punktewerte gegeben. Wähle einen lichdimensionalen Funktionenraum. Konstruiere nun eine Kurve in diesem Funktionenraum
Musterlösung zu Tutorium 1: Koordination des Informationssystems: Lücke-Theorem
 Musterlösung zu Tutorium 1: Koordination des Informationssystems: Lücke-Theorem 1.1 Kapitalwertbestimmung auf Basis kalkulatorischer Gewinne 1 a) Bestimmung des Kapitalwerts auf Basis von Zahlungen (übliche
Musterlösung zu Tutorium 1: Koordination des Informationssystems: Lücke-Theorem 1.1 Kapitalwertbestimmung auf Basis kalkulatorischer Gewinne 1 a) Bestimmung des Kapitalwerts auf Basis von Zahlungen (übliche
(Man sagt dafür auch, dass die Teilmenge U bezüglich der Gruppenoperationen abgeschlossen sein muss.)
 3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
3. Untergruppen 19 3. Untergruppen Nachdem wir nun einige grundlegende Gruppen kennengelernt haben, wollen wir in diesem Kapitel eine einfache Möglichkeit untersuchen, mit der man aus bereits bekannten
Varianz und Kovarianz
 KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
KAPITEL 9 Varianz und Kovarianz 9.1. Varianz Definition 9.1.1. Sei (Ω, F, P) ein Wahrscheinlichkeitsraum und X : Ω eine Zufallsvariable. Wir benutzen die Notation (1) X L 1, falls E[ X ]
1 Lineare Gleichungssysteme
 1 Lineare Gleichungssysteme Wenn man in der Schule an den Punkt der lineare Gleichungssysteme kommt, hat man normale Gleichungen und deren Umformungen schon behandelt. Und das nicht ohne Grund, denn die
1 Lineare Gleichungssysteme Wenn man in der Schule an den Punkt der lineare Gleichungssysteme kommt, hat man normale Gleichungen und deren Umformungen schon behandelt. Und das nicht ohne Grund, denn die
Mathematische Ökonometrie
 Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Mathematische Ökonometrie Ansgar Steland Fakultät für Mathematik Ruhr-Universität Bochum, Germany ansgar.steland@ruhr-uni-bochum.de Skriptum zur LV im SoSe 2005. Diese erste Rohversion erhebt keinen Anspruch
Konstruktion reeller Zahlen aus rationalen Zahlen
 Konstruktion reeller Zahlen aus rationalen Zahlen Wir nehmen an, daß der Körper der rationalen Zahlen bekannt ist. Genauer wollen wir annehmen: Gegeben ist eine Menge Q zusammen mit zwei Verknüpfungen
Konstruktion reeller Zahlen aus rationalen Zahlen Wir nehmen an, daß der Körper der rationalen Zahlen bekannt ist. Genauer wollen wir annehmen: Gegeben ist eine Menge Q zusammen mit zwei Verknüpfungen
Ausgewählte Lösungen zu den Übungsblättern 4-5
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Ausgewählte en zu den Übungsblättern -5 Aufgabe, Lineare Unabhängigkeit
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Vorlesung: Lineare Algebra (ME), Prof. Dr. J. Gwinner Ausgewählte en zu den Übungsblättern -5 Aufgabe, Lineare Unabhängigkeit
Diskrete Strukturen Kapitel 2: Grundlagen (Beweise)
 WS 2014/15 Diskrete Strukturen Kapitel 2: Grundlagen (Beweise) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_14
WS 2014/15 Diskrete Strukturen Kapitel 2: Grundlagen (Beweise) Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_14
Terme und Gleichungen
 Terme und Gleichungen Rainer Hauser November 00 Terme. Rekursive Definition der Terme Welche Objekte Terme genannt werden, wird rekursiv definiert. Die rekursive Definition legt zuerst als Basis fest,
Terme und Gleichungen Rainer Hauser November 00 Terme. Rekursive Definition der Terme Welche Objekte Terme genannt werden, wird rekursiv definiert. Die rekursive Definition legt zuerst als Basis fest,
Satz 18 (Satz von der totalen Wahrscheinlichkeit)
 Ausgehend von der Darstellung der bedingten Wahrscheinlichkeit in Gleichung 1 zeigen wir: Satz 18 (Satz von der totalen Wahrscheinlichkeit) Die Ereignisse A 1,..., A n seien paarweise disjunkt und es gelte
Ausgehend von der Darstellung der bedingten Wahrscheinlichkeit in Gleichung 1 zeigen wir: Satz 18 (Satz von der totalen Wahrscheinlichkeit) Die Ereignisse A 1,..., A n seien paarweise disjunkt und es gelte
Fehlerfortpflanzung. M. Schlup. 27. Mai 2011
 Fehlerfortpflanzung M. Schlup 7. Mai 0 Wird eine nicht direkt messbare physikalische Grösse durch das Messen anderer Grössen ermittelt, so stellt sich die Frage, wie die Unsicherheitsschranke dieser nicht-messbaren
Fehlerfortpflanzung M. Schlup 7. Mai 0 Wird eine nicht direkt messbare physikalische Grösse durch das Messen anderer Grössen ermittelt, so stellt sich die Frage, wie die Unsicherheitsschranke dieser nicht-messbaren
1. Gruppen. 1. Gruppen 7
 1. Gruppen 7 1. Gruppen Wie schon in der Einleitung erläutert wollen wir uns in dieser Vorlesung mit Mengen beschäftigen, auf denen algebraische Verknüpfungen mit gewissen Eigenschaften definiert sind.
1. Gruppen 7 1. Gruppen Wie schon in der Einleitung erläutert wollen wir uns in dieser Vorlesung mit Mengen beschäftigen, auf denen algebraische Verknüpfungen mit gewissen Eigenschaften definiert sind.
Lineare Abbildungen - I
 Lineare Abbildungen - I Definition. Seien V und W K-Vektorräume (über demselben K). Eine Abbildung F : V W heißt K-linear, wenn L1) F (v + w) = F (v) + F (w) v, w V L2) F (λv) = λf (v) v V, λ K. Somit
Lineare Abbildungen - I Definition. Seien V und W K-Vektorräume (über demselben K). Eine Abbildung F : V W heißt K-linear, wenn L1) F (v + w) = F (v) + F (w) v, w V L2) F (λv) = λf (v) v V, λ K. Somit
Mathematik für Biologen
 Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
Mathematik für Biologen Prof. Dr. Rüdiger W. Braun Heinrich-Heine-Universität Düsseldorf 11. November 2010 1 Erwartungswert und Varianz Erwartungswert Varianz und Streuung Rechenregeln Binomialverteilung
Übungsaufgaben Lösungen
 Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Übungsaufgaben Lösungen Stochastische Matrizen, Markov-Prozesse MV5.1 Eine N N-Matrix P heißt stochastisch, wenn ihre Matrixelemente nicht-negativ sind und alle Zeilensummen 1 ergeben. In Formeln: P ij
Grundlagen der Arithmetik und Zahlentheorie
 Grundlagen der Arithmetik und Zahlentheorie 1.0 Teilbarkeit In diesem Abschnitt werden wir einerseits die ganzen Zahlen an sich studieren und dabei besonders wichtige Zahlen, die Primzahlen, entsprechend
Grundlagen der Arithmetik und Zahlentheorie 1.0 Teilbarkeit In diesem Abschnitt werden wir einerseits die ganzen Zahlen an sich studieren und dabei besonders wichtige Zahlen, die Primzahlen, entsprechend
2.3 Basis und Dimension
 Lineare Algebra I WS 205/6 c Rudolf Scharlau 65 2.3 Basis und Dimension In diesem zentralen Abschnitt werden einige für die gesamte Lineare Algebra fundamentale Grundbegriffe eingeführt: Lineare Abhängigkeit
Lineare Algebra I WS 205/6 c Rudolf Scharlau 65 2.3 Basis und Dimension In diesem zentralen Abschnitt werden einige für die gesamte Lineare Algebra fundamentale Grundbegriffe eingeführt: Lineare Abhängigkeit
Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf
 Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf 1 Agenda Zinsrechnung Zinseszins Zeitwert des Geldes Strukturkongruente Refinanzierung Rendite Zinskurve 2 Das
Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf 1 Agenda Zinsrechnung Zinseszins Zeitwert des Geldes Strukturkongruente Refinanzierung Rendite Zinskurve 2 Das
8.2 Invertierbare Matrizen
 38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
Mathematik für. Wirtschaftswissenschaftler. Basiswissen mit Praxisbezug. 4., aktualisierte und erweiterte Auflage
 Mathematik für Wirtschaftswissenschaftler Basiswissen mit Praxisbezug 4., aktualisierte und erweiterte Auflage Knut Sydsaeter Peter Hammond mit Arne Strom Übersetzt und fach lektoriert durch Dr. Fred Böker
Mathematik für Wirtschaftswissenschaftler Basiswissen mit Praxisbezug 4., aktualisierte und erweiterte Auflage Knut Sydsaeter Peter Hammond mit Arne Strom Übersetzt und fach lektoriert durch Dr. Fred Böker
Mathematik und Logik
 Mathematik und Logik 5. Übungsaufgaben 2006-11-21 1. Beweisen Sie, daß die Aussage allgemeingültig ist. A = A Beweis. Dies ist ein Spezialfall von (((A = B) = B) = B) = (A = B), was wir wie folgt beweisen.
Mathematik und Logik 5. Übungsaufgaben 2006-11-21 1. Beweisen Sie, daß die Aussage allgemeingültig ist. A = A Beweis. Dies ist ein Spezialfall von (((A = B) = B) = B) = (A = B), was wir wie folgt beweisen.
Vertiefungskurs Mathematik
 Vertiefungskurs Mathematik Anforderungen für das Universitäts-Zertifikat im Schuljahr 01/13 Grundvoraussetzung: Teilnahme am Vertiefungskurs Mathematik in Klasse 11. Inhaltliche Voraussetzungen: Aussagenlogik
Vertiefungskurs Mathematik Anforderungen für das Universitäts-Zertifikat im Schuljahr 01/13 Grundvoraussetzung: Teilnahme am Vertiefungskurs Mathematik in Klasse 11. Inhaltliche Voraussetzungen: Aussagenlogik
2. Teilbarkeit. Euklidischer Algorithmus
 O. Forster: Einführung in die Zahlentheorie 2. Teilbarkeit. Euklidischer Algorithmus 2.1. Wir benutzen die folgenden Bezeichnungen: Z = {0, ±1, ±2, ±3,...} Menge aller ganzen Zahlen N 0 = {0, 1, 2, 3,...}
O. Forster: Einführung in die Zahlentheorie 2. Teilbarkeit. Euklidischer Algorithmus 2.1. Wir benutzen die folgenden Bezeichnungen: Z = {0, ±1, ±2, ±3,...} Menge aller ganzen Zahlen N 0 = {0, 1, 2, 3,...}
Logarithmische Skalen
 Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Mathematik Modul 3 -Arbeitsblatt A 3-7: LINEARE GLEICHUNGSSYSTEME MIT ZWEI VARIABLEN
 Schule Thema Bundesgymnasium für Berufstätige Salzburg Mathematik Modul 3 -Arbeitsblatt A 3-7: LINEARE GLEICHUNGSSYSTEME MIT ZWEI VARIABLEN Unterlagen LehrerInnenteam Sehr oft treten in der Mathematik
Schule Thema Bundesgymnasium für Berufstätige Salzburg Mathematik Modul 3 -Arbeitsblatt A 3-7: LINEARE GLEICHUNGSSYSTEME MIT ZWEI VARIABLEN Unterlagen LehrerInnenteam Sehr oft treten in der Mathematik
9.2 Invertierbare Matrizen
 34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
Lineare Algebra in der Oberstufe
 Lineare Algebra in der Oberstufe Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. April 2016 Stefan Ruzika 1: Schulstoff 11. April 2016 1 / 21 Übersicht Ziel dieses Kapitels
Lineare Algebra in der Oberstufe Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. April 2016 Stefan Ruzika 1: Schulstoff 11. April 2016 1 / 21 Übersicht Ziel dieses Kapitels
4. ggt und kgv. Chr.Nelius: Zahlentheorie (SS 2007) 9
 Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
Chr.Nelius: Zahlentheorie (SS 2007) 9 4. ggt und kgv (4.1) DEF: Eine ganze Zahl g heißt größter gemeinsamer Teiler (ggt) zweier ganzer Zahlen a und b, wenn gilt: GGT 0 ) g 0 GGT 1 ) g a und g b GGT 2 )
Lineare Differenzengleichungen und Polynome. Franz Pauer
 Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck, Technikerstr. 13/7, A-600 Innsbruck, Österreich. Franz.Pauer@uibk.ac.at Vortrag beim ÖMG-LehrerInnenfortbildungstag
Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck, Technikerstr. 13/7, A-600 Innsbruck, Österreich. Franz.Pauer@uibk.ac.at Vortrag beim ÖMG-LehrerInnenfortbildungstag
Vorlesung Mathematik I für Wirtschaftswissenschaftler. Universität Leipzig, WS 16/17
 Vorlesung Mathematik I für Wirtschaftswissenschaftler Universität Leipzig, WS 16/17 Prof. Dr. Bernd Kirchheim Mathematisches Institut kirchheim@math.uni-leipzig.de 1 / 1 Kapitel 1: Grundlagen 4 / 1 Kap.1
Vorlesung Mathematik I für Wirtschaftswissenschaftler Universität Leipzig, WS 16/17 Prof. Dr. Bernd Kirchheim Mathematisches Institut kirchheim@math.uni-leipzig.de 1 / 1 Kapitel 1: Grundlagen 4 / 1 Kap.1
Lineare Algebra und analytische Geometrie I Lösungsvorschlag zum 8. Tutoriumsblatt
 Mathematisches Institut der Universität München Wintersemester 24/5 Daniel Rost Lukas-Fabian Moser Lineare Algebra und analytische Geometrie I Lösungsvorschlag zum 8. Tutoriumsblatt Aufgabe T-. a) Die
Mathematisches Institut der Universität München Wintersemester 24/5 Daniel Rost Lukas-Fabian Moser Lineare Algebra und analytische Geometrie I Lösungsvorschlag zum 8. Tutoriumsblatt Aufgabe T-. a) Die
3.6 Eigenwerte und Eigenvektoren
 3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
Funktionale Programmierung ALP I. λ Kalkül WS 2012/2013. Prof. Dr. Margarita Esponda. Prof. Dr. Margarita Esponda
 ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
ALP I λ Kalkül WS 2012/2013 Berechenbarkeit - inspiriert durch Hilbert's Frage - im Jahr 1900, Paris - Internationaler Mathematikerkongress Gibt es ein System von Axiomen, aus denen alle Gesetze der Mathematik
Die Kalkulation von PKV-Tarifen unter Einbeziehung des Übertragungswertes
 Die Kalkulation von PKV-Tarifen unter Einbeziehung des Übertragungswertes Anna Wallner und Hans-Joachim Zwiesler Preprint Series: 2009-25 Fakultät für Mathematik und Wirtschaftswissenschaften UNIVERSITÄT
Die Kalkulation von PKV-Tarifen unter Einbeziehung des Übertragungswertes Anna Wallner und Hans-Joachim Zwiesler Preprint Series: 2009-25 Fakultät für Mathematik und Wirtschaftswissenschaften UNIVERSITÄT
Grundlagen der Theoretischen Informatik Musterlösungen zu ausgewählten Übungsaufgaben
 Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
Dieses Dokument soll mehr dazu dienen, Beispiele für die formal korrekt mathematische Bearbeitung von Aufgaben zu liefern, als konkrete Hinweise auf typische Klausuraufgaben zu liefern. Die hier gezeigten
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
4. Alternative Temporallogiken
 4. Alternative Temporallogiken Benutzung unterschiedlicher Temporallogiken entsprechend den verschiedenen Zeitbegriffen LTL: Linear Time Logic Ähnlich der CTL, aber jetzt einem linearen Zeitbegriff entspechend
4. Alternative Temporallogiken Benutzung unterschiedlicher Temporallogiken entsprechend den verschiedenen Zeitbegriffen LTL: Linear Time Logic Ähnlich der CTL, aber jetzt einem linearen Zeitbegriff entspechend
Lineare Algebra II. Prof. Dr. M. Rost. Übungen Blatt 12 (SS 2011) Abgabetermin: Donnerstag, 7. Juli.
 Lineare Algebra II Prof. Dr. M. Rost Übungen Blatt 12 (SS 2011) Abgabetermin: Donnerstag, 7. Juli http://www.math.uni-bielefeld.de/~rost/la2 Erinnerungen, Ergänzungen und Vorgriffe zur Vorlesung: Hier
Lineare Algebra II Prof. Dr. M. Rost Übungen Blatt 12 (SS 2011) Abgabetermin: Donnerstag, 7. Juli http://www.math.uni-bielefeld.de/~rost/la2 Erinnerungen, Ergänzungen und Vorgriffe zur Vorlesung: Hier
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Inhaltsverzeichnis. Inhaltsverzeichnis
 Inhaltsverzeichnis Inhaltsverzeichnis 1 Beweistechniken 1.1 Prädikatenlogik..................................... 1. Direkter Beweis.................................... 3 1.3 Indirekter Beweis....................................
Inhaltsverzeichnis Inhaltsverzeichnis 1 Beweistechniken 1.1 Prädikatenlogik..................................... 1. Direkter Beweis.................................... 3 1.3 Indirekter Beweis....................................
Eigenwerte. Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1)
 Eigenwerte 1 Eigenwerte und Eigenvektoren Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1) für einen Vektor x 0. Vektor x heißt ein
Eigenwerte 1 Eigenwerte und Eigenvektoren Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1) für einen Vektor x 0. Vektor x heißt ein
Vektorgeometrie. Inhaltsverzeichnis. Fragen und Antworten. (bitte nur für den Eigengebrauch verwenden)
 fua3673 Fragen und Antworten Vektorgeometrie (bitte nur für den Eigengebrauch verwenden) Inhaltsverzeichnis Vektorgeometrie im Raum. Fragen................................................. Allgemeines..........................................
fua3673 Fragen und Antworten Vektorgeometrie (bitte nur für den Eigengebrauch verwenden) Inhaltsverzeichnis Vektorgeometrie im Raum. Fragen................................................. Allgemeines..........................................
Die Firmen maximieren den Gewinn durch Wahl von y unter der Nebenbedingung der Produktionsmöglichkeiten f (y) 0
 Firmen Die Situation der Firmen wird sehr allgemein (und gewöhnungsbedürftig) beschrieben. Von den n Gütern die in der Ökonomie existieren benutzen die Firmen einen Teil zur Produktion (also als Input)
Firmen Die Situation der Firmen wird sehr allgemein (und gewöhnungsbedürftig) beschrieben. Von den n Gütern die in der Ökonomie existieren benutzen die Firmen einen Teil zur Produktion (also als Input)
A2.3 Lineare Gleichungssysteme
 A2.3 Lineare Gleichungssysteme Schnittpunkte von Graphen Bereits weiter oben wurden die Schnittpunkte von Funktionsgraphen mit den Koordinatenachsen besprochen. Wenn sich zwei Geraden schneiden, dann müssen
A2.3 Lineare Gleichungssysteme Schnittpunkte von Graphen Bereits weiter oben wurden die Schnittpunkte von Funktionsgraphen mit den Koordinatenachsen besprochen. Wenn sich zwei Geraden schneiden, dann müssen
14 Lineare Differenzengleichungen
 308 14 Lineare Differenzengleichungen 14.1 Definitionen In Abschnitt 6.3 haben wir bereits eine Differenzengleichung kennengelernt, nämlich die Gleichung K n+1 = K n q m + R, die die Kapitalveränderung
308 14 Lineare Differenzengleichungen 14.1 Definitionen In Abschnitt 6.3 haben wir bereits eine Differenzengleichung kennengelernt, nämlich die Gleichung K n+1 = K n q m + R, die die Kapitalveränderung
Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass
 Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass f Z (z) = Pr[Z = z] = x W X Pr[X + Y = z X = x] Pr[X = x] = x W X Pr[Y = z x] Pr[X = x] = x W X f X (x) f Y (z x). Den Ausdruck
Beweis: Mit Hilfe des Satzes von der totalen Wahrscheinlichkeit folgt, dass f Z (z) = Pr[Z = z] = x W X Pr[X + Y = z X = x] Pr[X = x] = x W X Pr[Y = z x] Pr[X = x] = x W X f X (x) f Y (z x). Den Ausdruck
Logik Vorlesung 3: Äquivalenz und Normalformen
 Logik Vorlesung 3: Äquivalenz und Normalformen Andreas Maletti 7. November 2014 Überblick Inhalt 1 Motivation und mathematische Grundlagen 2 Aussagenlogik Syntax und Semantik Äquivalenz und Normalformen
Logik Vorlesung 3: Äquivalenz und Normalformen Andreas Maletti 7. November 2014 Überblick Inhalt 1 Motivation und mathematische Grundlagen 2 Aussagenlogik Syntax und Semantik Äquivalenz und Normalformen
Vorkurs Mathematik. Vorlesung 5. Cauchy-Folgen
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Vorkurs Mathematik Vorlesung 5 Cauchy-Folgen Ein Problem des Konvergenzbegriffes ist, dass zur Formulierung der Grenzwert verwendet wird, den man unter Umständen
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Vorkurs Mathematik Vorlesung 5 Cauchy-Folgen Ein Problem des Konvergenzbegriffes ist, dass zur Formulierung der Grenzwert verwendet wird, den man unter Umständen
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
Mit Funktionen rechnen - ein wichtiges Thema der Sekundarstufe 2
 Mit Funktionen rechnen - ein wichtiges Thema der Sekundarstufe 2 Franz Pauer Institut für Fachdidaktik und Institut für Mathematik Universität Innsbruck Lehrer/innen/fortbildungstag Wien 2014 25. April
Mit Funktionen rechnen - ein wichtiges Thema der Sekundarstufe 2 Franz Pauer Institut für Fachdidaktik und Institut für Mathematik Universität Innsbruck Lehrer/innen/fortbildungstag Wien 2014 25. April
13. Klasse TOP 10 Grundwissen 13 Geradengleichungen 01
 . Klasse TOP 0 Grundwissen Geradengleichungen 0 Punkt-Richtungs-Form Geraden sind gegeben durch einen Aufpunkt A (mit Ortsvektor a) auf der Geraden und einen Richtungsvektor u: x = a + λ u, λ IR. (Interpretation:
. Klasse TOP 0 Grundwissen Geradengleichungen 0 Punkt-Richtungs-Form Geraden sind gegeben durch einen Aufpunkt A (mit Ortsvektor a) auf der Geraden und einen Richtungsvektor u: x = a + λ u, λ IR. (Interpretation:
Analytische Geometrie - Schnittwinkel. u 1, u 2 Richtungsvektoren der Geraden
 Analytische Geometrie - Schnittwinkel. Möglichkeiten und Formeln Gerade / Gerade: cos( ) = u u 2 u u 2 Gerade / Ebene: sin( ) = n u n u Ebene / Ebene: cos( ) = n n 2 n n 2 u, u 2 Richtungsvektoren der
Analytische Geometrie - Schnittwinkel. Möglichkeiten und Formeln Gerade / Gerade: cos( ) = u u 2 u u 2 Gerade / Ebene: sin( ) = n u n u Ebene / Ebene: cos( ) = n n 2 n n 2 u, u 2 Richtungsvektoren der
Differenzengleichungen. und Polynome
 Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-600 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung Mit linearen Differenzengleichungen
Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-600 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung Mit linearen Differenzengleichungen
UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN
 UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN VORLESUNG KOMMUTATIVE ALGEBRA, SOMMERSEMESTER 2007 1. Definitionen Ein kommutativer Ring mit Eins R ist ein Integritätsbereich, wenn er zumindest zwei
UNTERLAGEN ZUR TEILBARKEIT IN KOMMUTATIVEN RINGEN VORLESUNG KOMMUTATIVE ALGEBRA, SOMMERSEMESTER 2007 1. Definitionen Ein kommutativer Ring mit Eins R ist ein Integritätsbereich, wenn er zumindest zwei
Grundlagen Kondition Demo. Numerisches Rechnen. (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang
 Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Formale Methoden der Softwaretechnik 1 Vorlesung vom : Grundlage von Isabelle
 1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
1 Formale Methoden der Softwaretechnik 1 Vorlesung vom 16.11.09: Grundlage von Isabelle Christoph Lüth, Lutz Schröder Universität Bremen Wintersemester 2009/10 2 Fahrplan Teil I: Grundlagen der Formalen
Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf
 Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf 1 Agenda Zinsrechnung Zinseszins Zeitwert des Geldes Strukturkongruente Refinanzierung Rendite Zinskurve 2 Das
Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf 1 Agenda Zinsrechnung Zinseszins Zeitwert des Geldes Strukturkongruente Refinanzierung Rendite Zinskurve 2 Das
Rückblick auf die letzte Vorlesung. Bemerkung
 Bemerkung 1) Die Bedingung grad f (x 0 ) = 0 T definiert gewöhnlich ein nichtlineares Gleichungssystem zur Berechnung von x = x 0, wobei n Gleichungen für n Unbekannte gegeben sind. 2) Die Punkte x 0 D
Bemerkung 1) Die Bedingung grad f (x 0 ) = 0 T definiert gewöhnlich ein nichtlineares Gleichungssystem zur Berechnung von x = x 0, wobei n Gleichungen für n Unbekannte gegeben sind. 2) Die Punkte x 0 D
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Seminarvortrag aus Reiner Mathematik Existenz von Primitivwurzeln
 Seminarvortrag aus Reiner Mathematik Existenz von Primitivwurzeln Michael Kniely November 2009 1 Vorbemerkungen Definition. Sei n N +, ϕ(n) := {d [0, n 1] ggt (d, n) = 1}. Die Abbildung ϕ : N + N + heißt
Seminarvortrag aus Reiner Mathematik Existenz von Primitivwurzeln Michael Kniely November 2009 1 Vorbemerkungen Definition. Sei n N +, ϕ(n) := {d [0, n 1] ggt (d, n) = 1}. Die Abbildung ϕ : N + N + heißt
Topologische Grundbegriffe I. 1 Offene und Abgeschlossene Mengen
 Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
