Lineare Algebra in der Oberstufe
|
|
|
- Günter Bieber
- vor 7 Jahren
- Abrufe
Transkript
1 Lineare Algebra in der Oberstufe Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. April 2016 Stefan Ruzika 1: Schulstoff 11. April / 21
2 Übersicht Ziel dieses Kapitels Wiederholung des Schulstoffs zur Linearen Algebra der Oberstufe Schaffung einer gemeinsamen inhaltlichen Basis Inhalte: Lage von Punkten, Geraden & Ebenen in der Ebene, im Raum Abstände & Winkel Das Skalarprodukt & Orthogonalität Das Vektorprodukt Gauß-Verfahren zum Lösen von Gleichungssysteme Stefan Ruzika 1: Schulstoff 11. April / 21
3 Wiederholen Vertiefen Ausprobieren Textvorlage dieses Kapitels: Lambacher Schweizer Mathematik Qualifikationsphase Leistungskurs/Grundkurs Ernst Klett Verlag 2015 Das alte Mathe-Buch auskramen und lesen! Alte Aufgaben rechnen (zusätzlich zu den Übungsaufgaben)! Geogebra: Anschauung schulen! Stefan Ruzika 1: Schulstoff 11. April / 21
4 Punkte in der Ebene bzw. im Raum x 2 x 2 ( 3 P 1 = = (3, 4) 4) 4 P 1 = 3 3 x 1 x 1 a) in der Ebene R 2 x 3 b) im Raum R 3 Punkte in der Ebene bzw. im Raum können wir durch Angabe der Koordinaten spezifizieren. Stefan Ruzika 1: Schulstoff 11. April / 21
5 Abstände von Punkten x 2 Q P x 1 Wie berechnet man die Länge der Strecke PQ? Idee: zweimal Satz des Pythagoras anwenden x 3 Die Strecke PQ. Stefan Ruzika 1: Schulstoff 11. April / 21
6 Abstände von Punkten x 2 Q P x 1 Wie berechnet man die Länge der Strecke PQ? Idee: zweimal Satz des Pythagoras anwenden x 3 Die Strecke PQ. Den Abstand zweier Punkte P = (p 1, p 2, p 3 ) und Q = (q 1, q 2, q 3 ) berechnen wir durch PQ := ( 3 ) 1 2 (q 1 p 1 ) 2 + (q 2 p 2 ) 2 + (q 3 p 3 ) 2 = (q i p i ) 2 i=1 Stefan Ruzika 1: Schulstoff 11. April / 21
7 Vektoren Vektor: Tupel reeller Zahlen mit a) Richtung und b) Länge In der Ebene (in R 2 ): z. B. ( #» 3 OP = 4) Ortsvektor Der Ortsvektor (im Raum) 2 #» OP = 1 3 x 2 O #» OP P x 1 hat die Länge (auch: den Betrag) = 14 und den Gegenvektor #» OP = ( Stefan Ruzika 1: Schulstoff 11. April / 21 )
8 Vektoren Vektoren beschreiben Verschiebungen im Koordinatensystem. x 2 #» a x 1 Mit ( Vektoren ( kann ( man rechnen: ) ( a) + = = 4) 1) ) ( ( ) ( b) 2 = = 4) 2 4 8) Vektor + Vektor Reelle Zahl Vektor
9 Vektoren Vektoren beschreiben Verschiebungen im Koordinatensystem. x 2 #» b #» a x 1 Mit ( Vektoren ( kann ( man rechnen: ) ( a) + = = 4) 1) ) ( ( ) ( b) 2 = = 4) 2 4 8) Vektor + Vektor Reelle Zahl Vektor
10 Vektoren Vektoren beschreiben Verschiebungen im Koordinatensystem. x 2 #» a + #» b #» b #» a x 1 Mit ( Vektoren ( kann ( man rechnen: ) ( a) + = = 4) 1) ) ( ( ) ( b) 2 = = 4) 2 4 8) Vektor + Vektor Reelle Zahl Vektor Stefan Ruzika 1: Schulstoff 11. April / 21
11 Vektoren Vektoren beschreiben Verschiebungen im Koordinatensystem. x 2 x 2 #» a + #» b #» b 5 #» a #» a x 1 #» a x 1 Mit ( Vektoren ( kann ( man rechnen: ) ( a) + = = 4) 1) ) ( ( ) ( b) 2 = = 4) 2 4 8) Vektor + Vektor Reelle Zahl Vektor Stefan Ruzika 1: Schulstoff 11. April / 21
12 Linearkombination Einen Ausdruck wie λ #» v + µ #» w + ν #» u, wobei λ, µ, ν reelle Zahlen (sogenannte Koeffizienten) sind, heißt Linearkombination der Vektoren #» v, #» w, #» u, Stefan Ruzika 1: Schulstoff 11. April / 21
13 Linearkombination Einen Ausdruck wie λ #» v + µ #» w + ν #» u, wobei λ, µ, ν reelle Zahlen (sogenannte Koeffizienten) sind, heißt Linearkombination der Vektoren #» v, #» w, #» u, Frage: Für welche Werte gilt ( ( 3 0 λ + µ = 0? 4) 1) Stefan Ruzika 1: Schulstoff 11. April / 21
14 Linearkombination Einen Ausdruck wie λ #» v + µ #» w + ν #» u, wobei λ, µ, ν reelle Zahlen (sogenannte Koeffizienten) sind, heißt Linearkombination der Vektoren #» v, #» w, #» u, Frage: Für welche Werte gilt ( ( 3 0 λ + µ = 0? 4) 1) Und wie sieht es mit aus? λ λ λ = 0? 2 11 Stefan Ruzika 1: Schulstoff 11. April / 21
15 Linearkombination 2 Vektoren #» v, #» w heißen kollinear, wenn es eine reelle Zahl λ R gibt, so dass gilt: #» v = λ #» w Diese Bedingung ist äquivalent zu: #» v λ #» w = #» 0. Wir sagen: #» v und #» w sind linear abhängig. Kollinearität zweier Vektoren: der eine ist ein Vielfaches des anderen. Stefan Ruzika 1: Schulstoff 11. April / 21
16 Geraden Jede Gerade g lässt sich durch eine Gleichung der Form #» x = #» p + λ #» u, (λ R) beschreiben. Dabei nennen wir #» p Stützvektor und #» u Richtungsvektor. x 2 g x 1
17 Geraden Jede Gerade g lässt sich durch eine Gleichung der Form #» x = #» p + λ #» u, (λ R) beschreiben. Dabei nennen wir #» p Stützvektor und #» u Richtungsvektor. x 2 #» p g x 1
18 Geraden Jede Gerade g lässt sich durch eine Gleichung der Form #» x = #» p + λ #» u, (λ R) beschreiben. Dabei nennen wir #» p Stützvektor und #» u Richtungsvektor. x 2 #» u g #» p x 1 Stefan Ruzika 1: Schulstoff 11. April / 21
19 Geraden 7 Liegt der Punkt A = 5 auf der Geraden g : #» 3 5 x = 1 + λ 2? Die Punkte A = 2 und B = 6 liegen auf einer Geraden. 5 2 Bestimmen Sie eine Gleichung dieser Geraden. Beachte: Die Gleichung zur Beschreibung einer Geraden ist nicht eindeutig. Eine Gerade g kann also durch mehrere Gleichungen beschrieben werden. Stefan Ruzika 1: Schulstoff 11. April / 21
20 Lagebeziehungen von Geraden Zwei Geraden g und h im Raum können identisch sein. sich in einem gemeinsamen Punkt schneiden. zueinander parallel sein. zueinander windschief sein. Stefan Ruzika 1: Schulstoff 11. April / 21
21 Lagebeziehungen von Geraden So bestimmt man die Lagebeziehung zweier Geraden g : #» x = #» p + λ #» u und h : #» x = #» q + µ #» v : Sind die Richtungsvektoren #» u und #» v parallel zueinander? Stefan Ruzika 1: Schulstoff 11. April / 21
22 Lagebeziehungen von Geraden So bestimmt man die Lagebeziehung zweier Geraden g : #» x = #» p + λ #» u und h : #» x = #» q + µ #» v : Sind die Richtungsvektoren #» u und #» v parallel zueinander? Wenn ja: Liegt der Punkt P mit Ortsvektor #» p auf der Geraden h? Stefan Ruzika 1: Schulstoff 11. April / 21
23 Lagebeziehungen von Geraden So bestimmt man die Lagebeziehung zweier Geraden g : #» x = #» p + λ #» u und h : #» x = #» q + µ #» v : Sind die Richtungsvektoren #» u und #» v parallel zueinander? Wenn ja: Liegt der Punkt P mit Ortsvektor #» p auf der Geraden h? Wenn ja: g und h sind identisch. Stefan Ruzika 1: Schulstoff 11. April / 21
24 Lagebeziehungen von Geraden So bestimmt man die Lagebeziehung zweier Geraden g : #» x = #» p + λ #» u und h : #» x = #» q + µ #» v : Sind die Richtungsvektoren #» u und #» v parallel zueinander? Wenn ja: Liegt der Punkt P mit Ortsvektor #» p auf der Geraden h? Wenn ja: g und h sind identisch. Wenn nein: g und h sind parallel. Stefan Ruzika 1: Schulstoff 11. April / 21
25 Lagebeziehungen von Geraden So bestimmt man die Lagebeziehung zweier Geraden g : #» x = #» p + λ #» u und h : #» x = #» q + µ #» v : Sind die Richtungsvektoren #» u und #» v parallel zueinander? Wenn ja: Liegt der Punkt P mit Ortsvektor #» p auf der Geraden h? Wenn ja: g und h sind identisch. Wenn nein: g und h sind parallel. Wenn nein: Hat die Gleichung #» p + λ #» u = #» q + µ #» v eine Lösung? Stefan Ruzika 1: Schulstoff 11. April / 21
26 Lagebeziehungen von Geraden So bestimmt man die Lagebeziehung zweier Geraden g : #» x = #» p + λ #» u und h : #» x = #» q + µ #» v : Sind die Richtungsvektoren #» u und #» v parallel zueinander? Wenn ja: Liegt der Punkt P mit Ortsvektor #» p auf der Geraden h? Wenn ja: g und h sind identisch. Wenn nein: g und h sind parallel. Wenn nein: Hat die Gleichung #» p + λ #» u = #» q + µ #» v eine Lösung? Wenn ja: g und h schneiden sich. Stefan Ruzika 1: Schulstoff 11. April / 21
27 Lagebeziehungen von Geraden So bestimmt man die Lagebeziehung zweier Geraden g : #» x = #» p + λ #» u und h : #» x = #» q + µ #» v : Sind die Richtungsvektoren #» u und #» v parallel zueinander? Wenn ja: Liegt der Punkt P mit Ortsvektor #» p auf der Geraden h? Wenn ja: g und h sind identisch. Wenn nein: g und h sind parallel. Wenn nein: Hat die Gleichung #» p + λ #» u = #» q + µ #» v eine Lösung? Wenn ja: g und h schneiden sich. Wenn nein: g und h sind windschief. Stefan Ruzika 1: Schulstoff 11. April / 21
28 Skalarprodukt & Orthogonalität Für #» a = a 1 a 2 a 3 und #» b = b 1 b 2 b 3 definieren wir das Skalarprodukt von #» a und #» b als #» #» 3 a b := a1 b 1 + a 2 b 2 + a 3 b 3 = a i b i. i=1 Beachte: Beim Skalarprodukt verknüpfen wir multiplikativ zwei Vektoren und erhalten ein Skalar (also eine reelle Zahl). Dies ist schon die zweite Bedeutung von, die wir in dieser Vorlesung kennenlernen. Stefan Ruzika 1: Schulstoff 11. April / 21
29 Skalarprodukt & Orthogonalität 0 #» #» #» a und b seien nachfolgend beide ungleich dem Nullvektor 0 = 0. 0 #» a und #» b heißen orthogonal, wenn #» a #» b = 0 Es gilt: 4 2 #» #» a b = 1 9 = ( 1) = Also: #» a und #» b sind orthogonal; wir schreiben dafür auch: #» a #» b. Stefan Ruzika 1: Schulstoff 11. April / 21
30 Skalarprodukt & Orthogonalität Eigenschaften (Rechenregeln) Für das Skalarprodukt von Vektoren #» a, #» b und #» c gilt: 1 #» #» #» a b = b #» a (Kommutativität) 2 r #» a #» b = r ( #» a #» b ) für jede reelle Zahl r R (Assoziativität) 3 ( #» a + #» b ) #» c = #» a #» c + #» b #» c (Distributivität) 4 #» a #» a = #» a 2 Stefan Ruzika 1: Schulstoff 11. April / 21
31 Skalarprodukt & Orthogonalität Eigenschaften (Rechenregeln) Für das Skalarprodukt von Vektoren #» a, #» b und #» c gilt: 1 #» #» #» a b = b #» a (Kommutativität) 2 r #» a #» b = r ( #» a #» b ) für jede reelle Zahl r R (Assoziativität) 3 ( #» a + #» b ) #» c = #» a #» c + #» b #» c (Distributivität) 4 #» a #» a = #» a 2 Typische Aufgaben: Überprüfung der Orthogonalität zweier gegebener Geraden. Bestimmung zueinander orthogonaler Vektoren. Bestimmung fehlender Koordinaten von orthogonalen Vektoren. Orthogonalität bei geometrischen Figuren. Beweis der vier oben genannten Eigenschaften. Stefan Ruzika 1: Schulstoff 11. April / 21
32 Winkel zwischen Vektoren Für den Winkel α zwischen den Vektoren #» a und #» b gilt: #» a #» b = #» a #» b cos(α) mit 0 α 180 Stefan Ruzika 1: Schulstoff 11. April / 21
33 Winkel zwischen Vektoren Für den Winkel α zwischen den Vektoren #» a und #» b gilt: #» a #» b = #» a #» b cos(α) mit 0 α 180 Sei #» a = 2 3 und #» b = 1 Vektoren #» a und #» b : cos(α) =. Dann gilt für den Winkel α zwischen diesen beiden #» #» a b #» a #» b = = Also gilt: α 54, 0 Stefan Ruzika 1: Schulstoff 11. April / 21
34 Gauß-Verfahren Eine der häufigsten Aufgaben der Linearen Algebra / der Mathematik Lineare Gleichungssysteme (LGS) lösen. Carl Friedrich Gauß wiki/file:carl Friedrich Gauß.jpg Wie löst man ein LGS? Lineare Algebra Warum ist das so richtig? Lineare Algebra Wie löst man ein LGS schnell? Numerik Wie löst man ein LGS stabil? Numerik Wo muss man LGS in der Praxis lösen? Schule, Optimierung, Finanzmathematik, Computergrafik,... quasi immer mal wieder und überall! Stefan Ruzika 1: Schulstoff 11. April / 21
35 Gauß-Verfahren Der einfache Fall: Angenommen, es ist ein LGS in Zeilenstufenform gegeben: 2x 1 3x 2 + x 3 = 8 2x 2 + 5x 3 = 6 2x 3 = 4 Das lässt sich leicht lösen! Rechnung an der Tafel Stefan Ruzika 1: Schulstoff 11. April / 21
36 Gauß-Verfahren Gauß-Verfahren zum Lösen linearer Gleichungssysteme 1 Bringe das LGS durch Äquivalenzumformungen auf Zeilenstufenform. 2 Löse die Gleichungen der Zeilenstufenform schrittweise von unten nach oben. LGS: 3x 1 + 6x 2 2x 3 = 4 3x 1 + 2x 2 + x 3 = x 1 + 5x 2 5x 3 = 9 Kurzschreibweise in Matrixform: Rechnung an der Tafel Stefan Ruzika 1: Schulstoff 11. April / 21
37 Stefan Ruzika 1: Schulstoff 11. April / 21
Lineare Algebra in der Oberstufe
 Lineare Algebra in der Oberstufe Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 16. April 2016 Stefan Ruzika 1: Schulstoff 16. April 2016 1 / 32 Übersicht Ziel dieses Kapitels
Lineare Algebra in der Oberstufe Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 16. April 2016 Stefan Ruzika 1: Schulstoff 16. April 2016 1 / 32 Übersicht Ziel dieses Kapitels
Zusammenfassung der Analytischen Geometrie
 Zusammenfassung der Analytischen Geometrie 1. Rechnen mit Vektoren (Addition, Subtraktion, S-Multiplikation, Linearkombinationen) 1. Gegeben sind die Punkte A(2-6 ) und B(-1 14-4), 4 4 sowie die Vektoren
Zusammenfassung der Analytischen Geometrie 1. Rechnen mit Vektoren (Addition, Subtraktion, S-Multiplikation, Linearkombinationen) 1. Gegeben sind die Punkte A(2-6 ) und B(-1 14-4), 4 4 sowie die Vektoren
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
GRUNDLAGEN MATHEMATIK
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 1. Vektorrechnung und Geometrie Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 1. Vektorrechnung und Geometrie Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies
Grundwissen Abitur Geometrie 15. Juli 2012
 Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
d 2 b 2 c 2 d 3 b 3 c 3 , D a 1 d 1 c 1 v 3 Definiton (Verbindungsvektor): Zwei Punkte A(a 1 a 2 a 3 ) und B(b 1 b 2 b 3 ) legen den Vektor b 1 a 1
 2008/2009 Das Wichtigste in Kürze Klasse 3 Lineare Gleichungssysteme und Determinanten Definiton (Lineare Gleichungssysteme: Lineare Gleichungssysteme löst man entweder mit dem Gauß-Algorithmus oder nach
2008/2009 Das Wichtigste in Kürze Klasse 3 Lineare Gleichungssysteme und Determinanten Definiton (Lineare Gleichungssysteme: Lineare Gleichungssysteme löst man entweder mit dem Gauß-Algorithmus oder nach
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Mathematik Analytische Geometrie
 Mathematik Analytische Geometrie Grundlagen:. Das -Dimensionale kartesische Koordinatensystem: x x x. Vektoren und Ortsvektoren: a x = x x ist ein Vektor, der eine Verschiebung um x -Einheiten in x-richtung,
Mathematik Analytische Geometrie Grundlagen:. Das -Dimensionale kartesische Koordinatensystem: x x x. Vektoren und Ortsvektoren: a x = x x ist ein Vektor, der eine Verschiebung um x -Einheiten in x-richtung,
2.2 Kollineare und koplanare Vektoren
 . Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
. Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
(x 1. Vektoren. g: x = p + r u. p r (u1. x 2. u 2. p 2
 Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof. Dr. Ulrich Reif
 14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
14 Oktober 2008 1 Kurzskript zur Vorlesung Mathematik I für MB, WI/MB und andere Prof Dr Ulrich Reif Inhalt: 1 Vektorrechnung 2 Lineare Gleichungssysteme 3 Matrizenrechnung 4 Lineare Abbildungen 5 Eigenwerte
Zusammenfassung Mathe III. Themenschwerpunkt 3: Analytische Geometrie / lineare Algebra (ean) 1. Rechenregeln mit Vektoren
 Zusammenfassung Mathe III Themenschwerpunkt 3: Analytische Geometrie / lineare Algebra (ean) 1. Rechenregeln mit Vektoren Definition: (1) anschaulich: Ein Vektor ist eine direkt gerichtete Verbindung zweier
Zusammenfassung Mathe III Themenschwerpunkt 3: Analytische Geometrie / lineare Algebra (ean) 1. Rechenregeln mit Vektoren Definition: (1) anschaulich: Ein Vektor ist eine direkt gerichtete Verbindung zweier
Geometrie 3. Lagebeziehung zwischen geometrischen Objekten. 28. Oktober Mathe-Squad GbR. Lagebeziehung zwischen geometrischen Objekten 1
 Geometrie 3 Lagebeziehung zwischen geometrischen Objekten Mathe-Squad GbR 28. Oktober 2016 Lagebeziehung zwischen geometrischen Objekten 1 Lage zweier Geraden Geraden g : #» X = #» A + λ #» u mit λ R h
Geometrie 3 Lagebeziehung zwischen geometrischen Objekten Mathe-Squad GbR 28. Oktober 2016 Lagebeziehung zwischen geometrischen Objekten 1 Lage zweier Geraden Geraden g : #» X = #» A + λ #» u mit λ R h
Vektorräume. Stefan Ruzika. 24. April Mathematisches Institut Universität Koblenz-Landau Campus Koblenz
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 24. April 2016 Stefan Ruzika 3: Vektorräume 24. April 2016 1 / 20 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume Erinnerung:
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 24. April 2016 Stefan Ruzika 3: Vektorräume 24. April 2016 1 / 20 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume Erinnerung:
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
03. Vektoren im R 2, R 3 und R n
 03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
03 Vektoren im R 2, R 3 und R n Unter Verwendung eines Koordinatensystems kann jedem Punkt der Ebene umkehrbar eindeutig ein Zahlenpaar (x, y) zugeordnet werden P (x, y) Man nennt x und y die kartesischen
Vektorrechnung. 10. August Inhaltsverzeichnis. 1 Vektoren 2. 2 Grundlegende Rechenoperationen mit Vektoren 3. 3 Geometrie der Vektoren 5
 Vektorrechnung 0. August 07 Inhaltsverzeichnis Vektoren Grundlegende Rechenoperationen mit Vektoren 3 3 Geometrie der Vektoren 5 4 Das Kreuzprodukt 9 Vektoren Die reellen Zahlen R können wir uns als eine
Vektorrechnung 0. August 07 Inhaltsverzeichnis Vektoren Grundlegende Rechenoperationen mit Vektoren 3 3 Geometrie der Vektoren 5 4 Das Kreuzprodukt 9 Vektoren Die reellen Zahlen R können wir uns als eine
Skalarprodukt, Norm & Metrik
 Skalarprodukt, Norm & Metrik Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. Mai 2016 Stefan Ruzika 5: Skalarprodukt, Norm & Metrik 11. Mai 2016 1 / 13 Gliederung 1
Skalarprodukt, Norm & Metrik Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. Mai 2016 Stefan Ruzika 5: Skalarprodukt, Norm & Metrik 11. Mai 2016 1 / 13 Gliederung 1
H. Gruber, R. Neumann. Erfolg im Mathe-Abi. Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen
 H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Themen des Pflichtteils... Analysis Von der Gleichung
H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Themen des Pflichtteils... Analysis Von der Gleichung
Geometrie. Bei der Addition von Vektoren erhält man einen Repräsentanten des Summenvektors +, indem man die Repräsentanten von aneinanderfügt:
 Geometrie 1. Vektoren Die Menge aller zueinander parallelen, gleich langen und gleich gerichteten Pfeile werden als Vektor bezeichnet. Jeder einzelne Pfeil heißt Repräsentant des Vektors. Bei Ortsvektoren:
Geometrie 1. Vektoren Die Menge aller zueinander parallelen, gleich langen und gleich gerichteten Pfeile werden als Vektor bezeichnet. Jeder einzelne Pfeil heißt Repräsentant des Vektors. Bei Ortsvektoren:
Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra
 A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
A. Filler[-3mm] Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra, Teil 8 Folie 1 /27 Didaktik der Analysis und der Analytischen Geometrie/ Linearen Algebra 8. Das Skalarprodukt, metrische
Definition von R n. Parallelverschiebungen in R n. Definition 8.1 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R... R (n-mal), d.h.
 8 Elemente der linearen Algebra 81 Der euklidische Raum R n Definition von R n Definition 81 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R R (n-mal), dh R n = {(x 1, x 2,, x n ) : x
8 Elemente der linearen Algebra 81 Der euklidische Raum R n Definition von R n Definition 81 Unter dem Raum R n (n N) versteht man das kartesische Produkt R R R (n-mal), dh R n = {(x 1, x 2,, x n ) : x
Inhalt. Mathematik für Chemiker II Lineare Algebra. Vorlesung im Sommersemester Kurt Frischmuth. Rostock, April Juli 2015
 Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
Inhalt Mathematik für Chemiker II Lineare Algebra Vorlesung im Sommersemester 5 Rostock, April Juli 5 Vektoren und Matrizen Abbildungen 3 Gleichungssysteme 4 Eigenwerte 5 Funktionen mehrerer Variabler
00. Einiges zum Vektorraum R n
 00. Einiges zum Vektorraum R n In diesem einleitenden Kapitel werden die in der LV Einführung in die mathematischen Methoden erwähnten Konzepte über Vektoren (im R 2 und R 3 ) im Rahmen des n-dimensionalen
00. Einiges zum Vektorraum R n In diesem einleitenden Kapitel werden die in der LV Einführung in die mathematischen Methoden erwähnten Konzepte über Vektoren (im R 2 und R 3 ) im Rahmen des n-dimensionalen
Vorkurs Mathematik B
 Vorkurs Mathematik B Dr. Thorsten Camps Fakultät für Mathematik TU Dortmund 20. September 2011 Definition (R n ) Wir definieren: 1 Der R 2 sei die Menge aller Punkte in der Ebene. Jeder Punkt wird in ein
Vorkurs Mathematik B Dr. Thorsten Camps Fakultät für Mathematik TU Dortmund 20. September 2011 Definition (R n ) Wir definieren: 1 Der R 2 sei die Menge aller Punkte in der Ebene. Jeder Punkt wird in ein
Vektoren. Kapitel 13 Vektoren. Mathematischer Vorkurs TU Dortmund Seite 114 / 1
 Vektoren Kapitel 13 Vektoren Mathematischer Vorkurs TU Dortmund Seite 114 / 1 Vektoren 131 Denition: Vektoren im Zahlenraum Ein Vektor (im Zahlenraum) mit n Komponenten ist ein n-tupel reeller Zahlen,
Vektoren Kapitel 13 Vektoren Mathematischer Vorkurs TU Dortmund Seite 114 / 1 Vektoren 131 Denition: Vektoren im Zahlenraum Ein Vektor (im Zahlenraum) mit n Komponenten ist ein n-tupel reeller Zahlen,
Stefan Ruzika. 24. April 2016
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 24. April 2016 Stefan Ruzika 2: Körper 24. April 2016 1 / 21 Gliederung 1 1 Schulstoff 2 Körper Definition eines Körpers
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 24. April 2016 Stefan Ruzika 2: Körper 24. April 2016 1 / 21 Gliederung 1 1 Schulstoff 2 Körper Definition eines Körpers
Mögliche Lösung. Ebenen im Haus
 Lineare Algebra und Analytische Geometrie XX Ebenen im Raum Ebenen im Haus Ermitteln Sie die Koordinaten aller bezeichneten Punkte. Erstellen Sie für die Dachflächen E und E jeweils eine Ebenengleichung
Lineare Algebra und Analytische Geometrie XX Ebenen im Raum Ebenen im Haus Ermitteln Sie die Koordinaten aller bezeichneten Punkte. Erstellen Sie für die Dachflächen E und E jeweils eine Ebenengleichung
Geometrie. 1 Vektoren, Vektorielle analytische Geometrie der Ebene
 Geometrie Geometrie W. Kuhlisch Brückenkurs 207. Vektoren, Vektorrechnung und analytische Geometrie der Ebene 2. Vektorrechnung und analytische Geometrie des Raumes 3. Anwendungen in der Geometrie, Lagebeziehungen
Geometrie Geometrie W. Kuhlisch Brückenkurs 207. Vektoren, Vektorrechnung und analytische Geometrie der Ebene 2. Vektorrechnung und analytische Geometrie des Raumes 3. Anwendungen in der Geometrie, Lagebeziehungen
3 Vektoren. 3.1 Kartesische Koordinaten in Ebene und Raum. Höhere Mathematik 60
 Kartesische Koordinaten in Ebene und Raum 3 Vektoren 3.1 Kartesische Koordinaten in Ebene und Raum In der Ebene (mathematisch ist dies die Menge R 2 ) ist ein kartesisches Koordinatensystem festgelegt
Kartesische Koordinaten in Ebene und Raum 3 Vektoren 3.1 Kartesische Koordinaten in Ebene und Raum In der Ebene (mathematisch ist dies die Menge R 2 ) ist ein kartesisches Koordinatensystem festgelegt
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Basistext Geraden und Ebenen
 Basistext Geraden und Ebenen Parameterdarstellung Geraden Eine Gerade ist durch zwei Punkte P und Q, die auf der Geraden liegen, eindeutig festgelegt. Man benötigt zur Darstellung den Vektor. Dieser wird
Basistext Geraden und Ebenen Parameterdarstellung Geraden Eine Gerade ist durch zwei Punkte P und Q, die auf der Geraden liegen, eindeutig festgelegt. Man benötigt zur Darstellung den Vektor. Dieser wird
Teil II. Geometrie 19
 Teil II. Geometrie 9 5. Dreidimensionales Koordinatensystem Im dreidimensionalen Koordinatensystem gibt es acht Oktanten, oben I bis VI und unten VI bis VIII. Die Koordinatenachsen,x 2 und stehen jeweils
Teil II. Geometrie 9 5. Dreidimensionales Koordinatensystem Im dreidimensionalen Koordinatensystem gibt es acht Oktanten, oben I bis VI und unten VI bis VIII. Die Koordinatenachsen,x 2 und stehen jeweils
Lagebeziehung von Ebenen
 M8 ANALYSIS Lagebeziehung von Ebenen Es gibt Möglichkeiten für die Lagebeziehung zwischen zwei Ebenen. Die Ebenen sind identisch. Die Ebenen sind parallel. Die Ebenen schneiden sich in einer Geraden Um
M8 ANALYSIS Lagebeziehung von Ebenen Es gibt Möglichkeiten für die Lagebeziehung zwischen zwei Ebenen. Die Ebenen sind identisch. Die Ebenen sind parallel. Die Ebenen schneiden sich in einer Geraden Um
Vorkurs Mathematik Teil III. Lineare Algebra
 Vorkurs Mathematik Teil III. Lineare Algebra Inhalt 0. Inhalt 1. Lineare Gleichungssysteme und Gauß-Verfahren. Vektorrechnung 3. Lagebestimmungen von Punkt, Geraden und Ebenen 4. Skalarprodukt, Längen
Vorkurs Mathematik Teil III. Lineare Algebra Inhalt 0. Inhalt 1. Lineare Gleichungssysteme und Gauß-Verfahren. Vektorrechnung 3. Lagebestimmungen von Punkt, Geraden und Ebenen 4. Skalarprodukt, Längen
Formelsammlung Mathematik Grundkurs Inhalt
 Formelsammlung Mathematik Grundkurs Inhalt Inhalt...1 Trigonometrie Grundlagen... Vektoren...3 Skalarprodukt...4 Geraden...5 Abstandsberechnungen...6 Ebenen...7 Lineare Gleichungssysteme (LGS)...8 Gauß'sches
Formelsammlung Mathematik Grundkurs Inhalt Inhalt...1 Trigonometrie Grundlagen... Vektoren...3 Skalarprodukt...4 Geraden...5 Abstandsberechnungen...6 Ebenen...7 Lineare Gleichungssysteme (LGS)...8 Gauß'sches
Lineare Algebra: Theorie und Anwendungen
 Lineare Algebra: Theorie und Anwendungen Sommersemester 2012 Bernhard Burgeth Universität des Saarlandes c 2010 2012, Bernhard Burgeth 1 VEKTOREN IN DER EBENE UND IM RAUM 2 1 Vektoren in der Ebene und
Lineare Algebra: Theorie und Anwendungen Sommersemester 2012 Bernhard Burgeth Universität des Saarlandes c 2010 2012, Bernhard Burgeth 1 VEKTOREN IN DER EBENE UND IM RAUM 2 1 Vektoren in der Ebene und
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Wiederholung Vektoren/Geraden
 Wiederholung Vektoren/Geraden S. 55 Nr. 4a Stelle eine Vektorgleichung auf: x a + y b + z c = d. Bilde daraus ein LGS: x + 3y z = 1 x + y + z = 1 x + y + 5z = 3 1 3 1 1 oder in Matrixschreibweise: 1 1
Wiederholung Vektoren/Geraden S. 55 Nr. 4a Stelle eine Vektorgleichung auf: x a + y b + z c = d. Bilde daraus ein LGS: x + 3y z = 1 x + y + z = 1 x + y + 5z = 3 1 3 1 1 oder in Matrixschreibweise: 1 1
Mathematische Grundlagen für die Vorlesung. Differentialgeometrie
 Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Hauscurriculum Q2 Lineare Algebra/Analytische Geometrie Grundkurs März 2017
 Hauscurriculum Q2 Lineare Algebra/Analytische Geometrie Grundkurs März 2017 Übersicht: Q2.3 im Raum Q2.4 Matrizen zur Beschreibung von Q2.6 Vertiefung der Analytischen Geometrie (nur Grundkurs) verbindlich:
Hauscurriculum Q2 Lineare Algebra/Analytische Geometrie Grundkurs März 2017 Übersicht: Q2.3 im Raum Q2.4 Matrizen zur Beschreibung von Q2.6 Vertiefung der Analytischen Geometrie (nur Grundkurs) verbindlich:
Ausführliche Lösungen
 Bohner Ott Deusch Mathematik für berufliche Gymnasien Lineare Algebra Vektorgeometrie Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab. Auflage 6 ISBN 978--8-68-5 Das Werk und seine Teile
Bohner Ott Deusch Mathematik für berufliche Gymnasien Lineare Algebra Vektorgeometrie Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab. Auflage 6 ISBN 978--8-68-5 Das Werk und seine Teile
Vorlesung Mathematik 2 für Informatik
 Vorlesung Mathematik für Informatik Inhalt: Lineare Algebra Rechnen mit Vektoren und Matrizen Lineare Gleichungssysteme, GauÿAlgorithmus Vektorräume, Lineare Abbildungen Eigenwerte und Eigenvektoren Literatur
Vorlesung Mathematik für Informatik Inhalt: Lineare Algebra Rechnen mit Vektoren und Matrizen Lineare Gleichungssysteme, GauÿAlgorithmus Vektorräume, Lineare Abbildungen Eigenwerte und Eigenvektoren Literatur
Ebenen in Normalenform
 Ebenen in Normalenform Normalenvektoren und Einheitsvektoren Definition Normalenvektor Ein Normalenvektor einer Ebene ist ein Vektor, der senkrecht auf einer Ebene steht (siehe Seite 12). Berechnung eines
Ebenen in Normalenform Normalenvektoren und Einheitsvektoren Definition Normalenvektor Ein Normalenvektor einer Ebene ist ein Vektor, der senkrecht auf einer Ebene steht (siehe Seite 12). Berechnung eines
Grundlagen der Vektorrechnung
 Grundlagen der Vektorrechnung Ein Vektor a ist eine geordnete Liste von n Zahlen Die Anzahl n dieser Zahlen wird als Dimension des Vektors bezeichnet Schreibweise: a a a R n Normale Reelle Zahlen nennt
Grundlagen der Vektorrechnung Ein Vektor a ist eine geordnete Liste von n Zahlen Die Anzahl n dieser Zahlen wird als Dimension des Vektors bezeichnet Schreibweise: a a a R n Normale Reelle Zahlen nennt
Jürgen Roth Didaktik der Linearen Algebra und Analytischen Geometrie
 Jürgen Roth Didaktik der Linearen Algebra und Analytischen Geometrie Modul 12a: Fachdidaktische Bereiche juergen-roth.de/lehre/did_linalg_anageo/ Kapitel 5: Skalarprodukt 5.1 Inhalte Didaktik der Linearen
Jürgen Roth Didaktik der Linearen Algebra und Analytischen Geometrie Modul 12a: Fachdidaktische Bereiche juergen-roth.de/lehre/did_linalg_anageo/ Kapitel 5: Skalarprodukt 5.1 Inhalte Didaktik der Linearen
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat.
 1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
1. Vektoralgebra 1.0 Einführung Vektoren Ein Vektor ist eine Größe, welche sowohl einen Zahlenwert (Betrag) als auch eine Richtung hat. übliche Beispiele: Ort r = r( x; y; z; t ) Kraft F Geschwindigkeit
Anwendungsaufgaben zur Vektorrechnung (Abstände bestimmen)
 Anwendungsaufgaben zur Vektorrechnung (Abstände bestimmen) 1) a) Ein Flugzeug fliegt von A(4; 2; 5) nach B(12; 6; 10). In S(10; 10; 4,75) befindet sich die Spitze eines Berges. Wie weit fliegt das Flugzeug
Anwendungsaufgaben zur Vektorrechnung (Abstände bestimmen) 1) a) Ein Flugzeug fliegt von A(4; 2; 5) nach B(12; 6; 10). In S(10; 10; 4,75) befindet sich die Spitze eines Berges. Wie weit fliegt das Flugzeug
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 7 11. Mai 2010 Kapitel 8. Vektoren Definition 76. Betrachten wir eine beliebige endliche Anzahl von Vektoren v 1, v 2,..., v m des R n, so können
Mathematik für Naturwissenschaftler II SS 2010 Lektion 7 11. Mai 2010 Kapitel 8. Vektoren Definition 76. Betrachten wir eine beliebige endliche Anzahl von Vektoren v 1, v 2,..., v m des R n, so können
Grundsätzliches Produkte Anwendungen in der Geometrie. Vektorrechnung. Fakultät Grundlagen. Juli 2015
 Vektorrechnung Fakultät Grundlagen Juli 205 Fakultät Grundlagen Vektorrechnung Übersicht Grundsätzliches Grundsätzliches Vektorbegriff Algebraisierung der Vektorrechnung Betrag 2 Skalarprodukt Vektorprodukt
Vektorrechnung Fakultät Grundlagen Juli 205 Fakultät Grundlagen Vektorrechnung Übersicht Grundsätzliches Grundsätzliches Vektorbegriff Algebraisierung der Vektorrechnung Betrag 2 Skalarprodukt Vektorprodukt
Formelsammlung Analytische Geometrie
 Formelsammlung Analytische Geometrie http://www.fersch.de Klemens Fersch 6. August 6 Inhaltsverzeichnis 6 Analytische Geometrie 6. Vektorrechung in der Ebene......................................... 6..
Formelsammlung Analytische Geometrie http://www.fersch.de Klemens Fersch 6. August 6 Inhaltsverzeichnis 6 Analytische Geometrie 6. Vektorrechung in der Ebene......................................... 6..
1 lineare Gleichungssysteme
 Hinweise und Lösungen: http://mathemathemathe.de/lineare-algebra-grundlagen 1 lineare Gleichungssysteme Übung 1.1: Löse das lineare Gleichungssystem: I 3x + 3y + 7z = 13 II 1x 2y + 2, 5z = 1, 5 III 4x
Hinweise und Lösungen: http://mathemathemathe.de/lineare-algebra-grundlagen 1 lineare Gleichungssysteme Übung 1.1: Löse das lineare Gleichungssystem: I 3x + 3y + 7z = 13 II 1x 2y + 2, 5z = 1, 5 III 4x
Lernunterlagen Vektoren in R 2
 Die Menge aller reellen Zahlen wird mit R bezeichnet, die Menge aller Paare a 1 a 2 reeller Zahlen wird mit R 2 bezeichnet. Definition der Menge R 2 : R 2 { a 1 a 2 a 1, a 2 R} Ein Zahlenpaar a 1 a 2 bezeichnet
Die Menge aller reellen Zahlen wird mit R bezeichnet, die Menge aller Paare a 1 a 2 reeller Zahlen wird mit R 2 bezeichnet. Definition der Menge R 2 : R 2 { a 1 a 2 a 1, a 2 R} Ein Zahlenpaar a 1 a 2 bezeichnet
Denition 6.1 Eine Gerade ist die Menge aller Losungen (x; y) einer linearen Gleichung. y = A B x + C B : Ax + By = C mit 6= 0
 6 Der Vektorraum R n In den folgenden Wochen wenden wir uns der Linearen Algebra zu, die man als eine abstrakte Form des Rechnens mit Vektoren auassen kann. Ein zentrales Thema werden lineare Raume (=
6 Der Vektorraum R n In den folgenden Wochen wenden wir uns der Linearen Algebra zu, die man als eine abstrakte Form des Rechnens mit Vektoren auassen kann. Ein zentrales Thema werden lineare Raume (=
Outline. 1 Vektoren im Raum. 2 Komponenten und Koordinaten. 3 Skalarprodukt. 4 Vektorprodukt. 5 Analytische Geometrie. 6 Lineare Räume, Gruppentheorie
 Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
13. Klasse TOP 10 Grundwissen 13 Geradengleichungen 01
 . Klasse TOP 0 Grundwissen Geradengleichungen 0 Punkt-Richtungs-Form Geraden sind gegeben durch einen Aufpunkt A (mit Ortsvektor a) auf der Geraden und einen Richtungsvektor u: x = a + λ u, λ IR. (Interpretation:
. Klasse TOP 0 Grundwissen Geradengleichungen 0 Punkt-Richtungs-Form Geraden sind gegeben durch einen Aufpunkt A (mit Ortsvektor a) auf der Geraden und einen Richtungsvektor u: x = a + λ u, λ IR. (Interpretation:
Mathematische Formeln für das Studium an Fachhochschulen
 Mathematische Formeln für das Studium an Fachhochschulen von Richard Mohr. Auflage Hanser München 0 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 446 455 4 Zu Inhaltsverzeichnis schnell und portofrei
Mathematische Formeln für das Studium an Fachhochschulen von Richard Mohr. Auflage Hanser München 0 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 446 455 4 Zu Inhaltsverzeichnis schnell und portofrei
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Lineare Algebra/Analytische Geometrie I WiSe 2015/16
 Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Lineare Algebra/Analytische Geometrie I WiSe 25/6 Bearbeiten Sie bitte
Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs Lineare Algebra/Analytische Geometrie I WiSe 25/6 Bearbeiten Sie bitte
Lagebeziehungen zwischen Geraden und Ebenen mit Hilfe der Normalenform
 Lagebeziehungen zwischen Geraden und Ebenen mit Hilfe der Normalenform Bernhard Scheideler Albrecht-Dürer-Gymnasium Hagen Hilfen zur Analytischen Geometrie (). Dezember 0 Inhalt: Die Lagebeziehungen zwischen
Lagebeziehungen zwischen Geraden und Ebenen mit Hilfe der Normalenform Bernhard Scheideler Albrecht-Dürer-Gymnasium Hagen Hilfen zur Analytischen Geometrie (). Dezember 0 Inhalt: Die Lagebeziehungen zwischen
10.2 Linearkombinationen
 147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
Theorie 1 1 / 2 Grundbegriffe
 Theorie 1 1 / 2 Grundbegriffe Was ist ein Vektor? Wie lassen sich Vektoren darstellen? Theorie 1 2 / 2 Grundbegriffe Antwort : Ein Vektor ist die Menge aller gleichlangen, gleichgerichteten und gleichorientierten
Theorie 1 1 / 2 Grundbegriffe Was ist ein Vektor? Wie lassen sich Vektoren darstellen? Theorie 1 2 / 2 Grundbegriffe Antwort : Ein Vektor ist die Menge aller gleichlangen, gleichgerichteten und gleichorientierten
1 0,5 beschrieben. Sein Kurs wird durch den Vektor =
 1.) Ein rotes U-Boot ist auf Expedition im Ozean unterwegs. Es will ein Schiffswrack untersuchen. Seine Position lässt sich in einem Koordinatensystem mithilfe der Koordinaten U r ( 2-1,5-1 ) beschreiben.
1.) Ein rotes U-Boot ist auf Expedition im Ozean unterwegs. Es will ein Schiffswrack untersuchen. Seine Position lässt sich in einem Koordinatensystem mithilfe der Koordinaten U r ( 2-1,5-1 ) beschreiben.
Analytische Geometrie
 Analytische Geometrie Wiederholung (Klasse 0) zur Vektorrechnung Hausaufgabe ( Vorbereitung als Vortrag): C:\Users\Hagen\Documents\Dr. H. Fritsch\Eigene Dateien\Gymnasium-Muecheln\ Mathematik\Klasse \Kl--Wdhlg-Vektor.docx
Analytische Geometrie Wiederholung (Klasse 0) zur Vektorrechnung Hausaufgabe ( Vorbereitung als Vortrag): C:\Users\Hagen\Documents\Dr. H. Fritsch\Eigene Dateien\Gymnasium-Muecheln\ Mathematik\Klasse \Kl--Wdhlg-Vektor.docx
Box. Mathematik. Δ y = 1. Analytische Geometrie ZU DEN KERNCURRICULUM-LERNBEREICHEN:
 Box Mathematik Schülerarbeitsbuch 4 y C Δ x = 1 B 3 Δ y = 3 2 C Δ y = 1 1 A Δ x = 3 B x Niedersachsen 1 2 3 4 Analytische Geometrie ZU DEN KERNCURRICULUM-LERNBEREICHEN: Raumanschauung und Koordinatisierung
Box Mathematik Schülerarbeitsbuch 4 y C Δ x = 1 B 3 Δ y = 3 2 C Δ y = 1 1 A Δ x = 3 B x Niedersachsen 1 2 3 4 Analytische Geometrie ZU DEN KERNCURRICULUM-LERNBEREICHEN: Raumanschauung und Koordinatisierung
6. Vektor- und Koordinaten-Geometrie.
 6. Vektor- und Koordinaten-Geometrie. Jeder endlichen Menge, etwa der Menge kann man durch M = {,,, }. R 4 (M) = { a 1 + a 2 + a 3 + a 4 a i R } die Menge der formalen Linearkombinationen zuordnen. Es
6. Vektor- und Koordinaten-Geometrie. Jeder endlichen Menge, etwa der Menge kann man durch M = {,,, }. R 4 (M) = { a 1 + a 2 + a 3 + a 4 a i R } die Menge der formalen Linearkombinationen zuordnen. Es
Abstand zweier zueinander windschiefen Geraden
 Fachreferat aus dem Fach Mathematik Abstand zweier zueinander windschiefen Geraden Jakob Schöttl 2009-02-17 Inhaltsverzeichnis 1 Deklaration 1 2 Denition von windschief 2 3 Meine eigenen Versuche 2 3.1
Fachreferat aus dem Fach Mathematik Abstand zweier zueinander windschiefen Geraden Jakob Schöttl 2009-02-17 Inhaltsverzeichnis 1 Deklaration 1 2 Denition von windschief 2 3 Meine eigenen Versuche 2 3.1
Abitur 2013 Mathematik Geometrie V
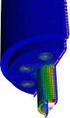
 Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Erfolg im Mathe-Abi 2010
 Gruber I Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Vorwort Vorwort Erfolg von Anfang an Das vorliegende Übungsbuch ist speziell auf die grundlegenden
Gruber I Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Vorwort Vorwort Erfolg von Anfang an Das vorliegende Übungsbuch ist speziell auf die grundlegenden
Geometrie. 1 Vektorielle analytische Geometrie der Ebene, Kegelschnitte
 Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Geometrie Geometrie W. Kuhlisch Brückenkurs 206. Vektorrechnung und analytische Geometrie der Ebene, Kegelschnitte 2. Vektorrechnung und analytische Geometrie des Raumes, Anwendungen in der Geometrie,
Lehrskript Mathematik Q12 Analytische Geometrie
 Lehrskript Mathematik Q1 Analytische Geometrie Repetitorium der analytischen Geometrie Eine Zusammenfassung der analytischen Geometrie an bayerischen Gymnasien von Markus Baur, StR Werdenfels-Gymnasium
Lehrskript Mathematik Q1 Analytische Geometrie Repetitorium der analytischen Geometrie Eine Zusammenfassung der analytischen Geometrie an bayerischen Gymnasien von Markus Baur, StR Werdenfels-Gymnasium
Vektorgeometrie. Inhaltsverzeichnis. Fragen und Antworten. (bitte nur für den Eigengebrauch verwenden)
 fua3673 Fragen und Antworten Vektorgeometrie (bitte nur für den Eigengebrauch verwenden) Inhaltsverzeichnis Vektorgeometrie im Raum. Fragen................................................. Allgemeines..........................................
fua3673 Fragen und Antworten Vektorgeometrie (bitte nur für den Eigengebrauch verwenden) Inhaltsverzeichnis Vektorgeometrie im Raum. Fragen................................................. Allgemeines..........................................
Lineare Abbildungen und Matrizen
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 31. Mai 2016 Stefan Ruzika 9: Lineare Abbildungen und Matrizen 31. Mai 2016 1 / 16 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 31. Mai 2016 Stefan Ruzika 9: Lineare Abbildungen und Matrizen 31. Mai 2016 1 / 16 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume
3 Vektorräume abstrakt
 Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
3. Übungsblatt Aufgaben mit Lösungen
 . Übungsblatt Aufgaben mit Lösungen Aufgabe : Gegeben sind zwei Teilmengen von R : E := {x R : x x = }, und F ist eine Ebene durch die Punkte A = ( ), B = ( ) und C = ( ). (a) Stellen Sie diese Mengen
. Übungsblatt Aufgaben mit Lösungen Aufgabe : Gegeben sind zwei Teilmengen von R : E := {x R : x x = }, und F ist eine Ebene durch die Punkte A = ( ), B = ( ) und C = ( ). (a) Stellen Sie diese Mengen
Mathematik-Aufgabenpool > Grundaufgaben zur Vektorrechnung I
 Michael Buhlmann Mathematik-Aufgabenpool > Grundaufgaben zur Vektorrechnung I Einleitung: Elemente der Vektorrechnung im dreidimensionalen reellen kartesischen x -x -x 3-Koordinatensystem sind Punkte P(p
Michael Buhlmann Mathematik-Aufgabenpool > Grundaufgaben zur Vektorrechnung I Einleitung: Elemente der Vektorrechnung im dreidimensionalen reellen kartesischen x -x -x 3-Koordinatensystem sind Punkte P(p
Das Skalarprodukt zweier Vektoren
 Beim Skalarprodukt zweier Vektoren werden die Vektoren so multipliziert, dass sich ein Skalar eine Zahl ergibt. Die Berechnung des Skalarproduktes ist ziemlich einfach, aber die weiteren Eigenschaften
Beim Skalarprodukt zweier Vektoren werden die Vektoren so multipliziert, dass sich ein Skalar eine Zahl ergibt. Die Berechnung des Skalarproduktes ist ziemlich einfach, aber die weiteren Eigenschaften
Einführung in das Skalarprodukt
 Die Homepage von Joachim Mohr Start Mathematik Einführung in das Skalarprodukt in Aufgaben Alle Lektionen und Texte der Delphi-Ecke sind in der gepackten Zip-Datei Delphi-Ecke (ohne Urlaubsbilder) (Stand:
Die Homepage von Joachim Mohr Start Mathematik Einführung in das Skalarprodukt in Aufgaben Alle Lektionen und Texte der Delphi-Ecke sind in der gepackten Zip-Datei Delphi-Ecke (ohne Urlaubsbilder) (Stand:
M Lernzusammenfassung - Vektoren -
 Christian Voigt M-Lernzusammenfassung 1 ABI M Lernzusammenfassung - Vektoren - Christian Voigt Version: 1.11 Christian Voigt M-Lernzusammenfassung 2 Inhaltsübersicht Allgemein... Namen... Addition... Vervielfachen...
Christian Voigt M-Lernzusammenfassung 1 ABI M Lernzusammenfassung - Vektoren - Christian Voigt Version: 1.11 Christian Voigt M-Lernzusammenfassung 2 Inhaltsübersicht Allgemein... Namen... Addition... Vervielfachen...
Analytische Geometrie, Vektorund Matrixrechnung
 Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Kapitel 1 Analytische Geometrie, Vektorund Matrixrechnung 11 Koordinatensysteme Eine Gerade, eine Ebene oder den Anschauungsraum beschreibt man durch Koordinatensysteme 111 Was sind Koordinatensysteme?
Mathematik für Naturwissenschaftler II
 Mathematik für Naturwissenschaftler II Dr Peter J Bauer Institut für Mathematik Universität Frankfurt am Main Sommersemester 27 Lineare Algebra Der mehrdimensionale Raum Vektoren Im Teil I dieser Vorlesung
Mathematik für Naturwissenschaftler II Dr Peter J Bauer Institut für Mathematik Universität Frankfurt am Main Sommersemester 27 Lineare Algebra Der mehrdimensionale Raum Vektoren Im Teil I dieser Vorlesung
5 Geraden im R Die Geradengleichung. Übungsmaterial 1
 Übungsmaterial 5 Geraden im R 5. Die Geradengleichung Eine Gerade ist eindeutig festgelegt durch zwei Punkte oder durch einen Punkt und eine Richtung. Beispiel: Die Gerade g durch die Punkte A(-//) und
Übungsmaterial 5 Geraden im R 5. Die Geradengleichung Eine Gerade ist eindeutig festgelegt durch zwei Punkte oder durch einen Punkt und eine Richtung. Beispiel: Die Gerade g durch die Punkte A(-//) und
Aufgabe A7/08 Die Ebene geht durch die Punkte 1,5 0 0,!0 3 0 und " Untersuchen
 Aufgabe A6/08 Gegeben sind die zwei parallelen Gerade und durch 2 3 1 6 : 9 4, : 2 8;, 4 1 5 2 Bestimmen Sie den Abstand der beiden Geraden. (Quelle Abitur BW 2008 Aufgabe 6) Aufgabe A7/08 Die Ebene geht
Aufgabe A6/08 Gegeben sind die zwei parallelen Gerade und durch 2 3 1 6 : 9 4, : 2 8;, 4 1 5 2 Bestimmen Sie den Abstand der beiden Geraden. (Quelle Abitur BW 2008 Aufgabe 6) Aufgabe A7/08 Die Ebene geht
, v 3 = und v 4 =, v 2 = V 1 = { c v 1 c R }.
 154 e Gegeben sind die Vektoren v 1 = ( 10 1, v = ( 10 1. Sei V 1 = v 1 der von v 1 aufgespannte Vektorraum in R 3. 1 Dann besteht V 1 aus allen Vielfachen von v 1, V 1 = { c v 1 c R }. ( 0 ( 01, v 3 =
154 e Gegeben sind die Vektoren v 1 = ( 10 1, v = ( 10 1. Sei V 1 = v 1 der von v 1 aufgespannte Vektorraum in R 3. 1 Dann besteht V 1 aus allen Vielfachen von v 1, V 1 = { c v 1 c R }. ( 0 ( 01, v 3 =
Vektorräume. 1. v + w = w + v (Kommutativität der Vektoraddition)
 Vektorräume In vielen physikalischen Betrachtungen treten Größen auf, die nicht nur durch ihren Zahlenwert charakterisiert werden, sondern auch durch ihre Richtung Man nennt sie vektorielle Größen im Gegensatz
Vektorräume In vielen physikalischen Betrachtungen treten Größen auf, die nicht nur durch ihren Zahlenwert charakterisiert werden, sondern auch durch ihre Richtung Man nennt sie vektorielle Größen im Gegensatz
Die komplexen Zahlen
 Die komplexen Zahlen Wir haben gesehen, dass die Menge R der reellen Zahlen einen angeordneten Körper bildet und dass für die Menge Q der rationalen Zahlen entsprechendes gilt. In beiden Körpern sind Gleichungen
Die komplexen Zahlen Wir haben gesehen, dass die Menge R der reellen Zahlen einen angeordneten Körper bildet und dass für die Menge Q der rationalen Zahlen entsprechendes gilt. In beiden Körpern sind Gleichungen
n n x a 1 a 2 = 0 n 1 x 1 + n 2 x 2 + ( n 1 a 1 n 2 a 2 )
 IX. Normalformen ================================================================== 9.1 Die Normalenform einer Geradengleichung im 2-dimensionalen Punktraum ----------------------------------------------------------------------------------------------------------------
IX. Normalformen ================================================================== 9.1 Die Normalenform einer Geradengleichung im 2-dimensionalen Punktraum ----------------------------------------------------------------------------------------------------------------
1 Vorlesungen: und Vektor Rechnung: 1.Teil
 1 Vorlesungen: 4.10.005 und 31.10.005 Vektor Rechnung: 1.Teil Einige in der Physik auftretende Messgrößen sind durch eine einzige Zahl bestimmt: Temperatur T K Dichte kg/m 3 Leistung P Watt = J/s = kg
1 Vorlesungen: 4.10.005 und 31.10.005 Vektor Rechnung: 1.Teil Einige in der Physik auftretende Messgrößen sind durch eine einzige Zahl bestimmt: Temperatur T K Dichte kg/m 3 Leistung P Watt = J/s = kg
& sind die Vektorkomponenten von und sind die Vektorkoordinaten von. A x. a) Der Betrag eines Vektors
 Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
Einführu hnung Was ist ein Vektor? In Bereichen der Naturwissenschaften treten Größen auf, die nicht nur durch eine Zahlenangabe dargestellt werden können, wie Kraft oder Geschwindigkeit. Zur vollständigen
Kapitel 3 Lineare Algebra
 Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
5. Wie bringt man einen Vektor auf eine gewünschte Länge? Zuerst bringt man ihn auf die Länge 1, dann multipliziert man mit der gewünschten Länge.
 1. Definition von drei Vektoren sind l.u. 2. Wie überprüft man 3 Vektoren mit Hilfe eines LGS auf lineare Unabhängigkeit? 3. Definition von Basis?... wenn sich der Nullvektor nur als triviale LK darstellen
1. Definition von drei Vektoren sind l.u. 2. Wie überprüft man 3 Vektoren mit Hilfe eines LGS auf lineare Unabhängigkeit? 3. Definition von Basis?... wenn sich der Nullvektor nur als triviale LK darstellen
Kapitel I: Vektorrechnung 2: Vektoren im Raum
 WS 1/14 - Prof Dr Manfred Leitz 2 Vektoren im Raum A Grundbegriffe B Rechnen mit Vektoren C Der euklidische Betrag D Das euklidische Skalarprodukt E Vektorprodukt und Spatprodukt F Geraden und Ebenen im
WS 1/14 - Prof Dr Manfred Leitz 2 Vektoren im Raum A Grundbegriffe B Rechnen mit Vektoren C Der euklidische Betrag D Das euklidische Skalarprodukt E Vektorprodukt und Spatprodukt F Geraden und Ebenen im
Vektor-Multiplikation Vektor- Multiplikation
 Vektor- Multiplikation a d c b Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Vektor-Multiplikation: Vektorprodukt Mittelschule, Berufsschule, Fachhochschule Elementare Programmierkenntnisse, Geometrie,
Vektor- Multiplikation a d c b Thema: Schultyp: Vorkenntnisse: Bearbeitungsdauer: Vektor-Multiplikation: Vektorprodukt Mittelschule, Berufsschule, Fachhochschule Elementare Programmierkenntnisse, Geometrie,
Elemente der Analysis II
 Elemente der Analysis II Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 8. Mai 2009 1 / 29 Bemerkung In der Vorlesung Elemente der Analysis I wurden Funktionen
Elemente der Analysis II Informationen zur Vorlesung: http://www.mathematik.uni-trier.de/ wengenroth/ J. Wengenroth () 8. Mai 2009 1 / 29 Bemerkung In der Vorlesung Elemente der Analysis I wurden Funktionen
Bild, Faser, Kern. Stefan Ruzika. 23. Mai Mathematisches Institut Universität Koblenz-Landau Campus Koblenz
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 23. Mai 2016 Stefan Ruzika 7: Bild, Faser, Kern 23. Mai 2016 1 / 11 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume 4 Basis
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 23. Mai 2016 Stefan Ruzika 7: Bild, Faser, Kern 23. Mai 2016 1 / 11 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume 4 Basis
