CSG (constructive solid geometry) mit mengentheoretischer Verknüpfung von Elementarobjekten.
|
|
|
- Nadine Brandt
- vor 6 Jahren
- Abrufe
Transkript
1 Kapitel 16 3D-Repräsentation Für 3-dimensionale Objekte gibt es mehrere Möglichkeiten der Repräsentation (d.h. Definition des Objekts) und der Darstellung (d.h. Projektion des Objekts auf den Bildschirm auch rendering genannt): Repräsentation Elementarobjekt mit Definitionspunkten, Drahtmodell, Flächenmodell mit Punkt- und Flächenliste und Normalen, CSG (constructive solid geometry) mit mengentheoretischer Verknüpfung von Elementarobjekten. Darstellung Punktmodell Drahtmodell mit sämtlichen Kanten, Drahtmodell mit Entfernung verdeckter Kanten, Flächenmodell mit Einfärbung, ohne abgewandte Flächen, Flächenmodell mit Einfärbung, ohne verdeckte Teile von Flächen, Flächenmodell mit Einfärbung, ohne verdeckte Teile von Flächen, mit Beleuchtungsmodell Körpermodell mit Berechnung von Schattenbildung, Spiegelungen und Brechungen. Zur Berechnung der Darstellung wird die Viewing-Pipeline benötigt, welche eine Transformation der Definitionspunkte vornimmt (Kapitel 15), die nicht sichtbaren Flächen entfernt (Kapitel 17) sowie das Rastern der projezierten Flächen durchführt (Kapitel 18). In diesem Kapitel werden die verschiedenen Repräsentationsarten behandelt und einige dazu gehörende Beispiele. 177
2 178 KAPITEL 16. 3D-REPRÄSENTATION 16.1 Elementarobjekte Für den Benutzer sollte die Beschreibung einer Szene durch Elementarobjekte erfolgen. Diese können unterschiedlich kompliziert sein, sollten aber durch wenige Parameter beschrieben werden können (Kugel, Quader, Pyramide, Kegel, Zylinder,...). Eine Kugel z.b. ist bereits durch Mittelpunkt und Radius eindeutig im Raum plaziert. Es ist sinnvoll, jedes Objekt in seinem eigenen, lokalen Modellkoordinatensystem zu definieren. Dessen Ursprung wird im Inneren des Objekts gewählt und das gesamte Objekt in ein Einheitsvolumen (z.b. 1 x, y, z +1) eingeschlossen. Für Orts- und Größenveränderungen sind Transformationen zuständig Drahtmodell In der nächsten Repräsentationsklasse wird das Elementarobjekt als Drahtmodell durch eine Liste von Kanten repräsentiert. Jede Kante besteht aus zwei Punkten im kartesischen Koordinatensystem. Beim Würfel verbinden die Kanten die Eckpunkte, bei einer Kugel werden die Längen- und Breitenkreise durch n-ecke angenähert, wobei mit n die Güte der Approximation steigt. Das Drahtmodell skizziert nur die Umrisse eines Objekts und enthält keine zusätzlichen Flächen- oder Volumeninformationen Flächenmodell Es werden Objekte durch approximierte oder analytische Flächen, z.b. durch eine Liste von konvexen Polygonen, repräsentiert. Ein solches Polygon wird durch seine Eckpunkte beschrieben, die durch Kanten verbunden sind und eine Fläche umschließen. Beim Würfel verbinden die Kanten die Eckpunkte, bei einer Kugel werden die Längen- und Breitenkreise durch n-ecke angenähert, wobei mit n die Güte der Approximation steigt. Punkteliste Flächenliste P 1 : (x 1,y 1,z 1 ) F 1 : p 1, p 2, p 4 P 2 : (x 2,y 2,z 2 ) F 2 : p 1, p 4, p 3 P 3 : (x 3,y 3,z 3 ) F 3 : p 1, p 3, p 3 P 4 : (x 4,y 4,z 4 ) F 4 : p 4, p 2, p 3 Zur vollständigen Beschreibung einer Fläche gehört noch die Angabe, welche Seite innen und welche Seite außen liegt. Dies geschieht durch Angabe des Normalenvektors: Er steht senkrecht auf der Fläche und zeigt von innen nach außen. Für die Approximation gekrümmter Flächen wird häufig pro Eckpunkt eine Normale verwendet.
3 16.4. FLÄCHENMODELL MIT HALBKANTENDARSTELLUNG Flächenmodell mit Halbkantendarstellung Jedes Objekt enthält eine Liste von Flächen, die von Halbkanten begrenzt werden. Die Halbkanten sind von außen betrachtet im Uhrzeigersinn orientiert und zeigen auf ihre jeweils linke Nachbarfläche sowie ihre Anfangs- und Endpunkte. Die Halbkantendarstellung eignet sich zur effizienten Entfernung von verdeckten Kanten und Flächen. Eine Kante zwischen Punkt P 1 und Punkt P 2, welche die Flächen F 1 und F 2 trennt, taucht einmal als Halbkante (P 1,P 2 ) in der Kantenliste zu F 2 auf mit einem Verweis auf die Nachbarfläche F 1 und ein weiteres Mal als (P 2,P 1 ) in der Kantenliste zu F 1 mit einem Verweis auf die Nachbarfläche F 2. Werden nun alle Halbkanten einer Fläche F 1 bearbeitet, so regelt die Sichtbarkeit von F 1 und die Sichtbarkeit der jeweils anstoßenden Fläche die Sichtbarkeit der jeweiligen Halbkante. Das doppelte Zeichnen einer Kante läßt sich vermeiden, indem bei jeder Fläche vermerkt wird, ob ihre Halbkanten bereits bearbeitet wurden. Auch die Flächennormalen können in der Datenstruktur gespeichert werden. P 4 h 11 h 12 F 3 P 2 h 10 h 2 P 3 F 1 h 9 h 7 h 1 h 3 h 4 h 5 F 4 F 2 h 8 h 6 P 4 P 1 P 4 Abbildung 16.1: Tetraeder mit 4 Knoten, 12 Halbkanten, 4 Flächen
4 180 KAPITEL 16. 3D-REPRÄSENTATION P 1 h 1 P 3 P 2 h 2 P 4 h 3 F 1 h 4 h 5 h 6 F 2 F 3 F 4 Flächenliste Punkteliste Abbildung 16.2: Objektstruktur für Tetraeder. Nicht gezeichnet sind Halbkanten für F 3 und F 4
5 16.5. POLYEDER Polyeder Abbildung 16.3 zeigt eine vom Projektionsalgorithmus erzeugte Szene mit Würfel und Tetraeder in der Drahtmodell-Darstellung mit gestrichelten Rückkanten. Abbildung 16.3: Vom Projektionsalgorithmus berechnete Drahtgitter-Darstellung Ein Würfel mit der Kantenlänge 1 hat im MC die homogenen Eckpunktkoordinaten (+0.5, +0.5, +0.5, 1), (+0.5, +0.5, 0.5, 1), (+0.5, 0.5, +0.5, 1), (+0.5, 0.5, 0.5, 1), ( 0.5, +0.5, +0.5, 1), ( 0.5, +0.5, 0.5, 1), ( 0.5, 0.5, +0.5, 1), ( 0.5, 0.5, 0.5, 1). Da jede der sechs Flächen des Würfels eben ist, gibt es pro Fläche nur einen Normalenvektor, der durch das Kreuzprodukt zweier benachbarter Kanten berechnet werden kann. Die Reihenfolge der Punkte ist dabei signifikant, da jeweils aufeinanderfolgende Punkte eine Kante bilden. Ein Quader entsteht aus dem Würfel durch ungleichmäßige Skalierung beim Modeling. Auch alle anderen Polyeder werden im MC in der Flächendarstellung definiert, ein Tetraeder beispielsweise mit Kantenlänge 1 und Schwerpunkt im Ursprung Gekrümmte Flächen Eine gekrümmte Oberfläche, die analytisch beschrieben werden kann, läßt sich beliebig gut durch Polygone approximieren. Die Gruppe der Objekte mit analytisch gekrümmter Oberfläche besteht aus zwei Typen: Während z.b. die Kugel nur aus einer solchen Fläche besteht, sind Zylinder und Kegel aus mehreren Flächen zusammengesetzt. Die Repräsentation der gekrümmten Körper erfolgt im Flächenmodell mit einer Flächen- und Eckpunkteliste sowie einer Normalenliste, die pro Eckpunkt die zugehörige Normale enthält.
6 182 KAPITEL 16. 3D-REPRÄSENTATION 16.7 Zylinder Der zur z-achse symmetrische Zylinder mit Höhe 2 und Radius 1 besteht aus einer Mantelfläche und zwei Deckflächen. Die beiden Kreisscheiben bei z = 1 und z = 1 lassen sich durch regelmäßige n- Ecke darstellen. Die Mantelfläche wird durch n Rechtecke approximiert. Dabei wachsen mit n sowohl die Genauigkeit der Approximation als auch der Rechenaufwand. Sei α = (2π)/n, so lauten für ein solches Rechteck die vier Eckpunkte und die zugehörigen Normalenvektoren: mit φ = k α, k {0,...,n 1}. Eckpunkt Normalenvektor (cos(φ), sin(φ), +1, 1) (cos(φ), sin(φ), 0, 0) (cos(φ + α),sin(φ + α),+1,1) (cos(φ + α),sin(φ + α),0,0) (cos(φ + α),sin(φ + α), 1,1) (cos(φ + α),sin(φ + α),0,0) (cos(φ), sin(φ), 1, 1) (cos(φ), sin(φ), 0, 0) Als Normalenvektor in einem Eckpunkt dieser Fläche wird also der tatsächliche Normalenvektor der Mantelfläche genommen. Dadurch erhalten aneinandergrenzende Flächen in ihren gemeinsamen Eckpunkten auch denselben Normalenvektor. Auf diese Weise erzeugt das Programm bei der späteren Beleuchtung den Eindruck eines stetigen Übergangs zwischen den Flächen. Der Betrachter nimmt statt einer n-eckigen Säule den Zylinder wahr. n = 8 y α MC x Normalen Abbildung 16.4: Zylinder im Grundriß mit Normalenvektoren der Mantelfläche
7 16.8. KUGEL Kugel Die Oberfläche einer Kugel mit Radius 1 kann beschrieben werden durch (sin(θ)cos(φ),sin(θ)sin(φ),cos(θ)),0 φ < 2π,0 θ < π. Zur Approximation durch Flächen wird der Vollwinkel in n Teile zerlegt: α = (2π)/n, n N gerade. Abbildung 16.5: Konstruktion einer Kugel mit Radius 1 im Ursprung Dadurch entstehen auf der Kugel n/2 gleichgroße Längenkreise und (n/2 1) verschieden große Breitenkreise. Diese schneiden n Dreiecke an jedem Pol und n(n/2 2) Vierecke aus der Kugeloberfläche. Die Ortsvektoren der Eckpunkte eines Dreiecks am Nordpol (θ = 0) lauten (0,0,+1,1),(sin(α)cos(φ),sin(α)sin(φ),cos(α),1),(sin(α)cos(φ+α),sin(α)sin(φ+α),cos(α),1), mit φ = k α, k {0,...,n 1}. Die Eckpunkte eines der Vierecke haben die Ortsvektoren (sin(θ) cos(φ), sin(θ) sin(φ), cos(θ), 1) (sin(θ)cos(φ + α),sin(θ)sin(φ + α),cos(θ),1) (sin(θ + α)cos(φ + α),sin(θ + α)sin(φ + α),cos(θ + α),1) (sin(θ + α)cos(φ),sin(θ + α)sin(φ),cos(θ + α),1) mit φ = k α,k N,k < n und θ = l α,l N,0 < l < (n/2 1). Als Normalenvektor wird in jedem Eckpunkt der Ortsvektor als Richtungsvektor (w = 0) eingetragen, denn der Radiusvektor steht senkrecht auf der Kugeloberfläche. Einen Ellipsoid erzeugt der Rendering-Algorithmus aus der Kugel durch ungleichmäßige Skalierung beim Modeling. Abbildung 16.6: Breiten- und Längengrade einer Kugel-Approximation
8 184 KAPITEL 16. 3D-REPRÄSENTATION 16.9 Bezier-Flächen Die in Kapitel 7.3 eingeführten Bezier-Kurven können auch zur Definition einer gekrümmten Fläche im Raum verwendet werden. Da eine Fläche zweidimensional ist, muß eine weitere Parameterdimension hinzugefügt werden, d.h. statt 0 t 1 gilt nun 0 u,v 1. Im folgenden Beispiel werden 16 Kontrollpunkte mit kubischen Bernsteinpolynomen gewichtet: P(u,v) = 3 3 i=0 j=0 B i,3 (u) B j,3 (v) P i, j / '( )* ! " +, : : # $ -. ; < % & Abbildung 16.7: Gitternetz mit 16 Kontrollpunkten für Bezier-Fläche im Raum Beim Verlängern einer Bezier-Fläche ist darauf zu achten, dass die neue Reihe von Kontrollpunkten tangential die bisherige Fläche verlängert, d.h. P i,2,p i,3 = Q i,0,q i,1 sind collinear und das Verhältnis der Abstände P i,3 P i,2 / Q i,1 Q i,0 ist konstant.! -. /0 *+,, ( ) & ' $ % " # Abbildung 16.8: Verlängerung einer Bezierfläche
9 NURBS-FLÄCHEN NURBS-Flächen Eine NURBS-Fläche sieht in homogenen Koordinaten folgendermaßen aus: q h (u,w) = n m i=0 j=0 P h i, jn i,k (u)m j,l (w) Die P h i, j sind die vierdimensionalen homogenen Stützpunkte. Die N i,k und die M j,l sind die nichtrationalen B-Spline-Basisfunktionen aus Kapitel 7. Um affine Koordinaten zu erreichen, wird wieder durch die homogenen Koordinaten dividiert: q(u,w) = n i=0 m j=0 h i, jp i, j N i,k (u)m j,l (w) n i=0 m j=0 h i, jn i,k (u)m j,l (w) = n m i=0 j=0 P i, j S i,k (u,w) wobei P i, j die dreidimensionalen Stützpunkte sind. Sie ergeben das Kontrollnetz für die Oberfläche. Bei den S i, j (u,w) handelt es sich um die biparametrisierten Flächenbasisfunktionen S i, j (u,w) = h i, j N i,k (u)m j,l (w) n i1=0 m j1=0 h i1, j1n i1,k (u)m j1,l (w) Die S i, j (u,w) sind nicht das Produkt der R i,k (u) und der R j,l (w) aus Kapitel 7. Sie haben aber ähnliche analytische Eigenschaften, so daß die NURBS-Fläche ähnliche analytische und geometrische Eigenschaften, wie die früher erwähnten NURBS-Kurven: Die S i, j (u,w) addieren für ein festes Paar von u und w zu 1. S i, j (u,w) 0 u,w Der maximale Grad der Basispolygone ist gleich der Zahl der Kontrollpunkte -1 in der entsprechenden Dimension. Eine NURBS-Kurve der Ordnung k,l (Grad k 1,l 1) ist überall C k 2,C l 2 stetig. NURBS-Flächen sind invariant bgzl. perspektivischer Projektion. Es genügt, die Stützpunkte mit der Viewing Pipeline zu transformieren und die eigentliche Interpolation im DC vorzunehmen. Wenn gilt h i, j 0 i, j, liegt die Fläche innerhalb der konvexen Hülle des Kontrollnetzes. Der Einfluß eines Stützpunktes ist begrenzt auf ±k/2, ±l/2 Interpolationsabschnitte in jeder Parameterdimension. Um die Normale der Fläche in einem beliebigen Punkt zu berechnen, müssen die Richtungsableitungen bzgl. u und w in diesem Punkt gebildet werden.
10 186 KAPITEL 16. 3D-REPRÄSENTATION CSG (constructive solid geometry) Sollen die beschriebenen Objekte auch im physikalischen Sinne realisierbar sein (zum Beispiel über wohldefinierte Volumen verfügen), so müssen die gespeicherten Oberflächen zusätzliche Eigenschaften erfüllen. Die zugrundeliegende Theorie heißt CSG (constructive solid geometry). Um solche Objekte zu erzeugen, beginnt man mit wohldefinierten Objekten und erzeugt durch regularisierte Mengenoperationen (Vereinigung), (Durchschnitt), \ (Differenz) neue, wiederum physikalisch sinnvolle Objekte. Hierbei bedeutet für die mengentheoretische Operation op {,,\} die regularisierte Operation op* den Abschluss des Inneren der Verknüpfung von A mit B: A op B = closure(interior(a op B)) Die hierarchische Struktur wird beschrieben durch einen binären Baum, dessen Blätter beschriftet sind mit den Elementarobjekten und dessen innere Knoten beschriftet sind mit den regularisierten Mengenoperationen (Vereinigung), (Durchschnitt), \ (Differenz). Die Wurzel repräsentiert das resultierende Objekt, welches aus den Elementarobjekten an den Blättern unter Anwendung der Operationen an den inneren Knoten konstruiert werden kann. Abbildung 16.9: Darstellung des Verknüpfungshierarchie (Beispiel aus Wikipedia)
11 OCTREE Octree Zur Verwaltung der räumlichen Anordung von Objekten im dreidimensionalen Raum eignet sich der Octree. Es handelt sich um die Erweiterung um die dritte Dimension des 2-dimensionalen Quadtree. Abbildung zeigt die Platzierung von 4 schwarzen Rechtecken A,B,C,D in der Ebene. Der zugehörige Quadtree teilt rekursiv die repräsentierte Fläche in 4 Quadranten ein und notiert an den Knoten, ob er nichts enthält (weiss), teilweise Objekte enthält (grau) oder ein Rechteck repräsentiert (schwarz). Abbildung 16.10: 4 Rechtecke in der Ebene mit zugehörigem Quadtree Abbildung zeigt die Platzierung von drei Würfeln A,B,C im Raum. Der zugehörige Octree teilt rekursiv den repräsentierten Raum in 8 Oktanten ein und notiert an einem Knoten, ob er nichts enthält (weiss), teilweise Objekte enthält (grau) oder einen Quader repräsentiert (farbig). Abbildung 16.11: 3 Quader im Raum mit zugehörigem Octree
12 188 KAPITEL 16. 3D-REPRÄSENTATION Java-Applet zur Wire-Frame-Projektion Abbildung 16.12: Screenshot vom 3D-wire-Applet
146
 145 netpbm PBM Portable Bitmap PGM Portable Greymap PPM Portable Pixmap PNM Portable Anymap Konvertierungsroutinen: anytopnm, asciitopgm, bmptoppm, giftopnm, pbmtopgm, pgmtopbm, pgmtoppm, ppmtopgm, pstopnm,
145 netpbm PBM Portable Bitmap PGM Portable Greymap PPM Portable Pixmap PNM Portable Anymap Konvertierungsroutinen: anytopnm, asciitopgm, bmptoppm, giftopnm, pbmtopgm, pgmtopbm, pgmtoppm, ppmtopgm, pstopnm,
Computergrafik 2016 Oliver Vornberger. Kapitel 16: 3D-Repräsentation
 Computergrafik 2016 Oliver Vornberger Kapitel 16: 3D-Repräsentation 1 Sequenz von Transformationen grün rot Kamera blau Modeling View Orientation View Mapping Device Mapping 2 Repräsentation + Darstellung
Computergrafik 2016 Oliver Vornberger Kapitel 16: 3D-Repräsentation 1 Sequenz von Transformationen grün rot Kamera blau Modeling View Orientation View Mapping Device Mapping 2 Repräsentation + Darstellung
Darstellungsarten für 3D-Körper. Boundary Representation (BRep):
 Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
Abitur 2016 Mathematik Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Approximationsverfahren für die Kurvendarstellung
 Approximationsverfahren für die Kurvendarstellung (a) Bézier-Kurven spezielle Form polynomialer Kurven spezifiziert durch n+1 Kontrollpunkte P 0, P 1,..., P n Kurve läuft nicht durch alle Kontrollpunkte,
Approximationsverfahren für die Kurvendarstellung (a) Bézier-Kurven spezielle Form polynomialer Kurven spezifiziert durch n+1 Kontrollpunkte P 0, P 1,..., P n Kurve läuft nicht durch alle Kontrollpunkte,
8. Modelle für feste Körper
 8. Modelle für feste Körper Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
8. Modelle für feste Körper Modell: Abbild der Realität, welches bestimmte Aspekte der Realität repräsentiert (und andere ausblendet) mathematische Modelle symbolische Modelle Datenmodelle Experimentalmodelle
Räumliche Bereichsintegrale mit Koordinatentransformation
 Räumliche Bereichsintegrale mit Koordinatentransformation Gegeben seien ein räumlicher Bereich, das heißt ein Körper K im R 3, und eine von drei Variablen abhängige Funktion f f(,, z). Die Aufgabe bestehe
Räumliche Bereichsintegrale mit Koordinatentransformation Gegeben seien ein räumlicher Bereich, das heißt ein Körper K im R 3, und eine von drei Variablen abhängige Funktion f f(,, z). Die Aufgabe bestehe
Vektorrechnung Aufgabe aus Abiturprüfung Bayern GK
 Vektorrechnung Aufgabe aus Abiturprüfung Bayern GK 1. In einem kartesischen Koordinatensystem sind der Punkt C(4 4, die Ebene E 1 : x 1 x +x 3 + = und die Gerade g: x = ( + λ( 1 gegeben. a Zeigen Sie,
Vektorrechnung Aufgabe aus Abiturprüfung Bayern GK 1. In einem kartesischen Koordinatensystem sind der Punkt C(4 4, die Ebene E 1 : x 1 x +x 3 + = und die Gerade g: x = ( + λ( 1 gegeben. a Zeigen Sie,
Oberflächenrepräsentationen Kontinuierliche Kurven Bezier-Kurven. Freiformflächen. Diskret
 Oberflächenrepräsentationen Kontinuierliche Kurven Bezier-Kurven Thomas Jung Freiformflächen NURBS Die Modellierung von Objekten erfordert die geeignete Repräsentation der Oberfläche Je nach Anforderung
Oberflächenrepräsentationen Kontinuierliche Kurven Bezier-Kurven Thomas Jung Freiformflächen NURBS Die Modellierung von Objekten erfordert die geeignete Repräsentation der Oberfläche Je nach Anforderung
Geometrierepräsentation
 Geometrierepräsentation Forderungen an Repräsentationsform: 1. mächtig (eine sinnvolle Menge von Objekten modellierbar) 2. eindeutig (es muß klar sein, was repräsentiert wird) H E D A F G C B Punkte, Linien,
Geometrierepräsentation Forderungen an Repräsentationsform: 1. mächtig (eine sinnvolle Menge von Objekten modellierbar) 2. eindeutig (es muß klar sein, was repräsentiert wird) H E D A F G C B Punkte, Linien,
Darstellung von Kurven und Flächen
 Darstellung von Kurven und Flächen Technische Universität Dresden Fakultät Informatik Institut für Software- und Multimediatechnik Dozent: Dr. Mascolous Referent: Gliederung / Einleitung 1 / 25 1. Kurven
Darstellung von Kurven und Flächen Technische Universität Dresden Fakultät Informatik Institut für Software- und Multimediatechnik Dozent: Dr. Mascolous Referent: Gliederung / Einleitung 1 / 25 1. Kurven
Mathematische Grundlagen
 Kapitel 2 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 2. 3D-Koordinatensystem Weit
Kapitel 2 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 2. 3D-Koordinatensystem Weit
Rechnen mit Vektoren. 1. Vektoren im Koordinatensystem Freie Vektoren in der Ebene
 Rechnen mit 1. im Koordinatensystem 1.1. Freie in der Ebene 1) Definition Ein Vektor... Zwei sind gleich, wenn... 2) Das ebene Koordinatensystem Wir legen den Koordinatenursprung fest, ferner zwei zueinander
Rechnen mit 1. im Koordinatensystem 1.1. Freie in der Ebene 1) Definition Ein Vektor... Zwei sind gleich, wenn... 2) Das ebene Koordinatensystem Wir legen den Koordinatenursprung fest, ferner zwei zueinander
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen
 Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
Bestimme ferner die Koordinaten des Bildpunktes von B bei der Spiegelung
 Vektoren - Skalar- und Vektorprodukt ================================================================== 1. Gegeben sind die Punkte A 1 2 3 und B 3 4 1 bzgl. eines kartesischen Koordina- tensystems mit
Vektoren - Skalar- und Vektorprodukt ================================================================== 1. Gegeben sind die Punkte A 1 2 3 und B 3 4 1 bzgl. eines kartesischen Koordina- tensystems mit
Abitur 2011 G8 Musterabitur Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
ein geeignetes Koordinatensystem zu verwenden.
 1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
Klausurenkurs zum Staatsexamen (WS 2016/17): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 6/7): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Algorithmische Geometrie: Voronoi Diagramme (Teil 2)
 Algorithmische Geometrie: Voronoi Diagramme (Teil 2) Nico Düvelmeyer WS 2009/2010, 12.1.2010 Überblick 1 Definition und grundlegende Eigenschaften (Wied.) 2 Bestimmung des Voronoi Diagramms Gleitebenenverfahren
Algorithmische Geometrie: Voronoi Diagramme (Teil 2) Nico Düvelmeyer WS 2009/2010, 12.1.2010 Überblick 1 Definition und grundlegende Eigenschaften (Wied.) 2 Bestimmung des Voronoi Diagramms Gleitebenenverfahren
Kollisionserkennung
 1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
1 Kollisionserkennung von Jens Schedel, Christoph Forman und Philipp Baumgärtel 2 1. Einleitung Wozu wird Kollisionserkennung benötigt? 3 - für Computergraphik 4 - für Simulationen 5 - für Wegeplanung
3D-Objektmodellierung
 3D-Objektmodellierung Beschränkung auf echte dreidimensionale Strukturen: keine isolierten Punkte, Kanten oder Flächen keine baumelnden Kanten oder Flächen Computergrafik: Modellierung dreidimensionaler
3D-Objektmodellierung Beschränkung auf echte dreidimensionale Strukturen: keine isolierten Punkte, Kanten oder Flächen keine baumelnden Kanten oder Flächen Computergrafik: Modellierung dreidimensionaler
-dimensionale Darstellungen
 1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
Teil 2: Kurven und Flächen. Kurven und Flächen. Kurven. Parametrische Objekte. Kurven: 1D-Objekte Flächen: 2D-Objekte, basierend auf Kurven
 Parametrische Objekte Kurven und Flächen Kurven: 1D-Objekte Flächen: 2D-Objekte, basierend auf Kurven Kurven Welche Form der Darstellung? Beispiel: 2D-Linie Explizit: y = k x + d x = (x, y) T Implzit:
Parametrische Objekte Kurven und Flächen Kurven: 1D-Objekte Flächen: 2D-Objekte, basierend auf Kurven Kurven Welche Form der Darstellung? Beispiel: 2D-Linie Explizit: y = k x + d x = (x, y) T Implzit:
Teil 2: Kurven und Flächen
 Parametrische Objekte Kurven und Flächen Kurven: 1D-Objekte Flächen: 2D-Objekte, basierend auf Kurven Kurven Welche Form der Darstellung? Beispiel: 2D-Linie Explizit: y = k x + d x = (x, y) T Implzit:
Parametrische Objekte Kurven und Flächen Kurven: 1D-Objekte Flächen: 2D-Objekte, basierend auf Kurven Kurven Welche Form der Darstellung? Beispiel: 2D-Linie Explizit: y = k x + d x = (x, y) T Implzit:
Wima-Praktikum 2: Bildsynthese-Phong
 Wima-Praktikum 2: Bildsynthese-Phong Wima-Praktikum 2: Prof. Dr. Lebiedz, M. Sc. Radic 1 Inhaltsverzeichnis 1 Einleitung 3 2 Kurze Beschreibung der Aufgabenstellung und dem Phong- Modell 3 3 Modellierung
Wima-Praktikum 2: Bildsynthese-Phong Wima-Praktikum 2: Prof. Dr. Lebiedz, M. Sc. Radic 1 Inhaltsverzeichnis 1 Einleitung 3 2 Kurze Beschreibung der Aufgabenstellung und dem Phong- Modell 3 3 Modellierung
Seminar 3-D Grafik Mathematische Grundlagen, Räume, Koordinatensysteme, Projektionen. Hermann Schwarz Marko Pilop
 Seminar 3-D Grafik Mathematische Grundlagen, Räume, Koordinatensysteme, Projektionen Hermann Schwarz Marko Pilop 2003-11-20 http://www.informatik.hu-berlin.de/~pilop/3d_basics.pdf {hschwarz pilop}@informatik.hu-berlin.de
Seminar 3-D Grafik Mathematische Grundlagen, Räume, Koordinatensysteme, Projektionen Hermann Schwarz Marko Pilop 2003-11-20 http://www.informatik.hu-berlin.de/~pilop/3d_basics.pdf {hschwarz pilop}@informatik.hu-berlin.de
Mathematische Grundlagen
 Kapitel 12 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 12.1 3D-Koordinatensystem Weit
Kapitel 12 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 12.1 3D-Koordinatensystem Weit
Koordinaten, Funktionen & Etwas Geometrie
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 26. Oktober 2009 Kartesische Koordinaten Ebene R 2 und Raum R 3 Allgemein: R n Punktmengen in der Ebene Graphen von Funktionen...im R 2 und
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 26. Oktober 2009 Kartesische Koordinaten Ebene R 2 und Raum R 3 Allgemein: R n Punktmengen in der Ebene Graphen von Funktionen...im R 2 und
Lage zweier Ebenen. Suche alle Punkte von E 1 die in E 2 enthalten sind. Setze also die Parameterform von E 1 in die Koordinatenform von E 2.
 LAGE Lage zweier Ebenen Suche alle Punkte von E die in E 2 enthalten sind. Setze also die Parameterform von E in die Koordinatenform von E 2. B = E : X E 2 : x + x 2 + x 3 = Parameterform (PF) in Koordinatenform
LAGE Lage zweier Ebenen Suche alle Punkte von E die in E 2 enthalten sind. Setze also die Parameterform von E in die Koordinatenform von E 2. B = E : X E 2 : x + x 2 + x 3 = Parameterform (PF) in Koordinatenform
Flächeninhalt, Volumen und Integral
 Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
Flächeninhalt, Volumen und Integral Prof. Herbert Koch Mathematisches Institut - Universität Bonn Schülerwoche 211 Hausdorff Center for Mathematics Donnerstag, der 8. September 211 Inhaltsverzeichnis 1
Abitur 2017 Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur 7 Mathematik Geometrie VI Gegeben sind die beiden bezüglich der x x 3 -Ebene symmetrisch liegenden Punkte A( 3 ) und B( 3 ) sowie der Punkt C( ). Teilaufgabe
Seite http://www.abiturloesung.de/ Seite Abitur 7 Mathematik Geometrie VI Gegeben sind die beiden bezüglich der x x 3 -Ebene symmetrisch liegenden Punkte A( 3 ) und B( 3 ) sowie der Punkt C( ). Teilaufgabe
Inhaltsverzeichnis. Inhaltsverzeichnis
 Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Inhaltsverzeichnis Inhaltsverzeichnis Einleitung 5 1 Zahlen 7 1.1 Zahlen und Zahlenmengen....................................... 7 1.2 Rechnen mit Zahlen und Termen....................................
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Michael Bender Martin Brill. Computergrafik. Ein anwendungsorientiertes Lehrbuch. 2., überarbeitete Auflage HANSER
 Michael Bender Martin Brill Computergrafik Ein anwendungsorientiertes Lehrbuch 2., überarbeitete Auflage HANSER Inhaltsverzeichnis Vorwort XI 1 Einleitung 1 1.1 Die Entwicklung der Computergrafik 1 1.2
Michael Bender Martin Brill Computergrafik Ein anwendungsorientiertes Lehrbuch 2., überarbeitete Auflage HANSER Inhaltsverzeichnis Vorwort XI 1 Einleitung 1 1.1 Die Entwicklung der Computergrafik 1 1.2
Prüfungsdauer: 120 Minuten
 Computergraphik und Multimediasysteme Seite 1 von 6 Klausur: Computergraphik II Probeklausur Semester: Prüfer: Prüfungsdauer: 1 Minuten Hilfsmittel: Schreibgeräte, Lineal, nichtprogrammierbarer Taschenrechner
Computergraphik und Multimediasysteme Seite 1 von 6 Klausur: Computergraphik II Probeklausur Semester: Prüfer: Prüfungsdauer: 1 Minuten Hilfsmittel: Schreibgeräte, Lineal, nichtprogrammierbarer Taschenrechner
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr 5, Thema, Aufgabe ) Sei V ein reeller Vektorraum. a) Wann nennt man eine Teilmenge U
Mathematische Probleme, SS 2013 Montag $Id: convex.tex,v /10/22 15:58:28 hk Exp $
 $Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
$Id: convex.tex,v 1.12 2013/10/22 15:58:28 hk Exp $ 3 Konvexgeometrie 3.1 Konvexe Polyeder Wir hatten einen konvexen Polyeder P im R n als die konvexe Hülle von endlich vielen Punkten definiert, wobei
Lernstraße zum Thema geometrische Körper. Vorbemerkungen. Liebe 10 a, nun sämtliche Arbeitsblätter; aufgrund einer Erkrankung
 Vorbemerkungen 02.06.2011 Liebe, nun sämtliche Arbeitsblätter; aufgrund einer Erkrankung meiner Kinder am Wochenende etwas später und aufgrund einer Bemerkung von Arian in der letzten Stunde etwas kürzer.
Vorbemerkungen 02.06.2011 Liebe, nun sämtliche Arbeitsblätter; aufgrund einer Erkrankung meiner Kinder am Wochenende etwas später und aufgrund einer Bemerkung von Arian in der letzten Stunde etwas kürzer.
2.3 Gekrümmte Oberflächen
 2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
2.3 Gekrümmte Oberflächen Jede Fläche im R 3 besitzt eine zweidimensionale Parameterdarstellung, so dass die Punkte der Fläche durch r(u, u 2 ) = x(u, u 2 )ê x + y(u, u 2 )ê y + z(u, u 2 )ê z beschrieben
Funktionen & Etwas Geometrie
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 22. Oktober 2008 Graphen von Funktionen...im R 2 und R 3...im R n Kreis & Kreisscheibe Kreis als Funktionsgraph Sphäre & Vollkugel Sphäre als
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 22. Oktober 2008 Graphen von Funktionen...im R 2 und R 3...im R n Kreis & Kreisscheibe Kreis als Funktionsgraph Sphäre & Vollkugel Sphäre als
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Hans Delfs. Übungen zu Mathematik III für Medieninformatik
 Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
2 Die Algebra der Matrizen
 Die Algebra der Matrizen Ein Hauptziel der Vorlesung zur Linearen Algebra besteht darin, Aussagen über die Lösungsmenge linearer Gleichungssysteme zu machen Etwa ob das Gleichungssystem x y + z 1 x + y
Die Algebra der Matrizen Ein Hauptziel der Vorlesung zur Linearen Algebra besteht darin, Aussagen über die Lösungsmenge linearer Gleichungssysteme zu machen Etwa ob das Gleichungssystem x y + z 1 x + y
2.4A. Reguläre Polyeder (Platonische Körper)
 .A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
.A. Reguläre Polyeder (Platonische Körper) Wie schon in der Antike bekannt war, gibt es genau fünf konvexe reguläre Polyeder, d.h. solche, die von lauter kongruenten regelmäßigen Vielecken begrenzt sind:
3.6 Einführung in die Vektorrechnung
 3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
3.6 Einführung in die Vektorrechnung Inhaltsverzeichnis Definition des Vektors 2 2 Skalare Multiplikation und Kehrvektor 4 3 Addition und Subtraktion von Vektoren 5 3. Addition von zwei Vektoren..................................
Mathematische Grundlagen
 Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Proseminar über multimediale Lineare Algebra und Analytische Geometrie
 Proseminar über multimediale Lineare Algebra und Analytische Geometrie Aufgabensteller: Dr. M. Kaplan Josef Lichtinger Montag, 1. Dezember 008 Proseminar WS0809 Inhaltsverzeichnis 1 Aufgabenstellung 3
Proseminar über multimediale Lineare Algebra und Analytische Geometrie Aufgabensteller: Dr. M. Kaplan Josef Lichtinger Montag, 1. Dezember 008 Proseminar WS0809 Inhaltsverzeichnis 1 Aufgabenstellung 3
Computergrafik. Michael Bender, Manfred Brill. Ein anwendungsorientiertes Lehrbuch ISBN Inhaltsverzeichnis
 Computergrafik Michael Bender, Manfred Brill Ein anwendungsorientiertes Lehrbuch ISBN 3-446-40434-1 Inhaltsverzeichnis Weitere Informationen oder Bestellungen unter http://www.hanser.de/3-446-40434-1 sowie
Computergrafik Michael Bender, Manfred Brill Ein anwendungsorientiertes Lehrbuch ISBN 3-446-40434-1 Inhaltsverzeichnis Weitere Informationen oder Bestellungen unter http://www.hanser.de/3-446-40434-1 sowie
0.1 Modellierung von Kurven und Flächen mittels B-Splines
 Vorlesung vom 28.04.06 Skript erstellt von Antonia Wittmers und Maria Gensel 0.1 Modellierung von Kurven und Flächen mittels B-Splines Das Wort Spline, übersetzt mit längliches, dünnes Stück Holz oder
Vorlesung vom 28.04.06 Skript erstellt von Antonia Wittmers und Maria Gensel 0.1 Modellierung von Kurven und Flächen mittels B-Splines Das Wort Spline, übersetzt mit längliches, dünnes Stück Holz oder
Boolesche Operationen und lokale Manipulationen
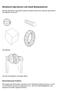 1 Boolesche Operationen und lokale Manipulationen Mit Hilfe Boolescher Operatoren werden komplexe Körper aus Instanzen generischer Grundkörper konstruiert.. Grundkörper Aus den Grundkörpern erzeugter Körper
1 Boolesche Operationen und lokale Manipulationen Mit Hilfe Boolescher Operatoren werden komplexe Körper aus Instanzen generischer Grundkörper konstruiert.. Grundkörper Aus den Grundkörpern erzeugter Körper
Beleuchtungsmodelle und Shading
 Beleuchtungsmodelle und Shading Andreas Spillner Computergrafik, WS 2018/2019 Ziel der Modellierung von Beleuchtung Baut auf dem Kapitel zu Licht und Farben auf. In die 3D-Szene werden Lichtquellen eingebracht.
Beleuchtungsmodelle und Shading Andreas Spillner Computergrafik, WS 2018/2019 Ziel der Modellierung von Beleuchtung Baut auf dem Kapitel zu Licht und Farben auf. In die 3D-Szene werden Lichtquellen eingebracht.
Computergraphik 1 ( )
 2008 Computergraphik 1 (186.461) Ausarbeitung für die schriftliche Prüfung Die Computergraphik stellt eine abwechslungsreiche und lohnende Schwerpunktbildung im Masterstudium Computergraphik & Digitale
2008 Computergraphik 1 (186.461) Ausarbeitung für die schriftliche Prüfung Die Computergraphik stellt eine abwechslungsreiche und lohnende Schwerpunktbildung im Masterstudium Computergraphik & Digitale
Darstellung von Kurven und Flächen
 Darstellung von Kurven und Flächen Proseminar Computergraphik, 10. Juni 2008 Christoph Dähne Seite 1 Inhalt Polygonnetze 3 Knotenliste 3 Kantenliste 3 Parametrisierte kubische Kurven 4 Definition 4 Stetigkeit
Darstellung von Kurven und Flächen Proseminar Computergraphik, 10. Juni 2008 Christoph Dähne Seite 1 Inhalt Polygonnetze 3 Knotenliste 3 Kantenliste 3 Parametrisierte kubische Kurven 4 Definition 4 Stetigkeit
Abitur 2010 Mathematik LK Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Kapitel 2: Mathematische Grundlagen
 [ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
[ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
Serie 6: Mehrfachintegrale und ihre Hauptsubstitutionen. D-ERDW, D-HEST, D-USYS Mathematik II FS 15 Dr. Ana Cannas. Bemerkungen:
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 6: Mehrfachintegrale und ihre Hauptsubstitutionen emerkungen: Die Aufgaben der Serie 6 bilden den Fokus der Übungsgruppen vom 3. März/2. April..
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 6: Mehrfachintegrale und ihre Hauptsubstitutionen emerkungen: Die Aufgaben der Serie 6 bilden den Fokus der Übungsgruppen vom 3. März/2. April..
7.4. Gradient, Niveau und Tangentialebenen
 7.4. Gradient Niveau und Tangentialebenen Wieder sei f eine differenzierbare Funktion von einer Teilmenge A der Ebene R -dimensionalen Raumes R n ) nach R. (oder des n Der Anstieg von f in einem Punkt
7.4. Gradient Niveau und Tangentialebenen Wieder sei f eine differenzierbare Funktion von einer Teilmenge A der Ebene R -dimensionalen Raumes R n ) nach R. (oder des n Der Anstieg von f in einem Punkt
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema, Aufgabe 4) Im R seien die beiden Ebenen E : 6 x + 4 y z = und E : + s + t 4 gegeben.
Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich D in R 3 ein Normalbereich, wenn er von der Form
 155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
155 Normalbereiche in R 2 sehen wie folgt aus: Analog ist ein Bereich in R 3 ein Normalbereich, wenn er von der Form = { (x,y,z) a x b,u(x) y o(x),ũ(x,y) z õ(x,y) } ist, wobei die Rollen der Koordinaten
Oberfläche von Körpern
 Definition Die Summe der Flächeninhalte der Flächen eines Körpers nennt man Oberflächeninhalt. Quader Der Oberflächeninhalt eines Quaders setzt sich folgendermaßen zusammen: O Q =2 h b+2 h l+2 l b=2 (h
Definition Die Summe der Flächeninhalte der Flächen eines Körpers nennt man Oberflächeninhalt. Quader Der Oberflächeninhalt eines Quaders setzt sich folgendermaßen zusammen: O Q =2 h b+2 h l+2 l b=2 (h
Lösungen der Übungsaufgaben III
 Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Mathematik für die ersten Semester (. Auflage): Lösungen der Übungsaufgaben III C. Zerbe, E. Ossner, W. Mückenheim 6. Man konstruiere die Winkelhalbierende eines beliebigen Winkels analog zur Konstruktion
Computergraphik I. Freiformkurven. aus: Farin Curven und Flächen im CAGD. Oliver Deussen Freiformkurven 1
 Freiformkurven aus: Farin Curven und Flächen im CAGD Oliver Deussen Freiformkurven 1 Definition für gebogene Kurven und Flächen Anwendungen: CAD: Automobil-, Flugzeug-, Schiffsbau Computergraphik: Objektmodellierung
Freiformkurven aus: Farin Curven und Flächen im CAGD Oliver Deussen Freiformkurven 1 Definition für gebogene Kurven und Flächen Anwendungen: CAD: Automobil-, Flugzeug-, Schiffsbau Computergraphik: Objektmodellierung
Polyedrische Approximation von Körpern mit Cabri 3D
 Heinz Schumann Polyedrische Approximation von Körpern mit Cabri 3D Die Approximation von konvexen Körpern, deren Oberfläche nicht aus Polygonen besteht, mittels einbeschriebener konvexer Polyeder ist notwendig,
Heinz Schumann Polyedrische Approximation von Körpern mit Cabri 3D Die Approximation von konvexen Körpern, deren Oberfläche nicht aus Polygonen besteht, mittels einbeschriebener konvexer Polyeder ist notwendig,
Stereometrie. Rainer Hauser. Dezember 2010
 Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
Stereometrie Rainer Hauser Dezember 2010 1 Einleitung 1.1 Beziehungen im Raum Im dreidimensionalen Euklid schen Raum sind Punkte nulldimensionale, Geraden eindimensionale und Ebenen zweidimensionale Unterräume.
35 Eine Säule mit quadratischem Querschnitt hat die Mantelfläche M=1.76m 2 und das Volumen V=0.088m 3. Wie hoch ist sie?
 BERECHNUNGSÜBUNGEN 1 Berechnen Sie angenähert die Masse der Luft in einem quaderförmigen Schulzimmer mit der Breite 6m, der Länge 7.m und der Höhe.6m. Die Dichte der Luft beträgt bei Raumtemperatur ca.
BERECHNUNGSÜBUNGEN 1 Berechnen Sie angenähert die Masse der Luft in einem quaderförmigen Schulzimmer mit der Breite 6m, der Länge 7.m und der Höhe.6m. Die Dichte der Luft beträgt bei Raumtemperatur ca.
Kapitel 8 Kollisionserkennung
 Kapitel 8 Kollisionserkennung Lukas Zimmer Gliederung Einführung Kollision mit einer Ebene Kugel - Ebene Quader - Ebene Räumliche Aufteilung Allgemeine Kugel Kollisionen Sliding Kollision von zwei Kugeln
Kapitel 8 Kollisionserkennung Lukas Zimmer Gliederung Einführung Kollision mit einer Ebene Kugel - Ebene Quader - Ebene Räumliche Aufteilung Allgemeine Kugel Kollisionen Sliding Kollision von zwei Kugeln
Gliederung. Körpergrundformen - Grundbegriffe Körpermodelle und netze
 Raumgeometrie K I N G A SZŰ C S F R I E D R I C H - S C H I L L E R - U N I V E R S I T Ä T J E N A F A K U L T Ä T F Ü R M A T H E M A T I K U N D I N F O R M A T I K A B T E I L U N G D I D A K T I K
Raumgeometrie K I N G A SZŰ C S F R I E D R I C H - S C H I L L E R - U N I V E R S I T Ä T J E N A F A K U L T Ä T F Ü R M A T H E M A T I K U N D I N F O R M A T I K A B T E I L U N G D I D A K T I K
Abitur 2010 Mathematik GK Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik GK Geometrie VI In einem kartesischen Koordinatensystem mit Ursprung O sind die Punkte A( ), B( ) und die Gerade g : x = O A + λ, λ R, gegeben.
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik GK Geometrie VI In einem kartesischen Koordinatensystem mit Ursprung O sind die Punkte A( ), B( ) und die Gerade g : x = O A + λ, λ R, gegeben.
Featurebasierte 3D Modellierung
 1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
1 Featurebasierte 3D Modellierung Moderne 3D arbeiten häufig mit einer Feature Modellierung. Hierbei gibt es eine Reihe von vordefinierten Konstruktionen, die der Reihe nach angewandt werden. Diese Basis
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Kopiervorlagen Geometrie (3) - Stereometrie
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Kopiervorlagen Geometrie (3) - Stereometrie Das komplette Material finden Sie hier: School-Scout.de Inhaltsverzeichnis Stereometrie
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Kopiervorlagen Geometrie (3) - Stereometrie Das komplette Material finden Sie hier: School-Scout.de Inhaltsverzeichnis Stereometrie
Geometrische Algorithmen Einige einfache Definitionen: Ist ein Punkt in einem Polygon? Punkt-in-Polygon-Problem. Das Punkt-in-Polygon-Problem
 Geometrische Algorithmen Einige einfache Definitionen: Punkt: im n-dimensionalen Raum ist ein n-tupel (n Koordinaten) Gerade: definiert durch zwei beliebige Punkte auf ihr Strecke: definiert durch ihre
Geometrische Algorithmen Einige einfache Definitionen: Punkt: im n-dimensionalen Raum ist ein n-tupel (n Koordinaten) Gerade: definiert durch zwei beliebige Punkte auf ihr Strecke: definiert durch ihre
3.1 Motivation. - Mit (mehreren) Koordinatentransformationen wird das Objektsystem in das Gerätesystem transformiert.
 3.1 Motivation Wichtige Grundlage der Bildwiedergabe auf dem Bildschirm oder anderen Ausgabegeräten sind Koordinatensysteme und Koordinatentransformationen im IR 2 und IR 3. Im allgemeinen unterscheidet
3.1 Motivation Wichtige Grundlage der Bildwiedergabe auf dem Bildschirm oder anderen Ausgabegeräten sind Koordinatensysteme und Koordinatentransformationen im IR 2 und IR 3. Im allgemeinen unterscheidet
Abitur 2013 Mathematik Geometrie V
 Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Sie braucht weniger Speicherplatz als das Polygon und
 Kapitel 7 Kurven Die bisher besprochenen 2D-Objekte haben bis auf den Kreis den Nachteil, daß sie im weitesten Sinne eckig sind. Wenn ein Objekt mit runder Form verlangt wird, z.b. ein Herz, ein Schiffsrumpf,
Kapitel 7 Kurven Die bisher besprochenen 2D-Objekte haben bis auf den Kreis den Nachteil, daß sie im weitesten Sinne eckig sind. Wenn ein Objekt mit runder Form verlangt wird, z.b. ein Herz, ein Schiffsrumpf,
Kapitel 1. Koordinaten im Raum. 1.1 Schrägbilder - Kavalier-Perspektive Koordinaten
 Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Solutions I Publication:
 WS 215/16 Solutions I Publication: 28.1.15 1 Vektor I 4 2 Ein Objekt A befindet sich bei a = 5. Das zweite Objekt B befindet sich bei b = 4. 2 3 (a) Die Entfernung von Objekt A zum Ursprung ist die Länge
WS 215/16 Solutions I Publication: 28.1.15 1 Vektor I 4 2 Ein Objekt A befindet sich bei a = 5. Das zweite Objekt B befindet sich bei b = 4. 2 3 (a) Die Entfernung von Objekt A zum Ursprung ist die Länge
entspricht der Länge des Vektorpfeils. Im R 2 : x =
 Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Norm (oder Betrag) eines Vektors im R n entspricht der Länge des Vektorpfeils. ( ) Im R : x = x = x + x nach Pythagoras. Allgemein im R n : x x = x + x +... + x n. Beispiele ( ) =, ( 4 ) = 5, =, 4 = 0.
Abitur 2011 G9 Abitur Mathematik GK Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur G9 Abitur Mathematik GK Geometrie VI Auf dem Boden des Mittelmeeres wurde ein antiker Marmorkörper entdeckt, der ersten Unterwasseraufnahmen zufolge die
Seite http://www.abiturloesung.de/ Seite Abitur G9 Abitur Mathematik GK Geometrie VI Auf dem Boden des Mittelmeeres wurde ein antiker Marmorkörper entdeckt, der ersten Unterwasseraufnahmen zufolge die
Aufgaben für den Mathematikunterricht. Inhaltsbereich 1: Raum und Form. 1.2 elementare geometrische Figuren kennen und herstellen
 Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle aus. Würfel Quader Pyramide Zylinder Kegel Kugel Ecken Kanten Flächen Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle
Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle aus. Würfel Quader Pyramide Zylinder Kegel Kugel Ecken Kanten Flächen Nr. 1 Geometrische Körper und ihre Eigenschaften Fülle die Tabelle
3D-Sicht, Projektionen
 Transformationen, deren Matrix als letzte Zeile nicht die Form: [... ] hat, gehören zur allgemeineren Klasse der perspektivischen Transformationen. Perspektivische Projektion von Punkten (,,z i ) auf (
Transformationen, deren Matrix als letzte Zeile nicht die Form: [... ] hat, gehören zur allgemeineren Klasse der perspektivischen Transformationen. Perspektivische Projektion von Punkten (,,z i ) auf (
Über die regelmäßigen Platonischen Körper
 Hermann König, Mathematisches Seminar Studieninformationstage an der Universität Kiel Über die regelmäßigen Platonischen Körper Winkelsumme im n-eck Zerlegung eines ebenen n-ecks in (n-2) Dreiecke, oben
Hermann König, Mathematisches Seminar Studieninformationstage an der Universität Kiel Über die regelmäßigen Platonischen Körper Winkelsumme im n-eck Zerlegung eines ebenen n-ecks in (n-2) Dreiecke, oben
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Rekonstruktion kontinuierlicher Daten Interpolation multivariater Daten Ulrich Rüde Lehrstuhl für Systemsimulation Sommersemester
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Rekonstruktion kontinuierlicher Daten Interpolation multivariater Daten Ulrich Rüde Lehrstuhl für Systemsimulation Sommersemester
Gundlagen Klasse 5/6 Geometrie. nach oben. Inhaltsverzeichnis
 Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Inhaltsverzeichnis Grundbegriffe der Geometrie Geometrische Abbildungen Das Koordinatensystem Schnittpunkt von Geraden Symmetrien Orthogonale Geraden Abstände Parallele Geraden Vierecke Diagonalen in Vielecken
Conservative Volumetric Visibility with Occluder Fusion
 Conservative Volumetric Visibility with Occluder Fusion Worum geht es? Ausgangspunkt komplexe Szene, wie Städte, Straßenzüge, etc. Ziel effiziente Berechnung von nicht sichtbaren Regionen Begriffe / Definitionen
Conservative Volumetric Visibility with Occluder Fusion Worum geht es? Ausgangspunkt komplexe Szene, wie Städte, Straßenzüge, etc. Ziel effiziente Berechnung von nicht sichtbaren Regionen Begriffe / Definitionen
4 x
 Quadratwurzeln und reelle Zahlen. Bestimme die Definitionsmenge des Wurzelterms in G = R a) T(x) = x b) x c) x d) x e) x +. Vereinfache a) 0 + 90 b) 6 7 + 08 7 7 c) 0 0 + d) 6. Mache den Nenner rational
Quadratwurzeln und reelle Zahlen. Bestimme die Definitionsmenge des Wurzelterms in G = R a) T(x) = x b) x c) x d) x e) x +. Vereinfache a) 0 + 90 b) 6 7 + 08 7 7 c) 0 0 + d) 6. Mache den Nenner rational
3.5 Methode des gleitenden Horizonts
 3.5 Methode des gleitenden Horizonts Für Flächen die durch eine Gleichung F (x, y, z) = 0 gegeben sind, lässt sich die Methode des gleitenden Horizonts anwenden. Dabei werden die sichtbaren Teile der Schnitte
3.5 Methode des gleitenden Horizonts Für Flächen die durch eine Gleichung F (x, y, z) = 0 gegeben sind, lässt sich die Methode des gleitenden Horizonts anwenden. Dabei werden die sichtbaren Teile der Schnitte
Triangulierungen von Punktmengen und Polyedern
 Triangulierungen von Punktmengen und Polyedern Vorlesung im Sommersemester 2 Technische Universität Berlin Jörg Rambau 2.4.2 Motivation und Beispiele Wir wollen hier den Begriff der Triangulierungen von
Triangulierungen von Punktmengen und Polyedern Vorlesung im Sommersemester 2 Technische Universität Berlin Jörg Rambau 2.4.2 Motivation und Beispiele Wir wollen hier den Begriff der Triangulierungen von
Klausurenkurs zum Staatsexamen (SS 2014): Lineare Algebra und analytische Geometrie 7
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 4): Lineare Algebra und analytische Geometrie 7 7. (Frühjahr, Thema 3, Aufgabe 4) Im R 3 seien die beiden Ebenen E : 6x+4y z = und E : +s +t 4 gegeben.
2.2 Kollineare und koplanare Vektoren
 . Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
. Kollineare und koplanare Vektoren Wie wir schon gelernt haben, können wir einen Vektor durch Multiplikation mit einem Skalar verlängern oder verkürzen. In Abbildung 9 haben u und v die gleiche Richtung,
Geometrie 2. Julian Fischer Julian Fischer Geometrie / 30
 Geometrie 2 Julian Fischer 6.7.2009 Julian Fischer Geometrie 2 6.7.2009 1 / 30 Themen 1 Bereichssuche und kd-bäume 1 Bereichssuche 2 kd-bäume 2 Divide and Conquer 1 Closest pair 2 Beispiel: Points (IOI
Geometrie 2 Julian Fischer 6.7.2009 Julian Fischer Geometrie 2 6.7.2009 1 / 30 Themen 1 Bereichssuche und kd-bäume 1 Bereichssuche 2 kd-bäume 2 Divide and Conquer 1 Closest pair 2 Beispiel: Points (IOI
I. Zahlen. Zahlensysteme 2035= Zahlenmengen 2035=5 407= Teilbarkeitsregeln. Runden Z H T
 I. Zahlen Zahlensysteme Unser Zahlensystem besteht aus den Ziffern 0 bis 9 (Dezimalsystem) und ist ein Stellenwertsystem; die Stelle einer Ziffer bestimmt ihren Wert in der Zahl. Das römische Zahlensystem
I. Zahlen Zahlensysteme Unser Zahlensystem besteht aus den Ziffern 0 bis 9 (Dezimalsystem) und ist ein Stellenwertsystem; die Stelle einer Ziffer bestimmt ihren Wert in der Zahl. Das römische Zahlensystem
Geometrie. Bei der Addition von Vektoren erhält man einen Repräsentanten des Summenvektors +, indem man die Repräsentanten von aneinanderfügt:
 Geometrie 1. Vektoren Die Menge aller zueinander parallelen, gleich langen und gleich gerichteten Pfeile werden als Vektor bezeichnet. Jeder einzelne Pfeil heißt Repräsentant des Vektors. Bei Ortsvektoren:
Geometrie 1. Vektoren Die Menge aller zueinander parallelen, gleich langen und gleich gerichteten Pfeile werden als Vektor bezeichnet. Jeder einzelne Pfeil heißt Repräsentant des Vektors. Bei Ortsvektoren:
KAPITEL 9 Splinefunktionen
 KAPITEL 9 Splinefunktionen 9.1 Splineräume und Approximationsgüte Bei der Behandlung von Splines ist es bequemer, statt mit dem Grad von Polynomen, mit der Ordnung k := Grad + 1 zu arbeiten. Für eine Knotenmenge
KAPITEL 9 Splinefunktionen 9.1 Splineräume und Approximationsgüte Bei der Behandlung von Splines ist es bequemer, statt mit dem Grad von Polynomen, mit der Ordnung k := Grad + 1 zu arbeiten. Für eine Knotenmenge
Übung (5) 4x 2y +2u 3v =1 3x 2u + v =0 2x +3y u +2v =0
 Übung (5). Lösen Sie folgendes lineare Gleichungssystem - sagen Sie zuvor, wie die Lösungsmenge aussehen sollte bzw. geometrisch zu interpretieren wäre: 4x y +u 3v = 3x u + v =0 x +3y u +v =0. Sagen Sie
Übung (5). Lösen Sie folgendes lineare Gleichungssystem - sagen Sie zuvor, wie die Lösungsmenge aussehen sollte bzw. geometrisch zu interpretieren wäre: 4x y +u 3v = 3x u + v =0 x +3y u +v =0. Sagen Sie
