Stabilität linearer Differentialgleichungssysteme 1-1
|
|
|
- Leopold Lorenz
- vor 6 Jahren
- Abrufe
Transkript
1 Stabilität linearer Differentialgleichungssysteme Ein lineares homogenes Differentialgleichungssystem mit konstanten Koeffizienten u = Au, u = (u 1,..., u n ) t, ist Stabilität linearer Differentialgleichungssysteme 1-1
2 Stabilität linearer Differentialgleichungssysteme Ein lineares homogenes Differentialgleichungssystem mit konstanten Koeffizienten u = Au, u = (u 1,..., u n ) t, ist stabil, wenn für alle Anfangswerte u(0); lim u(t) = 0 t Stabilität linearer Differentialgleichungssysteme 1-2
3 Stabilität linearer Differentialgleichungssysteme Ein lineares homogenes Differentialgleichungssystem mit konstanten Koeffizienten u = Au, u = (u 1,..., u n ) t, ist stabil, wenn für alle Anfangswerte u(0); lim u(t) = 0 t neutral stabil, wenn jede Lösung u(t) für alle t > 0 beschränkt bleibt und es Startwerte u(0) gibt, für die u(t) nicht gegen 0 konvergiert; Stabilität linearer Differentialgleichungssysteme 1-3
4 Stabilität linearer Differentialgleichungssysteme Ein lineares homogenes Differentialgleichungssystem mit konstanten Koeffizienten u = Au, u = (u 1,..., u n ) t, ist stabil, wenn für alle Anfangswerte u(0); lim u(t) = 0 t neutral stabil, wenn jede Lösung u(t) für alle t > 0 beschränkt bleibt und es Startwerte u(0) gibt, für die u(t) nicht gegen 0 konvergiert; instabil, wenn für einen Anfangswert u(0). lim u(t) = t Stabilität linearer Differentialgleichungssysteme 1-4
5 Stabilität lässt sich mit Hilfe der Eigenwerte λ von A charakterisieren. Notwendig und hinreichend ist, dass Re λ < 0 für alle Eigenwerte. Existiert hingegen ein Eigenwert mit Re λ > 0, so ist das System instabil. Stabilität linearer Differentialgleichungssysteme 1-5
6 Beispiel: zweidimensionales System ( u α 1 = Au, A = 1 α ) Stabilität linearer Differentialgleichungssysteme 2-1
7 Beispiel: zweidimensionales System ( u α 1 = Au, A = 1 α ) Eigenwerte λ ± = α ± i Stabilität linearer Differentialgleichungssysteme 2-2
8 Beispiel: zweidimensionales System ( u α 1 = Au, A = 1 α ) Eigenwerte λ ± = α ± i Re λ ± = α = stabil für α < 0 instabil für α > 0 Stabilität linearer Differentialgleichungssysteme 2-3
9 Beispiel: zweidimensionales System ( u α 1 = Au, A = 1 α ) Eigenwerte λ ± = α ± i Re λ ± = α = stabil für α < 0 instabil für α > 0 α = 0: u 1 = u 2, u 2 = u 1 = u 1 (t) = a cos t + b sin t, u 2 (t) = a sin t + b cos t Stabilität linearer Differentialgleichungssysteme 2-4
10 Beispiel: zweidimensionales System ( u α 1 = Au, A = 1 α ) Eigenwerte λ ± = α ± i Re λ ± = α = stabil für α < 0 instabil für α > 0 α = 0: u 1 = u 2, u 2 = u 1 = u 1 (t) = a cos t + b sin t, u 2 (t) = a sin t + b cos t beschränkte Lösungen = neutrale Stabilität Stabilität linearer Differentialgleichungssysteme 2-5
11 Klassifizierung reeller zweidimensionaler linearer Differentialgleichungssysteme Das qualitative Verhalten der Lösungen des Differentialgleichungssystems u = Au, u = (u 1, u 2 ) t, mit A einer reellen 2 2-Matrix lässt sich anhand der Jordan-Form ( ) λ s J = = Q 1 AQ, s {0, 1}, 0 ϱ von A klassifizieren (u = Qv v = Jv). Stabilität linearer Differentialgleichungssysteme 3-1
12 Klassifizierung reeller zweidimensionaler linearer Differentialgleichungssysteme Das qualitative Verhalten der Lösungen des Differentialgleichungssystems u = Au, u = (u 1, u 2 ) t, mit A einer reellen 2 2-Matrix lässt sich anhand der Jordan-Form ( ) λ s J = = Q 1 AQ, s {0, 1}, 0 ϱ von A klassifizieren (u = Qv v = Jv). Die folgenden Abbildungen zeigen jeweils den Verlauf typischer Lösungskurven. Stabilität linearer Differentialgleichungssysteme 3-2
13 Instabiler Sattel: λϱ < 0 Stabilität linearer Differentialgleichungssysteme 3-3
14 Instabiler Sattel: λϱ < 0 u 2 u 1 Stabilität linearer Differentialgleichungssysteme 3-4
15 Knoten: λϱ > 0, λ, ϱ R Stabilität linearer Differentialgleichungssysteme 3-5
16 Knoten: λϱ > 0, λ, ϱ R u 2 u 2 u 1 stabil, λ, ϱ < 0 instabil, λ, ϱ > 0 u 1 Stabilität linearer Differentialgleichungssysteme 3-6
17 Existiert keine Basis aus Eigenvektoren von A (s = 1), so spricht man von einem entarteten Knoten. Stabilität linearer Differentialgleichungssysteme 3-7
18 Existiert keine Basis aus Eigenvektoren von A (s = 1), so spricht man von einem entarteten Knoten. u 2 u 2 u 1 stabil, λ < 0 instabil, λ > 0 u 1 Stabilität linearer Differentialgleichungssysteme 3-8
19 Spirale: λ = r + iω = ϱ, rω 0 Stabilität linearer Differentialgleichungssysteme 3-9
20 Spirale: λ = r + iω = ϱ, rω 0 u 2 u 2 u 1 stabil, r < 0 instabil, r > 0 u 1 Stabilität linearer Differentialgleichungssysteme 3-10
21 Zentrum: λ = iω = ϱ, ω 0 Stabilität linearer Differentialgleichungssysteme 3-11
22 Zentrum: λ = iω = ϱ, ω 0 u 2 u 1 Stabilität linearer Differentialgleichungssysteme 3-12
23 Zusätzlich gibt es noch degenerierte Fälle, bei denen ein Eigenwert null ist. u 2 u 2 u 2 u 1 u 1 λ = 0, ϱ < 0 λ = 0, ϱ > 0 λ = 0, ϱ = 0, s = 1 In jedem dieser Fälle hat das Differentialgleichungssystem Ruhepunkte entlang der gesamten v 1 -Achse. u 1 Stabilität linearer Differentialgleichungssysteme 3-13
24 Beweis: Differentialgleichungssystem in Jordan-Form ( ) v λ s = v v 1 = λv 1 + sv 2 0 ϱ v 2 = ϱv 2 }{{} J Stabilität linearer Differentialgleichungssysteme 4-1
25 Beweis: Differentialgleichungssystem in Jordan-Form ( ) v λ s = v v 1 = λv 1 + sv 2 0 ϱ v 2 = ϱv 2 }{{} J (A) s = 0: Stabilität linearer Differentialgleichungssysteme 4-2
26 Beweis: Differentialgleichungssystem in Jordan-Form ( ) v λ s = v v 1 = λv 1 + sv 2 0 ϱ v 2 = ϱv 2 }{{} J (A) s = 0: allgemeine Lösung v 1 = αe λt, v 2 = βe ϱt mit α, β R Stabilität linearer Differentialgleichungssysteme 4-3
27 Beweis: Differentialgleichungssystem in Jordan-Form ( ) v λ s = v v 1 = λv 1 + sv 2 0 ϱ v 2 = ϱv 2 }{{} J (A) s = 0: allgemeine Lösung v 1 = αe λt, v 2 = βe ϱt mit α, β R (B) s = 1 ( = λ = ϱ): Stabilität linearer Differentialgleichungssysteme 4-4
28 Beweis: Differentialgleichungssystem in Jordan-Form ( ) v λ s = v v 1 = λv 1 + sv 2 0 ϱ v 2 = ϱv 2 }{{} J (A) s = 0: allgemeine Lösung v 1 = αe λt, v 2 = βe ϱt mit α, β R (B) s = 1 ( = λ = ϱ): allgemeine Lösung v 1 = (α + βt)e λt, v 2 = βe λt mit α, β R Stabilität linearer Differentialgleichungssysteme 4-5
29 Verschiedene Fälle Stabilität linearer Differentialgleichungssysteme 4-6
30 Verschiedene Fälle (i) λϱ < 0: Stabilität linearer Differentialgleichungssysteme 4-7
31 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 Stabilität linearer Differentialgleichungssysteme 4-8
32 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 ein Eigenwert positiv Stabilität linearer Differentialgleichungssysteme 4-9
33 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 ein Eigenwert positiv = lim t v(t) = Stabilität linearer Differentialgleichungssysteme 4-10
34 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 ein Eigenwert positiv = lim t v(t) = = instabil Stabilität linearer Differentialgleichungssysteme 4-11
35 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 ein Eigenwert positiv = lim t v(t) = = instabil (ii) λϱ > 0, λ, ϱ reell: Stabilität linearer Differentialgleichungssysteme 4-12
36 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 ein Eigenwert positiv = lim t v(t) = = instabil (ii) λϱ > 0, λ, ϱ reell: entweder beide Eigenwerte positiv oder negativ; entsprechend gilt lim t v(t) = oder 0 Stabilität linearer Differentialgleichungssysteme 4-13
37 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 ein Eigenwert positiv = lim t v(t) = = instabil (ii) λϱ > 0, λ, ϱ reell: entweder beide Eigenwerte positiv oder negativ; entsprechend gilt lim t v(t) = oder 0 = instabil oder stabil Stabilität linearer Differentialgleichungssysteme 4-14
38 Verschiedene Fälle (i) λϱ < 0: = λ ϱ, beide Eigenwerte reell (Produkt komplex konjugierter Eigenwerte positiv), und s = 0 ein Eigenwert positiv = lim t v(t) = = instabil (ii) λϱ > 0, λ, ϱ reell: entweder beide Eigenwerte positiv oder negativ; entsprechend gilt lim t v(t) = oder 0 = instabil oder stabil Die Aussage gilt auch im degenerierten Fall λ = ϱ, s = 1 aufgrund der Form (B) der allgemeinen Lösung. lim t 0 teλt = 0 für λ < 0 Stabilität linearer Differentialgleichungssysteme 4-15
39 (iii) λ = r + iω = ϱ, rω 0: Stabilität linearer Differentialgleichungssysteme 4-16
40 (iii) λ = r + iω = ϱ, rω 0: allgemeine Lösung ( ) v(t) = e rt αe iωt βe iωt } {{ } p(t) Stabilität linearer Differentialgleichungssysteme 4-17
41 (iii) λ = r + iω = ϱ, rω 0: allgemeine Lösung ( ) v(t) = e rt αe iωt βe iωt } {{ } p(t) p(t) beschränkt = Vorzeichen von r entscheidet Stabilitätstyp Stabilität linearer Differentialgleichungssysteme 4-18
42 (iii) λ = r + iω = ϱ, rω 0: allgemeine Lösung ( ) v(t) = e rt αe iωt βe iωt } {{ } p(t) p(t) beschränkt = Vorzeichen von r entscheidet Stabilitätstyp reelle Lösung spiralförmig u(t) = e rt (a Re(ξe iωt ) + b Im(ξe iωt )) mit a, b R und ξ dem (komplexen) Eigenvektor zu λ = r + iω Stabilität linearer Differentialgleichungssysteme 4-19
43 (iii) λ = r + iω = ϱ, rω 0: allgemeine Lösung ( ) v(t) = e rt αe iωt βe iωt } {{ } p(t) p(t) beschränkt = Vorzeichen von r entscheidet Stabilitätstyp reelle Lösung spiralförmig u(t) = e rt (a Re(ξe iωt ) + b Im(ξe iωt )) mit a, b R und ξ dem (komplexen) Eigenvektor zu λ = r + iω (iv) λ = iω = ϱ 0: Stabilität linearer Differentialgleichungssysteme 4-20
44 (iii) λ = r + iω = ϱ, rω 0: allgemeine Lösung ( ) v(t) = e rt αe iωt βe iωt } {{ } p(t) p(t) beschränkt = Vorzeichen von r entscheidet Stabilitätstyp reelle Lösung spiralförmig u(t) = e rt (a Re(ξe iωt ) + b Im(ξe iωt )) mit a, b R und ξ dem (komplexen) Eigenvektor zu λ = r + iω (iv) λ = iω = ϱ 0: analog zu (iii), Lösungen beschränkt und periodisch (Ellipsen) Stabilität linearer Differentialgleichungssysteme 4-21
45 (v-a) λ = 0, ϱ 0: Stabilität linearer Differentialgleichungssysteme 4-22
46 (v-a) λ = 0, ϱ 0: allgemeine Lösung (s = 0) v(t) = ( ) α βe ϱt Stabilität linearer Differentialgleichungssysteme 4-23
47 (v-a) λ = 0, ϱ 0: allgemeine Lösung (s = 0) v(t) = ( ) α βe ϱt ϱ < 0: v(t) für t beschränkt = neutral stabil Stabilität linearer Differentialgleichungssysteme 4-24
48 (v-a) λ = 0, ϱ 0: allgemeine Lösung (s = 0) v(t) = ( ) α βe ϱt ϱ < 0: v(t) für t beschränkt = neutral stabil ϱ > 0: v(t) für t unbeschränkt = instabil Stabilität linearer Differentialgleichungssysteme 4-25
49 (v-a) λ = 0, ϱ 0: allgemeine Lösung (s = 0) v(t) = ( ) α βe ϱt ϱ < 0: v(t) für t beschränkt = neutral stabil ϱ > 0: v(t) für t unbeschränkt = instabil (v-b) λ = 0 = ϱ, s = 1: Stabilität linearer Differentialgleichungssysteme 4-26
50 (v-a) λ = 0, ϱ 0: allgemeine Lösung (s = 0) v(t) = ( ) α βe ϱt ϱ < 0: v(t) für t beschränkt = neutral stabil ϱ > 0: v(t) für t unbeschränkt = instabil (v-b) λ = 0 = ϱ, s = 1: allgemeine Lösung instabil ( ) α + βt v(t) = β Stabilität linearer Differentialgleichungssysteme 4-27
51 Stabilitätsdiagramm Für ein zweidimensionales Differentialgleichungssystem u = Au, u = (u 1, u 2 ) t, lässt sich Stabilität mit Hilfe der Determinante und Spur der Matrix A charakterisieren. Notwendig und hinreichend für Stabilität ist Die Parabel det A > 0, Spur A < 0. ( ) Spur A 2 det A = λ = ϱ 2 trennt die qualitativ verschiedenen Fälle Spirale und Knoten. Stabilität linearer Differentialgleichungssysteme 5-1
52 Stabilitätsdiagramm Für ein zweidimensionales Differentialgleichungssystem u = Au, u = (u 1, u 2 ) t, lässt sich Stabilität mit Hilfe der Determinante und Spur der Matrix A charakterisieren. Notwendig und hinreichend für Stabilität ist Die Parabel det A > 0, Spur A < 0. ( ) Spur A 2 det A = λ = ϱ 2 trennt die qualitativ verschiedenen Fälle Spirale und Knoten. Bei dem Grenzfall λ = ϱ handelt es sich um einen (gegebenenfalls entarteten) Knoten. Stabilität linearer Differentialgleichungssysteme 5-2
53 det A stabile Spirale instabile Spirale λ = ωi neutrales Zentrum λ = < 0 λ = > 0 stabiler Knoten λ, < 0 λ, > 0 instabiler Knoten Spur A instabiler Sattel Stabilität linearer Differentialgleichungssysteme 5-3
54 Beweis: λ, ϱ Eigenwerte von A = det A = λϱ, Spur A = λ + ϱ Stabilität linearer Differentialgleichungssysteme 6-1
55 Beweis: λ, ϱ Eigenwerte von A = det A = λϱ, Spur A = λ + ϱ λ, ϱ R: Stabilität linearer Differentialgleichungssysteme 6-2
56 Beweis: λ, ϱ Eigenwerte von A = det A = λϱ, Spur A = λ + ϱ λ, ϱ R: Stabilität, d.h. λ, ϱ < 0 det A > 0 Spur A < 0 Stabilität linearer Differentialgleichungssysteme 6-3
57 Beweis: λ, ϱ Eigenwerte von A = det A = λϱ, Spur A = λ + ϱ λ, ϱ R: Stabilität, d.h. λ, ϱ < 0 λ = r + ωi, ϱ = r ωi: det A > 0 Spur A < 0 det A = r 2 + ω 2 > 0, gleiches Kriterium für Stabilität Spur A = 2r Stabilität linearer Differentialgleichungssysteme 6-4
58 Beweis: λ, ϱ Eigenwerte von A = det A = λϱ, Spur A = λ + ϱ λ, ϱ R: Stabilität, d.h. λ, ϱ < 0 λ = r + ωi, ϱ = r ωi: det A > 0 Spur A < 0 det A = r 2 + ω 2 > 0, gleiches Kriterium für Stabilität Spur A = 2r Übergang von komplexen zu reellen Eigenwerten ω 0, d.h. ( ) Spur A 2 λ = ϱ det A = 2 (abgebildete Parabel Knoten mit doppeltem Eigenwert) Stabilität linearer Differentialgleichungssysteme 6-5
59 Beispiel: Stabilität des Differentialgleichungssystems ( ) u 0 2 = u 1 α }{{} A in Abhängigkeit von dem reellen Parameter α Stabilität linearer Differentialgleichungssysteme 7-1
60 Beispiel: Stabilität des Differentialgleichungssystems ( ) u 0 2 = u 1 α }{{} A in Abhängigkeit von dem reellen Parameter α Charakterisierung mit Hilfe von det A = 2, Spur A = α Stabilität linearer Differentialgleichungssysteme 7-2
61 (i) α < 0: Stabilität linearer Differentialgleichungssysteme 7-3
62 (i) α < 0: stabil Stabilität linearer Differentialgleichungssysteme 7-4
63 (i) α < 0: stabil Knoten: d.h. α = det A (Spur A/2) 2 = (α/2) 2, Stabilität linearer Differentialgleichungssysteme 7-5
64 (i) α < 0: stabil Knoten: d.h. α 2 2 Spirale: d.h. 2 2 < α < 0 2 = det A (Spur A/2) 2 = (α/2) 2, det A > (Spur A/2) 2, Stabilität linearer Differentialgleichungssysteme 7-6
65 (i) α < 0: stabil Knoten: d.h. α 2 2 Spirale: d.h. 2 2 < α < 0 (ii) α = 0: 2 = det A (Spur A/2) 2 = (α/2) 2, det A > (Spur A/2) 2, Stabilität linearer Differentialgleichungssysteme 7-7
66 (i) α < 0: stabil Knoten: d.h. α 2 2 Spirale: d.h. 2 2 < α < 0 (ii) α = 0: neutrales Zentrum, Eigenwerte ±i 2 2 = det A (Spur A/2) 2 = (α/2) 2, det A > (Spur A/2) 2, Stabilität linearer Differentialgleichungssysteme 7-8
67 (i) α < 0: stabil Knoten: d.h. α 2 2 Spirale: d.h. 2 2 < α < 0 (ii) α = 0: neutrales Zentrum, Eigenwerte ±i 2 (iii) α > 0: 2 = det A (Spur A/2) 2 = (α/2) 2, det A > (Spur A/2) 2, Stabilität linearer Differentialgleichungssysteme 7-9
68 (i) α < 0: stabil Knoten: d.h. α 2 2 Spirale: d.h. 2 2 < α < 0 (ii) α = 0: neutrales Zentrum, Eigenwerte ±i 2 (iii) α > 0: instabil 2 = det A (Spur A/2) 2 = (α/2) 2, det A > (Spur A/2) 2, Stabilität linearer Differentialgleichungssysteme 7-10
69 (i) α < 0: stabil Knoten: d.h. α 2 2 Spirale: d.h. 2 2 < α < 0 (ii) α = 0: neutrales Zentrum, Eigenwerte ±i 2 (iii) α > 0: instabil Spirale: 2 = det A (Spur A/2) 2 = (α/2) 2, det A > (Spur A/2) 2, 0 < α < 2 2 Stabilität linearer Differentialgleichungssysteme 7-11
70 (i) α < 0: stabil Knoten: d.h. α 2 2 Spirale: d.h. 2 2 < α < 0 (ii) α = 0: neutrales Zentrum, Eigenwerte ±i 2 (iii) α > 0: instabil Spirale: 2 = det A (Spur A/2) 2 = (α/2) 2, det A > (Spur A/2) 2, 0 < α < 2 2 Knoten: 2 2 α Stabilität linearer Differentialgleichungssysteme 7-12
71 stabiler Knoten stabile Spirale neutrales Zentrum u 2 u 2 u 2 u 1 instabile Spirale u 1 instabiler Knoten u 1 u 2 u 2 u 1 u 1 Eigenlöungen u = ve λt zu reellen Eigenwerten fett Stabilität linearer Differentialgleichungssysteme 7-13
Abbildung 5.1: stabile und instabile Ruhelagen
Kapitel 5 Stabilität Eine intuitive Vorstellung vom Konzept der Stabilität vermitteln die in Abb. 5.1 dargestellten Situationen. Eine Kugel rollt unter dem Einfluss von Gravitation und Reibung auf einer
29.2 Lineare Differentialgleichungssysteme mit konstanten Koeffizienten Wir betrachten das homogene System. y = A y, t R, (1)
292 Lineare Differentialgleichungssysteme mit konstanten Koeffizienten Wir betrachten das homogene System y = A y, t R, ( wobei A C n n, und wollen ein Fundamentalsystem bestimmen Grundlegende Beobachtung:
Klassifikation planarer Systeme
Klassifikation planarer Systeme Dieser Vortrag thematisiert die Klassifikation planarer Systeme. Man klassifiziert planare Systeme um einen besseren Überblick über die verschiedenen Verhaltensweisen von
Serie 12: Eigenwerte und Eigenvektoren
D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr Ana Cannas Serie : Eigenwerte und Eigenvektoren Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom 7 und 9 Dezember Finden Sie für folgende
8. Übungsblatt Aufgaben mit Lösungen
8 Übungsblatt Aufgaben mit Lösungen Aufgabe 6: Matrix Bestimmen Sie die allgemeine reelle Lösung des Differentialgleichungssystems u x = Aux für die A =, 9 indem Sie das System auf eine einzelne gewöhnliche
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Lineare Algebra: Determinanten und Eigenwerte
: und Eigenwerte 16. Dezember 2011 der Ordnung 2 I Im Folgenden: quadratische Matrizen Sei ( a b A = c d eine 2 2-Matrix. Die Determinante D(A (bzw. det(a oder Det(A von A ist gleich ad bc. Det(A = a b
Lineare Algebra II 3. Übungsblatt
Lineare Algebra II 3. Übungsblatt Fachbereich Mathematik SS 2011 Prof. Dr. Kollross 27./28. April 2011 Susanne Kürsten Tristan Alex Minitest Aufgabe M1 (Formale Polynome) Betrachten Sie die folgenden Polynome
Prüfungsvorbereitungskurs Höhere Mathematik 3
Prüfungsvorbereitungskurs Höhere Mathematik 3 Differentialgleichungssysteme Marco Boßle Jörg Hörner Mathematik Online Frühjahr 20 PV-Kurs HM 3 DGlSysteme - Zusammenfassung Allgemeine Differentialgleichungssysteme.Ordnung
1.11 Eigenwertproblem Anwendungen von Eigenwerten und Eigenvektoren Lineare Rekursionen Lineare Differentialgleichungssysteme Bestimmung von
1.11 Eigenwertproblem Anwendungen von Eigenwerten und Eigenvektoren Lineare Rekursionen Lineare Differentialgleichungssysteme Bestimmung von Wachstumsraten Bestimmung von Maximal- und Minimalwerten von
Musterlösungen Blatt Mathematischer Vorkurs. Sommersemester Dr. O. Zobay. Matrizen
Musterlösungen Blatt 8 34007 Mathematischer Vorkurs Sommersemester 007 Dr O Zobay Matrizen Welche Matrixprodukte können mit den folgenden Matrizen gebildet werden? ( 4 5 A, B ( 0 9 7, C 8 0 5 4 Wir können
Blatt 1. Kinematik- Lösungsvorschlag
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
4.7 Lineare Systeme 1. Ordnung
3. Die allgemeine Lösung der inhomogenen Differentialgleichung lautet damit yx = y hom x + y inh x = c x + c 2 x + 8 x + 4 xlnx2 4 xlnx = C x + C 2 x + 4 xlnx2 4 xlnx. Wir haben c 2 + 8 zu C 2 zusammengefasst.
Klausur HM I H 2005 HM I : 1
Klausur HM I H 5 HM I : 1 Aufgabe 1 4 Punkte): Zeigen Sie mit Hilfe der vollständigen Induktion: n 1 1 + 1 ) k nn k n! für n. Lösung: Beweis mittels Induktion nach n: Induktionsanfang: n : 1 ) 1 + 1 k
Hauptachsentransformation: Eigenwerte und Eigenvektoren
Hauptachsentransformation: Eigenwerte und Eigenvektoren die bisherigen Betrachtungen beziehen sich im Wesentlichen auf die Standardbasis des R n Nun soll aufgezeigt werden, wie man sich von dieser Einschränkung
Drehachse und Drehwinkel
Drehachse und Drehwinkel Jede Drehung Q im R 3 besitzt eine Drehachse, d.h. lässt einen Einheitsvektor u invariant, und entspricht einer ebenen Drehung um einen Winkel ϕ in der zu u orthogonalen Ebene.
Jordan-Form. Eine komplexe quadratische Matrix A lässt sich durch eine Ähnlichkeitstranformation auf die Blockdiagonalform. = Q 1 AQ 0 J k J =
Jordan-Form Eine komplexe quadratische Matrix A lässt sich durch eine Ähnlichkeitstranformation auf die Blockdiagonalform J 1 0 J =... = Q 1 AQ 0 J k transformieren. Jordan-Form 1-1 Jordan-Form Eine komplexe
Gedämpfte harmonische Schwingung
Gedämpfte harmonische Schwingung Die Differentialgleichung u + 2ru + ω 2 0u = c cos(ωt) mit r > 0 modelliert sowohl eine elastische Feder als auch einen elektrischen Schwingkreis. Gedämpfte harmonische
Anleitung zu Blatt 4 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
Fachbereich Mathematik der Universität Hamburg WiSe / Dr Hanna Peywand Kiani 722 Anleitung zu Blatt 4 Differentialgleichungen I für Studierende der Ingenieurwissenschaften Lineare Differentialgleichungssysteme,
Lineare Algebra II. Prof. Dr. M. Rost. Übungen Blatt 7 (SS 2011) Abgabetermin: Donnerstag, 2. Juni.
Lineare Algebra II Prof. Dr. M. Rost Übungen Blatt 7 (SS 2011) Abgabetermin: Donnerstag, 2. Juni http://www.math.uni-bielefeld.de/~rost/la2 Erinnerungen, Ergänzungen und Vorgriffe zur Vorlesung: Eigenvektoren
Lineare Algebra II 11. Übungsblatt
Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
MC-Serie 11: Eigenwerte
D-ERDW, D-HEST, D-USYS Mathematik I HS 14 Dr. Ana Cannas MC-Serie 11: Eigenwerte Einsendeschluss: 12. Dezember 2014 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung
Lösungsskizzen zur Klausur
sskizzen zur Klausur Mathematik II Sommersemester 4 Aufgabe Es seien die folgenden Vektoren des R 4 gegeben: b = b = b 3 = b 4 = (a) Prüfen Sie ob die Vektoren b b 4 linear unabhängig sind bestimmen Sie
y hom (x) = C e p(x) dx
Gewöhnliche Differentialgleichungen F (x, y, y,..., y n ) = 0 Gleichung, die die Veränderliche x sowie die Funktion y = y(x) und ihre Ableitungen y,..., y n beinhaltet. Klassifiaktion: implizit F (...)
5 Gewöhnliche Differentialgleichungen
5 Gewöhnliche Differentialgleichungen 5.1 Einleitung & Begriffsbildung Slide 223 Natürliches Wachstum Eine Population bestehe zur Zeit t aus N(t) Individuen. Die Population habe konstante Geburts- und
Rückblick auf die letzte Vorlesung
Rückblick auf die letzte Vorlesung Lineare Differentialgleichungen Ausblick auf die heutige Vorlesung Lineare autonome Differentialgleichungen 2 Bestimmung des Fundamentalsystems 3 Jordansche Normalform
Differentialgleichungen
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Lösung 05 Klassische Theoretische Physik I WS 15/16. y a 2 + r 2. A(r) =
Karlsruher Institut für Technologie Institut für theoretische Festkörperphsik www.tfp.kit.edu Lösung Klassische Theoretische Phsik I WS / Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler Besprechung...
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
Karlsruher Institut für Technologie Institut für Analsis Dr. I. Anapolitanos Dipl.-Math. Sebastian Schwarz SS 07.05.07 Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik
Dynamische Systeme eine Einführung
Dynamische Systeme eine Einführung Seminar für Lehramtstudierende: Mathematische Modelle Wintersemester 2010/11 Dynamische Systeme eine Einführung 1. Existenz und Eindeutigkeit von Lösungen 2. Flüsse,
Gewöhnliche Differentialgleichungen
Gewöhnliche Differentialgleichungen Franz Hofbauer Eine Vorlesung für das Lehramtstudium Inhaltsverzeichnis Kapitel. Einleitung Kapitel 2. Differentialgleichungen erster und zweiter Ordnung 3. Lineare
tun, sondern nur mit der Reaktion auf verschiedene Anfangswerte.
2.3 Stabilität Eine wichtige Rolle spielt das Stabilitätsverhalten dynamischer Systeme. Wie üblich sei Φ die Fundamentalmatrix des linearen Systems ẋ = A(t)x + u. Im weiteren sei t fixiert, später wird
7 Lineare Abbildungen und Skalarprodukt
Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
9. Übungsblatt zur Mathematik I für Maschinenbau
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 9. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS /..-4.. Aufgabe G (Koordinatentransformation)
Mathematik für Studierende der Fachrichtungen Biologie, Chemie, Lebensmittelchemie und Erziehungswissenschaften Blatt 2
Fakultät Mathematik WS 27/8 Institut für Mathematische Stochastik / Institut für Analysis Dr. W. Kuhlisch, Dr. F. Morherr Mathematik für Studierende der Fachrichtungen Biologie, Chemie, Lebensmittelchemie
Serie 13. Analysis D-BAUG Dr. Cornelia Busch FS 2016
Analysis D-BAUG Dr. Cornelia Busch FS 2016 Serie 13 1. Prüfungsaufgabe 4, Winter 2014. Bestimmen Sie die Funktion, für die gilt: An jeder Stelle des Definitionsbereichs ist die Steigung des Graphen der
PROBEPRÜFUNG MATHEMATIK I UND II
PROBEPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften Für diese Probeprüfung sind ca 4 Stunden vorgesehen. Die eigentliche Prüfung wird signifikant
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 2
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 25): Lineare Algebra und analytische Geometrie 2 2. (Frühjahr 29, Thema 3, Aufgabe 3) Gegeben sei die reelle 3 3 Matrix 4 2 A = 2 7 2 R 3 3. 2 2 a)
BASISPRÜFUNG MATHEMATIK I UND II
ETH Zürich Sommer 015 Dr. Ana Cannas BASISPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften 1. Sei a) Ist das System lösbar? b) Lösen Sie das System
Mathematik II Frühjahrssemester 2013
Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Eigenwerte und Diagonalisierung
Eigenwerte und Diagonalisierung Wir wissen von früher: Seien V und W K-Vektorräume mit dim V = n, dim W = m und sei F : V W linear. Werden Basen A bzw. B in V bzw. W gewählt, dann hat F eine darstellende
Analysis von singulären Differentialgleichungen erster und zweiter Ordnung - Skalare Probleme
Analysis von singulären Differentialgleichungen erster und zweiter Ordnung - Skalare Probleme Jonathan Mosser 3. Juni 27 / 38 Vorbemerkungen Singularität Singuläre Probleme können auf zwei Arten formuliert
3.6 Eigenwerte und Eigenvektoren
3.6 Eigenwerte und Eigenvektoren 3.6. Einleitung Eine quadratische n n Matrix A definiert eine Abbildung eines n dimensionalen Vektors auf einen n dimensionalen Vektor. c A x c A x Von besonderem Interesse
Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen
Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Mathematik II Frühlingsemester 2015 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren
Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
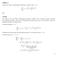Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Institut für Elektrotechnik und Informationstechnik. Aufgabensammlung zur. Systemtheorie
Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Systemtheorie Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski Dipl.-Ing. R. Besrat 05.04.2013 Übungsaufgaben zur Systemtheorie
Übungen zum Ferienkurs Analysis II
Übungen zum Ferienkurs Analysis II Implizite Funktionen und Differentialgleichungen 4. Umkehrbarkeit I Man betrachte die durch g(s, t = (e s cos(t, e s sin(t gegebene Funktion g : R R. Zeigen Sie, dass
Orthonormalisierung. ein euklidischer bzw. unitärer Vektorraum. Wir setzen
Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Seminar Gewöhnliche Differentialgleichungen
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Mathematik für Naturwissenschaftler, Pruscha & Rost Kap 7 Lösungen
Mathematik für Naturwissenschaftler, Pruscha & Rost Kap 7 Lösungen a) Es ist < x, y > α + + β β ( + α) und y α + + β α + + ( + α) (α + α + ) 6 α + α, also α, ± 5 + ± 9 4 ± 3 Es gibt also Lösungen: α, β
Lineare Algebra II 6. Übungsblatt
Lineare Algebra II 6 Übungsblatt Fachbereich Mathematik SS 2011 Prof Dr Kollross 18/19 Mai 2011 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minimalpolynom) Bestimmen Sie das Minimalpolynom der
Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt 4
Prof. Roland Gunesch Sommersemester Übungen zur Vorlesung Einführung in Dynamische Systeme Musterlösungen zu Aufgabenblatt 4 Analysieren Sie folgende mathematischen Modelle der Liebesbeziehung zwischen
Übungsaufgaben Mathematik 3 ASW Blatt 8 Lineare Differentialgleichungen 1. und 2. Ordnung mit konstanten Koeffizienten
Übungsaufgaben Mathematik 3 ASW Blatt 8 Lineare Differentialgleichungen und Ordnung mit konstanten Koeffizienten Prof Dr BGrabowski Lösung linearer Dgl Ordnung mittels Zerlegungssatz Aufgabe ) Lösen Sie
Stroppel Musterlösung , 180min. Aufgabe 1 (5 Punkte) Gegeben sei eine lineare Abbildung α: R 4 R 3 : x Ax mit. . Weiter sei b = A =
Stroppel Musterlösung 4. 9., 8min Aufgabe 5 Punkte Gegeben sei eine lineare Abbildung α: R 4 R 3 : x Ax mit 4 A =. Weiter sei b = 3 gegeben. Entscheiden Sie jeweils, ob die durch gekennzeichneten freien
R 3 und U := [e 2, e 3 ] der von e 2, e 3 erzeugte
![R 3 und U := [e 2, e 3 ] der von e 2, e 3 erzeugte](/thumbs/74/70162485.jpg "R 3 und U := [e 2, e 3 ] der von e 2, e 3 erzeugte")
Aufgabe ( Es seien e =, e = Untervektorraum (, e = ( R und U := [e, e ] der von e, e erzeugte Weiter sei G := {A GL(, R A e = e und A U U} (a Zeigen Sie, dass G eine Untergruppe von GL(, R ist (b Geben
Wiederholungsblatt Elementargeometrie LÖSUNGSSKIZZE
Wiederholungsblatt Elementargeometrie im SS 01 bei Prof. Dr. S. Goette LÖSUNGSSKIZZE Die Lösungen unten enthalten teilweise keine vollständigen Rechnungen. Es sind aber alle wichtigen Zwischenergebnisse
2.4 Gekoppelte lineare Differentialgleichungen
48 Kapitel 2 Lineare Algebra II 24 Gekoppelte lineare Differentialgleichungen Die Untersuchung der Normalformen von Matrizen soll nun auf die Lösung von gekoppelten Differentialgleichungen angewendet werden
Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom
Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom Eine Fragestellung, die uns im weiteren beschäftigen wird, ist das Finden eines möglichst einfachen Repräsentanten aus jeder Äquivalenzklasse
Lotka-Volterra-Gleichungen für mehr als zwei Populationen
Lotka-Volterra-Gleichungen für mehr als zwei Populationen Dennis Kunz 06.12.2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics Lotka-Volterra-Gleichungen für mehr als zwei
Die Abbildung (x 1 ;x 2 ) 7! (x 1 ;x 2 ; 1) ist eine Einbettung von R 2 in P 2 (als Mengen). Punkte mit z 6= 0 sind endliche" Punkte mit inhomogenen K
Kapitel IV Projektive Geometrie In diesem Kapitel wird eine kurze Einführung in die projektive Geometrie gegeben. Es sollen unendlich ferne Punkte mit Hilfe von homogene Koordinaten eingeführt werden und
6 Hauptachsentransformation
6 Hauptachsentransformation A Diagonalisierung symmetrischer Matrizen (6.1) Satz: Sei A M(n n, R) symmetrisch. Dann gibt es eine orthogonale n n-matrix U mit U t AU = D Diagonalmatrix Es folgt: Die Spalten
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 3 Der Axiator Eigenschaften des Axiators Bestimmung des Kegelschnitts Geometrische Betrachtungen Dualer Kegelschnitt Pol-Polare
Fachbereich Mathematik/Informatik 16. Juni 2012 Prof. Dr. H. Brenner. Mathematik für Anwender II. Testklausur mit Lösungen
Fachbereich Mathematik/Informatik 6. Juni 0 Prof. Dr. H. Brenner Mathematik für Anwender II Testklausur mit Lösungen Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Ein Skalarprodukt
Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 2016
Name, Vorname Matrikel-Nr. Aufg. Aufg.2 Aufg.3 Aufg.4 Σ Note bzw. Kennzeichen Klausur (Modulprüfung) zum Lehrerweiterbildungskurs 4Q Lineare Algebra/Analytische Geometrie II SoSe 206 Bearbeiten Sie bitte
HÖHERE MATHEMATIK 2, Übungen, Sommersemester Übungsblatt für den
. Übungsblatt für den 4. 3. 2008 () Die Gerade g sei durch die Gleichung 2x y = 3 gegeben. Bestimmen sie Gleichungen der beiden Geraden, die parallel zu g sind und den Abstand 2 von g haben. Bestimmen
y = A(x) y + b(x). (1) y = A(x) y (2)
73 5.2 Lineare Systeme Sei weiterhin IK = C oder IK = IR. Seien = I IR ein offenes Intervall, x 0 I, y 0 IK n, A: I IK n n und b: I IK n stetige matrix- bzw vektorwertige Funktionen. Wir betrachten komplexe
Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen
Kapitel XII Implizite Funktionen, der Umkehrsatz und Extrema unter Nebenbedingungen 53 Implizite Funktionen und allgemeine partielle Differenzierbarkeit 54 Der Umkehrsatz 55 Lokale Extrema unter Nebenbedingungen,
Wettbewerbs- und Symbiose-Modelle Von Jakob Foss
Wettbewerbs- und Symbiose-Modelle Von Jakob Foss Wettbewerbsmodell Das einfachste Wettbewerbsmodell für zwei Spezies lässt sich aus dem Lotka- Volterra Modell ableiten und sieht folgendermaßen aus: dn1
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 3
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 205/6): Lineare Algebra und analytische Geometrie 3 3. (Herbst 997, Thema 3, Aufgabe ) Berechnen Sie die Determinante der reellen Matrix 0 2 0 2 2
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
x 2 y + xp(x)y + q(x)y = 0, (1) wobei p(x) = Satz: Falls ρ 1, ρ 2 R, mit ρ 1 ρ 2 so gibt es für 0 < x < R ein Fundamentalsystem von (1) der Gestalt
Kurze Zusammenfassung der Vorlesung 6 Am Anfang werden wir einbisschen mehr den Potenzreihenansatz besprechen. Abgewandelter Potenzreihenansatz In Verallgemeinerung der Eulerschen Differentialgleichung
3 Satz von Fisher Tippett
Theorem 3.1 (Satz von Fisher Tippett; extremal types theorem). Eine Verteilung G ist eine Extremwertverteilung genau dann, wenn es c > 0, d R und γ R gibt mit G(t) = G γ (ct + d). { } Dabei ist G γ eine
Lineare Algebra und analytische Geometrie II
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 34 Die Diagonalisierbarkeit von Isometrien im Komplexen Satz 34.1. Es sei V ein endlichdimensionaler C-Vektorraum
Eigenwerte. Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1)
Eigenwerte 1 Eigenwerte und Eigenvektoren Ein Eigenwert einer quadratischen n n Matrix A ist ein Skalar λ C (eine komplexe Zahl) mit der Eigenschaft Ax = λx (1) für einen Vektor x 0. Vektor x heißt ein
Lineare Differentialgleichungen
Kapitel 3 Lineare Differentialgleichungen 31 Jordansche Normalform In diesem kurzen Abschnitt wiederholen wir einige Begriffe der linearen Algebra Sei A : n n eine lineare Abbildung mit zugehöriger Matrix
Lineare Algebra und analytische Geometrie II
Prof. Dr. H. Brenner Osnabrück SS 2016 Lineare Algebra und analytische Geometrie II Vorlesung 53 Norm von Endomorphismen und Matrizen Definition 53.1. Es seien V und W endlichdimensionale normierte K-
Zeige, daß A nichtsingulär ist und berechne die Inverse Matrix. Lösung: A ist nicht singulär, wenn det A 0. Ist das der Fall, so gilt
Algebra, Analytische Geometrie. 1. Sei 1, 0, 9 A := 1, 2, 3,. 2, 2, 2, Zeige, daß A nichtsingulär ist und berechne die Inverse Matrix. Lösung: A ist nicht singulär, wenn det A 0. Ist das der Fall, so gilt
H.J. Oberle Differentialgleichungen I WiSe 2012/ Stabilität. Wir betrachten ein allgemeines DGL-System erster Ordnung:
H.J. Oberle Differentialgleichungen I WiSe 2012/13 A. Allgemeines. 8. Stabilität Wir betrachten ein allgemeines DGL-System erster Ordnung: y (t) = f(t, y(t)) (8.1) mit y(t) R n, hinreichend glatter rechter
3 Lineare Differentialgleichungen
3 Lineare Differentialgleichungen In diesem Kapitel behandeln wir die allgemeine Theorie linearer Differentialgleichungen Sie werden zahlreiche Parallelen zur Theorie linearer Gleichungssysteme feststellen,
Finanzmathematik I Lösungvorschläge für Übungsblatt 1
Finanzmathematik I Lösungvorschläge für Übungsblatt 1 J. Widenmann ufgabe 1: Zu zeigen ist, dass Q die Definition Ü.1.1.2 erfüllt. Zunächst bemerken wir, dass Q wegen der nnahme f 0 Werte in R + annimmt.
Inhaltsverzeichnis INHALTSVERZEICHNIS 1
INHALTSVERZEICHNIS 1 Inhaltsverzeichnis 1 Die Parabel 2 1.1 Definition................................ 2 1.2 Bemerkung............................... 3 1.3 Tangenten................................ 3 1.4
Übungsblatt
Übungsblatt 3 3.5.27 ) Die folgenden vier Matrizen bilden eine Darstellung der Gruppe C 4 : E =, A =, B =, C = Zeigen Sie einige Gruppeneigenschaften: a) Abgeschlossenheit: Berechnen Sie alle möglichen
6 Die Schursche Normalform und einige Klassen von Matrizen
ME Lineare Algebra HT 28 111 6 Die Schursche Normalform und einige Klassen von Matrizen 61 Die Schur-Normalform und Hauptvektoren Für nichtdiagonalisierbare Matrizen gibt es andere Normalformen: Jordan-
Bericht zur Mathematischen Zulassungsprüfung im Mai 2010
Bericht zur Mathematischen Zulassungsprüfung im Mai 2 Heinz-Willi Goelden, Wolfgang Lauf, Martin Pohl Am 5. Mai 2 fand die Mathematische Zulassungsprüfung statt. Die Prüfung bestand aus einer 9-minütigen
Kapitel 5 (Ebene autonome Systeme) Abschnitt 5.1 (Reduktion auf skalare Di.gleichungen)
Abschnitt 5.1 Reduktion auf skalare Differenzialgleichungen 33 Kapitel 5 Ebene autonome Systeme Abschnitt 5.1 Reduktion auf skalare Di.gleichungen Aufgabe 1, Seite 190 Das gegebene System besitzt oensichtlich
KAPITEL 1. Einleitung
KAPITEL 1 Einleitung Wir beschäftigen uns in dieser Vorlesung mit Verfahren aus der Numerischen linearen Algebra und insbesondere dem sogenannten Mehrgitterverfahren zur Lösung linearer Gleichungssysteme
Tutorium Mathematik II, M Lösungen
Tutorium Mathematik II, M Lösungen März 03 *Aufgabe Bestimmen Sie durch Hauptachsentransformation Lage und Typ der Kegelschnitte (a) 3x + 4x x + 3x 4x = 0, (b) 3x + 4x x + 3x 4x 6 = 0, (c) 3x + 4x x +
2ml2 folgt die Form der Phasenraumtrajektorien zu
PDDr.S.Mertens Theoretische Physik I Mechanik J. Unterhinninghofen, M. Hummel Blatt WS 8/9 3..9. Phasenraumportrait eines Fadenpendels. Eine Masse m sei an einer masselosen Stange der Länge l aufgehängt,
Kapitel 1. Eigenwerttheorie für Matrizen. 1.1 Determinanten in höherer Dimension
Kapitel Eigenwerttheorie für Matrizen. Determinanten in höherer Dimension Wir beginnen damit, die Determinante einer Matrix auch für quadratische Matrizen mit mehr als 3 Zeilen einzuführen. Definition.
Orientierung der Vektoren b 1,..., b n. Volumen des von den Vektoren aufgespannten Parallelotops
15. DETERMINANTEN 1 Für n Vektoren b 1,..., b n im R n definiert man ihre Determinante det(b 1,..., b n ) Anschaulich gilt det(b 1,..., b n ) = Orientierung der Vektoren b 1,..., b n Volumen des von den
Lineare Differenzengleichungen
Lineare Differenzengleichungen Die Fibonacci-Zahlen F n sind definiert durch F 0 = 0 F 1 = 1 F n = F n 1 +F n 2 für n >= 2 Die letzte Zeile ist ein Beispiel für eine homogene lineare Differenzengleichung
Differentialgleichungen
Differentialgleichungen Das Handout ist Bestandteil der Vortragsfolien zur Höheren Mathematik; siehe die Hinweise auf der Internetseite vhm.mathematik.uni-stuttgart.de für Erläuterungen zur Nutzung und
51 Numerische Berechnung von Eigenwerten und Eigenvektoren
5 Numerische Berechnung von Eigenwerten und Eigenvektoren 5. Motivation Die Berechnung der Eigenwerte einer Matrix A IR n n als Lösungen der charakteristischen Gleichung (vgl. Kapitel 45) ist für n 5 unpraktikabel,
Homogene Systeme in höheren Dimensionen
56 4 Systeme von Differenzialgleichungen gefunden, so sind deren ilder, ' = T, Lösungen in den y-koordinaten. llerdings ist das uffinden einer geeigneten Transformation T gleichbedeutend mit der estimmung
Differentialgleichungen für Ingenieure WS 06/07
Differentialgleichungen für Ingenieure WS 06/07 5. Vorlesung, korrigierte Fassung Michael Karow Themen heute:. Gewöhnliche Lineare Differentialgleichungen. Ordnung mit konstanten Koeffizienten (a) Die
1 Ableitungen. Definition: Eine Kurve ist eine Abbildung γ : I R R n, γ besteht also aus seinen Komponentenfunktionen. a 1 + tx 1. eine Kurve.
1 Ableitungen Definition: Eine Kurve ist eine Abbildung γ : I R R n, γ besteht also aus seinen Komponentenfunktionen γ 1 (t) γ(t) = γ n (t) Bild(γ) = {γ(t) t I} heißt auch die Spur der Kurve Beispiel:1)
Definitionen. Merkblatt lineare Algebra. affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht
Seite 1 Definitionen affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht ähnliche Matrizen Matrizen, die das gleiche charakteristische Polynom haben
Bifurkationstheorie. 1. Verzweigungen stationärer Zustände
Bifurkationstheorie 1. Verzweigungen stationärer Zustände Die Lage, Anzahl und Stabilität der stationären Zustände von nichtlinearen Systemen hängt in der Regel noch von bestimmten Systemparametern ab.