Lösungsvorschläge zu ausgewählten Übungsaufgaben aus Storch/Wiebe: Lehrbuch der Mathematik Band 1, 3.Aufl. (Version 2010), Kapitel 6
|
|
|
- Siegfried Gerhardt
- vor 7 Jahren
- Abrufe
Transkript
1 Lösungsvorschläge zu ausgewählen Übungsaufgaben aus Sorch/Wiebe: Lehrbuch der Mahemaik Band, 3.Aufl. Version, Kapiel 6 6 Sammfunkionen und Inegrale Abschni 6.A, Variane zu Aufg. 5, p : Man gebe Sammfunkionen der folgenden raionalen Funkionen an, deren Parialbruchzerlegungen bereis in den Lösungen zu Abschni.B. besimm wurden , , Lösung: Uner Verwendung der bereis berechneen Parialbruchzerlegungen erhäl man: d + + d + d + d d Abschni 6.A, Variane zu Aufg. 5, p : ln 4 ln +, d + d d + d ln + ln + + arcan, d d + + d + + d +. + d + + d + ln ln + + arcan. + Man gebe eine Sammfunkion an zu +. Lösung: Wir verwenden Parialbruchzerlegung und machen dazu den Ansaz: + + a + + b + + c a+ + b + c+ + a+c + a+b+ c + a b+c + Der Vergleich der Koeffizienen von, und in den Zählern dieser Brüche liefer die Bedingungsgleichungen a+ c, a+ b+ c, a b+ c für a, b, und c, aus denen wir a 3, b, c errechnen. Es gil also: d 3 + d + d + 3 d 3 ln ln ln +..
2 Sorch/Wiebe, Band, Kapiel 6 Abschni 6.B, Teil von Aufg., p : Man berechne Sammfunkionen zu den folgenden Funkionen jeweils dor, wo sie auf R definier sind : sin, sin, cos, cos, Lösung: Parielle Inegraion liefer ln, arcan, arcsin, e sin, sin + cos, Mi der Subsiuion u, du d erhäl man +, sin d cos + lnln a, a, b R, a b. b, + ln, cos d cos + sin. sin d sin u du cos u cos. ln ln ln Parielle Inegraion liefer d ln d ln ln d, also d ln, ln d ln. Man häe hier auch die Subsiuion u ln, du d verwenden können: ln d u du u ln. Indem man zunächs parielle Inegraion verwende und dann u +, d.h. du d, subsiuier, sieh man: arcan d arcan d arcan + d arcan du u arcan ln u arcan ln +. Indem man zunächs parielle Inegraion verwende und dann u, d.h. du d, subsiuier, sieh man wegen arcsin / : du arcsin d arcsin d arcsin d arcsin + u arcsin + u arcsin +. Zweimalige parielle Inegraion bei der e jeweils inegrier und sin bzw. cos differenzier wird liefer e sin d e sin e cos d e sin e cos e sin d. Indem man das Inegral e sin d auf die linke Seie bring, folger man daraus e sin d e sin e cos e sin cos. Mi der Subsiuion u ln, du / d, e u und dann parieller Inegraion erhäl man: lnln d ln u du u ln u u ln lnln ln.
3 Sorch/Wiebe, Band, Kapiel 6 3 Mi der Subsiuion u + ln, du / d erhäl man d + ln du ln u ln + ln. u Indem wir die Subsiuion u : sin, also du cos d, verwenden, erhalen wir aus Inegral über eine raionale Funkion: cos cos d cos d cos sin d ln +u ln u ln +u u du u du du +u + u + sin ln sin + sin ln cos ln cos + sin cos d ein Mi den Halbwinkelformeln sin sin cos und sin + cos sowie an π und dem 4 Addiionsheorem des Tangens aus.e, Aufg. 9 ergib sich daraus cos d + sin ln sin ln sin + cos + sin cos sin + cos sin cos sin ln + cos cos sin ln sin + cos cos sin ln an + an ln an + an π 4 an an π ln an + π. 4 4 Indem man zunächs u, d.h. u, u du d subsiuier und dann pariell inegrier, sieh man cos d u cos u du u sin u sin u du u sin u+cos u sin + cos.. Indem wir die Subsiuion u : an, also arcan u, d du/+u, mi u +u an + an cos sin cos sin + cos, cos u +u an + an cos sin sin sin + sin cos verwenden, erhalen wir aus d ein Inegral über eine raionale Funkion: sin + cos sin + cos d du du u +u + u +u +u u u + du u du ln u ln u + u + ln u u + ln an + an Mi dem Addiionsheorem von Tangens aus.e, Aufg. 9 ergib sich an π 4 an π an π 8 8 an π, 8 also an π 8 + an π 8, d.h. an π 8 / + wegen an π >, und ferner 8 sin + cos d ln an + an ln an π + 8 an + an π 8 an an π 8 ln an π 8 + ln an + an π 8 an an π ln an π ln an + π. 8
4 4 Sorch/Wiebe, Band, Kapiel 6 Alernaiv kann man das berachee Inegral auch mi Hilfe von sin π 4 cos π 4 / auf das oben berechnee Inegral über / cos zurückführen: d sin + cos d sin sin π 4 + cos cos π 4 ln an π/4 + π 4 cos π 4 d ln an + π 8 Die beiden berechneen Sammfunkionen unerscheiden sich nur um die addiive Konsane ln an π 8.. Wir verwenden zunächs die Subsiuion u +, u u, also + 4 +, u + u + 4, d.h. d u u du, dann parielle Inegraion u + 4 und schließlich die Subsiuion u sinh, du cosh d : + d u u u du u + 3 u3 u u u + 4 du 4 3 u3 u u u u Arsinh u Arsinh Arsinh +. a Indem man die ganze Wurzel subsiuier, also u b, u b a, d.h. u b a u, sez mi d a bu du und dann Parialbruchzerlegung mach, sieh man u a a bu b d du a b du u u + du du u u+ + du u+ a b ln u u+ u a b ln u u u+ u+ u a b a b a b ln a b a b + a b a b a b ln + a b Sign b a + b a b a b ln a b + a b Sign b a b a b ln + a b Sign b. a b Dabei wurde benuz, dassa undb> gelen muss oder abera undb<, dami dieausgangsfunkion definier is. In jedem Fall gil dann a b a b. Schließlich is auch die Funkion a b ln a b + a b Sign b, die sich von dem berechneen Inegral nur a um eine addiive Konsane unerscheide, eine Sammfunkion zu b.
5 Sorch/Wiebe, Band, Kapiel 6 5 Abschni 6.B, Variane zu Aufg., p : Man berechne Sammfunkionen zu den folgenden Funkionen jeweils dor, wo sie auf R definier sind : sinh, sinh, ln, cos 3, cos 4, e cos e, sin 3, cos 3, sin cos 3, cosh, cosh sin sinh, cosh sin, sin ln, ln, +,, +, Lösung: Mi parieller Inegraion erhäl man, +, sin + cos, + 3 cos. sinh d cosh +, sin cos, ln, +, ln 4 cosh d cosh sinh., Die Subsiuion u, du d liefer sinh d sinh u du cosh u cosh. Parielle Inegraion liefer ln d ln d ln d ln 4 ln. Uner Verwendung von cos sin sieh man mi der Subsiuion u sin, du cos d : cos 3 d cos sin d u du u 3 u3 sin 3 sin3. Parielle Inegraion liefer unerverwendung von cos sin und cos d + sin cos : cos 4 d sin cos 3 3 sin cos sin d sin cos cos d 3 cos 4 d, also 4 cos 4 d sin cos sin cos, cos 4 d 4 sin cos sin cos. 8 Mi der Subsiuion u e, du e d sieh man e cos e d cos u du sin u sin e. Durch parielle Inegraion führ man berechnee Inegral über / cos zurück: cos 3 d cos cos d cos 3 sin cos + d cos 3 mi Hilfe von an cos d an cos an sin cos d cos sin +sin cos + ln cos ; auf das bereis weier ober d sin cos cos d, cos 3 d cos 3 sin cos + ln +sin cos. also Die Subsiuion u cos, du sin liefer Die vorsehende Subsiuion liefer ferner sin du cos 3 d u 3 u cos. sin d cos du u u cos.
6 6 Sorch/Wiebe, Band, Kapiel 6 Indem man zunächs u 3, d.h. u 3, 3u du d, subsiuier und dann zweimal pariell inegrier, sieh man sin 3 d 3u sin u du 3u cos u + 6 u cos u du 3u cos u + 6u sin u + 6 cos u 3 3 cos sin 3. Indem man zunächs u, d.h. u, u du d, subsiuier und dann zweimal pariell inegrier, sieh man cosh u cosh u du u sinh u 4 u sinh u du u sinh u 4u cosh u + 4 cosh u du u sinh u 4u cosh u + 4 sinh u sinh 4 cosh + 4 sinh. Mi der Subsiuion u sinh, du cosh d sieh man: cosh sin sinh d sin u du cos u cos sinh. Zweimalige parielle Inegraion liefer cosh sin d sinh sin sinh cos d sinh sin cosh cos also cosh sin d sinh sin cosh cos. cosh sin d, Indem man u ln, d.h. e u, e u du d, subsiuier, führ man das folgende Inegral auf das weier oben berechnee Inegral über e u sin u zurück: sin ln d e u sin u du eu sin u cos u sin ln cos ln. Parielle Inegraion liefer ln d d ln + ln. Parielle Inegraion liefer ebenfalls ln d d ln ln 4 ln. Uner Verwendung der Subsiuion u ln, du / d erhäl man ln 4 u 4 du 5 u5 5 ln 5. Übrigens könne man hier auch parielle Inegraion verwenden, wobei / inegrier und ln 4 differenzier wird. Das Ergebnis folg dann aus der Gleichung ln 4 d ln 5 4 ln ln 3 d, d. h. 5 ln 4 d ln 5. Mi der Subsiuion u ln, du / d, e u und dann parieller Inegraion erhäl man: ln u d e du ue u du ue u + e u du e u +u e ln +ln u ln. Übrigens könne man hier auch direk parielle Inegraion verwenden, wobei / inegrier und ln differenzier wird: ln d ln + ln. Mi der Subsiuion sinh,
7 Sorch/Wiebe, Band, Kapiel 6 7 d cosh, Arsinh bekomm man wegen cosh sinh und cosh, also cosh +sinh +, und mi Hilfe der nachfolgenden Subsiuion u cosh, du sinh : + d cosh sinh + sinh ln cosh cosh + ln sinh du sinh cosh du u ln u u+ Mi der Subsiuion sin, d cos, arcsin bekomm man wegen sin cos sin d cos du sin cos cos sin arcsin, wobei wir sin mi Hilfe parieller Inegraion aus sin sin cos + cos sin cos + sin sin cos sin berechnen. Die Subsiuion sinh, d cosh ergib wegen cosh sinh nach parieller Inegraion: + d cosh cosh sinh sinh cosh sinh + cosh, d.h. + cosh cosh sinh, und somi d cosh + Arsinh. Die Subsiuion cosh, d sinh ergib wegen cosh sinh nach parieller Inegraion: d sinh sinh cosh cosh sinh cosh + sinh, d.h. sinh sinh cosh, und somi d sinh Arcosh. Die Subsiuion sinh, d cosh ergib wegen cosh sinh nach parieller Inegraion: + cosh d sinh cosh sinh + + d Arsinh. Die Subsiuion u +, d.h. u +, + u + und u +, schließlich u 4u, d du, liefer mi nachfolgender parieller Inegraion: +u + d +u u u +u du u + + arcan +u +u + arcan u du +u arcan u +. Die Subsiuion u +, u +, u, u 4 u +, d 4u 3 4u du liefer + d u 4u 3 4u du 4u 4 4u du 4 5 u5 4 3 u3 4 5 u3 u
8 8 Sorch/Wiebe, Band, Kapiel 6 Wir verwenden zur Berechnung einer Sammfunkion zu /sin + cos die Subsiuion u an, also arcan u, d du/+u, mi u +u an + an u +u an + an cos sin sin + cos cos sin sin + cos und erhalen ein Inegral über eine raionale Funkion: d sin + cos du u +u + u +u +u ln u ln u 5 ln 5 cos cos, sin sin du u u 5 du u du u 5 u + 5 u 5 ln an an. 5 Wir verwenden wieder die Subsiuion u an, also arcan u, d du/+u, und erhalen ein Inegral über eine raionale Funkion: + 3 cos d du du u + 3 +u +u u u+ u+ du u du ln u+ ln u ln u+ u ln an + an. Abschni 6.B, Variane zu Aufg., p : Man berechne für m, n N die folgenden besimmen Inegrale: e ln d, e e ln ln d, + n d, n d, π sin m cos n, π sin m sin n, π cos m cos n. Lösung: Die Subsiuion u ln, du d/, mi u ln und ue ln e liefer: e ln d ue u u du 3 u3 3. Die Subsiuion u ln, du d/ mi ue ln e und ue ln e liefer: e e ln ln d ue ue ln u du u ln u u ln.
9 Sorch/Wiebe, Band, Kapiel 6 9 Die Subsiuion u +, du d, u liefer wegen u und u : + n u n u du u n u n+ du un+ n+ un+ u n+ u n+ n+ n+ n+ n+ + n+ n+ n 3 n+n+. Mi parieller Inegraion liefe die Rechnung übrigens folgendermaßen: + n +n+ n+ + + n+ n+ n+ + +n+ n+n+ n+ + n+ n+n+ n+n+ n+ n 3 n+n+. Mi Hilfe der Subsiuion u u, du d erhalen wir wegen u, u : n d u u n du u n u n+ +u n+ du un+ n+ un+ n+ + un+3 n+ 3 n+ n+ + n+ 3 n+n+ n+ 3. Mi zweimaliger parieller Inegraion liefe die Rechnung übrigens folgendermaßen: n n+ + n+ + n+ n+ n+ n+n+ n+ n+n+ n+3 n+n+n+3 + n+n+n+3. Mi sin m cos n sin m cos n + cos m sin n + sin m cos n cos m sin n sin m+n + sin m n bekomm man bei m n : π sin m cos n π sin m+n + π sin m n m+n cos m+n π m n cos m n π. Bei m n is sin m n und bei m n auch sin m+n. Das Ergebnis is dann in beiden Fällen auch gleich. Das Addiionsheorem sin m sin n cos m cos n +sin m sin n cos m cos n sin m sin n cos m n cos m+n liefer bei m n : π sin m sin n π cos m n π cos m+n m n sin m n π m+n sin m+n π.
10 Sorch/Wiebe, Band, Kapiel 6 Bei m n is cos m n und oben is das erse Inegral gleich π, während das zweie Inegral nach wie vor verschwinde; das Ergebnis is dann gleich π. Bei m n is auch cos m+n und beide Inegrale haben den Wer π; das Ergebnis is dann π. Das Addiionsheorem cos m cos n cos m+n + cos m n liefer bei m n π cos m cos n π cos m+n + π cos m n m+n sin m+n π + m n sin m n π +. Bei m n is cos m n und oben is der zweie Summand gleich π, während der erse Summand nach wie vor verschwinde; das Ergebnis is dann gleich π. Bei m n is auch cos m+ n und beide Summanden haben den Wer π; das Ergebnis is dann π. Auch die drei lezen Inegrale ließen sich durch zweimalige parielle Inegraion berechnen. Abschni 6.B, Aufg. 3, p : π/ π/ b Die Funkion f : [, ] K sei seig. Dann gil f sin f cos π π/ π/ f sin. Beweis: Die Subsiuion u π, du, π u liefer wegen sin π u cos u: π/ f sin f π/ sin π u du f π/ sin π u du f cos u du. Die Subsiuion u π, du, π u liefer wegen sin π u sin u: π/ π/ f sin f sin π u du π π/ π/ π π f sin π u du f sin u du Abschni 6.B, Aufg. 3, p : Für n N sei D n : an n, < π/. a Es is D :, D : ln cos und nd n+ an n nd n, n. b Für d n : D n π/4 is lim d n. n c Für m N is d m m m π 4 k, d m+ m ln k + k d Aus b und c folgere man noch einmal Beweis: a Offenbar is D D k k k + π 4 und k m k k ln. k k. k. Wegen ln cos an und ln cos ln is an ln cos für <π/. Ferner gil wegen an +an : nd n+ + nd n n an n+ + an n n an n an + an n ann.
11 Sorch/Wiebe, Band, Kapiel 6 b Da der Tangens im Inervall ], π/4] posiiv is, sind alle d n. Wegen anπ/4 is π D n+ dn+ 4 n D π n 4 n d n n. Es folg lim d n. n Bemerkung: Dies ergib sich auch aus dem folgenden allgemeinen Resula: Is f : [a, b] C seig mi b f < bis auf endlich viele Sellen in [a, b], so is lim n a f n. Zum Beweis können wir wegen b a f n b a f n annehmen, dass die Were von f in R + liegen. Ferner genüg es dann den Fall zu berachen, dass f nur an einer Selle c [a, b] den Wer ha. Sei dann ε > vorgegeben. Wir wählen ein Inervall posiiver Länge ε um c in [a, b]. Die Were von f auf dem Komplemen dieses Inervalls sind dann alle kleiner als C mi fesem C < und es gib ein n N mi f n ε/b a auf diesem Koplemen. Für n n gil dann b a f n ε + ε/b a b a ε. Für eine Verallgemeinerung siehe Band 3, 4.D, Aufg. 5. cwir verwenden Indukion überm N. Für m sind die angegebenen Formeln richig wegend : π 4 und d : ln. Der Schluss von m auf m+ ergib sich mi der Formel aus a und der Indukionsvoraussezung aus d m+ m+ d m m m+ m π 4 k m+ π k+ 4 m k und k+ k k d m+3 m+ d m+ m+ m ln m k m+ ln m+ k. k k d Wegen lim n d n folg aus der ersen Formel sofor der zweien Formel k k k lim m m k k k k k k k m k + lim k m k + π 4 k sowie aus ln ln. Abschni 6.B, Aufg. 6, p : Man gebe die Poenzreihenenwicklungen um an für die Funkionen ln + /, ln / und arcan / und gewinne dami ln + arcan n n π, n n ln n n n+ 6 m 6m : G. m n π 6, Der Wer G, des drien Inegrals heiß die C a a l a n s c h e K o n s a n e. Lösung: Die Logarihmusreihen ln + n n n und ln n jeweils für n < liefern n ln+ n n n n n n π und n n π 6 ln+ n n n n n und ln n n n, vgl. Beispiel 4.E.3, bekomm man n n. Mi den Summenformeln n n n n n n π, n
12 Sorch/Wiebe, Band, Kapiel 6 ln n n n n n Mi der Reihe des Arcusangens erhäl man arcan n n n n π 6. n n für < und folglich n+ arcan n n n n n+ n n n+ n n+ n+ n n+ m n 4m 4m+ m 6m 6m. Abschni 6.B, Variane zu Aufg. 6, p : Man berechne Aranh. Lösung: Mi Hilfe der Poenzreihenenwicklung von Aranh aus 4.B, Aufg. 6c bekomm man Aranh n n n+ n n+ n Abschni 6.B, Zusazaufgabe zu Aufg. 6, p : n Man zeige für die Caalansche Konsane G aus Aufg. 6 die Formeln G π 8 m Man folgere die Summenformeln und G 4m+3 m Beweis: Wie in den beiden vorsehenden Aufgaben gezeig, gil G arcan n ln + n π 6 4 π 6 π 8. ln τ τ + dτ. 4m+3 π 6 G, 4m+ π 6 + G. n n n+ π 8 n+ n m m m 4m+ 4m+3 4m+ + 4m+3 Differenzbildung liefer G π 8, woraus auch die angegebenen Summenformeln 4m+3 m sofor folgen. Mi parieller Inegraion erhäl man ferner G wegen arcan ln π 4 arcan arcan lim arcan ln lim arcan ln ln + und da man mi der Regel von de l Hôpial sieh: lim ln / lim + lim. ln + / / lim.,
13 Sorch/Wiebe, Band, Kapiel 6 3 Die Subsiuion /τ, /τ dτ liefer die zweie Inegraldarsellung. 6.C, Aufg. 3, p : a Der Flächeninhal des links in der folgenden Zeichnung skizzieren Einheiskreissekors {z C z, Arg z } mi dem Öffnungswinkel is / für π. b Der Flächeninhal des rechs in der folgenden Zeichnung skizzieren Einheishyperbelsekors zum Parameer is / für. c Der Flächeninhal der Ellipse {, y R /a + y/b } mi Halbachsen der Länge a und b is πab für a, b >. Beweis: a Is F der Flächeninhal des Dreiecks, das durch die -Achse, die Gerade durch den Nullpunk und cos, sin sowie die Parallele zur y-achse durch den Punk cos, begrenz wird, und is F A der Inhal der Fläche, die von dieser Parallelen, dem Kreis und der -Achse begrenz wird, so sieh man mi der Subsiuion cos τ, d sin τ dτ, cos und der durch parielle Inegraion zu erhalenden Formel sin τ dτ τ sin τ cos τ, dass der gesuche Flächeninhal folgenden Wer ha: F + F A cos sin cos sin cos + d + τ sin τ cos τ τ cos sin τ. + sin τ dτ b Is F der Flächeninhal des Dreiecks, das durch die -Achse, die Gerade durch den Nullpunk und cosh, sinh sowie die Parallele zur y-achse durch den Punk cosh, begrenz wird, und is F A der Inhal der Fläche, die von dieser Parallelen, der Hyperbel und der -Achse begrenz wird, so sieh man mi der Subsiuion cosh τ, d sinh τ dτ, cosh und der durch parielle Inegraion zu erhalenden Formel sinh τ dτ sinh τ cosh τ τ, dass der gesuche Flächeninhal folgenden Wer ha: F F A cosh sinh cosh sinh cosh d cosh sinh sinh τ cosh τ τ τ τ. sinh τ dτ c Die Gleichung der Ellipse is y ± b a a. Mi der Subsiuion a sin τ, d a cos τ dτ, a a sin π/, a a sin π/, und der durch parielle Inegraion zu erhalenden Formel cos τ dτ τ + sin τ cos τ sieh man, dass der gesuche Flächeninhal folgenden Wer ha: b a a a a d b a π/ π/ ab a a sin τ a cos τ dτ ab τ + sin τ cos τ τπ/ τ π/ πab. π/ π/ cos τ dτ
14 4 Sorch/Wiebe, Band, Kapiel 6 7 Uneigenliche Inegrale Abschni 7.A, Teil von Aufg., p : Man zeige, dass die folgenden uneigenlichen Inegrale eisieren und die angegebenen Were haben: + π ; + π ; π/ ; π an + π 4 π/ an ; + 4 ; + π ; ; e ; ln ; e e + 4 ; e a sin b b, falls a, b R, a > ; a + b Lösung: Wegen arcan /+ gil + arcan lim arcan lim arcan π π π, Da Nullselle von + 3 is, liefer Division mi Res die Produkdarsellung Wie in.b, Aufg. 3 berechnen wir die Parialbruchzerlegung und bekommen ln + 6 ln ln ln ln / 3 / lim arcan τ arcan π τ π 6 wegen anπ/6 sinπ/6 / cosπ/6 / 3 / ln + + arcan 3 3 π 3 3 Wie in.a, Aufg. berechnen wir die Fakorisierung und dann wie in.b, Aufg. 3 die beiden Parialbruchzerlegungen Dami bekommen wir: und
15 Sorch/Wiebe, Band, Kapiel ln + + ln ln π ln ln + + π + π 4 π arcan + arcan + + π, + 4 ln 4 + ln ln π ln ln + + π + π 4 π arcan + arcan + π, Bemerkung: Die Formelsammlungen von Bronsein-Semendjajew und Råde-Wesergren Springers Mahemaische Formeln geben für /+ 4 die Sammfunkion 4 ln arcan mi der obiges Inegral absurderweise wäre. Diese ha für ± die richige Ableiung, aber in eine Sprungselle der Höhe π/. Sie enseh aus der hier benuzen Sammfunkion durch falsches Anwenden des Addiionsheorems des Arcusangens. Ensprechendes gil für die Sammfunkion zu /+ 4. Teubners Taschenbuch der Mahemaik gib die richigen Sammfunkionen an. Die Subsiuion u, du liefer du u du u. u Die Subsiuion u, du liefer du u du u u.
16 6 Sorch/Wiebe, Band, Kapiel 6 Mi Hilfe der Subsiuion u an, arcan u, Inegrale auf bereis oben berechnee Inegrale zurückführen: π/ Es is u an +u du π 4 π, e e e. π/ u du lassen sich die beiden nächsen +u4 an Mi parieller Inegraion und der Regel von de l Hôpial sieh man: ln du +u 4 π π. ln ln ln lim ln lim ln / / lim + lim /. Mi der Subsiuion u e, du e, e sieh man e e + du u+ / u+ 4. Zweimalige parielle Inegraion liefer also + b a e a sin b a e a sin b b a e a cos b e a sin b b a e a cos b + b a b a Abschni 7.A, Variane zu Aufg., p : Man berechne die folgenden uneigenlichen Inegrale: + 3, cosh, π/ sin 3 cos, 3 + 8, e a cos b b a e a sin b, b a b a, + cosh, π 3 + 8, + 3 cos, + e,, e +, e a cos b e a sin b a + b. b e +, + arcan, e.
17 Sorch/Wiebe, Band, Kapiel 6 7 Lösung: Wie oben erhalen wir die Produkdarsellung und berechnen wie in.b, Aufg. 3 die Parialbruchzerlegung Dies liefer ln ln + 6 ln ln ln / 3 / lim arcan τ arcan π τ π 6 wegen anπ/6 sinπ/6 / cosπ/6 / 3 / ln + + arcan π 3 3 Mi Hilfe der Subsiuion u 4, du 4 3 und u, u, lim u sieh man arcan u du 4 u + 4 arcan u π 4 π π 4 4 π 6. π 4 π 6, Die Subsiuion u, u, du liefer u u du u u du du u u du u 3 u Mi Hilfe der Subsiuion u e +, e u, ln u, lim u erhäl man e + du u u u+ du u ln u+ u u und u, ln +. Indem wir die Subsiuion u : sinh, du cosh mi sinh, lim cosh verwenden, erhalen wir aus ein Inegral über eine raionale Funkion: cosh cosh cosh cosh cosh + sinh du +u arcan u π π.
18 8 Sorch/Wiebe, Band, Kapiel 6 Wegen coh / sinh und cosh sinh gil + cosh cosh sinh cosh cosh cosh sinh sinh cosh sinh sinh + sinh cosh + lim cosh sinh e e e + e +. Zweimalige parielle Inegraion liefer + e e Die Subsiuion u arcan, du + e + arcan e + e e liefer wegen arcanπ/4, lim + arcan u : u π/ π/ π/4 du u ln u π/ π/4 ln π ln π 4 ln π/ π/4 ln. Die Subsiuion u cos, du sin liefer wegen sin cos und sin π/, cos : π/ sin 3 cos u du u du u u 3/ du u 5 u5/ Mi parieller Inegraion, bei der cos im ersen Inegral inegrier und im zweien Inegral differenzier wird, sieh man: + cos cos + 3 cos 3 sin + sin cos sin sin cos, π + 3 cos sin cos cos π π π π. Bemerkung: Die beiden nächsen Inergale sind Spezialfälle von 7.B, Aufg. 4. Zur Berechnung von e + erweiern wir zunächs mi e, verwenden dann die Summenformel für die geomerische Reihe und die Verauschung von Inegraion und Summaion die möglich is, da e für ln eine konvergene Majorane für die Parialsummen der Reihe liefer. Anschließend benuzen wir parielle Inegraion und die Seigkei der gleichmäßig konvergenen Reihe k k+ + e k+ im k+ k Punk und schließlich die Summenformel aus Beispiel 4.E.3 :
19 Sorch/Wiebe, Band, Kapiel 6 9 lim > lim > e + k k k e +e lim > e k+ lim > e +e lim > k e k+ k k k+ e k+ k k k+ e k+ + k+ e k+ k + k+ e k+ k k+ π. Zur Berechnung von e erweiern wir zunächs mi e, verwenden dann die Summenformel für die geomerische Reihe und die Verauschung von Inegraion und Summaion die möglich is, da e für ln eine konvergene Majorane für die Parialsummen der Reihe liefer. Anschließend benuzen wir parielle Inegraion und die Seigkei der gleichmäßig konvergenen Reihe k+ + e k+ k+ k im Punk und schließlich die Summenformel aus Beispiel 4.E.3 : lim > lim > e k k e e lim > e k+ lim > k+ e k+ + k e e lim > k+ e k+ k+ e k+ k k + e k+ k+ e k+ k+ π 6. Abschni 7.A, Teil von Aufg., p : Man enscheide, ob die folgenden Inegrale konvergieren: + 3 +, Lösung: Für alle gil und folglich +. Da 3 + gil dies nach dem Majoranenkrierium auch für π/ an. nich konvergier, Die Subsiuion u cos, du sin, liefer π/ an π/ sin cos du u ln u. Abschni 7.A, Variane zu Aufg., p : Man enscheide, ob die folgenden Inegrale konvergieren: π/ cos und cosh.
20 Sorch/Wiebe, Band, Kapiel 6 + cos Lösung: Es gil cos sin sin + cos sin co sin cos +, sin d.h. cosh cos + sin π/ + konvergier nich. Mi der Subsiuion u e, du e, mi e, e e, sieh man wegen cosh e +e, dass das zweie Inegral ebenfalls nich konvergier: cosh e e e e du u u Abschni 7.A, Aufg. 6, p : f : R + R sei seig und monoon. Eisier e du u u u e. f, so is lim f. du u u+ Beweis: Nach dem Cauchy-Krierium gib es zu ε> ein mi + f < ε. Wegen der Seigkei von f gib es dann nach dem Mielwersaz der Inegralrechnung ein c zwischen und + mi f c < ε. Da f monoon is, muss dann lim f sein. Abschni 7.A, Teil von Aufg. 9, p : Mi 7.A.3 ese man die folgenden Reihen auf Konvergenz bzw. Divergenz: n3 n ln n lnln n ; n3 ln n ln n. Lösung: Da die Funkionen f / ln ln und / ln ln für 3 monoon fallend sind, können wir das Inegralkrierium 7.A.3 verwenden und haben die zugehörigen Inegrale auf Konvergenz zu esen. Die Subsiuion u ln, du /, e u e du, liefer u du. Für u e gil ln u, 3 ln ln ln 3 u u also e u e u ln u u u e und somi u u u e u e. Daher besiz das Inegral u du die konvergene Majorane ln 3 u u e u du e u du. ln 3 Die Subsiuion u ln, du /, e u du, gefolg von der Subsiuion ln u, d du/u, liefer ferner ln lnln du u ln u d ln. lnln 3 3 ln 3 lnln 3 Die erse Reihe is also konvergen, die zweie divergen. Abschni 7.A, Aufg., p : Für n N berechne man ln n. Lösung: Durch Indukion über n N zeigen wir zunächs lim ln n. Der Indukionsanfang n is rivial, und beim Schluss von n auf n+ verwenden wir die Regel von de l Hôpial: lim ln n+ lim ln n+ / lim n+ln n / / n+ lim ln n.
21 Sorch/Wiebe, Band, Kapiel 6 Durch Indukion über n N beweisen wir dami ln n n n!. Der Indukionsanfang n is bei 7.A, Aufg. bereis behandel worden. Der Schluss von n auf n+ folg durch parielle Inegraion: ln n+ ln n+ ln n+ n+ / ln n lim ln n+ n+ ln n n+ n n! n+ n+!. Abschni 7.A, Aufg., p : g sin und g cos eisieren für jede seige und monoone Funkion g : R + R mi lim g. Es is g sin π g sin g. Beweis: Da g monoon is und g für gegen geh, ha g in ganz R + dasselbe Vorzeichen und g is monoon fallend. Da das Vorzeichen von sin in den Inervallen [kπ, k+π] abwechselnd überall k+π posiiv bzw. überall negaiv is, sind somi auch die Inegrale I k : g sin abwechselnd bzw.. Nach dem verallgemeineren Mielwersaz der Inegralrechnung gil wegen der Monoonie von g k+π gkπ gkπ sin I k kπ k+π kπ g sin k+π kπ kπ gk+π sin gk+π, und die I k bilden eine monoon fallende Nullfolge. Das Leibniz-Krierium liefer nun die Konvergenz der alernierenden Reihe k I k gegen einen Grenzwer I mi I I g. Wir zeigen schließlich, dass auch das uneigenliche Inegral g sin gegen I konvergier. Sei dazu ε > vorgegeben. Dann gib es ein n mi k+π g sin I k I k I ε/ für alle k n. Wegen der Voraussezungen über g gib es ein S > mi g ε/π für alle S. Is nun Ma n π, S und is k : [/π], d.h. k n und k π < k + π, so folg mi der Dreiecksungleichung und dem Mielwersaz der Inegralrechnung g sin I g sin k +π k +π g sin I + k +π k +π g sin I g sin ε + k +π ε π k ε + πε π ε. Die Aussage über das ensprechende Kosinusinegral wird analog bewiesen oder durch die Subsiuion z + π auf ein Sinusinegral zurückgeführ.
22 Sorch/Wiebe, Band, Kapiel 6 Abschni 7.A, Aufg., p : Für alle z C ha Gz : Für z ai, a R, ergib sich e +z den Wer π. Beweis: Nach Beispiel 7.A. is G e cos a e a /4 π. e π. Wenn wir zeigen, dass G differenzierbar is mi G z für alle z C, so folg die erse Behaupung, da G nach Korollar 4.A.6 dann konsan is. Für z ai/, a R, ergib sich dann e ai/ e a /4+ai e e a /4 cos a i sin a, also π e ai/ d.h. e cos a e a /4 π. e e a /4 cos a i e e a /4 sin a e e a /4 cos a, Sei nun R R + beliebig. Es genüg, die Differenzierbarkeisaussage über G auf dem offenen Kreis E : {z C z < R} zu zeigen. Sezen wir z + iy,, y R, so gil für R, z E die Abschäzung Re+z Re++ iy + + y + + y z R, also e +z e Re+z e R e / und somi +z e +z e R +R e /. Auf E R folg z e +z +z e +z e R +R e /. Mi 7.A. gil e R +R e / 4e R 4e R e / e / + e R R e / + er R π e R R π + <. Daher is g : e R + R e / eine inegrierbare Majorane zu allen Funkionen z e +z, z E. Wir können folglich 7.A.9 anwenden und erhalen G z d dz e +z z e +z +z e +z e +z. Abschni 7.B, Aufg. a, p : Sei C mi Re >. Dann gil Ŵ ln. Beweis: Wir subsiuieren τ ln, e τ, e τ dτ und erhalen: ln τ e τ dτ τ e τ dτ Ŵ.
23 Sorch/Wiebe, Band, Kapiel 6 3 Abschni 7.B, Aufg. a, p : Seien, z C, z, und µ R +. Dann gil e zµ Ŵ/µ µz /µ. Beweis: Mi der Subsiuion τ z µ, also τ /µ, τ /µ z µ z /µ e zµ τ /µ e τ τ /µ dτ z µ z /µ µ z /µ dτ, erhäl man τ /µ e τ dτ µ z Ŵ. /µ µ
24 4 Sorch/Wiebe, Band, Kapiel 6 8 Approimaion von Inegralen Abschni 8.B, Zusazaufgabe, p : Man beweise ln e + ln. Dies is das Keks-Problem Nr. 7 der Uni Würzburg, vgl. hp:// keks. Beweis: Wir verwenden zunächs der Reihe nach die Summenformel für die geomerische Reihe, die Verauschung von Inegraion und Summaion die möglich is, da das uneigenliche Inegral über e eine konvergene Majorane is, die Subsiuion u k, die Summenformel k ln, ferner k und erhalen: ln e + ln u e u du Ŵ γ e ln +e k k γ ln + k ln ln u/k k k ln k k k e k+ k e u du. vgl. 7.B.7 sowie k k k k k k ln u e u du e u du ln e k k k ln k k e u du Nach Beispiel 8.B.4 besiz die Riemannsche Zea-Funkion ζs : eine Enwicklung der Form ks k ζs s + γ + c m s m um, woraus sich durch gliedweises Differenzieren ergib: m ζ s s + c m s m m mi geeigneen Koeffizienen c m, c m. Außerdem benuzen wir vgl. 6.A, Aufg. a k k k s k Durch Differenzieren erhalen wir daraus k s k ζs s ζs s s ζs. k k k ln k k s ln s ζs + s ζ s. Uner Verwendung der Poenzreihenenwicklung s e ln s ln s + ln s + folg: k k ln k k lim s ln s ζs + s ζ s lim ln ln s + s ln s + s + γ + + ln s ln s + s + c + lim γ ln ln + s ln + m c m s m γ ln ln
25 Sorch/Wiebe, Band, Kapiel 6 5 mi weieren Koeffizienen c m. Sez man dies oben ein, so bekomm man ln e + γ ln + k k ln k k ln, d.h. ln e + ln. Für die numerischen Berechnungen in den folgenden Aufgaben wurde das Programm Maple benuz. Abschni 8.C, Zusazaufgabe, p : Das Inegral I : e ha den Wer, a Man berechne I durch Rechnen mi Poenzreihen bis auf einen Fehler < 3. b Man berechne I mi der Trapezregel bis auf einen Fehler < 3. c Man berechne I mi der Simpson-Regel bis auf einen Fehler < 5. d Man berechne I uner Verwendung des Romberg-Verfahrens mi mindesens 8 Sellen hiner dem Komma. Lösung: a Da man Poenzreihen im Inneren des Konvergenzkreises gliedweise inegrieren darf, ergib sich I k k k! k k k k k! k k 4 k+ k! k k k+ k! ,7475, wobei der Fehler nach dem Leibniz-Krierium dem Berage nach höchsens gleich dem ersen nich berücksichigen Glied der Reihe is, also 5! 3 < 3 is. b Für f : e is f e, f 4 e, f e. f 3 besiz in [, ] nur die Nullselle, d.h. das globale Maimum M von f in diesem Inervall wird am Rande angenommen. Somi is M das Maimum von f und f, also Ma,,475. Für die Anzahl n der nowendigen Inervalle bei der Trapezregel gil die Abschäzung M 3/ n < 3, d.h. n> /,9. Wir nehmen also n3, h /3, k : k/3, und erhalen I T 3 h f +f + +f +f 3, c Wir schließen an die Lösung von b an. Weiere Ableiungen von f sind f e, f e. f 5 besiz im Inervall [, ] die Nullsellen und, , d.h. das globale Maimum M 4 von f 4 in diesem Inervall is gleich dem Maimum von f 4, f 4 7,35759, f 4, ,4948 also gleich. Für die Anzahl n der nowendigen Doppelinervalle bei der Simpson-Regel gil die Abschäzung M 4 5/ 88n 4 < 5, d.h. n > 4 /88 4,5. Wir nehmen also n 5, h /, k : k/, und erhalen I S 5 h 3 f +4f +f + +f 8 +4f 9 +f, d Das Romberg-Verfahren mi n is durch T m,k 4 k T 4 k m+,k T m,k gegeben, wobei T m, : T m die Were nach dem Trapezverfahren mi m Teilinervallen sind: T, T, T, T 4, T, T,... T m,k T m+k, T m+k, T m+k, T m+,k T m,k
26 6 Sorch/Wiebe, Band, Kapiel 6 In unserem Fall ergib sich der Wer I,746843, da das Romberg-Schema folgende Form ha:, ,73375,747843,74984, , , ,74686,746847,74684, ,746846,746843,746843,746843, ,746844,746843,746843,746843, Abschni 8.C, Zusazaufgabe, p : Mi Hilfe der Subsiuion u, du sieh man I : u + du 4 arcan u 4 arcan 4 π 4 π. a Man berechne I durch Rechnen mi Poenzreihen bis auf einen Fehler < 3. b Man berechne I mi der Trapezregel bis auf einen Fehler < 3. c Man berechne I mi der Simpson-Regel bis auf einen Fehler < 5. d Man berechne I uner Verwendung des Romberg-Verfahrens mi mindesens 8 Sellen hiner dem Komma. Lösung: a Da man Poenzreihen im Inneren des Konvergenzkreises gliedweise inegrieren darf und da die inegriere Reihe in den Punken auf seinem Rand, in denen sie konvergier, nach dem Abelschen Grenzwersaz noch seig is, liefer die Summenformel für die geomerische Reihe I lim < n 8 4 n lim < n n 8 n 4n+ lim < 999 n 4 n+ n 4 n+ 3,49654, n wobei der Fehler nach dem Leibniz-Krierium dem Berage nach n 8 4n+ 4n+ n 4 + < 3 is. b Für f : is f , f , f f besiz in [, ] nur die Nullsellen und,74538, d.h. das globale Maimum M von f in diesem Inervall wird am Rande angenommen oder in, Somi is M das Maimum von f, f, f,74538, also Ma, 8, 5 5. Für die Anzahl n der nowendigen Inervalle bei der Trapezregel gil die Abschäzung M 3/ n < 3, d.h. n> 5/ 45,6. Wir nehmen also n46, h /46, k : k/46, und erhalen I T 46 h f +f + +f 45 +f c Wir schließen an die Lösung von b an. Weiere Ableiungen von f sind f , f f 5 besiz im Inervall [, ] nur die Nullsellen, ,, , d.h. das globale Maimum M 4 von f 4 in diesem Inervall is gleich dem Maimum von f 4, f 4, f 4, , f 4, , also Ma ; 44 ; 3 ; Für die Anzahl n der nowendigen Doppelinervalle bei der Simpson-Regel gil dieabschäzungm 4 5/ 88n 4 < 5, d.h.n> /88,68. Wir nehmen also n, h /4, k : k/4, und erhalen I S h 3 f +4f +f + +f +4f 3 +f 4 3,
27 Sorch/Wiebe, Band, Kapiel 6 7 d Das Romberg-Verfahren mi n is durch T m,k 4 k T 4 k m+,k T m,k gegeben, wobei T m, : T m die Were nach dem Trapezverfahren mi m Teilinervallen sind: T, T, T, T 4, T, T,... T m,k T m+k, T m+k, T m+k, T m+,k T m,k In unserem Fall ergib sich der Wer I 3,459653, da das Romberg-Schema folgende Form ha:,, , , , , , , ,4584 3,4578 3, , , , , , , , , , , , , , , , ,459653
28 8 Sorch/Wiebe, Band, Kapiel 6 9 Einfache Differenzialgleichungen Abschni 9.A, Teil von Aufg., p : Man löse die folgende Differenzialgleichung mi gerennen Variablen: y e y cos. Lösung: Wir suchen ein Lösung y, die der Anfangsbedingung y y für, y R genüg. Da die Funkion e y keine Nullsellen besiz, gib es keine saionären Lösungen. Trennung der Variablen liefer e y y cos, e y e y e y y y y y e y dy cos d sin e y e y + sin sin ;, d.h. y ln e y + sin sin. Abschni 9.A, Variane zu Aufg., p : Man löse die folgenden Differenzialgleichungen mi gerennen Variablen: y y ln y y y sin sin, ; y y sin ; y + +y ; y y ; + ; y y cos ; y y cos. Lösung: Wir suchen jeweils Lösungen y, die der Anfangsbedingung y y für, y R genügen. Die Angabe des jeweiligen genauen Defiionsbereichs überlassen wir dem Leser. Die reche Seie der Differenzialgleichung y y ln y is nur füranfangswere y > und definier. Für y bekomm man die saionäre Lösung y. Bei y is y nirgendwo gleich, da u andernfalls nach Saz 9.A. konsan gleich wäre. Dann haben also ln y und ln y nach dem Zwischenwersaz ses das gleiche Vorzeichen, und Trennung der Variablen liefer y /y ln y /, d.h. für mi > gil: ln y ln ln ln y ln y y y y y dy y ln y ln y ln y, y y /. d ln ln ln ln, Für y ha y y sin die saionäre Lösung y. Bei y liefer Trennung der y Variablen y y sin, dy y y sin d, y + y cos + cos, y cos cos + /y, also y y + cos cos y cos cos +. Für y ha y + +y die saionäre Lösung y. Bei y is y nirgendwo gleich, da u andernfalls nach Saz 9.A. konsan gleich wäre. Dann haben also + y und +y nach dem Zwischenwersaz ses das gleiche Vorzeichen, und Trennung der Variablen liefer: y +y +, y y dy +y +, ln +y ln +y ln +y +y , also y + +y ep
29 Sorch/Wiebe, Band, Kapiel 6 9 Für y ± ha y y die saionären Lösungen y ±. Für y > is die reche Seie der Differenzialgleichung nich definier. Bei y < liefer Trennung der Variablen / y, d.h. arcsin y arcsin y y dy d, y sin arcsin y +. y y Für y ha y y die saionäre Lösung y. + Bei y is y nirgendwo gleich, da y andernfalls nach Saz 9.A. konsan gleich wäre. Dann haben also y und y nach dem Zwischenwersaz ses das gleiche Vorzeichen, und Trennung der Variablen liefer: y /y /+, folglich ln y y y ln y ln y dy y d + ln + ln + + ln +, y y + y +. + Für y ± ha y y cos die saionären Lösungen y ±. Für y > is die reche Seie der Differenzialgleichung nich definier. Bei y < liefer Trennung der Variablen y / y cos und folglich arcsin y arcsin y arcsin y y y y y dy y Die gesuche Lösung is also y sin arcsin y sin + sin. cos d sin sin. Für y ± ha y y cos die saionären Lösungen y ±. Bei y ± is y nirgendwo gleich ±, da y andernfalls nach Saz 9.A. konsan gleich ± wäre. Dann haben also y und y sowie +y und +y nach dem Zwischenwersaz ses das gleiche Vorzeichen, und Trennung der Variablen liefer y / y cos, folglich +y ln y y ln y + ln y + ln +y ln +y +y y y dy y + y y dy +y y +y y y +y e sin sin e sin e sin y dy y, cos d sin sin, +y c y e sin mi c : +y y e sin, y c e sin c e sin +.
30 3 Sorch/Wiebe, Band, Kapiel 6 Abschni 9.A, Teil von Aufg. 3, p : Man löse die homogene Differenzialgleichung y y +y. Lösung: Wir suchen eine Lösung y, die der Anfangsbedingung y y für, y R, genüg. Sei zunächs. Wir ransformieren die Differenzialgleichung durch die Subsiuion u : y/, d.h. u y y y y y +y y y/ +y/ y u +u u u u, +u in eine Differenzialgleichung für u mi gerennen Variablen und Anfangsbedingung u u : y /. Da u u die Nullsellen ± besiz, ha diese bei u ±, d.h. y ±, die saionären Lösungen u ±, d.h. y ±. Bei u ± is u niemals eine dieser Nullsellen von u + u, da u andernfalls nach Saz 9.A. konsan gleich einer davon wäre. Dann haben also u + u und u + u nach dem Zwischenwersaz ses das gleiche Vorzeichen, und Trennung der Variablen liefer für mi > : u u +u du u u d, ln u u u ln ln ln, u ln u + u u + u ln u u ln u u ln ln, u + u c mi c : u + u y + y c, u ± +, c y u ± + ± c +. Wegen y y ± y + y + ± y + y + ± y + is dabei das Vorzeichen Signy + zu wählen, d.h. es folg y + Signy + c +. Man beache, dass der Fall +y nich aufreen kann, da dafür die reche Seie der Differenzialgleichung nich definier is. Auch im Fall liefer die erhalene Funkion die Lösung y + Sign y y + des Anfangswerproblems, wie man leich besäig. Abschni 9.A, Variane zu Aufg. 3, p : Man löse die homogenen Differenzialgleichungen y y + y und y y4 4 y 3. Lösung: Wir suchen jeweils eine Lösung y, die deranfangsbedingung y y für, y R, genüg. Wir ransformieren die Differenzialgleichung y y + y durch die Subsiuion u : y/, d.h. u y y y u, in eine Differenzialgleichung für u mi gerennen Variablen und Anfangsbedingung u u : y /. Bei u >, d.h. y >, is die reche Seie der Differenzialgleichung nich definier. Für u ±, d.h. y ±, ha man die saionären Lösungen u ±, d.h. y ±. Bei u <, d.h. y <, liefer Trennung der Variablen für mi > : u u du d u, arcsin u arcsin u arcsin u u u ln ln, u sin ln + arcsin u sin ln cos arcsin u + cos ln u,
31 Sorch/Wiebe, Band, Kapiel 6 3 u sin ln u + cos ln u, y sin ln y + cos ln y. Wir ransformieren die Differenzialgleichung y y4 4 u y y y y y 3 y y 3 y durch die Subsiuion u : y/, d.h. u u 3 u 4 u 3, in eine Differenzialgleichung für u mi gerennen Variablen und Anfangsbedingung u u : y /. Bei u ±, d.h. y ±, bekomm man die saionären Lösungen u ±, d.h. y ±. Bei u ±, d.h. y ±, is u für kein eine dieser Nullsellen von u 4, da u andernfalls nach Saz 9.A. konsan gleich einer davon wäre. Dann haben also u 4 und u 4 nach dem Zwischenwersaz ses das gleiche Vorzeichen und Trennung der Variablen liefer für mi > : u u u 3 du u 4 d, 4 ln u4 u 4 4 ln u4 u u ln u 4 u 4 4 / u 4, u ± / 4+, y ± 4 y 4/4 4 / 4+ ± 4 y ln ln ln, Die Anfangsbedingung y erforder dabei das Vorzeichen Sign y, d.h. es is y Sign y 4 y Abschni 9.B, Teil von Aufg., p : Man löse die lineare Differenzialgleichung y + y e. Lösung: Wir suchen eine Lösung y, die der Anfangsbedingung y y für, y R, genüg. Die zugehörige homogene lineare Differenzialgleichung y + y ha ϕ ep d e als Lösung mi ϕ. Für die Sörfunkion g : e y ϕ y + g ϕ e y + e e e is die Lösung also e y e + e y e +. Abschni 9.B, Variane zu Aufg., p : Man löse die linearen Differenzialgleichungen y an y sin und y y + cos. Lösung: Wir suchen jeweils eine Lösung y, die deranfangsbedingung y y für, y R, genüg. Die zu y an y sin gehörende homogene lineare Differenzialgleichung y an y ha ϕ ep an d e ln cos +ln cos cos cos cos cos als Lösung mi ϕ, wobei und im selben Definiionsinervall des Tangens, also Inervall der Form ]k π, k+ π [, liegen sollen.
32 3 Sorch/Wiebe, Band, Kapiel 6 Für die Sörfunkion g : sin is die Lösung dann y ϕ y + g ϕ cos + y cos cos cos cos sin cos y cos + y cos cos cos + cos. Die zu y y + cos gehörende homogene lineare Differenzialgleichung y y ha d ϕ ep e ln ln für alle mi > als Lösung mi ϕ. Für die Sörfunkion g : cos is die Lösung dann y ϕ y + g ϕ y + Abschni 9.B, Teil von Aufg., p : cos / Man löse die folgenden Bernoullischen Differenzialgleichungen: y sin + sin. y 3 y + 3 y4, y + y 3 y 3, y y + y 5. Lösung: Wir suchen jeweils eine Lösung y, die deranfangsbedingung y y für, y R, genüg. Im Fall y is y die gesuche Lösung. Sei daher y. Bei y 3 y + 3 y4 handel es sich um eine Bernoullische Differenzialgleichung, die durch die Subsiuion u y 3 in die lineare Differenzialgleichung u 3y y 4 y 3 u + mi der Anfangsbedingung u u : y 3 überführ wird. Die zugehörige homogene lineare Differenzialgleichung u u ha die Lösung ϕ e, die der Anfangsbedingung ϕ genüg. Dann ha das Anfangswerproblem u u +, u u, die Lösung u e u + e e u e + e e u + e + e e u + +. Die gesuche Lösung des Ausgangsproblems is dann y 3 u 3 e y Im Fall y is y die gesuche Lösung von y + y 3 y 3. Sei daher y. Es handel es sich um eine Bernoullische Differenzialgleichung, die durch die Subsiuion u y in die lineare Differenzialgleichung u y y 3 4u 4 3 mi deranfangsbedingungu u : y überführ wird. Die zugehörige homogene lineare Differenzialgleichung u 4u ha die Lösung ϕ e, die der Anfangsbedingung ϕ genüg. Dann ha das Anfangswerproblem u 4u 4 3, u u, die Lösung
33 Sorch/Wiebe, Band, Kapiel 6 33 u e u + e 4 3 e u + e e u + e e e e u + e + e Die gesuche Lösung des Ausgangsproblems is dann y u 4e e e e u + +. e y + +. Im Fall y is y die gesuche Lösung von y y + y 5. Sei daher y. Es handel es sich um eine Bernoullische Differenzialgleichung, die durch die Subsiuion u y 4 in die lineare Differenzialgleichung u 4y y 5 4y 4 4 4u 4 mi der Anfangsbedingung u u : y 4 überführ wird. Die zugehörige homogene lineare Differenzialgleichung u 4u ha die Lösung ϕ e 4+4, die der Anfangsbedingung ϕ genüg. Dann ha das Anfangswerproblem u 4u 4, u u, die Lösung u e 4+4 u + e e 4+4 u e e 4 4 e 4+4 u + e e 4+4 e 4+4 u Die gesuche Lösung des Ausgangsproblems is dann y 4 u 4 e 4+4 u Abschni 9.B, Aufg. 5, p : Sei y f y + g eine lineare Differenzialgleichung erser Ordnung mi den seigen Funkionen f, g : [a, [ K, a R. Es gebe ein c R + mi f c für alle a. a Is g beschränk, so is auch jede Lösung y von y f y + g beschränk. b Gil lim g, so gil auch lim y für jede Lösung y der Gleichung y f y + g. Beweis: a Sei F : a f d. Dann is F F Lösung y von y f y + g mi ya y folg y e F y + a e F g y e F + a f d c für a. Für eine e F F g y e c + a e c g. Der erse Summand geh für gegen. Is g M für alle a, so is der zweie Summand beschränk durch M a e c M c eca M c. b Sei ε> vorgegeben. Nach Voraussezung gib es ein mi g εc/ für und es sei weierhin g M für alle a. Wegen lim e c gib es ein > mi y + M e c e c ca e c ε.
34 34 Sorch/Wiebe, Band, Kapiel 6 Sei y eine Lösung von y f y + g mi ya y. Dann gil für den zweien Summanden in der obigen Abschäzung von y : a e c g a e c g + e c g M a e c + εc e c M c e c e ca e c + ε e c M c e c e ca e c + ε, also y y e c + M c e c e ca e c + ε y + M e c e c ca e c + ε ε + ε ε für. Es folg lim y. Abschni 9.C, Aufg. 3b, p : Seien y bzw. y die Anzahlen der U 38 - bzw. U 35 -Aome in einer gegebenen Uranprobe zur Zei. Die Halbwerszeien von U 38 bzw. U 35 beragen T 4,5 9 Jahre bzw. T,7 9 Jahre. In einem Probesück habe das Verhälnis von U 38 und U 35 den Wer 37, 8. Uner der Annahme, dass zur Zei der Ensehung die Aneile von U 38 und U 35 gleich waren, berechne man das Aler der Probe. Lösung: Sei y die Anzahl der Aome eines Isoops mi der Halbwerszei T zur Zei, zur Anfangszei seien y Aome vorhanden. Die Zerfallsrae dy/ is proporional zu y, also dy/ λy, wobei λ > die Zerfallskonsane is. Es folg y y e λ. Wegen yt y folg e λt, d.h. λ ln /T. Für die Zerfallskonsanen von U 38 und U 35 ergib sich daraus λ,54 9 und λ,99 9 sowie λ λ, Mi Obigem folg 37,8 y y y e λ y e λ y y eλ λ e,836 9 e,836 9, woraus sich für das Aler der Probe der Wer 5,89 9 ergib. Das Aler der Erde wird heue mi ca. 4,5 9 Jahren angegeben. Abschni 9.C, Variane zu Aufg. 4, p : Die Luf in der Wüse habe abends um 8 Uhr eine Temperaur von 4 C; die Temperaur eines Seines, der dor in der Sonne gelegen ha, berage gleichzeiig 8 C. Von da an sinke die Temperaur T L der Luf. Die Temperaur des Seines T S ändere sich mi einer Rae, die proporional zur Temperaurdifferenz zwischen Luf und Sein is, d.h. zu jedem Zeipunk sei T S β T L T S N e w o n s c h e s A b k ü h l u n g s g e s e z. Man berechne die Temperaur des Seines um 4 Uhr am nächsen Morgen uner der Annahme β, a falls die Temperaur T L der Luf gleichmäßig um 4 C pro Sunde sink, b falls die Temperaur T L der Luf mi einer Abkühlungsrae sink, die proporional zur Temperaurdifferenz zwischen Luf und Sein is, d.h. Ṫ L α T L is, ewa mi dem Proporionaliäsfakor α 4. Lösung: a Es is T L 4 4, also T S β 4 4 T S. Diese lineare Differenzialgleichung ha die Lösung T S e β 8+ βe β 4 4 e β 4+e β e β β 4 4 e β β β. Für β und ergib sich die gesuche Temperaur zu 8+ 3e 5 8, C. b Es is T L + 3e α, also T S β + 3e α T S mi der Lösung T S e β 8 + βe β + 3e α 7e β + + 3β e α e β. β α Für α 4, β und ergib sich die gesuche Temperaur zu +e 5 +6e 5/ 5 C.
35 Sorch/Wiebe, Band, Kapiel 6 35 Abschni 9.C, Teil von Aufg. 5, p : Nach Torricellis Gesez ha Wasser, das aus einem bis zur Höhe h gefüllen Behäler aus einer kleinen Öffnung am Grunde des Behälers fließ, die Geschwindigkei c gh mi einer Konsanen c < c, die im Idealfall is. Is A die Fläche der Ausflussöffnung und ha der Behäler in der Höhe h den Querschni Fh, so erfüll h die Differenzialgleichung ḣ Ac gh/fh. Man beschreibe die Höhe h als Funkion der Zei und besimme die Zei, bis der Behäler leer is, für a ein zylindrisches Fass mi Radius R; b einen kegelförmigen Tricher mi Öffnungswinkel α. Lösung: a Es is Fh πr für alle Were von h. Wir haben also die Differenzialgleichung ḣ Ac h g πr für die Anfangsbedingung h H zu lösen und erhalen durch Trennen der Variablen: also h h H h h H h H dh A h πr c g A πr c g, A H πr c g. Wegen ht ergib sich für die gesuche Zei T : H A πr c g T, d.h. T πr Ac H g. b Wir bezeichnen die Höhe des Trichers mi H, seinen oberen Radius mi R und seinen uneren Radius mi r < R. Dann is s : an α R r. Die Querschnisfläche des Trichers in der Höhe h ha dann den H Radius r+hs und die Fläche Fh πr+hs. Wir haben also die Gleichung ḣ Ac h g πr+hs für die Anfangsbedingung h H zu lösen und erhalen durch Trennen der Variablen: Ac π h H h g H r+hs h dh Ac g π Ac g, π s h 3/ + rsh / + r h / dh 5 s h 5/ + 4r 3 sh3/ + r h / h H. Dies liefer eine Gleichung 5. Grades für h, aus der sich h, ewa mi dem Newon-Verfahren, besimmen läss. Für die gesuche Zei T, bis das Gefäß geleer is, ergib sich wegen ht : Ac g T π 5 s H 5/ 4r 3 sh 3/ r H / π, also T Ac g 5 s H 5/ sh 3/ +r H /. Mi ρ : sh/r erhäl man: T πr Ac H g 5 ρ + 3 ρ +. Im Fall r R is ρ, und wir erhalen die Formel aus a, im Fall A πr ergib sich einfach T H c g 5 ρ + 3 ρ +.
36 36 Sorch/Wiebe, Band, Kapiel 6 Abschni 9.C, Variane zu Aufg. 9, p : Ein Körper der Masse m falle aus der Ruhelage mi der Geschwindigkei v. Er unerliege dabei zwei Kräfen, nämlich der Schwerkraf mg und einer Widersandskraf der Form αv β mi Konsanen α >, β >. Berechnen Sie v und die Grenzgeschwindigkei lim v in den Fällen β und β. Lösung: Wegen Kraf Masse mal Beschleunigung gil die Kräfebilanz m v mg αv β. Dies is eine Differenzialgleichung mi gerennen Variablen für v. Trennung der Variablen liefer v dv g α m vβ. Sei zunächs β. Inegraion liefer m α ln g m α ln g α m v m α ln g α m v v g α m, v e g α/m. Auflösen nach v liefer g α m v e α/m g, d.h. v mg e α/m. Es folg: α mg lim v α. Sei nun β. Inegraion liefer mi Hilfe von 4.B, Aufg. 6b : v dv g α m v g v dv α mg v g α mg v anh αg m, v mg α α Aranh mg v v m α αg Aranh mg v, mg α anh αg m. Wegen lim anh folg mg lim v α. Abschni 9.C, Zusazaufgabe, p : Ein gleichmäßiger sarker Schneefall begann Sunden vor Miernach. Genau um Uhr fuhr ein Schneepflug los und räume mi konsaner Leisung, d.h. er schaffe immer die gleiche Menge Schnee pro Zeieinhei. In der zweien Sunde kam er nur halb so wei wie in der ersen Sunde, weil der Schnee inzwischen viel höher lag. Sellen Sie fes, wann es zu schneien begann, d.h. besimmen Sie. Lösung: Die Geschwindigkei des Schneepflugs sei v, die Anfangsgeschwindigkei sei v v und der zurückgelege Weg sei s. Wegen der Konsanz der Räumleisung und da die Schneehöhe proporional zur verflossenen Zei is, is die Geschwindigkei des Schneepflugs umgekehr proporional zur Zei, die sei dem Einsezen des Schneefalls verflossen is. Es gil also v : v : +, d.h. + v v, und mi ṡ v, s folg s v v + v ln + v ln + v ln v ln +. Wegen s 3 s is ln ln +, + 3. Es folg + + 3, +, d.h. + 5,68 Sunden 37 Minuen. Abschni 9.C, Zusazaufgabe, p : Das mechanische Zählwerk eines Kasseenrekorders zeige die Umdrehungszahl n der anfangs leeren Spule. Es sei n die zur Anzeige n gehörende Spieldauer. Bei Spielbeginn werde das Zählwerk auf gesell, d.h. es sei. Die Bandgeschwindigkei sei v 4,75 cm/sec. Man gebe n in Abhängigkei vom Radius R der leeren Spule und der Banddicke d an. Es sei n nach und n nach 8 Minuen erreich. Man berechne d und R.
37 Sorch/Wiebe, Band, Kapiel 6 37 Lösung: Es is n+h n + h R+nd π, also v dn lim n+h h R+nd π h h v folg: n v πrn + n πd. Einsezen der Were liefer R 4,5 mm und d,8 mm.. Daraus Abschni 9.D, Variane zu Aufg., p : Für die folgenden linearen Differenzialgleichungen besimme man alle komplewerigen und alle reellwerigen Lösungen: ÿ 3ẏ + y 3e + 4 ÿ 3ẏ 4y e, y 4ẏ + 4y + e, ÿ + ẏ + y + e, ÿ ẏ + y + sin 3, ÿ ẏ + y e + e sin, y + y + y e + e cos, y 3 ÿ + 4ẏ 6 e sin 3, y 3 ÿ + ẏ 5 e cos. Lösung: Die zu ÿ 3ẏ+y 3e +4 gehörende homogene lineare Differenzialgleichung ÿ 3ẏ+y mi konsanen Koeffizienen ha das charakerisische Polynom PX : X 3X + X X mi den Nullsellen und. Ihre sämlichen Lösungen sind also c e + c e, c, c K. Die inhomogene lineare Differenzialgleichung ÿ 3ẏ+y 3e lös man durch einen Ansaz vom Typ der rechen Seie. Da keine Nullselle von P is, erhäl man als eine Lösung 3/P e 3 6 e e. Die inhomogene lineare Differenzialgleichung ÿ 3ẏ + y 4e lös man ebenfalls durch einen Ansaz vom Typ der rechen Seie. Da keine Nullselle von P is, erhäl man als eine Lösung 4/Pe 4. Alle Lösungen der Ausgangsgleichung haben also die Form y c e + c e + e +, c, c K. Die zu ÿ 3ẏ 4y e gehörende homogene lineare Differenzialgleichung ÿ 3ẏ 4y mi konsanen Koeffizienen ha das charakerisische Polynom PX : X 3X 4 X 4X + mi den Nullsellen 4 und p,q-formel!. Ihre sämlichen Lösungen sind also c e 4 + c e, c, c K. Die inhomogene lineare Differenzialgleichung ÿ 3ẏ 4y e lös man durch einen Ansaz vom Typ der rechen Seie. Da keine Nullselle von P is, erhäl man als eine Lösung /Pe 6 e 3 e. Die inhomogene lineare Differenzialgleichung ÿ 3ẏ 4y e lös man ebenfalls durch einen Ansaz vom Typ der rechen Seie. Da keine Nullselle von P is, erhäl man als eine Lösung /Pe /4. Alle Lösungen der Ausgangsgleichung haben also die Form y c e 4 + c e 3 e + 4, c, c K. Die zu ÿ 4ẏ + 4y + e gehörende homogene Differenzialgleichung ÿ 4ẏ + 4y ha P X 4X+4 X mi der doppelen Nullselle als charakerisisches Polynom und daher e, e als Basis des Lösungsraums über R und über C. Die zugehörige inhomogene Differenzialgleichung mi recher Seie ha die Lösung /P e 4. Die inhomogene Differenzialgleichung mi recher Seie e ha die Lösung y /P e /6 e. Superposiion liefer die allgemeine Lösung y e + c e + c e, c, c K. Die zu ÿ + ẏ + y + e gehörende homogene Differenzialgleichung ÿ + ẏ + y ha P X + X+ X+ mi der doppelen Nullselle als charakerisisches Polynom und daher e, e als Basis des Lösungsraums über R und über C. Die zugehörige inhomogene Differenzialgleichung mi recher Seie lösen wir mi dem Ansaz y a+b e a+b und bekommen a, b 4, d.h. die Lösung 4. Die inhomogene Differenzialgleichung mi recher Seie e lösen wir mi dem Ansaz y he a e und bekommen a, d.h. die Lösung e. Superposiion liefer die allgemeine Lösung y 4 + e + c e + c e, c, c K.
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann
 Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Aufgaben zur Differenzialrechnung WS 06/07 Prof.Zacherl / Prof. Hollmann Aufgabe Im abgelaufenen Jahr haen einige große deusche Firmen hohe prozenuale Gewinnzuwächse. Gleichzeiig wurden eilweise massiv
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
7. Funktionalgleichung der Zeta-Funktion
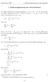 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Durch Modellierung beschreibt man Vorgänge aus der Natur sowie industrielle Prozesse
 Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Kapiel Modellierung Durch Modellierung beschreib man Vorgänge aus der Naur sowie indusrielle Prozesse mi mahemaischen Werkzeugen, zum Beispiel Gleichungen oder Ungleichungen. Modellierung geschieh durch
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Lösung - Serie 8. D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. MC-Aufgaben (Online-Abgabe) 1. Was für eine Kurve stellt die Parametrisierung
 D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
D-MAVT/D-MATL Analysis I HS 018 Dr. Andreas Seiger Lösung - Serie 8 MC-Aufgaben Online-Abgabe 1. Was für eine Kurve sell die Paramerisierung sin1 r = cos1, R dar? a Ein Kreis. Es gil x + y = sin 1 + cos
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Unendliche Folgen und Reihen
 . ) Zu Beginn befinde sich ein neu geborenes Kaninchenpaar K im Gehege (), ebenso zu Beginn des zweien Monas (), zu Beginn des drien Monas wird ein Kaninchenpaar K geboren (), zu Beginn des vieren Monas
. ) Zu Beginn befinde sich ein neu geborenes Kaninchenpaar K im Gehege (), ebenso zu Beginn des zweien Monas (), zu Beginn des drien Monas wird ein Kaninchenpaar K geboren (), zu Beginn des vieren Monas
4. Quadratische Funktionen.
 4-1 Funkionen 4 Quadraische Funkionen 41 Skalierung, Nullsellen Eine quadraische Funkion is von der Form f() = c 2 + b + a mi reellen Zahlen a, b, c; is c 0, so sprechen wir von einer echen quadraischen
4-1 Funkionen 4 Quadraische Funkionen 41 Skalierung, Nullsellen Eine quadraische Funkion is von der Form f() = c 2 + b + a mi reellen Zahlen a, b, c; is c 0, so sprechen wir von einer echen quadraischen
Ganzrationale Funktionenscharen. 4. Grades. Umfangreiche Aufgaben. Lösungen ohne CAS und GTR. Alle Methoden ganz ausführlich. Datei Nr.
 Ganzraionale Funkionenscharen. Grades Umfangreiche Aufgaben Lösungen ohne CAS und GTR Alle Mehoden ganz ausführlich Daei Nr. 7 Sand 3. Sepember 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
Ganzraionale Funkionenscharen. Grades Umfangreiche Aufgaben Lösungen ohne CAS und GTR Alle Mehoden ganz ausführlich Daei Nr. 7 Sand 3. Sepember 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Exponential- und Logarithmusfunktionen
 . ) Personen, Personen bzw. Personen ) Ewas weniger als Minuen. (Nach,... Minuen sind genau Personen informier.) ) Ja. Bereis um : Uhr sind (heoreisch) Personen informier. ) Informiere Miarbeierinnen und
. ) Personen, Personen bzw. Personen ) Ewas weniger als Minuen. (Nach,... Minuen sind genau Personen informier.) ) Ja. Bereis um : Uhr sind (heoreisch) Personen informier. ) Informiere Miarbeierinnen und
mathphys-online Abschlussprüfung Berufliche Oberschule 2009 Mathematik 12 Technik - A I - Lösung Teilaufgabe 1.0 Gegeben ist die reelle Funktion f( x)
 Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Abschlussprüfung Berufliche Oberschule 9 Mahemaik Technik - A I - Lösung Teilaufgabe. Gegeben is die reelle Funkion f( x) in der Definiionsmenge ID f = IR. Teilaufgabe. (4 BE) Unersuchen Sie das Verhalen
Zeit (in h) Ausflussrate (in l/h)
 Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
8.5 Uneigentliche Integrale Integrale über unbeschränkte Bereiche. f(x) dx. Integrale über unbeschränkte Funktionen mit Singularitäten am Rand
 8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Übungen zur Klausur 11M1 21/05/2008 Seite 1 von 5
 Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Seie von 5 Aufgabe : Eine ganzraionale Funkion. Grades habe die Nullsellen ; ;. Ihr Schaubild gehe durch P( 6). Besimme die Exremsellen. Skizziere den Graphen der Funkion. allgemeine Form einer Funkion.
Stammgruppe trifft sich zum Museumsrundgang Experte erklärt jeweils sein Plakat
 Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
 Abiurprüfung Mahemaik 007 Baden-Würemberg (ohne CAS) Pflicheil - Aufgaben Aufgabe : ( VP) Bilden Sie die erse Ableiung der Funkion f mi f () + = ( sin ). Aufgabe : ( VP) ln Berechnen Sie das Inegral e
Abiurprüfung Mahemaik 007 Baden-Würemberg (ohne CAS) Pflicheil - Aufgaben Aufgabe : ( VP) Bilden Sie die erse Ableiung der Funkion f mi f () + = ( sin ). Aufgabe : ( VP) ln Berechnen Sie das Inegral e
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen Hochschule Esslingen SS 2010 4 3 2 1 0 5 10 15 20 25 30 Fakulä Grundlagen (Hochschule Esslingen) SS 2010 1 / 9 Übersich 1 Vorberachungen Ableiungsbegri
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Übungsblatt 8 Musterlösung
 Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Masse, Kraft und Beschleunigung Masse:
 Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
ABITURPRÜFUNG 2002 LEISTUNGSFACH MATHEMATIK (HAUPTTERMIN)
 ABITURPRÜFUNG 00 LEISTUNGSFACH MATHEMATIK (HAUPTTERMIN) Arbeiszei: Hilfsmiel: 70 Minuen Taschenrechner (nich programmierbar, nich grafikfähig) Tafelwerk Der Prüfungseilnehmer wähl von den Aufgaben A1 und
ABITURPRÜFUNG 00 LEISTUNGSFACH MATHEMATIK (HAUPTTERMIN) Arbeiszei: Hilfsmiel: 70 Minuen Taschenrechner (nich programmierbar, nich grafikfähig) Tafelwerk Der Prüfungseilnehmer wähl von den Aufgaben A1 und
1. Schularbeit (6R) 24. Okt. 1997
 . Schularbei (6R). Ok. 997. Vereinfache und selle das Ergebnis mi posiiven Hochzahlen dar. Es sind dabei alle Rechenschrie anzugeben: 7 x x y 8 : x x y. Löse die folgende Wurzelgleichung ohne Verwendung
. Schularbei (6R). Ok. 997. Vereinfache und selle das Ergebnis mi posiiven Hochzahlen dar. Es sind dabei alle Rechenschrie anzugeben: 7 x x y 8 : x x y. Löse die folgende Wurzelgleichung ohne Verwendung
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Abschlussprüfung an Fachoberschulen in Bayern Mathematik mit CAS 2015 Analysis A2 Ausbildungsrichtung Technik
 MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
Zentrale schriftliche Abiturprüfungen im Fach Mathematik
 Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 9: Radioakiver Zerfall Beim radioakiven Zerfall einer Subsanz S 1 beschreib m 1 () die Masse der noch nich zerfallenen Subsanz zum Zeipunk mi
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
7. Gewöhnliche Differentialgleichungen
 1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
1 7. Gewöhnliche Differenialgleichungen DGL: Gewöhnliche DGL: Parielle DGL: Anfangs- oder Randbedingungen: Besimmungsgleichung für eine Funkion, in der die gesuchen Funkion und ihre Ableiungen vorkomm
Zeitreihenökonometrie
 ifo Insiu für Wirschafsforschung an der Universiä München Zeireihenökonomerie Kapiel 6 Nichsaionäre univariae Zeireihenmodelle ifo Insiu für Wirschafsforschung an der Universiä München Nichsaionäre Prozesse
ifo Insiu für Wirschafsforschung an der Universiä München Zeireihenökonomerie Kapiel 6 Nichsaionäre univariae Zeireihenmodelle ifo Insiu für Wirschafsforschung an der Universiä München Nichsaionäre Prozesse
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
22 Stetigkeit von Funktionen
 Abschni 22 Seigkei von Funkionen R Plao 47 22 Seigkei von Funkionen 221 Einührung Deiniion 221 Sei W D!Reine Funkion mi Deiniionsbereich D R a) an nenn die Funkion im Punk o 2 D seig, alls lim / D o /!
Abschni 22 Seigkei von Funkionen R Plao 47 22 Seigkei von Funkionen 221 Einührung Deiniion 221 Sei W D!Reine Funkion mi Deiniionsbereich D R a) an nenn die Funkion im Punk o 2 D seig, alls lim / D o /!
Traktrix DEMO. Text Nr Stand 11. Mai 2016 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK.
 Trkri Te Nr. 540 Snd. Mi 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mhe-cd.de 540 Trkri Vorwor Die Trkri is eine Kurve für gehobenemhemische Ansprüche. Ineressn is schon ihre mechnische
Trkri Te Nr. 540 Snd. Mi 06 FRIEDRICH W. BUCKEL INTERNETBIBLIOTHEK FÜR SCHULMATHEMATIK www.mhe-cd.de 540 Trkri Vorwor Die Trkri is eine Kurve für gehobenemhemische Ansprüche. Ineressn is schon ihre mechnische
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Aufgaben zur Zeitreihenanalyse (Kap. 3)
 Prof. Dr. Reinhold Kosfeld Fachbereich Wirschafswissenschafen Aufgaben zur Zeireihenanalyse (Kap. Aufgabe. Was verseh man uner einem sochasischen Prozess? Ein sochasischer Prozess is eine zeiliche Folge
Prof. Dr. Reinhold Kosfeld Fachbereich Wirschafswissenschafen Aufgaben zur Zeireihenanalyse (Kap. Aufgabe. Was verseh man uner einem sochasischen Prozess? Ein sochasischer Prozess is eine zeiliche Folge
Schriftliche Abiturprüfung Mathematik 2013
 Schrifliche Abiurprüfung Mahemaik 03 Aufgabe (NT 008, Nr) Pflicheil Bilden Sie die Ableiung der Funkion f mi f(x) = 3x e x+ und vereinfachen Sie so wei wie möglich ( VP) Aufgabe (HT 008, Nr ) G is eine
Schrifliche Abiurprüfung Mahemaik 03 Aufgabe (NT 008, Nr) Pflicheil Bilden Sie die Ableiung der Funkion f mi f(x) = 3x e x+ und vereinfachen Sie so wei wie möglich ( VP) Aufgabe (HT 008, Nr ) G is eine
Analysis: Exponentialfunktionen Analysis
 www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Mathematikaufgaben > Analysis > Funktionenscharen
 Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
Michael Buhlmann Mahemaikaugaben > Analysis > Funkionenscharen Augabe: Unersuche die ganz raionale Funkionenschar + 8 mi Parameer > 0 au: Nullsellen, Hoch- und Tiepunke, Monoonie, Wendepunke, Krümmung,
BESCHREIBUNG VON ZERFALLSPROZESSEN
 BESCHREIBUNG VON ZERFALLSPROZESSEN ab Ende der 1. Schulsufe Kreuze zu jedem angeführen Beispiel das richige mahemaische Modell an, begründe deine Enscheidung und beschreibe die Bedeuung der in den Modellen
BESCHREIBUNG VON ZERFALLSPROZESSEN ab Ende der 1. Schulsufe Kreuze zu jedem angeführen Beispiel das richige mahemaische Modell an, begründe deine Enscheidung und beschreibe die Bedeuung der in den Modellen
5.5. Abstrakte Abituraufgaben zu Exponentialfunktionen
 5.5. Absrake Abiuraufgaben zu Eponenialfunkionen Aufgabe : Kurvenunersuchung, Inegraion, Opimierungsaufgabe Gegeben is die Funkion f() ( ) e,5. a) Unersuchen Sie das Schaubild von f auf Achsenschnipunke,
5.5. Absrake Abiuraufgaben zu Eponenialfunkionen Aufgabe : Kurvenunersuchung, Inegraion, Opimierungsaufgabe Gegeben is die Funkion f() ( ) e,5. a) Unersuchen Sie das Schaubild von f auf Achsenschnipunke,
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Fit für die Q-Phase? Mathematiktraining für die Schüler und Schülerinnen des Beruflichen Gymnasiums Gelnhausen
 Fi für die Q-Phase? Mahemaikraining für die Schüler und Schülerinnen des. Gleichungen (mi und ohne Parameer) Löse folgende Gleichungen:. 4 7.6 e ( e )..7 4 4 k k. 6.8 6 0.4 4 4 4 49.9 cos..0 4.6. e e.7
Fi für die Q-Phase? Mahemaikraining für die Schüler und Schülerinnen des. Gleichungen (mi und ohne Parameer) Löse folgende Gleichungen:. 4 7.6 e ( e )..7 4 4 k k. 6.8 6 0.4 4 4 4 49.9 cos..0 4.6. e e.7
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Kapitel : Exponentielles Wachstum
 Wachsumsprozesse Kapiel : Exponenielles Wachsum Die Grundbegriffe aus wachsum 1.xmcd werden auch hier verwende! Wir verwenden im Beispiel 2 auch fas die gleiche Angabe wie in Beispiel 1 - lediglich eine
Wachsumsprozesse Kapiel : Exponenielles Wachsum Die Grundbegriffe aus wachsum 1.xmcd werden auch hier verwende! Wir verwenden im Beispiel 2 auch fas die gleiche Angabe wie in Beispiel 1 - lediglich eine
Übungen zur Ingenieur-Mathematik III WS 2009/10 Blatt = r cos t. mit 0 t 2π und interpretieren Sie das Ergebnis geometrisch.
 Übungen zur Ingenieur-Mahemaik III WS 9/ Bla 3 7.. Aufgabe 59: Berechnen Sie die Bogenlänge der Schraubenlinie r γ() := r h mi π und inerpreieren Sie das Ergebnis geomerisch. Lösung: Der Tangenialvekor
Übungen zur Ingenieur-Mahemaik III WS 9/ Bla 3 7.. Aufgabe 59: Berechnen Sie die Bogenlänge der Schraubenlinie r γ() := r h mi π und inerpreieren Sie das Ergebnis geomerisch. Lösung: Der Tangenialvekor
Die Lösungen der Übungsaufgaben werden durch folgendes Lemma etwas vereinfacht:
 Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
PHYSIK III. Serie 12, Musterlösung
 Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
Prof Dr Danilo Pescia Tel 044 633 50 pescia@solidphysehzch Winersemeser 06/07 wwwmicrosrucureehzch Serie, Muserlösung Niculin Saraz Tel 044 633 3 8 saraz@physehzch Reflexion Die Fresnel schen Formeln lauen:
Lösung Abiturprüfung 1994 Leistungskurs (Baden-Württemberg)
 Lösung Abiurprüfung 1994 Leisungskurs (Baden-Würemberg) Analysis I.1. a) D f = IR / { 1 } f x= = K besiz keine Nullsellen 1x f ' x= 8 1x = 8 K besiz keine Exremsellen senkreche Asymoe : x= 1 waagereche
Lösung Abiurprüfung 1994 Leisungskurs (Baden-Würemberg) Analysis I.1. a) D f = IR / { 1 } f x= = K besiz keine Nullsellen 1x f ' x= 8 1x = 8 K besiz keine Exremsellen senkreche Asymoe : x= 1 waagereche
