Atom- und Molekülphysik
|
|
|
- Gotthilf Lorenz
- vor 7 Jahren
- Abrufe
Transkript
1 Atom- und Molekülphysik nach den Vorlesungen von Prof. Dr. Lukas M. Eng (Sommersemester 2008) Herausgegeben von Jeffrey Kelling Felix Lemke Stefan Majewsky Stand: 23. Oktober 2008
2 Inhaltsverzeichnis Vorwort (zuerst lesen) 4 1 Allgemeines Aufgaben der Atom- und Molekülphysik Experimentelle Methoden Imaging Spektroskopie Entwicklung und Historie der Atomphysik Klassische Ansätze Das Rutherford-Bohr sche Atommodell Spektralserien und Energieniveauschema des H-Atoms Quantenmechanik Die zeitabhängige Schrödingergleichung Die stationäre Schrödingergleichung Die Schrödingergleichung im Nullpotential Die Schrödingergleichung im Zentralpotential Die Grobstruktur des H-Atoms Fein- und Hyperfeinstruktur des H-Atoms Normale Feinstrukturaufspaltung (Spin-Bahn-Kopplung) Relativistische Korrekturen Korrekturen für die endliche Ladungsdichte Lamb-Shift. Anomale Feinstrukturverschiebung Hyperfeinstruktur und Isotopieeffekt Verallgemeinerung der Quantenmechanik Operatoren. Eigenwerte. Eigenfunktionen. Quantenmechanischer Mittelwert Dirac-Schreibweise und Matrixdarstellung Postulate der Quantenmechanik Der quantenmechanische Oszillator Der Potentialtopf Unbegrenzter quadratischer Potentialtopf Begrenzter, quadratischer Potentialtopf Quantenmechanischer Tunneleffekt Auswahlregeln und Übergangsmatrixelemente Zweiniveausysteme. Einstein-Koeffizienten. Laser Atomstrukturen mit mehreren Elektronen Die elektrostatische Korrelation LS-Kopplung und jj-kopplung
3 6.3 Pauli-Prinzip. Symmetrie von Wellenfunktionen Die Struktur des He-Atoms Aufbauprinzip. Periodensystem der Atome Ionisationsenergien der Atome Spektrum der Alkali-Atome Spektrum der Erdalkali-Atome und Zweielektronen-Systeme Multiplett-Spektrum der Mehrelektronensystem Energiestruktur von Ionen Energiestruktur der inneren Elektronenschalen Atome in äußeren Feldern Zeeman-Effekt Normaler Zeeman-Effekt. Lorentz-Tripletts Anomaler Zeeman-Effekt Quadratischer Zeeman-Effekt: Diamagnetismus und Landaubereich Zusammenfassung Stark-Effekt Erste Ordnung der Störungsrechnung Zweite Ordnung der Störungsrechnung Starkeffekt für Zustände n > Parabolische Koordinaten Elektrische Feldionisation. Quantenmechanischer Tunneleffekt Molekülphysik Allgemeine Bemerkungen Definitionen Aufgaben der Molekülphysik Darstellung von Molekülen Analytik Bindungstypen Modellvorstellungen Kossel-Modell Lewis-Modell Quantenmechanische Modellvorstellung Einige spezielle Bindungen π- und σ-bindungen Hybridisierung Mehrfachbindungen. Mesomerie Bindungsverhältnisse in Festkörpern Rotations- und Schwingungsniveaus in Molekülen Stichwortverzeichnis 82
4 Vorwort Bevor Ihr beginnt, mit diesem Skript zu arbeiten, möchten wir Euch darauf hinweisen, dass dieses Skript weder den Besuch der Vorlesung noch das selbstständige Nacharbeiten des Stoffes ersetzt. Wer das nicht verstanden hat, bei dem kann die Benutzung des Skriptes für Probleme insbesondere im Verständnis des Stoffes sorgen. Das liegt daran, dass das Skript nicht als vorgekauter Wissensspeicher zu verstehen ist. Das hier ist eine Abschrift des Inhaltes, den die Vorlesung zu vermitteln versucht. Nicht enthalten sind zum Beispiel mündliche Kommentare des Professoren, auch wenn diese im individuellen Falle oft erst den Groschen fallen lassen. Gut geeignet ist das Skript einfach gesagt als Wissensstütze, also zum Beispiel zum schnellen Nachschlagen; außerdem zum Wiederholen früheren Stoffes, sofern ein ausreichendes Grundverständnis vorhanden ist. Nach diesen einleitenden Worten wünschen wir Euch viel Spaß bei der Arbeit mit diesem Skript und viel Erfolg beim Studium! Die AGeS-Redaktion P.S. Wir suchen immer Helfer, die unsere Skripte um neue Inhalte erweitern, Fehler suchen, oder das Layout ansprechender gestalten wollen. Wenn Ihr Lust habt, meldet Euch über unsere Webseite.
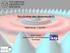
5 1.2 Experimentelle Methoden Seite 5 1 Allgemeines 1.1 Aufgaben der Atom- und Molekülphysik Die Atom- und Molekülphysik untersucht die physikalischen und chemischen Eigenschaften von Atomen und Molekülen sowie daraus resultierende optische, mechanische und elektronische Auswirkungen. Weiterhin sollen, wie in der Experimentalphysik, dazu nutzbare Methoden entwickelt, angewandt und diskutiert werden. Im Rahmen dieser Vorlesung werden die Erkenntnisse aus anderen Teilen der Physik, zum Beispiel der Quantenmechanik, genutzt, um die Eigenschaften einzelner Atome beschreiben zu können. Indem man untersucht, wie Atome sich unter Einfluss äußerer elektromagnetischer Felder verhalten, kann man zur Beschreibung von ganzen Molekülen gelangen. 1.2 Experimentelle Methoden Imaging Abbildung von Atomen und Molekülen auf atomarer Skala Spektroskopie Variation von Parametern einer äußeren Einwirkung (zum Beispiel Wellenlänge bei elektromagnetischen Wellen) Imaging Zur Untersuchung von Kristallen wird ein Feldionenmikroskop verwendet. In diesem ist eine Probe von einem mit einem Fluroeszenzfarbstoff beschichteten Schirm umgeben. Über eine kleine Öffnung, ein sogenanntes Inlet, werden Heliumatome eingelassen. Zwischen Schirm und Probe liegt eine Spannung an, sodass die Heliumatome bei Kontakt mit der Probe ionisiert und zum Schirm hin beschleunigt werden. Beim Auftreffen auf die Fluoreszenzschicht entsteht ein sichtbarer Leuchtpunkt, dessen Position Aussagen über die Struktur der Probe ermöglicht. Prinzipskizze zum Feldionenmikroskop Mit einen solchem Gerät lässt sich nur die Oberflächenstruktur der Probe untersuchen, nicht jedoch das sogenannte Bulk, das Innere des Festkörpers, welches konstante physikalische Eigenschaften aufweist.
6 1.3 Entwicklung und Historie der Atomphysik Seite 6 Beim Transmissionselektronenmikroskop (TEM) strahlt ein monochromatischer Elektronenstrahl durch eine Probe hindurch, wobei es zu Interferenz- und Beugungserscheinungen kommt. Über eine Fouriertransformation erhält man hieraus ein direktes Bild der Probe. Man erhält jedoch nur eine zweidimensionale Projektion der Probe. Nachteilig ist außerdem, dass die Messung in einem Hochvakuum stattfinden muss, um Streueffekte am Elektronenstrahl zu vermeiden und die Probe speziell präpariert werden muss, da die Schichtdicke maximal 10 nm betragen darf. Aufbau eines TEM Eine dritte Möglichkeit ist die Verwendung eines Rastersondenmikroskops. Hier ist insbesondere das Rastertunnelmikroskop (scanning tunneling microscope, STM) zu nennen, welches auch Kräfte und optische Eigenschaften in atomaren Strukturen abbilden kann Spektroskopie Schickt man zum Beispiel eine elektromagnetische Welle oder einen Teilchenstrom auf eine Probe, so werden Teile des Stromes gestreut, absorbiert, reflektiert und transmittiert. Diese Anteile Prinzip der Spektroskopie können durch Analysatoren qualitativ untersucht und mittels Detektoren quantifiziert werden. Um verlässliche Ergebnisse zu erhalten, muss man monochromatische Energieströme einsetzen (bei Licht nur eine Wellenlänge, bei Teilchen nur eine kinetische Energie für alle Teilchen). Durch das Spektroskopieren kann man zum Beispiel Informationen über atomare oder molekulare Abstände, Austrittarbeiten, Zustandsdichten oder die Spineinstellung eines Systems erhalten. Im Gegensatz zum Imaging findet die Spektroskopie nicht im r-raum statt, sondern im k-raum. Das heißt, es wird nicht ein direktes Bild geliefert, sondern die Fouriertransformation dieses Bildes. In diesem Zusammenhang ist das Babinet-Prinzip von besonderer Relevanz: Von der Beugung am Streuer kann man zur Beugung an der entsprechenden Apertur übergehen, denn das Beugungsbild zweier geometrisch komplementärer Blenden ist identisch. 1.3 Entwicklung und Historie der Atomphysik Um 500 v. Chr. stellten sich Philosophen wie Demokrit die Materie als aus unteilbaren (gr. atomos) Teilen zusammengesetzt vor. Im 12. Jh. fanden indische Philosophen weitere indirekte Indizien für diese These. In der Physik wurde dieses Problem mit dem Aufkommen der Newtonschen Axiome im 18. Jh. diskutierbar. Dalton nutzte die Idee der Atome, um 1808 das erste Periodensystem der Elemente aufzustellen. Zum Ende des 19. Jahrhunderts wurden mit der Röntgenstrahlung (1895) und der Radioaktivität (Becquerel, 1896) Effekte gefunden, die sich nur durch Vorgänge im Atom erklären ließen. Bereits im Jahre 1897 schätzte J. J. Thompson ab, dass ein Wasserstoff-Kern 1836-mal schwerer ist als ein Elektron.
7 1.3 Entwicklung und Historie der Atomphysik Seite 7 Im Jahr 1900, dem sogenannten Planckschen Jahr, postulierte Planck die Quantennatur und führte das Plancksche Wirkungsquantum zu deren Beschreibung ein nutzte Einstein die Quantentheorie, um den Photoeffekt zu erklären. Diese Quantisierung wurde erneut im Jahre 1914 durch den Franck-Hertz-Versuch nachgewiesen. Im Jahre 1911 zeigte Rutherford, dass die Masse eines Atomes zu großen Teilen in einem kleinen positiv geladenen Atomkern konzentriert ist, während die negativ geladene Atomhülle fast leer ist. Die moderne Quantenmechanik läutete de Broglie 1924 durch die Theorie des Welle-Teilchen-Dualismus ein.
8 2.1 Das Rutherford-Bohr sche Atommodell Seite 8 2 Klassische Ansätze 2.1 Das Rutherford-Bohr sche Atommodell Die Atomtheorie nach Thomson beschrieb das Atom als kontinuierlich verteilten Pudding aus Elektronen, der zum Beispiel α- Teilchen immer unter einem festen Winkel θ = 28 streut. Jedoch widersprach die Beobachtung großer Streuwinkel dieser These. Daraus konnte man schließen, dass die Masse in einem kleinen Bereich, dem Atomkern, vereinigt ist. Dieser Kern ist positiv geladen, die Streuung von α-teilchen im Thomsonschen negativ geladenen Elektronen umfliegen diesen Kern, sodass das Atommodell ganze Atom wieder elektrisch neutral ist. Dies würde aber dazu führen, dass die Elektronen aufgrund der Radialbeschleunigung Bremsstrahlung aussenden, wodurch sich ihre kinetische Energie verringern würde und sie deswegen aufgrund der Coulombkraft in den Kern stürzen würden. Um dieses Dilemma aufzulösen, postulierte Niels Bohr im Jahre 1913: 1. Es gibt bestimmte diskrete Bahnen, auf denen sich die Elektronen strahlungsfrei bewegen können. 2. Strahlungsaufnahme und -abgabe erfolgt durch Übergänge zwischen diesen diskreten Bahnen. Aus diesen Postulaten ergeben sicher einige Folgerungen: 1. Jede Bahn hat eine bestimmte Energie E n, hierbei ist n N die Hauptquantenzahl. Die tiefste Energie ist E Übergänge zwischen Bahnen sind ebenfalls scharf, die Energieänderung beträgt E = E n E n = h ν = ω. Ist E positiv, Energieniveaus im H-Atom so wird diese Energie als Photon abgegeben. Ist E negativ, muss diese Energie durch ein Photon zugeführt werden. 3. Die klassische Physik ist im Model von Bohr aufgrund des Korrespondenzprinzips wieder enthalten, wenn man das erforderliche E 0 gehen lässt und damit in das klassische Quasi- Kontinuum übergeht. Das Vorgehen ist nun, die Gesamtenergie klassisch auszurechnen, den Bahndrehimpuls des Elektrons einzusetzen und das Korrespondenzprinzip anzuwenden. Als Zentralkraft wirkt die Coulombkraft, es entsteht ein Gleichgewicht zur Zentrifugalkraft: 1 4π ε 0 Z e2 r 2 = m e ϕ 2 r ( ) Hierbei ist e der Betrag Ladung des Elektrons beziehungsweise Protons, r der Abstand des Elektrons vom Proton, m e die Elektronenruhemasse, Z die Kernladungszahl, ϕ die Winkelkoordinate und ϕ die
9 2.1 Das Rutherford-Bohr sche Atommodell Seite 9 Winkelgeschwindigkeit auf der Kreisbahn des Elektrons. Zu ϕ gehört ein Bahndrehimpuls p ϕ. Für die verschiedenen diskreten Bahnen ϕ n gibt es natürlich unterschiedliche Bahndrehimpulse p ϕn. Als Ansatz für den Zusammenhang zwischen diesen p ϕn wählen wir p ϕn+1 = p ϕn + C Mit ( ) erhalten wir ϕ n = p ϕ n m e r 2 r = 4π ε 0 p 2 ϕ n m e Z e 2 ( ) Die klassische Gesamtenergie ergibt sich als Summe der Energie im Coulomb-Potential und der kinetischen Energie: E g,kl = E p + E k E g,kl = 1 E g,kl = me 2 4π ε 0 Z e2 r + p2 ϕn 2m e r 2 ( Z e 2 4π ε 0 ) 2 1 p 2 ϕn Entsprechend ergibt sich eine Energieänderung für den Übergang von n zu n + 1: E = E g,kl,n+1 E g,kl,n = m ( ) e Z e 2 2 [ ] π ε 0 (p ϕn + C) 2 Die Frequenz des Umlaufes erhalten wir klassisch aus: ν kl,n = ϕ n 2π = p ϕn 2π m e r 2 Damit lässt sich auch eine Frequenzänderung für den Übergang von n zu n + 1 angeben: p 2 ϕ n ν kl = ν kl,n+1 ν kl,n Aufgrund des Korrespondenzprinzips muss diese Frequenzänderung mit der Energieänderung gemäß der Quantenphysik in der Beziehung E = h ν kl stehen. Unter der Voraussetzung p ϕn C, also für quasi dicht liegende Niveaus, erhält man daraus: C = p ϕn+1 p ϕn = h 2π = Die Niveaus sind also äquidistant. Der Bahndrehimpuls ist gleich dem klassischen Drehimpuls: n p ϕn = n = L n = L n Drehimpuls der Elektronen
10 2.2 Spektralserien und Energieniveauschema des H-Atoms Seite 10 Bisher hatten wir den Kern als fest betrachtet, die Elektronen bewegen sich auf Kreisbahnen um den Kern. Es ist aber auch möglich, dass sich der Kern im Atom bewegt. Zu Beschreibung dieses Systems verwenden wir Relativkoordinaten und eine reduzierte Masse (Zweikörperproblem): r = r e r k und m r = m e m k m e + m k Bei der Gesamtenergie und dem Gesamtdrehimpuls nimmt man nun die reduzierte Masse statt der Elektronenmasse, und kommt damit wieder auf gültige Werte. Aus dieser Betrachtung folgt: Zweikörperproblem im H-Atom 1. Die kleinste Umlaufbahn ist r n n=1 = r 1 = 4π ε 0 2 m e Ze 2 Beim H-Atom ist m r m e und Z = 1, damit ergibt sich der Bohrsche Radius r 1 a 0 0, 5 Å. 2. Die Gesamtenergie für die n-te Bahn ergibt sich zu E n = 1 2 m e 1+ me m k ( Z e 2 4πε 0 ) 2 1 n 2 = 2 1 2m r r 1 2 n 2 1 = E 1 n 2 = hc Z 2 R 1+ me mn 1 n 2 Darstellung mit kleinster Energie Darstellung mit Rydberg-Konstante 3. Frequenzbedingung: ν n+1,n = Z 2 c ( R me m k (n + 1) 2 1 ) n 2 Beispiel 2.1 zur Frequenzbedingung Für den Term m e /m k gilt bei den verschiedenen Wasserstoffisotopen: Wasserstoff: m e /m p Deuterium: m e /(2 m p ) Tritium: m e /(3 m p ) Damit ist bei den selteneren Wasserstoffisotopen das sonst sichtbare Spektrum in den UV-Bereich verschoben. 2.2 Spektralserien und Energieniveauschema des H-Atoms Beim Übergang von 0 zu n (diese Schreibweise für Zustände wird später erläutert) handelt es sich um eine Anregung, während ein Übergang von n zu 0 eine Abregung darstellt. Eine Anregung führt zu einer Erhöhung der Energie um E = E n E n = E n E 1 = hc Z 2 R (1 1n ) 1 + me m 2 H Übergang zwischen Zuständen Man definiert die Ionisationsenergie als die Energie, die nötig ist, um ein Elektron von einem Atom abzutrennen. Diese Energie erhält man durch Betrachtung des Übergangs aus dem Grundzustand n 0 des Elektrons mit der Hauptquantenzahl n 0 in den Zustand. Für das H-Atom ist E I = E 1 = hc Z 2 R 1 + me m H = 13,6 ev
11 2.2 Spektralserien und Energieniveauschema des H-Atoms Seite 11 Desweiteren definieren wir den Termwert T n als die dem absoluten Betrag des Energiewertes E n proportionale Wellenzahl (ν = 1/λ): Hieraus konnen wir schließen: 1. ν n,n = T n T n 2. λ n,n = 1/(T n T n ) T n = E n hc = R Z2 mit [T 1 + me n ] = cm 1 m H Anhand der n unterscheidet man verschiedene Serien von Spektrallinien, welche sich im spektralen Raum teilweise überlappen. Die Lyman-Serie geht vom Zielzustand n = 1 aus (also sind Werte n = 2, 3, 4,... möglich). Die Spektrallinien der Lyman-Serie liegen im tiefen Ultraviolettbereich (Deep Ultra Violet, DUV). Die Balmer-Serie tritt bei Übergängen zum Energieniveau n = 2 aus höheren Niveaus auf, Die Balmer-Serie ist sehr gut experimentell zugänglich, da die emittierte Strahlung im UV- und im sichtbaren Bereich liegt. Die Paschen-Serie besteht aus Rückfällen nach n = 3, die Strahlung ist infrarot. Die Brackett-Serie besteht aus Rückfällen nach n = 4, die Strahlung ist ebenfalls infrarot. Die Pfund-Serie besteht aus Rückfällen nach n = 5, die Strahlung ist nah-infrarot. In allen Formeln taucht die Kernladungszahl Z auf. Das liegt daran, dass sich die Überlegungen für das H-Atom auf andere Kerne in guter Näherung übertragen lassen. Allerdings darf keine Wechselwirkung zwischen Elektronen auftreten, deshalb gilt die Näherung nur, wenn das Atom soweit ionisiert ist, dass nur noch ein Elektron übrig ist. Das ist zum Beispiel bei He + mit Z = 2, Li 2+ mit Z = 3 oder auch bei U 91+ mit Z = 92 der Fall. Allgemein stimmt das Rutherford-Bohr-Modell im Groben sehr gut mit experimentellen Beobachtungen überein, allerdings nur für 1e -Übergange. Anwendungen der Wasserstoffübergänge Beim Laser wird Emission bei großen Quantenzahlen (meist n > 100) stimuliert. Die Lebensdauer τ n solcher Zustände ist sehr kurz, weswegen die spektrale Auflösung, also die Genauigkeit des emittierten Photonenstromes im Spektrum, sehr hoch ist: ν ν 0 = ω ω In der Astrophysik ist auch meistens n > 100, wodurch sich Frequenzen in der Größenordnung von 100 GHz ergeben können. Typisch ist hier das Auftreten von Elektroneneinfängen, bei denen ein Proton und ein Elektron sich zu einem angeregten H-Atom verbinden. p + e Hnj Hierbei ist n die Hauptquantenzahl des Energieniveaus des Elektrons, und j ist die Änderung des Hauptquantenzahl. j wird als griechischer Buchstabe notiert, zum Beispiel α für n = 1 und γ für n = 3 (entsprechend der Ordnung im griechischen Alphabet). Man schreibt also zum Beispiel H109β, wenn das Elektron von n = 109 nach n = 107 springt. Bei so hohen Quantenzahlen bewegen sich die Elektronen nicht mehr auf Kreisbahnen, sondern auf elliptischen Bahnen. Dadurch wird eine relativistische Betrachtung notwendig.
12 2.2 Spektralserien und Energieniveauschema des H-Atoms Seite 12 Im Jahre 1916 schlugen Bohr und Sommerfeld eine neue Theorie zur Erklärung der Elektronenbahnen mithilfe des Keplerschen Flächensatzes vor, bei dem die Energieniveaus E n nochmals durch Feinstrukturkonstanten α in Unterenergieniveaus E nα aufgespalten werden. Die Bohr-Sommerfeld- Theorie hat jedoch einige Probleme: Sie kann Übergangsintensitäten und chemische Bindungen nicht erklären und ist nur auf Systeme anwendbar, die lediglich ein Elektron enthalten und keine äußeren Felder beinhalten. Um diese Dinge zu erklären, benötigt man die Quantenmechanik.
13 3.1 Die zeitabhängige Schrödingergleichung Seite 13 3 Quantenmechanik Im Gegensatz zur klassischen Physik, in der wir von absoluter Gewissheit ausgehen, kann man in einer Quantentheorie für alles nur eine gewisse Wahrscheinlichkeit angeben. Es gibt verschiedene Quantentheorien: Die bereits erwähnte Bohr-Sommerfeld-Quantentheorie hat, wie oben dargestellt, viele Probleme und gilt als veraltet. Heute verwendet man die Theorien der Quantenmechanik nach Heisenberg und nach Schrödinger. 3.1 Die zeitabhängige Schrödingergleichung Beim Aufstellen der Schrödingergleichung geht man von dem 1924 von de Broglie postulierten Welle- Teilchen-Dualismus aus. Danach hat ein Teilchen eine Frequenz sowie eine Wellenlänge: ν = f = E h und λ = c ν = hc hν = h c E! = h p Hierbei ist c die Wellengeschwindigkeit, die nicht unbedingt gleich mit der Lichtgeschwindigkeit ist! Daraus folgt eine Beziehung für Energie und Impuls: E = p c Beispiel 3.1 Ein Virus im Körper hat die Masse m = 1 µg = 10 9 kg und die Geschwindigkeit v = 10 6 ms 1. Dann ist λ = h p = h m v = 6, m Die Wellenlänge dieses Virus ist um den Faktor 1000 kleiner als ein Atomkern, also wird man keine Welleneffekte beobachten können. Für ein nichtrelativistisches Elektron mit der kinetischen Energie E kin = 10 kev erhält man: E kin = p2 p = 2m e E kin λ = h 2m e p = h hc = 2me E kin 2me c 2 E kin Es ist hc = 1240 ev mm und m e c 2 = 511 kev, weswegen sich eine Wellenlänge von λ = 0,01226 nm ergibt. Das heißt, dass man in Atomen durchaus Effekte der Wellenmechanik beobachten kann. Der Ansatz von Schrödinger ist der Energiesatz: E tot = E kin + E pot = p2 2m + V ( r) ( )
14 3.2 Die stationäre Schrödingergleichung Seite 14 Schrödinger postulierte folgende Substitutionsregeln zur Umwandlung in eine Operatorgleichung: Das ergibt: E i t p i V ( r) Multiplikation mit V ( r) i ( i ) 2 = + V ( r) = 2 t 2m 2m 2 + V ( r) =: H Der rechte Term wird als Hamilton-Operator H bezeichnet. Diese Operatorgleichung kann auf eine (im Allgemeinen komplexe) Wellenfunktion Ψ angewendet werden. Diese Wellenfunktion beschreibt das Teilchensystem vollständig: i Ψ t = 2 2m 2 Ψ + V ( r) Ψ = HΨ Zeitabhängige Schrödingergleichung Nun fehlt noch eine physikalische Interpretation der Wellenfunktion Ψ( r, t). Man kann Ψ 2 = Ψ Ψ als Wahrscheinlichkeitsdichte auffassen, dass das Teilchen mit der Masse m unter Einfluss des Potentials V ( r) zur Zeit t im Raumelement dv = dx dy dz mit dem Mittelpunkt r zu finden ist. Die Wahrscheinlichkeit, dass sich das Teilchen irgendwo im Raum ist, ist gleich 100%: Ψ 2 dv = 1 Normierungsbedingung 3.2 Die stationäre Schrödingergleichung Die Zeitabhängigkeit soll aus der Schrödingergleichung eliminiert werden. Wir machen deshalb einen Separationsansatz: Ψ(x, y, z, t) = ψ(x, y, z) v(t) Einsetzen in die Schrödingergleichung ergibt: Wir dividieren durch v und ψ: i dv dt ψ = v Hψ i v dv dt = 1 ψ Hψ Den linken Term kann man gerade als Energie interpretieren. Damit ist E die Separationskonstante und es ergeben sich zwei Differentialgleichungen: dv v = E i dt und 1 ψ Hψ = E Die erste Differentialgleichung wird gelöst durch v(t) = v 0 exp ( i E ) t
15 3.4 Die Schrödingergleichung im Zentralpotential Seite 15 Es kann v 0 = 1 normiert werden, damit ergibt sich: Ψ( r, t) = ψ( r) exp ( i E ) t Die Wahrscheinlichkeitsdichte ist: Ψ 2 = Ψ Ψ = ψ ( r) exp (+i E ) t ψ( r) exp ( i E ) t = ψ 2 Die zweite Differentialgleichung ergibt bei Multiplikation mit ψ die Hψ = Eψ Stationäre Schrödingergleichung Hieraus folgen zum Beispiel die Energieeigenwerte im Wasserstoffatom. Diese sind abhängig vom jeweiligen atomaren System, dessen Potential V ( r) und Randbedingungen. Energiewerte können diskret (wie beim H-Atom) oder kontinuierlich (wie etwa beim harmonischen Oszillator) sein. Im Allgemeinen ist es ziemlich schwierig, exakte Werte für komplexere Systeme zu ermitteln. Meistens gelangt man nur mit numerischen Methoden, zum Beispiel durch Iteration, zum Ziel. 3.3 Die Schrödingergleichung im Nullpotential Wir betrachten das Potential V ( r) = 0, also ist F = grad V ( r) = 0. Wir beschränken uns für die Lösung auf den eindimensionalen Fall. Der Ansatz ist wiederum Ψ(x, t) = A exp [i(kx ωt)] Zunächst bestimmen wir die in der Schrödingergleichung vorkommenden Ableitungen: Ψ t = iω Ψ Ψ x = ik Ψ 2 Ψ x 2 = k 2 Ψ Eingesetzt ergibt sich: i ( iω) Ψ = 2 2m ( k2 ) Ψ ω = 2 k 2 2m = p2 2m = E Dieser Ansatz ist also gut für eindimensionale Fälle, somit auch für dreidimensionale Fälle. 3.4 Die Schrödingergleichung im Zentralpotential Wir haben nun als Potential V ( r) das radialsymmertische Coulomb-Potential. Aufgrund der nicht vorhandenen Zeitabhängigkeit dieses Potentials genügt die Lösung der zeitunabhängigen Schrödingergleichung Hψ = Eψ. Wir erwarten aufgrund der Struktur der Differentialgleichung, Energieeigenwerte E n und Eigenfunktionen ψ für den Hamilton-Operator des Coulombpotentials zu erhalten. Der Hamiltonoperator ist gegeben durch: H = 2 2m 2 Ze2 4πε 0 r
16 3.4 Die Schrödingergleichung im Zentralpotential Seite 16 Es erscheint sinnvoll, dieses Problem zur Lösung in Kugelkoordinaten zu übertragen: 2 = 2 x y z 2 = 1 ( ) ( ) r 2 r r r r }{{} 2 sin ϑ 1 sin ϑ + ϑ ϑ r }{{} 2 sin ϑ radialer Anteil polarer Anteil Wir verwenden wieder einen Separationsansatz: Es ergibt sich: [ 2 ΘΦ 2m r 2 d dr ( r 2 dr ) + RΘ dr r 2 sin ϑ ψ(x, y, z) = ψ(r, ϑ, ϕ) = R(r) Θ(ϑ) Φ(ϕ) ( d sin ϑ dθ ) + dϑ dϑ 2 ϕ 2 }{{} azimutaler Anteil ] RΘ r 2 sin 2 ϑ d2 Φ dϕ 2 +V c ( r) RΘΦ = RΘΦ E Zur Vereinfachung wird multipliziert mit 2m/ 2 (r 2 sin 2 ϑ)/(rθφ). ( sin2 ϑ R d r 2 dr ) sin ϑ ( dr dr Θ d sin ϑ dθ ) 2m dϑ dϑ 2 r2 sin 2 ϑ [E V c ( r)] = 1 Φ d2 Φ dϕ 2 Den linken von r und ϑ abhängigen Teil nennen wir ( ), der rechte Teil mit der Abhängigkeit von ϕ soll ( ) heißen. ( ) ergibt: d 2 Φ dϕ 2 Φ const. = 0 Der Lösungsansatz ist Φ(ϕ) = A exp (im l ϕ). Damit ist die bis jetzt unbekannte Separationskonstante durch m 2 l gegeben. Wir werden sehen, dass m l Z ist. Die Ganzzahl m l wird als magnetische Quantenzahl bezeichnet. Als Randbedingung nehmen wir die offensichtlich zu fordernde Periodizität Ψ(0) = Ψ(2π) = A und normieren A = 1. Zur Lösung von ( ) können wir die gefundene Separationskonstante m 2 l einsetzen. Wir dividieren durch sin 2 ϑ und separieren r und ϑ: m 2 ( l sin 2 ϑ 1 Θ sin ϑ d sin ϑ dθ ) = 1 ( dϑ dϑ R d r 2 dr ) + 2m dr dr 2 r2 [E V c ( r)] = const. Der linke Teil heißt jetzt ( ) und der rechte Teil wird vorübergehend ( ) genannt. Zur Separation verwenden wir die Separationskonstante l(l + 1). Wiederum werden wir sehen, dass l Z ist; l wird als Bahndrehimpulsquantenzahl bezeichnet. Nach der Lösung werden die Winkelfunktionen Θ und Φ zusammengefasst zu sphärischen Kugelfunktionen Y (ϑ, ϕ) = Θ(ϑ) Φ(ϕ). Wir nutzen noch die Differentialgleichung ( ) und erhalten: ( 1 ( ) sin ϑ d d sin ϑ 1 dϑ dϑ sin 2 ϑ d 2 ) dϕ 2 Y = l(l + 1) Y Die mathematische Physik hat gezeigt, dass diese Differentialgleichung durch assoziierte Legendre- Polynome gelöst wird. Diese haben die folgende Darstellung: ( P m l l (cos ϑ) = ( 1)m l 2 l (1 cos ϑ) m l/2 dl+m l cos 2 ϑ 1 ) l! d (cos ϑ) l+m l Hierbei ist l = 0, 1, 2,... der Grad des Legendre-Polynoms. Die ersten Polynome haben die Form: P0 0 (cos ϑ) = 1 P1 0 (cos ϑ) = cos ϑ P2 0(cos ϑ) = 1 2 (3 cos 2 ϑ 1 ) P3 0(cos ϑ) = 1 2 (5 cos 2 ϑ 3 cos ϑ )
17 3.4 Die Schrödingergleichung im Zentralpotential Seite 17 Die Lösung von ( ) ist also: Y = Y m l l (ϑ, ϕ) = Φ ml Θ ml,l(ϑ) = ( 1) ml (2l + 1) (l m l ) P m+l 4π (l + m l )! l (cos ϑ) Die folgenden Aufgaben werden dem geneigten Leser als simple Übungsaufgabe überlassen: (a) Zeigen Sie, dass gilt: Y m l l = ( 1) m l (Y m l l ) (b) Zeigen Sie, dass (Y m l l ) Y m l l dω = 1 ist. Hierbei ist dω ein Raumwinkelelement. (c) Zeigen Sie, dass durch die Legendre-Polynome ein vollständiges Orthogonalsystem gegeben ist, also dass gilt: (Y m l l ) Y m l l dω = δ l,l δ ml,m. l Nun schauen wir uns die Differentialgleichung ( ) an, diese lautete: ( 1 R d r 2 dr ) + 2m dr dr 2 r2 [E V c ( r)] = l (l + 1) Wir behaupten: Zum Beweis: r d dr [ d (r R) dr ] = r d [ R + r dr ] dr dr ( d r 2 dr ) = r d2 r R dr dr dr 2 = r dr dr +r dr dr +r2 d2 R dr 2 Zur Vereinfachung der Differentialgleichung substituieren wir r R( r) =: u( r): [ E u( r) = 2 2m d2 u( r) 2 ] l (l + 1) dr mr 2 + V c u( r) dr = 2r dr +r2 d2 R dr 2 = d ( r 2 dr ) dr dr In der Klammer steht ein neues effektives Potential, das zusätzlich zur Coulombkraft die Fliehkraft des Elektrons auf der Bahn l beschreibt: 2 l (l + 1) L 2mr 2 = 2 2I L entspricht dem Bahndrehimpuls (I ist das Trägheitsmoment des Elektrons). Es ergibt sich: L := l (l + 1) mit l = 0, 1, 2, 3,... Damit ist die Benennung von l als Bahndrehimpulsquantenzahl gerechtfertigt. Die Lösung von R( r) ergibt sich schließlich (siehe Quantenmechanik) zu: [ ( ) ] 2Z 3 (n l 1)! R n,l (r) = n a µ 2n (n + l)! e ϱ/2 ϱ l L 2l+1 n+l (ϱ) Hierbei sind: ϱ = nr L 2l+1 n+l (ϱ) = k=0 2Z r und a µ = 4π ε 0 2 n a µ µ e 2 und µ = m r = mm m + M Außerdem tauchen in der Lösung die assoziierten Laguerre-Polynome auf: ( 1) k+2l+1 (n + l)! 2 ϱ k (n r k)! (2l k)! k! mit n r = n l 1 n = 1, 2, 3,... l = 0, 1,..., n 1 Die Separation der ursprünglichen Schrödingergleichung war also erfolgreich. Was gilt für die R( r)?
18 3.4 Die Schrödingergleichung im Zentralpotential Seite 18 Die R( r) sind normiert: 0 R nl R nl dr = 1 R n,l exp( r/n) R n,0 (r = 0) 0 und R n,l 0 (r = 0) = 0 Betrachten wir nun die Darstellung der Kugelflächenfunktion Y : Y m l l ist normiert. Für l = 0 ist Y m l 0 räumlich isotrop, für m = 0 ist Yl 0 cos 2 ϑ. Es sind nur solche Y m l l definiert, für die m l l ist. Die übliche Darstellung für den Radialteil lautet: D(r) := r 2 R n,l (r) 2 Radiale Wahrscheinlichkeitsdichte Die radiale Wahrscheinlichkeitsdichte D(r) ist ein Mass für die Wahrscheinlichkeit, dass das Elektron sich im Intervall [r, r + dr] befindet. Alle Nullstellen von R n,l übertragen sich auf D. Außerdem kommt die Nullstelle r = 0 hinzu (welche eigentlich nur bei R n,l 0 vorkommt). Zur Bezeichnung: Den Bahndrehimpulsquantenzahlen werden Buchstaben zugeordnet. Bahndrehimpulsquantenzahl Orbitale s p d f g h i... Aus der Hauptquantenzahl n und dem Buchstaben für das Orbital ergibt sich die Elektronenkonfiguration, zum Beispiel 3d für n = 3 und l = 2. Die radiale Wahrscheinlichkeitsdichte D(r) hat unter anderem die folgenden Maxima: Konfiguration 1s 2p 3d 4f Abstand r a 0 4a 0 9a 0 16a 0 Nun betrachten wir die Funktion Φ(ϕ). Diese hing von der magnetischen Quantenzahl ab: Φ ml = A e im l ϕ mit m = 0, ±1, ±2,... Die Normierung ergibt A = 1/ 2π. Dann ist Φ ml 2 = 1/2π unabhängig von ϕ, daher hat das Elektron in gleichgroßen Winkelelementen dϕ 1 und dϕ 2 eine gleichgroße Aufenthaltswahrscheinlichkeit. (Die Lösung ist also in der xy-ebene isotrop.) Die Φ ml bilden ein Orthonormalsystem: 2π Es verbleibt noch Θ(ϑ) zu betrachten. Durch 0 Φ ml Φ m l dϕ = δ ml,m l Θ l,ml 2 sin ϑ dϑ = Θ l,ml Θ l,m l sin ϑ dϑ ist die Wahrscheinlichkeit gegeben, das Elektron in dem Intervall [ϑ, ϑ+ dϑ] zu finden. Die Normierung dieser Funktionen erfolgt wie folgt: 2π 0 Die Funktion Θ nimmt einige bekannte Formen an: Θ l,ml Θ 2 (l + m l )! l,m sin ϑ dϑ = δ l,l l (2l + 1) (l m l )!
19 3.5 Die Grobstruktur des H-Atoms Seite Für l = 0 und m l = 0 ergibt sich eine radial symmetrische Wellenfunktion Y 0 0 = 1/4π. Diese Funktion heißt s-wellenfunktion oder Kugelfunktion. 2. Für l = 1 und m l = 0 ergibt sich Y1 0 cos ϑ und daraus Y 0 1 (Y 1 0) cos 2 ϑ. Dies entspricht einer Dipolantenne, die in z-richtung strahlt. Für l = 1 und m l = ±1 ergibt sich Y ±1 1 sin ϑ und daraus Y ±1 1 (Y ±1 1 ) sin 2 ϑ. Dies entspricht einer Dipolantenne, die in der xy-ebene strahlt. Die Wellenfunktionen mit l = 1 heißen p-wellenfunktionen. 3. Für l = 2 und m l = 0 entspricht Y2 0 dem Feld einer Quadrupolantenne. Die Wellenfunktionen mit l = 2 heißen d-wellenfunktionen. Die allgemeine Lösung hat Eigenfunktionen ψ und damit auch Eigenwerte E i. Setzt man ψ in die Schrödingergleichung ein, erhält man: R E n = hc 1 + m M Z2 n 2 Dies ist analog zur Bohr-Rutherford-Theorie. Allerdings ist die Energie nur von der Hauptquantenzahl n abhängig, also haben alle Zustände die gleiche Energie, unabhängig von der Bahndrehimpulsquantenzahl l. Dieses Dilemma (mehrere Zustände mit derselben Energie) bezeichnet man als Entartung. Zur Darstellung der Wellenfunktionen benutzt man eine von White entwickelte Methode, bei der eine Spindel mit der Silhouette des Graphs von D(r) drehbar gelagert und durch einen Motor auf der z- Achse gedreht wird; es entsteht eine Bewegung in ϕ-richtung. Der polare Winkel ϑ wird mittels eines Holzprofils, welches die Form von Y m l l hat, zwischen 0 und π/2 eingestellt. Die Bewegung der Spindel wird mittels einer Kamera mit Langzeitbelichtung aufgezeichnet. 3.5 Die Grobstruktur des H-Atoms Die Quantenmechanik, insbesondere die Schrödingergleichung, wird angewendet auf das Zentralproblem mit dem Coulombpotential des H-Atomes. Man erhält eine Lösung mit drei Quantenzahlen: n = 1, 2, 3,... l = 0, 1, 2,... m l = l, l + 1,..., l 1, l Zu jedem n existieren n verschiedene l-werte, und zu jedem l existieren 2l + 1 verschiedene m l -Werte. Das System ist also überbestimmt. Wir wissen, dass es möglich ist, die Energien alleine durch n zu bestimmen, während die Eigenfunktionen durch alle drei Quantenzahlen beeinflusst werden. Die Energie eines Quantenzustandes ergibt sich aus: E n 1 n 2 Die E n sind also entartet, dabei ist die l-entartung n-fach und die m l -Entartung ist (2l + 1)-fach. Zum Beispiel haben für n = 2 die Zustände l = 0 (Konfiguration 2s) und l = 1 (Konfiguration 2p) die gleiche Energie, also ist die Energie zweifach l-entartet.
20 4.1 Normale Feinstrukturaufspaltung (Spin-Bahn-Kopplung) Seite 20 4 Fein- und Hyperfeinstruktur des H-Atoms Michelson und Morley beobachteten 1887, dass die Balmer-Linie des Wasserstoffspektrums eigentlich aus zwei sehr dicht nebeneinander liegenden Linien besteht. Ein erster vager Erklärungsversuch waren die von der Bohr-Sommerfeld-Theorie prognostizierten elliptischen Elektronenbahnen. Heute kennt man die genauen Ursachen und Probleme früherer Theorien: Das Elektron hat einen Elektronenspin S. Der Atomkern hat eine bestimmte Nukleonenstruktur. Es müssen einige relativistische und elektrodynamische Korrekturen vorgenommen werden. (Dafür nimmt man die Dirac-Gleichung, die relativistische Version der Schrödingergleichung. Die potentielle Energie setzt sich zusammen aus: H ges = H kin + H pot Anteil Ursache Größe H Coulomb Coulomb-Wechselwirkung 10 ev H fs Feinstruktur-Wechselwirkung 10 4 ev H QED Quantenelektrodynamik-Wechselwirkung 10 5 ev H hfs Hyperfeinstruktur-Wechselwirkung 10 5 ev H nukl Abweichungen aufgrund unterschiedlicher Nukleonenstruktur 10 8 ev 4.1 Normale Feinstrukturaufspaltung (Spin-Bahn-Kopplung) Die Niederländer Gaudsmith und Uhlenbeek postulieren 1925, dass das Elektron einen Spin haben muss. Damit ergibt sich eine neue Spinquantenzahl s = ±1/2. Daraus ergibt sich eine Spinquantenenergie E s = ± 1 2 Außerdem wird der Bahndrehimpuls L 2 = l (l + 1) 2 um den Spindrehimpuls erweitert: S 2 = s (s + 1) 2 S = s (s + 1) Drehimpulskopplung im Atom Neben der magnetischen Quantenzahl m l führt man eine magnetische Quantenzahl m s = ±1/2 ein. Man hat insgesamt zwei gekoppelte Drehimpulse L (des Atomes) und S (des Elektrons), es liegt also ein Kreisel vor. Die Kopplung zwischen L und S entspricht der normalen Feinstrukturaufspaltung. Sie folgt aus der Änderung des elektrischen Feldes (in der Größenordnung von 10 7 V/m zwischen Kern und Elektron, was zu einem Magnetfeld führt. Dieser Effekt soll jetzt quantifiziert werden.
21 4.1 Normale Feinstrukturaufspaltung (Spin-Bahn-Kopplung) Seite 21 Mit der Umlaufperiode T = 2π r/ v kann das bewegte Elektron als Strom aufgefasst werden: I = dq dt = e T = e v 2π r Entsprechend ergibt sich ein magnetisches Moment in der durch die Bewegung des Elektrons beschriebenen Stromschleife ( e l sei die Normale auf der Ebene, in der die Stromschleife liegt): µ l = I F = I πr 2 = e v 2π r πr2 = evr 2 = e 2m mrv = e 2m L Zur Quantifizierung der Kopplung Für L gibt es zwei Möglichkeiten: Im Bohrschen Modell ist L = l, damit ergibt sich 1 el µ l = 2m e l = l µ B e l = µ B L Das magnetische Moment ist also quantisiert. Das kleinstmögliche magnetische Moment ist: µ B = e 2m = 0, J/T Bohrsches Magneton Oben haben wir gesehen, dass µ l linear abhängig vom Bahndrehimpuls ist. Eine ähnliche Formel gilt auch für Spindrehimpulse, wenn man einen Korrekturfaktor einführt. µ l = g l µ B L µ s = gs µ B mit mit g l = 1 g s = 2 S Aus den Maxwell-Gleichungen folgt, dass die Bahnbewegung des Elektrons dazu führt, dass auf das Elektron ein Magnetfeld wirkt, was zu einer Änderung der potentiellen Energie führt: B = 1 c 2 v E E = 1 2 µ s B = 1 2 gs µ B S B Der Faktor 1/2 wurde 1926 von Thomas eingefügt, um relativistische Effekte zu beschreiben. Nun sehen wir uns die Lorentzkraft F = q ( v B) an, welche mit dem elektrischen Potential als F = V/ r r/ r quantifiziert ist. Das Magnetfeld ist damit: B = 1 r 1 ec 2 V r v r Der Bahndrehimpuls war L = m ( r v) = m ( v r), durch Kombination mit der obigen Gleichung ergibt sich: B = 1 r 1 emc 2 V r L Dies können wir, zusammen mit V/ r = e 2 /(4πε 0 r 2 ), in die obige Energieänderung einsetzen: E LS = e 2 4πε 0 2mc 2 S L r 3 ( ) 1 Wobei zu beachten ist, dass das magnetische Moment und der Drehimpuls per Konvention antiparallel sind.
22 4.1 Normale Feinstrukturaufspaltung (Spin-Bahn-Kopplung) Seite 22 Diese Energieänderung liegt in der Größenordnung von 10 4 ev. Das Magnetfeld hat eine Stärke von etwa 1 T. Die Wechselwirkung kann man sich so vorstellen: Der Bahndrehimpuls L generiert ein Magnetfeld B, welcher in S bzw. mu s ein Drehmoment erwirkt. Dadurch führen S und L eine Präzessionsbewegung um eine gemeinsame Achse, die auch quantisiert sein muss: J = L + S J = j (j + 1) Man wählt ein körperfestes Koordinatensystem, für das J um die z-achse präzediert. Dann präzediert L um die J-Achse und S um die L-Achse, wobei die letzte Präzession um den Faktor 1000 schneller läuft als die anderen. Im zeitlichen Mittel ist: J x = J y = 0 und J z = m j 0 Man führt also für die Quantenzahl j auch eine magnetische Quantenzahl m j ein, welche die Werte m j = j, j + 1,..., j 1, j annehmen kann. Nun wollen wir die Definition von J ausnutzen, um die Energieänderung zu vereinfachen: J = L + S J J = L L + S S + 2 S L S L ( ) = 1 2 J J L L S S S L = 1 2 [j (j + 1) l (l + 1) s (s + 1)] E LS = 2 4m 2 c 1 2 r V r [j (j + 1) l (l + 1) s (s + 1)] Damit wird das Energieniveau n für l 0 aufgespalten in zwei Zustände l + 1/2 und l 1/2. Bis jetzt haben wir nur das H-Atom betrachtet; allgemein gilt: E LS = α2 Z 2 n 2 E n Hiermit wird eine neue Konstante eingeführt. n l (l ) (l + 1) S L α := e2 4πε = 1 0 c 137, Feinstrukturkonstante Für J gilt wiederum, dass die x- und y-komponenten im Mittel verschwinden: Hierbei gilt: J x = J y = 0 und J z = m j m j = m l + m s Als allgemeine Schreibweise für die Zustände hat sich durchgesetzt: n (2s+1) L j Hierbei sind n die Hauptquantenzahl und 2s+1 die Multiplizität. L ist der Buchstabe für die Bahndrehimpulsquantenzahl l (als Großbuchstabe: S, P, D, F, G,...) und j ist die Drehimpulsquantenzahl. Wir wollen nun die Zustände für das H-Atom auflisten. Hier gilt j = l ± 1/2, wobei j > 0 sein soll.
23 4.1 Normale Feinstrukturaufspaltung (Spin-Bahn-Kopplung) Seite 23 n l j Bezeichung 1 0 1/2 1 2 S 1/ /2 2 2 S 1/ /2 2 2 P 1/ /2 2 2 P 3/ /2 3 2 S 1/ /2 3 2 P 1/ /2 3 2 P 3/ /2 3 2 D 3/ /2 3 2 D 5/ /2 4 2 S 1/ /2 4 2 P 1/ /2 4 2 P 3/ /2 4 2 D 3/ /2 4 2 D 5/ /2 4 2 F 5/ /2 4 2 F 7/2 Unser Ziel wird es nun sein, herauszufinden, unter welchen Umständen die einzelnen Niveaus besetzt werden können. Vorher führen wir nun noch zwei weitere Korrenturen zur Feinstruktur ein, zum einen die relativistische Geschwindigkeit der Elektronen, zum anderen die endliche Ladungsdichte am Ort des Kerns (für l = 0-Zustände) Relativistische Korrekturen Die relativistische Form des Hamiltonoperators lautet: H = p 2 c 2 + m 2 0 c4 m 0 c 2 +V ( r) }{{} kinetische Energie T Das bewirkt nur eine kleine Änderung gegenüber der nichtrelativistischen Rechnung. Entwicklung nach p führt auf: p2 p 4 T = + 1 2m 0 8 m O(p 6 ) 0 }{{ c2 } T Der erste Term entspricht der klassisch erwarteten kinetischen Energie T 0, der zweite Term ist ein Störungsterm. p 4 T = 1 8 m 2 0 = T 0 4 c2 2m 0 c 2 T 0 Die klassische kinetische Energie kann abgeschätzt werden durch: 1 T 0 E n V ( r) T = 2m 0 c 2 [E n V ( r)] 2 Beim Rechnen mit Störungen können wir die Erkenntnisse aus der Variationsrechnung anwenden: E rel = 1 2m 0 c [E 2 n V ( r)] 2 [ ] = 1 2m 0 c E 2 2 n 2E n Ze2 4πε 0 r + Z 2 e 4 (4πε 0 r) 2
24 4.2 Lamb-Shift. Anomale Feinstrukturverschiebung Seite 24 Klassich erhält man den Erwartungswert einer periodischen Funktion aus: f(t) = 1 T f(t) d 3 r In der Quantenmechanik muss mit der Wahrscheinlichkeitsdichte gewichtet werden: f( r) = f( r) ψ( r, t) 2 d 3 r Es ergibt sich damit: 1 = 1 r n 2 Z a 0 und 1 r 2 = 1 (l + 1/2) n 3 Z2 a 2 0 Daraus folgt für die Energiedifferenz zwischen nichtrelativistischer und relativistischer Rechnung: E rel = E n α2 Z 2 [ 3 n 2 4 n ] l + 1/ Korrekturen für die endliche Ladungsdichte Bei r = 0 findet sich für l = 0 (also die Zustände 1s, 2s, 3s und so weiter) eine endliche Ladung. Klassisch betrachtet kann dass Elektron nie am Ort des Kernes sein. In der Quantenmechanik muss man zur S-Wellenfunktion einen Korrekturterm hinzunehmen, der von Darwin entwickelt wurde (und hier nicht hergeleitet werden soll): E Darwin = π 2 2m c 2 Ze2 ψ n,l,ml (r = 0) 2 = E n (Zα)2 4πε 0 n Daraus folgt, dass es ein endlich großer Teil der Elektronenladung bei r = 0 liegt. Die Gesamtenergie des Elektrons ergibt sich mit allen Korrekturen zu: E n,j = E n + E fs = E n + E LS + E rel + E Darwin [ ( )] E n,j = E n 1 + Z2 α2 n n 2 j+1/2 3 4 Gesamtenergie des Elektrons mit Feinstrukturkorrekturen Die Energie hängt immer noch nicht von der Bahndrehimpulsquantenzahl ab, somit gibt es ab n = 3 weiterhin eine Entartung. Diese Entartung kann man auflösen, wenn man das Kernfeld nicht mehr als ideales Feld annimmt, sondern im Rahmen der Quantenelektrodynamik als quantisiert betrachtet. Dies führt zum sogenannten Lamb-Shift nach Willis E. Lamb. 4.2 Lamb-Shift. Anomale Feinstrukturverschiebung Bisher haben wir den Energieterm mithilfe der Spin-Bahn-Kopplung, der relativistischen Rechnung und der Darwinschen Näherung der Ladungsdichte für r = 0 korrigiert. Nun soll, wie in der Quantenelektrodynamik üblich, ein Feld als quantisiert angesehen werden: E = ( ω n ω + 1 ) 2 n ω
25 4.3 Hyperfeinstruktur und Isotopieeffekt Seite 25 Der tiefste Zustand liegt bei n ω = 0, also E = ω/2. Also existiert immer ein elektrisches Restfeld im Vakuum, die sogenannte Vakuumpolarisation. Aufgrund dieser Quantisierung kann sich das Elektron nicht auf einem festen Radius r 0 bewegen, sondern weicht zu einem neuen Radius r aus. Hierbei sind r 0 und r die Ortsvektoren des Elektrons ohne und mit Vakuumfeld. Die Differenz heißt d r = r r 0. Das Potential kann um r 0 entwickelt werden. Man beachte dabei, dass die Abweichungen im Mittel verschwinden, ihre Quadrate jedoch nicht. V ( r) = V ( r 0 + d r) = V ( r 0 ) + V } {{ d r } =0 im Mittel V (d r) 2 V ( r) = V (r 0 ) V (d r) 2 Die Bindungsenergie sinkt aufgrund dieses Effektes also ab, und zwar um etwa 10 2 % bis 10 5 %. E Lamb Z4 n 3 Man beachte, dass diese Korrektur nur bei S-Zuständen angewandt werden muss, da man nur dort eine Kreisbewegung hat. Damit haben zum Beispiel die Zustände 2 2 S 1/2 und 2 2 P 1/2 nicht mehr die gleiche Energie, Entartungen in höheren Bahndrehimpulsquantenzahlen bestehen jedoch weiterhin. 4.3 Hyperfeinstruktur und Isotopieeffekt Bisher haben wir den Atomkern als strukturlos betrachtet. Jetzt wollen wir nach den Überlegungen von Pauli (1924) eine Kernstruktur einführen. Die Gesamtmasse setzt sich aus der Masse der einzelnen Neutronen und Protonen zusammen. Damit haben wir neben dem Gesamtdrehimpuls J des Elektrons (Masse m e ) auch für den Atomkern (Masse m N ) einen Drehimpuls I. Neben der Drehimpulsquantenzahl j für das Elektron (die wie gehabt quantisiert ist) eine neue Zahl i = 0, 1/2, 1, 3/2,... ein, die außerdem mit einer magnetischen Quantenzahl m i = i, i + 1,..., i 1, i versehen ist. Es gilt nun: I = i(i + 1) In Analogie zum Elektron gibt es auch hier ein magnetisches Moment: µ I = g I µ N I mit µ N = e 2m p = m e m p µ B Hierbei ist g I der g-faktor des Kernes und µ N das kleinstmögliche Kernmagneton (in Analogie zum Bohrschen Magneton). Das magnetische Moment war beim Elektron relevant wegen des Elektronenspins. Auch hier gibt es einen zusätzlichen Eintrag im magnetischen Moment aufgrund eines Kernspins. Aufgrund des Massenverhältnisses von Kern und Elektron erwarten wir eine (gegenüber E fs um drei Größenordnungen kleinere) Korrektur der Elektronenenergie, falls µ N zu einem Magnetfeld koppelt: E hfs = µ I B( r = 0) Die relevanten Magnetfelder werden erzeugt durch den Elektronenspin sowie die Bahnbewegung des Elektrons. Beim Elektron war J = L + S der Gesamtdrehimpuls. Nun werden I und J gekoppelt zu einem neuen Drehimpuls: F x F = J + I = F y F z
26 4.3 Hyperfeinstruktur und Isotopieeffekt Seite 26 Wiederum sind die F x - und F y -Komponenten von F im zeitlichen Mittel gleich Null. Wir können zudem festellen, dass B J und µ i I ist. Das Quadrat von F ist E hfs = µ I B( r = 0) = A I J F 2 = I 2 + J I J mit I 2 = i(i + 1) 2 und J 2 = j(j + 1) 2 Es ergibt sich also: E hfs = 1 2 A C mit C = f(f + 1) i(i + 1) j(j + 1) und A = µ I B( r = 0) I J Man beachte, dass die I J-Präzession im Vergleich zur L S-Präzession sehr langsam verläuft. Beispiel 4.1 Hyperfeinstrukturaufspaltung im H-Atom Wir haben nur i = 1/2 und j = 1/2. Daraus ergibt ich für f: { 0 f = i ± j = 1 Der Grundzustand (n = 1) spaltet sich in zwei Niveaus auf und man erhält E hfs 1420 MHz. Dieser Effekt ist aber nur wichtig für niedrige Hauptquantenzahlen, da die Aufspaltung bei kleinen Hauptquantenzahlen wesentlich größer ist als bei großen (wegen der höheren Nähe zum Kern). Zur Hyperfeinstrukturaufspaltung kommen zwei Korrekturen: (a) Der Kern enthält noch nicht berücksichtigte magnetische und elektrische Multipole (aufgrund seines endlichen Volumens und der inhomogenen Ladungsverteilung). Die Abweichung vom Coulombpotential führt auf höhere Multipole, vor allem den elektrischen Quadrupol und den magnetischen Dipol. Für die Energie der Elektronen im Feld des Kerns galt bisher: E Coulomb = Z e 2 ϱ e 4π ε 0 r dω Die Ladungsdichte der Elektronen ϱ e ist isotrop. Nun betrachten wir als erste Abweichung die Energie des Kerns im Feld der Elektronen: E k = e ϱ k ϕ e dω Die Energiedifferenz E ist also E = E k E Coulomb als eine Abweichung vom idealen Modell einer punktförmigen Ladungsverteilcung im Kern. Für eine Quadrupolladungsdichte gilt zum Beispiel: E = E Q = eq ϕ zz(r = 0) 4 ( 3 2 cos2 ϕ 1 ) 2 Wir können nun ϕ e nach kleinen r entwickeln. eq = e r 2 (3 cos 2 ϕ 1 ) ϱ k dω Hierbei ist Q ein Wirkungsquerschnitt (in cm 2 ). Der Fall Q = 0 ist trivial (man hat wieder eine kugelförmige Verteilung). Ansonsten hat man eine Anisotropie (für Q > 0 eine Zigarre, für Q < 0 eine Oblate ).
27 4.3 Hyperfeinstruktur und Isotopieeffekt Seite 27 (b) Isotopieeffekt: Ein Atomkern besteht aus Z Protonen (Z 1), jeweils mit der Masse m p, und N Neutronen (N 0) mit der Masse m n. Die Massen von Neutron und Proton sind in etwa gleich. Somit haben wir insgesamt A = Z + N Nukleonen mit der Gesamtmasse m N A m p. Für Z = const. und N variabel haben wir verschiedene Isotope. Nun gibt es zwei Korrektureffekte: massenabhängiger Isotopieverschiebungseffekt (IVE): Analog zum Bohr-Rutherfordschen Masseneffekt haben wir eine reduzierte Masse: Die Energieeigenwerte ergeben sich nun zu: m r = m e m N m e + m N E n = hc Ry Z 2 n 2 [ 1 m ] e m N Zwei Isotope unterscheiden sich durch die verschiedenen Kernmassen: m N = A m p und m N = A m p E = hc Ry Z 2 [ 1 n 2 m e m 1 ] N m 1 N A }{{} 2 = A A A A Offensichtlicherweise ist dieser Effekt besonders stark für kleine Kerne. Für ein H-Atom haben wir in der Balmer-Serie etwa ν = 1, cm 1 und λ = 0,18 nm. Bei A > 30 ist der massenabhängige IVE kaum noch messbar. Volumen- oder Feldeffekt der IVE Dieser Effekt ist analog zum Lamb-Shift: Für A > 30 muss die endliche Ausdehnung der Kernladung beachtet werden. Das e -Potential muss also variiert werden. δ( E) = r 0 0 ϱ k δ( V ) 4πr 2 dr Hierbei ist δ( V ) die Variation der Kreisbahn durch die Kernladung. Dieser Effekt ist allerdings nur für kernnahe Bahnen wichtig, also für p- und s-schalen.
28 5.1 Operatoren. Eigenwerte. Eigenfunktionen. Quantenmechanischer Mittelwert Seite 28 5 Verallgemeinerung der Quantenmechanik Bisher hatten wir die Wellenmechanik des H-Atoms mithilfe der Schrödingergleichung beschrieben. Nun sollen eingeführt werden: 1. die Matrixdarstellung nach Heisenberg 2. die Dirac-Schreibweise für Vektoren 3. die Darstellung von Konfigurationen im Hilbertraum 4. die Anwendung auf Vielteilchensysteme (etwa für das Periodensystem oder den quantenmechanischen Tunneleffekt) 5.1 Operatoren. Eigenwerte. Eigenfunktionen. Quantenmechanischer Mittelwert Wir haben bereits den Hamiltonoperator H kennengelernt. Hψ = E ψ Hierbei ist ψ eine Eigenfunktion und E ein Eigenwert. Im Folgenden seien alle Operatoren durch Überstriche gekennzeichnet. Zu einem physikalischen Parameter A gibt es immer einen zugehörigen Operator A. Wir können über H einiges sagen: H ist ein linearer Operator. Allgemein gilt: (A + B)f = Af + Bf Der Operator ist hermitesch, das heißt, in Af = λ f ist λ immer reell. Zum Beweis integrieren wir über den Konfigurationsraum X (also den Hilbertraum). Dann muss gelten: f (F f) dx = (F f) f dx f (λf) dx = (λf) f dx λ f f dx = λ f f dx λ = λ Die Eigenfunktionen f n bilden ein Orthonormalsystem: f n f m dx = δ nm Im H-Atom sind diese Eigenfunktionen die ψ n,l,ml,s,m s,... Es gilt immer: ψ = c i ψ i und ψ ψ dx = c! i c i = 1 i i
10. Der Spin des Elektrons
 10. Elektronspin Page 1 10. Der Spin des Elektrons Beobachtung: Aufspaltung von Spektrallinien in nahe beieinander liegende Doppellinien z.b. die erste Linie der Balmer-Serie (n=3 -> n=2) des Wasserstoff-Atoms
10. Elektronspin Page 1 10. Der Spin des Elektrons Beobachtung: Aufspaltung von Spektrallinien in nahe beieinander liegende Doppellinien z.b. die erste Linie der Balmer-Serie (n=3 -> n=2) des Wasserstoff-Atoms
Atommodell führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen.
 Atommodell nach Rutherford 1911 führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen. Beobachtung: Fast alle Teilchen fliegen ungestört durch.
Atommodell nach Rutherford 1911 führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen. Beobachtung: Fast alle Teilchen fliegen ungestört durch.
Stark-Effekt für entartete Zustände
 Stark-Effekt für entartete Zustände Die Schrödingergleichung für das Elektron im Wasserstoff lautet H nlm = n nlm mit H = p2 e2 2 m e 4 r Die Eigenfunktion und Eigenwerte dieses ungestörten Systems sind
Stark-Effekt für entartete Zustände Die Schrödingergleichung für das Elektron im Wasserstoff lautet H nlm = n nlm mit H = p2 e2 2 m e 4 r Die Eigenfunktion und Eigenwerte dieses ungestörten Systems sind
10. Das Wasserstoff-Atom Das Spektrum des Wasserstoff-Atoms. im Bohr-Modell:
 phys4.016 Page 1 10. Das Wasserstoff-Atom 10.1.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
phys4.016 Page 1 10. Das Wasserstoff-Atom 10.1.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
Musterlösung 02/09/2014
 Musterlösung 0/09/014 1 Streuexperimente (a) Betrachten Sie die Streuung von punktförmigen Teilchen an einer harten Kugel vom Radius R. Bestimmen Sie die Ablenkfunktion θ(b) unter der Annahme, dass die
Musterlösung 0/09/014 1 Streuexperimente (a) Betrachten Sie die Streuung von punktförmigen Teilchen an einer harten Kugel vom Radius R. Bestimmen Sie die Ablenkfunktion θ(b) unter der Annahme, dass die
Der Gesamtbahndrehimpuls ist eine Erhaltungsgrösse (genau wie in der klassischen Mechanik).
 phys4.017 Page 1 10.4.2 Bahndrehimpuls des Elektrons: Einheit des Drehimpuls: Der Bahndrehimpuls des Elektrons ist quantisiert. Der Gesamtbahndrehimpuls ist eine Erhaltungsgrösse (genau wie in der klassischen
phys4.017 Page 1 10.4.2 Bahndrehimpuls des Elektrons: Einheit des Drehimpuls: Der Bahndrehimpuls des Elektrons ist quantisiert. Der Gesamtbahndrehimpuls ist eine Erhaltungsgrösse (genau wie in der klassischen
[ H, L 2 ]=[ H, L z. ]=[ L 2, L z. U r = Warum haben wir soviel Zeit mit L 2 verbracht? = x 2 2. r 1 2. y 2 2. z 2 = 2. r 2 2 r
![[ H, L 2 ]=[ H, L z. ]=[ L 2, L z. U r = Warum haben wir soviel Zeit mit L 2 verbracht? = x 2 2. r 1 2. y 2 2. z 2 = 2. r 2 2 r [ H, L 2 ]=[ H, L z. ]=[ L 2, L z. U r = Warum haben wir soviel Zeit mit L 2 verbracht? = x 2 2. r 1 2. y 2 2. z 2 = 2. r 2 2 r](/thumbs/71/65107015.jpg) Warum haben wir soviel Zeit mit L 2 verbracht? = x 2 2 y 2 2 z 2 = 2 r 2 2 r r 1 2 L r 2 ħ 2 11. Das Wasserstoffatom H = p2 2 U r μ = Masse (statt m, da m später als Quantenzahl verwendet wird) U r = e2
Warum haben wir soviel Zeit mit L 2 verbracht? = x 2 2 y 2 2 z 2 = 2 r 2 2 r r 1 2 L r 2 ħ 2 11. Das Wasserstoffatom H = p2 2 U r μ = Masse (statt m, da m später als Quantenzahl verwendet wird) U r = e2
9. Das Wasserstoff-Atom. 9.1 Das Spektrum des Wasserstoff-Atoms. im Bohr-Modell:
 09. Wasserstoff-Atom Page 1 9. Das Wasserstoff-Atom 9.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
09. Wasserstoff-Atom Page 1 9. Das Wasserstoff-Atom 9.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
Atommodell. Atommodell nach Bohr und Sommerfeld Für sein neues Atommodell stellte Bohr folgende Postulate auf:
 Für sein neues Atommodell stellte Bohr folgende Postulate auf: Elektronen umkreisen den Kern auf bestimmten Bahnen, wobei keine Energieabgabe erfolgt. Jede Elektronenbahn entspricht einem bestimmten Energieniveau
Für sein neues Atommodell stellte Bohr folgende Postulate auf: Elektronen umkreisen den Kern auf bestimmten Bahnen, wobei keine Energieabgabe erfolgt. Jede Elektronenbahn entspricht einem bestimmten Energieniveau
Aufbau von Atomen. Atommodelle Spektrum des Wasserstoffs Quantenzahlen Orbitalbesetzung Periodensystem
 Aufbau von Atomen Atommodelle Spektrum des Wasserstoffs Quantenzahlen Orbitalbesetzung Periodensystem Wiederholung Im Kern: Protonen + Neutronen In der Hülle: Elektronen Rutherfords Streuversuch (90) Goldatome
Aufbau von Atomen Atommodelle Spektrum des Wasserstoffs Quantenzahlen Orbitalbesetzung Periodensystem Wiederholung Im Kern: Protonen + Neutronen In der Hülle: Elektronen Rutherfords Streuversuch (90) Goldatome
(a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle?
 FK Ex 4-07/09/2015 1 Quickies (a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle? (b) Wie groß ist die Energie von Lichtquanten mit einer Wellenlänge von
FK Ex 4-07/09/2015 1 Quickies (a) Warum spielen die Welleneigenschaften bei einem fahrenden PKW (m = 1t, v = 100km/h) keine Rolle? (b) Wie groß ist die Energie von Lichtquanten mit einer Wellenlänge von
2. H Atom Grundlagen. Physik IV SS H Grundl. 2.1
 . H Atom Grundlagen.1 Schrödingergleichung mit Radial-Potenzial V(r). Kugelflächen-Funktionen Y lm (θ,φ).3 Radial-Wellenfunktionen R n,l (r).4 Bahn-Drehimpuls l.5 Spin s Physik IV SS 005. H Grundl..1 .1
. H Atom Grundlagen.1 Schrödingergleichung mit Radial-Potenzial V(r). Kugelflächen-Funktionen Y lm (θ,φ).3 Radial-Wellenfunktionen R n,l (r).4 Bahn-Drehimpuls l.5 Spin s Physik IV SS 005. H Grundl..1 .1
Φ muss eineindeutig sein
 phys4.018 Page 1 10.6.2 Lösungen für Φ Differentialgleichung: Lösung: Φ muss eineindeutig sein dies gilt nur für m l = 0, ±1, ±2, ±3,, ±l m l ist die magnetische Quantenzahl phys4.018 Page 2 10.6.3 Lösungen
phys4.018 Page 1 10.6.2 Lösungen für Φ Differentialgleichung: Lösung: Φ muss eineindeutig sein dies gilt nur für m l = 0, ±1, ±2, ±3,, ±l m l ist die magnetische Quantenzahl phys4.018 Page 2 10.6.3 Lösungen
H LS = W ( r) L s, (2)
 Vorlesung 5 Feinstruktur der Atomspektren Wir betrachten ein Wasserstoffatom. Die Energieeigenwerte des diskreten Spektrums lauten E n = mα c n, (1 wobei α 1/137 die Feinstrukturkonstante, m die Elektronmasse
Vorlesung 5 Feinstruktur der Atomspektren Wir betrachten ein Wasserstoffatom. Die Energieeigenwerte des diskreten Spektrums lauten E n = mα c n, (1 wobei α 1/137 die Feinstrukturkonstante, m die Elektronmasse
Ferienkurs der TU München- - Experimentalphysik 4 Wasserstoffatom, Feinstruktur und Atome im Magnetfeld. Jonas J. Funke
 Ferienkurs der TU München- - Experimentalphysik 4 Wasserstoffatom, Feinstruktur und Atome im Magnetfeld Lösung Jonas J. Funke 0.08.00-0.09.00 Aufgabe (Drehimpulsaddition). : Gegeben seien zwei Drehimpulse
Ferienkurs der TU München- - Experimentalphysik 4 Wasserstoffatom, Feinstruktur und Atome im Magnetfeld Lösung Jonas J. Funke 0.08.00-0.09.00 Aufgabe (Drehimpulsaddition). : Gegeben seien zwei Drehimpulse
Das Bohrsche Atommodell
 Das Bohrsche Atommodell Auf ein Elektron, welches im elektrischen Feld eines Atomkerns kreist wirkt ein magnetisches Feld. Der Abstand zum Atomkern ist das Ergebnis, der elektrostatischen Coulomb-Anziehung
Das Bohrsche Atommodell Auf ein Elektron, welches im elektrischen Feld eines Atomkerns kreist wirkt ein magnetisches Feld. Der Abstand zum Atomkern ist das Ergebnis, der elektrostatischen Coulomb-Anziehung
2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten
 Inhalt: 1. Regeln und Normen Modul: Allgemeine Chemie 2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten 3.Bausteine der Materie Atomkern: Elementarteilchen, Kernkräfte,
Inhalt: 1. Regeln und Normen Modul: Allgemeine Chemie 2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten 3.Bausteine der Materie Atomkern: Elementarteilchen, Kernkräfte,
Abb.15: Experiment zum Rutherford-Modell
 6.Kapitel Atommodelle 6.1 Lernziele Sie kennen die Entwicklung der Atommodelle bis zum linearen Potentialtopf. Sie kennen die Bohrschen Postulate und können sie auch anwenden. Sie wissen, wie man bestimmte
6.Kapitel Atommodelle 6.1 Lernziele Sie kennen die Entwicklung der Atommodelle bis zum linearen Potentialtopf. Sie kennen die Bohrschen Postulate und können sie auch anwenden. Sie wissen, wie man bestimmte
9. Moleküle. 9.1 Wasserstoff-Molekül Ion H Wasserstoff-Molekül H Schwerere Moleküle 9.4 Angeregte Moleküle. Physik IV SS
 9.1 Wasserstoff-Molekül Ion H + 9. Wasserstoff-Molekül H 9.3 Schwerere Moleküle 9.4 Angeregte Moleküle 9.1 9.1 Wasserstoff-Molekül Ion H + Einfachstes Molekül: H + = p + e p + Coulomb-Potenzial: Schrödinger-Gleichung:
9.1 Wasserstoff-Molekül Ion H + 9. Wasserstoff-Molekül H 9.3 Schwerere Moleküle 9.4 Angeregte Moleküle 9.1 9.1 Wasserstoff-Molekül Ion H + Einfachstes Molekül: H + = p + e p + Coulomb-Potenzial: Schrödinger-Gleichung:
Ferienkurs Experimentalphysik 4
 Ferienkurs Experimentalphysik 4 Probeklausur Markus Perner, Markus Kotulla, Jonas Funke Aufgabe 1 (Allgemeine Fragen). : (a) Welche Relation muss ein Operator erfüllen damit die dazugehörige Observable
Ferienkurs Experimentalphysik 4 Probeklausur Markus Perner, Markus Kotulla, Jonas Funke Aufgabe 1 (Allgemeine Fragen). : (a) Welche Relation muss ein Operator erfüllen damit die dazugehörige Observable
Übungsblatt 06. PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, oder 3. 6.
 Übungsblatt 06 PHYS400 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, (othmar.marti@uni-ulm.de) 2. 6. 2005 oder 3. 6. 2005 Aufgaben. Schätzen Sie die relativistische Korrektur E
Übungsblatt 06 PHYS400 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, (othmar.marti@uni-ulm.de) 2. 6. 2005 oder 3. 6. 2005 Aufgaben. Schätzen Sie die relativistische Korrektur E
14. Atomphysik. Inhalt. 14. Atomphysik
 Inhalt 14.1 Aufbau der Materie 14.2 Der Atomaufbau 14.2.1 Die Hauptquantenzahl n 14.2.2 Die Nebenquantenzahl l 14.2.3 Die Magnetquantenzahl m l 14.2.4 Der Zeemann Effekt 14.2.5 Das Stern-Gerlach-Experiment
Inhalt 14.1 Aufbau der Materie 14.2 Der Atomaufbau 14.2.1 Die Hauptquantenzahl n 14.2.2 Die Nebenquantenzahl l 14.2.3 Die Magnetquantenzahl m l 14.2.4 Der Zeemann Effekt 14.2.5 Das Stern-Gerlach-Experiment
14. Atomphysik Physik für E-Techniker. 14. Atomphysik
 14. Atomphysik 14.1 Aufbau der Materie 14.2 Der Atomaufbau 14.2.1 Die Hauptquantenzahl n 14.2.2 Die Nebenquantenzahl l 14.2.3 Die Magnetquantenzahl m l 14.2.4 Der Zeemann Effekt 14.2.5 Das Stern-Gerlach-Experiment
14. Atomphysik 14.1 Aufbau der Materie 14.2 Der Atomaufbau 14.2.1 Die Hauptquantenzahl n 14.2.2 Die Nebenquantenzahl l 14.2.3 Die Magnetquantenzahl m l 14.2.4 Der Zeemann Effekt 14.2.5 Das Stern-Gerlach-Experiment
Physik IV - Schriftliche Sessionsprüfung SS 2008
 Physik IV - Schriftliche Sessionsprüfung SS 2008 9:00 11:00, Donnerstag, 14. August 2008 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt 6 Aufgaben auf VIER Blättern. Es können insgesamt 60 Punkte
Physik IV - Schriftliche Sessionsprüfung SS 2008 9:00 11:00, Donnerstag, 14. August 2008 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt 6 Aufgaben auf VIER Blättern. Es können insgesamt 60 Punkte
Wiederholung der letzten Vorlesungsstunde:
 Wiederholung der letzten Vorlesungsstunde: Das Bohr sche Atommodell: Strahlenabsorption, -emission, Elektromagentische Strahlung, Wellen, Wellenlänge, Frequenz, Wellenzahl. Postulate: * Elektronen bewegen
Wiederholung der letzten Vorlesungsstunde: Das Bohr sche Atommodell: Strahlenabsorption, -emission, Elektromagentische Strahlung, Wellen, Wellenlänge, Frequenz, Wellenzahl. Postulate: * Elektronen bewegen
Vorlesung 24: Roter Faden: Wiederholung Quantisierung der Energien in QM. Emissions- und Absorptionsspektren der Atome
 Vorlesung 24: Roter Faden: Wiederholung Quantisierung der Energien in QM Franck-Hertz Versuch Emissions- und Absorptionsspektren der Atome Spektren des Wasserstoffatoms Bohrsche Atommodell Lösung der Schrödingergleichung
Vorlesung 24: Roter Faden: Wiederholung Quantisierung der Energien in QM Franck-Hertz Versuch Emissions- und Absorptionsspektren der Atome Spektren des Wasserstoffatoms Bohrsche Atommodell Lösung der Schrödingergleichung
Ferienkurs Experimentalphysik Lösung zur Übung 2
 Ferienkurs Experimentalphysik 4 01 Lösung zur Übung 1. Ermitteln Sie für l = 1 a) den Betrag des Drehimpulses L b) die möglichen Werte von m l c) Zeichnen Sie ein maßstabsgerechtes Vektordiagramm, aus
Ferienkurs Experimentalphysik 4 01 Lösung zur Übung 1. Ermitteln Sie für l = 1 a) den Betrag des Drehimpulses L b) die möglichen Werte von m l c) Zeichnen Sie ein maßstabsgerechtes Vektordiagramm, aus
Aufgabe 1: Wellenfunktion und Aufenthaltswahrscheinlichkeit
 Lösungsvorschlag Übung 8 Aufgabe : Wellenfunktion und Aufenthaltswahrscheinlichkeit a) Die Wahrscheinlichkeitsdichte ist eine Wahrscheinlichkeit pro Volumenelement. Die Wahrscheinlichkeit selbst ist eine
Lösungsvorschlag Übung 8 Aufgabe : Wellenfunktion und Aufenthaltswahrscheinlichkeit a) Die Wahrscheinlichkeitsdichte ist eine Wahrscheinlichkeit pro Volumenelement. Die Wahrscheinlichkeit selbst ist eine
Physikalisches Praktikum A 5 Balmer-Spektrum
 Physikalisches Praktikum A 5 Balmer-Spektrum Versuchsziel Es wird das Balmer-Spektrum des Wasserstoffatoms vermessen und die Rydberg- Konstante bestimmt. Für He und Hg werden die Wellenlängen des sichtbaren
Physikalisches Praktikum A 5 Balmer-Spektrum Versuchsziel Es wird das Balmer-Spektrum des Wasserstoffatoms vermessen und die Rydberg- Konstante bestimmt. Für He und Hg werden die Wellenlängen des sichtbaren
Thema heute: Aufbau der Materie: Das Bohr sche Atommodell
 Wiederholung der letzten Vorlesungsstunde: Erste Atommodelle, Dalton Thomson, Rutherford, Atombau, Coulomb-Gesetz, Proton, Elektron, Neutron, weitere Elementarteilchen, atomare Masseneinheit u, 118 bekannte
Wiederholung der letzten Vorlesungsstunde: Erste Atommodelle, Dalton Thomson, Rutherford, Atombau, Coulomb-Gesetz, Proton, Elektron, Neutron, weitere Elementarteilchen, atomare Masseneinheit u, 118 bekannte
Ferienkurs Experimentalphysik Übung 2 - Musterlösung
 Ferienkurs Experimentalphysik 4 00 Übung - Musterlösung Kopplung von Drehimpulsen und spektroskopische Notation (*) Vervollständigen Sie untenstehende Tabelle mit den fehlenden Werten der Quantenzahlen.
Ferienkurs Experimentalphysik 4 00 Übung - Musterlösung Kopplung von Drehimpulsen und spektroskopische Notation (*) Vervollständigen Sie untenstehende Tabelle mit den fehlenden Werten der Quantenzahlen.
Ein Lehrbuch für Studierende der Chemie im 2. Studienabschnitt
 Atom- und Molekülbau Ein Lehrbuch für Studierende der Chemie im 2. Studienabschnitt Von Peter C. Schmidt und Konrad G. Weil 147 Abbildungen, 19 Tabellen Georg Thieme Verlag Stuttgart New York 1982 Vorwort
Atom- und Molekülbau Ein Lehrbuch für Studierende der Chemie im 2. Studienabschnitt Von Peter C. Schmidt und Konrad G. Weil 147 Abbildungen, 19 Tabellen Georg Thieme Verlag Stuttgart New York 1982 Vorwort
8.3 Die Quantenmechanik des Wasserstoffatoms
 Dieter Suter - 409 - Physik B3 8.3 Die Quantenmechanik des Wasserstoffatoms 8.3.1 Grundlagen, Hamiltonoperator Das Wasserstoffatom besteht aus einem Proton (Ladung +e) und einem Elektron (Ladung e). Der
Dieter Suter - 409 - Physik B3 8.3 Die Quantenmechanik des Wasserstoffatoms 8.3.1 Grundlagen, Hamiltonoperator Das Wasserstoffatom besteht aus einem Proton (Ladung +e) und einem Elektron (Ladung e). Der
: Quantenmechanische Lösung H + 2. Molekülion und. Aufstellen der Schrödingergleichung für das H + 2
 H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
H + 2 Die molekulare Bindung : Quantenmechanische Lösung Aufstellen der Schrödingergleichung für das H + 2 Molekülion und Lösung Wichtige Einschränkung: Die Kerne sind festgehalten H Ψ(r) = E Ψ(r) (11)
Vorlesung Allgemeine Chemie (CH01)
 Vorlesung Allgemeine Chemie (CH01) Für Studierende im B.Sc.-Studiengang Chemie Prof. Dr. Martin Köckerling Arbeitsgruppe Anorganische Festkörperchemie Mathematisch-Naturwissenschaftliche Fakultät, Institut
Vorlesung Allgemeine Chemie (CH01) Für Studierende im B.Sc.-Studiengang Chemie Prof. Dr. Martin Köckerling Arbeitsgruppe Anorganische Festkörperchemie Mathematisch-Naturwissenschaftliche Fakultät, Institut
14. Atomphysik Aufbau der Materie
 14. Atomphysik 14.1 Aufbau der Materie 14.2 Der Atomaufbau 14.2.1 Die Hauptquantenzahl n 14.2.2 Die Nebenquantenzahl l 14.2.3 Die Magnetquantenzahl m l 14.2.4 Der Zeemann Effekt 14.2.5 Das Stern-Gerlach-Experiment
14. Atomphysik 14.1 Aufbau der Materie 14.2 Der Atomaufbau 14.2.1 Die Hauptquantenzahl n 14.2.2 Die Nebenquantenzahl l 14.2.3 Die Magnetquantenzahl m l 14.2.4 Der Zeemann Effekt 14.2.5 Das Stern-Gerlach-Experiment
n r 2.2. Der Spin Magnetische Momente In einem klassischen Atommodell umkreist das Elektron den Kern Drehimpuls
 2.2. Der Spin 2.2.1. Magnetische Momente In einem klassischen Atommodell umkreist das Elektron den Kern Drehimpuls Dies entspricht einem Kreisstrom. n r r I e Es existiert ein entsprechendes magnetisches
2.2. Der Spin 2.2.1. Magnetische Momente In einem klassischen Atommodell umkreist das Elektron den Kern Drehimpuls Dies entspricht einem Kreisstrom. n r r I e Es existiert ein entsprechendes magnetisches
ν und λ ausgedrückt in Energie E und Impuls p
 phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e [
 Vorlesung 4 Teilchen im externen Elektromagnetischen Feld Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e v B c ]. 1) Das elektrische
Vorlesung 4 Teilchen im externen Elektromagnetischen Feld Die Bewegungsgleichungen eines geladenen Teilchens im externen elektromagnetischen Feld sind bekannt d dt m v = e E + e v B c ]. 1) Das elektrische
8 Das Bohrsche Atommodell. 8. Das Bohrsche Atommodell
 1. Einführung 1.1. Quantenmechanik versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle:
1. Einführung 1.1. Quantenmechanik versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle:
SS 2015 Supplement to Experimental Physics 2 (LB-Technik) Prof. E. Resconi
 Quantenmechanik des Wasserstoff-Atoms [Kap. 8-10 Haken-Wolf Atom- und Quantenphysik ] - Der Aufbau der Atome Quantenmechanik ==> Atomphysik Niels Bohr, 1913: kritische Entwicklung, die schließlich Plancks
Quantenmechanik des Wasserstoff-Atoms [Kap. 8-10 Haken-Wolf Atom- und Quantenphysik ] - Der Aufbau der Atome Quantenmechanik ==> Atomphysik Niels Bohr, 1913: kritische Entwicklung, die schließlich Plancks
10 Teilchen und Wellen. 10.1 Strahlung schwarzer Körper
 10 Teilchen und Wellen Teilchen: m, V, p, r, E, lokalisierbar Wellen: l, f, p, E, unendlich ausgedehnt (harmonische Welle) Unterscheidung: Wellen interferieren 10.1 Strahlung schwarzer Körper JEDER Körper
10 Teilchen und Wellen Teilchen: m, V, p, r, E, lokalisierbar Wellen: l, f, p, E, unendlich ausgedehnt (harmonische Welle) Unterscheidung: Wellen interferieren 10.1 Strahlung schwarzer Körper JEDER Körper
10.7 Moderne Atommodelle
 10.7 Moderne Atommodelle Zu Beginn des 20. Jahrhunderts entwickelte Niels Bohr sein berühmtes Bohrsches Atommodell. Mit diesem Modell konnten die Atomhüllen von einfachen Atomen wie dem Wasserstoffatom
10.7 Moderne Atommodelle Zu Beginn des 20. Jahrhunderts entwickelte Niels Bohr sein berühmtes Bohrsches Atommodell. Mit diesem Modell konnten die Atomhüllen von einfachen Atomen wie dem Wasserstoffatom
Atome - Moleküle - Kerne
 Atome - Moleküle - Kerne Band I Atomphysik Von Univ.-Professor Dr. Gerd Otter und Akad.-Direktor Dr. Raimund Honecker III. Physikalisches Institut der Rheinisch-Westfälischen Technischen Hochschule Aachen
Atome - Moleküle - Kerne Band I Atomphysik Von Univ.-Professor Dr. Gerd Otter und Akad.-Direktor Dr. Raimund Honecker III. Physikalisches Institut der Rheinisch-Westfälischen Technischen Hochschule Aachen
Übungen Quantenphysik
 Ue QP 1 Übungen Quantenphysik Kernphysik Historische Entwicklung der Atommodelle Klassische Wellengleichung 5 Schrödinger Gleichung 6 Kastenpotential (Teilchen in einer Box) 8 Teilchen im Potentialtopf
Ue QP 1 Übungen Quantenphysik Kernphysik Historische Entwicklung der Atommodelle Klassische Wellengleichung 5 Schrödinger Gleichung 6 Kastenpotential (Teilchen in einer Box) 8 Teilchen im Potentialtopf
Probeklausur zur Vorlesung Physik III Sommersemester 17 (Dated: )
 Probeklausur zur Vorlesung Physik III Sommersemester 17 (Dated: 22.5.2017) Vorname und Name: Matrikelnummer: Hinweise Drehen Sie diese Seite nicht um, bis die Prüfung offiziell beginnt! Bitte legen Sie
Probeklausur zur Vorlesung Physik III Sommersemester 17 (Dated: 22.5.2017) Vorname und Name: Matrikelnummer: Hinweise Drehen Sie diese Seite nicht um, bis die Prüfung offiziell beginnt! Bitte legen Sie
Lösungsvorschlag Übung 9
 Lösungsvorschlag Übung 9 Aufgabe 1: Wellenfunktion und Aufenthaltswahrscheinlichkeit a Die Wahrscheinlichkeitsdichte ist eine Wahrscheinlichkeit pro Volumenelement. Die Wahrscheinlichkeit selbst ist eine
Lösungsvorschlag Übung 9 Aufgabe 1: Wellenfunktion und Aufenthaltswahrscheinlichkeit a Die Wahrscheinlichkeitsdichte ist eine Wahrscheinlichkeit pro Volumenelement. Die Wahrscheinlichkeit selbst ist eine
Vorlesung 21. Identische Teilchen und das Pauli-Prinzip
 Vorlesung 1 Identische Teilchen und das Pauli-Prinzip Identische Teilchen: Jede Art von Teilchen in der Natur definieren wir durch ihre Eigenschaften, z.b. Massen, Spins, Ladungen usw. Das bedeutet, dass
Vorlesung 1 Identische Teilchen und das Pauli-Prinzip Identische Teilchen: Jede Art von Teilchen in der Natur definieren wir durch ihre Eigenschaften, z.b. Massen, Spins, Ladungen usw. Das bedeutet, dass
12.8 Eigenschaften von elektronischen Übergängen. Übergangsfrequenz
 phys4.024 Page 1 12.8 Eigenschaften von elektronischen Übergängen Übergangsfrequenz betrachte die allgemeine Lösung ψ n der zeitabhängigen Schrödinger-Gleichung zum Energieeigenwert E n Erwartungswert
phys4.024 Page 1 12.8 Eigenschaften von elektronischen Übergängen Übergangsfrequenz betrachte die allgemeine Lösung ψ n der zeitabhängigen Schrödinger-Gleichung zum Energieeigenwert E n Erwartungswert
Physik IV - Schriftliche Sessionsprüfung Winter 2008/2009
 Physik IV - Schriftliche Sessionsprüfung Winter 2008/2009 9:00 11:00, Donnerstag, 29. Januar 2009, HG D 5.2 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt 6 Aufgaben auf FÜNF Blättern. Es können
Physik IV - Schriftliche Sessionsprüfung Winter 2008/2009 9:00 11:00, Donnerstag, 29. Januar 2009, HG D 5.2 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt 6 Aufgaben auf FÜNF Blättern. Es können
c = Ausbreitungsgeschwindigkeit (2, m/s) λ = Wellenlänge (m) ν = Frequenz (Hz, s -1 )
 2.3 Struktur der Elektronenhülle Elektromagnetische Strahlung c = λ ν c = Ausbreitungsgeschwindigkeit (2,9979 10 8 m/s) λ = Wellenlänge (m) ν = Frequenz (Hz, s -1 ) Quantentheorie (Max Planck, 1900) Die
2.3 Struktur der Elektronenhülle Elektromagnetische Strahlung c = λ ν c = Ausbreitungsgeschwindigkeit (2,9979 10 8 m/s) λ = Wellenlänge (m) ν = Frequenz (Hz, s -1 ) Quantentheorie (Max Planck, 1900) Die
7. Das Bohrsche Modell des Wasserstoff-Atoms. 7.1 Stabile Elektronbahnen im Atom
 phys4.08 Page 1 7. Das Bohrsche Modell des Wasserstoff-Atoms 7.1 Stabile Elektronbahnen im Atom Atommodell: positiv geladene Protonen (p + ) und Neutronen (n) im Kern negative geladene Elektronen (e -
phys4.08 Page 1 7. Das Bohrsche Modell des Wasserstoff-Atoms 7.1 Stabile Elektronbahnen im Atom Atommodell: positiv geladene Protonen (p + ) und Neutronen (n) im Kern negative geladene Elektronen (e -
Quantenchemie WS 2008/2009 Zusammenfassung 1. Teil
 Quantenchemie WS 2008/2009 Zusammenfassung 1. Teil 1. Grundlagen der Quantenmechanik (a) Wellenfunktion: Die Wellenfunktion Ψ(x, t) beschreibt den quantenmechanischen Zustand eines Teilchens am Ort x zur
Quantenchemie WS 2008/2009 Zusammenfassung 1. Teil 1. Grundlagen der Quantenmechanik (a) Wellenfunktion: Die Wellenfunktion Ψ(x, t) beschreibt den quantenmechanischen Zustand eines Teilchens am Ort x zur
Wiederholung der letzten Vorlesungsstunde:
 Wiederholung der letzten Vorlesungsstunde: Das (wellen-) quantenchemische Atommodell Orbitalmodell Beschreibung atomarer Teilchen (Elektronen) durch Wellenfunktionen, Wellen, Wellenlänge, Frequenz, Amplitude,
Wiederholung der letzten Vorlesungsstunde: Das (wellen-) quantenchemische Atommodell Orbitalmodell Beschreibung atomarer Teilchen (Elektronen) durch Wellenfunktionen, Wellen, Wellenlänge, Frequenz, Amplitude,
Aufgabe 49 (E): Bohrsches Atommodell (8 Punkte)
 UNIVERSITÄT KONSTANZ Fachbereich Physik Prof. Dr. Georg Maret (Experimentalphysik) Raum P 1009, Tel. (07531)88-4151 E-mail: Georg.Maret@uni-konstanz.de Prof. Dr. Matthias Fuchs (Theoretische Physik) Raum
UNIVERSITÄT KONSTANZ Fachbereich Physik Prof. Dr. Georg Maret (Experimentalphysik) Raum P 1009, Tel. (07531)88-4151 E-mail: Georg.Maret@uni-konstanz.de Prof. Dr. Matthias Fuchs (Theoretische Physik) Raum
Eigenschaften des Photons
 Eigenschaften des Photons Das Photon ist das Energiequant der elektromagnetischen Wellen, d.h. Licht hat wie von Einstein postuliert nicht nur Wellencharakter, sondern auch Teilchencharakter mit den oben
Eigenschaften des Photons Das Photon ist das Energiequant der elektromagnetischen Wellen, d.h. Licht hat wie von Einstein postuliert nicht nur Wellencharakter, sondern auch Teilchencharakter mit den oben
1. Zusammenfassung: Masse in der klassischen Mechanik. 2. Energie des klassischen elektromagnetischen Feldes
 2. Vorlesung 1. Zusammenfassung: Masse in der klassischen Mechanik + 1. Übungsaufgabe 2. Energie des klassischen elektromagnetischen Feldes Literatur: beliebiges Lehrbuch klassische Elektrodynamik z.b.
2. Vorlesung 1. Zusammenfassung: Masse in der klassischen Mechanik + 1. Übungsaufgabe 2. Energie des klassischen elektromagnetischen Feldes Literatur: beliebiges Lehrbuch klassische Elektrodynamik z.b.
1.4 Feinstruktur, Spin-Bahn Kopplung
 10 1.4 Feinstruktur, Spin-Bahn Kopplung Zu Beginn dieses Abschnitts wollen wir uns noch einmal einige zentrale Ergebnisse aus der Diskussion der stationären Lösungen für die Schrödinger Gleichung des Wasserstoffatoms
10 1.4 Feinstruktur, Spin-Bahn Kopplung Zu Beginn dieses Abschnitts wollen wir uns noch einmal einige zentrale Ergebnisse aus der Diskussion der stationären Lösungen für die Schrödinger Gleichung des Wasserstoffatoms
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie
 Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Ferienkurs Quantenmechanik I WKB-Näherung und Störungstheorie Sebastian Wild Freitag, 6.. Inhaltsverzeichnis Die WKB-Näherung. Grundlegendes............................. Tunnelwahrscheinlichkeit.......................
Atom-, Molekül- und Festkörperphysik
 Atom-, Molekül- und Festkörperphysik für LAK, SS 2016 Peter Puschnig basierend auf Unterlagen von Prof. Ulrich Hohenester 2. Vorlesung, 17. 3. 2016 Wasserstoffspektren, Zeemaneffekt, Spin, Feinstruktur,
Atom-, Molekül- und Festkörperphysik für LAK, SS 2016 Peter Puschnig basierend auf Unterlagen von Prof. Ulrich Hohenester 2. Vorlesung, 17. 3. 2016 Wasserstoffspektren, Zeemaneffekt, Spin, Feinstruktur,
8.2 Aufbau der Atome. auch bei der Entdeckung der Kathodenstrahlen schienen die Ladungsträger aus den Atomen herauszukommen.
 Dieter Suter - 404 - Physik B3 8.2 Aufbau der Atome 8.2.1 Grundlagen Wenn man Atome als Bausteine der Materie i- dentifiziert hat stellt sich sofort die Frage, woraus denn die Atome bestehen. Dabei besteht
Dieter Suter - 404 - Physik B3 8.2 Aufbau der Atome 8.2.1 Grundlagen Wenn man Atome als Bausteine der Materie i- dentifiziert hat stellt sich sofort die Frage, woraus denn die Atome bestehen. Dabei besteht
Für Geowissenschaftler. EP WS 2009/10 Dünnweber/Faessler
 Für Geowissenschaftler Termin Nachholklausur Vorschlag Mittwoch 14.4.10 25. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung und Quantenmechanik Photometrie Plancksches Strahlungsgesetze, Welle/Teilchen
Für Geowissenschaftler Termin Nachholklausur Vorschlag Mittwoch 14.4.10 25. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung und Quantenmechanik Photometrie Plancksches Strahlungsgesetze, Welle/Teilchen
Festkörperelektronik 4. Übung
 Festkörperelektronik 4. Übung Felix Glöckler 23. Juni 2006 1 Übersicht Themen heute: Feedback Spin Drehimpuls Wasserstoffatom, Bohr vs. Schrödinger Wasserstoffmolekülion, kovalente Bindung Elektronen in
Festkörperelektronik 4. Übung Felix Glöckler 23. Juni 2006 1 Übersicht Themen heute: Feedback Spin Drehimpuls Wasserstoffatom, Bohr vs. Schrödinger Wasserstoffmolekülion, kovalente Bindung Elektronen in
Eigenschaften des Photons
 Eigenschaften des Photons Das Photon ist das Energiequant der elektromagnetischen Wellen, d.h. Licht hat wie von Einstein postuliert nicht nur Wellencharakter, sondern auch Teilchencharakter mit den oben
Eigenschaften des Photons Das Photon ist das Energiequant der elektromagnetischen Wellen, d.h. Licht hat wie von Einstein postuliert nicht nur Wellencharakter, sondern auch Teilchencharakter mit den oben
Physik IV - Schriftliche Sessionsprüfung Sommer 2009
 Physik IV - Schriftliche Sessionsprüfung Sommer 2009 9:00 11:00, Samstag, 8. August 2009, HG F1 & HG F3 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt SECHS Aufgaben auf VIER SEITEN. Es können insgesamt
Physik IV - Schriftliche Sessionsprüfung Sommer 2009 9:00 11:00, Samstag, 8. August 2009, HG F1 & HG F3 Bitte zur Kenntnis nehmen: Es befinden sich insgesamt SECHS Aufgaben auf VIER SEITEN. Es können insgesamt
TC1 Grundlagen der Theoretischen Chemie
 TC1 Grundlagen der Theoretischen Chemie Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Praktikumsbetreuung: Robert Binder (rbinder@theochem.uni-frankfurt.de) Jan von Cosel (jvcosel@theochem.uni-frankfurt.de)
TC1 Grundlagen der Theoretischen Chemie Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Praktikumsbetreuung: Robert Binder (rbinder@theochem.uni-frankfurt.de) Jan von Cosel (jvcosel@theochem.uni-frankfurt.de)
Übungen zur Physik der Materie 1 Lösungsvorschlag Blatt 11 - Atomphysik. Aufgabe 28: Kurzfragen zur Atomphysik Teil 2
 Übungen zur Physik der Materie 1 Lösungsvorschlag Blatt 11 - Atomphysik Sommersemester 018 Vorlesung: Boris Bergues ausgegeben am 1.06.018 Übung: Nils Haag (Nils.Haag@lmu.de) besprochen am 6.06.018 Aufgabe
Übungen zur Physik der Materie 1 Lösungsvorschlag Blatt 11 - Atomphysik Sommersemester 018 Vorlesung: Boris Bergues ausgegeben am 1.06.018 Übung: Nils Haag (Nils.Haag@lmu.de) besprochen am 6.06.018 Aufgabe
Quantenmechanische Probleme in drei Raumdimensionen
 KAPITEL VI Quantenmechanische Probleme in drei Raumdimensionen VI. Dreidimensionaler Kastenpotential Der Vollständigkeit halber... VI. Teilchen in einem Zentralpotential In diesem Abschnitt werden die
KAPITEL VI Quantenmechanische Probleme in drei Raumdimensionen VI. Dreidimensionaler Kastenpotential Der Vollständigkeit halber... VI. Teilchen in einem Zentralpotential In diesem Abschnitt werden die
Einführung in die Quantentheorie der Atome und Photonen
 Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
4. Aufbau der Elektronenhülle 4.1. Grundlagen 4.2. Bohrsches Atommodell 4.3. Grundlagen der Quantenmechanik 4.4. Quantenzahlen 4.5.
 4. Aufbau der Elektronenhülle 4.. Grundlagen 4.. Bohrsches Atommodell 4.3. Grundlagen der Quantenmechanik 4.4. Quantenzahlen 4.5. Atomorbitale 4. Aufbau der Elektronenhülle 4.. Grundlagen 4.. Bohrsches
4. Aufbau der Elektronenhülle 4.. Grundlagen 4.. Bohrsches Atommodell 4.3. Grundlagen der Quantenmechanik 4.4. Quantenzahlen 4.5. Atomorbitale 4. Aufbau der Elektronenhülle 4.. Grundlagen 4.. Bohrsches
Übungen Atom- und Molekülphysik für Physiklehrer (Teil 2)
 Übungen Atom- und Molekülphysik für Physiklehrer (Teil ) Aufgabe 38) Welche J-Werte sind bei den Termen S, P, 4 P und 5 D möglich? Aufgabe 39) Welche Werte kann der Gesamtdrehimpuls eines f-elektrons im
Übungen Atom- und Molekülphysik für Physiklehrer (Teil ) Aufgabe 38) Welche J-Werte sind bei den Termen S, P, 4 P und 5 D möglich? Aufgabe 39) Welche Werte kann der Gesamtdrehimpuls eines f-elektrons im
Bewegung im elektromagnetischen Feld
 Kapitel 6 Bewegung im elektromagnetischen Feld 6. Hamilton Operator und Schrödinger Gleichung Felder E und B. Aus der Elektrodynamik ist bekannt, dass in einem elektrischen Feld E(r) und einem Magnetfeld
Kapitel 6 Bewegung im elektromagnetischen Feld 6. Hamilton Operator und Schrödinger Gleichung Felder E und B. Aus der Elektrodynamik ist bekannt, dass in einem elektrischen Feld E(r) und einem Magnetfeld
Entwicklung der Atommodelle
 Entwicklung der Atommodelle Entwicklung der Atommodelle Demokrit 460 v Chr. Nur scheinbar hat ein Ding eine Farbe, nur scheinbar ist es süß oder bitter; in Wirklichkeit gibt es nur Atome im leeren Raum.
Entwicklung der Atommodelle Entwicklung der Atommodelle Demokrit 460 v Chr. Nur scheinbar hat ein Ding eine Farbe, nur scheinbar ist es süß oder bitter; in Wirklichkeit gibt es nur Atome im leeren Raum.
Atome im elektrischen Feld
 Kapitel 3 Atome im elektrischen Feld 3.1 Beobachtung und experimenteller Befund Unter dem Einfluss elektrischer Felder kommt es zur Frequenzverschiebung und Aufspaltung in optischen Spektren. Dieser Effekt
Kapitel 3 Atome im elektrischen Feld 3.1 Beobachtung und experimenteller Befund Unter dem Einfluss elektrischer Felder kommt es zur Frequenzverschiebung und Aufspaltung in optischen Spektren. Dieser Effekt
Dr. Jan Friedrich Nr
 Übungen zu Experimentalphysik 4 - Lösungsvorschläge Prof. S. Paul Sommersemester 2005 Dr. Jan Friedrich Nr. 7 06.06.2005 Email Jan.Friedrich@ph.tum.de Telefon 089/289-2586 Physik Department E8, Raum 3564
Übungen zu Experimentalphysik 4 - Lösungsvorschläge Prof. S. Paul Sommersemester 2005 Dr. Jan Friedrich Nr. 7 06.06.2005 Email Jan.Friedrich@ph.tum.de Telefon 089/289-2586 Physik Department E8, Raum 3564
Die Schrödingergleichung II - Das Wasserstoffatom
 Die Schrödingergleichung II - Das Wasserstoffatom Das Wasserstoffatom im Bohr-Sommerfeld-Atommodell Entstehung des Emissionslinienspektrums von Wasserstoff Das Bohr-Sommerfeld sche Atommodell erlaubt für
Die Schrödingergleichung II - Das Wasserstoffatom Das Wasserstoffatom im Bohr-Sommerfeld-Atommodell Entstehung des Emissionslinienspektrums von Wasserstoff Das Bohr-Sommerfeld sche Atommodell erlaubt für
VL Landé-Faktor (Einstein-deHaas Effekt) Berechnung des Landé-Faktors Anomaler Zeeman-Effekt
 VL 14 VL13. Spin-Bahn-Kopplung (II) 13.1. Landé-Faktor (Einstein-deHaas Effekt) 13.2. Berechnung des Landé-Faktors 13.3. Anomaler Zeeman-Effekt VL14. Spin-Bahn-Kopplung (III) 14.1. Spin-Bahn-Kopplung 14.2.
VL 14 VL13. Spin-Bahn-Kopplung (II) 13.1. Landé-Faktor (Einstein-deHaas Effekt) 13.2. Berechnung des Landé-Faktors 13.3. Anomaler Zeeman-Effekt VL14. Spin-Bahn-Kopplung (III) 14.1. Spin-Bahn-Kopplung 14.2.
Aufspaltung der Energieniveaus von Atomen im homogenen Magnetfeld
 Simon Lewis Lanz 2015 simonlanzart.de Aufspaltung der Energieniveaus von Atomen im homogenen Magnetfeld Zeeman-Effekt, Paschen-Back-Effekt, Fein- und Hyperfeinstrukturaufspaltung Fließt elektrischer Strom
Simon Lewis Lanz 2015 simonlanzart.de Aufspaltung der Energieniveaus von Atomen im homogenen Magnetfeld Zeeman-Effekt, Paschen-Back-Effekt, Fein- und Hyperfeinstrukturaufspaltung Fließt elektrischer Strom
Molekulare Kerndynamik. Grundlagen
 Grundlagen Bei der Bestimmung der elektronischen Struktur von Molekülen haben wir bis jetzt den Fall betrachtet, daß die Kerne fest sind. Lösung der elektronischen Schrödingergleichung in einem festen
Grundlagen Bei der Bestimmung der elektronischen Struktur von Molekülen haben wir bis jetzt den Fall betrachtet, daß die Kerne fest sind. Lösung der elektronischen Schrödingergleichung in einem festen
Die Schrödingergleichung
 Vortrag im Rahmen der Vorlesung zu Spektralmethoden Magdalena Sigg Wanja Chresta 20. Mai 2008 Zusammenfassung ist die zentrale Gleichung der Quantenmechanik. Mit ihrer Hilfe werden Teilchen in gegebenen
Vortrag im Rahmen der Vorlesung zu Spektralmethoden Magdalena Sigg Wanja Chresta 20. Mai 2008 Zusammenfassung ist die zentrale Gleichung der Quantenmechanik. Mit ihrer Hilfe werden Teilchen in gegebenen
TC1 Grundlagen der Theoretischen Chemie
 TC1 Grundlagen der Theoretischen Chemie Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Topic: Wasserstoffatom Vorlesung: Mo 1h-12h, Do9h-1h Übungen: Do 8h-9h Web site: http://www.theochem.uni-frankfurt.de/tc1
TC1 Grundlagen der Theoretischen Chemie Irene Burghardt (burghardt@chemie.uni-frankfurt.de) Topic: Wasserstoffatom Vorlesung: Mo 1h-12h, Do9h-1h Übungen: Do 8h-9h Web site: http://www.theochem.uni-frankfurt.de/tc1
Gesamtdrehimpuls Spin-Bahn-Kopplung
 Gesamtdrehimpuls Spin-Bahn-Kopplung > 0 Elektron besitzt Bahndrehimpuls L und S koppeln über die resultierenden Magnetfelder (Spin-Bahn-Kopplung) Vektoraddition zum Gesamtdrehimpuls J = L + S Für J gelten
Gesamtdrehimpuls Spin-Bahn-Kopplung > 0 Elektron besitzt Bahndrehimpuls L und S koppeln über die resultierenden Magnetfelder (Spin-Bahn-Kopplung) Vektoraddition zum Gesamtdrehimpuls J = L + S Für J gelten
Elemente der Quantenmechanik III 9.1. Schrödingergleichung mit beliebigem Potential 9.2. Harmonischer Oszillator 9.3. Drehimpulsoperator
 VL 8 VL8. VL9. VL10. Das Wasserstoffatom in der klass. Mechanik 8.1. Emissions- und Absorptionsspektren der Atome 8.2. Quantelung der Energie (Frank-Hertz Versuch) 8.3. Bohrsches Atommodell 8.4. Spektren
VL 8 VL8. VL9. VL10. Das Wasserstoffatom in der klass. Mechanik 8.1. Emissions- und Absorptionsspektren der Atome 8.2. Quantelung der Energie (Frank-Hertz Versuch) 8.3. Bohrsches Atommodell 8.4. Spektren
Bohrsches Atommodell / Linienspektren. Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
 Bohrsches Atommodell / Linienspektren Quantenstruktur der Atome: Atomspektren Emissionslinienspektren von Wasserstoffatomen im sichtbaren Bereich Balmer Serie (1885): 1 / λ = K (1/4-1/n 2 ) 656.28 486.13
Bohrsches Atommodell / Linienspektren Quantenstruktur der Atome: Atomspektren Emissionslinienspektren von Wasserstoffatomen im sichtbaren Bereich Balmer Serie (1885): 1 / λ = K (1/4-1/n 2 ) 656.28 486.13
Das Wasserstoffatom Energiestufen im Atom
 11. 3. Das Wasserstoffatom 11.3.1 Energiestufen im Atom Vorwissen: Hg und Na-Dampflampe liefern ein charakteristisches Spektrum, das entweder mit einem Gitter- oder einem Prismenspektralapparat betrachtet
11. 3. Das Wasserstoffatom 11.3.1 Energiestufen im Atom Vorwissen: Hg und Na-Dampflampe liefern ein charakteristisches Spektrum, das entweder mit einem Gitter- oder einem Prismenspektralapparat betrachtet
Vorbemerkung. [disclaimer]
![Vorbemerkung. [disclaimer] Vorbemerkung. [disclaimer]](/thumbs/91/105086168.jpg) Vorbemerkung Dies ist ein abgegebener Übungszettel aus dem Modul physik4. Dieser Übungszettel wurde nicht korrigiert. Es handelt sich lediglich um meine Abgabe und keine Musterlösung. Alle Übungszettel
Vorbemerkung Dies ist ein abgegebener Übungszettel aus dem Modul physik4. Dieser Übungszettel wurde nicht korrigiert. Es handelt sich lediglich um meine Abgabe und keine Musterlösung. Alle Übungszettel
TP2: Elektrodynamik WS Arbeitsblatt 10 21/ Dipole und Multipole in stationären Feldern
 TP2: Elektrodynamik WS 2017-2018 Arbeitsblatt 10 21/22.12. 2017 Dipole und Multipole in stationären Feldern Die Multipolentwicklung ist eine hilfreiche Näherung zur Lösung der Poisson Gleichung, wenn eine
TP2: Elektrodynamik WS 2017-2018 Arbeitsblatt 10 21/22.12. 2017 Dipole und Multipole in stationären Feldern Die Multipolentwicklung ist eine hilfreiche Näherung zur Lösung der Poisson Gleichung, wenn eine
22. Wärmestrahlung. rmestrahlung, Quantenmechanik
 22. Wärmestrahlung rmestrahlung, Quantenmechanik Plancksches Strahlungsgesetz: Planck (1904): der Austausch von Energie zwischen dem strahlenden System und dem Strahlungsfeld kann nur in Einheiten von
22. Wärmestrahlung rmestrahlung, Quantenmechanik Plancksches Strahlungsgesetz: Planck (1904): der Austausch von Energie zwischen dem strahlenden System und dem Strahlungsfeld kann nur in Einheiten von
Quantenzahlen. A B z. Einführung in die Struktur der Materie 67
 Quantenzahlen Wir haben uns bis jetzt nur mit dem Grundzustand des H + 2 Moleküls beschäftigt Wie sieht es aus mit angeregten Zuständen wie z.b. 2p Zuständen im H Atom? Bezeichnung der Molekülorbitale
Quantenzahlen Wir haben uns bis jetzt nur mit dem Grundzustand des H + 2 Moleküls beschäftigt Wie sieht es aus mit angeregten Zuständen wie z.b. 2p Zuständen im H Atom? Bezeichnung der Molekülorbitale
Atome und ihre Eigenschaften
 Atome und ihre Eigenschaften Vom Atomkern zum Atom - von der Kernphysik zur Chemie Die Chemie beginnt dort, wo die Temperaturen soweit gefallen sind, daß die positiv geladenen Atomkerne freie Elektronen
Atome und ihre Eigenschaften Vom Atomkern zum Atom - von der Kernphysik zur Chemie Die Chemie beginnt dort, wo die Temperaturen soweit gefallen sind, daß die positiv geladenen Atomkerne freie Elektronen
Physikdepartment. Ferienkurs zur Experimentalphysik 4. Daniel Jost 09/09/15
 Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 09/09/15 Inhaltsverzeichnis Technische Universität München 1 Nachtrag: Helium-Atom 1 2 Röntgen-Spektren 2 3 Approximationen 6 3.1 Linear
Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 09/09/15 Inhaltsverzeichnis Technische Universität München 1 Nachtrag: Helium-Atom 1 2 Röntgen-Spektren 2 3 Approximationen 6 3.1 Linear
Das Rutherfordsche Atommodelle
 Dieses Lernskript soll nochmals die einzelnen Atommodelle zusammenstellen und die Bedeutung der einzelnen Atommdelle veranschaulichen. Das Rutherfordsche Atommodelle Entstehung des Modells Rutherford beschoss
Dieses Lernskript soll nochmals die einzelnen Atommodelle zusammenstellen und die Bedeutung der einzelnen Atommdelle veranschaulichen. Das Rutherfordsche Atommodelle Entstehung des Modells Rutherford beschoss
Atomphysik NWA Klasse 9
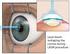 Atomphysik NWA Klasse 9 Atome wurden lange Zeit als die kleinsten Teilchen angesehen, aus denen die Körper bestehen. Sie geben den Körpern ihre chemischen und physikalischen Eigenschaften. Heute wissen
Atomphysik NWA Klasse 9 Atome wurden lange Zeit als die kleinsten Teilchen angesehen, aus denen die Körper bestehen. Sie geben den Körpern ihre chemischen und physikalischen Eigenschaften. Heute wissen
Einleitung Das Rutherford sche Atommodell Das Bohr sche Atommodell. Atommodelle [HERR] Q34 LK Physik. 25. September 2015
![Einleitung Das Rutherford sche Atommodell Das Bohr sche Atommodell. Atommodelle [HERR] Q34 LK Physik. 25. September 2015 Einleitung Das Rutherford sche Atommodell Das Bohr sche Atommodell. Atommodelle [HERR] Q34 LK Physik. 25. September 2015](/thumbs/49/25189684.jpg) Q34 LK Physik 25. September 2015 Geschichte Antike Vorstellung von Leukipp und Demokrit (5. Jahrh. v. Chr.); Begründung des Atomismus (atomos, griech. unteilbar). Anfang des 19. Jahrh. leitet Dalton aus
Q34 LK Physik 25. September 2015 Geschichte Antike Vorstellung von Leukipp und Demokrit (5. Jahrh. v. Chr.); Begründung des Atomismus (atomos, griech. unteilbar). Anfang des 19. Jahrh. leitet Dalton aus
Ferienkurs Quantenmechanik 2009
 Ferienkurs Quantenmechanik 2009 Grundlagen der Quantenmechanik Vorlesungsskript für den 3. August 2009 Christoph Schnarr Inhaltsverzeichnis 1 Axiome der Quantenmechanik 2 2 Mathematische Struktur 2 2.1
Ferienkurs Quantenmechanik 2009 Grundlagen der Quantenmechanik Vorlesungsskript für den 3. August 2009 Christoph Schnarr Inhaltsverzeichnis 1 Axiome der Quantenmechanik 2 2 Mathematische Struktur 2 2.1
Aufgabe 2: Quantenmechanisches Modell für pseudolineare Polyene
 Lösungsvorschlag Übung 10 Aufgabe 1: Ein Teilchen im eindimensionalen Kasten a Die Energiedifferenz zwischen zwei aufeinanderfolgenden Energie-Eigenwerten ist E n,n+1 = E n+1 E n ml n + 1 n 1.1 n + 1.
Lösungsvorschlag Übung 10 Aufgabe 1: Ein Teilchen im eindimensionalen Kasten a Die Energiedifferenz zwischen zwei aufeinanderfolgenden Energie-Eigenwerten ist E n,n+1 = E n+1 E n ml n + 1 n 1.1 n + 1.

 Erratum: Potentialbarriere E
Erratum: Potentialbarriere E