Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um:

Transkript

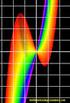
1 1 Grundlagen 1.1 Das Rechnen mit Zahlen Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um: N: natürliche Zahlen 1,,3,4,5,... Z: ganze Zahlen..., 3,, 1,0,1,,3,... Q: rationale Zahlen: das sind die Zahlen, die man als Quotient p q zweier ganzer Zahlen p und q schreiben kann. Es gibt auch nicht rationale (irrationale) Zahlen, z.b. oder π: R: reelle Zahlen: rationale und irrationale Zahlen. Wenn wir uns auf die positiven (negativen) Zahlen beschränken wollen, setzen wir ein hochgestelltes + ( ) Zeichen hinter unser Symbol, also Z +, Q + und R + sowie Z, Q und R. Beachte Z + = N. Wenn wir in unsere Zahlbereiche auch noch die 0 einschließen wollen, schreiben wir eine tiefergestellte 0 hinter unser Symbol, also bezeichnet z.b. N 0 die Zahlen 0,1,,3,... Diese Menge bezeichnet man auch als die Menge der nichtnegativen ganzen Zahlen! Potenzen Wir schreiben für das n-fache Produkt von a auch a n : a a a a = a n. a Basis, n Eponent. Für das Rechnen mit Potenzen gelten Rechenregeln, die wir aus der Schule als bekannt voraussetzen. Der Ausdruck 0 0 ist nicht definiert. Die Zahl n b heißt die n-te Wurzel von b. Wir setzen hier b 0 voraus sowie n b 0. Die n-te Wurzel aus b ist diejenige nichtnegative Zahl mit n = b. Wenn wir Ausdrücke der Form y betrachten, dann können wir entweder als feste Größe und y als die Variable, oder umgekehrt als Variable und y als fest betrachten. Im ersten Fall sprechen wir von Eponentialfunktionen, im zweiten Fall von Potenzfunktionen. Eponentialfunktionen Man macht sich das Verhalten der Eponentialfunktion am Besten an den zugehörigen Funktionsgraphen klar. Wir zeigen Ihnen hier einige Beispiele a mit a > 1 sowie 0 < a < 1. Beachten Sie den Unterschied: Ist a > 1, so ist die Funktion wachsend, ist 0 < a < 1, so ist sie fallend. Es gilt stets a 0 = 1, d.h. die Funktionsgraphen von a gehen stets durch den Punkt = 0, y = 1, unabhängig davon, wie a gewählt ist. 1

2 Einige Eponentialfunktionen a^ mit a> ^ ^ 1.1^ Hier müssen wir etwas aufpassen. Der Graph der Funktion 1.1 sieht sehr flach aus. Dem ist aber nicht so, wenn wir groß wählen. Dann zeigt auch der Graph von 1.1 eponentielles Wachstum: 1.1^

3 Einige Eponentialfunktionen a^ mit a< ^ ^ 5 0.9^ Potenzfunktionen Wir kommen nun zu Potenzfunktionen. Wir beginnen mit einigen Beispielen n mitn N.BeachtenSiedabeibitte,dassdie-Achse(manchmalauchAbszisse genannt) und die y-achse (Ordinate) nicht denselben Maßstab haben! 3

4 ^4 Einige Potenzfunktionen ^n ^ ^1 5 ^3 Wenn wir Potenzfunktionen n betrachten mit n Z, n < 0, so sehen die Funktionsgraphen etwas anders aus. Wir beschränken uns hierbei auf den Bereich > 0. Beachten Sie: m = 1 m, also z.b. = 1. Wir erhalten den Graphen von aus dem von, indem wir einfach die Kehrwerte der y-werte (also der Ordinatenwerte) des Graphen von bilden: 4

5 Einige Potenzfunktionen ^n, n<0 10 ^( 4) ^( 3) ^( ) 0 ^( 1) Hier sind nun einige Funktionsgraphen von Potenzfunktionen mit rationalen Eponenten. Wir müssen uns auf den Fall > 0 beschränken, weil z.b. Ausdrücke wie ( 1) 1/ = 1 gar nicht erklärt sind. Alle Graphen von Potenzfunktionen n gehen durch den Punkt = 1 und y = 1, weil stets 1 n = 1 gilt. Beachten Sie: p q = q p. 5

6 4 Einige Potenzfunktionen ^n 3 ^ ^( 1/) 1 ^( 1/5) ^(1/5) ^(1/) Logarithmus Die Umkehrung des Potenzierens ist das Logarithmieren. Gilt a = b, a,b > 0, a 1, so heißt der Logarithmus von b zur Basis a. Bezeichnung: = log a (b). Manchmal lassen wir die Angabe der Basis auch weg. Ist die Basis 10, sprechen wir vom dekadischen Logarithmus. Ist a die Eulersche Zahl e,718..., heißt der Logarithmus natürlich. Der natürliche Logarithmus wird meistens mit ln bezeichnet, der dekadische Logarithmus mit lg. Wir halten noch einmal eplizit fest: a log a (b) = b Für das Logarithmieren gelten Rechenregeln, die wir aus der Schule als bekannt voraussetzen. Für die konkrete Berechnung von Logarithmen benötigt man eigentlich nur die Kenntnis der Logarithmen zu einer bestimmten Basis: log a (b) = log c(b) log c (a). 6

7 Üblicherweise haben Studierende mit dem Logarithmieren etwas mehr Schwierigkeiten als mit den anderen Rechenregeln. Ähnlich wie im Fall von Eponentialund Potenzfunktionen zeigen wir Ihnen hier die Funktionsgraphen einiger Logarithmusfunktionen. Man beachte, dass log a () nur für a, > 0 sowie a 1 definiert sind. Es fällt auf: log a (1) = 0. Einige Logarithmusfunktionen log_0.5() 1 log_0.() log_1.5() log_3() Gleichungen und Ungleichungen Ein zentrales Thema der Algebra ist das Lösen von Gleichungen. Ganz einfach ist dies für sogenannte lineare Gleichungen a = b Wenn hier a 0 ist, können wir beide Seiten der Gleichung durch a dividieren und erhalten als Lösung = b a. Die positive Lösung einer Potenzgleichung der Form a = b, b > 0 ist = a b = b 1 a. Beachte: Der Ausdruck a b ist vereinbarungsgemäß immer positiv. Man beachte den Unterschied zur Eponentialgleichung a = b, a,b > 0, a 1 Die Lösung der Eponentialgleichung ist = log a (b). Die Lösungen von quadratischen Gleichungen der Form 7

8 a +b+c = 0, a 0 sollten aus der Schule bekannt sein. Die Lösungen für a 0 sind ± = b± b 4ac. a Machen wir uns noch einmal klar, wie man auf diese Lösung kommt. Wir setzen a 0 voraus: a +b+c = 0 + b a = c a + b ( ) b a + = c ( ) b a a + a ( + b ) = c a a + b 4a + b a = ± b 4ac a ± = b± b 4ac. a Weil es keine Wurzeln aus negativen Zahlen gibt, kann es passieren, dass eine quadratische Gleichung keine oder nur eine oder zwei Lösungen hat: Ist b 4ac > 0, so gibt es zwei Lösungen. Ist b 4ac = 0, so gibt es eine Lösung. Ist b 4ac < 0, so gibt es keine Lösungen. Beachten Sie, dass sich die Lösungsformel vereinfacht, wenn a = 1 ist. Wir erhalten dann als Lösung der Gleichung die sogenannte p-q-formel: Beispiel 1.1 Finde alle mit +p+q = 0 ± = p± p 4q Wir quadrieren beide Seiten und erhalten so + = 4. (1.1) (+) = 4. 8

9 also, weil (+) = +4+4, oder +4+4 = 4 +5 = 0 (5+) = 0. Das geht nur für = 0 oder = 5. Wir müssen jetzt aber aufpassen! Durch das Quadrieren der Gleichung haben wir vielleicht unerwünschte neue Lösungen erhalten. Beispiel: = 3, Quadrieren liefert = 9, als Lösungen also = ±3, aber = 3 war keine Lösung der ursprünglichen Gleichung! Wir müssen also, wenn wir beim Lösen von Gleichungen quadrieren, mit den erhaltenen Lösungen immer eine Probe machen, d.h. in die ursprüngliche Gleichung einsetzen. Wir machen also die Probe: Setzen wir 0 in die Gleichung (1.1) ein, so erhalten wir = 4, richtig. Beim Einsetzen von 5 ergibt sich 3 = 9, was falsch ist, da die Wurzel stets positiv ist! Ungleichungen Wir schreiben a < b falls a echt kleiner als b ist, also insbesondere a b. Wenn wir den Fall a = b auch zulassen wollen, schreiben wir a b. Wenn wir a < b < c schreiben meinen wir a < b und b < c (und damit natürlich auch a < c). Sinnlos ist ein Ausdruck der Form a < b > c. In den beiden folgenden Tabellen sind die wesentlichen Regeln für das Rechnen mit Ungleichungen zusammengefasst. Dabei steht [SU] für strikte Ungleichung, [U] für Ungleichung: [SU1] Aus a < b und b < c folgt a < c. [SU] Aus a < b folgt a+c < b+c. [SU3] Aus a < b und c < d folgt a+c < b+d. [SU4] Aus a < b und c > 0 folgt ac < bc. [SU5] Aus a < b folgt a > b. [SU6] Aus a < b, b > 0 und 0 < c < d folgt ac < bd. [SU7] Aus 0 < a < b folgt 1 a > 1 b. [SU8] Aus a < 0 < b folgt 1 a < 1 b. [SU9] Aus 0 < a < b folgt a < b. 9

10 [U1] Aus a b und b < c folgt a < c. [U] Aus a b und b c folgt a c. [U3] Aus a b folgt a+c b+c. [U4] Aus a b und c < d folgt a+c < b+d. [U5] Aus a b und c d folgt a+c b+d. [U6] Aus a b und c > 0 folgt ac bc. [U7] Aus a b folgt a b. [U8] Aus a b, b > 0 und 0 < c < d folgt ac < bd. [U9] Aus a b, b > 0 und 0 < c d folgt ac bd. [U10] Aus 0 < a b folgt 1 a 1 b. [U11] Aus 0 < a b folgt a b. Lernen Sie diese Regeln bitte nicht stur auswendig! Der Umgang mit Ungleichungen ist weitgehend selbsterklärend, wenn man nur beachtet, dass sich das Ungleichungszeichen umdreht wenn man mit einer negativen Zahl multipliziert (siehe [SU5] und [U7] sowie [SU8]). Es sei auch noch einmal auf [SU6] hingewiesen: Aus a < b, b > 0 und 0 < c < d folgt ac < bd Diese Aussage ist falsch für b 0: Setze a =, b = 1, c = 1, d = 3: Dann ist ac = nicht kleiner als bd = 3. Der Absolutbetrag Sei a eine reelle Zahl. Manchmal interessiert man sich nur für den Abstand von a zur 0, gleichgültig, ob a positiv oder negativ ist. Diesen Abstand nennt man den Betrag von a: { a falls a 0 a := a falls a < 0. Beachte: a > 0 falls a < 0. Das Zeichen := hier in der Definition bedeutet, das auf der linken Seite des Doppelpunktes ein neues Symbol durch Ausdrücke definiert wird, die auf der erchten Seite stehen (also auf der Seite des Gleichheitszeichens), und die schon bekannt sind. Wir haben hier ein erstes Beispiel, wo eine Funktion (hier die Betragsfunktion) durch eine Fallunterscheidung definiert wird. So etwas bereitet dem mathematischen Anfänger manchmal Probleme. Sie sollten sich aber rasch an solche Fallunterscheidungen gewöhnen, insbesondere bei der Untersuchung von Ungleichungen. Beispiel 1. 4 = 4, 4 = 4, 0 = 0, = Wir erhalten die beiden folgenden einfachen Regeln 10

11 a = a a b = a b. Von großer Bedeutung ist die Dreiecksungleichung a+b a + b Beispiel ( 5) = = 8 6 = = 8 (hier haben wir Gleichheit in der Dreiecksungleichung). Beispiel 1.4 Bestimme die Lösungsmenge der Ungleichung Wir formen diese Ungleichung um: < 5. (1.) < 4. Nun müssen wir aufpassen und zwei Fälle unterscheiden: Fall 1: > 0 Fall : < 0 1+ < 8 1 < 7 > 3 1+ > 8 (weil negativ ist!) 1 > 7 3 > Wir können jetzt aber nicht sagen, die Lösungsmenge besteht aus allen mit < 3, weil wir die Ungleichung < 3 ja nur unter der Voraussetzung < 0 erhalten haben. Die Lösungsmenge besteht in diesem Fall also aus allen < 0. Beachte, dass der Fall = 0 nicht auftreten kann. Wir erhalten: Die Ungleichung (1.) ist für alle mit < 0 sowie für alle mit > 3 gültig. 11

12 Beispiel 1.5 Bestimme die Lösungsmenge der Ungleichung 1 < +1 + (1.3) Wir multiplizieren beide Seiten mit ( 1)(+), um die Brüche zu beseitigen. Wir können das aber nur dann sorglos tun, wenn dieser Ausdruck positiv ist. Das ist der Fall für > 1 sowie für <. Fall 1: > 1 oder < < ( )(+) < ( 1)(+1) 4 < 1 4 < 1 Das bedeutet, dass die Ungleichung (1.3) für alle mit > 1 oder < gültig ist. Fall : < < 1 Nun gilt < ( )(+) > ( 1)(+1) 4 > 1 4 > 1 und das ist ganz offensichtlich nie erfüllt. Beachte auch hier wieder, dass die Fälle = sowie = 1 nicht behandelt werden müssen, da die in der Ungleichung auftretenden Ausdrücke in den Fällen gar nicht erklärt sind. Wir halten fest: Die Ungleichung (1.3) ist gültig für alle R mit < oder > 1. Wenn Sie wollen, können Sie durch Einsetzen von Werten dieses Ergebnis erhärten: = 0.3: Berechne zunächst die linke Seite = 17 7, dann die rechte Seite von.3 = Offensichtlich ist die linke Seite größer als die rechte Seite, die (1.3): 1.3 Ungleichung gilt also für = 0.3 nicht. =.1: Wir erhalten = < = 11. Die folgende Skizze illustriert das noch einmal: der durchgezogene Graph beschreibt die linke Seite, der gestrichelte Graph die rechte Seite der Ungleichung. 1

13 6 4 y Beispiel 1.6 Bestimme alle mit 3 > 0. (1.4) Um dieses Problem zu lösen, versuchen wir, die linke Seite der Ungleichung zu faktorisieren. Wir können zunächst ausklammern und bekommen ( ) > 0. Nun faktorisieren wir. Wir können das machen, indem wir die Nullstellen bestimmen. Die Nullstellen sind und 1, also = ( )(+1). Wir müssen also alle bestimmen mit ( )(+1) > 0. Das Produkt von 3 Zahlen (hier, und +1) ist größer als 0 wenn alle Zahlen > 0 sind oder wenn nur eine Zahl > 0 ist, die anderen beiden < 0. Alle Zahlen sind größer als 0 wenn > ist. Zwei Zahlen sind < 0 für 1 < < 0. Also: Die Ungleichung (1.4) ist für > sowie für 1 < < 0 gültig. Auch dies wird durch eine Skizze verdeutlicht: 13

14 Summen- und Produktzeichen Ein großer Vorteil der sehr formalen mathematischen Sprache ist es, komplizierte Zusammenhänge einfach und klar ausdrücken zu können. Gerade auch diese Eigenschaft der Mathematik macht sie zu einer geeigneten Hilfswissenschaft der Wirtschaftswissenschaften. Seien a 1,...,a n reelle Zahlen. Dann schreiben wir statt auch a 1 +a + +a n n i=1 (gelesen: Summe der a i mit i von 1 bis n). Der Laufinde i heißt Summationsinde, 1 und n sind die untere und obere Schranke. Die untere Schranke muss nicht 1 sein: 5 i = = = 50. i=3 Folgende einfachen Regeln gelten für den Umgang mit dem Summenzeichen: a i 14

15 n a = (n k +1)a (a ist konstant!) i=k n ca i i=k n (a i +b i ) = i=k n a i = i=k = c n i=k a i n a i + i=k m a i + i=k (ausklammern!) n i=k b i n i=m+1 a i für k m < n. Ähnlich wie das Summenzeichen kann man das Produktzeichen einführen: n a i = a k a k+1 a n. i=k Das Produktzeichen ist etwas weniger gebräuchlich als das Summenzeichen. Hier sind einfache Rechenregeln für den Umgang mit Π: n a = a n k+1 i=k n ca i i=k n (a i b i ) = i=k n i=k = c n k+1 n a i = ( i=k i=k n n a i n a i ) Die folgende Ungleichung(Cauchy-Schwarz-Ungleichung) ist manchmal sehr nützlich: i=k ( n ) n a i b i ( ai ) ( i=1 Beispiel 1.7 Setzen Sie die Zahlen i=1 i = 1 i = a i 3 b i 4 1 i=k n i=1 a i b i b i ) 15

16 ein und Sie erhalten (8+3) = 11 ( +3 ) (4 +1 ) = = 1. Man kann auch Gleichheit haben. Wähle und erhalte i = 1 i = a i 1 b i 4 (8+) = 100 = ( +( 1) ) (4 +( ) ) = 5 0 = Aussagen und Mengen In der Mathematik geht es um Aussagen. Eine Aussage ist ein statement, das entweder wahr oder falsch sein kann. Beides geht nicht! Äußerungen, die nicht die Eigenschaft haben, wahr oder falsch zu sein, gelten nicht als Aussagen. Beispiel 1.8 Das Bruttosozialprodukt der Bundesrepublik Deutschland ist höher als das der USA ist eine offenbar falsche Aussage. Gute Nacht, Freunde ist keine Aussage. Häufig hängen Aussagen auch von variablen Parametern ab. Wir sprechen dann von Aussageformen A(). Beispiel 1.9 Für alle natürlichen Zahlen gilt: ist Primzahl ist eine offenbar falsche Aussage. Eine richtige Aussage wäre: Für alle natürlichen Zahlen gilt, dass nicht negativ ist. Ein anderes Beispiel einer Aussageform ist: Unter allen Gütern gibt es mindestens ein Gut, dessen Preis sich verändert. Für Aussageformen führen wir folgende Bezeichnungen ein: A() gilt für alle : A() gilt für ein : A() A() Interessant wird es, wenn man Aussagen A und B miteinander verknüpft. Der Wahrheitswert der verknüpften Aussage hängt vom Wahrheitswert von A und B ab. Wir wollen das am Beispiel erläutern: Beispiel 1.10 Die Aussage Franz studiert Wirtschaftswissenschaften oder Mathematikïst wahr, wenn Franz mindestens eines der beiden Fächer Wirtschaft oder Mathematik studiert, eventuell auch beide. Die Aussage ist Verknüpfung 16

17 der beiden Aussagen Franz studiert Wirtschaftswissenschaften sowie Franz studiert Mathematik durch ein oder. Beachte: Die Aussage Franz studiert Wirtschaftswissenschaften oder Mathematik ist auch wahr, wenn Franz ganz fleißig ist und sowohl Wirtschaftswissenschaften als auch Mathematik studiert. Es handelt sich beim mathematischen oder nicht um ein entweder-oder. Konjunktion Seien A und B zwei Aussagen. Dann ist die Aussage A und B, geschrieben A B wahr, wenn beide Aussagen wahr sind. Die Aussage A und B ist falsch, wenn mindestens eine der beiden Aussagen A, B falsch ist. Man nennt dies auch die Konjunktion der Aussagen A und B. Disjunktion Seien A und B zwei Aussagen. Dann ist die Aussage A oder B, geschrieben A B wahr, wenn mindestens eine der Aussagen A oder B wahr ist. Die Aussage A oder B ist falsch, wenn sowohl A als auch B falsch sind. Man nennt dies auch die Disjunktion der Aussagen A und B. Man stellt dies häufig auch durch sogenannte Wahrheitstafeln dar. Das ist eine Tabelle, in die wir die möglichen Wahrheitswerte von A und B eintragen und dann die entsprechenden Wahrheitswerte der verknüpften Aussagen auswerten. Hier ist die Wahrheitstafel für die Konjunktion: und hier die für die Disjunktion: A B A B w w w f f w f f w f f f A B A B w w w f f w f f Kehrt man eine Aussage in ihr Gegenteil um, erhält man die Negation der Aussage. Bezeichnung: A. Klar ist, das eine negierte wahre Aussage falsch wird und umgekehrt. w w w f 17

18 Beispiel 1.11 Wir wollen die Aussage A Deutschland ist Eportweltmeister und Fussballvizeeuropameister negieren, d.h. wir suchen die Aussage, die wahr ist genau in den Fällen, in denen A falsch ist. A ist falsch, wenn eine der beiden Teilaussagen falsch ist, wenn also Deutschland nicht Eportweltmeister oder nicht Vizeeuropameister ist. Dieses Beispiel zeigt, wie wir eine Konjunktion negieren: A B = A B Ähnlich sieht es mit der Negation der Disjunktion aus: A B = A B Das Gleichheitszeichen soll hier bedeuten, dass die Aussagen auf den beiden Seiten denselben Wahrheitswert haben (also wahr oder falsch sind), wenn für A und B auf beiden Seiten die selben Aussagen eingesetzt werden. Schwierigkeit bereitet manchmal die Negation einer für alle sowie es gibt ein Aussage. A() = A() = A() A() Umgangssprachlich: Wenn eine Aussage A() nicht für alle gilt, dann muss es ein geben, für das diese Aussage nicht gilt. Und wenn es kein gibt für das eine Aussage A() wahr ist, dann ist A() für alle eine falsche Aussage. Beispiel 1.1 Sei A() die Aussage Der Preis des Gutes ist konstant. Wir wollen uns alle Aussagen anschauen, die wir mit A() mittels Negation sowie und bilden können: A() Die Preise aller Güter bleiben konstant. A() Die Preise aller Güter verändern sich. A() Nicht für alle Güter bleiben die Preise konstant. A() Nicht für alle Güter verändern sich die Preise. 18

19 A() Der Preis mindestens eines Gutes bleibt konstant. A() Der Preis mindestens eines Gutes verändert sich. A() Der Preis keines Gutes bleibt konstant. A() Der Preis keines Gutes verändert sich. Beachten Sie, dass hier die erste und achte, die zweite und siebte, die dritte und sechste sowie die vierte und fünfte Aussage jeweils gleich sind. Implikation und Äquivalenz Die Implikation (geschrieben A B) ist falsch, wenn A wahr ist, B aber falsch. In allen anderen Fällen ist die Implikation wahr. Sprechweise: Wenn A, dann B. Wahrheitstabelle: A B A B w w w f f w f f Das ist etwas gewöhnungsbedürftig, weil A B wahr ist wenn A falsch ist (aus etwas Falschem darf man alles folgern). Wenn die Aussage A B wahr ist, dann nennen wir A eine hinreichende Bedingung für B und B eine notwendige Bedingung für A. Gilt A B und B A, so nennt man die beiden Aussagen äquivalent. Bezeichnung: A B. Die zugehörige Wahrheitstafel ist w f w w A B A B w w w f f w f f Zwei Aussagen heißen also äquivalent, wenn sie beide wahr oder beide falsch sind. w f f w 19

20 Es sollte klar sein, wie zu definieren ist: A B bedeutet schlicht B A. Beispiel 1.13 Betrachte die Aussage Wenn die Inflation steigt, dann sinkt die Arbeitslosenquote. Wir überlegen uns, welche der folgenden Aussagen dazu äquivalent sind: 1. Damit die Arbeitslosenquote sinkt, muss die Inflation steigen.. Eine hinreichende Bedingung dafür, dass die Arbeitslosenquote sinkt, ist ein Anstieg der Inflation. 3. Die Arbeitslosenquote kann nur fallen wenn die Inflation steigt. 4. Wenn die Arbeitslosenquote nicht sinkt, dann steigt die Inflation nicht. 5. Die Inflation kann nur steigen wenn die Arbeitslosenquote sinkt. Offensichtlich bestehen alle diese Aussagen aus zwei Teilaussagen und Die Arbeitslosenquote sinkt (Aussage A) Die Inflation steigt. (Aussage B). Diese Aussagen sind unterschiedlich verknüpft. Wir wollen die Wahrheitstafeln für diese Verknüpfungen aufstellen. Die ursprüngliche Aussage lautet B A, und ihr Wahrheitswert wird zunächst bestimmt: A B B A (1) () (3) (4) (5) w w w w w w w w w f w f w f w w f w f w f w f f f f w w w w w w Also sind die Aussagen (), (4) und (5) äquivalent zur ursprünglichen Aussage. Wir wollen die Aussagen (1) bis (5) noch einmal analysieren: (1) A B () B A (3) A B (4) A B (5) B A Besonders interessant ist hier das vierte statement. Es zeigt, dass die Aussagen B A und A B äquivalent sind. Wir wollen das noch einmal ganz deutlich herausstellen: 0

21 (A B) ist äquivalent zu (B A) Einige Bemerkungen zu mathematischen Beweisen In der Mathematik hat man es stets mit Aussagen zu tun, die wahr oder falsch sind. Beispielsweise gilt für alle reellen Zahlen (a+b) = a +ab+b. Woher weiß man das? Man kann doch nicht alle reellen Zahlen einsetzen und schauen, ob diese Gleichung immer richtig ist. Das ist auch nicht nötig, denn man kann einen mathematischen Beweis für diese Aussage angeben. Ein Beweis für eine Aussage A ist eine Folge logischer Schlüsse, beginnend mit einer wahren Aussage B, an deren Ende A steht. Sie zeigen also die Gültigkeit der Aussage B A, wobei B aber eine wahre Aussage sein muss. Denn bedenken Sie: Aus einer falschen Aussage kann man alles folgern, also auch etwas Falsches. Sie wollen aber in einem Beweis ja gerade zeigen das etwas stimmt, also richtig ist. Sie dürfen, um eine Aussage A zu beweisen, auch nicht einfach von der Gültigkeit von A ausgehen und dann logisch auf die Gültigkeit einer wahren Aussage schließen und das als einen Beweis ansehen. Beispiel 1.14 Angenommen, jemand behauptet 3 = 4. Wenn wir die Gültigkeit dieser Aussage annehmen, können wir ja beide Seiten der Gleichung mit 0 multiplizieren. Wir erhalten so die Gleichung 0 = 0, die offenbar wahr ist. Ist deshalb aber 3 = 4 wahr? Natürlich nicht, weil wir von einer Aussage A auf etwas Wahres (die Aussage 0 = 0) geschlossen haben. Aber aus der Gültigkeit von 0 = 0 kann man natürlich nicht auf die Gültigkeit von A schlussfolgern. Beispiel 1.15 Wir wollen die folgende Aussage beweisen: Für alle reellen Zahlen 0 gilt +1 > 1. Fall 1: > 0 Dann ist + 1 = + 1 > 1, aber auch + 1 > ( 1) = 1, weil > für > 0, den Fall, den wir gerade betrachten. Weil +1 > 1 und +1 > ( 1), gilt sogar +1 = +1 > 1. Wir dürfen beide Seiten dieser Ungleichung durch dividieren, ohne dass sich das Ungleichungszeichen ändert, weil > 0. Das zeigt +1 > 1. Fall : < 0 Jetztist 1 = 1.Wirhaben1 > +1(weil < 0)und1 > 1 = 1

22 ( + 1). Damit gilt also 1 = 1 > + 1. Teilen wir die linke und rechte Seite dieser Ungleichung durch, so dreht sich das Ungleichungszeichen wegen < 0 um und wir erhalten wie im Fall 1 1 < +1. Das nächste Beispiel zeigt deutlich die Aufgabe eines mathematischen Beweises: Ein Beweis soll einen zweifelsfreien Grund angeben, warum eine Aussage richtig ist. Beispiel 1.16 Wir wollen die folgende Behauptung beweisen: Wenn in einem Schachbrett die diagonal gegenüberliegenden Eckfelder entfernt werden, kann das so entstehende Brett nicht mit Dominosteinen überdeckt werden, wobei jeder Dominostein genau zwei Felder des Schachbrettes überdeckt. Der Beweis ist ganz einfach: Jeder Dominostein überdeckt genau ein weißes und ein schwarzes Feld. Aber das Schachbrett, bei dem die Eckfelder entfernt wurden, hat nicht die gleiche Zahl weißer und schwarzer Felder! Manche Nicht-MathematikerInnen sind versucht, die Gültigkeit einer Aussageform A() zu beweisen, indem die Gültigkeit von A() für einige wenige Werte von nachgerechnet wird. Das ist natürlich kein Beweis! Beispiel 1.17 Angenommen, jemand behauptet n +n+41 sei für alle natürlichen Zahlen n eine Primzahl. Wir setzen ein und erhalten, dass n +n+41 eine Primzahl für alle Zahlen n zwischen 0 und 39 ist. Ist das ein Beweis? Nein! AußerdemistdieAussage,dassn +n+41fürallenatürlichenzahleneineprimzahl ist, falsch: Setzen Sie einfach n = 40 ein! Wir haben somit ein Gegenbeispiel gefunden. Etwas formaler. Wir hatten die Aufgabe zu entscheiden, ob eine Aussage A() für alle gilt. Um zu beweisen, dass die Aussage stets gilt, benötigen wir einen Beweis. Wenn wir aber zeigen wollen, dass die Aussage nicht immer gilt, genügt es, ein so anzugeben, dass A() falsch ist. Wir haben damit die Allgemeingültigkeit widerlegt. Im obigen Beispiel können wir die Behauptung, jede Zahl der Form n + n + 41 sei ein Primzahl, widerlegen, denn für n = 40 ist

23 n +n+41 offensichtlich keine Primzahl! Halten wir fest: Die Gültigkeit einer Aussage A() kann man nicht beweisen, indem man die Gültigkeit für einige Werte von überprüft. Man kann aber zeigen, dass die Aussage A() nicht allgemeingültig ist, wenn man nur ein Gegenbeispiel angibt, also ein g, für das A( g ) falsch ist. In den Wirtschaftswissenschaften werden Sie selten Beweise im mathematisch strengen Sinne finden. Der mathematische Beweis benötigt eakt angegebene Voraussetzungen, unter denen er funktioniert. Diese Voraussetzungen sind in den Wirtschaftswissenschaften häufig nicht so klar formulierbar. Viel häufiger tritt das Phänomen auf, dass man Aussagen widerlegt! Kehren wir zurück zu unserem Beispiel 1.13 über den Zusammenhang zwischen Arbeitslosenquote und Inflation. Dieser Zusammenhang ist heutzutage eindeutig durch etliche Gegenbeispiele widerlegt. Bis in die 80 er Jahre hinein wurde ein solcher Zusammenhang aber vermutet! 1.4 Mengen Ein zentrales Konzept für die Mathematik ist der Begriff der Menge. Eine Menge ist eine Zusammenfassung bestimmter, wohlunterschiedener Objekte. Von jedem dieser Objekte muss eindeutig feststehen, ob das Objekt zur Menge gehört oder nicht. Die Objekte heißen Elemente der Menge Ist a ein Element der Menge M, schreiben wir auch andernfalls a M a / M Die Elemente einer Menge sind immer alle verschieden. Es gibt unterschiedliche Möglichkeiten, Mengen zu beschreiben. Wir wollen die Menge M aller geraden ganzen Zahlen zwischen und 15 beschreiben: 1. Aufzählung M = {,4,6,8,10,1,14}. 3

24 . teilweise Aufzählung M = {,4,6,...,1,14} Hierbei muss man aufpassen, dass es nicht zu Missverständnissen kommt. 3. Beschreibung durch charakteristische Eigenschaften M := { : Z und und 15 und gerade}. Die leere Menge ist die Menge, die kein Element enthält. Beispiel 1.18 = { : wohnt in der Bundesrepublik Deutschland und ist im Jahre 1700 geboren} Die Mächtigkeit oder Ordnung einer Menge ist die Anzahl der Elemente in der Menge. Unsere oben betrachtete Menge M = {,4,6,8,10,1,14} hat also die Mächtigkeit 7. Schreibweise: M = Anzahl der Elemente in M. Falls M unendlich viele Elemente hat, schreiben wir M = ( : unendlich). Beziehungen zwischen Mengen Wir nennen A eine Teilmenge von B, wenn jedes Element aus A auch ein Element von B ist. Dabei darf auch A = B gelten. A B: A Teilmenge von B A B: A Teilmenge von B und A B Beachte, dass stets A A gilt. Ferner gilt für alle Mengen A. Beispiel 1.19 N Z Q R Die Menge aller Einwohner Magdeburgs ist eine Teilmenge der Menge aller Einwohner Deutschlands. Verknüpfung von Mengen Wir können Mengen schneiden oder vereinigen: A B = { : A oder B} Vereinigung A B = { : A und B} Schnitt 4

25 A B A B A A B B Achtung: Es gilt nicht A B = A + B, sondern A B = A + B A B Zwei Mengen heißen disjunkt, wenn ihr Schnitt leer ist. Für disjunkte Mengen gilt A B = A + B Manchmal wollen wir mehr als nur eine Menge vereinigen oder schneiden. Wir schreiben dann n A i = A 1 A... A n i=1 n A i = A 1 A... A n i=1 Die Differenz von Mengen ist wie folgt definiert: A\B = { : A und / B} 5

26 A B A\B Ist A eine Teilmenge von Ω, so schreiben wir statt Ω\A auch A oder, genauer, A Ω = Ω\A: Ω A A Beispiel 1.0 Wir betrachten die folgenden vier Mengen: A = { : R und 1 6} B = { : N und < 6} C = { : N und } D = { : R und < 6} 6

27 Dann gilt: Mengenalgebra A B = {1,,3,4,5} A\D = {6} A C = {,3,4,5,6} C \A = { : N und > 6} B C = {,3,4,5} B C = N A N = {1,,3,4,5,6} A R = { : R und ( < 1 oder > 6)} B N = {6,7,8,...}. Ähnlich wie für die Verknüpfung von Aussagen gibt es auch gewisse Rechenregeln für die Verknüpfung von Mengen. Wir geben im folgenden die wichtigsten Regeln an: Idempotenzgesetze A A = A A A = A Kommutativgesetze A B = B A A B = B A Assoziativgesetze A (B C) = (A B) C A (B C) = (A B) C Distributivgesetze A (B C) = (A B) (A C) A (B C) = (A B) (A C) Inklusionsgesetze A A B A B A 7

28 Man macht sich diese Regeln am besten anhand einiger Mengendiagramme (Venn-Diagramm) klar. Wir illustrieren hier nur das erste Distributivgesetz. Im ersten Diagramm sehen wir die Menge B C schraffiert. Danach vereinigen wir diese Menge mit A. Im letzten Bild haben wir die Mengen A B und A C jeweils unterschiedlich schraffiert und dadurch auch gleich den Schnitt (A B) (A C) gekennzeichnet. B B A B C A A (B C) C C B A (A B) (A C) Ähnliche Gesetze gelten für die Komplementbildung und die Mengendifferenz. Neue Mengen aus alten Mengen Die Potenzmenge einer Menge A ist die Menge aller Teilmengen von A. Bezeichnung: P(A). Ist A endlich, so gilt P(A) = A. Seien a 1,...a n irgendwelche Elemente. Wir nennen (a 1,a,...,a n ) ein n-tupel. Die Elemente müssen nicht unbedingt verschieden sein. Die Menge aller n-tupel (a 1,...,a n ) mit a i A i heißt das kartesische Produkt von A 1,...,A n. Bezeichnung: A 1 A A n. C 8

29 Beispiel 1.1 Sei A = {1,} und B = {a,b} und C = {b,c}. Dann gilt A (B C) = {(1,a),(1,b),(1,c),(,a), (,b),(,c)} (A B) (A C) = {(1,a),(1,b),(,a),(,b), (1,c),(,c)} A (B C) = {(1,b),(,b)} (A B) (A C) = {(1,b),(,b)} Diese Beispiele legen nahe (und man kann es auch beweisen), dass A (B C) = (A B) (A C) A (B C) = (A B) (A C) gilt. Im allgemeinen ist A B B A. 1.5 Relationen und Abbildungen Die Definition einer Relation ist ganz einfach: Eine Relation R zwischen zwei Mengen X und Y ist eine Teilmenge R X Y. Gilt X = Y, so heißt R eine Relation auf X. Man schreibt R y falls (,y) R. Beispiel 1. X: Menge der MathematikerInnen. Y: Menge der WirtschaftswissenschaftlerInnen. Eine Relation zwischen X und Y wird z.b. durch Mathematiker ist jünger als Wirtschaftswissenschaftler y erklärt. Sei X die Menge aller Frauen, Y die Menge aller Männer. Als Relation zwischen X und Y wählen wir verheiratet. A = {1,}, B = {,3}. Dann ist A B = {(1,),(1,3),(,),(,3)}. Wir erhalten z.b. folgende Relationen: R 1 = {(a,b) A B : a = b} = {(,)} R = {(a,b) A B : a < b} = {(1,),(1,3),(,3)} R 3 = {(a,b) A B : a b} = {(1,),(1,3),(,3),(,)} = A B R 4 = {(a,b) A B : a+b = } = 9

30 Man kann diese Relationen auch durch Graphen verdeutlichen. Dazu malen wir die Menge A und die Menge B auf und verbinden zwei Elemente mit einem Pfeil genau dann, wenn sie in Relation miteinander stehen: 1 R R 3 3 R 1 R 4 3 Diese Beispiele zeigen, dass an jedem Punkt kein, ein oder mehrere Pfeile beginnen können. Genauso kann an jedem Punkt kein, ein oder mehrere Pfeile ankommen. Solche Pfeildiagramme sind natürlich unhandlich, wenn die Mengen X und Y unendlich sind. Sind X und Y Zahlbereiche, können wir versuchen, die Menge der Punkte (, y) R in einem Koordinatensystem zu skizzieren. Abbildungen In den Wirtschaftswissenschaften haben wir es meistens mit Abbildungen zu tun. Eine Abbildung aus X nach Y ist eine Relation zwischen X und Y, so dass es zu jedem X höchstens ein y Y gibt, so dass und y in Relation zueinander stehen. Das Element y wird mit f() bezeichnet. 30

31 In unserer Pfeildarstellung bedeutet dies, dass in jedem Element X höchstens ein Pfeil beginnt: Beachte, dass nicht jedem X ein Funktionswert zugeordnet werden muss. Häufig wird gefordert, dass jedem X ein y so zugeordnet wird, dass und y in Relation stehen. Wir benutzen hier manchmal folgende Sprechweise: Wenn jedem X höchstens ein y zugeordnet wird, so sprechen wir von einer Funktion aus X nach Y. Wird jedem X genau ein f() zugeordnet, so wollen wir von einer Abbildung von X nach Y sprechen: Das ist manchmal ganz praktisch: Es hat Vorteile, wenn man komplizierte Funktionen hat wie etwa f() = , aufgefasst als Abbildung aus R nach R, wo man von vornherein gar nicht weiß, für welche der Nenner 0 wird, die Funktion also gar nicht definiert ist. Bezeichnung: f : X Y. Die Menge der X, für die f() erklärt ist, nennen wir den Definitionsbereich von f, bezeichnet mit D(f). Der Definitionsbereich D(f) muss nicht ganz X sein, wie die obigen Beispiele zeigen. Die Menge X heißt die Menge der unabhängigen Variablen, die Menge Y bezeichnet die abhängigen Variablen, denn wenn wir kennen, kennen wir auch f(). Beachten Sie bitte, dass der Definitionsbereich alle X enthält, für die es ein f() gibt, er ist also in einem gewissen Sinne maimal. Beispiel 1.3 Wir definieren f : R R durch f() = 1 1. Dieser Ausdruck ist natürlich nur erklärt, wenn 1 0. Also ist f eine Abbildung aus R nach R. Der Definitionsbereich ist R\{±1}. Die graphische Veranschaulichung: 31

32 4 y Beispiel 1.4 Wir betrachten f : R R definiert durch f() = lg (dekadischer Logarithmus). Wir haben schon gesehen, dass der Logarithmus nur für positive Zahlen erklärt ist. Der Definitionsbereich ist also R + :

33 Machen Sie sich bitte nicht zu viele Gedanken über die Frage, ob eine Abbildungen von oder aus einer Menge X erklärt ist. Wichtig ist nur, dass bei der 1 Beschreibung einer Abbildung durch eine Vorschrift, wie z.b. lg oder 1 zu beachten ist, dass diese Vorschrift für einige Werte von möglicherweise nicht definiert ist. Oft liegt das daran, dass man nicht durch 0 dividieren darf. Andere Möglichkeiten: Logarithmen oder Wurzeln negativer Zahlen sind nicht definiert. Manche trigonometrische Funktionen haben Stellen, wo sie nicht definiert sind, z.b. tan(π/) ist nicht definiert. Abbildungen werden oft auch Funktionen genannt. Meistens spricht man von Funktionen, wenn die Mengen X und Y Zahlbereiche sind. Wenn wir hier von Zahlbereichen sprechen, meinen wir nicht etwa nur R, sondern auch R, R 3 usw. Denken Sie daran: Ökonomische Daten hängen fast nie nur von einer Variablen ab. Injektiv, Surjektiv, Bijektiv Eine Abbildung f : X Y heißt injektiv wenn aus f( 1 ) = f( ) stets 1 = folgt. Die Abbildung heißt surjektiv, wenn es zu jedem y Y (mindestens) ein X gibt mit f() = y. Die Abbildung heißt bijektiv, wenn sie injektiv und surjektiv ist und es zu jedem X ein y gibt mit f() = y (f also insbesondere eine Abbildung von X nach Y ist). Für unsere Pfeildarstellung von Abbildungen bedeutet das folgendes: injektiv: in jedem y Y endet höchstens ein Pfeil surjektiv: in jedem y Y endet mindestens ein Pfeil bijektiv: in jedem y Y endet genau ein Pfeil und in jedem X beginnt genau ein Pfeil. 33

34 injektiv surjektiv bijektiv In allen drei Fällen haben wir Abbildungen, weil aus den linken Mengen an jedem Punkt nur höchstens ein Pfeil beginnt. Ist f eine injektive Abbildung, so definieren wir f 1 : Y X durch folgende Vorschrift: f 1 (y) =, wobei X durch die Eigenschaft f() = y bestimmt ist. Beachte, dass wegen der Injektivität eindeutig bestimmt ist. In unseren Pfeilbildern bedeutet dies einfach, dass wir jeden Pfeil umdrehen. Die Abbildung f 1 heißt die zu f inverse Abbildung. Beachte, dass auch f 1 injektiv ist. Ferner ist f bijektiv genau dann wenn f injektiv und surjektiv ist und zusätzlich f 1 auch surjektiv ist. 34

35 Bei einer bijektiven Abbildung geht von jedem Punkt in X genau ein Pfeil aus und in jedem Punkt aus Y endet genau ein Pfeil. Das heißt insbesondere, dass X und Y gleich viele Elemente haben. Verknüpfung von Abbildungen Seien f : X Y und g : Y Z zwei Abbildungen. Wir definieren die Abbildung g f : X Z wie folgt: (g f)() = g[f()]. Also: Wir wenden erst f auf an, dann auf den Wert f() die Abbildung g. Wichtigistes,sichzumerken,dassg f bedeutet,erstf unddanng anzuwenden. f g X Y Z g f 35

36 Funktionen einer Variablen.1 Einführende Beispiele Kostenfunktion und Stückkostenfunktion: Das Unternehmen Miel produziert hochwertige Waschmaschinen. Es hat monatliche Fikosten von Die sind unabhängig von der produzierten Menge. Pro produziertem Stück fallen variable Kosten (vor allem Material und Löhne) von 500 an. Die monatlichen Gesamtkosten des Unternehmens (in ) betragen dann K() = , wobei die Anzahl der im Monat produzierten Waschmaschinen ist. Bei 100 Waschmaschinen fallen also Gesamtkosten an in Höhe von bei 1000 Stück K(100) = , K(1000) = K heißt die Kostenfunktion. Wenn man nicht an den Gesamtkosten K interessiert ist, sondern an den Kosten pro produziertem Stück, so erhält man die Stückkostenfunktion S(). Sie ergibt sich aus der Kostenfunktion K() einfach durch In obigem Beispiel ist S() = K(). S() = Bei 100 produzierten Waschmaschinen ist das also bei 1000 Maschinen S(100) = 300, S(1000) = 670. = Weitere ökonomische Funktionen sind Nachfrage-Funktion (Preis-Absatz-Funktion): Sei p der Preis eines Gutes, N die nachgefragte (abgesetzte) Menge. Die Nachfragefunktion ist dann N(p). Üblicherweise wird N(p) kleiner, wenn der Preis p steigt. So könnte z.b. (p ausgedrückt in ) N(p) = p (.1) sein. Das heißt, bei einem Preis von 10 beträgt die Nachfrage Stück, bei einem Preis von 13 nur Stück. Oft wird auch umgekehrt die Funktion p(n) betrachtet. Angebotsfunktion: Sei p der Preis eines Gutes, A die vom Produzenten zu 36

37 dem Preis auf den Markt gebrachte Menge. Die Angebotsfunktion ist dann A(p). Angebotsfunktionen sind typischerweise monoton steigend. Erlösfunktion: Für N abgesetzte Güter zum Stückpreis p(n) ist der Erlös in Abhängigkeit von der Menge N E(N) = N p(n). Hierbei ist berücksichtigt, dass der Preis p von der Nachfrage N abhängt, typischerweise mit hoher Nachfrage steigt. In Abhängigkeit vom Preis p ist die Erlösfunktion E(p) = N(p) p. Wenn wir die Nachfragefunktion (.1) benutzen, erhalten wir E(p) = p 500p. Eine typische Frage ist: Für welchen Preis p wird der Erlös E(p) maimal. Solche und ähnliche Fragen werden wir mit etwas mathematischer Theorie beantworten können.. Grundlegende Begriffe und Bezeichnungen Eine Abbildung f : R R mit D(f) R heißt reellwertige Funktion einer reellen Variablen (Veränderlichen) wobei D(f) der bereits früher definierte Definitionsbereich von f ist. Die Menge W(f) := {f() : D(f)} heißt der Wertebereich von f. Erinnerung: D(f) = { R : Es gibt y R mit y = f()}, d.h. D(f) besteht aus all den, die man in f einsetzen kann. Wir nennen f() die Zuordnungsvorschrift und den Graph von f. G f = {(,y) D(f) R : y = f()} Viele Zuordnungsvorschriften haben einen natürlichen maimalen Definitionsbereich. Oft wird dann nur die Zuordnungsvorschrift angegeben, und es ist dann die zugehörige Funktion auf dem maimalen Definitionsbereich gemeint. Wenn aus dem Zusammenhang klar ist, was die Funktion f ist, schreiben wir auch einfach D statt D(f). 37

38 Beispiel.1 hat den maimalen Definitionsbereich R. 1 hat den maimalen Definitionsbereich R\{0}. Die schon vorher betrachtete Kostenfunktion K() = hat als Definitionsbereich R. In dem betrachteten Beispiel sind allerdings nur nicht-negative ganze Zahlen interessant (: Anzahl der Waschmaschinen) und nur bis zu einer gewissen Höhe, die durch die Maimalauslastung des Unternehmens gegeben ist. Dieses Beispiel zeigt, dass nicht alle Werte für, die mathematisch sinnvoll sind, auch im ökonomischen Sinn sinnvoll sind. In vielen Fällen ist f eine Funktion aus S nach T, wobei S,T R Teilmengen von R sind. In dem Fall schreibt man f : S T, f(). DieElementef()müsseninT liegen.derdefinitionsbereichvonf istindiesem Fall D(f) = { S : Es gibt y T mit y = f().} Ein Hilfsmittel zur Veranschaulichung einer Funktion f und ihres Graphen ist eine Wertetabelle, in der ausgewählte Werte von zusammen mit ihrem Funktionswert f() eingetragen werden. Beispiel. Wir setzen unser Beispiel K() = fort: K() Beispiel.3 f() = 3 ++1: f() Eine genauere Methode ist das Zeichnen der Graphen in ein Koordinatensystem. Der Graph zur oben angegebenen Funktion ist 38

39 Wir wollen uns in den folgenden Beispielen überlegen, ob die jeweiligen Funktionen f : R R injektiv, surjektiv oder bijektiv sind. Achtung: Es gibt Funktionen, die weder injektiv noch surjektiv noch bijektiv sind! Injektivität bedeutet, dass der Graph jeder Gerade mit der Gleichung y = a (a R) den Graphen G f von f höchstens einmal schneidet. Beachte, dass Gleichungen y = a Geraden parallel zur -Achse beschreiben. Surjektiv heißt, dass jede solche Gerade den Graphen mindestens einmal trifft, und bijektiv schließlich bedeutet, dass jede solche Gerade den Graphen genau einmal trifft, und dass gleichzeitig D(f) = R gilt. Sie müssen Surjektivität etwas anders interpretieren, wenn f : R A mit A R gilt. Surjektivität bedeutet dann, dass jede Gerade mit der Gleichung y = a mit a A den Graphen G f mindestens einmal trifft. Beispiel.4 f() = +4 30:

40 Diese Funktion ist weder injektiv noch surjektiv. Beispiel.5 f() = y Auch diese Funktion ist nicht surjektiv, denn f() ist niemals 0. Sie ist auch nicht injektiv, weil stets f( ) = f() gilt. Beispiel.6 S() = , D(S) = R y Diese Funktion ist injektiv und nimmt alle positiven Werte > 500 an. Wenn wir S also auffassen als eine Abbildung R + { R : > 500}, so ist S surjektiv (sogar bijektiv!). Beispiel.7 f() = 7 40

41 Diese Funktion heißt konstant Allgemein heißt eine Funktion mit der Vorschrift f() = c, wobei c eine Zahl unabhängig von ist, konstant. Konstante Funktionen sind nicht injektiv und nicht surjektiv. Beispiel.8 f() = 10 3: Die Abbildung f ist injektiv und surjektiv. Eine Funktion der Form f() = a +b heißt linear. Dabei sind a und b feste reelle Zahlen. Die Kostenfunktion K() = ist beispielsweise eine lineare Funktion. Beispiel.9 Ein Kopierladen erhebt die Kosten pro Fotokopie in Abhängigkeit von der Gesamtzahl der getätigten Kopien. Hierbei gelten folgende Preise: 41

42 Anzahl der Kopien 0 bis ab 100 Preis pro Kopie 0,05 0, Die Funktion k, die den Preis pro Kopie beschreibt, ist also gegeben durch 0,05 falls 0 49, k() = 0,04 falls 50 99, 0,03 falls 100. Ihr Graph sieht wie folgt aus: 0.05 ο ο Eine solche Funktion nennt man Treppenfunktion. Treppenfunktionen sind weder injektiv noch surjektiv. Achtung: Eigentlich ist unsere Funktion k() natürlich nur für ganzzahlige definiert. Wir haben bei der hier angegebenen Skizze aber beliebig reellwertig angenommen, was für die Visualisierung durchaus angemessen ist. Bei Funktionen mit Sprüngen wie in diesem Beispiel sollte man bei der Visualisierung deutlich machen, welche Punkte an den Sprungstellen zum Funktionsgraphen gehören. Wir malen einen fetten Punkt, wenn der Punkt dazugehört, sonst einen nicht ausgefüllten kleinen Kreis. Die Funktion K, die die Gesamtkosten des Kunden in Abhängigkeit von der Stückzahl angibt, ist 4

43 0,05 falls 0 49, K() = 0,04 falls 50 99, 0,03 falls 100. Ihr Graph sieht wie folgt aus: ο 3 ο Injektive Abbildungen haben eine schöne Eigenschaft. Beachten Sie dabei, dass der Wertebereich aus allen y R besteht, für die es ein gibt mit y = f(). Es handelt sich also um die Menge der reellen Zahlen, die wirklich als Bild von f auftreten. Ist die Funktion f : R R injektiv, hat den Definitionsbereich D und den Wertebereich W, so ist f : D W bijektiv. Dann heißt f 1 : W D, y wobei D mit f() = y die Umkehrfunktion zu f. Der Graph G f 1 = {(y,) W D y = f()} = {(y,) W D (,y) G f } entstehtausg f durchspiegelunganderwinkelhalbierendenmitdergleichung = y. Beispiel.10 Wir betrachten wieder die Stückkostenfunktion S() =

44 Für welche Stückzahl ergibt sich 1500? Wir lösen hierzu nach auf und erhalten = 170. = 1500 = 1000, Das ist die gesuchte Stückzahl, denn es ist nun S(170) = Lösen wir allgemein die Gleichung = y nach auf, so erhalten wir = y 500 und dies ist gerade die Umkehrfunktion, also S 1 (y) = y 500. Mit ihr lässt sich zu beliebigen Stückkosten die zugehörige Stückzahl ermitteln. Beispiel.11 Die Funktion f : R + 0 R+ 0 mit f() = ist bijektiv. Ihre Umkehrabbildung ist f 1 (y) = y. 4 3 y Beachte: Die Funktion f() = kann auch für alle R betrachtet werden, ist dann aber nicht injektiv, folglich gibt es dann auch keine Umkehrfunktion. Verknüpfung von Funktionen Aus gegebenen Funktionen können durch Verknüpfung mittels der Grundrechenarten neue Funktionen gebildet werden. 44

45 Seien f,g : R R Funktionen und λ R. Dann lassen sich auch die folgenden Funktionen definieren: λf : R R, mit (λf)() = λf(), f ±g : R R, mit (f ±g)() = f()±g(), f g : R R, mit f g : R R, mit f (f g)() = f() g(), f() () = g g(). Die Definitionsbereiche sind D(λf) = D(f), D(f ±g) = D(f) D(g), D(f g) = D(f) D(g), ( ) f D = { R : D(f) D(g) und g() 0}. g Wir erinnern daran, dass man auch f g (Verkettung von f und g) bilden kann. Der Definitionsbereich von f g sind diejenigen Elemente R, für die g() im Definitionsbereich von f liegt. Beispiel.1 Seien f() = 15 3, g() = 3+1. Dann sind (5f)() = 75 15, (f +g)() = +1, (f g)() = (15 3)( 3+1) = , ( ) f () = 15 3 g 3+1. Aus dem Definitionsbereich von f g weil g(1) = 0 und g(1/) = 0. müssen 1 und 1/ ausgeschlossen werden, Intervalle Seien a, b R mit a < b. Dann unterscheiden wir die folgenden Typen von 45

46 Intervallen Intervalle der Form [a,b] = { R : a b} abgeschlossenes Intervall, (a,b) = { R : a < < b} offenes Intervall, [a,b) = { R : a < b} (a,b] = { R : a < b} [a, ) = { R : a} (,b] = { R : b} (a, ) = { R : > a} (,b) = { R : < b} halboffene Intervalle. werden uneigentliche Intervalle genannt, die ersten beiden sind abgeschlossene, die letzten beiden offene Intervalle. Monotonie Neben Injektivität und Surjektivität spielen weitere Eigenschaften von Funktionen eine wichtige Rolle. Besonders wichtig ist die Monotonie: Seien f : R R eine Funktion und I R ein Intervall im Definitionsbereich von f. Gilt für alle 1, I mit 1 < f( 1 ) f( ) (bzw. f( 1 ) < f( )) (.) dann heißt f (streng) monoton wachsend in I. Gilt für alle 1, I mit 1 < f( 1 ) f( ) (bzw. f( 1 ) > f( )) dann heißt f (streng) monoton fallend in I. Die Funktion f heißt (streng) monoton wachsend auf dem ganzen Definitionsbereich, wenn die Bedingung (.) für alle 1, D(f) mit 1 < erfüllt ist. Entsprechendes gilt für (streng) monoton fallend Die Stückkostenfunktion S() = ist streng monoton fallend. Anschaulich bedeutet das: Je mehr Stücke produziert werden, so geringer sind die Stückkosten, um so effizienter ist also die Produktion. Wir halten folgenden interessanten Zusammenhang zwischen Monotonie und Injektivität fest: Ist f streng monoton wachsend (oder streng monoton fallend) dann ist f injektiv, hat also eine Umkehrfunktion. 46

47 Beispiel.13 Die Funktion f() = ist auf [0, ) streng monoton wachsend, auf(, ] streng monoton fallend. Wo genau sich das Wachstumsverhalten umkehrt, ist am Graphen nicht genau zu erkennen. Das werden wir später mit mathematischen Methoden ermitteln können. Können Funktionen nicht beliebig groß oder klein werden, spricht man von beschränkten Funktionen: Sei f : R R eine Funktion und sei D der Definitionsbereich. Gibt es ein c R mit f() c (bzw. f() c) für alle D, dann heißt f nach unten (bzw. oben) beschränkt. Ist f nach unten und nach oben beschränkt, dann heißt f beschränkt. Anders formuliert: Der Wertebereich W(f) ist beschränkt, also W(f) [a,b] für geeignete a,b R. Beispiel.14 Die Funktion f() = 4 mit dem Graphen ist nach unten beschränkt, weil f() 4 für alle R. Die Funktion ist aber nicht nach oben beschränkt. Beispiel.15 Die Funktion f() = 3 ist weder nach oben noch nach unten beschränkt. 47

48 Wir betrachten wieder die Kostenfunktion K() = auf dem Intervall [0, 000]. Dort ist K beschränkt, weil K() K(0) = K() K(000) = für alle [0,000]. Das Intervall [0,000] könnte aus ökonomischer Sicht relevant sein, wenn etwa die Maimalauslastung bei 000 produzierten Waschmaschinen liegt. Folgende Eigenschaft beschreibt eine gewisse Symmetrie des Funktionsgraphen: Sei f : R R eine Funktion mit D(f) = R, die Funktion ist also auf ganz R definiert. Gilt f( ) = f() für alle R, dann heißt f gerade. Wenn f( ) = f() für alle R gilt, dann heißt f ungerade. Der Graph einer geraden Funktion ist achsensymmetrisch zur y-achse, der einer ungeraden Funktion ist punktsymmetrisch bezüglich des Ursprungs des Koordinatensystems. 48

49 Beispiel.16 Die Funktion f() = 4 ist gerade, y die Funktion f() = 5 ist ungerade: 49

50 15 y Nullstellen Häufig interessiert man sich für die Werte der unabhängigen Variable einer Funktion, für die der Funktionswert 0 ist: Sei f : R R eine Funktion. Ist 0 D(f) eine reelle Zahl mit f( 0 ) = 0, dann heißt 0 eine Nullstelle von f. Der folgende Graph skizziert eine Funktion mit drei Nullstellen (3, 1 und 3): 50

51 Elementare Funktionen Trigonometrische Funktionen (Winkelfunktionen) Vorbemerkung. Wir definieren die Winkelfunktionen bezogen auf die Bogenlänge auf dem Einheitskreis, d.h. für [0,π]. Alternativ werden die Argumente der Winkelfunktionen in Winkelgraden angegeben. Hier entspricht der Winkelgrad α = 360 o der Bogenlänge = π, und Anteile am Vollkreiswinkel 360 o werden entsprechend in Anteile des Kreisumfangs umgerechnet: α = 360o t entspricht = π t d.h. die Bogenlänge zum Winkel α ist = π 180 α. (i) Sinus Als Winkelfunktion ist die Sinus-Funktion in folgender Weise definiert. Für einen Winkel α [0, π Gegenkathete ] ist sinα = Hypothenuse, wobei hier die (Längen der) Gegenkathete und Hypothenuse in einem rechtwinkligen Dreieck mit Scheitelwinkel α gemeint ist. Für α [ π,π] ist sinα = sin(π α). Für α [π,π] ist sinα = sin(α π). 51

52 Abbildung 1: Graphen von sin (rot) und cos (blau) Ist R, dann schreiben wir = mπ +α mit m Z, α [0,π), und setzensin = sinα. Dadurchist die Sinus-Funktion auf ganz R erklärt. Sie ist periodisch mit Periode π, d.h. sin( + π) = sin(). Ihr Wertebereich ist W(sin) = {y R : 1 y 1} = [ 1,1]. π/ α Gegenkathete Hypothenuse α Ankathete Diese Skizze zeigt noch einmal die Größen, die bei der Definition der trigonometrischen Funktionen eine Rolle spielen. (ii) Cosinus: Als Winkelfunktion ist die Cosinus-Funktion in folgender Weise definiert. Für einen Winkel α [0, π Ankathete ] ist cosα = Hypothenuse, wobei hier die (Länge der) Ankathete bzw. Hypothenuse in einem rechtwinkligen Dreieck mit Scheitelwinkel α gemeint ist. Für α [ π,π] ist cosα = cos(π α). Für α [π,π] ist cosα = cos(α π). Ist R, dann schreiben wir = mπ +α mit m Z, α [0,π), und setzen cos = cosα. Auch die Cosinus-Funktion ist periodisch mit Periode π. Ihr Wertebereich ist ebenfalls W(cos) = [ 1,1]. Es gilt 5