y = ( gt +C 3 )dt = 1 2 gt 2 +C 3 t +C 4. (9) (3) (4) ẋ(t = 0) = C 1 = v 0 cosα C 1 = v 0 cosα, ẏ(t = 0) = g 0+C 3 = v 0 sinα C 3 = v 0 sinα.
|
|
|
- Philipp Böhmer
- vor 6 Jahren
- Abrufe
Transkript
1 Kinematik und Dnamik Mechanik II) - Prof. Popov SoSe 13, KW 1 Lösunshinweise Seite 1 Kinematik der einachsien/räumichen Beweun Version vom 9. Jui 13 Tutorium Aufabe 4 a) Aus dem Diaramm at) über t wird die Forme für at) entnommen at) ist eine ineare Funktion mit Achsenabschnitt a und Steiun a t ): at) = a a t t. 1) Durch Interation eribt sich daraus mit der Randbedinun v) = ) die Geschwindikeit: vt) = a t)d t = [ a t a 4t t ] t=t t= = a t a 4t t ) st) wird emäß nebenstehender Skizze as der momentane Ort des Bas definiert. Danach ist s) =. Durch Interation der Geschwindikeit eribt sich: st) [ a st) = v t)d t = t a 3] t=t 1t t t= t ) = a t3 1t 3) In a diesen Formen ist t zunächst noch unbekannt. t wird bestimmt durch die Nebenbedinun, dass der Ba zu dieser Zeit das Rohr veräßt, aso st ) = t ) st ) = a t3 1t 1 = a t 1) 1 1 t = 5 = 5 1 a t = a 4) Wird jetzt4) in die Beziehun für die Geschwindikeit) einesetzt, eribt sich die Geschwindikeit beim Verassen des Rohres: vt ) = a t a ) = 3 4 a t b) = 3 4 a 1 5 4t t = a t a = 7 a 5) Die Beweun des Baes nach Verassen des Rohres ist eine zweidimensionae Beweun, die im Kartesischen, - Koordinatensstem über den Ortsvektor: r = e + e ) beschrieben wird. In diesem ortsfesten Koordinatensstem sind der zuehörie Geschwindikeits- und Bescheuniunsvektor erade: r = ẋ e +ẏ e und r = ẍ e +ÿ e. 7) Die - und Anteie der Beweun des Baes nach Verassen des Rohres können etrennt betrachet werden. In der -Richtun handet es sich um eine unbescheunite Beweun die Geschwindikeit beibt konstant). Es eribt sich demnach nach zweifacher unbestimmter Interation die Koordinate t ): ẋ = ẍdt = C 1, = ẋdt = C 1 dt = C 1 t +C. 8) Hierbei ist zu beachten, dass zur Abkürzun eine neue Zeitbezeichnun t eineführt wird, die ab dem Verassen des Rohres zäht: t = t t. Die Interationskonstanten C 1 und C sind später durch Anfansbedinunen zu bestimmen. Zunächst wird mit dem -Antei in der eichen Weise verfahren. In dieser Richtun wird der Ba Richtun Erdmittepunkt aso in neativer -Richtun) bescheunit: ẏ = ÿdt = dt = t +C 3, = t +C 3 )dt = 1 t +C 3 t +C 4. 9) Die vier Interationskonstanten sind aus vier Anfansbedinunen zu bestimmen. Zwei erhät man aus der Tatsache, dass die Geschwindikeit bei Verassen des Rohres bekannt ist: v = vt ) aus Geichun 5). Aus der v sinα v α v cosα nebenstehenden Skizze können die - und -Komponenten dieser Geschwindikeit abeesen werden. AB 1 ẋt = ) = v cosα 1) AB ẏt = ) = v sinα 11) Der Ursprun des, -Koordinatensstems iet am Ende des Abschussrohres. Somit erhät man zwei weitere Anfansbedinunen: AB 3 t = ) = 1) AB 4 t = ) = 13) Aus den Anfansbedinunen AB 1 und AB fot direkt: ẋt = ) = C 1 = v cosα C 1 = v cosα, ẏt = ) = +C 3 = v sinα C 3 = v sinα. Die weiteren Konstanten ereben sich durch Auswerten der Anfansbedinunen AB 3 und AB 4: t = ) = C 1 +C = C =, t = ) = 1 +C 3 +C 4 = C 4 =. Einsetzen der ermitteten Konstanten in die Geichunen 8) und 9) führt auf die Komponenten des Ortsvektors t ) und t ): t ) = v cosαt 14) t ) = t +v sinαt. 15)
2 Kinematik und Dnamik Mechanik II) - Prof. Popov SoSe 13, KW 1 Lösunshinweise Seite Kinematik der einachsien/räumichen Beweun Version vom 9. Jui 13 Gefrat ist nach der Weite bis zum Aufscha des Baes. Geichun 14) ibt den zurückeeten We zu jeder beiebien Zeit t an. Der Zeitpunkt des Aufschas t A äßt sich aus Gn. 15) ermitten. Im betrachteten,- Koordinatensstem befindet sich der Ba auf der Höhe t A ) = h: t A) = t A +t Av sinα = h t A v sinα t A h = t A1/ = v sinα ± v sin α + h Offensichtich ist der Wurzeausdruck rößer as der Summand davor, die Variante mit dem neative Vorzeichen würde aso insesamt zu einer Zeit t A < führen. Das ist nicht sinnvo, da der Aufscha erst nach dem Abschuss erfoen so. Die richtie Lösun ist deshab: t A = v sinα v + sin α + h Wird diese Beziehun in Geichun 14) einesetzt, so erhaten wir mit v = 7 a aus Geichun 5)) die Weite A, die ein Ba fiet: A = t v sinα v A) = + sin α + h ) v cosα c) Die Geichun für die senkrechte Ortskoordinate ist Geichun 15). Die Etrema dieser Geichun unter denen sich dann auch das esuchte Maimum befinden sote) erhät man übicherweise, indem man die Nustee der ersten Abeitun ermittet. Äquivaent dazu ist die foende Heranehensweise: Der Ba erreicht seine maimae Fuhöhe enau in dem Moment t M, in dem seine senkrechte Geschwindikeitskomponente ẏt ) erade Nu wird. ẏt ) = t M +v sinα! = t M = v sinα We Rϕ zurückeet die Läne des entsprecheden Kreisboensementes am Radumfan). Die Höhe des Mittepunktes verändert sich nicht. M und M seien die Koordinaten des Mittepunktes, dann it: M t) = Rϕt) M t) = R Die Koordinaten R und R des Vektors R, der vom Mittepunkt des Rades zum Punkt Titus weist, können der Skizze entnommen werden: R t) = Rsinϕt) R t) = Rcosϕt) Der Drehwinke ϕt) eribt sich aus der Anabe d dt ϕt) = ω = konst durch Interation. Die Interationskonstante ϕ ist Nu, wie man der Skizze zur Aufabensteun entnehmen kann. ϕt) = M ωd t+ϕ = ωt Die Koordinaten des Ortsvektors zum Punkt Titus ereben sich durch Addition von M und R: T t) M t) R t) = + T t) M t) R t) [ ] [ ] ϕt) sinϕt) ωt sinωt = R = R 1 cosϕt) 1 cosωt Die Koordinaten des Geschwindikeitsvektors ereben sich daraus durch Abeiten nach der Zeit: v t) ẋt t) 1 cosωt = = Rω v t) ẏ T t) sinωt Die Koordinaten des Bescheuniunsvektors ereben sich ebenso durch Abeiten: a t) v t) = = Rω sinωt a t) v t) cosωt R ϕ Nun ist die Höhe H M des Bas über dem Boden in diesem Moment eeben durch die senkrechte Ortskomponente Geichun 15)) zuzüich dem Abstand zwischen Koordinatenursprun am Ende des Abschußrohres) und dem Boden: H M = t M)+h = t M +t Mv sinα+h = v sin α + v sinα v sinα+h H M = 1 v sin α + h maimae Fuhöhe Aufabe 11 M sei der Ortsvektor des Radmittepunktes. Wenn das Rad sich um den Winke ϕ edreht hat, hat es dabei den
3 Kinematik und Dnamik Mechanik II) - Prof. Popov SoSe 13, KW 1 Lösunshinweise Seite 3 Kinematik der einachsien/räumichen Beweun Version vom 9. Jui 13 Hausaufaben Aufabe a) Es so zunächst der Abstand nach Abauf der Schrecksekunde bestimmt werden. Hierfür wird ein Koordinatensstem verwendet, dass seinen Ursprun an der Position von Auto B zum Zeitpunkt t = hat. Beide Autos beween sich bis zum Zeitpunkt t = T mit jeweis konstanter Geschwindikeit. Der Abstand der beiden Autos zum Zeitpunkt t = T ist dann erade: b) Mit unserem Erebnis für a und der Beziehun 19) eribt sich die esuchte Zeit: t G = v bzw. t = 3 v. ) Durch Einsetzen erhaten wir zudem die Strecke, emessen von der Position an der B beinnt zu bremsen: = s A t = T) s B t = T) = V A T + V B T = 1) Nun wird eine neue Zeit eineführt, die ab dem Zeitpunkt des Bremsens it: t = t T. Zusätzich wird ein neues Koordinatensstem eineführt, das seinen Ursprun an der Position von Auto B zum Zeitpunkt t = T bzw. t = hat. Die Bescheuniun des Waens B ist konstant und durch Interation erhaten wir die Geschwindikeit: v B t) = und die Position: s B t) = a d t+v B = a t +v, a t+v d t+s B = 1 a t +vt. In der eichen Weise verfahren wir mit der Beweun des Autos A: v A t) = s A t) = d t+v A = v, v d t+s A = vt +. Ein Zusammenstoß findet im Grenzfa t = t G erade dann statt wenn die foenden Bedinunen erfüt sind: s A t = t G) = s B t = t G), 17) v A t = t G) = v B t = t G). 18) Eine zu hohe Geschwindikeit des Autos B würde einen Zusammenstoß bewirken, umekehrt würde eine zu erine Geschwindikeit den Zusammenstoß änzich verhindern. Auswerten der Bedinun 18) führt auf: a t G +v = v t G = v a 19) und schießich mit der Bedinun 17) zu: 1 a v a ) v v a = v v a + a = v. Dies ist die notwenie Mindestbescheuninu, um einen Zusammenstoß erade noch zu verhindern. Mit den eebenen Zahenwerten und der Beziehun v B = v eribt sich die notwendie Bremsverzöerun: ) 1 m a s = m a = 5 m s. s B t ) = 3. 1) a)die zeitichen Veräufe von We und Geschwindikeit steen sich mit den in b) eebenen Werten foendermaßen dar: We st) in [m] Geschwindikeit vt) in [m/s] Zeit t in [s] s A t) s B t) Zeit t in [s] v A t) v B t)
4 Kinematik und Dnamik Mechanik II) - Prof. Popov SoSe 13, KW 1 Lösunshinweise Seite 4 Kinematik der einachsien/räumichen Beweun Version vom 9. Jui 13 Aufabe 5 eeben: rt) = +sinωt) I) Ort Geschwindikeit Bescheuniun t) = a t ẋt) = at ẍt) e. rt) = a1 t +vt+r ṙt) e. rt) = a1 st) e. ṡt) = LΩcosΩt st) = LΩ sinωt ] t) = u ω [1+e ωt e ωt ẏt) e. ÿt) = uωe ωt t) e. 1) ) ϕt) = e t ϕt) e. ϕt) = e t t) = Lcosλt v ẋt) = Lλsinλt v 3 ẍt) e. λ sinλt λ cosλt ϕ = Ω = konst ) dϕ dt = Ω 7) ϕt) d ϕ = Ωd t 8) ϕt) = Ωt 9) ϕ rcosψ rcosψsinϕ rcosψcosϕ ψ = θ = konst 3) dϕ dt = θ Bestimmun von ψ : ψt) ψ d ψ = θd t 31) ψt) ψ = θt 3) ψt) = θt+ψ II) z)! = zt) = +rt)sinψt) 33) t = = + +sinωφ ) sinψ) 34) = +sinψ : 35) = 1+sinψ 3) 1): ẏt) = r r ω t t t 1 ) 3 cos Ψt) t t 1 sin Ψt) ): ÿt) = 3r ) 5 t t 1 cos Ψt) 4 ) 3 +r ω t t t 1 sin Ψt) mit Ψt) = ω t t ) r ω t t 1 sin Ψt) 4r ω 4 t t t 1 cos Ψt) : 1 = sinψ 37) sinψ = 1 ψ = arcsin 1 ) 38) ψ = π ψt) = θt π ) 39) 4) ae bekannten Größen einsetzen ψ = 3 t) = rt)cosψt)cosϕt) 41) = +sinωt)cos θt π ) cos Ωt 4) Aufabe 8 Aufsteen eines Ortsvektors: rt) = t)e +t)e +zt)e z ) t) = +sinωt)cosψt)sinϕt) 43) = +sinωt)cos θt π ) sin Ωt 44) t) = rcosψcosϕ 3) t) = rcosψsinϕ 4) zt) = +rsinψ 5) z r ψ rcosψ rsinψ zt) = +rsinψ 45) = + +sinωt)sin θt π ) 4) Geschwindikeitsvektor: ẋ v = ẏ bzw v = ẋe +ẏe +że z 47) ż
5 Kinematik und Dnamik Mechanik II) - Prof. Popov SoSe 13, KW 1 Lösunshinweise Seite 5 Kinematik der einachsien/räumichen Beweun Version vom 9. Jui 13 [ ẋt) = +sinωt)cos θt π ) cosωt] 48) [ = +sinωt) cos θt π ) cos Ωt+ 49) [ +sinωt) cos θt π cosωt+ 5) )] +sinωt)cos θt π ) cosωt ) ] 51) [ = ΩcosΩtcos θt π ) cos Ωt+ 5) +sinωt) sin θt π ) ) θ cos Ωt+ 53) +sinωt)cos θt π ) sinωt ) ] Ω 54) t) und t) unterscheiden sich nur im etzten Term, anstatt cosωt steht sint, somit kann man ẏt) eich schreiben. [ ẏt) = ΩcosΩtcos θt π ) sin Ωt 55) +sinωt)θsin θt π ) sin Ωt+ 5) +sinωt)cos θt π ) ] ΩcosΩt 57) beachte Vorzeichen beim Abeiten) [ żt) = ΩcosΩtsin θt π ) + 58) +sinωt)θcos θt π )] 59)
Physik Mathematisches Pendel
 Physik Mathematisches Pende 1. Zie des Versuches Bestätiun der Schwinunseichun des mathematischen Pendes Bestimmun der Erdbescheuniun. Aufaben Indirekte Bestimmun von fünf Pendeänen i durch jeweiie Messun
Physik Mathematisches Pende 1. Zie des Versuches Bestätiun der Schwinunseichun des mathematischen Pendes Bestimmun der Erdbescheuniun. Aufaben Indirekte Bestimmun von fünf Pendeänen i durch jeweiie Messun
1. Aufgabe: (ca. 14 % der Gesamtpunkte)
 17. Auust 26 1. Aufabe: (ca. 14 % der Gesamtpunkte) Ein Punkt führt eine eradinie Beweun aus, bei der ṡ(s) d.h. die Geschwindikeit in Abhänikeit vom We durch das foende Diaramm eeben ist: s v 0 inear 0
17. Auust 26 1. Aufabe: (ca. 14 % der Gesamtpunkte) Ein Punkt führt eine eradinie Beweun aus, bei der ṡ(s) d.h. die Geschwindikeit in Abhänikeit vom We durch das foende Diaramm eeben ist: s v 0 inear 0
v A B A α h 1 h c) Wie lautet der Geschwindigkeitsvektor beim Auftreffen der Kugel im Punkt B?
 Institut für Mechanik Prof. Dr.-In. habil. P. Betsch Prof. Dr.-In. habil. Th. Seeli Prüfun in Dynamik 3. Auust 4 Aufabe ca. 0 % der Gesamtpunkte) H m v 0 y 0000 00000 00000 000 000 00 000 0 v A 000 00
Institut für Mechanik Prof. Dr.-In. habil. P. Betsch Prof. Dr.-In. habil. Th. Seeli Prüfun in Dynamik 3. Auust 4 Aufabe ca. 0 % der Gesamtpunkte) H m v 0 y 0000 00000 00000 000 000 00 000 0 v A 000 00
1. Aufgabe (ca. 26 % der Gesamtpunktzahl)
 Institut für Mechanik Prof. Dr.-In. habi. P. Betsch Prof. Dr.-In. habi. Th. Seei Moduprüfun Dynamik 08. März 207. Aufabe (ca. 26 % der Gesamtpunktzah) A m v A C h A B v B α h B h C D Ein as Punktmasse
Institut für Mechanik Prof. Dr.-In. habi. P. Betsch Prof. Dr.-In. habi. Th. Seei Moduprüfun Dynamik 08. März 207. Aufabe (ca. 26 % der Gesamtpunktzah) A m v A C h A B v B α h B h C D Ein as Punktmasse
Übungen zu Experimentalphysik 1 für MSE
 Physik-Department LS für Funktionee Materiaien WS 07/8 Übunen zu Experimentaphysik für MSE Prof. Dr. Peter Müer-Buschbaum, Dr. Voker Körstens, Dr. Neeima Pau, Sebastian Grott, Lucas Kreuzer, Simon Schaper,
Physik-Department LS für Funktionee Materiaien WS 07/8 Übunen zu Experimentaphysik für MSE Prof. Dr. Peter Müer-Buschbaum, Dr. Voker Körstens, Dr. Neeima Pau, Sebastian Grott, Lucas Kreuzer, Simon Schaper,
3. Kreisbewegung. Punkte auf einem Rad Zahnräder, Getriebe Drehkran Turbinen, Hubschrauberrotor
 3. Kreisbewegung Ein wichtiger technischer Sonderfall ist die Bewegung auf einer Kreisbahn. Dabei hat der Punkt zu jedem Zeitpunkt den gleichen Abstand vom Kreismittelpunkt. Beispiele: Punkte auf einem
3. Kreisbewegung Ein wichtiger technischer Sonderfall ist die Bewegung auf einer Kreisbahn. Dabei hat der Punkt zu jedem Zeitpunkt den gleichen Abstand vom Kreismittelpunkt. Beispiele: Punkte auf einem
Lösung 03 Klassische Theoretische Physik I WS 15/16. x 2n+1 (2n + 1)! = x 2n (2n)! + ( x) 2n (2n)! ( x) 2n+1
 Karlsruher Institut für Technoloie Institut für theoretische Festkörperphysik www.tfp.kit.edu Lösun 3 Klassische Theoretische Physik I WS 5/6 Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler
Karlsruher Institut für Technoloie Institut für theoretische Festkörperphysik www.tfp.kit.edu Lösun 3 Klassische Theoretische Physik I WS 5/6 Prof. Dr. G. Schön Punkte Sebastian Zanker, Daniel Mendler
Mathematischer Vorkurs für Physiker WS 2009/10
 TU München Prof. Dr. P. Vogl, Dr. S. Schlicht Mathematischer Vorkurs für Physiker WS 2009/10 Vorlesung 2, Montag nachmittag Differentiation und Integration von Vektorfunktionen Der Ortsvektor: Man kann
TU München Prof. Dr. P. Vogl, Dr. S. Schlicht Mathematischer Vorkurs für Physiker WS 2009/10 Vorlesung 2, Montag nachmittag Differentiation und Integration von Vektorfunktionen Der Ortsvektor: Man kann
4.1. Prüfungsfragen zu Schwingungen
 4.. Prüfunsfraen zu Schwinunen Aufabe : Unedäpfte Federschwinun (6) Zeie it Hife des. Newtonschen Aios und der Skizze rechts, dass eine Masse an einer Feder it der Federkonstanten D eine periodische Schwinun
4.. Prüfunsfraen zu Schwinunen Aufabe : Unedäpfte Federschwinun (6) Zeie it Hife des. Newtonschen Aios und der Skizze rechts, dass eine Masse an einer Feder it der Federkonstanten D eine periodische Schwinun
Musterlösungen (ohne Gewähr)
 Seite 1/17 Frae 1 ( 3 Punkte) Ein fahrendes Fahrzeu wird entsprechend dem Beschleuniunsverlauf a(t) abebremst. Zum Zeitpunkt t = hat es die Geschwindikeit v und befindet sich an der Position s =. Zum Zeitpunkt
Seite 1/17 Frae 1 ( 3 Punkte) Ein fahrendes Fahrzeu wird entsprechend dem Beschleuniunsverlauf a(t) abebremst. Zum Zeitpunkt t = hat es die Geschwindikeit v und befindet sich an der Position s =. Zum Zeitpunkt
Energiemethoden, Prof. Popov, WiSe 11/12, 4. Woche Lösungshinweise Seite 1 Lagrangesche-Gleichungen 1. Art. 3m 2 r. Somit sind.
 Eneriemethoen, Prof. Popov, WiSe 11/1, 4. Woche Lösunshinweise Seite 1 Tutorium Aufabe 47 Auf einer schiefen Ebene Neiunswinkel α befinet sich ein Sstem aus einem Klotz Masse m 1 un einem Vollzliner Masse
Eneriemethoen, Prof. Popov, WiSe 11/1, 4. Woche Lösunshinweise Seite 1 Tutorium Aufabe 47 Auf einer schiefen Ebene Neiunswinkel α befinet sich ein Sstem aus einem Klotz Masse m 1 un einem Vollzliner Masse
Übungen zum Ferienkurs Physik für Elektroingenieure Wintersemester 2015 / 16
 Übunen zum Ferienkurs Physik für Elektroinenieure Wintersemester 2015 / 16 Rupert Heider Nr. 1 17.03.2016 Aufabe 1 : Flieender Pfeil Sie schießen vom Boden aus einen Pfeil in einem Winkel α zur Horizontalen
Übunen zum Ferienkurs Physik für Elektroinenieure Wintersemester 2015 / 16 Rupert Heider Nr. 1 17.03.2016 Aufabe 1 : Flieender Pfeil Sie schießen vom Boden aus einen Pfeil in einem Winkel α zur Horizontalen
Berechnung von Sonnenuhren mit Vektorrechnung
 Berechnun on Sonnenuhren mit Vetorrechnun Übicherweise werden Sonnenuhren berechnet, indem zunächst die Koordinaten des Äquatorsystems (Deination der Sonne, Stundenwine der Sonne τ) mit Hife on ebener
Berechnun on Sonnenuhren mit Vetorrechnun Übicherweise werden Sonnenuhren berechnet, indem zunächst die Koordinaten des Äquatorsystems (Deination der Sonne, Stundenwine der Sonne τ) mit Hife on ebener
Mathematische Modellierung Lösungen zum 2. Übungsblatt
 Mathematische Modellierun Lösunen zum 2 Übunsblatt Klaus G Blümel Lars Hoeen 3 November 2005 Lemma 1 Unter Vernachlässiun der Luftreibun beschreibt ein Massepunkt, der im Punkt 0, 0) eines edachten Koordinatensystems
Mathematische Modellierun Lösunen zum 2 Übunsblatt Klaus G Blümel Lars Hoeen 3 November 2005 Lemma 1 Unter Vernachlässiun der Luftreibun beschreibt ein Massepunkt, der im Punkt 0, 0) eines edachten Koordinatensystems
Blatt 1. Kinematik- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik (T1) im SoSe 011 Blatt 1. Kinematik- Lösungsvorschlag Aufgabe 1.1. Schraubenlinie Die
2. Räumliche Bewegung
 2. Räumliche Bewegung Prof. Dr. Wandinger 1. Kinematik des Punktes TM 3 1.2-1 2. Räumliche Bewegung Wenn die Bahn des Punkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort
2. Räumliche Bewegung Prof. Dr. Wandinger 1. Kinematik des Punktes TM 3 1.2-1 2. Räumliche Bewegung Wenn die Bahn des Punkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort
a S 1 S 2 S G e z a/2 e y e x a/2 Abbildung 1: Werbetafel.
 VU Modellbildun Beispiele zu Kpitel : Mechnische Systeme 1.) Geeben ist die in Abbildun 1 drestellte Werbetfel mit der Msse m. Die Werbetfel ist mittels zwei Seilen S 1 und S n einer Wnd befestit. Außerdem
VU Modellbildun Beispiele zu Kpitel : Mechnische Systeme 1.) Geeben ist die in Abbildun 1 drestellte Werbetfel mit der Msse m. Die Werbetfel ist mittels zwei Seilen S 1 und S n einer Wnd befestit. Außerdem
Lösung zur Klausur Technische Mechanik III Universität Siegen, Fachbereich Maschinenbau,
 Lösun zur Klausur Technische Mechanik III Universität Sieen, Fachbereich Maschinenbau, 9.02.2008 Aufabe 1 (10 Punkte) y m 2 u M R MR v 0 h r x A l B s C Ein römischer Katapultwaen (Masse ) rollt beladen
Lösun zur Klausur Technische Mechanik III Universität Sieen, Fachbereich Maschinenbau, 9.02.2008 Aufabe 1 (10 Punkte) y m 2 u M R MR v 0 h r x A l B s C Ein römischer Katapultwaen (Masse ) rollt beladen
s t =. v s t h = gt, t = v t = a v t t =
 Michael Buhlmann Phsik > Mechanik > urf und urfparabel Innerhalb der Mechanik als Teilebiet der Phsik wird unter bestimmten Voraussetzunen earbeitet: Die Beweun eines Körpers im Raums wird zur Beweun eines
Michael Buhlmann Phsik > Mechanik > urf und urfparabel Innerhalb der Mechanik als Teilebiet der Phsik wird unter bestimmten Voraussetzunen earbeitet: Die Beweun eines Körpers im Raums wird zur Beweun eines
Pendel und Energiesatz
 A6 Pende und Eneriesatz -8-5 - -9-6 -3 3 6 9 5 8 Pende und Eneriesatz Dr Rüdier Schoz, Leibniz Universität Hannover Juni 4 A6 Pende und Eneriesatz Ziee In diesem Praktikumsversuch untersuchen Sie Pendebeweunen,
A6 Pende und Eneriesatz -8-5 - -9-6 -3 3 6 9 5 8 Pende und Eneriesatz Dr Rüdier Schoz, Leibniz Universität Hannover Juni 4 A6 Pende und Eneriesatz Ziee In diesem Praktikumsversuch untersuchen Sie Pendebeweunen,
Dynamik. Modulprüfung in Technischer Mechanik am 9. März Aufgaben. Name: Vorname: Matr.-Nr.: Fachrichtung: Hinweise:
 Moduprüfun in Technischer Mechanik a 9. März 16 Aufaben Nae: Vornae: Matr.-Nr.: Fachrichtun: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnunen üssen sauber und übersichtich sein. Die Benutzun roter
Moduprüfun in Technischer Mechanik a 9. März 16 Aufaben Nae: Vornae: Matr.-Nr.: Fachrichtun: Hinweise: Bitte schreiben Sie deutich esbar. Zeichnunen üssen sauber und übersichtich sein. Die Benutzun roter
Experimentalphysik 1
 Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg (ronja.berg@tum.de) Katharina Scheidt (katharina.scheidt@tum.de) Aufgabe 1: Superposition
Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg (ronja.berg@tum.de) Katharina Scheidt (katharina.scheidt@tum.de) Aufgabe 1: Superposition
2. Räumliche Bewegung
 2. Räumliche Bewegung Prof. Dr. Wandinger 1. Kinematik des Punktes TM 3 1.2-1 2. Räumliche Bewegung Wenn die Bahn des Punkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort
2. Räumliche Bewegung Prof. Dr. Wandinger 1. Kinematik des Punktes TM 3 1.2-1 2. Räumliche Bewegung Wenn die Bahn des Punkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort
2 Kinematik eines Massenpunkts in 2D und 3D
 2 Kinematik eines Massenpunkts in 2D und 3D Wir wollen die räumliche Bewegung eines Massenpunkts (Fliege im Zimmer, geworfener Stein, Planet im Sonnensystem, Stern in einem dichten Sternhaufen, etc.) mathematisch
2 Kinematik eines Massenpunkts in 2D und 3D Wir wollen die räumliche Bewegung eines Massenpunkts (Fliege im Zimmer, geworfener Stein, Planet im Sonnensystem, Stern in einem dichten Sternhaufen, etc.) mathematisch
(t - t ) (t - t ) bzw. δ ε. θ ε. (t - t ) Theorie A (WS2005/06) Musterlösung Übungsblatt ε= 0.1 ε= t ) = lim.
 Theorie A (WS5/6) Musterlösung Übungsblatt 7 6..5 Θ(t t [ t t ) = lim arctan( ) + π ] ε π ε ( ) d dt Θ(t t ) = lim ε π vergleiche Blatt 6, Aufg. b). + (t t ) ε ε = lim ε π ε ε + (t t ) = δ(t t ) Plot von
Theorie A (WS5/6) Musterlösung Übungsblatt 7 6..5 Θ(t t [ t t ) = lim arctan( ) + π ] ε π ε ( ) d dt Θ(t t ) = lim ε π vergleiche Blatt 6, Aufg. b). + (t t ) ε ε = lim ε π ε ε + (t t ) = δ(t t ) Plot von
Übungen zu Physik 1 für Maschinenwesen
 Physikdepartment E3 WS 0/ Übunen zu Physik für Maschinenwesen Prof. Dr. Peter Müller-Buschbaum, Dr. Eva M. Herzi, Dr. Volker Körstens, David Maerl, Markus Schindler, Moritz v. Sivers Vorlesun 0..0, Übunswoche
Physikdepartment E3 WS 0/ Übunen zu Physik für Maschinenwesen Prof. Dr. Peter Müller-Buschbaum, Dr. Eva M. Herzi, Dr. Volker Körstens, David Maerl, Markus Schindler, Moritz v. Sivers Vorlesun 0..0, Übunswoche
v(t) r(t) Die Bewegung eines Körpers auf einer Kreisbahn vom Radius r kann beschrieben werden durch
 Die Keisbeweun ================================================================== 1. Bescheibun de Keisbeweun y v(t) ϕ(t) (t) ϕ(t) x Die Beweun eines Köpes auf eine Keisbahn vom Radius kann beschieben
Die Keisbeweun ================================================================== 1. Bescheibun de Keisbeweun y v(t) ϕ(t) (t) ϕ(t) x Die Beweun eines Köpes auf eine Keisbahn vom Radius kann beschieben
4. An einem Federpendel schwingt eine Masse mit der Frequenz f = 0,8 Hz. Die Masse. 18. Kontrolle Physik LK
 18. Kontroe Physik LK 5.9.011 1. In eine U-Rohr wird eine Füssikeit zu Schwinen aneret. a) Überprüfen Sie, ob diese Schwinun haronisch veräuft, wenn Reibunsveruste unberücksichtit beiben. (5) b) Für die
18. Kontroe Physik LK 5.9.011 1. In eine U-Rohr wird eine Füssikeit zu Schwinen aneret. a) Überprüfen Sie, ob diese Schwinun haronisch veräuft, wenn Reibunsveruste unberücksichtit beiben. (5) b) Für die
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 2005/06
 Üunen zu: Theoretische Physik I klassische Mechanik W 2213 Toias Spraner - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teachin.html 9. Novemer 25 Üunslatt 1 Lösunsvorschla Aufae 1 klassisches
Üunen zu: Theoretische Physik I klassische Mechanik W 2213 Toias Spraner - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teachin.html 9. Novemer 25 Üunslatt 1 Lösunsvorschla Aufae 1 klassisches
Kapitel 2. Kinematik des Massenpunktes. 2.1 Einleitung. 2.2 Massenpunkt. 2.3 Ortsvektor
 Kapitel 2 Kinematik des Massenpunktes 2.1 Einleitung In diesem Kapitel behandeln wir die Bewegung von einem oder mehreren Körpern im Raum. Wir unterscheiden dabei zwischen Kinematik und Dynamik. Die Kinematik
Kapitel 2 Kinematik des Massenpunktes 2.1 Einleitung In diesem Kapitel behandeln wir die Bewegung von einem oder mehreren Körpern im Raum. Wir unterscheiden dabei zwischen Kinematik und Dynamik. Die Kinematik
Betrachtet man einen starren Körper so stellt man insgesamt sechs Freiheitsgrade der Bewegung
 Die Mechanik besteht aus drei Teilgebieten: Kinetik: Bewegungsvorgänge (Translation, Rotation) Statik: Zusammensetzung und Gleichgewicht von Kräften Dynamik: Kräfte als Ursache von Bewegungen Die Mechanik
Die Mechanik besteht aus drei Teilgebieten: Kinetik: Bewegungsvorgänge (Translation, Rotation) Statik: Zusammensetzung und Gleichgewicht von Kräften Dynamik: Kräfte als Ursache von Bewegungen Die Mechanik
1. Nach-Klausur - LK Physik Sporenberg - Q1/
 . Nach-Klausur - LK Physik Sporenber - / 0.04.03.Aufabe: Geeben ist eine flache Rechteckspule mit n 00 indunen, der Höhe h 0 cm, der Breite b 3,0 cm und den Anschlüssen und (siehe Skizze). Diese Spule
. Nach-Klausur - LK Physik Sporenber - / 0.04.03.Aufabe: Geeben ist eine flache Rechteckspule mit n 00 indunen, der Höhe h 0 cm, der Breite b 3,0 cm und den Anschlüssen und (siehe Skizze). Diese Spule
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 13
 Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Prof. C. Greiner, Dr. H. van Hees Sommersemester 014 Übungen zur Theoretischen Physik Lösungen zu Blatt 13 Aufgabe 51: Massenpunkt auf Kugel (a) Als generalisierte Koordinaten bieten sich Standard-Kugelkoordinaten
Institut für Allgemeine Mechanik der RWTH Aachen
 Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
Institut für Agemeine Mechanik der RWTH Aachen Prof. Dr.-Ing. D. Weichert 9.Übung Mechanik II SS 27 18.6.6 Abgabetermin 9.Übung: 25.7.6 14: Uhr 1. Aufgabe Der skizzierte, statisch unbestimmte aken wird
(0 4) 4 :( 2) Bestimmung von Geradengleichungen Aufgabe 1
 Bestimmun von Geradenleichunen Auabe Geeben ist die Geradenleichun (x) = -x +. Gesucht sind die Schnittpunkte mit den Koordinatenachsen. Lösun: Mit der y-achse (x=0): S y (0 ) Mit der x-achse (y=0): x
Bestimmun von Geradenleichunen Auabe Geeben ist die Geradenleichun (x) = -x +. Gesucht sind die Schnittpunkte mit den Koordinatenachsen. Lösun: Mit der y-achse (x=0): S y (0 ) Mit der x-achse (y=0): x
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 2005/06
 Übungen zu: Theoretische Physik I klassische Mechanik W 13 Tobias Spranger - Prof. Tom Kirchner WS 005/06 http://www.pt.tu-clausthal.de/qd/teaching.html. Dezember 005 Übungsblatt 7 Lösungsvorschlag 4 Aufgaben,
Übungen zu: Theoretische Physik I klassische Mechanik W 13 Tobias Spranger - Prof. Tom Kirchner WS 005/06 http://www.pt.tu-clausthal.de/qd/teaching.html. Dezember 005 Übungsblatt 7 Lösungsvorschlag 4 Aufgaben,
1. Lineare Funktionen
 Grundwissen zu den Geraden. Lineare Funktionen Geraden sind die Graphen linearer Funktionen. Dazu müssen wir zuerst den Beriff Funktion und dann den Beriff linear klären.. Funktion Eine Funktion ist eine
Grundwissen zu den Geraden. Lineare Funktionen Geraden sind die Graphen linearer Funktionen. Dazu müssen wir zuerst den Beriff Funktion und dann den Beriff linear klären.. Funktion Eine Funktion ist eine
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 2005/06
 Übungen zu: Theoretische Physik I klassische Mechanik W 3 Tobias Spranger - Prof. Tom Kirchner WS 5/6 http://www.pt.tu-clausthal.de/qd/teaching.html. Dezember 5 Übungsblatt 6 Lösungsvorschlag 3 ufgaben,
Übungen zu: Theoretische Physik I klassische Mechanik W 3 Tobias Spranger - Prof. Tom Kirchner WS 5/6 http://www.pt.tu-clausthal.de/qd/teaching.html. Dezember 5 Übungsblatt 6 Lösungsvorschlag 3 ufgaben,
Klassische Theoretische Physik II (Theorie B) Sommersemester 2016
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik II (Theorie B) Sommersemester 216 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 9. PD
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Klassische Theoretische Physik II (Theorie B) Sommersemester 216 Prof. Dr. Alexander Mirlin Musterlösung: Blatt 9. PD
Aufgabe 11: Windanlage
 Zentrale schritliche Abiturprüunen im Fach Mathematik Auabe 11: Windanlae Das Foto zeit einen Darrieus-Windenerie-Konverter. Der Wind setzt die drei Blätter um die vertikale Achse in Drehun; die Blätter
Zentrale schritliche Abiturprüunen im Fach Mathematik Auabe 11: Windanlae Das Foto zeit einen Darrieus-Windenerie-Konverter. Der Wind setzt die drei Blätter um die vertikale Achse in Drehun; die Blätter
Übungen zu Experimentalphysik 1 für MSE
 Physik-Department LS für Funktionelle Materialien WS 2017/18 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Dr. Neelima Paul, Sebastian Grott, Lucas Kreuzer,
Physik-Department LS für Funktionelle Materialien WS 2017/18 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Dr. Neelima Paul, Sebastian Grott, Lucas Kreuzer,
Technische Mechanik III Übungsblatt Nr. 3
 Institut für Technische Mechanik Prof. Dr.-In. C. Proppe Prof. Dr.-In. W. Seeann Nae: Testat: Terin: (jew. 19:00 Uhr) Vornae: Di., 25.11.2008 Matr. Nr.: Technische Mechanik III Übunsblatt Nr. 3 Thea: Newtonsches
Institut für Technische Mechanik Prof. Dr.-In. C. Proppe Prof. Dr.-In. W. Seeann Nae: Testat: Terin: (jew. 19:00 Uhr) Vornae: Di., 25.11.2008 Matr. Nr.: Technische Mechanik III Übunsblatt Nr. 3 Thea: Newtonsches
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 2
 Prof. C. Greiner, Dr. H. van Hees Sommersemester 214 Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 2 Aufgabe 5: otierendes Bezugssystem : das nertialsystem, : das rotierende System. d r = d r +
Prof. C. Greiner, Dr. H. van Hees Sommersemester 214 Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 2 Aufgabe 5: otierendes Bezugssystem : das nertialsystem, : das rotierende System. d r = d r +
Lösungen zu Übungsblatt 3
 PN1 Einführun in die Physik 1 für Chemiker und Bioloen Prof. J. Lipfert WS 2017/18 Übunsblatt 3 Lösunen zu Übunsblatt 3 Aufabe 1 Paris-Geschütz. a) Unter welchem Abschusswinkel θ hat das Geschütz seine
PN1 Einführun in die Physik 1 für Chemiker und Bioloen Prof. J. Lipfert WS 2017/18 Übunsblatt 3 Lösunen zu Übunsblatt 3 Aufabe 1 Paris-Geschütz. a) Unter welchem Abschusswinkel θ hat das Geschütz seine
1. Aufgabe: (ca % der Gesamtpunkte)
 Institut für Mechanik Prof. Dr.-In. habil. P. Betsch Prof. Dr.-In. habil. Th. Seeli Modulprüfun Dynamik 3. Auust 017 1. Aufabe: (ca..5 % der Gesamtpunkte) s P 1 m h P 3 P α l Eine Punktmasse m rutscht
Institut für Mechanik Prof. Dr.-In. habil. P. Betsch Prof. Dr.-In. habil. Th. Seeli Modulprüfun Dynamik 3. Auust 017 1. Aufabe: (ca..5 % der Gesamtpunkte) s P 1 m h P 3 P α l Eine Punktmasse m rutscht
Theoretische Physik I Mechanik Blatt 1
 PD Dr. S. Mertens S. Falkner, S. Mingramm Theoretische Physik I Mechanik Blatt 1 WS 27/28 8. 1. 27 1. Parabelbahn. Ein Punkt bewege sich auf der Kurve, die durch die Gleichung y 2 = 4ax + 4a 2 a > beschrieben
PD Dr. S. Mertens S. Falkner, S. Mingramm Theoretische Physik I Mechanik Blatt 1 WS 27/28 8. 1. 27 1. Parabelbahn. Ein Punkt bewege sich auf der Kurve, die durch die Gleichung y 2 = 4ax + 4a 2 a > beschrieben
Theoretische Physik: Mechanik
 Ferienkurs Theoretische Physik: Mechanik Sommer 213 Übung 2 - Lösung Technische Universität München 1 Fakultät für Physik 1 Schräger Wurf Ein Massepunkt der Masse m werde mit der Anfangsgeschwindigkeit
Ferienkurs Theoretische Physik: Mechanik Sommer 213 Übung 2 - Lösung Technische Universität München 1 Fakultät für Physik 1 Schräger Wurf Ein Massepunkt der Masse m werde mit der Anfangsgeschwindigkeit
(sin φ +tan αcos φ) (4)
 PDDr.S.Mertens Theoretische Physik I Mechanik J. Unterhinninhofen, M. Hummel Blatt WS 8/9 1.1.8 1. Wurf am Abhan. Sie stehen an einem Abhan, der den Steiunswinkel α hat, und wollen (4Pkt.) einen Stein
PDDr.S.Mertens Theoretische Physik I Mechanik J. Unterhinninhofen, M. Hummel Blatt WS 8/9 1.1.8 1. Wurf am Abhan. Sie stehen an einem Abhan, der den Steiunswinkel α hat, und wollen (4Pkt.) einen Stein
Lösung - Serie 7. D-MAVT/D-MATL Analysis I HS 2016 Dr. Andreas Steiger. 1. MC-Aufgaben (Online-Abgabe)
 D-MAVT/D-MATL Analysis I HS 016 Dr. Andreas Steiger Lösung - Serie 7 1. MC-Aufgaben Online-Abgabe 1. Gegeben sind die Kurven K 1 links und K rechts, die beide für wachsenden Parameter t von aussen nach
D-MAVT/D-MATL Analysis I HS 016 Dr. Andreas Steiger Lösung - Serie 7 1. MC-Aufgaben Online-Abgabe 1. Gegeben sind die Kurven K 1 links und K rechts, die beide für wachsenden Parameter t von aussen nach
Kinematik des Massenpunktes
 Technische Mechanik II Kinematik des Massenpunktes Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes Eindimensionale
Technische Mechanik II Kinematik des Massenpunktes Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Übersicht 1. Kinematik des Massenpunktes Eindimensionale
Experimentalphysik I: Mechanik
 Ferienkurs Experimentalphysik I: Mechanik Wintersemester 15/16 Übung 1 - Lösung Technische Universität München 1 Fakultät für Physik 1 Stein fällt in Brunnen Ein Stein fällt in einen Brunnen. Seine Anfangsgeschwindigkeit
Ferienkurs Experimentalphysik I: Mechanik Wintersemester 15/16 Übung 1 - Lösung Technische Universität München 1 Fakultät für Physik 1 Stein fällt in Brunnen Ein Stein fällt in einen Brunnen. Seine Anfangsgeschwindigkeit
1.2 Räumliche Bewegung. Aufgaben
 Technische Mechanik 3 1.2-1 Prof. Dr. Wandinger Aufgabe 1 1.2 Räumliche Bewegung Aufgaben Ein Flugzeug fliegt mit der Geschwindigkeit v F gegenüber der Luft einen angezeigten Kurs von 30. Der Wind weht
Technische Mechanik 3 1.2-1 Prof. Dr. Wandinger Aufgabe 1 1.2 Räumliche Bewegung Aufgaben Ein Flugzeug fliegt mit der Geschwindigkeit v F gegenüber der Luft einen angezeigten Kurs von 30. Der Wind weht
Physikalische Anwendungen Kinematik
 Physikalische Anwendungen Kinematik Zum Mathematik-Lehrbuch Notwendig und zunächst hinreichend (Shaker Verlag, Aachen) gibt es mehrere PDF-Dokumente mit ergänzenden Beispielen und Aufgaben, die die Anwendung
Physikalische Anwendungen Kinematik Zum Mathematik-Lehrbuch Notwendig und zunächst hinreichend (Shaker Verlag, Aachen) gibt es mehrere PDF-Dokumente mit ergänzenden Beispielen und Aufgaben, die die Anwendung
Übungen zur Theoretischen Physik 1 Lösungen zu Blatt 6 Hausübungen (Abgabe: )
 Prof. C. Greiner, Dr. H. van Hees Wintersemester 212/213 Übunen zur Theoretischen Physik 1 Lösunen zu Blatt 6 Hausübunen (Ababe: 14.12.212) (H14) Arbeit eines Kraftfeles (2 Punkte) r = (6m/s 2 t 2m/s,3m/s
Prof. C. Greiner, Dr. H. van Hees Wintersemester 212/213 Übunen zur Theoretischen Physik 1 Lösunen zu Blatt 6 Hausübunen (Ababe: 14.12.212) (H14) Arbeit eines Kraftfeles (2 Punkte) r = (6m/s 2 t 2m/s,3m/s
Herbst 2009 Seite 1/14. Gottfried Wilhelm Leibniz Universität Hannover Klausur Technische Mechanik III für Maschinenbau. Musterlösungen (ohne Gewähr)
 Seite 1/14 Frae 1 ( Punkte) Der skizzierte Mechanismus besteht aus drei Stäben, die über Drehelenke miteinander verbunden sind. Der Stab 1 wird mit der konstanten Winkeleschwindikeit ω 1 anetrieben. 3
Seite 1/14 Frae 1 ( Punkte) Der skizzierte Mechanismus besteht aus drei Stäben, die über Drehelenke miteinander verbunden sind. Der Stab 1 wird mit der konstanten Winkeleschwindikeit ω 1 anetrieben. 3
Technische Universität München Zentrum Mathematik
 ufabe 1. Diaraaerei echnische Universität München Zentru Matheatik Prof. Dr. Dr. Jüren Richter-Gebert, ernhard Werner Projective Geoetry 2 ( 2017) www-10.a.tu.de/projectivegeoetry217 Lösunen zu ufabenbatt
ufabe 1. Diaraaerei echnische Universität München Zentru Matheatik Prof. Dr. Dr. Jüren Richter-Gebert, ernhard Werner Projective Geoetry 2 ( 2017) www-10.a.tu.de/projectivegeoetry217 Lösunen zu ufabenbatt
2. Räumliche Bewegung
 2. Räumliche Bewegung Wenn die Bahn des Massenpunkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort im Raum zu bestimmen. Es muss ein Ortsvektor angegeben werden. Prof.
2. Räumliche Bewegung Wenn die Bahn des Massenpunkts nicht bekannt ist, reicht die Angabe einer Koordinate nicht aus, um seinen Ort im Raum zu bestimmen. Es muss ein Ortsvektor angegeben werden. Prof.
Theoretische Physik I: Lösungen Blatt Michael Czopnik
 Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
Theoretische Physik I: Lösungen Blatt 2 15.10.2012 Michael Czopnik Aufgabe 1: Scheinkräfte Nutze Zylinderkoordinaten: x = r cos ϕ y = r sin ϕ z = z Zweimaliges differenzieren ergibt: ẍ = r cos ϕ 2ṙ ϕ sin
v(t) = r(t) v(t) = a(t) = Die Kraft welche das Teilchen auf der Bahn hält muss entgegen dessen Trägheit wirken F = m a(t) E kin = m 2 v(t) 2
 Aufgabe 1 Mit: und ( x r(t) = = y) ( ) A sin(ωt) B cos(ωt) v(t) = r(t) t a(t) = 2 r(t) t 2 folgt nach komponentenweisen Ableiten ( ) Aω cos(ωt) v(t) = Bω sin(ωt) a(t) = ( ) Aω2 sin(ωt) Bω 2 cos(ωt) Die
Aufgabe 1 Mit: und ( x r(t) = = y) ( ) A sin(ωt) B cos(ωt) v(t) = r(t) t a(t) = 2 r(t) t 2 folgt nach komponentenweisen Ableiten ( ) Aω cos(ωt) v(t) = Bω sin(ωt) a(t) = ( ) Aω2 sin(ωt) Bω 2 cos(ωt) Die
5.1.5 Pendel = Sinusbewegung ******
 V55 5..5 ****** Motivation Dieser sehr schöne Versuch zeigt, dass die Projektion einer Kreisbewegung eine Sinusbewegung ergibt. Damit deckt sie sich mit einer simutanen Pendebewegung derseben Frequenz.
V55 5..5 ****** Motivation Dieser sehr schöne Versuch zeigt, dass die Projektion einer Kreisbewegung eine Sinusbewegung ergibt. Damit deckt sie sich mit einer simutanen Pendebewegung derseben Frequenz.
Teil II: Aufgaben zur Differential- und Integralrechnung Ohne Lösungsweg
 Staatliche Studienakademie Leipzi Brückenkurs Mathematik Studienrichtun Informatik 1. - 15. September 11 Teil II: Aufaben zur Differential- und Interalrechnun Ohne Lösunswe 1. Aufabe: Bilden Sie die ersten
Staatliche Studienakademie Leipzi Brückenkurs Mathematik Studienrichtun Informatik 1. - 15. September 11 Teil II: Aufaben zur Differential- und Interalrechnun Ohne Lösunswe 1. Aufabe: Bilden Sie die ersten
3. Kreisbewegung. Punkte auf einem Rad Zahnräder, Getriebe Drehkran Turbinen, Hubschrauberrotor
 3. Kreisbewegung Ein wichtiger technischer Sonderfall ist die Bewegung auf einer Kreisbahn. Dabei hat der Massenpunkt zu jedem Zeitpunkt den gleichen Abstand vom Kreismittelpunkt. Beispiele: Punkte auf
3. Kreisbewegung Ein wichtiger technischer Sonderfall ist die Bewegung auf einer Kreisbahn. Dabei hat der Massenpunkt zu jedem Zeitpunkt den gleichen Abstand vom Kreismittelpunkt. Beispiele: Punkte auf
(a) Transformation auf die generalisierten Koordinaten (= Kugelkoordinaten): ẏ = l cos(θ) θ sin(ϕ) + l sin(θ) cos(ϕ) ϕ.
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Lösungen zu Übungsblatt 3
 PN1 Einführun in die Physik für Chemiker 1 Prof. J. Lipfert WS 018/19 Übunsblatt 3 Lösunen zu Übunsblatt 3 Aufabe 1 Paris-Geschütz. a) Unter welchem Abschusswinkel θ hat das Geschütz seine maximale Reichweite
PN1 Einführun in die Physik für Chemiker 1 Prof. J. Lipfert WS 018/19 Übunsblatt 3 Lösunen zu Übunsblatt 3 Aufabe 1 Paris-Geschütz. a) Unter welchem Abschusswinkel θ hat das Geschütz seine maximale Reichweite
KIT SS Klassische Theoretische Physik II. V: Prof. Dr. M. Mühlleitner, Ü: Dr. M. Rauch. Klausur 2 Lösung. 11. Oktober 2012, Uhr
 KIT SS 1 Kassische Theoretische Physik II : Prof. Dr. M. Müheitner, Ü: Dr. M. Rauch Kausur Lösung 11. Oktober 1, 8-1 Uhr Aufgabe 1: Kurzfragen 4+4+=1 Punkte a Die Transformationen und zugehörigen Erhatungsgrößen
KIT SS 1 Kassische Theoretische Physik II : Prof. Dr. M. Müheitner, Ü: Dr. M. Rauch Kausur Lösung 11. Oktober 1, 8-1 Uhr Aufgabe 1: Kurzfragen 4+4+=1 Punkte a Die Transformationen und zugehörigen Erhatungsgrößen
Einführung. 2 Hydrostatik der Gase. 1 Hydrostatik der Flüssigkeiten. Sieben physikalische Basis-Größen. 2.1 Gesetz von Boyle-Mariotte.
 Foresaun Physik / Fakutät II / c Hochschue Hannover Version 1. uni 016 Einführun Hydrostatik der Gase. Sieen physikaische Basis-Größen. t [s] Zeit in Sekunden s [] Strecke in Metern [k] Masse in Kiora
Foresaun Physik / Fakutät II / c Hochschue Hannover Version 1. uni 016 Einführun Hydrostatik der Gase. Sieen physikaische Basis-Größen. t [s] Zeit in Sekunden s [] Strecke in Metern [k] Masse in Kiora
Übungen zu Theoretischer Mechanik (T1)
 Arnold Sommerfeld Center Ludwig Maximilians Universität München Prof. Dr. Viatcheslav Mukhanov Sommersemester 08 Übungen zu Theoretischer Mechanik T Übungsblatt 8, Besprechung ab 04.06.08 Aufgabe 8. Lineare
Arnold Sommerfeld Center Ludwig Maximilians Universität München Prof. Dr. Viatcheslav Mukhanov Sommersemester 08 Übungen zu Theoretischer Mechanik T Übungsblatt 8, Besprechung ab 04.06.08 Aufgabe 8. Lineare
27. Vorlesung Wintersemester
 27. Voresung Wintersemester 1 Nichtineare Dynamik: Agemeines Eine wichtige neue Erkenntnis zur kassischen Mechanik, die erst durch die Verwendung von Computern mögich war, ist die verbüffende Kompexität
27. Voresung Wintersemester 1 Nichtineare Dynamik: Agemeines Eine wichtige neue Erkenntnis zur kassischen Mechanik, die erst durch die Verwendung von Computern mögich war, ist die verbüffende Kompexität
1. Klausur Mechanik II WS 08/09, Prof. Dr. rer. nat. W. H. Müller Lehrstuhl für Koninuumsmechanik und Materialtheorie
 1. Kausur Mechanik II WS 08/09, Prof. Dr. rer. na. W. H. Müer Lehrsuh für Koninuusechanik und Maeriaheorie Theorieaufaben 1. Besien Sie den Breswe eines Auos, der nöi is, u seine kineische Enerie auf 1
1. Kausur Mechanik II WS 08/09, Prof. Dr. rer. na. W. H. Müer Lehrsuh für Koninuusechanik und Maeriaheorie Theorieaufaben 1. Besien Sie den Breswe eines Auos, der nöi is, u seine kineische Enerie auf 1
Physik 1 ET, WS 2012 Aufgaben mit Lösung 2. Übung (KW 44) Schräger Wurf ) Bootsfahrt )
 Physik ET, WS Aufaben mit Lösun. Übun (KW 44). Übun (KW 44) Aufabe (M.3 Schräer Wurf ) Ein Ball soll vom Punkt P (x, y ) (, ) aus unter einem Winkel α zur Horizontalen schrä nach oben eworfen werden. (a)
Physik ET, WS Aufaben mit Lösun. Übun (KW 44). Übun (KW 44) Aufabe (M.3 Schräer Wurf ) Ein Ball soll vom Punkt P (x, y ) (, ) aus unter einem Winkel α zur Horizontalen schrä nach oben eworfen werden. (a)
Klassische Theoretische Physik III (Elektrodynamik)
 WiSe 017/18 Klassische Theoretische Physik III (Elektrodynamik Vorlesung: Prof. Dr. D. Zeppenfeld Übung: Dr. M. Sekulla Übungsblatt 10 Ausgabe: Fr, 1.01.18 Abgabe: Fr, 19.01.17 Besprechung: Mi, 4.01.18
WiSe 017/18 Klassische Theoretische Physik III (Elektrodynamik Vorlesung: Prof. Dr. D. Zeppenfeld Übung: Dr. M. Sekulla Übungsblatt 10 Ausgabe: Fr, 1.01.18 Abgabe: Fr, 19.01.17 Besprechung: Mi, 4.01.18
Theoretische Mechanik
 Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 008 Theoretische Mechanik 4. Übung Lösungen 4. Spezielle Kraftgesetze Lösen Sie die
Prof. Dr. R. Ketzmerick/Dr. R. Schumann Technische Universität Dresden Institut für Theoretische Physik Sommersemester 008 Theoretische Mechanik 4. Übung Lösungen 4. Spezielle Kraftgesetze Lösen Sie die
21. Februar Korrektur
 Institut für Technische und Num. Mechanik Technische Mechanik II/III Profs. P. Eberhard, R. Seifried WS 0/ P. ebruar 0 Bachelor-Prüfun in Technischer Mechanik II/III ufabe (6 Punkte) Ein Ellipsentrainer
Institut für Technische und Num. Mechanik Technische Mechanik II/III Profs. P. Eberhard, R. Seifried WS 0/ P. ebruar 0 Bachelor-Prüfun in Technischer Mechanik II/III ufabe (6 Punkte) Ein Ellipsentrainer
Mathematik II: Übungsblatt 01: Lösungen
 N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
N.Mahnke Mathematik II: Übungsblatt 01: Lösungen Verständnisfragen: 1. Was versteht man unter einer parametrisierten ebenen Kurve? Eine parametrisierte ebene Kurve ist eine auf dem offenen Intervall ]t
Übungen zu Theoretischer Mechanik (T1)
 Arnod Sommerfed Center Ludwig Maximiians Universität München Prof. Dr. Viatchesav Muhanov Sommersemester 0 Übungen zu Theoretischer Mechani T) Übungsbatt 7, Besprechung ab.05.0 Aufgabe 7. Gedämpfter harmonischer
Arnod Sommerfed Center Ludwig Maximiians Universität München Prof. Dr. Viatchesav Muhanov Sommersemester 0 Übungen zu Theoretischer Mechani T) Übungsbatt 7, Besprechung ab.05.0 Aufgabe 7. Gedämpfter harmonischer
Formelsammlung: Physik I für Naturwissenschaftler
 Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 13. Dezember 212 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m]
Formelsammlung: Physik I für Naturwissenschaftler 1 Was ist Physik? Stand: 13. Dezember 212 Physikalische Größe X = Zahl [X] Einheit SI-Basiseinheiten Mechanik Zeit [t] = 1 s Länge [x] = 1 m Masse [m]
1.2 Räumliche Bewegung. Aufgaben
 Technische Mechanik 3 1.-1 Prof. Dr. Wandinger Aufgabe 1 1. Räumliche Bewegung Aufgaben Ein Flugzeug fliegt mit der Geschwindigkeit v F gegenüber der Luft einen angezeigten Kurs von 30. Der Wind weht mit
Technische Mechanik 3 1.-1 Prof. Dr. Wandinger Aufgabe 1 1. Räumliche Bewegung Aufgaben Ein Flugzeug fliegt mit der Geschwindigkeit v F gegenüber der Luft einen angezeigten Kurs von 30. Der Wind weht mit
Lagrange Formalismus
 Lagrange Formalismus Frank Essenberger FU Berlin 1.Oktober 26 Inhaltsverzeichnis 1 Oszillatoren 1 1.1 Fadenpendel.............................. 1 1.2 Stabpendel.............................. 3 1.3 U-Rohr................................
Lagrange Formalismus Frank Essenberger FU Berlin 1.Oktober 26 Inhaltsverzeichnis 1 Oszillatoren 1 1.1 Fadenpendel.............................. 1 1.2 Stabpendel.............................. 3 1.3 U-Rohr................................
Übungen zu Experimentalphysik 1 für MSE
 Physik-Department LS für Funktionelle Materialien WS 2014/15 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Daniel Moseguí González, Pascal Neibecker, Nitin
Physik-Department LS für Funktionelle Materialien WS 2014/15 Übungen zu Experimentalphysik 1 für MSE Prof. Dr. Peter Müller-Buschbaum, Dr. Volker Körstgens, Daniel Moseguí González, Pascal Neibecker, Nitin
Übungsblatt 05. PHYS1100 Grundkurs I (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti,
 Übungsblatt 05 PHYS1100 Grundkurs I (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, (othmar.marti@uni-ulm.de) 18. 11. 005 und 1. 11. 005 1 Aufgaben 1. Berechnen Sie für einen LKW von 40t Masse
Übungsblatt 05 PHYS1100 Grundkurs I (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, (othmar.marti@uni-ulm.de) 18. 11. 005 und 1. 11. 005 1 Aufgaben 1. Berechnen Sie für einen LKW von 40t Masse
Physik I Einführung in die Physik Mechanik
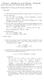 Physik I Einführung in die Physik Mechanik Winter 15/16, Prof. Thomas Müller, IEKP, KIT Aufgabenblatt ; Übung am 11.November (Mittwoch) 1. Sportwagen (a) Jeder Summand muss die Einheit m s haben, daher
Physik I Einführung in die Physik Mechanik Winter 15/16, Prof. Thomas Müller, IEKP, KIT Aufgabenblatt ; Übung am 11.November (Mittwoch) 1. Sportwagen (a) Jeder Summand muss die Einheit m s haben, daher
Solutions I Publication:
 WS 215/16 Solutions I Publication: 28.1.15 1 Vektor I 4 2 Ein Objekt A befindet sich bei a = 5. Das zweite Objekt B befindet sich bei b = 4. 2 3 (a) Die Entfernung von Objekt A zum Ursprung ist die Länge
WS 215/16 Solutions I Publication: 28.1.15 1 Vektor I 4 2 Ein Objekt A befindet sich bei a = 5. Das zweite Objekt B befindet sich bei b = 4. 2 3 (a) Die Entfernung von Objekt A zum Ursprung ist die Länge
1.4 Krummlinige Koordinaten I
 15 1.4 Krummlinige Koordinaten I (A) Motivation zur Definition verschiedener Koordinatensysteme Oft ist es sinnvoll und zweckmäßig Koordinatensysteme zu verwenden, die sich an der Geometrie und/oder Symmetrie
15 1.4 Krummlinige Koordinaten I (A) Motivation zur Definition verschiedener Koordinatensysteme Oft ist es sinnvoll und zweckmäßig Koordinatensysteme zu verwenden, die sich an der Geometrie und/oder Symmetrie
Übungen zu Physik I für Naturwissenschaftler Serie 1 Musterlösungen
 Übungen zu Physik I für Naturwissenschaftler Serie 1 Musterlösungen Denys Sutter, 25. September 217 Allgemeine Fragen 1. Dimensionsanalyse ist eine nützliche Methoe sich avon zu überzeugen, ass eine physikalische
Übungen zu Physik I für Naturwissenschaftler Serie 1 Musterlösungen Denys Sutter, 25. September 217 Allgemeine Fragen 1. Dimensionsanalyse ist eine nützliche Methoe sich avon zu überzeugen, ass eine physikalische
Musterlösung zur Übung am Donnerstag
 Musterösung zur Übung am Donnerstag Aufgabe 1: Strategie: 1. Man nimmt einen beiebigen Massepunkt m (z.b. Stein), hängt ihn an die Feder und enkt die Feder aus. Man misst die Schwingungsfrequenz (bzw.
Musterösung zur Übung am Donnerstag Aufgabe 1: Strategie: 1. Man nimmt einen beiebigen Massepunkt m (z.b. Stein), hängt ihn an die Feder und enkt die Feder aus. Man misst die Schwingungsfrequenz (bzw.
Ausführliche physikalische Beispiele Das mathematische Pendel
 Medizinische Physik und Biophysik (MPBP) Ausführiche physikaische Beispiee Das mathematische Pende Dip.-In. Dr. Friedrich Hanser SS z x m MPBP DAS MATHEMATISCHE PENDEL Inhatsverzeichnis Das mathematische
Medizinische Physik und Biophysik (MPBP) Ausführiche physikaische Beispiee Das mathematische Pende Dip.-In. Dr. Friedrich Hanser SS z x m MPBP DAS MATHEMATISCHE PENDEL Inhatsverzeichnis Das mathematische
Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 2008/09 Klausur ( )
 Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 1 Note Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 28/9 Klausur (6.2.29 Name: Studiengang: In die Wertung der Klausur
Nur vom Korrektor auszufüllen 1 2 3 4 5 6 7 8 9 1 Note Experimentalphysik für Naturwissenschaftler 1 Universität Erlangen Nürnberg WS 28/9 Klausur (6.2.29 Name: Studiengang: In die Wertung der Klausur
Tutorium zur Vorlesung Differential und Integralrechnung II Bearbeitungsvorschlag
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner SS 4 Blatt 5.6.4 Tutorium zur Vorlesung Differential und Integralrechnung II Bearbeitungsvorschlag 37. Wir bestimmen zunächst die Schnittpunkte
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner SS 4 Blatt 5.6.4 Tutorium zur Vorlesung Differential und Integralrechnung II Bearbeitungsvorschlag 37. Wir bestimmen zunächst die Schnittpunkte
Physik I Übung 4 - Lösungshinweise
 Physik I Übun 4 - Lösunshinweise Moritz Kütt WS 11/1 Stefan Reutter Stand:.1.11 Franz Fujara Aufabe 1 Postraub Es war im Jahre 189 als der berüchtite Ganoe Lanfuß-Bill mit seiner Bande einen leendären
Physik I Übun 4 - Lösunshinweise Moritz Kütt WS 11/1 Stefan Reutter Stand:.1.11 Franz Fujara Aufabe 1 Postraub Es war im Jahre 189 als der berüchtite Ganoe Lanfuß-Bill mit seiner Bande einen leendären
Kapitel 1. Kinematik des Punktes
 Kapitel 1 Kinematik des Punktes 1 2 Kinematik Die Lage eines Punkte P im Raum wird durch den Ortsvektor r(t) beschrieben. Aus der Verschiebung dr des Punktes P in eine Nachbarlage während der Zeit dt folgt
Kapitel 1 Kinematik des Punktes 1 2 Kinematik Die Lage eines Punkte P im Raum wird durch den Ortsvektor r(t) beschrieben. Aus der Verschiebung dr des Punktes P in eine Nachbarlage während der Zeit dt folgt
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 2005/06
 Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teaching.html 17. Januar 26 Übungsblatt 9 Lösungsvorschlag 4 Aufgaben,
Übungen zu: Theoretische Physik I klassische Mechanik W 2213 Tobias Spranger - Prof. Tom Kirchner WS 25/6 http://www.pt.tu-clausthal.de/qd/teaching.html 17. Januar 26 Übungsblatt 9 Lösungsvorschlag 4 Aufgaben,
1. Grundlagen der ebenen Kinematik
 Lage: Die Lage eines starren Körpers in der Ebene ist durch die Angabe von zwei Punkten A und P eindeutig festgelegt. Die Lage eines beliebigen Punktes P wird durch Polarkoordinaten bezüglich des Bezugspunktes
Lage: Die Lage eines starren Körpers in der Ebene ist durch die Angabe von zwei Punkten A und P eindeutig festgelegt. Die Lage eines beliebigen Punktes P wird durch Polarkoordinaten bezüglich des Bezugspunktes
Millikan Versuch. Redmann, Nigl, Wiessner, Köck. Entstehung des Versuches:
 Redmann, Nil, Wiessner, Köck Millikan Versuch Entstehun des Versuches: Anfan des 20. Jahrhunderts entstand die Frae, ob alle messbaren Ladunen auf eine kleinste Ladunseinheit zurückeführt werden können.
Redmann, Nil, Wiessner, Köck Millikan Versuch Entstehun des Versuches: Anfan des 20. Jahrhunderts entstand die Frae, ob alle messbaren Ladunen auf eine kleinste Ladunseinheit zurückeführt werden können.
10.3 Statische Momente, Schwerpunkte und Trägheitsmomente
 1.3 Sttische Momente, Schwerpunkte und Trägheitsmomente Sttisches Moment M g eines Mssenpunktes P (der Msse m) bezüglich einer Gerden g: M g := ml Msse Hebelrm l Abstnd von P zu g g 9 P l Bei n Mssenpunkten
1.3 Sttische Momente, Schwerpunkte und Trägheitsmomente Sttisches Moment M g eines Mssenpunktes P (der Msse m) bezüglich einer Gerden g: M g := ml Msse Hebelrm l Abstnd von P zu g g 9 P l Bei n Mssenpunkten
 THEORETISCHE PHYSIK C NACHKLAUSUR Prof. Dr. J. Kühn Dienstag, 27.4.2 Dr. S. Uccirati 7:3-2:3 Uhr Bewertungsschema für Bachelor Punkte Note < 4 5. 4-5.5 4.7 6-7.5 4. 8-9.5 3.7 2-2.5 3.3 22-23.5 3. 24-25.5
THEORETISCHE PHYSIK C NACHKLAUSUR Prof. Dr. J. Kühn Dienstag, 27.4.2 Dr. S. Uccirati 7:3-2:3 Uhr Bewertungsschema für Bachelor Punkte Note < 4 5. 4-5.5 4.7 6-7.5 4. 8-9.5 3.7 2-2.5 3.3 22-23.5 3. 24-25.5
2. Klausur zur Theoretischen Physik II
 PD Dr. Burkhard Dünwe SS 2006 Dipl.-Phys. Ulf D. Schiller 2. Klausur zur Theoretischen Physik II 22. Juli 2006 Name:............................................................ Matrikelnummer:...................................................
PD Dr. Burkhard Dünwe SS 2006 Dipl.-Phys. Ulf D. Schiller 2. Klausur zur Theoretischen Physik II 22. Juli 2006 Name:............................................................ Matrikelnummer:...................................................
Fallender Stein auf rotierender Erde
 Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 4 vom 13.05.13 Abgabe: 27. Mai Aufgabe 16 4 Punkte allender Stein auf rotierender Erde Wir lassen einen Stein der Masse m in einen
Übungen zu Theoretische Physik I - Mechanik im Sommersemester 2013 Blatt 4 vom 13.05.13 Abgabe: 27. Mai Aufgabe 16 4 Punkte allender Stein auf rotierender Erde Wir lassen einen Stein der Masse m in einen
K l a u s u r G k P h 11
 K l a u s u r G k P h Aufabe a) Aus welcher Höhe muß ein Körper frei fallen, damit er mit der Geschwin- dikeit auf den Boden aufschlät? v 8 km h b) Wie lane dauert der freie Fall des Körpers? Aufabe 2
K l a u s u r G k P h Aufabe a) Aus welcher Höhe muß ein Körper frei fallen, damit er mit der Geschwin- dikeit auf den Boden aufschlät? v 8 km h b) Wie lane dauert der freie Fall des Körpers? Aufabe 2
Blatt 10. Hamilton-Formalismus- Lösungsvorschlag
 Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik T) im SoSe 20 Blatt 0. Hamilton-Formalismus- Lösungsvorschlag Aufgabe 0.. Hamilton-Formalismus
Fakultät für Physik der LMU München Lehrstuhl für Kosmologie, Prof. Dr. V. Mukhanov Übungen zu Klassischer Mechanik T) im SoSe 20 Blatt 0. Hamilton-Formalismus- Lösungsvorschlag Aufgabe 0.. Hamilton-Formalismus
