V Im [TI + ~.] Lösungen der Aufgaben - = -+-. V ~ 1+7f. , v 12. Wo = (1L' 2 ' 7. x= Wo = j2iä. ~ X-Xt. b) x* = ~ + x' 13. D = 0,378.
|
|
|
- Fabian Müller
- vor 5 Jahren
- Abrufe
Transkript
1 Lösungen der Aufgaben ClC2 1. C=-- Cl + C2 oder = -+-. C Cl C2 3. Wo = /EA. ml 4 X" + {1 jg x = 0' {1L ' 2 {1jg Wo = (1L' a A 5. x = 2; b) x* = ~ + x' 2 ' 7. x= Wo = j2iä. L 8. S = (1, = ;;-;) = 0,289L., v WOR = /f; Wos= ~. 10. T = 84,3 Minuten. 11. T = 4 Im arccos _1_.. V ~ 1+7f 12. T = 2 V Im [TI + ~.] ~ X-Xt 13. D = 0, X m = 0,955 rnrn; A = 0,826; D = 0,131.
2 388 Lösungen der Aufgaben 15. A = 0,4; D = 0, D = 0,075; (xmaxh = 78,7%. 17. Xo = -V9; X4 = -1; 4,5 Halbschwingungen. 2)' 2 A 19. X.. - ( a - 43ß x 2 W x + Wox =, w ~ W O ; 20. x ~ ~ Ifi o 21. x - x: (8; _ ßX) i: + w5 (1 + 3:x 2 ) x = 0; W ~ w o A 8a x ~ - 3ß' 22. a) TiD x = acoth. 2Vl- D2' b) A 2a x TiD' ~ 23. Wo Vkrit = b sin 'Ij;. 24. ~ T 1 (. X r. x r ) -- - arcsln -A T Ti X - X r x +xr - = - arcsln -A -- ; 5,5s. 25. ~ T 1 2,;xx; - = 'f- arctan -A--' T Ti X - X r = 5560s/d. ~ T Fall a): Minus-Zeichen, Fall b): Plus-Zeichen. T = 4h2to. 26. h2 - h6' x = hto; X m = hoto. 27. Die Schwingung ist stabil wegen und LlED < LlE für ~ < o ~ o * 3mhL1 (Li + L 1L2 + Ln ~ = o 4 q (Li L ~ + L ~ ) ~ E> D ~ für E ~ > o ~ o,
3 n 28. 0,99792 < - < 1,00042; Wo 29. n:::: 14,14wo. n 1,83 < - < 2,24. Wo Lösungen der Aufgaben ( ßC) - co+- J 2' 31. Durch Einsetzen von y = al cos ~ + b1 sin ~ +... in (4.38) folgt a l c o[ s - ~ ~ + A + + b l~ s] i[ n - ~ ~ + + A... - =0. ~ ] Nullsetzen der eckigen Klammern ergibt Gi. (4.43). 32. vü=xo(d+k)=xo(d+)d2_1). 1 Dopt = "2..;J:"+k. 34. a) D = 1; b) Kriterium versagt, da FI = Vo von D unabhängig ist; c) Kriterium versagt ebenfalls, da F2 für D < 1 monoton und für D ::::: 1 konstant ist; v d) 2 F3 = 4;; Dopt ~ x(t)=n[t-2+(t+2)e-r] für O:::;T:::;TO; X(T) = n [TO - (2 + T - To)e-(r-ro) + (T + 2)e-r] für T:::: TO. 36. K7]4 v-. - )(1-7]2)2 + 4D27]2' 7]extr = J ~ -2D2) ( 1 ± )1-36D2(1 - D2); D :::; 0, ]2 B) u = 2D7] ; 1 C) u = 2" - 1; 7] v = 1; 2D V--' - 7], Gerade parallel zur u-achse im Abstand v = 1. Parabel wie im Falle A, nur mit reziprokem 7]-Maßstab.
4 390 Lösungen der Aufgaben 39. a) XR ;::; -xc; b) XR ;::; -Xc; T = --' 1 + 1]2 ' 4,36 < 1] < 00; o < 1] < 0,229. fj = 0,040 entsprechend 4% ] = 4,58; 1 Wo = 22,8-; s 10 = 1,88cm. 42. X max = 1,26 m. 43. Aus der Bedingung für eine 3 fache Wurzel der G l. (5.123) folgt \I 4Xo *. / 9ax*2 D* 3V3 ax*2 A * x = ~ ; 1] = VI + -8-; = 161]* da nur ein reeller Wert für i; existiert, können Sprünge nicht vorkommen. A X max ;::; V 37rxo sq' ] :s; 1] :s; ] mit 48. a = w o V O, 1 ~ 5 J. = C ('PI - JO,5 'P2 ) ; 1] = C ( v2 'PI + 'P2), 49. ~ mit beliebigem konstanten Faktor c (2 2).. ( 2) ga 82 0 'PI (! + 'P (! + ~ ' = P, l.. ( 2)" (2 2) ga 81 'PI (! + 'P (! + ~ ' = P. 2
5 51. W1 = I!; W2 = J 9 ~ ~ ~ ; = g2; a diese Werte sind nur reell für g < 2". 2. Lösungen der Aufgaben } -- _ a±0 --g, ( '1'10) - 1. '1'20 Wj ( '1'10 ) '1'20 W2 parallele Pendelschwingung der Stange, Drehschwingung um eine vertikale Achse durch den Schwerpunkt w6 - w 2 y = J.lW 2 x = 25mm. WI = )/2-1 Wo = 0,5412wo mit Wo = J! ~, )/2+ 1 W2 = Wo, W3 = /2 Wo = 1,3065wo, 55. W1 = 1,082wo; W2 = 1,414wo; W3 = 2,613wo mit Wo = J!;, TJ = J 4 _ TJ*2 57. (i = 1,2,3); für Wi =0 (i = 1); für Wi =1= (i = 2,3). CP3 = [ - 1 ' ~ ,035
6 392 Lösungen der Aufgaben 59. c.pi = c.pd Ni, i = 1,2,3, NI = 31,63Vkgm 2, N2 = 29,64Vkgm 2, N3 = 23,18Vkgm n = 2; 61.. TIff Wj = (2J - 1) 2" m' j = 1,2, JTIr2 G Wj = jti Lm' j = 1,2,3; j = 1: x/l = 1/2; j = 2: x/l = 1/4, 3/4; j = 3: x/l = 1/6, 1/2, 5/ h = 1,0122' hfp -; h* = 0,247/.1L. L p 64. Wj = )..;J ::3' j = 1,2; )..1 = 4,7300; )..2 = 7,8532. ~ W(F 1 = 0) = 0,07%, 67. a) Teilsystem I: Stab ohne Kugel, Teilsystem II: Feder-Kugel-System, nach Dunkerley: E E w1 ;:: 1 1 = 41}L 2 m = -4-- pu = 0,7116 pu' 2 w r + 2" w n TI ~ + E b2e/l 2 TI + 1
7 Lösungen der Aufgaben a) Teilsystem I: Torsionsstab ohne Drehmassen, Teilsystem II: Drehfeder-Drehmassen-System, b) (). 1T X 'PI X =S1ll 2L, Rayleigh- Quotient: 1 4QL2 J1 + 2J2 (7,-) 2 1T2G + Glp/L L!Clp J <P1 2 (x) dx 1 Gd = Gd m ' m' T + ~ 51T 3 Gd m {Gd {Gd 0,373y --;;-; :<::; Wl :<::; 0,383y --;;-;.
8 Literaturverzeichnis [1] Abraham, R.; Marsden, J.E.: Foundations of Mechanics. Reading 1978 [2] Argyris, J.H.: Die Methode der Finiten Elemente, Bd Braunschweig [3] Bathe, K.J.: Finite Elemente Methoden. Berlin u.a [4] Beletsky, V.V.: Reguläre und chaotische Bewegung starrer Körper. Stuttgart 1995 [5] Biezeno, C.B.; Grammel, R.: Technische Dynamik, 2 Bde. Berlin u.a [6] Collatz, L.: Eigenwertprobleme und ihre numerische Behandlung. Leipzig 1945 [7] Courant, R.; Hilbert, D.: Methoden der Mathematischen Physik 1,3. Aufl. Berlin, Heidelberg, New York 1968 [8] Den Hartog, I.P.: Mechanische Schwingungen, deutsche Übers. von G. Mesmer, 2. Auf!. Berlin u.a [9] Feigenbaum, M.J.: Quantitative Universality of a Class of Nonlinear Transformations. J. of Stat. Phys. 19, 1978, pp [10] Fischer, U.; Stephan, W.: Prinzipien und Methoden der Dynamik. Leipzig 1972 [11] Fryba, L.: Vibration ofsolids and Structures Under Moving Loads. Groningen 1972 [12] Geist, K.; Parlitz, U.; Lauterborn, W.: Comparison of Different Methods for Computing Ljapunov Exponents. Progress of Theoretical Physics 83, 1990, pp [13] Guckenheimer, J.; Holmes, P.J.: Nonlinear Oscillations, Dynamical Systems and Bifurcations. New York 1983 [14] Hagedorn, P.: Nichtlineare Schwingungen. Wiesbaden 1978 [15] Hagedorn, P.: Technische Schwingungslehre, Bd. 2, Lineare Schwingungen kontinuierlicher mechanischer Systeme. Berlin u.a [16] Hagedorn, P.; Otterbein, S.: Technische Schwingungslehre, Bd. 1, Lineare Schwingungen diskreter mechanischer Systeme. Berlin u.a [17] Kauderer, H.: Nichtlineare Mechanik. Berlin 1958 [18] Kersten, R.: Das Reduktionsverfahren in der Baustatik, 2. Aufl. Berlin, Heidelberg, New York 1982
9 Literaturverzeichnis 395 [19] Klotter, K: Technische Schwingungslehre, 2 Bde. Berlin u.a und 1960 [20] Knothe, K; WesseIs, H.: Finite Elemente. Berlin u.a [21] Kolousek, V.: Dynamik der Baukonstruktionen. Berlin u.a [22] Kreuzer, E.: Numerische Untersuchung nichtlinearer dynamischer Systeme. Berlin u.a [23] Kunick, A.; Steeb, W.-H.: Chaos in deterministischen Systemen. Mannheim 1986 [24] Lehr, E.: Schwingungstechnik, 2 Bde. Berlin 1930 und 1934 [25] Leven, R.W.; Koch, B.-P.; Pompe, B.: Chaos in dissipativen Systemen. Braunschweig 1989 [26] Link, M.: Finite Elemente in der Statik und Dynamik. Stuttgart 1994 [27] Magnus, K: Schwingungen, 4. Aufi. Stuttgart 1986 [28] Malkin, I.G.: Theorie der Stabilität einer Bewegung, deutsche Übers. von W. Hahn und R. Reißig. München 1959 [29] Meirovitch, L.: Computational Methods in Structural Dynamies. Alphen aan den Rijn 1980 [30] Minorsky, N.: Introduction to Non-Linear Mechanics. Ann Arbor 1947 [31] Moon, F.C.: Chaotic and Fractal Dynamics. New York 1992 [32] Müller, P.C.: Stabilität und Matrizen. Berlin, Heidelberg, New York 1977 [33] Müller, P.C.; Schiehlen, W.O.: Lineare Schwingungen. Wiesbaden 1976 und Stuttgart 1991 [34] Natke, H.G.: Baudynamik. Stuttgart 1989 [35] Parkus, H.: Mechanik der festen Körper. Wien, New York 1988 [36] PesteI, E.; Leckie, F.A.: Matrix Methods in Elastomechanics. New York 1963 [37] Pfeiffer, F.: Einführung in die Dynamik. Stuttgart 1989 [38] Poincare, H.: Les methodes nouvelles de la mecanique celeste. Vol. 1. Paris 1892 [39] Popp, K: Nichtlineare Schwingungen mechanischer Strukturen mit Füge- oder KontaktsteIlen. ZAMM 74,1994, S [40] Popp, K: Chaotische Bewegungen beim Duffing-Schwinger. In: Festschrift zum 70. Geburtstag von Prof. Dr. K Magnus. München 1982, pp [41] Popp, K; Hinrichs, N.; Oestreich, M.: Analysis of a Self Excited Friction Oscillator with External Excitation. In: Guran, A.; Pfeiffer, F.; Popp, K (Eds.) Dynamics with Friction, Part I. Singapore 1996 [42] Popp, K; Schiehlen, W.: Fahrzeugdynamik. Stuttgart 1993 [43] Riemer, M.; Wauer, J.; Wedig, W.: Mathematische Methoden der Technischen Mechanik. Berlin u.a [44] Schwarz, H.: Einführung in die moderne Systemtheorie. Braunschweig 1969
10 396 Literaturverzeichnis [45] Schwarz, H.R.: Methode der finiten Elemente. Stuttgart 1984 [46] Solodownikow, W.W.: Grundlagen der selbsttätigen Regelung, deutsche Bearbeitung von H. Kindler, 2 Bde. München 1959 [47] Stephan, W.; Postl, R.: Schwingungen elastischer Kontinua. Stuttgart 1995 [48] Stoker, J.J.: Non-linear Vibrations in Mechanical and Electrical Systems. New York 1950 [49] Thoma, M.: Theorie linearer Regelsysteme. Braunschweig 1973 [50] Thompson, J.M.T.; Stewart, H.B.: Nonlinear Dynamics and Chaos. Chichester 1986 [51] Troger, H.: Über chaotisches Verhalten einfacher mechanischer Systeme. ZAMM 62, 1982, T18-T27 [52] Truxal, J.G.: Entwurf automatischer Regelsysteme. Übers. aus dem Amerikanischen. Wien-München 1960 [53] U eda, Y.: Steady Motions Exhibited by Duffing's Equation: A Picture Book of Regular and Chaotic Motions. In: Holmes, P.J. (Ed.) New Approaches to Nonlinear Problems in Dynamies. Philadelphia 1980 [54] Uhrig, R.: Elastostatik und Elastokinetik in Matrizenschreibweise. Berlin, Heidelberg, New York 1973 [55] Ziegler, F.: Technische Mechanik der festen und flüssigen Körper. Wien, New York 1992 [56] Zurmühl, R.; Falk, S.: Matrizen und ihre Anwendungen, 5. Aufl., Teil 1. Grundlagen, Teil 2: Numerische Methoden. Berlin u.a und 1986
11 Sachverzeichnis Abbildung, diskrete 347 -, logistische 347 -, stroboskopische 356 Absolutdämpfung 213 aktive Entstörung 210 Amplitude 14 Amplituden-Frequenzgang 30, 193 Amplituden-Phasen-Charakteristik 194 Amplitudenverzerrung 207 Anfachungsgebiet 109 Anregungsbedingung 137 Anstückelverfahren 71, 201 Arnold-Zungen 380 Attraktor 349, 366 -, chaotischer oder seltsamer 366 Ausgangsfunktion 27 Ausgleichspendel 66 Balken mit Endkörper Längskraft 317 -, umlaufender 319 Balkenschwingungen 311 Bequemlichkeitshypothese 279, 326 Bernoulli 307 Bewegung, chaotische 346 Biegepfeil 55 Bifurkationsdiagramm 351 Blindarbeit 190 Blindleistung 188 Chaos 346 chaotische Bewegung 346 charakteristische Gleichung 247 charakteristischer Exponent 159 Coulombsche Reibung 91 d' Alembert 307 Dämpfung, äußere 327 -, durchdringende 277 -, innere 327 -, modale 279, 326 -, proportionale 279 -, vollständige 277 Dämpfungsgebiet 109 Dämpfungskräfte, quadratische 96 Dämpfungsmaß 80 Dämpfungsmatrix 277 Dehnstab 302 Dekrement, logarithmisches 86 Differentialgleichung, Duffingsche 226 -, Hillsche 159 -, Mathieusche 160 -, Meissnersche 168 -, Rayleighsche 145 -, Van der Poische 112, 129, 238 Differentialoperator 322, 324 -, positiv definit oder volldefinit 324 -, symmetrisch oder selbstadjungiert 324 Dimension, fraktale 358, von Attraktoren 371 Dirac-Funktion 175, 328 Diskretisierungsverfahren 331 Dissipationsfunktion 277, 285 dissipatives System 360 Drehschwinger 41, 49 Drehschwingerkette 286 Duffing 226 Duffing-Schwinger 382 Dunkerley 341 dynamische Versteifung 321 Eigenfunktion 309, 315 Eigenkreisfrequenz 14, 248, 274, 308, 315 Eigenschwingung 245, 249, 250, 310, 316 Eigenschwingungsform 310,316 Eigenvektor 266 Eigenwert 266, 315 Eigenwertaufgabe 266 Eigenwertproblem 323 Eigenzeit 80 Einfluß von Dämpfung 156 Eingangsfunktion 27 Einheitssprung 28 Einschwingvorgang 196 Einzugsbereich 366 elektrische Klingel 105 elektrischer Schwingkreis 49 Elementarfrequenzgang 283 elliptisches Integral 64
12 398 Sachverzeichnis Endmasse 340 Energie, kinetische 333 -, potentielle 334 Energiediagramm 52 Energiehaushalt 108 Entstörung, aktive 210 -, passive 210 Entwicklungssatz 325 Erregervektor 286 Erregung, harte 111 -, periodische 199 -, überkritische 187 -, unterkritische 187 -, weiche 111 Erschütterungsmesser 208 Exponent, charakteristischer 159 Fadenpendel 49, 151 Feder-Masse-Pendel 35 Feder-Masse-Schwinger 49, 180 Feigenbaumkonstante 351 Fenster, periodisches 351 Festreibung 91 Finite-Elemente-Methode 296 Fixpunkt 349 Frequenz 13 Frequenzfunktion 274 Frequenzgang 27 Frequenzgangmatrix 282 Frequenzgleichung 308, 315, 322 Frequenzreduktion 237 Froudesches Pendel 131 Funktion, zulässige 323, 332 Funktionalmatrix 370 Galerkin-Verfahren 335 Geysir 139 Gleichgewichtslage 14 Gleichrichterwirkung 237 Gleichung, charakteristische 247 Grenzzykel 109 -, stabile (instabile) 110 Hamiltonsches Integralprinzip 312 Harmonische-Balance-Methode 72, 115,218 harte Erregung 111 Hauptachsentransformation 251 Hauptkoordinaten 249, 251, 269 Hauptschwingung 245, 250, 310, 316 Helmholtzsche Kombinationstöne 235 Hillsche Differentialgleichung 159 Hochpaßkette 272 Holzer-Tolle 289 Hüllkurve 21, 84 Huygens-Steinersche Beziehung 65 hydraulischer Kippschwinger Stoßheber Widder 139 Hysterese 144 Integral, elliptische 64 Integrierbarkeit 361 Intermittenz 352 inverse Ortskurve 31, 194 Isoklinenmethode 74 Jacobi-Funktionen 63 Jacobimatrix 370 KAM-Theorie 361 Kennlinie bei trockener Reibung 132 Kippschwingungen 107, 137 Klingel, elektrische 105 Knotenpunkt 26 Kombinationsschwingungen 235 Kontinuumsschwingungen 302 Koppelschwingungen 34, 245 Koppelstärke 248 Körperpendel 49 Kreisabbildung 357 Kreiselmatrix 285 Kreisfrequenz 14 Kreuzschubkurbelgetriebe 17 Kupplungsstangen-Antrieb 149 Lagrangesche Gleichungen 246 Leistung 187 Ljapunov-Exponent 353, 368 logarithmisches Dekrement 86 Lösung, chaotische 358 -, periodische 358 -, quasiperiodische oder fastperiodische 358 -, subharmonische 358 Mäanderfunktion 200 Masseneinfluß der Feder 52 Massenmatrix 264 Materialdämpfung 327 Mathieusche Differentialgleichung 160 Meissnersche Differentialgleichung 164, 168 Melnikov-Methode 364 Messung, unterkritische 207 Methode der harmonischen Balance kleinen Schwingungen langsam veränderlichen Amplitude 121 -, modellgestützte 367 -, signalgestützte 367 Mitnahme-Effekt 242 Mittellage 14
13 Sachverzeichnis 399 Modalanalyse 317 Modalmatrix 269 Modulationsfrequenz 22 Nachführ-Regler 146 Nachgiebigkeitsmatrix, dynamische 282 Näherungsmethoden 71 nichtlineare Effekte 216 Nullphasenwinkel 18 Oberschwingungen 235 Orbit 349 -, homokliner 364 Orthogonalität 309 Ortskurve 27, 31, 193 -, inverse 31, 194 Oszillographenschleife 205 passive Entstörung 210 Pendellänge, reduzierte 65 Pendeluhr 110 Periode 13 Periodenverdoppelung 351 Pfeifgrenze 131 Phasenebene 22 Phasen-Frequenzgang 30, 193 Phasenfunktion 184 Phaseninstabilität 242 Phasenkurve 22, 368 Phasenporträt 22, 25, 88, 109, 134 Phasenraum 355 Phasenverlauf eines nichtlinearen Schwingers 229 Phasenverschiebung 19 Phasenverzerrung 207 Poincare-Abbildung 355, 368 Prüffunktion 28 Punkt, heterokliner 364 -, homokliner 364 Punkt-Abbildung 347 quadratische Dämpfungskräfte 96 Rampenfunktion 243 Randbedingungen 313 -, dynamische oder restliche 313, 323 -, geometrische oder wesentliche 313, 323 Rayleigh-Quotient 253, 267, 270, 325, 338 Rayleighsche Differentialgleichung 145 Rayleighsches Prinzip 339 reduzierte Pendellänge 65 Reibungspendel 132 Reibungsschwingungen 105, 131, 373 Relaisregelkreis 141 Relaisschwinger 68 Relativdämpfung 212 Relaxationsschwingungen 137 Resonanz 186, 282 Resonanzerscheinung 283 Resonanzfunktion 186 Resonanzkurven nichtlinearer Systeme 228 Restgrößenverfahren 289 Reversionspendel 66 Ritz-Ansatz 119 Ritz-Verfahren 332 Röhren-Generator 129 Röhrenkennlinie 130 Rollpendel 68 Rollschwinger 46 Rüttelrichtmoment 166 Saite 302 Sattelpunkt 27, 58 Saugkreis 263 Schaukelschwinger 152 Scheinresonanz 282 Schlagschwingungen eines Tragflügels 145 Schranke, obere 338 -, untere 341 Schrankenverfahren 331, 338 Schwebung 22, 198 Schwerependel 43, 148 Schwinger, nichtlinearer 91 Schwingerkette 271 Schwinger-Typ 105 Schwingkreis, elektrischer 38, 49 Schwingung, angefachte 16 -, aufschaukelnde 16 -, autonome 33 -, Differentialgleichung 32 -, Dreieck einer Flüssigkeitssäule 40 -, Entstehungsmechanismus 32 -, erzwungene 33, 171 -, fast periodische 14 -, freie 33 -, Freiheitsgrade 32 -, gedämpfte 16 -, gegenphasige 220 -, gleichphasige 220 -, harmonische 15 -, heteronome 33 -, modulierte 22 -, parametererregte 33, 147 -, Rechteck- 15 -, rheonome 147 -, Sägezahn- 15 -, selbsterregte 33, 104
14 400 Sachverzeichnis Schwingung, Sinus- 15 -, strämungserregte 106 -, Trapez- 15 -, ungedämpte 16 Schwingungen, Klassifikation 31 Schwingungs analyse 286 Schwingungsdauer 13 Schwingungsentstärung 212 Schwingungsisolierung 210 Schwingungsknoten 275 Schwingungsmeßgeräte 204 Schwingungsmesser 244 Schwingungstilger 262 Schwingungstilgung 283 Schwingungsweite 14 Schwingungszeit 13 Separatrix 27, 58 Simulation 367 Sinusschwingung 18 Southwell 341 Speichertyp 106 Sprungeffekt 230, 244 Sprungfunktion 28 Sprung-Übergangsfunktion 29, 174 stabile (instabile) Grenzzykel 110 Stabilität (Instabilität) im Großen Kleinen 111 Stabilitätskarte nach Ince/Strutt 161 Steifigkeitsmatrix 264 -, dynamische 282 Stoßerregung 123, 128 Stoßfunktion (Dirac-Funktion) 28 Stoß-Übergangsfunktion 175 Störungstheorie 361 Strudelpunkt 26, 88 Superpositionsprinzip 49 Synchronisierung 242 System, dissipatives 360 -, konservatives 360 -, nichtglattes 373 -, zeitdiskretes 347 Systemmatrix 286 Temperaturregelung 141 Teufelstreppe 378 Tiefpaßkette 272 Torsionsschwinger 49 Torsionsstab 302 Totzeit 144 Trägerfrequenz 22 Trägheitsradius 46 Trajektorie 349 tropfender Wasserhahn 139 Turbulenzdämpfung 96 Übergangsfunktion 27 Übertragungsfaktor 30 Übertragungsmatrizen-Verfahren 292 Uhrenpendel mit Festreibung 128 Unterschwingungen 236 Van der Polsehe Gleichung 112, 129, 238 Vektorbild 17 Verfahren der Beschreibungsfunktion harmonischen Balance 72, von Ritz und Galerkin 118 Vergleichsfunktion 323, 336 Vergrößerungsfunktion 30, 183, 185 Versteifung, dynamische 321 Verstimmungseffekt 169 Verzweigungsdiagramm 351 Volumenänderungsrate 365 Wachstum, exponentielles 347 -, logistisches 347 Wasserschlag 140 weiche Erregung 111 Welle, fortschreitende 307 -, stehende 307 Wellengeschwindigkeit 304 Wellengleichung 304 Wellenmesser 210 Windungszahl 358 Wirbelpunkt 25, 58 Wirkarbeit 190 Wirkleistung 188 Zeitkonstante 84 Zeitverlauf 367 Zieh-Erscheinung 242 Zungenfrequenzmesser 210 Zusatzfeder 340 Zusatzmasse 340 Zustandsgleichung 286 Zustandsgrößen 13, 285 Zustandsraum 355 Zustandsvektor 285 Zykloidenpendel 67
15 SPITZENTECHNOLOGIE BEI EINZELKOMPONENTEN - ZUKUNFTSORIENTIERTE SVSTEMLÖSUNGEN Vom klassischen Hersteller von Reifen und technischen Gummiprodukten haben wir uns zum Zulieferer für zukunftsweisende Systeme entwickelt. Mehr als Mitarbeiter beschäftigen sich in unseren deutschen und amerikanischen Technologiezentren damit, wegweisende Techniken zu gestalten und zum Erfolg zu führen. Wir bieten Ihnen spannende Aufgaben im Rahmen eines Direkteinstiegs, unterstützt durch den individuellen Einarbeitungsplan, oder in unserem zehnmonatigen, sehr praxisnahen Traineeprogramm. Doch ganz gleich, wie Sie starten: Sie haben bei uns alle Möglichkeiten, in einem intemationalen Umfeld voranz.ukommen. Nennen Sie es ruhig Karriere. wir nennen es Entfaltung Ihrer Fähigkeiten und Ihrer Persönlichkeit, die wir mit Hilfe professioneller PE-Programme unterstützen. Sie wollen mehr wissen? Dann sollten wir miteinander sprechen! Continental AG, Recruiting Office, Postfach 169, Hannover, oder per personaj@conti.de. oder besuchen Sie unsere Homepage: Die Continental AG, führender Technologiekonzern für automotive Systemtösungen, Reifen und technische Produkte. Umsatz 10,1 Mrd. und über Mitarbeiter in Wir verstehen uns als System-Entwicklungspartner unserer Kunden - weltwei1. (gntinentill
16 COMPENSER LEBEN & CO GMBH Postfach Berg Tel.: 08151/5768 Fax: 08151/ Stoß- und Schwingungsdämpfer, Federbeine, Ölbremsen Gasfedern Ihr Partner und Problemlöser zur Schwingungsdämpfung und Reduzierung von Stoßwirkungen. Prof. Dr.-Ing. P. Meinke IA Tlngenieurgesellschaft rur Angewandte Technologie mbh Leutstettener Str. 28 D Starnberg Tel: Fax: Systemanalysen Analyse komplexer rm:hanischer md mechatrooischer Systeme Fahueugf'ahrweg - Wechselwirkung von Eisenl:ehnen Ralsatzdynamik, Eirtgleisung;verhalten Dynamik von DIu;kma<;chinen Strukturdynamik großer elekttischer Antriebe Genaui@<eitortischeSystemeinihrer Lagerung Magnctlager Monitoring md Diagnose NichtlineareSysteme M=hinen-mdRotDrdynamik Systemanalyse durch Simulation and Animation Engineering in Mechanik und Elektronik Satelliten kommunikation und Navigation Anwendung von IN MARSA T Diensten, insbesondere C, D+ Entwicklung, Fertigung und Vertrieb von Transceivern und System lösungen Tracking und Tracing von Mobiles, Transportlogistik GPS - Anwendungen Hochgenaue Ortsbestimmungen, Gleislage - Vermessung Digitale Karten Software SIMPACK Analyse, Entwurf und Animation nichtiinearer Mehrkörpersysteme Fahrzeuge, Lagerungen, Roboter Antriebssysteme, Rad/Schiene - Modelle Software MEDYNA Simulation von Eisenbahnfahrzeugen, Fahrzeug/Fahrweg - Wechselwirkung, Maglev Fahrzeuge Laufstabilität und Fahrkomfort Rad/Schiene - Modul mit nichtelliptischer Kontaktfläche
17 Schwingungsschutz bieten wir für durch unsere Maschinen und Aggregate Gebäude und Gebäudeteile Gleisanlagen und Fahrwege Weitgespannte Bauwerke VISCO R Dämpfer. Tilger. GER Federelemente B GmbH GERB & Schwingungslsollerungen Co. KG ~ < ; ~ > \ ) 1 l< : 0> ~ D O q =:::. { i!p Tel.: (030) Fax: (030) < : > q O a o l l \ ) ~ < ; > Schwingungsisolierungen
Lösungen der Aufgaben
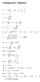 ösungen der Aufgaben. cc c oder. c c c c c. c c c. EA 3.. m 4. 5. fg fg x x,. a g xˆ, f. a 6. * * a ˆ ˆ ˆ ˆ ˆ* a a) x a x, b) x x, c) x xˆ* 7. x g 4a x, ga. a 4a x 8. s s, 89. g g 9. R, S.. T 84, 3 Minuten
ösungen der Aufgaben. cc c oder. c c c c c. c c c. EA 3.. m 4. 5. fg fg x x,. a g xˆ, f. a 6. * * a ˆ ˆ ˆ ˆ ˆ* a a) x a x, b) x x, c) x xˆ* 7. x g 4a x, ga. a 4a x 8. s s, 89. g g 9. R, S.. T 84, 3 Minuten
Schwingungen. Kurt Magnus Karl Popp Walter Sextro
 Kurt Magnus Karl Popp Walter Sextro Schwingungen Eine Einfuhrung in die physikalischen Grundlagen und die theoretische Behandlung von Schwingungsproblemen 8., uberarbeitete Auflage Mit 211 Abbildungen
Kurt Magnus Karl Popp Walter Sextro Schwingungen Eine Einfuhrung in die physikalischen Grundlagen und die theoretische Behandlung von Schwingungsproblemen 8., uberarbeitete Auflage Mit 211 Abbildungen
Eine Einführung in die theoretische Behandlung von Schwingungsproblemen
 Schwingungen Eine Einführung in die theoretische Behandlung von Schwingungsproblemen Von Dr. rer. nat. Dr.-Ing. E. h. Kurt Magnus Professor an dertechn. Universität München 4., durchgesehene Auflage Mit
Schwingungen Eine Einführung in die theoretische Behandlung von Schwingungsproblemen Von Dr. rer. nat. Dr.-Ing. E. h. Kurt Magnus Professor an dertechn. Universität München 4., durchgesehene Auflage Mit
Schwingungen. Kurt Magnus Karl Popp Walter Sextro
 Kurt Magnus Karl Popp Walter Sextro 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Schwingungen Eine Einführung
Kurt Magnus Karl Popp Walter Sextro 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Schwingungen Eine Einführung
Technische Schwingungslehre
 Technische Schwingungslehre Von Dipl.-Math. M. Knaebel Professor an der Fachhochschule für Technik Esslingen 5., überarbeitete und erweiterte Auflage Mit 219 Bildern, 41 Beispielen und 73 Aufgaben B. G.
Technische Schwingungslehre Von Dipl.-Math. M. Knaebel Professor an der Fachhochschule für Technik Esslingen 5., überarbeitete und erweiterte Auflage Mit 219 Bildern, 41 Beispielen und 73 Aufgaben B. G.
2. Schwingungen eines Einmassenschwingers
 Baudynamik (Master) SS 2017 2. Schwingungen eines Einmassenschwingers 2.1 Freie Schwingungen 2.1.1 Freie ungedämpfte Schwingungen 2.1.2 Federzahlen und Federschaltungen 2.1.3 Freie gedämpfte Schwingungen
Baudynamik (Master) SS 2017 2. Schwingungen eines Einmassenschwingers 2.1 Freie Schwingungen 2.1.1 Freie ungedämpfte Schwingungen 2.1.2 Federzahlen und Federschaltungen 2.1.3 Freie gedämpfte Schwingungen
Erzwungene Schwingungen
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung
Technische Schwingungslehre Prof. Dr.-Ing. habil. Michael Hanss. Aufgabensammlung mit Kurzlösungen
 Prof. Dr.-Ing. Prof. E.h. P. Eberhard / Prof. Dr.-Ing. M. Hanss SS 17 Ü1 Technische Schwingungslehre Prof. Dr.-Ing. habil. Michael Hanss Aufgabensammlung mit Kurzlösungen Sommersemester 017 Prof. Dr.-Ing.
Prof. Dr.-Ing. Prof. E.h. P. Eberhard / Prof. Dr.-Ing. M. Hanss SS 17 Ü1 Technische Schwingungslehre Prof. Dr.-Ing. habil. Michael Hanss Aufgabensammlung mit Kurzlösungen Sommersemester 017 Prof. Dr.-Ing.
4. Einführung in die Baudynamik
 Baustatik III SS 2017 4. Einführung in die Baudynamik 4.1 Allgemeine Vorbemerkungen 4.1.1 Bedeutungen der Baudynamik 4.1.2 Grundbegriffe und Klassifizierung 4.1.3 Modellierung der Bauwerksschwingungen
Baustatik III SS 2017 4. Einführung in die Baudynamik 4.1 Allgemeine Vorbemerkungen 4.1.1 Bedeutungen der Baudynamik 4.1.2 Grundbegriffe und Klassifizierung 4.1.3 Modellierung der Bauwerksschwingungen
2. Physikalisches Pendel
 2. Physikalisches Pendel Ein physikalisches Pendel besteht aus einem starren Körper, der um eine Achse drehbar gelagert ist. A L S φ S z G Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.2-1 2.1 Bewegungsgleichung
2. Physikalisches Pendel Ein physikalisches Pendel besteht aus einem starren Körper, der um eine Achse drehbar gelagert ist. A L S φ S z G Prof. Dr. Wandinger 6. Schwingungen Dynamik 2 6.2-1 2.1 Bewegungsgleichung
Rudolf Jürgler. Maschinendynamik. Dritte, neu bearbeitete Auflage. Mit 550 Abbildungen. Springer
 Rudolf Jürgler Maschinendynamik Dritte, neu bearbeitete Auflage Mit 550 Abbildungen Springer VII Inhaltsverzeichnis 1 Einleitung 1 2 Schwingungstechnische Grundbegriffe 3 2.1 Definition der Schwingung
Rudolf Jürgler Maschinendynamik Dritte, neu bearbeitete Auflage Mit 550 Abbildungen Springer VII Inhaltsverzeichnis 1 Einleitung 1 2 Schwingungstechnische Grundbegriffe 3 2.1 Definition der Schwingung
Klassische Mechanik. WILEY-VCH Verlag GmbH & Co. KGaA. Herbert Goldstein, Charles P. Poole, Jr., und John L Safko
 Herbert Goldstein, Charles P. Poole, Jr., und John L Safko Klassische Mechanik Dritte, vollständig überarbeitete und erweiterte Auflage WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Inhaltsverzeichnis Vorwort
Herbert Goldstein, Charles P. Poole, Jr., und John L Safko Klassische Mechanik Dritte, vollständig überarbeitete und erweiterte Auflage WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Inhaltsverzeichnis Vorwort
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Lineare und nichtlineare Schwingungen und Wellen
 Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik
 D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Oktober 2009 Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. D. Bestle Prinzip der
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Oktober 2009 Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. D. Bestle Prinzip der
Analyse nichtlinearer dynamischer Systeme der Elektrotechnik
 E. S. Philippow / W. G. Büntig Analyse nichtlinearer dynamischer Systeme der Elektrotechnik Einführung in die numerische Untersuchung einfacher Systeme Mit 198 Bildern und 27 Tabellen Carl Hanser Verlag
E. S. Philippow / W. G. Büntig Analyse nichtlinearer dynamischer Systeme der Elektrotechnik Einführung in die numerische Untersuchung einfacher Systeme Mit 198 Bildern und 27 Tabellen Carl Hanser Verlag
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik
 D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. Hon. Prof. (NUST) D. Bestle 1 Inhalt
D. Bestle Technische Mechanik III Schwingungen und Hydromechanik Arbeitsunterlagen zur Vorlesung Lehrstuhl Technische Mechanik und Fahrzeugdynamik Prof. Dr. Ing. habil. Hon. Prof. (NUST) D. Bestle 1 Inhalt
Hans Dresig Franz Holzweißig. Maschinendynamik. 7., bearbeitete Auflage Unter Mitarbeit von L. Rockhausen. Mit 237 Abbildungen.
 Hans Dresig Franz Holzweißig Maschinendynamik 7., bearbeitete Auflage Unter Mitarbeit von L. Rockhausen Mit 237 Abbildungen 4y Springer 0 Aufgaben und Gliederung der Maschinendynamik 1 1 Modellbildung
Hans Dresig Franz Holzweißig Maschinendynamik 7., bearbeitete Auflage Unter Mitarbeit von L. Rockhausen Mit 237 Abbildungen 4y Springer 0 Aufgaben und Gliederung der Maschinendynamik 1 1 Modellbildung
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Theoretische Physik: Mechanik
 Eckhard flebhan Theoretische Physik: Mechanik ELSEVIER SPEKTRUM AKADEMISCHER VERLAG Spektrum L AKADEMISCHER VI k_/l AKADEMISCHER VEHLAG Inhaltsverzeichnis Anmerkungen zur Theoretischen Physik 1 1 Vorbemerkungen
Eckhard flebhan Theoretische Physik: Mechanik ELSEVIER SPEKTRUM AKADEMISCHER VERLAG Spektrum L AKADEMISCHER VI k_/l AKADEMISCHER VEHLAG Inhaltsverzeichnis Anmerkungen zur Theoretischen Physik 1 1 Vorbemerkungen
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
3. Fluid-Struktur-Kopplung
 3. Fluid-Struktur-Kopplung Bei einer schwingenden Struktur muss die Normalkomponente der Schallschnelle mit der Normalkomponente der Geschwindigkeit an der Oberfläche der Struktur übereinstimmen. Dadurch
3. Fluid-Struktur-Kopplung Bei einer schwingenden Struktur muss die Normalkomponente der Schallschnelle mit der Normalkomponente der Geschwindigkeit an der Oberfläche der Struktur übereinstimmen. Dadurch
Ergebnis: Allg. Lösung der homogenen DGL ist Summe über alle Eigenlösungen: mit
 Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. 4. Dämpfungsmodelle. Elastodynamik 1 3.
 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 4. Dämpfungsmodelle 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische
0 Aufgaben und Gliederung der Maschinendynamik... 1
 Inhaltsverzeichnis 0 Aufgaben und Gliederung der Maschinendynamik... 1 1 Modellbildung und Kennwertermittlung... 7 1.1 Einteilung der Berechnungsmodelle...... 7 1.1.1 Allgemeine Grundsätze................................
Inhaltsverzeichnis 0 Aufgaben und Gliederung der Maschinendynamik... 1 1 Modellbildung und Kennwertermittlung... 7 1.1 Einteilung der Berechnungsmodelle...... 7 1.1.1 Allgemeine Grundsätze................................
Übung zu Mechanik 4 Seite 28
 Übung zu Mechanik 4 Seite 28 Aufgabe 47 Auf ein Fundament (Masse m), dessen elastische Bettung durch zwei Ersatzfedern dargestellt wird, wirkt die periodische Kraft F(t) = F 0 cos (Ω t). Die seitliche
Übung zu Mechanik 4 Seite 28 Aufgabe 47 Auf ein Fundament (Masse m), dessen elastische Bettung durch zwei Ersatzfedern dargestellt wird, wirkt die periodische Kraft F(t) = F 0 cos (Ω t). Die seitliche
Technische Schwingungslehre
 Technische Schwingungslehre Helmut Jäger Roland Mastel Manfred Knaebel Technische Schwingungslehre Grundlagen Modellbildung Anwendungen 8., überarbeitete Auflage Mit 250 Abbildungen, 74 Aufgaben und 40
Technische Schwingungslehre Helmut Jäger Roland Mastel Manfred Knaebel Technische Schwingungslehre Grundlagen Modellbildung Anwendungen 8., überarbeitete Auflage Mit 250 Abbildungen, 74 Aufgaben und 40
4. Dämpfungsmodelle. 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. Elastodynamik 3.
 4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
Schwingungslehre mit Maschinendynamik
 Eberhard Brommundt Delf Sachau Schwingungslehre mit Maschinendynamik 2., überarbeitete und erweiterte Auflage Mit 227 Abbildungen, 313 Aufgaben und zahlreichen Beispielen i Springer Vieweg Inhaltsverzeichnis
Eberhard Brommundt Delf Sachau Schwingungslehre mit Maschinendynamik 2., überarbeitete und erweiterte Auflage Mit 227 Abbildungen, 313 Aufgaben und zahlreichen Beispielen i Springer Vieweg Inhaltsverzeichnis
MATRIZEN. und Determinanten. und ihre Anwendung in Technik und Ökonomie. von Dr. rer. nat. Günter Dietrich und Prof. Dr.-Ing.
 MATRIZEN und Determinanten und ihre Anwendung in Technik und Ökonomie von Dr. rer. nat. Günter Dietrich und Prof. Dr.-Ing. Henry Stahl 5., neubearbeitete Auflage Mit 63 Bildern und 133 Beispielen und Lösungen
MATRIZEN und Determinanten und ihre Anwendung in Technik und Ökonomie von Dr. rer. nat. Günter Dietrich und Prof. Dr.-Ing. Henry Stahl 5., neubearbeitete Auflage Mit 63 Bildern und 133 Beispielen und Lösungen
Baudynamik (Master) SS 2017
 Baudynamik (Master) SS 7 3. Schwingungen mit zwei und mehr Freiheitsgraden 3. Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.. Einige Prinzipien der Mechanik 3.. Herleitung
Baudynamik (Master) SS 7 3. Schwingungen mit zwei und mehr Freiheitsgraden 3. Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.. Einige Prinzipien der Mechanik 3.. Herleitung
Das führt zu einer periodischen Hin- und Herbewegung (Schwingung) Applet Federpendel (http://www.walter-fendt.de)
 Elastische SCHWINGUNGEN (harmonische Bewegung) Eine Masse sei reibungsfrei durch elastische Kräfte in einer Ruhelage fixiert Wenn aus der Ruhelage entfernt wirkt eine rücktreibende Kraft Abb. 7.1 Biologische
Elastische SCHWINGUNGEN (harmonische Bewegung) Eine Masse sei reibungsfrei durch elastische Kräfte in einer Ruhelage fixiert Wenn aus der Ruhelage entfernt wirkt eine rücktreibende Kraft Abb. 7.1 Biologische
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
1. Einführung. Baudynamik (Master) SS 2017
 Baudynamik (Master) SS 2017 1. Einführung 1.1 Bedeutungen der Baudynamik 1.2 Grundbegriffe und Klassifizierung 1.3 Modellierung der Bauwerksschwingungen LEHRSTUHL FÜR BAUSTATIK 1 Baudynamik (Master) SS
Baudynamik (Master) SS 2017 1. Einführung 1.1 Bedeutungen der Baudynamik 1.2 Grundbegriffe und Klassifizierung 1.3 Modellierung der Bauwerksschwingungen LEHRSTUHL FÜR BAUSTATIK 1 Baudynamik (Master) SS
Dynamik hüpfender Bälle
 1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
3. Erzwungene Schwingungen
 3. Erzwungene Schwingungen 3.1 Grundlagen 3.2 Tilger 3.3 Kragbalken 3.4 Fahrbahnanregung 3.3-1 3.1 Grundlagen Untersucht wird die Antwort des Systems auf eine Anregung mit harmonischem Zeitverlauf. Bewegungsgleichung:
3. Erzwungene Schwingungen 3.1 Grundlagen 3.2 Tilger 3.3 Kragbalken 3.4 Fahrbahnanregung 3.3-1 3.1 Grundlagen Untersucht wird die Antwort des Systems auf eine Anregung mit harmonischem Zeitverlauf. Bewegungsgleichung:
Deterministisches Chaos
 Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Nichtglatte dynamische Systeme - Beispiele und Analysemethoden -
 - Beispiele und Analysemethoden - Popp, Karl Veröffentlicht in: Jahrbuch 1999 der Braunschweigischen Wissenschaftlichen Gesellschaft, S.73-77 J. Cramer Verlag, Braunschweig 73 KARL POPP, Neustadt/Nds.
- Beispiele und Analysemethoden - Popp, Karl Veröffentlicht in: Jahrbuch 1999 der Braunschweigischen Wissenschaftlichen Gesellschaft, S.73-77 J. Cramer Verlag, Braunschweig 73 KARL POPP, Neustadt/Nds.
1 Nicht-lineare dynamische Systeme
 1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
Dämpfung. . Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung. Elastodynamik 2 SS
 Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Dämpfung. Grundlagen. Viskose Dämpfung. Modale Dämpfung. Rayleigh-Dämpfung. Strukturdämpfung 5. Dämpfung 5-1 1. Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Mechanische Energie
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Physik III im Studiengang Elektrotechnik - Schwingungen und Wellen - Prof. Dr. Ulrich Hahn SS 28 Mechanik elastische Wellen Schwingung von Bauteilen Wasserwellen Akustik Elektrodynamik Schwingkreise elektromagnetische
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Schwingungslehre. mit Maschinendynamik. Eberhard Brommundt, Delf Sachau. Mit 210 Abbildungen und 286 Aufgaben. Teubner
 Eberhard Brommundt, Delf Sachau 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Schwingungslehre mit Maschinendynamik
Eberhard Brommundt, Delf Sachau 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Schwingungslehre mit Maschinendynamik
Physik für Oberstufenlehrpersonen. Frühjahrssemester Schwingungen und Wellen
 Physik für Oberstufenlehrpersonen Frühjahrssemester 2018 Schwingungen und Wellen Zum Einstieg in das neue Semester Schwingungen Schwingungen spielen bei natürlichen Prozessen bedeutende Rolle: -Hören und
Physik für Oberstufenlehrpersonen Frühjahrssemester 2018 Schwingungen und Wellen Zum Einstieg in das neue Semester Schwingungen Schwingungen spielen bei natürlichen Prozessen bedeutende Rolle: -Hören und
k = 1, 2,..., n (4.44) J k ϕ
 236 4 Torsionsschwinger und Längsschwinger ( J1 J2) M J M J2/ J1= 02, 10 0,5 8 1 + 6 2 max 4 5 2 10 2 bezogenes Moment 0 Bild 45 1 2 5 10 relatives Spiel ctϕ S/ M10 Maximales Moment infolge Spiel im Antrieb
236 4 Torsionsschwinger und Längsschwinger ( J1 J2) M J M J2/ J1= 02, 10 0,5 8 1 + 6 2 max 4 5 2 10 2 bezogenes Moment 0 Bild 45 1 2 5 10 relatives Spiel ctϕ S/ M10 Maximales Moment infolge Spiel im Antrieb
6 Eigenlösungen der eindimensionalen Wellengleichung
 39 Kontinuierliche Systeme lassen sich als Schwinger mit unendlich vielen Freiheitsgraden interpretieren. Daher ist ein ähnliches ösungsverhalten wie bei linearen diskreten Systemen zu erwarten, d.h. die
39 Kontinuierliche Systeme lassen sich als Schwinger mit unendlich vielen Freiheitsgraden interpretieren. Daher ist ein ähnliches ösungsverhalten wie bei linearen diskreten Systemen zu erwarten, d.h. die
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
 Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Teubner StudienbOcher Mechanik. K. Magnus / K. Popp Schwingungen
 Teubner StudienbOcher Mechanik K. Magnus / K. Popp Schwingungen Leitfaden der angewandten Mathematik und Mechanik LAMM Herausgegeben von Prof. Dr. Dr. h. c. mult. G. Hotz, SaarbrOcken Prof. Dr. P. Kall,
Teubner StudienbOcher Mechanik K. Magnus / K. Popp Schwingungen Leitfaden der angewandten Mathematik und Mechanik LAMM Herausgegeben von Prof. Dr. Dr. h. c. mult. G. Hotz, SaarbrOcken Prof. Dr. P. Kall,
1. Aufgabe: (ca. 14% der Gesamtpunkte)
 Institut für Mechanik Prof. Dr.-Ing. habil. P. Betsch Prof. Dr.-Ing. habil. Th. Seelig Prüfung in Baudynamik 23. Juli 2018 1. Aufgabe: (ca. 14% der Gesamtpunkte) a) Geben Sie Amplitude, Frequenz und Phasenverschiebung
Institut für Mechanik Prof. Dr.-Ing. habil. P. Betsch Prof. Dr.-Ing. habil. Th. Seelig Prüfung in Baudynamik 23. Juli 2018 1. Aufgabe: (ca. 14% der Gesamtpunkte) a) Geben Sie Amplitude, Frequenz und Phasenverschiebung
Parameterdef. an nichtl. Zweipolkennl.
 Parameterdef. an nichtl. Zweipolkennl. nichtlin. Zweipole Typen von Approximationsfunktionen KENNLINIENAPPROXIMATION Rektifikationsmethode y 5α 4α FUNKTION β < β > y = αx β β = 3α 2α α β < β =.5.5 2 2.5
Parameterdef. an nichtl. Zweipolkennl. nichtlin. Zweipole Typen von Approximationsfunktionen KENNLINIENAPPROXIMATION Rektifikationsmethode y 5α 4α FUNKTION β < β > y = αx β β = 3α 2α α β < β =.5.5 2 2.5
3. Erzwungene gedämpfte Schwingungen
 3. Erzwungene gedämpfte Schwingungen 3.1 Schwingungsgleichung 3.2 Unwuchtanregung 3.3 Weganregung 3.4 Komplexe Darstellung 2.3-1 3.1 Schwingungsgleichung F(t) m Bei einer erzwungenen gedämpften Schwingung
3. Erzwungene gedämpfte Schwingungen 3.1 Schwingungsgleichung 3.2 Unwuchtanregung 3.3 Weganregung 3.4 Komplexe Darstellung 2.3-1 3.1 Schwingungsgleichung F(t) m Bei einer erzwungenen gedämpften Schwingung
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: ) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung: Bei fortgeschrittenen
Manfred Knaebel Helmut Jäger Roland Mastel. Technische Schwingungslehre
 Manfred Knaebel Helmut Jäger Roland Mastel Technische Schwingungslehre Manfred Knaebel Helmut Jäger Roland Mastel Technische Schwingungslehre 7., korrigierte und überarbeitete Auflage Mit 247 Abbildungen,
Manfred Knaebel Helmut Jäger Roland Mastel Technische Schwingungslehre Manfred Knaebel Helmut Jäger Roland Mastel Technische Schwingungslehre 7., korrigierte und überarbeitete Auflage Mit 247 Abbildungen,
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
III. Schwingungen und Wellen
 III. Schwingungen und Wellen III.1 Schwingungen Physik für Mediziner 1 Schwingungen Eine Schwingung ist ein zeitlich periodischer Vorgang Schwingungen finden im allgemeinen um eine stabile Gleichgewichtslage
III. Schwingungen und Wellen III.1 Schwingungen Physik für Mediziner 1 Schwingungen Eine Schwingung ist ein zeitlich periodischer Vorgang Schwingungen finden im allgemeinen um eine stabile Gleichgewichtslage
Baudynamik. Jan Höffgen 18. Februar Koordinatensysteme 2
 Baudynamik Jan Höffgen 8. Februar 204 Inhaltsverzeichnis Koordinatensysteme 2 2 Bewegungsgleichungen 2 2. Allgemeines................................................ 2 2.2 Synthetische Methode nach d Alembert................................
Baudynamik Jan Höffgen 8. Februar 204 Inhaltsverzeichnis Koordinatensysteme 2 2 Bewegungsgleichungen 2 2. Allgemeines................................................ 2 2.2 Synthetische Methode nach d Alembert................................
F R. = Dx. M a = Dx. Ungedämpfte freie Schwingungen Beispiel Federpendel (a) in Ruhe (b) gespannt: Auslenkung x Rückstellkraft der Feder
 6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
6. Schwingungen Schwingungen Schwingung: räumlich und zeitlich wiederkehrender (=periodischer) Vorgang Zu besprechen: ungedämpfte freie Schwingung gedämpfte freie Schwingung erzwungene gedämpfte Schwingung
Experimentalphysik E1
 Experimentalphysik E1 Gedämpfte & erzwungene Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 16. Dez. 16 Harmonische Schwingungen Auslenkung
Experimentalphysik E1 Gedämpfte & erzwungene Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 16. Dez. 16 Harmonische Schwingungen Auslenkung
2. Freie Schwingungen
 2. Freie Schwingungen Die einfachsten schwingungsfähigen Systeme sind lineare Systeme: Die Rückstellkräfte sind proportional zur Auslenkung. Die Dämpfungskräfte sind proportional zur Geschwindigkeit. Bei
2. Freie Schwingungen Die einfachsten schwingungsfähigen Systeme sind lineare Systeme: Die Rückstellkräfte sind proportional zur Auslenkung. Die Dämpfungskräfte sind proportional zur Geschwindigkeit. Bei
Dynamik und Regelung Mechanischer Systeme
 Dynamik und Regelung Mechanischer Systeme Von Priv.-Doz. Dr.-Ing. habil. Hartmut Bremer Technische Universität München Mit 101 Bildern B. G.Teubner Stuttgart 1988 Inhalt s Verzeichnis Vorbemerkung: Der
Dynamik und Regelung Mechanischer Systeme Von Priv.-Doz. Dr.-Ing. habil. Hartmut Bremer Technische Universität München Mit 101 Bildern B. G.Teubner Stuttgart 1988 Inhalt s Verzeichnis Vorbemerkung: Der
f = f = f = Institut für Technische und Num. Mechanik Prof. P. Eberhard / Dr.-Ing. F. Fleißner WS 2017/18 P März 2018
 Institut für Technische und Num. Mechanik Maschinendynamik Prof. P. Eberhard / Dr.-Ing. F. Fleißner WS 2017/18 P 1 20. März 2018 Prüfung in Maschinendynamik Nachname, Vorname Aufgabe 1 (6 Punkte) Bestimmen
Institut für Technische und Num. Mechanik Maschinendynamik Prof. P. Eberhard / Dr.-Ing. F. Fleißner WS 2017/18 P 1 20. März 2018 Prüfung in Maschinendynamik Nachname, Vorname Aufgabe 1 (6 Punkte) Bestimmen
Experimentalphysik E1
 Experimentalphysik E1 Erzwungene & gekoppelte Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 10. Jan. 016 Gedämpfte Schwingungen m d x dt +
Experimentalphysik E1 Erzwungene & gekoppelte Schwingungen Alle Informationen zur Vorlesung unter : http://www.physik.lmu.de/lehre/vorlesungen/index.html 10. Jan. 016 Gedämpfte Schwingungen m d x dt +
Hochschule Düsseldorf University of Applied Sciences. 12. Januar 2017 HSD. Physik. Schwingungen III
 Physik Schwingungen III Wiederholung Komplexe Zahlen Harmonischer Oszillator DGL Getrieben Gedämpft Komplexe Zahlen Eulersche Formel e i' = cos ' + i sin ' Komplexe Schwingung e i!t = cos!t + i sin!t Schwingung
Physik Schwingungen III Wiederholung Komplexe Zahlen Harmonischer Oszillator DGL Getrieben Gedämpft Komplexe Zahlen Eulersche Formel e i' = cos ' + i sin ' Komplexe Schwingung e i!t = cos!t + i sin!t Schwingung
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
2. Freie gedämpfte Schwingungen
 2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
2. Freie gedämpfte Schwingungen
 2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
2. Freie gedämpfte Schwingungen Bei realen Systemen werden die Schwingungsausschläge mit der Zeit kleiner, und die Schwingung kommt zum Stillstand. Ursache sind Energieverluste durch Reibungs- und Dämpfungskräfte:
3 Zweidimensionale dynamische Systeme Oszillationen
 3 Zweidimensionale dynamische Systeme Oszillationen Lineare Systeme Ein Beispiel für ein zweidimensionales dynamisches System ist die Gleichung ẍ + ω 2 sin x = 0 für ebene Schwingungen eines reibungsfreien
3 Zweidimensionale dynamische Systeme Oszillationen Lineare Systeme Ein Beispiel für ein zweidimensionales dynamisches System ist die Gleichung ẍ + ω 2 sin x = 0 für ebene Schwingungen eines reibungsfreien
Poincaré-Schnitte. Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert
 Poincaré-Schnitte Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert Themen 1. Was sind Poincaré-Schnitte?. Anwendung: Poincaré-Schnitte Mathematica-Beispiel: Attraktor
Poincaré-Schnitte Ein Vortrag im Rahmen des Proseminars Theoretische Physik von Kai Hühn und Robin Mevert Themen 1. Was sind Poincaré-Schnitte?. Anwendung: Poincaré-Schnitte Mathematica-Beispiel: Attraktor
8 Freie Schwingungen kontinuierlicher Systeme
 51 Freie Schwingungen sind Lösungen der partiellen Differentialgleichung gegebene Anfangs- und Randbedingungen. Das Vorgehen ist die eindimensionale Wellengleichung und die Balkenbiegung einheitlich und
51 Freie Schwingungen sind Lösungen der partiellen Differentialgleichung gegebene Anfangs- und Randbedingungen. Das Vorgehen ist die eindimensionale Wellengleichung und die Balkenbiegung einheitlich und
8. Periodische Bewegungen
 8. Periodische Bewegungen 8.1 Schwingungen 8.1.1 Harmonische Schwingung 8.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 8.1.4 Erzwungene Schwingung 8. Periodische Bewegungen Schwingung Zustand y wiederholt
8. Periodische Bewegungen 8.1 Schwingungen 8.1.1 Harmonische Schwingung 8.1.2 Schwingungsenergie 9.1.3 Gedämpfte Schwingung 8.1.4 Erzwungene Schwingung 8. Periodische Bewegungen Schwingung Zustand y wiederholt
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Einführung in die Physik I. Schwingungen und Wellen 1
 Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Einführung in die Physik I Schwingungen und Wellen O. von der Lühe und U. Landgraf Schwingungen Periodische Vorgänge spielen in eine große Rolle in vielen Gebieten der Physik E pot Schwingungen treten
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen
 Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Physik III im Studiengang Elektrotechnik
 Physik III im Studiengang Elektrotechnik - harmonische Schwingungen - Prof. Dr. Ulrich Hahn WS 216/17 kinematische Beschreibung Auslenkungs Zeit Verlauf: ( t) ˆ cost Projektion einer gleichförmigen Kreisbewegung
Physik III im Studiengang Elektrotechnik - harmonische Schwingungen - Prof. Dr. Ulrich Hahn WS 216/17 kinematische Beschreibung Auslenkungs Zeit Verlauf: ( t) ˆ cost Projektion einer gleichförmigen Kreisbewegung
Systeme gewöhnlicher Di erentialgleichungen. Ordnung
 Systeme gewöhnlicher Di erentialgleichungen. Ordnung Systeme. Ordnung De nition Für eine gegebene n n-matrix A(x) =(a ij (x)) n i,j=, deren Elemente Funktionen von x sind und einer gegebenen rechten Seite
Systeme gewöhnlicher Di erentialgleichungen. Ordnung Systeme. Ordnung De nition Für eine gegebene n n-matrix A(x) =(a ij (x)) n i,j=, deren Elemente Funktionen von x sind und einer gegebenen rechten Seite
Physik mit dem PC. Von Dr. rer. nat. Ingo Bull Christian-Albrechts-Universität zu Kiel
 Physik mit dem PC Von Dr. rer. nat. Ingo Bull Christian-Albrechts-Universität zu Kiel B.G.Teubner Stuttgart Leipzig 1998 Inhalt 1 Einleitung 11 2 PC-Interfacetechnik 13 2.1 ADT-Interface am Enhanced Parallel
Physik mit dem PC Von Dr. rer. nat. Ingo Bull Christian-Albrechts-Universität zu Kiel B.G.Teubner Stuttgart Leipzig 1998 Inhalt 1 Einleitung 11 2 PC-Interfacetechnik 13 2.1 ADT-Interface am Enhanced Parallel
Rechenmethoden der Physik I (WS )
 Rechenmethoden der Physik I (WS 2009-2010) Vektoren Allgemeines: Kartesische Koordinaten. Komponenten, Vektoraddition, Einheitsvektoren Skalarprodukt: geometrische Bedeutung, Orthogonalität, Kronecker-Delta
Rechenmethoden der Physik I (WS 2009-2010) Vektoren Allgemeines: Kartesische Koordinaten. Komponenten, Vektoraddition, Einheitsvektoren Skalarprodukt: geometrische Bedeutung, Orthogonalität, Kronecker-Delta
Formelzusammenstellung
 Übung zu Mechanik 4 - ormelsammlung Seite 4 ormelzusammenstellung. Grundbegriffe Harmonische Schwingung Sinusschwingung: (t) sin ( t + ϕ) Schwingungsamplitude: Kreisfrequenz: Phasenwinkel: requenz: f Schwingungsdauer,
Übung zu Mechanik 4 - ormelsammlung Seite 4 ormelzusammenstellung. Grundbegriffe Harmonische Schwingung Sinusschwingung: (t) sin ( t + ϕ) Schwingungsamplitude: Kreisfrequenz: Phasenwinkel: requenz: f Schwingungsdauer,
Kleine Schwingungen vieler Freiheitsgrade
 Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
Kleine Schwingungen vieler Freiheitsgrade Betrachte System mit f Freiheitsgraden: (z.b. N Teilchen in 3 Dim.: f = 3N) Koordinaten: Geschwindigkeiten: Kinetische Energie: "Massenmatrix" Nebenbemerkung:
ÜBUNGSAUFGABEN PHYSIK SCHWINGUNGEN KAPITEL S ZUR. Institut für Energie- und Umwelttechnik Prof. Dr. Wolfgang Kohl UND WELLEN.
 ÜBUNGSAUFGABEN ZUR PHYSIK KAPITEL S SCHWINGUNGEN UND WELLEN Institut für Energie- und Umwelttechnik Prof. Dr. Wolfgang Kohl IEUT 10/05 Kohl 1. Schwingungen 10/2005-koh 1. Welche Auslenkung hat ein schwingender
ÜBUNGSAUFGABEN ZUR PHYSIK KAPITEL S SCHWINGUNGEN UND WELLEN Institut für Energie- und Umwelttechnik Prof. Dr. Wolfgang Kohl IEUT 10/05 Kohl 1. Schwingungen 10/2005-koh 1. Welche Auslenkung hat ein schwingender
Lehrgang der höheren Mathematik
 Lehrgang der höheren Mathematik Teil 1V/2 von W. I. Smirnow Mit 16 Abbildungen /-. \ D W VEB Deutscher Verlag der Wissenschaften Berlin 1989 Inhalt I. Allgemeine Theorie der partiellen Differentialgleichungen
Lehrgang der höheren Mathematik Teil 1V/2 von W. I. Smirnow Mit 16 Abbildungen /-. \ D W VEB Deutscher Verlag der Wissenschaften Berlin 1989 Inhalt I. Allgemeine Theorie der partiellen Differentialgleichungen
Regelungstechnik für Ingenieure
 Manfred Reuter Regelungstechnik für Ingenieure 7., überarbeitete und erweiterte Auflage Mit 322 Bildern Friedr. Vieweg & Sohn Braunschweig/Wiesbaden Inhaltsverzeichnis Formelzeichen 1 Einführung 1 1.1
Manfred Reuter Regelungstechnik für Ingenieure 7., überarbeitete und erweiterte Auflage Mit 322 Bildern Friedr. Vieweg & Sohn Braunschweig/Wiesbaden Inhaltsverzeichnis Formelzeichen 1 Einführung 1 1.1
Der Duffing-Oszillator
 11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
11.04.2006 Inhalt Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile Ruhelagen. Inhalt Erwartung im stationären Fall: eine instabile Ruhelage, zwei asymptotisch stabile
Versuch 3.14: Resonanzverhalten Nichtlinearer Oszillatoren
 Physikalisches Praktikum für Fortgeschrittene Technische Hochschule Darmstadt Abteilung A: Institut für Angewandte Physik Versuch 3.14: Resonanzverhalten Nichtlinearer Oszillatoren Vorbereitung: Resonanz,
Physikalisches Praktikum für Fortgeschrittene Technische Hochschule Darmstadt Abteilung A: Institut für Angewandte Physik Versuch 3.14: Resonanzverhalten Nichtlinearer Oszillatoren Vorbereitung: Resonanz,
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Baudynamik (Master) SS 2014
 Baudynamik (Master) SS 14 3. Schwingungen mit zwei und mehr Freiheitsgraden 3.1 Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.1.1 Einige Prinzipien der Mechanik 3.1. Herleitung
Baudynamik (Master) SS 14 3. Schwingungen mit zwei und mehr Freiheitsgraden 3.1 Einige Prinzipien der Mechanik und Herleitung der Schwingungsgleichungen 3.1.1 Einige Prinzipien der Mechanik 3.1. Herleitung
Differentialgleichungen
 Differentialgleichungen Eine Einführung unter besonderer Berücksichtigung der Anwendungen Von Dr. phil. Dr. h. c. mult. Lothar Collatz em. o. Professor an der Universität Hamburg 6., überarbeitete und
Differentialgleichungen Eine Einführung unter besonderer Berücksichtigung der Anwendungen Von Dr. phil. Dr. h. c. mult. Lothar Collatz em. o. Professor an der Universität Hamburg 6., überarbeitete und
Skript zum Ferienkurs Experimentalphysik 1
 Skript zum Ferienkurs Experimentalphysik 1 Christoph Buhlheller, Rebecca Saive, David Franke Florian Hrubesch, Wolfgang Simeth, Wolfhart Feldmeier 17. Februar 009 Inhaltsverzeichnis 1 Einleitung: Schwingungen
Skript zum Ferienkurs Experimentalphysik 1 Christoph Buhlheller, Rebecca Saive, David Franke Florian Hrubesch, Wolfgang Simeth, Wolfhart Feldmeier 17. Februar 009 Inhaltsverzeichnis 1 Einleitung: Schwingungen
Hochschule Düsseldorf University of Applied Sciences. 22. Dezember 2016 HSD. Physik. Schwingungen
 Physik Schwingungen Zusammenfassung Mechanik Physik Mathe Einheiten Bewegung Bewegung 3d Newtons Gesetze Energie Gravitation Rotation Impuls Ableitung, Integration Vektoren Skalarprodukt Gradient Kreuzprodukt
Physik Schwingungen Zusammenfassung Mechanik Physik Mathe Einheiten Bewegung Bewegung 3d Newtons Gesetze Energie Gravitation Rotation Impuls Ableitung, Integration Vektoren Skalarprodukt Gradient Kreuzprodukt
Schwingungen. Harmonische Schwingungen. t Anharmonische Schwingungen. S. Alexandrova FDIBA TU Sofia 1
 Schwingungen Harmonische Schwingungen x t Anharmonische Schwingungen x x t S. Alexandrova FDIBA TU Sofia 1 t ANHARMONISCHE SCHWINGUNGEN EHB : Kraft F = -k(x-x o ) Potentielle Energie: E p E p Parabel mit
Schwingungen Harmonische Schwingungen x t Anharmonische Schwingungen x x t S. Alexandrova FDIBA TU Sofia 1 t ANHARMONISCHE SCHWINGUNGEN EHB : Kraft F = -k(x-x o ) Potentielle Energie: E p E p Parabel mit
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
