MATHEMATIK UND VERSICHERUNGEN EINE ALLIANZ FÜRS LEBEN. Mitglied im DFG-Forschungszentrum Mathematik für Schlüsseltechnologien
|
|
|
- David Schulze
- vor 8 Jahren
- Abrufe
Transkript
1 MATHEMATIK UND VERSICHERUNGEN EINE ALLIANZ FÜRS LEBEN Teilnehmer: Thomas Benkert Sebastian Flach Wolfgang Schmidt Philip Wanninger Sebastian Schubert Gruppenleiter: Peggy Daume Graf-Münster-Gymnasium Graf-Münster-Gymnasium Graf-Münster-Gymnasium Graf-Münster-Gymnasium Andreas-Oberschule Humboldt-Universität, Mitglied im DFG-Forschungszentrum Mathematik für Schlüsseltechnologien Nach einer Einführung in die wirtschaftliche Welt der Versicherungen beschäftigte sich unsere Gruppe zunächst mit wahrscheinlichkeitstheoretischen Grundlagen. Dabei beschränkten wir uns auf die Begrie der Zufallsgröÿe, des Erwartungswertes, der Varianz und des fairen Spiels. Der Erwartungswert und das faire Spiel begegneten uns wieder im Äquivalenzprinzip, mit dem die Berechnung einer Nettoprämie für eine Lebensversicherung auf den Erlebensfall und für eine Versicherung auf den Todesfall erfolgte. Als nützliches Werkzeug zur Bestimmung der für die Nettoprämie notwendigen Todesund Überlebenswahrscheinlichkeiten lernten wir dabei Sterbetafeln kennen. 1
2 Mathematik und Versicherungen eine Allianz fürs Leben 1 Juristische Denition Versicherungsgeschäfte betreibt, wer, ohne daÿ ein innerer Zusammenhang mit einem Rechtsgeschäft anderer Art besteht, gegen Entgelt verpichtet ist ein wirtschaftliches Risiko dergestalt zu übernehmen, daÿ er a) anderen vermögenswerte Leistungen zu erbringen hat, wenn sich eine für deren wirtschaftliche Verhältnisse nachteilige, ihren Eintritt nach ungewisse Tatsache ereignet, um die dadurch verursachten Nachteile auszugleichen, oder b) anderen vermögenswerte Leistungen zu erbringen hat, wobei es von der Dauer des Lebens oder dem Eintritt oder dem Nichteintritt einer Tatsache im Laufe des menschlichen Lebens abhängt, ob oder wann in welchem Umfang zu leisten oder wie hoch das Entgelt ist, sofern der Risikoübernahme einer Kalkulation zugrunde liegt, wonach die dazu erforderlichen Mittel ganz oder im wesentlichen ganz durch die Gesamtheit der Entgelte aufgebracht werden. (Versicherungsaufsichtsgesetz) Aus der oben aufgeführten Denition ist zu erkennen, dass Versicherungen ungewisse/unvorhersehbare Ereignisse enthalten. Aus diesem Grund beschäftigten wir uns zunächst mit wahrscheinlichkeitstheoretischen Begrien und Denitionen. 2
3 2 Einführung in die Wahrscheinlichkeitstheorie 2.1 Zufallsgröÿen Sei Ω die Ergebnismenge eines Vorganges mit zufälligem Ergebnis. Eine Funktion X : Ω R heiÿt Zufallsgröÿe. Dabei wird jedem Ergebnis ω aus der Ergebnismenge Ω durch die Zufallsgröÿe X eine reelle Zahl X(ω) zugeordnet. Durch Zufallsgröÿen werden also messbare, in Zahlen ausdrückbare Eigenschaften der Ergebnisse erfasst. Die Verteilungen von Zufallsgröÿen werden meist in Tabellenform angegeben. Beispiel: Der Gewinnplan eines Würfelspiels sieht vor, nach dem Werfen dreier Würfel 2,00 auszuzahlen, wenn genau eine Sechs erscheint, 4,00 zu zahlen, wenn genau zwei Sechsen fallen und 8,00 zu zahlen, wenn alle drei Würfel eine Sechs zeigen. Der Einsatz des Spiels beträgt 1,20. In der folgenden Tabelle sind alle möglichen Werte des Nettogewinns (Dierenz von Auszahlung und Einsatz) und die dazugehörigen Wahrscheinlichkeiten angegeben. Nettogewinn in 1, 20 0, 80 2, 20 6, Wahrscheinlichkeit Eigenschaften einer Wahrscheinlichkeitsverteilung: Für alle A Ω P (Ω) = 1 P ( ) = 0 P (A) = 1 P (A) 2.2 Erwartungswert einer Zufallsgröÿe Wir betrachten erneut unser Beispiel mit den Würfeln und interessieren uns für folgendes Problem: Wie groÿ ist der durchschnittliche Nettogewinn, den man erzielen kann? Als Durchschnittswert aus vielen Beobachtungen ergibt sich in unserem Beispiel die Vorhersage: E(G) = 1, , , , = 0, 19. Der Spieler verliert im Schnitt pro Spiel 0,19. Dieser Durchschnittswert kann auch als Erwartungswert angesehen werden. 3
4 Denition: Sei X eine Zufallsgröÿe mit der folgenden Verteilung. X = x i x 1 x 2... x n P (X = x i ) p 1 p 2... p n Die Zahl E(X) = x 1 p 1 +x 2 p x n p n heiÿt Erwartungswert der Zufallsgröÿe X. Ein Spiel heiÿt fair, wenn der Erwartungswert E(X) des Reingewinns null ist. Andernfalls heiÿt das Spiel günstig oder ungünstig für den Spieler. Generell Ist E(G) > 0, so ist das Spiel für den Spieler günstig. Ist E(G) < 0, so ist das spiel für den Spieler ungünstig. Ist E(G) = 0, so ist das Spiel fair. Daraus folgt: In unserem Beispiel handelt es sich um ein für den Spieler ungünstiges Spiel. Eigenschaften des Erwartungswertes: Es seien X und Y Zufallsgröÿen. Dann gilt für alle a, b R: E(aX + b) = ae(x) + b, E(X + Y ) = E(X) + E(Y ). 2.3 Varianz einer Zufallsgröÿe Der Vollständigkeit halber denieren wir den Begri der Varianz einer Zufallsgröÿe, auch wenn diese nicht für die Versicherungsmathematik benötigt wird. Denition: Es sei X eine Zufallsgröÿe mit folgender Verteilung. X = x i x 1 x 2... x n P (X = x i ) p 1 p 2... p n Die Zahl V ar(x) = (x 1 E(X)) 2 p 1 + (x 2 E(X)) 2 p (x n E(X)) 2 p n heiÿt Varianz von X. σ = V ar(x) heiÿt Standardabweichung. 4
5 3 Arten der Lebensversicherung In der Lebensversicherungsmathematik unterscheidet man Versicherungen auf den Todesfall, auf den Erlebensfall sowie Mischformen beider. 1. Versicherungen auf den Todesfall Absicherung der Hinterbliebenen Versicherungsleistung wird fällig, wenn der Versicherungsnehmer innerhalb des Versicherungszeitraums stirbt 2. Versicherung auf den Erlebensfall Absicherung des Versicherungsnehmers Versicherungsleistung wird fällig, wenn der Versicherungsnehmer den Versicherungszeitraum überlebt 3. Gemischte kapitalbildende Lebensversicherung Mischform aus Versicherung auf Erlebens- und Todesfall 4 Sterbetafeln Bei einer Risiko- oder Kapitallebensversicherung hängen der Leistungsumfang der Versicherungen und die Zahlungsleistungen der Versicherungsnehmer vom zufälligen Zeitpunkt seines Todes ab. Bsp: Frau X: 40 Jahre alt, schlieÿt eine Lebensversicherung auf den Todesfall mit 2 Jahren Laufzeit und einer Versicherungssumme über ab. Den Betrag zahlt sie jährlich im Voraus. Wird die Versicherungsumme fällig, dann erfolgt die Zahlung üblicherweise am Ende des Versicherungsjahres. Für das Zufallsgeschehen sind folgende drei Szenarien denkbar: a) Frau X stirbt im 1. Jahr: 1 Jahresbeitrag bezahlt Versicherung zahlt nach 1 Jahr b) Frau X stirbt im 2. Jahr: 2 Jahresbeiträge bezahlt Versicherung zahlt nach zwei Jahren
6 c) Frau X stirbt nicht: 2 Jahresbeiträge bezahlt Versicherung zahlt nichts Die (erwartete) Gröÿe der zu zahlenden Versicherungsleistungen und der eingenommen Prämien berechnen wir mit Hilfe von Wahrscheinlichkeitsaussagen über die zufällige Lebensdauer der Menschen, die in sogenannten Sterbetafeln verankert sind. Da die zufällige Lebensdauer abhängig vom Geschlecht ist, gibt es Sterbetafeln für Männer und Frauen. Weitere Einussfaktoren (Gesundheitszustand, Region,...) bleiben meist unberücksichtigt. Die Sterbewahrscheinlichkeiten in den Sterbetafeln beruhen auf statistische Beobachtungen. 4.1 Die Bedeutung von q x und q y Die Sterbetafel (siehe Anhang) gibt zu jedem Alter x bzw. y und getrennt nach Geschlechtern (x = Männer, y = Frauen) die einjährige Sterbewahrscheinlichkeit q x bzw. q y dafür an, dass eine x-jährige (bzw. y-jährige) Person das Alter x + 1 bzw. y +1 nicht erreicht. (Achtung: In der Versicherungsmathematik geben x und y sowohl das Alter als auch das Geschlecht an.) Gibt T x die zufällige restliche Lebensdauer (es wird immer in ganzen Jahren gerechnet) ab dem Alter x an, so q x = P (T x < 1). Mit Hilfe der Regeln der Wahrscheinlichkeitsberechnung erhalten wir unsere einjährige Lebenswahrscheinlichkeit mit p x = 1 q x P (T x 1) = 1 P (T x < 1). Verträglichkeitsannahme: Die Wahrscheinlichkeit, dass ein x-jähriger das Alter s + t erreicht, ergibt sich als Produkt der Wahrscheinlichkeiten, dass er zunächst s Jahre überlebt und dann als x + s jähriger noch mindestens t weitere Jahre überlebt. Wir vereinbaren für die n-jährige Überlebenswahrscheinlichkeit die Schreibweise n p x. Für eine beliebige n-jährige Überlebenswahrscheinlichkeit gilt nach der Verträglichkeitsbedingung: np x = 1 p x 1 p x p x+n 1. 6
7 Die erwartete Anzahl der Lebenden des Alters x wird durch l x und l y beschrieben. Dabei wird von anfangs Neugeborenen ausgegangen. Es l x = x p 0. Zwischen l x und n p x gilt folgender Zusammenhang: Für beliebige Überlebenswahrscheinlichkeiten l x+n = l x n p x. (1) 5 Äquivalenzprinzip Die zentrale Frage unserer Untersuchungen lautete: Wie hoch sollen die Beträge der Versicherten sein, die jetzt im Voraus zu zahlen sind, damit sie den in der Zukunft liegenden Gegenleistungen des Versicherers mit hoher Wahrscheinlichkeit entsprechen? Man berechnet diesen Teil der LV-Prämie, die Nettoprämie, indem man von einem fairen Spiel ausgeht, das Gewinne und Kosten des Versicherungsunternehmens vernachlässigt. Summe der Prämie aller Versicherten eines LV-Unternehmens = Summe der Zahlungen des LV- Unternehmens an die betroenen Versicherten Als Grundlagen der Kalkulation der Nettoprämie dienen die folgenden Modellannahmen: Die Nettoprämie ist proportional zur Versicherungssumme. Diese wiederum wird vereinbart und ihre Auszahlung ist nicht an eine Schadenshöhe gebunden. Um die diversen Zahlungen vergleichbar zu machen, werden sie auf einen bestimmten Tag bezogen, sie werden diskontiert. Die Höhe der Nettoprämie ist abhängig vom Risiko und dem Sterbealter der Versicherten. In der Finanzmathematik wird davon ausgegangen, dass Geldbeträge durch Zinsen und Zinseszinsen wachsen. Ein Betrag k 0, der heute zu zahlen ist, hat in n Jahren bei i % Jahreszins den Wert k n = k 0 (1 + i 100 )n := r n k 0. Umgekehrt hat ein Betrag k n, der in n Jahren fällig ist, bei i % Jahreszinssatz heute den Barwert k 0 = kn := v n k r n 0. Die Faktoren r und v werden auch Aufzinsungs- und Abzinsungsfaktoren genannt. 7
8 Beispiel: Frau X, 40 Jahre alt, schlieÿt eine Lebensversicherung auf Todesfall über und mit einer Laufzeit von 2 Jahren ab.die Höhe der von ihr zu zahlenden Prämie sie N. Dann ergibt sich für die Verteilung der Versicherungsleistung und der Prämiezahlung Folgende: restl. Lebensdauer Prämienzahlung N N + N N + N 1,0325 1,0325 Leistung ,0325 Wahrscheinlichkeiten 1, (1,0325) 2 1, ,8 Für die erwarte Prämienleistung E(P 40 ) und die erwartete Versicherungsleistung E(L 40 ) ergibt sich: E(P 40 ) = N 1, (N + N 1, 699 ) 1, (N + N ) 0, 997 = 1, 968N 1, 0325 E(L 40 ) = , 0325 Nach dem Äquivalenzprinzip 1, , 669 (1, 0325) 2 E(L 40 ) = E(P 40 ) 152, 10 = 1, 968N N = 77, 28 = 152, 10 Die Nettoprämie für die Versicherung von Frau X beträgt fairerweise 77,28. Die im Internet für Frau X gefundenen Zahlbeiträge lagen zwischen 76,65 und 175,99. Zum Vergleich erfolgt die Berechnung der Lebensversicherung auf Erlebensfall. Beispiel: Herr Y, 40 Jahre alt, schlieÿt eine Lebensversicherung auf Erlebensfall über und einer Laufzeit von 2 Jahren ab. Dann ergibt sich für die Versicherungsleistung und die Prämienzahlung folgende Verteilung: restl. Lebensdauer Prämienzahlung N N + N N + N 1,0325 1,0325 Leistung (1,0325) 2 Wahrscheinlichkeit 2, ,816 0, 995
9 Die Berechnungen für die erwartete Prämienzahlung bzw. die erwartete Leistung ergeben folgende Werte: E(P 40 ) = 1, 966N E(L 40 ) = N = , 48 Die Nettoprämie beträgt fairerweise ,48. Nachdem wir zunächst einige konkrete Nettoprämien in verschiedenen Beispielen ausgerechnet hatten, gingen wir dazu über, allgemeine Formeln zu entwickeln. 5.1 n-jährige Lebenversicherung auf den Todesfall für eine männliche Person des Alters x Im Folgenden geben wir nur die allgemeinen Formeln zur Berechnung der erwarteten Leistungszahlungen E(L x ) und erwarteten Prämienzahlungen E(P x ) an. Auf eine Herleitung verzichten wir. Zur Berechnung der Nettoprämie muss nach dem Äquivalenzprinzip gelten: E(P x ) = E(L x ). Erklärung der verwendeten Variablen: S : Versicherungsleistung der Versicherung v : Abzinsungsfaktor mit v = 1 i, wobei i Rechnungszinssatz N : Nettoprämie k : abgelaufene Jahre Berechnung der erwarteten Leistungszahlung: Für die erwartete Leistungszahlung n 1 E(L x ) = N v k+1 kp x q x+k. Mit der Beziehung (1) erhalten wir für E(L x ) schlieÿlich: n 1 E(L x ) = N v k+1 (l x+k l x+k+1 ). Berechnung der erwarteten Prämienzahlung: Für die erwartete Prämienzahlung E(P x ) = S 1 n 1 v k l x+k. l x 9
10 5.2 n-jährige Lebenversicherung auf den Erlebensfall für eine männliche Person des Alters x Berechnung der erwarteten Leistungszahlung: Für die erwartete Leistungszahlung E(L x ) = S v n lx+n. l x Berechnung der erwarteten Prämienzahlung: Für die erwartete Prämienzahlung E(P x ) = N 1 n 1 l x v k l x+k. 5.3 n-jährige gemischte Kapitallebensversicherung für eine männliche Person des Alters x Berechnung der erwarteten Leistungszahlung: Ist T die Versicherungsleistung im Todesfall und W ist die Versicherungsleistung im Erlebensfall, so gilt für die erwartete Leistungszahlung: E(L x ) = W v n lx+k + T n 1 v k+1 (l x+k l x+k+1 ). l x l x Berechnung der erwarteten Prämienzahlung: Für die erwartete Prämienzahlung E(P x ) = N 1 n 1 l x v k l x+k. 6 Warum zahlt man mehr als die Nettoprämie? Bei sehr vielen Verträgen würde es mit sehr groÿer Wahrscheinlichkeit mindestens einmal vorkommen, dass die Summe der beanspruchten Leistungen gröÿer ist als die Summe der eingenommenen Prämien. Das Versicherungsunternehmen ist in diesem Fall vom sogenannten versicherungstechnischen Ruin bedroht. Versicherungsunternehmen sind gesetzlich verpichtet sich dagegen zu schützen. Daher werden beispielsweise individuelle Risikozuschläge (für Raucher, bestimmte Vorerkrankungen, Suchtkranke) für die einzelnen Versicherungsverträge eingearbeitet. Diese Risiken sind in Sterbetafeln nicht verankert. Versicherungsverträge verursachen Abschluss- und Verwaltungskosten. Diese Kosten werden bei der Berechnung des Versicherungsbeitrages berücksichtigt. 10
Kapitalversicherungen
 Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor
 Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung (Grundwissen)
 Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Tutorium zur Mathematik (WS 2004/2005) - Finanzmathematik Seite 1
 Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Erläuterungen zu Leitlinien zum Untermodul Krankenversicherungskatastrophenrisiko
 Erläuterungen zu Leitlinien zum Untermodul Krankenversicherungskatastrophenrisiko Die nachfolgenden Ausführungen in deutscher Sprache sollen die EIOPA- Leitlinien erläutern. Während die Leitlinien auf
Erläuterungen zu Leitlinien zum Untermodul Krankenversicherungskatastrophenrisiko Die nachfolgenden Ausführungen in deutscher Sprache sollen die EIOPA- Leitlinien erläutern. Während die Leitlinien auf
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003
 Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Kugel-Fächer-Modell. 1fach. 3fach. Für die Einzelkugel gibt es 3 Möglichkeiten. 6fach. 3! Möglichkeiten
 Kugel-Fächer-Modell n Kugeln (Rosinen) sollen auf m Fächer (Brötchen) verteilt werden, zunächst 3 Kugeln auf 3 Fächer. 1fach 3fach Für die Einzelkugel gibt es 3 Möglichkeiten } 6fach 3! Möglichkeiten Es
Kugel-Fächer-Modell n Kugeln (Rosinen) sollen auf m Fächer (Brötchen) verteilt werden, zunächst 3 Kugeln auf 3 Fächer. 1fach 3fach Für die Einzelkugel gibt es 3 Möglichkeiten } 6fach 3! Möglichkeiten Es
Lösungshinweise zur Einsendearbeit 2 SS 2011
 Lösungshinweise zur Einsendearbeit 2 zum Kurs 41500, Finanzwirtschaft: Grundlagen, SS2011 1 Lösungshinweise zur Einsendearbeit 2 SS 2011 Finanzwirtschaft: Grundlagen, Kurs 41500 Aufgabe Finanzierungsbeziehungen
Lösungshinweise zur Einsendearbeit 2 zum Kurs 41500, Finanzwirtschaft: Grundlagen, SS2011 1 Lösungshinweise zur Einsendearbeit 2 SS 2011 Finanzwirtschaft: Grundlagen, Kurs 41500 Aufgabe Finanzierungsbeziehungen
Tutorial: Homogenitätstest
 Tutorial: Homogenitätstest Eine Bank möchte die Kreditwürdigkeit potenzieller Kreditnehmer abschätzen. Einerseits lebt die Bank ja von der Vergabe von Krediten, andererseits verursachen Problemkredite
Tutorial: Homogenitätstest Eine Bank möchte die Kreditwürdigkeit potenzieller Kreditnehmer abschätzen. Einerseits lebt die Bank ja von der Vergabe von Krediten, andererseits verursachen Problemkredite
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Inhaltsübersicht Produktinformationsblatt zur Jahres-Reiserücktritts-Versicherung der Europäische Reiseversicherung AG
 Inhaltsübersicht Produktinformationsblatt zur Jahres-Reiserücktritts-Versicherung der Europäische Reiseversicherung AG 1. Produktinformationsblatt zur Jahres-Reiserücktritts-Versicherung mit Selbstbeteiligung
Inhaltsübersicht Produktinformationsblatt zur Jahres-Reiserücktritts-Versicherung der Europäische Reiseversicherung AG 1. Produktinformationsblatt zur Jahres-Reiserücktritts-Versicherung mit Selbstbeteiligung
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT
 GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Verteilungsmodelle. Verteilungsfunktion und Dichte von T
 Verteilungsmodelle Verteilungsfunktion und Dichte von T Survivalfunktion von T Hazardrate von T Beziehungen zwischen F(t), S(t), f(t) und h(t) Vorüberlegung zu Lebensdauerverteilungen Die Exponentialverteilung
Verteilungsmodelle Verteilungsfunktion und Dichte von T Survivalfunktion von T Hazardrate von T Beziehungen zwischen F(t), S(t), f(t) und h(t) Vorüberlegung zu Lebensdauerverteilungen Die Exponentialverteilung
Bereicherungsrecht Fall 2
 G hat bei der S-AG eine Lebensversicherung ihv. 300.000 abgeschlossen, als deren BegünsBgte seine Frau D benannt ist. Als die Finanzierung des gerade erworbenen Eigenheims die Möglichkeiten des G zu übersteigen
G hat bei der S-AG eine Lebensversicherung ihv. 300.000 abgeschlossen, als deren BegünsBgte seine Frau D benannt ist. Als die Finanzierung des gerade erworbenen Eigenheims die Möglichkeiten des G zu übersteigen
y 1 2 3 4 5 6 P (Y = y) 1/6 1/6 1/6 1/6 1/6 1/6
 Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Statistik für Prüfungskandidaten und Prüfungskandidatinnen Unabhängigkeit
Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Statistik für Prüfungskandidaten und Prüfungskandidatinnen Unabhängigkeit
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Swiss Life Vorsorge-Know-how
 Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Im weiteren werden die folgenden Bezeichnungen benutzt: Zinsrechnung
 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
.DXIPlQQLVFKHV5HFKQHQ =LQVUHFKQHQ. Für jeden Kaufmann unentbehrlich und vielseitig einsetzbar ist die Zinsrechnung. :DVVLQG=LQVHQ"
 =LQVUHFKQHQ Für jeden Kaufmann unentbehrlich und vielseitig einsetzbar ist die Zinsrechnung. :DVVLQG=LQVHQ" =LQV =LQVVDW]=LQVIX =HLW -DKU 0RQDW der Preis für die Nutzung eines Kapitals während einer bestimmten
=LQVUHFKQHQ Für jeden Kaufmann unentbehrlich und vielseitig einsetzbar ist die Zinsrechnung. :DVVLQG=LQVHQ" =LQV =LQVVDW]=LQVIX =HLW -DKU 0RQDW der Preis für die Nutzung eines Kapitals während einer bestimmten
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit
 Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
Eva Douma: Die Vorteile und Nachteile der Ökonomisierung in der Sozialen Arbeit Frau Dr. Eva Douma ist Organisations-Beraterin in Frankfurt am Main Das ist eine Zusammen-Fassung des Vortrages: Busines
Merkblatt Rentenversicherung
 Merkblatt Rentenversicherung Von einer privaten Rentenversicherung ist besonders jungen Leuten abzuraten. Allenfalls für Ältere um die 60 Jahre kann sich eine Rentenversicherung per Einmalzahlung lohnen,
Merkblatt Rentenversicherung Von einer privaten Rentenversicherung ist besonders jungen Leuten abzuraten. Allenfalls für Ältere um die 60 Jahre kann sich eine Rentenversicherung per Einmalzahlung lohnen,
Statistik I für Betriebswirte Vorlesung 5
 Statistik I für Betriebswirte Vorlesung 5 PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik 07. Mai 2015 PD Dr. Frank Heyde Statistik I für Betriebswirte Vorlesung 5 1 Klassische Wahrscheinlichkeitsdefinition
Statistik I für Betriebswirte Vorlesung 5 PD Dr. Frank Heyde TU Bergakademie Freiberg Institut für Stochastik 07. Mai 2015 PD Dr. Frank Heyde Statistik I für Betriebswirte Vorlesung 5 1 Klassische Wahrscheinlichkeitsdefinition
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
Das Persönliche Budget in verständlicher Sprache
 Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Das Persönliche Budget in verständlicher Sprache Das Persönliche Budget mehr Selbstbestimmung, mehr Selbstständigkeit, mehr Selbstbewusstsein! Dieser Text soll den behinderten Menschen in Westfalen-Lippe,
Was meinen die Leute eigentlich mit: Grexit?
 Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Was meinen die Leute eigentlich mit: Grexit? Grexit sind eigentlich 2 Wörter. 1. Griechenland 2. Exit Exit ist ein englisches Wort. Es bedeutet: Ausgang. Aber was haben diese 2 Sachen mit-einander zu tun?
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Themenschwerpunkt Sofortrente
 Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Kapitel 8.3: Kalkulation vom Hundert und im Hundert. Kapitel 8.4: Durchführung der Absatzkalkulation an einem Beispiel
 1 von 7 04.10.2010 15:59 Hinweis: Diese Druckversion der Lerneinheit stellt aufgrund der Beschaffenheit des Mediums eine im Funktionsumfang stark eingeschränkte Variante des Lernmaterials dar. Um alle
1 von 7 04.10.2010 15:59 Hinweis: Diese Druckversion der Lerneinheit stellt aufgrund der Beschaffenheit des Mediums eine im Funktionsumfang stark eingeschränkte Variante des Lernmaterials dar. Um alle
Ein gutes Gefühl, an alles gedacht zu haben. Die SV SterbegeldPolice.
 S V S t e r b eg e l d P o l i c e Ein gutes Gefühl, an alles gedacht zu haben. Die SV SterbegeldPolice. Was auch passiert: Sparkassen-Finanzgruppe www.sparkassenversicherung.de Sparkassen-Finanzgruppe
S V S t e r b eg e l d P o l i c e Ein gutes Gefühl, an alles gedacht zu haben. Die SV SterbegeldPolice. Was auch passiert: Sparkassen-Finanzgruppe www.sparkassenversicherung.de Sparkassen-Finanzgruppe
Vertical-Spreads Iron Condor Erfolgsaussichten
 www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
www.mumorex.ch 08.03.2015 1 Eigenschaften Erwartung Preis Long Calls Long Puts Kombination mit Aktien Vertical-Spreads Iron Condor Erfolgsaussichten www.mumorex.ch 08.03.2015 2 www.mumorex.ch 08.03.2015
Damit auch Sie den richtigen Weg nehmen können die 8 wichtigsten Punkte, die Sie bei der Beantragung Ihrer Krankenversicherung beachten sollten:
 Damit auch Sie den richtigen Weg nehmen können die 8 wichtigsten Punkte, die Sie bei der Beantragung Ihrer Krankenversicherung beachten sollten: Herzlich Willkommen bei der mehr-finanz24 GmbH Mit uns haben
Damit auch Sie den richtigen Weg nehmen können die 8 wichtigsten Punkte, die Sie bei der Beantragung Ihrer Krankenversicherung beachten sollten: Herzlich Willkommen bei der mehr-finanz24 GmbH Mit uns haben
 Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Download. Führerscheine Zinsrechnung. Schnell-Tests zur Lernstandserfassung. Jens Conrad, Hardy Seifert. Downloadauszug aus dem Originaltitel:
 Download Jens Conrad, Hardy Seifert Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung Downloadauszug aus dem Originaltitel: Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung
Download Jens Conrad, Hardy Seifert Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung Downloadauszug aus dem Originaltitel: Führerscheine Zinsrechnung Schnell-Tests zur Lernstandserfassung
Universität Bonn 28. Juli 2010 Fachbereich Rechts- und Wirtschaftswissenschaften Statistische Abteilung Prof. Dr. A. Kneip. KLAUSUR Statistik B
 Universität Bonn 28. Juli 2010 Fachbereich Rechts- und Wirtschaftswissenschaften Statistische Abteilung Prof. Dr. A. Kneip Sommersemester 2010 KLAUSUR Statistik B Hinweise zur Bearbeitung: Bei allen Teilaufgaben
Universität Bonn 28. Juli 2010 Fachbereich Rechts- und Wirtschaftswissenschaften Statistische Abteilung Prof. Dr. A. Kneip Sommersemester 2010 KLAUSUR Statistik B Hinweise zur Bearbeitung: Bei allen Teilaufgaben
Südbaden-Cup. Ausstieg Champions
 Südbaden-Cup Ausstieg Champions Beschreibung Der Ausstieg aus dem Turnier dient Spielern die eine weite Anreise haben sich aus dem Turnier zu verabschieden um noch am gleichen Tag heimzureisen und einen
Südbaden-Cup Ausstieg Champions Beschreibung Der Ausstieg aus dem Turnier dient Spielern die eine weite Anreise haben sich aus dem Turnier zu verabschieden um noch am gleichen Tag heimzureisen und einen
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Kapitalversicherungen
 Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Übungsaufgaben Tilgungsrechnung
 1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
Finanzmathematik. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.
 Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
PKV-Info. Lohnt der Wechsel innerhalb der PKV?
 PKV-Info Lohnt der Wechsel innerhalb der PKV? 2 Die Unternehmen der privaten Krankenversicherung (PKV) stehen miteinander im Wettbewerb. Das ist so gewollt, zum Nutzen der Versicherten. Denn jeder Wettbewerb
PKV-Info Lohnt der Wechsel innerhalb der PKV? 2 Die Unternehmen der privaten Krankenversicherung (PKV) stehen miteinander im Wettbewerb. Das ist so gewollt, zum Nutzen der Versicherten. Denn jeder Wettbewerb
Lebensversicherung. http://www.konsument.at/cs/satellite?pagename=konsument/magazinartikel/printma... OBJEKTIV UNBESTECHLICH KEINE WERBUNG
 Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
3.3. Aufgaben zur Binomialverteilung
 .. Aufgaben zur Binomialverteilung Aufgabe 1: Ziehen mit Zurücklegen und Binomialverteilung Ein sechsseitiger Würfel wird zehnmal geworfen. a) Wie groß ist die Wahrscheinlichkeit, nur beim ersten Mal die
.. Aufgaben zur Binomialverteilung Aufgabe 1: Ziehen mit Zurücklegen und Binomialverteilung Ein sechsseitiger Würfel wird zehnmal geworfen. a) Wie groß ist die Wahrscheinlichkeit, nur beim ersten Mal die
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Kapitalerhöhung - Verbuchung
 Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
Kapitalerhöhung - Verbuchung Beschreibung Eine Kapitalerhöhung ist eine Erhöhung des Aktienkapitals einer Aktiengesellschaft durch Emission von en Aktien. Es gibt unterschiedliche Formen von Kapitalerhöhung.
MI - Mission Impossible Sind Sie gut versichert? Ein kurzes Beispiel zur Versicherungsmathematik
 MI - Mission Impossible Sind Sie gut versichert? Ein kurzes Beispiel zur Versicherungsmathematik Seite 1 Vorstellung Organisation: Deutsche Aktuarvereinigung e.v. (DAV) berufsständische Vertretung der
MI - Mission Impossible Sind Sie gut versichert? Ein kurzes Beispiel zur Versicherungsmathematik Seite 1 Vorstellung Organisation: Deutsche Aktuarvereinigung e.v. (DAV) berufsständische Vertretung der
Profil A 49,3 48,2 50,7 50,9 49,8 48,7 49,6 50,1 Profil B 51,8 49,6 53,2 51,1 51,1 53,4 50,7 50 51,5 51,7 48,8
 1. Aufgabe: Eine Reifenfirma hat für Winterreifen unterschiedliche Profile entwickelt. Bei jeweils gleicher Geschwindigkeit und auch sonst gleichen Bedingungen wurden die Bremswirkungen gemessen. Die gemessenen
1. Aufgabe: Eine Reifenfirma hat für Winterreifen unterschiedliche Profile entwickelt. Bei jeweils gleicher Geschwindigkeit und auch sonst gleichen Bedingungen wurden die Bremswirkungen gemessen. Die gemessenen
Übung 2 Erfolgsrechnung
 Controlling in deutschen Unternehmen Übung 2 Erfolgsrechnung Dipl.-Kfm. Florian Böckling, MBA Dipl.-Kfm. Franz Zinser, MBA Lehrstuhl für Controlling Prof. Dr. Louis Velthuis Johannes Gutenberg-Universität
Controlling in deutschen Unternehmen Übung 2 Erfolgsrechnung Dipl.-Kfm. Florian Böckling, MBA Dipl.-Kfm. Franz Zinser, MBA Lehrstuhl für Controlling Prof. Dr. Louis Velthuis Johannes Gutenberg-Universität
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN
 HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
HIER GEHT ES UM IHR GUTES GELD ZINSRECHNUNG IM UNTERNEHMEN Zinsen haben im täglichen Geschäftsleben große Bedeutung und somit auch die eigentliche Zinsrechnung, z.b: - Wenn Sie Ihre Rechnungen zu spät
Korrigenda Handbuch der Bewertung
 Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
16 Risiko und Versicherungsmärkte
 16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Auftrag zum Fondswechsel
 Lebensversicherung von 1871 a.g. München Postfach 80326 München Auftrag zum Fondswechsel Versicherungsnummer Versicherungsnehmer Änderung zum: Bei fehlender Eintragung, findet die Änderung für den Switch
Lebensversicherung von 1871 a.g. München Postfach 80326 München Auftrag zum Fondswechsel Versicherungsnummer Versicherungsnehmer Änderung zum: Bei fehlender Eintragung, findet die Änderung für den Switch
einfache Rendite 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110
 Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Liechtensteinisches Landesgesetzblatt
 215.229.1 Liechtensteinisches Landesgesetzblatt Jahrgang 2001 Nr. 128 ausgegeben am 10. Juli 2001 Gesetz vom 16. Mai 2001 über den Versicherungsvertrag (Versicherungsvertragsgesetz, VersVG) Dem nachstehenden
215.229.1 Liechtensteinisches Landesgesetzblatt Jahrgang 2001 Nr. 128 ausgegeben am 10. Juli 2001 Gesetz vom 16. Mai 2001 über den Versicherungsvertrag (Versicherungsvertragsgesetz, VersVG) Dem nachstehenden
Box-and-Whisker Plot -0,2 0,8 1,8 2,8 3,8 4,8
 . Aufgabe: Für zwei verschiedene Aktien wurde der relative Kurszuwachs (in % beobachtet. Aus den jeweils 20 Quartaldaten ergaben sich die folgenden Box-Plots. Box-and-Whisker Plot Aktie Aktie 2-0,2 0,8,8
. Aufgabe: Für zwei verschiedene Aktien wurde der relative Kurszuwachs (in % beobachtet. Aus den jeweils 20 Quartaldaten ergaben sich die folgenden Box-Plots. Box-and-Whisker Plot Aktie Aktie 2-0,2 0,8,8
W-Rechnung und Statistik für Ingenieure Übung 11
 W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) Mathematikgebäude Raum 715 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) W-Rechnung und Statistik
W-Rechnung und Statistik für Ingenieure Übung 11 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) Mathematikgebäude Raum 715 Christoph Kustosz (kustosz@statistik.tu-dortmund.de) W-Rechnung und Statistik
MERKBLATT Zuschuss zu den Versicherungsbeiträgen der Kranken- und Pflegeversicherung zur Vermeidung von Hilfebedürftigkeit ( 26 SGB II)
 MERKBLATT Zuschuss zu den Versicherungsbeiträgen der Kranken- und Pflegeversicherung zur Vermeidung von Hilfebedürftigkeit ( 26 SGB II) Wer bekommt den Zuschuss? Überschreitet Ihr anzurechnendes Einkommen
MERKBLATT Zuschuss zu den Versicherungsbeiträgen der Kranken- und Pflegeversicherung zur Vermeidung von Hilfebedürftigkeit ( 26 SGB II) Wer bekommt den Zuschuss? Überschreitet Ihr anzurechnendes Einkommen
ikk-classic.de Gesetzliches Krankengeld für Selbstständige Kein Zusatzbeitrag 2010 Da fühl ich mich gut.
 ikk-classic.de Gesetzliches Krankengeld für Selbstständige Kein Zusatzbeitrag 2010 Da fühl ich mich gut. 2 Informationen Gesetzliches Krankengeld für Selbstständige Selbstständige haben die Möglichkeit,
ikk-classic.de Gesetzliches Krankengeld für Selbstständige Kein Zusatzbeitrag 2010 Da fühl ich mich gut. 2 Informationen Gesetzliches Krankengeld für Selbstständige Selbstständige haben die Möglichkeit,
AltersVorsorgen-Airbag
 1 Vertrag fu r 2x Schutz Dietmar Heinrich BCA OnLive 28.09.2015 1 Die Fakten im Überblick Über 21. Mio Deutsche glauben nicht, dass sie über eine ausreichende Altersvorsorge verfügen* 67 % der Deutschen
1 Vertrag fu r 2x Schutz Dietmar Heinrich BCA OnLive 28.09.2015 1 Die Fakten im Überblick Über 21. Mio Deutsche glauben nicht, dass sie über eine ausreichende Altersvorsorge verfügen* 67 % der Deutschen
ist die Vergütung für die leihweise Überlassung von Kapital ist die leihweise überlassenen Geldsumme
 Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
Information In der Zinsrechnung sind 4 Größen wichtig: ZINSEN Z ist die Vergütung für die leihweise Überlassung von Kapital KAPITAL K ist die leihweise überlassenen Geldsumme ZINSSATZ p (Zinsfuß) gibt
Kfz-Versicherung für Fahranfänger. mit der Lizenz zum Fahren
 Kfz-Versicherung für Fahranfänger mit der Lizenz zum Fahren startklar? Geschafft endlich der Führerschein! Nur das eigene Auto fehlt noch. Aber: Sie dürfen den Wagen Ihrer Eltern nutzen und so Ihr Können
Kfz-Versicherung für Fahranfänger mit der Lizenz zum Fahren startklar? Geschafft endlich der Führerschein! Nur das eigene Auto fehlt noch. Aber: Sie dürfen den Wagen Ihrer Eltern nutzen und so Ihr Können
Risiko und Versicherung - Übung
 Sommer 2009 Risiko und Versicherung - Übung Entscheidungstheoretische Grundlagen Renate Bodenstaff Vera Brinkmann r.bodenstaff@uni-hohenheim.de vera.brinkmann@uni-hohenheim.de https://insurance.uni-hohenheim.de
Sommer 2009 Risiko und Versicherung - Übung Entscheidungstheoretische Grundlagen Renate Bodenstaff Vera Brinkmann r.bodenstaff@uni-hohenheim.de vera.brinkmann@uni-hohenheim.de https://insurance.uni-hohenheim.de
Leichte-Sprache-Bilder
 Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Leichte-Sprache-Bilder Reinhild Kassing Information - So geht es 1. Bilder gucken 2. anmelden für Probe-Bilder 3. Bilder bestellen 4. Rechnung bezahlen 5. Bilder runterladen 6. neue Bilder vorschlagen
Dynamische Methoden der Investitionsrechnung
 4 Dynamische Methoden der Investitionsrechnung Lernziele Das Konzept des Gegenwartswertes erklären Den Überschuss oder Fehlbetrag einer Investition mit Hilfe der Gegenwartswertmethode berechnen Die Begriffe
4 Dynamische Methoden der Investitionsrechnung Lernziele Das Konzept des Gegenwartswertes erklären Den Überschuss oder Fehlbetrag einer Investition mit Hilfe der Gegenwartswertmethode berechnen Die Begriffe
Pfl egezusatzversicherung
 Pfl egezusatzversicherung Kinder haften für ihre Eltern! Seite 02/05 Pfl egezusatzversicherung Leistungsbeispiele aus der Praxis Im Jahr 2008 gab es in der gesetzlichen Pflegepflichtversicherung rund 2,1
Pfl egezusatzversicherung Kinder haften für ihre Eltern! Seite 02/05 Pfl egezusatzversicherung Leistungsbeispiele aus der Praxis Im Jahr 2008 gab es in der gesetzlichen Pflegepflichtversicherung rund 2,1
Bruchrechnung Wir teilen gerecht auf
 Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. : (+) : + Wir teilen einen Teil Eine halbe Minipizza auf Personen. :? Wir teilen
Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. Bruchrechnung Wir teilen gerecht auf Minipizzen auf Personen. : (+) : + Wir teilen einen Teil Eine halbe Minipizza auf Personen. :? Wir teilen
Was ist das Budget für Arbeit?
 1 Was ist das Budget für Arbeit? Das Budget für Arbeit ist ein Persönliches Geld für Arbeit wenn Sie arbeiten möchten aber nicht mehr in einer Werkstatt. Das gibt es bisher nur in Nieder-Sachsen. Und in
1 Was ist das Budget für Arbeit? Das Budget für Arbeit ist ein Persönliches Geld für Arbeit wenn Sie arbeiten möchten aber nicht mehr in einer Werkstatt. Das gibt es bisher nur in Nieder-Sachsen. Und in
A n a l y s i s Finanzmathematik
 A n a l y s i s Finanzmathematik Die Finanzmathematik ist eine Disziplin der angewandten Mathematik, die sich mit Themen aus dem Bereich von Finanzdienstleistern, wie etwa Banken oder Versicherungen, beschäftigt.
A n a l y s i s Finanzmathematik Die Finanzmathematik ist eine Disziplin der angewandten Mathematik, die sich mit Themen aus dem Bereich von Finanzdienstleistern, wie etwa Banken oder Versicherungen, beschäftigt.
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Sicherheit für eine unbeschwerte Zukunft: Jetzt gibt es 2 Versicherungen, die Sie doppelt entlasten!
 Sicherheit für eine unbeschwerte Zukunft: Jetzt gibt es 2 Versicherungen, die Sie doppelt entlasten! Eine Versicherung offener Kreditkarten- Ausstände Eine Versicherung geplanter Kreditkarten- Ausgaben*
Sicherheit für eine unbeschwerte Zukunft: Jetzt gibt es 2 Versicherungen, die Sie doppelt entlasten! Eine Versicherung offener Kreditkarten- Ausstände Eine Versicherung geplanter Kreditkarten- Ausgaben*
Arbeitskraftabsicherung. Zwei Fliegen mit einer Klappe. Arbeitskraftabsicherung über den Betrieb.
 Arbeitskraftabsicherung Zwei Fliegen mit einer Klappe. Arbeitskraftabsicherung über den Betrieb. Arbeitskraftabsicherung Die betriebliche Direktversicherung zur Absicherung der Arbeitskraft. Verlust der
Arbeitskraftabsicherung Zwei Fliegen mit einer Klappe. Arbeitskraftabsicherung über den Betrieb. Arbeitskraftabsicherung Die betriebliche Direktversicherung zur Absicherung der Arbeitskraft. Verlust der
Im Folgenden werden einige typische Fallkonstellationen beschrieben, in denen das Gesetz den Betroffenen in der GKV hilft:
 Im Folgenden werden einige typische Fallkonstellationen beschrieben, in denen das Gesetz den Betroffenen in der GKV hilft: Hinweis: Die im Folgenden dargestellten Fallkonstellationen beziehen sich auf
Im Folgenden werden einige typische Fallkonstellationen beschrieben, in denen das Gesetz den Betroffenen in der GKV hilft: Hinweis: Die im Folgenden dargestellten Fallkonstellationen beziehen sich auf
Wachstum 2. Michael Dröttboom 1 LernWerkstatt-Selm.de
 1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
1. Herr Meier bekommt nach 3 Jahren Geldanlage 25.000. Er hatte 22.500 angelegt. Wie hoch war der Zinssatz? 2. Herr Meiers Vorfahren haben bei der Gründung Roms (753. V. Chr.) 1 Sesterze auf die Bank gebracht
Montessori Verein Kösching e.v.
 Darlehensvertrag Zwischen dem Montessori Verein Kösching e.v. als Träger der Montessori-Schule Kösching - nachfolgend Schule genannt Und (Name, Vorname) (Straße, PLZ, Wohnort) - nachfolgend Darlehensgeber
Darlehensvertrag Zwischen dem Montessori Verein Kösching e.v. als Träger der Montessori-Schule Kösching - nachfolgend Schule genannt Und (Name, Vorname) (Straße, PLZ, Wohnort) - nachfolgend Darlehensgeber
Einführung in statistische Analysen
 Einführung in statistische Analysen Andreas Thams Econ Boot Camp 2008 Wozu braucht man Statistik? Statistik begegnet uns jeden Tag... Weihnachten macht Deutschen Einkaufslaune. Im Advent überkommt die
Einführung in statistische Analysen Andreas Thams Econ Boot Camp 2008 Wozu braucht man Statistik? Statistik begegnet uns jeden Tag... Weihnachten macht Deutschen Einkaufslaune. Im Advent überkommt die
infach Geld FBV Ihr Weg zum finanzellen Erfolg Florian Mock
 infach Ihr Weg zum finanzellen Erfolg Geld Florian Mock FBV Die Grundlagen für finanziellen Erfolg Denn Sie müssten anschließend wieder vom Gehaltskonto Rückzahlungen in Höhe der Entnahmen vornehmen, um
infach Ihr Weg zum finanzellen Erfolg Geld Florian Mock FBV Die Grundlagen für finanziellen Erfolg Denn Sie müssten anschließend wieder vom Gehaltskonto Rückzahlungen in Höhe der Entnahmen vornehmen, um
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
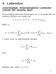 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
11.AsymmetrischeInformation
 .AsymmetrischeInformation Informationistnurwichtig,wenneineEntscheidungssituationdurcheinunsicheresUmfeld charakterisiertist.istesvielleichtso,daßauchdieunsicherheitselbstzueinereinschränkung derfunktionsfähigkeitvonmärktenführt?diesistinder
.AsymmetrischeInformation Informationistnurwichtig,wenneineEntscheidungssituationdurcheinunsicheresUmfeld charakterisiertist.istesvielleichtso,daßauchdieunsicherheitselbstzueinereinschränkung derfunktionsfähigkeitvonmärktenführt?diesistinder
1.3 Die Beurteilung von Testleistungen
 1.3 Die Beurteilung von Testleistungen Um das Testergebnis einer Vp zu interpretieren und daraus diagnostische Urteile ableiten zu können, benötigen wir einen Vergleichsmaßstab. Im Falle des klassischen
1.3 Die Beurteilung von Testleistungen Um das Testergebnis einer Vp zu interpretieren und daraus diagnostische Urteile ableiten zu können, benötigen wir einen Vergleichsmaßstab. Im Falle des klassischen
Arbeitsblatt Betriebliche Altersversorgung
 Arbeitsblatt Betriebliche Altersversorgung Im 3-Säulen-Modell der Alterssicherung ist die betriebliche Altersversorgung die zweite Säule. Die sogenannte Betriebsrente kann vom Arbeitgeber finanziert werden
Arbeitsblatt Betriebliche Altersversorgung Im 3-Säulen-Modell der Alterssicherung ist die betriebliche Altersversorgung die zweite Säule. Die sogenannte Betriebsrente kann vom Arbeitgeber finanziert werden
Sie haben das Recht, binnen vierzehn Tagen ohne Angabe von Gründen diesen Vertrag zu widerrufen.
 Widerrufsbelehrung Nutzt der Kunde die Leistungen als Verbraucher und hat seinen Auftrag unter Nutzung von sog. Fernkommunikationsmitteln (z. B. Telefon, Telefax, E-Mail, Online-Web-Formular) übermittelt,
Widerrufsbelehrung Nutzt der Kunde die Leistungen als Verbraucher und hat seinen Auftrag unter Nutzung von sog. Fernkommunikationsmitteln (z. B. Telefon, Telefax, E-Mail, Online-Web-Formular) übermittelt,
Klassische Risikomodelle
 Klassische Risikomodelle Kathrin Sachernegg 15. Jänner 2008 1 Inhaltsverzeichnis 1 Einführung 3 1.1 Begriffserklärung.................................. 3 2 Individuelles Risikomodell 3 2.1 Geschlossenes
Klassische Risikomodelle Kathrin Sachernegg 15. Jänner 2008 1 Inhaltsverzeichnis 1 Einführung 3 1.1 Begriffserklärung.................................. 3 2 Individuelles Risikomodell 3 2.1 Geschlossenes
Die Post hat eine Umfrage gemacht
 Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
Die Post hat eine Umfrage gemacht Bei der Umfrage ging es um das Thema: Inklusion Die Post hat Menschen mit Behinderung und Menschen ohne Behinderung gefragt: Wie zufrieden sie in dieser Gesellschaft sind.
R. Brinkmann http://brinkmann-du.de Seite 1 30.11.2013 Schriftliche Übung Mathematik Stochastik II (Nachschreiber) Jan. 2007
 R. Brinkmann http://brinkmann-du.de Seite 1 30.11.2013 Schriftliche Übung Mathematik Stochastik II (Nachschreiber) Jan. 2007 SG15/25D NAME: Lösungen 1. In einer Packung sind Glühbirnen, davon sind zwei
R. Brinkmann http://brinkmann-du.de Seite 1 30.11.2013 Schriftliche Übung Mathematik Stochastik II (Nachschreiber) Jan. 2007 SG15/25D NAME: Lösungen 1. In einer Packung sind Glühbirnen, davon sind zwei
CTI SYSTEMS S.A. CTI SYSTEMS S.A. 12, op der Sang. Fax: +352/2685-3000 L- 9779 Lentzweiler. Email: cti@ctisystems.com G.D.
 Z.I. Eselborn - Lentzweiler Phone: +352/2685-2000 12, op der Sang Fax: +352/2685-3000 L- 9779 Lentzweiler Email: cti@ctisystems.com G.D. Luxembourg URL: www.ctisystems.com Benutzung von Höhensicherungsgeräten
Z.I. Eselborn - Lentzweiler Phone: +352/2685-2000 12, op der Sang Fax: +352/2685-3000 L- 9779 Lentzweiler Email: cti@ctisystems.com G.D. Luxembourg URL: www.ctisystems.com Benutzung von Höhensicherungsgeräten
