Lineare Optimierung und ganzzahlige lineare Optimierung
|
|
|
- Berndt Schuler
- vor 6 Jahren
- Abrufe
Transkript
1 Definition 1: Problem LP: Lineare Optimierung und ganzzahlige lineare Optimierung geg.: m, n N, A Z m n, b Z m, c Z n ges.: x R n 0 mit c T x max Beispiel 1: (Gewinnmaximierung) Ax b Gerät Abteilung 1 Abteilung 2 Gewinn/Stück Ofen 2 Std. 1 Std. 30 Klimaanlage 1 Std. 2 Std. 50 Arbeitsleistung 8 Std/Tag 10 Std/Tag Frage: Wieviele Öfen und Klimaanlagen sollen hergestellt werden, um den Gesamtgewinn zu maximieren? Universität Paderborn PG AVESTA SS
2 Gerät Abteilung 1 Abteilung 2 Gewinn/Stück Ofen 2 Std. 1 Std. 30 Klimaanlage 1 Std. 2 Std. 50 Arbeitsleistung 8 Std/Tag 10 Std/Tag Modellierung: x 1 Öfen, x 2 Klimaanlagen. 2x 1 + x 2 8 x 1 + 2x x x 2 max LP : c = (30, 50) T «2 1 A = 1 2 b = (8, 10) T x = (x 1, x 2 ) T Maximiere c T x udn x 0 und Ax b. Universität Paderborn PG AVESTA SS
3 Graphische Lösung: 2x 1 + x 2 8, x 1 + 2x 2 10, 30x x 2 max 10 2x_1+x_2=8 8 Zulässige Lösungen liegen im 1. Quadranten links der roten Geraden Universität Paderborn PG AVESTA SS
4 Graphische Lösung: 2x 1 + x 2 8, x 1 + 2x 2 10, 30x x 2 max 10 2x_1+x_2=8 x_1+2x_2=10 Zulässige Lösungen liegen im 1. Quadranten links der roten Geraden unter der grünen Geraden Universität Paderborn PG AVESTA SS
5 Graphische Lösung: 2x 1 + x 2 8, x 1 + 2x 2 10, 30x x 2 max 10 2x_1+x_2=8 x_1+2x_2=10 8 Zulässige Lösungen liegen im magentafarbenen Polyeder Polyeder P der zulaessigen Loesungen Universität Paderborn PG AVESTA SS
6 Graphische Lösung: 2x 1 + x 2 8, x 1 + 2x 2 10, 30x x 2 max 10 2x_1+x_2=8 x_1+2x_2=10 30x_1+50x_2=500 8 Es existiert keine zulässige Lösung mit Zielfunktionswert Polyeder P der zulaessigen Loesungen Universität Paderborn PG AVESTA SS
7 Graphische Lösung: 2x 1 + x 2 8, x 1 + 2x 2 10, 30x x 2 max Verringern des Zielfunktionswertes 500 führt zum Verschieben der blauen Zielfunktionsgeraden in Richtung auf den Polyeder der zulässigen Lösungen x_1+x_2=8 x_1+2x_2=10 30x_1+50x_2=500 2 Polyeder P der zulaessigen Loesungen Universität Paderborn PG AVESTA SS
8 Graphische Lösung: 2x 1 + x 2 8, x 1 + 2x 2 10, 30x x 2 max 10 2x_1+x_2=8 x_1+2x_2=10 30x_1+50x_2=500 30x_1+50x_2=260 8 Es existiert eine zulässige Lösung mit Zielfunktionswert 260. Diese ist optimal. 6 4 Optimum = (2,4) 2 Polyeder P der zulaessigen Loesungen Universität Paderborn PG AVESTA SS
9 Geometrische Deutung (R n, +, ) mit komponentenweiser Addition und Multiplikation mit einem Skalar ist ein Vektorraum. U R n ist Unterraum, wenn U gegenüber + und abgeschlossen ist. Es gilt U ist Unterraum von R n U = {x R n Ax = 0, A R m n für ein m N}. Dann ist dim(u) = n rang(a). Für x R n, U Unterraum von R n ist ein affiner Unterraum definiert durch {x + y y U}. Es gilt U ist affiner Unterraum von R n genau dann wenn Für T R n ist U = {x R n Ax = b, A R m n, b R m für ein m N}. dim(t ) := min {dim(u)}. T U,Uaff.UR Universität Paderborn PG AVESTA SS
10 H R n mit dim(h) = n 1 heißt Hyperebene. Es ist dann H = {x R n a 1 x a n x n = b} mit a i R für alle i und mindestens einem a i 0. Jede Hyperebene H definiert zwei Halbräume H, H durch H = {x R n a 1 x a n x n b} H = {x R n a 1 x a n x n b} V R n heißt konvex, wenn für alle x, x V auch λx+(1 λ)x V für alle λ [0, 1]. Halbräume sind konvex, also ist auch ihr endlicher Durchschnitt konvex. Ist der Durchschnitt P endlich vieler Halbräume begrenzt und nicht leer, so heißt P Polyeder. ˆx P heißt Ecke von P Ist ˆx = λx + (1 λ)x, x, x P, so ist x = x = ˆx. Hyperebene H mit P H = {ˆx}. Universität Paderborn PG AVESTA SS
11 Jeder Polyeder ist die konvexe Hülle seiner Ecken. Ist V R n endlich, so ist die konvexe Hülle seiner Ecken conv(v ) ein Polyeder. Jede Ecke ˆx conv(v ) ist schon in V. Ist P = {x R n Ax b} beschränkt, so ist P ein Polyeder und eine optimale Lösung von Ax b, c T x max (Ax b, c T x min) wird an einer Ecke von P angenommen. Ist P = {x R n Ax b} unbeschränkt und ex. ein M R mit c T x M (c T x M) für alle x R n, so wird eine optimale Lösung von Ax b, c T x max (Ax b, c T x min) an einer Ecke von P angenommen. Es sei P R n m ein Polyeder. Dann ex. A Z m n, b N 0 m mit P = {x R n 0 Ax b}. Es sei A Z m n, b N m 0, c Z n mit rang(a) = m, P = {x R n 0 Ax b}, P und {c T x Ax b} ist nach oben beschränkt. Dann ist P ein Polyeder. Universität Paderborn PG AVESTA SS
12 Der LP-Löser Cplex Cplex ist ein kommerzielles Produkt zur Lösung von LPs (Cplex kann viel mehr). Binary steht unter /home-f/fg-monien/ilog/linux/cplex90/bin/i86 linux2 glibc2.2 gcc3.2/cplex Dokumentationen unter /home-f/fg-monien/ilog/doc/ Nach Aufruf können Inputs gelesen werden mit dem Kommando r <filename>. Eingabefiles in.lp-format haben eine einfache Struktur und müssen die Endung.lp haben. Nach dem Einlesen eines Problems kann durch das Kommando o die Optimierung gestartet werden. Nach der Optimierung kann man mit dem Kommando dis sol var - die Variablen der gefundenen Lösung anschauen. Notwendig vor Aufruf: setenv ILOG LICENSE FILE /home-f/fg-monien/ilog/linux/access.ilm Die Ausgabe von Cplex erscheint im Terminal und wird zusätzlich in das File cplex.log geschrieben. Universität Paderborn PG AVESTA SS
13 LP aus Beispiel 1: Inputfile LPexpl1.lp: \ Input file for cplex of Example 1 \ Maximize obj: 30 x x2 Subject To 2 x1 + x2 <= 8 x1 + 2 x2 <= 10 Bounds 0 <= x1 0 <= x2 End Universität Paderborn PG AVESTA SS
14 Ausgabe der Optimierung: CPLEX> r LPexpl1.lp Problem LPexpl1.lp read. Read time = sec. CPLEX> o Tried aggregator 1 time. No LP presolve or aggregator reductions. Presolve time = sec. Iteration log... Iteration: 1 Dual infeasibility = Iteration: 2 Dual objective = Dual - Optimal: Objective = e+02 Solution time = sec. Iterations = 2 (1) CPLEX> dis sol var - Variable Name Solution Value x x Universität Paderborn PG AVESTA SS
15 Beispiel 2: Problem MaxFlow: geg.: gerichteter Graph G = (V, E), s, t V und Kantenkapazitäten c e N für alle e E. ges.: ein Fluß f : E N 0 mit P e=(v,w) f(e) P e=(w,u) f(e) = 0 für alle w V \{s, t}, 0 f(e) c e für alle e E und P e=(s,v) f(e) P e=(v,s) f(e) maximal. Modellierung: Variablen x e [0, c e ]. Maximiere P e=(v,t) x e P e=(t,v) x e, so dass X e=(v,w) x e X e=(w,u) x e = 0 für alle w V \ {s, t}, x e 0 für alle e E, x e c e für alle e E. Universität Paderborn PG AVESTA SS
16 Bsp.: (Kapazitäten in rot) Maximize obj: fxt + fyt Subject To \ flow constraints: \ node u fsu + fvu - fuv - fux = 0 \ node v fsv + fuv + fxv - fvu - fvy = 0 \ node x fux + fyx - fxv - fxt = 0 \ node y fvy - fyx - fyt = 0 Bounds 0 <= fsu <= etc. End G s u v x y t Universität Paderborn PG AVESTA SS
17 CPLEX> r LPexpl2.lp... CPLEX> o... Dual - Optimal: Objective = e+01 Solution time = sec. Iterations = 3 (0) CPLEX> dis sol var - Variable Name Solution Value fxt fyt fsu fuv fux fsv fvy fyx All other variables in the range 1-10 are zero. G u s v x y t 4 4 Bei ganzzahligen Kapazitäten ist der Lösungsvektor f des Flussproblems auch automatisch ganzzahlig. Das gilt nicht für alle LPs. Universität Paderborn PG AVESTA SS
18 Beispiel 3: Problem Knapsack: geg.: p 1,..., p n, w 1,..., w n, d N 0. ges.: I [n], so dass P i I w i d und P i I p i maximal Bsp: d = w i p i Maximize obj: 2 x1 + 7 x2 + 4 x3 + 5 x4 + 3 x5 + 1 x6 + 6 x7 + 9 x8 + 8 x x10 Subject To 1 x1 + 2 x2 + 3 x3 + 4 x4 + 5 x5 + 6 x6 + 7 x7 + 8 x8 + 9 x x10 <= 20 Bounds 0 <= x1 <= 1... etc. End Cplex liefert eine Lösung x 1 =... = x 4 = x 8 = 1, x 10 = 0.2 mit Profit 29. Universität Paderborn PG AVESTA SS
19 Eine ganzzahlige (x i {0, 1}) optimale Lösung erhält man, wenn man im Cplex-Input vor das End die Anweisung Integers x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 setzt. Cplex liefert jetzt eine Lösung x 1 =... = x 4 = x 10 = 1 mit Profit 28. Probleme, die als LP modelliert werden können und bei denen jede optimale Lösung automatisch ganzzahlig ist gehören zur Komplexitätsklasse P. Zwar hat der Simplex-Algorithmus im schlimmsten Fall exponentielle Laufzeit, aber es gibt Polynomzeitalgorithmen zur Lösung des LP. Das Knapsack-Problem ist N P-vollständig. Unter der Voraussetzung, daß P N P muss es also Knapsack-Instanzen geben, deren Modellierung als LP keine ganzzahlige optimale Lösung hat. Universität Paderborn PG AVESTA SS
20 Definition 2: Problem IP: geg.: m, n N, A Z m n, b Z m, c Z n ges.: x N 0 n mit c T x max Ax b Das Problem IP ist N P-vollständig. Damit lassen sich theoretisch alle Probleme aus N P als IP modellieren. In der Praxis werden sehr viele Optimierungsprobleme aus N P als IP dargestellt und dann mit IP-Lösern wie Cplex bearbeitet. Universität Paderborn PG AVESTA SS
21 Universität Paderborn PG AVESTA SS
22 Ganzzahliges Optimierungsproblem: * * * Bei ganzzahligen Optimierungsproblemen liegen die zulässigen Punkte auf einem Gitter. Damit ist die Menge der zulässigen Lösungen nicht mehr konvex. * * ** * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * Universität Paderborn PG AVESTA SS
23 Beispiel 4: Problem Scheduling: geg.: m Maschinen mit Geschwindigkeiten c 1,..., c m N, n Jobs mit Lasten w 1,..., w n N. ges.: Eine Abbildung S : [n] [m], so daß max j [m] 8 >< X w i c j 9 >= >: i [n] >; S(i) = j {z } Makespan min Makespan 10 Universität Paderborn PG AVESTA SS
24 Modellierung: Variablen x i,j {0, 1} mit x i,j = 1 genau dann, wenn S(i) = j: max j [m] 8 < X : i [n] w i 9 = x i,j c j ; min X j [m] x i,j = 1 i [n] Um die Maximumsfunktion aufzulösen benutzt man eine neue Variable z R 0 : X i [n] z min x i,j w i c j z j [m] X j [m] x i,j = 1 i [n] Universität Paderborn PG AVESTA SS
25 Eingabe für Cplex: Minimize z Subject To \ alle Maschinenzeiten sind kleiner oder gleich z 5 x_0_ x_1_ x_2_ x_3_0 + 2 x_4_0 - z <= 0 10 x_0_1 + 3 x_1_1 + 5 x_2_1 + 7 x_3_1 + 4 x_4_1 - z <= 0 \ jeder Job wird genau einmal plaziert x_0_0 + x_0_1 = 1... x_4_0 + x_4_1 = 1 Bounds \ x_i_j sind 0,1 - Variablen 0 <= x_0_0 <= <= x_4_0 <= 1 Integers \ x_i_j sind ganzzahlig x_0_0... x_4_0 End Universität Paderborn PG AVESTA SS
26 Problem NashScheduling: geg.: m Maschinen mit Geschwindigkeiten c 1,..., c m, n Jobs mit (normierten) Laufzeiten w 1,..., w n. ges.: Eine Zuweisung der Jobs auf die Maschinen mit minimalem Makespan, unter der Bedingung daß kein Job seine Rechenzeit durch Auswahl einer anderen Maschine verbessern kann, solange alle anderen Jobs bei ihrer Wahl bleiben. geg.: mn, N, c 1,..., c m, w 1,..., w n N. ges.: z R 0, x {0, 1} [n] [m] mit z min, so daß P j [m] x ij = 1 für alle i [n] P w i i [n] c x ij z für alle j [m] j M (x i,j 1) + P n w k k=1 c x k,j P n w k j k=1 c x j k,j + w i c j für alle i [n], j, j [m], j j. wobei M eine Konstante ist, die groß genug ist, d.h. z.b. M = P i,j w i c j. Universität Paderborn PG AVESTA SS
27 Beispiel 5: Und nun noch ein Beispiel aus dem richtigen Leben: Der Kreisverband des FuLV Westfalen, Kreis Lippe, wollte für D-Juniorenmannschaften eine Hallenkreismeisterschaft ausrichten lassen. Die Ausrichtung wurde vom Verein FC Fortuna Schlangen übernommen. Es wurden 9 Mannschaften gemeldet, die Gemeinde Schlangen stellte an 4 Samstagen eine Sporthalle zur Verfügung. An diesen 4 Spieltagen musste jede Mannschaft einmal gegen jede andere Mannschaft spielen. Wie sollten die Spiele auf die 4 Spieltage verteilt werden? Wie generiert man einen Spielplan für eine Liga mit n Mannschaften? Universität Paderborn PG AVESTA SS
28 Um ein Schedule für n Mannschaften zu generieren, in dem jede Mannschaft genau einmal gegen jede andere Mannschaft spielt, gibt es einen einfachen Algorithmus: Mannschaft 1 bleibt immer an ihrem Platz, die anderen Mannschaften rotieren im Uhrzeigersinn usw. Es ist leicht zu zeigen, daß die Menge der Spielpaarungen nach allen Rotationen (inklusive der 0-ten) einen zulässigen Spielplan generiert. Jede Mannschaft hat an jedem Spieltag dieses Spielplanes genau ein Spiel. Wie kümmern uns hier nicht um die Frage, welche Mannschaften zuhause und welche auswärts spielen. Universität Paderborn PG AVESTA SS
29 1. Lösungsansatz für die Hallenkreismeisterschaft: Standardspielplan für 10 Mannschaften: Jetzt löschen wir die Spiele gegen 0 (= spielfrei) und verteilen die restlichen Spiele auf 4 Spieltage: Es ergeben sich einige unschöne Eigenschaften: so muss Mannschaft 9 am ersten Spieltag z.b. schon früh morgens anreisen, hat insgesamt 3 Spiele und davon ist eines auch noch das letzte des Tages. Dafür reist Mannschaft 9 am 2. Spieltag für ein einziges Spiel an, usw. Im Originalspielplan des Kreises mussten einige Mannschaften sagor zwei Spiele hintereinander spielen, hatten dann aber teilweise lange Pausen um auf ihr letztes Spiel des Tages zu warten. Das Resultat waren unzufriedene Trainer und unzufriedene Eltern. Universität Paderborn PG AVESTA SS
30 Optimierungsansatz: Wir benutzen 0, 1-Variablen x i,j,k,s mit der Bedeutung x i,j,k,s = 1 genau dann wenn Mannschaft i [n] gegen Mannschaft j [n] am Spieltag k [K] das Spiel s [S] spielt. Bedingungen: Jede Paarung wird genau einmal gespielt: X X x i,j,k,s = 1 i, j, j > i In jedem Slot wird höchstens ein Spiel gespielt: k s X X x i,j,k,s = 1 k, s i j Universität Paderborn PG AVESTA SS
31 Jedes Team spielt pro Tag mindestens n 1 und höchstens n 1 Spiele: X X n 1 x i,j,k,s, k j i s k X X ı n 1 x i,j,k,s k j i s Keine Mannschaft spielt zweimal hintereinander: x i,j,k,s + x i,j,k,s+1 1 i, j, j, k, s Zähle die Anzahl der Pausen der Länge p in zusätzlichen 0, 1-Variablen z i,k,s,p : k x i,j,k,s x i,j,k,s+p + z i,k,s,p 1, i, j, k, s, p Bestrafe Pausen der Länge p in der Zielfunktion mit Gewicht w p : X X X X w p z i,k,s,p min i k s p Universität Paderborn PG AVESTA SS
32 Beachte: z i,j,k,s,p = 1 heißt nicht, dass Mannschaft i am Tag k zwischen Spiel s und Spiel s+p immer frei hat (diese Bedingungen können auch linear beschrieben werden, sind aber komplexer), sondern nur, daß Mannschaft i Spiel s und Spiel s + p am Spieltag k spielen muss. Es ergab sich der folgende Spielplan: In dem optimierten Spielplan mussten an allen vier Spieltagen nur 4 Mannschaften (1,2,6,8) jeweils einmal eine Pause von 3 Spielen abwarten, traten 16 Spielpausen der Länge 2 und 16 Spielpausen der Länge 1 (bevorzugt) auf, spielte jede Mannschaft an jedem Spieltag genau 2 Spiele. Fazit: a) Optimierung hat echte Anwendungen in der Praxis! b) Kenntnisse über Optimierungsverfahren sind eine Grundvoraussetzung, um Optimierungspotenzial erkennen bzw. zu berechnen. Universität Paderborn PG AVESTA SS
6. Softwarewerkzeuge für die Lineare Programmierung
 6. Softwarewerkzeuge für die Lineare Programmierung Inhalt 6. Softwarewerkzeuge für die Lineare Programmierung GNU Linear Programming Kit Operations Research I Hochschule Bonn-Rhein-Sieg, SS 2013 314 GNU
6. Softwarewerkzeuge für die Lineare Programmierung Inhalt 6. Softwarewerkzeuge für die Lineare Programmierung GNU Linear Programming Kit Operations Research I Hochschule Bonn-Rhein-Sieg, SS 2013 314 GNU
Kombinatorische Optimierung
 Kombinatorische Optimierung Juniorprof. Dr. Henning Meyerhenke PARALLELES RECHNEN INSTITUT FÜR THEORETISCHE INFORMATIK, FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales
Kombinatorische Optimierung Juniorprof. Dr. Henning Meyerhenke PARALLELES RECHNEN INSTITUT FÜR THEORETISCHE INFORMATIK, FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales
Teil I. Lineare Optimierung
 Teil I Lineare Optimierung 5 Kapitel 1 Grundlagen Definition 1.1 Lineares Optimierungsproblem, lineares Programm. Eine Aufgabenstellung wird lineares Optimierungsproblem oder lineares Programm genannt,
Teil I Lineare Optimierung 5 Kapitel 1 Grundlagen Definition 1.1 Lineares Optimierungsproblem, lineares Programm. Eine Aufgabenstellung wird lineares Optimierungsproblem oder lineares Programm genannt,
Eigenschaften von LPs
 2 Lineare Programmierung Eigenschaften von LPs Eigenschaften von LPs Definition 24 Eine Menge K IR n heißt konvex gdw für je zwei Punkte Punkte x (1) K und x (2) K auch jeder Punkt mit 0 λ 1 zu K gehört
2 Lineare Programmierung Eigenschaften von LPs Eigenschaften von LPs Definition 24 Eine Menge K IR n heißt konvex gdw für je zwei Punkte Punkte x (1) K und x (2) K auch jeder Punkt mit 0 λ 1 zu K gehört
VORLESUNG 12 Lineare Optimierung (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt)
 VORLESUNG 12 Lineare Optimierung (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 53 Wiederholung! Basis-Startlösung berechnet! Künstliche Variablen! Erkennung von unlösbaren Problemen! Eliminierung
VORLESUNG 12 Lineare Optimierung (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 53 Wiederholung! Basis-Startlösung berechnet! Künstliche Variablen! Erkennung von unlösbaren Problemen! Eliminierung
Optimierung für Wirtschaftsinformatiker: Lineare Programme
 Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Optimierung für Wirtschaftsinformatiker: Lineare Programme Dr. Nico Düvelmeyer Dienstag, 31. Mai 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Lineare Programme Allgemeine Form 2 Spezielle Darstellungen
Computer Science Department - High Performance and Web Computing Group. Optimierungsprobleme
 Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
Optimierungsprobleme Häufig in Alltagssituationen anzutreffen (z.b. Kauf eines Gerätes) Optimierungsprobleme (OPs) sind Probleme, die i.a. viele zulässige Lösungen besitzen Jeder Lösung ist ein bestimmter
1 Lineare Optimierung, Simplex-Verfahren
 1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
1 Lineare Optimierung, Simplex-Verfahren 1.1 Einführung Beispiel: In einer Fabrik werden n Produkte A 1, A 2,..., A n hergestellt. Dazu werden m Rohstoffe B 1, B 2,..., B m (inklusive Arbeitskräfte und
Kap. 4: Lineare Programmierung
 Kap. 4: Lineare Programmierung Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 13./14. VO A&D WS 08/09 27.11./2.12.2008 Petra Mutzel Alg. & Dat.
Kap. 4: Lineare Programmierung Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 13./14. VO A&D WS 08/09 27.11./2.12.2008 Petra Mutzel Alg. & Dat.
4.4 Quadratische Optimierungsprobleme
 4.4 Quadratische Optimierungsprobleme 1. Quadratische Programme (QP) 1 2 xt P x + q T x + r s.t. Gx h (4.34) wobei P S n +, G R (m n) und A R (p n) Zielfunktion (ZF) ist (konvex) quadratisch Nebenbedingungen
4.4 Quadratische Optimierungsprobleme 1. Quadratische Programme (QP) 1 2 xt P x + q T x + r s.t. Gx h (4.34) wobei P S n +, G R (m n) und A R (p n) Zielfunktion (ZF) ist (konvex) quadratisch Nebenbedingungen
VORLESUNG 11 Lineare Optimierung (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt)
 VORLESUNG Lineare Optimierung (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 3 Wiederholung! Lineare Programme häufig geeignete Modellierung von Optimierungsproblemen! Verschiedene Darstellungen sind
VORLESUNG Lineare Optimierung (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 3 Wiederholung! Lineare Programme häufig geeignete Modellierung von Optimierungsproblemen! Verschiedene Darstellungen sind
Optimierung I. Dr. Ulf Lorenz F2.413
 Optimierung I Dr. Ulf Lorenz F2.413 flulo@upb.de Organisation Dozent: Dr. Ulf Lorenz F2.413 Fürstenallee 11 email: flulo@upb.de WWW: http://www.upb.de/cs/flulo (hier auch aktuelle Infos + Ü-Zettel) Vorlesungen:
Optimierung I Dr. Ulf Lorenz F2.413 flulo@upb.de Organisation Dozent: Dr. Ulf Lorenz F2.413 Fürstenallee 11 email: flulo@upb.de WWW: http://www.upb.de/cs/flulo (hier auch aktuelle Infos + Ü-Zettel) Vorlesungen:
2. Optimierungsprobleme 6
 6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
Effiziente Algorithmen Lineares Programmieren 216. Schwache Dualität
 Effiziente Algorithmen Lineares Programmieren 216 Schwache Dualität Sei wieder z = max{ c T x Ax b, x 0 } (P ) und w = min{ b T u A T u c, u 0 }. (D) x ist primal zulässig, wenn x { x Ax b, x 0 }. u ist
Effiziente Algorithmen Lineares Programmieren 216 Schwache Dualität Sei wieder z = max{ c T x Ax b, x 0 } (P ) und w = min{ b T u A T u c, u 0 }. (D) x ist primal zulässig, wenn x { x Ax b, x 0 }. u ist
Optimierungsprobleme. B. Langfeld, M. Ritter, B. Wilhelm Diskrete Optimierung: Fallstudien aus der Praxis
 Optimierungsprobleme Instanz eines Optimierungsproblems zulässiger Bereich (meist implizit definiert) Zielfunktion Optimierungsrichtung opt {max, min} Optimierungsproblem Menge von Instanzen meist implizit
Optimierungsprobleme Instanz eines Optimierungsproblems zulässiger Bereich (meist implizit definiert) Zielfunktion Optimierungsrichtung opt {max, min} Optimierungsproblem Menge von Instanzen meist implizit
Das Linear Ordering Problem Exakte Lösungsverfahren. für NP-schwierige. VO Algorithm Engineering
 Das Linear Ordering Problem Exakte Lösungsverfahren VO Algorithm Engineering für NP-schwierige Professor Dr. Petra Mutzel kombinatorische Lehrstuhl für Algorithm Engineering, LS11 Optimierungsprobleme
Das Linear Ordering Problem Exakte Lösungsverfahren VO Algorithm Engineering für NP-schwierige Professor Dr. Petra Mutzel kombinatorische Lehrstuhl für Algorithm Engineering, LS11 Optimierungsprobleme
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung
 Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung Dr. Nico Düvelmeyer Freitag, 24. Juni 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Dualität Motivation Duales LP Dualitätssätze
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung Dr. Nico Düvelmeyer Freitag, 24. Juni 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Dualität Motivation Duales LP Dualitätssätze
6 Korrektheit des Simplexalgorithmus
 6 Korrektheit des Simplexalgorithmus Folgerung: Es sei L: Ax = b, c T x max LP und A B nicht-degenerierte PZB von L und es gebe c r := c r c B A B A r > 0 a) Falls a r := A B a r 0, dann L unbeschränkt
6 Korrektheit des Simplexalgorithmus Folgerung: Es sei L: Ax = b, c T x max LP und A B nicht-degenerierte PZB von L und es gebe c r := c r c B A B A r > 0 a) Falls a r := A B a r 0, dann L unbeschränkt
8. Konvexe Polytope. Tobias Boelter. Mittwoch, 5. März TopMath Frühlingsschule
 1 / 31 8. Konvexe Tobias Boelter TopMath Frühlingsschule Mittwoch, 5. März 2014 2 / 31 Es können auch nicht konvexe untersucht werden, wir beschränken uns hier aber auf konvexe. Mit einem Polytop ist hier
1 / 31 8. Konvexe Tobias Boelter TopMath Frühlingsschule Mittwoch, 5. März 2014 2 / 31 Es können auch nicht konvexe untersucht werden, wir beschränken uns hier aber auf konvexe. Mit einem Polytop ist hier
Inhalt. 8.1 Motivation. 8.2 Optimierung ohne Nebenbedingungen. 8.3 Optimierung unter Nebenbedingungen. 8.4 Lineare Programmierung
 8. Optimierung Inhalt 8.1 Motivation 8.2 Optimierung ohne Nebenbedingungen 8.3 Optimierung unter Nebenbedingungen 8.4 Lineare Programmierung 8.5 Kombinatorische Optimierung 2 8.1 Motivation Viele Anwendungen
8. Optimierung Inhalt 8.1 Motivation 8.2 Optimierung ohne Nebenbedingungen 8.3 Optimierung unter Nebenbedingungen 8.4 Lineare Programmierung 8.5 Kombinatorische Optimierung 2 8.1 Motivation Viele Anwendungen
Optimierung. Optimierung. Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung Fabian Kuhn
 Optimierung Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung 1 Assignment Problem (Zuordnungsproblem) Gewichtetes Perfektes Bipartites Matching agents Costs tasks Weise jedem Agenten genau
Optimierung Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung 1 Assignment Problem (Zuordnungsproblem) Gewichtetes Perfektes Bipartites Matching agents Costs tasks Weise jedem Agenten genau
Optimierung. Optimierung. Vorlesung 8 Lineare Programmierung III: Simplex Algorithmus Fabian Kuhn
 Optimierung Vorlesung 8 Lineare Programmierung III: Simplex Algorithmus 1 Resource Allocation Beispiel aus Vorlesung 6 Primales LP: Duales LP: max 3 4 2 2 4 2 8 3 6 0, 0, 0 min 4 8 6 2 3 3 4 2 2 0, 0,
Optimierung Vorlesung 8 Lineare Programmierung III: Simplex Algorithmus 1 Resource Allocation Beispiel aus Vorlesung 6 Primales LP: Duales LP: max 3 4 2 2 4 2 8 3 6 0, 0, 0 min 4 8 6 2 3 3 4 2 2 0, 0,
Optimierung für Nichtmathematiker
 Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS2010/11 1 / 1 Teil IV Konvexe und ganzzahlige Optimierung Vorlesung 11 IV Konvexe und ganzzahlige Optimierung 2 / 34 Inhaltsübersicht 29Lineare Optimierung
Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS2010/11 1 / 1 Teil IV Konvexe und ganzzahlige Optimierung Vorlesung 11 IV Konvexe und ganzzahlige Optimierung 2 / 34 Inhaltsübersicht 29Lineare Optimierung
3. Grundlagen der Linearen Programmierung
 3. Grundlagen der linearen Programmierung Inhalt 3. Grundlagen der Linearen Programmierung Lineares Programm Grafische Lösung linearer Programme Normalform Geometrie linearer Programme Basislösungen Operations
3. Grundlagen der linearen Programmierung Inhalt 3. Grundlagen der Linearen Programmierung Lineares Programm Grafische Lösung linearer Programme Normalform Geometrie linearer Programme Basislösungen Operations
VORLESUNG 14 Lineare Optimierung, Dualität (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt)
 VORLESUNG 14 Lineare Optimierung, Dualität (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 96 H. Meyerhenke: Kombinatorische Optimierung Dualität bei linearen Programmen Def.: Es sei (L): c T x max
VORLESUNG 14 Lineare Optimierung, Dualität (Viele Folien nach Ulf Lorenz, jetzt TU Darmstadt) 96 H. Meyerhenke: Kombinatorische Optimierung Dualität bei linearen Programmen Def.: Es sei (L): c T x max
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung
 Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung 18.3.14-20.3.14 Dr. Florian Lindemann Moritz Keuthen, M.Sc. Technische Universität München Garching, 19.3.2014 Kursplan Dienstag, 18.3.2014
Rechnerpraktikum zu Grundlagen der Nichtlinearen Optimierung 18.3.14-20.3.14 Dr. Florian Lindemann Moritz Keuthen, M.Sc. Technische Universität München Garching, 19.3.2014 Kursplan Dienstag, 18.3.2014
Schranken für zulässige Lösungen
 Schranken für zulässige Lösungen Satz 5.9 Gegeben seien primales und duales LP gemäß der asymmetrischen Form der Dualität. Wenn x eine zulässige Lösung des primalen Programms und u eine zulässige Lösung
Schranken für zulässige Lösungen Satz 5.9 Gegeben seien primales und duales LP gemäß der asymmetrischen Form der Dualität. Wenn x eine zulässige Lösung des primalen Programms und u eine zulässige Lösung
1 Der Simplex Algorithmus I
 1 Nicoletta Andri 1 Der Simplex Algorithmus I 1.1 Einführungsbeispiel In einer Papiermühle wird aus Altpapier und anderen Vorstoffen feines und grobes Papier hergestellt. Der Erlös pro Tonne feines Papier
1 Nicoletta Andri 1 Der Simplex Algorithmus I 1.1 Einführungsbeispiel In einer Papiermühle wird aus Altpapier und anderen Vorstoffen feines und grobes Papier hergestellt. Der Erlös pro Tonne feines Papier
Inhalt. 1. Flußprobleme. 2. Matching. 3. Lineares Programmieren. 4. Ganzzahliges Programmieren. 5. NP-Vollständigkeit. 6. Approximationsalgorithmen
 Effiziente Algorithmen Einführung 1 Inhalt 1. Flußprobleme 2. Matching. Lineares Programmieren 4. Ganzzahliges Programmieren 5. NP-Vollständigkeit 6. Approximationsalgorithmen 7. Backtracking und Branch-and-Bound
Effiziente Algorithmen Einführung 1 Inhalt 1. Flußprobleme 2. Matching. Lineares Programmieren 4. Ganzzahliges Programmieren 5. NP-Vollständigkeit 6. Approximationsalgorithmen 7. Backtracking und Branch-and-Bound
Scheduling und Lineare ProgrammierungNach J. K. Lenstra, D. B. Shmoys und É.
 Scheduling und Lineare ProgrammierungNach J. K. Lenstra, D. B. Shmoys und É. Tardos Janick Martinez Esturo jmartine@techfak.uni-bielefeld.de xx.08.2007 Sommerakademie Görlitz Arbeitsgruppe 5 Gliederung
Scheduling und Lineare ProgrammierungNach J. K. Lenstra, D. B. Shmoys und É. Tardos Janick Martinez Esturo jmartine@techfak.uni-bielefeld.de xx.08.2007 Sommerakademie Görlitz Arbeitsgruppe 5 Gliederung
Innere-Punkt-Methoden
 Innere-Punkt-Methoden Johannes Stemick 26.01.2010 Johannes Stemick () Innere-Punkt-Methoden 26.01.2010 1 / 28 Übersicht 1 Lineare Optimierung 2 Innere-Punkt-Methoden Path-following methods Potential reduction
Innere-Punkt-Methoden Johannes Stemick 26.01.2010 Johannes Stemick () Innere-Punkt-Methoden 26.01.2010 1 / 28 Übersicht 1 Lineare Optimierung 2 Innere-Punkt-Methoden Path-following methods Potential reduction
Grundlagen der Optimierung. Übung 6
 Technische Universität Chemnitz Chemnitz, 2. November 24 Prof. Dr. R. Herzog, J. Blechschmidt, A. Schäfer Abgabe am 28. November 24 Grundlagen der Optimierung Übung 6 Aufgabe 2: Verschiedene Verfahren
Technische Universität Chemnitz Chemnitz, 2. November 24 Prof. Dr. R. Herzog, J. Blechschmidt, A. Schäfer Abgabe am 28. November 24 Grundlagen der Optimierung Übung 6 Aufgabe 2: Verschiedene Verfahren
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Sätze PLUS Es gilt für A, B R n n : det(ab) = det A det B (Determinantenmultiplikationssatz)
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Sätze PLUS Es gilt für A, B R n n : det(ab) = det A det B (Determinantenmultiplikationssatz)
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Für n N ist die Matrix-Exponentialfunktion
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Für n N ist die Matrix-Exponentialfunktion
Lineare Programmierung (2)
 Inhalt Rückblick Motivation - linearen Programmierung Flussprobleme Multiple Warenflüsse Fortsetzung Simplex Algorithmus Initialisierung Fundamentalsatz der linearen Programmierung schwache Dualität Dualität
Inhalt Rückblick Motivation - linearen Programmierung Flussprobleme Multiple Warenflüsse Fortsetzung Simplex Algorithmus Initialisierung Fundamentalsatz der linearen Programmierung schwache Dualität Dualität
Modellieren mit AMPL
 Modellieren mit AMPL Elisabeth Gassner Mathematische Modelle in den Wirtschaftswissenschaften Prof. R. E. Burkard 27. April 2007 E. Gassner (Mathematische Modelle) AMPL 27. April 2007 1 / 21 Überblick
Modellieren mit AMPL Elisabeth Gassner Mathematische Modelle in den Wirtschaftswissenschaften Prof. R. E. Burkard 27. April 2007 E. Gassner (Mathematische Modelle) AMPL 27. April 2007 1 / 21 Überblick
Operations Research. Flüsse in Netzwerken. Flüsse in Netzwerken. Unimodularität. Rainer Schrader. 2. Juli Gliederung.
 Operations Research Rainer Schrader Flüsse in Netzwerken Zentrum für Angewandte Informatik Köln 2. Juli 2007 1 / 53 2 / 53 Flüsse in Netzwerken Unimodularität Gliederung Netzwerke und Flüsse bipartite
Operations Research Rainer Schrader Flüsse in Netzwerken Zentrum für Angewandte Informatik Köln 2. Juli 2007 1 / 53 2 / 53 Flüsse in Netzwerken Unimodularität Gliederung Netzwerke und Flüsse bipartite
Simplex-Verfahren. Kapitel 4. Simplex-Verfahren. Peter Becker (H-BRS) Operations Research I Sommersemester / 298
 Kapitel 4 Simplex-Verfahren Peter Becker (H-BRS) Operations Research I Sommersemester 24 86 / 298 Inhalt Inhalt 4 Simplex-Verfahren Dualer Simplexalgorithmus Vermeidung von Zyklen Peter Becker (H-BRS)
Kapitel 4 Simplex-Verfahren Peter Becker (H-BRS) Operations Research I Sommersemester 24 86 / 298 Inhalt Inhalt 4 Simplex-Verfahren Dualer Simplexalgorithmus Vermeidung von Zyklen Peter Becker (H-BRS)
Lineare Optimierung und Simplex-Algorithmus
 Lineare Optimierung und Simplex-Algorithmus Problemstellung Beispiel : Unser Unternehmen verfügt über drei Maschinen A, B, C, mit denen zwei verschiedene Produkte P, P2 hergestellt werden. Die Maschinen
Lineare Optimierung und Simplex-Algorithmus Problemstellung Beispiel : Unser Unternehmen verfügt über drei Maschinen A, B, C, mit denen zwei verschiedene Produkte P, P2 hergestellt werden. Die Maschinen
Das Lagrange-duale Problem
 Das Lagrange-duale Problem Tobias Kulke 29. April 2010 1 Einführung Für jedes Paar (λ, ν) mit λ 0 liefert die Langrange-duale Funktion ( ) p g(λ, ν) = inf L(x, λ, ν) = inf f 0 (x) + λ i f i (x) + ν i h
Das Lagrange-duale Problem Tobias Kulke 29. April 2010 1 Einführung Für jedes Paar (λ, ν) mit λ 0 liefert die Langrange-duale Funktion ( ) p g(λ, ν) = inf L(x, λ, ν) = inf f 0 (x) + λ i f i (x) + ν i h
Lineare und kombinatorische Optimierung
 Lineare und kombinatorische Optimierung Theorie, Algorithmen und Anwendungen Prof. Dr. Peter Becker Fachbereich Informatik Hochschule Bonn-Rhein-Sieg Wintersemester 2017/18 Peter Becker (H-BRS) Lineare
Lineare und kombinatorische Optimierung Theorie, Algorithmen und Anwendungen Prof. Dr. Peter Becker Fachbereich Informatik Hochschule Bonn-Rhein-Sieg Wintersemester 2017/18 Peter Becker (H-BRS) Lineare
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 7 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 200 Prof. Dr. Klaus Höllig (IMNG)
Numerische Lineare Algebra Vorlesung 7 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 200 Prof. Dr. Klaus Höllig (IMNG)
Approximationsalgorithmen für NP-harte Optimierungsprobleme
 Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 18 Was tun mit NP-harten Problemen? Viele praxisrelevante
Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 18 Was tun mit NP-harten Problemen? Viele praxisrelevante
Vorlesung Lineare Optimierung (Sommersemester 2010)
 1 Vorlesung Lineare Optimierung (Sommersemester 2010) Kapitel 6: Die Geometrie der Linearen Optimierung Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Juni 2010) Gliederung 2 Das
1 Vorlesung Lineare Optimierung (Sommersemester 2010) Kapitel 6: Die Geometrie der Linearen Optimierung Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Juni 2010) Gliederung 2 Das
Wiederholung zu Flüssen
 Universität Konstanz Methoden der Netzwerkanalyse Fachbereich Informatik & Informationswissenschaft SS 2008 Prof. Dr. Ulrik Brandes / Melanie Badent Wiederholung zu Flüssen Wir untersuchen Flüsse in Netzwerken:
Universität Konstanz Methoden der Netzwerkanalyse Fachbereich Informatik & Informationswissenschaft SS 2008 Prof. Dr. Ulrik Brandes / Melanie Badent Wiederholung zu Flüssen Wir untersuchen Flüsse in Netzwerken:
Approximationsalgorithmen für NP-harte Optimierungsprobleme
 Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 4. Januar 2011 Berthold Vöcking, Informatik 1 () Vorlesung
Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 4. Januar 2011 Berthold Vöcking, Informatik 1 () Vorlesung
Eine kurze Beschreibung zu AMPL und CPLEX
 Welchen Kuchen backt Bernd Brezel? Lineare Optimierung Eine kurze Beschreibung zu AMPL und CPLEX Prof. Dr. Andrea Walther Institut für Mathematik Universität Paderborn 1 1 Das allgemeines Vorgehen Zur
Welchen Kuchen backt Bernd Brezel? Lineare Optimierung Eine kurze Beschreibung zu AMPL und CPLEX Prof. Dr. Andrea Walther Institut für Mathematik Universität Paderborn 1 1 Das allgemeines Vorgehen Zur
Perlen der Informatik I Wintersemester 2012 Aufgabenblatt 7
 Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
Klausurrepetitorium ABWL
 Klausurrepetitorium ABWL Planungs- und Südwestfälische Industrie- und Handelskammer 9. August 5 Dr. Friedhelm Kulmann, Sandra Rudolph 9.8.5 Gliederung. Nichtlineare Optimierungsprobleme.. Quadratisches
Klausurrepetitorium ABWL Planungs- und Südwestfälische Industrie- und Handelskammer 9. August 5 Dr. Friedhelm Kulmann, Sandra Rudolph 9.8.5 Gliederung. Nichtlineare Optimierungsprobleme.. Quadratisches
Unimodularität. Kapitel 1. Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206
 Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
Kapitel 1 Unimodularität Peter Becker (H-BRS) Operations Research II Wintersemester 2015/16 11 / 206 Inhalt 1 Unimodularität Total unimodulare Matrizen Inzidenzmatrix Optimierungsprobleme auf Graphen Peter
Anwendungen der Wirtschaftsmathematik und deren Einsatz im Schulunterricht
 Anwendungen der Wirtschaftsmathematik und deren Einsatz im Schulunterricht Beispiele wirtschaftsmathematischer Modellierung Lehrerfortbildung, Speyer, Juni 2004-1- Beispiele wirtschaftsmathematischer Modellierung
Anwendungen der Wirtschaftsmathematik und deren Einsatz im Schulunterricht Beispiele wirtschaftsmathematischer Modellierung Lehrerfortbildung, Speyer, Juni 2004-1- Beispiele wirtschaftsmathematischer Modellierung
Insbesondere sind nach dieser Definition also auch die leere Menge und einpunktige Teilmengen konvex.
 Konvexe Mengen 2 Wie am Ende des vorigen Kapitels bereits erwähnt, ist die notwendige Gradientenbedingung aus Satz 1.4.6 für konvexe Zielfunktionen auch hinreichend. Diese Tatsache mag als erste Motivation
Konvexe Mengen 2 Wie am Ende des vorigen Kapitels bereits erwähnt, ist die notwendige Gradientenbedingung aus Satz 1.4.6 für konvexe Zielfunktionen auch hinreichend. Diese Tatsache mag als erste Motivation
Effiziente Algorithmen I
 H 10. Präsenzaufgabenblatt, Wintersemester 2015/16 Übungstunde am 18.01.2015 Aufgabe Q Ein Reiseveranstalter besitzt ein Flugzeug, das maximal p Personen aufnehmen kann. Der Veranstalter bietet einen Flug
H 10. Präsenzaufgabenblatt, Wintersemester 2015/16 Übungstunde am 18.01.2015 Aufgabe Q Ein Reiseveranstalter besitzt ein Flugzeug, das maximal p Personen aufnehmen kann. Der Veranstalter bietet einen Flug
Kapitel 9: Lineare Programmierung Gliederung
 Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Proseminar Lineare Algebra WS 08/09 Prof. Dr. O. Bogopolski 1. Vortrag: Lineare Gleichungen. am 11. März von Maximilian Wahner
 Proseminar Lineare Algebra WS 08/09 Prof. Dr. O. Bogopolski 1 Vortrag: Lineare Gleichungen am 11. März 2009 von Maximilian Wahner Technische Universität Dortmund Fakultät für Mathematik Proseminar Lineare
Proseminar Lineare Algebra WS 08/09 Prof. Dr. O. Bogopolski 1 Vortrag: Lineare Gleichungen am 11. März 2009 von Maximilian Wahner Technische Universität Dortmund Fakultät für Mathematik Proseminar Lineare
Dualitätssätze der linearen Optimierung
 Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Kapitel 9 Dualitätssätze der linearen Optimierung Sei z = c T x min! Ax = b 9.1 x 0 mit c, x R n, b R m, A R m n ein lineares Programm. Definition 9.1 Duales lineares Programm. Das lineare Programm z =
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Graphenalgorithmen Maximaler Fluss Einleitung Flussnetzwerke Ford-Fulkerson Fulkerson Methode Maximales bipartites Matching
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Graphenalgorithmen Maximaler Fluss Einleitung Flussnetzwerke Ford-Fulkerson Fulkerson Methode Maximales bipartites Matching
5 Lineare Gleichungssysteme und Determinanten
 5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
6. Woche: Lineare Codes, Syndrom, Gilbert-Varshamov Schranke. 6. Woche: Lineare Codes, Syndrom, Gilbert-Varshamov Schranke 107/ 238
 6 Woche: Lineare Codes, Syndrom, Gilbert-Varshamov Schranke 6 Woche: Lineare Codes, Syndrom, Gilbert-Varshamov Schranke 107/ 238 Erinnerung: Der Vektorraum F n 2 Schreiben {0, 1} n als F n 2 Definition
6 Woche: Lineare Codes, Syndrom, Gilbert-Varshamov Schranke 6 Woche: Lineare Codes, Syndrom, Gilbert-Varshamov Schranke 107/ 238 Erinnerung: Der Vektorraum F n 2 Schreiben {0, 1} n als F n 2 Definition
Einführung in die Mathematik des Operations Research
 Universität zu Köln Mathematisches Institut Prof. Dr. F. Vallentin Einführung in die Mathematik des Operations Research Sommersemester 3 en zur Klausur (7. Oktober 3) Aufgabe ( + 3 + 5 = Punkte). Es sei
Universität zu Köln Mathematisches Institut Prof. Dr. F. Vallentin Einführung in die Mathematik des Operations Research Sommersemester 3 en zur Klausur (7. Oktober 3) Aufgabe ( + 3 + 5 = Punkte). Es sei
Netzwerk-Simplex. MinCostFlow als Lineares Programm. 1 of 12 Netzwerksimplex
 Netzwerk-Simplex MinCostFlow als Lineares Programm of 2 Netzwerksimplex MinCostFlow geg: gerichteter Graph G, Kapazitäten u R R 0 { }, Bedarfe b V R, Pfeilkosten c R R ges: zulässiger b-fluss f mit minimalen
Netzwerk-Simplex MinCostFlow als Lineares Programm of 2 Netzwerksimplex MinCostFlow geg: gerichteter Graph G, Kapazitäten u R R 0 { }, Bedarfe b V R, Pfeilkosten c R R ges: zulässiger b-fluss f mit minimalen
3.2 Lineare Optimierung (Entscheidungen unter Sicherheit)
 3. Lineare Optimierung (Entscheidungen unter Sicherheit) Betrachtet wird hier der Fall Θ = (bzw. die Situation u(a, ϑ) bzw. l(a,ϑ) konstant in ϑ Θ für alle a A). Da hier keine Unsicherheit über die Umweltzustände
3. Lineare Optimierung (Entscheidungen unter Sicherheit) Betrachtet wird hier der Fall Θ = (bzw. die Situation u(a, ϑ) bzw. l(a,ϑ) konstant in ϑ Θ für alle a A). Da hier keine Unsicherheit über die Umweltzustände
maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j];
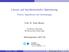
![maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j]; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum {j in P} (1/a[j]) * X[j] <= beta; subject to Grenzen {j in P}: 0 <= X[j] <= u[j];](/thumbs/64/50698761.jpg) AMPL-Modell für beliebige Produkte (myprod.mod) set P; param a {j in P}; param beta; param c {j in P}; param u {j in P}; var X {j in P}; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum
AMPL-Modell für beliebige Produkte (myprod.mod) set P; param a {j in P}; param beta; param c {j in P}; param u {j in P}; var X {j in P}; maximize Profit: sum {j in P} c[j] * X[j]; subject to Zeit: sum
OPERATIONS-RESEARCH (OR)
 OPERATIONS-RESEARCH (OR) Man versteht darunter die Anwendung mathematischer Methoden und Modelle zur Vorbereitung optimaler Entscheidungen bei einem Unternehmen. Andere deutsche und englische Bezeichnungen:
OPERATIONS-RESEARCH (OR) Man versteht darunter die Anwendung mathematischer Methoden und Modelle zur Vorbereitung optimaler Entscheidungen bei einem Unternehmen. Andere deutsche und englische Bezeichnungen:
Inhaltsübersicht für heute:
 Inhaltsübersicht für heute: Dualität Anwendung: Spieltheorie Komplementarität und Sensitivitätsanalyse Spaltengenerierung Schnittebenenverfahren Welchen Simplex wann? Inhaltsübersicht für heute: Dualität
Inhaltsübersicht für heute: Dualität Anwendung: Spieltheorie Komplementarität und Sensitivitätsanalyse Spaltengenerierung Schnittebenenverfahren Welchen Simplex wann? Inhaltsübersicht für heute: Dualität
Geometrische Deutung linearer Abbildungen
 Geometrische Deutung linearer Abbildungen Betrachten f : R n R n, f(x) = Ax. Projektionen z.b. A = 1 0 0 0 1 0 0 0 0 die senkrechte Projektion auf die xy-ebene in R 3. Projektionen sind weder injektiv
Geometrische Deutung linearer Abbildungen Betrachten f : R n R n, f(x) = Ax. Projektionen z.b. A = 1 0 0 0 1 0 0 0 0 die senkrechte Projektion auf die xy-ebene in R 3. Projektionen sind weder injektiv
Approximationsalgorithmen. 19. Dezember / 28
 Approximationsalgorithmen 19. Dezember 2017 1 / 28 Optimierungsprobleme Das Ziel: Bearbeite schwierige Optimierungsprobleme der Form opt y f (x, y) so dass L(x, y). Die Zielfunktion f (x, y) ist zu minimieren
Approximationsalgorithmen 19. Dezember 2017 1 / 28 Optimierungsprobleme Das Ziel: Bearbeite schwierige Optimierungsprobleme der Form opt y f (x, y) so dass L(x, y). Die Zielfunktion f (x, y) ist zu minimieren
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
 Gliederung der Vorlesung 1. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege 4. Minimale spannende Bäume 5. Färbungen und Cliquen 6. Traveling Salesman Problem 7. Flüsse in Netzwerken
Gliederung der Vorlesung 1. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege 4. Minimale spannende Bäume 5. Färbungen und Cliquen 6. Traveling Salesman Problem 7. Flüsse in Netzwerken
β 1 x :=., und b :=. K n β m
 44 Lineare Gleichungssysteme, Notations Betrachte das lineare Gleichungssystem ( ) Sei A = (α ij ) i=,,m j=,n α x + α x + + α n x n = β α x + α x + + α n x n = β α m x + α m x + + α mn x n = β m die Koeffizientenmatrix
44 Lineare Gleichungssysteme, Notations Betrachte das lineare Gleichungssystem ( ) Sei A = (α ij ) i=,,m j=,n α x + α x + + α n x n = β α x + α x + + α n x n = β α m x + α m x + + α mn x n = β m die Koeffizientenmatrix
1 Rotating Calipers. 2 Antipodal und Copodal. 3 Distanzen Rechtecke Eigenschaften
 1 Rotating Calipers 2 3 Rotating Calipers - Algorithmus Konvexes Polygon mit parallelen Stützgeraden Rotating Calipers - Finder Shamos lässt 1978 zwei Stützgeraden um ein Polygon rotieren Zwei Stützgeraden
1 Rotating Calipers 2 3 Rotating Calipers - Algorithmus Konvexes Polygon mit parallelen Stützgeraden Rotating Calipers - Finder Shamos lässt 1978 zwei Stützgeraden um ein Polygon rotieren Zwei Stützgeraden
Probleme aus NP und die polynomielle Reduktion
 Probleme aus NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 15. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Probleme aus NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 15. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
Operations Research. Ganzzahlige lineare Programme. ganzzahlige lineare Programme. Ganzzahlige lineare Programme. Rainer Schrader. 25.
 Operations Research Rainer Schrader Ganzzahlige lineare Programme Zentrum für Angewandte Informatik Köln 25. Juni 2007 1 / 49 2 / 49 Ganzzahlige lineare Programme Gliederung ganzzahlige lineare Programme
Operations Research Rainer Schrader Ganzzahlige lineare Programme Zentrum für Angewandte Informatik Köln 25. Juni 2007 1 / 49 2 / 49 Ganzzahlige lineare Programme Gliederung ganzzahlige lineare Programme
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2015
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2015 4. April 2016 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2015 4. April 2016 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
Die Lagrange-duale Funktion
 Die Lagrange-duale Funktion Gregor Leimcke 21. April 2010 1 Die Lagrangefunktion Wir betrachten das allgemeine Optimierungsproblem wobei minimiere f 0 über D sodass f i 0, i = 1,..., m 1.1 D = h i = 0,
Die Lagrange-duale Funktion Gregor Leimcke 21. April 2010 1 Die Lagrangefunktion Wir betrachten das allgemeine Optimierungsproblem wobei minimiere f 0 über D sodass f i 0, i = 1,..., m 1.1 D = h i = 0,
Die Größe A(n, d) und optimale Codes
 Die Größe A(n, d) und optimale Codes Definition Optimaler Code Wir definieren A(n, d) = max{m binärer (n, M, d) Code} Ein (n, M, d)-code heißt optimal, falls M = A(n, d). Bestimmung von A(n, d) ist offenes
Die Größe A(n, d) und optimale Codes Definition Optimaler Code Wir definieren A(n, d) = max{m binärer (n, M, d) Code} Ein (n, M, d)-code heißt optimal, falls M = A(n, d). Bestimmung von A(n, d) ist offenes
= ( n x j x j ) 1 / 2
 15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
LinOpt - Tool zur Visualisierung eines multikriteriellen Optimierungsproblems
 LinOpt Tool zur Visualisierung eines multikriteriellen Optimierungsproblems Erstellt von Michael Berklmeir, Michael Haarnagell, Stefan Kraus, Stephan Roser im Rahmen einer Seminararbeit am Lehrstuhl für
LinOpt Tool zur Visualisierung eines multikriteriellen Optimierungsproblems Erstellt von Michael Berklmeir, Michael Haarnagell, Stefan Kraus, Stephan Roser im Rahmen einer Seminararbeit am Lehrstuhl für
Kuhn-Tucker Bedingung
 Kapitel 13 Kuhn-Tucker Bedingung Josef Leydold Mathematik für VW WS 017/18 13 Kuhn-Tucker Bedingung 1 / Optimierung unter Nebenbedingungen Aufgabe: Berechne das Maximum der Funktion f (x, y) g(x, y) c,
Kapitel 13 Kuhn-Tucker Bedingung Josef Leydold Mathematik für VW WS 017/18 13 Kuhn-Tucker Bedingung 1 / Optimierung unter Nebenbedingungen Aufgabe: Berechne das Maximum der Funktion f (x, y) g(x, y) c,
6 Lineare Optimierung
 6 Lineare Optimierung Um die Aufgabenstellung deutlich zu machen, beginnen wir mit einem (natürlich sehr vereinfachten) Beispiel: Produtionsplan einer (zugegebenermaßen sehr leinen) Schuhfabri. Hergestellt
6 Lineare Optimierung Um die Aufgabenstellung deutlich zu machen, beginnen wir mit einem (natürlich sehr vereinfachten) Beispiel: Produtionsplan einer (zugegebenermaßen sehr leinen) Schuhfabri. Hergestellt
Optimierungsalgorithmen
 Optimierungsalgorithmen Jakob Puchinger Algorithmen und Datenstrukturen 2 Arbeitsbereich für Algorithmen und Datenstrukturen Institut für Computergraphik und Algorithmen Technische Universität Wien Übersicht
Optimierungsalgorithmen Jakob Puchinger Algorithmen und Datenstrukturen 2 Arbeitsbereich für Algorithmen und Datenstrukturen Institut für Computergraphik und Algorithmen Technische Universität Wien Übersicht
Minimumproblem. Definition 4.7. Ein LP der Form. unter den Nebenbedingungen. d ij x j b i (i =1,...,m)
 Minimumproblem Definition 4.7 Ein LP der Form nx Minimiere Z = c j x j j=1 unter den Nebenbedingungen nx d ij x j b i (i =1,...,m) j=1 und den Vorzeichenbedingungen x j 0(j =1,...,n) heißt Minimumproblem.
Minimumproblem Definition 4.7 Ein LP der Form nx Minimiere Z = c j x j j=1 unter den Nebenbedingungen nx d ij x j b i (i =1,...,m) j=1 und den Vorzeichenbedingungen x j 0(j =1,...,n) heißt Minimumproblem.
Der n-dimensionale Raum
 Der n-dimensionale Raum Mittels R kann nur eine Größe beschrieben werden. Um den Ort eines Teilchens im Raum festzulegen, werden schon drei Größen benötigt. Interessiert man sich für den Bewegungszustand
Der n-dimensionale Raum Mittels R kann nur eine Größe beschrieben werden. Um den Ort eines Teilchens im Raum festzulegen, werden schon drei Größen benötigt. Interessiert man sich für den Bewegungszustand
INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS
 Julian Arz, Timo Bingmann, Sebastian Schlag INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS KIT Julian Universität Arz, des Timo LandesBingmann, Baden-Württemberg Sebastian und Schlag nationales 2.
Julian Arz, Timo Bingmann, Sebastian Schlag INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS KIT Julian Universität Arz, des Timo LandesBingmann, Baden-Württemberg Sebastian und Schlag nationales 2.
3 Polytope. 3.1 Polyeder
 28 3 Polytope 3.1 Polyeder Polytope in der Ebene und im Raum standen neben Kreis und Kugel schon während der griechischen Antike im Mittelpunkt des mathematischen (und philosophischen) Interesses. Durch
28 3 Polytope 3.1 Polyeder Polytope in der Ebene und im Raum standen neben Kreis und Kugel schon während der griechischen Antike im Mittelpunkt des mathematischen (und philosophischen) Interesses. Durch
Probeklausur Optimierung
 Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
Universität Hamburg Fakultät für Mathematik, Informatik und Naturwissenschaften Dr. Nico Düvelmeyer Hamburg, 4. Juli 2011 Probeklausur Optimierung Bitte selber ausfüllen: Name: (darf anonymisiert werden)
Mehrkriterielle Optimierung mit Metaheuristiken
 Sommersemester 2006 Mehrkriterielle Optimierung mit Metaheuristiken (Vorlesung) Prof. Dr. Günter Rudolph Fachbereich Informatik Lehrstuhl für Algorithm Engineering (LS XI) Fachgebiet Computational Intelligence
Sommersemester 2006 Mehrkriterielle Optimierung mit Metaheuristiken (Vorlesung) Prof. Dr. Günter Rudolph Fachbereich Informatik Lehrstuhl für Algorithm Engineering (LS XI) Fachgebiet Computational Intelligence
Lösungsskizzen zu den Klausuraufgaben zum Kurs 1142 Algorithmische Mathematik. a 0 = 0 =
 Lösungsskizzen zu den Klausuraufgaben zum Kurs 4 Algorithmische Mathematik 4KSL3 6 Punkte Aufgabe. Die Folge (a n ) n N natürlicher Zahlen a n sei rekursiv definiert durch a 0 = 0, a n = a n + n falls
Lösungsskizzen zu den Klausuraufgaben zum Kurs 4 Algorithmische Mathematik 4KSL3 6 Punkte Aufgabe. Die Folge (a n ) n N natürlicher Zahlen a n sei rekursiv definiert durch a 0 = 0, a n = a n + n falls
Mathematik II für Studierende der Informatik (Analysis und lineare Algebra) im Sommersemester 2018
 (Analysis und lineare Algebra) im Sommersemester 2018 5. April 2018 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
(Analysis und lineare Algebra) im Sommersemester 2018 5. April 2018 Zu der Vorlesung wird ein Skript erstellt, welches auf meiner Homepage veröffentlicht wird: http://www.math.uni-hamburg.de/home/geschke/lehre.html
7.1 Matrizen und Vektore
 7.1 Matrizen und Vektore Lineare Gleichungssysteme bestehen aus einer Gruppe von Gleichungen, in denen alle Variablen nur in der 1. Potenz vorkommen. Beispiel Seite 340 oben: 6 x 2 = -1 + 3x 2 = 4 mit
7.1 Matrizen und Vektore Lineare Gleichungssysteme bestehen aus einer Gruppe von Gleichungen, in denen alle Variablen nur in der 1. Potenz vorkommen. Beispiel Seite 340 oben: 6 x 2 = -1 + 3x 2 = 4 mit
Entscheidungsbäume. Definition Entscheidungsbaum. Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen?
 Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Entscheidungsbäume Frage: Gibt es einen Sortieralgorithmus mit o(n log n) Vergleichen? Definition Entscheidungsbaum Sei T ein Binärbaum und A = {a 1,..., a n } eine zu sortierenden Menge. T ist ein Entscheidungsbaum
Wiederholung. Wir gehen von LP s in Standardform aus, wobei A R m n vollen Zeilenrang hat: minc T x A x = b
 Wiederholung Wir gehen von LP s in Standardform aus, wobei A R m n vollen Zeilenrang hat: minc T x A x = b x 0. x R n heißt Basislösung, wenn Ax = b und rang(a J ) = J, wobei J = {j x (j) 0}; Basislösung
Wiederholung Wir gehen von LP s in Standardform aus, wobei A R m n vollen Zeilenrang hat: minc T x A x = b x 0. x R n heißt Basislösung, wenn Ax = b und rang(a J ) = J, wobei J = {j x (j) 0}; Basislösung
Lineare Gleichungssysteme
 Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
Studientag zur Algorithmischen Mathematik
 Studientag zur Algorithmischen Mathematik Lineare Optimierung Winfried Hochstättler Diskrete Mathematik und Optimierung FernUniversität in Hagen 1. Juli 2012 Outline Lineares Programm (LP) in Standardform
Studientag zur Algorithmischen Mathematik Lineare Optimierung Winfried Hochstättler Diskrete Mathematik und Optimierung FernUniversität in Hagen 1. Juli 2012 Outline Lineares Programm (LP) in Standardform
11. BASIS, UNTERRAUM, und DIMENSION
 11. BASIS, UNTERRAUM, und DIMENSION 1 Basen werden zu unterschiedlichen Zwecken benutzt: Um lineare Abbildungen in ihrer Matrixdarstellung zu vereinfachen, um die Dimension von Vektorräumen und ihren Unterräumen
11. BASIS, UNTERRAUM, und DIMENSION 1 Basen werden zu unterschiedlichen Zwecken benutzt: Um lineare Abbildungen in ihrer Matrixdarstellung zu vereinfachen, um die Dimension von Vektorräumen und ihren Unterräumen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 7. Dezember 2017 INSTITUT FÜR THEORETISCHE 0 07.12.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 7. Dezember 2017 INSTITUT FÜR THEORETISCHE 0 07.12.2017 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
H. Meyerhenke: Kombinatorische Optimierung. Paralleles Rechnen, Institut für Theoretische Informatik, Fakultät für Informatik
 VORLESUNG 13 Smoothed Analysis des Simplex-Algorithmus Nach Heiko Röglin, Universität Bonn, Vorlesungsskript Introduction to Smoothed Analysis vom 9. Januar 2012 78 Wiederholung Simplex-Algorithmus! Korrektheit:!
VORLESUNG 13 Smoothed Analysis des Simplex-Algorithmus Nach Heiko Röglin, Universität Bonn, Vorlesungsskript Introduction to Smoothed Analysis vom 9. Januar 2012 78 Wiederholung Simplex-Algorithmus! Korrektheit:!
Newton-Verfahren zur gleichungsbeschränkten Optimierung. 1 Gleichungsbeschränkte Optimierungsprobleme
 Newton-Verfahren zur gleichungsbeschränkten Optimierung Armin Farmani Anosheh (afarmani@mail.uni-mannheim.de) 3.Mai 2016 1 Gleichungsbeschränkte Optimierungsprobleme Einleitung In diesem Vortrag geht es
Newton-Verfahren zur gleichungsbeschränkten Optimierung Armin Farmani Anosheh (afarmani@mail.uni-mannheim.de) 3.Mai 2016 1 Gleichungsbeschränkte Optimierungsprobleme Einleitung In diesem Vortrag geht es
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 29.11.2013 Alexander Lytchak 1 / 13 Wiederholung Der Rang einer linearen Abbildung ist gleich dem Spaltenrang der darstellenden
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 29.11.2013 Alexander Lytchak 1 / 13 Wiederholung Der Rang einer linearen Abbildung ist gleich dem Spaltenrang der darstellenden
