x (k+1) = Φ(x (k) ), k = 0,1,... lim k x(k) = x = A 1 b,

Transkript

1 Ì Ð ÎÁÁÁ ÁØ Ö Ø Ú Ä ÙÒ Ð Ò Ö Ö Ð ÙÒ Ý Ø Ñ

2

3 ÅÓØ Ú Ø ÓÒ Ö Ø Å Ø Ó Ò Û Ù Ð Ñ Ò Ø ÓÒ Ú Ö ¹ Ö Ò Ò Ö ÖÓ Ñ Ò ÓÒ Ò n Ö Ù ÛÒ (O(n 3 )) Ô Þ ÐÐ Ö ÒÒ ØÞØ Å ØÖ Þ Òº Ù Û ÁØ Ö Ø Ú Î Ö Ö Ò Ò ÓÖÑ Ñ Ø x (k+1) = Φ(x (k) ), k = 0,1,... lim k x(k) = x = A 1 b, ÛÓ Φ(x (k) ) Þ ÒØ Ù Û ÖØ Ø Û Ö Ò ÒÒº ½

4

5 ¾ ÃÓÒ ØÖÙ Ø ÓÒ ÚÓÒ ÁØ Ö Ø ÓÒ Ú Ö Ö Ò A R n n Ö ÙÐÖ b R n ÙÒ x R n Ò ÙØ Ä ÙÒ ÚÓÒ Ax = b Ë Ö Ò Û Ö A = B +(A B) ÛÓ B R n n Ö ÙÐÖ Ó Ø Ax = b Bx+(A B)x = b x = B 1 (B A)x+B 1 b x = (I B 1 A)x+B 1 b =: Φ(x) Ö Ø ÜÔÙÒ Ø Ø Ö Ø ÓÒ x (k+1) = Φ(x (k) ) = (I B 1 A)x (k) +B 1 b, k = 0,1,... Á Ø B = A Ó Ø x (1) = A 1 b = x Ü Ø Ä ÙÒ º Ö ÓÐÐØ B A Ò B 1 ³ Ò ³ ÞÙ Ö Ò Ò Ò Å ØÖ Ü T := I B 1 A Ø ÁØ Ö Ø ÓÒ Ñ ØÖ Üº Ë ØÞ ¾ º½ µ Ë Ò Î ØÓÖÒÓÖÑ ÙÒ T ÞÙ ÓÖ Ò Ø Å ¹ ØÖ ÜÒÓÖÑº ÐØ T < 1, T = I B 1 A Ó Ø ÜÔÙÒ Ø Ð ÙÒ x = Φ(x) Ò Ù Ò Ä ÙÒ ÙÒ ÞÛ Ö x = A 1 bº ÁØ Ö Ø ÓÒ Ú Ö Ö Ò x (k+1) = Tx (k) + B 1 b, k = 0,1,... ÓÒÚ Ö ÖØ ÒÒ Ö ÐÐ x (0) R n Ò Ä ÙÒ x ÙÒ ÐØ ÔÖ ÓÖ Ð Ö ØÞÙÒ x (k) x T k 1 T x(1) x (0), k N. µ ÁØ Ö Ø ÓÒ Ú Ö Ö Ò

6 ½ ¾ ÃÓÒ ØÖÙ Ø ÓÒ ÚÓÒ ÁØ Ö Ø ÓÒ Ú Ö Ö Ò x (k+1) = Tx (k) + B 1 b, k = 0,1,... ÓÒÚ Ö ÖØ Ò Ù ÒÒ Û ÒÒ ρ(t) < 1 ÐØº Û Å Ø Φ(x) = Tx+B 1 b ÓÐ Ø Û Ò Φ(x) Φ(y) = Tx+B 1 b Ty B 1 b = T(x y) T x y ÙÒ T < 1 Φ ÓÒØÖ Ö Ò Øº Ù Ò Ò a) Ö Ò Ö Ù Ñ Ò Ò ÜÔÙÒ Ø ØÞ Ë ØÞ ½ º¾µº Ë ØÞ ¾½º Ø ρ(t) = inf{ T : T Ø ÞÙ ÓÖ Ò Ø Å ØÖ ÜÒÓÖÑ}. ÐØ ÒÙÒ ρ(t) < 1 Ó Ü Ø ÖØ Ð Ó Ò ÞÙ ÓÖ Ò Ø Å ØÖ ÜÒÓÖÑ Ñ Ø T < 1 ÙÒ ÃÓÒÚ Ö ÒÞ ÓÐ Ø Ù a)º Ë ÒÙÒ x (k) ÓÒÚ Ö ÒØ Ñ Ø lim k x (k) = x = A 1 b. Ö Ò Ð Ö f (k) = x (k) x ÐØ f (k+1) = x (k+1) x = Tx (k) +B 1 b Tx B 1 b = T(x (k) x) = Tf (k) ÙÒ lim k f (k) = 0 Ò ÎÓÖÖ Ù ØÞÙÒ Ö ÐÐ f (0) R n º Ë ÒÙÒ Ô Þ ÐÐ f (0) Ò ÒÚ ØÓÖ ÚÓÒ T ÞÙÑ ÒÛ ÖØ λº ÒÒ ÐØ f (k) = Tf (k 1) =... = T k f (0) = λ k f (0) Ï Ò lim k f (k) = 0 ÑÙ ÒÒ λ < 1 ÐØ Òº λ Ò Ð Ö ÒÛ ÖØ Û Ö ÑÙ ρ(t) < 1 Òº Ñ Ö ÙÒ Ö Å ØÖ Ü T = ( ) ÐØ T = T Z = 1.2 > 1 Ö T 2 = ρ(t T T) = ρ(t) = < 1º ÃÓÒØÖ Ø ÓÒ Ò Ø ÒÒ Ò Ñ ÐÐ Ñ Ø 2 Ö Ò Ø Ñ Ø Ò Û Ò Û Ö Ò

7 ¾ Â Ó ¹ ÙÒ Ù¹Ë Ð¹Î Ö Ö Ò Ï Ö Ö Ò A = D L U Ñ Ø D = diag(a 11,a 22,...,a nn ) a 12 a 1n. L = a , U = a n 1n. a n1 a nn Ù Ö Ñ º º D Ø ÒÚ ÖØ Ö Öº a ii 0, i = 1,...,n, Ï Ð Ò Û Ö B = D Ó Ø T J := I D 1 A ÙÒ Û Ö Ö ÐØ Ò Î Ö Ö Ò x (k+1) = T J x (k) + D 1 b = (I D 1 A)x (k) + D 1 b = D 1 (D A)x (k) + D 1 b = D 1 [(L + U)x (k) + b] ÓÑÔÓÒ ÒØ ÒÛ Ö Ø Ö i = 1,...,n x (k+1) i = [ n j=1 (L+U) ijx (k) = 1 a ii [ j=1,j i a ii j + b i ] a ij x (k) j b i ] Î Ö Ö Ò Ø Â Ó ¹ Ó Ö ÑØ Ö ØØÚ Ö Ö Òº Ï Ð Ò Û Ö B = D L Ó Ø T GS = I (D L) 1 A ÙÒ Û Ö Ö ÐØ Ò Î Ö Ö Ò x (k+1) = T GS x (k) + (D L) 1 b = (I (D L) 1 A)x (k) + (D L) 1 b = (D L) 1 [(D L A) x (k) + b] }{{} =U.

8 ½ ¾ Â Ó ¹ ÙÒ Ù¹Ë Ð¹Î Ö Ö Ò (D L)x (k+1) = Ux (k) + b ÃÓÑÔÓÒ ÒØ ÒÛ Ö Ø Ö i = 1,...,n (Dx (k+1) ) i = (Lx (k+1) ) i + (Ux (k) ) i + b i i 1 a ii x (k+1) i = a ij x (k+1) j a ij x (k) j + b i x (k+1) i = 1 a ii j=1 [ i 1 j=1 j=i+1 a ij x (k+1) j + j=i+1 a ij x (k) j b i ] Î Ö Ö Ò Ø Ù¹ Ë Ð¹ Ó Ö ÒÞ Ð Ö ØØÚ Ö Ö Ò Ö Ö ÒÙÒ ÚÓÒ x (k+1) i ÓÒ Ö Ò Ø Ò ÃÓÑÔÓÒ ÒØ Ò, 1 j i 1 Ö Ø Ø Û Ö Òº x (k+1) j Ë ØÞ ¾ º½ µ Á Ø A R n n ØÖ Ø ÓÒ Ð ÓÑ Ò ÒØ ÐØ Ð Ó a ii > j=1,j i a ij, i = 1,...,n, Ó ÓÒÚ Ö ÖØ Â Ó ¹Î Ö Ö Ò ÙÒ Ò ÚÓÑ ËØ ÖØÚ ØÓÖ x (0) R n º µ Ë Ò a ii 0, i = 1,...,n ÙÒ Ö Ö ÙÖ Ú Ò ÖØ Ò Ð Ò p 1,...,p n Ñ Ø ÐØ p i := i 1 j=1 a ij a ii p i + j=i+1 p := max i=1,...,n p i < 1. a ij a ii ÒÒ ÓÒÚ Ö ÖØ Ù¹Ë Ð¹Î Ö Ö Ò ÙÒ Ò ÚÓÑ ËØ ÖØÚ ¹ ØÓÖ x (0) R n º Û µ ÐØ Ty = I D 1 A = max i=1,...,n δ ij a ij = max i=1,...,n j=1 j=1,j i a ij a ii a ii < 1 Ò ÎÓÖÖ Ù ØÞÙÒ º ÙÔØÙÒ ÓÐ Ø ÒÒ Ù Ë ØÞ ¾ º½ µ º µ Ë x R n Ñ Ø x = max i=1,...,n x i = 1 ÙÒ

9 ¾ Â Ó ¹ ÙÒ Ù¹Ë Ð¹Î Ö Ö Ò ½ ÒÒ Ø z = T GS x = (I (D L) 1 A)x = (D L) 1 (D L A)x = (D L) 1 Ux. i 1 a ij z i = z j a ii j=1 j=i+1 À ÖÐ ØÙÒ Ù¹Ë Ð¹Î Ö Ö Ò µº x = 1 Ø Ö ÐØ Ò Û Ö z 1 j=1 j=2 a ij a ii x j a 1j a 11 = p 1 < 1 ÒÒ Ñ ÐØ z j p j Ö j = 1,...,i 1º ÒÒ ÐØ i 1 a ij z i a ii p a ij j + = p i < 1 a ii j=i+1 Ð Ó Ø z < 1 ÙÒ Û Ò Ö ÃÓÑÔ Ø Ø ÚÓÒ {x R n : x = 1} ÓÐ Ø T GS = max x =1 T GSx < 1 ÃÓÖÓÐÐ Ö ¾ º¾ Ö ØÖ Ø ÓÒ Ð ÓÑ Ò ÒØ Å ØÖ Þ Ò A R n n ÓÒ¹ Ú Ö ÖØ Ù¹Ë Ð¹Î Ö Ö Ò ÙÒ Ò ÚÓÑ ËØ ÖØÛ ÖØ x (0) R n º Û ÐØ Ò ÎÓÖ Ù ØÞÙÒ p 1 = j=2 a ij a ii < 1 ÙÒ ÐÐ p 1,...,p i 1 < 1 Ò Ó Ø Ù p i = < i 1 j=1 a ij a ii j=1,j i p j + a ij a ii j=i+1 < 1. Ñ Ö ÙÒ Ö ØÖ Ø ÓÒ Ð ÓÑ Ò ÒØ Å ØÖ Þ Ò A R n n ÐØ Ø Ø T GS T J < 1. a ij a ii

10 ½ ¼ ¾ Â Ó ¹ ÙÒ Ù¹Ë Ð¹Î Ö Ö Ò ËØÓ Ö» ÙÐ Ö µ Ö ÓÒ Ø ÒØ ÓÖ Ò Ø Å ØÖ Þ Ò A R n n º º Å ØÖ Þ Ò A = D L U Ö ÐØ ÒÛ ÖØ ÚÓÒ C(α) := αd 1 L + α 1 D 1 U, α R + ÙÒ Ò ÚÓÒ α Ò ÐØ Ó Ö ρ(t GS ) = ρ(t j ) 2. ÃÓÒÚ Ö ÖØ Ð Ó Â Ó ¹Î Ö Ö Ò Ö Ò ÓÒ Ø ÒØ ÓÖ Ò Ø Å ¹ ØÖ Ü Ó Ù Ù¹Ë Ð¹Î Ö Ö Ò ÙÒ ÞÛ Ö ÓÔÔ ÐØ Ó Ò ÐÐº

11 ¾ Ê Ð Ü Ø ÓÒ Ú Ö Ö Ò ÁØ Ö Ø ÓÒ Ú Ö Ö Ò Ò Ø ÐØ x (k+1) = (I B 1 A)x (k) + B 1 b = x (k) B 1 Ax (k) + B 1 b = x (k) + x (k), ÛÓ x (k) = x (k+1) x (k) = B 1 Ax (k) +B 1 b Øº Á Ö Ò Ò Ê Ð Ü Ø ÓÒ Ô Ö Ñ Ø Ö ω R + Ò ÙÖ x (k+1) = x (k) + ω x (k), ÙÑ ÃÓÒÚ Ö ÒÞ Î Ö Ö Ò ÞÙ Ð ÙÒ Òº Â Ó ¹Ê Ð Ü Ø ÓÒ Ú Ö Ö Ò B = Dµ x (k+1) = x (k) + ω( D 1 Ax (k) + D 1 b) = (I ωd 1 A)x (k) + ωd 1 b = T JOR (ω)x (k) + ωd 1 b, k = 0,1,... ÃÓÑÔÓÒ ÒØ ÒÛ Ö Ø x (k+1) i = x (k) i + ω a ii (b i j=1 = (1 ω)x (k) i + ω a ii (b i a ij x (k) j ) j=1,j i a ij x (k) j ). Ë ØÞ ¾ º½ Å ØÖ Ü T J = I D 1 A ÒÙÖ Ö ÐÐ ÒÛ ÖØ λ 1 λ 2... λ n Ñ Ø Ð Ò Ö ÙÒ Ò Ò ÒÚ ØÓÖ Ò v 1,...,v n ÙÒ ÐØ ρ(t J ) < 1º ÒÒ ØÞØ Å ØÖ Ü T JOR (ω) ÒÛ ÖØ ÙÒ ÐØ Ñ Ø µ i := 1 ω +ωλ i, i = 1,...,n

12 ½ ¾ ¾ Ê Ð Ü Ø ÓÒ Ú Ö Ö Ò Û Å Ø Ö ÐØ Ò Û Ö 2 ω opt := 2 λ 1 λ n ρ(t JOR (ω opt )) ρ(t JOR (ω)) ω 0. (I D 1 A)v i = T j v i = λ i v i, i = 1,...,n T JOR (ω)v i = (I ωd 1 A)v i = [(1 ω)i + ω(i D 1 A)]v i = (1 ω +ωλ i )v i, i = 1,...,n. Ð Ó Ò µ i (ω) := 1 ω+ωλ i ÒÛ ÖØ ÚÓÒ T JOR (ω) ÙÒ ÐØ µ 1 (ω) µ 2 (ω)... µ n (ω). ÓÐÐ ÒÙÒ ω opt > 0 Ó Û ÐØ Û Ö Ò ρ(t JOR (ω opt )) = max i=1,...,n µ i(ω opt ) max i=1,...,n µ i(ω) = ρ(t JOR (ω)) Ö ÐÐ ω > 0 ÐØº À ÖÞÙ ÓÐÐØ ÐØ Ò ÒÒ Û Ò µ n (ω opt ) = µ 1 (ω opt ) 1 ω opt +ω opt λ n = (1 ω opt +ω opt λ 1 ) 2 ω opt = > 0, 2 λ 1 λ n λ i = Tr(T J ) = Tr(I D 1 A) = 0 i=1 Ñ Ò ÒÛ ÖØ ÚÓÒ T J ÙÒØ Ö Ð ÎÓÖÞ Ò Òº Á Ø ÒÙÒ ω > ω opt Ó ÐØ ÙÒ Ñ Ø µ 1 (ω) = 1 ω(1 λ 1 ) < 1 ω opt (1 λ 1 ) = µ 1 (ω opt ) < 0 ρ(t JOR (ω)) µ 1 (ω) > µ 1 (ω opt ) = ρ(t JOR (ω opt )). Ò ÐÐ ω < ω opt Û Ø Ñ Ò Ò ÐÓ º Ù¹Ë Ð¹Ê Ð Ü Ø ÓÒ Ú Ö Ö Ò ËÇÊ¹Î Ö Ö Òµ

13 ¾ Ê Ð Ü Ø ÓÒ Ú Ö Ö Ò ½ x (k+1) i = x (k) i + ω( x (k) ) i = x (k) i + ω a ii (b i i 1 j=1 = (1 ω)x (k) i + ω a ii (b i i = 1,...,n k = 0,1,... Å ØÖ Ü¹Ë Ö Û a ij x (k+1) j i 1 j=1 j=i a ij x (k+1) j a ij x (k) j ) j=i+1 a ij x (k) j (I ωd 1 L)x (k+1) = [(1 ω)i + ωd 1 U]x (k) + ωd 1 b D 1 (D ωl)x (k+1) = D 1 [(1 ω)d+ωu]x (k) + ωd 1 b x (k+1) = (D ωl) 1 [(1 ω)d +ωu]x (k) + ω(d ωl) 1 b = T SOR (ω)x (k) + ω(d ωl) 1 b Ñ Ø Ö ÁØ Ö Ø ÓÒ Ñ ØÖ Ü T SOR (ω) := (D ωl) 1 [(1 ω)d+ωu]. Ë ØÞ ¾ º¾ A R n n Ñ Ø a ii 0, i = 1,...,nº ÒÒ ÐØ Ö ω R ρ(t SOR (ω)) ω 1 Û Ò µ 1,...,µ n ÒÛ ÖØ ÚÓÒ T SOR (ω)º ÒÒ ÓÐ Ø n µ i = det(t SOR (ω)) ÑÒ Ø i=1 = det((d ωl) 1 )det([(1 ω)d +ωu]) = det(d 1 )det((1 ω)d) = det(d 1 )(1 ω) n det(d) = (1 ω) n. ρ(t SOR (ω)) = max i=1,...,n µ i 1 ω. ÃÓÖÓÐÐ Ö ¾ º ËÇÊ¹Î Ö Ö Ò ÓÒÚ Ö ÖØ Ø Ò Ö ω (0,2)º ω > 1 ÇÚ ÖÖ Ð Ü Ø ÓÒ ω < 1 ÍÒ ÖÖ Ð Ü Ø ÓÒ SOR = ËÙ Ú ÇÚ ÖÊ Ð Ü Ø ÓÒ )

14 ½ ¾ Ê Ð Ü Ø ÓÒ Ú Ö Ö Ò Ë ØÞ ¾ º µ Á Ø A R n n ÝÑÑ ØÖ ÔÓ Ø Ú Ò Ø Ó ÓÒÚ Ö ÖØ ËÇÊ¹Î Ö Ö Ò Ò Ù ÒÒ Û ÒÒ ω (0,2) Øº µ A R n n ÓÒ Ø ÒØ ÓÖ Ò Ø ÙÒ σ(t J ) = σ(i D 1 A) Rº ÖÒ Ö ρ := ρ(t J ) < 1. ÒÒ ÐØ µ ËÇÊ¹Î Ö Ö Ò ÓÒÚ Ö ÖØ Ö ÐÐ ω (0,2)º µ Å Ø Ö Ï Ð ω opt := ρ 2 ÐØ ρ(t SOR (ω opt )) ρ(t SOR (ω)) Ö ÐÐ ω (0,2) ÛÓ Øº ρ(t SOR (ω opt )) = 1 1 ρ ρ 2 Û ºÅ Ø Ö ³ÆÙÑ Ö Ð Ò Ö Ö Ð ÙÒ Ý Ø Ñ ³ Î Û ½ º

15 ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò ÒÙÒ Ô Þ ÐÐ A R n n ÝÑÑ ØÖ ÔÓ Ø Ú Ò Ø Ô µ º º A = A T ÙÒ x,ax 2 = x T Ax > 0 x R n \{0}. Ë ØÞ ¾ º½ Á Ø x Ä ÙÒ ÚÓÒ Ax = b Ñ Ø Ò Ö Ô ¹Å ØÖ Ü A R n n Ó ÐØ F(x) = min v R nf(v), ÛÓ F : R n R Ò ÖØ Ø ÙÖ F(v) = 1 a ik v k v i 2 i=1 k=1 = 1 2 v,av 2 b,v 2. b i v i i=1 Û Ö Ô ÖØ ÐÐ Ò Ð ØÙÒ Ò ÚÓÒ ÐØ F (v) = a jk v k b j. v j Ð Ó Ø ÙÒ k=1 F(v) = Av b 2 F v i v j (v) = a ij, À ¹Å ØÖ Ü ÚÓÒ F º Ä ÙÒ x ÚÓÒ Ax = b Ö ÐÐØ Ð Ó F(x) = Ax b = 0 ÙÒ 2 F(x) = A > 0 Ð Ó Ø x Ò Å Ò ÑÙÑ ÚÓÒ F º F(v) = Av b = 0 Ò ÒÓØÛ Ò ÃÖ Ø Ö ÙÑ Ø ÑÙ Å Ò ÑÙÑ Av = b Ð Ò Ð Ó Ø x Ò ÙØ ÐÓ Ð Å Ò ÑÙÑ ÚÓÒ F º

16 ½ ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò Þ ÒÙÒ Ö Î ØÓÖ r := Av b Û Ö Ê Ù ÒÚ ØÓÖ ÞÙ v ¹ Ò ÒÒØº Á Å Ò Ñ Ö F(v) Ø Ö Ø Ú ÙÑ Ò Æ ÖÙÒ Ò x ÞÙ Ö ÐØ Òº Á Ø Ò Ê ØÙÒ Ú ØÓÖ p R n \{0} Ò Ó Ø ÑÑ Ò Û Ö Ù ¹ Ò ÚÓÒ v R n Ò t R Ñ Ø F(v +t p) = minf(v +tp). t R Ï Ö Ò Ö Ò ϕ : R R ÙÖ ϕ(t) := F(v+tp) ÙÒ ÖÖ Ò Ò ϕ(t) = F(v +tp) = 1 2 v +tp,a(v+tp) 2 b,v +tp 2 Ø ÒÒ = 1 2 v,av 2 + t p,av t2 p,ap 2 b,v 2 t b,p 2 = 1 2 t2 p,ap 2 + t p,av b 2 + F(v) Ñ Ø r = Av b º A Ô Ø Û Ö ÙÖ ϕ (t) = 0 t = p,r 2 p,ap 2 =: t v A := v,av 2, v R n Ò ÆÓÖÑ Ò ÖØ Ó Ò ÒÒØ Ò Ö ÒÓÖÑº ÁÒ ÓÒ Ö Ø p,ap 2 > 0 p 0º Ç Ò Ö Ø t = 0 p,v 2 = 0 Ð Ó ÐÐ Ö Ê ØÙÒ Ú ØÓÖ p ÓÖ¹ Ø Ó ÓÒ Ð ÞÙÑ Ê Ù ÒÚ ØÓÖ v Û ÐØ ÛÙÖ º Ä ÑÑ ¾ º¾º Á Ø v = v +t p Ó ÐØ p,r 2 = 0 ÛÓ r = Av b Øº Û Ø p,r 2 = p,av b 2 = p,a(v +t p) b 2 = p,r+t Ap 2 = p,r 2 + t p,ap 2 = 0. Ò ÙÐ ÁÒØ ÖÔÖ Ø Ø ÓÒ n = 2 Æ Ú ÙÑ Ò Ò {v R n : F(v) = ÓÒ Ø} Ò ÓÒÞ ÒØÖ ÐÐ Ô Ò ÙÑ x

17 ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò ½ p x v r v r Å Ð Ï Ð ÚÓÒ p p = F(v) = (Av b) = r. ÖØ ÞÙÖ Å Ø Ó Ø Ð Ø Ò Ø v (k+1) = v (k) λ k (Av (k) b), k = 0,1,... ÃÓÒÚ Ö ÒÞ Ø Ö ÙÒØ Ö ÍÑ ØÒ Ò Ö Ð Ò Ñº Ö Ï Ð ÓÒ Ù ÖØ Ê ØÙÒ pº Ò Ø ÓÒ ¾ º º Û Î ØÓÖ Ò p,q R n Ò ÓÒ Ù ÖØ Ó Ö A¹ ÓÖØ Ó ÓÒ Ð ÐÐ Ö Ò Ô ¹Å ØÖ Ü A ÐØ p,q A := p,aq 2 = 0. ÒÒ Ñ Ò x (i),i = 0,...,k ÓÒ Ø ÑÑØ ÙÒ r 0,...,r k Ñ Ø r i = Ax (i) b ÞÙ Ö Ò Ê Ù ÒÚ ØÓÖ Òº ÖÒ Ö p 0 = r 0 º Ö k¹ø ËÙ Ö ØÙÒ p k ØÞ Ò Û Ö p k = r k + k 1 α j p j j=0 ÙÒ Ö Ò Ò α 0,...,α m 1 R Ó p k ÞÙ ÐÐ Ò Ò Ö Ò ËÙ Ö ¹ ØÙÒ Ò p 0,...,p k 1 ÓÒ Ù ÖØ Ø ÙÒ ØÞ Ò ÚÓÖÖ Ù Ö Ø ÐØº ÖØ Ö i = 0,...,k 1 ÞÙ p i,p j A = 0 0 i < j k 1

18 ½ ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò 0 = p k,ap i 2 = r k,ap i 2 + k 1 α j p j,ap i 2 j=0 ÙÒ Ñ Ø ÞÙ = r k,ap i 2 + α i p i,ap i 2 α i = r k,ap i 2 p i,ap i 2. ÖØ ÞÙ Ñ ÚÓÖÐÙ Ò Î Ö Ö Ò Ï Ð x (0) R n,p 0 := r 0 = Ax (0) bº ÁØ Ö Ö Ö k = 0,1,... λ k := p k,r k 2 p k,ap k 2 ; x (k+1) := x (k) +λ k p k ; r r+1 := r k + λ k Ap k º Û ÚÓÒ Ä ÑÑ ¾ º¾µ p k+1 := r k+1 Ë ØÞ ¾ º ÐØ k j=0 r k+1,ap j 2 p j,ap j 2 p j. µ p k,ap i 2 = 0, 0 i < k µ U k+1 := span{p 0,...,p k } = span{r 0,...,r n } ÙÒ dimu k+1 = k +1 µ r k U k µ x (k) = A 1 b r k = 0 p k = 0 µ U k+1 = span{r 0,Ar 0,...,A k r 0 } µ r k,ap i 2 = 0, 0 i < k 1 º Û µ ÃÐ Ö Ò ÃÓÒ ØÖÙ Ø ÓÒº µ ÁÒ Ù Ø ÓÒ Ö k k = 0 p 0 = r 0 R n \{0} ÙÔØÙÒ º Ë ÙÔØÙÒ Ö k 0 Û Òº p 0,...,p k+1 ÓÖØ Ó ÓÒ Ð Þ Ð Ë Ð ÖÔÖÓ Ù Ø u,av 2 Ò ÓÐ Ødim{p 0,...,p k,p k+1 } = dimu k+2 = k +2º Æ ÃÓÒ ØÖÙ Ø ÓÒ ÐØ p k+1 r k+1 = k α j p j U k+1 j=0 ÙÒ ÓÑ Ø U k+2 = span{u k+1,p k+1 } = span{u k+1,r k+1 }. µ Ï Ö Û Ò Û Ö Ò Ù Ø Ú r 1,r 0 2 = r 0,r 0 2 p 0,r 0 2 p 0,Ap 0 2 Ap 0,r 0 2 = 0,

19 ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò ½ p 0 = r 0 Øº ÐØ ÙÔØÙÒ Ö k Ó Ø Ñ Ø η U k ÖÒ Ö ÐØ r k+1,η 2 = r k,η }{{} 2 +λ k Ap k,η }{{} 2 =0 nach Ind.vor. =0 nach a) r k+1,p k 2 = r k,p k 2 p k,r k 2 p k,ap k 2 p k,ap k 2 = 0 ÙÒ Ñ Ø ÙÔØÙÒ º µ x k = A 1 b r k = 0 Ð Öº Á Ø r k = 0 Ó Ø p k = 0 Ò ÃÓÒ ØÖÙ Ø ÓÒº Á Ø p k = 0 Ó Ø r k U k Ò µ Ö Ø Ù r k U k Ò µº Ð Ó Ø r k = 0º µ ÁÒ Ù Ø ÓÒ Ò k k = 0 Ð Öº ÐØ ÙÔØÙÒ Ö kº Ù µ ÓÐ Ø ÓÛ Ð Ó Ø r k U k+1 = span{r 0,...,r k } = span{r 0,...,A k r 0 } Ap k AU k+1 = span{ar 0,...,A k+1 r 0 }. r k+1 = r k +λ k Ap k span{r 0,...,A k+1 r 0 }. Ù µ ÓÐ Ø dimu k+2 = k +2 Ð Ó Ø U k+2 = span{r 0,...,A k+1 r 0 }. µ Ö i < k 1 ÐØ p i U k 1 ÙÒ ÓÑ Ø Ap i U k Ò µº ÓÐ Ð ÐØ Û Ò µ r k,ap i 2 = 0 Å Ø À Ð ÚÓÒ Ë ØÞ ¾ º ÒÒ Ò Û Ö Ò Ê Ò Ù Û Ò Î Ö Ö Ò Ú ÖÖ Ò ÖÒº Ù µ Ð ÖØ p k = r k Ù µ Ð ÖØ k 1 j=0 r k,ap j 2 p j,ap j 2 p j = r k r k,ap k 1 2 p k 1,Ap p 1 2 p k 1 0 = r k+1,r k 2 = r k +λ k Ap k,r k 2 λ k = r k,r k 2 Ap k,r k 2 ÙÒ ÓÑ Ø ÐØ r k,r k 2 = p k,r k 2 º Ù Ö Ñ

20 ½ ¼ ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò Ap k = 1 λ k (r k+1 r k ) Ø ÓÐ Ø ÒÓ r k+1,ap k 2 = r k+1,r k+1 r k b)c) = p k,ap k 2 p k,r k+1 r k 2 r k+1,r k+1 2 p k,r k 2. ËÓÑ Ø Ö ÐØ Ò Û Ö Ò ÐØ ÓÖÑ Î Ö Ö Ò Ö ÃÓÒ Ù ÖØ Ò Ö ÒØ Ò ¹Î Ö Ö Òµ Ï Ð x (0) R n r 0 := Ax (0) b, p 0 := r 0, α 0 := r º ÁØ Ö Ö Ö k = 0,1,... ÐÐ α k 0 Ø Ò Ö r k := Ap k x (k+1) := x (k) +λ k p k ; r k+1 := r k +λ k v k ; α k+1 := r k ; p k+1 := r k+1 + α k+1 α k p k. Þ ÒÙÒ Ö Î ØÓÖÖ ÙÑ ; λ k := α k r k,p k 2 ; U k := span{r 0,...,A k 1 r 0 } Ø ÃÖÝÐÓÚ¹ÍÒØ ÖÖ ÙÑ Ö Ñ Ò ÓÒ kº Ö ¹Î Ö Ö Ò ÐØ Ø Ø x (k) x (0) + span{p 0,...,p k 1 } 27.4 e) = x (0) +U k. ÐØ Ó Ö Ë ØÞ ¾ º Ö ÁØ Ö ÖØ Ò ¹Î Ö Ö Ò ÐØ F(x (k) ) = min v x 0 +U k F(v). Û Ö Ð η U k \{0} ÙÒ Û Ò x (k) x 0 +U k ÐØ Ñ Ø Ö ØÐ ÙÒ ϕ(t) := F(x (k) +tη) ÙÒ ÓÑ Ø ϕ (t) = η,aη 2 + η,ax (k) b 2, ϕ (0) = η,ax (k) b 2,

21 ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò ½ ½ Û Ö Ù Ë ØÞ ¾ º µ ÓÐ Øº f(x (k) ) = min v x0 +U k F(v) r k = Ax (k) b U k ÃÓÖÓÐÐ Ö ¾ º Ü Ø Ö Ê ÒÙÒ Ò Ø ¹Î Ö Ö Ò Ò ÔØ Ø Ò n Ë Ö ØØ Ò Ñ Ø Ö Ü Ø Ò Ä ÙÒ x (n) = x = A 1 bº Û ÓÐ Ø Ù Ë ØÞ ¾ º ÙÒ dimu k = kº ÁÑ ÐÐ Ñ Ò Ò Ò Ø ¹Î Ö Ö Ò Ù ÖÙÒ ÚÓÒ ÊÙÒ ÙÒ ¹ Ð ÖÒ Ò Ø Ò n Ë Ö ØØ Òº Å Ò ÒÒ ÓÐ Ò ÃÓÒÚ Ö ÒÞÖ ÙÐØ Ø Û Òº Ë ØÞ ¾ º ÃÓÒÚ Ö ÒÞ ¹Î Ö Ö Ò µ Á Ø A R n n Ô ÙÒ x = A 1 b Ó ÐØ Ö ÁØ Ö ÖØ Ò x (k) ¹Î Ö Ö Ò ( ) k κ 1 x (k) x A 2 x (0) x A κ+1 ÛÓ ËÔ ØÖ Ð ÓÒ Ø ÓÒ ÚÓÒ A Øº κ = λ max = A 2 A 1 2 λ min Û ËØÓ Ö» ÙÐ Ö ÃÓÒÚ Ö ÒÞ Û Ò Ø Ò Ø Ð Ó ÚÓÒ Ö ÃÓÒ Ø ÓÒ ÚÓÒ A º

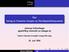
22 ½ ¾ ¾ Î Ö Ö Ò Ö ÓÒ Ù ÖØ Ò Ö ÒØ Ò x 2 x = A ( 1) b x (3) x (2) p 2 p 1 x (1) x (0) x 1 Æ Ú ÙÑ Ò Ò {v R n : F(v) = F(x (k) )} ÙÒ ÃÓÒÚ Ö ÒÞÚ ÖÐ Ù ¹Î Ö Ö Ò Ö n = 2º