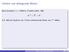
Herbstsemester v T A 1 u. = I + uv T A 1 uvt A 1 + uv T A 1 uv T A 1. = I + uv T A 1 u(1 + vt A 1 u)v T A 1

Transkript

1 Dr. V. Gradinaru K. Imeri Herbstsemester 2018 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie 11 Aufgabe 11.1 Sherman-Morrison-Woodbury-Formel In dieser Aufgabe üben wir die Anwendung des Matrixkalküls und das Rechnen mit Blockmatrizen im Zusammenhang mit einer wichtigen Formel für die Inverse von Matrizen, die durch die Modifikation einer invertierbaren Matrix durch ein Tensorprodukt (äusseres Produkt) hervorgeht. Gegeben seien eine invertierbare Matrix A R n n, n N, und zwei beliebige Vektoren u, v R n, für die gelte 1 + v T A 1 u a) Zeigen Sie, dass (A + uv T ) 1 A 1 A 1 uv T A v T A 1 u. Hinweis: Machen Sie sich zuerst klar, wie man nachweist, dass eine Matrix die Inverse einer anderen Matrix ist. Danach läuft die Lösung der Aufgabe auf ein ziemlich mechanisches Anwenden der Rechenregeln für das Matrixprodukt hinaus. Wichtig ist, dass man sieht, wann sich bestimmte Matrixprodukte auf blosse Zahlen reduzieren, denn dann lassen sie sich natürlich mit anderen Matrixprodukten vertauschen. Lösung: Man will zeigen, dass (A + uv T )(A + uv T ) 1 I. Also: (A + uv T )(A 1 A 1 uv T A v T A 1 u ) AA 1 + uv T A 1 AA 1 uv T A 1 + uv T A 1 uv T A v T A 1 u I + uv T A 1 uvt A 1 + uv T A 1 uv T A v T A 1 u I + uv T A 1 u(1 + vt A 1 u)v T A v T A 1 u I + uv T A 1 uv T A 1 (1 + vt A 1 u) 1 + v T A 1 u I + uv T A 1 uv T A 1 I. 11.1b) Wir betrachten nun das folgende lineare Gleichungssystem in Blockmatrixform: [ ][ ] [ ] A u x b v T 1 ζ 0 (11.1.1) Geben Sie die Matrixnotation eines linearen Gleichungssystem mit n Gleichungen und n Unbekannten an, das vom Vektor x aus der Lösung von (11.1.1) erfüllt wird. Hinweis: Das logische Vorgehen ist natürlich die Elimination von ζ. Seite 1

2 Lösung: Ausmultiplizieren von (11.1.1) ergibt: Einsetzen von ζ v T x in (11.1.2) ergibt Ax + uζ b (11.1.2) v T x ζ 0 Ax + uv T x b (A + uv T )x b. Aufgabe 11.2 Rang-Eins Modifikation In dieser Aufgabe sehen wir eine Möglichkeit, wie wir durch Rang-Eins-Matrizen modifizierte lineare Gleichungssysteme mit wenig Aufwand lösen können, sofern wir die Lösung der Originalgleichung kennen. Wir betrachten eine Matrix A R n n, für welche gilt A A T. Weiter nehmen wir einen Vektor u R n \ {0} und definieren die Matrizen M ± : A ± uu T. 11.2a) Zeigen Sie, dass Bild(M ± ) Bild(A) + Bild(uu T ). Bemerkung: Wir nehmen an, dass Rang A m n. Bedenken Sie, dass Rang uu T 1, da dim Kern(uu T ) dim Kern(u T ) n 1. Dann folgt aus der Aufgabe, dass Rang M ± m + 1. Lösung: Wir schreiben die Definition von Bild(M ± ) aus: Bild(M ± ) {( A ± uu T ) x : x R n} x 1 x 1(A) :,1 + + x n (A) :,n ± u T x u : x. R n R x n x 1 (A) :,1 + + x n (A) :,n + x n+1 u : x. x n Rn+1 x n+1 x 1 x 1(A) :,1 + + x n (A) :,n : x. R n + {x n+1u : x n+1 R} x n Bild(A) + Bild(uu T ). 11.2b) Zeigen Sie, dass M ± invertierbar ist, sofern gilt, dass A invertierbar ist und u T A 1 u / { 1, 1}. Hinweis: Die Sherman-Morrison-Woodbury-Formel könnte hier sehr hilfreich werden. Lösung: Wir können die Sherman-Morrison-Woodbury-Identität direkt verwenden. Sie gilt gerade für invertierbare Matrizen A R n n und Vektoren u R n, so dass u T A 1 u / { 1, 1}, und stellt die gesuchte Inverse dar: (M ± ) 1 (A ± uu T ) 1 A 1 A 1 uu T A 1 1 ± u T A 1 u. Seite 2 x 1

3 11.2c) Für gegebene Lösung x R n und rechte-seite-vektor b R n soll u so bestimmt werden, dass gilt M + x b, oder M x b. (11.2.1) Hinweis: (1) Machen Sie den Ansatz r : b Ax und betrachten Sie die Fälle (a) r 0, (b) r R n \ {0}. (2) Zeigen Sie im Fall (1b), dass für ein geeignetes u R n gelten muss: u span{r}. Machen Sie dann den Ansatz u : αr für ein α R. (3) Machen Sie bei der weiteren Rechnung im Fall (1b) eine weitere Fallunterscheidung nach dem Vorzeichen von r T x R. Lösung: Wir formen die beiden Gleichungen um. M ± x b ( A ± uu T ) x b ±u u T x R b Ax :r (11.2.2) Wenn r 0 gilt, dann wählen wir u 0 und die Gleichung ist erfüllt. Andernfalls, also für r R n \ {0}, machen wir den Ansatz u : αr und setzen diesen in (11.2.2) ein. Wir erhalten Wir unterscheiden nun drei verschiedene Fälle: ±α 2 r r T x r R ±α 2 r T x 1. (11.2.3) Sofern r T x 0, ist die Gleichung (11.2.3) nie erfüllt. Wir erhalten folglich keine Lösung. Im Falle r T x < 0 müssen wir r T x > 0 betrachten, damit wir die Wurzel ziehen und α berechnen können. Wir erhalten α 1 r T x. In diesem Fall gilt die Gleichung (11.2.1) für M x b. Für r T x > 0 müssen wir, damit die Wurzel davon (und somit α) definiert ist, die Gleichung M + x b verwenden. Wir erhalten α 1. r T x Aufgabe 11.3 Lineare Regression in der Signalverarbeitung Die lineare Ausgleichsrechnung spielt auch eine grosse Rolle in der modernen Signalverarbeitung, zum Beispiel, wenn es um das Ausmessen von Übertragungskanälen geht. Man erhält auf diese Weise etwa die Werte für die Gewichte in der Point-Spread-Function, die die Verzerrung von Pixelbildern in optischen Übertragungssystemen beschreibt. In dieser Aufgabe behandeln wir aber einen einfacheren, eindimensionalen Fall, nämlich die Störung eines zeitdiskreten Signals bei der Übertragung. Seite 3

4 Abbildung 11.1: Übertragungskanal und zeitdiskrete Signale auf Senderseite (links) und Empfängerseite (rechts) Wir betrachten ein zeitdiskretes Signal, welches gegeben ist durch die Folge von Werten x 1,..., x m, m N, die die Signalamplituden zu festen Abtastzeitpunkten angeben. Diese Signale werden durch einen linearen Übertragungkanal (in Abbildung 11.1 mit einem blauen Pfeil symbolisiet) geschickt, wobei vorher und nachher Funktstille herrscht. Leider ist der Kanal nicht perfekt, so dass sich zeitlich benachbarte Signalwerte gegenseitig beeinflussen, ein Phänomen, das man als Übersprechen bezeichnet. Daher besteht das am anderen Ende des Kanals empfangene Signal aus einer anderen Folge von Werten y 1,..., y m. Der Zusammenhang zwischen dem empfangenen und gesendeten Signal ist näherungsweise gegeben durch wobei wir annehmen, dass gilt x 0 x m+1 0. y i βx i 1 + αx i + βx i+1, i 1,..., m, (11.3.1) Die Aufgabe besteht nun darin, die unbekannten Übersprechparameter α und β aus den gemessenen Signalen zu ermitteln und zwar durch Lösen eines überbestimmten linearen Gleichungssystems mit der Methode der kleinsten Quadrate aus der Vorlesung. 11.3a) Stellen Sie das überbestimmte lineare Gleichungssystem für das Schätzproblem auf. Hinweis: Die Herausforderung besteht darin, die Koeffizientenmatrix A, die Unbekannten x und die rechte Seite b aus (11.3.1) richtig zu identifizieren. Dabei ist Vorsicht geboten, denn die Notation in (11.3.1) kann leicht in die Irre führen; die x i sind keine Unbekannten! Lösung: Setze A x 1 x 2 x 2 x 1 + x 3 x 3 x 2 + x 4. x m 1 x m, x. x m 2 + x m x m 1 Dann ist unser überbestimmtes Gleichungssystem Ax b. [ ] α β y 1 y 2 y m und b b) Geben Sie die Normalengleichungen für das überbestimmte lineare Gleichungssystem aus Teilaufgabe 11.3a) an. Geben Sie die Einträge der Matrix der Normalengleichung explizit an. Seite 4

5 Lösung: Die Normalengleichung von Ax b ist A Ax A b und, zur Erinnerung, die Lösung der Normalengleichung ist die beste Lösung zur Minimierung der Fehlers b Ax. Wir schreiben Dann gilt C 11 m i1 x2 i. Weiter gilt m 1 C 12 C 21 x 1 x 2 + m i2 x 1 x 2 [ ] x 2 x 1 + x 3 C A T x1 x A 2... x m x 3 x 2 + x 4. x 2 x 1 + x 3... x m 1.. i2 x m m 1 x i (x i 1 + x i+1 ) + x m 1 x m x 1 x 2 + m 1 m 1 x i x i 1 + x i x i+1 2 x i x i+1. i1 Für den letzten Eintrag in C erhalten wir m 1 C 22 x i2 i1 (x i 1 + x i+1 ) 2 + x 2 m 2 m 2 i2 i2 m 1 x 2 i + 2 i2 x m 1 m 1 x i x i 1 + Berechnen wir nun A T b. Wir erhalten [ m A T b i1 x ] iy i x 2 y 1 + x m 1 y m + m 1 i2 y. i(x i 1 + x i+1 ) i2 x i 1 x i+1 + x x 2 m. x i x i+1 + x m x m c) Für welche Signale x 1, x 2,..., x m können wir keine eindeutige Kleinste-Quadrate-Lösung erwarten? Hier geben theoretische Resultate aus der linearen Algebra dem Ingenieur Hinweise darauf, wie der die Messung durchzuführen hat. Hinweis: Erinnern Sie sich an eine Bedingung an die Systemmatrix, die die Eindeutigkeit der Kleinste- Quadrate-Lösung sicherstellt. Überlegen Sie sich dann, wann die Matrix des überbestimmten Gleichungssystems aus Teilaufgabe 11.3a) keinen vollen Spaltenrang hat. Dies führt auf ein Eigenwertproblem. Um Eigenvektoren zu finden, probieren Sie schliesslich Eingangssignale der Form ( x l (x l j) m j1 R m, l {1,..., m} mit x l j : sin π jl ), j 1,..., m. m + 1 Lösung: Es muss Rang(A) 2 gelten, damit die Normalengleichungen eine eindeutige Lösung besitzen. Damit hingegen Rang(A) 1, muss gelten, dass x i 1 + x i+1 λx i für alle i. Wir schreiben diese Gleichungen in Matrixform auf: Mx : x λx (11.3.2) Seite 5

6 Falls nun x l ein Eigenvektor von M ist, gilt Mx l λ l x l. Wir folgen dem Tipp und machen den Ansatz: ( x l (x l j) m j1 R m, l {1,..., m} mit x l j : sin π jl ), j 1,..., m. (11.3.3) m + 1 Einsetzen in (11.3.2) ergibt: ( sin π x l i 1 + x l i+1 λ l x i ) ( + sin π (i 1)l m + 1 (i + 1)l m + 1 ) λ l x i. (11.3.4) Als nächstes verwendet man die trigonometrischen Identitäten sin(a + b) sin(a) cos(b) + cos(a) sin(b) und sin(a b) sin(a) cos(b) cos(a) sin(b). Damit wird aus (11.3.4) für a π il l m+1 und b ±π m+1 : ) ( ) ( ) πil πl x l i 1 + x l i+1 2 sin cos m + 1 m + 1 ( πl 2 cos m + 1 :λ l x l i, l 1,..., m. Somit ist gezeigt, dass x l tatsächlich ein Eigenvektor von M ist. Als nächstes zeigen wir, dass für x x l die Spalten von A linear abhängig sind: ( ) πl x l i 1 + x l i+1 2 cos x l i, l 1,..., m, m + 1 ( ) πl A :,2 2 cos A :,1 m + 1 Das bedeutet Rang(A) 1. Daraus folgt, dass auch A T A nicht mehr vollen Rang hat, sobald x ein Eigenvektor von M ist. Aufgabe 11.4 Lineare Rekursion: Das Räuber-Beute-Modell Eine Anwendung linearer Rekursionen ist die Vorhersage der dynamischen Entwicklung der Altersstruktur einer Population. Darüber hinaus sind lineare Rekursionen sehr wichtig für die mathematische Modellierung von Populationsdynamik, denn die natürlichen Rhythmen von Tag und Nacht und Jahreszeiten legen eine Entwicklung in Zeitschritten nahe. Um qualitative und quantitative Vorhersagen aus solchen Modellen zu treffen, ist die Diagonalisierung der Rekursionsmatrix das entscheidende Hilfsmittel. Dieses Werkzeug stellt die lineare Algebra bereit. Wir betrachten ein zeitdiskretes Räuber-Beute-Modell, welches repräsentiert wird durch die parameterabhängigen Rekursionsgleichungen q k, q k+1 α + 6, k N 0, (11.4.1) 5 q k, wobei die Population der Räuber und q k die Population der Beute zum Zeitpunkt t k darstellt, und in Abhängigkeit vom reellen Parameter α [0, 1]. Offensichtlich impliziert das Modell (11.4.1) ein exponentielles Wachstum der Beutepopulation, wenn keine Räuber vorhanden sind (Koeffizient 6 5 ), eine exponentielle Abnahme der Räuberpopulation, falls es keine Beutetiere gibt (Koeffizient 3 5 ), Seite 6

7 ein reduziertes Wachstum oder sogar ein Schrumpfen der Beutepopulation in Gegenwart von vielen Räubern (Koeffizient α), eine weniger starke Abnahme oder sogar eine Zunahme der Räuberpopopulation, wenn viele Beutetiere vorhanden sind (Koeffizient 3 5 ). Zum Zeitpunkt t 0 seien die Anfangswerte gegeben durch (p 0, q 0 ) R a) Stellen Sie das Räuber-Beute Modell in der Form einer linearen Rekursion gemäss dar, wobei A R 2 2, x k R 2 für alle k N. x k+1 Ax k (11.4.2) Lösung: Wir definieren x k : [ q k ]. Somit erhalten wir aus (11.4.1) [ 3 ] x k α 6 x k. (11.4.3) 5 :A 11.4b) Für welche(n) Wert(e) von α gibt es [ p 0 q 0 ] 0 so, dass p 0 und q k q 0 für alle k N? Hinweis: Natürlich muss man nur herausfinden, wann p 1 p 0 und q 1 q 0. Die Berechnung von Eigenwerten ist für diese Teilaufgabe nicht notwendig. Lösung: Wir betrachten die Gleichung (11.4.2) für k 0 und setzen dort die Bedingungen p 1 p 0 und q 1 q 0 ein: [ α 1 5 [ α x 0 Ax 0. ] [ ] x ] [ ] x Wir erhalten folglich eine nichttriviale Lösung, falls 2 5α 0 gilt, beziehungsweise α 2 5. Für dieses α bleibt die Folge {(, q k )} k N konstant. 11.4c) Berechnen Sie die Eigenwerte der Matrix A in Abhängigkeit des Parameters α [0, 9 20 ). Lösung: Wir berechnen die Eigenwerte von A, indem wir das charakteristische Polynom von A berechnen und dessen Nullstellen bestimmen. [ 3 p A (λ) : det (A λi n ) det 5 λ ] ( )( ) α 5 λ 5 λ 5 λ + α 5 λ α λ Die Eigenwerte sind die Nullstellen des charakteristischen Polynoms von A, p A (λ). Sie lauten λ 1, ± α ± 9 20α 10. (11.4.4) Seite 7

8 11.4d) Analysieren Sie das Verhalten von (, q k ) für t k in Abhängigkeit des reellen Parameters α > 0. Genauer, für welche Werte von α (0, 9 20 ) gilt p2 k + q2 k < für alle k N und alle Startwerte (p 0, q 0 ) R 2? Hinweis: Man hat die Beträge aller Eigenwerte der Rekursionsmatrix in Abhängigkeit vom Parameter zu inspizieren. Lösung: Wir betrachten die Diskriminante in (11.4.4). Für α [0, 9 20 ) gilt, dass D 9 20α > 0. Somit sind die Eigenwerte λ 1, λ 2 von A immer reell und verschieden voneinander. Die Folge x k [ q k ], beziehungsweise die Rekursion (11.4.3), lässt sich deshalb in der Eigenbasis zu den Eigenwerten λ 1, ± 9 20α 10 darstellen. Wir erhalten mithilfe der Basiswechselmatrix S die Darstellung der Rekursion in der Eigenbasis, y k S 1 x k. ( S } 1 {{ x k+1 } S 1 Ax k S 1 A k x 0 S 1 SD k S 1) x 0 D k S } 1 {{ x } 0. :y k+1 :y 0 y k+1 D k y 0. Wir bemerken, dass diese Folge y k genau dann beschränkt bleibt für alle y 0, sofern gilt λ 1 1, λ 2 1 (siehe Konvergenzkriterium für geometrische Folgen aus der Analysisvorlesung). Wir erhalten λ 1, α 10 ± ± 9 20α α 1 α 2 5, was aufgrund der Monotonizität von λ 1,2 in Abhängigkeit von α dazu führt, dass die Folge y k (und somit auch x k ) beschränkt ist für alle α [ 2 5, 9 20 ), und divergiert für α [0, 2 5 ). 11.4e) Schreiben Sie eine MATLAB-Funktion function [p,q] raeuber beute modell( alpha ), welche einen konkreten reellen Wert α > 0 als Eingabe nimmt und das Verhalten des Räuber-Beute Modells [ über ] eine lange Zeitdauer [0, t 100 ] simuliert, wobei t k 0.1 k. Als Startwerte wählen wir 300 [ ] x 0. Die Funktion soll die Werte für p 600 k, q k über diesen Zeitraum plotten und x 100 p 100 q 100 zurückgeben. Überprüfen Sie so Ihre Berechnungen in Teilaufgabe 11.4d). Lösung: Listing 11.1: MATLAB-Funktion aus Teilaufgabe 11.4e) 1 f u n c t i o n [p,q] raeuber_beute_modell(alpha) 2 % Diese Funktion nimmt den Parameter \alpha >0 und gibt 3 % p und q zurueck, welche die Werte [p^100,q^100] der Rekursion 4 % [p^k,q^k] [0.6, 0.2; -alpha, 1.2] [p^k,q^k] 5 % repraesentieren. 6 % Seite 8

9 7 % Schrittweite 0.1, t_00, t_100100* t 0:0.1:10; 9 N 101; 10 % Startwerte 11 x0 [300;600]; 12 % Rekursionsmatrix A 13 A [0.6, 0.2; - alpha, 1.2]; 14 % Inizialisierung der Vektoren p_vec, q_vec. 15 p_vec z e r o s (N,1); 16 p_vec(1)x0(1); 17 q_vec z e r o s (N,1); 18 q_vec(1)x0(2); % Ausfuehrung der Rekursion 100 mal 21 f o r k2:n 22 x A*[p_vec(k-1,1);q_vec(k-1,1)]; 23 p_vec(k,1) x(1); 24 q_vec(k,1) x(2); 25 end % Plotten der Folgen x^k, k0,..., f i g u r e ; 29 p l o t (t, p_vec, -xr, t, q_vec, -*b ) 30 x l a b e l ( t_k ) 31 y l a b e l ( p_k, q_k ) 32 legend( p_k, q_k ) % Ausgaben 35 p p_vec(n); 36 q q_vec(n); 37 end Aufgabe 11.5 Die Spur diagonalisierbarer Matrizen In dieser Aufgabe lernen wir eine spezielle Funktion auf dem Raum der quadratischen Matrizen kennen, die Spur. Sie steht in enger Beziehung zum Spektrum einer Matrix. Die Spur einer quadratischen Matrix M R n n ist definiert als Spur M : n (M) j,j. (11.5.1) j1 11.5a) Bestimmen Sie die Dimension des Unterraums U : { M R n n : Spur M 0 } R n n. Hinweis: Sie können U als Kern einer Matrix charakterisieren. Dann sieht man, dass diese Matrix nur ein Zeilenvektor ist. Seite 9

10 q k q k , q k 300, q k t k t k (a) Plot für α 0.45 (b) Plot für α q k q k , q k 450, q k t k t k (c) Plot für α 0.4 (d) Plot für α 0.39 Abbildung 11.2: Plot-Ausgaben der MATLAB-Funktion aus Teilaufgabe 11.4e) für verschiedene Parameter α. Lösung: Wir schreiben die Matrix M als Vektor. Wir definieren für jede Matrix M R n n den Vektor v M (M) :,1 (M) :,2. (M) :,n R n2. Für die Matrix A R 1,n2 mit {1 j { 1, n + 2, 2n + 3, 3n + 4,..., n(n 2) + n 1, n 2} (A) 1,j :. 0 sonst gilt Somit erhalten wir Spur M Av M. dim U dim { M R n n : Spur M 0 } dim { M R n n : Av M 0 } dim Kern(A) n 2 1. Seite 10

11 11.5b) Zeigen Sie, dass gilt Lösung: Spur (BC) Spur BC Spur CB, B, C R n n. (11.5.2) n j1 k1 n b jk c kj n k1 j1 n c kj b jk Spur (CB), wobei b ij den ij-eintrag der Matrix B bezeichnet und c kj den kj-eintrag von C. Bemerkung: Beachten Sie aber, dass im Allgemeinen Spur (ABC) Spur (BAC)! Als einfaches Gegenbeispiel betrachten Sie die Matrizen [ ] [ ] [ ] A, B, C Explizites ausrechnen ergibt Spur (ABC) 35 und Spur (BAC) c) Sei A R n n diagonalisierbar, mit wobei S R n n invertierbar ist. Zeigen Sie, dass gilt A S diag(λ 1,..., λ n ) S 1, (11.5.3) :D Spur A n λ j. (11.5.4) Bemerkung: Die Identität (11.5.4) bietet ein nützliches Hilfsmittel zur Überprüfung der Korrektheit von berechneten Eigenwerten. Hinweis: Verwenden Sie Teilaufgabe 11.5b). Lösung: Wir benutzen Teilaufgabe 11.5b) und die Zerlegung in (11.5.3): Spur A (11.5.3) Spur ( SD :B S 1 ) (11.5.2) :C j1 Spur ( S } 1 {{ S } D) Spur (D) I n n λ j. j1 Aufgabe 11.6 Fourier-Matrizen Die Tatsache, dass selbst reelle Polynome komplexe Nullstellen haben können, zwingt uns dazu, im Zusammenhang mit der Diagonalisierung von Matrizen in C zu rechnen. Das ist auch einer der tieferen Gründe für die grosse Bedeutung komplexer Zahlen in Wissenschaft und Technik. Machen Sie also nicht Ihren Mathematikprofessor dafür verantwortlich, dass Sie sich mit komplexen Zahlen herumschlagen müssen, sondern die Weigerung mancher reeller Polynome, ausschliesslich reelle Nullstellen zu haben. Eine sehr wichtige Familie komplexer Matrizen sind die Fouriermatrizen F n (Fkl n)n k,l1 Cn n, n N, definiert durch ( ) 2πi Fkl n : exp (k 1)(l 1), 1 k, l n. n Dabei bezeichnet i C die imaginäre Einheit (i 2 1). Seite 11

12 11.6a) Zeigen Sie, dass für alle n N gilt, dass F H n F n n I n, wobei das hochgestellte H die komplex konjugierte Transponierte einer Matrix bezeichnet (die hermitesch Transponierte). Hinweis: Aus der Analysis sollten die folgenden Rechenregeln für die komplexe Exponentialfunktion bekannt sein: exp(2πik) 1 für jedes k Z, exp(kz) (exp(z)) k für alle k Z, z C, exp(z) exp(z) für alle z C. Erinnern Sie sich ausserdem an die geometrische Summenformel n 1 q k 1 qn 1 q k0 für alle q C \ {1}, n N. Lösung: Wir schreiben w exp ( ) 2πi n. Dann gilt ( ) 2πi w m exp n m für m Z, ( ) 2πi w n exp n n exp(2πi) 1, ( ) ( ) ( 2πi 2πi w m exp n m exp n m exp 2πi ) n m w m. Da F n kl exp( 2πı n (k 1)(l 1)), erhalten wir F n kl F n lk w(k 1)(l 1) für alle 1 l, k n. Anders gesagt, Fn T F n, und damit Fn H F n. Definiere A Fn H F n. Wir wollen zeigen, dass A ni n. Die Definition von A (A lj ) als Produkt zweier Matrizen gibt uns n n n A lj (Fn H ) lk (F n ) kj w (l 1)(k 1) w (k 1)(j 1) w ( l+1)(k 1) w (k 1)(j 1) k1 k1 n w (k 1)(1 l+j 1) k1 n w (k 1)(j l). k1 Wir unterscheiden die folgenden zwei Fälle: 1. Falls l j, dann a ll n w (k 1)(l l) k1 Das heisst a ll n für 1 l n. 2. Falls l j, dann a lj n w (k 1)(j l) k1 k1 n w (k 1) 0 k1 n 1 n. k1 n n 1 (w j l ) (k 1) (w j l ) (k) 1 (wj l ) n 1 (w j l ) 0 1 (w j l ) 0. k1 Das heisst a jl 0, falls j l. Zusammen erhalten wir A ni n, also F H n F n ni n. k0 Seite 12

13 11.6b) Mit welcher komplexen Zahl muss man F n multiplizieren, um eine unitäre Matrix zu erhalten? Lösung: Falls wir F n : 1 n F n definieren, erhalten wir mit 11.6a), dass F H n F n 1 n F H n F n 1 n ni n I n, also ist F n unitär. 11.6c) Es bezeichne e (k) R n den k-ten Einheitsvektor. Die zyklische Permutationsmatrix P n R n n ist definiert durch P n [e (2), e (3),..., e (n 1), e (n), e (1) ]. Zeigen Sie, dass diese Matrix durch die Fouriermatrix diagonalisiert wird, dass es also eine Diagonalmatrix D C n n so gibt, dass P n F n F n D. Bestimmen Sie auch die Diagonaleinträge von D. Hinweis: Erinnern Sie sich daran, dass AS SD, D diag(λ 1,..., λ n ), genau dann wenn die Spalten s l, l 1,..., n, von S erfüllen, dass As l λ l s l, l 1,..., n. Lösung: Wir schreiben P n (p n i,j )n i,j1 und F n (fi,j n )n i,j1 (w(i 1)(j 1) ) n i,j1. Bedenken Sie, dass p n i,i 1 1, pn 1,n 1 und pn i,j 0 für die übrigen Fälle von (i, j). Dann haben wir für den (l, k)-ten Eintrag der folgenden Matrix ({ ) n (P n F n ) l,k p l,j fj,k n fn,k n, falls l 1, f n j1 l 1,k, falls l 2, l,k l,k ({ ) ({ ) w (n 1)(k 1), falls l 1, w (k 1) w n(k 1), falls l 1, w (l 2)(k 1), falls l 2, w (k 1) w (l 1)(k 1), falls l 2, l,k l,k ({ ) ({ ) w (k 1) w n(k 1), falls l 1, w (k 1) 1, falls l 1, w (k 1) w (l 1)(k 1), falls l 2, w (k 1) f n l,k l,k, falls l 2, l,k ( ) w (k 1) fl,k n Wir haben gezeigt, dass l,k, (P n F n ) :,k w (k 1) (F n ) :,k, Mit dem Hinweis folgt D : diag(1, w 1,..., 1, w (n 1) ) haben wir P n F n F n D. Aufgabe 11.7 Orthogonalität von Eigenvektoren normaler Matrizen Satz 7.4 im Buch garantiert die lineare Unabhängigkeit von Eigenvektoren einer Matrix A C n n, die zu verschiedenen Eigenwerten von A gehören. Für eine spezielle Klasse von Matrizen, nämlich die normalen Matrizen, kann man eine viel stärkere Aussage einfach beweisen, nämlich den folgenden Satz: Seite 13

14 Satz. Erfüllt die Matrix A C n n die Bedingung AA H A H A, (11.7.1) ist sie also vertauschbar mit ihrer konjugiert Transponierten A H, so sind jeweils zwei Eigenvektoren, die zu verschiedenen Eigenwerten gehören, orthogonal. Beachten Sie, dass wir in dieser Aufgabe konsequent mit komplexen Matrizen und Vektoren rechnen. 11.7a) Zeigen Sie, dass für eine Matrix, die (11.7.1) erfüllt, gilt: Kern(A) Kern(A H ). Hinweis: Verwenden Sie die Rechenregeln für das Standard-Skalarprodukt in C n. Lösung: : x Kern(A) Ax 0 x H A H Ax 0 0 Ax 2 A H AAA H x } H {{ A } A H x 0 (A H x) }{{ H } A H x 2 Def. Norm A H x 0 x Kern(A H ) : (A H ) H A 1. Teil Kern(A H ) Kern((A H ) H ) Kern(A) 11.7b) Zeigen Sie, dass aus der Eigenschaft (11.7.1) der Matrix A C n n folgt: (A λi n )(A λi n ) H (A λi n ) H (A λi n ) für alle λ C. Hinweis: Für komplexe Matrizen gelten die gleichen Rechenregeln wie für reelle Matrizen. Lösung: (A λi n )(A λi n ) H (A λi n )(A H λ H I H n ) AA }{{ H } λ H AIn H λ I n A H + λλ H A H A (I na H ) H (A H I n) H In H A A H A H I n A H A λ H I H n A λa H I n + λλ H I H n I n (A H λ H I H n )A (A H λ H I H n )λi n (A H λ H I H n )(A λi n ) (A λi n ) H (A λi n ) λ 2 λ H λ I n I H n Seite 14

15 11.7c) Beweisen Sie, dass jeder Eigenvektor von A auch ein Eigenvektor von A H ist und umgekehrt. Hinweis: Aus der Definition von Eigenvektoren wissen wir, dass sie Elemente des Kerns von bestimmten Matrizen sind. Diese Matrizen sind uns bereits in der vorherigen Teilaufgabe begegnet. Geht Ihnen ein Licht auf? Teilaufgabe 11.7a)! Lösung: Av λv (A λi n )v 0 v Kern(A λi n ) 11.7a),11.7b) v Kern((A λi n ) H ) v Kern(A H λ H I H n ) (A H λi H n )v 0 A H v λv 11.7d) Beweisen Sie nun den obigen Satz unter Verwendung des Ergebnisses von Teilaufgabe 11.7c). Hinweis: Orthogonalität von zwei Eigenvektoren v 1 und v 2 zu den Eigenwerten λ 1 und λ 2 bedeutet: v 1, v 2 0. Wir wissen λ 1 λ 2. Es genügt also, λ 1 v 1, v 2 λ 2 v 1, v 2 zu zeigen. Lösung: Da wir annehmen, dass λ 1 λ 2, reicht es zu zeigen, dass gilt: λ 1 v 1, v 2 λ 2 v 1, v 2. Daraus folgt trivialerweise, dass v 1, v 2 0 sein muss, denn Nun gilt λ 1 v 1, v 2 (λ 1 λ 2 ) v 1, v 2 v 1, v Def SP Def und 11.7c) λ 1 v 1, v 2 A H v 1, v 2 A H v 1 λ 1 v 1 Def SP v 1, Av 2 Def v 2 Def SP v1, λ 2 v 2 λ 2 v 1, v 2. Seite 15