Fourier-Reihen & Fourier - Transformation
|
|
|
- Gerd Bader
- vor 7 Jahren
- Abrufe
Transkript
1 Fourier-Reihen & Fourier - ransformation Prof. Dr. Karlheinz Blanenbach Hochschule Pforzheim iefenbronner Str Pforzheim Überblic / Anwendungen: Die Fourier-ransformation dient beispielsweisezur Analyse von Signalen (Signalverarbeitung), der Filterung und der Analyse von Schwingungen. Empfohlene Literatur: - Böhme: Analysis, Springer - Latusse et al. : Lehr- und Übungsbuch Mathemati V, Fachbuchverlag Leipzig-Köln - Papula : Mathemati für Ingenieure und Naturwissenschaftler, Band, Vieweg - Westermann : Mathemati für Ingenieure mit MAPLE, Band, Springer - Burg et al. : Höhere Mathemati für Ingenieure, Band III, eubner - ilman Butz: Fourier-ransformation für Fußgänger, eubner Blanenbach / WS / 3.9.
2 . Fourier - Reihenentwiclung (Wiederholung aus. Sem) Fourier-Reihenentwiclung warum, wozu?: - Methode zur Darstellung von Funtionen durch (unendliche) Reihen gut für Mirocontroller falls mathematische Funtion nicht im Compiler implementiert ist oder eingebaute Compilerfuntion zu langsam. - Anwendungen: Differentiation, Integration, Spetrum,. Einschub zur Wiederholung: Allgemeines zu Reihen Anwendungen: - Darstellung von Funtionen mit Reihen Numeri - Integrierbareit von 'unlösbaren' Integralen - Frequenzanalyse nach FOURIER - In der echni sind viele Zusammenhänge als Reihen angenähert (oft auch, weil eine exate Formel existiert bzw. experimentell ermittelt) Bsp: Hooe sches Gesetz, -abhängiger Längenausdehnung bzw. eletrischer Widerstand: X = X o ( + ) Definition: a + a + a a n +... = a n n (R - ) a n : n-tes Reihenglied Reihe ist - onvergent, wenn a n n = S (Grenzwert S existiert, S < ) (R - ) - divergent: Grenzwert S existiert nicht a n = n Ideal: Unendliche Reihe Reale Numeri: endliche Reihe a n N n = <s N > (R - 3) Partialsumme Blanenbach / WS / 3.9.
3 Vorgehensweise bei Reihen: ) existiert S? ) wenn ja (onvergent), bestimme S bzw. <s N > Beispiele: n n = = divergent... = onvergent? n n Reihendefinitionen: - geometrisch : a n = a q n- - alternierend : a - a + a Potenzreihe : a + a x + a x² + (Polynom) - arithmetisch : a n = a + (n-) d - harmonisch : a n = / n Geometrische Reihen Def.: n a q = a + aq + aq² + aq³ +... (R - 4) n Konvergenzbed.: q < Summe: S a für q < (R - 5) q n Bsp:... n n 4 q = / also onvergent, a = S Blanenbach / WS /
4 Alternierende Reihen n Def.: n a = a - a + a 3 - a (R - 6) n Leibnitz - Konvergenzriterium: ) a n > a n+ (R - 7) ) lim a n n alternierende Reihe onvergent, wenn beide Bed. erfüllt n n n Bsp:... 3 a n = /n Leibnitz: ) n n ) lim n n Reihe ist onvergent Potenzreihen Def.: n a x n = a n o + a x + a x + a 3 x (R - 8) mit a n R Potenzreihe = Polynom Konvergenzradius r a n lim (R - 9) n an - onvergent : x < r - divergent : x > r - eine Aussage : x = r n x x x Bsp:... n! n r a lim a n n n lim n (n )! n! lim(n ) n Reihe onvergent für alle x R (Faultät > Potenz) Blanenbach / WS /
5 Potenzdarstellung von Funtionen onvergente Potenzreihe stellt eine reelle Zahl dar: y f(x) n a x n (R - ) n somit gilt auch: d - Differential y' f'( x) dx n an x n n n a x n n - Integral F x f x dx a x dx a x n n ( ) ( ) n n n n n C Bsp: ( ) n x n - x + x² - x³ +... mit a =, q = -x : geometrische Reihe n ( x) x n für x < f(x) = / (+x) (Summe) Diff. und Int. Mit obiger Reihendefinition und Summe Diff: f (x) = -/(+x)² = - + x - 3x² +... = ( ) n n n x n (so erhält man auch Summen von neuen Reihen) Int : dx f( x) dx ln( x) x zu Fuß unmöglich aus Formelsammlung n ( x) n dx x x² x³ 3... C = ln(+x)! C aus ln = für x= C = ln(+x) x x²/ + x³/3 Anwendung: Numeri Blanenbach / WS /
6 Beispiele von Potenzreihen (aus Papula Formelsammlung) Blanenbach / WS /
7 MacLaurin - Reihe Kann y = f(x) in eine onvergente Potenzreihe entwicelt werden, so ist dies nur mit der ML - Reihe möglich: n (n) f'() f''() f () n f () n f (x) f() x x²... x x (R - )!! n! n! n Achtung: Entwiclung nur um x =! Beispiele: - lineare Näherung f(x) f() + f () x F = + D x Hooesches Gesetz für Feder R = R o + R o aus R o ( + ) V = V o + V o aus V o ( + ) - f(x) = e x f(x) = f (x) = f (x) =..= e x f() = f () = f () =..= e = e x = + x/! + x²/! + x³/3! - y = x² - f() = - f (x) = x ; f () = - f (x) = ; f () = - f und folgende: Null f(x) = + + / x² + + = x² Blanenbach / WS /
8 aylor - Reihe - allgemeiner Fall der MacLaurin - Reihe für x = - Entwiclung um beliebigen Wert x, der beannt sein muß - h ist Abstand von x n (n) f'(xo ) f''(xo ) f (xo ) n f (xo ) n f (xo h) f(xo ) h h²... h h (R - )!! n! n! n Bsp: e,4 e =,78 beannt -> x o =, x o + h =,4 h =,4 f( +,4) = e + e h + e /! h² + e /3! h³ +... = e ( + h + h²/ + h³/ ) Vergleich (an der afel) MacLaurin und aylor für f(x) = e x mit x =, für aylor : e xo mit x o = also e =,7 beannt Exat: 7,389 n MacLaurin aylor e =, e =,7 3, 5,44 5, 6,8 3 6,33 7,5 4 7, 7,36 5 7,7 7,38 Mit aylor-reihe ommt man schneller, d.h. für leiner n, dem exaten Wert näher. Blanenbach / WS /
9 Näherungspolynome (aus Papula Formelsammlung) liefern (nur) in der Nähe des Nullpunte brauchbare Ergebnisse! (Bsp: sinx = x und e -x = - x geht für größere x, z.b. schief ) Blanenbach / WS /
10 . Fourier Reihen Vorteil Fourier im Vergleich zu aylor- und MacLaurin-Reihe: - basiert auf periodischen Vorgängen, welche technische Schwingungen besser als Potenzreihen beschreiben! - Analyse des Frequenzspetrums ( Fouriertrafo) Fourier-Analyse von Musiinstrumenten rel. Lautstäre rompete rel. Lautstäre Horn f o f o 3f o 4f o 5f o Frequenz f o f o 3f o 4f o 5f o Frequenz rel. Lautstäre Oboe rel. Lautstäre Clarinette f o f o 3f o 4f o 5f o Frequenz f o f o 3f o 4f o 5f o Frequenz Allerdings: Idealisierte Betrachtung (scharfe Peas) für Reihen. Bei Messung und Fourier-ransformation verbreitern sich diese Peas. Blanenbach / WS / 3.9.
11 Periodische Funtionen Def.: f(t + P) = f(t) mit P = n n =,,,, : Periodendauer Beispiele einfachster periodischer Funtionen: - y = A cos t - y = A sin t y A Periodendauer t mit A : Amplitude = / : Kreisfrequenz, wichtig bei Fourier-Reihe: sin(t), cos(t), aus f = / : Frequenz = f Integrationseigenschaften periodischer Funtionen: Verschieben der Integrationsgrenzen ist erlaubt: ( ) = ( ) Def.: - Gerade Funtion : g (t) = g (-t) symmetrisch zur Y-Achse - Ungerade Funtion : u (-t) = -u (t) symmetrisch zum Ursprung Beispiele: - Cosinus : y = A cos t : y (t) = y (-t) gerade - Sinus : y = A sin t : y (-t) = -y (t) ungerade Hausaufgabe : Rechtec-, Dreiec-, Kippspannung, Gleichgerichteter Sinus, Blanenbach / WS / 3.9.
12 .. Definition der Fourier Reihe Ziel: Zerlegung einer periodischen Funtion nach Sinus und Cosinus Def.: f (t) a a cost b sint o f(x) a o a cos x b sin x mit den Fourier Koeffizienten ( reelle ganze Zahlen): relative Zeit t Ort x Amplitude (Periode mit = /) a (DC-Anteil) f(t) dt f(x) dx a f(t) cos(t) dt f(x) cosx dx b f(t) sin( t) dt f(x) sinx dx Bemerungen Die Integrationsgrenzen önnen verschoben werden. Salopp formuliert: Man muß nur darauf achten, dass über eine ganze Periode integriert wird: o o f(t)dt f(t)dt Man findet auch oft eine Fourier-Reihenentwiclung nach x. In der echni meist zeitabhängige Messwerte etc. deshalb Zeit (Periode ) verwenden! Vereinfachung für folgende Fälle (Symmetrie): Funtion Definition alle Bsp. gerade f(-t) = f(t) b = cos ungerade f(-t) = - f(t) a = (inl. a o ) sin d.h. Approximation nur durch Sinus bzw. Cosinus! Blanenbach / WS / 3.9.
13 Vereinfachung für Rechnung mit Periode : Def.: f (t) ao a cost b sint ao A sin t mit A a b ; tan, Rest siehe oben a b Anmerung: Dirichletsche Bedingungen Die Entwiclung einer periodischen Funtion in eine Fourier-Reihe ist unter folgenden Voraussetzungen (sog. Dirichletsche Bedingungen) möglich:. Das Periodenintervall lässt sich in endlich viele eilintervalle zerlegen, in denen die Funtion stetig und monoton ist. In den Unstetigeitsstellen existiert sowohl der lins- als auch rechtsseitige Grenzwert (es ommen nur Sprungunstetigeiten mit endlichen Sprüngen in Betracht) Diese Bedingung ist z.b. nicht für angens als periodische Funtion erfüllt! Beispiele: zu. : Rechtec- bzw. Sägezahnsignal sind stetig und monoton in eilintervallen zu. : Dreiecsfuntion an der Spitze Unstetigeit mit endlichem Sprung Hilfreiche Integrale und Definitionen : für cos dt für - t sin - t dt für alle - sin sin cos ( ) cos ( ) - cos cos cos ( ) cos ( ) - sin cos sin( ) sin( ) Blanenbach / WS /
14 Bsp: Fourier-Reihe eines Sägezahn-Signales f( t) t für t für t f(t) mit f(t + ) = f(t) = t Kochrezept :. Bestimmung von aus Periodendauer: = (hier, aus Defintion, siehe auch Sizze); Definition der Periodendauer = /f = / = = / =. Sind Dirichletsche Bedingungen erfüllt? 3. Symmetrie? (vereinfacht Rechnung): ungerade Funtion, da f(-t) = -f(t) alle a = (inl a o ) 4. DC-Anteil? hier einer wg. Symmetrie (3.) 5. Berechnung der Fourieroeffizienten b f t sin t dt (Verschiebung der Integrationsgrenzen möglich) mit f(t) = t (s.o.), = und = : b tsin tdt t cos t sin t b Produt Integration ² Bem.: sin() = sin({-}) = b cos ( ) cos( ) ( ) cos cos( ) cos cos( ) cos( ) Blanenbach / WS /
15 b cos Klappt das im Mirocontroller? Nein, da ungenau Überlegung zur Vereinfachung: Welche Werte nehmen die b s an? cos() wird für alle s (reelle ganze Zahlen) nur + oder - b gerade ungerade ( ) 6. Explizites Hinschreiben der Fourier-Reihe f ( t) b sin ( t) hier : ( ) sin ( t) Def. Rel. Amplitude, Frequenz 7. Explizite Beschreibung der ersten Glieder 3 Amplitude - + /3 f(t) sint - sint + /3 sin3t Hier: = (s.o.) (Bedeutung) Grundfrequenz des Sägezahns. harmonische Oberwelle. harmonische Oberwelle Blanenbach / WS /
16 Fourier-Darstellung Sägezahn y 4 Sägezahn (nicht maßstäblich) bis = bis = bis = t Nullstellen-Versatz durch EXCEL-Schrittweite b Fourier - Koeffizienten Sägezahn (Spetrum),8,6,4,,8,6,4, Liniendiagramm, da einzelne disrete 'x-werte', hier Die b s fallen relativ langsam, da die Spitzen des Sägezahnes nachgebildet werden müssen. Blanenbach / WS /
17 Beispiele für Fourier-Reihen (aus Papula Mathematische Formelsammlung) Blanenbach / WS /
18 Blanenbach / WS /
19 Blanenbach / WS /
20 Rechtecsignal Gegeben: f (t) für t für t. Bestimmung von aus Periodendauer: = = / Definition Kreisfrequenz = / =. Sind Dirichletsche Bedingungen erfüllt? 3. Symmetrie? (vereinfacht Rechnung): ungerade Funtion, da f(-t) = -f(t) alle a = (inl a o ) 4. DC-Anteil? hier einer wg. Symmetrie (3.) auch aus Sizze: ein DC-Anteil (DC = ) erennbar a = 5. Berechnung der Fourieroeffizienten b f t sin ( t) dt sin( t) dt sin ( t) dt b cos ( t) cos ( t ) b cos( ) cos( ) cos( ) cos( ) cos( ) cos( ) Blanenbach / WS / 3.9.
21 - gerade = cos= + () = b = - ungerade = cos= - () = + b = 4 / ist aber ungeschict besser : ungerade durch - ausdrücen b 4 () ( ) ( ) 6. Explizites Hinschreiben der Fourier-Reihe f(t) a o a cos t b sin t 4 f ( t) sin {( ) t } ( ) 7. Explizite Beschreibung der ersten Glieder Die ersten 3 Glieder der Reihenentwiclung: f (t) 4 sint 4 sin3t 3 4 sin5t 5 4 sint 3 sin3t sin5t 5 Blanenbach / WS / 3.9.
22 Rechtec-Signal durch Fourier-Reihe approximiert Blanenbach / WS / 3.9.
23 Komplexe Darstellung der Fourier-Reihe es galt: (t) a a cost b sint f (Reihe) o mit e j = cos jsin (Euler) erhält man: cost = / (e jt + e -jt ) sint = / j (e jt - e -jt ) a cost + b sint = / (a - jb ) e jt + / (a + jb ) e -jt Substitution: c c - j t j t f (t) ao ce c e wegen: c e jt c e jt folgt: f(t) c e jt bzw. f(x) c e j x - entspricht negativen Frequenzen! a o C o mit C j t f(t) e dt C f(x) e j x dx Beziehungen zwischen a, b, A und C : C o = a o ; a = Re {C } ; b = - Im {C } ; A C a² b² Blanenbach / WS /
24 Blanenbach / WS / Beispiel: Rechtecfuntion omplex f(x) = f(x + ) ungerade j gerade und mit j j j j j j j NR e e j e j dx e dx e x f C j j erweitern j u j j x j x j x j sin cos ) ( sin ) ( cos : ) ( ) ( x dx dx e x f C x j Damit lautet die omplexe Fourier-Reihe ausgeschrieben: ( ) ( ) ( )
25 Beginn: =, -, +, -3, +3 Ziel: f(x) reell Blanenbach / WS /
26 .. Fourier - ransformation echni: - Meßzeit begrenzt, nicht - oft nicht periodische Funtionen (z.b. Sprache) deshalb Fourier-Reihe oft nicht Mittel der Wahl - ric des Fourier-Integrales hierbei: periodische Fortsetzung - Ergebnis der Fourier-ransformation ist ein ontinuierliches Spetrum Fourier-Reihe Fourier-Integral f(t) f(t) Messung periodische Fortsetzung Signal Messung t + <-----> Periode - / + / Messzeit t Spetrum a disret a ontinuierlich f f Blanenbach / WS /
27 Vergleich Fourier- Reihe und Fourier ransformation Blanenbach / WS /
28 Fourier ransformation Bezeichnung: f(t) F() omplexe Darstellung (e jt = cost jsint) Definition der Integrale Summe Integral Einzelglieder Fourier-ransformierte disret ontinuierlich Fourier- Reihe f(t) c e - für c.c. jt C f(t) e j t dt Fourier- Integral jt f( t) F( ) e d jt F( ) f( t) e dt F() ist Fouriertransformierte von f(t) : Spetraldarstellung im Allgemeinen omplex, d.h. Amplitude + Phase ACHUNG: - Nie = / verwenden wie bei Fourier-Reihe! - Vereinfachung für reelle gerade bzw. ungerade Funtionen f(t) siehe 9! Aufsplittung von F() in Real- und Imaginärteil e -jt = cost - jsint : F( ) jt f ( t) e dt f ( t) cos( t) dt j f ( t) sin( t) dt F( ) R( ) j I( ) F( ) R²( ) I ²( ) : Betrag ( ) I R ( ) ( ) : Phase A() = F() : Amplitudenspetrum : Praxis! Blanenbach / WS /
29 Blanenbach / WS /
30 Beispiele Rechtec-Signale vs. Opti (Beugung) Blanenbach / WS /
31 abelle Fourier-ransformierte (aus Föllinger, HÜHIG) Vergleiche Rechtecimpuls und sinx/x (Si) Blanenbach / WS /
32 Blanenbach / WS /
33 Blanenbach / WS /
34 Blanenbach / WS /
35 Fourier-ransformierte und Fensterfuntionen Vorgehensweise: Erfassung (z.b. Oszi) und Multipliation im Zeitbereich mit Fensterfuntion Fensterfuntionen dämpfen die Nebenzipfel (Frequenz im Original nicht vorhanden!) zu Lasten der Amplitude des Hauptmaximums Blanenbach / WS /
36 Weitere Fensterfuntionen (aus Butz: F für Fußgänger, eubner) Blanenbach / WS /
37 Frequenz Auflösung verschiedener Fensterfuntionen (aus Butz: F für Fußgänger, eubner) Gegeben ist folgende Funtion: f(t) = cos(t) + - cos(,5 t) + -3 cos(,5 t) + -3 cos( t) + -4 cos(,75 t) + -5 cos(3t) Frequenz,5,5,75 3 Amplitude Frage: Mit welcher Fensterfuntion wird das Signal mit benachbarten Frequenzen und teilweise geringen Amplituden aufgelöst? Blanenbach / WS /
38 Fourier-Fenster-Funtion: Rechtec Spaltfuntion (Zoom, s.u.) Verbreiterung des Hz-Peas F (Amplitudenspetrum), Fouriertransformierte einer zeitlich begrenzten Cosinusschwingung fo = Hz, Meßdauer s : gemessene Schwingungen,8,6,4, f /Hz F (Amplitudenspetrum) Fouriertransformierte einer zeitlich begrenzten Cosinusschwingung fo = Hz, Meßdauer s : gemessene Schwingungen f /Hz Nebenzipfeldämpfung durch mehr Perioden, aber Gefahr der Unterabtastung Blanenbach / WS /
39 Beispiel: Fourier-ransformation eines RLC-Schwingreis mit schwacher Dämpfung Amplitude Gedämpfte Schwingungen Einhüllende, Zeit -,5 - schw ach gedämpft Kriechfall Aperiodischer Grenzfall rel. Amplitude F gedämpfte Schwingung 8 6 A (d=,) A (d =,5) A (d = ) 4,5,5,5 rel. Frequenz (w/w s ) Blanenbach / WS /
40 Übungsaufgaben Fourier-Reihen und -ransformation. Entwicle die Funtion a f (t) a für t t t,, mit f(t+) = f(t) in eine Fourier-Reihe und sizziere das Ergebnis. a, 4,... 4a sint sin3t sin5t Lsg: b f(t)... mit 4, 3, sin t. Entwicle die Funtion f( t) für sin t t t mit f(t+) = f(t) in eine Fourier-Reihe (ipp: = und sizziere das Ergebnis. 4 cost cos4t sin6t Lsg: f(t)... mit a ungerade = ; a gerade = 4/(-²) Berechne Fouriertransformierte eines Dreiecimpulses und sizziere das Ergebnis f(t) A - mess/ t Lösung: 8A m (F ) sin² ² m 4. Berechne die F des doppelten Rechtecpuls und sizziere das Ergebnis f(t) -3-3 t Lösung: F( ) 4 sin cos Blanenbach / WS /
Fourier-Reihen, Fourier- und Laplace - Transformation
 Fourier-Reihen, Fourier- und Laplace - Transformation Prof. Dr. Karlheinz Blankenbach Hochschule Pforzheim Tiefenbronner Str. 65 7575 Pforzheim Überblick / Anwendungen: - Fourier: Analyse von Schwingungen
Fourier-Reihen, Fourier- und Laplace - Transformation Prof. Dr. Karlheinz Blankenbach Hochschule Pforzheim Tiefenbronner Str. 65 7575 Pforzheim Überblick / Anwendungen: - Fourier: Analyse von Schwingungen
Fourier - Transformation
 Fourier - Transformation Kurzversion 2. Sem. Prof. Dr. Karlheinz Blankenbach Hochschule Pforzheim, Tiefenbronner Str. 65 75175 Pforzheim Überblick / Anwendungen / Motivation: Die Fourier-Transformation
Fourier - Transformation Kurzversion 2. Sem. Prof. Dr. Karlheinz Blankenbach Hochschule Pforzheim, Tiefenbronner Str. 65 75175 Pforzheim Überblick / Anwendungen / Motivation: Die Fourier-Transformation
FOURIERREIHEN. a) Periodische Funktionen. 3) Rechteckschwingung. b) Stückweise stetige Funktionen. Skizze= Sägezahnschwingung
 FOURIERREIHEN 1. Grundlagen a) Periodische Funtionen Beispiele: 1) f( x) = sin( x+ π / 3), T = 2 π /. 2) f( t) = cos( ωt+ ϕ), T = 2 π / ω. 3) Rechtecschwingung, 1< t < f() t =, f( t+ 2) = f() t 1, < t
FOURIERREIHEN 1. Grundlagen a) Periodische Funtionen Beispiele: 1) f( x) = sin( x+ π / 3), T = 2 π /. 2) f( t) = cos( ωt+ ϕ), T = 2 π / ω. 3) Rechtecschwingung, 1< t < f() t =, f( t+ 2) = f() t 1, < t
Kapitel 2: Fourieranalyse. Analoge, periodische Signale
 ZHW, NM, 5/, Rur Kapitel : Fourieranalyse Analoge, periodische Signale Inhaltsverzeichnis. EINLEIUNG.... LINEARER MIELWER... 3. LEISUNG UND EFFEKIVWER...3 4. WINKELFUNKIONEN...3 5. FOURIERREIHE...4 6.
ZHW, NM, 5/, Rur Kapitel : Fourieranalyse Analoge, periodische Signale Inhaltsverzeichnis. EINLEIUNG.... LINEARER MIELWER... 3. LEISUNG UND EFFEKIVWER...3 4. WINKELFUNKIONEN...3 5. FOURIERREIHE...4 6.
Messung der Schallgeschwindigkeit über Resonanz
 Messung der Schallgeschwindigeit über Resonanz Lautsprecher Mirofon Frequenzgenerator/Wechselspannung und Verstärer Oszillosop mit Darstellung der Anregung (Kanal 1) und des Mirofon- Signals (Kanal 2)
Messung der Schallgeschwindigeit über Resonanz Lautsprecher Mirofon Frequenzgenerator/Wechselspannung und Verstärer Oszillosop mit Darstellung der Anregung (Kanal 1) und des Mirofon- Signals (Kanal 2)
Fourierreihen. Definition. Eine Funktion f(x) heißt periodisch mit der Periode T, wenn f(x + T ) = f(x)
 Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
Fourier-Reihen und Fourier-Transformation
 Fourier-Reihen und Fourier-Transformation Matthias Dreÿdoppel, Martin Koch, Bernhard Kreft 25. Juli 23 Einleitung Im Folgenden sollen dir und die Fouriertransformation erläutert und mit Beispielen unterlegt
Fourier-Reihen und Fourier-Transformation Matthias Dreÿdoppel, Martin Koch, Bernhard Kreft 25. Juli 23 Einleitung Im Folgenden sollen dir und die Fouriertransformation erläutert und mit Beispielen unterlegt
Mathematik I Herbstsemester 2018 Kapitel 6: Potenzreihen
 Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
), wobei. ) bezeichnete. Wir schreiben. s n. , falls dieser existiert.
 7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
7.7. Potenzreihen Unendliche Reihen waren reelle oder omplexe Folgen der Form (s n ), wobei n s n f f 0 + f +... f n die n-te Partialsumme zur Folge (f n ) bezeichnete. Wir schreiben Konvergenzriterien
Fourieranalyse und Diskrete Cosinus Transformation (DCT)
 Fourieranalyse und Disrete Cosinus Transformation (DCT) Eine Ausarbeitung für den Physileistungsurs 12.2 Philipp Julian Münzel, Juni 2005 Mathematical analysis is as extensive as Nature herself Jean Baptiste
Fourieranalyse und Disrete Cosinus Transformation (DCT) Eine Ausarbeitung für den Physileistungsurs 12.2 Philipp Julian Münzel, Juni 2005 Mathematical analysis is as extensive as Nature herself Jean Baptiste
Analysis I Mathematik für InformatikerInnen II SoSe 12 Musterlösungen zur Prüfungsklausur vom 18. Juli 2012
 Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
:. (engl.: first harmonic frequency)
 5 Fourier-Reihen 5.1 Schwingungsüberlagerung 5.2 "Oberschwingungen" f 0 :. (engl.: fundamental frequency) :. (engl.: first harmonic frequency) Jede ganzzahlige (n) vielfache Frequenz von f 0 nennt man
5 Fourier-Reihen 5.1 Schwingungsüberlagerung 5.2 "Oberschwingungen" f 0 :. (engl.: fundamental frequency) :. (engl.: first harmonic frequency) Jede ganzzahlige (n) vielfache Frequenz von f 0 nennt man
Praktikumsbeispiele zum Lehrgebiet WR II, Numerische Mathematik und CAS Serie Approximation
 TU Ilmenau Institut für Mathemati FG Numerische Mathemati und Informationsverarbeitung PD Dr. W. Neundorf Datei: pb approx.tex Pratiumsbeispiele zum Lehrgebiet WR II, Numerische Mathemati und CAS Serie
TU Ilmenau Institut für Mathemati FG Numerische Mathemati und Informationsverarbeitung PD Dr. W. Neundorf Datei: pb approx.tex Pratiumsbeispiele zum Lehrgebiet WR II, Numerische Mathemati und CAS Serie
Ferienkurs der TU München- - Analysis 2 Fourierreihen und Taylorreihen. Marcus Jung, Jonas J. Funke
 Ferienkurs der U München- - Analysis Fourierreihen und aylorreihen Lösung Marcus Jung, Jonas J. Funke 3.8. FOURIERREIHEN Fourierreihen Aufgabe. Sei f : R R stetig und periodisch mit Fourierkoeffizienten
Ferienkurs der U München- - Analysis Fourierreihen und aylorreihen Lösung Marcus Jung, Jonas J. Funke 3.8. FOURIERREIHEN Fourierreihen Aufgabe. Sei f : R R stetig und periodisch mit Fourierkoeffizienten
Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften
 Department Mathemati der Universität Hamburg WiSe 20/202 Dr. Hanna Peywand Kiani Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften Reelle Zahlenreihen 6.2.20 Die ins Netz gestellten
Department Mathemati der Universität Hamburg WiSe 20/202 Dr. Hanna Peywand Kiani Anleitung zu Blatt 4 Analysis I für Studierende der Ingenieurwissenschaften Reelle Zahlenreihen 6.2.20 Die ins Netz gestellten
FK03 Mathematik I: Übungsblatt 9 Lösungen
 FK03 Mathematik I: Übungsblatt 9 Lösungen Verständnisfragen. Welche zwei Beispiele sind in der Vorlesung für die Anwendung von transzendenten Funktionen behandelt worden? Schnittpunktsbestimmung zwischen
FK03 Mathematik I: Übungsblatt 9 Lösungen Verständnisfragen. Welche zwei Beispiele sind in der Vorlesung für die Anwendung von transzendenten Funktionen behandelt worden? Schnittpunktsbestimmung zwischen
9 Fourieranalyse von nichtsinusförmigen periodischen Wechselgrößen und nichtperiodische Größen
 9 Fourieranalyse von nichtsinusförmigen periodischen Wechselgrößen und nichtperiodische Größen 95 9. Fourierreihenentwiclung von analytisch gegebenen nichtsinusförmigen periodischen Wechselgrößen Nichtsinusförmige
9 Fourieranalyse von nichtsinusförmigen periodischen Wechselgrößen und nichtperiodische Größen 95 9. Fourierreihenentwiclung von analytisch gegebenen nichtsinusförmigen periodischen Wechselgrößen Nichtsinusförmige
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
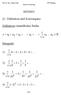 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
Blatt 11.4: Deltafunktion und Fourierreihen
 Faultät für Physi R: Rechenmethoden für Physier, WiSe 215/16 Dozent: Jan von Delft Übungen: Benedit Bruognolo, Dennis Schimmel, Fraue Schwarz, uas Weidinger http://homepages.physi.uni-muenchen.de/~vondelft/ehre/15r/
Faultät für Physi R: Rechenmethoden für Physier, WiSe 215/16 Dozent: Jan von Delft Übungen: Benedit Bruognolo, Dennis Schimmel, Fraue Schwarz, uas Weidinger http://homepages.physi.uni-muenchen.de/~vondelft/ehre/15r/
Spektralanalyse. Spektralanalyse ist derart wichtig in allen Naturwissenschaften, dass man deren Bedeutung nicht überbewerten kann!
 Spektralanalyse Spektralanalyse ist derart wichtig in allen Naturwissenschaften, dass man deren Bedeutung nicht überbewerten kann! Mit der Spektralanalyse können wir Antworten auf folgende Fragen bekommen:
Spektralanalyse Spektralanalyse ist derart wichtig in allen Naturwissenschaften, dass man deren Bedeutung nicht überbewerten kann! Mit der Spektralanalyse können wir Antworten auf folgende Fragen bekommen:
Die komplexen Zahlen und Skalarprodukte Kurze Wiederholung des Körpers der komplexen Zahlen C.
 Die omplexen Zahlen und Salarprodute Kurze Wiederholung des Körpers der omplexen Zahlen C. Erinnerung an die Definition von exp, sin, cos als Potenzreihen C C Herleitung der Euler Formel Definition eines
Die omplexen Zahlen und Salarprodute Kurze Wiederholung des Körpers der omplexen Zahlen C. Erinnerung an die Definition von exp, sin, cos als Potenzreihen C C Herleitung der Euler Formel Definition eines
SiSy1, Praktische Übung 3. Fourier-Analyse (periodischer Signale) kann als Fourier-Reihe 1 beschrieben werden:
 /5 Fourier-Analyse (periodischer Signale) Grundlagen Ein periodisches, kontinuierliches Signal x(t) der Periodendauer kann als Fourier-Reihe beschrieben werden: wie folgt ( ) = c k x t + e j k 2πf t k=
/5 Fourier-Analyse (periodischer Signale) Grundlagen Ein periodisches, kontinuierliches Signal x(t) der Periodendauer kann als Fourier-Reihe beschrieben werden: wie folgt ( ) = c k x t + e j k 2πf t k=
Analysis1-Klausuren in den ET-Studiengängen (Ba) ab 2007
 Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Analysis-Klausuren in den ET-Studiengängen (Ba) ab 7 Im Folgenden finden Sie die Aufgabenstellungen der bisherigen Klausuren Analysis im Bachelorstudium der ET-Studiengänge sowie knapp gehaltene Ergebnisangaben.
Programmierung und Angewandte Mathematik
 Programmierung und Angewandte Mathematik C++ /Scilab Programmierung und Einführung in das Konzept der objektorientierten Anwendungen zu wissenschaftlichen Rechnens SS 2012 Inhalt Steckbrief der Funktion
Programmierung und Angewandte Mathematik C++ /Scilab Programmierung und Einführung in das Konzept der objektorientierten Anwendungen zu wissenschaftlichen Rechnens SS 2012 Inhalt Steckbrief der Funktion
Abgabe: KW 11. Aufgabe 2-0a: Berechnen Sie die Grenzwerte der Funktionen. x 2 x. lim. lim
 . Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
. Übung zur Höheren Mathemati Abgabe: KW Aufgabe -a: Berechnen Sie die Grenzwerte der Funtionen 5 4 lim ln ln lim e lim sin lim (sin ) Aufgabe -b: Bestimmen Sie Definitionsbereich, Nullstellen, Polstellen,
Als Summendarstellung der komplexen Zahl bezeichnen wir den bekannten Ausdruck
 A.1 MATHEMATISCHE GRUNDLAGEN In diesem Abschnitt werden die mathematischen Grundlagen zusammengestellt, die für die Behandlung von Übertragungssystemen erforderlich sind. Unter anderem sind dies die komplexen
A.1 MATHEMATISCHE GRUNDLAGEN In diesem Abschnitt werden die mathematischen Grundlagen zusammengestellt, die für die Behandlung von Übertragungssystemen erforderlich sind. Unter anderem sind dies die komplexen
,Faltung. Heavisidefunktion σ (t), Diracimpuls δ (t) Anwendungen. 1) Rechteckimpuls. 2) Sprungfunktionen. 3) Schaltvorgänge
 Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Komplexe Analysis für ITET und RW/CSE. Serie 11
 Prof. Dr. F. Da Lio R. Gantner Frühlingssemester 5 Komplexe Analysis für ITET und RW/CSE ETH Zürich D-MATH Serie Aufgabe. Fourierreihen (.a Sei f p die ungerade periodische Fortsetzung der Funktion f :
Prof. Dr. F. Da Lio R. Gantner Frühlingssemester 5 Komplexe Analysis für ITET und RW/CSE ETH Zürich D-MATH Serie Aufgabe. Fourierreihen (.a Sei f p die ungerade periodische Fortsetzung der Funktion f :
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Systemtheorie Teil A - Zeitkontinuierliche Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 6 Musterlösungen Spektrum von Signalen 6. Approximation eines periodischen Signals
Systemtheorie Teil A - Zeitkontinuierliche Signale und Systeme - Musterlösungen Manfred Strohrmann Urban Brunner Inhalt 6 Musterlösungen Spektrum von Signalen 6. Approximation eines periodischen Signals
Aufgabe 2-1: Berechnen Sie die folgenden unbestimmten / bestimmten Integrale mittels Substitution.
 . Übung zur Höheren Mathemati Abgabe: 6..8, 8: Uhr Aufgabe -: Berechnen Sie die folgenden unbestimmten / bestimmten Integrale mittels Substitution. sin d cos d tan tan 4 sinh 7 sinh 5 e) f) 8 d 4 ln()
. Übung zur Höheren Mathemati Abgabe: 6..8, 8: Uhr Aufgabe -: Berechnen Sie die folgenden unbestimmten / bestimmten Integrale mittels Substitution. sin d cos d tan tan 4 sinh 7 sinh 5 e) f) 8 d 4 ln()
Klausur - Analysis 1
 Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Prof. Dr. László Széelyhidi Analysis I, WS 22 Klausur - Analysis Lösungen Aufgabe. i Punt Definieren Sie, wann x n eine Cauchyfolge ist. Lösung : x n heisst Cauchyfolge wenn es zu jedem ε > ein N N gibt,
Anwendungen der Fourier-Entwicklung in der Elektrotechnik 1 / 22
 Anwendungen der Fourier-Entwicklung in der Elektrotechnik 1 / Unser heutiges Ziel Reaktion eines Netzwerks auf ein periodisches Eingangssignal oder speziell Wie reagiert ein RC-Glied auf periodische Erregung?
Anwendungen der Fourier-Entwicklung in der Elektrotechnik 1 / Unser heutiges Ziel Reaktion eines Netzwerks auf ein periodisches Eingangssignal oder speziell Wie reagiert ein RC-Glied auf periodische Erregung?
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Formelanhang Mathematik II
 Formelanhang Mathematik II Mechatronik 2. Sem. Prof. Dr. K. Blankenbach Wichtige Formeln: - Euler: e j = cos() + j sin() ; e -j = cos() - j sin() - Sinus mit Phase: Übersicht Differentialgleichungen (DGL)
Formelanhang Mathematik II Mechatronik 2. Sem. Prof. Dr. K. Blankenbach Wichtige Formeln: - Euler: e j = cos() + j sin() ; e -j = cos() - j sin() - Sinus mit Phase: Übersicht Differentialgleichungen (DGL)
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Taylor-Reihenentwicklung. Bemerkungen. f(z) = a k (z z 0 ) k mit a k,z 0,z C. z k z C. f (k) (x 0 ) (x x 0 ) k mit x 0,x R.
 8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
8.2 Potenzreihen Definition: Eine Reihe der Form f(z) = a ( ) mit a,z 0,z C heißt (omplexe) Potenzreihe zum Entwiclungspunt z 0 C. Beispiel: Die (omplexe) Exponentialfuntion ist definiert durch die Potenzreihe
Vorlesung Mathematik 2 für Ingenieure (Sommersemester 2016)
 1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 3. Übung WS 17/18: Woche vom
 Übungsaufgaben 3. Übung WS 17/18: Woche vom 3. 10. - 7. 10. 017 Fourierreihen: 16. b,c,e,o), 16.3 a, b), 16.4 a) auch reelle Fourierreihe) Klausureinsicht zu Mathematik II 11.8. 017): 30.10.17, 7.00-8.30
Übungsaufgaben 3. Übung WS 17/18: Woche vom 3. 10. - 7. 10. 017 Fourierreihen: 16. b,c,e,o), 16.3 a, b), 16.4 a) auch reelle Fourierreihe) Klausureinsicht zu Mathematik II 11.8. 017): 30.10.17, 7.00-8.30
1. Aufgabe (6 Punkte) Zeigen Sie mit Hilfe der vollständigen Induktion, dass folgende Gleichheit gilt für alle n N, n 2. k (k + 1)! = 1 1 n!.
 . Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
. Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
NAE Nachrichtentechnik und angewandte Elektronik
 Inhaltsverzeichnis: NAE Nachrichtentechni und angewandte Eletroni hema Unterpunt Seite Deinitionen zur Fourier-Analse Grundschwingung 5- eilschwingungen 5- Oberwellen 5- Harmonische 5- Amplitude und Phasenlage
Inhaltsverzeichnis: NAE Nachrichtentechni und angewandte Eletroni hema Unterpunt Seite Deinitionen zur Fourier-Analse Grundschwingung 5- eilschwingungen 5- Oberwellen 5- Harmonische 5- Amplitude und Phasenlage
Hochschule Düsseldorf University of Applied Sciences. 12. Januar 2017 HSD. Physik. Schwingungen III
 Physik Schwingungen III Wiederholung Komplexe Zahlen Harmonischer Oszillator DGL Getrieben Gedämpft Komplexe Zahlen Eulersche Formel e i' = cos ' + i sin ' Komplexe Schwingung e i!t = cos!t + i sin!t Schwingung
Physik Schwingungen III Wiederholung Komplexe Zahlen Harmonischer Oszillator DGL Getrieben Gedämpft Komplexe Zahlen Eulersche Formel e i' = cos ' + i sin ' Komplexe Schwingung e i!t = cos!t + i sin!t Schwingung
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
Anmerkung: Falls f(x) nicht ganz glatt ist, sondern nur stückweise stetig differenzierbar ist (d.h. Sprünge hat), gilt (Satz v.
 Fourier-Reihen für periodische Funktionen Sei periodisch, mit Periode L: Auch für diesen Fall gilt die Fourier- Reihen-Darstellung (b.3), mit : (b.3) (und stückweise stetig differenzierbar) (c.5) Integral
Fourier-Reihen für periodische Funktionen Sei periodisch, mit Periode L: Auch für diesen Fall gilt die Fourier- Reihen-Darstellung (b.3), mit : (b.3) (und stückweise stetig differenzierbar) (c.5) Integral
Parseval-Identität: Seien zwei Funktionen v. mit Fourier-Reihen: dann gilt: Parseval-Identität. Speziell:
 Parseval-Identität: Seien zwei Funktionen v. mit Fourier-Reihen: dann gilt: (kühnes Vertauschen von Integral und Summe!) Parseval-Identität Speziell: Anmerkung: beide Seiten kann man als Skalarprodukt
Parseval-Identität: Seien zwei Funktionen v. mit Fourier-Reihen: dann gilt: (kühnes Vertauschen von Integral und Summe!) Parseval-Identität Speziell: Anmerkung: beide Seiten kann man als Skalarprodukt
f(t) = a 2 + darstellen lasst Periodische Funktionen.
 7. Fourier-Reihen Viele Prozesse der Ingenieur- und Naturwissenschaften verlaufen periodisch oder annahernd periodisch, wie die Schwingungen einer Saite, Spannungs- und Stromverlaufe in Wechselstromkreisen
7. Fourier-Reihen Viele Prozesse der Ingenieur- und Naturwissenschaften verlaufen periodisch oder annahernd periodisch, wie die Schwingungen einer Saite, Spannungs- und Stromverlaufe in Wechselstromkreisen
Folgen und Reihen. Thomas Blasi
 Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Zwischenprüfung Winter 2016 Analysis I D-BAUG
 ETH Zürich Zwischenprüfung Winter 216 Analysis I D-BAUG Dr. Meike Akveld Wichtige Hinweise Prüfungsdauer: 9 Minuten. Zugelassene Hilfsmittel: Keine, ausser das verteilte Blatt mit Standardintegralen. Es
ETH Zürich Zwischenprüfung Winter 216 Analysis I D-BAUG Dr. Meike Akveld Wichtige Hinweise Prüfungsdauer: 9 Minuten. Zugelassene Hilfsmittel: Keine, ausser das verteilte Blatt mit Standardintegralen. Es
1 + t dt = ( t) k dt. ( 1) k. k + 1 tk+1
 6 POTENZREIHEN 161 Wir wollen diese Gleichung für x < 1 noch auf andere Weise herleiten. Es ist ln(1 + x) = x 1 x 1 + t dt = ( t) dt. Die geometrische Reihe = ( t) ist nach dem Majorantenriterium für t
6 POTENZREIHEN 161 Wir wollen diese Gleichung für x < 1 noch auf andere Weise herleiten. Es ist ln(1 + x) = x 1 x 1 + t dt = ( t) dt. Die geometrische Reihe = ( t) ist nach dem Majorantenriterium für t
Fourier-Reihen. Definition. Eine auf R definierte Funktion f heißt periodisch mit der Periode T 0, wenn f(x + T ) = f(x) x R.
 Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
5. Fourier-Transformation
 5. Fourier-Transformation 5.1 Definition 5.2 Eigenschaften 5.3 Transformation reeller Funktionen 5.4 Frequenzbereich und Zeitbereich 2.5-1 5.1 Definition Definition: Die Fourier-Transformation einer Funktion
5. Fourier-Transformation 5.1 Definition 5.2 Eigenschaften 5.3 Transformation reeller Funktionen 5.4 Frequenzbereich und Zeitbereich 2.5-1 5.1 Definition Definition: Die Fourier-Transformation einer Funktion
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Punktweise Konvergenz stückweise glatter Funktionen. 1 Vorbereitungen
 Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
VIII. Fourier - Reihen
 VIII. Fourier - Reihen Dieses Kapitel enthält eine kurze Einführung in die mathematische Beschreibung von Schwingungen. Übersicht über den Inhalt von Kapitel VIII: 5. Der Satz von Fejér 53. Die Parsevalsche
VIII. Fourier - Reihen Dieses Kapitel enthält eine kurze Einführung in die mathematische Beschreibung von Schwingungen. Übersicht über den Inhalt von Kapitel VIII: 5. Der Satz von Fejér 53. Die Parsevalsche
HTBLA Neufelden Fourierreihen Seite 1 von 14. Peter Fischer
 HTBLA Neufelden Fourierreihen Seite von 4 Peter Fischer pe.fischer@atn.nu Fourierreihen Mathematische / Fachliche Inhalte in Stichworten: Fourierreihe, Fourierkoeffizienten, gerade und ungerade Funktionen,
HTBLA Neufelden Fourierreihen Seite von 4 Peter Fischer pe.fischer@atn.nu Fourierreihen Mathematische / Fachliche Inhalte in Stichworten: Fourierreihe, Fourierkoeffizienten, gerade und ungerade Funktionen,
4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter
 4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1 Grundbegriffe 4.2 Frequenzspektren, Fourier-Transformation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterführende Literatur (z.b.): Beate Meffert, Olaf Hochmuth: Werkzeuge
Systemtheorie. Vorlesung 20: Eigenschaften der Fourier-Transformation. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 2: Eigenschaften der Fourier-Transformation Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Fourier-Transformation Eigenschaften der Fourier-Transformation Definitionsgleichungen
Systemtheorie Vorlesung 2: Eigenschaften der Fourier-Transformation Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Fourier-Transformation Eigenschaften der Fourier-Transformation Definitionsgleichungen
Periodische Funktionen, Fourier Reihen
 Kapitel 1: Periodische Funktionen, Fourier Reihen 1.1 Grundlegende Begriffe Periodische Funktionen Definition: Eine Funktion f : R R oder f : R C) heißt periodisch mit der Periode T, falls für alle t R
Kapitel 1: Periodische Funktionen, Fourier Reihen 1.1 Grundlegende Begriffe Periodische Funktionen Definition: Eine Funktion f : R R oder f : R C) heißt periodisch mit der Periode T, falls für alle t R
Erfüllt eine Funktion f für eine feste positive Zahl p und sämtliche Werte t des Definitionsbereichs die Gleichung
 34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
4. Übung für Übungsgruppen Musterlösung
 Grundlagenveranstaltung Systemtheorie WS 6/7 (H.S. Stiehl, AB Kognitive Systeme, FB Informatik der Universität Hamburg). Übung für Übungsgruppen Musterlösung (N. Stein, Institut für Angewandte Physik,
Grundlagenveranstaltung Systemtheorie WS 6/7 (H.S. Stiehl, AB Kognitive Systeme, FB Informatik der Universität Hamburg). Übung für Übungsgruppen Musterlösung (N. Stein, Institut für Angewandte Physik,
Mathematik I Herbstsemester 2018 Kapitel 5: Integralrechnung
 Mathematik I Herbstsemester 208 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 70 5. Integralrechnung Grundbegriffe Das bestimmte Integral als Flächeninhalt Der Fundamentalsatz Partielle
Mathematik I Herbstsemester 208 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 70 5. Integralrechnung Grundbegriffe Das bestimmte Integral als Flächeninhalt Der Fundamentalsatz Partielle
Zeitfunktionen. Kapitel Elementarfunktionen
 Kapitel Zeitfunktionen Systeme werden durch Eingangsgrößen (Ursache, Eingangssignal, Erregung) angeregt und man interessiert sich für die Ausgangsgrößen (Wirkung, Ausgangssignal, Antwort). Die praktisch
Kapitel Zeitfunktionen Systeme werden durch Eingangsgrößen (Ursache, Eingangssignal, Erregung) angeregt und man interessiert sich für die Ausgangsgrößen (Wirkung, Ausgangssignal, Antwort). Die praktisch
5. Fourier-Transformation
 Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Klausur zur Vorlesung Analysis 1 (240003) 1. Termin: Aufgaben und Lösungen
 Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Prof Dr M Kaßmann Wintersemester 9/ Faultät für Mathemati Universität Bielefeld Klausur zur Vorlesung Analysis () Termin: 5 Aufgaben Lösungen Aufgaben: Die omplexen Lösungen der Gleichung z = i sind (
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson 2004
 4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
Runde 9, Beispiel 57
 Runde 9, Beispiel 57 LVA 8.8, Übungsrunde 9,..7 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 3..7 Angabe Seien y, z C N und c, d C N ihre Spektralwerte. Außerdem bezeichne (x k ) k die N - periodische
Runde 9, Beispiel 57 LVA 8.8, Übungsrunde 9,..7 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 3..7 Angabe Seien y, z C N und c, d C N ihre Spektralwerte. Außerdem bezeichne (x k ) k die N - periodische
Die komplexen Zahlen werden definiert als die geordneten Paare z = (x, y) reeller Zahlen x, y R, zusammen mit den Rechenoperationen
 2 Komplexe Zahlen 2.1 Definition Die omplexen Zahlen werden definiert als die geordneten Paare z = (x, y) reeller Zahlen x, y R, zusammen mit den Rechenoperationen z 1 + z 2 (x 1, y 1 ) + (x 2, y 2 ) :=
2 Komplexe Zahlen 2.1 Definition Die omplexen Zahlen werden definiert als die geordneten Paare z = (x, y) reeller Zahlen x, y R, zusammen mit den Rechenoperationen z 1 + z 2 (x 1, y 1 ) + (x 2, y 2 ) :=
Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik
![Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation. Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik](/thumbs/48/24765147.jpg) Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 4 Fourier-Transformation 3
Nachrichtentechnik [NAT] Kapitel 4: Fourier-Transformation Dipl.-Ing. Udo Ahlvers HAW Hamburg, FB Medientechnik Sommersemester 25 Inhaltsverzeichnis Inhalt Inhaltsverzeichnis 4 Fourier-Transformation 3
1 k k konvergent? und
 28 Reihen 27 28 Reihen Aufgabe: Sind die Reihen ( + und onvergent? 28. Komplexe Reihen. a Für eine Folge (a in C heißt die Reihe a onvergent, falls die Folge der Partialsummen (s n := n a onvergiert. In
28 Reihen 27 28 Reihen Aufgabe: Sind die Reihen ( + und onvergent? 28. Komplexe Reihen. a Für eine Folge (a in C heißt die Reihe a onvergent, falls die Folge der Partialsummen (s n := n a onvergiert. In
Analoge Signale und Systeme im Zeit- und Frequenzbereich
 . Zeitbereich Analoge Signale und Systeme im Zeit- und Frequenzbereich. Zeitbereich. Die Sprungfuntion h(t) Eine um die Zeit τ zeitverschobene Sprungfuntion schreibt sich also h(t-τ).. Der Dirac-Impuls
. Zeitbereich Analoge Signale und Systeme im Zeit- und Frequenzbereich. Zeitbereich. Die Sprungfuntion h(t) Eine um die Zeit τ zeitverschobene Sprungfuntion schreibt sich also h(t-τ).. Der Dirac-Impuls
9 Fourier-Transformation
 9 Fourier-Transformation Zoltán Zomotor Versionsstand: 5. September 2015, 18:26 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
9 Fourier-Transformation Zoltán Zomotor Versionsstand: 5. September 2015, 18:26 Die nummerierten Felder bitte mithilfe der Videos ausfüllen: http://www.z5z6.de This work is based on the works of Jörn Loviscach
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 2017/18, am
 Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
Mathematik I Herbstsemester 2018 Kapitel 3: Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 39 3. Differentialrechnung Einführung Ableitung elementarer Funktionen Ableitungsregeln Kettenregel Ableitung
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 39 3. Differentialrechnung Einführung Ableitung elementarer Funktionen Ableitungsregeln Kettenregel Ableitung
0.1 Formale Potenzreihen und Konvergenz
 0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
2 Komplexe Zahlen. 2.1 Grundlagen. Aufgabe Aufgabe Aufgabe 2.1.3
 2 Komplexe Zahlen 2.1 Grundlagen Aufgabe 2.1.1 Sei z 1 = 2 + und =. Stellen Sie a) z 1 +, b) z 1, c) z 1. zeichnerisch dar und berechnen Sie die Werte. Aufgabe 2.1.2 Berechnen Sie die folgenden Werte,
2 Komplexe Zahlen 2.1 Grundlagen Aufgabe 2.1.1 Sei z 1 = 2 + und =. Stellen Sie a) z 1 +, b) z 1, c) z 1. zeichnerisch dar und berechnen Sie die Werte. Aufgabe 2.1.2 Berechnen Sie die folgenden Werte,
Ferienkurs Analysis 1
 TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
TECHNISCHE UNIVERSITÄT MÜNCHEN Ferienurs Analysis 1 Potenzreihen, Exponentialfuntion, Stetigeit, Konvergenz, Grenzwert Henri Thoma 1.03.014 Inhaltsverzeichnis 1. Potenzreihen:... 1. Exponentialfuntion...
Probeklausur zur Analysis für Informatiker
 Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
Lehrstuhl A für Mathemati Prof. Dr. R. Stens Aachen, den 28. Januar 20 Probelausur zur Analysis für Informatier Musterlösung Aufgabe Zeigen Sie, dass für alle n N gilt. 2n+ ( ) + Beweis durch vollständige
g(x) := (x 2 + 2x + 4) sin(x) für z 1 := 1 + 3i und z 2 := 1 + i. Geben Sie das Ergebnis jeweils
 . Aufgabe Punkte a Berechnen Sie den Grenzwert n + n + 3n. b Leiten Sie die folgenden Funktionen ab. Dabei ist a R eine Konstante. fx : lnx e a, gx : x + x + 4 sinx c Berechnen Sie z z und z z in der Form
. Aufgabe Punkte a Berechnen Sie den Grenzwert n + n + 3n. b Leiten Sie die folgenden Funktionen ab. Dabei ist a R eine Konstante. fx : lnx e a, gx : x + x + 4 sinx c Berechnen Sie z z und z z in der Form
SS 2016 Höhere Mathematik für s Studium der Physik 21. Juli Probeklausur. Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert.
 SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
HOCHSCHULBÜCHER FÜR MATHEMATIK H.GRELL, K.MARUHN U N D W.RINOW BAND 14 FOURIERREIHEN VON G.P. TOLSTOW MIT 51 A B B I L D U N G E N
 fc HOCHSCHULBÜCHER FÜR MATHEMATIK H E R A U S G E G E B E N VON H.GRELL, K.MARUHN U N D W.RINOW BAND 14 FOURIERREIHEN VON G.P. TOLSTOW MIT 51 A B B I L D U N G E N 1955 VEB DEUTSCHER VERLAG DER WISSENSCHAFTEN
fc HOCHSCHULBÜCHER FÜR MATHEMATIK H E R A U S G E G E B E N VON H.GRELL, K.MARUHN U N D W.RINOW BAND 14 FOURIERREIHEN VON G.P. TOLSTOW MIT 51 A B B I L D U N G E N 1955 VEB DEUTSCHER VERLAG DER WISSENSCHAFTEN
Konvergenz und Stetigkeit
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 12. Dezember 2007 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 12. Dezember 2007 Konvergenz Definition Fourierreihen Obertöne Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld
 ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
konvergent falls eine allgemeine ("gutmütige") Funktion. Frage: kann man sie in der darstellen mittels einer Potenzreihe in
 C5 Funktionen: Taylorreihen & Fourieranalysis C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen
C5 Funktionen: Taylorreihen & Fourieranalysis C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen
Trignonometrische Funktionen 6a
 Schuljahr 2015/16 andreas.kucher@uni-graz.at Institute for Mathematics and Scientific Computing Karl-Franzens-Universität Graz Graz, November 23, 2015 Winkelmaße Winkelmaß bis 6. Klasse: Grad (0 360 )
Schuljahr 2015/16 andreas.kucher@uni-graz.at Institute for Mathematics and Scientific Computing Karl-Franzens-Universität Graz Graz, November 23, 2015 Winkelmaße Winkelmaß bis 6. Klasse: Grad (0 360 )
Unendliche Reihen - I
 Unendliche Reihen - I Zur Wiederholung. Sei eine Folge ( ) N aus R (bzw. C) gegeben (die Folge der Summanden). Die Folge (s n ) n N in der Form Die Reihe mit s n = n heißt unendliche Reihe und wird geschrieben.
Unendliche Reihen - I Zur Wiederholung. Sei eine Folge ( ) N aus R (bzw. C) gegeben (die Folge der Summanden). Die Folge (s n ) n N in der Form Die Reihe mit s n = n heißt unendliche Reihe und wird geschrieben.
Höhere Mathematik II. Variante A
 Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
Lehrstuhl II für Mathematik Prof Dr E Triesch Höhere Mathematik II SoSe 5 Variante A Zugelassene Hilfsmittel: Als Hilfsmittel zugelassen sind zehn handbeschriebene DinA4-Blätter (Vorder- und Rückseite
MAI-Übungsaufgaben im SS02
 MAI-Übungsaufgaben im SS02 Prof. Dr. Th. Risse SS 2002 Knappe Rückmeldungen zu den jeweiligen Übungsaufgaben (wie soll man sonst aus Fehlern lernen?) mit einer Bewertungstabelle ganz am Ende! 1 Übungsaufgaben,
MAI-Übungsaufgaben im SS02 Prof. Dr. Th. Risse SS 2002 Knappe Rückmeldungen zu den jeweiligen Übungsaufgaben (wie soll man sonst aus Fehlern lernen?) mit einer Bewertungstabelle ganz am Ende! 1 Übungsaufgaben,
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK
 ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
ANALYSIS FÜR INFORMATIKER ÜBUNGSBLATT WEIHNACHTSGESCHENK Dr. J. Giannoulis, M.Sc. S. Metzler, Dipl. Math. K. Tichmann WS 00/ Trainingseinheit 0 Sript Kartieren Sie grob die Inhalte des Sripts. Welche Werzeuge,
