Schülerworkshop Computertomographie Mathematik als Schlüsseltechnologie
|
|
|
- Thilo Kohler
- vor 6 Jahren
- Abrufe
Transkript
1 Schülerworkshop Computertomographie Mathematik als Schlüsseltechnologie Norbert Köckler 1. und 2. Juni 2007 Computertomographie und lineare Gleichungssysteme
2 Überblick zum CT-Vortrag 1. Einleitung Wer hats erfunden und was sind MRT und CT? 2. Das Prinzip eines Tomographen als Diashow. 3. Halbwertsdicke, Strahlenintensitäten und die Tomographieformel. 4. Was und wie wird gemessen und was wird berechnet? 5. Am Ende steht ein lineares Gleichungssystem!
3 Eine Reise durch das Gehirn Ein Gehirn in Schichten Bilder entstehen bei einer: Computer-Tomographie (Röntgenstrahlen) Magnet-Resonanz-Tomographie (Magnetfelder & Radiowellen)
4 Wer hat es ermöglicht? Johann Radon österreichischer Mathematiker Entwickelte 1917 ein mathematische Verfahren die sog. RadonTransformation. Die Radon-Transformation war damals noch fern jeglicher Anwendung.
5 Wer hat es erfunden? Allen M.Cormack amerikanischer Physiker Leistete die physikalischen Vorarbeit. Godfrey M. Hounsfield * 1919 britischer Ingenieur Entwickelte den ersten Prototypen eines CT. Sie erhielten für Ihre Arbeit den Nobelpreis in Medizin Die Nobelpreisträger für Medizin The Nobel Foundation
6 CT als interdisziplinäre Technologie (1/2) Physik Medizin Ermöglicht die Geräte Fordert gewisse Eigenschaften Informatik Mathematik Konstruiert ICs, stellt Datenstrukturen bereit Ermöglicht die Lösung der Gleichungen
7 CT als interdisziplinäre Technologie (2/2) Physik Medizin Modelliert neue Versuchsanordnung Erwartet spezielle Darstellung Informatik Mathematik Präsentiert neue Visualisierungen Erfindet schnelle Algorithmen zur Bildbearbeitung
8 CT oder MRT? Was heißt Tomographie? Computer-Tomographie (CT) CT, Quelle: Philips Tomos = Schichten + Graphie = Schreiben Magnet-Resonanz-Tomographie (MRT) MRT, Foto: Frank Luerweg
9 Prinzip der Tomographie als Diashow(1/9) Die Bestandteile einer Computer-Tomographie (Modell) Monitor StrahlenEmpfänger StrahlenSender Computer Patient
10 Prinzip der Tomographie als Diashow(9/9)...aus den geschwächten Strahlintensitäten das Schichtbild berechnet. Alle Bilder werden gespeichert.
11 CT in echt Das Foto zeigt eine reale Untersuchungssituation. Im Vordergrund erkennt man die Steuerung mit Computer und Bildschirm, im Hintergrund liegt eine Patientin auf dem Schlitten, der während der Untersuchung in das ringförmige CT-Gerät eingefahren war. Der Schlitten steht nun wieder vor dem Gerät und in Sekundenschnelle zeigt der Monitor das Auswertungsbild.
12 Verringerung der Intensität innerhalb von Schichten Wir lassen Röntgenstrahlung auf ein homogenes Material einwirken. Es sei bekannt, für welche Schichtdicke die Intensität der Strahlung beim Durchgang durch diese Schicht genau auf den halben Wert absinkt Eine Halbwertsdicke 100% 50% Noch eine Halbwertsdicke 25% Halbwertsdicke d h : Die Schichtdicke einer homogenen Schicht, bei der durchgehende Strahlung auf den halben Wert absinkt, wird Halbwertsdicke genannt.
13 Formel für die Intensitätsabnahme Die Intensität lässt sich beschreiben durch den Ansatz: d I d =I 0 e I d abhängig von: der Eingangsintensität I 0, Dabei ist die Intensität dem Absorptionskoeffizienten, der die Intensitätsabnahme pro Längeneinheit beschreibt, der bereits durchlaufenden Länge d.
14 Berechnung des Absorptionskoeffizienten Wir kennen das Ergebnis, wenn die Strahlung genau eine Halbwertsdicke eines homogenen Materials durchlaufen hat: d h I d h =I 0 e oder kurz: d h e =I 0 0,5 =0,5 Wir wenden die Umkehrfunktion ln x auf beide Seiten an: d h=ln 0,5 Wir erhalten somit für den Absorptionskoeffizienten: 1 ln 0,5 ln 2 = = dh dh
15 Wie sieht es mit inhomogenen Schichten aus? Zerlegung der inhomogenen Schicht in homogene Teilschichten: I 0 d2 d1 d3 d 4 I d 1 d 2 d 3 d Die Eingangsintensität für die zweite Schicht ist die Ausgangsintensität der ersten Schicht usw. Somit erhalten wir: 1 d 1 I d =I 0 e 2 d 2 e 3 d 3 e 4 d 4 e 1 d 1 2 d 2 3 d 3 4 d 4 =I 0 e Logarithmieren der Gleichung führt zur Tomographieformel: ln I d = 1 d 1 2 d 2 3 d 3 4 d 4 I 0
16 Wie läuft die Messung ab? Betrachten wir die Messung von einem 3x3 Objekt. Während der Untersuchung hat sich die Anordnung um das Objekt gedreht. Dabei wurden die Zellen einer Schicht mehrfach vom Strahlenbündel durchleuchtet. Zur Bestimmung der Dichteverteilung werden die Messwerte herangezogen, die die einzelnen Strahlen beim Durchlaufen von Zellen, die auf ihrem Weg lagen, geliefert haben. Wie vorher überlegt, nimmt die Intensität der Strahlen auf dem Weg vom Sender zum Empfänger abhängig vom Gewebe ab.
17 Mit welchen Daten wird gerechnet Betrachten wir genau eine Messung und nummerieren die Zellen durch: Dieser Strahl trifft Z7 und Z8 Weglänge in Zelle Z5 Z7 Z8 Z9 Z4 Z5 Z6 Z1 Z2 Z3 Die Strahlenintensität wird von dem Empfänger gemessen. Welche Zellen von den Strahlen getroffen worden sind, muss berechnet werden. Die Weglänge muss ebenfalls berechnet werden.
18 Getroffene Zellen und Weglänge Strahlen können mit einer Geradengleichung beschrieben werden. Welche Zellen trifft der Strahl mit der Gleichung g x =x 1? Der Strahl trifft die Zellen Z4 und Z8! Wie groß ist die Weglänge in den getroffenen Zellen? 3 2. Z8 Z9 Z4 Z5 Z6 Z1 Z2 Z3 2 Nach dem Satz von Pythagoras ist die Weglänge in jeder Zelle gleich Z
19 Schichten in Zellen einteilen Diskretisierung (1/2) Die eigentliche Aufgabe ist es, den Intensitätsverlust unendlich vieler Strahlen entlang einer Geraden kontinuierlich zu messen. Dabei ist der Abschwächungskoeffizient eine kontinuierliche Funktion. Man bekommt eine unendliche Menge von Integralen, unter denen die gesuchte Funktion steht: b I1 x dx= ln I a 0 Radon hat 1917 gezeigt, dass man aus unendlich vielen solchen Messungen die dreidimensionale Verteilung der Abschwächung berechnen kann.
20 Schichten in Zellen einteilen Diskretisierung (2/2) Rechnerisch lässt sich das nicht durchführen. Deshalb zerlegt man die durchstrahlte Scheibe in endlich viele Zellen, in denen der Abschwächungskoeffizient als konstant angenommen wird. Diese Diskretisierung liefert pro Strahl eine Gleichung der Form I1 L1 1 L2 2 Ln n= ln I0 Dabei sind n : die berechnete Anzahl der durchstrahlten Zellen, L j : die berechnete Länge des Strahls in Zelle Z j, I 0 : die gegebene Eingangsintensität, I 1 : die gemessene Ausgangsintensität, j : der unbekannte Abschwächungskoeffizient in Zelle Z j.
21 Lineares Gleichungssystem 1. Während sich der Empfänger und Sender um das Objekt drehen, werden die Intensitäten der Strahlen durch die Zellanordnung gemessen. 2. Für jeden Strahl wird über die Tomographieformel eine lineare Gleichung aufgestellt. 3. Es wird ein lineares Gleichungssystem (LGS) aufgebaut. 4. Die Unbekannten des LGS sind die Absorptionskoeffizienten der vom Strahl getroffenen Zellen. 5. Durch Lösen des LGS erhält man die Absorptionskoeffizienten. 6. Diese Dichtewerte stellt man als Farbwert dar und erhält so ein Bild der Schicht.
22 Fragestellung zum Lösen von linearen Gleichungssystemen Wie viele Gleichungen benötigt man für eine sinnvolle Lösung? Wenn die Schicht mit einem n n Raster dargestellt wird, reichen dann stets n n Messungen aus? Müssen es genau n n Gleichungen/Messungen sein? Für ein Raster von ergeben sich Unbekannte. Wie löst man ein so großes Gleichungssystem? Im folgenden Vortrag werden wir uns mit diesen Fragen befassen!
23 Literaturquellen (1/2) Ich danke den Kollegen Loch und Schwebinghaus für die Genehmigung Ihre Internetseiten zu benutzen. Der größte Teil der bis hierher gesehenen Seiten, Bilder und Animationen stammt aus dem MathePrisma-Projekt, siehe unten unter 6. 1 GABOR T. HERMAN, Image Reconstruction from Projections: The Fundamentals of Computerized Tomography, Academic Press, New York, KIRCHGRABER, HARTMANN, HRSG., Lineare Gleichungssysteme - Ein Leitprogramm in Mathematik, ETH Zürich, KIRCHGRABER, STOFFER, Von gut und schlecht gestellten Problemen und ihrer Bedeutung (zum Beispiel für die Gesundheit), ETH Zürich, HOCHBRUCK, SAUTTER, Mathematik fürs Leben am Beispiel der Computertomographie, Universität Düsseldorf, Math. Semesterberichte 49, (2002). 5 CROY, KABADSHOW, Computertomographie CT (Projektarbeit Jugend forscht), Chemnitz, TU Freiberg, KARL-HEINZ LOCH, ULRICH SCHWEBINGHAUS, CT-Projekt im MathePrisma der Uni Wuppertal,
24 Bildquellen (2/2) Wir danken für die Bereitstellung der Fotos: Folie 5: Allan M. Cormack und Godfrey N. Hounsfield, The Nobel Foundation Folie 7: MRT-Untersuchung, Frank Luerweg Folie 17, Nebenpfad Realsituation: CT-Untersuchung, Philips CT-Tomograph, zugleich Startbild in der Modellmaschine II, Philips Film und Titelfotos einer Realuntersuchung, mit Genehmigung einer nicht namentlich genannten Patientin
Verbindung Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1
 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 1 Aspekte der Analysis und der Linearen Algebra!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 2 Arbeitsauftrag für Gruppenarbeit
Methode der kleinsten Quadrate
 1. Phase: Methode der kleinsten Quadrate Einführung Im Vortrag über das CT-Verfahren hat Herr Köckler schon auf die Methode der kleinsten Quadrate hingewiesen. Diese Lösungsmethode, welche bei überbestimmten
1. Phase: Methode der kleinsten Quadrate Einführung Im Vortrag über das CT-Verfahren hat Herr Köckler schon auf die Methode der kleinsten Quadrate hingewiesen. Diese Lösungsmethode, welche bei überbestimmten
Computertomographie. Die Idee
 Computertomographie Außermathematische Anwendungen im Mathematikunterricht WS 202/3 Franz Embacher, Universität Wien Die Idee Die Idee der Computertomographie besteht darin, aus der Abschwächung (Absorption)
Computertomographie Außermathematische Anwendungen im Mathematikunterricht WS 202/3 Franz Embacher, Universität Wien Die Idee Die Idee der Computertomographie besteht darin, aus der Abschwächung (Absorption)
Anwendungen der Linearen Algebra
 Anwendungen der Linearen Algebra mit MATLAB Bearbeitet von Günter M. Gramlich 1. Auflage 2004. Buch. 179 S. Hardcover ISBN 978 3 446 22655 5 Format (B x L): 14,5 x 21 cm Gewicht: 265 g Weitere Fachgebiete
Anwendungen der Linearen Algebra mit MATLAB Bearbeitet von Günter M. Gramlich 1. Auflage 2004. Buch. 179 S. Hardcover ISBN 978 3 446 22655 5 Format (B x L): 14,5 x 21 cm Gewicht: 265 g Weitere Fachgebiete
VOM RÖNTGENBILD ZUM COMPUTERTOMOGRAMM
 VOM RÖNTGENBILD ZUM COMPUTERTOMOGRAMM REFERAT IM RAHMEN DES FACHSEMINARS WS2009/10 AUSARBEITUNG BEI PROF. KARL-OTTO LINN BJÖRN SAßMANNSHAUSEN 1 0. INHALT 1. Vorwort... 3 2. Geschichte Der Computertomogrphie...
VOM RÖNTGENBILD ZUM COMPUTERTOMOGRAMM REFERAT IM RAHMEN DES FACHSEMINARS WS2009/10 AUSARBEITUNG BEI PROF. KARL-OTTO LINN BJÖRN SAßMANNSHAUSEN 1 0. INHALT 1. Vorwort... 3 2. Geschichte Der Computertomogrphie...
Physikalische Grundlagen der Röntgentechnik und Sonographie
 Physikalische Grundlagen der Röntgentechnik und Sonographie PD Dr. Frank Zöllner Computer Assisted Clinical Medicine Faculty of Medicine Mannheim University of Heidelberg Theodor-Kutzer-Ufer 1-3 D-68167
Physikalische Grundlagen der Röntgentechnik und Sonographie PD Dr. Frank Zöllner Computer Assisted Clinical Medicine Faculty of Medicine Mannheim University of Heidelberg Theodor-Kutzer-Ufer 1-3 D-68167
Zerstörungsfreie Materialprüfung
 Zerstörungsfreie Materialprüfung Projekt 3 Andreas Neubauer Institut für Industriemathematik Johannes Kepler Universität Linz Teilnehmer: Bianca Brandl, Stefanie Hartl, Tobias Hermann, Jannik Hildebrandt,
Zerstörungsfreie Materialprüfung Projekt 3 Andreas Neubauer Institut für Industriemathematik Johannes Kepler Universität Linz Teilnehmer: Bianca Brandl, Stefanie Hartl, Tobias Hermann, Jannik Hildebrandt,
Ü b u n g s b l a t t 11
 Mathe für Physiker I Wintersemester 0/04 Walter Oevel 8. 1. 004 Ü b u n g s b l a t t 11 Abgabe von Aufgaben am 15.1.004 in der Übung. Aufgabe 91*: (Differentialgleichungen, Separation. 10 Bonuspunkte
Mathe für Physiker I Wintersemester 0/04 Walter Oevel 8. 1. 004 Ü b u n g s b l a t t 11 Abgabe von Aufgaben am 15.1.004 in der Übung. Aufgabe 91*: (Differentialgleichungen, Separation. 10 Bonuspunkte
Logarithmische Skalen
 Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Logarithmische Skalen Arbeitsblatt Logarithmische Skalen ermöglichen dir eine übersichtlichere Darstellung von Kurvenverläufen vor allem dann, wenn sie sich über sehr große Zahlenbereiche erstrecken. 1
Überbestimmte lineare Gleichungssysteme
 Überbestimmte lineare Gleichungssysteme Fakultät Grundlagen September 2009 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme Übersicht 1 2 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme
Überbestimmte lineare Gleichungssysteme Fakultät Grundlagen September 2009 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme Übersicht 1 2 Fakultät Grundlagen Überbestimmte lineare Gleichungssysteme
DR. ARZT MUSTER MEIN TEAM MEIN TEAM. Ich freue mich, dass Sie meine Ordination gewählt haben. Herzlich willkommen in meiner Ordination!
 1 DR. ARZT MUSTER FA für Radiologie 2 Herzlich willkommen in meiner Ordination! Ich freue mich, dass Sie meine Ordination gewählt haben. 3 4 Dr. Arzt Muster MEIN TEAM Medizinstudium in Wien Ausbildung
1 DR. ARZT MUSTER FA für Radiologie 2 Herzlich willkommen in meiner Ordination! Ich freue mich, dass Sie meine Ordination gewählt haben. 3 4 Dr. Arzt Muster MEIN TEAM Medizinstudium in Wien Ausbildung
F CT1 Verschiedene Abtastverfahren in der Computertomographie
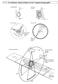 F CT1 Verschiedene Abtastverfahren in der Computertomographie AB CT1 Prinzip der Computertomographie AB CT1 Prinzip der Computertomographie - Musterlösung Kollimatoren blenden ein etwa bleistiftdickes
F CT1 Verschiedene Abtastverfahren in der Computertomographie AB CT1 Prinzip der Computertomographie AB CT1 Prinzip der Computertomographie - Musterlösung Kollimatoren blenden ein etwa bleistiftdickes
18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus
 18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus Conrad Donau 8. Oktober 2010 Conrad Donau 18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus 8. Oktober 2010 1 / 7 18.1 Wiederholung: Ebenen in R 3
18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus Conrad Donau 8. Oktober 2010 Conrad Donau 18. Matrizen 2: Gleichungssysteme, Gauß-Algorithmus 8. Oktober 2010 1 / 7 18.1 Wiederholung: Ebenen in R 3
Mathematischer Vorkurs Lösungen zum Übungsblatt 5
 Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Differenzengleichungen. und Polynome
 Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-600 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung Mit linearen Differenzengleichungen
Lineare Differenzengleichungen und Polynome Franz Pauer Institut für Mathematik, Universität Innsbruck Technikerstr. 13/7, A-600 Innsbruck, Österreich franz.pauer@uibk.ac.at 1 Einleitung Mit linearen Differenzengleichungen
Lineare Gleichungssysteme
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 5. Dezember 2007 Definition : Tomographie (Fortsetzung) : Tomographie Definition: Ein lineares Gleichungssystem (LGS) ist ein System von n
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 5. Dezember 2007 Definition : Tomographie (Fortsetzung) : Tomographie Definition: Ein lineares Gleichungssystem (LGS) ist ein System von n
Funktionsweise und Rekonstruktionsverfahren SPECT & SPECT/CT. C. Schütze
 Funktionsweise und Rekonstruktionsverfahren SPECT & SPECT/CT C. Schütze Gammakamera und SPECT-Systeme http://www.healthcare.siemens.com, http://www.healthcare.philips.com, http://www.miegermany.de Grundprinzip
Funktionsweise und Rekonstruktionsverfahren SPECT & SPECT/CT C. Schütze Gammakamera und SPECT-Systeme http://www.healthcare.siemens.com, http://www.healthcare.philips.com, http://www.miegermany.de Grundprinzip
Lineare Gleichungssysteme
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 28. November 2011 Definition Beispiel: Wassermengen und Konzentrationen in einem Fluss Beispiel Zeilenstufenform Beispiel (Fortsetzung) Anhang
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 28. November 2011 Definition Beispiel: Wassermengen und Konzentrationen in einem Fluss Beispiel Zeilenstufenform Beispiel (Fortsetzung) Anhang
Interpolation und Integration mit Polynomen
 Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
Interpolation und Integration mit Polynomen Philipp Andrea Zardo Universität Kassel 23. Februar 2006 / Kassel Outline 1 Einleitung Was ist numerische Mathematik? Die eulersche e-funktion Ein Wurzelalgorithmus
Optimierung in der Strahlentherapie
 Optimierung in der Strahlentherapie G. Gramlich gramlich@fh-ulm.de FH Ulm Optimierung in der Strahlentherapie p.1/28 Inhalt Worum geht s? Optimierung in der Strahlentherapie p.2/28 Inhalt Worum geht s?
Optimierung in der Strahlentherapie G. Gramlich gramlich@fh-ulm.de FH Ulm Optimierung in der Strahlentherapie p.1/28 Inhalt Worum geht s? Optimierung in der Strahlentherapie p.2/28 Inhalt Worum geht s?
Bildgebende Systeme in der Medizin
 10/27/2011 Page 1 Hochschule Mannheim Bildgebende Systeme in der Medizin Computer-Tomographie Faculty of Medicine Mannheim University of Heidelberg Theodor-Kutzer-Ufer 1-3 D-68167 Mannheim, Germany Friedrich.Wetterling@MedMa.Uni-Heidelberg.de
10/27/2011 Page 1 Hochschule Mannheim Bildgebende Systeme in der Medizin Computer-Tomographie Faculty of Medicine Mannheim University of Heidelberg Theodor-Kutzer-Ufer 1-3 D-68167 Mannheim, Germany Friedrich.Wetterling@MedMa.Uni-Heidelberg.de
Numerische Lineare Algebra
 Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
Numerische Lineare Algebra Vorlesung 5 Prof. Dr. Klaus Höllig Institut für Mathematischen Methoden in den Ingenieurwissenschaften, Numerik und Geometrische Modellierung SS 21 Prof. Dr. Klaus Höllig (IMNG)
5 Eigenwerte und die Jordansche Normalform
 Mathematik für Ingenieure II, SS 9 Freitag 6 $Id: jordantex,v 7 9/6/ :8:5 hk Exp $ 5 Eigenwerte und die Jordansche Normalform 5 Die Jordansche Normalform Nachdem wir bisher das Vorgehen zur Berechnung
Mathematik für Ingenieure II, SS 9 Freitag 6 $Id: jordantex,v 7 9/6/ :8:5 hk Exp $ 5 Eigenwerte und die Jordansche Normalform 5 Die Jordansche Normalform Nachdem wir bisher das Vorgehen zur Berechnung
Vortrag Computertomographie
 Vortrag Computertomographie Alexander Kohlheyer Seminar Bildverarbeitung in der Medizin Universität Koblenz Inhalt 1. Historie 2. Aufbau und grobe Funktionsweise eines CT 3. Physik der Röntgenstrahlung
Vortrag Computertomographie Alexander Kohlheyer Seminar Bildverarbeitung in der Medizin Universität Koblenz Inhalt 1. Historie 2. Aufbau und grobe Funktionsweise eines CT 3. Physik der Röntgenstrahlung
Lagebeziehung von Ebenen
 M8 ANALYSIS Lagebeziehung von Ebenen Es gibt Möglichkeiten für die Lagebeziehung zwischen zwei Ebenen. Die Ebenen sind identisch. Die Ebenen sind parallel. Die Ebenen schneiden sich in einer Geraden Um
M8 ANALYSIS Lagebeziehung von Ebenen Es gibt Möglichkeiten für die Lagebeziehung zwischen zwei Ebenen. Die Ebenen sind identisch. Die Ebenen sind parallel. Die Ebenen schneiden sich in einer Geraden Um
Grundlagen der Computer-Tomographie
 Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
6.2. Prüfungsaufgaben zur Lösbarkeit von LGS
 6.. Prüfungsaufgaben zur Lösbarkeit von LGS Aufgabe : Lösbarkeit von LGS () Berechne mit Hilfe des Gauß-Verfahrens die Lösungsmengen der drei folgenden inhomogenen Gleichungssysteme. Gib außerdem die Lösungsmengen
6.. Prüfungsaufgaben zur Lösbarkeit von LGS Aufgabe : Lösbarkeit von LGS () Berechne mit Hilfe des Gauß-Verfahrens die Lösungsmengen der drei folgenden inhomogenen Gleichungssysteme. Gib außerdem die Lösungsmengen
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Höhere Mathematik III
 Universität Stuttgart Fachbereich Mathematik Prof. Dr. J. Pöschel Dr. D. Zimmermann Dipl.-Math. K. Sanei Kashani Blatt 5 Höhere Mathematik III el, kb, mecha, phs Vortragsübungen (Musterlösungen) 7..4 Aufgabe
Universität Stuttgart Fachbereich Mathematik Prof. Dr. J. Pöschel Dr. D. Zimmermann Dipl.-Math. K. Sanei Kashani Blatt 5 Höhere Mathematik III el, kb, mecha, phs Vortragsübungen (Musterlösungen) 7..4 Aufgabe
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Höhere Mathematik II für Ingenieurinnen und Ingenieure Beispiele zur 10. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 7. Juni 2017 Höhere Mathematik II für Ingenieurinnen und Ingenieure Beispiele zur 10. Übung Wenn
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, 7. Juni 2017 Höhere Mathematik II für Ingenieurinnen und Ingenieure Beispiele zur 10. Übung Wenn
Lineare Funktionen. Das rechtwinklige (kartesische) Koordinatensystem. Funktionen
 Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
Das rechtwinklige (kartesische) Koordinatensystem Funktionen Funktion: Eine Funktion ist eine eindeutige Zuordnung. Jedem x D wird genau eine reelle Zahl zugeordnet. Schreibweise: Funktion: f: x f (x)
Computertomographie (CT), Magnetresonanztomographie (MRT) und Ultraschall (US)
 Computertomographie (CT), Magnetresonanztomographie (MRT) und Ultraschall (US) Prof. Dr. Willi Kalender, Ph.D. Institut für Medizinische Physik Universität Erlangen-Nürnberg www.imp.uni-erlangen,de 3D
Computertomographie (CT), Magnetresonanztomographie (MRT) und Ultraschall (US) Prof. Dr. Willi Kalender, Ph.D. Institut für Medizinische Physik Universität Erlangen-Nürnberg www.imp.uni-erlangen,de 3D
6 Symmetrische Matrizen und quadratische Formen
 Mathematik für Ingenieure II, SS 009 Dienstag 3.6 $Id: quadrat.tex,v.4 009/06/3 4:55:47 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6.3 Quadratische Funktionen und die Hauptachsentransformation
Mathematik für Ingenieure II, SS 009 Dienstag 3.6 $Id: quadrat.tex,v.4 009/06/3 4:55:47 hk Exp $ 6 Symmetrische Matrizen und quadratische Formen 6.3 Quadratische Funktionen und die Hauptachsentransformation
2. Schulaufgabe aus der Mathematik Lösungshinweise
 2. Schulaufgabe aus der Mathematik Lösungshinweise Gruppe A (a) Allgemein ist eine Geradengleichung in der Form g(x) = m x+b gegeben, wobei m die Steigung der Geraden und b der y-achsenabschnitt, also
2. Schulaufgabe aus der Mathematik Lösungshinweise Gruppe A (a) Allgemein ist eine Geradengleichung in der Form g(x) = m x+b gegeben, wobei m die Steigung der Geraden und b der y-achsenabschnitt, also
Prüfung zur Vorlesung Mathematik I/II
 Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Dr. A. Caspar ETH Zürich, August 2011 D BIOL, D CHAB Prüfung zur Vorlesung Mathematik I/II Bitte ausfüllen! Name: Vorname: Legi-Nr.: Nicht ausfüllen! Aufgabe Punkte Kontrolle 1 2 3 4 5 6 Total Vollständigkeit
Das Wichtigste auf einen Blick
 Das Wichtigste auf einen Blick Zusammenfassung Geometrie.Parameterform einer Geraden Eine Gerade ist wie auch in der Analysis durch zwei Punkte A, B im Raum eindeutig bestimmt einer der beiden Punkte,
Das Wichtigste auf einen Blick Zusammenfassung Geometrie.Parameterform einer Geraden Eine Gerade ist wie auch in der Analysis durch zwei Punkte A, B im Raum eindeutig bestimmt einer der beiden Punkte,
Röntgen Physik und Anwendung
 Röntgen Physik und Anwendung Entstehung und Beschreibung von Röntgenstrahlung Was ist der wesentliche Unterschied zwischen Röntgen-Photonen und Photonen, die bei Phosphoreszenz/Lumineszenz entstehen? Begründen
Röntgen Physik und Anwendung Entstehung und Beschreibung von Röntgenstrahlung Was ist der wesentliche Unterschied zwischen Röntgen-Photonen und Photonen, die bei Phosphoreszenz/Lumineszenz entstehen? Begründen
Volumenakquise. Vortrag von Benjamin Gayer
 10.11.11 1 Volumenakquise Vortrag von Benjamin Gayer Einführung Bildquelle: http://www.medical.siemens.com/siemens/de_de/rg_marcom_fbas/files/patienteninformationen/ct_geschichte_technologie. pdf 10.11.11
10.11.11 1 Volumenakquise Vortrag von Benjamin Gayer Einführung Bildquelle: http://www.medical.siemens.com/siemens/de_de/rg_marcom_fbas/files/patienteninformationen/ct_geschichte_technologie. pdf 10.11.11
Dentale Volumentomographie (DVT) Grundlagen
 Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze c 2009 1 / 28 Dentale Volumentomographie Definition Bei der
Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze Dentale Volumentomographie (DVT) Grundlagen Priv.-Doz. Dr. Ralf Schulze c 2009 1 / 28 Dentale Volumentomographie Definition Bei der
Themenheft mit viel Trainingsmaterial (Siehe Vorwort!) Unabhänge Vektoren und Erzeugung von Vektoren Gauß-Algorithmus Rang einer Matrix.
 LINEARE ALGEBRA Lösbarkeit von linearen Gleichungssystemen Themenheft mit viel Trainingsmaterial (Siehe Vorwort!) Unabhänge Vektoren und Erzeugung von Vektoren Gauß-Algorithmus Rang einer Matrix Gleichungssysteme
LINEARE ALGEBRA Lösbarkeit von linearen Gleichungssystemen Themenheft mit viel Trainingsmaterial (Siehe Vorwort!) Unabhänge Vektoren und Erzeugung von Vektoren Gauß-Algorithmus Rang einer Matrix Gleichungssysteme
Systeme von Differentialgleichungen. Beispiel 1: Chemische Reaktionssysteme. Beispiel 2. System aus n Differentialgleichungen 1. Ordnung: y 1.
 Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Systeme von Differentialgleichungen Beispiel : Chemische Reaktionssysteme System aus n Differentialgleichungen Ordnung: y (x = f (x, y (x,, y n (x Kurzschreibweise: y y 2 (x = f 2(x, y (x,, y n (x y n(x
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik II für biw/ciw/mach/mage/vt
 Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Karlsruher Institut für Technologie Institut für Algebra und Geometrie PD Dr. F. Hettlich Dr. S. Schmitt Dipl.-Math. J. Kusch Karlsruhe, den 09.06.20 Lösungen zum 9. Übungsblatt zur Vorlesung Höhere Mathematik
Differentialgleichungen sind überall!
 Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Übungsblatt
 Übungsblatt 3 3.5.27 ) Die folgenden vier Matrizen bilden eine Darstellung der Gruppe C 4 : E =, A =, B =, C = Zeigen Sie einige Gruppeneigenschaften: a) Abgeschlossenheit: Berechnen Sie alle möglichen
Übungsblatt 3 3.5.27 ) Die folgenden vier Matrizen bilden eine Darstellung der Gruppe C 4 : E =, A =, B =, C = Zeigen Sie einige Gruppeneigenschaften: a) Abgeschlossenheit: Berechnen Sie alle möglichen
Rekonstruktion dynamischer Kardio-CT-Daten
 Seminar Kardiologie Dipl.-Phys. Stefan Wesarg Rekonstruktion dynamischer Kardio-CT-Daten Vortrag von Florian Nöll Überblick 1. Die Bedeutung der Computertomographie und wie man eine CT durchführt 2. Evolution
Seminar Kardiologie Dipl.-Phys. Stefan Wesarg Rekonstruktion dynamischer Kardio-CT-Daten Vortrag von Florian Nöll Überblick 1. Die Bedeutung der Computertomographie und wie man eine CT durchführt 2. Evolution
Vektoren - Basiswechsel
 Vektoren - Basiswechsel Grundprinzip Für rein geometrische Anwendungen verwendet man üblicherweise die Standardbasis. Damit ergibt sich in den Zahlenangaben der Koordinaten kein Unterschied zu einem Bezug
Vektoren - Basiswechsel Grundprinzip Für rein geometrische Anwendungen verwendet man üblicherweise die Standardbasis. Damit ergibt sich in den Zahlenangaben der Koordinaten kein Unterschied zu einem Bezug
Nichtlineare Gleichungssysteme
 Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Mathematik II Frühlingsemester 2015 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren
 Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 12 8. Juni 2010 Kapitel 10. Lineare Gleichungssysteme (Fortsetzung) Umformung auf obere Dreiecksgestalt Determinantenberechnung mit dem Gauß-Verfahren
Mathematik für Naturwissenschaftler II SS 2010 Lektion 12 8. Juni 2010 Kapitel 10. Lineare Gleichungssysteme (Fortsetzung) Umformung auf obere Dreiecksgestalt Determinantenberechnung mit dem Gauß-Verfahren
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Gleichungen mit mehreren Unbekannten Kap. 2.5 Seite 124
 Gleichungen mit mehreren Unbekannten Kap. 2.5 Seite 24 Gleichungen mit mehreren Unbekannten kennen Sie bereits von den Funktionsgleichungen: y = 3x 4 oder y = x 2 2x + 5. Bereits diese beiden e zeigen,
Gleichungen mit mehreren Unbekannten Kap. 2.5 Seite 24 Gleichungen mit mehreren Unbekannten kennen Sie bereits von den Funktionsgleichungen: y = 3x 4 oder y = x 2 2x + 5. Bereits diese beiden e zeigen,
Grundlagen der Physik 3 Lösung zu Übungsblatt 2
 Grundlagen der Physik 3 Lösung zu Übungsblatt 2 Daniel Weiss 17. Oktober 2010 Inhaltsverzeichnis Aufgabe 1 - Zustandsfunktion eines Van-der-Waals-Gases 1 a) Zustandsfunktion.................................
Grundlagen der Physik 3 Lösung zu Übungsblatt 2 Daniel Weiss 17. Oktober 2010 Inhaltsverzeichnis Aufgabe 1 - Zustandsfunktion eines Van-der-Waals-Gases 1 a) Zustandsfunktion.................................
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg
 Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Pflichtteilaufgaben zu Gegenseitige Lage, Abstand, Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz wwwmathe-aufgabencom September 6 Abituraufgaben (Haupttermin) Aufgabe
Wichtige Eigenschaften
 Technik und Dosisaspekte M. Sadick Institut für Klinische Radiologie und Nuklearmedizin Wichtige Eigenschaften Schnittbildverfahren: überlagerungsfrei verzerrungsfrei maßstabsgetreu digital streustrahlenarm
Technik und Dosisaspekte M. Sadick Institut für Klinische Radiologie und Nuklearmedizin Wichtige Eigenschaften Schnittbildverfahren: überlagerungsfrei verzerrungsfrei maßstabsgetreu digital streustrahlenarm
Allgemeines Gleichungssystem mit zwei Gleichungen und zwei Variablen. Der erste Index bezeichnet die Nummer der Zeile, der zweite die der Spalte.
 Lineare Gleichungssysteme. Einleitung Lineare Gleichungssysteme sind in der Theorie und in den Anwendungen ein wichtiges Thema. Theoretisch werden sie in der Linearen Algebra untersucht. Die Numerische
Lineare Gleichungssysteme. Einleitung Lineare Gleichungssysteme sind in der Theorie und in den Anwendungen ein wichtiges Thema. Theoretisch werden sie in der Linearen Algebra untersucht. Die Numerische
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Dr. H. Macholdt 7. September 2005 1 Motivation Viele Probleme aus dem Bereich der Technik und der Naturwissenschaften stellen uns vor die Aufgabe mehrere unbekannte Gröÿen gleichzeitig
Lineare Gleichungssysteme Dr. H. Macholdt 7. September 2005 1 Motivation Viele Probleme aus dem Bereich der Technik und der Naturwissenschaften stellen uns vor die Aufgabe mehrere unbekannte Gröÿen gleichzeitig
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Aufgabenkomplex 4: Vektorfunktionen, Differenzialgleichungen, Eigenwertprobleme
 Technische Universität Chemnitz 04. Juni 00 Fakultät für Mathematik Höhere Mathematik I. Aufgabenkomple 4: Vektorfunktionen, Differenzialgleichungen, Eigenwertprobleme Letzter Abgabetermin:. Juni 00 (in
Technische Universität Chemnitz 04. Juni 00 Fakultät für Mathematik Höhere Mathematik I. Aufgabenkomple 4: Vektorfunktionen, Differenzialgleichungen, Eigenwertprobleme Letzter Abgabetermin:. Juni 00 (in
Lösungen zu den Übungen zur Einführung in die Spektroskopie für Studenten der Biologie (SS 2011)
 Universität Konstanz Fachbereich Biologie Priv.-Doz. Dr. Jörg H. Kleinschmidt http://www.biologie.uni-konstanz.de/folding/home.html Datum: 26.5.211 Lösungen zu den Übungen zur Einführung in die Spektroskopie
Universität Konstanz Fachbereich Biologie Priv.-Doz. Dr. Jörg H. Kleinschmidt http://www.biologie.uni-konstanz.de/folding/home.html Datum: 26.5.211 Lösungen zu den Übungen zur Einführung in die Spektroskopie
$Id: linabb.tex,v /01/09 13:27:34 hk Exp hk $
 Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 7 11. Mai 2010 Kapitel 8. Vektoren Definition 76. Betrachten wir eine beliebige endliche Anzahl von Vektoren v 1, v 2,..., v m des R n, so können
Mathematik für Naturwissenschaftler II SS 2010 Lektion 7 11. Mai 2010 Kapitel 8. Vektoren Definition 76. Betrachten wir eine beliebige endliche Anzahl von Vektoren v 1, v 2,..., v m des R n, so können
2.3 Abschirmung von Betastrahlen. Aufgabe. Welche Stoffe eignen sich zur Abschirmung von β-strahlen?
 Naturwissenschaften - Physik - Radioaktivität - 2 Strahlenarten und ihre Eigenschaften (P7300800) 2.3 Abschirmung von Betastrahlen Experiment von: Phywe Gedruckt: 6.0.203 6:22:32 intertess (Version 3.06
Naturwissenschaften - Physik - Radioaktivität - 2 Strahlenarten und ihre Eigenschaften (P7300800) 2.3 Abschirmung von Betastrahlen Experiment von: Phywe Gedruckt: 6.0.203 6:22:32 intertess (Version 3.06
Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern
 Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern Vorlesung Robotik SS 016 Kalmanfiter () Kalman-Filter: optimaler rekursiver Datenverarbeitungsalgorithmus optimal hängt vom gewählten
Kalmanfiter (1) Typische Situation für den Einsatz von Kalman-Filtern Vorlesung Robotik SS 016 Kalmanfiter () Kalman-Filter: optimaler rekursiver Datenverarbeitungsalgorithmus optimal hängt vom gewählten
Übungsblatt 05 PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
 Übungsblatt 05 PHYS300 Grundkurs IIIb Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, othmar.marti@physik.uni-ulm.de) 5. 2. 2003 oder 2.. 2004 Aufgaben. In einer Leitung, die parallel zur x-achse
Übungsblatt 05 PHYS300 Grundkurs IIIb Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti, othmar.marti@physik.uni-ulm.de) 5. 2. 2003 oder 2.. 2004 Aufgaben. In einer Leitung, die parallel zur x-achse
Analytische Geometrie
 Analytische Geometrie Wiederholung (Klasse 0) zur Vektorrechnung Hausaufgabe ( Vorbereitung als Vortrag): C:\Users\Hagen\Documents\Dr. H. Fritsch\Eigene Dateien\Gymnasium-Muecheln\ Mathematik\Klasse \Kl--Wdhlg-Vektor.docx
Analytische Geometrie Wiederholung (Klasse 0) zur Vektorrechnung Hausaufgabe ( Vorbereitung als Vortrag): C:\Users\Hagen\Documents\Dr. H. Fritsch\Eigene Dateien\Gymnasium-Muecheln\ Mathematik\Klasse \Kl--Wdhlg-Vektor.docx
Einführung FEM 1D - Beispiel
 p. 1/28 Einführung FEM 1D - Beispiel /home/lehre/vl-mhs-1/folien/vorlesung/4_fem_intro/deckblatt.tex Seite 1 von 28 p. 2/28 Inhaltsverzeichnis 1D Beispiel - Finite Elemente Methode 1. 1D Aufbau Geometrie
p. 1/28 Einführung FEM 1D - Beispiel /home/lehre/vl-mhs-1/folien/vorlesung/4_fem_intro/deckblatt.tex Seite 1 von 28 p. 2/28 Inhaltsverzeichnis 1D Beispiel - Finite Elemente Methode 1. 1D Aufbau Geometrie
Numerisches Programmieren, Übungen
 Technische Universität München SoSe 3 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Jürgen Bräckle Numerisches Programmieren, Übungen Musterlösung 3. Übungsblatt:
Technische Universität München SoSe 3 Institut für Informatik Prof. Dr. Thomas Huckle Dipl.-Inf. Christoph Riesinger Dipl.-Math. Jürgen Bräckle Numerisches Programmieren, Übungen Musterlösung 3. Übungsblatt:
Serie 8: Fakultativer Online-Test
 Prof Norbert Hungerbühler Lineare Algebra I Serie 8: Fakultativer Online-Test ETH Zürich - D-MAVT HS 215 1 Diese Serie besteht nur aus Multiple-Choice-Aufgaben und wird nicht vorbesprochen Die Nachbesprechung
Prof Norbert Hungerbühler Lineare Algebra I Serie 8: Fakultativer Online-Test ETH Zürich - D-MAVT HS 215 1 Diese Serie besteht nur aus Multiple-Choice-Aufgaben und wird nicht vorbesprochen Die Nachbesprechung
Lineare Algebra für D-ITET, D-MATL, RW. Beispiellösung für Serie 10. Aufgabe ETH Zürich D-MATH. Herbstsemester Dr. V. Gradinaru D.
 Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
2. Spezielle anwendungsrelevante Funktionen
 2. Spezielle anwendungsrelevante Funktionen (1) Affin-lineare Funktionen Eine Funktion f : R R heißt konstant, wenn ein c R mit f (x) = c für alle x R existiert linear, wenn es ein a R mit f (x) = ax für
2. Spezielle anwendungsrelevante Funktionen (1) Affin-lineare Funktionen Eine Funktion f : R R heißt konstant, wenn ein c R mit f (x) = c für alle x R existiert linear, wenn es ein a R mit f (x) = ax für
1 Kurvenuntersuchung /40
 00 Herbst, (Mathematik) Aufgabenvorschlag B Kurvenuntersuchung /40 Die Tragflächen des berühmten Flugzeuges Junkers Ju-5 können an der Nahtstelle zum Flugzeugrumpf mithilfe der Funktionen f und g mit 8
00 Herbst, (Mathematik) Aufgabenvorschlag B Kurvenuntersuchung /40 Die Tragflächen des berühmten Flugzeuges Junkers Ju-5 können an der Nahtstelle zum Flugzeugrumpf mithilfe der Funktionen f und g mit 8
Klausur Mathematik I
 Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
Klausur Mathematik I E-Techniker/Mechatroniker/Informatiker/W-Ingenieure). März 007 Hans-Georg Rück) Aufgabe 6 Punkte): a) Berechnen Sie alle komplexen Zahlen z mit der Eigenschaft z z = und z ) z ) =.
6 Bestimmung linearer Funktionen
 1 Bestimmung linearer Funktionen Um die Funktionsvorschrift einer linearen Funktion zu bestimmen, muss man ihre Steigung ermitteln. Dazu sind entweder Punkte gegeben oder man wählt zwei Punkte P 1 ( 1
1 Bestimmung linearer Funktionen Um die Funktionsvorschrift einer linearen Funktion zu bestimmen, muss man ihre Steigung ermitteln. Dazu sind entweder Punkte gegeben oder man wählt zwei Punkte P 1 ( 1
5 Lineare Gleichungssysteme und Determinanten
 5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
5 Lineare Gleichungssysteme und Determinanten 51 Lineare Gleichungssysteme Definition 51 Bei einem linearen Gleichungssystem (LGS) sind n Unbekannte x 1, x 2,, x n so zu bestimmen, dass ein System von
Mathematik 1, Teil B. Inhalt:
 FH Emden-Leer Fachb. Technik, Abt. Elektrotechnik u. Informatik Prof. Dr. J. Wiebe www.et-inf.fho-emden.de/~wiebe Mathematik 1, Teil B Inhalt: 1.) Grundbegriffe der Mengenlehre 2.) Matrizen, Determinanten
FH Emden-Leer Fachb. Technik, Abt. Elektrotechnik u. Informatik Prof. Dr. J. Wiebe www.et-inf.fho-emden.de/~wiebe Mathematik 1, Teil B Inhalt: 1.) Grundbegriffe der Mengenlehre 2.) Matrizen, Determinanten
Praktikum zur Vorlesung Einführung in die Geophysik
 Praktikum zur Vorlesung Einführung in die Geophysik Hinweise zum Praktikum: Messunsicherheit und Fehlerrechnung Stefan Wenk, Prof. Thomas Bohlen TU Bergakademie Freiberg Institut für Geophysik www.geophysik.tufreiberg.de/pages/studenten/praktika/nebenfaechlerpraktikum.htm
Praktikum zur Vorlesung Einführung in die Geophysik Hinweise zum Praktikum: Messunsicherheit und Fehlerrechnung Stefan Wenk, Prof. Thomas Bohlen TU Bergakademie Freiberg Institut für Geophysik www.geophysik.tufreiberg.de/pages/studenten/praktika/nebenfaechlerpraktikum.htm
Anfängerpraktikum D11 - Röntgenstrahlung
 Anfängerpraktikum D11 - Röntgenstrahlung Vitali Müller, Kais Abdelkhalek Sommersemester 2009 1 Messung des ersten Spektrums 1.1 Versuchsaufbau und Hintergrund Es sollte das Spektrum eines Röntgenapparates
Anfängerpraktikum D11 - Röntgenstrahlung Vitali Müller, Kais Abdelkhalek Sommersemester 2009 1 Messung des ersten Spektrums 1.1 Versuchsaufbau und Hintergrund Es sollte das Spektrum eines Röntgenapparates
Die Kettenlinie. Zwischen 2 Masten sei ein Kabel der Länge l gespannt, wobei natürlich für die Größe des Abstandes der Masten gilt: AB < l
 Zwischen Masten sei ein Kabel der Länge l gespannt, wobei natürlich für die Größe des Abstandes der Masten gilt: AB < l Fragen: (1) Wie weit hängt das Kabel durch? ( d =?) () Wie groß ist die Seilspannung
Zwischen Masten sei ein Kabel der Länge l gespannt, wobei natürlich für die Größe des Abstandes der Masten gilt: AB < l Fragen: (1) Wie weit hängt das Kabel durch? ( d =?) () Wie groß ist die Seilspannung
Vorwort. Οψις γὰρ τῶν ἀδήλων τὰ φαινόμενα. (Die Phänomene eröffnen eine Sicht auf das Verborgene.) ANAXAGORAS
 Vorwort Οψις γὰρ τῶν ἀδήλων τὰ φαινόμενα. (Die Phänomene eröffnen eine Sicht auf das Verborgene.) ANAXAGORAS Es gibt keine mathematische Definition inverser Probleme. In TechnikundNaturwissenschaft hat
Vorwort Οψις γὰρ τῶν ἀδήλων τὰ φαινόμενα. (Die Phänomene eröffnen eine Sicht auf das Verborgene.) ANAXAGORAS Es gibt keine mathematische Definition inverser Probleme. In TechnikundNaturwissenschaft hat
Einführung in die linearen Funktionen. Autor: Benedikt Menne
 Einführung in die linearen Funktionen Autor: Benedikt Menne Inhaltsverzeichnis Vorwort... 3 Allgemeine Definition... 3 3 Bestimmung der Steigung einer linearen Funktion... 4 3. Bestimmung der Steigung
Einführung in die linearen Funktionen Autor: Benedikt Menne Inhaltsverzeichnis Vorwort... 3 Allgemeine Definition... 3 3 Bestimmung der Steigung einer linearen Funktion... 4 3. Bestimmung der Steigung
Perlen der Informatik I Wintersemester 2012 Aufgabenblatt 7
 Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
Technische Universität München WS 2012 Institut für Informatik Prof. Dr. H.-J. Bungartz Prof. Dr. T. Huckle Prof. Dr. M. Bader Kristof Unterweger Perlen der Informatik I Wintersemester 2012 Aufgabenblatt
9. Vorlesung Wintersemester
 9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
4. Übungsblatt zur Mathematik I für Maschinenbau
 Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 4. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS /..-7.. Aufgabe G (Geraden im R ) Bestimmen
Fachbereich Mathematik Prof. Dr. M. Joswig Dr. habil. Sören Kraußhar Dipl.-Math. Katja Kulas 4. Übungsblatt zur Mathematik I für Maschinenbau Gruppenübung WS /..-7.. Aufgabe G (Geraden im R ) Bestimmen
Minimale Anzahl von Hinweisen bei Sudoku
 Minimale Anzahl von Hinweisen bei Sudoku Sascha Kurz sascha.kurz@uni-bayreuth.de (basierend auf Arbeiten von Ariane Papke und Gary McGuire et al.) Oberseminar Effizienz dezentraler Strukturen, Bayreuth,
Minimale Anzahl von Hinweisen bei Sudoku Sascha Kurz sascha.kurz@uni-bayreuth.de (basierend auf Arbeiten von Ariane Papke und Gary McGuire et al.) Oberseminar Effizienz dezentraler Strukturen, Bayreuth,
Grundlagen der radiologischen Diagnostik
 Grundlagen der radiologischen Diagnostik Mit den wachsenden technischen Möglichkeiten entwickeln sich immer bessere Methoden, um Verletzungen oder andere Krankheitsbilder zu diagnostizieren. Trotz aller
Grundlagen der radiologischen Diagnostik Mit den wachsenden technischen Möglichkeiten entwickeln sich immer bessere Methoden, um Verletzungen oder andere Krankheitsbilder zu diagnostizieren. Trotz aller
Übungen Theoretische Physik I (Mechanik) Blatt 5 ( )
 TU München Prof. P. Vogl Beispiel 1: Übungen Theoretische Physik I (Mechanik) Blatt 5 (26.08.11) Nach Gompertz (1825) wird die Ausbreitung von Rostfraß auf einem Werkstück aus Stahl durch eine lineare
TU München Prof. P. Vogl Beispiel 1: Übungen Theoretische Physik I (Mechanik) Blatt 5 (26.08.11) Nach Gompertz (1825) wird die Ausbreitung von Rostfraß auf einem Werkstück aus Stahl durch eine lineare
Einführung des Integrals. Integralrechnung. Der Hauptsatz. Stammfunktionen. Einführung des Integrals
 Einführung des Integrals 15 14 Integralrechnung Einführung des Integrals Stammfunktionen Hauptsatz lächen Mittelwerte Rotationsvolumen Das Integral wird aus einer geometrischen ragestellung hergeleitet:
Einführung des Integrals 15 14 Integralrechnung Einführung des Integrals Stammfunktionen Hauptsatz lächen Mittelwerte Rotationsvolumen Das Integral wird aus einer geometrischen ragestellung hergeleitet:
Aufgabenblatt 1: Abgabe am vor der Vorlesung
 Aufgabenblatt 1: Abgabe am 17.09.09 vor der Vorlesung Aufgabe 1. a.) (1P) Geben Sie die Lösungsmenge der folgenden Gleichung an: 6x + y = 10. Zeichnen Sie die Lösungsmenge in ein Koordinatensystem. b.)
Aufgabenblatt 1: Abgabe am 17.09.09 vor der Vorlesung Aufgabe 1. a.) (1P) Geben Sie die Lösungsmenge der folgenden Gleichung an: 6x + y = 10. Zeichnen Sie die Lösungsmenge in ein Koordinatensystem. b.)
4 Der Gauß Algorithmus
 4 Der Gauß Algorithmus Rechenverfahren zur Lösung homogener linearer Gleichungssysteme Wir betrachten ein GLS (1) a 11 x 1 + a 1 x + + a 1n x n = a 1 x 1 + a x + + a n x n = a m1 x 1 + a m x + + a mn x
4 Der Gauß Algorithmus Rechenverfahren zur Lösung homogener linearer Gleichungssysteme Wir betrachten ein GLS (1) a 11 x 1 + a 1 x + + a 1n x n = a 1 x 1 + a x + + a n x n = a m1 x 1 + a m x + + a mn x
Zeilenstufenform eines Gleichungssystems
 Zeilenstufenform eines Gleichungssystems Ein lineares Gleichungssystem mit einer m n-koeffizientenmatrix lässt sich mit Gauß-Transformationen auf Zeilenstufenform (Echelon-Form) transformieren: Ax = b...
Zeilenstufenform eines Gleichungssystems Ein lineares Gleichungssystem mit einer m n-koeffizientenmatrix lässt sich mit Gauß-Transformationen auf Zeilenstufenform (Echelon-Form) transformieren: Ax = b...
Das lineare Gleichungssystem
 26/27 Grundwissen Analytische Geometrie I m1 as lineare Gleichungssystem Man startet zuerst mit der Betrachtung eines linearen Gleichungssystem mit zwei Unbekannten.(Genaueres siehe Skript) Einführung
26/27 Grundwissen Analytische Geometrie I m1 as lineare Gleichungssystem Man startet zuerst mit der Betrachtung eines linearen Gleichungssystem mit zwei Unbekannten.(Genaueres siehe Skript) Einführung
Primzahlen im Schulunterricht wozu?
 Primzahlen im Schulunterricht wozu? Franz Pauer Institut für Fachdidaktik und Institut für Mathematik Universität Innsbruck Tag der Mathematik Graz 6. Februar 2014 Einleitung Eine (positive) Primzahl ist
Primzahlen im Schulunterricht wozu? Franz Pauer Institut für Fachdidaktik und Institut für Mathematik Universität Innsbruck Tag der Mathematik Graz 6. Februar 2014 Einleitung Eine (positive) Primzahl ist
Einführungsbeispiel Kostenfunktion
 Einführungsbeispiel Kostenfunktion Sie bauen eine Fabrik für Luxusautos auf und steigern die Produktion jeden Monat um 1000 Stück. Dabei messen Sie die jeweiligen Kosten und stellen sie grafisch dar. Die
Einführungsbeispiel Kostenfunktion Sie bauen eine Fabrik für Luxusautos auf und steigern die Produktion jeden Monat um 1000 Stück. Dabei messen Sie die jeweiligen Kosten und stellen sie grafisch dar. Die
Mathematik fürs Leben am Beispiel der Computertomographie
 Mathematische Semesterberichte manuscript No. (will be inserted by the editor) Marlis Hochbruck Jörg-M. Sautter Mathematik fürs Leben am Beispiel der Computertomographie Eingegangen am??.??.2001 / Angenommen
Mathematische Semesterberichte manuscript No. (will be inserted by the editor) Marlis Hochbruck Jörg-M. Sautter Mathematik fürs Leben am Beispiel der Computertomographie Eingegangen am??.??.2001 / Angenommen
Mathematischer Vorkurs
 Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite 1 / 170 Vollständige Induktion Kapitel 13 Vollständige Induktion Mathematischer Vorkurs TU Dortmund Seite 117 / 170 Vollständige
Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite 1 / 170 Vollständige Induktion Kapitel 13 Vollständige Induktion Mathematischer Vorkurs TU Dortmund Seite 117 / 170 Vollständige
H. Gruber, R. Neumann. Erfolg im Mathe-Abi. Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen
 H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Themen des Pflichtteils... Analysis Von der Gleichung
H. Gruber, R. Neumann Erfolg im Mathe-Abi Übungsbuch für den Pflichtteil Baden-Württemberg mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Themen des Pflichtteils... Analysis Von der Gleichung
