Viewing Pipeline. Kapitel Die synthetische Kamera
|
|
|
- Gisela Bretz
- vor 5 Jahren
- Abrufe
Transkript
1 Kapitel 15 Viewing Pipeline Die Abbildung dreidimensionaler Objekte auf dem Bildschirm wird in eine Reihe von Elementartransformationen erlegt: Konstruktion von komplexen Senen aus elementaren Objekten (Modeling), Festlegen der Bildebene (View Orientation), Projektion auf ein normiertes Gerät (View Mapping), Abbildung auf ein Ausgabegerät (Device Mapping) Die snthetische Kamera V N (x max, max ) Auge = PRP = NRP U VPD VRC V RP N (x min, min ) Abbildung 15.1: Parameter ur Beschreibung der snthetischen Kamera 165
2 166 KAPITEL 15. VIEWING PIPELINE Die Parameter ur Durchführung der 3D-auf-2D-Abbildung (viewing transformation) sind im wesentlichen die Position und Orientierung einer snthetischen Kamera und ein Punkt in der Sene, auf den die Kamera fokussiert ist: Der View Reference Point (V RP). Die View Plane ist die Bildebene, auf die die Sene projiiert wird. Diese ist definiert durch die View Plane Normal N, die Richtung, aus der die Kamera die Sene aufnimmt, und den V RP. Die Kamera befindet sich im PRP (Projection Reference Point oder Normal Reference Point (NRP)), der dem Augenpunkt eines natürlichen Betrachters entspricht. Die Orientierung der Kamera wird durch den View Up Vector (VUV oder VUP) festgelegt. Durch Projektion des VUV in die View Plane erhält man den Vektor V. Der Vektor U in der View Plane wird so gewählt, daß U, V, N ein rechtshändiges kartesisches Koordinatensstem bilden, das sogenannte View Reference Coordinate Sstem VRC mit dem V RP als Ursprung und dem Augenpunkt PRP auf der positiven N-Achse bei N = V PD (View Plane Distance). Die beiden Punkte in den UV -Koordinaten der Viewplane (x min, min ), (x max, max ) legen das sogenannte View Window fest, d.h., was von der Sene u sehen ist (entspricht der Brennweite eines Kameraobjektivs). Der sichtbare Teil kann noch weiter eingeschränkt werden durch Angabe einer front plane und einer back plane. Sene N Auge back plane window front plane Abbildung 15.2: Einschränkung des sichtbaren Teils Bemerkung: Zur Berechnung der Projektion auf die Bildebene ist es unerheblich, wo die Bildebene in der Sene arrangiert ist Viewing Pipeline Die fotorealistische Darstellung von 3D-Objekten einer Sene auf den 2D-Bildschirm läßt sich beschreiben durch eine Sequen von Transformationen, genannt Viewing Pipeline. Folgende Informationen sind erforderlich: Jedes Objekt wird beschrieben durch Modellkoordinaten (.B. Würfel ist beschrieben durch Mittelpunkt (0,0,0) und Kantenlänge 1). Die Sene wird beschrieben durch eine Menge von Objekten, deren Lage und Größe in Weltkoordinaten beschrieben sind.
3 15.2. VIEWING PIPELINE 167 Die Beleuchtung wird beschrieben durch eine Menge von Lichtquellen, der Lage und Ausrichtung in Weltkoordinaten beschrieben sind. Die snthetische Kamera wird beschrieben durch U,V,N,V PD,(x max, max ),(x min, min ). Folgende Abkürungen werden verwendet: MC WC VRC NPC DC model coordinate sstem world coordinate sstem view reference coordinate sstem normalied projection coordinate sstem device coordinate sstem Jedes Polgon durchläuft die folgende Viewing-Pipeline: 1.) Modeling: MC WC Beschreibe Polgonpunkte in Weltkoordinaten (dies geschieht durch Translation, Rotation und Skalierung). 2.) View Orientation: WC VRC Beschreibe Polgonpunkte bgl. des UV N-Sstems (dies geschieht durch Wechsel des Koordinatensstems, anschließend ist die Sene beschrieben mit x-ebene = Bildebene, das Auge liegt bei = V PD). 3.) View Mapping: VRC NPC Transformiere die Sene derart, daß der sichtbare (= im Pramidenstumpf aus view window, front plane, back plane liegende) Teil abgebildet wird auf einen Einheitswürfel, dessen Vorderund Rückseite der front plane bw. back plane entsprechen. 4.) Device Mapping: NPC DC Bilde jeden Bildpunkt auf Gerätekoordinaten ab = übernimm x,-koordinaten; liefert Tiefeninformation Modeling-Transformationen Punkt 1.) wird Modeling genannt: Das Anordnen von Objekten aus dem Modellkoordinatensstem (MC) u einer Sene in dem sogenannten Weltkoordinatensstem (WC). Im MC liegen die Objekte als Prototpen vor. Ihre Definitionspunkte sind unabhängig von der späteren Größe und Position im WC in Modellkoordinaten gegeben. Der Ursprung des MC befindet sich sinnvollerweise im Zentrum des Objekts. Erst durch das Modeling erhalten die Objekte im WC ihre individuelle Größe, Orientierung und Position. Dieses wird im wesentlichen durch drei Arten von Transformationen realisiert: Translation, Rotation und Skalierung View Orientation Zur Abbildung einer dreidimensionalen Sene aus den Weltkoordinaten auf den Bildschirm muß eine natürliche Betrachtersicht (View Orientation) definiert werden. Eine solche Betrachtersicht besteht aus den Viewing-Parametern
4 168 KAPITEL 15. VIEWING PIPELINE Betrachterstandpunkt PRP (Projection Reference Point; auch Eepoint), Blickrichtung V RP (View Reference Point), vertikale Orientierung VUV (View Up Vector) oder VUP (View Up Point), Blickwinkel (Brennweite). Der fiktive Betrachter blickt vom PRP in Richtung V RP und kippt dabei die Kamera so um die Blickrichtung, daß VUP von ihm aus gesehen vertikal nach oben eigt. Der Blickwinkel entspricht der Brennweite und regelt den Bildausschnitt (Zooming). Durch diese Parameter wird das VRC (View Reference Coordinate Sstem) definiert mit V RP als Ursprung und PRP auf der positiven -Achse. Die x-ebene wird als View Plane beeichnet und steht senkrecht auf der Blickrichtung. Die -Achse ist gegeben durch die Projektion von VUP in die View Plane. Deshalb darf VUP nicht parallel ur Blickrichtung sein. Das VRC hat die gleiche Metrik wie das WC. Es handelt sich also um einen Wechsel des Koordinatensstems. Die entsprechende Matrix, die den Wechsel vom WC ins VRC durchführt ergibt sich, wenn man die Vektoren U, V und N und die homogenen Koordinaten des V RP bgl. des WC als Spaltenvektoren nebeneinander schreibt und diese Matrix anschließend invertiert. Der Abstand wischen V RP und PRP wird als V PD (View Plane Distance) beeichnet. WC VUP View Plane NRP V RP VRC x Abbildung 15.3: Definition des VRC Für die Anwendung des Viewings ergeben sich im Programm verschiedene Möglichkeiten: Soll ein Objekt von verschiedenen Seiten betrachtet werden, so wird V RP in das Objekt gelegt. Durch PRP läßt sich nun die Blickrichtung frei wählen. Der Vektor VUP kann dabei konstant bleiben, sofern nicht senkrecht von oben oder unten geschaut wird. Soll sich die Sene bei konstantem Standpunkt um den Betrachter drehen, wird PRP festgesett. Durch Veränderung des V RP bewegt sich dann die Sene vor dem Auge des Betrachters. Der VUP kann dabei konstant bleiben, solange er nicht kollinear um Vektor durch V RP und PRP wird. Eine weitere Möglichkeit sind Animationen, bei denen sich.b. der Beobachter vorwärts in die Sene hineinbewegt. Dieser Effekt läßt sich durch Verschieben von V RP und PRP um denselben Vektor erielen.
5 15.2. VIEWING PIPELINE View Volume Bei einer Kamera ist der maximal abbildbare Ausschnitt einer Sene durch das Objektiv festgelegt. Im Programm wird ur Erielung desselben Effekts ein rechteckiger Ausschnitt aus der Bildebene das Window gewählt. Das Seitenverhältnis entspricht dem des Ausgabegeräts. Durch das View Window und die gewählte Projektion wird ein Bildraum definiert, der View Volume genannt wird. Nur jene Objekte und Objektteile, die sich innerhalb dieses Bildraumes befinden, werden auf die Bildebene (und dadurch in das View Window) abgebildet. View Plane View Window α NRP VRC V RP V PD Abbildung 15.4: Definition des View Windows x Die Form des Bildraumes ist bei der perspektivischen Projektion eine unendliche Pramide, deren Spite im Projektionsentrum PRP (Projection Reference Point) liegt und deren Kanten durch die Eckpunkte des View Windows verlaufen. Hierbei wird im Programm der Betrachterstandpunkt PRP als Projektionsentrum gewählt. Back Plane Front Plane View Window V RP x VRC PRP(= NRP) FPD 0 BPD Abbildung 15.5: Bildraum bei perspektivischer Projektion Die Begrenung des Bildraumes in Richtung der -Achse des VRC erfolgt durch wei ur View Plane parallele Ebenen, die Front und Back Plane genannt werden. Die Front Plane liegt vom Projektionsentrum PRP aus gesehen vor der Back Plane. Ihre -Komponenten werden als Front Plane Distance (FPD) und Back Plane Distance (BPD) beeichnet. Es gilt BPD < FPD. Mit diesen Ebenen können Teile der Sene von der Projektion auf die Bildebene ausgeschlossen werden. Speiell bei der perspektivischen Projektion erweist sich diese Möglichkeit als notwendig, da sonst sehr nahe Objekte
6 170 KAPITEL 15. VIEWING PIPELINE alle anderen verdecken bw. sehr weit entfernte als nicht mehr erkennbare (d.h. u kleine) Figuren abgebildet würden. Mit Front und Back Plane ergibt sich als View Volume ein Pramidenstumpf View Mapping Statt nun das View Volume aus dem VRC direkt auf den Bildschirm u projiieren, wird im Programm eine weitere Transformation durchgeführt, die nicht nur ur Effiiensteigerung des Algorithmus führt, sondern auch die Projektion der Sene auf die Bildebene erleichert: Der Bildraum wird in einen ur Bildebene normal ausgerichteten Einheitswürfel (0 x 1;0 1;0 1) umgewandelt. Anstelle mehrerer unterschiedlicher Projektionen muß so anschließend nur noch die orthogonale Parallelprojektion auf die Ebene = 0 durchgeführt werden. Das sogenannte View Mapping wird deshalb auch als Ausgabe auf einen normierten Bildschirm beeichnet. Das Koordinatensstem, in dem sich der Einheitswürfel befindet, heißt Normalied Projection Coordinate Sstem (NPC). Der Betrachterstandpunkt befindet sich im Unendlichen auf der positiven -Achse und hat die homogenen Koordinaten (0,0,1,0). Vom Betrachter aus gesehen liegt im NPC der Punkt (0,0,0) links unten hinten und (1,1,1) rechts oben vorne. (0,1,0) x VRC frustum VRC NPC (0,0,1) NPC x (1,0,0) Abbildung 15.6: View Mapping Bei der perspektivischen Projektion wird in einem ersten Schritt der Pramidenstumpf, der den Bildraum darstellt und frustum genannt wird, auf einen regelmäßigen Pramidenstumpf abgebildet. Dessen Grundfläche ist ein Quadrat, das mit jeder Seitenfläche einen Winkel von 45 einschließt. Dabei werden die -Koordinaten nicht und die x- und -Koordinaten proportional ur -Koordinate verändert, was einer Scherung an der -Achse entspricht. Im weiten Schritt wird der regelmäßige Pramidenstumpf in den normierten Einheitswürfel transformiert. Dau müssen die x- und - Koordinaten proportional u den reiproken -Werten skaliert werden. Die Front Plane entspricht im NPC der Ebene = 1 und die Back Plane der Ebene = 0. Beide Schritte werden im Programm u einer Transformationsmatrix usammengefaßt. Bei deren Anwendung auf die homogenen Koordinaten ist u beachten, daß die resultierenden Punkte im allgemeinen w-werte ungleich 1 haben, die affinen Koordinaten also erst nach der Division durch w vorliegen. Außerdem ist diese Abbildung nur beüglich der x- und -Koordinaten linear. In -Richtung werden die Werte durch die Scherung im weiten Schritt reiprok vererrt, d.h., äquidistante Punkte längs der -Achse im VRC häufen sich im NPC bei = 0 nahe der Back Plane.
7 15.2. VIEWING PIPELINE 171 Zur Erleichterung der Herleitung wird unächst das Koordinatensstem so transformiert, daß der PRP im Ursprung sitt. Danach wird das Koordinatensstem an der x-ebene gespiegelt, indem die - Koordinaten mit -1 multipliiert werden. Danach ist das Koordinatensstem linkshändig. Es seien d min,d und d max die Abstände der Frontplane, Bildebene und Backplane vom Augenpunkt. Zur Durchführung von Punkt 3.) der Viewing Pipeline wird unächst die abgeschnittene Pramide (= frustum) transformiert in einen smmetrischen Pramidenstumpf mit quadratischer Grundfläche und Kanten unter 45. (d,d) ( max,d) 45 Auge Auge ( min,d) Bildebene ( d, d) Abbildung 15.7: Überführung in Pramidenstumpf Es müssen also die -Koordinaten proportional ur -Koordinate verändert werden. Dies entspricht einer Scherung an der -Achse, so daß die Achse vom PRP um Zentrum des ViewWindows mti der - Achse usammenfällt. Zusätlich wird in -Richtung so skaliert, daß die Grundseite des entstandenen Pramidenstumpfs eine Kantenlänge von 2d bekommt: = k 1 + k 2 = Punkt ( max,d) soll abgebildet werden auf (d,d); Punkt ( min,d) soll abgebildet werden auf ( d,d). Durch Lösen des Gleichungssstems d = k 1 max + k 2 d d = k 1 min + k 2 d erhält man k 1 = 2d max min, k 2 = max + min max min Analoge Überlegungen für die x-werte ergibt: k 1 = 2d x max x min, k 2 = x max + x min x max x min
8 172 KAPITEL 15. VIEWING PIPELINE Als nächstes wird die regelmäßige Pramide in den Einheitswürfel (0 x 1,0 1,0 1) transformiert. Die front plane entspricht der Ebene = 0 und die back plane der Ebene = 1. (d max,d max ) (1,1) 1 (d min,d min ) Auge 0 back view plane front ( d min,d min ) back view plane front Abbildung 15.8: Überführung in Einheitswürfel Da die -Werte proportional u den reiproken -Werten skaliert werden müssen, ergibt sich als Transformation = k 1 + k 2 = k 3 + k 4 1 Der Kehrwert von im Term u ist nur möglich, indem durch einen geeigneten Eintrag in der vierten Zeile der noch u konstruierenden Transformationsmatrix erreicht wird, dass die vierte Komponente des transformierten Punktes den Wert enthält. Bei der üblichen Auswertung einer homogenen Koordinate wird dann durch geteilt. Durch diesen Trick müssen aber neben dem Term für und dem für x auch der Term u den Kehrwert von eingebaut bekommen. Punkt (d max,d max ) soll abgebildet werden auf (1,1), Punkt ( d min,d min ) soll abgebildet werden auf (0,0). Durch Lösen des Gleichungssstems 1 = k 1 + k 2 dmax d max
9 15.2. VIEWING PIPELINE 173 erhält man 0 = k 1 + k 2 d min d min k 1 = 1 2, k 2 = 1 2. Durch Lösen des Gleichungssstems erhält man k 3 = 1 = k 3 + k 4 0 = k 3 + k 4 1 d max 1 d min d max d max d min, k 4 = d min d max d max d min. Die x-werte werden analog u den -Werten skaliert. Insgesamt ergibt sich somit x = x 2 1 = d max = d min d max 1 d max d min d max d min. Zwar wird hierdurch die Sene im vorderen -Bereich nicht-linear gestaucht, ur Bestimmung der Sichtbarkeit reichen die ermittelten -Werte jedoch aus, da ihre Ordnung erhalten bleibt. Durch Verknüpfen der beiden letten Transformationen erhält man in Schritt 3.) als Transformationsmatrix d x max x 0 1 min 2 (1 x min + x max x max x ) 0 min 0 d 1 max min 2 (1 min + max max ) 0 min 0 0 d max d max d min d max d min d max d min die den sichtbaren Teil der Sene in den Einheitswürfel transformiert. Um wieder ein rechtshändiges Koordinatensstem u erhalten, wird unächst das Koordinatensstem so transformiert, daß die Back Plane in die x-ebene verschoben wird. Abschließend wird wieder an der x-ebene gespiegelt.
10 174 KAPITEL 15. VIEWING PIPELINE Device Mapping Die abschließende Projektion der Sene in Schritt 4.) aus dem NPC auf den Bildschirm wird als Device Mapping beeichnet. Der Einheitswürfel enthält dank der vorangegangenen Transformationen die gesamte darustellende Seneninformation. Die Abbildung muß lediglich die x- und -Koordinaten aus dem NPC so in die Bildschirmkoordinaten DC (Device Coordinate Sstem) transformieren, daß eine anschließende Rundung die ganahligen Koordinaten der Pixel ergibt. DC ist auf den meisten Bildschirmen ein linkshändiges Koordinatensstem. (Die -Achse eigt nach unten, oben links ist der Ursprung (0, 0).) Die Anahl der Pixel im Ausgabefenster ist flexibel und betrage horiontal xsie und vertikal sie. In x-richtung muß dann das Intervall [0, 1] auf die diskreten Werte {0,...,xsie 1} und in -Richtung [0,1] umgekehrt auf {sie 1,...,0} abgebildet werden. Die -Koordinaten dienen später ur Bestimmung und Unterdrückung verdeckter Flächen, die sich durch die Staffelung der Objekte in der Tiefe des Bildraumes ergeben. (0,1,0) back plane NPC DC DC Displa xsie x front plane (0,0,1) NPC x (1,0,0) sie Abbildung 15.9: Device Mapping Die Transformationsmatrix entspricht einer Skalierung um den Vektor (xsie, sie, 1) konkateniert mit einer Translation des Ursprungs in die linke untere Ecke des Bildschirms (0,sie,0). T NPC DC = xsie sie 0 sie Für die Projektion werden einfach die x- und -Werte übernommen; die -Werte sind erforderlich ur Regelung der Sichtbarkeit.
11 15.2. VIEWING PIPELINE Zusammenfassung Abbildung eigt den Ablauf der Transformationen im Überblick. Diese Viewing Pipeline wird von den Eckpunkten aller Polgone durchlaufen, aus denen sich die Sene usammensett. MC Modeling Coordinate Sstem MC WC Modeling WC World Coordinate Sstem WC VRC View Orientation VRC View Reference Coordinate Sstem VRC NPC View Mapping NPC Normalied Projection Coordinate Sstem NPC DC Device Mapping DC Device Coordinate Sstem Abbildung 15.10: Transformationspipeline
12 176 KAPITEL 15. VIEWING PIPELINE 15.3 Clipping Jedes Polgon, das die Viewing Pipeline durchläuft, kostet Rechenaufwand ur Transformation seiner Eckpunte und damit Zeit. Noch mehr Zeit kostet das Schattieren des Polgons, das wir später noch kennenlernen werden. Da nur der Teil der Sene, der sich im f rustum befindet, später auf dem Bilbschirm u sehen sein wird, ist es sinnvoll, den unsichtbaren Teil der Sene so früh wie möglich im Ablauf der Viewing Pipeline losuwerden. Im average case dürfen die Punkte als gleichverteilt im Raum angenommen werden. Der unsichtbare Teil der Sene wird also im Allgemeinen einen nicht u vernachlässigenden Anteil an der Gesamtsene haben. Um den unsichtbaren Teil ausublenden, müssen wir die gesamte Sene auf irgendeiner Stufe der Viewing Pipeline am f rustum clippen. Wir wollen wei Stufen, die sich anbieten, näher betrachten: Clipping im WC Clipping im NPC Zunächst gehen wir davon aus, daß neben den MC-Koordinaten auch die WC-Koordinaten für jeden Polgonpunkt vorliegen Clipping im WC Diese Strategie beginnt damit, die Ebenengleichungen für die sechs Seiten des f rustums im WC u bestimmen. Bei einer Kamerafahrt muß dies im Allgemeinen für jedes Frame neu geschehen. Der Aufwand ist aber unabhängig von der Sene und ihrer Komplexität. Jeder Polgonpunkt wird durch Auswertung der Ebenengleichung an jeder der sechs Seiten geclippt. Wenn ein Polgon eine oder mehrere der Seiten schneidet, müssen noch die neuen Polgonpunkte berechnet werden, indem die Schnittpunkte der Polgonkanten mit den Seiten ermittelt werden. Nur die verbleibenden Punkte müssen ins DC transformiert und auf dem Bildschirm angeeigt werden. Dau ist eine Multiplikation mit der Matrix WC DC notwendig Clipping im NPC Zunächst müssen alle Polgonpunkte mit der Matrix WC NPC ins NPC transformiert werden. Dann wird die dreidimensionale Erweiterung des 2D-Polgon-Clippings von Cohen und Sutherland durchgeführt. Es wird für jeden Punkt ein 6-Bit-Bereichscode bestimmt, der angibt, ob ein Punkt im View Volume (der Einheitswürfel) liegt oder nicht. Dieser Code läßt sich besonders einfach bestimmen, da die Clippingebenen unabhängig von der Sene und der Lage der Kamera immer die Seiten des Einheitswürfels sind. Es reicht also ein einfacher Vergleich mit den Werten 0 bw. 1, um ein Bit des Bereichscodes festulegen. Falls eine Polgonkante eine oder mehrere der Seiten schneidet müssen wieder die neuen Polgonpunkte errechnet werden. Danach müssen die verbleibenden Punkte mit einer weiteren Multiplikation (mit NPC DC) in Bildschirmkoordinaten gebracht und angeeigt werden.
13 15.3. CLIPPING Vergleich der beiden Vorgehensweisen Beim Clipping im WC spart man eine Transformation aller Punkte im Gegensat um Clipping im NPC. Dafür ist das eigentliche Clipping eines Polgon(punkte)s etwas aufwändiger als im weiten Fall. Auch die Schnittpunktberechnung ist im NPC etwas günstiger als im WC. Beim Clipping im WC muß das f rustum noch ins WC gebracht werden. Dieser Vorgang hat konstanten Aufwand und fällt ab einer gewissen Senengröße nicht mehr ins Gewicht. Die Zahl der Punkte, die nach dem Clipping übrig bleibt ist in beiden Fällen gleich, damit auch der Aufwand für die abschließsende Transformation. Man kann nicht entscheiden, welche Strategie die bessere ist, denn die Effiien der mathematischen Operationen auf dem verwendeten Proessor bw. in der verwendeten Programmiersprache spielen eine Rolle. Der unnötige Aufwand der durch die Transformation der unsichtbaren Punkte ins NPC entsteht, läßt sich folgendermaßen abschäten: Angenommen die gane Sene passe in einen Würfel der Kantenlänge g. Dann hat sie ein Volumen von g 3. Der Betrachter stehe im Schwerpunkt des Würfels und blicke so in die Sene, daß das View Window genau einer Würfelseite entspricht. Dann sieht er fünf Sechstel der Sene nicht. Bei gleichverteilten Punkten entspricht das auch fünf Sechstel unnötig vom WC ins NPC transformierten Punkte. Jede Transformation verursacht 16 Multiplikationen und 12 Additionen. Die Entscheidung, ob ein Punkt im Frustum liegt, kostet im NPC sechs Vergleiche (die Hälfte der Vergleiche findet gegen 0 statt, was vermutlich nochmal schneller als ein beliebiger Vergleich ist). Dieselbe Entscheidung kostet im WC 18 Multiplikationen und 6 Vergleiche. D.h. das Clipping im WC ist pro Knoten wei Mutliplikationen teurer. Allerding braucht man im NPC usätlichen Speicherplat für die NPC-Koordinaten und den Bereichscode. Wenn die WC-Koordinaten allerdings nicht vorliegen, sondern für jedes Frame neu aus den MC- Koordinaten errechnet werden müssen, sieht es etwas anders aus. Dann bleibt der Aufwand des Clipping im NPC gleich, denn der erste Schritt besteht jett in einer Transformation mit MC NPC. Der Aufwand des Clipping im WC steigt aber um eine Transformation MC WC für jeden Polgonpunkt. Trotdem hat die parallele Speicherung der WC-Koordinaten ihre Berechtigung. Sie werden für die Beleuchtung benötigt (hier allerdings nur die der sichtbaren Punkte) und viele Datenstrukturen, die die Bestimmung des sichtbaren Teils der Sene wesentlich effiienter machen, arbeiten auf den WC- Koordinaten Umgebungsclipping Eine weitere Effiiensteigerung wird möglich durch die Verwendung eines Umgebungsclippings. Hier wird ein Cluster von mehreren, komplexen Objekten mit einem großen Quader umgeben. Ergibt ein erster Clipping-Test, dass dieser Quader außerhalb des Frustums liegt, so erübrigen sich alle Clipping-Abfragen bgl. seiner inneren Objekte.
Computergrafik 2010 Oliver Vornberger
 Computergrafik 21 Oliver Vornberger Kapitel 15: Viewing Pipeline Vorlesung vom 31.5.1 1 Sequen von Transformationen grün rot Kamera blau Modeling View Orientation View Mapping Device Mapping 2 Die synthetische
Computergrafik 21 Oliver Vornberger Kapitel 15: Viewing Pipeline Vorlesung vom 31.5.1 1 Sequen von Transformationen grün rot Kamera blau Modeling View Orientation View Mapping Device Mapping 2 Die synthetische
156 KAPITEL 13. 3D-TRANSFORMATIONEN 1. Translation um (,Z ;,Z ;,Z ), 2. Skalierung um (s ;s ;s ), 3. Translation um (Z ;Z ;Z ). Die Transformationsmat
 Kapitel 13 3D-Transformationen 13.1 Translation Mit homogenen Koordinaten lat sich der um den Translationsvektor t =(t ;t ;t )verschobene Punkt P =(; ; ) in der folgenden Form darstellen: ( 0 ; 0 ; 0 ):=(
Kapitel 13 3D-Transformationen 13.1 Translation Mit homogenen Koordinaten lat sich der um den Translationsvektor t =(t ;t ;t )verschobene Punkt P =(; ; ) in der folgenden Form darstellen: ( 0 ; 0 ; 0 ):=(
3 Koordinatentransformationen
 8 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 3 Koordinatentransformationen Für die Darstellung von dreidimensionalen Objekten wird grundsätlich eine Reihe von Transformationen ausgeführt, die von den
8 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 3 Koordinatentransformationen Für die Darstellung von dreidimensionalen Objekten wird grundsätlich eine Reihe von Transformationen ausgeführt, die von den
14 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE. x y
 4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
3.5 Transformationen im Raum
 3.5 Transformationen im Raum Translation Die Verschiebung eines Punktes (,,) T um den Translationsvektor (t,t,t ) T ergibt den Punkt (,, ) T mit 1 t 1 t 1 t 1 + t + t = = + t 1 1 1 T(t,t,t ) Computergrafik
3.5 Transformationen im Raum Translation Die Verschiebung eines Punktes (,,) T um den Translationsvektor (t,t,t ) T ergibt den Punkt (,, ) T mit 1 t 1 t 1 t 1 + t + t = = + t 1 1 1 T(t,t,t ) Computergrafik
Transformationen im 3D-Raum
 Thomas Jung Repräsentation von 3D-Oberflächen Aufbau von Szenen Transformationen im 3D-Raum Projektionstranformationen Anwendung in OpenGL Geometrietransformationen bilden die Basis für die Computergrafik
Thomas Jung Repräsentation von 3D-Oberflächen Aufbau von Szenen Transformationen im 3D-Raum Projektionstranformationen Anwendung in OpenGL Geometrietransformationen bilden die Basis für die Computergrafik
Projektion. Ebene geometrische Projektionen
 Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Schattenwurf mit Perspective Shadow Maps
 16. April 2010 Xpiriax Software Wer wir sind und was wir machen Hobby-Entwicklerteam, zur Zeit 6 Personen gegründet Anfang 2008 Schwerpunkte: Spiele- & 3D-Engine-Programmierung Ziele: Erfahrung, Arbeitsproben,
16. April 2010 Xpiriax Software Wer wir sind und was wir machen Hobby-Entwicklerteam, zur Zeit 6 Personen gegründet Anfang 2008 Schwerpunkte: Spiele- & 3D-Engine-Programmierung Ziele: Erfahrung, Arbeitsproben,
3.1 Motivation. - Mit (mehreren) Koordinatentransformationen wird das Objektsystem in das Gerätesystem transformiert.
 3.1 Motivation Wichtige Grundlage der Bildwiedergabe auf dem Bildschirm oder anderen Ausgabegeräten sind Koordinatensysteme und Koordinatentransformationen im IR 2 und IR 3. Im allgemeinen unterscheidet
3.1 Motivation Wichtige Grundlage der Bildwiedergabe auf dem Bildschirm oder anderen Ausgabegeräten sind Koordinatensysteme und Koordinatentransformationen im IR 2 und IR 3. Im allgemeinen unterscheidet
3D-Transformationen. Kapitel Translation Skalierung
 Kapitel 3 3D-Transformationen Wie im weidimensionalen Fall, werden die Definitionspunkte der Objekte als Spaltenvektoren mit homogener Koordinate geschrieben. Die notwendigen Transformationen werden wieder
Kapitel 3 3D-Transformationen Wie im weidimensionalen Fall, werden die Definitionspunkte der Objekte als Spaltenvektoren mit homogener Koordinate geschrieben. Die notwendigen Transformationen werden wieder
Computergrafik Sommersemester 2004 Übungen
 Sommersemester 4 Freiwillige Zusatzübung Aufgabe 6: Transformationen im zweidimensionalen aum Berechnen Sie die Transformationsmatri, die eine Szene zuerst um 3 Grad um den Ursprung dreht und anschließend
Sommersemester 4 Freiwillige Zusatzübung Aufgabe 6: Transformationen im zweidimensionalen aum Berechnen Sie die Transformationsmatri, die eine Szene zuerst um 3 Grad um den Ursprung dreht und anschließend
Koordinatensysteme und Clipping
 Koordinatensysteme und Clipping Michael Olp Inhaltsverzeichnis 1 Einführung in die perspektivische Projektion 1 1.1 Projektion von Liniensegmenten....... 1 2 Koordinatensysteme 2 2.1 Modeling....................
Koordinatensysteme und Clipping Michael Olp Inhaltsverzeichnis 1 Einführung in die perspektivische Projektion 1 1.1 Projektion von Liniensegmenten....... 1 2 Koordinatensysteme 2 2.1 Modeling....................
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
3. Analyse der Kamerabewegung Video - Inhaltsanalyse
 3. Analyse der Kamerabewegung Video - Inhaltsanalyse Stephan Kopf Bewegungen in Videos Objektbewegungen (object motion) Kameraoperationen bzw. Kamerabewegungen (camera motion) Semantische Informationen
3. Analyse der Kamerabewegung Video - Inhaltsanalyse Stephan Kopf Bewegungen in Videos Objektbewegungen (object motion) Kameraoperationen bzw. Kamerabewegungen (camera motion) Semantische Informationen
Kapitel 3: Geometrische Transformationen
 [ Computeranimation ] Kapitel 3: Geometrische Transformationen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 3. Geometrische Transformationen
[ Computeranimation ] Kapitel 3: Geometrische Transformationen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 3. Geometrische Transformationen
Erinnerung. Arbeitsschritte der Computergraphik. Modellierung. Animation. Rendering. Ausgabemedium. Generierung
 Erinnerung Arbeitsschritte der Computergraphik Modellierung Animation Generierung Ausgabemedium Graphik/-Pipeline Wandelt die Beschreibung einer Szene im dreidimensionalen Raum in eine zweidimensionale
Erinnerung Arbeitsschritte der Computergraphik Modellierung Animation Generierung Ausgabemedium Graphik/-Pipeline Wandelt die Beschreibung einer Szene im dreidimensionalen Raum in eine zweidimensionale
3D-Sicht, Projektionen
 Transformationen, deren Matrix als letzte Zeile nicht die Form: [... ] hat, gehören zur allgemeineren Klasse der perspektivischen Transformationen. Perspektivische Projektion von Punkten (,,z i ) auf (
Transformationen, deren Matrix als letzte Zeile nicht die Form: [... ] hat, gehören zur allgemeineren Klasse der perspektivischen Transformationen. Perspektivische Projektion von Punkten (,,z i ) auf (
Legt man die vom Betrachter aus gesehen vor den, wird die spätere Konstruktion kleiner als die Risse. Legt man die hinter das Objekt, wird die perspek
 Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Mathematische Grundlagen
 Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Mathematische Grundlagen Oliver Deussen Mathematische Grundlagen 1 Affine Räume um Zeichenebene bzw. Raum zu beschreiben, muß vorher ein Koordinatensystem festgelegt werden durch geometrische Fragestellungen
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Verdeckung Graphische DV und BV, Regina Pohle, 20. Verdeckung Einordnung in die Inhalte der Vorlesung Einführung mathematische und
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Verdeckung Graphische DV und BV, Regina Pohle, 20. Verdeckung Einordnung in die Inhalte der Vorlesung Einführung mathematische und
Mathematische Grundlagen
 Kapitel 2 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 2. 3D-Koordinatensystem Weit
Kapitel 2 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 2. 3D-Koordinatensystem Weit
geschlossene Schachtel mit einem kleinen Loch
 Kameramodellierung Lochkamera Kamerakonstante Kamerazentrum geschlossene Schachtel mit einem kleinen Loch ideale Kamera: Loch hat keine Ausdehnung die Strahlen sind ein Büschel von Geraden Abbildung erfolgt
Kameramodellierung Lochkamera Kamerakonstante Kamerazentrum geschlossene Schachtel mit einem kleinen Loch ideale Kamera: Loch hat keine Ausdehnung die Strahlen sind ein Büschel von Geraden Abbildung erfolgt
Computergrafik Universität Osnabrück, Henning Wenke,
 Computergrafik Universität Osnabrück, Henning Wenke, 2012-06-04 Kapitel VIII: Per Primitive Operations Primitive I 3 Primitive II Elementare grafische Grundform Besteht in OpenGL aus Folge von 1-3 Vertices
Computergrafik Universität Osnabrück, Henning Wenke, 2012-06-04 Kapitel VIII: Per Primitive Operations Primitive I 3 Primitive II Elementare grafische Grundform Besteht in OpenGL aus Folge von 1-3 Vertices
Übungsserie 5 Die Gerade
 Kantonsschule Solothurn Übungen Vektorrechung RYS Übungsserie Die Gerade Bestimme eine Parametergleichung durch die wei Punkte A( -) und B( -) b) Liegen die Punkte P( -8) und Q( -) auf dieser Geraden?
Kantonsschule Solothurn Übungen Vektorrechung RYS Übungsserie Die Gerade Bestimme eine Parametergleichung durch die wei Punkte A( -) und B( -) b) Liegen die Punkte P( -8) und Q( -) auf dieser Geraden?
Kapitel 2: Mathematische Grundlagen
 [ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
[ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
Computergrafik Universität Osnabrück, Henning Wenke,
 Computergrafik Universität Osnabrück, Henning Wenke, 2012-05-30 Korrektur: Kugelkoordinaten II r und θ konstant: Rand einer Kreisscheibe parallel zur xy Ebene z θ fest y θ konstant, r R : Kegel, ausgehend
Computergrafik Universität Osnabrück, Henning Wenke, 2012-05-30 Korrektur: Kugelkoordinaten II r und θ konstant: Rand einer Kreisscheibe parallel zur xy Ebene z θ fest y θ konstant, r R : Kegel, ausgehend
Anschauliche Parallelrisse und Hauptrisse
 Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
Anschauliche Parallelrisse und Hauptrisse Seit frühester Kindheit wirst du im täglichen Leben immer wieder mit Bildern konfrontiert, sei es in Form von Bauanleitungen oder Produktinformationen. Du solltest
Hans Delfs. Übungen zu Mathematik III für Medieninformatik
 Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
Hans Delfs Übungen zu Mathematik III für Medieninformatik 1 RÄUMLICHE DARSTELLUNGEN VON OBJEKTEN 1 1 Räumliche Darstellungen von Objekten Der Einheitswürfel ist der achsenparallele Würfel in A 3, der von
7.3 Lorentz Transformation
 26 KAPITEL 7. SPEZIELLE RELATIVITÄTSTHEORIE 7.3 Lorent Transformation In diesem Abschnitt sollen die Transformationen im 4-dimensionalen Minkowski Raum betrachtet werden. Dabei wollen wir uns auf solche
26 KAPITEL 7. SPEZIELLE RELATIVITÄTSTHEORIE 7.3 Lorent Transformation In diesem Abschnitt sollen die Transformationen im 4-dimensionalen Minkowski Raum betrachtet werden. Dabei wollen wir uns auf solche
Seminar 3-D Grafik Mathematische Grundlagen, Räume, Koordinatensysteme, Projektionen. Hermann Schwarz Marko Pilop
 Seminar 3-D Grafik Mathematische Grundlagen, Räume, Koordinatensysteme, Projektionen Hermann Schwarz Marko Pilop 2003-11-20 http://www.informatik.hu-berlin.de/~pilop/3d_basics.pdf {hschwarz pilop}@informatik.hu-berlin.de
Seminar 3-D Grafik Mathematische Grundlagen, Räume, Koordinatensysteme, Projektionen Hermann Schwarz Marko Pilop 2003-11-20 http://www.informatik.hu-berlin.de/~pilop/3d_basics.pdf {hschwarz pilop}@informatik.hu-berlin.de
Advanced Computer Graphics Erweiterung zur 6. Übung
 Advanced Computer Graphics Erweiterung zur 6. Übung M.Sc. Tristan Nauber Advanced Computer Graphics: Übung 6 Model-View-Projection Transformationen Model-View-Projection Gegeben Gesucht y Modell Kamera
Advanced Computer Graphics Erweiterung zur 6. Übung M.Sc. Tristan Nauber Advanced Computer Graphics: Übung 6 Model-View-Projection Transformationen Model-View-Projection Gegeben Gesucht y Modell Kamera
Abbildung von Weltkoordinaten nach Bildkoordinaten
 Abbildung von Weltkoordinaten nach Bildkoordinaten Werner Mayer 28. Februar 24 Zusammenfassung Dieses Dokument beschreibt die Abbildungsvorschrift von 3D-Punkten nach Pixelkoordinaten eines Bildes. Dabei
Abbildung von Weltkoordinaten nach Bildkoordinaten Werner Mayer 28. Februar 24 Zusammenfassung Dieses Dokument beschreibt die Abbildungsvorschrift von 3D-Punkten nach Pixelkoordinaten eines Bildes. Dabei
Grundlagen der Spieleprogrammierung
 Grundlagen der Spieleprogrammierung Sommer 23 Grundlagen der Spieleprogrammierung Teil I: 3D-Graphik Kapitel 2: Die Mathematik Peter Sturm Universität Trier Outline. Übersicht und Motivation 2. Mathematische
Grundlagen der Spieleprogrammierung Sommer 23 Grundlagen der Spieleprogrammierung Teil I: 3D-Graphik Kapitel 2: Die Mathematik Peter Sturm Universität Trier Outline. Übersicht und Motivation 2. Mathematische
C A R L V O N O S S I E T Z K Y. Transformationen. Johannes Diemke. Übung im Modul OpenGL mit Java Wintersemester 2010/2011
 C A R L V O N O S S I E T Z K Y Transformationen Johannes Diemke Übung im Modul OpenGL mit Java Wintersemester 2010/2011 Motivation Transformationen Sind Grundlage vieler Verfahren der Computergrafik Model-
C A R L V O N O S S I E T Z K Y Transformationen Johannes Diemke Übung im Modul OpenGL mit Java Wintersemester 2010/2011 Motivation Transformationen Sind Grundlage vieler Verfahren der Computergrafik Model-
Kapitel 1. Koordinaten im Raum. 1.1 Schrägbilder - Kavalier-Perspektive Koordinaten
 Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Kapitel Koordinaten im Raum Schrägbilder - Kavalier-Perspektive Koordinaten Im Raum benötigt man drei Angaben, um die Lage eines Punktes zu beschreiben So beschreiben Geographen durch N5 0"E07 38 7"H5m
Abitur 2011 G8 Musterabitur Mathematik Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Seite http://www.abiturloesung.de/ Seite Abitur G8 Musterabitur Mathematik Geometrie VI In einem kartesischen Koordinatensystem ist ein Würfel W der Kantenlänge gegeben. Die Eckpunkte G ( ) und D ( ) legen
Analytische Geometrie Spatprodukt
 Analytische Geometrie Spatprodukt David Schmid, Reto Da Forno Kantonsschule Schüpfheim Januar 2005 Analytische Geometrie: Das Spatprodukt 1 Das Spatprodukt Hinweis: Die Vektoren werden aus darstellungstechnischen
Analytische Geometrie Spatprodukt David Schmid, Reto Da Forno Kantonsschule Schüpfheim Januar 2005 Analytische Geometrie: Das Spatprodukt 1 Das Spatprodukt Hinweis: Die Vektoren werden aus darstellungstechnischen
0 1 0 b Die inverse Funktion muss die Translation um b sein und hat daher die homogene Matrix b b 1
 Homogene Koorinaten Aufgabe. In homogener Darstellung ist ie Translation f R 4 R 4 um einen Vektor b R 3 eine lineare Funktion un kann aher urch eine Matri Vektor Multiplikation realisiert weren. Wie sieht
Homogene Koorinaten Aufgabe. In homogener Darstellung ist ie Translation f R 4 R 4 um einen Vektor b R 3 eine lineare Funktion un kann aher urch eine Matri Vektor Multiplikation realisiert weren. Wie sieht
Abitur 2016 Mathematik Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik Geometrie V Betrachtet wird der abgebildete Würfel A B C D E F G H. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen
Vektoren - Die Basis
 Vektoren - Die Basis Motivation (Als Vereinfachung - der Schreibarbeit - wählen wir meistens Vektoren in R 2.) Eigentlich ist ja Alles klar! Für einen Vektor a gilt a = ( a x a y )! Am Ende werden wir
Vektoren - Die Basis Motivation (Als Vereinfachung - der Schreibarbeit - wählen wir meistens Vektoren in R 2.) Eigentlich ist ja Alles klar! Für einen Vektor a gilt a = ( a x a y )! Am Ende werden wir
Merkhilfe Vektorrechnung
 Merkhilfe Vektorrechnung 1. Was ist ein Vektor? 2. Verbindungsvektor AB =? 3. Punkte A und B, Gerade g Punkte A, B und C, Ebene E 4. Mitte M der Strecke AB OM =? a 1 a = a 2, b 1 b = b 2 a 3 b 3 5. Betrag
Merkhilfe Vektorrechnung 1. Was ist ein Vektor? 2. Verbindungsvektor AB =? 3. Punkte A und B, Gerade g Punkte A, B und C, Ebene E 4. Mitte M der Strecke AB OM =? a 1 a = a 2, b 1 b = b 2 a 3 b 3 5. Betrag
-dimensionale Darstellungen
 1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
1.9 2 1 2 -dimensionale Darstellungen Auf einer Fläche F (2 dimensional) wird eine Operation ausgeführt Zum Beispiel wir eine Verschiebung um den Vektor t durchgeführt. Gemeint ist der Körper, der überstrichen
Projektionen von geometrischen Objekten
 Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
3D-Transformationen. Kapitel Translation Skalierung
 Kapitel 13 3D-Transformationen Wie im weidimensionalen Fall, werden die Definitionspunkte der Objekte als Spaltenvektoren mit homogener Koordinate geschrieben. Die notwendigen Transformationen werden wieder
Kapitel 13 3D-Transformationen Wie im weidimensionalen Fall, werden die Definitionspunkte der Objekte als Spaltenvektoren mit homogener Koordinate geschrieben. Die notwendigen Transformationen werden wieder
Inhaltsverzeichnis. 1 Hardwaregrundlagen
 Inhaltsverzeichnis 1 Hardwaregrundlagen 2.1 Koordinatentransformationen 2.2 Transformationen in der Ebene 2.3 Transformationen im Raum 3 Repräsentation und Modellierung von Objekten 4 Rasterung 5 Visibilität
Inhaltsverzeichnis 1 Hardwaregrundlagen 2.1 Koordinatentransformationen 2.2 Transformationen in der Ebene 2.3 Transformationen im Raum 3 Repräsentation und Modellierung von Objekten 4 Rasterung 5 Visibilität
Shader. Computer Graphics: Shader
 Computer Graphics Computer Graphics Shader Computer Graphics: Shader Inhalt Pipeline Memory Resources Input-Assembler Vertex-Shader Geometry-Shader & Stream-Output Rasterizer Pixel-Shader Output-Merger
Computer Graphics Computer Graphics Shader Computer Graphics: Shader Inhalt Pipeline Memory Resources Input-Assembler Vertex-Shader Geometry-Shader & Stream-Output Rasterizer Pixel-Shader Output-Merger
2D-Clipping. Kapitel Clipping von Linien. y max. y min x min. x max
 Kapitel 5 2D-Clipping Ziel: Nur den Teil einer Szene darstellen, der innerhalb eines Fensters sichtbar ist. y max y min x min x max Abbildung 5.1: Clip-Fenster 5.1 Clipping von Linien Zu einer Menge von
Kapitel 5 2D-Clipping Ziel: Nur den Teil einer Szene darstellen, der innerhalb eines Fensters sichtbar ist. y max y min x min x max Abbildung 5.1: Clip-Fenster 5.1 Clipping von Linien Zu einer Menge von
Transformation Allgemeines Die Lage eines Punktes kann durch einen Ortsvektor (ausgehend vom Ursprung des Koordinatensystems
 Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
Transformation - 1 1. Allgemeines 2. Zwei durch eine Translation verknüpfte gleichartige Basissysteme 3. Zwei durch eine Translation verknüpfte verschiedenartige Basissysteme (noch gleiche Orientierung)
7.6. Prüfungsaufgaben zu Normalenformen
 7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
7.6. Prüfungsaufgaben zu Normalenformen Aufgabe () Gegeben sind die Gerade g: x a + r u mit r R und die Ebene E: ( x p ) n. a) Welche geometrische Bedeutung haben die Vektoren a und u bzw. p und n? Veranschaulichen
Lösbarkeit linearer Gleichungssysteme
 Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Lösbarkeit linearer Gleichungssysteme Lineares Gleichungssystem: Ax b, A R m n, x R n, b R m L R m R n Lx Ax Bemerkung b 0 R m Das Gleichungssystem heißt homogen a A0 0 Das LGS ist stets lösbar b Wenn
Transformation - 3. Für "übliche" Anwendungen in der Geometrie ist es sinnvoll, bei Transformationen eine gleiche
 Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
Transformation - 3 Wiederholung und spezielle Angaben im Zusammenhang mit Kreis-Berechnungen 1. Problemstellung Im Zusammenhang mit der Berechnung von Schnittflächen kann es sinnvoll sein, die Berechnung
Analytische Geometrie - Schnittwinkel. u 1, u 2 Richtungsvektoren der Geraden
 Analytische Geometrie - Schnittwinkel. Möglichkeiten und Formeln Gerade / Gerade: cos( ) = u u 2 u u 2 Gerade / Ebene: sin( ) = n u n u Ebene / Ebene: cos( ) = n n 2 n n 2 u, u 2 Richtungsvektoren der
Analytische Geometrie - Schnittwinkel. Möglichkeiten und Formeln Gerade / Gerade: cos( ) = u u 2 u u 2 Gerade / Ebene: sin( ) = n u n u Ebene / Ebene: cos( ) = n n 2 n n 2 u, u 2 Richtungsvektoren der
Softwareprojekt Spieleentwicklung
 Softwareprojekt Spieleentwicklung Prototyp I (2D) Prototyp II (3D) Softwareprojekt 12.04. 19.04. 26.04. 03.05. 31.05. Meilenstein I 28.06. Meilenstein II Prof. Holger Theisel, Tobias Günther, OvGU Magdeburg
Softwareprojekt Spieleentwicklung Prototyp I (2D) Prototyp II (3D) Softwareprojekt 12.04. 19.04. 26.04. 03.05. 31.05. Meilenstein I 28.06. Meilenstein II Prof. Holger Theisel, Tobias Günther, OvGU Magdeburg
2D-Punkt-Transformationen
 Zur Erinnerung Drehung eines beliebigen Punktes B um den Winkel θ um den Koordinaten-Ursprung zum Punkt B : x B r cosα y B r sin α [r, α: Hilfsgrößen ] x B r cos(α+θ) r (cosα cosθ sinα sinθ) x B cosθ y
Zur Erinnerung Drehung eines beliebigen Punktes B um den Winkel θ um den Koordinaten-Ursprung zum Punkt B : x B r cosα y B r sin α [r, α: Hilfsgrößen ] x B r cos(α+θ) r (cosα cosθ sinα sinθ) x B cosθ y
Lösungsvorschlag zum zweiten Übungsblatt
 Lösungsvorschlag zum zweiten Übungsblatt Aufgabe Wir zeigen, daß die Drehung um den Ursprung um 9 und die Spiegelung an der x-achse nicht kommutieren. Die Matrix für die Drehmatrix lautet in diesem Fall
Lösungsvorschlag zum zweiten Übungsblatt Aufgabe Wir zeigen, daß die Drehung um den Ursprung um 9 und die Spiegelung an der x-achse nicht kommutieren. Die Matrix für die Drehmatrix lautet in diesem Fall
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Computergraphik Grundlagen
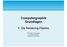 Computergraphik Grundlagen V. Die Rendering-Pipeline Prof. Stefan Schlechtweg Hochschule Anhalt Fachbereich Informatik Inhalt Lernziele 1. Der Begriff Rendering 2. Die Rendering-Pipeline Geometrische Modellierung
Computergraphik Grundlagen V. Die Rendering-Pipeline Prof. Stefan Schlechtweg Hochschule Anhalt Fachbereich Informatik Inhalt Lernziele 1. Der Begriff Rendering 2. Die Rendering-Pipeline Geometrische Modellierung
Mathematische Grundlagen
 Kapitel 12 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 12.1 3D-Koordinatensystem Weit
Kapitel 12 Mathematische Grundlagen In diesem Kapitel werden die mathematischen Grundlagen dargelegt, die für die Darstellung von dreidimensionalen Objekten notwendig sind. 12.1 3D-Koordinatensystem Weit
Projektionen. wie schon immer... Page 1. Computergraphik
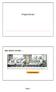 Projektionen wie schon immer... Comutergrahik Page Bilereugung? Welt & Bilmoell Comutergrahik Grahics Piline Moeling Transformations Illumination (Shaing) Viewing Transformation (Persctive / Orthograhic)
Projektionen wie schon immer... Comutergrahik Page Bilereugung? Welt & Bilmoell Comutergrahik Grahics Piline Moeling Transformations Illumination (Shaing) Viewing Transformation (Persctive / Orthograhic)
2.11 Clipping von Linien
 2.11 Clipping von Linien Sollen Objekte in der Bildebene innerhalb eines Fensters dargestellt werden, so wird ein Verfahren benötigt, mit dem alle außerhalb des Fensters liegenden Objektteile abgeschnitten
2.11 Clipping von Linien Sollen Objekte in der Bildebene innerhalb eines Fensters dargestellt werden, so wird ein Verfahren benötigt, mit dem alle außerhalb des Fensters liegenden Objektteile abgeschnitten
How To Create A Panorama Image From A Photoelectric Image From An Image From The Camera (I)
 Chapter 3 Image Registration Distributed Algorithms for Einführung (I) Definition: Image Registration Gegeben: 2 Bilder der gleichen Szene aber aufgenommen aus unterschiedlichen Perspektiven Gesucht: Transformation,
Chapter 3 Image Registration Distributed Algorithms for Einführung (I) Definition: Image Registration Gegeben: 2 Bilder der gleichen Szene aber aufgenommen aus unterschiedlichen Perspektiven Gesucht: Transformation,
Abitur 2013 Mathematik Geometrie V
 Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
Seite 1 http://www.abiturloesung.de/ Seite Abitur 1 Mathematik Geometrie V Teilaufgabe b ( BE) Ein auf einer horizontalen Fläche stehendes Kunstwerk besitzt einen Grundkörper aus massiven Beton, der die
(7) Normal Mapping. Vorlesung Computergraphik II S. Müller. Dank an Stefan Rilling U N I V E R S I T Ä T KOBLENZ LANDAU
 (7) Normal Mapping Vorlesung Computergraphik II S. Müller Dank an Stefan Rilling Einleitung Die Welt ist voller Details Viele Details treten in Form von Oberflächendetails auf S. Müller - 3 - Darstellung
(7) Normal Mapping Vorlesung Computergraphik II S. Müller Dank an Stefan Rilling Einleitung Die Welt ist voller Details Viele Details treten in Form von Oberflächendetails auf S. Müller - 3 - Darstellung
Darstellungsarten für 3D-Körper. Boundary Representation (BRep):
 Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
Darstellungsarten für 3D-Körper Boundary Representation (BRep): Darstellung eines (verallgemeinerten) Polyeders durch das System seiner Ecken, Kanten und Facetten Abspeichern durch (Teilgraphen des) vef-graphen
3. Analyse der Kamerabewegung Video - Inhaltsanalyse
 3. Analyse der Kamerabewegung Video - Inhaltsanalyse Stephan Kopf Bewegungen in Videos Objektbewegungen (object motion) Kameraoperationen bzw. Kamerabewegungen (camera motion) Semantische Informationen
3. Analyse der Kamerabewegung Video - Inhaltsanalyse Stephan Kopf Bewegungen in Videos Objektbewegungen (object motion) Kameraoperationen bzw. Kamerabewegungen (camera motion) Semantische Informationen
Kreis - Tangente. 2. Vorbemerkung: Satz des Thales Eine Möglichkeit zur Bestimmung der Tangente benutzt den Satz des Thales.
 Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
8. Projektionsarten und Perspektive
 8. Projektionsarten un Perspektive Projektionen: transformieren 3D-Objekte in 2D-Biler (mathematisch: lineare Abb., aber nicht bijektiv ugehörige Matri singulär,.h. Determinante ) Projektion ist Grunaufgabe
8. Projektionsarten un Perspektive Projektionen: transformieren 3D-Objekte in 2D-Biler (mathematisch: lineare Abb., aber nicht bijektiv ugehörige Matri singulär,.h. Determinante ) Projektion ist Grunaufgabe
Axonometrie. 11 Axonometrien. Grundrissaxonometrie x : y : z = 1 : 1 : 1
 11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
Kapitel 2 Lineare Algebra II. 2.1 Lineare Abbildungen
 Kapitel 2 Lineare Algebra II 21 Lineare Abbildungen Die mit der Vektorraumstruktur verträglichen Abbildungen zwischen Vektorräumen werden als linear bezeichnet Genauer definiert man: 21 Definition Eine
Kapitel 2 Lineare Algebra II 21 Lineare Abbildungen Die mit der Vektorraumstruktur verträglichen Abbildungen zwischen Vektorräumen werden als linear bezeichnet Genauer definiert man: 21 Definition Eine
Abstände und Zwischenwinkel
 Abstände und Zwischenwinkel Die folgenden Grundaufgaben wurden von Oliver Riesen, KS Zug, erstellt und von Stefan Gubser, KS Zug, überarbeitet. Aufgabe 1: Bestimme den Abstand der beiden Punkte P( 3 /
Abstände und Zwischenwinkel Die folgenden Grundaufgaben wurden von Oliver Riesen, KS Zug, erstellt und von Stefan Gubser, KS Zug, überarbeitet. Aufgabe 1: Bestimme den Abstand der beiden Punkte P( 3 /
Lineare Algebra und Computer Grafik
 Lineare Algebra und Computer Grafik Kurze Zusammenfassung (Stand: 3 Juli 2) Prof Dr V Stahl Copyright 28 by Volker Stahl All rights reserved V Stahl Lineare Algebra und Computer Grafik Zusammenfassung
Lineare Algebra und Computer Grafik Kurze Zusammenfassung (Stand: 3 Juli 2) Prof Dr V Stahl Copyright 28 by Volker Stahl All rights reserved V Stahl Lineare Algebra und Computer Grafik Zusammenfassung
Affine Koordinatentransformationen
 Affine Koordinatentransformationen Medieninformatik IL Andreas Unterweger Vertiefung Medieninformatik Studiengang ITS FH Salzburg Wintersemester 017/18 Andreas Unterweger (FH Salzburg) Affine Koordinatentransformationen
Affine Koordinatentransformationen Medieninformatik IL Andreas Unterweger Vertiefung Medieninformatik Studiengang ITS FH Salzburg Wintersemester 017/18 Andreas Unterweger (FH Salzburg) Affine Koordinatentransformationen
Transformation - Homogene Koordinaten. y + b )
 Transformation - Homogene Koordinaten In der "üblichen" Behandlung werden für die Verschiebung (Translation) und die Drehung (Rotation) verschiedene Rechenvorschriften benutzt - einmal Addition von Vektoren
Transformation - Homogene Koordinaten In der "üblichen" Behandlung werden für die Verschiebung (Translation) und die Drehung (Rotation) verschiedene Rechenvorschriften benutzt - einmal Addition von Vektoren
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Abitur 2011 G9 Abitur Mathematik GK Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur G9 Abitur Mathematik GK Geometrie VI Auf dem Boden des Mittelmeeres wurde ein antiker Marmorkörper entdeckt, der ersten Unterwasseraufnahmen zufolge die
Seite http://www.abiturloesung.de/ Seite Abitur G9 Abitur Mathematik GK Geometrie VI Auf dem Boden des Mittelmeeres wurde ein antiker Marmorkörper entdeckt, der ersten Unterwasseraufnahmen zufolge die
Computergrafik 1. 2D Rendering
 Computergrafik 2D Rendering Hearn/Baker 32., 3.4-3.6,5. 5.8, 6. 6.8, 6. Based on material b Werner Purgathofer, Gerhard Reitmar and Dieter Schmalstieg 2D Racasting Inhalt Einfaches Rendering Model 2D Transformationen
Computergrafik 2D Rendering Hearn/Baker 32., 3.4-3.6,5. 5.8, 6. 6.8, 6. Based on material b Werner Purgathofer, Gerhard Reitmar and Dieter Schmalstieg 2D Racasting Inhalt Einfaches Rendering Model 2D Transformationen
Lineare Transformationen und Determinanten. 10-E Ma 1 Lubov Vassilevskaya
 Lineare Transformationen und Determinanten 10-E Ma 1 Lubov Vassilevskaya Lineare Transformation cc Definition: V und W sind zwei Vektorräume. Eine Funktion T nennt man eine lineare Transformation von V
Lineare Transformationen und Determinanten 10-E Ma 1 Lubov Vassilevskaya Lineare Transformation cc Definition: V und W sind zwei Vektorräume. Eine Funktion T nennt man eine lineare Transformation von V
13 Lösen von Gleichungssystemen
 Vorkurs Mathematik 2 3 LÖSEN VON GLEICHUNGSSYSTEMEN 3 Lösen von Gleichungssystemen Zu Beginn des Kurses haben wir folgendes Gleichungssystem gelöst: 2 + 3y = 5 () + 2y = 4 (2) In diesem Beispiel haben
Vorkurs Mathematik 2 3 LÖSEN VON GLEICHUNGSSYSTEMEN 3 Lösen von Gleichungssystemen Zu Beginn des Kurses haben wir folgendes Gleichungssystem gelöst: 2 + 3y = 5 () + 2y = 4 (2) In diesem Beispiel haben
Bildverarbeitung: 3D-Geometrie. D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13
 Bildverarbeitung: 3D-Geometrie D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
Bildverarbeitung: 3D-Geometrie D. Schlesinger () Bildverarbeitung: 3D-Geometrie 1 / 13 Lochkamera Modell C Projektionszentrum, Optische Achse, Bildebene, P Hauptpunkt (optische Achse kreuzt die Bildebene),
3D-Darstellungen mit Maxima
 Kapitel 5 3D-Darstellungen mit Maxima 5.1 noch einmal: Kavalier-Perspektive 5.1.1 Würfel Wir haben schon festgestellt, dass die Matrix einer Abbildung schon durch die Bilder der drei Einheitspunkte (1
Kapitel 5 3D-Darstellungen mit Maxima 5.1 noch einmal: Kavalier-Perspektive 5.1.1 Würfel Wir haben schon festgestellt, dass die Matrix einer Abbildung schon durch die Bilder der drei Einheitspunkte (1
Eigenwerte und Eigenvektoren
 Vortrag Gmnasium Birkenfeld Von der mathematischen Spielerei zur technischen Anwendung Vortrag Gmnasium Birkenfeld. Vektoren und Matrizen Wir betrachten einen Punkt P (, ) in der Ebene eines rechtwinklig
Vortrag Gmnasium Birkenfeld Von der mathematischen Spielerei zur technischen Anwendung Vortrag Gmnasium Birkenfeld. Vektoren und Matrizen Wir betrachten einen Punkt P (, ) in der Ebene eines rechtwinklig
Lineare Funktionen. Aufgabe 1. Sei f R 2 R definiert durch. x 1 + 3x Beweisen Sie ausführlich, dass f linear ist.
 Lineare Funktionen Aufgabe. Sei f R R definiert durch x f = x x + 3x. Beweisen Sie ausführlich, dass f linear ist. Aufgabe. Die Funktionen (nicht erschrecken sind definiert durch + ( (R n R m (R n R m
Lineare Funktionen Aufgabe. Sei f R R definiert durch x f = x x + 3x. Beweisen Sie ausführlich, dass f linear ist. Aufgabe. Die Funktionen (nicht erschrecken sind definiert durch + ( (R n R m (R n R m
Lineare Algebra Übungen
 Dr Andreas Maurischat Aachen 9 September 7 Lineare Algebra Übungen Vorkurs Mathematik 7 RWTH Aachen Aufgaben um Kapitel (Vektorrechnung Aufgabe Im R sind die Punkte P = (; ; Q = (; ; R = ( ; ; gegeben
Dr Andreas Maurischat Aachen 9 September 7 Lineare Algebra Übungen Vorkurs Mathematik 7 RWTH Aachen Aufgaben um Kapitel (Vektorrechnung Aufgabe Im R sind die Punkte P = (; ; Q = (; ; R = ( ; ; gegeben
++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen dx+ey+f = 0 1.1
 Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
Aufgaben zu Kapitel 9
 9 9 a) b) Ist oder, so ist offenbar Sind und kollinear, also eta λ, so ist λ λ λ λ λ λ λ λ λ Sei umgekehrt und sei Dann ist mindestens eine Komponente on, eta ungleich Aus folgt: ------ ------ und ferner
9 9 a) b) Ist oder, so ist offenbar Sind und kollinear, also eta λ, so ist λ λ λ λ λ λ λ λ λ Sei umgekehrt und sei Dann ist mindestens eine Komponente on, eta ungleich Aus folgt: ------ ------ und ferner
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Rang einer Matrix. 1-E1 Ma 1 Lubov Vassilevskaya
 Rang einer Matrix 1-E1 Ma 1 Lubov Vassilevskaya Unterdeterminante einer nichtquadratischen Matrix M ist eine nichtquadratische 2,3-Matrix: M = 6 2 3 0 5 7 Durch Streichen einer der drei Spalten kann man
Rang einer Matrix 1-E1 Ma 1 Lubov Vassilevskaya Unterdeterminante einer nichtquadratischen Matrix M ist eine nichtquadratische 2,3-Matrix: M = 6 2 3 0 5 7 Durch Streichen einer der drei Spalten kann man
Computergrafik 1 Beleuchtung
 Computergrafik 1 Beleuchtung Kai Köchy Sommersemester 2010 Beuth Hochschule für Technik Berlin Überblick Lokale Beleuchtungsmodelle Ambiente Beleuchtung Diffuse Beleuchtung (Lambert) Spiegelnde Beleuchtung
Computergrafik 1 Beleuchtung Kai Köchy Sommersemester 2010 Beuth Hochschule für Technik Berlin Überblick Lokale Beleuchtungsmodelle Ambiente Beleuchtung Diffuse Beleuchtung (Lambert) Spiegelnde Beleuchtung
Kapitel 4: Schattenberechnung
 Kapitel 4: Schattenberechnung 1 Überblick: Schattenberechnung Motivation Schattenvolumen Shadow Maps Projektive Schatten 2 Motivation Wesentlich für die Wahrnehmung einer 3D-Szene Eigentlich ein globaler
Kapitel 4: Schattenberechnung 1 Überblick: Schattenberechnung Motivation Schattenvolumen Shadow Maps Projektive Schatten 2 Motivation Wesentlich für die Wahrnehmung einer 3D-Szene Eigentlich ein globaler
Computergrafik 1 3D Rendering
 Computergrafik 3D Rendering Hearn/Baker 5.9-6,7.-9,7. Based on material b Werner Purgathofer and Dieter Schmalstieg Creating an Illusion The environment The imaging process = rendering The camera 2 Rendering
Computergrafik 3D Rendering Hearn/Baker 5.9-6,7.-9,7. Based on material b Werner Purgathofer and Dieter Schmalstieg Creating an Illusion The environment The imaging process = rendering The camera 2 Rendering
In den vorigen Abschnitten wurden die globalen kartesischen Koordinaten der Atome eines Moleküls transformiert.
 4 MATRXDARSTELLUNG VON SYMMETREOPERATONEN 33 4.8 Lokale Koordinatenachsen m Gegensat um globalen Koordinatensstem, das für das gesamte Molekül gilt, sind lokale Koordinatenachsen individuell für jedes
4 MATRXDARSTELLUNG VON SYMMETREOPERATONEN 33 4.8 Lokale Koordinatenachsen m Gegensat um globalen Koordinatensstem, das für das gesamte Molekül gilt, sind lokale Koordinatenachsen individuell für jedes
Analytische Geometrie - Das Lotfußpunktverfahren - Gerade/Gerade (R 3 )
 Analytische Geometrie - Das Lotfußpunktverfahren - Gerade/Gerade R 3 ) Gerade - Gerade in R 3 ) Der Fall sich schneidender Geraden ist uninteressant. Es existiert dann ein beliebiger Abstand je nach der
Analytische Geometrie - Das Lotfußpunktverfahren - Gerade/Gerade R 3 ) Gerade - Gerade in R 3 ) Der Fall sich schneidender Geraden ist uninteressant. Es existiert dann ein beliebiger Abstand je nach der
MaTHEMATISCHE GRUNDLAGEN BUGA-AR TELESCOPE. Marko HeRBERTZ
 MaTHEMATISCHE GRUNDLAGEN BUGA-AR TELESCOPE Marko HeRBERTZ Wiederholung: Objekt-, Welt- und Kamerakoordinaten Kugelkoordinaten in kartesische Mögliche Schwierigkeiten Kameralinse Lage der Festung Lagerichtige
MaTHEMATISCHE GRUNDLAGEN BUGA-AR TELESCOPE Marko HeRBERTZ Wiederholung: Objekt-, Welt- und Kamerakoordinaten Kugelkoordinaten in kartesische Mögliche Schwierigkeiten Kameralinse Lage der Festung Lagerichtige
6. Analytische Geometrie : Geraden in der Ebene
 M 6. Analtische Geometrie : Geraden in der Ebene 6.. Vektorielle Geradengleichung Eine Gerade ist durch einen Punkt A und einen Richtungsvektor r eindeutig bestimmt. Durch die Einführung eines Parameters
M 6. Analtische Geometrie : Geraden in der Ebene 6.. Vektorielle Geradengleichung Eine Gerade ist durch einen Punkt A und einen Richtungsvektor r eindeutig bestimmt. Durch die Einführung eines Parameters
Technische Universität München Zentrum Mathematik
 Technische Universität München Zentrum Mathematik Michael Strobel Geometriekalküle WS 217/18 http://www-m1.ma.tum.de/geometriekalkuelews1718 Lösungen zu Aufgabenblatt 7 (29. Februar 217) Aufgabe 1. Abstand
Technische Universität München Zentrum Mathematik Michael Strobel Geometriekalküle WS 217/18 http://www-m1.ma.tum.de/geometriekalkuelews1718 Lösungen zu Aufgabenblatt 7 (29. Februar 217) Aufgabe 1. Abstand
Lösungen zu der Stationsarbeit: Parametergleichungen von Geraden/Lagebeziehung von Geraden
 Lösungen zu der Stationsarbeit: Parametergleichungen von Geraden/Lagebeziehung von Geraden Lösung zur Pflichtaufgabe a) b) Würfel: A( ), B( ), C( ), D( ), E( ), F( ), G( ), H( ) Pyramide: A( ), B( ), C(
Lösungen zu der Stationsarbeit: Parametergleichungen von Geraden/Lagebeziehung von Geraden Lösung zur Pflichtaufgabe a) b) Würfel: A( ), B( ), C( ), D( ), E( ), F( ), G( ), H( ) Pyramide: A( ), B( ), C(
Computergrafik 1 Transformationen
 Computergrafik 1 Transformationen Kai Köchy Sommersemester 2010 Beuth Hochschule für Technik Berlin Überblick Repräsentationen, Primitiven Transformationen in 2D Skalierung Translation Rotation Scherung
Computergrafik 1 Transformationen Kai Köchy Sommersemester 2010 Beuth Hochschule für Technik Berlin Überblick Repräsentationen, Primitiven Transformationen in 2D Skalierung Translation Rotation Scherung
(6) View Transformation. Vorlesung Computergrafik T. Grosch
 (6) Vie Transformation Vorlesng Comptergrafik T. Grosch Wiederholng Transformationen Translation, Rotation, Skalierng Matrien OpenGL: Modelie Matri Hete Kamera seten (Vie Transformation) Transformation
(6) Vie Transformation Vorlesng Comptergrafik T. Grosch Wiederholng Transformationen Translation, Rotation, Skalierng Matrien OpenGL: Modelie Matri Hete Kamera seten (Vie Transformation) Transformation
Lineare Abbildungen (Teschl/Teschl 10.3, 11.2)
 Lineare Abbildungen (Teschl/Teschl.3,.2 Eine lineare Abbildung ist eine Abbildung zwischen zwei Vektorräumen, die mit den Vektoroperationen Addition und Multiplikation mit Skalaren verträglich ist. Formal:
Lineare Abbildungen (Teschl/Teschl.3,.2 Eine lineare Abbildung ist eine Abbildung zwischen zwei Vektorräumen, die mit den Vektoroperationen Addition und Multiplikation mit Skalaren verträglich ist. Formal:
