Differentialrechnung. Mathematik I für Chemiker. Daniel Gerth
|
|
|
- Paul Hoch
- vor 5 Jahren
- Abrufe
Transkript
1 Differentialrechnung Mathematik I für Chemiker Daniel Gerth
2 Überblick Differentialrechnung Dieses Kapitel erklärt: Was man unter den Ableitungen einer Funktion versteht. Wie man die Ableitungen einer Funktion herleitet. Wie man weitergehend als in Kapitel Abbildungen und Funktionen charakteristische Stellen einer Funktion mit Hilfe ihrer Ableitungen bestimmt. Wie man allgemeine, unter Umständen kompliziert strukturierte Funktionen durch mathematisch einfache Funktionen annähert. Daniel Gerth (JKU) Differentialrechnung 2 / 1
3 Inhaltsverzeichnis Daniel Gerth (JKU) Differentialrechnung 3 / 1
4 Einleitung. Motivation Wie stark ist eine Funktion gekrümmt? Auf welche Weise lässt sich eine gegebene Funktion durch Polynome annähern? Wie lassen sich Nullstellen von Funktionen numerisch schnell und effizient berechnen? Der Anwendungsbereich der Differentialrechnung ist unmöglich in nur wenigen Worten zusammenfassen. Mit den Begriffen und den Zusammenhängen rund um die Steigung einer Funktion steht ein Apparat von Hilfsmitteln zur Verfügung, um viele Untersuchungen erheblich zu erleichtern. In diesem Kapitel werden wir die grundlegende Idee der Differentialrechnung kennenlernen, um später auf ihre unterschiedlichen Anwendungen einzugehen. Genug Motivation...??? Daniel Gerth (JKU) Differentialrechnung 4 / 1
5 Grundidee Diese ist sehr einfach: Ersetzt man eine Funktion f(x) nahe einer Stelle x 0 durch ihre Tangente t(x), so macht man nahe x 0 nur kleine Fehler. Die Tangente ist dabei als lineare Funktion viel leichter zu handhaben, als die Funktion f selbst. Daniel Gerth (JKU) Differentialrechnung 5 / 1
6 Definition 1.1 Sei f : D R eine Funktion und x 0 D ein innerer Punkt von D. Dann heißt f differenzierbar an der Stelle x 0, falls der Grenzwert f f(x) f(x 0 ) f(x 0 + h) f(x 0 ) (x 0 ) := lim = lim x x 0 x x 0 h 0 h existiert. f (x 0 ) heißt erste Ableitung von f an der Stelle x 0. Die Funktion f heißt differenzierbar in M D, falls sie in jedem Punkt x 0 M differenzierbar ist. Man nennt die Funktion dann die erste Ableitung von f. f : M R, x f (x), Daniel Gerth (JKU) Differentialrechnung 6 / 1
7 Geometrische Interpretation Für h 0 geht die Sekante s(x) durch (x 0, f(x 0 )) und (x 0 + h, f(x 0 + h)) in eine Tangente t(x) über. Die erste Ableitung f (x 0 ) ist also die Steigung der Tangente t an f im Punkt x 0. Daniel Gerth (JKU) Differentialrechnung 7 / 1
8 Höhere Ableitungen Ist eine Funktion f in x 0 differenzierbar, und ist ihre Ableitung f in x 0 wiederum differenzierbar, so erhält man durch erneutes Differenzieren die so genannte zweite Ableitung von f an der Stelle x 0 : f (x 0 ) := (f ) (x 0 ) := lim x x 0 f (x) f (x 0 ) x x 0. Entsprechend wird (für n N) die n te Ableitung f (n) (x 0 ) = (f (n 1) ) (x 0 ) von f an der Stelle x 0 definiert. (Dabei ist f (0) (x 0 ) := f(x 0 ) zu setzen.) Schreibweise: Für die ersten drei Ableitungen schreibt man f, f und f. Ab n = 4 schreibt man zumeist f (n). Daniel Gerth (JKU) Differentialrechnung 8 / 1
9 Schreibweise. Differentialquotient Leibniz-Notation f (x 0 ) = df dx (x 0) = d dx f(x 0), f (x 0 ) = d2 f dx 2 (x 0) = d2 dx 2 f(x 0) = df dx (x 0),. f (n) (x 0 ) = dn f dx n (x 0) = dn dx n f(x df (n 1) 0) = (x 0 ) dx Wenn f von der Zeit t abhängt, wird die Ableitung von f zum Zeitpunkt t 0 auch mit f(t 0 ) notiert (diese Schreibweise wird von den Physikern sehr gerne verwendet). Differenzenquotient (die Steigung der Sekante des Graphen von f durch die Punkte (x 0, f(x 0 )) und (x,f(x))). y x = y y 0 x x 0 = f(x) f(x 0) x x 0. Obwohl die Differenzen y und x jeweils gegen null konvergieren, besitzt der y im Fall x der Differenzierbarkeit einen endlichen Grenzwert. Die erste Ableitung von f an der Stelle x 0 wird daher auch als Differentialquotient bezeichnet. Daniel Gerth (JKU) Differentialrechnung 9 / 1
10 Beispiele Die konstante Funktion f 1 (x) = c (c R) ist differenzierbar mit f 1(x) = 0, denn f 1 (x + h) f 1 (x) h = c c h = 0 0, h 0. Die lineare Funktion f 2 (x) = ax (a R) ist differenzierbar mit f 2(x) = a, denn f 2 (x + h) f 2 (x) h = a(x + h) ax h = ah h = a a, h 0. Die quadratische Funktion f 3 (x) = x 2 ist differenzierbar mit f 3(x) = 2x, denn f 3 (x + h) f 3 (x) h = (x + h)2 x 2 h = 2hx + h2 h = 2x + h 2x, h 0. Daniel Gerth (JKU) Differentialrechnung 10 / 1
11 Elementare Funktionen und ihre Ableitungen f(x) x n (n R) e x sin(x) cos(x) tan(x) ln(x) f (x) nx n 1 e x cos(x) sin(x) 1 cos 2 (x) 1 x Mit Hilfe der Ableitungsdefinition bestimme man die erste Ableitung von f(x) = 1 x. Daniel Gerth (JKU) Differentialrechnung 11 / 1
12 Beispiel für eine nicht differenzierbare Funktion Die Funktion f(x) = x ist in x 0 = 0 nicht differenzierbar, denn aber f(0 + h) f(0) h 0 lim = lim = 1, h 0+ h h 0+ h f(0 + h) f(0) h 0 lim = lim = 1 1. h 0 h h 0 h Der Differenzenquotient besitzt also keinen Grenzwert für h 0. Der bei x 0 = 0 auftretende Knick ist typisch für Funktionen, die stetig, aber nicht differenzierbar sind. Es ist offensichtlich, dass man in diesem Punkt keine eindeutig bestimmte Tangente finden kann. Daniel Gerth (JKU) Differentialrechnung 12 / 1
13 Satz 1.2 (Bezug zur Stetigkeit) Ist f : D R in x 0 D differenzierbar, dann ist f in x 0 auch stetig. Beweisidee: f(x) f(x 0 ) = f(x) f(x 0) x x 0 } {{ } f (x 0) (x x 0 ) 0, x x 0. }{{} 0 Achtung: Wie das Beispiel f(x) = x zeigt, gibt es sehr wohl stetige Funktionen, die nicht differenzierbar sind. Die Umkehrung von Satz 1.2 ist also falsch! Differenzierbarkeit ist somit eine stärkere Eigenschaft als Stetigkeit. Daniel Gerth (JKU) Differentialrechnung 13 / 1
14 Präzisierung des Linearisierungsgedankens Wir wollen noch einmal den Bezug der Funktion f zu ihrer Tangente t nahe x 0 aufgreifen. Dabei hilft folgende alternative Charakterisierung der Differenzierbarkeit: Satz 1.3 Eine Funktion f : D R ist genau dann in x 0 D differenzierbar, wenn es eine Zahl a R und eine Funktion ϕ : D R gibt mit f(x) = f(x 0 ) + a(x x 0 ) + ϕ(x) (1) und ϕ(x) x x 0 0 für x x 0. In diesem Fall gilt a = f (x 0 ). Daniel Gerth (JKU) Differentialrechnung 14 / 1
15 Präzisierung des Linearisierungsgedankens Mit der Tangentenfunktion t(x) = f(x 0 ) + f (x 0 )(x x 0 ) liest sich (1) für eine differenzierbare Funktion f als Grob gesprochen: f(x) = t(x) + ϕ(x) mit ϕ(x) x x 0 0, x x 0. Funktion = Tangente + Restterm, wobei der Restterm für x x 0 schneller als linear gegen Null geht. Visualisierung: Daniel Gerth (JKU) Differentialrechnung 15 / 1
16 Satz 2.1 Regeln für die Ableitung Sind f, g : D R differenzierbar in x 0 D, dann sind cf (c R), f ± g, fg und f/g (falls g(x 0 ) 0) in x 0 differenzierbar. Dabei gelten folgende Regeln: (cf) (x 0 ) = cf (x 0 ) (für c R), (f ± g) (x 0 ) = f (x 0 ) ± g (x 0 ) (Summenregel), (fg) (x 0 ) = f (x 0 )g(x 0 ) + f(x 0 )g (x 0 ) (Produktregel), ( ) f g (x0 ) = f (x 0)g(x 0) f(x 0)g (x 0) g(x 0) (Quotientenregel). 2 Daniel Gerth (JKU) Differentialrechnung 16 / 1
17 Beispiele Finden Sie die Ableitungen von f 1 (x) = 7x 2 + 4x 8, f 2 (x) = (x + 1)e x, f 3 (x) = ex x, f 4 (x) = 1 x n für n N. Daniel Gerth (JKU) Differentialrechnung 17 / 1
18 Satz 2.2 (Kettenregel) Ist f : D f R in x 0 D f differenzierbar und g : D g R in f(x 0 ) D g differenzierbar, dann ist (g f) ebenfalls in x 0 differenzierbar mit (g f) (x 0 ) = g (f(x 0 )) f (x 0 ). (2) Die Multiplikation mit f (x 0 ) in (2) nennt man Nachdifferenzieren. Außerdem sind für g und f die Begriffe äußere und innere Ableitung gebräuchlich. In Leibniz-Notation schreibt man für (2) mitunter kurz dg dx = dg df df dx. Man bestimme die Ableitung von h(x) = (x 2 4) 5 (x R). Daniel Gerth (JKU) Differentialrechnung 18 / 1
19 Satz 2.3 (Ableitung der Umkehrfunktion) Die reelle Funktion f : D W sei in x 0 D differenzierbar und besitze die Umkehrfunktion f 1 : W D. Ist f (x 0 ) 0 und ist f 1 stetig in f(x 0 ), dann ist f 1 in f(x 0 ) differenzierbar mit (f 1 ) (f(x 0 )) = 1 f (x 0 ) bzw. (f 1 ) (y 0 ) = 1 f (x 0 ) für y 0 = f(x 0 ). Leibniz-Notation: dx dy = 1 dy dx für y = f(x) bzw. x = f 1 (y). Daniel Gerth (JKU) Differentialrechnung 19 / 1
20 Beispiel Für y = f(x) = sin(x), x ( π 2, π 2 ), gilt f (x) = cos(x) 0. Desweiteren ist f 1 (y) = arcsin(y) stetig. Damit gilt nach Satz 2.3 arcsin (y) = 1 sin (x) = 1 cos(x) = 1 1 =. 1 sin 2 (x) 1 y 2 Bestimmen Sie die auf diese Weise die Ableitungen von f 1 (x) = e x und f 2 (x) = x. Daniel Gerth (JKU) Differentialrechnung 20 / 1
21 Logarithmisches Differenzieren Die Kettenregel liefert für positive differenzierbare Funktionen f die Gleichung (ln(f(x))) = f (x) f(x) bzw. f (x) = (ln(f(x))) f(x). Beispiel Für f(x) = x x (x > 0) gilt (x x ) = (ln(x x )) x x = (x ln x) x = (1 + ln x)x x. Man bestimme die Ableitung der Funktion f(x) = x 1 (x 2)(x 3). Daniel Gerth (JKU) Differentialrechnung 21 / 1
22 Ableitungen elementarer Funktionen Die folgenden Tabellen sollten Sie am besten auswendig lernen. Die Ableitungen aller anderen Funktionen können Sie mit Hilfe von Definitionen und der Regel aus vorherigem Abschnitt leicht herleiten. Potenz- und Exponentialfunktionen, Logarithmen f(x) x n (n R) e x ln(x) a x (a > 0) log a (x) f (x) nx n 1 e x 1 x a x ln(a) 1 x ln(a) Trigonometrische Funktionen f(x) sin(x) cos(x) tan(x) cot(x) f (x) cos(x) sin(x) 1 cos 2 (x) = 1 + tan2 (x) 1 sin 2 (x) Daniel Gerth (JKU) Differentialrechnung 22 / 1
23 Ableitungen elementarer Funktionen Arkusfunktionen f(x) arcsin(x) arccos(x) arctan(x) arccot(x) f (x) 1 1 x x x x 2 Berechnen Sie die Ableitungen der tan(x), arctan(x), arcsin(x) und anderer Funktionen aus den oben angegebenentabellen. Daniel Gerth (JKU) Differentialrechnung 23 / 1
24 Extrema, Wachstum und Krümmung differenzierbarer Funktionen Definition 4.1 Sei f : D R eine reelle Funktion. Ein Punkt x D heißt lokales Maximum (lokales Minimum) von f, wenn es ein ε > 0 gibt, so dass f(x 0 ) f(x) (f(x 0 ) f(x)) für alle x D (x 0 ε, x 0 + ε). (3) x 0 heißt lokales Extremum von f, wenn x 0 ein lokales Maximum oder ein lokales Minimum von f ist. Bei einem lokalen Extremum x 0 betrachtet man also nur das Verhalten der Funktion f sehr nahe bei x 0. Das Gegenstück sind globale Extrema, bei denen die Beziehung f(x 0 ) f(x) bzw. f(x 0 ) f(x) aus (3) für alle x D gelten muss. Daniel Gerth (JKU) Differentialrechnung 24 / 1
25 Zeichnen Sie die Graphen der Funktion f : R R, f(x) = 2 cos(2x); g : [0, ) R, g(x) = 1 1+x cos(x) (qualitativ reicht), und machen Sie sich den Unterschied zwischen global und lokal auch graphisch klar. Daniel Gerth (JKU) Differentialrechnung 25 / 1
26 Satz 4.2 (Notwendige Bedingung für lokale Extrema) Ist x 0 (a, b) ein lokales Extremum der differenzierbaren Funktion f : (a, b) R, dann gilt f (x 0 ) = 0. (4) Mit Satz 4.2 kann man also die Kandidaten finden, die für ein lokales Extremum überhaupt in Frage kommen. Nur für diese wird man dann einen konkreten Nachweis versuchen. Graphische Darstellung: An einem Extremalstelle x 0 besitzt die Funktion f aus Satz 4.2 eine horizontale Tangente. Daniel Gerth (JKU) Differentialrechnung 26 / 1
27 Satz 4.3 (Hinreichende Bedingung für lokale Extrema) Sei f : (a, b) R zweimal differenzierbar mit stetiger zweiter Ableitung und f (x 0 ) = 0 für ein x 0 (a, b). Dann ist x 0 Stelle eines lokalen Minimums, wenn f (x 0 ) > 0, Stelle eines lokalen Maximums, wenn f (x 0 ) < 0. Bestimmen Sie die lokalen und globalen Extrema von f(x) = x 3 2x + 4. Analysieren Sie das Verhalten von f(x) = x n (n = 2, 4, 5) im Hinblick auf die Sätze 4.2 und 4.3 und das tatsächliche Auftreten von Extrema. Daniel Gerth (JKU) Differentialrechnung 27 / 1
28 Satz 4.4 (Bedingung für ein Extremum) Sei f : (a, b) R eine k Mal differenzierbare Funktion mit stetiger k ter Ableitung und k 2. Gilt für eine Stelle x 0 (a, b), dass f (x 0 ) = f (x 0 ) =... = f (k 1) (x 0 ) = 0 und f (k) (x 0 ) 0, so besitzt die Funktion f an der Stelle x 0 genau dann ein Extremum, falls k eine gerade Zahl ist. Dann ist x 0 Stelle eines lokalen Minimums, wenn f (k) (x 0 ) > 0, Stelle eines lokalen Maximums, wenn f (k) (x 0 ) < 0. Analysieren Sie das Verhalten von f(x) = x n (n = 2, 4, 5) im Hinblick auf den Satz 4.4. Daniel Gerth (JKU) Differentialrechnung 28 / 1
29 Der Mittelwertsatz und Folgerungen daraus Satz 4.5 Ist f : [a, b] R stetig und in (a, b) differenzierbar, und gilt f(a) = f(b), dann gibt es ein ξ (a, b) mit f (ξ) = 0. Graphische Darstellung: Beweiseidee: f nimmt auf [a, b] Maximum und Minimum an. (Warum?) Liegen Maximum und Minimum auf dem Intervallrand, so ist f(x) = 0 auf [a, b], d.h. f (x) = 0 für alle x (a, b). Ansonsten gibt es ein lokales Extremum ξ (a, b). Für dieses gilt f (ξ) = 0 nach Satz 4.2. Daniel Gerth (JKU) Differentialrechnung 29 / 1
30 Die Voraussetzung f(a) = f(b) = 0 kann durch folgende Modifikation entfernt werden: Satz 4.6 (Mittelwertsatz) Ist f : [a, b] R stetig und in (a, b) differenzierbar, dann gibt es ein ξ (a, b) mit Graphische Darstellung: f (ξ) = f(b) f(a). (5) b a Die Funktion nimmt an mindestens einer Zwischenstelle ξ den Anstieg der Sekante s durch (a, f(a)) und (b, f(b)) an. Daniel Gerth (JKU) Differentialrechnung 30 / 1
31 Monotonie Mit dem Mittelwertsatz lässt sich sofort ein Ergebnis zur Bestimmung des Monotonieverhaltens einer differenzierbaren Funktion herleiten: Folgerung 4.7 Sei f : [a, b] R stetig und differenzierbar in (a, b). Ist f (x) = 0 für alle x (a, b), so ist f konstant. Ist f (x) 0 (bzw. f (x) 0) für alle x (a, b), so ist f monoton wachsend (bzw. fallend). Ist f (x) > 0 (bzw. f (x) < 0) für alle x (a, b), so ist f streng monoton wachsend (bzw. fallend) Daniel Gerth (JKU) Differentialrechnung 31 / 1
32 Die Funktion f(x) = x 3 ist streng monoton wachsend, da aus x < y immer x 3 < y 3 folgt. Versuchen Sie sich an einem Nachweis mittels Folgerung 4.7. Daniel Gerth (JKU) Differentialrechnung 32 / 1
33 Krümmungsverhalten Definition 4.8 Eine reelle Funktion f : D R heißt konvex (bzw. konkav) im Intervall I D, wenn für alle x, y I und alle λ (0, 1) gilt. f(λx + (1 λ)y) λf(x) + (1 λ)f(y) (bzw. f(λx + (1 λ)y) λf(x) + (1 λ)f(y)) (6) Veranschaulichung: Die Sekante durch (x, f(x)) und (y, f(y)) verläuft in [x, y] oberhalb (bzw. unterhalb) des Graphen von f. Graphische Darstellung: Daniel Gerth (JKU) Differentialrechnung 33 / 1
34 Konvexität und Differenzierbarkeit Satz 4.9 Ist die Funktion f : (a, b) R differenzierbar, so definieren wir für jedes z (a, b) die Tangentenfunktion t z : x f(z) + f (z)(x z). f ist in (a, b) genau dann konvex (bzw. konkav), wenn für alle z (a, b) und alle x (a, b) gilt. f(x) t z (x) (bzw. f(x) t z (x)) Veranschaulichung: Jede Tangente an f verläuft unterhalb (bzw. oberhalb) des Graphen von f. Daniel Gerth (JKU) Differentialrechnung 34 / 1
35 Satz 4.10 Ist die Funktion f : (a, b) R differenzierbar, dann ist f genau dann konvex (bzw. konkav) in (a, b), wenn f in (a,b) monoton wachsend (bzw. fallend) ist. Ist f zweimal differenzierbar, dann ist f in (a, b) genau dann konvex (bzw. konkav), wenn f (x) 0 (bzw. f (x) 0) für alle x (a, b) gilt. Daniel Gerth (JKU) Differentialrechnung 35 / 1
36 Graphische Darstellung: Untersuchen Sie das Krümmungsverhalten der Funktionen f 1 (x) = x n (n N), f 2 (x) = e x, f 3 (x) = ln(x), f 4 (x) = cos(x) mit Hilfe von dem gegebenen Satz. Daniel Gerth (JKU) Differentialrechnung 36 / 1
37 Wende- und Sattelpunkte Definition 4.11 Ein Punkt (x 0, f(x 0 )) des Graphen, an dem sich das Krümmungsverhalten einer Funktion f ändert, heißt Wendepunkt von f. Die Stelle x 0 heißt Wendestelle. Die Tangente in einem Wendepunkt heißt Wendetangente. Einen Wendepunkt mit horizontaler Tangente nennt man auch Sattelpunkt. Daniel Gerth (JKU) Differentialrechnung 37 / 1
38 Satz 4.12 Ist f : (a, b) R zweimal differenzierbar und (x 0, f(x 0 )) ein Wendepunkt von f, dann ist f (x 0 ) = 0. Ist f : (a, b) R dreimal differenzierbar und gilt für ein x 0 (a, b) sowohl f (x 0 ) = 0 als auch f (x 0 ) 0, dann ist (x 0, f(x 0 )) ein Wendepunkt von f. Daniel Gerth (JKU) Differentialrechnung 38 / 1
39 Kurvendiskussion Eine Kurvendiskussion setzt sich aus den folgenden Teilaufgaben zusammen: Definitionsbereich. Auf welcher (möglichst großen) Menge D ist die Funktion f definiert? Wertebereich. Welche Werte kann f(x) (x D) annehmen? Symmetrie. Ist f gerade oder ungerade? Nullstellen. Löse f(x) = 0. Extrema. Bestimme die Lösungen x E von f (x) = 0. Wendepunkte. Bestimme die Lösungen x W von f (x) = 0. Verhalten an Polstellen. Ist f eine rationale Funktion, bestimme die Pole x P von f (Nullstellen des Nennerpolynoms) und berechne lim f(x) sowie lim f(x). x x P x x P + Verhalten im Unendlichen. Berechne lim f(x) sowie lim f(x). x x Monotoniebereiche. Untersuche Vorzeichen von f (x). Krümmungsverhalten. Untersuche Vorzeichen von f (x). Graphische Darstellung. Daniel Gerth (JKU) Differentialrechnung 39 / 1
40 Das Newton-Verfahren zur Nullstellenbestimmung Im vorherigen Kapitel (Abschnitt 3) hatten wir das Bisektionsverfahren zur Lösung von Gleichungen der Form f(x) = 0 (7) kennengelernt (f soll stetig sein). In diesem Abschnitt wollen wir ein weiteres Verfahren, das so genannte Newton-Verfahren, kennen lernen: Ist f zusätzlich auch differenzierbar, so liefert uns das im Folgenden beschriebene, in der Praxis weit verbreitete Verfahren eine schnelle und damit effiziente Methode zur numerischen Bestimmung der Nullstellen von f. Ziel ist die Bestimmung einer Lösung x von (7) ausgehend von einem Startwert x 0, der möglichst in der Nähe von x liegt. Daniel Gerth (JKU) Differentialrechnung 40 / 1
41 Das Newton-Verfahren Graphische Darstellung. Idee Man berechnet im n ten Schritt die Nullstelle x n der Tangente t auf f in x n 1. Diese wird als neue Näherung für x verwendet. Natürlich wird man zu Beginn einen Startwert x 0 wählen müssen. (???) Daniel Gerth (JKU) Differentialrechnung 41 / 1
42 Herleitung der Verfahrensvorschrift Wir stellen die Bedingung t(x n ) = f(x n 1 ) + f (x n 1 )(x n x n 1 )! = 0. Umstellen nach x n führt auf die Verfahrenvorschrift des Newton-Verfahrens: x n = x n 1 f(x n 1) f, (n = 1, 2,...). (8) (x n 1 ) Daniel Gerth (JKU) Differentialrechnung 42 / 1
43 Beispiel Für das Beispiel f(x) = e x + x 2 liefert (8) die Vorschrift x n = x n 1 ex n 1 + x n 1 2 e x n Ausgehend vom Startwert x 0 = 0 liefert die Berechnung folgende Werte: n x n f(x n) Daniel Gerth (JKU) Differentialrechnung 43 / 1
44 Konvergenzeigenschaften Wenn das Newton-Verfahren konvergiert, dann wesentlich schneller als das Bisektionsverfahren (Faustformel: in jedem Schritt Verdopplung der Anzahl korrekter Dezimalstellen). Voraussetzung für Konvergenz ist aber, dass der Startwert x 0 genügend nahe bei x liegt ( lokal konvergentes Verfahren ). Ist f : R R dagegen zweimal stetig differenzierbar, d.h. f ist stetig, sowie konvex, und besitzt f eine reelle Nullstelle, so konvergiert die Newton-Folge für jeden Startwert x 0 mit f(x 0 ) 0. Bestimmen Sie die Nullstellen der Funktion f(x) = x + e x. Vergleichen Sie die Anzahl der Schritte für das Newton-Verfahren und das Bisektionsverfahren (sehen Sie das Übungstutorium). Berechnen Sie die Nullstellen der Funktion f(x) = arctan(x). Wählen Sie als den Startwert x 0 = 1.5 und zeigen Sie, dass das Verfahren divergiert. Machen Sie sich die letzten beiden Aussagen an den Beispielen f(x) = x 2 1 und f(x) = x 2 e x graphisch klar. Daniel Gerth (JKU) Differentialrechnung 44 / 1
45 Der Satz von Bernoulli- de l Hospital Wenn wir f(x) lim x x 0 g(x) berechnen möchten, aber sowohl die Zähler- und Nennerfunktion gegen 0 oder (d.h. 0 0 oder ) gehen, was erwarten wir dann? Existiert dennoch ein Grenzwert? Wie untersuchen wir dies? Solche Probleme werden häufig leichter, wenn Differenzierbarkeit gegeben ist. Falls f und g aber differenzierbar sind, so stellt der folgende Satz von Bernoullide l Hospital ein verblüffend einfaches Werkzeug zur Verfügung. Daniel Gerth (JKU) Differentialrechnung 45 / 1
46 Satz 6.1 (Regeln von Bernoulli- de l Hospital) Seien f, g : (a, b) R differenzierbare Funktionen, und für x 0 (a, b) gelte entweder lim f(x) = lim g(x) = 0 x x 0 x x 0 oder lim x x 0 f(x) = lim x x 0 g(x) = ±. Ferner sei g (x) 0 für alle x in einer Umgebung von x 0 und f (x) lim x x 0 g = α mit α R {± }. (x) Dann gilt f(x) lim x x 0 g(x) = lim f (x) x x 0 g (x) = α. Daniel Gerth (JKU) Differentialrechnung 46 / 1
47 Plausibilitätsargument zum Satz 6.1 Nahe einer Stelle x 0 mit f(x 0 ) = g(x 0 ) = 0 gilt f(x) f (x 0 )(x x 0 ) und g(x) g (x 0 )(x x 0 ). Damit also Beispiele sin(x) cos(x) lim = lim = 1, x 0 x x 0 1 lim x x 3 e x = lim x 3x 2 e x = lim x f(x) g(x) f (x 0 ) g (x 0 ). 6x e x = lim x sin(2x 2) 2 cos(2x 2) lim x 1 2x 2 = lim = 2 cos(0) = 1 1 x 1 4x e x = 0, Berechnen Sie die folgenden Grenzwerte x sin(x) lim x 0 x sin(x), e αx x lim für α > 0. Wie kann man aus letzterem einem Aussage über lim x x α, β > 0 gewinnen? sin 2 (x) x 3 und lim x x. Daniel Gerth (JKU) x 0 Differentialrechnung 47 / 1 lim x 0 e αx x β für
48 Bemerkungen Die Bedeutung der l Hospitalschen Regeln wird vom Anfänger oft überschätzt und endet in nervenaufreibenden Rechnungen ohne Ergebnis. Betrachten Sie dazu zum Beispiel e x e x lim x e x + e x Daniel Gerth (JKU) Differentialrechnung 48 / 1
49 Bemerkungen Die Bedeutung der l Hospitalschen Regeln wird vom Anfänger oft überschätzt und endet in nervenaufreibenden Rechnungen ohne Ergebnis. Betrachten Sie dazu zum Beispiel lim x e x e x e x + e x ( 1 e 2x ) = lim x 1 + e 2x = 1. Häufig ist es günstiger, bei der Grenzwertberechnung für unbestimmte Ausdrücke wie 0 0 oder auf Potenzreihen zurückgreifen. Daniel Gerth (JKU) Differentialrechnung 48 / 1
50 Totales Differential und Fehlerfortpflanzung Wir kommen noch einmal auf die Leibniz-Schreibweise y (x 0 ) = dy dx (x 0) zurück und wollen die Ausdrücke dx und dy näher fassen. Definition 7.1 (Totales Differential) Sei f : D R eine in x 0 differenzierbare Funktion. Für eine beliebige Zahl dx = x x 0 heißt dy := f (x 0 )dx = f (x 0 )(x x 0 ) totales Differential von f bei x 0. Daniel Gerth (JKU) Differentialrechnung 49 / 1
51 Geometrische Bedeutung dy ist die Änderung der Funktionswerte der Tangente bei Änderung des Arguments um dx. Idee für Fehlerfortpflanzung Approximiert man f nahe x 0 durch die Tangente, so gilt näherungsweise f(x) f(x 0 ) =: y dy = f (x 0 )dx. Daniel Gerth (JKU) Differentialrechnung 50 / 1
52 Praktische Anwendung In Experimenten ist häufig der Einfluss des Fehlers x einer Messgröße x auf den Fehler y einer berechneten Zielgröße y = f(x) von Interesse. Mit dem totalen Differential und der eben beschriebenen Idee ergibt sich die Näherungsformel y f (x) x. Beispiel aus der Thermodynamik Für ein ideales Gas ist die Entropie S(T, V ) = C V ln(t ) + R ln(v ) + S 0, wobei C V die Molwärme bei konstantem Volumen ist. Dann ist das totale Differential der Entropie ds = S S dt + T V dv = C V T dt + R V dv. Daniel Gerth (JKU) Differentialrechnung 51 / 1
53 Der Satz von Taylor Mir der ersten Ableitung waren wir in der Lage, Funktionen nahe einer Stelle x 0 linear zu approximieren. Statt linearer Funktionen kann man auch Polynome höherer Ordnung verwenden und damit ggf. noch bessere Ergebnisse erreichen. Illustration der Idee Die Funktion f(x) = cos(x) (rot) lässt sich nahe x 0 = 0 durch die Tangente t(x) = 1 approximieren (grün). Besser ist jedoch die Approximation durch T 2 (x) = x2 (blau) oder durch T 4 (x) = x x4 (rot). Daniel Gerth (JKU) Differentialrechnung 52 / 1
54 Satz 8.1 (Satz von Taylor) Sei f : I R eine auf offenen Intervall I (n + 1) mal differenzierbare Funktion; x 0, x I. Dann gibt es eine Zahl ξ zwischen x und x 0, so dass mit dem Taylor-Polynom n ter Ordnung T n (x) = n k=0 f (k) (x 0 ) (x x 0 ) k k! f(x) = T n (x) + R n (x) = f(x 0 ) + f (x 0 )(x x 0 ) + f (x 0 ) 2 und dem Lagrangeschen Restglied R n (x) = f (n+1) (ξ) (n + 1)! (x x 0) n+1. (x x 0 ) f (n) (x 0 ) (x x 0 ) n n! Daniel Gerth (JKU) Differentialrechnung 53 / 1
55 Beispiel Es sei f(x) = sin(x). Wir wollen die Funktion um die Stelle x 0 = 0 approximieren. Die Funktion f ist ersichtlich unendlich oft differenzierbar. Es gilt f (x) = cos(x), f (x) = sin(x), f (x) = cos(x), f (4) (x) = f, f (5) = f,... und somit f(x 0 ) = 0, f (x 0 ) = 1, f (x 0 ) = 0, f (x 0 ) = 1, f (4) (x 0 ) = 0,.... Die ersten 6 Taylor-Polynome lauten also T 1 (x) = 0 + 1(x 0) = x, T 2 (x) = 0 + 1(x 0) (x 0)2 = x, T 3 (x) = 0 + 1(x 0) (x 0)2 1 6 (x 0)3 = x 1 6 x3, T 4 (x) = x 1 6 x3, T 5 (x) = T 6 (x) = x 1 6 x x5. Daniel Gerth (JKU) Differentialrechnung 54 / 1
56 Graphische Darstellung f(x) = sin(x) (blau) mit den Taylorpolynomen T 1 (x) = T 2 (x)(grün), T 3 (x) = T 4 (x) (rot) und T 5 (x) = T 6 (x) (türkis) im Entwicklungspunkt x 0 = 0. Entwickeln Sie die Funktion f(x) = e x um die Stelle x 0 = 0 und berechnen Sie das Taylorpolynom der Ordnung 2. Schätzen Sie den Fehler mit dem Lagrangeschen Restglied ab. Daniel Gerth (JKU) Differentialrechnung 55 / 1
57 Taylor-Reihen Verhält sich das Restglied gutartig, so approximieren die Taylorpolynome T n die Funktion f mit größer werdendem n nahe x 0 immer besser. Im günstigsten Fall lässt sich f in einer Umgebung von x 0 durch eine Taylor-Reihe darstellen: f(x) = n=0 f (n) (x 0 ) (x x 0 ) n für alle x mit x x 0 < ε. n! Daniel Gerth (JKU) Differentialrechnung 56 / 1
58 Wichtige Taylor-Reihen (1 x) 1 x n x < 1 sin(x) n=0 n=0 ( 1) n x 2n+1 (2n+1)! x R e x n=0 x n n! x R cos(x) n=0 ( 1) n x 2n (2n)! x R ln(1 + x) n=1 ( 1) n+1 x n n x ( 1, 1] Daniel Gerth (JKU) Differentialrechnung 57 / 1
59 Warnung Es soll aber vor dem Trugschluss gewarnt werden, der Satz von Taylor garantiere die Entwickelbarkeit jeder unendlich oft differenzierbaren Funktion in eine Taylor-Reihe. Vielmehr gilt: Es gibt Fälle, in denen die Taylor-Reihe für x x 0 überhaupt nicht konvergiert. Es gibt Fälle, in denen die Taylor-Reihe für x x 0 konvergiert, aber mit der eigentlichen Funktion f nichts zu tun hat. Daniel Gerth (JKU) Differentialrechnung 58 / 1
60 Ziele erreicht? Sie sollten nun (bzw. nach Abschluss der Übungen / Tutorien) den Ableitungsbegriff und die Idee der linearen Approximation tiefgreifend verstanden haben, Funktionen sicher auf Differenzierbarkeit untersuchen und deren Ableitung mit Diffenzenquotient oder Ableitungsregeln sicher bestimmen können, alle Punkte einer Kurvendiskussion sicher ausführen können, Taylor-Polynome sicher berechnen können und wissen was man unter einer Taylor-Reihe versteht, über Newton-Verfahren und Fehlerfortpflanzung grob Bescheid wissen. Sie sind sich nicht sicher oder meinen nein? Sie wissen schon... Daniel Gerth (JKU) Differentialrechnung 59 / 1
4 Differentialrechnung in einer Variablen
 4 Differentialrechnung in einer Variablen Die Infinitesimalrechnung ist ein weiteres großes analytisches Konzept, ohne das moderne Naturwissenschaften undenkbar sind. Die Entwicklung erfolgte unabhängig
4 Differentialrechnung in einer Variablen Die Infinitesimalrechnung ist ein weiteres großes analytisches Konzept, ohne das moderne Naturwissenschaften undenkbar sind. Die Entwicklung erfolgte unabhängig
4 Differentialrechnung in einer Variablen
 4 Differentialrechnung in einer Variablen Die Infinitesimalrechnung ist ein weiteres großes analytisches Konzept, ohne das moderne Naturwissenschaften undenkbar sind. Die Entwicklung erfolgte unabhängig
4 Differentialrechnung in einer Variablen Die Infinitesimalrechnung ist ein weiteres großes analytisches Konzept, ohne das moderne Naturwissenschaften undenkbar sind. Die Entwicklung erfolgte unabhängig
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de SS 2017 Vorlesung 7 MINT Mathkurs SS 2017 1 / 25 Vorlesung 7 (Lecture 7) Differentialrechnung differential
Vorlesung Analysis I WS 07/08
 Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Vorlesung Analysis I WS 07/08 Erich Ossa Vorläufige Version 07/12/04 Ausdruck 8. Januar 2008 Inhaltsverzeichnis 1 Grundlagen 1 1.1 Elementare Logik.................................. 1 1.1.A Aussagenlogik................................
Übersicht. 1. Motivation. 2. Grundlagen
 Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Übersicht 1. Motivation 2. Grundlagen 3. Analysis 3.1 Folgen, Reihen, Zinsen 3.2 Funktionen 3.3 Differentialrechnung 3.4 Extremwertbestimmung 3.5 Nichtlineare Gleichungen 3.6 Funktionen mehrerer Variabler
Mathematischer Vorkurs NAT-ING II
 Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Mathematischer Vorkurs NAT-ING II (02.09.2013 20.09.2013) Dr. Jörg Horst WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 252 Kapitel 7 Differenzierbarkeit Mathematischer Vorkurs TU Dortmund Seite
Anwendungen der Differentialrechnung
 KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
KAPITEL 7 Anwendungen der Differentialrechnung 7.1 Maxima und Minima einer Funktion................. 141 7.2 Mittelwertsatz............................ 144 7.3 Kurvendiskussion..........................
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Kapitel 7. Differentialrechnung. Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56
 Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
2015, MNZ. Jürgen Schmidt. Vorkurs. Mathematik. Ableiten. Tag WS 2015/16
 Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
Vorkurs 4. Mathematik Ableiten WS 2015/16 Tag Einführendes Beispiel Vernachlässigen wir den Luftwiderstand, so können wir in hinreichender Näherung für den freien Fall eines Körpers s(t) = 5t 2 als Weg-Zeit-Abhängigkeit
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
Kapitel 5: Differentialrechnung
 Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
Kapitel 5: Differentialrechnung Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz Stefan Ruzika (KO) Kapitel 5: Differentialrechnung 1 / 23 Gliederung 1 Grundbegriffe 2 Abbildungen
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Vorlesung Mathematik für Ingenieure 1 (Wintersemester 2008/09)
 Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
Vorlesung Mathematik für Ingenieure (Wintersemester 2008/09) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 9. November 2008) Die
Mathematik I Herbstsemester 2018 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Mathematik I Herbstsemester 2018 Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 55 4. Anwendungen der Differentialrechnung Monotonie Krümmung Linearisierung einer Funktion Extremwerte
Differentiation und Taylorentwicklung. Thomas Fehm
 Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Differentiation und Taylorentwicklung Thomas Fehm 4. März 2009 1 Differentiation in R 1.1 Grundlagen Definition 1 (Ableitung einer Funktion) Es sei f eine Funktion die auf dem Intervall I R definiert ist.
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 6: Differenzialrechnung einer Veränderlichen Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. Dezember 2011)
Kapitel 16 : Differentialrechnung
 Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
5 Differenzialrechnung für Funktionen einer Variablen
 5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
5 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
x 1 keinen rechtsseitigen Grenzwert x 0+ besitzen. (Analog existiert der linksseitige Grenzwert nicht.)
 Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Differentialrechnung 1 Grenzwerte Gegeben sei ein Intervall I R, a I {, } und f : I\{a} R. Die Funktion f kann sehr wohl auch an der Stelle x = a erklärt sein, wir wollen aber nur wissen wie sich die Funktion
Vorkurs Mathematik-Physik, Teil 2 c 2016 A. Kersch
 Differentialrechnung. Definition Vorkurs Mathematik-Physik, Teil c 06 A. Kersch Geometrische Interpretation Die Ableitung einer Funktion f() an einer Stelle = 0 ist über den Grenzwert des Differenzenquotienten
Differentialrechnung. Definition Vorkurs Mathematik-Physik, Teil c 06 A. Kersch Geometrische Interpretation Die Ableitung einer Funktion f() an einer Stelle = 0 ist über den Grenzwert des Differenzenquotienten
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen
 Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
Kapitel 5. Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen
6 Di erentialrechnung, die Exponentialfunktion
 6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
6 Di erentialrechnung, die Exonentialfunktion 6. Exonentialfunktion Wir führen die Exonentialfunktion ein, die eine stetige Funktion mit folgenden Eigenschaften ist: ex(x + y) =ex(x)ex(y) (8) ex(0) =,
19.2 Mittelwertsatz der Differentialrechnung
 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
19 Mittelwertsätze der Differentialrechnung mit Anwendungen 19.1 Satz von Rolle 19.2 Mittelwertsatz der Differentialrechnung 19.4 Globaler Wachstumssatz 19.6 Verallgemeinerter Mittelwertsatz der Differentialrechnung
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mathematik 1 Bachelorstudiengang Maschinenbau
 Mathematik 1 Bachelorstudiengang Maschinenbau Prof. Dr. Stefan Etschberger Hochschule Augsburg Sommersemester 2012 7. Differentialrechnung einer Veränderlichen 7.2. Differentialquotient und Ableitung
Mathematik 1 Bachelorstudiengang Maschinenbau Prof. Dr. Stefan Etschberger Hochschule Augsburg Sommersemester 2012 7. Differentialrechnung einer Veränderlichen 7.2. Differentialquotient und Ableitung
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 6. (n+1)!. Daraus folgt, dass e 1/x < (n+
 D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
Analysis I. Guofang Wang , Universität Freiburg
 Universität Freiburg 10.1.2017, 11.1.2017 Definition 1.1 (Ableitung) Die Funktion f : I R n hat in x 0 I die Ableitung a R n (Notation: f (x 0 ) = a), falls gilt: f(x) f(x 0 ) lim = a. (1.1) x x 0 x x
Universität Freiburg 10.1.2017, 11.1.2017 Definition 1.1 (Ableitung) Die Funktion f : I R n hat in x 0 I die Ableitung a R n (Notation: f (x 0 ) = a), falls gilt: f(x) f(x 0 ) lim = a. (1.1) x x 0 x x
Mathematik zum Mitnehmen
 Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Mathematik zum Mitnehmen Zusammenfassungen und Übersichten aus Arens et al., Mathematik Bearbeitet von Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth
Thema 5 Differentiation
 Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
Thema 5 Differentiation Definition 1 Sei f : D R. Dann ist f im Punkt x 0 differenzierbar, falls f(x) f(x 0 ) x x 0 x x 0 auf der Menge D \ {x 0 } existiert. Der Limes ist dann die Ableitung von f im Punkt
2 Differenzialrechnung für Funktionen einer Variablen
 2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
2 Differenzialrechnung für Funktionen einer Variablen Ist f eine ökonomische Funktion, so ist oft wichtig zu wissen, wie sich die Funktion bei kleinen Änderungen verhält. Beschreibt etwa f einen Wachstumsprozess,
Kapitel 5 Differential- und Integralrechnung in einer Variablen
 Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
Mathematischer Vorbereitungskurs für das MINT-Studium
 Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de WS 2016/2017 Vorlesung 7 MINT Mathkurs WS 2016/2017 1 / 20 Stetigkeit einer Funktion (continuity of a
Mathematischer Vorbereitungskurs für das MINT-Studium Dr. B. Hallouet b.hallouet@mx.uni-saarland.de WS 2016/2017 Vorlesung 7 MINT Mathkurs WS 2016/2017 1 / 20 Stetigkeit einer Funktion (continuity of a
1 Höhere Ableitungen 2. 2 Mittelwertsatz und Monotonie 3. 3 Konvexe und konkave Funktionen 5. 4 Lokale und globale Extremalstellen 7
 Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Analysis I. 8. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 8. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 9, 207 Grenzwerte Korollar 5.2.2 (Bernoulli-de l Hôpital) Seien f, g : [a, b] R stetig und differenzierbar
Analysis I 8. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching April 9, 207 Grenzwerte Korollar 5.2.2 (Bernoulli-de l Hôpital) Seien f, g : [a, b] R stetig und differenzierbar
(1 + z 2j ) = 1 z2n+2. 1 z. (1 + z)(1 z) 1 z. 1 z. (1 + z 2j ) = 1 z. 1 z 1 z
 Aufgabe Zeigen Sie mit vollständiger Induktion: Für alle n N gilt (8 Punkte) n ( + z 2j ) = 2n+, wobei z C, z, eine komplexe Zahl ist Lösung [8 Punkte] Induktionsanfang: n = : ( + z 2j ) = ( + z 2 ) =
Aufgabe Zeigen Sie mit vollständiger Induktion: Für alle n N gilt (8 Punkte) n ( + z 2j ) = 2n+, wobei z C, z, eine komplexe Zahl ist Lösung [8 Punkte] Induktionsanfang: n = : ( + z 2j ) = ( + z 2 ) =
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Aufgabe 98 12.12.2012 Untersuchen Sie die Funktion f W R! R mit f.x/
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Aufgabe 98 12.12.2012 Untersuchen Sie die Funktion f W R! R mit f.x/
9. Übungsblatt zur Vorlesung Mathematik I für Informatik
 Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Fachbereich Mathematik Prof. Dr. Thomas Streicher Dr. Sven Herrmann Dipl.-Math. Susanne Pape 9. Übungsblatt zur Vorlesung Mathematik I für Informatik Wintersemester 2009/2010 8./9. Dezember 2009 Gruppenübung
Analysis 1 für Informatiker (An1I)
 Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
dx nf(x 0). dx f(n 1) (x 0 ) = dn
 4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
3.2 Funktionsuntersuchungen mittels Differentialrechnung
 3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
3. Funktionsuntersuchungen mittels Differentialrechnung 46 3. Funktionsuntersuchungen mittels Differentialrechnung In diesem Abschnitt betrachten wir Funktionen f: D, welche je nach Bedarf zumindest ein-
16. Differentialquotient, Mittelwertsatz
 16. Differentialquotient, Mittelwertsatz Gegeben sei eine stetige Funktion f : R R. Wir suchen die Gleichung der Tangente t an die Kurve y = f(x) im Punkt (x, f(x ), x R. Das Problem dabei ist, dass vorderhand
16. Differentialquotient, Mittelwertsatz Gegeben sei eine stetige Funktion f : R R. Wir suchen die Gleichung der Tangente t an die Kurve y = f(x) im Punkt (x, f(x ), x R. Das Problem dabei ist, dass vorderhand
Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften:
 1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
Kompetenz: Verinnerlichung des Mittelwertsatzes Daraus ergibt sich leicht der wichtige Mittelwertsatz der Differentialrechnung:
 16 Mittelwertsätze und Anwendungen 71 16 Mittelwertsätze und Anwendungen Lernziele: Konzepte: Konvexität und Konkavität Resultate: Mittelwertsätze der Differentialrechnung Methoden: Regeln von de l Hospital
16 Mittelwertsätze und Anwendungen 71 16 Mittelwertsätze und Anwendungen Lernziele: Konzepte: Konvexität und Konkavität Resultate: Mittelwertsätze der Differentialrechnung Methoden: Regeln von de l Hospital
HM I Tutorium 9. Lucas Kunz. 19. Dezember 2018
 HM I Tutorium 9 Lucas Kunz 19. Dezember 2018 Inhaltsverzeichnis 1 Theorie 2 1.1 Definition der Ableitung............................ 2 1.2 Ableitungsregeln................................ 2 1.2.1 Linearität................................
HM I Tutorium 9 Lucas Kunz 19. Dezember 2018 Inhaltsverzeichnis 1 Theorie 2 1.1 Definition der Ableitung............................ 2 1.2 Ableitungsregeln................................ 2 1.2.1 Linearität................................
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung
 Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik I Herbstsemester 2014 Kapitel 4: Anwendungen der Differentialrechnung www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Klausurenkurs zum Staatsexamen (WS 2016/17): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 206/7): Differential und Integralrechnung 3 3. (Herbst 20, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende
Differentialrechnung
 Differentialrechnung Um Funktionen genauer zu untersuchen bzw. sie zu analysieren, ist es notwenig, etwas über ihren Verlauf, as qualitative Verhalten er Funktion, sagen zu können. Das heisst, wir suchen
Differentialrechnung Um Funktionen genauer zu untersuchen bzw. sie zu analysieren, ist es notwenig, etwas über ihren Verlauf, as qualitative Verhalten er Funktion, sagen zu können. Das heisst, wir suchen
Differentialrechnung
 Kapitel 7 Differentialrechnung Josef Leydold Auffrischungskurs Mathematik WS 2017/18 7 Differentialrechnung 1 / 75 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f
Kapitel 7 Differentialrechnung Josef Leydold Auffrischungskurs Mathematik WS 2017/18 7 Differentialrechnung 1 / 75 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f = f ( 0 + ) f ( 0 ) = f
Differentialrechnung. Kapitel 7. Differenzenquotient. Graphische Interpretation des Differentialquotienten. Differentialquotient
 Differenzenquotient Sei f : R R eine Funktion. Der Quotient Kapitel 7 Differentialrechnung f = f 0 + f 0 = f 0 0 heißt Differenzenquotient an der Stelle 0., Sekante 0, f 0 f 0 Josef Leydold Auffrischungskurs
Differenzenquotient Sei f : R R eine Funktion. Der Quotient Kapitel 7 Differentialrechnung f = f 0 + f 0 = f 0 0 heißt Differenzenquotient an der Stelle 0., Sekante 0, f 0 f 0 Josef Leydold Auffrischungskurs
differenzierbare Funktionen
 Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Der Differenzenquotient
 Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Der Differenzenquotient Von den linearen Funktionen kennen wir den Begriff des Differenzenquotienten k = y 2 y 1 x 2 x 1 mit dem die Steigung einer Geraden festgelegt wird. Der Begriff des Differentialkoeffizienten
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 5. x 1 2x 3 = lim 6x
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 5. MC-Aufgaben Online-Abgabe. Durch zweifache Anwendung der Regel von Bernoulli-de l Hôpital folgt Stimmt diese Überlegung? lim x x 3 +
Die elementaren Funktionen (Überblick)
 Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
Die elementaren Funktionen (Überblick) Zu den elementaren Funktionen zählen wir die Potenz- und die Exponentialfunktion, den Logarithmus, sowie die hyperbolischen und die trigonometrischen Funktionen und
5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 115
 5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 5 Satz 5.5.2 (Ableitung der Umkehrfunktion einer Winkelfunktionen) Die Umkehrfunktionen der trigonometrischen Funktionen sind nach Satz 5.2.3 auf den
5.5. UMKEHRFUNKTIONEN TRIGONOMETRISCHER FUNKTIONEN 5 Satz 5.5.2 (Ableitung der Umkehrfunktion einer Winkelfunktionen) Die Umkehrfunktionen der trigonometrischen Funktionen sind nach Satz 5.2.3 auf den
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
Tutorium: Analysis und lineare Algebra. Differentialrechnung. Steven Köhler. mathe.stevenkoehler.de Steven Köhler
 Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
Tutorium: Analysis und lineare Algebra Differentialrechnung Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Differenzenquotient Der Di erenzenquotient ist de niert als f(x) x f(x) f(x 0)
V.1 Konvergenz, Grenzwert und Häufungspunkte
 V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
Modul Grundbildung Analysis WiSe 10/11. A.: Wurde in diesem Kapitel behandelt. C.: Weitere Fragen (Nicht nur für die Klausur interessant)
 Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
23 Konvexe Funktionen und Ungleichungen
 23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
23 Konvexe Funktionen und Ungleichungen 231 Konvexe Funktionen 232 Kriterien für Konvexität 233 Streng konvexe Funktionen 235 Wendepunkte 237 Ungleichung von Jensen 2310 Höldersche Ungleichung 2311 Minkowskische
GRUNDLAGEN MATHEMATIK
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 4. Differentialrechnung Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 4. Differentialrechnung Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies
Klausurenkurs zum Staatsexamen (WS 2015/16): Differential und Integralrechnung 3
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 25/6): Differential und Integralrechnung 3 3. (Herbst 2, Thema 3, Aufgabe 2) Gegeben ist für m R die Funktion f m : ], 2π[ R; f m (x) = Folgende Tatsachen
f(f 1 (w)) = w f 1 (f(z)) = z Abbildung 21: Eine Funktion und ihre Umkehrfunktion
 Mathematik für Naturwissenschaftler I 2.8 2.8 Umkehrfunktionen 2.8. Definition Sei f eine Funktion. Eine Funktion f heißt Umkehrfunktion, wenn f (w) = z für w = f(z). f darf nicht mit f(z) = (f(z)) verwechselt
Mathematik für Naturwissenschaftler I 2.8 2.8 Umkehrfunktionen 2.8. Definition Sei f eine Funktion. Eine Funktion f heißt Umkehrfunktion, wenn f (w) = z für w = f(z). f darf nicht mit f(z) = (f(z)) verwechselt
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 6. Übung: Woche vom bis
 Übungsaufgaben 6. Übung: Woche vom 17. 11. bis 21. 11. 2014 Heft Ü1: 9.1 (d,n,t); 9.2 (b,h,i); 9.3 (b,e); 9.4 (b,e,f) Übungsverlegung (einmalig!): Gruppe VIW 02 nach Mo., 5. DS; WIL C 204 (für Mittwoch,
Übungsaufgaben 6. Übung: Woche vom 17. 11. bis 21. 11. 2014 Heft Ü1: 9.1 (d,n,t); 9.2 (b,h,i); 9.3 (b,e); 9.4 (b,e,f) Übungsverlegung (einmalig!): Gruppe VIW 02 nach Mo., 5. DS; WIL C 204 (für Mittwoch,
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
MIA Analysis einer reellen Veränderlichen WS 06/07. Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen
 Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Version 01.02. Januar 2007 MIA Analysis einer reellen Veränderlichen WS 06/07 Kurzfassung Martin Schottenloher Kapitel VI. Differenzierbare Funktionen in einer Veränderlichen In diesem Kapitel werden differenzierbare
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann
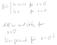 Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Ableitungen höherer Ordnung: Sei f : D R eine differenzierbare Funktion. Ist die Ableitung f : D R ihrerseits in jedem Punkt x D differenzierbar, dann heißt f (x) = (f ) (x) die zweite Ableitung von f
Mathematischer Vorkurs
 Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite / 50 Kapitel 5 Mathematischer Vorkurs TU Dortmund Seite 54 / 50 Scheitel S Schenkel α Winkelbereich Winkel werden in Grad
Mathematischer Vorkurs Dr. Agnes Lamacz Mathematischer Vorkurs TU Dortmund Seite / 50 Kapitel 5 Mathematischer Vorkurs TU Dortmund Seite 54 / 50 Scheitel S Schenkel α Winkelbereich Winkel werden in Grad
Kapitel 6 Folgen und Stetigkeit
 Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
x e x sin(x) lim oder lim bestimmen lassen.
 Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Es folgt nun noch ein Nachtrag zum Thema Grenzwerte von Funktionen. Wir hatten in Abschnitt 2.6 Beispiele von Funktionen gesehen, bei denen die üblichen Grenzwertregeln nicht weiterhelfen, etwa bei Quotienten
Kapitel 7 Differentialrechnung
 Kapitel 7 Differentialrechnung 245 Kapitel 7.1 Grundbegriffe 246 Der Differentialquotient und das Integral sind die Kernbegriffe der Analysis. Ableitung und Integralbegriff werden durch gewisse Grenzwerte
Kapitel 7 Differentialrechnung 245 Kapitel 7.1 Grundbegriffe 246 Der Differentialquotient und das Integral sind die Kernbegriffe der Analysis. Ableitung und Integralbegriff werden durch gewisse Grenzwerte
1 Höhere Ableitungen 2. 2 Mittelwertsatz und Monotonie 3. 3 Konvexe und konkave Funktionen 5. 4 Lokale und globale Extremalstellen 7
 Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Universität Basel 4 Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematik 1 Dr. Thomas Zehrt Kurvendiskussionen Inhaltsverzeichnis 1 Höhere Ableitungen 2 2 Mittelwertsatz und
Serie 13: Online Test
 D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
D-ERDW, D-HEST, D-USYS Mathematik I HS 13 Dr. Ana Cannas Serie 13: Online Test Einsendeschluss: 31. Januar 214 Bei allen Aufgaben ist genau eine Antwort richtig. Lösens des Tests eine Formelsammlung verwenden.
Übungen zu Einführung in die Analysis
 Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
Übungen zu Einführung in die Analysis (Nach einer Zusammengestellung von Günther Hörmann) Sommersemester 2011 Vor den folgenden Aufgaben werden in den ersten Wochen der Übungen noch jene zur Einführung
2 Stetigkeit und Differenzierbarkeit
 2.1) Sei D R. a) x 0 R heißt Häufungspunkt von D, wenn eine Folge x n ) n N existiert mit x n D,x n x 0 und lim n x n = x 0. D sei die Menge der Häufungspunkte von D. b) x 0 D heißt innerer Punkt von D,
2.1) Sei D R. a) x 0 R heißt Häufungspunkt von D, wenn eine Folge x n ) n N existiert mit x n D,x n x 0 und lim n x n = x 0. D sei die Menge der Häufungspunkte von D. b) x 0 D heißt innerer Punkt von D,
7 Integralrechnung für Funktionen einer Variablen
 7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
7 Integralrechnung für Funktionen einer Variablen In diesem Kapitel sei stets D R, und I R ein Intervall. 7. Das unbestimmte Integral (Stammfunktion) Es sei f : I R eine Funktion. Eine differenzierbare
Wirtschafts- und Finanzmathematik
 Wirtschafts- und Finanzmathematik für Betriebswirtschaft und International Management Wintersemester 2017/18 04.10.2017 Einführung, R, Grundlagen 1 11.10.2017 Grundlagen, Aussagen 2 18.10.2017 Aussagen
Wirtschafts- und Finanzmathematik für Betriebswirtschaft und International Management Wintersemester 2017/18 04.10.2017 Einführung, R, Grundlagen 1 11.10.2017 Grundlagen, Aussagen 2 18.10.2017 Aussagen
Lösungen zu Aufgabenblatt 10P
 Analysis Prof. Dr. Peter Becker Fachbereich Informatik Sommersemester 05 9. Juni 05 Lösungen zu Aufgabenblatt 0P Aufgabe (Funktionsgrenzwerte) Berechnen Sie die folgenden Grenzwerte: cos(x) x cos( x )
Analysis Prof. Dr. Peter Becker Fachbereich Informatik Sommersemester 05 9. Juni 05 Lösungen zu Aufgabenblatt 0P Aufgabe (Funktionsgrenzwerte) Berechnen Sie die folgenden Grenzwerte: cos(x) x cos( x )
Eigenschaften stetiger Funktionen Buch Kap. 2.5
 Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
Eigenschaften stetiger Funktionen Buch Kap. 2.5 Satz 2.6: (Nullstellensatz) Ist f : [a, b] R stetig und haben f (a) und f (b) unterschiedliche Vorzeichen, so besitzt f in (a, b) mindestens eine Nullstelle.
2.6 Lokale Extrema und Mittelwertsatz
 2.6. Lokale Etrema und Mittelwertsatz 49 2.6 Lokale Etrema und Mittelwertsatz In diesem Kapitel bezeichne f stets eine reellwertige Funktion, definiert auf einem abgeschlossenen Intervall [a, b]. Unter
2.6. Lokale Etrema und Mittelwertsatz 49 2.6 Lokale Etrema und Mittelwertsatz In diesem Kapitel bezeichne f stets eine reellwertige Funktion, definiert auf einem abgeschlossenen Intervall [a, b]. Unter
f(x 0 ) = lim f(b k ) 0 0 ) = 0
 5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
Höhere Mathematik 1 Übung 9
 Aufgaben, die in der Präsenzübung nicht besprochen wurden, können in der darauf folgenden übung beim jeweiligen übungsleiter bzw. bei der jeweiligen übungsleiterin abgegeben werden. Diese Abgabe ist freiwillig
Aufgaben, die in der Präsenzübung nicht besprochen wurden, können in der darauf folgenden übung beim jeweiligen übungsleiter bzw. bei der jeweiligen übungsleiterin abgegeben werden. Diese Abgabe ist freiwillig
3 Folgen, Reihen und stetige Funktionen
 Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Definition: Differenzierbare Funktionen
 Definition: Differenzierbare Funktionen 1/12 Definition. Sei f :]a, b[ R eine Funktion. Sie heißt an der Stelle ξ ]a, b[ differenzierbar, wenn der Grenzwert existiert. f(ξ + h) f(ξ) lim h 0 h = lim x ξ
Definition: Differenzierbare Funktionen 1/12 Definition. Sei f :]a, b[ R eine Funktion. Sie heißt an der Stelle ξ ]a, b[ differenzierbar, wenn der Grenzwert existiert. f(ξ + h) f(ξ) lim h 0 h = lim x ξ
bestimmt werden. Allein die Regel (5.4) würde wegen g(x) = 2, folglich erhalten wir den korrekten lim
 bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
bestimmt werden. Allein die Regel (5.4) würde wegen f (x) lim x g (x) = lim 2e 2x = lim x e x x 2ex = 0 dengrenzwert0für(5.5)liefern.dasistaberfalsch,dennwegen lim 0 ist lim x g(x) = 2, folglich erhalten
4 Differenzierbarkeit
 7 4 DIFFERENZIERBARKEIT Sei dazu 0 < ρ < s < r. Dann gilt lim sup k k a k
7 4 DIFFERENZIERBARKEIT Sei dazu 0 < ρ < s < r. Dann gilt lim sup k k a k
Differenzialrechnung. Mathematik-Repetitorium
 Differenzialrechnung 5.1 Die Ableitung 5.2 Differentiation elementarer Funktionen 5.3 Differentiationsregeln 5.4 Höhere Ableitungen 5.5 Partielle Differentiation 5.6 Anwendungen Differenzialrechnung 1
Differenzialrechnung 5.1 Die Ableitung 5.2 Differentiation elementarer Funktionen 5.3 Differentiationsregeln 5.4 Höhere Ableitungen 5.5 Partielle Differentiation 5.6 Anwendungen Differenzialrechnung 1
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Staatsexamen Herbst 2017 Differential- und Integralrechnung, Thema I
 Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Staatsexamen Herbst 17 Differential- und Integralrechnung, Thema I 1. a) Die Aussage ist wahr! Sei s R der Reihenwert der Reihe k=1 Da a n = s n s n 1 für n, ist also b) Die Aussage ist falsch! a k, also
Tutorium: Analysis und Lineare Algebra
 Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
Tutorium: Analysis und Lineare Algebra Vorbereitung der Bonusklausur am 25.06.2018 20. Juni 2018 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2018 Steven Köhler 20. Juni 2018 Konvergenz
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf. SBP Mathe Grundkurs 2
 SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
SBP Mathe Grundkurs 2 # 0 by Clifford Wolf SBP Mathe Grundkurs 2 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
