W 1 Deterministisches Chaos
|
|
|
- Brit Fürst
- vor 7 Jahren
- Abrufe
Transkript
1 niversität Potsdam nstitut für Physik und Astronomie Physikalisches Praktikum für Fortgeschrittene 011 W 1 Deterministisches Chaos Die Gesetze der klassischen Physik sind deterministisch, d.h. dynamische Systeme werden durch Bewegungsdifferenzialgleichungen modelliert, die eine eindeutige Vorschrift zur Berechnung der zeitlichen Systementwicklung aus einem Anfangszustand darstellen. Trotz dieser Determiniertheit zeigt die numerische Berechnung der Bahnkurve oder die Beobachtung z.b. eines gekickten Rotationspendels, dass insbesondere bei größeren Schwingungsamplituden die Pendelbewegung außerordentlich komplex und unregelmäßig verläuft [7]. Obwohl durch die deterministische Dynamik eindeutig vorherbestimmt, ist es praktisch nicht mehr möglich, das Verhalten des Systems mittelfristig vorauszusagen, denn schon kleinste Veränderungen der Anfangsbedingungen (infinitesimale Störungen) führen schnell zu völlig verschiedenen Trajektorien. Die Dynamik solcher Systeme erscheint ungeordnet, chaotisch. Das starke Kausalitätsprinzip, wonach ähnliche rsachen auch ähnliche Wirkungen haben, wird offensichtlich verletzt. Dies eröffnet eine völlig neue Sichtweise zur Beurteilung dynamischer Prozesse. Als populäre Metapher für die extrem sensitive Abhängigkeit der chaotischen Dynamik von deren Anfangsbedingungen hat der Meteorologe E.N. Lorenz ( ) als einen denkbaren Vorgang den Schmetterlingseffekt genannt, wonach schon der Flügelschlag eines Schmetterlings an einem Ort u.. einen Tornado an einem anderen Ort auslösen kann. Chaotisches Verhalten wird durch die Nichtlinearität der Bewegungsgleichungen verursacht. Chaos ist mithin untrennbar mit Nichtlinearität verbunden und Nichtlinearität ist fundamental für das gesamte Naturgeschehen. Doch weil im allgemeinen die analytische ntegration eines nichtlinearen Differenzialgleichungssystems mit enormen mathematischen Problemen verbunden ist, wurde Nichtlinearität lange Zeit wie ein Ärgernis verdrängt oder als Ausnahme empfunden. Man beschränkte sich auf die ntersuchung der wenigen nichtlinearen Bewegungsprobleme, die sich in hinreichender Näherung durch eine lineare Differenzialgleichung beschreiben lassen. Korrekturtipps und Verbesserungsvorschläge werden dankbar entgegengenommen. Bitte an udo.schwarz@uni-potsdam.de senden. Zur Vertiefung des Themas besuchen Sie bitte das Wahlpflichtmodul Nichtlineare Dynamik im 5. und 6. Semester der Bachelor-Ausbildung und im 1. und. Semester der Master-Ausbildung. 1
2 Erst als durch die rasante Entwicklung der Computer auch eine leistungsstarke Rechentechnik zur Verfügung stand, konnte auch die Dynamik nichtlinearer Systeme genauer analysiert werden. Dabei wurde schnell klar, dass Nichtlinearität statt einer Ausnahme der eigentlich viel interessantere und bedeutungsvollere Normalfall ist. Auch ist Chaos nicht einfach mit nordnung oder Regellosigkeit gleichzusetzen. An die Stelle von Gleichförmigkeit oder Periodizität treten andere Ordnungsbegriffe, die eng mit Selbstähnlichkeit, Skaleninvarianz und niversalität verbunden sind. m vorliegenden Experiment ist ein spezieller elektrischer Schwingkreis (Chua-System) mit veränderlicher Steuerspannung C (Kontrollparameter des Systems) zu untersuchen. Dabei kann der zeitliche Verlauf der Spannung im Schwingkreis als Funktion der Steuerspannung C und insbesondere deren Entwicklung über das typische Bifurkationsszenario ins Chaos verfolgt werden. Für jeden Schwingungszustand lassen sich die Zeitverläufe der Spannungen digital registrieren und damit das Frequenzspektrum und der Phasenraum darstellen. 1 Aufgabenstellung 1. nter LabVEW ist auf der Basis vorhandener Bausteine (V = Virtuelle nstrumente) im Zusammenhang mit einer Multifunktionskarte ein Programm zur Steuerung, Messwerterfassung, -darstellung und Datenspeicherung zu erstellen.. Die nichtlineare Strom-Spannungs-Kennlinie der Chua-Diode ist aufzunehmen. 3. Das Zeitverhalten der Schwingschaltung ist als Funktion des Steuerparameters (Steuerspannung an den Kapazitätsdioden) zu registrieren. Dabei ist die Schwingung über mehrere typische Entwicklungsstadien in den chaotischen Bereich zu steuern. 4. Aus den Messkurven der Aufgabe 3 sind a) das Feigenbaum-Diagramm zu konstruieren, b) die Feigenbaum-Konstante abzuschätzen und c) für jede charakteristische Entwicklungsstufe das Zeitverhalten, die Bahnprojektion der Schwingung auf die zweidimensionale - Ebene des Phasenraums sowie das Frequenzspektrum darzustellen und d) die Abhängigkeit der Grundfrequenz vom Steuerparameter zu veranschaulichen. 5. Für das Standard-Beispiel unimodaler iterierter Abbildungen [, 4, 6, 7, 8], für die logistische Abbildung, siehe map, x n+1 = ax n (1 x n ) mit a (0, 4], x [0, 1], (1) sind das Bifurkationsdiagramm x (a), wobei x Punkte des Attraktors sind, und die Ljapunov-Exponenten λ(a) zu berechnen und zu diskutieren.
3 Physikalische Grundlagen.1 Der Chua-Schwingkreis Der Chua-Oszillator (Abb. 1) ist ein einfaches elektronisches System, das die Hauptphänomene der Chaos-Theorie experimentell zugänglich macht. Das System besteht aus fünf linearen Elementen und einem nichtlinearen Element, der sog. Chua-Diode. R 1 1 L R C C 1 Chua-Diode Abbildung 1: Chua Oszillator Der Chua-Oszillator lässt sich durch ein nichtlineares Differenzialgleichungssystem d 1 dt d dt d dt = 1 [ ] 1 f( 1 ), C 1 R 1 = 1 ( ) 1 +, C R 1 = 1 L ( + R ) beschreiben. Die Funktion f() charakterisiert die nichtlineare Strom-Spannungs-Kennlinie der Chua-Diode. n dimensionsfreier Form lauten die Gleichungen ẋ = α(y h(x)), ẏ = x y + z, ż = βy γz, wobei h(x) eine nichtlineare Funktion ist. α, β, und γ sind Konstanten. Der im Versuch untersuchte Schwingkreis wird in Abb. gezeigt. Der Schwingkreis unterscheidet sich vom Standard-Chua-System durch den zusätzlichen Widerstand R 3 und die 3
4 Kapazitätsdiode C D. Der aus einer Spule mit der nduktivität L und einem Kondensator mit der Kapazität C bestehende Schwingkreis wird durch den eingerahmten aktiven Schaltungsteil, die Chua-Diode, angeregt. An die Chua-Diode wird die Arbeitsspannung A angelegt. nfolge der nichtlinearen Kennlinie der Chua-Diode verläuft die Schwingung in einem Doppel-Mulden-Potenzial, das bei kleinen Schwingungsamplituden (starke Dämpfung) durch das parabelförmige Potenzial des harmonischen (d.h. linearen) Oszillators angenähert werden kann. Mittels der Kapazität C 1 lässt sich die Schwingungsdämpfung beeinflussen. Hierzu liegt in Reihe zu C 1 eine Kapazitätsdiode, deren Kapazität durch die äußere Spannung C variierbar ist. Mit wachsender Kapazität C 1 wirkt diese zunehmend als Kurzschlussbrücke, wodurch die Schwingung zunehmend gedämpft wird. Der Dämpfungswiderstand R 1 entkoppelt C von C 1 und ließe sich ebenfalls zur Schwingungsdämpfung nutzen. n Abhängigkeit von der Steuerspannung (d. h. von C D ) beobachtet man vier unterschiedliche Zustände: Keine Schwingungen (Ruhezustand, der wie auch alle anderen Regimes des Chua-Oszillators, von elektronischem Rauschen überlagert ist), periodische Schwingungen und chaotische Schwingungen ( Typen). Das entspricht der Existenz eines Fixpunktes, von Grenzzyklen bzw. chaotischen One-Scroll- und Double-Scroll-Attraktoren im Phasenraum des Systems. PC 1 Multi O R 1 L R C C 1 C D ( C ) C Chua-Diode A R 3 Abbildung : Schema des Versuches. Der Chua-Oszillator wird durch den Computer gesteuert und die Spannungen 1 und werden gemessen und in digitaler Form im Computer gespeichert. 4
5 . Darstellung der chaotischen Bewegung..1 Darstellung im Feigenbaum-Diagramm Der Weg ins Chaos über eine Bifurkationskaskade wird als Bifurkationsszenario bezeichnet. Dabei wird ein Kontrollparameter oder Steuerparameter (bei der Chua-Schwingschaltung C ) kontinuierlich erhöht. Bei C = C1 wird der Übergang vom Fixpunkt zum Grenzzyklus beobachtet. Bei C = C findet die erste Periodenverdopplung statt. Mit wachsendem C werden in zunehmend kürzeren Abständen immer mehr Bifurkationen beobachtet, bis die Schwingung schließlich bei C = C in eine chaotische Bewegung übergeht. Die Verzweigungspunkte ( C, C4...) lassen sich bequem aus dem Feigenbaum - Diagramm dieser Entwicklung ablesen. Dazu werden die beobachteten Schwingungsamplituden der Grenzzyklen über dem Steuerparameter C aufgetragen... Darstellung im Phasenraum Nach dem Einschwingen ergibt sich für die Grundschwingung als Attraktor ein stabiler Grenzzyklus, der sich im Phasenraum dieses Bewegungsvorganges und in der Projektion auf die 1 - -Ebene als eine in sich geschlossene Kurve zeigt. Die Abweichung von der Ellipsen-Form zeigt, dass keine harmonische Schwingung vorliegt. Die Bifurkationen offenbaren sich recht eindrucksvoll in einer mit C zunehmenden Aufspaltung der Phasenkurve zu einer zweifachen, vierfachen bzw. achtfachen Schleifenbahn usw., bis bei genügend hohem C das Überschwingen in die zweite Potenzial-Mulde und schließlich chaotisches Verhalten zu beobachten ist. Die nun nicht mehr in sich geschlossenen Bahnkurven zeigen dennoch interessante Muster, die darauf hindeuten, dass auch das Chaos von bestimmten Ordnungsprinzipien beherrscht wird. Dass die Bahn sich mehrfach schneidet bedeutet keinen Widerspruch zur Determiniertheit der Bewegung, denn die dreidimensionale Trajektorie wird auf eine Ebene projiziert. Bei kontinuierlichen Systemen sind mindestens drei effektive Freiheitsgrade für deterministisch-chaotisches Verhalten erforderlich...3 Darstellung im Frequenzspektrum (Spektrale Leistungsdichte) Die mit jeder Bifurkation einhergehende Periodenverdopplung lässt sich auch eindrucksvoll durch das Fourier-Spektrum der Schwingung nachweisen: Nach jeder Bifurkation taucht ein neuer Peak bei der halben Vorgängerfrequenz auf. nformieren Sie sich bei Wikipedia zu folgenden Begriffen: spektrale Leistungsdichte, Periodogramm, Leistungs-Spektrum, Power-Spektrum...4 Die Dynamik der logistischen Abbildung Überraschenderweise zeigen einige diskrete Abbildungen ein ganz ähnliches Bifurkationsszenario wie physikalische Systeme. Deshalb wurde das Studium des Feigenbaum- Diagramms der wohl bekanntesten diskreten Abbildung, der logistischen Abbildung (eingeführt in 1845 bei Verhulst für die Beschreibung der Populationsdynamik. Siehe: en.wikipedia.org/wiki/logistic map), in das vorstehende Experiment mit einbezogen. Die Ähnlichkeit des Verhaltens von kontinuierlichen Systemen und iterierten Abbildungen ist 5
6 nicht zufällig: Man kann beweisen, dass die Dynamik der Signalamplituden (maximalen Werten) des Chua-Systems annähernd durch eine eindimensionale Abbildung beschrieben wird. 3 Messverfahren Die Experimentsteuerung und Datenerfassung erfolgt über eine Multifunktionskarte 604 der Firma National nstruments. Diese Karte verfügt über analoge und digitale Ein- und Ausgänge sowie Zähl-Kanäle. Für die Kommunikation mit der Karte wird das Softwarepaket LabVEW (N) verwendet, nachdem die Kanäle der Karte softwaremäßig konfiguriert worden sind. Die Programmierung in LabVEW bedient sich grafischer Symbole. Damit ist es möglich, ohne spezielle Programmiererfahrung nach kurzer Einarbeitung erste Prozessabläufe zu programmieren. LabVEW verwendet das vertraute Modell der grafischen Blockschaltbilder. Ein Programm-Modul wird als virtuelles nstrument (V) bezeichnet, dessen Aussehen und Funktionalität sich an einem realen nstrument orientiert. Mit Lab- VEW kann man wissenschaftliche Applikationen lösen, ohne sich dabei mit Syntax und Semantik einer Text orientierten Programmiersprache auseinandersetzen zu müssen. Die Möglichkeit, Prozesse und Algorithmen durch Diagramme darzustellen, erlaubt dem Anwender, seine deen und Aufgaben in einer sehr natürlichen und intuitiven Art zu veranschaulichen. Dem Einsteiger wird für den Versuch eine Bibliothek von Vs, mit denen eine Programmierung in einer Ebene möglich ist, bereitgestellt. 4 Tipps zur Versuchsdurchführung und -auswertung Zur Erinnerung für die LabVEW-Handhabung wird das Online-Tutorial [5] empfohlen. Als weiterführende Literatur stehen die Quellen [1,] in der Handbibliothek zur Verfügung. Verwenden Sie das virtuelle nstrument (V) Kennlinie, um die --Kennlinie aufzunehmen. Dazu müssen Sie die Schaltung umbauen (s. Abb. ), d.h., die Steuerspannung C auf die Chua-Diode legen und die Spannung 3 = R 3 messen. Überlegen Sie, wie man an der aufgebauten Schaltung die --Kennlinie der Diode aufnehmen kann. Die Kennlinie ist abzuspeichern. Die Bereiche der Kennlinie sind quantitativ auszuwerten. nter Verwendung der im Palettensatz Chaos bereitgestellten virtuellen nstrumente finden Sie ein Steuer- und Mess-Programm, das folgende Aufgaben erfüllt: kontinuierliche Wiederholung der Messung bis zum manuellen Abbruch nitialisierung der Analog-nput-Funktion (A-Funktion) mit Eingabe der Gerätenummer 1, der Namen der Messkanäle, Bereitstellung einer maximalen Speichertiefe von Punkten, Start der A-Messung für eine einzugebende aktuelle Speichertiefe mit einer während der Abarbeitung der Routine veränderbaren Abtastrate Wiederholte Auslesung des Messwert-Speichers und nachfolgende Verarbeitung der Werte 6
7 PC Multi O C Chua-Diode 3 R 3 Abbildung 3: Schaltung zur Messung der --Kennlinie der Chua-Diode Grafische Darstellung der zeitlichen Spannungsverläufe Aufarbeitung des Daten-Arrays in a) zwei eindimensionale Arrays zur Verarbeitung durch diskrete Fourier-Transformation und Anzeige des Frequenzspektrums und b) in ein Cluster zur Phasenraum-Darstellung gleichzeitig während der Routine variable manuelle Eingabe des Wertes für die Analog-Output-Funktion Speicherung der aktuellen Messdaten als ASC-File nach Abbruch der Routine Für eine günstige Wahl der Samplingrate wiederholen Sie das Thema diskrete Fourier- Transformation und Frequenzanalyse. Frage: Was besagt das Abtast-Theorem? Die Steuerspannung C wird langsam erhöht, bis 1 bzw. einen periodischen Spannungs- Verlauf zeigen. Durch weiteres vorsichtiges Erhöhen des Steuerparameters C gelangt man über eine Folge von Bifurkationen zu Grenzzyklen mit zunehmender Periodenlänge und schließlich zum Chaos. nsbesondere sind die Bifurkationspunkte möglichst genau zu ermitteln. Zusätzlich sind für ausgewählte Steuerparameter zwischen den Bifurkationspunkten Messungen mit einer solchen Samplingrate zu registrieren, die in der anschließenden Auswertung die Bestimmung der auftretenden Schwingungsamplituden zulassen. Zu jedem Datensatz sind die Werte der Steuerspannung und der Samplingrate (zur Reproduktion der Zeitachse) zu notieren. Die detaillierte Auswertung und Darstellung der Ergebnisse erfolgt z.b. mit Hilfe von ORGN. 7
8 Zur Darstellung des Feigenbaum-Diagramms werden die Amplituden über dem Steuerparameter aufgetragen. 5 Chaos bei der logistischen Abbildung 5.1 Berechnung des Bifurkationsdiagramms Für die teration der Abbildung (Gl. 1) ist ein Computer-Programm zu schreiben. Die folgenden Schritte sind zu realisieren: a (0, 4] wählen für beliebigen Startwert x 0 (0, 1) die Abbildung ca. 30 mal iterieren, um auf den Attraktor zu gelangen. Dieser Trajektorien-Abschnitt ist zu verwerfen. die teration dann auf dem Attraktor mit x 30 beginnen und die Trajektorie speichern die gespeicherten Werte gegen a plotten a neu wählen und alles wiederholen Frage: Warum muss man die ersten terationsschritte ignorieren? 5. Der Ljapunov - Exponent Ein Maß für die sensitive Abhängigkeit der Bewegungen von deren Anfangsbedingungen, d.h. Stabilität der Bahnen, ist der maximale Ljapunov-Exponent λ max (Chua System ist dreidimensional und hat deswegen 3 Ljapunov-Exponenten). Der chaotischen Bewegung entspricht λ max > 0. Eindimensionale Abbildungen x n+1 = f(x n ) werden durch nur einen Ljapunov-Exponenten λ charakterisiert [6, 7, 8]: N 1 λ = lim N 1 ld f (x i ), N i=0 wobei x i Punkte auf dem jeweiligen Attraktor A(a) sind. Berechnen Sie λ(a) für verschiedene Kontrollparameter a (0, 4] der logistischen Abbildung (Gl. 1). Literatur [1] Argyris, J., Faust, G., Haase, M.: Die Erforschung des Chaos, 1994 und 010 [] Goldstein, H., Poole, C.P., Safko, J.L.: Klassische Mechanik, 3., vollst. berarb. und erw. Auflage, 006 8
9 [3] Jamal, R., Krauss, P.: LabVEW Das Grundlagenbuch, 1998 und Jamal, R., H. Pichlik: LabVEW Das Anwenderbuch, 1999 [4] Jetschke, G.: Mathematik der Selbstorganisation: Qualitative Theorie nichtlinearer dynamischer Systeme und gleichgewichtsferner Strukturen in Physik, Chemie und Biologie, 1989 und 009 [5] LabVEW - eine online-einführung. a568199/p / [6] Leven, R.W., Koch, B.P., Pompe, B.: Chaos in dissipativen Systemen, 1989 und 1994 [7] Schuster, H.G.: Deterministic Chaos. An ntroduction, 1988, 1995, 008 [8] Strogatz, S.H.: Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering, 1994, 1997, 00 [9] Worg, R.: Deterministisches Chaos - Wege in die nichtlineare Dynamik,
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
1 Nicht-lineare dynamische Systeme
 1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1. Vorwort zum Versuch Ziel des Versuchs Aufgabenstellung Aufgaben zur Vorbereitung Versuchsdurchführung...
 Albert-Ludwigs-Universität Freiburg Fakultät für Physik Fortgeschrittenenpraktikum I FP I Deterministisches Chaos Inhalt A. Versuchsanleitung: Seite 1. Vorwort zum Versuch... 2 2. Ziel des Versuchs...
Albert-Ludwigs-Universität Freiburg Fakultät für Physik Fortgeschrittenenpraktikum I FP I Deterministisches Chaos Inhalt A. Versuchsanleitung: Seite 1. Vorwort zum Versuch... 2 2. Ziel des Versuchs...
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
 Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Jan Henrik Sylvester. 10. Februar 2003
 Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Seminar über gewöhnliche Differentialgleichungen Chaos in eindimensionalen diskreten dynamischen Systemen: Das Feigenbaum-Szenario Die logistische Abbildung Jan Henrik Sylvester 10. Februar 2003 1 Die
Lyapunov-Exponenten. Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems:
 Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Analyse des Langzeitverhaltens ( t ) eines physikalischen Systems: - t tritt bei konkreten beobachteten Systemen nicht auf t >> τ (τ: charakteristische Systemzeit) - t: Dauer der Beobachtung, Prognosezeitraum,...
Erzwungene Schwingungen
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum S4 Erzwungene Schwingungen Dieses Experiment enthält zwei Bestandteile: Es werden Zusammehänge zwischen erregender und erregter Schwingung
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Feigenbaum, Chaos und die RG
 Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
Feigenbaum, Chaos und die RG 9. Juli 27 Lara Becker Bildquelle: [7] Nichtlineare Systeme und Chaos nichtlineare Systeme in letzter Zeit wieder reges Forschungsgebiet Ermöglichung der Untersuchung nicht-integrabler
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Elektrische Schwingungen
 Dr. Angela Fösel & Dipl. Phys. Tom Michler Revision: 14.10.2018 Ein elektrischer Schwingkreis ist eine (resonanzfähige) elektrische Schaltung aus einer Spule (L) und einem Kondensator (C), die elektrische
Dr. Angela Fösel & Dipl. Phys. Tom Michler Revision: 14.10.2018 Ein elektrischer Schwingkreis ist eine (resonanzfähige) elektrische Schaltung aus einer Spule (L) und einem Kondensator (C), die elektrische
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Ergebnis: Allg. Lösung der homogenen DGL ist Summe über alle Eigenlösungen: mit
 Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Zusammenfassung: Lineare DGL mit konstanten Koeffizienten (i) Suche Lösung für homogene DGL per Exponential-Ansatz: e-ansatz: Zeitabhängigkeit nur im Exponenten! zeitunabhängiger Vektor, Ergebnis: Allg.
Chaos im getriebenen nicht-linearen Pendel
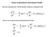 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
 3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften
HARMONIK ZWISCHEN ORDNUNG UND CHAOS
 HARMONIK ZWISCHEN ORDNUNG UND CHAOS Grundstrukturen der Natur und ihre Wahrnehmung durch den Hörenden Menschen Vortrag auf dem Harmonik-Symposion 2010 am 2. Mai 2010 Hans G. Weidinger 1. Was ist Harmonik?
HARMONIK ZWISCHEN ORDNUNG UND CHAOS Grundstrukturen der Natur und ihre Wahrnehmung durch den Hörenden Menschen Vortrag auf dem Harmonik-Symposion 2010 am 2. Mai 2010 Hans G. Weidinger 1. Was ist Harmonik?
Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality
 Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Physik mit dem PC. Von Dr. rer. nat. Ingo Bull Christian-Albrechts-Universität zu Kiel
 Physik mit dem PC Von Dr. rer. nat. Ingo Bull Christian-Albrechts-Universität zu Kiel B.G.Teubner Stuttgart Leipzig 1998 Inhalt 1 Einleitung 11 2 PC-Interfacetechnik 13 2.1 ADT-Interface am Enhanced Parallel
Physik mit dem PC Von Dr. rer. nat. Ingo Bull Christian-Albrechts-Universität zu Kiel B.G.Teubner Stuttgart Leipzig 1998 Inhalt 1 Einleitung 11 2 PC-Interfacetechnik 13 2.1 ADT-Interface am Enhanced Parallel
x=r cos y=r sin } r2 =x 2 y 2
 6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Die Darstellung nichtlinearer Bewegungsabläufe
 Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
 Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Theoretische Physik 2 (Theoretische Mechanik)
 Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Theoretische Physik 2 (Theoretische Mechanik) Prof. Dr. Th. Feldmann 15. Januar 2014 Kurzzusammenfassung Vorlesung 21 vom 14.1.2014 6. Hamilton-Mechanik Zusammenfassung Lagrange-Formalismus: (generalisierte)
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
2.9 Gedämpfter Harmonischer Oszillator
 72 KAPITEL 2. DYNAMIK EINES MASSENPUNKTES 2.9 Gedämpfter Harmonischer Oszillator In diesem Abschnitt wollen wir die Bewegung eines Massenpunktes betrachten, der sich in einer Raumrichtung x in einer Harmonischen
72 KAPITEL 2. DYNAMIK EINES MASSENPUNKTES 2.9 Gedämpfter Harmonischer Oszillator In diesem Abschnitt wollen wir die Bewegung eines Massenpunktes betrachten, der sich in einer Raumrichtung x in einer Harmonischen
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Chaos - Nichtlineare Dynamik
 Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Flüsse, Fixpunkte, Stabilität
 1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
1 Flüsse, Fixpunkte, Stabilität Proseminar: Theoretische Physik Yannic Borchard 7. Mai 2014 2 Motivation Die hier entwickelten Formalismen erlauben es, Aussagen über das Verhalten von Lösungen gewöhnlicher
durch Ratengleichungen der Form t t = F 2 N 1 t, N 2 t d N 1 t
 5. Wechselwirkungen zwischen verschiedenen Spezies Allgemein kann man die zeitliche Entwicklung zweier Spezies N 1 und N 2 durch Ratengleichungen der Form d N 1 t d N 2 t = F 1 N 1 t, N 2 t, t = F 2 N
5. Wechselwirkungen zwischen verschiedenen Spezies Allgemein kann man die zeitliche Entwicklung zweier Spezies N 1 und N 2 durch Ratengleichungen der Form d N 1 t d N 2 t = F 1 N 1 t, N 2 t, t = F 2 N
120 Gekoppelte Pendel
 120 Gekoppelte Pendel 1. Aufgaben 1.1 Messen Sie die Schwingungsdauer zweier gekoppelter Pendel bei gleichsinniger und gegensinniger Schwingung. 1.2 Messen Sie die Schwingungs- und Schwebungsdauer bei
120 Gekoppelte Pendel 1. Aufgaben 1.1 Messen Sie die Schwingungsdauer zweier gekoppelter Pendel bei gleichsinniger und gegensinniger Schwingung. 1.2 Messen Sie die Schwingungs- und Schwebungsdauer bei
Stabile periodische Bewegungen (Grenzzyklen)
 Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
4.5 Gekoppelte LC-Schwingkreise
 4.5. GEKOPPELTE LC-SCHWINGKEISE 27 4.5 Gekoppelte LC-Schwingkreise 4.5. Versuchsbeschreibung Ein elektrischer Schwingkreis kann induktiv mit einem zweiten erregten Schwingkreis 2 koppeln. Der Kreis wird
4.5. GEKOPPELTE LC-SCHWINGKEISE 27 4.5 Gekoppelte LC-Schwingkreise 4.5. Versuchsbeschreibung Ein elektrischer Schwingkreis kann induktiv mit einem zweiten erregten Schwingkreis 2 koppeln. Der Kreis wird
Motivation. Motivation 2
 Grenzzyklen 1 Motivation Grenzzyklen modellieren von selbst oszillierende Systeme Stabile Grenzzyklen kleine Abweichungen in den Anfangsbedingungen gehen in Grenzzyklus über Beispiele: Van-der-Pol Schwingkreis
Grenzzyklen 1 Motivation Grenzzyklen modellieren von selbst oszillierende Systeme Stabile Grenzzyklen kleine Abweichungen in den Anfangsbedingungen gehen in Grenzzyklus über Beispiele: Van-der-Pol Schwingkreis
Praktikum. Modellbildung und Simulation. Stichworte: Modellbildung Analoge Simulation Digitale Simulation
 Praktikum Stichworte: Modellbildung Analoge Simulation Digitale Simulation Aufgabenstellung und Lösungsidee - Kennenlernen verschiedener Methoden zur Modellbildung eines mechanisches Schwingers - Abbildung
Praktikum Stichworte: Modellbildung Analoge Simulation Digitale Simulation Aufgabenstellung und Lösungsidee - Kennenlernen verschiedener Methoden zur Modellbildung eines mechanisches Schwingers - Abbildung
Chaos am invertierten Pendel
 Physikalisches Praktikum für Fortgeschrittene, Teil A Chaos am invertierten Pendel Versuch 5.1 Gruppe 14 W.Bender (walter.bender@rwth-aachen.de), J.Luckas (c.hihiro@gmx.de) INHALTSVERZEICHNIS Inhaltsverzeichnis
Physikalisches Praktikum für Fortgeschrittene, Teil A Chaos am invertierten Pendel Versuch 5.1 Gruppe 14 W.Bender (walter.bender@rwth-aachen.de), J.Luckas (c.hihiro@gmx.de) INHALTSVERZEICHNIS Inhaltsverzeichnis
Untersuchungen am magnetischen Doppelpendel - Spaceball
 Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel
Untersuchungen am magnetischen Doppelpendel - Spaceball I. Silz, H. J. Schlichting, V. Nordmeier Universität - Gesamthochschule Essen, 45141 Essen 1. Einleitung Galt das Pendel lange Zeit als ein Paradebeispiel
Schnelle Fouriertransformation (FFT)
 Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
Lineare und nichtlineare Schwingungen und Wellen
 Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
Lineare und nichtlineare Schwingungen und Wellen Von Prof. Dr. sc. nat. ETH Fritz Kurt Kneubühl Eidgenössische Technische Hochschule Zürich unter Mitwirkung von Dr. sc. nat. ETH Damien Philippe Scherrer
Resonanz Versuchsvorbereitung
 Versuche P1-1,, Resonanz Versuchsvorbereitung Thomas Keck, Gruppe: Mo-3 Karlsruhe Institut für Technologie, Bachelor Physik Versuchstag: 0.1.010 1 1 Vorwort Im Praktikumsversuch,,Resonanz geht es um freie
Versuche P1-1,, Resonanz Versuchsvorbereitung Thomas Keck, Gruppe: Mo-3 Karlsruhe Institut für Technologie, Bachelor Physik Versuchstag: 0.1.010 1 1 Vorwort Im Praktikumsversuch,,Resonanz geht es um freie
Protokoll zum Anfängerpraktikum
 Protokoll zum Anfängerpraktikum Elektromagnetischer Schwingkreis Gruppe, Team 5 Sebastian Korff Frerich Max 8.5.6 Inhaltsverzeichnis. Einleitung -3-. Versuchsdurchführung -5-. Eigenfrequenz und Dämpfung
Protokoll zum Anfängerpraktikum Elektromagnetischer Schwingkreis Gruppe, Team 5 Sebastian Korff Frerich Max 8.5.6 Inhaltsverzeichnis. Einleitung -3-. Versuchsdurchführung -5-. Eigenfrequenz und Dämpfung
Elektromagnetische Schwingkreise
 Grundpraktikum der Physik Versuch Nr. 28 Elektromagnetische Schwingkreise Versuchsziel: Bestimmung der Kenngrößen der Elemente im Schwingkreis 1 1. Einführung Ein elektromagnetischer Schwingkreis entsteht
Grundpraktikum der Physik Versuch Nr. 28 Elektromagnetische Schwingkreise Versuchsziel: Bestimmung der Kenngrößen der Elemente im Schwingkreis 1 1. Einführung Ein elektromagnetischer Schwingkreis entsteht
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen
 Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Zentralabitur 2007 Physik Schülermaterial Aufgabe II LK Bearbeitungszeit: 300 min
 Thema: Abklingprozesse Aufgabenstellung In den folgenden Aufgaben werden anhand des radioaktiven Zerfalls und der gedämpften elektromagnetischen Schwingung zwei Abklingprozesse betrachtet. Außerdem werden
Thema: Abklingprozesse Aufgabenstellung In den folgenden Aufgaben werden anhand des radioaktiven Zerfalls und der gedämpften elektromagnetischen Schwingung zwei Abklingprozesse betrachtet. Außerdem werden
Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos. Wintersemester 2018/ M. Zaks
 Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos Wintersemester 2018/19 22.01.2019 M. Zaks hintergrund Kontext: Wettervorhersage. Entstehung von Luftbewegungen infolge der thermischen
Vorlesung 14. Lorenz-Attraktor: erstes Beispiel vom dynamischen Chaos Wintersemester 2018/19 22.01.2019 M. Zaks hintergrund Kontext: Wettervorhersage. Entstehung von Luftbewegungen infolge der thermischen
E 21 - Gekoppelte Schwingungen
 14.11.08 PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER LGyGe Versuch: E 21 - Gekoppelte Schwingungen 1. Grundlagen Zur Vorbereitung müssen Sie sich mit den folgenden physikalischen Begriffen, Vorgängen und Verfahren
14.11.08 PHYSIKALISCHES PRAKTIKUM FÜR ANFÄNGER LGyGe Versuch: E 21 - Gekoppelte Schwingungen 1. Grundlagen Zur Vorbereitung müssen Sie sich mit den folgenden physikalischen Begriffen, Vorgängen und Verfahren
I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N
 Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Lars Knapik Geophysikalisch-Meteorologisches Seminar Zusammenfassung des Vortrags vom 26.06.2008 I N T E R M I T T E N Z U N D S T R U K T U R F U N K T I O N E N Selbstähnlichkeit Um Intermittenz zu erklären
Elektrischer Schwingkreis
 Fakultät für Technik Bereich Informationstechnik Elektrischer Schwingkreis Name 1: Name 2: Name 3: Gruppe: Datum: 2 1 Allgemeines Im Versuch Mechanischer Schwingkreis haben Sie einen mechanischen Schwingkreis
Fakultät für Technik Bereich Informationstechnik Elektrischer Schwingkreis Name 1: Name 2: Name 3: Gruppe: Datum: 2 1 Allgemeines Im Versuch Mechanischer Schwingkreis haben Sie einen mechanischen Schwingkreis
Inhalt der Vorlesung A1
 PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
PHYSIK Physik A/B1 A WS SS 17 13/14 Inhalt der Vorlesung A1 1. Einführung Methode der Physik Physikalische Größen Übersicht über die vorgesehenen Themenbereiche. Teilchen A. Einzelne Teilchen Beschreibung
Institut für Elektrotechnik und Informationstechnik. Aufgabensammlung zur. Systemtheorie
 Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Systemtheorie Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski Dipl.-Ing. R. Besrat 05.04.2013 Übungsaufgaben zur Systemtheorie
Institut für Elektrotechnik und Informationstechnik Aufgabensammlung zur Systemtheorie Prof. Dr. techn. F. Gausch Dipl.-Ing. C. Balewski Dipl.-Ing. R. Besrat 05.04.2013 Übungsaufgaben zur Systemtheorie
Versuch 3.14: Resonanzverhalten Nichtlinearer Oszillatoren
 Physikalisches Praktikum für Fortgeschrittene Technische Hochschule Darmstadt Abteilung A: Institut für Angewandte Physik Versuch 3.14: Resonanzverhalten Nichtlinearer Oszillatoren Vorbereitung: Resonanz,
Physikalisches Praktikum für Fortgeschrittene Technische Hochschule Darmstadt Abteilung A: Institut für Angewandte Physik Versuch 3.14: Resonanzverhalten Nichtlinearer Oszillatoren Vorbereitung: Resonanz,
Kondensator und Spule
 Hochschule für angewandte Wissenschaften Hamburg Naturwissenschaftliche Technik - Physiklabor http://www.haw-hamburg.de/?3430 Physikalisches Praktikum ----------------------------------------------------------------------------------------------------------------
Hochschule für angewandte Wissenschaften Hamburg Naturwissenschaftliche Technik - Physiklabor http://www.haw-hamburg.de/?3430 Physikalisches Praktikum ----------------------------------------------------------------------------------------------------------------
Übung Systemtheorie und Regelungstechnik I - WS08/09 Übungstermin 1 am Universität des Saarlandes
 Übung Systemtheorie und Regelungstechnik I - WS08/09 Übungstermin 1 am 22.11.2008 Universität des Saarlandes Aufgabe 1.1: Gegeben ist der schematische Aufbau eines Mischers: Auf den Antriebsstrang Antriebsstrang
Übung Systemtheorie und Regelungstechnik I - WS08/09 Übungstermin 1 am 22.11.2008 Universität des Saarlandes Aufgabe 1.1: Gegeben ist der schematische Aufbau eines Mischers: Auf den Antriebsstrang Antriebsstrang
Diskrete Populationsmodelle für Einzelspezies
 Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
SINIS Simulation nichtlinearer Systeme
 In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
In: Deutsche Physikalische Gesellschaft (Hrsg.): Didaktik der Physik. Bremen 21. Berlin: Lehmanns ISBN 3-931253-87-2 SINIS Simulation nichtlinearer Systeme O.Busse, V. Nordmeier, H.J. Schlichting Universität
Fixpunkte und Stabilitätsanalyse
 Fixpunkte und Stabilitätsanalyse 1 Themenüberblick Motivation 1D-Probleme Bifurkationen 2D-Probleme Fixpunkttypen Lotka-Volterra-Modelle 2 Motivation Bisher: Lineare Dynamik Jetzt: Nichtlineare Systeme
Fixpunkte und Stabilitätsanalyse 1 Themenüberblick Motivation 1D-Probleme Bifurkationen 2D-Probleme Fixpunkttypen Lotka-Volterra-Modelle 2 Motivation Bisher: Lineare Dynamik Jetzt: Nichtlineare Systeme
1. Bestimmen Sie die Phasengeschwindigkeit von Ultraschallwellen in Wasser durch Messung der Wellenlänge und Frequenz stehender Wellen.
 Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 10/015 M Schallwellen Am Beispiel von Ultraschallwellen in Wasser werden Eigenschaften von Longitudinalwellen betrachtet. Im ersten
Universität Potsdam Institut für Physik und Astronomie Grundpraktikum 10/015 M Schallwellen Am Beispiel von Ultraschallwellen in Wasser werden Eigenschaften von Longitudinalwellen betrachtet. Im ersten
Deterministisches Chaos
 . Institut für Mathematik und Physik Albert-Ludwigs-Universität Freiburg im Breisgau 26. Juni 2012 I Inhaltsverzeichnis 1 Vorwort zum Versuch 1 2 Ziel des Versuchs 1 3 Aufgabenstellung 2 4 Aufgaben zur
. Institut für Mathematik und Physik Albert-Ludwigs-Universität Freiburg im Breisgau 26. Juni 2012 I Inhaltsverzeichnis 1 Vorwort zum Versuch 1 2 Ziel des Versuchs 1 3 Aufgabenstellung 2 4 Aufgaben zur
Partielle Differentialgleichungen
 http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
http://www.free background wallpaper.com/background wallpaper water.php Partielle Differentialgleichungen 1 E Partielle Differentialgleichungen Eine partielle Differentialgleichung (Abkürzung PDGL) ist
Deterministisches Chaos
 Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Heinz Georg Schuster Deterministisches Chaos Eine Einführung Weinheim New York Basel Cambridge Tokyo Einleitung 1 1 Experimente und einfache Modelle 7 1.1 Experimente zum Deterministischen Chaos 7 Das
Algorithmen für Chaos und Fraktale
 Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
Dynamik hüpfender Bälle
 1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
1 Dynamik hüpfender Bälle Proseminar: Theoretische Physik Florian Döhle 2. Juli 2014 2 Video Chaotische Bewegung Video Periodische Bewegung 3 Gliederung 1 Motivation 2 Aufstellen und Fixpunktanalyse der
GP Getriebenes Pendel
 GP Getriebenes Pendel Blockpraktikum Frühjahr 7 (Gruppe ) 5. April 7 Inhaltsverzeichnis 1 Einführung Theoretische Grundlagen 3 Versuchsdurchführung 3 4 Messergebnisse und Auswertung 3 4.1 Abhängigkeit
GP Getriebenes Pendel Blockpraktikum Frühjahr 7 (Gruppe ) 5. April 7 Inhaltsverzeichnis 1 Einführung Theoretische Grundlagen 3 Versuchsdurchführung 3 4 Messergebnisse und Auswertung 3 4.1 Abhängigkeit
Praktikum I PP Physikalisches Pendel
 Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Veränderung in gestalteter Beziehung
 Dr. Dr. Strunk Veränderung in gestalteter Beziehung 1 complexity-research.com Veränderung in gestalteter Beziehung Dipl.-Psych. Dr. Dr. Guido Strunk 1. VORTRAG... 2 2. FEEDBACKSYSTEME NICHTLINEALITÄT...
Dr. Dr. Strunk Veränderung in gestalteter Beziehung 1 complexity-research.com Veränderung in gestalteter Beziehung Dipl.-Psych. Dr. Dr. Guido Strunk 1. VORTRAG... 2 2. FEEDBACKSYSTEME NICHTLINEALITÄT...
Versuchsprotokoll E208: Fourriertransformation und nichtlinearer Oszillator Fortgeschrittenenpraktikum Physik Universität Bonn
 Versuchsprotokoll E208: Fourriertransformation und nichtlinearer Oszillator Fortgeschrittenenpraktikum Physik Universität Bonn Alexander Rothkegel, Frank Fremerey unter Anleitung von Ursula Meyer 1. Juni
Versuchsprotokoll E208: Fourriertransformation und nichtlinearer Oszillator Fortgeschrittenenpraktikum Physik Universität Bonn Alexander Rothkegel, Frank Fremerey unter Anleitung von Ursula Meyer 1. Juni
Ökologische Gleichungen für zwei Spezies
 Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
Ökologische Gleichungen für zwei Spezies Florian Kern 06.Dezember 2011 Josef Hofbauer and Karl Sigmund: Evolutionary Games and Population Dynamics, Cambridge, Kapitel 4 Inhaltsverzeichnis 1 Satz von der
Probestudium der Physik 2011/12
 Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
Probestudium der Physik 2011/12 Karsten Kruse 2. Mechanische Schwingungen und Wellen - Theoretische Betrachtungen 2.1 Der harmonische Oszillator Wir betrachten eine lineare Feder mit der Ruhelänge l 0.
5. Vorlesung Wintersemester
 5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
5. Vorlesung Wintersemester 1 Bewegung mit Stokes scher Reibung Ein dritter Weg, die Bewegungsgleichung bei Stokes scher Reibung zu lösen, ist die 1.1 Separation der Variablen m v = αv (1) Diese Methode
(a) Transformation auf die generalisierten Koordinaten (= Kugelkoordinaten): ẏ = l cos(θ) θ sin(ϕ) + l sin(θ) cos(ϕ) ϕ.
 Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Karlsruher Institut für Technologie Institut für Theorie der Kondensierten Materie Theoretische Physik B - Lösungen SS 10 Prof. Dr. Aleander Shnirman Blatt 5 Dr. Boris Narozhny, Dr. Holger Schmidt 11.05.010
Drehschwingungen, Elektrische Schwingungen, Dämpfung
 Aufgaben 18 Schwingungen Drehschwingungen, Elektrische Schwingungen, Dämpfung Lernziele - sich aus dem Studium eines schriftlichen Dokumentes neue Kenntnisse erarbeiten können. - die Analogie zwischen
Aufgaben 18 Schwingungen Drehschwingungen, Elektrische Schwingungen, Dämpfung Lernziele - sich aus dem Studium eines schriftlichen Dokumentes neue Kenntnisse erarbeiten können. - die Analogie zwischen
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
 Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
 Vorwort Dynamische Systeme können durch mathematische Gleichungen modelliert werden, die eine eindeutige Vorschrift zur Berechnung der zeitlichen Entwicklung des Systemzustandes darstellen, so daß die
Vorwort Dynamische Systeme können durch mathematische Gleichungen modelliert werden, die eine eindeutige Vorschrift zur Berechnung der zeitlichen Entwicklung des Systemzustandes darstellen, so daß die
Seminar Fraktale. Kapitel 13 Dynamical Systems. Von Dirk Simon
 Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Seminar Fraktale Kapitel 13 Dynamical Systems Von Dirk Simon Übersicht Einführung und Definitionen Dynamische Systeme Attraktoren Chaos Ein paar Beispiele Anwendungen Einführung Anwendung für f r Dynamische
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester Physik-Institut der Universität Zürich
 Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Iterationsverfahren und Stabilitätsuntersuchung
 1 FÜR INTERESSIERTE! NICHT TESTRELEVANT 1! Iterationsverfahren und Stabilitätsuntersuchung Unter Iterationsverfahren versteht man rekursive numerische Methoden mit welchen auch analytisch nicht lösbare
1 FÜR INTERESSIERTE! NICHT TESTRELEVANT 1! Iterationsverfahren und Stabilitätsuntersuchung Unter Iterationsverfahren versteht man rekursive numerische Methoden mit welchen auch analytisch nicht lösbare
Nichtlineare Prozesse in der Elektrochemie II
 Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
Nichtlineare Prozesse in der Elektrochemie II 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert,
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Gedämpfte harmonische Schwingung
 Gedämpfte harmonische Schwingung Die Differentialgleichung u + 2ru + ω 2 0u = c cos(ωt) mit r > 0 modelliert sowohl eine elastische Feder als auch einen elektrischen Schwingkreis. Gedämpfte harmonische
Gedämpfte harmonische Schwingung Die Differentialgleichung u + 2ru + ω 2 0u = c cos(ωt) mit r > 0 modelliert sowohl eine elastische Feder als auch einen elektrischen Schwingkreis. Gedämpfte harmonische
Fibonacci Zahlen: 3. Hamiltonsche Systeme. 3.1 Hamilton Dynamik. Teilverhältnis beim `goldenen Schnitt : definiert als. mit
 Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Fibonacci Zahlen: definiert als Bemerkungen: (1) ist das Teilverhältnis beim `goldenen Schnitt : mit A T B und (2) Alle Zahlen, deren Darstellung als Kettenbruch auf endet, heißen `noble Zahlen. (3) Entwicklung
Übungsblatt 2: Modellierung und Linearisierung (Abgabe am von 8:00-8:15 im Vorlesungs-Hörsaal) Prof. Dr. Moritz Diehl
 Vorlesung Systemtheorie und Regelungstechnik (SR Albert-Ludwigs-Universität Freiburg Sommersemester 2014 Übungsblatt 2: Modellierung und Linearisierung (Abgabe am 21.5.2014 von 8:00-8:15 im Vorlesungs-Hörsaal
Vorlesung Systemtheorie und Regelungstechnik (SR Albert-Ludwigs-Universität Freiburg Sommersemester 2014 Übungsblatt 2: Modellierung und Linearisierung (Abgabe am 21.5.2014 von 8:00-8:15 im Vorlesungs-Hörsaal
3 Zweidimensionale dynamische Systeme Oszillationen
 3 Zweidimensionale dynamische Systeme Oszillationen Lineare Systeme Ein Beispiel für ein zweidimensionales dynamisches System ist die Gleichung ẍ + ω 2 sin x = 0 für ebene Schwingungen eines reibungsfreien
3 Zweidimensionale dynamische Systeme Oszillationen Lineare Systeme Ein Beispiel für ein zweidimensionales dynamisches System ist die Gleichung ẍ + ω 2 sin x = 0 für ebene Schwingungen eines reibungsfreien
1.2 Schwingungen von gekoppelten Pendeln
 0 1. Schwingungen von gekoppelten Pendeln Aufgaben In diesem Experiment werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken
0 1. Schwingungen von gekoppelten Pendeln Aufgaben In diesem Experiment werden die Schwingungen von zwei Pendeln untersucht, die durch eine Feder miteinander gekoppelt sind. Für verschiedene Kopplungsstärken
Abiturprüfung Physik, Grundkurs. Induktionsspannungen an einer im Magnetfeld schwingenden Leiterschaukel
 Seite 1 von 8 Abiturprüfung 2009 Physik, Grundkurs Aufgabenstellung: Aufgabe 1: Induktionsspannungen an einer im Magnetfeld schwingenden Leiterschaukel Ein Kupferstab der Länge L = 14 cm hängt wie in Abbildung
Seite 1 von 8 Abiturprüfung 2009 Physik, Grundkurs Aufgabenstellung: Aufgabe 1: Induktionsspannungen an einer im Magnetfeld schwingenden Leiterschaukel Ein Kupferstab der Länge L = 14 cm hängt wie in Abbildung
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Klassische Mechanik. WILEY-VCH Verlag GmbH & Co. KGaA. Herbert Goldstein, Charles P. Poole, Jr., und John L Safko
 Herbert Goldstein, Charles P. Poole, Jr., und John L Safko Klassische Mechanik Dritte, vollständig überarbeitete und erweiterte Auflage WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Inhaltsverzeichnis Vorwort
Herbert Goldstein, Charles P. Poole, Jr., und John L Safko Klassische Mechanik Dritte, vollständig überarbeitete und erweiterte Auflage WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Inhaltsverzeichnis Vorwort
Eine Einführung in die theoretische Behandlung von Schwingungsproblemen
 Schwingungen Eine Einführung in die theoretische Behandlung von Schwingungsproblemen Von Dr. rer. nat. Dr.-Ing. E. h. Kurt Magnus Professor an dertechn. Universität München 4., durchgesehene Auflage Mit
Schwingungen Eine Einführung in die theoretische Behandlung von Schwingungsproblemen Von Dr. rer. nat. Dr.-Ing. E. h. Kurt Magnus Professor an dertechn. Universität München 4., durchgesehene Auflage Mit
Grundpraktikum Physik. Poggendorf sche Kompensationsmethode und Wheatstone sche Brückenschaltung
 Grundpraktikum Physik Anleitung zum Versuch Nr. 23 Poggendorf sche Kompensationsmethode und Wheatstone sche Brückenschaltung Stand: 02.11.2017 Versuchsziel: Stromlose Messung ohmscher Widerstände und Kapazitiver
Grundpraktikum Physik Anleitung zum Versuch Nr. 23 Poggendorf sche Kompensationsmethode und Wheatstone sche Brückenschaltung Stand: 02.11.2017 Versuchsziel: Stromlose Messung ohmscher Widerstände und Kapazitiver
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06
 Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 8 1 d Alembertsches Prinzip und Lagrangegleichungen 1. Art Teil II 2 Das d Alembertsche Prinzip für N-Teilchensysteme
Ergänzende Materialien zur Vorlesung Theoretische Mechanik, WS 2005/06 Dörte Hansen Seminar 8 1 d Alembertsches Prinzip und Lagrangegleichungen 1. Art Teil II 2 Das d Alembertsche Prinzip für N-Teilchensysteme
Thema: Schwingung eines Hohlkörpers
 Abitur 9 Physik Klausur Hannover, 75 arei LK Semester Bearbeitungszeit: 9 min Thema: Schwingung eines Hohlkörpers 1 Aufgabe In einem Hohlkörper befindet sich ein Magnet (Abb1) In seiner Ruhelage schwebt
Abitur 9 Physik Klausur Hannover, 75 arei LK Semester Bearbeitungszeit: 9 min Thema: Schwingung eines Hohlkörpers 1 Aufgabe In einem Hohlkörper befindet sich ein Magnet (Abb1) In seiner Ruhelage schwebt
7.4 Gekoppelte Schwingungen
 7.4. GEKOPPELTE SCHWINGUNGEN 333 7.4 Gekoppelte Schwingungen Als Beispiel für 2 gekoppelte Schwingungen betrachten wir das Doppelpendel, das in Abb. 7.19 dargestellt ist. Zunächst vernachlässigen wir die
7.4. GEKOPPELTE SCHWINGUNGEN 333 7.4 Gekoppelte Schwingungen Als Beispiel für 2 gekoppelte Schwingungen betrachten wir das Doppelpendel, das in Abb. 7.19 dargestellt ist. Zunächst vernachlässigen wir die
