a) f(5) = 82,0 repräsentiert die Einwohneranzahl in Deutschland im Jahr Also 82 Millionen Einwohnerzahl.
|
|
|
- Marielies Eberhardt
- vor 5 Jahren
- Abrufe
Transkript
1 Hausaufgabenlösungen Lambacher Schweizer Mathematik Qualifikationsphase Leistungskurs / Grundkurs Nordrhein-Westfalen ISBN Seite 12 Aufgabe 1 a) f(5) = 82,0 repräsentiert die Einwohneranzahl in Deutschland im Jahr Also 82 Millionen Einwohnerzahl. Der Ausdruck f(6) f(5,5) 0,1 gibt die durchschnittliche Änderungsrate (also die 6 5,5 durchschnittliche Geschwindigkeit) zwischen das 5,5. und das 6. Jahr an. In diesem Zeitraum hat sich die Einwohnerzahl um 0,1 Millionen Einwohner pro Jahr verringert. b) T (1) = 25 bedeutet, dass nach einer Minute die Temperatur 25 Grad beträgt nach zehn Minuten (f(10)= 1) 1 Grad. = 1 gibt die durchschnittliche Änderungsrate von der. bis zur 5. Minute Der Ausdruck T(5) T() 5 an. Demnach steigt die Temperatur in diesem Zeitraum um einen Grad Celsius pro Minute an. c) v(5) = 25 gibt die Geschwindigkeit von 25 Meter pro Sekunde in der fünften Sekunde an. v (8) = 16 gibt die Beschleunigung von 16 Meter pro Quadratsekunde in der achten Sekunde an. Aufgabe 2 a) Skizze: b) f(x) = 0,25 x 2 (x 2)(x + 1) + 1 f(x) = ( 0,25 x + 0,5x 2 )(x + 1) + 1 f(x) = 0,25 x + 0,5x 0,25x + 0,5x f (x) = x + 0,75x 2 + x + 1
2 Seite 1 a) (A) () ; (B) (); (C) (1); (D) (2) b) (A) f(x) = x + 8 x2 1 f (x) = x x (B) f(x) = (x + 1) f (x) = 2x + 2 (C) f(x) = 2 cos(x) f (x) = 2 sin(x) (D) f(x) = 11 5 x x2 + 1 f (x) = 5 x x Aufgabe a) f(x) = 2x f (x) = x = x Ι : 1 = x b) g(x) = x x 1 g (x) = x 2 = x 2 Ι + 8 = x 2 Ι 8 = x2 Ι
3 8 = x = x 2 Aufgabe 5 a) f(x) = 2 x 2 6x + 6,5 f (x) = x 6 g(x) = x 8x x g (x) = x 2 16x + 16 h(x) = x 5x 2 + h (x) = x 10x b) 0 = x 6 Ι = x Ι 6 = x f ( 6 ) = 2 (6 ) 2 6 ( 6 ) + 6,5 = 2 E ( 6 ; 2) 0 = x 2 16x + 16 Ι 0 = x 2 16 x + 16 x 1,2 = 8 ± ( 8 ) 2 x 1 = 16 x 2 = g ( ) = ( ) 8 ( 2 ) + 16 ( ) = g () = () 8 () () = 0 E 1 ( ; )
4 E 2 ( ; 0) 0 = x 10x 0 = x (x 2 10) x 1 = 0 und x 2 10 = 0 Ι + 10 x 2 = 10 Ι x 2 = 10 Ι x 2 = 10 x = 10 2 h ( 10 ) = ( 10) 5 ( 10 ) + = 9 2 h ( 10 ) = ( 10 ) 5 ( 10 ) + = 9 E 1 ( 10 ; 9 ) E 2 ( 10 ; 9 ) c) GTR nutzen Aufgabe 6 a) Falsch. Nur Nullstellen der ersten Ableitung sind potentielle Extremstellen der Funktion. b) Richtig. Da die Ableitungsfunktion an der Stelle 2 eine Nullstelle hat und die Steigung vor und nach der Nullstelle im positiven Bereich ist, handelt es sich hier um einen Sattelpunkt. c) g hat eine Extremstelle und einen Sattelpunkt. d) Richtig. Mit wachsendem x wächst auch f(x) oder bleibt gleich. e) g hat einen Tiefpunkt und einen Sattelpunkt.
5 Aufgabe 7 a) f(t) = 0,01 t + 0,2 t 2 2,08 t + 6,8 f (t) = 0,0 t 2 + 0,6 t 2,08 1 = 0,0 t 2 + 0,6 t 2,08 Ι 1 0 = 0,0 t 2 + 0,6 t,08 0 = t 2 6 t + 08 Ι ( 0,0) x 1,2 = 2 ± ( 2 2 ) 08 x 1 = 1 x 2 = 22 Um 1 Uhr und um ca. 7 Uhr steigt die Temperatur um einen Grad Celsius pro Stunde. b) 0 = 0,0 t 2 + 0,6 t 2,08 Ι ( 0,0) 0 = t 2 6 t x 1,2 = 2 ± ( 2 2 ) 208 x 1 = 52 x 2 = f ( 52 ) = 0,01 (52 ) + 0,2 ( 52 2 ) 2,08 ( ) + 6,8 = 27 f() = 0,01 () + 0,2 () 2 2,08 () + 6,8 = Höchste Temperatur um ca. 17 Uhr mit 1,85 Grad Celsius Tiefsttemperatur um Uhr mit Grad Celsius. Seite 1 Aufgabe 8 a) f(x) = x + 1 b) f (x) = x 2 Aufgabe 11
6 a) f(x) = 1 x x 2 + 8x + 1 f (x) = x 2 6x + 8 f () = 2 6 () + 8 = 0 b) = x 2 6x + 8 Ι 0 = x 2 6x + 5 x 1,2 = ± 2 5 x 1 = 5 x 2 = 1 f(5) = 1 (5) (5) (5) + 1 = 2 f(1) = 1 (1) (1) (1) + 1 = 19 P 1 (5 ; 2 ), P 2 ( 1 ; 19 ) c) f (x) = x 2 6x + 8 Ι Quadratische Ergänzung f (x) = x 2 6x f (x) = x 2 6x f (x) = (x 2 6x + 2 ) f (x) = (x ) = (x ) 2 1 Ι = (x ) 2 Ι ±1 = x Ι + x 1 = und x 2 = 2 Außerhalb des Intervalls [2; ] haben besitzt die Funktion eine positive Steigung. Aufgabe 12 Die Funktionen sind parallel zu einander. Aufgabe 1 a) Falsch. Die Werte sollten positiv sein. b) Richtig. Es handelt sich nämlich um eine Parabel. c) Das gilt nicht immer.
7 d) Das gilt nicht immer. Es könnte sich auch um einen Sattelpunkt handeln. e) Richtig. f) Das gilt nicht immer. Die Nullstellen der ersten Ableitung sind nur potentielle Extremstellen. Aufgabe 1 a) m = T(2) T(0) 2 m = m = ,5 In den ersten beiden Stunden sind die Temperatur mit einer Geschwindigkeit von,5 Grad Celsius pro Stunde. b) Mit GTR Seite 15 Aufgabe 15 a) Mit GTR b) m 1 = r(1) r(0,5) 0,5 π 8π m 1 = 0,26 0,5 m 2 = r(1,5) r(1) 0,5 9 8π π m 2 = 0,18 0,5 Im ersten Intervall wächst der Radius um 0,26 Meter pro Liter und im zweiten Intervall wächst der Radius um 0,18 Meter pro Liter. c) Mit GTR Aufgabe 16 a)
8 f(t) = 0,000t 0,02t + 0,605t 2 f (t) = 0,0012t 0,072t 2 + 1,21t f (t) = 0,006t 2 0,1t + 1,21 f (t) = 0,0072t 0,1 0 = 0,006t 2 0,1t + 1,21 Ι 0,006 0 = t 2 0t t 1,2 = 20 ± t 1 28 t 2 12 f (28) = 0,0072 (28) 0,1 = f (12) = 0,0072 (12) 0,1 = höchst Geschwindigkeit zum Zeitpunkt 12 Sekunden erreicht. b) m = f(0) f(20) 20 m = c) GRT Aufgabe 17 a) Alles trifft zu. b) Alles trifft zu. = 5,1 5,1 m s 1,2 km h c) Der blaue Graph trifft nicht zu. Aufgabe 18 a) (1) Die Extremstelle sollte bei 0 sein und es müsste ein Hochpunkt sein, weil die Steigung zu erst positiv ist und anschließend negativ. (2) Die Extremstellen sollten bei -1 und 1 sein. Bei -1 sollte der Tiefpunkt sein und bei 1 der Hochpunkt.
9 () Die Extremstellen sollten bei -2 und 0 sein. Bei -2 sollte der Hochpunkt liegen und bei 0 der Tiefpunkt. b) Skizze Aufgabe 19 Individuelle Lösung Seite 17 Aufgabe 1 a) [- ; -2] rechtsgekrümmt ; [-2; 1] linksgekrümmt; [1;,5] rechtsgekrümmt; [,5; ] linksgekrümmt b) [- ; ] linksgekrümmt c) [- ; 1] linksgekrümmt; [1; ] rechtsgekrümmt; [;6] linksgekrümmt; [6 ; 8] rechtsgekrümmt; [8 ; ] linksgekrümmt Aufgabe 2 a) linksgekrümmt x 1 ; x, rechtsgekrümmt x ; x 5, linksgekrümmt x 5 ; x 7 b) f(x) = 1 12 x 9 8 x2 f (x) = 1 x 9 x f (x) = x 2 9 f ( ) = ( ) 2 9 = 27 linksgekrümmt im Intervall f ( 1) = ( 1) 2 9 = 5 rechtgekrümmt im Intervall f (2) = (2) 2 9 = 7 linksgekrümmt im Intervall Aufgabe a) f(x) = x 2 + 2x + f (x) = 2x + 2 f (x) = 2 Funktion ist rechtgekrümmt. b)
10 f(x) = x x f (x) = x 2 1 f (x) = 6x [ ; 0] rechtsgekrümmt, [0 ; ]linksgekrümmt c) f (x) = x x 2 9x 5 f (x) = x 2 6 x 9 f (x) = 6x 6 [ ; 1] rechtsgekrümmt, [1 ; ]linksgekrümmt d) f(x) = x + x 2 f (x) = x + 2x f (x) = 12x linksgekrümmt e) f(x) = x 6x 2 f (x) = x 12x f (x) = 12x = 12x 2 12 x 1 = 1 ; x 2 = 1 [ ; 1] linksgekrümmt, [ 1,1] rechtsgekrümmt, [1; ]linksgekrümmt f) f(x) = 1 x + x 2 2 f (x) = x + 6x f (x) = x = x linksgekrümmt g) f(x) = 1 x6 20x 2 f (x) = 2x 5 0x f (x) = 10x 0 0 = 10x 0 x 1 = 2; x 2 = 2 [ ; 2] linksgekrümmt; [ 2; 2] rechtsgekrümmt; [2; ]linksgekrümmt h) f(x) = 1 20 x x + 2 x f (x) = 1 x + 2x x2
11 f (x) = x + 6x 2 + 9x 0 = x + 6x 2 + 9x 0 = x(x 2 + 6x + 9) x 1 = 0 und x 2 + 6x + 9 = 0 x 1,2 = ± ( ) 2 9 x 1,2 = [ ; ] linksgekrümmt, [ ; ]rechtsgekrümmt i) f(x) = (x + 2) 2 (x 1) 2 [ ; 1,5]rechtsgekrümmt, [ 1,5; 0,25]linkgekrümmt, [0,25; ]rechtsgekrümmt siehe GTR Aufgabe a) Erste Ableitung positiv, zweite Ableitung negativ b) Erste Ableitung negativ, zweite Ableitung positiv c) Erste Ableitung negativ, zweite Ableitung positiv Seite 18 Aufgabe 6 a) A: f(x) negativ; f (x) positiv; f (x) positiv B: f(x) 0; f (x) positiv; f (x) positiv C: f(x) positiv; f (x) positiv; f (x) positiv b) A: f(x) negativ; f (x) positiv ; f (x) negativ B f(x) 0; f (x) positiv; f (x) negativ C: f(x) positiv; f (x) 0; f (x) negativ D: f(x) positiv; f (x) negativ; f (x) 0 E: f(x) 0; f (x) 0; f (x) positv F: f(x) positiv; f (x) positiv; f (x) positiv c) A: f(x) negativ; f (x) positiv; f (x) negativ B: f(x) negativ; f (x) 0 ; f (x) negativ C: f(x) 0; f (x) positiv; f (x) 0 D: f(x) positiv; f (x) positiv; f (x) positiv
12 Aufgabe 7 a) An x 2 am kleinsten und x am größten b) x 1 am kleinsten und x 6 am größten c) Bei der zweiten Ableitung handelt es sich um eine Parabel Aufgabe 8 Siehe GRT Aufgabe 9 a) Wenn f eine Funktion zweiten Grades ist und f eine lineare Funktion. b) Nein x kein auch Null annehmen. c) Nein. Beispiel Sattelpunkt. Aufgabe 10 a) Lösung suchen Seite 20 Aufgabe 1 a) f(x) = x x 2 Notwendige Bedingung f (x) = 0 f (x) = x 2 6x 0 = x 2 6x 0 = x(x 6) 0 = x 1 0 = x 6 Ι +6 6 = x Ι 2 = x 2 Hinreichende Bedingung f (x E ) 0 f (x) = 6x 6 f (0) = 6(0) 6 = 6 < 0 HP f (2) = 6(2) 6 = 6 > 0 TP Punktberechnung f (0) = (0) (0) 2 = 0 HP (0; 0)
13 f (2) = (2) (2) 2 = 6 TP (2; 6) b) f(x) = x 12x Notwendige Bedingung f (x) = 0 f (x) = x = x 2 12 Ι = x 2 Ι = x 2 Ι 2 = x 1 und 2 = x 2 Hinreichende Bedingung f (x E ) 0 f (x) = 6x f (2) = 6(2) = 12 > 0 TP f ( 2) = 6( 2) = 12 < 0 HP Punktberechnung f ( 2) = ( 2) 12( 2) = 16 HP ( 2; 16) f (2) = (2) 12(2) = 16 TP (2; 16) c) f(x) = 1 x 2 x2 + 1 Notwendige Bedingung f (x) = 0 f (x) = x 2 x 0 = x 2 x 0 = x(x ) 0 = x 1 0 = x 0 = x Ι + = x 2 Hinreichende Bedingung f (x E ) 0 f (x) = 2x
14 f (0) = 2(0) = < 0 HP f () = 2() = > 0 TP Punktberechnung f (0) = 1 (0) 2 (0)2 + 1 = 1 HP (0; 1) f () = 1 () 2 ()2 + 1 = 16 TP (; 7 2 ) d) f(x) = x + 6x 2 Notwendige Bedingung f (x) = 0 f (x) = x x 0 = x x 0 = x( x + 12) 0 = x 1 0 = x + 12 Ι = x Ι ( ) = x 2 Hinreichende Bedingung f (x E ) 0 f (x) = 6x + 12 f (0) = 6(0) + 12 = 12 > 0 TP f () = 6() + 12 = 12 > 0 HP Punktberechnung f (0) = (0) + (0) 2 = 0 TP (0; 0) f () = () + 6() 2 = 2 TP (; 2) e) f(x) = 1 6 x + 2x Notwendige Bedingung f (x) = 0 f (x) = 1 2 x2 + 2
15 0 = 1 2 x2 + 2 Ι 2 2 = 1 2 x2 = x 2 Ι ( 2) Ι 2 = x 1 und 2 = x 2 Hinreichende Bedingung f (x E ) 0 f (x) = x f (2) = (2) = 2 < 0 HP f ( 2) = ( 2) = 2 > 0 TP Punktberechnung f (2) = 1 6 (2) + 2(2) = 8 HP (2; 8 ) f ( 2) = 1 6 ( 2) + 2( 2) = 8 TP ( 2; 8 ) f) f(x) = 1 x + x 2 9x Notwendige Bedingung f (x) = 0 f (x) = x 2 + 8x 9 0 = x 2 + 8x 9 x 1,2 = ± () x 1 = 1 und x 2 = 9 Hinreichende Bedingung f (x E ) 0 f (x) = 2x + 8 f (1) = 2(1) + 8 = 10 > 0 TP f ( 9) = 2( 9) + 8 = 10 < 0 HP Punktberechnung f (1) = 1 (1) + (1) 2 9(1) = 1 TP (1; 1 ) f ( 9) = 1 ( 9) + ( 9) 2 9( 9) = 162 HP ( 9; 162) Aufgabe 2
16 a) Nullstellen f(x) = x x 2 + x 0 = x x 2 + x 0 = x(x 2 x + ) 0 = x 1 x 2, = 2 ± (2) 2 x 2 = und x = 1 Hoch- und Tiefpunkte f (x) = x 2 8x + f (x) = 6x 8 Notwendige Bedingung 0 = x 2 8x + Ι 0 = x 2 8 x + 1 x 1,2 = ± ( ) 2 1 x 1 = und x 2 = 7 9 Hinreichende Bedingung f ( + 7 ) = 2 7 Tiefpunkt 9 f ( 7 ) = 2 7 Hochpunkt 9 Punktberechnung f ( ) 2,11 TP ( ; 2,11) f ( 7 9 ) 0,6 HP ( 7 9 ; 0,6) b) Nullstellen
17 f(x) = x + x 2 x 0 = x + x 2 x 0 = x( x 2 + x ) 0 = x 1 x 2, = 1 ± ( )2 keine weiteren Nullstellen Hoch- und Tiefpunkte f (x) = x 2 + 2x f (x) = 6x + 2 Notwendige Bedingung 0 == x 2 + 2x Ι ( ) 0 = x 2 2 x + 1 x 1,2 = 1 ± ( 1 ) 2 1 keine Hoch oder Tiefpunkte vorhanden c) Nullstellen f(x) = x x 2 0 = x x 2 0 = x 2 (x 2 ) 0 = x 1,2 0 = x 2 Ι + = x 2 Ι x = 2 und x = 2 Hoch- und Tiefpunkte f (x) = 16x 8x f (x) = 8x 2 8 Notwendige Bedingung 0 = 16x 8x 0 = x(16x 2 8) 0 = x 1
18 0 = 16x 2 8 Ι = 16x 2 Ι = x2 Ι x 1 = 1 2 und x 2 = 1 2 Hinreichende Bedingung f (0) = 8 Hochpunkt f ( 1 ) = 16 Tiefpunkt 2 f ( 1 ) = 16 Tiefpunkt 2 Punktberechnung f ( 1 2 ) = 1 TP ( 1 2 ; 1) f ( 1 2 ) = 1 TP ( 1 2 ; 1) f(0 ) = 0 HP (0 ; 0) d) Nullstellen f(x) = 1 x 1 x x 2 0 = 1 x 1 x x 2 0 = x 2 ( 1 x2 1 x 1) 0 = x 1,2 0 = 1 x2 1 x 1 Ι 0 = x 2 x x 2, = 1 2 ± ( 1 2 )2 +
19 x 2 = und x = Hoch- und Tiefpunkte f (x) = x x 2 2x f (x) = x 2 2x 2 Notwendige Bedingung 0 = x x 2 2x 0 = x ( x2 x 2) 0 = x 1 0 = x2 x 2 Ι 0 = x 2 x 2 x 2, = 8 ± ( 2 8 ) + 2 x 1 = und x 2 = Hinreichende Bedingung f (0) = 2 Hochpunkt f ( ) 1,66 Tiefpunkt 6 f ( ) 0,91 Hochpunkt 6 Punktberechnung f ( ) 1,75 TP ( ; 1,75) f ( ) 0,5 HP ( ; 0,5) f(0) = 0 HP (0; 0)
20 e) Nullstellen f(x) = ( x 2) 0 = (x 2) Ι ( 1) 0 = (x 2) Ι 0 = x 2 Ι = x 1 Hoch- und Tiefpunkte f (x) = ( x 2) 2 f (x) = 6(x 2) Notwendige Bedingung 0 = ( x 2) 2 Ι ( ) 0 = ( x 2) 2 Ι 0 = x 2 Ι = x 1 Hinreichende Bedingung f (2) = 0 Sattelpunkt Punktberechnung f(0) = 0 SP (0; 0) f) Nullstellen f(x) = (x 2 1) 2 0 = (x 2 1) 2 Ι 0 = x 2 1 Ι = x 2 Ι 1 = x 1, 1 = x 2 Hoch- und Tiefpunkte f (x) = x (x 2 1) f (x) = 12x 2 Notwendige Bedingung
21 0 = x (x 2 1) = x x 0 = x x 0 = x(x 2 ) 0 = x 1 0 = x 2 Ι + = x 2 Ι 1 = x 2 Ι 1 = x 2 und x = 1 f (0) = > 0 HP f (1) = 8 < 0 TP f ( 1) = 8 < 0 TP Punktberechnung f(0) = 1 HP(0; 1) f(1) = 0 TP(1; 0) f( 1) = 0 TP ( 1; 0) g) f(x) = (x 2 2)(x 2 ) Nullstellen 0 = (x 2 2) (x 2 ) 0 = x 2 2 ± 2 = x 1,2 0 = x 2 ±2 = x 2, Hoch- und Tiefpunkte f(x) = (x 2 2)(x 2 ) f(x) = x 6x f (x) = x 12x f (x) = 12 x 2 12 Notwendige Bedingung 0 = x 12x
22 0 = x(x 2 12) 0 = x 1 0 = x 2 12 Ι = x 2 Ι = x 2 Ι = x 2 und = x Hinreichende Bedingung f (0) = 1 < 0 HP f ( ) = 2 > 0 TP f ( ) = 2 > 0 TP Punktberechnung f(0) = 8 HP (0; 8) f( ) = 1 TP ( ; 1) f( ) = 1 TP ( ; 1) h) f(x) = x (x 2 ) Nullstellen 0 = x (x 2 ) 0 = x 1 0 = x 2 Ι + = x 2 Ι 2 = x 2 und 2 = x Hoch- und Tiefpunkt f(x) = x x f (x) = x 2 f (x) = 6x Notwendige Bedingung 0 = x 2 Ι +
23 = x 2 Ι = x2 Ι = x 1 und = x 2 Hinreichende Bedingung f ( ) = 6 > 0 TP f ( ) = = 6 ( ) < 0 HP Punktberechnung f ( ),08 HP ( ;,08) f ( ),08 TP ( ;,08) i) f (x) = x (x + 6)( x 1) Nullstellenberechnung 0 = x (x + 6)( x 1) x 1 = 0, x 2 = 6, x = 1 Hoch- und Tiefpunkte f(x) = (x 2 + 6x)( x 1) = x x 2 + 6x 2 6x = x + 5x 2 6x f (x) = x x 6 f (x) = 6x + 10 Notwendige Bedingung 0 = x x 6 Ι 0 = x x 2 x 1,2 = 5 ± ( 5 ) x 1 0,52 ; x 2,85
24 Hinreichende Bedingung f (0,52) = 1,12 > 0 TP f (,85) = 1,1 < 0 HP Punktberechnung f(0,52) 1,6 TP(0,52 ; 1,6) f(,85) 0,15 HP (,85; 0,15) Aufgabe f(x) = 0,25t 12t 2 + 1t 0 = 0,25t 12t 2 + 1t 0 = t(0,25t 2 12t + 1) 0 = t 1 0 = 0,25t 2 12t + 1 Ι 0 = t 2 8t x 2, = 2 ± (2) x 2, = 2 f (x) = 0,75t 2 2t + 1 f (x) = 1,5 t 2 0 = 0,75t 2 2t + 1 Ι: 0,75 0 = t 2 + 2t x 1,2 = 16 ± (16) x 1 = 8 und x 2 = 2 f (8) = 12 < 0 HP f (2) = 12 > 0 TP f(8) = 512 HP (8; 512) f(2) = 0 TP (2; 0) Die Nullstellen gegeben an, wann kein Wasser mehr in den Stausee zufließt. Einmal zum Zeitpunkt Null, also am Anfang der Messung und am Ende der Messung zum Zeitpunkt 2. Die Extremstellen geben die höchste bzw. niedrigste Zuflussgeschwindigkeiten an. Die Höchste Zuflussgeschwindigkeit ist zum Zeitpunkt 8 erreicht und beträgt 512 m Zuflussgeschwindigkeit ist am Ende der Messung erreicht und beträgt 0 m h. h die niedrigste
25 Aufgabe a) richtig. Zwischen den x-werten 0 und 1 sowie 1 und 2 kann man Vorzeichenwechsel registrieren. b) falsch. Die zweite Ableitung wäre eine Geradenfunktion hätte somit höchstens nur eine Nullstelle. c) Meines Erachtens falsch. Es müsste f (0) < 0 gelten d) falsch. An der Stelle x = 0 hat der Graph eine Nullstelle. Seite 21 Aufgabe 5 a) f (x) negativ, Gerade mit negativer Steigung ; f (x) negativ Parallele zur x Achse b) f (x) positiv, nach oben geöffenete Parabel ; f (x) positiv, Gerade mit positiver Steigung c) f (x) positiv, nach oben geöffnete Parabel; f (x) positiv, Gerade mit positiver Steigung Aufgabe 8 a) Die Extremstellen der Funktion f sind die Nullstellen der ersten Ableitung. Im Intervall [ ; 2] ist die Funktion linksgekrümmt und im Intervall [ 2; ] rechtsgekrümmt. b) Mit GTR lösen Aufgabe 9 a) f(x) = 0,25x x und g(x) = 0,2x 5 0,75x f (x) = x x 2 0 = x x 2 0 = x 2 (x ) 0 = x 1 0 = x Ι + = x 2 g (x) = x x 0 = x (x ) 0 = x 1
26 0 = x Ι + = x 2 b) f (x) = x 2 6x f (0) = 0 Sattelpunkt f () = 9 Tiefpunkt g (x) = x 9x 2 g (0) = 0 Sattelpunkt g () = 27 Tiefpunkt c) Mit GTR lösen Aufgabe 10 a) f(x) = x 2 b) f(x) =? c) f(x) = x d) f(x) = sin (x) e) Mit dem GTR Aufgabe 11 a) Richtig, weil es sich um eine Parabel handelt. b) Richtig c) Richtig d) Das gilt aber nicht immer. Seite 22 Aufgabe 12
27 Seite 187 Aufgabe a) Überprüfung der Richtungsvektoren: 2 6 ( 1 ) = k ( ) 1 2 = 6k Ι ( 6) 1 = k Ι ( ) 1 = k Ι 1 = k 1 = k 1 = k Somit sind die Geraden parallel zueinander oder identisch Überprüfung ob die Geraden parallel sind: ( 0) = ( 1) + t ( ) Ι ( 1) ( 1) = t ( ) 1 2 = 6t Ι ( 6) 1 = t Ι ( ) 1 = t Ι 1 = t 1 = t 1 = t Da die Skalare Größen nicht übereinstimmen sind die Geraden parallel. b) Überprüfung der Richtungsvektoren: 2 0 ( 0) = k ( 1 ) = 0 0 = k 1 = k Somit schneiden sich die Geraden oder sind windschief zueinander. Überprüfung ob sich die Geraden schneiden: s ( 0) = ( ) + t ( 1 ) Ι t ( 1 ) s ( 0) t ( 1 ) = ( ) 1 1 I. 2 s = 2 Ι (2) II. t = Ι ( 1) III. s + t = t = und s = 1 in III. einsetzen III. 1 + ( ) = 2 = Widerspruch Somit sind die Geraden windschief zueinander.
28 c) Überprüfung der Richtungsvektoren: 1 2 ( 0) = k ( 1) = 2k 0 = k 1 = k Somit schneiden sich die Geraden oder sind windschief zueinander. Überprüfung ob sich die Geraden schneiden: ( 1) + s ( 0) = ( 2) + t ( 1) Ι t ( 1) Ι ( 1) s ( 0) t ( 1) = ( 2) ( 1) I. s 2t = II. t = 1 Ι ( 1) III. s t = t = 1; t in III. einsetzen: II. s ( 1) = Ι 1 s = 2 t und s in III. einsetzen I. 2 2( 1) = = = Somit schneiden sich die Geraden. Berechnung des Schnittpunktes t in Gerade h einsetzen: 2 2 h: x = ( 2) + ( 1) ( 1) = ( 1) 1 Der Schnittpunkt lautet S (2/1/) d) Überprüfung der Richtungsvektoren: 1 0,5 ( 2) = k ( ) 1 = 0,5 k Ι ( 0,5) 2 = k 2 = k 0 = 0 k Somit schneiden sich die Geraden oder sind windschief zueinander. Überprüfung ob sich die Geraden schneiden: ,5 0,5 5 ( 5) + s ( 2) = ( 15) + t ( 1 ) Ι t ( 1 ) Ι ( 5)
29 1 0,5 5 5 s ( 2) t ( 1 ) = ( 15) ( 5) I. s + 0,5t = 10 II. 2s t = 20 Ι + 2 I III. 0 = 0 2s + 2s t + t = s = 0 Ι s = 10 s in II. einsetzen. II. 2 ( 10) t = t = 20 Ι + 20 t = 0 t = 0 t und s in I. einsetzen II ,5 0 = = 10 Somit schneiden sich die Geraden. Berechnung des Schnittpunktes t in Gerade h einsetzen: 5 0,5 5 h: x = ( 15) + 0 ( ) = ( 15) 1 Der Schnittpunkt lautet S (-5/-15/1) S.188 Aufgabe 1 a) Entfernung von Punkt A und C: ΙAC Ι = (10 2) 2 + (15 5) 2 + (1) 2 ΙAC Ι = (8) 2 + (10) 2 + (1) 2 = ,85 Der Punkt C 12,85 km vom Startplatz A entfernt. b) Überprüfung der Richtungsvektoren. Zuerst muss man jedoch den Richtungsvektor des Ballons aufstellen. 2 AB = ( 8 5) 1
30 2 AB = ( ) 1 Überprüfung der Richtungsvektoren: 0 2 ( 60) = k ( ) = 2k Ι 2 60 = k Ι 60 = k 15 = k 20 = k 60 = k Somit schneiden sich die Geraden oder sind windschief zu einander. Also es könnte zu einer Kollision kommen. Überprüfung ob sich die Geraden schneiden: ( 5) + s ( ) = ( 15) + t ( 60) Ι t ( 60) Ι ( 5) s ( ) t ( 60) = ( 15) ( 5) s ( ) t ( 60) = ( 10) I. 2s + 0t = 8 II. s + 60t = 10 III. s 60t = 1 II. + III. s = 11 Ι s = 11 s in III. einsetzen: t = 1 Ι 60 t = 1,75 Ι ( 60)
31 t = 7 20 s und t in I. einsetzen: = = 8 Somit sind die Geraden windschief zu einander. Die Flugobjekte werden nicht kollidieren. c) Die Koordinaten sind in Kilometer angegeben und die Veränderung der Positionen wurde in Stunden gemessen. Die Geschwindigkeit wird dann Kilometer pro Stunde (km/h) angeben. Länge des Richtungsvektors des Ballons: ΙAB Ι = (2) 2 + () 2 + (1) 2 = 1,7 Der Ballon fliegt mit meiner Geschwindigkeit von,7 km/h. Länge des Richtungsvektors des Flugzeugs: Ιu Ι = ( 0) 2 + ( 60) 2 + (60) 2 = 8100 = 90 Das Flugzeug fliegt mit einer Geschwindigkeit von 90 km/h. Seite 22 Aufgabe 6 a) Aufstellen einer Geradengleichung: 9 g AB : x = ( 5) + t ( 7 5) g AB : x = ( 5) + t ( 2) 7 0 b) Aufstellen einer Ebenengleichung: 6 2 E: x = ( 5) + t ( 2) + s ( 6) 7 0 c) Überprüfung der Spanvektoren:
32 6 2 ( 2) ( 6) = ( 6) + 0 ( ) = 0 0 Da das Skalarprodukt Null ist, sind die Spanvektoren rechtswinklig zu einander. Mit anderen Worten, die Eimerketten und die Fahrtrichtung des Baggers sind senkrecht zu einander. d) 6 2 E: x = ( 5) + t ( 2) + s ( 6) 7 0 Anpassung des Vektors der Fahrtrichtung: 6 18 ( 2) = ( 6 ) 0 0 Länge des Vektors u : Ιu Ι = (2) 2 + ( 6) 2 + ( ) 2 = 7 LE Anpassung des Vektors der Eimerketten: ( 6) = ( 0) E 1 : x = ( 5) + t ( 6 ) + s ( 0) Für t = 1 und s = 1 erhält man die Längen des Ebenenstücks. Seite 2 Aufgabe 1 0 a) E: x 2 + x = 0 n = ( ) Für Punkt A gilt dann: 0 g A : x = ( 1) + t ( ) 7 in E einsetzen: ( 1 + t) + ( 7 + t) = 0 + 9t t = 0
33 t = 0 Ι 25 Ι 25 t = 1 Lotfußpunkt (F) berechnen: 0 g A : x = ( 1) + ( 1) ( ) = ( ) 7 Berechnung des Abstandes Punkt / Ebene: ΙAF Ι = ( ) 2 + ( + 1) 2 + ( 7) 2 = 5 LE Für Punkt B gilt: Ι ( p b ) n 0 Ι = d Berechnung des Einheitsvektors der Normale: Ιn Ι = (0) 2 + () 2 + (5) 2 = 5 n 0 = Punkt P auf der Ebene als Ortsvektor: 2 ( ) ( ) Berechnung des Abstandes Punkt zur Ebene: 2 6 [( ) ( 8 )] = d [( 12)] ( ) = d ( ) Ι Ι = 20 = d 5 Für Punkt C gilt:
34 Berechnung des Abstandes Punkt zur Ebene: 2 [( ) ( )] = d ( ) 5 [( 1)] = d ( ) = 5 = d b) Berechnung des Einheitsvektors der Normale: Ιn Ι = (12) 2 + (6) 2 + ( ) 2 = 16 n 0 = 8 1 Punkt auf der Ebene berechnen: ( ) 1 12 [x ( 2,5)] ( 6 ) = 0 x = ( 0,5),5 6,5 Für Punkt A:
35 2 [( 0,5) ( 0 )] 6,5 8 1 = d ( ) 5 [( 0,5)],5 8 1 = ,5 8,5 = 9 16 = d ( ) Für Punkt B: 1 [( 0,5) ( 8,5 )] 6,5 0, = [( 8 )] = = Ι 12Ι = 12 = d ( ) ( ) Für Punkt C: [( 0,5) ( 20 )] 6,5 1, = [ ( 20,5 )] 7, = , ,75 = 29 8 = d ( ) ( ) c) Normale berechnen mit dem Kreuzprodukt der Spannvektoren: n = ( 1 ( 1) + 5 0) = ( 1 ) ( 1) 5 n 0 = ( 26)
36 6 Punkt auf der Ebene mit s= 1 und r = 1 ( 6 ) Für Punkt A gilt dann: 6 2 [( 6 ) ( )] = [ ( 2 )] 5 16 ( 26) ( 26) = = = d Für Punkt B gilt dann: 6 8 [( 6 ) ( 6 )] ( 26)
Abitur Mathematik Baden-Württemberg 2012
 Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Analysis: Klausur Analysis
 Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
 Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
K2 MATHEMATIK KLAUSUR 2. Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
K2 MATHEMATIK KLAUSUR 2 06.12.2013 Aufgabe PT WTA WTGS Darst. Gesamtpunktzahl Punkte (max 27 15 15 3 60 Punkte Notenpunkte PT 1 2 3 4 5 6 7 8 P. (max 2 3 2 4 5 3 4 4 Punkte WT Ana a b Summe P. (max 8 7
Lösungen zur Prüfung 2014: Pflichtteil
 Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Teil A hilfsmittelfreier Teil
 Klassenarbeit GYM Klasse 10 Seite 1 Datum: Thema: Ableitungen Name: Zeit: Erreichte Punkte: Note: Hilfsmittel: keine Teil A hilfsmittelfreier Teil Aufgabe 1: (6 Punkte) Bestimme jeweils mithilfe geeigneter
Klassenarbeit GYM Klasse 10 Seite 1 Datum: Thema: Ableitungen Name: Zeit: Erreichte Punkte: Note: Hilfsmittel: keine Teil A hilfsmittelfreier Teil Aufgabe 1: (6 Punkte) Bestimme jeweils mithilfe geeigneter
Analysis. Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente. Gymnasium Klasse 10
 Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Analysis Ganzrationale Funktionen: Nullstellen, Extrempunkte, Monotonie, Verhalten im Unendlichen, Tangente Gymnasium Klasse 1 Hilfsmittel: wissenschaftlicher Taschenrechner Alexander Schwarz März 18 1
Lösungsvorschlag Vorbereitung KA2 K
 Lösungsvorschlag Vorbereitung KA K 4..7 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet
Lösungsvorschlag Vorbereitung KA K 4..7 Pflichtteil (etwa 40 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet
Mathematisches Thema Quadratische Funktionen 1. Art Anwenden. Klasse 10. Schwierigkeit x. Klasse 10. Mathematisches Thema
 Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
Förderaufgaben EF Arbeitsblatt 1 Abgabe Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung.
 Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Lagebeziehung von Ebenen
 M8 ANALYSIS Lagebeziehung von Ebenen Es gibt Möglichkeiten für die Lagebeziehung zwischen zwei Ebenen. Die Ebenen sind identisch. Die Ebenen sind parallel. Die Ebenen schneiden sich in einer Geraden Um
M8 ANALYSIS Lagebeziehung von Ebenen Es gibt Möglichkeiten für die Lagebeziehung zwischen zwei Ebenen. Die Ebenen sind identisch. Die Ebenen sind parallel. Die Ebenen schneiden sich in einer Geraden Um
MATHEMATIK KLAUSUR V. Gesamtpunktzahl /30 Notenpunkte. (1) Bestimmen Sie die erste Ableitung der folgenden Funktionen: f(x) = 3x sin(x) + x ln(2x)
 MATHEMATIK KLAUSUR V 296216 Aufgabe 1 2 3 4 5 6 7 8 9 Punkte (max 4 2 3 3 3 3 5 6 1 Punkte Gesamtpunktzahl /3 Notenpunkte (1 Bestimmen Sie die erste Ableitung der folgenden Funktionen: (2 Berechnen Sie
MATHEMATIK KLAUSUR V 296216 Aufgabe 1 2 3 4 5 6 7 8 9 Punkte (max 4 2 3 3 3 3 5 6 1 Punkte Gesamtpunktzahl /3 Notenpunkte (1 Bestimmen Sie die erste Ableitung der folgenden Funktionen: (2 Berechnen Sie
Analysis: Trigonometr. Funktionen Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben
 Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
Analysis Trigonometrische Funktionen Pflicht- und Wahlteilaufgaben Gymnasium Oberstufe J oder J Alexander Schwarz www.mathe-aufgaben.com Dezember 0 Pflichtteilaufgaben (ohne GTR): Aufgabe : Leite die folgenden
2) 2 4 in der größtmöglichen Definitionsmenge
 Abschlussprüfung Berufliche Oberschule 009 Mathematik 13 Nichttechnik - A I - Lösung Teilaufgabe 1.0 Gegeben ist die Funktion f( x) ln ( x ) 4 in der größtmöglichen Definitionsmenge D f IR. Ihr Graph wird
Abschlussprüfung Berufliche Oberschule 009 Mathematik 13 Nichttechnik - A I - Lösung Teilaufgabe 1.0 Gegeben ist die Funktion f( x) ln ( x ) 4 in der größtmöglichen Definitionsmenge D f IR. Ihr Graph wird
KOMPETENZHEFT ZU STAMMFUNKTIONEN
 KOMPETENZHEFT ZU STAMMFUNKTIONEN 1. Aufgabenstellungen Aufgabe 1.1. Finde eine Funktion F (x), die F (x) = f(x) erfüllt. a) f(x) = 5 x 2 2 x + 8 e) f(x) = 1 + x x 2 b) f(x) = 1 x4 10 f) f(x) = e x + 2
KOMPETENZHEFT ZU STAMMFUNKTIONEN 1. Aufgabenstellungen Aufgabe 1.1. Finde eine Funktion F (x), die F (x) = f(x) erfüllt. a) f(x) = 5 x 2 2 x + 8 e) f(x) = 1 + x x 2 b) f(x) = 1 x4 10 f) f(x) = e x + 2
K2 MATHEMATIK KLAUSUR 3
 K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
K2 MATHEMATIK KLAUSUR 3 NACHTERMIN 2..23 Aufgabe PT WTA WTGS Gesamtpunktzahl Punkte (max 3 5 5 6 Punkte Notenpunkte PT 2 3 4 5 6 7 8 9 P. (max 2 2 3 4 5 3 4 4 3 Punkte WT Ana a b c Summe P. (max 8 4 3
Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS. 16. Jänner Mathematik. Teil-2-Aufgaben. Korrekturheft
 Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS 16. Jänner 2018 Mathematik Teil-2-Aufgaben Korrekturheft Aufgabe 1 Funktion a) Lösungserwartung: Mögliche Vorgehensweise: f (x) = 2 a
Standardisierte kompetenzorientierte schriftliche Reifeprüfung AHS 16. Jänner 2018 Mathematik Teil-2-Aufgaben Korrekturheft Aufgabe 1 Funktion a) Lösungserwartung: Mögliche Vorgehensweise: f (x) = 2 a
Hauptprüfung 2007 Aufgabe 3
 Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Hauptprüfung Abiturprüfung 2017 (ohne CAS) Baden-Württemberg
 Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Hauptprüfung Abiturprüfung 217 (ohne CAS) Baden-Württemberg Wahlteil Analysis A2 Hilfsmittel: GTR und Merkhilfe allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com Mai 217 1 Aufgabe A
Hauptprüfung Abiturprüfung Baden-Württemberg
 Hauptprüfung Abiturprüfung 18 Baden-Württemberg Teil 4: Hilfsmittel WTR und Merkhilfe Vektorgeometrie berufliche Gymnasien (AG, BTG, EG, SG, TG, WG) Alexander Schwarz www.mathe-aufgaben.com Juni 18 1 Lineare
Hauptprüfung Abiturprüfung 18 Baden-Württemberg Teil 4: Hilfsmittel WTR und Merkhilfe Vektorgeometrie berufliche Gymnasien (AG, BTG, EG, SG, TG, WG) Alexander Schwarz www.mathe-aufgaben.com Juni 18 1 Lineare
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
LÖSUNGEN Kurvendiskussion
 M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
Abschlussprüfung Mathematik 12 Nichttechnik A I - Lösung
 GS.06.0 - m_nt-a_lsg_gs.pdf Abschlussprüfung 0 - Mathematik Nichttechnik A I - Lösung Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( x) D f = IR. x x x mit der Definitionsmenge Teilaufgabe. (7
GS.06.0 - m_nt-a_lsg_gs.pdf Abschlussprüfung 0 - Mathematik Nichttechnik A I - Lösung Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( x) D f = IR. x x x mit der Definitionsmenge Teilaufgabe. (7
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
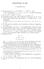 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Lösungserwartungen und Lösungsschlüssel zur 4. M-Schularbeit. ja nein ja nein ja nein
 Lösungserwartungen und Lösungsschlüssel zur 4. M-Schularbeit 6. Klasse I) Mathematische Grundkompetenzen 1) Lösung: S x = ( 1 3 0 ) S y = ( 0-10 ) 2 Punkte für die richtigen Schnittpunkte. 2) Lösung: x
Lösungserwartungen und Lösungsschlüssel zur 4. M-Schularbeit 6. Klasse I) Mathematische Grundkompetenzen 1) Lösung: S x = ( 1 3 0 ) S y = ( 0-10 ) 2 Punkte für die richtigen Schnittpunkte. 2) Lösung: x
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation
 5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Anwendungsaufgaben zur Vektorrechnung (Abstände bestimmen)
 Anwendungsaufgaben zur Vektorrechnung (Abstände bestimmen) 1) a) Ein Flugzeug fliegt von A(4; 2; 5) nach B(12; 6; 10). In S(10; 10; 4,75) befindet sich die Spitze eines Berges. Wie weit fliegt das Flugzeug
Anwendungsaufgaben zur Vektorrechnung (Abstände bestimmen) 1) a) Ein Flugzeug fliegt von A(4; 2; 5) nach B(12; 6; 10). In S(10; 10; 4,75) befindet sich die Spitze eines Berges. Wie weit fliegt das Flugzeug
1. Fall: 2. Fall: Lösungsblatt zu: Differentialquotient. Tipp: Nullstellen. Tipp: Es reicht, wenn einer der Faktoren Null wird.
 Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
( 0 ( x) d) Die Funktionsgleichung der Funktion 1 lautet: f( Für x 2 = 0 : Wähle die Werte -1 und 1. Überprüfe x1 = 1,
 Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Mathematik GK m1/m2/m3, 2. Kl. Funktionenuntersuchung Lösung A
 Aufgabe 1: Kurvendiskussion Führe eine vollständige Funktionsuntersuchung für die Funktion f x = 1 2 x5 1 4 x4 3 2 x3 durch. Dazu gehören alle Teilaufaben, wie sie im Unterricht besprochen wurden und auf
Aufgabe 1: Kurvendiskussion Führe eine vollständige Funktionsuntersuchung für die Funktion f x = 1 2 x5 1 4 x4 3 2 x3 durch. Dazu gehören alle Teilaufaben, wie sie im Unterricht besprochen wurden und auf
Polynome. Ein Term der Form. mit n und a 0 heißt Polynom. Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms.
 Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Zusammenfassung Abitursstoff Mathematik
 Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Abkürzungen & Begriffe
 A Bedeutungen Abkürzungen & Begriffe Abzisse ist ein normaler x-wert [ Ordinate] arcsin, arccos, arctan sind die korrekten Bezeichnungen für: sin -, cos -, tan -. [Die üblichen Bezeichnungen sin -, cos
A Bedeutungen Abkürzungen & Begriffe Abzisse ist ein normaler x-wert [ Ordinate] arcsin, arccos, arctan sind die korrekten Bezeichnungen für: sin -, cos -, tan -. [Die üblichen Bezeichnungen sin -, cos
K2 MATHEMATIK KLAUSUR 4. Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
Übungsaufgaben Analysis hilfsmittelfrei
 Übungsaufgaben Analysis hilfsmittelfrei Aufgabe 1 Der Graph der Funktion f (x) = 0,5x3+ 1,5x2+ 4,5x 3,5 hat im Punkt T( 1 6) einen relativen (lokalen) Tiefpunkt und im Punkt H(3 10) einen relativen (lokalen)
Übungsaufgaben Analysis hilfsmittelfrei Aufgabe 1 Der Graph der Funktion f (x) = 0,5x3+ 1,5x2+ 4,5x 3,5 hat im Punkt T( 1 6) einen relativen (lokalen) Tiefpunkt und im Punkt H(3 10) einen relativen (lokalen)
Bayern Musterlösung zu Klausur Analysis, Aufgabengruppe I
 Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Selbsteinschätzungstest Auswertung und Lösung
 Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Mathematik im Berufskolleg II
 Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
5. Probeklausur - Lösung
 EI M5 2011-12 MATHEMATIK 5. Probeklausur - Lösung 1. Aufgabe (2 Punkte) Bilde die erste Ableitung der Funktion f mit sin für reelle Zahlen x. Hier haben wir unter der Wurzel noch eine Funktion, daher benutzen
EI M5 2011-12 MATHEMATIK 5. Probeklausur - Lösung 1. Aufgabe (2 Punkte) Bilde die erste Ableitung der Funktion f mit sin für reelle Zahlen x. Hier haben wir unter der Wurzel noch eine Funktion, daher benutzen
Abitur 2013 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
Abitur 2010 Mathematik LK Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.
 1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
1 Abiturprüfung Mathematik 2017 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analysis A 2 Lösungen der Aufgaben A 2.1 und A 2.2 klaus_messner@web.de www.elearning-freiburg.de 2 Aufgabe A 2.1
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit x f(x) = (x + 5) e. Aufgabe : ( VP) Gegeben ist die Funktion
Ü b u n g s a r b e i t
 Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Abschlussaufgabe Nichttechnik - Analysis II
 Analysis NT GS - 0.06.06 - m06_ntalsg_gs.mcd Abschlussaufgabe 006 - Nichttechnik - Analysis II.0 Gegeben sind die reellen Funktionen fx ( ) mit ID f = ID g = IR. ( ) = x und gx ( ) = fx ( ) +. Zeigen Sie,
Analysis NT GS - 0.06.06 - m06_ntalsg_gs.mcd Abschlussaufgabe 006 - Nichttechnik - Analysis II.0 Gegeben sind die reellen Funktionen fx ( ) mit ID f = ID g = IR. ( ) = x und gx ( ) = fx ( ) +. Zeigen Sie,
. Ihr Schaubild sei &. a) Geben Sie die Asymptoten von & an. b) Bestimmen Sie den Schnittpunkt der Tangente an & im Punkt 1 1 mit der Achse.
 Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
K2 KLAUSUR 2. Aufgabe Punkte (max) Punkte. (1) Bestimmen Sie die Ableitung von f(x) = 2 x
 K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Prüfungsteil 1, Aufgabe 3. Analysis. Nordrhein-Westfalen 2012 GK. Aufgabe a (1) Aufgabe a (2) Abitur Mathematik: Musterlösung
 Abitur Mathematik: Prüfungsteil 1, Aufgabe 3 Nordrhein-Westfalen 2012 GK Aufgabe a (1) 1. SCHRITT: BEDINGUNG FÜR PUNKTSYMMETRIE ZUM URSPRUNG PRÜFEN Der Graph der Funktion : ist genau dann punktsymmetrisch
Abitur Mathematik: Prüfungsteil 1, Aufgabe 3 Nordrhein-Westfalen 2012 GK Aufgabe a (1) 1. SCHRITT: BEDINGUNG FÜR PUNKTSYMMETRIE ZUM URSPRUNG PRÜFEN Der Graph der Funktion : ist genau dann punktsymmetrisch
Pflichtteil Pflichtteil Pflichtteil Abiturprüfung Mathematik 2013 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen Pflichtteil Aufgabe : Bilden Sie die erste Ableitung der Funktion mit +5 ( VP) Verwende Produkt- und Kettenregel
Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen Pflichtteil Aufgabe : Bilden Sie die erste Ableitung der Funktion mit +5 ( VP) Verwende Produkt- und Kettenregel
(Quelle Abitur BW 2004) Gegeben sind die Schaubilder der Funktion mit, ihrer Ableitungsfunktion, einer Stammfunktion von und der Funktion mit.
 Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
Eigenschaften von Funktionen
 Eigenschaften von Funktionen Mag. Christina Sickinger HTL v 1 Mag. Christina Sickinger Eigenschaften von Funktionen 1 / 48 Gegeben sei die Funktion f (x) = 1 4 x 2 1. Berechnen Sie die Steigung der Funktion
Eigenschaften von Funktionen Mag. Christina Sickinger HTL v 1 Mag. Christina Sickinger Eigenschaften von Funktionen 1 / 48 Gegeben sei die Funktion f (x) = 1 4 x 2 1. Berechnen Sie die Steigung der Funktion
3.3 Linkskurve, Rechtskurve Wendepunkte
 166 FUNKTIONSUNTERSUCHUNGEN 3.3 Linkskurve, Rechtskurve Wendepunkte Einführung (1) Anschauliche Erklärung des Begriffs Wendepunkt Bei Motorradrennen lässt sich beobachten, wie sich die Motorradfahrer beim
166 FUNKTIONSUNTERSUCHUNGEN 3.3 Linkskurve, Rechtskurve Wendepunkte Einführung (1) Anschauliche Erklärung des Begriffs Wendepunkt Bei Motorradrennen lässt sich beobachten, wie sich die Motorradfahrer beim
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Funktionstypen und ihre Schaubilder 1
 Funktionstypen und ihre Schaubilder 1 Funktionen können Nullstellen, Extremstellen, Sattelstellen, Wendestellen, Polstellen bzw. deren Schaubilder (Kurven) können Schnittpunkte mit der x-achse, Extrempunkte
Funktionstypen und ihre Schaubilder 1 Funktionen können Nullstellen, Extremstellen, Sattelstellen, Wendestellen, Polstellen bzw. deren Schaubilder (Kurven) können Schnittpunkte mit der x-achse, Extrempunkte
Inhalt der Lösungen zur Prüfung 2011:
 Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Inhalt der Lösungen zur Prüfung : Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 6 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 6 Pflichtteil Lösungen zur Prüfung
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung
 Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
Abschlussprüfung Berufliche Oberschule 2017 Mathematik 12 Nichttechnik - A I - Lösung
 Abschlussprüfung Berufliche Oberschule Mathematik Nichttechnik - A I - Lösung Teilaufgabe. Gegeben ist die ganzrationale Funktion g dritten Grades mit D g IR, deren Graph G g in untenstehender Abbildung
Abschlussprüfung Berufliche Oberschule Mathematik Nichttechnik - A I - Lösung Teilaufgabe. Gegeben ist die ganzrationale Funktion g dritten Grades mit D g IR, deren Graph G g in untenstehender Abbildung
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Abituraufgaben allg. bildendes Gymnasium Pflichtteil 2007 BW Aufgabe A1
 Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 1. Aufgabe A2 Berechnen Sie das Integral. Aufgabe A3 Lösen Sie die Gleichung 2 0. Aufgabe A4 Gegeben ist die Funktion mit. a) Bestimmen Sie die Punkte
Aufgabe A1 Bilden Sie die Ableitung der Funktion mit 1. Aufgabe A2 Berechnen Sie das Integral. Aufgabe A3 Lösen Sie die Gleichung 2 0. Aufgabe A4 Gegeben ist die Funktion mit. a) Bestimmen Sie die Punkte
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
G13 KLAUSUR 1. (1) (2 VP) Bilden Sie die erste Ableitung der Funktion f mit. f(x) = e 2x+1 x
 G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
Baden-Württemberg: Abitur 2014 Pflichtteil Lösungen. Für die Ableitungsfunktion werden die Produkt- und Kettenregel benötigt:
 Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Lösungen Aufgabe : Zunächst wird die Funktionsgleichung von f umgeschrieben in 0,5 x f(x) = x e Für die Ableitungsfunktion werden die Produkt-
Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Lösungen Aufgabe : Zunächst wird die Funktionsgleichung von f umgeschrieben in 0,5 x f(x) = x e Für die Ableitungsfunktion werden die Produkt-
Vektorgeometrie. 1. Vektoren eingeben, Norm, Skalarprodukt. 2 In einem kartesischen Koordinatensystem sind die Vektoren. , v. und. gegeben.
 Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
Vektorgeometrie 1. Vektoren eingeben, Norm, Skalarprodukt 2 In einem kartesischen Koordinatensystem sind die Vektoren u 14, 5 11 10 v 2 und w 5 gegeben. 10 10 a) Zeigen Sie, dass die Vektoren einen Würfel
Vollständige Kurvendiskussion mit Erläuterungen
 Vollständige Kurvendiskussion mit Erläuterungen Aufgabe: Gegeben ist die Funktion =³ 3 +. Führen Sie eine vollständige Kurvendiskussion durch. 1.) Ableitungen: =3 6+1 =6 6 =6 (relevant für die Steigung
Vollständige Kurvendiskussion mit Erläuterungen Aufgabe: Gegeben ist die Funktion =³ 3 +. Führen Sie eine vollständige Kurvendiskussion durch. 1.) Ableitungen: =3 6+1 =6 6 =6 (relevant für die Steigung
Die Funktion ist gegeben durch ; 0. a) Die Tangente an den Graphen von im Punkt verläuft durch 0 0,5. Bestimmen Sie die Koordinaten von.
 Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
Hauptprüfung Fachhochschulreife Baden-Württemberg
 Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Hauptprüung Fachhochschulreie 204 Baden-Württemberg Augabe 2 Analysis Hilsmittel: graikähiger Taschenrechner Beruskolleg Alexander Schwarz www.mathe-augaben.com September 204 Gegeben ist die Funktion mit
Abitur 2011 G8 Musterabitur Mathematik Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur G Musterabitur Mathematik Geometrie V In einem kartesischen Koordinatensystem beschreibt die x x -Ebene eine flache Landschaft, in der sich ein Flughafen
Seite http://www.abiturloesung.de/ Seite Abitur G Musterabitur Mathematik Geometrie V In einem kartesischen Koordinatensystem beschreibt die x x -Ebene eine flache Landschaft, in der sich ein Flughafen
Differentialrechnung. Mathematik W14. Christina Sickinger. Berufsreifeprüfung. v 1 Christina Sickinger Mathematik W14 1 / 79
 Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
Abitur 2010 Mathematik GK Geometrie VI
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik GK Geometrie VI In einem kartesischen Koordinatensystem mit Ursprung O sind die Punkte A( ), B( ) und die Gerade g : x = O A + λ, λ R, gegeben.
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik GK Geometrie VI In einem kartesischen Koordinatensystem mit Ursprung O sind die Punkte A( ), B( ) und die Gerade g : x = O A + λ, λ R, gegeben.
MATHEMATIK K1 EINSTIEGSARBEIT (OHNE GTR)
 MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
Aufgabe 2: Analysis (WTR)
 Abitur Mathematik: Nordrhein-Westfalen 2013 Aufgabe 2 a) (1) STARTPUNKT BERECHNEN Der x Wert des Startpunktes ist mit 8 gegeben. Der zugehörige y Wert ist 8 1 50 8 3 106 8 4,24. 4 25 Der Startpunkt liegt
Abitur Mathematik: Nordrhein-Westfalen 2013 Aufgabe 2 a) (1) STARTPUNKT BERECHNEN Der x Wert des Startpunktes ist mit 8 gegeben. Der zugehörige y Wert ist 8 1 50 8 3 106 8 4,24. 4 25 Der Startpunkt liegt
Wahlteil: Analysis I 1
 Abitur Mathematik: Wahlteil: Analysis I 1 Baden-Württemberg 2012 Aufgabe I 1 a) 1. SCHRITT: KOORDINATEN DES NÖRDLICHSTEN PUNKTES N BESTIMMEN Der nördlichste Punkt N entspricht dem Hochpunkt des Graphen
Abitur Mathematik: Wahlteil: Analysis I 1 Baden-Württemberg 2012 Aufgabe I 1 a) 1. SCHRITT: KOORDINATEN DES NÖRDLICHSTEN PUNKTES N BESTIMMEN Der nördlichste Punkt N entspricht dem Hochpunkt des Graphen
c) Am Punkt R( ) ändert das U-Boot seine Fahrtrichtung und fährt in Richtung des Vektors w = 13
 Lineare Algebra / Analytische Geometrie Grundkurs Aufgabe 9 U-Boot Während einer Forschungsfahrt tritt ein U-Boot am Punkt P(100 0 540) alle Angaben in m in den Überwachungsbereich seines Begleitschiffes
Lineare Algebra / Analytische Geometrie Grundkurs Aufgabe 9 U-Boot Während einer Forschungsfahrt tritt ein U-Boot am Punkt P(100 0 540) alle Angaben in m in den Überwachungsbereich seines Begleitschiffes
Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR.
 Lösung A1.1 Lösungslogik GTR-Einstellungen: Y1=6000, Y2= 1 Y3=4000 Y4= 1 Y5=5000 Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR. Zeitraum Änderungsrate
Lösung A1.1 Lösungslogik GTR-Einstellungen: Y1=6000, Y2= 1 Y3=4000 Y4= 1 Y5=5000 Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR. Zeitraum Änderungsrate
(x 1. Vektoren. g: x = p + r u. p r (u1. x 2. u 2. p 2
 Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Mathematische Behandlung der Natur- und Wirtschaftswissenschaften I. f(x) := e x + x.
 Technische Universität München WS 009/0 Fakultät für Mathematik Prof. Dr. J. Edenhofer Dipl.-Ing. W. Schultz Übung Lösungsvorschlag Mathematische Behandlung der Natur- und Wirtschaftswissenschaften I Aufgabe
Technische Universität München WS 009/0 Fakultät für Mathematik Prof. Dr. J. Edenhofer Dipl.-Ing. W. Schultz Übung Lösungsvorschlag Mathematische Behandlung der Natur- und Wirtschaftswissenschaften I Aufgabe
Standards Differentialrechnung (Vorschlag erarbeitet von Melanie Schönauer im Rahmen einer FBA/ 0809; Betreuung der FBA durch Dr.
 Standards Differentialrechnung (Vorschlag erarbeitet von Melanie Schönauer im Rahmen einer FBA/ 0809; Betreuung der FBA durch Dr. Walter Mayer) 1. Der Punkt P(1/y) liegt auf dem Graphen der Funktion f(x)
Standards Differentialrechnung (Vorschlag erarbeitet von Melanie Schönauer im Rahmen einer FBA/ 0809; Betreuung der FBA durch Dr. Walter Mayer) 1. Der Punkt P(1/y) liegt auf dem Graphen der Funktion f(x)
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 7 Wahlteil Analysis Wahlteil Analysis 7 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 8 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Bestimmen Sie jeweils die Lösungsmenge der Gleichung: 1. Bestimmen Sie jeweils die Lösungsmenge der Gleichung:
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
Abiturprüfung Mathematik Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil Aufgabe : Bilden Sie die Ableitung der Funktion f
K2 KLAUSUR MATHEMATIK
 K2 KLAUSUR MATHEMATIK NACHTERMIN 16.02.2012 Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 (max) 2 2 3 4 5 3 4 3 Wahlteil Analysis Aufgabe a b c (max) 10 3 5 Wahlteil Geometrie Aufgabe a b c (max) 7 4 5 Gesamtpunktzahl
K2 KLAUSUR MATHEMATIK NACHTERMIN 16.02.2012 Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 (max) 2 2 3 4 5 3 4 3 Wahlteil Analysis Aufgabe a b c (max) 10 3 5 Wahlteil Geometrie Aufgabe a b c (max) 7 4 5 Gesamtpunktzahl
