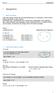
A b, d, B a, b, c, d, e somit gilt: A B. A 4, 5, 6, B 4, 5, 6 somit gilt: A B

Transkript

1 1 1.1 egriff der Menge Unter einer Menge versteht man die Zusammenfassung von voneinander unterscheidbaren Dingen (Elementen) zu einem Ganzen. Eine Menge kann in aufzählender Form, mithilfe eines Mengenbildes (Venn-Diagramm) oder in beschreibender Form angegeben werden. Dabei bezeichnen wir Mengen mit grossen uchstaben, die Elemente von Mengen meist mit kleinen uchstaben. eispiel ufzählende Form = {a, b, c} a ist Element von (man schreibt: a ) b ist Element von (man schreibt: b ) c ist Element von (man schreibt: c ) d ist nicht Element von (man schreibt: d ) Mengenbild (Venn-Diagramm) a b c 1.2 eziehungen zwischen Mengen Teilmenge ist eine Teilmenge von, falls jedes Element von auch Element von ist. (man schreibt: ) a c b d e eispiel b, d, a, b, c, d, e somit gilt: chtung Jede Menge ist Teilmenge von sich selbst: Die leere Menge ist Teilmenge jeder Menge: und leere Menge Gleichheit von Mengen Zwei Mengen und sind gleich, wenn sie dieselben Elemente enthalten. (man schreibt: ) eispiel 4, 5, 6, 4, 5, 6 somit gilt: 1

2 1.3 Verknüpfungen von Mengen (Mengenoperationen) Durchschnittsmenge Die Durchschnittsmenge der beiden Mengen und ist die Menge aller Elemente, die zu und zu gehören. x x x logische 'und' man liest: «gleich geschnitten mit ist die Menge aller x für die gilt, x ist Element von und x ist Element von» Vereinigungsmenge Die Vereinigungsmenge der beiden Mengen und ist die Menge aller Elemente, die zu oder zu oder zu beiden Mengen gehören. 1 x x x logische 'oder' man liest: «gleich vereinigt mit ist die Menge aller x für die gilt, x ist Element von oder x ist Element von» Differenzmenge Die Differenzmenge \ ist die Menge aller Elemente von, die nicht zu gehören. \ x x x logische 'und' man liest: «gleich ohne ist die Menge aller x für die gilt, x ist Element von und x ist nicht Element von» \ 1 Das logische Zeichen (für oder ) bedeutet oder im nicht ausschliessenden Sinn. Die ussage Neriah ruft an oder schreibt einen rief lässt im nicht ausschliessenden Sinn drei Möglichkeiten zu: 1. Neriah ruft an, schreibt aber keinen rief. 2. Neriah ruft nicht an, schreibt aber einen rief. 3. Neriah ruft an und schreibt einen rief. 2

3 Rechenregeln (Schaltalgebra) Logische Verknüpfungen lassen sich mit einer besonderen rt von Mathematik darstellen. Man spricht von der Schaltalgebra, die aus der ooleschen lgebra hervorgeht. ufgrund des binären Zahlensystems kennt die Schaltalgebra nur zwei Konstanten: die 0 und die 1. Es gelten folgenden Regeln (Vorrangigkeit und indungsstärke): a. UND bindet stärker als ODER b. Klammern binden stärker als UND c. Negationszeichen binden stärker als Klammern (siehe Kapitel 1.8) uf die angewandt, bedeutet dies: eweis = anschaulich: grün = rot «geschnitten» mit hellblau = anschaulich: grün = rot «vereinigt» mit hellblau Fazit Das Resultat kann von der Klammersetzung abhängen. Legen Sie deshalb die Reihenfolge der Mengenoperationen eindeutig mit Klammern fest! 3

4 Merke Leere Menge Die Menge, die kein Element besitzt, heisst leere Menge. Man bezeichnet sie mit 0 (durchgestrichene Null). Die Schreibweise { } ist nach DIN nicht vorgesehen. Wir werden die Schreibweise { } trotzdem verwenden. Diese Schreibweise wirkt einem Missverständnis entgegen: Die leere Menge ist nicht nichts, sondern etwas, das nichts enthält. Für die leere Menge treffen wir folgende Vereinbarungen: Die leere Menge gehört zu den endlichen Mengen. Die leere Menge ist eine Teilmenge jeder Menge. Unterscheiden Sie: { } Leere Menge, die kein Element enthält. {0} Menge mit dem einzigen Element Null. Elementfremd (disjunkt) Zwei Mengen und heissen elementfremd (disjunkt), falls gilt:. Eselsbrücke für ls Eselsbrücke für das logische «UND» können Sie sich für das Symbol den nfangsbuchstaben für das englische «ND» merken. Verwechslung von \ mit / Verwechseln Sie das Symbol für «ohne» nicht mit dem Symbol für die Division: \ nicht mit / verwechseln! Unterschied und ei der Schreibweise bzw. steht links immer ein Element, rechts wird die Menge angegeben! ei der Schreibweise bzw. steht links und rechts immer eine Menge: eispiele: 5 2, 3 1, 2, 3, 4, 5 Element bzw. Menge Menge Menge usnahme, wenn eine Menge von Mengen ist: 1, 2, 2 ist korrekt! rbeitstechnik Verwenden Sie Farben wenn Sie Mengen schraffieren müssen. Markieren Sie die einzelnen rbeitsschritte mit unterschiedlichen Farben. Ein eispiel sehen Sie auf der Vorderseite. Die Menge wird in drei rbeitsschritten schraffiert! 4

5 1.4 Übungen 1. Geben Sie alle Teilmengen der Menge = {a, b, c} an. Sie erhalten damit die Menge aller Teilmengen von (siehe 1.11 Potenzmenge). Menge aller Teilmengen der Menge : { {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}, { }} 2. Zeigen Sie anhand von eispielen: Eine Menge von n Elementen besitzt 2 n Teilmengen. nzahl Elemente = {a} = {a, b} Teilmengen {{ }, {a}} {{ }, {a}, {b}, {a, b}} = {a, b, c} { {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}, { }} n 2 n 3. Ein Vater hat vier Kinder: nna, erta, yril und Doris. Er kann einen Nachmittag allein (im Wirtshaus), mit einem seiner Kinder, mit zweien, mit dreien oder mit allen Kindern verbringen. uf wie viele rten kann er den Nachmittag verbringen? nzahl Elemente K = {a, b, c, d} 4 Elemente somit 2 4 = 16 Möglichkeiten Teilmengen { {a}, {b}, {c}, {d}, {a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}, {a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}, {a, b, c, d}, { }} Tipp: Damit keine Kombination vergessen geht Wahrheitstabelle verwenden! a b c d Teilmengen Vorgehen für Tabelle { } {d} {c} {c, d} {b} {b, d} {b, c} {b, c, d} {a} {a, d} {a, c} {a, c, d} {a, b} {a, b, d} {a, b, c} {a, b, c, d} 1. für jedes Element eine Spalte eröffnen 2. nzahl Zeilen = 2 n 3. Spalte 4 mit 0, 1, 0, 1 usw. (1 Null, 1 Eins) 4. Spalte 3 mit 0, 0, 1, 1, usw. (2 Nullen, 2 Einsen) 5. Spalte 2 mit 0, 0, 0, 0, 1, 1, 1, 1 usw. (4 Nullen, 4 Einsen) 6. Spalte 1 (8 Nullen, 8 Einsen) Dieses Verfahren funktioniert für beliebige nzahl Elemente! 5

6 6 4. Schraffieren Sie die angegeben Mengen. 5. Schraffieren Sie die angegeben Mengen. = = = =

7 7 6. Schraffieren Sie die angegeben Mengen.

8 7. Gegeben sind vier Mengen = {a, b, d, f}, = {c, d, e, f, g}, = {d, e, f}, D = {i, j, k}. a. ilden Sie die folgenden Mengen:,,,, \, \ Sie sollen dabei erkennen:,, jedoch \ \ Man sagt: Für den Durchschnitt und für die Vereinigung zweier Mengen gilt das Kommutativgesetz (Vertauschungsgesetz). Tipp: Elemente zuerst in Venn-Diagramm eintragen! a, b, c, d, e, f, g a d g c a, b, c, d, e, f, g d, f b f e d, f a, b c, e, g b. ilden Sie die folgenden Mengen: \, \,,, D, und D c g c d e f g d f e j k i D c, g c, d, e, f, g d, e, f c, d, e, f, g, i, j, k c. erechnen Sie:?,? und \? a, b, d, f a, b, d, f \ d. Was ist richtig, was ist falsch? Kreuzen Sie die richtigen ussagen an. b richtig falsch b richtig falsch richtig falsch richtig falsch richtig falsch richtig falsch richtig falsch richtig falsch e. erechnen Sie:?,?, \?, \? \ \ 8

9 8. Ergänzen Sie korrekt. us folgt: \ 9. Setzen Sie das passende Zeichen ein:,,, oder a. 1 {1, 2, 3} b. {1, 2} {1, 2, 3} c. {1} {1, 2, 3} d. {1, 2, 3} {1, 3, 2} e. 0 {1, 2, 3} f. {0} {0, 1, 2, 3} g. 0 {0, 1, 2, 3} h. { } {{ }, {1}, {2, 3}} i. { } {1, 2, 3} 10. Welche je zwei der angegebenen Mengen sind zueinander disjunkt? = {1, 3, 5}, = {1, 2, 3}, = {2, 4, 6}, D = {a, b} D D D 9

10 1.5 Übungen (alte M-Prüfungen) 1. Luzern 1993 Der Hersteller von 3 Waschmitteln, und stellt durch Umfrage bei 250 Haushalten fest: 15 Haushalte verwenden alle drei Waschmittel, 35 Haushalte Waschmittel und, 20 Haushalte und, 25 Haushalte und, 40 Haushalte nur, 10 Haushalte nur, 95 Haushalte verwenden keines der drei Waschmittel. a. Zeichnen Sie ein Venn-Diagramm b. Wie viele Haushalte verwenden nur Waschmittel? c. In welchem Verhältnis sind die drei Waschmittel anzubieten? Geg: 1. Schritt 2. Schritt 3. Schritt 4. Schritt G 250, 15, 35, 20, 25, 0, G \ \ 40, \ 1 95 Ges: 5. Schritt 6. Schritt 7. Schritt \?, : :? Lösung: \ \ \ \ \ G \ somit: b. \ Haushalte verwenden nur Waschmittel. c. : : 100: 80: 40 5: 4 : 2 Die Waschmittel sind im Verhältnis 5:4:2 : : anzubieten. 10

11 2. rig 1998 Von den SchülerInnen einer Klasse spielen 6 kein Instrument. 10 SchülerInnen spielen Violine und 7 spielen Klavier. Ferner gibt es 12 FlötenspielerInnen in der Klasse, von denen alle mit usnahme von dreien noch mindestens ein weiteres Instrument spielen, nämlich 6 Violine und 5 Klavier. Von den ViolinistInnen spielen 3 kein weiteres Instrument. Wie viele SchülerInnen a. zählt die Klasse? b. spielen nur Klavier? c. spielen alle drei Instrumente? d. spielen Violine und Klavier? Geg: 1. Schritt 2. Schritt G\ V K F 6, V 10, K 7, F 12, F\ V K 3, V F 6, KF 5, V\ KF 3 Ges: 3. Schritt 4. Schritt 5. Schritt G?, K\ V F?, V K F?, V K? Lösung: V K K F \V V K F V F \K V K \F K\ V F F 6 somit: a. G Die Klasse besteht aus 23 Lernenden. b. K\ V F 1 1 Lernender spielt nur Klavier. c. V K F 2 2 Lernende spielen alle Instrumente. d. V K 3 3 Lernende spielen Violine und Klavier. 11

12 3. iel 1999 In einem Handelsbetrieb arbeiten insgesamt 130 Personen, hauptsächlich in den ereichen Einkauf (E), Verkauf (V) und dministration (). 16 ngestellte sind auf verschiedenen Spezialgebieten, z.. EDV, hauffeure, Kantine etc., tätig. ufgrund ihrer usbildung können 80 Personen in der dministration, 50 Personen im Verkauf und 40 Personen im Einkauf eingesetzt werden. Kenntnisse in dministration und Verkauf haben 24 Personen, 8 Personen davon auch im Einkauf. 14 Personen kennen sich im Einkauf und Verkauf aus. Tragen Sie die entsprechenden ngaben in untenstehendes Venn-Diagramm ein und vervollständigen Sie das Mengendiagramm. E V Geg: G 130, G\ E V 16, , V 5, 0 E 40, V 24 E V 8 E V Ges: Mengendiagramm 16 Lösung: 1. E V 8 2. V \ E E V \ V \ E E \ V Kern der ufgab e 6. E \ V \ E V

13 4. ern 2000 (*) Eine schulinterne Umfrage zeigt, dass von den erfassten Personen 42 keinen Sport treiben. 62 efragte betätigen sich als Leichtathleten (L) und 49 spielen Rakett-allspiele (R). 84 efragte gaben an, Fussball (F) zu spielen, von denen alle ausser 21 noch mindestens eine weitere Sportart treiben, nämlich 40 Leichtathletik und 35 Rakett-allspiele. 20 Leichtathleten üben keine weitere Sportart aus. Stellen Sie die edingungen in einem Diagramm dar und beantworten Sie die folgenden Fragen: a. Wie viele Personen wurden mit der Umfrage erfasst? b. Wie viele Personen spielen nur Fussball oder nur Rakett-allspiele? c. Für wie viele Personen trifft folgende edingung zu: (R F)\(L F)? Geg: Ges: Lösung: 1. Schritt 2. Schritt G \ L R F 42, L 62, R 49, F 84, F \ R L 21, F L 40, F R 35, L \ R F Schritt G?, F\ L R R\ L F?, R F \ L F? nur Fussball nur Rakett-allspiele L R R F \ L L R F L F \R L R \F R\ L F F 42 somit: a. G b. F\ L R\ L F nur Fussball nur Rakett-allspiele c. R F \ L F R F \ L 23 13

14 5. Luzern 1999 (*) Für die folgenden Teilaufgaben a. bis d. benutzen Sie bitte das untenstehende Venn- Diagramm. Dabei bedeuten die Mengen: Personen mit guten Sprachkenntnissen in spanisch = S, italienisch = I, französisch = F. a. Für eine freie Stelle einer internationalen Firma bewerben sich 29 Personen. 15 Personen können gut spanisch, 10 italienisch und 4 sprechen alle drei Sprachen. 9 Personen sprechen mindestens italienisch und französisch. 8 ewerberinnen können nur spanisch. 3 Personen haben gute Spanisch- und Französisch-, aber keine guten Italienischkenntnisse. Es hat dreimal so viele ewerberinnen, die keine dieser Sprachen sprechen als ewerberinnen, die nur französisch sprechen. Schreiben Sie die Zahl der entsprechenden ewerberinnen in die einzelnen Teilmengen ein und stellen Sie eine Gleichung auf, damit Sie die unbekannten Zahlen berechnen können. b. Wie viele ewerberinnen sprechen französisch? c. Wie viele ewerberinnen haben Kenntnisse in mindestens 2 dieser Sprachen? d. Schraffieren Sie im Venn-Diagramm die Menge (S \ F) (I F). S I Geg: G 29, S 15, I 10, S I F 4, IF 9, S \ IF 8, S F \ I 3, G \ S IF 3x, F \ S I x x = 2 Ges: F?, S I IF F S? F 3x = 6 Lösung: 1. S IF 4 2. IF \ S S \ IF 8 4. S F \ I 3 5. S I \ F I \ S F x 3x x 2 8. F S I IF F S

15 somit: a. x 3x x 2 siehe oben Punkt 7 b. 14 Personen sprechen französisch. c. 12 Personen haben Kenntnisse von mindestens 2 Sprachen. d. Siehe nachfolgendes Venn-Diagramm! S I x = 2 F 3x = 6 S \ F IF 15

16 1.6 Zahlenmengen Die natürlichen Zahlen N Die Menge der natürlichen Zahlen ist die Menge mit den Elementen 0, 1, 2, 3, 4, 5, Sie wird wie folgt notiert: * N 0, 1, 2, 3, 4, 5, N 1, 2, 3, 4, 5, Im ereich der natürlichen Zahlen kann man unbeschränkt addieren und multiplizieren. Die Subtraktion und die Division führen in der Regel aus dem ereich der natürlichen Zahlen hinaus ? das Ergebnis ist keine natürliche Zahl 12? das Ergebnis ist keine natürliche Zahl 7 Die ganzen Zahlen Z Die Menge der ganzen Zahlen ist die Menge mit den Elementen, 3, 2, 1, 0, 1, 2, 3, Sie wird wie folgt notiert: Z, 3, 2, 1, 0, 1, 2, 3, Im ereich der ganzen Zahlen kann man unbeschränkt addieren, subtrahieren und multiplizieren. Die Division führt in der Regel aus dem ereich der ganzen Zahlen hinaus. 12? das Ergebnis ist keine natürliche Zahl 7 Die rationalen Zahlen Q (ruchzahlen) Die Division zweier Zahlen ist in Z nicht immer ausführbar; sie erfordert daher eine Erweiterung des Zahlenraumes. Sie erfolgt durch die Einführung der ruchzahlen oder kurz rüche. Die Menge der rationalen Zahlen wird wie folgt notiert: a Q a Z b Z \ 0 b und Im ereich der rationalen Zahlen kann man unbeschränkt addieren, subtrahieren und multiplizieren und dividieren. Lediglich das Wurzelziehen (und andere «höhere» Rechenoperationen) führt in der Regel aus dem ereich der rationalen Zahlen hinaus. 2? das Ergebnis ist keine rationale Zahl Jede Division führt entweder zu einer endlichen (d. h. die Division «geht auf») oder periodischen Dezimalzahl. Die Darstellung als Dezimalzahl lässt erkennen, dass diese Schreibweise nur eine nnäherung darstellt. 1 0, das Ergebnis ist eine periodische Dezimalzahl 7 Jede endliche oder periodische Dezimalzahl lässt sich als ruchzahl schreiben. 16

17 Irrationale Zahlen I Die Menge der irrationalen Zahlen ist die Menge aller unendlichen, jedoch nicht periodischen Dezimalzahlen., 2 oder 0, Diese Zahlen lassen sich also nicht als ruchzahl schreiben. Reelle Zahlen R Die Menge der reellen Zahlen enthält die rationalen und die irrationalen Zahlen: R Q I. Wie aus dem Venn-Diagramm ersichtlich ist, sind alle Zahlenmengen letztlich Teilmengen von R. Es gilt somit: Q Z R N I N Z Q R und I R 17

18 1.7 Grundmenge (ezugsmenge) Vielfach ist es sinnvoll, eine Grundmenge G anzugeben. Das sind alle jene Dinge, die überhaupt in etracht gezogen werden. ei der Lösung von Gleichungen verwendet man immer eine Grundmenge G. Wenn man nicht eine spezielle Grundmenge angibt, dann wählt man in der Regel R als Grundmenge. G = N bedeutet: Grundmenge ist die Menge der natürlichen Zahlen G = Z bedeutet: Grundmenge ist die Menge der ganzen Zahlen G = Q bedeutet: Grundmenge ist die Menge der rationalen Zahlen 1.8 Komplementmenge (Negation) Die Komplementmenge oder das Komplement einer Menge ergänzt die Menge zur Grundmenge. G man schreibt: Negationszeichen G G \ man liest: nicht eispiele G 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3 4, 5, 6, 7, 8, 9, 10 N N G x x 16, x x 10 10, 11, 12, 13, 14, 15 G a, b, c,, z, a, b, c,, p q, r, s, t,, z 1.9 Mächtigkeit einer Menge Zwei Mengen und sind gleichmächtig, wenn jedem Element von eindeutig ein Element von zugeordnet werden kann und umgekehrt. man schreibt: b a c d Die beiden Mengen a, b, c, d und 1, 2, 3, 4 sind zwar nicht gleich sind jedoch gleichmächtig. ei endlichen Mengen ist die Mächtigkeit einer Menge gleich der nzahl ihrer Elemente. esteht die Menge aus 4 Elementen, so schreibt man kurz 4. chtung: Die senkrechten Striche stehen für die Mächtigkeit und nicht für die etragsfunktion!, sie 18

19 1.10 Produktmenge (Pfeildiagramm) (*) Unter der Produktmenge aus und versteht man die Menge aller Paare (x, y), wobei x und y ist. Zahlenpaare kann man auch in einem Koordinatensystem eintragen. man schreibt: Kreuz a b Die Mächtigkeit von x ist gleich der Mächtigkeit von multipliziert mit der Mächtigkeit von : eispiel a, b, 1, 2, 3 a, 1, a, 2, a, 3, b, 1, b, 2, b, Hinweis: Innerhalb der runden Klammern müssen Sie auf die Reihenfolge achten:a, 1 1, a Innerhalb der geschweiften Klammer kommt es nicht auf die Reihenfolge an! Potenzmenge (*) Unter der Potenzmenge versteht man die Menge aller Teilmengen einer gegebenen Grundmenge. Man notiert die Potenzmenge von meist als P(). Jede Menge mit n Elementen hat genau 2 n n Teilmengen: P 2 eispiele a P, a a, b P, a, b, a, b Hinweis: Typische nwendung Schaltungssynthese in der Digitaltechnik Frage: Wie viele verschiedene Kombinationen sind mit zwei Schaltern S 1 und S 2 möglich? S, S P, S, S, S, S Lösung: Eingänge usgang S 1 S 2 Z aus aus? aus ein? ein aus? ein ein? Durch den Einsatz einer «Wahrheitstabelle» kann verhindert werden, dass gleiche Kombinationen mehrfach vorkommen, beziehungsweise einzelne Kombinationen vergessen werden! 19

20 1.12 Übungen 1. Setzen Sie ein Kreuz, falls die links angegebene Zahl eine natürliche Zahl, ganze Zahl, rationale Zahl etc. ist. natürliche Zahl ganze Zahl rationale Zahl irrationale Zahl 7 x x x x 3 x x x 3 x x 0.34 x x reelle Zahl 3 4 x x 2. Gegeben sind G 1, 4, 9,, 100 und 4, 16, 25, 81, 100 1, 9, 36, 49, 64. estimmen Sie. 3. Gegeben sind G N und Menge der geraden Zahlen. estimmen Sie. Menge der ungeraden Zahlen 4. Geben Sie die Mächtigkeit für jede der Mengen,,, D und E an: a, b, c, d 1, 2, 3, 4, 5 2, 4, 6, 8, 10 D 0 E Welche dieser Mengen sind gleichmächtig? D 1 E 0 und sind gleichmächtig 5. (*) Gegeben sind a, b, c, d und u, v, w Welche Mächtigkeit haben x und x?. ilden Sie x und x. a,u, a,v, a,w, b,u, b,v, b,w, c,u, c,v, c,w, d,u, d,v, d,w u,a, u,b, u,c, u,d, v,a, v,b, v,c, v,d, w,a, w,b, w,c, w,d und

21 6. (*) Gegeben sind a, b, c, d, e und 2, 4, 6, 8, 10, 12 Welche Mächtigkeit hat x? Gegeben ist a, b, c, d. a. ilden Sie die Menge aller Teilmengen von. b. Welche Mächtigkeit hat diese Menge? Teilmengen, a, b, c, d, a,b, a,c, a,d, b,c, b,d, c,d, a,b,c, a,b,d, a,c,d, b,c,d, a,b,c,d 4 Teilmengen Wie viele Teilmengen hat eine Menge mit der Mächtigkeit 10? '024 Teilmengen 9. (*) Gegeben ist a, b, c. ilden Sie x. a,a, a,b, a,c, b,a, b,b, b,c, c,a, c,b, c,c 10. (*) Geben Sie wenigstens fünf Elemente der Menge Z x Z an. Z Z 3,6, 3,7, 5, 8, 13,0, 34,78, Punkte im Koordinatensystem 11. Vergewissern Sie sich, dass Sie folgende egriffe kennen: Menge, Element, Gleichheit von Mengen, Teilmenge, Menge aller Teilmengen, Durchschnitt, Vereinigung, disjunkt, Differenzmenge, Mächtigkeit einer Menge, Gleichmächtigkeit, (*) Produktmenge, N, Z, Q, I, R. 12. Welche natürlichen Zahlen zwischen 45 und 55 geben durch 6 dividiert höchstens 9? x 45 x x 55 x 54 L 46,47,48,49,50,51,52,53,

22 13. Welche natürlichen Zahlen ergeben zu 7 addiert mehr als 12 und mit 7 multipliziert weniger als 63? x 7 12 x 7 63 x 5 x 9 L 6,7, Übungen, Frommenwiler Lösen Sie die folgenden ufgaben: Nummer Seite emerkungen 8 (a, c und d) (a und c) 251 alle möglichen Teilmengen 16 (c und d) (a und b) 252 alle möglichen Teilmengen 20 (a bis d) 252 Venn-Diagramm zeichnen 21 (a bis g) (a bis f) 253 mehrere Lösungen möglich Venn-Diagramm zeichnen 22