3D-Computergrafik. Rastergrafik
|
|
|
- Friedrich Kohler
- vor 8 Jahren
- Abrufe
Transkript
1 3D-Computergrafik Rastergrafik
2 Notation von Polygonen Polygone werden nach 2D abgebildet Für weitere Betrachtungen reicht also zunächst: Betrachtung 2D-Prmitiven Erörtern der Aufgaben der Computergrafik im 2D-Fall
3 Vom Modell zum Bild: Vorüberlegungen Spezialfall: 2D-Computergraphik Bezug nehmend auf den allgemeinen Prozess der Bilderzeugung mit dem Rechner ergeben sich bei der 2D-Bilderzugung folgende Aufgaben: Abbildung der Vision eines Bildes eines Benutzers in einer geeigneten Modellbeschreibung im Rechner, Überführung des Modells in eine Form, die am Bildschirm ausgegeben werden kann.
4 Vom Modell zum Bild: Vorüberlegungen Voraussetzung: Vision eines 2D-Bildes eines Benutzers durch Positionierung von 2D-Primitiven möglich Solche 2D-Primitive sind z. B. Linie, Kreis, Ellipse, Rechteck, Vieleck (Polygon) etc.
5 Aufgabenstellung: Zielformulierung und Motivation Gesucht ist also grundsätzlich 1. eine Datenstruktur, die es erlaubt, die 2D-Primitive im Rechner abzubilden 2. spezielles Programm, dass die 2D-Primitive aus der Modellbeschreibung in die spezifische Beschreibung des Ausgabegeräts überführt Am weitesten verbreitet sind hierbei rasterorientiert arbeitende Ausgabegeräte.
6 Aufgabenstellung: Zielformulierung und Motivation Das bedeutet bei einer Ausgabe auf einem rasterorientierten Datensichtgerät (Monitor), Speicherung in einer Bitmap oder Ausgabe auf einen Drucker 1. die Überführung der idealen 2D-Primitive aus der Modellbeschreibung in die entsprechenden Rasterprimitive des Ausgabegeräts und 2. die Transformation der der Koordinaten der 2D-Primitive aus dem Koordinatensystem des Modells in das gerätespezifische Koordinatensystem. Ausgegeben wird auf den rasterorientiert arbeitenden Ausgabegeräten ein Rasterbild.
7 Rasterbilder Vor- und Nachteile Vorteile: Einfache Speicherung (Anordnung der Elemente) Viele Nachbearbeitungsmöglichkeiten (vgl. Bildverarbeitung)
8 Rasterbilder Vor- und Nachteile Nachteile: Diskretisierung einer geometrischen Beschreibung erforderlich Treppenstufen-Effekte (Aliasing) beim Transformieren (Vergrößern, Rotieren) Hoher Speicherplatzbedarf
9 Rasterbilder nähere Betrachtung Ein Rasterbild B als Matrix mit R Spalten und L Zeilen: B = (b(x, y)) wobei x der Spaltenindex mit 0 x R 1 und y der Zeilenindex mit 0 y L 1 ist. Das Bildelement besitzt dabei den Wert b(x, y).
10 Rasterbilder nähere Betrachtung Der Farbwert c ist eine (irgendwie geartete) Kombination von Farbkanälen c = K(v 0,, v n ) v V wobei V das zu Grunde liegende Farbmodell repräsentiert.
11 Rasterbilder nähere Betrachtung Ferner lässt sich ein Bild wie folgt betrachten: B = (b(x, y, n)) wobei n der Kanalzähler für ein zu Grunde liegendes Farbmodell mit N Farbkanälen ist mit 0 n N.
12 Anforderungen an Algorithmen Rasterungsalgorithmen werden oft gebraucht, sind daher zeitkritisch. Anforderungen: keine aufwändigen Operationen (Multiplikation, Division sind aufwändiger als Addition), möglichst mittels Integer-Arithmetik implementieren, möglichst einfach strukturierte Algorithmen.
13 Vorausgehende Betrachtungen Wie sollen schließlich später die gerasterten Primitive vorliegen? Rasterbild ist aus Pixeln zusammengesetzt. Pixel stammt vom englischen picture element und kennzeichnet die kleinste unteilbare Einheit eines Rasterbildes. Die Pixel im Rasterbild sind gitterförmig angeordnet in Zeilen und Spalten, sind alle gleich groß, werden angesehen als Quadrate, die eine bestimmte Fläche überdecken, alle Pixel eines Rasterbildes bedecken dieses vollständig (es gibt keine Lücken).
14 Zusammenfassung: Eigenschaften von Pixeln Position in der Bildmatrix, angegeben in Koordinaten der Bildmatrix, also als Wertepaar (Spalte, Zeile), Grundlage hierfür bildet das Koordinatensystem der Bildmatrix beliebiger Farbwert, Größe (Ausdehnung) der Rechteckfläche des Pixels
15 2D-Rastergrafik Einführung
16 Abstraktion: Pixelmodell für Entwurf von Algorithmen Konzentration auf das Wesentliche: Bild besteht aus gleichmäßigem Gitter An Gitterkreuzungspunkten befinden sich die Bildelemente Vereinfachung der Bildelemente: keine Ausdehnung sind ein- oder ausgeschaltet
17 Abstraktion: Pixelmodell für Entwurf von Algorithmen Bildelemente stehen in Relation zueinander: Vierernachbarschaft Achternachbarschaft NW N NE Nachbarschafts-Beziehung wird gemäß der Himmelsrichtungen kodiert W E SW S SE
18 2D Rastergrafik Rastern von Linien
19 Anforderungen Linien sollten gerade aussehen Linien sollten gleichmäßig hell erscheinen Helligkeit sollte unabhängig von Richtung sein Endpunkte sollten exakt sein Linien sollen konstante Dicke haben Linienalgorithmus soll schnell sein
20 Linien mathematisch Gegeben: zwei Punkte P 1 (x 1, y 1 ) und P 2 (x 2, y 2 ) Gesucht: Beschreibung der Linie zwischen P 1 und P 2 setzen: x = x 2 x 1 y = y 2 y 1 Anstieg m = y/ x
21 Linie: Mathematische Beschreibung erste Möglichkeit: parametrische Beschreibung man erhält: y = x 1 + t(x 2 x 1 ) = x 1 + t x y = y 1 + t(y 2 y 1 ) = y 1 + t y für t = 0 den Punkt (x 1, y 1 ) für t = 1 den Punkt (x 2, y 2 ) Alle Punkte der Linie erhält man, wenn man für t alle Werte aus [0,1] einsetzt.
22 Linie: Mathematische Beschreibung zweite Möglichkeit: Beschreibung über Anstieg y = mx + n m = y/ x n: y-koordinate des Schnittpunkts mit der y-achse dritte Möglichkeit: implizite Beschreibung der Linie F(x, y) = ax + by + c = 0 Für alle Punkte auf der Gerade ist obige Gleichung erfüllt.
23 Naiver Algorithmus Gegeben: zwei Punkte P 1 (x 1, y 1 ) und P 2 (x 2, y 2 ) jeweils Integer- Koordinaten Gesucht: alle Pixel, die auf der Linie liegen erster Schritt: Geradengleichung y = mx + n aufstellen Einfachster Weg: Iteration von x 1 nach x 2 im Pixelabstand, entsprechende y-werte berechnen, runden, zeichnen double m = (y2-y1)/(x2-x1) ; for (int x = x1; x <= x2; x++) { double y = m*x + n; setpixel( x, round( y )); }
24 Naiver Algorithmus double m = (y2-y1)/(x2-x1); for (int x = x1; x <= x2; x++) { double y = m*x + n; setpixel( x, round( y )); } Rechnen mit Gleitkommawerten bei y und m Division und Multiplikation verbrauchen Zeit Runden Was ist mit senkrechten Linien m nicht definiert Aussehen der Linien bei verschiedenen Anstiegen
25 ?
26 DDA (Digital Differential Analyzer) DDA = Digital Differential Analyzer Man wandert der Linie in kleinen Schritten entlang und zeichnet alle Pixel, in denen ein Schritt endet Schrittweite Pixelbreite, damit Keine Löcher Schrittweite erhält man z. B. durch mehrmaliges Halbieren der Gesamtlänge
27 DDA (Digital Differential Analyzer) int Length, I; double X, Y, Xinc, Yinc; Length = abs(x2 - X1); if (abs(y2 - Y1) > Length) Length = abs(y2-y1); Xinc = (X2 - X1) / Length; Yinc = (Y2 - Y1) / Length; X = X1; Y = Y1; while(x < X2){ } setpixel(round(x), Round(Y)); X = X + Xinc; Y = Y + Yinc; Probleme: Division Runden
28 Bresenham-Algorithmus auch Mittelpunktschema für Linien, Midpoint-Line-Algorithmus genannt Lösen der Probleme der anderen Ansätze, also ausschließlich Integer-Arithmetik keine Division, keine komplizierten Multiplikationen Einschränkungen: Pixel liegen auf Integer-Gitter (keine wirkliche Einschränkung) Anstieg der Linie kleiner 1, d. h. Linie befindet sich im 1. Oktanten (0 a 45 ) (auch keine Einschränkung, die eine Verallgemeinerung ausschließt)
29 Vorüberlegungen implizite Geradengleichung F(x, y) = ax + by + c = 0 liefert eine Antwort auf die Frage, auf welcher Seite der Geraden ein gegebener Punkt P(x 1, y 1 ) liegt ist F(x 1, y 1 ) > 0 P liegt unterhalb der Geraden ist F(x 1, y 1 ) < 0 P liegt oberhalb der Geraden ist F(x 1, y 1 ) = 0 liegt auf der Geraden dabei ist: a = y b = x
30 Mittelpunktschema für Linien Annahme: Steigung der Linie zwischen 0 und 1 gerade gesetztes Pixel ist P P NE E Welches der beiden Pixel E oder NE muss als nächstes gesetzt werden? Entscheidung, welches der beiden Pixel näher am Schnittpunkt der Linie mit dem Pixelgitter liegt das für jedes Pixel
31 Mittelpunktschema für Linien P NE M E leichter zu bestimmen: liegt der Mittelpunkt M zwischen E und NE oberhalb oder unterhalb der Linie momentane Position P(x, y) Koordinaten von M: M(x + 1, y + ½) F(M) = F(x + 1, y + ½) wenn F(M) > 0, dann geht Linie über M vorbei NE nächstes Pixel wenn F(M) 0, dann geht Linie unter M vorbei E nächstes Pixel wähle d = F(M)=F(x + 1, y + ½) als Entscheidungsvariable
32 Mittelpunktschema für Linien Berechnen von F(M) für ein Pixel, Zeichnen des Pixels, Berechnen von F(M) für das neue Pixel Fragestellung: Kann F(M) für das neue Pixel aus dem F(M) für das gerade berechnete Pixel bestimmt werden? möglicherweise einfachere Berechnungen schrittweise Weitergehen von Pixel i zu Pixel i + 1 Inkrementeller Algorithmus
33 Mittelpunktschema für Linien y + 2 y + 1 y NE M P E x x + 1 x + 2 M 1 M 2 Fall 1: NE als nächstes Pixel ausgewählt F(M) = F((x + 1), (y + ½)) = a(x + 1) + b(y + ½) + c dann ist M 1 der nächste Mittelpunkt F(M 1 ) = F((x + 2), (y + 3 / 2 )) = a(x + 2) + b(y + 3 / 2 ) + c Differenz zwischen beiden: F(M 1 ) F(M) = a + b F(M 1 ) = F(M) + a + b mit a = y und b = x F(M 1 ) = F(M) + y x d = d + y x NE = y x
34 Mittelpunktschema für Linien y + 2 y + 1 y NE M P E x x + 1 x + 2 M 1 M 2 Fall 2: E als nächstes Pixel ausgewählt F(M) = F((x + 1), (y + ½)) = a(x + 1) + b(y + ½) + c dann ist M 2 der nächste Mittelpunkt F(M 2 ) = F((x + 2), (y + ½)) = a(x + 2) + b(y + ½) + c Differenz zwischen beiden: F(M 2 ) F(M) = a F(M 2 ) = F(M) + a mit a = y: F(M 1 ) = F(M) + y d = d + y E = y
35 Mittelpunktschema für Linien Idee für den Algorithmus: beginne beim ersten Pixel berechne die Entscheidungsvariable d=f(m) für dieses Pixel entscheide, ob E oder NE das nächste Pixel ist zeichne das Pixel aktualisiere d entsprechend der Wahl von E oder NE wiederhole, solange der Endpunkt nicht erreicht ist Offene Frage: Initialer Wert von d?
36 Mittelpunktschema für Linien Initialer Wert von d? Startpunkt der Linie sei (x 0,y 0 ) erster Mittelpunkt ist dann F((x 0 + 1), (y 0 +½)) = a(x 0 + 1) + b(y 0 +½) + c = ax 0 + a + by 0 + ½b + c = F(x 0, y 0 ) + a + ½b Startpunkt (x 0, y 0 ) liegt auf der Linie, also F(x 0, y 0 )=0 Initialer Wert der Entscheidungsvariable d = a + ½b aber: keine Integer-Werte Es interessiert nur das Vorzeichen von d. Multiplikation von F(x, y) mit 2 hat keinen Effekt auf das Vorzeichen Initialer Wert der Entscheidungsvariable d = 2a + b Inkremente: NE = 2 y 2 x und E = 2 y
37 void midpoint-line(int xo, int yo, int xe, int ye, int color) { int dx = xe - xo; int dy = ye - yo; int d = 2 * dy - dx; int incre = 2 * dy; int icrne = 2 * (dy - dx); int x = xo; int y = yo; setpixel(xo, yo, color); while (x<xe) { if (d<=0) { d+=incre; x++; } else { d += incrne; x++; y++; } setpixel(x, y, color); } }
38 Beispiel: Linie von (0,0) nach (5,3) Initiale Werte: x = 5, y = 3, E = 6, NE = 4 Entscheidungsvariable d = x=0, y=0, setpixel(0,0,color) d=1>0 Auswahl NE d=d+d NE =1-4=-3 x=x+1=1, y=y+1=1 x=1, y=1, setpixel(1,1,color) d=-3<0 Auswahl E d=d+d E =-3+6=3 x=x+1=2, y=1 x=2, y=1, setpixel(2,1,color) d=3>0 Auswahl NE d=d+d NE =3-4=-1 x=x+1=3, y=y+1=2 x=3, y=2, setpixel(3,2,color) d=-1<0 Auswahl E d=d+d E =-1+6=5 x=x+1=4, y=2 x=4, y=2, setpixel(4,2,color) d=5>0 Auswahl NE d=d+d NE =5-4=1 x=x+1=5, y=y+1=3 x=5, y=3, setpixel(5,3,color)
39 Zusammenfassung Algorithmus arbeitet ausschließlich mit: Integer-Arithmetik Additionen Inkrementeller Algorithmus, d. h. Positionen der Pixel werden nach und nach aus denen der vorherigen berechnet kleine Schleifenkörper Implementierung in Hardware möglich
40 Probleme und Erweiterungen Beschränkung des Anstiegs auf 0 m 45 kein wirkliches Problem Algorithmus kann erweitert werden auf alle möglichen Anstiege (Vertauschen von x und y, Vorzeichen, etc.) lange Linien werden Pixel für Pixel gezeichnet Erweiterungen, die gleich zwei Pixel im Voraus berechnen Linie setzt sich aus Mustern zusammen Muster finden und als Gesamtheit setzen
41 Algorithmen der Rastergrafik Rastern von Kreisen 41
42 Kreise mathematisch Gegeben: Zentrum und Radius allgemeine Kreisgleichung für einen Kreis mit dem Zentrum im Ursprung: F(x, y) = x 2 + y 2 = r 2 alle Punkte (x, y), die diese Gleichung erfüllen, liegen auf dem Kreis Kreisgleichung, wenn Mittelpunkt nicht im Ursprung liegt, sondern an der Position (x c, y c ): F(x, y) = (x x c ) 2 + (y y c ) 2 = r 2 42
43 Naiver Algorithmus Auflösen der Kreisgleichung nach y: Schleife über alle x von r bis r Probleme: aufwändige Berechnung Wurzel Quadrate Lücken in der Umgebung von x = r 2 y = r - x 2 43
44 Parametrischer Algorithmus löst Problem der Lücken in den Bereichen nahe x = r Idee: Übergang zur Kreisgleichung in Parameterform x = r cos sowie y = r sin Schleife über in gleichen, geeignet groß gewählten Schritten Probleme hier: Berechnung der Winkelfunktionen nicht akzeptabel Lösung über Lookup-Tabellen denkbar, jedoch immer noch ineffizient 44
45 Symmetrie des Kreises ( x, y) (x, y) Verringerung der Anzahl der Rechenoperationen durch Nutzung der Symmetrie des Kreises ( y, x) (y, x) ( y, x) (y, x) ( x, y) (x, y) void circlepoints( int x, int y ) { setpixel( x, y ); setpixel( y, x ); setpixel( y, -x ); setpixel( x, -y ); setpixel( -x, -y ); setpixel( -y, -x ); setpixel( -y, x ); setpixel( -x, y ); } 45
46 Bresenham-Algorithmus Herangehensweise wie bei Geraden Ziele: Integer-Arithmetik Eliminieren aufwändiger Operationen Finden eines inkrementellen Algorithmus Basis: implizite Gleichung des Kreises Die Funktion F(x, y) = x 2 + y 2 r 2 ist Null für Punkte auf der Kreislinie ist negativ für Punkte innerhalb des Kreises ist positiv für Punkte außerhalb des Kreises 46
47 Grundidee Berechnung für den zweiten Oktanten gerade P gesetztes E Pixel ist P Welches der beiden Pixel E oder SE muss Mals nächstes M 1 gesetzt werden? SE Entscheidung, welches der beiden Pixel näher am Schnittpunkt des Kreises Mmit 2 dem Pixelgitter liegt Vorgehensweise für jedes Pixel erzeuge alle anderen Oktanten über Symmetrie 47
48 Grundidee Liegt M innerhalb oder außerhalb des Kreises entspricht in diesem Oktanten: liegt M ober- oder unterhalb der Kreislinie P E Momentane Position P(x, y) Koordinaten von MM: M M(x + 1, y ½) 1 F(M) = F(x + 1, SE y ½) wenn F(M) < 0, dann geht Kreis über M vorbei E nächstes Pixel M 2 wenn F(M) 0, dann geht Kreis unter M vorbei SE nächstes Pixel wähle d = F(M) = F(x + 1, y ½) als Entscheidungsvariable 48
49 Grundidee Fall 1: d < 0 E als nächstes Pixel ausgewählt F(M) P = F((x + E1), (y ½)) = (x + 1) 2 + (y ½) 2 r 2 dann ist M 1 der Mnächste M 1 Mittelpunkt SE F(M 1 ) = F((x + 2), (y ½)) = (x + 2) 2 +(y ½) 2 r 2 Differenz zwischen beiden: F(M 1 ) F(M) = 2x + 3 d = d + (2x + 3) E = (2x + 3) M 2 49
50 Grundidee P E M M 1 SE M 2 Fall 2: d 0 SE als nächstes Pixel ausgewählt F(M) = F((x + 1), (y ½)) = (x + 1) 2 + (y ½) 2 r 2 dann ist M 2 der nächste Mittelpunkt F(M 2 ) = F((x + 2) = (y 3 / 2 )) = (x + 2) 2 + (y 3 / 2 ) 2 r 2 Differenz zwischen beiden: F(M 2 ) F(M) = 2x 2y + 5 d = d + (2x 2y + 5) SE = (2x 2y + 5) 50
51 Grundidee Initialer Wert von d erstes Pixel des Kreises (besser: des berechneten Kreisausschnittes) ist P(0, r) Erster Mittelpunkt ist damit M(1, r ½) d = F(1, r ½) = (r ½) 2 r 2 = 5 / 4 r allerdings: kein Integer-Wert neue Entscheidungsvariable h = d 1 / 4 Anfangswert: h start = 1 r Entscheidungskriterium: d < 0 wird zu h < ¼ da die Berechnung von h mit ganzzahligen Werten beginnt und h nur ganzzahlig (durch E, SE ) inkrementiert wird, kann h ¼ durch h < 0 ersetzt werden 51
52 Algorithmus void MidpointCircle (int radius) { int x = 0; /* Initialisierung */ int y = radius; int d = 1 - radius; circlepoints (x, y); } while (y > x) { if (d < 0) { /* Auswahl von E */ d = d + 2 x +3; x = x + 1 } else { /* Auswahl von SE */ d := d + 2 (x-y) + 5; x := x + 1; y := y - 1; } circlepoints (x, y) } 52
53 Beispiel 6 3 Beispiel: Kreis um (0,0) Radius 6 Initialisierung: x = 0, y = 6, d = x=0, y=6, d=-5, circlepoints(0,0) d=-5<0 Auswahl E d=d+2x+3=-2 x=x+1=1 circlepoints(1,6) d=-2<0 Auswahl E d=d+2x+3=5 x=x+1=2 circlepoints(2,6) d=5>0 Auswahl SE d=d+2(x-y)+5=2 x=x+1=3, y=y-1=5 circlepoints(3,5) d=5>0 Auswahl SE d=d+2(x-y)+5=3 x=x+1=4, y=y-1=4 circlepoints(4,4) 53
54 Beispiel (x,y) (y,x) (y,-x) (x,-y) (-x,-y) (-y,-x) (-y,x) (-x,y) (0,6) (6,0) (6,-0) (0,-6) (-0,-6) (-6,-0) (-6,0) (-0,6) (1,6) (6,1) (6,-1) (1,-6) (-1,-6) (-6,-1) (-6,1) (-1,6) (2,6) (6,2) (6,-2) (2,-6) (-2,-6) (-6,-2) (-6,2) (-2,6) (3,5) (5,3) (5,-3) (3,-5) (-3,-5) (-5,-3) (-5,3) (-3,5) (4,4) (4,4) (4,-4) (4,-4) (-4,-4) (-4,-4) (-4,4) (-4,4) 54
55 Erweiterungen Algorithmus ist relativ effizient, weil: inkrementeller Algorithmus Integer-Arithmetik nur ein Achtel des Kreises muss berechnet werden Aber: immer noch Multiplikationen notwendig, um die Inkremente zu berechnen zur Erinnerung: E = (2x + 3) und SE = (2x 2y + 5) Linienalgorithmus arbeitet mit konstanten Inkrementen Geht das hier auch? Idee: Berechnen der Inkremente E und SE auch inkrementell dazu: betrachten nicht nur einen Pixelschritt, sondern zwei 55
56 Differenzen zweiter Ordnung Fall 1: im aktuellen Schritt wurde E gewählt Bewertungspunkt (aktuelles Pixel) wandert von (x, y) nach (x + 1, y) Inkremente am alten Pixel (x, y) waren: Ealt = 2x + 3 SEalt = 2x 2y + 5 Inkremente am neuen Pixel wären: eneu = 2(x + 1) + 3 SEneu = 2(x + 1) 2y + 5 Differenzen zwischen beiden: eneu Ealt = 2 SEneu SEalt = 2 56
57 Differenzen zweiter Ordnung Fall 2: im aktuellen Schritt wurde SE gewählt Bewertungspunkt (aktuelles Pixel) wandert von (x, y) nach (x + 1, y 1) Inkremente am alten Pixel (x, y) waren Ealt =2x +3 SEalt =2x 2y + 5 Inkremente am neuen Pixel wären: Eneu =2(x + 1) +3 SEneu =2(x + 1) 2(y 1) + 5 Differenzen zwischen beiden: Eneu Ealt = 2 SEneu SEalt = 4 57
58 Algorithmus void MidpointCircle(int radius) { int x = 0; int y = radius; int d = 1 radius; int deltae = 3; int deltase = 2 * radius + 5; circlepoints(x, y); /* draws 8 points */ while (y > x) { if (d < 0) { /* select E */ d += deltae; deltae += 2; deltase += 2; } else { /* select SE */ d += deltase; deltae += 2; deltase += 4; y ; } x++; circlepoints(x, y); } } 58
59 Algorithmen der Rastergrafik Rastern von Ellipsen 59
60 Grundlegendes Gleichung der Ellipse mit Mittelpunkt im Ursprung F(x, y) = b 2 x 2 + a 2 y 2 a 2 b 2 = 0 hier nur achsenparallele Ellipsen Algorithmus für ersten Quadranten reicht aus, Rest durch Spiegelungen Ziel: inkrementeller Mittelpunkt-Algorithmus b -a a -b 60
61 Herleitung für den Algorithmus Schwierigkeit: zwei Gebiete mit entweder Auswahl zwischen E und SE oder Auswahl zwischen SE und S Grenze: Punkt, an dem die Ellipse den Anstieg 1 hat hier ohne Herleitung: Übergang, der erste Mittelpunkt, für den gilt: y 2 (y ½) b 2 (x 1) E Tangentenanstieg = 1 SE E SE 61
62 Herleitung für Algorithmus Gebiet 1: Mittelpunkt liegt zwischen E und SE d alt = F(x + 2, y ½) =b 2 (x + 1) 2 + a 2 (y ½) 2 a 2 b 2 Wahl von E als nächstes Pixel: d neu = F(x + 2, y ½) =b 2 (x + 2) 2 + a 2 (y ½) 2 a 2 b 2 E = d neu d alt = b 2 (2x + 3) Wahl von SE als nächstes Pixel: d neu = F(x + 2, y 3 / 2 ) =b 2 (x + 2) 2 + a 2 (y 3 / 2 ) 2 a 2 b 2 E = d neu d alt = b 2 (2x + 3) + a 2 ( 2y + 2) Gebiet 2: Mittelpunkt liegt zwischen SE und S analog 62
63 Herleitung für Algorithmus Initialer Wert für d es ist (0, b) das erste Pixel, damit (1, b ½) der erste Mittelpunkt F(1, b ½) = b 2 + a 2 (b ½) 2 a 2 b 2 = b 2 + a 2 ( b + ¼) = d Beim Wechsel der Gebiete ist ein neuer Initialwert für d zu berechnen, er liegt zwischen S und SE bei (x + ½, y 1) F(x + ½, y 1) = b 2 (x + ½) 2 + a 2 (y 1) 2 a 2 b 2 = d sonst Algorithmus wie beim Kreis Ausnutzen der vierfachen Symmetrie 63
64 Algorithmus void MidpointEllipse(int a, int b, int color) { int x = 0; int y = b; double d1 = b*b-a*a*b-(a*a/4); ellipsepoints( x, y ); while( a*a*(y-0.5) > b*b*(x-1)) { if d1 < 0 { d1 += b*b*(2*x+3)} else { d1 += (b*b*(2*x+3)+a*a*(-2*y+2)); y--; } x++ ellipsepoints( x, y ); } d2 = b*b*(x+.5)*(x+.5)+a*a*(y-1)*(y-1)-a*a*b*b; while(y > 0) { if d2 < 0 { d2 += b*b*(2*x+2)+a*a*(-2*y+3); x++; } else { d2 += a*a*(-2*y+3) } y--; ellipsepoints( x, y ); } } 64
65 Zusammenfassung Ellipse Algorithmus kann natürlich noch erweitert werden: Ellipsen nicht im Ursprung (trivial) Ellipsen nicht achsenparallel (schwierig) Differenzen zweiter Ordnung (trivial) Float-Berechnungen (schwieriger) aber auch hier inkrementeller Algorithmus relativ einfache Berechnungen Aufgrund der Eigenschaften der Ellipsen machen sich eigenständige Algorithmen für sehr schmale Ellipsen (a oder b sehr klein) bezahlt. 65
66 Zusammenfassung Rasteralgorithmen werden oft aufgerufen, daher besondere Anforderungen: schnell einfach Integer-Arithmetik inkrementelle Algorithmen nach dem Mittelpunkt-Schema Linien, Kreise, Ellipsen erweiterbar für allgemeine Lagen der Primitive Beispiel für Herleitung von Algorithmen in der Rastergraphik 66
67 Offene Fragen Rasterung allgemeiner Kurven würde Rahmen sprengen Bisher waren alle Linien genau ein Pixel breit, was passiert, wenn man dickere Linien haben möchte? nächstes Kapitel Beim Rastern wurden bisher alle Pixel mit einer Farbwert gesetzt, das führt zu unschönen Artefakten Aliasing Wie kann man dem begegnen? Antialiasing übernächstes Kapitel Was passiert mit dem Inneren von Figuren Binnenstrukturen? Füllen überübernächstes Kapitel 67
68 Rasteralgorithmen Breite bzw. dicke Primitive 68
69 Breite Primitive bisher: Alle Linien sind genau 1 Pixel breit. vorgestellte Algorithmen eignen sich sehr gut dafür aber: Wie wird verfahren, wenn die Linien dicker sein sollen? Welche Probleme treten dabei auf? Wie kann man diese lösen? 69
70 Breite Primitive Ansatz: anstelle eines Pixels werden an jedem Punkt mehrere Pixel gezeichnet Fragen: Wie sieht die Pixelgruppe aus, die gezeichnet werden soll (rund, rechteckig, etc.) Wie ist die Orientierung der Pixelgruppe insbesondere, wenn sie nicht rund ist? Wie sehen die Linienenden aus? Wie sehen Knotenpunkte aus, an denen zwei Linien aneinanderstoßen? Drei Methoden für breite Primitive: Pixelwiederholung Bewegliche Pinsel Ränder zeichnen und dazwischen füllen 70
71 Pixelwiederholung Duplizieren von Pixeln in Zeilen oder Spalten funktioniert gut für Linien spaltenweises Duplizieren für Anstieg 1 < m < 1 zeilenweises Duplizieren sonst 71
72 Probleme Linienenden sind immer horizontal oder vertikal gerade. Horizontale und vertikale Linien haben eine sichtbar unterschiedliche Breite im Vergleich zu schrägen Linien. Sei t die Breite einer Linie (in Pixeln) Horizontale und vertikale Linien haben die Breite t. 45 -Linien haben eine Breite von t / 2. Geradzahlige Linienbreiten Welches Pixel liegt genau auf der berechneten Linie? Ober- und Unterkante (rechte/linke Kante) fallen aus 72
73 Bewegliche Pinsel Pinsel hinterlässt ein spezifisches Pixelmuster (Footprint) Bewegen des Pinsels entlang der gerasterten Linie und Zeichnen des Musters an jeder Stelle Probleme: Linienenden nicht an der genauen Pixelposition Unterschiedliche Breite der Linien bei unterschiedlichen Anstiegen Viele Pixel werden mehrfach gesetzt Aussehen der Linie stark abhängig vom Aussehen des Pixelmusters 73
74 74
75 Ränder zeichnen und Füllen Anstelle der Rasterung eines Primitivs werden zwei gerastert, mit Abstand t / 2 vom idealen Primitiv. Der Raum zwischen den beiden Primitiven wird dann gefüllt. Eigenschaften bzw. auftretende Probleme: funktioniert auch mit geradzahligen Linienbreiten Breite nicht abhängig vom Anstieg Probleme beim Finden der versetzten Linien Geraden sind unproblematisch Kreise sind unproblematisch Ellipsen sind problematisch Kurven, die t / 2 von einer Ellipse entfernt gezeichnet werden, sind keine Ellipsen allgemeine Kurven funktionieren nicht 75
76 76
77 Rasteralgorithmen Kantenglättung Antialiasing 77
78 Antialiasing Neues Problem: Treppenstufen-Effekte beim Zeichnen von Linien, Details gehen verloren, etc. Aliasing Ursachen: Diskretisierung eines kontinuierlichen Signals unterschiedliche Abtastfrequenzen (Abtasttheorem) Lösung: Antialiasing verschiedene Verfahren je nach Anwendung hier insbesondere: Antialiasing beim Rastern von Linien erhöht die Qualität von Graphiken in Hardware verfügbar 78
79 Aliasing-Beispiele Treppenstufen Binnen- Strukturen: Details gehen verloren 79
80 Aliasing-Beispiele Moiré-Muster und Verwischen bei Texturen 80
81 Methoden Allgemeines Verfahren: Erhöhen der Auflösung des Zielbildes und Zusammenfassen mehrerer Pixel zu einem Supersampling Einbau in die Rasterungs-Algorithmen Adaptive Anpassung der Pixelfarbe (Grauwert) an die Entfernung von der exakten Linie Gewichtete Flächenbewertung Ungewichtete Flächenbewertung 81
82 Supersampling einfachste Methode: Bild wird in einer höheren Auflösung gesampled (berechnet) danach: Downsampling auf die gewünschte Auflösung (gewichtetes Mittel der Sub-Pixel, die auf einen Pixel abgebildet werden) Praktikable Ansätze unterscheiden sich in: Auswahl der Super-Auflösung Lage der Subpixel zum Pixel an sich (Gitter) Auswahl des Downsampling-Filters einfaches Averaging Box-Filter Convolution 82
83 Einfaches Supersampling wähle eine höhere Auflösung für ein virtuelles Bild z. B. dreifache Auflösung stelle das Bild mit dieser höheren Auflösung dar 83
84 Einfaches Supersampling fasse jeweils n Pixel des virtuellen Bildes zu einem Pixel des Ergebnisbildes zusammen (im Beispiel jeweils 3 3 Pixel) W W S W S S S S S Mittelwert der Farben bilden 66% S 84
85 Einfaches Supersampling Ausgabe des Ergebnisbildes 85
86 Flächenbewertungs-Algorithmen Anwendung direkt bei der Rasterkonvertierung von Primitiven (Linien, etc.) Geometrische Linie hat keine Breite, aber: eine gerasterte Linie ist (wenigstens) 1 Pixel breit Geometrischer Umriss einer Linie = langes, schmales Rechteck Rechteckfläche überlappt Pixelgrundflächen teilweise, ungleichmäßig Bisherige Vereinfachung: Pixel gesetzt oder nicht zu grob führt zu Treppenstufen-Effekten 86
87 Ungewichtete Flächenbewertung Idee: Pixelhelligkeit proportional zum Anteil der Überdeckung dem Linienrechteck dosieren Annahme: Jedes Pixel hat quadratische Grundfläche der Größe 1 1 = Rasterzelle. Grad der Überdeckung Rasterzelle/Linienumriss = Pixel-Helligkeit Helligkeit 0% Überdeckung 100% 87
88 Gewichtete Flächenbewertung Helligkeitsbestimmung bei ungewichteter Flächenbewertung: Leuchtvolumen als Würfel, Anteil der überdeckten Linienfläche Realität: Pixelgrundflächen sind keine Quadrate sondern Kreise, daher Leuchtvolumen eher als Zylinder ansehen 88
89 Gewichtete Flächenbewertung Pixelflächen auch nicht gleichmäßig hell ausgeleuchtet, heller im Zentrum, Licht fällt auch in Nachbarpixelzellen, daher Leuchtvolumen als Kegel mit größerer Grundfläche Gewichtete Flächenbewertung: Anteil der Pixelhelligkeit entspricht abgeschnittenem Volumenanteil des Kegels 89
90 Gupta-Sproull-Linien Verbindung von gewichteter Flächenbewertung mit dem Bresenham-Algorithmus für Linien Geometrisches Modell: Mittelpunkte der Pixel auf Gitterpunkten mit Abstand 1 Pixel besitzen Einfluss- Bereich, der einer Kreisscheibe mit Radius 1 entspricht Linie besitzt Dicke t Abstand Pixel zu Gerade wird durch den Abstand Pixelmittelpunkt zur Mittellinie des Primitivs bestimmt 90
91 Gupta-Sproull-Linien Ablauf des Verfahrens 1. Berechne Rasterpunkt (Bresenham) 2. Berechne Distanz D zwischen Rasterpunkt und Linie 3. Gehe einen Schritt entlang der y-achse aufwärts und berechne Du 4. Gehe einen Schritt entlang der y-achse abwärts und berechne Dl 5. mit größerem D, Dl, Du ergibt sich kleinerer Grauwert 6. Jede Linie ist somit 3 Pixel dick Grauwerte können vorberechnet werden 1. max. Abstand ist 1.5, unterteilen je nach Anzahl der Graustufen (16, 256, etc.) 2. Abspeichern in Tabelle und Lookup über Abstand 91
92 Zusammenfassung Antialiasing Vorteile Eckige Kanten und harte Übergänge werden reduziert Pixel- und Linien-Flimmern wird reduziert Nachteile Verringerte Schärfe Kleine Schriften werden beschädigt Größere Datenmengen Längere Rechenzeiten 92
93 Quellen Foley, van Dam, Feiner, Hughes: Computer Graphics, Principles and Practice. Zweite Auflage, Addison Wesley. ISBN Bernhard Preim: Computergraphik 1. Universität Magdeburg, Vorlesungsskript, Juli
6.2 Scan-Konvertierung (Scan Conversion)
 6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
6.2 Scan-Konvertierung (Scan Conversion) Scan-Konvertierung ist die Rasterung von einfachen Objekten (Geraden, Kreisen, Kurven). Als Ausgabemedium dient meist der Bildschirm, der aus einem Pixelraster
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Graphische Grundalgorithmen Graphische DV und BV, Regina Pohle, 4. Algorithmen für graphische Primitive 1 Einordnung in die Inhalte
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Graphische Grundalgorithmen Graphische DV und BV, Regina Pohle, 4. Algorithmen für graphische Primitive 1 Einordnung in die Inhalte
Computergraphik Grundlagen
 Computergraphik Grundlagen X. Rasterung Linien und Kreise Prof. Stefan Schlechtweg Hochschule Anhalt Fachbereich Informatik Inhalt Lernziele 1. Was ist ein Pixel? 2. Rasterung 3. Pixelgraphik Vor- und
Computergraphik Grundlagen X. Rasterung Linien und Kreise Prof. Stefan Schlechtweg Hochschule Anhalt Fachbereich Informatik Inhalt Lernziele 1. Was ist ein Pixel? 2. Rasterung 3. Pixelgraphik Vor- und
Plotten von Linien ( nach Jack Bresenham, 1962 )
 Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Plotten von Linien ( nach Jack Bresenham, 1962 ) Ac Eine auf dem Bildschirm darzustellende Linie sieht treppenförmig aus, weil der Computer Linien aus einzelnen (meist quadratischen) Bildpunkten, Pixels
Die Rasterbildtechnik
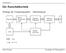 Die Rasterbildtechnik Anfänge der Computergraphik: Vektordisplays Oliver Deussen Grundlagen der Rastergraphik 1 Vorteile von Vektordisplays: - geringer Speicheraufwand (Display-Liste statt Pixelfeld) -
Die Rasterbildtechnik Anfänge der Computergraphik: Vektordisplays Oliver Deussen Grundlagen der Rastergraphik 1 Vorteile von Vektordisplays: - geringer Speicheraufwand (Display-Liste statt Pixelfeld) -
Computergraphik I. Scan Conversion: Lines & Co. Einordnung in die Pipeline. G. Zachmann Clausthal University, Germany zach@tu-clausthal.
 11/4/10 lausthal omputergraphik I Scan onversion of Lines. Zachmann lausthal University, ermany zach@tu-clausthal.de Einordnung in die Pipeline Rasterisierung der Objekte in Pixel Ecken-Werte interpolieren
11/4/10 lausthal omputergraphik I Scan onversion of Lines. Zachmann lausthal University, ermany zach@tu-clausthal.de Einordnung in die Pipeline Rasterisierung der Objekte in Pixel Ecken-Werte interpolieren
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Antialiasing Graphische DV und BV, Regina Pohle, 5. Antialiasing 1 Einordnung in die Inhalte der Vorlesung Einführung mathematische
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Antialiasing Graphische DV und BV, Regina Pohle, 5. Antialiasing 1 Einordnung in die Inhalte der Vorlesung Einführung mathematische
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Aufgabe 1. Zunächst wird die allgemeine Tangentengleichung in Abhängigkeit von a aufgestellt:
 Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
Aufgabe 1 1.1. Bestimmung von D max : 1. Bedingung: x >0 ; da ln(x) nur für x > 0 definiert ist. 2. Bedingung: Somit ist die Funktion f a nur für x > 0 definiert und sie besitzt eine Definitionslücke an
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Formelsammlung zur Kreisgleichung
 zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
zur Kreisgleichung Julia Wolters 6. Oktober 2008 Inhaltsverzeichnis 1 Allgemeine Kreisgleichung 2 1.1 Berechnung des Mittelpunktes und Radius am Beispiel..... 3 2 Kreis und Gerade 4 2.1 Sekanten, Tangenten,
Im Original veränderbare Word-Dateien
 Computergrafik Bilder, Grafiken, Zeichnungen etc., die mithilfe von Computern hergestellt oder bearbeitet werden, bezeichnet man allgemein als Computergrafiken. Früher wurde streng zwischen Computergrafik
Computergrafik Bilder, Grafiken, Zeichnungen etc., die mithilfe von Computern hergestellt oder bearbeitet werden, bezeichnet man allgemein als Computergrafiken. Früher wurde streng zwischen Computergrafik
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen.
 13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
13. Lineare DGL höherer Ordnung. Eine DGL heißt von n-ter Ordnung, wenn Ableitungen y, y, y,... bis zur n-ten Ableitung y (n) darin vorkommen. Sie heißt linear, wenn sie die Form y (n) + a n 1 y (n 1)
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Mathematischer Vorbereitungskurs für Ökonomen
 Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Die reellen Lösungen der kubischen Gleichung
 Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
Die reellen Lösungen der kubischen Gleichung Klaus-R. Löffler Inhaltsverzeichnis 1 Einfach zu behandelnde Sonderfälle 1 2 Die ganzrationale Funktion dritten Grades 2 2.1 Reduktion...........................................
32. Algorithmus der Woche Kreise zeichnen mit Turbo Programmoptimierung: Wie kann man die Zahl der Rechenoperationen minimieren?
 32. Algorithmus der Woche Kreise zeichnen mit Turbo Programmoptimierung: Wie kann man die Zahl der Rechenoperationen minimieren? Autor Leif Kobbelt, RWTH Aachen Dominik Sibbing, RWTH Aachen Hast Du schon
32. Algorithmus der Woche Kreise zeichnen mit Turbo Programmoptimierung: Wie kann man die Zahl der Rechenoperationen minimieren? Autor Leif Kobbelt, RWTH Aachen Dominik Sibbing, RWTH Aachen Hast Du schon
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
DIFFERENTIALGLEICHUNGEN
 DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
DIFFERENTIALGLEICHUNGEN GRUNDBEGRIFFE Differentialgleichung Eine Gleichung, in der Ableitungen einer unbekannten Funktion y = y(x) bis zur n-ten Ordnung auftreten, heisst gewöhnliche Differentialgleichung
( ) als den Punkt mit der gleichen x-koordinate wie A und der
 ETH-Aufnahmeprüfung Herbst 05 Mathematik I (Analysis) Aufgabe [6 Punkte] Bestimmen Sie den Schnittwinkel α zwischen den Graphen der Funktionen f(x) x 4x + x + 5 und g(x) x x + 5 im Schnittpunkt mit der
ETH-Aufnahmeprüfung Herbst 05 Mathematik I (Analysis) Aufgabe [6 Punkte] Bestimmen Sie den Schnittwinkel α zwischen den Graphen der Funktionen f(x) x 4x + x + 5 und g(x) x x + 5 im Schnittpunkt mit der
Abiturprüfung Mathematik 2008 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe Für jedes t f t () + t R ist die Funktion f t gegeben durch = mit R. Das Schaubild von f t heißt K t.. (6 Punkte)
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen?
 Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Welche Lagen können zwei Geraden (im Raum) zueinander haben? Welche Lagen können zwei Ebenen (im Raum) zueinander haben? Welche Lagen kann eine Gerade bezüglich einer Ebene im Raum einnehmen? Wie heiÿt
Monatliche Grundgebühr: 5,00 Zeitabhängige Nutzung: Feiertags/Sonntags: 0,04 /min
 Aufgabe 1: Wortvorschriften Gib zu den Wortvorschriften je eine Funktionsgleichung an: a) Jeder Zahl wird das Doppelte zugeordnet b) Jeder Zahl wird das um 6 verminderte Dreifache zugeordnet c) Jeder Zahl
Aufgabe 1: Wortvorschriften Gib zu den Wortvorschriften je eine Funktionsgleichung an: a) Jeder Zahl wird das Doppelte zugeordnet b) Jeder Zahl wird das um 6 verminderte Dreifache zugeordnet c) Jeder Zahl
Behörde für Bildung und Sport Abitur 2008 Lehrermaterialien zum Leistungskurs Mathematik
 Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
Die Näherung durch die Sekante durch die Punkte A und C ist schlechter, da der Punkt C weiter von A entfernt liegt.
 LÖSUNGEN TEIL 1 Arbeitszeit: 50 min Gegeben ist die Funktion f mit der Gleichung. Begründen Sie, warum die Steigung der Sekante durch die Punkte A(0 2) und C(3 11) eine weniger gute Näherung für die Tangentensteigung
LÖSUNGEN TEIL 1 Arbeitszeit: 50 min Gegeben ist die Funktion f mit der Gleichung. Begründen Sie, warum die Steigung der Sekante durch die Punkte A(0 2) und C(3 11) eine weniger gute Näherung für die Tangentensteigung
Die Gleichung A x = a hat für A 0 die eindeutig bestimmte Lösung. Für A=0 und a 0 existiert keine Lösung.
 Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Lineare Gleichungen mit einer Unbekannten Die Grundform der linearen Gleichung mit einer Unbekannten x lautet A x = a Dabei sind A, a reelle Zahlen. Die Gleichung lösen heißt, alle reellen Zahlen anzugeben,
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen
 Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Elemente der Analysis I Kapitel 2: Einführung II, Gleichungen Prof. Dr. Volker Schulz Universität Trier / FB IV / Abt. Mathematik 8. November 2010 http://www.mathematik.uni-trier.de/ schulz/elan-ws1011.html
Die Größe von Flächen vergleichen
 Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
Vertiefen 1 Die Größe von Flächen vergleichen zu Aufgabe 1 Schulbuch, Seite 182 1 Wer hat am meisten Platz? Ordne die Figuren nach ihrem Flächeninhalt. Begründe deine Reihenfolge. 1 2 3 4 zu Aufgabe 2
Das Mathematik-Abitur im Saarland
 Informationen zum Abitur Das Mathematik-Abitur im Saarland Sie können Mathematik im Abitur entweder als grundlegenden Kurs (G-Kurs) oder als erhöhten Kurs (E-Kurs) wählen. Die Bearbeitungszeit für die
Informationen zum Abitur Das Mathematik-Abitur im Saarland Sie können Mathematik im Abitur entweder als grundlegenden Kurs (G-Kurs) oder als erhöhten Kurs (E-Kurs) wählen. Die Bearbeitungszeit für die
Quadratische Gleichungen
 Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Quadratische Gleichungen Aufgabe: Versuche eine Lösung zu den folgenden Zahlenrätseln zu finden:.) Verdoppelt man das Quadrat einer Zahl und addiert, so erhält man 00..) Addiert man zum Quadrat einer Zahl
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
!(0) + o 1("). Es ist damit möglich, dass mehrere Familien geschlossener Orbits gleichzeitig abzweigen.
 Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Bifurkationen an geschlossenen Orbits 5.4 167 der Schnittabbldung konstruiert. Die Periode T (") der zugehörigen periodischen Lösungen ergibt sich aus =! + o 1 (") beziehungsweise Es ist also t 0 = T (")
Lineare Gleichungssysteme
 Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Lineare Gleichungssysteme 1 Zwei Gleichungen mit zwei Unbekannten Es kommt häufig vor, dass man nicht mit einer Variablen alleine auskommt, um ein Problem zu lösen. Das folgende Beispiel soll dies verdeutlichen
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
LU-Zerlegung. Zusätze zum Gelben Rechenbuch. Peter Furlan. Verlag Martina Furlan. Inhaltsverzeichnis. 1 Definitionen.
 Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Zusätze zum Gelben Rechenbuch LU-Zerlegung Peter Furlan Verlag Martina Furlan Inhaltsverzeichnis Definitionen 2 (Allgemeine) LU-Zerlegung 2 3 Vereinfachte LU-Zerlegung 3 4 Lösung eines linearen Gleichungssystems
Vermessung und Verständnis von FFT Bildern
 Vermessung und Verständnis von FFT Bildern Viele Auswertungen basieren auf der "Fast Fourier Transformation" FFT um die (ungewünschten) Regelmäßigkeiten im Schliffbild darzustellen. Die Fourier-Transformation
Vermessung und Verständnis von FFT Bildern Viele Auswertungen basieren auf der "Fast Fourier Transformation" FFT um die (ungewünschten) Regelmäßigkeiten im Schliffbild darzustellen. Die Fourier-Transformation
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Dynamische Mathematik mit GeoGebra 30. März 1. April 2009
 Dynamische Mathematik mit GeoGebra 30. März 1. April 2009 Angebote für Fortgeschrittene Thema 1 Gegeben ist ein beliebiges Dreieck. Über die Seiten des Dreiecks werden Quadrate errichtet. In zwei Ecken
Dynamische Mathematik mit GeoGebra 30. März 1. April 2009 Angebote für Fortgeschrittene Thema 1 Gegeben ist ein beliebiges Dreieck. Über die Seiten des Dreiecks werden Quadrate errichtet. In zwei Ecken
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit sin() f() =. Aufgabe : ( VP) Berechnen Sie das Integral ( )
SUDOKU - Strategien zur Lösung
 SUDOKU Strategien v. /00 SUDOKU - Strategien zur Lösung. Naked Single (Eindeutiger Wert)? "Es gibt nur einen einzigen Wert, der hier stehen kann". Sind alle anderen Werte bis auf einen für eine Zelle unmöglich,
SUDOKU Strategien v. /00 SUDOKU - Strategien zur Lösung. Naked Single (Eindeutiger Wert)? "Es gibt nur einen einzigen Wert, der hier stehen kann". Sind alle anderen Werte bis auf einen für eine Zelle unmöglich,
Quadratische Funktionen (Parabeln)
 Quadratische Funktionen (Parabeln) Aufgabe: Gegeben ist die quadratische Funktion = () x. Berechne mit Hilfe einer Wertetabelle die Funktionswerte von bis + im Abstand 0,. Zeichne anschließend die Punkte
Quadratische Funktionen (Parabeln) Aufgabe: Gegeben ist die quadratische Funktion = () x. Berechne mit Hilfe einer Wertetabelle die Funktionswerte von bis + im Abstand 0,. Zeichne anschließend die Punkte
Lösungsmethoden gewöhnlicher Differentialgleichungen (Dgl.)
 Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Lösungsmethoden gewöhnlicher Dierentialgleichungen Dgl) Allgemeine und partikuläre Lösung einer gewöhnlichen Dierentialgleichung Eine Dierentialgleichung ist eine Gleichung! Zum Unterschied von den gewöhnlichen
Repetitionsaufgaben: Lineare Gleichungen
 Kantonale Fachschaft Mathematik Repetitionsaufgaben: Lineare Gleichungen Zusammengestellt von Hannes Ernst, KSR Lernziele: - Lineare Gleichungen von Hand auflösen können. - Lineare Gleichungen mit Parametern
Kantonale Fachschaft Mathematik Repetitionsaufgaben: Lineare Gleichungen Zusammengestellt von Hannes Ernst, KSR Lernziele: - Lineare Gleichungen von Hand auflösen können. - Lineare Gleichungen mit Parametern
1 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R
 C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
C H R I S T O P H D R Ö S S E R D E R M A T H E M A T I K V E R F Ü H R E R L Ö S U N G E N Seite 7 n Wenn vier Menschen auf einem Quadratmeter stehen, dann hat jeder eine Fläche von 50 mal 50 Zentimeter
Vorkurs Mathematik Übungen zu Polynomgleichungen
 Vorkurs Mathematik Übungen zu en 1 Aufgaben Lineare Gleichungen Aufgabe 1.1 Ein Freund von Ihnen möchte einen neuen Mobilfunkvertrag abschließen. Es gibt zwei verschiedene Angebote: Anbieter 1: monatl.
Vorkurs Mathematik Übungen zu en 1 Aufgaben Lineare Gleichungen Aufgabe 1.1 Ein Freund von Ihnen möchte einen neuen Mobilfunkvertrag abschließen. Es gibt zwei verschiedene Angebote: Anbieter 1: monatl.
Vorkurs Mathematik Übungen zu Differentialgleichungen
 Vorkurs Mathematik Übungen zu Differentialgleichungen Als bekannt setzen wir die folgenden Umformungen voraus: e ln(f(x)) = f(x) e f(x)+c = e f(x) e c e ln(f(x)) +c = f(x) e c = f(x) c f ( g(x) ) g (x)
Vorkurs Mathematik Übungen zu Differentialgleichungen Als bekannt setzen wir die folgenden Umformungen voraus: e ln(f(x)) = f(x) e f(x)+c = e f(x) e c e ln(f(x)) +c = f(x) e c = f(x) c f ( g(x) ) g (x)
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Der Frosch als Vektorgrafik
 Der Frosch als Vektorgrafik Einen Frosch erstellen und dabei typische Arbeitsweisen in CorelDraw kennen lernen Den auf der Titelseite von Draw dargestellten Frosch wollen wir nun nach basteln. Die benötigten
Der Frosch als Vektorgrafik Einen Frosch erstellen und dabei typische Arbeitsweisen in CorelDraw kennen lernen Den auf der Titelseite von Draw dargestellten Frosch wollen wir nun nach basteln. Die benötigten
Vektoren mit GeoGebra
 Vektoren mit GeoGebra Eine Kurzanleitung mit Beispielen Markus Hohenwarter, 2005 In GeoGebra kann mit Vektoren und Punkten konstruiert und gerechnet werden. Diese Kurzanleitung gibt einen Überblick über
Vektoren mit GeoGebra Eine Kurzanleitung mit Beispielen Markus Hohenwarter, 2005 In GeoGebra kann mit Vektoren und Punkten konstruiert und gerechnet werden. Diese Kurzanleitung gibt einen Überblick über
Bilderzeugung Pixel. Daniela Glatz Jasmin Rießle. Sommersemester 2012
 Bilderzeugung Pixel Daniela Glatz Jasmin Rießle Sommersemester 2012 Bilderzeugung Pixel Inhaltsverzeichnis Definition: Was ist ein Pixel? Aufbau eines digitalen Pixels Auflösung Interpolation Farbe Pixelanimation
Bilderzeugung Pixel Daniela Glatz Jasmin Rießle Sommersemester 2012 Bilderzeugung Pixel Inhaltsverzeichnis Definition: Was ist ein Pixel? Aufbau eines digitalen Pixels Auflösung Interpolation Farbe Pixelanimation
Info zum Zusammenhang von Auflösung und Genauigkeit
 Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
Da es oft Nachfragen und Verständnisprobleme mit den oben genannten Begriffen gibt, möchten wir hier versuchen etwas Licht ins Dunkel zu bringen. Nehmen wir mal an, Sie haben ein Stück Wasserrohr mit der
DAS ABI-PFLICHTTEIL Büchlein
 DAS ABI-PFLICHTTEIL Büchlein für Baden-Württemberg Alle Originalaufgaben Haupttermine 004 0 Ausführlich gerechnete und kommentierte Lösungswege Mit vielen Zusatzhilfen X π Von: Jochen Koppenhöfer und Pascal
DAS ABI-PFLICHTTEIL Büchlein für Baden-Württemberg Alle Originalaufgaben Haupttermine 004 0 Ausführlich gerechnete und kommentierte Lösungswege Mit vielen Zusatzhilfen X π Von: Jochen Koppenhöfer und Pascal
Mathematik. UND/ODER Verknüpfung. Ungleichungen. Betrag. Intervall. Umgebung
 Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Mathematik UND/ODER Verknüpfung Ungleichungen Betrag Intervall Umgebung Stefan Gärtner 004 Gr Mathematik UND/ODER Seite UND Verknüpfung Kommentar Aussage Symbolform Die Aussagen Hans kann schwimmen p und
Simulation LIF5000. Abbildung 1
 Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
Simulation LIF5000 Abbildung 1 Zur Simulation von analogen Schaltungen verwende ich Ltspice/SwitcherCAD III. Dieses Programm ist sehr leistungsfähig und wenn man weis wie, dann kann man damit fast alles
Umgekehrte Kurvendiskussion
 Umgekehrte Kurvendiskussion Bei einer Kurvendiskussion haben wir eine Funktionsgleichung vorgegeben und versuchen ihre 'Besonderheiten' herauszufinden: Nullstellen, Extremwerte, Wendepunkte, Polstellen
Umgekehrte Kurvendiskussion Bei einer Kurvendiskussion haben wir eine Funktionsgleichung vorgegeben und versuchen ihre 'Besonderheiten' herauszufinden: Nullstellen, Extremwerte, Wendepunkte, Polstellen
Woraus besteht ein Bild? 28.02.2008 (c) Winfried Heinkele 2006 2
 Woraus besteht ein Bild? 28.02.2008 (c) Winfried Heinkele 2006 2 Was ist ein Pixel? Die durch das Objektiv einer Kamera auf einen Film oder einen elektronischen Bildsensor projizierte Wirklichkeit ist
Woraus besteht ein Bild? 28.02.2008 (c) Winfried Heinkele 2006 2 Was ist ein Pixel? Die durch das Objektiv einer Kamera auf einen Film oder einen elektronischen Bildsensor projizierte Wirklichkeit ist
Download. Mathematik üben Klasse 8 Funktionen. Differenzierte Materialien für das ganze Schuljahr. Jens Conrad, Hardy Seifert
 Download Jens Conrad, Hard Seifert Mathematik üben Klasse 8 Funktionen Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Funktionen Differenzierte
Download Jens Conrad, Hard Seifert Mathematik üben Klasse 8 Funktionen Differenzierte Materialien für das ganze Schuljahr Downloadauszug aus dem Originaltitel: Mathematik üben Klasse 8 Funktionen Differenzierte
10.1 Auflösung, Drucken und Scannen
 Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
Um einige technische Erläuterungen kommen wir auch in diesem Buch nicht herum. Für Ihre Bildergebnisse sind diese technischen Zusammenhänge sehr wichtig, nehmen Sie sich also etwas Zeit und lesen Sie dieses
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Erstellen von x-y-diagrammen in OpenOffice.calc
 Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
Erstellen von x-y-diagrammen in OpenOffice.calc In dieser kleinen Anleitung geht es nur darum, aus einer bestehenden Tabelle ein x-y-diagramm zu erzeugen. D.h. es müssen in der Tabelle mindestens zwei
www.mathe-aufgaben.com
 Abiturprüfung Mathematik 008 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe 1: ( VP) x Gegeben ist die Funktion f mit f(x). x Bilden Sie die Ableitung von f und fassen Sie diese so weit wie
Abiturprüfung Mathematik 008 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe 1: ( VP) x Gegeben ist die Funktion f mit f(x). x Bilden Sie die Ableitung von f und fassen Sie diese so weit wie
5. Lineare Funktionen
 5. Lineare Funktionen Lernziele: -Eine lineare Funktion grafisch darstellen -Geradengleichung (Funktionsgleichung einer linearen Funktion) -Deutung von k- und d-wert -Grafische Lösung von Gleichungssystemen
5. Lineare Funktionen Lernziele: -Eine lineare Funktion grafisch darstellen -Geradengleichung (Funktionsgleichung einer linearen Funktion) -Deutung von k- und d-wert -Grafische Lösung von Gleichungssystemen
Public-Key-Algorithmen WS2015/2016
 Public-Key-Algorithmen WS2015/2016 Lernkontrollfragen Michael Braun Was bedeuten die kryptographischen Schutzziele Vertraulichkeit, Integrität, Nachrichtenauthentizität, Teilnehmerauthentizität, Verbindlichkeit?
Public-Key-Algorithmen WS2015/2016 Lernkontrollfragen Michael Braun Was bedeuten die kryptographischen Schutzziele Vertraulichkeit, Integrität, Nachrichtenauthentizität, Teilnehmerauthentizität, Verbindlichkeit?
Funktionen (linear, quadratisch)
 Funktionen (linear, quadratisch) 1. Definitionsbereich Bestimme den Definitionsbereich der Funktion f(x) = 16 x 2 2x + 4 2. Umkehrfunktionen Wie lauten die Umkehrfunktionen der folgenden Funktionen? (a)
Funktionen (linear, quadratisch) 1. Definitionsbereich Bestimme den Definitionsbereich der Funktion f(x) = 16 x 2 2x + 4 2. Umkehrfunktionen Wie lauten die Umkehrfunktionen der folgenden Funktionen? (a)
Arbeitspunkt einer Diode
 Arbeitspunkt einer Diode Liegt eine Diode mit einem Widerstand R in Reihe an einer Spannung U 0, so müssen sich die beiden diese Spannung teilen. Vom Widerstand wissen wir, dass er bei einer Spannung von
Arbeitspunkt einer Diode Liegt eine Diode mit einem Widerstand R in Reihe an einer Spannung U 0, so müssen sich die beiden diese Spannung teilen. Vom Widerstand wissen wir, dass er bei einer Spannung von
Einführung in. Logische Schaltungen
 Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Einführung in Logische Schaltungen 1/7 Inhaltsverzeichnis 1. Einführung 1. Was sind logische Schaltungen 2. Grundlegende Elemente 3. Weitere Elemente 4. Beispiel einer logischen Schaltung 2. Notation von
Korrelation (II) Korrelation und Kausalität
 Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Computer Vision I. Nikos Canterakis. Lehrstuhl für Mustererkennung, Universität Freiburg
 Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 6 Endliche Kameras Die Lochkamera Die Projektive Kamera Die projektive Kamera Spalten von P Zeilen von P Hauptpunkt und Hauptachse
Nikos Canterakis Lehrstuhl für Mustererkennung, Universität Freiburg Gliederung 6 Endliche Kameras Die Lochkamera Die Projektive Kamera Die projektive Kamera Spalten von P Zeilen von P Hauptpunkt und Hauptachse
Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])
![Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Erstellen einer Collage. Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu])](/thumbs/29/13170670.jpg) 3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
3.7 Erstellen einer Collage Zuerst ein leeres Dokument erzeugen, auf dem alle anderen Bilder zusammengefügt werden sollen (über [Datei] > [Neu]) Dann Größe des Dokuments festlegen beispielsweise A4 (weitere
Diese Prozesse und noch viele andere Tricks werden in der Digitalfotografie mit Hilfe von Bildbearbeitungsprogrammen, wie z. B. Gimp, bewältigt.
 Workflows mit Gimp Workflows sind Arbeitsabläufe, in denen man ein rohes Bildmaterial in ein ansehnliches Foto verwandelt. Denn das, was die Kamera sieht, entspricht selten unseren Vorstellungen eines
Workflows mit Gimp Workflows sind Arbeitsabläufe, in denen man ein rohes Bildmaterial in ein ansehnliches Foto verwandelt. Denn das, was die Kamera sieht, entspricht selten unseren Vorstellungen eines
Abituraufgabe zur analytischen Geometrie, Hessen 2013, B2, Grundkurs (TR)
 Abituraufgabe zur analytischen Geometrie, Hessen 2013, B2, Grundkurs (TR) 1 Bei Ausgrabungen wurden die Überreste einer 4500 Jahre alten Pyramide entdeckt. Die Abbildung zeigt die Ansicht der Pyramidenruine
Abituraufgabe zur analytischen Geometrie, Hessen 2013, B2, Grundkurs (TR) 1 Bei Ausgrabungen wurden die Überreste einer 4500 Jahre alten Pyramide entdeckt. Die Abbildung zeigt die Ansicht der Pyramidenruine
Berechnung der Erhöhung der Durchschnittsprämien
 Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Graphic Coding. Klausur. 9. Februar 2007. Kurs A
 Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Graphic Coding Klausur 9. Februar 2007 Kurs A Name: Matrikelnummer: Hinweise - Es sind keine Hilfsmaterialien erlaubt. (Keine Bücher, Taschenrechner, Handys) - Sie haben zwei Stunden Zeit. - Insgesamt
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lösungsvorschlag für die Probeklausuren und Klausuren zu Algebra für Informations- und Kommunikationstechniker bei Prof. Dr.
 Lösungsvorschlag für die Probeklausuren und Klausuren zu Algebra für Informations- und Kommunikationstechniker bei Prof. Dr. Kurzweil Florian Franzmann André Diehl Kompiliert am 10. April 2006 um 18:33
Lösungsvorschlag für die Probeklausuren und Klausuren zu Algebra für Informations- und Kommunikationstechniker bei Prof. Dr. Kurzweil Florian Franzmann André Diehl Kompiliert am 10. April 2006 um 18:33
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Zahlen auf einen Blick
 Zahlen auf einen Blick Nicht ohne Grund heißt es: Ein Bild sagt mehr als 1000 Worte. Die meisten Menschen nehmen Informationen schneller auf und behalten diese eher, wenn sie als Schaubild dargeboten werden.
Zahlen auf einen Blick Nicht ohne Grund heißt es: Ein Bild sagt mehr als 1000 Worte. Die meisten Menschen nehmen Informationen schneller auf und behalten diese eher, wenn sie als Schaubild dargeboten werden.
Systeme 1. Kapitel 6. Nebenläufigkeit und wechselseitiger Ausschluss
 Systeme 1 Kapitel 6 Nebenläufigkeit und wechselseitiger Ausschluss Threads Die Adressräume verschiedener Prozesse sind getrennt und geschützt gegen den Zugriff anderer Prozesse. Threads sind leichtgewichtige
Systeme 1 Kapitel 6 Nebenläufigkeit und wechselseitiger Ausschluss Threads Die Adressräume verschiedener Prozesse sind getrennt und geschützt gegen den Zugriff anderer Prozesse. Threads sind leichtgewichtige
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Paper Computer Science Experiment. Computation (NP-Vollständigkeit) Steinerbäume
 Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Steinerbäume Unterrichtsform Entdeckendes Lernen, Einzelarbeit, Lernen am Modell Voraussetzung Bäume
Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Steinerbäume Unterrichtsform Entdeckendes Lernen, Einzelarbeit, Lernen am Modell Voraussetzung Bäume
Lichtbrechung an Linsen
 Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Sammellinsen Lichtbrechung an Linsen Fällt ein paralleles Lichtbündel auf eine Sammellinse, so werden die Lichtstrahlen so gebrochen, dass sie durch einen Brennpunkt der Linse verlaufen. Der Abstand zwischen
Dokumentation zum Projekt Multimediale Lehre Fluidmechanik an der Technischen Universität Graz
 Dokumentation zum Projekt Multimediale Lehre Fluidmechanik an der Technischen Universität Graz Andreas Aigner email: andreasa@sbox.tu-graz.ac.at. Januar 00 Inhaltsverzeichnis Theorie. Stromfunktion...........................
Dokumentation zum Projekt Multimediale Lehre Fluidmechanik an der Technischen Universität Graz Andreas Aigner email: andreasa@sbox.tu-graz.ac.at. Januar 00 Inhaltsverzeichnis Theorie. Stromfunktion...........................
Platinen mit dem HP CLJ 1600 direkt bedrucken ohne Tonertransferverfahren
 Platinen mit dem HP CLJ 1600 direkt bedrucken ohne Tonertransferverfahren Um die Platinen zu bedrucken, muß der Drucker als allererstes ein wenig zerlegt werden. Obere und seitliche Abdeckungen entfernen:
Platinen mit dem HP CLJ 1600 direkt bedrucken ohne Tonertransferverfahren Um die Platinen zu bedrucken, muß der Drucker als allererstes ein wenig zerlegt werden. Obere und seitliche Abdeckungen entfernen:
4 Aufzählungen und Listen erstellen
 4 4 Aufzählungen und Listen erstellen Beim Strukturieren von Dokumenten und Inhalten stellen Listen und Aufzählungen wichtige Werkzeuge dar. Mit ihnen lässt sich so ziemlich alles sortieren, was auf einer
4 4 Aufzählungen und Listen erstellen Beim Strukturieren von Dokumenten und Inhalten stellen Listen und Aufzählungen wichtige Werkzeuge dar. Mit ihnen lässt sich so ziemlich alles sortieren, was auf einer
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
 Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Universität Bonn, Institut für Angewandte Mathematik. WS 2012/2013 Prüfung Angewandte Mathematik und Statistik - Agrarwiss. /ELW
 Universität Bonn, Institut für Angewandte Mathematik Dr. Antje Kiesel WS 2012/2013 Prüfung Angewandte Mathematik und Statistik - Agrarwiss. /ELW 08.03.2013 Matrikelnummer Platz Name Vorname 1 2 3 4 5 6
Universität Bonn, Institut für Angewandte Mathematik Dr. Antje Kiesel WS 2012/2013 Prüfung Angewandte Mathematik und Statistik - Agrarwiss. /ELW 08.03.2013 Matrikelnummer Platz Name Vorname 1 2 3 4 5 6
Abituraufgabe zur Analysis, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Analysis, Hessen 2009, Grundkurs (TR) Gegeben ist die trigonometrische Funktion f mit f(x) = 2 sin(2x) 1 (vgl. Material 1). 1.) Geben Sie für die Funktion f den Schnittpunkt mit der y
Abituraufgabe zur Analysis, Hessen 2009, Grundkurs (TR) Gegeben ist die trigonometrische Funktion f mit f(x) = 2 sin(2x) 1 (vgl. Material 1). 1.) Geben Sie für die Funktion f den Schnittpunkt mit der y
2.8 Grenzflächeneffekte
 - 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
- 86-2.8 Grenzflächeneffekte 2.8.1 Oberflächenspannung An Grenzflächen treten besondere Effekte auf, welche im Volumen nicht beobachtbar sind. Die molekulare Grundlage dafür sind Kohäsionskräfte, d.h.
Grundlagen von Corel Draw
 Grundlagen von Corel Draw Allgemeines Corel Draw ist ein so genanntes Vektorgrafik-Programm. Der Vorteil von Vektorgrafiken besteht darin, dass die Qualität auch beim Vergrößern im Gegensatz zu Bitmap-Bildern
Grundlagen von Corel Draw Allgemeines Corel Draw ist ein so genanntes Vektorgrafik-Programm. Der Vorteil von Vektorgrafiken besteht darin, dass die Qualität auch beim Vergrößern im Gegensatz zu Bitmap-Bildern
computer graphics & visualization
 Entwicklung und Implementierung echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs Motivation
Entwicklung und Implementierung echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs echtzeitfähiger Verfahren zur Darstellung von reflektierenden Objekten auf GPUs Motivation
n 0 1 2 3 4 5 6 7 8 9 10 11 12 S n 1250 1244, 085 1214, 075 1220, 136 1226, 167 Nach einem Jahr beträgt der Schuldenstand ca. 1177,09.
 Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
